Calculation of shells by analytical methods

M. Tort¹, E. Oñate^1,2

¹ Universitat Politècnica de Catalunya (UPC), Barcelona, Spain

² Centre Internacional de Metodes Numerics a l'Enginyeria - CIMNE, Barcelona, Spain

Resum

Las formas de revolución generadas por estructuras de láminas son los elementos más simples y logrados del arte arquitectónico clásico. Así pues, la motivación principal de este texto es presentar las herramientas básicas para entender el funcionamiento de este tipo de estructuras y que el lector pueda diseñarlas sin ningún tipo de problemas.

El texto se centrará en el análisis de las dos láminas más comunes. En primer lugar la cúpula y en segundo lugar el muro cilíndrico. Una vez analizadas las dos tipologías estudiaremos la unión entre ambas y de este análisis aparecerá el anillo de borde necesario en muchos casos.

Summary

The forms of revolution generated by shell structures are the simplest of classical art. Thus, the main motivation of this paper is present the basic tools for understanding shell behavior and the reader can design it without any problems.

The text will focus on analyzing the two most common shells. First the dome and second cylindrical wall. Having analyzed the two types we will look the union between these two types and see the ring edge necessary in many cases.

Capítulo 1

1 Introducción

“En este espacio de tres dimensiones que la providencia ha deparado a la humanidad, no puede ésta prescindir de ellas para sus construcciones.” Es en esta idea en la que se basa mi trabajo. Por norma general, actualmente la preparación técnica referente a los tipos estructurales se limita a considerar solamente una dimensión, y en algun caso dos, pero en ningún caso se entiende la estructura como un conjunto de tres dimensiones.

Las formas de revolución generadas por estructuras laminares son los elementos más simples y logrados del arte arquitectónico clásico. Es la solución más natural, más sencilla y, a su vez, más cargada de sentido técnico para cubrir un área sin soportes intermedios con el mínimo material, de manera que definamos sin apenas intención, el volumen que estamos buscando. Así pues, la motivación principal de este texto es persentar las herramientas básicas para entender el funcionamiento de este tipo de estructuras y que el lector pueda diseñarlas sin ningún tipo de problemas.

Para comprender el comportamiento de cualquier tipología de estructura es imprescindible profundizar en los esfuerzos y deformaciones que predominan y que marcan la forma que tienen de trabajar. Es por esta razón por la que estudiaremos las láminas desde el punto de vista analítico, consiguiendo de esta manera que el lector tenga suficientes conocimientos para tratar de optimizar sus diseños. No obstante, compararemos los resultados obtenidos con los que obtendriamos realizando el estudio con el método de los elementos finitos ya que esta no es una herramienta de trabajo de la cual podamos prescindir.

Como ya hemos comentado, las estructuras de lámina son un campo con muchas posibilidades. En este texto solo se pertende profundizar en las más importantes. El texto se centrará en el análisis de las dos láminas más comunes. En primer lugar la cúpula y en segundo lugar el muro cilíndrico. Una vez analizadas las dos tipologías estudiaremos la unión entre ambas y de este análisis aparecerá el anillo de borde necesario en muchos casos.

1.1 Antecedentes

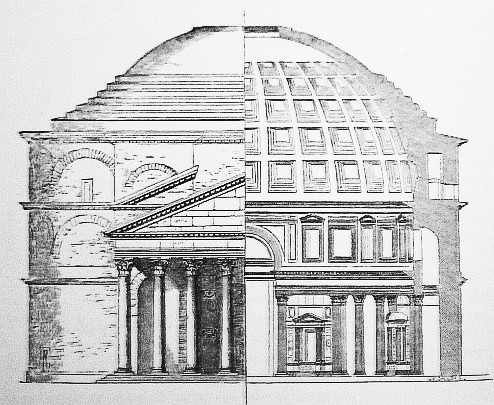
Una de las primeras construcciones de gran importancia diseñadas mediante elementos constructivos de lámina es el Panteón de Agripa (Roma), un templo circular construido en Roma a principios del Imperio Romano dedicado a todos los dioses.

Figura 1: El Pantenón en un grabado de Giovanni Battista Piranesi.

Como se puede observar en las imágenes, el templo se compone de una amplia sala redonda adosada al pórtico de un templo clásico. El diámetro de la sala es de 43.3m y consigue una altura hasta el óculo de 43.3m. A su vez, esta sala se compone de un tambor cilíndrico de 6.4m metros de espesor que sostiene una cúpula que como podemos apreciar está aligerada. El grueso de la cúpula varia de 6.4m en el arranque a 1.2m alrededor del óculo.

Figura 2: Sección y Alzado del Pantenón.

Se podría decir que el siguiente hito histórico en la utilización de elementos de lámina los podemos encontrar a principios de siglo pasado en Los Hangares de Orly (1921) de Eugène Freyssinet. Se trata de un sistema de láminas plegadas que suponen un récord mundial. No solo en sus dimensiones sinó en los metros cúbicos de hormigón empleados por volumen útil de construcción; a esto se le añade una mano de obra muy reducida y una gran velocidad de ejecución, inusual en obras de hormigón armado, gracias al ingenio en el proceso constructivo basado en la repetición y en los medios auxiliares.

Figura 3: Hangares de Orly

Lo curioso de esta obra es que el proyectista,como él mismo reconoce, en ningún momento tuvo presente la repercusión estética de su trabajo. "`Es en los hangares de Orly donde un acercamiento entre la ausencia de intenciones artísticas y la potencia de efectos es más chocante. Estas edificaciones fueron objeto de un concurso entre constructores. Mi sociedad había presentado un precio tan considerablemente inferior a todos los demás concursantes que temían haber sufrido un error en nuestra evaluación; sobre todo porque, presionados por otros trabajos, dispusimos de poco tiempo para el estudio del anteproyecto. Despues de largos tanteos llegué a combinar formas no empleadas hasta entonces, susceptibles de ser realizadas por medios mecánicos con poca mano de obra y tales que una amplia solidez del edificio se encontrase asegurada, mediante un débil gasto de materiales. No buscaba más, y ni un segundo pensé en los posibles efectos artísticos. Sin embargo, éstos son sorprendentes…Y no es debida únicamente a las desacostrumbadas dimensiones de la nave; es,ante todo, una sensación de equilibrio, de armonía y de orden; una convicción espontánea de que cada detalle es justo tal y como debía ser, con una satisfacción de la sensibilidad idéntica a la que sentimos ante una obra de arte conseguida"'¹. Estas líneas reflejan la potencia que presentan este tipo de estructuras ya que con el mínimo uso de material y con altas posibilidades de mecanización de la producción podemos obtener un diseño óptimo desde el punto de vista estético y de funcionamiento estructural del sistema. En resumen, con el mínimo esfuerzo obtendremos el máximo resultado.

Figura 4: Hangar Roma y Turin Exibition Hall

Sobre la misma época, cabe destacar dos diseñadores también importantes. En primer lugar, tenemos a Pier Luigi Nervi con obras tan importantes como el Hangar de las Fuerzas Aerias Italianas (Roma) o el Turin Exibition Hall que se muestran en la figura 4. Por otro lado tenemos a Eduardo Torroja Miret, autor de obras como el Mercado de Algeciras o el Frontón de Recoletos entre muchas otras destacables.

Figura 5: Mercado de Algeciras.

Figura 6: Frontón de Recoletos.

Para finalizar nuestro recorrido histórico, no podemos olvidar hacer referencia a obras más contemporáneas como el Centre de nouvelles industries et technologies situado en la Defense de París , el oceanográfico de Valencia, la gasolinera de Heinz Isler en la autopista entre Bern y Zurich o bien el Palau Blaugrana de Francesc Cavalé y Josep Soteras.

Figura 7: Láminas de doble curvatura I.

Figura 8: Láminas de doble curvatura II.

(¹) Eugène Freyssinet, José A. Fernandez. Grupo 2c Ediciones

1.2 Comportamiento general de las láminas

1.2.1 Teoría general de láminas

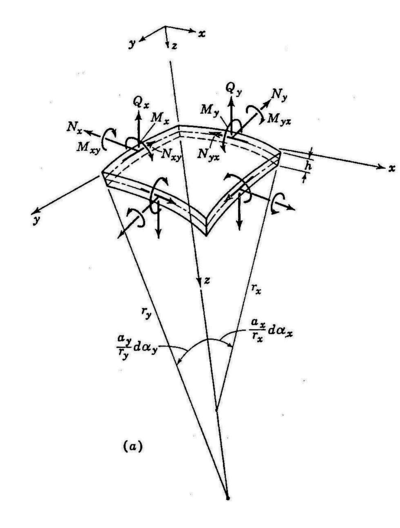
Definición 1: Losa curvada cuyo espesor h es relativamente pequeño comparado con sus otras dimensiones y comparado con sus radios de curvatura ${\textstyle r_{x}}$ y ${\textstyle r_{y}}$.

Figura 9: Elemento diferencial de lámina delgada

(0) Relaciones esfuerzos-tensión

${\begin{array}{cc}N_{x}=\int _{\frac {-h}{2}}^{\frac {h}{2}}\sigma _{x}\,(1-{\frac {z}{r_{y}}})\,dz&N_{y}=\int _{\frac {-h}{2}}^{\frac {h}{2}}\sigma _{y}\,(1-{\frac {z}{r_{x}}})\,dz\\N_{xy}=\int _{\frac {-h}{2}}^{\frac {h}{2}}\tau _{xy}\,(1-{\frac {z}{r_{y}}})\,dz&N_{yx}=\int _{\frac {-h}{2}}^{\frac {h}{2}}\tau _{yx}\,(1-{\frac {z}{r_{x}}})\,dz\\Q_{x}=\int _{\frac {-h}{2}}^{\frac {h}{2}}\tau _{xz}\,(1-{\frac {z}{r_{y}}})\,dz&Q_{y}=\int _{\frac {-h}{2}}^{\frac {h}{2}}\tau _{yz}\,(1-{\frac {z}{r_{x}}})\,dz\\M_{x}=\int _{\frac {-h}{2}}^{\frac {h}{2}}\sigma _{x}\,z(1-{\frac {z}{r_{y}}})\,dz&M_{y}=\int _{\frac {-h}{2}}^{\frac {h}{2}}\sigma _{y}\,z(1-{\frac {z}{r_{x}}})\,dz\\M_{xy}=\int _{\frac {-h}{2}}^{\frac {h}{2}}\tau _{xy}\,z\,(1-{\frac {z}{r_{y}}})\,dz&M_{yx}=\int _{\frac {-h}{2}}^{\frac {h}{2}}\tau _{yx}\,z\,(1-{\frac {z}{r_{x}}})\,dz\\\end{array}}$

Hipótesis 1: Como ${\textstyle z/r_{y}}$ y ${\textstyle z/r_{x}}$ son despreciables por definición de lámina delgada, podemos decir que:

${\begin{array}{cc}N_{xy}=N_{yx}&M_{xy}=M_{yx}\end{array}}$

Hipótesis 2: Se acepta la teoría de pequeñas deformaciones. Es decir, las deformaciones de la lámina bajo carga son suficientemente pequeñas para que los cambios de geometría de ésta no afecten al equilibrio estático del sistema.

Hipótesis 3: Comportamiento lineal-elástico del material, con lo que conseguimos una relación directa entre tensión y deformación.

Hipótesis 4: [Normalidad] Puntos sobre la normal a la superficie media antes de la deformación permanecen sobre la normal a la superficie media deformada.

Hipótesis 5: [Love-Kirchhoff] Se desprecian las deformaciones de la lámina debida a los cortantes ${\textstyle Q_{x}}$ y ${\textstyle Q_{y}}$.

Teniendo en cuenta estas hipótesis previas ya podemos plantear el esquema general que nos llevará a la formulación completa de la Teoría general de láminas delgadas.

${\begin{array}{l|}{\hbox{Equilibrio (5 ec.-8 inc.)}}\\{\hbox{Relación deformación-desplazamientos (6ec.-8inc.)}}\\{\hbox{Relación tensión-deformación (3ec.-6inc.)}}\\{\hbox{Relación esfuerzos-deformación (6ec.-3inc.)}}\\{\hbox{Relación esfuerzos-desplazamientos (6ec.-3inc.)}}\\\end{array}}{\begin{array}{c}{\hbox{Formulación completa}}\\{\hbox{(11ec.-11inc.)}}\end{array}}$

(1) Equilibrio

Sobre el elemento diferencial que se muestra en la figura  9 podemos imponer 6 condiciones de equilibrio:

${\begin{array}{ccc}\sum X=0&\sum Y=0&\sum Z=0\\\sum M_{x}=0&\sum M_{y}=0&\sum M_{z}=0\\\end{array}}$

Si aceptamos la hipótesis 0, podemos establecer que ${\textstyle \sum M_{z}\neq 0}$ con lo que como se había anunciado, las condiciones de equilibrio nos dan 5 ecuaciones i 8 incógnitas.

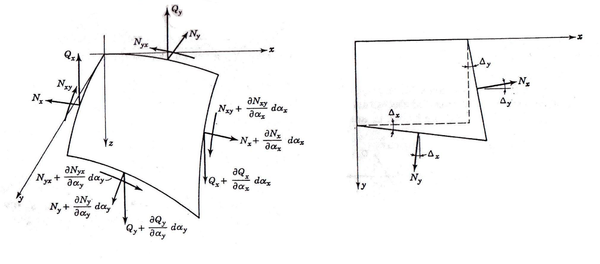
Figura 10: Equilibrio sobre el elemento diferencial

En primer lugar tenemos que estudiar el elemento diferencial de la figura 9 donde nos aparecen los términos ${\textstyle a_{x}}$ y ${\textstyle a_{y}}$. Éstos los debemos entender como funciones de radio de curvatura que varian sobre los ejes ${\textstyle y}$ y ${\textstyle x}$ respectivamente y a la vez cumplen las siguientes condiciones:

${\begin{array}{ccc}{\begin{array}{c}a_{x}(y=0)=r_{x}\\a_{y}(x=0)=r_{y}\\\end{array}}&\left.{\frac {a_{x}}{r_{x}}}\,d\alpha _{x}\right|_{y=0}=d\alpha _{y}&\left.{\frac {a_{y}}{r_{y}}}\,d\alpha _{y}\right|_{x=0}=d\alpha _{x}\\\end{array}}$

Consideramos primero los esfuerzos ${\textstyle N_{x}}$ descritas claramente en la figura 10:

$-N_{x}\,a_{y}\,d\alpha _{y}\,+{\Big (}N_{x}+{\frac {\partial N_{x}}{\partial \alpha _{x}}}\,d\alpha _{x}{\Big )}\,{\Big (}a_{y}+{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,d\alpha _{x}{\Big )}\,d\alpha _{y}$

(1)

El segundo término de la expresión (1) puede desarrollarse dando lugar a:

$N_{x}\,{\frac {\partial a_{y}}{\partial \alpha _{y}}}\,d\alpha _{x}\,d\alpha _{y}\,+\,a_{y}\,{\frac {\partial N_{x}}{\partial \alpha _{x}}}\,d\alpha _{x}\,d\alpha _{y}\,+\,{\frac {\partial N_{x}}{\partial \alpha _{x}}}\,d\alpha _{x}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,d\alpha _{x}\,d\alpha _{y}$

(2)

Asimismo, los dos primeros términos de (2) pueden combinarse del siguiente modo:

${\frac {\partial (N_{x}\,a_{y})}{\partial \alpha _{x}}}\,d\alpha _{x}\,d\alpha _{y}$

(3)

y el tercer término puede ser despreciado por ser de segundo orden. De este modo la expresión (1) puede ser reescrita por la (3).

Ahora vamos a considerar los esfuerzos ${\textstyle N_{y}}$ que no actuan en el eje x pero si tienen una cierta componente como se puede observar en la figura 10.

$-N_{y}\,a_{x}\,d\alpha _{x}\,\Delta _{x}$

(4)

donde ${\textstyle \Delta _{x}}$ se puede entender como:

$\Delta _{x}={\frac {(\partial a_{y}/\partial \alpha _{x})\,d\alpha _{x}\,d\alpha _{y}}{a_{x}\,d\alpha _{x}}}={\frac {\partial a_{y}}{\partial \alpha _{x}}}\,{\frac {d\alpha _{y}}{a_{x}}}$

(5)

Si introducimos la expresión (5) en la (4) obtendremos la siguiente expresión:

$-N_{y}\,a_{x}\,d\alpha _{x}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,{\frac {d\alpha _{y}}{a_{x}}}=-N_{y}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,d\alpha _{x}\,d\alpha _{y}$

(6)

Del mismo modo, se puede observar que los esfuerzos ${\textstyle N_{xy}}$ también tienen componente en la dirección x que puede ser determinada con la evaluación del ángulo:

$\Delta _{y}={\frac {(\partial a_{x}/\partial \alpha _{y})\,d\alpha _{y}\,d\alpha _{x}}{a_{y}\,d\alpha _{y}}}={\frac {\partial a_{x}}{\partial \alpha _{y}}}\,{\frac {d\alpha _{x}}{a_{y}}}$

(7)

y la componente total será:

$-N_{xy}\,a_{y}\,d\alpha _{y}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,{\frac {d\alpha _{x}}{a_{y}}}=N_{xy}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,d\alpha _{y}\,d\alpha _{x}$

(8)

Por lo que hace a los esfuerzos ${\textstyle N_{yx}}$ obtendremos una expresión similar a la (1):

$-N_{yx}\,a_{x}\,d\alpha _{x}\,+{\Big (}N_{yx}+{\frac {\partial N_{yx}}{\partial \alpha _{y}}}\,d\alpha _{y}{\Big )}\,{\Big (}a_{x}+{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,d\alpha _{y}{\Big )}\,d\alpha _{x}$

(9)

Que del mismo modo que en la expresión (3) puede reducirse a:

${\frac {\partial (N_{yx}\,a_{x})}{\partial \alpha _{y}}}\,d\alpha _{x}\,d\alpha _{y}$

(10)

Por ahora ya se han considerado todos los esfuerzos que actuan sobre el plano de la lámina, pero no nos podemos olvidar de los esfuerzos cortantes que también darán componente sobre el eje x como se puede ver en la figura 11.

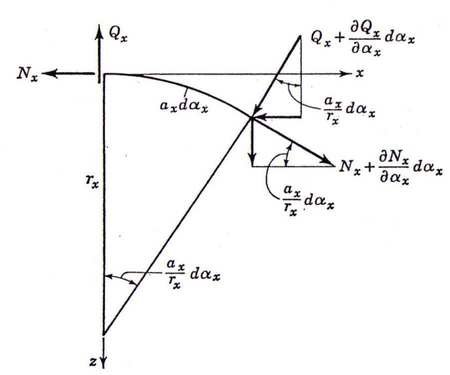
Figura 11: Esfuerzos cortantes

La componente de ${\textstyle Q_{x}}$ sobre el eje x es:

$-{\Big (}Q_{x}\,+\,{\frac {\partial Q_{x}}{\partial \alpha _{x}}}\,d\alpha _{x}{\Big )}{\Big (}a_{y}\,+{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,d\alpha _{x}{\Big )}\,d\alpha _{y}\,{\frac {a_{x}}{r_{x}}}\,d\alpha _{x}$

(11)

Si desarrollamos la expresión y despreciamos los términos de orden superior obtenemos:

$-Q_{x}\,a_{y}\,d\alpha _{y}\,{\frac {a_{x}}{r_{x}}}\,d\alpha _{x}$

(12)

Por lo que hace al esfuerzo ${\textstyle Q_{y}}$, solamente tendremos contribución sobre el eje x si ${\textstyle a_{x}}$ y ${\textstyle a_{y}}$ no son radios principales de curvatura. En la figura 12 se muestra el elemento detallando la distancia total que obtiene en la esquina ${\textstyle z_{x}+z_{y}+z_{xy}}$ donde:

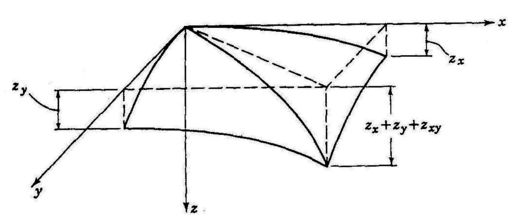
Figura 12: Curvatura del elemento diferencial

$z_{x}$ $={\frac {1}{a_{x}}}\,{\frac {\partial z}{\partial \alpha _{x}}}\,a_{x}\,d\alpha _{x}$ $z_{y}$ $={\frac {1}{a_{y}}}\,{\frac {\partial z}{\partial \alpha _{y}}}\,a_{y}\,d\alpha _{y}$ $z_{xy}$ $={\frac {1}{a_{x}\,a_{y}}}\,{\frac {\partial }{\partial \alpha _{y}}}\,{\big (}{\frac {\partial z}{\partial \alpha _{x}}}{\big )}\,a_{x}\,a_{y}\,d\alpha _{x}\,d\alpha _{y}={\frac {a_{x}\,a_{y}}{r_{xy}}}\,d\alpha _{x}\,d\alpha _{y}$

(13)

donde el giro de la superficie ${\textstyle 1/r_{xy}}$ se expresa como:

${\frac {1}{r_{xy}}}={\frac {1}{a_{x}\,a_{y}}}\,{\frac {\partial }{\partial \alpha _{y}}}\,{\big (}{\frac {\partial z}{\partial \alpha _{x}}}{\big )}$

(14)

De esta manera, la componente de ${\textstyle Q_{y}}$ en la dirección x será:

$Q_{y}\,a_{x}\,d\alpha _{x}\,{\frac {a_{y}\,d\alpha _{y}}{r_{xy}}}$

(15)

Finalmente combinando las expresiones (3), (6), (8), (10), (12), (15) y añadiendo el efecto de las cargas ${\textstyle (p_{x},p_{y},p_{z})}$ encontraremos la condición de equilibrio de los esfuerzos resultantes sobre el eje x ${\textstyle (\sum {X=0)}}$:

$\sum {X}={\frac {\partial (N_{x}\,a_{y})}{\partial \alpha _{x}}}\,-\,N_{y}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,+\,N_{xy}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,+\,{\frac {\partial (N_{yx}\,a_{x})}{\partial \alpha _{y}}}\,-\,Q_{y}\,{\frac {a_{x}\,a_{y}}{r_{xy}}}\,-\,Q_{x}\,a_{y}\,{\frac {a_{x}}{r_{x}}}\,+\,p_{x}\,a_{x}\,a_{y}=0$

(16)

Siguiendo el mismo esquema para las demás condiciones de equilibrio planteadas, llegamos a las siguientes ecuaciones de equilibrio:

$\sum {X}$ $={\frac {\partial (N_{x}\,a_{y})}{\partial \alpha _{x}}}\,-\,N_{y}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,+\,N_{xy}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,+\,{\frac {\partial (N_{yx}\,a_{x})}{\partial \alpha _{y}}}\,-\,Q_{y}\,{\frac {a_{x}\,a_{y}}{r_{xy}}}\,-\,Q_{x}\,a_{y}\,{\frac {a_{x}}{r_{x}}}\,+\,p_{x}\,a_{x}\,a_{y}=0$ $\sum {Y}$ $={\frac {\partial (N_{y}\,a_{x})}{\partial \alpha _{y}}}\,-\,N_{x}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,+\,N_{yx}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,+\,{\frac {\partial (N_{xy}\,a_{y})}{\partial \alpha _{x}}}\,-\,Q_{x}\,{\frac {a_{x}\,a_{y}}{r_{xy}}}\,-\,Q_{y}\,a_{x}\,{\frac {a_{y}}{r_{y}}}\,+\,p_{y}\,a_{x}\,a_{y}=0$ $\sum {Z}$ $={\frac {\partial (Q_{x}\,a_{y})}{\partial \alpha _{x}}}\,+\,{\frac {\partial (Q_{y}\,a_{x})}{\partial \alpha _{y}}}\,+\,N_{x}\,{\frac {a_{x}\,a_{y}}{r_{x}}}\,+\,(N_{xy}+N_{yx})\,{\frac {a_{x}\,a_{y}}{r_{x}y}}\,+\,N_{y}\,{\frac {a_{x}\,a_{y}}{r_{y}}}\,p_{z}\,a_{x}\,a_{y}=0$ $\sum {M_{x}}$ $=-{\frac {\partial (M_{y}\,a_{x})}{\partial \alpha _{y}}}\,+\,M_{x}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,-\,M_{yx}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,+\,{\frac {\partial (M_{xy}\,a_{y})}{\partial \alpha _{x}}}\,+\,Q_{y}\,a_{x}\,a_{y}=0$ $\sum {M_{y}}$ $=-{\frac {\partial (M_{x}\,a_{y})}{\partial \alpha _{x}}}\,+\,M_{y}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,+\,M_{xy}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,-\,{\frac {\partial (M_{yx}\,a_{x})}{\partial \alpha _{y}}}\,+\,Q_{x}\,a_{x}\,a_{y}=0$

(17)

(2) Relaciones deformación-desplazamientos

En la figura 13 se muestra el elemento diferencial después de la deformación donde se puede observar que la deformación unitaria sobre el eje x ${\textstyle (\epsilon _{x0})}$ será:

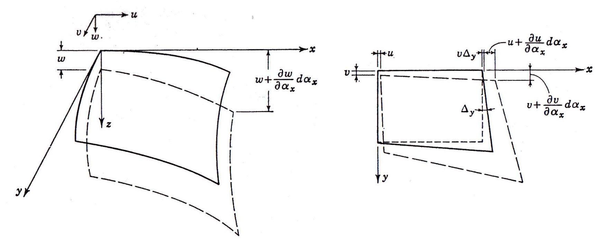
Figura 13: Elemento diferencial deformado

$\epsilon _{x0}={\frac {1}{a_{x}}}\,{\frac {\partial u}{\partial \alpha _{x}}}\,+\,{\frac {v}{a_{x}\,a_{y}}}\,{\frac {\partial a_{x}}{\partial a_{y}}}\,-\,{\frac {w}{r_{x}}}$

Donde el primer término representa la extensión sobre el eje x, el segundo la extensión debida al movimiento lateral del elemento y el tercero el acortamiento debido al descenso del radio de curvatura. Siguiendo el mismo criterio, podemos encontrar las demas deformaciones unitarias y angulares:

$\epsilon _{x0}$ $={\frac {1}{a_{x}}}\,{\frac {\partial u}{\partial \alpha _{x}}}\,+\,{\frac {v}{a_{x}\,a_{y}}}\,{\frac {\partial a_{x}}{\partial a_{y}}}\,-\,{\frac {w}{r_{x}}}$ $\epsilon _{y0}$ $={\frac {1}{a_{y}}}\,{\frac {\partial u}{\partial \alpha _{y}}}\,+\,{\frac {v}{a_{y}\,a_{x}}}\,{\frac {\partial a_{y}}{\partial a_{x}}}\,-\,{\frac {w}{r_{y}}}$ $\gamma _{xy0}$ $={\frac {1}{a_{x}}}\,{\frac {\partial v}{\partial \alpha _{x}}}\,+\,{\frac {1}{a_{y}}}\,{\frac {\partial u}{\partial \alpha _{y}}}\,-\,{\frac {u}{a_{x}\,a_{y}}}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,-\,{\frac {v}{a_{x}\,a_{y}}}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,-\,{\frac {2\,w}{r_{xy}}}$

(18)

Los giros de la lámina se pueden expresar como:

$\phi _{x}$ $={\frac {u}{r_{x}}}\,+\,{\frac {\partial w}{a_{x}\,\partial \alpha _{x}}}\,+\,{\frac {v}{r_{xy}}}$ $\phi _{y}$ $={\frac {v}{r_{y}}}\,+\,{\frac {\partial w}{a_{y}\,\partial \alpha _{y}}}\,+\,{\frac {u}{r_{xy}}}$

(19)

Y finalmente, si entendemos la curvatura como la variación del giro por longitud de arco ${\textstyle (ad\alpha )}$, la expresión de las curvaturas es:

$\chi _{x}$ $={\frac {1}{a_{x}}}\,{\frac {\partial \phi _{x}}{\partial \alpha _{x}}}\,+\,{\frac {\phi _{y}}{a_{x}\,a_{y}}}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}$ $\chi _{y}$ $={\frac {1}{a_{y}}}\,{\frac {\partial \phi _{y}}{\partial \alpha _{y}}}\,+\,{\frac {\phi _{x}}{a_{x}\,a_{y}}}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}$ $2\chi _{xy}$ $={\frac {1}{a_{y}}}\,{\frac {\partial \phi _{x}}{\partial \alpha _{y}}}\,+\,{\frac {1}{a_{x}}}\,{\frac {\partial \phi _{y}}{\partial \alpha _{x}}}\,-\,{\frac {\phi _{x}}{a_{x}\,a_{y}}}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,-\,{\frac {\phi _{y}}{a_{x}\,a_{y}}}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}$

(20)

La deformación ${\textstyle \epsilon _{x}}$ entendida como una distancia ${\textstyle z}$ medida desde la superficie media, es una composición de la deformación ${\textstyle \epsilon _{x0}}$ debida al esfuerzo axil y a la deformación debida a la flexión:

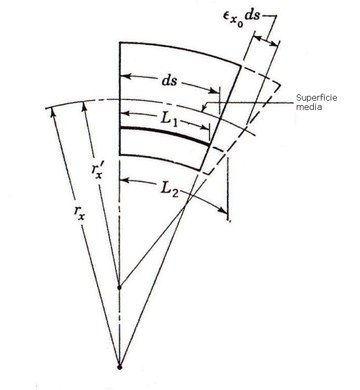
Figura 14: Deformación de la superficie media

$\epsilon _{x}$ $={\frac {L_{2}-L_{1}}{L_{1}}}$ $L_{1}$ $=ds\,{\Big (}1-{\frac {z}{r_{x}}}{\Big )}$ $L_{2}$ $=ds\,(1+\epsilon _{x0})\,{\Big (}1-{\frac {z}{r'_{x}}}{\Big )}$ $\epsilon _{x}$ $={\frac {1-z/r'_{x}+\epsilon _{x0}\,(1-z/r'_{x})-1+z/r_{x}}{1-z/r_{x}}}$

(21)

Si despreciamos los términos ${\textstyle z/r_{x}}$ y ${\textstyle z/r'_{x}}$ con respecto a la unidad, obtenemos:

$\epsilon _{x}\,=\,\epsilon _{x0}\,-\,z\,{\Big (}{\frac {1}{r'_{x}}}-{\frac {1}{r_{x}}}{\Big )}$

De esta manera, obtenemos las deformaciones de la superficie media:

$\epsilon _{x}$ $=\epsilon _{x0}-z\,\chi _{x}$ $\epsilon _{y}$ $=\epsilon _{y0}-z\,\chi _{y}$ $\gamma _{xy}$ $=\gamma _{xy0}-2\,z\,\chi _{xy}$

(22)

(3) Relaciones tensión-deformación

Llegados a este punto, necesitamos acotar el problema para poderlo afrontar de forma directa. Para ello tenemos que añadir las siguientes hipótesis:

Hipótesis 6: Material Lineal Elástico

Hipótesis 7: Material Isotrópico

Hipótesis 8: Material Homogéneo

Sin más, la relación tensión-deformación será la correspondiente a las ecuaciones constitutivas para material elástico lineal e isótropo.

$\epsilon _{x}$ $={\frac {1}{E}}\,[\sigma _{x}-\nu \,(\sigma _{y}+\sigma _{z})]$ $\epsilon _{y}$ $={\frac {1}{E}}\,[\sigma _{y}-\nu \,(\sigma _{x}+\sigma _{z})]$ $\gamma _{xy}$ $={\frac {\tau _{xy}}{G}}$

(23)

Como ya hemos visto anteriormente ${\textstyle \sigma _{z}=0}$ y por lo tanto obtenemos las siguientes expresiones:

$\sigma _{x}$ $={\frac {E}{1-\nu ^{2}}}\,(\epsilon _{x}+\nu \,\epsilon _{y})$ $\sigma _{y}$ $={\frac {E}{1-\nu ^{2}}}\,(\epsilon _{y}+\nu \,\epsilon _{x})$ $\tau _{xy}$ $=G\,\gamma _{xy}$

(24)

Donde ${\textstyle G}$ es el módulo de deformación a cortante y vale:

$G={\frac {E}{2\,(1+\nu )}}$

(25)

(4) Relaciones esfuerzos-deformación

Si combinamos los puntos (0), (3) y la ecuación 22 e integramos alrededor de ${\textstyle h}$, podemos obtener las siguientes relaciones:

$N_{x}$ $=K\,(\epsilon _{x0}+\nu \,\epsilon _{y0})$ $N_{y}$ $=K\,(\epsilon _{y0}+\nu \,\epsilon _{x0})$ $N_{xy}$ $=N_{yx}\,=\,Gh\gamma _{xy0}$ $M_{x}$ $=-D\,(\chi _{x}\,+\,\nu \chi _{y})$ $M_{y}$ $=-D\,(\chi _{y}\,+\,\nu \chi _{x})$ $M_{xy}$ $=-M_{yx}\,=\,{\frac {Gh^{3}}{6}}\,\chi _{xy}\,=\,D(1-\nu )\,\chi _{xy}$

(26)

Donde:

${\begin{array}{ll}{\hbox{Rigidez axial}}&K={\frac {Eh}{1-\nu ^{2}}}\\{\hbox{Rigidez a cortante}}&G={\frac {E}{2\,(1+\nu )}}\\{\hbox{Rigidez a flexión}}&D={\frac {Eh^{3}}{12\,(1-\nu ^{2})}}\end{array}}$

(27)

(5) Relaciones esfuerzos-desplazamientos

Finalmente si juntamos los puntos (4) y (2) podemos obtener las ecuaciones que relacionan los esfuerzos con los desplazamientos.

$N_{x}$ $=K\,{\Big [}{\frac {1}{a_{x}}}\,{\frac {\partial u}{\partial \alpha _{x}}}\,+\,{\frac {v}{a_{x}\,a_{y}}}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,-\,{\frac {w}{r_{x}}}\,+\,\nu {\Big (}{\frac {1}{a_{y}}}\,{\frac {\partial v}{\partial \alpha _{y}}}\,+\,{\frac {u}{a_{x}\,a_{y}}}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,-\,{\frac {w}{r_{y}}}{\Big )}{\Big ]}$ $N_{y}$ $=K\,{\Big [}{\frac {1}{a_{y}}}\,{\frac {\partial v}{\partial \alpha _{y}}}\,+\,{\frac {u}{a_{x}\,a_{y}}}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,-\,{\frac {w}{r_{y}}}\,+\,\nu {\Big (}{\frac {1}{a_{x}}}\,{\frac {\partial u}{\partial \alpha _{x}}}\,+\,{\frac {v}{a_{x}\,a_{y}}}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,-\,{\frac {w}{r_{x}}}{\Big )}{\Big ]}$ $N_{xy}$ $=N_{yx}\,=\,Gh\,{\Big (}{\frac {1}{a_{x}}}\,{\frac {\partial v}{\partial \alpha _{x}}}\,+\,{\frac {1}{a_{y}}}\,{\frac {\partial u}{\partial \alpha _{y}}}\,-\,{\frac {u}{a_{x}\,a_{y}}}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,-\,{\frac {v}{a_{x}\,a_{y}}}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,-\,{\frac {2w}{r_{xy}}}{\Big )}$ $M_{x}$ $=-D{\Big [}{\frac {1}{a_{x}}}\,{\frac {\partial \phi _{x}}{\partial \alpha _{x}}}\,+\,{\frac {\phi _{y}}{a_{x}\,a_{y}}}{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,+\,\nu \,{\Big (}{\frac {1}{a_{y}}}\,{\frac {\partial \phi _{y}}{\partial \alpha _{y}}}\,+\,{\frac {\phi _{x}}{a_{x}\,a_{y}}}{\frac {\partial a_{y}}{\partial \alpha _{x}}}{\Big )}{\Big ]}$ $M_{y}$ $=-D{\Big [}{\frac {1}{a_{y}}}\,{\frac {\partial \phi _{y}}{\partial \alpha _{y}}}\,+\,{\frac {\phi _{x}}{a_{x}\,a_{y}}}{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,+\,\nu \,{\Big (}{\frac {1}{a_{x}}}\,{\frac {\partial \phi _{x}}{\partial \alpha _{x}}}\,+\,{\frac {\phi _{y}}{a_{x}\,a_{y}}}{\frac {\partial a_{x}}{\partial \alpha _{y}}}{\Big )}{\Big ]}$ $M_{xy}$ $=-M_{xy}\,=\,{\frac {D(1-\nu )}{2}}\,{\Big (}{\frac {1}{a_{y}}}{\frac {\partial \phi _{x}}{\partial \alpha _{y}}}\,+\,{\frac {1}{a_{x}}}{\frac {\partial \phi _{y}}{\partial \alpha _{x}}}\,-\,{\frac {\phi _{x}}{a_{x}\,a_{y}}}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}-\,{\frac {\phi _{y}}{a_{x}\,a_{y}}}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}{\Big )}$

(28)

De esta manera hemos descrito la teoría general de láminas de forma análoga como se podría describir la teoría general de vigas delgadas. Si combinamos las ecuaciones 28 y 17 obtendremos el sistema resultante con 11 ecuaciones y 11 incógnitas.

1.2.2 Simplificaciones de la teoría general

Como ya hemos visto, la teoría general nos lleva a un sistema diferencial con 11 ecuaciones y 11 incógnitas. En la práctica, solo muy pocos casos pueden ser estudiados de este modo por lo engorroso que resulta su cálculo. Así pues, mediante simplificaciones y asumiendo ciertas hipótesis podemos llegar a formulaciones mucho más asequibles.

(1) Teoría de láminas de curvatura reducida

Esta teoría asume las siguientes hipótesis:

Hipótesis 1: La pendiente de la lámina es reducida.

Hipótesis 2: La curvatura de la superficie es pequeña.

Hipótesis 3: Las reacciones en el contorno se limitan a los esfuerzos ${\textstyle N_{x}}$, ${\textstyle N_{x}}$, ${\textstyle N_{xy}}$, que actúan contenidas en la superficie media de la lamina.

Hipótesis 4: Los cambios de curvatura son pequeños.

Si tenemos en cuenta estas condiciones, podemos decir que ${\textstyle a_{x}}$ y ${\textstyle a_{y}}$ son constantes, por lo que sus derivadas serán nulas y términos como ${\textstyle \partial (N_{x}\,a_{y})/\partial \alpha _{x}}$ pasaran a, ${\textstyle a_{y}\,\partial (N_{x})/\partial \alpha _{x}}$ con lo que las ecuaciones de equilibrio se reducen a:

${\frac {1}{a_{x}}}\,{\frac {\partial N_{x}}{\partial \alpha _{x}}}\,+\,{\frac {1}{a_{y}}}\,{\frac {\partial N_{yx}}{\partial \alpha _{y}}}\,+\,p_{x}\,=\,$ ${\frac {1}{a_{y}}}\,{\frac {\partial N_{y}}{\partial \alpha _{y}}}\,+\,{\frac {1}{a_{x}}}\,{\frac {\partial N_{xy}}{\partial \alpha _{x}}}\,+\,p_{y}\,=\,$ ${\frac {1}{a_{x}}}\,{\frac {\partial Q_{x}}{\partial \alpha _{x}}}\,+\,{\frac {1}{a_{y}}}\,{\frac {\partial Q_{y}}{\partial \alpha _{y}}}\,+\,{\frac {N_{x}}{r_{x}}}\,+\,{\frac {2N_{xy}}{r_{xy}}}\,+\,{\frac {N_{y}}{r_{y}}}\,+\,p_{z}=0$ $-$ ${\frac {1}{a_{y}}}\,{\frac {\partial M_{y}}{\partial \alpha _{y}}}\,+\,{\frac {1}{a_{x}}}\,{\frac {\partial M_{xy}}{\partial \alpha _{x}}}\,+\,Q_{y}\,=\,$ $-$ ${\frac {1}{a_{x}}}\,{\frac {\partial M_{x}}{\partial \alpha _{x}}}\,-\,{\frac {1}{a_{y}}}\,{\frac {\partial M_{yx}}{\partial \alpha _{y}}}\,+\,Q_{x}\,=\,$

(29)

Si seguimos desarrollando, podemos llegar a la ecuación siguiente:

$N_{x}$ $=K\,{\Big [}{\frac {1}{a_{x}}}\,{\frac {\partial u}{\partial \alpha _{x}}}\,-\,{\frac {w}{r_{x}}}\,+\,\nu {\Big (}{\frac {1}{a_{y}}}\,{\frac {\partial v}{\partial \alpha _{y}}}\,-\,{\frac {w}{r_{y}}}{\Big )}{\Big ]}$ $N_{y}$ $=K\,{\Big [}{\frac {1}{a_{y}}}\,{\frac {\partial v}{\partial \alpha _{y}}}\,-\,{\frac {w}{r_{y}}}\,+\,\nu {\Big (}{\frac {1}{a_{x}}}\,{\frac {\partial u}{\partial \alpha _{x}}}\,-\,{\frac {w}{r_{x}}}{\Big )}{\Big ]}$ $N_{xy}$ $=Gh\,{\Big (}{\frac {1}{a_{x}}}\,{\frac {\partial v}{\partial \alpha _{x}}}\,+\,{\frac {1}{a_{y}}}\,{\frac {\partial u}{\partial \alpha _{y}}}\,-\,{\frac {2w}{r_{xy}}}{\Big )}$ $M_{x}$ $=-D{\Big (}{\frac {1}{a_{x}^{2}}}\,{\frac {\partial ^{2}w}{\partial \alpha _{x}^{2}}}\,+\,\nu \,{\frac {1}{a_{y}^{2}}}\,{\frac {\partial ^{2}w}{\partial \alpha _{y}^{2}}}{\Big )}$ $M_{y}$ $=-D{\Big (}{\frac {1}{a_{y}^{2}}}\,{\frac {\partial ^{2}w}{\partial \alpha _{y}^{2}}}\,+\,\nu \,{\frac {1}{a_{x}^{2}}}\,{\frac {\partial ^{2}w}{\partial \alpha _{x}^{2}}}{\Big )}$ $M_{xy}$ $=D(1-\nu )\,{\Big (}{\frac {1}{a_{x}\,a_{y}}}\,{\frac {\partial ^{2}w}{\partial \alpha _{x}\,\partial \alpha _{y}}}{\Big )}$

(30)

(2) Ecuación de la placa plana

Siguiendo con las hipótesis hasta ahora mencionadas, si sustituimos los valores de ${\textstyle Q_{x}}$ y ${\textstyle Q_{y}}$ en la ecuación 29 obtenemos la siguiente ecuación:

${\frac {1}{a_{x}^{2}}}\,{\frac {\partial ^{2}M_{x}}{\partial \alpha _{x}^{2}}}\,-\,{\frac {1}{a_{x}\,a_{y}}}\,{\frac {\partial ^{2}M_{xy}}{\partial \alpha _{x}\,\partial \alpha _{y}}}\,+\,{\frac {1}{a_{y}^{2}}}\,{\frac {\partial ^{2}M_{y}}{\partial \alpha _{y}^{2}}}\,+\,{\frac {N_{x}}{r_{x}}}\,+\,{\frac {2N_{xy}}{r_{xy}}}\,+\,{\frac {N_{y}}{r_{y}}}\,+\,p_{z}\,=\,$

(31)

Finalmente, si sustituimos la ecuación 30 en 31 obtendremos:

$-\nabla ^{4}w\,+\,{\frac {1}{D}}\,{\Big (}{\frac {N_{x}}{r_{x}}}\,+\,{\frac {2N_{xy}}{r_{xy}}}\,+\,{\frac {N_{y}}{r_{y}}}{\Big )}\,=\,-{\frac {p_{z}}{D}}$

(32)

Al estudiar el caso concreto de la placa plana, podemos decir que ${\textstyle r_{x}=r_{y}=r_{xy}=\infty }$ y por lo tanto, podemos reducir la ecuación 32 a:

${\begin{array}{cc}\nabla ^{4}w\,=\,{\frac {p_{z}}{D}}&\,\,\,{\hbox{Ecuación de la placa delgada}}\end{array}}$

(33)

1.2.3 Método general de análisis

El primer paso para resolver un problema de lámina delgada es reducir la formulación general a una ecuación con una incógnita, tal y como hemos hecho en las simplificaciones anteriores.

En general, ésta es una ecuación diferencial lineal de octavo orden cuya solución incluye la evalución de ocho constantes de integración más una solución particular. Así pues, necesitamos ocho condiciones de contorno. Por lo que hace a la solución particular, incluirá las cargas superficiales y se suele aproximar mediante la teoría de la membrana.

De esta manera, el método contempla la solución de dos ecuaciones:

a) Solución homogénea de la ecuación diferencial donde suprimimos las cargas.
b) Solución particular, donde sí tenemos en cuenta las cargas. En muchos casos podemos demostrar que esta solución puede simplificarse con la teoría de la membrana sin perder representativamente precisión.

Así pues, podemos esquematizar el método general de la siguiente manera:

1. Podemos considerar que las cargas son resistidas en su totalidad por los esfuerzos de membrana.
2. En general podemos ver que las deformaciones producidas por estos esfuerzos no son compatibles con las condiciones de contorno.
3. Para restaurar la compatibilidad debemos imponer esfuerzos hiperestáticos que encontraremos resolviendo las ecuaciones de compatibilidad o equilibrio en el contorno de la lámina.

Como podemos ver, este método no se separa del discurso clásico de la estática que usamos con frecuencia para resolver todo tipo de estructuras (vigas, pórticos, placas,…

1.2.4 Teoría de la membrana

Definición 2: Cuerpo elástico de pequeño espesor y escasa rigidez flexional que solo puede resistir tensiones sobre la superficie media.

Si suprimimos los esfuerzos de flexión de la ecuación de equilibrio 17 obtenemos la siguiente ecuación, cuya solución resulta relativamente sencilla.

La teoría de la membrana puede establecer ciertas bases razonables de diseño siempre y cuando se cumplan las siguientes condiciones:

a) Los desplazamientos debidos a los esfuerzos de membrana produciran deformaciones a flexión despreciables.
b) Las cargas se distribuiran sin problema sobre la superficie de la lámina
c) Los contornos pueden sustituir los esfuerzos y permitir el desplazamiento requerido por los esfuerzos de membrana resultantes.

${\frac {\partial (N'_{x}\,a_{y})}{\partial \alpha _{x}}}\,-\,N'_{y}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,+\,N'_{xy}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,+\,{\frac {\partial (N'_{yx}\,a_{x})}{\partial \alpha _{y}}}\,+\,p_{x}\,a_{x}\,a_{y}$ $=0$ ${\frac {\partial (N'_{y}\,a_{x})}{\partial \alpha _{y}}}\,-\,N'_{x}\,{\frac {\partial a_{x}}{\partial \alpha _{y}}}\,+\,N'_{yx}\,{\frac {\partial a_{y}}{\partial \alpha _{x}}}\,+\,{\frac {\partial (N'_{xy}\,a_{y})}{\partial \alpha _{x}}}\,+\,p_{y}\,a_{x}\,a_{y}$ $=0$ ${\frac {N'_{x}}{r_{x}}}\,+\,{\frac {(N'_{xy}+N_{yx})}{r_{xy}}}\,\,+\,{\frac {N'_{y}}{r_{y}}}\,p_{z}$ $=$ $0$

(34)

1.3 Análisis de láminas mediante el MEF

Como ya hemos comentado, una vez analizada cada tipología de lámina analiticamente compararemos el resultado obtenido con el vertido con cualquier programa de elementos finitos. Para ello es necesario conocer como trabajan dichos programas y las hipótesis básicas sobre las que trabajan. De esta manera, a continuación se explicará como se analiza mediante elementos finitos estructuras de lámina.

1.3.1 Análisis de láminas con elementos planos

Tipológicamente las láminas pueden considerarse una generalización de las placas al caso de superficie media no plana. Es precisamente esta no coplanaridad la que confiere el carácter resistente de las láminas al permitir la aparición de esfuerzos axiales (esfuerzos de membrana) que, juntamente con los de flexión, contribuyen a dotar a las láminas de una capacidad portante muy superior a la de las placas.

En general, podemos decir que las láminas son a las placas, lo que los arcos (o las estructuras reticulares) son a las vigas. Por lo tanto, un buen conocimiento de la influencia del axil en arcos y pórticos favorecerá sin duda a la comprensión del funcionamiento estructural de las estructuras laminares.

La obtención de las ecuaciones de una lámina (equilibrio, constitutivas y cinemáticas) es complicada, debido precisamente a la curvatura de su superficie media. Una de las maneras más sencillas de sortear este problema es estudiar el comportamiento de una lámina como si estuviese compuesta de elementos planos de tamaño pequeño¹.

Como concepto general, este análisis discretiza la lámina en pequeños elementos planos que se trataran como elementos de placa. Lógicamente cuanto mayor sea la discretización mejor será la aproximación adoptada. Este concepto se esquematiza muy claramente en la figura siguiente.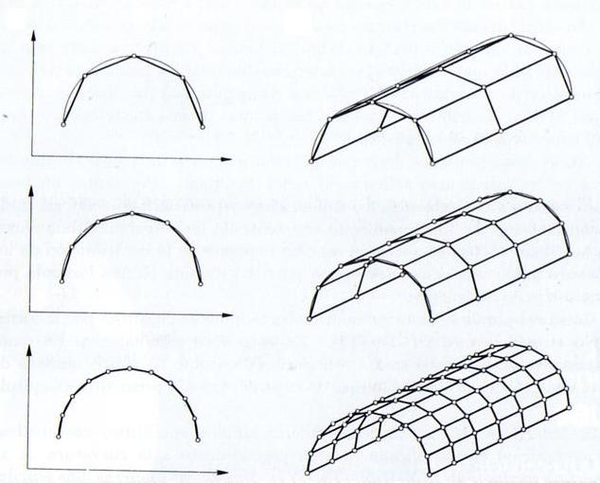

Figura 15: Discretización de arcos y láminas cilíndricas en elementos planos.

La formulación de láminas planas está descrita de forma rigurosa en el capítulo 10 de la referencia [6].

Los elementos de lámina plana más utlizados en la práctica son los siguientes:

1. Combinación de elementos de tensión plana cuadrilátero isoparamétrico de cuatro nodos con cualquier elemento de placa de Reissner-Mindlin análogos de cuatro nodos.
2. Combinación de elementos de tensión plana cuadriláteros isoparemétricos de ocho y nueve nodos con elementos de placa de Reissner-Mindlin del mismo número de nodos.
3. Combinación de elementos de tensión plana triangulares con los de placa de Reissner-Mindlin del mismo número basados en deformaciones de cortante impuestas.

Para los ejemplos que realizaremos en este texto, trabajaremos con la tercera opción, trabjando con elementos triangulares que optimizan mejor el tiempo de cálculo respecto a los grados de libertad.

(¹) Eugenio Oñate. Cálculo de Estructuras por el Método de Elementos Finitos. Análisis estático lineal Capítulo 10. CIMNE. Barcelona, 1995

1.3.2 Análisis de láminas con elementos tridimensionales

Como es obvio, cualquier tipología estructural puede modelizarse mediante sólidos tridimensionales. Los problemas 3D representan sin duda un mayor esfuerzo de cálculo por elementos finitos; es por esta razón por lo que se suele simplificar el análisis reduciéndolo a la mínima dimensión posible. Aún así hay ciertos casos en los que resulta complicado reducir las dimensiones del problema y por lo tanto se tiende a utilizar el análisis tridimensional.

En muchas ocasiones, al estudiar el apoyo de las cúpulas, es necesario instalar un anillo perimetral para absorver las reacciones de la lámina. Dicho anillo no es más que una viga curva bajo el borde de la lámina. En este caso conviven dos tipologias estructurales: elementos de lámina y elementos de viga. Modelizar dicho sistema puede resultar complejo y se escapa del objetivo de este estudio. En el capítulo 13 de la referencia [6] se explica como modelizar dicho sistema pero no hay ningún programa comercial que disponga de dicho cálculo. Así pues, este problema será estudiado mediante elementos tridimensionales cuya formulación podemos encontrar en el capítulo 7 de la referencia [6].

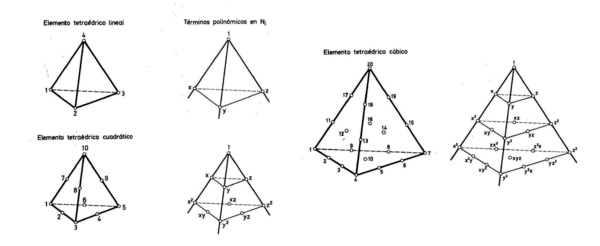
Los elementos más utilizados, y los que utlizaremos en este texto, son los elementos tetraédricos lineales (4 nodos). Al igual que los elementos triangulares en estudios en 2D, los tetraédricos optimizan el tiempo de cálculo respecto a los grados de libertad proporcionando una precisión suficiente para los calculos realizados. Otros elementos para sólidos tridimensionales utilizados pueden ser: elementos hexaédricos rectos Lagrangianos, elementos hexaédricos rectos Serendípitos, elementos tetraédricos cuadráticos (10 nodos) o elementos tetraédricos cúbicos (20 nodos). Los dos primeros no llegan nunca al nivel de optimización del tiempo de cálculo que obtenemos con elementos tetraédricos; mientras que los segundos nos darían una mayor precisión pero nos disparan el tiempo de cálculo.

Figura 16: Elementos tetraédricos.

1.4 Tipologías de láminas y principales características

Como ya hemos comentado, las estructuras de lámina presentan un gran abanico de posibilidades, entre las tipologías más utilizadas estan las siguientes:

1.4.1 Cúpulas

Superfície de revolución generada a partir de una línea curva llamada meridiano. Las cúpulas permiten cubrir una gran superfície sin ningún apoyo intermedio.

Estas láminas pueden adoptar distintas formas según su método constructivo, variando en función de la forma de planta y el perfil de acuerdo a la cónica utilizada. Así pues tenemos entre otras, cúpulas semiesféricas, semielipsoides de planta circular o elipsoides de planta elíptica.

Las cúpulas se caracterizan por trabajar a compresión en la totalidad de la superfície como si de un arco se tratara. En el caso en que el apoyo no sea tangencial al meridiano, se generará una reacción horizontal que deberemos intentar resisistir con algún refuerzo perimetral tipo anillo rigidizador. Este análisis se tratará con mayor detalle en los capítulos 2 y 4.

1.4.2 Muros de lámina cilíndrica

Este tipo de lámina suele ser utilizada para depósitos de almacenamiento de fluidos, por lo que estarán sometidos a importantes presiones internas. Asimismo también pueden ser utilizadas como muros para las estructuras de torres. En este texto se trataran estructuras que tengan forma de superficie de revolución, en concreto se trataran los cilindros circulares verticales.

Como veremos más adelante, estas estructuras trabajan prácticamente en toda su altura a tracción en el caso más habitual de presión interna (almacenamiento de fluidos), por lo que en estructuras de gran envergadura suele ser interesante un pretensado de las zonas más solicitadas.

En ocasiones es necesario unir cúpula a muros cilíndricos, por lo que el muro deberá resistir la reacción horizontal ya bien por su propia rigidez o ayudado por un refuerzo perimetral. Este análisis, lo estudiaremos en el capítulo 4.

1.4.3 Placas plegadas

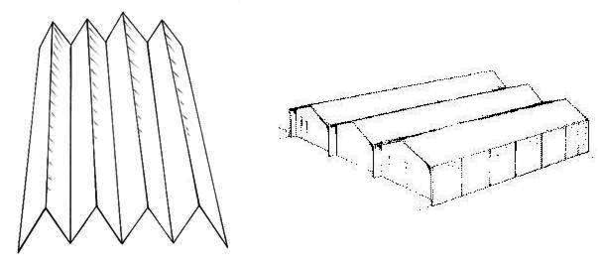
Las placas plegadas son estructuras de placa a las que para aumentar su eficiencia estructural se refuerza con nervaduras, eliminando así parte del material de la zona próxima al plano neutro. Normalmente se consideran junto a las láminas delgadas, ya que su comportamiento en el conjunto de la estructura es similar. Si comparamos un segmento de cilindro con una serie de placas delgadas, podremos comprobar que los dos sistemas tienen aproximadamente los mismos esfuerzos. Si la serie tiende a infinito nos acercamos a la lámina cilíndrica en el límite. Sucede algo similar a la relación entre una viga de gran luz y una viga en celosía, el comportamiento discreto llevado al límite se aproxima mucho al comportamiento continuo.

Figura 17: Ejemplos de placas plegadas.

El sistema estructural de placas plegadas es eficiente por su alta rigidez y su baja relación peso-superficie, lo cual motivó su uso en el pasado. Actualmente, el requerimiento de moldes y cimbras especiales lo convirtió en una alternativa cara y por lo tanto su uso actual es escaso. Así pues, en este trabajo no se va analizar con detalle esta tipología estructural.

1.4.4 Láminas cilíndricas

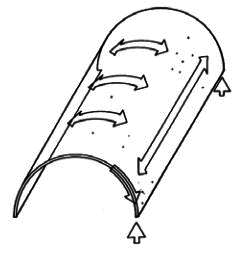
Este tipo de láminas suele utilizarse para cubrir superfícies lineales sin apoyos intermedios. Consiste en cortar la lámina cilíndrica circular del deposito vertical y abatirla tal y como vemos en la figura 18. Los Hangares de Orly son un ejemplo claro de lámina cilíndrica construída mediante láminas plegadas.

Figura 18: Comportamiento de la lámina cilíndrica.

El comportamiento estructural del sistema es muy claro y se puede entender como una serie de arcos consecutivos que descargan sus compresiones sobre una viga de borde. Esta viga puede tener el apoyo garantizado en toda su longitud o bien puede estar apoyada en apoyos transversales intermedios. El primer caso es relativamente sencillo de calcular mientras que en el segundo se deberá compatibilizar el comportamiento de los tres elementos, lo que nos complicara bastante el cálculo.

1.4.5 Hiperboloides y paraboloides hiperbólicos

La utilización de superficies de revolución no tiene límites, y ha dado lugar a formas muy distintas de cúpula como los hiperboloides. Actualmente se empiezan a utilizar superfícies de doble curvatura, es decir, con formas cóncavo-convexas, trabajando a tracción y realizadas con hormigón pretensado, asegurando por si mismo la estanqueidad del conjunto.

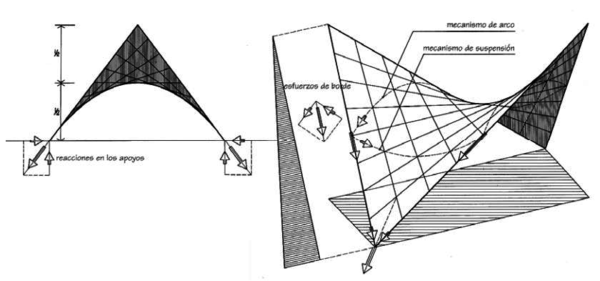
El paraboloide hiperbólico ofrece la ventaja de inscribirse bien en un cuadrilátero formado por cuatro bordes rector. La membrana puede dar reacciones tangenciales solamente, sobre el borde sin provocar flexiones de éste. Esta forma surge como resultado de una búsqueda basada en un principio económico fundamental: evitar en la medida de lo posible, los esfuerzos de flexión mediante la forma adecuada.

Figura 19: Comportamiento del paraboloide hiperbólico.

1.5 Cimbras hinchables

Como ya hemos comentado con anterioridad, este texto tiene por objetivo facilitar y aproximar al lector a los tipos estructurales racionalmente más perfectos pero muy poco utilizados en la actualidad.

La razón de su desuso, recae en dos grandes hechos: el primero es el desconocimeinto del análisis de su comportamiento por parte del diseñador, para ello se dedica la mayor parte del texto a intentar acercar el análisis al lector. Y en segundo lugar y muy importante, el procedimiento constructivo de estas estructura resulta muy complicado y se situa muy lejos en cuanto a costes de la construcción industrializada de los forjados tradicionales. Este problema es más difícil de solucionar, pero desde mi punto de vista, debemos trabajar en la dirección de facilitar y economizar su construcción ya que si se consigue se estarán ejecutando estructuras fáciles de construir utilizando el mínimo material posible.

Un ejemplo ingenioso para la construcción de cúpulas es el método inventado por Dante Bin, utilizando cimbras hinchables:

1.5.1 El método Binshell

En 1960 Dante Bini, arquitecto italiano, alcanzó los primeros éxitos sobre el uso de una cimbra soportada por aire en la construcción de domos de hormigón. Su idea consistió, de manera general, en colocar a "nivel de piso" todo el acero y hormigón requerido, que después erigió a través de la presurización de la cimbra; logrando con ello la formación y construcción del domo. Con esta técnica, logró reducir la mayor parte de las dificultades constructivas; además de disminuir los altos costos de construcción. Desde entonces se han construido más de 1500 domos alrededor del mundo utilizando esta técnica.

Las sucesivas fases del proceso constructivo, que se describen en la figura 20, son las siguientes:

Figura 20: Proceso constructivo del método Binshell.

Nivelación del terreno: construcción del anillo perimetral circular que como hemos comentado servirá para rigidizar la estructura definitiva pero además este proceso sirve para anclar la membrana neumática interna y la externa. Deben colocarse también los conductos de aducción de aire, por debajo de dicho anillo.

Extendido y fijación de la membrana flexible: su borde se fija a un tubo rígido anclado debidamente al anillo rigidizador.

Ferralla: se monta el armado convenientemente solapado, se introducen por el interior de resortes o muelles helicoidales de acero, que formando una malla, se anclan asimismo al anillo; al inflarse la membrana, los resortes se alargan paulatinamente al aumentar el paso de la hélice, adaptando su desarrollo al de la membrana; las barras de acero consecutivas deslizan una sobre otra, a lo largo de sus zonas de libre solape.

Puesta en obra del hormigón: se trata de hormigón que normalmente hoy puede colocarse con bomba; el hormigón se fabrica con aditivos plastificantes para mejorar su trabajabilidad y sobre todo con aditivos retardadores del proceso de fraguado; cuyos efectos duran unas 8 horas desde el inicio del hormigonado (que para un diámetro de 40m puede durar 2 o 3 horas más 1 hora de extendido).

Membrana exterior: sirve de encofrado externo para contener el hormigón fresco furante la operación de inflado y elevación de la membrana neumática y para contener el hormigón también en las operaciones de vibrado. También sirve como película para mejorar los procesos de fraguado y primer endurecimiento.

Vibrado: antes de inflar la membrana, se coloca un sistema especial de vibración sujeto a un eje central fijado a las armaduras; la vibración procede helicoidalmente sobre la membrana externa una vez ha alcanzado el estado final a plena presurización.

Inflado: el aire impulsado, penetra bajo la membrana flexible, que se eleva paulatinamente y con ella el hormigón fresco y la ferralla encima.

Desinflado (o descimbrado):después del vibrado, la presión del aire se mantiene a un nivel constante hasta que el hormigón haya endurecido suficientemente (entre 1 o 3 días). Se retira primero la membrana externa y se inspecciona la superfície para repasar con morteros eventuales defectos o irregularidades superficiales; el desinflado se practica gradualmente en unos 30 o 60 minutos hasta reducir la presión a cero.

2 Cúpulas

2.1 Simplificaciones de la teoría general y formulación concreta

Definición 1: Lámina delgada formada por una superficie de revolución generada a partir de la rotación de un plano curvo llamado meridiano.

1. Tensiones de membrana para cúpulas cargadas simétricamente con respecto a su eje de revolución.
Para estudiar este tipo de láminas, usaremos el siguiente sistema de coordenadas polares.

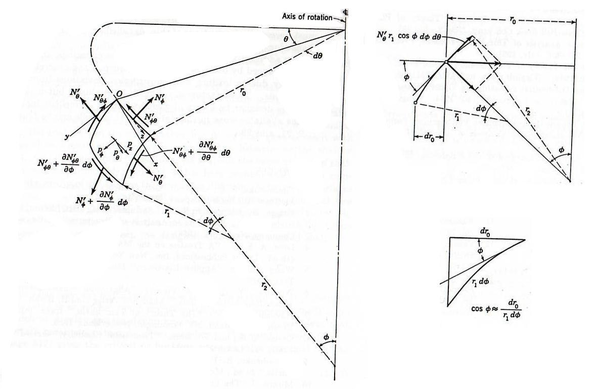
Figura 21: Elemento diferencial de cúpula.

$\alpha _{x}$ $=\theta$ $a_{x}$ $=r_{0}$ $r_{x}$ $=r_{2}$ $r_{0}$ $=r_{2}\sin \phi$ $N'_{xy}$ $=N'_{\theta \phi }$ $\alpha _{y}$ $=\phi$ $a_{y}$ $=r_{1}$ $r_{y}$ $=r_{1}$ $N'_{x}$ $=N'_{\theta }$ $N'_{y}$ $=N'_{\phi }$

(35)

De esta manera la ecuación 34; considerando que ${\textstyle r_{xy}=\infty }$ y simetría de revolución; se puede reducir a:

${\frac {\partial N'_{\theta }}{\partial \theta }}r_{1}\,+\,N'_{\theta \phi }{\frac {r_{0}}{\partial \phi }}\,+\,{\frac {\partial (N'_{\phi \theta }r_{0})}{\partial \phi }}\,+\,p_{\theta }r_{0}r_{1}$ $=$ $0$ ${\frac {\partial (N'_{\phi }r_{0})}{\partial \phi }}\,-\,N'_{\theta }{\frac {\partial r_{o}}{\partial \phi }}\,+\,{\frac {\partial N'_{\phi \theta }}{\partial \theta }}r_{1}\,+\,p_{\phi }r_{0}r_{1}$ $=$ $0$ ${\frac {N'_{\theta }}{r_{2}}}\,+\,{\frac {N'_{\phi }}{r_{1}}}\,+\,p_{z}$ $=$ $0$

(36)

Si además asumimos también que la carga es simétrica con respecto al eje de revolución, se anula la variación respecto al eje ${\textstyle \theta }$ y por lo tanto pasamos de ${\textstyle \partial \phi }$ a ${\textstyle d\phi }$. De esta manera obtenemos que la carga circumferencial es nula y que los esfuerzos cortantes resultantes se desprecian a lo largo de los círculos meridianos y paralelos. Finalmente obtenemos la ecuación de la membrana para cúpulas simétricas tanto geométricamente como de carga.

${\frac {d(N'_{\phi \theta }r_{0})}{d\phi }}\,-\,N'_{\theta }\,{\frac {dr_{0}}{d\phi }}\,+\,p_{\theta }r_{0}r_{1}$ $=$ $0$ ${\frac {N'_{\theta }}{r_{2}}}\,+\,{\frac {N'_{\phi }}{r_{1}}}\,+\,p_{z}$ $=$ $0$

(37)

De la figura 21 podemos observar que:

$\cos \phi \approx {\frac {dr_{0}}{r_{1}d_{\phi }}}$

Por lo que podemos reescribir la primera expresión de la ecuación 37 por:

${\frac {d(N'_{\phi \theta }r_{0})}{d\phi }}\,-\,N'_{\theta }\,r_{1}\cos \phi \,+\,p_{\theta }r_{0}r_{1}=0$

A partir de la segunda expresión de 37 podemos llegar a:

$N'_{\theta }=-{\frac {r_{0}}{\sin \phi }}{\Big (}{\frac {N'_{\phi }}{r_{1}}}+p_{z}{\Big )}$

(38)

Así pues si combinamos la ecuación 38 con la primera de la ecuación 37 obtendremos la siguiente expresión:

$\sin \phi \,{\frac {d(N'_{\phi }r_{0})}{d\phi }}\,+\,\sin \phi \,{\frac {r_{0}}{\sin \phi }}{\Big (}{\frac {N'_{\phi }}{r_{1}}}+p_{z}{\Big )}r_{1}\cos _{\phi }\,+\,\sin \phi \,p_{\phi }\,r_{0}r_{1}=0$

(39)

Finalmente, si integramos la ecuación 39:

$\int _{0}^{\phi }\sin \phi \,{\frac {d(N'_{\phi }r_{0})}{d\phi }}d\phi \,+\,\int _{0}^{\phi }N'_{\phi }r_{0}\cos \phi \,d\phi =-{\frac {1}{2\pi }}\int _{0}^{\phi }(p_{\phi }\sin \phi +p_{z}\cos \phi {)2}\pi r_{0}r_{1}\,d\phi$

(40)

Obtendremos, utilizando integración por partes, la siguiente expresión:

$N'_{\phi }=-{\frac {1}{2\pi r_{0}\sin \phi }}\int _{0}^{\phi }(p_{\phi }\sin \phi +p_{z}\cos \phi )(2\pi r_{0})r_{1}d\phi$

(41)

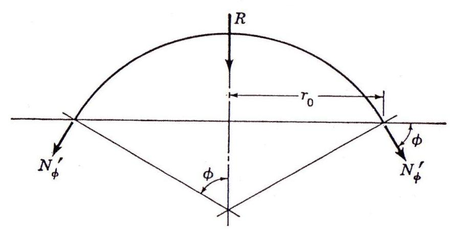
Figura 22: Resultante vertical derivada de la integración de las cargas.

Donde ${\textstyle \int _{0}^{\phi }r_{1}d\phi }$ integra la carga vertical alrededor del meridiano (tal y como se describe en la figura 22). Si suponemos la carga resultante de esta integración R. y por lo tanto ${\textstyle N'_{\phi }}$ y ${\textstyle N'_{\theta }}$ se expresaran de la siguiente manera:

$N'_{\phi }$ $=-{\frac {R}{2\pi r_{0}\sin \phi }}$ $N'_{\theta }$ $={\frac {R}{2\pi \sin ^{2}\phi }}-p_{z}{\frac {r_{0}}{\sin \phi }}$

(42)

1. CÚPULAS ESFÉRICAS CON CARGA UNIFORME A LO LARGO DE LA SUPERFICIE

En este caso ${\textstyle r_{1}=r_{2}=a}$, ${\textstyle p_{\phi }=q\sin \phi }$ y ${\textstyle p_{z}=q\cos \phi }$, entonces tenemos

$R=2\pi a^{2}q\int _{0}^{\phi }\sin \phi d\phi =2\pi a^{2}q(1-\cos \phi )$

y por lo tanto la ecuación 42 se reduce a:

$N'_{\phi }$ $=-aq{\frac {1}{1+\cos \phi }}$ $N'_{\theta }$ $=aq{\big (}{\frac {1}{1+\cos \phi }}-\cos \phi {\big )}$

(43)

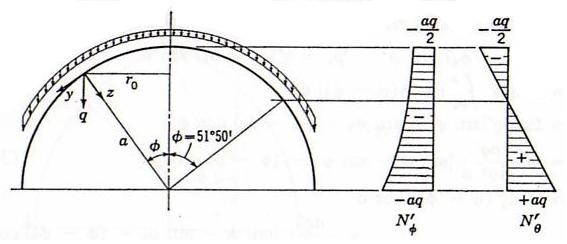
El comportamiento de este tipo de cúpulas queda muy bien descrito en la figura 23.

Figura 23: Evolución de $N'_{\phi }$ y $N'_{\theta }$ a lo largo de $\phi$.

En pocos casos sucede que el apoyo de la cúpula sea tangente al meridiano sinó que habitualmente suele ser un apoyo horizontal por lo que se presenta una incopatibilidad ya que el apoyo no soporta la reacción horizontal derivada del ${\textstyle N'_{\phi }(H'_{\phi }=N'_{\phi }\,\cos \phi )}$. Se deberá por lo tanto, en estos casos, añadir un anillo rigidizador que resista dicha reacción cuya solución estudiaremos más adelante.

2. CÚPULAS ESFÉRICAS CON CARGA EXTERNA UNIFORME

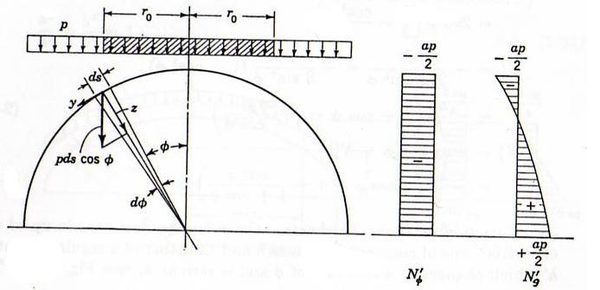
En este caso ${\textstyle p_{z}=q\cos ^{2}\phi }$, ${\textstyle p_{\phi }=psin\phi \cos \phi }$ y ${\textstyle p_{\theta }=0}$. Así pues se puede comprobar que ${\textstyle R=p\pi r_{0}^{2}=pa^{2}\pi \sin ^{2}\phi }$ y por lo tanto

$N'_{\phi }$ $=-{\frac {ap}{2}}$ $N'_{\theta }$ $=-{\frac {ap}{2}}\cos 2\phi$

(44)

En la figura 24 se puede observar que ${\textstyle N'_{\phi }}$ es constante alrededor de ${\textstyle \phi }$ mientras que ${\textstyle N'_{\theta }}$ pasa de compresión tracción anulandose para ${\textstyle \phi =45^{\circ }}$.

Figura 24: Evolución de $N'_{\phi }$ y $N'_{\theta }$ a lo largo de $\phi$.

3. CÚPULAS CON CARGA EXTERIOR UNIFORME

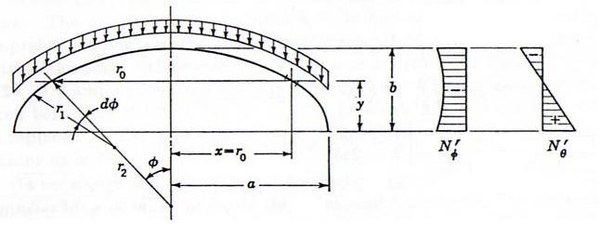
En este caso asumiremos que ${\textstyle p_{z}=p}$ y ${\textstyle p_{\phi }=p_{\theta }=0}$ y por lo tanto ${\textstyle R=2\pi a^{2}p\int _{0}^{\phi }\sin \phi \cos \phi d\phi }$ y por lo tanto los esfuerzos de membrana serán:

$N'_{\phi }$ $=-{\frac {\pi a^{2}p\sin ^{2}\phi }{2a\sin ^{2}\phi }}=-{\frac {ap}{2}}$ $N'_{\theta }$ $=-a{\big (}p-{\frac {ap}{2a}}{\big )}=-{\frac {ap}{2}}$

(45)

4. CÚPULAS ELÍPTICAS

Figura 25: Evolución de $N'_{\phi }$ y $N'_{\theta }$ a lo largo de $y$.

Como ya conocemos, la ecuación de la elipse para coordenadas cartesianas es:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

Donde ${\textstyle a}$ es el radio mayor ,${\textstyle b}$ el menor y ${\textstyle x}$ corresponde a ${\textstyle r_{0}}$ radio del círculo paralelo.

$x=r_{0}=a{\sqrt {1-{\frac {y^{2}}{b^{2}}}}}={\frac {a}{b}}{\sqrt {b^{2}-y^{2}}}$

${\frac {dy}{dx}}={\frac {1}{dx/dy}}=-\tan \phi =-{\frac {b}{ay}}{\sqrt {b^{2}-y^{2}}}$

Entonces

$\sin \phi ={\frac {dy}{ds}}={\frac {dy}{\sqrt {dy^{2}+dx^{2}}}}={\frac {dy/dx}{\sqrt {(dy/dx)^{2}+1}}}={\frac {-\tan \phi }{\sqrt {1+\tan ^{2}\phi }}}={\frac {-b{\sqrt {b^{2}-y^{2}}}}{\sqrt {b^{4}+y^{2}(a^{2}-b^{2})}}}$

(46)

Con el mismo planteamiento encontraríamos

$\cos \phi ={\frac {ay}{\sqrt {b^{4}+y^{2}(a^{2}-b^{2})}}}$

(47)

Así pues, los dos principales radios de curvatura son:

$r_{1}={\frac {[b^{4}+y^{2}(a^{2}-b^{2})]^{(}3/2)}{ab^{4}}}$

$r_{2}={\frac {a}{b^{2}}}{\sqrt {b^{4}+y^{2}(a^{2}-b^{2})}}$

En este caso concreto trabajaremos con ${\textstyle p_{z}=q\cos \phi }$, ${\textstyle p_{\phi }=q\sin \phi }$ y ${\textstyle p_{\theta }=0}$ y por lo tanto ${\textstyle R=2\pi q\int _{0}^{\phi }xds}$. Donde ${\textstyle x}$ la hemos encontrado antes y ${\textstyle ds}$:

$ds=dy{\sqrt {1+{\Big (}{\frac {dx}{dy}}{\Big )}^{2}}}$

$ds=dy{\sqrt {1+{\frac {a^{2}y^{2}}{b^{2}(b^{2}-y^{2})}}}}$

$R=2\pi q\int _{y}^{b}{{\frac {a}{b}}{\sqrt {b^{2}-y^{2}}}{\sqrt {\frac {b^{2}(b^{2}-y^{2})+a^{2}y^{2}}{b^{2}(b^{2}-y^{2})}}}}dy$

Entonces:

$R=2\pi a^{2}q{\Bigg [}{\frac {1}{2}}-{\frac {y}{2ab^{2}}}{\sqrt {b^{4}+y^{2}(a^{2}-b^{2})}}+{\frac {b^{2}}{2a{\sqrt {a^{2}-b^{2}}}}}\log {\bigg (}{\frac {b(a+{\sqrt {a^{2}-b^{2}}})}{y{\sqrt {a^{2}-b^{2}}}+{\sqrt {b^{4}+y^{2}(a^{2}-b^{2})}}}}{\bigg )}{\Bigg ]}$

(48)

Vamos a llamar C a la parte contenida entre paréntesis y por lo tanto:

$R=2\pi a^{2}qC$

Los valores de los esfuerzos de membrana pueden obtenerse a partir de la ecuación eq:ecup008) y obtendremos las siguientes expresiones que definen claramente el comportamiento que avanzabamos en la figura fig:fig:cupula005.

$N'_{\phi }$ $=-{\frac {R}{2\pi r_{0}\sin \phi }}=-{\frac {a^{2}qCb^{2}}{\sin ^{2}\phi \,a{\sqrt {b^{4}+y^{2}(a^{2}-b^{2})}}}}$

(49)

Ahora usando las relaciones obtenidas en la ecuación 46 obtendremos:

$N'_{\phi }$ $=-{\frac {a^{2}qb^{2}C[b^{4}+(a^{2}-b^{2})]}{b^{2}(b^{2}-y^{2})a{\sqrt {b^{4}+y^{2}(a^{2}-b^{2})}}}}=-{\frac {qa^{2}}{b}}{\frac {C}{(b^{2}-y^{2})/b^{2}}}{\frac {\sqrt {b^{4}+y^{2}(a^{2}-b^{2})}}{ab}}$

(50)

Para tratar de simplificar la ecuación obtenida llamaremos Q a:

$Q={\sqrt {1-{\frac {a^{2}-b^{2}}{a^{2}}}{\Big (}a-{\frac {y^{2}}{b^{2}}}{\Big )}}}={\frac {\sqrt {b^{4}+y^{2}(a^{2}-b^{2})}}{ab}}$

Por lo que hace a $N'_{\theta }$ sabemos que:

$N'_{\theta }=-r_{2}{\Big (}p_{z}+{\frac {N'_{\phi }}{r_{1}}}{\Big )}=-r_{2}q\cos \phi -{\frac {N'_{\phi }}{r_{1}}}r_{2}$

Y por lo tanto usando la ecuación 47 podemos llegar a:

${\frac {r_{2}}{r_{1}}}={\frac {a^{2}b^{2}}{b^{4}+y^{2}(a^{2}-b^{2})}}={\frac {1}{Q^{2}}}$

$N'_{\theta }=-{\frac {aq\cos \phi {\sqrt {b^{4}+y^{2}(a^{2}-b^{2})}}}{b^{2}}}+{\frac {a^{q}}{b}}{\frac {C}{[1-(y^{2}/b^{2})]Q}}$

$N'_{\theta }=-{\frac {a^{2}qy{\sqrt {b^{4}+y^{2}(a^{2}-b^{2})}}}{b^{2}{\sqrt {b^{4}+y^{2}(a^{2}-b^{2})}}}}+{\frac {a^{q}}{b}}{\frac {C}{[1-(y^{2}/b^{2})]Q}}$

Ahora ya podemos determinar los esfuerzos de membrana de una cúpula elíptica.

${\begin{array}{l}N'_{\phi }&=-{\frac {qa^{2}}{b}}{\frac {CQ}{1-(y^{2}/b^{2})}}\\N'_{\theta }&=-{\frac {qa^{2}}{b}}{\Big [}{\frac {y}{b}}-{\frac {Cb^{2}}{(b^{2}-y^{2})Q}}{\Big ]}\end{array}}$

(51)

5. CÚPULAS CÓNICAS

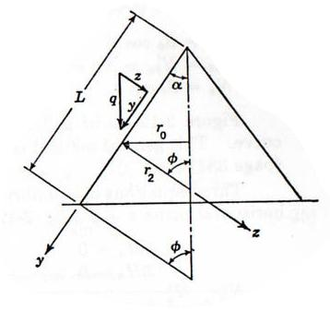
Figura 26: Descripción geométrica de una cúpula cónica.

Para este tipo de cúpulas se puede considerar:

${\begin{array}{l}\phi &=\pi /2-\alpha &=constante\\\end{array}}$

${\begin{array}{l}r_{1}=\infty \,;\,r_{2}=r_{0}/\cos \alpha \,;\,r_{0}=y\sin \alpha \\\end{array}}$

En este caso para cargas muertas sobre una lámina de espesor uniforme partimos de:

${\begin{array}{l}p_{z}=q\sin \alpha \,;\,p_{y}=q\cos \alpha \,;\,p_{x}=0\\\end{array}}$

$R=\int _{0}^{y}{2\pi r_{0}q}dy=\pi qy^{2}\sin \alpha$

Finalmente podemos obtener los esfuerzos de membrana que son:

${\begin{array}{l}N'_{\phi }&=-{\frac {qy}{2\cos \alpha }}\\N'_{\theta }&=-yq\tan \alpha \sin \alpha \end{array}}$

(52)

(b) Desplazamientos de membrana para cúpulas cargadas simétricamente con respecto a su eje de revolución.

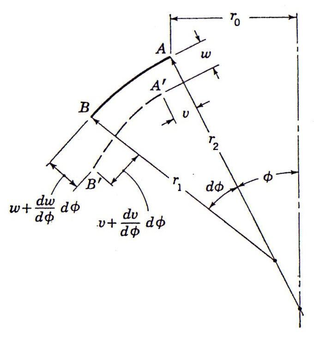
Figura 27: Desplazamientos sobre el elemento diferencial de cúpula.

Las deformaciones de la superfície media que vimos en el capítulo anterior son para este caso:

$\alpha _{x}$ $=\theta$ $a_{x}$ $=r_{0}$ $r_{x}$ $=r_{2}$ $\epsilon _{x0}$ $=\epsilon _{\theta }$ $\alpha _{y}$ $=\phi$ $a_{y}$ $=r_{1}$ $r_{y}$ $=r_{1}$ $\epsilon _{y0}$ $=\epsilon _{\phi }$

(53)

$\epsilon _{\theta }$ $={\frac {1}{r_{0}}}{\frac {\partial u}{\partial \theta }}+{\frac {v}{r_{0}r_{1}}}{\frac {\partial r_{0}}{\partial \phi }}-{\frac {w}{r_{2}}}$ $\epsilon _{\phi }$ $={\frac {1}{r_{1}}}{\frac {\partial v}{\partial \phi }}+{\frac {u}{r_{0}r_{1}}}{\frac {\partial r_{1}}{\partial \theta }}-{\frac {w}{r_{1}}}$

(54)

Gracias a la simetría podemos decir que:

${\frac {\partial r_{1}}{\partial \theta }}={\frac {\partial u}{\partial \theta }}=0$ ${\hbox{y}}$ $\,\,\,\,{\frac {\partial r_{0}}{\partial \phi }}=r_{1}\cos {\phi }$

De la figura 27, podemos obtener:

$\epsilon _{\theta }$ $={\frac {v}{r_{0}}}\cos {\phi }-{\frac {w}{r_{2}}}$ $\epsilon _{\phi }$ $={\frac {1}{r_{1}}}{\frac {dv}{d\phi }}-{\frac {w}{r_{1}}}$

Y combinando estas dos ecuaciones podemos llegar a:

${\frac {dv}{d\phi }}-v\cot {\phi }$ $=r_{1}\epsilon _{\phi }-r_{2}\epsilon _{\theta }$

(55)

Ahora a partir de las relaciones tensión-deformación de la teoría de la elasticidad, podemos deducir:

$\epsilon _{\theta }$ $={\frac {1}{Eh}}(N'_{\phi }-\nu N'_{\theta })\epsilon _{\phi }$ $={\frac {1}{Eh}}(N'_{\theta }-\nu N'_{\phi })$

(56)

Finalmente combinamos la ecuación 55 y 56 obtenemos la siguiente ecuación diferencial:

${\frac {dv}{d\phi }}-v\cot {\phi }$ $={\frac {1{N'_{\phi }}(r_{1}+\nu r_{2})-N'_{\theta }(r_{2}+\nu r_{1})}{Eh}}$

(57)

Si llamamos ${\textstyle f(\phi )}$ al segundo término de la ecuación anterior:

${\frac {dv}{d\phi }}-$ $v\cot {\phi }=f(\phi )$ $v=\sin {\phi }$ ${\big (}\int {\frac {f(\phi )}{\sin {\phi }}}d\phi {+}C{\big )}$

(58)

Donde ${\textstyle C}$ es una constante determinada por las condiciones de contorno.

Encontrada ${\textstyle v}$, podemos encontrar ${\textstyle w}$ ya que:

$w=v\cot {\phi }-r_{2}\epsilon _{\theta }=v\cot {\phi }-{\frac {r_{2}}{Eh}}(N'_{\theta }-\nu N'_{\phi })$

Como vimos en el capítulo anterior:

$\phi _{y}=\Delta _{\phi }={\frac {v}{r_{1}}}+{\frac {dw}{r_{1}d\phi }}$

(59)

En el análisis que se presenta a continuación los valores de ${\textstyle v}$ y ${\textstyle w}$ no son utilizados mientras que si que usaremos el movimiento horizontal ${\textstyle \Delta _{H}}$ y la rotación ${\textstyle \Delta _{\phi }}$.

$\Delta _{H}=r_{0}\epsilon _{\theta }={\frac {1}{Eh}}(N'_{\theta }-\nu N'_{\phi })r_{0}={\frac {r_{2}\sin {\phi }}{Eh}}(N'_{\theta }-\nu N'_{\phi })$

(60)

Para bordes rígidos sabemos que ${\textstyle w=0}$ y por lo tanto

$\Delta _{\phi }={\frac {dw}{r_{1}d\phi }}={\frac {\cot {\phi }}{r_{1}}}{\frac {dv}{d\phi }}-{\frac {d}{r_{1}d\phi }}{\Big [}{\frac {r_{2}}{Eh}}(N'_{\theta }-\nu N'_{\phi }{\Big ]}$

(61)

Si tomamos ahora la ecuación 57 y la simplificamos para ${\textstyle v=0}$, obtendremos:

${\frac {dv}{d\phi }}={\frac {1}{Eh}}{\big [}N'_{\phi }(r_{1}+\nu r_{2})-N'_{\theta }(r_{2}+\nu r_{1}){\big ]}$

Por lo que finalmente obtenemos:

$\Delta _{\phi }={\frac {\cot {\phi }}{r_{1}Eh}}{\Big [}N'_{\phi }(r_{1}+\nu r_{2})-N'_{\theta }(r_{2}+\nu r_{1}){\Big ]}-{\frac {d}{r_{1}d\phi }}{\Big (}{\frac {\Delta _{H}}{\sin {\phi }}}{\Big )}$

(62)

Por analizar un ejemplo buscamos los desplazamientos en el contorno para una cúpula esférica de espesor constante donde ${\textstyle r_{1}=r_{2}=a}$, ${\textstyle v=0}$ y ${\textstyle N'_{\phi }}$ y ${\textstyle N'_{\theta }}$ las encontramos de las ecuaciones 43:

$\Delta _{H}$ $={\frac {a^{2}q}{Eh}}{\Big (}{\frac {1+\nu }{1+\cos {\phi }}}-\cos {\phi }{\Big )}\sin {\phi }$ $\Delta _{\phi }$ $=-{\frac {aq}{Eh}}(2+\nu )\sin {\phi }$

(63)

(c) Flexión en láminas de revolución bajo cargas simétricas respecto a su eje de rotación.

Para una lámina simétrica, la ecuación general de equilibrio 17 se reduce a:

$r_{1}{\frac {\partial N_{\theta }}{\partial \theta }}+_{\theta \phi }{\frac {\partial r_{0}}{\partial \phi }}+{\frac {\partial (N_{\phi \theta }r_{0})}{\partial \phi }}-Q_{\theta }r_{1}\sin {\phi }+p_{\theta }r_{0}r_{1}$ $=0$ ${\frac {\partial (N_{\phi }r_{0})}{\partial \phi }}-N_{\theta }{\frac {\partial r_{0}}{\partial \phi }}+r_{1}{\frac {\partial N_{\theta \phi }}{\partial \theta }}-Q_{\phi }r_{0}+p_{\phi }r_{0}r_{1}$ $=0$ $r_{1}{\frac {\partial Q_{\theta }}{\partial \theta }}+{\frac {\partial (Q_{\phi }r_{0})}{\partial \phi }}+N_{\theta }r_{1}\sin {\phi }+N_{\phi }r_{0}+p_{z}r_{0}r_{1}$ $=0$ $-{\frac {\partial (M_{\phi }r_{0})}{\partial \phi }}+M_{\theta }{\frac {\partial r_{0}}{\partial \phi }}+r_{1}{\frac {\partial M_{\theta \phi }}{\partial \theta }}+Q_{\phi }r_{0}r_{1}$ $=0$ $-r_{1}{\frac {\partial M_{\theta }}{\partial \theta }}+M_{\theta \phi }{\frac {\partial r_{0}}{\partial \phi }}-{\frac {\partial (M_{\phi \theta }r_{0})}{\partial \phi }}+Q_{\theta }r_{0}r_{1}$ $=0$

(64)

Asimismo, para carga axisimétrica y con ${\textstyle \partial r_{0}/\partial \phi =r_{1}\cos {\phi }}$se reduce a:

${\frac {d(N_{\phi }r_{0})}{d\phi }}-N_{\theta }r_{1}\cos {\phi }-Q_{\phi }r_{0}+p_{\phi }r_{0}r_{1}$ $=0$ ${\frac {d(Q_{\phi }r_{0})}{d\phi }}+N_{\theta }r_{1}\sin {\phi }+N_{\phi }r_{0}+p_{z}r_{0}r_{1}$ $=0$ $-{\frac {d(M_{\phi }r_{0})}{d\phi }}+M_{\theta }r_{1}\cos {\phi }+Q_{\phi }r_{0}r_{1}$ $=0$

(65)

Del mismo modo que las ecuaciones obtenidas en el primer capítulo y simplificadas para el caso de simetría de revolución, obtendremos las siguientes ecuaciones:

$N_{\theta }$ $=K{\Big (}{\frac {v}{r_{0}}}\cos {\phi }-{\frac {w}{r_{2}}}+{\frac {\nu }{r_{1}}}{\frac {dv}{d\phi }}-{\frac {\nu w}{r_{1}}}{\Big )}$ $N_{\phi }$ $=K{\Big (}{\frac {1}{r_{1}}}{\frac {dv}{d\phi }}-{\frac {w}{r_{1}}}+{\frac {\nu v}{r_{0}}}\cos {\phi }-{\frac {\nu w}{r_{2}}}{\Big )}$ $M_{\theta }$ $=-D{\Big [}{\Big (}{\frac {v}{r_{1}}}+{\frac {dw}{r_{1}d\phi }}{\Big )}{\frac {\cos {\phi }}{r_{0}}}+{\frac {\nu }{r_{1}}}{\frac {d}{d\phi }}{\Big (}{\frac {v}{r_{1}}}+{\frac {dw}{r_{1}d\phi }}{\Big )}{\Big ]}$ $M_{\phi }$ $=-D{\Big [}{\frac {1}{r_{1}}}{\frac {d}{d\phi }}{\Big (}{\frac {v}{r_{1}}}+{\frac {dw}{r_{1}d\phi }}{\Big )}+\nu {\Big (}{\frac {v}{r_{1}}}+{\frac {dw}{r_{1}d\phi }}{\frac {\cos {\phi }}{r_{0}}}{\Big )}{\Big ]}$

(66)

De esta manera, con las ecuaciones 65 y 66 obtendremos el sistema de 7 ecuaciones con 7 incógnitas ${\textstyle (N_{\phi },N_{\theta },Q_{\phi },M_{\phi },M_{\theta },v\,\,{\hbox{y}}\,\,w)}$. Este sistema se puede reducir a 2 ecuaciones introduciendo 2 variables nuevas,

$V={\frac {1}{r_{1}}}{\Big (}v+{\frac {dw}{d\phi }}{\Big )}$ $\,\,\,\,{\hbox{y}}\,\,\,\,U=r_{2}Q_{\phi }$

(67)

donde ${\textstyle V=\phi _{y}}$, ángulo de rotación respecto a la tangente del meridiano.

Como en el apartado a), podemos reemplazar la primera ecuación de equilibrio por una expresión de equilibrio vertical basada en la teoría de la membrana.

$2\pi r_{0}N_{\phi }\sin {\phi }+2\pi r_{0}Q_{\phi }\cos {\phi }+R=0\rightarrow N_{\phi }=-Q_{\phi }\cot {\phi }-{\frac {R}{2\pi r_{0}\sin _{\phi }}}$

(68)

Si sustituimos esta ecuación en la segunda ecuación de equilibrio, obtendremos la siguiente expresión:

$N_{\theta }=-{\frac {1}{r_{1}\sin {\phi }}}{\frac {d(Q_{\phi }r_{0})}{d_{\phi }}}+{\frac {Q_{\phi }r_{0}\cot {\phi }}{r_{1}\sin {\phi }}}+{\frac {R}{2\pi r_{1}\sin ^{2}{\phi }}}-p_{z}{\frac {r_{0}}{\sin {\phi }}}$

(69)

Se puede observar en las últimas ecuaciones que el último término de la 68 y los dos últimos de eq:ecup034 corresponden a los esfuerzos obtenidos anteriormente de la teoría de la membrana. Así pues:

$N_{\phi }$ $=-{\frac {1}{r_{2}}}U\cot {\phi }+N'_{\phi }$ $N_{\theta }$ $=-{\frac {1}{r_{1}}}{\frac {dU}{d\phi }}+N'_{\theta }$

(70)

Las dos primeras ecuaciones de la 66 pueden ser reordenadas de la siguiente manera:

${\frac {dv}{d\phi }}-w$ $={\frac {r_{1}}{Eh}}(N_{\phi }-\nu N_{\theta })$ $v\cot {\phi }-w$ $={\frac {r_{2}}{Eh}}(N_{\theta }-\nu N_{\phi })$

(71)

Con lo que conseguimos eliminar la incógnita ${\textstyle w}$ y obtener una sola ecuación:

${\frac {dv}{d\phi }}-v\cot {\phi }$ $={\frac {1{(r_{1}+\nu r_{2})N_{\phi }}-(r_{2}+\nu r_{1})N_{\theta }}{Eh}}$

(72)

Ahora derivamos la segunda ecuación de 71 con respecto a ${\textstyle \phi }$ obtendremos:

${\frac {dv}{d\phi }}\cot {\phi }-{\frac {v}{\sin ^{2}{\phi }}}-{\frac {dw}{d\phi }}$ $={\frac {d}{d\phi }}{\Big [}{\frac {r_{2}}{Eh}}(N_{\theta }-\nu N_{\phi }){\Big ]}$

y combinamos las dos últimas ecuaciones para obtener la siguiente expresión:

$v+{\frac {dw}{d\phi }}$ $=r_{1}V$ $={\frac {\cot {\phi }{(r_{1}+\nu r_{2})N_{\phi }}-(r_{2}+\nu r_{1})N_{\theta }}{Eh}}-{\frac {d}{d\phi }}{\Big [}{\frac {r_{2}}{Eh}}(N_{\theta }-\nu N_{\phi }){\Big ]}$

(73)

Ahora sustituimos 70 en la ecuación anterior (73) para obtener la siguiente ecuación:

${\frac {r_{1}}{r_{1}^{2}}}{\frac {d^{2}U}{d\phi ^{2}}}+{\frac {1}{r_{1}}}{\Big [}{\frac {d}{d\phi }}{\Big (}{\frac {r_{2}}{r_{1}}}{\Big )}+{\frac {r_{2}}{r_{1}}}\cot {\phi }-{\frac {r_{2}}{r_{1}h}}{\frac {dh}{d\phi }}{\Big ]}{\frac {dU}{d\phi }}-{\frac {1}{r_{1}}}{\Big (}{\frac {r_{1}}{r_{2}}}\cot ^{2}{\phi }-\nu -{\frac {\nu }{h}}{\frac {dh}{d\phi }}\cot {\phi }{\Big )}U+$ $+{\frac {\nu r_{2}}{r_{1}}}{\frac {dN'_{\phi }}{d\phi }}+{\frac {1}{r_{1}}}{\Big (}\nu {\frac {dr_{2}}{d\phi }}+\nu r_{2}\cot {\phi }+r_{1}\cot {\phi }-{\frac {\nu r_{2}}{h}}{\frac {dh}{d\phi }}{\Big )}N'_{\phi }-{\frac {r_{2}}{r_{1}}}{\frac {dN'_{\theta }}{d\phi }}-$ $-{\frac {1}{r_{1}}}{\Big (}{\frac {dr_{2}}{d\phi }}+r_{2}\cot {\phi }+\nu r_{1}\cot {\phi }-{\frac {r_{2}}{h}}{\frac {dh}{d\phi }}{\Big )}N'_{\theta }=EhV$

(74)

Si introducimos la variable V en la segunda parte de 66 obtendremos las expresiones:

$M_{\theta }$ $=-D{\Big (}V{\frac {\cot {\phi }}{r_{2}}}+{\frac {\nu }{r_{1}}}{\frac {dV}{d\phi }}{\Big )}$ $M_{\phi }$ $=-D{\Big (}{\frac {1}{r_{1}}}{\frac {dV}{d\phi }}+\nu {\frac {V\cot {\phi }}{r_{2}}}{\Big )}$

(75)

Finalmente combinamos estas dos ecuaciones con la ecuación de ${\textstyle V}$ y obtendremos:

${\frac {r_{2}}{r_{1}^{2}}}{\frac {d^{2}V}{d\phi ^{2}}}+{\frac {1}{r_{1}}}{\Big [}{\frac {d}{d\phi }}{\Big (}{\frac {r_{2}}{r_{1}}}{\Big )}+{\frac {r_{2}}{r_{1}}}\cot {\phi }+3{\frac {r_{2}}{r_{1}h}}{\frac {dh}{d\phi }}{\Big ]}{\frac {dV}{d\phi }}-{\frac {1}{r_{1}}}{\Big (}\nu -{\frac {3\nu \cot {\phi }}{h}}{\frac {dh}{d\phi }}+{\frac {r_{2}}{r_{1}}}\cot ^{2}{\phi }{\Big )}V=-{\frac {U}{D}}$

(76)

De esta manera a partir de las ecuaciones 75 y 76, podemos obtener una solución general para una lámina que forma una superfície de revolución bajo cargas axisimétricas. La integración de estas dos ecuaciones no es fácil por lo que plantearemos una simplificación correcta para la mayoria de estructuras de lámina de hormigón.

Consideraremos una cúpula esférica de espesor constante donde ${\textstyle r_{1}=r_{2}=a}$ con lo que 75 y 76 se reducen a:

${\frac {d^{2}Q_{\phi }}{d\phi ^{2}}}+\cot {\phi }{\frac {dQ_{\phi }}{d\phi }}-(\cot ^{2}{\phi }-\nu )Q_{\phi }-\nu {\frac {dN'_{\phi }}{d\phi }}+(1+\nu )\cot {\phi }N'_{\phi }-{\frac {dN'_{\phi }}{d\phi }}-(1+\nu )\cot {\phi }N'_{\theta }=EhV$ ${\frac {d^{2}V}{d\phi ^{2}}}+\cot {\phi }{\frac {dV}{d\phi }}-(\cot ^{2}{\phi }+\nu )V=-{\frac {a^{2}Q_{\phi }}{D}}$

(77)

Ahora entenderemos la solución de este problema como composición de dos: por un lado la solución derivada de la teoría de la membrana para cargas superficiales y en segundo lugar la solución de flexión que permite tener en cuenta las condiciones de contorno.

Entonces deberemos despreciar los efectos de los esfuerzos de membrana en las ecuaciones de flexión ya que ya han sido consideradas en la teoría de la membrana, por lo que ${\textstyle N'_{\theta }}$ y ${\textstyle N'_{\phi }}$ se excluyen de 77.

Ahora debemos asumir que los efectos de borde se comportan de forma similar a una función de amortiguamiento rápido que incluye el término ${\textstyle e^{\lambda \phi }}$ por lo que los términos ${\textstyle d^{2}Q_{\phi }/d\phi ^{2}}$ serán considerablemente mayores que ${\textstyle dQ_{\phi }/d\phi }$ y ${\textstyle Q_{\phi }}$.

A partir de estas simplificaciones, podremos reducir las ecuaciones 77 a:

${\frac {d^{2}Q_{\phi }}{d\phi ^{2}}}=EhV$ ${\frac {d^{2}V}{d\phi ^{2}}}=-{\frac {a^{2}Q_{\phi }}{D}}$

(78)

Y combinando las dos ecuaciones llegaremos a definir la siguiente ecuación diferencial de cuarto orden:

${\frac {d^{4}Q_{\phi }}{d\phi ^{4}}}+4\lambda ^{4}Q_{\phi }=0$

(79)

donde ${\textstyle \lambda ^{4}=3(1-\nu ^{2}){\big (}{\frac {a}{h}}{\big )}^{2}}$

La solución general de la ecuación diferencial es:

$Q_{\phi }=C_{1}e^{\lambda \phi }\cos {\lambda \phi }+C_{2}e^{\lambda \phi }\sin {\lambda \phi }+C_{3}e^{-\lambda \phi }\cos {\lambda \phi }+C_{4}e^{-\lambda \phi }\sin {\lambda \phi }$

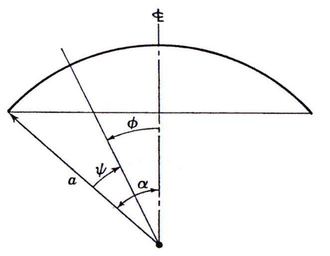
Figura 28: Variables sobre el eje de rotación de la cúpula.

$C_{3}$

y ${\textstyle C_{4}}$ se anulan ya que los efectos de borde estan localizados en ${\textstyle \phi =\alpha }$ y disminuyen rápidamente al aumentar ${\textstyle \phi }$ por lo que ${\textstyle e^{-\lambda \phi }}$ no es aplicable.

Entonces:

$Q_{\phi }=C_{1}e^{\lambda \phi }\cos {\lambda \phi }+C_{2}e^{\lambda \phi }\sin {\lambda \phi }$

Realizamos un cambio simple de variable y obtendremos:

$Q_{\phi }=Ce^{-\lambda \psi }\sin({\lambda \psi {+\gamma }})$

(80)

A partir de esta solución ya podemos encontrar los esfuerzos resultantes:

$N_{\phi }$ $=-Q_{\phi }\cot {\phi }=-\cot(\alpha {-\psi })Ce^{-\lambda \psi }\sin {(\lambda \psi {+\gamma })}$ $N_{\theta }$ $=-{\frac {dQ_{\phi }}{d\phi }}=-\lambda {\sqrt {2}}Ce^{-\lambda \psi }\sin {(\lambda \psi {+\gamma }-{\frac {\pi }{4}})}$

(81)

También obtendremos los desplazamientos horizontales (despreciando el efecto de ${\textstyle \nu }$) y la rotación:

$\Delta _{H}$ $=-{\frac {a\sin(\alpha {-\psi })}{Eh}}{\Big [}\lambda {\sqrt {2}}Ce^{-\lambda \psi }\sin {{\Big (}\lambda \psi {+\gamma }-{\frac {\pi }{4}}{\Big )}}{\Big ]}$ $\Delta _{\phi }$ $=V={\frac {1}{Eh}}{\frac {d^{2}Q_{\phi }}{d\phi ^{2}}}={\frac {2\lambda ^{2}}{Eh}}Ce^{-\lambda \psi }\cos(\lambda \psi {+\gamma })$

(82)

Y finalmente podemos encontrar los momentos sustituyendo la segunda ecuación de 82 en la 75 y despreciando ${\textstyle V}$ al compararlo con ${\textstyle {\frac {dV}{d\phi }}}$:

$M_{\phi }$ $=-{\frac {D}{a}}{\frac {dV}{d\phi }}={\frac {a}{\lambda {\sqrt {2}}}}Ce^{-\lambda \psi }\sin {(\lambda \psi {+\gamma }+{\frac {\pi }{4}})}$ $M_{\theta }$ $=-{\frac {\nu D}{a}}{\frac {dV}{d\phi }}=\nu M_{\phi }$

(83)

1. CÙPULA SOMETIDA A UN MOMENTO $M_{\alpha }$ EN SU PIE

En este caso para ${\textstyle \phi =\alpha }$ tenemos que ${\textstyle M_{\phi }=M_{\alpha }}$ y ${\textstyle N_{\phi }=0}$. Y para ${\textstyle \psi =0}$ tenemos que ${\textstyle N_{\alpha }=0=-\cot {\alpha }C\sin {(\lambda \psi {+\gamma })}}$ y por lo tanto ${\textstyle \gamma }$ tiene que anularse.

Entonces, de la ecuación 83 obtenemos:

$M_{\alpha }={\frac {a}{\lambda {\sqrt {2}}}}C\sin({\frac {\pi }{4}})\rightarrow C={\frac {2M_{\alpha }\lambda }{a}}$

Con lo que queda resuelto el problema obteniendo la rotación en ${\textstyle \phi =\alpha }$

$\Delta _{\alpha }={\frac {2\lambda ^{2}}{Eh}}{\frac {M_{\alpha }2\lambda }{a}}={\frac {4\lambda ^{3}M_{\alpha }}{Eah}}$

Y el desplazamiento horizontal en el mismo punto:

$\Delta _{H}={\frac {2\lambda ^{2}\sin {\alpha }}{Eh}}M_{\alpha }$

2. CÚPULA SOMETIDA A CARGA HORIZONTAL $H$ UNIFORME EN SU PIE

En este caso para ${\textstyle \phi =\alpha }$ tenemos que ${\textstyle M_{\alpha }=0}$ y ${\textstyle N_{\alpha }=H\cos {\alpha }}$. Entonces de la ecuación 83 podemos extraer que ${\textstyle \gamma =-{\frac {\pi }{4}}}$ y de 81 obtendremos que ${\textstyle C={\frac {2H\sin {\alpha }}{\sqrt {2}}}}$. Por lo tanto la solución al problema en este supuesto será:

$\Delta _{\alpha }={\frac {2\lambda ^{2}\sin {\alpha }}{Eh}}H$

$\Delta _{H}={\frac {2a\lambda ^{\sin }^{2}{\alpha }}{Eh}}H$




	CASO 1	CASO 2
${\textstyle N_{\phi }}$	$-{\frac {2\lambda }{a}}\cot {\alpha {-\psi }}e^{-\lambda \psi }\sin {\lambda \psi }M_{\alpha }$	$-{\sqrt {2}}\cot(\alpha {-\psi })\sin {\alpha }e^{-\lambda \psi }\sin {\big (}\lambda \psi -{\frac {\pi }{4}}{\big )}H$
${\textstyle N_{\theta }}$	$-{\frac {2{\sqrt {2}}\lambda ^{2}}{a}}e^{-\lambda \psi }\sin {\big (}\lambda \psi -{\frac {\pi }{4}}{\big )}M_{\alpha }$	$-2\lambda \sin {\alpha }e^{-\lambda \psi }\sin {{\big (}\lambda \psi -{\frac {\pi }{2}}{\big )}H}$
${\textstyle M_{\phi }}$	${\sqrt {2}}e^{-\lambda \psi }sin{\big (}\lambda \psi +{\frac {\pi }{4}}{\big )}M_{\alpha }$	${\frac {a}{\lambda }}\sin {\alpha }e^{-\lambda \psi }\sin {\lambda \psi }H$
${\textstyle \Delta _{\alpha }}$	${\frac {4\lambda ^{3}M_{\alpha }}{Eah}}$	${\frac {2\lambda ^{2}\sin {\alpha }}{Eh}}H$
${\textstyle \Delta _{H}}$	${\frac {2\lambda ^{2}\sin {\alpha }}{Eh}}M_{\alpha }$	${\frac {2a\lambda \sin ^{2}{\alpha }}{Eh}}H$

2.2 Ejemplos de aplicación

Una vez vistas las herramientas que debemos utilizar, estudiaremos el problema de una cúpula esférica sometida a carga gravitatoria (carga muerta y sobrecarga), cambio de temperatura y sobrecarga de viento.

Los datos para el problema son los siguientes:

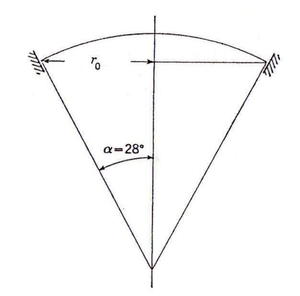
Figura 29: Aplicación cúpula esférica.

$r_{1}$ $=r_{2}=a=28.80m$ $h$ $=10cm$ $\alpha$ $=28^{\circ }$ $r_{0}$ $=a\sin {\alpha }=13.50m$ $\nu$ $={\frac {1}{6}}=0.167$ $\Delta T$ $=-5.25^{\circ }C$ $q$ $=4.30kPa$ $\lambda$ $={\sqrt {3(1-\nu ^{2}){\Big (}{\frac {a}{h}}{\Big )}^{2}}}=22$

(84)

El planteamiento que adoptaremos para solucionar este problema se basa en el utilizado en cualquier estructura hiperestática. En un primer momento estudiaremos las deformaciones de membrana suponiendo que los bordes están libres (Errores). Para solucionar la incompatibilidad que se genera, impondremos unos esfuerzos hiperestáticos ${\textstyle H}$, ${\textstyle M_{\alpha }}$ que restauraran la compatibilidad que exijan las condiciones de contorno.

En primera lugar resolveremos el caso con carga uniforme sobre la superfície de la lámina:

Errores(Deformaciones de la teoría de la membrana)

Obtendremos las deformaciones de las ecuaciones de 62:

$\Delta _{H}$ $={\frac {a^{2}q}{Eh}}{\Big (}{\frac {1+\nu }{1+\cos {\phi }}}-\cos {\phi }{\Big )}\sin {\phi }=-1010{\frac {q}{E}}$ $\Delta _{\phi }$ $={\frac {aq}{Eh}}(2+\nu )\sin {\phi }=290{\frac {q}{E}}$

(85)

Correcciones (Deformaciones debidas a esfuerzos hiperestáticos en el contorno)

Como hemos comentado, aplicamos dos esfuerzos en los bordes (${\textstyle H}$ y ${\textstyle M_{\alpha }}$) que generaran las siguientes deformaciones. En el caso de ${\textstyle M_{\alpha }}$ obtendremos:

$\Delta _{\alpha }$ $={\frac {4\lambda ^{3}M_{\alpha }}{Eah}}={\frac {14600}{E}}M_{\alpha }$ $\Delta _{H}$ $={\frac {2\lambda ^{2}\sin {\alpha }}{Eh}}M_{\alpha }={\frac {4500}{E}}M_{\alpha }$

(86)

En el caso de ${\textstyle H}$ obtendremos:

$\Delta _{\alpha }$ $={\frac {2\lambda ^{2}\sin {\alpha }}{Eh}}H={\frac {4500}{E}}M_{\alpha }$ $\Delta _{H}$ $={\frac {2a\lambda \sin ^{2}{\alpha }}{Eh}}H={\frac {2740}{E}}M_{\alpha }$

(87)

Compatibilidad (desplazamiento y giro nulo en el pie de la cúpula)

$\sum \Delta _{H}$ $=0\rightarrow {4500}M_{alpha}+2740H=1010q$ $\sum \Delta _{\alpha }$ $=0\rightarrow {14600}M_{alpha}+4500H=-290q$

(88)

Resolvemos el sistema y obtenemos:

$M_{\alpha }$ $=-1.16kN\cdot m/m$ $H$ $=3.50kN/m$

(89)

Con estos resultados, utilizando la tabla solución de los dos casos anteriores y asumiendo el principio de superposición, podemos obtener los esfuerzos de la cúpula como suma algebraica de los tres casos:

$N_{\phi }(\psi ,M_{\alpha },H)=N'_{\phi }(\psi )+N_{\phi }(\psi ,M_{\alpha )}+N_{\phi }(\psi ,H)$

$N_{\theta }(\psi ,M_{\alpha },H)=N'_{\theta }(\psi )+N_{\theta }(\psi ,M_{\alpha )}+N_{\theta }(\psi ,H)$

$M_{\phi }(\psi ,M_{\alpha },H)=M'_{\phi }(\psi )+M_{\phi }(\psi ,M_{\alpha )}+M_{\phi }(\psi ,H)$

Los resultados que describen las figuras siguientes se detallan en las tablas adjuntas:




(deg)	(rad)	-\psi	e^-		-45º	+45º	-90º
0.0000	0.0000	1.8800	1.0000	0.0000	-0.7070	0.7070	-1.0000
1.0000	0.0175	1.9600	0.6800	0.3750	-0.3910	0.9210	-0.9270
2.0000	0.0349	2.0500	0.4640	0.6940	-0.0170	1.0000	-0.7190
5.0000	0.0873	2.3600	0.1470	0.9400	0.9060	0.4230	0.3420
10.0000	0.1750	3.0800	0.0210	-0.6430	0.0870	-0.9960	0.7660
20.0000	0.3490	7.2000	0.0004	0.9850	0.5740	0.8190	-0.1740
28.0000	0.4890		0.0000	-0.9700	-0.5150	-0.8570	0.2420

Figura 30: Cúpula esférica sometida a carga uniforme




Esfuerzos resultantes bajo carga gravitatoria uniforme
	0º	1º	2º	5º	10º	20º	28º
N'_	-65.67	-65.52	-65.38	-64.50	-64.65	-62.02	-62.02
N__1(-H)	3.06	1.17	0.00	-0.73	0.00	0.00	0.00
N__2(M_)	0.00	0.88	1.17	0.58	-0.15	0.00	0.00
N_	-62.60	-63.48	-64.21	-64.65	-64.79	-62.02	-62.02
N'_	-43.78	-44.95	-46.11	-49.76	-54.43	-60.56	-62.02
N__1(-H)	71.21	45.24	23.64	-3.65	-1.17	0.00	0.00
N__2(M_)	-38.82	-14.59	-0.44	7.44	1.17	0.00	0.00
N_	-11.38	-14.30	-22.91	-45.97	-54.43	-60.56	-62.02
M'_	0.00	0.00	0.00	0.00	0.00	0.00	0.00
M__1(-H)	0.00	0.55	0.69	0.24	0.09	0.00	0.00
M__2(M_)	-1.16	-1.02	-0.75	-0.10	0.12	0.00	0.00
M_	-1.16	-0.47	-0.06	0.190	0.01	0.00	0.00

Ahora someteremos la cúpula a un cambio de temperatura ${\textstyle \Delta T}$ y estudiaremos los esfuerzos resultantes:

Errores(Deformaciones de la teoría de la membrana)

El único error en este caso es el desplazamiento lateral debido al gradiente de temperatura que resulta ser:

$\Delta _{H}=D_{10}=r_{0}\Delta T\epsilon =-13.50\cdot {5.25}\cdot {1.15}\cdot {10}^{-5}=-8.10\cdot {10}^{-4}m$

Para facilitar los cálculos posteriores multiplicaremos dicha deformación por el módulo de deformación elástico ${\textstyle E=2.1\cdot {10}^{7}}$:

$ED_{10}=-17000kN/m$

Correcciones (Deformaciones debidas a esfuerzos hiperestáticos en el contorno)

Las correcciones en este caso son las mismas que en el caso de carga uniforme.

Compatibilidad (desplazamiento y giro nulo en el pie de la cúpula)

Aplicamos compatibilidad como en el caso anterior y obtenemos:

$\sum \Delta _{H}$ $=0\rightarrow {4500}M_{alpha}+2740H=17000$ $\sum \Delta _{\alpha }$ $=0\rightarrow {14600}M_{alpha}+4500H=0$

(90)

Resolvemos el sistema y obtenemos:

$M_{\alpha }$ $=-3.90kN\cdot m/m$ $H$ $=12.60kN/m$

(91)

Los resultados en este caso serán los siguientes:




Esfuerzos resultantes bajo cambio de temperatura
	0º	1º	2º	5º	10º	20º	28º
N'_	0.00	0.00	0.00	0.00	0.00	0.00	0.00
N__1(-H)	10.94	4.23	1.17	-2.63	0.00	0.00	0.00
N__2(M_alpha)	0.00	2.92	3.79	1.90	-0.15	0.00	0.00
N_	10.94	7.15	4.96	-0.73	-0.15	0.00	0.00
N'_	0.00	0.00	0.00	0.00	0.00	0.00	0.00
N__1(-H)	255.38	161.98	85.37	-12.84	-4.09	0.00	0.00
N__2(M_alpha)	-128.42	-48.16	-1.46	23.93	0.29	0.00	0.00
N_	126.96	113.83	83.91	11.09	-3.79	0.00	0.00
M'_	0.00	0.00	0.00	0.00	0.00	0.00	0.00
M__1(-H)	0.00	1.82	2.45	0.89	0.29	0.00	0.00
M__2(M_alpha)	-3.78	-3.38	-2.45	-0.31	0.44	0.00	0.00
M_	-3.78	-1.56	0.00	0.58	0.73	0.00	0.00

2.3 Comparación con MEF

Como ya hemos comentado, el cálculo analítico no es la única herramienta para el cálculo de láminas. Podemos encontrar herramientas muy potentes como por ejemplo el método de los elementos finitos, que te permite realizar un cálculo muy preciso en muy poco tiempo. En nuestro caso, hemos introducido la geométria del problema estudiado en el programa de cálculo por elementos finitos GiD.

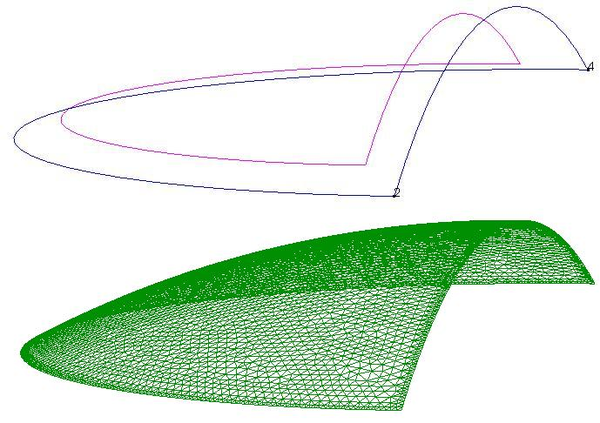
Figura 31: Geometría y mallado de la cúpula

Como se puede observar en la figura, solo hemos estudiado la mitad de la estructura para evitar problemas al generar la malla y sobretodo para ahorrar tiempo de cálculo. Así pues deberemos añadir a las condiciones de contorno, las condiciones de simétria en el corte.

Para este caso, hemos utilizado elementos de lámina triangulares de longitud 0.15m dando lugar a la malla de la figura 31.

Una vez introducidas las condiciones de contorno, las propiedades del material y las cargas actuantes, se inicia el cálculo de la solución, que durará aproximadamente 5 minutos.

Los resultados obtenidos que se muestran a continuación, describen claramente un comportamiento similar al de la solución encontrada analíticamente (figura 30) y por lo tanto podemos afirmar que la solución vertida por el ordenador es correcta.

Figura 32: Esfuerzo $N_{\phi }$ alrededor de la cúpula

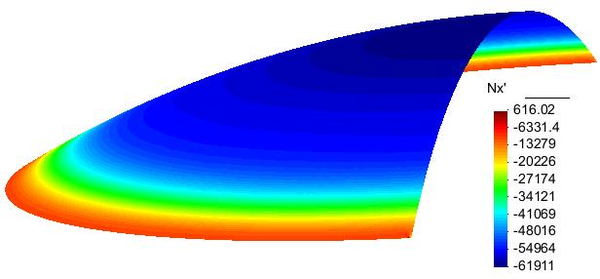
Figura 33: Esfuerzo $N_{\theta }$ alrededor de la cúpula

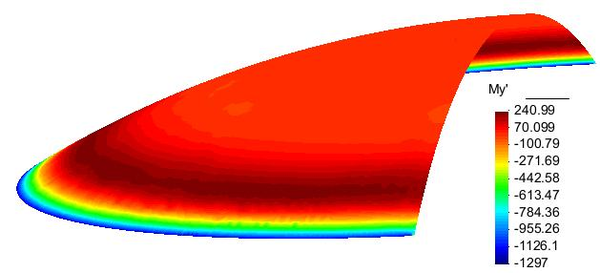
Figura 34: Esfuerzo $M_{\phi }$ alrededor de la cúpula

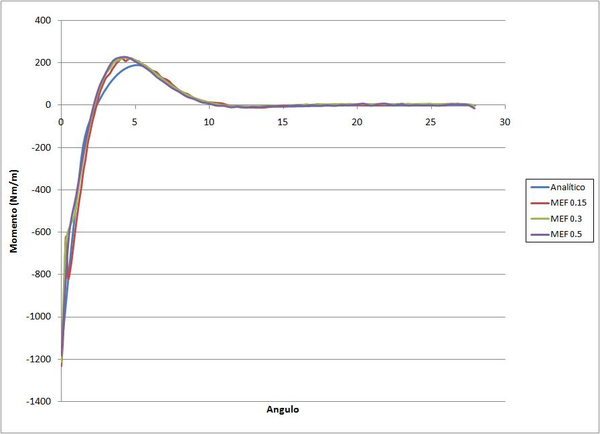
Figura 35: Comparación cálculo analítico vs MEF.

En la figura anterior se muestra el gráfico comparativo entre la solución analítica y la solución por el método de los elementos finitos. En concreto se ha comparado el momento ${\textstyle M_{phi}}$ a lo largo del meridiano. En este se pueden observar dos detalles importantes; en primer lugar podemos ver que la solución por el MEF ha convergido para un tamaño de la malla de 0.15m. Y en segundo lugar, se puede constatar que los dos cálculos no solo presentan comportamiento similares, sino que los resultados también coinciden salvo en los puntos de mayor momento donde hay un pequeño error. No tenemos que olvidar que el cálculo por el MEF es aproximado y por lo tanto siempre encontraremos pequeños errores.

Una vez más,se demuestra la necesidad de utilizar un cálculo analítico previo para comprobar que la solución que nos da el ordenador es correcta y cumple con teoría estudiada. El cálculo analítico nos será de gran utilidad para detectar posibles errores al introducir los datos de partida del problema (cargas, condiciones de contorno o propiedades del material).

3 Muros de láminas cilíndricas (Depósitos)

3.1 Simplificaciones de la teoría general y formulación concreta

1. Tensiones de membrana para láminas cilíndricas circulares.

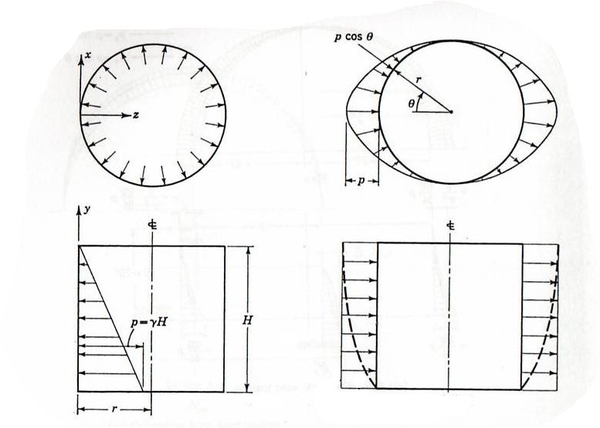
Para estudiar este tipo de láminas, utilizaremos un sistema de coordenadas cilíndricas:

Figura 36: Sistema de referencia para láminas cilíndricas.

$\alpha _{x}$ $=\theta$ $a_{x}$ $=r$ $r_{x}$ $=r$ $N'_{x}$ $=N'_{\theta }$ $\alpha _{y}$ $=y$ $a_{y}$ $=1$ $r_{y}$ $=\infty$ $N'_{xy}$ $=N'_{\theta y}$

(92)

En los casos en que ${\textstyle r}$ es constante, la ecuación general de la teoría de la membrana 34 puede reducirse a:

${\frac {\partial N'_{\theta }}{\partial \theta }}+r{\frac {\partial N'_{y\theta }}{\partial y}}+p_{\theta }r$ $=0$ $r{\frac {\partial N'_{y}}{\partial y}}+{\frac {\partial N'_{\theta y}}{\partial \theta }}+p_{y}r$ $=0$ ${\frac {N'_{\theta }}{r}}+p_{z}$ $=0$

(93)

De la tercera ecuación podemos encontrar fácilmente:

$N'_{\theta }=-p_{z}r$

La primera ecuación puede ser reescrita como:

${\frac {\partial N'_{y\theta }}{\partial y}}=-{\frac {1}{r}}{\frac {\partial N'_{\theta }}{\partial \theta }}-p_{\theta }$

Y la segunda como:

${\frac {\partial N'_{y}}{\partial y}}=-{\frac {1}{r}}{\frac {\partial N'_{\theta y}}{\partial \theta }}-p_{y}$

Si intregamos estas dos últimas expresiones, obtenemos un sistema fácil de resolver.

$N'_{\theta }$ $=-p_{z}r$ $N'_{y\theta }$ $=-\int {\Big (}{\frac {1}{r}}{\frac {\partial N'_{\theta }}{\partial \theta }}+p_{\theta }{\Big )}dy+f_{1}(\theta )$ $N'_{y}$ $=-\int {\Big (}{\frac {1}{r}}{\frac {\partial N'_{\theta y}}{\partial \theta }}+p_{y}{\Big )}dy+f_{2}(\theta )$

(94)

Considerando las cargas descritas en la figura 36 obtendremos los correspondientes esfuerzos de membrana.

1. Muro cilíndrico cargado por presión interna.

En este caso tenemos que ${\textstyle p_{\theta }=p_{y}=0}$ y ${\textstyle p_{z}=pf(y)}$, donde ${\textstyle p_{z}}$ es independiente de ${\textstyle \theta }$. Por lo tanto 94 se reduce a:

$N'_{\theta }$ $=-rpf(y)$ $N'_{y\theta }$ $=f_{1}(\theta )$ $N'_{y}$ $=-\int {\Big (}{\frac {1}{r}}{\frac {\partial }{\partial \theta }}f_{1}(\theta ){\Big )}dy+f_{2}(\theta )$

(95)

Podemos decir que ${\textstyle f_{1}(\theta )=f_{2}(\theta )=0}$ ya que son efectos de borde que pueden se impuestos en el análisis de las presiones.

Si consideramos carga hidrostática con el eje ${\textstyle y}$ ascendente, sabemos que:

$p_{z}=-\gamma (H-y)$

Por lo tanto:

$N'_{\theta }$ $=\gamma (H-y)r$ $N'_{y\theta }$ $=N'_{y}=0$

(96)

2. Muro cilíndrico cargado por presión externa.

En el caso en que la carga fuera constante alrededor de ${\textstyle \theta }$, el resultado sería el mismo que 96 pero con el signo cambiado. Así pues consideraremos carga de viento con variación sobre ${\textstyle \theta }$, por lo que tenemos ${\textstyle p_{\theta }=p_{y}=0}$ y ${\textstyle p_{z}=p\cos {\theta }}$.

La ecuación 94 se reduce a:

$N'_{\theta }$ $=-pr\cos {\theta }$ $N'_{y\theta }$ $=-py\sin {\theta }+f_{1}{\theta }$ $N'_{y}$ $=-{\frac {p}{r}}\cos {\theta }{\Big (}Hy-{\frac {y^{2}}{2}}{\Big )}+f_{2}(\theta )$

(97)

Para ${\textstyle y=H}$, ${\textstyle N'_{y\theta }=0}$ por lo que:

$f_{1}(\theta )=pH\sin {\theta }\rightarrow N'_{y\theta }=p(H-y)\sin {\theta }$

Finalmente para ${\textstyle y=H}$, ${\textstyle N'_{y}=0}$ por lo que:

$f_{2}(\theta )={\frac {pH^{2}}{2r}}\cos {\theta }\rightarrow N'_{y}={\frac {p}{2r}}(H-y)^{2}\cos {\theta }$

(b) Desplazamientos de membrana para láminas cilíndricas cargadas simétricamente con respecto a su eje de revolución.

En el caso de tener solo carga de presión, tenemos que ${\textstyle u=\partial /\partial \theta =0}$ y las deformaciones de la ecuación 18 con ${\textstyle r_{y}=\infty }$ pasa a ser:

$\epsilon _{x0}$ $=-{\frac {w}{r_{x}}}=-{\frac {w}{r}}$ $\epsilon _{y0}$ $={\frac {dv}{dy}}$ $\gamma _{xy0}$ $=0$

(98)

Las rotaciones descritas en 19 pasan a:

$\phi _{x}$ $={\frac {1}{a_{x}}}{\frac {\partial w}{\partial \alpha _{x}}}={\frac {1}{r}}{\frac {dw}{d\theta }}=0$ $\phi _{y}$ $={\frac {1}{a_{y}}}{\frac {\partial w}{\partial \alpha _{y}}}={\frac {dw}{dy}}$

(99)

Ahora, con las tensiones de membrana encontradas para carga hidrostática, podemos encontrar el desplazamiento ${\textstyle w}$:

$\epsilon _{x0}=\epsilon _{\theta }={\frac {N'_{\theta }}{Eh}}={\frac {\gamma r}{Eh}}(H-y)=-{\frac {w}{r}}\rightarrow w=-{\frac {\gamma r^{2}}{Eh}}(H-y)$

(100)

Por lo que hace a las rotaciones, si consideramos ${\textstyle h=ctt}$ obtendremos:

$\phi _{y}={\frac {\gamma r^{2}}{Eh}}$

(101)

En el caso de tener espesor con variación lineal ${\textstyle (h=h_{0}(1-\alpha y))}$ obtendremos:

$w$ $=-{\frac {\gamma r^{2}(H-y)}{Eh_{0}(1-\alpha y)}}$ $\phi _{y}$ $={\frac {1-H\alpha }{1-2\alpha y+\alpha ^{2}y^{2}}}{\frac {\gamma r^{2}}{Eh_{0}}}$

(102)

(c) Flexión en láminas cilíndricas bajo carga simétrica respecto su eje de revolución.

En la ecuación general de equilibrio, sustituiremos los términos correspondientes a cilindros circulares:

$\alpha _{x}$ $=\theta$ $a_{x}$ $=r$ $r_{x}$ $=r$ $r_{xy}$ $=\infty$ $\alpha _{y}$ $=y$ $a_{y}$ $=1$ $r_{y}$ $=\infty$

(103)

y obtendremos:

${\frac {\partial N_{\theta }}{\partial \theta }}+{\frac {\partial N_{y\theta }}{\partial y}}r-Q_{\theta }+p_{\theta }r$ $=0$ ${\frac {\partial N_{y}}{\partial y}}r+{\frac {\partial N_{\theta y}}{\partial \theta }}+p_{y}r$ $=0$ ${\frac {\partial Q_{\theta }}{\partial \theta }}+{\frac {\partial Q_{y}}{\partial y}}r+N_{\theta }+p_{z}r$ $=0$ $-{\frac {\partial M_{y}}{\partial y}}r+{\frac {\partial M_{\theta y}}{\partial \theta }}+Q_{y}r$ $=0$ $-{\frac {\partial M_{\theta }}{\partial \theta }}-{\frac {\partial M_{y\theta }}{\partial y}}r+Q_{\theta }r$ $=0$

(104)

Para carga axisimétrica, ${\textstyle u=\partial /\partial \theta =0}$ y por lo tanto de la 28 obtenemos que:

$N_{y\theta }=N_{\theta y}=M_{y\theta }=M_{\theta y}=0$

Y podemos reducir la 104 a:

${\frac {dN_{y}}{dy}}r+p_{y}r$ $=0$ ${\frac {dQ_{y}}{dy}}r+N_{\theta }+p_{z}r$ $=0$ $-{\frac {dM_{y}}{dy}}r+Q_{y}r$ $=0$

(105)

De las ecuaciones de 105, la primera es completamente independiente de las demás. Para cargas axisimétricas, las cargas ${\textstyle p_{y}}$ son directamente soportadas por la resultante ${\textstyle N_{y}}$. En el caso en que ${\textstyle N_{y}=0}$, la flexión en cilindros circulares, se puede describir mediante dos ecuaciones de equilibrio con tres incógnitas (${\textstyle Q_{y}}$, ${\textstyle N_{\theta }}$ y ${\textstyle M_{y}}$). Para resolver este problema, debemos utilizar la ecuación 28 que en este caso será:

$N_{y}$ $=K{\Big (}{\frac {dv}{dy}}-\nu {\frac {w}{r}}{\Big )}$ $N_{x}$ $=N_{\theta }=K{\Big (}-{\frac {w}{r}}+\nu {\frac {dv}{dy}}{\Big )}$ $M_{y}$ $=-D{\Big (}{\frac {d\phi _{y}}{dy}}{\Big )}$

(106)

Como ${\textstyle N_{y}=0}$, tenemos que:

${\frac {dv}{dy}}=\nu {\frac {w}{r}}$

Que sustituyendo en la segunda ecuación obtendremos:

$N_{\theta }=-K(1-\nu ^{2}){\frac {w}{r}}=-{\frac {Ehw}{r}}$

(107)

y con ${\textstyle \phi _{y}=dw/dy}$:

$M_{y}=-D{\frac {d^{2}w}{dy^{2}}}$

(108)

Así pues, la ecuación 105 se puede reducir a una sola expresión:

${\frac {dM_{y}}{dy}}=Q_{y}\rightarrow r{\frac {d^{2}M_{y}}{dy^{2}}}+N_{\theta }+p_{z}r=0$

(109)

Introducimos los esfuerzos ${\textstyle N_{\theta }}$ y ${\textstyle M_{y}}$ encontradas en la ecuaciones anteriores y obtendremos la expresión general de láminas cilíndricas.

${\frac {d^{2}}{dy^{2}}}{\Big (}D{\frac {d^{2}w}{dy^{2}}}{\Big )}+{\frac {Ehw}{r^{2}}}=p_{z}$

(110)

La solución de dicha ecuación resulta sencilla en el caso en que la lámina tenga un espesor constante y por lo tanto una ${\textstyle D}$ constante. En este caso la ecuación 110 pasa a:

$D{\frac {d^{4}w}{dy^{4}}}+{\frac {Eh}{r^{2}}}w=p_{z}$

(111)

Esta ecuación presenta una cierta similitud con la ecuación de la viga elástica:

$EI{\frac {d^{4}w}{dy^{4}}}+kw=p_{z}$

donde ${\textstyle kw}$ son las reacciones. En el caso de láminas cilíndricas, usaremos el parametro

$\beta ^{4}={\frac {Eh}{4r^{2}D}}={\frac {3(1-\nu ^{2})}{r^{2}h^{2}}}$

(112)

por lo que la ecuación 111 se puede reescribir como:

${\frac {d^{4}w}{dy^{4}}}+4\beta ^{4}w={\frac {p_{z}}{D}}$

(113)

Cuya solución resulta ser:

$w=e^{\beta y}(C_{1}\cos {\beta y}+C_{2}\sin {\beta y})+e^{-\beta y}(C_{3}\cos {\beta y}+C_{4}\sin {\beta y})+f(y)$

(114)

$f(y)$

es la solución particular que en este caso será la solución de la teoría de la membrana ${\textstyle w=p_{z}r^{2}/Eh\,\,}$ y ${\textstyle C_{1}}$,${\textstyle C_{2}}$,${\textstyle C_{3}}$ y ${\textstyle C_{4}}$ son constantes de integración que dependen de las condiciones de contorno del cilíndro.

En el caso en que el cilindro es suficientemente largo, los efectos de ${\textstyle Q_{0}}$ y ${\textstyle M_{0}}$ en uno de los contornos es despreciable en el otro controno, por lo que cada borde puede ser tratado de forma independiente. De esta manera la ecuación 114 se reduce hasta el punto de poderse resolver solamente con dos constantes. Podemos observar que ${\textstyle e^{\beta y}}$ aumenta con ${\textstyle y}$, por lo que no nos permitirá localizar efectos de contorno hasta que ${\textstyle C_{1}=C_{2}=0}$, por lo que:

$w=e^{-\beta y}(C_{3}\cos {\beta y}+C_{4}\sin {\beta y})$

(115)

En primer lugar, debemos determinar los esfuerzos ${\textstyle Q_{0}}$ y ${\textstyle M_{0}}$ en los contornos libres.

$M_{y}$ $=-D{\Big (}{\frac {d^{2}w}{dy^{2}}}{\Big )}_{y=0}=M_{0}$ $Q_{y}$ $={\Big (}{\frac {dM_{y}}{dy}}{\Big )}_{y=0}=-D{\Big (}{\frac {d^{3}w}{dy^{3}}}{\Big )}_{y=0}=Q_{0}$

(116)

Derivamos la ecuación 115 las veces que haga falta para obtener:

${\frac {d^{2}w}{dy^{2}}}$ $=2\beta ^{2}e^{-\beta y}(C_{3}\sin {\beta y}-C_{4}\cos {\beta y})$ ${\frac {d^{3}w}{dy^{3}}}$ $=2\beta ^{3}e^{-\beta y}[C_{3}(\cos {\beta y}-\sin {\beta y})+C_{4}(\cos {\beta y}+\sin {\beta y})]$

(117)

Entonces para ${\textstyle y=0}$ obtendremos.

$M_{0}$ $=2\beta ^{2}DC_{4}\rightarrow C_{4}={\frac {M_{0}}{2\beta ^{2}D}}$ $Q_{0}$ $=-2\beta ^{3}D(C_{3}+C_{4})\rightarrow C_{3}=-{\frac {1}{2\beta ^{2}D}}(Q_{0}+\beta M_{0})$

(118)

Resuelto el problema, no resulta difícil encontrar el desplazamiento ${\textstyle w}$ y la rotación ${\textstyle dw/dy}$. En el caso del análisis de láminas cilíndricas, el punto de interés suele ser ${\textstyle y=0}$, con lo que tenemos:

$(w)_{y=0}$ $=-{\frac {1}{2\beta ^{3}D}}(\beta M_{0}+Q_{0})$ ${\Big (}{\frac {dw}{dy}}{\Big )}_{y=0}$ $={\frac {1}{2\beta ^{2}D}}(2\beta M_{0}+Q_{0})$

(119)

Asimismo diferenciando la ecuación 115 obtendremos la siguiente tabla:




	$w=-{\frac {1}{2\beta ^{3}D}}$
	${\frac {dw}{dy}}={\frac {1}{2\beta ^{2}D}}$
	${\frac {d^{2}w}{dy^{2}}}=-{\frac {1}{2\beta D}}$
	${\frac {d^{3}w}{dy^{3}}}=-{\frac {1}{D}}$
	$\phi (\beta y)=(\cos {\beta y}+\sin {\beta y}),e^{\beta y}$
	$\psi (\beta y)=(\cos {\beta y}-\sin {\beta y}),e^{\beta y}$
	$\theta (\beta y)=\cos {\beta y},e^{\beta y}$
	$\xi (\beta y)=\sin {\beta y},e^{\beta y}$

Obtendremos también las expresiones de los esfuerzos de la lámina:

$N_{\theta }$ $=-{\frac {Ehw}{r}}$ $M_{\theta }$ $=\nu M_{y}$ $M_{y}$ $=-D{\frac {d^{2}w}{dy^{2}}}$ $Q_{y}$ $=-D{\frac {d^{3}w}{dy^{3}}}$

(120)

En la siguiente tabla se detallan los valores de los resultados obtenidos para diferentes valores de ${\textstyle \beta y}$.




${\textstyle \beta y}$	$\phi (\beta y)$	$\psi (\beta y)$	$\theta (\beta y)$	$\xi (\beta y)$	$\beta y$	$\phi (\beta y)$	$\psi (\beta y)$	$\theta (\beta y)$	$\xi (\beta y)$
0.0000	1.0000	1.0000	1.0000	0.0000	3.5000	-0.0389	-0.0177	-0.0283	-0.0106
0.1000	0.9907	0.8100	0.9003	0.0903	3.6000	-0.0366	-0.0124	-0.0245	-0.0121
0.2000	0.9651	0.6398	0.8024	0.1627	3.7000	-0.0341	-0.0079	-0.0210	-0.0131
0.3000	0.9267	0.4888	0.7077	0.2189	3.8000	-0.0314	-0.0040	-0.0177	-0.0137
0.4000	0.8784	0.3564	0.6174	0.2610	3.9000	-0.0286	-0.0008	-0.0147	-0.0139
0.5000	0.8231	0.2415	0.5323	0.2908	4.0000	-0.0258	0.0019	-0.0120	-0.0139
0.6000	0.7628	0.1431	0.4530	0.3099	4.1000	-0.0231	0.0040	-0.0095	-0.0136
0.7000	0.6997	0.0599	0.3798	0.3199	4.2000	-0.0204	0.0057	-0.0074	-0.0131
0.8000	0.6354	-0.0093	0.3131	0.3223	4.3000	-0.0179	0.0070	-0.0054	-0.0124
0.9000	0.5712	-0.0657	0.2527	0.3185	4.4000	-0.0155	0.0079	-0.0038	-0.0117
1.0000	0.5083	-0.1108	0.1988	0.3096	4.5000	-0.0132	0.0085	-0.0023	-0.0109
1.1000	0.4476	-0.1457	0.1510	0.2967	4.6000	-0.0111	0.0089	-0.0011	-0.0100
1.2000	0.3899	-0.1716	0.1091	0.2807	4.7000	-0.0092	0.0090	-0.0001	-0.0091
1.3000	0.3355	-0.1897	0.0729	0.2626	4.8000	-0.0075	0.0089	0.0007	-0.0082
1.4000	0.2849	-0.2011	0.0419	0.2430	4.9000	-0.0059	0.0087	0.0014	-0.0073
1.5000	0.2384	-0.2068	0.0158	0.2226	5.0000	-0.0045	0.0084	0.0019	-0.0065
1.6000	0.1959	-0.2077	-0.0059	0.2018	5.1000	-0.0033	0.0079	0.0023	-0.0056
1.7000	0.1576	-0.2047	-0.0235	0.1812	5.2000	-0.0023	0.0075	0.0026	-0.0049
1.8000	0.1234	-0.1985	-0.0376	0.1610	5.3000	-0.0014	0.0069	0.0028	-0.0042
1.9000	0.0932	-0.1899	-0.0484	0.1415	5.4000	-0.0006	0.0064	0.0029	-0.0035
2.0000	0.0667	-0.1794	-0.0563	0.1231	5.5000	0.0000	0.0058	0.0029	-0.0029
2.1000	0.0439	-0.1675	-0.0618	0.1057	5.6000	0.0005	0.0052	0.0029	-0.0023
2.2000	0.0244	-0.1548	-0.0652	0.0896	5.7000	0.0010	0.0046	0.0028	-0.0018
2.3000	0.0080	-0.1416	-0.0668	0.0748	5.8000	0.0013	0.0041	0.0027	-0.0014
2.4000	-0.0056	-0.1282	-0.0669	0.0613	5.9000	0.0015	0.0036	0.0025	-0.0010
2.5000	-0.0166	-0.1149	-0.0658	0.0491	6.0000	0.0017	0.0031	0.0024	-0.0007
2.6000	-0.0254	-0.1019	-0.0636	0.0383	6.1000	0.0018	0.0026	0.0022	-0.0004
2.7000	-0.0320	-0.0895	-0.0608	0.0287	6.2000	0.0019	0.0022	0.0020	-0.0002
2.8000	-0.0369	-0.0777	-0.0573	0.0204	6.3000	0.0019	0.0018	0.0018	0.0000
2.9000	-0.0403	-0.0666	-0.0534	0.0132	6.4000	0.0018	0.0015	0.0017	0.0002
3.0000	-0.0423	-0.0563	-0.0493	0.0070	6.5000	0.0018	0.0011	0.0015	0.0003
3.1000	-0.0431	-0.0469	-0.0450	0.0019	6.6000	0.0017	0.0009	0.0013	0.0004
3.2000	-0.0431	-0.0383	-0.0407	-0.0024	6.7000	0.0016	0.0006	0.0011	0.0005
3.3000	-0.0422	-0.0306	-0.0364	-0.0058	6.8000	0.0015	0.0004	0.0010	0.0006
3.4000	-0.0408	-0.0237	-0.0323	-0.0085	6.9000	0.0014	0.0002	0.0008	0.0006

3.2 Ejemplos de aplicación

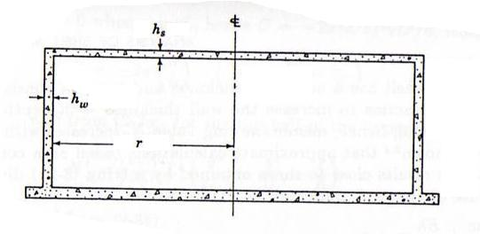
3.2.1 Muro cilíndrico con forjado circular superior y con carga hidrostática.

Figura 37: Muro cilíndrico con forjado circular superior y con carga hidrostática.

Errores(Deformaciones debidas a la teoría de la membrana).

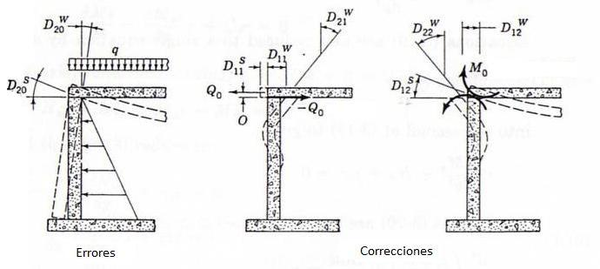
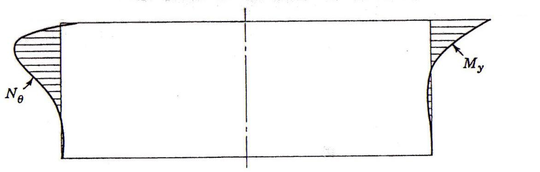
Como se decribe en la imagen siguiente,las deformaciones de membrana son el giro del forjado¹ y giro del tanque en cabeza, debido al empuje hidrostático del fluido.

Figura 38: Sistema de referencia para láminas cilíndricas.

$D_{20}^{s}$ $=-{\frac {qr}{16D_{s}}}{\Big [}{\frac {3+\nu }{1+\nu }}a^{2}-r^{2}{\Big ]}=-{\frac {qr}{16D_{s}}}{\Big (}{\frac {12}{7}}{\Big )}$ $D_{s}$ $={\frac {Eh_{s}^{3}}{12(1-\nu ^{2})}}=2.46\cdot {10}^{-3}E\rightarrow D_{20}^{s}=24600{\frac {q}{E}}$

(121)

$\phi _{y}$ $=D_{20}^{w}=-{\frac {\gamma r^{2}}{Eh}}=-11.10{\frac {\gamma }{E}}$

(122)

Correcciones (Deformaciones debidas a esfuerzos hiperestáticos en todos los bordes).

Aplicamos un momento ${\textstyle M_{0}}$ y un cortante ${\textstyle Q_{0}}$ para conseguir la compatibilidad. Los desplazamientos del deposito son:

$\Delta _{H}(-Q_{0})$ $=D_{11}^{w}={\frac {1}{2\beta ^{3}D_{w}}}Q_{0}=260{\frac {Q_{0}}{E}}$ $D_{w}={\frac {Eh_{w}^{3}}{12(1-\nu ^{2})}}=4.75\cdot {10}^{-3}E$ $\beta ^{4}={\frac {3(1-\nu ^{2})}{r^{2}h^{2}}}=0.30m^{-4}$ $\beta ^{3}=0.40m^{-3}\,;\beta ^{2}=0.55m^{-2}\,;\beta =0.74m^{-1}$ $\Delta \phi (-Q_{0})$ $=D_{21}^{w}={\frac {-1}{2\beta ^{2}D_{w}}}Q_{0}=-195{\frac {Q_{0}}{E}}$ $\Delta _{H}(-M_{0})$ $=D_{12}^{w}={\frac {-1}{2\beta ^{2}D_{w}}}M_{0}=-195{\frac {M_{0}}{E}}$ $\Delta \phi (-M_{0})$ $=D_{22}^{w}={\frac {M_{0}}{\beta D_{w}}}=285{\frac {M_{0}}{E}}$

(123)

Por lo que hace al forjado circular, los esfuerzos impuestos generan un desplazamiento horizontal y una rotación.

$\Delta _{H}^{s}$ $=D_{11}^{s}={\frac {r}{Eh_{s}}}(1-\nu )Q_{0}={\frac {22.5}{E}}Q_{0}$ $\Delta _{\phi }^{s}$ $=D_{22}^{s}={\frac {M_{0}r}{D_{s}(1+\nu )}}={\frac {2900}{E}}M_{0}$

(124)

Compatibilidad de deformaciones.

Planteamos las ecuaciones de compatibilidad y obtenemos los esfuerzos introducidos:

$\sum {\Delta _{H}}$ $=0\rightarrow 285Q_{0}-195M_{0}=11.1\gamma$ $\sum {\Delta \phi }$ $=0\rightarrow {-195}Q_{0}+3185M_{0}=-24600q$

(125)

$Q_{0}=4.1\gamma \cdot {10}^{-2}-5.5q$

$M_{0}=2.5\gamma \cdot {10}^{-3}-8.1q$

En el caso en que ${\textstyle \gamma =0}$, los resultados al problema son los descritos en la tabla y figura siguientes:

Figura 39: Esfuerzos resultantes al someter el forjado a la carga $q$




${\textstyle y}$	$\beta y$	$Ew(y)$	${\frac {d^{2}w(y)}{dy^{2}}}$	$N_{\theta }(y)$	$M_{y}(y)$	$y$	$\beta y$	$Ew(y)$	${\frac {d^{2}w(y)}{dy^{2}}}$	$N_{\theta }(y)$	$M_{y}(y)$
0.00	0.00	129.63	8.10	-6.00	-8.10	3.10	2.29	-127.71	-0.49	5.91	0.49
0.10	0.07	12.15	7.55	-0.56	-7.55	3.20	2.37	-111.71	-0.50	5.17	0.50
0.20	0.15	-89.49	6.99	4.14	-6.99	3.30	2.44	-96.71	-0.50	4.48	0.50
0.30	0.22	-176.17	6.45	8.16	-6.45	3.40	2.52	-82.89	-0.50	3.84	0.50
0.40	0.30	-248.93	5.91	11.52	-5.91	3.50	2.59	-70.10	-0.49	3.25	0.49
0.50	0.37	-309.41	5.38	14.32	-5.38	3.60	2.66	-58.35	-0.48	2.70	0.48
0.60	0.44	-358.38	4.88	16.59	-4.88	3.70	2.74	-47.66	-0.46	2.21	0.46
0.70	0.52	-396.89	4.39	18.37	-4.39	3.80	2.81	-37.89	-0.45	1.75	0.45
0.80	0.59	-426.02	3.92	19.72	-3.92	3.90	2.89	-29.18	-0.43	1.35	0.43
0.90	0.67	-447.01	3.48	20.69	-3.48	4.00	2.96	-21.24	-0.41	0.98	0.41
1.00	0.74	-460.31	3.07	21.31	-3.07	4.10	3.03	-14.37	-0.38	0.67	0.38
1.10	0.81	-467.18	2.68	21.63	-2.68	4.20	3.11	-8.15	-0.36	0.38	0.36
1.20	0.89	-468.40	2.32	21.69	-2.32	4.30	3.18	-2.71	-0.34	0.13	0.34
1.30	0.96	-464.60	1.98	21.51	-1.98	4.40	3.26	1.96	-0.31	-0.09	0.31
1.40	1.04	-456.89	1.67	21.15	-1.67	4.50	3.33	5.98	-0.29	-0.28	0.29
1.50	1.11	-445.15	1.38	20.61	-1.38	4.60	3.40	9.37	-0.27	-0.43	0.27
1.60	1.18	-430.78	1.12	19.94	-1.12	4.70	3.48	12.27	-0.24	-0.57	0.24
1.70	1.26	-414.11	0.89	19.17	-0.89	4.80	3.55	14.68	-0.22	-0.68	0.22
1.80	1.33	-395.19	0.68	18.30	-0.68	4.90	3.63	16.44	-0.20	-0.76	0.20
1.90	1.41	-375.10	0.49	17.37	-0.49	5.00	3.70	17.88	-0.18	-0.83	0.18
		0.00
2.00	1.48	-353.89	0.32	16.38	-0.32	5.10	3.77	18.99	-0.16	-0.88	0.16
2.10	1.55	-332.03	0.17	15.37	-0.17	5.20	3.85	19.61	-0.14	-0.91	0.14
2.20	1.63	-309.73	0.04	14.34	-0.04	5.30	3.92	20.19	-0.12	-0.93	0.12
2.30	1.70	-287.31	-0.07	13.30	0.07	5.40	4.00	20.29	-0.11	-0.94	0.11
2.40	1.78	-265.25	-0.17	12.28	0.17	5.50	4.07	20.07	-0.09	-0.93	0.09
2.50	1.85	-243.43	-0.25	11.27	0.25	5.60	4.14	19.82	-0.08	-0.92	0.08
2.60	1.92	-222.02	-0.32	10.28	0.32	5.70	4.22	19.54	-0.07	-0.90	0.07
2.70	2.00	-201.37	-0.37	9.32	0.37	5.80	4.29	18.93	-0.05	-0.88	0.05
2.80	2.07	-181.64	-0.42	8.41	0.42	5.90	4.37	18.16	-0.04	-0.84	0.04
2.90	2.15	-162.70	-0.45	7.53	0.45	6.00	4.44	17.52	-0.03	-0.81	0.03
3.00	2.22	-144.57	-0.47	6.69	0.47	6.10	4.51	16.70	-0.02	-0.77	0.02

(¹) Deformaciones obtenidas en Teoría de placas y láminas de S. Timoshenko y S. Woinowsky-Krieger.

3.2.2 Muro cilíndrico conectado a su cimentación

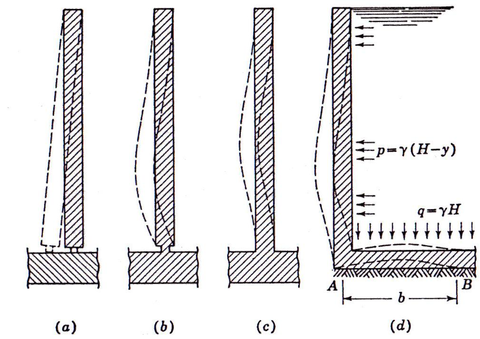
Tenemos que distinguir entre 4 tipos de apoyo diferente:

1. Libre deslizamiento: en este caso, la teoría de la membrana nos dará la solución completa.
2. Apoyo de bisagra: el efecto de un cortante radial, debe superponerse a la solución de la teoría de la membrana.
3. Apoyo fijo: en este caso aparecerá un momento y un cortante en la base del muro.
4. Apoyo parcialmente fijo: se considera una cierta rotación en la base de manera que el momento que aparece se ve reducido.

Figura 40: Tipologias de apoyos en cimentación.

Ahora estudiaremos los 4 tipos para el ejemplo anteriormente estudiado.

3.2.2.1 Libre deslizamiento

Como hemos comentado, la solución es la de la teoría de la membrana (equación 96). Este caso no presenta momentos.

3.2.2.2 Apoyo de bisagra

Errores

$w=-{\frac {\gamma r^{2}H}{Eh}}=-1080{\frac {\gamma }{E}}$

(126)

Correcciones

$\Delta _{H}(Q_{0})={\frac {1}{2\beta ^{3}D}}Q_{0}=262{\frac {Q_{0}}{E}}$

(127)

Compatibilidad

$\sum {\Delta _{H}}=0\rightarrow 262Q_{0}-1080\gamma =0\rightarrow Q_{0}=4.10\gamma \overbrace {=} ^{\gamma =10kN/m^{2}}41kN/m$

(128)

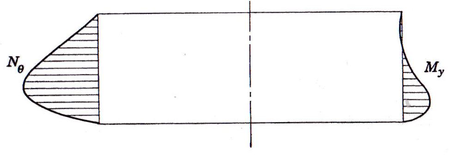
Ahora, teniendo en cuenta el efecto del ${\textstyle Q_{0}}$ encontrado, superpondremos el efecto de la teoría de la membrana y de dicho cortante hiperestático y obtendremos el resultado que se detalla en la imagen siguiente:

Figura 41: Esfuerzos en deposito bajo carga hidrostática (apoyo de bisagra)

Sustituyendo el esfuerzo hiperestático obtenido en las ecuaciones 120 y combinandolas con la solución de la teoría de la membrana, obtenemos el siguiente resultado:




${\textstyle y}$	$\beta y$	$Ew(y)$	${\frac {d^{2}w(y)}{dy^{2}}}$	$N_{\theta }(y)$	$M_{y}(y)$	$y$	$\beta y$	$Ew(y)$	${\frac {d^{2}w(y)}{dy^{2}}}$	$N_{\theta }(y)$	$M_{y}(y)$
0.00	0.00	-10758.44	0.00	-2.12	0.00	3.10	2.29	717.59	-4.19	-279.22	4.19
0.10	0.07	-9963.40	-3.81	-30.73	3.81	3.20	2.37	720.82	-3.62	-271.17	3.62
0.20	0.15	-9176.95	-7.05	-58.94	7.05	3.30	2.44	716.51	-3.10	-262.77	3.10
0.30	0.22	-8405.57	-9.77	-86.45	9.77	3.40	2.52	704.68	-2.62	-254.02	2.62
0.40	0.30	-7653.56	-12.02	-113.07	12.02	3.50	2.59	687.46	-2.18	-245.03	2.18
0.50	0.37	-6928.44	-13.84	-138.44	13.84	3.60	2.66	665.95	-1.77	-235.83	1.77
0.60	0.44	-6232.37	-15.26	-162.46	15.26	3.70	2.74	640.13	-1.41	-226.44	1.41
0.70	0.52	-5568.57	-16.34	-185.00	16.34	3.80	2.81	612.16	-1.07	-216.94	1.07
0.80	0.59	-4939.20	-17.10	-205.93	17.10	3.90	2.89	580.96	-0.78	-207.30	0.78
0.90	0.67	-4346.41	-17.59	-225.18	17.59	4.00	2.96	548.68	-0.52	-197.60	0.52
1.00	0.74	-3790.20	-17.82	-242.73	17.82	4.10	3.03	514.25	-0.29	-187.81	0.29
1.10	0.81	-3272.72	-17.85	-258.49	17.85	4.20	3.11	480.90	-0.08	-178.06	0.08
1.20	0.89	-2792.89	-17.69	-272.50	17.69	4.30	3.18	446.48	0.09	-168.27	-0.09
1.30	0.96	-2350.72	-17.37	-284.77	17.37	4.40	3.26	412.05	0.24	-158.48	-0.24
1.40	1.04	-1946.20	-16.92	-295.30	16.92	4.50	3.33	378.70	0.37	-148.73	-0.37
1.50	1.11	-1576.11	-16.36	-304.23	16.36	4.60	3.40	345.35	0.48	-138.99	-0.48
1.60	1.18	-1241.52	-15.70	-311.52	15.70	4.70	3.48	313.07	0.57	-129.29	-0.57
1.70	1.26	-941.36	-14.98	-317.22	14.98	4.80	3.55	282.95	0.63	-119.70	-0.63
1.80	1.33	-671.33	-14.21	-321.52	14.21	4.90	3.63	253.90	0.69	-110.15	-0.69
1.90	1.41	-432.49	-13.40	-324.38	13.40	5.00	3.70	225.93	0.73	-100.66	-0.73
2.00	1.48	-221.62	-12.56	-325.94	12.56	5.10	3.77	199.03	0.75	-91.21	-0.75
2.10	1.55	-38.73	-11.71	-326.21	11.71	5.20	3.85	174.29	0.76	-81.87	-0.76
2.20	1.63	120.49	-10.86	-325.38	10.86	5.30	3.92	151.69	0.77	-72.62	-0.77
2.30	1.70	257.13	-10.02	-323.50	10.02	5.40	4.00	130.18	0.77	-63.43	-0.77
2.40	1.78	371.17	-9.19	-320.58	9.19	5.50	4.07	109.74	0.76	-54.28	-0.76
2.50	1.85	465.84	-8.37	-316.77	8.37	5.60	4.14	91.45	0.74	-45.23	-0.74
2.60	1.92	543.30	-7.59	-312.15	7.59	5.70	4.22	75.31	0.72	-36.29	-0.72
2.70	2.00	604.62	-6.84	-306.79	6.84	5.80	4.29	60.25	0.69	-27.39	-0.69
2.80	2.07	650.89	-6.12	-300.73	6.12	5.90	4.37	46.26	0.66	-18.54	-0.66
2.90	2.15	684.24	-5.44	-294.08	5.44	6.00	4.44	34.43	0.63	-9.79	-0.63
3.00	2.22	706.83	-4.79	-286.92	4.79	6.10	4.51	23.67	0.59	-1.10	-0.59

3.2.2.3 Apoyo fijo

Errores

$w$ $=-1080{\frac {\gamma }{E}}$ ${\frac {dw}{dy}}$ $={\frac {\gamma r^{2}}{Eh}}=180{\frac {\gamma }{E}}$

(129)

Correcciones

$\Delta _{H}(-Q_{0})=262{\frac {Q_{0}}{E}}\,\,\,\,\,\,\,$ $\Delta _{\phi }(-Q_{0})=-195{\frac {Q_{0}}{E}}$ $\Delta _{H}(M_{0})=-195{\frac {Q_{0}}{E}}\,\,\,\,\,\,\,$ $\Delta _{\phi }(M_{0})=-286{\frac {Q_{0}}{E}}$

(130)

Compatibilidad

$\Delta _{H}$ $=0\rightarrow 262Q_{0}-195M_{0}=1080\gamma$ $\Delta _{\phi }$ $=0\rightarrow {-195}Q_{0}+286M_{0}=-180\gamma$

(131)

Resolviendo el sistema y calculando para ${\textstyle \gamma =10kN/m^{2}}$ obtenemos los siguientes resultados:

$Q_{0}$ $=7.41\gamma =74.1kN/m$ $M_{0}$ $=4.43\gamma =44.3kN/m$

(132)

La distribución de los esfuerzos en este caso será de este tipo:

Figura 42: Esfuerzos en depósito bajo carga hiperestática (apoyo fijo)

Sustituyendo los esfuerzos hiperestáticos obtenidos en las ecuaciones 120 y combinándolas con la solución de la teoría de la membrana, obtenemos el siguiente resultado:




${\textstyle y}$	$\beta y$	$Ew(y)$	${\frac {d^{2}w(y)}{dy^{2}}}$	$N_{\theta }(y)$	$M_{y}(y)$	$y$	$\beta y$	$Ew(y)$	${\frac {d^{2}w(y)}{dy^{2}}}$	$N_{\theta }(y)$	$M_{y}(y)$
0.00	0.00	-10841.89	44.30	1.74	-44.30	3.10	2.29	71.98	-7.18	-249.33	7.18
0.10	0.07	-10630.77	37.19	0.17	-37.19	3.20	2.37	162.97	-6.62	-245.35	6.62
0.20	0.15	-10342.31	30.69	-4.99	-30.69	3.30	2.44	240.36	-6.07	-240.73	6.07
0.30	0.22	-9988.17	24.77	-13.18	-24.77	3.40	2.52	303.27	-5.54	-235.44	5.54
0.40	0.30	-9578.70	19.40	-23.94	-19.40	3.50	2.59	354.74	-5.03	-229.62	5.03
0.50	0.37	-9130.96	14.58	-36.47	-14.58	3.60	2.66	395.85	-4.53	-223.33	4.53
0.60	0.44	-8651.43	10.28	-50.47	-10.28	3.70	2.74	426.60	-4.05	-216.55	4.05
0.70	0.52	-8149.36	6.45	-65.51	-6.45	3.80	2.81	450.02	-3.60	-209.43	3.60
0.80	0.59	-7632.96	3.10	-81.22	-3.10	3.90	2.89	464.17	-3.18	-201.89	3.18
0.90	0.67	-7111.27	0.18	-97.17	-0.18	4.00	2.96	472.94	-2.78	-194.10	2.78
1.00	0.74	-6586.87	-2.36	-113.25	2.36	4.10	3.03	473.51	-2.41	-185.92	2.41
1.10	0.81	-6068.82	-4.50	-129.04	4.50	4.20	3.11	471.73	-2.06	-177.64	2.06
1.20	0.89	-5560.32	-6.32	-144.38	6.32	4.30	3.18	464.56	-1.74	-169.11	1.74
1.30	0.96	-5064.83	-7.82	-159.12	7.82	4.40	3.26	453.09	-1.45	-160.38	1.45
1.40	1.04	-4588.36	-9.03	-172.98	9.03	4.50	3.33	439.27	-1.19	-151.54	1.19
1.50	1.11	-4126.80	-9.99	-186.14	9.99	4.60	3.40	422.00	-0.94	-142.54	0.94
1.60	1.18	-3688.97	-10.71	-198.21	10.71	4.70	3.48	403.24	-0.72	-133.47	0.72
1.70	1.26	-3275.51	-11.22	-209.16	11.22	4.80	3.55	384.07	-0.53	-124.38	0.53
1.80	1.33	-2882.09	-11.56	-219.17	11.56	4.90	3.63	362.53	-0.35	-115.18	0.35
1.90	1.41	-2515.82	-11.72	-227.93	11.72	5.00	3.70	340.37	-0.20	-105.96	0.20
2.00	1.48	-2173.42	-11.75	-235.58	11.75	5.10	3.77	317.56	-0.06	-96.70	0.06
2.10	1.55	-1857.50	-11.65	-242.00	11.65	5.20	3.85	294.35	0.05	-87.43	-0.05
2.20	1.63	-1564.57	-11.44	-247.37	11.44	5.30	3.92	273.30	0.15	-78.25	-0.15
2.30	1.70	-1295.27	-11.15	-251.63	11.15	5.40	4.00	250.76	0.24	-69.01	-0.24
2.40	1.78	-1052.17	-10.79	-254.69	10.79	5.50	4.07	227.57	0.31	-59.74	-0.31
2.50	1.85	-831.17	-10.35	-256.72	10.35	5.60	4.14	206.56	0.37	-50.56	-0.37
2.60	1.92	-630.96	-9.89	-257.79	9.89	5.70	4.22	187.72	0.42	-41.49	-0.42
2.70	2.00	-452.18	-9.38	-257.87	9.38	5.80	4.29	168.24	0.45	-32.39	-0.45
2.80	2.07	-294.59	-8.84	-256.96	8.84	5.90	4.37	148.98	0.47	-23.30	-0.47
2.90	2.15	-155.18	-8.29	-255.22	8.29	6.00	4.44	132.76	0.50	-14.35	-0.50
3.00	2.22	-31.76	-7.74	-252.73	7.74	6.10	4.51	116.75	0.50	-5.41	-0.50

3.2.2.4 Apoyo parcialmente fijo

Como se puede ver en la figura 40, la solera proporciona un apoyo monolítico de manera que muro y cimentación trabajan solidariamente a fin de reducir los esfuerzos hiperestáticos en la base.

Para estudiar este caso, tendremos que realizar la siguiente aproximación. Consideramos la losa como una serie de vigas de ancho constante y de longitud ${\textstyle b}$, donde actua una carga vertical ${\textstyle q}$ y un momento ${\textstyle M}$. Para la losa considerada, el ancho no será constante, por lo que se considerará que varia de la unidad en el extremo hasta cero en el centro.

A partir de esta aproximación podemos escribir dos ecuaciones teniendo en cuenta que no habrá deformación relativa entre los puntos A y B y no hay rotación en el punto B.

$\phi _{A}$ $={\frac {1}{3D_{s}}}Mb-{\frac {qb^{3}}{24D_{s}}}$ $\phi _{B}$ $={\frac {1}{6D_{s}}}Mb-{\frac {qb^{3}}{24D_{s}}}=0$

(133)

de donde obtenemos que:

$b$ $=2{\sqrt {\frac {M}{q}}}$ $\phi _{A}$ $={\frac {1}{3D_{s}}}{\sqrt {\frac {M_{0}^{3}}{q}}}$

(134)

El valor de ${\textstyle b}$ debe ser mucho menor en relación a la distancia ${\textstyle r}$ para que ${\textstyle D_{s}}$ se pueda considerar constante a lo largo de la longitud ${\textstyle b}$.

Errores

$w$ $=-1080{\frac {\gamma }{E}}$ ${\frac {dw}{dy}}$ $={\frac {\gamma r^{2}}{Eh}}=180{\frac {\gamma }{E}}$

(135)

Correcciones

$\Delta _{H}(-Q_{0})=262{\frac {Q_{0}}{E}}\,\,\,\,\,\,\,$ $\Delta _{\phi }(-Q_{0})=-195{\frac {Q_{0}}{E}}$ $\Delta _{H}(M_{0})=-195{\frac {Q_{0}}{E}}\,\,\,\,\,\,\,$ $\Delta _{\phi }(M_{0})=-286{\frac {Q_{0}}{E}}$

(136)

Incluimos ademas la flexibilidad de la losa.

$\Delta _{H_{s}}$ $={\frac {Q_{0}r}{Eh}}(1-\nu )={\frac {22.5Q_{0}}{E}}$ $\Delta _{\phi _{s}}$ $=0$ $\phi _{A_{s}}$ $={\frac {1}{3D_{s}}}{\sqrt {\frac {M_{0}^{3}}{q}}}={\frac {13.5}{E}}{\sqrt {\frac {M_{0}^{3}}{q}}}$

(137)

Compatibilidad

$\sum \Delta _{H}$ $=0\rightarrow 22.5Q_{0}+262Q_{0}-195M_{0}=1080\gamma$ $\sum \Delta _{\phi }$ $=0\rightarrow {-195}Q_{0}+286M_{0}+13.5{\sqrt {\frac {M_{0}^{3}}{q}}}=-180\gamma$

(138)

Resolviendo el sistema para ${\textstyle \gamma =10kN/m^{3}}$ y ${\textstyle q=H\gamma =61kN/m^{2}}$ obtenemos el siguiente resultado:

$M_{0}=36.7kN\cdot m/m\rightarrow b=1.55m$

$Q_{0}=63kN/m$

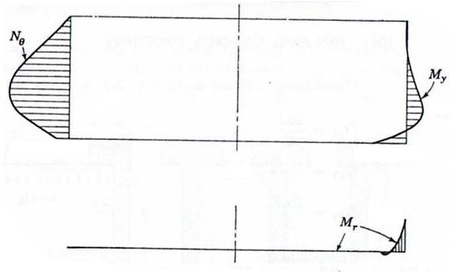
La distribución de los esfuerzos a lo largo de la lámina y de la solera es la siguiente:

Figura 43: Esfuerzos en deposito y solera bajo carga hiperestática (apoyo parcialmente fijo)

Sustituyendo los esfuerzos hiperestáticos obtenidos en las ecuaciones 120 y combinándolas con la solución de la teoría de la membrana, obtenemos el siguiente resultado:




${\textstyle y}$	$\beta y$	$Ew(y)$	${\frac {d^{2}w(y)}{dy^{2}}}$	$N_{\theta }(y)$	$M_{y}(y)$	$y$	$\beta y$	$Ew(y)$	${\frac {d^{2}w(y)}{dy^{2}}}$	$N_{\theta }(y)$	$M_{y}(y)$
0.00	0.00	-9404.98	36.70	-64.78	-36.70	3.10	2.29	87.85	-6.11	-250.07	6.11
0.10	0.07	-9198.81	30.66	-66.13	-30.66	3.20	2.37	163.36	-5.63	-245.36	5.63
0.20	0.15	-8928.91	25.14	-70.42	-25.14	3.30	2.44	227.30	-5.15	-240.12	5.15
0.30	0.22	-8605.19	20.13	-77.21	-20.13	3.40	2.52	278.95	-4.69	-234.31	4.69
0.40	0.30	-8236.39	15.60	-86.09	-15.60	3.50	2.59	320.92	-4.25	-228.06	4.25
0.50	0.37	-7836.95	11.54	-96.38	-11.54	3.60	2.66	354.13	-3.82	-221.39	3.82
0.60	0.44	-7412.31	7.92	-107.84	-7.92	3.70	2.74	378.59	-3.41	-214.33	3.41
0.70	0.52	-6970.27	4.70	-120.10	-4.70	3.80	2.81	396.89	-3.02	-206.97	3.02
0.80	0.59	-6517.71	1.90	-132.85	-1.90	3.90	2.89	407.39	-2.66	-199.26	2.66
0.90	0.67	-6062.21	-0.55	-145.74	0.55	4.00	2.96	413.38	-2.33	-191.34	2.33
1.00	0.74	-5605.90	-2.65	-158.67	2.65	4.10	3.03	412.50	-2.01	-183.10	2.01
1.10	0.81	-5156.37	-4.43	-171.28	4.43	4.20	3.11	409.71	-1.71	-174.77	1.71
1.20	0.89	-4716.24	-5.93	-183.46	5.93	4.30	3.18	402.42	-1.44	-166.23	1.44
1.30	0.96	-4288.37	-7.17	-195.06	7.17	4.40	3.26	391.57	-1.19	-157.53	1.19
1.40	1.04	-3877.73	-8.15	-205.88	8.15	4.50	3.33	378.80	-0.97	-148.74	0.97
1.50	1.11	-3480.80	-8.92	-216.05	8.92	4.60	3.40	363.19	-0.76	-139.81	0.76
1.60	1.18	-3104.92	-9.49	-225.25	9.49	4.70	3.48	346.37	-0.57	-130.84	0.57
1.70	1.26	-2750.60	-9.89	-233.46	9.89	4.80	3.55	329.30	-0.41	-121.85	0.41
1.80	1.33	-2414.05	-10.13	-240.84	10.13	4.90	3.63	310.32	-0.27	-112.77	0.27
1.90	1.41	-2101.22	-10.24	-247.12	10.24	5.00	3.70	290.86	-0.14	-103.67	0.14
2.00	1.48	-1809.27	-10.22	-252.44	10.22	5.10	3.77	270.91	-0.02	-94.54	0.02
2.10	1.55	-1540.36	-10.11	-256.69	10.11	5.20	3.85	250.70	0.07	-85.41	-0.07
2.20	1.63	-1291.42	-9.90	-260.01	9.90	5.30	3.92	232.38	0.16	-76.36	-0.16
2.30	1.70	-1062.94	-9.63	-262.39	9.63	5.40	4.00	212.86	0.23	-67.25	-0.23
2.40	1.78	-857.07	-9.30	-263.72	9.30	5.50	4.07	192.85	0.29	-58.13	-0.29
		0.00	0.00					0.00	0.00
2.50	1.85	-670.26	-8.91	-264.17	8.91	5.60	4.14	174.72	0.34	-49.09	-0.34
2.60	1.92	-501.35	-8.49	-263.79	8.49	5.70	4.22	158.48	0.37	-40.14	-0.37
2.70	2.00	-350.82	-8.04	-262.56	8.04	5.80	4.29	141.75	0.40	-31.16	-0.40
2.80	2.07	-218.45	-7.57	-260.49	7.57	5.90	4.37	125.24	0.41	-22.20	-0.41
2.90	2.15	-101.64	-7.09	-257.69	7.09	6.00	4.44	111.34	0.44	-13.35	-0.44
3.00	2.22	1.48	-6.60	-254.27	6.60	6.10	4.51	97.65	0.44	-4.52	-0.44

3.3 Comparación con MEF

Siguiendo el mismo criterio que en el capítulo anterior, estudiaremos el segundo ejemplo analizado (muro cilindrico con apoyo fijo en la base sometido a carga hidrostática) con el programa de cálculo por elementos finítos GiD. En este caso, también ahorraremos tiempo de cálculo reduciendo la estructura a un cuarto e imponiendo las condiciones de contorno de simetría en los dos cortes.

De esta manera, la geometría que introducimos es la siguiente

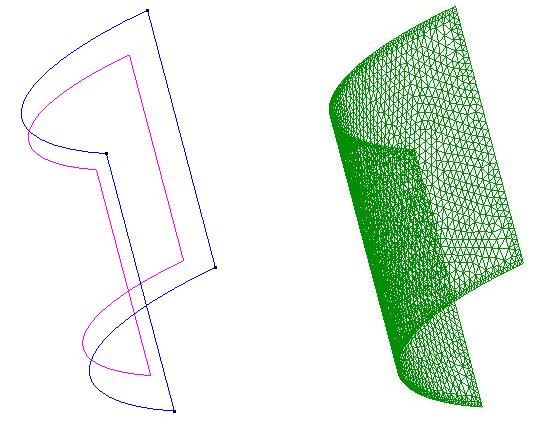
Figura 44: Geometria y mallado del deposito.

Para este ejemplo también usaremos elementos de lámina triangulares de longitud 0.20m. Una vez aplicadas las condiciones de contorno e introducidas las cargas y características del material en el modelo, ya podemos iniciar el cálculo.

Analizando la solución vertida por el programa, podemos observar que otra vez, cumple con el comportamiento que preveía el cálculo analítico.

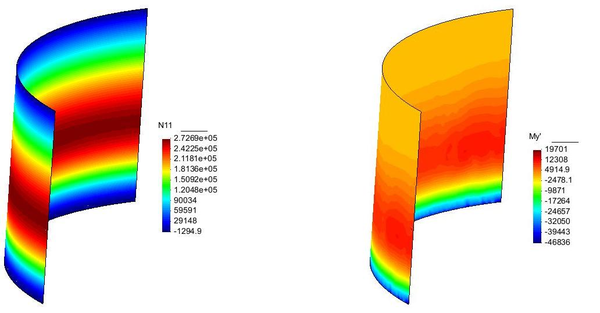
Figura 45: Esfuerzo $N_{\theta }$ alrededor del tanque.

En este caso, podemos extraer las gráficas ${\textstyle N_{\theta }(y)}$ y ${\textstyle M_{y}(y)}$ que habíamos presentado en la figura(42) y compararlas entre ellas. Podemos observar que el resultado obtenido por el MEF al converger la solución(tamaño 0.20) es una muy buena aproximación ya que presenta exactamente el mismo comportamiento y el error numérico es mínimo.

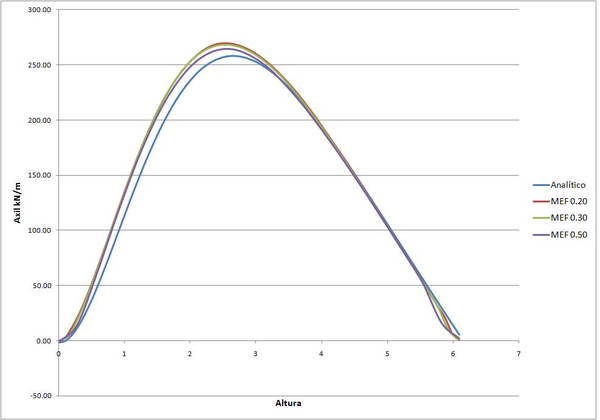
Figura 46: Comparación cálculo analítico vs MEF del esfuerzo $N_{\theta }$ alrededor de $y$.

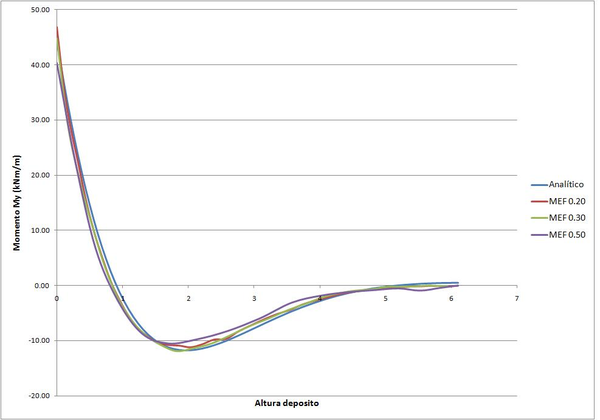
Figura 47: Comparación cálculo analítico vs MEF del esfuerzo $M_{y}$ alrededor de $y$.

4 Cúpulas conectadas a muros cilíndricos

En el cápitulo 2 solo tuvimos en cuenta cúpulas apoyadas sobre cimentación tangencial al meridiano. En éstas observamos que la flexión se puede restringir generalmente a la zona cercana a los apoyos. En la figura 48 podemos comprobar el caso más general de apoyo de una cúpula.

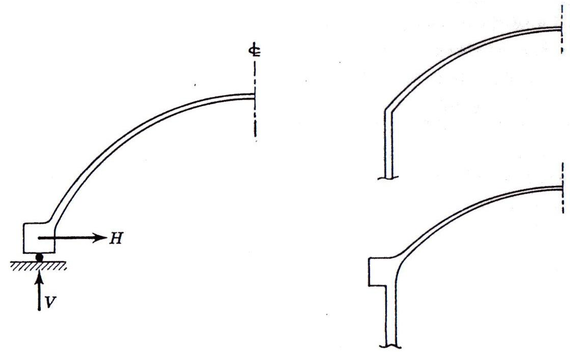
Figura 48: Apoyos habituales para cúpulas.

En este caso, el esfuerzo de membrana ${\textstyle N'_{\alpha }}$ no puede ser contrarestados por un soporte vertical ya que tenemos la componente horizontal (${\textstyle H=-N'_{\alpha }\cos {\alpha }}$). Para ello, deberemos pensar en una restricción como un anillo de borde, un muro cilíndrico o bien la combinación de ambas.

Para estudiar este caso, debemos dar una expresión para las fuerzas, momentos y deformaciones de un anillo circular. Una vez hecho este análisis, lo combinaremos con los resultados obtenidos en los capítulos 2 y 3.

4.1 Anillos circulares

Estudiaremos un anillo de sección rectangular constante como muestran las figuras siguientes. Este anillo está sometido a una fuerza (H) y una fuerza vertical (V) uniformemente distribuidas.

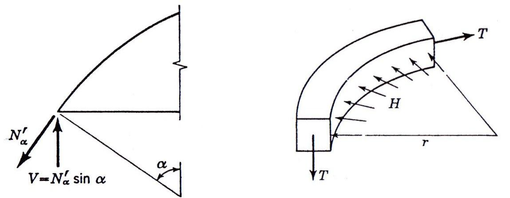
Figura 49: Esfuerzos resultantes sore el anillo circular.

En el caso de la fuerza horizontal, sabemos que causa un esfuerzo constante en el anillo (T):

$T=Hr$

y una deformación circunferencial

$\epsilon _{c}={\frac {T}{EA_{R}}}\rightarrow \Delta _{c}={\frac {2\pi r}{EA_{R}}}T$

y por lo tanto un cambio de radio de

$\Delta _{H}={\frac {rT}{EA_{R}}}\rightarrow \Delta _{H}={\frac {r^{2}}{EA_{R}\Delta \Delta }}H$

En segundo lugar, podemos considerar un momento radial ${\textstyle (M_{\alpha })}$ uniformemente distribuido sobre el anillo (Figura (50)). Si consideramos la mitad del anillo y tomamos momentos alrededor del eje ${\textstyle x}$, obtendremos por equilibrio:

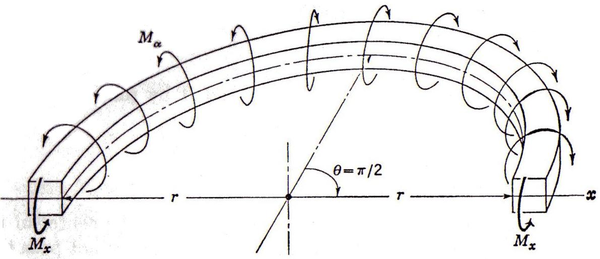
Figura 50: Momento flector uniformemente repartido sobre el anillo circular.

$M_{x}=2\int _{0}^{\pi /2}{M_{\alpha }r\cos {\theta }}d\theta =2M_{\alpha }r[\sin {\theta }]_{0}^{\pi /2}=2M_{\alpha }r$

En el caso del anillo entero ${\textstyle M_{x}=M_{\alpha }r}$.

Por la teoría de vigas elásticas, sabemos que en una sección:

$\sigma _{\theta }={\frac {M_{x}y}{I_{R}}}\rightarrow \epsilon _{c}={\frac {M_{x}y}{EI_{R}}}\rightarrow \Delta _{c}=2\pi r{\frac {M_{x}y}{I_{R}}}$

Y por lo tanto el cambio de radio será:

$\Delta _{H}={\frac {rM_{x}y}{EI_{R}}}\rightarrow \Delta _{H}={\frac {r^{2}y}{EI_{R}}}M_{\alpha }$

El giro de la sección será facilmente calculable

$\Delta _{\alpha }={\frac {\Delta _{H}}{y}}\rightarrow \Delta _{\alpha }={\frac {r^{2}}{EI_{R}}}M_{\alpha }$

Estas últimas ecuaciones, nos darán los movimientos del anillo para una fuerza ${\textstyle H}$ y un momento radial ${\textstyle M_{\alpha }}$. Para una mejor aproximación usaremos ${\textstyle r}$ como el radio interior.

Finalmente para una sección rectangular las ecuaciones mencionadas son:

$\Delta _{H}={\frac {r^{2}}{Ebd}}H\,\,\,;\,\,\,\Delta _{H}={\frac {12r^{2}y}{Ebd^{3}}}M_{\alpha }\,\,\,;\,\,\,\Delta _{\alpha }={\frac {12r^{2}}{Ebd^{3}}}M_{\alpha }$

(139)

4.2 Análisis de cúpulas conectadas a un anillo circunferencial

Consideramos la cúpula conectada monolíticamente al anillo y el anillo apoyado libremente a la cimentación tal y como se ve en la figura siguiente (51).

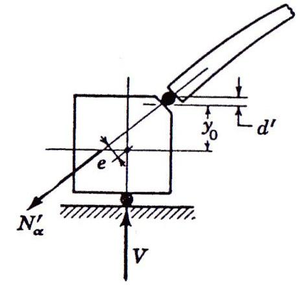
Figura 51: Cúpula conectada a anillo circular

Errores(Deformaciones de membrana)

La componente horizontal de ${\textstyle N'_{\alpha }}$ se pasa por equilibrio a la tensión del anillo como ${\textstyle T=N'_{\alpha }a\sin {\alpha }\cos {\alpha }}$ ya que el radio de la cúpula es ${\textstyle a=r/\sin {\alpha }}$.

Las deformaciones de membrana serán: movimiento horizontal y giro del borde de la cúpula ${\textstyle (\Delta _{H}^{D}y\Delta _{\alpha }^{D})}$ y del anillo ${\textstyle (\Delta _{H}^{R}y\Delta _{\alpha }^{R})}$. Las dos primeras dependen de la carga y las sacaremos del capítulo 2, mientras que las dos segundas las obtendremos de la ecuación 139.

La deformación de membrana será en el caso en que ${\textstyle N'_{\alpha }}$ pase por el centro de gravedad del anillo.

$\Delta _{H}={\frac {r^{2}}{EA_{R}}}={\frac {r^{2}}{EA_{R}}}N'_{\alpha }\cos {\alpha }$

De lo contrario, se generará un momento radial ${\textstyle M_{\alpha }=N'_{\alpha }e}$ por lo que a la deformación horizontal se le tendrá que añadir:

$\Delta _{H}={\frac {r^{2}y}{EI_{R}}}M_{\alpha }={\frac {r^{2}yN'_{\alpha }e}{EI_{R}}}\rightarrow \Delta _{H}^{R}={\frac {r^{2}}{EA_{R}}}N'_{\alpha }\cos {\alpha }+{\frac {r^{2}yN'_{\alpha }e}{EI_{R}}}$

Lógicamente, necesitaremos encontrar el desplazamiento en la unión cúpula-anillo.

$\Delta _{H}^{R}(y_{0}=d/2)={\Big (}{\frac {r^{2}}{EA_{R}}}\cos {\alpha }+{\frac {r^{2}y_{0}e}{EI_{R}}}{\Big )}N'_{\alpha }$

Y el giro en dicho punto será:

$\Delta _{\alpha }=-{\frac {r^{2}e}{EI_{R}}}N'_{\alpha }$

En el caso de que ${\textstyle N'_{\alpha }}$ pase por el centro de gravedad del anillo (${\textstyle e=0}$) y por lo tanto ${\textstyle \Delta _{\alpha }=0}$ y no hay giro.

En el caso de anillo rectangular.

$\Delta _{H}^{R}={\big (}\cos {\alpha }+{\frac {12y_{o}e}{d^{2}}}{\big )}{\frac {r^{2}N'_{\alpha }}{Ebd}}\,\,\,;\,\,\,\Delta _{\alpha }=-{\frac {12r^{2}eN'_{\alpha }}{Ebd^{3}}}$

(140)

Correcciones (Esfuerzos hiperestáticos)

Para contrarrestar las deformaciones de membrana, aplicamos una fuerza y un momento hiperestáticos ${\textstyle (H_{0},M_{0})}$. Consideramos primero ${\textstyle H_{0}}$ aplicado en ${\textstyle y_{0}}$, luego:

$\Delta _{H}^{R}(H_{0})={\Big (}{\frac {1}{A_{R}}}+{\frac {y_{0}^{2}}{I_{R}}}{\Big )}{\frac {r^{2}}{E}}H_{0}$

$\Delta _{\alpha }^{R}(H_{0})=-{\frac {r^{2}y_{0}}{EI_{R}}}H_{0}$

Ahora consideramos el momento ${\textstyle M_{0}}$

$\Delta _{H}^{R}(M_{0})=-{\frac {r^{2}y_{0}}{EI_{R}}}M_{0}$

$\Delta _{\alpha }^{R}(M_{0})={\frac {r^{2}M_{0}}{EI_{R}}}$

Para una sección rectangular estas deformaciones serán:

$\Delta _{H}^{R}(H_{0})$ $={\Big (}1+{\frac {12y_{0}^{2}}{d^{2}}}{\Big )}{\frac {r^{2}}{Ebd}}H_{0}$ $\Delta _{\alpha }^{R}(H_{0})$ $=-{\frac {12r^{2}y_{0}}{Ebd^{3}}}H_{0}$ $\Delta _{H}^{R}(M_{0})$ $=-{\frac {12r^{2}y_{0}}{Ebd^{3}}}M_{0}$ $\Delta _{\alpha }^{R}(M_{0})$ $={\frac {12r^{2}}{Ebd^{3}}}M_{0}$

(141)

Estos valores se pueden combinar ahora con las deformaciones hiperestáticas de la cúpula:

$\Delta _{H}(H_{0})=\Delta _{H}^{D}(H_{0})+\Delta _{H}^{R}(H_{0})$

$\Delta _{\alpha }(H_{0})=\Delta _{\alpha }^{D}(H_{0})+\Delta _{\alpha }^{R}(H_{0})$

$\Delta _{H}(M_{0})=\Delta _{H}^{D}(M_{0})+\Delta _{H}^{R}(M_{0})$

$\Delta _{\alpha }(M_{0})=\Delta _{\alpha }^{D}(M_{0})+\Delta _{\alpha }^{R}(M_{0})$

Compatibilidad

Impondremos la misma condición que en los casos anteriores para encontrar los esfuerzos hiperestáticos (${\textstyle H_{0},M_{0}}$).

$\sum \Delta _{H}=0$

$\sum \Delta _{\alpha }=0$

4.2.1 Ejemplo de aplicación

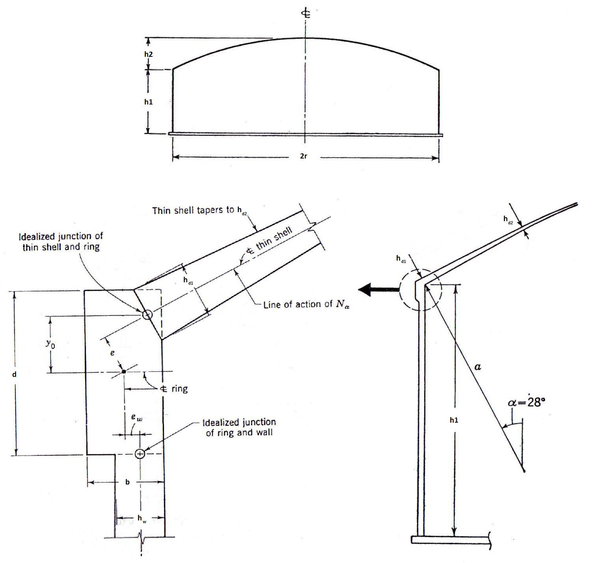
Figura 52: Ejemplo de aplicación cúpula conectada a anillo circular

$r$ $=13.5m\,\,\,\,\,\,$ $a=28.8m$ $h_{1}$ $=6.7m\,\,\,\,\,\,$ $h_{2}=3.35m$ $h_{D_{1}}$ $=15cm\,\,\,\,\,\,$ $h_{D_{2}}=6.3cm$ $\nu$ $=0\,\,\,\,\,\,$

(142)

Consideraremos ${\textstyle h_{D}=11cm}$ y obtendremos una buena aproximación.

Errores

$N'_{\alpha }=-aq{\frac {1}{1+\cos {\alpha }}}=-15.30q$

(143)

$e$ $=10.5cm\,\,\,\,\,\,$ $d=44.30cm$ $e_{w}$ $=3.80cm\,\,\,\,\,\,$ $b=20.30cm$ $y_{0}$ $=15.40cm\,\,\,\,\,\,$

(144)

La deformación de membrana del anillo será:

$\Delta _{H_{R}}={\Big (}{\frac {r^{2}}{EA_{R}}}\cos {\alpha }+{\frac {r^{2}y_{0}e}{EI_{R}}}{\Big )}N'_{\alpha }=-41000{\frac {q}{E}}$

$\Delta _{\alpha _{R}}=-{\frac {12r^{2}eN'_{alpha}}{Ebd^{3}}}=199000{\frac {q}{E}}$

Y la deformación de membrana de la cúpula:

$\Delta _{H_{D}}={\frac {a^{2}q}{Eh_{D}}}{\Big (}{\frac {1}{1+\cos {\alpha }}}-\cos {\alpha }{\Big )}\sin {\alpha }=-1270{\frac {q}{E}}$

$\Delta _{\alpha _{D}}=-{\frac {aq}{Eh}}2\sin {\alpha }=250.5{\frac {q}{E}}$

Por lo que la deformación de membrana del conjunto será:

$\Delta _{H}=-42270{\frac {q}{E}}$

$\Delta _{\alpha }=199250{\frac {q}{E}}$

Correcciones (Esfuerzos hiperestáticos)

Aparecen los esfuerzos hiperestáticos (${\textstyle M_{0}}$ y ${\textstyle Q_{0}}$) para intentar restaurar la compatibilidad del sistema (${\textstyle \lambda =21.5}$).

${\begin{array}{ll}\Delta _{\alpha _{D}}(H_{0})={\frac {2\lambda ^{2}\sin {\alpha }}{Eh}}H_{0}=4020{\frac {H_{0}}{E}}&\Delta _{\alpha _{R}}(H_{0})=-{\frac {12r^{2}y_{0}}{Ebd^{3}}}H_{0}=-19100{\frac {H_{0}}{E}}\\\Delta _{H_{D}}(M_{0})={\frac {2\lambda ^{2}\sin {\alpha }}{Eh}}H_{0}=4020{\frac {M_{0}}{E}}&\Delta _{H_{R}}(M_{0})=-{\frac {12r^{2}y_{0}}{Ebd^{3}}}M_{0}=-19100{\frac {M_{0}}{E}}\\\Delta _{H_{D}}(H_{0})={\frac {2a\lambda \sin ^{2}{\alpha }}{Eh}}=2500{\frac {H_{0}}{E}}&\Delta _{H_{R}}(H_{0})={\Big (}1+{\frac {12r^{2}y_{0}}{d^{2}}}{\Big )}{\frac {r^{2}}{Ebd}}=4950{\frac {H_{0}}{E}}\\\Delta _{\alpha _{D}}(H_{0})={\frac {4\lambda ^{3}}{ah}}{\frac {M_{0}}{E}}6=12800{\frac {M_{0}}{E}}&\Delta _{\alpha _{R}}(H_{0})={\frac {12r^{3}}{Ebd^{3}}}M_{0}=124000{\frac {M_{0}}{E}}\\\end{array}}$

(145)

$\Delta _{H}$ $=7450{\frac {H_{0}}{E}}-15100{\frac {M_{0}}{E}}$ $\Delta _{\alpha }$ $=-15100{\frac {H_{0}}{E}}+136800{\frac {M_{0}}{E}}$

(146)

Compatibilidad

$\sum {\Delta _{H}}$ $=0$ $\sum {\Delta _{\alpha }}$ $=0$

(147)

Del sistema obtenemos que ${\textstyle H_{0}=3.47q}$ y ${\textstyle M_{0}=-1.075q}$.

Obtenidos ${\textstyle H_{0}}$ y ${\textstyle M_{0}}$, podemos encontrar los esfuerzos sobre la cúpula hayando los esfuerzos debidos a cada uno de los esfuerzos hiperestáticos y combinándolos con la solución de la teoría de la membrana. El resultado final es el descrito en la tabla siguiente.




${\textstyle \phi }$	$N_{\theta }(M)$	$N_{\theta }(H)$	$N'_{\theta }$	$N_{\theta }$	$M_{\phi }$	$\phi$	$N_{\theta }(M)$	$N_{\theta }(H)$	$N'_{\theta }$	$N_{\theta }$	$M_{\phi }$
0.00	34.87	21.70	-10.13	46.44	-1.08	14.00	0.25	0.06	-13.33	-13.02	-0.01
0.25	28.64	19.67	-10.21	38.10	-0.88	14.25	0.23	0.06	-13.37	-13.07	-0.01
0.50	23.01	17.67	-10.28	30.40	-0.70	14.50	0.21	0.06	-13.40	-13.13	-0.01
0.75	17.97	15.73	-10.36	23.35	-0.55	14.75	0.19	0.06	-13.44	-13.18	-0.01
1.00	13.51	13.87	-10.43	16.95	-0.41	15.00	0.18	0.06	-13.47	-13.24	-0.01
1.25	9.60	12.11	-10.50	11.20	-0.29	15.25	0.16	0.06	-13.51	-13.29	0.00
1.50	6.20	10.45	-10.58	6.08	-0.18	15.50	0.14	0.06	-13.54	-13.35	0.00
1.75	3.28	8.91	-10.65	1.55	-0.09	15.75	0.12	0.05	-13.58	-13.40	0.00
2.00	0.81	7.49	-10.72	-2.41	-0.01	16.00	0.11	0.05	-13.61	-13.45	0.00
2.25	-1.25	6.20	-10.79	-5.84	0.05	16.25	0.09	0.05	-13.64	-13.50	0.00
2.50	-2.94	5.02	-10.86	-8.77	0.10	16.50	0.08	0.04	-13.68	-13.55	0.00
2.75	-4.29	3.97	-10.93	-11.25	0.14	16.75	0.06	0.04	-13.71	-13.60	0.00
3.00	-5.34	3.03	-10.99	-13.30	0.17	17.00	0.05	0.04	-13.74	-13.65	0.00
3.25	-6.13	2.21	-11.06	-14.98	0.20	17.25	0.04	0.03	-13.77	-13.69	0.00
3.50	-6.68	1.49	-11.13	-16.32	0.21	17.50	0.03	0.03	-13.80	-13.73	0.00
3.75	-7.03	0.87	-11.19	-17.36	0.22	17.75	0.03	0.03	-13.82	-13.77	0.00
4.00	-7.21	0.34	-11.26	-18.13	0.23	18.25	0.01	0.02	-13.88	-13.85	0.00
4.25	-7.24	-0.11	-11.32	-18.67	0.23	18.50	0.01	0.02	-13.91	-13.88	0.00
4.50	-7.16	-0.47	-11.39	-19.02	0.23	18.75	0.00	0.01	-13.93	-13.92	0.00
4.75	-6.97	-0.77	-11.45	-19.19	0.22	19.00	0.00	0.01	-13.96	-13.95	0.00
5.00	-6.70	-1.00	-11.51	-19.21	0.21	19.25	-0.01	0.01	-13.98	-13.98	0.00
5.25	-6.37	-1.18	-11.58	-19.12	0.20	19.50	-0.01	0.01	-14.00	-14.00	0.00
5.50	-6.00	-1.30	-11.64	-18.94	0.19	19.75	-0.01	0.01	-14.03	-14.03	0.00
5.75	-5.59	-1.39	-11.70	-18.68	0.18	20.00	-0.01	0.00	-14.05	-14.06	0.00
6.00	-5.16	-1.44	-11.76	-18.36	0.16	20.25	-0.01	0.00	-14.07	-14.08	0.00
6.25	-4.73	-1.45	-11.82	-18.00	0.15	20.50	-0.01	0.00	-14.09	-14.10	0.00
6.50	-4.29	-1.44	-11.88	-17.61	0.13	20.75	-0.01	0.00	-14.11	-14.12	0.00
6.75	-3.86	-1.41	-11.94	-17.21	0.12	21.00	-0.01	0.00	-14.13	-14.15	0.00
7.00	-3.44	-1.37	-11.99	-16.79	0.11	21.25	-0.01	0.00	-14.15	-14.16	0.00
7.25	-3.03	-1.30	-12.05	-16.39	0.09	21.50	-0.01	0.00	-14.17	-14.18	0.00
7.50	-2.65	-1.23	-12.11	-15.99	0.08	21.75	-0.01	0.00	-14.19	-14.20	0.00
7.75	-2.29	-1.15	-12.16	-15.60	0.07	22.00	-0.01	0.00	-14.20	-14.22	0.00
8.00	-1.96	-1.07	-12.22	-15.24	0.06	22.25	-0.01	0.00	-14.22	-14.23	0.00
8.25	-1.65	-0.98	-12.27	-14.90	0.05	22.50	-0.01	0.00	-14.23	-14.25	0.00
8.50	-1.37	-0.89	-12.32	-14.58	0.04	22.75	-0.01	0.00	-14.25	-14.26	0.00
8.75	-1.11	-0.81	-12.38	-14.29	0.03	23.00	-0.01	0.00	-14.26	-14.27	0.00
9.00	-0.88	-0.72	-12.43	-14.03	0.03	23.25	-0.01	0.00	-14.28	-14.29	0.00
9.25	-0.68	-0.64	-12.48	-13.79	0.02	23.50	-0.01	0.00	-14.29	-14.30	0.00
9.50	-0.49	-0.56	-12.53	-13.58	0.01	23.75	-0.01	0.00	-14.30	-14.31	0.00
9.75	-0.34	-0.49	-12.58	-13.40	0.01	24.00	-0.01	0.00	-14.31	-14.32	0.00
10.00	-0.20	-0.42	-12.63	-13.25	0.01	24.25	0.00	0.00	-14.32	-14.33	0.00
10.25	-0.08	-0.35	-12.68	-13.12	0.00	24.50	0.00	0.00	-14.33	-14.34	0.00
10.50	0.01	-0.29	-12.73	-13.01	0.00	24.75	0.00	0.00	-14.34	-14.35	0.00
10.75	0.09	-0.24	-12.77	-12.92	0.00	25.00	0.00	0.00	-14.35	-14.36	0.00
11.00	0.16	-0.19	-12.82	-12.85	-0.01	25.25	0.00	0.00	-14.36	-14.36	0.00
11.25	0.21	-0.15	-12.87	-12.81	-0.01	25.50	0.00	0.00	-14.37	-14.37	0.00
11.50	0.25	-0.11	-12.91	-12.77	-0.01	25.75	0.00	0.00	-14.37	-14.38	0.00
11.75	0.28	-0.08	-12.96	-12.76	-0.01	26.00	0.00	0.00	-14.38	-14.38	0.00
12.00	0.30	-0.05	-13.00	-12.75	-0.01	26.25	0.00	0.00	-14.38	-14.39	0.00
12.25	0.31	-0.03	-13.04	-12.76	-0.01	26.50	0.00	0.00	-14.39	-14.39	0.00
12.50	0.31	0.00	-13.09	-12.78	-0.01	26.75	0.00	0.00	-14.39	-14.39	0.00
12.75	0.31	0.01	-13.13	-12.80	-0.01	27.00	0.00	0.00	-14.39	-14.40	0.00
13.00	0.31	0.03	-13.17	-12.84	-0.01	27.25	0.00	0.00	-14.40	-14.40	0.00
13.25	0.30	0.04	-13.21	-12.88	-0.01	27.50	0.00	0.00	-14.40	-14.40	0.00
13.50	0.28	0.05	-13.25	-12.92	-0.01	27.75	0.00	0.00	-14.40	-14.40	0.00
13.75	0.27	0.05	-13.29	-12.97	-0.01	28.00	0.00	0.00	-14.40	-14.40	0.00

En la gráfica siguiente se observa el comportamiento de la cúpula ante los esfuerzos aplicados.

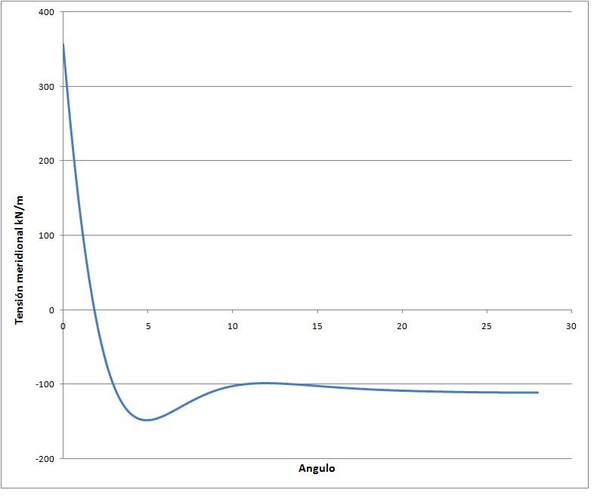
Figura 53: Cúpula conectada al anillo rigidizador.

4.2.2 Comparación con MEF

En el caso de tener que modelizar con elementos finitos estructuras compuestas por elementos de lámina y elementos de biga, no podemos hacerlo mediante elementos de lámina como hemos hecho hasta ahora. En este caso deberiamos analizar el problema con algún programa que permita combinar ambos componentes o utilizar elementos tridimensionales.

En este caso utilizaremos elementos tridimensionales tretaedricos de tamaño 0.30m obteniendo la geometría y el mallado que se muestra a continuación:

Figura 54: Cúpula conectada al anillo rigidizador.

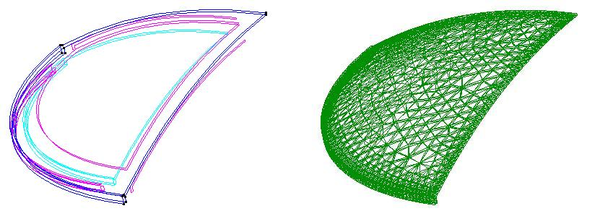
Figura 55: Geometría y mallado del conjunto cúpula-anillo.

Al analizar el problema en tres dimensiones, no podemos extraer momentos, por lo que trabajaremos con la tensión como resultado. Del mismo modo, el programa GiD no permite en 3D exportar gráficas sobre un contorno curvo por lo que tendremos que comparar los resultados puntualmente.

El resultado vertido por el ordenador es el siguiente:

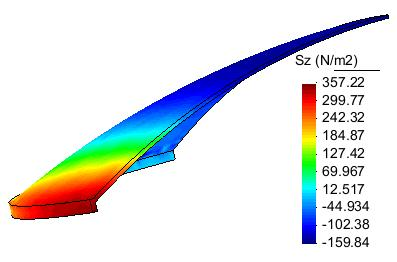
Figura 56: Tensión meridional obtenida con MEF..

Si contrastamos el gráfico anterior con el de la figura 53 podemos ver que los comportamientos de la lámina descritos en ambos resultados son muy parecidos. Asimismo, desde el punto de vista numérico, si comparamos la tensión máxima en la unión cúpula-anillo, podemos comprobar que es exactamente la misma (${\textstyle \sigma =357.2237821N/m2}$ y ${\textstyle \sigma _{MEF}=357.22N/m2}$). De esta manera, podemos concluir una vez más que el método de los elementos finítos nos dará una fiel aproximación a la solución analítica.

4.3 Análisis de cúpula conectada a un muro cilíndrico

En algunos casos, puede ser interesante resistir los empujes de membrana meridionales mediante la construcción de la cúpula conectada directamente al muro cilíndrico. Esto sucederá como veremos para cargas pequeñas, ya que de lo contrario el espesor que necesitaremos de muro será más costoso que instalar un anillo circular.

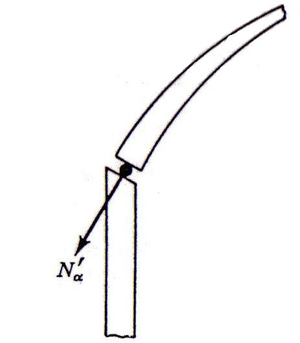
Figura 57: Cúpula conectada a muro circular

Errores

Considerando que la cúpula esta sostenida totalmente sobre el muro, tenemos un esfuerzo radial ${\textstyle N'_{\alpha }}$ que se descompondrá en dos componentes:

$H=N'_{\alpha }\cos {\alpha }$

$V=N'_{\alpha }\sin {\alpha }$

Estas componentes darán lugar a las deformaciones de membrana del muro (${\textstyle \Delta _{H_{W}}}$ y ${\textstyle \Delta _{\phi _{W}}}$). La componente ${\textstyle H}$ producirá la siguiente deformación:

$\Delta _{H_{W}}={\frac {N'_{\alpha }\cos {\alpha }}{2\beta ^{3}D}}$

$\Delta _{\phi _{W}}=-{\frac {N'_{\alpha }\cos {\alpha }}{2\beta ^{2}D}}$

Correcciones (Esfuerzos hiperestáticos)

Como en todos lo ejemplos anteriores tendremos las deformaciones debidas a los esfuerzos hiperestáticos (${\textstyle M_{0}}$ y ${\textstyle Q_{0}}$).

$\Delta _{H}(Q_{0})=\Delta _{H_{W}}(Q_{0})+\Delta _{H_{D}}(Q_{0})$

$\Delta _{H}(M_{0})=\Delta _{H_{W}}(M_{0})+\Delta _{H_{D}}(M_{0})$

$\Delta _{\phi }(Q_{0})=\Delta _{\phi _{W}}(Q_{0})+\Delta _{\phi _{D}}(Q_{0})$

$\Delta _{\phi }(M_{0})=\Delta _{\phi _{W}}(M_{0})+\Delta _{\phi _{D}}(M_{0})$

Compatibilidad

Escribimos otra vez la ecuación de compatibilidad de deformaciones y encontramos los esfuerzos hiperestáticos (${\textstyle M_{0}}$ y ${\textstyle Q_{0}}$).

4.3.1 Ejemplo de aplicación

En este caso, tenemos una varación del espesor del tanque de la base hasta la unión cúpula muro. Bien, una buena aproximación sería coger el espesor de la unión (${\textstyle h_{w}=13cm)}$).

Errores (deformaciones de membrana)

Siendo

$\beta ^{4}={\frac {Eh}{4r^{2}D}}={\frac {3(1-\nu ^{2})}{r^{2}h_{w}^{2}}}=0.9022\rightarrow \beta =0.9746$

y

$D_{w}={\frac {Eh_{w}^{3}}{12(1-\nu ^{2})}}=1.71\cdot {10}^{-4}E$

Obtenemos las deformaciones de membrana:

${\begin{array}{ll}\Delta _{H_{D}}=-1270{\frac {q}{E}}&\Delta _{H_{w}}={\frac {N'_{\alpha }\cos {\alpha }}{2\beta ^{3}D_{W}}}=-42700{\frac {q}{E}}\\\Delta _{\alpha _{D}}=250.5{\frac {q}{E}}&\Delta _{\alpha _{D}}=-{\frac {N'_{\alpha }\cos {\alpha }}{2\beta ^{2}D_{W}}}=41517.28{\frac {q}{E}}\\\end{array}}$

(148)

$\Delta _{H_{0}}$ $=-43990{\frac {q}{E}}$ $\Delta _{\alpha _{0}}$ $=41780{\frac {q}{E}}$

(149)

Correcciones (deformaciones hiperestáticas)

${\begin{array}{ll}\Delta _{\alpha _{D}}(H_{0})={\frac {2\lambda ^{2}\sin {\alpha }}{Eh}}H_{0}=4020{\frac {H_{0}}{E}}&\Delta _{\alpha _{w}}(H_{0})={\frac {-1}{2\beta ^{2}D_{w}}}H_{0}=-3085{\frac {H_{0}}{E}}\\\Delta _{H_{D}}(M_{0})={\frac {2\lambda ^{2}\sin {\alpha }}{Eh}}H_{0}=4020{\frac {M_{0}}{E}}&\Delta _{H_{w}}(M_{0})={\frac {-1}{2\beta ^{2}D_{w}}}M_{0}=-3085{\frac {M_{0}}{E}}\\\Delta _{H_{D}}(H_{0})={\frac {2a\lambda \sin ^{2}{\alpha }}{Eh}}=2500{\frac {H_{0}}{E}}&\Delta _{H_{w}}(H_{0})={\frac {1}{2\beta ^{3}D_{w}}}H_{0}=3165{\frac {H_{0}}{E}}\\\Delta _{\alpha _{D}}(H_{0})={\frac {4\lambda ^{3}}{ah}}{\frac {M_{0}}{E}}6=12800{\frac {M_{0}}{E}}&\Delta _{\alpha _{w}}(H_{0})={\frac {M_{0}}{\beta D_{w}}}=6010{\frac {M_{0}}{E}}\\\end{array}}$

(150)

$\Delta _{H}$ $=5695{\frac {H_{0}}{E}}-935{\frac {M_{0}}{E}}$ $\Delta _{\alpha }$ $=-935{\frac {H_{0}}{E}}+18800{\frac {M_{0}}{E}}$

(151)

Compatibilidad

$\sum {\Delta _{H}}$ $=0$ $\sum {\Delta _{\alpha }}$ $=0$

(152)

Del sistema obtenemos que ${\textstyle H_{0}=8.15q}$ y ${\textstyle M_{0}=-2.62q}$.

Dichos esfuerzos generan los siguientes esfuerzos sobre el muro alrededor del eje y. Hay que aclarar que ${\textstyle y=0}$ corresponde al punto de aplicación de los esfuerzos hiperestáticos, es decir, la unión cúpula-muro.




${\textstyle y}$	$\beta y$	$Ew(y)$	${\frac {d^{2}w(y)}{dy^{2}}}$	$N_{\theta }(y)$	$M_{y}(y)$	$y$	$\beta y$	$Ew(y)$	${\frac {d^{2}w(y)}{dy^{2}}}$	$N_{\theta }(y)$	$M_{y}(y)$
0.00	0.00	-15451.43	2.62	148.79	-2.62	3.40	3.38	570.99	-0.04	-5.50	0.04
0.10	0.10	-14572.79	1.86	140.33	-1.86	3.50	3.48	525.13	-0.02	-5.06	0.02
0.20	0.20	-13591.37	1.20	130.88	-1.20	3.60	3.58	478.02	0.00	-4.60	0.00
0.30	0.30	-12544.84	0.64	120.80	-0.64	3.70	3.68	430.37	0.01	-4.14	-0.01
0.40	0.40	-11460.98	0.17	110.37	-0.17	3.80	3.78	384.45	0.03	-3.70	-0.03
0.50	0.50	-10369.02	-0.22	99.85	0.22	3.90	3.87	338.73	0.04	-3.26	-0.04
0.60	0.60	-9289.01	-0.53	89.45	0.53	4.00	3.97	297.01	0.04	-2.86	-0.04
0.70	0.70	-8235.00	-0.78	79.30	0.78	4.10	4.07	256.93	0.05	-2.47	-0.05
0.80	0.79	-7226.24	-0.97	69.59	0.97	4.20	4.17	217.77	0.05	-2.10	-0.05
0.90	0.89	-6268.42	-1.11	60.36	1.11	4.30	4.27	184.78	0.05	-1.78	-0.05
1.00	0.99	-5372.41	-1.20	51.73	1.20	4.40	4.37	151.17	0.06	-1.46	-0.06
1.10	1.09	-4540.94	-1.26	43.73	1.26	4.50	4.47	122.19	0.05	-1.18	-0.05
1.20	1.19	-3778.16	-1.28	36.38	1.28	4.60	4.57	97.85	0.05	-0.94	-0.05
1.30	1.29	-3086.67	-1.28	29.72	1.28	4.70	4.67	74.33	0.05	-0.72	-0.05
1.40	1.39	-2464.66	-1.25	23.73	1.25	4.80	4.77	53.90	0.05	-0.52	-0.05
1.50	1.49	-1910.29	-1.21	18.40	1.21	4.90	4.87	36.56	0.05	-0.35	-0.05
1.60	1.59	-1420.29	-1.15	13.68	1.15	5.00	4.97	20.76	0.04	-0.20	-0.04
1.70	1.69	-992.81	-1.08	9.56	1.08	5.10	5.07	8.78	0.04	-0.08	-0.04
1.80	1.79	-626.13	-1.01	6.03	1.01	5.20	5.17	-1.65	0.04	0.02	-0.04
1.90	1.89	-313.97	-0.93	3.02	0.93	5.30	5.27	-9.82	0.03	0.09	-0.03
2.00	1.99	-53.14	-0.85	0.51	0.85	5.40	5.36	-15.71	0.03	0.15	-0.03
2.10	2.09	162.63	-0.76	-1.57	0.76	5.50	5.46	-22.33	0.02	0.22	-0.02
2.20	2.19	334.98	-0.68	-3.23	0.68	5.60	5.56	-26.68	0.02	0.26	-0.02
2.30	2.28	473.08	-0.60	-4.56	0.60	5.70	5.66	-28.76	0.02	0.28	-0.02
2.40	2.38	576.32	-0.53	-5.55	0.53	5.80	5.76	-30.12	0.02	0.29	-0.02
2.50	2.48	650.04	-0.46	-6.26	0.46	5.90	5.86	-31.47	0.01	0.30	-0.01
2.60	2.58	700.44	-0.39	-6.74	0.39	6.00	5.96	-30.56	0.01	0.29	-0.01
2.70	2.68	727.50	-0.33	-7.01	0.33	6.10	6.06	-31.91	0.01	0.31	-0.01
2.80	2.78	738.13	-0.27	-7.11	0.27	6.20	6.16	-30.27	0.01	0.29	-0.01
2.90	2.88	733.07	-0.22	-7.06	0.22	6.30	6.26	-28.63	0.00	0.28	0.00
3.00	2.98	714.67	-0.18	-6.88	0.18	6.40	6.36	-26.99	0.00	0.26	0.00
3.10	3.08	688.92	-0.14	-6.63	0.14	6.50	6.46	-24.63	0.00	0.24	0.00
3.20	3.18	654.38	-0.10	-6.30	0.10	6.60	6.56	-24.53	0.00	0.24	0.00
3.30	3.28	613.31	-0.07	-5.91	0.07	6.70	6.66	-22.17	0.00	0.21	0.00

Sobre la cúpula, los esfuerzos hiperestáticos generaran los esfuerzos descritos en la tabla siguiente:




${\textstyle \phi }$	$N_{\theta }(M)$	$N_{\theta }(H)$	$N'_{\theta }$	$N_{\theta }$	$M_{\phi }$	$\phi$	$N_{\theta }(M)$	$N_{\theta }(H)$	$N'_{\theta }$	$N_{\theta }$	$M_{\phi }$
0.00	84.99	52.89	-10.13	127.75	-2.62	14.00	0.61	0.14	-13.33	-12.58	-0.02
0.25	69.79	47.94	-10.21	107.52	-2.16	14.25	0.57	0.15	-13.37	-12.65	-0.02
0.50	56.07	43.07	-10.28	88.86	-1.75	14.50	0.52	0.15	-13.40	-12.73	-0.02
0.75	43.80	38.35	-10.36	71.79	-1.37	14.75	0.47	0.15	-13.44	-12.81	-0.01
1.00	32.93	33.81	-10.43	56.31	-1.04	15.00	0.43	0.15	-13.47	-12.90	-0.01
1.25	23.39	29.51	-10.50	42.40	-0.75	15.25	0.38	0.15	-13.51	-12.98	-0.01
1.50	15.11	25.48	-10.58	30.01	-0.50	15.50	0.34	0.14	-13.54	-13.06	-0.01
1.75	8.00	21.72	-10.65	19.08	-0.28	15.75	0.30	0.13	-13.58	-13.15	-0.01
2.00	1.98	18.26	-10.72	9.53	-0.10	16.00	0.26	0.13	-13.61	-13.23	-0.01
2.25	-3.04	15.10	-10.79	1.27	0.06	16.25	0.22	0.12	-13.64	-13.30	-0.01
2.50	-7.16	12.24	-10.86	-5.77	0.18	16.50	0.19	0.11	-13.68	-13.38	-0.01
2.75	-10.45	9.67	-10.93	-11.71	0.29	16.75	0.16	0.10	-13.71	-13.45	0.00
3.00	-13.02	7.39	-10.99	-16.62	0.37	17.00	0.13	0.09	-13.74	-13.52	0.00
3.25	-14.93	5.38	-11.06	-20.62	0.43	17.25	0.10	0.08	-13.77	-13.58	0.00
3.50	-16.28	3.62	-11.13	-23.79	0.47	17.50	0.08	0.07	-13.80	-13.64	0.00
3.75	-17.14	2.11	-11.19	-26.23	0.50	17.75	0.06	0.06	-13.82	-13.70	0.00
4.00	-17.58	0.82	-11.26	-28.01	0.52	18.25	0.03	0.05	-13.88	-13.80	0.00
4.25	-17.66	-0.26	-11.32	-29.24	0.52	18.50	0.01	0.04	-13.91	-13.85	0.00
4.50	-17.44	-1.15	-11.39	-29.98	0.52	18.75	0.00	0.03	-13.93	-13.89	0.00
4.75	-16.98	-1.87	-11.45	-30.30	0.50	19.00	-0.01	0.03	-13.96	-13.93	0.00
5.00	-16.33	-2.44	-11.51	-30.28	0.49	19.25	-0.01	0.02	-13.98	-13.97	0.00
5.25	-15.53	-2.87	-11.58	-29.97	0.46	19.50	-0.02	0.02	-14.00	-14.01	0.00
5.50	-14.61	-3.18	-11.64	-29.43	0.44	19.75	-0.02	0.01	-14.03	-14.04	0.00
5.75	-13.62	-3.39	-11.70	-28.71	0.41	20.00	-0.03	0.01	-14.05	-14.07	0.00
6.00	-12.58	-3.50	-11.76	-27.84	0.38	20.25	-0.03	0.01	-14.07	-14.09	0.00
6.25	-11.52	-3.54	-11.82	-26.88	0.35	20.50	-0.03	0.00	-14.09	-14.12	0.00
6.50	-10.45	-3.52	-11.88	-25.85	0.32	20.75	-0.03	0.00	-14.11	-14.14	0.00
6.75	-9.40	-3.45	-11.94	-24.78	0.28	21.00	-0.03	0.00	-14.13	-14.16	0.00
7.00	-8.38	-3.33	-11.99	-23.70	0.25	21.25	-0.03	0.00	-14.15	-14.19	0.00
7.25	-7.39	-3.18	-12.05	-22.62	0.22	21.50	-0.03	0.00	-14.17	-14.20	0.00
7.50	-6.46	-3.00	-12.11	-21.57	0.20	21.75	-0.03	0.00	-14.19	-14.22	0.00
7.75	-5.59	-2.81	-12.16	-20.55	0.17	22.00	-0.03	-0.01	-14.20	-14.24	0.00
8.00	-4.77	-2.60	-12.22	-19.59	0.15	22.25	-0.03	-0.01	-14.22	-14.25	0.00
8.25	-4.02	-2.39	-12.27	-18.68	0.12	22.50	-0.03	-0.01	-14.23	-14.27	0.00
8.50	-3.33	-2.18	-12.32	-17.83	0.10	22.75	-0.02	-0.01	-14.25	-14.28	0.00
8.75	-2.70	-1.96	-12.38	-17.04	0.08	23.00	-0.02	-0.01	-14.26	-14.29	0.00
9.00	-2.14	-1.76	-12.43	-16.33	0.07	23.25	-0.02	-0.01	-14.28	-14.30	0.00
9.25	-1.65	-1.56	-12.48	-15.68	0.05	23.50	-0.02	-0.01	-14.29	-14.31	0.00
9.50	-1.21	-1.36	-12.53	-15.10	0.04	23.75	-0.02	-0.01	-14.30	-14.32	0.00
9.75	-0.82	-1.18	-12.58	-14.59	0.03	24.00	-0.01	-0.01	-14.31	-14.33	0.00
10.00	-0.49	-1.02	-12.63	-14.14	0.02	24.25	-0.01	-0.01	-14.32	-14.34	0.00
10.25	-0.21	-0.86	-12.68	-13.75	0.01	24.50	-0.01	-0.01	-14.33	-14.35	0.00
10.50	0.03	-0.72	-12.73	-13.41	0.00	24.75	-0.01	0.00	-14.34	-14.36	0.00
10.75	0.23	-0.59	-12.77	-13.13	-0.01	25.00	-0.01	0.00	-14.35	-14.36	0.00
11.00	0.39	-0.47	-12.82	-12.90	-0.01	25.25	-0.01	0.00	-14.36	-14.37	0.00
11.25	0.51	-0.37	-12.87	-12.72	-0.01	25.50	-0.01	0.00	-14.37	-14.37	0.00
11.50	0.61	-0.27	-12.91	-12.58	-0.02	25.75	0.00	0.00	-14.37	-14.38	0.00
11.75	0.68	-0.19	-12.96	-12.47	-0.02	26.00	0.00	0.00	-14.38	-14.38	0.00
12.00	0.73	-0.12	-13.00	-12.40	-0.02	26.25	0.00	0.00	-14.38	-14.39	0.00
12.25	0.75	-0.06	-13.04	-12.35	-0.02	26.50	0.00	0.00	-14.39	-14.39	0.00
12.50	0.76	-0.01	-13.09	-12.33	-0.02	26.75	0.00	0.00	-14.39	-14.39	0.00
12.75	0.76	0.03	-13.13	-12.34	-0.02	27.00	0.00	0.00	-14.39	-14.40	0.00
13.00	0.74	0.07	-13.17	-12.36	-0.02	27.25	0.00	0.00	-14.40	-14.40	0.00
13.25	0.72	0.09	-13.21	-12.40	-0.02	27.50	0.00	0.00	-14.40	-14.40	0.00
13.50	0.69	0.12	-13.25	-12.45	-0.02	27.75	0.00	0.00	-14.40	-14.40	0.00
13.75	0.65	0.13	-13.29	-12.51	-0.02	28.00	0.00	0.00	-14.40	-14.40	0.00

4.3.2 Comparación con MEF

Como en los anteriores cálculos por elementos finitos, en este también trabajaremos solo con la mitad de la estructura y aplicaremos condiciones de simetría en el corte. Como los dos elementos estructurales estudiados son estructuras de lámina, podremos estudiar el conjunto con elementos finítos de lámina. La malla se construirá apartir de elementos triangulares de un tamaño de 0.3m tal y como se ve en la figura siguiente:

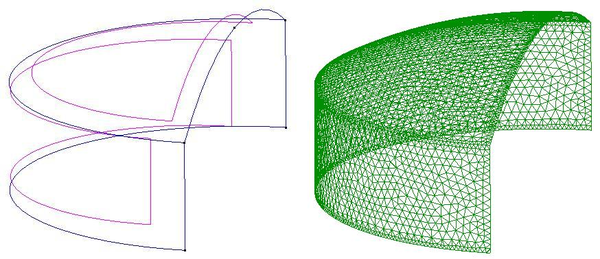
Figura 58: Geometría y mallado del sistema

Una vez generada la malla e impuestas las condiciones de contorno,cargas y materiales utilizados ya podemos arrancar el cálculo de la estructura que durará unos 20 minutos. Analizaremos el resultado obtenido de ${\textstyle M_{y}}$ ya que podremos comparar con facilidad y encontrar el error si lo hubiese.

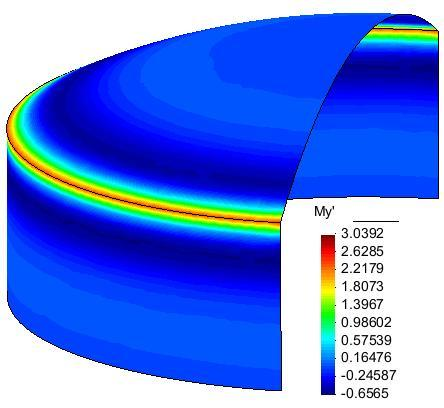
Figura 59: Esfuerzo $M_{y}$ alrededor del eje $y$.

Ahora dibujamos el gráfico obtenido anteriormente de la solución analítica comparandolo con los datos obtenido del MEF:

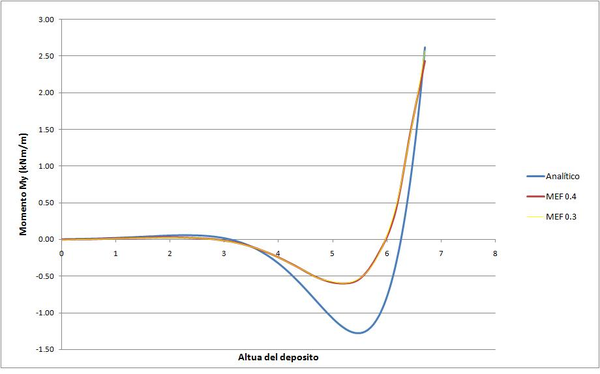
Figura 60: Comparación cálculo analítico vs MEF del esfuerzo $M_{y}$ alrededor de $y$.

En este caso, los dos resultados presentan el mismo comportamiento pero el valor máximo es mayor en el caso del cálculo analítico. En este ejemplo se demuestra que el método de los elementos finítos es una simple aproximación que debe ser contrastada siempre para evitar posibles errores.

4.4 Análisis de cúpula conectada a muro cilíndrico mediante anillo rigidizador

En la mayoría de los casos, no podemos conectar directamente la cúpula al muro, ya que nos obligaría a tener un espesor de muro muy grande, por lo que habitualmente resulta interesante un refuerzo circumferencial en la cabeza del muro. Para estudiar este caso analizaremos directamente el ejemplo utilizado hasta ahora.

Errores(Deformaciones de membrana)

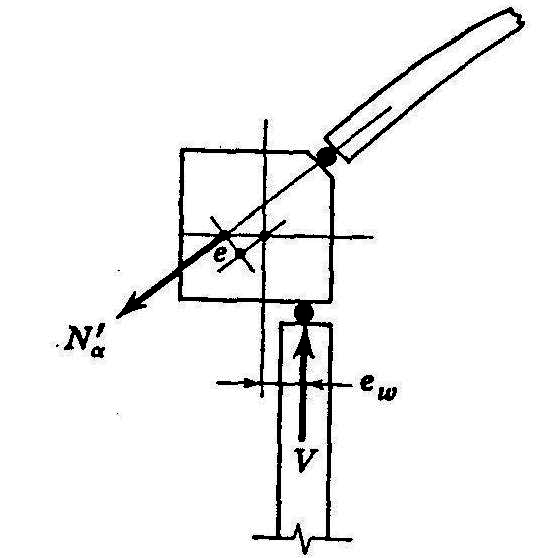
Figura 61: Sistema básico de la etructura

En este caso, tendremos 6 desplazamientos de membrana. En primer lugar, tenemos la deformación de membrana de la cúpula:

$\Delta _{H_{D}}$ $={\frac {aq^{2}}{Eh_{D}}}{\Big (}{\frac {1}{1+\cos {\alpha }}}-\cos {\alpha }{\Big )}\sin {\alpha }=-1270{\frac {q}{E}}$ $\Delta _{\alpha _{D}}$ $=-{\frac {aq}{Eh}}2\sin {\alpha }=250{\frac {q}{E}}$

(153)

Después tendremos la deformación del anillo en su fibra superior. En este caso habrá que añadir un momento adicional derivado de la excentricidad del muro, por lo que ${\textstyle e_{t}=e+e_{w}\sin {\alpha }}$.

$\Delta _{H_{R_{s}}}$ $={\Big (}\cos {\alpha }+{\frac {12y_{0}e_{t}}{d^{2}}}{\Big )}{\frac {r^{2}}{Ebd}}N'_{\alpha }=-63200{\frac {q}{E}}$ $\Delta _{\alpha _{R_{s}}}$ $=-{\frac {12r^{2}e_{t}}{Ebd^{3}}}N'_{\alpha }=232800{\frac {q}{E}}$

(154)

Finalmente tenemos la deformacion de la fibra inferior del anillo derivada del esfuerzo de membrana ${\textstyle N'_{\alpha }}$.

$\Delta _{H_{R_{i}}}$ $={\Big (}-\cos {\alpha }+{\frac {6e_{t}}{d}}{\Big )}{\frac {r^{2}}{Ebd}}N'_{\alpha }=-24200{\frac {q}{E}}$ $\Delta _{\alpha _{R_{i}}}$ $={\frac {12r^{2}e_{t}}{Ebd^{3}}}N'_{\alpha }=-232800{\frac {q}{E}}$

(155)

De esta manera, las deformaciones de membrana serán:

$\Delta _{H_{0s}}$ $=-64470{\frac {q}{E}}$ $\Delta _{\alpha _{0s}}$ $=233050{\frac {q}{E}}$ $\Delta _{H_{0i}}$ $=-24200{\frac {q}{E}}$ $\Delta _{\alpha _{0i}}$ $=-232800{\frac {q}{E}}$

(156)

Correcciones (Esfuerzos hiperestáticos)

En este caso tendremos dos pares de esfuerzos hiperestáticos (${\textstyle H_{0s}}$, ${\textstyle M_{0s}}$, ${\textstyle H_{0i}}$ y ${\textstyle M_{0i}}$), uno para cada unión.

En primer lugar estudiaremos el desplazamiento en la unión cúpula-anillo (superior):

$\Delta _{H_{s}}(H_{0s})_{D}$ $={\frac {2a\lambda \sin ^{2}{\alpha }}{Eh}}H_{0s}=2500{\frac {H_{0s}}{E}}$ $\Delta _{H_{s}}(M_{0s})_{D}$ $={\frac {2\lambda ^{2}\sin {\alpha }}{Eh}}M_{0s}=4020{\frac {M_{0s}}{E}}$ $\Delta _{H_{s}}(H_{0s})_{R}$ $={\Big (}1+{\frac {12y_{0}^{2}}{d^{2}}}{\Big )}{\frac {r^{2}}{Ebd}}H_{0s}=4970{\frac {H_{0s}}{E}}$ $\Delta _{H_{s}}(M_{0s})_{R}$ $=-{\frac {12r^{2}y_{0}}{Ebd^{3}}}M_{0s}=-19000{\frac {M_{0s}}{E}}$ $\Delta _{H_{s}}(H_{0i})_{R}$ $=-{\Big (}1-{\frac {6y_{0}}{d}}{\Big )}{\frac {r^{2}}{Ebd}}H_{0i}=2200{\frac {H_{0i}}{E}}$ $\Delta _{H_{s}}(M_{0i})_{R}$ $={\frac {12r^{2}y_{0}}{Ebd^{3}}}M_{0i}=19000{\frac {M_{0i}}{E}}$

(157)

$\Delta _{H_{s}}=7470{\frac {H_{0s}}{E}}-14980{\frac {M_{0s}}{E}}+2200{\frac {H_{0i}}{E}}+19000{\frac {M_{0i}}{E}}$

Ahora analizaremos el giro en el mismo punto:

$\Delta _{\alpha _{s}}(H_{0s})_{D}$ $={\frac {2\lambda ^{2}\sin {\alpha }}{Eh}}H_{0s}=4020{\frac {H_{0s}}{E}}$ $\Delta _{\alpha _{s}}(M_{0s})_{D}$ $={\frac {4\lambda ^{3}}{ahE}}M_{0s}=12800{\frac {M_{0s}}{E}}$ $\Delta _{\alpha _{s}}(H_{0s})_{R}$ $=-{\frac {12r^{2}y_{0}}{Ebd^{3}}}H_{0s}=-19000{\frac {H_{0s}}{E}}$ $\Delta _{\alpha _{s}}(M_{0s})_{R}$ $={\frac {12r^{2}}{Ebd^{3}}}M_{0s}=123900{\frac {M_{0s}}{E}}$ $\Delta _{\alpha _{s}}(H_{0i})_{R}$ $={\frac {-6r^{2}}{bd^{2}E}}H_{0i}=-27400{\frac {H_{0i}}{E}}$ $\Delta _{\alpha _{s}}(M_{0i})_{R}$ $=-{\frac {12r^{2}}{Ebd^{3}}}M_{0i}=-123900{\frac {M_{0i}}{E}}$

(158)

$\Delta _{\alpha _{s}}=-14980{\frac {H_{0s}}{E}}+136700{\frac {M_{0s}}{E}}-27400{\frac {H_{0i}}{E}}-123900{\frac {M_{0i}}{E}}$

Una vez analizada la junta cúpula-anillo, podemos analizar el desplazamiento en la junta anillo-muro:

$\Delta _{H_{i}}(H_{0i})_{W}$ $={\frac {1}{2\beta ^{3}D_{W}}}H_{0i}=3160{\frac {H_{0i}}{E}}$ $\Delta _{H_{i}}(M_{0i})_{W}$ $={\frac {-1}{2\beta ^{2}D_{W}}}M_{0i}=-3080{\frac {M_{0i}}{E}}$ $\Delta _{H_{i}}(H_{0i})_{R}$ $={\frac {4r^{2}}{Ebd}}H_{0i}=8100{\frac {H_{0i}}{E}}$ $\Delta _{H_{i}}(M_{0i})_{R}$ $={\frac {6r^{2}}{Ebd^{2}}}M_{0i}=27400{\frac {M_{0i}}{E}}$ $\Delta _{H_{i}}(H_{0s})_{R}$ $=-{\Big (}1-{\frac {6y_{0}}{d}}{\Big )}{\frac {r^{2}}{Ebd}}H_{0s}=2200{\frac {H_{0s}}{E}}$ $\Delta _{H_{i}}(M_{0s})_{R}$ $=-{\frac {6r^{2}}{Ebd^{2}}}M_{0s}=-27400{\frac {M_{0s}}{E}}$

(159)

$\Delta _{H_{i}}=2200{\frac {H_{0s}}{E}}-27400{\frac {M_{0s}}{E}}+11260{\frac {H_{0i}}{E}}+24320{\frac {M_{0i}}{E}}$

Finalmente, solo faltará encontrar el giro en la fibra inferior del anillo (anillo-muro):

$\Delta _{\alpha _{i}}(H_{0i})_{W}$ $=-{\frac {-1}{2\beta ^{2}D_{W}}}H_{0i}=-3080{\frac {H_{0i}}{E}}$ $\Delta _{\alpha _{i}}(M_{0i})_{W}$ $=-{\frac {1}{\beta D_{W}}}M_{0i}=6010{\frac {M_{0i}}{E}}$ $\Delta _{\alpha _{i}}(H_{0i})_{R}$ $={\frac {6r^{2}}{Ebd^{2}}}H_{0i}=27400{\frac {H_{0i}}{E}}$ $\Delta _{\alpha _{i}}(M_{0i})_{R}$ $={\frac {12r^{2}}{Ebd^{3}}}M_{0i}=123900{\frac {M_{0i}}{E}}$ $\Delta _{\alpha _{i}}(H_{0s})_{R}$ $={\frac {12r^{2}y_{0}}{Ebd^{3}}}H_{0s}=19000{\frac {H_{0s}}{E}}$ $\Delta _{\alpha _{i}}(M_{0s})_{R}$ $=-{\frac {12r^{2}}{Ebd^{3}}}M_{0s}=-123900{\frac {M_{0s}}{E}}$

(160)

$\Delta _{\alpha _{i}}=19000{\frac {H_{0s}}{E}}-123900{\frac {M_{0s}}{E}}+24320{\frac {H_{0i}}{E}}+129900{\frac {M_{0i}}{E}}$

Compatibilidad

En este caso, tendremos que imponer 4 condiciones de compatibilidad de deformaciones:

$\sum {\Delta _{H_{s}}}$ $=0$ $\sum {\Delta _{\alpha _{s}}}$ $=0$ $\sum {\Delta _{H_{i}}}$ $=0$ $\sum {\Delta _{\alpha _{i}}}$ $=0$

(161)

De esta manera obtenemos un sistema de 4 ecuaciones con 4 incógnitas, que podemos resolver con facilidad para obtener los esfuerzos hiperestáticos:

$H_{0s}=+7.25q\,\,\,\,\,\,M_{0s}=-2.50q$

$H_{0i}=-2.98q\,\,\,\,\,\,M_{0i}=-1.10q$

Dichos esfuerzos generan en el depósito los siguientes esfuerzos alrededor del eje y. Es necesario aclarar que ${\textstyle y=0}$ corresponde al punto de aplicación de los esfuerzos hiperestáticos, es decir, la unión muro-anillo.




${\textstyle y}$	$\beta y$	$Ew(y)$	${\frac {d^{2}w(y)}{dy^{2}}}$	$N_{\theta }(y)$	$M_{y}(y)$	$y$	$\beta y$	$Ew(y)$	${\frac {d^{2}w(y)}{dy^{2}}}$	$N_{\theta }(y)$	$M_{y}(y)$
0.00	0.00	-5256.75	1.10	50.62	-1.10	3.40	3.38	198.88	-0.07	-1.92	0.07
0.10	0.10	-5009.68	0.82	48.24	-0.82	3.50	3.48	184.54	-0.07	-1.78	0.07
0.20	0.20	-4717.35	0.58	45.43	-0.58	3.60	3.58	169.44	-0.08	-1.63	0.08
0.30	0.30	-4393.76	0.37	42.31	-0.37	3.70	3.68	153.86	-0.08	-1.48	0.08
0.40	0.40	-4049.33	0.19	38.99	-0.19	3.80	3.78	138.65	-0.08	-1.34	0.08
0.50	0.50	-3695.09	0.04	35.58	-0.04	3.90	3.87	123.26	-0.07	-1.19	0.07
0.60	0.60	-3338.86	-0.09	32.15	0.09	4.00	3.97	109.07	-0.07	-1.05	0.07
0.70	0.70	-2986.17	-0.19	28.76	0.19	4.10	4.07	95.32	-0.07	-0.92	0.07
0.80	0.79	-2644.59	-0.26	25.47	0.26	4.20	4.17	81.71	-0.06	-0.79	0.06
0.90	0.89	-2316.65	-0.32	22.31	0.32	4.30	4.27	70.20	-0.06	-0.68	0.06
1.00	0.99	-2006.91	-0.37	19.33	0.37	4.40	4.37	58.30	-0.05	-0.56	0.05
1.10	1.09	-1716.76	-0.40	16.53	0.40	4.50	4.47	47.98	-0.05	-0.46	0.05
1.20	1.19	-1448.19	-0.41	13.95	0.41	4.60	4.57	39.24	-0.04	-0.38	0.04
1.30	1.29	-1202.66	-0.42	11.58	0.42	4.70	4.67	30.72	-0.04	-0.30	0.04
1.40	1.39	-979.90	-0.42	9.44	0.42	4.80	4.77	23.24	-0.03	-0.22	0.03
1.50	1.49	-779.64	-0.41	7.51	0.41	4.90	4.87	16.83	-0.03	-0.16	0.03
1.60	1.59	-600.98	-0.39	5.79	0.39	5.00	4.97	10.93	-0.03	-0.11	0.03
1.70	1.69	-443.65	-0.37	4.27	0.37	5.10	5.07	6.39	-0.02	-0.06	0.02
1.80	1.79	-307.30	-0.35	2.96	0.35	5.20	5.17	2.38	-0.02	-0.02	0.02
1.90	1.89	-189.90	-0.33	1.83	0.33	5.30	5.27	-0.80	-0.02	0.01	0.02
2.00	1.99	-90.48	-0.30	0.87	0.30	5.40	5.36	-3.15	-0.01	0.03	0.01
2.10	2.09	-7.03	-0.27	0.07	0.27	5.50	5.46	-5.81	-0.01	0.06	0.01
2.20	2.19	60.90	-0.25	-0.59	0.25	5.60	5.56	-7.63	-0.01	0.07	0.01
2.30	2.28	116.55	-0.22	-1.12	0.22	5.70	5.66	-8.63	-0.01	0.08	0.01
2.40	2.38	159.52	-0.19	-1.54	0.19	5.80	5.76	-9.32	0.00	0.09	0.00
2.50	2.48	191.71	-0.17	-1.85	0.17	5.90	5.86	-10.01	0.00	0.10	0.00
2.60	2.58	215.20	-0.15	-2.07	0.15	6.00	5.96	-9.88	0.00	0.10	0.00
2.70	2.68	230.01	-0.12	-2.21	0.12	6.10	6.06	-10.57	0.00	0.10	0.00
2.80	2.78	238.53	-0.11	-2.30	0.11	6.20	6.16	-10.13	0.00	0.10	0.00
2.90	2.88	241.08	-0.09	-2.32	0.09	6.30	6.26	-9.68	0.00	0.09	0.00
3.00	2.98	238.40	-0.07	-2.30	0.07	6.40	6.36	-9.24	0.00	0.09	0.00
3.10	3.08	232.76	-0.06	-2.24	0.06	6.50	6.46	-8.49	0.00	0.08	0.00
3.20	3.18	223.55	-0.04	-2.15	0.04	6.60	6.56	-8.58	0.00	0.08	0.00
3.30	3.28	211.60	-0.03	-2.04	0.03	6.70	6.66	-7.83	0.00	0.08	0.00

Por lo que hace al esfuerzo ${\textstyle N_{\theta }}$, deberemos encontrar el esfuerzo debido a cada uno de los esfuerzos hiperestáticos y combinarlo con la solución de la teoría de la membrana. El resultado final es el descrito en la tabla siguiente.




${\textstyle \phi }$	$N_{\theta }(M)$	$N_{\theta }(H)$	$N'_{\theta }$	$N_{\theta }$	$M_{\phi }$	$\phi$	$N_{\theta }(M)$	$N_{\theta }(H)$	$N'_{\theta }$	$N_{\theta }$	$M_{\phi }$
0.00	81.10	50.47	-10.13	121.43	-2.50	14.00	0.58	0.14	-13.33	-12.61	-0.02
0.25	66.59	45.75	-10.21	102.13	-2.09	14.25	0.54	0.14	-13.37	-12.68	-0.01
0.50	53.50	41.10	-10.28	84.32	-1.72	14.50	0.50	0.15	-13.40	-12.76	-0.01
0.75	41.80	36.59	-10.36	68.03	-1.38	14.75	0.45	0.15	-13.44	-12.84	-0.01
1.00	31.42	32.26	-10.43	53.26	-1.08	15.00	0.41	0.14	-13.47	-12.92	-0.01
1.25	22.32	28.16	-10.50	39.98	-0.81	15.25	0.37	0.14	-13.51	-13.00	-0.01
1.50	14.42	24.31	-10.58	28.15	-0.58	15.50	0.32	0.13	-13.54	-13.09	-0.01
1.75	7.63	20.73	-10.65	17.72	-0.37	15.75	0.28	0.13	-13.58	-13.17	-0.01
2.00	1.89	17.43	-10.72	8.60	-0.20	16.00	0.25	0.12	-13.61	-13.24	-0.01
2.25	-2.90	14.41	-10.79	0.72	-0.05	16.25	0.21	0.11	-13.64	-13.32	-0.01
2.50	-6.83	11.68	-10.86	-6.01	0.07	16.50	0.18	0.10	-13.68	-13.39	-0.01
2.75	-9.97	9.23	-10.93	-11.67	0.17	16.75	0.15	0.09	-13.71	-13.46	0.00
3.00	-12.42	7.05	-10.99	-16.37	0.25	17.00	0.12	0.09	-13.74	-13.53	0.00
3.25	-14.25	5.13	-11.06	-20.18	0.32	17.25	0.10	0.08	-13.77	-13.59	0.00
3.50	-15.54	3.46	-11.13	-23.21	0.36	17.50	0.08	0.07	-13.80	-13.65	0.00
3.75	-16.36	2.01	-11.19	-25.54	0.40	17.75	0.06	0.06	-13.82	-13.71	0.00
4.00	-16.77	0.78	-11.26	-27.25	0.42	18.25	0.03	0.05	-13.88	-13.81	0.00
4.25	-16.85	-0.25	-11.32	-28.42	0.43	18.50	0.01	0.04	-13.91	-13.85	0.00
4.50	-16.64	-1.10	-11.39	-29.13	0.43	18.75	0.00	0.03	-13.93	-13.90	0.00
4.75	-16.20	-1.78	-11.45	-29.44	0.43	19.00	-0.01	0.03	-13.96	-13.94	0.00
5.00	-15.58	-2.32	-11.51	-29.42	0.42	19.25	-0.01	0.02	-13.98	-13.97	0.00
5.25	-14.82	-2.74	-11.58	-29.13	0.40	19.50	-0.02	0.02	-14.00	-14.01	0.00
5.50	-13.94	-3.03	-11.64	-28.61	0.38	19.75	-0.02	0.01	-14.03	-14.04	0.00
5.75	-13.00	-3.23	-11.70	-27.93	0.36	20.00	-0.03	0.01	-14.05	-14.07	0.00
6.00	-12.00	-3.34	-11.76	-27.11	0.33	20.25	-0.03	0.01	-14.07	-14.09	0.00
6.25	-10.99	-3.38	-11.82	-26.19	0.31	20.50	-0.03	0.00	-14.09	-14.12	0.00
6.50	-9.97	-3.36	-11.88	-25.21	0.28	20.75	-0.03	0.00	-14.11	-14.14	0.00
6.75	-8.97	-3.29	-11.94	-24.19	0.26	21.00	-0.03	0.00	-14.13	-14.16	0.00
7.00	-7.99	-3.18	-11.99	-23.16	0.23	21.25	-0.03	0.00	-14.15	-14.18	0.00
7.25	-7.06	-3.03	-12.05	-22.14	0.21	21.50	-0.03	0.00	-14.17	-14.20	0.00
7.50	-6.17	-2.86	-12.11	-21.14	0.18	21.75	-0.03	0.00	-14.19	-14.22	0.00
7.75	-5.33	-2.68	-12.16	-20.17	0.16	22.00	-0.03	-0.01	-14.20	-14.24	0.00
8.00	-4.55	-2.48	-12.22	-19.25	0.14	22.25	-0.03	-0.01	-14.22	-14.25	0.00
8.25	-3.83	-2.28	-12.27	-18.38	0.12	22.50	-0.02	-0.01	-14.23	-14.26	0.00
8.50	-3.18	-2.08	-12.32	-17.58	0.10	22.75	-0.02	-0.01	-14.25	-14.28	0.00
8.75	-2.58	-1.87	-12.38	-16.83	0.08	23.00	-0.02	-0.01	-14.26	-14.29	0.00
9.00	-2.05	-1.68	-12.43	-16.15	0.07	23.25	-0.02	-0.01	-14.28	-14.30	0.00
9.25	-1.57	-1.48	-12.48	-15.53	0.05	23.50	-0.02	-0.01	-14.29	-14.31	0.00
9.50	-1.15	-1.30	-12.53	-14.98	0.04	23.75	-0.01	-0.01	-14.30	-14.32	0.00
9.75	-0.78	-1.13	-12.58	-14.49	0.03	24.00	-0.01	-0.01	-14.31	-14.33	0.00
10.00	-0.47	-0.97	-12.63	-14.07	0.02	24.25	-0.01	-0.01	-14.32	-14.34	0.00
10.25	-0.20	-0.82	-12.68	-13.70	0.01	24.50	-0.01	0.00	-14.33	-14.35	0.00
10.50	0.03	-0.68	-12.73	-13.38	0.01	24.75	-0.01	0.00	-14.34	-14.36	0.00
10.75	0.22	-0.56	-12.77	-13.12	0.00	25.00	-0.01	0.00	-14.35	-14.36	0.00
11.00	0.37	-0.45	-12.82	-12.90	-0.01	25.25	-0.01	0.00	-14.36	-14.37	0.00
11.25	0.49	-0.35	-12.87	-12.73	-0.01	25.50	0.00	0.00	-14.37	-14.37	0.00
11.50	0.58	-0.26	-12.91	-12.59	-0.01	25.75	0.00	0.00	-14.37	-14.38	0.00
11.75	0.65	-0.18	-12.96	-12.49	-0.01	26.00	0.00	0.00	-14.38	-14.38	0.00
12.00	0.69	-0.12	-13.00	-12.42	-0.02	26.25	0.00	0.00	-14.38	-14.39	0.00
12.25	0.72	-0.06	-13.04	-12.38	-0.02	26.50	0.00	0.00	-14.39	-14.39	0.00
12.50	0.73	-0.01	-13.09	-12.37	-0.02	26.75	0.00	0.00	-14.39	-14.39	0.00
12.75	0.72	0.03	-13.13	-12.37	-0.02	27.00	0.00	0.00	-14.39	-14.40	0.00
13.00	0.71	0.06	-13.17	-12.40	-0.02	27.25	0.00	0.00	-14.40	-14.40	0.00
13.25	0.69	0.09	-13.21	-12.43	-0.02	27.50	0.00	0.00	-14.40	-14.40	0.00
13.50	0.66	0.11	-13.25	-12.48	-0.02	27.75	0.00	0.00	-14.40	-14.40	0.00
13.75	0.62	0.13	-13.29	-12.54	-0.02	28.00	0.00	0.00	-14.40	-14.40	0.00

4.4.1 Comparación con MEF

En este caso, como en el ejemplo de la cúpula conectada al anillo, estamos mezclando elementos de lámina con elementos de biga por lo que analizaremos el problema mediante una modelización en tres dimensiones con elementos tretaédricos. La malla utilizada que se muestra a continuación es de un tamaño de 0.10m. Como se puede observar, hemos trabajado con un cuarto de la estructura con el fin de reducir al máximo el tiempo de cálculo, lo que nos permitirá refinar en gran medida la malla. Así pues al introducir los datos debemos insertar las condiciones de simetría en los cortes.

Figura 62: Cúpula conectada a muro cilíndrico mediante anillo rigidizador.

Figura 63: Geometría y mallado del sistema estructural.

Una vez introducidas las condiciones de contorno, la carga sobre la cúpula y definido el material, arrancamos el cálculo que para la maya descrita durará aproximadamente unos 30 minutos. Como trabajamos en 3D deberemos analizar las tensiones meridionales.

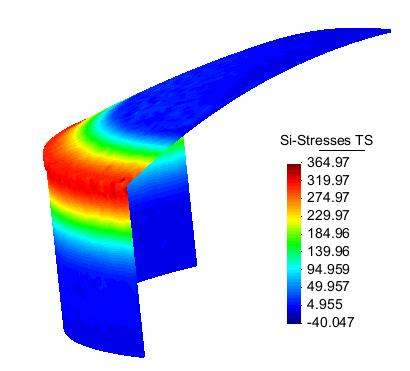
Figura 64: Tensiones meridionales a lo largo de la lámina.

Como se puede observar en el gráfico siguiente, no conseguimos que la solución por el MEF converja y por lo tanto no podemos decir que la solución vertida por el ordenador sea correcta. Este es uno de los problemas importantes que presenta el método de los elementos finitos, no podemos tomar cualquier solución que nos de el problema como buena porque puede suceder que el procedimiento numérico no haya concluido.

Aún así, podemos decir que el cálculo computacional responde al comportamiento determinado por el cálculo analítico y a medida que refinamos la malla se acerca más a este; por lo que podemos decir que si el ordenador nos lo permitiera, la solución convergente volvería a ser una aproximación fiel del comportamiento de la teoría estudiada en este texto.

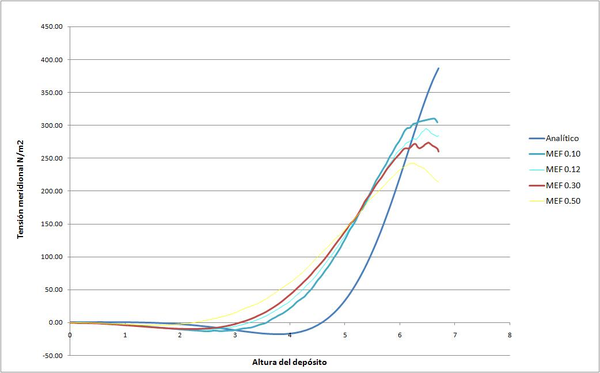
Figura 65: Comparación cálculo analítico vs MEF de la tensión meridional.

4.5 Peretensado del anillo rigidizador

Como hemos podido comprobar, al conectar el anillo a la cúpula este se ve altamente traccionado por lo que resulta de un gran interes pretensarlo.

El análisis de esta fuerza, sigue la misma linea que los estudiados hast ahora y resulta mu sencillo.

Errores

La única fuerza del sistema (${\textstyle F}$, fuerza del pretensado), tendrá su componente horizontal sobre el anillo:

$H_{F}={\frac {F}{r+b}}$

Dicha componente generará las siguientes deformaciones, teniendo en cuenta que ${\textstyle e_{f}}$ es la excentricidad de la fuerza del pretensado con respecto al cetro de gravedad.

$\Delta _{H}={\Big (}{\frac {1}{A_{R}}}+{\frac {y_{0}e_{F}}{I_{R}}}{\Big )}{\frac {r^{2}}{E}}H_{F}$

$\Delta _{\alpha }=-{\frac {r^{2}e_{F}}{EI_{R}}}H_{F}$

Normalmente no se suele aplicar ninguna excentricidad al pretensado, pero para un cálculo preciso, tendríamos que considerar una excentricidad accidental.

Correcciones(Esfuerzos hiperestáticos) y Compatibilidad

Igual que en el análisis cúpula-anillo, obtenemos las deformaciones debidas a los esfuerzos hiperestátcos (${\textstyle H_{0}}$ y ${\textstyle M_{0}}$) e imponemos compatibilidad de desplazamientos en la junta. Hay que tener cuidado con el uso del pretensado ya que en el caso de tener un anillo muy flexible, la fuerza del pretensado puede llegar a causar compresiones adicionales en el borde de la cúpula. En el caso de anillo rígido, la mayor parte de la fuerza del pretensado la recibe el anillo.

Agradecimientos

No quisiera terminar este texto sin agradecer de forma breve la ayuda que me han procurado las personas que he tenido cerca durante estos últimos tres años y que me han ayudado en el duro camino de estos años de carrera y sobretodo en la redacción de este trabajo.

En primer lugar, me gustaría agradecer a mi familia el apoyo y la confianza que desde el primer día me ha brindado. En segundo lugar, quisiera dar las gracias a mi pareja Verónica por apoyarme durante estos tres años y echarme una mano en los momentos difíciles y siempre que lo he necesitado. Sin ninguna duda, este camino no hubiese sido tan fácil de no ser por mi pareja y mi familia.

Finalmente, quiero dar las gracias a los profesores Eugenio Oñate y Francisco Zarate por darme la primera idea para arrancar este trabajo y por los consejos que me ha dado durante la elaboración de este estudio.

A todos ellos, muchas gracias.

Marc Tort Baños

BIBLIOGRAFÍA

[1] David P. Billington. Thin shel concrete structures. McGraw-Hill. USA 1965.
[2] S. Timoshenko y S. Woinowsky-Krieger Teoría de placas y láminas. URMO, S.A. de Ediciones Nueva York 1959.
[3] Juan Cerdó Pons. Cálculo simplificado de láminas cilíndricas. Colección Seinor nº10. Madrid, 1991.
[4] José Ángel Jurado y Santiago Hernández. Análisis Estructural de placas y láminas. Tórulco Edicións. La Coruña, 2002.
[5] Eduardo Torroja Miret. Razón y Ser de los tipos estructurales. CSIC. Madrid, 1991.

[6] Eugenio Oñate. Cálculo de Estructuras por el Método de Elementos Finitos. Análisis estático lineal. CIMNE. Barcelona, 1995.