Computational fluid dynamics indicators to improve cardiovascular pathologies diagnosis

Dedicated to my father...

Acknowledgments

First I would like to deeply thank Anne-Beatrice, Victoria and Anna for their patience, encouragement and support throughout my PhD. I would like also to express my gratitude to my parents, Ibrahim and Ana, my brother and sister, Yusef and Sara for their constant moral support. From the start, you always trust in me. Muchas gracias por apoyarme, comprenderme y animarme durante todos estos años fuera de casa.

I would like also to express my sincere gratitude to my supervisor, Prof.Eugenio Oñate for giving me the opportunity to join the International Center for Numerical Methods in Engineering (CIMNE) and work under his supervision. He has strongly supported my work with deep enthusiasm and worthy ideas. His aptitude to go straight to the point together with his talent in studying and solving problems have made a crucial contribution to the outcome of this work. I wish also to thank Prof.Miguel Cervera and Prof.Raimon Jané for their continuous interest, support and guidance during this monograph.

I would like to warmly thank all of the former and present members of CIMNE who made the work place a friendly environment and who are now, more friends than colleagues: to Jorge S.Pérez with whom we had a great collaboration and interesting technical, for his continuous support in my research (Jorge, eres un crack y lo sabes); to Carlos Labra, Enrique Ortega, Ariel Eijo, Temo, Giovana Gavidia, Ilaria and Maurizio Bordone with whom I shared the office during years for his endless good mood, kindness and all of the discussions we had; to Riccardo Rossi, Pooyan Dadvand, Carlos Roig and Jordi Cotela for their support in the integration of the 1D implementation and reduced model into KRATOS and for their kindness and all of the interesting technical discussions we had; to Joaquin (Cartagena) for his endless confidence, friendship and 'salad-shared'; Adrian Silisque, Elke Pahl and Steffen Mohr who made Barcelona a place to enjoy; to GID Department for always being so nice, ready to help and supportive; to Miguel Angel y Lucia for your really good mood, to Alberto for listen and support me during his stage at Barcelona, you showed me a new way of living and Joaquin Arteaga, thanks to you I am writing this. Further thanks to all of the people who work at CIMNE. It was great working with you all. Thank you for your work and your motivation.

Sincere thanks to CIMNE-TIC department: Jordi Jimenez who is always positive and always enthusiastic and motivated by new projects, to Sergio Valero, maestro Sensei, maestro programador, Angel Priegue (Alias Cruchi) 'tranquilo Edu no pasa nada', Cruchi thanks for your patience and thank for the 'Cafe-relaxing time in plaza mayor' on Friday evening, Aleki who always bring a great atmosphere to the office; Claudio Zinggerling for your professionalism and all of the discussions we had on different subjects and his friendly support; Andy for his friendliness; Pedro for his vitality, Francesc Campá for his good mood and friendship and Alberto Tena for his kindness,...por cierto, la undécima ESTA DADA!!!

Many great collaborations in the clinical setting were possible during the project. To those who contributed, thank you. Special thanks go to Dr.Francesc Carreras, Dr.Pedro Hion-Li at the Hospital Sant Pau i Creu Blanca, Dr.Xavier Alomar at Clinica Creu Blanca and Jean-Paul Aben at Pie Medical Imaging, all of whom gave me the chance to discover the clinical environment and freely shared with me their inestimable knowledge.

Last, but not least, my gratitude also goes to Administration and Project Management departments, Anna, Cecilia, Maëlle, Merce, Sandra, Irene, Marí Carmen, Francisco, Cristina, among others, for your help in making easy the administrative processes.

Further thanks to all of co-authors have contributed to the achievement of this monograph, thank you very much. This work would not be possible without your support.

Most of all, I would like to warmly thank all the friends from Palencia and Valladolid. You always have been there.

Presentation

The studies included in the monograph belong to the same research line, leading to three papers already published in international journals.

Paper 1.

Title: A Reduced Order Model based on Coupled 1D/3D Finite Element Simulations for an Efficient Analysis of Hemodynamics Problems.
Authors: E.Soudah, R.Rossi, S.Idelsohn, E.Oñate
Journal: Journal of Computational Mechanics. (2014) 54:1013-1022.
DOI: 10.1007/s00466-014-1040-2

Paper 2.

Title: CFD Modelling of Abdominal Aortic Aneurysm on Hemodynamic Loads using a Realistic Geometry with CT.

Authors: E.Soudah, E.Y.K. Ng, T.H Loong, M.Bordone, P. Uei and N.Sriram.

Journal: Computational and Mathematical Methods in Medicine. Volume 2013 - 472564, 01/06/2013.

DOI: 10.1155/2013/472564

Paper 3.

Title: Mechanical stress in abdominal aortic aneurysms using artificial neural networks.

Authors: Eduardo Soudah, José F. Rodríguez, Roberto López

Journal of Mechanics in Medicine and Biology. Vol. 15, No. 3 (2015) 1550029

DOI: 10.1142/S0219519415500293

Articles are reprinted with permission, and have been reformatted to fit the layout of the Monogrpah.

Abstract

In recent years, the study of computational hemodynamics within anatomically complex vascular regions has generated great interest among clinicians. The progress in computational fluid dynamics, image processing and high-performance computing have allowed us to identify the candidate vascular regions for the appearance of cardiovascular diseases and to predict how this disease may evolve. In this monograph we attempt to introduce into medicine the computational predictive paradigm that has been used in engineering for many years. Several groups have tried to create predictive models for cardiovascular pathologies, but they have not yet begun to use them in clinical practice. Our final aim is to go further and obtain predictive variables to be used in the clinical field.

We try to predict the evolution of aortic abdominal aneurysm, aortic coarctation and coronary artery disease in a personalized way for each patient. We propose diagnostic indicators that can improve the diagnosis and predict the evolution of the disease more efficiently than the methods used until now. In particular, a new methodology for computing diagnostic indicators based on computational hemodynamics and medical imaging is proposed. We have worked with data of anonymous patients to create real predictive technology that will allow us to continue advancing in personalized medicine and generate a more sustainable health systems. The objective of this monograph is therefore to develop predictive models for cardiovascular pathologies by merging medical imaging and computational techniques at a clinical level.

It is expected in the near future that larger databases of patient-specific computational models will be available to doctors. These data can be used with predictive models to improve diagnosis and to define personalized therapies and treatments.

Resumen

Durante los últimos años, el estudio de las enfermedades cardiovasculares mediante el uso técnicas computacionales ha generado muchas expectativas en el campo de la medicina. Los avances realizados en técnicas de procesamiento de imágenes, métodos computacionales y el uso de grandes procesadores de cálculo han permitido identificar y correlacionar variables hemodinámicas con los estados incipientes o de desarrollo de patologías cardiovasculares. Hoy en día la medicina se basa en el diagnóstico, pero en esta monografía queremos tratar de introducir el concepto de medicina computacional preventiva. El objetivo principal es desarrollar modelos preventivos basados en indicadores de diagnóstico para patologías cardiovasculares combinando procesamiento de imágenes y técnicas computacionales.

En esta monografía, tratamos de predecir la evolución de aneurismas abdominales, la formación del trombo intraluminal en el interior del saco aneurismático, el estudio de la ateroesclerosis y de la coartación de aorta, así como, posibles problemas derivados de la válvula aórtica de manera personalizada. Para entender cómo una patología cardiovascular evoluciona y cuándo va a convertirse en un riesgo para la salud, es necesario desarrollar una metodología eficiente que permita calcular indicadores de diagnóstico. En esta monografía, hemos propuesto indicadores de diagnóstico basados en técnicas computacionales e imágenes médicas que pueden mejorar el diagnóstico y a la vez predecir la evolución de una patología de manera más eficiente que los métodos utilizados hasta ahora. Sin embargo, el objetivo final es llevar dichos indicadores a la práctica clínica. Actualmente estamos trabajando con datos de pacientes anónimos para crear una gran base de datos que nos permita avanzar en la medicina personalizada y en la generación de sistemas de salud más sostenibles. Es de esperar que en el futuro existan estas bases de datos a disposición de los médicos, y que estos datos sirvan para mejorar el diagnóstico y definir tratamientos personalizados.

1 Introduction

Clinical evidences have always allowed us to identify the candidate vascular regions for the appearance of cardiovascular diseases and to predict how these diseases may evolve. These clinical evidences are usually based on biological markers or anatomical indicators. However, over the last few years, thanks to the progress in computational hemodynamics, imaging processing, geometry reconstruction techniques and the increase in high-performance computing, variables such as, wall shear stress, wall elasticity, vorticity, turbulent kinetic energy, flow patterns or pressure drop, among others, have become new clinical evidences or diagnostic indicators (DIs), especially for cardiovascular diseases (CVD). Previously, patient-specific simulations were typically applied in advanced stages of disease progression, and consequently, from a medical point of view were a diagnosis-costly ineffective. In that sense, computational hemodynamics has emerged as a promising tool to estimate these new DIs and it's playing a key role in the understanding of CVD hemodynamics. The correlation of these new DIs with patient-specific data is needed to predict the development of cardiovascular pathologies and to improve the surgical strategies. In fact, these DIs are increasingly becoming a clinical reference standard for early diagnosis, treatment and prognosis allowing a better stratification of patients with disease stage adapted therapy instead of escalating to the most aggressive and costly therapy. Therefore, the precise knowledge and understanding of computational hemodynamics has become a necessity of the medical community, which includes the cardiovascular physiology, medical imaging and Computational Fluid Dynamics (CFD).

The purpose of this chapter is to give an outline of the most common diagnostic indicators used in cardiovascular diseases, as well as, the objectives and the methodology used in this monograph.

1.1 Biomechanical forces

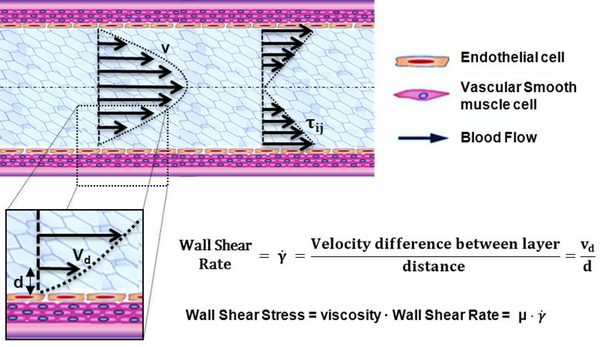
It is well-known that the interactions of pulsatile blood flow with arterial geometries generate complex biomechanical forces on the vessel wall with spatial and temporal variations [1]. Those biomechanical forces act over the internal layer of the arteries, endothelium. The endothelium produces a wide array of biochemical signals (homeostatic mediators) under physiological conditions [2][3] keeping the artery healthy. A key stimulus to maintain the protective status of the endothelial lining at the inner vessel wall is the tangential force that blood flow exerts on it; this tangential force is known as wall shear stress (WSS) (see figure 1). Fluctuations of the wall shear stress provoke changes in the biochemical signals[4], may arise the initiation and progression some cardiovascular diseases. For example, the growth or possibly rupture of the aneurysm wall[5], plaque instability in the carotid bifurcation[6][7] or in the coronaries [8][9], thrombus formation[10][11] or playing an important role in atherogenesis[12][13]. From a clinical stand point, the assessment of hemodynamic forces within the cardiovascular system circulation is still a challenge for the medical community, due to the three dimensional blood flow patterns close to the arterial wall needs to be measured in vivo. For that reason, computational hemodynamics has emerged as important tool for the clinician, allowing to quantify those hemodynamic forces and to correlate with the progression of cardiovascular pathologies.

Figure 1: Biomechanical forces acting on the arterial wall. Blood pressure and blood flow induce forces in the vascular system that lead the initiation or progression of some cardiovascular diseases. Blood pressure produces a force directed perpendicular to the vessel wall. As a consequence, the cylindrical structure will be stretched circumferentially, resulting in a circumferential stress. In contrast, the force induced by a difference in movement of blood and the non-moving vessel wall leads to stress and strain parallel to the surface of endothelial cells. Due to its shearing deformation, this is called a shear stress. This shear stress exerts its main effects through the activation of mechanosensitive receptors and signalling pathways.

1.2 Diagnostic Indicators

As pointed out, blood flow induces a reaction force ${\textstyle F_{\mu }}$ over vessel wall. The reaction force depends of the contact surface, blood-surface interface and velocity gradient between the vessel wall and blood adjacent layers[14]. For a viscous isotropic incompressible fluid, the constitutive relation between ${\textstyle \tau _{ij}}$ and the strain rate tensor ${\textstyle d_{ij}=1/2\cdot (u_{i,j}+u_{j,i})}$ is:

$\mathbf {\tau _{ij}} =2\cdot \mu \cdot d_{ij}=\mu \left({\frac {\delta u_{i}}{\delta x_{j}}}+{\frac {\delta u_{j}}{\delta x_{i}}}\right)$

(1.1)

where ${\textstyle \mu }$ is fluid dynamic viscosity, where u the fluid velocity, $\delta /x_{i,j}$ is the distance to the vessel wall and ${\textstyle \tau }$${\textstyle _{ij}}$ is the wall shear stress. If ${\textstyle \tau }$${\textstyle _{ij}}$ is proportional to the deviatoric stress tensor (relation between the shear stress and the strain rate is linear), the fluid is known as Newtonian fluid. And when the relation between the deviatoric shear stress and the strain rate tensor is nonlinear, the fluid is known as Non-Newtonian fluid. Therefore, the relationship between the deviatoric stress tensor and the strain rate tensor models defined the rheological behavior of a fluid. Perktold et al.[14] pointed out how the errors deriving from employing a Newtonian model for blood yield non-essential differences in flow characteristics and wall shear stress distributions. In this monograph, a rigid wall (no slippage is allowed) and blood (see appendix 8) as Newtonian fluid are considered, therefore WSS can be defined as:

$\mathbf {\tau _{ij}} =\mathbf {WSS} =\mu \cdot {\dot {\gamma }}=\mu \cdot {\frac {\delta u_{j}}{\delta x_{i}}}$

(1.2)

where ${\textstyle {\dot {\gamma }}}$(sec${\textstyle ^{-}1}$) is the shear rate ($\delta u_{j}/\delta x_{i}$), where u$_{j}$ is the parallel blood fluid velocity to the wall and x$_{i}$ the normal distance to the arterial wall. Usually, WSS distributions is normalized by the average parent vessel WSS in the same patient to allow comparison among different patients[15][16]. Figure 2 shows the blood flood hemodynamic forces acting on vessel wall.

Figure 2: Hemodynamic forces that act on blood vessels. Wall shear stress (WSS) is proportional to the product of the blood viscosity ($\mu$) and the spatial gradient of blood velocity at the wall (dv/dy).

When analyzing a cardiac flow (pulsating flow), it may be of interest to quantify the average load at a certain instant of the cardiac cycle, as time averaged WSS (TAWSS).

$TAWSS={\frac {1}{T}}\cdot \left|\int _{0}^{T}\mathbf {WSS} \cdot dt\right|$

(1.3)

where WSS is the instantaneous shear stress vector and T is the duration of the cycle. Another parameter related to WSS oscillations is the oscillatory shear index (OSI)[6]:

$OSI={\frac {1}{2}}\left[1-{\frac {\left|\int _{0}^{T}\mathbf {WSS} \cdot dt\right|}{\int _{0}^{T}\left|\mathbf {WSS} \right|\cdot dt}}\right]$

(1.4)

Oscillatory shear index is used to identify regions on the vessels wall subjected to highly oscillating WSS values during the cardiac cycle. For example, a purely oscillatory flow with equal forward and backward contributions will produce an OSI of 0.5; however, in unidirectional flows the OSI will be identically zero. High OSI induces region with perturbed endothelial alignment. These regions are usually associated with bifurcations flows and vortex formation that are strictly related to atherosclerotic plaque formation and fibrointimal hyperplasia.

Based on wall shear stress, and its temporal and spatial variations, other indices have been proposed to capture the mechanobiological effects over the endothelium[17], such us, relative residence time(RRT)[18], particle residence time(PRT)[19] or endothelial cell activation potential (ECAP)[11]. Relative Residence Time (RRT) is defined as the state of disturbed flow. The residence time of the blood near the wall is reflected by combination of WSS and OSI. Mathematically, RRT is inversely proportional to the magnitude of the time-averaged WSS vector:

$RRT={\frac {1}{(1-2\cdot OSI)\cdot TAWSS}}$

(1.5)

The particle residence time describes flow stagnation or recirculation, for example in the abdominal aneurysm [11] or cerebral aneurysm [20]. ECAP is defined the endothelial susceptibility, and correlate the TAWSS with the OSI:

$ECAP={\frac {OSI}{TAWSS}}$

(1.6)

The main purpose of this index is to identify local regions of the wall that can be exposed to pro-thrombotic WSS stimuli. Higher values of the ECAP index will thereby correspond to situations of large OSI and small TAWSS, that is, i.e. in abdominal aneurysm, intraluminal thrombus (ILT) development.

Nowadays, the combination of these WSS based-indicators are employed as promising hemodynamic predictors of the cardiovascular pathologies. Although, computational methods, medical imaging resolution and acquisition speed have increased over the past decades, assessment of WSS is still challenging in complex flow geometries [21][22][23][24]. For that reason, a good modelization combined with a numerical simulation is still needed (see figure 3).

Figure 3: Diagnostic Indicators in a patient-specific model

Other importance feature in many cardiovascular diseases is the helical flow patterns and turbulent blood flow, characterized by fast random temporal and spatial velocities fluctuations[25]. These irregular and rapid fluctuations are not present in healthy situations, and play also a key role in some cardiovascular pathologies. The helical flow patterns show a measure(index) of blood flow complexity, and therefore, is an important factor in the development of cardiovascular disease, as shown in figure 4. Given the fluid flow velocity vector field u, the vorticity vector field w is the curl of the velocity field:

$\mathbf {w} =\nabla \left.\times \right.\mathbf {u}$

(1.7)

Basically, the vorticity vector points along the axis of spin, and the magnitude of the vorticity vector encodes the rate of spin. Given the vorticity vector field, mathematicians introduce several useful additional concepts: vortex lines, vortex sheets and vortex tubes. Technically speaking, vortex lines are the integral curves of the vorticity vector field; this simply means that vortex lines are curves which are tangent to the vorticity field at each point. Vortex sheets, meanwhile, are surfaces which are tangent to the vorticity field at all points. Vortex tubes are three-dimensional regions obtained by taking a 2 dimensional area orthogonal to the vorticity field, and then taking all the vortex lines through that area. Now, the helicity (h) is defined as the inner product of the velocity and the vorticity:

$\mathbf {h} =\mathbf {u} ~\mathbf {w}$

(1.8)

Thus, if the streamlines of the fluid are orthogonal to the vorticity, then the helicity is zero. This is the case with a transverse vortex. In the case of a longitudinal vortex, the helicity is non-zero, and measures how tightly the streamlines corkscrew along a vortex tube. In fact, the helicity of a vortex tube can be defined by integrating the helicity field:

$\mathbf {H} =\int {}{}\mathbf {u} \cdot (\nabla \left.x\right.\mathbf {u} )\cdot d^{3}r$

(1.9)

It is a theorem of inviscid fluid mechanics that the helicity of a vortex tube is preserved over time. However, if a vortex tube is stretched, then its cross sectional area decreases, and the magnitude of the vorticity w increases, lowering the pressure at the center of the vortex. So, from a blood flow dynamics, the stretching of longitudinal vortex tubes could be a indicators of a cardiovascular pathology [26]. These effects are directly correlated with the oscillatory shear index [6].

Figure 4: Left: Streamlines in a healthy aorta. Right: Streamlines in unhealthy aorta

Another index to evaluate blood complexity is to measure the Turbulent Kinetic Energy (TKE). The velocity and the turbulent kinetic energy combined can give a visualization of disturbed flow. Increased level of TKE indicates more turbulent flow, and it is undesirable for the cardiovascular system. For this reason, analyzing and understanding energy transfer and dissipation in some cardiovascular pathologies is important for the clinician. From mathematical point of view, the turbulent kinetic energy is calculated and defined as half sum of the variance of the velocity fluctuations:

$TKE={\frac {1}{2}}\cdot ({\overline {{u'}^{2}}}+{\overline {{v'}^{2}}}+{\overline {{w'}^{2}}})$

(1.10)

The pressure is also an important indicator about the arteries status, due to represents the hemodynamic forces within the cardiovascular system circulation. Nowadays, the pressure drop (or gradient) has been evaluated as powerful predictors of epicardial coronary disease or aortic Coarctation. From a clinical standpoint, the assessment of hemodynamic forces within the coronaries circulation (or Aorta) is still difficult, because pressure can be only measured invasively and flow cannot be measured directly with Doppler ultrasound in small deep coronary vessels, as the coronaries. For that reason, computational hemodynamic becomes a promising tool to estimate the pressure non-invasively. For example, pressure-derived myocardial Fractional Flow Reserve index(FFR) is the standard goal for determining the physiological significance of a coronary stenosis[27]. FFR index is calculated as the ratio of the distal pressure to the stenosis/coartaction by the proximal pressure to the lesion in a non-rest situation (or maximum effort). Furthermore, the clinicians are able to reproduce several patient-conditions modifying the boundary conditions of computational model, based only on a medical image. The clinicians should simulate a non-inducing stress situation to the patient reducing the intervention costs. The capability of computing the pressure drop without pressure-wire has gained wide acceptance in the clinical community in the recent years[28][29].

1.2.1 Clinical practice & Diagnostic Indicators

The purpose of this section is doing a review of how the diagnostic indicators (above mentioned) can be applied into a clinical practice.

1.2.1.1 Atherosclerosis

Atherosclerosis is a disease in which plaque builds up inside your arteries. Plaque is made up of fat, cholesterol, calcium, and other substances found in the blood. Over time, plaque hardens and narrows your arteries, and in advanced phases of atherosclerosis, plaque becomes vulnerable. This limits the flow of oxygen-rich blood to your organs and other parts of your body and a possible rupture of vulnerable (or unstable) plaque exposes thrombogenic material, such as collagen to the circulation and eventually induces thrombus formation in the lumen. Plaque rupture can occur whenever plaque stress exceeds the plaque strength and thus the prediction of plaque rupture may be augmented by accurate assessment of hemodynamic forces [30]. Atherosclerosis can affect any artery in the body, including arteries in the heart, brain, arms, legs, pelvis, and kidneys, and mainly affects middle and large sized arteries near side branches and at the inner bend of curved segments. At these locations, the average normalized drag force of the flowing blood acting on the vessel wall, the wall shear stress (WSS), is low and/or turbulent leading to endothelial dysfunction and ingress of lipids into the vessel wall, initiating an inflammatory response. Thus in the early phases of the disease WSS can predict locations of plaque initiation and progression[31].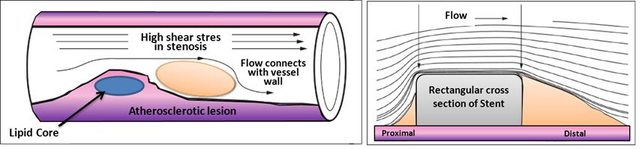

Figure 5: Left, Atherosclerosis lesion. Right, Flow around rectangular section of stent

In more advanced stages of disease, when plaque growth results in lumen narrowing, the local WSS patterns will change such that certain plaque regions to mainly located upstream- are exposed to elevated WSS[32]. Evidence is accumulating that the elevated WSS influences plaque composition in such a way that it induces local weakening of the plaque, making plaque regions exposed to high WSS prone to rupture[33][34] [35]. Clinical studies confirmed these findings: plaque rupture, both in coronary arteries and carotid arteries are observed more frequently in the upstream of the plaque[36][37][38]. Shear stress with a low mean or maximum value and varying direction (oscillating shear stress) has been associated with development of plaque vulnerability. As a result, different diseases may develop based on which arteries are affected, for example, acute myocardial infarction is mainly triggered by rupture of so-called vulnerable plaques in the coronary arteries linked with the coronary stenosis. In [39] there is a review comparing the localization of atherosclerotic lesions with the distribution of haemodynamic indicators calculated using computational fluid dynamics.

1.2.1.2 Coronary Artery Disease

Coronary artery disease(CAD) is the most common type of heart disease and cause of heart attacks. CAD is caused by abnormal narrowing of the coronary arteries (coronary stenosis) resulting in reduction of blood flow to the heart. The stenosis impedes to deliver oxygen to the heart muscle, which provoking heart attack. This disease is directly related with the atherosclerosis plaque. When stenosis occurs, the common clinical practice for decision taking related to the need (or not) of implanting a stent in a obstructed coronary artery requires the measurement of the Fractional Flow Reserve (FFR). FFR is derived from measuring the ratio of aortic pressure and pressure beyond a stenosis. Stenting is a specialized treatment for coronary arteries that are narrowed or blocked by plaques. It involves placing a balloon into the narrowed portion of the coronary artery with a surrounding wire mesh (stent). When the balloon is expanded, the stent remains in the vessel keeping the plaque pushed outwards, to let blood flow to the heart pass by.

From the technical point of view, invasive FFR measurement is often flawed by submaximal hyperemia (underestimating the stenosis severity) and by issues related to the guiding catheter[27]. A large guiding catheter may interfere with maximum blood flow and a guiding catheter with side holes may influence proximal coronary pressure and interfere with intracoronary administration of adenosine. Animal studies have suggested that a significant portion of subjects undergoing invasive FFR with adenosine do not achieve maximal hyperemia[40]. This suggests that the physiologic significance of some lesions may be underestimated when using standard current vasodilator doses and that higher, potentially toxic doses, may be needed in order to achieve maximal hyperemia. From clinical point of view, invasive FFR is unable to depict the coronary culprit lesion in cases of serial coronary lesions or in case of lesions in side branches of bifurcations[41][42]. For this reason less than 10% of European patients are subject to an invasive FFR measurement.

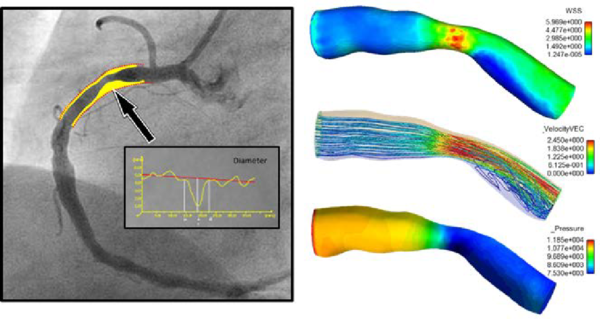
Figure 6: Streamline and wall shear stress in a coronary artery

In recent years, several alternative methods based on Computational Fluid Dynamics (CFD) have been proposed for non-invasive estimation of coronary blood flow circulation [43]. CFD has been applied to coronary computed tomography angiography for computation of FFR. However, accuracy of method[44][45] and diagnostic accuracy remains suboptimal[46]. The main challenges for such methods are the lack of patient-specific data including anatomy, patient-specific boundary conditions, the condition of the microvasculature of the myocardium, and the large-scale computational resources required for the complex calculations. In [47] pressure gradients are computed using CFD in which the geometry of the aorta is extracted from MRA. Additional MR Phase contrast imaging is performed to measure the velocity which is used as boundary conditions. In [28] lumped parameter models of the heart, systemic circulation and coronary microcirculation are coupled to a patient specific 3D model of the aortic root and epicardial coronary arteries extracted from CTA. Disadvantages of these approaches are that all calculations are performed exclusively in 3D as well as the fact that the calculations cannot be performed during intervention because of the need for CT. Moreover, one vital piece of information is still missing in CFD, namely the condition of the coronary circulatory auto-regulation, also known as the patients cardiac flow reserve. This results in a method that is of high computational complexity. A recent study applied CFD to three dimensional X-ray angiography for the computation of the FFR incorporating the coronary flow reserve[48]. However, this method requires X-ray angiographic imaging during hyperemia which is a burden to the patient. Placing known side effects of adenosine into perspective; reduced blood flow to the heart which might worsen symptoms in patients with coronary heart diseases or even cause a heart attack, this is clearly an undesired situation especially during diagnostic coronary angiography.

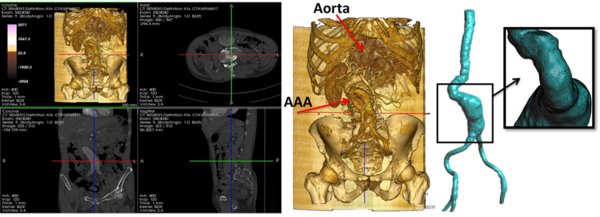
1.2.1.3 Aortic Aneurysms

The aortic dilatation is an asymptomatic disease with complicated and lethal sharp pains that can occur anywhere in the human aorta. By definition, if the aorta diameter at least is 50% greater than the normal size of the aorta produces what is called aneurysm. And if this occurs in the thoracic aorta is termed a Thoracic Aortic Aneurysm(TAA), in the abdominal aorta is named Abdominal Aortic Aneurysm(AAA). However, the aneurysm pathogenesis is still unknown.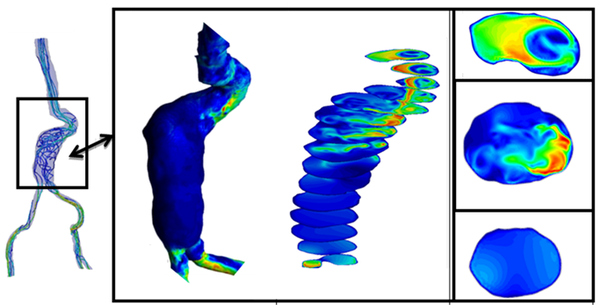

Figure 7: Diagnostic Indicators in Aortic Abdominal Aneurysm. Streamlines, wall shear stress and velocity profiles at different sections of the aneurismatic sac.

It is thought that the initial dilatation is caused partly by degeneration of the medial elastin and smooth muscles in the arterial wall or by the effect of the wall shear stress. Vessel wall remodeling as a result of shear stress alteration is accompanied by synthesis and secretion of NO, growth factors and metalloproteins, which contribute to aneurysm pathogenesis. Genetics and risk factors like smoking, hypertension, chronic obstructive pulmonary disease(COPD), inflammation and atherosclerosis play key roles in aneurysms genesis and progression[49]. In this context, there are few predictors of the aorta dilatation available in the clinical practice. Mainly, they are based on the aortic diameter and increasing aortic size. Currently, the accepted values have been changing over time and they are actually being discussed by the groups with experience, for example, [50][51] in TAA patients or [52][53] in AAA patients. There is also a hemodynamic factor of parietal stress in the aortic dilatation, which is currently a little-known factor. Prior works, related TAA, have confirmed the presence of different flux in bicuspid aortic valve without aortic dilation compared to tricuspid aortic valves patterns by using cardiac magnetic resonance imaging (cardiac MRI). Abnormal flow patterns have been also detected in aneurysms located in the ascending aorta which confirms flow jets to the anterolateral wall of the aorta [54]. It is also known that shear stresses play an important role in the initiation, progression and rupture of aneurysms[55][56]. Vorticity inside the aneurysm is connected to aneurysm plaque or thrombus formation [5][11]. Figure 7 shows some DI's in an Aortic Abdominal Aneurysm(AAA)[15].

1.2.1.4 Aortic Coarctation

Aortic coarctation(CoA) occurs approximately in 10% of patients with congenital heart defects and represents a narrowing of the descending aorta (see paper 1). Due to the reduction in the aorta descending diameter, high pressure gradients can appear across the CoA, resulting in an increased cardiac workload in the left ventricle during systole [57]. The narrowing of the aorta creates a flow jet with high velocity, inducing a very complex turbulent flow field. Recently, researchers has characterized changes of hemodynamic parameters such as pulse blood pressure, aortic capacitance, and wall shear stress due to the presence of an aortic coarctation [57][58][59]. Hemodynamic changes caused by the coarctation can result in endothelial dysfunction [60], provoking non normal values of TAWSS or elevated OSI for CoA patients.

1.3 Objectives

The general objective in this monograph is improving computational hemodynamics to develop patient specific diagnostic indicators for an early identification of cardiovascular pathologies(and its progress). To reach this goal, this monograph attempts to improve the prior mathematical models used for cardiovascular system for a deeper understanding on the response of the cardiovascular system to:

• improve diagnostics and therapeutical procedures for Aorta Coarctation (paper 1 in Chapter 2),
• study the mechanical factors that may be important in triggering the onset of aneurysms (paper 2 in Chapter 3 and paper 3 in Chapter 4),
• combine medical images with computational hemodynamic to estimate DI's (Chapter 5) and
• use medical images data to generate computational model (paper 4 in Chapter 5).

Other applications studied based on the methodology developed in this monograph were, (i) study of new mechanical factor related to the AAA and (ii) studied the effect of vorticity and the eccentricity of the aortic bicuspid valve (in Chapter 5).

From the methodology point of view, a new methodology to compute diagnostic indicators based on computational hemodynamics has been proposed. In order to compute the pressure drop under different patient-specific situations, a reduced-order model has been developed in paper 1. The reduced-order method was implemented as part of the C++ finite element library KRATOS[61]. KRATOS is a multiphysics simulation open source (LGPL licence) framework based on the stabilized Finite Element Method for analysis of the Navier-Stokes equations in viscous flows. Efficient and parallel solvers for 3D fluid problems have been implemented in KRATOS that allow tackling large problems using supercomputers if available. The 1D model developed in this monograph was also implemented as new elements inside KRATOS. Blood was modeled as a Newtonian fluid with constant density and different outlet conditions were implemented. In appendix 9 a detail description of the implementation is shown.

Additionally, the diagnostic indicators have been correlated with the patient-specific geometry (paper 2). Once a 3D model of a vascular tree is obtained, the geometry is meshed having special attention in the near-wall region(boundary layer) using the tetrahedral (3D) elements. A good boundary layer mesh allows to properly capturing the sharp velocity gradients. The Navier-Stokes equations (see section 1.4.2) were solved with TDYN[62] to model blood flow in the normal and aneurysmatic abdominal aortas. For the 3D model, rigid wall was assumed and no-slip boundary condition was applied at the luminal wall. A volumetric/mass flow rate was applied at the inlet and a pressure wave was applied at the outlets. A python script implemented to compute WSS-based diagnostic indicator is shown in appendix 10. A new procedure to segment the aorta using 4D flow Cardiac Magnetic Resonance (CMR) data has been also proposed. Beyond this, 4D flow CMR visualization offer a qualitative and comprehensive descriptions of the flow fields than any other in-vivo imaging technique (in chapter 5). The velocity data provided by 4D flow CMR has been complementary to the higher resolution velocity fields computed by the CFD in order to estimate the WSS. We have also developed an algorithm to compute WSS based on the 4D flow CMR data. To compute vorticity and helicity from a velocity field a Vascular Modeling Toolkit (VMTK)[26] and TDYN[62] were used. In spite of this, a new diagnostic indicator to estimate coronary artery disease based on computational hemodynamics has been also proposed (in chapter 5).

In this monograph, blood has been considered as incompressible and Newtonian fluid, and we will focus on the systemic arterial system and coronary circulation. Further information about cardiovascular physiology can be found in appendix 8. In the following, a brief summary of the methods employed to reach the objectives of this monograph is given in the next section. For a complete description of the methodology used in this monograph see papers 1-4 in chapter 2-5, respectively.

1.4 Methodology

1.4.1 Patient-specific modelling

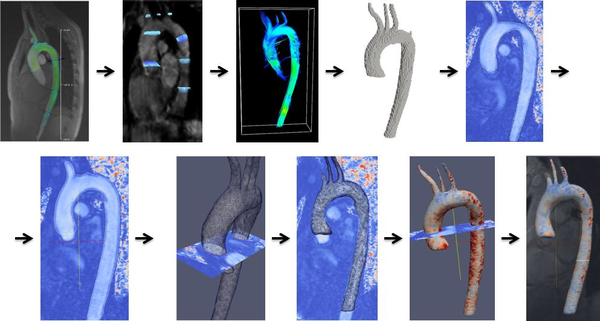
Patient-specific modeling is the development of computational models of human physiology that are individualized to patient-specific data[63]. Imaging data can be stored in the Digital Imaging and Communication in Medicine (DICOM) format [64]. The DICOM format file contains two parts: the header which stores detailed information about the patient such as name, type of scan, ages, dimension of the image and the voxel, image position, and so forth. The second data set contains information of each scanned image. Segmentation of medical image was required to extract the geometry of the region of interest (or analysis). The segmentation process can include several procedures as threshold, region growing, centerline, among others, followed by 3D anatomical reconstruction to obtain a coarse solid model[65] . During threshold, a range of gray scale values are selected such that the region to be selected is of the best contrast. After the regions of interest are extracted, the voxels are labelling together with an identificator to create the 3D geometry.

In previous work[65] an efficient methodology for pre-processing medical images to generate computational meshes for numerical simulation is explained. A schematic flowchart for creating and validating a 3D patient-specific model is shown in figure 5 of [65]. Aneurysm models (patient-specific geometries) of paper 2 were reconstructed from computer tomography-angiography (CTA) scan using the diagnostic software ITK-SNAP[66] and DIPPO[67].

Figure 8: Left CT DICOM (sagital, coronal and axial images) of patient with Aortic Abdominal Aneurysm. Center CT volume render of Aortic Abdominal Aneurysm illustrating the Abdominal sac. Right computational patient-specific model and computational mesh

Both image processing programs employ active contour (deformable models) which move under the action of external forces according to the image intensity and first and second spatial image gradients. A schematic diagram depicting the segmentation of medical image at various locations of the abdominal aneurysm is shown in figure 8. Coronary models of chapter 5 were reconstructed from X-ray coronary angiography (XA). At the moment, X-ray coronary angiography is the standard technique for anatomical assessment and the diagnosis of coronary arteries. The 3D coronary models reconstructed was based on two bi-dimensional images taken from different perspectives. Then the reconstruction of abdominal aneurysm anatomy or coronary into a computational mesh (computer model) is performed based on the segmentation information. To generate the computational mesh GiD pre and ostprocessor[67] and the open source Vascular Modeling Toolkit (VMTK) [26] were used.

Next, a list of freely available tools for medical image processing and mesh generation using in the appended papers is outlined; VTK[68] is an open-source software toolkit for visualization, computer graphics and image processing with a great online community and numerous examples. VTK is cross platform with implementations for Windows, Mac Os and Linux. Users can code in C++, Java, Phyton or TCL. Knowlegde of VTK means that developers can take advantage of other tools such as ITK or ITK-SNAP, to name a few. ITK[69] is an open-source, cross-platform system that sits on top of VTK. It provides developers with an extensive suite of software tools for image analysis. ITK-SNAP[66] is a freely available tool built on ITK and VTK for image manipulation. The source code for ITK-SNAP is part of ITK Applications, so developers can add their own modifications. DCMTK[70] is a collection of libraries and applications for reading, writing and otherwise manipulating DICOM images. It works with multiple operating systems. VMTK[26] is collection of applications for pre and postprocessing medical images.

1.4.1.1 4D flow cardiovascular magnetic resonance imaging

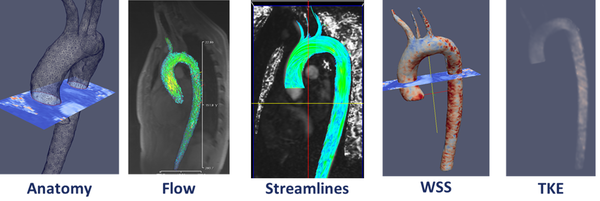
At present, 4D flow cardiovascular magnetic resonance imaging (4D CMRI) sequences are being a promising tool to visualize and quantify 4D (3D+t) blood flow. From these sequences the raw data can be obtained and conveniently processed, allowing visualization of the blood flow patterns in any segment of the cardiovascular tree[71][72][73]. Nevertheless, the visualization of these images entails an important manual work, becoming a very time-dependent task and then turning out to be not useful in the current clinical practice. Therefore, it is important to improve the technology and the methods of automatic representation of the 4D blood flows, in particular for the WSS analysis. In chapter 5, it is demonstrated that 4D flow CMRI technique is a reliable tool to provide the boundary conditions for the Computational Fluid Dynamics(CFD) in order to estimate the WSS within the entire thoracic aorta in a short computation time. Our image-based CFD methodology exploits the morphological MRI for geometry modelling and 4D flow CMRI for setting the boundary conditions for the fluid dynamics modelling. The aim is to evaluate visualization of well-defined aortic blood flow features and the associated wall shear stress by the combination of both techniques. In that sense, CIMNE has developed a home-made ad-hoc software (Aorta4D) oriented to make progress in this field of work [72][74][73]. Aorta4D will afford analysis and spatially visualization of the registered 3-directional blood flow velocities, and perform a 3D semi-automatic segmentation based on the 4D flow CMRI data.

1.4.2 Computational hemodynamics

In this section we will limit to the essential description of mathematical equations and the most important dimensionless parameters to characterize the blood flow[75]. In this monograph, we consider blood as an homogeneous, incompressible, constant-density (${\textstyle \rho =}$1050 kg/m${\textstyle ^{3}}$), Newtonian fluid with constant viscosity (${\textstyle \mu =}$0.0035 Pa.s). and vascular walls are modeled as non-permeable and rigid walls (see appendix 8.1). Under these assumptions, the conservation of mass and momentum in the compact form are described by the following system of partial differential equations (1.11):

${\begin{array}{rcll}\rho \cdot \left(\displaystyle {\frac {\partial \mathbf {u} }{\partial \mathbf {t} }}+(\mathbf {u} \cdot \bigtriangledown \mathbf {u} )\right)+\nabla p-\nabla \cdot (\mu \bigtriangleup \mathbf {u} )&=&\rho \cdot \mathbf {f} &\qquad {\textrm {in}}\Omega (0,t){\textrm {}}\\\nabla u&=&0&\qquad {\textrm {in}}\Omega (0,t){\textrm {}}\end{array}}$

(1.11)

where ${\textstyle \Omega }$ is a three-dimensional domain, u denotes the blood velocity, p is the pressure field, ${\textstyle \rho }$ density, ${\textstyle \mu }$ the dynamic viscosity of the fluid and f the volumetric acceleration. Volumetric forces(${\textstyle \rho \cdot \mathbf {f} }$) and thermal effects are not considered in this monograph. The spatial discretization of the Navier-Stokes equations has been done by means of the finite element method (FEM), while for the time discretization an iterative algorithm that can be considered as an implicit fractional step method has been used [62][61]. Blood flow can be characterized by the Reynolds and Womersley [76] dimensionless number. These numbers correlate the inertial and viscous forces of the previous equation 1.11. The Womersley number(${\textstyle \alpha }$) is a dimensionless parameter that represents the ratio between oscillatory inertial forces and viscous forces. Physically, the Womersley number can be interpret as the ratio of artery diameter to the laminar boundary layer growth over the pulse period (characteristic frequency):

$\alpha ={\frac {D}{2}}\cdot {\sqrt {\frac {w\rho }{\mu }}}$

(1.12)

where w the characteristic frequency and D is the characteristic diameter. If ${\textstyle \alpha }$ is high, the fluid is non-viscous, and if ${\textstyle \alpha }$ is low, the viscosity of the fluid is high. Womersley number characterizes the unsteady of the blood flow. The ratio of the inertial force to the viscous forces is the dimensionless parameter called Reynolds number:

$Re={\frac {U^{2}\rho }{\frac {\mu u}{D}}}={\frac {LU\rho }{\mu }}$

(1.13)

When we have a large Reynolds number inertial forces are dominant over viscous forces and viceversa. This naturally leads us to the role of Reynolds number as the key parameter which identifies the transition of the flow to turbulence. Usually, Reynolds number suggests that in most arteries of the cardiovascular system the flow is laminar. The exceptions are the flow in severely stenotic vessels, where the flow regime can be become transitional or turbulent. Turbulence blood flow implies fluctuating pressure acting on the arterial wall, and fluctuating, increased shear stress, which can be provoke post-stenotic dilation or atherogenesis. In this monograph, blood flow has being considering laminar. Figure 9 shows the full process from the medical image to the numerical simulation: aortic abdominal aneurism imaging, geometry modelling, finite elements meshing and mechanical and hemodynamics numerical simulation.

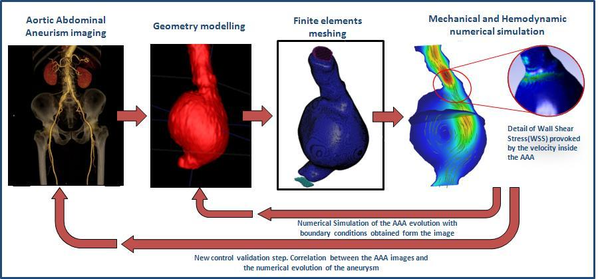
Figure 9: From the medical image to the simulation

1.4.2.1 Patient-specific boundary conditions

It is well known that to estimate properly the DI's, the specific patient-specific boundary conditions are needed. Several authors [77][78][79] have noted how inlet velocity profiles and flow waveform shapes play an non-negligible role on wall shear stress or pressure distributions. Nowadays, there are several medical techniques to perform velocity measurements inside large arteries in vivo and non-invasively, as Doppler Utrasound or phase-contrast magnetic resonance. Using these acquired data into the computational hemodynamical model will provide us enough information to define our simulation. It should be pointed out that the conditions measured depend on physical activity and posture of the patient [80]. In paper 2 and chapter 7 the technique uses to acquire the velocity information for the prescription of patient-specific boundary conditions was phase-contrast magnetic resonance.

Acquisition of boundary conditions by phase-contrast magnetic resonance: At present Cardiac Magnetic Resonance Imaging (CMRI) image is the only non-invasive imaging modality that can measure 3D blood velocity in a 3D representation, and that allows visualization of spatial velocity distribution velocity in a two-dimensional plane (2D). This technique is valuable non-invasively tool for evaluation of the cardiovascular flow patterns owing to its unique possibility to simultaneously acquire sectional imaging without restriction, anatomy (magnitude image) and blood flow velocities(phase image) with a single scan. The majority of the commercial systems offer the bi-dimensional phase-contrast sequence to quantify blood velocity and derivative cardiac flow. These sequences are reliable and precise methods to calculate stroke volume for pulmonary/systemic flow ratios estimation (Qp:Qs) and to calculate volume regurgitation in valvular insufficiencies [81][82]. At present, the phase-contrast sequences are being developed to allow obtaining information of the 4D flow (see 1.4.1.1).

Boundary conditions from multiscale modeling of circulation: Another approach to impose the boundary conditions is to use reduced models, as 1D model or 0D (lumped) models. 1D and 0D models are mathematical models able to reproduce the systemic and pulmonary circulation. Figure 10 shows a standard approach to provide realistic local boundary conditions for 3D CFD simulations at the specific arterial domain using 1D models of the entire arterial tree and 0D models at the distal ends[83]. 1D model solves the Navier-Stokes equations under some assumptions (see appendix 9) and lumped models (0D models) can be derived from electrical circuit analogies where blood flow is represented by the current and arterial pressure by the voltage. Usually the electrical components of these circuits are resistances, inductances and capacitors. Where resistances represent arterial and peripheral resistance that occur as a result of viscous dissipation inside the vessels, capacitors represent volume compliance of the vessels that allows them to store large amounts of blood, and inductors represent inertia of the blood[75]. The values of these electrical components can be estimated from physical data of the subject [84][85]. This approach is quite used because it is capable to account for the effect of local pathological conditions on the whole circulatory system, providing realistic boundary conditions for the 3D problem [75][79][86].

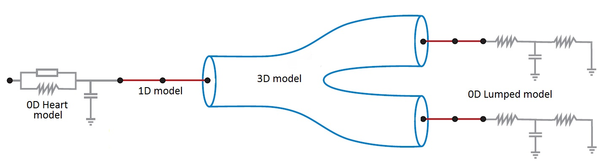
Figure 10: Coupling of 0D heart model, with 1D model (Systemic Circulation), 3D model (patient-specific geometry) and 0D lumped models (terminal resistance) to perform a computational analysis

1.4.3 Postprocessing

Output data were imported into GiD for post-processing[67]. A python script to compute WSS-based indicators was performed into EnSight[87] (see appendix 10).

2 A Reduced Order Model based on Coupled 1D/3D Finite Element Simulations for an Efficient Analysis of Hemodynamics Problems

Title: A Reduced Order Model based on Coupled 1D/3D Finite Element Simulations for an Efficient Analysis of Hemodynamics Problems.

Authors: E.Soudah, R.Rossi, S.Idelsohn, E.Oñate.

Journal: Journal of Computational Mechanics. (2014) 54:1013-1022.

Received: 18 February 2014 / Accepted: 30 April 2014 / Published online: 23 May 2014

DOI: 10.1007/s00466-014-1040-2

Scientific contribution: Design of a new methodology to estimate the pressure drop in aortic coarctation under different scenarios. The methodology is based on the integration a 1D numerical model (see appendix 9) into a reduced order model based on 3D CFD formulation.

Contribution to the paper: The principal author developed and implemented the 1D model and the reduced order model into the KRATOS Multi-Physics software (www.cimne.com/kratos)([61]).

Article reprinted with permission. Electronic version of an article published as: copyright Springer-Verlag Berlin Heidelberg 2014. Print ISSN 0178-7675. Online ISSN 1432-0924. Journal No: 00466 http://www.springer.com/

3 CFD Modelling of Abdominal Aortic Aneurysm on Hemodynamic Loads using a Realistic Geometry with CT

Title: CFD Modelling of Abdominal Aortic Aneurysm on Hemodynamic Loads using a Realistic Geometry with CT.

Authors: E.Soudah, E.Y.K. Ng, T.H Loong, M.Bordone, P. Uei and N.Sriram.

Journal: Computational and Mathematical Methods in Medicine. Volume 2013-472564, 01/06/2013. (OPEN ACCESS JOURNAL)

DOI: 10.1155/2013/472564

Scientific contribution: Computational fluid dynamics studies of abdominal aortic aneurysms (AAA) to find a correlation between hemodynamics parameters and geometrical factors.

Contribution to the paper: The principal author developed the segmentation and mesh procedures together with M.Bordone and T.H Loong. He also had a major active part in the interpretation of the results together with E.Y.K. Ng, P. Uei and N.Sriram. This overall work was carried out in collaboration with Tan Tock Seng Hospital and Nanyang Technological University of Singapore under the NTU-NHG Innovation Seed Grant Project no. ISG/11007.

4 Mechanical Stress in Abdominal Aneuryms using Artificial Neural networks

Title: Mechanical stress in abdominal aortic aneurysms using artificial neural networks.

Authors: Eduardo Soudah, José F. Rodríguez, Roberto López

Journal of Mechanics in Medicine and Biology. Vol. 15, No. 3 (2015) 1550029

DOI: 10.1142/S0219519415500293

Scientific contribution: Combination of artificial neural networks with computational mechanics procedures to estimate the principal stresses in the aneurismatical sac in idealized AAA geometries.

Contribution to the paper: Pres and post processing tools for mesh generation for numerical simulations. Development, implementation and application of the artificial neural model together with José F. Rodríguez and Roberto López. This overall work was carried out in collaboration with Group of Applied Mechanics and Bioengineering from University of Zaragoza.

Article reprinted with permission.Electronic version of an article published as:

Journal of Mechanics in Medicine and Biology. Vol. 15, No. 3 (2015) 1550029

DOI: 10.1142/S0219519415500293

copyright World Scientific Publishing Company.

http://www.worldscientific.com/worldscinet/jmmb

5 Estimation of Wall Shear Stress using 4D flow Cardiovascular MRI and Computational Fluid Dynamics

Title: Estimation of Wall Shear Stress using 4D flow Cardiovascular MRI and Computational Fluid Dynamics (article in preparation)

Scientific contribution: Designed new methodology to estimate the Wall Shear Stress(WSS) using 4D flow cardiovascular MR data and computational fluid dynamics. The methodology proposed is based on interpolate the data acquired from the 4D flow CMR sequence into a patient-specific refined-mesh computational mesh. This paper is a proof-of-concept to validate WSS using CFD data.

Contribution to the paper: This work is being carried out in collaboration with the E.T.S. d'Enginyeries Industrial i Aeronáutica de Terrassa (ETSEIAT), UPC and the Unidad de Imagen Cardiaca, Servicio de Cardiología, Hospital de la Santa Creu i Sant Pau. The simulation in the OPENFOAM software([88]) was performed during the final career project of Jordi Casacuberta in the ETSEIAT. The author of this monograph has developed the algorithm and the methodology for the calculation of the WSS using 4D flow CMR data in collaboration with Jorge S.Pérez (CIMNE). The author of this monograph has also contributed in the segmentation and the analysis of results.

6 Related Work

Thanks to the scientific contributions of paper 1, paper 2, paper 3 and paper 4, in this chapter the following applications have been studied:

• Qualitative evaluation of flow patterns in the Ascending Aorta with 4D phase contrast sequences.
• Study new mechanical factors related to the Abdominal Aortic Aneurysm.

6.1 Qualitative evaluation of flow patterns in the Ascending aorta with 4D phase contrast sequences

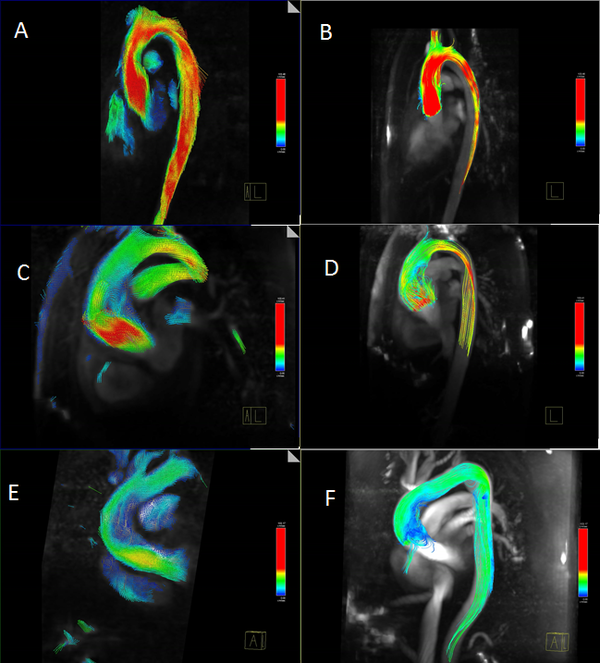
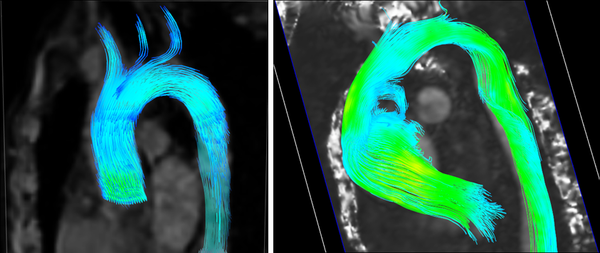
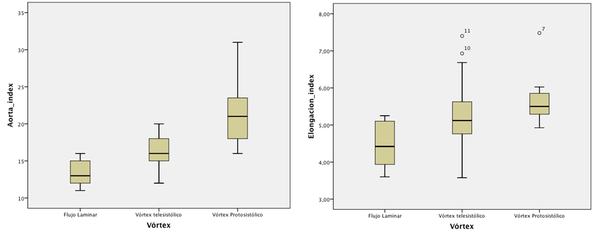
4D Phase Contrast Cardiac Magnetic Resonance(4D-PC-CMR) sequences allow to obtain three-dimensional flow images (see section 1.4.1.1) and to analyze of the patient-specific characteristics of intravascular flows under normal and pathological conditions. In clinical practice, these sequences allow to advance the understanding of the pathophysiology of vascular diseases through the interaction between flow and anatomy. Besides of this, it also help to understand the origin of diagnostic errors of 2D flow PC sequences. The aim of this study is to describe and characterize qualitatively different patterns of systolic flow in the Ascending Aorta(AoAsc) against to its aortic diameter with different degrees of root dilatation and against the different aortic valve pathologies using 4D PC Cardio MR sequences.

Figure 11: Blood flow patterns in ascending aorta, left (velocity vector), right (streamlines). A and B show a laminar flow with maximum speed in the center of the aortic flow. C and D show a turbulent flow into the dilation of the aorta with an eccentric jet. D and E show a turbulent flow into the elongation of the aorta with an eccentric jet.

All the patients (31 patients) who participated in this trial were volunteered and provided written consent to be part of this study. This study was reviewed and approved by the Ethics Committee of the Hospital Sant Pau i Creu Blanca, Barcelona, Spain. The 31 patients have different aortic problems, 12 patients suffer cardiomyopathy, 6 patients have a dilated aorta, 4 patients have aortic valve disease, 1 patient has a mitral valve disease, 1 patient has an atrial fibrillation and another suffers syncope, as well as 5 were healthy volunteers. For each patient an anatomy/flow cross-sectional of AoAsc was done. The flow pattern studied was: (i) at the Valsalva sinus (SV), where the flow adopts a uniformity velocity with a peak in the middle of the aorta (see figure 11.A and 11.B) or an eccetric flow jet with a maximun speed located at the periphery (see figure 11.C and 11.D), and (ii) at the AoAsc level, where the flow keep constast along the systole phase (see figure 11.A and 11.B) or the Systolic Turbulent Flow (FTS) can be defined as vortices or circular paths in opposite direction to the normal aortic systolic flow (see figure 11.D and 11.E). The AoAsc diameter was measured to the level of the bifurcation of the pulmonary artery, and the elongation of the aorta was defined as the maximum distance from the front wall of the AoAsc to the rear wall of the descending aorta at the level also to the bifurcation of the pulmonary artery. Jet's direction is defined as maximum velocity in the streamline related to the perpendicular plane at the aortic root.

In 29 patients (93.5%) the left ventricular ejection fraction was normal. The aortic valve was bicuspid in 4 patients and 3 of them show a dilated AoAsc.The average diameter of the AoAsc was 16.80${\textstyle \pm }$4.41mm. The mean aortic elongation diameter was 5.15${\textstyle \pm }$0.99cm. From the 4D sequences, 15 patients have a central jet at the Valsalva sinus (48.4%) and 16 patients have an eccentric jet (51.6% 10 patients have laminar flow at the AoAsc level (32%), 13 patients show a vortex during the systolic phase(42%) and 8 patient during the protosystolic phase(26%) (see figure 11). Statistical correlation between FTS against the AoAsc diameter and elongation of the aorta was done 12. The analysis shows that the diameter of the AoAsc has a significant linear relationship with the flow pattern in aortic systolic, which indicates higher prevalence of turbulence flow (proto-systolic vs systolic) for a higher aortic diameter (figure 12). The flow characteristics in the AoAsc were analyzed by two independent clinicians getting a good concordance. The jet eccentricity in the SV indicates a trend (p = 0.06) for the FTS origin in AoAsc. The presence of a bicuspid valve is also associated with the formation of vortices (p = 0.047), although when it is adjusted by the AoAsc's diameter, statistical significance (P = 0.48) decreases.

Figure 12: Left, Aortic index versus flow characteristics. Right, Aortic elongation versus flow characteristics.

6.1.1 Conclusions

The flow pattern during systolic phase in the ascending aorta changes progressively from laminar flow with directional jet in not-dilated aortas to turbulent flow with eccentricity jet in dilated aortas. Other factors, such as bicuspid aortic valve can increase the turbulence effect but there are not essential to provoke it. This study was done in collaboration with Dr.Francecs Carreras, Dr.Chi-Hion Pedro Li and Dr.Xavier Alomar from Hospital Sant Pau i Creu Blanca and Clinica Creu Blanca, Barcelona, Spain, respectively. The equipment used was a Magnetom Verio 3T Siemens, Erlangen, Germany.

6.2 Study new mechanical factor related to the Abdominal Aortic Aneurysm

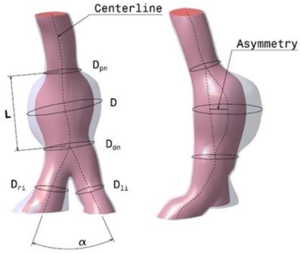
The primary goal of this further work was to motivate a new phenomenological approach for identifying regions of possible formation of Intra Luminal Thrombus (ILT) on an intact but susceptible endothelium within AAAs. Following the idea of paper 2, CFD Modelling of Abdominal Aortic Aneurysm on Hemodynamic Loads using a Realistic Geometry with CT, thirteen new patients with infrarenal aneurysms from Clinical Hospital of Valladolid (Spain) have been studied. The patients chosen for this study were selected during the first stages of the AAA's development. All the patients who participated in this trial analysis volunteered and provide written consent to be part of the study. This study was reviewed and approved by the Ethics Committee of the Clinical Hospital of Valladolid (Spain). To characterize the AAA shape and size, the main geometrical AAA parameters were determined using the lumen center line [66][26] of the segmented images. Twelve indices were defined and computed for the thirteen AAA patient-specific models. Figure 13 shows the seven geometrical parameters defined (AAA morphometry).

Figure 13: Abdominal Aneuryms 1D geometrical parameters. D: maximum transverse diameter, D$_{pn}$: neck proximal diameter(smallest diameter of the infrarenal artery, just before the AAA), D$_{dn}$: neck distal diameter (smallest diameter of the aorta, just after the AAA), L: aneurismal length (length between proximal and distal necks), D$_{li}$: left iliac diameter (left iliac diameter), D$_{ri}$: right iliac diameter (right iliac diameter) and $\alpha$ is the angle between the right and left iliac arteries.

Another four geometrical indices[15] were defined: ${\textstyle \gamma }$(saccular index) assesses the length of the AAA region, this region will be affected by the formation and further development of the ILT, ${\textstyle \chi }$ (deformation rate) characterizes the deformation of the aorta, relation between D${\textstyle _{pn}}$ and D, ${\textstyle \epsilon }$ (tortuosity index) is the ratio of the length of the curve to the distance between the proximal and distal neck and ${\textstyle \beta }$ (symmetry index) is the result of the non-symmetry expansion of the aneurysm sac. Next table 1 shows the parameters for the 13 new cases analyzed.

90

Table. 1 Geometrical parameters of the 13 AAA cases analyzed

	$V_{AAA}$	$D$	$D_{pn}$	$D_{dn}$	$L$	$D_{li}$	$D_{ri}$	$\gamma$	$\chi$	$\epsilon$	$\beta$	$\alpha$
n	(mm${\textstyle ^{3}}$)	(mm)	(mm)	(mm)	(mm)	(mm)	(mm)
1	49223,2	30,34	19,77	23,36	80,42	14,74	12,50	0,377	1,533	0,0389	0,460	56,70
2	43623,0	33,07	26,91	29,70	82,71	15,73	17,62	0,399	1,22	0,022	0,60	57,20
3	51862,0	42,96	20,90	17,82	102,19	12,22	11,85	0,420	2,056	0,140	0,769	50,62
4	55935,0	41,39	24,53	33,56	94,23	18,27	12,32	0,439	1,687	0,0308	0,529	66,27
5	44386,1	34,80	20,88	30,35	109,71	20,23	15,16	0,317	1,667	0,0660	0,490	61,87
6	32740,0	33,51	20,53	23,92	114,88	15,50	13,01	0,29	1,632	0,0147	0,380	64,33
7	40608,0	40,05	32,18	34,86	104,16	23,43	15,67	0,384	1,245	0,0383	0,430	54,67
8	83186,0	50,99	24,23	39,33	105,47	14,81	21,45	0,483	2,104	0,0445	0,748	43,01
9	46676,0	37,28	23,45	24,28	89,19	11,44	11,45	0,417	1,590	0,0645	0,573	38,67
10	45780,0	40,88	25,60	25,90	80,38	9,90	11,18	0,508	1,597	0,0817	0,642	25,56
11	43130,0	42,23	22,02	30,15	85,50	21,63	19,94	0,493	1,918	0,0409	0,709	48,96
12	30538,0	29,81	20,71	19,00	92,39	15,70	11,88	0,322	1,439	0,0655	0,505	43,77
13	51388,0	37,52	33,39	21,66	99,12	12,20	14,80	0,378	1,124	0,0343	0,755	40,58

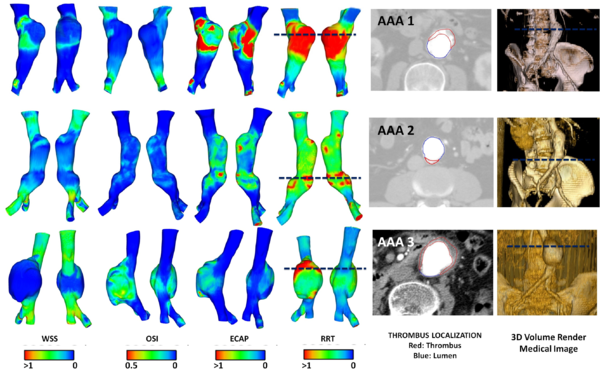
The hemodynamic variables for the thirteen abdominal aneurysms were obtained using image-based CFD under realistic flow conditions. The AAA simulations were performed for three cardiac cycles, and the results from the last cardiac cycle were used to compute the WSS-based diagnostic indicators (WSS(eq.1.2), OSI(eq.1.4), ECAP(eq.1.6) and RRT(eq.1.5)). Depending on the complexity of the AAA model, a 3D mesh consisted of 1.000.000 ${\textstyle \pm 15\%}$ tetrahedral elements. A boundary layer was created to capture properly the velocities close to the wall. Next image shows the WSS, OSI, ECAP and RRT values for three different AAAs.

Figure 14: Spatial distribution of WSS, OSI, ECAP and RRT in three abdominal aortic aneurysm. For each AAA, anterior and posterior views of the lesions. On the right, 3D volume render and a CT slice showing the localization of the incipient thrombus (red line: thrombus, blue line: lumen). Dark Blue line represents the localization of the CT slice.

6.2.1 Conclusions

The computed WSS-based diagnostic indicators combined with the geometrical factors may provide more information about ILT development for a complex AAA geometries. The results show that aneurysmal wall regions with increased flow and high tortuosity index may be prone to thrombus deposition, and consequently, ILT formation. Higher values of the RRT and ECAP indices correspond to the areas with ILT, as is shown in figure 14. A preliminary analysis of the thirteen AAA confirmed that the length, asymmetry and saccular index significantly influence in the WSS-based diagnostic indicators, which highlight the weight of these variables on the ILT development and the rupture-prone AAA areas. No correlations between maximum diameter and WSS-based diagnostic indicators were obtained, as might be expected. This finding is in agreement with the strategy adopted in the research, all the AAAs considered have a diameter around 40 mm, and therefore the rupture risk is not significant. The study shows that WSS-based diagnostic indicators may provide important additional information on aneurysm progression on a patient-specific basis. Based on this preliminary study, it is possible to hypothesize that the characterization of AAA morphometry and its influence on the regional and temporal distribution of the hemodynamical variables would be necessary for patient-specific assessment of rupture risk and ILT development. To improve the reliability of the results, would be needed to expand the number of cases in the study. The methodology here developed could be an indicative that other indices like, asymmetry, deformation rate, AAA length, saccular index, are important and could also be readily incorporated into surgeon's decision making, instead of the classical maximum diameter criterion.

7 Conclusions and Future work

7.1 Conclusions

The increasing availability and efficiency of computational tools for patient-specific simulations provides useful data to understand the psychopathology of cardiovascular diseases. The rationale for this monograph is to reinforce the clinical utility of computational hemodynamics, contributing to its translation into clinical practice through the diagnostic indicators. The results of this monograph will provide useful quantitative data for proof-of-concept studies. Hopefully, this will enable clinicians to gain insights, develop intuitions, and provide constructive feedback and guidance for the development of more representative models. Moreover, the increasing sophistication of therapeutic solutions for cardiovascular pathologies require the development of tools for quantitative patient-specific simulations to aid therapeutic planning through the assessment of pre-operative scenarios and the prediction of therapeutic intervention outcomes. The integration of technical developments into prototypes will allow the clinicians to become acquainted with the newly developed technology underpinning exploitation in new products. It should be noted that part of the development performed during this monograph is being integrated into clinical prototypes. Another general objective of this monograph is to generate and share a common technology infrastructure, resources and knowledge across/between clinical practice, physics and bio-engineering. The key findings of the four papers and related work are summarized below.

In this monograph we have developed a geometrical multiscale framework for simulation cardiovascular diseases under different physiological and pathological conditions. The cardiovascular diseases studied under this multiscale framework were the Aorta Coartaction and Coronary Disease, but, the technology underlying is applicable to other common cardiovascular conditions, including peripheral, cerebrovascular, and reno-vascular disease, and may be used to determine whether vascular stenosis are hemodynamically significant as well as the relative benefit of therapeutic interventions. In this line, we have also proposed a new coronary indicator to evaluate the stenosis without hyperemia condition (under evaluation). At the same time, we have developed and validated a 1D numerical model coupled with the reduced order model. A 1D-reduced order model validation for other groups of people or patients could also be useful for research and clinical outcome analysis. The 1D model is able to describe the pulse wave dynamics and the interaction between the heart and the circulatory system. We have also studied the hemodynamics factors that may be important in triggering the onset of aneurysms correlated with the patient-specific anatomy. The hemodynamics factor and the geometry are directly related with the ILT formation. More AAA cases are needed to define a direct correlation between the hemodynamics factors and AAA development. Quantification of WSS, as well as other WSS-based indicators, are of crucial importance for the understanding of the development of cardiovascular pathologies as, aneurysm or arteriosclerosis. In this way, the feasibility of CFD as a predictive tool to use for treatment planning of cardiovascular diseases has been demonstrated. A methodology to obtain computational meshes from medical image has been defined. A new procedure to segment the aorta using 4D flow CMR data has also been proposed. Beyond this, 4D flow CMR visualization offers a more qualitative and comprehensive description of the flow fields than any other in-vivo imaging technique. The velocity data provided by 4D flow CMR has been complementary to the higher resolution velocity fields computed by the CFD in order to estimate the WSS. We have also developed an algorithm to compute WSS based on the 4D flow CMR data. Based on that approach other diagnostic indicators could be estimated, as pulse wave velocity(PWV)[89], turbulent kinetic energy[90], relative pressure fields[91] or volume and kinetic energy of ventricular flow compartments[92]. For full details refer to the 'Results sections of papers.

7.2 Limitations and Future work

The diagnostic indicators obtained in this monograph need to be validated and reproducible if they are to be useful for clinical workflows. Multicenter studies are necessary to establish the repeatability of various aspects of the technique used in the papers across centers. Widespread clinical usage would be facilitated by further integration into the standard clinical environment. The methodology developed in this monograph makes the process more robust and transparent, in the way that the models can be incorporated into clinical workflows. This means to develop interfaces and put them in a clinical context (in connection with imaging and clinical data accessed directly from the hospital's computer system) where physicians can use it. Several improvements and further possibilities are offered on the basis on the present papers.

The presented techniques are currently employed for patient-specific modeling of aorta and coronary arteries acquired from different modalities, both from geometric and fluid-dynamics points of view. A study (still to be published) on 20 coronary models reconstructed at Pie Medical Imaging (PMI), Maastricht, Netherlands has further demonstrated the validity of the computation method proposed. The coronary index for all 20 models will be computed in 1 hour with full automation and acceptable results. Further work will consist on reduce the computational time to be useful in a clinical routine and setting properly the hyperemia conditions of the patients. Another study (still to be published) on 23 Abdominal aneurysm model reconstructed at the International Center of numerical Methods in Engineering (CIMNE), Barcelona, Spain and Mechanical Engineering Division, CARTIF Technological, Valladolid, Spain has the objective to correlate the Intra Luminal Thrombus (ILT) with the hemodynamics parameters and the geometrical factor, in the sense of predicting the ILT evolution based only on the geometrical factor. Another indices can be estimated, for example, the flow-induced platelet activation (TFP) proposed by [11]. The main purpose of this index is to identify local regions of the wall that at the same time were exposed to prothrombotic WSS stimuli and a flow rich in activated platelets. TFP is defined as:

$TFP=ECAP\cdot PLAP={\frac {OSI\cdot PLAP}{TAWSS}}$

(7.1)

where PLAP is the PLatelet Activation Potential recently proposed [93]. TFP index combines the ECAP-based on WSS and the fluid shear history-based PLAP obtained by particle tracking. Briefly, the PLAP is a non-dimensional scalar index that represents the magnitude of shear rates that a fluid particle accumulates while travelling throughout the fluid domain.

$PLAP(x,t)=\int _{t-2T}^{t}|D(x(\tau ),\tau )|d\tau$

(7.2)

where |D(x(${\textstyle \tau }$),${\textstyle \tau }$)| is the Frobenius norm of the symmetric part of the spatial gradient of velocity tensor, t is the time of injection of the particle and 2T indicates how long the particle has been tracked. Collecting particle information for multiple cardiac cycles allows one to capture flow stagnation events that might be of importance in thrombogenesis [93].

Two new collaborations with the Hospital Sant Pau i Creu Blanca, Barcelona, Spain are now beginning. Both are related with the 4D flow CMR acquisition, Aortic Dissection and Portal pressure. Related to the Aortic Dissection, the objective is to improve the clinical intervention procedure, we are going to combine 4D flow CMR sequences with CFD to estimate the relative pressure in the true and false lumen. And related to the Portal pressure, the goal is to use 4D flow CMR sequence to estimate the flow and pressure in the Portal system with the objective of check the liver function. Besides of the clinical applications, a prototype of the software (AORTA4D) to visualize and quantify 4D flow CMR data is currently being developed in collaboration with GiD Department of CIMNE.

Several improvements and further technological possibilities are offered on the basis on the present papers. In the current papers there are a number of limitations to obtain the hemodynamics parameters that can be gradually removed. For instance, the autoregulation phenomenon, in response to hemodynamic stimuli, which is an important issue in coronary blood flow mechanisms, was not considered in the related work and it could be included in the future. For the 1D model used in the Paper 1, small distal vessels such as arterioles, capillaries, venules and veins were not modeled directly and may need to be investigated in detail. In that line, a more robust methodology to estimate the lumped parameters in patient-specific models would be needed. Addition of the pulmonary circulation could also close the circulation loop and make an even more useful model. For paper 2, the interaction between arterial blood flow and intraluminal thrombus was not taken into account, and it could play an important role in the development of some abdominal aneurysms, as well as, it would be needed to increase the number of the cases to get more evidences with the hemodynamics parameters obtained. For paper 4, the constitutive arterial model used for the AAA did not take into account the fiber distributions and the model used were geometrical model. About 4D flow CMR technologies there are still some uncertainties related to the clinical use, chapter 6 and chapter 7. Derived flow parameters, need further development or validation for clinical use, to include measurements of WSS, pressure difference, TKE or intracardiac flow components. The accuracy on the acquisition parameters measured is quite dependent of the clinical sequence (image-protocol) used. In our particular case, the WSS is quite dependent of the spatial resolution, therefore an accurate segmentation is needed. We are working on new segmentation algorithm (see figure 15). Additionally, a validation protocol using a phantom model would be needed.

Figure 15: Preliminary concept of automatic segmentation of the Aorta based on 4D MRI data

8 Cardiovascular physiology

The purpose of this appendix is to introduce which are the basics of the cardiovascular physiology. This brief overview of the cardiovascular physiology is only included for the purpose of providing essential information to scientists without a background in medicine. In this appendix the macroscopic and microscopic structure of arterial walls, blood modeling and cardiovascular system is briefly explained. For a more detailed exposition of the different mechanical/rheological characteristics of cardiovascular system and the overall functioning of the blood vessel see Tortora et al.[94].

8.1 Cardiovascular physiology

Cardiovascular physiology is the study of the cardiovascular system, specifically addressing the physiology of the heart (cardiac physiology) and blood vessels (circulatory physiologic) (see figure 16[95]). The cardiovascular system is a pressurized closed system responsible for transporting nutrients, hormones, and cellular waste throughout the body. From a physical point of view, there are three independent circuits:

• Systemic Circulation: The former brings oxygenated blood from the heart, thought arteries and capillaries, to the various organs (systemic arterial system) and then brings it back to heart (systemic venous system). The systemic arterial system is an extensive high-pressure system; hence the structure of its blood vessels reflects the high pressures to which they are subjected. The systemic venous system acts as a collecting system, returning blood from the capillary networks to the heart passively down a pressure gradient.
• Pulmonary circulation: The latter pumps the venous blood into the pulmonary artery where it enters the pulmonary system, through the pulmonary veins, get oxygenated and is finally received by the heart, ready to be sent to the systemic circulation (where the blood is pumped through the aortic valve into the aorta).
• The coronary circulation arises from the aorta and provides a blood supply to the myocardium, the heart muscle

Figure 16: The cardiovascular system is a close loop. The heart is a pump that circulates blood through the system. Arteries take blood away from the heart (systemic circulation) and veins (pulmonary circulation) carry blood back to the heart.

This monograph will focus on systemic arterial system and coronary circulation.

8.1.1 Blood Vessels

The blood vessels are the part of the circulatory system that transport blood throughout the body. The vascular system is composed of arteries, arterioles, capillaries, venules and veins (see figure 17[96]). The three main types of blood vessels are:

1. Arteries, which carry blood away from the heart at relatively high pressure,
2. Veins, which carry blood back to the heart at relatively low pressure and
3. Capillaries, which provide the link between the arterial and venous blood vessels.

Regarding the small vessels mention that arterioles are the smallest branches of the arterial network. Arterioles vary in diameter ranging from 0.3 mm to 0.4 mm. Any artery with a diameter smaller than 0.5 mm is considered to be an arteriole. Capillaries are specialized for diffusion of substances across their wall. Capillaries are the smallest vessels of the blood circulatory system and form a complex inter linking network. Pressure is essentially lost in the capillaries. As the capillaries begin to thicken and merge, they become venules. Venules eventually become veins and head back to the heart.

In general, arteries are roughly subdivided into two types: elastic (or large arteries) and muscular (or small arteries). Elastic arteries have relatively large diameters and are located close to the heart (for example, the aorta, the carotid and iliac arteries), while muscular arteries are located at the periphery (for example, femoral, celiac, cerebral arteries). The walls of all the blood vessels, except the capillaries which are only one cell thick, have the same basic components but the proportion of the components varies with function. Therefore, the structure of the vessels in the different parts of the circulatory or vascular system varies and the differences relate directly to the function of each type of vessel (see table 2). Arteries are not just tubes through which the blood flows.

Table. 2 Vessel Type

Vessels	Diameter of lumen (mm)	Wall thickness (mm)	Mean pressure (kPa)
Aorta	25	2	12.5
Large arteries	1-10	1	12
Small arteries	0.5-1	1	12
Arteriole	0.01-0.5	0.03	7
Capillary	0.006-0.01	0.001	3
Venule	0.01-0.5	0.003	1.5
Vein	0.5-15	0.5	1
Vein cava	30	1.5	0.5

All blood vessels, except capillaries, are composed of three distinct layers (tunica intima, tunica media and tunica externa or adventicia) surrounding a central blood carrying canal (known as the lumen). The constituents of arterial walls from the mechanical perspective are important to researchers interested in constitutive issues.

• Tunica intima. The tunica intima is the innermost layer of the artery. It composed of a lining layer of highly specialized multi-functional flattened epithelial cells termed endothelium. This sits on a basal lamina; beneath this is a very thin layer of fibro-collagenous support tissue.
• Tunica media. The tunica media is the middle layer in a blood vessel wall and is a complex three-dimensional network of smooth muscle cells reinforced by organized layers of elastic tissue which form elastic laminae. The tunica media is particularly prominent in arteries, being relatively indistinct in veins and virtually non-existent in very small vessels. From the mechanical perspective, the media is the most significant layer in a healthy artery.
• Tunica Adventicia. The tunica adventitia or externa is the outermost layer of blood vessels. It is composed largely of collagen, but smooth muscle cells may be present, particularly in veins. The tunica adventitia is often the most prominent layer in the walls of veins. Within the tunica adventitia of vessels with thick walls (such as large arteries and veins) are small blood vessels which send penetrating branches into the media to supply it with blood.

Veins do not have as many elastic fibers as arteries. Veins do have valves, which keep the blood from pooling and flowing back to the legs under the influence of gravity. When these valves break down, as often happens in older or inactive people, the blood does flow back and pool in the legs. The result is varicose veins, which often appear as large purplish tubes in the lower legs.

Figure 17: The human circulatory system (simplified). Red indicates oxygenated blood (arterial system), blue indicates deoxygenated (venous system).

8.1.2 Blood Modelling

Blood is a suspension of cells into a fluid called plasma. It delivers oxygen and nutrients to the cells and remove CO${\textstyle _{2}}$ and waste products. Blood also enables hormones and other substances to be transported between tissues and organs. The blood makes up about 7% of the weight of a human body, with a volume of about 5 litters in an average adult. Understanding blood physiology depends on understanding the components of blood. Blood is made up of plasma (about 55%) and cellular elements (about 45% These cellular elements include red blood cells (also called RBCs or erythrocytes), white blood cells (also called leukocytes) and platelets (also called thrombocyte) suspended in a plasma. Plasma is essentially a blood aqueous solution containing 92% water, 8% blood plasma proteins, and trace amounts of other materials (i.e albumin or globulin). Plasma has many functions as involving colloid, osmotic effects, transport, signaling, immunity and clotting.

• 5${\textstyle \ast }$10${\textstyle ^{12}}$ erythrocytes or red cells (45.0% of blood volume)in a woman 4.800.000 and in a men 5.400.400 erythrocytes per mm${\textstyle ^{3}}$ (or microliter) Size: disc biconcave 7 or 7.5 ${\textstyle \mu }$m of diameter. Erythrocytes are responsible for the exchange of oxygen and CO${\textstyle _{2}}$ with the cells.
• 9${\textstyle \ast }$10${\textstyle ^{9}}$ leukocytes or white cells(1.0% of blood volume) 4.500 y 11.500 per mm${\textstyle ^{3}}$ (or microliter) in the blood. Size: between 8 and 20 ${\textstyle \mu }$m. Leukocytes play a major role in the human immune system.
• 3${\textstyle \ast }$10${\textstyle ^{11}}$ thrombocytes (${\textstyle {>}}$1.0% of blood volume): Platelets are responsible for blood clotting (coagulation).

Blood viscosity is a measure of the resistance of blood to flow. The blood viscosity increases as the percentage of cells in the blood increases: more cells mean more friction, which means a greater viscosity. The percentage of the blood volume occupied by red blood cells is called the haematocrit. With a normal haematocrit of about 40 (that is, approximately 40% of the blood volume is red blood cells and the remainder plasma), the viscosity of whole blood (cells plus plasma) is about 3 times that the viscosity of the water. Other factors influencing blood viscosity include temperature, where an increase in temperature results in a decrease in viscosity. This is particularly important in hypothermia, where an increase in blood viscosity will provoke problems with blood circulation.

Blood compressibility is the relation between all of its components and their volume fraction or a measure of the relative volume change of a fluid as a response to a pressure change. The 92% of the blood is water, and how the water has a high relation of compressibility, blood can be consider an incompressible fluid. Mathematically, it is mean that the mass is conserved within the domain.

Usually, for small arteries (less than 1mm in diameter) blood is consider as Non-Newtonian fluid, however in medium/large arteries blood may be considered as Newtonian fluid. To explain this behaviour it is necessary to explain which the Fahraeus-Lindqvist effect is. Fahraeus-Lindqvist effect is characterized by a decrease in the apparent blood viscosity as the arteries diameter decreases below 500 mm. The minimum apparent viscosity is reached when the tube diameter is higher than 8 mm, upon further decreases in tube diameter, the apparent viscosity increases very rapidly. The physical reason behind the Fahraeus-Lindqvist effect is the formation of a cells-free layer near the wall of the tube[14]. The layer is devoid of RBCs and has a reduced local viscosity. The extent of the cell-free layer, which depends on the vessel size and haematocrit, is a major factor that determinate the apparent viscosity of the blood. The core of the tube, on the contrary, is rich with RBCs and has a higher local viscosity. However, in large arteries with internal diameter > 500 mm, although the blood density depends on the red cells concentration, the blood may be considered a homogeneous fluid with standard behavior (Newtonian fluid)[14]. The viscosity ${\textstyle \mu }$ of the fluid is proportional to ${\textstyle \tau }$${\textstyle _{ij}}$. Therefore, the rheological properties of blood depends on the vessels size, for instance, when the vessel diameter reduces to size comparable with the one of the red cells (below 12${\textstyle \mu }$m), blood cannot be considered as continuum any longer, therefore, blood is a complex fluid whose flow properties are significantly affected by the arrangement, orientation and deformability of red blood cells.

9 Numerical Model

One-Dimensional (1D) models of blood flow have been extensively used to study wave propagation phenomena in arteries. These models allow us to investigate physical mechanisms underlying changes in pressure and flow pulse waveforms that are produced by cardiovascular disease, however these models do not taken into account the effects provoked by the 3D geometry. In this appendix, the 1D mathematical formulation and the reduced model used in paper 1 ('A Reduced Order Model based on Coupled 1D/3D Finite Element Simulations for an Efficient Analysis of Hemodynamics Problems.) are briefly explained.

9.1 1D Mathematical Model

A preliminary basic knowledge about the cardiovascular system was given in appendix 8. We introduce an one-dimensional mathematical model to describe the flow motion in arteries and its interaction with the wall displacement in order to provide a better understanding of the hemodynamics in large vessels. In absence of branching, a short of an artery may be considered as a cylindrical compliant tube, and it can be described by using a curvilinear cylindrical coordinate system ${\textstyle \mathrm {(r,\Theta ,z)} }$ with the corresponding base unit vector ${\textstyle \mathrm {(e_{r},e_{\Theta },e_{z})} }$ radial, circumferential and axil unit vector, respectively, as show in figure 18. The vessel extends from ${\textstyle \mathrm {z=0} }$ to ${\textstyle \mathrm {z=L} }$ and this length ${\textstyle \mathrm {L} }$ is constant with time, therefore, the spatial domain ${\textstyle \mathrm {\Omega _{c}} }$ in cylindrical coordinate is defined as follows:

Figure 18: Section of an artery with the principal geometrical parameters

$\Omega _{c}=\{\mathrm {(r,\Theta ,z)} :0\leqslant \mathrm {r} \leqslant \mathrm {R(z,t)} ;\mathrm {\Theta } \epsilon [0,2\Pi );\mathrm {z} \epsilon (0,L);\Delta t>0\}$

(9.1)

Defined our domain, the following assumptions must be taken into account in order to deduce the one-dimensional mathematical model:

• Radial displacements. The wall displaces along the radial direction solely, thus at each point on the tube surface we may write ${\textstyle \mathrm {\eta =\eta \cdot e_{r}} }$, where ${\textstyle \mathrm {\eta =R_{z}-R_{0}} }$ is the displacement with respect to a reference radius ${\textstyle \mathrm {R_{0}} }$.
• Axial symmetry. All quantities are independent from the angular coordinate ${\textstyle \mathrm {\Theta } }$. As a consequence, every axial section, ${\textstyle \mathrm {z=constant} }$, remains circular during the wall motion. The arteries radius ${\textstyle \mathrm {R} }$ is a function of ${\textstyle \mathrm {z} }$ and ${\textstyle \mathrm {t} }$. A generic axial section will be indicated by ${\textstyle \mathrm {S=S(z,t)} }$ where,

$S(z,t)=\{(r,\Theta ,z):0\leqslant r\leqslant R(z,t);\Theta \epsilon [0,2\Pi );\Delta t>0\}$

(9.2)

and, its measure ${\textstyle \mathrm {A} }$ is given by

$A(z,t)=\int _{S}\,d\sigma =\pi R^{2}(z,t)=\pi \cdot \left[R_{0}(z)+\eta (z,t)\right]^{2}$

(9.3)

• Dominance axial velocity, the velocity components orthogonal to the ${\textstyle \mathrm {z} }$ axis are negligible compared to the component along ${\textstyle \mathrm {z} }$. The latter is indicated by ${\textstyle \mathrm {u_{z}} }$ and its expression in cylindrical coordinates reads:

$u_{z}(r,z,t)={\overline {u}}(z,t)\cdot s\cdot \left[{\frac {r}{R(z,t)}}\right]$

(9.4)

where ${\textstyle \mathrm {\overline {u}} }$ is the mean velocity in each axial section and ${\textstyle \mathrm {s} }$ is a velocity profile.

${\overline {u}}(z,t)={\frac {1}{A}}\cdot \int _{S}u_{z}\,d\sigma$

(9.5)

• Constant pressure, we assume that the pressure ${\textstyle \mathrm {P} }$ is constant on each axial section ${\textstyle \mathrm {S} }$, so that it depends only on ${\textstyle \mathrm {z} }$ and ${\textstyle \mathrm {t} }$.

${\overline {p}}(z,t)=\int _{S}p_{z}\,d\sigma$

(9.6)

• No body forces. We neglect body forces.

The resulting state variables are

${\overline {Q}}(z,t)=\int _{S}(z,t)u_{z}\,d\sigma =A(z,t)\cdot {\overline {u}}$ $A(z,t)=\int _{{\mathcal {S}}(z,t)}d\sigma =\pi R^{2}(z,t)$

(9.7)

where ${\textstyle A}$ is the cross-sectional area and ${\textstyle Q}$ is the volumetric flow rate.

Therefore, we have three independent variables ${\textstyle \mathrm {(A,u,p)} }$, or equivalently ${\textstyle \mathrm {(A,Q,p)} }$. Thus, we require three independent equations to get a solution. These three equations will be provided by equations of conservations of mass and momentum and an algebraic law that link the pressure and area of the artery.

9.1.1 Conservation equations

The conservation equations reflect a certain physical amount of a continuous medium that must always be satisfied and which are not limited in their application to the material. By applying the conservation equations in the domain ${\textstyle \Omega }$ the body ${\textstyle \beta }$ leads to an integral relationship. Since the integral relationship must hold for any sub-domain of the body, then the conservation equations can be expressed as partial differential equations. Before continuing with the conservation equations, the material time derivative of an integral relationship to any property space is defined by

${\dfrac {d}{dt}}\int _{\Omega }(\bullet )=\int _{\Omega }({\dfrac {d(\bullet )}{dt}}+{\mathcal {r}}(\bullet )\cdot \mathbf {v} )d\Omega$

(9.8)

which is the Reynold's transport theorem.

9.1.2 Conservation of the mass

A fundamental law of Newtonian mechanics is the conservation of the mass, also called continuity equation, contained in a material volume. Considering the vessel shown in figure 18 as our control volume, the principle of mass conservation requires that the rate of change of mass within the domain ${\textstyle \Omega _{t}}$ plus the net mass flux out of the control volume is zero.

Denoting the vessel volume as

$V(t)=\int _{0}^{L}Adz,$

(9.9)

where ${\textstyle L}$ is the length of the vessel and assuming there are no infiltration through the side walls, the mass conservation can be written as

$\rho {\dfrac {dV(t)}{dt}}+\rho Q(L,t)-\rho Q(0,t)=0$

(9.10)

where ${\textstyle \rho }$ is the blood density. If infiltration does occur we must add a source term to this equation [97]. To determine the one-dimensional equation of mass conservation, we insert the volume into equation 9.10 and, note that

$Q(L,t)-Q(0,t)=\int _{0}^{L}{\dfrac {\partial Q}{\partial z}}dz,$

we obtain

$\rho {\dfrac {d}{dt}}\int _{0}^{L}A(z,t)dz+\rho \int _{0}^{L}{\dfrac {\partial Q}{\partial z}}dz=0.$

If we assume ${\textstyle L}$ is independent of time we can take the time derivative inside the integral to arrive at

$\rho \int _{0}^{L}{\Biggl \{}{\dfrac {\partial A}{\partial t}}+{\dfrac {\partial Q}{\partial z}}{\Biggr \}}dz=0$

Since we have not specified the length ${\textstyle L}$, the control volume is arbitrary and so the above equation must be true for any value of ${\textstyle L}$ and so in general we require that the integrand is zero. We therefore obtain the differential one-dimensional mass conservation equation:

${\dfrac {\partial A}{\partial t}}+{\dfrac {\partial Q}{\partial z}}={\dfrac {\partial A}{\partial t}}+{\dfrac {\partial (uA)}{\partial z}}=0$

(9.11)

9.1.3 Conservation of the momentum

The momentum equation, also called the equation of motion, is a relation equating the rate of change of momentum of a selected portion of the body and the some of all forces acting on that portion. Again we consider the vessel as our control volume and assume that there is no flux through the side walls in the ${\textstyle z}$-direction. In this case, it states that the rate of change of momentum within the integration domain ${\textstyle \Omega _{t}}$ plus the net flux of the momentum out of the domain itself is equal to the applied forces on the domain and can be expressed over an arbitrary length ${\textstyle L}$ as

${\dfrac {\partial }{\partial t}}\int _{0}^{L}\rho Qdz+(\alpha \rho Qu)_{L}-(\alpha \rho Qu)_{0}=F$

(9.12)

where ${\textstyle F}$ is defined as the applied forces in the z-direction acting on the domain. The equation 9.12 includes the momentum-flux correction coefficient ${\textstyle \alpha }$, also called Coriolis coefficient, which accounts for the fact that the momentum flux calculated with averaged quantities (${\textstyle {\bar {u}}}$) does not consider non-linearity of sectional integration of flux momentum. So we may assume

${\dfrac {\partial }{\partial t}}\int _{S}\rho {\tilde {u}}^{2}A\equiv \alpha \rho {\tilde {u}}^{2}A=\alpha \rho Q{\tilde {u}}\quad \Rightarrow \quad \alpha (z,t)={\dfrac {\int _{S}{\tilde {u}}^{2}d\sigma }{A{\tilde {u}}^{2}}}={\dfrac {\int _{S}{\tilde {s}}^{2}d\sigma }{A}}$

(9.13)

In general, the coefficient ${\textstyle \alpha }$ vary in time and space, yet in our model it is taken constant as a consequence of 9.5 It is immediate to verify that ${\textstyle \alpha \geq 1}$.

The axial velocity profile s(y) is chosen a priori through the power-law relation

$s(y)=\gamma ^{-1}(\gamma +2)(1-y^{\gamma })$

(9.14)

where ${\textstyle y}$ is the radial coordinate and ${\textstyle \gamma }$ is a proper coefficient. Commonly accepted approximation are ${\textstyle \gamma =2}$ (${\textstyle \alpha =4/3}$), which corresponds to the Poiseuille solution (parabolic velocity profile), while ${\textstyle \gamma =9}$ (${\textstyle \alpha =1.1}$) leads to a more physiological flat profile, following the Womersley theory. The blood profile trend with these values are shown in figure 19.

We will see that the choice of ${\textstyle \alpha =1}$, which indicates a completely flat velocity profile, would lead to certain simplification in our analysis.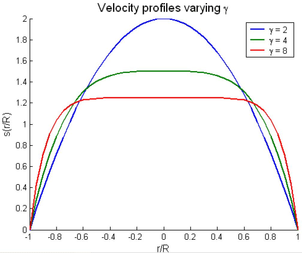

Figure 19: Blood flow profile adopting different values of $\gamma$.

To complete the equation 9.12 we need to define the applied forces ${\textstyle \mathbf {F} }$ which typically involve a pressure and a viscous force contribution,

$F=(PA)_{0}-(PA)_{L}+\int _{0}^{L}\int _{\partial S}{\hat {P}}n_{z}dsdz+\int _{0}^{L}fdz$

(9.15)

where ${\textstyle \partial S}$ represents the boundary of the section ${\textstyle S}$, ${\textstyle n_{z}}$ is the ${\textstyle z}$-component of the surface normal and f stands for the friction force per unit of length. The pressure force acting on the side walls, given by the double integral, can be simplified since we assumed both constant sectional pressure and axial symmetry of the vessel; so we have

$\int _{0}^{L}\int _{\partial S}{\hat {P}}n_{z}dsdz=\int _{0}^{L}P{\dfrac {\partial A}{\partial z}}dz$

(9.16)

If we finally combine equations 9.12,9.15 and 9.16 we obtain the momentum conservation for the computation domain expressed as

${\dfrac {d}{dt}}\int _{0}^{L}PQdz+(\alpha \rho Qu)_{L}-(\alpha \rho Qu)_{0}=(PA)_{0}-(PA)_{L}+\int _{0}^{L}P{\dfrac {\partial A}{\partial z}}dz+\int _{0}^{L}fdz$

(9.17)

To obtain the one-dimensional differential equation for the momentum we note that

$(\alpha \rho Qu)_{L}-(\alpha \rho Qu)_{0}=\int _{0}^{L}{\dfrac {\partial (\alpha \rho Qu)}{\partial z}}dz$ $(PA)_{0}-(PA)_{L}=-\int _{0}^{L}{\dfrac {\partial (PA)}{\partial z}}dz$

which inserted into 9.17, taking ${\textstyle L}$ independent of time and ${\textstyle \rho }$ constant, gives

$\rho \int _{0}^{L}{\Biggl \{}{\dfrac {\partial Q}{\partial t}}+{\dfrac {\partial (\alpha Qu)}{\partial z}}{\Biggr \}}dz=\int _{0}^{L}{\Biggl \{}-{\dfrac {\partial (PA)}{\partial z}}+P{\dfrac {\partial A}{\partial z}}+f{\Biggr \}}dz$

Once again this relationship is satisfied for an arbitrary length ${\textstyle L}$ and therefore can only be true when the integrands are equal. So the one-dimensional equation for the momentum conservation becomes

${\dfrac {\partial Q}{\partial t}}+\alpha {\dfrac {\partial }{\partial z}}{\Biggl (}{\dfrac {Q^{2}}{A}}{\Biggr )}=-{\frac {A}{\rho }}{\dfrac {\partial P}{\partial z}}+{\frac {f}{\rho }}$

(9.18)

The viscous term in the equation 9.15 can be taken proportional to the averaged velocity ${\textstyle {\bar {u}}}$, thus we write

${\dfrac {f}{\rho }}=K_{R}{\dfrac {Q}{A}}$

Therefore we finally obtain the equation of the momentum continuity

${\dfrac {\partial Q}{\partial t}}+\alpha {\dfrac {\partial }{\partial z}}{\Biggl (}{\dfrac {Q^{2}}{A}}{\Biggr )}=-{\frac {A}{\rho }}{\frac {\partial P}{\partial z}}+K_{r}{\bar {u}}$

(9.19)

where ${\textstyle K_{R}}$ is a strictly positive quantity that represents the viscous resistance of the flow per unit length of tube. It depends on the kinematic viscosity ${\textstyle \nu ={\frac {\mu }{\rho }}}$ of the fluid and the velocity profile s chosen. For a power law profile ${\textstyle s(y)}$, we have ${\textstyle K_{R}=2\pi \nu (\gamma +2)}$. In particular, for a parabolic profile ${\textstyle K_{R}=8\pi \nu }$, while for a flat profile we obtain ${\textstyle K_{R}=22\pi \nu }$.

9.1.4 Vessel wall constitutive model

Once we obtained the two governing equations 9.11 and 9.19, it is possible to write the one-dimensional system as

${\dfrac {\partial A}{\partial t}}+{\dfrac {\partial Q}{\partial z}}=0$ ${\dfrac {\partial Q}{\partial t}}+{\dfrac {\partial }{\partial z}}(\alpha {\dfrac {Q^{2}}{A}})+{\dfrac {A}{\rho }}{\dfrac {\partial P}{\partial z}}+K_{R}{\dfrac {Q}{A}}=0$

(9.20)

for all $z$ ${\textstyle \in (0,L)}$ and t ${\textstyle >}$ 0, where the unknown variables are ${\textstyle A}$, ${\textstyle Q}$ and ${\textstyle P}$. The system of equations 9.20 may be also expressed alternatively in terms of the variables ${\textstyle (A,{\bar {u}})}$ instead ${\textstyle (A,Q)}$.

${\dfrac {\partial A}{\partial t}}+{\dfrac {\partial A{\bar {u}}}{\partial z}}=0$ ${\dfrac {\partial {\bar {u}}}{\partial t}}+{\bar {u}}{\dfrac {\partial {\bar {u}}}{\partial z}}+{\dfrac {1}{\rho }}{\dfrac {\partial P}{\partial z}}+K_{R}{\bar {u}}=0$

(9.21)

As we can notice the number of unknown variables is greater than the number of equations (three against two); therefore we must provide another equation in order to close the system. A possibility is to introduce an algebraic relation linking the area of the vessel and pressure to the wall deformation. For the paper 1 we have considered the Generalised string model [98], which is written in the following form

$\rho _{w}h_{0}{\dfrac {\partial ^{2}\eta }{\partial t^{2}}}-{\tilde {\gamma }}{\dfrac {\partial \eta }{\partial t}}-{\tilde {a}}{\dfrac {\partial ^{2}\eta }{\partial z^{2}}}-{\tilde {c}}{\dfrac {\partial ^{3}\eta }{\partial t\partial z^{2}}}+{\tilde {b}}\eta =(P-P_{ext}),\qquad z\in (0,L),t>0$

(9.22)

We may identify the physical significance of the various terms:

• Inertia term: $\rho _{w}h_{0}{\dfrac {\partial ^{2}\eta }{\partial t^{2}}}$, proportional to the wall acceleration
• Voigt viscoelastic term: ${\tilde {\gamma }}{\dfrac {\partial \eta }{\partial t}}$, viscoelastic term, proportional to the radial displacement velocity
• Longitudinal pre-stress state of the vessel: ${\tilde {a}}{\dfrac {\partial ^{2}\eta }{\partial z^{2}}}$,
• Viscoelastic term: ${\tilde {c}}{\dfrac {\partial ^{3}\eta }{\partial t\partial z^{2}}}$,
• Elastic term: ${\tilde {b}}\eta$.

Besides ${\textstyle \rho _{w}}$ is the vessel density, ${\textstyle h_{0}}$ is the wall thickness, ${\textstyle {\tilde {a}}}$, ${\textstyle {\tilde {b}}}$ and ${\textstyle {\tilde {c}}}$ are three positive coefficients. We can develop the last term of 9.22 being

$\eta =R-R_{0}\qquad \Rightarrow \qquad \eta ={\dfrac {{\sqrt {A}}-{\sqrt {A_{0}}}}{\sqrt {\pi }}},\quad \quad A_{0}=\pi R_{0}^{2}$

Elastic model

The elastic response is the dominating effect, while the other terms are less important. Consequently, a first model is obtained by neglecting all derivatives in 9.22. Pressure and area will then be related by the following algebraic law

${\tilde {b}}={\dfrac {Eh_{0}}{kR_{0}^{2}}}={\dfrac {\pi Eh_{0}}{kA_{0}}},\qquad k=1-\nu ^{2}$

where ${\textstyle E}$ is the Young modulus of elasticity and ${\textstyle \nu }$ represents the Poisson ratio, typically taken to be ${\textstyle \nu =0.5}$ (then ${\textstyle k=0.75}$) since biological tissue is practically incompressible. We have taken ${\textstyle k=1}$.

$P-P_{ext}={\tilde {b}}\eta =\beta {\dfrac {{\sqrt {A}}-{\sqrt {A_{0}}}}{A_{0}}}$

(9.23)

where

$\beta =Eh_{0}{\sqrt {\pi }}$

is in general a function of z trough the Young modulus E. In a more general setting, the algebraic relationship may be expressed as

$P=P_{ext}+\psi (A;A_{0},\beta )$

(9.24)

where we outlined that the pressure will depend not only on ${\textstyle A}$, but also on ${\textstyle A_{0}}$ and on a set of coefficients ${\textstyle \beta ={\beta _{1},\beta _{2},\dots ,\beta _{n}}}$ which accounts for the physical and mechanical characteristics of the arterial vessel. Both ${\textstyle A_{0}}$ and ${\textstyle \mathbf {\beta } }$ are given functions of ${\textstyle z}$, but they do not vary in time. It is required that ${\textstyle \psi }$ be at least a ${\textstyle C^{1}}$ function of its arguments and be defined for each positive value of ${\textstyle A}$ and ${\textstyle A_{0}}$. In addition we must have, for all the allowable values of ${\textstyle A}$, ${\textstyle A_{0}}$ and ${\textstyle \beta }$ that

${\dfrac {\partial \psi }{\partial A}}>0,\qquad \psi (A_{0};A_{0},\beta )=0$

There are several examples of algebraic pressure-area relationship for one-dimensional models of arterial flow Langewouters_1984,Smith_2003; here we assumed the relationship 9.23, where ${\textstyle \beta =\beta _{1}}$ and, for the sake of simplicity, ${\textstyle P_{ext}=0}$. The function ${\textstyle \psi }$ can be written as

$\psi (A;A_{0},\beta _{1})=\beta _{1}{\dfrac {{\sqrt {A}}-{\sqrt {A_{0}}}}{A_{0}}}$

(9.25)

It is useful introduce the Moens-Korteweg velocity

$c_{1}(A;A_{0},\beta )={\sqrt {{\dfrac {A}{\rho }}{\dfrac {\partial \psi }{\partial A}}}}$

which represents the propagation speed of waves along the cylindrical vessels. In our case may be readily computes as

$c_{1}={\sqrt {\dfrac {\beta }{2\rho A_{0}}}}A^{\frac {1}{4}}$

(9.26)

Taking into account 9.23 the system 9.20 can be written in the conservation form

${\dfrac {\partial \mathbf {U} }{\partial t}}+{\dfrac {\partial \mathbf {F(U)} }{\partial z}}=\mathbf {S(U)} ,\quad z\in (0,L),\quad t>0$

(9.27)

where

$\mathbf {U} ={\begin{bmatrix}A\\Q\end{bmatrix}}$

(9.28)

are the conservative variables,

$\mathbf {F(U)} ={\begin{bmatrix}Q\\\alpha {\dfrac {Q^{2}}{A}}+C_{1}\end{bmatrix}}$

the corresponding fluxes, and

$\mathbf {S(U)} ={\begin{bmatrix}0\\-K_{R}{\dfrac {Q}{A}}+{\dfrac {\partial C_{1}}{\partial A_{0}}}{\dfrac {dA_{0}}{dz}}+{\dfrac {\partial C_{1}}{\partial \beta }}{\dfrac {d\beta }{dz}}\end{bmatrix}}$

a source term of the system. In our modelling, ${\textstyle A_{0}}$ and ${\textstyle \beta _{1}}$ are taken constant along the axial direction ${\textstyle z}$ because we assume that both the initial area ${\textstyle A_{0}}$ and the Young modulus ${\textstyle E}$ do not vary in space; so the expression of ${\textstyle \mathbf {S} }$ accounts only for the friction term depending on ${\textstyle K_{R}}$.

${\textstyle C_{1}}$ is a primitive of the wave speed ${\textstyle c_{1}}$, given by

$C_{1}(A;A_{0},\beta )=\int _{A_{0}}^{A}c_{1}^{2}(\tau ;A_{0},\beta )d\tau$

Applying the relationship 9.26 and 9.25, we obtain

$c_{1}={\sqrt {\dfrac {\beta _{1}}{2\rho A_{0}}}}A^{\frac {1}{4}}\quad \Rightarrow \quad C_{1}={\frac {\beta _{1}}{3\rho A_{0}}}A^{\frac {3}{2}}$

(9.29)

9.1.5 Characteristic analysis

One of the methods for solving non-linear hyperbolic system of partial differential equations, like the one-dimensional elastic model 9.27 , is the characteristic analysis [78]. After some simple manipulations the system 9.27 may be written in the quasi-linear form:

${\dfrac {\partial \mathbf {U} }{\partial t}}+\mathbf {H(U)} {\dfrac {\partial \mathbf {U} }{\partial z}}=\mathbf {B} (\mathbf {U} ),\qquad z\in (0,L),t>0$

(9.30)

where

$\mathbf {H(U)} ={\begin{bmatrix}0&1\\{\dfrac {A}{\rho }}{\dfrac {\partial \psi }{\partial A}}-\alpha {\bar {u}}^{2}&2\alpha {\bar {u}}\end{bmatrix}}={\begin{bmatrix}0&1\\c_{1}^{2}-\alpha {\Bigg (}{\dfrac {Q}{A}}{\Bigg )}^{2}&2\alpha {\dfrac {Q}{A}}\end{bmatrix}}$

is the Jacobian matrix. If ${\textstyle A_{0}}$ and ${\textstyle \beta }$ are constant ${\textstyle \mathbf {B} =-\mathbf {S} }$. Considering 9.30, we can calculate the eigenvalues for the matrix ${\textstyle \mathbf {H(U)} }$

$\lambda _{1,2}=\alpha {\dfrac {Q}{A}}\pm c_{\alpha }$

(9.31)

where

$c_{\alpha }={\sqrt {c_{1}^{2}+\alpha (\alpha -1){\dfrac {Q^{2}}{A^{2}}}}}$

Since the Coriolis coefficient ${\textstyle \alpha \geq 1}$ (we considered, for simplicity, ${\textstyle \alpha =1}$), ${\textstyle c_{\alpha }}$ is a real number; besides, under the assumption that ${\textstyle A>0}$, indeed a necessary condition to have physical relevant solution, ${\textstyle c_{1}>0}$; therefore we have ${\textstyle c_{\alpha }>0}$ which means ${\textstyle \mathbf {H} }$ has two real distinct eigenvalues and so, by definition, the system 9.30 is strictly hyperbolic. For typical values of velocity, vessel section and mechanical parameter ${\textstyle \beta _{1}}$ encountered in main arteries under physiologically conditions, we find that ${\textstyle \lambda _{1}>0}$ and ${\textstyle \lambda _{2}<0}$, i.e., the flow is sub-critical everywhere. Furthermore, it may be shown [99] that the flow is smooth. Discontinuities, which would normally appear when treating a non -linear hyperbolic system, do not have the time to form on out context because of the pulsatility of the boundary conditions. Afterwards this considerations, from now on we will assume sub-critical regime and smooth solutions.

Let ${\textstyle (\mathbf {l} _{1},\mathbf {l} _{2})}$ and ${\textstyle (\mathbf {r_{1}} ,\mathbf {r_{2}} )}$ be two couples of left and right eigenvectors of ${\textstyle \mathbf {H} }$. The matrices ${\textstyle \mathbf {R} }$, ${\textstyle \mathbf {L} }$ and ${\textstyle \mathbf {\Lambda } }$ are defined as

$\mathbf {L} ={\begin{bmatrix}\mathbf {l} _{1}^{T}\\\mathbf {l} _{2}^{T}\end{bmatrix}},\quad \mathbf {R} ={\begin{bmatrix}\mathbf {r} _{1}&\mathbf {r} _{2}\end{bmatrix}},\quad \mathbf {\Lambda } ={\begin{bmatrix}\lambda _{1}&0\\0&\lambda _{2}\end{bmatrix}}$

(9.32)

Since left and right eigenvalues are mutually orthogonal, we choose them so that ${\textstyle \mathbf {L} \mathbf {R} =\mathbf {I} }$, being ${\textstyle \mathbf {I} }$ the identity matrix. Matrix ${\textstyle \mathbf {H} }$ may then be decomposed as

$\mathbf {H} =\mathbf {R} \mathbf {\Lambda } \mathbf {L}$

and the system 9.30 takes the equivalent form

$\mathbf {L} {\dfrac {\partial \mathbf {U} }{\partial t}}+\mathbf {\Lambda } \mathbf {L} {\dfrac {\partial \mathbf {U} }{\partial z}}+\mathbf {L} \mathbf {B(U)} =0$

(9.33)

If there exist two quantities ${\textstyle W_{1}}$ and ${\textstyle W_{2}}$ which satisfy

${\dfrac {\partial W_{1}}{\partial \mathbf {U} }}=\mathbf {l_{1}} ,\quad {\dfrac {\partial W_{2}}{\partial \mathbf {U} }}=\mathbf {l_{2}}$

(9.34)

we will call them characteristic variables of the hyperbolic system. By setting ${\textstyle \mathbf {W} =[W_{1},W_{2}]^{T}}$ the system 9.33 may be elaborated into

${\dfrac {\partial \mathbf {W} }{\partial t}}+\mathbf {\Lambda } {\dfrac {\partial \mathbf {W} }{\partial z}}+\mathbf {G} =0$

(9.35)

where

$\mathbf {G} =\mathbf {L} \mathbf {B} -{\dfrac {\partial \mathbf {W} }{\partial A_{0}}}{\dfrac {dA_{0}}{dz}}-{\dfrac {\partial \mathbf {W} }{\partial \beta }}{\dfrac {d\beta }{dz}}$

Under the assumption that ${\textstyle A_{0}}$ and ${\textstyle \beta _{1}}$ are constant in space and taking ${\textstyle \mathbf {B} }$ negligible, the equation 9.35 becomes

${\dfrac {\partial \mathbf {W} }{\partial t}}+\mathbf {\Lambda } {\dfrac {\partial \mathbf {W} }{\partial z}}=0$

which is a system of decoupled scalar equation written as

${\dfrac {\partial W_{i}}{\partial t}}+\mathbf {\lambda _{i}} {\dfrac {\partial W_{i}}{\partial z}}=0$

(9.36)

From 9.36 we have ${\textstyle W_{1}}$ and ${\textstyle W_{2}}$ are constant along two characteristics curves in the (z,t) plane 20 described by the differential equations

${\dfrac {dz}{dt}}=\lambda _{1}\quad ,\quad {\dfrac {dz}{dt}}=\lambda _{2}$

Figure 20: Diagram of characteristics in the (z,t) plane. The solution on the point $R$ is obtained by the superimposition of the two characteristics $W_{1}$ and $W_{2}$.

The expression for the left eigenvectors ${\textstyle \mathbf {l} _{1}}$ and ${\textstyle \mathbf {l} _{2}}$ is given by

$\mathbf {l} _{1}=\xi {\begin{bmatrix}c_{\alpha }-\alpha {\bar {u}}\\1\end{bmatrix}},\quad \mathbf {l} _{2}=\xi {\begin{bmatrix}-c_{\alpha }-\alpha {\bar {u}}\\1\end{bmatrix}},$

(9.37)

where ${\textstyle \xi =\xi (A,{\bar {u}})}$ is any arbitrary smooth function of its arguments with ${\textstyle \xi >0}$. Here we have expressed ${\textstyle \mathbf {l} _{1}}$ and ${\textstyle \mathbf {l} _{2}}$ as functions of ${\textstyle (A,{\bar {u}})}$ instead of ${\textstyle (A,Q)}$ in order to simplify the next developments.

For an hyperbolic system of two equations is always possible to find the characteristic variables (or, equivalently, the Riemann invariants) locally, that is in a small neighbourhood of any point ${\textstyle \mathbf {U} }$ [100], yet the existence of global characteristic is not in general guaranteed. However, assuming ${\textstyle \alpha =1}$ the relationship 9.37 take the much simpler form

${\dfrac {\partial W_{1}}{\partial A}}=\xi c_{1},\qquad {\dfrac {\partial W_{1}}{\partial {\bar {u}}}}=\xi A$ (9.38) ${\dfrac {\partial W_{2}}{\partial A}}=-\xi c_{1},\qquad {\dfrac {\partial W_{2}}{\partial {\bar {u}}}}=\xi A$ (9.39)

We now show that a set of global characteristic variables do exist for the problem at hand. Since we note, from 9.38, that ${\textstyle W_{1,2}}$ are exact differentials being

${\dfrac {\partial ^{2}W_{i}}{\partial A\partial {\bar {u}}}}={\dfrac {\partial ^{2}W_{i}}{\partial {\bar {u}}\partial A}}$

for any values of ${\textstyle A}$ and ${\textstyle {\bar {u}}}$, we also have that ${\textstyle c_{1}}$ does not depend on ${\textstyle {\bar {u}}}$ and then, from above relationship we obtain

$c_{1}{\dfrac {\partial \xi }{\partial {\bar {u}}}}=\xi +A{\dfrac {\partial \xi }{\partial A}}$

In order to satisfy this relation we have to choose ${\textstyle g=g(A)}$ such that ${\textstyle g=-A{\dfrac {\partial g}{\partial A}}}$. To do this we can take ${\textstyle g=A^{-1}}$. As a consequence we can write

$\partial W_{1}={\dfrac {c_{1}}{A}}\partial A+\partial {\bar {u}},\quad \partial W_{2}=-{\dfrac {c_{1}}{A}}\partial A+\partial {\bar {u}}$

(9.40)

Taking ${\textstyle (A_{0},0)}$ as a reference state for our variables ${\textstyle (A_{0},{\bar {u}})}$ we can integrate the above relationships obtaining

$W_{1}={\bar {u}}+\int _{A_{0}}^{A}{\dfrac {c_{1}(\epsilon )}{\epsilon }}d\epsilon ,\qquad W_{2}={\bar {u}}-\int _{A_{0}}^{A}{\dfrac {c_{1}(\epsilon )}{\epsilon }}d\epsilon$

(9.41)

Introducing the expression 9.29 for ${\textstyle c_{1}}$ we have

$W_{1,2}={\dfrac {Q}{A}}\pm 4{\Bigg (}{\sqrt {\dfrac {\beta _{1}}{2\rho A_{0}}}}A^{\frac {1}{4}}-c_{0}{\Bigg )}$

(9.42)

with ${\textstyle c_{0}}$ is the wave speed related to the reference state. We finally can write the variables ${\textstyle (A,Q)}$ in terms of the characteristic ones,

$A={\Bigg (}{\dfrac {2\rho A_{0}}{\beta _{1}}}{\Bigg )}^{2}{\Bigg (}{\dfrac {W_{1}-W_{2}}{8}}{\Bigg )}^{4},\qquad Q=A{\dfrac {W_{1}+W_{2}}{2}}$

(9.43)

allowing in particular, the implementation of boundary and compatibility conditions, that we will discuss in the next section.

9.1.6 Boundary conditions

By the characteristic analysis of the one-dimensional model we pointed out the hyperbolic nature of the one-dimensional system of blood flow in arteries; consequently the solution is given by the superimposition of two waves whose eigenvalues ${\textstyle \lambda _{1,2}}$ represent the propagation speeds of such waves. As we have seen previously, they always have opposite sign and so blood flow is sub-critical; under this condition, we need an initial condition along all the spatial domain and two boundary conditions to close the governing system: one at the inlet section ${\textstyle z=0}$ and the other at the outlet ${\textstyle z=L}$ (see figure 21).

Figure 21: Boundary and initial conditions of the hyperbolic system.

Figure 22: One-dimensional model with absorbing conditions.

Different type of boundary conditions can be imposed. An important class of boundary conditions is represented by the so-called non-reflecting or absorbing boundary conditions [101], which allows the simple wave associated with the characteristics to enter or leave the domain without spurious reflections (see Figure 22). Absorbing boundary conditions can be imposed by defining values for the wave entering the domain; in our case we have ${\textstyle \lambda _{1}>0}$ and ${\textstyle \lambda _{2}<0}$ so ${\textstyle W_{1}}$ is the entering characteristic in ${\textstyle z=0}$ and ${\textstyle W_{2}}$ the inlet characteristic in ${\textstyle Z=L}$. In Hedstrom [102], non-reflecting boundary conditions for an hyperbolic problem are written as

$\mathbf {l} _{1}\cdot {\Bigg [}{\dfrac {\partial \mathbf {U} }{\partial t}}-\mathbf {B} (\mathbf {U} ){\Bigg ]}_{x=0}=0,\quad \mathbf {l} _{2}\cdot {\Bigg [}{\dfrac {\partial \mathbf {U} }{\partial t}}-\mathbf {B} (\mathbf {U} ){\Bigg ]}_{x=L}=0$

When there is an explicit formulation of the characteristic variables, it is possible impose the boundary conditions directly in terms of incoming characteristics, for example

$W_{1}(t)=g_{1}(t),\qquad {\hbox{in}}\quad z=0,t>0$

being ${\textstyle g_{1}(t)}$ a given function. However, the problem rarely have boundary data in terms of variable characteristics, they are normally expressed in terms of physical variables.

In addition to absorbing boundary conditions based on characteristic variables, it may impose a function that describes the temporal trend on the edge of one of the unknown functions of the problem, then the flux flow ${\textstyle Q}$ (or the speed ${\textstyle u}$) or the area ${\textstyle A}$. Conditions of this type are typically used on the proximal node ${\textstyle z=0}$ and can be expressed as follows:

$Q(0,t)=g_{q}(t),\quad t>0$ $A(0,t)=g_{a}(t),\quad t>0$

The boundary conditions imposed by the knowledge of the physical variables are reflective. Therefore, if we impose such a condition in the proximal node, the incoming characteristic variable, that we denoted by ${\textstyle W_{2}}$, will be partially reflected in the computational domain. This is a real physical phenomenon.

The initial conditions are the conditions to be imposed by defining the value of ${\textstyle A(z,t)}$ and ${\textstyle Q(z,t)}$ along the spatial domain ${\textstyle z\in (0,L)}$ at the initial time ${\textstyle t=0}$. For instance if we require the area at the initial time, the initial condition is expressed as

$A(z,t)=A_{0}(z),\quad z\in (0,L)$

9.1.6.1 Terminals lumped parameter

The assumptions made for the 1-D model become less appropriate with decreasing the size of the arteries; for example, the blood flow in the larger arteries is pulsatile and is dominated by inertia while in the capillaries is almost stable and dominant by the viscosity. Consequently, the 1-D model should be limited until at the distal section of the domain ${\textstyle (z=L)}$. We have seen a first approach which imposes not reflective boundary conditions in the vessels terminals 9.44, but this solution is not adherent to reality. We then introduce the lumped parameter models (0-D) who consider the fact that the pressure waves are physically in part reflected and partly absorbed. These models coupled with the one-dimensional constitutive equation 9.27 leads to a multiscale framework 1-D/0-D. Therefore, the hemodynamic effects of the blood vessels after the distal section limit are generally simulated using a lumped parameter model governed by ordinary differential equations that relate the pressure with the flow at the outlet of the 1-D model [103].

Expressing the system 9.30 in terms of ${\textstyle (A,P,Q)}$ with ${\textstyle Q=A{\bar {u}}}$ and linearising around the state of reference ${\textstyle (A_{0},0,0)}$, with ${\textstyle \beta }$ an ${\textstyle A_{0}}$ be constant along ${\textstyle z}$, is obtained.

$C_{1D}{\dfrac {\partial p}{\partial t}}+{\dfrac {\partial q}{\partial z}}=0$ $L_{1D}{\dfrac {\partial q}{\partial t}}+{\dfrac {\partial p}{\partial z}}=-R_{1D}q$ $p={\dfrac {a}{C_{1D}}}$

(9.44)

where ${\textstyle a}$,${\textstyle p}$ and ${\textstyle q}$ are the perturbation variables for area, pressure and volume flux, respectively ${\textstyle (A_{0}+a,p,q)}$ and

$R_{1D}={\dfrac {\rho c_{0}}{A_{0}}},\qquad C_{1D}={\dfrac {A_{0}}{\rho c_{0}^{2}}},\qquad L_{1D}={\dfrac {\rho }{A_{0}}}$

(9.45)

are the viscous resistance to flow, wall compliance and blood inertia, respectively, per unit of length of vessel ${\textstyle l}$. Integrating system 9.44 over the length ${\textstyle l}$ yields the lumped parameter model, where the variables are ${\textstyle R_{0D}=R_{1D}l}$, ${\textstyle C_{0D}=C_{1D}l}$, ${\textstyle L_{0D}=L_{1D}l}$ and ${\textstyle {\hat {p}}={\frac {1}{l}}\int _{0}^{l}pdz,{\hat {q}}={\frac {1}{l}}\int _{0}^{l}qdz}$ are the mean pressure and flow over the whole domain. In physiological conditions pulsatile waves travel at a speed greater compared to that of the blood, then ${\textstyle {\hat {p}}=p_{in}}$ and ${\textstyle {\hat {q}}=q_{out}}$. Therefore, the final 0-D model is the following:

$C_{0D}{\dfrac {\partial p_{in}}{\partial t}}+q_{out}-q_{in}=0$ $L_{0D}{\dfrac {\partial q_{out}}{\partial t}}+R_{0D}q_{out}+p_{out}-p_{in}=0$

(9.46)

where ${\textstyle q_{in}=q(0,t)}$, ${\textstyle q_{out}=q(L,t)}$, ${\textstyle p_{in}=p(0,t)}$ and ${\textstyle p_{out}=p(L,t)}$ are the flows and pressures at the inlet and outlet of the 0-D domain. As it is represented in Figure 23, the system 9.46 is analogous to an electric circuit, in which the role of the flow and pressure are played by the current and potential, ${\textstyle R_{0D}}$ corresponds to an electric resistance, ${\textstyle C_{0D}}$ to a capacitance and ${\textstyle L_{0D}}$ to an inductance [104].

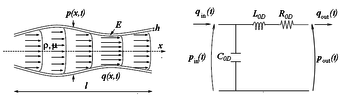
Figure 23: 1-D arterial vessel domain (left) and the equivalent 0-D system discretises at first order in space (right).

Table. 3 Analogy between hydraulic and electrical network.

Hydraulic	Physiological variables	Electric
Pressure ${\textstyle P[Pa]}$	Blood pressure ${\textstyle [mmHg]}$	Voltage ${\textstyle V}$
Flow rate ${\textstyle Q[m^{3}/s]}$	Blood flow rate ${\textstyle [L/s]}$	Current ${\textstyle I}$
Volume ${\textstyle V[m^{3}]}$	Blood volume ${\textstyle [L]}$	Charge ${\textstyle q[C]}$
Viscosity ${\textstyle \eta }$	Blood viscosity ${\textstyle \mu [Pa\cdot s]}$	Electrical resistance ${\textstyle R}$
Elastic coefficient	Vessel's wall compliance	Capacitance ${\textstyle C}$
Inertance	Blood inertia	Inductance ${\textstyle L}$

9.1.7 Implementation

The nonlinear hyperbolic system 9.27 has been discretized using a Taylor-Galerkin scheme [105], which is the finite element equivalent of Lax-Wendroff (based on the expansion in Taylor series) stabilisation for the finite difference method. This method may result in short computational times, and is second order accurate in both time and space.

Considering the equation 9.27 and having ${\textstyle \mathbf {H} ={\dfrac {\partial \mathbf {F} }{\partial \mathbf {U} }}}$ we may write

${\dfrac {\partial \mathbf {U} }{\partial t}}=\mathbf {S} -{\dfrac {\partial \mathbf {F} }{\partial z}}$ ${\dfrac {\partial ^{2}\mathbf {U} }{\partial t^{2}}}={\dfrac {\partial \mathbf {S} }{\partial \mathbf {U} }}{\dfrac {\partial \mathbf {U} }{\partial t}}-{\dfrac {\partial }{\partial z}}{\Bigg (}\mathbf {H} {\dfrac {\partial \mathbf {U} }{\partial t}}{\Bigg )}$ $={\dfrac {\partial \mathbf {S} }{\partial \mathbf {U} }}{\Bigg (}\mathbf {S} -{\dfrac {\partial \mathbf {F} }{\partial z}}{\Bigg )}-{\dfrac {\partial \mathbf {H} \mathbf {B} }{\partial z}}+{\dfrac {\partial }{\partial z}}{\Bigg (}\mathbf {H} {\dfrac {\partial \mathbf {F} }{\partial z}}{\Bigg )}$

(9.47)

For simplicity the dependence of ${\textstyle \mathbf {S} }$ and ${\textstyle \mathbf {F} }$ from ${\textstyle \mathbf {U} }$ is dropped. Starting from the above equations, we now consider the time intervals ${\textstyle (t^{n},t^{n+1})}$, for ${\textstyle n=0,1,\dots ,T}$; then we discretize the equation in time using a Taylor series which includes first and second order derivatives if ${\textstyle \mathbf {U} }$. Therefore we obtain the following semi-discrete schemes for the approximation ${\textstyle \mathbf {U} ^{n+1}}$ of ${\textstyle \mathbf {U} (t^{n+1})}$:

• Taylor-Galerkin scheme:

$\mathbf {u} ^{n+1}=\mathbf {u} ^{n}+\Delta t\mathbf {u} _{t}^{n}+{\dfrac {\Delta t^{2}}{2}}\mathbf {u} _{tt}^{n}$

(9.48)

$\mathbf {U} ^{n+1}=\mathbf {U} ^{n}-\Delta t{\dfrac {\partial }{\partial z}}{\Bigg (}\mathbf {F} ^{n}+{\dfrac {\Delta t}{2}}\mathbf {H} ^{n}\mathbf {S} ^{n}{\Bigg )}+{\dfrac {\Delta t^{2}}{2}}{\Bigg [}\mathbf {S} _{\mathbf {U} }^{n}{\dfrac {\partial \mathbf {F} ^{n}}{\partial z}}-{\dfrac {\partial }{\partial z}}{\Bigg (}\mathbf {H} ^{n}{\dfrac {\partial \mathbf {F} ^{n}}{\partial z}}{\Bigg )}{\Bigg ]}$ $+\Delta t{\Bigg (}\mathbf {S} ^{n}+{\dfrac {\Delta t}{2}}\mathbf {S} _{\mathbf {U} }^{n}\mathbf {S} ^{n}{\Bigg )},\qquad n=0,1,\dots$

(9.49)

where ${\textstyle \mathbf {S} _{\mathbf {U} }^{n}={\dfrac {\partial \mathbf {S} ^{n}}{\partial \mathbf {U} }}}$ and ${\textstyle \mathbf {F} ^{n}}$, stands for ${\textstyle \mathbf {F(U^{n})} }$, just as ${\textstyle \mathbf {H} ^{n}}$, ${\textstyle \mathbf {S} ^{n}}$ and ${\textstyle \mathbf {S} _{\mathbf {U} }^{n}}$; the value ${\textstyle \mathbf {U} ^{0}}$ is given by the initial conditions.

For each time interval ${\textstyle (t^{n},t^{n+1})}$ we apply a spatial discretization carried out using the Galerkin finite element method. To this purpose we subdivide the domain ${\textstyle \Omega =\{z:z\in (0,L)\}}$, which is the 1-D counterpart of the 3-D domain ${\textstyle \Omega _{t}}$, into a finite number ${\textstyle N_{el}}$ of linear elements length ${\textstyle l}$ (Figure 24).

Figure 24: One-dimensional mesh representing a vessel.

Moreover we introduce a trial function space, ${\textstyle {\mathcal {T}}}$, and a weighting function space, ${\textstyle {\mathcal {W}}}$. These spaces are both defined to consist of all suitably smooth functions and to be such that

${\mathcal {T}}={\Big \{}\mathbf {U} (z,t)|\mathbf {U} (z,0)=\mathbf {U} ^{0}(z){\hbox{ on }}\Omega _{t}\quad {\hbox{at}}\quad t=t^{0}{\Big \}},\qquad {\mathcal {W}}={\Big \{}{\mathcal {W}}(\mathbf {z} ){\Big \}}$

Considering the scheme, we multiply the equation 9.49 for the weight function ${\textstyle \mathbf {W} }$ and we integrate it over the domain ${\textstyle \Omega _{t}}$ obtaining, for ${\textstyle \forall t>0t^{0}}$

$\int _{\Omega }{\Bigg (}\mathbf {U} ^{n+1}-\mathbf {U} ^{n}{\Bigg )}d\Omega =-\Delta t{\Bigg [}\int _{\Omega }{\dfrac {\partial \mathbf {W} }{\partial z}}\mathbf {F} _{LW}^{n}d\Omega -\int _{\Omega }\mathbf {S} _{LW}^{n}\mathbf {W} d\Omega {\Bigg ]}-$ $-{\dfrac {\Delta t^{2}}{2}}{\Bigg [}\int _{\Omega }{\dfrac {\partial \mathbf {W} }{\partial z}}\mathbf {S_{U}} ^{n}\mathbf {F} ^{n}-\int _{\Omega }{\dfrac {\partial \mathbf {W} }{\partial z}}{\dfrac {\partial \mathbf {F} ^{n}}{\partial z}}\mathbf {H} ^{n}{\Bigg ]}-$ $-\Delta t{\Bigg [}N_{i}{\bar {\mathbf {F} }}_{r}^{n}|_{z=L}-N_{i}{\bar {\mathbf {F} }}_{l}^{n}|_{z=0}{\Bigg ]}$

(9.50)

where we have assumed

$\mathbf {F} _{LW}^{n}(\mathbf {U} _{j})=\mathbf {F} ^{n}+{\dfrac {\Delta t}{2}}\mathbf {H} ^{n}\mathbf {S} ^{n}$

and

$\mathbf {S} _{LW}^{n}(\mathbf {U} _{j})=\mathbf {S} ^{n}+{\dfrac {\Delta t}{2}}\mathbf {S_{U}} ^{n}\mathbf {S} ^{n}$

Starting from the weak form of the problem 9.50 we build the subspaces ${\textstyle {\mathcal {T}}^{h}}$ and ${\textstyle {\mathcal {W}}^{h}}$ for the trial and weighting function spaces ${\textstyle {\mathcal {T}}}$ and ${\textstyle {\mathcal {W}}}$ defining them as

${\mathcal {T}}^{h}={\Bigg \{}{\hat {\mathbf {U} }}(z,t)|{\hat {\mathbf {U} }}(z,t)=\sum _{j=1}^{N}\mathbf {U} _{j}(t)N_{j}(z);\quad \mathbf {U} (t^{0})={\bar {\mathbf {U} }}(z_{j})=\mathbf {U} _{j}^{0}{\Bigg \}}$ ${\mathcal {W}}^{h}={\Bigg \{}{\mathcal {W}}(z,t)|{\mathcal {W}}(z)=\sum _{j=1}^{N}W_{j}(t)N_{j}(z){\Bigg \}}$

(9.51)

where ${\textstyle N_{j}}$ is the standard linear finite element shape function (Figure 25) associated to the ${\textstyle j-th}$ node, located at ${\textstyle z=z_{j}}$, and ${\textstyle \mathbf {U} _{j}}$ and ${\textstyle {\hat {\mathbf {U} }}}$ at the node ${\textstyle j}$. Since we are using the Galerkin method, the base shape functions defined above are used as weighting.

Figure 25: Sketch of a 1D linear shape function.

Adopting the following notation

$(W,U)_{\Omega _{e}}=\int _{\Omega _{e}}W\cdot Ud\Omega ,$

and considering the sum of each element contribution

$\int _{\Omega }\dots =\sum _{el}\int _{\Omega _{e}}\dots ,$

the equation 9.50 becomes

$\sum _{el}(N_{i},N_{j})_{\Omega _{e}}(\mathbf {U} _{j}^{n+1}-\mathbf {U} _{j}^{n})=\Delta t\sum _{el}[(N_{i,z},N_{j})_{\Omega _{e}}\mathbf {F} _{LW}^{n}(\mathbf {U} _{j})+N_{i},N_{j})_{\Omega _{e}}\mathbf {S} _{LW}^{n}(\mathbf {U} _{j})]-$ $-{\dfrac {\Delta t^{2}}{2}}\sum _{el}{\Bigg (}(N_{i},N_{j})_{\Omega _{e}}\mathbf {S_{U}} ^{n}(\mathbf {U} _{j}){\dfrac {\partial \mathbf {F} _{j}^{n}}{\partial z}}{\Bigg )}-$ $-{\dfrac {\Delta t^{2}}{2}}\sum _{el}{\Bigg (}(N_{i,z},N_{j})_{\Omega _{e}}\mathbf {H} _{j}^{n}(\mathbf {U} _{j}){\dfrac {\partial \mathbf {F} _{j}^{n}}{\partial z}}{\Bigg )}-$ $-\Delta t{\Bigg [}N_{i}{\bar {\mathbf {F} }}_{r}^{n}|_{z=L}-N_{i}{\bar {\mathbf {F} }}_{l}^{n}|_{z=0}{\Bigg ]}$

(9.52)

For what concerns the border nodes, we have to consider the boundaries condition. Starting from the equation 9.52, we have the term of boundary conditions represented by

$\Delta t{\Bigg [}N_{i}{\bar {\mathbf {F} }}_{r}^{n}|_{z=L}-N_{i}{\bar {\mathbf {F} }}_{l}^{n}|_{z=0}{\Bigg ]},\qquad i=1,2$

which implies the knowledge of the flux terms depending from the values of ${\textstyle A}$ and ${\textstyle Q}$ at inlet and outlet sections of the domain. To extract them from the characteristic information ${\textstyle W_{1}(0,t)}$ and ${\textstyle W_{2}(L,t)}$ we need an additional expression for the other characteristic variables ${\textstyle W_{2}(0,t)}$ and ${\textstyle W_{1}(L,t)}$ to recover ${\textstyle \mathbf {U} (A,Q)}$ using the equation 9.43. To this purpose we adopted a technique based on the extrapolation of the outgoing characteristics. Having the friction parameter ${\textstyle K_{r}}$ small with respect to the other equation terms in 9.27, we assume that at the boundary points ${\textstyle z=0}$ and ${\textstyle z=L}$ the flow is generated by the characteristic system 9.36. At a generic time step ${\textstyle n}$ we have ${\textstyle \mathbf {U} ^{n}}$ known and we linearise the eigenvalues ${\textstyle \lambda _{1,2}}$ of 9.27 by taking their values at respective boundary for ${\textstyle t=t^{n}}$. The solution corresponding to this linearised problem at time ${\textstyle t^{n+1}}$ gives

$W_{2}^{n+1}(0)=W_{2}^{n}(-\lambda _{2}^{n}(0)\Delta t)$ $W_{1}^{n+1}(L)=W_{1}^{n}(-\lambda _{1}^{n}(L)\Delta t)$

which is a first-order approximation of the outgoing characteristic variables from the previous step. By using these information together with the values of ${\textstyle W_{1}^{n+1}(0)}$ and ${\textstyle W_{2}^{n+1}(L)}$ , we are able to compute, through 9.43, the required boundary data.

We choose to use, for time integration, both a second and fourth order explicit Runge-Kutta scheme; such methods are diffused in computational fluid dynamics, and show good properties, e.g ease of programming, simple treatment of boundary conditions and good stability. Regarding the stability, the second order Taylor-Galerkin scheme entails a time step limitations. A linear stability analysis [106] indicates that the following Courant-Friedrichs-Lewy condition should be satisfied

$\Delta t\leq {\dfrac {\sqrt {3}}{3}}\min _{0\leq i\leq N}{\Bigg [}{\dfrac {h_{i}}{\max(\lambda _{1,i},\lambda _{1,i+1})}}{\Bigg ]}$

(9.53)

where ${\textstyle \lambda _{1,i}}$ here indicates the value of ${\textstyle \lambda _{1}}$ at mesh node ${\textstyle z_{i}}$. This condition, which is necessary to obtain the stability of a method explicitly imposes a constraint on the choice of the discretization time and space of the method used; it corresponds to a CFL number of ${\textstyle {\frac {\sqrt {3}}{3}}}$.

9.1.7.1 Branching

The vascular system is characterized by the presence of branching. The flow in a bifurcation is intrinsically 3-D, however may be still described by means of a 1-D model. In order to manage a branching zone, when using a 1-D formulation, we follow a technique called domain decomposition [107]. The numerical solver accounts for the treatment of two types of bifurcation: the bifurcation 2-1 typical of the arterial system and the bifurcation 1-1 which represents two vessel linked together with different mechanical properties.

9.1.7.2 Bifurcation 1-2

The bifurcation 1-2 represents the typical branching of the arterial system. As we have introduced we have used the domain decomposition method to solve this problem. We divide the domain ${\textstyle \Omega }$ into three partitions ${\textstyle \Omega _{1}}$,${\textstyle \Omega _{2}}$ and ${\textstyle \Omega _{3}}$ as is showed at Figure 26; doing this we have 3 sub-problems which must be coupled imposing adequate boundary conditions. Then we have to evaluate 6 variables, ${\textstyle (A_{i},Q_{i})}$ with ${\textstyle i=1,2,3}$, corresponding to the problem unknowns, area and flow rate for each one of the vessels composing the branching.

Figure 26: Domain decomposition of a bifurcation 1-2.

From the decomposition of the governing system into characteristic variables we know that the system can be interpreted in terms of a forward and backward travelling waves. Considering the model of a splitting bifurcation shown in Figure 26, we denote the parent vessel by an index 1 and its two daughter vessels by the indices 2 and 3, respectively. The simplest condition we can impose to require the mass conservation through the bifurcation and therefore the flow rate balance can be written

$Q_{1}=Q_{2}+Q_{3}$

remembering that the flow moves from the sub-domain ${\textstyle \Omega _{1}}$ to the sub-domain ${\textstyle \Omega _{2}}$ and ${\textstyle \Omega _{3}}$. Other two assumptions can be obtained from the requirement of continuity of the momentum flux at the bifurcation. This lead to consider the total pressure term continuous at the boundary. So we may write

$P_{1}+{\dfrac {1}{2}}\rho {\Bigg (}{\dfrac {Q_{1}}{A_{1}}}{\Bigg )}^{2}=P_{2}+{\dfrac {1}{2}}\rho {\Bigg (}{\dfrac {Q_{2}}{A_{2}}}{\Bigg )}^{2}$

$P_{1}+{\dfrac {1}{2}}\rho {\Bigg (}{\dfrac {Q_{1}}{A_{1}}}{\Bigg )}^{2}=P_{3}+{\dfrac {1}{2}}\rho {\Bigg (}{\dfrac {Q_{3}}{A_{3}}}{\Bigg )}^{2}$

The remaining three relationship can be derived using the characteristic variables. The parent vessel can only reach the junction by a forward travelling wave. This wave is denoted as ${\textstyle W_{1}^{1}}$, where the superscript is the vessel number while the subscript stands for the forward direction. Similarly, the characteristics variables of daughter vessels, which can reach the bifurcation only by backwards travelling wave, are represent by ${\textstyle W_{2}^{2}}$ and ${\textstyle W_{2}^{3}}$.

$W_{1}^{1}={\dfrac {Q_{1}}{A_{1}}}+4{\sqrt {\dfrac {\beta _{1}}{2\rho A_{01}}}}A_{1}^{1/4}=u_{1}+4(c_{1}-c_{0}^{1})$ $W_{2}^{1}={\dfrac {Q_{2}}{A_{2}}}-4{\sqrt {\dfrac {\beta _{2}}{2\rho A_{02}}}}A_{2}^{1/4}=u_{2}+4(c_{2}-c_{0}^{2})$ $W_{2}^{2}={\dfrac {Q_{3}}{A_{3}}}-4{\sqrt {\dfrac {\beta _{3}}{2\rho A_{03}}}}A_{3}^{1/4}=u_{3}+4(c_{3}-c_{0}^{3})$

where ${\textstyle c_{0}^{1}}$,${\textstyle c_{0}^{2}}$and ${\textstyle c_{0}^{3}}$ are the values of the wave speed evaluated using the area ${\textstyle A_{0}}$ in the vessels 1,2 and 3. In summary, the resulting system which determines the values ${\textstyle (A_{1},Q_{1})}$,${\textstyle (A_{2},Q_{2})}$ and ${\textstyle (A_{3},Q_{3})}$ at the bifurcation is the following

$W_{1}^{1}={\dfrac {Q_{1}}{A_{1}}}+4{\sqrt {\dfrac {\beta _{1}}{2\rho A_{01}}}}A_{1}^{1/4}$ $W_{2}^{1}={\dfrac {Q_{2}}{A_{2}}}-4{\sqrt {\dfrac {\beta _{2}}{2\rho A_{02}}}}A_{2}^{1/4}$ $W_{2}^{2}={\dfrac {Q_{3}}{A_{3}}}-4{\sqrt {\dfrac {\beta _{3}}{2\rho A_{03}}}}A_{3}^{1/4}$ $Q_{1}=Q_{2}+Q_{3}$ $P_{1}+{\dfrac {1}{2}}\rho {\Bigg (}{\dfrac {Q_{1}}{A_{1}}}{\Bigg )}^{2}=P_{2}+{\dfrac {1}{2}}\rho {\Bigg (}{\dfrac {Q_{2}}{A_{2}}}{\Bigg )}^{2}$ $P_{1}+{\dfrac {1}{2}}\rho {\Bigg (}{\dfrac {Q_{1}}{A_{1}}}{\Bigg )}^{2}=P_{3}+{\dfrac {1}{2}}\rho {\Bigg (}{\dfrac {Q_{3}}{A_{3}}}{\Bigg )}^{2}$

(9.54)

We can solve it through the Newton-Raphson technique for differential systems of non-linear equations.This type of modelling does not consider the geometry of the junctions. For instance, the angle between the various vessels are not take into account.

9.1.7.3 Bifurcation 1-1

The discontinuity at the interface between arteries with different materials(mechanical behaviour) or geometrical properties is solved with a similar process used in the treatment of the bifurcations 2-1. Following the domain decomposition method adopted before, we proceed by splitting the problem in two sub-domains ${\textstyle \Omega _{1}}$ and ${\textstyle \Omega _{2}}$, and solving the following non-linear system for the interface variables, namely

$W_{1}={\dfrac {Q_{1}}{A_{1}}}+4{\sqrt {\dfrac {\beta _{1}}{2\rho A_{01}}}}A_{1}^{1/4}$ $W_{2}={\dfrac {Q_{2}}{A_{2}}}-4{\sqrt {\dfrac {\beta _{2}}{2\rho A_{02}}}}A_{2}^{1/4}$ $Q_{1}=Q_{2}$ $P_{1}+{\dfrac {1}{2}}\rho {\Bigg (}{\dfrac {Q_{1}}{A_{1}}}{\Bigg )}^{2}=P_{2}+{\dfrac {1}{2}}\rho {\Bigg (}{\dfrac {Q_{2}}{A_{2}}}{\Bigg )}^{2}$

(9.55)

Again, We solve the non-linear system obtained through the Newton-Raphson method. In both systems 9.54 and 9.55, it has been verified that the determinant of the Jacobian is different from zero for all allowable values of the parameters, thus guaranteeing that the Newton iteration is well-posed [108].

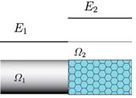
Figure 27: Domain decomposition of a bifurcation 1-1.

9.1.7.4 Coupling 1-D and 3D-reduced model

In order to consider into the 1D model an external pressure drop, we need to modify the total pressure term (9.55) adding the function f${\textstyle ^{3D}}$(k${\textstyle _{1}}$,k${\textstyle _{2}}$):

$P_{i}+{\frac {1}{2}}\rho {\frac {{Q_{i}}^{2}}{{A_{i}}^{2}}}=P_{j}+{\frac {1}{2}}\rho {\frac {{Q_{j}}^{2}}{{A_{j}}^{2}}}+{f^{3D}}_{j}(k_{1},k_{2})$

(9.56)

where indexes ${\textstyle {\hbox{i}}}$ and ${\textstyle {\hbox{j}}}$ denote the parent and the daughter vessels respectively and the function f${\textstyle ^{3D}}$(k${\textstyle _{1}}$,k${\textstyle _{2}}$) denotes the external pressure drop (or energy losses). In our case f${\textstyle ^{3D}}$ is the pressure drop of the 3D model.

${f^{3D}}_{j}(k_{1},k_{2})=k_{1}Q_{j}+k_{2}\mid Q_{j}\mid Q_{j}$

(9.57)

k${\textstyle _{1}}$ and k${\textstyle _{2}}$ are the viscous and turbulent coefficients that should be adjusted according to the pressure drop between the inlet/outlet planes defined in the 3D model.

Personalized 3D reduced order model In our particular case, firstly we need to solve the 3D problem (real case). To estimate the coefficients k1 and k2 of the equation (9.57), at each time step t${\textstyle _{n}}$, we calculate and store the mean values of the flow and the pressure at the inlet and the outlet of our 3D domain. Using these values we choose k${\textstyle _{1}}$ and k${\textstyle _{2}}$ that minimizes the sum of squared pressure drop by least squares method. In this way we are able to capture the energy losses provoked by the geometry of our 3D model, and take into account in the 1D model.

9.1.8 Coupling 1-D and 0-D models

The existence and uniqueness of the solution of a coupled problem between the 0-D model system 9.46 and the hyperbolic 1-D system 9.35, has been proven by Formaggia [109] for a sufficiently small time so that the characteristic curve leaving the 1-D/0-D interface does not intersect with incoming characteristic curves. Numerically, the coupling problem between a 1-D domain and a 0-D model is established through the solution of a Riemann problem at the interface (Figure 28). An intermediate state ${\textstyle (A^{*},U^{*})}$ originates at time ${\textstyle t+\Delta t}$ from the states ${\textstyle (A_{L},U_{L})}$ and ${\textstyle (A_{R},U_{R})}$ at time ${\textstyle t}$. The state ${\textstyle (A_{L},U_{L})}$ corresponds to the end point of the 1-D domain, and ${\textstyle (A_{R},U_{R})}$ is a virtual state selected so that ${\textstyle (A^{*},U^{*})}$ satisfies the relation between ${\textstyle A^{*}}$ and ${\textstyle U^{*}}$ dictated by system 9.46. The 1-D and 0-D variables at the interface are related through ${\textstyle q_{in}=A^{*}U^{*}}$ and ${\textstyle p_{in}={\frac {\beta }{A_{0}}}({\sqrt {A^{*}}}-{\sqrt {A_{0}}})}$, and ${\textstyle p_{out}}$ is prescribed as a constant parameter that represents the pressure at which flow to the venous system ceases.

Figure 28: Coupling 1-D/0-D model.

According to the method of characteristics, if ${\textstyle G=0}$ equation 9.35 leads to

$W_{1}(A^{*},U^{*})=W_{1}(A_{L},U_{L})$ (9.58) $W_{2}(A^{*},U^{*})=W_{2}(A_{R},U_{R})$ (9.59)

Solving 9.58 for ${\textstyle A^{*}}$ and ${\textstyle U^{*}}$ yields

$A^{*}={\Bigg [}{\sqrt {\dfrac {2\rho A_{0}}{\beta }}}{\dfrac {W_{1}(A_{L},U_{L})-W_{2}(A_{R},U_{R})}{8}}+A_{0}^{\frac {1}{4}}{\Bigg ]}^{4}$

(9.60)

$U^{*}={\dfrac {W_{1}(A_{L},U_{L})+W_{2}(A_{R},U_{R})}{2}}$

(9.61)

The 1-D outflow boundary condition is imposed by enforcing that either ${\textstyle U_{R}=U_{L}}$, which reduces Eq. 9.60 to

$A_{R}={\Bigg [}2(A^{*})^{\frac {1}{4}}-(A_{L})^{\frac {1}{4}}{\Bigg ]}^{4}$

(9.62)

or ${\textstyle A_{R}=A_{L}}$, which reduces Eq. 9.61 to

$U_{R}=2U^{*}-U_{L}$

(9.63)

9.1.8.1 Terminal resistance (R) model

This model simulates the peripheral circulation as a purely resistive load ${\textstyle Rp}$, (R${\textstyle _{0D}}$=Rp, L${\textstyle _{0D}}$=0, C${\textstyle _{0D}}$= 0) (Figure 23) and in which the state ${\textstyle (A^{*},U^{*})}$ satisfies

$A^{*}U^{*}={\dfrac {P(A^{*})-p_{out}}{R_{p}}}$

(9.64)

Combining with 9.46 we leads to a non-linear equation

${\mathcal {F}}(A^{*})=R_{p}{\Bigg [}{\Big [}U_{L}+4c(A_{L}){\Big ]}A^{*}-4c(A^{*})A^{*}{\Bigg ]}-{\dfrac {\beta }{A_{0}}}{\Bigg (}{\sqrt {A^{*}}}-{\sqrt {A_{0}}}{\Bigg )}+p_{out}=0$

(9.65)

which is solved using Newton-Raphson method, with the initial value of ${\textstyle A^{*}=A_{L}}$. Once ${\textstyle A^{*}}$ has been obtained, ${\textstyle U^{*}}$ is calculated from Eq. 9.61. If we consider both ${\textstyle C}$ and ${\textstyle L}$ equal to zero, we lead to the single terminal resistance model.

9.1.8.2 Three-element (RCR) Windkessel model

This model accounts for the resistance and the compliance of the peripheral vessels using the ${\textstyle RCR}$ Windkessel model, which accounts for the cumulative effects of all distal vessels (small arteries, arterioles and capillaries). The three-element Windkessel model consists of two resistances ${\textstyle R_{1}}$ and ${\textstyle R_{2}}$ and a capacitor ${\textstyle C}$. According to Section 9.1.8.1, we consider ${\textstyle R_{1}}$ to let any incoming wave reach the ${\textstyle CR_{2}}$ system without being reflected. Waves are reflected by the ${\textstyle CR_{2}}$ system, which is governed by

$C{\dfrac {dP_{c}}{dt}}=A^{*}U^{*}-{\dfrac {p_{c}-p_{out}}{R_{2}}}$

(9.66)

The first resistance, ${\textstyle R_{1}}$, is introduced in order to absorb the incoming waves and reduces artificial wave reflections. It satisfies

$A^{*}U^{*}={\dfrac {P(A^{*})-(p_{c})^{n}}{R_{1}}}$

(9.67)

where ${\textstyle (p_{C})^{n}}$ is the pressure at ${\textstyle C}$ at the time step ${\textstyle n}$. It is determining by solving at every time step ${\textstyle n}$ the first-order time discretisation of the Eq. 9.66

$p_{C}^{n}=p_{C}^{n-1}-{\dfrac {\Delta t}{C}}A^{*}U^{*}$

(9.68)

The coupling is solved as for the ${\textstyle R}$ terminal resistance model, but with ${\textstyle p_{out}=p_{c}}$ and ${\textstyle R_{1}=R_{p}}$

${\mathcal {F}}(A^{*})=R_{1}{\Bigg [}{\Big [}U_{L}+4c(A_{L}){\Big ]}A^{*}-4c(A^{*})A^{*}{\Bigg ]}-{\dfrac {\beta }{A_{0}}}{\Bigg (}{\sqrt {A^{*}}}-{\sqrt {A_{0}}}{\Bigg )}+p_{c}=0$

(9.69)

Again, once ${\textstyle A^{*}}$ is obtained by Netwon-Rapshon, we can proceed to calculated ${\textstyle U^{*}}$, int his case from 9.67.

9.1.9 Validation

A validation against in-vivo data is very difficult because some of the geometrical and elastic properties of the biological system are very complicated to measure. This is the reason because experimental replicas of the cardiovascular system to assess numerical tool are commonly used. To validate the 1D formulation implemented, the experimental model developed by Matthys et al. has been used [103] (1:1 silicone human arterial network). The silicone network is connected proximal to a pulsatile pump providing for a periodic input flow with the following settings: 70 ${\textstyle bpm}$ and a stroke volume of 70 ${\textstyle ml}$, creating a mean pressure of approximately 100 ${\textstyle mmHg}$ at the aortic root, these are typical values of a normal healthy person. Outflow boundary conditions were set of terminal resistance tubes connected to overflow reservoirs, creating a closed loop hydraulic system which induces a back pressure of 3.2 ${\textstyle mmHg}$. A 65–35${\textstyle \%}$ water–glycerol mixture, with density ${\textstyle \rho }$ = 1050 ${\textstyle kg\cdot m^{3}}$ and viscosity ${\textstyle \mu }$ =5 ${\textstyle mPa\cdot s}$, was used to simulate the blood. The elastic wall properties of the silicone sample have a constant Young's modulus of 1.2 ${\textstyle MPa}$. The properties of the silicone network are summarize in table 4[103], as we can see the measurement report an interval of confidence, which unfortunately will affect the comparison between the experimental data and our results. For the simulations we have used the mean values show in the table 4.

Although the experimental set-up is only an approximation to the human systemic circulation, it is able to reproduce pulse waveforms with significant physiological features in the aortic vessels. Figure 30 shows some of the main physiological features of pulse pressure, velocity and flow rate described previously. We observe that the numerical solver is able to describe the peaking and steepening pulse pressure as we move away from the heart, and a reduction in amplitude of the flow with the distance from the heart.

Figure 29: a) Plan view schematic of the hydraulic model. 1: Pump (left heart); 2: catheter access; 3: aortic valve; 4: peripheral resistance tube; 5: stiff plastic tubing (veins); 6: venous overflow; 7: venous return conduit; 8: buffering reservoir; 9: pulmonary veins. (b) Topology and references labels of the arteries simulated, whose properties are given in table 4. (c) Detail of the pump and the aorta.

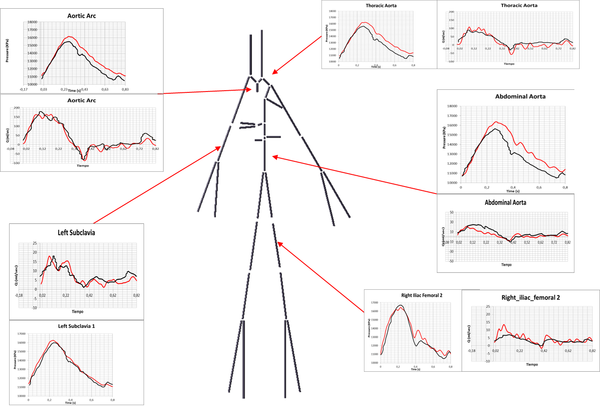
Figure 30: Simulated physiological(blank line) versus numerical results(red line) features of pressure and flow rate in difference section of the cardiovascular system.

Table. 4 Properties of the 37 silicon vessels used in the in-vitro model. The interval of confidence of the geometrical measurements is indicated in the heading.

n	Arterial segment	l [cm]	r [cm]	h [mm]	c[${\textstyle ms^{-1}}$]	$R_{p}[GPa\cdot s\cdot m^{-3}]$
		$\pm$2.0%	$\pm$3.5%	$\pm$2.5%
1.	Ascending Aorta	3.6	1.440	0.51	5.21	-
2.	Innonimate	2.8	1.100	0.35	4.89	-
3.	R. Carotid	14.5	0.537	0.28	6.35	2.67
4.	R. Subclavian I	21.8	0.436	0.27	6.87	-
5.	R. Subclavian II	16.5	0.334	0.16	6.00	-
6.	R. radial	23.5	0.207	0.15	6.78	3.92
7.	R. ulnar	17.7	0.210	0.21	8.81	3.24
8.	Aortic arch I	2.1	1.300	0.50	5.41	-
9.	L. Carotid	17.8	0.558	0.31	6.55	3.11
10.	Aortic arch II	2.9	1.250	0.41	4.98	-
11.	L. Subclavian I	22.7	0.442	0.22	6.21	-
12.	L. Subclavian II	17.5	0.339	0.17	6.26	-
13.	L. radial	24.5	0.207	0.21	8.84	3.74
14.	L. ulnar	1.91	0.207	0.16	7.77	3.77
15.	Thoracic Aorta I	5.6	1.180	0.43	5.29	-
16.	Intercostals	19.5	0.412	0.27	7.07	2.59
17.	Thoracic Aorta II	7.2	1.100	0.34	4.84	-
18.	Celiac I	3.8	0.397	0.20	6.20	-
19.	Celiac II	1.3	0.431	1.25	14.9	-
20.	Splenic	19.1	0.183	0.13	7.24	3.54
21.	Gastric	19.8	0.192	0.11	6.73	4.24
22.	Hepatic	18.6	0.331	0.21	6.95	3.75
23.	Abdominal Aorta I	6.2	0.926	0.33	5.19	-
24.	L. renal	12.0	0.259	0.19	7.39	3.46
25.	Abdominal Aorta II	7.0	0.790	0.35	5.83	-
26.	R. renal	11.8	0.255	0.16	6.95	3.45
27.	Abdominal Aorta III	10.4	0.780	0.30	5.41	-
28.	R. iliac-femoral I	20.5	0.390	0.21	6.47	-
29.	R. iliac-femoral II	21.6	0.338	0.15	5.89	-
30.	R. iliac-femoral III	20.6	0.231	0.20	8.04	-
31.	L. iliac-femoral I	20.1	0.402	0.20	6.19	-
32.	L. iliac-femoral II	19.5	0.334	0.16	6.11	-
33.	L. iliac-femoral III	20.7	0.226	0.13	6.67	-
34.	R. anterior tibial	16.3	0.155	0.15	8.47	5.16
35.	R. posterior tibial	15.1	0.153	0.12	7.73	5.65
36.	L. posterior tibial	14.9	0.158	0.11	7.23	4.59
37.	L. anterior tibial	12.6	0.156	0.10	7.01	3.16

10 Python Script

10.1 Phyton Script

# ------------------------------------------------------------
# SHEAR FORCE SECTION
# ------------------------------------------------------------
# Ok. For this routine, Shear Stress components is NOT GIVEN,
# and therefore calculated with the velocity gradient, fluid dynamic
# viscosity, and fluid shear routine therefore, we will have to do
# some pre-operations.
# ------------------------------------------------------------
# NOTE:
# Using Solution (FAQ) "Fluid Forces, Drag Calculations in
# EnSight" (#3), under "II. Shear Forces" steps a-i we have:
#
##################################################
#Procedure:
# a. in the fluid domain surrounding the surface, define vx,
# vy, vx, the velocity components, as three new scalars
# b. using the Grad operator in the variable calculator, compute the
# gradient of each of these components in the fluid, resulting
# in new gradient vectors of these components,
# i.e. grad_vx, grad_vy, grad_vz
# c. these gradients must be mapped from the fluid onto the surface.
# This is done either by using the Case Map feature in EnSight, or
# creating an isosurface (velocity = 0.) or a clip plane that
# corresponds to the surface of interest.
# d. Compute the fluid shear stress components using the FluidShear
# function in the variable calculator and the mapped velocity gradients.
# A value for the fluid’s dynamic viscosity must be provided.
# This may also be a scalar variable.
# e. Create a fluid shear stress vector from these components using
# the MakeVect function in the variable calculator.
# f. We need the tangential component of the fluid shear stress
# vector in order to integrate the shear stress forces and moments.
# The tangential component may be displayed by projecting
# this from the Feature Detail Editor (Vector Arrows)
# g. Compute the tangential component of the shear stress.
# This is done using vector algebra.
# First, create a surface normal vector variable using
# the Normal function in the variable calculator.
# Next, dot this with the shear stress vector, and multiply
# this product by the surface normal vector.
# This produces the normal component of the shear stress vector.
# The tangential component is now computed by subtracting this normal
# component from the shear stress vector, or Vt = V - Vn, where V
# represents the shear stress vector.
# h. We now use the tangential component of the surface shear stress,
# itself a vector, to compute a shear stress force vector,
# simple by multiplying the x/y/z components of the tangential
# component of the shear stress by the incremental surface area.
# Part #1 is Fluid Domain
# Part #2 is the Wall of interest.
# vel_name is velocity vector
# Begin
vel_name = "_VelocityVEC"
fluid_part_num = 2
surface_part_num = 1
viscosity = 3.5
tbegin=0
tend=4
num_steps = tend-tbegin+1 #added 1 for total num timesteps if start
# from 0
ensight.part.select_begin(fluid_part_num)
ensight.variables.activate(vel_name)
#
# b. With ONLY fluid part(s) selected...
# Calculate a gradient vector from each component these velocity
# components
ensight.part.select_begin(fluid_part_num)
# Note gradient function requires additional step of extracting
# vector components of velocity prior to calling it. You cannot,
# for example, directly reference Velocity[X], and etc.
ensight.variables.evaluate("VelX = "+vel_name+"[X]")
ensight.variables.evaluate("VelY = "+vel_name+"[Y]")
ensight.variables.evaluate("VelZ = "+vel_name+"[Z]")
ensight.variables.evaluate("GradU = Grad(plist,VelX)")
ensight.variables.evaluate("GradV = Grad(plist,VelY)")
ensight.variables.evaluate("GradW = Grad(plist,VelZ)")
# c. Now select boundary part(s).
# Map the 3 component gradient vectors from the fluid part(s)
# to the surface part(s) via CaseMap using 1 case on itself.
# Case Map CaseMap(2D or 3D part(s), case to map from, scalar/vector/
# tensor). Finds the specified scalar, vector, or tensor variable
# values for the specified part(s) from the indicated case.
ensight.part.select_begin(surface_part_num)
ensight.variables.evaluate("CaseMap_GradU = CaseMap(plist,1,GradU,1)")
ensight.variables.evaluate("CaseMap_GradV = CaseMap(plist,1,GradV,1)")
ensight.variables.evaluate("CaseMap_GradW = CaseMap(plist,1,GradW,1)")
#
# d. With boundary part(s) selected...
# Compute the Fluid Shear stress (Tau) components
# Compute the fluid shear stress components using the FluidShear
# function in the variable calculator and the mapped velocity
# gradients. A value for the fluid’s dynamic viscosity must
# be provided. This may also be a scalar variable.
ensight.variables.evaluate("TauU = FluidShear(plist,CaseMap_GradU," +
str(viscosity) + ")")
ensight.variables.evaluate("TauV = FluidShear(plist,CaseMap_GradV," +
str(viscosity) + ")")
ensight.variables.evaluate("TauW = FluidShear(plist,CaseMap_GradW," +
str(viscosity) + ")")
#
# e. With boundary part(s) selected...
# Create the fluid shear stress vector
# Create a fluid shear stress vector from these components using
# the MakeVect function in the variable calculator.
ensight.variables.evaluate("Tau = MakeVect(plist,TauU,TauV,TauW)")
#
# f. With boundary part(s) selected...
# You can visually inspect the vector arrows of Tau on the boundary
# part by creating these vector arrows and displaying the tangential
# component
# g. With boundary part(s) selected...
# Compute the decomposed tangential vector components of the Tau:
# 1. Computing the surface Normal vector on the boundary part(s)
ensight.variables.evaluate("Normal = Normal(plist)")
# 2. Creating the decomposed normal vector component of the Tau
# vector: by dotting Tau with the surface Normal and
# multiplying this scalar by the surface Normal again.
ensight.variables.evaluate("TauN = DOT(Tau,Normal)*Normal")
# 3. Creating the decomponed tangential vector component of the
# Tau vector: by subtracting, i.e. TauT = Tau - TauN
ensight.variables.evaluate("TauT = Tau-TauN")
#
# h. With boundary part(s) selected...
# Compute the element shear-stress force
# 1. Extract the 3 component scalars from TauT
ensight.variables.evaluate("TauTx = TauT[X]")
ensight.variables.evaluate("TauTy = TauT[Y]")
ensight.variables.evaluate("TauTz = TauT[Z]")
# 2. Compute the element area scalar
ensight.variables.evaluate("EleSize = EleSize(plist)")
# 3. Compute the tangential shear-stress component forces
ensight.variables.evaluate("FtauTx = TauTx*EleSize")
ensight.variables.evaluate("FtauTy = TauTy*EleSize")
ensight.variables.evaluate("FtauTz = TauTz*EleSize")
#
# i. With boundary part(s) selected...
# Now, sum up each shear-stress force component into constant values
ensight.variables.evaluate("sumFSX = StatMoment(plist,FtauTx,0)")
ensight.variables.evaluate("sumFSY = StatMoment(plist,FtauTy,0)")
ensight.variables.evaluate("sumFSZ = StatMoment(plist,FtauTz,0)")
# These three constant variables should contain the components of the
# shear stress. Grab the variables from EnSight to be able to store
# in a python register or print
sumFX=ensight.ensvariable("sumFX")
sumFY=ensight.ensvariable("sumFY")
sumFZ=ensight.ensvariable("sumFZ")
sumFSX=ensight.ensvariable("sumFSX")
sumFSY=ensight.ensvariable("sumFSY")
sumFSZ=ensight.ensvariable("sumFSZ")
# place these variables into storage array for printing
print "---------------- Force Summary --------------------"
print " Fx Fy Fz"
print "Shear Force : ",sumFSX[0], sumFSY[0], sumFSZ[0]
ensight.part.select_begin(surface_part_num)
# WSS = TauU,TauV,TauW
#|WSS| =Mod_Tau
ensight.variables.evaluate("Mod_Tau=SQRT(TauU^2+TauV^2+TauW^2)")
ensight.variables.evaluate("I_Mod_WSS = TempMean(plist,Mod_Tau, "
+ str(tbegin) + " , " + str(tend) + ")")
ensight.variables.evaluate("I_WSS = TempMean(plist,Tau, "
+ str(tbegin) + " , " + str(tend) + ")")
ensight.variables.evaluate("Mod_I_WSS=SQRT(I_WSS[X]^2+I_WSS[Y]^2+
I_WSS[Z]^2)")
ensight.variables.evaluate("OSI=0.5*(1-(Mod_I_WSS/I_Mod_WSS))")
ensight.variables.evaluate("RRT = 1/((1-2*OSI)*Mod_I_WSS)")
ensight.variables.evaluate("ECAP = OSI/Mod_I_WSS")

References

[1] Kwak, Brenda R. and Bäck, Magnus and Bochaton-Piallat, Marie-Luce and Caligiuri, Giuseppina and Daemen, Mat J.A.P. and Davies, Peter F. and Hoefer, Imo E. and Holvoet, Paul and Jo, Hanjoong and Krams, Rob and Lehoux, Stephanie and Monaco, Claudia and Steffens, Sabine and Virmani, Renu and Weber, Christian and Wentzel, Jolanda J. and Evans, Paul C. (2014) "Biomechanical factors in atherosclerosis: mechanisms and clinical implications", Volume 35. The Oxford University Press. European Heart Journal 43 3013–3020

[2] S. M. Wasserman and J. N. Topper. (2004) "Adaptation of the endothelium to fluid flow: in vitro analyses of gene expression and in vivo implications", Volume 9. Vascular Medicine 1 35-45

[3] DePaola N, and Gimbrone MA, and et al. (1992) "Vascular endothelium responds to fluid shear stress gradients", Volume 12. Arteriosclerosis, Thrombosis, and Vascular Biology 11 1254-1257.

[4] White, C. R., and M. Haidekker, and et al. (2001) "Temporal gradients in shear, but not spatial gradients, stimulate endothelial cell proliferation.", Volume 103. Circulation 20 2508-2513

[5] J. Biasetti, and F. Hussain and T. C. Gasser. (2011) "Blood flow and coherent vortices in the normal and aneurysmatic aortas: a fluid dynamical approach to intra-luminal thrombus formation", Volume 8. Journal of The Royal Society Interface 1449-1461

[6] D. N. Ku, and D. P. Giddens, and C. K. Zarins, and S. Glagov. (1985) "Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low oscillating shear stress.", Volume 5. Arteriosclerosis, Thrombosis, and Vascular Biology. 3 293-302

[7] K. S. Cunningham and A. I. Gotlieb. (2005) "The role of shear stress in the pathogenesis of atherosclerosis", Volume 85. Laboratory investigation, 1 9-23

[8] Samady, H. and Eshtehardi P., and McDaniel, M. C. and Suo, J. and Dhawan, S. S. and Maynard, C. and Timmins L. H., and Quyyumi A.A. and Giddens D. P. (2011) "Coronary artery wall shear stress is associated with progression and transformation of atherosclerotic plaque and arterial remodeling in patients with coronary artery disease.", Volume 124. Circulation 7 779-788

[9] Wentzel, Jolanda J. and Chatzizisis, Yiannis S. and Gijsen, Frank J.H. and Giannoglou, George D. and Feldman, Charles L. and Stone, Peter H. (2012) "Endothelial shear stress in the evolution of coronary atherosclerotic plaque and vascular remodelling: current understanding and remaining questions", Volume 96. The Oxford University Press. Cardiovascular Research 2 234-243

[10] J. Biasetti, and P. G. Spazzini, and J. Swedenborg and T. C. Gasser. (2012) "An integrated fluid-chemical model toward modeling the formation of intra-luminal thrombus in abdominal aortic aneurysms", Volume 3. Frontiers in Physiology 266

[11] Di Achille, P. and Tellides, G. and Figueroa, C. A. and Humphrey, J. D. (2014) "A haemodynamic predictor of intraluminal thrombus formation in abdominal aortic aneurysms", Volume 470. The Royal Society. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 2172

[12] A. Malek and S. Alper and S. Izumo. (1999) "Hemodynamic shear stress and its role in atherosclerosis.", Volume 282. The Journal of the American Medical Association 21 2035-2042

[13] Chatzizisis YS, and Coskun AU, and Jonas M, and Edelman ER, and Feldman CL, and Stone PH. (2007) "Role of endothelial shear stress in the natural history of coronary atherosclerosis and vascular remodeling: molecular, cellular, and vascular behavior.", Volume 49. Elsevier Inc. Journal of the American College of Cardiology 25 2379-93

[14] Perktold. (1991) "Pulsatile non-Newtonian Blood Flow in Three-Dimensional Carotid Bifurcation Models: A Numerical Study of Flow Phenomena Under Different Bifurcation Angles.", Volume 13. Journal of Biomedical Engineering 507-515

[15] Soudah, E. and Ng, E. and Loong, Th. and Bordone, M. and Pua, U. and Narayanan, S. (2013) "CFD Modelling of Abdominal Aortic Aneurysm on Hemodynamic Loads using a Realistic Geometry with CT", Volume 2564. Computational and Mathematical Methods in Medicine 9

[16] Xiang J, and Natarajan SK, and Tremmel M, Ma D, and Mocco J, and Hopkins LN, and Siddiqui AH, and Levy EI, Meng H. (2011) "Hemodynamic-Morphologic Discriminants for Intracranial Aneurysm Rupture", Volume 42. Stroke 1 144-52

[17] Lee SW, and Antiga L, and Steinman DA. (2009) "Correlations among indicators of disturbed flow at the normal carotid bifurcation.", Volume 131. J. Biomechanical Engineering

[18] Himburg, Heather A. and Grzybowski, Deborah M. and Hazel, Andrew L. and LaMack, Jeffrey A. and Li, Xue-Mei and Friedman, Morton H. (2004) "Spatial comparison between wall shear stress measures and porcine arterial endothelial permeability", Volume 286. American Physiological Society. American Journal of Physiology - Heart and Circulatory Physiology 5 H1916–H1922

[19] Suh G-Y, and Les AS, and Tenforde AS, and et al. (2011) "Quantification of Particle Residence Time in Abdominal Aortic Aneurysms Using Magnetic Resonance Imaging and Computational Fluid Dynamics.", Volume 39. Annals of biomedical engineering. 2 864-883.

[20] Sugiyama S, and Niizuma K, and Nakayama T, and Shimizu H, and Endo H, and Inoue T, and Fujimura M, and Ohta M, and Takahashi A, and Tominaga T. (2013) "Relative residence time prolongation in intracranial aneurysms: a possible association with atherosclerosis.", Volume 73. Neurosurgery 5 767-76

[21] Potters, WV. and van Ooij, P. and Marquering, H. and vanBavel, E. and Nederveen, AJ. (2015) "Volumetric arterial wall shear stress calculation based on cine phase contrast MRI.", Volume 41. Journal of Magnetic Resonance Imaging 2 505-16

[22] Markl, M. and Wallis, W. and Harloff, A. (2011) "Reproducibility of flow and wall shear stress analysis using flow-sensitive four-dimensional MRI", Volume 33. Journal of Magnetic Resonance Imaging 988-94

[23] Barker AJ and Markl M and Berk J and Lorenz R and Bock J and Bauer S. (2012) "Bicuspid aortic valve is associated with altered wall shear stress in the ascending aorta.", Volume 5. Circulation: Cardiovascular Imaging 457-66.

[24] Potters, Wouter V. and Marquering, Henk A. and VanBavel, Ed. and Nederveen, Aart J. (2014) "Measuring Wall Shear Stress Using Velocity-Encoded MRI", Volume 7. Current Cardiovascular Imaging Reports 9257

[25] Morbiducci, Umberto and Ponzini, Raffaele and Rizzo, Giovanna and Cadioli, Marcello and Esposito, Antonio and Montevecchi, FrancoMaria and Redaelli, Alberto. (2011) "Mechanistic insight into the physiological relevance of helical blood flow in the human aorta: an in vivo study", Volume 10. Springer-Verlag. Biomechanics and Modeling in Mechanobiology 3 339-355

[26] Antiga L, and Piccinelli M, and Botti L, and Ene-Iordache B, and Remuzzi A, and Steinman DA. (2008) "An image-based modeling framework for patient-specific computational hemodynamics.", Volume 46. Medical & Biological Engineering & Computing 1097-1112

[27] Pijls, Nico HJ and Sels, Jan-Willem EM. (2012) "Functional measurement of coronary stenosis", Volume 59. Am Coll Cardio Found. Journal of the American College of Cardiology 12 1045-1057

[28] Taylor, CA. and Timothy, A. and Min, James K. (2013) "Computational Fluid Dynamics Applied to Cardiac Computed Tomography for Noninvasive Quantification of Fractional Flow Reserve", Volume 61. Journal of the American College of Cardiology 22

[29] van den Wijngaard, Jeroen. and Schwarz, Janina. and van Horssen, Pepijn. and van Lier, Monique. and Dobbe, Johannes. and Spaan, Jos. and Siebes, Maria. (2013) "3D Imaging of vascular networks for biophysical modeling of perfusion distribution within the heart", Volume 46. Elsevier. Journal of Biomechanics 2 229–239

[30] Choi, Gilwoo and Lee, Joo Myung and Kim, Hyun-Jin and Park, Jun-Bean and Sankaran, Sethuraman and Otake, Hiromasa and Doh, Joon-Hyung and Nam, Chang-Wook and Shin, Eun-Seok and Taylor, Charles A. and Koo, Bon-Kwon. (2015) "Coronary Artery Axial Plaque Stress and its Relationship With Lesion GeometryApplication of Computational Fluid Dynamics to Coronary CT Angiography", Volume 8. JACC: Cardiovascular Imaging 10 1156-1166

[31] Slager, CJ and Wentzel, JJ and Gijsen, FJH and Schuurbiers, JCH and Van der Wal, AC and Van der Steen, AFW and Serruys, PW. (2005) "The role of shear stress in the generation of rupture-prone vulnerable plaques", Volume 2. Nature Publishing Group. Nature Clinical Practice Cardiovascular Medicine 8 401–407

[32] Gijsen, Frank JH and Wentzel, Jolanda J and Thury, Attila and Mastik, Frits and Schaar, Johannes A and Schuurbiers, Johan CH and Slager, Cornelis J and van der Giessen, Wim J and de Feyter, Pim J and van der Steen, Anton FW and others. (2008) "Strain distribution over plaques in human coronary arteries relates to shear stress", Volume 295. Am Physiological Soc. American Journal of Physiology-Heart and Circulatory Physiology 4 H1608–H1614

[33] Groen, Harald C and Gijsen, Frank JH and van der Lugt, Aad and Ferguson, Marina S and Hatsukami, Thomas S and van der Steen, Anton FW and Yuan, Chun and Wentzel, Jolanda J. (2007) "Plaque Rupture in the Carotid Artery Is Localized at the High Shear Stress Region A Case Report", Volume 38. Am Heart Assoc. Stroke 8 2379–2381

[34] Fukumoto, Yusaku and Hiro, Takafumi and Fujii, Takashi and Hashimoto, Genta and Fujimura, Tatsuhiro and Yamada, Jutaro and Okamura, Takayuki and Matsuzaki, Masunori. (2008) "Localized elevation of shear stress is related to coronary plaque rupture: a 3-dimensional intravascular ultrasound study with in-vivo color mapping of shear stress distribution", Volume 51. Journal of the American College of Cardiology. Journal of the American College of Cardiology 6 645–650

[35] Gijsen, Frank and van der Giessen, Alina and van der Steen, Anton and Wentzel, Jolanda. (2013) "Shear stress and advanced atherosclerosis in human coronary arteries", Volume 46. Elsevier. Journal of biomechanics 2 240–247

[36] Lovett, Joanna K and Rothwell, Peter M. (2003) "Site of carotid plaque ulceration in relation to direction of blood flow: an angiographic and pathological study", Volume 16. Karger Publishers. Cerebrovascular Diseases 4 369–375

[37] de Weert TT, and Cretier S, and Groen HC, and et al. (2009) "Atherosclerotic plaque surface morphology in the carotid bifurcation assessed with multidetector computed tomography angiography", Volume 40. Stroke 4 1334-1340

[38] Zarins CK, and Giddens DP, and Bharadvaj BK, and Sottiurai VS, and Mabon RF, and Glagov S. (1985) "Carotid bifurcation atherosclerosis: Quantitative correlation of plaque localization with flow velocity profiles and wall shear stress.", Volume 53. Circulation Research 502-514

[39] Peiffer V, and Sherwin SJ, and Weinberg PD. (2103) "Does low and oscillatory wall shear stress correlate spatially with early atherosclerosis? A systematic review", Volume 99. Cardiovascular Research. 2 242-50

[40] Jeremias, Allen and Filardo, Steven D and Whitbourn, Robert J and Kernoff, Robert S and Yeung, Alan C and Fitzgerald, Peter J and Yock, Paul G. (2000) "Effects of intravenous and intracoronary adenosine 5-triphosphate as compared with adenosine on coronary flow and pressure dynamics", Volume 101. Am Heart Assoc. Circulation 3 318–323

[41] Koo, Bon-Kwon and Kang, Hyun-Jai and Youn, Tae-Jin and Chae, In-Ho and Choi, Dong-Joo and Kim, Hyo-Soo and Sohn, Dae-Won and Oh, Byung-Hee and Lee, Myoung-Mook and Park, Young-Bae and others. (2005) "Physiologic assessment of jailed side branch lesions using fractional flow reserve", Volume 46. Am Coll Cardio Found. Journal of the American College of Cardiology 4 633–637

[42] De Bruyne, Bernard and Pijls, Nico HJ and Heyndrickx, Guy R and Hodeige, Dominique and Kirkeeide, Richard and Gould, K Lance. (2000) "Pressure-derived fractional flow reserve to assess serial epicardial stenoses theoretical basis and animal validation", Volume 101. Am Heart Assoc. Circulation 15 1840-1847

[43] Siebes, Maria and Ventikos, Yiannis. (2010) "The role of biofluid mechanics in the assessment of clinical and pathological observations", Volume 38. Springer. Annals of biomedical engineering 3 1216–1224

[44] Koo, Bon-Kwon and Erglis, Andrejs and Doh, Joon-Hyung and Daniels, David V and Jegere, Sanda and Kim, Hyo-Soo and Dunning, Allison and DeFrance, Tony and Lansky, Alexandra and Leipsic, Jonathan and others. (2011) "Diagnosis of ischemia-causing coronary stenoses by noninvasive fractional flow reserve computed from coronary computed tomographic angiograms: results from the prospective multicenter DISCOVER-FLOW (Diagnosis of Ischemia-Causing Stenoses Obtained Via Noninvasive Fractional Flow Reserve) study", Volume 58. Am Coll Cardio Found. Journal of the American College of Cardiology 19 1989–1997

[45] Min, James K and Leipsic, Jonathon and Pencina, Michael J and Berman, Daniel S and Koo, Bon-Kwon and van Mieghem, Carlos and Erglis, Andrejs and Lin, Fay Y and Dunning, Allison M and Apruzzese, Patricia and others. (2012) "Diagnostic accuracy of fractional flow reserve from anatomic CT angiography", Volume 308. American Medical Association. Journal of the American Medical Association 12 1237–1245

[46] Wijns, William. (2012) "The One-Stop Shop Offering Both Coronary Anatomy and Myocardial Perfusion: May Well Be Opening Soon, Around the Corner??", Volume 5. Journal of the American College of Cardiology. JACC: Cardiovascular Imaging 11 1112–1114

[47] Tayllamin, Bruno and Moreno, Ramiro and Nicoud, Franck and Chau, Ming and Rousseau, Hervé. (2011) "CFD-based functional imaging for arteries: in vitro validation". AFM, Maison de la Mécanique, 39/41 rue Louis Blanc-92400 Courbevoie

[48] Tu, Shengxian and Barbato, Emanuele and Koszegi, Zsolt and Yang, Junqing and Sun, Zhonghua and Holm, Niels R. and Tar, Balezs and Li, Yingguang and Rusinaru, Dan and Wijns, William and Reiber, Johan H.C. (2014) "Fractional Flow Reserve Calculation From 3-Dimensional Quantitative Coronary Angiography and TIMI Frame Count A Fast Computer Model to Quantify the Functional Significance of Moderately Obstructed Coronary Arteries", Volume 7. JACC: Cardiovascular Interventions 7 768-777

[49] Choke, E. and Cockerill, G. and Wilson, W.R.W. and Sayed, S. and Dawson, J. and Loftus, I. and Thompson, M.M. (2005) "A Review of Biological Factors Implicated in Abdominal Aortic Aneurysm Rupture", Volume 30. European Journal of Vascular and Endovascular Surgery. Elsevier. European Journal of Vascular and Endovascular Surgery 3 227-244

[50] Ryan R. Davies, and Amy Gallo, and Michael A. Coady, and George Tellides, and Donald M. Botta, and Brendan Burke, and Marcus P. Coe, and Gary S. Kopf, and John A. Elefteriades. (2006) "Novel Measurement of Relative Aortic Size Predicts Rupture of Thoracic Aortic Aneurysms", Volume 81. The Annals of Thoracic Surgery 1 169-177

[51] Christoph A Nienaber and Rachel E Clough. (2015) "Management of acute aortic dissection", Volume 385. The Lancet: Cardiovascular & Vascular Medicine 9970 800-811

[52] Samarth S. Raut, and Santanu Chandra, and Judy Shum, and Christopher B. Washington, and Satish C. Muluk, and Ender A. Finol and José F. Rodríguez. (2013) "Biological, Geometric and Biomechanical Factors Influencing Abdominal Aortic Aneurysm Rupture Risk: A Comprehensive Review", Volume 3. Recent Patents on Medical Imaging 44-59

[53] Raut SS, and Chandra S, and Shum J, and Finol EA. (2013) "The role of geometric and biomechanical factors in abdominal aortic aneurysm rupture risk assessment.", Volume 41. Annals of Biomedical Engineering 7 1459-77

[54] den Reijer PM, and Sallee D, and van der Velden P, and Zaaijer ER, and Parks WJ, and Ramamurthy S, and Robbie TQ, and Donati G, and Lamphier C, and Beekman RP, and Brummer ME. (2010) "Hemodynamic predictors of aortic dilatation in bicuspid aortic valve by velocity-encoded cardiovascular magnetic resonance.", Volume 12. Journal of Cardiovascular Magnetic Resonance 4

[55] Marcelo A. Castro. (2013) "Understanding the Role of Hemodynamics in the Initiation, Progression, Rupture, and Treatment Outcome of Cerebral Aneurysm from Medical Image-Based Computational Studies", Volume 2013. ISRN Radiology 17

[56] Tejas Canchi, and S. D. Kumar, and E. Y. K. Ng, and Sriram Narayanan. (2015) "A Review of Computational Methods to Predict the Risk of Rupture of Abdominal Aortic Aneurysms", Volume 2015. Hindawi. BioMed Research International 12

[57] LaDisa, John F. and Dholakia, Ronak J. and Figueroa, C. Alberto and Vignon-Clementel, Irene E. and Chan, Frandics P. and Samyn, Margaret M. and Cava, Joseph R. and Taylor, Charles A. and Feinstein, Jeffrey A. (2011) "Computational Simulations Demonstrate Altered Wall Shear Stress in Aortic Coarctation Patients Treated by Resection with End-to-end Anastomosis", Volume 6. Blackwell Publishing Inc. Congenital Heart Disease 5 432–443

[58] LaDisa JF, and Alberto Figueroa C, and Vignon-Clementel IE, and Kim HJ, and Xiao N, and Ellwein LM, and Chan FP, and Feinstein JA, and Taylor CA. (2011) "Computational simulations for aortic coarctation: representative results from a sampling of patients.", Volume 133. Journal of Biomechanical Engineering 9

[59] Lantz J, and Ebbers T, and Engvall J, and Karlsson M. (2013) "Numerical and experimental assessment of turbulent kinetic energy in an aortic coarctation.", Volume 46. Journal Biomechanics 11 1851-1858

[60] Menon, Arjun and Eddinger, Thomas J and Wang, Hongfeng and Wendell, David C and Toth, Jeffrey M and LaDisa, John F. (2012) "Altered hemodynamics, endothelial function, and protein expression occur with aortic coarctation and persist after repair", Volume 303. American Physiological Society. American Journal of Physiology. Heart and Circulatory Physiology 11 H1304–H1318

[61] Dadvand P and Rossi R and Oñate E. (2010) "An object-oriented environment for developing finite element codes for multi-disciplinary applications.", Volume 17. Archives of Computational Methods in Engineering 253-297

[62] COMPASSIS. (2012) "TDYN: Theoretical Background."

[63] Neal, Maxwell Lewis and Kerckhoffs, Roy. (2010) "Current progress in patient-specific modeling.", Volume 1. Oxford Journals. Briefings in Bioinformatics 11 111-26

[64] The National Electrical Manufacturers Association. (1992, 1993, 1994, 1995.) "Digital Imaging and Communications in Medicine (DICOM).". NEMA Publications

[65] M.Cerrolaza, G.Gavidia, E.Soudah, M. Martín-Landrove. (2014) "Modelling human tissues an efficient integrated methodology.", Volume 26. Biomedical Engineering: Applications, Basis and Communications. No 1. 1450012.

[66] Paul A. Yushkevich and Joseph Piven and Cody Hazlett, Heather and Gimpel Smith, Rachel and Sean Ho and James C. Gee and Guido Gerig. (2006) "User-Guided 3D Active Contour Segmentation of Anatomical Structures: Significantly Improved Efficiency and Reliability", Volume 31. Neuroimage 3 1116–1128

[67] CIMNE. (2010) "GID. The personal pre and postprocessor."

[68] Schroeder, Will and Martin, Ken and Lorensen, Bill "The Visualization Toolkit, Third Edition". Kitware Inc.

[69] Ibáñez, L. and Schroeder, W. and Ng, L. and Cates, J. (2003) "The ITK Software Guide". Kitware

[70] "DCMTK - DICOM Toolkit"

[71] Markl, Michael and Draney, Mary T and Hope, Michael D and Levin, Jonathan M and Chan, Frandics P and Alley, Marcus T and Pelc, Norbert J and Herfkens, Robert J. (2004) "Time-resolved 3-dimensional velocity mapping in the thoracic aorta: visualization of 3-directional blood flow patterns in healthy volunteers and patients", Volume 28. LWW. Journal of computer assisted tomography 4 459–468

[72] Lantz, J. and Renner, J. and Karlsson, M. (2011) "Wall shear stress in a subject specific human aorta. influence of fluid-structure interaction", Volume 4. World Scientific Publishing. Internal Journal of Applied Mechanics 3 759-778

[73] Sven Petersson and Petter Dyverfeldt and Tino Ebbers. (2012) "Assessment of the Accuracy of MRI Wall Shear Stress Estimation using Numerical Simulations", Volume 36. Journal of Magnetic Resonance Imaging 128-138

[74] Stalder, A. F. and Frydrychowicz, A. and Russe, M. F. and Korvink, J. G. and Hennig, J. and Li, K. and Markl, M. (2011) "Assessment of flow instabilities in the healthy aorta using flow-sensitive MRI". Journal of Magnetic Resonance Imaging 33 839-846

[75] L. Formaggia and F. Nobile and A. Quarteroni and A. Veneziani. (1999) "Multiscale modelling of the circulatory system: a preliminary analysis.", Volume 2. Computing and Visualization in Science. 75-83

[76] J. R. Womersley. (1955) "Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known.", Volume 127. Journal Physiology 553-563

[77] J. S. Milner, and J. A. Moore, and B. K. Rutt, and D. A. Steinman. (1998) "Hemodynamics of human carotid artery bifurcations: computational studies with models reconstructed from magnetic resonance imaging of normal subjects.", Volume 28. Journal of Vascular Surgery, 143-156

[78] A. Quarteroni and L. Formaggia. (2002) "Mathematical modelling and numerical simulation of the cardiovascular system"

[79] Taylor, C.A. and Figueroa, CA. (2009) "Patient-Specific Modeling of Cardiovascular Mechanics", Volume 11. Annual Review of Biomedical Engineering 1 109-134

[80] Lau, Kevin D. and Figueroa Alvarez, Alberto. (2015) "Simulation of short-term pressure regulation during the tilt test in a coupled 3D-0D closed-loop model of the circulation", Volume 14. Biomechanics and Modeling in Mechanobiology 4 915–929

[81] Lotz, J. (2007) "Flow measurements in cardiac MRI", Volume 47. Radiologe; 4 333-41

[82] Srichai, M. B. and Lim, R. P. and Wong, S. and Lee Vs. (2009) "Cardiovascular applications of phase-contrast MRI", Volume 192. American Journal of Roentgenology 3 662-75

[83] van de Vosse F, and Stergiopulos N. (2011) "Pulse wave propagation in the arterial tree.", Volume 43. Annual Review of Fluid Mechanics 467-499

[84] Pant, S. and Fabreges, B. and Gerbeau, J. and Vignon-Clementel I. (2014) "A methodological paradigm for patient-specific multi-scale CFD simulations: From clinical measurements to parameter estimates for individual analysis.", Volume 30. International Journal for Numerical Methods in Biomedical Engineering 1614-1648.

[85] Mahmoud Ismail, and Wolfgang A. Wall, and Michael W. Gee. (2013) "Adjoint-based inverse analysis of windkessel parameters for patient-specific vascular models", Volume 244. Journal of Computational Physics 113-130

[86] Adelmo Cristiano Innocenza Malossi. (2012) "Partitioned Solution of Geometrical Multiscale Problems for the Cardiovascular System: Models, Algorithms, and Applications.". Ecole Polytechnique Federale de Lausanne

[87] 2014 CEI Inc., EnSight. All Rights Reserved. "CEO EnSight"

[88] The OpenFOAM Foundation. All Rights Reserved. "Free Open Source CFD. OpenFOAM"

[89] Markl M, and Wallis W, and Strecker C, and Gladstone BP, and Vach W, Harloff A. (2012) "Analysis of pulse wave velocity in the thoracic aorta by flow-sensitive four-dimensional MRI: reproducibility and correlation with characteristics in patients with aortic atherosclerosis.", Volume 35. Journal of Magnetic Resonance Imaging 5 1162-8

[90] Petersson, S., Dyverfeldt, P., Sigfridsson, A., Lantz, J., Carlholl, C.-J. and Ebbers, T. (2015) "Quantification of turbulence and velocity in stenotic flow using spiral three-dimensional phase-contrast MRI.". Magnetic Resonance in Medicine

[91] Donati F, and Figueroa CA, and Smith NP, and Lamata P, and Nordsletten DA. (2015) "Non-invasive pressure difference estimation from PC-MRI using the work-energy equation.", Volume 26. Medical Image Analysis 1 159-172.

[92] Eriksson J, Bolger AF, Ebbers T, Carlholl CJ. (2013) "Four-dimensional blood flow-specific markers of LV dysfunction in dilated cardiomyopathy.", Volume 15. European Heart Journal Cardiovascular Imaging 5 417-24

[93] Shadden, ShawnC. and Hendabadi, Sahar. (2013) "Potential fluid mechanic pathways of platelet activation", Volume 12. Springer-Verlag. Biomechanics and Modeling in Mechanobiology 3 467-474

[94] Tortora, G.J. and Derrickson, B. (2006) "Principios de anatomía y fisiología". Médica Panamericana

[95] Pearson Education Inc. (2013) "Hypertension and Physiology of the Heart, Pearson Education Inc"

[96] Wikipedia. (2004) "Circulatory system –- Wikipedia, The Free Encyclopedia"

[97] J. J. Wang and K. H. Parker. (2004) "Wave propagation in a model of the arterial circulation", Volume 37. Journal Biomechanics 457-470

[98] A. Quarteroni and R. Sacco. (2000) "Matematica Numerica"

[99] Canic.S and Kim.H. (2003) "Mathematical analysis of the quasilinear effects in a hyperbolic model of blood flow through compliant axisymmetric vessels". Mathematical Methods in Applied Sciences

[100] E. Godlewski and P. A. Raviart. (1996) "Numerical approximation of hyperbolic systems of conservation laws"

[101] K. Thompson. (1987) "Time dependent boundary conditions for hyperbolic systems", Volume 68. Journal of Computational Physics 1-24

[102] Hedstrom G. W. (1979) "Non-reflecting boundary conditions for nonlinear hyperbolic systems". Journal of Computational Physics

[103] Matthys, KS and Alastruey, J and Peiro, J and Khir, AW and Segers, P and Verdonck, PR and Parker, KH and Sherwin, SJ. (2007) "Pulse wave propagation in a model human arterial network: Assessment of 1-D numerical simulations against in vitro measurements", Volume 40. Journal of Biomechanics 3476–3486

[104] I. Kokalari and T. Karaja and M. Guerrisi. (2013) "Review on lumped parameter method for modeling the blood flow in systemic arteries". Journal Biomedical Science and Engineering

[105] J. Donea and S. Giuliani and L. Quartapelle. (1984) "Time-accurate solutions of advenction-diffusion problems by finite elements", Volume 71. Computer Methods in Applied Mechanics and Engineering 93-122

[106] L. Quartapelle. (1993) "Numerical Solution of the Incompressible Navier-Stokes Equations"

[107] A. Quarteroni and A. Valli. (1999) "Domain decomposition methods for partial differential equation"

[108] D. Formaggia and D. Lamponi and A. Quarteroni. (1992) "One-dimensional model for blood flow in arteries". Journal of Engineering. Mathematics

[109] M. A. Fernandez and V. Mlsic and A. Quarteroni. (2005) "Analysis of a geometrical multiscale blood flow model based on the coupling of ODE's and hyperbolic PDE's", Volume 4. SIAM Journal Multiscale Modeling. Simulation 215-236