A machine learning based methodology for anomaly detection in dam behaviour

Abstract

Dam behaviour is difficult to predict with high accuracy. Numerical models for structural calculation solve the equations of continuum mechanics, but are subject to considerable uncertainty as to the characterisation of materials, especially with regard to the foundation. As a result, these models are often incapable to calculate dam behaviour with sufficient precision. Thus, it is difficult to determine whether a given deviation between model results and monitoring data represent a relevant anomaly or incipient failure.

By contrast, there is a tendency towards automatising dam monitoring devices, which allows for increasing the reading frequency and results in a greater amount and variety of data available, such as displacements, leakage, or interstitial pressure, among others.

This increasing volume of dam monitoring data makes it interesting to study the ability of advanced tools to extract useful information from observed variables.

In particular, in the field of Machine Learning (ML), powerful algorithms have been developed to face problems where the amount of data is much larger or the underlying phenomena is much less understood.

In this monograph, the possibilities of machine learning techniques are analysed for application to dam structural analysis based on monitoring data. The typical characteristics of the data sets available in dam safety are taking into account, as regards their nature, quality and size.

A critical literature review is performed, from which the key issues to consider for implementation of these algorithms in dam safety are identified.

A comparative study of the accuracy of a set of algorithms for predicting dam behaviour is carried out, considering radial and tangential displacements and leakage flow in a 100-m high dam. The results suggest that the algorithm called “Boosted Regression Trees” (BRT) is the most suitable, being more accurate in general, while flexible and relatively easy to implement.

The possibilities of interpretation of the mentioned algorithm are evaluated, to identify the shape and intensity of the association between external variables and the dam response, as well as the effect of time. The tools are applied to the same test case, and allow more accurate identification of the time effect than the traditional statistical method.

Finally, a methodology for the implementation of predictive models based on BRT for early detection of anomalies is presented, together with its implementation in an interactive tool that provides information on dam behaviour, through a set of selected devices. It allows the user to easily verify whether the actual data for each of these devices are within a pre-defined normal operation interval.

Resumen

El comportamiento estructural de las presas de embalse es difícil de predecir con precisión. Los modelos numéricos para el cálculo estructural resuelven bien las ecuaciones de la mecánica de medios continuos, pero están sujetos a una gran incertidumbre en cuanto a la caracterización de los materiales, especialmente en lo que respecta a la cimentación. Como consecuencia, frecuentemente estos modelos no son capaces de calcular el comportamiento de las presas con suficiente precisión. Así, es difícil discernir si un estado que se aleja en cierta medida de la normalidad supone o no una situación de riesgo estructural.

Por el contrario, muchas de las presas en operación cuentan con un gran número de aparatos de auscultación, que registran la evolución de diversos indicadores como los movimientos, el caudal de filtración, o la presión intersticial, entre otros. Aunque hoy en día hay muchas presas con pocos datos observados, hay una tendencia clara hacia la instalación de un mayor número de aparatos que registran el comportamiento con mayor frecuencia.

Como consecuencia, se tiende a disponer de un volumen creciente de datos que reflejan el comportamiento de la presa, lo cual hace interesante estudiar la capacidad de herramientas desarrolladas en otros campos para extraer información útil a partir de variables observadas.

En particular, en el ámbito del aprendizaje automático (machine learning), se han desarrollado algoritmos muy potentes para entender fenómenos cuyo mecanismo es poco conocido, acerca de los cuales se dispone de grandes volúmenes de datos.

En esta monografía se hace un análisis de las posibilidades de las técnicas más recientes de aprendizaje automático para su aplicación al análisis estructural de presas basado en los datos de auscultación. Para ello se tienen en cuenta las características habituales de las series de datos disponibles en las presas, en cuanto a su naturaleza, calidad y cantidad.

Se ha realizado una revisión crítica de la bibliografía existente, a partir de la cual se han identificado los aspectos clave a tener en cuenta para implementación de estos algoritmos en la seguridad de presas.

Se ha realizado un estudio comparativo de la precisión de un conjunto de algoritmos para la predicción del comportamiento de presas considerando desplazamientos radiales, tangenciales y filtraciones. Para ello se han utilizado datos reales de una presa bóveda. Los resultados sugieren que el algoritmo denominado “Boosted Regression Trees” (BRTs) es el más adecuado, por ser más preciso en general, además de flexible y relativamente fácil de implementar.

Adicionalmente, se han identificado las posibilidades de interpretación del citado algoritmo para extraer la forma e intensidad de la asociación entre las variables exteriores y la respuesta de la presa, así como el efecto del tiempo. Las herramientas empleadas se han aplicado al mismo caso piloto, y han permitido identificar el efecto del tiempo con más precisión que el método estadístico tradicional.

Finalmente, se ha desarrollado una metodología para la aplicación de modelos de predicción basados en BRTs en la detección de anomalías en tiempo real. Esta metodología se ha implementado en una herramienta informática interactiva que ofrece información sobre el comportamiento de la presa, a través de un conjunto de aparatos seleccionados. Permite comprobar a simple vista si los datos reales de cada uno de estos aparatos se encuentran dentro del rango de funcionamiento normal de la presa.

Nomenclature

${\textstyle a}$ Magnitude of the artificial anomaly introduced

${\textstyle {a}_{1}\dots {a}_{10}}$ Coefficients in the HST formula

${\textstyle d}$ Number of days since 1 January

${\textstyle F\left({x}_{i}\right)}$ Output of predictive model for ${\textstyle {t}_{i}}$

${\textstyle {F}_{n}\left({X}^{j}\right)}$ Output of an ensemble model at iteration ${\textstyle n}$

${\textstyle f_{m}({X}^{j})}$ Weak learner fitted at iteration ${\textstyle m}$

${\textstyle {F}_{2}}$ Index of accuracy of anomaly detection models

${\textstyle h}$ Reservoir level

${\textstyle s}$ Argument of the trigonometrical functions in the HST model. ${\textstyle s=2\pi d{/}{365.25}}$

${\textstyle Mn}$ ${\textstyle n}$ Version of a BRT model

${\textstyle min}$ minimum

${\textstyle \mu }$ Residuals average

${\textstyle N}$ Number of records in a period

${\textstyle \nu }$ Regularisation parameter

${\textstyle p}$ Number of inputs

${\textstyle R}$ Model residuals (prediction-observation)

${\textstyle {\sigma }^{2}}$ Variance

${\textstyle {S}_{m}}$ Subsample of a training set used to fit ${\textstyle f_{m}({X}^{j})}$

${\textstyle {sd}_{res}}$ Standard deviation of the residuals

${\textstyle t}$ time

${\textstyle {t}_{det}}$ Detection time

${\textstyle {X}^{j}}$ Input variable

${\textstyle {x}_{i}^{j}}$ Observed value for input ${\textstyle {X}^{j}}$ at time ${\textstyle {t}_{i}}$

${\textstyle {x}_{k}^{j}}$ Equally-spaced values of ${\textstyle {X}^{j}}$ to be used in PDPs

${\textstyle Y}$ Measured response variable

${\textstyle {\hat {Y}}}$ Predicted response variable

${\textstyle {y}_{i}}$ Observed value of the output variable at time ${\textstyle {t}_{i}}$

${\textstyle {\bar {{y}_{i}}}}$ Mean of ${\textstyle {y}_{i}}$

ANFIS Adaptive Neuro-Fuzzy System

ARX Auto-Regressive Exogenous

BRT Boosted regression Trees

FEM Finite Element Method

GA Genetic Algorithms

HST Hydrostatic Season Time

HSTT Hydrostatic Season Temperature Time

KNN K-Nearest Neighbours

MARS Multivariate Adaptive Regression Splines

ML Machine Learning

MLP Multi Layer Perceptron

MLR Multilinear regression

NN Neural Network

PCA Principal Component Analysis

RF Random Forest

SVM Support Vector Machine

ACA Agencia Catalana de l'Aigua

ARV Average Relative Variance

KDE Kernel Density Estimation

MAE Mean Absolute Error

MINECO Ministerio de Economía y Competitividad

MSE Mean Squared Error

OOR Out of range

PDP Partial dependence plot

RI Relative Influence

1 Introduction and Objectives

1.1 Introduction

Dams play a key role in our society, since they provide essential services to our way of living, such as flood defence, water storage and power generation. Moreover, an eventual failure might have catastrophic consequences in terms of casualties, economic and environmental losses, as was unfortunately verified in the past [1].

As a consequence, safe dam operation needs to be ensured, and potentially anomalous performance shall be detected as early as possible, to avoid serious malfunctioning or failure. While the first objective is achieved by means of an appropriate maintenance program both for the structure and the hydro-electromechanical devices, failure prevention by early detection of anomalies is primarily based on surveillance tasks [2], [3].

In turn, surveillance is based on two main pillars [2]: a) visual inspection and b) monitoring of dam and foundation. Its main objective is to reduce the probability of failure [3].

Lombardi [4] formulated the objectives of dam and foundation monitoring in a concise way, by posing four questions to be answered:

1. Does the dam behave as expected/predicted?
2. Does the dam behave as in the past?
3. Does any trend exist which could impair its safety in the future?
4. Was any anomaly in the behaviour of the dam detected?

The answer to these questions requires the analysis of dam monitoring data two ways:

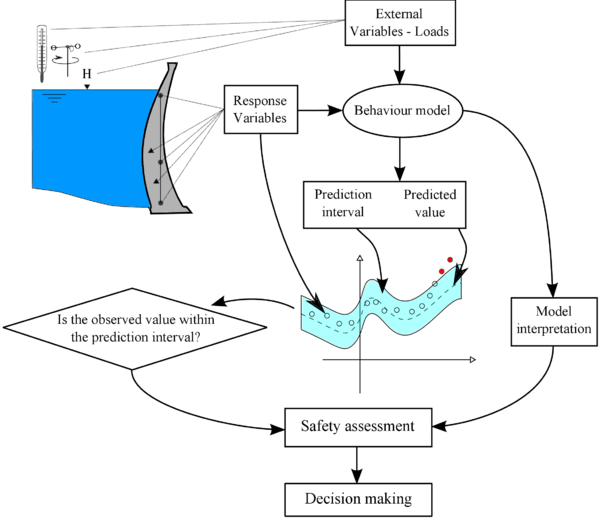
• In the short term (some times “on-line”), the measurements of some devices are compared to reference values, which correspond to the dam response to the concurring loads in “normal” or “safe” condition. These reference values and associated prediction intervals above and below them are obtained from some behaviour model, which accounts for the actual value of the acting loads. Those measurements outside the cited interval are considered as potential symptoms of anomalous behaviour, hence further verified.
• In the medium to long term, behaviour models and observed data are analysed to draw conclusions on the overall dam performance. In particular, the association between each load and output is observed, and the evolution over time is evaluated.

The result of this analysis is essential in dam safety assessment and decision making, together with the rest of available information about dam construction and operation, including visual inspection. Figure 1 shows schematically the monitoring data analysis process.

Figure 1: Flow diagram of dam monitoring data analysis.

1.2 Motivation

Dam monitoring data analysis, and the answer to the above mentioned questions, require a behaviour model that provides an estimate on the response of the structure at a given time, taking into account the acting loads.

Existing models can be classified as follows [5]:

• Deterministic: typically based on the finite element method (FEM), these methods calculate the dam response on the basis of the physical governing laws.
• Statistical: exclusively based on dam monitoring data.
• Hybrid: deterministic models which parameters have been adjusted to fit the observed data.
• Mixed: comprised by a deterministic model to predict the dam response to hydrostatic pressure, and a statistical one to consider deformation due to thermal effects.

Numerical models based on the FEM provide useful estimates of dam displacements and stresses, but are subject to a significant degree of uncertainty in the characterisation of the materials, especially with respect to the structural behaviour of the foundation and the thermal evolution of the dam body in concrete (particularly arch) dams. Other assumptions and simplifications have to be made, regarding geometry and boundary conditions. These tools are essential during the initial stages of the life cycle of the structure, provided that not enough data are available to build data-based predictive models. However, their results are often not accurate enough for a precise assessment of dam safety.

This is more acute when dealing with determined variables such as leakage in concrete dams and their foundations, due to the intrinsic features of the physical process, which is often non-linear [6], and responds to threshold and delayed effects [7], [8]. Numerical analysis cannot deal with such a phenomenon, because comprehensive information about the location, geometry and permeability of each fracture would be needed. Other phenomena are also difficult to reproduce with numerical models, such as the beginning of failure by concrete plasticising or cracking, although tools have been developed for this purpose [9].

These drawbacks are shared by all approaches that make use of a FEM model: deterministic, hybrid and mixed.

Many of the dams in operation have a number of monitoring devices that record the evolution of various indicators such as displacements, leakage flow or pore water pressure, among others. Although there are still many dams with few observed data, there is a clear trend towards the installation of a larger number of devices with higher data acquisition frequency [3]. As a result, there is an increasing amount of information on dam performance.

Statistical tools employed in regular engineering practice for dam monitoring data analysis are relatively simple. They are frequently limited to graphical exploration of the time series of data [10], along with simple statistical models [3], [11]. The hydrostatic-season-time (HST) model [12] is the most widely applied, and the only generally accepted by practitioners.

HST is based on multiple linear regression considering the three most influential external variables: hydrostatic load, air temperature and time. It often provides useful estimations of displacements in concrete dams [13], and does not require air temperature time series data (it is assumed to follow a constant yearly cycle). Moreover, the resulting model is easily interpretable, since the contribution of each input is assumed to be cumulative.

Nonetheless, HST also features conceptual limitations that damage the prediction accuracy [13] and may lead to misinterpretation of the results [14]. For example, it is based on the assumption that the hydrostatic load and the temperature are independent, whereas it is well known that they are coupled, since the thermal field is influenced by the the water temperature in the upstream face [15]. On another note, it lacks flexibility, since the functions have to be defined beforehand, and thus may not represent the true behaviour of the structure [7]. Also, they are not well-suited to model non-linear interactions between input variables [6].

In the recent years, non-parametric techniques have emerged as an alternative to HST for building data-based behaviour models [16], e.g. support vector machines (SVN) [17], neural networks (NN) [18], adaptive neuro-fuzzy systems (ANFIS) [19], among others [16]. In general, these tools are more suitable to model non-linear cause-effect relations, as well as interaction among external variables, as that previously mentioned between hydrostatic load and temperature. On the contrary, they are typically more difficult to interpret, what led them to be termed as “black box” models (e.g. [20]). As a consequence, the vast majority of related works are limited to the verification of their prediction accuracy when estimating determined output variables (e.g. [21], [22], [23]).

Therefore, dam engineers face a dilemma: the HST model is widely known and used and easily interpretable. However, it is based on some incorrect assumptions, and its accuracy can be increased. On the other hand, more flexible and accurate models are available, but they are more difficult to implement and analyse.

The research aims at solving this issue by exploring the possibilities of machine learning algorithms to improve dam monitoring data analysis and safety assessment.

1.3 Objectives

The main objective is the development of a methodology for dam behaviour analysis based on machine learning, efficient in early detection of anomalies. To achieve that goal, the following specific objectives need to be fulfilled:

1. Literature review on data-based models for dam monitoring data analysis, with focus on the following topics:

• Critical analysis of relevant articles and conference proceedings.
• Identification of areas to improve in the field of dam monitoring data interpretation.
• Revision of the statistical and machine learning tools with potential for application to the problem to be solved.
• Verification of the applicability of each tool to predict output variables of different nature.
• Analysis of the key methodological issues as regards the implementation of predictive models in day-to-day practice.
• Selection of a group of algorithms for a more detailed analysis.

2. Algorithm selection, in terms of accuracy, flexibility, robustness and ease of implementation.

3. Analysis of the effect of the training set size, to have an estimate on the time period required from the first filling before having the possibility of employing some data-based behaviour model.

4. Identification of tools for interpretation of ML models, i.e., analysis of the influence of each input on dam response and retrospective assessment of dam performance to detect potential changes in time.

5. Implementation of the methodology in a software tool for anomaly detection, with the following functionalities:

• Accuracy: the better the prediction of the model fits the actual response of the dam, the more reliable the conclusions drawn from its interpretation [24]. Moreover, a more accurate model will result in a narrower prediction interval which in turn would allow earlier anomaly detection.
• Flexibility: each dam typology presents different characteristics in terms of the most influential loads, the strength and nature of their association with dam response, the most representative output variables and the potential failure modes, among other aspects. The behaviour model should ideally be able to adapt to highly different situations.
• Interpretability: model analysis should throw information on the nature and intensity of the association between each input and response, and in particular on the time effect, i.e., whether dam performance changed over time, and which way.
• Ability to detect anomalies: a criterion to determine a prediction interval around the model prediction is required, to classify upcoming observations of different output variables as “normal” or “potentially anomalous”.
• Ability to identify extraordinary situations due to load combination.
• A graphical user interface for its practical application, including tools for data exploration, model fitting and anomaly detection.

1.4 Publications

This monograph is presented as a compendium of articles, previously published in indexed scientific journals. The list and the association with this document follows:

Chapter 2 contains a summary of the articles related to the literature review:

• Salazar, F., Morán, R., Toledo, M.Á., Oñate, E. Data-Based Models for the Prediction of Dam Behaviour: A Review and Some Methodological Considerations. Archives of Computational Methods in Engineering (2015). doi:10.1007/s11831-015-9157-9
• Salazar, F., Toledo, M.Á., Discussion on “Thermal displacements of concrete dams: Accounting for water temperature in statistical models”, Engineering Structures, Available online 13 August 2015, ISSN 0141-0296,

  http://dx.doi.org/10.1016/j.engstruct.2015.08.001.

Chapter 3 is a summary of the article dealing with algorithm selection, based on a comparison of candidate techniques:

• Salazar, F., Toledo, M.Á., Oñate, E., Morán, R. An empirical comparison of machine learning techniques for dam behaviour modelling, Structural Safety, Volume 56, September 2015, Pages 9-17, ISSN 0167-4730,

  http://dx.doi.org/10.1016/j.strusafe.2015.05.001.

Chapter 4 focuses on model interpretation, and is associated with the fourth paper in the compendium:

• Salazar, F., Toledo, M.Á., Oñate, E., Suárez, B. Interpretation of dam deformation and leakage with boosted regression trees, Engineering Structures, Volume 119, 15 July 2016, Pages 230-251, ISSN 0141-0296,

  http://dx.doi.org/10.1016/j.engstruct.2016.04.012.

The overall methodology for anomaly detection is described in Chapter 5. It takes into account the conclusions of the precedent works, and is the subject of another article currently under review.

Finally, part of the work was presented in the following conferences:

Salazar, F., Oñate, E., Toledo, M.Á. Posibilidades de la inteligencia artificial en el análisis de auscultación de presas. III Jornadas de Ingeniería del Agua, Valencia (Spain), October 2013 (in Spanish). Salazar, F., Morera, L., Toledo, M.Á., Morán, R., Oñate, E. Avances en el tratamiento y análisis de datos de auscultación de presas. X Jornadas Españolas de Presas, Spancold, Sevilla (Spain), February 2015 ¹ (in Spanish). Salazar, F., Oñate, E., Toledo, M.Á. Nuevas técnicas para el análisis de datos de auscultación de presas y la definición de indicadores cuantitativos de su comportamiento, IV Jornadas de Ingeniería del Agua, Córdoba (Spain), October 2015. Salazar, F., González, J.M., Toledo, M.Á., Oñate, E. A methodology for dam safety evaluation and anomaly detection based on boosted regression trees. 8${\textstyle ^{th}}$ European Workshop on Structural Health Monitoring, Bilbao (Spain), July 2016.

A copy of the post-print version of the articles is included in Appendix 7, while the works presented in conferences form Appendix 8.

Therefore, Chapters 2, 3 and 4 include a summary of the methods and results of the correspondent articles, while Chapter 5 contains the final part of the research, in which the previous results were taken into account.

(¹) Section 3 of this paper was carried out by León Morera

2 State of the art review

2.1 Introduction

A literature review was performed on a selection of articles and conference proceedings featuring examples of application of data-based models in dam behaviour modelling. This chapter includes a summary of this analysis.

In what follows, ${\textstyle Y\in \mathbb {R} }$ stands for some response variable (e.g. displacement, leakage flow, crack opening, etc.), which is estimated in terms of a set of inputs ${\textstyle {X}^{j}}$: ${\textstyle Y\approx {\hat {Y}}=F({X}^{j})}$. The observed values are denoted as ${\textstyle (x_{i}^{j},y_{i}),i=1,...,N}$, where ${\textstyle N}$ is the number of observations and ${\textstyle j=1\dots p}$ refer to the dimensions of the input space.

2.2 Statistical and machine learning techniques used in dam monitoring analysis

2.2.1 Models based on linear regression

2.2.1.1 The Hydrostatic-Season-Time model (HST)

Linear regression is the simplest statistical technique, appropriate to reproduce certain phenomena. It is also the basis of the most popular data-based behaviour model in dam engineering: the Hydrostatic-Season-Time (HST). It was first proposed by Willm and Beaujoint in 1967 [12].

It is based on the assumption that the dam response is a linear combination of three effects:

${\hat {Y}}={F}_{1}\left(h\right)+{F}_{2}\left(s\right)+{F}_{3}\left(t\right)$

(2.1)

• A reversible effect of the hydrostatic load which is commonly considered in the form of a fourth-order polynomial of the reservoir level (${\textstyle h}$) ([5], [25], [7]):

${F}_{1}\left(h\right)=a_{0}+a_{1}h+a_{2}h^{2}+a_{3}h^{3}+a_{4}h^{4}$

(2.2)

• A reversible influence of the air temperature, which is assumed to follow an annual cycle. Its effect is approximated by the first terms of the Fourier transform:

${F}_{2}\left(s\right)=a_{5}cos(s)+a_{6}sen(s)+a_{7}sen^{2}(s)+$ $a_{8}sen(s)cos(s)$

(2.3)

where ${\textstyle s=2\pi d{/}{365.25}}$ and d is the number of days since 1 January.

• An irreversible term due to the evolution of the dam response over time. A combination of monotonic time-dependant functions is frequently considered. The original form is [12]:

${F}_{3}\left(t\right)=a_{9}log(t)+a_{10}{e}^{t}$

(2.4)

The model parameters ${\textstyle a_{1}...a_{10}}$ are adjusted by the least squares method: the final model is based on the values which minimise the sum of the squared deviations between the model predictions and the observations.

The main advantages are:

• It frequently provides useful estimations of displacements in concrete dams [13].
• It is simple and thus easily interpretable: the effect of each external variable can be isolated in a straightforward manner, since they are assumed to be cumulative.
• Since the thermal effect is considered as a periodic function, the time series of air temperature are not required. This widens the possibilities of application, as only the reservoir level variation needs to be available to build an HST model.
• It is well known by practitioners and frequently applied in several countries [13].

It also features relevant limitations:

• The functions have to be defined beforehand, and thus may not represent the true behaviour of the structure [7].
• The governing variables are supposed to be independent, although some of them have been proven to be correlated [26].
• They are not well-suited to model non-linear interactions between input variables [6].

Several alternatives have been proposed to overcome these shortcomings. Penot et al. [27] introduced the HSTT method, in which the thermal periodic effect is corrected according to the actual air temperature.

Related approaches also based on linear regression were applied in dam safety, often by means of the addition of further input variables following some heuristics or after a trial-and-error process [18], [6], [7], [11], [28]. In all cases, the need to make a priori assumptions about the model remains, although variable selection procedures have also been proposed, such as Stojanovic et al. [29], who combined greedy MLR with variable selection by means of genetic algorithms (GA).

2.2.1.2 Consideration of delayed effects

It is well known that dams respond to certain loads with some delay [8]. The most typical examples are the change in pore pressure in an earth-fill dam due to reservoir level variation [30] and the influence of the air temperature in the thermal field in a concrete dam body [7].

Several alternatives have been proposed to account for these effects. The most popular is based on an enrichment of the linear regression by including moving averages or gradients of some explanatory variables in the set of predictors. Guedes and Coelho [31] predicted the leakage flow on the basis of the mean reservoir level over the course of a five-days period. Sánchez Caro [32] included the 30 and 60 days moving average of the reservoir level in the conventional HST formulation to predict the radial displacements of El Atazar Dam. Further examples are due to Popovici et al. [33] and Crépon and Lino [34].

A more formal alternative to conventional HST to account for delayed effects was proposed by Bonelli [35], [25]. It was intended to account for the delayed response of an arch dam in terms of the temperature field, with the final aim of predicting radial displacements. Lombardi et al. [4] suggested an equivalent formulation, also to compute the thermal response of the dam to changes in air temperature. Although the formulation differs from a multiple linear regression, its numerical integration leads to a predictive model which is a linear combination of:

• the value of the predictors at ${\textstyle {t}_{i}}$ and ${\textstyle {t}_{i-1}}$.
• the value of the output variable at ${\textstyle {t}_{i-1}}$.

which is the conventional form of a first order auto-regressive exogenous (ARX) model.

This is the most enriched version of multiple linear regression, where predictors of different types are combined. This gives greater flexibility to the algorithm to adapt to different situations or response variables. By contrast, the number of potential inputs can become very large, which generally leads to the need for some variable selection procedure. For example, Piroddi and Spinelli [36] applied a specific algorithm for selecting 11 out of 40 predictors considered. Principal component analysis (PCA) was also employed for variable selection (e.g. [37], [38], [6]).

A further drawback of linear regression with many input variables is that model interpretation becomes difficult, since the contribution of each predictor is harder to isolate.

Moreover, the use of the previous (lagged) value of the output to calculate a prediction for current record may induce to question a) whether the observed previous value or the precedent prediction should be used, and b) whether the model parameters should be readjusted at every time step.

In addition, current and previous values of response variables different from the target variable (e.g. radial displacements or leakage) can be considered as inputs. They implicitly encompass information from unrecorded or unknown phenomena, so the resulting model will probably be more accurate. However, it can also “learn” the anomalous behaviour and consider it as normal, in which case it would be inappropriate to detect anomalies.

The higher accuracy obtained by increasing the information given to the model invites exploring the utility of this approach, keeping their limitations in mind.

2.2.2 Machine learning based models

Among the non-conventional data-based algorithms, neural networks (NNs) are by far the most popular in the field of dam monitoring data analysis. NN models are flexible, and allow modelling complex and highly non-linear phenomena. Most of the published works employ the conventional multi-layer perceptron (MLP) and some sigmoid as the activation function.

These models often result in greater accuracy than MLR, due to the higher flexibility. However, the results are highly dependent on some issues to be determined by the user:

1. The network architecture, i.e., number of layers and perceptrons in each layer, which is not known beforehand. Some authors focus on the definition of an efficient algorithm for determining an appropriate network architecture [39], whereas others use conventional cross-validation [18] or a simple trial and error procedure [40].
2. The training process, which may reach a local minimum of the error function. The probability of occurrence of this event can be reduced by introducing a learning rate parameter [40].
3. The stopping criterion, to avoid over-fitting. Various alternatives are suitable for solving this issue, such as early stopping and regularisation [41].

The fitting procedures greatly differ among authors. While Simon et al. [7] trained an MLP with three perceptrons in one hidden layer for 200,000 iterations, Tayfur et al. [40] used regularisation with 5 hidden neurons and 10,000 iterations. Neither of them followed any specific criterion to set the number of neurons. For his part, Mata [18] tested NN architectures with one hidden layer having 3 to 30 neurons on an independent test data set. He repeated the training of each NN model 5 times with different initialisation of the weights.

It can be concluded that NNs share some of the target features (flexibility, accuracy), but lack ease for implementation and robustness. Model interpretation is not straightforward, and the results depend on the initialisations, so several models need to be trained and their results averaged to increase robustness. Moreover, only numerical inputs can be considered, which need to be normalised for model fitting (and de-normalised afterwards).

Other ML approaches were also applied in dam safety, such as Adaptive neuro-fuzzy systems (ANFIS) ([21], [42]), Support Vector Machines (SVM) ([43], [17]), or K-nearest neighbours (KNN) ([44]). They mostly share the mentioned properties of NNs: greater flexibility and accuracy, more difficult interpretation and potential over-fitting.

2.3 Methodological issues

Although each algorithm has its peculiarities, they all need to face intrinsic aspects of the problem to be solved, which can be analysed independently of the selected technique. Some of them have been mentioned before as variable selection. Others are specific to data-based prediction tasks, and in particular to the dam behaviour problem.

2.3.1 Input selection

The vast majority of statistical and ML algorithms are highly dependent on the inputs considered, which results in a need for input variable selection. The issue has arisen in combination with the use of NN [45], [46], [47], [48], [49], ARX [36], MLR [29] and ANFIS models [21].

The selection of predictors can be useful to reduce the dimensionality of the problem (essential for ARX models), as well as to facilitate the interpretation of the results.

The criterion to be used depends on the type of data available, the main objective of the study (prediction or interpretation), and the characteristics of the phenomenon to be modelled. Engineering judgement is thus essential to make these decisions.

By contrast, some ML algorithms are insensitive to the presence of highly-correlated or uninformative predictors, such as those based on decision trees. Boosted regression trees (BRTs) and random forests (RFs) stand out among those included in this category, though they are relatively new and unknown for most dam engineers.

2.3.2 Model interpretation

There is an obvious interest in model interpretation to analyse the effect of each input on dam response, once the parameters have been fitted. This contributes to answer the first question posed by Lombardi [4]: does the dam behave as expected/predicted? For example, an arch dam is expected to move in the downstream direction in front of a combination of high hydrostatic load and low temperature.

The evolution over time is particularly relevant, since it is related to the second and third questions [4]:

• Does the dam behave as in the past?
• Does any trend exist which could impair its safety in the future?

The effect of time, hydrostatic load and temperature can be easily obtained from an HST model, since it is based on the assumption that they are additive. However, it was already mentioned that they are actually correlated. Paraphrasing Breiman [24], when a pre-defined model is fit to data, ``the conclusions drawn are about the model's mechanism, not about nature's mechanism ¹. Moreover, “if the model is a poor emulation of nature, the conclusions may be wrong”.

Therefore, the interpretation of a more accurate predictive model will offer more reliable conclusions. The price to be paid for the greater flexibility and accuracy is the more difficult interpretation.

The vast majority of published studies are limited to the analysis of model accuracy for the output variable under consideration, as compared to HST. Only a few come to deal with model interpretation, that is, to analyse the strength and nature of the contribution of each action to the dam response. They are often limited to cases where a low number of inputs are considered (e.g. [18], [50], [7], [33]).

(¹) Breiman employs “nature” to denote any phenomenon partially understood, which associates the predictor variables to the outcome. In this research, ``nature's mechanism is homologous to “dam behaviour”

2.3.3 Training and validation sets

Accuracy is the main (and most obvious) measure of model performance, i.e. how well the model predictions fit to the observed data. However, it is well known that an increase in the number of parameters results in models more susceptible to over-fit. The higher complexity of ML algorithms has a similar effect as regards over-fitting. Hence, model accuracy must be computed properly.

It has been proven that the prediction accuracy of a data-based model, measured on the training data, is an overestimation of its overall performance [51]. Therefore, part of the available data needs to be reserved for model accuracy estimation (validation set). In principle, any sub-setting of the available data into training and validation sets is acceptable, provided the data are independent and identically distributed (i.i.d.).

This is not the case in dam monitoring series, which are time-dependant in general. Moreover, the amount of available data is limited, what in turn limits the size of the training and validation sets. Ideally, both should cover all the range of variation of the most influential variables.

On another note, a minimum amount of data is necessary to build a predictive model with appropriate generalisation ability. Some authors estimate the minimum period to be 5 [5] to 10 years [52], though it is case-dependent.

A further problem for the application of data-based models is that transient phenomena take place during the first years of operation [4]. Therefore, data from that period should be analysed in detail, since it might not be representative of subsequent dam performance.

In spite of these issues, many authors use the training set for computing model generalisation capability, or use a small sample for validation. This raises doubts about the actual accuracy of these models, in particular of those more strictly data-based, such as NN or SVM.

The deviation between predictions and observations is essential for dam behaviour assessment [4]. Moreover, the prediction intervals are typically based on some multiple of the standard deviation of the residuals. Hence, the proper estimation of model accuracy, over an adequate validation set, is fundamental from a practical viewpoint.

This topic is covered in depth in Chapter 5.

2.3.4 Practical implementation

Despite the increasing amount of literature on the use of advanced data-based tools, very few examples described their practical integration in dam safety analysis. The vast majority were limited to the model accuracy assessment, by quantifying the model error with respect to the actual measured data.

The information provided by reliable automated systems, based on highly accurate models, can be a great support for decision making regarding dam safety [3], [2].

To achieve that goal, the outcome of the predictive model must be transformed into a set of rules that determine whether the system should issue a warning. The actions to be taken need to be defined on a case-by-case basis, taking into consideration the relevance of each device as regards the overall dam safety [4].

Actually, an overall analysis of the most representative instruments is recommended, to identify (and discard) any isolated reading error. Cheng and Zheng [43] proposed a procedure for calculating normal operating thresholds (“control limits”), and a qualitative classification of potential anomalies: a) extreme environmental variable values, b) global structure damage, c) instrument malfunctions and d) local structure damage.

A more accurate analysis could be based on the consideration of the major potential modes of failure to obtain the corresponding behaviour patterns and an estimate of how they would be reflected on the monitoring data. Mata et al. [53] employed this idea to develop a system that takes the measurements of several devices and classifies them as correspondent to normal or accidental situation. This scheme can be easily implemented in an automatic system, though requires a detailed analysis of the possible failure modes, and their numerical simulation to provide data with which to train the classifier.

2.4 Conclusions

There is a growing interest in the application of innovative tools in dam monitoring data analysis. Although only HST is fully implemented in engineering practice, the number of publications on the application of other methods has increased considerably in recent years, specially NN.

It seems clear that the models based on ML algorithms can offer more accurate estimates of the dam behaviour than the HST method in many cases. In general, they are more suitable to reproduce non-linear effects and complex interactions between input variables and dam response.

However, most of the published works refer to specific case studies, certain dam typologies or determined outputs. Many focus on radial displacements in arch dams, although this typology represents roughly 5% of dams in operation worldwide.

A useful data-based algorithm should be versatile to face the variety of situations presented in dam safety: different typologies, outputs, quality and volume of data available, among others. Data-based techniques should be capable of dealing with missing values and robust to reading errors.

These tools must be employed rigorously, given their relatively high number of parameters and flexibility, what makes them susceptible to over-fit the training data. It is thus essential to check their generalisation capability on an adequate validation data set, not used for fitting the model parameters.

The main limitation of these methods is their inability to extrapolate, i.e., to generate accurate predictions outside the range of variation of the training data. Therefore, before applying these models for predicting the dam response in a given situation, it should be checked whether the load combination under consideration lies within the values of the input variables in the training data set.

From a practical viewpoint, data-based models should also be user-friendly and easily understood by civil engineering practitioners, typically unfamiliar with computer science, who have the responsibility for decision making.

Finally, two overall conclusions can be drawn from the review:

• ML techniques can be highly valuable for dam safety analysis, though some issues remain unsolved.
• Regardless of the technique used, engineering judgement based on experience is critical for building the model, for interpreting the results, and for decision making with regard to dam safety.

3 Algorithm Selection

3.1 Introduction

In view of the conclusions of the literature review, a set of ML algorithms were selected for a detailed comparative analysis. The main features were already known, but there was a need for testing their appropriateness to build dam behaviour models.

A selection of algorithms were faced to a practical case study, and the results were compared. Specifically, the following techniques were considered: random forests (RF), boosted regression trees (BRT), support vector machines (SVM) and multivariate adaptive regression splines (MARS). Both HST and NN were also used for comparison purposes. Similar analyses had been previously performed in other fields of engineering, such as the prediction of urban water demand [54].

3.2 Case study

The data used for the study correspond to La Baells dam. It is a double curvature arch dam, with a height of 102 m, which entered into service in 1976. The monitoring system records the main indicators of the dam performance: displacement, temperature, stress, strain and leakage. The data were provided by the Catalan Water Agency (Agencia Catalana de l'Aigua, ACA), the dam owner, for research purposes. Among the available records, the study focused on 14 variables: 10 correspond to displacements measured by pendulums (five radial and five tangential), and four to leakage flow. Several variables of different types were considered in order to obtain more reliable conclusions. The details of the available data are included in the article, whereas the location of each monitoring device is depicted in Figure 2.

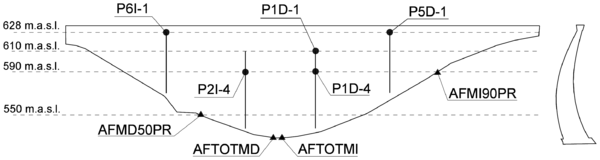
Figure 2

The specific features of dam monitoring data analysis were taken into account to design the experiment. In all cases, approximately 40% of the records (from 1998 to 2008) were left out as the testing set. This is a large proportion compared with previous studies, which typically leave 10-20 % of the available data for testing [21], [18], [44]. A larger test set was selected in order to increase the reliability of the results.

On another note, it is well known that the early years of operation often correspond to a transient state, non-representative of the quasi-stationary response afterwards [4]. In such a scenario, using those years for training a predictive model would be inadvisable. This might lead to question the optimal size of the training set in achieving the best accuracy ([52], [6]). The available time series for La Baells dam span from 1979 to 2008. To analyse this issue, four different training sets were chosen to fit each model, spanning five, 10, 15 and 18 years of records. In all cases, the training data used correspond to the closest time period to the test set (e.g. periods 1993-1997, 1988-1997, 1983-1997, and 1979-1997, respectively).

The predictor set included inputs related to the environmental actions: air temperature and hydrostatic load. A time-dependent term was also added, to account for possible variations in dam behaviour over the period of analysis. Several variables derived from those actually measured at the dam site (reservoir level and the average daily temperature) were also included. They are listed in Table 1.

Table. 1 Predictor variables considered.

Code	Group	Type	Period (days)
Level	Hydrostatic load	Original	-
Lev007	Hydrostatic load	Moving average	7
Lev014			14
Lev030			30
Lev060			60
Lev090			90
Lev180			180
Tair	Air temperature	Moving average	1
Tair007			7
Tair014			14
Tair030			30
Tair060			60
Tair090			90
Tair180			180
Rain	Rainfall	Accumulated	1
Rain030			30
Rain060			60
Rain090			90
Rain180			180
NDay	Time	Original	-
Year			-
Month	Season	Original	-
n010	Hydrostatic load	Rate of variation	10
n020			20
n030			30

The variable selection was performed according to dam engineering practice. Both displacements and leakage are strongly dependant on hydrostatic load. Air temperature is well known to affect displacements, in the form of a delayed action. It may also influence leakage flow (as Seifart et al. reported for Itaipú Dam [55]), although it is uncertain (Simon et al. observed no dependency [7]). Both the air temperature and some moving averages were included in the analysis.

A relatively large set of predictors was used to capture every potential effect, overlooking the high correlation among some of them. The comparison sought to be as unbiased as possible, thus all the models were built using the same inputs¹ and data pre-process (only normalisation was performed when necessary). While it is acknowledged that this procedure may favour the techniques that better handle noisy or scarcely important variables, theoretically all learning algorithms should discard them automatically during the model fitting.

(¹) with the exceptions of MARS and HST, as explained in the article

3.3 Results and discussion

Table 2, contains the mean absolute error (MAE) for each target and model, computed as:

$MAE={\frac {{\sum }_{i=1}^{N}\left|{y}_{i}-F\left({x}_{k}^{j}\right)\right|}{N}}$

(3.1)

where ${\textstyle N}$ is the size of the training (or test) set, ${\textstyle y_{i}}$ are the observed outputs and ${\textstyle F(x_{i})}$ the predicted values.

Table. 2 MAE for each output and model, fitted on the whole training set (18 years). The values within 10% from the minimum are highlighted in bold, and the minimum MAE are also underlined. The results correspond to the test set.

Type	Target	RF	BRT	NN	SVM	MARS	HST
Radial (mm)	P1DR1	1.70	0.93	0.58	0.75	2.32	1.35
	P1DR4	1.05	0.71	0.68	0.76	1.50	1.37
	P2IR4	0.94	0.97	1.02	1.05	0.85	1.12
	P5DR1	0.86	0.70	0.64	1.35	0.89	0.88
	P6IR1	1.47	0.69	0.72	0.60	1.67	0.91
Tangential (mm)	P1DT1	0.24	0.25	0.52	0.35	0.55	0.47
	P1DT4	0.15	0.15	0.18	0.19	0.22	0.20
	P2IT4	0.13	0.11	0.13	0.12	0.14	0.10
	P5DT1	0.40	0.22	0.19	0.38	0.47	0.18
	P6IT1	0.28	0.27	0.39	0.94	0.39	0.51
Leakage (l/min)	AFMD50PR	1.24	0.90	2.11	4.25	1.74	2.24
	AFMI90PR	0.18	0.15	0.07	0.33	0.25	0.28
	AFTOTMD	1.82	1.60	3.04	5.38	1.85	2.60
	AFTOTMI	0.91	0.42	0.83	1.49	1.49	1.11

It can be seen that models based on ML techniques mostly outperform the reference HST method. NN models yield the highest accuracy for radial displacements, whereas BRT models are better on average both for tangential displacements and leakage flow. It should be noted that the MAE for some tangential displacements is close to the measurement error of the device (${\textstyle \pm 0.1mm}$).

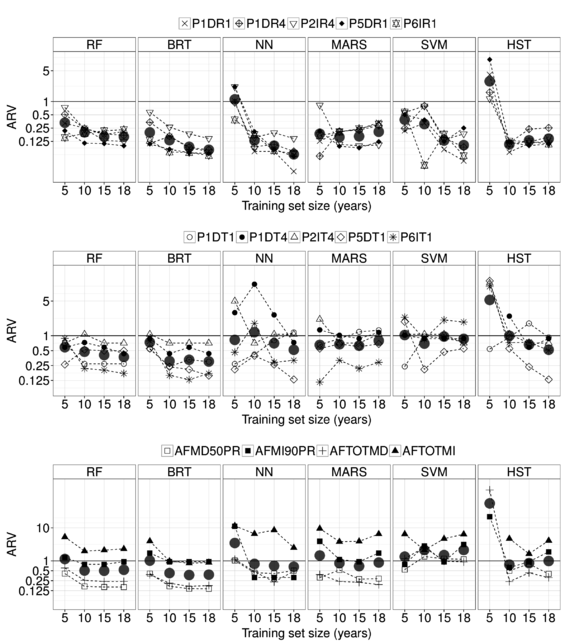
The effect of the training set size is depicted in Figure 3, where the model accuracy is measured in terms of the average relative variance (ARV) [56]:

$ARV={\frac {{\sum }_{i=1}^{N}{\left({y}_{i}-F\left({x}_{k}^{j}\right)\right)}^{2}}{{\sum }_{i=1}^{N}{\left({y}_{i}-{\bar {{y}_{i}}}\right)}^{2}}}={\frac {MSE}{{\sigma }^{2}}}$

(3.2)

where ${\textstyle {\bar {y}}}$ is the output mean. Given that ARV denotes the ratio between the mean squared error (MSE) and the variance (${\textstyle \sigma ^{2}}$), it accounts both for the magnitude and the deviation of the target variable. Furthermore, a model with ARV=1 is as accurate a prediction as the mean of the observed outputs.

Although the use of the whole training set is optimal for six out of 14 targets, significant improvements are reported in some cases by eliminating some of the early years. Surprisingly, for two of the outputs, the lower MAE corresponds to a model trained over five years, which in principle was assumed to be too small a training set. MARS is especially sensitive to the size of the training data. The MARS models trained on five years improve the accuracy for P1DR4 and P6IT1 by 13.3 % and 14.8 % respectively.

Figure 3: ARV for each model and training set size. Models with $ARV>1.0$ are less accurate than the sample mean. The average values for each output, algorithm and training set size are plotted with black dots. Note the logarithmic scale of the vertical axis. Top: radial displacements. Middle: tangential displacements. Bottom: leakage flow. Some HST models trained over 5 years are out of the range of the vertical axis, thus highly inaccurate. The results correspond to the test set.

These results strongly suggest that it is advisable to select carefully the most appropriate training set size. This should be done by leaving an independent test set.

3.4 Conclusions

It was found that the accuracy of currently applied methods for predicting dam behaviour can be substantially improved by using ML techniques.

The sensitivity analysis to the training set size shows that removing the early years of dam life cycle can be beneficial. In this work, it has resulted in a decrease in MAE in some cases (up to 14.8% Hence, the size of the training set should be considered as an extra parameter to be optimised during training.

Some of the techniques analysed (MARS, SVM, NN) are more susceptible to further tuning than others (RF, BRT), given that they have more hyper-parameters and are more sensitive to the presence of correlated or uninformative inputs. As a consequence, the former might have a larger margin for improvement than the latter.

However, both detailed tuning and careful variable selection increase the computational cost and complicate the analysis. Since the objective is the extension of these techniques for the prediction of a large number of variables of many dams, the simplicity of implementation is an aspect to be considered in model selection.

In this sense, BRT showed to be the best choice: it was the most accurate for five of the 14 targets; easy to implement; robust with respect to the training set size; able to consider any kind of input (numeric, categorical or discrete), and not sensitive to noisy and low relevant predictors.

4 Model Interpretation

4.1 Introduction

As a result of the comparative analysis, BRT was selected as the most appropriate tool to achieve the research objectives. In this stage, the possibilities of interpretation were investigated to:

1. Identify the effect of each external variable on the dam behaviour
2. Detect the temporal evolution of the dam response
3. Provide meaningful information to draw conclusions about dam safety

For this purpose, the same data from La Baells Dam were employed, though the analysis focused on 12 variables: 8 corresponded to radial displacements measured by pendulums (along the upstream-downstream direction), and four to leakage flow. The location of each monitoring device is depicted in Figure 4.1.

Geometry and location of the targets considered for model interpretation. Left: view from downstream. Right: highest cross-section.

Since BRT models automatically discard those predictors not associated with the output [57], the initial model considered the same inputs as described in section 3. All the calculations were performed on a training set covering the period 1980-1997, and the model accuracy was assessed for a validation set correspondent to the years 1998-2008.

4.2 Methods

4.2.1 Boosted regression trees

BRT models are built by combining two algorithms: a set of single models are fitted by means of decision trees [58], and their output is combined to compute the overall prediction using boosting [59]. For the sake of completeness, a short description of both techniques follow, although excellent introductions can be found in [60], [61], [62], [20].

4.2.1.1 Regression trees

Regression trees were first proposed as statistical models by Breiman et al. [58]. They are based on the recursive division of the training data in groups of “similar” cases. The output of a regression tree is the mean of the output variable for the observations within each group.

When more than one predictor is considered (as usual), the best split point for each is computed, and the one which results in greater error reduction is selected. As a consequence, non-relevant predictors are automatically discarded by the algorithm, as the error reduction for a split in a low relevant predictor will generally be lower than that in an informative one.

Other interesting properties of regression trees are:

• They are robust against outliers.
• They require little data pre-processing.
• They can handle numerical and categorical predictors.
• They are appropriate to model non-linear relations, as well as interaction among predictors.

By contrast, regression trees are unstable, i. e., small variations in the training data lead to notably different results. Also, they are not appropriate for certain input-output relations, such as a straight ${\textstyle 45^{\circ }}$ line [62].

4.2.1.2 Boosting

Boosting is a general scheme to build ensemble prediction models [59]. It is based on the generation of a (frequently high) number of simple models (also referred to as “weak learners”) on altered versions of the training data. The overall prediction is computed as a weighted sum of the output of each model in the ensemble. The rationale behind the method is that the average of the prediction of many simple learners can outperform that from a complex one [63].

The idea is to fit each learner to the residual of the previous ensemble. The main steps of the original boosting algorithm when using regression trees and the squared-error loss function can be summarised as follows [64]:

1. Start predicting with the average of the observations (constant):

$F_{0}\left({X}^{j}\right)={f}_{0}\left({X}^{j}\right)={\bar {y}}_{i}$

2. For ${\textstyle m=1}$ to ${\textstyle M}$
   1. Compute the prediction error on the training set:

   ${\tilde {y}}_{i}={y}_{i}-F_{m-1}\left(x_{i}^{j}\right)$

   2. Draw a random sub-sample of the training set (${\textstyle S_{m}}$)
   3. Consider ${\textstyle S_{m}}$ and fit a new regression tree to the residuals of the previous ensemble:

   ${\tilde {y}}_{i}\approx {f}_{m}\left({X}^{j}\right),i\in S_{m}$

   4. Update the ensemble:

   $F_{m}({X}^{j})\Leftarrow F_{m-1}({X}^{j})+f_{m}({X}^{j})$

3. ${\textstyle F_{M}}$ is the final model

It is generally accepted that this procedure is prone to over-fitting, because the training error decreases with each iteration [64]. To overcome this problem, it is convenient to add a regularization parameter ${\textstyle \nu \in (0,1)}$, so that step (d) turns into:

$F_{m}({X}^{j})\Leftarrow F_{m-1}({X}^{j})+\nu \cdot f_{m}({X}^{j})$

Some empirical analyses showed that relatively low values of ${\textstyle \nu }$ (below 0.1) greatly improve generalisation capability [59]. In practice, it is common to set the regularisation parameter and consider a number of trees such that the training error stabilises [60]. Subsequently, a certain number of terms are pruned using for example cross-validation. This is the approach employed in this work, with ${\textstyle \nu =0.01}$ and a maximum of 1,000 trees. It was verified that the training error reached the minimum before adding the maximum number of trees.

Five-fold cross-validation was applied to determine the amount of trees in the final ensemble. The process was repeated using trees of depth 1 and 2 (interaction.depth), and the most accurate for each target was selected. The rest of the parameters were set to their default values [65].

All the calculations were performed in the R environment [66].

Several procedures to interpret ML models, often termed “black box” models, can be found in the literature. In this work, the relative influence (RI) of each predictor and the partial dependence plots (PDP) were employed.

4.2.2 Relative influence (RI)

BRT models are robust against the presence of uninformative predictors, as they are discarded during the selection of the best split. Moreover, it seems reasonable to think that the most relevant predictors are more frequently selected during training. In other words, the relative influence (RI) of each input is proportional to the frequency with which they appear in the ensemble. Friedman [59] proposed a formulation to compute a measure of RI for BRT models based on this intuition. Both the relative presence and the error reduction achieved are considered in the computation. The results are normalised so that they add up to 100.

Based on this measurement, the most influential variables were identified for each output, and the results were interpreted in relation to dam behaviour. In order to facilitate the analysis, the RI was plotted as word clouds [67]. These plots resemble histograms, with the advantage of being more appropriate to visualise a greater set of variables. The code representing each predictor was displayed with a font size proportional to its relative influence with the library “wordcloud” [68].

Furthermore, two degrees of variable selection were applied, based on the RI of each predictor. First, a BRT model (M1) was trained with all the variables considered (section 5.2.3). Second, the inputs with ${\textstyle RI\left({X}^{j}\right)>min\left(RI\left({X}^{j}\right)\right)+sd\left(RI\left({X}^{j}\right)\right)}$ were selected to build a new model (M2). This criteria is heuristic and based on the 1-SE rule proposed by Breiman et al. [58]. Finally, a model with three predictors was generated (M3), featuring the more relevant variables of each group: temperature, time and reservoir level for radial displacements, and rainfall, time and level for leakage flows.

These three versions were generated to analyse the effect of the presence of uninformative variables in the predictor set. Moreover, the simplest model facilitates the analysis, as the effect of each action is concentrated in one single predictor.

In this sense, the temporal evolution is particularly relevant for dam safety evaluation, as it can help to identify a progressive deterioration of the dam or the foundation, which might result in a serious fault if not corrected.

4.2.3 Partial dependence plots

Multi-linear regression models and HST in particular are based on the assumption that the input variables are statistically independent, so the prediction is computed as the sum of their contributions. As a result, the effect of each predictor in the response can be easily identified, by plotting ${\textstyle F({X}^{j}),\forall j=1...p}$.

This method is not appropriate for BRT models, as interactions among predictors are accounted for. While this results in more flexibility, it also implies that the identification of the relation between predictors and response is not straightforward.

Nonetheless, it is possible to examine the predictor-response relationship by means of the partial dependence plots [59]. This tool can be applied to any black box model, as it is based on the marginal effect of each predictor on the output, as learned by the model. Let ${\textstyle {X}^{j}}$ be the variable of interest. A set of equally spaced values are defined along its range: ${\textstyle {X}^{j}={x}_{k}^{j}}$. For each of those values, the average of the model predictions is computed:

${\bar {F}}\left({x}_{k}^{j}\right)={\frac {1}{N}}\sum _{i=1}^{N}F\left({x}_{i}^{j},{x}_{i}^{jc}\right)$

(4.1)

where ${\textstyle {x}_{i}^{jc}}$ is the value for all inputs other than ${\textstyle {X}^{j}}$ for the observation ${\textstyle i}$.

Similar plots can be obtained for interactions among inputs: the average prediction is computed for couples of fixed ${\textstyle {x}_{k}^{j}}$, where ${\textstyle j}$ takes two different values. Hence, the results can be plotted as a three-dimensional surface (section 4.3.3). In this work, partial dependence plots were restricted to the simplest model, which considered three predictors. Therefore, three 3D plots allowed investigating the pairwise interactions among all the inputs considered in the simplified model.

4.2.4 Overall procedure

The complete process comprised the following steps:

1. Fit a BRT model on the training data with the variables in table 1 (M1).
2. Compute the RI and generate the word cloud.
3. Select the most relevant predictors with the 1-SE rule [58] and fit a new BRT model (M2).
4. Build a simple BRT model (M3) with the most influential variable of each group (temperature, level and time for displacements, and rainfall, level and time for leakage).
5. Generate the univariate and bivariate partial dependence plots for the simplest model.
6. Compute the goodness of fit for each model in both the training and the validation sets.

4.3 Results

4.3.1 Effect of input selection

Table 3 contains the error indices for each target. For those models with variable selection, the predictors are also listed. The results show that BRT efficiently discarded irrelevant inputs, since the fitting accuracy was similar for each version in most cases (i.e., the presence of uninformative predictors did not damage the fitting accuracy).

0.9 !

Table. 3 Accuracy of each model and target for the training and validation sets. The results and inputs considered by the most accurate version are highlighted in bold.

	Train		Validation
Target	MAE	ARV	MAE	ARV	Inputs
P1DR1	0.64	0.03	0.91	0.08	All
	0.68	0.03	0.81	0.06	Tair090,Level,NDay,Lev007,Lev014
	0.69	0.03	0.78	0.06	NDay,Tair090,Level
P1DR4	0.46	0.03	0.65	0.08	All
	0.50	0.03	0.66	0.08	Level,Tair090,NDay,Lev007,Lev014,Lev030
	0.51	0.03	0.67	0.08	NDay,Tair090,Level
P2IR1	0.66	0.03	1.03	0.09	All
	0.85	0.05	1.09	0.09	Tair090,Level,Lev007,Lev014
	0.71	0.04	0.98	0.08	NDay,Tair090,Level
P2IR4	0.48	0.05	0.90	0.14	All
	0.61	0.06	0.93	0.14	Level,Tair090,Lev007,Lev014,Lev030
	0.53	0.06	0.94	0.16	NDay,Tair090,Level
P5DR1	0.66	0.05	0.82	0.08	All
	0.64	0.05	0.87	0.10	Tair060,Level,Tair030
	0.83	0.08	0.93	0.11	NDay,Tair060,Level
P5DR3	0.25	0.03	0.47	0.21	All
	0.33	0.05	0.55	0.22	Tair060,Level,Tair030
	0.31	0.04	0.52	0.24	NDay,Tair060,Level
P6IR1	0.60	0.04	0.80	0.09	All
	0.65	0.05	0.78	0.08	Tair060,Tair030,Level,NDay
	0.83	0.08	0.85	0.1	NDay,Tair060,Level
P6IR3	0.23	0.02	0.40	0.08	All
	0.37	0.05	0.67	0.17	Tair060,Level,Tair030
	0.29	0.03	0.43	0.09	NDay,Tair060,Level
AFMD50PR	1.28	0.16	0.93	0.19	All
	1.45	0.17	1.36	0.28	Level,Lev014,Lev007
	1.16	0.14	1.23	0.48	NDay,Rain090,Level
AFMI90PR	0.08	0.09	0.15	0.51	All
	0.08	0.10	0.12	0.45	Lev007,NDay,Level,Lev014,Lev030
	0.08	0.10	0.12	0.46	NDay,Rain030,Lev007
AFTOTMD	1.64	0.15	1.67	0.37	All
	1.87	0.19	1.73	0.45	Level,Lev007,Lev014
	1.69	0.18	1.97	0.52	NDay,Rain180,Level
AFTOTMI	0.41	0.11	0.44	0.40	All
	0.44	0.12	0.44	0.42	NDay,Lev060,Lev014,Lev007,Lev030,Lev180,Lev090,Level
	0.54	0.18	0.46	0.60	NDay,Rain180,Lev060

4.3.2 Relative influence

The analysis of the wordclouds of RI allowed identifying some interesting features of La Baells dam behaviour. As for the radial displacements, (Figure 4.3.2), the thermal inertia was observed as higher RI for Tair060 and Tair090 than for Tair (which in fact resulted negligible). By contrast, the reservoir level at the date of the record was always more influential than all the moving averages, what reveals an immediate response of the dam to this load.

Other conclusions derived from Figure 4.3.2 are:

• The thermal inertia was lower near the abutments.
• The RI of the temperature with respect to that of the hydrostatic load increased from the foundation towards the crown, and from the centre to the abutments.
• The dam behaviour is sensibly symmetrical.

Word clouds for the radial displacements analysed.

The same analysis for the leakage flows revealed a clear different behaviour between the right (AFMD50PR and AFTOTMD) and the left margins (AFMI90PR and AFTOTMI). While the former responded mainly to the hydrostatic load, with little inertia, the latter showed a remarkable dependence on time, as well as a greater relevance of several rolling means of reservoir level. Figure 4.3.2 shows the word clouds for the leakage flows.

Word clouds for the leakage measurement locations analysed.

The low inertia with respect to the hydrostatic load suggests that most of the leakage flow comes from the reservoir, while the effect of rainfall is negligible.

4.3.3 Partial dependence plots (PDPs)

The resulting PDPs allowed verifying that the dam “behaved as expected”, in terms of the first question posed by Lombardi. Figure 4.3.3 contains the univariate PDP for P1DR1, which shows that higher hydrostatic load and lower air temperature are associated with displacement towards downstream and vice-versa.

Partial dependence plot for P1DR1. Movement towards downstream correspond to lower values in the vertical axis, and vice-versa.

Similar plots can be generated in 3D, which allow investigating the pairwise interactions for all the inputs considered (Figure 4.3.3).

3D PDPs for the main acting loads and P1DR1.

The analysis of the leakage flows (Figure 4.3.3) confirmed that the time effect was irrelevant in the right abutment, except by certain erratic behaviour in the first two years and in the last three. On the contrary, a sharp decrease in leakage flow was revealed around 1983 for both locations in the left abutment, and a lower decrease in later years.

The shape of the effect of the hydrostatic load is sensibly exponential, with low influence for reservoir level below 610 m.a.s.l.

Partial dependence plot for leakage flows.

The PDPs also provide information to answer the second and third questions, by means of analysing the partial dependence on time. In the particular case of P1DR1, these plots show a step around 1991-1992 for the whole ranges of level and temperature, which might represent some change in dam response (Figures 4.3.3 and 4.3.3. This issue was object of further verification.

First, an HST model was fitted and similarly interpreted (Figure 4.3.3). The time effect was a linear trend towards downstream, in contrast with the step suggested by the BRT model.

On another note, the average reservoir level in the period 1991-1997 was significantly higher than before 1991, and might be the cause of the step registered in Figures 4.3.3 and 4.3.3: it represents a greater displacement towards downstream in the most recent period, which is consistent with the higher average hydrostatic load.

Contribution of time, temperature and hydrostatic load on P1DR1, as derived from the interpretation of HST.

To clarify the divergence in the results, a new BRT model was fitted to artificial data generated by plugging actual time series of reservoir level into the HST model, while removing the time-dependent terms:

${\hat {P1DR1}}_{mod}=a_{1}h+a_{2}h^{2}+a_{3}h^{3}+a_{4}h^{4}+a_{5}h^{5}$ (4.2) $+a_{8}cos(s)+a_{9}sin(s)$ $+a_{10}sin^{2}(s)+a_{11}sin(s)cos(s)$

The artificial time series data maintains the original reservoir level variation, and thus the higher load in the 1991-1997 period. Figure 4.3.3 contains the partial dependence plot for this BRT model, which clearly shows that the independence of the artificial data with respect to time was correctly captured. This result confirms that the step in the time dependence captured by BRT is not a consequence of the higher hydrostatic load in 1991-1997.

Partial dependence plot for the artificial time-independent data. P1DR1. It should be noted that time influence is negligible.

4.4 Conclusions

The interpretation of BRT models resulted in meaningful information on dam behaviour and the effect of each input variable. It allowed verifying that the dam response was in agreement with intuition (e.g. higher hydrostatic load generated displacement towards downstream), and isolating the evolution over time.

The observation of the relative influence of each predictor allowed detecting the thermal inertia of the dam, its symmetrical behaviour, as well as the high variation over time for the leakage flows in the left abutment.

Moreover, the analysis of the time effect suggested that partial dependence plots based on BRT models are more effective to identify performance changes, as they are not coerced by the shape of the regression functions that need to be defined a priori for HST.

5 Anomaly detection

5.1 Introduction

In the precedent sections, the first three questions posed in Chapter 1 were answered: BRT models allowed to study the dam response to the main loads, the relevance of each of the potential inputs, and the evolution over time. The high accuracy of BRTs imply that the conclusions drawn from the model interpretation are reliable.

However, the main objective of dam safety is to prevent failures, for which anomalies need to be detected at early stage. This refers to the fourth question: “was any anomaly in the behaviour of the dam detected?” [4]. The capability of predictive models to identify anomalies has been much less frequently studied than their accuracy. Mata et al. [53] developed a model based on linear discriminant analysis for the early detection of developing failure scenarios. This methodology belongs to the Type 2 among those defined by Hodge and Austin [69]: the system is trained with both normal and abnormal behaviour data, and classifies new inputs as belonging to one of those categories. The drawback of this approach is that the failure mode must be defined beforehand and simulated with sufficient accuracy to provide the training data. Hence, the system is specific for the failure mode considered.

Jung et al. [70] used a similar approach: abnormal situations were defined based on the discrepancy between model predictions and observed data. They focused on embankment dam piezometer data, and only the reservoir level was considered as external variable (although they acknowledge that the rainfall can also be influential). It is not clear whether this methodology could be applied to other dam typologies or response variables.

Cheng and Zeng [43] presented a methodology based on the definition of some control limits, which depend on the prediction error of a regression model. In addition, they proposed a classification of anomalies based on the trend of the deviation and on how the overall deviance is distributed among the devices considered. It has the advantage of being simultaneously applied to a set of devices, although the case study presented is simple and the test period considered very short (30 days), as compared to the available data (1,555 days).

Other examples of application of advanced tools together with prediction intervals have been published by Gamse and Oberguggenberger [71], who employed the procedure of probabilistic quality control, Yu et al. [11], based on principal component analysis (PCA), Kao and Loh [47], who used PCA together with neural networks (NN), Li et al. [23], who considered the autocorrelation of the residuals and Loh et al. [48], who presented models for short and long term prediction.

Most of these works follow a conceptually similar methodology: a prediction model is built, the density function of the residuals is calculated and used to define the prediction intervals, which are applied to detect anomalies. In all cases, the efficiency is verified by means of its application to a short period of records. As an exception, Jung et al. [70] and Mata et al. [53] used abnormal data obtained from finite element models (FEM).

In this Chapter, the results of the previous stages are implemented in a methodology for early detection of anomalies, with the following innovative features:

• The prediction model is based on boosted regression trees (BRTs), which showed to be more accurate than other machine learning and statistical tools in previous works [22].
• Causal, non-causal and auto-regressive models are considered and jointly analysed.
• Artificially-generated data are taken as reference. They were obtained from a FEM model considering the coupling between thermal and hydrostatic loads. This allows to identify normal and abnormal behaviour, as observed by some authors ([70], [53]). In this work, the FEM results are compared to actually observed data to verify their reliability.
• A methodology is proposed to neglect false anomalies due to the occurrence of extraordinary loads. It is based on the values of the two main actions (thermal and hydrostatic).
• Three types of anomalies are considered, affecting both to isolated devices and to the whole structure.
• Although radial displacements in an arch dam were selected for the case study, the method can be applied to other dam typologies and response variables. Moreover, it adapts well to different amount and type of input variables, due to the great flexibility and robustness of BRTs.

The outputs considered correspond to the same radial displacements employed in Chapter 4 (Figure 4.1).

5.2 Methods

5.2.1 Prediction intervals

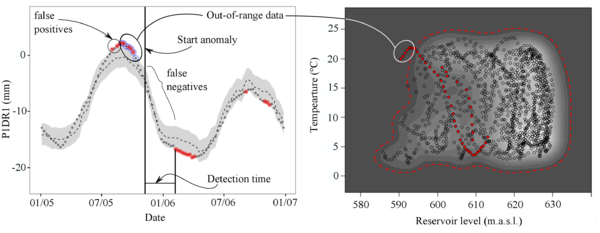
As mentioned above, most of the published works on the application of data-based models in dam monitoring are limited to the assessment of the model accuracy. However, the main practical utility of these models is the early detection of anomalies, for which it is necessary to compare the predictions with monitoring readings, and verify whether they fall within a predefined range. If the residual density function follows a normal distribution, that range can be defined in terms of the standard deviation of the residuals. For example, Kao and Loh [47] presented the 99% prediction intervals for models based on neural networks, while Jung et al. [70] tested 1, 2 and 3 standard deviations of the residuals as the width of the prediction interval.

Based on the results of a preliminary study [72], the prediction interval was set to ${\textstyle \left[\mu -2{sd}_{res},\mu +2{sd}_{res}\right]}$, being ${\textstyle \mu }$ and ${\textstyle {sd}_{res}}$ the mean and the standard deviation of the residuals, respectively. Special attention was paid to the determination of a realistic residual distribution. It is well known that the accuracy of a machine learning prediction model must be calculated from a data set not used for model fitting [73] (validation set). In the case of time series, this validation set should be more recent in time than the training data, since in practice the model is used for predicting a time period subsequent to the training data [51].

The hold-out cross-validation method meets this requirement, with the most recent data in the hold-out set (Figure 4).

Figure 4: Hold-out cross-validation scheme.

However, this implies discarding the most recent data for the model fit, which are generally the most useful, since they represent the most similar behaviour to that to be predicted (assuming there may be a gradual change in behaviour over time). Moreover, the validation data may be biased, if they correspond, for instance, to a especially warm (or cold) period.

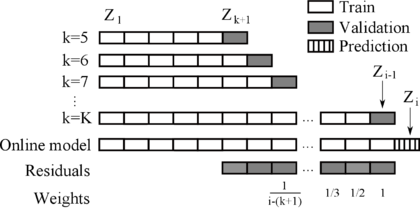
To overcome these drawbacks while maintaining good estimate of the prediction error, an approach based on the hold-out cross validation method suggested by Arlot and Celisse [51] for non-stationary time series data was employed.

The proposed method takes into account the following specific aspects of dam behaviour: a) changes in the dam-foundation system are generally gradual, and b) dam behaviour models are typically revised annually, coinciding with the update of safety reports.

Let us consider that a behaviour model is to be fitted at the beginning of year ${\textstyle {Z}_{i}}$, to be applied for anomaly detection during that year. The available data corresponds to the years ${\textstyle {Z}_{1}\dots {Z}_{i-1}}$, with ${\textstyle {Z}_{1}}$ being the initial year of dam operation. With the simple hold-out method, a model is fitted with data in years ${\textstyle {Z}_{1}\dots {Z}_{i-2}}$, whose accuracy is evaluated on data in ${\textstyle {Z}_{i-1}}$.

In this work, a minimum training period of 5 years was considered. This value was chosen in view of the results of previous studies [22], and the evolution of model accuracy on the reference data, as described in section 5.3.2. Then, an iterative process was followed to reduce potential bias in the loads during ${\textstyle {Z}_{i-1}}$. A set of predictions is generated as follows:

• For ${\textstyle k=5\dots i-2}$
• Fit a model ${\textstyle {M}_{k}}$ trained with the period ${\textstyle {Z}_{1}\dots {Z}_{k}}$.
• Compute ${\textstyle {R}_{k}}$ as the residuals of ${\textstyle {M}_{k}}$ when predicting year ${\textstyle {Z}_{k+1}}$.
• Compute the mean (${\textstyle {\mu }_{k}}$) and standard deviation (${\textstyle {sd}_{res,k}}$) of ${\textstyle {R}_{k}}$

At the end of the process, residuals for a set of models ${\textstyle {M}_{k},k=5\cdots i-2}$ are obtained, with the particularity that they are computed over different time periods, always subsequent to the training set ${\textstyle \left({Z}_{6}\cdots {Z}_{i-1}\right)}$. That is, the amount of observations in the training sample increases, and are used to predict the following year. The potential bias of some abnormal loads for one year is compensated by averaging, while a realistic prediction error is achieved, since it is always based on precedent data. A similar approach was employed by Herrera et al. to estimate demand in water supply networks, who employed the term growing window strategy [54].

Additionally, since the model accuracy typically increases as the training data grows, the actual model accuracy for the application period (year ${\textstyle {Z}_{i}}$) will be more similar to that obtained for ${\textstyle {Z}_{i-1}}$. Hence, ${\textstyle {R}_{i-2}}$ is more representative of the expected model performance for ${\textstyle {Z}_{i}}$. To account for this issue, the prediction intervals are based on a weighted average of ${\textstyle {\mu }_{k}}$ and ${\textstyle {sd}_{res,k}}$. In particular, the weights for each year decrease geometrically from the most recent to the first available. A schematic representation of the procedure is included in Figure 5.

Figure 5: Graphical representation of the weighted growing-window cross-validation procedure. The prediction interval is estimated as a function of the weighted average of the standard deviation of the residuals for previous years, each one is computed from a model trained with a different training set.

Finally, to take advantage of all the available data, a model is fitted with the entire period ${\textstyle {Z}_{1}\dots {Z}_{i-1}}$, with which the predictions for the following year (${\textstyle {Z}_{i}}$) are computed.

Since the test set becomes part of the validation period in the subsequent years, the residuals generated during the application of the model in the test period can be added to those computed for previous years, so that there is no need to repeat the whole process: the previous residuals can be employed to obtain the new prediction interval, after updating the correspondent weights.

5.2.2 Causal and non-causal models

BRT models are robust against the presence of uninformative or highly correlated predictors [59], [74]. Hence, variable selection is much less influential for tree-based methods than for other machine learning tools [57]. This property was employed to build BRT models of three types.

The first is a causal model, as that described in section 3.2, which considers as predictors those inputs related to air temperature, hydrostatic load and time (Table 1). A priori, a model of this type is expected to detect reading errors and changes in dam behaviour. However, its accuracy might be improved, since the response of the dam may depend on variables not considered, such as the maximum and minimum daily temperatures, or the solar radiation.

The second version is the Non-Causal model. In addition to the predictors described above, dam response variables were also considered as inputs. This means that each radial displacement is included in the input set to predict other radial displacements. This version will in principle give greater precision, since the record from a neighbouring device (e.g. another station of the same pendulum) implicitly contains the effect of external variables not considered in the causal version. By contrast, this model might not be able to detect anomalies affecting several devices. For example, a slide in a block of a concrete gravity dam will be reflected in all stations of the correspondent plumb line; therefore, the relation between the hydrostatic load and the displacement would be abnormal, while the relationship between several readings of the same pendulum could be normal.

Finally, an auto-regressive with exogenous inputs (ARX) [75] model was also fitted for each output, where the lagged values of all radial displacements were added to the Non-Causal model input set¹. Specifically, the response at time ${\textstyle {t}_{i}}$ is estimated based on the readings at ${\textstyle {t}_{i-1}}$ and ${\textstyle {t}_{i-2}}$, both for the variable to predict and other response variables.

One of the objectives of this work is to test the ability of all three models to detect various types of abnormalities, and draw conclusions for practical purposes.

(¹) The ARX model is also non-causal, in the sense that variables with non-causal relation with the outputs are included as predictors. The acronym ARX was employed to distinguish both models when necessary, although they are occasionally jointly referred to as “non-causal models”. For the sake of clarity, the capitalised version (“Non-Causal”) is used to specifically refer to the second model, excluding the ARX.

5.2.3 Case study

As in previous analyses, La Baells arch dam was also selected as the case study (Section 3.2). In this case, the air temperature and the reservoir level time series were considered as inputs to a FEM model. The results of this model in terms of radial displacements at the location of the pendulums were extracted and compared to the actual measurements. The objective was to check that the FEM model could provide realistic data to generate reference time series of dam behaviour. These artificial data are free from any temporal variation (the reference numerical model does not vary with time; only environmental loads do).

The dam was considered as a three-dimensional solid discretised in hexahedral serendipity 27-node elements. A portion of the foundation was also included, resulting in a total of 13,029 nodes and 2,530 elements. The thermal and mechanical problems were solved separately on the resulting finite element mesh (Figure 5.2.3). The material properties are shown in table 4.

Table. 4 Material properties considered in the FEM model.

Property	Dam	Foundation
Young modulus ${\textstyle (N\cdot {m}^{-2})}$	$4.76\cdot {10}^{10}$	$3.10\cdot {10}^{10}$
Poisson ratio	0.25	0.25
Density ${\textstyle (kg\cdot {m}^{-3})}$	2,400	3,000
Thermal conductivity ${\textstyle (W\cdot ^{\circ }{K}^{-1}\cdot {m}^{-1})}$	2.4	2.2
Thermal expansion coefficient	${10}^{-5}$	${10}^{-5}$
Specific heat ${\textstyle (J\cdot {kg}^{-1}\cdot ^{\circ }{K}^{-1})}$	982	950

For the thermal problem, a transient computation was run over the 1981-2008 period with time step of 30 days. The temperature was imposed in both dam faces, with different values for the wet and dry areas. For the boundaries below the reservoir level, the temperature was considered as equal to that of the water, which in turn was estimated by means of the Bofang formula [76]. Although it allows accounting for the temperature variation with depth, a unique value was considered in this work for all the wetted boundaries, equal to that obtained for 50% depth. For the dry faces, the 30-days moving average of air temperature was imposed, to take into account the thermal inertia. The result was increased by 2 degrees to account for the solar radiation, following the approach proposed by Pérez and Martínez for Spanish dams in the North-East region [77]. The temperature evolution for the first year was repeated 4 times to ensure that the result was not influenced by the initial conditions.

The mechanical response was assumed to be elastic and instantaneous (without inertia), hence for each time step, the hydrostatic load correspondent to the actual reservoir level was applied.

The results of both models (thermal and mechanical) were added, and the displacement evolution at the location of the monitoring devices were extracted. The model results, which are generated in global axes, were later transformed to the local axes correspondent to the radial displacements, as measured by the monitoring devices.

Finally, weekly values were obtained via interpolation, according to the average reading frequency for the available data.

In addition to radial displacements, also the temperature evolution in the dam body was compared to observed data from several thermometers embedded in the dam body.

The goodness of fit of the FE model was computed in terms of the mean absolute error (MAE) (equation 3.1).

5.2.4 Anomalies

As described in the previous section, the reference time series were those obtained with the FEM model for the 1980-2008 period, where the boundary conditions and loads correspond to the reservoir level and air temperature actually measured in the dam site. Three different types of anomalies were later introduced to modify those data:

• Scenario 1: Progressive breakdown of an isolated device. An increasing value was added to the reference series, with constant rate (a mm ${\textstyle \cdot }$ year-1).
• Scenario 2: The same as scenario 1, though the magnitude of the deviation is constant (a mm)
• Scenario 3: Imposed displacement of the left abutment. The data for this scenario were obtained from a modified FEM model representing a hypothetical sliding of the left abutment. For that purpose, the boundary condition at that region was set to ${\textstyle a}$ mm both in x and y axes (instead of null displacement, as for the reference case).

It is important to note that the anomaly of scenario 3 affects differently to each of the devices analysed. Since a displacement in the left abutment was imposed, the results in the left half of the dam body are anomalous. However, those in the right half are not affected. This can be observed in Figure 6, which depicts the displacement field in the dam body generated by the imposed anomaly with ${\textstyle a=2mm}$.

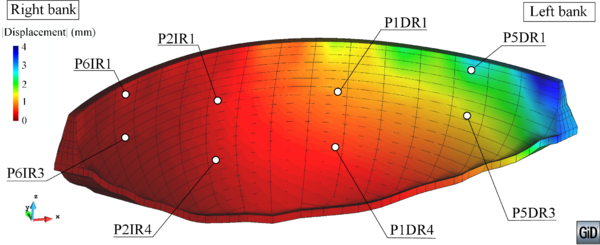
Figure 6: Displacement field resulting from the anomaly in scenario 3. View from downstream.

Table 5 contains the mean absolute deviation between the reference and the anomalous time series for each device for ${\textstyle a=2mm}$. Since the anomaly in scenario 3 does not affect to some devices, those values considered as abnormal by the system will be false positives.

Table. 5 Discrepancy between the normal displacements, as computed with the FEM model, and those imposed in scenario 3 for $a=2mm$. Mean absolute error (mm).

Device	MAE (mm)	Device	MAE (mm)
P1DR1	0.61	P5DR1	1.42
P1DR4	0.52	P5DR3	1.05
P2IR1	0.10	P6IR1	0.02
P2IR4	0.13	P6IR3	0.01

For each scenario, the performance of the three models considered (causal, Non-Causal and auto-regressive) was analysed. 4,000 anomalous cases were generated, where the following parameters were randomly selected:

• Initial date of abnormal period
• Anomaly scenario
• Output variable (Scenarios 1 and 2)
• Magnitude: 0.5, 1.0 or 2.0 mm ${\textstyle \cdot }$ year -1 for scenario 1; 0.5, 1.0 or 2.0 mm for scenario 2; 1.0 or 2.0 mm for scenario 3.

Each anomalous case was presented to all three models to compare their ability for anomaly detection. This was computed in terms of the detection time (${\textstyle {t}_{det}}$), defined as the elapsed time from the start of the anomaly until the first observation considered anomalous by each model, measured in days (Figure 7). Since the abnormal period was limited to 1 year, the models which did not detect any anomaly were assigned a ${\textstyle {t}_{det}}$ value of 365 days.

Moreover, the effectiveness of an anomaly detection system also depends on the number of false positives (observations considered abnormal by the model, which are actually normal) and false negatives (abnormal values not detected as such by the model). The two most commonly used metrics to account for these are precision (equation 5.1) and recall (equation 5.2). The comparison was mainly based on the ${\textstyle {F}_{2}}$ index [70], which jointly considers precision and recall, giving more importance to the latter (Eq. 5.3).

$precision={\frac {truepositives}{truepositives+falsepositives}}$

(5.1)

$recall={\frac {truepositives}{truepositives+falsenegatives}}$

(5.2)

${F}_{2}=(1+{2}^{2}){\frac {precision\cdot recall}{4\cdot precision+recall}}$

(5.3)

However, these indexes are not useful for model performance assessment when analysing the unaffected devices in scenario 3. In these cases, there are not true positives (all records are normal, since these devices are not affected by the anomaly). Hence, both precision and recall equal zero. Nonetheless, it is highly relevant to know whether the proposed models correctly identify these records within the prediction interval. For that purpose, scenario 3 was analysed by means of the amount of false positives, whose computation depends on the device. For those in the left half of the dam body (as viewed from upstream), which are actually anomalous, the observations above the upper limit of the prediction interval are considered as false positives, since they would imply a deviation towards upstream (while the actual anomaly corresponds to a displacement in the downstream direction). By contrast, for the unaffected devices, every record outside the prediction interval is a false positive, both above the upper limit and below the lower limit of the interval.

5.2.5 Load combination verification

In general, model accuracy is dependent on the values of the input variables. The more input data available for similar situations to that to be predicted, the more accuracy is to be expected. In dam behaviour, it will depend on the thermal and hydrostatic loads.

This effect is more important when input values are out of the training data range [78]. In particular, the accuracy of data-based models as BRTs may decrease dramatically when extrapolating.

Cheng et al. [43] defined a possible abnormal state of the dam (State 3), that “may be caused by extreme environmental values variables”. In this work, this issue was explicitly verified, and out-of-range (OOR) instances were considered as potential false positives.

This verification was carried out following an original procedure, specifically designed for the dam behaviour problem, where there are three main loads: thermal, mechanical (hydrostatic head) and temporal.

If the behaviour of the dam does not change over time, the importance of time variable is negligible. This was checked when fitting BRT models to the reference data, which correspond to time-independent dam behaviour. The inclusion of these variables is useful for retrospective analysis, as confirmed in Chapter 4. In practice, a previously trained model is employed to predict future values. Hence, it is obvious that the model prediction is an extrapolation in time axis and thus does not need to be verified.

As for the other two loads (thermal and hydrostatic), the simplest approach would be to check whether their values for the test period are greater (lower) than the maximum (minimum) within the training data set. However, that would not consider that both effects are coupled: the water temperature is different to that of the air, hence the water surface elevation affects the boundary condition in the upstream dam face and, as a result, conditions the thermal response of the dam [26].

Moreover, there is not a widely accepted agreement on what extrapolation is and how to handle it [78]. In dam behaviour modelling, it seems obvious that a hydrostatic load above the maximum in the training set is out-of-range. However, a more detailed definition seems appropriate to account for the “empty space phenomenon” [79], i.e., the existence of areas without training samples within the range of the inputs.

To account for this issue, a procedure that takes into consideration the combination of both loads is proposed:

1. The training data are plotted in the (Reservoir level, Air temperature) plane.
2. A two-dimensional density function is computed by means of the kernel density estimation (KDE) method.
3. The training instance with lower density value is localised, and the corresponding isoline is plotted.
4. The input values for the new data are plotted on the same plane. Those falling outside the isoline are considered as OOR.

With this procedure, it is taken into account that the predictive accuracy can be poor for a load combination not previously presented, even though their values, if considered separately, are within the training range. An example of this issue is presented in Figure 7.

Figure 7: Model performance indicators. Left: typical output plot, with the observations (circles), the predictions (dotted line), and the prediction interval (shaded area). Before the start of anomaly, some data fall outside the prediction interval (in red). Of those, some are false positives, whereas others correspond to out-of-range inputs (blue circles), since they fall in a low-density region in the 2D density plot (right). In this case, a combination of high temperature and low reservoir level was presented for the first time in dam history.

5.3 Results and discussion

5.3.1 FEM model accuracy

Figure 8 shows the comparison between the observed radial displacements for P1DR1 and those obtained with the FE model for the period 1994-2008. Results for other outputs are similar (Table 6). The FEM model accuracy is comparable to that obtained in previous Chapters with data-based models 2.

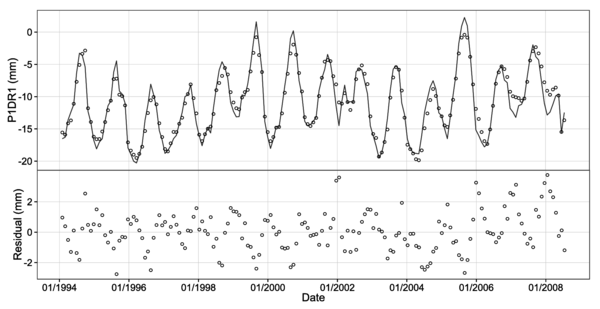
Figure 8: FEM results versus observations for P1DR1.

Table. 6 Deviation between the radial displacements as computed with the FEM and the actual records for the 1994-2008 period. Mean absolute error.

Output	MAE (mm)	Output	MAE (mm)
P1DR1	0.70	P5DR1	0.81
P1DR4	0.65	P5DR3	1.01
P2IR1	1.08	P6IR1	0.96
P2IR4	0.98	P6IR3	0.58

As regards the temperature, Figure 9 shows the numerical results and the observed data for 4 thermometers and the January 2007 - June 2008 period. Both the devices and the time period correspond to the results published by Santillán et al. [15], who employed a highly detailed thermal model for the same case study.

Figure 9: Comparison between numerical and measured temperature in 4 locations within the dam body.

Since predicting the thermal response is not the main objective of this analysis, relevant simplifications were employed to generate the reference data (neglecting the variation in water temperature with depth, using a relatively large time step). Nonetheless, the temperature within the dam body was well captured.

This, together with the results for displacements, confirm that the resulting data series mostly reproduce the dam response to the main loads. Therefore, they are representative of the normal behaviour of the dam and useful to evaluate the ability of the methodology to detect anomalies.

5.3.2 Prediction accuracy

The performance of all models on the reference data (without anomalies) was first assessed. The objectives are:

1. Verify the evolution of the prediction accuracy over time
2. Check the effect of averaging the standard deviation
3. Compare all models in terms of false positives
4. Evaluate the efficiency of the criterion to detect out-of-range data

For that purpose, the iterative process described in section 5.2.1 was followed, i.e., each model is re-fitted yearly over an increasing training set, and the prediction interval is updated as a function of the actualised value of the weighted average of the residual standard deviation. Since the dam-foundation behaviour is time-independent for the reference case, the variation in model accuracy is due to the increase of training data.

Figure 10 shows the evolution of both the raw and the weighted average of the residual standard deviation for all devices and models. Some conclusions can be drawn:

• As expected, the accuracy of the Non-Causal and ARX models model is higher, since the non-causal inputs implicitly contain information regarding external variables not considered in the causal version.
• The inclusion of lagged variables in the ARX model is not relevant, as compared to the Non-Causal one.
• The raw values show high variance, especially for the causal model, which is eliminated by averaging
• The time evolution of the weighted standard deviation of the residuals is similar for all models: a sharp decrease in the first years, followed by quasi-constant behaviour. Nonetheless, the causal model requires more data to reach the low-slope part of the curve.

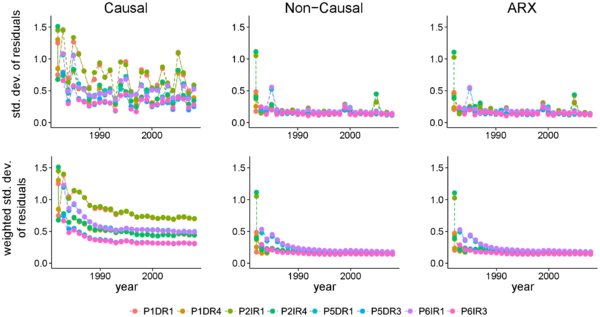
Figure 10: Time evolution of the prediction accuracy for all models and outputs. Top: standard deviation of residuals per year. Bottom: weighted average.

Table 7 contains the amount of false positives for all targets and models, as well as those correspondent to out-of-range inputs. Although the prediction interval for the causal model is wider (due to the higher residual standard deviation), it also generates a greater quantity of false positives. However, the average amount is low in all cases, as compared to the total amount of records (1,464). Moreover, the procedure to identify out-of-range inputs reduces the false positives by 27 % for the causal model and by 45% for both the non-causal and the ARX. As a result, the mean percentage of false positives is 8.0, 2.8 and 2.6 % respectively. It should be noticed that the results for the non-causal and ARX models are lower than the theoretical percentage of values outside the interval within 2 times the standard deviation in a normal distribution (5%

Table. 7 Amount of false positives.

Model	Causal		Non-Causal		ARX
Target	False pos.	OOR	False pos.	OOR	False pos.	OOR
P1DR1	179	53	91	40	82	35
P1DR4	178	54	89	42	75	38
P2IR1	184	54	89	41	85	35
P2IR4	198	54	95	50	75	38
P5DR1	125	31	50	21	51	21
P5DR3	164	49	72	31	68	30
P6IR1	129	31	51	21	50	21
P6IR3	171	42	63	27	65	28
Mean	166	46	75	34	69	31

5.3.3 Anomaly detection

Figure 11 (a) shows the ${\textstyle {F}_{2}}$ results as a function of the model and the anomaly magnitude ${\textstyle a}$ for scenarios 1 and 2. As expected, the larger anomalies were more easily detected in all cases. As for the input variables, Non-Causal model performed better on average, especially for small anomalies and as compared to the causal model. Again, the inclusion of lagged variables generated a minor effect, in this case towards slightly poorer performance.

Figure 11: ${F}_{2}$ index for scenarios 1 and 2.

The results for Scenario 3 are more interesting to analyse, since they correspond to a realistic anomaly affecting the overall dam behaviour. Since the effect of this anomaly is different on each output, the results are presented in terms of the true detection time ${\textstyle {t}_{d}}$ per device, i. e., the elapsed time until the first record identified as a deviation towards downstream. Figure 12 shows the results.

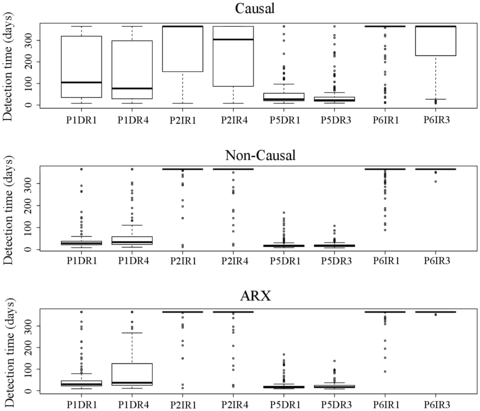
Figure 12: Detection time (days) per target and model for scenario 3.

A perfect model would feature null detection time for the affected devices (P1DR1, P1DR4, P5DR1 and P5DR3), and 365 days for the remaining (P2IR1, P2IR4, P6IR1 and P6IR3). Both the Non-Causal and the ARX models showed almost perfect performance. As regards the causal model, the anomaly in the most affected devices (P5DR1 and P5DR3) is detected almost instantly, but is less effective for P1DR1 and P1DR4, whose deviation from the reference behaviour is low (see Table 6). The detection time for P1DR1 and P1DR4 is around two months, with high variation up to 300 days.

A complete assessment of the model performance requires analysing the amount of false positives. They correspond to any value outside the prediction interval for the targets in the right half of the dam body, and to anomalies correspondent to deviations towards upstream for those in the left region. Figure 13 shows these results.

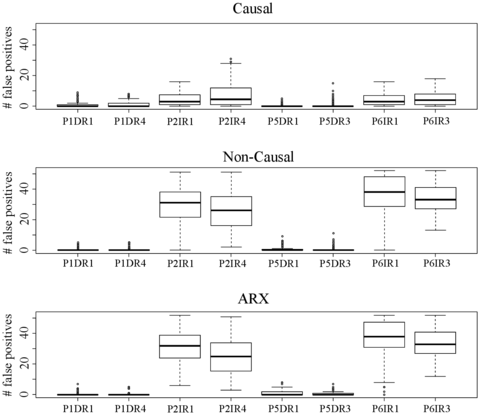
Figure 13: False positives per target and model for scenario 3.

It can be observed that the causal model is clearly more effective in this regard: both the Non-Causal and the ARX models classify around half of the observations for the unaffected devices as abnormal (there are 52 observations in the period of analysis). This result is due to the nature of the inputs for each model. For example, the Non-Causal model generates a prediction for P6IR1 based on the value of P5DR1 (among other inputs, but this is particularly important for being symmetrical within the dam body). In scenario 3, P5DR1 deviates towards downstream with respect to the reference (training) period. Since that input is anomalous, the resulting prediction is also wrong. In this case, the model interprets that the value of P6IR1 falls in the upstream side of the prediction interval.

This issue is highly relevant, since the final aim of the system is not only to detect a potentially anomalous behaviour, but also to support the correct identification of the cause, and then the decision making. In fact, similar results would have been obtained had the devices been analysed jointly in scenarios 1 and 2: a real deviation towards downstream in some device is (in general) correctly identified by the non-causal models, but that same value would generate an incorrect prediction for other devices, of opposite sign.

Causal models do not give these spurious results, since they predict the dam response only based on the external variables, at the cost of a generally higher detection time.

A straightforward option to avoid this behaviour is to discard non-causal models. However, their good performance for detecting true anomalies suggests that they can be useful overall.

As an alternative, the outputs whose value is identified as anomalous by the Non-Causal model can be removed from the input set. This requires re-training, but it can still offer accurate results, thanks to the flexibility of BRTs.

A new set of 240 cases was run for scenario 3 and the Non-Causal model. The results shown in Figure 14 confirm that the removal of abnormal variables is effective against false positives, while maintaining the ability for anomaly detection. The model performance is only poorer for P2IR1 (unaffected by the anomaly in scenario 3): the detection time is lower than 365 days, which indicates the existence of false positives. Nonetheless, the average detection time is still 270 days, and the total amount of false positives is lower than 10 %

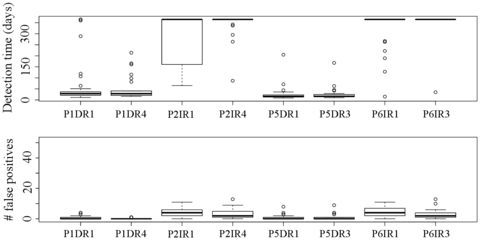
Figure 14: Detection time and false positives per target for scenario 3 and the Non-Causal model, once the anomalous variables are removed from the input set.

This approach was implemented in a new interactive tool, which was developed to present the results for all devices involved. It is based on the shiny library [80], and includes two plots for each model (Figure 15).

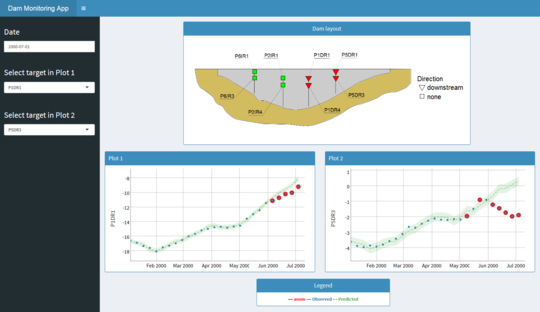
Figure 15: Interface of the dam monitoring data analysis tool for a case from scenario 3. The imposed displacement in the left abutment is correctly identified.

First, each device is plotted on its actual location within the dam body, with a symbol that is a function of the deviation between prediction and observation for the date under consideration. Then, the evolution of observations and predictions for the most recent period is plotted for two devices selected by the user. Figure 15 shows the application interface for one of the anomalies from scenario 3. It can be observed that the anomaly is correctly localised.

With this tool, the user jointly receives the overall information on all devices under consideration, and a more detailed plot of the selected output, where the value of the deviation, as well as the trend, can be observed. In this version, devices whose residuals are lower than two times the standard deviation are plotted in green; those between two and three times are depicted in yellow, and those above three times are shown in red. The shapes correspond to the direction of the deviation (upstream or downstream), as interpreted by each model. This criterion can be tailored to the user preferences.

5.4 Summary and conclusions

A methodology for early detection of anomalies in dam behaviour was presented, which includes a prediction model based on BRT, a criterion for detecting anomalies based on the residual density function, and a procedure for realistic estimation of the prediction interval. Also, extraordinary loads are identified by jointly considering the two most important external loads (hydrostatic load and temperature).

Causal models (which only consider external variables) and non-causal (including both internal and lagged variables as predictors) were compared in terms of detection time for three different anomaly scenarios. The results showed that non-causal models are more effective for the detection of anomalies, both affecting to isolated devices (Scenarios 1 and 2), and those resulting from an overall malfunction of the dam (Scenario 3).

In the case study considered, the inclusion of lagged variables had minor effect both in the model accuracy and the detection time. This suggests that the Non-Causal model (without lagged variables) might be a better choice due to its higher simplicity.

Causal models were more robust as regards the precision (when accounting for false positives). In abnormal periods, the prediction of non-causal models for unaffected devices is often wrong because it is partially based on anomalous data (that from the devices actually affected by the anomaly). This type of behaviour is a consequence of the nature of the model itself, and is the price to pay in exchange for a greater ability for early detection of anomalies.

However, an updated version of the Non-Causal model, where the anomalous variables are removed from the input set, avoided the above-mentioned issue, and showed to be as effective for anomaly detection as the original Non-Causal, and even more robust against false positives than the causal model. Hence, this approach is the best option to provide useful information to the dam safety managers. To that end, it was implemented in an interactive on-line tool, which shows the devices whose behaviour is interpreted as potentially abnormal by the predictive model, together with the plot of the evolution of predictions and observations for all relevant outputs.

This tool can be used as a support for decision making, since it facilitates the identification of a potential deviation from normal behaviour. Thus, it can be used as an indicator to generate a warning which might lead to intensify the dam safety monitoring activity.

6 Achievements, Conclusions and Future Research Lines

6.1 Achievements

A comprehensive literature review on data-based models for dam behaviour estimation was performed. A selection of articles was analysed, paying attention to the essential aspects of model building and assessment. The weaknesses of the published works were highlighted, and conclusions were drawn on criteria for building data-based dam behaviour models.

The possibilities of 5 state-of-the-art machine learning algorithms for dam behaviour modelling were analysed. Two of them had seldom been applied in this field before (neural networks and support vector machines), while the rest (random forests, boosted regression trees and multi-adaptive regression splines) had, to the best of my knowledge, never been used in dam safety to date. Their prediction accuracy was computed for 14 output variables of three different types (radial and tangential displacements, and leakage), correspondent to a real 100-m high arch dam. Issues related to the training algorithms and criteria to determine the value of the meta-parameters were addressed.

As a result of the previous analysis, BRT models were selected for further assessment. Based on the same case study, the effectiveness of the available tools (partial dependence plots and variable importance measure) for BRT model interpretation was verified. The results of the variable importance measure were presented in an innovative way: as wordclouds. This kind of plots are well known and often employed in other fields, and showed to be useful for agile interpretation of the results.

The effect of the inclusion of non-causal inputs was assessed, leading to the non-causal models. They showed to be even more accurate, though new issues arose regarding their implementation in dam safety assessment. Criteria for overcoming them were proposed, as well as for the practical implementation of data-based predictive models for the early detection of anomalies:

• A methodology to neglect false anomalies due to the occurrence of extraordinary loads.
• An innovative approach to obtain a realistic estimate of the model accuracy.
• A residual-based criterion to determine the prediction interval (range of safe operation).

These criteria were applied to develop an interactive tool for dam monitoring data analysis and anomaly detection that allows on-line control of dam performance at a glance. Both the code of the application and images of the user interface are included in Section 9.3.

A second interactive tool was also developed, which makes use of the “shiny” [80] and “ggplot2” [81] libraries within RStudio [82]. It has the following functionalities:

1. Data Import is designed to load time series data to be analysed and used to build predictive models. Alternatively, a previously fitted model can be loaded for its analysis.
2. Data Exploration allows pseudo-4D representation of dam monitoring data. Time series for all installed devices (both external and response variables) can be plotted. The user can select which variable to plot in the horizontal and vertical axes. The values are depicted with shape and colour dependent on two extra variables, also selected by the user. In this same section, time series of several outputs can be jointly plotted, together with some external variable in a secondary y-axis. This plot is based on the library “dygraphs” [83], which is highly interactive.
3. Model Fitting is designed to build BRT models to estimate different output variables for users unfamiliar with RStudio. The following parameters can be tuned:
• Output variable to predict
• Inputs to consider (the resulting model can thus be causal or non-causal)
• Training parameters (number of trees, shrinkage, interaction depth and bag fraction)
• Training and validation periods

The output of the application is a plot with predictions and observations, together with the residuals and the MAE for the training and prediction sets.

4. Interpretation includes plots showing the input variable importance: a bar chart with the 5 most important variables and a wordcloud with all inputs. Also, partial dependence plots for three predictors selected by the user.

6.2 Conclusions

The main conclusions of the research can be summarised as follows:

• Machine-learning and other advanced data-based tools are becoming familiar in the field of dam safety. The amount of published papers on the field increased in the recent years, most of which showed that the accuracy of deterministic or statistical models can be increased. However, most of them referred to specific case studies, certain dam typologies or determined outputs, and did not deal with model interpretation. As a result, these tools are far from being fully implemented in day-to-day practice.
• ML models typically feature a relatively high amount of parameters. This makes them flexible, but also susceptible to over-fit the training data. Hence, it is essential to check their generalisation capability on an adequate validation data set, not used for fitting the model parameters.
• Among the ML tools analysed, Boosted Regression Trees resulted to be advantageous from an overall viewpoint, since they showed to be more accurate on average for different type of output variables, easy to implement, robust with respect to the training set size, able to consider any kind of input (numeric, categorical or discrete), and low sensitive to noisy and low relevant predictors.
• Nonetheless, other ML algorithms such as Neural Networks, Support Vector Machines or Multi-Adaptive Regression Splines, produced more accurate predictions for some response variables. Moreover, some of them allow further tuning (e.g. variable selection). Therefore, if the main objective is to achieve the best possible fit, the analysis should not be limited to a single technique.
• The accuracy of data-based models as BRTs may decrease dramatically when extrapolating, so the conclusions drawn from their interpretation should be analysed carefully when those situations arise. In this sense, a load combination that presents for first time in dam history is an extraordinary situation, even though the values of the loads are within the historical range, when considered separately. As an example, it was found that the model predictions were unreliable in situations with a combination of low hydrostatic load and air temperature, although both were higher than the respective historical minimum.
• The application of BRT models to make predictions for a more recent period than that used for training, involves extrapolation over time (provided that some time dependent predictor is considered). Hence, results should be analysed carefully, in particular if the time effect seems relevant. This applies to any data-based model considering time as input, including HST.
• The removal of the early years of dam life cycle from the training set can be beneficial, though results suggest that its influence depends on the algorithm. While it resulted in a decrease in MAE above 10 % for some response variables, BRT accuracy showed lower dependency. Nonetheless, the size of the training set should be considered as an extra parameter to be optimised during training.
• The minimum required training period to obtain a model with reasonable accuracy can be estimated in 5 years, although this value is highly case-dependent. The aspects that influence this minimum are:

• The load combinations acting during the first years of operation: for example, if the reservoir level remains low, a data-based model will be highly inaccurate when estimating dam response in front of the design flood.
• The behaviour of dam and foundation during the first filling and the subsequent months. Although transient phenomena are frequent, their magnitude can differ greatly from case to case.
• The algorithm used to generate the model, and the input variables considered. In particular, non-causal models can be highly accurate with a shorter training period.

• Non-causal models (which include both external and response variables as inputs) are more accurate than causal ones for dam behaviour modelling, and more effective for early detection of anomalies. The reason is that the response variables implicitly provide information that is not included in the causal variables. However, it should be noted that if an anomaly affects several response variables, models that include them as inputs will probably give spurious results. This effect was actually observed in the case study, although they were still advantageous after removing the anomalous variables from the input set.
• BRT models can be efficiently interpreted as regards the relevant questions to be solved in dam safety assessment. Partial dependence plots show the contribution of each input to the output under consideration, as well as the performance evolution over time. Variable importance measures allow identifying the thermal inertia, as well as the relative influence of each acting load. The results are objective and reliable, since no a priori assumptions need to be made on the shape and intensity of the association between each input and the dam response.
• In spite of the observed advantages of ML algorithms, their results should be checked, when possible, against those provided by other means, such as deterministic models. Also, all available information about the dam behaviour should be taken into account, especially that obtained by visual inspection. Ultimately, engineering judgement based on experience is critical for building the model, interpreting the results, and making decisions with regard to dam safety.

6.3 Future research lines

Future research lines can be drawn from the results of the work, as well as from identified open issues:

• The work focused on BRTs because a robust and highly adaptive algorithm was looked for. However, other tools may be equally or more convenient in certain cases, depending on the variable to predict, the available information, and the characteristics of the dam. As an example, MARS provided greater accuracy in 3 of the 14 variables analysed in the comparative study, and always with a shorter training period. More sophisticated approaches such as the committees of experts (which can be of different nature) could also throw more accurate predictions. A more detailed discussion of this and similar algorithms might determine in which conditions they can be more effective.
• Data-based models obviously require a minimum amount of data to be generated. This means that they cannot be employed during the initial stage of dam life cycle, and in particular during the first filling. In this period, only numerical models are available, thought they also require real data for calibration. Interesting information might be obtained from the application of data-based models on numerically generated data, to narrow prediction intervals in the initial years of dam operation.
• The joint application and analysis of numerical and data-based models can also be advantageous in subsequent stages of dam life cycle, when enough monitoring data is available to build predictive models. Numerical models can be employed to estimate dam response in front of extraordinary loads, to enlarge and enrich the training data. Also, they can be modified to simulate potential anomalies or modes of failure, to generate response data to feed the data-based model. Research on this topic might reveal further possibilities.
• This research was based on the assumption that the time series data available were accurate and complete. Actually, data for the case study presented a low amount of missing values, which were simply interpolated. In the general case, it is highly frequent that long periods of data for determined sensors are missing. This prevents the inclusion of such variables among the inputs or output set, unless the missing values are imputed. Research is necessary to formulate criteria for missing value imputation. They should be dependent, at least, on the type of variable and the length of the missing period. Linear interpolation is appropriate for some variables (e.g. weekly mean temperature) if the missing period is short, but that is not the case in general.
• Many of the dams in operation were built decades ago, and their monitoring data is heterogeneous, incomplete or hand-written. In some cases, the lack of information might make impossible to apply any data-based model. A general picture of the quality of monitoring data would allow to develop tools and criteria to import data into an appropriate format and take full advantage of the available information.
• Flexibility was one of the premises throughout the research. BRTs were chosen because of their accuracy, but also because they automatically adapt to a variety of situations in terms of input variables availability and strength and shape of input-output association. Nonetheless, application of the tool and methodology to a set or real dams of different typologies would reveal specific issues to be solved.
• When an anomaly that affects several response variables occur, the non-causal models that rely on such variables as inputs give false positives on the unaffected devices. In the implementation developed, this problem is avoided by simply eliminating all variables considered anomalous in a first iteration. A more detailed study of this issue could allow developing a general criterion for identifying variables that are in fact abnormal, taking full advantage of all available information.
• The application developed displays the observations of the selected devices with different colour, depending on whether the system considered them as normal or abnormal. These colours are drawn over a front view of the dam, with each device in its actual location. In case of incipient failure, it could be useful to identify the potential causes, taking into account the dam typology, and the number and location of devices whose measure is identified as anomalous. A more detailed study, would allow defining colour patterns associated to potential failure modes.

BIBLIOGRAPHY

[1] Duffaut, Pierre. (2013) "The traps behind the failure of Malpasset arch dam, France, in 1959", Volume 5. Elsevier. Journal of Rock Mechanics and Geotechnical Engineering 5 335–341

[2] International Commission on Large Dams. (2000) "Automated dam monitoring systems. Guidelines and case histories". ICOLD B-118

[3] International Commission on Large Dams. (2012) "Dam surveillance guide". ICOLD B-158

[4] Lombardi, G. (2004) "Advanced data interpretation for diagnosis of concrete dams". Technical Report, CISM

[5] Swiss Committee on Dams. (2003) "Methods of analysis for the prediction and the verification of dam behaviour". Technical Report, ICOLD

[6] Chouinard, Luc and Roy, Vincent. (2006) "Performance of Statistical Models for dam Monitoring Data". Joint International Conference on Computing and Decision Making in Civil and Building Engineering, Montreal, June 14–16

[7] Simon, A. and Royer, M. and Mauris, F. and Fabre, J.P. (2013) "Analysis and Interpretation of Dam Measurements using Artificial Neural Networks". Proceedings of the 9th ICOLD European Club Symposium, Venice, Italy

[8] Lombardi, G. and Amberg, F. and Darbre, G.R. (2008) "Algorithm for he prediction of functional delays in the behaviour of concrete dams". Hydropower and Dams 3 111-116

[9] Papadrakakis, Manolis and Papadopoulos, Vissarion and Lagaros, Nikos D and Oliver, Javier and Huespe, Alfredo E and Sánchez, Pablo. (2008) "Vulnerability analysis of large concrete dams using the continuum strong discontinuity approach and neural networks", Volume 30. Elsevier. Structural Safety 30(3) 217–235

[10] Myers, B.K. and Scofield, D.H. (2008) "Providing improved dam safety monitoring using existing staff resources: Fern Ridge Dam case study". Proceedings of 28th Annual USSD Conference

[11] Yu, Hong and Wu, ZhongRu and Bao, TengFei and Zhang, Lan. (2010) "Multivariate analysis in dam monitoring data with PCA", Volume 53(4). Science China Technological Sciences 1088–1097

[12] Willm, G. and Beaujoint, N. (1967) "Les méthodes de surveillance des barrages au service de la production hydraulique d'Electricité de France-Problèmes ancients et solutions nouvelles". 9th ICOLD Congres 529-550, Q34-R30. [in French]

[13] Tatin, M and Briffaut, M and Dufour, F and Simon, A and Fabre, J-P. (2015) "Thermal displacements of concrete dams: Accounting for water temperature in statistical models", Volume 91. Elsevier. Engineering Structures 26–39

[14] Amberg, F. (2009) "Interpretative models for concrete dam displacements". 23th ICOLD Congress

[15] Santillán, D and Salete, E and Vicente, DJ and Toledo, MÁ. (2014) "Treatment of Solar Radiation by Spatial and Temporal Discretization for Modeling the Thermal Response of Arch Dams", Volume 140. American Society of Civil Engineers. Journal of Engineering Mechanics 11

[16] Salazar, Fernando and Morán, Rafael and Toledo, Miguel Á and Oñate, Eugenio. (2015) "Data-Based Models for the Prediction of Dam Behaviour: A Review and Some Methodological Considerations". Springer. Archives of Computational Methods in Engineering 1–21

[17] Rankovic, Vesna and Grujovic, Nenad and Divac, Dejan and Milivojevic, Nikola. (2014) "Development of support vector regression identification model for prediction of dam structural behaviour", Volume 48. Elsevier. Structural Safety 33–39

[18] J. Mata. (2011) "Interpretation of concrete dam behaviour with artificial neural network and multiple linear regression models", Volume 3. Engineering Structures 3(3) 03 - 910

[19] Demirkaya, Seyfullah. (2010) "Deformation analysis of an arch dam using ANFIS". Proceedings of the second international workshop on application of artificial intelligence and innovations in engineering geodesy. Braunschweig, Germany 21–31

[20] Auret, Lidia and Aldrich, Chris. (2011) "Empirical comparison of tree ensemble variable importance measures", Volume 105. Elsevier. Chemometrics and Intelligent Laboratory Systems 2 157–170

[21] Rankovic, Vesna and Grujovic, Nenad and Divac, Dejan and Milivojevic, Nikola and Novakovic, Aleksandar. (2012) "Modelling of dam behaviour based on neuro-fuzzy identification", Volume 35. Elsevier. Engineering Structures 107–113

[22] Salazar, F and Toledo, MA and Oñate, E and Morán, R. (2015) "An empirical comparison of machine learning techniques for dam behaviour modelling", Volume 56. Elsevier. Structural Safety 9–17

[23] Li, Fuqiang and Wang, Zhenyu and Liu, Guohua. (2013) "Towards an Error Correction Model for dam monitoring data analysis based on Cointegration Theory", Volume 43. Structural Safety 12–20

[24] Breiman, Leo and others. (2001) "Statistical modeling: The two cultures (with comments and a rejoinder by the author)", Volume 16. Institute of Mathematical Statistics. Statistical Science 3 199–231

[25] Bonelli, Stéphane and Félix, H. (2001) "Interpretation of measurement results, delayed response analysis of temperature effect". Proceedings of the Sixth ICOLD Benchmark Workshop on Numerical Analysis of Dams

[26] Tatin, M. and Briffaut, M. and Dufour, F. and Simon, A. and Fabre, J.P. (2013) "Thermal Displacements of Concrete Dams: Finite Element and Statistical Modelling". 9th ICOLD European Club Symposium

[27] Penot, Isabelle and Daumas, Bruno and Fabre, J.P. (2005) "Monitoring behaviour". Water Power and Dam Construction

[28] Carrere, A. and Noret-Duchene, C. (2001) "Interpretation of an arch dam behaviour using enhanced statistical models". Proceedings of the Sixth ICOLD Benchmark Workshop on Numerical Analysis of Dams

[29] Stojanovic, B. and Milivojevic, M. and Ivanovic, M. and Milivojevic, N. and Divac, D. (2013) "Adaptive system for dam behavior modeling based on linear regression and genetic algorithms", Volume 65. Advances in Engineering Software 182–190

[30] Bonelli, Stéphane and Radzicki, Krzysztof. (2008) "Impulse response function analysis of pore pressure in earthdams", Volume 12. European Journal of Environmental and Civil Engineering 3 243–262

[31] Guedes, Q.M. and Coelho, P.S.M. (1985) "Statistical behaviour model of dams". 15th ICOLD Congres Q56-R16, 319-334

[32] Sánchez Caro, Francisco Javier. (2007) "Dam safety: contributions to the deformation analysis and monitoring as an element of prevention of pathologies of geotechnical origin". PhD Thesis, UPM

[33] Popovici, A. and Ilinca, C. and Ayvaz, T. (2013) "The performance of the neural networks to model some response parameters of a buttress dam to environment actions". Proceedings of the 9th ICOLD European Club Symposium, Venice, Italy

[34] Crépon, O. and Lino, M. (1999) "An analytical approach to monitoring". Water Power and Dam Construction

[35] Bonelli, Stéphane and Royet, P. (2001) "Delayed response analysis of dam monitoring data". Proceedings of the Fifth ICOLD European Symposium on Dams in a European Context

[36] Piroddi, Luigi and Spinelli, William. (2003) "Long-range nonlinear prediction: a case study", Volume 4. IEEE. 42nd IEEE Conference on Decision and Control 3984–3989

[37] Mata, J. and Tavares de Castro, A. and Sá da Costa, J. (2014) "Constructing statistical models for arch dam deformation", Volume 21. Structural Control Health Monitoring 21(3) 423–437

[38] Chouinard, L. and Bennett, D. and Feknous, N. (1995) "Statistical Analysis of Monitoring Data for Concrete Arch Dams", Volume 9. Journal of Performance of Constructed Facilities 4 286–301

[39] Santillán, D. and Fraile-Ardanuy, J. and Toledo, M.Á. (2014) "Seepage prediction in arch dams by means of artificial neural networks", Volume V(3). Water Technology and Science

[40] Tayfur, Gokmen and Swiatek, Dorota and Wita, Andrew and Singh, Vijay P. (2005) "Case study: Finite element method and artificial neural network models for flow through Jeziorsko earthfill dam in Poland", Volume 131 (6). Journal of Hydraulic Engineering 431–440

[41] Hastie, Trevor and Tibshirani, Robert and Firedman, Jerome. (2009) "The Elements of Statistical Learning - Data Mining, Inference, and Prediction". Springer, 2 Edition

[42] Xu, HongZhong and Li, XueHong. (2012) "Inferring rules for adverse load combinations to crack in concrete dam from monitoring data using adaptive neuro-fuzzy inference system", Volume 55(1). Science China Technological Sciences 136–141

[43] Cheng, Lin and Zheng, Dongjian. (2013) "Two online dam safety monitoring models based on the process of extracting environmental effect", Volume 57. Elsevier. Advances in Engineering Software 48–56

[44] Saouma, VICTOR and Hansen, ERIC and Rajagopalan, BALAJI. (2001) "Statistical and 3D Nonlinear Finite Element Analysis of Schlegeis Dam". Proceedings of the Sixth ICOLD Benchmark Workshop on Numerical Analysis of Dams 17–19

[45] Demirkaya, S. and Balcilar, M. (2012) "The contribution of Soft Computing Techniques for the interpretation of Dam Deformation". Proceedings of the FIG working week

[46] Rankovic, Vesna and Novakovic, Aleksandar and Grujovic, Nenad and Divac, Dejan and Milivojevic, Nikola. (2014) "Predicting piezometric water level in dams via artificial neural networks", Volume 24(5). Springer. Neural Computing and Applications, 1115–1121

[47] Kao, Ching-Yun and Loh, Chin-Hsiung. (2013) "Monitoring of long-term static deformation data of Fei-Tsui arch dam using artificial neural network-based approaches", Volume 20. Wiley Online Library. Structural Control and Health Monitoring 3 282–303

[48] Loh, Chin-Hsiung and Chen, Chia-Hui and Hsu, Ting-Yu. (2011) "Application of advanced statistical methods for extracting long-term trends in static monitoring data from an arch dam", Volume 10. SAGE Publications. Structural Health Monitoring 6 587–601

[49] Panizzo, A. and Petaccia, A. (2009) "Analysis of monitoring data for the safety control of dams using neural networks". New Trends in Fluid Mechanics Research. Springer 344–347

[50] Santillán, D and Fraile-Ardanuy, Jesús and Toledo, MA. (2013) "Dam seepage analysis based on artificial neural networks: The hysteresis phenomenon". IEEE. Neural Networks (IJCNN), The 2013 International Joint Conference on 1–8, IEEE

[51] Arlot, Sylvain and Celisse, Alain and others. (2010) "A survey of cross-validation procedures for model selection", Volume 4. The author, under a Creative Commons Attribution License. Statistics surveys 40–79

[52] De Sortis, A and Paoliani, P. (2007) "Statistical analysis and structural identification in concrete dam monitoring", Volume 29. Elsevier. Engineering Structures 1 110–120

[53] Mata, J and Leito, N Schclar and de Castro, A Tavares and da Costa, J Sá. (2014) "Construction of decision rules for early detection of a developing concrete arch dam failure scenario. A discriminant approach", Volume 142. Elsevier. Computers & Structures 142:45–53

[54] Herrera, Manuel and Torgo, Luís and Izquierdo, Joaquín and Pérez-García, Rafael. (2010) "Predictive models for forecasting hourly urban water demand", Volume 387. Elsevier. Journal of Hydrology 1 141–150

[55] Seifard, L.A. and Szpilman, A. and Piasentin, C. (1985) "Itaipu structures. Evaluation of their performance". 15th ICOLD Congress, 287-317, Q56-R15

[56] Weigend, Andreas S and Huberman, Bernardo A and Rumelhart, David E. (1992) "Predicting sunspots and exchange rates with connectionist networks". Proc. of the 1990 NATO Workshop on Nonlinear Modeling and Forecasting (Santa Fe, NM) Volume 12 395–432, Addison-Wesley, Redwood, CA.

[57] Friedman, Jerome H and Meulman, Jacqueline J. (2003) "Multiple additive regression trees with application in epidemiology", Volume 22. Wiley Online Library. Statistics in medicine 9 1365–1381

[58] Breiman, Leo. (1984) "Classification and regression trees". Chapman & Hall/CRC

[59] Friedman, J.H. (2001) "Greedy function approximation: a gradient boosting machine". JSTOR. Annals of Statistics 1189 - 1232

[60] Ridgeway, Greg. (2007) "Generalized Boosted Models: A guide to the gbm package", R package vignette. URL http://CRAN.R-project.org/package=gbm

[61] Leathwick, JR and Elith, J and Francis, MP and Hastie, T and Taylor, P. (2006) "Variation in demersal fish species richness in the oceans surrounding New Zealand: an analysis using boosted regression trees", Volume 321. Marine Ecology Progress Series 267–281

[62] Elith, Jane and Leathwick, John R and Hastie, Trevor. (2008) "A working guide to boosted regression trees", Volume 77. Wiley Online Library. Journal of Animal Ecology 4 802–813

[63] Schapire, Robert E. (2003) "The boosting approach to machine learning: An overview". Nonlinear estimation and classification. Springer 149–171

[64] Alexandre Michelis. (2012) "Traditional versus non-traditional boosting algorithms". University of Manchester

[65] G. Ridgeway with contributions from others. (2013) "gbm: Generalized Boosted Regression Models", R package version 2.1

[66] R Core Team. (2013) "R: A Language and Environment for Statistical Computing". R Foundation for Statistical Computing, Viena, Austria

[67] Kaser, Owen and Lemire, Daniel. (2007) "Tag-cloud drawing: Algorithms for cloud visualization". arXiv preprint cs/0703109

[68] Ian Fellows. (2014) "wordcloud: Word Clouds". R package version 2.5.

[69] Hodge, Victoria J and Austin, Jim. (2004) "A survey of outlier detection methodologies", Volume 22. Springer. Artificial Intelligence Review 2 85–126

[70] Jung, In-Soo and Berges, Mario and Garrett, James H and Poczos, Barnabas. (2015) "Exploration and evaluation of AR, MPCA and KL anomaly detection techniques to embankment dam piezometer data", Volume 29. Elsevier. Advanced Engineering Informatics 4 902–917

[71] Gamse, Sonja and Oberguggenberger, Michael. (2016) "Assessment of long-term coordinate time series using hydrostatic-season-time model for rock-fill embankment dam". Wiley Online Library. Structural Control and Health Monitoring

[72] Salazar, F and González, JM and Toledo, MA and Oñate, E. (2016) "A methodology for dam safety evaluation and anomaly detection based on boosted regression trees". Proceedings of the 8th European Workshop on Structural Health Monitoring, Bilbao, Spain

[73] Hyndman, Rob J and Athanasopoulos, George. (2014) "Forecasting: principles and practice". OTexts

[74] Salazar, Fernando and Toledo, Miguel Á and Oñate, Eugenio and Suárez, Benjamín. (2016) "Interpretation of dam deformation and leakage with boosted regression trees", Volume 119. Elsevier. Engineering Structures 230–251

[75] Palumbo, P. and Piroddi, L. and Lancini, S. and Lozza, F. (2001) "NARX modeling of radial crest displacements of the Schlegeis Arch Dam". Proceedings of the Sixth ICOLD Benchmark Workshop on Numerical Analysis of Dams, Salzburg, Austria

[76] Bofang, Z. (1997) "Prediction of water temperature in deep reservoirs", Volume 8. REED BUSINESS PUBLISHING. Dam Engineering 13–26

[77] Pérez, JL and Martínez, E . (1995) "La acción térmica del medio ambiente como solicitación de diseño en proyectos de presas españolas", Volume 3349. Rev Obras Públicas 79–90

[78] Ebert, Tobias and Belz, Julian and Nelles, Oliver. (2014) "Interpolation and extrapolation: Comparison of definitions and survey of algorithms for convex and concave hulls". IEEE. Computational Intelligence and Data Mining (CIDM), 2014 IEEE Symposium on 310–314

[79] Verleysen, Michel and others. (2003) "Learning high-dimensional data", Volume 186. IOS PRESS. Nato Science Series Sub Series III Computer And Systems Sciences 141–162

[80] Winston Chang and Joe Cheng and JJ Allaire and Yihui Xie and Jonathan McPherson. (2016) "shiny: Web Application Framework for R"

[81] Hadley Wickham. (2009) "ggplot2: elegant graphics for data analysis". Springer New York

[82] RStudio Team. (2015) "RStudio: Integrated Development Environment for R". RStudio, Inc., Boston, MA

[83] Dan Vanderkam and JJ Allaire and Jonathan Owen and Daniel Gromer and Petr Shevtsov and Benoit Thieurmel. (2016) "dygraphs: Interface to 'Dygraphs' Interactive Time Series Charting Library", R package version 1.1.1.3.

Appendix A. Articles in the compilation

A.1 Data-based models for the prediction of dam behaviour. A review and some methodological considerations

Title: Data-based models for the prediction of dam behaviour. A review and some methodological considerations First Author: Fernando Salazar González. CIMNE - International Center for Numerical Methods in Engineering Second Author: Rafael Morán Moya. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Third Author: Miguel Á. Toledo Municio. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Fourth Author: Eugenio Oñate Ibáñez de Navarra. CIMNE - International Center for Numerical Methods in Engineering Journal: Archives of Computational Methods in Engineering D.O.I. 10.1007/s11831-015-9157-9 Impact Factor 4.214

A.2 Discussion on “Thermal displacements of concrete dams: Accounting for water temperature in statistical models”

Title: Discussion on “Thermal displacements of concrete dams: Accounting for water temperature in statistical models” First Author: Fernando Salazar González. CIMNE – International Center for Numerical Methods in Engineering

Second Author: Miguel Á. Toledo Municio. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Journal: Engineering Structures D.O.I. 10.1016/j.engstruct.2015.08.001. Impact Factor 1.893

A.3 An empirical comparison of machine learning techniques for dam behaviour modelling

Title: An empirical comparison of machine learning techniques for dam behaviour modelling

First Author: Fernando Salazar González. CIMNE – International Center for Numerical Methods in Engineering Second Author: Miguel Á. Toledo Municio. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Third Author: Eugenio Oñate Ibáñez de Navarra. CIMNE - International Center for Numerical Methods in Engineering Fourth Author: Rafael Morán Moya. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Journal: Structural Safety D.O.I. 10.1016/j.strusafe.2015.05.001 Impact Factor 2.086

A.4 Interpretation of dam deformation and leakage with boosted regression trees

Title: Interpretation of dam deformation and leakage with boosted regression trees First Author: Fernando Salazar González. CIMNE - International Center for Numerical Methods in Engineering Second Author: Miguel Á. Toledo Municio. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Third Author: Eugenio Oñate Ibáñez de Navarra. CIMNE - International Center for Numerical Methods in Engineering Fourth Author: Benjamín Suárez Arroyo. CIMNE - International Center for Numerical Methods in Engineering Journal: Engineering Structures D.O.I. 10.1016/j.engstruct.2016.04.012 Impact Factor 1.893

Appendix B. Other publications

B.1 Posibilidades de la inteligencia artificial en el análisis de auscultación de presas

Title: Posibilidades de la inteligencia artificial en el análisis de auscultación de presas First Author: Fernando Salazar González. CIMNE - International Center for Numerical Methods in Engineering Second Author: Miguel Á. Toledo Municio. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Third Author: Eugenio Oñate Ibáñez de Navarra. CIMNE - International Center for Numerical Methods in Engineering Conference: III Jornadas de Ingeniería del Agua. La protección contra los riesgos hídricos (JIA 2013) Date-Location: October 2013 - Valencia (Spain) ISBN 978-84-267-2070-2

B.2 Avances en el tratamiento y análisis de datos de auscultación de presas

Title: Avances en el tratamiento y análisis de datos de auscultación de presas First Author: Fernando Salazar González. CIMNE - International Center for Numerical Methods in Engineering Second Author: León Morera. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Third Author: Miguel Á. Toledo Municio. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Fourth Author: Rafael Morán. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Fifth Author: Eugenio Oñate Ibáñez de Navarra. CIMNE – International Center for Numerical Methods in Engineering Conference: X Jornadas Españolas de Presas Date-Location: February 2015 - Sevilla (Spain)

B.3 Nuevas técnicas para el análisis de datos de auscultación de presas y la definición de indicadores cuantitativos de su comportamiento

Title: Nuevas técnicas para el análisis de datos de auscultación de presas y la definición de indicadores cuantitativos de su comportamiento First Author: Fernando Salazar González. CIMNE - International Center for Numerical Methods in Engineering Second Author: Miguel Á. Toledo Municio. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Third Author: Eugenio Oñate Ibáñez de Navarra. CIMNE - International Center for Numerical Methods in Engineering Fourth Author: León Morera. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Fifth Author: Rafael Morán. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Conference: III Jornadas de Ingeniería del Agua. La precipitación y los procesos erosivos (JIA 2015) Date-Location: October 2013 - Córdoba (Spain)

B.4 A methodology for dam safety evaluation and anomaly detection based on boosted regression trees

Title: A methodology for dam safety evaluation and anomaly detection based on boosted regression trees First Author: Fernando Salazar González. CIMNE - International Center for Numerical Methods in Engineering Second Author: José M. González. CIMNE - International Center for Numerical Methods in Engineering Third Author: Miguel Á. Toledo Municio. Technical University of Madrid (UPM). Department of Civil Engineering: Hydraulics, Energy and Environment. Fourth Author: Eugenio Oñate Ibáñez de Navarra. CIMNE - International Center for Numerical Methods in Engineering Conference: 8${\textstyle ^{th}}$ European Workshop on Structural Health Monitoring Date-Location: July 2016 - Bilbao (Spain)

Appendix C. Code

C.1 Introduction

In this appendix, the code for the interactive tools is included. They all make use of the Shiny library and are formed by three files:

• global.R includes general instructions
• server.R contains the calculations
• ui.R controls the user interface

All files should be placed in the same directory, together with a data folder where the input data should be stored in an appropriate format to be read from global.R

C.2 Dam Monitoring App

C.2.1 User interface

Upload tab

Figure C.1: Dam Monitoring App. Welcome tab. File upload.

Data exploration

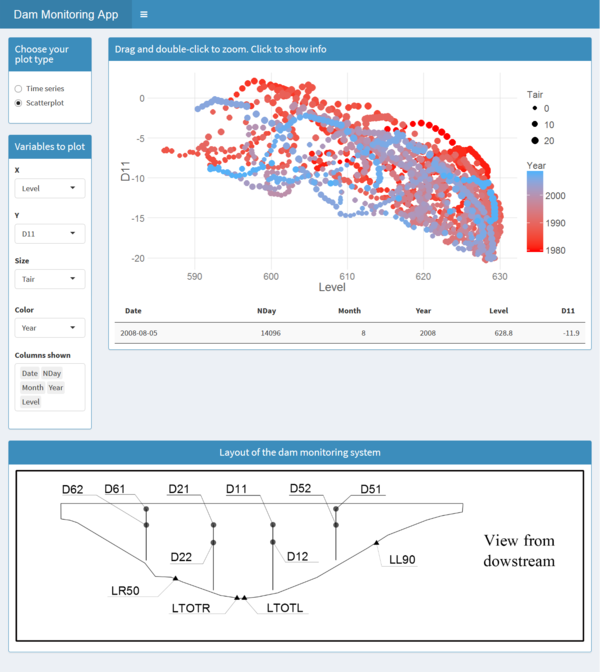
Figure C.2: Tab for data exploration. User interface for scatterplot.

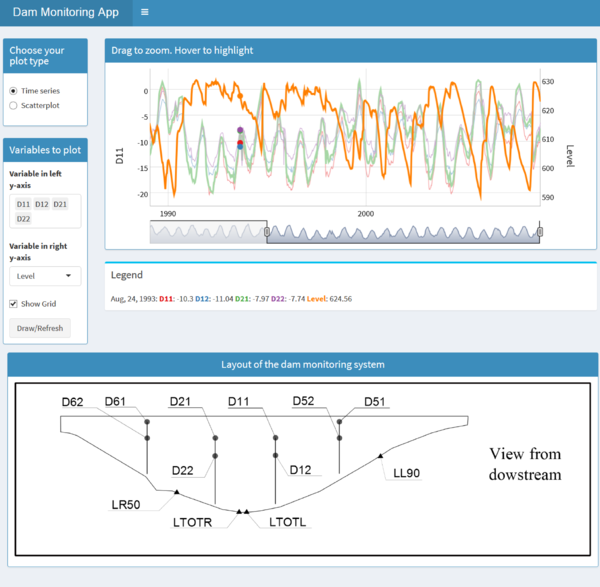
Figure C.3: Tab for data exploration. User interface for time series plot.

Model fitting

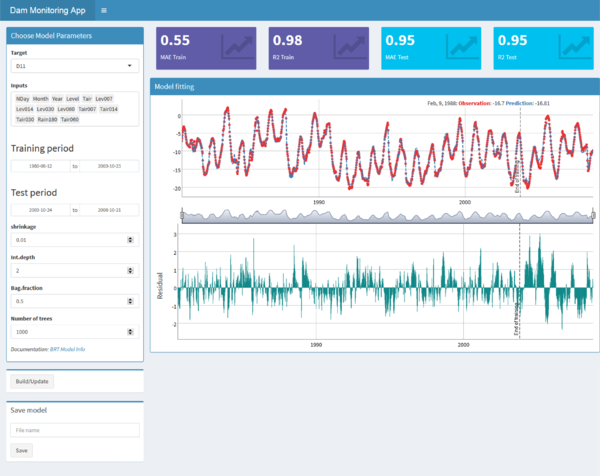
Figure C.4: Tab for model fitting. User interface.

Model interpretation

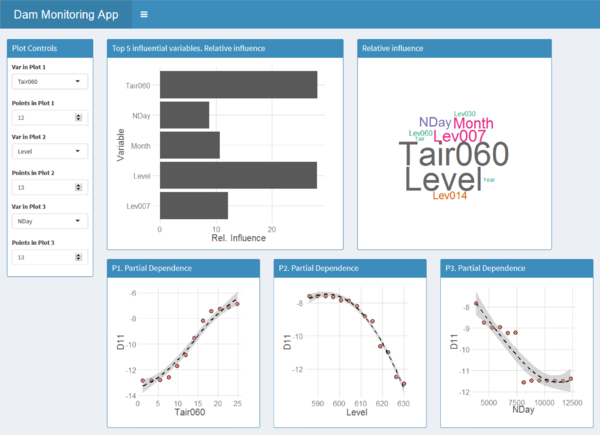
Figure C.5: Tab for model interpretation. User interface.

C.3 Anomaly Detection App

This application requires an image of the dam, also stored in the “data” folder.

9.3.1 User interface

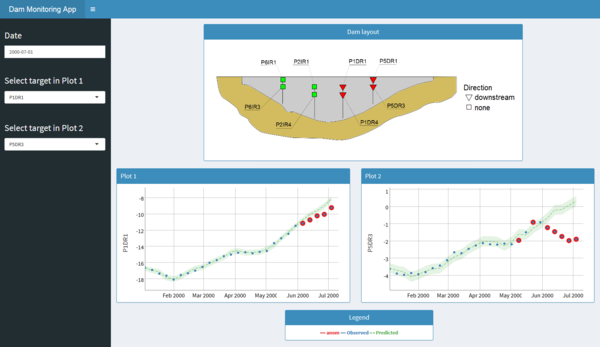
Figure C.6: Anomaly detection application. User interface