A Study on the Coffee Spilling Phenomena in the Low Impulse Regime

Abstract

When a half-full Bordeaux glass is oscillated sideways at 4 Hz, calm waves of wine gently ripple upon the surface. However, when a cylindrical mug is subject to the same motion, it does not take long for the liquid to splash aggressively against the cup and ultimately spill. This is a manifestation of the same principles that also make us spill coffee when we walk. In this study, we first investigate the physical properties of the fluid-structure interaction of the coffee cup; in particular, the frequency spectrum of each oscillating component is examined methodically. It is revealed that the cups oscillation is not monochromatic: harmonic modes exist, and their proportions are significant. As a result, although the base frequency of the cup is considerably displaced from the resonance region, maximum spillage is initiated by the second harmonic mode of driving force that the cup exerts on its contents. Thus, we spill coffee. As an application of these experimental findings, a number of methods to reduce liquid spillage are investigated. Most notably, an alternative method to hold the cup is suggested; in essence, by altering the mechanical structure of the cup-holding posture, we can effectively suppress the higher frequency components of the driving force and thus stabilize the liquid oscillation. In an attempt to rationalize all we have investigated above, a mechanical model is proposed. Due to practicalities, rather than to construct a dynamical system using Newtons equation of motion, we choose to utilize the Euler-Lagrangian equations. Extensive simulation studies reveal that our model, crude in its form, successfully embodies the essential facets of reality. This liberates us to make two predictions that were beyond our experimental limits: the change in magnitude of the driving force and the temporal stabilization process.

Introduction

Rarely do we manage to carry coffee around without spilling it once (Fig. 1 ). In fact, due to the very commonness of the phenomenon, we tend to dismiss questioning it beyond simply exclaiming: “Jenkins! You have too much coffee in your cup!”

Fig. 1. Rarely do we walk without spilling coffee.

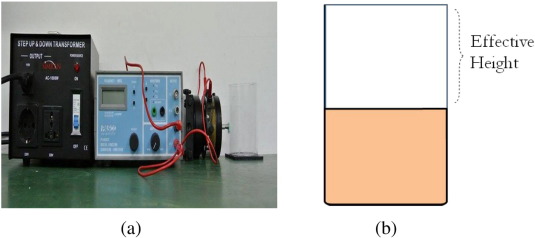
However, the coffee spilling phenomenon is deceivingly simple. As a counter-intuitive example, prepare two liquid containers with distinct geometrical structures; here, we consider a wine glass and a normal sized cylindrical mug. We first pour the same amount of coffee inside each container. Then, using a mechanical vibrator connected to a function generator (Fig. 2 a), we impose a horizontal excitation X  = X₀  cos (2πft ) to each liquid container, where X denotes the containers horizontal position and f is set to 2 Hz. This effectively simulates the human walking motion. Intuitively, since the amount of coffee is the same in each container, the amount spillage due to the oscillation should be fairly similar as well. However, this is not the case. As clearly shown in Fig. 3 b, the liquid motion inside the wine glass is aggressive while that of the cylindrical cup is comparatively steady; consequently, the quantity of spillage is significantly different. When the driving frequency “f ” is changed to 4 Hz, we are again surprised. Essentially, the liquid behavior inside each container is completely reversed: while the coffee inside the wine glass remains close to its equilibrium, the coffee inside the cylindrical cup oscillates violently (Fig. 3 c and d). Such experiment results are enough to show that the amount of liquid may not be the sole reason behind spilling coffee.

Fig. 2. (a) A mechanical setup to maintain a fixed frequency during oscillation. (b) A diagram of the effective cup height.

Fig. 3. Oscillations at (a), (b) 2 Hz and (c), (d) 4 Hz.

Indeed, the spilling of coffee is a manifestation of multiple interactions, ranging from the body-hand coordination to the resonance properties of the cup-coffee interaction. Thus, in order to gain clearer insight, the coffee spilling phenomenon is divided into two regimes: the low impulse regime and the high impulse regime. The term “impulse” indicates the maximum magnitude of the impulse that the cup experiences. Not surprisingly, the physical properties of each regime are pronouncedly different. In the low impulse regime, the interaction between the cup and coffee is considered as a periodic function; thus, the oscillation properties are researched extensively. However, in the high impulse regime, the interaction between the cup and coffee is momentary and aggressive. Oscillation phenomena carry less importance in such a regime. Spilling from casual walking falls under the former regime; spilling after slamming into a colleague falls under the latter. In the present paper, the low impulse regime is set to be the main focus of study.

Also, the effective cup height (which is defined to be the height of the cup minus the liquid equilibrium level [[[#f0010|Fig. 2]] b]) is not considered as a variable in this study for two reasons. First, the role of the effective height of the cup in spilling is rather straight forward. If the effective height of the cup is large enough, the coffee is unlikely to spill unless it is flipped over. On the other hand, if the effective height of the cup is close to zero, that is, if the cup is filled to its brim, the liquid is much more likely to spill. Thus, the taller the cup and lesser the coffee, the less you spill. Such a relationship is not investigated to further extent in this study. Second, as much as it is simple, the role of effective cup height is also absolute; due to the dominant role of the effective cup height, it is treated as a classification rather than a variable.

Thus, in this paper, we study the conditions that maximize the amplitude of coffee oscillation under the low impulse regime. In the Experiment Studies section, the liquid oscillation properties and the cups motion properties are investigated. Here, a surprising feature of the hand (cup) movement during walking is realized from its frequency spectrum. Then, combining the results from each investigation, it will be revealed how the interplay between the cup and coffee leads to spilling. By applying this knowledge, a number of methods to reduce coffee spilling are presented as well. Next, in the Model Studies section, two mechanical models of the “normal hand” posture and the “claw-hand” posture are proposed. They are each modeled by the oscillating-pivot single pendulum and the oscillating-pivot double pendulum; both models are constructed upon the bold assumption that coffee, at least in this study, can be treated as a simple pendulum. Surprisingly, simulation studies reveal that both models successfully predict the important physical properties discovered through experiment. We then conclude the paper with a summary of our discoveries.

Coffee spilling has also been extensively researched by Mayer and Krechetnikov (2012) . They present the conditions under which coffee spills for various walking speeds and initial liquid levels, followed by a spherical pendulum model to reflect such investigations. Kulczycki et al. (2013) have also taken a different approach on the subject; based on an appropriate Steklov eigenvalue problem, their research puts a focus on the geometrical properties of the fluid. However, as it will be shown throughout this paper and reiterated in the conclusion section, the experiment conclusion and mechanical models constructed in this research are profoundly different from former studies.

Experiment Studies

From experience, we know that our carrying hand is usually strong enough to be essentially unaffected by the coffees impact on the cup. This subtle insight immensely simplifies the situation: instead of analyzing both directions of influence, we can limit ourselves to one. In other words, we interpret the coffee-cup system as a forced harmonic oscillator. The driving force, which is synchronized with the carrying hands motion, is directly exerted on the liquid from the inner walls of the cup. If the driving frequency corresponds to the resonance frequency of coffee, the sloshing amplitude reaches its maximum and leads to spilling. Thus, the question that we must investigate is clear: what are the resonance conditions of this forced oscillator?

Throughout this research, the following equipment/software have been utilized: PASCO Function Generator (PI-9587), PASCO Mechanical Vibrator (SF-9324), Samsung Galaxy S4 accelerometer, MATLAB, and IDLE (Python).

Liquid Oscillation Properties

In order to determine the resonance conditions, the first and foremost information that must be acquired is the resonance frequency of the oscillator. Here, the oscillator is coffee. From the assumption that our liquid in consideration is incompressible, irrotational, and inviscid, the following equation predicts the natural frequencies of the various modes of fluid oscillation in an upright cylindrical container (Ibrahim, 2005  ;  Mayer and Krechetnikov, 2012 ).

${\omega }_{mn}^{2}={\frac {g{\epsilon }_{mn}}{R}}tanh\left({\frac {{\epsilon }_{mn}H}{R}}\right)\left[1+\right.$$\left.{\frac {\sigma }{\rho g}}{\left({\frac {{\epsilon }_{mn}}{R}}\right)}^{2}\right]$

( 1)

ω_{m  , n} is the angular frequency of an oscillation mode corresponding to a specific (m , n ) where m  = 0 , 1 , 2… and n  = 1 , 2 , 3…. H  , ρ , and σ are the height, density, and surface tension of the liquid, respectively. R is the cup radius, and g is the gravitational acceleration. ϵ_{m  , n} is defined by the relation ϵ_{m  , n}  = ϵ_{m  , 0}  + (n  − 1)π where ϵ_{m  , 0} is the solution to J_m^′ (ϵ ) = 0 and J is the m th order Bessel function of the first kind.

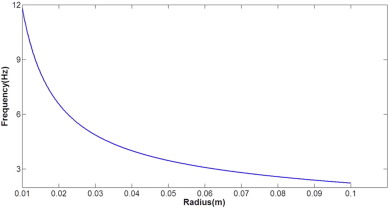
Of the various modes of oscillation, our main interest is the first antisymmetric mode. This is because of two reasons: the first antisymmetric mode involves the largest amount of liquid mass movement, and as we will see in the following section, its frequency corresponds to the driving frequency (at least approximately). Thus, by substituting the parameters in equation Eq. (1) with the generic cup dimensions (Amplifer, n.d. ) of 82 mm diameter and 95 mm height, the generic σ and ρ values for coffee, ¹ and ϵ₁₁  = 1.841, we calculate the first antisymmetric mode frequency to be approximately 3.95 Hz. Indeed, this value is dependent on the specific dimensions of the cup, and it is helpful to have a sense of how much the natural frequency would change according to the radius of the cup. Such a relationship is illustrated in Fig. 4 . Interestingly, the equation predicts a different amount of change in the natural frequency when the radius is either increased or decreased: an increase in the radius will not cause the natural frequency to change as much as it would if it was decreased.

Fig. 4. The natural frequencies as the radius changes.

The first antisymmetric mode can also easily be observed in the lab. Using the same mechanical device that was utilized in the introduction, we oscillate the container for one period and record its subsequent surface waves. In order to avoid unnecessary effects such as the liquid surface breaking or other modes of oscillation being excited, the amplitude of the mechanical vibrator was set to be 2 cm and the frequency was fixed at 2 Hz. These are also reasonable values that correspond to human walking motion.

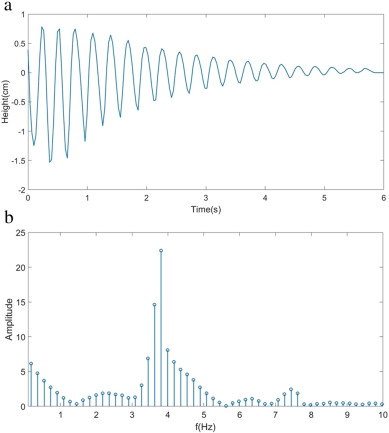
By using the color difference between the coffee and the background, we track one point on the liquid surface and plot its height relative to the equilibrium level. The final graph is presented in Fig. 5 a.

Fig. 5. (a) The relative height of a point on the liquid surface while it oscillates. (b) A FFT analysis of (a) reveals that the oscillation is fairly close to 3.8 Hz.

Visually, the damping oscillation seems to be monochromatic with an exponentially decreasing envelope. The former observation can be easily verified from the frequency spectrum (Fig. 5 b), which reveals that the damping oscillation indeed has a single dominant frequency of approximately 3.8 Hz. This value is slightly below the predicted frequency of 3.95 Hz, most likely due to the viscosity of coffee and other unconsidered frictional forces that arise from the cup-coffee interactions.² The second speculation is a bit trickier. The decreasing envelope is directly related to the damping coefficient γ; however, without sufficient knowledge of the input energy and the rate of dissipation, the damping coefficient defined as the following definition cannot be accurately calculated (Sauret et al., 2015 ).

$\gamma ={\frac {<{\overset {\cdot }{E}}_{l}>}{2E}}$

Instead, γ is determined by using an exponential curve fit of the enveloped curve of the damping oscillation. The damping coefficient is revealed to be approximately 0.674 rad/s, with r-square value of 0.9774. A parameter that can greatly increase this value is discussed in the Suppressing Resonance section.

Cup Motion Properties

After investigating the oscillator properties, the next step is to analyze the driving force: the cup. The cup is synchronized with our hands motion, which is directly influenced by our bodily movements. Such body-hand coordination properties have been extensively researched in biomechanical studies (Pontzer et al ., 2009  ; Collins et al ., 2009  ; Donker, 2002  ;  Anderson and Pandy, 2001 ), and it is revealed that the hands swaying motion during locomotion is dictated by our lower bodys “up and down” movements (Pontzer et al. (2009) coin the term “passive mass damper” for our hands swaying motion). However, we need to be cautious of the fact that the specific mechanism of the hands control of the cup may change according to how we hold the cup. While such deviations will be investigated in the Suppressing Resonance section and the Model Studies section, for now, we stick to the normal hand posture, as illustrated in Fig. 6 a.

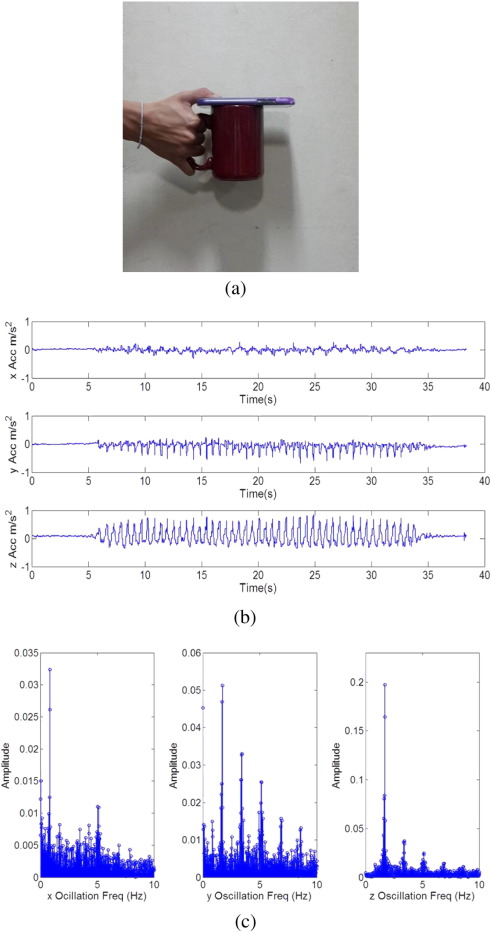
Fig. 6. (a) A simple apparatus to measure the acceleration that the cup experiences during locomotion. The acceleration data is recorded on the phone, which is stably fixed on the cup. In order to ensure that the weight of the cup did not change too much, the total weight of the apparatus was set to be equal to that of a 2 = 3 full cup. (b) The acceleration time plot in each orientation of measurement. There is a clear periodic tendency. (c) The FFT result in each orientation of measurement. The y-axis oscillation clearly exhibits harmonic frequencies; the second harmonic frequency coincides with the resonant frequency of coffee. Due to our up-and-down motion during walking, the z-axis oscillation exhibits strong periodicity of 2 Hz; this is our normal perceived frequency of walking.

In this research, two methods were employed in order to measure the acceleration of the cup during locomotion. The first method, which turned out to be unsuccessful, was to utilize image processing tools. The idea was to track the center of mass of the cup while the cup holder casually walked. That way, it would be possible to extract the time plot of the cups position, and subsequently, the time plot of the acceleration of the cup (by taking a second order derivative of the position data). However, this method was unsuccessful due to two main reasons. First, the image data was not sensitive enough. If the data is obtained over a long distance, one would inevitably have to zoom-out; this directly reduces the number of pixels, resulting in an insufficient amount of data. On the other hand, if we zoom in as much as we want to, the data collection time span is greatly limited. Unfortunately, we are stuck in a Heisenberg uncertainty principle-like situation in which we cannot achieve both measurements with desired quality at the same time. Second, the visual data was limited to only one plane of oscillation. Although the plane parallel to the walking direction is indeed where most of the action occurs, it would be better if data from all three planes of oscillation could be acquired as well. Such issues were solved by adopting the second method: utilizing an accelerometer.³

The second method proved to be quite successful. The apparatus, as shown in Fig. 6 a, is straightforward. By fixing an accelerometer (or, equivalently, a smartphone) to the top of the mug, we record all three directions of acceleration. Since the mug is a hard body, we expect the acceleration measured on any part of the mug to be equal; the accelerometer was also strapped to the bottom of the mug in order to verify that the experiment results were indeed independent of the position of the accelerometer.⁴

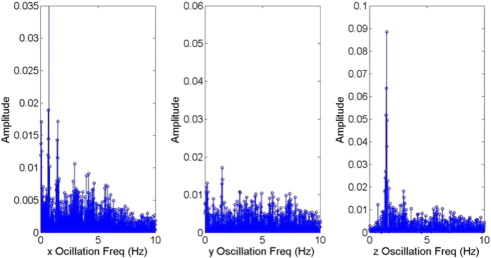
Representative acceleration plots in each orientation and their respective FFT analysis results are presented in Fig. 6 b and c. The vertical axis is the normalized relative amplitude of each frequency component. Here, the y-axis is the walking direction, the z-axis is the direction perpendicular to the ground, and the x-axis is the remaining sideways direction. From the acceleration time plot, the difference in the maximum magnitude of acceleration in each axis is highlighted. The z-axis acceleration has the biggest magnitude, and the x-axis acceleration is almost negligible in magnitude compared to the other two. This matches our expectations, since the up-and-down motion of walking is visually much larger than that of sideways swaying. According to the results of Pontzer et al. (2009) , the frequency of the z-axis oscillation should be synchronized with our lower-body movements.

Another interesting observation can be made from the frequency spectrum in each axis. In the acceleration time plot, the z-axis oscillation seems to have a smaller frequency than the y-axis oscillation; this is counter-intuitive, since we expect the cup motion to be have the same frequency as our body (up-and-down oscillation) itself. In order to shine a light on such observation, a FFT analysis is conducted on each acceleration plot.

Indeed, the FFT results are quite enlightening. Let us first take note of the y-axis frequency spectrum (Fig. 6 c). Evidently, the cup does not oscillate at the same frequency of our body. In fact, the motion is not even close to being purely sinusoidal: at least five or more distinct harmonic frequencies are contained in the motion. This directly goes against the daily assumption that our hand simply goes up and down when we walk. Instead, the cup-carrying hand undergoes a complex oscillation that is less than perfectly synchronized with our bodily motions. We should note that such intricate oscillations do not stem from the arm itself, but rather the extra degree of freedom that the wrist allows in the cup motion. Another significant observation is made by examining the specific values of the frequency components in the y-axis oscillation. Among the distinct harmonic frequencies, the second harmonic frequency coincides with 3.5–4 Hz, which is the resonance frequency of coffee in regular sized (Amplifer, n.d. ) cylindrical cups. In other words, as we casually walk, our hand oscillates in such a way that resonates with the first antisymmetric mode of coffee oscillation; thus, the likelihood of coffee spilling is maximized. It is important to realize that resonance would not likely occur if higher-frequency modes did not exist in our hand motion. For example, would one still spill coffee if the cup was strapped around ones waist? The answer is probably “No,” since, as we saw in the introduction, coffee does not spill as much when it is simply driven at 2 Hz. Again, the particularity of the cup motion that allows higher-frequency oscillation is highlighted.

Now we shift our focus to the other two results (Fig. 6 c). First, the z-axis oscillation clearly exhibits a dominant frequency close to 1.7 Hz. There also exist higher frequencies, but they are rather insignificant compared to the dominant frequency. This is reflected in our experience that the walking motion is largely composed of up-and-down motions, and that the frequency of such up-and-down motion is what we normally perceive to be the walking frequency. Although it cannot initiate a significant level of coffee sloshing, the z-axis oscillation at 1.7 Hz can still amplify the first antisymmetric mode in two ways. First, since 1.7 Hz is close to half of the resonance frequency, the z-axis oscillation can increase the amplitude of the coffee once every two cycles after the first antisymmetric mode is excited by y-axis oscillations. Second, there is the possibility of subharmonic resonance, as in the parametrically driven pendulum (Butikov, 2002  ;  Rudnick, 1969 ). However, such behavior was neither experimentally nor mathematically investigated thoroughly in this research. Next, it is notable that the x-axis oscillation has a dominant frequency of approximately 1 Hz, which is the half of the walking frequency itself. This reflects the sideways swaying motion of our hands when we walk, which, evidently, occurs once every two walking cycles. The x-axis oscillation, combined with y-axis oscillation, can cause the liquid to circulate around inside the cup.

Suppressing Resonance

So far, we have succeeded in uncovering the basic mechanism behind coffee spilling: resonance. By investigating the frequency properties of the coffee and cup motion, it is now evident that walking excites the first antisymmetric mode of coffee oscillation. It was also realized that such excitation is enabled by the biomechanical particularity of the hand motion. Now we ask the practical question: how do we stop spilling? The suggested solution is rather straight forward. Since the culprit behind spilling is resonance, preventing resonance would be sufficient to significantly reduce the probability of spilling. This can be achieved by altering either the coffees resonance frequency or the cup motion itself. A number of possible methods to implement such changes are discussed here.

The first suggested method is to change the way we walk. By walking backwards, we are able to significantly change the frequency characteristics of our hand motion. Using the same experiment setup shown in 6a, we conduct a FFT analysis of the cups acceleration when we walk backwards. In order to ensure the consistency of the result, the experiment was repeated five times. A representative result is shown in Fig. 7 .

Fig. 7. Frequency spectrum of backwards walking.

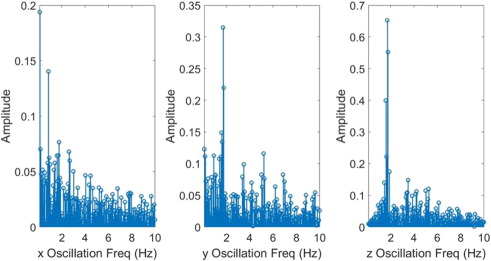
A notable change in the y-oscillation frequency spectrum is highlighted. Compared to normal walking, the frequency spectrum is more evenly distributed, and the presence of higher-frequency modes is greatly reduced; in fact, there does not seem to be a dominant frequency at all. Evidently, the resonance frequency of coffee is no longer a significant component in the frequency spectrum of the cup. Thus, the first antisymmetric mode now has a lesser chance of being excited, leading to a subsequent decrease in the probability of coffee spilling. Perhaps this is due to the fact that we are not used to walking backwards. Since we are not accustomed to backwards walking, our motion in the walking direction becomes irregular, and our body starts to heavily rely on sideways swinging motion in order to keep balance. This also accounts for the subtle changes in the x-axis and z-axis oscillations as well: the 1.7 Hz component has become more dominant in the z-axis, and the case is similar for 1 Hz in the x-axis.

Of course, walking backwards may be less of a practical method to prevent coffee spilling than a mere physical speculation. A few trials will soon reveal that walking backwards, much more than suppressing resonance, drastically increases the chances of tripping on a stone or crashing into a passing by colleague who may also be walking backwards (this would most definitely lead to spillage).

Fortunately, the second suggested method is a bit more realistic. By changing the way we hold the cup, it is also possible to suppress resonance; the proposed method of cup-holding is illustrated in Fig. 8 , and it is named as the claw-hand posture. As it will be explained further in the Model Studies section, such a method of holding the cup is mechanically equivalent to adding another oscillatory component to our system. Again, the same mechanical device used in former experiments is used to record the acceleration that the cup undergoes in the claw-hand posture. Then, we investigate changes in the frequency spectrum of the recorded data. A representative FFT analysis result is given in Fig. 9 . The change in the y-oscillation frequency spectrum is similar to that of walking backwards: the higher-frequency harmonic modes have been reduced greatly, although the dominant frequency near 1.7 Hz remains significant. Thus, we expect the claw-hand posture to have similar effects on the coffee oscillation as walking backwards.

Fig. 8. The “claw-hand” method of carrying coffee.

Fig. 9. Frequency spectrum of the claw-hand posture.

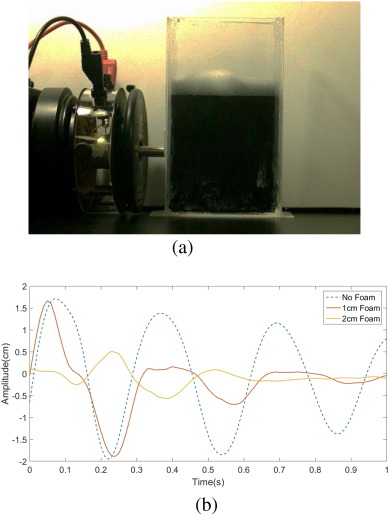
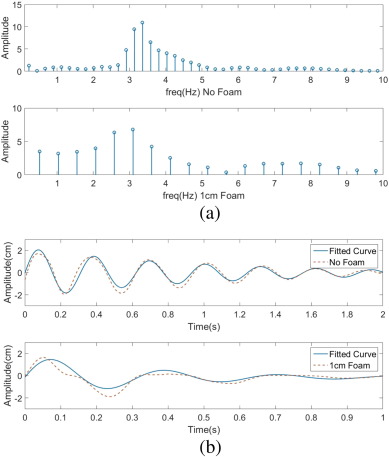
We also propose the method of adding a foam layer to the liquid surface. Such a method was extensively researched by Sauret, Boulogne, Cappello, Dressaire, and Stone. Their study demonstrates that a relatively thin layer of foam can be effective in damping liquid sloshing (refer to Sauret et al., 2015 ). A similar but simplified experiment is conducted in this study. The experiment apparatus illustrated in Fig. 10 a is used to observe the surface oscillations when a layer of foam was added—a Hele-Shaw cell is used due to the technical difficulties of analyzing the surface oscillation in a 3-dimensional container. Three samples are analyzed: the no-foam sample, 1 cm foam sample, and the 2 cm foam sample. The foaming solution is composed of 90% water and 10% glycerol, and the experiments are performed over a short timespan (about 1 s) so that the decay of the foam layer would be negligible. Again, using the color difference between the coffee and the background, we track one point on the liquid surface. The time plot of the relative height in each sample is presented in Fig. 10 b. From the frequency spectra in Fig. 11 a, we observe that the damping frequency decreases from approximately 3.3 Hz to 3 Hz.⁵ Then, from the fitted curve (Fig. 11 b) of the no-foam sample 1 cm foam sample, we note that damping coefficient nearly triples in its value (from 1.025 rad/s to 2.928 rad/s); according to Sauret et al. (2015) , this is a result of the energy dissipation in the wall boundary layer.

Fig. 10. (a) A mechanical device to observe the effect of adding foam. Due to technical difficulties, a Hele-Shaw cell is used instead of a cylindrical container. (b) The time plot of the relative height in each sample. A drastic decrease in the amplitude as a foam layer added can be observed.

Fig. 11. (a) The frequency spectra of the no-foam sample (top) and the 1 cm foam sample (bottom). A shift in the dominant frequency to the left can be observed. (b) The fitted curves are plotted with the original data plots. When 1 cm of foam layer was added, the damping coefficient γ increased to 2.93 rad/s from 2.23 rad/s and the angular frequency ωd decreased to 19.83 rad/s from 20.16 rad/s. The R2 value for each curve fit is 0.8877 (no foam) and 0.7668 (1 cm foam).

There is also the method of changing the cups resonance property itself. In Fig. 4 , it is evident that a decrease in the radius of the cup can significantly increase the resonance frequency; by dividing the cup into smaller cylindrical cells, as shown in Fig. 12 , the liquid oscillation is sufficiently displaced from the resonance domain. However, such an effect is not quantified in this research.⁶

Fig. 12. By dividing the cup into smaller cylindrical cells, we can displace the oscillation from resonance.

Model Studies

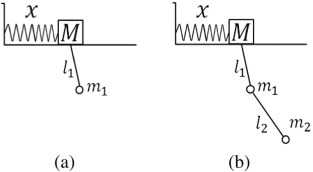
Although a full biomechanical description of the coffee spilling phenomenon is beyond the scope of this study, a simplified mechanical model is proposed and analyzed in order to gain further insight into the dynamics of the phenomenon. So far, we have examined two distinct ways of carrying coffee: the normal hand posture and the claw-hand posture. For each posture, a mechanical model that encompasses such differences is constructed and compared to experiment findings. The proposed mechanical models are illustrated in Fig. 13 a and b. In both models, the coffees impact on the cup motion is no longer ignored. Also, for simplicitys sake, the walking frequency is set to be 2 Hz and the first antisymmetric mode is set to be 4 Hz (the actual values are approximately 1.7 Hz and 3.8 Hz). For the normal hand posture, the arm is depicted by a simple harmonic oscillator of mass M. Since the arm itself is not flexible, it is considered to oscillate at 2 Hz, perfectly synchronized with the bodily oscillations. Thus, M and the spring constant k are decided so that the natural frequency of M under a small displacement would equal 2 Hz. Next, the coffee is depicted by a simple pendulum; the simple pendulum oscillating at f corresponds to coffee being driven at an external driving force of frequency f . Here, l₁ is decided so that the natural frequency of the simple pendulum would equal that of the first antisymmetric mode, which is 4 Hz.

Fig. 13. Two mechanical models are proposed. (a) is the “normal hand” posture and (b) is the “claw-hand” posture.

Indeed, at first, this does not seem to be a physically sound analogy. However, as illustrated in Fig. 14 , the first antisymmetric mode of liquid oscillation somewhat resembles the simple pendulum in the sense that the center of mass oscillates with respect to a fixed point above the liquid surface. Also, as it will be revealed below, the implications of this analogy is astonishingly consistent with experiment results. The claw-hand model is similarly constructed as well. The only modification for the claw-hand model is that the simple pendulum is now a double pendulum; the claw-hand posture essentially adds one more degree of freedom to the generalized coffee-cup coordinate system. Seemingly subtle, this extra degree of freedom will later on prove itself to have a significant effect on the frequency spectrum of the cup motion. In the following two subsections, the Euler–Lagrange equations for each mechanical model is solved and investigated extensively.

Fig. 14. A depiction of the first antisymmetric mode and a simple pendulum. The colored circles represent the center of mass of liquid.

Normal Hand Posture: Oscillating-pivot Simple Pendulum

The generalized coordinate system for the oscillating-pivot simple pendulum and their relevant parameters can be expressed as the following.

$\left({\begin{array}{c}q_{1}\\q_{2}\end{array}}\right)=\left({\begin{array}{c}x\\{\theta }_{1}\end{array}}\right)$

$\left({\begin{array}{c}M\\m_{1}\\l1\\k\\g\end{array}}\right)=\left({\begin{array}{c}1kg\\0.1kg\\1.55cm\\157.9137{\frac {N}{m}}\\9.81{\frac {m}{s^{2}}}\end{array}}\right)$

Next, the systems kinetic energy, potential energy, and the Lagrangian are calculated to be the following equations.

$L_{normal}=T-V$ $T={\frac {M{\overset {\cdot }{x}}^{2}}{2}}+{\frac {m_{1}}{2}}\left\{{\overset {\cdot }{x}}^{2}+{\left(l_{1}{\overset {\cdot }{\theta }}_{1}\right)}^{2}+2{\overset {\cdot }{x}}{\overset {\cdot }{\theta }}_{1}l_{1}cos\left({\theta }_{1}\right)\right\}$ $v=-m_{1}gl_{1}cos\left({\theta }_{1}\right)+{\frac {kx^{2}}{2}}$

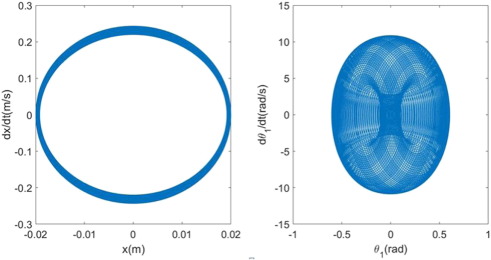
The corresponding Euler–Lagrange equations are integrated by the Runge–Kutta method, with initial values set to be {x , θ₁ } = {2 cm, 0.1 rad} and timespan t  = [0 s, 60 s]. The representative phase diagrams are illustrated in Fig. 15 .

Fig. 15. Phase diagrams for the normal hand model.

The arm, represented by x, clearly follows a monochromatic cycle. On the other hand, the coffee, represented by θ₁ , follows a more complex trajectory. In order to determine the frequency characteristics of each oscillator (the arm and coffee), a FFT analysis is conducted again on each data set. The result is illustrated in Fig. 16 .

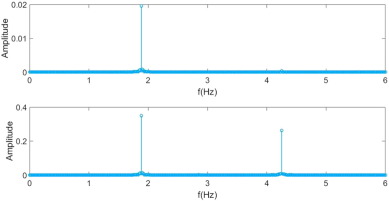
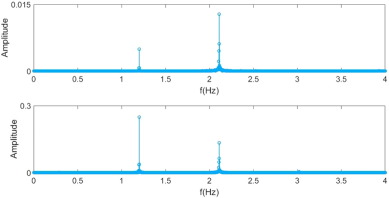
Fig. 16. FFT analysis of the normal hand model. The frequency spectrum of each generalized coordinate x  , θ1 is shown from top to bottom. The timespan is 60 s.

The upper graph is the frequency spectrum of x and the lower graph is the frequency spectrum of θ₁ . Indeed, the arm oscillates monochromatically at 2 Hz as our body would during actual walking. What is surprising is the result for θ₁ . Just as we have discovered in our former experiments, the coffee is excited at 4 Hz, even though the arm itself oscillates at 2 Hz. Although a definitive conclusion cannot be made without further biomechanical insight, our model suggests that such particularities of the cup motion may indeed be a result of the extra degree of freedom that the wrist provides. Also, our model shows that the characteristics of walking can be simulated in well-defined dynamical systems such as this one.

Another interesting observation can be made when the timespan is greatly extended. For example, the frequency spectra of x and m₁ are illustrated in Fig. 17 when the timespan is extended to 500 s.

Fig. 17. FFT analysis of the normal hand model. The frequency spectrum of each generalized coordinate x  , θ1 is shown from top to bottom. The timespan is 500 s.

A conspicuous shift in the frequency spectrum has occurred: the high frequency component (4 Hz) of m₁ has disappeared and a low frequency component (1–1.5 Hz) has newly appeared. In other words, as the time elapsed, the system evolved into a stable state in which only low frequency oscillations remained. This may be a potential answer to the thought-provoking question: “If one were to walk for an infinite amount of time, would coffee be inevitably spilt at some point?” If we only considered the fact that our hand motion resonates with coffee, the answer appears to be “Yes.” However, as our model suggests, if our hand motion evolves into an oscillation state that does not resonate with coffee, the answer may certainly be “No.” Of course, since we usually do not walk for 500 s or more with a cup of coffee, such stabilization hardly ever takes place; our mechanical model merely suggests the possibility of it.

Claw-hand Posture: Oscillating-pivot Double Pendulum

The generalized coordinate system for the oscillating-pivot double pendulum and their relevant parameters can be expressed as the following.

$\quad \left({\begin{array}{c}q_{1}\\q_{2}\\q_{3}\end{array}}\right)=\left({\begin{array}{c}x\\{\theta }_{1}\\{\theta }_{2}\end{array}}\right)$

$\left({\begin{array}{c}M\\m_{1}\\m_{2}\\l1\\l2\\k\\g\end{array}}\right)=\left({\begin{array}{c}1kg\\0.1kg\\0.1kg\\15cm\\1.55cm\\157.9137{\frac {N}{m}}\\9.81{\frac {m}{s^{2}}}\end{array}}\right)$

Now, there is an extra m₂ and l₂ term involved. Consequently, the systems kinetic energy, potential energy, and the Lagrangian take a more complex form than the oscillating-pivot simple pendulum.

$L_{clawhand}=T-V$

$T={\frac {M}{2}}{\overset {\cdot }{x}}^{2}+{\frac {m_{1}}{2}}\left\{{\overset {\cdot }{x}}^{2}+\right.$$\left.{\left(l_{1}{\overset {\cdot }{\theta }}_{1}\right)}^{2}+\right.$$\left.2{\overset {\cdot }{x}}{\overset {\cdot }{{\theta }_{1}}}l_{1}cos\left({\theta }_{1}\right)\right\}+$${\frac {m_{2}}{2}}\left\{{\overset {\cdot }{x}}+{\left(l_{1}{\overset {\cdot }{{\theta }_{1}}}\right)}^{2}+\right.$$\left.{\left(l_{2}{\overset {\cdot }{{\theta }_{2}}}\right)}^{2}+\right.$$\left.2l_{1}l_{2}{\overset {\cdot }{{\theta }_{1}}}{\overset {\cdot }{{\theta }_{2}}}cos\left({\theta }_{1}+\right.\right.$$\left.\left.{\theta }_{2}\right)\right\}+m_{2}{\overset {\cdot }{x}}\left\{l_{1}\quad {\overset {\cdot }{{\theta }_{1}}}cos\left({\theta }_{1}\right)+\right.$$\left.l_{2}{\overset {\cdot }{{\theta }_{2}}}cos\left({\theta }_{2}\right)\right\}$

$V={\frac {kx^{2}}{2}}-m_{1}g\left\{x+l_{1}cos\left({\theta }_{1}\right)\right\}-$$m_{2}g\left\{x+l_{1}cos\left({\theta }_{1}\right)+l_{2}cos\left({\theta }_{2}\right)\right\}$

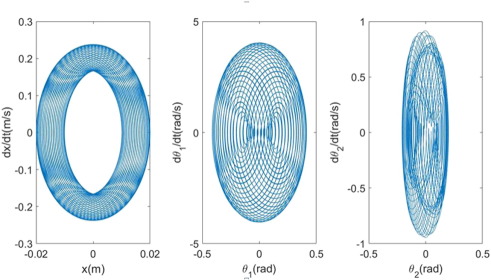
Again, the corresponding Euler–Lagrange equations are integrated by the Runge–Kutta method. The initial values are set to be {x , θ₁ , θ₂ } = {2cm, 0.1rad, 0.1rad} and time span t  = [0s, 60s]. The representative phase diagrams are illustrated in Fig. 18 . Compared to the claw-hand model, a visual difference in the phase diagram for coffee (represented by θ₁ in Fig. 15 and θ₂ in Fig. 18 ) is evident. Such a difference can quantified through a FFT analysis of the claw-hand model, as shown in Fig. 19 .

Fig. 18. Phase diagrams for the claw-hand model.

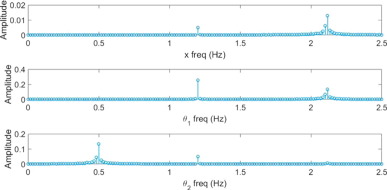
Fig. 19. FFT analysis of the claw-hand model. The frequency spectrum of each generalized coordinate x  , θ1  , θ2 is shown from top to bottom. The timespan is 60 s.

As expected, mass M oscillates at a frequency close to 2 Hz. Although the motion is not as purely sinusoidal as the normal hand model, it is still fairly monochromatic. But as we shift our focus to the next two frequency spectra, a notable deviation from that of the normal hand model is observed. While in the normal hand model, the dominant frequency was increased as we shifted from the main oscillator (M) to the subsequent oscillator (θ₁ ), the case for the claw-hand model is completely the opposite. Starting from approximately 2 Hz, the dominant frequency is halved for each subsequent oscillator (θ₁ , θ₂ ). Ultimately, the driving frequency of the cup (θ₂ ) is pronouncedly displaced from the resonance frequency. Although our experiment results for the claw-hand posture suggest a less extreme effect, our model successfully predicts that the claw-hand posture may indeed suppress resonance. The slight deviation from actual experiment results most likely arises from the fact that, in reality, θ₁ and θ₂ cannot oscillate as independently as described by the claw-hand model; the actual claw-hand posture should be an in-between state of the normal hand model and the claw-hand model.

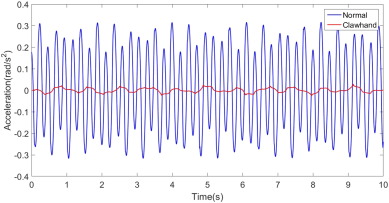
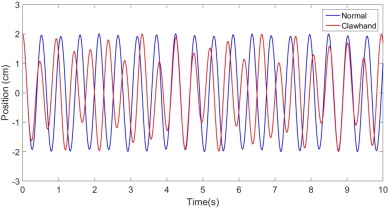
Additionally, the difference in the magnitude of the coffees acceleration in each mechanical model is compared in Fig. 20 . Even though the amplitude of the M oscillation is similar, as can be seen in Fig. 21 , the consequent acceleration that the coffee oscillator undergoes has a notable difference in magnitude. Since the magnitude of acceleration is directly proportional to the magnitude of impulse that an oscillator is given in one cycle, we expect such a difference in magnitude to have significant effects on the consequent coffee oscillation. Although we are currently under the low impulse regime, it is interesting that such a difference in the magnitude of impulse can be predicted by our mechanical model. Again, since the magnitude of acceleration in the claw-hand model is significantly smaller, the claw-hand posture is less likely to spill coffee.

Fig. 20. A comparison of the angular acceleration that θ1 in the normal hand model (blue) and θ2 in the claw-hand model (red) undergoes.

Fig. 21. A comparison of the amplitude of oscillation that M undergoes in each model. The blue line is the normal hand model and the red line is the claw-hand model.

Discussion and Conclusion

In this study, we researched how spillage is maximized in the low impulse regime. Resonance was the key. By approximating the coffee-cup system to a forced harmonic oscillator, we first determined the resonance frequency of the first antisymmetric mode of coffee oscillation. Then, we confirmed that the driving force was not monochromatic: the frequency spectrum of the coffee cups acceleration during locomotion revealed modes of higher frequency. Among these modes, the second dominant frequency corresponded to the resonance frequency of coffee, resulting in maximum spillage. This is pronouncedly different from former findings of Mayer and Krechetnikov (2012) , for their research assumed that the driving force due to walking is monochromatic; consequently, the resonance conditions investigated in their research differ from ours.

Moreover, we showed that either walking backwards or holding the cup with the claw-hand posture led to significant changes in the driving force frequency spectrum, suggesting a method to suppress resonance. The effect of foam layers in a Hele-Shaw cell was also examined; we showed that the damping frequency decreases and the damping coefficient increases when a foam layer was added (extensive studies on the foam layer is done by Sauret et al., 2015 ). An alternative cup design that would suppress resonance was also suggested, depicted in Fig. 12 .

Finally, we constructed two mechanical models: the normal hand posture and the claw-hand posture. In both models, phase diagrams demonstrated clear periodicity in the base oscillator (M, corresponding to the arm) but complex cycles for the endmost oscillators (θ₁ for the normal hand model and θ₂ for the claw-hand model). From the frequency spectrum of each endmost oscillator, the physical properties realized in previous experiments were successfully reconstructed: θ₁ in the normal hand model carried a 4 Hz component and θ₂ in the claw-hand model oscillated at a frequency lower than 2 Hz. Predictions regarding the amplitude of acceleration were made as well. Another theoretical finding was that the endmost oscillator in the normal hand model stabilized to a lower frequency mode as time elapsed—this may account for the fact that spillage is less likely to occur later on during walking motion.

References

1. Amplifer, n.d Amplifer, n.d. The Standard Coffee Mug Dimensions http://blog.ampli.fi/the-standard-coffee-mug-dimensions/ .
2. Anderson and Pandy, 2001 F.C. Anderson, M.G. Pandy; Dynamic optimization of human walking; J. Biomech. Eng., 5 (123) (2001) http://dx.doi.org/10.1115/1.1392310
3. Butikov, 2002 E. Butikov; Subharmonic resonances of the parametrically driven pendulum; J. Phys. A Math. Gen., 35 (2002)
4. Collins et al., 2009 S.H. Collins, P.G. Adamczyk, A.D. Kuo; Dynamic arm swinging in human walking; Proc. R. Soc. B Biol. Sci. (2009) http://dx.doi.org/10.1098/rspb.2009.0664
5. Donker, 2002 S.F. Donker; Flexibility of Human Walking: A Study on Interlimb Coordination; (2002)
6. Ibrahim, 2005 R.A. Ibrahim; Liquid Sloshing Dynamics: Theory and Applications; Cambridge University Press (2005)
7. Kulczycki et al., 2013 T. Kulczycki, M. Kwasnicki, B. Siudeja; Spilling from a cognac glass; (2013) (http://arxiv.org/abs/1311.7296 )
8. Mayer and Krechetnikov, 2012 H.C. Mayer, R. Krechetnikov; Walking with coffee: why does it spill?; Phys. Rev. E, 85 (046117) (2012) http://dx.doi.org/10.1103/PhysRevE.85.046117
9. Pontzer et al., 2009 H. Pontzer, J.H. Holloway, D.A. Raichlen, D.E. Lieberman; Control and function of arm swing in human walking and running; J. Exp. Biol., 212 (2009) http://dx.doi.org/10.1098/rspb.2009.0664
10. Rudnick, 1969 J. Rudnick; Subharmonics and the transition to chaos; Lecture Notes in Physics, Springer (1969), pp. 115–129
11. Sauret et al., 2015 A. Sauret, F. Boulogne, J. Cappello, E. Dressaire, H.A. Stone; Damping of liquid sloshing by foams; Phys. Fluids, 27 (022103) (2015) http://dx.doi.org/10.1063/1.4907048
12. Sobolik et al., 2002 V. Sobolik, V. Tovcigrecko, M. Delgado, R. Zitny, K. Allaf; Viscosity and electrical conductivity of concentrated solutions of soluble coffee; J. Food Eng., 51 (2002) http://dx.doi.org/10.1016/S0260–8774(01)00042–5

Notes

1. The surface tension of a generic cup of coffee has been researched by Sobolik et al. (2002) to be approximately 0.037 N/m at 40^°  C.

2. Indeed, the natural frequency should be derived from the relation  ω_r  = (ω₀²  − 2γ² )^1/2 and ω_d  = (ω₀²  − γ² )^1/2 where ω_d is (2π  × 3.8 Hz) and ω_r is the resonance frequency. However, the damping coefficient is determined to be approximately (0.674 rad/s). Considering that ω_d is around 570 rad² /s² , the difference between ω_d  and ω₀ is negligible.

3. Unfortunately, accelerometers are infamous for their inaccuracy and high level of noise. However, since we are mostly concerned with information related to frequency, and noise signals are random by definition, the most essential data extracted from the accelerometer would be fairly reliable. A noise test was conducted in order to confirm that no dominant frequency was shown in a FFT analysis.

4. There exists the issue that the cup also undergoes a nodding motion as we walk, which would mean that the “x, y, z” orientations recorded by the accelerometer slightly change during motion. And, as we will mention later, such an extra degree of freedom is what allows the cups intricate oscillation. However, the magnitude of the nodding motion itself is much smaller in scale compared to the other orientations of oscillation. Thus, we ignore the changes in the axis during locomotion.

5. The deviation from the values in Fig. 5 a is due to the distinct geometries of the Hele-Shaw cell and a cylindrical cup.

6. The cleaning of such a cup would indeed be quite a tedious job.