Generalized finite difference solution for the Motz Problem

Abstract

In this paper, it is presented a formulation of a generalized finite difference scheme to solve the Motz problem. It is based on a general difference scheme defined by an optimality condition, which has been developed to solve Poisson-like equations whose domains are approximated by a wide variety of grids over general regions. Numerical examples showing second-order accuracy of the calculated solutions are presented.

Keywords: Generalized finite difference, Motz problem

1. The Motz problem

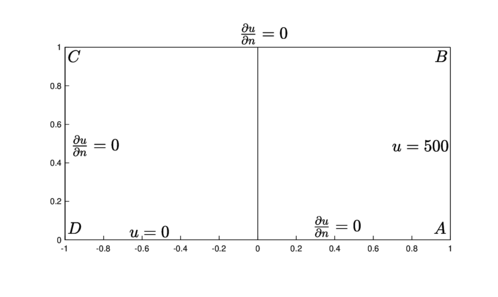
The Motz problem is a benchmark for the Laplace equation problem that is often used for testing various special numerical methods; it was proposed in the literature for the solution of elliptic boundary value problems with boundary singularities. The boundary value problem is stated as follows (Figure 1)

${\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=0,\qquad -1\leq x\leq 1,\quad 0\leq y\leq 1$ $u|_{\overline {OD}}=0$ $u|_{\overline {AB}}=500$ ${\frac {\partial u}{\partial n}}|_{{\overline {OA}}\cup {\overline {BC}}\cup {\overline {CD}}}=0.$

A singularity similar to that at the origin appears analogously in several hydrological applications, often related to an abrupt change in the boundary condition, particularly in groundwater infiltration in the alternation of pervious and impervious boundary zones.

Figure 1. Motz problem domain and boundary conditions

The closed-form solution of Motz problem is given as a series

$u=\sum _{i=0}^{\infty }A_{i}r^{(i+{\frac {1}{2}})}\cos \left[\left(i+{\frac {1}{2}}\right)\theta \right],$

(1)

where ${\textstyle r}$ and ${\textstyle \theta }$ are the polar coordinates; its convergence ratio is 2, and therefore valid over the whole domain (Figure 1).

Several papers discuss the accurate numerical calculation of the coefficients ${\textstyle A_{i}}$. Lu [1] calculated them with 17 significant digits using a collocation Treftz method. Li et al. [2] used a special boundary approximation method to derive the leading coefficients of the asymptotic solution expansion. Similar approaches were followed by Li [3] and Arad et al. [4], who employed boundary methods combined with least-squares and penalty method techniques to handle the boundary information, and by Georgiou [5], who employed Lagrange multipliers.

Some other authors focus on solving the Motz problem using different numerical techniques. Bernal and Kindelan [6] thoroughly discussed the performance of the radial basis function method in the solution of the Motz problem, including the global radial basis function method due to Kansa [7], as well as Shu's local differential quadrature method based on radial basis functions [8]. They showed that the exponential convergence obtained by increasing resolution and increasing the shape parameter is lost due to the presence of the singularity. The accuracy of the solution can be increased by using collocation at some boundary nodes to restore the convergence of the method, although it is necessary to use functions similar to the terms in equation (1), which are capable of capturing the behaviour of the solution near the discontinuity.

To produce an accurate solution based on the flexibility of meshfree methods, Hong [9] addressed a singular basis function enrichment technique in a meshless method, using the leading terms of the local series expansion at the boundary singularity, as enrichment functions for a local approximation space constructed to calculate the solution. The enrichment technique is derived from the Generalized Finite Element Method (GFEM) and produces accurate results, although it requires smooth global support basis functions and basis enrichment to produce the numerical solution.

The aforementioned papers give an insight into the different approaches considered in the problem. Finite elements and radial basis functions can be certainly used to produce accurate results near the singularity, although it is also possible to consider the little restrictive and more versatile alternative given by the Generalized Finite Differences Method (GFDM), which has recently been used to produce satisfactory approximations to solve differential equations in a wide number of applications modeled over irregular regions; for instance, on structured grids, a Generalized Crank Nicolson scheme is presented in [10]. Chávez et al showed a stable calculation of the solution of nonlinear Richards equation which avoids oscillations in high gradient regions in [11], and Tinoco et al addressed the conditions for stability in general schemes in [12].

The GFDM is not limited to a grid structure, and can also be applied on unstructured grids and even as a meshless method in clouds of points: Benito et al studied its use on parabolic and hyperbolic equations [13], advection-diffusion equations [14], seismic wave problems [15] and nonlinear elliptic equations [16] . Fan et al have applied general finite differences on Burgers equation [17], obstacle problems [18], shallow water equations [19] and natural double convection problems [20].

In this paper, bearing in mind the engineering applications where the use of GFDM has been successfully applied, this paper shows an accurate numerical approximation to the solution of Motz problem.

It is organized as follows: generalized finite differences are presented in Section 2. The description of the meshes used is given in Section 3. Numerical tests are described in Section 4; discussion and conclusions in Section 5, followed by conclusions in Section 6.

2. General finite differences

A very common and widely used discretization procedure to approximate the solutions of differential equations is the finite difference method. This is because it can be easily applied in block-rectangular regions.

The well-known classic schemes for the first and second-order derivatives can be easily deduced from basic analytical considerations or by straightforward application of the Taylor theorem. Despite the basic idea of the theorem is quite simple, its use leads to more complicated schemes on non-rectangular regions when the geometry associated with the scheme changes. Nevertheless, when symmetry is involved, very interesting approaches can be considered; like those due to Liszka [21] for regular hexagonal geometries and to Benito [22,13] for slightly perturbed clouds of nodes.

In the following paragraphs, we discuss the use of a general difference scheme that can be calculated by considering a set of nodes ${\textstyle p_{0}=(x_{0},y_{0}),p_{1}=(x_{1},y_{1}),p_{2}=(x_{2},y_{2}),...,p_{k}=(x_{k},y_{k})}$ where the solution of a differential equation is evaluated or approximated. For these nodes it is required to find coefficients ${\textstyle \Gamma _{0},\Gamma _{1},...,\Gamma _{k}}$ in such a way that consistency condition is fulfilled. In other words, the local truncation error to approximate the second-order linear operator

$L(u,A(x,y),B(x,y),C(x,y),D(x,y),E(x,y))=$ $A(x,y){\frac {\partial ^{2}u}{\partial x^{2}}}+B(x,y){\frac {\partial ^{2}u}{\partial y^{2}}}+C(x,y){\frac {\partial u}{\partial x}}+D(x,y){\frac {\partial u}{\partial y}}+E(x,y)u$

(2)

at the grid point ${\textstyle p_{0}}$ employing the combination

$L_{0}:=\sum _{l=0}^{k}\Gamma _{l}(p_{0},p_{l},A(x_{0},y_{0}),B(x_{0},y_{0}),C(x_{0},y_{0}),D(x_{0},y_{0}),E(x_{0},y_{0}))u(p_{l}),$

(3)

must satisfy the condition

$\tau (p_{0}):=[L(u,A(x,y),B(x,y),C(x,y),D(x,y),E(x,y))]_{(x_{0},y_{0})}-L_{0}\to 0$

(4)

as ${\textstyle p_{1},...p_{k}\to p_{0}}$ [23].

The coefficients ${\textstyle \Gamma _{l}}$ may change from one inner grid point to another in an irregular region, since they depend on the positions of the nodes ${\textstyle p_{i}}$ relative to ${\textstyle p_{0}}$. Nevertheless, in the case of nearly rectangular grids and the Laplace equation, since the coefficients ${\textstyle \Gamma _{l}}$ are invariant under rotations and translations, essentially one set of coefficients is required.

For the sake of brevity, in the following paragraphs the coefficient

$\Gamma _{l}(p_{0},p_{l},A(x_{l},y_{l}),B(x_{l},y_{l}),C(x_{l},y_{l}),D(x_{l},y_{l}),E(x_{l},y_{l}))$

will be denoted as ${\textstyle \Gamma _{l}}$.

Let ${\textstyle \Delta x_{l}}$ and ${\textstyle \Delta y_{l}}$ be the ${\textstyle x}$ and ${\textstyle y}$ components of ${\textstyle p_{l}-p_{0}}$, respectively. Thus, the local truncation error ${\textstyle \tau (p_{0})}$ (up to second-order) yields

$\tau (p_{0})=$ $\left(E(x_{0},y_{0})-\sum _{i=0}^{k}\Gamma _{i}\right)u(p_{0})+\left(C(x_{0},y_{0})-\sum _{i=1}^{k}\Gamma _{i}\Delta x_{i}\right){\frac {\partial u}{\partial x}}(p_{0})+$ $\left(D(x_{0},y_{0})-\sum _{i=1}^{k}\Gamma _{i}\Delta y_{i}\right){\frac {\partial u}{\partial y}}(p_{0})+\left(A(x_{0},y_{0})-\sum _{i=1}^{k}{\frac {\Gamma _{i}(\Delta x_{i})^{2}}{2}}\right){\frac {\partial ^{2}u}{\partial x^{2}}}(p_{0})+$ $\left(-\sum _{i=1}^{k}\Gamma _{i}\Delta x_{i}\Delta y_{i}\right){\frac {\partial ^{2}u}{\partial x\partial y}}(p_{0})+\left(B(x_{0},y_{0})-\sum _{i=1}^{k}{\frac {\Gamma _{i}(\Delta y_{i})^{2}}{2}}\right){\frac {\partial ^{2}u}{\partial y^{2}}}(p_{0})+$ ${\mathcal {O}}\left(\max\{\Delta x_{i},\Delta y_{i}\}\right)^{3}.$

Therefore, assuming smoothness of ${\textstyle u}$, to get second-order local consistency the coefficients of the derivatives of ${\textstyle u}$ at the right-hand side of the expansion must satisfy the linear system

$\left({\begin{array}{rrrrr}1&&1&...&1\\0&&\Delta x_{1}&...&\Delta x_{q}\\0&&\Delta y_{1}&...&\Delta y_{q}\\0&&(\Delta x_{1})^{2}&...&(\Delta x_{q})^{2}\\0&&\Delta x_{1}\Delta y_{1}&...&\Delta y_{q}\Delta z_{q}\\0&&(\Delta y_{1})^{2}&...&(\Delta y_{q})^{2}\\\end{array}}\right)\left({\begin{array}{c}\Gamma _{0}\\\Gamma _{1}\\\Gamma _{2}\\\cdot \\\cdot \\\cdot \\\Gamma _{q}\\\end{array}}\right)=\left({\begin{array}{c}E(x_{0},y_{0})\\C(x_{0},y_{0})\\D(x_{0},y_{0})\\2A(x_{0},y_{0})\\0\\2B(x_{0},y_{0})\\\end{array}}\right).$

(5)

One must note that, in general, this system is not well-determined. This poses the calculation of the coefficients in terms of a well studied algebraic problem which can be solved robustly. Hence, the main question is how to produce a solution of equation (5) which provides a consistent second-order scheme. Several alternatives are possible, for example, in [10], an efficient heuristic calculation to solve numerically the diffusion equation was proposed. It was based on an unconstrained optimization problem for every inner grid point. To apply it, first, we separate the first equation of the matrix system (5)

$\sum _{i=0}^{q}\Gamma _{i}=E(x_{0},y_{0})$

(6)

and then we solve the system

$M\Gamma =\beta ,$

(7)

where

$M=\left({\begin{array}{clcl}\Delta x_{1}&...&\Delta x_{q}\\\Delta y_{1}&...&\Delta y_{q}\\(\Delta x_{1})^{2}&...&(\Delta x_{q})^{2}\\\Delta x_{1}\Delta y_{1}&...&\Delta x_{q}\Delta y_{q}\\(\Delta y_{1})^{2}&...&(\Delta y_{q})^{2}\\\end{array}}\right),$

(8)

$\Gamma =\left({\begin{array}{c}\Gamma _{1}\\\Gamma _{2}\\.\\.\\.\\\Gamma _{q}\\\end{array}}\right),\quad \beta =\left({\begin{array}{c}C(x_{0},y_{0})\\D(x_{0},y_{0})\\2A(x_{0},y_{0})\\0\\2B(x_{0},y_{0})\\\end{array}}\right).$

(9)

Next, ${\textstyle \Gamma _{0}}$ is obtained from equation (6).

Equation (7) defines the generalized finite differences in general grids. To solve it is straightforward when the grid is rectangular or nearly rectangular, and a sufficient number of nodes or symmetries are available.

In irregular grids or clouds of points, which lack symmetry, the system defined by ${\textstyle M}$ is underdetermined if ${\textstyle q>6}$, which means that, in that case, at least seven neighbor nodes around ${\textstyle p_{0}}$ are required to get local consistency.

On the other hand, in a rather regular structured -or mapping- grid, symmetries reduce the number of required neighbors. An important consequence is that the symmetric location of nodes around the central node avoids rank deficiency of ${\textstyle M}$ in the system (7).

3. Grids and stencils

The main issue to consider when solving the Motz problem is the singularity in the partial derivative ${\textstyle {\frac {\partial u}{\partial x}}}$ at the origin of coordinates. The usual approach to produce an accurate approximation at that point is to refine the grid around it. However, this causes not only an increase in the computational cost, but often the results are not satisfactory due to the high gradient values of the solution on the positive ${\textstyle x}$-axis; even with robust techniques as those based on radial basis functions [6], a special treatment is required near the origin. Some other approaches, like that of Hong, require a rather sophisticated process of patch mapping to produce accurate results [9].

When finite differences are considered, it is important to emphasize that the method has been successfully applied to problems with strong boundary layers, for instance, by Ivanenko [24] and Pereyra [25], when the equidistribution principle is addressed. In other words, the key is to produce a suitably adapted grid through a simple procedure. In this paper, to derive the rule that controls the refinement around the origin, the clue is given by the shape of the significative terms in the closed-form solution series of equation (1).

Bearing in mind the equidistribution principle as discussed by Ivanenko, since the graph of the solution ${\textstyle u(x)}$ is monotonic along the positive ${\textstyle x}$-axis, and resembles that of a boundary layer, there is a mapping ${\textstyle \xi \mapsto x=\xi ^{\alpha }}$ such that the expression

${\frac {\partial u}{\partial \xi }}={\frac {\partial u}{\partial x}}{\frac {\partial x}{\partial \xi }}$

(10)

is constant. According to eq. (1), each term in the solution along such axis equals ${\textstyle x^{(i+{\frac {1}{2}})}}$, ${\textstyle i=0,1,...}$. Therefore, the constant right-hand side of (10) takes the form

${\frac {\partial u}{\partial x}}{\frac {\partial x}{\partial \xi }}=\left[{\frac {\partial x}{\partial \xi }}\right]\left[\left(i+{\frac {i}{2}}\right)x^{i-{\frac {1}{2}}}\right],\qquad i=0,1,...$

This implies that the partial derivative ${\textstyle {\frac {\partial x}{\partial \xi }}}$ must have the form ${\textstyle x^{({\frac {1}{2}}-i)}}$ and, in consequence, the grid refinement is of the form

$\xi \mapsto x=\xi ^{\frac {2}{2i+1}},\qquad i=0,1,...$

(11)

According to the estimations presented by Lu [1], the first five coefficients in the equation (1) are the significative ones: Those terms correspond to ${\textstyle i=0,1,...,5}$. Since the value ${\textstyle i>1}$ in equation (11) represents an increase in the distance between the grid nodes around the origin, only the value ${\textstyle i=0}$, which corresponds to ${\textstyle \alpha =2}$, is considered.

Thus, the mesh adaptation procedure is as follows:

1. The grid for the whole domain of the problem is generated in the first step as a regular rectangular grid.
2. Every cell is subdivided into two triangles in the second step to define six neighbours in the stencil for every inner grid node.
3. Finally, the grid is adapted by modifying the grid coordinates following the mapping given by equation(11).

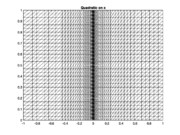
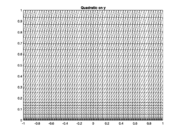
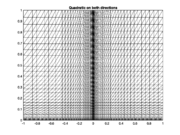
In the numerical tests, the interval ${\textstyle [1.5,2.5]}$ was considered for the exponent ${\textstyle \alpha }$. For comparison purposes, the mapping was applied to the ${\textstyle x}$-axis (Type I grids), to the ${\textstyle y}$-axis (Type II grids), and both axes (Type III). An example of the grids corresponding to the different distributions is shown in Figure 2.

Figure 2. Examples of the kinds of grids used in the tests

The three kinds of grids define a regular location of neighbors at the inner nodes: star-shaped subgrids with 6 neighbours that can be used to approximate the derivatives in the left-hand side of equation (6); an example of such subgrid can be seen in Figure 3. The Laplacian operator is approximated at the point ${\textstyle p_{0}}$, and the corresponding neighbours are ${\textstyle p_{1}}$, ${\textstyle p_{2}}$, ${\textstyle p_{3}}$, ${\textstyle p_{4}}$, ${\textstyle p_{5}}$, and ${\textstyle p_{6}}$. The values ${\textstyle h_{1}}$, ${\textstyle h_{2}}$, ${\textstyle k_{1}}$, and ${\textstyle k_{2}}$ are the step size lengths in the stencil. Bearing in mind equation (5), this poses a problem with 6 equations and ${\textstyle k=7}$ unknowns; since the values ${\textstyle h_{1}}$, ${\textstyle h_{2}}$, ${\textstyle k_{1}}$, and ${\textstyle k_{2}}$ are non zero, after preconditioning of equation (6) by scaling, the rank of ${\textstyle M}$ is equal to five, which allows a robust calculation of the coefficients and leaves one degree of freedom available.

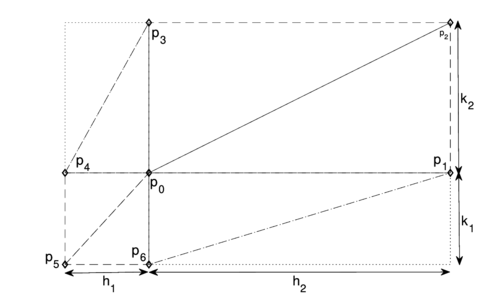
Figure 3. Selection of neighbours for an inner grid node

Regarding the boundary condition, a straightforward discretization using the GFDM method was addressed in [26]: at a boundary node of a structured grid, equation (7) is evaluated at its five neighbors, taking the right-hand side ${\textstyle \beta }$ to define the directional derivative. However, since the neighbors are often not balanced around the boundary node, such selection might produce first approximations which could cause loss of order in the Motz problem with the grids considered here.

In this paper, we define an ad hoc ghost point to avoid loss of accuracy. The boundary condition

${\frac {\partial u}{\partial n}}(p_{0})=l_{x}{\frac {\partial u}{\partial x}}+l_{y}{\frac {\partial u}{\partial y}}$

where ${\textstyle n=(l_{x},l_{y})}$ is the outer normal vector at ${\textstyle p_{0}}$, is approximated using the scheme of equation (5) with ${\textstyle A=B=E=0}$ and ${\textstyle C=l_{x}}$, ${\textstyle D=l_{y}}$ using 7 points: a ghost point ${\textstyle p_{g}}$, and the nodes ${\textstyle p_{0}}$, ${\textstyle p_{1}}$, ${\textstyle p_{2}}$, ${\textstyle p_{3}}$, ${\textstyle p_{4}}$ and ${\textstyle p_{5}}$ (Figure 4), which yields the equation (12)

$l_{x}{\frac {\partial u}{\partial x}}+l_{y}{\frac {\partial u}{\partial y}}\approx {\hat {\Gamma }}_{g}u(p_{g})+\sum _{l=0}^{k}{\hat {\Gamma }}_{l}u(p_{l}),$

(12)

or, in other words,

$u(p_{g})={\frac {1}{{\hat {\Gamma }}_{g}}}{\frac {\partial u}{\partial n}}(p_{0})-\sum _{l=0}^{k}{\frac {{\hat {\Gamma }}_{l}}{{\hat {\Gamma }}_{g}}}u(p_{l}).$

(13)

For convenience, the ghost point ${\textstyle p_{g}}$ is calculated in such a way that ${\textstyle p_{0}}$ is the midpoint of ${\textstyle p_{g}}$ and ${\textstyle p_{c}}$, the latter being the centroid of the nodes ${\textstyle p_{0}}$, ${\textstyle p_{1}}$, ${\textstyle p_{2}}$, ${\textstyle p_{3}}$, ${\textstyle p_{4}}$, and ${\textstyle p_{5}}$ (Figure 4).

The value of ${\textstyle u(p_{g})}$ given by the equation (13) is substituted in the approximation to the Laplacian (equation (7) at ${\textstyle p_{0}}$ using the same 7 points ${\textstyle p_{g}}$, ${\textstyle p_{0}}$, ${\textstyle p_{1}}$, ${\textstyle p_{2}}$, ${\textstyle p_{3}}$, ${\textstyle p_{4}}$, and ${\textstyle p_{5}}$, which eliminates the value of ${\textstyle u(p_{g})}$.

Te assembled system for the whole grid becomes sparse as the number of grid points per side increases; it was solved using a sparse lu decomposition to produces the approximation to the solution of the problem.

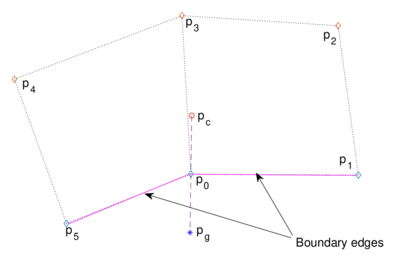
Figure 4. Selection of ghost point at a boundary node of a general structured grid with Neumann condition

4 Numerical tests

Several tests were performed with ${\textstyle m}$ and ${\textstyle 2m-1}$ nodes per side on the ${\textstyle y}$ and ${\textstyle x}$ directions, respectively, varying ${\textstyle m}$ from 31 to 351. Grids of the three types in the previous section were generated, and the Motz problem was solved using the proposed scheme for every grid size and distribution. An example of the finite difference discretization described in the previous section is sketched in Figure 5.

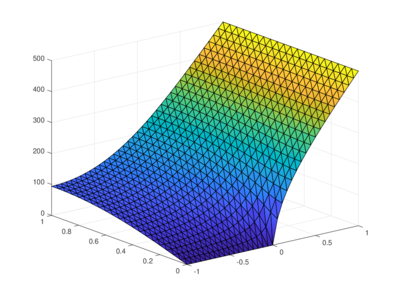
Figure 5. Grid and calculated solution

To assess the accuracy of the numerical solution, since the approximation was calculated using structured grids, the quadratic error

$\epsilon ={\sqrt {\sum _{i,j}\left[u_{i,j}-u(p_{i,j})\right]^{2}A_{i,j}}},$

(14)

was used, where ${\textstyle u_{i,j}}$ is the solution calculated using the difference scheme at the point ${\textstyle p_{i,j}}$, ${\textstyle u}$ is the exact solution (equation (1)) at the same point, and ${\textstyle A_{i,j}}$ is the area of the rhombus defined by the nodes ${\textstyle p_{i+1,j},p_{i-1,j},p_{i,j+1},p_{i,j-1}}$.

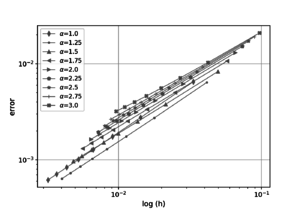
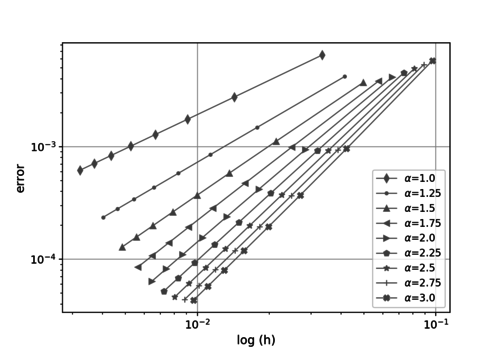
The measure of the roughness of the grid is given by the meh norm ${\textstyle h}$; the log graph of the mean square errors versus the grid norm for the type I and II grids are shown in Figures 6 and 7. One can note that there is a clear convergence tendency on all the tests despite the boundary singularity. But, when only a nonuniform distribution either along the ${\textstyle x}$ or the ${\textstyle y}$-axis is used, the second-order approximation is lost, in a similar way as reported by Bernal using radial basis functions. The best results are obtained with the grids which are non-uniform on ${\textstyle x}$ and ${\textstyle y}$, as can be seen in Figure 7.

Figure 6. Log values of the quadratic errors, nonuniform node distribution on $x$ or $y$

Figure 7. Log values of the quadratic errors, nonuniform node distribution on $x$ and $y$

The values of the errors, grid norms, and estimated convergence order are shown in Tables 1 to 3. The values in the last table show that, indeed, quadratic convergence is obtained when the same nonuniform node distribution along both axes is used, even in the presence of the boundary singularity.

Table 1. Quadratic errors and approximation order for type I grids

${\textstyle \alpha }$	$m$	$n$	$h$	$\epsilon$	Order
1.00	31	61	3.3333E-02	6.4941E-03	––
1.00	71	141	1.4286E-02	2.7556E-03	1.01
1.00	111	221	9.0909E-03	1.7489E-03	1.01
1.00	151	301	6.6667E-03	1.2810E-03	1.00
1.00	191	381	5.2632E-03	1.0106E-03	1.00
1.00	231	461	4.3478E-03	8.3446E-04	1.00
1.00	271	541	3.7037E-03	7.1060E-04	1.00
1.00	311	621	3.2258E-03	6.1877E-04	1.00
1.25	31	61	4.1492E-02	6.4057E-03	––
1.25	71	141	1.7825E-02	2.7333E-03	1.01
1.25	111	221	1.1351E-02	1.7503E-03	0.99
1.25	151	301	8.3264E-03	1.2920E-03	0.98
1.25	191	381	6.5746E-03	1.0260E-03	0.98
1.25	231	461	5.4318E-03	8.5207E-04	0.97
1.25	271	541	4.6275E-03	7.2925E-04	0.97
1.25	311	621	4.0306E-03	6.3784E-04	0.97

Table 2. Quadratic errors and approximation order for type II grids

${\textstyle \alpha }$	$m$	$n$	$h$	$\epsilon$	Order
1.00	31	61	0.033333	0.0064941	––
1.00	71	141	0.014286	0.0027556	1.01
1.00	111	221	0.0090909	0.0017489	1.01
1.00	151	301	0.0066667	0.001281	1.00
1.00	191	381	0.0052632	0.0010106	1.00
1.00	231	461	0.0043478	0.00083446	1.00
1.00	271	541	0.0037037	0.0007106	1.00
1.00	311	621	0.0032258	0.00061877	1.00
1.25	31	61	0.041492	0.0060306	––
1.25	71	141	0.017825	0.0026189	0.99
1.25	111	221	0.011351	0.0016827	0.98
1.25	151	301	0.0083264	0.001243	0.98
1.25	191	381	0.0065746	0.00098714	0.98
1.25	231	461	0.0054318	0.00081951	0.97
1.25	271	541	0.0046275	0.00070109	0.97
1.25	311	621	0.0040306	0.00061294	0.97

Table 3. Quadratic errors and approximation order for type III grids

${\textstyle \alpha }$	$m$	$n$	$h$	$\epsilon$	Order
2.00	71	141	2.8367E-02	9.3949E-04	1.77
2.00	111	221	1.8099E-02	4.1865E-04	1.80
2.00	151	301	1.3289E-02	2.3926E-04	1.81
2.00	191	381	1.0499E-02	1.5584E-04	1.82
2.00	231	461	8.6767E-03	1.1006E-04	1.82
2.00	271	541	7.3937E-03	8.2131E-05	1.83
2.00	311	621	6.4412E-03	6.3786E-05	1.83
2.25	31	61	7.3442E-02	4.5265E-03	––
2.25	71	141	3.1856E-02	9.2020E-04	1.91
2.25	111	221	2.0338E-02	3.8741E-04	1.93
2.25	151	301	1.4938E-02	2.1315E-04	1.94
2.25	191	381	1.1803E-02	1.3496E-04	1.94
2.25	231	461	9.7560E-03	9.3190E-05	1.94
2.25	271	541	8.3140E-03	6.8259E-05	1.95
2.25	311	621	7.2434E-03	5.2179E-05	1.95
2.50	31	61	8.1262E-02	4.9361E-03	––
2.50	71	141	3.5333E-02	9.2007E-04	2.02
2.50	111	221	2.2573E-02	3.7194E-04	2.02
2.50	151	301	1.6583E-02	1.9951E-04	2.02
2.50	191	381	1.3106E-02	1.2407E-04	2.02
2.50	231	461	1.0834E-02	8.4506E-05	2.02
2.50	271	541	9.2336E-03	6.1224E-05	2.02
2.50	311	621	8.0450E-03	4.6380E-05	2.02
2.75	31	61	8.9015E-02	5.3606E-03	––
2.75	71	141	3.8796E-02	9.3491E-04	2.10
2.75	111	221	2.4802E-02	3.6799E-04	2.08
2.75	151	301	1.8227E-02	1.9446E-04	2.07
2.75	191	381	1.4407E-02	1.1975E-04	2.06
2.75	231	461	1.1911E-02	8.0998E-05	2.06
2.75	271	541	1.0152E-02	5.8375E-05	2.05
2.75	311	621	8.8459E-03	4.4042E-05	2.05
3.00	31	61	9.6704E-02	5.7955E-03	––
3.00	71	141	4.2248E-02	9.6029E-04	2.17
3.00	111	221	2.7026E-02	3.7142E-04	2.13
3.00	151	301	1.9867E-02	1.9454E-04	2.10
3.00	191	381	1.5707E-02	1.1915E-04	2.09
3.00	231	461	1.2987E-02	8.0299E-05	2.08
3.00	271	541	1.1070E-02	5.7715E-05	2.07
3.00	311	621	9.6462E-03	4.3453E-05	2.06

5. Results and discussion

Several assertions can be drawn from the numerical results. First, despite the presence of the boundary singularity, the results are accurate enough. This is certainly a strength of the proposed finite difference scheme, which is rather simple. Since the main differences between the scheme discussed in this paper and the standard five-point scheme for the Laplacian are the addition of two extra “diagonal” nodes in the inner grid nodes and the use of a suitable grid spacing, this suggests that the proposed stencils are suitable to produce accurate results.

The convergence orders in table 3 must be highlighted. Having in mind the presence of the singularity and the simplicity of the addressed difference stencils, this is indeed a remarkable result. Since the boundary node redistribution was defined by a very simple rule, this suggests that it is unnecessary to consider another kind of grids or more complex refinements near the singularity to solve the Motz problem, although, it must be acknowledged that the mesh adapting strategy was proposed ad hoc for it. Naturally, the numerical treatment of different singularities in other problems require a different application of the equidistribution principle.

6. Conclusions

Indeed, generalized finite differences can be used to solve the Motz problem numerically. The numerical results show that generalized finite differences produce accurate solutions to a complicated benchmark problem, and the most noteworthy fact is that this can be done even with very simple structured grids. This is an important feature of the GFDM method, considering the difficulty of the problem. Thinking about the solution to several linear and nonlinear problems with this method which appear in the literature [27,10,22,13], it is certainly a reliable numerical tool.

The results are very encouraging since boundary configurations similar to those of Motz problem appear in several relevant applications, for instance, in interfaces between different media in infiltration problems, or advection-diffusion problems with sources and sinks along the boundary. Both problems are currently under investigation and advances in this sense will be reported in a future paper.

Acknowledgments

We want to thank CIC-UMSNH 9.16, and Aula-CIMNE Morelia for the financial support for this work.

References

[1] Lu T.T., Hu H.Y., Li Z.C. Highly accurate solutions of Motz's and the cracked beam problems. Engineering Analysis with Boundary Elements, 28:1387–1403, 2004.

[2] Li Z.C., Mathon R., Sermer P. Boundary methods for solving elliptic problems with singularities and interfaces. SIAM Journal of Numerical Analysis, 24:487–498, 1987.

[3] Li Z.C. An approach for combining the Ritz-Galerkin and Finite-Element Methods. Journal of Approximation Theory, 39:132-152, 1983.

[4] Arad M., Yosibash Z., Ben-Dor G., Yakhot A. Computing flux intensity factors by a boundary method for elliptic equations with singularities. Communications in Numerical Methods in Engineering, 14:657–670, 1998.

[5] Georgiou G.C., Olson L., Smyrlis Y.S. A singular function boundary integral method for the Laplace equation. Communications in Numerical Methods in Engineering, 12:127-134, 1996.

[6] Bernal F., Kindelan, M. Radial basis function solution of the Motz problem. Engineering Computations, 27:606–620, 2010.

[7] Kansa E.J. Multiquadrics, a scattered data approximation scheme with applications to computational fluid dynamics II: solutions to parabolic, hyperbolic and elliptic partial differential equations. Computers and Mathematics with Applications, 19:147–161, 1990.

[8] Shu C., Ding H., Yeo K.S. Local radial basis function-based differential quadrature method and its application to solve two-dimensional incompressible Navier-Stokes equations. Computer Methods in Applied Mechanics and Engineering, 192:941–954, 2003.

[9] Hong W.T. Enriched meshfree method for an accurate numerical solution of the Motz problem. Advances in Mathematical Physics, 2016:1-12, 2016.

[10] Domínguez-Mota F.J., Mendoza-Armenta S., Tinoco-Guerrero G., Tinoco-Ruiz J.G. Finite difference schemes satisfying an optimality condition for the unsteady heat equation. Mathematics and Computers in Simulation, 106:76–83, 2014.

[11] Chávez-Negrete C., Domínguez-Mota F.J., Santana-Quinteros D. Numerical solution of Richards' equation of water flow by generalized finite differences. Computers and Geotechnics, 101:168–175, 2018.

[12] Tinoco-Guerrero G., Domínguez-Mota F.J., Gaona-Arias A., Ruiz-Zavala M.L., Tinoco-Ruiz J.G. A stability analysis for a generalized finite-difference scheme applied to the pure advection equation. Mathematics and Computers in Simulation, 147:293–300, 2018.

[13] Benito J.J., Ureña F., Gavete L. Solving parabolic and hyperbolic equations by the generalized finite difference method. Journal of Computational and Applied Mathematics, 209:208–233, 2007.

[14] Benito J.J., Ureña F., Gavete, L. Application of the generalized finite difference method to solve the advection-diffusion equation. Journal of Computational and Applied Mathematics, 235:1849–1855, 2011.

[15] Benito J.J., Ureña F., Salete E., Gavete, L. A note on the application of the generalized finite difference method to seismic wave propagation in 2D. Journal of Computational and Applied Mathematics, 236:3016–3025, 2012.

[16] Gavete L., Ureña F., Benito J.J., García A., Ureña M., Salete E. Solving second order non-linear elliptic partial differential equations using generalized finite difference method. Journal of Computational and Applied Mathematics, 318:378–387, 2017.

[17] Fan C.M., Li P.W. Generalized finite difference method for solving two-dimensional Burgers' equations. Procedia Engineering, 79:55–60, 2014.

[18] Chan H.F., Fan C.M., Kuo C.W. Generalized finite difference method for solving two-dimensional non-linear obstacle problem. Engineering Analysis with Boundary Elements, 37:1189–1196, 2013.

[19] Li P.W., Fan C.M. Generalized finite difference method for two-dimensional shallow water equations. Engineering Analysis with Boundary Elements, 80:58–71, 2017.

[20] Li P.W. , Chen W., Fu Z.J., Fan C.M. Generalized finite difference method for solving the double-diffusive natural convection in fluid-saturated porous media. Engineering Analysis with Boundary Elements 95:175–186, 2018.

[21] Liszka T., Orkisz J. The finite difference method at arbitrary irregular grids and its application in applied mechanics. Computers and Structures, 11:83–95, 1980.

[22] Benito J.J., Ureña F., Gavete L., Alonso B. A posteriori error estimator and indicator in generalized finite differences. Application to improve the approximated solution of elliptic PDEs. International Journal of Computer Mathematics, 85:359–370, 2008.

[23] Celia, M., Gray, W. Numerical Methods for Differential Equations: fundamental concepts for scientific and engineering applications. Prentice-Hall, 1992.

[24] Ivanenko, S. In Selected chapters on grid generation and applications. B. Azarenok (Ed.), Russian Academy of Sciences, 2009.

[25] Pereyra V., Sewell G. A singular function boundary integral method for the Laplace equation. Numer. Math., 23:261-268, 1975.

[26] Domínguez-Mota F.J., Mendoza S., Tinoco-Ruiz J.G, Tinoco-Guerrero G. Numerical solution of Poisson-like equations with Robin boundary conditions using a finite difference scheme defined by an optimality condition. Proceedings of MASCOT 2011, 17, 101-110, 2011.

[27] Domínguez-Mota F.J., Equihua M., Mendoza S., Tinoco-Ruiz J.G. Solución de ecuaciones diferenciales elípticas en regiones planas irregulares usando mallas convexas generadas por métodos variacionales empleando elementos finitos. Rev. Int. Mét. Num. Cálc. Dis. Ing., 26:187–194, 2010.