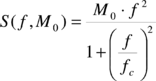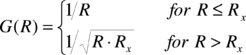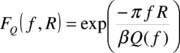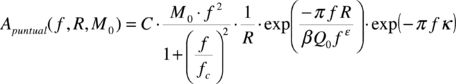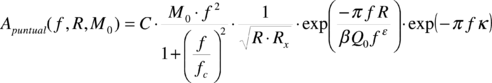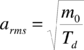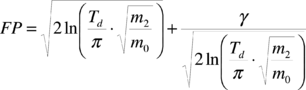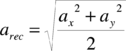ABSTRACT
A numerical procedure for the calibration of a source spectrum model to find the optimal combination of seismological parameters and derive unbiased ground motion prediction equations is presented, using available accelerogram recordings as calibration target. The source spectrum model is used to compute the radiated spectra of SH-waves for different seismic moments and hypocentral distances, combining point (far field) and finite (near field) source models. The expected value of the peak ground acceleration is computed from the radiated spectra using random vibrations theory. A genetic algorithm is used to search for the source spectrum parameters that best fit the available strong motion recordings. The procedure can be applied to any region with statistically significant accelerogram records.
The proposed methodology is used to derive spectral ground motion prediction equations compatible with the seismo-tectonic environment of Colombia, using 206 strong motion recordings as the calibration target. The obtained ground motion prediction equations are compared with those used in the latest national seismic hazard assessment study of Colombia. The comparison shows that the strong ground motion prediction equations obtained using the proposed methodology have lower residual bias, showing reasonable matching between them and the real strong motion recordings.
INTRODUCCIÓN
Los sismos se definen como un proceso de liberación súbita de energía mecánica debido a cambios en el estado de esfuerzos y deformaciones en zonas de interacción de placas tectónicas, o dentro de ellas. Su efecto inmediato es la transmisión de esa energía mecánica y su difusión mediante ondas de diversos tipos, a través de la corteza terrestre. Su ocurrencia, dentro marcos de tiempo de vida humana, es poco probable, mientras que sus consecuencias pueden ser devastadoras.
El análisis tradicional de amenaza sísmica se realiza de manera probabilista (PSHA por sus siglas en inglés Probabilistic Seismic Hazard Analysis), en el cual se determinan las tasas de excedencia de los parámetros de intensidad de movimiento (e.g. la aceleración máxima del terreno o las aceleraciones espectrales) en cada punto del territorio de análisis. Estas tasas de excedencia dan cuenta del número de veces por año que se espera se iguale o exceda una intensidad de movimiento particular en el sitio de interés.
Para realizar un análisis de amenaza probabilista, es fundamental la definición de funciones de atenuación que representen de manera adecuada los procesos de transformación que sufren las ondas sísmicas al transitar por la corteza terrestre. Estos procesos están asociados al gasto de la energía de movimiento principalmente por el avance y expansión del frente de onda y la anelasticidad del medio. Dentro de los avances recientes de la sismología moderna está la solución del espectro de amplitudes de Fourier (EAF) de aceleración en un medio continuo, por efecto de un rompimiento súbito de cortante puro en una dislocación con geometría conocida. Estos modelos están basados en formulaciones sismológicas clásicas, las cuales permiten definir la forma matemática de los desplazamientos de las fuentes cuando ocurre un sismo, así como el contenido de frecuencia que genera dicho movimiento, para diferentes mecanismos de dislocación. Es decir, es posible calcular, suponiendo un medio homogéneo e isotrópico y un semi-espacio infinito, la forma del EAF en cualquier parte de un territorio, conociendo la magnitud y localización del hipocentro de un terremoto particular.
Si bien son muchas las funciones de atenuación de movimiento fuerte disponibles en la literatura, cada una determinada a partir de información de una región particular y mediante suposiciones y consideraciones también particulares, no existe en la actualidad una metodología general de obtención de funciones de atenuación que sea aplicable en cualquier territorio que cuente con instrumentación sísmica adecuada y que esté basada en la solución teórica de las amplitudes espectrales. En esta monografía se propone el desarrollo de una metodología numérica para la calibración de un modelo de espectro de fuente a partir de información acelerográfica disponible. Esta metodología será aplicable a cualquier territorio donde se cuente con una muestra representativa de mediciones de movimiento sísmico.
1. FUNCIONES DE ATENUACIÓN DEL MOVIMIENTO FUERTE
El peligro que induce la actividad sísmica sobre regiones aledañas a poblaciones o asentamientos humanos, ha derivado en la necesidad de establecer parámetros que definan el nivel de la amenaza y metodologías generales que permitan estimar dichos parámetros.
Los parámetros que definen el nivel de peligro en un modelo de amenaza sísmica se conocen como parámetros de movimiento fuerte. Estos parámetros definen la intensidad del movimiento en el sitio de análisis. Su estimación se hace por medio de ecuaciones conocidas como funciones de atenuación, las cuales dependen principalmente de la distancia de la fuente sismogénica al sitio, la magnitud sísmica, y el tipo de mecanismo focal de ruptura.
1.1 PARÁMETROS DE MOVIMIENTO FUERTE
Los parámetros de movimiento fuerte permiten definir la amenaza en un área en particular, por lo cual se constituyen en el objetivo primordial de los estudios y análisis de amenaza sísmica. El movimiento del terreno se caracteriza por tener variables representativas tanto en amplitud, como frecuencia y duración. Algunos parámetros logran caracterizar el movimiento en uno de estos componentes, mientras otros pueden caracterizar los tres. Dada la complejidad asociada al tránsito de las ondas sísmicas por la corteza terrestre, resulta imposible reproducir perfectamente el movimiento del terreno en un sitio determinado, por muy complejo que sea el modelo que se adopte. De acuerdo con esto, la elección del modelo de estimación del movimiento fuerte debe hacerse de acuerdo con los alcances del estudio que se realice. La Tabla 1.1 presenta algunos de los parámetros de movimiento más empleados en ingeniería sísmica, indicando su capacidad de representar alguna de sus características primordiales.
| Característica del movimiento fuerte | ||||
| Parámetro de movimiento fuerte | Amplitud | Contenido frecuencial | Duración | |
| Aceleración, velocidad o desplazamiento máximo | PGA, PGV, PGD | x | ||
| Espectro de Fourier | EAF | x | x | x |
| Espectro de respuesta | ER | x | X | |
| Duración | Td | x | ||
La manera más sencilla y común de definir un movimiento fuerte es a partir de un acelerograma. Un acelerograma es simplemente una representación gráfica de aceleración contra tiempo. Esta gráfica contiene toda la información necesaria asociada al movimiento, como por ejemplo los valores de amplitud máxima, contenido frecuencial y duración. Esta señal de aceleración puede ser convertida a velocidad o desplazamiento, mediante la integración numérica directa del registro. Los acelerogramas se registran en estaciones acelerográficas, provistas de sensores en tres ejes ortogonales. Uno de esos ejes se hace coincidir con la vertical, mientras los otros dos se hacen coincidir con las direcciones cardinales NS y EO respectivamente.
Uno de los principales componentes en un análisis de amenaza sísmica es el estudio de las funciones de atenuación de los parámetros de intensidad que caracterizan el movimiento fuerte. La mayor parte de la energía de un sismo se libera en forma de ondas de esfuerzo, que se desplazan por la corteza de la tierra. Dado que la magnitud está relacionada con la energía liberada en la zona de ruptura, la intensidad de dichas ondas se encuentra relacionada con la magnitud. Los efectos de la magnitud son principalmente: el aumento en la amplitud de la intensidad, la variación en el contenido frecuencial y el aumento en la duración de la vibración.
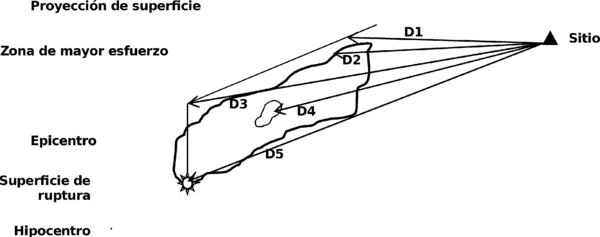
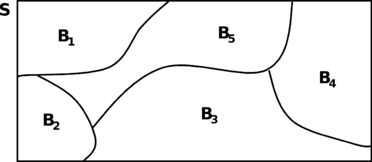
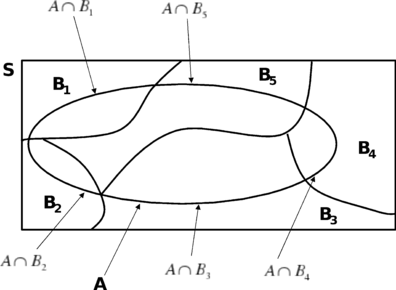
A medida que las ondas se desplazan por el medio rocoso, son absorbidas parcial y progresivamente por los materiales por los que transitan. Como resultado, la energía por unidad de volumen varía en función de la distancia. Dado que la intensidad está relacionada con la energía de las ondas, se encuentra también relacionada con la distancia. Muchas funciones de atenuación relacionan la intensidad en términos de algún parámetro de movimiento fuerte, con una de las distancias presentadas en la Figura 1.1, las cuales caracterizan de diferente manera el origen del movimiento vibratorio.
La distancia D1 representa la distancia del sitio a la proyección en superficie del plano de falla. D2 es la distancia a la superficie de falla. D3 es la distancia epicentral. D4 corresponde a la distancia hasta la zona en la superficie de falla que liberó una mayor cantidad de energía (conocida comúnmente como distancia a la ruptura o Rrup), la cual no necesariamente corresponde con el hipocentro. Y por último D5 es la distancia hipocentral.
La aceleración máxima (PGA) es el parámetro más empleado en los estudios de amenaza sísmica para representar el movimiento del terreno, por lo cual se han propuesto diversos modelos de atenuación de este parámetro con la distancia y las propiedades del medio transmisor. A medida que se cuenta con mayor cantidad de registros de sismos, es posible refinar las funciones de atenuación, lo que deriva en una frecuente publicación de correlaciones nuevas y más refinadas. El nivel de refinamiento aumenta a medida que se desarrollan métodos de procesamiento más avanzados. Un sinnúmero de funciones de atenuación de aceleración máxima han sido desarrolladas a nivel mundial en las últimas décadas, dada la alta relevancia de este insumo dentro de los análisis de amenaza sísmica.
Desarrollos similares a los realizados para la aceleración máxima del terreno han derivado en la obtención de funciones de atenuación de la velocidad máxima horizontal (PGV) y el desplazamiento máximo (PGD), a partir de registros acelerográficos integrados.
Dada la importancia que ha tenido el espectro de respuesta dentro de la práctica de la ingeniería sísmica, se han desarrollado relaciones de atenuación para obtener las ordenadas del espectro de manera directa. Esto puede realizarse a partir de regresiones sobre espectros calculados a registros acelerográficos de zonas con buena instrumentación sísmica.
Alternativamente, se puede calibrar un modelo teórico de las características físicas de una fuente, medio de tránsito de ondas, y comportamiento de la respuesta en el sitio, para predecir la forma del espectro de amplitudes de Fourier (EAF). A partir de la solución del rompimiento instantáneo sobre una superficie esférica en un medio perfectamente elástico, es posible estimar las amplitudes del espectro de Fourier.
La duración del movimiento aumenta al aumentar la magnitud sísmica. Sin embargo, la variación con la distancia depende de cómo se defina el parámetro. Para duraciones basadas en amplitudes de aceleración absoluta, como la determinada con el umbral de duración, tienden a disminuir a medida que aumenta la distancia, dado que la aceleración absoluta disminuye de la misma manera. Duraciones basadas en aceleraciones relativas se incrementan con la distancia, derivando en duraciones muy largas aun cuando las amplitudes sean muy pequeñas.
1.2 FUNCIONES DE ATENUACIÓN BASADAS EN EL ESPECTRO DE FUENTE
Recientemente se han desarrollado una gran variedad de modelos de atenuación, generalmente basados en datos históricos de mediciones de movimiento en estaciones acelerográficas. A partir de regresiones sobre los datos disponibles es posible establecer tendencias y dispersiones de las intensidades de movimiento en función de la magnitud sísmica y la distancia fuente-sitio. Dentro de los desarrollos recientes vale la pena mencionar las llamadas funciones de atenuación de nueva generación (NGA) (Abrahamson & Silva 2008; Boore & Atkinson 2008; Campbell & Bozorgnia 2008, Chiou & Youngs 2008; Idriss 2008).
Por otra parte, desde hace más de 30 años la sismología moderna ha estudiado el problema de propagación de las ondas sísmicas por la corteza terrestre, y ha derivado expresiones matemáticas que permiten caracterizar la forma del espectro de amplitudes de Fourier del movimiento fuerte para una magnitud y una distancia conocidas. Estos modelos se conocen como modelos de espectro de fuente (Aki, 1967; Brune, 1970). Estos modelos están basados en formulaciones sismológicas clásicas, las cuales permiten definir la forma matemática de los desplazamientos de las fuentes cuando ocurre un sismo, así como el contenido frecuencial del movimiento fuerte, para diferentes mecanismos de dislocación.
Aki (1967) dedujo la forma del EAF de desplazamiento, asociado al paso de las ondas de cortante (ondas S) por un punto del campo lejano, en función de la densidad de masa del medio por donde transitan las ondas, la velocidad de las ondas de cortante en el medio, la distancia fuente-sitio, el momento sísmico, el patrón de radiación, y la frecuencia de esquina. Brune (1970) convirtió el modelo de Aki (1967) a aceleración multiplicando por la frecuencia al cuadrado, para obtener el EAF de aceleraciones en un medio ideal y un semi-espacio infinito.
Una porción de la energía que transmiten las ondas sísmicas a la corteza terrestre se transforma en deformación elástica. Otra porción se disipa por procesos viscosos, comportamiento no lineal de las rocas o en forma de calor. Por tanto, en la atenuación de la intensidad del movimiento se considera el efecto de la atenuación anelástica. Knopoff (1964) determinó que este efecto está controlado por un parámetro conocido como absorción anelástica. Este parámetro ha sido ampliamente usado en la sismología moderna para establecer la calidad de las rocas en términos de disipación de energía sísmica.
Por otra parte, el espectro de Brune (1970) predice una amplitud constante para valores de frecuencia superiores a la frecuencia de esquina. Esto no es posible en la realidad dado que se estaría considerando una disponibilidad energética infinita para el movimiento sísmico. Se ha observado en espectros de aceleración para sismos reales, que a medida que aumenta la distancia al foco sísmico, las altas frecuencias son filtradas por el medio y las amplitudes de aceleración decaen de forma más rápida que lo predicho por la atenuación geométrica. Hanks (1982) introdujo una frecuencia de corte al modelo de espectro de fuente que permite modelar el decaimiento de la energía en alta frecuencia.
Singh et.al. (1989) condensaron los anteriores parámetros en un modelo de espectro de fuente que considera la atenuación anelástica y el decaimiento de la energía en alta frecuencia, junto con consideraciones particulares que involucran el comportamiento observado de ciertos parámetros del modelo en función de la frecuencia y de la distancia. El resultado es un modelo de espectro de fuente que permite describir suficientemente bien el tránsito de las ondas S por la corteza, y determinar la forma teórica del EAF de aceleración en cualquier punto del territorio de análisis.
Considerando la aleatoriedad inherente al movimiento fuerte inducido por la ocurrencia de terremotos, se puede emplear la teoría de vibraciones aleatorias para determinar el valor esperado de la intensidad de movimiento a partir del EAF. Singh et.al. (1989) emplean los trabajos de Cartwright y Longuett-Higgins (1956), y Davenport (1964), con el fin de determinar el valor esperado de la intensidad máxima de movimiento en el dominio temporal como función de momentos de área del EAF. El procedimiento puede ampliarse a ordenadas espectrales, al multiplicar el EAF calculado por la función de transferencia de un oscilador de un grado de libertad, caracterizado por un periodo fundamental de vibración y un porcentaje de amortiguamiento respecto al crítico.
En décadas pasadas varios autores han usado modelos de espectro de fuente para derivar funciones de atenuación (Ordaz y Singh, 1992; Atkinson 1995; Gallego 1999; Tavaloki y Pezeshk, 2005; Zafarani y Soghrat, 2012). Cabe resalar el trabajo de Gallego (1999), quién calibró el modelo de espectro de fuente propuesto por Singh et.al. (1989) con datos acelerográficos recolectados por la Red Nacional de Acelerógrafos de Colombia, y propuso funciones de atenuación de la aceleración espectral para el territorio colombiano.
2. CALIBRACIÓN DEL MODELO DE ESPECTRO DE FUENTE
En el marco del análisis probabilista de amenaza sísmica, las funciones de atenuación proveen los momentos de probabilidad de la intensidad de movimiento fuerte distribuida Lognormal, para magnitudes y distancias dentro de su rango de validez. Deben representar de manera adecuada los parámetros sismológicos asociados a la ruptura, los procesos de transformación que sufren las ondas sísmicas al viajar por la corteza terrestre y, adicionalmente, deben estar dadas en términos de variables físicas con relevancia en ingeniería, como lo son la aceleración máxima del terreno (PGA), y la aceleración espectral (Sa).
Los parámetros asociados a la fuente, trayectoria y atenuación local, que son relevantes en la atenuación del movimiento fuerte, pueden ser modelados mediante el uso de un modelo de espectro de fuente, el cual combina el escalamiento de fuente, propagación geométrica, atenuación del medio de tránsito y atenuación local, para proveer una solución teórica de las amplitudes espectrales del movimiento fuerte.
En la formulación del espectro de fuente, las fuentes sísmicas son consideradas como discontinuidades en un medio homogéneo e isotrópico, y los terremotos se modelan como dislocaciones de cortante puro. Usando estas suposiciones básicas, la forma del Espectro de Amplitudes de Fourier (EAF) a nivel de la roca firme puede ser calculada para cualquier ubicación. Una vez se ha calculado el EAF, la esperanza matemática de los valores máximos del movimiento fuerte, en el dominio del tiempo, se calcula aplicando las herramientas dadas en la teoría de vibraciones aleatorias. El enfoque mencionado permite el cálculo de la esperanza matemática de parámetros pico del movimiento fuerte, como lo es el PGA, en cualquier ubicación, dado un momento sísmico (el cual está asociado a la magnitud) y una distancia. Cuando se repite el cálculo para muchas magnitudes y distancias, se obtiene una función de atenuación.
El modelo de espectro de fuente depende de un número importante de variables que definen el proceso de ruptura de la corteza y la calidad del medio de tránsito de las ondas sísmicas, por lo tanto su uso para generar funciones de atenuación no es
directo. Dada la alta no linealidad de la solución de la esperanza matemática del movimiento fuerte, un procedimiento numérico de calibración fue desarrollado, con el fin de determinar el conjunto de parámetros sismológicos que mejor se ajustan a las intensidades reales medidas mediante una red de acelerógrafos. En esta monografía, el primer parámetro objetivo de calibración es PGA. A la aceleración espectral se le da un tratamiento un poco diferente, el cual se presenta más adelante en este capítulo.
2.1 ESPERANZA MATEMÁTICA DE PGA
Para cualquier magnitud y distancia a la ruptura, el EAF radiado, de ondas SH, es calculado y la esperanza matemática de PGA (E{PGA}) es determinada aplicando teoría de vibraciones aleatorias. En esa monografía se usa como base el modelo de espectro de fuente propuesto por Singh et.al. (1989).
El modelo de espectro radiado de ondas SH considera todos los procesos relevantes en la atenuación del movimiento fuerte. Está basado en la formulación del espectro de fuente de Brune (1970), con términos adicionales que dan cuenta de la anelasticidad del medio de tránsito, atenuación local y el tipo de ondas predominante en la atenuación geométrica. Singh et. al. (1989) define espectros de fuente puntual y fuente finita para campo lejano y campo cercano, respectivamente.
2.1.1 Modelo de fuente puntual
El espectro de amplitudes de Fourier de aceleración A(f,R,M0), asumiendo un modelo de fuente ω-2, puede escribirse como:
|
(2.1) |
en donde f es la frecuencia, R la distancia, M0 el momento sísmico, C es una constante relacionada con el medio de tránsito de las ondas sísmicas, S(f,M0) es el término de fuente, G(R) es el término de la propagación geométrica, FQ(f,R) es el filtro de anelasticidad y Fκ(f,R) es el filtro de atenuación local o filtro kappa.
El término constante es,
|
(2.2) |
en donde RθΦ es el patrón de radiación, F es un factor de amplificación por superficie libre, P es un factor de partición de la energía en dos componentes ortogonales, ρ es la densidad del medio y β es su velocidad de onda de cortante. Aup es un factor de corrección por la amplificación inducida en las ondas S por su propagación hacia arriba a través de capas de material con velocidad de onda de cortante progresivamente menor (Boore, 1986). A pesar de ser dependiente de la frecuencia, es aproximadamente 2 para f >1Hz. En este trabajo se asumió Aup = 2 para todas las frecuencias.
El término de fuente, para una fuente ω-2, está dado por (Brune 1970),
|
(2.3) |
|
(2.4) |
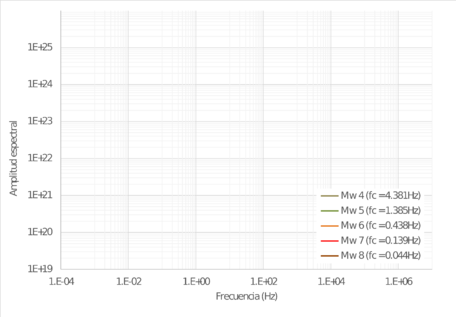
en donde Δσ es la caída de esfuerzos y fc es la frecuencia de esquina. La Figura 2.1 presenta de manera gráfica el término de fuente como función de la frecuencia y la magnitud. Se presenta también la frecuencia de esquina obtenida para cada magnitud, asumiendo un valor constate de Δσ = 210 mbar.
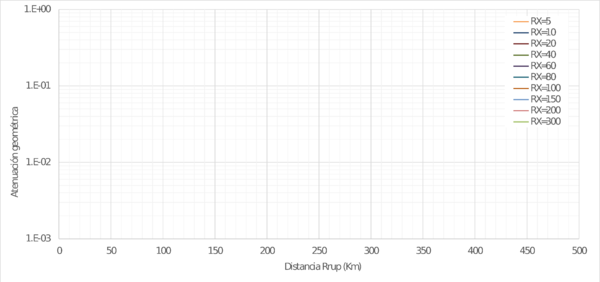
El término de propagación geométrica es,
|
(2.5) |
Este término da cuenta de la predominancia de ondas de cuerpo en la propagación cuando R≤Rx, y de ondas de superficie para R>Rx. Por lo tanto, Rx es la distancia en la cual se espera que cambie el tipo de ondas predominantes. Las ondas superficiales son predominantes para distancias mayores a 100 Km. La Figura 2.2 presenta de manera gráfica el término de atenuación geométrica como función de la distancia y para varios valores de Rx.
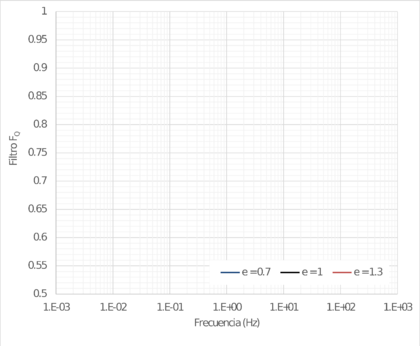
El filtro de anelasticidad es,
|
(2.6) |
en donde Q(f) es el factor de calidad de las rocas Q (Knopoff, 1964) dependiente de la frecuencia. En este trabajo se asume una dependencia de Q con la frecuencia de la forma ![]() , la cual es una versión generalizada de la función asumida en trabajos previos (Castro et al. 1990; Ordaz y Singh 1992; Atkinson 1995; Tavaloki y Pezeshk 2005; Singh et al. 2007; Hassani et al. 2011). Es importante anotar que para valores de ε < 1, FQ funciona como un filtro pasa-bajas, lo cual es su intención. En el caso en que ε = 1, Q sería proporcional a la frecuencia y el filtro FQ resultaría siendo constante para una distancia dada. Valores de ε > 1 resultan en un FQ pasa-altas, lo cual es inconsistente dado que el espectro radiado no sería de tipo ω-2. Por lo tanto, ε debe siempre ser menor a 1. La Figura 2.3 presenta esta situación de manera gráfica. Se muestran los valores del filtro FQ para ε = 0.7, 1 y 1.3 y para una distancia fija de 50 Km. El caso ε =1.3 presentado en la Figura 2.3 es inconsistente con la formulación ω-2 del espectro de fuente.
, la cual es una versión generalizada de la función asumida en trabajos previos (Castro et al. 1990; Ordaz y Singh 1992; Atkinson 1995; Tavaloki y Pezeshk 2005; Singh et al. 2007; Hassani et al. 2011). Es importante anotar que para valores de ε < 1, FQ funciona como un filtro pasa-bajas, lo cual es su intención. En el caso en que ε = 1, Q sería proporcional a la frecuencia y el filtro FQ resultaría siendo constante para una distancia dada. Valores de ε > 1 resultan en un FQ pasa-altas, lo cual es inconsistente dado que el espectro radiado no sería de tipo ω-2. Por lo tanto, ε debe siempre ser menor a 1. La Figura 2.3 presenta esta situación de manera gráfica. Se muestran los valores del filtro FQ para ε = 0.7, 1 y 1.3 y para una distancia fija de 50 Km. El caso ε =1.3 presentado en la Figura 2.3 es inconsistente con la formulación ω-2 del espectro de fuente.
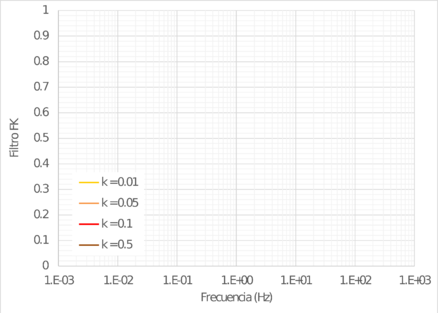
El filtro de atenuación local (o filtro kappa) es,
|
(2.7) |
El filtro de atenuación local está asociado al hecho que las amplitudes de alta frecuencia se atenúan mucho más rápido de lo predicho por la anelasticidad y atenuación geométrica, debido principalmente a condiciones particulares en cercanía a la superficie, que pueden variar de ubicación en ubicación. Este filtro da cuenta de la disminución en la amplitud espectral para f > fmax, siendo fmax la frecuencia de corte introducida por Hanks en 1982. La Figura 2.4 muestra la variación del filtro Fκ con la frecuencia, para varios valores de κ.
Gallego y Ordaz (1999) emplean en su formulación del espectro de fuente, un κ dependiente de la distancia, de la siguiente forma
|
(2.8) |
en donde κ1 y Q1 son constantes que dependen del medio de tránsito de las ondas. En esta formulación κ es proporcional a la distancia, presentando diferencias de uno o dos órdenes de magnitud entre distancias muy cortas y muy largas. Estas diferencias pueden inducir una sobreestimación de la amenaza para distancias cortas, y una subestimación para distancias largas. Por esta razón se prefirió mantener un κ constante como en la formulación original del espectro de fuente de Singh et.al. (1989).
Aplicando las definiciones anteriores a la ecuación 2.1 se obtiene, para R≤Rx (predominancia de ondas de cuerpo)
|
(2.9) |
y para R>Rx (predominancia de ondas de superficie)
|
(2.10) |
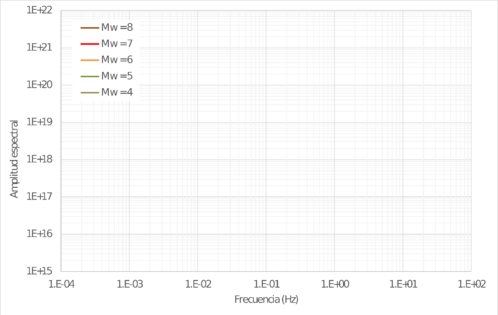
La Figura 2.5 presenta varios EAF teóricos calculados a manera de ejemplo, y su variación con la magnitud. Los espectros mostrados son para: R = 16 Km, Rx = 100 Km, C=233, Δσ = 210 mbar, β=3,5 Km/s, ρ = 2.5 Ton/m3, Q0 = 700, ε = 0.9 y κ = 0.015.
2.1.2 Modelo de fuente finita
Con el fin de considerar que en el campo cercano el rompimiento no puede ser considerado puntual, Singh et.al. (1989) proponen un modelo de fuente finita que está basado en la definición de una zona de ruptura de geometría circula, formada por muchos diferenciales de área, cada uno de los cuales puede modelarse como fuente puntual. El espectro de campo cercano resultante, calculado en un punto localizado sobre el eje del círculo de ruptura es
|
(2.11) |
en donde α=2π/β Q0, r0 es el radio del área de ruptura y E1 es la integral exponencial (Abramowitz y Stegun, 1964). El modelo de fuente puntual es válido únicamente para f >=fc. Para frecuencias menores, el modelo indica amplitudes espectrales casi constantes. Esta característica hace que sea imposible aplicar el modelo de fuente finita solo. La banda de baja frecuencia del espectro radiado (f <fc) estará siempre definida por el modelo de fuente puntual. Esto tiene sentido dado que el espectro es de tipo ω-2 incluso para el campo cercano. Por otra parte, el modelo de fuente puntual predice amplitudes espectrales muy grandes para la banda de frecuencias centrales (fc<f<fmax), para grandes momentos sísmicos. Esta situación se corrige en el modelo de fuente finita dado que este modelo se satura dada la naturaleza finita del rompimiento. En este modelo, todos los diferenciales de área que componen la zona de ruptura aportan amplitud al espectro radiado, pero aquellos ubicados cerca del perímetro de la zona aportan menos que los ubicados cerca al centro. Por esta razón, se define el espectro radiado como el mínimo entre los espectros calculados con los modelos de fuente finita y puntual.
|
(2.12) |
2.1.3 Valor esperado de PGA
Dada la naturaleza aleatoria de los registros de movimiento fuerte, la teoría de vibraciones aleatorias puede ser usada para determinar el valor esperado de PGA (E{PGA}) como función del EAF de aceleración. De los trabajos de Cartwright y Longuett-Higgins (1956) y Davenport (1964) se puede establecer que
|
(2.13) |
en donde arms es la aceleración cuadrática media y FP es el valor esperado de la máxima razón PGA/ arms. arms y FP se calculan como sigue
|
(2.14) |
|
(2.15) |
en donde Td es la duración de la fase intensa, γ es la constante de Euler (γ = 0.577...) y mn son los momentos de orden n del EAF,
|
(2.16) |
De acuerdo con Herman (1985), la duración de la fase intensa puede obtenerse como
|
(2.17) |
2.2 PROCEDIMIENTO PARA LA CALIBRACIÓN DEL MODELO PARA PGA
La metodología presentada permite el cálculo de la esperanza matemática de PGA como función del EAF de aceleración radiado. E{PGA} puede entonces ser expresado como una función de todos los parámetros involucrados en su formulación.
|
(2.18) |
En esta monografía, los parámetros de la función presentada en la ecuación 2.18 son las variables de calibración. Sin embargo, no todas las variables en la ecuación 2.18 son susceptibles de calibración. Dado que la magnitud y la distancia son conocidas, M0 y R son removidos del conjunto de variables. M0 es función de la magnitud de momento (Mw) como se indica en Hanks y Kanamori (1979). Para el desarrollo de esta monografía, se asumieron los valores ρ = 2.5 Ton/m3 y β = 3.5 Km/s. Rx fue definido por Gallego y Ordaz (1999) como 100 Km para el territorio colombiano, valor que se mantiene en este trabajo. El conjunto final de parámetros sismológicos es: Δσ, ε, Q0, κ, y RθΦ. La cantidad E{PGA} está entonces definida mediante una función altamente no lineal en un espacio de 6 dimensiones, por lo cual la aplicación de métodos estadísticos clásicos de ajuste es impráctica. Por lo tanto, en este trabajo de desarrolló un algoritmo genético con el fin de buscar el conjunto óptimo de parámetros sismológicos que mejor se ajusten a los valores de PGA observados en los registros acelerográficos.
En el algoritmo genético implementado en esta monografía, los individuos corresponden a diferentes modelos de atenuación de movimiento fuerte. El genotipo de estos individuos es el conjunto de parámetros sismológicos seleccionados para la calibración. La evolución inicia con una población de individuos generados aleatoriamente, y sigue un proceso iterativo en el cual los individuos son cruzados y mutados (es decir, su genotipo es modificado) para dar vida a la población de la siguiente generación. En cada generación, el ajuste de cada individuo de la población (es decir, el sesgo que presenta a los valores observados de PGA) es evaluado.
En este estudio se implementó un enfoque de Evolución Forzada (EF), en el cual el individuo con el mejor ajuste (al cual se le denomina “campeón”) es cruzado con todos los demás individuos de su generación, creando así la siguiente generación. Este enfoque garantiza que el ajuste obtenido en cada generación es, al menos, tan bueno como el de la generación anterior. La nueva generación de individuos es usada en la siguiente iteración del algoritmo. El algoritmo termina cuando se alcanza un máximo número de generaciones, o cuando se obtiene un ajuste suficientemente bueno.
2.2.1 Estructura del algoritmo
Inicialización
Un conjunto de cientos o miles de individuos es creado como población inicial. Todos los individuos son creados mediante la selección aleatoria de los valores de los parámetros sismológicos que componen su genotipo, dentro de rangos predefinidos. Estos rangos permiten restringir los valores de estos parámetros solamente a valores con un sentido físico lógico.
Selección
Dentro de cada generación, el ajuste de los individuos es determinado por su capacidad de reducir el sesgo respecto a los valores observados de PGA. Para cada individuo, la cantidad E{PGA} es calculada junto con los residuales para cada registro acelerográfico. Los residuales (Re) se calculan como sigue
|
|
(2.19) |
en donde arec es la aceleración nominal registrada en cada acelerograma,
|
(2.20) |
en donde ax es la componente ortogonal x del movimiento fuerte (típicamente la componente E-W) y ay es la componente y (típicamente la N-S). La componente vertical es descartada en este procedimiento.
En seguida, para cada individuo se calcula el sesgo de la siguiente manera
|
(2.21) |
El individuo con el menor sesgo será declarado campeón y será cruzado con todos los otros individuos de su generación.
Cruce y mutación
Las operaciones de cruce y mutación son ejecutadas luego de la selección del individuo campeón. Estas operaciones permiten la creación de nuevos individuos para la siguiente generación. El cruce se lleva a cabo por medio de una mezcla aleatoria de los parámetros sismológicos de los individuos “padres” (uno de los cuales es siempre el campeón), de manera que el individuo “hijo” resultante tiene en su genotipo información de ambos padres. El tamaño de la población se mantiene siempre constante.
Dada la alta no linealidad del problema, no es posible asegurar que el individuo campeón corresponda a uno con el mínimo sesgo global. Por lo tanto, los individuos son aleatoriamente mutados durante la evolución con el fin de evitar el estancamiento en un mínimo sesgo local.
Finalización
Un mínimo sesgo aceptable y un máximo número de generaciones deben ser definidos con el fin de limitar el número total de iteraciones. Cuando alguno de los dos se alcanza, el algoritmo finaliza. El individuo campeón de la última generación contiene la combinación óptima de parámetros sismológicos que definen el modelo de espectro de fuente y proveerá el menor sesgo.
2.3 EXPANSIÓN A ORDENADAS ESPECTRALES
El procedimiento de cálculo puede ser expandido para calcular funciones de atenuación de la aceleración espectral, mediante la multiplicación del EAF de aceleración teórico por la función de transferencia de un oscilador de un grado de libertad (O1GDL). El espectro de respuesta de aceleración es de gran importancia para fines de ingeniería, dado que provee la máxima aceleración inducida sobre un O1GDL de comportamiento elástico durante la ocurrencia de un terremoto.
La función de transferencia de un O1GDL de periodo de vibración T y coeficiente de amortiguamiento ζ está dada por,
|
(2.22) |
El EAF de aceleración de la respuesta del O1GDL (Aosc) se calcula multiplicando su función de transferencia por el EAF radiado,
|
(2.23) |
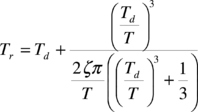
El valor esperado de la aceleración espectral se calcula de Aosc usando teoría de vibraciones aleatorias, de la misma manera que para PGA, con una modificación para dar cuenta del cambio en la duración de la fase intensa. Td es reemplazado en la ecuación 38 por la duración de la respuesta del O1GDL (Tr). Tr se calcula según lo indicado por Joyner y Boore (1988).
|
(2.24) |
2.3.1 Procedimiento para la calibración del modelo para ordenadas espectrales
La metodología presentada permite el cálculo de la esperanza matemática de la aceleración espectral como función del EAF de aceleración radiado, modificado por la función de transferencia de un O1GDL con periodo fundamental de vibración T. El valor esperado de la aceleración espectral correspondiente, Sa(T), puede ser expresado como:
|
(2.25) |
Los términos asociados al EAF de la aceleración espectral son los mismos asociados a PGA (constante, de fuente, propagación geométrica, atenuación anelástica y atenuación local) más el término asociado a la respuesta elástica de un O1GDL. El único término que tiene una dependencia directa con el periodo estructural es el término de respuesta de un O1GDL. Este término no cuenta con parámetros libres que puedan ser susceptibles de calibración. Por lo tanto, debe seleccionarse de los parámetros libres del modelo sismológico, aquellos que puedan ser empleados para ajustar el modelo a las ordenadas espectrales.
Dentro del conjunto de parámetros sismológicos, se selección Q0 como parámetro susceptible de calibración para ordenadas espectrales. Esta selección tiene que ver con la clara dependencia de Q con la frecuencia, así mismo como la independencia de todos los demás parámetros (M0, R, Rx, Δσ, ε, κ, ρ, β y RθΦ con la frecuencia. Se consideró entonces que los parámetros sismológicos no dependientes de la frecuencia, quedarían establecidos por el resultado del procedimiento de calibración sobre PGA. Esto implica entonces que en el cálculo del valor esperado de las aceleraciones espectrales, los parámetros Rx, Δσ, ε, κ, ρ, β y RθΦ son constantes, es decir:
|
(2.26) |
Dado que M0, R y T son cantidades conocidas, el único parámetro libre es Q0. De esta manera, se aplica el mismo algoritmo de ajuste que para la calibración de PGA sobre Sa(T). Vale la pena hacer notar que la ejecución del algoritmo genético en este caso resulta en una búsqueda aleatoria de valores de Q0.
3. OBTENCIÓN DE FUNCIONES DE ATENUACIÓN PARA COLOMBIA
Con el fin de implementar y probar la metodología propuesta, se presenta en esta sección la construcción de funciones de atenuación para el territorio colombiano, calibradas con registros acelerográficos de sismos ocurridos en el país.
El territorio colombiano constituye una amplia región de interacción tectónica, en la cual interactúan las placas Caribe, Suramérica y Nazca. La totalidad del territorio se encuentra ubicado sobre la placa Suramérica. Al occidente, la placa Nazca subduce la placa Suramérica a lo largo de la Costa Pacífica colombiana, teniendo asociado a este movimiento sismos de alta magnitud. Las deformaciones inducidas en la corteza por efecto de la interacción entre las placas Nazca y Suramérica, son absorbidas por un conjunto de sistemas de fallas corticales, dentro de los cuales resaltan el sistema Romeral, de tipo transcurrente, y el sistema Frontal de la Cordillera Oriental ubicado en el piedemonte llanero, y de tipo inverso (falla de cabalgamiento). Al norte, el principal rasgo sismotectónico lo constituye la zona de compresión entre las placas Suramérica y Caribe, la cual induce deformaciones que son absorbidas por movimientos transcurrentes de los sistemas Oca en Colombia y San Sebastián en Venezuela.
3.1 BASE DE DATOS DE MOVIMIENTO FUERTE
Los registros de movimiento fuerte fueron obtenidos de la Red Nacional de Acelerógrafos de Colombia (RNAC), operada por el Servicio Geológico Colombiano. La base de datos contiene un total de 284 acelerogramas crudos (no corregidos) registrados a nivel de roca firme para un periodo de 14 años desde 1994 a 2008, para terremotos con magnitud de momento Mw superior a 4.4. Registros posteriores no han sido incluidos en este estudio, pero no han ocurrido sismos importantes en Colombia desde entonces.
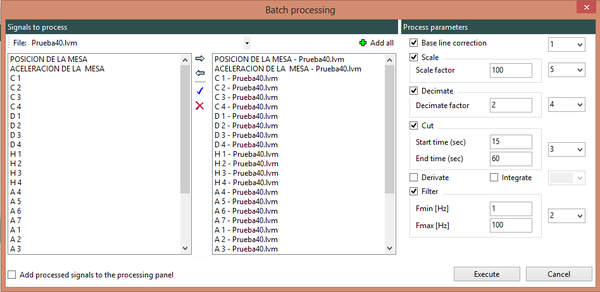
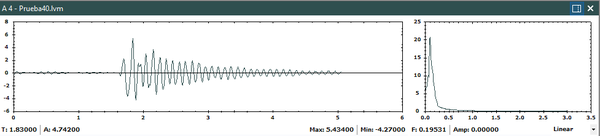
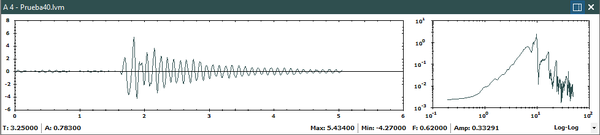
Los 284 acelerogramas fueron sometidos a un procesamiento que incluyó: corrección de instrumento (ganancia) y de línea base (fase 1 del procesamiento) y filtrado
pasabanda y diezmado a un intervalo de tiempo uniforme (fase 2 del procesamiento). Después de este proceso, la base de datos fue depurada con el fin de descartar
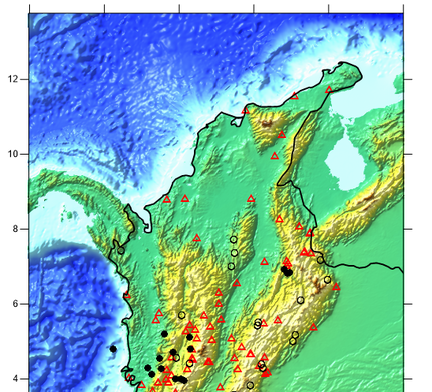
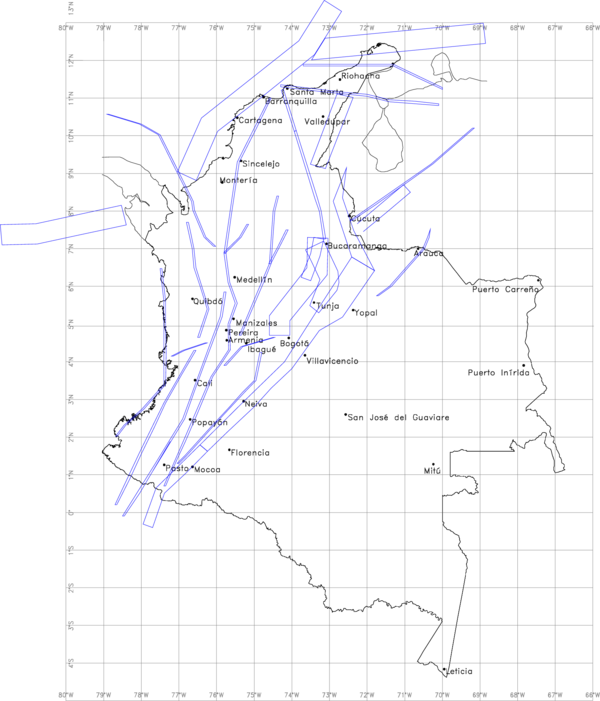
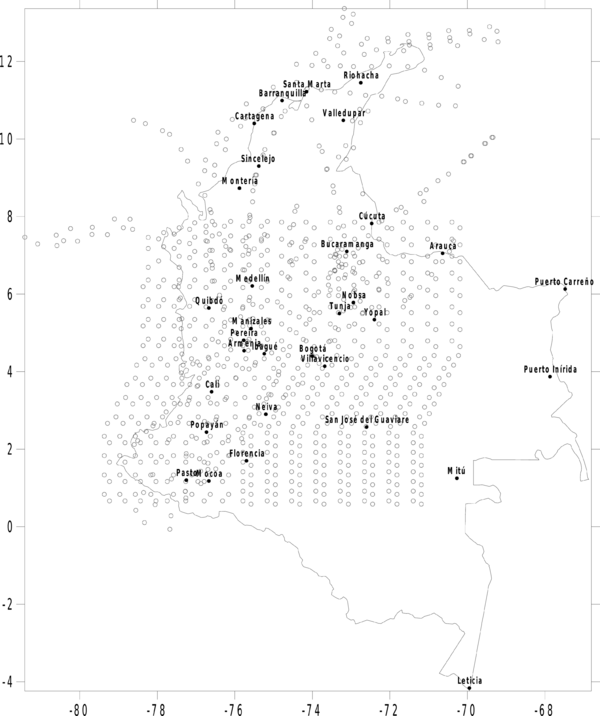
registros erróneos o de muy bajo PGA. La base de datos definitiva cuenta con 206 registros acelerográficos. Finalmente, los registros se dividieron en dos conjuntos: sismos corticales y sismos de subducción. Los grupos quedaron conformados por 87 acelerogramas asociados a 22 terremotos corticales y 119 acelerogramas asociados a 15 terremotos de subducción (ver Tabla 3.1). La Figura 3.1 muestra la ubicación de los epicentros de los terremotos usados en la calibración, junto con la ubicación de los acelerógrafos de la RNAC.
Los 284 acelerogramas fueron sometidos a un procesamiento que incluyó: corrección de instrumento (ganancia) y de línea base (fase 1 del procesamiento) y filtrado pasabanda y diezmado a un intervalo de tiempo uniforme (fase 2 del procesamiento). Después de este proceso, la base de datos fue depurada con el fin de descartar registros erróneos o de muy bajo PGA. La base de datos definitiva cuenta con 206 registros acelerográficos. Finalmente, los registros se dividieron en dos conjuntos: sismos corticales y sismos de subducción. Los grupos quedaron conformados por 87 acelerogramas asociados a 22 terremotos corticales y 119 acelerogramas asociados a 15 terremotos de subducción (ver Tabla 3.1). La Figura 3.1 muestra la ubicación de los epicentros de los terremotos usados en la calibración, junto con la ubicación de los acelerógrafos de la RNAC.
| Nombre del sismo | Tipo | Fecha | Mw | Profundidad [Km] | Número de acelerogramas |
| Páez | Cortical | 06/06/1994 | 6.1 | 1 | 1 |
| Santa Isabel | Cortical | 9/19/1994 | 4.6 | 1 | 2 |
| Tauramena | Cortical | 1/19/1995 | 6.2 | 25 | 5 |
| Calima | Subducción | 02/08/1995 | 6.4 | 102 | 7 |
| Risaralda | Subducción | 8/19/1995 | 6.4 | 110 | 4 |
| Zaragoza | Cortical | 06/11/1996 | 5.1 | 5 | 4 |
| Sipi | Subducción | 09/11/1996 | 4.6 | 100 | 10 |
| Juradó | Cortical | 11/04/1996 | 6.1 | 5 | 4 |
| El Dovio | Subducción | 11/17/1996 | 4.5 | 110 | 11 |
| Nido de Bucaramanga | Subducción | 01/01/1997 | 5.8 | 160 | 5 |
| Sipi | Subducción | 2/19/1997 | 5.6 | 120 | 6 |
| Nido de Bucaramanga | Subducción | 06/11/1997 | 5.8 | 170 | 3 |
| Cubarral | Cortical | 7/17/1997 | 4.8 | 5 | 24 |
| Génova | Subducción | 09/02/1997 | 6.8 | 230 | 12 |
| Argelia | Subducción | 12/10/1997 | 4.4 | 100 | 1 |
| Génova | Subducción | 12/11/1997 | 6.4 | 220 | 1 |
| Chameza | Cortical | 02/10/1998 | 4.5 | 5 | 6 |
| Landazuri | Cortical | 03/06/1998 | 4.8 | 5 | 2 |
| Cimitarra | Cortical | 03/08/1998 | 4.9 | 5 | 25 |
| Armenia | Cortical | 1/25/1999 | 5.8 | 5 | 1 |
| Guayabetal | Cortical | 06/01/1999 | 4.6 | 5 | 2 |
| Sativasur | Cortical | 7/17/1999 | 5 | 5 | 7 |
| Trujillo | Subducción | 7/19/1999 | 4.9 | 130 | 1 |
| Betulia | Subducción | 11/08/1999 | 6.2 | 160 | 8 |
| Fortul | Cortical | 1/17/2000 | 5.3 | 5 | 2 |
| El Bagre | Cortical | 3/28/2000 | 4.7 | 5 | 5 |
| Tuluá | Subducción | 9/22/2001 | 5.6 | 180 | 1 |
| La Uribe | Cortical | 11/23/2002 | 5 | 5 | 9 |
| Colombia | Cortical | 1/22/2003 | 4.6 | 5 | 1 |
| Sotará | Cortical | 8/18/2004 | 4.6 | 5 | 1 |
| Océano Pacífico | Subducción | 11/15/2004 | 6.6 | 24 | 2 |
| Toro | Cortical | 03/08/2005 | 4.6 | 5 | 1 |
| Tadó | Subducción | 4/21/2005 | 4.7 | 90 | 4 |
| Puracé | Cortical | 03/06/2007 | 4.4 | 5 | 1 |
| Andes | Cortical | 4/24/2007 | 4.7 | 15 | 14 |
| Cubará | Cortical | 6/20/2007 | 5.1 | 5 | 11 |
| Quetame | Cortical | 5/28/2008 | 5.1 | 1 | 2 |
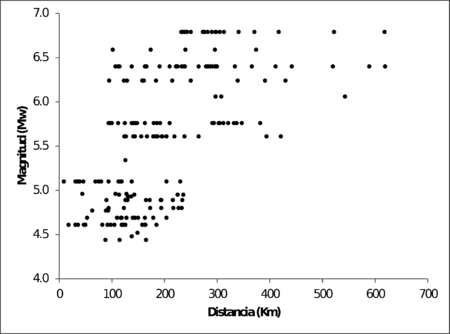
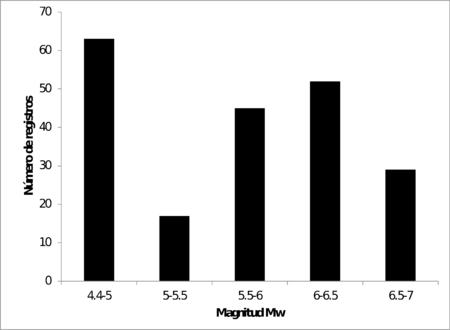
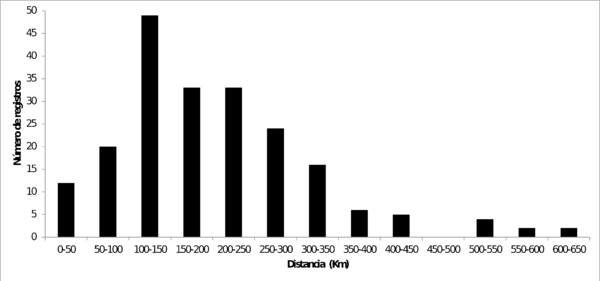
La magnitud fue expresada de manera uniforme en escala de magnitud de momento Mw. La distribución de magnitudes y distancias se presenta en la Figura 3.2. Las magnitudes van de 4.4 a 6.8 Mw, y las distancias van de 88 a 619 Km. La Figura 3.3 muestra un histograma de las magnitudes sobre rangos uniformes. La Figura 3.4 presenta un histograma de las distancias. Estos histogramas muestran que el número de registros puede asumirse como distribuido uniformemente en las magnitudes pero no en las distancias. El intervalo de distancias central (de 100 a 300 Km) tiene más del 65% de todos los registros. Para distancias mayores a 400Km, solamente se cuenta con 13 acelerogramas. La estimación del movimiento fuerte para distancias mayores a 400 Km es de gran importancia en el caso Colombiano, dada la posibilidad de ocurrencia de un sismo de gran magnitud en la zona de subducción de la costa pacífica, que afecte la ciudad de Bogotá debido a los importantes efectos de sitio que ahí se presentan. Por otra parte, la máxima magnitud disponible es 6.8 Mw, que es un valor bajo comparado con las máximas magnitudes esperadas en las fuentes sismogénicas colombianas (AIS 2010, Salgado et.al. 2010). Estos vacíos en los datos limitan la aplicabilidad de técnicas de regresión para la generación de funciones de atenuación en Colombia. El procedimiento aquí propuesto parece proveer una solución práctica en este caso.
3.2 FUNCIONES DE ATENUACIÓN DE PGA PARA COLOMBIA
El procedimiento de calibración propuesto ha sido aplicado para obtener el conjunto de parámetros sismológicos del modelo de espectro de fuente que mejor se ajustan a los valores de PGA observados. Se calibraron funciones de atenuación para sismos corticales y de subducción por separado. La Tabla 3.2 presenta los rangos iniciales para los parámetros sismológicos, definidos previamente a la calibración.
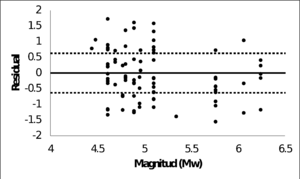
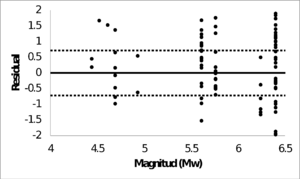
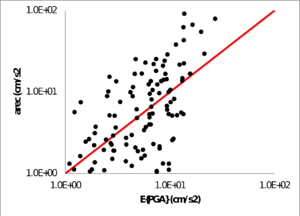
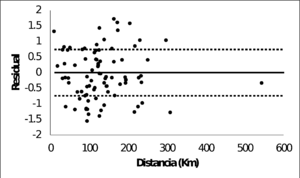
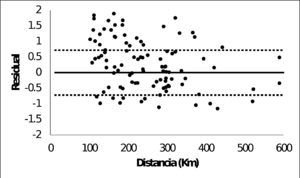
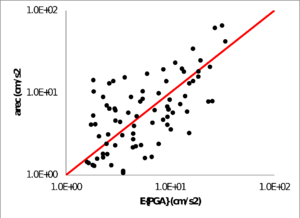
Los parámetros sismológicos resultantes se presentan en la Tabla 3.3, junto con el sesgo y desviación estándar finales. Los valores de los parámetros son lógicos desde el punto de vista de su significado físico. Los residuales se presentan en la Figura 3.5 para ambos modelos (cortical y subducción), mostrando su variación con la distancia y con la magnitud. La Figura 3.5 presenta adicionalmente el sesgo y la desviación obtenidos para cada modelo. Los sesgos finales son muy cercanos a cero, lo cual indica en términos prácticos que la estimación de PGA usando el procedimiento propuesto se puede considerar como no sesgada, lo cual es una característica muy deseable en las funciones de atenuación. La Figura 3.6 muestra la relación entre el PGA calculado (E{PGA}) y la intensidad nominal o PGA observado (arec). Los resultados muestran un muy buen ajuste entre los PGA calculados y observados.
| Parámetro | Unidades | Mínimo | Máximo |
| Bar | 50 | 250 | |
| ε | 0.8 | 1 | |
| Qo | - | 50 | 800 |
| k | - | 0.005 | 0.04 |
| - | 0.55 | 0.65 |
| Mecanismo focal | [bar] | Qo | ε | k | Sesgo | Desviación estándar | |
| Cortical | 235.9 | 723.1 | 0.9 | 0.0333 | 0.642 | 0.0009 | 0.63 |
| Subducción | 210.3 | 477.9 | 0.91 | 0.0346 | 0.623 | 0.0008 | 0.72 |
|
|
|
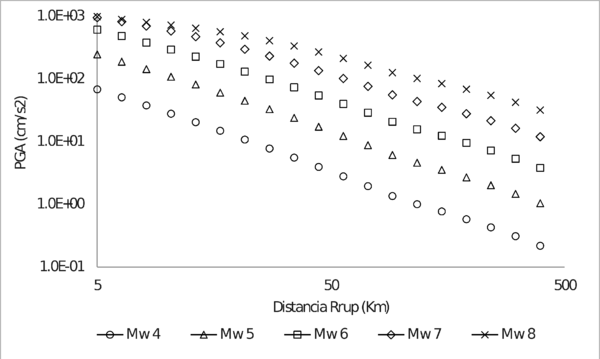
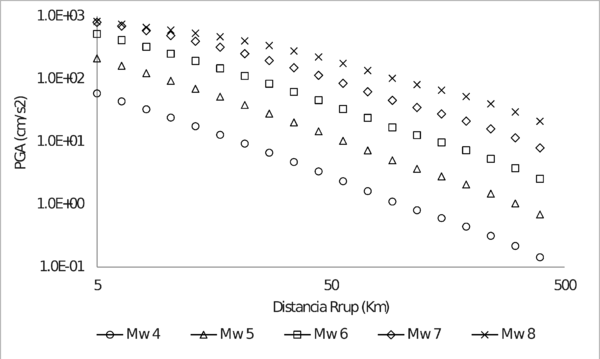
La Figura 3.7 y Figura 3.8 presentan las funciones de atenuación obtenidas en términos de PGA y calculadas con los parámetros de la Tabla 3.3, para sismos corticales y de subducción, respectivamente. Estas funciones de atenuación han sido definidas para distancias entre 5 y 500 Km y magnitudes entre 4 y 8 Mw.
3.3 FUNCIONES DE ATENUACIÓN DE LA ACELERACIÓN ESPECTRAL PARA COLOMBIA
El procedimiento de calibración propuesto, se ejecutó para obtener funciones de atenuación de la aceleración espectral para O1GDL con 0.05, 0.1, 0.15, 0.3, 0.5, 1.0, 1.5, 2.0, 2.5, y 3.0 segundos de periodo fundamental de vibración, y ζ = 5%. El rango de variación de Q0 es el mismo presentado en la Tabla 3.2. Se calibraron funciones de atenuación para sismos corticales y de subducción. Los valores de Q0 obtenidos en cada caso, junto con el correspondiente sesgo y desviación estándar, se presentan en la Tabla 3.4. Los valores obtenidos para Q0 se presentan de manera gráfica, como función del periodo estructural, en la Figura 3.9.
Dentro de este trabajo, en definitiva, se obtuvieron dos modelos de atenuación finales, uno por cada tipo de terremotos, los cuales se generan mediante el ensamblaje de los modelos de atenuación particulares de cada periodo estructural y PGA. Estos modelos de atenuación tienen, en todos los casos, sesgos cercanos a cero, lo cual indica que son insesgados en todas las ordenadas espectrales. Adicionalmente, sus desviaciones estándar están dentro de los valores normales reportados en la literatura.
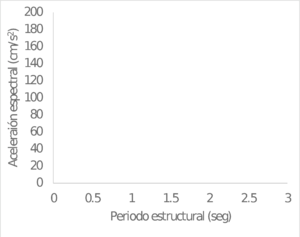
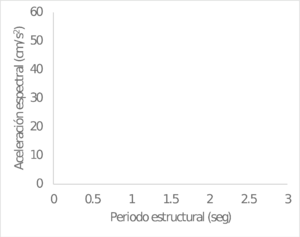
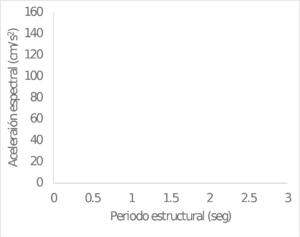
La Figura 3.10 presenta dos ejemplos de espectros de respuesta (ζ = 5%) para magnitudes y distancias arbitrarias, para el modelo de sismos corticales, y la Figura 3.11 presenta los espectros de respuesta para el modelo de sismos de subducción.
| T (seg) | Cortical | Subducción | ||||
| Q0 | Sesgo | Desviación estándar | Q0 | Sesgo | Desviación estándar | |
| 0.05 | 241.2 | -0.0027 | 0.76 | 355.9 | 0.0172 | 0.72 |
| 0.10 | 257.8 | 0.0053 | 0.78 | 356.9 | 0.0143 | 0.76 |
| 0.15 | 344.3 | 0.0154 | 0.78 | 406.9 | 0.0208 | 0.75 |
| 0.30 | 578.3 | 0.0015 | 0.72 | 382.2 | 0.0232 | 0.72 |
| 0.50 | 390.4 | 0.0009 | 0.68 | 253.2 | 0.0075 | 0.70 |
| 1.00 | 319.2 | -0.0010 | 0.66 | 165.5 | 0.0483 | 0.70 |
| 1.50 | 302.3 | -0.0008 | 0.64 | 146.8 | -0.0492 | 0.72 |
| 2.00 | 371.2 | -0.0046 | 0.67 | 149.6 | -0.1402 | 0.74 |
| 2.50 | 510.9 | 0.0033 | 0.70 | 124.8 | 0.0334 | 0.71 |
| 3.00 | 954.9 | -0.0003 | 0.72 | 132.8 | -0.0540 | 0.73 |
|
|
| Mw=5; R=35 Km | Mw=8; R=150 Km |
|
|
| Mw=5; R=35 Km | Mw=8; R=150 Km |
|
|
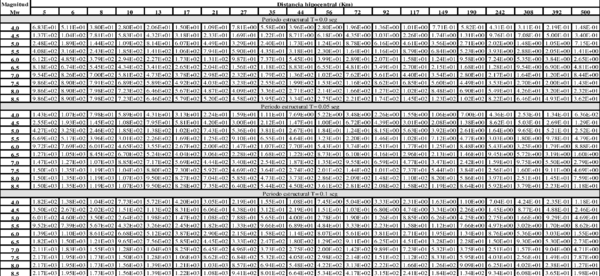
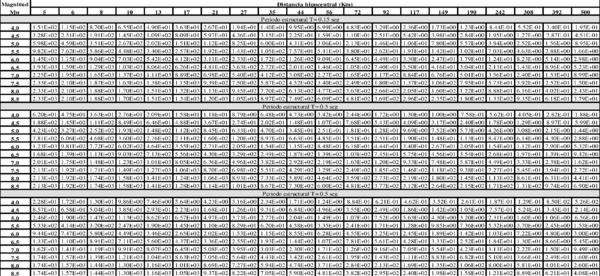
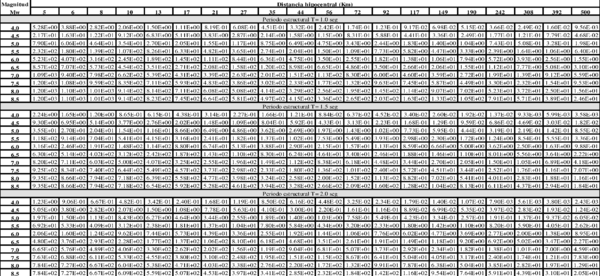
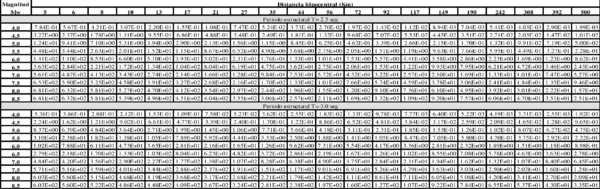
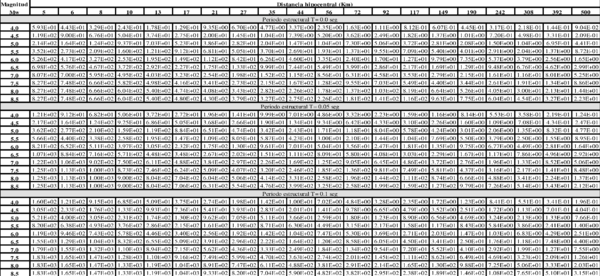
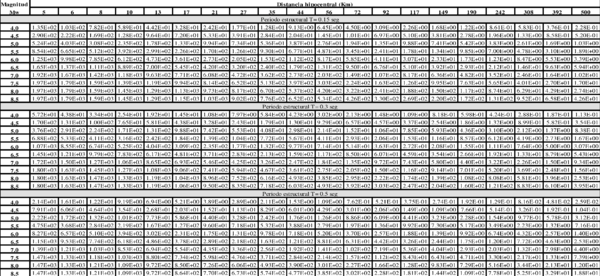
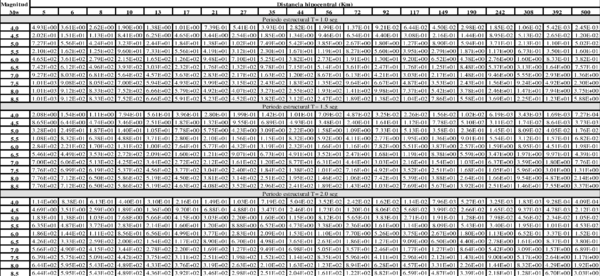
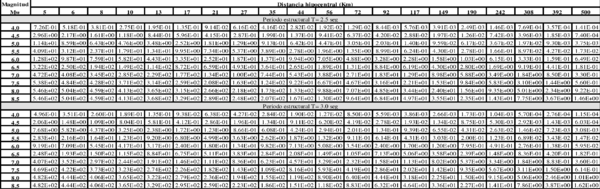
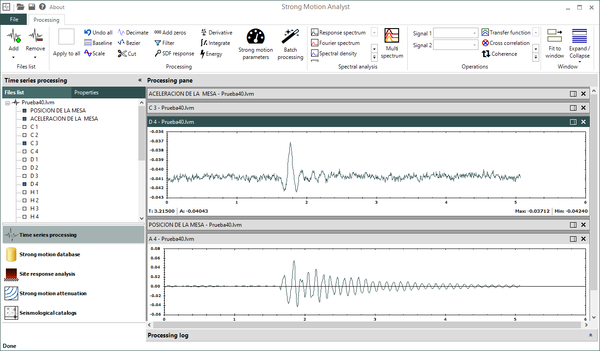
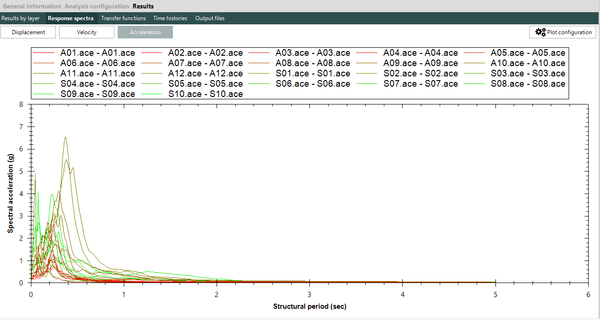
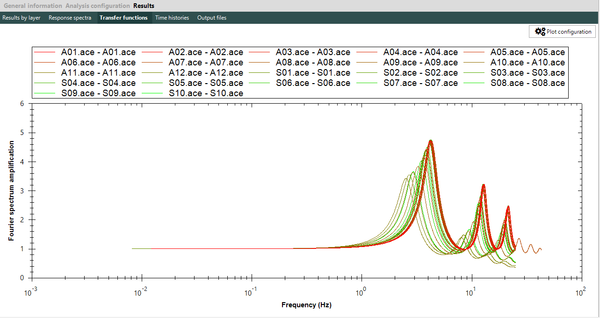
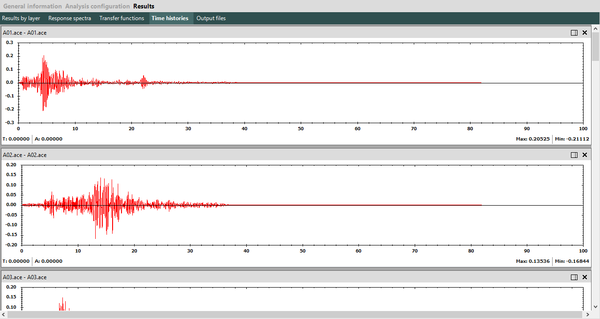
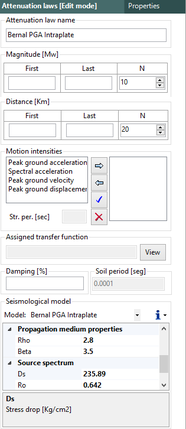
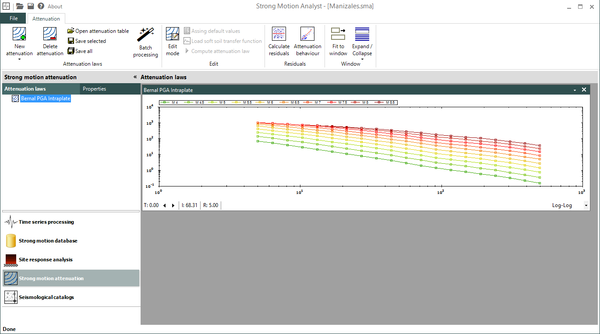
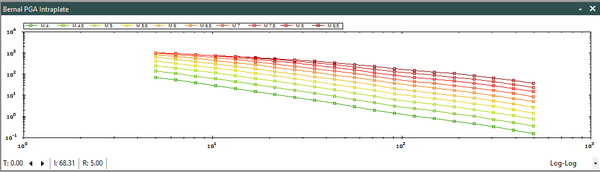
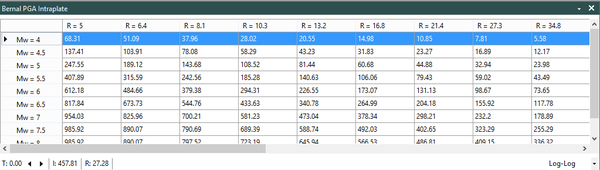
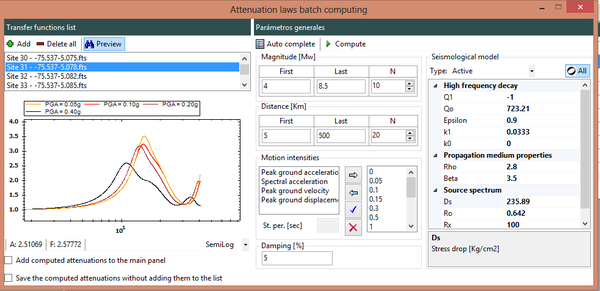
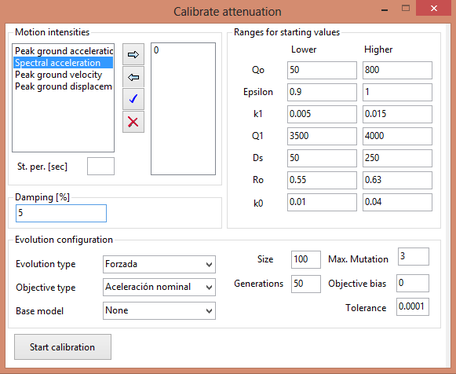
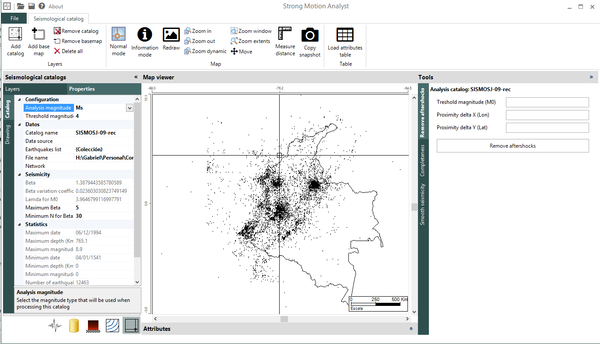
Dado que no existe una expresión simple para calcular PGA o aceleraciones espectrales, usando los resultados de esta monografía, el Anexo A contiene tablas de valores de PGA y aceleración espectral para diferentes combinaciones de magnitud y distancia, y para los periodos estructurales definidos en este trabajo. Es posible construir funciones de atenuación para PGA o aceleración espectral para combinaciones diferentes de magnitud, distancia o periodo estructural, usando el programa Strong Motion Analyst, y el cual es un software académico de libre uso que implementa los procedimientos acá contenidos y los parámetros sismológicos resultantes. El Anexo C presenta una breve descripción de este programa.
3.4 COMPARACIÓN CON FUNCIONES DE ATENUACIÓN PREVIAMENTE APLICADAS AL CASO COLOMBIANO
Las funciones de atenuación obtenidas son comparadas con las que fueron usadas en el Estudio General de Amenaza Sísmica de Colombia (AIS 2010, Salgado et.a. 2010). Esas funciones de atenuación son: Campbell strike (Campbell, 1997) y Gallego y Ordaz (1999) para sismos corticales, y Campbell reverse (Campbell 1997) y Gallego y Ordaz (1999) para sismos de subducción; todas ellas a nivel de roca firme. Se calcularon los residuales para todas estas funciones de atenuación usando la base de datos de acelerogramas de este trabajo. Los sesgos y desviaciones estándar resultantes para PGA, se presentan en la Tabla 3.5, en comparación con los obtenidos para las funciones de atenuación acá desarrolladas.
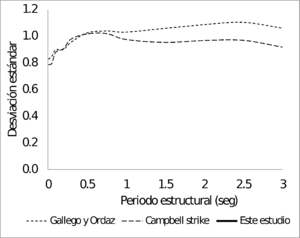
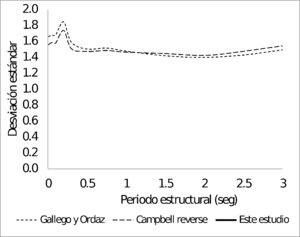
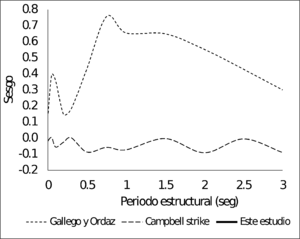
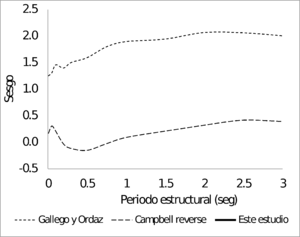
La Figura 3.12 presenta los sesgos y desviaciones estándar, en función del periodo estructural, del modelo de atenuación para sismos corticales obtenido en esta monografía, en comparación con los modelos correspondientes usados en el Estudio General de Amenaza Sísmica de Colombia (AIS 2010, Salgado et.a. 2010). La Figura 3.13 presenta la misma comparación para los modelos de subducción.
| Cortical | Subducción | ||||
| Función de atenuación | Sesgo | Desviación estándar | Función de atenuación | Sesgo | Desviación estándar |
| Campbell strike | 0.018 | 0.79 | Campbell reverse | 0.02 | 1.56 |
| Gallego y Ordaz | 0.155 | 0.83 | Gallego y Ordaz | 1.248 | 1.66 |
| Este trabajo | 0.0009 | 0.63 | Este trabajo | 0.0008 | 0.72 |
|
|
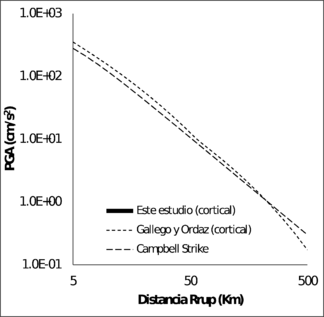
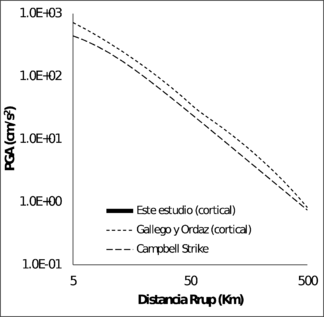
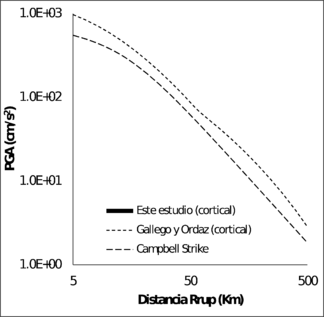
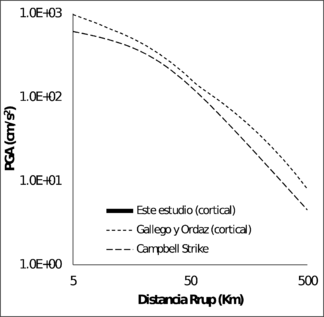
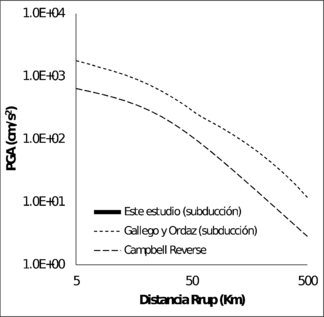
La Figura 3.14 muestra la comparación de las funciones de atenuación para sismos corticales y la Figura 3.15 muestra la misma comparación para as funciones de sismos de subducción, para los modelos de PGA. En el caso de las funciones de atenuación de sismos corticales, para magnitudes mayores a 6, la función obtenida en esta monografía está siempre por encima de los otros modelos. En el caso de las funciones para sismos de subducción, la propuesta por Gallego y Ordaz (1999) predice valores de PGA muy por encima que los dado por el modelo propuesto en este trabajo, para distancias a la ruptura superiores a 80 Km.
| Mw = 5.0 | Mw = 6.0 |
|
|
| Mw = 7.0 | Mw = 8.0 |
|
|
| Mw = 5.0 | Mw = 6.0 |
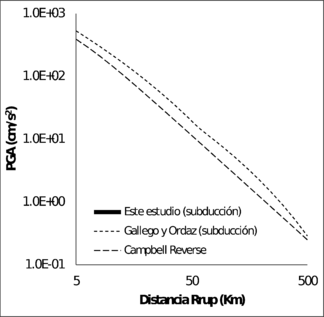
|
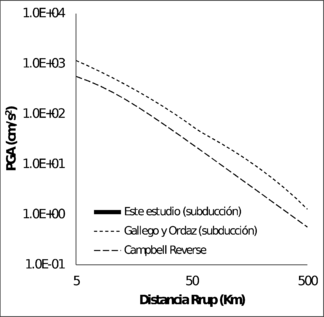
|
| Mw = 7.0 | Mw = 8.0 |
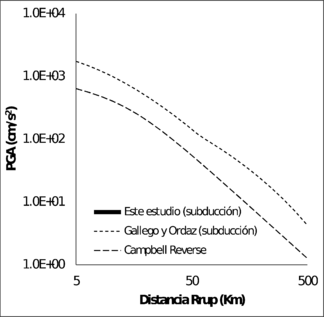
|
|
El modelo de espectro de fuente presentado permite entonces construir funciones de atenuación de movimiento fuerte por medio de la calibración de los parámetros sismológicos que definen la forma del EAF. Esta formulación es particularmente útil en regiones con densidad no uniforme de datos en el rango de magnitudes y distancias de aplicación. En el caso colombiano, el modelo permite estimar los momentos de probabilidad de intensidades de movimiento fuerte que son insesgadas con relación a los datos acelerográficos existentes, y que tienen desviaciones estándar aceptables.
4. EVALUACIÓN DE LA AMENAZA SÍSMICA DE COLOMBIA
El cálculo de la amenaza sísmica emplea las definiciones y métodos presentados anteriormente, para establecer el nivel de peligro esperado en un sitio o zona determinada, bajo la influencia de la actividad sísmica de fuentes aledañas. Históricamente los ingenieros, geólogos y sismólogos se han preocupado por desarrollar metodologías de cálculo que representan cada vez mejor el comportamiento de las fuentes, el tránsito de las ondas dentro del medio rocoso, la respuesta de los suelos y la respuesta estructural en el sitio de interés.
En las últimas décadas se ha desarrollado el enfoque probabilista en los análisis de amenaza sísmica, con el fin de involucrar de manera analítica la incertidumbre asociada con las variables que intervienen en el peligro sísmico de una región. Parámetros como la frecuencia de ocurrencia de determinado sismo, la probabilidad de que ocurra en un sitio específico, probabilidades de excedencia de intensidades sísmicas, entre otros, son incluidos en los modelos de cálculo, para conformar un análisis probabilista de amenaza sísmica (PSHA por sus siglas en inglés).
La evaluación probabilista de la amenaza sísmica se basa en la ecuación propuesta por Esteva (1970) para el cálculo de tasas de excedencia de medidas de intensidad de movimiento sísmico, como función de las características de generación de los terremotos y la atenuación de las ondas sísmicas a su paso por la corteza terrestre, la cual a su vez es una aplicación del teorema de la probabilidad total. Por lo tanto la tasa de excedencia de alguna medida de intensidad asociada a la ocurrencia de un evento de amenaza, en un punto particular del territorio de análisis, se puede calcular como la suma ponderada de la probabilidad de excedencia del nivel de intensidad para el cual se está calculando, para todos los escenarios que definen la amenaza, usando como factores de ponderación las frecuencias anuales de ocurrencia de los terremotos.
Por lo tanto, para calcular las tasas de excedencia de valores de intensidad es necesario construir un conjunto de escenarios estocásticos, mutuamente excluyentes y colectivamente exhaustivos, cada uno con una distribución geográfica de
momentos de probabilidad que caractericen las medidas de intensidad de movimiento fuerte
Desde hace más de 30 años se ha desarrollado una metodología robusta de evaluación probabilista de la amenaza sísmica, mediante la cual es posible involucrar de manera analítica la incertidumbre asociada a variables como la tasa de ocurrencia de terremotos en una región, la magnitud y ubicación de los sismos y la atenuación de la energía del movimiento fuerte. La metodología de evaluación probabilista de la amenaza sísmica fue establecida inicialmente por Cornell (1968) y Esteva (1970), y puede resumirse en cuatro pasos principales, según lo establece Reiter (1990):
- 1. Caracterización de las fuentes generadoras de terremotos con influencia en el sitio de análisis, en términos de su geometría y distribución de probabilidad de inicio de la ruptura en el área definida.
- 2. Definición de la sismicidad de las fuentes consideradas, a partir del registro histórico de eventos ocurridos sobre su geometría (catálogo sísmico) y sus características sismotectónicas. Existen diferentes modelos de recurrencia de magnitudes para caracterizar la tasa de ocurrencia de terremotos.
- 3. Estimación de parámetros de movimiento fuerte en el sitio de análisis. Esto se lleva a cabo empleando funciones de atenuación de movimiento que consideren la incertidumbre asociada a la estimación de los parámetros.
- 4. Finalmente se combinan las incertidumbres asociadas a localización, tamaño y atenuación y se obtienen las tasas anuales de excedencia de parámetros de movimiento fuerte.
4.1 MODELO DE FUENTES Y SISMICIDAD
La caracterización de las fuentes generadoras de terremotos puede hacerse mediante diferentes geometrías. Es usual modelar las fuentes como planos en el espacio, dado que esta geometría se ajusta muy bien a las características generales de las zonas de deformación y rompimiento de la corteza terrestre. Es usual también asignar una probabilidad uniforme a la ocurrencia de los terremotos dentro de la geometría de las fuentes. Dado que esta suposición implica que toda la energía del terremoto es irradiada desde el hipocentro, Der-Kiureghian y Ang (1977) plantearon una manera de considerar el tamaño de la superficie de ruptura dentro de análisis de amenaza. Relaciones entre la magnitud sísmica y el tamaño de la zona de ruptura, considerando fuentes planas pueden encontrarse en Brune (1970), Singh et al. (1982) o Wells y Coppersmith (1994). Dentro del alcance del análisis probabilista de amenaza sísmica, no se han propuesto mayores avances respecto a este tema.
Con relación a la caracterización de la sismicidad de las fuentes, es decir, establecer la tasa de ocurrencia de los terremotos, existen una serie de modelos de recurrencia de magnitudes que son directamente aplicables en el análisis. Dentro de los más representativos se encuentran la ley de recurrencia de Gutenberg y Richter (1944) y variaciones como la ley Gutenberg y Richter acotada, y la ley de recurrencia del terremoto característico, esta última empleada en diversas investigaciones (Youngs y Coppersmith, 1985; Wu et. al. 1995). Si bien estos modelos permiten establecer la recurrencia de magnitudes en una fuente a partir de la información histórica disponible, no permiten caracterizar la ocurrencia de terremotos dentro de una ventana de tiempo. Es común entonces considerar que el proceso de generación de terremotos en una fuente sigue un proceso de Poisson, es decir, se considera que el número de ocurrencias en una ventana de tiempo dada es independiente del número de ocurrencias en cualquier otra ventana de tiempo, o en otras palabras, que el proceso no tiene memoria. Esta manera de ver la recurrencia de magnitudes permite establecer tanto la distribución de probabilidad de la ocurrencia de terremotos de diferente magnitud, como la distribución de probabilidad del tiempo entre la ocurrencia de dos terremotos consecutivos. El modelo de recurrencia de Poisson ha sido usado en una gran cantidad de investigaciones sobre amenaza sísmica, a tal punto que es el modelo de recurrencia más ampliamente usado hoy en día. Cornell y Winterstein (1986) mostraron que el modelo de recurrencia Poissoniano es adecuado para la caracterización de la sismicidad de las fuentes, excepto en casos particulares en los cuales toda la amenaza esté controlada por una sola fuente con un fuerte comportamiento de recurrencia del terremoto característico. Por este motivo y otras razones asociadas a la simplicidad, facilidad de uso y carencia de información para la aplicación de modelos más sofisticados, el modelo de recurrencia de Poisson se puede considerar como el más apropiado para el análisis de amenaza sísmica.
En el modelo poissoniano, la actividad de la i-ésima fuente sísmica se especifica en términos de la tasa de excedencia de las magnitudes, li(M), generadas por esta fuente. La tasa de excedencia de magnitudes mide qué tan frecuentemente se generan temblores con magnitud superior a una específica. Para la mayor parte de las fuentes sísmicas, la función li(M) es una versión modificada de la relación de Gutenberg y Richter. En estos casos, la sismicidad queda descrita como,
|
|
(4.1) |
en donde M0 es la mínima magnitud o magnitud umbral. l0, βi, y Mu son parámetros que definen la tasa de excedencia de cada una de las fuentes sísmicas. Estos parámetros, diferentes para cada fuente, se estiman mediante procedimientos estadísticos de máxima verosimilitud e información experta. De esta manera, cada una de las fuentes sismogénicas queda caracterizada mediante los siguientes de parámetros de sismicidad:
- Recurrencia de magnitudes: se identifica mediante el parámetro β que representa la pendiente promedio de la curva de recurrencia de magnitudes (curva de número de eventos con magnitud mayor que M, versus magnitud sísmica M) en la zona de magnitudes bajas.
- Magnitud máxima Mu: se estima con base en la máxima longitud de ruptura posible de cada una de las fuentes y en otras características morfotectónicas.
- Tasa de recurrencia de sismos con magnitud mayor que la de umbral λ0: corresponde al número promedio de eventos por año de sismos con magnitud mayor que M0 que ocurren en una determinada fuente.
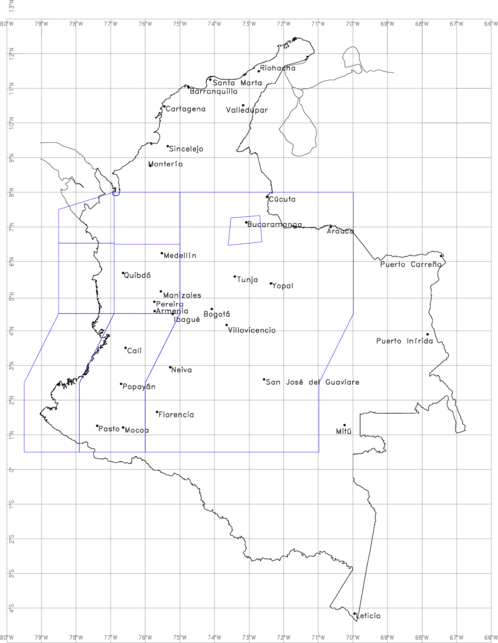
Se evaluó la amenaza sísmica de Colombia a nivel de roca firme, usando el modelo de atenuación desarrollado en esta monografía. El modelo de fuentes empleado ha sido tomado del Estudio General de Amenaza Sísmica de Colombia (AIS 2010, Salgado et.al. 2010). Se tienen un total de 39 fuentes, 31 de las cuales son de tipo cortical, y 8 de subducción. En la Tabla 4.1 se presentan los parámetros de sismicidad asignados a las fuentes sismogénicas colombianas. Las Figura 4.1 presenta la geometría de las fuentes de tipo cortical y la Figura 4.2 la geometría de las fuentes de tipo subducción.
| Fuente | M0 | λ | β | CV β | Mu |
| Arco de Dabeiba | 4 | 2.63 | 1.80 | 0.091 | 6.9 |
| Bahía Solano | 4 | 2.98 | 1.30 | 0.086 | 7.5 |
| Benioff Intermedia Sur | 4 | 1.85 | 3.85 | 0.070 | 8.0 |
| Benioff Intermedia Centro | 4 | 5.80 | 1.49 | 0.061 | 8.0 |
| Benioff Intermedia Norte | 4 | 2.17 | 1.91 | 0.100 | 8.0 |
| Benioff Profunda | 4 | 5.70 | 2.02 | 0.062 | 7.5 |
| Boconó | 4 | 4.93 | 2.03 | 0.066 | 7.4 |
| Bucaramanga Santa Marta Norte | 4 | 0.13 | 1.33 | 0.440 | 6.5 |
| Bucaramanga Santa Marta Centro | 4 | 0.87 | 2.27 | 0.160 | 6.5 |
| Bucaramanga Santa Marta Sur | 4 | 0.93 | 3.31 | 0.154 | 6.9 |
| Cauca | 4 | 5.00 | 2.62 | 0.066 | 7.5 |
| Cimitarra | 4 | 0.59 | 2.97 | 0.196 | 6.5 |
| Compresión Caribe SE | 4 | 0.59 | 1.65 | 0.196 | 6.5 |
| Compresión Carive SW | 4 | 0.70 | 2.29 | 0.179 | 6.1 |
| Cuiza | 4 | 0.76 | 1.74 | 0.171 | 6.6 |
| Espíritu Santo | 4 | 0.22 | 2.04 | 0.333 | 6.5 |
| Fallas del Magdalena | 4 | 0.28 | 1.10 | 0.288 | 7.0 |
| Frontal Cordillera Oriental Norte | 4 | 1.48 | 1.50 | 0.122 | 8.0 |
| Frontal Cordillera Oriental Centro | 4 | 2.61 | 1.50 | 0.091 | 8.0 |
| Frontal Cordillera Oriental Sur | 4 | 2.37 | 2.26 | 0.090 | 8.0 |
| Garrapatas | 4 | 0.26 | 3.00 | 0.302 | 6.5 |
| Ibagué | 4 | 0.26 | 1.58 | 0.302 | 6.9 |
| Junín | 4 | 0.15 | 2.19 | 0.408 | 7.0 |
| Murindó | 4 | 3.59 | 1.44 | 0.078 | 7.5 |
| Nido de Bucaramanga | 4 | 32.10 | 1.88 | 0.026 | 6.5 |
| Normal Panamá Pacífico | 4 | 2.20 | 1.83 | 0.100 | 7.1 |
| Oca | 4 | 1.63 | 2.06 | 0.116 | 6.5 |
| Palestina | 4 | 0.98 | 1.69 | 0.151 | 6.5 |
| Perijá | 4 | 0.59 | 3.07 | 0.196 | 6.5 |
| Puerto Rondón | 4 | 0.24 | 1.80 | 0.316 | 6.7 |
| Romeral | 4 | 0.54 | 2.03 | 0.119 | 7.6 |
| Romeral Norte | 4 | 0.46 | 1.88 | 0.223 | 6.5 |
| Salinas | 4 | 1.63 | 1.91 | 0.116 | 6.5 |
| Suárez | 4 | 1.33 | 2.47 | 0.129 | 6.5 |
| Subducción Norte | 4 | 3.15 | 1.33 | 0.083 | 8.6 |
| Subducción Centro | 4 | 2.46 | 1.29 | 0.094 | 8.6 |
| Subducción Sur | 4 | 16.30 | 1.95 | 0.036 | 8.9 |
| Uribante-Caparro | 4 | 0.87 | 1.60 | 0.160 | 7.0 |
4.2 AMENAZA SÍSMICA DE COLOMBIA A NIVEL DE TERRENO FIRME
Una vez determinada la tasa de actividad de cada una de las fuentes sísmicas, es necesario evaluar los efectos que, en términos de intensidad sísmica, produce cada una de ellas en un sitio de interés. Para ello se requiere saber qué intensidad se presentaría en el sitio en cuestión, hasta ahora supuesto en terreno firme, si en la i-ésima fuente ocurriera un temblor con magnitud dada.
La intensidad de movimiento fuerte, s, se modela como una variable aleatoria con el fin de incorporar de manera racional la incertidumbre asociada a su estimación. En la práctica común de la ingeniería sísmica, el interés se centra en la estimación de parámetros de movimiento de amplitud máxima (PGA, PGV y PGD), así como ordenadas del espectro de respuesta. Es usual representar estos parámetros de movimiento fuerte como variables aleatorias distribuidas lognormal, con momentos de probabilidad dados por la función de atenuación.
Una vez conocidas la sismicidad de las fuentes y los patrones de atenuación de las ondas generadas en cada una de ellas, puede calcularse la amenaza sísmica considerando la suma de los efectos de la totalidad de las fuentes sísmicas y la distancia entre cada fuente y el sitio donde se encuentra la estructura. La amenaza, expresada en términos de las tasas de excedencia de intensidades s, se calcula como,
|
(4.2) |
en donde la sumatoria abarca la totalidad de las fuentes sísmicas N, y Pr(S>s|M,Ri) es la probabilidad de que la intensidad exceda un cierto valor, dadas la magnitud del sismo M, y la distancia entre la i-ésima fuente y el sitio Ri. Las funciones λi(M) son las tasas de actividad de las fuentes sísmicas. La integral se realiza desde M0 hasta Mu, lo que indica que se toma en cuenta, para cada fuente sísmica, la contribución de todas las magnitudes.
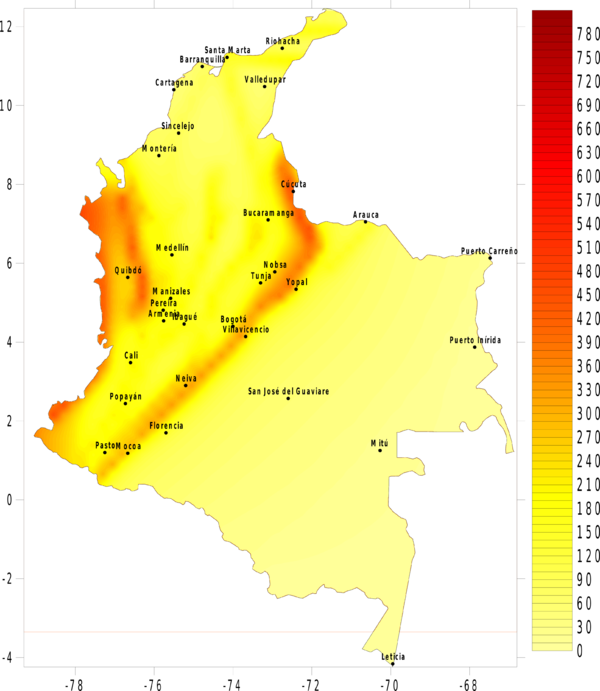
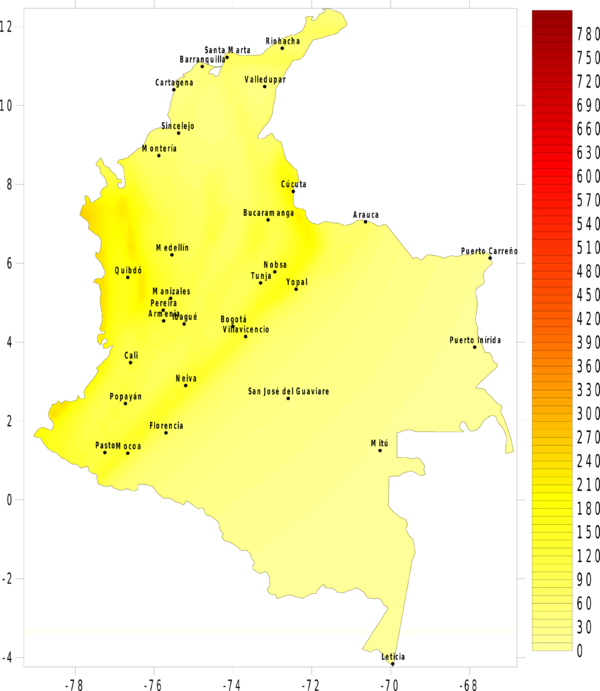
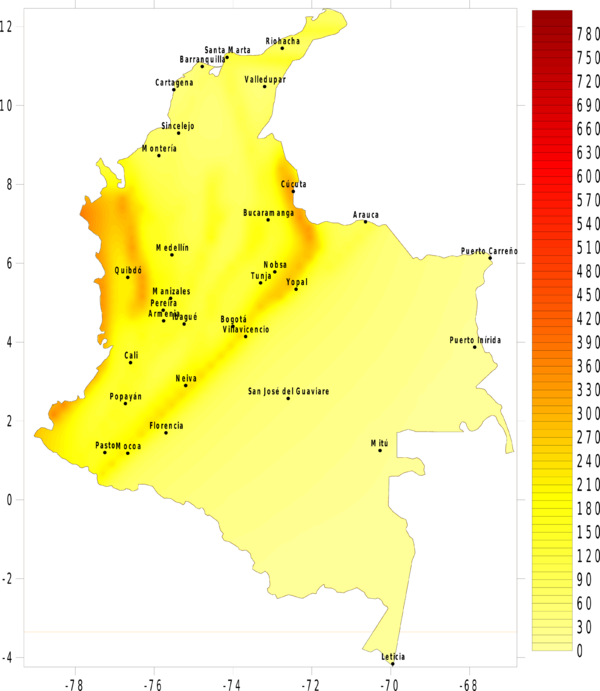
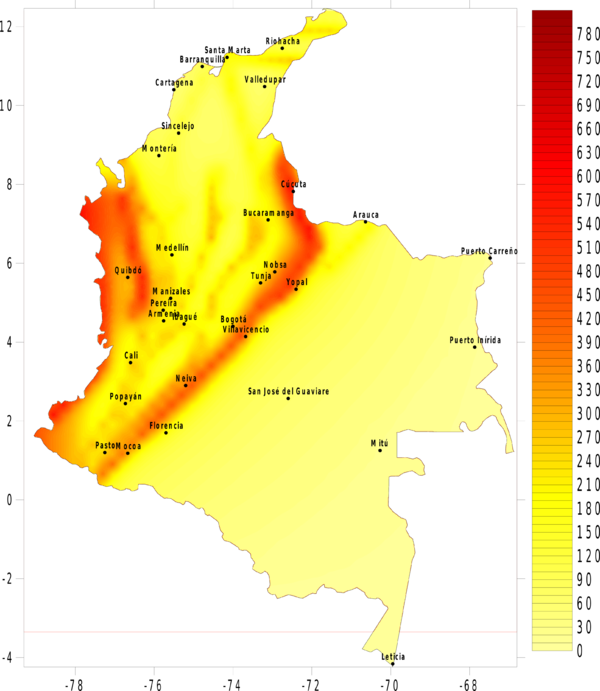
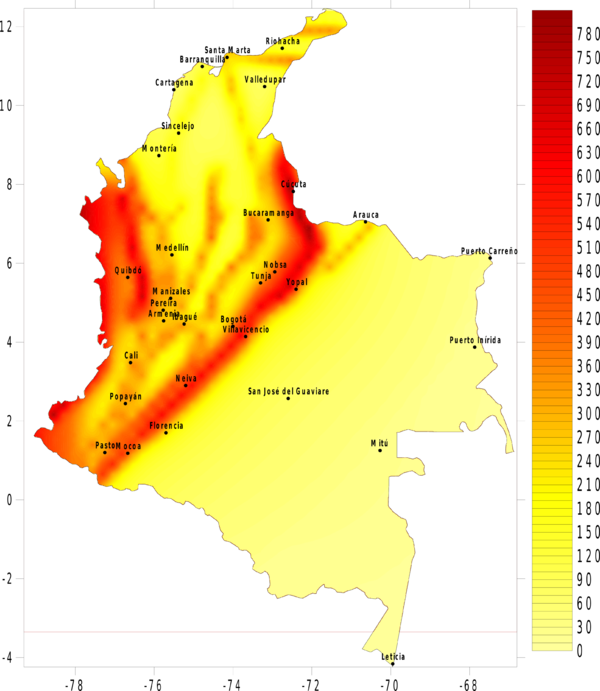
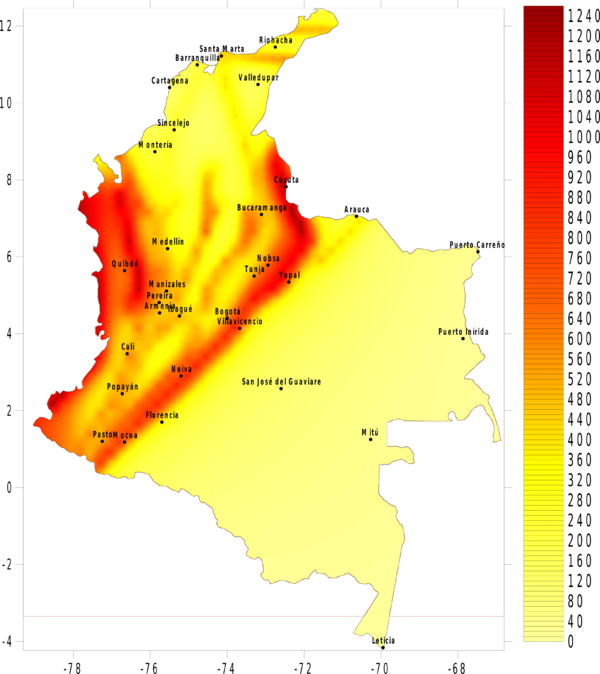
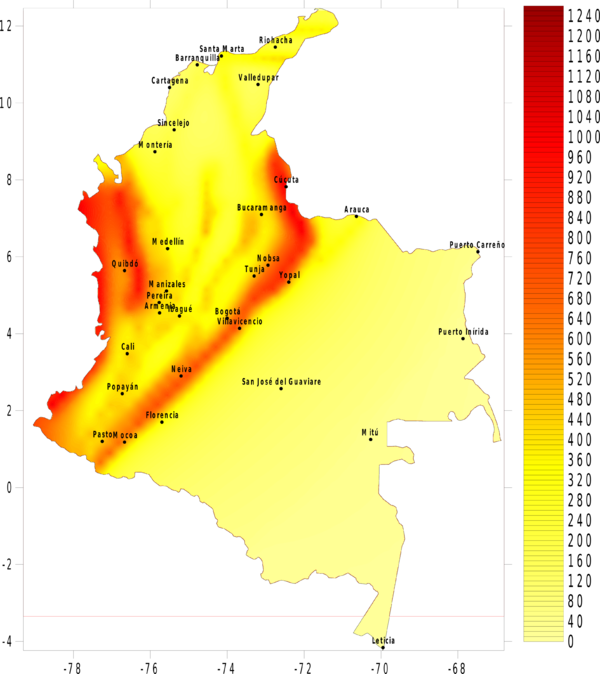
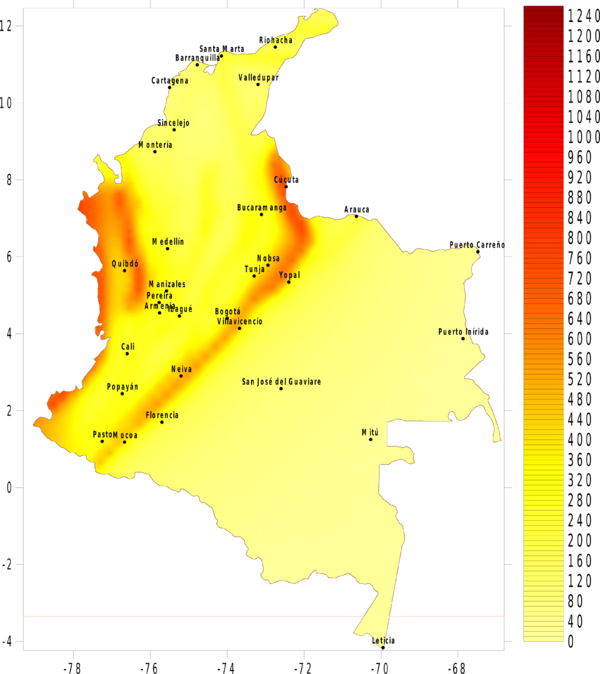
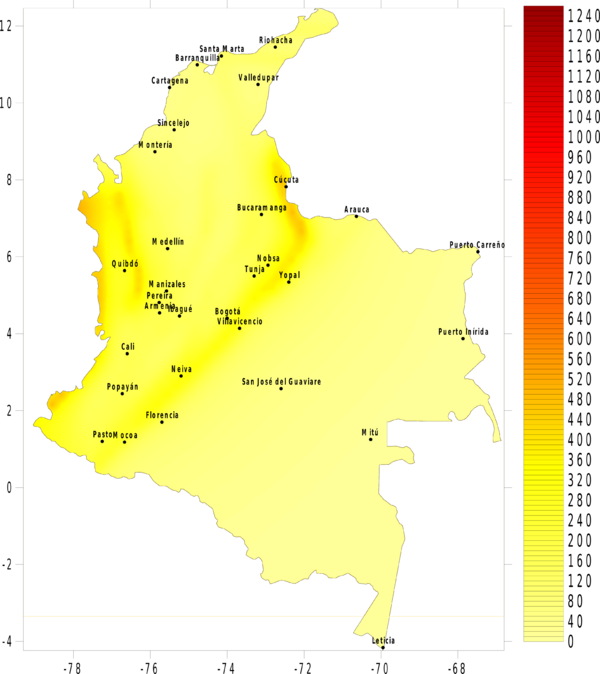
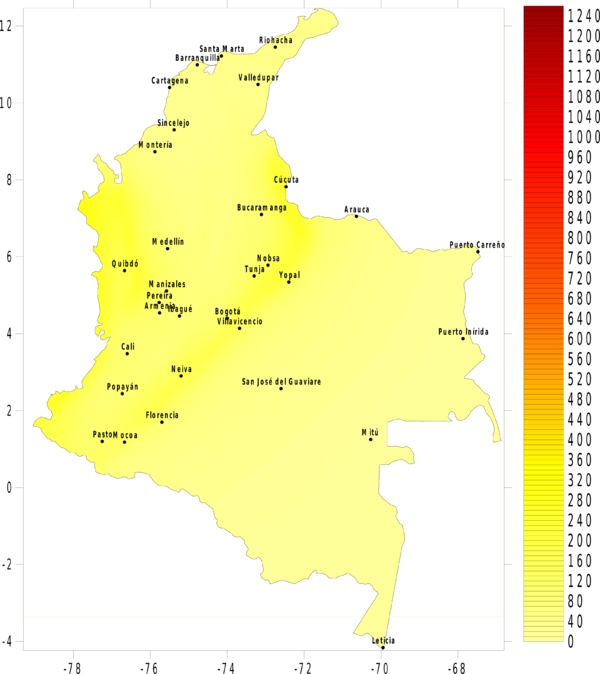
La amenaza o el peligro sísmico se expresa, entonces, en términos de la tasa de excedencia de valores dados de intensidad sísmica. Si se leen los valores de intensidad correspondientes a valores fijos de tasa de excedencia (o alternativamente periodos de retorno) en cada uno de los nodos de la malla de cálculo, es posible generar mapas de amenaza sísmica. La Figura 4.3 presenta el mapa de amenaza uniforme para Colombia, en términos del PGA, para 500 años de periodo de retorno. En el Anexo B de este documento, se presenta el conjunto de mapas de amenaza sísmica generado para Colombia, en particular mapas de amenaza uniforme en términos de PGA para 100, 250, 500, 1000 y 2500 años de periodo de retorno, y mapas en términos de la aceleración espectral, para 500 años de periodo de retorno y para periodos estructurales de 0.15, 0.3, 0.5, 1.0, y 2.0 segundos.
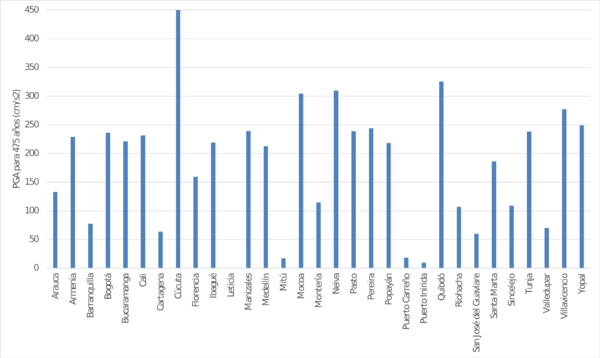
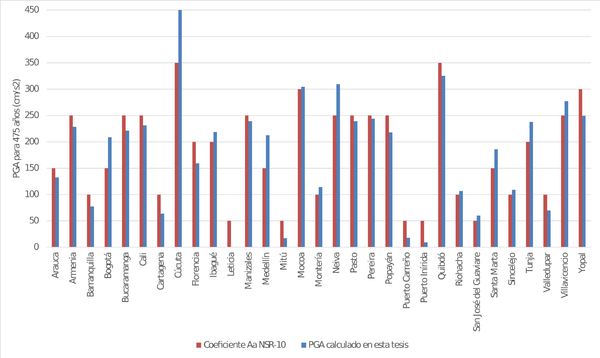
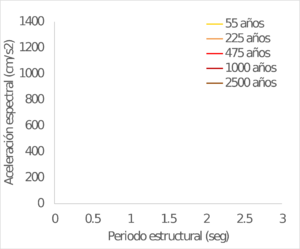
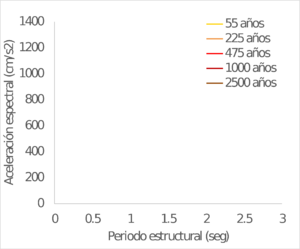
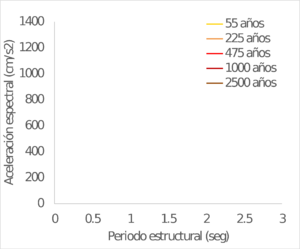
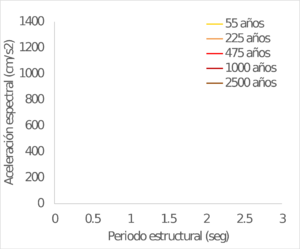
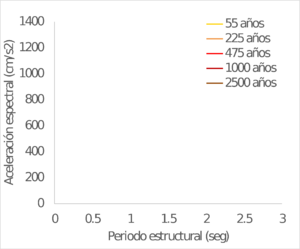
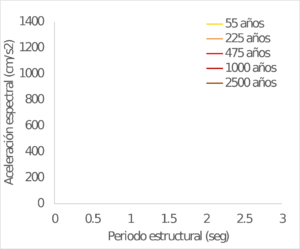
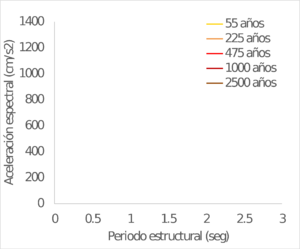
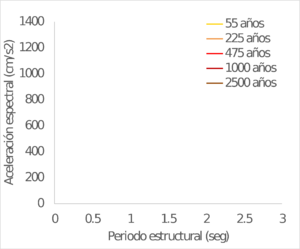
Los resultados se obtienen también para ubicaciones seleccionadas dentro del área urbana de las capitales de departamento en Colombia. La Figura 4.4 muestra el valor calculado de PGA para 475 años de periodo de retorno. Por su parte la Figura 4.5 presenta una comparación entre los valores de PGA calculados en este trabajo y los exigidos en la Norma Colombiana de Construcciones Sismo Resistentes – NSR 10 (AIS, 2010) para el diseño estructural de edificaciones nuevas (coeficiente Aa). Finalmente, la Figura 4.6 y la Figura 4.7 muestran los espectros de amenaza uniforme para varias ciudades seleccionadas en Colombia.
| ARMENIA | BARRANQUILLA |
|
|
| BOGOTÁ | BUCARAMANGA |
|
|
| CALI | IBAGUÉ |
|
|
| MANIZALES | MEDELLÍN |
|
|
| PASTO | POPAYÁN |
|
|
| VILLAVICENCIO | YOPAL |
|
|
Los resultados presentados muestran, en términos de probabilidad, las intensidades sísmicas que puede esperarse que ocurran en cualquier ubicación dentro del territorio colombiano. Estos resultados son de gran utilidad para la definición de coeficientes sísmicos de diseño para edificaciones e infraestructura. Las normas de construcción deben basar sus requerimientos de diseño en estudios de amenaza que provean resultados como los aquí presentados. La selección del periodo de retorno de diseño está asociada con la aversión al riesgo que tiene la sociedad. En el caso colombiano, por ejemplo, las edificaciones se diseñan, por ley, para aceleraciones sísmicas con 475 años de periodo de retorno, lo cual corresponde a una probabilidad de excedencia del 10% en 50 años. Esto quiere decir que, en un lapso de tiempo de 50 años se espera que se superen, con 10% de probabilidad, las aceleraciones para las cuales la estructura funciona dentro de su rango elástico. Más allá del rango elástico, se espera que ocurran daños estructurales y no estructurales en la construcción, pero sin colapso. Es este el nivel de riesgo sísmico, desde una perspectiva de la ingeniería estructural, que la sociedad colombiana ha aceptado. Es evidente entonces la importancia de un enfoque probabilista de evaluación de la amenaza con fines de toma de decisiones.
La evaluación de la amenaza sísmica aquí presentada fue adoptada por la Asociación Colombiana de Ingeniería Sísmica para la definición de coeficientes de diseño dentro de la versión más reciente del Código Colombiano de Puentes (AIS e INVIAS, 2014). En general puede observarse que los resultados se encuentran en el mismo orden de magnitud que los valores contenidos en la norma NSR-10 (ver Figura 4.5).
4.2.1 Representación por escenarios
Adicionalmente a los resultados anteriores, con fines de evaluación del riesgo, la amenaza sísmica debe representarse por medio de una colección de escenarios, tal y como se indica en el Anexo D de este documento. En este caso, se definieron un total de 22324 escenarios de amenaza, cada uno calculado para 11 medidas de intensidad, que corresponden a aceleraciones espectrales para periodos estructurales de 0.0, 0.05, 0.1, 0.15, 0.3, 0.5, 1.0, 1.5, 2.0, 2.5 y 3.0 segundos. Cada escenario, en cada medida de intensidad, contiene dos mallas de valores que corresponden a la mediana y a la desviación estándar del logaritmo natural de la aceleración. Estas mallas dan cuenta de la variación espacial de la aceleración tras la ocurrencia de un sismo.
Con el fin de incluir de manera directa el resultado de la evaluación de la amenaza en el cálculo del riesgo, manteniendo de manera rigurosa la representación por escenarios, dicho resultado debe almacenarse en el formato AME (Torres et.al. 2013), el cual es un formato raster multicapa diseñado específicamente para amenazas naturales. Los cálculos fueron realizados en el programa CRISIS 2007 (Ordaz et.al. 2007). En este caso, se emplea el formato .AME Paramétrico. Este tipo de no almacena valores de intensidad, sino que almacena parámetros para poder reconstruir los valores de intensidad asociados a un escenario, cuando el usuario lo necesite. Esto produce archivos de tamaño muy reducido, aunque la evaluación de intensidad en tiempo real es relativamente lenta. Algunos de los parámetros necesarios para reconstruir la intensidad son: la magnitud del sismo, su posición focal, las ecuaciones de atenuación que deben usarse y el tamaño de la ruptura.
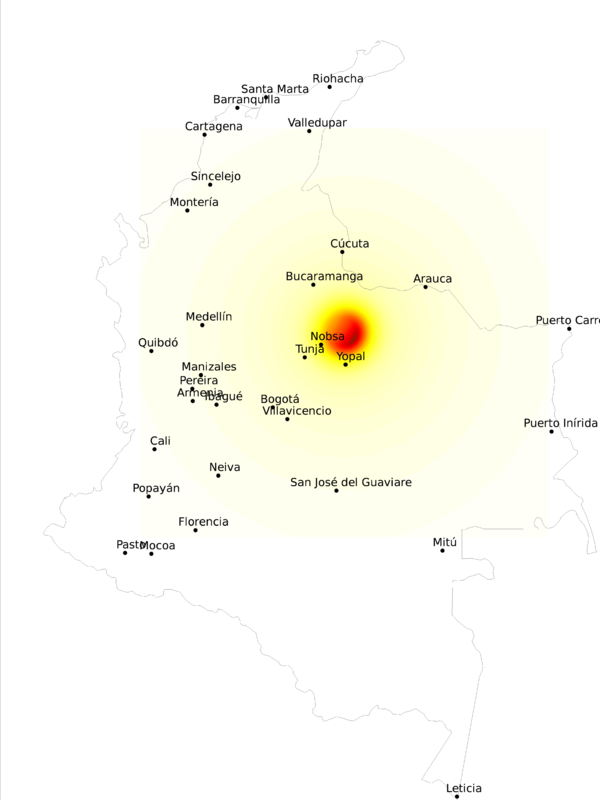
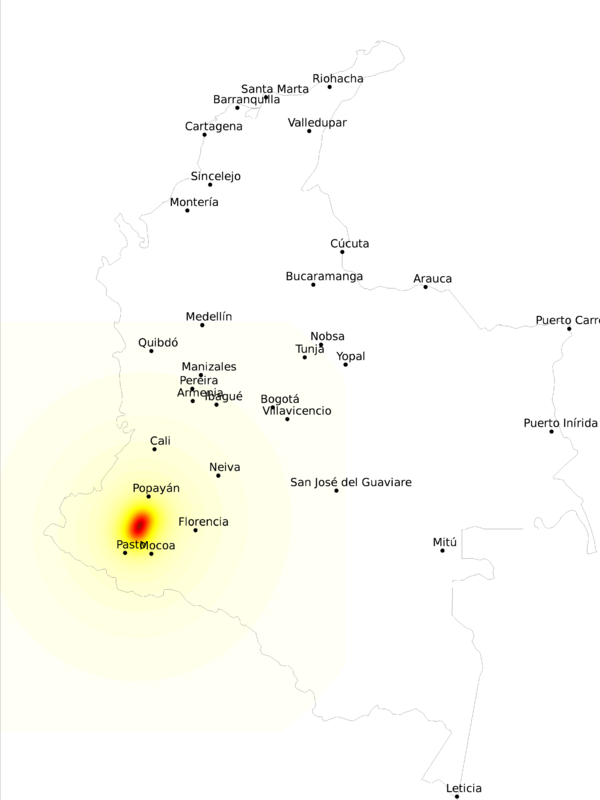
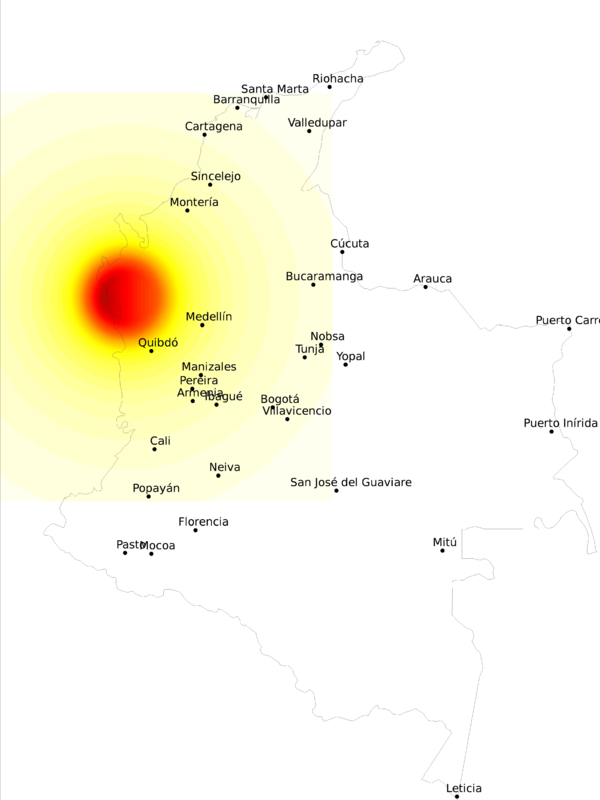
En la Figura 4.8 se presentan los epicentros de los terremotos incluidos en el conjunto de escenarios. La ubicación está, por supuesto, condicionada a la geometría de las fuentes sismogénicas. A modo de ejemplo, de la Figura 4.9 a la Figura 4.11 se presenta la distribución espacial de la mediana de PGA para tres escenarios seleccionados al azar dentro del conjunto.
Esta representación de la amenaza por escenarios, permite proceder al cálculo del riesgo de manera directa, conociendo de antemano los elementos expuestos y su vulnerabilidad. Es posible también obtener los resultados de amenaza sísmica integrada, es decir las curvas de amenaza en cada ubicación del territorio, directamente del conjunto de escenarios sísmicos. Es, por lo tanto, una representación más integral de la amenaza del territorio colombiano, dado que provee más información acerca del potencial de ocurrencia de terremotos.
REFERENCIAS
Abrahamson, N. y Silva, W. 2008. Summary of the Abrahamson & Silva NGA Ground-Motion Relations. Earthquake Spectra, Vol 24, N° 1, pp 67-98. Febrero 2008.
Abramowitz, M., and Stegun, I. A. 1964. Handbook of mathematical functions. National Bureau of Standards. Applied Mathematics Series.
Asociación Colombiana de Ingeniería Sísmica (AIS). 2010. Estudio General de Amenaza Sísmica de Colombia. Comité AIS-300
Asociación Colombiana de Ingeniería Sísmica (AIS). 2014. Código Colombiano de Puentes. Comité AIS-200
Aki, K. 1967. Scaling Law of Seismic Spectrum. Journal of Geophysical Research, 72, pp. 1217-1231.
Atkinson, G. M. 1995. Attenuation and Source Parameters of Earthquakes in the Cascadia Region. Bull. Seism. Soc. Am, Vol. 85, No. 5, pp. 1327-1342
Bazurro, P., y Cornell, .A. C. 2004. Nonlinear Soil-Site Effects in Probabilistic Seismic-Hazard Analysis. Bulletin of the Seismological Society of America, 94-6, pp. 2110-2123.
Boore, D. M. y Atkinson, G. M. 2008. Ground-Motion Prediction Equations for the Average Horizontal Component of PGA, PGV, and 5%-Damped PSA at Spectral Periods between 0.01 s and 10.0 s. Earthquake Spectra, Vol 24, N° 1, pp 99-138. Febrero 2008.
Brune, J.N. 1970. Tectonic Stress and the Spectra of Seismic S Waves from Earth. Journal of Geophysical Research, 75, pp. 4997-5009.
Campbell, K.W. 1997. Empirical near-source attenuation relationships for horizontal and vertical components of peak ground acceleration, peak ground velocity, and pseudo-absolute acceleration response spectra. Seismological Research Letters. 68(1), 154 -179.
Campbell, K. W. y Bozorgnia, Y. 2008. NGA Ground Motion Model for the Geometric Mean Horizontal Component of PGA,PGV,PGD and 5% Damped Linear Elastic Response Spectra for Periods Ranging from 0.01 to 10 s. Earthquake Spectra, Vol 24, N° 1, pp 139-172. Febrero 2008.
Cartwright, D. E. y Longuett-Higgins, M. S. 1956. The Statistical Distribution of the Maxima of a Random Function. Proc. Roy. Soc. London, 237, pp. 212-232.
Castro, R. R., Anderson, J. G. and Singh, S. K. 1990. Site response, attenuation and source spectra of S waves along the Guerrero, Mexico, subduction zone. Bull. Seism. Soc. Am, Vol. 80, No. 6, pp. 1481-1503
Chiou, B. S.-J. & Youngs, R. R. 2008. An NGA Model for the Average Horizontal Component of Peak Ground Motion and Response Spectra. Earthquake Spectra, Vol 24, N° 1, pp 173-216. Febrero 2008.
Cornell, C.A. 1968. Engineering Seismic Risk Analysis. Bulletin of the Seismological Society of America, 58, pp. 1583-1606
Cornell, C.A. y Winterstein, S. R. 1986. Applicability of the Poisson Earthquake-Occurrence Model. Seismic Hazard Methodology for the Central and Eastern United States, EPRI Research Report NP-4726, Electric Power Research Institute, Palo Alto, California
Davenport, A.G. 1964. Note on the Distribution of the Largest Value of a Random Function with Application to Gust Loading. Proc. Inst. C. E., 28, pp. 187-196.
Der-Kiureghian, A. y Ang, A. H. S. 1977. A Fault-Rupture Model for Seismic Risk Analysis. Bulletin of the Seismological Society of America, 67, pp. 1173-1194
Esteva, L. 1970. Seismic Risk and Seismic Design Decisions. En: Hansen, R. J. (ed.). Seismic Design of Nuclear Power Plant. MIT Press, Cambridge, Massachusetts
Gallego, M. 1999. Estimación del Riesgo Sísmico en la República de Colombia. Tesis de Maestría. División de Estudios de Posgrado, UNAM.
Gallego, M., and Ordaz, M. 1999. Construcción de leyes de atenuación para Colombia a partir de espectros fuente y teoría de vibraciones aleatorias. Revista internacional de ingeniería de estructuras. Vol. 4, 1, pp 45-60.
Gautschi, W. & Cahill, W. F. 1965. Exponential integral and related functions. Handbook of mathematical functions. Abramowitz, M. & Stegun, I. (Ed). Dover publications, NewYork.
Gutenberg, B. y Richter, C. F. 1944. Frequency of Earthquakes in California. Bulletin of the Seismological Society of America, 34, pp. 1985-1988
Hanks, T. C. & Kanamori, H. 1979. A moment magnitude scale. J. Geophys. Res. 84, pp. 2348–2350.
Hanks, T. C. 1982. fmax. Bull. Seism. Soc. Am, VoL 72, No. 6, pp. 1867-187
Hassani, B., Zafarani, H., Farjoodi, J. and Ansari, A. 2011. Estimation of site amplification, attenuation and source spectra of S-waves in the East-Central Iran. Soil Dynamics and Earthquake Engineering 31 (2011) 1397–1413
Hermann, R B. 1985. An extension of random vibration theory estimates of strong ground motion to large distances, Bull. Seism. Soc. Am, 73, pp. 157-171.
Joyner, W.B., y Boore, D.M. 1988. Measurement, characterization and prediction of strong ground motion. Earthquake Engineering and Soil Dynamics II, Proc. Am. Soc. Civil Eng. Geotech. Eng. Div. Specialty Conf. Junio 27-30, 1998, Park City, Utah.
Kramer, S. 1996. Geotechnical Earthquake Engineering. Prentice Hall.
Knopoff, L. 1964. Q. Review of Geophysics, 2, pp. 625-660.
Ordaz, M., and Singh, S. K. 1992. Source spectra and spectral attenuation of seismic waves from Mexican earthquakes, and evidence of amplification in the hill zone of Mexico City. Bull. Seism. Soc. Am, Vol. 82, No. 1, pp. 24-43
Ordaz, M., Aguilar, A. y Arboleda, J. 2007. CRISIS2007: Program for Computing Seismic Hazard. Instituto de Ingeniería. Universidad Nacional Autónoma de México.
Salgado M. 2010. Evaluación probabilista y espectral de la amenaza sísmica de Colombia: Estudio general con fines de diseño sismo resistente. Universidad de Los Andes. Bogotá, Colombia.
Salgado M., Bernal G., Yamín L., Cardona O. 2010. Evaluación de la amenaza sísmica de Colombia. Actualización y uso en las nuevas normas colombianas de diseño sismo resistente NSR-10. Rev. de Ing. 32: 28-37. Universidad de Los Andes, Bogotá, Colombia.
Singh, S. K., Apsel, R., Fried, J., y Brune, J. N. 1982. Spectral Attenuation of SH Waves along the Imperial Fault. Bulletin of the Seismological Society of America, 72, pp. 2003-2016.
Singh, S. K., Ordaz, M., Anderson, J.G., Rodriguez, M., Quaas, R., Mena, E., Ottaviani, M., and Almora, D. 1989. Analysis of near source strong ground motion recordings along the Mexican subduction zone. Bull. Seism. Soc. Am. 70, pp. 903-914.
Singh, S. K., Iglesias, A., García, D., Pacheco, J. F. and Ordaz, M. 2007. Q of Lg Waves in the Central Mexican Volcanic Belt. Bull. Seism. Soc. Am, Vol. 97, No. 4, pp. 1259–1266
Reiter, L. 1990. Earthquake Hazard Analysis - Issues and Insights. Columbia University Press, New York, 254 pp
Singh, S. K., Bazan, E., y Esteva, L. 1980. Expected Earthquake Magnitude from a Fault. Bulletin of the Seismological Society of America, Vol. 70, N° 3, pp. 903-914, Junio 1980.
Singh, S. K., Ordaz, M., Anderson, J.G., Rodriguez, M., Quaas, R., Mena, E., Ottaviani, M., y Almora, D. 1989. Analysis of Near Source Strong Ground Motion Recordings along the Mexican Subduction Zone. Bulletin of the Seismological Society of America, 70, pp. 903-914.
Tavakoli, B., and Pezeshk, S. 2005. Empirical-Stochastic Ground-Motion Prediction for Eastern North America. Bull. Seism. Soc. Am, Vol. 95, No. 6, pp. 2283–2296
Torres, M. A., Jaimes, M. A., Reinoso, E., Ordaz, M. 2013. Event-based approach for probabilistic flood risk assessment. International Journal of River Basin Management. DOI: 10.1080/15715124.2013.847844
Wells, D. L. y Coppersmith, K. J. 1994. New Empirical Relationships among Magnitude, Rupture Length, Rupture Width, Rupture Area, and Surface Displacement. Bulletin of the Seismological Society of America, Vol. 84, N° 4, pp. 974-1002, Agosto 1994.
Wu, S.-C., Cornell, C.A., Winterstein, S.R. 1995 A hybrid recurrence model and its implication on seismic hazad results. Bulletin of the Seismological Society of America, 85-1, pp. 1-16.
Youngs, R. R. y Coppersmith, K. J. 1985. Implications of Fault Slip Rates and Earthquake Recurrence Models to Probabilistic Seismic Hazard Assessments. Bulletin of the Seismological Society of America, 75, pp. 939-964
Zafarani, H. and Soghrat, M. 2012. Simulation of Ground Motion in the Zagros Region of Iran Using the Specific Barrier Model and the Stochastic Method. Bull. Seism. Soc. Am, Vol. 102, No. 5, pp. 2031–2045
Anexo A. Tablas de atenuación
Los valores de intensidad dados en las tablas son aceleraciones espectrales elásticas correspondientes al periodo estructural indicado. Los valores están expresados en cm/s2.
Sismos corticales
Sismos de subducción
Anexo B. Mapas de amenaza sísmica de Colombia
En este anexo se presentan los mapas de amenaza sísmica calculados para Colombia. Se incluyen mapas de amenaza uniforme, en términos del PGA, para periodos de retorno de 100, 250, 500, 1000 y 2500 años. También se presentan mapas en términos de la aceleración espectral, para 500 años de periodo de retorno, periodos estructurales de 0.15, 0.3, 0.5, 1.0, y 2.0 segundos, y un coeficiente de amortiguamiento respecto al crítico de 5%.
Anexo C. Programa Strong Motion Analyst
Strong Motion Analyst (SMA) es un programa de computador cuyo objetivo es el procesamiento de información sismológica, haciendo uso de metodologías del estado del arte. Dentro del contexto de esta monografía, SMA fue aplicado con tres objetivos principales:
- Construir una base de datos de movimiento fuerte, en la cual se almacenan como registros individuales las señales obtenidas en estaciones acelerográficas, en sus tres componentes ortogonales, así como las propiedades generales de la estación y del sismo que fue registrado.
- El procesamiento de las señales contenidas en la base de datos, con el fin de corregir el contenido de frecuencia y otras características importantes de las mismas.
- La implementación del método de calibración del modelo de espectro de fuente presentado en esta monografía.
Adicionalmente a lo mencionado, SMA permite realizar otros procesamientos de interés dentro de la ingeniería sísmica y la sismología. SMA es un programa modular, en donde cada módulo funciona de manera independiente, pero guardando total compatibilidad con los demás módulos del programa. Los módulos actualmente disponibles en la versión 1.0 de SMA son:
- Procesamiento de señales. Este módulo incluye una serie de herramientas para el procesamiento de señales contra el tiempo. La medida de amplitud de la señal puede ser cualquier tipo de medida física, aunque muchos de los procesos tienen sentido cuando se trata de señales de aceleración (acelerogramas).
- Base de datos de movimiento fuerte. SMA incluye una base de datos de acelerogramas, tomados de dos fuentes principales: la Red Nacional de Acelerógrafos de Colombia y el proyecto NGA del PEER. Este módulo da acceso a los datos contenidos en una base de datos Access, permite hacer consultas sobre dicha base de datos y da la opción de agregar al módulo de procesamiento de señales los acelerogramas que el usuario desee. En esta base de datos se almacena también la información asociada a la estación acelerográfica de registro y al sismo que generó el movimiento fuerte.
- Análisis de respuesta de sitio. En este módulo el usuario puede modelar la repuesta dinámica unidimensional de estratigrafías de suelo blando, mediante un modelo no lineal (lineal equivalente) y la matriz propagadora de Thompson-Haskel. SMA permite almacenar toda la información asociada a la ubicación geográfica del sitio, su estratigrafía, propiedades mecánicas estáticas y dinámicas de los estratos de suelo y permite obtener resultados para señales seleccionadas del módulo de procesamiento.
- Atenuación del movimiento fuerte. El cálculo de funciones de atenuación a partir del modelo de espectro de fuente está implementado en este módulo. SMA permite al usuario definir todas las variables involucradas en la generación de las funciones de atenuación, de manera que pueden obtenerse funciones personalizadas y específicas para una región en la cual se conozcan los parámetros sismológicos que conforman el modelo. Los modelos de atenuación generados pueden ser exportados en formato compatible con el programa CRISIS (versiones 2003 en adelante) (Ordaz et. al.). Adicionalmente el módulo permite realizar análisis de residuales con respecto a acelerogramas cargados al módulo de procesamiento desde la base de datos de movimiento fuerte. Finalmente, en este módulo se encuentra implementado el procedimiento para la calibración de funciones de atenuación del movimiento fuerte.
- Catálogos sismológicos. Este módulo permite al usuario realizar procesamientos básicos sobre catálogos sismológicos. Adicionalmente a la presentación del catálogo en un mapa, el programa permite remover réplicas, hacer análisis de completitud y calcular mallas de parámetros de sismicidad suavizada para análisis simplificados de amenaza sísmica. Estas mallas son compatibles con el programa CRISIS (versiones 2012 y 2014) (Ordaz et. al.)
Adicionalmente a los módulos listados, se encuentran actualmente en desarrollo otros módulos complementarios que serán liberados en la medida en que sean terminados y probados. Los módulos en desarrollo son:
- Análisis modal NExT/ERA. Las técnicas de identificación modal de estructuras son ampliamente usadas en el mundo para determinar variaciones en el comportamiento dinámico de estructuras indispensables y obtener modelos de daño y patología estructural. Estas técnicas permiten determinar, con un alto grado de confiabilidad, los modos principales de vibración de una estructura a partir de señales de vibración libre registradas en diversas ubicaciones de la misma. Dentro de las técnicas de identificación modal disponibles en la literatura, NExT/ERA ha probado ser una de las más robustas y de implementación directa en sistemas computacionales. NExT/ERA son las siglas para Natural Excitation Technique / Eigenvalue Regression Analysis. SMA implementará esta metodología para la identificación modal de estructuras a partir de registros de vibración libre.
- Análisis de vibraciones. Las vibraciones estructurales asociadas a fuentes no sísmicas, como por ejemplo el hincado de pilotes cerca de una construcción, la cercanía a vías de tráfico pesado o la sismicidad inducida por actividades de minería, pueden afectar de manera significativa la seguridad de una estructura y la de sus ocupantes. En la actualidad existen una serie de normativas que determinan los niveles mínimos de vibración aceptables dentro de la estructura y en sus alrededores. SMA implementará metodologías para determinar, a partir de vibraciones registradas en una estructura, si la amplitud y contenido frecuencial de dichas vibraciones puede afectar o no la estructura o a sus ocupantes, en función de lo establecido en la normativa internacional.
- Selección de señales. Es práctica común dentro de la ingeniería sísmica, y en particular en la evaluación de la amenaza sísmica o para la microzonificación sísmica de ciudades, la selección de acelerogramas compatibles con la amenaza. SMA implementará una metodología para la selección automática de estas señales a partir de un análisis de desagregación de la amenaza sísmica, el cual indica los rangos de distancia y magnitud que contribuyen de manera más significativa a la amenaza en una ubicación particular.
- Interacción dinámica suelo-estructura. Es ampliamente reconocida la importancia de la interacción dinámica suelo-estructura en la definición de movimientos sísmicos para una edificación particular. Cuando la cimentación es profunda, o la estructura tiene niveles enterrados, la respuesta dinámica del suelo y la respuesta estructural no pueden tratarse separadamente. SMA implementará las metodologías originalmente implementadas en el software FLUSH (Lysmer et.al., 1991), el cual es de código fuente abierto. Estas metodologías, originalmente desarrolladas en lenguaje FORTRAN, serán traducidas a Visual Basic .NET con el fin de hacer uso de las herramientas ya programadas dentro de SMA.
SMA ha sido desarrollado en su totalidad en inglés, con el fin de permitir su uso y aplicación por parte de investigadores de todas partes del mundo. SMA está disponible para descarga por internet en el siguiente enlace:
http://www.engsoftwaresolutions.com/downloads/SMA.zip
Requerimientos e instalación
SMA es un programa desarrollado en Visual Basic .NET para sistema operativo Windows 7 o superior. La compatibilidad del programa con versiones anteriores de Windows es limitada o nula.
Los requerimientos de hardware mínimos para la instalación de SMA en los computadores personales (PC) son los siguientes:
- Procesador Dual Core (o superior) y velocidad del procesador superior a 2.0 GHz.
- Una capacidad libre en disco duro de 5.0 Gb.
- 2048 Mb de memoria RAM.
- Tarjeta de video 16Mb.
En términos de software, SMA requiere de la instalación previa de los siguientes programas:
- Microsoft .NET Framework 4.0.
- Microsoft Office 2007 o superior. SMA hace uso en particular de los programas Access y Excel.
SMA se distribuye como freeware, mediante un paquete instalador secuencial el cual se encarga de manera automática de copiar los archivos del programa a la ubicación determinada en el computador y de dar los accesos al usuario. Para ejecutar el instalador, debe hacerse doble clic sobre el paquete de instalación SetupSMA.msi y seguir de manera cuidadosa todos los pasos.
Interfaz de usuario
SMA es un programa diseñado con una interfaz amigable y de fácil uso. El programa se inicia por defecto en el módulo de procesamiento de señales. La interfaz de SMA está dividida en tres regiones principales: la cinta de herramientas, el panel de navegación y el panel de procesamiento.
La cinta de herramientas contiene todas las herramientas y opciones de procesamiento del módulo que se encuentre activo. Las herramientas se encuentran organizadas en grupos de acuerdo con el tipo de procesamiento para el cual sirven. El panel de navegación contiene el acceso a los módulos del programa, así como herramientas de navegación dentro de los archivos o conjuntos de datos que se presentan y trabajan en cada módulo. Finalmente, el panel de procesamiento presenta al usuario de manera visual el objeto que se está procesando y el resultado del procesamiento aplicado. A continuación se detalla el uso de los módulos actualmente disponibles en la versión 1.0 de SMA.
Procesamiento de señales
El módulo de procesamiento de señales de SMA permite procesar señales de intensidad contra el tiempo, dentro de una ambiente de procesamiento amigable y de fácil uso.
Para inicial el uso del módulo, deben agregarse señales a la lista de archivos. SMA permite adicionar señales de diversas fuentes:
- Acelerogramas en archivo de texto de múltiples columnas.
- Señales registradas en acelerómetros CMAC (desarrollados por la Universidad de los Andes).
- Archivos de texto multi-canal de LabView.
- Generación de señales sintéticas de ruido gaussiano o acelerogramas sintéticos.
Al adicionar un archivo, el programa lo adiciona al listado de archivos. En este ejemplo, se agregará un archivo de texto multi-canal de LabView. El archivo se presenta como un nodo del listado, que al expandirse da acceso a todos los canales.
Al hacer doble clic sobre el nombre de los canales, estos se adicionan al panel de procesamiento.
Las señales se presentan en ventanas individuales, en las cuales se indica el nombre del canal y del archivo correspondiente, los pares tiempo-amplitud en función de la ubicación del sensor sobre el gráfico, y los valores máximo y mínimo de la amplitud señal graficada.
Estas ventanas de señal pueden colapsarse haciendo doble clic sobre la barra de encabezado para facilitar la visualización de múltiples canales.
Las herramientas de procesamiento disponibles se describen a continuación:
- Apply to all. Al seleccionar esta opción, el procesamiento se efectuará sobre todas las señales cargadas al panel. De no estar seleccionado, se procesará solamente la seleccionada (la ventana con el encabezado resaltado en verde).
- Undo all. Permite deshacer todo el procesamiento y volver a la señal originalmente cargada al programa.
- Baseline. Corrige la línea base de la señal.
- Scale. Permite escalar la señal en amplitud.
- Decimate. Permite diezmar la señal, es decir, eliminar datos para reducir la frecuencia de muestreo.
- Bezier. Permite aumentar de manera sintética el número de datos de la señal, al aplicar una interpolación de Bezier de orden 4.
- Cut. permite recortar una porción de la señal entre dos instantes de tiempo definidos.
- Add zeros. Añade valores de amplitud cero al comienzo o final de la señal. Esto es útil para alinear la fase intensa de señales.
- Filter. Permite filtrar el contenido de frecuencia de la señal. Es posible aplicar filtros pasa-bajas, pasa-altas, pasa-banda, o band-stop.
- SDF response. Calcula la respuesta de un oscilador de un grado de libertad ante la señal indicada. Aunque esta función opera en todos los casos, solamente tiene sentido cuando la intensidad de la señal es aceleración.
- Derivative. Obtiene la derivada de la señal respecto al tiempo.
- Integrate. Obtiene la integral de la señal respecto al tiempo.
- Energy. Calcula la energía asociada al movimiento mediante el uso del teorema de Parseval. Solo tiene sentido para señales de aceleración.
- Strong motion parameters. Esta función permite determinar una serie de parámetros de movimiento fuerte ampliamente usados en ingeniería sísmica. Los parámetros calculados son (solo tiene sentido para señales de aceleración):
- Aceleración pico del terreno (PGA)
- Velocidad pico del terreno (PGV)
- Desplazamiento pico del terreno (PGD)
- Relación PGV/PGA
- Aceleración RMS (Root Mean Square)
- Velocidad RMS
- Desplazamiento RMS
- Intensidad de Arias (Ia)
- Intensidad característica (Ic)
- Aceleración efectiva de diseño (EDA)
- Densidad específica de energía (SED)
- Velocidad absoluta acumulativa (CAV)
- Intensidad del espectro de aceleración (ASI)
- Intensidad del espectro de velocidad (VSI)
- Intensidad de Housner (HI)
- Duración total
- Duración significativa
- Periodo predominante (Tp)
- Periodo promedio (Tm)
- Fecuencia promedio (fm)
Adicionalmente, SMA incluye una herramienta de procesamiento por lotes, mediante la cual es posible realizar procesamiento básico a un gran número de señales, sin necesidad de cargarlas al panel de procesamiento (botón Batch processing). Una vez adicionadas las señales a procesar, se establecen los parámetros de procesamiento, y su orden de aplicación a la derecha.
SMA también admite operaciones de análisis espectral sobre las señales. Las operaciones admitidas son:
- Espectro de respuesta.
- Espectro de Fourier.
- Densidad espectral de respuesta.
- Diagrama de Husid.
- Diagrama de flujo de energía.
El resultado de aplicar este tipo de análisis se presenta en la ventana de espectros a la derecha de la señal, dado que no corresponden a procesamientos que impliquen cambios en la señal misma. A continuación se muestran algunos ejemplos.
SMA admite también la comparación del resultado del análisis espectral de múltiples señales, mediante la herramienta Multi spectrum. En la ventana de multi spectrum se muestran los espectros de todas las señales cargadas al procesamiento.
Finalmente, SMA admite operaciones entre señales. Las operaciones admitidas son:
- Función de transferencia.
- Correlación cruzada.
- Suma.
- Resta.
- Odograma.
A modo de ejemplo, se presenta el resultado de operar con las dos señales presentadas a continuación. Debe indicarse al programa cual es la señal 1 y cual la señal 2.
SMA mantiene un registro de todo el procesamiento efectuado, el cual puede consultarse en la parte inferior del panel de procesamiento. De esta manera, el usuario sabe en todo momento cual ha sido el procesamiento efectuado a las señales disponibles.
Base de datos de movimiento fuerte
La base de datos de movimiento fuerte de SMA incluye registros de la Red Nacional de Acelerógrafos de Colombia (hasta el 2010) y todos los acelerogramas usados en el proyecto NGA (2005) del PEER.
En la pantalla del módulo, se presenta el listado de acelerogramas disponibles, junto con toda la información asociada a cada uno, así como una previsualización de las señales.
Las propiedades asociadas a cada registro de la base de datos son:
- Nombre del sismo.
- Fecha y hora de ocurrencia del sismo.
- País.
- Nombre de la estación acelerográfica.
- Fuente de los datos.
- Tipo de suelo (según clasificación NEHRP).
- Coordenadas geográficas WGS84 de la ubicación del epicentro.
- Coordenadas geográficas WGS 84 de la ubicación de la estación.
- Distancias epicentral, hipocentral, Rrup y Joyner-Boore.
- Profundidad del hipocentro.
- Tipo de mecanismo focal.
- Magnitudes Mw, ML, Ms y mb.
- Intensidades máximas PGA, PGV y PGD.
- Duración de la señal.
- Frecuencia de muestreo.
En el panel de previsualización pueden efectuarse las operaciones de análisis espectral mencionadas anteriormente en el módulo de procesamiento de señales, para las 3 componentes del registro (norte-sur, este-oeste y vertical).
Dado que la información está almacenada en una base de datos, pueden hacerse consultas para obtener solamente registros de interés. SMA trae herramientas de consultas (filtro) predeterminadas por nombre del evento, estación, fecha de ocurrencia, ubicación epicentral, mecanismo focal, magnitud y distancia. Adicionalmente, el usuario puede definir consultas personalizadas en lenguaje SQL para obtener los registros que sean de su interés.
Finalmente, todos los registros de la base de datos pueden agregarse como señales al módulo de procesamiento.
Respuesta dinámica de suelos
El módulo de respuesta dinámica de suelos permite calcular la respuesta sísmica de estratigrafías de suelo blando haciendo uso de la matriz propagadora de Thompson-Haskel y del método lineal equivalente de análisis no-lineal.
Debe añadirse un nuevo perfil para poder comenzar. El módulo admite tantos perfiles como el usuario desee. A modo de ejemplo, se presentan en este documento algunos perfiles de la ciudad de Manizales, previamente configurados en SMA.
En la pantalla del módulo, se presentan todos los perfiles disponibles. Al seleccionar alguno de los perfiles, se muestra la información del mismo.
En el panel de procesamiento, la información asociada al sitio de cálculo se presenta en tres pestañas: información general, configuración de análisis y resultados.
En la pestaña de información general, se presentan los datos del sitio de sondeo, junto con un mapa de localización respecto a un mapa de referencia definido por el usuario. El mapa de referencia puede ser cualquier archivo en formato ESRI Shapefile.
En la pestaña de configuración de análisis, se introduce al programa la información solicitada en lo que se refiere a las propiedades estáticas y dinámicas de los suelos que conforman los diferentes estratos. También se establecen las propiedades básicas de las señales sísmicas a emplear.
Finalmente, una vez configurado el sitio, se procede al cálculo de la respuesta dinámica, y se obtienen los resultados del análisis. Estos resultados se presentan en varias categorías: resultados por capa, espectros de respuesta, funciones de transferencia y acelerogramas en superficie.
En particular, los acelerogramas resultantes en superficie pueden ser adicionados al módulo de procesamiento de SMA.
Atenuación del movimiento fuerte
Este módulo de SMA fue ampliamente usado en este trabajo, en particular en lo que corresponde a la calibración de un modelo de espectro de fuente. El módulo permite construir funciones de atenuación con base en el modelo de espectro de fuente usado en esta monografía, a partir de la definición de los parámetros sismológicos necesarios, así como de un rango de magnitudes, distancias y periodos estructurales de análisis.
El programa permite crear funciones de atenuación con un mismo modelo sismológico para todas las ordenadas del espectro de respuesta, o con modelos individuales para cada ordenada. A modo de ejemplo, se presenta en este documento la creación de una función de atenuación de único modelo sismológico. La información a llenar se presenta en el panel de navegación a la izquierda de la pantalla.
El programa incluye los parámetros sismológicos del modelo de atenuación calibrado en esta monografía para el territorio colombiano, así como los propuestos por Gallego y Ordaz (1999). Adicionalmente el usuario puede definir sus propios parámetros para obtener un modelo personalizado. Una vez ingresados los datos se procede a la generación de la función de atenuación. Pueden generarse tantas como el usuario desee.
Las funciones de atenuación se presentan en ventanas individuales, en las cuales puede navegarse por todas las ordenadas del espectro que se definieron, y puede consultarse la información en forma gráfica o de tabla.
Las funciones de atenuación pueden exportarse a formato de texto .atn, compatible con el programa CRISIS (versiones 2003 en adelante), desarrollado por el profesor Mario Ordaz y otros en el Instituto de Ingeniería de la UNAM (México), el cual es un sistema ampliamente usado en el mundo para evaluaciones probabilistas de amenaza sísmica.
Es posible generar funciones de atenuación considerando los efectos locales, mediante la adición de una función de transferencia del espectro de Fourier, definida para diferentes niveles de PGA en la base de un depósito de suelo blando. Este procedimiento puede también ejecutarse en SMA mediante el procesamiento por lotes de funciones de atenuación (botón Batch processing).
Se cargan entonces tantas funciones de transferencia como funciones de atenuación quieran generarse, las cuales pueden previsualizarse directamente en la ventana del procesamiento por lotes. Se configuran los parámetros de generación de las funciones de atenuación, y se selecciona el modelo sismológico a usar. En seguida, el programa inicia el cálculo y escribe directamente el archivo .atn compatible con CRISIS en un directorio especificado por el usuario. Las funciones generadas pueden también ser agregadas al panel de procesamiento.
SMA incluye también herramienta para el procesamiento de residuales y el cálculo de sesgos y desviaciones estándar de las funciones de atenuación calculadas. Para ejecutar estos procesos, deben agregarse al módulo de procesamiento las señales base de comparación desde la base de datos de movimiento fuerte de SMA. Es posible también calibrar un modelo de atenuación usando la metodología propuesta en esta monografía, dando clic en el botón Calibrate attenuation.
Catálogos sismológicos
Por último, la versión 1.0 de SMA incluye un módulo de procesamiento de catálogos sismológicos, en el cual pueden realizarse operaciones básicas comunes en análisis simológico.
Para adicionar un catálogo, debe ingresarse un archivo de Excel en donde se consigna toda la información requerida por SMA acerca del catálogo sismológico. Una vez cargado el catálogo, SMA despliega un mapa con la ubicación de los epicentros, así como todas las propiedades básicas del catálogo. Pueden también agregarse capas base de referencia en formato ESRI Shapefile.
Las herramientas disponibles en el módulo son la remoción de réplicas, análisis de completitud y sismicidad suavizada. Para remover réplicas, debe definirse una magnitud umbral y distancias de proximidad en grados para la búsqueda de los terremotos que precedieron el movimiento sísmico principal. Una vez removidas las réplicas, puede adicionarse el catálogo resultante como nuevo catálogo o remplazarse el original.
La herramienta de análisis de completitud permite determinar el año de completitud del catálogo, para una magnitud umbral. Deben definirse criterios de búsqueda sobre la curva de número de terremotos acumulados en el tiempo, de los cuales SMA trae valores por defecto. Una vez definidos estos parámetros, el programa despliega una gráfica de completitud indicando el año aproximado de completitud del catálogo para la magnitud seleccionada.
Finalmente, SMA permite calcular parámetros de sismicidad suavizada para análisis aproximados de amenaza sísmica. Los parámetros calculados son λ0, que corresponde a la tasa anual de recurrencia de terremotos para una magnitud umbral, β que es la pendiente de la curva de recurrencia de magnitudes en la zona de magnitudes bajas, y CV(β), que es el coeficiente de variación de β. Estos parámetros se almacenan en formato raster GRD binario de Surfer 6, y son compatibles con el programa CRISIS (versiones 2012 y 2014) para la evaluación de la amenaza sísmica.
Anexo D. Representación de la amenaza sísmica para la evaluación probabilista del riesgo
La amenaza sísmica se mide usando su frecuencia de ocurrencia y su severidad, esta última siendo caracterizada a través de parámetros de movimiento fuerte calculados en cada ubicación geográfica. La evaluación de riesgos se basa en la frecuencia histórica de ocurrencia de los terremotos y la intensidad de movimiento que producen. Una vez que los parámetros que caracterizan la ocurrencia del fenómeno se definen desde un punto de vista físico, es necesario generar un conjunto de escenarios estocásticos que, analíticamente hablando, permiten definir todas las formas posibles en que la amenaza sísmica puede manifestarse en la región de análisis, en función de su frecuencia y severidad.
La amenaza se caracteriza entonces, en cada punto de análisis en el territorio de estudio, a través de la distribución de la probabilidad de la medida de intensidad asociada a su severidad, definida en términos de su valor central y su medida de dispersión, la cual da cuenta de la incertidumbre asociada con la ocurrencia de dicho grado de intensidad en el territorio. Es importante señalar que, en lo que respecta a la evaluación del riesgo sísmico, la dispersión es altamente relevante para la correcta cuantificación de las pérdidas, dado que un mismo escenario puede causar una correlación de pérdida, es decir, afectación simultánea a varios elementos expuestos en un área extensa.
La razón por la cual debe representarse la amenaza como una colección de escenarios está relacionada directamente con la evaluación del riesgo. Es representación permite aplicar la metodología probabilista de análisis de riesgo de manera directa, y permite incluir de manera racional las incertidumbres asociadas a la amenaza.
Como se mencionó anteriormente, el objetivo del análisis probabilista del riesgo es la caracterización, también probabilista, de las pérdidas esperadas sobre un conjunto de elementos expuestos, dada la ocurrencia de terremotos. Dado que hay incertidumbre en la estimación de la pérdida, esta es entonces modelada como una variable aleatoria. En términos generales, interesa conocer lo siguiente acerca de la pérdida:
- El universo de todas las pérdidas posibles, es decir, el dominio de la variable aleatoria que describe la pérdida.
- La función de densidad de probabilidad de la pérdida, la cual está definida dentro del dominio de la variable.
En términos generales, un evento de pérdida A, definido dentro del universo de todas las pérdidas posibles (o espacio de muestreo) S, se puede representar en un diagrama de conjuntos como se muestra en la Figura D.1. El evento A es un subconjunto de S, el cual es definido de manera totalmente arbitraria, es decir, su definición depende exclusivamente de a que pregunta se quiere contestar. En este sentido, el evento A puede estar definido, por ejemplo, como el conjunto de pérdidas mayores a 10 millones, o como el conjunto de pérdidas menores a 100 millones, o incluso como el conjunto de pérdidas entre 10 y 100 millones. Esto significa que A es definido por el tomador de decisiones, en función del tipo de decisiones que quiera tomar. Ahora bien, la definición de A en sí misma no es de interés; interesa conocer la probabilidad de A, denotada como P(A). Entonces si, por ejemplo, A está definido como el conjunto de pérdidas mayores a 10 millones, lo que realmente interesa conocer es la probabilidad de que la pérdida sea mayor a 10 millones, es decir P(A).
Dado que los eventos A son definidos de manera arbitraria, resulta inconveniente realizar el análisis de riesgo para un conjunto A específico. Se requiere encontrar una manera mediante la cual sea posible determinar P(A) para cualquier evento A de interés. Esto se logra subdividiendo el espacio de muestreo S en un número finito de eventos base conocidos, B (Figura D.2).
Los eventos base B deben cumplir las siguientes características:
- Ser mutuamente excluyentes. En términos matemáticos esto significa que los conjuntos nunca se intersectan, es decir, su intersección es el conjunto vacío. En términos del análisis de riesgo esto quiere decir que los eventos de pérdida B no pueden ocurrir simultáneamente.
- Ser colectivamente exhaustivos. En términos matemáticos esto implica que la unión de todos los conjuntos B es igual al espacio de muestreo S. En términos del análisis de riesgo esto significa que los eventos B, en conjunto, representan de manera integral el universo de todas las pérdidas posibles.
Ahora bien, para poder determinar P(A), para un evento A cualquiera, hacemos uso de las intersecciones que se producen entre el evento A y los eventos base B (Figura D.3).
Dado que el evento A se puede definir como la unión de sus intersecciones con los eventos base B, y recurriendo al tercer axioma de la teoría de la probabilidad1, podemos definir a P(A) como la suma, para todos los eventos base B, de la probabilidad de ocurrencia de las intersecciones:
Para cualquier evento base Bj, definimos la probabilidad P(A|Bj) como la probabilidad condicional de A, dado que Bj ha ocurrido. Esta probabilidad condicional está dada por:
(D.2)
Nótese que se asume que Bj ha ocurrido. Esto significa que el espacio de muestreo S es ahora reemplazado por un nuevo espacio de muestro, Bj, y P(A|Bj) no es más que la probabilidad de A en ese nuevo espacio. De esta manera, reemplazando la ecuación D.2 en la ecuación D.1, llegamos a la solución de P(A), que no es más que la definición del teorema de la probabilidad total:
(D.3)
Esta ecuación indica la probabilidad de ocurrencia de cualquier evento de pérdida sobre el espacio S.
Haciendo uso de la ecuación D.3 podemos calcular la probabilidad de cualquier evento A. La Tabla D.1 muestra, a modo de ejemplo, tres eventos A arbitrarios y su medida de probabilidad calculada con la Ecuación 3.
| Eventos arbitrarios A | Probabilidad |
| Pérdidas mayores a 10 millones | |
| Pérdidas menores a 100 millones | |
| Pérdidas entre 10 y 100 millones | |
En resumen, dentro del contexto del análisis de riesgo, la definición de los eventos de interés A es totalmente arbitraria, por lo tanto su probabilidad P(A) se calcula como función de la distribución de probabilidad de la pérdida para cada evento base Bj. Esto implica que los eventos base B no pueden ser definidos de manera arbitraria.
En análisis de riesgo, la colección de eventos base B se construye a partir de la definición de escenarios de amenaza. Se define entonces una colección de escenarios de amenaza, usualmente generados de manera estocástica, los cuales representan de manera integral todas las formas como la amenaza puede manifestarse en el territorio de análisis. Estos escenarios deben cumplir las siguientes características:
- Ser mutuamente excluyentes.
- Ser colectivamente exhaustivos.
- Admitir una medida de probabilidad temporal, generalmente conocida como su frecuencia anual de ocurrencia.
- Admitir una medida de probabilidad espacial mediante la definición de su medida de intensidad como una variable aleatoria.
La medida de intensidad a la que se hace referencia corresponde a la variable física que representa la severidad del fenómeno en el territorio de análisis. Para el caso de los terremotos, las medidas de intensidad comúnmente usadas son las amplitudes máximas del movimiento fuerte en el terreno (PGA, PGV, PGD), así como las ordenadas del espectro de respuesta (Sa).
Dado que el número de escenarios que representan de manera integral la amenaza sísmica en un territorio cualquiera puede ser de decenas o centenas de miles, Torres et.al. (2013) proponen el uso de un formato computacional llamado .AME, el cual es un formato raster multicapa diseñado específicamente para amenazas naturales, y que permite un manejo adecuado, en términos computacionales, de la información asociada a los escenarios.
(1) El tercer axioma de la probabilidad establece que, para una colección contable de eventos mutuamente excluyentes, la probabilidad de su unión es igual a la suma de las probabilidades individuales.
Document information
Published on 01/01/2015
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?