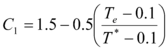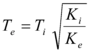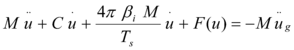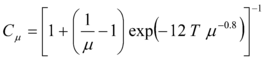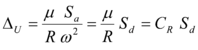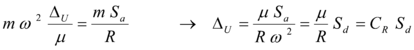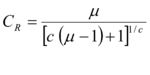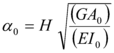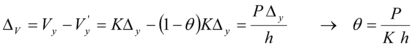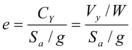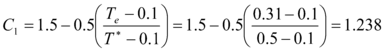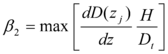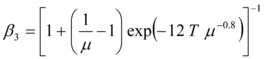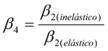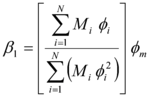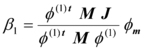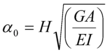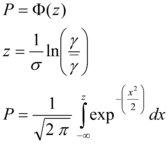PRESENTACIÓN
En la última década se han desarrollado importantes investigaciones en los Estados Unidos de Norte América, para evaluar en forma rápida la vulnerabilidad sísmica de las estructuras, a partir del cálculo de la deriva máxima de piso. Estas investigaciones han sido efectuadas en base a sismos registrados fundamentalmente en el área de California y teniendo en cuenta los materiales y sistemas constructivos que ahí utilizan.
Para todos es conocido, que la peligrosidad sísmica del Estado de California es diferente de la peligrosidad sísmica de América del Sur y algo similar se puede indicar con respecto a los materiales y sistemas constructivos. Por este motivo es que la Escuela Superior Politécnica del Ejército ESPE, Ecuador, apoyó la realización del proyecto de investigación científica, denominado: “Evaluación rápida de la deriva máxima de piso para evaluar la vulnerabilidad sísmica de estructuras de Hormigón Armado”.
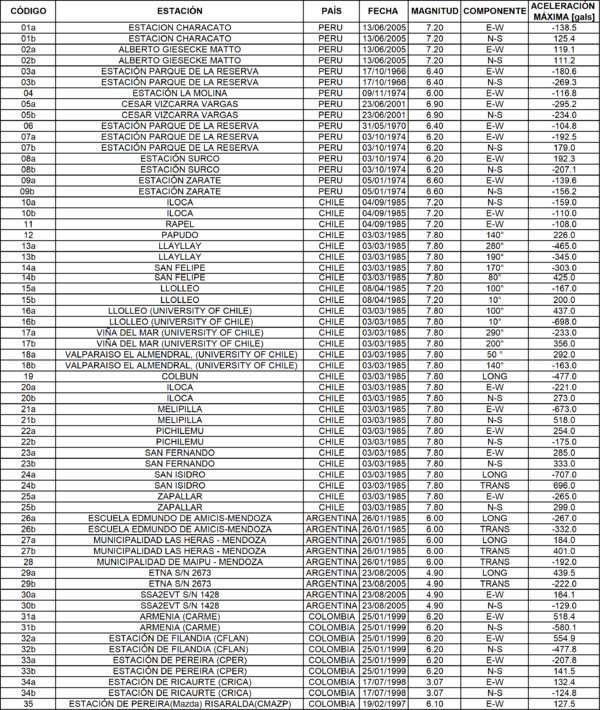
En esta investigación se obtienen relaciones entre el desplazamiento máximo inelástico con respecto al desplazamiento máximo elástico, de sistemas de un grado de libertad, pero a partir de sismos registrados en: Colombia, Ecuador, Perú, Argentina y Chile. En ninguno de los países indicados se cuenta con suficientes acelerogramas, de eventos sísmicos cuya aceleración máxima del suelo sea mayor al 10% de la aceleración de la gravedad, que permitan tener una muestra bastante confiable a partir del cual se pueda realizan un estudio estadístico pero al trabajar en conjunto se tuvo 63 registros, que es un número considerable.
De igual manera se encuentran relaciones entre la deriva máxima de piso con respecto a la deriva global del edificio pero trabajando con materiales y sistemas estructurales de Ecuador. Para el efecto se han considerado edificios de hormigón armado de uno a seis pisos de alto, conformados por vigas de poco peralte y columnas, sin muros de corte. Este tipo de construcción, que son bastante flexibles, también se las encuentra en países vecinos.
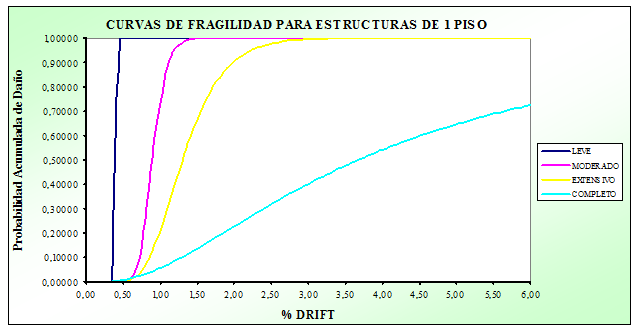
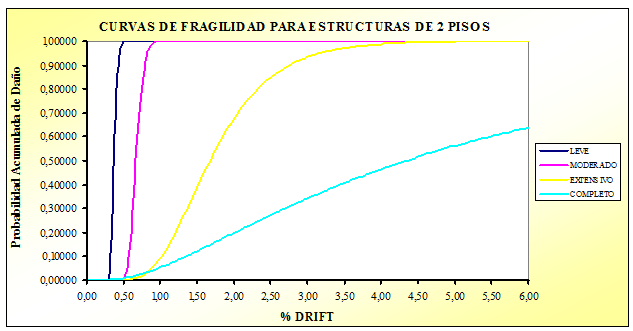
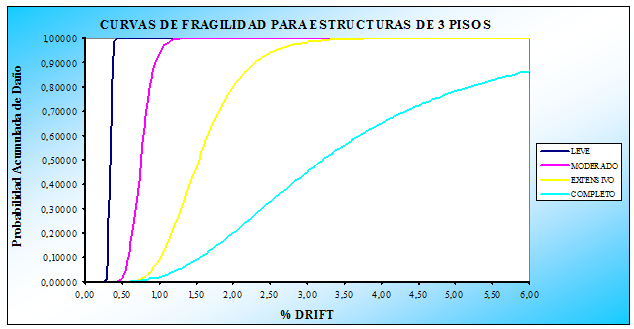
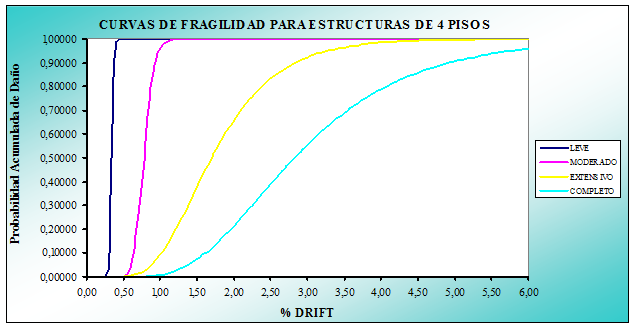
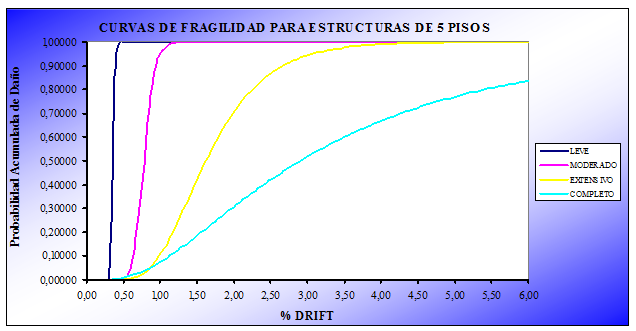
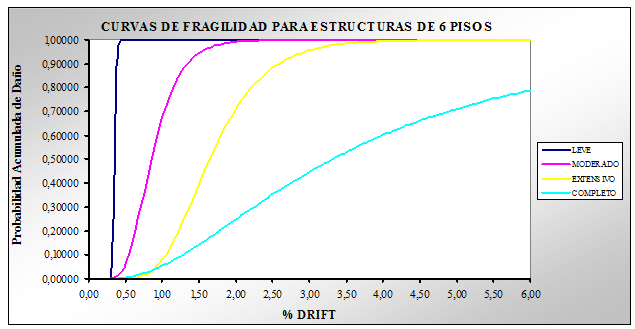
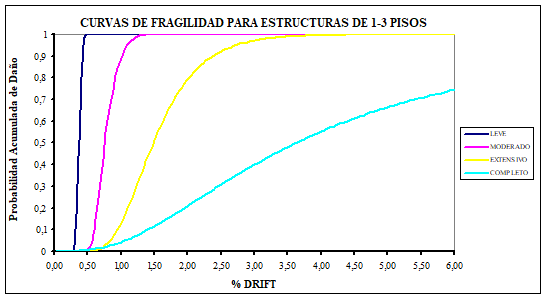
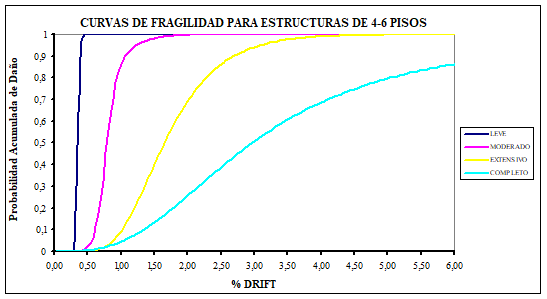
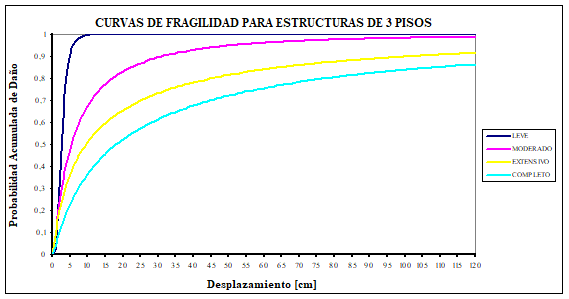
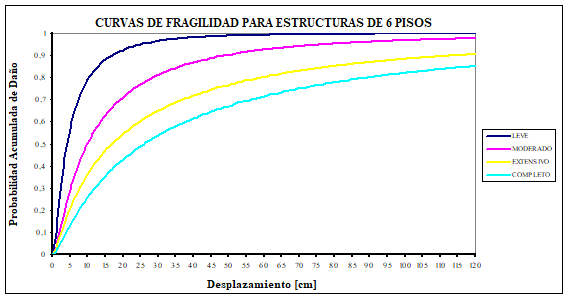
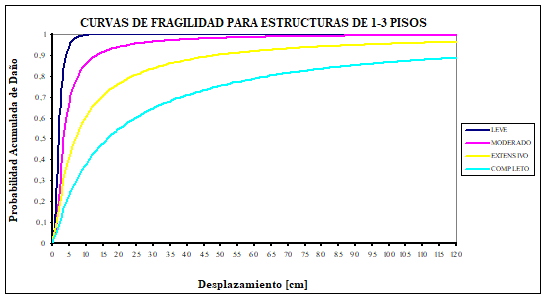
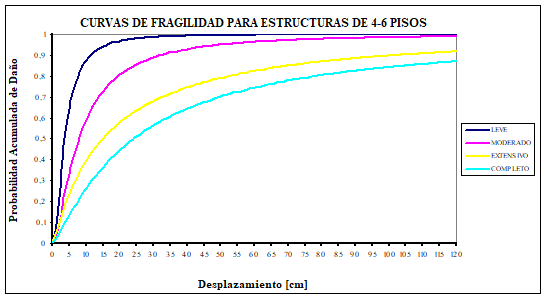
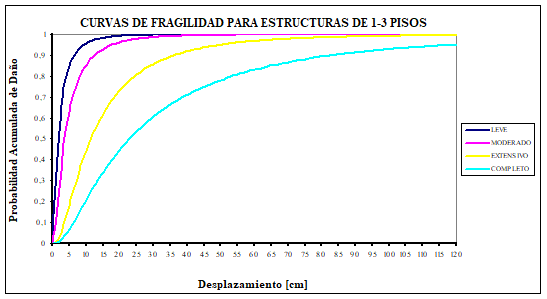
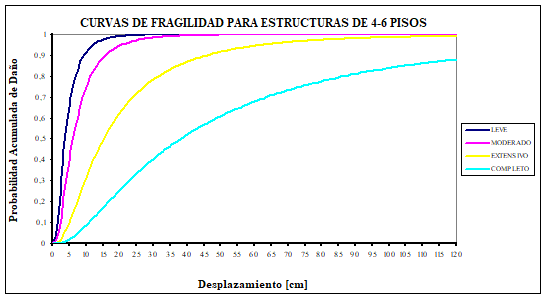
Uno de los objetivos de la investigación era mostrar mediante la elaboración de curvas de fragilidad que las construcciones bajas, de uno a seis pisos, que se están realizando en buena parte del Ecuador responden a un nivel de diseño sísmico bajo que no está acorde con la alta peligrosidad sísmica del País caracterizada por una aceleración máxima del suelo en roca del 40% de la aceleración de la gravedad.
Se presentan dos metodologías de cálculo para encontrar la deriva máxima de piso, en la que los parámetros que intervienen en su formulación han sido obtenidos en base a registros de Sur América y a sistemas constructivos de Ecuador. La bondad de estas metodologías se ha comprobado, comparando con los resultados que se obtienen del análisis no lineal, paso a paso de más de mil resultados, hallando una muy buena correlación en los resultados medios.
En la segunda metodología se halla la deriva máxima de piso, a partir del análisis lineal elástico multiplicando por un parámetro de corrección; esta metodología puede ser aplicable cuando se tengan pocos edificios a evaluar. En cambio la primera metodología que contempla cinco parámetros es aplicable a un gran número de edificios, si se tienen muy pocas estructuras la incertidumbre es alta.
Finalmente, deseo dejar constancia de mi agradecimiento a las autoridades de la Escuela Superior Politécnica del Ejército, por haber financiado el proyecto: “Evaluación rápida de la deriva máxima de piso para evaluar la vulnerabilidad sísmica de estructuras de Hormigón Armado”. Así como también a Paúl Guerrero, Carlos Bobadilla, Carolina Robalino, Gonzalo Huidobro, Diego Quisanga y Anuar González, que participaron en este proyecto.
CAPÍTULO 1. MÉTODO DEL COEFICIENTE DE DESPLAZAMIENTO
Se presenta el Método del Coeficiente de Desplazamiento y se analizan cada uno de los coeficientes que intervienen en su formulación, en base a las contribuciones científicas que han realizado varios investigadores. De esta manera, se pretende que el lector utilice el método con mayor conocimiento de causa y se vaya viendo el estado del arte del tema principal que interesa cual es la evaluación rápida de la deriva máxima de piso.
De igual manera se presentan recomendaciones, para el cálculo de algunos coeficientes que intervienen en el método, orientadas al análisis sísmico de estructuras conformadas por vigas y columnas de hormigón armado.
1.1 ANTECEDENTES
Dentro de las nuevas filosofías de diseño sísmico de estructuras se tiene, el Análisis y Diseño Sísmico por Desempeño, mediante la cual se pretende tener un control del comportamiento que va a tener una edificación ante varias acciones sísmicas a las que puede estar sujeta la construcción durante la vida útil de la misma. Comportamiento en términos estructurales y económicos.
Para verificar el desempeño de una estructura que ha sido ya diseñada, la Agencia Federal para el Manejo de Emergencias, FEMA 273 (1997) y FEMA 356 (2000), presentan dos métodos de análisis, el primero de ellos se denomina “Método del Coeficiente del Desplazamiento” y el segundo “Método del Espectro de Capacidad”. En este capítulo se aborda el primero de ellos cuyo objetivo fundamental es predecir en forma rápida y confiable cual es el desplazamiento lateral máximo que se espera en una estructura ante una determinada acción sísmica.
Varias investigaciones sirvieron de base para la propuesta de FEMA 273, en este capítulo se presentan dos, con cierto detalle, el realizado por Shimazaki y Sozen (1984) y el estudio de Miranda (1991). De igual manera una vez que se publicó el Método del Coeficiente de Desplazamientos numerosos investigadores han realizado estudios tendientes a dar mayor precisión y seguridad al método, entre estos trabajos se tienen los desarrollados por Whittaker et al (1998); Miranda (2000); Miranda y Reyes (2002); Lee et al (1999); Gupta y Krawinkler (2000). Los mismos que también son presentados en el presente capítulo y que sirvieron de base para la nueva publicación de FEMA-356 en que se aborda el tema.
1.2 DESCRIPCIÓN DEL MÉTODO
La Agencia Federal para el Manejo de Emergencias, de los Estados Unidos de Norte América, en su guía para la Rehabilitación Sísmica de Edificios, FEMA-356 (2000), propone la siguiente ecuación para encontrar el Desplazamiento máximo en el tope de un edificio ![]() .
.
|
|
(1.1) |
siendo ![]() la aceleración espectral elástica asociada al período fundamental efectivo
la aceleración espectral elástica asociada al período fundamental efectivo ![]() y los coeficientes
y los coeficientes ![]() y
y ![]() son factores de ajuste los mismos que se indican a continuación pero antes es importante indicar que la ecuación ( 1.1 ) es general para cualquier tipo de estructura pero en este capítulo se presentan los factores para estructuras de hormigón armado sin muros de corte solo con vigas y columnas.
son factores de ajuste los mismos que se indican a continuación pero antes es importante indicar que la ecuación ( 1.1 ) es general para cualquier tipo de estructura pero en este capítulo se presentan los factores para estructuras de hormigón armado sin muros de corte solo con vigas y columnas.
-
 es un factor de modificación que relaciona el desplazamiento espectral y el desplazamiento en el tope del edificio, con valores que van desde 1 para edificaciones de 1 piso hasta 1.5 para edificios de más de 10 pisos. Es un factor de paso del sistema de un grado de libertad, 1gdl., al sistema de múltiples grados de libertad que corresponde al edificio. En la tabla 1.1 se presentan los valores de este factor en función del número de pisos de la estructura analizada.
es un factor de modificación que relaciona el desplazamiento espectral y el desplazamiento en el tope del edificio, con valores que van desde 1 para edificaciones de 1 piso hasta 1.5 para edificios de más de 10 pisos. Es un factor de paso del sistema de un grado de libertad, 1gdl., al sistema de múltiples grados de libertad que corresponde al edificio. En la tabla 1.1 se presentan los valores de este factor en función del número de pisos de la estructura analizada.
-
El valor de ![]() no es más que el factor de participación modal en el tope del edificio y se evalúa analíticamente con la siguiente ecuación.
no es más que el factor de participación modal en el tope del edificio y se evalúa analíticamente con la siguiente ecuación.
|
|
(1.2) |
donde ![]() es la masa del nivel i;
es la masa del nivel i; ![]() es la ordenada de la forma modal fundamental en el nivel i;
es la ordenada de la forma modal fundamental en el nivel i; ![]() es el número de pisos;
es el número de pisos; ![]() es la amplitud del modo fundamental en la azotea o cubierta del edificio.
es la amplitud del modo fundamental en la azotea o cubierta del edificio.
donde ![]() es el período que define el punto de cambio del segmento de aceleración constante al segmento de velocidad constante;
es el período que define el punto de cambio del segmento de aceleración constante al segmento de velocidad constante; ![]() es el período fundamental efectivo. Para valores de
es el período fundamental efectivo. Para valores de ![]() comprendidos entre 0.1 y
comprendidos entre 0.1 y ![]() , se recomienda interpolar linealmente. En consecuencia
, se recomienda interpolar linealmente. En consecuencia ![]() se evaluará con la siguiente ecuación:
se evaluará con la siguiente ecuación:
|
|
(1.3) |
El período ![]() se evalúa con la siguiente ecuación:
se evalúa con la siguiente ecuación:
|
|
(1.4) |
donde ![]() es la rigidez inicial de la estructura que se la obtiene de la curva de capacidad sísmica resistente, que relaciona el cortante basal con el desplazamiento lateral máximo;
es la rigidez inicial de la estructura que se la obtiene de la curva de capacidad sísmica resistente, que relaciona el cortante basal con el desplazamiento lateral máximo; ![]() es una rigidez secante a la curva de capacidad que pasa por el punto cuya ordenada es igual a 0.6 del cortante de fluencia
es una rigidez secante a la curva de capacidad que pasa por el punto cuya ordenada es igual a 0.6 del cortante de fluencia ![]() ;
; ![]() es el período de vibración inicial de la estructura en el rango elástico.
es el período de vibración inicial de la estructura en el rango elástico.
FEMA-356 establece que ![]() para
para ![]() . Para el caso de que
. Para el caso de que ![]() se tiene:
se tiene:
|
|
(1.5) | |
| (1.6) |
donde ![]() es el valor de la masa modal efectiva, para estructuras de 1 y 2 pisos
es el valor de la masa modal efectiva, para estructuras de 1 y 2 pisos ![]() ; para estructuras de más de 3 pisos
; para estructuras de más de 3 pisos ![]() Por otra parte
Por otra parte ![]() es el peso total de la estructura y
es el peso total de la estructura y ![]() es el cortante a nivel de fluencia de la estructura. De tal manera que si se desea utilizar la ecuación (1.5) para calcular
es el cortante a nivel de fluencia de la estructura. De tal manera que si se desea utilizar la ecuación (1.5) para calcular ![]() se necesita conocer el valor de
se necesita conocer el valor de ![]() por este motivo es preferible utilizar la ecuación (1.3)
por este motivo es preferible utilizar la ecuación (1.3)
-
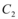 es un factor que toma en cuenta los efectos de degradación de rigidez, pérdida de resistencia y el estrangulamiento de los ciclos histeréticos, en la respuesta del desplazamiento máximo. Este factor, está en función del nivel de desempeño que se espera de la edificación como se aprecia en la tabla 1.2
es un factor que toma en cuenta los efectos de degradación de rigidez, pérdida de resistencia y el estrangulamiento de los ciclos histeréticos, en la respuesta del desplazamiento máximo. Este factor, está en función del nivel de desempeño que se espera de la edificación como se aprecia en la tabla 1.2
-
|
|
(1.7) |
donde ![]() viene definida por la relación entre la rigidez post fluencia con relación a la rigidez elástica del modelo bilineal de la curva de capacidad sísmica resistente;
viene definida por la relación entre la rigidez post fluencia con relación a la rigidez elástica del modelo bilineal de la curva de capacidad sísmica resistente; ![]() fue definido en la ecuación (1.6). El valor de
fue definido en la ecuación (1.6). El valor de ![]() obtenido con (1.7) será menor a:
obtenido con (1.7) será menor a:
|
|
(1.8) |
siendo ![]() el período fundamental elástico;
el período fundamental elástico; ![]() es el factor de estabilidad de piso que está en función de la deriva de piso, lo que dificulta el cálculo ya que lo que se pretende conocer es el desplazamiento lateral máximo en el tope del edificio.
es el factor de estabilidad de piso que está en función de la deriva de piso, lo que dificulta el cálculo ya que lo que se pretende conocer es el desplazamiento lateral máximo en el tope del edificio.
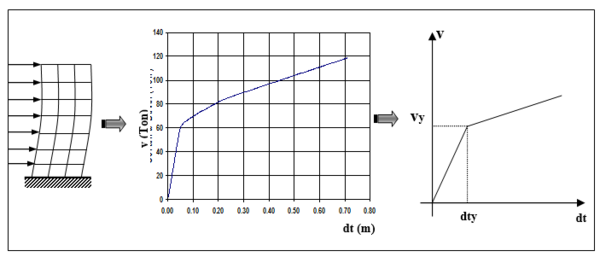
La curva de capacidad sísmica resistente se obtiene mediante la Técnica del Pushover que consiste en aplicar cargas laterales monotónicas crecientes en una dirección hasta llevar al colapso a la estructura, Aguiar (2003). En la figura 1.1 se ilustra su cálculo, a la izquierda se aprecia un pórtico plano sometido a cargas laterales, se realiza un análisis no lineal estático y para cada incremento de carga se obtiene el cortante basal ![]() y el desplazamiento lateral máximo
y el desplazamiento lateral máximo ![]() ; en base a estos puntos se determina la curva de capacidad la misma que se indica en la parte central de la figura 1.1, de ésta gráfica se obtiene el modelo bilineal respectivo conformado por una zona elástica y una zona inelástica, como se aprecia a la derecha de la figura 1.1. El punto de cruce de estas dos rectas es el punto de fluencia que tiene un cortante
; en base a estos puntos se determina la curva de capacidad la misma que se indica en la parte central de la figura 1.1, de ésta gráfica se obtiene el modelo bilineal respectivo conformado por una zona elástica y una zona inelástica, como se aprecia a la derecha de la figura 1.1. El punto de cruce de estas dos rectas es el punto de fluencia que tiene un cortante ![]() y un desplazamiento
y un desplazamiento ![]() .
.
La pendiente, de la curva central de la figura 1.1, para un desplazamiento lateral de 0, es la rigidez inicial ![]() que consta en la ecuación ( 1.4 ) y la pendiente de la derecha de la figura 1.1, para el rango elástico, es el valor de
que consta en la ecuación ( 1.4 ) y la pendiente de la derecha de la figura 1.1, para el rango elástico, es el valor de ![]() .
.
La ecuación ( 1.1 ) plantea que el desplazamiento espectral ![]() asociado al período al período de vibración
asociado al período al período de vibración ![]() , y que es igual a
, y que es igual a ![]() , sea modificado debido al comportamiento inelástico mediante el factor
, sea modificado debido al comportamiento inelástico mediante el factor ![]() , el mismo que ha sido obtenido de estudios estadísticos empleando, por lo regular un modelo bilineal, sin considerar degradación de resistencia, degradación de rigidez y efecto de cierre de grietas, que son fundamentales en el análisis no lineal. La inclusión de estos factores en el método se lo corrige por medio del factor
, el mismo que ha sido obtenido de estudios estadísticos empleando, por lo regular un modelo bilineal, sin considerar degradación de resistencia, degradación de rigidez y efecto de cierre de grietas, que son fundamentales en el análisis no lineal. La inclusión de estos factores en el método se lo corrige por medio del factor ![]() . Por otra parte en el rango inelástico se debe tener en cuenta el efecto
. Por otra parte en el rango inelástico se debe tener en cuenta el efecto ![]() , especialmente cuando la estructura está sometida a grandes deformaciones, este efecto se lo considera por medio del factor
, especialmente cuando la estructura está sometida a grandes deformaciones, este efecto se lo considera por medio del factor ![]() . Finalmente para pasar todos estos valores del sistema de 1 gdl., al sistema con múltiples grados de libertad se lo hace por medio del factor de participación modal
. Finalmente para pasar todos estos valores del sistema de 1 gdl., al sistema con múltiples grados de libertad se lo hace por medio del factor de participación modal ![]() , evaluado en el último piso.
, evaluado en el último piso.
1.3 ALGUNOS TRABAJOS ANTERIORES
Las investigaciones realizadas por Newmark y Rosenblueth, (1971); Newmark y Hall, (1982) y otros científicos aportaron al desarrollo del Método del Coeficiente de Desplazamiento. Únicamente para no alargar la exposición se indican dos estudios en el presente apartado, el desarrollado por Shimazaki y Sozen (1984) y el efectuado por Miranda (1991) que aportaron a la definición del coeficiente ![]() .
.
1.3.1 Estudio de Shimazaki y Sozen
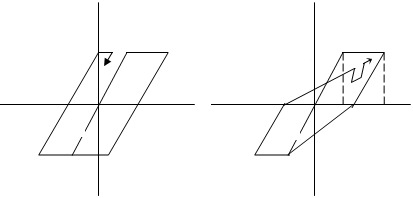
Shimazaki y Sozen (1984) estudiaron la respuesta sísmica elástica e inelástica de un conjunto de osciladores de 1gdl., ante la acción de tres eventos sísmicos empleando cinco modelos de histéresis y aplicando el Método de Newmark, con un valor de ![]() . En este capítulo solo se presentan los resultados obtenidos con dos de ellos y son los modelos mostrados en la figura 1.2; el de la izquierda, es el modelo elasto plasto perfecto que no contempla deterioro de rigidez en la descarga, ni deterioro de resistencia, ni efecto de cierre de grietas. El otro, es el modelo simplificado de Takeda que se aprecia a la derecha de la figura 1.2. Se destaca que en todos los modelos de histéresis el valor de
. En este capítulo solo se presentan los resultados obtenidos con dos de ellos y son los modelos mostrados en la figura 1.2; el de la izquierda, es el modelo elasto plasto perfecto que no contempla deterioro de rigidez en la descarga, ni deterioro de resistencia, ni efecto de cierre de grietas. El otro, es el modelo simplificado de Takeda que se aprecia a la derecha de la figura 1.2. Se destaca que en todos los modelos de histéresis el valor de ![]() , es decir en el rango inelástico la rigidez del sistema es nula.
, es decir en el rango inelástico la rigidez del sistema es nula.
Se presentan los resultados obtenidos ante el registro de la componente N-S del sismo de El Centro de 1940 y se lo hace para tres casos que corresponden a: ![]() ;
; ![]() ; y,
; y, ![]() . Donde
. Donde ![]() es el período elástico del oscilador de 1gdl;
es el período elástico del oscilador de 1gdl; ![]() es aproximadamente el período de transición entre la región de aceleración constante y la región de velocidad constante del espectro de respuesta.
es aproximadamente el período de transición entre la región de aceleración constante y la región de velocidad constante del espectro de respuesta.
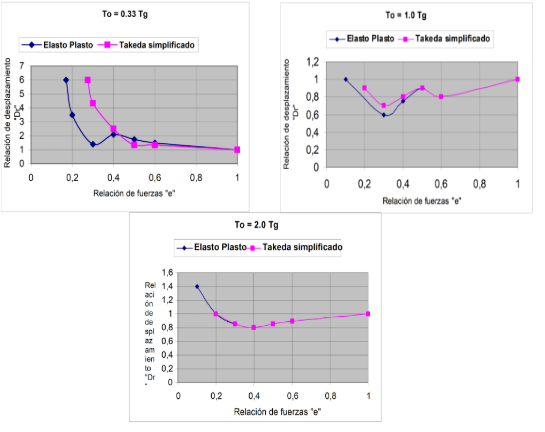
En la figura 1.3, se presentan estos resultados en función de la relación de fuerzas ![]() y de la relación de desplazamientos
y de la relación de desplazamientos ![]() definidos de la siguiente manera:
definidos de la siguiente manera:
|
|
(1.9) | |
| (1.10) |
donde ![]() es el cortante a nivel de fluencia del oscilador de 1gdl,
es el cortante a nivel de fluencia del oscilador de 1gdl, ![]() es el peso del oscilador,
es el peso del oscilador, ![]() es la aceleración del espectro de respuesta elástica asociada al período
es la aceleración del espectro de respuesta elástica asociada al período ![]() , y,
, y, ![]() es la aceleración de la gravedad. Por otro lado,
es la aceleración de la gravedad. Por otro lado, ![]() es el máximo desplazamiento inelástico y
es el máximo desplazamiento inelástico y ![]() es el máximo desplazamiento elástico.
es el máximo desplazamiento elástico.
En el estudio, se encontró que para relaciones de ![]() el desplazamiento máximo elástico es aproximadamente igual al desplazamiento máximo inelástico, razón por la cual en la figura 1.3 sé grafica hasta
el desplazamiento máximo elástico es aproximadamente igual al desplazamiento máximo inelástico, razón por la cual en la figura 1.3 sé grafica hasta ![]() . Existe amplificación de los desplazamientos inelásticos para valores de
. Existe amplificación de los desplazamientos inelásticos para valores de ![]() menores a la unidad. Tener
menores a la unidad. Tener ![]() implica que la capacidad sísmica es mayor que la demanda sísmica . Por otra parte se aprecia que para
implica que la capacidad sísmica es mayor que la demanda sísmica . Por otra parte se aprecia que para ![]() el modelo de histéresis poco influye en la respuesta sísmica, lo que se aprecia en las gráficas para
el modelo de histéresis poco influye en la respuesta sísmica, lo que se aprecia en las gráficas para ![]() y
y ![]() .
.
Finalmente para ![]() se aprecia que la respuesta inelástica es mucho mayor que la respuesta elástica especialmente para valores de
se aprecia que la respuesta inelástica es mucho mayor que la respuesta elástica especialmente para valores de ![]() . Además para este rango la respuesta dinámica depende del modelo de histéresis.
. Además para este rango la respuesta dinámica depende del modelo de histéresis.
1.3.2 Estudio de Miranda, 1991
Miranda (1991) analizó la respuesta sísmica de 31000 sistemas de 1gdl ante la acción de 124 registros sísmicos que habían sido obtenidos en suelo duro o rocoso, suelo aluvional y suelo suave. La mayor parte de estos sismos fueron registrados en California en el período comprendido entre 1985 y 1991. También incluyó los sismos de Chile de 1985, de Michoacán de 1985 y de San Salvador de 1986.
Para el análisis no lineal consideró un modelo bilineal con una rigidez post fluencia igual al 3% de la rigidez elástica y trabajó con un amortiguamiento viscoso. Obtuvo relaciones del Desplazamiento Inelástico con respecto al Desplazamiento Elástico para los tres tipos de suelo indicados en el párrafo anterior. El análisis contempló ductilidades de desplazamiento igual a 1, 2, 3, 4, 5 y 6.
Los resultados reportados por Miranda (1991) fueron muy similares a los reportados por Shimazaki y Sozen (1984) y sus principales conclusiones se resumen a continuación:
- Para suelos aluvionales, halló similares relaciones a las indicadas en el párrafo anterior.
- Para suelo suave, encontró que para valores similares a
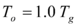 , los valores medios de los desplazamientos inelásticos fueron entre 30 y 40% menores a los valores medios de los desplazamientos elásticos. Pero para
, los valores medios de los desplazamientos inelásticos fueron entre 30 y 40% menores a los valores medios de los desplazamientos elásticos. Pero para  los desplazamientos inelásticos son sustancialmente más grandes que los desplazamientos elásticos.
los desplazamientos inelásticos son sustancialmente más grandes que los desplazamientos elásticos.
- Para suelo suave, encontró que para valores similares a
1.4 ALGUNOS TRABAJOS POSTERIORES
En el presente apartado se presentan los trabajos realizados por Whittaker et al (1998); y Miranda (2000). El objetivo principal está centrado en el valor del coeficiente ![]() propuesto por FEMA, se presenta este factor con la nomenclatura utilizada por los mencionados investigadores. Posteriormente se describe el trabajo de Lee et al (1999) que permite determinar el coeficiente
propuesto por FEMA, se presenta este factor con la nomenclatura utilizada por los mencionados investigadores. Posteriormente se describe el trabajo de Lee et al (1999) que permite determinar el coeficiente ![]() , y los estudios de Gupta y Krawinkler, sobre el efecto
, y los estudios de Gupta y Krawinkler, sobre el efecto ![]() que está asociados a
que está asociados a ![]() .
.
1.4.1 Estudio de Whittaker, Constantinou y Tsopelas
Existen tres aspectos a resaltar en el trabajo desarrollado por Whittaker et al (1998), el primero de ellos tiene que ver con la demanda sísmica considerada, el segundo con la ecuación diferencial con la cual trabajaron el problema dinámico y el tercero sobre los resultados obtenidos.
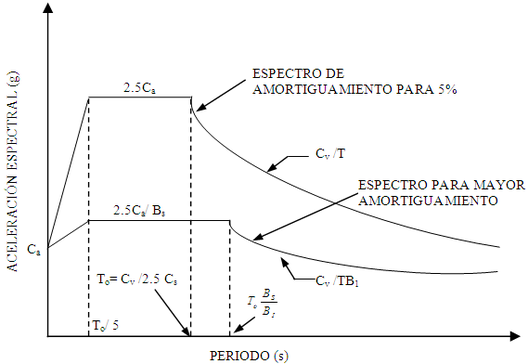
Con respecto a la demanda sísmica, consideraron 20 registros horizontales, correspondientes a 10 terremotos ocurridos en los Estados Unidos de Norte América y cuya magnitud fue mayor a 6.5. Los acelerogramas de estos sismos fue escalada de tal manera que el espectro de respuesta promedio de todos ellos sea muy similar al que se reporta el código UBC-97 y que consta en FEMA 273/274 (1997). El escalamiento fue realizado de tal forma que se conservó la frecuencia de los sismos y las características del evento. En la figura 1.4 se indica la forma del Espectro del UBC-97 pero se debe manifestar que trabajaron con un perfil de suelo que está entre C o D, que corresponde a un suelo de dureza intermedia tendiendo a duro. Consideraron ![]() y
y ![]()
En la parte superior de la figura 1.4 aparece el espectro de diseño elástico del UBC-97 para un 5% de amortiguamiento efectivo ![]() y en la parte inferior el espectro inelástico para valores mayores de amortiguamiento. Los valores de
y en la parte inferior el espectro inelástico para valores mayores de amortiguamiento. Los valores de ![]() y
y ![]() están en función del valor del factor de amortiguamiento efectivo
están en función del valor del factor de amortiguamiento efectivo ![]() y se indican en la tabla 1.3. El análisis sísmico fue realizado con el espectro promedio de los 10 terremotos utilizados con las indicaciones anotadas anteriormente.
y se indican en la tabla 1.3. El análisis sísmico fue realizado con el espectro promedio de los 10 terremotos utilizados con las indicaciones anotadas anteriormente.
El segundo aspecto que llama la atención, se refiere a la ecuación diferencial utilizada para definir el sistema de 1gdl. Esta es:
|
|
(1.11) |
donde ![]() son el desplazamiento, velocidad y la aceleración de la masa relativo al suelo;
son el desplazamiento, velocidad y la aceleración de la masa relativo al suelo; ![]() es la aceleración del suelo,
es la aceleración del suelo, ![]() es la masa del sistema;
es la masa del sistema; ![]() es el amortiguamiento que se considera de tipo viscoso;
es el amortiguamiento que se considera de tipo viscoso; ![]() es la fuerza restauradora del sistema, para el rango elástico vale
es la fuerza restauradora del sistema, para el rango elástico vale ![]() , siendo
, siendo ![]() la rigidez elástica. Para el rango plástico la rigidez va cambiando de acuerdo al punto del modelo de histéresis en que se encuentra;
la rigidez elástica. Para el rango plástico la rigidez va cambiando de acuerdo al punto del modelo de histéresis en que se encuentra; ![]() es el período secante asociado al máximo desplazamiento. Finalmente,
es el período secante asociado al máximo desplazamiento. Finalmente, ![]() es otro coeficiente de amortiguamiento. De tal manera que el amortiguamiento del sistema está definido por dos valores que son
es otro coeficiente de amortiguamiento. De tal manera que el amortiguamiento del sistema está definido por dos valores que son ![]() y
y ![]() . Para el rango elástico y para amortiguamiento viscoso se tiene:
. Para el rango elástico y para amortiguamiento viscoso se tiene:
donde ![]() es el período en el rango elástico. Para un amortiguamiento en el rango inelástico se tiene:
es el período en el rango elástico. Para un amortiguamiento en el rango inelástico se tiene:
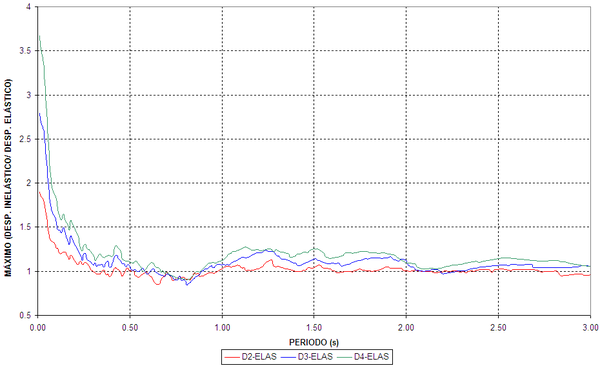
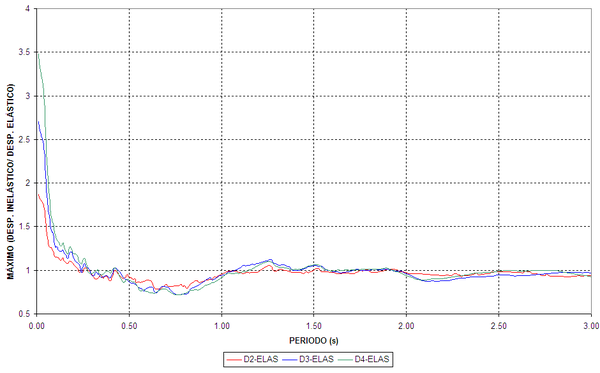
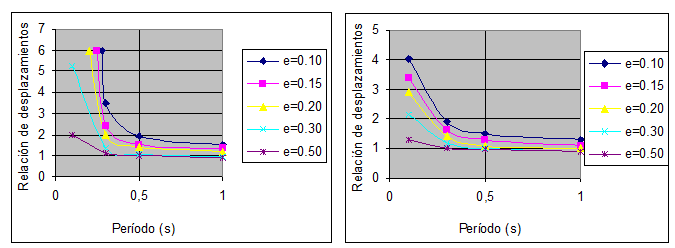
Con relación a los resultados, en la figura 1.5 se indica el valor de ![]() que relaciona el desplazamiento medio inelástico con el desplazamiento medio elástico en función del período. Las curvas de la izquierda, corresponden al caso en que la rigidez post fluencia tiene un valor
que relaciona el desplazamiento medio inelástico con el desplazamiento medio elástico en función del período. Las curvas de la izquierda, corresponden al caso en que la rigidez post fluencia tiene un valor ![]() , siendo
, siendo ![]() la relación entre la rigidez inelástica con relación a la rigidez elástico del modelo bilineal. A la derecha, se presentan las curvas para el caso en que
la relación entre la rigidez inelástica con relación a la rigidez elástico del modelo bilineal. A la derecha, se presentan las curvas para el caso en que ![]() .
.
De la figura 1.5 se desprende que para valores de período mayores que 0.5 s., el valor medio del desplazamiento inelástico es aproximadamente igual al desplazamiento elástico para valores de ![]() . Se destaca que el período de 0.5 s., corresponde aproximadamente a la zona de transición donde la aceleración es constante. La correlación es mejor para el caso de
. Se destaca que el período de 0.5 s., corresponde aproximadamente a la zona de transición donde la aceleración es constante. La correlación es mejor para el caso de ![]() Para valores de
Para valores de ![]() la diferencia entre el desplazamiento inelástico y desplazamiento elástico es significativa especialmente para períodos menores a 0.5 s. Whittaker et al (1998) concluyen que el valor del factor máximo de
la diferencia entre el desplazamiento inelástico y desplazamiento elástico es significativa especialmente para períodos menores a 0.5 s. Whittaker et al (1998) concluyen que el valor del factor máximo de ![]() , recomendado por FEMA-273, es mayor para valores de
, recomendado por FEMA-273, es mayor para valores de ![]() De igual forma se aprecia que para
De igual forma se aprecia que para ![]() y para todos los valores de
y para todos los valores de ![]() los valores de
los valores de ![]() son mayores a los recomendados por FEMA-273.
son mayores a los recomendados por FEMA-273.
|
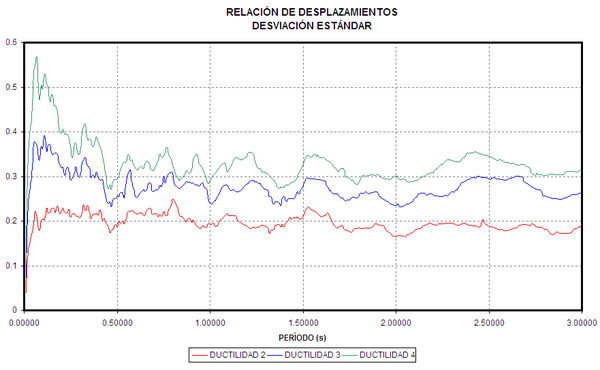
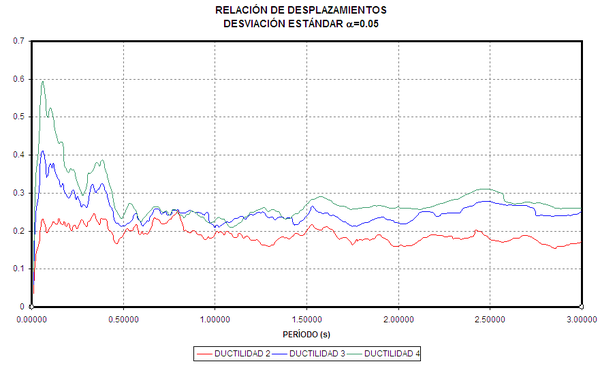
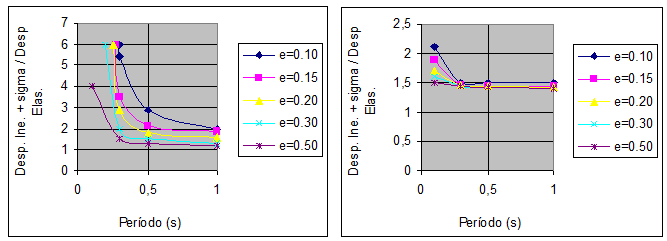
Por otra parte, con los datos estadísticos obtenidos se presenta en la figura 1.6, a la izquierda, la relación entre el desplazamiento inelástico medio más una desviación estándar, con relación al desplazamiento elástico y a la derecha la relación entre el mismo numerador anterior con relación al desplazamiento inelástico medio. Todo esto para valores de ![]() . En la figura de la izquierda, se aprecia que para valores de período menores a 0.3 s., la relación entre los desplazamientos considerando la desviación estándar es mucho mayor a la relación en que no se considera la desviación estándar a tal punto que Whittaker y Constantinou (1998) indican que el valor de 1.5 como cota máxima recomendado por FEMA 273 es bajo. Esto se aprecia mejor en el gráfico de la derecha de la figura 1.6, en que los valores entre el desplazamiento medio inelástico más una desviación estándar con respecto a los desplazamientos medios inelásticos son mayores a 1.5 para períodos menores a 0.5 segundos.
. En la figura de la izquierda, se aprecia que para valores de período menores a 0.3 s., la relación entre los desplazamientos considerando la desviación estándar es mucho mayor a la relación en que no se considera la desviación estándar a tal punto que Whittaker y Constantinou (1998) indican que el valor de 1.5 como cota máxima recomendado por FEMA 273 es bajo. Esto se aprecia mejor en el gráfico de la derecha de la figura 1.6, en que los valores entre el desplazamiento medio inelástico más una desviación estándar con respecto a los desplazamientos medios inelásticos son mayores a 1.5 para períodos menores a 0.5 segundos.
|
1.4.2 Estudio de Miranda, 2000
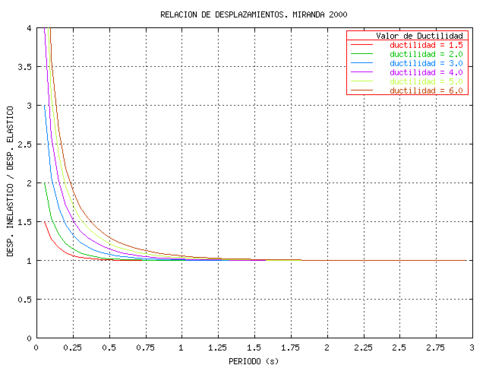
Miranda (2000) realiza un estudio en base a 264 registros de aceleración, correspondientes a 12 terremotos registrados en el estado de California, con el propósito de ver la relación que existe entre los desplazamientos máximos inelásticos con relación a los desplazamientos máximos elásticos en sistemas de 1gdl. Para la respuesta no lineal consideró demandas de ductilidad igual a 1.5, 2.0, 3.0, 4.0, 5.0 y 6.0. Varios parámetros fueron tomados en cuenta para el análisis, entre ellos se destacan:
- Efecto de Suelo, para lo cual clasificó los 264 registros en 78 registros correspondientes a perfiles de suelo tipo A y B, 76 registros a perfil tipo C y 110 registros a perfil tipo D. La definición de los perfiles de suelo son la estipulada por el UBC-97. Del estudio encontró que el suelo no influye mayormente en la relación del desplazamiento inelástico máximo con respecto al desplazamiento máximo elástico. Lógicamente que en el suelo tipo D se tendrá los mayores valores de esta relación pero no es significativa. Posteriormente, Akkar y Miranda (2005) reconocen que el suelo si influye en la relación del desplazamiento máximo inelástico con relación al desplazamiento máximo elástico.an>
- Efecto de Magnitud, se separó los registros en: 68 de magnitudes comprendidas entre 5.7 y 6.2; 92 registros con magnitudes entre 6.3 y 6.9 y 78 registros con magnitudes entre 7.0 y 7.8. Nuevamente el estudio reportó que la magnitud no influye significativamente en la relación entre el desplazamiento máximo inelástico con relación al elástico.
- Efecto de la distancia de ruptura, para el efecto se trabajó con 78 registros cuya distancia epicentral está entre 1 y 20 Km; 92 registros con distancia epicentral comprendida entre 20.1 y 45.0 Km, y 82 registros con distancia epicentral comprendida entre 45.1 y 160 Km. El estudio demostró que el efecto de la distancia epicentral no influye significativamente en la relación del desplazamiento máximo inelástico con relación al desplazamiento elástico.
Miranda (2000) en el estudio encontró la respuesta no lineal de 78600 sistemas de 1gdl correspondientes a los 264 registros de aceleraciones del suelo, trabajando con 50 períodos y 6 niveles de demandas de ductilidad. En base a esta información encontró la siguiente relación:
|
|
(1.12) |
donde ![]() es la relación entre el desplazamiento máximo inelástico con relación al desplazamiento máximo elástico, es un valor medio de los valores obtenidos;
es la relación entre el desplazamiento máximo inelástico con relación al desplazamiento máximo elástico, es un valor medio de los valores obtenidos; ![]() es la demanda de ductilidad y
es la demanda de ductilidad y ![]() es el período de vibración del sistema de 1 gdl. La ecuación de
es el período de vibración del sistema de 1 gdl. La ecuación de ![]() fue obtenida utilizando un análisis de regresión no lineal empleando el Método de Levenberg-Marquardt. En la figura 1.7, se presenta la variación de
fue obtenida utilizando un análisis de regresión no lineal empleando el Método de Levenberg-Marquardt. En la figura 1.7, se presenta la variación de ![]() en función del período
en función del período ![]() para diferentes valores de ductilidad. Del estudio se desprende además:
para diferentes valores de ductilidad. Del estudio se desprende además:
- La relación del valor medio del desplazamiento inelástico más una desviación estándar con relación al valor medio del desplazamiento elástico para valores de período mayores a 1.2 s., variaban entre 1.07 para ductilidades de 1.5 a 1.47 para ductilidades de 6. De tal manera que el valor de 1.5 propuesto por FEMA-273 asociado a una desviación estándar es un valor aceptable. Para períodos menores a 1.2 s., el valor de 1.5 consideran un poco alto.
1.5 MÉTODOS INDIRECTOS
Miranda (2001) denomina Métodos Indirectos de estimación del desplazamiento máximo lateral a los que se obtienen en función de la ductilidad ![]() y del factor de reducción de las fuerzas sísmicas
y del factor de reducción de las fuerzas sísmicas ![]() , empleando la siguiente ecuación:
, empleando la siguiente ecuación:
|
|
(1.13) |
las variables todavía no definidas son: ![]() que es el desplazamiento máximo inelástico,
que es el desplazamiento máximo inelástico, ![]() que es la frecuencia natural de vibración;
que es la frecuencia natural de vibración; ![]() es el desplazamiento espectral asociado al período de vibración
es el desplazamiento espectral asociado al período de vibración ![]() ; y,
; y, ![]() el coeficiente que relaciona el desplazamiento máximo inelástico con el desplazamiento máximo elástico y que también es igual a la relación de
el coeficiente que relaciona el desplazamiento máximo inelástico con el desplazamiento máximo elástico y que también es igual a la relación de ![]() .
.
Los métodos directos son aquellos que se derivan, del estudio dinámico de estructuras de 1 gdl ante varías acciones sísmicas, para encontrar la relación entre el desplazamiento máximo inelástico y el desplazamiento máximo elástico. Uno de estos métodos corresponde al trabajo realizado por Miranda, que se presentó en el apartado anterior, quien denominó ![]() a esta relación. Antes de proceder con el estudio conviene demostrar la ecuación ( 1.13 ), Vidic et al (1994).
a esta relación. Antes de proceder con el estudio conviene demostrar la ecuación ( 1.13 ), Vidic et al (1994).
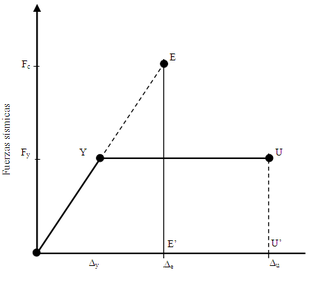
Si en un sistema de 1gdl, cuando este supera el punto de fluencia Y, indicado en la figura 1.8, y si se continúa con el análisis elástico, llegaría en un momento determinado hasta el punto E, que está asociado a la fuerza elástica ![]() y al desplazamiento elástico
y al desplazamiento elástico ![]() . En la figura 1.8 las rectas que unen el origen con el punto Y, y con el punto U, definen el modelo elasto perfectamente plástico en el cual ante la misma acción sísmica no se llega al punto E sino hasta el punto U que está asociado a la fuerza de fluencia
. En la figura 1.8 las rectas que unen el origen con el punto Y, y con el punto U, definen el modelo elasto perfectamente plástico en el cual ante la misma acción sísmica no se llega al punto E sino hasta el punto U que está asociado a la fuerza de fluencia ![]() y al desplazamiento
y al desplazamiento ![]() . En otras palabras dado un sistema de 1 gdl en el cual se realiza un análisis elástico ante una acción sísmica que se sabe va a producir daño en el sistema si se realiza un análisis elástico se llega al punto E pero si se hace un análisis inelástico se llega al punto U.
. En otras palabras dado un sistema de 1 gdl en el cual se realiza un análisis elástico ante una acción sísmica que se sabe va a producir daño en el sistema si se realiza un análisis elástico se llega al punto E pero si se hace un análisis inelástico se llega al punto U.
Se define el factor ![]() como la relación entre la fuerza elástica con relación a la fuerza de fluencia. La fuerza elástica no es más que la masa multiplicada por la aceleración de tal manera que:
como la relación entre la fuerza elástica con relación a la fuerza de fluencia. La fuerza elástica no es más que la masa multiplicada por la aceleración de tal manera que:
|
|
(1.14) |
Por otra parte, la pendiente de la que va del origen de coordenadas hasta el punto Y, es la rigidez ![]() , de tal manera que
, de tal manera que ![]() pero de la dinámica de estructuras se sabe que
pero de la dinámica de estructuras se sabe que ![]() . De tal manera que:
. De tal manera que:
|
|
(1.15) |
Se sabe que la ductilidad ![]() , de donde
, de donde ![]() Al sustituir esta expresión en la ecuación ( 1.15 ) y luego al igualar con la ecuación ( 1.14 ) se tiene:
Al sustituir esta expresión en la ecuación ( 1.15 ) y luego al igualar con la ecuación ( 1.14 ) se tiene:
Una vez que se ha demostrado la ecuación ( 1.13 ) se presenta a continuación los resultados del trabajo realizado por Nassar y Krawinkler (1991) quienes estudiaron la respuesta de sistemas de 1gdl ante 15 terremotos registrados en el estado de California, sobre suelo firme y aluvial. Del estudio realizado obtuvieron la siguiente expresión para el factor de reducción de la fuerza sísmica, que ellos lo denominan, ![]() .
.
|
|
(1.16) | |
| (1.17) |
donde ![]() es una función del período
es una función del período ![]() y del cociente entre la rigidez post fluencia y rigidez elástica que se ha denominado
y del cociente entre la rigidez post fluencia y rigidez elástica que se ha denominado ![]() . Los valores de a y b en función de la variable
. Los valores de a y b en función de la variable ![]() se indican en la tabla 1.4.
se indican en la tabla 1.4.
De tal manera que el factor ![]() para los estudios realizados por Nassar y Krawinkler (1991) resulta:
para los estudios realizados por Nassar y Krawinkler (1991) resulta:
|
|
(1.18) |
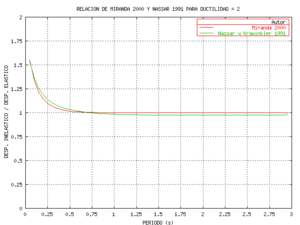
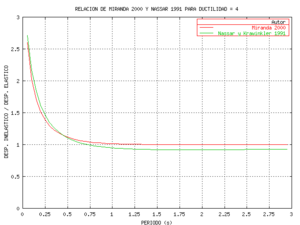
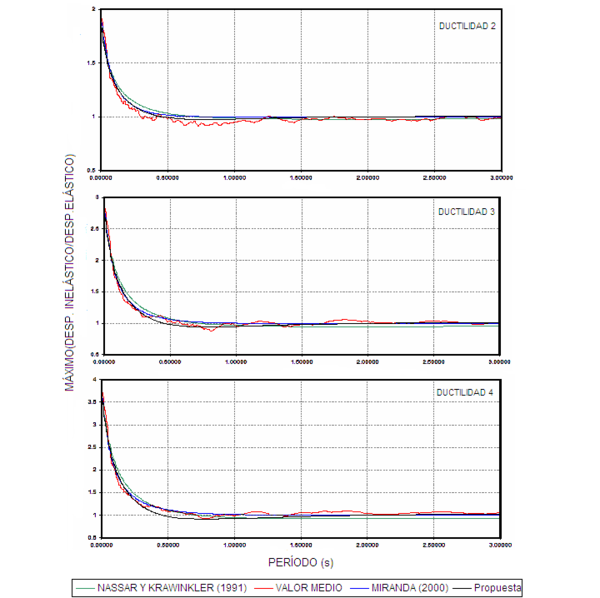
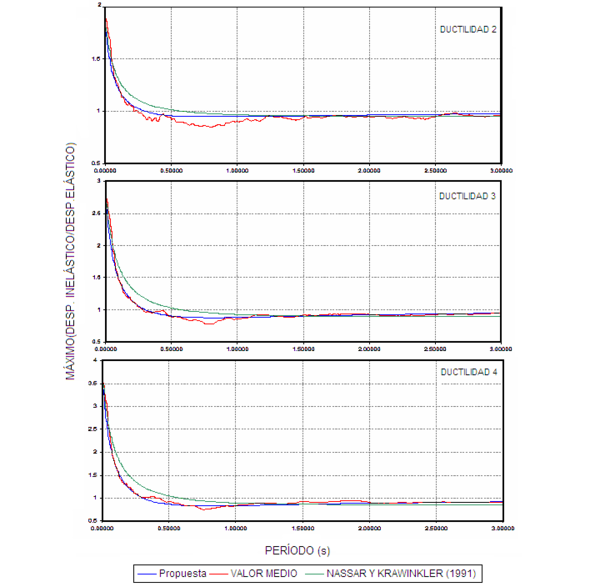
En la figura 1.9 se comparan las curvas que se obtienen al utilizar las ecuaciones de ![]() propuesto por Miranda (2000) y
propuesto por Miranda (2000) y ![]() propuesto por Nassar y Krawinkler (1991). Es valida ésta comparación ya que en los dos casos trabajaron con sismos del estado de California. La comparación se la va a realizar para el caso de
propuesto por Nassar y Krawinkler (1991). Es valida ésta comparación ya que en los dos casos trabajaron con sismos del estado de California. La comparación se la va a realizar para el caso de ![]() , que corresponde al modelo elásto perfectamente plástico que fue con el cual se obtuvo
, que corresponde al modelo elásto perfectamente plástico que fue con el cual se obtuvo ![]() . A la izquierda de la figura 1.9 se presentan los resultados para
. A la izquierda de la figura 1.9 se presentan los resultados para ![]() , y a la derecha para
, y a la derecha para ![]() .
.
En la figura 1.9 se aprecia una muy buena correlación entre los valores obtenidos de ![]() y
y ![]() . Se destaca que
. Se destaca que ![]() corresponde a un método directo y que
corresponde a un método directo y que ![]() corresponde a un método indirecto, con los cuales se puede predecir el desplazamiento inelástico máximo que se espera en sistemas de 1gdl en función del desplazamiento máximo elástico.
corresponde a un método indirecto, con los cuales se puede predecir el desplazamiento inelástico máximo que se espera en sistemas de 1gdl en función del desplazamiento máximo elástico.
1.6 ANÁLISIS DEL FACTOR C0
En el Método del Coeficiente de Desplazamiento, ![]() , es el factor de paso del sistema de 1 gdl., al sistema de múltiples grados de libertad, también conocido como factor de participación evaluado en el tope del edificio, el mismo que se analiza en el presente apartado. Para el efecto se estudian dos trabajos el uno realizado por Miranda (1999) en que resuelve un sistema continuo conformado por una viga de flexión que está acoplada a una viga de corte, considerando sección constante y el otro el estudio de Miranda y Reyes (2002) en que resuelven el mismo sistema continuo pero considerando sección variable.
, es el factor de paso del sistema de 1 gdl., al sistema de múltiples grados de libertad, también conocido como factor de participación evaluado en el tope del edificio, el mismo que se analiza en el presente apartado. Para el efecto se estudian dos trabajos el uno realizado por Miranda (1999) en que resuelve un sistema continuo conformado por una viga de flexión que está acoplada a una viga de corte, considerando sección constante y el otro el estudio de Miranda y Reyes (2002) en que resuelven el mismo sistema continuo pero considerando sección variable.
Para el caso de sección constante, Miranda (1999) encuentra en forma aproximada que el factor de participación ![]() se evalúa con la siguiente ecuación:
se evalúa con la siguiente ecuación:
|
|
(1.19) | |
| (1.20) |
donde ![]() es la forma modal en el piso j, pero que no se calcula de un problema de valores y vectores propios sino evaluando el desplazamiento lateral
es la forma modal en el piso j, pero que no se calcula de un problema de valores y vectores propios sino evaluando el desplazamiento lateral ![]() en el piso j, ante un determinado patrón de cargas y normalizándolo con respecto al desplazamiento en el tope del edificio
en el piso j, ante un determinado patrón de cargas y normalizándolo con respecto al desplazamiento en el tope del edificio ![]() ; N es el número total de pisos, la variable
; N es el número total de pisos, la variable ![]() se mide desde la base del edificio y
se mide desde la base del edificio y ![]() es la altura total del edificio.
es la altura total del edificio.
Para el caso de carga lateral actuando en el sistema continuo y para el comportamiento de una estructura que trabaja como una viga de flexión (edificios en base a muros de corte) a partir de las ecuaciones ( 1.19 ) y ( 1.20 ) se obtiene, en forma aproximada.
Al reemplazar las sumatorias indicadas se tiene:
|
|
(1.21) |
De tal manera que ![]() se puede evaluar únicamente en base al número de pisos N, como se indica en la ecuación ( 1.21 ) que fue obtenida por Algan (1982).
se puede evaluar únicamente en base al número de pisos N, como se indica en la ecuación ( 1.21 ) que fue obtenida por Algan (1982).
Miranda y Reyes (2002) resuelven el sistema acoplado de la viga de flexión con la viga de corte en función del parámetro adimensional ![]() que se indica a continuación:
que se indica a continuación:
|
|
(1.22) |
siendo ![]() la rigidez al corte y
la rigidez al corte y ![]() la rigidez a flexión. Para edificios con muros de corte el valor de
la rigidez a flexión. Para edificios con muros de corte el valor de ![]() es menor a 2; para edificios con un sistema dual formado por muros de corte y vigas y columnas el valor de
es menor a 2; para edificios con un sistema dual formado por muros de corte y vigas y columnas el valor de ![]() se encuentra entre 1.5 y 6. Finalmente para edificios en base a vigas y columnas, el valor de
se encuentra entre 1.5 y 6. Finalmente para edificios en base a vigas y columnas, el valor de ![]() está entre 5 y 20. La evaluación de
está entre 5 y 20. La evaluación de ![]() se realiza en forma similar a la indicada para sección constante pero con la solución que presentan Miranda y Reyes (2002).
se realiza en forma similar a la indicada para sección constante pero con la solución que presentan Miranda y Reyes (2002).
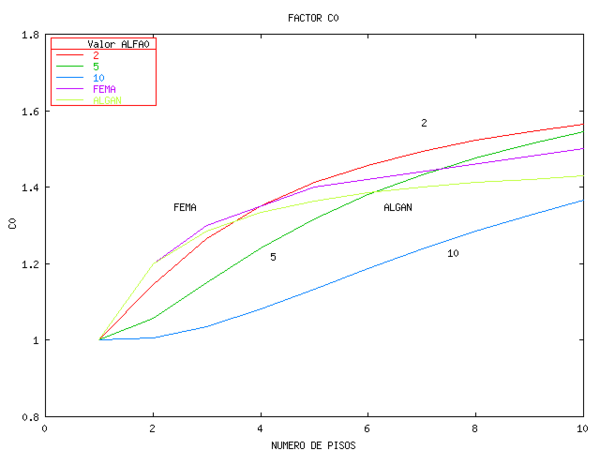
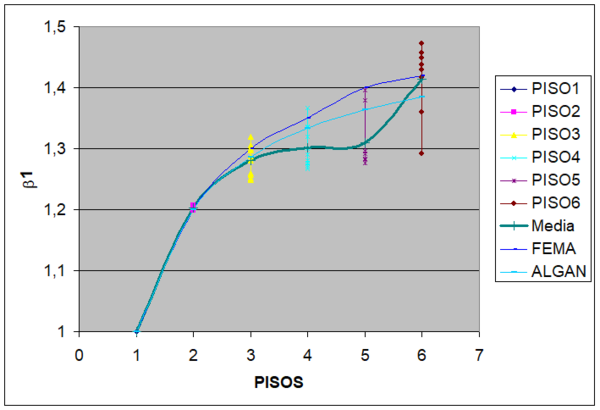
En la figura 1.10 se presentan las curvas que se obtienen a partir de los resultados de Miranda y Reyes (2002), para sección constante y para ![]() =2 que vendría a ser el límite superior de edificios con muros de corte; para
=2 que vendría a ser el límite superior de edificios con muros de corte; para ![]() que es el límite inferior para el caso de edificios con vigas y columnas; para
que es el límite inferior para el caso de edificios con vigas y columnas; para ![]() que es un caso intermedio de edificios con vigas y columnas. En estos tres casos se ha considerado que la carga actuante es triangular. Se indica también lo que se obtiene con la propuesta de Algan y también se indica lo recomendado por FEMA 356 en el Método del Coeficiente de los Desplazamientos.
que es un caso intermedio de edificios con vigas y columnas. En estos tres casos se ha considerado que la carga actuante es triangular. Se indica también lo que se obtiene con la propuesta de Algan y también se indica lo recomendado por FEMA 356 en el Método del Coeficiente de los Desplazamientos.
Se presentan las curvas hasta 10 pisos porque para un edificio de mayor número de pisos convendría analizarlo con un método más exacto como el Método del Espectro de Capacidad. En la figura 1.10 se aprecia que la propuesta de FEMA se correlaciona bastante bien con los coeficientes que se obtienen de la ecuación deducida por Algan. Para edificios menores a 5 pisos la curva obtenida para ![]() se aproxima bastante bien a las curvas halladas con FEMA 356 y Algan pero para edificios de más de 6 pisos la curva
se aproxima bastante bien a las curvas halladas con FEMA 356 y Algan pero para edificios de más de 6 pisos la curva ![]() reporta valores altos.
reporta valores altos.
Al trabajar con los valores obtenidos para ![]() se tendrían valores bajos para edificios menores a 5 pisos y luego valores similares a los de FEMA 356 y Algan para edificios entre 6 y 8 pisos y valores altos para edificios de más de 8 pisos. En la tabla 1.5 se indican los valores que se hallan para
se tendrían valores bajos para edificios menores a 5 pisos y luego valores similares a los de FEMA 356 y Algan para edificios entre 6 y 8 pisos y valores altos para edificios de más de 8 pisos. En la tabla 1.5 se indican los valores que se hallan para ![]() en función del número de pisos.
en función del número de pisos.
1.7 ANÁLISIS DEL FACTOR C1
En base a los estudios presentados en este capítulo se concluye que el valor de ![]() recomendado por FEMA para
recomendado por FEMA para ![]() es adecuado toda vez que para períodos largos el desplazamiento máximo inelástico es aproximadamente igual al desplazamiento máximo elástico. En consecuencia se cumple muy bien la regla de igual desplazamiento para
es adecuado toda vez que para períodos largos el desplazamiento máximo inelástico es aproximadamente igual al desplazamiento máximo elástico. En consecuencia se cumple muy bien la regla de igual desplazamiento para ![]() .
.
Para ![]() , FEMA-356 recomienda que
, FEMA-356 recomienda que ![]() , éste valor parece adecuado para estructuras con un valor de
, éste valor parece adecuado para estructuras con un valor de ![]() . Para estructuras con un valor de
. Para estructuras con un valor de ![]() y
y ![]() se recomienda que
se recomienda que ![]() . Independiente del valor de
. Independiente del valor de ![]() se ha visto en los estudios presentados y en otros, se ha visto los resultados de sistemas de 1 gdl ante sismos de múltiples frecuencias, duración moderada y sin pulsos largos que
se ha visto en los estudios presentados y en otros, se ha visto los resultados de sistemas de 1 gdl ante sismos de múltiples frecuencias, duración moderada y sin pulsos largos que ![]() . De tal manera que es una buena opción considerar
. De tal manera que es una buena opción considerar ![]() para el caso de
para el caso de ![]() para
para ![]() .
.
Para el rango de valores de período efectivo entre 0.1 y ![]() es muy adecuado la interpolación lineal pero teniendo en cuenta el valor de
es muy adecuado la interpolación lineal pero teniendo en cuenta el valor de ![]() para
para ![]() , valdrá
, valdrá ![]() para el caso de que
para el caso de que ![]() , caso contrario
, caso contrario ![]() .
.
Se destaca que posteriormente en este libro se presentarán los resultados de una investigación realizada por el autor de este texto con sismos registrados en Colombia, Perú, Chile y Argentina en que se determina el parámetro ![]() .
.
1.8 ANÁLISIS DEL FACTOR C2
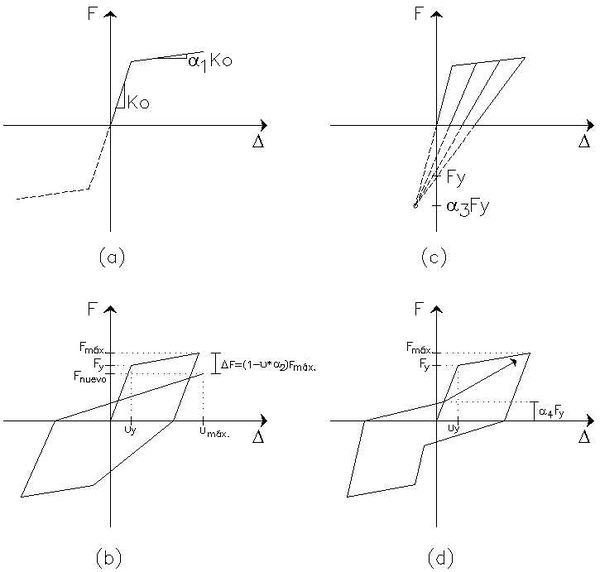
Es muy escasa la información que proporciona FEMA-356 con relación al factor ![]() , razón por la cual se recurre al trabajo desarrollado por Lee et al (1999), quienes estudiaron el comportamiento no lineal de un conjunto de sistemas de 1 gdl., ante 40 sismos registrados en Estados Unidos de Norte América, Alaska, México y el Salvador. El objetivo del estudio fue ver como influye en la respuesta no lineal cuatro parámetros que definen a los modelos de histéresis. Estos parámetros se indican en la figura 1.11 y son:
, razón por la cual se recurre al trabajo desarrollado por Lee et al (1999), quienes estudiaron el comportamiento no lineal de un conjunto de sistemas de 1 gdl., ante 40 sismos registrados en Estados Unidos de Norte América, Alaska, México y el Salvador. El objetivo del estudio fue ver como influye en la respuesta no lineal cuatro parámetros que definen a los modelos de histéresis. Estos parámetros se indican en la figura 1.11 y son:
De acuerdo a FEMA, ![]() , es un factor de corrección que considera el deterioro de resistencia, deterioro de rigidez en la descarga y el efecto de cierre de grietas. Es decir no toma en cuenta el factor
, es un factor de corrección que considera el deterioro de resistencia, deterioro de rigidez en la descarga y el efecto de cierre de grietas. Es decir no toma en cuenta el factor ![]() . Lee et al (1999) en su estudio lo que hallaron fue en que porcentaje se incrementa o disminuye el factor de reducción de las fuerzas sísmicas
. Lee et al (1999) en su estudio lo que hallaron fue en que porcentaje se incrementa o disminuye el factor de reducción de las fuerzas sísmicas ![]() debido al modelo de histéresis pero como se vio en los Métodos Indirectos al sacar la inversa se encuentra el factor de corrección con el que se obtienen los desplazamientos inelásticos.
debido al modelo de histéresis pero como se vio en los Métodos Indirectos al sacar la inversa se encuentra el factor de corrección con el que se obtienen los desplazamientos inelásticos.
Por efecto del deterioro de resistencia el valor de ![]() disminuye con relación a los valores que se obtienen del modelo elasto perfectamente plástico. Los valores para diferentes valores de
disminuye con relación a los valores que se obtienen del modelo elasto perfectamente plástico. Los valores para diferentes valores de ![]() se indican en la tabla 1.6. En la última columna de esta tabla se indica el valor promedio. Se aprecia que conforme se incrementa la ductilidad el valor disminuye.
se indican en la tabla 1.6. En la última columna de esta tabla se indica el valor promedio. Se aprecia que conforme se incrementa la ductilidad el valor disminuye.
| Ductilidad | Promedio | ||||
| 2 | 98 | 96 | 94 | 91 | 94.75 |
| 3 | 97 | 94 | 92 | 89 | 93.00 |
| 4 | 96 | 93 | 90 | 87 | 91.50 |
| 5 | 95 | 91 | 88 | 85 | 89.75 |
| 6 | 95 | 91 | 87 | 84 | 89.25 |
| Ductilidad | Promedio | ||||
| 2 | 99 | 97 | 94 | 91 | 95.25 |
| 3 | 99 | 97 | 94 | 91 | 95.25 |
| 4 | 99 | 97 | 94 | 91 | 95.25 |
| 5 | 99 | 97 | 94 | 91 | 95.25 |
| 6 | 99 | 97 | 94 | 91 | 95.25 |
En la tabla 1.7 se indica la variación de ![]() en función de la demanda de ductilidad y del parámetro
en función de la demanda de ductilidad y del parámetro ![]() . Se observa que este parámetro no cambia con la ductilidad y como era de esperarse mientras más pequeño es
. Se observa que este parámetro no cambia con la ductilidad y como era de esperarse mientras más pequeño es ![]() el factor
el factor ![]() disminuye más.
disminuye más.
| Ductilidad | Promedio | ||||
| 2 | 99 | 98 | 97 | 94 | 97.00 |
| 3 | 99 | 98 | 96 | 94 | 96.75 |
| 4 | 98 | 97 | 96 | 94 | 96.25 |
| 5 | 98 | 97 | 96 | 93 | 96.00 |
| 6 | 98 | 97 | 95 | 93 | 95.75 |
En la tabla 1.8 se aprecia la variación de ![]() en función del parámetro
en función del parámetro ![]() que cuantifica el efecto de cierre de grietas que se produce cuando un elemento ingresa al rango no lineal y empieza a deformarse en sentido contrario.
que cuantifica el efecto de cierre de grietas que se produce cuando un elemento ingresa al rango no lineal y empieza a deformarse en sentido contrario.
Al obtener la inversa del producto de los valores promedios indicados en la última columna de las tablas 5 a 7 se encuentra el valor de ![]() y se indican en la tabla 1.9 para diferentes valores de ductilidad.
y se indican en la tabla 1.9 para diferentes valores de ductilidad.
1.9 ANÁLISIS DEL FACTOR C3
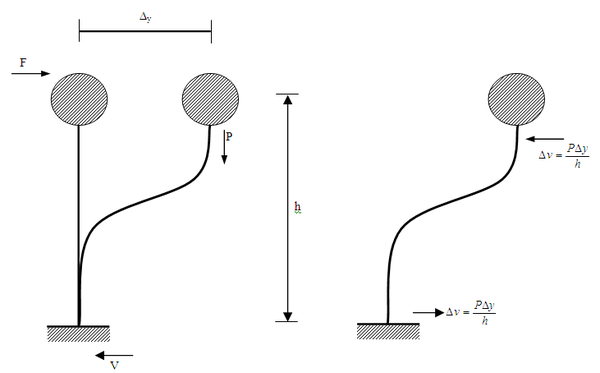
Con el propósito de entender mejor el efecto ![]() y la curva de capacidad sísmica, se analiza un sistema de un 1 gdl., como el mostrado en la figura 1.12 en el cual debido a la aplicación de una fuerza lateral F se genera en la base un corte basal V y la estructura se deforma
y la curva de capacidad sísmica, se analiza un sistema de un 1 gdl., como el mostrado en la figura 1.12 en el cual debido a la aplicación de una fuerza lateral F se genera en la base un corte basal V y la estructura se deforma ![]() . En la estructura deformada actúa la carga vertical P que tiende a volcar al sistema con un momento igual a
. En la estructura deformada actúa la carga vertical P que tiende a volcar al sistema con un momento igual a ![]() , siendo h la altura del sistema. Para contrarrestar este momento de volteo se necesitan un par de cortantes que en la figura 1.12 se han denominado
, siendo h la altura del sistema. Para contrarrestar este momento de volteo se necesitan un par de cortantes que en la figura 1.12 se han denominado ![]() , y que tienen por magnitud:
, y que tienen por magnitud: ![]() .
.
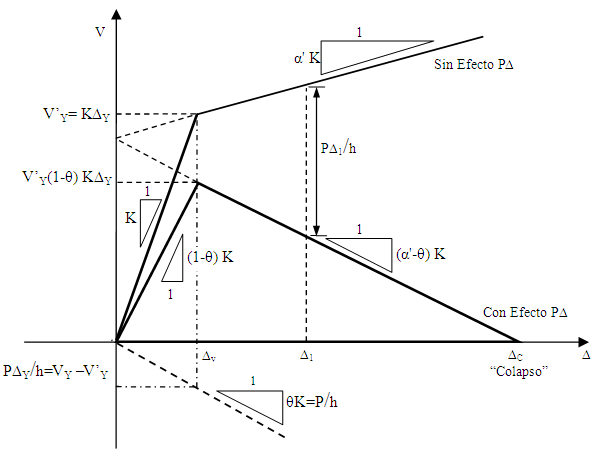
En la figura 1.13 se presenta, el modelo bilineal, de la curva de capacidad sísmica resistente de ese sistema de 1 gdl., sin y con efecto ![]() . Modelo propuesto por Gupta y Krawinkler (2000). Se ha denominado
. Modelo propuesto por Gupta y Krawinkler (2000). Se ha denominado ![]() a la relación entre la rigidez inelástica con relación a la rigidez elástica
a la relación entre la rigidez inelástica con relación a la rigidez elástica ![]() pero sin considerar el efecto
pero sin considerar el efecto ![]() . Cuando se considera el efecto
. Cuando se considera el efecto ![]() el cortante de fluencia
el cortante de fluencia ![]() disminuye en una magnitud
disminuye en una magnitud ![]() y pasa el punto
y pasa el punto ![]() a
a ![]() que vale
que vale ![]() . Siendo
. Siendo ![]() el coeficiente de estabilidad de piso.
el coeficiente de estabilidad de piso.
Se aprecia también en la figura 1.13 el modelo bilineal de la curva de capacidad, para el sistema de 1 gdl., considerando el efecto ![]() . La pendiente del rango inelástico vale
. La pendiente del rango inelástico vale ![]() , y la pendiente de la zona elástica vale
, y la pendiente de la zona elástica vale ![]() . Si la pendiente del rango inelástico es negativa se presentará el colapso.
. Si la pendiente del rango inelástico es negativa se presentará el colapso.
Numéricamente se tiene:
La misma relación se obtiene en base al triángulo rectángulo que aparece en el cuarto cuadrante del modelo indicado en la figura 1.13.
La rigidez ![]() . Al reemplazar este valor en el factor de estabilidad de piso se halla:
. Al reemplazar este valor en el factor de estabilidad de piso se halla: ![]() . Lo importante de la deducción numérica y del modelo presentado era entender que el efecto
. Lo importante de la deducción numérica y del modelo presentado era entender que el efecto ![]() puede ser muy crítico en estructuras cuya rigidez post fluencia tiene un valor bastante bajo ya que al considerar el efecto
puede ser muy crítico en estructuras cuya rigidez post fluencia tiene un valor bastante bajo ya que al considerar el efecto ![]() esta pendiente decae y se presenta el colapso. FEMA reconoce este problema y recomienda que si el valor de
esta pendiente decae y se presenta el colapso. FEMA reconoce este problema y recomienda que si el valor de ![]() es mayor a 0% la estructura no tendrá problemas de
es mayor a 0% la estructura no tendrá problemas de ![]() y se considera
y se considera ![]() . Se destaca que
. Se destaca que ![]() es la relación entre la rigidez inelástica con relación a la rigidez elástica de la curva de capacidad sísmica.
es la relación entre la rigidez inelástica con relación a la rigidez elástica de la curva de capacidad sísmica.
En el sistema de 1 gdl., se consideró por facilidad el punto de fluencia para la explicación del efecto ![]() pero se pudo haber considerado cualquier otro desplazamiento. Para sistemas de múltiples grados de libertad el factor de estabilidad de piso queda:
pero se pudo haber considerado cualquier otro desplazamiento. Para sistemas de múltiples grados de libertad el factor de estabilidad de piso queda:
|
|
(1.23) |
donde el subíndice i representa el piso; ![]() es la carga vertical actuante desde el piso i hasta el tope del edificio;
es la carga vertical actuante desde el piso i hasta el tope del edificio; ![]() es el desplazamiento relativo del piso
es el desplazamiento relativo del piso ![]() ;
; ![]() es el cortante del piso
es el cortante del piso ![]() ;
; ![]() es la altura del entrepiso
es la altura del entrepiso ![]() . Para cada piso se debe evaluar
. Para cada piso se debe evaluar ![]() . Finalmente
. Finalmente ![]() se evalúa con la ecuación ( 1.8 )
se evalúa con la ecuación ( 1.8 )
1.10 PROPUESTA PARA ESTRUCTURAS CON VIGAS Y COLUMNAS
Luego del análisis de los trabajos que se han presentado, sin considerar la investigación realizada en la ESPE la misma que es presentada en los siguientes capítulos, se recomienda para estructuras de hormigón armado conformadas por vigas y columnas, proceder de la siguiente manera para encontrar el desplazamiento lateral máximo ante una acción sísmica definida por su espectro al utilizar el Método del Coeficiente de Desplazamiento:
- 1. Encontrar la curva de capacidad sísmica resistente en tres dimensiones de preferencia o en dos dimensiones. Existen programas como IDARC, DRAIN, SAP2000, Ruaumoko, CEINCI3, entre otros con los cuales se puede hallar esta curva aplicando la técnica del pushover.
- 2. Definir el modelo bilineal de la curva de capacidad sísmica resistente y determinar las coordenadas del punto de fluencia, la rigidez elástica, la rigidez inelástica, el valor de
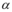 que relaciona la rigidez inelástica con respecto a la elástica y el período fundamental efectivo
que relaciona la rigidez inelástica con respecto a la elástica y el período fundamental efectivo 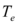 . Si el valor de
. Si el valor de 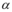 menor a 0 tendrá problemas de efecto
menor a 0 tendrá problemas de efecto 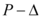 .
.
- 4. En función del número de pisos determinar el coeficiente
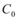 se trabaja con los valores hallados para
se trabaja con los valores hallados para 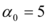 . En el capítulo 3 en base al análisis de 60 estructuras, que responden a la forma como se construye en el Ecuador, se ve que los valores reportados con la fórmula de Algan se aproximan bastante bien a los valores hallados. Sin embargo en este capítulo se trabaja con los valores indicados en la tabla 1.5.
. En el capítulo 3 en base al análisis de 60 estructuras, que responden a la forma como se construye en el Ecuador, se ve que los valores reportados con la fórmula de Algan se aproximan bastante bien a los valores hallados. Sin embargo en este capítulo se trabaja con los valores indicados en la tabla 1.5.
Si ![]() y
y ![]() se recomienda que
se recomienda que ![]() . Si
. Si ![]() se tiene:
se tiene:
Si ![]() y
y ![]() interpolar linealmente entre
interpolar linealmente entre ![]() que es el valor para
que es el valor para ![]() , y
, y ![]() que corresponde a
que corresponde a ![]() . Lógicamente que se debe imponer un valor de
. Lógicamente que se debe imponer un valor de ![]() y calcular en forma iterativa.
y calcular en forma iterativa.
| Ductilidad | 2 | 3 | 4 | 5 | 6 |
| |
1.14 | 1.17 | 1.19 | 1.22 | 1.23 |
En forma preliminar el desplazamiento lateral máximo es igual al producto ![]() con lo que se puede establecer la ductilidad
con lo que se puede establecer la ductilidad ![]() toda vez que se conoce el desplazamiento de fluencia
toda vez que se conoce el desplazamiento de fluencia ![]() .
.
- 8. Se encuentra el Desplazamiento Lateral en el tope con la siguiente ecuación.
La ecuación reporta el valor máximo medio. Si a este valor se multiplica por 1.5 se tendrá una cota superior del desplazamiento lateral máximo. De tal forma que es conveniente encontrar un rango de valores para ![]() .
.
- 9. Con el valor medio de
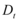 que reporta la ecuación y con el valor máximo (multiplicado por 1.5) se ingresa a la curva de capacidad resistente y a los archivos de resultados del programa utilizado en el análisis con el pushover y se encuentra las secciones que van a ingresar al rango no lineal, la demanda de ductilidad por curvatura de sus elementos, los desplazamientos de cada uno de los pisos y las distorsiones de piso. En fin importante información que no ha sido tratada en este capítulo pero que está detallada en Aguiar (2003).
que reporta la ecuación y con el valor máximo (multiplicado por 1.5) se ingresa a la curva de capacidad resistente y a los archivos de resultados del programa utilizado en el análisis con el pushover y se encuentra las secciones que van a ingresar al rango no lineal, la demanda de ductilidad por curvatura de sus elementos, los desplazamientos de cada uno de los pisos y las distorsiones de piso. En fin importante información que no ha sido tratada en este capítulo pero que está detallada en Aguiar (2003).
1.11 EJEMPLO 1: DESPLAZAMIENTO LATERAL
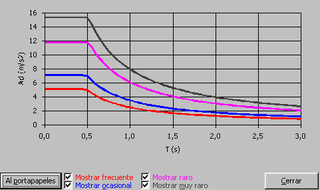
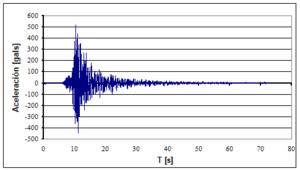
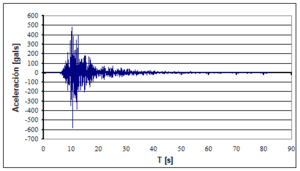
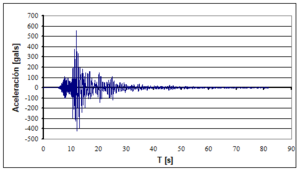
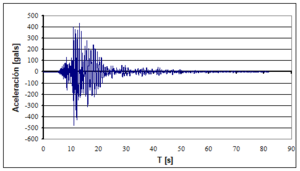
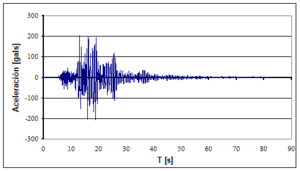
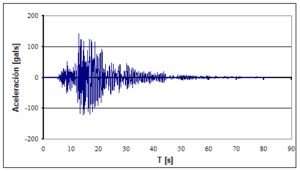
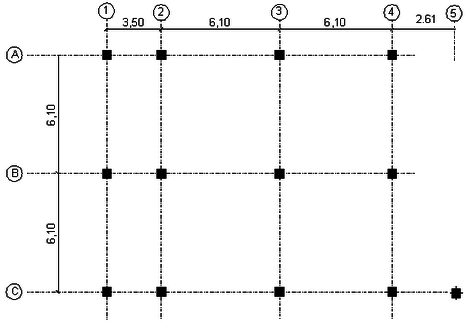
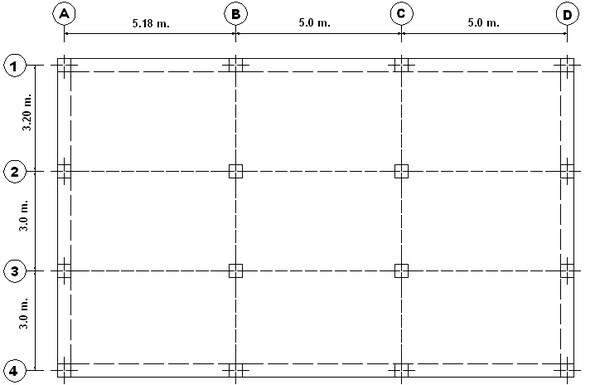
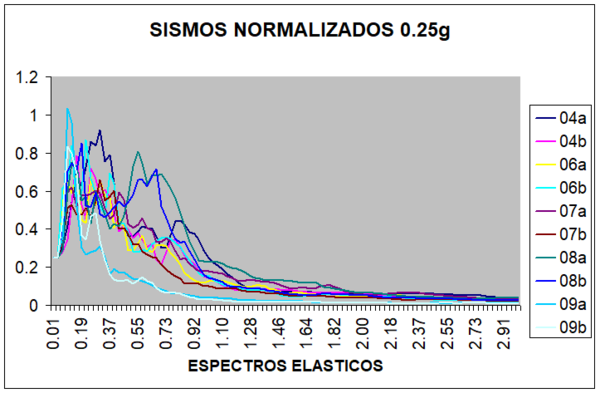
Encontrar los desplazamientos laterales máximos de la estructura de cuatro pisos indicada, a la izquierda de la figura 1.14. Ante los cuatro eventos sísmicos mostrados a la derecha de la figura 1.14. Si la curva de capacidad sísmica resistente, en tres dimensiones, del modelo bilineal está definida por:
De los espectros de la figura 14 se tiene que ![]() que corresponde al punto donde la aceleración deja de ser constante. El análisis no lineal estático se lo realizó con el programa CEINCI3 descrito en Aguiar (2003) y entre otros resultados se obtuvo que el período de vibración inicial es 0.31 s., y de acuerdo a los datos del problema se tiene:
que corresponde al punto donde la aceleración deja de ser constante. El análisis no lineal estático se lo realizó con el programa CEINCI3 descrito en Aguiar (2003) y entre otros resultados se obtuvo que el período de vibración inicial es 0.31 s., y de acuerdo a los datos del problema se tiene:
Por ser estructura de 4 pisos el valor de ![]() Para determinar
Para determinar ![]() es conveniente calcular
es conveniente calcular ![]() , para ello se considera dato del problema que el peso
, para ello se considera dato del problema que el peso ![]() .
.
| Sismo | |
|
|
|
|
|
|
| Frecuente | 507.2 | 0.549 | 1.238 | 1.14 | 1.469 | 1.0 | 1.750 |
| Ocasional | 710.1 | 0.392 | 1.475 | 1.14 | 2.057 | 1.0 | 2.085 |
| Raro | 1176.0 | 0.237 | 2.425 | 1.19 | 3.403 | 1.0 | 3.578 |
| Muy Raro | 1528.8 | 0.182 | 2.900 | 1.22 | 4.431 | 1.0 | 4.387 |
En la tabla 1.10 se indica: los cuatro sismos de análisis, la aceleración espectral que se encuentra para el período efectivo, el valor de ![]() , se aprecia que únicamente para el sismo frecuente el valor es mayor a 0.4 y para los otros sismos el valor de
, se aprecia que únicamente para el sismo frecuente el valor es mayor a 0.4 y para los otros sismos el valor de ![]() es menor a 0.4 Por lo tanto, para el sismo frecuente se tiene:
es menor a 0.4 Por lo tanto, para el sismo frecuente se tiene:
Para los otros sismos se debe imponer un valor de ductilidad para hallar ![]() , para el sismo ocasional se considera
, para el sismo ocasional se considera ![]() , para el sismo raro
, para el sismo raro ![]() y para el muy raro
y para el muy raro ![]() . Luego para el sismo ocasional se encuentra:
. Luego para el sismo ocasional se encuentra:
Al proceder de igual manera con los sismos raro y muy raro se encuentran los restantes valores de ![]() que se indican en la tabla 1.10.
que se indican en la tabla 1.10.
Por otra parte para las ductilidades indicadas los valores de ![]() son 1.14; 1.19; y 1.22. El primer valor es para ductilidad igual a 2. Se considera el valor 1.14 también para el sismo frecuente.
son 1.14; 1.19; y 1.22. El primer valor es para ductilidad igual a 2. Se considera el valor 1.14 también para el sismo frecuente.
Por ser el valor ![]() >0% el valor de
>0% el valor de ![]() de acuerdo a FEMA-356. Finalmente en la tabla 1.11 se indican en la tercera columna los desplazamientos laterales que se obtienen al aplicar la fórmula recomendada por FEMA. En la cuarta columna se hallan las ductilidades las mismas que se encuentran dividiendo el desplazamiento máximo para el desplazamiento a nivel de fluencia, para el rango elástico
de acuerdo a FEMA-356. Finalmente en la tabla 1.11 se indican en la tercera columna los desplazamientos laterales que se obtienen al aplicar la fórmula recomendada por FEMA. En la cuarta columna se hallan las ductilidades las mismas que se encuentran dividiendo el desplazamiento máximo para el desplazamiento a nivel de fluencia, para el rango elástico ![]() . Se considera que los valores iniciales de
. Se considera que los valores iniciales de ![]() son bastante adecuados por lo que no se recalcula el valor de
son bastante adecuados por lo que no se recalcula el valor de ![]() .
.
| Sismo | |
(cm) |
|
Método del
Espectro de Capacidad (cm) |
| Frecuente | 507.2 | 2.161 | 1.00 | 4.03 |
| Ocasional | 710.1 | 3.604 | 1.29 | 5.64 |
| Raro | 1176.0 | 10.242 | 3.66 | 9.73 |
| Muy Raro | 1528.8 | 16.326 | 5.83 | 12.50 |
En la última columna de la tabla 1.11 se indica los desplazamientos que se obtienen con el Método del Espectro de Capacidad, aplicando el programa CEINCI3, se aprecia que existe una buena correlación con los desplazamientos obtenidos con el Método del Coeficiente de Desplazamiento.
1.12 CONCLUSIONES
Se ha presentado y analizado cada uno de los coeficientes que intervienen en el Método del Coeficiente de Desplazamiento recomendado por la Agencia Federal para el Manejo de Emergencias, FEMA para encontrar el desplazamiento lateral máximo en el tope del edificio ante cargas sísmicas. En este estudio se dan recomendaciones, sobre algunos coeficientes del método, para edificios de hormigón armado conformados por vigas y columnas y se ha indicado una secuencia de cálculo. Del estudio realizado se desprenden las siguientes conclusiones:
REFERENCIAS
- 1. Aguiar R., (2003), Análisis Sísmico por Desempeño, Centro de Investigaciones Científicas. Escuela Politécnica del Ejército, 342 p, Quito.
- 2. Akkar D., and Miranda E., (2005), “Statistical evaluation of approximate methods for estimating maximum deformation demands on existing structures”, Journal of Structures Engineering, 131 (1), 160-172.
- 3. American Society of Civil Engineers, (2000), Pre-standard and commentary for the seismic rehabilitation of buildings, FEMA 356, Federal Emergency Management Agency Washington, D.C.
- 4. Algan B., (1982), Drift and damage considerations in earthquake resistan design of reinforced concrete buildings, Ph.D thesis, University of Illinois, Urbana. Illinois.
- 5. FEMA (1997), NEHRP provisions for the seismic rehabilitation of buildings, Federal Emergency Management Agency. Rep. FEMA 273 (Guidelines) and 274 (Comentary), Washington, D.C.
- 6. Gupta A., and Krawinkler H., (2000), “Dynamic P-Delta effects for flexible inelastic steel structures”, Journal of Structural Engineering, 126 (1), 145-154.
- 7. Lee L., Hang S., and Oh Y., ( 1999) , “Determination of ductility factor considering different hysteretic models”, Earthquake Engineering and Structural Dynamics, 28, 957-977.
- 8. Miranda E., (1991), Seismic upgrading and evaluation of existing buildings, Ph.D. thesis, Dept. of Civil. Engineering., University of California Berkeley, California.
- 9. Miranda E., (1999), “Approximate seismic lateral deformation demands in multistory buildings”, Journal of Structural Engineering, 125 (4), 417-425
- 10. Miranda E., (2000), “Inelastic displacement ratios for structures on firm sites”, Journal of Structural Engineering, 126 (10), 1150-1159.
- 11. Miranda E., (2001), “Estimation of inelastic deformation demands of SDOF systems”, Journal of Structural Engineering, 127 (9), 1005-1012.
- 12. Miranda E., Reyes C., (2002), “Aproximate lateral drift demands in multistory buildings with nonuniform stiffness”, Journal of Structural Engineering, 128 (7), 840-849.
- 13. Nassar A., and Krawinkler H., (1991), “Seismic demands for SDOF and MDOF systems”, John Blume Earthquake Engineering. Ctr. Dept. of Civil Engineering, Rep. 95, Stanford University, Stanford, California.
- 14. Newnark N., and Hall W., (1982), Earthquake Spectra and Design. Earthquake Engineering Research Institute, Berkeley, California.
- 15. Newmark N., and Rosenblueth E., (1971), Fundamentals of Earthquake Engineering, Prentice Hall Inc., Englewood Cliffs, N.J.
- 16. Shimazaki K., and Sozen M., (1984), “Seismic drift of reinforced concrete structures” Res. Rep., Hazama-Gumi Ltd., Tokio, Japan (in Japanese); and draft report (in English).
- 17. UBC (1997), Uniform Building Code, International Conference of Building Officials, ICBO, 3 Vol, Whittier, CA, USA.
- 18. Vidic T., Fajfar P., and Fischinger M., (1994), “Consistent inelastic design spectra: Strength an Displacement”, Earthquake Engineering and Structural Dynamics, 23, 507-521.
- 19. Whittaker A., Constantinou M., and Tsopelas P., (1998), “Displacement estimates for Performance-Based Seismic Design”, Journal of Structural Engineering, 124 (8), 905-912.
CAPÍTULO 2. DERIVA MÁXIMA DE PISO
Se presenta un modelo para evaluar, en forma rápida, la deriva máxima de piso en edificios de hormigón armado conformado por vigas y columnas, se analizan las variables que intervienen y se analiza el probable comportamiento que tendrán edificios de 1 a 10 pisos con demandas de ductilidad entre 1 y 4, situados en la zona de mayor peligrosidad sísmica del Ecuador y en cuatro perfiles de suelo. El modelo está orientado a la evaluación de zonas urbanas.
2.1 ANTECEDENTES
Una variable muy utilizada para correlacionar el daño de una edificación ante terremotos es la deriva de piso ![]() . Por ejemplo, el comité VISION 2000 establece la siguiente correlación. Si
. Por ejemplo, el comité VISION 2000 establece la siguiente correlación. Si ![]() no hay daño en la estructura; si
no hay daño en la estructura; si ![]() el daño que se espera en la estructura es leve; si
el daño que se espera en la estructura es leve; si ![]() el daño en la estructura es moderado; si
el daño en la estructura es moderado; si ![]() el daño en la estructura es extensivo y si
el daño en la estructura es extensivo y si ![]() el daño es completo.
el daño es completo.
Reyes (1999) realizó un acopio de varios trabajos experimentales para correlacionar el daño con la deriva máxima de piso, unos cuantos valores de ese trabajo se indican en la tabla 2.1. Se observa que a mayor ductilidad ![]() de la estructura mayor es la deriva de piso esperado y mayor es el daño. De igual manera se aprecia que las estructuras conformada por una losa plana y columnas no tienen un buen comportamiento sísmico ya que con un valor de
de la estructura mayor es la deriva de piso esperado y mayor es el daño. De igual manera se aprecia que las estructuras conformada por una losa plana y columnas no tienen un buen comportamiento sísmico ya que con un valor de ![]() se tiene un colapso incipiente.
se tiene un colapso incipiente.
Relacionando los valores de la tabla 2.1, con las recomendaciones de VISION 2000, para estructuras de hormigón armado sin muros de corte o contravientos, un daño leve significa que el agrietamiento no es considerable en la estructura. Cuando el agrietamiento es considerable y se ha iniciado la fluencia de la estructura el daño es moderado. El colapso en la tabla 2.1 se aprecia que en marcos dúctiles se inicia en 0.03 y en marcos con ductilidad limitada en 0.015.
En el diseño sísmico de un edificio de Hormigón Armado H.A., el proyectista estructural inicia su labor imponiéndose una ductilidad. Ahora bien, ¿Ante ese valor de ![]() que deriva máxima de piso espera?, este es uno de los objetivos del presente capítulo, para lo cual se indica un modelo para evaluar
que deriva máxima de piso espera?, este es uno de los objetivos del presente capítulo, para lo cual se indica un modelo para evaluar ![]() rápidamente.
rápidamente.
Otra aplicación, se tiene en una construcción existente de H.A., si se desea conocer en forma rápida la deriva máxima ante un sismo representado mediante un espectro. El valor de ![]() dará la pauta sobre la necesidad de reforzar o no el edificio. La forma exacta de hacerlo sería mediante análisis no lineal en tres dimensiones, a lo mejor si es para un solo edificio es factible realizar el análisis no lineal pero si se tiene un gran número de construcciones y se desea establecer la vulnerabilidad de ese conjunto con fines de establecer una prima de seguro no queda otra opción que recurrir a una evaluación rápida como la que aquí se presenta.
dará la pauta sobre la necesidad de reforzar o no el edificio. La forma exacta de hacerlo sería mediante análisis no lineal en tres dimensiones, a lo mejor si es para un solo edificio es factible realizar el análisis no lineal pero si se tiene un gran número de construcciones y se desea establecer la vulnerabilidad de ese conjunto con fines de establecer una prima de seguro no queda otra opción que recurrir a una evaluación rápida como la que aquí se presenta.
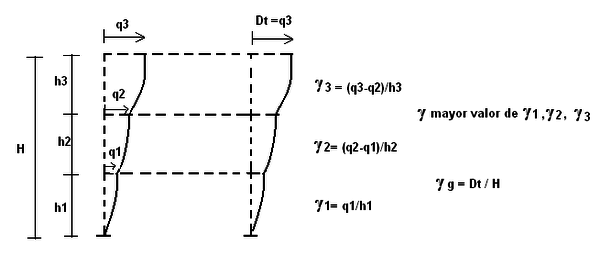
De tal manera que es muy importante conocer, en forma rápida la deriva máxima de piso de un edificio ![]() , para el efecto se presenta en este capítulo dos trabajos, el primero presentado por Miranda (1997) y el segundo el desarrollado por Gupta y Krawinkler (2000,a). El primero está orientado a estructuras de H.A. y el segundo a estructuras de acero. Pero antes de ello conviene repasar que se entiende por deriva de piso, para ello en la figura 2.1 se presenta una estructura deformada por cargas sísmicas y los corrimientos laterales por piso se han identificado con las variables
, para el efecto se presenta en este capítulo dos trabajos, el primero presentado por Miranda (1997) y el segundo el desarrollado por Gupta y Krawinkler (2000,a). El primero está orientado a estructuras de H.A. y el segundo a estructuras de acero. Pero antes de ello conviene repasar que se entiende por deriva de piso, para ello en la figura 2.1 se presenta una estructura deformada por cargas sísmicas y los corrimientos laterales por piso se han identificado con las variables ![]() y
y ![]() .
.
El desplazamiento lateral máximo de piso se denominó en el capítulo anterior como ![]() En consecuencia de acuerdo a la nomenclatura de la figura 2.1 se tiene
En consecuencia de acuerdo a la nomenclatura de la figura 2.1 se tiene ![]() . La deriva de piso
. La deriva de piso ![]() no es más que el desplazamiento relativo de piso dividido para la altura de entrepiso, de tal manera que en cada piso se tiene una deriva y el valor de
no es más que el desplazamiento relativo de piso dividido para la altura de entrepiso, de tal manera que en cada piso se tiene una deriva y el valor de ![]() es el mayor valor de todas las derivas de piso.
es el mayor valor de todas las derivas de piso.
Por otra parte, se define la deriva global ![]() como la relación entre el desplazamiento máximo en el tope
como la relación entre el desplazamiento máximo en el tope ![]() dividida para la altura total del edificio
dividida para la altura total del edificio ![]() .
.
2.1.1 Trabajo de Miranda, 1997
Miranda (1997) propone la siguiente ecuación para calcular la deriva máxima de entrepiso.
|
|
(2.1) |
donde ![]() es un factor de amplificación que permite encontrar el desplazamiento lateral máximo en el tope de un edificio a partir del desplazamiento lateral máximo de un sistema de un grado de libertad, 1 gdl. En el capítulo anterior a este coeficiente FEMA-356 lo denomina
es un factor de amplificación que permite encontrar el desplazamiento lateral máximo en el tope de un edificio a partir del desplazamiento lateral máximo de un sistema de un grado de libertad, 1 gdl. En el capítulo anterior a este coeficiente FEMA-356 lo denomina ![]() ;
; ![]() es un factor de amplificación que permite determinar la deriva máxima de entrepiso a partir de la deriva global de la estructura;
es un factor de amplificación que permite determinar la deriva máxima de entrepiso a partir de la deriva global de la estructura; ![]() es un factor de amplificación que sirve para calcular los desplazamientos laterales máximos inelásticos a partir de los desplazamientos laterales máximos elásticos en el sistema de 1 gdl. En el capítulo anterior a este coeficiente se denominó
es un factor de amplificación que sirve para calcular los desplazamientos laterales máximos inelásticos a partir de los desplazamientos laterales máximos elásticos en el sistema de 1 gdl. En el capítulo anterior a este coeficiente se denominó ![]() ;
; ![]() es un factor que sirve para determinar el cociente entre la deriva máxima de entrepiso y la deriva global pero calculado en una estructura con comportamiento elástico lineal con relación a la misma relación pero calculada con comportamiento inelástico;
es un factor que sirve para determinar el cociente entre la deriva máxima de entrepiso y la deriva global pero calculado en una estructura con comportamiento elástico lineal con relación a la misma relación pero calculada con comportamiento inelástico; ![]() es la altura total del edificio y
es la altura total del edificio y ![]() es el desplazamiento espectral elástico para el período efectivo. En los siguientes apartados se presentará con detalle cada uno de los términos que constan en la ecuación ( 2.1 ).
es el desplazamiento espectral elástico para el período efectivo. En los siguientes apartados se presentará con detalle cada uno de los términos que constan en la ecuación ( 2.1 ).
2.1.2 Trabajo de Gupta y Krawinkler
Gupta y Krawinkler (2000,a) proponen la siguiente ecuación para el cálculo de la deriva máxima global, se indica con la nomenclatura utilizada por ellos.
|
|
(2.2) |
donde ![]() es el factor de amplificación que relaciona el desplazamiento espectral elástico en un sistema de 1 gdl con la deriva global del edificio;
es el factor de amplificación que relaciona el desplazamiento espectral elástico en un sistema de 1 gdl con la deriva global del edificio; ![]() es el factor que relaciona la deriva global elástica con la deriva global inelástica;
es el factor que relaciona la deriva global elástica con la deriva global inelástica; ![]() es el factor de amplificación que toma en cuenta el efecto
es el factor de amplificación que toma en cuenta el efecto ![]() en la deriva global inelástica;
en la deriva global inelástica; ![]() es el factor de modificación que relaciona la deriva de piso con la deriva global. Las restantes variables ya fueron definidas.
es el factor de modificación que relaciona la deriva de piso con la deriva global. Las restantes variables ya fueron definidas.
El trabajo de Gupta y Krawinkler, está orientado a estructuras de acero, se lo presenta con el propósito de ver que coeficientes considera y de alguna manera compararlos con los propuestos por Miranda (1997) no para aplicarlos en estructuras de H.A. pero si para tener más elementos de juicio. Como este trabajo está orientado a estructuras de H.A. a continuación se detalla en forma muy rápida los coeficientes que intervienen en el modelo de Gupta y Krawinkler.
El coeficiente ![]() es similar a
es similar a ![]() . Es más para estructuras de acero cuyo período este alrededor de los 2 segundos o más Gupta y Krawinkler proponen que
. Es más para estructuras de acero cuyo período este alrededor de los 2 segundos o más Gupta y Krawinkler proponen que ![]() , para otros valores de período
, para otros valores de período ![]() . Estructuras de H.A. que tengan un período de 2 segundos o más son edificios muy altos y sería conveniente en dichas estructuras obtener la deriva máxima de piso con procedimientos más exactos.
. Estructuras de H.A. que tengan un período de 2 segundos o más son edificios muy altos y sería conveniente en dichas estructuras obtener la deriva máxima de piso con procedimientos más exactos.
El coeficiente ![]() es similar a
es similar a ![]() que se presentará con detenimiento en apartados posteriores. El coeficiente
que se presentará con detenimiento en apartados posteriores. El coeficiente ![]() no aparece en la ecuación ( 2.1 ), un estudio detallado de este coeficiente en inglés se tiene en Gupta y Krawinkler (2000,b) y en el capítulo anterior se presentan las ecuaciones de cálculo siguientes:
no aparece en la ecuación ( 2.1 ), un estudio detallado de este coeficiente en inglés se tiene en Gupta y Krawinkler (2000,b) y en el capítulo anterior se presentan las ecuaciones de cálculo siguientes:
|
|
(2.3) |
donde el subíndice i representa el piso; ![]() es la carga vertical actuante desde el piso i hasta el tope del edificio;
es la carga vertical actuante desde el piso i hasta el tope del edificio; ![]() es el desplazamiento relativo del piso
es el desplazamiento relativo del piso ![]() ;
; ![]() es el cortante del piso
es el cortante del piso ![]() ;
; ![]() es la altura del entrepiso
es la altura del entrepiso ![]() . Para cada piso se debe evaluar
. Para cada piso se debe evaluar ![]() y con el mayor valor se determina
y con el mayor valor se determina ![]() .
.
El coeficiente ![]() es similar a
es similar a ![]() . Como se habrá podido apreciar son muy parecidas las dos ecuaciones. Como se indicó, en los siguientes apartados se presentará con detalle los coeficientes de la ecuación propuesta por Miranda (1997) pero antes de ello es conveniente tratar sobre el cálculo del período fundamental, con el propósito de ver si se aplica este período en lugar de calcular el período efectivo, que como se vio en el capítulo anterior se requiere de un programa de computación para obtener la curva de capacidad sísmica resistente, empleando la técnica del pushover, lo cual demanda tiempo.
. Como se habrá podido apreciar son muy parecidas las dos ecuaciones. Como se indicó, en los siguientes apartados se presentará con detalle los coeficientes de la ecuación propuesta por Miranda (1997) pero antes de ello es conveniente tratar sobre el cálculo del período fundamental, con el propósito de ver si se aplica este período en lugar de calcular el período efectivo, que como se vio en el capítulo anterior se requiere de un programa de computación para obtener la curva de capacidad sísmica resistente, empleando la técnica del pushover, lo cual demanda tiempo.
2.2 PERÍODO FUNDAMENTAL
La filosofía del artículo es evaluar la deriva máximo de piso de una manera rápida, razón por la cual no tiene sentido evaluar el período de una estructura resolviendo el problema de vibración libre sin amortiguamiento a más que demanda tiempo ya que se debe determinar la matriz de rigidez y de masas del sistema, el resultado no es “exacto” ya que no se toma en cuenta los elementos no estructurales, la interacción suelo estructura y sobre todo la acción sísmica. En efecto la acción sísmica si influye en el cálculo del período fundamental como lo han demostrado Goel y Chopra (1997) y esto se desea traer a colocación en el presente apartado.
Algunos códigos recomiendan el cálculo del período fundamental ![]() con expresiones que han sido obtenidas de registros sísmicos en varios edificios, como los indicados en la tabla 2.2, que tiene la particularidad de que estos registros tuvieron una aceleración máxima del suelo mayor a 0.15 g., siendo g., la aceleración de la gravedad, de tal manera que los edificios en los cuales fueron registrados superaron el punto de agrietamiento pero no el de fluencia.
con expresiones que han sido obtenidas de registros sísmicos en varios edificios, como los indicados en la tabla 2.2, que tiene la particularidad de que estos registros tuvieron una aceleración máxima del suelo mayor a 0.15 g., siendo g., la aceleración de la gravedad, de tal manera que los edificios en los cuales fueron registrados superaron el punto de agrietamiento pero no el de fluencia.
Los datos de la tabla 2.2 se encuentran en Goel y Chopra (1997) y fueron registrados en edificios de H.A. conformados por vigas y columnas. En la referencia indicada, se tiene un total de 68 valores de período e incluyen a registros con aceleraciones del suelo menores a 0.15 g., en la tabla 2.2 se anotaron los registros que superan 0.15 g. Con estos datos y con un análisis de regresión encuentran que la ecuación que mejor se ajusta, es la siguiente:
|
|
(2.4) |
La relación encontrada por Goel y Chopra reporta valores superiores de período en relación a la recomendada por el UBC-97 y que ha sido acogida por varios códigos. La ecuación del UBC-97 para edificios de H.A. conformada por vigas y columnas es:
|
|
(2.5) |
En la figura 2.1 se presentan los períodos encontrados en edificios cuya aceleración máxima del suelo fue superior a 0.15 g., y que constan en la tabla 2.2, con una línea continua se han unido los períodos longitudinal y transversal. Se ha dibujado además la curva que se obtiene con la ecuación (2.4) y la que se halla con la ecuación (2.5). Esta última se identifica con el título de “códigos”. Se aprecia que mejor se ajusta la ecuación propuesta por Goel y Chopra; la misma tendencia se tiene con los 68 valores de períodos con los cuales obtuvieron la relación entre la altura del edificio ![]() , y el período fundamental T.
, y el período fundamental T.
En las ecuaciones (2.4) y (2.5) la altura H debe expresarse en pies, si se desea colocar en metros estas ecuaciones cambian a:
|
|
(2.6) |
Existen algunos trabajos, para obtener el período fundamental en función de la altura del edificio o del número de pisos. Para el efecto, han trabajado con vibración ambiental, con vibración forzada o a partir de los registros sísmicos. Solo dos de las conclusiones de estos estudios, se resumen a continuación:
- 1. Miranda (1991) encontró que el período fundamental obtenido a partir de registros sísmicos es mayor que el período fundamental encontrado por vibración ambiental
 , es mayor en un 33% aproximadamente. Esto se debe a que con vibración ambiental, los elementos no estructurales no intervienen a diferencia de lo que sucede cuando actúa un sismo. Miranda (1991) encontró la siguiente relación:
, es mayor en un 33% aproximadamente. Esto se debe a que con vibración ambiental, los elementos no estructurales no intervienen a diferencia de lo que sucede cuando actúa un sismo. Miranda (1991) encontró la siguiente relación: 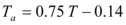 donde
donde  es el período encontrado a partir de registros sísmicos.
es el período encontrado a partir de registros sísmicos.
- 2. Midorikawa (1990) presenta las siguientes fórmulas para hallar el período fundamental:
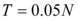 , para Chile en que las estructuras son a base de muros de corte;
, para Chile en que las estructuras son a base de muros de corte; 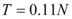 para México en estructuras sin muros de corte con vigas y columnas;
para México en estructuras sin muros de corte con vigas y columnas; 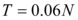 para Japón en que los edificios incluyen muros de corte.
para Japón en que los edificios incluyen muros de corte.
Para tomar en cuenta la variación del período que se puede tener al utilizar una determinada ecuación, es conveniente trabajar por lo menos con tres ecuaciones de períodos y hallar un rango de variación de la deriva de entrepiso y un valor medio de la misma.
Adelantando resultados, que se presentarán en capítulos posteriores, se destaca que la deriva máxima de piso que se halla con la ecuación (2.1) o similares, depende radicalmente del período que se utiliza. De tal forma que se debe tener especial cuidado, en la selección de la o las ecuaciones, que se utilicen en la evaluación del período. FEMA-356 indica que se calcule con el período efectivo pero esto demanda un tiempo considerable en preparar los datos para encontrar la curva de capacidad sísmica resistente.
2.3 ANÁLISIS DE LOS COEFICIENTES
En este apartado se analizan los coeficientes ![]() y
y ![]() que intervienen en la ecuación ( 2.1 ). Se destaca que en los siguientes capítulos de este libro se presentará el resultado de la investigación realizada en el Centro de Investigaciones Científicas de la ESPE para calcular
que intervienen en la ecuación ( 2.1 ). Se destaca que en los siguientes capítulos de este libro se presentará el resultado de la investigación realizada en el Centro de Investigaciones Científicas de la ESPE para calcular ![]() ,
, ![]() y
y ![]() en base a la forma de construir en el Ecuador y ante sismos registrados en Colombia, Ecuador, Perú, Chile y Argentina.
en base a la forma de construir en el Ecuador y ante sismos registrados en Colombia, Ecuador, Perú, Chile y Argentina.
Sea ![]() el desplazamiento lateral máximo en el tope del edificio y sea
el desplazamiento lateral máximo en el tope del edificio y sea ![]() el desplazamiento lateral máximo en el sistema de 1 gdl., la relación entre estas dos variables viene dada por el factor
el desplazamiento lateral máximo en el sistema de 1 gdl., la relación entre estas dos variables viene dada por el factor ![]() , de la siguiente manera:
, de la siguiente manera:
Miranda y Reyes (2002) a partir de la solución de un sistema continuo, de una viga de corte acoplado a una viga de flexión, encuentran las ecuaciones que permiten calcular ![]() para diferentes valores de
para diferentes valores de ![]() . En base a estas ecuaciones en el capítulo anterior se trabajó con los valores de
. En base a estas ecuaciones en el capítulo anterior se trabajó con los valores de ![]() indicados en la tabla 2.3.
indicados en la tabla 2.3.
| Piso | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| |
1.00 | 1.06 | 1.15 | 1.24 | 1.32 | 1.38 | 1.43 | 1.48 | 1.51 | 1.55 |
Los valores de la tabla 2.3 se obtienen reemplazando ![]() en las ecuaciones desarrolladas por Miranda y Reyes (2002) para el caso de sección constante. El valor de
en las ecuaciones desarrolladas por Miranda y Reyes (2002) para el caso de sección constante. El valor de ![]() viene definido por:
viene definido por:
siendo ![]() la rigidez al corte y
la rigidez al corte y ![]() la rigidez a flexión. Los ejercicios que se desarrollan en este capítulo se hacen en base a los valores indicados en la tabla 2.3. En el siguiente capítulo se verá que para las construcciones de Ecuador, son muy bajos los valores de la tabla 2.3 para edificios de 1 a 6 pisos.
la rigidez a flexión. Los ejercicios que se desarrollan en este capítulo se hacen en base a los valores indicados en la tabla 2.3. En el siguiente capítulo se verá que para las construcciones de Ecuador, son muy bajos los valores de la tabla 2.3 para edificios de 1 a 6 pisos.
Sea ![]() la deriva global del edificio, en donde
la deriva global del edificio, en donde ![]() es el desplazamiento lateral máximo en el tope del edificio y
es el desplazamiento lateral máximo en el tope del edificio y ![]() la altura total del edificio y sea:
la altura total del edificio y sea: ![]()
|
|
(2.8) |
donde ![]() es la deriva del piso j definida como la relación entre el desplazamiento relativo de piso con relación a la altura de piso
es la deriva del piso j definida como la relación entre el desplazamiento relativo de piso con relación a la altura de piso ![]() . El desplazamiento relativo, es igual al desplazamiento en el piso j+1 que se ha denominado
. El desplazamiento relativo, es igual al desplazamiento en el piso j+1 que se ha denominado ![]() menos el desplazamiento del piso j, identificada por
menos el desplazamiento del piso j, identificada por ![]() . Miranda (1999) al trabajar con un sistema continuo, determina en forma aproximada la deriva de piso j como la derivada de la función desplazamiento con respecto a la variable z como se indica en la ecuación ( 2.8 ). La variable
. Miranda (1999) al trabajar con un sistema continuo, determina en forma aproximada la deriva de piso j como la derivada de la función desplazamiento con respecto a la variable z como se indica en la ecuación ( 2.8 ). La variable ![]() se mide desde la base del edificio. Con esta notación se tiene:
se mide desde la base del edificio. Con esta notación se tiene:
|
|
(2.9) |
Por lo tanto ![]() , es un factor que transforma la deriva global de un edificio, en la deriva de piso. Al tener en cuenta la ecuación ( 2.8 ) en que la deriva de piso es la derivada, se obtiene de la ecuación ( 2.9 ) el valor de
, es un factor que transforma la deriva global de un edificio, en la deriva de piso. Al tener en cuenta la ecuación ( 2.8 ) en que la deriva de piso es la derivada, se obtiene de la ecuación ( 2.9 ) el valor de ![]() pero lo que interesa es el valor máximo de la deriva de piso, razón por la cual:
pero lo que interesa es el valor máximo de la deriva de piso, razón por la cual:
|
|
(2.10) |
Para el caso de sección constante, Miranda y Reyes (2002) reportan una solución analítica y para los casos de sección variable la solución debe obtenerse con la ayuda del ordenador. En la tabla 2.4 se indican algunos valores de ![]() para el caso de carga triangular en función del parámetro
para el caso de carga triangular en función del parámetro ![]() , que relaciona la rigidez lateral en el tope del edificio con relación a la rigidez lateral en la base del edificio.
, que relaciona la rigidez lateral en el tope del edificio con relación a la rigidez lateral en la base del edificio.
| |
|
|
| |
| |
1.39 | 1.34 | 1.28 | 1.24 |
| |
1.46 | 1.40 | 1.33 | 1.25 |
Si el proyectista estructural no calcula ![]() ni
ni ![]() puede considerar
puede considerar ![]() en forma aproximada.
en forma aproximada.
Existen varias propuestas para el factor ![]() para pasar los desplazamientos laterales máximos elásticos a los desplazamientos laterales máximos inelásticos. Uno de esos trabajos es el recomendado por Miranda (2000) el mismo que se indica a continuación:
para pasar los desplazamientos laterales máximos elásticos a los desplazamientos laterales máximos inelásticos. Uno de esos trabajos es el recomendado por Miranda (2000) el mismo que se indica a continuación:
|
|
(2.11) |
donde ![]() es la demanda de ductilidad y
es la demanda de ductilidad y ![]() es el período de vibración del sistema de 1gdl. En el capítulo anterior se presentó el origen de ésta ecuación. La ecuación (2.11) es el resultado del análisis de sistemas de 1 gdl., ante 264 acelerogramas, de sismos registrados en los Estados Unidos de Norte América.
es el período de vibración del sistema de 1gdl. En el capítulo anterior se presentó el origen de ésta ecuación. La ecuación (2.11) es el resultado del análisis de sistemas de 1 gdl., ante 264 acelerogramas, de sismos registrados en los Estados Unidos de Norte América.
La ecuación (2.11) permite encontrar el factor ![]() en función de la ductilidad
en función de la ductilidad ![]() . Desde un punto de vista, de diseño sísmico por desempeño, el proyectista puede conocer que deriva máxima de piso espera en un edificio para una determinada demanda de ductilidad y con esa deriva de piso a priori saber el grado de daño, como se vio en el apartado 2.1.
. Desde un punto de vista, de diseño sísmico por desempeño, el proyectista puede conocer que deriva máxima de piso espera en un edificio para una determinada demanda de ductilidad y con esa deriva de piso a priori saber el grado de daño, como se vio en el apartado 2.1.
Otras ecuaciones para el cálculo de ![]() son las recomendadas por FEMA 273 y FEMA 356 que se indicaron en el capítulo anterior.
son las recomendadas por FEMA 273 y FEMA 356 que se indicaron en el capítulo anterior.
![]() es un factor que permite calcular, el cociente entre la relación de la deriva máxima de entrepiso y la deriva global, en una estructura con comportamiento inelástico con respecto a la relación de la deriva máxima de entrepiso y la deriva global, en una estructura con comportamiento elástico. En otras palabras es el parámetro
es un factor que permite calcular, el cociente entre la relación de la deriva máxima de entrepiso y la deriva global, en una estructura con comportamiento inelástico con respecto a la relación de la deriva máxima de entrepiso y la deriva global, en una estructura con comportamiento elástico. En otras palabras es el parámetro ![]() calculado en forma inelástica con relación a este mismo parámetro obtenido en forma elástica.
calculado en forma inelástica con relación a este mismo parámetro obtenido en forma elástica.
|
|
(2.12) |
Ante un sismo la distribución de fuerzas en altura es diferente si se lo analiza con comportamiento elástico a que si se lo analiza con comportamiento inelástico y consecuentemente serán diferentes sus distorsiones. El factor ![]() depende de la ductilidad
depende de la ductilidad ![]() y del número de pisos
y del número de pisos ![]() .
.
|
|
(2.13) |
2.3.5 Comentarios a la Ecuación propuesta por Miranda
Sea ![]() el desplazamiento lateral máximo en un edificio y
el desplazamiento lateral máximo en un edificio y ![]() la deriva máxima que se espera en algún piso de la estructura, de acuerdo al modelo presentado se tiene:
la deriva máxima que se espera en algún piso de la estructura, de acuerdo al modelo presentado se tiene:
De esta manera se ha demostrado la ecuación (2.1). Ahora bien si se compara está ecuación con la propuesta por Gupta y Krawinkler se aprecia que falta un factor que tome en cuenta el efecto ![]() , su evaluación se debe realizar con la ecuación (2.3) que demanda conocer un poco más a la estructura y a lo mejor no está en la filosofía de evaluación rápida de la deriva máxima de piso.
, su evaluación se debe realizar con la ecuación (2.3) que demanda conocer un poco más a la estructura y a lo mejor no está en la filosofía de evaluación rápida de la deriva máxima de piso.
Un factor que si hay como incorporar en la ecuación (2.1) es el efecto del deterioro de rigidez en la descarga, el deterioro de resistencia y el efecto de cierre de grietas, todo esto debido al comportamiento no lineal. La mayor parte de estudios que se han realizado para obtener ![]() no consideran estos efectos en el modelo constitutivo del material. El trabajo de Miranda (2000) por ejemplo solo considera incremento de rigidez post fluencia en el modelo. De tal manera, que se propone, que la ecuación para el cálculo de
no consideran estos efectos en el modelo constitutivo del material. El trabajo de Miranda (2000) por ejemplo solo considera incremento de rigidez post fluencia en el modelo. De tal manera, que se propone, que la ecuación para el cálculo de ![]() sea:
sea:
|
|
(2.14) |
Lee et al (1999) en base al estudio del efecto de los modelos de histéresis de sistemas de 1 gdl ante la acción de 40 sismos, encuentra cual es el efecto de considerar: incremento de rigidez pos fluencia en el modelo con relación a los resultados que se obtienen con el modelo Elasto Perfectamente Plástico EPP, el efecto de considerar deterioro de la rigidez en la descarga con relación al modelo EPP, efecto del deterioro de resistencia con relación al EPP y efecto de cierre de grietas con relación al EPP. En base a los valores medios de los últimos tres efectos, en el capítulo anterior se recomendó los valores de ![]() que se indican en la tabla 2.5.
que se indican en la tabla 2.5.
| Ductilidad | 1 | 2 | 3 | 4 | 5 | 6 |
| |
1.00 | 1.14 | 1.17 | 1.19 | 1.22 | 1.23 |
2.4 APLICACIÓN
Se calculan las distorsiones máximas de piso, que se esperan en estructuras de 1 a 10 pisos de H.A., conformadas por vigas y columnas; si estas se encuentran en la zona de mayor peligrosidad sísmica del Ecuador que está definida por un valor ![]() La altura de cada entrepiso es de 3.0 m. El cálculo se realiza para valores de ductilidad de 1 a 4. Se considera que las estructuras se hallan en cada uno, de los cuatro perfiles de suelo que estipula el Código Ecuatoriano de la Construcción CEC-2000. Las ecuaciones que definen el espectro elástico, del CEC-2000, son las siguientes y la forma del espectro se indica en la figura 2.2
La altura de cada entrepiso es de 3.0 m. El cálculo se realiza para valores de ductilidad de 1 a 4. Se considera que las estructuras se hallan en cada uno, de los cuatro perfiles de suelo que estipula el Código Ecuatoriano de la Construcción CEC-2000. Las ecuaciones que definen el espectro elástico, del CEC-2000, son las siguientes y la forma del espectro se indica en la figura 2.2
|
|
(2.15) | |
| (2.16) | ||
| (2.17) |
Donde: ![]() es el coeficiente de importancia,
es el coeficiente de importancia, ![]() es el factor de amplificación de la respuesta dinámica,
es el factor de amplificación de la respuesta dinámica, ![]() es el factor de amplificación por efecto del perfil de suelo,
es el factor de amplificación por efecto del perfil de suelo, ![]() es la aceleración máxima de suelo que se obtiene de estudios de peligrosidad sísmica para un período de retorno de 475 años. Los valores de
es la aceleración máxima de suelo que se obtiene de estudios de peligrosidad sísmica para un período de retorno de 475 años. Los valores de ![]() y
y ![]() se indican en la tabla 2.6. En el presente apartado el período fundamental se obtiene aplicando la ecuación propuesta por Goel y Chopra (1997).
se indican en la tabla 2.6. En el presente apartado el período fundamental se obtiene aplicando la ecuación propuesta por Goel y Chopra (1997).
| Perfil de suelo | |
|
|
|
| S1 | 0.50 | 2.50 | 2.5 | 1.0 |
| S2 | 0.52 | 3.11 | 3.0 | 1.2 |
| S3 | 0.82 | 4.59 | 2.8 | 1.5 |
| S4 | 2.00 | 10.00 | 2.5 | 2.0 |
En la figura 2.3 se presentan los resultados obtenidos al utilizar la ecuación ( 2.1 ), la curva inferior de cada uno de los gráficos corresponde a ![]() y la superior a
y la superior a ![]() . Del análisis de esta gráfica se desprende:
. Del análisis de esta gráfica se desprende:
- Las menores distorsiones de piso se presentan en suelo S1, luego S2, S3 y S4.
- En un perfil de suelo S1 y S2 el daño que se espera en la estructura, de acuerdo a VISION 2000, es moderado.
- En perfil de suelo S3 las edificaciones menores a 6 pisos presentan un daño moderado en la estructura y las de 7 pisos o más el daño es extensivo. El comentario es similar en un perfil de suelo S4 pero a partir de los 8 pisos el daño es extensivo.
2.5 INFLUENCIA DEL PERÍODO
Para ver la influencia que tiene la fórmula que se utiliza para evaluar el período fundamental en la deriva máxima de piso; en la figura 2.4, se presentan los resultados que se obtuvieron en un perfil de suelo S2 y para una demanda de ductilidad de 3. En las figuras, en lugar de escribir deriva máxima de piso se ha escrito drift.
Las ecuaciones utilizadas para encontrar el período son: ![]() propuesta por Goel y Chopra (1997);
propuesta por Goel y Chopra (1997); ![]() recomendada por el UBC-97;
recomendada por el UBC-97; ![]() obtenida experimentalmente en México y
obtenida experimentalmente en México y ![]() muy utilizada en varios lugares. Todas estas fórmulas son recomendadas para estructuras de H.A., conformadas por vigas y columnas, sin muros de corte. Del análisis de la figura 2.4 se desprende lo siguiente:
muy utilizada en varios lugares. Todas estas fórmulas son recomendadas para estructuras de H.A., conformadas por vigas y columnas, sin muros de corte. Del análisis de la figura 2.4 se desprende lo siguiente:
- Existe gran dispersión en las distorsiones de piso obtenidas con las diferentes fórmulas, especialmente para estructuras menores a 5 pisos.
La ecuación propuesta por Goel y Chopra (1997) aproximadamente reporta valores medios, en relación a las otras curvas, como se aprecia en la figura 2.5 en que se ha dibujado la curva que se obtiene con los cuatro valores de períodos y se observa que prácticamente coincide con la curva que se obtiene al utilizar la ecuación de Goel y Chopra (1997). Un resultado similar se encontró con los restantes perfiles de suelo y demandas de ductilidad.
2.6 INPORTANCIA DE INCORPORAR 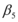
En el capítulo 13 de Aguiar (2003) se analiza el comportamiento sísmico de la estructura de 3 pisos, indicada en la figura 2.6, empleando el Método del Espectro de Capacidad. Esta estructura, se halla ubicada en la zona de mayor peligrosidad sísmica del Ecuador y sobre un suelo tipo S2.
La deriva máxima de piso que se obtiene por el Método del Espectro de Capacidad es ![]() y tiene una demanda de ductilidad
y tiene una demanda de ductilidad ![]() , para el sentido X-X que es el más crítico. Ahora bien, se desea encontrar en forma aproximada la deriva máxima de piso, utilizando la figura 2.3 para suelo tipo S2. Infiriendo el valor, para
, para el sentido X-X que es el más crítico. Ahora bien, se desea encontrar en forma aproximada la deriva máxima de piso, utilizando la figura 2.3 para suelo tipo S2. Infiriendo el valor, para ![]() se halla que la deriva máxima de piso es
se halla que la deriva máxima de piso es ![]() .
.
En la tabla 2.5, el valor de ![]() para ductilidad 4 es 1.19. Por lo tanto, si se multiplica este valor por 0.009 se obtiene
para ductilidad 4 es 1.19. Por lo tanto, si se multiplica este valor por 0.009 se obtiene ![]() que se aproxima bastante al valor encontrado de
que se aproxima bastante al valor encontrado de ![]() .
.
2.7 CONCLUSIONES
Se ha presentado un modelo para evaluar, en forma rápida, la deriva máxima de piso en edificios de Hormigón Armado, conformado por vigas y columnas y se lo ha aplicado al Ecuador, en estructuras de 1 a 10 pisos situadas en cuatro perfiles de suelo y el cálculo se realizó para demandas de ductilidad que varían entre 1 y 4. Del estudio realizado, se desprenden las siguientes conclusiones.
- El modelo cumple con su objetivo de tener una idea rápida del probable desempeño sísmico de una estructura y puede ser utilizada para un diagnóstico preliminar de estructuras existentes o para tener una visión del probable desempeño de una estructura que se está diseñando.
- La ecuación para calcular el período fundamental propuesta por Goel y Chopra es una buena opción para ser aplicable en estructuras de H.A., conformada por vigas y columnas en el Ecuador. Los resultados que se obtuvieron prácticamente son valores medios a los que se obtienen con otras relaciones que también son aplicables a la tipología mencionada.
REFERENCIAS
- 20. Aguiar R., (2003), Análisis Sísmico por Desempeño, Centro de Investigaciones Científicas. Escuela Politécnica del Ejército, 342 p, Quito.
- 21. Algan B., (1982), Drift and damage considerations in earthquake resistan design of reinforced concrete buildings, Ph.D thesis, University of Illinois, Urbana. Illinois.
- 22. American Society of Civil Engineers, (2000), Pre-standard and commentary for the seismic rehabilitation of buildings, FEMA 356, Federal Emergency Management Agency Washington, D.C.
- 23. FEMA (1997), NEHRP provisions for the seismic rehabilitation of buildings, Federal Emergency Management Agency. Rep. FEMA 273 (Guidelines) and 274 (Comentary), Washington, D.C.
- 24. Goel R., and Chopra A., (1997), “Period formulas for moment-resisting frame buildings”, Journal of Structural Engineering, 123 (11), 1454-1461.
- 25. Gupta A., and Krawinkler H., (2000,a), “Estimation of seismic drift demands for frame structures”, Earthquake Engineering and Structural Dynamics, 28, 1287-1305.
- 26. Gupta A., and Krawinkler H., (2000,b), “Dynamic P-Delta effects for flexible inelastic steel structures”, Journal of Structural Engineering, 126 (1), 145-154.
- 27. Lee L., Hang S., and Oh Y., ( 1999) , “Determination of ductility factor considering different hysteretic models”, Earthquake Engineering and Structural Dynamics, 28, 957-977.
- 28. Midorikawa S., (1990), Ambient vibration test of building in Santiago and Viña del Mar, Report on the Chile-Japan Joint study project on seismic design of structures. Pontificia Universidad Católica de Chile, Escuela de Ingeniería, Departamento de Ingeniería Estructural, Santiago, Chile.
- 29. Miranda E., (1997), “Estimation of maximum interstory drift demands in displacement-based design” Seismic design methodologies for the next generation of codes, Krawinkler H., and Fajfar P., editor, Balkema.
- 30. Miranda E., (1999), “Approximate seismic lateral deformation demands in multistory buildings”, Journal of Structural Engineering, 125 (4), 417-425
- 31. Miranda E., (2000), “Inelastic displacement ratios for structures on firm sites”, Journal of Structural Engineering, 126 (10), 1150-1159.
- 32. Miranda E., (2001), “Estimation of inelastic deformation demands of SDOF systems”, Journal of Structural Engineering, 127 (9), 1005-1012.
- 33. Miranda E., Reyes C., (2002), “Aproximate lateral drift demands in multistory buildings with nonuniform stiffness”, Journal of Structural Engineering, 128 (7), 840-849.
- 34. Reyes C., (1999), El estado límite de servicio en el diseño sísmico de edificios, Tesis Doctoral. División de estudios de postgrado de la Facultad de Ingeniería, Universidad Nacional Autónoma de México, México D.F.
- 35. SEAOC (1995), Vision 2000 Report on performance based seismic engineering of buildings, Structural Engineers Association of California, Volume I, Sacramento.
- 36. UBC (1997), Uniform Building Code, International Conference of Building Officials, ICBO, 3 Vol, Whittier, CA, USA.
CAPÍTULO 3 PARÁMETRO 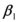
Se presentan los resultados del cálculo del parámetro ![]() en 60 estructuras de hormigón armado de dos y tres vanos y de uno a seis pisos, de hormigón armado y se comparan los resultados, con los que se obtienen de la solución de una viga de flexión acoplada a una viga de corte de sección constante; lo propio se hace con el modelo anterior pero de sección variable. Se comparan además con los recomendados por FEMA 356. En base a todo este estudio se recomiendan valores de
en 60 estructuras de hormigón armado de dos y tres vanos y de uno a seis pisos, de hormigón armado y se comparan los resultados, con los que se obtienen de la solución de una viga de flexión acoplada a una viga de corte de sección constante; lo propio se hace con el modelo anterior pero de sección variable. Se comparan además con los recomendados por FEMA 356. En base a todo este estudio se recomiendan valores de ![]() a ser utilizados en la evaluación de la deriva máxima de piso de edificios de hormigón armado.
a ser utilizados en la evaluación de la deriva máxima de piso de edificios de hormigón armado.
3.1 ANTECEDENTES
En el capítulo anterior se estudió y se propuso el cálculo de la deriva máxima de piso, en edificios de hormigón armado, con la siguiente ecuación.
|
|
(3.1) |
Miranda (1997) propuso la ecuación (3.1) sin el parámetro ![]() . Ahora a partir de este capítulo, se va a presentar los trabajos desarrollados en el Centro de Investigaciones Científicas, CEINCI, de la Escuela Politécnica del Ejército para determinar cada uno de los parámetros que intervienen en la ecuación (3.1) en base a la forma como se construye en el Ecuador, a los materiales que se emplean y sobre todo a los sismos registrados en América Latina.
. Ahora a partir de este capítulo, se va a presentar los trabajos desarrollados en el Centro de Investigaciones Científicas, CEINCI, de la Escuela Politécnica del Ejército para determinar cada uno de los parámetros que intervienen en la ecuación (3.1) en base a la forma como se construye en el Ecuador, a los materiales que se emplean y sobre todo a los sismos registrados en América Latina.
Lastimosamente, se dispone de muy pocos acelerogramas de eventos sísmicos registrados en el Ecuador, a pesar de que en el País, se han registrado sismos muy fuertes como el del 4 de agosto de 1998 que afectó a Bahía de Caráquez y que tuvo una magnitud de 7.1, de acuerdo a la Red Sísmica del Austro, Aguiar et al (1998). O el sismo del 2 de octubre de 1995, que causó el colapso del puente colgante sobre el río Upano, fue un sismo superficial de magnitud 6.8. Aguiar (2000). De estos dos sismos, que son recientes, se dispone de un acelerograma cuya aceleración máxima del suelo es menor a 0.10 g.
Habría sido interesante realizar la investigación exclusivamente con sismos registrados en el Ecuador, pero ante esta carencia se decidió trabajar con acelerogramas de sismos registrados en Colombia, Perú, Chile y Argentina; con una condición, cual es, que la aceleración máxima del registro sea mayor al 10% de la aceleración de la gravedad. De Ecuador se consideró un solo registro por lo anotado en el párrafo anterior.
Volviendo al tema central, se debe manifestar que en los últimos cinco años del siglo XX, en los Estados Unidos de Norte América se presentaron varios trabajos para evaluar en forma rápida la deriva máxima de piso de edificios de hormigón armado. Lo que se ha hecho es transferencia de conocimientos es así como en los dos primeros capítulos de este libro se presentó el estado del arte sobre este tema.
Pero no podemos aplicar esas investigaciones realizadas en países de gran liderazgo científico sin adaptarlo a la realidad ecuatoriana. Por este motivo cada uno de los parámetros que intervienen en la ecuación ( 3.1 ) han sido investigados en el CEINCI-ESPE y se proponen ecuaciones o valores para ser utilizados en la evaluación de la deriva máxima de piso de edificios de hormigón armado sin muros de corte de 1 a 6 pisos.
3.2 TRABAJOS REALIZADOS
El parámetro ![]() permite obtener el desplazamiento lateral máximo en un sistema de múltiples grados de libertad a partir del desplazamiento lateral máximo en un sistema de 1 gdl., y se encuentra con la siguiente ecuación.
permite obtener el desplazamiento lateral máximo en un sistema de múltiples grados de libertad a partir del desplazamiento lateral máximo en un sistema de 1 gdl., y se encuentra con la siguiente ecuación.
|
|
(3.2) |
Donde ![]() es la masa del nivel i;
es la masa del nivel i; ![]() es la ordenada de la forma modal fundamental en el nivel i;
es la ordenada de la forma modal fundamental en el nivel i; ![]() es el número de pisos;
es el número de pisos; ![]() es la amplitud del modo fundamental en la azotea. La ecuación (3.2) fue presentada en el capítulo 1 como ecuación ( 1.2 ). Otra forma de escribir es:
es la amplitud del modo fundamental en la azotea. La ecuación (3.2) fue presentada en el capítulo 1 como ecuación ( 1.2 ). Otra forma de escribir es:
|
|
(3.3) |
Siendo ![]() el modo de vibración uno;
el modo de vibración uno; ![]() es la matriz de masas,
es la matriz de masas, ![]() es un vector que para el caso plano es unitario y
es un vector que para el caso plano es unitario y ![]() fue indicado en el párrafo anterior. De tal manera que
fue indicado en el párrafo anterior. De tal manera que ![]() no es más que el factor de participación del modo uno multiplicado por
no es más que el factor de participación del modo uno multiplicado por ![]() .
.
| Número
de pisos |
Valor de |
| 1 | 1.0 |
| 2 | 1.2 |
| 3 | 1.3 |
| 5 | 1.4 |
| Más de 10 pisos | 1.5 |
En el capítulo 1 también se manifestó que FEMA-356 recomienda los valores indicados en la tabla 3.1 para edificios de hormigón armado sin muros de corte.
Por otra parte, en capítulos anteriores, se mostró la ecuación propuesta por Algan (1982) para calcular ![]() , la misma que fue obtenida a partir de una viga de corte acoplada a una de flexión pero de sección constante. Esta ecuación es:
, la misma que fue obtenida a partir de una viga de corte acoplada a una de flexión pero de sección constante. Esta ecuación es:
|
|
(3.4) |
Donde ![]() es el número de pisos. De igual forma en los capítulos anteriores, se presentó los valores de
es el número de pisos. De igual forma en los capítulos anteriores, se presentó los valores de ![]() que se obtienen al aplicar las ecuaciones deducidas por Miranda y Reyes ( 2002 ) para un valor de
que se obtienen al aplicar las ecuaciones deducidas por Miranda y Reyes ( 2002 ) para un valor de ![]() . El parámetro
. El parámetro ![]() se halla con la siguiente ecuación.
se halla con la siguiente ecuación.
|
|
(3.5) |
Siendo ![]() la rigidez al corte y
la rigidez al corte y ![]() la rigidez a flexión. El trabajo de Miranda y Reyes (2002) es para una viga de flexión acoplada a una viga de corte pero de sección variable.
la rigidez a flexión. El trabajo de Miranda y Reyes (2002) es para una viga de flexión acoplada a una viga de corte pero de sección variable.
3.3 CÁLCULO DE 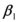
Se analizaron 6 estructuras de 1 a 6 pisos con la configuración en planta indicada en la figura 3.1, que tiene dos vanos en cada dirección, con luces de 4.0 m., y altura de entrepiso de 3 metros. Se utilizó un hormigón, con una resistencia máxima a la compresión de 21 MPa.
El coeficiente de elasticidad se obtuvo con la siguiente expresión: ![]() . El valor de
. El valor de ![]() se encontró en forma aproximada, utilizando la siguiente expresión:
se encontró en forma aproximada, utilizando la siguiente expresión: ![]() .
.
Adicionalmente, se analizaron 54 estructuras de 1 a 6 pisos con la distribución en planta mostrada en la figura 3.2. En este caso, se tiene 3 vanos en cada dirección de 5.0 m., cada uno y altura de entrepisos iguales que miden 3.0 m., cada una. Las dimensiones de las columnas y vigas de cada edificio, fueron proporcionados por los siguientes profesores de la facultad de Ingeniería Civil de la ESPE.
Los edificios analizados son simétricos en planta y elevación, debido a que la metodología que se está presentando para evaluar en forma rápida la deriva máxima de piso es aplicable a estructuras simétricas.
La tendencia en el Ecuador es construir edificios flexibles, es así como por ejemplo en una estructura de 2 pisos con la distribución en planta indicada en la figura 3.2 se llegó a obtener un período fundamental elástico de 0.8 s., trabajando con inercias gruesas. La mayor parte de los períodos fundamentales de las estructuras de 2 pisos analizadas están entre 0.5 y 0.6 s., que se consideran altos. Para tener una idea de la sección transversal de las columnas y vigas, se indica de una de ellas. Para un edificio de 3 pisos, las columnas son de 40/40 para los dos primeros pisos y 35/35 en el tercer piso; las vigas son de 40/30. La primera dimensión es la base y la segunda la altura de la sección transversal; se ha indicado las dimensiones de una estructura, las otras están en ese orden, esto es para el caso de luces de 5 m.
3.4 RESULTADOS
En la figura 3.3, se presentan los valores de ![]() obtenidos en el estudio; para estructuras de un piso se tiene
obtenidos en el estudio; para estructuras de un piso se tiene ![]() . Para estructuras de 2 pisos, los valores están alrededor de 1.2; y a medida que aumenta el número de pisos, la dispersión se incrementa, así para estructuras de 3 pisos el valor mínimo encontrado fue de 1.257 y el valor máximo de 1.319. etc.
. Para estructuras de 2 pisos, los valores están alrededor de 1.2; y a medida que aumenta el número de pisos, la dispersión se incrementa, así para estructuras de 3 pisos el valor mínimo encontrado fue de 1.257 y el valor máximo de 1.319. etc.
En la figura 3.3, con línea gruesa se muestra la curva que une los valores medios en cada caso y también se indican los valores hallados con la fórmula de Algan y los recomendados por FEMA 356, se aprecia que los valores obtenidos con la ecuación de ALGAN se aproxima mejor a los valores medios encontrados en el estudio, razón por la cual se recomienda utilizar la ecuación de Algan para determinar el parámetro ![]() .
.
Se destaca que los valores que se obtienen al utilizar el modelo de viga de flexión acoplado a una viga de corte, para el caso de sección variable y para valores de ![]() son bastante bajos razón por la que no se dibujaron en la figura 1.3.
son bastante bajos razón por la que no se dibujaron en la figura 1.3.
Las estructuras analizadas tenían valores de ![]() y al obtener valores de
y al obtener valores de ![]() con las ecuaciones de Miranda y Reyes (2002) para valores de
con las ecuaciones de Miranda y Reyes (2002) para valores de ![]() altos, los valores de
altos, los valores de ![]() son muy bajos, encontrándose muy por debajo de los valores hallados en el estudio.
son muy bajos, encontrándose muy por debajo de los valores hallados en el estudio.
3.5 CONCLUSIONES
Se ha obtenido el valor de ![]() de 60 estructuras de 1 a 6 pisos, de dos y tres vanos, encontrando que los valores que se obtienen con la fórmula de Algan se aproximan mejor que los valores recomendados por FEMA 356, a los valores hallados en el estudio. Por lo tanto el valor de
de 60 estructuras de 1 a 6 pisos, de dos y tres vanos, encontrando que los valores que se obtienen con la fórmula de Algan se aproximan mejor que los valores recomendados por FEMA 356, a los valores hallados en el estudio. Por lo tanto el valor de ![]() para encontrar la deriva máxima de piso en estructuras de hormigón armado sin muros de corte se evaluará con la siguiente ecuación:
para encontrar la deriva máxima de piso en estructuras de hormigón armado sin muros de corte se evaluará con la siguiente ecuación:
REFERENCIAS
- 37. Aguiar R., Torres M., Romo M., y Caiza P. (1998), El Sismo de Bahía, Centro de Investigaciones Científicas. Escuela Politécnica del Ejército, 125 p, Quito.
- 38. Aguiar R., (200), Sismo de Macas de 1995, Centro de Investigaciones Científicas. Escuela Politécnica del Ejército, 74 p, Quito.
- 39. Algan B., (1982), Drift and damage considerations in earthquake resistan design of reinforced concrete buildings, Ph.D thesis, University of Illinois, Urbana. Illinois.
- 40. American Society of Civil Engineers, (2000), Pre-standard and commentary for the seismic rehabilitation of buildings, FEMA 356, Federal Emergency Management Agency Washington, D.C.
- 41. Miranda E., (1997), “Estimation of maximum interstory drift demands in displacement-based design” Seismic design methodologies for the next generation of codes, Krawinkler H., and Fajfar P., editor, Balkema.
- 42. Miranda E., Reyes C., (2002), “Aproximate lateral drift demands in multistory buildings with nonuniform stiffness”, Journal of Structural Engineering, 128 (7), 840-849.
CAPÍTULO 4 PARÁMETRO 
Se obtiene la respuesta no lineal de 120 edificios de Hormigón Armado de 1 a 10 pisos, compuestos por vigas y columnas, sin muros de corte, ante la acción de 32 acelerogramas registrados en Colombia, Ecuador, Perú, Argentina y Chile. Con el propósito de encontrar el parámetro que relaciona la deriva máxima de piso con respecto a la deriva global, que se denomina ![]() . Este parámetro sirve para evaluar en forma rápida la deriva máxima de piso.
. Este parámetro sirve para evaluar en forma rápida la deriva máxima de piso.
Al multiplicar los 120 edificios por los 32 acelerogramas se obtiene 3840 casos analizados, en base a los cuales se determina el parámetro ![]() en función del número de pisos.
en función del número de pisos.
4.1 INTRODUCCIÓN
La Agencia Federal para el Manejo de Emergencias, FEMA-356, recomienda la siguiente ecuación para el cálculo del desplazamiento lateral máximo en el tope de un edificio.
|
|
(4.1) |
El significado de cada una de las variables de ( 4.1 ) fue indicado en el capítulo 1. Ahora si se divide el desplazamiento lateral máximo ![]() para la altura total del edificio
para la altura total del edificio ![]() se obtiene la deriva global del edificio. Para encontrar la deriva máxima de piso
se obtiene la deriva global del edificio. Para encontrar la deriva máxima de piso ![]() en función de la deriva global se utiliza la siguiente expresión.
en función de la deriva global se utiliza la siguiente expresión.
|
|
(4.2) |
Se destaca que la deriva piso es igual al desplazamiento lateral relativo de piso dividido para la altura de entrepiso, de tal manera que en cada piso se tiene una deriva y el mayor valor de todos ellos, es el que se utiliza en la ecuación ( 4.2 ).
En este trabajo, se presenta una fórmula para encontrar ![]() la misma que es obtenida a partir de la respuesta no lineal de 120 estructuras de hormigón armado sin muros de corte, de 1 a 10 pisos ante la acción de 32 registros sísmicos. De tal manera, que se obtiene
la misma que es obtenida a partir de la respuesta no lineal de 120 estructuras de hormigón armado sin muros de corte, de 1 a 10 pisos ante la acción de 32 registros sísmicos. De tal manera, que se obtiene ![]() a partir de 3840 reportes de la relación entre la deriva máxima de piso con relación a la deriva global.
a partir de 3840 reportes de la relación entre la deriva máxima de piso con relación a la deriva global.
4.2 ESTRUCTURAS Y SISMOS DE ANÁLISIS
En la figura 4.1 se indica la planta tipo de los edificios analizados, las luces son de 4.0 m., la altura de los entrepisos son de 3.0 m., el hormigón utilizado tiene una resistencia máxima a la compresión de 21 MPa. Y el acero un límite de fluencia de 420 MPa. En Huidobro (2006) se indica las secciones de las vigas, columnas y armadura de los elementos.
Las estructuras responden a una forma constructiva del Ecuador y de algunos países latinoamericanos, cuya tendencia es no tener vigas descolgadas, por este motivo el ancho de las vigas es mayor que el peralte, no son vigas banda ya que si aparece una pequeña dimensión fuera de la losa. Para tener una idea de las dimensiones utilizadas se indica que en las construcciones de 1 piso las vigas fueron de 20/20, en las de 6 pisos de 60/30 y en las de 10 pisos de 100/40; la primera dimensión corresponde a la base y la segunda a la altura de la sección transversal. Para las edificaciones de 1 piso las columnas son de 20/20, para las de 6 pisos de 45/45 y para las de 10 pisos de 65/65; las dimensiones se han expresado en centímetros.
El refuerzo longitudinal de columnas varió desde una cuantía del 1% al 2% y el de vigas de 0.5% al 1.5%, se tienen 12 casos para cada piso, los mismos que se indican en la tabla 4.1.
Los estribos colocados en vigas y columnas son de 8 mm., de diámetro espaciados a 10 cm., en los extremos del elemento y 20 cm., en el centro de luz, son estribos simples.
| Caso | Cuantía de columna | Cuantía de armadura inferior de viga | Cuantía de la armadura superior de viga |
| 1 | 1.0 | 0.50 | 0.75 |
| 2 | 1.0 | 0.75 | 1.00 |
| 3 | 1.0 | 1.00 | 1.25 |
| 4 | 1.0 | 1.25 | 1.50 |
| 5 | 1.5 | 0.50 | 0.75 |
| 6 | 1.5 | 0.75 | 1.00 |
| 7 | 1.5 | 1.00 | 1.25 |
| 8 | 1.5 | 1.25 | 1.50 |
| 9 | 2.0 | 0.50 | 0.75 |
| 10 | 2.0 | 0.75 | 1.00 |
| 11 | 2.0 | 1.00 | 1.25 |
| 12 | 2.0 | 1.25 | 1.50 |
| CÓDIGO | ESTACIÓN | PAÍS | FECHA | MAGNITUD | ACELERACIÓN
MÁXIMA [gals] |
| 05a | CESAR VIZCARRA VARGAS | PERU | 23/06/2001 | 6.9 | -295.2 |
| 05b | CESAR VIZCARRA VARGAS | PERU | 23/06/2001 | 6.9 | 234.0 |
| 03b | PARQUE DE LA RESERVA | PERU | 17/10/1966 | 6.4 | -180.6 |
| 08b | ESTACIÓN SURCO | PERU | 03/10/1974 | 6.2 | -207.1 |
| 07a | PARQUE DE LA RESERVA | PERU | 03/10/1974 | 6.2 | -192.5 |
| 08a | ESTACION SURCO | PERU | 03/10/1974 | 6.2 | 192.3 |
| 09b | ESTACION ZARATE | PERU | 05/01/1974 | 6.6 | -156.2 |
| 36 | ESTACION | PERU | 392 | ||
| 31a | ARMENIA (CARME) | COLOMBIA | 25/01/1999 | 6.2 | 518.4 |
| 31b | ARMENIA (CARME) | COLOMBIA | 25/01/1999 | 6.2 | -680.1 |
| 32a | FILANDIA (CFLAN) | COLOMBIA | 25/01/1999 | 6.2 | 554.9 |
| 32b | FILANDIA (CFLAN) | COLOMBIA | 25/01/1999 | 6.2 | -477.8 |
| 33a | PEREIRA (CPER) | COLOMBIA | 25/01/1999 | 6.2 | -207.8 |
| 33b | PEREIRA (CPER) | COLOMBIA | 25/01/1999 | 6.2 | -141.5 |
| 34a | RICAURTE (CRICA) | COLOMBIA | 17/07/1996 | 3.07 | 132.4 |
| 34b | RICAURTE (CRICA) | COLOMBIA | 17/07/1996 | 3.07 | -124.8 |
| 35 | PEREIRA(MAZDA) | COLOMBIA | 19/02/1997 | 6.10 | 127.5 |
| 37 | QUINDIO | COLOMBIA | 25/01/1999 | 580.10 | |
| 38 | QUINDIO | COLOMBIA | 25/01/1999 | 477.80 | |
| 39 | QUINDIO | COLOMBIA | 25/01/1999 | 141.50 | |
| 40 | REGIONAL | COLOMBIA | 17/07/1998 | 132.40 | |
| 41 | REGIONAL | COLOMBIA | 17/07/1998 | 124.8 | |
| 30a | SSA2EVT S/N 1428 | ARGENTINA | 23/08/2005 | 4.9 | 164.07 |
| 30B | SSA2EVT S/N 1428 | ARGENTINA | 23/08/2005 | 4.9 | -128.96 |
| 18a | VALPARAISO EL ALMENDRAL | CHILE | 09/03/1985 | 7.8 | 292.0 |
| 19 | COLBUN | CHILE | 09/03/1985 | 7.8 | 477.0 |
| 18b | VALPARAISO EL ALMENDRAL | CHILE | 09/03/1985 | 7.8 | -163.0 |
| 17b | VIÑA DEL MAR (UNIVERSITY OF CHILE) | CHILE | 09/03/1985 | 7.8 | 356.0 |
| 17a | VIÑA DEL MAR (UNIVERSITY OF CHILE) | CHILE | 09/03/1985 | 7.8 | -233.0 |
| 16b | LLOLLEO(UNIVERSITY OF CHILE) | CHILE | 09/03/1985 | 7.8 | -698.0 |
| 15a | LLOLLEO | CHILE | 08/04/1985 | 7.2 | -167.0 |
| 14a | SAN FELIPE | CHILE | 09/03/1985 | 7.8 | -303.0 |
| 40 e | ESMERALDAS | ECUADOR | 06/1988 | 210.19 |
En la tabla 4.2, se indican los datos más relevantes de los 32 acelerogramas utilizados en el estudio y que fueron registrados de la siguiente manera: 8 en Chile, 14 en Colombia, 7 en Perú, 2 en Argentina y 1 en Ecuador. Son registros cuya aceleración máxima es mayor al 10% de la aceleración de la gravedad, de tal forma que la estructura trabaja en el rango no lineal.
4.3 ANÁLISIS NO LINEAL Y RESULTADOS
Se empleó el programa IDARC (Inelastic Damage Análisis of Reinforced Concrete Structures) para encontrar la respuesta no lineal en el tiempo, de los 120 edificios, ante cada uno de los sismos especificados en la tabla 4.2. El programa considera el modelo de Kent y Park (1971) para el comportamiento del hormigón y el modelo trilineal para el comportamiento del acero, que contempla incremento de resistencia en la zona de endurecimiento. Por otra parte, se utilizó el modelo de histéresis de Park et al (1987) que contempla deterioro de rigidez en la descarga, deterioro de resistencia y efecto pinching o de cierre de grietas.
En la figura 4.2, se presentan los resultados obtenidos para los cuatro primeros casos que corresponden a una cuantía de acero de 1% en columnas. En el eje horizontal se presenta el número de pisos y en el eje vertical el valor de ![]() . Se aprecia que la mayor parte de resultados están agrupados pero existen algunos casos en que los valores obtenidos de
. Se aprecia que la mayor parte de resultados están agrupados pero existen algunos casos en que los valores obtenidos de ![]() tienen valores altos. Huidobro (2006), Bobadilla (2006) y Robalino (2006).
tienen valores altos. Huidobro (2006), Bobadilla (2006) y Robalino (2006).
4.4 VALORES MEDIOS
Para cada caso, se obtuvo la curva de valores medios y están indicados en los gráficos de la figura 4.2, con una línea más gruesa sin embargo de ello en la figura 4.3 se presentan estas curvas para los 12 casos. En la figura 4.3, se aprecia que las curvas inferiores corresponden a los casos en que se tiene mayor cuantía de acero longitudinal en columnas.
En la tabla 4.3, se presentan los valores medios encontrados para cada caso de análisis, que son los puntos de la gráfica de la figura 4.3. En la última columna de la tabla 4.3 se aprecia que el valor de ![]() inicia en 1 para un piso y luego se va incrementando hasta los 6 pisos, ahí se mantiene constante hasta el piso 7 y luego decrece. En la figura 4.4 se presenta esta curva de valores medios y en la figura 4.5 la curva de desviación estándar.
inicia en 1 para un piso y luego se va incrementando hasta los 6 pisos, ahí se mantiene constante hasta el piso 7 y luego decrece. En la figura 4.4 se presenta esta curva de valores medios y en la figura 4.5 la curva de desviación estándar.
En forma general la desviación estándar, ![]() está alrededor de 0.15 pero para 7 pisos se tiene el mayor de
está alrededor de 0.15 pero para 7 pisos se tiene el mayor de ![]() y es de 0.276; para 1 piso
y es de 0.276; para 1 piso ![]() ya que la deriva máxima de piso es igual a la deriva global.
ya que la deriva máxima de piso es igual a la deriva global.
| Piso | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Med |
| 1 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 2 | 1.06 | 1.10 | 1.18 | 1.24 | 1.10 | 1.08 | 1.09 | 1.15 | 1.13 | 1.09 | 1.07 | 1.07 | 1.11 |
| 3 | 1.30 | 1.41 | 1.53 | 1.55 | 1.24 | 1.28 | 1.37 | 1.41 | 1.22 | 1,23 | 1.26 | 1.31 | 1.34 |
| 4 | 1.46 | 1.61 | 1.69 | 1.75 | 1.37 | 1.39 | 1.44 | 1.51 | 1.35 | 1.34 | 1.39 | 1.41 | 1.48 |
| 5 | 1.59 | 1.74 | 1.87 | 1.94 | 1.44 | 1.47 | 1.55 | 1.60 | 1.42 | 1.45 | 1.44 | 1.46 | 1.58 |
| 6 | 1.70 | 1.78 | 1.79 | 1.98 | 1.63 | 1.58 | 1.58 | 1.61 | 1.62 | 1.53 | 1.54 | 1.55 | 1.66 |
| 7 | 1.64 | 1.73 | 2.10 | 2.28 | 1.54 | 1.59 | 1.56 | 1.59 | 1.54 | 1.52 | 1.43 | 1.41 | 1.66 |
| 8 | 1.69 | 1.68 | 1.86 | 1.98 | 1.52 | 1.44 | 1.51 | 1.48 | 1.48 | 1.41 | 1.38 | 1.40 | 1.57 |
| 9 | 1.69 | 1.64 | 1.67 | 1.84 | 1.51 | 1.42 | 1.36 | 1.38 | 1.47 | 1.35 | 1.29 | 1.29 | 1.49 |
| 10 | 1.59 | 1.76 | 1.75 | 1.77 | 1.30 | 1.29 | 1.31 | 1.33 | 1.27 | 1.24 | 1.25 | 1.16 | 1.42 |
4.4 AJUSTE DE CURVA
En la figura 4.4, se aprecia que los puntos tienen una tendencia de una parábola de segundo grado, con está idea como base, se utilizó el programa MATH GRAPHER que utiliza el Método de Levenberg Marquardt para hallar los coeficientes de la parábola en función del número de pisos ![]() . La ecuación encontrada es la siguiente:
. La ecuación encontrada es la siguiente:
|
|
(4.3) |
En la figura 4.6 se presentan la curva de valores medios de ![]() obtenida en el estudio, con la curva encontrada mediante el ajuste y que está descrita en la ecuación ( 4.3 ), se aprecia una buena aproximación lo cual queda reflejado en la tabla 4.4, donde se obtiene el error medio
obtenida en el estudio, con la curva encontrada mediante el ajuste y que está descrita en la ecuación ( 4.3 ), se aprecia una buena aproximación lo cual queda reflejado en la tabla 4.4, donde se obtiene el error medio ![]() está alrededor del 1%. Se define el error medio de la siguiente manera:
está alrededor del 1%. Se define el error medio de la siguiente manera:
|
|
(4.4) |
Donde ![]() es el valor medio encontrado en el estudio;
es el valor medio encontrado en el estudio; ![]() es el valor encontrado mediante la ecuación ( 4.3 ) y
es el valor encontrado mediante la ecuación ( 4.3 ) y ![]() es el número de puntos.
es el número de puntos.
4.5 OTROS TRABAJOS
Miranda y Reyes (2002) resuelven una viga de corte acoplada a una viga de flexión, de sección variable y presentan una ecuación bastante extensa para determinar el parámetro ![]() . En base a esta ecuación Aguiar (2005) determina los valores de
. En base a esta ecuación Aguiar (2005) determina los valores de ![]() los mismos que se indican en la tabla 4.5.
los mismos que se indican en la tabla 4.5.
| |
|
|
| |
| |
1.39 | 1.34 | 1.28 | 1.24 |
| |
1.46 | 1.40 | 1.33 | 1.25 |
Siendo ![]() relaciona la rigidez lateral en el tope del edificio con respecto a la rigidez lateral en la base del edificio y
relaciona la rigidez lateral en el tope del edificio con respecto a la rigidez lateral en la base del edificio y ![]() viene definido por:
viene definido por:
|
|
(4.5) |
En la que ![]() es la rigidez al corte y
es la rigidez al corte y ![]() es la rigidez a flexión. Esta ecuación ha sido ya presentada en capítulos anteriores.
es la rigidez a flexión. Esta ecuación ha sido ya presentada en capítulos anteriores.
Por el modelo numérico de cálculo utilizado ![]() no depende del número de pisos y a medida que se incrementa el valor de
no depende del número de pisos y a medida que se incrementa el valor de ![]() el valor de
el valor de ![]() también se incrementa. Miranda y Reyes (2002) recomiendan que cuando no se evalué
también se incrementa. Miranda y Reyes (2002) recomiendan que cuando no se evalué ![]() se considere
se considere ![]() de tal manera que esta cantidad viene a ser un valor medio.
de tal manera que esta cantidad viene a ser un valor medio.
Por otra parte Zavala et al (2004) al analizar estructuras de hormigón armado, sin muros de corte, determinan ![]() en función del período fundamental efectivo y los valores que encuentran están entre 1.4 y 1.6 para períodos comprendidos entre 0.4 y 1.2 s., para períodos menores a 0.4 s., los valores van decreciendo.
en función del período fundamental efectivo y los valores que encuentran están entre 1.4 y 1.6 para períodos comprendidos entre 0.4 y 1.2 s., para períodos menores a 0.4 s., los valores van decreciendo.
De tal manera que los valores de ![]() encontrados en el presente estudio se encuentran en el rango de valores de otros estudios similares con la característica de que es muy sencillo determinar este parámetro ya que depende únicamente del número de pisos de la estructura.
encontrados en el presente estudio se encuentran en el rango de valores de otros estudios similares con la característica de que es muy sencillo determinar este parámetro ya que depende únicamente del número de pisos de la estructura.
4.7 CONCLUSIONES
Del análisis no lineal, paso a paso, de 120 edificios de hormigón armado, sin muros de corte de 1 a 10 pisos, ante la acción de 32 acelerogramas registrados en Colombia, Ecuador, Perú, Argentina y Chile se ha determinado el parámetro ![]() que relaciona la deriva máxima de piso con respecto a la deriva global. Encontrando la siguiente ecuación, en función del número de pisos
que relaciona la deriva máxima de piso con respecto a la deriva global. Encontrando la siguiente ecuación, en función del número de pisos ![]() .
.
El valor de ![]() siempre será mayor a la unidad. La ecuación encontrada reportó un error que está ligeramente superior al 1% con respecto a los valores medios obtenidos en el estudio.
siempre será mayor a la unidad. La ecuación encontrada reportó un error que está ligeramente superior al 1% con respecto a los valores medios obtenidos en el estudio.
REFERENCIAS
- 49. Aguiar R., (2005), “Evaluación rápida del drift de un edificio de H.A.”, Revista SIGMA. Revista del Colegio de Ingenieros Civiles de Pichincha, 2 (6), Quito, Ecuador.
- 50. American Society of Civil Engineers, (2000), Pre-standard and Commentary for the Seismic Rehabilitation of Buildings, FEMA-356, Federal Emergency Management Agency, Wahington, D.C.
- 51. Bobadilla C., (2006), Curvas de fragilidad y evaluación rápida de la vulnerabilidad de estructuras, Tesis de grado. Facultad de Ingeniería Civil. Escuela Politécnica del Ejército, 214 p, Quito, Ecuador.
- 52. Ghobarah A., Aly N. and El-Attar M. (1997) “Performance level criteria and evaluation. A critical review of proposed guidelines”. Seismic design methodology for the next generation of codes. Fajfar and Krawinkler Editors, Balkema, Slovenia.
- 53. Huidobro G., (2006), Relación entre la deriva de piso y la deriva global para evaluar la vulnerabilidad sísmica de las estructuras, Tesis de Grado. Facultad de Ingeniería Civil. Escuela Politécnica del Ejército, Quito, Ecuador.
- 54. Kent D., and Park R., (1971), “Flexural members with confined concrete”, Journal of Structural Division, ASCE, Vol. 97, ST7, 1969-1990.
- 55. Miranda E., Reyes C., (2002), “Aproximate lateral drift demands in multistory buildings with nonuniform stiffness”, Journal of Structural Engineering, 128 (7), 840-849.
- 56. Park Y., Reinhorn A., and Kunnath S., (1987), IDARC: Inelastic Damage Analysys of Reinforced Concrete Frame-Shear-Wall Structures, Technical Report NCEER-87-0008, State University of New York at Buffalo.
- 57. Robalino C., (2006) Capacidad sísmica de las estructuras considerando la interacción suelo estructura. Tesis de Grado. Facultad de Ingeniería Civil. Escuela Politécnica del Ejército, Quito.
- 58. Zavala C., Scaletti H., Proaño R., (2004), “Estimación de la respuesta sísmica en estructuras en base a sistemas de 1 gdl para el cálculo de la vulnerabilidad sísmica”, Presentación en Power Point. Seminario Internacional de Vulnerabilidad y Riesgo Sísmico, Lima, Perú.
CAPÍTULO 5 PARÁMETRO 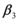
Se presenta la obtención del parámetro ![]() que relaciona el desplazamiento lateral máximo inelástico con respecto al desplazamiento lateral máximo elástico, en sistemas de un grado de libertad, la misma que sirve para evaluar en forma rápida la deriva máxima de piso. Para obtener este parámetro se trabajó con 63 acelerogramas de eventos registrados en América del Sur y cuya aceleración máxima del suelo fue mayor al 10% de la aceleración de la gravedad.
que relaciona el desplazamiento lateral máximo inelástico con respecto al desplazamiento lateral máximo elástico, en sistemas de un grado de libertad, la misma que sirve para evaluar en forma rápida la deriva máxima de piso. Para obtener este parámetro se trabajó con 63 acelerogramas de eventos registrados en América del Sur y cuya aceleración máxima del suelo fue mayor al 10% de la aceleración de la gravedad.
5.1 INTRODUCCIÓN
Existen una gran cantidad de modelos de daño a nivel de: elementos, piso o estructura completa, para cuantificar el comportamiento de una estructura ante una acción sísmica, Aguiar y Barbat (1998). Modelos, que toman como parámetro la cantidad de energía disipada, el número de ciclos que la estructura incursiona en el rango no lineal, la demanda de ductilidad, etc. Para calcular el daño con estos modelos, se debe realizar un análisis no lineal dinámico en dos o tres dimensiones, que demanda bastante tiempo en la entrada de datos de los programas de ordenador que existen y en el análisis de los reportes.
Una alternativa, para no calcular los índices de daño y tener una idea bastante clara del comportamiento sísmico de una estructura es determinar la distorsión máxima de piso ![]() , o drift en lengua inglesa, ya que se ha visto que se relaciona bastante bien con el daño estructural y no estructural, Bertero et al (1991), Moehle (1992 y 1996). De ahí, la necesidad de contar con una ecuación apropiada, para evaluar en forma rápida la deriva máxima de piso. En el capítulo 2 se había propuesto la siguiente ecuación.
, o drift en lengua inglesa, ya que se ha visto que se relaciona bastante bien con el daño estructural y no estructural, Bertero et al (1991), Moehle (1992 y 1996). De ahí, la necesidad de contar con una ecuación apropiada, para evaluar en forma rápida la deriva máxima de piso. En el capítulo 2 se había propuesto la siguiente ecuación.
|
|
(5.1) |
En el capítulo 3 se presentó la investigación realizada para determinar el parámetro ![]() que permite pasar el desplazamiento lateral encontrado en un sistema de 1 gdl a un sistema de múltiples grados de libertad. De igual manera, en el capítulo 4, se presentó los estudios para encontrar el parámetro
que permite pasar el desplazamiento lateral encontrado en un sistema de 1 gdl a un sistema de múltiples grados de libertad. De igual manera, en el capítulo 4, se presentó los estudios para encontrar el parámetro ![]() que relaciona la deriva de piso máxima con respecto a la deriva global de la estructura.
que relaciona la deriva de piso máxima con respecto a la deriva global de la estructura.
Ahora, en el presente capítulo, en base a sismos registrados en América del Sur, con aceleraciones mayores de 0.1 g., siendo g la aceleración de la gravedad, se determina el factor ![]() que relaciona el desplazamiento máximo inelástico con relación al desplazamiento máximo elástico en sistemas de 1 gdl.
que relaciona el desplazamiento máximo inelástico con relación al desplazamiento máximo elástico en sistemas de 1 gdl.
Con el propósito de ilustrar la importancia de conocer la deriva de piso máxima, en la figura 5.1 se presenta la curva de capacidad sísmica resistente de una estructura, que relaciona el drift o deriva máxima de piso con el cortante basal. Esta curva es obtenida mediante la aplicación de la técnica del empujón o pushover, Aguiar (2002 y 2003). Se han determinado tres puntos notables en la curva que son el punto de agrietamiento del concreto, el de fluencia del acero y el de capacidad última.
Con relación a estos puntos Ghobarah (2004) presenta el desempeño sísmico de la estructura, en la parte superior se aprecia el comportamiento estructural clasificado en: elástico, inelástico y colapso. En la parte intermedia el daño clasificado en: menor, reparable, irreparable, severo y extremo. Finalmente, en la parte inferior el desempeño de acuerdo a la recomendación del comité VISION 2000, que lo define como: inmediatamente ocupacional, operacional, seguridad de vida, prevención del colapso y cerca de colapso.
El desempeño que se espera en una estructura está en función del sismo de análisis, tema que no se aborda en este capítulo para no desviar la atención del estudio. Pero en relación a la figura 5.1 se presentan en la tabla 5.1, valores referenciales propuestos por Ghobarah et al (1997) para definir el daño y así tener una idea del estado en que se encuentra una edificación en base al drift máximo de piso o al drift global.
| Daño → | Menor | Reparable | Irreparable | Severo | Extremo |
| Desempeño | Agrietamiento | Fluencia de acero | Inicio de Mecanismo | Mecanismo Global | Degradación notable de resistencia |
| Descripción de los daños | Grietas ligeramente visibles | Grietas | Grietas abiertas y pérdida de recubrimiento | Grietas muy anchas y mayor pérdida de recubrimiento | Deformaciones permanentes visibles |
| Índice de daño | 0.05 | 0.14 | 0.40 | 0.60 | Mayor de 0.60 |
| Cuantificación de desempeño | Grietas menores de 0.3 mm. | Grietas menores de 1 mm. | Grietas entre 1 y 2 mm. | Grietas mayores de 2 mm. | Grietas anchas y profundas. Dilatación de los elementos |
| Drift de piso | 0.005 | 0.011 | 0.023 | 0.046 | > 0.060 |
| Drift global | 0.003 | 0.008 | 0.018 | 0.040 | >0.049 |
5.2 OTRAS RELACIONES DE 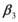
Sea ![]() el desplazamiento lateral máximo inelástico, en un sistema de 1 gdl y sea
el desplazamiento lateral máximo inelástico, en un sistema de 1 gdl y sea ![]() el desplazamiento espectral elástico. La relación que existe entre
el desplazamiento espectral elástico. La relación que existe entre ![]() y
y ![]() , es la siguiente:
, es la siguiente:
|
|
(5.2) |
Existen varias propuestas para el factor ![]() , aquí únicamente se presentan dos; la desarrollada por Miranda (2000), que ya fue analizada en el capítulo 2 y la de Nassar y Krawinkler (1991) que fue presentada en el capítulo 1. La propuesta de Miranda (2000) es:
, aquí únicamente se presentan dos; la desarrollada por Miranda (2000), que ya fue analizada en el capítulo 2 y la de Nassar y Krawinkler (1991) que fue presentada en el capítulo 1. La propuesta de Miranda (2000) es:
|
|
(5.3) |
donde ![]() es la demanda de ductilidad y
es la demanda de ductilidad y ![]() es el período de vibración del sistema. Se destaca que Miranda (2000) trabajo con un modelo elasto perfectamente plástico, de tal manera que la ecuación (5.3) es aplicable a estructuras en las cuales
es el período de vibración del sistema. Se destaca que Miranda (2000) trabajo con un modelo elasto perfectamente plástico, de tal manera que la ecuación (5.3) es aplicable a estructuras en las cuales ![]() . Siendo
. Siendo ![]() la relación entre la rigidez post fluencia con respecto a la rigidez elástica. Por otro lado, la ecuación propuesta por Nassar y Krawinkler (1991) es la siguiente:
la relación entre la rigidez post fluencia con respecto a la rigidez elástica. Por otro lado, la ecuación propuesta por Nassar y Krawinkler (1991) es la siguiente:
|
|
(5.4) | |
| (5.5) |
donde ![]() es una función del período
es una función del período ![]() y del valor de
y del valor de ![]() descrito en el párrafo anterior. Los valores de a y b en función de
descrito en el párrafo anterior. Los valores de a y b en función de ![]() se indican en la tabla 5.2.
se indican en la tabla 5.2.
| |
|
|
| 0.00 | 1.00 | 0.42 |
| 0.02 | 1.00 | 0.37 |
| 0.10 | 0.80 | 0.29 |
La ecuación de ![]() que se obtiene en este estudio, en base a sismos registrados en América del Sur será comparada con las ecuaciones propuestas por Miranda (2000) y por Nassar y Krawinkler (1991) por este motivo es que se ha vuelto a copiar otra vez estas ecuaciones.
que se obtiene en este estudio, en base a sismos registrados en América del Sur será comparada con las ecuaciones propuestas por Miranda (2000) y por Nassar y Krawinkler (1991) por este motivo es que se ha vuelto a copiar otra vez estas ecuaciones.
5.3 REGISTROS SÍSMICOS
En la figura 5.2, se presentan los epicentros de los 15 sismos considerados en el estudio y en la tabla 5.3 se dan los parámetros más importantes de cada uno de los 63 registros de los 15 sismos.
Se aprecia que todos los eventos tienen una aceleración máxima del suelo mayor a 0.10 g., de igual manera se observa que en algunas estaciones solo se tiene una componente sísmica, esto se debe a que la otra componente tuvo una aceleración máxima menor a 0.10 g.
Varios de los registros sísmicos de Colombia, corresponden al sismo que afectó al Eje Cafetero de Colombia el 25 de enero de 1999, que puso en evidencia el mal comportamiento que tuvieron las estructuras diseñadas antes de la normativa sísmica de 1984 y el buen comportamiento sísmico que tuvieron las edificaciones diseñadas después de 1984 en base a las nuevas normativas sismo resistentes.
En los registros sísmicos de Chile se considera el sismo del 3 de marzo de 1985 que tuvo una magnitud de 7.8 y que causó poco daño en las estructuras de hormigón armado con relación a la gran magnitud del sismo. El poco daño se debe, en parte, a que la mayor parte de las estructuras de Chile son con muros de corte; no es raro encontrar edificaciones menores a cinco pisos con muros de corte, en Chile, lo que no sucede en Ecuador donde las construcciones menores a cinco pisos son sin muros de corte. La deriva máxima de piso permitida por la Normativa Chilena es del 1% y para que eso se cumpla las construcciones deben ser muy rígidas en cambio la deriva máxima permitida por el Código Ecuatoriano de la Construcción es del 2% tal vez esta sea una de las razones por que las construcciones de Ecuador son más flexibles. Se destaca que tanto en la Norma Sísmica de Chile de 1996, como en el Código Ecuatoriano de la Construcción del 2000, la zona de mayor peligrosidad sísmica de los dos países, tienen un valor de 0.4 g.
Si se piensa que la deriva máxima de piso permitida por la Normativa Chilena es muy exigente, más lo es la de la Normativa Técnica de Perú de 2003, que establece una deriva máxima de piso de 0.7%. De tal manera, para que las estructuras de Perú cumplan con esta condición deberán ser más rígidas que las de Chile. En Ecuador, Perú y Chile, la zona de mayor peligrosidad sísmica de los respectivos países en las normativas sísmicas vigentes, establecen una aceleración máxima del suelo del 40% de la aceleración de la gravedad sin embargo, en Ecuador se diseñan estructuras más flexibles.
5.4 RESULTADOS
El parámetro ![]() relaciona el desplazamiento lateral máximo inelástico con respecto al desplazamiento lateral máximo elástico en sistemas de 1 gdl. En otras palabras relaciona los espectros inelásticos de desplazamiento con respecto a los espectros elásticos de desplazamiento. Se obtuvieron espectros inelásticos para ductilidades de 2, 3 y 4. Para la obtención de los espectros se utilizó el programa DEGTRA .
relaciona el desplazamiento lateral máximo inelástico con respecto al desplazamiento lateral máximo elástico en sistemas de 1 gdl. En otras palabras relaciona los espectros inelásticos de desplazamiento con respecto a los espectros elásticos de desplazamiento. Se obtuvieron espectros inelásticos para ductilidades de 2, 3 y 4. Para la obtención de los espectros se utilizó el programa DEGTRA .
A manera de ejemplo del trabajo realizado, en la figura 5.3, se presentan la relación entre el espectro de desplazamiento inelástico con respecto al espectro de desplazamiento elástico del sismo registrado el 13 de junio de 2005 en Characato, Perú, que corresponde al evento cuyo código es 01a en la tabla 5.3; a la izquierda se presenta dicha relación para ![]() y a la derecha para
y a la derecha para ![]() . Guerrero (2005).
. Guerrero (2005).
Tanto para la gráfica izquierda, como derecha de la figura 5.3; la curva superior es la relación de espectros para una ductilidad de 4, la curva de la mitad para una ductilidad de 3 y la inferior para una ductilidad de 2. Nótese para los tres casos que cuando el período tiende a cero la relación del espectro inelástico con relación al espectro elástico tiende a la ductilidad.
Cada uno de los espectros se obtuvo para 300 puntos hasta un período de 3 s., de tal manera que el intervalo de período con que se trabajó fue de 0.0033 s. Por otra parte los espectros se hallaron para un factor de amortiguamiento ![]() .
.
Se obtuvieron espectros elásticos para los 53 sismos; espectros inelásticos para ductilidades de 2, 3 y 4 para un modelo elasto perfectamente plástico. De tal forma que se encontraron 159 espectros inelásticos para ![]() y 159 espectros inelásticos para
y 159 espectros inelásticos para ![]() . Por lo tanto, se obtuvieron 371 espectros sumando los espectros elásticos, si esta cantidad se multiplica por 300 puntos se tiene 1113000 valores, con los cuales se encontró las ecuaciones para el parámetro
. Por lo tanto, se obtuvieron 371 espectros sumando los espectros elásticos, si esta cantidad se multiplica por 300 puntos se tiene 1113000 valores, con los cuales se encontró las ecuaciones para el parámetro ![]() .
.
Una vez que se obtuvo la relación espectral de desplazamiento, para cada evento sísmico, se encontró los valores medios de esta relación para cada país, así por ejemplo, en la figura 5.4 se muestran los valores medios para ![]() en la parte superior y para
en la parte superior y para ![]() en la parte inferior, para el Perú. Se aprecia que para valores de período superiores a 0.5 s., la tendencia de la relación tiende a la unidad especialmente para el caso de que
en la parte inferior, para el Perú. Se aprecia que para valores de período superiores a 0.5 s., la tendencia de la relación tiende a la unidad especialmente para el caso de que ![]() ; para
; para ![]() esta tendencia es mayor a la unidad. Para períodos menores a 0.5 s., la relación es mayor que la unidad.
esta tendencia es mayor a la unidad. Para períodos menores a 0.5 s., la relación es mayor que la unidad.
5.5 VALORES MEDIOS
Por otra parte, se encontró los valores medios del parámetro ![]() , de todos los sismos separados, obviamente para los dos valores de
, de todos los sismos separados, obviamente para los dos valores de ![]() , los mismos que se presentan en la figura 5.5, para
, los mismos que se presentan en la figura 5.5, para ![]() , y en la figura 5.6, para
, y en la figura 5.6, para ![]() , Guerrero (2005). Se indican los valores medios para ductilidades de 2, 3 y 4, se aprecia que para un período igual a cero el valor de
, Guerrero (2005). Se indican los valores medios para ductilidades de 2, 3 y 4, se aprecia que para un período igual a cero el valor de ![]() tiende al valor de la ductilidad.
tiende al valor de la ductilidad.
En la figura 5.5, se aprecia que ![]() tiende a la unidad para períodos mayores a 0.5 s., y en la figura 5.6, se observa que los valores de
tiende a la unidad para períodos mayores a 0.5 s., y en la figura 5.6, se observa que los valores de ![]() son ligeramente menores a la unidad para el mismo rango de períodos. De igual manera se aprecia en las dos figuras que el valor de
son ligeramente menores a la unidad para el mismo rango de períodos. De igual manera se aprecia en las dos figuras que el valor de ![]() difiere muy poco con la ductilidad para períodos mayores a 0.5 s., para valores menores a este período, la ductilidad si influye en el valor de
difiere muy poco con la ductilidad para períodos mayores a 0.5 s., para valores menores a este período, la ductilidad si influye en el valor de ![]() .
.
5.6 DESVIACIÓN ESTÁNDAR
En la figura 5.7, se presenta la desviación estándar de ![]() para ductilidades de 2 a 4, para
para ductilidades de 2 a 4, para ![]() , y en la figura 5.8, lo propio pero para
, y en la figura 5.8, lo propio pero para ![]() . Para el primer caso, se aprecia en forma general, que la desviación estándar se encuentra entre 0.2 y 0.3; para el segundo caso se encuentra entre 0.2 y 0.25.
. Para el primer caso, se aprecia en forma general, que la desviación estándar se encuentra entre 0.2 y 0.3; para el segundo caso se encuentra entre 0.2 y 0.25.
Es importante notar que para períodos cortos, caso de las construcciones de 1 y 2 pisos, la desviación estándar llega a valores de 0.6 Por esta razón se recomienda que en la evaluación rápida de la deriva máxima de pisos, para el caso de construcciones de 1 piso se sume la cantidad de 0.5 al parámetro ![]() que se obtenga con la fórmula propuesta en el estudio y que se indicó en el capítulo 2. A las de 2 pisos se sume 0.3
que se obtenga con la fórmula propuesta en el estudio y que se indicó en el capítulo 2. A las de 2 pisos se sume 0.3
5.7 AJUSTE DE CURVAS
Para el ajuste de las curvas se utilizó el método de Levenberg Marquart que está implementado en el programa MATH GRAPHER. La forma de la ecuación a ajustar es la propuesta por Nassar y Krawinkler que se indica a continuación:
Los coeficientes ![]() y
y ![]() , son los que van a determinarse con los datos del estudio. En la figura 5.9, se indica a manera de ejemplo el ajuste realizado con los valores medios de la curva obtenida para
, son los que van a determinarse con los datos del estudio. En la figura 5.9, se indica a manera de ejemplo el ajuste realizado con los valores medios de la curva obtenida para ![]() y
y ![]() . Los valores que se encontraron para este caso son:
. Los valores que se encontraron para este caso son: ![]() y
y ![]() .
.
Al proceder de igual forma con los restantes datos se hallaron los valores de ![]() y
y ![]() que se indican en la tabla 5.4
que se indican en la tabla 5.4
| Ductilidad | |
| ||
| |
|
|
| |
| 2 | 1.590 | 0.318 | 1.080 | 0.213 |
| 3 | 2.180 | 0.396 | 1.290 | 0.256 |
| 4 | 2.440 | 0.428 | 1.370 | 0.274 |
| Promedio | 2.070 | 0.381 | 1.247 | 0.248 |
En la figura 5.10, se presentan los valores medios de ![]() obtenidos en el estudio, la ecuación de Miranda, la ecuación de Nassar y Krawinkler y la encontrada en este estudio, denominada …propuesta… con los valores “a” y “b” indicados en la tabla 5.4; esta figura corresponde al caso de
obtenidos en el estudio, la ecuación de Miranda, la ecuación de Nassar y Krawinkler y la encontrada en este estudio, denominada …propuesta… con los valores “a” y “b” indicados en la tabla 5.4; esta figura corresponde al caso de ![]() .
.
La figura 5.11, es similar a la figura 5.10 pero con los valores de ![]() ; en esta figura no se incluye la ecuación de Miranda debido a que el autor obtuvo la ecuación para
; en esta figura no se incluye la ecuación de Miranda debido a que el autor obtuvo la ecuación para ![]() .
.
La ecuación propuesta, es la que mejor se aproxima a los valores medios de ![]() , como se aprecia en las figuras 5.10 y 5.11 y numéricamente se demuestra en la tabla 5.5, en que se ha presentado el error medio, que se obtiene con cada una de las ecuaciones, se define el error medio
, como se aprecia en las figuras 5.10 y 5.11 y numéricamente se demuestra en la tabla 5.5, en que se ha presentado el error medio, que se obtiene con cada una de las ecuaciones, se define el error medio ![]() de la siguiente manera:
de la siguiente manera:
donde ![]() es el valor medio de
es el valor medio de ![]() encontrado en el estudio,
encontrado en el estudio, ![]() es el valor de
es el valor de ![]() que se halla con la ecuación de ajuste y
que se halla con la ecuación de ajuste y ![]() es el número de puntos.
es el número de puntos.
| DUCTILIDAD | MIRANDA (2000) | NASSAR (1991) | PROPUESTA |
| 2 | 0.034 | 0.030 | 0.027 |
| 3 | 0.032 | 0.063 | 0.031 |
| 4 | 0.048 | 0.105 | 0.067 |
En la tabla 5.6, se presentan los errores medios para el caso de ![]() ; se aprecia que con la ecuación propuesta se tiene el menor error, en forma categórica. Para
; se aprecia que con la ecuación propuesta se tiene el menor error, en forma categórica. Para ![]() la ecuación propuesta da muy buenos resultados para ductilidades de 2 y 3, para ductilidad de 4 la ecuación de Miranda es una mejor aproximación.
la ecuación propuesta da muy buenos resultados para ductilidades de 2 y 3, para ductilidad de 4 la ecuación de Miranda es una mejor aproximación.
| DUCTILIDAD | NASSAR (1991) | PROPUESTA |
| 2 | 0.046 | 0.034 |
| 3 | 0.062 | 0.024 |
| 4 | 0.088 | 0.034 |
Al utilizar la ecuación propuesta por Miranda, en los datos que se obtienen para ![]() , el error medio que se obtiene, para todas las ductilidades es mayor a los indicados en la tabla 5.6. Esto es muy importante tener en cuenta ya que la mayor parte de estructuras tienen valores de
, el error medio que se obtiene, para todas las ductilidades es mayor a los indicados en la tabla 5.6. Esto es muy importante tener en cuenta ya que la mayor parte de estructuras tienen valores de ![]() mayores a cero.
mayores a cero.
5.8 COMENTARIOS
La información de los registros sísmicos, con los cuales se trabajó en este capítulo, no especifica en forma clara el tipo de suelo en que fueron registrados. Por esta razón, no se clasificaron los registros en función del perfil de suelo. Se destaca que Akkar y Miranda (2005) recomiendan que el parámetro ![]() tenga la siguiente forma:
tenga la siguiente forma:
|
|
(5.6) |
Donde: ![]() es el período de vibración del sistema,
es el período de vibración del sistema, ![]() período característico que depende del perfil de suelo,
período característico que depende del perfil de suelo, ![]() y
y ![]() , parámetros que se obtienen del ajuste y
, parámetros que se obtienen del ajuste y ![]() es el factor de resistencia lateral.
es el factor de resistencia lateral.
Por otra parte, Chopra, (2005), recomienda que el parámetro ![]() tenga la siguiente forma:
tenga la siguiente forma:
|
|
(5.7) |
|
|
(5.8) |
Donde ![]() es el factor de reducción de las fuerzas sísmicas por ductilidad,
es el factor de reducción de las fuerzas sísmicas por ductilidad, ![]() han sido ya indicados,
han sido ya indicados, ![]() y
y ![]() son parámetros que se hallan del ajuste. De tal manera que se recomienda calcular
son parámetros que se hallan del ajuste. De tal manera que se recomienda calcular ![]() en función del tipo de suelo.
en función del tipo de suelo.
5.9 CONCLUSIONES
En base a la respuesta lineal y no lineal, de sistemas de un grado de libertad, sometidas a la acción de 63 acelerogramas registrados en América del Sur, con aceleraciones mayores a 0.10 g., se ha determinado el parámetro ![]() que relaciona el desplazamiento máximo inelástico con relación al desplazamiento máximo elástico, encontrando la siguiente expresión:
que relaciona el desplazamiento máximo inelástico con relación al desplazamiento máximo elástico, encontrando la siguiente expresión:
Se destaca que para construcciones de 1 piso al valor obtenido de ![]() con la ecuación se le debe sumar 0.5 y a las construcciones de 2 pisos se sumará 0.3
con la ecuación se le debe sumar 0.5 y a las construcciones de 2 pisos se sumará 0.3
A Mario Ordaz del Instituto de Ingeniería de la UNAM por habernos facilitado el programa DEGTRA; a Rodolfo Saragoni de la Universidad de Chile, por sus comentarios; a INGEOMINAS de Colombia, a Miguel Tornello de CEREDETEC de Argentina y al CISMID de Perú, por habernos facilitado los registros sísmicos.
REFERENCIAS
- 59. Aguiar R., (2002), Sistema de Computación CEINCI3 para evaluar daño sísmico en los Países Bolivarianos, Centro de Investigaciones Científicas. Escuela Politécnica del Ejército, 302 p, Quito, Ecuador.
- 60. Aguiar R., (2003) Análisis Sísmico por Desempeño, Centro de Investigaciones Científicas. Escuela Politécnica del Ejército, 342 p, Quito, Ecuador.
- 61. Aguiar R., y Barbat A., (1998), “Global damage index methodology for reinforced concrete building structures subjected to seismic actions”, Fourth World Congress on Computational Mechanics, 20 p, Buenos Aires, Argentina.
- 62. Akkar D., and Miranda E., (2005), “Statistical evaluation of approximate methods for estimating maximum deformation demands on existing structures”, Journal of Structures Engineering, 131 (1), 160-172.
- 63. Bertero V., Anderson J., Krawinkler H., and Miranda E., (1991), “Design guidelines for ductility and drift limits: Review of the state of the practice and state of the art in ductility and drift-based earthquake-resistant design of buildings”, Earthquake Engineering Research Center, Report No UCB/EERC-91/15 , University of California, Berkeley, California.
- 64. CEC-2000, “Código Ecuatoriano de la Construcción”, XIII Jornadas Nacionales de Ingeniería Estructural. Pontificia Universidad Católica del Ecuador, 325-350, Quito.
- 65. Chopra A., (2005) “Estimating seismic demands for performance-based engineering of buildings”, Congreso Chileno de Sismología e Ingeniería Antisísmica. IX Jornadas, 34 p, Concepción, Chile.
- 66. FEMA (1997), NEHRP provisions for the seismic rehabilitation of buildings, Federal Emergency Management Agency. Rep. FEMA 273 (Guidelines) and 274 (Comentary), Washington, D.C.
- 67. Ghobarah A., Aly N. and El-Attar M. (1997) “Performance level criteria and evaluation. A critical review of proposed guidelines”. Seismic design methodology for the next generation of codes. Fajfar and Krawinkler Editors, Balkema, Slovenia.
- 68. Ghobarah A. (2004), “On drift limits associated with different damage levels”, International workshop on performance based seismic design. Department of Civil Engineering, Mc. Master University, June 28- July 1, 2004.
- 69. Guerrero P., (2005), Determinación rápida de la deriva de piso. Análisis de la relación entre el desplazamiento inelástico máximo esperado con el desplazamiento calculado para la respuesta elástica lineal en sistemas de 1 gdl. Tesis de Grado. Facultad de Ingeniería Civil. Escuela Politécnica del Ejército, Quito.
- 70. Moehle J., (1992), “Displacement-based design of reinforced concrete structures” Earthquake Spectra, Vol 8, 403-428.
- 71. Moehle J., (1996), “Displacement-based seismic design criteria”, Proceeding of the eleventh world conference on earthquake engineering, Acapulco, México.
- 72. Nassar A., and Krawinkler H., (1991), “Seismic demands for SDOF and MDOF systems”, John Blume Earthquake Engineering. Ctr. Dept. of Civil Engineering, Rep. 95, Stanford University, Stanford, California.
- 73. Norma NCh 433. Of. 96, (1996), Diseño Sísmico de Edificios, Instituto de Normalización INN-Chile, 42 p, Santiago.
- 74. Ordaz M., (2005) Programa DEGTRA, Instituto de Ingeniería. Universidad Nacional Autónoma de México, UNAM, México.
- 75. SEAOC (1995), Vision 2000 Report on performance based seismic engineering of buildings, Structural Engineers Association of California, Volume I, Sacramento.
- 76. SENCICO (2003), Reglamento Nacional de Construcciones. Norma Técnica de Edificación E.030. Diseño Sismorresistente, Servicio Nacional de Normalización, Capacitación e Investigación para la Industria de la Construcción, 38 p, Lima.
CAPÍTULO 6 PARÁMETRO 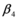
Se ha encontrado la respuesta lineal y no lineal de 72 estructuras de hormigón armado, sin muros de corte, ante la acción de 27 registros sísmicos de Colombia, Ecuador, Perú, Chile y Argentina y se ha determinado la relación que existe, entre el cálculo inelástico con el cálculo elástico de la deriva máxima de piso con respecto a la deriva global. De los 1944 valores obtenidos, se presenta una ecuación para ésta relación, la misma que sirve para la evaluación rápida de la deriva de piso máxima.
6.1 INTRODUCCIÓN
En la última década varios investigadores, Ordaz et al (2005), Olarte et al (2005), Zavala et al (2004), Gupta y Krawinkler (2000), entre otros, se encuentran trabajando en una metodología para evaluar en forma rápida la vulnerabilidad sísmica de las estructuras a partir de la deriva máxima de piso. Para el efecto han propuesto expresiones de cálculo en base a registros sísmicos y sistemas constructivos de la región en que viven. Tres de los trabajos citados parten de la ecuación propuesta por Miranda (1997) para evaluar la deriva máxima de piso y es la siguiente:
|
|
(6.1) |
donde ![]() es el valor de paso del sistema de un grado de libertad al sistema de múltiples grados de libertad, fue estudiado en el capítulo 3;
es el valor de paso del sistema de un grado de libertad al sistema de múltiples grados de libertad, fue estudiado en el capítulo 3; ![]() es un factor de amplificación que permite determinar la distorsión máxima de entrepiso a partir de la deriva global de la estructura, estudiado en el capítulo 4;
es un factor de amplificación que permite determinar la distorsión máxima de entrepiso a partir de la deriva global de la estructura, estudiado en el capítulo 4; ![]() es un factor que permite calcular los desplazamientos laterales máximos con comportamiento inelástico a partir de los máximos desplazamientos laterales con comportamiento elástico, estudiado en capítulo 5;
es un factor que permite calcular los desplazamientos laterales máximos con comportamiento inelástico a partir de los máximos desplazamientos laterales con comportamiento elástico, estudiado en capítulo 5; ![]() es un factor que sirve para determinar el cociente entre la distorsión máxima de entrepiso y la distorsión global pero calculado en una estructura con comportamiento inelástico con relación a la misma relación pero calculada con comportamiento elástico, que se analiza en el presente capítulo;
es un factor que sirve para determinar el cociente entre la distorsión máxima de entrepiso y la distorsión global pero calculado en una estructura con comportamiento inelástico con relación a la misma relación pero calculada con comportamiento elástico, que se analiza en el presente capítulo; ![]() es la altura total del edificio y
es la altura total del edificio y ![]() es el desplazamiento espectral elástico asociado al período efectivo
es el desplazamiento espectral elástico asociado al período efectivo ![]() de la estructura.
de la estructura.
En este trabajo se determina el parámetro ![]() , a partir del análisis sísmico de 72 estructuras que responden a la forma como se construye en el Ecuador, ante la acción de 27 registros sísmicos de: Colombia ( 9), Ecuador (1), Perú (7), Chile (8) y Argentina (2). De esta forma se calibra el parámetro
, a partir del análisis sísmico de 72 estructuras que responden a la forma como se construye en el Ecuador, ante la acción de 27 registros sísmicos de: Colombia ( 9), Ecuador (1), Perú (7), Chile (8) y Argentina (2). De esta forma se calibra el parámetro ![]() para ser utilizado en futuros estudios de vulnerabilidad sísmica de estructuras situadas en Sur América y que tengan similares características a las aquí analizadas.
para ser utilizado en futuros estudios de vulnerabilidad sísmica de estructuras situadas en Sur América y que tengan similares características a las aquí analizadas.
6.2 PARÁMETRO 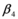
Se había definido la deriva global ![]() como la relación entre el desplazamiento lateral máximo
como la relación entre el desplazamiento lateral máximo ![]() con respecto a la altura total del edificio y la deriva máxima de piso
con respecto a la altura total del edificio y la deriva máxima de piso ![]() como el mayor valor de las derivas de cada piso las mismas que se obtienen dividiendo el desplazamiento relativo de piso para la altura del entrepiso. El parámetro
como el mayor valor de las derivas de cada piso las mismas que se obtienen dividiendo el desplazamiento relativo de piso para la altura del entrepiso. El parámetro ![]() , se define de la siguiente manera:
, se define de la siguiente manera:
|
|
(6.2) |
El numerador de la ecuación (6.2) representa la relación entre la deriva máxima de piso con respecto a la deriva global pero calculada mediante análisis no lineal y el denominados representa la misma relación pero obtenida mediante análisis lineal. Miranda (1999) considera a ![]() como un factor de seguridad al cálculo de la deriva máxima de piso y recomienda la siguiente ecuación para su evaluación:
como un factor de seguridad al cálculo de la deriva máxima de piso y recomienda la siguiente ecuación para su evaluación:
|
|
(6.3) |
Donde ![]() es la demanda de ductilidad y
es la demanda de ductilidad y ![]() es el número de pisos de la estructura. La ecuación que se obtiene en este estudio se comparará con la ecuación ( 6.3 ).
es el número de pisos de la estructura. La ecuación que se obtiene en este estudio se comparará con la ecuación ( 6.3 ).
6.3 ESTRUCTURAS Y SISMOS DE ANÁLISIS
Se analizaron 72 estructuras de hormigón armado de 1 a 6 pisos con la configuración en planta indicada en la figura 6.1. La armadura longitudinal de las columnas varió de 1% a 2% y la armadura longitudinal de las vigas varió de 0.5% a 1.5%, los casos considerados de armado se indican en la tabla 6.1; el refuerzo transversal tanto de vigas como de columnas se consideró de 8 mm., de diámetro espaciado cada 10 en los extremos del elemento y cada 20 cm., en el centro de luz.
| Caso | Cuantía de columna | Cuantía de armadura inferior de viga | Cuantía de la armadura superior de viga |
| 1 | 1.0 | 0.50 | 0.75 |
| 2 | 1.0 | 0.75 | 1.00 |
| 3 | 1.0 | 1.00 | 1.25 |
| 4 | 1.0 | 1.25 | 1.50 |
| 5 | 1.5 | 0.50 | 0.75 |
| 6 | 1.5 | 0.75 | 1.00 |
| 7 | 1.5 | 1.00 | 1.25 |
| 8 | 1.5 | 1.25 | 1.50 |
| 9 | 2.0 | 0.50 | 0.75 |
| 10 | 2.0 | 0.75 | 1.00 |
| 11 | 2.0 | 1.00 | 1.25 |
| 12 | 2.0 | 1.25 | 1.50 |
La carga vertical varió desde 400 Kg/m2 para las estructuras de 1 piso a 700 kg/m2 para las estructuras de 6 pisos. El hormigón utilizado tiene una resistencia máxima a la comprensión de 21 MPa y el acero un límite de fluencia de 420 MPa.
Se consideró el modelo de Kent y Park (1971) para el comportamiento del hormigón confinado y el modelo trilineal para el acero que contempla incremento de resistencia en la zona de endurecimiento. Por otra parte se utilizó el modelo de histéresis de Park et al (1987) que contempla deterioro de rigidez en la descarga, deterioro de resistencia y efecto pinching o de cierre de grietas. Todo esto para el análisis no lineal que fue realizado mediante la utilización del programa IDARC.
Los 27 registros sísmicos utilizados en el estudio se indican en la tabla 6.2 y fueron seleccionados por que la aceleración máxima es mayor al 10% de la aceleración de la gravedad.
| CÓDIGO | ESTACIÓN | PAÍS | FECHA | MAGNITUD | ACELERACIÓN
MÁXIMA [gals] |
| 05ª | CESAR VIZCARRA VARGAS | PERU | 23/06/2001 | 6.9 | -295.2 |
| 05b | CESAR VIZCARRA VARGAS | PERÚ | 23/06/2001 | 6.9 | 234.0 |
| 03b | PARQUE DE LA RESERVA | PERU | 17/10/1966 | 6.4 | -180.6 |
| 08b | ESTACIÓN SURCO | PERU | 03/10/1974 | 6.2 | -207.1 |
| 07ª | PARQUE DE LA RESERVA | PERU | 03/10/1974 | 6.2 | -192.5 |
| 08ª | ESTACION SURCO | PERU | 03/10/1974 | 6.2 | 192.3 |
| 09b | ESTACION ZARATE | PERU | 05/01/1974 | 6.6 | -156.2 |
| 31ª | ARMENIA (CARME) | COLOMBIA | 25/01/1999 | 6.2 | 518.4 |
| 31b | ARMENIA (CARME) | COLOMBIA | 25/01/1999 | 6.2 | -680.1 |
| 32ª | FILANDIA (CFLAN) | COLOMBIA | 25/01/1999 | 6.2 | 554.9 |
| 32b | FILANDIA (CFLAN) | COLOMBIA | 25/01/1999 | 6.2 | -477.8 |
| 33ª | PEREIRA (CPER) | COLOMBIA | 25/01/1999 | 6.2 | -207.8 |
| 33b | PEREIRA (CPER) | COLOMBIA | 25/01/1999 | 6.2 | -141.5 |
| 34ª | RICAURTE (CRICA) | COLOMBIA | 17/07/1996 | 3.07 | 132.4 |
| 34b | RICAURTE (CRICA) | COLOMBIA | 17/07/1996 | 3.07 | -124.8 |
| 35 | PEREIRA(MAZDA) RISARALDA(CMAZPA) | COLOMBIA | 19/02/1997 | 6.10 | 127.5 |
| 30ª | SSA2EVT S/N 1428 | ARGENTINA | 23/08/2005 | 4.9 | 164.07 |
| 30B | SSA2EVT S/N 1428 | ARGENTINA | 23/08/2005 | 4.9 | -128.96 |
| 18ª | VALPARAISO EL ALMENDRAL | CHILE | 09/03/1985 | 7.8 | 292.0 |
| 19 | COLBUN | CHILE | 09/03/1985 | 7.8 | 477.0 |
| 18b | VALPARAISO EL ALMENDRAL | CHILE | 09/03/1985 | 7.8 | -163.0 |
| 17b | VIÑA DEL MAR (UNIVERSITY OF CHILE) | CHILE | 09/03/1985 | 7.8 | 356.0 |
| 17ª | VIÑA DEL MAR (UNIVERSITY OF CHILE) | CHILE | 09/03/1985 | 7.8 | -233.0 |
| 16b | LLOLLEO(UNIVERSITY OF CHILE) | CHILE | 09/03/1985 | 7.8 | -698.0 |
| 15ª | LLOLLEO | CHILE | 08/04/1985 | 7.2 | -167.0 |
| 14ª | SAN FELIPE | CHILE | 09/03/1985 | 7.8 | -303.0 |
| 40 | ESMERALDAS | ECUADOR | 06/1989 | 210.19 |
6.4 RESULTADOS
Los resultados del análisis no lineal, que corresponden al numerador de ( 6.2 ) se detallan en Huidobro (2006) y Bobadilla (2006), estos se obtuvieron utilizando el programa IDARC. Los resultados del análisis lineal que corresponden al denominador de la ecuación (6.2) se detallan en González (2006) los mismos que se encontraron utilizando el programa LINEAL desarrollado por Aguiar (2005).
Para el análisis no lineal interviene la armadura longitudinal y transversal; en cambio para el análisis lineal no interviene esta armadura. Por lo tanto, para obtener el numerador de la ecuación ( 6.2 ) se ejecutó el programa IDARC 1944 veces, que resulta de la multiplicación de las 72 estructuras por los 27 sismos. Para obtener el denominador de la ecuación ( 6.2 ) se ejecutó el programa LINEAL 162 veces, que se obtiene multiplicando las 6 estructuras tipo de 1 a 6 pisos por los 27 sismos.
En la figura 6.2, se presentan los valores de ![]() obtenidos con la ecuación (6.2) para las estructuras analizadas cuya armadura longitudinal corresponde al caso 1 indicado en la tabla 6,1. En la figura 6.3, se indican los resultados para el caso 2 y en la figura 6.4, para el caso 3. Esto con el propósito de mostrar parte de los valores obtenidos.
obtenidos con la ecuación (6.2) para las estructuras analizadas cuya armadura longitudinal corresponde al caso 1 indicado en la tabla 6,1. En la figura 6.3, se indican los resultados para el caso 2 y en la figura 6.4, para el caso 3. Esto con el propósito de mostrar parte de los valores obtenidos.
En cada figura presentada ( 6.2 a 6.4) y para las diferentes estructuras se han dibujado 27 puntos que corresponden a los sismos de análisis. Con línea continua y uniendo todos los pisos se presenta la curva de valores medios. Con relación a los tres casos presentados se realizan los siguientes comentarios.
- Las curvas de valores medios empiezan en la 1, para estructuras de 1 pisos y terminan en un valor cercano a 1.2 para las estructuras de 6 pisos.
- Existen valores que son menorea a la unidad, lo que significa que el denominador de la ecuación ( 6.2 ) fue mayor al numerador.
6.5 VALORES MEDIOS Y AJUSTE
En la figura 6.5 se muestran las curvas de valores medios obtenidas para los 12 casos de armado considerados en el estudio. De esta gráfica se realizan los siguientes comentarios.
- Todas las curvas de valores medios tienen la misma tendencia, en forma general.
- Las curvas que tienen mayores valores corresponden a los casos en que la cuantía del refuerzo longitudinal de columnas fue del 1% y las curvas que tienen los menores valores son aquellas en que la cuantía de columnas es del 2%.
- Para estructuras de 1 pisos, los valores son la unidad como era de esperarse. Luego los valores más bajos se observan en las estructuras de 2 pisos y así sucesivamente. Para las estructuras de 5 pisos se tienen los mayores valores.
- Con línea un poco más gruesa, se indica la curva de los valores medios de todas estas curvas. Esta curva se vuelve a mostrar en la figura 6.6.
En la figura 6.6 se aprecia que la tendencia de la curva de valores medios de todos los casos, que viene a representar la curva media de los 1944 valores obtenidos en el estudio, tiende a ser lineal con una pendiente positiva razón por la cual se ajustó estos puntos con la recta indicada en la ecuación ( 6.4 ) y que está en función del número de pisos ![]() .
.
|
|
(6.4) |
En la figura 6.7 se presenta las desviaciones estándar encontradas para las estructuras de 1 a 6 pisos, la mayor desviación se tiene para los edificios de 5 pisos, con un valor de 0.135, realmente son bajos los valores encontrados y esto se debe a que los puntos encontrados estaban bastante agrupados.
6.6 DISCUSIÓN
En la figura 6.8 se compara la curva obtenida en el estudio con las curvas propuestas por Miranda (1999) para ductilidades de 2, 3 y 4. Se observa que la curva propuesta reporta valores similares a los que reporta la ecuación de Miranda lo cual da seguridad a la investigación realizada.
Para estructuras de 1 piso, el valor de ![]() tiene que ser 1 ya que la deriva máxima de piso es igual a la deriva global de la estructura, esto es valido tanto para el análisis lineal como no lineal. En el estudio realizado se tiene que
tiene que ser 1 ya que la deriva máxima de piso es igual a la deriva global de la estructura, esto es valido tanto para el análisis lineal como no lineal. En el estudio realizado se tiene que ![]() para estructuras de 1 piso y los valores que se obtienen con la ecuación propuesta por Miranda (1999) reporta valores ligeramente mayores.
para estructuras de 1 piso y los valores que se obtienen con la ecuación propuesta por Miranda (1999) reporta valores ligeramente mayores.
No se trata de ver si la ecuación propuesta en el estudio es mejor o peor que la recomendada por Miranda (1999), en buena hora que reporta resultados parecidos. Lo que se quería es tener una ecuación que responda al sistema como se construye en el Ecuador y que se tome en cuenta los sismos que se registran en América del Sur.
6.7 CONCLUSIONES
Se ha encontrado el parámetro ![]() , que sirve para la evaluación rápida de la deriva máxima de pisos, después de haber encontrado la respuesta en el tiempo de 72 estructuras de hormigón armado, sin muros de corte, ante la acción de 27 acelerogramas de eventos sísmicos registrados en Colombia, Ecuador, Perú, Chile y Argentina. La respuesta en el tiempo se obtuvo de dos maneras, la primera utilizando un programa de análisis no lineal y la segunda empleando un programa de análisis lineal. Del estudio realizado se obtuvo la siguiente ecuación:
, que sirve para la evaluación rápida de la deriva máxima de pisos, después de haber encontrado la respuesta en el tiempo de 72 estructuras de hormigón armado, sin muros de corte, ante la acción de 27 acelerogramas de eventos sísmicos registrados en Colombia, Ecuador, Perú, Chile y Argentina. La respuesta en el tiempo se obtuvo de dos maneras, la primera utilizando un programa de análisis no lineal y la segunda empleando un programa de análisis lineal. Del estudio realizado se obtuvo la siguiente ecuación:
Donde ![]() es el número de pisos. La ecuación propuesta deberá utilizarse para determinar el parámetro
es el número de pisos. La ecuación propuesta deberá utilizarse para determinar el parámetro ![]() en la evaluación de la deriva máxima de piso en edificios de hormigón armado, sin muros de corte, situados en América del Sur
en la evaluación de la deriva máxima de piso en edificios de hormigón armado, sin muros de corte, situados en América del Sur
REFERENCIAS
- 77. Aguiar R., (2005) Programa LINEAL para hallar la respuesta en el tiempo de estructuras. Centro de Investigaciones Científicas. Escuela Politécnica del Ejército, Quito.
- 78. Bobadilla C., (2006) Curvas de Fragilidad y evaluación rápida de la vulnerabilidad sísmica de estructuras, Tesis de Grado. Facultad de Ingeniería Civil, Escuela Politécnica del Ejército, Quito.
- 79. González A., (2006) Evaluación rápida de la deriva máxima de piso. Cálculo del parámetro
 , Tesis de Grado. Escuela de Ingeniería Civil. Universidad Técnica de Manabí, Portoviejo.
, Tesis de Grado. Escuela de Ingeniería Civil. Universidad Técnica de Manabí, Portoviejo.
- 80. Gupta A., and Krawinkler H., (2000), “Estimation of seismic drift demands for frame structures”, Earthquake Engineering and Structural Dynamics, 28, 1287-1305.
- 81. Huidobro G., (2006), Relación entre la deriva máxima de piso y la deriva global en Estructuras de Hormigón Armado, Tesis de Grado. Facultad de Ingeniería Civil. Escuela Politécnica del Ejército, Quito.
- 82. Kent D., and Park R., (1971), “Flexural members with confined concrete”, Journal of Structural Division, ASCE, Vol. 97, ST7, 1969-1990.
- 83. Miranda E., (1997), “Estimation of maximum interstory drift demands in displacement-based design” Seismic design methodologies for the next generation of codes, Krawinkler H., and Fajfar P., editor, Balkema.
- 84. Miranda E., (1999), “Approximate seismic lateral deformation demands in multistory buildings”, Journal of Structural Engineering, 125 (4), 417-425.
- 85. Olarte J., Aguilar Z., Zavala C., Romaní S., Escobar R., (2005), “Estimación de la pérdida máxima probable PML en Lima y Callao: Aplicación a la Industria Aseguradora Peruana”. XIX Simposio Internacional Últimos Avances en la Ingeniería Sísmica y Gestión del Riesgo de los Desastres, 19 p, Lima.
- 86. Ordaz M., Miranda E., Reinoso E., Santa Cruz S., (2005), “Modelo de estimación de pérdidas por sismo en México con fines de seguro”, XIX Simposio Internacional Últimos Avances en la Ingeniería Sísmica y Gestión del Riesgo de los Desastres, 33 p, Lima.
- 87. Park Y., Reinhorn A., and Kunnath S., (1987), IDARC: Inelastic Damage Analysys of Reinforced Concrete Frame-Shear-Wall Structures, Technical Report NCEER-87-0008, State University of New York at Buffalo.
- 88. Valles R., Reinhorn A., Kunnath S., Li C., and Madan A., (1996), IDARC2D Version 4.0: A computer program for the inelastic damage analysis of buildings, National Center for Earthquake Engineering Research. Headquartered at the State University of New York at Buffalo, Technical Report NCEER-96-0010, 189 p. New York.
- 89. Zavala C., Scaletti H., Proaño R., (2004), “Estimación de la respuesta sísmica de estructuras en base a sistemas de 1 gdl para el cálculo de la vulnerabilidad sísmica”, Seminario Internacional Vulnerabilidad y Riesgo Sísmico, CISMID. Universidad Nacional de Ingeniería, 36 p, Lima, Perú.
CAPÍTULO 7. METODOLOGÍA PROPUESTA PARA LA EVALUACIÓN RÁPIDA DE LA DERIVA MÁXIMA DE PISO
Se presenta una metodología para evaluar en forma rápida la deriva máxima de pisos en edificios de hormigón armado conformados por vigas y columnas, sin muros de corte, en la que cada uno de los parámetros que intervienen en el cálculo, han sido obtenidos a partir de sismos registrados en Colombia, Ecuador, Perú, Chile y Argentina. Además se ha considerado la forma como se construye en el Ecuador, la calidad del acero y el hormigón que usualmente se utiliza en las construcciones.
Posteriormente, se obtiene la deriva máxima de piso de 72 edificios, de 1 a 6 pisos, ante la acción de 25 registros sísmicos, mediante análisis no lineal dinámico y se comparan los 1800 resultados obtenidos con los valores que se encuentran al aplicar la metodología rápida de evaluación.
7.1 INTRODUCCIÓN
Uno de los objetivos de este libro era presentar una metodología para evaluar en forma rápida y a la vez confiable, la deriva máxima de piso, de edificios de hormigón armado, sin muros de corte, para ello se propuso la siguiente ecuación:
|
|
(7.1) |
En la que se ha incrementado el parámetro ![]() a la propuesta realizada por Miranda (1997, 1999). Cada uno de los parámetros que intervienen en la evaluación han sido investigados y sus resultados se han presentado en los capítulos anteriores, ahora únicamente se mostrará la ecuación o valores de cálculo.
a la propuesta realizada por Miranda (1997, 1999). Cada uno de los parámetros que intervienen en la evaluación han sido investigados y sus resultados se han presentado en los capítulos anteriores, ahora únicamente se mostrará la ecuación o valores de cálculo.
La ecuación ( 7.1 ) es la que se utilizará para encontrar la deriva máxima de piso, bajo el título de metodología rápida y cuyos valores serán comparados con los que reporta el programa IDARC al realizar un análisis no lineal dinámico, paso a paso.
Una vez que se determina la deriva máxima de piso, ante una acción sísmica dada se puede inferir el desempeño de la misma, utilizando los valores recomendados por Ghobarah (2004) o por el comité VISION 2000 (1995). También se puede encontrar el desempeño utilizando las curvas de fragilidad, que se indican en el capítulo 9 de este libro, para cuatro niveles de daño denominadas: leve, moderado, extensivo y completo.
7.2 PARÁMETRO 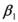
En el capítulo 3, se encontró que la ecuación que mejor se ajusta a los resultados obtenidos, al analizar 60 estructuras de 1 a 6 pisos, en las cuales se calculó ![]() es la siguiente:
es la siguiente:
|
|
(7.2) |
Donde ![]() es el número de pisos. Se recuerda que
es el número de pisos. Se recuerda que ![]() es el parámetro que permite obtener el desplazamiento lateral máximo, en la cubierta, en un sistema de múltiples grados de libertad a partir del desplazamiento lateral máximo de un sistema de 1 gdl. La ecuación ( 7.2 ) fue propuesta por Algan (1982).
es el parámetro que permite obtener el desplazamiento lateral máximo, en la cubierta, en un sistema de múltiples grados de libertad a partir del desplazamiento lateral máximo de un sistema de 1 gdl. La ecuación ( 7.2 ) fue propuesta por Algan (1982).
7.3 PARÁMETRO 
Se analizaron 120 estructuras de hormigón armado de 1 a 10 pisos ante la acción de 32 acelerogramas, de sismos registrados en Colombia, Ecuador, Perú, Argentina y Chile. De tal manera que se obtuvieron 3840 valores del parámetro ![]() . En el capítulo 4, se detalla el trabajo realizado, sin embargo se destaca que se realizó un análisis no lineal dinámico, de cada uno de los 3840 casos y se hallo la relación entre la deriva máxima de piso y la deriva global y la ecuación que mejor se aproxima a los resultados obtenidos es:
. En el capítulo 4, se detalla el trabajo realizado, sin embargo se destaca que se realizó un análisis no lineal dinámico, de cada uno de los 3840 casos y se hallo la relación entre la deriva máxima de piso y la deriva global y la ecuación que mejor se aproxima a los resultados obtenidos es:
|
|
(7.3) |
Donde ![]() es el número de pisos de la estructura. El valor de
es el número de pisos de la estructura. El valor de ![]() , tiene que ser mayor o igual a la unidad. Se hace notar, que el parámetro
, tiene que ser mayor o igual a la unidad. Se hace notar, que el parámetro ![]() se obtuvo del análisis de edificios de 1 a 10 pisos pero la comparación de la deriva máxima de piso utilizando la metodología rápida y el análisis no lineal se realiza con edificios de 1 a 6 pisos.
se obtuvo del análisis de edificios de 1 a 10 pisos pero la comparación de la deriva máxima de piso utilizando la metodología rápida y el análisis no lineal se realiza con edificios de 1 a 6 pisos.
7.4 PARÁMETRO 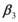
El parámetro ![]() relaciona el desplazamiento lateral máximo inelástico con respecto al desplazamiento lateral máximo elástico, en sistemas de 1 gdl, con este recordatorio se debe manifestar que en base al análisis de 63 acelerogramas registrados en Colombia, Perú, Chile y Argentina se obtuvo la siguiente ecuación:
relaciona el desplazamiento lateral máximo inelástico con respecto al desplazamiento lateral máximo elástico, en sistemas de 1 gdl, con este recordatorio se debe manifestar que en base al análisis de 63 acelerogramas registrados en Colombia, Perú, Chile y Argentina se obtuvo la siguiente ecuación:
|
|
(7.4) | |
| (7.5) | ||
| (7.6) |
Siendo ![]() la relación entre la rigidez post fluencia con respecto a la rigidez elástica de la curva de capacidad sísmica resistente que relaciona el cortante basal con el desplazamiento lateral máximo. Siempre se deberá considerar
la relación entre la rigidez post fluencia con respecto a la rigidez elástica de la curva de capacidad sísmica resistente que relaciona el cortante basal con el desplazamiento lateral máximo. Siempre se deberá considerar ![]() , mayor que 1. Adicionalmente y como se indicó en el capítulo 5 para estructuras de 1 piso se deberá sumar la cantidad de 0.5 y para las de dos pisos la cantidad de 0.3.
, mayor que 1. Adicionalmente y como se indicó en el capítulo 5 para estructuras de 1 piso se deberá sumar la cantidad de 0.5 y para las de dos pisos la cantidad de 0.3.
7.5 PARÁMETRO 
Para el cálculo de ![]() se analizaron 72 estructuras de 1 a 6 pisos ante la acción de 27 registros sísmicos de Colombia (9), Ecuador (1), Perú (7), Chile (8) y Argentina(2), de tal manera que se obtuvieron 1944 valores de
se analizaron 72 estructuras de 1 a 6 pisos ante la acción de 27 registros sísmicos de Colombia (9), Ecuador (1), Perú (7), Chile (8) y Argentina(2), de tal manera que se obtuvieron 1944 valores de ![]() empleando la ecuación (7.7).
empleando la ecuación (7.7).
|
|
(7.7) |
El parámetro ![]() no es más que la relación del parámetro
no es más que la relación del parámetro ![]() calculado en el rango inelástico, con relación al parámetro
calculado en el rango inelástico, con relación al parámetro ![]() calculado en el rango elástico. Del estudio realizado que se presentó en el capítulo 6, se obtuvo la siguiente ecuación, en función del número de pisos
calculado en el rango elástico. Del estudio realizado que se presentó en el capítulo 6, se obtuvo la siguiente ecuación, en función del número de pisos ![]() .
.
|
|
(7.8) |
7.6 PARÁMETRO 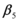
Los estudios realizados para determinar los parámetros ![]() ,
, ![]() y
y ![]() no contemplan deterioro de rigidez en la descarga, deterioro de resistencia en un ciclo de histéresis y efecto de cierre de grietas. Estos tres factores, son incluidos en el modelo numérico de cálculo de la deriva máxima de piso mediante el parámetro
no contemplan deterioro de rigidez en la descarga, deterioro de resistencia en un ciclo de histéresis y efecto de cierre de grietas. Estos tres factores, son incluidos en el modelo numérico de cálculo de la deriva máxima de piso mediante el parámetro ![]() y se recomiendan los valores indicados en la tabla 7.1 que están en función de la ductilidad del sistema
y se recomiendan los valores indicados en la tabla 7.1 que están en función de la ductilidad del sistema ![]() . En el capítulo 2, se presentó el trabajo de Lee et al (1999) que sirvió de base para la formulación de
. En el capítulo 2, se presentó el trabajo de Lee et al (1999) que sirvió de base para la formulación de ![]() .
.
| Ductilidad | 1 | 2 | 3 | 4 | 5 | 6 |
| |
1.00 | 1.14 | 1.17 | 1.19 | 1.22 | 1.23 |
7.7 PERÍODO EFECTIVO
El período efectivo ![]() con el cual se ingresa al espectro elástico para calcular el desplazamiento
con el cual se ingresa al espectro elástico para calcular el desplazamiento ![]() , de acuerdo a FEMA 356 se evalúa con la siguiente ecuación:
, de acuerdo a FEMA 356 se evalúa con la siguiente ecuación:
|
|
(7.9) |
donde ![]() es la rigidez inicial de la estructura que se la obtiene de la curva de capacidad sísmica resistente, que relaciona el cortante basal con el desplazamiento lateral máximo;
es la rigidez inicial de la estructura que se la obtiene de la curva de capacidad sísmica resistente, que relaciona el cortante basal con el desplazamiento lateral máximo; ![]() es una rigidez secante a la curva de capacidad que pasa por el punto cuya ordenada es igual a 0.6 del cortante de fluencia
es una rigidez secante a la curva de capacidad que pasa por el punto cuya ordenada es igual a 0.6 del cortante de fluencia ![]() ;
; ![]() es el período de vibración inicial de la estructura en el rango elástico. Emplear esta ecuación implica conocer la curva de capacidad sísmica resistente y para ello se debe suministrar la geometría de la estructura y la armadura longitudinal y transversal de cada uno de sus elementos, lo que demanda un tiempo apreciable que no estaría de acuerdo con la filosofía de la metodología rápida de evaluación de la deriva máxima de piso, por lo que se recomienda calcular tres valores de
es el período de vibración inicial de la estructura en el rango elástico. Emplear esta ecuación implica conocer la curva de capacidad sísmica resistente y para ello se debe suministrar la geometría de la estructura y la armadura longitudinal y transversal de cada uno de sus elementos, lo que demanda un tiempo apreciable que no estaría de acuerdo con la filosofía de la metodología rápida de evaluación de la deriva máxima de piso, por lo que se recomienda calcular tres valores de ![]() y hallar tres valores espectrales de
y hallar tres valores espectrales de ![]() y por ende tres derivas de piso máximo con la ecuación (7.1) y de estas encontrar el valor medio.
y por ende tres derivas de piso máximo con la ecuación (7.1) y de estas encontrar el valor medio.
Se propone el cálculo de ![]() con las siguientes ecuaciones, la primera es la obtenida de registros sísmicos con aceleraciones mayores al 15% de la aceleración de la gravedad en edificios de hormigón armado sin muros de corte, de tal manera que las estructuras sobrepasaron el punto de agrietamiento, la ecuación propuesta por Goel y Chopra (1997) es:
con las siguientes ecuaciones, la primera es la obtenida de registros sísmicos con aceleraciones mayores al 15% de la aceleración de la gravedad en edificios de hormigón armado sin muros de corte, de tal manera que las estructuras sobrepasaron el punto de agrietamiento, la ecuación propuesta por Goel y Chopra (1997) es:
|
|
(7.10) |
Donde ![]() es la altura total del edificio expresada en metros. La segunda ecuación que se propone para el cálculo de
es la altura total del edificio expresada en metros. La segunda ecuación que se propone para el cálculo de ![]() es la propuesta por el UBC-97 que se indica a continuación:
es la propuesta por el UBC-97 que se indica a continuación:
|
|
(7.11) |
De igual manera la altura total se expresa en metros. La tercera ecuación es la obtenida en México, en edificios de hormigón armado sin muros de corte y es la siguiente:
|
|
(7.12) |
7.8 ESTRUCTURAS Y SISMOS DE ANÁLISIS
La geometría y armado de las 72 estructuras de 1 a 6 pisos que se analizaron se indicó en el capítulo 4 del libro, únicamente para recordar la planta tipo se indica en la figura 7.1, como complemento a la información se debe manifestar que la carga vertical varió desde 400 Kg/m2 para las estructuras de 1 piso a 700 kg/m2 para las estructuras de 6 pisos.
| CÓDIGO | ESTACIÓN | PAÍS | FECHA | MAGNITUD | ACELERACIÓN
MÁXIMA [gals] |
| 05ª | CESAR VIZCARRA VARGAS | PERU | 23/06/2001 | 6.9 | -295.2 |
| 05b | CESAR VIZCARRA VARGAS | PERÚ | 23/06/2001 | 6.9 | 234.0 |
| 03b | PARQUE DE LA RESERVA | PERU | 17/10/1966 | 6.4 | -180.6 |
| 08b | ESTACIÓN SURCO | PERU | 03/10/1974 | 6.2 | -207.1 |
| 07ª | PARQUE DE LA RESERVA | PERU | 03/10/1974 | 6.2 | -192.5 |
| 08ª | ESTACION SURCO | PERU | 03/10/1974 | 6.2 | 192.3 |
| 09b | ESTACION ZARATE | PERU | 05/01/1974 | 6.6 | -156.2 |
| 31ª | ARMENIA (CARME) | COLOMBIA | 25/01/1999 | 6.2 | 518.4 |
| 31b | ARMENIA (CARME) | COLOMBIA | 25/01/1999 | 6.2 | -680.1 |
| 32ª | FILANDIA (CFLAN) | COLOMBIA | 25/01/1999 | 6.2 | 554.9 |
| 32b | FILANDIA (CFLAN) | COLOMBIA | 25/01/1999 | 6.2 | -477.8 |
| 33ª | PEREIRA (CPER) | COLOMBIA | 25/01/1999 | 6.2 | -207.8 |
| 33b | PEREIRA (CPER) | COLOMBIA | 25/01/1999 | 6.2 | -141.5 |
| 35 | PEREIRA(MAZDA) | COLOMBIA | 19/02/1997 | 6.10 | 127.5 |
| 30ª | SSA2EVT S/N 1428 | ARGENTINA | 23/08/2005 | 4.9 | 164.07 |
| 30B | SSA2EVT S/N 1428 | ARGENTINA | 23/08/2005 | 4.9 | -128.96 |
| 18ª | VALPARAISO EL ALMENDRAL | CHILE | 09/03/1985 | 7.8 | 292.0 |
| 19 | COLBUN | CHILE | 09/03/1985 | 7.8 | 477.0 |
| 18b | VALPARAISO EL ALMENDRAL | CHILE | 09/03/1985 | 7.8 | -163.0 |
| 17b | VIÑA DEL MAR | CHILE | 09/03/1985 | 7.8 | 356.0 |
| 17ª | VIÑA DEL MAR | CHILE | 09/03/1985 | 7.8 | -233.0 |
| 16b | LLOLLEO | CHILE | 09/03/1985 | 7.8 | -698.0 |
| 15ª | LLOLLEO | CHILE | 08/04/1985 | 7.2 | -167.0 |
| 14ª | SAN FELIPE | CHILE | 09/03/1985 | 7.8 | -303.0 |
| 40 | ESMERALDAS | ECUADOR | 06/1989 | 210.19 |
El hormigón utilizado tiene una resistencia máxima a la comprensión de 21 MPa y el acero un límite de fluencia de 420 MPa. Los acelerogramas con los cuales se obtuvo la deriva máxima de piso utilizando el programa IDARC, mediante análisis no lineal dinámico, se presentan en la tabla 7.2. Se destaca que es análisis no lineal dinámico ya que con el programa IDARC se puede realizar también un análisis no lineal estático para encontrar la curva de capacidad sísmica empleando la técnica del pushover.
7.9 ANÁLISIS NO LINEAL Y RESULTADOS
Se analizaron 1800 valores que corresponden a las 72 estructuras sometidas a los 25 registros indicados en la tabla 7.2. El análisis se realizó de dos maneras, la primera utilizando el programa IDARC y la segunda empleando la ecuación ( 7.1 ). Para el primer caso, se encontró la respuesta no lineal, paso a paso, de un pórtico central del edificio; interesaba ver únicamente la distorsión máxima de piso y la demanda de ductilidad la misma, que en la mayoría de los casos fue superior a 4. Posteriormente se evaluó la deriva máxima de piso por medio de la ecuación (7.1) empleando los parámetros ![]() a
a ![]() que han sido indicados en este capítulo. Se destaca que en la metodología rápida se obtuvo primero los espectros de desplazamiento elástico de cada uno de los sismos y los desplazamientos espectrales,
que han sido indicados en este capítulo. Se destaca que en la metodología rápida se obtuvo primero los espectros de desplazamiento elástico de cada uno de los sismos y los desplazamientos espectrales, ![]() se hallaron para los tres períodos indicados en las ecuaciones (7.10) a (7.12) y luego se obtuvo un promedio de los valores obtenidos de
se hallaron para los tres períodos indicados en las ecuaciones (7.10) a (7.12) y luego se obtuvo un promedio de los valores obtenidos de ![]() el mismo que se reemplazó en la ecuación (7.1).
el mismo que se reemplazó en la ecuación (7.1).
Se denomina ![]() a la deriva máxima de piso obtenida con el programa IDARC y
a la deriva máxima de piso obtenida con el programa IDARC y ![]() a la deriva máxima de piso encontrada con la ecuación (7.1). Para poder visualizar los resultados en una sola figura se define la relación
a la deriva máxima de piso encontrada con la ecuación (7.1). Para poder visualizar los resultados en una sola figura se define la relación ![]() . Si esta relación tiende a 1 significa que la aproximación de la deriva máxima de piso que se encuentra en forma rápida con la ecuación (7.1) reporta muy buenos resultados. En la figura 7.2 se presenta esta relación para los 1800 puntos.
. Si esta relación tiende a 1 significa que la aproximación de la deriva máxima de piso que se encuentra en forma rápida con la ecuación (7.1) reporta muy buenos resultados. En la figura 7.2 se presenta esta relación para los 1800 puntos.
La línea continua de la figura 7.2, que une a todos los pisos, corresponde al valor medio encontrado con los valores de cada piso, se aprecia que una gran cantidad de puntos se encuentra bajo la línea de valores medios, el promedio sube por que existen valores que presentan una muy alta relación ![]() .
.
El valor medio para los edificios de 4, 5 y 6 pisos es prácticamente la unidad lo que significa que la evaluación de la deriva máxima de piso, con los parámetros propuestos en este estudio, para la metodología rápida es muy buena; para los edificios de 3 pisos el valor medio es de 2.649, que se considera aceptable. En cambio para las estructuras de 1 y 2 pisos la diferencia entre la deriva máxima que reporta el programa IDARC con la deriva máxima que se obtiene con la metodología rápida es considerable. Esto se debe a que las estructuras de 1 y 2 pisos tienen un período bastante bajo y los valores espectrales ![]() asociados son bajos para los casos en que la relación
asociados son bajos para los casos en que la relación ![]() es alta.
es alta.
En la tabla 7.3 se indican los valores medios encontrados para las estructuras analizadas y que corresponde a la línea continua que une los diferentes pisos en la figura 7.2.
| Número de pisos | Valor medio |
| 1 | 8.220 |
| 2 | 4.449 |
| 3 | 2.649 |
| 4 | 1.314 |
| 5 | 0.783 |
| 6 | 0.667 |
7.10 ANÁLISIS CON INERCIAS AGRIETADAS
Los valores medios indicados en la tabla 7.3 son bastante buenos pero se hallan mejores resultados, si el período fundamental se encuentra resolviendo el problema de valores y vectores propios, a partir de la matriz de masa y de la matriz de rigidez. Esta matriz de rigidez se obtiene con inercias agrietadas. El Código Ecuatoriano de la Construcción, establece los siguientes valores para encontrar la rigidez agrietada de vigas y columnas.
Donde ![]() es la rigidez a flexión calculada con la inercia gruesa; para las vigas, se considera, la rigidez a flexión es el 50% de la rigidez a flexión gruesa y para columnas el 80% de la rigidez a flexión gruesa. Con estos valores se halló el período.
es la rigidez a flexión calculada con la inercia gruesa; para las vigas, se considera, la rigidez a flexión es el 50% de la rigidez a flexión gruesa y para columnas el 80% de la rigidez a flexión gruesa. Con estos valores se halló el período.
El período de vibración encontrado con inercias agrietadas es mayor que el reportado con las ecuaciones (7.10) a (7.12). Con estos períodos, se encontró el desplazamiento espectral de cada uno de los sismos y se halló la deriva de piso máxima empleando la ecuación (7.1).
Posteriormente, se halló la relación entre la deriva de piso que reporta el programa IDARC que se ha denominado ![]() con la deriva de piso de la metodología rápida, los resultados de esta relación se indican en la figura 7.3 para los 1800 casos analizados.
con la deriva de piso de la metodología rápida, los resultados de esta relación se indican en la figura 7.3 para los 1800 casos analizados.
Al comparar las figuras 7.2 y 7.3 se aprecia que mejores resultados se obtienen al encontrar el período con inercias agrietadas. En efecto los valores medios son los indicados en la tabla 7.4 y se aproximan en todos los casos a la unidad.
| Número de pisos | Valor medio |
| 1 | 1.1944 |
| 2 | 1.2789 |
| 3 | 1.1964 |
| 4 | 0.8705 |
| 5 | 0.6639 |
| 6 | 0.6405 |
7.11 CONCLUSIONES
En base a sismos registrados en Colombia, Ecuador, Perú, Chile y Argentina y tomando en cuenta la forma como se construye los edificios de hormigón armado en el Ecuador, se han determinado varios parámetros que intervienen en la evaluación de la deriva máxima de piso mediante una sola ecuación, que se ha denominado metodología rápida. Posteriormente, se analizaron 1800 resultados de las derivas máximas de piso que se obtuvieron al utilizar un programa de análisis no lineal dinámico, como es el IDARC y se comparó los resultados con los que se encuentran con la ecuación que contempla cinco parámetros y de los valores medios se desprenden las siguientes conclusiones:
- Al encontrar el período de vibración con inercias agrietadas, la deriva máxima de piso que se obtiene con la metodología rápida propuesta se aproxima muy bien a las derivas máximas de piso que reporta el programa IDARC. El valor medio de los 1800 casos analizados está alrededor de 1.
- Si se obtiene el período de vibración en base a fórmulas aproximadas, la deriva de piso hallada con la metodología rápida reporta resultados satisfactorios para edificios de 3, 4, 5 y 6 pisos. Para las estructuras de 1 y 2 pisos la diferencia es apreciable.
REFERENCIAS
- 90. Algan B., (1982), Drift and damage considerations in earthquake resistan design of reinforced concrete buildings, Ph.D thesis, University of Illinois, Urbana. Illinois.
- 91. American Society of Civil Engineers, (2000), Pre-standard and commentary for the seismic rehabilitation of buildings, FEMA 356, Federal Emergency Management Agency Washington, D.C.
- 92. ATC-40, (1996) Seismic evaluation and retrofit of concrete buildings, Applied Technology Council, Redwood City, California.
- 93. Bertero V., (1995), “Tri-service manual methods in VISION 2000”, Part 2, Appendix J, Structural Engineers Association of California, Sacramento.
- 94. Chopra A., Goel K., (2002), “A modal pushover analysis procedure for estimating seismic demands for buildings”, Earthquake Engineering and Structural Dynamics, Vol 31, 561-582.
- 95. FEMA (1997), NEHRP provisions for the seismic rehabilitation of buildings, Federal Emergency Management Agency. Rep. FEMA 273 (Guidelines) and 274 (Comentary), Washington, D.C.
- 96. Goel R., and Chopra A., (1997), “Period formulas for moment-resisting frame buildings”, Journal of Structural Engineering, 123 (11), 1454-1461.
- 97. Lee L., Hang S., and Oh Y., ( 1999) , “Determination of ductility factor considering different hysteretic models”, Earthquake Engineering and Structural Dynamics, 28, 957-977.
- 98. Miranda E., (1997), “Estimation of maximum interstory drift demands in displacement-based design” Seismic design methodologies for the next generation of codes, Krawinkler H., and Fajfar P., editor, Balkema.
- 99. SEAOC (1995), Vision 2000 Report on performance based seismic engineering of buildings, Structural Engineers Association of California, Volume I, Sacramento.
- 100. Shimazaki K., and Sozen M., (1984), “Seismic drift of reinforced concrete structures” Res. Rep., Hazama-Gumi Ltd., Tokyo, Japan (in Japanese); and draft report (in English).
- 101. UBC (1997), Uniform Building Code, International Conference of Building Officials, ICBO, 3 Vol, Whittier, CA, USA.
- 102. Valles R., Reinhorn A., Kunnath S., Li C., and Madan A., (1996), IDARC2D Version 4.0: A computer program for the inelastic damage analysis of buildings, National Center for Earthquake Engineering Research. Headquartered at the State University of New York at Buffalo, Technical Report NCEER-96-0010, 189 p. New York.
CAPÍTULO 8. NUEVA METODOLOGÍA Y PARÁMETRO 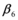
Se encuentra, en primer lugar, una relación entre la deriva máxima de piso calculada en forma inelástica con respecto a la deriva máxima de piso calculada en forma elástica, de 72 estructuras de hormigón armado, que tienen dos vanos en cada dirección de 4.0m., de luz, sin muros de corte, ante la acción de 27 acelerogramas registrados en Colombia, Ecuador, Perú, Chile y Argentina.
Posteriormente, se presenta la nueva metodología de cálculo para evaluar la deriva máxima de piso en el rango no lineal, a partir de la respuesta elástica y se verifica la bondad de esta metodología al analizar 72 estructuras, que tienen tres vanos de 5.0 m., cada uno, en cada dirección, ante la acción de 4 acelerogramas normalizados a 0.4 g., registrados en el Perú.
8.1 INTRODUCCIÓN Y NUEVA METODOLOGÍA
En el capítulo 7, se presentó una metodología para evaluar la deriva máxima de piso empleando la siguiente ecuación:
|
|
(8.1) |
Cada uno de los parámetros que intervienen en ( 8.1 ) han sido investigados y presentados en los capítulos anteriores. Se vio en el capítulo 7, que la ecuación reporta muy buenos resultados, siempre y cuando se encuentre el período de vibración resolviendo el problema de valores y vectores propios, calculando para el efecto la matriz de rigidez con inercias agrietadas. Este cálculo implica el uso de un programa de computación; ya que se va a utilizar un programa se propone el cálculo de la deriva máxima de piso a partir del análisis sísmico lineal, de una estructura, paso a paso.
El uso de un programa de análisis dinámico elástico es mucho más fácil que el uso de un programa de análisis dinámico inelástico. Por esta razón se plantea encontrar la deriva máxima de piso inelástico a partir de la deriva máxima de piso, que se encuentra con un programa de análisis elástico, mediante la siguiente ecuación:
|
|
(8.2) |
Donde ![]() es la deriva máxima de piso que se obtiene con un programa de análisis lineal elástico;
es la deriva máxima de piso que se obtiene con un programa de análisis lineal elástico; ![]() es la relación entre la deriva máxima de piso en el rango inelástico con respecto a la deriva máxima de piso en el rango elástico.
es la relación entre la deriva máxima de piso en el rango inelástico con respecto a la deriva máxima de piso en el rango elástico.
8.2 ESTRUCTURAS Y SISMOS DE ANÁLISIS PARA OBTENER 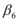
Se analizaron 72 estructuras de hormigón armado de 1 a 6 pisos, las mismas que están detalladas en el capítulo 6, ante los 27 sismos que se indican en dicho capítulo. Para las estructuras de 1 piso, se tienen 12 casos de análisis dependiendo de la armadura longitudinal utilizada, lo propio se tiene con las estructuras de 2 pisos, etc. Se destaca que las estructuras tienen 2 vanos en planta de 4.0 m., cada uno, ya que se analizan posteriormente 72 estructuras, para ver la bondad de la nueva metodología propuesta para evaluar la deriva máxima de piso pero ahora las estructuras tienen 3 vanos de 5.0 m., de luz cada uno. Los sismos de análisis son registros cuya aceleración máxima es mayor a 0.1 g, siendo g la aceleración de la gravedad para el cálculo del parámetro ![]() .
.
Para el análisis no lineal se utilizó el programa IDARC desarrollado en el Centro de Investigaciones de Ingeniería Sísmica, de la Universidad de New York y Buffalo. Por otra parte, para el análisis lineal se empleó el programa LINEAL desarrollado en el Centro de Investigaciones Científicas, de la Escuela Politécnica del Ejército. Con los dos programas se halló la respuesta en el tiempo utilizando algoritmos paso a paso y se determinó la deriva máxima en el rango no lineal ![]() , y en el rango lineal
, y en el rango lineal ![]() . Finalmente utilizando la ecuación (8.2) se encontró
. Finalmente utilizando la ecuación (8.2) se encontró ![]() .
.
8.3 RESULTADOS DEL PARÁMETRO 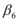
En la figura 8.1, se indica en abscisas el número de pisos de las estructuras estudiadas y en ordenadas el valor de ![]() ; los comentarios de estos resultados son los siguientes:
; los comentarios de estos resultados son los siguientes:
- En las estructuras de un piso se tiene mayor dispersión de valores, le sigue las de dos y tres pisos.
- Los valores medios encontrados, se indican con línea continua y sus valores se indican en la tabla 8.1
En la figura 8.2, se indican los valores medios encontrados en el estudio y se encontró que la curva que mejor se aproxima a los valores medios, es una parábola, definida por la siguiente ecuación:
|
|
(8.3) |
Siendo ![]() el número de pisos. En la nueva metodología de cálculo se empleará en primer lugar la ecuación ( 8.3 ) para hallar el parámetro
el número de pisos. En la nueva metodología de cálculo se empleará en primer lugar la ecuación ( 8.3 ) para hallar el parámetro ![]() y este valor se multiplicará por la deriva máxima de piso que se encuentre del análisis sísmico, paso a paso, pero utilizando un programa de Análisis lineal elástico.
y este valor se multiplicará por la deriva máxima de piso que se encuentre del análisis sísmico, paso a paso, pero utilizando un programa de Análisis lineal elástico.
8.4 RESULTADOS DE NUEVA METODOLOGÍA
Se analizaron 72 estructuras de 1 a 6 pisos, con la distribución en planta indicada en la figura 8.3, se tienen 3 vanos en cada dirección de 5.0 m., cada uno. La altura de los entrepisos es igual y mide 3.0 m. Las dimensiones de las columnas y vigas se indican en Quisanga (2006). De igual manera se consideró los 12 casos de armadura indicados en el capítulo 6, se recuerda que el refuerzo transversal para vigas y columnas está compuesto por 1 ![]() de 8 mm., @ 10 cm., en los extremos del elemento y @ 20 cm., en el centro de luz.
de 8 mm., @ 10 cm., en los extremos del elemento y @ 20 cm., en el centro de luz.
Los registros sísmicos empleados se indican en la tabla 8.2, los mismos que fueron normalizados al 40% de la aceleración de la gravedad. Si bien la aceleración máxima de estos registros es mayor al 10% de la aceleración de la gravedad se los normalizó a 0.4 g., para que todos tengan la misma aceleración y sea igual a la estipulada en la zona de mayor peligrosidad sísmica del Código Ecuatoriano de la Construcción y de varios países de América del Sur. Los eventos sísmicos seleccionados fueron registrados en el Perú.
| Cód | Fecha | Magnitud | Distancia
Epicentral ( km) |
Duración
(s) |
Aceleración
Máxima (gal) |
Componente | Suelo |
| 04 a | 9-11-74 | 6.0 | 80.55 | 39.42 | 116.785 | E-W | Arcilloso |
| 06 a | 31-05-70 | 6.4 | 369.17 | 45.02 | 104.818 | E-W | Grava |
| 07 a | 30-10-74 | 6.2 | 59.74 | 97.96 | 192.489 | E-W | Grava |
| 07 b | 30-10-74 | 6.2 | 59.74 | 97.96 | 178.951 | N-S | Grava |
Como se ha indicado, se encontró la respuesta en el tiempo mediante análisis no lineal, utilizando el programa IDARC y la respuesta lineal, empleando el programa LINEAL Aguiar (2005). Luego se determinó las respuestas máximas de desplazamientos laterales en cada piso y con esos valores se hallo la deriva máxima en cada piso. Finalmente la deriva máxima de piso.
Sea ![]() la deriva máxima de piso hallada mediante análisis no lineal, que se considera la solución exacta y sea
la deriva máxima de piso hallada mediante análisis no lineal, que se considera la solución exacta y sea ![]() la deriva máxima de piso encontrada mediante análisis lineal. Al multiplicar
la deriva máxima de piso encontrada mediante análisis lineal. Al multiplicar ![]() por
por ![]() se encuentra la deriva máxima de piso, en forma aproximada que en la ecuación (8.2) se denominó
se encuentra la deriva máxima de piso, en forma aproximada que en la ecuación (8.2) se denominó ![]() . Se denomina
. Se denomina ![]() a la relación entre
a la relación entre ![]() con respecto a
con respecto a ![]() . Si este factor tiende a la unidad la metodología propuesta es muy buena.
. Si este factor tiende a la unidad la metodología propuesta es muy buena.
|
|
(8.4) |
En la figura 8.4, se muestran los valores de ![]() encontrados en el estudio. Se aprecia que las estructuras de 1 piso, la dispersión de resultados es pequeña y para las estructuras de 2 a 6 pisos la dispersión es similar y varía entre 1 y 4, aproximadamente. Los valores medios se indican con línea continua y se encuentran entre 1.25 y 2, en la tabla 8.3 se indican estos valores que demuestran que la metodología propuesta reporta muy buenos resultados tanto en la dispersión como en los valores medios.
encontrados en el estudio. Se aprecia que las estructuras de 1 piso, la dispersión de resultados es pequeña y para las estructuras de 2 a 6 pisos la dispersión es similar y varía entre 1 y 4, aproximadamente. Los valores medios se indican con línea continua y se encuentran entre 1.25 y 2, en la tabla 8.3 se indican estos valores que demuestran que la metodología propuesta reporta muy buenos resultados tanto en la dispersión como en los valores medios.
| Estructuras de | Valor medio de |
Desviación estándar de |
| 1 piso | 1.26 | 0.26 |
| 2 pisos | 1.38 | 0.54 |
| 3 pisos | 1.51 | 0.54 |
| 4 pisos | 1.79 | 0.54 |
| 5 pisos | 2.00 | 0.67 |
| 6 pisos | 1.90 | 0.69 |
8.5 CONCLUSIONES
Dos temas que están relacionados, se han presentado en este capítulo, el primero que tiene relación con la determinación del parámetro ![]() y el segundo con la nueva metodología de cálculo de la deriva máxima de piso en edificios de hormigón armado, en forma rápida.
y el segundo con la nueva metodología de cálculo de la deriva máxima de piso en edificios de hormigón armado, en forma rápida.
Para el primer tema se determino el parámetro ![]() del análisis de 72 estructuras sometidas a la acción de 27 registros sísmicos dando un total de 1944 valores, con los cuales se obtuvo la siguiente relación, en función del número de pisos, la misma que es valida para edificios de hormigón armado de 1 a 6 pisos, sin muros de corte.
del análisis de 72 estructuras sometidas a la acción de 27 registros sísmicos dando un total de 1944 valores, con los cuales se obtuvo la siguiente relación, en función del número de pisos, la misma que es valida para edificios de hormigón armado de 1 a 6 pisos, sin muros de corte.
Para verificar la nueva metodología de cálculo de la deriva máxima de piso se realizó el estudio en 72 estructuras ante 4 registros sísmicos. Estudio en el que se comparó la deriva máxima de piso hallada con la metodología propuesta con relación a la que se obtiene de un análisis no lineal. La comparación es bastante buena debido a que las dispersiones obtenidas son bajas y los valores promedios están entre 1.25 y 2.0.
REFERENCIAS
- 103. Aguiar R., (2005) Programa LINEAL para hallar la respuesta en el tiempo de estructuras. Centro de Investigaciones Científicas. Escuela Politécnica del Ejército, Quito.
- 104. Quisanga D., (2006) Curvas de fragilidad para las diferentes zonas sísmicas del Ecuador e influencia del refuerzo transversal, Tesis de grado. Facultad de Ingeniería Civil. Escuela Politécnica del Ejército.
- 105. Valles R., Reinhorn A., Kunnath S., Li C., and Madan A., (1996), IDARC2D Version 4.0: A computer program for the inelastic damage analysis of buildings, National Center for Earthquake Engineering Research. Headquartered at the State University of New York at Buffalo, Technical Report NCEER-96-0010, 189 p. New York.
CAPÍTULO 9. CURVAS DE FRAGILIDAD
En base al análisis no lineal, de estructuras de hormigón armado de 1 a 6 pisos y que responden a una forma de construcción en el Ecuador, se obtienen curvas de fragilidad de desplazamiento lateral máximo, las mismas que se aproximan bastante bien a las propuestas por HAZUS para el nivel de diseño sísmico bajo y están muy distantes de las curvas de fragilidad presentadas por HAZUS para los niveles de diseño sísmico moderado y alto.
Se analizaron 119 estructuras constituidas por vigas y columnas, sin muros de corte, ante la acción de nueve registros sísmicos de Colombia, cuya aceleración máxima del suelo es mayor al 10% de la aceleración de la gravedad y se obtuvieron curvas de fragilidad para cuatro niveles de daño denominados: leve, moderado, extensivo y completo.
Finalmente, como caso práctico, se encuentran las curvas de fragilidad para dos estructuras de 4 y 5 pisos ubicadas en la ciudad de Macas, para 10 registros sísmicos normalizados al 25% de la aceleración de la gravedad y se comparan los resultados con las curvas de fragilidad que se indican en los párrafos anteriores.
9.1 INTRODUCCIÓN
Para la realización de estudios de vulnerabilidad sísmica se necesita tener curvas de fragilidad, tema que es abordado en el presente capítulo. Existen varias formas de obtenerlas, las mismas que se indican a continuación: i) mediante observaciones de campo, luego de haberse registrado un sismo. ii) en forma experimental en el laboratorio. iii) en forma analítica mediante simulación y iv) métodos basados en la opinión de expertos.
En este estudio se optó por la tercera forma, para el efecto se analizaron 119 estructuras ante la acción de 9 sismos, se encontró la respuesta no lineal, paso a paso y se determinaron los desplazamientos laterales máximos y la deriva de piso máxima ya que el interés era encontrar curvas de fragilidad para esos Parámetros Estructural, PE.
Las curvas de fragilidad, que se obtienen en este capítulo, son gráficas en las cuales en el eje de las X, se especifica el PE., y en el eje de las Y, la Probabilidad de excedencia P. Como el problema se trabaja en forma probabilística, se tiene que definir una función de distribución que mejor se ajuste a los datos. En el trabajo, se emplea una …función de distribución lognormal…, que tiene la siguiente forma:
|
|
(9.1) |
Donde ![]() es el valor medio del parámetro estructural,
es el valor medio del parámetro estructural, ![]() es la desviación estándar del parámetro estructural seleccionado, IS es la Intensidad Sísmica,
es la desviación estándar del parámetro estructural seleccionado, IS es la Intensidad Sísmica, ![]() estado de daño en el punto discreto i. Entonces, la ecuación representa la probabilidad de que el estado de daño sea mayor o igual al estado de daño en el punto discreto i para un determinado nivel de intensidad sísmica. El término de la derecha de la ecuación ( 9.1 ) se acostumbra escribirla como
estado de daño en el punto discreto i. Entonces, la ecuación representa la probabilidad de que el estado de daño sea mayor o igual al estado de daño en el punto discreto i para un determinado nivel de intensidad sísmica. El término de la derecha de la ecuación ( 9.1 ) se acostumbra escribirla como ![]() .
.
Antes de explicar con mayor detalle la ecuación ( 9.1 ) conviene mencionar que en otros estudios se han utilizado otras funciones de distribución, por ejemplo, Ordaz et al (2005) emplea una función de distribución tipo ![]() que trae inmersa a la función gamma
que trae inmersa a la función gamma ![]() la misma que es aplicada para México.
la misma que es aplicada para México.
Para obtener curvas de fragilidad de la deriva máxima de piso ![]() , habrá que reemplazar esta variable en PE, quedando la función de distribución lognormal de la siguiente manera:
, habrá que reemplazar esta variable en PE, quedando la función de distribución lognormal de la siguiente manera:
|
|
(9.2) | |
| (9.3) |
Las curvas de fragilidad dan una idea muy clara del comportamiento de una estructura ante una acción sísmica, representa la probabilidad de que la respuesta exceda, para el presente caso, una determinada distorsión de piso. Posteriormente se verá que con las curvas de fragilidad se obtiene una probabilidad de daño para un valor dado de ![]() .
.
Ghobarah et al (1997) define cinco niveles de desempeño, en función de la deriva máxima de piso o distorsión máxima de piso ![]() , los mismos que se indican en la tabla 9.1; esta clasificación es la que se utilizó en el estudio. En la tabla 9.1 se indica además en forma general el nivel de daño en cada clasificación y el desempeño.
, los mismos que se indican en la tabla 9.1; esta clasificación es la que se utilizó en el estudio. En la tabla 9.1 se indica además en forma general el nivel de daño en cada clasificación y el desempeño.
9.2 ESTRUCTURAS Y SISMOS DE ANÁLISIS
Se han analizado 119 estructuras de hormigón armado de 1 a 6 pisos, las mismas que se encuentran descritas en Bobadilla (2005) y responden a la forma como se construye en el Ecuador. Las de un piso tienen columnas de 20/20 cm. y las de seis pisos columnas de 45/45 cm. Las luces son de 4.0 m. y la altura de entrepiso es de 3.0 m. En capítulos anteriores ya se ha descrito las características de estas estructuras, por lo que se omite dar más detalles al respecto.
Setenta y dos edificios de 1 a 6 pisos fueron analizados ante los nueve registros sísmicos, que se indican en la tabla 9.2, lo que da un total de 648 casos. Adicionalmente, se estudió el comportamiento de 44 estructuras más pero no ante todos los eventos sísmicos, con lo que se tiene un total de 692 casos; se analizaron estas 44 estructuras adicionales para tener como mínimo 20 datos en cada grupo de análisis.
| Reg. | Estación | País | Fecha | Magnitud | Comp | Distan.
Epic. (km.) |
Aceler.
Máxima (Gal.) |
| 1 | Armenia (Carme) | Colombia | 25/01/99 | 6.20 | E-W | 13 | 518,4 |
| 2 | Armenia (Carme) | Colombia | 25/01/99 | 6.20 | N-S | 13 | -580.1 |
| 3 | Finlandia (C Flan) | Colombia | 25/01/99 | 6.20 | E-W | 33 | 554.9 |
| 4 | Finlandia (C Flan) | Colombia | 25/01/99 | 6.20 | N-S | 33 | -477.8 |
| 5 | Pereira (C Per) | Colombia | 25/01/99 | 6.20 | E-W | 48 | -207.8 |
| 6 | Pereira (C Per) | Colombia | 25/01/99 | 6.20 | N-S | 48 | 141.5 |
| 7 | Ricaurte (C Rica) | Colombia | 17/07/98 | 3.07 | E-W | 637 | 132.4 |
| 8 | Ricaurte (C Rica) | Colombia | 17/07/98 | 3.07 | N-S | 637 | -124.8 |
| 9 | Pereira (C Mazpa) | Colombia | 19/02/97 | 6.10 | E-W | 154 | 127.7 |
Se aprecia en la tabla 9.2 que la aceleración máxima de los registros utilizados supera el 10% de la aceleración de la gravedad, no se quería trabajar con sismos de menor aceleración para tener un comportamiento no lineal en las estructuras. La mayor parte de los acelerogramas corresponden al sismo que afectó al eje cafetero de Colombia, el 25 de enero de 1999, que fue un sismo superficial con una profundidad focal de 17 km., y está asociado al fallamiento de Romeral, (Aguiar 1999). En la figura 9.1 se indican los acelerogramas del sismo de enero de 1999 considerados en el estudio, se aprecia que el tiempo de duración fue de aproximadamente 25 s., y que la fase intensa, la que causa daño tuvo una duración que está alrededor de los 9 s.
9.3 ANÁLISIS NO LINEAL Y CLASIFICACIÓN
Se empleó el programa IDARC (Inelastic Damage Análisis of Reinforced Concrete Structures) para encontrar la respuesta no lineal en el tiempo, de cada estructura ante cada uno de los sismos especificados en la tabla 9.2. El programa considera el modelo de Kent y Park (1971) para el comportamiento del hormigón y el modelo trilineal para el comportamiento del acero que contempla incremento de resistencia en la zona de endurecimiento. Por otra parte se utilizó el modelo de histéresis de Park et al (1987) que contempla deterioro de rigidez en la descarga, deterioro de resistencia y efecto pinching o de cierre de grietas. Se realizó un análisis en dos dimensiones.
Una vez que se obtuvo la respuesta en el tiempo, se clasificaron los casos de acuerdo a la deriva máxima de piso. Se clasificó teniendo en cuenta los valores indicados en la primera columna de la tabla 9.1; esta clasificación se indica en la tabla 9.3. Al margen de la determinación de las curvas de fragilidad, vale la pena destacar que la mayor parte de casos van a tener un daño moderado (191) y leve (183). Aguiar y Bobadilla (2005).
Se destaca que hay 154 casos en que la deriva máxima de piso es mayor que 0.023 y que han sido clasificadas como daño completo pero esto no significa que van a colapsar, se van a presentar grietas mayores de 2 mm., pero no necesariamente colapsan.
Las cifras indicadas en la tabla 9.3 deben llamar a la reflexión a los proyectistas estructurales ya que se está diseñando y construyendo, como que el Ecuador no fuera un país con una alta peligrosidad sísmica. Las dimensiones de las columnas que se utilizan son muy bajas, el tener vigas de pequeño peralte no ayudan a una respuesta adecuada y el utilizar estribos simples de 8 mm., de diámetro completan el panorama por el cual las estructuras en general no tienen un buen comportamiento sísmico.
| Pisos | Sin Daño | Daño Leve | Daño Moderado | Daño Extensivo | Daño Completo |
| 1 | --- | 20 | 27 | 20 | 41 |
| 2 | --- | 20 | 45 | 20 | 32 |
| 3 | --- | 32 | 41 | 21 | 21 |
| 4 | --- | 46 | 37 | 20 | 20 |
| 5 | 11 | 44 | 21 | 21 | 20 |
| 6 | 12 | 21 | 20 | 39 | 20 |
| TOTAL | 23 | 183 | 191 | 141 | 154 |
9.4 ESTUDIO ESTADÍSTICO
Para cada tipo de estructuras, en función del número de pisos, se tienen cuatro grupos de datos, correspondientes a daño: leve, moderado, extensivo y completo. Con cada uno de esos grupos, que se indican en la tabla 9.3, se analizó si las respuestas obtenidas corresponden efectivamente a una función de distribución lognormal. A manera de ejemplo en la tabla 9.4, se indica la forma como se trabajó con las derivas máximas de piso obtenidas para el grupo de datos de daño completo en edificaciones de 2 pisos.
Las derivas máximas de piso, se trabajó en porcentaje, para no tener problema con el cálculo de la integral, indicada en la ecuación ( 9.3 ) ya que valores muy pequeños dan problemas en la obtención de la integral, que dicho sea de paso no existe una solución analítica exacta, por lo que debe resolverse la integral, con métodos numéricos.
En la segunda columna de la tabla 9.4, se indica el valor medio del rango y en la tercera columna la frecuencia de los datos reportados. Con estas columnas se obtuvo el …polígono de frecuencias … que se indica, a la izquierda, de la figura 9.2.
En la cuarta columna, se tiene el límite superior del rango que viene a representar el valor de z, de la ecuación ( 9.3 ) es decir es el límite superior de la integral, la quinta columna, es la probabilidad acumulada que se encuentra con la ecuación ( 9.3 ). La sexta columna, se obtiene por diferencia de valores de los datos de la quinta columna y representa el área bajo cada rango. Finalmente la última columna, se obtiene multiplicando la sexta columna por el número total de datos. Con los datos de la cuarta columna y de la última columna, se halla la …curva normalizada… que se indica, a la derecha, de la figura 9.2 y que demuestra que la función de distribución lognormal se ajusta bastante bien a las distorsiones de piso máximas obtenidas. Se ha utilizado la nomenclatura descrita en Downie y Heath (1983).
9.5 CURVAS DE FRAGILIDAD DE DERIVAS DE PISO
Una vez demostrado que los resultados obtenidos se ajustan a una distribución lognormal, se procedió a obtener las curvas de fragilidad, las mismas que se indican en las figuras 9.3 a 9.8, aplicando las ecuaciones ( 9.2 ) y ( 9.3 ). La primera, corresponde a las estructuras de 1 piso y la última, a las de seis pisos. Se destaca que todas las edificaciones estaban conformadas por vigas y columnas, no tenían muros de corte.
| PISO | LEVE | MODERADO | EXTENSIVO | COMPLETO | ||||
| Valor Medio | Desv.
Estándar |
Valor Medio | Desv.
Estándar |
Valor Medio | Desv.
Estándar |
Valor Medio | Desv.
Estándar | |
| (%) | (%) | (%) | (%) | (%) | (%) | (%) | (%) | |
| 1 | 0.397 | 0.050 | 0.896 | 0,175 | 1,303 | 0,327 | 3,675 | 0,818 |
| 2 | 0.378 | 0.093 | 0.674 | 0,120 | 1,674 | 0,388 | 3,708 | 0,912 |
| 3 | 0.346 | 0.066 | 0.750 | 0,188 | 1,530 | 0,317 | 3,213 | 0,567 |
| 4 | 0.343 | 0.071 | 0.776 | 0,146 | 1,698 | 0,399 | 2,822 | 0,434 |
| 5 | 0.361 | 0.066 | 0.778 | 0,154 | 1,620 | 0,388 | 2,901 | 0,737 |
| 6 | 0.358 | 0.057 | 0.854 | 0,187 | 1,643 | 0,352 | 2,957 | 0,740 |
En la tabla 9.5, se indica el valor medio y la desviación estándar de las derivas máximas de piso, para los cuatro niveles de daño. En base a estos valores se obtuvieron las curvas de fragilidad, que se han mostrado en las figuras 9.3 a 9.8.
Posteriormente, se agruparon los resultados en dos grupos, de uno a tres pisos y de cuatro a seis pisos, los valores medios y la desviación estándar para estos grupos se presenta en la tabla 9.6 y las correspondientes curvas de fragilidad en las figuras 9.9 y 9.10.
| PISO | LEVE | MODERADO | EXTENSIVO | COMPLETO | ||||
| Valor Medio | Desv.
Estándar |
Valor Medio | Desv.
Estándar |
Valor Medio | Desv.
Estándar |
Valor Medio | Desv.
Estándar | |
| (%) | (%) | (%) | (%) | (%) | (%) | (%) | (%) | |
| 1-3 | 0.374 | 0.070 | 0.773 | 0.161 | 1.503 | 0.344 | 3.532 | 0.766 |
| 4-6 | 0.354 | 0.064 | 0.803 | 0.162 | 1.654 | 0.380 | 2.893 | 0.637 |
El Código Ecuatoriano de la Construcción, CEC-2000 establece como deriva máxima de piso el 2 %. Con esta cantidad, al ingresar a la figura 9.9 o 9.10, se aprecia, en forma aproximada, que tendrán un 80% de daño extensivo y un 20% de daño completo, cantidades muy altas.
9.6 CURVAS DE FRAGILIDAD DE HAZUS
La Agencia Federal para el Manejo de Emergencias, FEMA por sus siglas en Inglés, publicó en 1999 el programa HAZUS que proviene de Hazards U.S. en que indica una metodología para la estimación de las pérdidas por sismos y más que eso presenta información muy práctica, la misma que puede ser utilizada en la evaluación de la vulnerabilidad sísmica de una ciudad en forma bastante rápida.
Entre la información, se tienen las curvas de fragilidad, tema que se aborda en éste capítulo. En efecto HAZUS 99, presenta estas curvas para cuatro niveles de diseño denominados: pre-norma, bajo, moderado y alto; para cada uno de estos niveles de diseño, se tiene un límite de la deriva máxima de piso ![]() , los mismos que se indican en las tabla 9.7 y 9.8 para los cuatro niveles de daño, denominados: leve, moderado, extensivo y completo.
, los mismos que se indican en las tabla 9.7 y 9.8 para los cuatro niveles de daño, denominados: leve, moderado, extensivo y completo.
| Niveles de daño | Niveles de diseño | |||
| Pre-norma | Bajo | Moderado | Alto | |
| Leve | 0.0040 | 0.0050 | 0.0050 | 0.0050 |
| Moderado | 0.0064 | 0.0080 | 0.0087 | 0.0100 |
| Extensivo | 0.0160 | 0.0020 | 0.0233 | 0.0300 |
| Completo | 0.0400 | 0.0500 | 0.0600 | 0.0800 |
| Niveles de daño | Niveles de diseño | |||
| Pre-norma | Bajo | Moderado | Alto | |
| Leve | 0.0027 | 0.0033 | 0.0033 | 0.0033 |
| Moderado | 0.0043 | 0.0053 | 0.0058 | 0.0067 |
| Extensivo | 0.0107 | 0.0133 | 0.0156 | 0.0200 |
| Completo | 0.0267 | 0.0333 | 0.0400 | 0.0533 |
Los valores de las derivas máximas de piso, en el umbral del nivel de daño indicadas en las tablas 9.7 y 9.8, corresponden a estructuras de hormigón armado, sin muros de corte, de 1 a 3 pisos y de 4 a 7 pisos, respectivamente que HAZUS 99 las denomina C1L y C1M. Se destaca que HAZUS 99 presenta valores similares para 36 tipologías estructurales. En Aguiar (2002) se presenta un estudio bastante detallado del programa HAZUS 99.
En este trabajo se han analizado 119 estructuras de hormigón armado de 1 a 6 pisos, que corresponden a los casos C1L y C1M, obteniendo las curvas de fragilidad, las mismas que han sido comparadas con las reportadas por HAZUS 99 con el propósito de ver si son aplicables estas curvas a las construcciones de Ecuador y para comparar a que nivel de diseño sísmico se aproximan más las construcciones de Ecuador.
9.7 CURVAS DE FRAGILIDAD DE DESPLAZAMIENTOS
Para cada grupo de datos indicados en la tabla 9.3, se encontró el valor medio de los desplazamientos obtenidos ![]() y la correspondiente desviación estándar
y la correspondiente desviación estándar ![]() las mismas que se indican en la tabla 9.9 y que sirvieron de base para la obtención de las curvas de fragilidad de desplazamientos. Para no alargar la exposición, en la figura 9.11, se indica esta curva para estructuras de 3 pisos y en la figura 9.12, para estructura de 6 pisos.
las mismas que se indican en la tabla 9.9 y que sirvieron de base para la obtención de las curvas de fragilidad de desplazamientos. Para no alargar la exposición, en la figura 9.11, se indica esta curva para estructuras de 3 pisos y en la figura 9.12, para estructura de 6 pisos.
Con el propósito de comparar las curvas de fragilidad obtenidas, con las que reporta el programa HAZUS 99, los datos obtenidos del estudio se agruparon en dos, el primero que contiene los resultados de las estructuras de 1 a 3 pisos y el segundo con los resultados de 4 a 6 pisos. En la tabla 9.10, se indican los valores medios y la desviación estándar para estos dos grupos. Las curvas que se obtienen para estos dos grupos se indican en las figuras 9.13 y 9.14.
| PISO | LEVE | MODERADO | EXTENSIVO | COMPLETO | ||||
| Valor Medio | Desv.
Estándar |
Valor Medio | Desv.
Estándar |
Valor Medio | Desv.
Estándar |
Valor Medio | Desv.
Estándar | |
| (cm.) | (cm.) | (cm.) | (cm.) | (cm.) | (cm.) | (cm.) | (cm.) | |
| 1 | 1.174 | 0.0164 | 2.6882 | 0.5155 | 3.9641 | 0.9895 | 12.5502 | 1.3842 |
| 2 | 2.1954 | 0.5979 | 3.8331 | 0.7096 | 10.4608 | 1.2490 | 20.5316 | 1.7036 |
| 3 | 2.5793 | 0.4984 | 5.3882 | 1.3696 | 9.5647 | 1.8479 | 18.1957 | 1.7394 |
| 4 | 3.1805 | 0.6448 | 6.9864 | 1.1527 | 11.9424 | 1.7463 | 23.3404 | 0.6785 |
| 5 | 4.0867 | 0.7726 | 7.4300 | 0.8102 | 15.2093 | 1.2297 | 23.1213 | 0.8645 |
| 6 | 4.1561 | 1.0938 | 10.0666 | 1.2437 | 16.8875 | 1.4928 | 26.2543 | 1.4690 |
| PISO | LEVE | MODERADO | EXTENSIVO | COMPLETO | ||||
| Valor Medio | Desv.
Estándar |
Valor Medio | Desv.
Estándar |
Valor Medio | Desv.
Estándar |
Valor Medio | Desv.
Estándar | |
| (cm.) | (cm.) | (cm.) | (cm.) | (cm.) | (cm.) | (cm.) | (cm.) | |
| 1-3 | 1.631 | 0.371 | 3.970 | 0.865 | 7.997 | 1.362 | 17.093 | 1.609 |
| 4-6 | 3.808 | 0.837 | 8.161 | 1.069 | 14.680 | 1.490 | 24.239 | 1.004 |
HAZUS 99 presenta cuatro curvas de fragilidad similares a la de la figura 9.13 y otras cuatro similares a las de la figura 9.14, que corresponden a los niveles de diseño denominados: pre código, bajo, moderado y alto. El nivel de diseño denominado pre código sirve para estructuras que no se hallan en zonas sísmicas, el nivel de diseño llamado bajo para estructuras que se hallan en zonas de muy baja sismicidad, el nivel de diseño moderado para aquellas que se encuentran en zonas de moderada intensidad y el nivel de diseño denominado alto para estructuras que se hallan en zonas de alta peligrosidad sísmica.
Las curvas de fragilidad obtenidas y mostradas en las figuras 9.13 y 9.14 se compararon con las de HAZUS 99 para los cuatro niveles de diseño y se encontró que las que mejor se aproximan son las correspondientes al nivel de diseño sísmico denominado bajo.
En la figuras 9.15 y 9.16 se presentan las curvas de fragilidad de HAZUS 99 para las estructuras C1L y C1M, respectivamente, para el nivel de diseño bajo.
En la figura 9.17 se presentan las curvas de fragilidad, encontradas en el estudio y las de HAZUS 99 para el caso de 1 a 3 pisos, se aprecia que para los niveles de daño leve y moderado las curvas de fragilidad encontradas en este estudio son prácticamente las mismas que las de HAZUS pero para los niveles de daño extensivo y completo existe cierta diferencia y radica en que el nivel de daño que se espera con las curvas de fragilidad obtenidas en el estudio es mayor que las reportada por HAZUS para desplazamientos laterales máximos que están en el orden de 20 cm., y 30 cm., para daño extensivo y completo. Para desplazamientos mayores las curvas se aproximan bastante.
Para estructuras de 1 a 3 pisos el desplazamiento lateral máximo, por lo general será menor a 30 cm., por lo que se puede indicar que las curvas de fragilidad de HAZUS 99 reportan menor porcentaje de daño acumulado para los niveles denominados extensivo y completo.
En la figura 9.18 se comparan las cuatro curvas de fragilidad obtenidas en el estudio para estructuras de 4 a 6 pisos, con las reportadas por HAZUS 99 para el nivel de diseño sísmico bajo. La aproximación es muy buena para el daño leve y existe diferencia para los restantes niveles de daño, se aprecia que HAZUS, reporta mayor daño acumulado para los niveles: moderado y extensivo. Se destaca que HAZUS, trabajó en este grupo denominado C1M con estructuras de 4 a 7 pisos y en el estudio se trabajó con estructuras de 4 a 6 pisos.
9.8 ANALISIS DE ESTRUCTURAS UBICADAS EN MACAS
Se presentan las curvas de fragilidad de dos edificios de hormigón armado de la ciudad de Macas, el uno tiene 4 pisos y el otro 5 pisos, las curvas de fragilidad se han obtenido para 10 eventos sísmicos normalizados a 0.25 g., que es la aceleración máxima estipulada en el Código Ecuatoriano de la Construcción para la ciudad de Macas, que se halla ubicada al sur oriente del Ecuador.
Las curvas de fragilidad obtenidas, han sido comparadas con las curvas de fragilidad presentadas en los apartados anteriores ya que Macas se halla ubicada en una zona de moderada intensidad, donde se les puede admitir un nivel de diseño sísmico bajo pero en Macas las construcciones tienen un buen nivel sismo resistente. En efecto la mayor parte de construcciones tienen estribos dobles en las columnas y están espaciados a 10 cm., o menos como en el caso de la fotografía 1, en que el espaciamiento es de 7 cm. Normalmente en columnas colocan estribos de 10 mm., de diámetro y en vigas de 8 mm., de diámetro.
9.8.1 Estructuras de análisis
En la figura 9.19 se indica la distribución en planta de la estructura de 4 pisos, incluido un mezanine, que se denominará estructura 1. Tiene dos tipos de columnas, las tipo 1, son de 50/50 y van hasta el nivel 5.0 m., y las tipo 2, son de 40/40, todas tienen estribos dobles como los indicados en la fotografía 9.1 de 10 mm., de diámetro @ 10 cm., en los extremos y 15 cm., en el centro de luz.
Las vigas tienen un ancho de 30 cm., y un peralte de 50 cm., en todos los pisos del edificio, lo que cambia es el armado longitudinal, los estribos utilizados son de 8 mm., de diámetro espaciados cada 10 cm., y 20 cm., en los extremos del elemento y centro de luz, respectivamente.
La estructura 2 es de 5 pisos, en la figura 9.20 se muestra la distribución en planta de las columnas, se aprecia que en el un sentido las luces son de 5.0 m., y una de 5.18 m.; en el otro sentido las luces son de 3.0 m., y una de 3.20 m. Todas las columnas, son de 40/40, en todos los pisos y están armadas con 12 hierros de 16 mm., de diámetro y tienen estribos dobles como los de la fotografía 1 espaciados a 10 cm., en los extremos y 20 cm., en el centro de luz.
Las vigas en la dirección de las luces de 3.0 m., son de 20/20 y en el sentido transversal donde las luces son de 5.0 m., son de 20 cm., de base por 40 cm., de peralte; los estribos son de 8 mm., de diámetro cada 10 y 20 cm.
La altura del primer piso es de 3.50 m., del segundo piso al cuarto es de 2.70 m., y la altura del último piso es de 2.40 m. De tal manera que el primer piso tiene mayor altura que los pisos superiores.
El hormigón utilizado, en las dos estructuras, tiene una resistencia a la compresión máxima de 210 kg/cm2 y el acero un límite de fluencia de 4200 kg/cm2.
9.8.2 Sismos de análisis
En la tabla 9.11 se indican los registros sísmicos considerados en el estudio, los mismos que fueron registrados o sentidos en el Perú. Entre otros datos se indica la aceleración máxima del registro aunque se destaca que todos los sismos fueron normalizados a una aceleración máxima de 0.25 g. que es igual a 245 gals ya que en Macas el sismo de diseño tiene una aceleración máxima del suelo en roca de 245 gals.
Los espectros de respuesta elásticos de los registros sísmicos utilizados, se indican en la figura 9.21. Nótese en todos ellos, para un período igual a cero, inician en 0.25 ya que están normalizados a 0.25 g. El registro cuyo código es 09 a sobrepasa la aceleración de la gravedad, para un período que está alrededor de 0.15 s. También se aprecia que hasta períodos de 0.8 s., se tienen aceleraciones espectrales superiores a 0.6 g. De tal manera que las estructuras estarán sometidas a aceleraciones importantes.
Adelantando los resultados, se debe indicar que los menores desplazamientos de la estructura 1 se obtuvo para el sismo del 5 de enero de 1974, cuyos registros son el 09 a y 09 b. Para estos dos eventos se aprecia que para períodos mayores a 0.4 s., la aceleración es menor a 0.15 g. Las estructuras analizadas tienen un período que es mayor a 0.4 s.
| Cód. | Fecha | Magnitud | Componente | Aceleración
Máxima (gals) |
Distancia
Epicentral (km.) |
Duración
(s.) |
| 04 a | 09/11/74 | 6.0 | E-W | 116.785 | 80.55 | 39.42 |
| 04 b | 09/11/74 | 6.0 | N-S | 93.710 | 80.55 | 39.42 |
| 06 a | 31/05/70 | 6.4 | E-w | 104.818 | 369.17 | 45.02 |
| 06 b | 31/05/70 | 6.4 | N-S | 97.749 | 369.17 | 45.02 |
| 07 a | 03/10/74 | 6.20 | E-W | 192.5 | 59.74 | 97.96 |
| 07 b | 03/10/74 | 6.20 | N-S | 179.0 | 59.74 | 97.96 |
| 08 a | 03/10/74 | 6.20 | E-W | 192.3 | 63.89 | 97.96 |
| 08 b | 03/10/74 | 6.20 | N-S | 207.1 | 63.89 | 97.96 |
| 09 a | 05/01/74 | 6.60 | E-W | 139.6 | 90.10 | 32.80 |
| 09 b | 05/01/74 | 6.60 | N-S | 156.2 | 90.10 | 32.80 |
9.8.3 Resultados del análisis no lineal
Se encontró la respuesta en el tiempo, empleando el programa IDARC, que ha sido ya descrito en otros capítulos del libro. Los desplazamientos laterales máximos para la estructura 1 y para el pórtico B se indican en la tabla 9.12 y para la estructura 2 en la tabla 9.13, que corresponden al pórtico 2.
| Piso | 04 a | 04 b | 06 a | 06 b | 07 a | 07 b | 08 a | 08 b | 09 a | 09 b |
| 4 | 87.27 | 57.48 | 37.50 | 59.58 | 53.58 | 26.85 | 64.51 | 64.78 | 13.18 | 15.23 |
| 3 | 50.25 | 35.54 | 23.23 | 33.77 | 33.16 | 17.39 | 40.80 | 37.60 | 7.62 | 8.61 |
| 2 | 17.47 | 16.91 | 8.89 | 15.81 | 13.74 | 9.13 | 16.25 | 14.11 | 4.04 | 6.28 |
| 1 | 5.63 | 5.92 | 3.50 | 5.44 | 4.68 | 3.28 | 5.34 | 4.53 | 1.55 | 2.39 |
| Piso | 04 a | 04 b | 06 a | 06 b | 07 a | 07 b | 08 a | 08 b | 09 a | 09 b |
| 5 | 46.94 | 57.36 | 52.10 | 39.94 | 72.19 | 35,05 | 96,60 | 51,36 | 15,36 | 8,99 |
| 4 | 41.28 | 49.39 | 41.82 | 37.30 | 64.05 | 30,20 | 84,31 | 42,05 | 12,46 | 8,38 |
| 3 | 32.41 | 36.93 | 35.11 | 31.05 | 55.60 | 23,76 | 64,49 | 29,80 | 9,42 | 7,07 |
| 2 | 22.21 | 24.68 | 25.88 | 20.85 | 40.12 | 17,51 | 39,97 | 21,84 | 6,91 | 5,01 |
| 1 | 11.53 | 12.03 | 12.68 | 11.11 | 19.18 | 9,42 | 16,42 | 10,74 | 3,77 | 3,20 |
9.8.4 Curva de fragilidad de Estructura 1
En la tabla 9.14, se presentan las derivas máximas de piso ![]() encontradas en la estructura 1, se aprecia que la menor deriva es 0.0017 que no genera daño y la mayor deriva es 0.0116 que si genera daño pero esto es lo que se espera en el diseño sismo resistente, para un sismo de 0.25 g., en Macas. El valor medio de las derivas máximas de piso
encontradas en la estructura 1, se aprecia que la menor deriva es 0.0017 que no genera daño y la mayor deriva es 0.0116 que si genera daño pero esto es lo que se espera en el diseño sismo resistente, para un sismo de 0.25 g., en Macas. El valor medio de las derivas máximas de piso ![]() es 0.00602 y la desviación estándar
es 0.00602 y la desviación estándar ![]() es 0.00316. Con estos valores, se halló la curva de fragilidad, que se indica en la figura 9.22. Para poder comparar ésta curva, con las otras que se presentaron en apartados anteriores, en la figura 9.23 se incluye la misma y se aprecia, que el daño esperado es moderado, lo cual demuestra un buen comportamiento sísmico de la estructura.
es 0.00316. Con estos valores, se halló la curva de fragilidad, que se indica en la figura 9.22. Para poder comparar ésta curva, con las otras que se presentaron en apartados anteriores, en la figura 9.23 se incluye la misma y se aprecia, que el daño esperado es moderado, lo cual demuestra un buen comportamiento sísmico de la estructura.
| Sismo | 04 a | 04 b | 06 a | 06 b | 07 a | 07 b | 08 a | 08 b | 09 a | 09 b |
| Drift | 0.0116 | 0.0069 | 0.0045 | 0.0080 | 0.0064 | 0.0030 | 0.0077 | 0.0085 | 0.0017 | 0.0021 |
| |
0.00602 | |||||||||
| |
0.00316 | |||||||||
9.8.5 Curva de fragilidad de Estructura 2
Se procede en forma similar a la estructura 1, es así como en la tabla 9.15 se tienen las derivas de piso máximas para la estructura 2, las mismas que son menores a la estructura 1.
| Sismo | 04 a | 04 b | 06 a | 06 b | 07 a | 07 b | 08 a | 08 b | 09 a | 09 b |
| Drift | 0.004 | 0.005 | 0.005 | 0.004 | 0.008 | 0.003 | 0.009 | 0.005 | 0.001 | 0.001 |
| |
0.00438 | |||||||||
| |
0.00255 | |||||||||
Se destaca que las curvas de fragilidad, que se indican en las figuras 9.24 y 9.25 corresponden al pórtico 2 de la estructura 2. El pórtico 2 tiene vigas de 20/40. En la dirección perpendicular las vigas son de 20/20 pero las luces son menores. Se aprecia que la curva de fragilidad hallada para la estructura 2 tiene menor comportamiento que la curva de fragilidad hallada para la estructura 1.
9.9 CONCLUSIONES
Se han analizado 72 estructuras ante la acción de 9 sismos y también de 44 estructuras más con lo que se tiene un gran total de 692 casos, en base a los cuales se han determinado curvas de fragilidad de deriva de piso máxima y de desplazamiento lateral máximo, en edificios de hormigón armado de 1 a 6 pisos. Estas curvas están clasificadas para cuatro niveles de daño denominados: leve, moderado, extensivo y completo. Del estudio realizado se desprende la siguiente conclusión.
- Las curvas de fragilidad obtenidas en el estudio se aproximan bastante bien con las curvas de fragilidad de HAZUS 99 para el nivel de diseño sísmico bajo. Esto debe ser un llamado de atención ya que el nivel de diseño sísmico bajo se lo utiliza en zonas de baja sismicidad y el Ecuador es un País con un alto peligro sísmico. De tal manera que la tendencia de tener vigas con poco peralte, columnas con dimensiones mínimas y estribos simples de 8 mm., de diámetro tanto en vigas como en columnas no son adecuados para el Ecuador.
Por otra parte, se obtuvo las curvas de fragilidad de dos estructuras de 4 y 5 pisos, ubicadas en la ciudad de Macas y se halló que las mismas tienen un buen comportamiento sísmico para la zona en la cual se encuentran. En efecto las curvas de fragilidad obtenidas para 10 registros sísmicos normalizados a 0.25 g., que es la aceleración estipulada por el CEC-2000, demuestran que se espera daño moderado en estas edificaciones, que significa que las grietas que se van a producir serán menores a 1 mm.
REFERENCIAS
- 106. Aguiar R., Bobadilla C., (2005), “Curvas de fragilidad para estructuras de H/A de Ecuador menores a siete pisos”, Revista Ciencia. Centro de Investigaciones Científicas. Escuela Politécnica del Ejército, 8 (2), 81-88, Quito, Ecuador.
- 107. Aguiar R., (2002), Sistema de Computación CEINCI3 para evaluar daño sísmico en los Países Bolivarianos, Centro de Investigaciones Científicas. Escuela Politécnica del Ejército, 302 p, Quito-Ecuador
- 108. Aguiar R., (1999), Sismo de Colombia. Eje Cafetero 1999, Centro de Investigaciones Científicas. Escuela Politécnica del Ejército, 164 p, Quito, Ecuador.
- 109. Bobadilla C., (2005) Curvas de Fragilidad y evaluación rápida de la vulnerabilidad sísmica de estructuras, Tesis de Grado, Facultad de Ingeniería Civil. Escuela Politécnica del Ejército, Quito.
- 110. Downie N., and Heath R., (1983), Métodos Estadísticos Aplicados, Ediciones del Castillo, S.A., 373 p., Madrid, España.
- 111. Ghobarah A., Aly N. and El-Attar M. (1997) “Performance level criteria and evaluation. A critical review of proposed guidelines”. Seismic design methodology for the next generation of codes. Fajfar and Krawinkler Editors, Balkema, Slovenia.
- 112. HAZUS 99, (1999), Earthquake loss estimation methodology, Federal Emergency Management Agency, FEMA and National Institute of Building Sciences NIBS, Vol 5, Chapter 5, Washington D.C.
- 113. Kent D., and Park R., (1971), “Flexural members with confined concrete”, Journal of Structural Division, ASCE, Vol. 97, ST7, 1969-1990.
- 114. Ordaz M., Miranda E., Reinoso E., Santa Cruz S., (2004), “Modelo de estimación de pérdidas por sismo en México con fines de seguro, XIX Simposio Internacional: “Últimos avances en la Ingeniería Sísmica y gestión del riesgo de los desastres”, 33 p., Lima, Perú.
- 115. Park Y., Reinhorn A., and Kunnath S., (1987), IDARC: Inelastic Damage Analysys of Reinforced Concrete Frame-Shear-Wall Structures, Technical Report NCEER-87-0008, State University of New York at Buffalo.
Document information
Published on 01/01/2006
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?