Updated Lagrangian mixed finite element formulation for quasi and fully incompressible fluids

Latest revision as of 10:17, 7 June 2019

Published in Computational Mechanics, Vol. 54 (6), pp. 1583-1596, 2014
DOI: 10.1007/s00466-014-1078-1

Abstract

We present a mixed velocity-pressure finite element formulation for solving the updated Lagrangian equations for quasi and fully incompressible fluids. Details of the governing equations for the conservation of momentum and mass are given in both differential and variational form. The finite element interpolation uses an equal order approximation for the velocity and pressure unknowns. The procedure for obtaining stabilized FEM solutions is outlined. The solution in time of the discretized governing conservation equations using an incremental iterative segregated scheme is described. The linearization of these equations and the derivation of the corresponding tangent stiffness matrices is detailed. Other iterative schemes for the direct computation of the nodal velocities and pressures at the updated configuration are presented. The advantages and disadvantages of choosing the current or the updated configuration as the reference configuration in the Lagrangian formulation are discussed.

Keywords: Updated Lagrangian formulation, incompressible fluids, finite element method, incremental solution, tangent matrix, mixed formulation, stabilized method

1 INTRODUCTION

In Lagrangian analysis procedures, the motion of the particles of a deforming body is followed in time. In Eulerian formulations, on the other hand, attention is focused in the motion of the material through a stationary control volume. Lagrangian methods have been traditionally used for the numerical analysis of solids and structures, while Eulerian methods are typical in computational fluid dynamics [2,4,5,36,40,41].

Despite this evidence, the use of a Lagrangian description for solving fluid dynamics problems using the finite element method (FEM) [10,41] and different meshless and mesh-based particle-based numerical techniques [6,7,12],[16]–[20],[25,26] [29]–[35],[37,38] has received much attention in recent years. Of particular interest are numerical procedures, such as the Particle Finite Element Method (PFEM) [16,25,26,29,31], that combine the advantage of particle-based procedures with the formalism and accuracy of the FEM.

Despite the increasing interest in the Lagrangian approach for solving the equations of fluid mechanics using the FEM, there are few references to the derivation of incremental iterative solution schemes using linearized forms of the discretized Lagrangian equations for fluid flow problems. An early attempt in this direction was reported by Radovitzky and Ortiz [34] who derived the tangent matrix for the FEM Lagrangian analysis of compressible flows using a Newton-Rapsohn type iterative scheme.

The goal of this paper is to present a mixed velocity-pressure formulation for the finite element analysis of quasi and fully incompressible fluids using an updated Lagrangian formulation. We advocate an equal order interpolation for the velocity and pressure variables which invariably requires using an adequate stabilization scheme for the mass balance equation in order to obtain accurate numerical results. In the paper we derive in some detail both the continuum and discretized (FEM) forms of the equations governing the motion of the fluid in the updated Lagrangian description. An incremental Newton-Raphson type iterative staggered scheme for the solution in time of the non linear discretized equations is detailed. The derivations are carried out first using the current configuration as the reference configuration in the Lagrangian description of the motion. The expression of the different matrices and vectors involved in the incremental iterative scheme is given. The particular form of the FEM equations when the updated configuration is taken as the reference configuration is presented. The direct transient solution of the nodal velocities and pressures using monolithic and staggered schemes is also presented for completeness.

The chapter concludes with a discussion of the computational advantages and disadvantages of choosing the current or the the updated configuration as the reference configuration in the Lagrangian description.

In the next section the basic concepts of the motion of a fluid are briefly revisited. These concepts are standard and can be found in many books on computational solid and fluid mechanics and fluid-structure interaction, among others [2,3,4,5,13,36]. This introductory section aims to set up the updated Lagrangian framework where the governing equations for the fluid are written and subsequently solved with the FEM using a mixed velocity-pressure formulation.

2 MOTION. DISPLACEMENT, VELOCITY AND ACCELERATION

We will consider a domain containing a fluid which evolves in time due to external and internal forces and prescribed velocities from an initial configuration at time ${\textstyle t={}^{0}t}$ (typically ${\textstyle {}^{0}t=0}$ ) to a current configuration at time ${\textstyle t={}^{n}t}$ . The fluid volume ${\textstyle V}$ and its boundary ${\textstyle \Gamma }$ at the initial and current configurations are denoted as ( ${\textstyle {}^{0}V,{}^{0}\Gamma }$ ) and ( ${\textstyle {}^{n}V,{}^{n}\Gamma }$ ), respectively. The goal is to find the domain that the fluid occupies, as well as the velocities, strain rates and stresses (the deviatoric stresses and the pressure) in the so-called updated configuration at time ${\textstyle {}^{n+1}t={}^{n}t+\Delta t}$ (Figure 1). In the following a left superindex denotes the configuration of the fluid domain where the variable is computed.

Figure 1: Initial (

), current (

) and updated (

) configurations of a fluid domain

with Neumann (

) and Dirichlet (

) boundaries. Trajectory of a material point

and velocity (

) and displacement (

) vectors of the point at each configuration.

,

and

denote schematically the trajectories of the overall domain between two configurations.

The motion of the fluid domain is described by

(1)

where ${\textstyle {}^{t}{x}}$ is the position of the material point ${\textstyle {}^{0}{x}}$ laying on the initial configuration at time ${\textstyle t}$ . The coordinates ${\textstyle {}^{t}{x}}$ give the spatial position of a point and are called spatial or Eulerian coordinates. The function ${\textstyle {\boldsymbol {\phi }}}$ maps the initial configuration into the current configuration at time ${\textstyle t}$ . The position of the points in the current and initial configurations at time ${\textstyle t={}^{n}t}$ and ${\textstyle t={}^{0}t}$ , respectively are expressed by

{\begin{array}{l}{}^{n}{x}={\boldsymbol {\phi }}({}^{0}{x},{}^{n}t)\quad {\hbox{or}}\quad {}^{n}x_{i}=\phi _{i}({}^{n}{x},{}^{n}t)\\{}^{0}{x}={\boldsymbol {\phi }}({}^{0}{x},{}^{0}t)\quad {\hbox{or}}\quad {}^{0}x_{i}=\phi _{i}({}^{0}{x},{}^{0}t)\end{array}}

(2)

Thus the mapping ${\textstyle {\boldsymbol {\phi }}({}^{0}{x},{}^{0}t)}$ is the identity mapping.

In the Lagrangian description (also called the material description) the independent variables are the material coordinates ${\textstyle {}^{0}{x}}$ of the point on the initial configuration and the time ${\textstyle t}$ . In the Eulerian description, on the other hand, the independent coordinates are the spatial coordinates ${\textstyle {}^{t}{x}}$ and the time ${\textstyle t}$ [4,5].

The displacement of a material point is given by the difference between its position at time ${\textstyle t}$ and its original position, so

(3)

where ${\textstyle {u}=[u_{1},u_{2},u_{3}]^{T}}$ is the displacement vector of a point.

For ${\textstyle t={}^{n}t}$ we have

(4)

The velocity vector is the rate of change of the position vector for a material point, i.e. the time derivative of ${\textstyle \phi ({}^{0}{x},t)}$ with ${\textstyle {}^{0}{x}}$ held constant (also called the material time derivative or total derivative). The velocity vector is usually written as (using Eq.(3) and noting that the coordinates ${\textstyle {}^{0}{x}}$ are fixed)

(5)

The velocity vector of a material point in the current configuration is written as

(6)

The acceleration vector is the rate of change of the velocity vector of a material point (i.e. the material time derivative of the velocity vector) and it can be written as

(7)

and

(8)

Eq.(7) is the material form of the acceleration. Note the difference of Eq.(7) with the expression of the acceleration written in the Eulerian description which involves the convective terms [2,4,5,13,36,41].

In the total Lagrangian description the various equations and variables are referred to the initial configuration which is taken as the reference configuration. In the updated Lagrangian description, either the current or the updated configurations can be taken as the reference configuration [2,4,5,13,36].

For simplicity, in the first part of this work the current configuration will be taken as the reference configuration for the derivation of the incremental FEM equations. The reason is that the current configuration remain fixed during the iterative solution process. The particularization for the case when the updated configuration is taken as the reference configuration is presented in the last part of the paper.

The displacement increment vector ${\textstyle \Delta {u}({}^{0}{x},t)=[\Delta u_{1},\Delta u_{2},\Delta u_{3}]^{T}}$ of a material point between the updated and the current configurations is defined as

(9)

The displacement increment of a material point can be computed from the velocity as

(10)

where ${\textstyle {}^{\tau }{v}}$ is the velocity vector of the points laying on the trajectory followed by the material point between times ${\textstyle {}^{n}t}$ and ${\textstyle {}^{n+1}t}$ (Figure 1). The integral of Eq.(10) can be approximated in a number of ways (see Remark 4).

3 MOMENTUM EQUATIONS AND BOUNDARY CONDITIONS

Let us assume that at time ${\textstyle {}^{n+1}t}$ the fluid occupies a volume ${\textstyle {}^{n+1}V}$ with a boundary ${\textstyle {}^{n+1}\Gamma }$ . The fluid is subjected to body forces ${\textstyle {}^{n+1}b_{i}}$ acting over the volume ${\textstyle {}^{n+1}V}$ and surface tractions ${\textstyle {}^{n+1}t_{i}^{p}}$ acting on the part of the boundary termed as ${\textstyle {}^{n+1}\Gamma _{t}}$ , where index ${\textstyle i}$ denotes the component of the force along the ${\textstyle i}$ th cartesian axis (Figure 1).

The equations of internal equilibrium between the applied body forces and the Cauchy stresses ${\textstyle \sigma _{ij}}$ in the fluid are expressed by the momentum equations written in the updated configuration as [2,4,5,13,36]

(11)

where ${\textstyle {}^{n+1}r_{m_{i}}}$ is the ${\textstyle i}$ th momentum equation, ${\textstyle {}^{n+1}\rho }$ , ${\textstyle {}^{n+1}v_{i}}$ and ${\textstyle {}^{n+1}a_{i}}$ are the fluid density and the ${\textstyle i}$ th component of the velocity and the acceleration at time ${\textstyle {}^{n+1}t}$ and ${\textstyle n_{s}}$ is the number of space dimensions ( ${\textstyle n_{s}=3}$ for three dimensional (3D) problems). Note that ${\textstyle \sigma _{ij}}$ is always referred to the updated configuration, i.e. ${\textstyle \sigma _{ij}\equiv {}^{n+1}\sigma _{ij}}$ .

In Eq.(11) and in the following, the standard summation convention for repeated indices is adopted, unless otherwise specified.

The boundary conditions are

(12)

(13)

where ${\textstyle {}^{n+1}v_{i}^{p}}$ is the prescribed value of the ${\textstyle i}$ th velocity component at the external boundary ${\textstyle {}^{n+1}\Gamma _{v}}$ with ${\textstyle {}^{n+1}\Gamma _{v}\cup {}^{n+1}\Gamma _{t}={}^{n+1}\Gamma }$ . In Eq.(13) ${\textstyle n_{j}}$ is the ${\textstyle j}$ th component of the unit normal to the boundary ${\textstyle {}^{n+1}\Gamma _{t}}$ where the prescribed surface tractions ${\textstyle {}^{n+1}t_{i}^{p}}$ are applied.

The goal is to obtain the geometry of the updated configuration ${\textstyle {}^{n+1}V}$ , as well as the velocities and stresses in ${\textstyle {}^{n+1}V}$ that satisfy Eqs.(11)–(13).

4 PRINCIPLE OF VIRTUAL POWER IN THE UPDATED CONFIGURATION

The principle of virtual power (PVP) can be written in the updated configuration as [2,4,5]

(14)

where ${\textstyle {}^{n+1}\delta A}$ , ${\textstyle {}^{n+1}\delta U}$ and ${\textstyle {}^{n+1}\delta W}$ are the virtual powers due to the acceleration terms, the stresses and the external loads acting on ${\textstyle {}^{n+1}V}$ , respectively given by [2,4,5]

${}^{n+1}\delta A=\int _{{}^{n+1}V}\delta {v}^{T}{~}^{n+1}\rho ~{}^{n+1}{a}~d~{}^{n+1}V$	(15)
${}^{n+1}\delta U=\int _{{}^{n+1}V}\left\{\delta {D}\right\}^{T}\left\{{\boldsymbol {\sigma }}\right\}d~{}^{n+1}V$	(16)
${}^{n+1}\delta W=\int _{{}^{n+1}V}\delta {v}^{T}{~}^{n+1}{b}~d{~}^{n+1}V+\int _{{}^{n+1}\Gamma _{t}}\delta {v}^{T}{~}^{n+1}{t}~d~{}^{n+1}\Gamma$	(17)

In Eq.(15)–(16) ${\textstyle \delta {v}}$ , ${\textstyle {b}}$ and ${\textstyle {t}}$ are the virtual velocity vector, the body forces vector and the surface tractions vector, respectively defined for 3D problems as

(18)

In Eq.(16) ${\textstyle {\boldsymbol {\sigma }}}$ is the Cauchy stress tensor and ${\textstyle \delta {D}}$ is the virtual rate of deformation tensor defined as

(19)

where ${\textstyle \delta v_{i}}$ is the ${\textstyle i}$ th component of the virtual velocity.

In the following ${\textstyle \left\{{A}\right\}}$ , where A is a symmetric tensor, will denote the vector representation of A. Hence, in Eq.(16) ${\textstyle \left\{{\boldsymbol {\sigma }}\right\}}$ and ${\textstyle \left\{\delta {D}\right\}}$ are the Cauchy stress vector and the rate of deformation vector, respectively defined in Voigt notation [4,5] as

$\left\{{\boldsymbol {\sigma }}\right\}=\left[\sigma _{11},\sigma _{22},\sigma _{33},\sigma _{12},\sigma _{13},\sigma _{23}\right]^{T}$	(20.a)
$\left\{\delta {D}\right\}=\left[\delta D_{11},\delta D_{22},\delta D_{33},\delta D_{12},\delta D_{13},\delta D_{23}\right]^{T}$	(20.b)

Similarly, ${\textstyle \left[{A}\right]}$ will denote hereonwards the matrix form of tensor ${\textstyle A}$ .

Remark 1. The PVP can be obtained by applying the standard weighted residual method to the governing equations (11) and (13) using the virtual velocities ${\textstyle \delta v_{i}}$ as weighting functions [4].

Remark 2. Tensor ${\textstyle \delta {D}}$ can be interpreted as the variation of the rate of deformation tensor ${\textstyle D}$ defined in terms of the velocities at the updated configuration as

(21)

5 TRANSFORMATION TO THE CURRENT CONFIGURATION. LAGRANGIAN STRESS AND STRAIN MEASURES

In the following sections we will use the current configuration as the reference configuration for computing the internal virtual due to the acceleration terms and the stresses, as well as for subsequently performing the linearization of its discretized form via the FEM. The alternative of using the updated configuration as the reference configuration is presented in Section 12.

After the standard transformations of continuum mechanics [2,4,5,13,36] the internal virtual power at the updated configuration due to the acceleration terms and the stresses can be expressed in terms of material parameters, integrals, strain rates and stress measures evaluated at the current configuration ${\textstyle {}^{n}V}$ as

(22.a)

(22.b)

where ${\textstyle \delta {\dot {E}}}$ and ${\textstyle {S}}$ are the material virtual strain rate tensor and the second Piola-Kirchhoff stress tensor, respectively. The relationship between the material strain rate tensor ${\textstyle {\dot {E}}}$ and the rate of deformation tensor ${\textstyle {D}}$ and between the stress tensors ${\textstyle {\boldsymbol {\sigma }}}$ and ${\textstyle {S}}$ is [2,4,5,13,36]

(23)

where F is the deformation gradient and ${\textstyle J}$ is the Jacobian, respectively defined as

(24)

From the expression of ${\textstyle {\dot {E}}}$ of Eq.(23) we can deduce

(25)

Remark 3. The material strain rate tensor can also be obtained from the time derivative of the Green-Lagrange strain tensor ${\textstyle {E}}$ as [2,4,5]

(26)

where ${\textstyle {C}={F}^{T}{F}}$ is the right Cauchy-Green tensor and ${\textstyle {\dot {F}}={\frac {d}{dt}}({F})}$ . The expression of ${\textstyle \delta {\dot {E}}}$ is obtained by writing the variation of ${\textstyle {\dot {E}}}$ with respect to the velocities as

(27)

A useful explicit expression of the material strain rate tensor components in terms of the velocities ${\textstyle {}^{n+1}v_{i}}$ and the displacement increments ${\textstyle \Delta u_{i}}$ is

(28.a)

with

(28.b)

From Eqs.(5) we deduce

(29.a)

with

(29.b)

6 SPLIT OF THE INTERNAL VIRTUAL POWER INTO DEVIATORIC AND VOLUMETRIC COMPONENTS

The Cauchy stress tensor can be split in its deviatoric component ${\textstyle {\boldsymbol {\sigma }}'}$ and the hydrostatic pressure component ${\textstyle p}$ as

(30)

where ${\textstyle {I}_{3}}$ is the ${\textstyle 3\times 3}$ identity matrix.

Note that in incompressible fluid mechanics the pressure ${\textstyle p}$ is an independent variable. Also, unless otherwise specified we will assume that ${\textstyle p}$ is the pressure at the updated configuration (i.e. ${\textstyle p={~}^{n+1}p}$ ).

Substituting Eq.(30) into the internal virtual power expression in Eq.(16) gives

(31)

where ${\textstyle D_{v}}$ is the volumetric strain rate given by

(32)

It can be proven that [4,5,13,36]

(33)

where ${\textstyle {\dot {E}}_{v}}$ is the volumetric material strain rate,

(34.a)

(34.b)

and ${\textstyle C_{ij}^{-1}}$ is the element ${\textstyle ij}$ of tensor ${\textstyle {C}^{-1}}$ .

The internal virtual power expression of Eq.(31) can be written in the current configuration as follows.

Substituting the Cauchy stress split of Eq.(30) into the expression of the second Piola-Kirchhoff stress tensor of Eq.(23) gives

(35)

where

(36)

is the deviatoric second Piola-Kirchhoff stress tensor. ${\textstyle {S}'}$ is usually called the (true) deviatoric component of ${\textstyle S}$ [4,5,13,36].

Substituting Eq.(35) into (22.b) gives

(37)

with

(38)

Eq.(37) can also be obtained from Eq.(31) using the relationship between ${\textstyle {D},~{\boldsymbol {\sigma }}'}$ and ${\textstyle D_{v}}$ with ${\textstyle {\dot {E}}}$ , ${\textstyle {S}'}$ and ${\textstyle {\dot {E}}_{v}}$ , respectively and the expression ${\textstyle d^{n+1}V=Jd^{n}V}$ [2,4,5].

Substituting Eqs.(15), (22.a) and (37) into (14), the PVP in the updated configuration can be written in terms of the pressure, the deviatoric second Piola-Kirchhoff stresses and the virtual Green-Lagrange strains computed in the current configuration as

{\begin{array}{r}\displaystyle \int _{{}^{n}V}\delta {v}^{T}{~}^{n}\rho {~}^{n+1}{a}d{~}^{n}V+\int _{{}^{n}V}\left(\left\{\delta {\dot {E}}\right\}^{T}\left\{{S}'\right\}+J\delta {\dot {E}}_{v}p\right)d{~}^{n}V-\\-\displaystyle \int _{{}^{n+1}V}\delta {v}^{T}{~}^{n+1}{b}~d{~}^{n+1}V-\int _{{}^{n+1}\Gamma _{t}}\delta {v}^{T}{~}^{n+1}{t}~d{~}^{n+1}\Gamma =0\end{array}}

(39)

The vector form of tensors ${\textstyle \delta {\dot {E}}}$ and ${\textstyle {S}}$ in Eq.(39) is

(40.a)

(40.b)

Note that the contribution of the external forces in Eq.(39) is computed at the updated configuration and this requires using the correct expression for the density and the surface tractions on ${\textstyle {}^{n+1}V}$ (see also Remark 5).

7 CONSTITUTIVE RELATIONSHIP FOR THE DEVIATORIC STRESSES

The relationship between the deviatoric Cauchy stresses ${\textstyle {\sigma '}_{ij}}$ and the rates of deformation ${\textstyle D_{ij}}$ for a Newtonian fluid is written as

(41)

where ${\textstyle {D'}_{kl}}$ are the deviatoric rates of deformation. The rates of deformation ${\textstyle D_{ij}}$ are obtained in terms of the velocities by Eq.(21).

The components of the fourth order constitutive tensor ${\textstyle {c}}$ in the updated configuration are

(42)

where ${\textstyle \mu }$ is the viscosity of the fluid.

Eq.(41) can be written in vector form as

(43)

with

{\begin{array}{l}\left\{{\boldsymbol {\sigma }}'\right\}=\left[\sigma '_{11},\sigma '_{22},\sigma '_{33},\sigma '_{12},\sigma '_{13},\sigma '_{23}\right]^{T}\\\left\{{D}\right\}=\left[D_{11},D_{22},D_{33},2D_{12},2D_{13},2D_{23}\right]^{T}\end{array}}

(44)

and the constitutive matrix ${\textstyle [{c}]}$ is given by (for 3D problems)

\left[{c}\right]=\mu \left[\displaystyle {\begin{matrix}\displaystyle {\frac {4}{3}}&\displaystyle -{\frac {2}{3}}&\displaystyle -{\frac {2}{3}}&0&0&0\\[.25cm]&\displaystyle {\frac {4}{3}}&\displaystyle -{\frac {2}{3}}&0&0&0\\[.25cm]&&\displaystyle {\frac {4}{3}}&0&0&0\\{\hbox{ Sym.}}&&&1&0&0\\&&&&1&0\\&&&&&1\end{matrix}}\right]

(45)

The constitutive equation (41) can be transformed to the current configuration to yield the relationship between the deviatoric second Piola-Kirchhoff stresses and the material strain rates as

(46)

The constitutive tensor in the current configuration ${\textstyle \left[{\boldsymbol {\cal {C}}}\right]}$ is obtained from its counterpart in the updated configuration as [36]

(47)

The vector form of Eq.(46) is written as

(48)

Matrix ${\textstyle \left[{\boldsymbol {\cal {C}}}\right]}$ is obtained by applying Voigt rule to the terms of tensor ${\textstyle {\boldsymbol {\cal {C}}}}$ [4,5].

8 THE MASS BALANCE EQUATION

The mass balance equation in the updated configuration is written for a quasi-incompressible fluid as

(49)

where ${\textstyle c}$ is the speed of sound in the fluid. For a fully incompressible fluid ${\textstyle c=\infty }$ and Eq.(49) reduces to the standard form ${\textstyle D_{v}=0}$ . The quasi-incompressible form will be retained here and this will allow us to account for the effect of the (small) compressibility in most fluids.

Eq.(49) can be written in terms of the bulk modulus of the fluid ${\textstyle \kappa }$ defined as ${\textstyle \kappa =\rho c^{2}}$ . For convenience we will retain the form of Eq.(49).

The variational form of the mass balance equation is obtained via the standard weighted residual method [41] as

(50)

where ${\textstyle q}$ are appropriate test functions with dimensions of pressure [4,5,41].

The integral expression (50) can be written in the current configuration using Eq.(33) as

(51)

In the derivation of Eq.(51) we have used the standard expressions [4,5]

(52)

Eqs.(39) and (51) together with the constitutive relationship (47) and the boundary conditions (12) complete the set of governing variational equations for a fluid in the updated Lagrangian description. The solution of these equations with the FEM is described in the next section.

9 FINITE ELEMENT DISCRETIZATION

We interpolate the velocities and the pressure in terms of their nodal values in the standard finite element fashion [28,39,41]. For a mesh of ${\textstyle n}$ -noded ${\textstyle C^{\circ }}$ continuous elements we can write

(53)

where

{\bar {v}}=\left\{{\begin{matrix}{\bar {v}}^{1}\\{\bar {v}}^{2}\\\vdots \\{\bar {v}}^{N}\end{matrix}}\right\}\quad {\hbox{with }}{\bar {v}}^{i}=[{\bar {v}}_{1}^{i},{\bar {v}}_{2}^{i},{\bar {v}}_{3}^{i}]^{T}\quad ,\quad {\bar {p}}=[{\bar {p}}_{1},{\bar {p}}_{2},\cdots ,{\bar {p}}_{N}]^{T}

(54.a)

where ${\textstyle N}$ is the total number of nodes in the mesh, ${\textstyle {\bar {v}}_{j}^{i}}$ and ${\textstyle {\bar {p}}^{i}}$ are ${\textstyle j}$ th velocity component and the pressure unknowns for node ${\textstyle i}$ ,

{\begin{array}{l}{N}_{v}=[{N}_{1}^{v},{N}_{2}^{v},\cdots ,{N}_{N}^{v}]\quad ,\quad {N}_{i}^{v}=N_{i}^{v}{I}_{3}\\{N}_{p}=[{N}_{1}^{p},{N}_{2}^{p},\cdots ,{N}_{N}^{p}]\end{array}}

(54.b)

In Eq.(54.b) ${\textstyle {N}_{i}^{v}}$ and ${\textstyle N_{i}^{p}}$ are the global shape functions [28,39] for the velocity and pressure interpolations for node ${\textstyle i}$ , respectively.

The velocity and pressure increments and the virtual velocities are interpolated in terms of their nodal values in the same fashion as in Eq.(53).

The strain rate vector ${\textstyle \left\{{\dot {E}}\right\}}$ and its virtual expression ${\textstyle \left\{\delta {\dot {E}}\right\}}$ are respectively expressed in terms of the nodal velocities ${\textstyle {\bar {v}}}$ and their virtual values ${\textstyle \delta {\bar {v}}}$ via Eqs.(28.a), (29.a) and (53) as

(55)

The actual and virtual volumetric material strain rates are related to the virtual velocities as

(56)

In the above equations ${\textstyle {B}}$ is the material strain rate matrix given by

(57)

where

{\begin{array}{l}{}_{n}{B}_{i}^{0}=\left[{\begin{matrix}{}_{n}N_{i,1}^{v}&0&0\\0&{}_{n}N_{i,2}^{v}&0\\0&0&{}_{n}N_{i,3}^{v}\\{}_{n}N_{i,2}^{v}&{}_{n}N_{i,1}^{v}&0\\{}_{n}N_{i,3}^{v}&0&{}_{n}N_{i,1}^{v}\\0&{}_{n}N_{i,3}^{v}&{}_{n}N_{i,2}^{v}\end{matrix}}\right]~~{\hbox{and}}~~{B}_{i}^{L}={}_{n}{B}_{i}^{0}{L}^{T}~~{\hbox{with}}~~{L}=\left[{\begin{matrix}l_{11}&l_{12}&l_{13}\\l_{21}&l_{22}&l_{23}\\l_{31}&l_{32}&l_{33}\end{matrix}}\right]\end{array}}

(58.a)

are the linear and non linear counterparts of the material strain rate matrix, respectively. The components of ${\textstyle {}_{n}{B}_{i}^{0}}$ and ${\textstyle {L}}$ are

(58.b)

The deviatoric second Piola-Kirchhoff stresses are related to the nodal velocities via Eqs.(47) and (55) as

(59)

Remark 4. The displacement increment ${\textstyle \Delta u_{i}}$ can be computed in terms of the velocity in a number of ways. A popular choice is

(60.a)

where ${\textstyle {~}^{n+\alpha }v_{i}}$ is the velocity at ${\textstyle t=t_{n}+\alpha \Delta t}$ where ${\textstyle \alpha }$ is a positive number ( ${\textstyle 0\leq \alpha \leq 1}$ ). The value of ${\textstyle {~}^{n+\alpha }v_{i}}$ is typically computed as

(60.b)

9.1 Discretized form of the PVP

Substituting Eqs.(53), (55) and (56) into the PVP (Eq.(39)) we obtain, after simplifying the virtual velocities

(61)

where ${\textstyle {}^{n+1}{\bar {r}}_{m}}$ is the residual vector of the discretized momentum equations in the updated configuration and ${\textstyle {\dot {\bar {v}}}\equiv {\partial {}^{n+1}{\bar {v}} \over \partial t}}$ is the nodal acceleration vector.

Eq.(61) can be written in a more compact form as

(62)

where

(63)

In Eq.(62) ${\textstyle {}^{n+1}{g}_{v}}$ and ${\textstyle {}^{n+1}{g}_{p}}$ are internal force vectors contributed by the deviatoric second Piola-Kirchhoff stresses and the pressure, respectively and ${\textstyle {}^{n+1}{f}_{m}}$ is the external force vector.

Recall that the internal force vectors at the current configuration are obtained in terms of expressions at the updated configuration.

Remark 5. The computation of the body force vector ${\textstyle {}^{n+1}{b}}$ in Eq.(63) for the case of selfweight requires computing the density at the updated configuration as ${\textstyle {}^{n+1}\rho ={\frac {1}{J}}{}^{n}\rho }$ . We also note that the surface tractions ${\textstyle {}^{n+1}{t}}$ are applied on the boundary of the updated configuration ${\textstyle {}^{n+1}\Gamma }$ , which requires the accurate identification of this boundary.

The acceleration term in Eq.(62) can be approximated in a number of manners. A backward Euler scheme gives

(64)

9.2 Discretization of the mass conservation equation

The arbitrary pressure test functions ${\textstyle q}$ are interpolated in the same fashion as the pressure as

(65)

where vector ${\textstyle {\bar {q}}}$ contains the nodal values of ${\textstyle q}$ .

Substituting the expression of ${\textstyle {\dot {E}}_{v}}$ in term of ${\textstyle {}^{n+1}{\bar {v}}}$ from Eq.(56) and Eq.(65) in the variational form of the mass balance equation (Eq.(51)) we obtain, after eliminating the pressure test functions ${\textstyle {\bar {q}}}$

(66)

where ${\textstyle {}^{n+1}{\bar {r}}_{v}}$ is the residual vector of the discretized mass conservation equation, ${\textstyle {\dot {\bar {p}}}={\partial {~}^{n+1}{\bar {p}} \over \partial t}}$ and the terms of ${\textstyle {M}_{p}}$ and ${\textstyle {}^{n}{Q}}$ are

(67)

9.3 Stabilization of the mass conservation equation

It is well known that the FEM solutions for the fully incompressible limit are unstable for some particular forms of the approximation for the velocities and the pressure [10,39,41]. This is the case, for instance, when an equal order interpolation is chosen for the velocity components and the pressure (i.e. ${\textstyle N_{i}^{v}=N_{i}^{p}}$ ). This problem can be overcome by using finite element approximations for ${\textstyle {v}}$ and ${\textstyle p}$ satisfying the so-called LBB conditions [10,39,41], or else by introducing stabilization terms into the discretized mass balance equation [10,41]. In this work the later approach is chosen for obtaining stabilized numerical solutions.

In essence all stabilized formulations modify the discretized form of the mass balance equation as

(68)

where ${\textstyle {}^{n+1}{\bar {r}}_{v}}$ was defined in Eq.(66) and ${\textstyle {}^{n+1}{\bar {r}}_{s}}$ is a stabilization mass balance vector which expression can be typically written as

(69)

where ${\textstyle {\boldsymbol {\cal {S}}}}$ is a stabilization matrix and ${\textstyle {}^{n+1}{f}_{s}}$ is a force vector that depends on the nodal velocities and pressures. The form of ${\textstyle {\boldsymbol {\cal {S}}}}$ and ${\textstyle {f}_{s}}$ is different for each stabilization method. Typically, ${\textstyle {\boldsymbol {\cal {S}}}}$ and ${\textstyle {}^{n+1}{f}_{s}}$ contain integrals over the volume and the Neumann boundary of the analysis domain and are both a function of the so-called stabilization parameters which expression also depends on the particular stabilization method chosen [3,8,9,10,15,31,37,41].

The derivation of a stabilized mixed velocity-pressure formulation for incompressible fluids exceeds the objectives of this paper. Details can be obtained in the references cited in the previous paragraphs.

A particular stabilized Lagrangian formulation with excellent mass conservation features based on the Finite Calculus (FIC) theory [21]–[24],[27,30] can be found in [31].

10 INCREMENTAL SOLUTION FOR THE NODAL VELOCITIES AND PRESSURES

We will derive next an incremental iterative procedure for solving the discretized form of the equations for conservation of linear momentum and mass conservation in a segregated form. This requires the linearization of Eqs.(61) and (68) with respect to the nodal velocity and pressure unknowns, respectively. The linearization procedure takes advantage from the fact that the reference configuration (i.e. the current configuration ${\textstyle {}^{n}V}$ ) remains fixed during the linearization process.

10.1 Linearization of the discretized momentum equations with respect to the nodal velocities

We linearize the residual vector ${\textstyle {}^{n+1}{\bar {r}}_{m}}$ of Eq.(61) with respect to the nodal velocities ${\textstyle {\bar {v}}}$ as

(70)

Expression (70) is the directional derivative of the residual vector ${\textstyle {}^{n+1}{\bar {r}}_{m}}$ at a point ${\textstyle {x}}$ in the direction of the nodal velocity vector ${\textstyle d{\bar {v}}}$ (hereafter called nodal velocity pseudo-increment vector). The same definition applies to the directional derivative of a matrix or a scalar depending on the space coordinate ${\textstyle {x}}$ , the nodal velocities ${\textstyle {\bar {v}}}$ and the nodal pressures ${\textstyle {\bar {p}}}$ [4,5,36].

Using the expression of vector ${\textstyle {}^{n+1}{\bar {r}}_{m}}$ of Eq.(62) in Eq.(70) and neglecting the changes of vector ${\textstyle {}^{n+1}{f}_{m}}$ with the velocity, gives

\delta _{\bar {v}}{}^{n+1}{\bar {r}}_{m}={\frac {1}{\Delta t}}{M}_{v}d{\bar {v}}+\int _{{}^{n}V}{\Big \{}{B}^{T}{\Big [}\delta _{\bar {v}}\left\{\mathbf {S} '\right\}+\left(\delta _{\bar {v}}J\left\{{C}^{-1}\right\}+{J}\delta _{\bar {v}}\left\{{C}^{-1}\right\}\right)p+

(71)

After some algebra detailed in the Appendix, the following linearized form of ${\textstyle {}^{n+1}{\bar {r}}_{m}}$ with respect to the nodal velocities is found

(72)

where matrices ${\textstyle {M}_{v}}$ and ${\textstyle {}^{n}{Q}}$ were given in Eq.(67) and ${\textstyle {}^{n}{K}_{c}}$ and ${\textstyle {K}_{\sigma }}$ are the constitutive and initial stress matrices, respectively. The expression of these matrices is

(73)

The form of matrices ${\textstyle {G}}$ and ${\textstyle {\hat {S}}'}$ is given in the Appendix.

The expression of the tangent constitutive tensor ${\textstyle {\boldsymbol {\cal {C}}}_{T}}$ is (see Appendix)

(74)

Tensor ${\textstyle {\boldsymbol {\cal {C}}}_{T}}$ contains contributions from the constitutive tensor ${\textstyle {\boldsymbol {\cal {C}}}}$ of Eq.(46), the time step and the pressure. This form of ${\textstyle {\boldsymbol {\cal {C}}}_{T}}$ is very similar to that used for incompressible continua [4,5,13,36]. It can be shown that tensor ${\textstyle {\boldsymbol {\cal {I}}}}$ is symmetric (see Appendix) and, hence, the tangent constitutive tensor ${\textstyle {\boldsymbol {\cal {C}}}_{T}}$ is symmetric [4,5,13,36].

10.2 Linearization of the nodal pressures with respect to the nodal velocities. Derivation of the tangent matrix

From Eq.(66) we can obtain the directional derivative of the nodal pressure variables in the direction of the nodal velocity increments. Using a trapezoidal rule for approximating the time derivative term gives

(75)

where ${\textstyle \theta }$ is a time parameter such that ${\textstyle 0<\theta \leq 1}$ . A value ${\textstyle \theta =1}$ defines a backward Euler scheme [39,41].

From Eq.(75) it is straightforward to obtain

(76)

Substituting Eq.(76) into (72) gives the final linearized form of the momentum equations in terms of the nodal velocities increments as

(77)

where ${\textstyle (\cdot )^{i}}$ denotes values at the ${\textstyle i}$ th iteration and the tangent matrix ${\textstyle ^{n}{K}_{T}}$ is

(78)

with ${\textstyle {M}_{v}}$ , ${\textstyle {K}_{c}}$ and ${\textstyle {K}_{\sigma }}$ defined in Eqs.(63) and (72) and the tangent “bulk” matrix ${\textstyle {K}_{p}}$ is

(79)

In practice, ${\textstyle {K}_{p}}$ is computed using the diagonal form of ${\textstyle {M}_{p}}$ , i.e.

(80)

where ${\textstyle {M}_{pD}={diag}({M}_{p})}$ .

The incremental form of the momentum equations can written as

(81)

Solution of Eq.(81) yields the nodal velocity increments ${\textstyle d{\bar {v}}}$ for the ${\textstyle i}$ th iteration.

Remark 6. For fully incompressible fluids ( ${\textstyle c=\infty }$ ) a large but finite value of ${\textstyle c}$ is used in practice. This allows to eliminate the pressure DOFs in the momentum equations via Eq.((76)).

Remark 7. The tangent “bulk” stiffness matrix ${\textstyle \mathbf {K} _{p}}$ in the tangent matrix ${\textstyle \mathbf {K} _{T}}$ accounts for the changes of the pressure due to the velocity. Including matrix ${\textstyle \mathbf {K} _{p}}$ in ${\textstyle \mathbf {K} _{T}}$ has proven to be essential for the fast convergence, mass preservation and overall accuracy of the iterative solution in all cases [11]. The ${\textstyle \theta }$ parameter in ${\textstyle {K}_{p}}$ (Eq.(79)) has the role of preventing the ill-conditioning of ${\textstyle \mathbf {K} _{T}}$ for very large values of the speed of sound in the fluid that lead to a dominant role of the terms of the tangent bulk stiffness matrix ${\textstyle {K}_{p}}$ . Clearly, the value of the terms of ${\textstyle {K}_{p}}$ can also be limited by reducing the time step size. This, however, leads to an increase in the overall cost of the computations [11]. An adequate selection of ${\textstyle \theta }$ improves the convergence of the iterative process and leads to a more accurate numerical solution with reduced mass loss, even for large time steps [11]. These considerations, however, do not affect the value of ${\textstyle c}$ within matrix ${\textstyle {M}_{p}}$ in Eq.(67) that vanishes for the fully incompressible case ( ${\textstyle c=\infty }$ ).

10.3 Linearization of the stabilized mass conservation equation with respect to the nodal pressures

The stabilized mass conservation equation (68) is linearized with respect to the nodal pressure pseudo-increment vector ${\textstyle d{\bar {p}}}$ using Eqs.(66), (68) and (69) as

(82)

Using Eqs.(67)–(68) and a backward Euler scheme for approximating the time derivative of the nodal pressure in Eq.(67) gives

(83)

In the derivation of Eq.(83) we have neglected the pressure dependence of the terms of matrix ${\textstyle {\boldsymbol {\cal {S}}}}$ and ${\textstyle {}^{n+1}{f}_{s}}$ in Eq.(69).

The incremental form of the mass balance equation is therefore

(84)

Solution of Eq.(84) yields the nodal pressure pseudo-increment vector ${\textstyle d{\bar {p}}}$ at the ${\textstyle i}$ th iteration.

10.4 Incremental solution of the discretized equations

An incremental Newton-Raphson type iterative solution scheme for the stabilized velocity-pressure formulation is as follows.

Within a time increment ${\textstyle [n,n+1]}$ :

Initialize variables: ${\textstyle ({}^{n+1}{x},{}^{n+1}{\bar {v}}^{1},{}^{n+1}{\bar {p}}^{1},{}^{n+1}{\bar {r}}_{m},{}^{n+1}{\hat {r}}_{v})\equiv ({}^{n}{x},{}^{n}{\bar {v}},{}^{n}{\bar {p}},{}^{n}{\bar {r}}_{m},{}^{n}{\hat {r}}_{v})}$ .
Iteration loop = ${\textstyle i=1,\cdots ,NITER}$

For each iteration

Compute the nodal velocity pseudo-increments ,

(from Eq.(81)) from

(85)

Update the nodal velocities :

(86)

Compute the nodal pressure pseudo-increments ,

. From Eq.(84),

(87)

Update the nodal pressures :

(88)

Update the nodal displacement increments ${\textstyle \Delta {u}}$ using Eq.(60.a) and the approximate value for the nodal velocities ${\textstyle {}^{n+1}{\bar {v}}^{i+1}}$ .

Update the nodal coordinates in the updated configuration as

(89)

Compute the material derivative of the Green strains ${\dot {E}}_{ij}$ and the deviatoric second Piola-Kirchhoff stresses ${S'}_{ij}$ (from Eqs.(55) and (45)).
Compute the momentum and mass balance residuals : ${\textstyle ^{n+1}{\bar {r}}_{m}^{i+1}}$ and ${\textstyle ^{n+1}{\hat {r}}_{v}^{i+1}}$

Check convergence

(90)

where ${\textstyle \Vert \cdot \Vert }$ denotes the quadratic norm and ${\textstyle e_{m}}$ and ${\textstyle e_{v}}$ are prescribed error tolerances for the discretized residuals of the momentum and mass balance equations, respectively.

If both conditions (90) are satisfied then make ${\textstyle n\leftarrow n+1}$ and proceed to the next time increment. Otherwise, make the iteration counter ${\textstyle i\leftarrow i+1}$ and repeat Steps 1–9.

Remark 8. An alternative convergence criteria based on the nodal velocities and pressures can be defined as

$\Vert ^{n+1}{\bar {v}}^{i+1}-{}^{n+1}{\bar {v}}^{i}\Vert \leq e_{\bar {v}}\Vert ^{n+1}{\bar {v}}^{i}\Vert$	(91.a)
$\Vert ^{n+1}{\bar {p}}^{i+1}-^{n+1}{\bar {p}}^{i}\Vert \leq e_{\bar {p}}\Vert ^{n+1}{\bar {p}}^{i}\Vert$	(91.b)

where ${\textstyle e_{\bar {v}}}$ and ${\textstyle e_{\bar {p}}}$ are error tolerances.

Remark 9. The nodal velocity and pressure increment vectors ${\textstyle \Delta {\bar {v}}}$ and ${\textstyle \Delta {\bar {p}}}$ can be computed at the end of each time step as

(92)

where ${\textstyle {}^{n+1}{\bar {v}}}$ and ${\textstyle {}^{n+1}{\bar {p}}}$ denote the converged values at the end of the iteration loop. Clearly, ${\textstyle \Delta {\bar {v}}}$ and ${\textstyle \Delta {\bar {p}}}$ can also be obtained by adding up the pseudo-increment vectors ${\textstyle d{\bar {v}}}$ and ${\textstyle d{\bar {p}}}$ within the iterative solution.

Remark 10. The nodal pressures ${\textstyle ^{n+1}{\bar {p}}^{i+1}}$ can be directly obtained from Eq.(68), after substitution of Eqs.(66) and (69), as

(93)

The rest of the iterative solution scheme is similar to that described above. Eq.(93) substitutes Eqs.(87) and (88) and the convergence of the nodal pressures is verified by Eq.(91.b).

Remark 11. For a fully incompressible fluid ${\textstyle c=\infty }$ and matrix ${\textstyle {M}_{p}=0}$ in Eqs.(67), (87) and (93).

The problem can still be accurately solved in this case using an adequate expression for the stabilization matrix ${\textstyle {\boldsymbol {\cal {S}}}}$ . The form of ${\textstyle {\boldsymbol {\cal {S}}}}$ presented in [31] includes a Laplacian term over the whole domain ${\textstyle \Omega }$ and an integral along the Neumann boundary ${\textstyle \Gamma _{t}}$ . The boundary term in ${\textstyle {\boldsymbol {\cal {S}}}}$ avoids the need for prescribing the pressure on the domain boundary. If a standard Laplacian form is chosen for ${\textstyle {\boldsymbol {\cal {S}}}}$ , then the value of the pressure has to be prescribed in strong form at some boundary points in order to obtain good results [41].

11 DIRECT ITERATIVE SOLUTION OF THE NODAL VELOCITIES AND PRESSURES

Substituting the FEM approximation for the velocities and the pressure (53) into Eq.(64) and assuming a Newtonian fluid with a constitutive equation given by Eq.(47), the following matrix expression of the discretized momentum equations can be obtained

(94)

where ${\textstyle {M}_{v}}$ , ${\textstyle {}^{n}{Q}}$ and ${\textstyle {}^{n+1}{f}_{m}}$ have been defined previously and

(95)

Combining Eq.(94) with the stabilized mass balance equation (68) and using Eq.(66) gives the following matrix system for the nodal velocities and pressures

\left[{\begin{matrix}{M}_{v}&{0}\\{0}&-{M}_{p}\end{matrix}}\right]\left\{{\begin{matrix}{\dot {\bar {v}}}\\{\dot {\bar {p}}}\end{matrix}}\right\}+\left[{\begin{matrix}{K}_{v}&{Q}\\{Q}^{T}&-{\boldsymbol {\cal {S}}}\end{matrix}}\right]\left\{{\begin{matrix}{}^{n+1}{\bar {v}}\\{}^{n+1}{\bar {p}}\end{matrix}}\right\}-\left\{{\begin{matrix}{}^{n+1}{f}_{m}\\{}^{n+1}{f}_{s}\end{matrix}}\right\}={0}

(96)

Eq.(96) can be written in a compact (monolithic) form as

(97)

where

{M}=\left[{\begin{matrix}{M}_{v}&{0}\\{0}&-{M}_{p}\end{matrix}}\right]~~,~~{K}=\left[{\begin{matrix}{K}_{v}&{Q}\\{Q}^{T}&-{\boldsymbol {\cal {S}}}\end{matrix}}\right]~~,~~{~}^{n+1}{\bar {a}}=\left\{{\begin{matrix}{}^{n+1}{\bar {v}}\\{}^{n+1}{\bar {p}}\end{matrix}}\right\}~~,~~{}^{n+1}{f}=\left\{{\begin{matrix}{}^{n+1}{f}_{m}\\{}^{n+1}{f}_{s}\end{matrix}}\right\}

(98)

11.1 Monolithic solution scheme

Eq.(98) is the basis for deriving monolithic iterative time integration schemes for directly computing the nodal velocities and pressure at the updated configuration. For instance, the standard backward Euler scheme gives

(99)

with ${\textstyle {H}^{i}={\frac {1}{\Delta t}}{M}+{K}_{v}^{i}}$ .

The values of ${\textstyle {}^{n+1}{\bar {a}}}$ can be directly found by solving Eq.(99) iterative.

The non linearity of matrix ${\textstyle {}^{n}{K}_{v}}$ emanates from the non linear terms in the material strain rate matrix ${\textstyle {B}^{L}}$ involving the displacement increments (Eqs.(9)).

11.2 Segregated solution scheme

The nodal velocities and pressures at the updated configuration can be also computed starting from Eq.(97) using a segregated iterative scheme as follows

(100)

(101)

Eqs.(100) and (101) are solved sequentially and iteratively until convergence for the nodal velocities and pressures is found.

The above iterative scheme can be considered as a simplification of the more accurate incremental iterative segregated scheme described in Section 10.4.

Remark 12. A variant of the iteration matrix in the left hand side of Eq.(100) can be used by adding the bulk stiffness matrix ${\textstyle {K}_{p}}$ to matrix ${\textstyle {H}^{i}}$ [11,31].

12 PARTICULARIZATION FOR THE UPDATED CONFIGURATION

The finite element formulation presented in the previous sections can be particularized for the case when the updated configuration ${\textstyle {~}^{n+1}{V}}$ is chosen as the reference configuration.

The particularization is simple if we note that now ${\textstyle \Delta u_{i}=0}$ . Hence, ${\textstyle {L}=0}$ and ${\textstyle {B}^{L}={0}}$ (see Eq.(58.a)). Also all the space derivatives are taken with respect to the updated coordinates ${\textstyle {~}^{n+1}x_{i}}$ and the integrals are carried out in the updated configuration ${\textstyle {~}^{n+1}V}$ . In addition, the tangent constitutive tensor ${\textstyle {\boldsymbol {\cal {C}}}_{T}={c}}$ . The expressions of the relevant matrices and vectors for this case are given in Box 1.

13 PROS AND CONS OF USING THE CURRENT OR THE UPDATED CONFIGURATION AS THE REFERENCE CONFIGURATION

We have shown in the previous sections that either the current or the updated configuration can be indistinctly used as the reference configuration for the finite element analysis of quasi and fully incompressible fluids using a Lagrangian formulation. Both choices imply solving a non linear system of equations. However, the nature of the non-linearity is different for each case.

If the current configuration is chosen as the reference configuration, all integrals in the tangent matrix are performed on the known configuration ${\textstyle {}^{n}V}$ which remains fixed during the iterative solution process. The non-linearity affects, however, the non linear terms of the material strain rate matrix (i.e. ${\textstyle {B}^{L}}$ ) and also the constitutive tensor ${\textstyle {\boldsymbol {\cal {C}}}}$ that involves the deformation gradient. A simplification of the tangent stiffness matrix for this case can be introduced by neglecting ${\textstyle {B}^{L}}$ in the material strain rate matrix and assuming that ${\textstyle {F}={C}={I}_{3}}$ and, hence, ${\textstyle {\boldsymbol {\cal {C}}}_{T}={c}}$ .

If, on the other hand, the updated configuration is chosen as the reference configuration, then all the integrals in the tangent matrix are computed in the unknown configuration ${\textstyle {}^{n+1}V}$ , which should be updated at each iteration. On the other hand, the expression for the material strain rate matrix is linear and also ${\textstyle {\boldsymbol {\cal {C}}}_{T}={c}}$ . A simplification of the iterative process can be introduced by keeping the tangent matrix constant for a fixed number of iterations.

Indeed the above mentioned simplifications can affect the convergence rate of the iterative solution and should be implemented with care.

Which reference configuration should be chosen can be problem dependent and, certainly, the choice will affect the organization of the computer program and its efficiency. What should be kept in mind is that the final solution, i.e. the geometry of the updated configuration and the velocities and stresses on ${\textstyle {}^{n+1}V}$ , should be identical in both cases.

In previous works of the authors with the Particle Finite Element Method (PFEM) the current configuration ${\textstyle {}^{n}V}$ was typically chosen as the reference configuration with the simplified form for the tangent matrix as explained above and also neglecting the initial stress matrix terms in ${\textstyle {K}_{T}}$ [16,17,25,26,29,31]. Recent experiences indicate that using the updated configuration ${\textstyle {}^{n+1}V}$ as the reference configuration can be advantageous in many Lagrangian flow problems. The topic is still open for research and hopefully this paper will be useful for choosing the adequate FEM expressions for each case.

14 CONCLUDING REMARKS

We have presented a mixed velocity-pressure finite element formulation for solving the updated Lagrangian equations for quasi and fully incompressible fluids. The finite element interpolation uses an equal order approximation for the velocity and pressure unknowns. We have detailed a number of iterative algorithms for solving the non-linear stabilized FEM equations for the velocities and the pressure at the nodes using incremental and direct solution schemes. The algorithms presented are useful for the study of Lagrangian flows, as well as for solving fluid-structure-interaction problems using a unified Lagrangian finite element formulation for modelling both the fluid and the structure [11,17].

The choice of the current or the updated configurations as the reference Lagrangian configuration is still an open topic. Researchers interested in Lagrangian CFD procedures will find in this paper the equations to be used for each case, from which simplifications or further computational refinements can be made.

ACKNOWLEDGEMENTS

This work was partially supported by the Advanced Grant project SAFECON of the European Research Council (ERC).

References

[1] S. Badia, R. Codina, Unified stabilized finite element formulation for the Stokes and the Darcy problems. SIAM J. on Numerical Analysis, 47, 1971–2000, 2009.

[2] K.J. Bathe, Finite element procedures. Prentice-Hall, 1996.

[3] Y. Bazilevs, K Takizawa, T.E Tezduyar, Computational Fluid-Structure Interaction: Methods and Applications, Wiley, 2013.

[4] T. Belytschko, W.K. Liu and B. Moran, Non linear finite element for continua and structures. 2d Edition, Wiley, 2013.

[5] J. Bonet and R.D. Wood, Non linear continuum mechanics for finite element analysis. Wiley, 2nd Edition, 2008.

[6] J.U. Brackbill, D.B. Kothe, H.M. Ruppel, FLIP: A low-dissipation, particle-in-cell method for fluid flow. Computer Physics Communications, 48, 25–38, 1988.

[7] D. Burgess, D. Sulsky, J.U. Brackbill, Mass matrix formulation of the FLIP particle-in-cell method. Journal of Computational Physics, 103 (1), 1–15, 1992.

[8] R. Codina, Stabilized finite element approximation of transient incompressible flows using orthogonal subscales. Comput. Meth. Appl. Mech. Engrg., 191, 4295–4321, 2002.

[9] R. Codina, H. Coppola-Owen, P. Nithiarasu and C. Liu, Numerical comparison of CBS and SGS as stabilization techniques for the incompressible Navier-Stokes equations. Int. J. Numer. Meth. Engng., 66, 1672–1689, 2006.

[10] J. Donea and A. Huerta, Finite Element Methods for Flow Problems. Wiley, 2003.

[11] A. Franci, E. Oñate, J.M. Carbonell, Unified Lagrangian formulation for analysis of fluid-structure interaction problems. Research Report PI-400, CIMNE, Barcelona 2013.

[12] F.H. Harlow, The particle-in-cell computing method for fluid dynamics. Methods Comput. Phys., 3, 219, 1963.

[13] G.A. Holzaphel, Non linear solid mechanics. Wiley, 2000.

[14] A. Huerta, Y. Vidal, J. Bonet, Updated Lagrangian formulation for corrected Smooth Particle Hydrodynamics. Int. J. of Computational Methods, 3 (4), 383–399, 2006.

[15] T.J.R. Hughes, G. Scovazzi, L.P. Franca, Multiscale and stabilized methods. Encyclopedia of Comput. Mechanics. E. Stein, R. de Borst and T.J.R. Hughes (Eds.), Vol. 3 Fluids, 5–60, Wiley, 2004.

[16] S.R. Idelsohn, E. Oñate, F. Del Pin, The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves. Int. J. Num. Meth. Eng., 61(7), 964–989, 2004.

[17] S.R. Idelsohn, J. Marti, A. Limache, E. Oñate Unified Lagrangian formulation for elastic solids and incompressible fluids: Application to fluid-structure interaction problems via the PFEM. Comput. Meth. Appl. Mech. Engrg., 197 (19-20), 1762–1776, 2008.

[18] S. Li, W.K. Liu, Meshfree and particle methods and their applications. Appl. Mech. Rev., 55, 1, 2002.

[19] W.K. Liu, Y. Chen, S. Jun, J.S. Chen, T. Belytschko, C. Pan, R.A. Uras, C.T. Chang, Overview and applications of the Reproducing Kernel Particle Methods. Arch Comput Methods Eng., 3 (1), 3–80, 1996.

[20] M.B. Liu and G.R. Liu, Smoothed particle hydrodynamics (SPH): an overview and recent developments. Arch Comput Methods Eng., Vol. 17, 25–-76, 2010.

[21] E. Oñate, Derivation of stabilized equations for advective-diffusive transport and fluid flow problems. Comput. Meth. Appl. Mech. Engrg. 151, 233–267, 1998.

[22] E. Oñate, A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation. Comput Methods Appl Mech Engrg., 182(1–2), 355–370, 2000.

[23] E. Oñate, Multiscale computational analysis in mechanics using finite calculus: an introduction. Comput. Meth. Appl. Mech. Engrg., 192(28-30), 3043–3059, 2003.

[24] E. Oñate, Possibilities of finite calculus in computational mechanics. Int. J. Numer. Meth. Engng., 60(1), 255–281, 2004.

[25] E. Oñate, S.R. Idelsohn, F. Del Pin, R. Aubry, The particle finite element method. An overview. Int. J. Comput. Methods, 1(2), 267–307, 2004.

[26] E. Oñate, J. García, S.R. Idelsohn, F. Del Pin, FIC formulations for finite element analysis of incompressible flows. Eulerian, ALE and Lagrangian approaches. Comput. Meth. Appl. Mech. Engrg. 195(23-24), 3001–3037, 2006.

[27] E. Oñate, A. Valls, J. García, Computation of turbulent flows using a finite calculus-finite element formulation. Int. J. Numer. Meth. Engng., 54, 609–637, 2007.

[28] E. Oñate, Structural analysis with the finite element method. Linear statics. Volume 1. Basis and Solids. CIMNE-Springer, 2009.

[29] E. Oñate, M.A. Celigueta, S.R. Idelsohn, F. Salazar, B. Suárez, Possibilities of the particle finite element method for fluid-soil-structure interaction problems. Computational Mechanics, 48(3), 307–318, 2011.

[30] E. Oñate, S.R. Idelsohn, C. Felippa, Consistent pressure Laplacian stabilization for incompressible continua via higher-order finite calculus. Int. J. Numer. Meth. Engng, 87 (1-5), 2011, 171–195.

[31] E. Oñate, A. Franci, J.M. Carbonell, Lagrangian formulation for finite element analysis of incompressible fluids with reduced mass losses. Int. J. Numer. Meth. Fluids, 2013. DOI:0.1002/fld.3870.

[32] E. Oñate, P. Nadukandi, S.R. Idelsohn, P1/P0+ elements for incompressible flows with discontinuous material properties. Comput. Meth. Appl. Mech. Engrg., 271, 185–209, 2014, .

[33] N.A. Patankar, D.D. Joseph, Lagrangian numerical simulation of particulate flows. Int. J. of Multiphase Flow, 27 (10), 1685–-1706, 2001.

[34] R. Radovitzky and M. Ortiz, Lagrangian finite element analysis of newtonian fluid flows. Int. J. Numer. Meth. Engng., 43, 607–619, 1998.

[35] B. Ramaswamy and M. Kawahara, Lagrangian finite element analysis applied to viscous free surface fluid flow. Int. J. Num. Meth. Fluids, 7, 953–984, 1986.

[36] P. Wriggers, Non linear finite element methods. Springer, 2008.

[37] T.E. Tezduyar, Finite elements for flow problems with moving boundaries and interfaces. Arch. for Comput. Methods Eng., 8, 83–130, 2001.

[38] D.Z. Zhang, Q. Zou, W.B. VanderHeyden, X. Ma, Material point method applied to multiphase flows. Journal of Computational Physics, 227 (6), 3159-3173, 2008.

[39] O.C. Zienkiewicz, R.L. Taylor, J.Z. Zhu, The Finite Element Method. Vol. 1 The Basis. Elsevier, 6th Edition, 2005.

[40] O.C. Zienkiewicz, R.L. Taylor, The Finite Element Method. Vol. 2 Solid and Structural Mechanics. Elsevier, 6th Edition, 2005.

[41] O.C. Zienkiewicz, R.L. Taylor and P. Nithiarasu, The Finite Element Method. Vol. 3 Fluid Dynamics. Elsevier, 6th Edition, 2005.

APPENDIX A. LINEARIZATION OF THE MOMENTUM EQUATIONS WITH RESPECT TO THE NODAL VELOCITIES

Using the expression of ${\textstyle {}^{n+1}{\bar {r}}_{m}}$ of Eq.(62) and neglecting the changes of the external vector ${\textstyle {}^{n+1}{\bar {f}}_{m}}$ with the velocity (accounting for these changes is possible and will lead to additional terms in the tangent matrix), we can write

\delta _{\bar {v}}{}^{n+1}{\bar {r}}_{m}={\frac {1}{\Delta t}}{M}_{v}d{\bar {v}}+\int _{{}^{n}V}{\Big \{}{B}^{T}{\Big [}\delta _{\bar {v}}\left\{\mathbf {S} '\right\}+\left(\delta _{\bar {v}}J\left\{{C}^{-1}\right\}+{J}\delta _{\bar {v}}\left\{{C}^{-1}\right\}\right)p+

(A.1)

Introducing Eqs.(55) and (59) into (A.1) gives after some algebra [4,5,36]

(A.2)

(A.3)

(A.4)

where

(A.5)

It can be shown that tensor ${\textstyle {\boldsymbol {\cal {I}}}}$ is symmetric [4,5].

On the other hand,

(A.6a)

with

{\begin{array}{l}{G}=\left[{\begin{matrix}{\bar {G}}&{\bar {0}}&{\bar {0}}\\{\bar {0}}&{\bar {G}}&{\bar {0}}\\{\bar {0}}&{\bar {0}}&{\bar {G}}\end{matrix}}\right]~~,~~{\bar {G}}=\left[{\begin{matrix}{}_{n}N_{1,1}^{v}&0&0&{}_{n}N_{2,1}^{v}&0&0&\cdots &{}_{n}N_{n,1}^{v}\\{}_{n}N_{1,2}^{v}&0&0&{}_{n}N_{2,2}^{v}&0&0&\cdots &{}_{n}N_{n,2}^{v}\\{}_{n}N_{1,3}^{v}&0&0&{}_{n}N_{2,3}^{v}&0&0&\cdots &{}_{n}N_{n,3}^{v}\end{matrix}}\right]\\[1cm]{\hat {S}}'=\left[{\begin{matrix}{S}'&{0}&{0}\\{0}&{S}'&{0}\\{0}&{0}&{S}'\end{matrix}}\right]~~,~~{0}=\left[{\begin{matrix}0&0&0\\0&0&0\\0&0&0\end{matrix}}\right]~~,~~{\bar {0}}=\left\{{\begin{matrix}0\\0\\0\end{matrix}}\right\}\end{array}}

(A.6b)

with ${\textstyle {}_{n}N_{i,j}^{v}}$ defined in Eq.(58.b).

In the derivation of Eqs.(A.3), (A.4) and (A.6a) we have assumed that ${\textstyle d(\Delta u_{i})=du_{i}=\Delta t~d({}^{n+\alpha }v_{i})=\Delta t~dv_{i}}$ . This relationship follows from Eq.(60.a).

Substituting Eqs.(A.2)–(A.4) and (A.6a) and the interpolation for the pressure (Eq.(53)) into (A.1) yields the linearized form of the residual vector of the discretized momentum equations as

(A.7)

where matrices ${\textstyle {M}_{v}}$ and ${\textstyle {Q}}$ were given in Eq.(67) and ${\textstyle {K}_{c}}$ and ${\textstyle {K}_{\sigma }}$ are the constitutive and initial stress matrices, respectively. The expression of these matrices is

(A.8)

The tangent constitutive tensor ${\textstyle {\boldsymbol {\cal {C}}}_{T}}$ is deduced from Eqs.(A.1)-(A.4) as

(A.9)

It is straightforward to show that tensor ${\textstyle {\boldsymbol {\cal {C}}}_{T}}$ is symmetric.

Latest revision as of 10:17, 7 June 2019

Abstract

1 INTRODUCTION

2 MOTION. DISPLACEMENT, VELOCITY AND ACCELERATION

3 MOMENTUM EQUATIONS AND BOUNDARY CONDITIONS

4 PRINCIPLE OF VIRTUAL POWER IN THE UPDATED CONFIGURATION

5 TRANSFORMATION TO THE CURRENT CONFIGURATION. LAGRANGIAN STRESS AND STRAIN MEASURES

6 SPLIT OF THE INTERNAL VIRTUAL POWER INTO DEVIATORIC AND VOLUMETRIC COMPONENTS

7 CONSTITUTIVE RELATIONSHIP FOR THE DEVIATORIC STRESSES

8 THE MASS BALANCE EQUATION

9 FINITE ELEMENT DISCRETIZATION

9.1 Discretized form of the PVP

9.2 Discretization of the mass conservation equation

9.3 Stabilization of the mass conservation equation

10 INCREMENTAL SOLUTION FOR THE NODAL VELOCITIES AND PRESSURES

10.1 Linearization of the discretized momentum equations with respect to the nodal velocities

10.2 Linearization of the nodal pressures with respect to the nodal velocities. Derivation of the tangent matrix

10.3 Linearization of the stabilized mass conservation equation with respect to the nodal pressures

10.4 Incremental solution of the discretized equations

11 DIRECT ITERATIVE SOLUTION OF THE NODAL VELOCITIES AND PRESSURES

11.1 Monolithic solution scheme

11.2 Segregated solution scheme

12 PARTICULARIZATION FOR THE UPDATED CONFIGURATION

13 PROS AND CONS OF USING THE CURRENT OR THE UPDATED CONFIGURATION AS THE REFERENCE CONFIGURATION

14 CONCLUDING REMARKS

ACKNOWLEDGEMENTS

References

APPENDIX A. LINEARIZATION OF THE MOMENTUM EQUATIONS WITH RESPECT TO THE NODAL VELOCITIES

Document information

Document Score

Share this document

claim authorship

@@ Line 1: / Line 1: @@
-==1 Title, abstract and keywords<!-- Your document should start with a concise and informative title. Titles are often used in information-retrieval systems. Avoid abbreviations and formulae where possible. Capitalize the first word of the title.
+Published in ''Computational Mechanics'', Vol. 54 (6), pp. 1583-1596, 2014<br />
+DOI: 10.1007/s00466-014-1078-1
-Provide a maximum of 6 keywords, and avoiding general and plural terms and multiple concepts (avoid, for example, 'and', 'of'). Be sparing with abbreviations: only abbreviations firmly established in the field should be used. These keywords will be used for indexing purposes.
+==Abstract==
-An abstract is required for every document; it should succinctly summarize the reason for the work, the main findings, and the conclusions of the study. Abstract is often presented separately from the article, so it must be able to stand alone. For this reason, references and hyperlinks should be avoided. If references are essential, then cite the author(s) and year(s). Also, non-standard or uncommon abbreviations should be avoided, but if essential they must be defined at their first mention in the abstract itself. -->==
+We present a mixed velocity-pressure finite element formulation for solving the updated Lagrangian equations for quasi and fully incompressible fluids. Details of the governing equations for the conservation of momentum and mass are given in both differential and variational form. The finite element interpolation  uses an equal  order approximation for the velocity and pressure unknowns. The procedure for obtaining stabilized FEM solutions is outlined. The  solution in time of the discretized governing conservation equations using an incremental iterative segregated scheme is described. The linearization of these equations and the derivation of the corresponding tangent stiffness matrices is detailed. Other iterative  schemes for the direct computation of  the nodal velocities and pressures at the updated configuration are presented. The advantages and disadvantages of choosing the current or the updated configuration as the reference configuration in the Lagrangian formulation are discussed.
+'''Keywords''': Updated Lagrangian formulation, incompressible fluids, finite element method, incremental solution, tangent matrix, mixed formulation, stabilized method
+==1 INTRODUCTION==
+In Lagrangian analysis procedures, the motion of the particles of a deforming body is followed in time. In  Eulerian formulations, on the other hand, attention is focused in the motion of the material through a stationary control volume. Lagrangian methods have been traditionally used for the numerical analysis of solids and structures, while Eulerian methods are typical in computational fluid dynamics <span id='citeF-2'></span><span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-36'></span><span id='citeF-40'></span><span id='citeF-41'></span>[[#cite-2|[2,4,5,36,40,41]]].
-==2 The main text<!-- You can enter and format the text of this document by selecting the ‘Edit’ option in the menu at the top of this frame or next to the title of every section of the document. This will give access to the visual editor. Alternatively, you can edit the source of this document (Wiki markup format) by selecting the ‘Edit source’ option.
+Despite this evidence,  the use of a Lagrangian description for solving fluid dynamics problems using the finite element method (FEM) <span id='citeF-10'></span><span id='citeF-41'></span>[[#cite-10|[10,41]]] and different meshless and mesh-based particle-based numerical techniques <span id='citeF-6'></span><span id='citeF-7'></span><span id='citeF-12'></span>[[#cite-6|[6,7,12]]],<span id='citeF-16'></span>[[#cite-16|[16]]]&#8211;<span id='citeF-20'></span>[[#cite-20|[20]]],<span id='citeF-25'></span><span id='citeF-26'></span>[[#cite-25|[25,26]]] <span id='citeF-29'></span>[[#cite-29|[29]]]&#8211;<span id='citeF-35'></span>[[#cite-35|[35]]],<span id='citeF-37'></span><span id='citeF-38'></span>[[#cite-37|[37,38]]] has received much attention in recent years. Of particular interest are numerical procedures, such as the Particle Finite Element Method (PFEM) <span id='citeF-16'></span><span id='citeF-25'></span><span id='citeF-26'></span><span id='citeF-29'></span><span id='citeF-31'></span>[[#cite-16|[16,25,26,29,31]]], that combine the advantage of particle-based procedures with the formalism and accuracy of the FEM.
-Most of the documents in Scipedia are written in English (write your manuscript in American or British English, but not a mixture of these). Anyhow, specific publications in other languages can be published in Scipedia. In any case, the documents published in other languages must have an abstract written in English.
+Despite the increasing interest in the Lagrangian approach for solving the equations of   fluid mechanics using the FEM, there are few references to the derivation of incremental iterative solution schemes using linearized forms of the discretized Lagrangian equations for fluid flow problems. An early attempt in this direction was reported by Radovitzky and Ortiz <span id='citeF-34'></span>[[#cite-34|[34]]] who derived the tangent matrix for the FEM Lagrangian analysis of compressible flows using a Newton-Rapsohn type iterative scheme.
+The goal of this paper is to present a mixed velocity-pressure formulation for the finite element analysis of quasi and fully incompressible fluids using an updated Lagrangian formulation. We advocate an equal order interpolation for the velocity and pressure variables which invariably requires using an adequate stabilization scheme for the mass balance equation in order to obtain accurate numerical results. In the paper we derive in some detail both the continuum and discretized (FEM) forms of the  equations governing the motion of the fluid in the updated Lagrangian description. An incremental Newton-Raphson type  iterative staggered scheme for the solution in time of the non linear discretized equations is detailed. The derivations are carried out first using the current configuration as the reference configuration in the Lagrangian description of the motion.  The expression of the different matrices and vectors involved in the incremental iterative scheme is given. The particular form of the FEM equations when the updated configuration is taken as the reference configuration is presented. The  direct transient solution of the nodal velocities and pressures using  monolithic and staggered schemes is also presented for completeness.
-.1 Subsections
+The chapter concludes with a discussion of the computational advantages and disadvantages of choosing the current or the the updated configuration as the reference configuration in the Lagrangian description.
-Divide your article into clearly defined and numbered sections. Subsections should be numbered 1.1, 1.2, etc. and then 1.1.1, 1.1.2, ... Use this numbering also for internal cross-referencing: do not just refer to 'the text'. Any subsection may be given a brief heading. Capitalize the first word of the headings.
+In the next section the basic concepts of the motion of a fluid are briefly revisited. These concepts are standard and can be found in many books on computational solid and fluid mechanics and fluid-structure interaction, among others <span id='citeF-2'></span><span id='citeF-3'></span><span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-13'></span><span id='citeF-36'></span>[[#cite-2|[2,3,4,5,13,36]]]. This introductory section  aims to set up the updated Lagrangian framework where the governing equations for the fluid are written and subsequently solved with the FEM using a mixed velocity-pressure formulation.
+==2 MOTION. DISPLACEMENT, VELOCITY AND ACCELERATION==
-.2 General guidelines
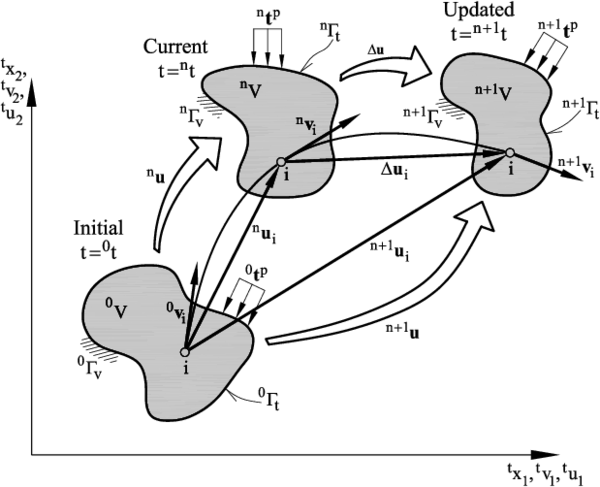
+We will consider a domain containing a fluid which evolves in time due to external and internal forces and prescribed velocities from an ''initial configuration'' at time <math display="inline">t={}^0 t</math> (typically <math display="inline">{}^0t =0</math>) to a ''current configuration'' at time <math display="inline">t={}^n t</math>. The fluid volume <math display="inline">V</math> and its boundary <math display="inline">\Gamma </math> at the initial and current configurations are denoted as (<math display="inline">{}^0 V, {}^0 \Gamma </math>) and (<math display="inline">{}^n V, {}^n \Gamma </math>), respectively. The goal is to find the domain that the fluid occupies, as well as the velocities, strain rates and stresses (the deviatoric stresses and the pressure) in the so-called ''updated configuration'' at time <math display="inline">{}^{n+1} t= {}^n t+\Delta t</math> (Figure 1). In the following a left superindex denotes the configuration of the fluid domain where the variable is computed.
-Some general guidelines that should be followed in your manuscripts are:
+<div id='img-1'></div>
+{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;"
+|-
+|[[Image:draft_Samper_857768298-Figura1.png|600px|Initial (t =⁰t), current (t=ⁿt) and updated (t=ⁿ⁺¹ t) configurations of a fluid domain V with Neumann (Γₜ) and Dirichlet (Γ<sub>v</sub>) boundaries. Trajectory of a material point i and velocity  (v<sub>i</sub>) and displacement (u<sub>i</sub>) vectors of the point at each configuration. ⁿu, ⁿ⁺¹, u and ∆u denote schematically the trajectories of the overall domain between two configurations.]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" | '''Figure 1:''' Initial (<math>t ={}^0 t</math>), current (<math>t={}^n t</math>) and updated (<math>t={}^{n+1} t</math>) configurations of a fluid domain <math>V</math> with Neumann (<math>\Gamma _t</math>) and Dirichlet (<math>\Gamma _v</math>) boundaries. Trajectory of a material point <math>i</math> and velocity  (<math>{v}_i</math>) and displacement (<math>{u}_i</math>) vectors of the point at each configuration. <math>{}^n {u}</math>, <math>{}^{n+1}, {u}</math> and <math>\Delta {u}</math> denote schematically the trajectories of the overall domain between two configurations.
+|}
-*  Avoid hyphenation at the end of a line.
+The motion of the fluid domain is described by
-*  Symbols denoting vectors and matrices should be indicated in bold type. Scalar variable names should normally be expressed using italics.
+<span id="eq-1"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^t{x} =  \boldsymbol{\phi } ({}^0 {x} ,t) \quad \hbox{or}\quad {}^t x_i = \phi _i ({}^0 {x} ,t)    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (1)
+|}
-*  Use decimal points (not commas); use a space for thousands (10 000 and above).
+where <math display="inline">{}^t{x}</math> is the position of the material point <math display="inline">{}^0 {x}</math> laying on the initial configuration at time <math display="inline">t</math>. The coordinates <math display="inline">{}^t{x}</math> give the spatial position of a point and are called ''spatial'' or ''Eulerian coordinates''. The function <math display="inline">\boldsymbol{\phi }</math> maps the initial configuration into the current configuration at  time <math display="inline">t</math>. The position of the points in the current  and initial configurations at time <math display="inline">t={}^n t</math> and <math display="inline">t={}^0  t</math>, respectively are expressed by
-*  Follow internationally accepted rules and conventions. In particular use the international system of units (SI). If other quantities are mentioned, give their equivalent in SI.
+<span id="eq-2"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\begin{array}{l}{}^n {x} = \boldsymbol{\phi }({}^0 {x} ,{}^n t) \quad \hbox{or}\quad {}^n x_i = \phi _i ({}^n {x} ,{}^n t)\\ {}^0 {x} = \boldsymbol{\phi } ({}^0 {x} ,{}^0 t) \quad \hbox{or}\quad {}^0 x_i = \phi _i ({}^0 {x} ,{}^0 t)  \end{array}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (2)
+|}
+Thus the mapping <math display="inline">\boldsymbol{\phi }({}^0 {x} , {}^0t)</math> is the identity mapping.
-.3 Tables, figures, lists and equations
+In the Lagrangian description (also called the ''material description'') the independent variables are the material coordinates <math display="inline">{}^0 {x}</math> of the point on the initial configuration and the time <math display="inline">t</math>. In the Eulerian description, on the other hand, the independent coordinates are the spatial coordinates <math display="inline">{}^t{x}</math> and the time <math display="inline">t</math> <span id='citeF-4'></span><span id='citeF-5'></span>[[#cite-4|[4,5]]].
-Please insert tables as editable text and not as images. Tables should be placed next to the relevant text in the article. Number tables consecutively in accordance with their appearance in the text and place any table notes below the table body. Be sparing in the use of tables and ensure that the data presented in them do not duplicate results described elsewhere in the article.
+The displacement of a material point is given by the difference between its position at time <math display="inline">t</math> and its original position, so
-Graphics may be inserted directly in the document and positioned as they should appear in the final manuscript.
+<span id="eq-3"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{u} ({}^0 {x} ,t) = \boldsymbol{\phi } ({}^0 {x} ,t) - \boldsymbol{\phi }({}^0 {x} ,{}^0 t) = {}^t{x} - {}^0 {x}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (3)
+|}
-Number the figures according to their sequence in the text. Ensure that each illustration has a caption. A caption should comprise a brief title. Keep text in the illustrations themselves to a minimum but explain all symbols and abbreviations used. Try to keep the resolution of the figures to a minimum of 300 dpi. If a finer resolution is required, the figure can be inserted as supplementary material
+where <math display="inline">{u} = [u_1,u_2,u_3]^T</math> is the displacement vector of a point.
-For tabular summations that do not deserve to be presented as a table, lists are often used. Lists may be either numbered or bulleted. Below you see examples of both.
+For <math display="inline">t = {}^n t</math> we have
-. The first entry in this list
+<span id="eq-4"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^n{u} \equiv {u} ({}^0{x} ,{}^n t)  = {}^n {x} - {}^0 {x}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (4)
+|}
-. The second entry
+The velocity vector  is the rate of change of the position vector for a material point, i.e. the time derivative of <math display="inline">\phi ({}^0 {x} ,t)</math>  with <math display="inline">{}^0 {x}</math> held constant (also called ''the material time derivative'' or ''total derivative''). The velocity vector is usually written as (using Eq.([[#eq-3|3]]) and noting that the coordinates <math display="inline">{}^0 {x}</math> are fixed)
-.1. A subentry
+<span id="eq-5"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^t{v} = [{}^tv_1,{}^tv_2,{}^tv_3]^T  \equiv {v} ({}^0 {x} ,t) = \frac{\partial \boldsymbol{\phi }({}^0 {x} ,t) }{\partial t}= \frac{\partial {u} ({}^0 {x} ,t) }{\partial t} \equiv  \dot {u}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (5)
+|}
-. The last entry
+The velocity vector of a material point in the current configuration is written as
-* A bulleted list item
+<span id="eq-6"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^n{v} = [{}^n v_1,{}^n v_2,{}^n v_3]^T \equiv  {v} ({}^0{x} ,{}^n t)    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+|}
-* Another one
+The acceleration vector  is the rate of change of the velocity vector of a material point (i.e. the material time derivative of the velocity vector) and it can be written as
-You may choose to number equations for easy referencing. In that case they must be numbered consecutively with Arabic numerals in parentheses on the right hand side of the page. Below is an example of formulae that should be referenced as eq. (1].
+<span id="eq-7"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^t {a} = {a} ({}^0{x} ,t) \equiv  \frac{\partial {v}({}^0 {x} ,t) }{\partial t}= \frac{\partial ^2 {u} ({}^0 {x} ,t) }{\partial t^2} =   \ddot {u}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (7)
+|}
+and
-.4 Supplementary material
+<span id="eq-8"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^n{a} =[{}^n a_1,{}^n a_2,{}^n a_3]^T = {a} ({}^0{x} ,{}^n t)    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (8)
+|}
-Supplementary material can be inserted to support and enhance your article. This includes video material, animation sequences, background datasets, computational models, sound clips and more. In order to ensure that your material is directly usable, please provide the files with a preferred maximum size of 50 MB. Please supply a concise and descriptive caption for each file. -->==
+Eq.([[#eq-7|7]]) is the ''material form'' of the acceleration. Note the difference of Eq.([[#eq-7|7]]) with the expression of the acceleration written in the Eulerian description which involves the convective terms <span id='citeF-2'></span><span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-13'></span><span id='citeF-36'></span><span id='citeF-41'></span>[[#cite-2|[2,4,5,13,36,41]]].
+In the ''total Lagrangian description''  the various equations and variables are referred to the initial configuration which is taken as the ''reference configuration''. In the ''updated Lagrangian description'',  either the current or the updated configurations can be taken as the ''reference configuration'' <span id='citeF-2'></span><span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-13'></span><span id='citeF-36'></span>[[#cite-2|[2,4,5,13,36]]].
+For simplicity, in the first part of this work the current configuration will be taken  as the reference configuration for the derivation of the incremental FEM equations. The reason is that the current configuration remain fixed during the iterative solution process. The particularization for the case when the updated configuration is taken as the reference configuration is presented in the last part of the paper.
+The displacement increment vector <math display="inline">\Delta {u}({}^0 {x} ,t) = [\Delta u_1,\Delta u_2,\Delta u_3]^T</math>  of a material point between the updated and the current configurations is defined as
-==3 Bibliography<!--
+<span id="eq-9"></span>
-Citations in text will follow a citation-sequence system (i.e. sources are numbered by order of reference so that the first reference cited in the document is [1], the second [2], and so on) with the number of the reference in square brackets. Once a source has been cited, the same number is used in all subsequent references. If the numbers are not in a continuous sequence, use commas (with no spaces) between numbers. If you have more than two numbers in a continuous sequence, use the first and last number of the sequence joined by a hyphen
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\Delta {u} \equiv \Delta {u}({}^0 {x} ,t) = \boldsymbol{\phi } ({}^0 {x} , {}^{n+1}t) - \boldsymbol{\phi }({}^0 {x} ,{}^n t) = {}^{n+1}{x} - {}^n {x}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (9)
+|}
-You should ensure that all references are cited in the text and that the reference list. References should preferably refer to documents published in Scipedia. Unpublished results should not be included in the reference list, but can be mentioned in the text. The reference data must be updated once publication is ready. Complete bibliographic information for all cited references must be given following the standards in the field (IEEE and ISO 690 standards are recommended). If possible, a hyperlink to the referenced publication should be given. See examples for Scipedia’s articles [1], other publication articles [2], books [3], book chapter [4], conference proceedings [5], and online documents [6], shown in references section below. -->==
+The displacement increment of a material point can be computed from the velocity as
+<span id="eq-10"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\Delta {u} = \int _{{}^n t}^{{}^{n+1}t} {}^\tau {v}d\tau    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (10)
+|}
+where <math display="inline">{}^\tau {v}</math> is the velocity vector of the points laying on the trajectory followed by the material point between times <math display="inline">{}^n t</math> and <math display="inline">{}^{n+1}t</math> (Figure [[#img-1|1]]). The integral of Eq.([[#eq-10|10]]) can be approximated in a number of ways (see Remark 4).
+==3 MOMENTUM EQUATIONS AND BOUNDARY CONDITIONS==
-==4 Acknowledgments<!-- Acknowledgments should be inserted at the end of the document, before the references section. -->==
+Let us assume that at time <math display="inline">{}^{n+1} t</math> the fluid occupies a volume <math display="inline">{}^{n+1} V</math> with a boundary <math display="inline">{}^{n+1}\Gamma </math>.  The fluid is subjected to body forces <math display="inline">{}^{n+1}b_i</math> acting over the volume <math display="inline">{}^{n+1} V</math> and surface tractions <math display="inline">{}^{n+1} t_i^p</math> acting on the part of the boundary termed as <math display="inline">{}^{n+1}\Gamma _t</math>, where index <math display="inline">i</math> denotes the component of the force along the <math display="inline">i</math>th cartesian axis (Figure 1).
+The equations of internal equilibrium between the applied body forces and the Cauchy stresses <math display="inline">\sigma _{ij}</math> in the fluid are expressed by the ''momentum equations'' written in the ''updated configuration'' as <span id='citeF-2'></span><span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-13'></span><span id='citeF-36'></span>[[#cite-2|[2,4,5,13,36]]]
+<span id="eq-11"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1} r_{m_i}  :={}^{n+1} \rho ~ {}^{n+1} a_i-{\partial \sigma _{ij} \over \partial x_j}- {}^{n+1}b_i=0 \quad \hbox{in }{}^{n+1} V\quad ,\quad i,j = 1,\cdots ,n_s  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (11)
+|}
+where <math display="inline">{}^{n+1} r_{m_i}</math> is the <math display="inline">i</math>th momentum equation, <math display="inline">{}^{n+1} \rho </math>, <math display="inline">{}^{n+1} v_i</math> and <math display="inline">{}^{n+1} a_i</math> are the fluid density and the <math display="inline">i</math>th component of the velocity and the acceleration at time <math display="inline">{}^{n+1} t</math> and <math display="inline">n_s</math> is the number of space dimensions (<math display="inline">n_s=3</math> for three dimensional (3D) problems). Note that <math display="inline">\sigma _{ij}</math> is always referred to the updated configuration, i.e. <math display="inline">\sigma _{ij} \equiv {}^{n+1}\sigma _{ij}</math>.
-==5 References<!--[1] Author, A. and Author, B. (Year) Title of the article. Title of the Publication. Article code. Available: http://www.scipedia.com/ucode.
+In Eq.([[#eq-11|11]]) and in the following, the standard summation convention for repeated indices is adopted, unless otherwise specified.
-[2] Author, A. and Author, B. (Year) Title of the article. Title of the Publication. Volume number, first page-last page.
+The boundary conditions are
-[3] Author, C. (Year). Title of work: Subtitle (edition.). Volume(s). Place of publication: Publisher.
+<span id="eq-12"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1} v_i-{}^{n+1} v_i^p =0 \quad \hbox{on }{}^{n+1} \Gamma _v  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (12)
+|}
-[4] Author of Part, D. (Year). Title of chapter or part. In A. Editor & B. Editor (Eds.), Title: Subtitle of book (edition, inclusive page numbers). Place of publication: Publisher.
+<span id="eq-13"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\sigma _{ij}n_j - {}^{n+1} t_i^p =0 \quad \hbox{on }{}^{n+1} \Gamma _t  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (13)
+|}
-[5] Author, E. (Year, Month date). Title of the article. In A. Editor, B. Editor, and C. Editor. Title of published proceedings. Paper presented at title of conference, Volume number, first page-last page. Place of publication.
+where <math display="inline">{}^{n+1}v_i^p</math>  is the prescribed value of the <math display="inline">i</math>th velocity component at the external boundary <math display="inline">{}^{n+1} \Gamma _v</math>  with <math display="inline">{}^{n+1} \Gamma _v \cup {}^{n+1} \Gamma _t = {}^{n+1} \Gamma </math>. In Eq.([[#eq-13|13]]) <math display="inline">n_j</math> is the <math display="inline">j</math>th component of the unit normal to the boundary <math display="inline">{}^{n+1}\Gamma _t</math> where the prescribed surface tractions <math display="inline">{}^{n+1} t_i^p</math> are applied.
-[6] Institution or author. Title of the document. Year. [Online] (Date consulted: day, month and year). Available: http://www.scipedia.com/document.pdf.
+The goal is to obtain the geometry of the updated configuration <math display="inline">{}^{n+1}V</math>, as well as the velocities and stresses in <math display="inline">{}^{n+1}V</math> that satisfy Eqs.([[#eq-11|11]])&#8211;([[#eq-13|13]]).
--->==
+==4 PRINCIPLE OF VIRTUAL POWER IN THE UPDATED CONFIGURATION==
+The principle of virtual power (PVP) can be written in the updated configuration  as <span id='citeF-2'></span><span id='citeF-4'></span><span id='citeF-5'></span>[[#cite-2|[2,4,5]]]
+<span id="eq-14"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1} \delta A + {}^{n+1} \delta U - {}^{n+1}\delta W=0  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (14)
+|}
+where <math display="inline">{}^{n+1} \delta A</math>, <math display="inline">{}^{n+1}\delta U</math> and <math display="inline">{}^{n+1}\delta W</math> are the virtual powers due to the acceleration terms, the stresses and the external loads acting on <math display="inline">{}^{n+1}V</math>, respectively given by <span id='citeF-2'></span><span id='citeF-4'></span><span id='citeF-5'></span>[[#cite-2|[2,4,5]]]
+<span id="eq-15"></span>
+<span id="eq-16"></span>
+<span id="eq-16"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1}\delta A = \int _{{}^{n+1}V}\delta{v}^T {~}^{n+1}\rho ~ {}^{n+1} {a} ~ d ~{}^{n+1}V</math>
+| style="width: 5px;text-align: right;white-space: nowrap;" | (15)
+|-
+| style="text-align: center;" | <math>   {}^{n+1}\delta U = \int _{{}^{n+1}V}\left\{\delta {D}\right\}^T  \left\{{\boldsymbol \sigma }\right\}d ~ {}^{n+1}V </math>
+| style="width: 5px;text-align: right;white-space: nowrap;" | (16)
+|-
+| style="text-align: center;" | <math> {}^{n+1}\delta W = \int _{{}^{n+1}V} \delta{v}^T   {~}^{n+1} {b} ~ d{~}^{n+1}V + \int _{{}^{n+1}\Gamma _t} \delta{v}^T {~}^{n+1}{t}~ d ~ {}^{n+1}\Gamma  </math>
+| style="width: 5px;text-align: right;white-space: nowrap;" | (17)
+|}
+|}
+In Eq.([[#eq-15|15]])&#8211;([[#eq-16|16]]) <math display="inline">\delta{v}</math>, <math display="inline">{b}</math> and <math display="inline">{t}</math> are the virtual velocity vector, the body forces vector and the surface tractions vector, respectively defined for 3D problems as
+<span id="eq-18"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta{v} = [\delta v_1,\delta v_2,\delta v_3]^T ~~,~~  {b}= [b_1,b_2,b_3]^T ~~,~~ {t}= [t_1,t_2,t_3]^T    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (18)
+|}
+In Eq.([[#eq-16|16]]) <math display="inline">{\boldsymbol \sigma }</math> is the Cauchy stress tensor and <math display="inline">\delta {D}</math> is the virtual rate of deformation tensor defined as
+<span id="eq-19"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta {D}_{ij}= \frac{1}{2} \left({\partial \delta v_i \over \partial {~}^{n+1} x_j}  +  {\partial \delta v_j \over \partial {~}^{n+1} x_i}\right)  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (19)
+|}
+where <math display="inline">\delta v_i</math> is the <math display="inline">i</math>th component of the virtual velocity.
+In the following <math display="inline">\left\{{A} \right\}</math>, where '''A''' is a symmetric tensor, will denote the vector representation of '''A'''. Hence, in Eq.([[#eq-16|16]]) <math display="inline">\left\{{\boldsymbol \sigma }\right\}</math> and <math display="inline">\left\{\delta {D}\right\}</math> are the Cauchy stress vector and the rate of deformation vector, respectively defined in Voigt notation <span id='citeF-4'></span><span id='citeF-5'></span>[[#cite-4|[4,5]]] as
+<span id="eq-20.a"></span>
+<span id="eq-20.b"></span>
+<span id="eq-20.b"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left\{{\boldsymbol \sigma }\right\}=  \left[\sigma _{11},\sigma _{22},\sigma _{33},\sigma _{12},\sigma _{13},\sigma _{23}   \right]^T</math>
+| style="width: 5px;text-align: right;white-space: nowrap;" | (20.a)
+|-
+| style="text-align: center;" | <math>   \left\{\delta {D}\right\}=  \left[\delta D_{11},\delta D_{22}, \delta D_{33},\delta D_{12},\delta D_{13},\delta D_{23} \right]^T    </math>
+| style="width: 5px;text-align: right;white-space: nowrap;" | (20.b)
+|}
+|}
+Similarly, <math display="inline">\left[{A} \right]</math> will denote hereonwards the matrix form of tensor <math display="inline">A</math>.
+'''Remark 1.''' The PVP can be obtained by applying the standard weighted residual method to the governing equations ([[#eq-11|11]]) and ([[#eq-13|13]]) using the virtual velocities <math display="inline">\delta v_i</math> as weighting functions <span id='citeF-4'></span>[[#cite-4|[4]]].
+'''Remark 2.''' Tensor <math display="inline">\delta {D}</math> can be interpreted as the variation of the rate of deformation tensor <math display="inline">D</math> defined in terms of the velocities at the updated configuration as
+<span id="eq-21"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{D}_{ij} = \frac{1}{2} \left({\partial {~}^{n+1} v_i \over \partial {~}^{n+1}x_j}+{\partial {~}^{n+1} v_j \over \partial {~}^{n+1}x_i}   \right)        </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (21)
+|}
+==5 TRANSFORMATION TO THE CURRENT CONFIGURATION. LAGRANGIAN STRESS AND STRAIN MEASURES==
+In the following sections we will use the current configuration as the reference configuration for computing the internal virtual due to the acceleration terms and the stresses, as well as  for subsequently performing  the linearization of its discretized  form via the FEM. The alternative of using the updated configuration as the reference configuration is presented in Section 12.
+After the standard transformations  of continuum mechanics  <span id='citeF-2'></span><span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-13'></span><span id='citeF-36'></span>[[#cite-2|[2,4,5,13,36]]] the internal virtual power at the updated configuration due to the acceleration terms and the stresses can be expressed in terms of material parameters, integrals, strain rates and stress measures evaluated at the ''current configuration'' <math display="inline">{}^{n}V</math> as
+<span id="eq-22.a"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1}\delta A = \int _{{}^{n}V} \delta{v}^T {~}^n \rho {~}^{n+1} {a} ~d {~}^{n}V  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (22.a)
+|}
+<span id="eq-22.b"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1}\delta U = \int _{{}^{n}V} \left\{\delta \dot{E} \right\}^T  \left\{{S}\right\}d {}^{n}V  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (22.b)
+|}
+where <math display="inline">\delta \dot{E}</math> and <math display="inline">{S}</math> are the material virtual strain rate tensor and the second Piola-Kirchhoff stress tensor, respectively. The relationship between the material strain rate tensor <math display="inline">\dot{E}</math> and the rate of deformation tensor <math display="inline">{D}</math> and between the stress tensors <math display="inline">{\boldsymbol \sigma }</math> and <math display="inline">{S}</math> is <span id='citeF-2'></span><span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-13'></span><span id='citeF-36'></span>[[#cite-2|[2,4,5,13,36]]]
+<span id="eq-23"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\dot{E}=  {F}^T  {D}{F} \quad , \quad {S} =J {F}^{-1} {\boldsymbol \sigma } {F}^{-T}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (23)
+|}
+where '''F''' is the deformation gradient and <math display="inline">J</math> is the Jacobian, respectively defined as
+<span id="eq-24"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>F_{ij}= \frac{\partial {~}^{n+1}{x}_i}{\partial {~}^n {x}_j}\quad ,\quad J=\vert {F}\vert   </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (24)
+|}
+From the expression of <math display="inline">\dot{E}</math> of Eq.([[#eq-23|23]]) we can deduce
+<span id="eq-25"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta \dot{E}= {F}^T \delta {D}{F}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (25)
+|}
+'''Remark 3.''' The material strain rate tensor can also be obtained from the time derivative of the Green-Lagrange strain tensor <math display="inline">{E}</math> as <span id='citeF-2'></span><span id='citeF-4'></span><span id='citeF-5'></span>[[#cite-2|[2,4,5]]]
+<span id="eq-26"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\dot{E} = \frac{d}{dt}({E}) = \frac{d}{dt} \left(\frac{1}{2}\left({C}-{I}   \right)\right)=\frac{1}{2}  \frac{d}{dt}{C}= \frac{1}{2}  \frac{d}{dt} ({F}^T {F}) = \frac{1}{2} ({F}^T \dot {F} + \dot {F}^T {F} )     </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (26)
+|}
+where <math display="inline">{C}=  {F}^T {F}</math>  is the right Cauchy-Green tensor and <math display="inline">\dot {F} = \frac{d}{dt}({F})</math>.  The expression of <math display="inline">\delta \dot{E}</math>  is obtained by writing the variation of <math display="inline"> \dot{E}</math> with respect to the velocities as
+<span id="eq-27"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta \dot{E} =\frac{1}{2} \left({F}^T \delta \dot {F}+ \delta \dot {F}^T {F} \right)  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (27)
+|}
+A useful explicit expression of the material strain rate tensor components in terms of the velocities <math display="inline">{}^{n+1}v_i</math> and the displacement increments <math display="inline">\Delta u_i</math> is
+<span id="eq-28.a"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\dot E_{ij}= \frac{1}{2} \left({}^{n+1}_n v_{i,j} +{}^{n+1}_n v_{j,i} + {}^{n+1}_n v_{k,i} ~{}_n \Delta u_{k,j} + {}^{n+1}_n v_{k,j} ~{}_n \Delta  u_{k,i}   \right)  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (28.a)
+|}
+with
+<span id="eq-28.b"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1}_n v_{i,j} = {\partial {~}^{n+1} v_i \over \partial {~}^n x_j}\quad ,\quad ~{}_n \Delta u_{i,j} = {\partial \Delta u_i \over \partial {~}^n x_j}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (28.b)
+|}
+From Eqs.([[#5 TRANSFORMATION TO THE CURRENT CONFIGURATION. LAGRANGIAN STRESS AND STRAIN MEASURES|5]]) we deduce
+<span id="eq-29.a"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta \dot{E}_{ij}= \frac{1}{2} \left({}_n \delta v_{i,j}~ +  {}_n \delta  v_{j,i}+{}_n \delta v_{k,i}~ {}_n \Delta u_ {k,j}+ {}_n \delta v_{k,j} ~{}_n \Delta u_{k,i} \right)  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (29.a)
+|}
+with
+<span id="eq-29.b"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}_n \delta v_{i,j} = \frac{\partial \delta v_i}{\partial {}^n x_j}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (29.b)
+|}
+==6 SPLIT OF THE INTERNAL VIRTUAL POWER INTO DEVIATORIC AND VOLUMETRIC COMPONENTS==
+The Cauchy stress tensor can be split in its deviatoric component <math display="inline">{\boldsymbol \sigma }'</math> and the hydrostatic pressure component <math display="inline">p</math> as
+<span id="eq-30"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{\boldsymbol \sigma } ={\boldsymbol \sigma }' + p {I}_3  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (30)
+|}
+where <math display="inline">{I}_3</math>  is the <math display="inline">3\times 3</math> identity matrix.
+Note that in incompressible fluid mechanics the pressure <math display="inline">p</math> is an independent variable. Also, unless otherwise specified we will assume that <math display="inline">p</math> is the pressure at the updated configuration (i.e. <math display="inline">p= {~}^{n+1}p</math>).
+Substituting Eq.([[#eq-30|30]]) into the internal virtual power expression in Eq.([[#eq-16|16]]) gives
+<span id="eq-31"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1} \delta U = \int _{{}^{n+1}V}\left\{\delta {D}\right\}^T \left(\left\{{\boldsymbol \sigma }'\right\}+{m} p  \right)d{~}^{n+1}V = \left(\int _{{}^{n+1}V}\left\{\delta {D}\right\}^T \left\{{\boldsymbol \sigma }'\right\}+ \delta D_v p \right)d{~}^{n+1}V  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (31)
+|}
+where <math display="inline">D_v</math> is the ''volumetric strain rate'' given by
+<span id="eq-32"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>D_v = D_{ii}= {m}^T \left\{{D}\right\}\quad \hbox{with}\quad {m}= [1,1,1,0,0,0]^T  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (32)
+|}
+It can be proven that  <span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-13'></span><span id='citeF-36'></span>[[#cite-4|[4,5,13,36]]]
+<span id="eq-33"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>D_v = \dot E_v \quad \hbox{with}\quad \dot E_v= \left\{\dot {E}\right\}^T \left\{{C}^{-1} \right\}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (33)
+|}
+where <math display="inline"> \dot E_v</math> is the volumetric material strain rate,
+<span id="eq-34.a"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left\{{E}' \right\}= \left[\dot E_{11},  \dot E_{22},\dot E_{33},2\dot E_{12},2\dot E_{13},2\dot E_{23}  \right]^T  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (34.a)
+|}
+<span id="eq-34.b"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left\{{C}^{-1} \right\}=\left[C^{-1}_{11},  C^{-1}_{22},C^{-1}_{33},C^{-1}_{12},C^{-1}_{13},C^{-1}_{23}  \right]^T  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (34.b)
+|}
+and <math display="inline">C_{ij}^{-1}</math> is the element <math display="inline">ij</math> of tensor <math display="inline">{C}^{-1}</math>.
+The  internal virtual power expression of Eq.([[#eq-31|31]]) can be written in the ''current configuration'' as follows.
+Substituting the Cauchy stress split of Eq.([[#eq-30|30]]) into the expression of the second Piola-Kirchhoff  stress tensor of Eq.([[#eq-23|23]]) gives
+<span id="eq-35"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{S} = J {F}^{-1} {\boldsymbol \sigma }'  {F}^{-T} + p J {C}^{-1} = {S}' + p J {C}^{-1}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (35)
+|}
+where
+<span id="eq-36"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{S}' = J {F}^{-1} {\boldsymbol \sigma }'  {F}^{-T}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (36)
+|}
+is the  deviatoric second Piola-Kirchhoff stress tensor. <math display="inline"> {S}'</math> is usually called the ''(true) deviatoric component'' of <math display="inline">S</math> <span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-13'></span><span id='citeF-36'></span>[[#cite-4|[4,5,13,36]]].
+Substituting Eq.([[#eq-35|35]]) into ([[#eq-22.b|22.b]]) gives
+<span id="eq-37"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1}\delta U = \int _{{}^{n}V} \left(\left\{\delta \dot {E}\right\}^T  \left\{{S}'\right\}+ J\delta \dot E_v p \right)d{}^{n}V  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (37)
+|}
+with
+<span id="eq-38"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left\{{S}'\right\}{= [S'}_{11}{,S'}_{22}{,S'}_{33}{,S'}_{12}{,S'}_{13}{,S'}_{23}]^T\quad , \quad  \delta \dot E_v = \left\{\delta \dot {E}\right\}^T  \left\{{C}^{-1}\right\}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (38)
+|}
+Eq.([[#eq-37|37]]) can also be obtained from Eq.([[#eq-31|31]]) using the relationship between <math display="inline">{D},~{\boldsymbol \sigma }'</math> and <math display="inline">D_v</math> with <math display="inline">\dot {E}</math>, <math display="inline">{S}'</math> and <math display="inline">\dot E_v</math>, respectively and the expression <math display="inline">d^{n+1}V =Jd^nV</math> <span id='citeF-2'></span><span id='citeF-4'></span><span id='citeF-5'></span>[[#cite-2|[2,4,5]]].
+Substituting Eqs.([[#eq-15|15]]), ([[#eq-22.a|22.a]]) and ([[#eq-37|37]]) into ([[#eq-14|14]]), the PVP in the updated configuration can be written in terms of the pressure,  the deviatoric second Piola-Kirchhoff stresses and the virtual Green-Lagrange strains computed in the current configuration as
+<span id="eq-39"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\begin{array}{r}  \displaystyle \int _{{}^{n}V} \delta{v}^T {~}^n \rho {~}^{n+1} {a}  d {~}^{n}V   +\int _{{}^{n}V} \left(\left\{\delta \dot {E}\right\}^T  \left\{{S}'\right\}+ J\delta \dot E_v p \right)d{~}^{n}V -\\ - \displaystyle \int _{{}^{n+1}V} \delta{v}^T  {~}^{n+1}{b}~ d{~}^{n+1} V - \int _{{}^{n+1}\Gamma _t} \delta{v}^T {~}^{n+1} {t}~d {~}^{n+1} \Gamma = 0\end{array} </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (39)
+|}
+The vector form of tensors <math display="inline">\delta \dot {E}</math> and <math display="inline">{S}</math> in Eq.([[#eq-39|39]]) is
+<span id="eq-40.a"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left\{\delta \dot {E}\right\}= [\delta \dot E_{11}, \delta \dot E_{22},\delta \dot E_{33},2\delta \dot E_{12},2\delta \dot E_{13},2\delta \dot E_{23}]^T  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (40.a)
+|}
+<span id="eq-40.b"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left\{{S}\right\}= [S_{11},S_{22},S_{33},S_{12},S_{13},S_{23}]^T  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (40.b)
+|}
+Note that the contribution of the external forces in Eq.([[#eq-39|39]]) is computed at the updated configuration and this requires using the correct expression for the density and the surface tractions on <math display="inline">{}^{n+1}V</math> (see also Remark 5).
+==7 CONSTITUTIVE RELATIONSHIP FOR THE DEVIATORIC STRESSES==
+The relationship between the deviatoric Cauchy stresses <math display="inline">{\sigma '}_{ij}</math> and the rates of deformation <math display="inline">D_{ij}</math> for a Newtonian fluid is written as
+<span id="eq-41"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{\sigma '}_{ij} ={c}_{ijkl}{ D'}_{kl} = {c}_{ijkl} \left(D_{kl}- \frac{1}{3} D_v \delta _{kl}\right)  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (41)
+|}
+where <math display="inline">{D'}_{kl}</math> are the deviatoric rates of deformation. The rates of deformation <math display="inline">D_{ij}</math> are obtained in terms of the velocities by Eq.([[#eq-21|21]]).
+The components of the fourth order constitutive tensor <math display="inline">{c}</math> in the updated configuration are
+<span id="eq-42"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{c}_{ijkl} =\mu \left(\delta _{ik} \delta _{jl} + \delta _{il} \delta _{jk}\right)  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (42)
+|}
+where <math display="inline">\mu </math> is the viscosity of the fluid.
+Eq.([[#eq-41|41]]) can be written in vector form as
+<span id="eq-43"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left\{{\boldsymbol \sigma }'\right\}= \left[{c}\right]\left\{{D}\right\}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (43)
+|}
+with
+<span id="eq-44"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\begin{array}{l}\left\{{\boldsymbol \sigma }'\right\}=  \left[\sigma' _{11},  \sigma' _{22},\sigma' _{33},\sigma' _{12},\sigma' _{13},\sigma' _{23}  \right]^T\\ \left\{{D}\right\}= \left[D_{11},  D_{22},D_{33},2D_{12},2D_{13},2D_{23}  \right]^T  \end{array}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (44)
+|}
+and the constitutive matrix <math display="inline">[{c}]</math> is given by (for 3D problems)
+<span id="eq-45"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left[{c}\right]=\mu \left[\displaystyle \begin{matrix}\displaystyle \frac{4}{3} & \displaystyle -\frac{2}{3} & \displaystyle -\frac{2}{3} &0&0&0\\[.25cm] & \displaystyle \frac{4}{3} & \displaystyle -\frac{2}{3} &0&0&0\\[.25cm] & &\displaystyle \frac{4}{3} &0&0&0\\ \hbox{ Sym.} &&& 1 &0&0\\ &&&&1&0\\ &&&&&1  \end{matrix} \right]  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (45)
+|}
+The constitutive equation ([[#eq-41|41]]) can be transformed to the current configuration to yield the relationship between the deviatoric second Piola-Kirchhoff stresses and the material strain rates  as
+<span id="eq-46"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{S'}_{ij} = {\cal C}_{ijkl} \dot E_{kl}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (46)
+|}
+The constitutive tensor in the current configuration <math display="inline">\left[\boldsymbol{\cal C}\right]</math> is obtained from its counterpart in the updated configuration as <span id='citeF-36'></span>[[#cite-36|[36]]]
+<span id="eq-47"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{\cal C}_{ijkl} = F^{-1}_{Ai} F^{-1}_{Bj}F^{-1}_{Ck}F^{-1}_{Dl} c_{ABCD}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (47)
+|}
+The vector form of Eq.([[#eq-46|46]]) is written as
+<span id="eq-48"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left\{\mathbf{S}' \right\}= \left[\boldsymbol{\cal C}\right]\left\{\dot {E}\right\}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (48)
+|}
+Matrix <math display="inline">\left[\boldsymbol{\cal C}\right]</math> is obtained by applying Voigt rule to the terms of tensor <math display="inline">\boldsymbol{\cal C}</math> <span id='citeF-4'></span><span id='citeF-5'></span>[[#cite-4|[4,5]]].
+==8 THE MASS BALANCE EQUATION==
+The mass balance equation in the updated configuration is written for a quasi-incompressible fluid as
+<span id="eq-49"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1} r_v:= - \frac{1}{{}^{n+1}\rho c^2}\frac{\partial p}{\partial t}+D_v =0 \quad \hbox{in } {}^{n+1}V   </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (49)
+|}
+where <math display="inline">c</math> is the speed of sound in the fluid. For a fully incompressible fluid <math display="inline">c=\infty </math> and Eq.([[#eq-49|49]]) reduces to the standard form <math display="inline">D_v =0</math>. The quasi-incompressible form will be retained here and this will allow us to account for the effect of the (small) compressibility in most fluids.
+Eq.([[#eq-49|49]]) can be written in terms of the ''bulk modulus'' of the fluid <math display="inline">\kappa </math> defined as <math display="inline">\kappa = \rho c^2</math>. For convenience we will retain the form of Eq.([[#eq-49|49]]).
+The variational form of the mass balance equation is obtained via the standard weighted residual method <span id='citeF-41'></span>[[#cite-41|[41]]] as
+<span id="eq-50"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\int _{{}^{n+1}V} q \left(- \frac{1}{{}^{n+1}\rho c^2}\frac{\partial p}{\partial t}+D_v   \right)d {~}^{n+1}V=0  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (50)
+|}
+where <math display="inline">q</math> are appropriate  test functions with dimensions of pressure <span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-41'></span>[[#cite-4|[4,5,41]]].
+The integral expression ([[#eq-50|50]]) can be written in the current configuration  using Eq.([[#eq-33|33]]) as
+<span id="eq-51"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\displaystyle \int _{{}^{n}V} q \left(- \frac{J^2}{{}^{n}\rho c^2}\frac{\partial p}{\partial t}+J\dot E_v   \right)d{~}^{n}V=0  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (51)
+|}
+In the derivation of Eq.([[#eq-51|51]]) we have used the standard expressions <span id='citeF-4'></span><span id='citeF-5'></span>[[#cite-4|[4,5]]]
+<span id="eq-52"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n}\rho = {}^{n+1}\rho J \quad \hbox{and}\quad d {~}^{n+1}V = J d {~}^{n}V    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (52)
+|}
+Eqs.([[#eq-39|39]]) and ([[#eq-51|51]]) together with the constitutive relationship ([[#eq-47|47]]) and the  boundary conditions ([[#eq-12|12]]) complete the set of governing variational equations for a  fluid in the updated Lagrangian description. The solution of these equations with the FEM is described in the next section.
+==9 FINITE ELEMENT DISCRETIZATION==
+We interpolate the velocities and the pressure in terms of their nodal values in the standard finite element fashion <span id='citeF-28'></span><span id='citeF-39'></span><span id='citeF-41'></span>[[#cite-28|[28,39,41]]]. For a mesh of <math display="inline">n</math>-noded <math display="inline">C^\circ </math> continuous elements we can write
+<span id="eq-53"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1} {v}= {N}_v {}^{n+1} \bar{v}\quad ,\quad p = {N}_p  {}^{n+1}\bar{p}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (53)
+|}
+where
+<span id="eq-54.a"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\bar{v} = \left\{\begin{matrix}\bar{v}^1\\ \bar{v}^2\\\vdots \\ \bar{v}^N    \end{matrix} \right\}\quad \hbox{with } \bar{v}^i = [\bar v^i_1,\bar v^i_2, \bar v^i_3]^T\quad ,\quad  \bar{p} = [\bar p_1,\bar p_2,\cdots ,\bar p_N]^T  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (54.a)
+|}
+where <math display="inline">N</math> is the total number of nodes in the mesh, <math display="inline">\bar v^i_j</math> and <math display="inline">\bar{p}^i</math> are <math display="inline">j</math>th velocity component and the pressure unknowns for node <math display="inline">i</math>,
+<span id="eq-54.b"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\begin{array}{l}{N}_v = [{N}^v_1,{N}^v_2,\cdots ,{N}^v_N ]\quad ,\quad {N}^v_i= N^v_i{I}_3\\ {N}_p = [{N}^p_1,{N}^p_2,\cdots ,{N}^p_N ]\end{array}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (54.b)
+|}
+In Eq.([[#eq-54.b|54.b]]) <math display="inline">{N}^v_i</math> and <math display="inline">N^p_i</math> are the ''global  shape functions'' <span id='citeF-28'></span><span id='citeF-39'></span>[[#cite-28|[28,39]]] for the velocity and pressure interpolations for node <math display="inline">i</math>, respectively.
+The velocity and pressure increments and the virtual velocities are interpolated in terms of their nodal values in the same fashion as in Eq.([[#eq-53|53]]).
+The  strain rate vector <math display="inline">\left\{\dot {E}\right\}</math> and its virtual expression <math display="inline">\left\{\delta \dot {E}\right\}</math> are respectively expressed in terms of the nodal velocities <math display="inline">\bar{v}</math> and their virtual values <math display="inline">\delta \bar{v}</math> via Eqs.([[#eq-28.a|28.a]]), ([[#eq-29.a|29.a]]) and ([[#eq-53|53]]) as
+<span id="eq-55"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left\{\dot {E}\right\}= {B} {}^{n+1} \bar{v} \quad ,\quad \left\{\delta \dot {E}\right\}= {B} \delta \bar {v}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (55)
+|}
+The actual and virtual volumetric material strain rates are related to the virtual velocities as
+<span id="eq-56"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\dot {E}_v  = \left\{{C}^{-T}\right\}{B}{~}^{n+1} \bar{v} \quad ,\quad \delta \dot {E}_v =\delta \bar{v}^T {B}^T\left\{{C}^{-1}\right\}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (56)
+|}
+In the above equations <math display="inline">{B}</math> is the material strain rate matrix given by
+<span id="eq-57"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{B} = [{B}_1,{B}_2,\cdots , {B}_N]^T \quad , \quad {B}_i =  {}_n{B}_i^0+{B}_i^L  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (57)
+|}
+where
+<span id="eq-58.a"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\begin{array}{l}{}_n{B}_i^0 = \left[ \begin{matrix}{}_nN^v_{i,1} &0&0\\ 0&{}_nN^v_{i,2} &0\\ 0&0&{}_nN^v_{i,3}\\ {}_nN^v_{i,2} &{}_nN^v_{i,1} &0\\ {}_nN^v_{i,3}&0&{}_nN^v_{i,1}\\  0&{}_nN^v_{i,3}&{}_nN^v_{i,2}  \end{matrix}\right]~~\hbox{and}~~  {B}_i^L ={}_n{B}_i^0 {L}^T  ~~\hbox{with}~~ {L}= \left[\begin{matrix}l_{11} & l_{12} & l_{13}\\ l_{21} & l_{22} & l_{23}\\ l_{31} & l_{32} & l_{33}  \end{matrix}\right]         \end{array}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (58.a)
+|}
+are the linear and non linear counterparts of the material strain rate matrix, respectively. The components of <math display="inline"> {}_n{B}_i^0</math> and <math display="inline">{L}</math> are
+<span id="eq-58.b"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}_nN^v_{i,j}= {\partial N^v_i \over \partial {}^n x_j}  \quad , \quad  l_{ij} =\sum \limits _{k=1}^n {}_nN^v_{k,j} \Delta u_k    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (58.b)
+|}
+The deviatoric second Piola-Kirchhoff stresses are related to the nodal velocities via Eqs.([[#eq-47|47]]) and ([[#eq-55|55]]) as
+<span id="eq-59"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left\{\mathbf{S}' \right\}=\left[\boldsymbol{\cal C}\right]\left\{\dot {E}\right\}= \left[\boldsymbol{\cal C}\right]{B} {~}^{n+1} \bar{v}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (59)
+|}
+'''Remark 4.''' The displacement increment <math display="inline">\Delta u_i</math> can be computed in terms of the velocity in a  number of ways. A popular choice is
+<span id="eq-60.a"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\Delta u_i =  \Delta t   {~}^{n+\alpha } v_i            </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (60.a)
+|}
+where <math display="inline">{~}^{n+\alpha } v_i </math> is the velocity at <math display="inline">t=t_n + \alpha \Delta t</math> where <math display="inline">\alpha </math> is a positive number (<math display="inline">0\le \alpha \le 1</math>). The value of <math display="inline">{~}^{n+\alpha } v_i </math> is typically computed as
+<span id="eq-60.b"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{~}^{n+\alpha } v_i  = (1-\alpha )^n v_i +  \alpha {}^{n+1} v_i            </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (60.b)
+|}
+===9.1 Discretized form of the PVP===
+Substituting Eqs.([[#eq-53|53]]),  ([[#eq-55|55]]) and ([[#eq-56|56]]) into the PVP (Eq.([[#eq-39|39]])) we obtain, after simplifying the virtual velocities
+<span id="eq-61"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1} \bar {r}_m := \int _{{}^{n}V} {}^n\rho {N}_v^T {N}_v {\dot{\bar {v}}}d {~}^{n}V   +\int _{{}^{n}V} {B}^T \left[\left\{\mathbf{S}' \right\}+ J  \left\{{C}^{-1}\right\}{p} \right]d {~}^{n}V - </math>
+|-
+| style="text-align: center;" | <math> \int _{{}^{n+1}V} {N}_v^T {~}^{n+1}{b} ~ d {~}^{n+1} V - \int _{{}^{n+1}\Gamma } {N}_v^T {~}^{n+1} {t}~d{~}^{n+1}\Gamma ={0}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (61)
+|}
+where <math display="inline">{}^{n+1} \bar {r}_m</math> is the residual vector of the discretized momentum equations in the updated configuration and <math display="inline"> {\dot{\bar {v}}} \equiv {\partial {}^{n+1} \bar {v} \over \partial t}</math> is the nodal acceleration vector.
+Eq.([[#eq-61|61]]) can be written in a more compact form as
+<span id="eq-62"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\displaystyle {}^{n+1} \bar {r}_m := {M}_v {\dot{\bar{v}}} + {}^{n+1} {g}_v + {}^{n+1} {g}_p - {}^{n+1} {f}_m    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (62)
+|}
+where
+<span id="eq-63"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{M}_v = \!\!\int _{{}^{n}V} {}^n\rho {N}_v^T {N}_v d ~{}^nV ~ , ~   {}^{n+1}{g}_v = \!\!\int _{{}^{n}V} {B}^T {S}' d {~}^{n} V  ~,~  {}^{n+1}{g}_p= \!\!\int _{{}^{n}V} {B}^T  J \left\{{C}^{-1}\right\}p d {~}^{n} V</math>
+|-
+| style="text-align: center;" | <math>   {}^{n+1} {f}_m = \!\!\int _{{}^{n+1}V}  {N}_v^T {~}^{n+1}~{b} ~d{~}^{n+1} V + \!\!\int _{{}^{n+1}\Gamma }  {N}_v^T {~}^{n+1}{t}~ d{~}^{n+1} V    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (63)
+|}
+In Eq.([[#eq-62|62]]) <math display="inline">{}^{n+1} {g}_v</math>  and <math display="inline">{}^{n+1}{g}_p</math> are internal force vectors contributed by the deviatoric second Piola-Kirchhoff stresses and the pressure, respectively and <math display="inline">{}^{n+1} {f}_m</math> is the external force vector.
+Recall that the internal force vectors at the current configuration are obtained in terms of expressions at the updated configuration.
+'''Remark 5.''' The computation of the body force vector <math display="inline">{}^{n+1}{b}</math> in Eq.([[#eq-63|63]]) for the case of selfweight requires computing the density at the updated configuration as <math display="inline">{}^{n+1}\rho = \frac{1}{J}{}^n\rho </math>. We also note that the surface tractions <math display="inline">{}^{n+1}{t}</math> are applied on the boundary of the updated configuration <math display="inline">{}^{n+1}\Gamma </math>, which requires the accurate identification of this boundary.
+The acceleration term in Eq.([[#eq-62|62]]) can be approximated in a number of manners. A backward Euler scheme gives
+<span id="eq-64"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1} \bar {r}_m := {M}_v \frac{{}^{n+1} \bar{v}-{}^{n}  \bar{v} }{\Delta t}+ {}^{n+1} {g}_v + {}^{n+1} {g}_p - {}^{n+1} {f}_m =0    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (64)
+|}
+===9.2 Discretization of the mass conservation equation===
+The arbitrary pressure test functions <math display="inline">q</math> are interpolated in the same fashion as the pressure as
+<span id="eq-65"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>q= {N}_p \bar{q}= \bar {q}^T{N}_p^T  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (65)
+|}
+where vector <math display="inline"> \bar{q}</math> contains the nodal values of <math display="inline">q</math>.
+Substituting the expression of <math display="inline">\dot {E}_v</math> in term of <math display="inline">{}^{n+1} \bar{v}</math> from Eq.([[#eq-56|56]]) and Eq.([[#eq-65|65]]) in the variational form of the mass balance equation (Eq.([[#eq-51|51]])) we obtain, after eliminating the pressure test functions <math display="inline">\bar{q}</math>
+<span id="eq-66"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\displaystyle {}^{n+1} \bar {r}_v : = - {M}_p {\dot{\bar{p}}} + {Q}^T {~}^{n+1} \bar {v}={0}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (66)
+|}
+where <math display="inline">{}^{n+1} \bar {r}_v</math> is the residual vector of the discretized mass conservation equation, <math display="inline"> {\dot{\bar {p}}} = {\partial {~}^{n+1} \bar {p} \over \partial t}</math> and the terms of <math display="inline">{M}_p</math> and <math display="inline">{}^{n}{Q}</math> are
+<span id="eq-67"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>M_{p_{ij}}=\int _{{}^{n}V} \frac{J^2}{^n\rho c^2}N^p_i N^p_j d{~}^{n}V ~~,~~{Q}= \int _{{}^{n}V} {B}^T \left\{{C}^{-1}\right\}{N}_p J d {~}^{n} V   </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (67)
+|}
+===9.3 Stabilization of the mass conservation equation===
+It is well known that  the FEM  solutions for the fully incompressible limit are unstable for some particular forms of the approximation for the velocities and the pressure <span id='citeF-10'></span><span id='citeF-39'></span><span id='citeF-41'></span>[[#cite-10|[10,39,41]]]. This is the case, for instance, when an equal order interpolation is chosen for the velocity components and the pressure (i.e. <math display="inline">N^v_i = N^p_i</math>). This problem can be overcome by using finite element approximations for <math display="inline">{v}</math> and <math display="inline">p</math> satisfying the so-called LBB conditions <span id='citeF-10'></span><span id='citeF-39'></span><span id='citeF-41'></span>[[#cite-10|[10,39,41]]], or else by introducing stabilization terms into the discretized mass balance equation <span id='citeF-10'></span><span id='citeF-41'></span>[[#cite-10|[10,41]]]. In this work the later approach is chosen for obtaining stabilized numerical solutions.
+In essence all stabilized formulations modify the discretized form of the  mass balance equation as
+<span id="eq-68"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\displaystyle  {}^{n+1} \hat {r}_v := {}^{n+1} \bar {r}_v +  ^{n+1} \bar {r}_s =0  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (68)
+|}
+where <math display="inline">{}^{n+1} \bar {r}_v</math> was defined in Eq.([[#eq-66|66]])  and <math display="inline">{}^{n+1} \bar {r}_s</math> is a stabilization mass balance vector which expression can be typically written as
+<span id="eq-69"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1} \bar {r}_s = -  \boldsymbol{\cal S} {~}^{n+1} \bar {p}+  {}^{n+1} {f}_s   </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (69)
+|}
+where <math display="inline">\boldsymbol{\cal S}</math> is a stabilization matrix and <math display="inline">{}^{n+1}{f}_s</math> is a force vector that depends on the nodal velocities and pressures. The form of <math display="inline">\boldsymbol{\cal S}</math> and <math display="inline">{f}_s</math> is different for each stabilization method. Typically, <math display="inline">\boldsymbol{\cal S}</math> and <math display="inline">{}^{n+1}{f}_s</math> contain integrals  over the volume and the Neumann boundary of the analysis domain and are both a function of the so-called stabilization parameters which expression also depends on the particular stabilization method chosen <span id='citeF-3'></span><span id='citeF-8'></span><span id='citeF-9'></span><span id='citeF-10'></span><span id='citeF-15'></span><span id='citeF-31'></span><span id='citeF-37'></span><span id='citeF-41'></span>[[#cite-3|[3,8,9,10,15,31,37,41]]].
+The derivation of a stabilized  mixed velocity-pressure formulation for incompressible fluids exceeds the objectives of this paper. Details can be obtained in the references cited in the previous paragraphs.
+A particular stabilized Lagrangian formulation with excellent mass conservation features based on the Finite Calculus (FIC) theory <span id='citeF-21'></span>[[#cite-21|[21]]]&#8211;<span id='citeF-24'></span>[[#cite-24|[24]]],<span id='citeF-27'></span><span id='citeF-30'></span>[[#cite-27|[27,30]]] can be found in <span id='citeF-31'></span>[[#cite-31|[31]]].
+==10 INCREMENTAL SOLUTION FOR THE NODAL VELOCITIES AND PRESSURES==
+We will derive next an incremental iterative procedure for solving the discretized form of the equations for conservation of linear momentum and mass conservation in a segregated form. This requires the linearization of Eqs.([[#eq-61|61]]) and ([[#eq-68|68]]) with respect to the nodal velocity and pressure unknowns, respectively. The linearization procedure takes advantage from the fact that the reference configuration (i.e. the current configuration <math display="inline">{}^{n}V</math>) remains fixed during the linearization process.
+===10.1 Linearization of the discretized  momentum equations with respect to the nodal velocities===
+We linearize the residual vector <math display="inline">{}^{n+1} \bar {r}_m</math> of Eq.([[#eq-61|61]]) with respect to the nodal velocities <math display="inline">\bar {v}</math> as
+<span id="eq-70"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta _{\bar v} {}^{n+1} \bar {r}_m ({x},\bar {v},\bar {p})   = \frac{d}{d\epsilon }\Bigg|_{\epsilon =0}  {}^{n+1} \bar {r}_m  ({x},\bar {v}+\epsilon d\bar{v},\bar {p})    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (70)
+|}
+Expression ([[#eq-70|70]]) is the directional derivative of the residual vector <math display="inline">{}^{n+1} \bar {r}_m</math> at a point <math display="inline">{x}</math> in the direction of the nodal velocity vector <math display="inline">d\bar {v}</math> (hereafter called ''nodal velocity pseudo-increment vector''). The same definition applies to the directional derivative of a matrix or a scalar depending on the space coordinate <math display="inline">{x}</math>, the nodal velocities <math display="inline">\bar {v}</math> and the nodal pressures <math display="inline">\bar {p}</math> <span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-36'></span>[[#cite-4|[4,5,36]]].
+Using the expression of vector <math display="inline">{}^{n+1} \bar {r}_m</math> of Eq.([[#eq-62|62]]) in Eq.([[#eq-70|70]]) and neglecting the changes of vector <math display="inline">{}^{n+1} {f}_m</math> with the  velocity,  gives
+<span id="eq-71"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta _{\bar v} {}^{n+1} \bar {r}_m = \frac{1}{\Delta t}{M}_v d \bar {v}+      \int _{{}^{n}V} \Big\{{B}^T \Big[\delta _{\bar v}\left\{\mathbf{S}' \right\}+ \left(\delta _{\bar v} J\left\{{C}^{-1}\right\}+ {J} \delta _{\bar v} \left\{{C}^{-1}\right\}\right)p + </math>
+|-
+| style="text-align: center;" | <math>  + J \left\{{C}^{-1}\right\}\delta _{\bar v}p\Big]+ \delta _{\bar v} {B}^T  \left\{\mathbf{S}' \right\}\Big\}d{~}^{n} V  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (71)
+|}
+After some algebra detailed in the Appendix, the following linearized form of <math display="inline">{}^{n+1}\bar{r}_m</math> with respect to the nodal velocities is found
+<span id="eq-72"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta _v  {}^{n+1}\bar{r}_m   = \left(\frac{1}{\Delta t}{M}_v +  {K}_c + {K}_\sigma \right)  d \bar {v}+  {Q}  {\delta }_{\bar v}^{n+1}\bar {p}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (72)
+|}
+where matrices <math display="inline">{M}_v</math> and <math display="inline">{}^{n} {Q}</math> were given in Eq.([[#eq-67|67]]) and <math display="inline">{}^n{K}_c</math> and <math display="inline">{K}_\sigma </math> are the constitutive and initial stress matrices, respectively. The expression of these matrices is
+<span id="eq-73"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{K}_c = \!\!\int _{{}^{n}V}{B}^T [\boldsymbol{\cal C}_T] {B} d {~}^{n}V ~~ ,~~  {K}_\sigma = \Delta t \!\int _{{}^{n}V}{G}^T \hat{S}' {G}d {~}^{n}V  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (73)
+|}
+The form of matrices <math display="inline">{G}</math> and <math display="inline">\hat{S}'</math> is given in the Appendix.
+The expression of the tangent constitutive tensor <math display="inline">\boldsymbol{\cal C}_T</math> is (see Appendix)
+<span id="eq-74"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\boldsymbol{\cal C}_T = \boldsymbol{\cal C} + J  \Delta t ~p ({C}^{-1}\otimes {C}^{-1} - 2 \boldsymbol{\cal I})    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (74)
+|}
+Tensor <math display="inline">\boldsymbol{\cal C}_T</math> contains contributions from the  constitutive tensor <math display="inline">\boldsymbol{\cal C}</math> of Eq.([[#eq-46|46]]), the time step and  the pressure. This form of <math display="inline">\boldsymbol{\cal C}_T</math> is very similar to that used for incompressible continua <span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-13'></span><span id='citeF-36'></span>[[#cite-4|[4,5,13,36]]].  It can be shown that tensor <math display="inline">\boldsymbol{\cal I}</math> is symmetric (see Appendix) and, hence, the tangent constitutive tensor <math display="inline">\boldsymbol{\cal C}_T</math> is symmetric <span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-13'></span><span id='citeF-36'></span>[[#cite-4|[4,5,13,36]]].
+===10.2 Linearization of the nodal pressures with respect to the nodal velocities. Derivation of the tangent matrix===
+From  Eq.([[#eq-66|66]]) we can obtain the directional derivative of the nodal pressure variables in the direction of the nodal velocity increments. Using a trapezoidal rule for approximating the time derivative term gives
+<span id="eq-75"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{M}_p\frac{1}{\theta \Delta t} ({~}^{n+1}\bar {p} - {}^{n+\theta }\bar {p}) + {Q}^T \bar {v} = {0}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (75)
+|}
+where <math display="inline">\theta </math> is a time parameter such that <math display="inline">0<\theta \le 1</math>. A value <math display="inline">\theta =1</math> defines a backward Euler scheme <span id='citeF-39'></span><span id='citeF-41'></span>[[#cite-39|[39,41]]].
+From Eq.([[#eq-75|75]]) it is straightforward to obtain
+<span id="eq-76"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{\delta }_{\bar v} {~}^{n+1}\bar {p}= \theta \Delta t {M}_p^{-1} {Q}^T d \bar {v}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (76)
+|}
+Substituting Eq.([[#eq-76|76]]) into ([[#eq-72|72]]) gives the final linearized form of the momentum equations in terms of the nodal velocities increments as
+<span id="eq-77"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{\delta }_{\bar v} {}^{n+1}\bar {r}_m =  {K}_T^i d \bar {v}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (77)
+|}
+where <math display="inline">(\cdot )^i</math> denotes values at the <math display="inline">i</math>th iteration and the tangent matrix <math display="inline"> ^n {K}_T</math> is
+<span id="eq-78"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\displaystyle  {K}_T = \frac{1}{\Delta t} {M}_v +  {K}_c +  {K}_\sigma +  {K}_p   </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (78)
+|}
+with <math display="inline">{M}_v</math>, <math display="inline"> {K}_c</math> and <math display="inline">{K}_\sigma </math>  defined in Eqs.([[#eq-63|63]]) and ([[#eq-72|72]]) and the tangent “bulk” matrix <math display="inline">{K}_p</math> is
+<span id="eq-79"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{K}_p = \theta \Delta t  {Q} {M}_p^{-1}  {Q}^T  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (79)
+|}
+In practice, <math display="inline"> {K}_p</math> is computed using the diagonal form of <math display="inline">{M}_p</math>, i.e.
+<span id="eq-80"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{K}_p = \theta \Delta t {Q} {M}_{pD}^{-1}  \bar{Q}^T  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (80)
+|}
+where <math display="inline">{M}_{pD} ={diag}({M}_p)</math>.
+The incremental form of the momentum equations can written as
+<span id="eq-81"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1}\bar {r}_{m} \simeq {}^{n+1}\bar {r}_{m}^i + {\delta }_{\bar v} {~}^{n+1}\bar {r}_m = {}^{n+1}\bar {r}_m^i + {K}_T^i d \bar {v} =0  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (81)
+|}
+Solution of Eq.([[#eq-81|81]]) yields the nodal velocity increments <math display="inline">d \bar {v}</math> for the <math display="inline">i</math>th iteration.
+'''Remark 6.''' For fully incompressible fluids (<math display="inline">c=\infty </math>) a large but finite value of <math display="inline">c</math> is used in practice. This allows to eliminate the pressure DOFs in the momentum equations via Eq.(([[#eq-76|76]])).
+'''Remark 7.''' The tangent “bulk” stiffness matrix <math display="inline">\mathbf{K}_p</math> in the tangent matrix <math display="inline">\mathbf{K}_T</math>  accounts for the changes of the pressure due to the velocity. Including matrix <math display="inline">\mathbf{K}_p</math> in <math display="inline">\mathbf{K}_T</math> has proven to be essential for the fast convergence, mass preservation and overall accuracy of the iterative solution in all cases <span id='citeF-11'></span>[[#cite-11|[11]]].      The <math display="inline">\theta </math> parameter in <math display="inline">{K}_p</math> (Eq.([[#eq-79|79]]))  has the role of preventing the ill-conditioning of <math display="inline">\mathbf{K}_T</math> for very large values of the speed of sound in the fluid that lead to a dominant role of the terms of the tangent bulk stiffness matrix <math display="inline">{K}_p</math>. Clearly, the value of the terms of <math display="inline">{K}_p</math> can also be limited by reducing the time step size. This, however, leads to an increase in the overall cost of the computations <span id='citeF-11'></span>[[#cite-11|[11]]]. An adequate selection of <math display="inline">\theta </math>  improves the convergence of the iterative process and leads to a more accurate numerical solution with reduced mass loss, even for large time steps <span id='citeF-11'></span>[[#cite-11|[11]]]. These considerations, however, do not affect the value of <math display="inline">c</math> within matrix <math display="inline">{M}_p</math> in Eq.([[#eq-67|67]]) that vanishes for the fully incompressible case (<math display="inline">c =\infty </math>).
+===10.3 Linearization of the stabilized mass conservation equation with respect to the nodal pressures===
+The stabilized mass conservation equation ([[#eq-68|68]]) is linearized with respect to the nodal pressure pseudo-increment vector <math display="inline">d \bar {p}</math> using Eqs.([[#eq-66|66]]), ([[#eq-68|68]]) and ([[#eq-69|69]])  as
+<span id="eq-82"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta _{\bar p} {}^{n+1} \hat {r}_v ({x},\bar {v},\bar {p})= \frac{d}{d\epsilon }\Bigg|_{\epsilon =0} {}^{n+1} \hat{r}_v ({x},\bar {v},\bar {p}+\epsilon d \bar {p})    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (82)
+|}
+Using  Eqs.([[#eq-67|67]])&#8211;([[#eq-68|68]]) and a backward Euler scheme for approximating the time derivative of the nodal pressure in Eq.([[#eq-67|67]]) gives
+<span id="eq-83"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta _{\bar p} {~}^{n+1} \hat {r}_v   = - \left(\frac{1}{\Delta t} {M}_p + \boldsymbol{\cal S}\right)d \bar {p}   </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (83)
+|}
+In the derivation of Eq.([[#eq-83|83]]) we have neglected the pressure dependence of the terms of matrix <math display="inline"> \boldsymbol{\cal S}</math> and <math display="inline">{}^{n+1} {f}_s</math> in Eq.([[#eq-69|69]]).
+The incremental form of the mass balance equation is therefore
+<span id="eq-84"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{}^{n+1}{\hat{r}}_v \simeq {}^{n+1}{\hat{r}}_v^i +  \delta _{\bar p} {~}^{n+1}{\hat{r}}_v = {}^{n+1}{\hat{r}}_v^i - \left(\frac{1}{\Delta t}{M}_p + \boldsymbol{\cal S}^i   \right)d \bar {p}=0  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (84)
+|}
+Solution of Eq.([[#eq-84|84]])  yields the ''nodal pressure pseudo-increment vector'' <math display="inline">d \bar {p}</math> at the <math display="inline">i</math>th iteration.
+===10.4 Incremental solution of the discretized equations===
+An incremental Newton-Raphson type iterative solution scheme for the stabilized velocity-pressure formulation is as follows.
+Within a time increment <math display="inline">[n,n+1]</math>:
+*  Initialize variables: <math display="inline">({}^{n+1} {x}, {}^{n+1}\bar {v}^{1}, {}^{n+1}\bar {p}^{1}, {}^{n+1}\bar {r}_m, {}^{n+1}\hat {r}_v) \equiv ({}^{n} {x},{}^{n}\bar {v},{}^{n}\bar {p},{}^{n}\bar {r}_m, {}^{n}\hat{r}_v)</math>.
+* Iteration loop = <math display="inline">i=1,\cdots , NITER</math>
+<br/>
+''For each iteration''
+<br/>
+<ol>
+<li>'''Compute the nodal velocity pseudo-increments''' , <math display="inline">d \bar {v}</math> (from Eq.([[#eq-81|81]])) from
+<span id="eq-85"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>
+{K}_T^i d \bar {v}= - {}^{n+1}\bar {r}_m^i ({}^{n+1}{\bar{v}}^i, {}^{n+1}{\bar{p}}^i)    </li>
+</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (85)
+|}
+<li>'''Update the nodal velocities''' :
+<span id="eq-86"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>
+^{n+1} \bar {v}^{i+1}=^{n+1} \bar {v}^i + d \bar {v}    </li>
+</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (86)
+|}
+<li>'''Compute the nodal pressure pseudo-increments''' , <math display="inline">d\bar {p}</math>. From Eq.([[#eq-84|84]]),
+<span id="eq-87"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>
+\left(\frac{1}{\Delta t} {M}_p +\boldsymbol{\cal S}^i\right)d \bar {p} = ^{n+1}\hat {r}_v^i ({}^{n+1} \bar {v}^{i+1},{}^{n+1} \bar {p}^{i})    </li>
+</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (87)
+|}
+<li>'''Update the nodal pressures''' :
+<span id="eq-88"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>
+^{n+1} \bar {p}^{i+1}= ^{n+1} \bar {p}^{i} + d\bar {p}     </li>
+</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (88)
+|}
+<li>Update the nodal displacement increments <math display="inline">\Delta {u}</math> using Eq.([[#eq-60.a|60.a]]) and the approximate value for the nodal velocities <math display="inline">{}^{n+1} \bar {v}^{i+1}</math>.   </li>
+<li>Update the nodal coordinates in the updated configuration as
+<span id="eq-89"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>
+{}^{n+1} {x}^{i+1} = {}^{n+1} {x}^i + \Delta {u}      </li>
+</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (89)
+|}
+<li>'''Compute the material derivative of the Green strains <math>\dot E_{ij}</math> and the deviatoric second Piola-Kirchhoff stresses <math>{S'}_{ij}</math>'''  (from Eqs.([[#eq-55|55]]) and ([[#eq-45|45]])).    </li>
+<li>'''Compute the momentum and mass balance residuals''' : <math display="inline">^{n+1}\bar {r}_m^{i+1}</math> and <math display="inline">^{n+1}\hat {r}_v^{i+1}</math>    </li>
+<li>'''Check convergence'''
+<span id="eq-90"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>
+\begin{array}{l}
+\Vert ^{n+1}\bar {r}_m^{i+1} \Vert  \le  e_m \Vert {}^n{f}_v\Vert \\[.5cm]   \Vert ^{n+1}\hat {r}_v^{i+1} \Vert  \le  e_v {~}^{n}V    </li>
+\end{array}
+</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (90)
+|}
+where <math display="inline">\Vert \cdot \Vert </math> denotes the quadratic norm and <math display="inline">e_m</math> and <math display="inline">e_v</math> are prescribed error tolerances for the discretized residuals of the momentum and mass balance equations, respectively.
+If both conditions ([[#eq-90|90]]) are satisfied then make <math display="inline">n\leftarrow n+1</math> and proceed to the next time increment. Otherwise, make the iteration counter <math display="inline">i\leftarrow i+1</math> and repeat Steps 1&#8211;9.
+</ol>
+'''Remark 8.''' An alternative convergence criteria based on the  nodal velocities and pressures can be defined as
+<span id="eq-91.a"></span>
+<span id="eq-91.b"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\Vert ^{n+1}\bar {v}^{i+1} - {}^{n+1}\bar {v}^i\Vert  \le  e_{\bar v} \Vert ^{n+1}\bar {v}^i\Vert </math>
+| style="width: 5px;text-align: right;white-space: nowrap;" | (91.a)
+|-
+| style="text-align: center;" | <math>      \Vert ^{n+1}\bar {p}^{i+1} - ^{n+1}\bar {p}^i\Vert  \le  e_{\bar p} \Vert ^{n+1}\bar {p}^i\Vert  </math>
+| style="width: 5px;text-align: right;white-space: nowrap;" | (91.b)
+|}
+|}
+where <math display="inline">e_{\bar v}</math> and <math display="inline">e_{\bar p}</math> are error tolerances.
+'''Remark 9.''' The  nodal velocity and pressure increment vectors <math display="inline">\Delta \bar {v}</math> and <math display="inline">\Delta \bar {p}</math> can be computed at the end of each time step as
+<span id="eq-92"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\Delta \bar {v} =   {}^{n+1}\bar {v}- {}^{n}\bar {v}\quad \hbox{and}\quad \Delta \bar {p} =   {}^{n+1}\bar {p} - {}^{n}\bar {p}                </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (92)
+|}
+where <math display="inline">{}^{n+1}\bar {v}</math> and <math display="inline">{}^{n+1}\bar {p}</math> denote the converged values at the end of the iteration loop. Clearly, <math display="inline">\Delta \bar {v}</math> and <math display="inline">\Delta \bar {p}</math> can also be obtained by adding up the pseudo-increment vectors <math display="inline">d\bar {v}</math> and <math display="inline">d\bar {p}</math> within the iterative solution.
+'''Remark 10.''' The nodal pressures <math display="inline">^{n+1}\bar {p}^{i+1}</math> can be directly obtained from Eq.([[#eq-68|68]]), after substitution of Eqs.([[#eq-66|66]]) and ([[#eq-69|69]]), as
+<span id="eq-93"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left(\frac{1}{\Delta t} {M}_p +   \boldsymbol{\cal S}^i  \right){}^{n+1} \bar {p}^{i+1}= {Q}^T {~}^{n+1} \bar {v}^{i+1} + \frac{1}{\Delta t} {M}_p {~}^{n} \bar{p} + {}^{n+1} {f}_s  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (93)
+|}
+The rest of the iterative solution scheme is similar to that described above. Eq.([[#eq-93|93]]) substitutes  Eqs.([[#eq-87|87]]) and ([[#eq-88|88]]) and the convergence of the nodal pressures is verified by Eq.([[#eq-91.b|91.b]]).
+'''Remark 11.''' For a fully incompressible fluid <math display="inline">c = \infty </math> and matrix <math display="inline">{M}_p=0</math> in Eqs.([[#eq-67|67]]), ([[#eq-87|87]]) and ([[#eq-93|93]]).
+The problem can still be accurately solved in this case using an adequate expression for the stabilization matrix <math display="inline">\boldsymbol{\cal S}</math>. The form of <math display="inline">\boldsymbol{\cal S}</math> presented in <span id='citeF-31'></span>[[#cite-31|[31]]]  includes a Laplacian term over the whole domain <math display="inline">\Omega </math> and an integral along the Neumann boundary <math display="inline">\Gamma _t</math>. The boundary term in <math display="inline">\boldsymbol{\cal S}</math> avoids the need for prescribing the pressure on the domain boundary. If a standard Laplacian form is chosen for <math display="inline">\boldsymbol{\cal S}</math>, then the value of the pressure has to be prescribed in strong form at some boundary points in order to obtain good results <span id='citeF-41'></span>[[#cite-41|[41]]].
+==11 DIRECT ITERATIVE SOLUTION OF THE NODAL VELOCITIES AND PRESSURES==
+Substituting the FEM approximation for the velocities and the pressure ([[#eq-53|53]]) into Eq.([[#eq-64|64]]) and assuming a Newtonian fluid with a constitutive equation given by Eq.([[#eq-47|47]]), the following matrix expression of the discretized momentum equations can be obtained
+<span id="eq-94"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\displaystyle {}^{n+1} \bar {r}_m := {M}_v {\dot{\bar{v}}} +  {K}_v {~}^{n+1} \bar{v} + {Q}{~}^{n+1} \bar {p}-{}^{n+1} {f}_m=0  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (94)
+|}
+where <math display="inline">{M}_v</math>, <math display="inline">{}^{n}{Q}</math> and <math display="inline">{}^{n+1} {f}_m</math> have been defined previously and
+<span id="eq-95"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{K}_v = \int _{{}^{n}V} {B}^T \left[ \boldsymbol{\cal C}\right]{B} d {~}^{n} V    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (95)
+|}
+Combining Eq.([[#eq-94|94]]) with the stabilized mass balance equation ([[#eq-68|68]]) and using Eq.([[#eq-66|66]]) gives the following matrix system for the nodal velocities and pressures
+<span id="eq-96"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left[\begin{matrix}{M}_v & {0} \\  {0}& -  {M}_p      \end{matrix}   \right]\left\{\begin{matrix}{\dot{\bar{v}}}\\ {\dot{\bar{p}}}  \end{matrix} \right\}+ \left[\begin{matrix}{K}_v & {Q}\\ {Q}^T & -  \boldsymbol{\cal S} \end{matrix} \right]\left\{\begin{matrix}{}^{n+1} \bar{v}\\ {}^{n+1} \bar{p}  \end{matrix} \right\}- \left\{\begin{matrix}{}^{n+1} {f}_m\\ {}^{n+1} {f}_s   \end{matrix} \right\}={0}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (96)
+|}
+Eq.([[#eq-96|96]]) can be written in a compact (monolithic) form as
+<span id="eq-97"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{M} {\dot{\bar{a}}} +  {K} {~}^{n+1} \bar{a} -{}^{n+1} {f}=0    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (97)
+|}
+where
+<span id="eq-98"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{M}=\left[\begin{matrix}{M}_v & {0}\\ {0} & -{M}_p \end{matrix} \right]~~ ,~~  {K} = \left[\begin{matrix}{K}_v & {Q}\\ {Q}^T & -  \boldsymbol{\cal S}\end{matrix} \right]~~ ,~~ {~}^{n+1} \bar{a} = \left\{\begin{matrix}{}^{n+1} \bar{v}\\ {}^{n+1} \bar{p}  \end{matrix} \right\}~~ ,~~ {}^{n+1} {f} = \left\{\begin{matrix}{}^{n+1} {f}_m\\ {}^{n+1} {f}_s   \end{matrix} \right\}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (98)
+|}
+===11.1 Monolithic solution scheme===
+Eq.([[#eq-98|98]]) is the basis for deriving monolithic iterative time integration schemes for directly computing the nodal velocities and pressure at the updated configuration. For instance, the standard backward Euler scheme gives
+<span id="eq-99"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{H}^i {~}^{n+1} \bar{a}^{i+1}  = {}^{n+1} {f}^i + \frac{1}{\Delta t}{M} {}^{n} \bar{a}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (99)
+|}
+with <math display="inline"> {H}^i = \frac{1}{\Delta t} {M} + {K}_v^i</math>.
+The values of <math display="inline">{}^{n+1} \bar{a}</math> can be directly found by solving Eq.([[#eq-99|99]]) iterative.
+The  non linearity of matrix <math display="inline">{}^{n}{K}_v</math> emanates from the non linear  terms in the material strain rate matrix <math display="inline">{B}^L</math> involving the displacement increments (Eqs.([[#9 FINITE ELEMENT DISCRETIZATION|9]])).
+===11.2 Segregated solution scheme===
+The nodal velocities and pressures at the updated configuration can be also computed starting from Eq.([[#eq-97|97]]) using a segregated iterative scheme as follows
+<span id="eq-100"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left[\frac{1}{\Delta t} {M}_v +  {K}_v^i \right]{~}^{n+1} \bar{v}^{i+1} = {}^{n+1} {f}_m - {Q} {~}^{n+1} {p}^i    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (100)
+|}
+<span id="eq-101"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\left[\frac{1}{\Delta t} {M}_p +  \boldsymbol{\cal S}^i \right]{~}^{n+1} \bar{p}^{i+1} = {~}^{n+1}  {f}_s + {Q}^T  {~}^{n+1} \bar{v}^{i+1} + \frac{1}{\Delta t} {M}_p  {~}^{n} \bar{p}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (101)
+|}
+Eqs.([[#eq-100|100]]) and ([[#eq-101|101]]) are solved sequentially and iteratively until convergence for the nodal velocities and pressures is found.
+The above iterative scheme can be considered as a simplification of the more accurate incremental iterative segregated scheme described in Section 10.4.
+'''Remark 12.''' A variant of the iteration matrix in the left hand side of Eq.([[#eq-100|100]]) can be used by adding the bulk stiffness matrix <math display="inline">{K}_p</math> to matrix <math display="inline">{H}^i</math> <span id='citeF-11'></span><span id='citeF-31'></span>[[#cite-11|[11,31]]].
+==12 PARTICULARIZATION FOR THE UPDATED CONFIGURATION==
+The finite element formulation presented in the previous sections can be particularized for the case when the updated configuration <math display="inline">{~}^{n+1} {V}</math> is chosen as the reference configuration.
+The particularization is simple if we note that now <math display="inline">\Delta u_i=0</math>. Hence, <math display="inline">{L}=0</math> and <math display="inline">{B}^L ={0}</math> (see Eq.([[#eq-58.a|58.a]])). Also all the space derivatives are taken with respect to the updated coordinates <math display="inline">{~}^{n+1}x_i</math> and the integrals are carried out in the updated configuration <math display="inline">{~}^{n+1}V</math>. In addition, the tangent constitutive tensor <math display="inline">\boldsymbol{\cal C}_T ={c}</math>. The expressions of the relevant matrices and vectors for this case are given in Box 1.
+==13 PROS AND CONS OF USING THE CURRENT OR THE UPDATED CONFIGURATION AS THE REFERENCE CONFIGURATION==
+We have shown in the previous sections that either the current or the updated configuration can be indistinctly  used as the reference configuration for the finite element analysis of quasi and fully incompressible fluids  using a Lagrangian formulation. Both choices imply solving a non linear system of equations. However, the nature of the non-linearity is different for each case.
+If the current configuration is chosen as the reference configuration, all integrals in the tangent matrix are performed on the known configuration <math display="inline">{}^nV</math> which remains fixed during the iterative solution process. The non-linearity affects, however, the non linear terms of the material strain rate matrix (i.e. <math display="inline">{B}^L</math>) and also the constitutive tensor <math display="inline">\boldsymbol{\cal C}</math> that involves the deformation gradient. A simplification of the tangent stiffness matrix  for this case can be introduced by neglecting <math display="inline">{B}^L</math> in the material strain rate matrix and assuming that <math display="inline">{F}={C}={I}_3</math> and, hence, <math display="inline">\boldsymbol{\cal C}_T ={c}</math>.
+If, on the other hand, the updated configuration is chosen as the reference configuration, then all the integrals in the tangent matrix are computed in the unknown configuration <math display="inline">{}^{n+1}V</math>, which should be updated at each iteration. On the other hand, the expression for the material strain rate matrix is linear and also <math display="inline">\boldsymbol{\cal C}_T ={c}</math>. A simplification of the iterative process can be introduced by keeping the tangent matrix constant for a fixed number of iterations.
+Indeed the above mentioned simplifications can affect the convergence rate of the iterative solution and should be implemented with care.
+Which reference configuration should be chosen can be problem dependent and, certainly, the choice will affect the organization of the computer program and its efficiency. What should be kept in mind is that the final solution, i.e. the geometry of the updated configuration and the velocities and stresses on <math display="inline">{}^{n+1}V</math>, should be identical in both cases.
+In previous works of the authors with the Particle Finite Element Method (PFEM) the ''current'' configuration <math display="inline">{}^nV</math> was typically chosen as the reference configuration with the simplified form for the tangent matrix as explained above and also neglecting the initial stress matrix terms in <math display="inline">{K}_T</math> <span id='citeF-16'></span><span id='citeF-17'></span><span id='citeF-25'></span><span id='citeF-26'></span><span id='citeF-29'></span><span id='citeF-31'></span>[[#cite-16|[16,17,25,26,29,31]]]. Recent experiences indicate that using the updated configuration <math display="inline">{}^{n+1}V</math> as the reference configuration can be advantageous in many Lagrangian flow problems. The topic is still open for research  and hopefully  this paper will be useful for choosing  the adequate FEM expressions for each case.
+==14 CONCLUDING REMARKS==
+We have presented a mixed velocity-pressure finite element formulation for solving the updated Lagrangian equations for quasi and fully incompressible fluids. The finite element interpolation  uses an equal order approximation for the velocity and pressure unknowns. We have detailed a number of iterative algorithms for  solving the non-linear stabilized FEM equations for the velocities and the  pressure at the nodes using incremental and direct solution schemes. The algorithms presented are  useful for the study of Lagrangian  flows, as well as for solving fluid-structure-interaction problems using a unified Lagrangian finite element formulation for modelling both the fluid and the structure <span id='citeF-11'></span><span id='citeF-17'></span>[[#cite-11|[11,17]]].
+The choice of the current or the updated configurations as the reference Lagrangian configuration is still an open topic. Researchers interested in Lagrangian CFD procedures will find in this paper the equations to be used for each case, from which simplifications or further computational refinements can be made.
+==ACKNOWLEDGEMENTS==
+This work was partially supported by the Advanced Grant project SAFECON of the European Research Council (ERC).
+==References==
+<div id="cite-1"></div>
+'''[1]'''  S. Badia, R. Codina, Unified stabilized finite element formulation for the Stokes and the Darcy problems. ''SIAM J. on Numerical Analysis'', 47, 1971&#8211;2000, 2009.
+<div id="cite-2"></div>
+'''[[#citeF-2|[2]]]'''  K.J. Bathe, ''Finite element procedures''. Prentice-Hall, 1996.
+<div id="cite-3"></div>
+'''[[#citeF-3|[3]]]'''  Y. Bazilevs, K Takizawa, T.E Tezduyar, ''Computational Fluid-Structure Interaction: Methods and Applications'', Wiley, 2013.
+<div id="cite-4"></div>
+'''[[#citeF-4|[4]]]'''  T. Belytschko, W.K. Liu and B. Moran, ''Non linear finite element for continua and structures''. 2d Edition, Wiley, 2013.
+<div id="cite-5"></div>
+'''[[#citeF-5|[5]]]'''  J. Bonet and R.D. Wood, ''Non linear continuum mechanics for finite element analysis''. Wiley, 2nd Edition, 2008.
+<div id="cite-6"></div>
+'''[[#citeF-6|[6]]]'''  J.U. Brackbill, D.B. Kothe, H.M. Ruppel, FLIP: A low-dissipation, particle-in-cell method for fluid flow. ''Computer Physics Communications'', 48, 25&#8211;38, 1988.
+<div id="cite-7"></div>
+'''[[#citeF-7|[7]]]'''  D. Burgess, D. Sulsky, J.U. Brackbill, Mass matrix formulation of the FLIP particle-in-cell method. ''Journal of Computational Physics'', 103 (1), 1&#8211;15, 1992.
+<div id="cite-8"></div>
+'''[[#citeF-8|[8]]]'''  R. Codina, Stabilized finite element approximation of transient incompressible flows using orthogonal subscales. ''Comput. Meth. Appl. Mech. Engrg.'', 191, 4295&#8211;4321, 2002.
+<div id="cite-9"></div>
+'''[[#citeF-9|[9]]]'''  R. Codina, H. Coppola-Owen, P. Nithiarasu and C. Liu, Numerical comparison of CBS and SGS as stabilization techniques for the incompressible Navier-Stokes equations. ''Int. J. Numer. Meth. Engng.'', 66, 1672&#8211;1689, 2006.
+<div id="cite-10"></div>
+'''[[#citeF-10|[10]]]'''  J. Donea and A. Huerta, ''Finite Element Methods for Flow Problems''. Wiley, 2003.
+<div id="cite-11"></div>
+'''[[#citeF-11|[11]]]'''  A. Franci, E. Oñate, J.M. Carbonell, Unified Lagrangian formulation for analysis of fluid-structure interaction problems. Research Report PI-400, CIMNE, Barcelona 2013.
+<div id="cite-12"></div>
+'''[[#citeF-12|[12]]]''' F.H. Harlow, The particle-in-cell computing method for fluid dynamics. ''Methods Comput. Phys.'', 3, 219, 1963.
+<div id="cite-13"></div>
+'''[[#citeF-13|[13]]]'''  G.A. Holzaphel, ''Non linear solid mechanics''. Wiley, 2000.
+<div id="cite-14"></div>
+'''[14]'''  A. Huerta, Y. Vidal,  J. Bonet, Updated Lagrangian formulation for corrected Smooth Particle Hydrodynamics. ''Int. J. of Computational Methods'',  3 (4), 383&#8211;399, 2006.
+<div id="cite-15"></div>
+'''[[#citeF-15|[15]]]'''  T.J.R. Hughes, G. Scovazzi, L.P. Franca, Multiscale and stabilized methods. Encyclopedia of Comput. Mechanics. E. Stein, R. de Borst and T.J.R. Hughes (Eds.), Vol. 3 Fluids, 5&#8211;60, Wiley, 2004.
+<div id="cite-16"></div>
+'''[[#citeF-16|[16]]]'''  S.R. Idelsohn, E. Oñate, F. Del Pin,  The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves. ''Int. J. Num. Meth. Eng.'', 61(7), 964&#8211;989, 2004.
+<div id="cite-17"></div>
+'''[[#citeF-17|[17]]]'''  S.R. Idelsohn, J. Marti, A. Limache, E. Oñate Unified Lagrangian formulation for elastic solids and incompressible fluids: Application to fluid-structure interaction problems via the PFEM. ''Comput. Meth. Appl. Mech. Engrg.'', 197 (19-20), 1762&#8211;1776, 2008.
+<div id="cite-18"></div>
+'''[18]'''  S. Li, W.K. Liu, Meshfree and particle methods and their applications. ''Appl. Mech. Rev.'', 55, 1, 2002.
+<div id="cite-19"></div>
+'''[19]'''  W.K. Liu, Y. Chen, S. Jun, J.S. Chen, T. Belytschko, C. Pan, R.A. Uras, C.T. Chang, Overview and applications of the Reproducing Kernel Particle Methods.  ''Arch Comput Methods Eng.'', 3 (1), 3&#8211;80, 1996.
+<div id="cite-20"></div>
+'''[[#citeF-20|[20]]]'''  M.B. Liu and G.R. Liu, Smoothed particle hydrodynamics (SPH): an overview and  recent developments. ''Arch Comput Methods Eng.'', Vol. 17, 25–-76, 2010.
+<div id="cite-21"></div>
+'''[[#citeF-21|[21]]]'''  E. Oñate,  Derivation of stabilized  equations for advective-diffusive transport and fluid flow  problems. ''Comput. Meth. Appl. Mech. Engrg.'' 151, 233&#8211;267, 1998.
+<div id="cite-22"></div>
+'''[22]'''  E. Oñate, A stabilized finite element method  for incompressible viscous flows using a finite increment calculus formulation.  ''Comput Methods Appl Mech Engrg.'',  182(1&#8211;2), 355&#8211;370, 2000.
+<div id="cite-23"></div>
+'''[23]'''  E. Oñate,  Multiscale computational analysis in mechanics using    finite calculus: an introduction. ''Comput. Meth. Appl. Mech. Engrg.'',    192(28-30), 3043&#8211;3059, 2003.
+<div id="cite-24"></div>
+'''[[#citeF-24|[24]]]'''   E. Oñate, Possibilities of finite calculus in computational  mechanics. ''Int. J. Numer. Meth. Engng.'', 60(1), 255&#8211;281, 2004.
+<div id="cite-25"></div>
+'''[[#citeF-25|[25]]]'''  E. Oñate, S.R. Idelsohn, F. Del Pin, R. Aubry, The particle    finite element method. An overview. ''Int. J. Comput. Methods'',     1(2), 267&#8211;307, 2004.
+<div id="cite-26"></div>
+'''[[#citeF-26|[26]]]'''  E. Oñate, J. García,  S.R. Idelsohn, F. Del Pin,  FIC    formulations for finite element analysis of incompressible flows. Eulerian,    ALE and Lagrangian approaches.  ''Comput. Meth. Appl. Mech. Engrg.''    195(23-24), 3001&#8211;3037, 2006.
+<div id="cite-27"></div>
+'''[[#citeF-27|[27]]]'''  E. Oñate, A. Valls, J. García, Computation of turbulent flows using a finite calculus-finite element formulation. ''Int. J. Numer. Meth. Engng.'', 54, 609&#8211;637, 2007.
+<div id="cite-28"></div>
+'''[[#citeF-28|[28]]]'''   E. Oñate,  ''Structural analysis with the finite element method. Linear statics. Volume 1. Basis and Solids''.  CIMNE-Springer, 2009.
+<div id="cite-29"></div>
+'''[[#citeF-29|[29]]]'''  E. Oñate, M.A. Celigueta, S.R. Idelsohn, F. Salazar, B. Suárez, Possibilities of the particle finite element method for fluid-soil-structure interaction problems. ''Computational Mechanics'', 48(3), 307&#8211;318, 2011.
+<div id="cite-30"></div>
+'''[[#citeF-30|[30]]]'''  E. Oñate, S.R. Idelsohn, C. Felippa,  Consistent pressure Laplacian stabilization for incompressible continua via higher-order finite calculus. ''Int. J. Numer. Meth. Engng'', 87 (1-5), 2011, 171&#8211;195.
+<div id="cite-31"></div>
+'''[[#citeF-31|[31]]]'''  E. Oñate, A. Franci, J.M. Carbonell, Lagrangian formulation for finite element analysis of incompressible fluids with reduced mass losses. ''Int. J. Numer. Meth. Fluids'', 2013. DOI:0.1002/fld.3870.
+<div id="cite-32"></div>
+'''[32]'''  E. Oñate, P. Nadukandi, S.R. Idelsohn, P1/P0+ elements for incompressible  flows  with discontinuous material properties. ''Comput. Meth. Appl. Mech. Engrg.'', 271, 185&#8211;209, 2014, .
+<div id="cite-33"></div>
+'''[33]'''  N.A. Patankar, D.D. Joseph, Lagrangian numerical simulation of particulate flows. ''Int. J. of Multiphase Flow'', 27 (10), 1685–-1706, 2001.
+<div id="cite-34"></div>
+'''[[#citeF-34|[34]]]'''  R. Radovitzky and M. Ortiz, Lagrangian finite element analysis of newtonian fluid flows. ''Int. J. Numer. Meth. Engng.'', 43, 607&#8211;619, 1998.
+<div id="cite-35"></div>
+'''[[#citeF-35|[35]]]'''  B. Ramaswamy and M. Kawahara, Lagrangian finite element analysis applied to viscous free surface fluid flow. ''Int. J. Num. Meth. Fluids'', 7, 953&#8211;984, 1986.
+<div id="cite-36"></div>
+'''[[#citeF-36|[36]]]'''   P. Wriggers, ''Non linear finite element methods''. Springer, 2008.
+<div id="cite-37"></div>
+'''[[#citeF-37|[37]]]'''  T.E. Tezduyar, Finite elements for flow problems with moving boundaries and interfaces. ''Arch. for Comput. Methods Eng.'', 8, 83&#8211;130, 2001.
+<div id="cite-38"></div>
+'''[[#citeF-38|[38]]]'''  D.Z. Zhang, Q. Zou, W.B. VanderHeyden, X. Ma, Material point method applied to multiphase flows. ''Journal of Computational Physics'', 227 (6), 3159-3173, 2008.
+<div id="cite-39"></div>
+'''[[#citeF-39|[39]]]'''  O.C. Zienkiewicz, R.L. Taylor, J.Z. Zhu, ''The Finite Element Method. Vol. 1 The Basis''. Elsevier, 6th Edition, 2005.
+<div id="cite-40"></div>
+'''[[#citeF-40|[40]]]'''  O.C. Zienkiewicz, R.L. Taylor, ''The Finite Element Method. Vol. 2 Solid and Structural Mechanics''. Elsevier, 6th Edition, 2005.
+<div id="cite-41"></div>
+'''[[#citeF-41|[41]]]'''  O.C. Zienkiewicz, R.L. Taylor and P. Nithiarasu, ''The Finite Element Method. Vol. 3 Fluid Dynamics''. Elsevier, 6th Edition, 2005.
+==APPENDIX A. LINEARIZATION OF THE MOMENTUM EQUATIONS WITH RESPECT TO THE NODAL VELOCITIES==
+Using the expression of <math display="inline">{}^{n+1}\bar{r}_m</math> of Eq.([[#eq-62|62]]) and neglecting the changes of the external vector <math display="inline">{}^{n+1}\bar{f}_m</math>  with the velocity (accounting for these changes is possible and will lead to additional terms in the tangent matrix), we can write
+<span id="eq-A1"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta _{\bar v} {}^{n+1} \bar {r}_m = \frac{1}{\Delta t}{M}_v d \bar {v}+      \int _{{}^{n}V} \Big\{{B}^T \Big[\delta _{\bar v}\left\{\mathbf{S}' \right\}+ \left(\delta _{\bar v} J\left\{{C}^{-1}\right\}+ {J} \delta _{\bar v} \left\{{C}^{-1}\right\}\right)p + </math>
+|-
+| style="text-align: center;" | <math>  + J \left\{{C}^{-1}\right\}\delta _{\bar v}p\Big]+ \delta _{\bar v} {B}^T  \left\{\mathbf{S}' \right\}\Big\}d{~}^{n} V  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (A.1)
+|}
+Introducing Eqs.([[#eq-55|55]]) and ([[#eq-59|59]]) into ([[#eq-A1|A.1]]) gives after some algebra <span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-36'></span>[[#cite-4|[4,5,36]]]
+<span id="eq-A2"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta _{\bar v} \left\{\mathbf{S}' \right\}= [\boldsymbol{\cal C}]\delta _{\bar v} \left\{\dot {E}\right\} = [\boldsymbol{\cal C}] {B} d \bar {v}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (A.2)
+|}
+<span id="eq-A3"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta _{\bar v} J \left\{{C}^{-1}\right\}= J {C}^{-1} \otimes {C}^{-1} \delta _{\bar v} \left\{{E}\right\} = J \Delta t{C}^{-1} \otimes {C}^{-1} {B} d \bar {v}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (A.3)
+|}
+<span id="eq-A4"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>J \delta _{\bar v} \left\{{C}^{-1}\right\}= - 2 J \boldsymbol{\cal I} \delta _{\bar v} \left\{{E}\right\}= -2 J \Delta t \boldsymbol{\cal I} {B} d \bar {v}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (A.4)
+|}
+where
+<span id="eq-A5"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\boldsymbol{\cal I}_{ijkl}= \frac{1}{2} \left[({C}^{-1})_{ik} ({C}^{-1})_{jl}- ({C}^{-1})_{il}({C}^{-1})_{jk}\right]   </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (A.5)
+|}
+It can be shown that tensor <math display="inline">\boldsymbol{\cal I}</math> is symmetric <span id='citeF-4'></span><span id='citeF-5'></span>[[#cite-4|[4,5]]].
+On the other hand,
+<span id="eq-A6.a"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta _{\bar v} {B}^T  \left\{{S}' \right\}= \Delta t {G}^T \hat{S}'{G}   d \bar {v}  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (A.6a)
+|}
+with
+<span id="eq-A6.b"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\begin{array}{l}{G}=\left[ \begin{matrix}\bar {G} &  \bar {0} &  \bar {0}\\ \bar {0} &\bar {G}&\bar {0}\\ \bar {0} & \bar {0}& \bar {G} \end{matrix}\right] ~~,~~ \bar {G} =  \left[ \begin{matrix}{}_nN^v_{1,1} &0&0& {}_nN^v_{2,1}&0&0& \cdots &  {}_nN^v_{n,1}\\ {}_nN^v_{1,2} &0&0& {}_nN^v_{2,2}&0&0& \cdots &  {}_nN^v_{n,2}\\ {}_nN^v_{1,3} &0&0& {}_nN^v_{2,3}&0&0& \cdots &  {}_nN^v_{n,3}  \end{matrix}\right]\\[1cm] \hat {S}' = \left[ \begin{matrix}{S}' &  {0} &   {0}\\ {0} & {S}'& {0}\\  {0} & {0}&  {S}' \end{matrix}\right]~~,~~ {0} = \left[ \begin{matrix}0&0&0\\ 0&0&0\\ 0&0&0  \end{matrix}\right]~~,~~ \bar {0} = \left\{ \begin{matrix}0\\0\\0  \end{matrix}\right\} \end{array}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (A.6b)
+|}
+with <math display="inline">{}_nN^v_{i,j}</math> defined in Eq.([[#eq-58.b|58.b]]).
+In the derivation of Eqs.([[#eq-3|A.3]]), ([[#eq-4|A.4]]) and ([[#eq-A6.a|A.6a]]) we have assumed that <math display="inline"> d(\Delta u_i)= du_i =\Delta t ~d ({}^{n+\alpha }v_i) = \Delta t ~dv_i</math>. This relationship follows from Eq.([[#eq-60.a|60.a]]).
+Substituting Eqs.([[#eq-2|A.2]])&#8211;([[#eq-4|A.4]]) and ([[#eq-6.a|A.6a]]) and the interpolation for the pressure (Eq.([[#eq-53|53]])) into ([[#eq-A1|A.1]]) yields the linearized form of the residual vector of the discretized momentum equations  as
+<span id="eq-A7"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\delta _v  {}^{n+1}\bar{r}_m =\frac{1}{\Delta t}{M}_v  d \bar {v} +  \left\{\int _{{}^{n}V}\left[{B}^T [\boldsymbol{\cal C}_T] {B}+ {G}^T \hat{S}{G}\right]d {~}^{n}V            \right\}d \bar {v}  + </math>
+|-
+| style="text-align: center;" | <math> +\left\{\int _{{}^{n}V} {B}^T \left\{{C}^{-1}\right\}{N}_p J d {~}^{n}V     \right\}{\delta }_{\bar v}^{n+1}\bar {p}= \left(\frac{1}{\Delta t}{M}_v +  {K}_c + {K}_\sigma \right)  d \bar {v}+  {Q}  {\delta }_{\bar v}^{n+1}\bar {p}    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (A.7)
+|}
+where matrices <math display="inline">{M}_v</math> and <math display="inline">{Q}</math> were given in Eq.([[#eq-67|67]]) and <math display="inline">{K}_c</math> and <math display="inline">{K}_\sigma </math> are the constitutive and initial stress matrices, respectively. The expression of these matrices is
+<span id="eq-A8"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>{K}_c = \!\!\int _{{}^{n}V}{B}^T [\boldsymbol{\cal C}_T] {B} d {~}^{n}V ~~ ,~~  {K}_\sigma =\!\!\int _{{}^{n}V}{G}^T \hat{S}' {G}d {~}^{n}V  </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (A.8)
+|}
+The tangent constitutive tensor <math display="inline">\boldsymbol{\cal C}_T</math> is deduced from Eqs.([[#eq-1|A.1]])-([[#eq-4|A.4]]) as
+<span id="eq-9"></span>
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\boldsymbol{\cal C}_T = \boldsymbol{\cal C} + J \Delta t p ({C}^{-1}\otimes {C}^{-1} - 2 \boldsymbol{\cal I})    </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (A.9)
+|}
+It is straightforward to show that tensor <math display="inline">\boldsymbol{\cal C}_T</math> is symmetric.