Published in Computational Mechanics, Vol. 54 (6), pp. 1583-1596, 2014
DOI: 10.1007/s00466-014-1078-1
Abstract
We present a mixed velocity-pressure finite element formulation for solving the updated Lagrangian equations for quasi and fully incompressible fluids. Details of the governing equations for the conservation of momentum and mass are given in both differential and variational form. The finite element interpolation uses an equal order approximation for the velocity and pressure unknowns. The procedure for obtaining stabilized FEM solutions is outlined. The solution in time of the discretized governing conservation equations using an incremental iterative segregated scheme is described. The linearization of these equations and the derivation of the corresponding tangent stiffness matrices is detailed. Other iterative schemes for the direct computation of the nodal velocities and pressures at the updated configuration are presented. The advantages and disadvantages of choosing the current or the updated configuration as the reference configuration in the Lagrangian formulation are discussed.
Keywords: Updated Lagrangian formulation, incompressible fluids, finite element method, incremental solution, tangent matrix, mixed formulation, stabilized method
1 INTRODUCTION
In Lagrangian analysis procedures, the motion of the particles of a deforming body is followed in time. In Eulerian formulations, on the other hand, attention is focused in the motion of the material through a stationary control volume. Lagrangian methods have been traditionally used for the numerical analysis of solids and structures, while Eulerian methods are typical in computational fluid dynamics [2,4,5,36,40,41].
Despite this evidence, the use of a Lagrangian description for solving fluid dynamics problems using the finite element method (FEM) [10,41] and different meshless and mesh-based particle-based numerical techniques [6,7,12],[16]–[20],[25,26] [29]–[35],[37,38] has received much attention in recent years. Of particular interest are numerical procedures, such as the Particle Finite Element Method (PFEM) [16,25,26,29,31], that combine the advantage of particle-based procedures with the formalism and accuracy of the FEM.
Despite the increasing interest in the Lagrangian approach for solving the equations of fluid mechanics using the FEM, there are few references to the derivation of incremental iterative solution schemes using linearized forms of the discretized Lagrangian equations for fluid flow problems. An early attempt in this direction was reported by Radovitzky and Ortiz [34] who derived the tangent matrix for the FEM Lagrangian analysis of compressible flows using a Newton-Rapsohn type iterative scheme.
The goal of this paper is to present a mixed velocity-pressure formulation for the finite element analysis of quasi and fully incompressible fluids using an updated Lagrangian formulation. We advocate an equal order interpolation for the velocity and pressure variables which invariably requires using an adequate stabilization scheme for the mass balance equation in order to obtain accurate numerical results. In the paper we derive in some detail both the continuum and discretized (FEM) forms of the equations governing the motion of the fluid in the updated Lagrangian description. An incremental Newton-Raphson type iterative staggered scheme for the solution in time of the non linear discretized equations is detailed. The derivations are carried out first using the current configuration as the reference configuration in the Lagrangian description of the motion. The expression of the different matrices and vectors involved in the incremental iterative scheme is given. The particular form of the FEM equations when the updated configuration is taken as the reference configuration is presented. The direct transient solution of the nodal velocities and pressures using monolithic and staggered schemes is also presented for completeness.
The chapter concludes with a discussion of the computational advantages and disadvantages of choosing the current or the the updated configuration as the reference configuration in the Lagrangian description.
In the next section the basic concepts of the motion of a fluid are briefly revisited. These concepts are standard and can be found in many books on computational solid and fluid mechanics and fluid-structure interaction, among others [2,3,4,5,13,36]. This introductory section aims to set up the updated Lagrangian framework where the governing equations for the fluid are written and subsequently solved with the FEM using a mixed velocity-pressure formulation.
2 MOTION. DISPLACEMENT, VELOCITY AND ACCELERATION
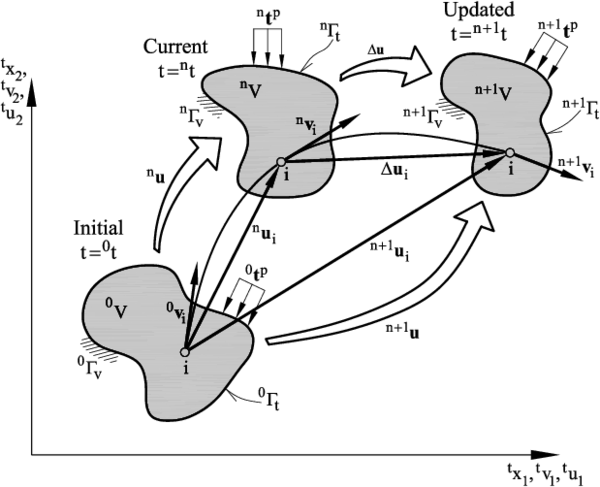
We will consider a domain containing a fluid which evolves in time due to external and internal forces and prescribed velocities from an initial configuration at time (typically ) to a current configuration at time . The fluid volume and its boundary at the initial and current configurations are denoted as () and (), respectively. The goal is to find the domain that the fluid occupies, as well as the velocities, strain rates and stresses (the deviatoric stresses and the pressure) in the so-called updated configuration at time (Figure 1). In the following a left superindex denotes the configuration of the fluid domain where the variable is computed.
The motion of the fluid domain is described by
|
|
(1) |
where is the position of the material point laying on the initial configuration at time . The coordinates give the spatial position of a point and are called spatial or Eulerian coordinates. The function maps the initial configuration into the current configuration at time . The position of the points in the current and initial configurations at time and , respectively are expressed by
|
|
(2) |
Thus the mapping is the identity mapping.
In the Lagrangian description (also called the material description) the independent variables are the material coordinates of the point on the initial configuration and the time . In the Eulerian description, on the other hand, the independent coordinates are the spatial coordinates and the time [4,5].
The displacement of a material point is given by the difference between its position at time and its original position, so
|
|
(3) |
where is the displacement vector of a point.
For we have
|
|
(4) |
The velocity vector is the rate of change of the position vector for a material point, i.e. the time derivative of with held constant (also called the material time derivative or total derivative). The velocity vector is usually written as (using Eq.(3) and noting that the coordinates are fixed)
|
|
(5) |
The velocity vector of a material point in the current configuration is written as
|
|
(6) |
The acceleration vector is the rate of change of the velocity vector of a material point (i.e. the material time derivative of the velocity vector) and it can be written as
|
|
(7) |
and
|
|
(8) |
Eq.(7) is the material form of the acceleration. Note the difference of Eq.(7) with the expression of the acceleration written in the Eulerian description which involves the convective terms [2,4,5,13,36,41].
In the total Lagrangian description the various equations and variables are referred to the initial configuration which is taken as the reference configuration. In the updated Lagrangian description, either the current or the updated configurations can be taken as the reference configuration [2,4,5,13,36].
For simplicity, in the first part of this work the current configuration will be taken as the reference configuration for the derivation of the incremental FEM equations. The reason is that the current configuration remain fixed during the iterative solution process. The particularization for the case when the updated configuration is taken as the reference configuration is presented in the last part of the paper.
The displacement increment vector of a material point between the updated and the current configurations is defined as
|
|
(9) |
The displacement increment of a material point can be computed from the velocity as
|
|
(10) |
where is the velocity vector of the points laying on the trajectory followed by the material point between times and (Figure 1). The integral of Eq.(10) can be approximated in a number of ways (see Remark 4).
3 MOMENTUM EQUATIONS AND BOUNDARY CONDITIONS
Let us assume that at time the fluid occupies a volume with a boundary . The fluid is subjected to body forces acting over the volume and surface tractions acting on the part of the boundary termed as , where index denotes the component of the force along the th cartesian axis (Figure 1).
The equations of internal equilibrium between the applied body forces and the Cauchy stresses in the fluid are expressed by the momentum equations written in the updated configuration as [2,4,5,13,36]
|
|
(11) |
where is the th momentum equation, , and are the fluid density and the th component of the velocity and the acceleration at time and is the number of space dimensions ( for three dimensional (3D) problems). Note that is always referred to the updated configuration, i.e. .
In Eq.(11) and in the following, the standard summation convention for repeated indices is adopted, unless otherwise specified.
The boundary conditions are
|
|
(12) |
|
|
(13) |
where is the prescribed value of the th velocity component at the external boundary with . In Eq.(13) is the th component of the unit normal to the boundary where the prescribed surface tractions are applied.
The goal is to obtain the geometry of the updated configuration , as well as the velocities and stresses in that satisfy Eqs.(11)–(13).
4 PRINCIPLE OF VIRTUAL POWER IN THE UPDATED CONFIGURATION
The principle of virtual power (PVP) can be written in the updated configuration as [2,4,5]
|
|
(14) |
where , and are the virtual powers due to the acceleration terms, the stresses and the external loads acting on , respectively given by [2,4,5]
|
In Eq.(15)–(16) , and are the virtual velocity vector, the body forces vector and the surface tractions vector, respectively defined for 3D problems as
|
|
(18) |
In Eq.(16) is the Cauchy stress tensor and is the virtual rate of deformation tensor defined as
|
|
(19) |
where is the th component of the virtual velocity.
In the following , where A is a symmetric tensor, will denote the vector representation of A. Hence, in Eq.(16) and are the Cauchy stress vector and the rate of deformation vector, respectively defined in Voigt notation [4,5] as
|
Similarly, will denote hereonwards the matrix form of tensor .
Remark 1. The PVP can be obtained by applying the standard weighted residual method to the governing equations (11) and (13) using the virtual velocities as weighting functions [4].
Remark 2. Tensor can be interpreted as the variation of the rate of deformation tensor defined in terms of the velocities at the updated configuration as
|
|
(21) |
5 TRANSFORMATION TO THE CURRENT CONFIGURATION. LAGRANGIAN STRESS AND STRAIN MEASURES
In the following sections we will use the current configuration as the reference configuration for computing the internal virtual due to the acceleration terms and the stresses, as well as for subsequently performing the linearization of its discretized form via the FEM. The alternative of using the updated configuration as the reference configuration is presented in Section 12.
After the standard transformations of continuum mechanics [2,4,5,13,36] the internal virtual power at the updated configuration due to the acceleration terms and the stresses can be expressed in terms of material parameters, integrals, strain rates and stress measures evaluated at the current configuration as
|
|
(22.a) |
|
|
(22.b) |
where and are the material virtual strain rate tensor and the second Piola-Kirchhoff stress tensor, respectively. The relationship between the material strain rate tensor and the rate of deformation tensor and between the stress tensors and is [2,4,5,13,36]
|
|
(23) |
where F is the deformation gradient and is the Jacobian, respectively defined as
|
|
(24) |
From the expression of of Eq.(23) we can deduce
|
|
(25) |
Remark 3. The material strain rate tensor can also be obtained from the time derivative of the Green-Lagrange strain tensor as [2,4,5]
|
|
(26) |
where is the right Cauchy-Green tensor and . The expression of is obtained by writing the variation of with respect to the velocities as
|
|
(27) |
A useful explicit expression of the material strain rate tensor components in terms of the velocities and the displacement increments is
|
|
(28.a) |
with
|
|
(28.b) |
From Eqs.(5) we deduce
|
|
(29.a) |
with
|
|
(29.b) |
6 SPLIT OF THE INTERNAL VIRTUAL POWER INTO DEVIATORIC AND VOLUMETRIC COMPONENTS
The Cauchy stress tensor can be split in its deviatoric component and the hydrostatic pressure component as
|
|
(30) |
where is the identity matrix.
Note that in incompressible fluid mechanics the pressure is an independent variable. Also, unless otherwise specified we will assume that is the pressure at the updated configuration (i.e. ).
Substituting Eq.(30) into the internal virtual power expression in Eq.(16) gives
|
|
(31) |
where is the volumetric strain rate given by
|
|
(32) |
It can be proven that [4,5,13,36]
|
|
(33) |
where is the volumetric material strain rate,
|
|
(34.a) |
|
|
(34.b) |
and is the element of tensor .
The internal virtual power expression of Eq.(31) can be written in the current configuration as follows.
Substituting the Cauchy stress split of Eq.(30) into the expression of the second Piola-Kirchhoff stress tensor of Eq.(23) gives
|
|
(35) |
where
|
|
(36) |
is the deviatoric second Piola-Kirchhoff stress tensor. is usually called the (true) deviatoric component of [4,5,13,36].
Substituting Eq.(35) into (22.b) gives
|
|
(37) |
with
|
|
(38) |
Eq.(37) can also be obtained from Eq.(31) using the relationship between and with , and , respectively and the expression [2,4,5].
Substituting Eqs.(15), (22.a) and (37) into (14), the PVP in the updated configuration can be written in terms of the pressure, the deviatoric second Piola-Kirchhoff stresses and the virtual Green-Lagrange strains computed in the current configuration as
|
|
(39) |
The vector form of tensors and in Eq.(39) is
|
|
(40.a) |
|
|
(40.b) |
Note that the contribution of the external forces in Eq.(39) is computed at the updated configuration and this requires using the correct expression for the density and the surface tractions on (see also Remark 5).
7 CONSTITUTIVE RELATIONSHIP FOR THE DEVIATORIC STRESSES
The relationship between the deviatoric Cauchy stresses and the rates of deformation for a Newtonian fluid is written as
|
|
(41) |
where are the deviatoric rates of deformation. The rates of deformation are obtained in terms of the velocities by Eq.(21).
The components of the fourth order constitutive tensor in the updated configuration are
|
|
(42) |
where is the viscosity of the fluid.
Eq.(41) can be written in vector form as
|
|
(43) |
with
|
|
(44) |
and the constitutive matrix is given by (for 3D problems)
|
|
(45) |
The constitutive equation (41) can be transformed to the current configuration to yield the relationship between the deviatoric second Piola-Kirchhoff stresses and the material strain rates as
|
|
(46) |
The constitutive tensor in the current configuration is obtained from its counterpart in the updated configuration as [36]
|
|
(47) |
The vector form of Eq.(46) is written as
|
|
(48) |
Matrix is obtained by applying Voigt rule to the terms of tensor [4,5].
8 THE MASS BALANCE EQUATION
The mass balance equation in the updated configuration is written for a quasi-incompressible fluid as
|
|
(49) |
where is the speed of sound in the fluid. For a fully incompressible fluid and Eq.(49) reduces to the standard form . The quasi-incompressible form will be retained here and this will allow us to account for the effect of the (small) compressibility in most fluids.
Eq.(49) can be written in terms of the bulk modulus of the fluid defined as . For convenience we will retain the form of Eq.(49).
The variational form of the mass balance equation is obtained via the standard weighted residual method [41] as
|
|
(50) |
where are appropriate test functions with dimensions of pressure [4,5,41].
The integral expression (50) can be written in the current configuration using Eq.(33) as
|
|
(51) |
In the derivation of Eq.(51) we have used the standard expressions [4,5]
|
|
(52) |
Eqs.(39) and (51) together with the constitutive relationship (47) and the boundary conditions (12) complete the set of governing variational equations for a fluid in the updated Lagrangian description. The solution of these equations with the FEM is described in the next section.
9 FINITE ELEMENT DISCRETIZATION
We interpolate the velocities and the pressure in terms of their nodal values in the standard finite element fashion [28,39,41]. For a mesh of -noded continuous elements we can write
|
|
(53) |
where
|
|
(54.a) |
where is the total number of nodes in the mesh, and are th velocity component and the pressure unknowns for node ,
|
|
(54.b) |
In Eq.(54.b) and are the global shape functions [28,39] for the velocity and pressure interpolations for node , respectively.
The velocity and pressure increments and the virtual velocities are interpolated in terms of their nodal values in the same fashion as in Eq.(53).
The strain rate vector and its virtual expression are respectively expressed in terms of the nodal velocities and their virtual values via Eqs.(28.a), (29.a) and (53) as
|
|
(55) |
The actual and virtual volumetric material strain rates are related to the virtual velocities as
|
|
(56) |
In the above equations is the material strain rate matrix given by
|
|
(57) |
where
|
|
(58.a) |
are the linear and non linear counterparts of the material strain rate matrix, respectively. The components of and are
|
|
(58.b) |
The deviatoric second Piola-Kirchhoff stresses are related to the nodal velocities via Eqs.(47) and (55) as
|
|
(59) |
Remark 4. The displacement increment can be computed in terms of the velocity in a number of ways. A popular choice is
|
|
(60.a) |
where is the velocity at where is a positive number (). The value of is typically computed as
|
|
(60.b) |
9.1 Discretized form of the PVP
Substituting Eqs.(53), (55) and (56) into the PVP (Eq.(39)) we obtain, after simplifying the virtual velocities
|
|
(61) |
where is the residual vector of the discretized momentum equations in the updated configuration and is the nodal acceleration vector.
Eq.(61) can be written in a more compact form as
|
|
(62) |
where
|
|
(63) |
In Eq.(62) and are internal force vectors contributed by the deviatoric second Piola-Kirchhoff stresses and the pressure, respectively and is the external force vector.
Recall that the internal force vectors at the current configuration are obtained in terms of expressions at the updated configuration.
Remark 5. The computation of the body force vector in Eq.(63) for the case of selfweight requires computing the density at the updated configuration as . We also note that the surface tractions are applied on the boundary of the updated configuration , which requires the accurate identification of this boundary.
The acceleration term in Eq.(62) can be approximated in a number of manners. A backward Euler scheme gives
|
|
(64) |
9.2 Discretization of the mass conservation equation
The arbitrary pressure test functions are interpolated in the same fashion as the pressure as
|
|
(65) |
where vector contains the nodal values of .
Substituting the expression of in term of from Eq.(56) and Eq.(65) in the variational form of the mass balance equation (Eq.(51)) we obtain, after eliminating the pressure test functions
|
|
(66) |
where is the residual vector of the discretized mass conservation equation, and the terms of and are
|
|
(67) |
9.3 Stabilization of the mass conservation equation
It is well known that the FEM solutions for the fully incompressible limit are unstable for some particular forms of the approximation for the velocities and the pressure [10,39,41]. This is the case, for instance, when an equal order interpolation is chosen for the velocity components and the pressure (i.e. ). This problem can be overcome by using finite element approximations for and satisfying the so-called LBB conditions [10,39,41], or else by introducing stabilization terms into the discretized mass balance equation [10,41]. In this work the later approach is chosen for obtaining stabilized numerical solutions.
In essence all stabilized formulations modify the discretized form of the mass balance equation as
|
|
(68) |
where was defined in Eq.(66) and is a stabilization mass balance vector which expression can be typically written as
|
|
(69) |
where is a stabilization matrix and is a force vector that depends on the nodal velocities and pressures. The form of and is different for each stabilization method. Typically, and contain integrals over the volume and the Neumann boundary of the analysis domain and are both a function of the so-called stabilization parameters which expression also depends on the particular stabilization method chosen [3,8,9,10,15,31,37,41].
The derivation of a stabilized mixed velocity-pressure formulation for incompressible fluids exceeds the objectives of this paper. Details can be obtained in the references cited in the previous paragraphs.
A particular stabilized Lagrangian formulation with excellent mass conservation features based on the Finite Calculus (FIC) theory [21]–[24],[27,30] can be found in [31].
10 INCREMENTAL SOLUTION FOR THE NODAL VELOCITIES AND PRESSURES
We will derive next an incremental iterative procedure for solving the discretized form of the equations for conservation of linear momentum and mass conservation in a segregated form. This requires the linearization of Eqs.(61) and (68) with respect to the nodal velocity and pressure unknowns, respectively. The linearization procedure takes advantage from the fact that the reference configuration (i.e. the current configuration ) remains fixed during the linearization process.
10.1 Linearization of the discretized momentum equations with respect to the nodal velocities
We linearize the residual vector of Eq.(61) with respect to the nodal velocities as
|
|
(70) |
Expression (70) is the directional derivative of the residual vector at a point in the direction of the nodal velocity vector (hereafter called nodal velocity pseudo-increment vector). The same definition applies to the directional derivative of a matrix or a scalar depending on the space coordinate , the nodal velocities and the nodal pressures [4,5,36].
Using the expression of vector of Eq.(62) in Eq.(70) and neglecting the changes of vector with the velocity, gives
|
|
(71) |
After some algebra detailed in the Appendix, the following linearized form of with respect to the nodal velocities is found
|
|
(72) |
where matrices and were given in Eq.(67) and and are the constitutive and initial stress matrices, respectively. The expression of these matrices is
|
|
(73) |
The form of matrices and is given in the Appendix.
The expression of the tangent constitutive tensor is (see Appendix)
|
|
(74) |
Tensor contains contributions from the constitutive tensor of Eq.(46), the time step and the pressure. This form of is very similar to that used for incompressible continua [4,5,13,36]. It can be shown that tensor is symmetric (see Appendix) and, hence, the tangent constitutive tensor is symmetric [4,5,13,36].
10.2 Linearization of the nodal pressures with respect to the nodal velocities. Derivation of the tangent matrix
From Eq.(66) we can obtain the directional derivative of the nodal pressure variables in the direction of the nodal velocity increments. Using a trapezoidal rule for approximating the time derivative term gives
|
|
(75) |
where is a time parameter such that . A value defines a backward Euler scheme [39,41].
From Eq.(75) it is straightforward to obtain
|
|
(76) |
Substituting Eq.(76) into (72) gives the final linearized form of the momentum equations in terms of the nodal velocities increments as
|
|
(77) |
where denotes values at the th iteration and the tangent matrix is
|
|
(78) |
with , and defined in Eqs.(63) and (72) and the tangent “bulk” matrix is
|
|
(79) |
In practice, is computed using the diagonal form of , i.e.
|
|
(80) |
where .
The incremental form of the momentum equations can written as
|
|
(81) |
Solution of Eq.(81) yields the nodal velocity increments for the th iteration.
Remark 6. For fully incompressible fluids () a large but finite value of is used in practice. This allows to eliminate the pressure DOFs in the momentum equations via Eq.((76)).
Remark 7. The tangent “bulk” stiffness matrix in the tangent matrix accounts for the changes of the pressure due to the velocity. Including matrix in has proven to be essential for the fast convergence, mass preservation and overall accuracy of the iterative solution in all cases [11]. The parameter in (Eq.(79)) has the role of preventing the ill-conditioning of for very large values of the speed of sound in the fluid that lead to a dominant role of the terms of the tangent bulk stiffness matrix . Clearly, the value of the terms of can also be limited by reducing the time step size. This, however, leads to an increase in the overall cost of the computations [11]. An adequate selection of improves the convergence of the iterative process and leads to a more accurate numerical solution with reduced mass loss, even for large time steps [11]. These considerations, however, do not affect the value of within matrix in Eq.(67) that vanishes for the fully incompressible case ().
10.3 Linearization of the stabilized mass conservation equation with respect to the nodal pressures
The stabilized mass conservation equation (68) is linearized with respect to the nodal pressure pseudo-increment vector using Eqs.(66), (68) and (69) as
|
|
(82) |
Using Eqs.(67)–(68) and a backward Euler scheme for approximating the time derivative of the nodal pressure in Eq.(67) gives
|
|
(83) |
In the derivation of Eq.(83) we have neglected the pressure dependence of the terms of matrix and in Eq.(69).
The incremental form of the mass balance equation is therefore
|
|
(84) |
Solution of Eq.(84) yields the nodal pressure pseudo-increment vector at the th iteration.
10.4 Incremental solution of the discretized equations
An incremental Newton-Raphson type iterative solution scheme for the stabilized velocity-pressure formulation is as follows.
Within a time increment :
- Initialize variables: .
- Iteration loop =
For each iteration
- Compute the nodal velocity pseudo-increments , (from Eq.(81)) from
(85) - Update the nodal velocities :
(86) - Compute the nodal pressure pseudo-increments , . From Eq.(84),
(87) - Update the nodal pressures :
(88) - Update the nodal displacement increments using Eq.(60.a) and the approximate value for the nodal velocities .
- Update the nodal coordinates in the updated configuration as
(89) - Compute the material derivative of the Green strains and the deviatoric second Piola-Kirchhoff stresses (from Eqs.(55) and (45)).
- Compute the momentum and mass balance residuals : and
- Check convergence
(90) where denotes the quadratic norm and and are prescribed error tolerances for the discretized residuals of the momentum and mass balance equations, respectively.
If both conditions (90) are satisfied then make and proceed to the next time increment. Otherwise, make the iteration counter and repeat Steps 1–9.
Remark 8. An alternative convergence criteria based on the nodal velocities and pressures can be defined as
|
where and are error tolerances.
Remark 9. The nodal velocity and pressure increment vectors and can be computed at the end of each time step as
|
|
(92) |
where and denote the converged values at the end of the iteration loop. Clearly, and can also be obtained by adding up the pseudo-increment vectors and within the iterative solution.
Remark 10. The nodal pressures can be directly obtained from Eq.(68), after substitution of Eqs.(66) and (69), as
|
|
(93) |
The rest of the iterative solution scheme is similar to that described above. Eq.(93) substitutes Eqs.(87) and (88) and the convergence of the nodal pressures is verified by Eq.(91.b).
Remark 11. For a fully incompressible fluid and matrix in Eqs.(67), (87) and (93).
The problem can still be accurately solved in this case using an adequate expression for the stabilization matrix . The form of presented in [31] includes a Laplacian term over the whole domain and an integral along the Neumann boundary . The boundary term in avoids the need for prescribing the pressure on the domain boundary. If a standard Laplacian form is chosen for , then the value of the pressure has to be prescribed in strong form at some boundary points in order to obtain good results [41].
11 DIRECT ITERATIVE SOLUTION OF THE NODAL VELOCITIES AND PRESSURES
Substituting the FEM approximation for the velocities and the pressure (53) into Eq.(64) and assuming a Newtonian fluid with a constitutive equation given by Eq.(47), the following matrix expression of the discretized momentum equations can be obtained
|
|
(94) |
where , and have been defined previously and
|
|
(95) |
Combining Eq.(94) with the stabilized mass balance equation (68) and using Eq.(66) gives the following matrix system for the nodal velocities and pressures
|
|
(96) |
Eq.(96) can be written in a compact (monolithic) form as
|
|
(97) |
where
|
|
(98) |
11.1 Monolithic solution scheme
Eq.(98) is the basis for deriving monolithic iterative time integration schemes for directly computing the nodal velocities and pressure at the updated configuration. For instance, the standard backward Euler scheme gives
|
|
(99) |
with .
The values of can be directly found by solving Eq.(99) iterative.
The non linearity of matrix emanates from the non linear terms in the material strain rate matrix involving the displacement increments (Eqs.(9)).
11.2 Segregated solution scheme
The nodal velocities and pressures at the updated configuration can be also computed starting from Eq.(97) using a segregated iterative scheme as follows
|
|
(100) |
|
|
(101) |
Eqs.(100) and (101) are solved sequentially and iteratively until convergence for the nodal velocities and pressures is found.
The above iterative scheme can be considered as a simplification of the more accurate incremental iterative segregated scheme described in Section 10.4.
Remark 12. A variant of the iteration matrix in the left hand side of Eq.(100) can be used by adding the bulk stiffness matrix to matrix [11,31].
12 PARTICULARIZATION FOR THE UPDATED CONFIGURATION
The finite element formulation presented in the previous sections can be particularized for the case when the updated configuration is chosen as the reference configuration.
The particularization is simple if we note that now . Hence, and (see Eq.(58.a)). Also all the space derivatives are taken with respect to the updated coordinates and the integrals are carried out in the updated configuration . In addition, the tangent constitutive tensor . The expressions of the relevant matrices and vectors for this case are given in Box 1.
13 PROS AND CONS OF USING THE CURRENT OR THE UPDATED CONFIGURATION AS THE REFERENCE CONFIGURATION
We have shown in the previous sections that either the current or the updated configuration can be indistinctly used as the reference configuration for the finite element analysis of quasi and fully incompressible fluids using a Lagrangian formulation. Both choices imply solving a non linear system of equations. However, the nature of the non-linearity is different for each case.
If the current configuration is chosen as the reference configuration, all integrals in the tangent matrix are performed on the known configuration which remains fixed during the iterative solution process. The non-linearity affects, however, the non linear terms of the material strain rate matrix (i.e. ) and also the constitutive tensor that involves the deformation gradient. A simplification of the tangent stiffness matrix for this case can be introduced by neglecting in the material strain rate matrix and assuming that and, hence, .
If, on the other hand, the updated configuration is chosen as the reference configuration, then all the integrals in the tangent matrix are computed in the unknown configuration , which should be updated at each iteration. On the other hand, the expression for the material strain rate matrix is linear and also . A simplification of the iterative process can be introduced by keeping the tangent matrix constant for a fixed number of iterations.
Indeed the above mentioned simplifications can affect the convergence rate of the iterative solution and should be implemented with care.
Which reference configuration should be chosen can be problem dependent and, certainly, the choice will affect the organization of the computer program and its efficiency. What should be kept in mind is that the final solution, i.e. the geometry of the updated configuration and the velocities and stresses on , should be identical in both cases.
In previous works of the authors with the Particle Finite Element Method (PFEM) the current configuration was typically chosen as the reference configuration with the simplified form for the tangent matrix as explained above and also neglecting the initial stress matrix terms in [16,17,25,26,29,31]. Recent experiences indicate that using the updated configuration as the reference configuration can be advantageous in many Lagrangian flow problems. The topic is still open for research and hopefully this paper will be useful for choosing the adequate FEM expressions for each case.
14 CONCLUDING REMARKS
We have presented a mixed velocity-pressure finite element formulation for solving the updated Lagrangian equations for quasi and fully incompressible fluids. The finite element interpolation uses an equal order approximation for the velocity and pressure unknowns. We have detailed a number of iterative algorithms for solving the non-linear stabilized FEM equations for the velocities and the pressure at the nodes using incremental and direct solution schemes. The algorithms presented are useful for the study of Lagrangian flows, as well as for solving fluid-structure-interaction problems using a unified Lagrangian finite element formulation for modelling both the fluid and the structure [11,17].
The choice of the current or the updated configurations as the reference Lagrangian configuration is still an open topic. Researchers interested in Lagrangian CFD procedures will find in this paper the equations to be used for each case, from which simplifications or further computational refinements can be made.
ACKNOWLEDGEMENTS
This work was partially supported by the Advanced Grant project SAFECON of the European Research Council (ERC).
References
[1] S. Badia, R. Codina, Unified stabilized finite element formulation for the Stokes and the Darcy problems. SIAM J. on Numerical Analysis, 47, 1971–2000, 2009.
[2] K.J. Bathe, Finite element procedures. Prentice-Hall, 1996.
[3] Y. Bazilevs, K Takizawa, T.E Tezduyar, Computational Fluid-Structure Interaction: Methods and Applications, Wiley, 2013.
[4] T. Belytschko, W.K. Liu and B. Moran, Non linear finite element for continua and structures. 2d Edition, Wiley, 2013.
[5] J. Bonet and R.D. Wood, Non linear continuum mechanics for finite element analysis. Wiley, 2nd Edition, 2008.
[6] J.U. Brackbill, D.B. Kothe, H.M. Ruppel, FLIP: A low-dissipation, particle-in-cell method for fluid flow. Computer Physics Communications, 48, 25–38, 1988.
[7] D. Burgess, D. Sulsky, J.U. Brackbill, Mass matrix formulation of the FLIP particle-in-cell method. Journal of Computational Physics, 103 (1), 1–15, 1992.
[8] R. Codina, Stabilized finite element approximation of transient incompressible flows using orthogonal subscales. Comput. Meth. Appl. Mech. Engrg., 191, 4295–4321, 2002.
[9] R. Codina, H. Coppola-Owen, P. Nithiarasu and C. Liu, Numerical comparison of CBS and SGS as stabilization techniques for the incompressible Navier-Stokes equations. Int. J. Numer. Meth. Engng., 66, 1672–1689, 2006.
[10] J. Donea and A. Huerta, Finite Element Methods for Flow Problems. Wiley, 2003.
[11] A. Franci, E. Oñate, J.M. Carbonell, Unified Lagrangian formulation for analysis of fluid-structure interaction problems. Research Report PI-400, CIMNE, Barcelona 2013.
[12] F.H. Harlow, The particle-in-cell computing method for fluid dynamics. Methods Comput. Phys., 3, 219, 1963.
[13] G.A. Holzaphel, Non linear solid mechanics. Wiley, 2000.
[14] A. Huerta, Y. Vidal, J. Bonet, Updated Lagrangian formulation for corrected Smooth Particle Hydrodynamics. Int. J. of Computational Methods, 3 (4), 383–399, 2006.
[15] T.J.R. Hughes, G. Scovazzi, L.P. Franca, Multiscale and stabilized methods. Encyclopedia of Comput. Mechanics. E. Stein, R. de Borst and T.J.R. Hughes (Eds.), Vol. 3 Fluids, 5–60, Wiley, 2004.
[16] S.R. Idelsohn, E. Oñate, F. Del Pin, The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves. Int. J. Num. Meth. Eng., 61(7), 964–989, 2004.
[17] S.R. Idelsohn, J. Marti, A. Limache, E. Oñate Unified Lagrangian formulation for elastic solids and incompressible fluids: Application to fluid-structure interaction problems via the PFEM. Comput. Meth. Appl. Mech. Engrg., 197 (19-20), 1762–1776, 2008.
[18] S. Li, W.K. Liu, Meshfree and particle methods and their applications. Appl. Mech. Rev., 55, 1, 2002.
[19] W.K. Liu, Y. Chen, S. Jun, J.S. Chen, T. Belytschko, C. Pan, R.A. Uras, C.T. Chang, Overview and applications of the Reproducing Kernel Particle Methods. Arch Comput Methods Eng., 3 (1), 3–80, 1996.
[20] M.B. Liu and G.R. Liu, Smoothed particle hydrodynamics (SPH): an overview and recent developments. Arch Comput Methods Eng., Vol. 17, 25–-76, 2010.
[21] E. Oñate, Derivation of stabilized equations for advective-diffusive transport and fluid flow problems. Comput. Meth. Appl. Mech. Engrg. 151, 233–267, 1998.
[22] E. Oñate, A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation. Comput Methods Appl Mech Engrg., 182(1–2), 355–370, 2000.
[23] E. Oñate, Multiscale computational analysis in mechanics using finite calculus: an introduction. Comput. Meth. Appl. Mech. Engrg., 192(28-30), 3043–3059, 2003.
[24] E. Oñate, Possibilities of finite calculus in computational mechanics. Int. J. Numer. Meth. Engng., 60(1), 255–281, 2004.
[25] E. Oñate, S.R. Idelsohn, F. Del Pin, R. Aubry, The particle finite element method. An overview. Int. J. Comput. Methods, 1(2), 267–307, 2004.
[26] E. Oñate, J. García, S.R. Idelsohn, F. Del Pin, FIC formulations for finite element analysis of incompressible flows. Eulerian, ALE and Lagrangian approaches. Comput. Meth. Appl. Mech. Engrg. 195(23-24), 3001–3037, 2006.
[27] E. Oñate, A. Valls, J. García, Computation of turbulent flows using a finite calculus-finite element formulation. Int. J. Numer. Meth. Engng., 54, 609–637, 2007.
[28] E. Oñate, Structural analysis with the finite element method. Linear statics. Volume 1. Basis and Solids. CIMNE-Springer, 2009.
[29] E. Oñate, M.A. Celigueta, S.R. Idelsohn, F. Salazar, B. Suárez, Possibilities of the particle finite element method for fluid-soil-structure interaction problems. Computational Mechanics, 48(3), 307–318, 2011.
[30] E. Oñate, S.R. Idelsohn, C. Felippa, Consistent pressure Laplacian stabilization for incompressible continua via higher-order finite calculus. Int. J. Numer. Meth. Engng, 87 (1-5), 2011, 171–195.
[31] E. Oñate, A. Franci, J.M. Carbonell, Lagrangian formulation for finite element analysis of incompressible fluids with reduced mass losses. Int. J. Numer. Meth. Fluids, 2013. DOI:0.1002/fld.3870.
[32] E. Oñate, P. Nadukandi, S.R. Idelsohn, P1/P0+ elements for incompressible flows with discontinuous material properties. Comput. Meth. Appl. Mech. Engrg., 271, 185–209, 2014, .
[33] N.A. Patankar, D.D. Joseph, Lagrangian numerical simulation of particulate flows. Int. J. of Multiphase Flow, 27 (10), 1685–-1706, 2001.
[34] R. Radovitzky and M. Ortiz, Lagrangian finite element analysis of newtonian fluid flows. Int. J. Numer. Meth. Engng., 43, 607–619, 1998.
[35] B. Ramaswamy and M. Kawahara, Lagrangian finite element analysis applied to viscous free surface fluid flow. Int. J. Num. Meth. Fluids, 7, 953–984, 1986.
[36] P. Wriggers, Non linear finite element methods. Springer, 2008.
[37] T.E. Tezduyar, Finite elements for flow problems with moving boundaries and interfaces. Arch. for Comput. Methods Eng., 8, 83–130, 2001.
[38] D.Z. Zhang, Q. Zou, W.B. VanderHeyden, X. Ma, Material point method applied to multiphase flows. Journal of Computational Physics, 227 (6), 3159-3173, 2008.
[39] O.C. Zienkiewicz, R.L. Taylor, J.Z. Zhu, The Finite Element Method. Vol. 1 The Basis. Elsevier, 6th Edition, 2005.
[40] O.C. Zienkiewicz, R.L. Taylor, The Finite Element Method. Vol. 2 Solid and Structural Mechanics. Elsevier, 6th Edition, 2005.
[41] O.C. Zienkiewicz, R.L. Taylor and P. Nithiarasu, The Finite Element Method. Vol. 3 Fluid Dynamics. Elsevier, 6th Edition, 2005.
APPENDIX A. LINEARIZATION OF THE MOMENTUM EQUATIONS WITH RESPECT TO THE NODAL VELOCITIES
Using the expression of of Eq.(62) and neglecting the changes of the external vector with the velocity (accounting for these changes is possible and will lead to additional terms in the tangent matrix), we can write
|
|
(A.1) |
Introducing Eqs.(55) and (59) into (A.1) gives after some algebra [4,5,36]
|
|
(A.2) |
|
|
(A.3) |
|
|
(A.4) |
where
|
|
(A.5) |
It can be shown that tensor is symmetric [4,5].
On the other hand,
|
|
(A.6a) |
with
|
|
(A.6b) |
with defined in Eq.(58.b).
In the derivation of Eqs.(A.3), (A.4) and (A.6a) we have assumed that . This relationship follows from Eq.(60.a).
Substituting Eqs.(A.2)–(A.4) and (A.6a) and the interpolation for the pressure (Eq.(53)) into (A.1) yields the linearized form of the residual vector of the discretized momentum equations as
|
|
(A.7) |
where matrices and were given in Eq.(67) and and are the constitutive and initial stress matrices, respectively. The expression of these matrices is
|
|
(A.8) |
The tangent constitutive tensor is deduced from Eqs.(A.1)-(A.4) as
|
|
(A.9) |
It is straightforward to show that tensor is symmetric.
Document information
Published on 01/01/2014
DOI: 10.1007/s00466-014-1078-1
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?