| Line 1: | Line 1: | ||
| − | |||
| Line 6: | Line 5: | ||
==“The Idealized steel profile”, a computational method for the design of reinforcing steel in concrete structures== | ==“The Idealized steel profile”, a computational method for the design of reinforcing steel in concrete structures== | ||
| − | <span style="text-align: center; font-size: 75%;">Luis Fernando Verduzco Martínez[1], Alejandro Hernández Martínez | + | <span style="text-align: center; font-size: 75%;">Luis Fernando Verduzco Martínez[1], Alejandro Hernández Martínez, Humberto Esqueda Oliva [3] |
</span> | </span> | ||
| Line 12: | Line 11: | ||
<span style="text-align: center; font-size: 75%;">[1]lf.verduzcomartinez@ugto.mx | <span style="text-align: center; font-size: 75%;">[1]lf.verduzcomartinez@ugto.mx | ||
| − | [2] alejandro.hernandez@ugtomx.onmicrosoft.com | + | [2] alejandro.hernandez@ugtomx.onmicrosoft.com |
| − | <span id="fnc-1"></span>[[#fn-1|<sup>1</sup>]] | + | [3] esquedah@yahoo.com <span id="fnc-1"></span>[[#fn-1|<sup>1</sup>]] Resúmen |
| − | + | Se presenta el desarrollo y modelación matemática y numérica de un nuevo método computacional llamado “El perfil idealizado de acero” para el diseño de acero de refuerzo en estructuras de concreto reforzado. En el presente trabajo se mostrará su aplicación para columnas de concreto prismáticas sólidas de sección rectangular y circular sometidas a flexo-compresión biaxial, de acuerdo a los componentes y criterios de diseño y análisis para este tipo de estructuras, adaptando la modelación numérica para ambas geometrías, así como respetando los criterios que establecen las <span id='citeF-3'></span>[[#cite-3|[3]]]. | |
| − | + | ||
| − | Se presenta el desarrollo y modelación matemática y numérica de un nuevo método computacional llamado | + | |
Se probará al final dicho método para el diseño de diversos modelos experimentales de concreto reforzado bajo ciertas combinaciones de cargas a partir de un análisis estructural previo, haciendo comparaciones de los resultados de acuerdo a eficiencia estructural y geometría en la variación de varios paramétros de diseño y objetivos específicos. | Se probará al final dicho método para el diseño de diversos modelos experimentales de concreto reforzado bajo ciertas combinaciones de cargas a partir de un análisis estructural previo, haciendo comparaciones de los resultados de acuerdo a eficiencia estructural y geometría en la variación de varios paramétros de diseño y objetivos específicos. | ||
| − | + | Palabras clave: criterios de diseño, acero de refuerzo, concreto reforzado, formulación matemática, métodos computacionales Abstract | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | It is presented the mathematical and numerical devolpement and modelling of a new computational method named | + | It is presented the mathematical and numerical devolpement and modelling of a new computational method named “The idealized steel profile” for the design of reinforcing steel in concrete structures. Hereby it will be shown its application for solid prismatic concrete columns of both rectangular and circular cross sections subjected to flexo-compression stresses in two directions, according to the design components and analysis criteria stablished for this type of structures following the <span id='citeF-3'></span>[[#cite-3|[3]]]. |
At the end such method will be tested for various experimental structural models under certain load combinations from a structural analysis made previously, making comparisons between the results according to certain design criteria and requirements such as structural efficiency, costs and geometry following various specific design goals. | At the end such method will be tested for various experimental structural models under certain load combinations from a structural analysis made previously, making comparisons between the results according to certain design criteria and requirements such as structural efficiency, costs and geometry following various specific design goals. | ||
| − | + | keywords: design criteria, reinforcing steel, reinforced concrete, mathematical formulation, computational methods | |
<span id="fn-1"></span> | <span id="fn-1"></span> | ||
| − | <span style="text-align: center; font-size: 75%;">([[#fnc-1|<sup>1</sup>]]) Universidad de Guanajuato,Aula CIMNE-UG, Guanajuato, Guanajuato, México 2019. </span> | + | <span style="text-align: center; font-size: 75%;">([[#fnc-1|<sup>1</sup>]]) Universidad de Guanajuato, Aula CIMNE-UG, Guanajuato, Guanajuato, México 2019. </span> |
==1 Introducción== | ==1 Introducción== | ||
| Line 63: | Line 57: | ||
* Desarrollar la formulación matemática y numérica para la programación en un lenguaje de programación, tanto para secicones de geometría ciruclar y rectangular, de acuerdo a los criterios de diseño y análisis que establecen las <span id='citeF-3'></span>[[#cite-3|[3]]] | * Desarrollar la formulación matemática y numérica para la programación en un lenguaje de programación, tanto para secicones de geometría ciruclar y rectangular, de acuerdo a los criterios de diseño y análisis que establecen las <span id='citeF-3'></span>[[#cite-3|[3]]] | ||
| − | |||
* Hacer un estudio de precios unitarios y costos de proveedores de acerero, así como de equipo y mano de obra en general para armar el acero de refuerzo | * Hacer un estudio de precios unitarios y costos de proveedores de acerero, así como de equipo y mano de obra en general para armar el acero de refuerzo | ||
| − | |||
* Insertar estos costos en el programa al momento del diseño | * Insertar estos costos en el programa al momento del diseño | ||
| − | |||
* Realizar las simulaciones y ejecución de experimentos requeridos para analizar el comportamiento de diferentes modelos estructurales de columnas ante diferentes condiciones de carga, haciendo comparaciones entre los diversos resultados referente a costos finales, eficiencias estructurales y geometrías | * Realizar las simulaciones y ejecución de experimentos requeridos para analizar el comportamiento de diferentes modelos estructurales de columnas ante diferentes condiciones de carga, haciendo comparaciones entre los diversos resultados referente a costos finales, eficiencias estructurales y geometrías | ||
| Line 80: | Line 71: | ||
El desarrollo de los métodos numéricos más famosos por aquellos grandes científicos, matemáticos e ingenieros han servido de inspiración para muchos investigadores en la ingeniería y ciencia más que para desarrollar la aplicación de los existentes a problemas, desarrollar los suyos propios con la potencia de las computadoras. | El desarrollo de los métodos numéricos más famosos por aquellos grandes científicos, matemáticos e ingenieros han servido de inspiración para muchos investigadores en la ingeniería y ciencia más que para desarrollar la aplicación de los existentes a problemas, desarrollar los suyos propios con la potencia de las computadoras. | ||
| − | Se han desarrolaldo desde el uso de las computadoras innumerables métodos computacionales en el análisis y diseño de las estructuras. Tal vez el más famoso y usado de todos es el | + | Se han desarrolaldo desde el uso de las computadoras innumerables métodos computacionales en el análisis y diseño de las estructuras. Tal vez el más famoso y usado de todos es el Método del Elementos Finito <span id='citeF-6'></span>[[#cite-6|[6]]] cuyas aplicaciones van desde el análisis elástico de elementos estructurales, hasta la simulación numérica de fluidos. Desde su primera aparición en 1956 el mismo método ha evulocionado y desarrollado para crear diferentes versiones del mismo dependiendo de su aplicación. |
Sin embargo, de manera general, cada vez que se quiere hacer una mejora en un análisis y/o diseño estructural en cuánto a rápidez y aproximaciones de soluciones deseadas se crea un nuevo método numérico computacional. Ya que con solo hecho de implementar la potencia de una computadora para encontrar una solución de un problema se requiere de un ajuste de datos, desarrollo de modelos matemáticos, encontrar coeficientes o iterar operaciones aritméticas, y eso, en sí, lo vuelve un método numérico computacional. | Sin embargo, de manera general, cada vez que se quiere hacer una mejora en un análisis y/o diseño estructural en cuánto a rápidez y aproximaciones de soluciones deseadas se crea un nuevo método numérico computacional. Ya que con solo hecho de implementar la potencia de una computadora para encontrar una solución de un problema se requiere de un ajuste de datos, desarrollo de modelos matemáticos, encontrar coeficientes o iterar operaciones aritméticas, y eso, en sí, lo vuelve un método numérico computacional. | ||
| Line 106: | Line 97: | ||
Las columnas de concreto reforzado pueden clasificarse como columnas cortas, intermedias y columnas largas.<span id="fnc-2"></span>[[#fn-2|<sup>1</sup>]] Es necesario tener esto en cuenta para entender cómo funciona el programa, ya que el análisis de las columnas preceden del mismo mecanismo de falla de estos tipos de columnas. | Las columnas de concreto reforzado pueden clasificarse como columnas cortas, intermedias y columnas largas.<span id="fnc-2"></span>[[#fn-2|<sup>1</sup>]] Es necesario tener esto en cuenta para entender cómo funciona el programa, ya que el análisis de las columnas preceden del mismo mecanismo de falla de estos tipos de columnas. | ||
| − | + | Columnas cortas: La carga que pueden soportar está regida por las dimensiones de su sección transversal y por la resistencia de los materiales de que está construida. | |
| − | + | Columnas intermedias: La falla es por una combinación de aplastamiento y pandeo. | |
| − | + | Columnas largas: La capacidad de carga axial en estás columnas se ve reducida a causa de los momentos secundarios resultates debidos a la deformacion por flexión de la columna. | |
El presente trabajo trata únicamente con columnas cortas. | El presente trabajo trata únicamente con columnas cortas. | ||
<span id="fn-2"></span> | <span id="fn-2"></span> | ||
| − | <span style="text-align: center; font-size: 75%;">([[#fnc-2|<sup>1</sup>]]) Jack C. McCormac, Rusell H. Brown, | + | <span style="text-align: center; font-size: 75%;">([[#fnc-2|<sup>1</sup>]]) Jack C. McCormac, Rusell H. Brown, “Diseño de concreto reforzado”, 14va edición, Alfaomega(2015), p.257.</span> |
===6.2 Tipos de columnas de concreto=== | ===6.2 Tipos de columnas de concreto=== | ||
| Line 124: | Line 115: | ||
<span id="fn-3"></span> | <span id="fn-3"></span> | ||
| − | <span style="text-align: center; font-size: 75%;">([[#fnc-3|<sup>1</sup>]]) Jack C. McCormac, Rusell H. Brown, | + | <span style="text-align: center; font-size: 75%;">([[#fnc-3|<sup>1</sup>]]) Jack C. McCormac, Rusell H. Brown, “Diseño de concreto reforzado”, 14th edition, Alfaomega (2015), p. 258.</span> |
===6.3 Conceptos generales de diseño=== | ===6.3 Conceptos generales de diseño=== | ||
| Line 148: | Line 139: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>P_{oc} = (0.85)f{'}_{c}(A_{c}-A_{s})+f_{y}(A_{s}) </math> | + | | style="text-align: center;" | <math> P_{oc} = (0.85)f{'}_{c}(A_{c}-A_{s})+f_{y}(A_{s}) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (1) | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | ||
|} | |} | ||
| − | Cabe resaltar que se está considerando el área de acero en la contribución de la resistencia del concreto a compresión (primer término de la | + | Cabe resaltar que se está considerando el área de acero en la contribución de la resistencia del concreto a compresión (primer término de la Ecuación [[#eq-1|1]], que puede influir considerablemente en los cálculos. |
Por otra parte, la carga máxima a tensión que el elemento puede soportar está dada por: | Por otra parte, la carga máxima a tensión que el elemento puede soportar está dada por: | ||
| Line 163: | Line 154: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>P_{ot} = (f_{y}(A_{s})) </math> | + | | style="text-align: center;" | <math> P_{ot} = (f_{y}(A_{s})) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (2) | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | ||
| Line 177: | Line 168: | ||
<br />a. Se aborda el análisis mediante propuestas de geometría de la sección de la columna que permanecerán fijas, haciendo variar únicamente el área de acero de refuerzo. | <br />a. Se aborda el análisis mediante propuestas de geometría de la sección de la columna que permanecerán fijas, haciendo variar únicamente el área de acero de refuerzo. | ||
| + | <br />b. Un elemento puede alcanzar su resistencia bajo innumerables combinaciones de carga axial y momento flexionante. Estas combinaciones varían desde una capa axial máxima (<math>P_{oc}</math>) sin momento de flexión, hasta un momento (<math>M_{o}</math>) sin fuerza axial. | ||
| − | <br /> | + | <br />c. El lugar geométrico de las combinaciones de carga axial y momento flexionante con las que un elemento puede alcanzar su resistencia se representa gráficamente por medio de un ''diagrama de interacción" Figura [[#img-1|1]]. |
| + | <br />d. Cuando al aumentar la carga externa, el momento y la carga axial crecen en la misma proporción, la historia de carga queda representada por una recta desde el origen, con una pendiente igual al cociente <math display="inline">P/M=1/e</math>. Figura [[#img-1|1]]. | ||
| + | <br />e. Existen solo dos modos principales de falla de elementos sujetos a flexo-compresión: falla en compresión y falla en tensión: | ||
| − | + | <br />1. Falla a compresión: Se produce por aplastamiento del concreto. El acero del lado más comprimido fluye, en tanto que el lado opuesto no fluye en tensión | |
| − | + | <br />2. Falla en tensión: Se produce cuando el acero de un lado fluye en tensión antes de que se produzca el aplastamiento del concreto en el lado opuesto más comprimido.<p> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <br />1. | + | |
| − | <br />2. | + | |
</p> | </p> | ||
| − | <br />f. El diagrama de interacción de un elemento puede obtenerse a partir de las hipótesis descritas para el cálculo de la resistencia de elementos sujetos a flexión pura, considerando que ahora la sumatoria de fuerzas debe ser igual a la carga | + | <br />f. El diagrama de interacción de un elemento puede obtenerse a partir de las hipótesis descritas para el cálculo de la resistencia de elementos sujetos a flexión pura, considerando que ahora la sumatoria de fuerzas debe ser igual a la carga P aplicada.<p> |
| − | + | ||
| − | + | ||
| − | + | </p> NOTA: Lo anterior aplica para cualquier geometría. | |
<div id='img-1'></div> | <div id='img-1'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig4_1.png|396px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig4_1.png|396px|Diagrama de interacción típico. (Dibujo propio.)]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 1:''' | + | | colspan="1" | '''Figura 1:''' Diagrama de interacción típico. (Dibujo propio.) |
|} | |} | ||
====Fórmula de Bresler==== | ====Fórmula de Bresler==== | ||
| − | Bresler desarrolló una expresión muy simple para columnas rectangulares para calcular los valores máximos de la carga de compresión que | + | Bresler desarrolló una expresión muy simple para columnas rectangulares para calcular los valores máximos de la carga de compresión que actúa a excentricidades <math>e_{x}</math> y <math>e_{y}</math> en secciones rectangulares con refuerzo simétrico. Ecuación [[#eq-3|3]]. Dicha solución surgió ante la necesidad de evitar realizar los cálculos para determinar una superficie de interacción<span id="fnc-5"></span>[[#fn-5|<sup>2</sup>]], reduciendo el problemas a una combinación de soluciones más simples; dos de flexo-compresión en un plano de simetría y una de compresión axial. |
<span id="eq-3"></span> | <span id="eq-3"></span> | ||
| Line 215: | Line 201: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\frac{1}{P_{R}}=\frac{1}{P_{rx}}+\frac{1}{P_{ry}}-\frac{1}{P_{oc}} </math> | + | | style="text-align: center;" | <math> \frac{1}{P_{R}}=\frac{1}{P_{rx}}+\frac{1}{P_{ry}}-\frac{1}{P_{oc}} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (3) | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
|} | |} | ||
| − | Donde: <math | + | Donde: <math>P_{R}</math>=Carga normal resistente sobre la sección transversal del elemento actuando a excentricidades <math>e_{x}</math> y <math>e_{y}</math>. |
| − | <math | + | <math>P_{rx}</math>=Carga normal resistente a una excentricidad de <math>e_{y}</math>. |
| − | <math | + | <math>P_{ry}</math>=Carga normal resistente a una excentricidad de <math>e_{x}</math>. |
| − | La | + | La Ecuación [[#eq-3|3]] verifica los ensayes disponibles dentro del 20 por ciento de aproximación, y representa una familia de planos que aproximan los puntos de la superficie de interacción. Figura [[#img-2|2]]. <div id='img-2'></div> |
| − | + | ||
| − | <div id='img-2'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig4.png|420px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig4.png|420px|Superficie de interacción típica. Tomada de:]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 2:''' | + | | colspan="1" | '''Figura 2:''' Superficie de interacción típica. Tomada de: |
|} | |} | ||
| − | + | Otro enfoque para analizar columnas sujetas a carga axial y flexión en dos planos Ecuación [[#eq-4|4]] a es partir de la cual se desprende otra expresión simplificada para calcular la eficiencia de un elemento cuando la relación <math>P_{R}/P_{oc}<0.1</math>. Ecuación [[#eq-9|9]] (que es la se presenta en las NTC-2017 [ntc17]) a las cuáles se hará referencia a continuación. | |
| − | Otro enfoque para analizar columnas sujetas a carga axial y flexión en dos planos | + | |
<span id="eq-4"></span> | <span id="eq-4"></span> | ||
| Line 244: | Line 227: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>(\frac{P_{u}-P_{nb}}{P_{ot}-P_{nb}})+(\frac{M_{ux}}{M_{nbx}}^{1.5})+(\frac{M_{uy}}{M_{nby}}^{1.5})=1.0 </math> | + | | style="text-align: center;" | <math> (\frac{P_{u}-P_{nb}}{P_{ot}-P_{nb}})+(\frac{M_{ux}}{M_{nbx}}^{1.5})+(\frac{M_{uy}}{M_{nby}}^{1.5})=1.0 </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (4) | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) | ||
| Line 253: | Line 236: | ||
<math>P_{nb}</math>=Resistencia nominal a carga axial en la condición balanceada. | <math>P_{nb}</math>=Resistencia nominal a carga axial en la condición balanceada. | ||
| − | <math>M_{nbx}</math> y <math>M_{nby}</math>=Momentos nominales resistentes en la condición balanceada alrededor de los ejes | + | <math>M_{nbx}</math> y <math>M_{nby}</math>=Momentos nominales resistentes en la condición balanceada alrededor de los ejes X y Y recpectivamente. |
| − | <math>M_{ux}</math> y <math>M_{uy}</math>=Momentos nominales aplicados alrededor de los ejes | + | <math>M_{ux}</math> y <math>M_{uy}</math>=Momentos nominales aplicados alrededor de los ejes X y Y respectivamente. |
<span id="fn-4"></span> | <span id="fn-4"></span> | ||
| − | <span style="text-align: center; font-size: 75%;">([[#fnc-4|<sup>1</sup>]]) González Cuevas, Fco. Robles Fernández, | + | <span style="text-align: center; font-size: 75%;">([[#fnc-4|<sup>1</sup>]]) González Cuevas, Fco. Robles Fernández,“Aspectos básicos del Concreto Reforzado”, 4ª edición, Limusa (2005). Capítulo 6, p. 127-155.</span> |
<span id="fn-5"></span> | <span id="fn-5"></span> | ||
| Line 265: | Line 248: | ||
===6.4 Normativa=== | ===6.4 Normativa=== | ||
| − | Anteriormente se presentaron hipótesis generales de diseño con concreto, porque son de tales hipótesis en que los reglamentos de construcción se basan. Para desarrollar éste proyecto se hizo referencia a las | + | Anteriormente se presentaron hipótesis generales de diseño con concreto, porque son de tales hipótesis en que los reglamentos de construcción se basan. Para desarrollar éste proyecto se hizo referencia a las Normas Técnicas complementarias para el diseño y construcción de estructuras de concreto del Reglamento de Construcciones de la Ciudad de México (NTC-2017), que aunque se basan en las hipótesis anteriores no presentan tal cual los mismos criterios de diseño, y que son cuestionados mucho por la sociedad ingenieril. Veamos que proponen estas normas. |
====6.4.1 Carga axial==== | ====6.4.1 Carga axial==== | ||
| Line 277: | Line 260: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>f{''}c=0.85(f{'}c) </math> | + | | style="text-align: center;" | <math> f{''}c=0.85(f{'}c) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (5) | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) | ||
|} | |} | ||
| − | De modo que la ecuación | + | De modo que la ecuación Ecuación [ [[#eq-1|1]]] se transforma a: |
<span id="eq-6"></span> | <span id="eq-6"></span> | ||
| Line 290: | Line 273: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>P_{oc}=F_{R}((f{''}c)(A_{c}-A_{s})+f_{y}(A_{s})) </math> | + | | style="text-align: center;" | <math> P_{oc}=F_{R}((f{''}c)(A_{c}-A_{s})+f_{y}(A_{s})) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (6) | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | ||
|} | |} | ||
| − | De modo que la ecuación | + | De modo que la ecuación Ecuación [ [[#eq-2|2]]] se transforma a: |
<span id="eq-7"></span> | <span id="eq-7"></span> | ||
| Line 303: | Line 286: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>P_{ot}=F_{R}(f_{y})(A_{s}) </math> | + | | style="text-align: center;" | <math> P_{ot}=F_{R}(f_{y})(A_{s}) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (7) | | style="width: 5px;text-align: right;white-space: nowrap;" | (7) | ||
|} | |} | ||
| − | Para una mejor interpretación de los factores mecionados se puede hacer referencia a la | + | Para una mejor interpretación de los factores mecionados se puede hacer referencia a la Figura [[#img-3|3]], que es el bloque de transformación equivalente de esfuerzos de las hipótesis de las NTC-2017. |
<div id='img-3'></div> | <div id='img-3'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-Fig5.png|576px| | + | |[[Image:Draft_Verduzco Martinez_325285613-Fig5.png|576px|Hipótesis de las NTC-2017 sobre la distribución de deformaciones y esfuerzos en la zona de compresión. Adaptada de: <span id='citeF-3'></span>[[#cite-3|[3]]]]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 3:''' | + | | colspan="1" | '''Figura 3:''' Hipótesis de las NTC-2017 sobre la distribución de deformaciones y esfuerzos en la zona de compresión. Adaptada de: <span id='citeF-3'></span>[[#cite-3|[3]]] |
|} | |} | ||
| − | + | Donde: <math> C=ab(f{''}_{c}) </math> <math> 0.65<=(\beta _{1}=1.05-\frac{f{'}_{c}}{1400})<=0.85 </math> | |
| − | Donde: | + | |
| − | + | ||
| − | <math>C=ab(f{''}_{c}) </math> | + | |
| − | + | ||
| − | <math> | + | |
| − | + | ||
| − | 0.65<=(\beta _{1}=1.05-\frac{f{'}_{c}}{1400})<=0.85 </math> | + | |
====6.4.2 Compresión y flexión en dos direcciones==== | ====6.4.2 Compresión y flexión en dos direcciones==== | ||
| − | <span id="fnc-7"></span>[[#fn-7|<sup>2</sup>]] | + | <span id="fnc-7"></span>[[#fn-7|<sup>2</sup>]] Se usará la expresión siguiente (que es derivada de la fórmula de Bresler) para el cálculo de la carga máxima actuante en la sección a cierta excentricidad. |
| − | + | ||
| − | Se usará la expresión siguiente (que es derivada de la fórmula de | + | |
<span id="eq-8"></span> | <span id="eq-8"></span> | ||
| Line 338: | Line 312: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>P_{R}=\frac{1}{\frac{1}{P_{rx}}+\frac{1}{P_{ry}}-\frac{1}{P_{oc}}} </math> | + | | style="text-align: center;" | <math> P_{R}=\frac{1}{\frac{1}{P_{rx}}+\frac{1}{P_{ry}}-\frac{1}{P_{oc}}} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (8) | | style="width: 5px;text-align: right;white-space: nowrap;" | (8) | ||
|} | |} | ||
| − | Para valores de <math | + | Para valores de <math>\frac{P_{R}}{P_{oc}}<0.1</math>, se usará la expresión siguiente: |
<span id="eq-9"></span> | <span id="eq-9"></span> | ||
| Line 351: | Line 325: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\frac{M_{ux}}{M_{rx}}+\frac{M_{uy}}{M_{ry}}<=1.0 </math> | + | | style="text-align: center;" | <math> \frac{M_{ux}}{M_{rx}}+\frac{M_{uy}}{M_{ry}}<=1.0 </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (9) | | style="width: 5px;text-align: right;white-space: nowrap;" | (9) | ||
|} | |} | ||
| − | Donde: | + | Donde: <math>M_{ux}</math> y <math>M_{uy}</math> son los momentos actuantes alrededor de los ejes X, Y, respectivamente. |
| − | + | ||
| − | <math>M_{ux}</math> y <math>M_{uy}</math> son los momentos actuantes alrededor de los ejes X, Y, respectivamente. | + | |
<math>M_{rx}</math> y <math>M_{ry}</math> son los momentos resistentes de diseño alrededor de los mismos ejes. | <math>M_{rx}</math> y <math>M_{ry}</math> son los momentos resistentes de diseño alrededor de los mismos ejes. | ||
<span id="fn-6"></span> | <span id="fn-6"></span> | ||
| − | <span style="text-align: center; font-size: 75%;">([[#fnc-6|<sup>1</sup>]]) El factor de reducción <math>F_{R}</math>, que para el caso de columnas con carga axial es de 0.8 | + | <span style="text-align: center; font-size: 75%;">([[#fnc-6|<sup>1</sup>]]) El factor de reducción <math>F_{R}</math>, que para el caso de columnas con carga axial es de 0.8 <span id='citeF-3'></span>[[#cite-3|[3]]]</span> |
<span id="fn-7"></span> | <span id="fn-7"></span> | ||
| − | <span style="text-align: center; font-size: 75%;">([[#fnc-7|<sup>2</sup>]]) González Cuevas, Fco. Robles Fernández, | + | <span style="text-align: center; font-size: 75%;">([[#fnc-7|<sup>2</sup>]]) González Cuevas, Fco. Robles Fernández, “Aspectos básicos del Concreto Reforzado”, 4ª edición, Limusa (2005). Capítulo 6, p. 148.</span> |
==7 El método del perfil idealizado de acero== | ==7 El método del perfil idealizado de acero== | ||
| Line 372: | Line 344: | ||
===7.1 Secciones rectangulares-modelo matemático=== | ===7.1 Secciones rectangulares-modelo matemático=== | ||
| − | Empleando las hipótesis de diseño anteriormente descritas se ha idealizado el acero de refuerzo de un elemento como se muestra. | + | Empleando las hipótesis de diseño anteriormente descritas se ha idealizado el acero de refuerzo de un elemento como se muestra. Figura [[#img-4|4]] <div id='img-4'></div> |
| − | + | ||
| − | <div id='img-4'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-Fig6.png|193px| | + | |[[Image:Draft_Verduzco Martinez_325285613-Fig6.png|193px|Sección rectangular idealizada de concreto reforzado.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 4:''' | + | | colspan="1" | '''Figura 4:''' Sección rectangular idealizada de concreto reforzado. |
|} | |} | ||
| − | |||
Para estas secciones se desarrolló un método puramente matemático con ecuaciones que definieran la resistencia de la columna de acuerdo a la ubicación del eje neutro de esfuerzos en la sección siguiendo paramétros de geometrías. También se desarrolló un método numérico que resulta más sencillo de programar y se meustra justo después. | Para estas secciones se desarrolló un método puramente matemático con ecuaciones que definieran la resistencia de la columna de acuerdo a la ubicación del eje neutro de esfuerzos en la sección siguiendo paramétros de geometrías. También se desarrolló un método numérico que resulta más sencillo de programar y se meustra justo después. | ||
| − | Tomando como referencia la siguiente figura | + | Tomando como referencia la siguiente figura Figura [[#img-5|5]]: <div id='img-5'></div> |
| − | + | ||
| − | <div id='img-5'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-perfilacero1.png|308px| | + | |[[Image:Draft_Verduzco Martinez_325285613-perfilacero1.png|308px|Sección rectangular idealizada de concreto reforzado.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 5:''' | + | | colspan="1" | '''Figura 5:''' Sección rectangular idealizada de concreto reforzado. |
|} | |} | ||
| − | + | Donde: <math>t</math> = espesor de la sección transversal del acero de refuerzo idealizado como un refuerzo constante alrededor de la sección. | |
| − | Donde: | + | |
| − | + | ||
| − | <math>t</math> = espesor de la sección transversal del acero de refuerzo idealizado como un refuerzo constante alrededor de la sección. | + | |
===7.2 Casos de análisis para el cálculo de la resistencia del acero=== | ===7.2 Casos de análisis para el cálculo de la resistencia del acero=== | ||
| − | De acuerdo a la distribución lineal de las deformaciónes unitarias y el comportamiento elasto-plástico del acero, se podrían derivar cinco casos de análisis respecto a las diferentes posiciones del eje neutro en el cálculo de nuestro diagrama de interacción, de acuerdo a los tipos de geometrías a que los mismos estados de esfuerzos (debido a dichas posiciones del eje neutro) sobre la sección transversal del elemento dan lugar. Estas configuraciones de geometrías de esfuerzos se pueden transformar consecuentemente a fuerzas puntuales | + | De acuerdo a la distribución lineal de las deformaciónes unitarias y el comportamiento elasto-plástico del acero, se podrían derivar cinco casos de análisis respecto a las diferentes posiciones del eje neutro en el cálculo de nuestro diagrama de interacción, de acuerdo a los tipos de geometrías a que los mismos estados de esfuerzos (debido a dichas posiciones del eje neutro) sobre la sección transversal del elemento dan lugar. Estas configuraciones de geometrías de esfuerzos se pueden transformar consecuentemente a fuerzas puntuales Figura [[#img-6|6]], con las que se pueden calcular el momento actuante respecto al eje neutro elástico de la sección transversal de todo el elemento de concreto. |
<div id='img-6'></div> | <div id='img-6'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig12.png|492px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig12.png|492px|Geometrías de bloques de distribución de esfuerzos para cierta posición del eje neutro.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 6:''' | + | | colspan="1" | '''Figura 6:''' Geometrías de bloques de distribución de esfuerzos para cierta posición del eje neutro. |
|} | |} | ||
| Line 414: | Line 378: | ||
Se presenta la siguiente metodología de manera general para el análisis de las fuerzas y momentos de flexión resultantes, con la que se podrá conceptualizar y segmentar la manera en que se desarrollaron las fórmulas y ecuaciones. | Se presenta la siguiente metodología de manera general para el análisis de las fuerzas y momentos de flexión resultantes, con la que se podrá conceptualizar y segmentar la manera en que se desarrollaron las fórmulas y ecuaciones. | ||
| − | + | Para las fuerzas resultantes resistentes: | |
Para cada bloque (<math>i</math>) en un determinado estado de esfuerzos: | Para cada bloque (<math>i</math>) en un determinado estado de esfuerzos: | ||
* Determiar la longitud de la configuración geométrica de esfuerzos (<math display="inline">L</math>) en dirección al peralte de la sección. | * Determiar la longitud de la configuración geométrica de esfuerzos (<math display="inline">L</math>) en dirección al peralte de la sección. | ||
| − | |||
* Determinar el área efectiva bajo esfuerzos <math display="inline">2tL</math> | * Determinar el área efectiva bajo esfuerzos <math display="inline">2tL</math> | ||
| − | |||
* Determinar la fuerza resultante que define la geometría de dicha configuración de esfuerzos | * Determinar la fuerza resultante que define la geometría de dicha configuración de esfuerzos | ||
| Line 429: | Line 391: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> F_{i} = \left\{ \begin{array}{ll} 2E_{ac}tL\varepsilon & \mathrm{si } \varepsilon{<}=0.0021 \\ 2f_{y}tL & \mathrm{si } \varepsilon{>0.0021} \end{array} \right. </math> |
| − | + | ||
| − | F_{i} = \left\{ \begin{array}{ll} | + | |
| − | + | ||
| − | 2E_{ac}tL\varepsilon & \mathrm{si } \varepsilon{<}=0.0021 \\ 2f_{y}tL & \mathrm{si } \varepsilon{>0.0021} \end{array} \right. </math> | + | |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (10) | | style="width: 5px;text-align: right;white-space: nowrap;" | (10) | ||
|} | |} | ||
| − | Donde: | + | Donde: <math>E_{ac}=\frac{fy}{\varepsilon _{y}}=\frac{4200 \frac{kg}{cm^2}}{0.0021}</math><p> <math>E_{ac}=2e10 \frac{kg}{cm^{2}}</math> </p> |
| − | + | * Sumar todas las fuerzas resultantes de cada configuración geométrica de esfuerzos para obtener la resultante resistente: <math>F_{R}=\sum _{i=1}^{i=no.bloques}F_{i}</math> | |
| − | <math>E_{ac}=\frac{fy}{\varepsilon _{y}}=\frac{4200 \frac{kg}{cm^2}}{0.0021}</math> | + | |
| − | + | ||
| − | <p> <math | + | |
| − | + | ||
| − | </p> | + | |
| − | * Sumar todas las fuerzas resultantes de cada configuración geométrica de esfuerzos para obtener la resultante resistente: | + | |
| − | + | ||
| − | <math>F_{R}=\sum _{i=1}^{i=no.bloques}F_{i}</math> | + | |
| − | + | Para los momentos resultantes resistentes: | |
Para cada configuración geométrica (<math>i</math>) en un determinado estado de esfuerzos: | Para cada configuración geométrica (<math>i</math>) en un determinado estado de esfuerzos: | ||
* Determiar la profundidad <math display="inline">d_{i}</math> del centroide de la configuración geométrica sobre el que actúa la fuerza resultante. | * Determiar la profundidad <math display="inline">d_{i}</math> del centroide de la configuración geométrica sobre el que actúa la fuerza resultante. | ||
| − | |||
* Determinar la distancia de ese punto respecto al eje centroidal de la sección transversal <math display="inline">\frac{1}{2}h-d_{i}</math> | * Determinar la distancia de ese punto respecto al eje centroidal de la sección transversal <math display="inline">\frac{1}{2}h-d_{i}</math> | ||
| + | * Determiar el Momento resultante equivalente: <math>M_{i}=F_{i}(\frac{1}{2}h-d_{i})</math> | ||
| + | * Sumar todas los momentos resultantes producidos por cada configuración geométrica de esfuerzos para obtener el momento de flexión resultante resistente: <math>M_{R}=\sum _{i=1}^{i=no.bloques}M_{i}</math> | ||
| − | + | Tomar en cuenta que por ahora solo se está considerando el acero de refuerzo. De modo que para calcular el volumen de estas configuraciones geométricas de deformaciones (o fuerzas resultantes), se analiza el área de las dos partes laterales del perfil idealizado de acero Figura [[#img-5|5]] y la de la parte superior e inferior por separado. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Tomar en cuenta que por ahora solo se está considerando el acero de refuerzo. De modo que para calcular el volumen de estas configuraciones geométricas de deformaciones (o fuerzas resultantes), se analiza el área de las dos partes laterales del perfil idealizado de acero | + | |
Para las partes laterales se toma referencia de la metodología descrita para esta geometría; tomando en cuenta una variación lineal de esfuerzos a lo largo de tales. | Para las partes laterales se toma referencia de la metodología descrita para esta geometría; tomando en cuenta una variación lineal de esfuerzos a lo largo de tales. | ||
| − | A diferencia de las partes superior en inferior en que se toma un esfuerzo constante a lo largo de la longitud de tales partes. De forma que aquí entrarán en lugar las fuerzas (<math>F_{a}</math> y <math>F_{b}</math>) | + | A diferencia de las partes superior en inferior en que se toma un esfuerzo constante a lo largo de la longitud de tales partes. De forma que aquí entrarán en lugar las fuerzas (<math>F_{a}</math> y <math>F_{b}</math>) Ecuación [ [[#eq-11|11]]] y Ecuación [ [[#eq-12|12]]] para todos los casos, representando las fuerzas resitentes resultantes que actuarán en los centroides de las partes superior en inferior del perfil de acero, supuestas como <math>d_{1}</math> y <math>d_{2}</math>, respectivamente. <div id='img-7'></div> |
| − | + | ||
| − | <div id='img-7'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-perfilacero1.png|308px| | + | |[[Image:Draft_Verduzco Martinez_325285613-perfilacero1.png|308px|Sección rectangular idealizada de concreto reforzado.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 7:''' | + | | colspan="1" | '''Figura 7:''' Sección rectangular idealizada de concreto reforzado. |
|} | |} | ||
| Line 485: | Line 426: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{a}=\varepsilon _{a}E_{ac}t(b-2rec) </math> | + | | style="text-align: center;" | <math> F_{a}=\varepsilon _{a}E_{ac}t(b-2rec) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (11) | | style="width: 5px;text-align: right;white-space: nowrap;" | (11) | ||
| Line 496: | Line 437: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{b}=\varepsilon _{b}E_{ac}t(b-2rec) </math> | + | | style="text-align: center;" | <math> F_{b}=\varepsilon _{b}E_{ac}t(b-2rec) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (12) | | style="width: 5px;text-align: right;white-space: nowrap;" | (12) | ||
|} | |} | ||
| − | + | Nota: La convención de signos será: Compresión (-) y Tensión (+). | |
====7.2.2 Caso 1: se presenta una configuración geométrica de esfuerzos rectangular en tensión==== | ====7.2.2 Caso 1: se presenta una configuración geométrica de esfuerzos rectangular en tensión==== | ||
| Line 510: | Line 451: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>-\infty{<}c<=\frac{30}{51}d_{1} </math> | + | | style="text-align: center;" | <math> -\infty{<}c<=\frac{30}{51}d_{1} </math> |
|} | |} | ||
|} | |} | ||
| Line 516: | Line 457: | ||
Ver Demostración 1.1 en Anexo 1 [p. actual] | Ver Demostración 1.1 en Anexo 1 [p. actual] | ||
| − | En éste caso el elemento de concreto no se producen momentos de flexión por los bloques de estados de esfuerzo, únicamente fuerzas axiales a tensión. | + | En éste caso el elemento de concreto no se producen momentos de flexión por los bloques de estados de esfuerzo, únicamente fuerzas axiales a tensión. Figura [[#img-8|8]] <div id='img-8'></div> |
| − | + | ||
| − | <div id='img-8'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig8.png|512px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig8.png|512px|a) Diagrama de distribución de deformaciones. Caso 1. a) En alguna posición de c dentro del rango permitido, b) c está en el limite superior del rango permitido. Dibujo propio. Ver Demostración 1.1 en Anexo 1 [p. actual]]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 8:''' | + | | colspan="1" | '''Figura 8:''' a) Diagrama de distribución de deformaciones. Caso 1. a) En alguna posición de c dentro del rango permitido, b) c está en el limite superior del rango permitido. Dibujo propio. Ver Demostración 1.1 en Anexo 1 [p. actual] |
|} | |} | ||
| − | |||
Donde: | Donde: | ||
<math>d_{1}=rec+\frac{1}{2}(t)</math> | <math>d_{1}=rec+\frac{1}{2}(t)</math> | ||
| − | <math | + | <math>d_{2}=h-rec-\frac{1}{2}(t)</math> Por lo tanto, de las ecuaciones Ecuación [[#eq-11|11]] y Ecuación [[#eq-12|12]]: |
| − | + | ||
| − | Por lo tanto, de las ecuaciones | + | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 539: | Line 475: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{a}=0.0021E_{ac}t(b-2rec) </math> | + | | style="text-align: center;" | <math> F_{a}=0.0021E_{ac}t(b-2rec) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (13) | | style="width: 5px;text-align: right;white-space: nowrap;" | (13) | ||
| Line 549: | Line 485: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{b}=0.0021E_{ac}t(b-2rec) </math> | + | | style="text-align: center;" | <math> F_{b}=0.0021E_{ac}t(b-2rec) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (14) | | style="width: 5px;text-align: right;white-space: nowrap;" | (14) | ||
| Line 560: | Line 496: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{1}=2(t)(d_{2}-d_{1})E_{ac}(0.0021) </math> | + | | style="text-align: center;" | <math> F_{1}=2(t)(d_{2}-d_{1})E_{ac}(0.0021) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (15) | | style="width: 5px;text-align: right;white-space: nowrap;" | (15) | ||
| Line 570: | Line 506: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{1}=0 </math> | + | | style="text-align: center;" | <math> M_{1}=0 </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (16) | | style="width: 5px;text-align: right;white-space: nowrap;" | (16) | ||
| Line 583: | Line 519: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{R}=F_{1}+F_{a}+F_{b} </math> | + | | style="text-align: center;" | <math> F_{R}=F_{1}+F_{a}+F_{b} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (17) | | style="width: 5px;text-align: right;white-space: nowrap;" | (17) | ||
| Line 593: | Line 529: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{R}=M_{1} </math> | + | | style="text-align: center;" | <math> M_{R}=M_{1} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (18) | | style="width: 5px;text-align: right;white-space: nowrap;" | (18) | ||
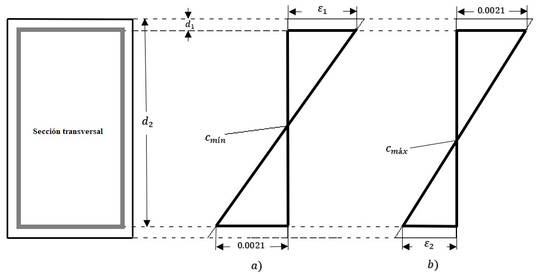
| Line 607: | Line 543: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\frac{30}{51}d_{1}<c<=d_{1} </math> | + | | style="text-align: center;" | <math> \frac{30}{51}d_{1}<c<=d_{1} </math> |
|} | |} | ||
|} | |} | ||
| − | Hágase referencia a | + | Hágase referencia a Figura [[#img-9|9]] para visualizar este rango. <div id='img-9'></div> |
| − | + | ||
| − | <div id='img-9'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig9.png|383px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig9.png|383px|a) Diagrama de configuracion geométrica de deformaciones en el límite inferior del eje neutro. b) Diagrama de configuración geométrica de deformaciones en el límite superior del eje neutro. c) Diagrama de configuración geométrica de deformaciones para cualquier posición del eje neutro dentro de rango permitido. (Dibujo propio). Ver Demostración 2.1 en Anexo 1 [p. actual]]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 9:''' | + | | colspan="1" | '''Figura 9:''' a) Diagrama de configuracion geométrica de deformaciones en el límite inferior del eje neutro. b) Diagrama de configuración geométrica de deformaciones en el límite superior del eje neutro. c) Diagrama de configuración geométrica de deformaciones para cualquier posición del eje neutro dentro de rango permitido. (Dibujo propio). Ver Demostración 2.1 en Anexo 1 [p. actual] |
|} | |} | ||
| − | + | Por lo tanto, de las ecuaciones Ecuación [[#eq-11|11]] y Ecuación [[#eq-12|12]]: | |
| − | Por lo tanto, de las ecuaciones | + | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 628: | Line 561: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{a}=0.0021E_{ac}t(b-2rec) </math> | + | | style="text-align: center;" | <math> F_{a}=0.0021E_{ac}t(b-2rec) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (19) | | style="width: 5px;text-align: right;white-space: nowrap;" | (19) | ||
| Line 638: | Line 571: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{b}=0.0021E_{ac}t(b-2rec) </math> | + | | style="text-align: center;" | <math> F_{b}=0.0021E_{ac}t(b-2rec) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (20) | | style="width: 5px;text-align: right;white-space: nowrap;" | (20) | ||
|} | |} | ||
| − | Ahora, con las variables definidas anteriormente y la figura | + | Ahora, con las variables definidas anteriormente y la figura Figura [[#img-9|9]], se pueden deducir las siguientes ecuaciones para calcular la fuerza resultante y el momento de flexión resultante resistente en el acero. |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 650: | Line 583: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{1}=2(t)(\varepsilon )(h_{3}-(d_{1}-c))E_{ac} </math> | + | | style="text-align: center;" | <math> F_{1}=2(t)(\varepsilon )(h_{3}-(d_{1}-c))E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (21) | | style="width: 5px;text-align: right;white-space: nowrap;" | (21) | ||
| Line 660: | Line 593: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{1}=F_{1}(d_{1}+\frac{1}{2}(h_{3}-(d_{1}-c)-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{1}=F_{1}(d_{1}+\frac{1}{2}(h_{3}-(d_{1}-c)-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (22) | | style="width: 5px;text-align: right;white-space: nowrap;" | (22) | ||
| Line 671: | Line 604: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{2}=2(t)\frac{1}{2}(0.0021-\varepsilon )(h_{3}-(d_{1}-c))E_{ac} </math> | + | | style="text-align: center;" | <math> F_{2}=2(t)\frac{1}{2}(0.0021-\varepsilon )(h_{3}-(d_{1}-c))E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (23) | | style="width: 5px;text-align: right;white-space: nowrap;" | (23) | ||
| Line 681: | Line 614: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{2}=F_{2}(d_{1}+\frac{2}{3}(h_{3}-(d_{1}-c))-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{2}=F_{2}(d_{1}+\frac{2}{3}(h_{3}-(d_{1}-c))-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (24) | | style="width: 5px;text-align: right;white-space: nowrap;" | (24) | ||
| Line 691: | Line 624: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{3}=2(t)(d_{2}-h_{3}-c)(0.0021)E_{ac} </math> | + | | style="text-align: center;" | <math> F_{3}=2(t)(d_{2}-h_{3}-c)(0.0021)E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (25) | | style="width: 5px;text-align: right;white-space: nowrap;" | (25) | ||
| Line 701: | Line 634: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{3}=F_{3}(c+h_{3}+\frac{1}{2}(d_{2}-c-h_{3})-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{3}=F_{3}(c+h_{3}+\frac{1}{2}(d_{2}-c-h_{3})-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (26) | | style="width: 5px;text-align: right;white-space: nowrap;" | (26) | ||
| Line 714: | Line 647: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{R}=F_{1}+F_{2}+F_{3}+F_{a}+F_{b} </math> | + | | style="text-align: center;" | <math> F_{R}=F_{1}+F_{2}+F_{3}+F_{a}+F_{b} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (27) | | style="width: 5px;text-align: right;white-space: nowrap;" | (27) | ||
| Line 726: | Line 659: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{R}=M_{1}+M_{2}+M_{3}+F_{a}(d_{1}-\frac{1}{2}h)+F_{b}(d_{2}-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{R}=M_{1}+M_{2}+M_{3}+F_{a}(d_{1}-\frac{1}{2}h)+F_{b}(d_{2}-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (28) | | style="width: 5px;text-align: right;white-space: nowrap;" | (28) | ||
| Line 740: | Line 673: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>d_{1}<c<=\frac{30}{9}d_{1} </math> | + | | style="text-align: center;" | <math> d_{1}<c<=\frac{30}{9}d_{1} </math> |
|} | |} | ||
|} | |} | ||
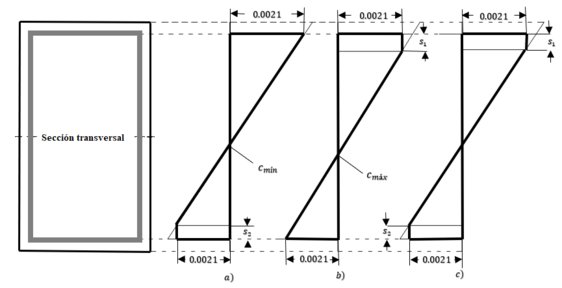
| − | Hágase referencia a | + | Hágase referencia a Figura [[#img-10|10]] para visualizar este rango. <div id='img-10'></div> |
| − | + | ||
| − | <div id='img-10'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig11.png|448px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig11.png|448px|a) Sección transversal, b) Configuraciones geométricas de deformaciones en el límite inferior del rango permitido del eje neutro, c) Configuraciones geométricas de deformaciones en el límite superior del rango permitido del eje neutro. Dibujo propio. Ver Demostración 3.1 en Anexo 1 [p. actual]]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 10:''' | + | | colspan="1" | '''Figura 10:''' a) Sección transversal, b) Configuraciones geométricas de deformaciones en el límite inferior del rango permitido del eje neutro, c) Configuraciones geométricas de deformaciones en el límite superior del rango permitido del eje neutro. Dibujo propio. Ver Demostración 3.1 en Anexo 1 [p. actual] |
|} | |} | ||
| − | |||
Donde: | Donde: | ||
| − | <math>h_{2}=\frac{21}{30}c</math> | + | <math>h_{2}=\frac{21}{30}c</math> De modo que para definir las ecuaciones Ecuación [[#eq-11|11]] y Ecuación [[#eq-12|12]] se tiene: |
| − | + | ||
| − | De modo que para definir las ecuaciones | + | |
<math>\varepsilon _{a}=(1-\frac{d_{1}}{c})(0.003)</math> | <math>\varepsilon _{a}=(1-\frac{d_{1}}{c})(0.003)</math> | ||
| − | <math | + | <math>\varepsilon _{b}=0.0021</math> Y para las fuerzas y momentos resistentes resultantes, se tiene: |
| − | + | ||
| − | Y para las fuerzas y momentos resistentes resultantes, se tiene: | + | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 771: | Line 697: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{1}=-\frac{1}{2}(c-d_{1})(\varepsilon _{a})(2t)E_{ac} </math> | + | | style="text-align: center;" | <math> F_{1}=-\frac{1}{2}(c-d_{1})(\varepsilon _{a})(2t)E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (29) | | style="width: 5px;text-align: right;white-space: nowrap;" | (29) | ||
| Line 781: | Line 707: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{1}=F_{1}(d_{1}+\frac{1}{3}(c-d_{1})-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{1}=F_{1}(d_{1}+\frac{1}{3}(c-d_{1})-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (30) | | style="width: 5px;text-align: right;white-space: nowrap;" | (30) | ||
| Line 791: | Line 717: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{2}=\frac{1}{2}h_{2}(0.0021)(2t)E_{ac} </math> | + | | style="text-align: center;" | <math> F_{2}=\frac{1}{2}h_{2}(0.0021)(2t)E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (31) | | style="width: 5px;text-align: right;white-space: nowrap;" | (31) | ||
| Line 801: | Line 727: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{2}=F_{2}(c+\frac{2}{3}h_{2}-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{2}=F_{2}(c+\frac{2}{3}h_{2}-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (32) | | style="width: 5px;text-align: right;white-space: nowrap;" | (32) | ||
| Line 811: | Line 737: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{3}=0.0021(d_{2}-c-h_{2})(2t))E_{ac} </math> | + | | style="text-align: center;" | <math> F_{3}=0.0021(d_{2}-c-h_{2})(2t))E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (33) | | style="width: 5px;text-align: right;white-space: nowrap;" | (33) | ||
| Line 821: | Line 747: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{3}=F_{3}((c+h_{2})+\frac{1}{2}(d_{2}-c-h_{2})-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{3}=F_{3}((c+h_{2})+\frac{1}{2}(d_{2}-c-h_{2})-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (34) | | style="width: 5px;text-align: right;white-space: nowrap;" | (34) | ||
| Line 831: | Line 757: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{R}=F_{1}+F_{2}+F_{3}-F_{a}+F_{b} </math> | + | | style="text-align: center;" | <math> F_{R}=F_{1}+F_{2}+F_{3}-F_{a}+F_{b} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (35) | | style="width: 5px;text-align: right;white-space: nowrap;" | (35) | ||
| Line 841: | Line 767: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{R}=M_{1}+M_{2}+M_{3}-F_{a}(d_{1}-\frac{1}{2}h)+F_{b}(d_{2}-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{R}=M_{1}+M_{2}+M_{3}-F_{a}(d_{1}-\frac{1}{2}h)+F_{b}(d_{2}-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (36) | | style="width: 5px;text-align: right;white-space: nowrap;" | (36) | ||
| Line 855: | Line 781: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\frac{60}{102}t>=\frac{9}{51}h-\frac{60}{51}rec </math> | + | | style="text-align: center;" | <math> \frac{60}{102}t>=\frac{9}{51}h-\frac{60}{51}rec </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (37) | | style="width: 5px;text-align: right;white-space: nowrap;" | (37) | ||
|} | |} | ||
| − | + | Nota: Ver Demostración CE.1 en Anexo 1. p. actual | |
| − | De la misma demostración se puede ver, que para calcular <math | + | De la misma demostración se puede ver, que para calcular <math>C_{min}</math> y <math>C_{max}</math>: <math>C_{min}=30(\frac{d_{2}}{51})</math> |
| − | <math | + | <math>C_{max}=30(\frac{d_{1}}{9})</math> <div id='img-11'></div> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | <div id='img-11'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig14.png|540px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig14.png|540px|Diagrama de configuraciones geométricas de deformaciones para el caso especial. a) Para la posición del eje neutro en el límite inferior, b) Para la posición del eje neutro en el límite superior. Dibujo propio.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 11:''' | + | | colspan="1" | '''Figura 11:''' Diagrama de configuraciones geométricas de deformaciones para el caso especial. a) Para la posición del eje neutro en el límite inferior, b) Para la posición del eje neutro en el límite superior. Dibujo propio. |
|} | |} | ||
| − | + | Por lo tanto, haciendo referencia a la Figura [[#img-11|11]], para las ecuaciones Ecuación [[#eq-11|11]] y Ecuación [[#eq-12|12]]: | |
| − | Por lo tanto, haciendo referencia a la | + | |
<math>\varepsilon _{a}=(1-\frac{d_{1}}{c})(0.003)</math> | <math>\varepsilon _{a}=(1-\frac{d_{1}}{c})(0.003)</math> | ||
| − | <math | + | <math>\varepsilon _{b}=(\frac{d_{2}}{c}-1)(0.003)</math> Y las fuerzas y momentos resistentes se calcularían como: |
| − | + | ||
| − | Y las fuerzas y momentos resistentes se calcularían como: | + | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 889: | Line 808: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{1}=-\frac{1}{2}\varepsilon _{a}E_{ac}(c-d_{1})2t </math> | + | | style="text-align: center;" | <math> F_{1}=-\frac{1}{2}\varepsilon _{a}E_{ac}(c-d_{1})2t </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (38) | | style="width: 5px;text-align: right;white-space: nowrap;" | (38) | ||
| Line 899: | Line 818: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{1}=-F_{1}(d_{1}+\frac{1}{3}(c-d_{1})) </math> | + | | style="text-align: center;" | <math> M_{1}=-F_{1}(d_{1}+\frac{1}{3}(c-d_{1})) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (39) | | style="width: 5px;text-align: right;white-space: nowrap;" | (39) | ||
| Line 909: | Line 828: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{2}=\frac{1}{2}\varepsilon _{b}E_{ac}(d_{2}-c)2t </math> | + | | style="text-align: center;" | <math> F_{2}=\frac{1}{2}\varepsilon _{b}E_{ac}(d_{2}-c)2t </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (40) | | style="width: 5px;text-align: right;white-space: nowrap;" | (40) | ||
| Line 919: | Line 838: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{2}=F_{2}(d_{2}-\frac{1}{3}(d_{2}-c)) </math> | + | | style="text-align: center;" | <math> M_{2}=F_{2}(d_{2}-\frac{1}{3}(d_{2}-c)) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (41) | | style="width: 5px;text-align: right;white-space: nowrap;" | (41) | ||
| Line 929: | Line 848: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{R}=F_{1}+F_{2}-F_{a}+F_{b} </math> | + | | style="text-align: center;" | <math> F_{R}=F_{1}+F_{2}-F_{a}+F_{b} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (42) | | style="width: 5px;text-align: right;white-space: nowrap;" | (42) | ||
| Line 939: | Line 858: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{R}=M_{1}+M_{2}-F_{a}(d_{1}-\frac{1}{3}h)+F_{b}(d_{2}-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{R}=M_{1}+M_{2}-F_{a}(d_{1}-\frac{1}{3}h)+F_{b}(d_{2}-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (43) | | style="width: 5px;text-align: right;white-space: nowrap;" | (43) | ||
| Line 946: | Line 865: | ||
====7.2.6 Caso 3-4: Se presentan configuraciones geométricas de deformaciónes triangular y rectangular a compresión, así como a tensión.==== | ====7.2.6 Caso 3-4: Se presentan configuraciones geométricas de deformaciónes triangular y rectangular a compresión, así como a tensión.==== | ||
| − | <math | + | <math>\frac{30}{9}d_{1}<c<=\frac{30}{51}d_{2}</math> |
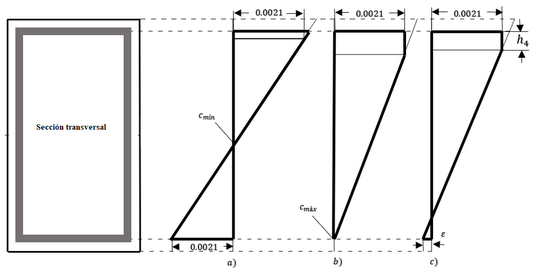
| − | Hágase referencia a | + | Hágase referencia a Figura [[#img-10|10]] para visualizar este rango. <div id='img-12'></div> |
| − | + | ||
| − | <div id='img-12'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-caso34.png|562px| | + | |[[Image:Draft_Verduzco Martinez_325285613-caso34.png|562px|a) Diagrama de configuraciones geométricas de deformaciones para el límite inferior del rango permitido del eje neutro, b) Diagrama de configuraciones geométricas de deformaciones para el límite superior del rango permitido del eje neutro. c) Diagrama configuraciones geométricas de deformaciones para cualquiera posición del eje neutro entre el rango permitido. Caso 3-4.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 12:''' | + | | colspan="1" | '''Figura 12:''' a) Diagrama de configuraciones geométricas de deformaciones para el límite inferior del rango permitido del eje neutro, b) Diagrama de configuraciones geométricas de deformaciones para el límite superior del rango permitido del eje neutro. c) Diagrama configuraciones geométricas de deformaciones para cualquiera posición del eje neutro entre el rango permitido. Caso 3-4. |
|} | |} | ||
| − | |||
Donde: <math>s_{1}=\frac{9}{30}c-d_{1}</math> | Donde: <math>s_{1}=\frac{9}{30}c-d_{1}</math> | ||
| − | <math | + | <math>s_{2}=h-\frac{51}{30}c-d_{1}</math> Por lo tanto, para las ecuaciones Ecuación [[#eq-11|11]] y Ecuación [[#eq-12|12]]: |
| − | + | ||
| − | Por lo tanto, para las ecuaciones | + | |
<math>\varepsilon _{a}=0.0021</math> | <math>\varepsilon _{a}=0.0021</math> | ||
| − | <math | + | <math>\varepsilon _{b}=0.0021</math> Y las fuerzas y momentos resistentes se calcularían como: |
| − | + | ||
| − | Y las fuerzas y momentos resistentes se calcularían como: | + | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 975: | Line 887: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{1}=-2t(0.0021)(s_{1})E_{ac} </math> | + | | style="text-align: center;" | <math> F_{1}=-2t(0.0021)(s_{1})E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (44) | | style="width: 5px;text-align: right;white-space: nowrap;" | (44) | ||
| Line 985: | Line 897: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{1}=F_{1}(d_{1}+\frac{1}{2}(s_{1})-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{1}=F_{1}(d_{1}+\frac{1}{2}(s_{1})-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (45) | | style="width: 5px;text-align: right;white-space: nowrap;" | (45) | ||
| Line 995: | Line 907: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{2}=-\frac{1}{2}2t(0.0021)(c-s_{1}-d_{1})E_{ac} </math> | + | | style="text-align: center;" | <math> F_{2}=-\frac{1}{2}2t(0.0021)(c-s_{1}-d_{1})E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (46) | | style="width: 5px;text-align: right;white-space: nowrap;" | (46) | ||
| Line 1,005: | Line 917: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{2}=F_{2}(d_{1}+s_{1}+\frac{1}{3}((c-d_{1}-s_{1}))-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{2}=F_{2}(d_{1}+s_{1}+\frac{1}{3}((c-d_{1}-s_{1}))-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (47) | | style="width: 5px;text-align: right;white-space: nowrap;" | (47) | ||
| Line 1,015: | Line 927: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{3}=\frac{1}{2}2t(0.0021)(d_{2}-c-s_{2})E_{ac} </math> | + | | style="text-align: center;" | <math> F_{3}=\frac{1}{2}2t(0.0021)(d_{2}-c-s_{2})E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (48) | | style="width: 5px;text-align: right;white-space: nowrap;" | (48) | ||
| Line 1,025: | Line 937: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{3}=F_{3}(d_{2}-s_{2}-\frac{1}{3}(d_{2}-c-s_{2})-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{3}=F_{3}(d_{2}-s_{2}-\frac{1}{3}(d_{2}-c-s_{2})-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (49) | | style="width: 5px;text-align: right;white-space: nowrap;" | (49) | ||
| Line 1,035: | Line 947: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{4}=2t(0.0021)(s_{2})E_{ac} </math> | + | | style="text-align: center;" | <math> F_{4}=2t(0.0021)(s_{2})E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (50) | | style="width: 5px;text-align: right;white-space: nowrap;" | (50) | ||
| Line 1,045: | Line 957: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{4}=F_{4}(d_{2}-\frac{1}{2}s_{2})-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{4}=F_{4}(d_{2}-\frac{1}{2}s_{2})-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (51) | | style="width: 5px;text-align: right;white-space: nowrap;" | (51) | ||
| Line 1,055: | Line 967: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{R}=F_{1}+F_{2}+F_{3}+F_{4}-F_{a}-F_{b} </math> | + | | style="text-align: center;" | <math> F_{R}=F_{1}+F_{2}+F_{3}+F_{4}-F_{a}-F_{b} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (52) | | style="width: 5px;text-align: right;white-space: nowrap;" | (52) | ||
| Line 1,065: | Line 977: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{R}=M_{1}+M_{2}+M_{3}+M_{4} | + | | style="text-align: center;" | <math>\begin{array}{l} M_{R}=M_{1}+M_{2}+M_{3}+M_{4}\\ -F_{a}(d_{1}-\frac{1}{2}h)-F_{b}(d_{2}-\frac{1}{2}h) \end{array}</math> |
| − | + | ||
| − | + | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (53) | | style="width: 5px;text-align: right;white-space: nowrap;" | (53) | ||
| Line 1,074: | Line 984: | ||
====7.2.7 Caso 4: Se presenta una configuración geométrica de deformaciones triangular y una rectangular a compresión; y una triangular a tensión.==== | ====7.2.7 Caso 4: Se presenta una configuración geométrica de deformaciones triangular y una rectangular a compresión; y una triangular a tensión.==== | ||
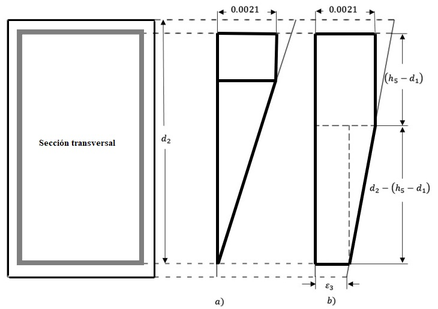
| − | <math | + | <math>\frac{30}{51}d_{2}<c<=d_{2}</math> |
| − | Para el cálculo de las fuerzas y momentos de flexión resultantes resistentes ha de hacerse referencia tanto a la | + | Para el cálculo de las fuerzas y momentos de flexión resultantes resistentes ha de hacerse referencia tanto a la Figura [[#img-13|13]].. <div id='img-13'></div> |
| − | + | ||
| − | <div id='img-13'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig16.png|533px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig16.png|533px|a) Diagrama configuraciones geométricas de deformaciones para el límite inferior del rango permitido del eje neutro. b) Diagrama de configuraciones geométricas de deformaciones para el límite superior del rango permitido del eje neutro. c) Diagrama de configuraciones geométricas de deformaciones para cualquiera posición del eje neutro entre su rango permitido. Caso 4.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 13:''' | + | | colspan="1" | '''Figura 13:''' a) Diagrama configuraciones geométricas de deformaciones para el límite inferior del rango permitido del eje neutro. b) Diagrama de configuraciones geométricas de deformaciones para el límite superior del rango permitido del eje neutro. c) Diagrama de configuraciones geométricas de deformaciones para cualquiera posición del eje neutro entre su rango permitido. Caso 4. |
|} | |} | ||
| − | |||
Donde: <math>h_{4}=(1-\frac{21}{30}-\frac{d_{1}}{c})c</math> | Donde: <math>h_{4}=(1-\frac{21}{30}-\frac{d_{1}}{c})c</math> | ||
| − | <math | + | <math>\varepsilon=0.003(\frac{d_{2}}{c}-1)</math> Nota: Ver demostración 4.1 en Anexo 1 p. actual |
| − | + | Por lo tanto, para las ecuaciones Ecuación [[#eq-11|11]] y Ecuación [[#eq-12|12]]: | |
| − | + | ||
| − | Por lo tanto, para las ecuaciones | + | |
<math>\varepsilon _{a}=0.0021</math> | <math>\varepsilon _{a}=0.0021</math> | ||
| − | <math | + | <math>\varepsilon _{b}=\varepsilon </math> Entonces las fuerzas y momentos resistentes se calculan como: |
| − | + | ||
| − | Entonces las fuerzas y momentos resistentes se calculan como: | + | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,105: | Line 1,008: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{1}=-2t(0.0021)h_{4}E_{ac} </math> | + | | style="text-align: center;" | <math> F_{1}=-2t(0.0021)h_{4}E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (54) | | style="width: 5px;text-align: right;white-space: nowrap;" | (54) | ||
| Line 1,115: | Line 1,018: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{1}=F_{1}((d_{1}+\frac{1}{2}h_{4})-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{1}=F_{1}((d_{1}+\frac{1}{2}h_{4})-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (55) | | style="width: 5px;text-align: right;white-space: nowrap;" | (55) | ||
| Line 1,125: | Line 1,028: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{2}=-\frac{1}{2}2t(0.0021)(c-d_{1}-h_{4})E_{ac} </math> | + | | style="text-align: center;" | <math> F_{2}=-\frac{1}{2}2t(0.0021)(c-d_{1}-h_{4})E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (56) | | style="width: 5px;text-align: right;white-space: nowrap;" | (56) | ||
| Line 1,135: | Line 1,038: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{2}=F_{2}(\frac{2}{3}(d_{1}+h_{4}+\frac{1}{2}c)-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{2}=F_{2}(\frac{2}{3}(d_{1}+h_{4}+\frac{1}{2}c)-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (57) | | style="width: 5px;text-align: right;white-space: nowrap;" | (57) | ||
| Line 1,145: | Line 1,048: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{3}=\frac{1}{2}2t\varepsilon (d_{2}-c)E_{ac} </math> | + | | style="text-align: center;" | <math> F_{3}=\frac{1}{2}2t\varepsilon (d_{2}-c)E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (58) | | style="width: 5px;text-align: right;white-space: nowrap;" | (58) | ||
| Line 1,155: | Line 1,058: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{3}=F_{3}((\frac{1}{3}c+\frac{2}{3}d_{2})-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{3}=F_{3}((\frac{1}{3}c+\frac{2}{3}d_{2})-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (59) | | style="width: 5px;text-align: right;white-space: nowrap;" | (59) | ||
| Line 1,165: | Line 1,068: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{R}=F_{1}+F_{2}+F_{3}-F_{a}+F_{b} </math> | + | | style="text-align: center;" | <math> F_{R}=F_{1}+F_{2}+F_{3}-F_{a}+F_{b} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (60) | | style="width: 5px;text-align: right;white-space: nowrap;" | (60) | ||
| Line 1,175: | Line 1,078: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{R}=M_{1}+M_{2}+M_{3}-F_{a}(d_{1}-\frac{1}{2}h)+F_{b}(d_{2}-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{R}=M_{1}+M_{2}+M_{3}-F_{a}(d_{1}-\frac{1}{2}h)+F_{b}(d_{2}-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (61) | | style="width: 5px;text-align: right;white-space: nowrap;" | (61) | ||
| Line 1,182: | Line 1,085: | ||
====7.2.8 Caso 5. Se presentan dos bloques rectangulares y uno triangular, todos a compresión.==== | ====7.2.8 Caso 5. Se presentan dos bloques rectangulares y uno triangular, todos a compresión.==== | ||
| − | <math | + | <math>d_{2}<c<=\frac{30}{9}d_{2}</math> Para visualizar este rango hágase referencia a la siguietne figura Figura [[#img-14|14]] y a la demostración que se indíca en la leyenda de la misma figura. <div id='img-14'></div> |
| − | + | ||
| − | Para visualizar este rango hágase referencia a la siguietne figura | + | |
| − | + | ||
| − | <div id='img-14'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig18.png|438px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig18.png|438px|a) Diagrama de configuraciones geométricas de deformaciones en el límite inferior del eje neutro. b) Diagrama de configuraciones geométricas de deformaciones en el límite superior del eje neutro. Caso 5. Dibujo propio. Ver demostración 5.1 en Anexo 1 p. actual]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 14:''' | + | | colspan="1" | '''Figura 14:''' a) Diagrama de configuraciones geométricas de deformaciones en el límite inferior del eje neutro. b) Diagrama de configuraciones geométricas de deformaciones en el límite superior del eje neutro. Caso 5. Dibujo propio. Ver demostración 5.1 en Anexo 1 p. actual |
|} | |} | ||
| − | |||
Donde: <math>h_{5}=\frac{9}{30}c</math> | Donde: <math>h_{5}=\frac{9}{30}c</math> | ||
| − | <math | + | <math>\varepsilon _{3}=0.0021-\frac{0.003}{c}(d_{2}-h_{5})</math> Por lo tanto, para las ecuaciones Ecuación [[#eq-11|11]] y Ecuación [[#eq-12|12]]: |
| − | + | ||
| − | Por lo tanto, para las ecuaciones | + | |
<math>\varepsilon _{a}=0.0021</math> | <math>\varepsilon _{a}=0.0021</math> | ||
| − | <math | + | <math>\varepsilon _{b}=\varepsilon _{3}</math> Y las fuerzas y momentos resutaltantes resistentes se calculan como: |
| − | + | ||
| − | Y las fuerzas y momentos resutaltantes resistentes se calculan como: | + | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,211: | Line 1,105: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{1}=-2t(0.0021)(h_{5}-d_{1})E_{ac} </math> | + | | style="text-align: center;" | <math> F_{1}=-2t(0.0021)(h_{5}-d_{1})E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (62) | | style="width: 5px;text-align: right;white-space: nowrap;" | (62) | ||
| Line 1,221: | Line 1,115: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{1}=F_{1}(\frac{1}{2}(h_{5}+d_{1})-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{1}=F_{1}(\frac{1}{2}(h_{5}+d_{1})-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (63) | | style="width: 5px;text-align: right;white-space: nowrap;" | (63) | ||
| Line 1,231: | Line 1,125: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{2}=-\frac{1}{2}2t(0.0021-\varepsilon _{b})(d_{2}-h_{5})E_{ac} </math> | + | | style="text-align: center;" | <math> F_{2}=-\frac{1}{2}2t(0.0021-\varepsilon _{b})(d_{2}-h_{5})E_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (64) | | style="width: 5px;text-align: right;white-space: nowrap;" | (64) | ||
| Line 1,241: | Line 1,135: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{2}=F_{2}(\frac{2}{3}(h_{5}+\frac{1}{2}d_{2})-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{2}=F_{2}(\frac{2}{3}(h_{5}+\frac{1}{2}d_{2})-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (65) | | style="width: 5px;text-align: right;white-space: nowrap;" | (65) | ||
| Line 1,251: | Line 1,145: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{3}=-\varepsilon _{b}(d_{2}-h_{5})2tE_{ac} </math> | + | | style="text-align: center;" | <math> F_{3}=-\varepsilon _{b}(d_{2}-h_{5})2tE_{ac} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (66) | | style="width: 5px;text-align: right;white-space: nowrap;" | (66) | ||
| Line 1,261: | Line 1,155: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{3}=F_{3}(\frac{1}{2}(d_{2}+h_{5})-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{3}=F_{3}(\frac{1}{2}(d_{2}+h_{5})-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (67) | | style="width: 5px;text-align: right;white-space: nowrap;" | (67) | ||
| Line 1,271: | Line 1,165: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{R}=F_{1}+F_{2}+F_{3}-F_{a}-F_{b} </math> | + | | style="text-align: center;" | <math> F_{R}=F_{1}+F_{2}+F_{3}-F_{a}-F_{b} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (68) | | style="width: 5px;text-align: right;white-space: nowrap;" | (68) | ||
| Line 1,281: | Line 1,175: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{R}=M_{1}+M_{2}+M_{3}-F_{a}(d_{1}-\frac{1}{2}h)-F_{b}(d_{2}-\frac{1}{2}h) </math> | + | | style="text-align: center;" | <math> M_{R}=M_{1}+M_{2}+M_{3}-F_{a}(d_{1}-\frac{1}{2}h)-F_{b}(d_{2}-\frac{1}{2}h) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (69) | | style="width: 5px;text-align: right;white-space: nowrap;" | (69) | ||
| Line 1,288: | Line 1,182: | ||
====7.2.9 Caso 6. Un bloque rectangular de esfuerzos en compresión==== | ====7.2.9 Caso 6. Un bloque rectangular de esfuerzos en compresión==== | ||
| − | <math | + | <math>c>\frac{30}{9}d_{2}</math> <div id='img-15'></div> |
| − | + | ||
| − | <div id='img-15'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig20.png|313px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig20.png|313px|Diagrama de configuraciones geométricas de deformaciones a compresión pura (el eje neutro esta localizado justo en el límite inferior de su rango permitido)). Caso 6. (Dibujo propio.) Ver demostración 6.1 en Anexo 1. actual]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 15:''' | + | | colspan="1" | '''Figura 15:''' Diagrama de configuraciones geométricas de deformaciones a compresión pura (el eje neutro esta localizado justo en el límite inferior de su rango permitido)). Caso 6. (Dibujo propio.) Ver demostración 6.1 en Anexo 1. actual |
|} | |} | ||
| − | + | En este caso la sección resistirá únicamente fuerzas axiales a compresión, y no momentos de flexión, Figura [[#img-15|15]] pues el bloque se esfuerzos que se genera tiene como punto de acción justo el eje de centroide de la sección misma. | |
| − | En este caso la sección resistirá únicamente fuerzas axiales a compresión, y no momentos de flexión, | + | |
Por lo tanto: | Por lo tanto: | ||
| Line 1,307: | Line 1,198: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{1}=-0.0021(d_{2}-d_{1})E_{ac}2t </math> | + | | style="text-align: center;" | <math> F_{1}=-0.0021(d_{2}-d_{1})E_{ac}2t </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (70) | | style="width: 5px;text-align: right;white-space: nowrap;" | (70) | ||
| Line 1,317: | Line 1,208: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{R}=F_{1}-F_{a}-F_{b} </math> | + | | style="text-align: center;" | <math> F_{R}=F_{1}-F_{a}-F_{b} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (71) | | style="width: 5px;text-align: right;white-space: nowrap;" | (71) | ||
| Line 1,327: | Line 1,218: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{R}=0 </math> | + | | style="text-align: center;" | <math> M_{R}=0 </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (72) | | style="width: 5px;text-align: right;white-space: nowrap;" | (72) | ||
| Line 1,334: | Line 1,225: | ||
====7.2.10 Casos de análisis para el concreto==== | ====7.2.10 Casos de análisis para el concreto==== | ||
| − | Lo que se pretende aquí es encontrar el área neta del concreto bajo esfuerzos para cualquier valor en la profundidad del eje neutro | + | Lo que se pretende aquí es encontrar el área neta del concreto bajo esfuerzos para cualquier valor en la profundidad del eje neutro Figura [[#img-17|17]]. Al ser una sección rectangular, el análisis se simplifica a un solo caso, ya que el área variará uniformemente a lo largo de todo el peralte de la sección, ya sea respecto al eje X o Y. A partir de esa área neta se determinará el volumen del bloque de esfuerzos-deformaciones resultante de compresión en unidades de Fuerza, y posteriormente el momento de flexión resultante respecto al eje del centroide de la sección como sigue: |
<div id='img-16'></div> | <div id='img-16'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig21.png|465px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig21.png|465px|Diagrama de bloque equivalente de esuferzos de compresión en el concreto. Dibujo propio.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 16:''' | + | | colspan="1" | '''Figura 16:''' Diagrama de bloque equivalente de esuferzos de compresión en el concreto. Dibujo propio. |
|} | |} | ||
| Line 1,350: | Line 1,241: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>C=-abf{''}c </math> | + | | style="text-align: center;" | <math> C=-abf{''}c </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (73) | | style="width: 5px;text-align: right;white-space: nowrap;" | (73) | ||
| Line 1,361: | Line 1,252: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M_{c}=-C(\frac{h}{2}-\frac{a}{2}) </math> | + | | style="text-align: center;" | <math> M_{c}=-C(\frac{h}{2}-\frac{a}{2}) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (74) | | style="width: 5px;text-align: right;white-space: nowrap;" | (74) | ||
| Line 1,369: | Line 1,260: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig22.png|398px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig22.png|398px|Diagrama tridimensional del bloque equivalente de esfuerzos de compresión en el concreto. Dibujo propio.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 17:''' | + | | colspan="1" | '''Figura 17:''' Diagrama tridimensional del bloque equivalente de esfuerzos de compresión en el concreto. Dibujo propio. |
|} | |} | ||
===7.3 Secciones rectangulares-modelo numérico=== | ===7.3 Secciones rectangulares-modelo numérico=== | ||
| − | Siguiendo la misma idealización del perfil de acero que en el modelo matemático se tiene | + | Siguiendo la misma idealización del perfil de acero que en el modelo matemático se tiene Figura [[#img-18|18]]: <div id='img-18'></div> |
| − | + | ||
| − | <div id='img-18'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-numerico_rec_modelo.png|257px| | + | |[[Image:Draft_Verduzco Martinez_325285613-numerico_rec_modelo.png|257px|Modelo geométrico para la metodología numérica de análisis: Dibujo propio.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 18:''' | + | | colspan="1" | '''Figura 18:''' Modelo geométrico para la metodología numérica de análisis: Dibujo propio. |
|} | |} | ||
| + | Donde: <math>dA_{ac}=dL(t)</math> | ||
| − | + | <math>L=h-2rec</math> | |
| − | <math> | + | <math>dL=\frac{L}{nElementos}</math> |
| − | <math | + | <math>nElementos=</math> Número de elementos |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
====7.3.1 Cálculo de la resistencia del acero==== | ====7.3.1 Cálculo de la resistencia del acero==== | ||
| − | + | Metodología Para la determinación de la resistencia de carga axial y flexión se sigue la siguiente metodología: | |
| − | + | * Determinar la distancia de cada segmento de perfil con respecto a la fibra superior más alejada de la sección transversal del elemento de concreto <math display="inline">d</math>.<p> Para las partes superior e inferior del perfil se tiene: | |
| − | + | ||
| − | * Determinar la distancia de cada segmento de perfil con respecto a la fibra superior más alejada de la sección transversal del elemento de concreto <math display="inline">d</math>.<p> | + | |
| − | + | ||
| − | Para las partes superior e inferior del perfil se tiene: | + | |
<span id="eq-75"></span> | <span id="eq-75"></span> | ||
| Line 1,412: | Line 1,294: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> F_{a}=\varepsilon _{a}E_{ac}t(b-2rec) </math> |
| − | + | ||
| − | F_{a}=\varepsilon _{a}E_{ac}t(b-2rec) </math> | + | |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (75) | | style="width: 5px;text-align: right;white-space: nowrap;" | (75) | ||
| Line 1,425: | Line 1,305: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> F_{b}=\varepsilon _{b}E_{ac}t(b-2rec) </math> |
| − | + | ||
| − | F_{b}=\varepsilon _{b}E_{ac}t(b-2rec) </math> | + | |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (76) | | style="width: 5px;text-align: right;white-space: nowrap;" | (76) | ||
| Line 1,437: | Line 1,315: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> M_{a,b}=F_{a}(d_{1}-\frac{1}{2}h)+F_{b}(d_{2}-\frac{1}{2}h) </math> |
| − | + | ||
| − | M_{a,b}=F_{a}(d_{1}-\frac{1}{2}h)+F_{b}(d_{2}-\frac{1}{2}h) </math> | + | |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (77) | | style="width: 5px;text-align: right;white-space: nowrap;" | (77) | ||
|} | |} | ||
| − | Donde: | + | Donde: <math>\varepsilon _{a}=(1-\frac{d_{1}}{c})(0.003)</math></p><p> <math>\varepsilon _{b}=(\frac{d_{2}}{c}-1)(0.003)</math></p><p> <math>d_{1}=rec+\frac{1}{2}(t)</math></p><p> <math>d_{2}=h-rec-\frac{1}{2}(t)</math> Mientras que para los costados del perfil se tiene: |
| − | + | ||
| − | <math>\varepsilon _{a}=(1-\frac{d_{1}}{c})(0.003)</math> | + | |
| − | + | ||
| − | </p><p> <math | + | |
| − | + | ||
| − | Mientras que para los costados del perfil se tiene: | + | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,457: | Line 1,327: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> F_{R}=2\sum _{i=1}^{nElementos}E_{ac}\varepsilon (dA_{ac}) </math> |
| − | + | ||
| − | F_{R}=2\sum _{i=1}^{nElementos}E_{ac}\varepsilon (dA_{ac}) </math> | + | |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (78) | | style="width: 5px;text-align: right;white-space: nowrap;" | (78) | ||
| Line 1,469: | Line 1,337: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> M_{R}=\sum _{i=1}^{nElementos}-2E_{ac}\varepsilon (dA_{ac})(\frac{1}{2}h-d) </math> |
| − | + | ||
| − | M_{R}=\sum _{i=1}^{nElementos}-2E_{ac}\varepsilon (dA_{ac})(\frac{1}{2}h-d) </math> | + | |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (79) | | style="width: 5px;text-align: right;white-space: nowrap;" | (79) | ||
|} | |} | ||
| − | Donde: | + | Donde: <math>t</math> = Espesor del perfil</p><p> <math>rec</math> = recubrimiento</p><p> <math>h</math> = peralte de la sección</p><p> <math>\varepsilon _{a}=(1-\frac{d}{c})(0.003)</math></p><p> </p> |
| − | + | * A partir de ahí se cálcula <math display="inline">\varepsilon </math> en función de c, cuidando únicamente la siguiente restricción <math display="inline">[-0.0021<\varepsilon <0.0021]</math>.<p> </p> | |
| − | <math>t</math> | + | |
| − | + | ||
| − | = Espesor del perfil</p><p> <math | + | |
| − | + | ||
| − | </p> | + | |
| − | * A partir de ahí se cálcula <math display="inline">\varepsilon </math> en función de | + | |
| − | + | ||
| − | </p> | + | |
* Y finalmente calcular la fuerza y momento resultantes resistentes:<p> | * Y finalmente calcular la fuerza y momento resultantes resistentes:<p> | ||
| Line 1,493: | Line 1,351: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> F_{R}=F_{a}+F_{b}+2\sum _{i=1}^{nElementos}E_{ac}\varepsilon (dA_{ac}) </math> |
| − | + | ||
| − | F_{R}=F_{a}+F_{b}+2\sum _{i=1}^{nElementos}E_{ac}\varepsilon (dA_{ac}) </math> | + | |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (80) | | style="width: 5px;text-align: right;white-space: nowrap;" | (80) | ||
| Line 1,505: | Line 1,361: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> M_{R}=F_{a}(d_{1}-\frac{1}{2}h)+F_{b}(d_{2}-\frac{1}{2}h)+\sum _{i=1}^{nElementos}-2E_{ac}\varepsilon (dA_{ac})(\frac{1}{2}h-d) </math> |
| − | + | ||
| − | M_{R}=F_{a}(d_{1}-\frac{1}{2}h)+F_{b}(d_{2}-\frac{1}{2}h)+\sum _{i=1}^{nElementos}-2E_{ac}\varepsilon (dA_{ac})(\frac{1}{2}h-d) </math> | + | |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (81) | | style="width: 5px;text-align: right;white-space: nowrap;" | (81) | ||
| Line 1,520: | Line 1,374: | ||
==8 Columnas circulares== | ==8 Columnas circulares== | ||
| − | Análogo a la idealización del acero de refuerzo de columnas rectangulares, se ha idealizado el acero de refuerzo en éste tipo de columnas como se muestra en la siguiente figura | + | Análogo a la idealización del acero de refuerzo de columnas rectangulares, se ha idealizado el acero de refuerzo en éste tipo de columnas como se muestra en la siguiente figura Figura [[#img-19|19]]. <div id='img-19'></div> |
| − | + | ||
| − | <div id='img-19'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig23.png|302px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig23.png|302px|Idealización de una sección circular de concreto reforzado. Dibujo propio.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 19:''' | + | | colspan="1" | '''Figura 19:''' Idealización de una sección circular de concreto reforzado. Dibujo propio. |
|} | |} | ||
| − | + | Donde: <math>t</math> = Espesor del perfil | |
| − | Donde: | + | |
| − | + | ||
| − | <math>t</math> = Espesor del perfil | + | |
<math>rec</math> = recubrimiento | <math>rec</math> = recubrimiento | ||
| − | <math>d_{ma}</math> = diámetro de la sección del elemento | + | <math>d_{ma}</math> = diámetro de la sección del elemento Nota: El recubrimiento se mide desde el borde de la sección de la columna al centro del espesor del refuerzo ficticio. |
| − | + | ||
| − | + | ||
A diferencia de la geometría rectangular, para la ciruclar resultó bastante complejo analizar la distribución de esfuerzos mediante el enfoque de análisis planteado originalmente (determinando la geometría de las configuraciones de estados de deformaciones, por lo que simplificó con el siguiente planteamiento: | A diferencia de la geometría rectangular, para la ciruclar resultó bastante complejo analizar la distribución de esfuerzos mediante el enfoque de análisis planteado originalmente (determinando la geometría de las configuraciones de estados de deformaciones, por lo que simplificó con el siguiente planteamiento: | ||
| Line 1,544: | Line 1,391: | ||
===8.1 Cálculo de la resistencia del acero=== | ===8.1 Cálculo de la resistencia del acero=== | ||
| − | Lo que se hará es tratar el perfil de acero como una línea circular y subdividirla en pequeños segmentos con espesor <math>t</math>, | + | Lo que se hará es tratar el perfil de acero como una línea circular y subdividirla en pequeños segmentos con espesor <math>t</math>, Figura [[#img-20|20]], aunque en realidad cada segmento se tratará como un punto al que le corresponderá una cierta condición de esfuerzos dependiendo de su ubicación en el plano cartesiano de referencia y del caso del cual se trate. <div id='img-20'></div> |
| − | + | ||
| − | <div id='img-20'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig27.png|499px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig27.png|499px|Esquema de análisis para las condiciones de esfuerzos en el acero de refuerzo. Dibujo propio.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 20:''' | + | | colspan="1" | '''Figura 20:''' Esquema de análisis para las condiciones de esfuerzos en el acero de refuerzo. Dibujo propio. |
|} | |} | ||
| + | Donde: <math>dA_{ac}=dL(t)</math> | ||
| − | + | <math>L=\Pi (d_{ma}-2rec)</math> | |
| − | + | ||
| − | <math | + | |
| − | + | ||
| − | + | ||
| − | <math | + | <math>dL=\frac{L}{n}</math> |
| − | <math | + | <math>n=</math> Número de elementos |
====8.1.1 Metodología==== | ====8.1.1 Metodología==== | ||
| Line 1,568: | Line 1,410: | ||
Para la determinación de la resistencia de carga axial y flexión se sigue la siguiente metodología: | Para la determinación de la resistencia de carga axial y flexión se sigue la siguiente metodología: | ||
| − | * Determinar la distancia de cada segmento de perfil con respecto a la fibra más alejada de la sección transversal del elemento de concreto <math display="inline">d</math>.<p> | + | * Determinar la distancia de cada segmento de perfil con respecto a la fibra más alejada de la sección transversal del elemento de concreto <math display="inline">d</math>.<p> </p> |
| − | + | * A partir de ahí se cálcula <math display="inline">\varepsilon </math> en función de c, cuidando únicamente la siguiente restricción <math display="inline">[-0.0021<\varepsilon <0.0021]</math>.<p> </p> | |
| − | </p> | + | |
| − | * A partir de ahí se cálcula <math display="inline">\varepsilon </math> en función de | + | |
| − | + | ||
| − | </p> | + | |
* Y finalmente calcular la fuerza y momento resultantes resistentes:<p> | * Y finalmente calcular la fuerza y momento resultantes resistentes:<p> | ||
| Line 1,581: | Line 1,419: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> F_{R}=\sum _{i=1}^{nElementos}E_{ac}\varepsilon (dA_{ac}) </math> |
| − | + | ||
| − | F_{R}=\sum _{i=1}^{nElementos}E_{ac}\varepsilon (dA_{ac}) </math> | + | |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (82) | | style="width: 5px;text-align: right;white-space: nowrap;" | (82) | ||
| Line 1,593: | Line 1,429: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> M_{R}=\sum _{i=1}^{nElementos}-E_{ac}\varepsilon (dA_{ac})(\frac{1}{2}d_{ma}-d) </math> |
| − | + | ||
| − | M_{R}=\sum _{i=1}^{nElementos}-E_{ac}\varepsilon (dA_{ac})(\frac{1}{2}d_{ma}-d) </math> | + | |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (83) | | style="width: 5px;text-align: right;white-space: nowrap;" | (83) | ||
| Line 1,606: | Line 1,440: | ||
A diferencia de las columnas de sección rectangular, en las circulares el diferencial de área al cambiar el eje neutro no será uniforme. | A diferencia de las columnas de sección rectangular, en las circulares el diferencial de área al cambiar el eje neutro no será uniforme. | ||
| − | También podremos transformar ésta área de compresión en un bloque equivalente de esfuerzos, y para poder hacer ésto será necesario cálcular el centroide del área real de compresión en cada posición del eje neutro y a partir de ahí calcular el momento de flexión resistente de la sección. | + | También podremos transformar ésta área de compresión en un bloque equivalente de esfuerzos, y para poder hacer ésto será necesario cálcular el centroide del área real de compresión en cada posición del eje neutro y a partir de ahí calcular el momento de flexión resistente de la sección. Figura [[#img-21|21]]. <div id='img-21'></div> |
| − | + | ||
| − | <div id='img-21'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig47.png|539px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig47.png|539px|Diagrama de distribución de esfuerzos para el concreto. Dibujo propio.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 21:''' | + | | colspan="1" | '''Figura 21:''' Diagrama de distribución de esfuerzos para el concreto. Dibujo propio. |
|} | |} | ||
| − | |||
Donde: <math>a=\beta (c)</math> | Donde: <math>a=\beta (c)</math> | ||
| − | <math | + | <math>f{''}_{c}=F_{R}(0.85)f^{'}c</math> Para calcular ésta fuerza de compresión tomaremos el siguiente sistema de referencia: Figura [[#img-22|22]], para definir integrales para calcular el área efectiva de compresión del concreto en cualquier posición del eje neutro. <div id='img-22'></div> |
| − | + | ||
| − | Para calcular ésta fuerza de compresión tomaremos el siguiente sistema de referencia: | + | |
| − | + | ||
| − | <div id='img-22'></div> | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig48.png|567px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig48.png|567px|Sistema de referencia cartesiano para el análisis de la distribución de esfuerzos de compresión en el concreto. Dibujo propio.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 22:''' | + | | colspan="1" | '''Figura 22:''' Sistema de referencia cartesiano para el análisis de la distribución de esfuerzos de compresión en el concreto. Dibujo propio. |
|} | |} | ||
| − | |||
Subdividiremos el análisis en dos casos para simplificación: | Subdividiremos el análisis en dos casos para simplificación: | ||
| − | + | Cuando <math>a<\frac{1}{2}d_{ma}</math> | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,639: | Line 1,465: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{co}=f{''}c \int _{-z(y_{co}=a)}^{z(y_{co}=a)}(a-y_{co})\mathrm{d}z </math> | + | | style="text-align: center;" | <math> F_{co}=f{''}c \int _{-z(y_{co}=a)}^{z(y_{co}=a)}(a-y_{co})\mathrm{d}z </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (84) | | style="width: 5px;text-align: right;white-space: nowrap;" | (84) | ||
| Line 1,649: | Line 1,475: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{co}\cdot Y_{co}=f{''}c \int _{-z(y_{co}=a)}^{z(y_{co}=a)}(a-y_{co})... | + | | style="text-align: center;" | <math>\begin{array}{l} F_{co}\cdot Y_{co}=f{''}c \int _{-z(y_{co}=a)}^{z(y_{co}=a)}(a-y_{co})...\\ (\frac{1}{2}d_{ma}-\frac{1}{2}(a+y_{co})))\mathrm{d}z \end{array}</math> |
| − | + | ||
| − | + | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (85) | | style="width: 5px;text-align: right;white-space: nowrap;" | (85) | ||
|} | |} | ||
| − | + | Cuando <math>a>=\frac{1}{2}d_{ma}</math> | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,663: | Line 1,487: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{co}=f{''}c (\Pi (\frac{1}{2}d_{ma})^{2}-... | + | | style="text-align: center;" | <math>\begin{array}{l} F_{co}=f{''}c (\Pi (\frac{1}{2}d_{ma})^{2}-...\\ ...-\int _{-z(y_{co}=d_{ma}-a)}^{z(y_{co}=d_{ma}-a)}((d_{ma}-a)-y_{co})\mathrm{d}z) \end{array}</math> |
| − | + | ||
| − | + | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (86) | | style="width: 5px;text-align: right;white-space: nowrap;" | (86) | ||
| Line 1,675: | Line 1,497: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>F_{co}\cdot Y_{co}=f{''}c (-\int _{-z(y_{co}=d_{ma}-a)}^{z(y_{co}=d_{ma}-a)}((d_{ma}-... | + | | style="text-align: center;" | <math>\begin{array}{l} F_{co}\cdot Y_{co}=f{''}c (-\int _{-z(y_{co}=d_{ma}-a)}^{z(y_{co}=d_{ma}-a)}((d_{ma}-...\\ ...-a)-y_{co})(-(\frac{1}{2}d_{ma}-...\\ ...-\frac{1}{2}(d_{ma}-a-y_{co}))\mathrm{d}z) \end{array}</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (87) | | style="width: 5px;text-align: right;white-space: nowrap;" | (87) | ||
| Line 1,694: | Line 1,512: | ||
Se establece un cierto número de puntos para determinar los diagramas de interacción, determinado los valores <math>P_{ot}</math>, <math>P_{oc}</math> como los límites del rango de las fuerzas del diagrama de interacción, pudiendo extraer una fuerza respectiva a cada punto del mismo que tendrá el papel de raíz en el método numérico a emplear para el cálculo de su respectivo momento resistente. | Se establece un cierto número de puntos para determinar los diagramas de interacción, determinado los valores <math>P_{ot}</math>, <math>P_{oc}</math> como los límites del rango de las fuerzas del diagrama de interacción, pudiendo extraer una fuerza respectiva a cada punto del mismo que tendrá el papel de raíz en el método numérico a emplear para el cálculo de su respectivo momento resistente. | ||
| − | El método numérico empleado para la aproximación de ráices es el llamado ''Método de la | + | El método numérico empleado para la aproximación de ráices es el llamado ''Método de la Falsa posición. Anexo 3 p. actual |
===10.1 Cálculo de la eficiencia mecánica-estructural=== | ===10.1 Cálculo de la eficiencia mecánica-estructural=== | ||
| Line 1,700: | Line 1,518: | ||
Para cada condición de fuerza actuante en la columna se determinará la respectiva eficiencia estructural que hay entre ésta condición y la resistencia que el diagrama de interacción índica. | Para cada condición de fuerza actuante en la columna se determinará la respectiva eficiencia estructural que hay entre ésta condición y la resistencia que el diagrama de interacción índica. | ||
| − | La diferencia en el cálculo de éstas eficiencias en columnas circulares y rectangulares es que en las rectangulares se deberán extraer de los diagramas de interacción calculados en el sentido de <math>x</math> y <math>y</math> la carga resistente y el momento resistente (<math>M_{rx}, M_{ry}, P_{rx}, P_{ry}</math> | + | La diferencia en el cálculo de éstas eficiencias en columnas circulares y rectangulares es que en las rectangulares se deberán extraer de los diagramas de interacción calculados en el sentido de <math>x</math> y <math>y</math> la carga resistente y el momento resistente (<math>M_{rx}, M_{ry}, P_{rx}, P_{ry}</math> [p. actual]), y para las circulares al ser su sección simétrica respecto a cualquier eje, se calculará la eficiencia respecto a una sola dirección, extrayendo la carga resistente y el momento resistente (<math>M_{r}, P_{r}</math>) del diagrama de interacción calculado. |
| − | Para lo anterior se empleará geometría analítica con el sistema cartesiano de los propios diagramas de interacción | + | Para lo anterior se empleará geometría analítica con el sistema cartesiano de los propios diagramas de interacción Figura [[#img-23|23]] calculando el punto de intersección entre dos rectas imaginarias A y B, tal que A partirá del origen pasando por alguna condición de fuerza actuante prolongándose hasta el borde del diagrama de interacción, y B será tal que una el punto anterior <math>(M_{i}, P_{i})</math> y posterior <math>(M_{i+1}, P_{i+1})</math> del punto en el cual la recta A intersecta al diagrama de interacción. <div id='img-23'></div> |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-diagintreferencia.png|375px| | + | |[[Image:Draft_Verduzco Martinez_325285613-diagintreferencia.png|375px|Diagrama de interacción en el plano cartesiano de referencia para el programa.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 23:''' | + | | colspan="1" | '''Figura 23:''' Diagrama de interacción en el plano cartesiano de referencia para el programa. |
|} | |} | ||
De modo que el cálculo del momento resistente para una respectiva condición se cálcula como: | De modo que el cálculo del momento resistente para una respectiva condición se cálcula como: | ||
| Line 1,741: | Line 1,559: | ||
===10.2 Cálculo de área requerida de acero=== | ===10.2 Cálculo de área requerida de acero=== | ||
| − | Ya determinada la eficiencia mecánica estructural para cada condición de carga actuante se determinará a continuación la más crítica, y a partir de ésta se cálculará el espesor del perfil de acero simplemente iterando el valor de <math>t</math> con un cierto incremento <math>dt</math>, hasta llegar a un rango de eficiencia crítica requerida, establecida a priori, pues está será la eficiencia que nos servirá de comparación para seguir iterando o no. | + | Ya determinada la eficiencia mecánica estructural para cada condición de carga actuante se determinará a continuación la más crítica, y a partir de ésta se cálculará el espesor del perfil de acero simplemente iterando el valor de <math>t</math> con un cierto incremento <math>dt</math>, hasta llegar a un rango de eficiencia crítica requerida, establecida a priori, pues está será la eficiencia que nos servirá de comparación para seguir iterando o no. Figura [ [[#img-24|24]]] |
<div id='img-24'></div> | <div id='img-24'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-condcritica.png|359px| | + | |[[Image:Draft_Verduzco Martinez_325285613-condcritica.png|359px|Condición de carga crítica de diseño.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 24:''' | + | | colspan="1" | '''Figura 24:''' Condición de carga crítica de diseño. |
|} | |} | ||
==11 Determinación del acero de refuerzo== | ==11 Determinación del acero de refuerzo== | ||
| − | Una vez que se ha determinado el área de acero a emplear para que se alcance la eficiencia deseada, se debe transformar esa área ficticia de acero en varillas corrugadas, distribuyéndolas uniformemente en la sección (obedeciendo las hipótesis de diseño de la | + | Una vez que se ha determinado el área de acero a emplear para que se alcance la eficiencia deseada, se debe transformar esa área ficticia de acero en varillas corrugadas, distribuyéndolas uniformemente en la sección (obedeciendo las hipótesis de diseño de la Sección [[#6.3.2 Flexo-compresión|6.3.2]]), por lo que sólo se admitirán números pares de varillas. |
El programa genera un arreglo matricial de propuestas de número de varillas, desde 4 (para columnas rectangulares) o 6 (para columnas circulares), calculando para cada diámetro el número de varillas requeridas, tomando como referencia los tipos de varillas disponibles comercialmente. | El programa genera un arreglo matricial de propuestas de número de varillas, desde 4 (para columnas rectangulares) o 6 (para columnas circulares), calculando para cada diámetro el número de varillas requeridas, tomando como referencia los tipos de varillas disponibles comercialmente. | ||
| Line 1,759: | Line 1,577: | ||
El usuario podrá elegir no sólo el diámetro del acero de refuerzo, sino también la distribución de éstas en la sección (solo para las columnas rectangulares, ya que para circulares la distribución es simétrica respecto a cualquier eje de simetría), de manera que siempre se respete la separación mínima o distancia libre entre varillas <math>S_{min}=\frac{3}{2}TMA</math>. Aunque por defecto lo que usualmente se busca es la opción que resulte la más eficiente o la más económica. De manera que el usuario también podrá elegir que criterio es el más conveniente. | El usuario podrá elegir no sólo el diámetro del acero de refuerzo, sino también la distribución de éstas en la sección (solo para las columnas rectangulares, ya que para circulares la distribución es simétrica respecto a cualquier eje de simetría), de manera que siempre se respete la separación mínima o distancia libre entre varillas <math>S_{min}=\frac{3}{2}TMA</math>. Aunque por defecto lo que usualmente se busca es la opción que resulte la más eficiente o la más económica. De manera que el usuario también podrá elegir que criterio es el más conveniente. | ||
| − | Cabe mencionar que la distribución del acero de refuerzo tiene influencia en la eficiencia mecánica de los elementos, y para cada opción de número de varillas/diámetro le corresponderá un buen número de configuraciones de éstas en las sección, por lo que el programa hará también un análisis de eficiencia de cada opción disponible, pero ahora tratando al acero de refuerzo precisamente como varillas de acero, para verificar cuáles cumplen con el rango requerido de eficiencia que se establecio a priori, una vez hecho esto, el programa seleccionará la opción más eficiente. | + | Cabe mencionar que la distribución del acero de refuerzo tiene influencia en la eficiencia mecánica de los elementos, y para cada opción de número de varillas/diámetro le corresponderá un buen número de configuraciones de éstas en las sección, por lo que el programa hará también un análisis de eficiencia de cada opción disponible, pero ahora tratando al acero de refuerzo precisamente como varillas de acero, para verificar cuáles cumplen con el rango requerido de eficiencia que se establecio a priori, una vez hecho esto, el programa seleccionará la opción más eficiente. </span> |
{| class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;" | {| class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;" | ||
|+ style="font-size: 75%;" |<span id='table-1'></span>Tabla. 1 Tabla de tipos de varillas comerciales en México | |+ style="font-size: 75%;" |<span id='table-1'></span>Tabla. 1 Tabla de tipos de varillas comerciales en México | ||
| Line 1,809: | Line 1,627: | ||
|} | |} | ||
| + | <span style="text-align: center; font-size: 75%;"> | ||
==12 Diseño de experimento== | ==12 Diseño de experimento== | ||
| Line 1,820: | Line 1,639: | ||
====12.1.1 Datos de entrada==== | ====12.1.1 Datos de entrada==== | ||
| − | + | </span> | |
{| class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;" | {| class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;" | ||
|+ style="font-size: 75%;" |<span id='table-2'></span>Tabla. 2 Datos de entrada para el diseño de acero de refuerzo en columnas rectangulares | |+ style="font-size: 75%;" |<span id='table-2'></span>Tabla. 2 Datos de entrada para el diseño de acero de refuerzo en columnas rectangulares | ||
| Line 1,840: | Line 1,659: | ||
|} | |} | ||
| − | Con las siguientes combinaciones de carga para ambas estructuras: | + | <span style="text-align: center; font-size: 75%;"> Con las siguientes combinaciones de carga para ambas estructuras: |
| − | + | ||
| + | </span> | ||
{| class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;" | {| class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;" | ||
|+ style="font-size: 75%;" |<span id='table-3'></span>Tabla. 3 Combinaciones de carga resultantes de un análisis estructural previo para ambos modelos estructurales. | |+ style="font-size: 75%;" |<span id='table-3'></span>Tabla. 3 Combinaciones de carga resultantes de un análisis estructural previo para ambos modelos estructurales. | ||
| Line 1,871: | Line 1,690: | ||
|} | |} | ||
| + | <span style="text-align: center; font-size: 75%;"> | ||
====12.1.2 Resultados==== | ====12.1.2 Resultados==== | ||
| Line 1,876: | Line 1,696: | ||
Una vez hecho el análisis de resistencia con las cargas y datos dados se obtienen los siguientes diagramas de interacción, tabla de eficiencias estructurales para cada modelo estructural con los grosores resultantes del perfil idealizado de acero, distribución óptima en costo y eficiencia de varillas de acero en cada modelo estructural y sus respectivas tablas de eficiencia con dicha opción de varillado: | Una vez hecho el análisis de resistencia con las cargas y datos dados se obtienen los siguientes diagramas de interacción, tabla de eficiencias estructurales para cada modelo estructural con los grosores resultantes del perfil idealizado de acero, distribución óptima en costo y eficiencia de varillas de acero en cada modelo estructural y sus respectivas tablas de eficiencia con dicha opción de varillado: | ||
| − | + | Eficiencia estructural con espesores de perfiles idealizados de acero resultantes: | |
<div id='img-25'></div> | <div id='img-25'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-ef_tabla_t_colrec01.png|375px| | + | |[[Image:Draft_Verduzco Martinez_325285613-ef_tabla_t_colrec01.png|375px|Tabla de eficiencias con espesor de perfil (t) resultante-Modelo estructural 01.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 25:''' | + | | colspan="1" | '''Figura 25:''' Tabla de eficiencias con espesor de perfil (t) resultante-Modelo estructural 01. |
|} | |} | ||
<div id='img-26'></div> | <div id='img-26'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-ef_tabla_t_colrec02.png|384px| | + | |[[Image:Draft_Verduzco Martinez_325285613-ef_tabla_t_colrec02.png|384px|Tabla de eficiencias con espesor de perfil (t) resultante-Modelo estructural 02.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 26:''' | + | | colspan="1" | '''Figura 26:''' Tabla de eficiencias con espesor de perfil (t) resultante-Modelo estructural 02. |
|} | |} | ||
| − | + | Diagramas de interacción con espesor de perfil (t) resultante para cada modelo: | |
| − | + | Nota:Los puntos rojos representan las condiciones de carga en ese sentido. <div id='img-27'></div> | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-diagIntPerfilX_rec_col01.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-diagIntPerfilX_rec_col01.png|525px|Diagrama de interacción en X con espesor de perfil (t) resultante-Modelo estructural 01.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 27:''' | + | | colspan="1" | '''Figura 27:''' Diagrama de interacción en X con espesor de perfil (t) resultante-Modelo estructural 01. |
|} | |} | ||
<div id='img-28'></div> | <div id='img-28'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-diagIntPerfilY_rec_col01.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-diagIntPerfilY_rec_col01.png|525px|Diagrama de interacción en Y con espesor de perfil (t) resultante-Modelo estructural 01.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 28:''' | + | | colspan="1" | '''Figura 28:''' Diagrama de interacción en Y con espesor de perfil (t) resultante-Modelo estructural 01. |
|} | |} | ||
<div id='img-29'></div> | <div id='img-29'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-diagIntPerfilX_rec_col02.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-diagIntPerfilX_rec_col02.png|525px|Diagrama de interacción en X con espesor de perfil (t) resultante-Modelo estructural 02.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 29:''' | + | | colspan="1" | '''Figura 29:''' Diagrama de interacción en X con espesor de perfil (t) resultante-Modelo estructural 02. |
|} | |} | ||
<div id='img-30'></div> | <div id='img-30'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-diagIntPerfilY_rec_col02.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-diagIntPerfilY_rec_col02.png|525px|Diagrama de interacción en Y con espesor de perfil (t) resultante-Modelo estructural 02.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 30:''' | + | | colspan="1" | '''Figura 30:''' Diagrama de interacción en Y con espesor de perfil (t) resultante-Modelo estructural 02. |
|} | |} | ||
| − | + | Opciones de distribución de varillas disponibles resultantes: | |
<div id='img-31'></div> | <div id='img-31'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-opciones_var_rec_01.png|288px| | + | |[[Image:Draft_Verduzco Martinez_325285613-opciones_var_rec_01.png|288px|Tabla de opciones disponibles de varillado-Modelo 01.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 31:''' | + | | colspan="1" | '''Figura 31:''' Tabla de opciones disponibles de varillado-Modelo 01. |
|} | |} | ||
<div id='img-32'></div> | <div id='img-32'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-opciones_var_rec_02.png|292px| | + | |[[Image:Draft_Verduzco Martinez_325285613-opciones_var_rec_02.png|292px|Tabla de opciones disponibles de varillado-Modelo 02.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 32:''' | + | | colspan="1" | '''Figura 32:''' Tabla de opciones disponibles de varillado-Modelo 02. |
|} | |} | ||
| − | + | Distribución de varillado óptima en costo y eficiencia | |
<div id='img-33'></div> | <div id='img-33'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-seccion_col01_rec.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-seccion_col01_rec.png|525px|Distribución de opción óptima de varillado en costo y eficiencia estructural correspondiente a la opción 3 Tabla [[#img-31|31]]-Modelo 01]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 33:''' | + | | colspan="1" | '''Figura 33:''' Distribución de opción óptima de varillado en costo y eficiencia estructural correspondiente a la opción 3 Tabla [[#img-31|31]]-Modelo 01 |
|} | |} | ||
<div id='img-34'></div> | <div id='img-34'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-seccion_rec_col02.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-seccion_rec_col02.png|525px|Distribución de opción óptima de varillado en costo y eficiencia estructural correspondiente a la opción 1 Tabla [[#img-32|32]]-Modelo 02]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 34:''' | + | | colspan="1" | '''Figura 34:''' Distribución de opción óptima de varillado en costo y eficiencia estructural correspondiente a la opción 1 Tabla [[#img-32|32]]-Modelo 02 |
|} | |} | ||
Tomando como referencia las distribuciones de varillas en la sección para cada modelo con las tablas de opciones disponibles de varillado, se puede notar que el programa al tomar la opción más económica, hace la selección tomando en cuenta también la mejor eficiencia estructural, que aunque no es la más eficiente de manera absoluta, si lo es con respecto al costo más bajo, ya que se pueden presentar mismos costos óptimos con diferentes eficiencias estrucrales. | Tomando como referencia las distribuciones de varillas en la sección para cada modelo con las tablas de opciones disponibles de varillado, se puede notar que el programa al tomar la opción más económica, hace la selección tomando en cuenta también la mejor eficiencia estructural, que aunque no es la más eficiente de manera absoluta, si lo es con respecto al costo más bajo, ya que se pueden presentar mismos costos óptimos con diferentes eficiencias estrucrales. | ||
| − | + | Diagramas de interacción para las opciones de varillado óptimas en costo para cada modelo estructural: | |
<div id='img-35'></div> | <div id='img-35'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-diagIntVarX_rec_col01.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-diagIntVarX_rec_col01.png|525px|Diagrama de interacción en X con varillas resultantes-Modelo estructural 01.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 35:''' | + | | colspan="1" | '''Figura 35:''' Diagrama de interacción en X con varillas resultantes-Modelo estructural 01. |
|} | |} | ||
<div id='img-36'></div> | <div id='img-36'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-diagIntVarY_rec_col01.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-diagIntVarY_rec_col01.png|525px|Diagrama de interacción en Y con varillas resultantes-Modelo estructural 01.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 36:''' | + | | colspan="1" | '''Figura 36:''' Diagrama de interacción en Y con varillas resultantes-Modelo estructural 01. |
|} | |} | ||
<div id='img-37'></div> | <div id='img-37'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-diagIntVarX_rec_col02.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-diagIntVarX_rec_col02.png|525px|Diagrama de interacción en X con varillas resultantes-Modelo estructural 02.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 37:''' | + | | colspan="1" | '''Figura 37:''' Diagrama de interacción en X con varillas resultantes-Modelo estructural 02. |
|} | |} | ||
<div id='img-38'></div> | <div id='img-38'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-diagIntVarY_rec_col02.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-diagIntVarY_rec_col02.png|525px|Diagrama de interacción en X con varillas resultantes-Modelo estructural 02.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 38:''' | + | | colspan="1" | '''Figura 38:''' Diagrama de interacción en X con varillas resultantes-Modelo estructural 02. |
|} | |} | ||
| Line 1,991: | Line 1,811: | ||
====12.2.1 Datos de entrada==== | ====12.2.1 Datos de entrada==== | ||
| − | + | </span> | |
{| class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;" | {| class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;" | ||
|+ style="font-size: 75%;" |<span id='table-4'></span>Tabla. 4 Datos de entrada para el diseño de acero de refuerzo en columnas circulares | |+ style="font-size: 75%;" |<span id='table-4'></span>Tabla. 4 Datos de entrada para el diseño de acero de refuerzo en columnas circulares | ||
| Line 2,008: | Line 1,828: | ||
|} | |} | ||
| − | Con las siguientes combinaciones de carga para ambas estructuras: | + | <span style="text-align: center; font-size: 75%;"> Con las siguientes combinaciones de carga para ambas estructuras: |
| − | + | ||
| + | </span> | ||
{| class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;" | {| class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;" | ||
|+ style="font-size: 75%;" |<span id='table-5'></span>Tabla. 5 Combinaciones de carga resultantes de un análisis estructural previo para ambos modelos estructurales. | |+ style="font-size: 75%;" |<span id='table-5'></span>Tabla. 5 Combinaciones de carga resultantes de un análisis estructural previo para ambos modelos estructurales. | ||
| Line 2,033: | Line 1,853: | ||
|} | |} | ||
| + | <span style="text-align: center; font-size: 75%;"> | ||
====12.2.2 Resultados==== | ====12.2.2 Resultados==== | ||
| Line 2,038: | Line 1,859: | ||
Una vez hecho el análisis de resistencia con las cargas y datos dados se obtienen los siguientes diagramas de interacción, tabla de eficiencias estructurales para cada modelo estructural con los grosores resultantes del perfil idealizado de acero, distribución óptima en costo y eficiencia de varillas de acero en cada modelo estructural y sus respectivas tablas de eficiencia con dicha opción de varillado: | Una vez hecho el análisis de resistencia con las cargas y datos dados se obtienen los siguientes diagramas de interacción, tabla de eficiencias estructurales para cada modelo estructural con los grosores resultantes del perfil idealizado de acero, distribución óptima en costo y eficiencia de varillas de acero en cada modelo estructural y sus respectivas tablas de eficiencia con dicha opción de varillado: | ||
| − | + | Eficiencia estructural con espesores de perfiles idealizados de acero resultantes: | |
<div id='img-39'></div> | <div id='img-39'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-ef_cir_01_perfil.png|237px| | + | |[[Image:Draft_Verduzco Martinez_325285613-ef_cir_01_perfil.png|237px|Tabla de eficiencias con espesor de perfil (t) resultante-Modelo estructural 01.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 39:''' | + | | colspan="1" | '''Figura 39:''' Tabla de eficiencias con espesor de perfil (t) resultante-Modelo estructural 01. |
|} | |} | ||
<div id='img-40'></div> | <div id='img-40'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-ef_cir_02_perfil.png|237px| | + | |[[Image:Draft_Verduzco Martinez_325285613-ef_cir_02_perfil.png|237px|Tabla de eficiencias con espesor de perfil (t) resultante-Modelo estructural 02.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 40:''' | + | | colspan="1" | '''Figura 40:''' Tabla de eficiencias con espesor de perfil (t) resultante-Modelo estructural 02. |
|} | |} | ||
| − | + | Diagramas de interacción con espesor de perfil (t) resultante para cada modelo: | |
<div id='img-41'></div> | <div id='img-41'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-diagIntPerfil_cir01.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-diagIntPerfil_cir01.png|525px|Diagrama de interacción con espesor de perfil (t) resultante-Modelo estructural 01.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 41:''' | + | | colspan="1" | '''Figura 41:''' Diagrama de interacción con espesor de perfil (t) resultante-Modelo estructural 01. |
|} | |} | ||
<div id='img-42'></div> | <div id='img-42'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-diagIntPerfil_cir02.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-diagIntPerfil_cir02.png|525px|Diagrama de interacción con espesor de perfil (t) resultante-Modelo estructural 02.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 42:''' | + | | colspan="1" | '''Figura 42:''' Diagrama de interacción con espesor de perfil (t) resultante-Modelo estructural 02. |
|} | |} | ||
| − | + | Opciones de distribución de varillas disponibles resultantes: | |
<div id='img-43'></div> | <div id='img-43'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-ef_opc_cir_01.png|196px| | + | |[[Image:Draft_Verduzco Martinez_325285613-ef_opc_cir_01.png|196px|Tabla de opciones disponibles de varillado-Modelo 01.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 43:''' | + | | colspan="1" | '''Figura 43:''' Tabla de opciones disponibles de varillado-Modelo 01. |
|} | |} | ||
<div id='img-44'></div> | <div id='img-44'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-ef_opc_cir_02.png|198px| | + | |[[Image:Draft_Verduzco Martinez_325285613-ef_opc_cir_02.png|198px|Tabla de opciones disponibles de varillado-Modelo 02.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 44:''' | + | | colspan="1" | '''Figura 44:''' Tabla de opciones disponibles de varillado-Modelo 02. |
|} | |} | ||
| − | + | Distribución de varillado óptima en costo y eficiencia | |
<div id='img-45'></div> | <div id='img-45'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-seccion_cir01.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-seccion_cir01.png|525px|Distribución de opción óptima de varillado en costo y eficiencia estructural correspondiente a la opción 2 Tabla [[#img-43|43]]-Modelo 01]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 45:''' | + | | colspan="1" | '''Figura 45:''' Distribución de opción óptima de varillado en costo y eficiencia estructural correspondiente a la opción 2 Tabla [[#img-43|43]]-Modelo 01 |
|} | |} | ||
<div id='img-46'></div> | <div id='img-46'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-seccion_cir02.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-seccion_cir02.png|525px|Distribución de opción óptima de varillado en costo y eficiencia estructural correspondiente a la opción 1 Tabla [[#img-44|44]]-Modelo 02]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 46:''' | + | | colspan="1" | '''Figura 46:''' Distribución de opción óptima de varillado en costo y eficiencia estructural correspondiente a la opción 1 Tabla [[#img-44|44]]-Modelo 02 |
|} | |} | ||
| − | + | Diagramas de interacción para las opciones de varillado óptimas en costo para cada modelo estructural: | |
<div id='img-47'></div> | <div id='img-47'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-diagIntVar_cir01.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-diagIntVar_cir01.png|525px|Diagrama de interacción con varillas resultantes-Modelo estructural 01.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 47:''' | + | | colspan="1" | '''Figura 47:''' Diagrama de interacción con varillas resultantes-Modelo estructural 01. |
|} | |} | ||
<div id='img-48'></div> | <div id='img-48'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-diagIntVar_cir02.png|525px| | + | |[[Image:Draft_Verduzco Martinez_325285613-diagIntVar_cir02.png|525px|Diagrama de interacción con varillas resultantes-Modelo estructural 02.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 48:''' | + | | colspan="1" | '''Figura 48:''' Diagrama de interacción con varillas resultantes-Modelo estructural 02. |
|} | |} | ||
==13 Discusión y conclusiones== | ==13 Discusión y conclusiones== | ||
| − | El método aparte de ser muy fácil de programar en una computadora ofrece una nueva forma para analizar y diseñar estructuras de concreto reforzado. Sin duda que aún queda mucho por desarrollar y este puede | + | El método aparte de ser muy fácil de programar en una computadora ofrece una nueva forma para analizar y diseñar estructuras de concreto reforzado. Sin duda que aún queda mucho por desarrollar y este puede es el comienzo de nuevas investigaciones en material de optimización de estrucruras de concreto, ya que como tal este método también se implementó en le presente trabajo una optimización, aunque con un método muy sencillo de búsqueda, más sin embargo los resultados obtenidos son los óptimos de acuerdo a los requerimientos de diseño. |
==14 Agradecimientos== | ==14 Agradecimientos== | ||
| − | Agradezco a la Universidad de Guanajuato, mi casa de estudios, por esta oportunidad, así como especial agradecimiento al Aula CIMNE-UG, que representó para mi un espacio de ideas y centro de exploración organizacional. A mi director de tesis el Dr. Alejandro Hernández Martínez y a mi tutor proyectos en el Aula CIMNE a la cual también dicho trabajo forma parte, el MC. Humberto Esqueda Oliva, pues | + | Agradezco a la Universidad de Guanajuato, mi casa de estudios, por esta oportunidad, así como especial agradecimiento al Aula CIMNE-UG, que representó para mi un espacio de ideas y centro de exploración organizacional. A mi director de tesis el Dr. Alejandro Hernández Martínez y a mi tutor proyectos en el Aula CIMNE a la cual también dicho trabajo forma parte, el MC. Humberto Esqueda Oliva, pues con el Aula CIMNE se desarrolló el programa computacional como tal en lenguaje C principalmente con MatLab para la parte gráfica, y para la parametrización visual de los elementos estructurales y su acero de refuerzo. |
==15 Anexo 1. Demostraciones de las variables envueltas en los casos de análisis de columnas rectangulares== | ==15 Anexo 1. Demostraciones de las variables envueltas en los casos de análisis de columnas rectangulares== | ||
| Line 2,134: | Line 1,955: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig49.png|332px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig49.png|332px|Demostración 1.1 para el caso 1 de columnas rectangulares.Dibujo propio.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 49:''' | + | | colspan="1" | '''Figura 49:''' Demostración 1.1 para el caso 1 de columnas rectangulares.Dibujo propio. |
|} | |} | ||
Por relación de triángulos: | Por relación de triángulos: | ||
| Line 2,149: | Line 1,970: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig50.png|395px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig50.png|395px|Demostración 2.1 para el Caso 2 de columnas rectangulares]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 50:''' | + | | colspan="1" | '''Figura 50:''' Demostración 2.1 para el Caso 2 de columnas rectangulares |
|} | |} | ||
<math>s=h_{3}+c-d_{1}</math> | <math>s=h_{3}+c-d_{1}</math> | ||
| Line 2,170: | Line 1,991: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig51.png|181px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig51.png|181px|Demostración 3.1 para el Caso 3 de columnas rectangulares]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 51:''' | + | | colspan="1" | '''Figura 51:''' Demostración 3.1 para el Caso 3 de columnas rectangulares |
|} | |} | ||
Por relación de triángulos: | Por relación de triángulos: | ||
| Line 2,189: | Line 2,010: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig52.png|326px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig52.png|326px|Demostración CE.1 para el Caso Especial de columnas rectangulares]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 52:''' | + | | colspan="1" | '''Figura 52:''' Demostración CE.1 para el Caso Especial de columnas rectangulares |
|} | |} | ||
De modo que se deberá cumplir la siguiente relación: | De modo que se deberá cumplir la siguiente relación: | ||
| Line 2,218: | Line 2,039: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig53.png|185px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig53.png|185px|Demostración 4.1 del Caso 4.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 53:''' | + | | colspan="1" | '''Figura 53:''' Demostración 4.1 del Caso 4. |
|} | |} | ||
Por relaciones trigonométricas: | Por relaciones trigonométricas: | ||
| Line 2,239: | Line 2,060: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig54.png|147px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig54.png|147px|Demostración 5.1 para el Caso 5.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 54:''' | + | | colspan="1" | '''Figura 54:''' Demostración 5.1 para el Caso 5. |
|} | |} | ||
Por relaciones trigonométricas: | Por relaciones trigonométricas: | ||
| Line 2,252: | Line 2,073: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Verduzco Martinez_325285613-fig55.png|146px| | + | |[[Image:Draft_Verduzco Martinez_325285613-fig55.png|146px|Demostración 6.1 para el Caso 6]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 55:''' | + | | colspan="1" | '''Figura 55:''' Demostración 6.1 para el Caso 6 |
|} | |} | ||
Por relaciones trigonométricas: | Por relaciones trigonométricas: | ||
| Line 2,318: | Line 2,139: | ||
|} | |} | ||
| − | Sustituyendo la | + | Sustituyendo la Ecuación [ [[#eq-88|88]]] en Ecuación [ [[#eq-92|92]]]. |
<span id="eq-94"></span> | <span id="eq-94"></span> | ||
| Line 2,352: | Line 2,173: | ||
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | '''[1]''' Adolfo Iván Jiménez P. y Dra. Sonia Elda Ruiz Gómez, | + | '''[1]''' Adolfo Iván Jiménez P. y Dra. Sonia Elda Ruiz Gómez, Factores óptimos de cargas para el diseño de columnas esbeltas, Tesis de Licenciatura, UNAM, México, 2013 <div id="cite-2"></div> |
| − | '''[2]''' Steven C. Chapra, Raymond P. Canale, | + | '''[2]''' Steven C. Chapra, Raymond P. Canale, Métodos numéricos para ingenieros, Quinta edición, McGraw Hill <div id="cite-3"></div> |
| − | '''[[#citeF-3|[3]]]''' Gaceta Oficial de la Ciudad de México, | + | '''[[#citeF-3|[3]]]''' Gaceta Oficial de la Ciudad de México, Normas técnicas complementarias de la Ciudad de México, 2017, Normas Técnicas Complementarias para Diseño y Construcción de Estructuras de Concreto 2017 <div id="cite-4"></div> |
| − | '''[[#citeF-4|[4]]]''' González Cuevas, Fco. Robles Hernández, | + | '''[[#citeF-4|[4]]]''' González Cuevas, Fco. Robles Hernández, Aspectos básicos del concreto reforzado, 4ta edición, Limusa 2005 <div id="cite-5"></div> |
| − | '''[5]''' Jack McCormac y Rusell H. Brows, | + | '''[5]''' Jack McCormac y Rusell H. Brows, Diseño de concreto reforzado, 14va edición, Alfaomega, 2015 <div id="cite-6"></div> |
'''[[#citeF-6|[6]]]''' Turner, M. J., Clough, R. W., Martin H. C. and Topp, L. J. Stiffness and Deflection Analysis of Complex Structures . Journal of the Aeronautical Sciences, Vol. 23 No. 9, 1956 pp. 805-823. <div id="cite-7"></div> | '''[[#citeF-6|[6]]]''' Turner, M. J., Clough, R. W., Martin H. C. and Topp, L. J. Stiffness and Deflection Analysis of Complex Structures . Journal of the Aeronautical Sciences, Vol. 23 No. 9, 1956 pp. 805-823. <div id="cite-7"></div> | ||
| − | '''[7]''' Yoeber Castro Atau, “Sistematización de detalles, habilitación y armado de acero ASTM A615 para construcciones de concreto armado: impacto técnico, económico y ambiental”, Universidad Nacional de San Cristobal de Huamanga, 2010 | + | '''[7]''' Yoeber Castro Atau, “Sistematización de detalles, habilitación y armado de acero ASTM A615 para construcciones de concreto armado: impacto técnico, económico y ambiental”, Universidad Nacional de San Cristobal de Huamanga, 2010 |
| + | |||
| + | </span> | ||
Revision as of 22:16, 28 September 2020
“El Perfil idealizado de acero”, un método computacional para el diseño de acero de refuerzo en estructuras de concreto
“The Idealized steel profile”, a computational method for the design of reinforcing steel in concrete structures
Luis Fernando Verduzco Martínez[1], Alejandro Hernández Martínez, Humberto Esqueda Oliva [3]
[1]lf.verduzcomartinez@ugto.mx
[2] alejandro.hernandez@ugtomx.onmicrosoft.com
[3] esquedah@yahoo.com 1 Resúmen
Se presenta el desarrollo y modelación matemática y numérica de un nuevo método computacional llamado “El perfil idealizado de acero” para el diseño de acero de refuerzo en estructuras de concreto reforzado. En el presente trabajo se mostrará su aplicación para columnas de concreto prismáticas sólidas de sección rectangular y circular sometidas a flexo-compresión biaxial, de acuerdo a los componentes y criterios de diseño y análisis para este tipo de estructuras, adaptando la modelación numérica para ambas geometrías, así como respetando los criterios que establecen las [3].
Se probará al final dicho método para el diseño de diversos modelos experimentales de concreto reforzado bajo ciertas combinaciones de cargas a partir de un análisis estructural previo, haciendo comparaciones de los resultados de acuerdo a eficiencia estructural y geometría en la variación de varios paramétros de diseño y objetivos específicos.
Palabras clave: criterios de diseño, acero de refuerzo, concreto reforzado, formulación matemática, métodos computacionales Abstract
It is presented the mathematical and numerical devolpement and modelling of a new computational method named “The idealized steel profile” for the design of reinforcing steel in concrete structures. Hereby it will be shown its application for solid prismatic concrete columns of both rectangular and circular cross sections subjected to flexo-compression stresses in two directions, according to the design components and analysis criteria stablished for this type of structures following the [3].
At the end such method will be tested for various experimental structural models under certain load combinations from a structural analysis made previously, making comparisons between the results according to certain design criteria and requirements such as structural efficiency, costs and geometry following various specific design goals.
keywords: design criteria, reinforcing steel, reinforced concrete, mathematical formulation, computational methods
(1) Universidad de Guanajuato, Aula CIMNE-UG, Guanajuato, Guanajuato, México 2019.
1 Introducción
En los proyectos de diseño y análisis estructural de elementos de concreto reforzado se requiere de análisis numéricos que evocan muchas iteraciones para llegar a un resultado que sea tanto estructural como económicamente eficiente; con el uso de métodos numéricos podemos llegar a estas soluciones muy rápidamente.
El uso de métodos numéricos y programación se ha convertido en una herrmienta necesaria para la automatización de procesos y optimización en tiempos y recursos en el diseño de infraestructura civil. Resulta útil como ingeniero en cualquier área en que se este trabajando, tener conocimientos y habilidades de computación y programación, ya sea en una o en varias plataformas e interfaces de lenguajes de programación.
El presente trabajo está orientado precisamente a usar programación y métodos numéricos en la practica diaria en el diseño de análisis de infraestructura civil, en éste caso se determinará el acero de refuerzo necesario en columnas de concreto para que resistan ciertas condiciones de carga.
En la práctica común, la determinación del acero de refuerzo necesario en elementos de concreto se realiza mediante aproximaciones empíricas basadas en la experiencia; el proceso se vuelve bastante tardado y cansado.
Expondremos pues, el diseño de un software, cuya principal función es la de determinar una configuración de varillas de acero de refuerzo para elementos de concreto sometidos a flexo-compresión, que resulte la más eficiente estructuralmente o la más económica. Para ello el diseñador únicamente tendrá que definir las dimensiones en función de los requerimientos estructurales y/o de espacio. Pueden ser estos elementos columnas cortas y/o largas, pilas, pilotes o incluso dados de cimentación.
El programa tiene la capacidad de analizar elementos estructurales de concreto con secciones circulares y rectangulares. Usualmente, por cuestiones constructivas se requieren geometrías de secciones que no sean complejas y que sean uniformes.
Como resultdos de éste programa se obtienen tanto propuestas como recomendaciones de disposiciónes y arreglos del refuerzo, es decir, no solo se obtienen las opciones de número de varillas con su respectivo diámetro, sino también el acomodo que pudieran tener éstas e indicando además la eficiencia crítica estructural para cada arreglo. El programa selecciona ya sea el arreglo más eficiente etructuralmente o el más barato (de acuerdo a las preferencias del constructor) para cada columna, para luego calcular los volúmenes de materiales requridos (acero, concreto y cimbra) e integrar el presupuesto del proyecto; pasando de la etapa de diseño del proyecto a la elaboración de la cotización en cuestión de segundos. Diversos softwares comerciales de análisis y diseño estructural no hacen esto, de ellos se obitenen únicamente resultados de un análisis con las geometrías y el refuerzo que el diseñador propone inicialmente.
Las aplicaciones y alcances que puede tener éste enfoque de análisis son de gran potencial en el diseño de estructuras de concreto, ya que podría adaptarse a cualquier geometría, cambiando la forma en que se diseñan y analizan elementos de concreto reforzado de hoy en adelante.
2 Objetivo
Diseñar un programa que sea capaz de determinar los posibles arreglos de acero de refuerzo para cualquier número de columnas que se trate, así como seleccionar la opción más eficiente o barata para cada columna, calculando los volumenes de materiales requeridos para finalmente integrar la cotización del proyecto.
3 Metodología general
Se presenta la siguiente metodología de manera general para el desarrollo de las funciones del programa de optimización (consideraciones para análisis estructural, optimización, exportación de reportes y resultados).
- Desarrollar la formulación matemática y numérica para la programación en un lenguaje de programación, tanto para secicones de geometría ciruclar y rectangular, de acuerdo a los criterios de diseño y análisis que establecen las [3]
- Hacer un estudio de precios unitarios y costos de proveedores de acerero, así como de equipo y mano de obra en general para armar el acero de refuerzo
- Insertar estos costos en el programa al momento del diseño
- Realizar las simulaciones y ejecución de experimentos requeridos para analizar el comportamiento de diferentes modelos estructurales de columnas ante diferentes condiciones de carga, haciendo comparaciones entre los diversos resultados referente a costos finales, eficiencias estructurales y geometrías
4 Materiales y métodos
4.1 Métodos numéricos computacionales con aplicación a diseño de estructuras
Los métodos numéricos constituyen técnicas mediante las cuales es posible formular problemas matemáticos con resolución mediante operaciones aritméticas. Con el desarrollo de las computadoras digitales eficientes y rápidas, el papel de los métodos numéricos en ingeniería aumento considerablemente.
Antes de las computadoras se gastaba bastante energía en la técnica misma de solución, en lugar de usarla en la definición del problema. Esto debido al trabajo monótono que se requería para obtener resultados numéricos aceptables. Ahora, al usar la potencia de una comutadora se obtienen soluciones directamente, sin tener que recurrir a simplifaciones o soluciones análiticas que pueden resultar complejas. Gracias a esto, es posible dar más importancia ahora a la interpretación de la solución y su incorporación al sistema total del problema.
El desarrollo de los métodos numéricos más famosos por aquellos grandes científicos, matemáticos e ingenieros han servido de inspiración para muchos investigadores en la ingeniería y ciencia más que para desarrollar la aplicación de los existentes a problemas, desarrollar los suyos propios con la potencia de las computadoras.
Se han desarrolaldo desde el uso de las computadoras innumerables métodos computacionales en el análisis y diseño de las estructuras. Tal vez el más famoso y usado de todos es el Método del Elementos Finito [6] cuyas aplicaciones van desde el análisis elástico de elementos estructurales, hasta la simulación numérica de fluidos. Desde su primera aparición en 1956 el mismo método ha evulocionado y desarrollado para crear diferentes versiones del mismo dependiendo de su aplicación.
Sin embargo, de manera general, cada vez que se quiere hacer una mejora en un análisis y/o diseño estructural en cuánto a rápidez y aproximaciones de soluciones deseadas se crea un nuevo método numérico computacional. Ya que con solo hecho de implementar la potencia de una computadora para encontrar una solución de un problema se requiere de un ajuste de datos, desarrollo de modelos matemáticos, encontrar coeficientes o iterar operaciones aritméticas, y eso, en sí, lo vuelve un método numérico computacional.
5 Antecedentes de construcción con concreto reforzado
Tan solo desde el punto de vista ambiental, en la construcción, la tecnología del concreto armado se antepone a filosofías de sustentabilidad; la manipulación de aceros de construcción ASTM A615 (barras lisas y corrugadas) en forma desmedida desde la concepción de los diseños de refuerzos previos hasta su empleo en la construcción origina altos grados de desperdicios de acero, por efectos de cortes, doblados ineficinetes, o simplemente por una falta de diseño óptimo de este en las estructuras, tal que cumpla con todas las restricciones de eficiencia estructural al mismo tiempo que se use el mínimo posible.
5.1 El acero de refuerzo en la industria de la construcción
En obras de concreto armado, se generan entre el 7% al 27% de desperdicios de aceros ASTM A615 en forma de barras corrugadas. Estas barras se fabrican tanto de acero laminado en caliente como acero trabajado en frío. Los diámetros usuales de barras producidas en México varían de , a , aunque algunos productores han fabricado barras corrugadas de , y .
El acero de refuerzo se produce además en otras más diversas formas para todo tipo de elementos de concreto, también las hay barras lisas, barras de acero helicoidales para la forticiación y reforzamiento de rocas, taludes y suelos a manera de perno de fijación. Incluso se fabrican como mallas cuadriculares (transpuestas en doble sentido) principalemtne para estructuras de losas y cimentaciones.
El tener un mejor control en la cantidad de acero que se usa para este tipo de estructuras en la construcción es primordial hoy en día para mitigar los impactos ambientales y económicos a que se enfrenta un país, pues la industria de la construcción siempre será de gran peso e influencia en cualquier región del mundo. Es imprescindible el desarrollo de tecnología que pueda favorecer el control en diseño y construcción de estas estructuras.
6 Columnas de concreto reforzado
Es el elemento estructural vertical empleado para sostener la carga de la edificación o estructura principal que se trate. Se utiliza principalemente por la libertad que proporciona para distribuir espacios al tiempo que cumple con la función de soportar el peso de la construcción.
Las formas, armados y las específicaciones de las columnas estarán en razón directa del tipo de esfeurzos y condiciones en general a que estas sean expuestas.
6.1 Clasificación de columnas de concreto
Las columnas de concreto reforzado pueden clasificarse como columnas cortas, intermedias y columnas largas.1 Es necesario tener esto en cuenta para entender cómo funciona el programa, ya que el análisis de las columnas preceden del mismo mecanismo de falla de estos tipos de columnas.
Columnas cortas: La carga que pueden soportar está regida por las dimensiones de su sección transversal y por la resistencia de los materiales de que está construida.
Columnas intermedias: La falla es por una combinación de aplastamiento y pandeo.
Columnas largas: La capacidad de carga axial en estás columnas se ve reducida a causa de los momentos secundarios resultates debidos a la deformacion por flexión de la columna.
El presente trabajo trata únicamente con columnas cortas.
(1) Jack C. McCormac, Rusell H. Brown, “Diseño de concreto reforzado”, 14va edición, Alfaomega(2015), p.257.
6.2 Tipos de columnas de concreto
El tipo de columnas de concreto depende de la forma de la sección transversal, así como de su tipo de refuerzo 1. Hay columnas de concreto con refuerzo en forma de varillas longitudinales de acero, con restricción lateral (helicoidal o con estribos cerrados).
Generalmente las columnas con estribos tienen una sección transversal rectangular, mientras que las columnas zunchadas suelen tener sección trasnversal circular, pero también pueden fabricarse con secciones rectangulares, octogonales, entre otras formas. Las espirales en comparación de los estribos incrementan en mayor medida la resistencia debido al aumento de la eficiencia del efecto de confinamiento del refuerzo transversal; aunque, en algunos casos, aumentando también los costos de construcción.
(1) Jack C. McCormac, Rusell H. Brown, “Diseño de concreto reforzado”, 14th edition, Alfaomega (2015), p. 258.
6.3 Conceptos generales de diseño
Es necesario entender las hipótesis empleadas en el diseño de concreto reforzado, para comprender de donde provienen algunos factores, y números incluídos en el análisis.
6.3.1 Carga axial
Si se somete un espécimen de concreto simple con relación alto ancho de dos a una carga axial de compresión, la carga máxima se llegará a una deformación unitaria del orden de 0.002. Arbitrariamente se toma como 100 por ciento la resistencia de un espécimen con relación de esbeltez igual a dos. [4]
Para relaciones de esbeltez mayores que dos, la resistencia baja, hasta llegar al 85 por ciento, aproximadamente. Por consiguiente, la resistencia de un elemento de concreto simple sujeto a compresión axial puede estimarse como el producto del 85 por ciento del esfuerzo medido en cilindro de control , ensayado en las mismas condiciones, multiplicado por el área de la sección transversal del elemento. Este factor de reducción, 0.85, es solo un promedio de resultados de ensayes en miembros colados verticalmente.
Cuando se le adiciona el refuerzo longitudinal a un espécimen de concreto simple y se le añade también el refuerzo transversal necesario para mantener las barras longitudinales en su posición durante el colado, la carga máxima se obtendrá ahora a una deformación unitaria del orden de 0.0021. La falla, en cambio, se produce a una deformación unitaria de 0.003 o 0.004, si el ensaye es de corta duración.
La resistencia adicional sobre la de un prisma de concreto simple debido a la adición del refuerzo longitudinal en compresión se puede estimar como el producto del área del acero por el esfuerzo de fluencia
Por lo tanto, la resistencia o carga máxima a compresión que un prisma de concreto con refuerzo longitudinal puede alcanzar esta dada por la siguiente expresión:.
|
|
(1) |
Cabe resaltar que se está considerando el área de acero en la contribución de la resistencia del concreto a compresión (primer término de la Ecuación 1, que puede influir considerablemente en los cálculos.
Por otra parte, la carga máxima a tensión que el elemento puede soportar está dada por:
|
|
(2) |
En la que solo interviene el acero, ya que el concreto se agrieta y no contribuye a la resistencia.
6.3.2 Flexo-compresión
Consideraciones generales de análisis
a. Se aborda el análisis mediante propuestas de geometría de la sección de la columna que permanecerán fijas, haciendo variar únicamente el área de acero de refuerzo.
b. Un elemento puede alcanzar su resistencia bajo innumerables combinaciones de carga axial y momento flexionante. Estas combinaciones varían desde una capa axial máxima () sin momento de flexión, hasta un momento () sin fuerza axial.
c. El lugar geométrico de las combinaciones de carga axial y momento flexionante con las que un elemento puede alcanzar su resistencia se representa gráficamente por medio de un diagrama de interacción" Figura 1.
d. Cuando al aumentar la carga externa, el momento y la carga axial crecen en la misma proporción, la historia de carga queda representada por una recta desde el origen, con una pendiente igual al cociente . Figura 1.
e. Existen solo dos modos principales de falla de elementos sujetos a flexo-compresión: falla en compresión y falla en tensión:
1. Falla a compresión: Se produce por aplastamiento del concreto. El acero del lado más comprimido fluye, en tanto que el lado opuesto no fluye en tensión
2. Falla en tensión: Se produce cuando el acero de un lado fluye en tensión antes de que se produzca el aplastamiento del concreto en el lado opuesto más comprimido.
f. El diagrama de interacción de un elemento puede obtenerse a partir de las hipótesis descritas para el cálculo de la resistencia de elementos sujetos a flexión pura, considerando que ahora la sumatoria de fuerzas debe ser igual a la carga P aplicada.
NOTA: Lo anterior aplica para cualquier geometría.
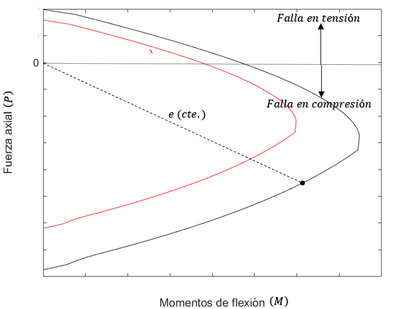
|
| Figura 1: Diagrama de interacción típico. (Dibujo propio.) |
Fórmula de Bresler
Bresler desarrolló una expresión muy simple para columnas rectangulares para calcular los valores máximos de la carga de compresión que actúa a excentricidades y en secciones rectangulares con refuerzo simétrico. Ecuación 3. Dicha solución surgió ante la necesidad de evitar realizar los cálculos para determinar una superficie de interacción2, reduciendo el problemas a una combinación de soluciones más simples; dos de flexo-compresión en un plano de simetría y una de compresión axial.
|
|
(3) |
Donde: =Carga normal resistente sobre la sección transversal del elemento actuando a excentricidades y .
=Carga normal resistente a una excentricidad de .
=Carga normal resistente a una excentricidad de .
La Ecuación 3 verifica los ensayes disponibles dentro del 20 por ciento de aproximación, y representa una familia de planos que aproximan los puntos de la superficie de interacción. Figura 2.
|
| Figura 2: Superficie de interacción típica. Tomada de: |
Otro enfoque para analizar columnas sujetas a carga axial y flexión en dos planos Ecuación 4 a es partir de la cual se desprende otra expresión simplificada para calcular la eficiencia de un elemento cuando la relación . Ecuación 9 (que es la se presenta en las NTC-2017 [ntc17]) a las cuáles se hará referencia a continuación.
|
|
(4) |
Donde: =Carga axial nominal aplicada
=Resistencia nominal a carga axial en la condición balanceada.
y =Momentos nominales resistentes en la condición balanceada alrededor de los ejes X y Y recpectivamente.
y =Momentos nominales aplicados alrededor de los ejes X y Y respectivamente.
(1) González Cuevas, Fco. Robles Fernández,“Aspectos básicos del Concreto Reforzado”, 4ª edición, Limusa (2005). Capítulo 6, p. 127-155.
(2) Es el espacio geométrico de los valores de carga axial que la sección de un elemento es capaz de resistir, en todos sus planos.
6.4 Normativa
Anteriormente se presentaron hipótesis generales de diseño con concreto, porque son de tales hipótesis en que los reglamentos de construcción se basan. Para desarrollar éste proyecto se hizo referencia a las Normas Técnicas complementarias para el diseño y construcción de estructuras de concreto del Reglamento de Construcciones de la Ciudad de México (NTC-2017), que aunque se basan en las hipótesis anteriores no presentan tal cual los mismos criterios de diseño, y que son cuestionados mucho por la sociedad ingenieril. Veamos que proponen estas normas.
6.4.1 Carga axial
En las NTC-2017 se considera necesario hacer una modificación en el valor de mediante Factores de carga y Factores de Resistencia 1. En el apartado de concreto se específica que para el cálculo de resistencias se utilice una resistencia reducida a la compresión del concreto denominada . Cuyo valor es:
|
|
(5) |
De modo que la ecuación Ecuación [ 1] se transforma a:
|
|
(6) |
De modo que la ecuación Ecuación [ 2] se transforma a:
|
|
(7) |
Para una mejor interpretación de los factores mecionados se puede hacer referencia a la Figura 3, que es el bloque de transformación equivalente de esfuerzos de las hipótesis de las NTC-2017.
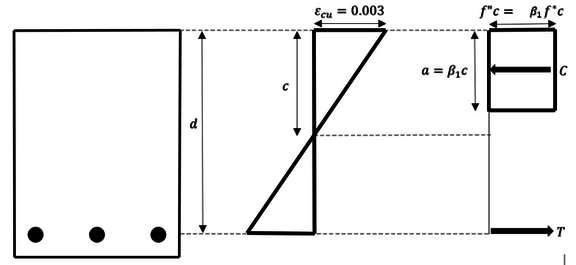 ] ]
|
| Figura 3: Hipótesis de las NTC-2017 sobre la distribución de deformaciones y esfuerzos en la zona de compresión. Adaptada de: [3] |
Donde:
6.4.2 Compresión y flexión en dos direcciones
2 Se usará la expresión siguiente (que es derivada de la fórmula de Bresler) para el cálculo de la carga máxima actuante en la sección a cierta excentricidad.
|
|
(8) |
Para valores de , se usará la expresión siguiente:
|
|
(9) |
Donde: y son los momentos actuantes alrededor de los ejes X, Y, respectivamente.
y son los momentos resistentes de diseño alrededor de los mismos ejes.
(1) El factor de reducción , que para el caso de columnas con carga axial es de 0.8 [3]
(2) González Cuevas, Fco. Robles Fernández, “Aspectos básicos del Concreto Reforzado”, 4ª edición, Limusa (2005). Capítulo 6, p. 148.
7 El método del perfil idealizado de acero
7.1 Secciones rectangulares-modelo matemático
Empleando las hipótesis de diseño anteriormente descritas se ha idealizado el acero de refuerzo de un elemento como se muestra. Figura 4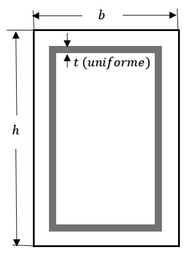
|
| Figura 4: Sección rectangular idealizada de concreto reforzado. |
Para estas secciones se desarrolló un método puramente matemático con ecuaciones que definieran la resistencia de la columna de acuerdo a la ubicación del eje neutro de esfuerzos en la sección siguiendo paramétros de geometrías. También se desarrolló un método numérico que resulta más sencillo de programar y se meustra justo después.
Tomando como referencia la siguiente figura Figura 5: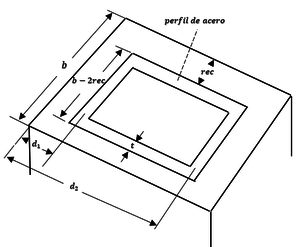
|
| Figura 5: Sección rectangular idealizada de concreto reforzado. |
Donde: = espesor de la sección transversal del acero de refuerzo idealizado como un refuerzo constante alrededor de la sección.
7.2 Casos de análisis para el cálculo de la resistencia del acero
De acuerdo a la distribución lineal de las deformaciónes unitarias y el comportamiento elasto-plástico del acero, se podrían derivar cinco casos de análisis respecto a las diferentes posiciones del eje neutro en el cálculo de nuestro diagrama de interacción, de acuerdo a los tipos de geometrías a que los mismos estados de esfuerzos (debido a dichas posiciones del eje neutro) sobre la sección transversal del elemento dan lugar. Estas configuraciones de geometrías de esfuerzos se pueden transformar consecuentemente a fuerzas puntuales Figura 6, con las que se pueden calcular el momento actuante respecto al eje neutro elástico de la sección transversal de todo el elemento de concreto.
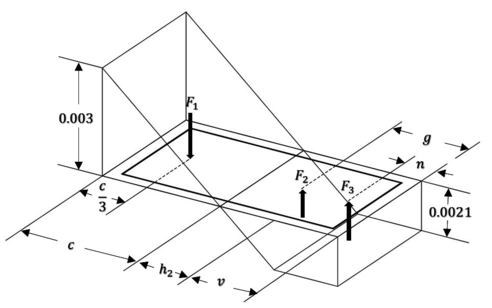
|
| Figura 6: Geometrías de bloques de distribución de esfuerzos para cierta posición del eje neutro. |
7.2.1 Metodología
Se presenta la siguiente metodología de manera general para el análisis de las fuerzas y momentos de flexión resultantes, con la que se podrá conceptualizar y segmentar la manera en que se desarrollaron las fórmulas y ecuaciones.
Para las fuerzas resultantes resistentes:
Para cada bloque () en un determinado estado de esfuerzos:
- Determiar la longitud de la configuración geométrica de esfuerzos () en dirección al peralte de la sección.
- Determinar el área efectiva bajo esfuerzos
- Determinar la fuerza resultante que define la geometría de dicha configuración de esfuerzos
|
|
(10) |
- Sumar todas las fuerzas resultantes de cada configuración geométrica de esfuerzos para obtener la resultante resistente:
Para los momentos resultantes resistentes:
Para cada configuración geométrica () en un determinado estado de esfuerzos:
- Determiar la profundidad del centroide de la configuración geométrica sobre el que actúa la fuerza resultante.
- Determinar la distancia de ese punto respecto al eje centroidal de la sección transversal
- Determiar el Momento resultante equivalente:
- Sumar todas los momentos resultantes producidos por cada configuración geométrica de esfuerzos para obtener el momento de flexión resultante resistente:
Tomar en cuenta que por ahora solo se está considerando el acero de refuerzo. De modo que para calcular el volumen de estas configuraciones geométricas de deformaciones (o fuerzas resultantes), se analiza el área de las dos partes laterales del perfil idealizado de acero Figura 5 y la de la parte superior e inferior por separado.
Para las partes laterales se toma referencia de la metodología descrita para esta geometría; tomando en cuenta una variación lineal de esfuerzos a lo largo de tales.
A diferencia de las partes superior en inferior en que se toma un esfuerzo constante a lo largo de la longitud de tales partes. De forma que aquí entrarán en lugar las fuerzas ( y ) Ecuación [ 11] y Ecuación [ 12] para todos los casos, representando las fuerzas resitentes resultantes que actuarán en los centroides de las partes superior en inferior del perfil de acero, supuestas como y , respectivamente.
|
| Figura 7: Sección rectangular idealizada de concreto reforzado. |
|
|
(11) |
|
|
(12) |
Nota: La convención de signos será: Compresión (-) y Tensión (+).
7.2.2 Caso 1: se presenta una configuración geométrica de esfuerzos rectangular en tensión
|
|
Ver Demostración 1.1 en Anexo 1 [p. actual]
En éste caso el elemento de concreto no se producen momentos de flexión por los bloques de estados de esfuerzo, únicamente fuerzas axiales a tensión. Figura 8Donde:
Por lo tanto, de las ecuaciones Ecuación 11 y Ecuación 12:
|
|
(13) |
|
|
(14) |
|
|
(15) |
|
|
(16) |
Entonces, la fuerza y el momento neto resistente queda como:
|
|
(17) |
|
|
(18) |
7.2.3 Caso 2. Se presentan dos configuraciones geométricas rectangulares y una triangular, todas a tensión
Dando continuidad al caso anterior, el rango en el cual estará la profundidad del eje neutro para éste caso es:
|
|
Por lo tanto, de las ecuaciones Ecuación 11 y Ecuación 12:
|
|
(19) |
|
|
(20) |
Ahora, con las variables definidas anteriormente y la figura Figura 9, se pueden deducir las siguientes ecuaciones para calcular la fuerza resultante y el momento de flexión resultante resistente en el acero.
|
|
(21) |
|
|
(22) |
|
|
(23) |
|
|
(24) |
|
|
(25) |
|
|
(26) |
Quedando, la fuerza y momento neto resistente como:
|
|
(27) |
De modo que el momento par resistente del acero en éste caso, estará dado por:
|
|
(28) |
7.2.4 Caso 3; Se presenta una configuración geométrica de deformaciones triangular a compresión, una triangular a tensión y una rectangular a tensión
Para que esto ocurra, la profundidad del eje neutro deberá estar entre el siguiente rango:
|
|
Donde:
De modo que para definir las ecuaciones Ecuación 11 y Ecuación 12 se tiene:
Y para las fuerzas y momentos resistentes resultantes, se tiene:
|
|
(29) |
|
|
(30) |
|
|
(31) |
|
|
(32) |
|
|
(33) |
|
|
(34) |
|
|
(35) |
|
|
(36) |
7.2.5 Caso especial. Se presentan únicamente configuraciones geométricas triangulares de deformaciones
Para que se dé éste caso, se debe dar la siguiente relación entre el espesor del perfil , el peralte de la sección y el recubrimiento .
|
|
(37) |
Nota: Ver Demostración CE.1 en Anexo 1. p. actual
De la misma demostración se puede ver, que para calcular y :
Por lo tanto, haciendo referencia a la Figura 11, para las ecuaciones Ecuación 11 y Ecuación 12:
Y las fuerzas y momentos resistentes se calcularían como:
|
|
(38) |
|
|
(39) |
|
|
(40) |
|
|
(41) |
|
|
(42) |
|
|
(43) |
7.2.6 Caso 3-4: Se presentan configuraciones geométricas de deformaciónes triangular y rectangular a compresión, así como a tensión.
Hágase referencia a Figura 10 para visualizar este rango.
Donde:
Por lo tanto, para las ecuaciones Ecuación 11 y Ecuación 12:
Y las fuerzas y momentos resistentes se calcularían como:
|
|
(44) |
|
|
(45) |
|
|
(46) |
|
|
(47) |
|
|
(48) |
|
|
(49) |
|
|
(50) |
|
|
(51) |
|
|
(52) |
|
|
(53) |
7.2.7 Caso 4: Se presenta una configuración geométrica de deformaciones triangular y una rectangular a compresión; y una triangular a tensión.
Para el cálculo de las fuerzas y momentos de flexión resultantes resistentes ha de hacerse referencia tanto a la Figura 13..
Donde:
Nota: Ver demostración 4.1 en Anexo 1 p. actual
Por lo tanto, para las ecuaciones Ecuación 11 y Ecuación 12:
Entonces las fuerzas y momentos resistentes se calculan como:
|
|
(54) |
|
|
(55) |
|
|
(56) |
|
|
(57) |
|
|
(58) |
|
|
(59) |
|
|
(60) |
|
|
(61) |
7.2.8 Caso 5. Se presentan dos bloques rectangulares y uno triangular, todos a compresión.
Para visualizar este rango hágase referencia a la siguietne figura Figura 14 y a la demostración que se indíca en la leyenda de la misma figura.Donde:
Por lo tanto, para las ecuaciones Ecuación 11 y Ecuación 12:
Y las fuerzas y momentos resutaltantes resistentes se calculan como:
|
|
(62) |
|
|
(63) |
|
|
(64) |
|
|
(65) |
|
|
(66) |
|
|
(67) |
|
|
(68) |
|
|
(69) |
7.2.9 Caso 6. Un bloque rectangular de esfuerzos en compresión
En este caso la sección resistirá únicamente fuerzas axiales a compresión, y no momentos de flexión, Figura 15 pues el bloque se esfuerzos que se genera tiene como punto de acción justo el eje de centroide de la sección misma.
Por lo tanto:
|
|
(70) |
|
|
(71) |
|
|
(72) |
7.2.10 Casos de análisis para el concreto
Lo que se pretende aquí es encontrar el área neta del concreto bajo esfuerzos para cualquier valor en la profundidad del eje neutro Figura 17. Al ser una sección rectangular, el análisis se simplifica a un solo caso, ya que el área variará uniformemente a lo largo de todo el peralte de la sección, ya sea respecto al eje X o Y. A partir de esa área neta se determinará el volumen del bloque de esfuerzos-deformaciones resultante de compresión en unidades de Fuerza, y posteriormente el momento de flexión resultante respecto al eje del centroide de la sección como sigue:
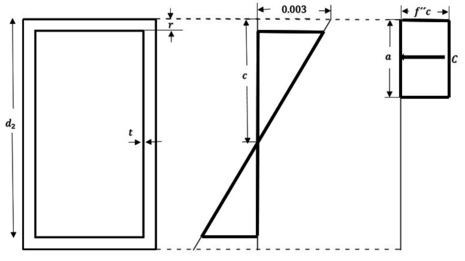
|
| Figura 16: Diagrama de bloque equivalente de esuferzos de compresión en el concreto. Dibujo propio. |
|
|
(73) |
|
|
(74) |
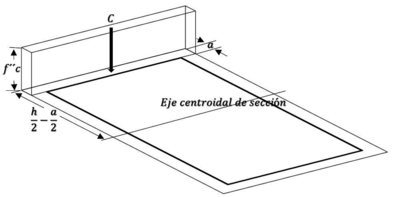
|
| Figura 17: Diagrama tridimensional del bloque equivalente de esfuerzos de compresión en el concreto. Dibujo propio. |
7.3 Secciones rectangulares-modelo numérico
Siguiendo la misma idealización del perfil de acero que en el modelo matemático se tiene Figura 18: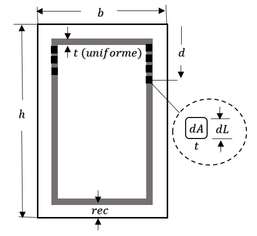
|
| Figura 18: Modelo geométrico para la metodología numérica de análisis: Dibujo propio. |
Donde:
Número de elementos
7.3.1 Cálculo de la resistencia del acero
Metodología Para la determinación de la resistencia de carga axial y flexión se sigue la siguiente metodología:
- Determinar la distancia de cada segmento de perfil con respecto a la fibra superior más alejada de la sección transversal del elemento de concreto .
Para las partes superior e inferior del perfil se tiene:
|
|
(75) |
|
|
(76) |
|
|
(77) |
Mientras que para los costados del perfil se tiene:
|
|
(78) |
|
|
(79) |
= recubrimiento
= peralte de la sección
- A partir de ahí se cálcula en función de c, cuidando únicamente la siguiente restricción .
- Y finalmente calcular la fuerza y momento resultantes resistentes:
|
|
(80) |
|
|
(81) |
7.3.2 Cálculo de la resistencia del concreto
Se sigue la misma forma que en el modelo matemático. Sección 7.2.10
8 Columnas circulares
Análogo a la idealización del acero de refuerzo de columnas rectangulares, se ha idealizado el acero de refuerzo en éste tipo de columnas como se muestra en la siguiente figura Figura 19.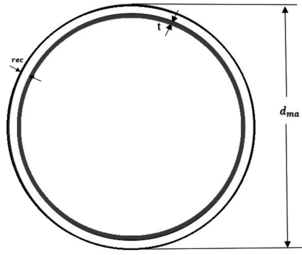
|
| Figura 19: Idealización de una sección circular de concreto reforzado. Dibujo propio. |
Donde: = Espesor del perfil
= recubrimiento
= diámetro de la sección del elemento Nota: El recubrimiento se mide desde el borde de la sección de la columna al centro del espesor del refuerzo ficticio.
A diferencia de la geometría rectangular, para la ciruclar resultó bastante complejo analizar la distribución de esfuerzos mediante el enfoque de análisis planteado originalmente (determinando la geometría de las configuraciones de estados de deformaciones, por lo que simplificó con el siguiente planteamiento:
8.1 Cálculo de la resistencia del acero
Lo que se hará es tratar el perfil de acero como una línea circular y subdividirla en pequeños segmentos con espesor , Figura 20, aunque en realidad cada segmento se tratará como un punto al que le corresponderá una cierta condición de esfuerzos dependiendo de su ubicación en el plano cartesiano de referencia y del caso del cual se trate.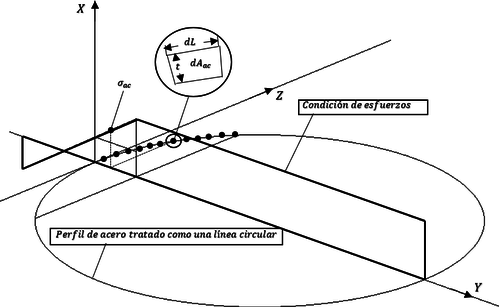
|
| Figura 20: Esquema de análisis para las condiciones de esfuerzos en el acero de refuerzo. Dibujo propio. |
Donde:
Número de elementos
8.1.1 Metodología
Para la determinación de la resistencia de carga axial y flexión se sigue la siguiente metodología:
- Determinar la distancia de cada segmento de perfil con respecto a la fibra más alejada de la sección transversal del elemento de concreto .
- A partir de ahí se cálcula en función de c, cuidando únicamente la siguiente restricción .
- Y finalmente calcular la fuerza y momento resultantes resistentes:
|
|
(82) |
|
|
(83) |
8.2 Casos de análisis para el concreto
A diferencia de las columnas de sección rectangular, en las circulares el diferencial de área al cambiar el eje neutro no será uniforme.
También podremos transformar ésta área de compresión en un bloque equivalente de esfuerzos, y para poder hacer ésto será necesario cálcular el centroide del área real de compresión en cada posición del eje neutro y a partir de ahí calcular el momento de flexión resistente de la sección. Figura 21.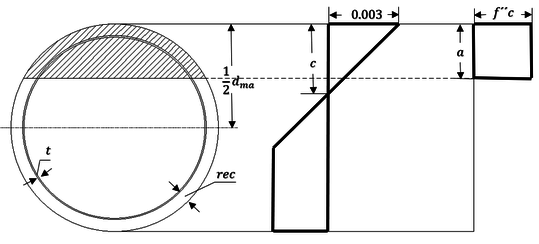
|
| Figura 21: Diagrama de distribución de esfuerzos para el concreto. Dibujo propio. |
Donde:
Para calcular ésta fuerza de compresión tomaremos el siguiente sistema de referencia: Figura 22, para definir integrales para calcular el área efectiva de compresión del concreto en cualquier posición del eje neutro.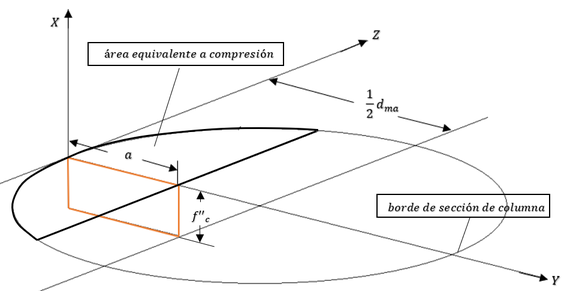
|
| Figura 22: Sistema de referencia cartesiano para el análisis de la distribución de esfuerzos de compresión en el concreto. Dibujo propio. |
Subdividiremos el análisis en dos casos para simplificación:
Cuando
|
|
(84) |
|
|
(85) |
Cuando
|
|
(86) |
|
|
(87) |
9 Geometría y propiedades mecánicas de los materiales
Recordando que el objetivo es determinar un arreglo de refuerzo tal que cumpla con un rango de eficiencia aceptable ante ciertos elementos mecánicos actuantes al que la estructura concreto estaría sometidos, manteniendo constante la geometría de las sección propuesta inicialmente. Por lo que nuestros datos de entrada serán el número de elementos a diseñar, para cada elemento se indicará la resistencia a compresión simple del concreto , la resistencia a la fluencia del acero , y el recubrimiento .
El programa también necesitará las fuerzas actuantes en la columna para su diseño. Dichas fuerzas se determinan normalmente mediante un análisis estructural, el cual es común que se realice en algún software para tal fin. A partir de éste punto se determinará un valor inicial del espesor del perfil idealizado de acero , acomodado en la secicón de concreto de tal manera que se respete el recubrimiento deseado, para así comenzar con las iteraciones de actualización de los diagramas de interacción de las columnas hasta que la condición mecánica actuante más crítica sea cubierta.
10 Cálculo de los diagramas de interacción
Se establece un cierto número de puntos para determinar los diagramas de interacción, determinado los valores , como los límites del rango de las fuerzas del diagrama de interacción, pudiendo extraer una fuerza respectiva a cada punto del mismo que tendrá el papel de raíz en el método numérico a emplear para el cálculo de su respectivo momento resistente.
El método numérico empleado para la aproximación de ráices es el llamado Método de la Falsa posición. Anexo 3 p. actual
10.1 Cálculo de la eficiencia mecánica-estructural
Para cada condición de fuerza actuante en la columna se determinará la respectiva eficiencia estructural que hay entre ésta condición y la resistencia que el diagrama de interacción índica.
La diferencia en el cálculo de éstas eficiencias en columnas circulares y rectangulares es que en las rectangulares se deberán extraer de los diagramas de interacción calculados en el sentido de y la carga resistente y el momento resistente ( [p. actual]), y para las circulares al ser su sección simétrica respecto a cualquier eje, se calculará la eficiencia respecto a una sola dirección, extrayendo la carga resistente y el momento resistente () del diagrama de interacción calculado.
Para lo anterior se empleará geometría analítica con el sistema cartesiano de los propios diagramas de interacción Figura 23 calculando el punto de intersección entre dos rectas imaginarias A y B, tal que A partirá del origen pasando por alguna condición de fuerza actuante prolongándose hasta el borde del diagrama de interacción, y B será tal que una el punto anterior y posterior del punto en el cual la recta A intersecta al diagrama de interacción.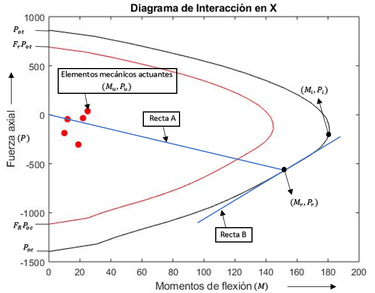
|
| Figura 23: Diagrama de interacción en el plano cartesiano de referencia para el programa. |
De modo que el cálculo del momento resistente para una respectiva condición se cálcula como:
|
|
(88) |
Y su fuerza resistente respectiva como:
|
|
(89) |
Ver demostración Anexo 1. p. actual
Ahora ya se pueden aplicar las fórmulas que índican las NTC-2017 p. actual, para calcular las eficiencias de cada condición mecánica actuante.
10.2 Cálculo de área requerida de acero
Ya determinada la eficiencia mecánica estructural para cada condición de carga actuante se determinará a continuación la más crítica, y a partir de ésta se cálculará el espesor del perfil de acero simplemente iterando el valor de con un cierto incremento , hasta llegar a un rango de eficiencia crítica requerida, establecida a priori, pues está será la eficiencia que nos servirá de comparación para seguir iterando o no. Figura [ 24]
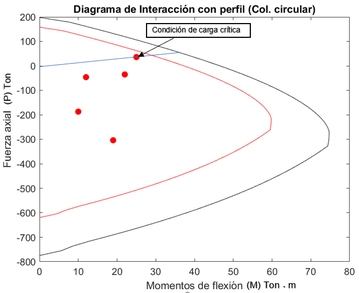
|
| Figura 24: Condición de carga crítica de diseño. |
11 Determinación del acero de refuerzo
Una vez que se ha determinado el área de acero a emplear para que se alcance la eficiencia deseada, se debe transformar esa área ficticia de acero en varillas corrugadas, distribuyéndolas uniformemente en la sección (obedeciendo las hipótesis de diseño de la Sección 6.3.2), por lo que sólo se admitirán números pares de varillas.
El programa genera un arreglo matricial de propuestas de número de varillas, desde 4 (para columnas rectangulares) o 6 (para columnas circulares), calculando para cada diámetro el número de varillas requeridas, tomando como referencia los tipos de varillas disponibles comercialmente.
El usuario podrá elegir no sólo el diámetro del acero de refuerzo, sino también la distribución de éstas en la sección (solo para las columnas rectangulares, ya que para circulares la distribución es simétrica respecto a cualquier eje de simetría), de manera que siempre se respete la separación mínima o distancia libre entre varillas . Aunque por defecto lo que usualmente se busca es la opción que resulte la más eficiente o la más económica. De manera que el usuario también podrá elegir que criterio es el más conveniente.
Cabe mencionar que la distribución del acero de refuerzo tiene influencia en la eficiencia mecánica de los elementos, y para cada opción de número de varillas/diámetro le corresponderá un buen número de configuraciones de éstas en las sección, por lo que el programa hará también un análisis de eficiencia de cada opción disponible, pero ahora tratando al acero de refuerzo precisamente como varillas de acero, para verificar cuáles cumplen con el rango requerido de eficiencia que se establecio a priori, una vez hecho esto, el programa seleccionará la opción más eficiente.
| Tipo (octavo) | área | ||
12 Diseño de experimento
Para cada tipo de geometría se probó un modelo estructural de experimentación con diferentes valores de .
12.1 Columnas rectangulares
En un análisis estructural hecho previamente se proponen las siguientes geometrías y :
12.1.1 Datos de entrada
Con las siguientes combinaciones de carga para ambas estructuras:
12.1.2 Resultados
Una vez hecho el análisis de resistencia con las cargas y datos dados se obtienen los siguientes diagramas de interacción, tabla de eficiencias estructurales para cada modelo estructural con los grosores resultantes del perfil idealizado de acero, distribución óptima en costo y eficiencia de varillas de acero en cada modelo estructural y sus respectivas tablas de eficiencia con dicha opción de varillado:
Eficiencia estructural con espesores de perfiles idealizados de acero resultantes:

|
| Figura 25: Tabla de eficiencias con espesor de perfil (t) resultante-Modelo estructural 01. |

|
| Figura 26: Tabla de eficiencias con espesor de perfil (t) resultante-Modelo estructural 02. |
Diagramas de interacción con espesor de perfil (t) resultante para cada modelo:
Nota:Los puntos rojos representan las condiciones de carga en ese sentido.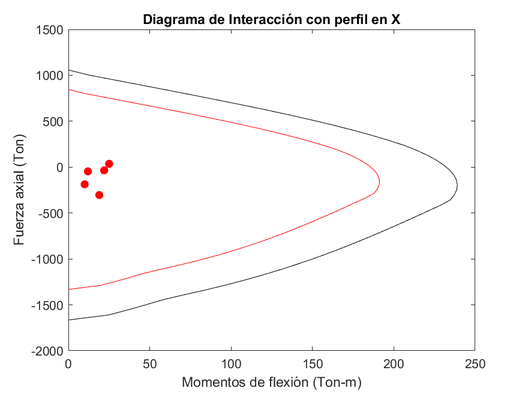
|
| Figura 27: Diagrama de interacción en X con espesor de perfil (t) resultante-Modelo estructural 01. |
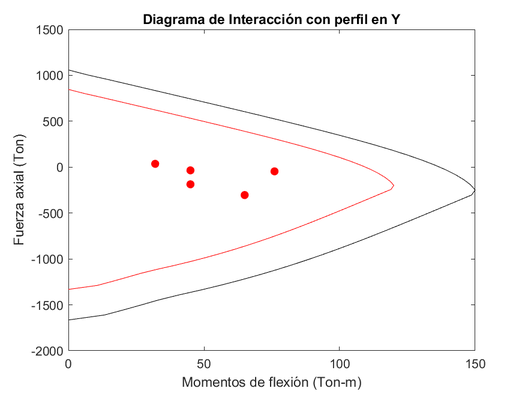
|
| Figura 28: Diagrama de interacción en Y con espesor de perfil (t) resultante-Modelo estructural 01. |
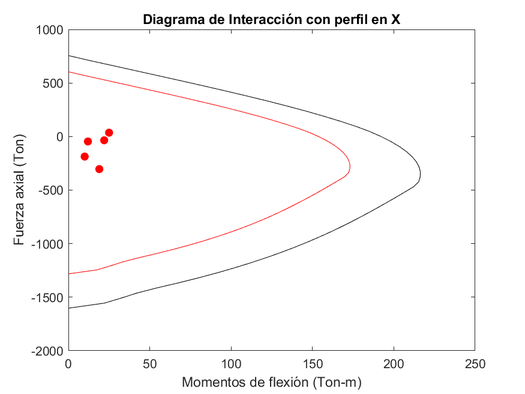
|
| Figura 29: Diagrama de interacción en X con espesor de perfil (t) resultante-Modelo estructural 02. |
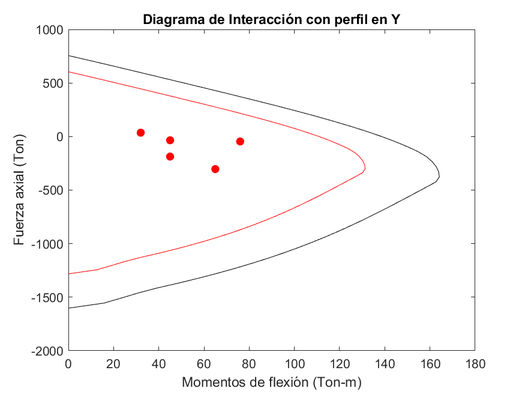
|
| Figura 30: Diagrama de interacción en Y con espesor de perfil (t) resultante-Modelo estructural 02. |
Opciones de distribución de varillas disponibles resultantes:
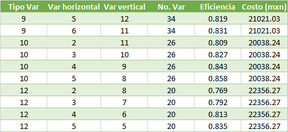
|
| Figura 31: Tabla de opciones disponibles de varillado-Modelo 01. |
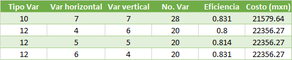
|
| Figura 32: Tabla de opciones disponibles de varillado-Modelo 02. |
Distribución de varillado óptima en costo y eficiencia
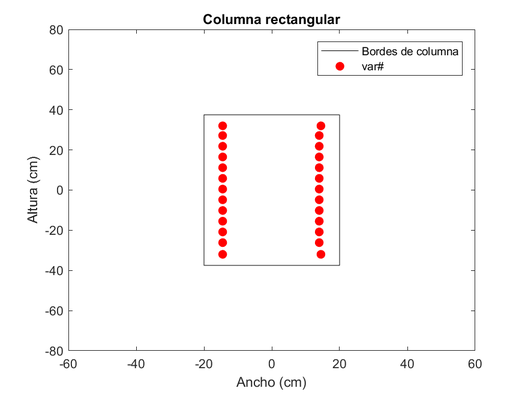
|
| Figura 33: Distribución de opción óptima de varillado en costo y eficiencia estructural correspondiente a la opción 3 Tabla 31-Modelo 01 |
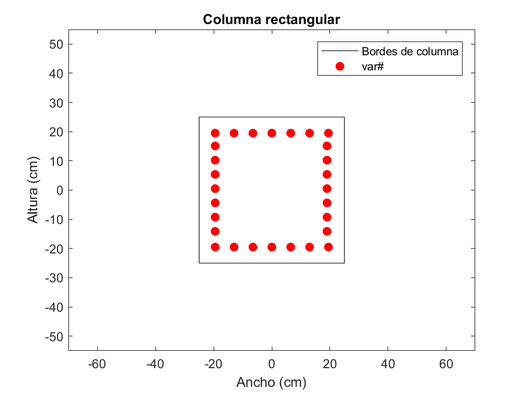
|
| Figura 34: Distribución de opción óptima de varillado en costo y eficiencia estructural correspondiente a la opción 1 Tabla 32-Modelo 02 |
Tomando como referencia las distribuciones de varillas en la sección para cada modelo con las tablas de opciones disponibles de varillado, se puede notar que el programa al tomar la opción más económica, hace la selección tomando en cuenta también la mejor eficiencia estructural, que aunque no es la más eficiente de manera absoluta, si lo es con respecto al costo más bajo, ya que se pueden presentar mismos costos óptimos con diferentes eficiencias estrucrales.
Diagramas de interacción para las opciones de varillado óptimas en costo para cada modelo estructural:
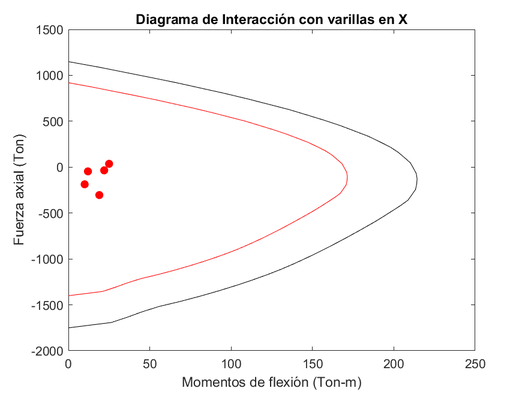
|
| Figura 35: Diagrama de interacción en X con varillas resultantes-Modelo estructural 01. |
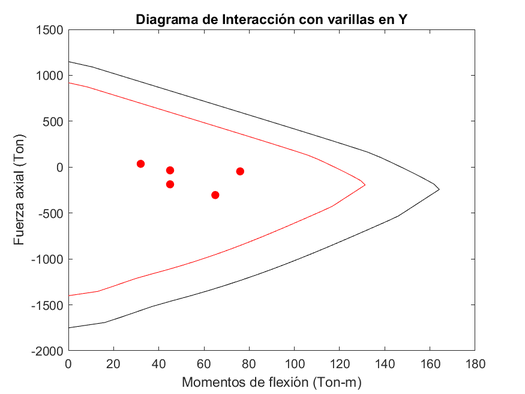
|
| Figura 36: Diagrama de interacción en Y con varillas resultantes-Modelo estructural 01. |
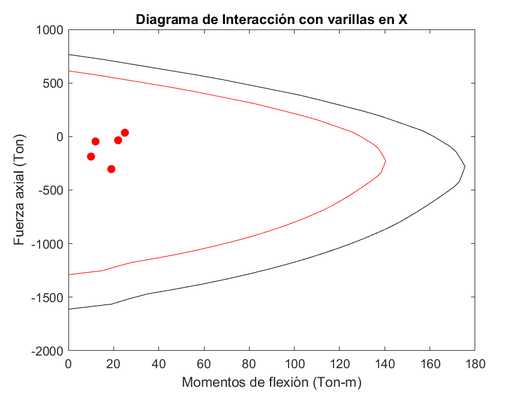
|
| Figura 37: Diagrama de interacción en X con varillas resultantes-Modelo estructural 02. |
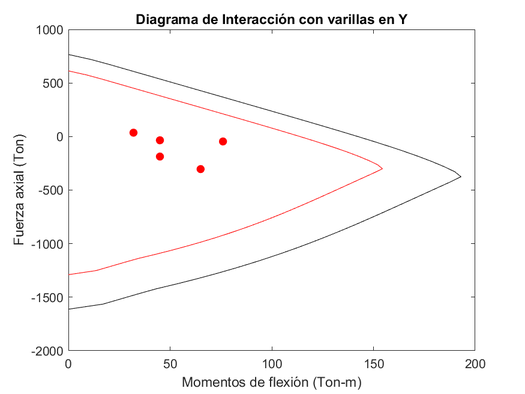
|
| Figura 38: Diagrama de interacción en X con varillas resultantes-Modelo estructural 02. |
12.2 Columnas circulares
12.2.1 Datos de entrada
Con las siguientes combinaciones de carga para ambas estructuras:
12.2.2 Resultados
Una vez hecho el análisis de resistencia con las cargas y datos dados se obtienen los siguientes diagramas de interacción, tabla de eficiencias estructurales para cada modelo estructural con los grosores resultantes del perfil idealizado de acero, distribución óptima en costo y eficiencia de varillas de acero en cada modelo estructural y sus respectivas tablas de eficiencia con dicha opción de varillado:
Eficiencia estructural con espesores de perfiles idealizados de acero resultantes:
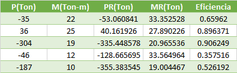
|
| Figura 39: Tabla de eficiencias con espesor de perfil (t) resultante-Modelo estructural 01. |
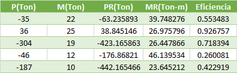
|
| Figura 40: Tabla de eficiencias con espesor de perfil (t) resultante-Modelo estructural 02. |
Diagramas de interacción con espesor de perfil (t) resultante para cada modelo:
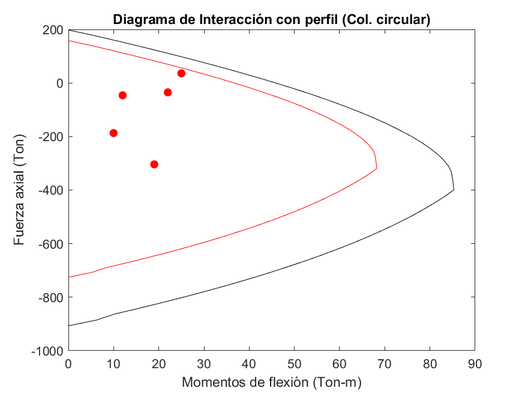
|
| Figura 41: Diagrama de interacción con espesor de perfil (t) resultante-Modelo estructural 01. |
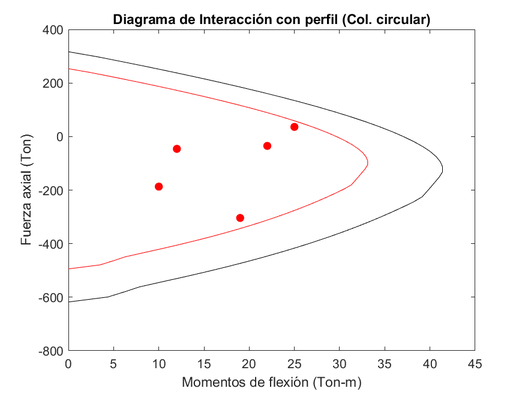
|
| Figura 42: Diagrama de interacción con espesor de perfil (t) resultante-Modelo estructural 02. |
Opciones de distribución de varillas disponibles resultantes:
| Figura 43: Tabla de opciones disponibles de varillado-Modelo 01. |
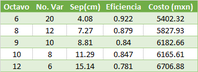
|
| Figura 44: Tabla de opciones disponibles de varillado-Modelo 02. |
Distribución de varillado óptima en costo y eficiencia
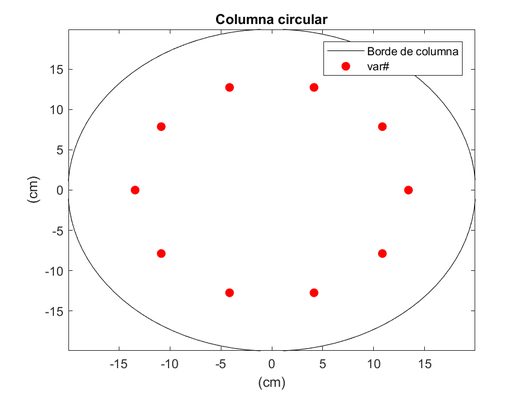
|
| Figura 45: Distribución de opción óptima de varillado en costo y eficiencia estructural correspondiente a la opción 2 Tabla 43-Modelo 01 |
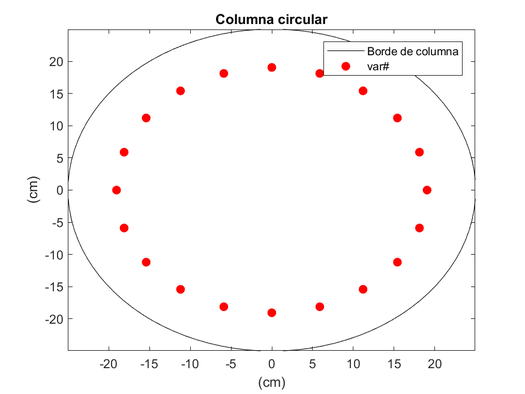
|
| Figura 46: Distribución de opción óptima de varillado en costo y eficiencia estructural correspondiente a la opción 1 Tabla 44-Modelo 02 |
Diagramas de interacción para las opciones de varillado óptimas en costo para cada modelo estructural:
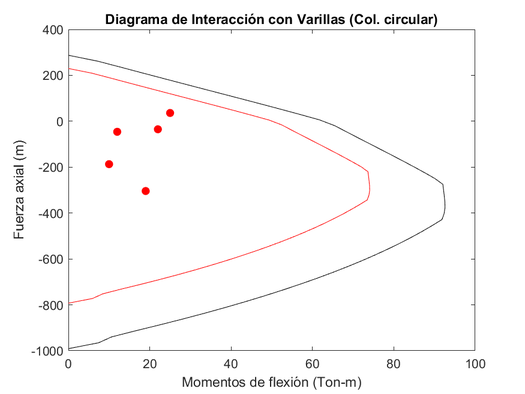
|
| Figura 47: Diagrama de interacción con varillas resultantes-Modelo estructural 01. |
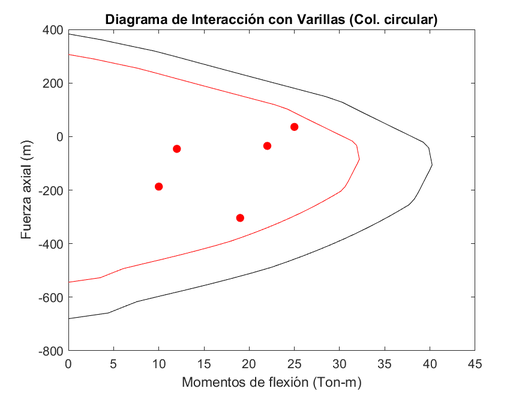
|
| Figura 48: Diagrama de interacción con varillas resultantes-Modelo estructural 02. |
13 Discusión y conclusiones
El método aparte de ser muy fácil de programar en una computadora ofrece una nueva forma para analizar y diseñar estructuras de concreto reforzado. Sin duda que aún queda mucho por desarrollar y este puede es el comienzo de nuevas investigaciones en material de optimización de estrucruras de concreto, ya que como tal este método también se implementó en le presente trabajo una optimización, aunque con un método muy sencillo de búsqueda, más sin embargo los resultados obtenidos son los óptimos de acuerdo a los requerimientos de diseño.
14 Agradecimientos
Agradezco a la Universidad de Guanajuato, mi casa de estudios, por esta oportunidad, así como especial agradecimiento al Aula CIMNE-UG, que representó para mi un espacio de ideas y centro de exploración organizacional. A mi director de tesis el Dr. Alejandro Hernández Martínez y a mi tutor proyectos en el Aula CIMNE a la cual también dicho trabajo forma parte, el MC. Humberto Esqueda Oliva, pues con el Aula CIMNE se desarrolló el programa computacional como tal en lenguaje C principalmente con MatLab para la parte gráfica, y para la parametrización visual de los elementos estructurales y su acero de refuerzo.
15 Anexo 1. Demostraciones de las variables envueltas en los casos de análisis de columnas rectangulares
Caso 1
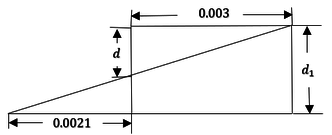
|
| Figura 49: Demostración 1.1 para el caso 1 de columnas rectangulares.Dibujo propio. |
Por relación de triángulos:
Caso 2
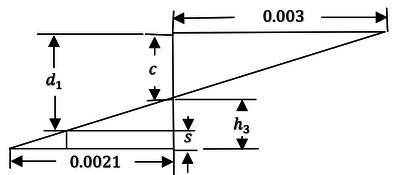
|
| Figura 50: Demostración 2.1 para el Caso 2 de columnas rectangulares |
Por relación de triángulos:
Entonces:
Caso 3
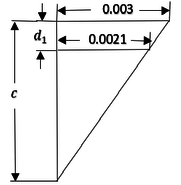
|
| Figura 51: Demostración 3.1 para el Caso 3 de columnas rectangulares |
Por relación de triángulos:
Entonces:
Caso especial
Sea la razón de distribución líneal de esfuerzos para el limite máximo del caso especial, y la razón de distribución líneal de esfuerzos para el límite mínimo:
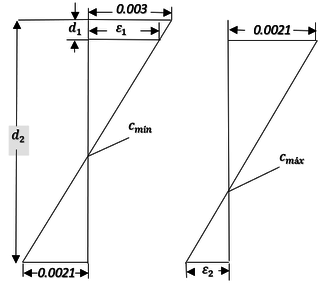
|
| Figura 52: Demostración CE.1 para el Caso Especial de columnas rectangulares |
De modo que se deberá cumplir la siguiente relación:
Luego: Y simplificando, se tiene:
Y ahora, por relaciones trigonométricas
Y además:
Caso 4
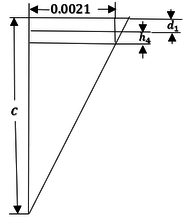
|
| Figura 53: Demostración 4.1 del Caso 4. |
Por relaciones trigonométricas:
Por lo tanto:
O también:
Caso 5
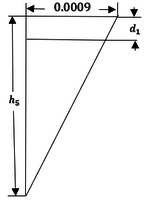
|
| Figura 54: Demostración 5.1 para el Caso 5. |
Por relaciones trigonométricas:
Caso 6
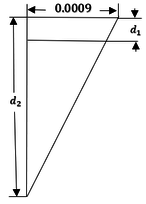
|
| Figura 55: Demostración 6.1 para el Caso 6 |
Por relaciones trigonométricas:
Entonces:
16 Anexo 2. Demostraciones del desarrollo del programa
16.1 Geometría analítica para el cálculo de eficiencias mecánicas
Ecuación de la recta A:
|
|
(90) |
Ecuación de la recta B:
|
|
(91) |
Igualando las ecuaciones anteriores por compatibilidad:
|
|
(92) |
Despejando x de la ecuación anterior:
|
|
(93) |
Sustituyendo la Ecuación [ 88] en Ecuación [ 92].
|
|
(94) |
Donde:
17 Referencias bibliográficas
BIBLIOGRAFÍA
[1] Adolfo Iván Jiménez P. y Dra. Sonia Elda Ruiz Gómez, Factores óptimos de cargas para el diseño de columnas esbeltas, Tesis de Licenciatura, UNAM, México, 2013 [2] Steven C. Chapra, Raymond P. Canale, Métodos numéricos para ingenieros, Quinta edición, McGraw Hill [3] Gaceta Oficial de la Ciudad de México, Normas técnicas complementarias de la Ciudad de México, 2017, Normas Técnicas Complementarias para Diseño y Construcción de Estructuras de Concreto 2017 [4] González Cuevas, Fco. Robles Hernández, Aspectos básicos del concreto reforzado, 4ta edición, Limusa 2005 [5] Jack McCormac y Rusell H. Brows, Diseño de concreto reforzado, 14va edición, Alfaomega, 2015 [6] Turner, M. J., Clough, R. W., Martin H. C. and Topp, L. J. Stiffness and Deflection Analysis of Complex Structures . Journal of the Aeronautical Sciences, Vol. 23 No. 9, 1956 pp. 805-823.[7] Yoeber Castro Atau, “Sistematización de detalles, habilitación y armado de acero ASTM A615 para construcciones de concreto armado: impacto técnico, económico y ambiental”, Universidad Nacional de San Cristobal de Huamanga, 2010
Document information
Published on 07/01/21
Submitted on 07/01/21
Volume 5, 2021
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?
![a) Diagrama de distribución de deformaciones. Caso 1. a) En alguna posición de c dentro del rango permitido, b) c está en el limite superior del rango permitido. Dibujo propio. Ver Demostración 1.1 en Anexo 1 [p. actual]](/wd/images/thumb/6/6d/Draft_Verduzco_Martinez_325285613-fig8.png/512px-Draft_Verduzco_Martinez_325285613-fig8.png)
![a) Diagrama de configuracion geométrica de deformaciones en el límite inferior del eje neutro. b) Diagrama de configuración geométrica de deformaciones en el límite superior del eje neutro. c) Diagrama de configuración geométrica de deformaciones para cualquier posición del eje neutro dentro de rango permitido. (Dibujo propio). Ver Demostración 2.1 en Anexo 1 [p. actual]](/wd/images/thumb/c/c3/Draft_Verduzco_Martinez_325285613-fig9.png/383px-Draft_Verduzco_Martinez_325285613-fig9.png)
![a) Sección transversal, b) Configuraciones geométricas de deformaciones en el límite inferior del rango permitido del eje neutro, c) Configuraciones geométricas de deformaciones en el límite superior del rango permitido del eje neutro. Dibujo propio. Ver Demostración 3.1 en Anexo 1 [p. actual]](/wd/images/thumb/8/8b/Draft_Verduzco_Martinez_325285613-fig11.png/448px-Draft_Verduzco_Martinez_325285613-fig11.png)