Abstract
This thesis develops a numerical tool (the Virtual Wind Tunnel, VWT) for the resolution of problems involving fluid flow around structures. Due to the limitations that traditional methods may have in this context, the VWT is based on the use of fixed mesh technologies (CutFEM-type) combined with an implicit representation of the embedded bodies.
One of the main contributions of the thesis is the use of such fixed mesh methods to solve lightweight thin-walled structures problems. Hence, two embedded formulations capable of representing the flow around bodies with and without internal volume are proposed. The first one results in a simpler implementation and lower computational effort but can only represent a slip behavior of the wall. The second one gets rid of such limitation by including a Nitsche imposition of the Navier-slip condition, thus allowing modelling any wall behavior as a wall law would do.
The applicability range of the VWT includes the fluid–structure interaction problem (FSI). To that purpose an improvement for the boundary condition imposition of the FM-ALE algorithm mesh motion problem is also proposed. Moreover, the implementation, which has been conceived to be easily extended to any other coupled problem, is also treated.
The validation of the technologies within the VWT includes multiple theoretical test cases as well as feasible industrial applications. Among these, the FSI analysis of a 4-point tent during a strong wind episode deserves to be highlighted as it showcases the achievement of the initial objective of the thesis.
Resumen
spanish En esta tesis se desarrolla una herramienta numérica (el Virtual Wind Tunnel, VWT) para la resolución de problemas que involucran el flujo de un fluido alrededor de una estructura. Debido a las limitaciones que los métodos tradicionales pueden tener en este contexto, el VWT se basa en el empleo de técnicas de malla fija (tipo CutFEM) combinadas con una descripción implícita de los cuerpos embebidos.
Una de las principales contribuciones de la tesis es el empleo de dichos métodos de malla fija para resolver problemas de estructuras ligeras de pared delgada. Así pues, se proponen dos formulaciones embebidas capaces de representar el flujo alrededor de un cuerpo con o sin volumen interno. La primera de ellas resulta en una implementación más sencilla así como en un menor coste computacional pero únicamente puede reprentar un comportamiento deslizante de la pared. La segunda elimina esta limitación incluyendo una imposición mediante el método de Nitsche de la condición de Navier-slip, permitiendo así modelar cualquier comportamiento del mismo modo que lo haría una ley de pared.
El rango de aplicabilidad del VWT incluye el problema de interacción fluido–estructura (FSI). A tal propósito se plantea una mejora para la imposición de las condiciones de contorno del problema de movimiento de la malla del algoritmo FM-ALE. Asimismo, también se hace especial hincapié en la implementación, que ha sido concebida para ser fácilmente extensible a cualquier otro problema acoplado.
La validación de las tecnologías implementadas en el VWT incluyen múltiples casos teóricos así como posibles aplicaciones industriales. Entre éstas se destaca el análisis FSI de una 4-point tent durante un episodio de viento severo ya que demuestra la consecución del objetivo inicial de la tesis.
Acknowledgements
First of all, I would like to acknowledge the Spanish Minister of Science, Innovation and Universities (Ministerio de Ciencia, Innovación y Universidades) and the International Center for Numerical Methods in Engineering (CIMNE) for the financial support during these four years. In this regard, the International Graduate School of Science and Engineering (IGSSE) of the Technische Universität München (TUM) is also acknowledged. Furthermore, I also thank the Oskar von Miller Forum (OvMF) for the accommodation during my international stay.
My gratitude extends to my two directors. I thank Prof. Eugenio Oñate for allowing me to work in such an interesting topic and for the confidence in me to achieve the objectives of this thesis. This work would not have been completed without the help of Prof. Rossi. Riccardo, many thanks for always having time to invest on this. I hope this is just the very fist one of many upcoming research successes.
The entire Kratos team deserve to be acknowledged by its own merits. Among all the developers, I particularly thank Dr. Jordi Cotela, Dr. Eduardo Soudah, Dr. Antonia Larese, Dr. Pooyan Dadvand, Carlos A. Roig (aka Charlie), Philipp Bucher and (soon Dr.) Vicente Mataix. Jordi, thanks for the valuable discussions (possibly lessons) about fluid dynamics and turbulence as well as for the coding advises. I also thank you for the fun during my stay in Munich. Edu, thanks for giving me the chance of applying my research in the biomedical field and for constantly try to find new opportunities for the group (by the way, you still owe me some hours of conversation). Antonia, thanks for all the help since I became your student for the first time. I want to also thank the KratosCore-man Pooyan for the enormous help while developing the level set algorithms as well as for the C++ and design patterns guidelines. The guy who silently makes everything work must be acknowledged too. Charlie, thanks for all the help with the compilation and debugging weird issues. I also thank the guy who has most probably reviewed the entire Kratos many times to force all of us to do things properly. Philipp, thanks for all the code reviews and brilliant suggestions. At this point, I must also thank the coolest office mate I ever had. Vicente, thanks for allowing me to constantly tease you, for the laughs during the tough moments and for being always disposed to help. I want to also thank the rest of CIMNE staff, specially the GiD team and the rookies that brought fresh air to the office a few years ago.
My gratitude also goes for the Bavarian colleagues in the Statik Chair. I personally thank Prof. Roland Wüchner for all the help and the guys of the Raum 0101.Z1.026, which I can confirm is the loudest office in the Chair. Thanks Andreas, Altug, Íñigo and Tobi for making me feel like at home during my stay.
Furthermore, I would like to express my gratitude to Prof. Miguel Cervera for the confidence in me to lecture one of his subjects. In this regard, I also acknowledge my teaching colleague Alejandro Cornejo as well as my colleague in the Department Gabriel Barbat.
There are people that has contributed to make this thesis possible without realizing. Here I want to thank my friends Toni (aka Kaborza), Ana, Enric (aka Epi), Eva María (aka Kpo), Dani Rey, Laura Cuni and Carlos (aka Carlutus). I also thank my long term teammates Víctor, Ortuño, Samu (aka Chino), Fer and Javi, as well as the last seasons joins Nachete, Nacho (aka Bibi), Andreu, Antonio and Lluís. These lists lack the important former teammates Álex, Adri, Joaquín (aka Maka), Bistu, Aitor and Manolo. All of them made me (temporally) forget about the troubles that raised during the prosecution of this thesis.
Last but not least, I want to also thank my family. Gracias Elena por acompañarme durante estos años y conseguir siempre hacerme reír, especialmente en los momentos más duros. Agradecer a mi madre María Luisa Martínez por su amor incondicional y por constantemente cuidar de nosotros. Gustaríame tamén dedicar unas palabras a o recordo da miña avoa Hortensia. Finalmente, mi más sentido agradecimiento es para mi padre Juan Francisco Zorrilla. Gracias Papa por enseñarme como luchar frente a las adversidades, por siempre confiar ciegamente en mí y por constantemente empujarme a dar un paso más allá. Esta tesis es una consecuencia de todo lo que he aprendido de ti.
input-ch2-StateArt input-ch3-NavierStokes input-ch4-CMAME_emb_1 input-ch5-AusasNavierSlip input-ch6-BIO input-ch7-CMAME_fsi input-ch8-Conclusions
1 Introduction
1.1 Fluid dynamics. A brief historical survey
Since the ancient era, humans have tried to tame the fluids for their own benefit. In the very beginning, this was limited to take profit of the wind thrust for navigation purposes. The earliest evidence of the use of a sail appears on a painted ceramic disk dating between 5500 and 5000 BC which was found in the current Kuwait. This discovery suggests that primitive wind sailing was already known in the Ubaid 3 period of the Mesopotamian empire [1]. Later on, the watermill appeared during the Hellenistic period (early 3rd century BC) in Byzantium and Alexandria to harness power from water [2,3].
These technologies kept evolving during centuries. Hence, the advances in sail navigation made possible the goods commerce as well as the culture exchange among all the civilizations in the Mediterranean sea and, after the 15th century, around the world. Watermills also evolved, to be more efficient or to become windmills, which appeared in the current Iran in the mid 9th century to generate power from the wind [4]. Although these are only two examples it is clear that these and other fluid-related technologies helped to write the history of mankind.
Furthermore, the technological advances nourished the interest on the theoretical comprehension of the mechanics of fluids. In this context, the Archimedes' principle (250 BC) can be considered as the very first theoretical milestone, which became the base for the hydrostatics studies of the ancient Greek philosophers. A few centuries later, the middle age Islamic physicists took the lead on this. This allowed them to reach a deep comprehension about the hydraulics of many engineering structures.
The breakthrough into modern fluid dynamics came in the 16th century from the hand of Leonardo da Vinci (1452-1519). Based on the observation of nature, da Vinci achieved an empirical understanding of some of the most complex fluid dynamics phenomena. Some of these are the first description of a pressure lift force, which can be understood as the first theory of flight, or the first explanation of turbulence, which he did from the observation of the water flow patterns that generate behind obstacles in rivers.
Nonetheless, the 17th and 18th centuries can be considered as the most prolific times for the theory of fluid dynamics thanks to the contributions of many brilliant mathematicians. Among all of them, Isaac Newton (1643-1727), Daniel Bernoulli (1700-1782), Leonhard Euler (1707-1783) and Jean le Rond d'Alembert (1717-1783) stand out. Isaac Newton settled the foundations with his well-known laws of motion and studies about the friction and viscosity (Principia, 1687). Later on, Daniel Bernoulli proved that the gradient of pressure is proportional to the acceleration of the fluid in his theory of the motion of fluids (Hydrodynamica, 1738). In 1757 Leonhard Euler posed his famous Euler differential equations for inviscid flows. Just one year later, Jean le Rond d'Alembert proved that the drag of a body of any shape moving through a fluid with no viscosity is zero (1758). This phenomenon was known from then on as the d'Alembert paradox.
During the 19th century the effort was put on adding a friction term to Euler's equations in order to overcome the d'Alembert paradox and obtain the results observed in nature. This was achieved in 1822 by Claude-Louis Navier (1785-1836), who proposed the addition of an extra molecular viscosity term. Although several authors published works in this regard, it took two decades to find the first mathematical reversible derivation of the new viscous Euler equations, which was presented by George Gabriel Stokes (1819-1903) in 1845. Hereafter, these equations were known as the Navier-Stokes equations. In 1851 George Gabriel Stokes also derived the well-known Stokes' law for the calculation of the drag force exerted on spherical objects in high viscous flows.
Viscosity and turbulence have been possibly the major theoretical concerns of contemporary fluid dynamics. In 1883 Osborne Reynolds (1842-1912) demonstrated with his famous experiment how the transition from laminar to turbulent flow occurs. 20 years later, Ludwig Prandtl (1875-1953) presented his viscous boundary layer theory (1904) which has been the basis for most of the aerospace technological advances of the past century [5]. Besides these, the contributions of Theodore von Karman (1881-1963), Geoffrey Ingram Taylor (1886-1975) and Andrey Nikolaevich Kolmogorov (1903-1987) aiming at understanding the turbulence also deserve to be mentioned.
The eruption of the World Ward in the beginning of the 20th century came with an astonishing evolution of the aerospace engineering, which promoted the construction of experimental wind tunnel facilities. The wind tunnels proliferation continued until the end of the World War II and allowed scientists and engineers to properly visualize and accurately measure the flow passing through objects for first time in history. This capability turned into a deep empirical knowledge that made possible the amazing aerodynamic advances of the past century.
Although numerical methods were used from long time ago, it was the apparition of modern computers during the second half of the 20th century what effectively enabled the virtual resolution of real-life problems by using computational techniques. Hence, the constantly growing computational power paced the apparition of a widespread range of numerical techniques since the 50s. It was however during the 60s and the 70s when the aircraft industry, mainly Boeing and NASA, effectively drove the Computational Fluid Dynamics (CFD) forward by developing numerical techniques to solve simplified inviscid models, namely the potential and Euler equations. Thanks to this, CFD methods could be applied for the first time to the resolution of real engineering problems. During the 80s and the 90s CFD technologies advanced further on and achieved the resolution of the complete Navier-Stokes equations, helping CFD methods to populate other engineering fields such as the automotive, biomedical or civil engineering.
In addition, during the early 80s commercial CFD codes came into the open market to become one of the daily used Computer-Aided Engineering (CAE) tools. Nowadays, commercial and open-source CFD codes provide technicians, designers and researchers with a virtual wind tunnel toolbox on their own laptops. Thus, CFD have become in an indispensable part of any design process involving fluids, making possible the development of technologies that have helped to achieve the all-times most rapid mankind evolution.
1.2 The fluid–structure interaction problem
From the previous section, it can be concluded that the comprehension of the interaction mechanisms that appear after the immersion of a body into a fluid has been one of the most important scientific challenges of the past centuries. In a wide range of applications, such as the hydrostatic analysis of massive civil engineering structures or the laminar flow analysis in open water channels, the fluid dynamics analysis can be efficiently achieved without considering the deformation of the “wet” bodies. However, there are lots of engineering and natural phenomena in which such simplification is no longer valid, leading to the so called Fluid–Structure Interaction (FSI) problems.
At this point, it is important to remark that the resolution of a fluid dynamics problem with and without considering such fluid–structure interaction mechanisms can lead to a completely different response. Hence, the FSI problem can be somehow considered as the union of a fluid dynamics and a solid mechanics problems such that the solution of each one of them is linked to the one of the other. This mutual dependency comes from the fact that the structure is deformable under the action of the fluid load. At the same time, the structure deformation implies a modification in the fluid problem geometry, which turns into a change in the load distribution over the structure.
Nowadays this might seem kind of obvious, but uncontrolled FSI is behind some of the most famed engineering failures of the modern era. For instance, fluttering, which is a dynamic instability that causes self-oscillation of fluid-surrounded slender bodies, is understood to be the main cause of the Tacoma Narrows bridge collapse in 1940 as well as the Braniff International Airways flight 542 crash in 1959.
Furthermore, there also exists lots of natural phenomena, such as the flapping of animal wings or the hydrodynamics of fish fins that are indeed FSI problems [6,7,8]. The study of such animal motion mechanisms from a computational perspective [9,10] is of great value for the development of novel technologies such as newfangled unmanned vehicles. Such natural phenomena also include many of the human body processes, mainly those related to the circulatory and respiratory systems. The numerical simulation of these has helped the clinicians in the decision making in front of cardiovascular [11,12,13] and airways [14] diseases, in the development of new prosthetic devices such as artificial heart valves [15,16,17], and more recently, in the study of the mechanics of blood cell motion [18].
More specifically, there are also lots of civil engineering structures that are affected by the FSI problem. These can be basically summarized in thin-walled structures [19], namely membranes and shells, and slender structures such as bridge decks [20], chimneys, elevated tanks that suffer from sloshing during earthquakes [21,22] or the blades of wind energy harvesting mills [23].
In some cases, the FSI effects can be efficiently reproduced using reduced order models [24] (e.g. water hammer in fluid ducts). However, such simplifications are no longer possible in the vast majority of applications since the interaction mechanisms involve a three-dimensional behavior. This thesis focuses on the latter, particularly in those problems that involve lightweight thin-walled structures.
1.3 Lightweight thin–walled structures
Since their appearance in the mid past century, the interest in the use of highly flexible thin–walled structural solutions has been constantly growing. In this regard, the German architect and engineer Frei Otto (1925-2015) must be acknowledged as the pioneer in the design of lightweight structures. Under the idea of creating more sustainable structures in a world with resources shortages, Frei Otto abandoned the traditional structural design in favour of more efficient and creative solutions based on the use of metal reinforced tensile membranes and cables [25]. Although this new technology was initially used for basic structures, such as the Musikpavillon in the 1955 Kassel Federal Garden exhibition (Fig. 1.1a), their advantages rapidly became apparent and encouraged their use as permanent solutions for the roof covers of the 1967 Montreal World Expo German pavilion and the 1972 Munich Olympic Stadium (Olympiastadion München) (Fig. 1.1b).

|

|
| (a) Kassel Federal Garden exhibition Musikpavillon (1955). | (b) Olympiastadion München interior view (1972). |
| Figura 1.1: Evolution of lightweight structures by Frei Otto. | |
The pioneer understanding of how structures must be conceived that Frei Otto had impinged the current structural design criteria, which have evolved to use of much more efficient materials such as reinforced textile composites. Even though such extremely lightweight structures can be also employed as roof covers or shadowing structures (Fig. 1.2), their versatility and resource-saving manufacturing opens a wide variety of novel applications.

|
| Figura 1.2: Textile roof cover in the airport of München. |
For instance, these can be used for the creation of temporary rapid deployment inflatable structures that can serve as emergency shelters, exposition pavilions or hangars (Fig. 1.3) [26]. Furthermore, they can also be used for the creation of foldable or moving structures capable of adapting their shape according to the environmental conditions (Fig. 1.4). Last but not least, there are other problems out of the civil engineering scope, such as the optimization of sail navigation or the design of parachutes, that could directly benefit from the research on this field.

|

|
| (a) Exterior view. | (b) Interior view. |
| Figura 1.3: Inflatable 75m span hangar in Saudi Arabia (courtesy of Buildair). | |

|

|
| (a) Shading structure closed. | (b) Shading structure opened. |
| Figura 1.4: Convertible shading roof in the Prophet's Mosque in Medina. In summer the umbrellas open to provide shade while in winter they do so to prevent the day warmth from escaping (courtesy of SL Rash GmbH). | |
It is clear that the structural safety analysis of this family of structures depends hugely on the characterization of the mechanical properties of the textile materials they are composed of. Their response is also strongly influenced by the wind load they are subjected to.
Normally, the structural integrity under the action of wind loads is ensured by the accomplishment of the design codes requirements. Unfortunately, these newfangled structural solutions are commonly out of the scope of the standards, and thus require alternative ways to guarantee safety and reliability. Moreover, they are prone to suffer from aeroelastic effects, which should definitively be considered in the response assessment, owing to their extremely flexible nature.
Even though wind tunnel facilities have been of great benefit to characterize the flow around flexible objects, they have some inherent drawbacks. On the one hand, wind tunnels involve enormous construction and operation costs that compromise their economic viability. This turns into an increased cost per experiment, which restricts their use to reference research centers or big private companies. On the other hand, depending on the dimensions of the problem and of the ones of the wind tunnel, the experiment may require the use of a reduced scale model. In some applications this might compromise the quality of the results as it is not always possible to properly reproduce the scale effects in the reduced experiment in such a way that the aeroelastic behavior of the real structure is represented. In this context, numerical simulation arises as a feasible alternative to overcome these limitations, which surely appear in the FSI wind analysis of lightweight structures.
1.4 Objectives
The main objective of this thesis is the development of a numerical tool, henceforth the Virtual Wind Tunnel (VWT), for the reliable resolution of FSI numerical experiments. It has to be emphasized that the VWT must be capable of dealing with any type of structure, namely volumetric and membrane-like bodies.
Considering that the target application is the resolution of extremely flexible structures under the action of severe wind loads, the VWT must be robust enough to cope with extremely large displacements and/or rotations. On top of this, there might be cases in which the analysed bodies can suffer from self-contact and wrinkling.
In this context, the traditional Arbitrary Lagrangian-Eulerian (ALE) approaches that have been traditionally used for similar purposes are prone to suffer from element deterioration. Hence, rather than focusing on the Computational Solid Mechanics (CSM) problem, this work focuses on the developing of embedded Finite Element (FE) methods for the robust resolution of CFD and FSI problems involving thin-walled structures. It is pointed out that efficiency is crucial for the effective technology transfer of the VWT to real engineering applications, in which the computational times must be in accordance to the project development ones. In consequence, all the techniques in this work take this as an essential requirement.
At the end of this thesis, the VWT tool will help to
- extend the use of CFD and FSI simulations to the civil engineering field as it already occurs in other engineering disciplines (e.g. aerospace engineering)
- study the aeroelasticity phenomena that occur in extremely flexible structures that cannot be tested in real wind tunnel facilities. The better understanding of these during the design phase would allow optimizing the geometry and materials of the structure, thus reducing the construction overall cost and material consumption.
- optimize and simplify the design process by reducing the amount of required wind tunnel experiments, something that should turn into a more efficient project development.
Last but not least, it is due mentioning that all the implementations of this work must remain as open source software. In order to fulfil this requirement the VWT will be developed within the Kratos Multiphysics open source framework [27,28].
1.5 Contents
First of all, it has to be clearly stated that this document is conceived as a compendium of publications. Therefore, three of the chapters are made as a brief introduction to the corresponding paper and the postprint submitted to the journal.
Chapter 2 presents the state of the art on fixed mesh CFD methods and FSI coupling. In Chapter 3 the quasi–incompressible Navier–Stokes stabilized formulation used throughout the thesis is derived. Chapter 4 is the first paper of the compendium and presents a discontinuous embedded formulation for the CFD analysis of slip thin-walled bodies. This formulation is enhanced in Chapter 5 to deal with both stick and slip thin-walled bodies. Chapter 6 is the second paper of the compendium and validates the formulation described in Chapter 5 with data from in vitro biomedical experiments. The extension of the embedded CFD solver to FSI problems is studied in the third paper of the compendium, which is collected in Chapter 7. In Chapter 8 embedded CFD methods are exploited to efficiently deal with extremely large wind engineering problems. Finally, the conclusions and further work lines are discussed in Chapter 9.
2 State of the art
This chapter reviews the state of the art on the use of fixed mesh techniques in CFD and FSI problems. The first section describes how this family of numerical methods can help to efficiently solve the VWT target applications. Secondly, the implicit representation of geometries is briefly discussed, particularly focusing on the discontinuous level set representation of membrane-like bodies. The third section reviews the characteristic features of each one of the literature fixed mesh approaches in order to choose the suitable one for the problems at hand. The forth section reviews the literature on the chosen alternative. The fifth section presents the common issues that appear when fixed mesh methods are applied to moving interface problems. Finally, the last section reviews the coupling techniques to approach the FSI problem, specially that one applied in this thesis.
2.1 Fixed mesh methods. Motivation
This thesis aims at creating a framework for the FSI analysis of any type of bodies, with a particular emphasis on the lightweight thin-walled structures. Taking into account that these are highly deformable structures, the traditional Arbitrary Lagrangian-Eulerian (ALE) methods [29] might lack robustness since the mesh motion problem tends to yield degenerated elements, namely highly distorted or even inverted, when large displacements and rotations of the boundaries appear. Moreover, problems involving thin-walled bodies might also fall into topology changes if self-contact or wrinkling appears.
Having said this, it can be easily guessed that the selection of the fluid-structure interface tracking technique becomes crucial for the robust and efficient resolution of the problems at hand. Taking this into account, mesh-based approaches can be classified according to how the analysed bodies are represented in body conforming (also known as body fitted) and non-conforming approaches.
Even though body conforming purely Lagrangian methods such as the Particle Finite Element Method (PFEM) [30,31] are a robust alternative for the interface tracking in moving boundary problems, they rapidly become prohibitive as remeshing is required at each time step. Alternatively, the CFD domain can be meshed regardless the analysed objects to decouple the computational mesh (henceforth denoted as background mesh) from the immersed geometries, which are no longer represented by the boundaries of the mesh. Instead, the analysed bodies are implicitly characterized on the background mesh from their skin representation by using techniques such as the level set method [32].
Although this introduces an extra complexity to the problem, the implicit representation of boundaries becomes advantageous for the interface tracking. Hence, all the potential mesh updating issues that may appear under the presence of large boundary displacements and rotations are bypassed since the ALE mesh motion problem is substituted by a simple update of the implicit representation of the bodies. On top of that, topology changes are naturally dealt with without requiring any operation in the background fixed mesh.
Furthermore, the use of an implicit representation also optimizes the simulation pipeline since the preprocess becomes much more efficient. On the one hand, it avoids all the manual repairing operations such as the removal of holes, overlapped surfaces or duplicated entities that are required to create a volume mesh from a “dirty” input geometry. These operations, which can amount up to the 50% of the total simulation time for real engineering cases [33], can be completely bypassed as the geometrical defects are filtered by the level set calculation algorithm, which is a more robust and effective operation [34,35]. On the other hand, it is also known that the creation of a volume mesh from a thin-walled geometry is a rather troublesome operation, specially when complex curved geometries are involved. This is because the original membrane geometry needs to be duplicated in order to generate the volume mesh. These two geometrical entities tend to intersect each other when working in the machine precision limit, thus leading to a failure of the meshing operation. Using an implicit representation of the volumeless immersed bodies automatically avoids such limitation.
2.2 Level set representation of immersed geometries
At this point, it is clear that using a level set representation is of great utility in some applications. This section briefly describes the basics of implicit representations and how they can be applied depending on the volumetric nature of the analysed geometries.
The main idea behind any level set method relies on the calculation of a signed distance function such that its zero isosurface matches, as closely as possible, the skin of the analysed bodies. Even though all the level set algorithms are based on the intersection between the background and overlapped skin meshes, they can be classified according to their treatment of the volumetric nature of the bodies. Hence, those bodies that feature a well defined internal volume are typically represented using a continuous level set algorithm (Fig. 2.1). In this case the distance is computed node-by-node and the inside/outside concept is treated using computer graphics techniques such as the raycasting [36]. These methods always return a smooth and continuous representation of the immersed bodies.
Unfortunately, these methods are not valid for membrane-like bodies as the inside/outside concept becomes meaningless in this case. In consequence, volumeless bodies cannot be represented in terms of a nodal-based distance function. Nevertheless, it is possible to describe these in terms of an element-based level set. As it can be observed in Fig. 2.2, such capability comes however at the price of having a potentially discontinuous distance function, meaning that the same node can have different distance sign and value depending on the element considered. This is exploited in the subsequent chapters, as well as in [37,38,39,40], to model a wide variety of thin-walled structures such as boat sails, lightweight membranes or thin biological tissues.
2.3 Level set methods for CFD and FSI problems
Prior to any further discussion, it is interesting to mention that the first FSI numerical approach was based on a non-conforming mesh method. It was presented in the early 70s by Prof. Peskin and relies on the addition of an artificial body force to consider the immersed structure motion into the fluid problem [41].
Introducing the use of a level set-based representation of the immersed geometries opens the possibility to use a wide variety of methods such as the eXtended Finite Element Method (xFEM) [42,43,44,45], the Immersed Boundary Method (IBM) [46,47,48,34,35,49], the Embedded Boundary Method (EBM) (also known as Cut-FEM) [50] or the Shifted Boundary Method (SBM) [51,52]. Regardless this thesis only considers traditional FE discretizations, the novel Immersogeometric approaches [16,53] that combine exact geometries and embedded formulations also deserve to be mentioned.
Table 2.1 compares the aforementioned methods according to different criteria. The first one is the computational effort in terms of locality and matrix graph preservation, according to which xFEM is the most expensive technique as it requires the introduction of extra Degrees Of Freedom (DOFs) associated with the FE enrichment unknowns. Aside of introducing the need for blending elements, which turns into a more expensive distributed memory assembly because of the communication overhead, this also requires the system matrix graph to be reconstructed each time the level set is updated.
The second criterion compares the BC imposition. In this regard, the IBM is possibly the most straightforward approach, as it allows direct imposition of the BC. However, this is not done over the interface but on its closest dry nodes, something that makes the method prone to suffer from mass conservation issues. The SBM method aims at overcoming this limitation by imposing a modified boundary value that takes into account the distance between the interface and the closest dry nodes where the BC is enforced. Contrariwise, the xFEM and the EBM rely on a weak BC imposition. This is normally done using variational techniques such as the penalty method [54,37], the Nitsche method [55,56,57,58,59,60] or the Lagrange multipliers method [61]. Although the weak imposition entails an extra complexity, that might turn into accuracy and stability issues, it allows to consistently enforce the BC over the level set intersections, which are the best non-conforming representation of the immersed geometries that can be implicitly achieved.
Last but not least, the table compares the capability of the methods to be applied to membrane-like bodies. As it can be observed, any method that requires an interior (i.e. dry node) for the BC imposition becomes no longer valid for the simulation of thin-walled geometries, meaning that only the xFEM and the EBM can be applied for such purpose.
Taking into account that industrial CFD and FSI problems likely involve a huge number of DOFs, the chosen alternative must be as computationally efficient as possible. Considering that only the xFEM and the EBM fulfill the thin-walled bodies requirement, the more suitable method for the target applications is the EBM owing to the absence of blending elements and the ability to keep the initial system matrix graph during the entire simulation.
| xFEM | IBM | SBM | EBM | ||
| Computational effort | Local | No | Yes | Yes | Yes |
| Keeps matrix graph | No | Yes | Yes | Yes | |
| BC imposition | Direct | No | Yes | Yes* | No |
| over | Yes | No | No | Yes | |
| Thin-walled bodies | Yes | No | No | Yes | |
2.4 The Embedded Boundary Method. An overview
After having selected the EBM as reference fixed mesh approach, this section briefly reviews its basis as well as the different alternatives that can be employed for the weak imposition of the level set BC. To ease the discussion, from now on the fluid computational domain is denoted as while the immersed objects skin representation is denoted as .
The first distinguishable feature of the EBM is that the computational domain is not conformed by the element faces but by the intersections of the level set function with the background mesh elements. Aside of being a more accurate representation of the analysed bodies, this enables the application of the method to thin-walled bodies. This is schematically depicted in Fig. 2.3, which recovers the previously presented volumetric (Fig. 2.1) and volumeless (Fig. 2.2) toy examples to show their corresponding embedded computational domain.
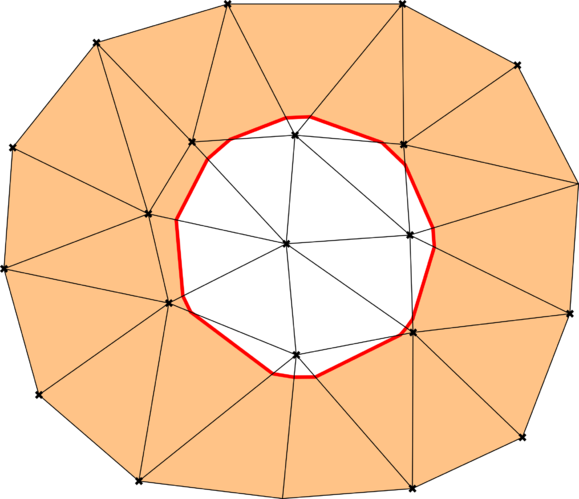
|
|
| (a) Continuous level set case. | (b) Discontinuous level set case. |
| Figura 2.3: EBM sketch for the examples in Figs. 2.1 and 2.2. Light orange denotes the active computational domain (). Red lines denote the level set intersections () that represent the embedded skin. | |
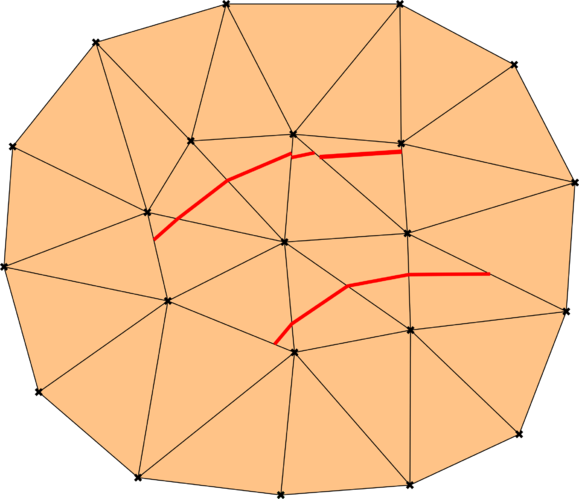
From the previous images it can be deduced that an auxiliary splitting operation is required in each intersected element to perform the integration properly. As it is depicted in Fig. 2.4, the division of the parent geometry in a set of smaller ones allows relocating the integration points such that only the “wet” part of the cut elements is integrated. The same procedure is equivalently applied to thin-walled bodies (Fig. 2.4b) to consistently integrate both (“wet”) sides of the membrane bodies.
Once the volume integration has been performed, the fluid BC needs to be imposed over the either continuous or discontinuous level set intersections that conform (highlighted in red in Figs. 2.3 and 2.4). Although it is possible to create new nodes from the splitting pattern to strongly impose the BC [34], this operation is commonly done in a weak (i.e. variational) sense. There is a wide variety of methods that can be used for such purpose, leading to different flavors of the EBM. In the following a brief review of all the approaches that have been successfully applied to CFD problems is presented.
The most extended approach to weakly enforce the BCs in the context of EBM methods is possibly the Nitsche method [55,62], which has been applied for the imposition of the stick (no-slip) condition in both Stokes [58] and Navier-Stokes [16,59] problems. The modified Nitsche method for no-slip conditions in [56] should be also acknowledged because of its simplicity and remarkable good performance. Regarding the slip wall behavior, the Nitsche method is used in [57] to enforce a pure slip condition. In [60] this is extended to the Navier-slip condition.
The Lagrange multipliers method can be alternatively used to impose Dirichlet BCs [63,64]. In [57] a Lagrange multiplier approach for the imposition of the pure slip condition in Stokes flows is presented. Furthermore, the Lagrange multipliers technique in [61], which is based on a static condensation, deserves to be highlighted after its ability to keep constant the number of DOFs.
Unfortunately, all the aforementioned EBM approaches require a well-defined internal volume. In consequence, none of the methods above can be directly applied for the analysis of thin-walled bodies, thus precluding the simulation of membrane and shell structures. This could be achieved in an IBM fashion by adding an artificial volume force body [41,65,66,67]. However this kind of methods might lack accuracy and suffer from mass conservation issues in some applications. In [9] an EMB ghost cell method able to work with any type of bodies (volumetric and volumeless) is presented. Nonetheless, such capability comes at the price of having a no longer purely local method as the BC imposition requires the element neighbors. Alternatively, the approach in [54] addresses the problem in a EBM-like manner by introducing a modified FE space in combination with a penalty imposition of the no penetration BC. An important advantage of this method is that the graph of the discrete stiffness matrix is preserved, something that becomes crucial when the level set function needs to constantly updated (i.e. FSI problems).
After having reviewed the literature on Cut-FEM approaches it can be noted that the volumetric problem is pretty well resolved. There is a wide variety of approaches that can efficiently and robustly deal with the problem at hand. Among these, the approaches in [56] and [60] are used in this work for the volumetric no-slip and slip (in a general Navier-slip sense) wall behavior modeling.
However, there is still room for the research on the application of the EBM to the resolution of CFD problems involving thin-walled bodies. More specifically, there is no purely local approach in the literature capable of representing the discontinuities arising from the immersion of membrane-like structures. The chapters 4 and 5 of this thesis aim at accomplishing such objective.
2.5 Fixed mesh methods and moving bodies
The enhanced robustness that fixed mesh approach have to deal with arbitrary large displacements and rotations comes at the price of some particularities that require to be taken care of. These are the small cut instability and the historical data initialization.
2.5.1 Small cut instability
As it can be easily guessed from its name, this problem is an instability that pops up when there is an ill-conditioned intersection between the level set and the background mesh. Even though the concept of ill-conditioned intersection varies depending on the fixed mesh approach used, it can be generalized to any intersection of the embedded skin that occurs extremely close to one node of the background mesh, which is equivalent to say that close to zero values of the level set are potentially ill-conditioned. It is important to note that no distinction is done yet between continuous and discontinuous level set functions, meaning that zero values of the distance function are always ill-defined. For those cases involving volumetric bodies represented by continuous distance functions, the previous definition can be restricted to those level set values close to zero that yield an almost empty element.
The small cut instability commonly appears when the interface moves across the background mesh. Nonetheless, it may also happen in problems involving a steady interface, specially in those ones involving poorly defined input geometries. In consequence, an auxiliary strategy to prevent this undesired situation is always demanded to robustly apply any fixed mesh method.
There are several approaches to prevent the convergence of the problem to be ruined by the ill-conditioned cuts. Some of these are the ghost penalty method [50] or the ghost cell method [68]. Although the stability and robustness of these methods is proved, they require the neighbors of the ill-conditioned elements to be applied. This adds a search operation that turns into an extra computational overhead, which might be particularly relevant when distributed memory platforms are used.
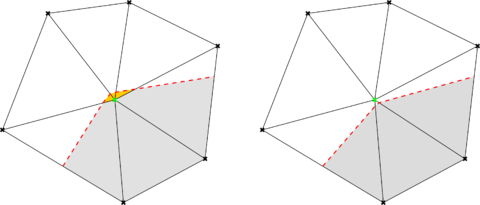
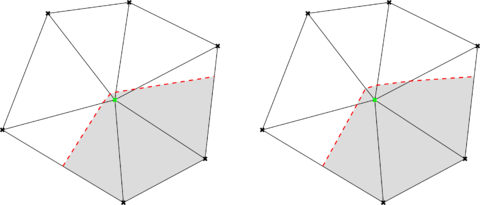
Alternatively, the ill-conditioned cuts can be avoided rather than controlled by using a level set quality check and correction algorithm. This approach starts from the idea that the level set is indeed a representation of the real geometry, whose quality is directly related to the background mesh element size. Taking this into consideration, the distance can be slightly modified by a small quantity depending on the element size without incurring in a noticeable error. For the continuous level set case, this means to avoid the “almost empty” intersections (highlighted in light orange in Fig. 2.5) by slightly moving the interface towards the positive distance side. Likewise, for the discontinuous level set case ill-conditioned cuts can be avoided by slightly modifying the close to zero elemental level set values (Fig. 2.6). This approach arises as a more computationally efficient (almost) purely local alternative that only requires one synchronization operation. The capability of this apporach to robustly deal with the problems at hand is evinced in Chapters 6, 7 and 8, where it is applied to complex real-life geometries.
|
| Figura 2.5: Continuous distance check and correction. Grey regions represent the computational domain . Red dashed lines represent the level set intersections . Before (left) and after (right). |
|
| Figura 2.6: Discontinuous distance check and correction. Grey regions represent the computational domain . Red dashed lines represent the level set intersections . Before (left) and after (right). |
2.5.2 Consistent initialization of values. The FM-ALE method
This issue appears when the level set function, regardless its continuous/discontinuous nature, evolves in time. As it is graphically described in Fig. 2.7, when the distance function modifies its spatial configuration the background mesh nodes that used to lie in one side of the level set might end up in the other one. In consequence, the historical data of these nodes is no longer valid, thus leading to a wrong approximation of all the inertial terms involved in the problems.
It is due mentioning that no distinction is done between continuous and discontinuous distance functions, as the historical values need to be consistently updated in both cases. While in the continuous level set case (volumetric bodies) it is needed to consistently initialize the historical values in those nodes that change their status from “dry” to “wet”, in the discontinuous level set case (volumeless bodies) it is required to do so as the historical data becomes meaningless as soon as the nodes move from one side to the other of the immersed thin-walled body. Having said this, it can be easily guessed that the proper treatment of this issue is crucial for the application of fixed mesh methods to any moving boundaries problem (i.e. FSI).
The consistent historical data initialization can be achieved in an ALE-fashion by using the Fixed Mesh–Arbitrary Lagrangian Eulerian (FM–ALE) method. The FM–ALE was firstly described in [69] to address this issue in moving boundaries embedded CFD problems. In [70] the authors extend the method to solid mechanics and FSI problems. Similarly, they do so for free-surface problems involving floating objects in [71,72].
The main idea behind the FM-ALE method is to retrieve the consistent historical values from the so called virtual mesh, which is created as a copy of the background mesh used in the resolution of the problem. Each time the level set changes its spatial configuration, the virtual mesh is accordingly deformed by solving a mesh motion problem. Then all the historical values, as well as the mesh velocity, can be projected from the virtual mesh to the background one. Once the projection is completed, the deformation of the virtual mesh is reverted back to the initial position.
It is due mentioning that this last step is the key of success of the method when it is used in presence of arbitrary large movements of the embedded interfaces. Hence, bringing back the virtual mesh to its original position each time the FM–ALE algorithm is applied implies that the mesh motion problem most likely involves small displacements and rotations, thus avoiding the common element distortion issues associated to body conforming ALE approaches. Besides that, reverting the mesh deformation also makes the problem presumably cheaper in terms of the computational effort.
2.6 Fluid-Structure Interaction
This section reviews the ingredients that are required to extend the embedded CFD solver to FSI problems. Hence, the different alternatives that can be selected to achieve the coupling are reviewed. The last part of the section focuses in detail on the particular choice of this work. To ease the discussion, the fluid and structure domains are denoted as and from now on. Similarly, their corresponding FSI interfaces are denoted as and .
2.6.1 Coupling schemes
For a coupled problem of any type it is required to satisfy the interface transmission conditions to guarantee that the coupling is effectively achieved. Such transmission conditions are of course problem dependent and thus need to be particularized depending on the physics to be coupled. For the FSI specific case these are the interface force equilibrium as well as the mass continuity, which demands that and spatial configurations match.
To ensure that the transmission conditions of the problem are accomplished, a coupling scheme is required. These can be classified according to how the transmission conditions are imposed in Dirichlet-Neumann (DN), Neumann-Neumann (NN) and Robin-type schemes (i.e. Robin-Robin (RR) or Neumann-Robin (NR)).
Owing to its proved well performance in the FSI field [73,74,75,54], the DN coupling scheme is selected as reference coupling scheme in this thesis. In short, the DN scheme consists in enforcing a Dirichlet BC in one subdomain and a Neumann BC in the other one. The Dirichlet condition is commonly applied in the lower density subdomain, which in the FSI case is likely . In consequence, the Neumann BC is applied over as a surface load whose value comes from the stress in the fluid boundary. For a thorough review on the stability and performance of the DN scheme, as well as on its interaction with several time discretization techniques the reader is referred to [76].
Furthermore, the implementation of the DN scheme is reasonably simple and does not require to modify the subdomain formulations. This last feature becomes crucial for the efficient application of non-intrusive coupling algorithms like the ones that are to be exploited in chapter 7 of this thesis.
Nevertheless, it has to be mentioned that there exist cases in which the DN may lack convergence or suffer from stability issues [77]. In this context, NN and Robin-type schemes arise as a feasible alternative to overcome these limitations. Although these applications are out of the scope of this thesis, the reader is referred to [78,79] and [80,81] for more information regarding RR and NR schemes.
2.6.2 Implementation of coupling schemes
The previously defined transmission conditions require a coupling strategy to ensure that they are satisfied in all the coupling interfaces. Such strategies can be classified according to how the coupled problem is solved in monolithic and partitioned (also known as staggered) strategies.
The idea behind any monolithic strategy is to put together all the subdomain contributions, together with the corresponding transmission conditions, in a unique large system of equations. This approach has been successfully applied in the resolution of body conforming FSI problems in [82,30]. More related to this thesis is the method in [70], where the authors present a monolithic FSI technique based on a non-conforming discretization in both the fluid and the structure subdomains.
Although monolithic strategies are possibly the most robust approach for the resolution of strongly coupled FSI problems, they tend to yield poorly conditioned systems of equations, which might eventually impede the use of fast iterative solvers. Besides this, the implementation of a monolithic strategy is rather intrusive and likely requires the development of a new solver for the specific purpose of the coupling.
Partitioned strategies avoid these disadvantages by keeping a separated solver for each one of the subdomain problems, meaning that the fulfillment of the transmission conditions is achieved by exchanging information between the coupled subdomains. Although the convergence rate of partitioned strategies might be suboptimal, they allow reusing already existing, possibly robust and thoroughly validated, specific solvers. This idea brings up the concept of black-box coupling [83,84,85], in which the coupling strategy is also requested to not interfere with the subdomain solvers more than to get and set information. Hence, the subdomain solvers are considered as a sort of black boxes that return a solution for the input data, that must be provided according to their Application Programming Interface (API).
In the framework of this thesis, this makes possible to directly use the already existent structural mechanics module of Kratos Multiphysics in order to focus the implementation effort on the development of the embedded CFD technologies and its extension to FSI problems.
Partitioned strategies can be further classified according to how many times the information is exchanged per time step. On the one hand, there are the loosely-coupled (or explicit) strategies in which the information is exchanged once per time step [86]. This is obviously the cheapest approach in terms of computational and implementation effort. However, they might lack convergence when there is strong interaction between subdomains or when the added mass effects are important [87,88,89].
On the other hand, there are the strongly-coupled (or implicit) strategies in which the information exchange occurs in an iterative manner until a certain convergence criterion is reached. Depending on how the information is used within each iteration, it is possible to distinguish between Jacobi and Gauss–Seidel strongly-coupled strategies. While in Jacobi-type iterations the information exchange occurs at the same time, allowing the parallel resolution of the subdomain problems, in Gauss-Seidel iterations this is done in a sequential manner, enabling the use of the latest information obtained in one subdomain to solve the other one within the same iteration.
The iterative nature of Gauss-Seidel approaches makes them more suitable for the target applications of this thesis. Although their convergence rate might be not as good as that of monolithic approaches, it can be astonishingly improved, specially when facing strongly coupled problems, by using them in combination with convergence acceleration algorithms.
Finally, it is interesting to point out that there exist some semi-implicit strategies that are somehow between the explicit and implicit ones. A very detailed review about several semi-implicit approaches can be found in [81].
2.6.3 Black-box interface residual minimization techniques
The choice of a Gauss–Seidel iterative strategy requires the definition of an interface residual function such that its minimization ensures the fulfilment of the problem transmission conditions. As the interface residual is completely problem dependent, it is assumed to be already defined for the discussion at hand. Hence, the literature review in this subsection focuses on the residual minimization rather than on its definition, which will be addressed in chapter 7.
As it is commented above, the use of a black-box coupling strategy implies restricted access to the subdomain solvers. The most straightforward approach that accomplishes with such requirement is a fixed-point iteration with relaxation. Although convergence can be achieved using a constant relaxation parameter, these methods are commonly used in combination with dynamic relaxation formulas. Among all of them, the second order Aitken scheme is possibly the most extended technique in the FSI community [73,75] owing to its reasonably good performance and relatively easy implementation.
Alternatively, the interface residual problem can be considered as a vector of unknowns to be minimized. Hence, the problem can be posed as a Newton–Raphson (N–R) iterative procedure, leading to the so called Jacobian-based residual minimization techniques. Ideally, the exact Jacobian that minimizes the vector interface residual could be computed by accessing the subdomain solvers. However, this intentionally precluded by the selection of a black-box coupling strategy. Nevertheless, the exact Jacobian calculation can be avoided by using Jacobian-free Newton-Krylov (JFNK) [90,14] or Quasi-Newton (QN) [84] methods.
Rather than approximating the complete interface Jacobian, JFNK methods are based on approximating its projection onto the iteration update vector by using a finite differences formula. Owing to the inherent non-linearity of the FSI problem, such projection needs to be linearized by introducing a small perturbation, which needs to be selected by the user. Although this issue can be addressed by using a formula to automatically do that [91], the optimal value for the small perturbation is still completely problem dependent.
In this context, QN methods arise as an alternative to avoid the selection of the perturbation constant. Unlike JFNK methods, QN approaches approximate the complete interface Jacobian by means of a linearized formula that takes the information from the previous FSI iterations. The different QN methods can be characterized according to how such Jacobian approximation formula is conceived [92].
Among all of them, the Broyden's iteration scheme should be acknowledged as the first QN method applied to FSI problems [91]. A more popular approach is the Interface Quasi-Newton with Inverse Jacobian from Least Squares model (IQN-ILS) [93,92], as well as its block equations version (IBQN-ILS) [92]. In [92] the authors prove that the performance of the IQN-ILS overcomes that of Aitken and of Interface-GMRES schemes for all the reported examples. A very similar approach to the IQN-ILS is the MultiVector Quasi-Newton (MVQN) algorithm presented in [84]. Although the authors report that it converges slightly faster than the IQN-ILS, this comes at the price of requiring a matrix inversion, whose size equals the interface residual one, each time the Jacobian is approximated. This disadvantage has been recently overcome in [94].
Considering that QN approaches involve a rather large number of matrix operations, each QN iteration is possibly more computationally expensive than that one of a JFNK technique. Notwithstanding this, they are reported to be the most efficient Jacobian-free approach in terms of total number of iterations. Taking into account that the computational bottleneck in partitioned FSI problems is likely the resolution of the CFD problem, the reduction of the total coupling iterations is what effectively turns into a performance improvement. Taking this into account, the embedded FSI coupling Gauss-Seidel technique presented in chapter 7 will be based on the use of QN algorithms. More specifically, the MVQN is chosen as reference black-box convergence accelerator owing to its reported good performance.
input-ch2-StateArt input-ch3-NavierStokes input-ch4-CMAME_emb_1 input-ch5-AusasNavierSlip input-ch6-BIO input-ch7-CMAME_fsi
This section presents the quasi–incompressible Navier-Stokes formulation that serves as basis for all the embedded CFD developments of this thesis. Firstly, the viscous incompressible Navier-Stokes governing equations as well as the inclusion an extra pseudo–compressibility term are discussed. Secondly, the FE discretization and the subscales stabilization technique are introduced. In the third section the variational form of the problem is derived together with some notes on its symbolic implementation. Finally, the correctness of the implementation is proven by the method of manufactured solutions.
This thesis focuses on the resolution of CFD and FSI problems involving viscous fluids. Considering that the Mach number (Ma) of the target applications is below 0.3, the flow can be considered as incompressible and thus modeled with the well-known viscous incompressible Navier–Stokes (N–S) equations [29,95].
In this context, the Cauchy stress tensor can be defined as
|
|
(3.1) |
where denotes the velocity, the pressure, the symmetric gradient operator, the 2nd order identity tensor and the 4th order viscous constitutive tensor.
Although any viscous constitutive relation could be used, only isotropic Newtonian fluids are considered in this thesis. Hence, the viscous constitutive tensor reads
|
|
(3.2) |
where denotes the tensor product and the 4th order symmetric identity tensor. and are the viscosity constants. The first one represents the dynamic viscosity while the second one can be computed as after taking the Stokes' assumption, which is valid in those cases in which the compressibility of the medium is negligible.
Inserting the previous definition of into the balance of linear momentum and mass conservation equations yields the viscous incompressible N–S equations
|
being the density and the vector of volumetric (body) forces. and denote the partial time derivative and the gradient operator. is the convective velocity, which is defined from the mesh velocity as .
At this point, it is important to provide some remarks about the convective term in Eq. 3.3.a since it strongly affects the applicability and convergence of the method. The first one concerns the inclusion of , which equals in a fixed mesh Eulerian framework. Although this is a valid simplification, it would impede the application of the FM–ALE algorithm in chapter 7. In consequence, it is convenient to keep such ALE definition of the convective velocity .
The second one concerns the non–linearity. As it is evinced in [96], it is convenient to do a Picard linearization of the convective term for the sake of the non-linear iteration robustness. Hence, the convective velocity is linearized as , where superscript denote the current iteration. In consequence, the convective term turns into , which is the correct Picard linearization that ensures stability and proper convection of information [96].
With regard to the mass conservation equation, when dealing with purely incompressible fluids it is customary assumed that , meaning that that the pressure field is defined up to a constant. In the standard body fitted case, this issue is immediately fixed by imposing a Neumann BC in any part of the domain. Unfortunately, this solution might be no longer valid when working with a level set-based fixed mesh approach. This is due to the fact that, despite the level set is a robust and always defined operation, there are situations in which isolated closed domains of fluid (i.e. “bubbles”) can appear. Taking into account that such undesired fluid cavities are likely related to poorly defined input files (e.g. stl) or to moving boundary problems involving complex geometries, it is impossible to a priori known their location. Trying to locate them in order to apply a Neumann BC is not a feasible solution since this is an extremely expensive, and possibly non-deterministic operation.
Alternatively, the unbounded pressure issue can be readily fixed if a slight compressibility is included in the formulation. This can be achieved by rewriting the density time derivative in Eq. 3.3.b such that a state equation linking the density to the pressure field can be introduced. For almost incompressible fluids, it is possible to take the simplified speed of sound equation of state
|
|
(3.4) |
Hence, developing the material time derivative of the density in Eq. 3.3.b as
|
|
which is equivalent to
|
|
allows to get rid of the density partial time derivative by inserting Eq. 3.4 as
|
|
By further assuming that , which physically means that the density space fluctuations are negligible, the term can be neglected to give
|
|
(3.5) |
Combining this last equation with the momentum conservation law in Eq. 3.3.a yields the final form of the quasi-incompressible N–S equations
|
It is important to mention that the fully-incompressible form is recovered as the sound speed . This makes possible to effectively deactivate the pseudo-compressible term in those cases in which isolated fluid cavities are not expected to appear. In chapter 5 a test example that proves the capability of this approach to deal with such undesired scenarios is presented.
3.2 Discrete form and stabilization
The FE discretization of mixed formulations, such as the Stokes (or N–S) equations, is commonly associated to saddle point problems [97]. These give rise to numerical artifacts and spurious oscillations, which most probably ruin the solution, when the discretizations of the mixed variables are not compatible between them. In this context, the Ladyzhenskaya–Babuska–Brezzi (LBB) condition, also known as inf–sup condition, provides a criterion to distinguish between stable and unstable discretizations. For more details on inf–sup stable and unstable FE discretizations, the reader is referred to [98,95].
Aiming to keep the embedded elemental splitting as simple as possible, this thesis only considers simplex elements with same velocity and pressure interpolation order (i.e. linear triangles and tetrahedra [99]). Furthermore, simplex elements are the most straightforward approach to generate unstructured grids around complex geometries. However, they are inf–sup unstable and therefore require the use of a stabilization technique to avoid spurious oscillations. Note that using an inf–sup stable discretization would require the use of higher order approximations, which in the context of EBM would turn into an extremely cumbersome implementation of the splitting algorithms.
There is a wide variety of stabilization techniques that have been proved to be effective for similar N–S problems. Some of these are the Streamline Upwind/Petrov–Galerkin (SUPG) [100,101], the Galerkin Least-Squares (GLS) [102], the Finite Increment Calculus (FIC) [103] or the Variational MultiScales (VMS) [104,105], which is the adopted one.
The VMS method relies on the separation of the solution fields and in two scales as
|
and being the velocity and pressure FE resolvable scales. Contrariwise, and are the subscales representing the velocity and pressure fluctuations that cannot be captured by the FE solution and thus need to be modeled.
The previous separation of scales can be inserted into Eq. 3.6 to yield
|
At this point it is required to define a model for the subscales and , which are assumed to have a bubble shape that implies zero value of all their boundary integrals [104]. In general terms, it can be said that the subscales are built as a projection of the FE residuals onto the space of the small scales. In consequence, the nature of such projection defines the subscale model to end up with. Hence, assuming an identity projection operator leads to the Algebraic Sub-Grid Scales (ASGS) [106] while considering an orthogonal one, which implies the assumption that the subscales space is orthogonal to the FE one, leads to the Orthogonal SubScales(OSS) [107]. Owing to its remarkably good performance and simplicity, which turns into a more efficient implementation, the ASGS is the option selected in this work.
Hence, the ASGS velocity and pressure subscales can be calculated from the momentum and mass conservation discrete residuals and as
|
being and the stabilization constants, which are taken from [106] and computed as
|
where and , is the convective velocity norm and is the element size, which is computed as the average of the heights associated to each node of the element. is a parameter bounded between 0 and 1 that allows considering the time step value in the calculation of .
Note that the previous subscales definition (Eq. 3.9) introduces a dependency on the FE solution through the algebraic momentum and mass conservation residuals, which are defined as
|
Besides this, Eq. 3.8 also shows the time dependent nature of the subscales. Considering such time dependency leads to a so called dynamic subscales formulation. Conversely, neglecting it by assuming that as well as leads to a quasi-static subscales formulation. Even though the dynamic approach has superior characteristics [108], these come at the cost of increasing the complexity of the formulation. Moreover, they also involve a huge increase in the memory consumption as they introduce the need of storing the subscales historical data for each integration point. Taking these considerations into account, the quasi-static approach is the preferred option in this thesis.
3.3 Variational form and automatic differentiation
After having defined the stabilized governing equations, the variational (weak) form of the problem needs to be derived. To do that, the velocity and pressure test functions and are defined. For the sake of simplicity, it is also convenient to use the standard notation for the inner product volume integral. Likewise, the inner product boundary integrals can be denoted as .
Hence, the Galerkin FE functional to be minimized is built as the inner product volume integral of the test functions times the FE residuals as
|
|
(3.12) |
Note that Eq. 3.12 involves the complete FE residuals, which include not only the FE solution but also the subscales. After introducing the scales separation and the quasi-static subscales assumption, the complete FE residuals and read as
|
Inserting these into the Galerkin functional above yields the stabilized quasi–incompressible Navier–Stokes Galerkin functional
|
|
(3.14) |
Taking into account that this formulation is to be discretized using simplicial elements, integration by parts is demanded for getting rid of as higher order derivatives as possible. After doing so and dropping all the remaining higher order terms, the final Galerkin functional to be implemented reads as
|
|
(3.15) |
being the Cauchy traction vector, computed as , and the outwards unit normal vector. Note that this equation already takes into account the subscales null boundary value assumption.
The algebraic form of the discrete functional in Eq. 3.15 can be automatically obtained by using a Computer Algebra System (CAS). Among all the available alternatives, in this work the Python library Sympy [109] is used. Aside of being a much more efficient alternative to the traditional implementation in terms of the human effort, following a symbolic implementation ensures that the differentiation of the functional is always correct since this is automatically performed by the CAS library. This limits the possible error sources to the definition of the Galerkin functional, and thus minimizes the potential implementation mistakes.
Therefore, the elemental Left Hand Side matrix () and Right Hand Side vector () can be automatically obtained by expressing the symbolic functional in terms of the nodal test functions ( and ) and the nodal unknowns ( and ). Then, assuming a symbolic description of the shape functions and of their derivatives, allows obtaining the elemental by automatic differentiation as
|
|
(3.16) |
while the elemental can be similarly derived as
|
|
(3.17) |
The symbolic implementation of the quasi–incompressible Navier–Stokes stabilized formulation presented in this chapter is available in the Kratos Multiphysics repository.
Last but not least, it is due mentioning that this section assumes previous knowledge on the FE method. In case more details about the basis of the method are required, the reader is referred to [110,99]. Concerning the specific application of the FE method to CFD problems, the reader is referred to [111,29,95].
3.4 Validation
This section validates the FE implementation of the quasi–incompressible Navier–Stokes formulation previously described. To that purpose the Method of Manufactured Solutions (MMS) is used [112,113]. The problem geometry consists in a 1x1m square while the material properties and are equal to 103 and 10-4. The speed of sound velocity is set to 104 in order to introduce the effect of the pseudo–compressible term.
The problem is solved for two different source terms that correspond to two different transient solutions. First the source term
|
|
that corresponds to the sinusoidal transient field
|
|
is set.
Secondly, the experiment is repeated for the source term
|
|
which corresponds to the non-linear transient field
|
|
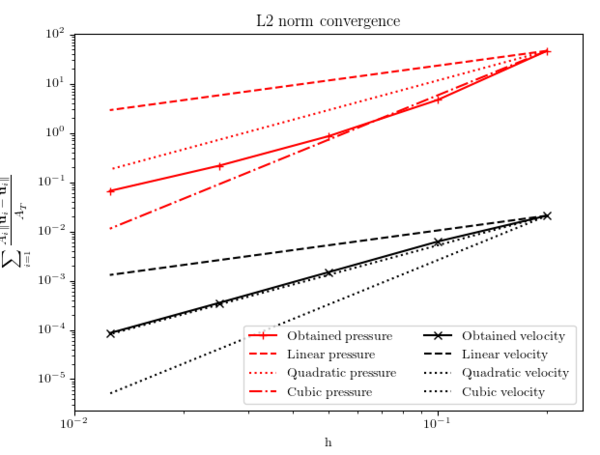
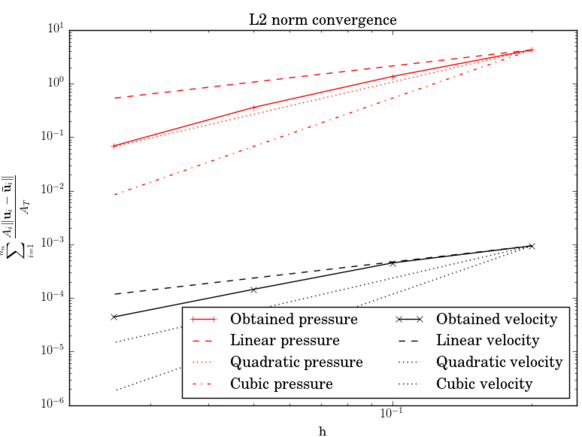
Fig. 3.1 collects the weighted average error for both the velocity and pressure fields after 1s of simulation. In both cases it can be observed that the velocity and pressure convergence rates match the expected and ones.
|
|
| (a) Sinusoidal transient field. | (b) Non-linear transient field. |
| Figura 3.1: Manufactured solution experiments results. | |
4 A modified Finite Element formulation for the imposition of the slip boundary condition over embedded volumeless geometries
4.1 Article data
Title: A modified Finite Element formulation for the imposition of the slip boundary condition over embedded volumeless geometries
Authors: R. Zorrilla, A. Larese and R. Rossi
Journal: Computer Methods in Applied Mechanics and Engineering 353 (2019) 123–157
Received: 2 May 2018 / Accepted: 10 May 2019 / Available online: 15 May 2019
DOI: 10.1016/j.cma.2019.05.007
4.2 Scientific contribution
This chapter collects the first paper of the compendium, which presents a novel embedded mesh method for the resolution of Navier–Stokes problems. Even though the proposed formulation is capable of dealing with any type of body, it is intended to be used in combination with discontinuous level set functions to allow the resolution of CFD problems involving embedded thin-walled bodies.
The proposal is based on the substitution of the standard FE space by an alternative one in those elements that are intersected by the level set. Such alternative space, which was firstly proposed in [114], makes possible the representation of both the velocity and pressure discontinuities arising from the immersion of any body. In addition to this, a no penetration condition is weakly imposed by doing a convenient integration by parts of the mass conservation equation and the addition of an extra term that penalizes the normal projection of the embedded wall velocity. Taking into account that no constraint is enforced in the tangential direction, the imposition is equivalent to a slip BC.
The paper also discusses alternative approaches to impose the slip condition, namely a MultiFreedom Constraint (MFC) approach for body fitted discretizations and a Nitsche-based imposition of the Navier-slip BC for volumetric embedded bodies. These alternative approaches are also applied to validate the discontinuous embedded proposal. The accuracy of the method is proved as well as its ability to keep the convergence order of the modified FE space. Furthermore, the chapter also showcases a potential real application that the proposed technique could have in the context of membrane structures CFD by solving the flow around two boat sails.
The results obtained in this chapter are a very first step towards the final VWT objective. More specifically, this chapter settles the basis of the discontinuous embedded Navier–Stokes formulations that are to be exploited in the subsequent chapters for the resolution of more complex CFD and FSI problems.
5.1 Introduction
This chapter advances further in the investigation of embedded CFD methods for thin-walled bodies. Hence, taking as starting point the purely-slip formulation presented in Chapter 4, this chapter introduces some enhancements in order to extend the applicability range of the method to any wall behavior from the slip to the stick (no-slip) limits. This is achieved by substituting the slip BC by a general Navier-slip BC, which can be somehow understood as a linear wall law. In addition, the BC enforcement is also improved by substituting the penalty-based method by a Nitsche imposition.
The chapter is organized as follows. First of all the discontinuous Nitsche-based method for the Navier-slip BC imposition is presented. Secondly, the new proposal is validated by solving several examples, which involve different wall behaviors ranging from the slip to the no-slip limits. Moreover, a potential industrial application is also presented. The last section collects the conclusions and further enhancements.
The formulation in this chapter has been submitted for its publication in Computer Methods in Applied Mechanics and Engineering (CMAME). The current status of the paper is under review.
This section presents a novel formulation for the imposition of the Navier-slip BC over embedded thin-walled bodies. Hence, the substitution of the standard FE space by the Ausas discontinuous one is also introduced in order to represent the discontinuities arising from the immersion of a (possibly thin-walled) body. However, the space substitution is combined in this case with the Navier-slip Nitsche method presented in [60]. Although this might seem a simple mixture of the ideas in Chapter 4 with the ones in [60], it is not obvious that the combination of the Ausas FE space with a stick wall behavior works out of the box owing to the worse interpolation properties featured by the Ausas FE space. In the following, the properties of the Ausas FE space are briefly recalled to ease the comprehension of the rest of the chapter. The next subsections present the Nitsche method for the imposition of the Navier-slip BC and a more accurate alternative to calculate the drag force when the Ausas FE space is involved.
5.2.1 The Ausas Finite Element space
The Ausas FE space was initially conceived to represent the discontinuities arising from the resolution of two-phase flow problems [114,115]. In this thesis, the ability of the Ausas FE space to disconnect the solution fields in the two sides of the level set intersection is exploited to directly embed thin-walled bodies without requiring any interface operation.
A particularly interesting feature of the Ausas FE space is that it is conforming with the standard FE one. Hence, no special treatment of the blending elements (the elements neighbouring the intersected ones) is required, thus leading to a purely local formulation. This becomes in a great advantage for the extension of the formulation to distributed memory platforms.
Aiming to describe the main geometrical features of the Ausas FE space, Fig. 5.1 depicts the same intersected element example that the original authors used in their proposal. By inspecting the Ausas shape functions that are obtained from the corresponding division in subelements, it can be observed that:
- the shape function values along an intersected edge are constant. Note that in the green side the shape function at the intersection points Q and P takes the same value as in A (Fig. 5.1b). On the other hand, in the red side the value at the intersection point P takes the same value as in B (Fig. 5.1c). The same can be observed for Q and C (Fig. 5.1d).
- in consequence, the shape functions values are constant in one of the split sides (the green one in Fig. 5.1a), and thus lead to an always constant interpolation with no gradient. Hence, only piecewise constant functions can be exactly reproduced.
- in the non-constant side, the shape function gradients are approximatively null in the intersection normal direction.
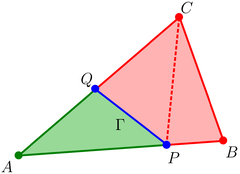
|
|
| (a) Partition of ABC following the interface PQ. | (b) |
|
|
| (c) | (d) |
| Figura 5.1: Ausas shape functions for the intersected finite element ABC (source [114]). | |
This subsection presents the general Navier-slip BC as well as the Nitsche method that is employed for its imposition. As it has been already mentioned, this technique is based on the work by Winter et. al. in [60], which is adapted to be used in combination with the aforementioned Ausas FE space.
In short, the Navier-slip BC can be understood as a sort of linear wall law whose behaviour is regulated by the slip length parameter as
|
|
(5.1) |
where and denote the tangential wall velocity and the normal to the wall direction. As it can be observed, the Navier-slip BC approaches the completely stick condition as while it tends to the slip limit as .
From a numerical perspective, the general Navier-slip BC is defined as the conjunction of a no penetration constraint in the normal direction and a shear force imposition in the tangential one. While the first one is enforced on the normal projection of the velocity, the second is a boundary value imposition of the tangential projection of the viscous traction, meaning that the general Navier-slip condition is indeed a Robin-type BC. Accordingly, the Navier-slip BC can be split in a normal and a tangential contribution as
|
in which and are the velocity and the tangential traction to be imposed over the embedded boundary. and are the normal and tangential projection operators, which can be computed as and .
The imposition of the BC in Eq. 5.2 is achieved by using a stabilized Nitsche method in both the normal and tangential directions. The Nitsche imposition of the normal component reads
|
|
(5.3) |
while the tangential one is
|
|
(5.4) |
is the penalty constant while . The choice leads to the adjoint inconsistent Nitsche formulation, which enjoys improved inf-sup stability for any value of [60]. Even though optimal convergence is not guaranteed for the velocity L2-error in this case, the adjoint inconsistent formulation is taken owing to its reported better stability properties. is a stabilization constant defined as
|
|
(5.5) |
It is important to remark that these two constraints need to be integrated in both sides of the level set interface after the ability of the Ausas FE space to completely disconnect the positive and negative sides of the intersection. Hence, the problem somehow translates to impose the same constraint in two different but overlapping interfaces.
In addition, it is also important to point out that the Ausas FE space reduces the approximation properties within the cut elements, so exactly where the Nitsche terms are active. This effect is particularly relevant since, depending on the splitting pattern, the gradient of the velocity and of the test functions is kinematically forced to be zero on one of the sides of the cut. In this context, the verification of the correct imposition of the Navier-slip BC is fundamental.
5.2.3 Drag calculation
Owing to the worse interpolation properties featured by the Ausas FE space, the boundary traction calculation might be inaccurate, specially under the presence of important wall shear effects. This section aims to address such undesired situation, which might limit the extension of the method to FSI problems.
In general terms, the computation of the embedded boundary traction can be performed by integrating the formula
|
|
(5.6) |
over the level set intersections. Alternatively, it can be assumed that the Navier-Slip condition requires , or equivalently that , and rewrite Eq. 5.6 in the form
|
|
(5.7) |
These two expressions are equivalent in the continuum and when a “standard” FE formulation is employed. Not so however in the case of using Ausas shape functions, since in presence of zero velocity gradients would predict a zero skin friction in the first while the second would correctly estimate a skin friction provided that the tangential velocity is non-zero on the cut boundary (even when the gradient is zero in the immediate vicinity of the intersection).
In order to explain such inconsistency, the use of Ausas shape functions can be re-interpreted as the use of the standard FE space subjected to the additional constraint that the solution needs to be piecewise constant along each cut edge. The action of such geometric constraint is fundamental in the way equilibrium is established in the vicinity of the immersed objects. Indeed, the constraint allows forces to be transmitted from the cut boundary to the surrounding nodes without the need of producing a gradient in the solution, and is the reason for which the effective tangential stress can be non-zero in the vicinity of the embedded boundaries.
5.3 Validation
This section collects the benchmarking of the proposed formulation. To ensure that all the examples can be reproduced, the geometry, BCs and simulation settings are detailed prior to the results assessment.
In the following all the examples are listed with a brief description of their motivation
- 2D straight channel: this is a simple test case to check the implementation and convergence rates of the formulation considering three different wall behaviors (slip, intermediate and no-slip).
- 2D flow inside a ring: to obtain the convergence rates of the formulation when dealing with faceted approximations of curved geometries. The influence of the Nitsche constant is also evaluated with this example.
- 2D flow around pressurized cylinder: to prove the utility of the pseudo-compressible term to keep the pressure bounded when isolated fluid cavities appear.
- 2D elbow with internal wall: to test the performance of the formulation with a more complex geometry.
- 2D flow around thin-walled arch profile: to assess the performance of the proposed technique to solve high Re flows. This example is conceived as a 2D idealization of the final 3D example.
- 3D flow around a sailboat: this example presents a potential industrial application that consists in the CFD analysis of a sailboat.
5.3.1 2D straight channel
The objective of this very first example is to preliminary assess the correctness and convergence rates of the proposed formulation. Thus, the geometry and boundary conditions have been selected to be as simple as possible.
The geometry consists in a 2D 1.1x2m rectangular channel. The discontinuous level set function is set such that the effective width of the channel is 1m. Regarding the wall behaviour, the bottom edge is considered as a no-slip boundary while the embedded top one is tested with both slip and no-slip BCs. Moreover, an extra intermediate case in which the embedded skin equals 10-1m is also solved.
The material properties are selected such that the Re number is 100. This is achieved by setting the density to 1kg/m3 and the viscosity to and 10-2kg/ms.
A second order Backward Differentiation Formula (BDF2) scheme is used for the time discretization. To ensure that the steady state solution is reached, 20 time steps of 100s are solved.
The problem is solved for a set of structured meshes, whose characteristic element size and edge subdivisions are collected in Table 5.1.
| Mesh 0 | Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 | Mesh 5 | |
| Element size [m] | 0.2 | 0.0667 | 0.0333 | 0.0016 | 0.0083 | 0.0042 |
| Short edge divisions | 5 | 15 | 30 | 65 | 120 | 241 |
| Long edge divisions | 10 | 30 | 60 | 130 | 240 | 480 |
5.3.1.1 Slip interface
In this case the flow is induced by applying a volume force of 0.5m/s2 in the horizontal direction. The problem reaches a steady state that can be characterized by the rigid body movement
|
Table 5.2 collects the -norm of both the velocity and pressure errors. Fig. 5.2a and Fig. 5.2b depict the previous results. As it can be observed, the convergence order is for the velocity field while it is superlinear for the pressure one, meaning that the obtained convergence rates match the linear FE ones even though the Ausas FE space is limited to a convergence rate [114]. Such improved convergence is a particularity of the current test case, which is not affected by the null gradient limitation of the Ausas shape functions since the analytical solution gradient is zero in the top embedded boundary.
Finally, Fig. 5.3 presents the velocity field for three different mesh refinement levels (meshes 1, 3 and 5 in Table 5.1). The obtained solution matches the parabolic rigid body movement in Eq. 5.8.a in all cases. It can be also observed that, as expected, the gradient tends to zero in the region close to the embedded boundary as the mesh is refined.
| Mesh 0 | Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 | Mesh 5 | |
| 2.41253 | 0.950292 | 0.129366 | 0.007083 | 0.001888 | 0.000479 | |
| 0.056811 | 0.009313 | 0.001444 | 0.000376 | 0.000144 | 0.000051 |
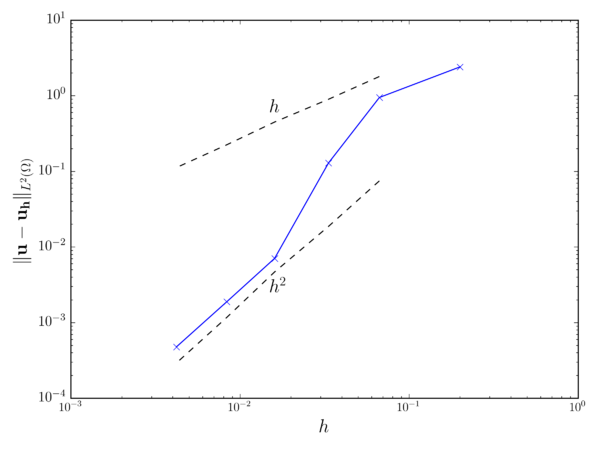
|
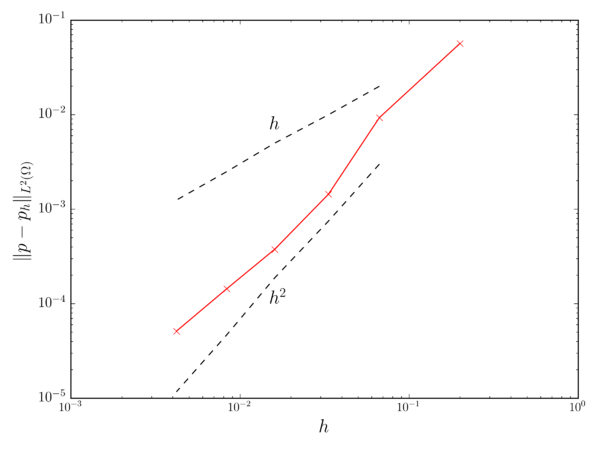
|
| (a) Velocity convergence. | (b) Pressure convergence. |
| Figura 5.2: 2D straight channel (slip interface). Solid lines represent the obtained results. Dashed lines represent and convergence rates. | |
|
|
| (a) Mesh 1. | (b) Mesh 3. |
| |
| (c) Mesh 5. | |
| Figura 5.3: 2D straight channel (slip interface). Coarse, medium and fine meshes field. | |
5.3.1.2 No-slip interface
Instead of using a body force to induce the flow, in this case a pressure gradient between the inlet and the outlet is applied. Hence, the pressure is fixed to 1Pa in the left edge and to 0Pa in the right one. This, in combination with the no-slip behaviour in both top and bottom boundaries, leads to the well known pressure driven flow between two steady plates benchmark, also known as Poiseuille flow. The steady state analytical solution of the Poiseuille flow can be particularised for the above mentioned material properties as
|
Table 5.3 collects the -norm of the velocity and pressure errors. The results exhibit a convergence rate around for both velocity and pressure fields (Figs. 5.4a and 5.4b).
Fig. 5.5 depicts the obtained solution for three different mesh refinement levels (meshes 1, 3 and 5 in Table 5.1). The expected parabolic velocity profile can be noted in all cases. However, the peak value in the channel mid axis is far from the analytical solution value (6.25m/s) in the coarsest mesh. Regarding the pressure, the horizontal linear gradient can be observed in all cases.
Furthermore, it is worth to comment about the perturbations in the solution close to the embedded boundary, which can be clearly noted in the coarsest mesh pressure field (Fig. 5.4b). These are the direct consequence of the inability of the Ausas FE space to represent a gradient in one side of the intersected elements, which forces the solution in the embedded boundary vicinity to accommodate according to such extra constraint.
| Mesh 0 | Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 | Mesh 5 | |
| 3.1982 | 1.06859 | 0.28365 | 0.07003 | 0.035238 | 0.014591 | |
| 0.067731 | 0.02977 | 0.012579 | 0.004407 | 0.001754 | 0.000556 |
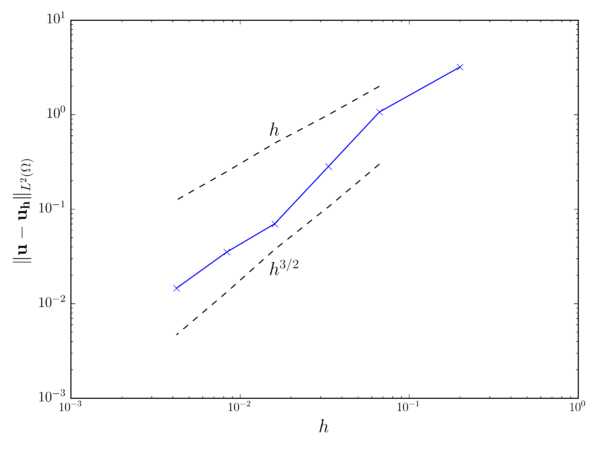
|
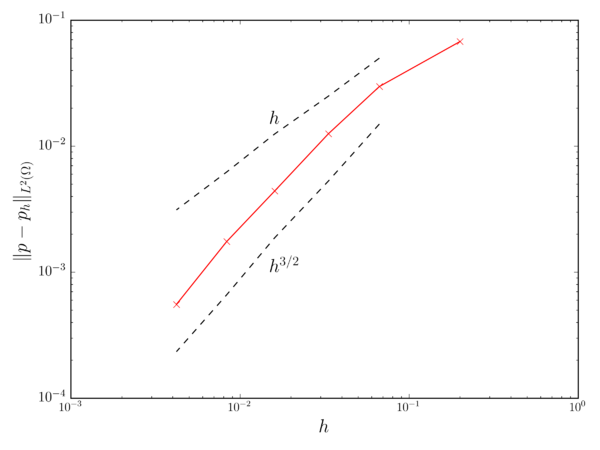
|
| (a) Velocity convergence. | (b) Pressure convergence. |
| Figura 5.4: 2D straight channel (no-slip interface). Solid lines represent the obtained results. Dashed lines represent and convergence rates. | |
5.3.1.3 Slip length 10-1 interface
This last variant of the straight channel test checks the performance of the proposed technique when it is applied in a wall law fashion. This means to introduce a controlled wall friction such that the embedded skin behavior is between the slip and no-slip limits. Hence, the slip length is set to 10-1m in the embedded boundary. The inlet profile is accordingly imposed in the left edge while the bottom edge velocity is fixed to [1,0]m/s.
These settings yield the analytical velocity and pressure steady state solution
|
which exerts a 0.0182N total horizontal drag force over the embedded boundary.
Table 5.4 collects the -norm of both the velocity and pressure errors as well as the -norm of the horizontal drag force error. These results are presented for three different values of the penalty constant . As it can be observed in Fig. 5.6, the convergence rate of the three analysed magnitudes is in all cases around , which is in line with the results previously obtained for the pure no-slip case. Besides that, it can be also noted that the convergence rate of the formulation is not affected by the value. As expected, the error constant minimizes for smaller values.
Complementary, Fig. 5.7 shows the obtained velocity fields for three mesh refinement levels (meshes 1, 3 and 5 in Table 5.1). The expected linear velocity profile can be clearly identified in all cases.
Finally, it has to be highlighted that, even though this test involves a very simple geometry, the obtained results are a very first, but essential, proof of convergence required prior to the application of the proposed technique to more realistic scenarios.
| Mesh 0 | Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 | Mesh 5 | ||
| = 10-1 | 0.026176 | 0.008904 | 0.001587 | 8.78378e-05 | 4.5824e-05 | 2.21285e-05 | |
| 0.015735 | 0.005540 | 0.000865 | 3.40915e-05 | 1.56027e-05 | 9.09062e-06 | ||
| 0.034265 | 0.023253 | 0.019279 | 0.018424 | 0.018315 | 0.018247 | ||
| = 10-2 | 0.027379 | 0.009778 | 0.002054 | 0.00023 | 0.000162 | 8.08048e-05 | |
| 0.019098 | 0.006327 | 0.001165 | 0.000164 | 8.69214e-05 | 4.38793e-05 | ||
| 0.033049 | 0.022813 | 0.019053 | 0.018319 | 0.018256 | 0.018219 | ||
| = 10-3 | 0.027548 | 0.009871 | 0.002102 | 0.000322 | 0.000174 | 8.67592e-05 | |
| 0.019457 | 0.006407 | 0.001196 | 0.000177 | 9.52864e-05 | 4.74011e-05 | ||
| 0.032919 | 0.022768 | 0.01903 | 0.018308 | 0.01825 | 0.018216 |
|
|
| (a) Mesh 1. | (b) Mesh 3. |
| |
| (c) Mesh 5. | |
| Figura 5.7: 2D straight channel (Slip length 10-1 interface). Coarse, medium and fine meshes velocity field. | |
5.3.2 2D flow inside a ring
The aim of this test is to obtain the convergence rates of the presented formulation, in both the slip and no-slip limits, when dealing with polygonal approximations of curved boundaries. It is known that the imposition of a slip BC over faceted approximations of curved boundaries can be problematic [57]. This is explained by the fact that the slip BC requires the velocity to be parallel to each face of the discrete polygonal approximation. In consequence, the unique solution that fulfills such requirement in the vertices that are shared between faces is the null velocity. As it is observed in [57,37], this can lead to a wrong velocity approximation in the slip wall, specially in those cases that present an insufficient discretization of the curved boundary.
The geometry of the problem consists in two concentric cylinders separated by an interior fluid cavity. The inner cylinder radius is 0.5m while the outer one is 1.0m, meaning that the fluid domain can be described as . The fluid is initially at rest and a unit angular velocity is imposed in the outer cylinder to induce the flow. The pressure is fixed to zero along the outer cylinder boundary to obtain a radially symmetric solution.
With regard to the material properties, the dynamic viscosity and density are 1.0kg/m3 and 10-3kg/ms. A second order BDF2 scheme is used for the time discretization. To ensure that the steady state solution is reached, 10 time steps of 200s are solved.
A centered structured mesh is used in all the refinement levels of the study. Note that the outer cylinder is completely meshed disregarding the inner one, which is represented by a radial discontinuous distance function. The characteristic element size together with the number of radial and perimeter subdivisions are collected in Table 5.5. Fig. 5.8 shows the Mesh 1 refinement level in Table 5.5. More specifically, Fig. 5.8a depicts the centered structured pattern while Fig. 5.8b details the discontinuous level set function intersection pattern.
In the following, the convergence of the obtained solutions when a slip and no-slip BC is imposed over the inner boundary is studied by means of the analytical solutions, which can be easily obtained from the mass and momentum conservation equations written in polar coordinates.
| Mesh 0 | Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 | Mesh 5 | Mesh 6 | |
| Element size [m] | 0.1428 | 0.06667 | 0.03448 | 0.01754 | 0.00884 | 0.00444 | 0.00223 |
| Radial divisions | 7 | 15 | 29 | 57 | 113 | 225 | 449 |
| Perimeter divisions | 21 | 43 | 85 | 169 | 337 | 673 | 1345 |

|

|
| (a) Mesh capture. | (b) Level set intersection pattern. |
| Figura 5.8: 2D flow inside a ring test case geometry (mesh 1). | |
5.3.2.1 Slip interface
In order to ensure a slip-like behavior, the slip length is set to 108 in all the cases presented in this subsection. The Nitsche penalty constant is 0.1 in all the examples. The analytical solution can be expressed in polar coordinates as
|
Table 5.6 collects the -norm of the velocity and pressure errors. For both velocity and pressure fields, the results display a superlinear convergence rate close to (Figs. 5.9a and 5.9b), which is in line with slip straight channel observations as well as with the results in [114,37].
The obtained velocity and pressure fields are shown for three of the mesh refinement levels (mesh 0, 3 and 6) in Fig. 5.11. At first sight, it can be easily observed that the coarsest mesh solution if far from the expected slip behavior. However, the method converges to the slip solution as the mesh is refined. These observations are in agreement with the ones in [57] about the resolution of a similar Stokes problem using a Nitsche imposition of the slip BC. The same issues are also reported in Chapter 4 when solving the same test but using the Navier-Stokes embedded discontinuous purely slip formulation. Having said this, the deterioration of the convergence rates to a superlinear rate below the expected one is presumably associated to the polygonal approximation of curved boundaries rather than to the Nitsche imposition of the slip BC.
| Mesh 0 | Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 | Mesh 5 | Mesh 6 | |
| 0.372217 | 0.265875 | 0.173553 | 0.092081 | 0.040315 | 0.016052 | 0.006761 | |
| 0.148217 | 0.084728 | 0.055737 | 0.030523 | 0.013681 | 0.005508 | 0.002329 |
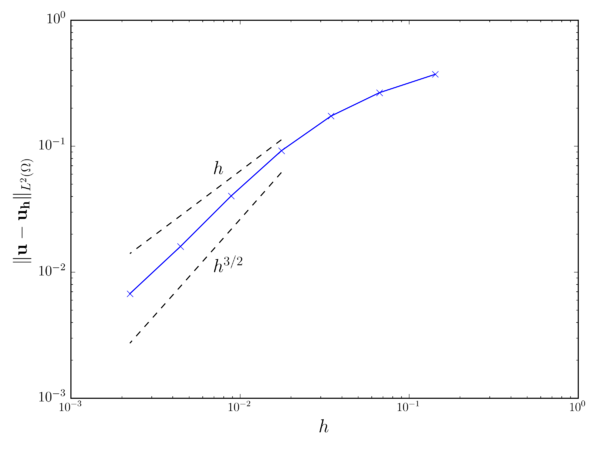
|
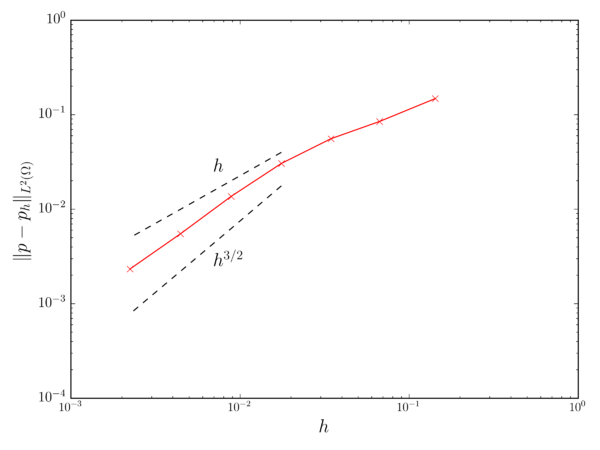
|
| (a) Velocity convergence. | (b) Pressure convergence. |
| Figura 5.9: 2D flow inside a ring (slip interface). Solid lines represent the obtained results. Dashed lines represent and convergence rates. | |
Complementary, the sensitivity of the formulation to the value of the penalty constant when is also assessed. To that purpose, the same example is solved but using the finest mesh and a set of values ranging from from 10-4 to 102. Table 5.7 collects the velocity and pressure error -norms for all the values. These results are also depicted in Fig. 5.10. It can be observed that both error norms minimize for values between 0.1 and 10, being the minimum values around the unit value.
| 102 0 | 101 | 100 | 10-1 | 10-2 | 10-3 | 10-4 | |
| 0.066914 | 0.010858 | 0.003796 | 0.006761 | 0.03991 | 0.183505 | 0.319047 | |
| 0.022297 | 0.003725 | 0.0013086 | 0.002329 | 0.013493 | 0.057347 | 0.092092 |
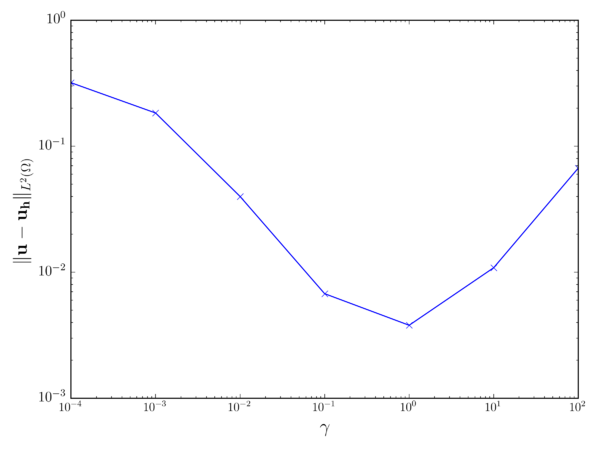
|
Pressure error norm. |
| (a) Velocity error norm. | (b) Pressure error norm. |
| Figura 5.10: 2D flow inside a ring (slip interface). Error norms for different values. | |
5.3.2.2 No-slip interface
In this case the slip length is set to 0 to enforce a no-slip wall behavior in the embedded interface. The Nitsche penalty constant is kept as 0.1. As in the slip case, the results and convergence assessment are based on the analytical solution, which in in polar coordinates reads as
|
Table 5.8 collects the velocity and pressure error -norms. These values are also depicted in Figs. 5.9a and 5.9b. It can be observed that both velocity and pressure fields exhibit a linear convergence rate. Such deteriorated convergence rate can be again associated to the inability of the Ausas FE space to properly capture the shear effects within the intersected elements.
Fig. 5.11 depicts the solution for three of the mesh refinement levels (meshes 0, 3 and 6). It can be observed that the solution tends to the analytical one as the mesh is refined.
| Mesh 0 | Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 | Mesh 5 | Mesh 6 | |
| 0.083878 | 0.047655 | 0.024639 | 0.012780 | 0.006550 | 0.003318 | 0.001670 | |
| 0.055474 | 0.015289 | 0.006531 | 0.003074 | 0.001510 | 0.000751 | 0.000374 |
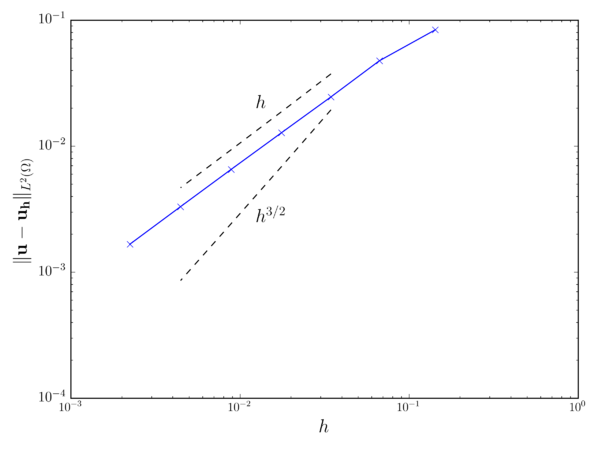
|
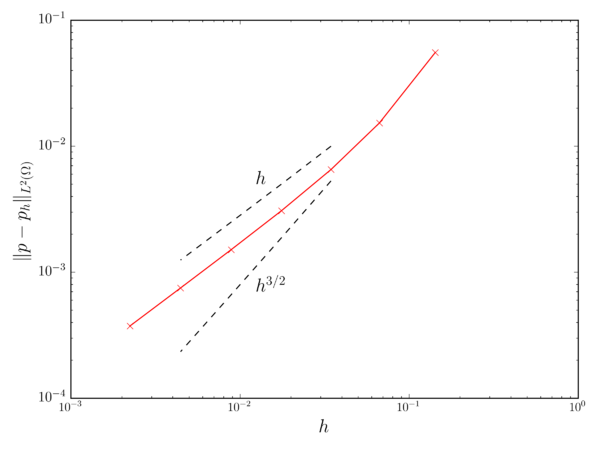
|
| (a) Velocity convergence. | (b) Pressure convergence. |
| Figura 5.12: 2D flow inside a ring (no-slip interface). Solid lines represent the obtained results. Dashed lines represent and convergence rates. | |
5.3.3 2D flow around pressurized cylindrical membrane
This example is specifically conceived to prove the capability of the pseudo-compressible term in Eq. 3.6.b to prevent the pressure field to blow up when isolated cavities of fluid appear.
To that purpose this test solves the fluid flow around an embedded cylindrical membrane that is filled with fluid. After the ability of the Ausas FE space to disconnect both sides of the level set, the embedded cylinder becomes in an isolated fluid cavity with no pressure constraint, and thus requires the pseudo-compressibility term in the mass conservation equation to keep the pressure bounded.
The problem geometry consists in a 1x5m channel containing a 0.1m radius cylinder. Assuming that the bottom left corner of the channel coincides with the origin, the center of the cylinder is located in the (1.25,0.5)m coordinates. With regard to the fluid properties, and are set to 1.0kg/m3 and 10-2kg/ms. The speed of sound velocity is equal to 103m/s, which is a feasible value for a liquid medium. Inside the cylinder (Figs. 5.14a and 5.14b), a volume force equal to m/s2 is applied to ensure that the initial solution (zero velocity and pressure) is not in equilibrium.
A constant inlet velocity profile of 1m/s is imposed in the left edge of the channel while a symmetry condition (zero normal velocity and free tangential velocity) is enforced in the top and bottom walls. In order to get a steady state solution, the cylinder is modeled as a slip body by setting the slip length to 108. Furthermore, it is important to clearly state that the pressure is not fixed in any point of the computational domain.
The time discretization is done using a BDF2 scheme with a constant time step equal to 1s. To ensure that the steady solution is reached, the simulation is run for a total time of 100s. The channel is meshed with a structured grid made with around 200k linear triangular elements, whose average size is 7e-3m.
Figs. 5.14c and 5.14e depict the obtained solution. As expected, the flow around the cylinder presents an upstream stagnation point and a symmetric steady wake. Inside the cylinder (Fig. 5.14d and 5.14f), the expected hydrostatic solution can be clearly identified too. These results prove that the addition of a slight compressibility is enough to keep the pressure bounded, and therefore to ensure convergence, despite the presence of isolated fluid cavities with no pressure constraint.
Finally, it is important to spend some words on the relevance that these results have for the application of the proposed technique to real life problems involving “dirty” input geometries. Although in this case the unbounded pressure issue could be immediately tackled by fixing the pressure in any point inside the cylinder, this is likely impossible to be done in a real scenario since complex geometries can be rarely described using an analytical level set functions as the cylinder case. Hence, the use of the quasi-incompressible form of the N–S equations is of great utility for the extension of the proposed method to either real geometries or complex moving domains as it makes possible to automatically handle such unbounded pressure cavities regardless their a priori unknown location.
5.3.4 2D elbow with internal wall
This example, which was firstly proposed in [116], consists in a curved 2D pipe conforming an elbow shape (Fig. 5.15). A zero-thickness wall is placed inside the curved pipe, generating two separated fluid ducts whose cross section area varies in space. Even though for such a simple geometry the zero-thickness wall could be alternatively modelled by duplicating the interface nodes, in this case it is represented using a discontinuous level set function.
![2D elbow with internal wall. Problem geometry (source [116]).](/wd/images/thumb/3/3b/Draft_Samper_633963255-test-elbow_geometry.png/450px-Draft_Samper_633963255-test-elbow_geometry.png)
|
| Figura 5.15: 2D elbow with internal wall. Problem geometry (source [116]). |
The previously described elbow geometry is solved considering a slip interface, as was done by the original authors in [116], as well as a no-slip one. The obtained solutions are compared with the ones obtained with a body fitted reference solver as well as with the literature data. Furthermore, the analytical values, which can be easily obtained from the mass conservation principle, are also considered in the results assessment.
With regard to the fluid properties, they are selected such that the Re number is unitary. Considering the width of each one of the ducts as reference length, the unit Re number can be achieved by setting the density to 1kg/m3, the dynamic viscosity to 1kg/ms and a constant inlet velocity of 1m/s. In all cases the outer walls are assumed to have null velocity (no-slip condition) and the pressure is fixed to zero along the outlet. The BDF2 time scheme is used for the time discretization with a constant time time step of 10-2s. The total simulation time is 1s, which is enough to reach a steady solution.
5.3.4.1 Slip interface
For the sake of a fair comparison, the meshes employed in this case are set as similar as possible to the reference ones in [116]. Hence, four structured grids (denoted as coarse, medium, fine and very fine) are used. Table 5.9 collects the number of elements of each one of the refinement levels together with the reference ones in [116].
| Mesh | Reference | Present work |
| Coarse | 2400 | 2300 |
| Medium | 9600 | 8900 |
| Fine | 38400 | 36200 |
| Very fine | 153600 | 147000 |
Considering that the reference solution assumes a slip behavior of the intermediate wall, the slip length is set to 108, which is a large enough value to yield a wall behavior close to the slip limit.
Prior to any convergence assessment, the solution obtained with the medium refinement mesh is presented in Fig. 5.16. As it can be observed, the flow discontinuities arising from the introduction of the zero-thickness intermediate wall are perfectly captured by the formulation. As expected, a pressure gradient appears in the right duct due to the contraction generated by the wall. This turns into a flow acceleration to preserve the inlet flow rate. On the contrary, the left duct pressure gradient is almost constant since there is no variation in the cross section. The minor differences between the inlet and outlet pressure values are due to the local energy losses that occur when the flow changes its direction in the elbow.
![Velocity modulus [m/s].](/wd/images/thumb/4/49/Draft_Samper_633963255-test-elbow_new_ausas_velocity_medium-22cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-test-elbow_new_ausas_velocity_medium-22cm-0cm-0cm-0cm.png)
|
![Pressure [Pa].](/wd/images/thumb/7/7d/Draft_Samper_633963255-test-elbow_new_ausas_pressure_medium-22cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-test-elbow_new_ausas_pressure_medium-22cm-0cm-0cm-0cm.png)
|
| (a) Velocity modulus [m/s]. | (b) Pressure [Pa]. |
| Figura 5.16: 2D elbow with internal wall (slip interface). Medium mesh solution. | |
Figs. 5.17 and 5.18 collect the results assessment. On the one hand, Fig. 5.17 compares the obtained medium mesh outlet y-velocity with the reference, body fitted and Chapter 4 ones. A good correlation can be observed between all the values. Minor differences can only be observed between the penalty-based formulation and the Nitsche-based one, being the Nitsche-based formulation slightly more accurate in the values close to the embedded wall. This is more noticeable in the right duct due to the higher fluid velocity.
On the other hand, Fig. 5.18 depicts the convergence of the outlet y-velocity when the mesh is refined. It can be noted that the obtained values converge to the reference ones. This is even more evident in the values close to the embedded wall (Table 5.10), which significantly improve upon refinement.
|
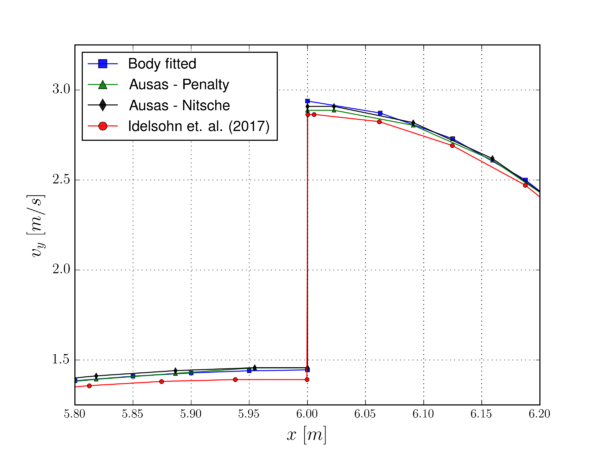
|
| (a) General view. | (b) Interface region zoom. |
| Figura 5.17: 2D elbow with internal wall (slip interface). Outlet comparison [m/s]. | |
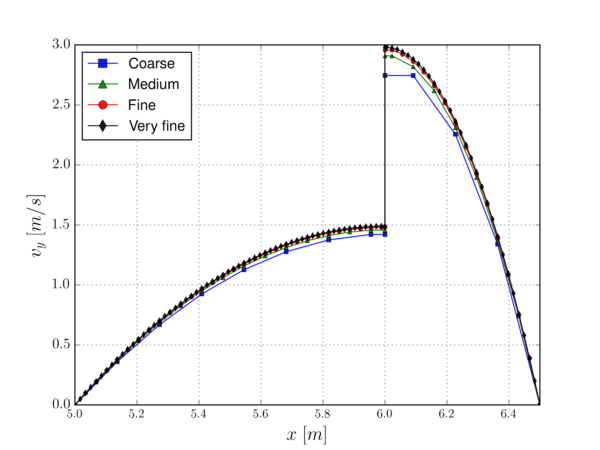
|
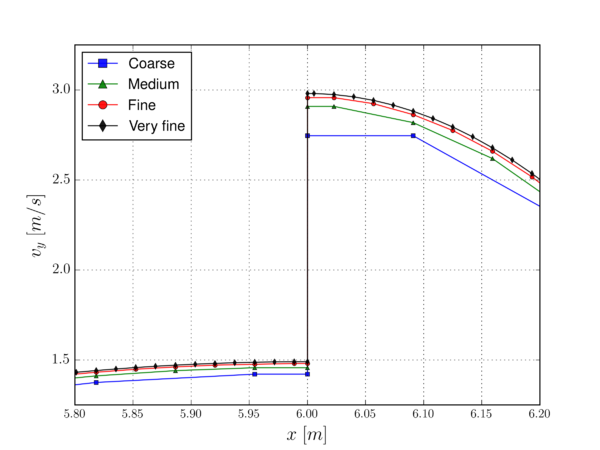
|
| (a) General view. | (b) Interface region zoom. |
| Figura 5.18: 2D elbow with internal wall (slip interface). Outlet convergence [m/s]. | |
Finally, Table 5.10 compares the outlet maximum y-component velocity values with the analytical solution ones. According to [116], if it is considered that the flow is parabolic in both sides of the intermediate wall, it can be proven that the analytical maximum velocity is 1.5m/s in the left duct and 3m/s in the right one. The absolute errors that are obtained taking these two values as reference are collected in Table 5.10. Once again, it can be observed that the values converge to the expected solution as the mesh is refined.
| abs. err. | abs. err. | |||
| Expected | 1.5 | - | 3.0 | - |
| Coarse | 1.4213 | 0.0787 | 2.7459 | 0.2541 |
| Medium | 1.4569 | 0.0431 | 2.9089 | 0.0911 |
| Fine | 1.4805 | 0,0196 | 2.9574 | 0,0426 |
| Very fine | 1.4902 | 0,0098 | 2.9804 | 0,0196 |
5.3.4.2 No-slip interface
In this section the 2D elbow test case is modified to consider a no-slip behavior in the intermediate embedded wall. Although the geometry is the same, it is convenient to modify the inlet to consider a parabolic profile in both ducts according to the no-slip wall behaviour. However, preliminary tests showed that the flow rate might be influenced by the level intersection pattern in the inlet owing to the Ausas FE space interpolation properties. Therefore, the inlet function is not imposed along the entire left edge but along the 75% of the length of each duct to ensure that the intersection pattern does not affect the inflow. Thus, the bottom duct inlet function reads as
|
|
(5.13) |
while the top one is
|
|
(5.14) |
Note that these parabolic functions preserve the original benchmark flow rates.
Taking into account the influence that the no-slip boundary condition has in the solution, a new set of finer meshes is used to properly capture the expected parabolic velocity profile. The new mesh sizes are collected in Table 5.11.
| Mesh | Element size |
| Body fitted | 0.01 |
| Embedded (coarse) | 0.07 |
| Embedded (medium) | 0.0175 |
| Embedded (fine) | 0.01 |
Fig. 5.19 depicts the medium mesh embedded solution. As expected, the imposition of the no-slip constraint in the intermediate wall yields a symmetric parabolic profile in both ducts. Furthermore, the pressure gradient required to keep the inlet flow rate also appears in both ducts.
![Velocity modulus [m/s].](/wd/images/thumb/e/e2/Draft_Samper_633963255-test-elbow_no_slip_ausas_constant_inlet_velocity_medium-22cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-test-elbow_no_slip_ausas_constant_inlet_velocity_medium-22cm-0cm-0cm-0cm.png)
|
![Pressure [Pa].](/wd/images/thumb/1/1b/Draft_Samper_633963255-test-elbow_no_slip_ausas_constant_inlet_pressure_medium-22cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-test-elbow_no_slip_ausas_constant_inlet_pressure_medium-22cm-0cm-0cm-0cm.png)
|
| (a) Velocity modulus [m/s]. | (b) Pressure [Pa]. |
| Figura 5.19: 2D elbow with internal wall (no-slip interface). Medium mesh solution. | |
Fig. 5.20 compares the three mesh refinements with the reference body fitted solution, proving that the Nitsche embedded solution converges to the reference one as the mesh is refined. It is worth mentioning that the lower accuracy solutions have a higher peak velocity value. This is explained by the inability of the Ausas FE space to properly capture the solution in the elements intersected by the no-slip embedded wall. Considering that no velocity gradient can be captured in one side of these elements, the velocity becomes null (in a variational sense) over the entire element (Fig. 5.20b). In consequence, the flow needs to accelerate in the rest of the duct to keep the inlet flow rate.
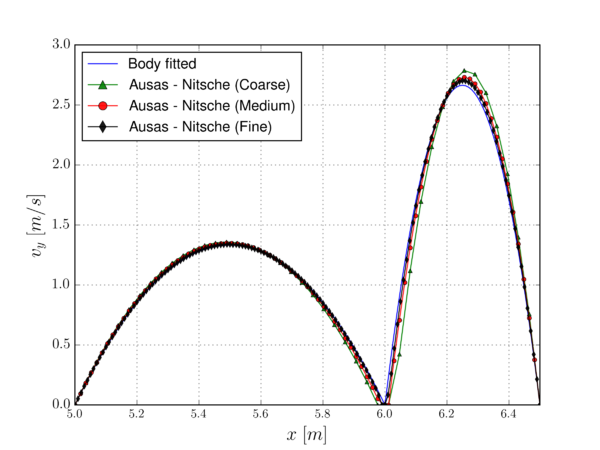
|
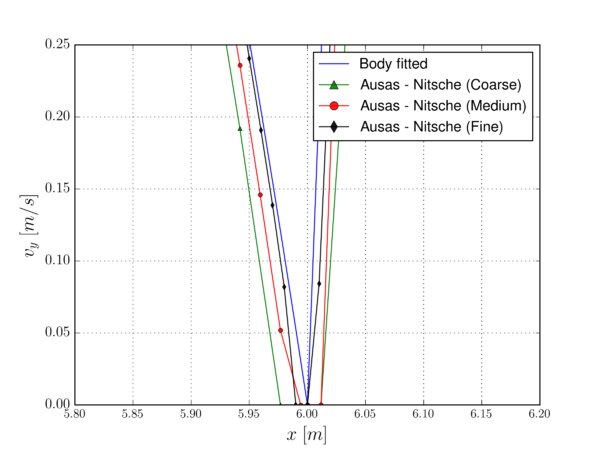
|
| (a) General view. | (b) Interface region zoom. |
| Figura 5.20: 2D elbow with internal wall (no-slip interface). Outlet [m/s]. | |
Similarly to what has been done for the slip case, Table 5.12 compares the reference analytical values, which can be easily obtained considering a parabolic flow and mass conservation, with the three refinement levels ones. Again, it can be observed that the no-slip solution converges to the reference one as the mesh is refined.
| abs. err. | abs. err. | |||
| Expected | 1.3332 | - | 2.6664 | - |
| Coarse | 1.3577 | 0.0245 | 2.7874 | 0.121 |
| Medium | 1.3492 | 0.016 | 2.7304 | 0.064 |
| Fine | 1.3370 | 0.0038 | 2.7011 | 0.0347 |
5.3.5 2D flow around thin-walled arch profile
This example is conceived to be a transition case between the more academic examples presented so far and the real application in the next subsection. Hence, the objective is to assess the performance of the formulation when very large Re are involved but still keeping an elementary 2D geometry.
The problem geometry consists in a 20x100m rectangular channel in which a 4m chord and 1m height arch geometry is placed. Note that the embedded arch geometry is thought to be reasonably similar to the cross-section of a real 3D thin-walled structure (e.g. a sail or lightweight roof cover). Assuming that the bottom left corner of the channel is placed in the (0,0)m coordinates, the arch can be created from the three points (-2,-0.5), (0,0.5) and (2,-0.5)m. These geometry settings yield a 5% blockage coefficient. The material properties are set such that the Re is 105. Taking the height of the arch as reference length for the Re calculation, this can be achieved by setting and to 1kg/m3 and 10-5kg/ms.
The BCs are rather simple. A constant inlet velocity of 1m/s is imposed in the left edge of the channel while the pressure is fixed to 0Pa in the right one. A symmetry BC (zero normal velocity and free tangential velocity) is imposed in the top and bottom edges. Concerning the embedded body BC, two scenarios are considered. The former is an ideal slip case, in which the slip length is set to 108m, whereas the latter entails a stick condition, whose slip length is equal to 10-3m. Note that this value is of the same order of magnitude as the corresponding theoretical boundary layer thickness.
Both the embedded and the reference body fitted meshes have around 320k linear triangular elements. It is important to point out that in the body fitted case the boundary edges representing the analysed arch geometry are duplicated in order to model the velocity and pressure discontinuities. Concerning the time discretization, the BDF2 scheme is used again. In all cases the time step is 0.05s.
5.3.5.1 Slip interface
Fig. 5.21 presents the time evolution of the drag and lift forces. As it can be observed, both the body fitted and the embedded solutions reach a steady state solution with null horizontal drag force. Concerning the vertical lift force, the embedded solution one is 1.60N while body fitted reference one is 1.66N. Although the steady values are similar, it can be observed that the embedded solution is more chaotic during the initial transient phase, and thus requires more time to approach the steady state.
Complementary, Figs. 5.22 and 5.23 compare the body fitted and embedded steady state solutions, which are in remarkably good agreement. Besides, it can be observed the steady solution presents a symmetric pattern that, according to the d'Alembert's paradox, explains the null horizontal drag component.
![Drag force [N].](/wd/images/thumb/7/7d/Draft_Samper_633963255-0cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-0cm-0cm-0cm-0cm.png)
|
![Lift force [N].](/wd/images/thumb/7/7d/Draft_Samper_633963255-0cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-0cm-0cm-0cm-0cm.png)
|
| (a) Drag force [N]. | (b) Lift force [N]. |
| Figura 5.21: 2D flow around thin-walled arch profile (slip interface). Drag and lift evolution. | |
|
|
| (a) Body fitted. | (b) Embedded. |
| Figura 5.22: 2D flow around thin-walled arch profile (slip interface). Velocity modulus [m/s]. | |
|
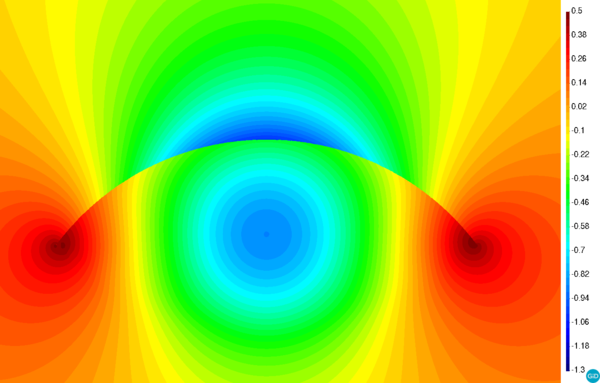
|
| (a) Body fitted. | (b) Embedded. |
| Figura 5.23: 2D flow around thin-walled arch profile (slip interface). Pressure [Pa]. | |
5.3.5.2 No-slip interface
As it is done in the slip interface case, Fig. 5.24 presents the time evolution of the drag and lift forces. Since in this case the solution is no longer steady, this information is accompanied with the corresponding histograms. It can be observed that the embedded and body fitted drag force histograms are in really good agreement, being the average drag value around the 0.2N (Fig. 5.24b). To what concerns the lift force, the embedded values are more disperse than the body fitted ones (Fig. 5.24d).
Fig. 5.25 depicts a velocity and pressure snapshot of the obtained embedded solution. The presence of a stagnation point in the front end of the arch can be noted as well as the velocity and pressure discontinuities that arise after embedding the arch geometry.
Moreover, the turbulent nature of the flow, which separates in the top part of the arch, can be also observed. Small vortexes appear after the separation point, whose location is approximately at one quarter of the total arch length. Besides these, a larger vortex appears in the trailing part of the arch.
Last but not least, it is important to highlight the capability of the method to correctly impose not only the slip condition but a wall law-like one. This capability would be of great utility for the extension of the proposed technique to real engineering applications, in which the resolution of the boundary layer is normally not affordable.
![Velocity modulus [m/s].](/wd/images/thumb/4/47/Draft_Samper_633963255-test-simple_sails_EMB_1e-3_v_close_2-12cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-test-simple_sails_EMB_1e-3_v_close_2-12cm-0cm-0cm-0cm.png)
|
![Pressure [Pa].](/wd/images/thumb/8/8f/Draft_Samper_633963255-test-simple_sails_EMB_1e-3_p_close_2-12cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-test-simple_sails_EMB_1e-3_p_close_2-12cm-0cm-0cm-0cm.png)
|
| (a) Velocity modulus [m/s]. | (b) Pressure [Pa]. |
| Figura 5.25: 2D flow around thin-walled arch profile (no-slip interface). Embedded solution. | |
5.3.6 3D flow around a sailboat
The objective of this last example is to showcase the capabilities of the discontinuous Navier-slip formulation to efficiently solve real engineering problems. In order to exploit the ability of the method to conveniently deal with membrane-like bodies, the chosen geometry consists in a real 3D sailboat. It is due mentioning that no reference solution of any type is available for the problem at hand. Hence, this example only represents a proof-of-concept of a potential industrial application.
Figs. 5.26a and 5.27a depict the geometry of the sailboat, which has been provided by Juan Kouyoumdjian Naval Architects. The length and beam of the hull are 18.3m and 5.75m while the height of mast, whose axis is placed in the origin, is around 27m.
The computational domain is a 80m radius and 70m height cylinder centered in the (13.8,0,16.5)m coordinates (Fig. 5.28). The lateral surface of the cylinder is divided in two regions. The light green one represents the outlet, which comprises one quarter of the total skin, while the light pink one is the inlet.
Aiming to exploit the features of the method, the input geometrical entities are separated in two sets according to their volume nature. On the one hand, those entities that conform bodies with well defined internal volume (i.e. the hull and the mast), that is to say, those ones that can be straightforwardly represented using a body conforming discretization, are collected in one set. On the other hand, another set containing all the surfaces that represent the membrane sails is created.
By doing so it is possible to take advantage of the implicit representation to avoid the volume meshing of the thin-walled sails. Hence, the mainsail as well as the headsails are considered as four independent embedded volumeless bodies which are represented by a discontinuous level set function.
Unlike the previous examples, in which the level set can be computed with a simple analytical function, this example requires the use of a level set calculation algorithm [117]. Figs. 5.26 and 5.27 compare the input boat geometry to the one used in the resolution of the problem, which includes the level set representation of the sails. Although the this is in general terms very accurate, the boundaries of the reconstructed geometry exhibit a “saw-toothed” pattern. This behavior, which is also reported for a similar case in [37], is a consequence of the nature of the level set method, which cannot represent the partial intersections that do not split the element in two complete parts.

|

|
| (a) Original geometry. | (b) Computational model. |
| Figura 5.26: 3D flow around a sailboat. Sailboat top-side view. | |

|

|
| (a) Original geometry | (b) Computational model. |
| Figura 5.27: 3D flow around a sailboat. Sailboat top-rear view. | |
|
| Figura 5.28: 3D flow around a sailboat. Computational domain. |
The boundary conditions are rather simple. Both the hull and the mast are slip. The same behaviour is also imposed in the top and bottom surfaces of the computational domain. In the outlet surface the pressure is fixed to 0Pa. In the inlet surface a wind velocity of 15knots (7.72m/s) is imposed in the (1,0,1) direction, which is rotated with respect to the alignment of the hull. With regard to the Navier-slip BC in the embedded sails, the slip length is set to 10-2m while the penalty constant is equal to 0.25. The problem is run for 20s using a time step of 0.025s. The computational domain is meshed with 3.3M linear tetrahedra. Fig. 5.29 shows a detail the body conforming volume mesh surrounding the hull and the mast.

|
| Figura 5.29: 3D flow around a sailboat. Hull and mast mesh detail. |
Despite the lack of reference results, the obtained velocity and pressure fields are convincing. As it can be observed in Fig. 5.30c, the discontinuous Navier-slip formulation is capable of representing the pressure discontinuity between the two sides of the embedded sails. More specifically, a positive overpressure appears in the windward region of the sails (Fig. 5.30a) while a suction occurs in the leeward one (Fig. 5.30b). Such pressure discontinuity generates the wind thrust of the sailboat.
Figs. 5.31, 5.32, 5.33 and 5.34 present a set of horizontal cross sections of the velocity vector field. It is interesting to comment the effect that the slip length has in the solution, which can be clearly noted in the front sail, specially in the plane equal to 5m cross section (Fig. 5.32). Even though the flow separation that occurs in the front edge of the sail, the velocity is neither null nor maximum in the sail surface. Instead, it behaves as a wall law, which is expected to be the nature of the Navier-slip BC. Despite the lack of a more rigorous study about the effect that more feasible values of the could have in the solution, the results of these preliminary experiments appear to be promising from the industrial application perspective.
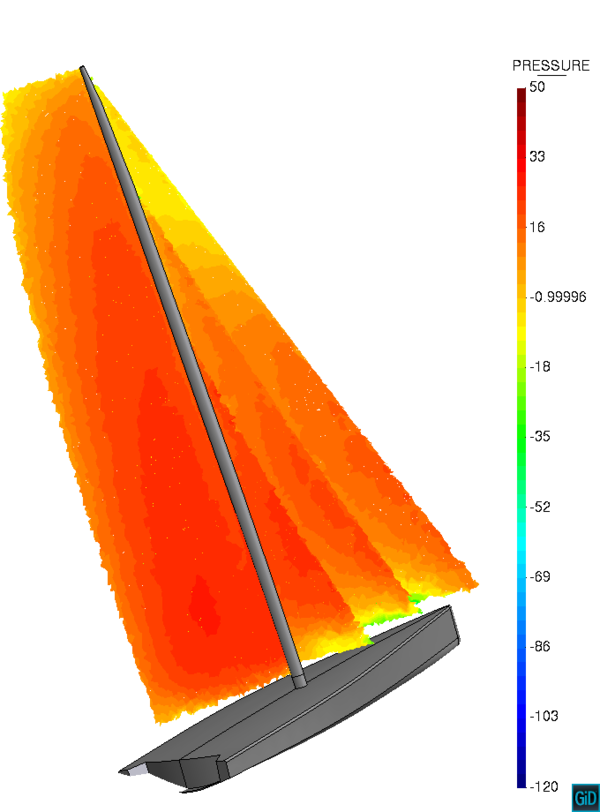
|

|
| (a) Boat detail (windward). | (b) Boat detail (leeward). |
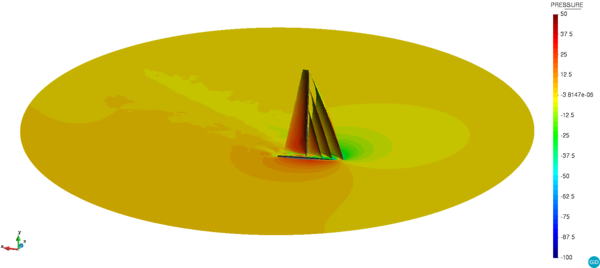
| |
| (c) Computational domain cross section. | |
| Figura 5.30: 3D flow around a sailboat. Pressure field [Pa]. | |
![3D flow around a sailboat. Velocity field cross section at height 1m [m/s].](/wd/images/thumb/3/3c/Draft_Samper_633963255-test-boat_sails_case_1_v_cross_section_1-4cm-0cm-4cm-0cm.png/480px-Draft_Samper_633963255-test-boat_sails_case_1_v_cross_section_1-4cm-0cm-4cm-0cm.png)
|
| Figura 5.31: 3D flow around a sailboat. Velocity field cross section at height 1m [m/s]. |
![3D flow around a sailboat. Velocity field cross section at height 5m [m/s].](/wd/images/thumb/3/3e/Draft_Samper_633963255-test-boat_sails_case_1_v_cross_section_5-4cm-0cm-4cm-0cm.png/480px-Draft_Samper_633963255-test-boat_sails_case_1_v_cross_section_5-4cm-0cm-4cm-0cm.png)
|
| Figura 5.32: 3D flow around a sailboat. Velocity field cross section at height 5m [m/s]. |
![3D flow around a sailboat. Velocity field cross section at height 12.5m [m/s].](/wd/images/thumb/3/34/Draft_Samper_633963255-test-boat_sails_case_1_v_cross_section_125-4cm-0cm-4cm-0cm.png/480px-Draft_Samper_633963255-test-boat_sails_case_1_v_cross_section_125-4cm-0cm-4cm-0cm.png)
|
| Figura 5.33: 3D flow around a sailboat. Velocity field cross section at height 12.5m [m/s]. |
![3D flow around a sailboat. Velocity field cross section at height 20m [m/s].](/wd/images/thumb/0/0d/Draft_Samper_633963255-test-boat_sails_case_1_v_cross_section_20-4cm-0cm-4cm-0cm.png/480px-Draft_Samper_633963255-test-boat_sails_case_1_v_cross_section_20-4cm-0cm-4cm-0cm.png)
|
| Figura 5.34: 3D flow around a sailboat. Velocity field cross section at height 20m [m/s]. |
5.4 Conclusion
This chapter presents a novel embedded formulation for the weak imposition of the Navier-slip BC in viscous incompressible Navier-Stokes flows. The proposal is valid not only for volumetric bodies but also for membrane-like ones that feature no internal volume.
The new formulation relies on the use of the Ausas discontinuous FE space in combination with a Nitsche-based imposition of the Navier-slip BC. Provided a discontinuous level set function representing the immersed objects, the Ausas FE space is able to capture the velocity and pressure jumps inside the intersected elements. On top of that, the Navier-slip BC that is enforced in the level set intersections makes possible to represent any wall behaviour from the slip to the no-slip limits.
Furthermore, the proposed technique has neither blending elements nor extra degrees of freedom. While the former becomes relevant when working in distributed memory environments (MPI), the latter avoids the need of reconstructing the system matrix graph each time the level set is updated.
The convergence and accuracy of the method is assessed by solving several examples, which consider different values of the slip length ranging from the slip to the no-slip limits. For values close to the slip limit, the velocity and pressure convergence rates are around , which is in accordance with the interpolation properties of the Ausas FE space [114,37]. However, the convergence rates deteriorate to when the slip length approaches the no-slip limit. Such degradation can be perfectly expected owing to the inability of the Ausas FE space to properly represent the gradients in the intersected elements. Nonetheless, the wall shear effects are roughly recovered upon mesh refinement as the thickness of the constant solution (or null gradient) region is reduced.
Complementary, the ability of the compressibility term in the mass conservation equation to keep the pressure bounded is proved by solving one example involving isolated fluid cavities with no Neumann BC. These results are crucial for the application of the method either to ill-conditioned level set functions coming from “dirty” input geometries or to complex moving boundary problems.
The experimental campaign is completed with two examples involving high Re turbulent flows. While the first one involves a simple 2D geometry, the second one is a feasible industrial application that evinces the utility of the method to completely get rid of the pre-processing difficulties that arise when trying to create a volume mesh from a thin-walled structure. In these two examples the viscous Navier-slip approach is proved to be a reasonable alternative to the more expensive boundary layer mesh plus no-slip condition combination.
Finally, it is interesting to point out the further enhancements and arising work lines. The first one is to couple the proposed tool with a structural mechanics solver to build a FSI framework for the analysis of highly flexible membrane and shell structures. Another interesting application in the biomedical engineering context is the modelling of the fluid flow around thin biological tissues [40]. There is also room for more theoretical advances. In this regard, the method could be enhanced to work in combination with a discontinuous edge-based level set function. This would help to handle some of the partial element intersection issues reported in the sailboat example.
input-ch2-StateArt input-ch3-NavierStokes input-ch4-CMAME_emb_1 input-ch5-AusasNavierSlip
6 Computational modeling of the fluid flow in type B aortic dissection using a modified Finite Element embedded formulation
6.1 Article data
Title: Computational modeling of the fluid flow in type B aortic dissection using a modified Finite Element embedded formulation
Authors: R. Zorrilla, E.Soudah and R. Rossi
Journal: Biomechanics and Modelling in Mechanobiology (2020)
Received: 2 September 2019 / Accepted: 14 January 2020 / Available online: 23 January 2020
DOI: 10.1007/s10237-020-01291-x
6.2 Scientific contribution
This chapter presents the second paper of the compendium. The objective of the article is to further validate the formulation developed in Chapter 5 by solving the flow in a type B Aortic Dissection (AD) phantom model. Although this application is far from the civil engineering field, it has been chosen since the data from previous numerical simulations and in vitro experiments is available. Furthermore, this article also aims at applying the methods developed in this thesis to other engineering disciplines. More specifically, this paper proves that the proposed discontinuous embedded formulation can be efficiently employed for the resolution of CFD problems involving thin biological tissues.
After a brief revision of the state of the art about CFD modeling of the AD disease, the article presents the in vitro experiment that is reproduced. The original in vitro experiment presents four variants of the phantom model [118], which differ in the number and size of the tears in the intimal flap. The results show that the embedded solutions obtained with the formulation in Chapter 5 are in really good agreement with both the experimental data in [118] as well as with the body fitted CFD simulation results presented in [119].
Additionally, the article also describes a simple procedure that might help the clinicians in the decision making before the AD fenestration surgery. Although the idea might seem rather simple, it can serve as a complementary tool to assess which is the optimal position for the fenestration re-entry tears when used in combination with patient specific geometries. Finally, it is important to highlight that the findings of this chapter can be considered as a first step towards the application of the proposed techniques to more complex biomedical problems involving thin-walled bodies such as the FSI analysis of hearth valves.
7 An embedded Finite Element framework for the resolution of strongly coupled Fluid–Structure Interaction problems. Application to volumetric and membrane-like structures
7.1 Article data
Title: An embedded Finite Element framework for the resolution of strongly coupled Fluid–Structure Interaction problems. Application to volumetric and membrane-like structures
Authors: R. Zorrilla, R. Rossi, R. Wüchner and E. Oñate
Journal: Computer Methods in Applied Mechanics and Engineering 368 (2020) 113179
Received: 28 January 2020 / Accepted: 23 May 2020 / Available online: 2 June 2020
DOI: 10.1016/j.cma.2020.113179
7.2 Scientific contribution
This chapter presents the last paper of the compendium. In short, the main contribution of the paper is the collection of all the previously developed CFD technologies to extend the applicability range of the embedded framework to FSI problems. It is important to highlight the capability of the novel embedded FSI toolbox to efficiently deal with any type of bodies, including membrane-like geometries.
For the sake of versatility, the FSI coupling is done in a black-box fashion using QN convergence accelerators within a Gauss-Seidel subdomain iteration. The paper discusses the particularities of the embedded FSI coupling, including a proposal for the imposition of the FM-ALE BCs. In addition, the article details the object oriented implementation, which is done according to code sustainability criteria in order to straightforwardly use the same implementation, not only in the body fitted case, but also in the resolution of other coupled problems (e.g. Conjugate Heat Transfer).
The embedded FSI solver is validated by solving several examples involving both volumetric and thin-walled bodies. The obtained solutions are compared, whenever it is possible, with reference data from the literature as well as with the results obtained with an alternative body fitted solver. The article proves that both the accuracy and the efficiency, which is measured in terms of the number of FSI subdomain iterations, are barely affected by the EBM method employed in the resolution of the CFD problem.
It is also interesting to highlight that the article presents one test example that entails extremely large rotations which would definitively have required remeshing if a body fitted solver would have been used. This benchmark showcases the enhanced robustness that the embedded solver has when dealing with such challenging scenarios.
Finally, the last example targets the main objective stated at the early beginnings of the thesis: the efficient and robust simulation of extremely lightweight civil engineering structures. Hence, the FSI analysis of a 4-point tent structure during an extreme wind episode is solved using the developed FSI framework. The results prove that the VWT numerical tool is production-ready and thus prepared to be applied to real engineering problems.
8 Towards predictive territory planning
Predictive territory planning could be defined as all the social, political and technical actions that need to be taken in advance to ensure the sustainable management and evolution of a populated regions. Hence, the predictive territory planning is a holistic concept in which multiple knowledge areas are involved. Among all of them, this chapter focuses on how the computational wind engineering, used in combination with level set methods, can help to achieve such challenging objective.
The chapter is organized as follows. First of all, the advantages of using a level set discretization to deal with dirty input geometries are discussed. Secondly, an application case of such techniques to analyse the wind flow over a city digital model is shown. The last section collects some thoughts about the applicability of the method to real management strategies.
8.1 Introduction
Nowadays, Computer Aided Design (CAD) is a well established tool in the design pipeline of all the engineering areas. Thanks to CAD modelling, it is relatively easy to sketch and modify any conceptual design, regardless the complexity of its geometrical features. This, in combination with numerical analysis has allowed designers and engineers to have a rapid virtual prototyping lab in their own laptops.
Having said this, it is clear that the ideal scenario would be to directly use the CAD model created during the design stage to run the simulation, avoiding thus the need of generating an intermediate simulation model from the CAD-based geometry. This idea gave rise to the so called IsoGeometric Analysis (IGA) [120,33] or ImmersoGeometric Analysis methods [16,53] in which the simulation is done on top of the CAD geometries.
Unfortunately, there are cases in which the CAD model is not suitable for the numerical analysis and thus requires modifications to become simulation-compatible. On the one hand, it might happen that the CAD model has a high level of detail which is neither required nor suitable for the numerical simulation. This situation commonly happens when dealing with CAD models from architecture or civil engineering projects, in which the level of detail required to do the blueprints or the measurements is much beyond that one demanded to do an accurate CFD analysis of the structure. On the other hand, it might also happen that the input geometry is given in a low fidelity format such as the STereoLithography (stl). These “dirty” input geometries can be rarely meshed out of the box since the mesh generation algorithms are rather sensitive to the geometrical imperfections.
Traditionally, these issues have been addressed by manually repairing the input geometries. This implies to clean up and fix all the possible defects, namely duplicated entities, holes and overlapped surfaces, in order to create a watertight meshable geometry. As it can be easily guessed, this task rapidly turns into an extremely time and effort consuming, or even unaffordable, operation, specially when dealing with real complex geometries. Indeed, the geometrical repairing and meshing are reported to take up to the 50% of the total simulation time in real engineering applications [33].
In this context, the body conforming preprocess bottleneck can be avoided by using an implicit description of the bodies. By doing so the defects of the input geometry are automatically filtered by the level set calculation algorithm, which is an always defined operation, meaning that all the human geometrical operations are completely bypassed. Hence, thanks to the robustness of the level set calculation operation the preprocessing of complex geometries is extremely simplified and accelerated as it only requires the generation of an unfitted background computational mesh. Furthermore, this opens the possibility of using of fast Octree-based algorithms [121] to generate the background mesh, which can be upgraded later on by using a distance-based anisotropic refinement [122].
These ideas are presented in Fig. 8.1 for an Aston Martin Vanquish CAD model. As it can be observed in Fig. 8.1a, the stl input geometry features a high level of detail which makes impossible to create a watertight volume mesh out of the box. Instead of repairing the stl file, something that seems a priori to be extremely complicated, the geometry can be implicitly represented in the background mesh. For a reasonable level of discretization, the distance calculation algorithm yields the level set function depicted in Fig. 8.1b, which features a sufficient level of detail to run a CFD simulation.

|

|
| (a) Input stl geometry. | (b) Level set representation. |
| Figura 8.1: Aston Martin Vanquish level set calculation test. | |
8.2 A civil engineering application: city wind flow
In this section the previously described advantages of implicit geometry representations are exploited in the context of predictive territory planning. More specifically, the application at hand consists in the wind CFD analysis of a portion of a real city.
To efficiently achieve this, the computational domain is created as a prismatic vertical extrusion of the region of interest boundaries. Then the bottom face of the prism is removed such that the inferior part of the computational domain matches the ground surface, whose geometry can be obtained from a digital terrain elevation model. Once this operation is completed, the computational domain is ready to be meshed.
Note that so far only the terrain, with no buildings over it, is represented by the volume mesh boundaries. Taking into account that the public databases from which the buildings geometries can be retrieved commonly involve a rather poor quality, repairing the input files representing the buildings is fairly impossible when large urban areas are to be analysed. Instead, the input file describing the building geometries can be literally thrown into the computational domain in order to implicitly represent these in the volume mesh.
This approach is applied to solve the wind flow over a vast extension (2.5x1.5km) of the Montigala district of the city of Badalona (Spain). Fig. 8.2 depicts a map of the region of interest while Fig. 8.3 does so with the computational model, including the level set representation of the buildings and the computational box wire frame. As it can be observed, the ground is described by the lower surface of the computational box (Fig. 8.3a) while Figs. 8.3b and 8.3c zoom in the buildings implicit representation. The 62M elements background mesh yields a resolution around 1m, which is considered enough taking into account that the objective of this kind of analysis is to have an overall understanding of the flow over a vast region of terrain. A constant air inlet of 10m/s is imposed in the south-west side of the domain (left edge in Fig. 8.2). With regard to the wall behavior, both the computational domain faces and the embedded skin are modeled as slip walls as the boundary layer viscous effects cannot be properly represented with this mesh resolution. Owing to the dimensions of the problem, it is impossible to solve it in a desktop machine and the use of an HPC facility is thus required. In this case the problem is solved in the in-house cluster Acuario using 192 MPI processes.
Fig. 8.4 presents some streamlines from the obtained velocity field. It can be observed that the distance based approach is capable of capturing the main features of the wind effects, also including the urban canyon phenomenon (Fig. 8.4b), which is of particular interest in the urban wind engineering context.
|
| Figura 8.2: Wind flow over cities. Montigala district (Badalona, Spain) domain of interest. |
|
Streamlines detail 1. |
| (a) Complete view. | (b) Streamlines detail 1. |
| Streamlines detail 2. | |
| (c) Streamlines detail 2. | |
| Figura 8.4: Wind flow over cities. Montigala district (Badalona, Spain). Obtained streamlines. | |
8.3 Conclusion
This chapter aims at exploiting the robustness of the implicit level set representation from a completely different perspective. This is to simplify the preprocessing of extremely “dirty” input geometries in the context of civil wind engineering. Hence, all the tedious geometrical repairing operations, which might be unaffordable in complex scenarios as the one presented in the previous section, are automatically bypassed thanks to the inherent capabilities of the distance calculation algorithm. However, such enhanced robustness comes at the price of requiring a way finer volume mesh discretization to achieve a reasonably accurate resolution of the embedded boundaries. In consequence, a scalable MPI implementation, as well as the access to an HPC facility, becomes mandatory to efficiently transfer this technology to real applications.
It is important to remark that the results in this chapter are a proof-of-concept of a future research line that arises from the main developments of this thesis. Hence, this chapter only focuses on the modeling simplification, meaning that other important aspects of the wind engineering such as the turbulent wind inlet BC are not considered yet. Despite this, the obtained results are promising and make possible the gradual addition of extra features.
A feasible enhancement that would be of great utility in the civil engineering field is the combination of the embedded CFD solver with a pollutant transport one in order to assess how an accidental or chimney contaminant plume would affect a region. Furthermore, the ideas in this chapter can be perfectly used in combination with a body conforming representation. This opens the possibility to select a building of interest, in which the wind effects require to be accurately captured, with an embedded representation of the surroundings.
input-ch2-StateArt input-ch3-NavierStokes input-ch4-CMAME_emb_1 input-ch5-AusasNavierSlip input-ch6-BIO input-ch7-CMAME_fsi input-ch8-Cities
9 Conclusion
This last chapter presents the closure of the work. To that purpose, the achievements of each one of the previous chapters are discussed first. Secondly, the generic conclusions that arise after having finished the thesis are presented as a closure. Finally, the last section outlines the future research lines and improvements.
9.1 Achievements
The first remarkable scientific contribution of this thesis is the discontinuous Navier–Stokes embedded formulation for the imposition of the slip BC presented in Chapter 4. Such formulation, which is intended to be used in combination with a discontinuous level set representation, modifies the standard FE space in the intersected elements by the Ausas discontinuous one. This substitution, in combination with a weak imposition of the no penetration BC, namely slip BC, allows the resolution of CFD problems involving not only volumetric bodies but also thin-walled ones. The experiments, which involve low and high Re cases, show that the convergence rate of the Ausas FE space is kept. Furthermore, the method is of the same order of accuracy as the body fitted and embedded approaches that the tests compare to.
In Chapter 5 the discontinuous slip formulation is enhanced by including a Nitsche-based imposition of the general Navier-slip condition. Aside of keeping the capability of the previous formulation to deal with membrane-like bodies, this improved version makes possible to model any wall behaviour from the slip to the no-slip limits. The experiments show a convergence rate around when the wall BC approaches the slip limit. However, the convergence rate deteriorates to when the wall effects become relevant, that is to say when the wall BC approaches the no-slip limit. This is associated to the inability of the Ausas FE space to properly capture the gradient in the intersected elements.
Concerning the computational efficiency, none of these formulations have neither blending elements nor extra DOFs. This becomes in an advantage when working in a distributed memory environment since there is no extra communication overhead. Furthermore, the matrix graph calculation is not required to be constructed each time the level set is updated, something that would definitively be a computational bottleneck when dealing with moving boundary problems (i.e. FSI).
Complementary, Chapter 5 proves the utility of the pseudo-compressibility term that is added to the mass conservation equation in Chapter 3. Hence, the ability of such extra term to keep the pressure bounded is evinced by solving a test case involving an isolated fluid cavity with no Neumann BC. It has to be highlighted that this feature becomes crucial for the application of the developed methods to real engineering problems involving ill-conditioned level set functions, which may come either from “dirty” input geometries as it is discussed in Chapter 8, or from moving boundary problems involving complex bodies.
In Chapter 6 the discontinuous Navier-slip formulation is further validated by reproducing an in vitro experiment that consists in a phantom model of the aortic dissection cardiovascular disease. The obtained results are in agreement with both the experimental data and the literature numerical simulations. Besides this, the results also prove the utility of the formulation to model the flow around thin biological tissues.
Chapter 7 extends all the previous embedded CFD developments to be applied in the resolution of FSI problems. In other words, it can be said that the thesis objective of creating the VWT framework is ultimately accomplished in this chapter. The FSI coupling is achieved by the use of a black-box embedded interface residual Gauss-Seidel iteration that makes possible the resolution of strongly coupled problems. The robustness and performance of the embedded FSI solver is tested by solving several examples involving both volumetric and thin-walled structures. In addition, the accuracy and efficiency are also assessed by comparing the obtained results with the ones of a body fitted solver. The results prove that using a non-conforming discretization in the fluid domain neither compromises the quality nor the convergence of the solution.
Chapter 7 also includes an improvement for the BC imposition of the FM-ALE algorithm mesh motion problem. This enhancement, whose computational cost is negligible compared with the rest of the FM-ALE operations, allows treating the embedded interfaces in a sort of Lagrangian manner such that the movement of the FM-ALE virtual mesh coincides (in a variational sense) with the embedded skin within the cut elements. This improvement ensures that the movement is large enough to guarantee a proper initialization of the historical variables but also small enough to prevent the common element distortion issues associated to mesh motion problems. Complementary, Chapter 7 details the implementation of the embedded FSI coupling by providing the guidelines to build an easily extensible black-box coupling framework based on object oriented design patterns.
Furthermore, it is important to highlight that the last example in Chapter 7 entails the simulation of a real scale extremely lightweight membrane structure during a strong wind episode. The results confirm the capability of the embedded FSI solver to robustly deal with the target application established at the beginning of the thesis.
Last but not least, Chapter 8 presents an alternative civil engineering application in which level set based approaches can be useful. In this case the robustness of the level set method, which makes possible to efficiently deal with poor quality input geometries, is exploited to easily generate large scale wind flow simulations.
9.2 Closure
After having discussed all the achievements in the previous section, it can be said that fixed mesh methods can play an important role in nowadays computational engineering. Thanks to the level set representation of the bodies, this family of methods can easily deal with arbitrary moving interfaces and thus bypass all the common problems that ALE-based body conforming approaches have. Furthermore, level set based approaches can also help to make the preprocess more efficient, specially when dealing with “dirty” input geometries or when a volume mesh has to be created from a volumeless thin-walled structure.
These advantages come however at the price of requiring some extra complexities, such as the weak BC imposition or the use (and implementation) of an efficient level set calculation algorithm. Besides this, body conforming approaches are always slightly more accurate than embedded ones. Aside of the fact that the weak BC imposition may affect in this regard, the implicit representation of geometries is inherently less accurate than the body fitted one since some geometrical features, such as sharp corners in volumetric bodies and partial intersections in thin-walled ones, cannot be represented by a level set function. As a consequence, the unique way to minimize such geometrical representation error is to refine the mesh in those regions where the embedded bodies are expected to move across.
Taking into account such disadvantages, the embedded approach should not be considered as a substitute of the standard body conforming ones. Instead, it has to be thought of as an always robust alternative to be applied in those cases in which the standard methods are expected to perform badly.
Recalling the motivation of the thesis in Chapter 1, it can be said that the initially stated objectives have been all accomplished. The embedded framework that has been developed is capable of dealing with both CFD and FSI problems involving any type of bodies, including membrane-like ones, which was one of the main demands. Altogether, these developments are the so called VWT, which can be considered ready to be applied in the resolution of real civil engineering problems.
9.3 Future research lines
This section briefly describes which are the remaining improvements and future work lines arising from this thesis. These have been divided in three categories: implementation, technical advances and other applications.
Regarding the missing implementations, they be summarized in two main tasks. The first and more urgent one is the MPI implementation of some auxiliary utilities, which are mainly related to the FM-ALE algorithm. The second one is the development and validation of a user-friendly Graphical User Interface (GUI). Right now only a mock-up version of the VWT GUI is available. These two requirements are mandatory for the effective application of the VWT toolbox in real industrial projects.
Concerning the technical improvements, these aim at limiting the effect of the implicit representation accuracy issues discussed in the previous section. On the one hand, using an edge-based level set function instead of the current elemental one could help to detect those partial intersections that occur when a thin-walled skin geometry does not completely split an element. Once such partial intersections are detected, the boundary artifacts commented in Chapter 7 could be addressed by including an extra variational term. On the other hand, both the CFD and FSI embedded solvers could benefit from the use of a level set-based anisotropic mesh refinement strategy. This would substantially help to recover the geometrical details that are lost because of the implicit representation.
Complementary, the MVQN convergence accelerator can be also improved to avoid the inverse Jacobian matrix storage, which might involve a great memory consumption when dealing with large FSI problems. Some experiments have been carried out in this regard using a recursive implementation of the inverse Jacobian approximation. After some preliminary tests, the alternative implementation seems to be valid. Nevertheless, a thorough validation is still pending, specially to assess how the number of recursive steps used in the approximation of the Jacobian (i.e. buffer size) affects the FSI coupling convergence.
Finally, it is important to highlight that the VWT developments can be exploited in other engineering fields. Chapter 6 proves that the embedded CFD solver can be efficiently applied in the resolution of problems that involve fluid flow around biological tissues. The next step is to use the embedded FSI solver to solve problems that require introducing the deformation of the tissues such as the blood flow through the tricuspid or mitral hearth valves. Moreover, embedded methods are understood to be one of the few options that can efficiently deal with topology changes without requiring remeshing. In this regard, it could be also interesting to apply the embedded FSI solver to problems involving contact or membrane wrinkling (e.g. folding/unfolding sails or parachutes). Preliminary fluid-structure-contact interaction experiments combining the embedded FSI solver with an implicit mortar contact formulation showed promising results.
BIBLIOGRAFÍA
[1] R. Carter. (2006) "Boat remains and maritime trade in the Persian Gulf during the sixth and fifth millennia BC", Volume 80. Cambridge University Press. Antiquity 307 52-63
[2] J.P. Oleson. (1984) "Greek and Roman mechanical water-lifting devices: the history of a technology", Volume 16. Springer Science & Business Media
[3] Wikander, rjan and others. (2000) "Handbook of ancient water technology". Brill Leiden
[4] A. Lucas. (2006) "Wind, water, work: ancient and medieval milling technology", Volume 8. Brill
[5] M. Gad-el-Hak, Mohamed. (1998) "Fluid Mechanics from the Beginning to the Third Millennium", Volume 14. International Journal of Engineering Education
[6] C.P. Ellington and C. van den Berg and A.P. Willmott and A.L.R. Thomas. (1996) "Leading-edge vortices in insect flight", Volume 384. Nature 6610 626-630
[7] G.K. Taylor and R.L. Nudds and A.L.R. Thomas. (2003) "Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency", Volume 425. Nature 6959 707-711
[8] J. Young and S.M. Walker and R.J. Bomphrey and G.K. Taylor and A.L.R. Thomas. (2009) "Details of Insect Wing Design and Deformation Enhance Aerodynamic Function and Flight Efficiency", Volume 325. American Association for the Advancement of Science. Science 5947 1549–1552
[9] R. Mittal and H. Dong and M. Bozkurttas and F.M. Najjar and A. Vargas and A. von Loebbecke. (2008) "A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries", Volume 227. Journal of Computational Physics 10 4825 - 4852
[10] Hong Zhao and Jonathan B. Freund and Robert D. Moser. (2008) "A fixed-mesh method for incompressible flow-structure systems with finite solid deformations", Volume 227. Journal of Computational Physics 6 3114 - 3140
[11] C. Alberto Figueroa and Irene E. Vignon-Clementel and Kenneth E. Jansen and Thomas J.R. Hughes and Charles A. Taylor. (2006) "A coupled momentum method for modeling blood flow in three-dimensional deformable arteries", Volume 195. Computer Methods in Applied Mechanics and Engineering 41 5685 - 5706
[12] Taelman, Liesbeth and Bols, Joris and Degroote, Joris and Muthurangu, Vivek and Panzer, Joseph and Vierendeels, Jan and Segers, Patrick. (2016) "Differential impact of local stiffening and narrowing on hemodynamics in repaired aortic coarctation: an FSI study", Volume 54. Medical & Biological Engineering & Computing 2 497–510
[13] Ryzhakov, Pavel and Soudah, Eduardo and Dialami, Narges. (2019) "Computational modeling of the fluid flow and the flexible intimal flap in type B aortic dissection via a monolithic Arbitrary Lagrangian/Eulerian fluid-structure interaction model", Volume n/a. International Journal for Numerical Methods in Biomedical Engineering n/a e3239
[14] Küttler, U. and Gee, M. and Förster, Ch. and Comerford, A. and Wall, W. A. (2010) "Coupling strategies for biomedical fluid–structure interaction problems", Volume 26. International Journal for Numerical Methods in Biomedical Engineering 3–4 305–321
[15] S.K. Dahl and J. Vierendeels and J. Degroote and S. Annerel and L.R. Hellevik and B. Skallerud. (2012) "FSI simulation of asymmetric mitral valve dynamics during diastolic filling", Volume 15. Taylor & Francis. Computer Methods in Biomechanics and Biomedical Engineering 2 121-130
[16] D. Kamensky and M.-C. Hsu and D. Schillinger and J.A. Evans and A. Aggarwal and Y. Bazilevs and M.S. Sacks and T.J.R. Hughes. (2015) "An immersogeometric variational framework for fluid-structure interaction: Application to bioprosthetic heart valves", Volume 284. Computer Methods in Applied Mechanics and Engineering 1005 - 1053
[17] M.D. de Tullio and G. Pascazio. (2016) "A moving-least-squares immersed boundary method for simulating the fluid-structure interaction of elastic bodies with arbitrary thickness", Volume 325. Journal of Computational Physics 201 - 225
[18] Hugo Casquero and Yongjie Jessica Zhang and Carles Bona-Casas and Lisandro Dalcin and Hector Gomez. (2018) "Non-body-fitted fluid-structure interaction: Divergence-conforming B-splines, fully-implicit dynamics, and variational formulation", Volume 374. Journal of Computational Physics 625-653
[19] M. Glück and M. Breuer and F. Durst and A. Halfmann and E. Rank. (2001) "Computation of fluid-structure interaction on lightweight structures", Volume 89. Journal of Wind Engineering and Industrial Aerodynamics 14 1351 - 1368
[20] R. Scotta and M. Lazzari and E. Stecca and J. Cotela and R. Rossi. (2016) "Numerical wind tunnel for aerodynamic and aeroelastic characterization of bridge deck sections", Volume 167. Computers & Structures 96 - 114
[21] Idelsohn, S. R. and Marti, J. and Souto-Iglesias, A. and Oñate, E. (2008) "Interaction between an elastic structure and free-surface flows: experimental versus numerical comparisons using the PFEM", Volume 43. Computational Mechanics 1 125-132
[22] Oñate, Eugenio and Franci, Alessandro and Carbonell, Josep M. (2014) "Lagrangian formulation for finite element analysis of quasi-incompressible fluids with reduced mass losses", Volume 74. International Journal for Numerical Methods in Fluids 10 699-731
[23] M. Saeedi and R. Wüchner and K.-U. Bletzinger. (2016) "Fluid-Structure interaction analysis and performance evaluation of a membrane blade", Volume 753. IOP Publishing. Journal of Physics: Conference Series 102009
[24] R. Livaolu and A. Doangün. (2006) "Simplified seismic analysis procedures for elevated tanks considering fluid-structure-soil interaction", Volume 22. Journal of Fluids and Structures 3 421 - 439
[25] Otto, Frei and Trostel, Rudolf and Schleyer, Friedrich Karl. (1967) "Tensile structures: design, structure, and calculation of buildings of cables, nets, and membranes", Volume 69. MIT Press London
[26] Oñate, Eugenio and Flores, Fernando G. and Marcipar, Javier. (2008) "Membrane Structures Formed by Low Pressure Inflatable Tubes. New Analysis Methods and Recent Constructions". Textile Composites and Inflatable Structures II. Springer Netherlands 163–196
[27] P. Dadvand and R. Rossi and E. Oñate. (2010) "An Object-oriented Environment for Developing Finite Element Codes for Multi-disciplinary Applications", Volume 17. Archives of Computational Methods in Engineering 3 253–297
[28] P. Dadvand and R. Rossi and M. Gil and X. Martorell and J. Cotela and E. Juanpere and S.R. Idelsohn and E. Oñate. (2013) "Migration of a generic multi-physics framework to HPC environments", Volume 80. Computers & Fluids 301 - 309
[29] J. Donea and A. Huerta and J.-Ph. Ponthot and A. Rodríguez-Ferran. (2004) "Arbitrary Lagrangian-Eulerian Methods". Encyclopedia of Computational Mechanics. American Cancer Society
[30] Ryzhakov, P. B. and Rossi, R. and Idelsohn, S. R. and Oñate, E. (2010) "A monolithic Lagrangian approach for fluid–structure interaction problems", Volume 46. Computational Mechanics 6 883–899
[31] Alessandro Franci and Eugenio Oñate and Josep Maria Carbonell. (2016) "Unified Lagrangian formulation for solid and fluid mechanics and FSI problems", Volume 298. Computer Methods in Applied Mechanics and Engineering 520 - 547
[32] S.Osher and R. Fedkiw. (2003) "Level Set Methods and Dynamic Implicit Surfaces", Volume 153. Springer-Verlag New York, 1 Edition
[33] J.A. Cottrell and T.J.R. Hughes and Y. Bazilevs. (2009) "Isogeometric analysis: toward integration of CAD and FEA". John Wiley & Sons
[34] Löhner, Rainald and Baum, Joseph D. and Mestreau, Eric and Sharov, Dmitri and Charman, Charles and Pelessone, Daniele. (2004) "Adaptive embedded unstructured grid methods", Volume 60. International Journal for Numerical Methods in Engineering 3 641-660
[35] R. Löhner and J.R. Cebral and F.E. Camelli and S. Appanaboyina and J.D. Baum and E.L. Mestreau and O.A. Soto. (2008) "Adaptive embedded and immersed unstructured grid techniques", Volume 197. Comput. Methods Appl. Mech. Engrg. 25 2173-2197
[36] Scott D Roth. (1982) "Ray casting for modeling solids", Volume 18. Computer Graphics and Image Processing 2 109 - 144
[37] R. Zorrilla and A. Larese and R. Rossi. (2019) "A modified Finite Element formulation for the imposition of the slip boundary condition over embedded volumeless geometries", Volume 353. Computer Methods in Applied Mechanics and Engineering 123 - 157
[38] R. Zorrilla and A. Larese and R. Rossi. (3020under review) "A discontinuous Nitsche based Finite Element formulation for the imposition of the general Navier-slip boundary condition over embedded volumeless geometries". Computer Methods in Applied Mechanics and Engineering
[39] R. Zorrilla and R. Rossi and R. Wüchner and E. Oñate. (2020) "An embedded Finite Element framework for the resolution of strongly coupled FluidStructure Interaction problems. Application to volumetric and membrane-like structures", Volume 368. Elsevier BV. Computer Methods in Applied Mechanics and Engineering 113179
[40] Zorrilla, Rubén and Soudah, Eduardo and Rossi, Riccardo. (2020) "Computational modeling of the fluid flow in type B aortic dissection using a modified finite element embedded formulation". Biomechanics and Modeling in Mechanobiology
[41] C.S. Peskin. (1972) "Flow patterns around heart valves: A numerical method", Volume 10. Journal of Computational Physics 2 252 - 271
[42] T. Sawada and A. Tezuka. (2011) "LLM and X-FEM based interface modeling of fluid–thin structure interactions on a non-interface-fitted mesh", Volume 48. Computational Mechanics 3 319–332
[43] L.C. Foucard and F.J. Vernerey. (2015) "An X-FEM-based numerical-asymptotic expansion for simulating a Stokes flow near a sharp corner", Volume 102. International Journal for Numerical Methods in Engineering 2 79-98
[44] Frédéric Alauzet and Benoit Fabreges and Miguel A. Fernández and Mikel Landajuela. (2016) "Nitsche-XFEM for the coupling of an incompressible fluid with immersed thin-walled structures", Volume 301. Computer Methods in Applied Mechanics and Engineering 300 - 335
[45] Schott, B. and Shahmiri, S. and Kruse, R. and Wall, W.A. (2016) "A stabilized Nitsche-type extended embedding mesh approach for 3D low- and high-Reynolds-number flows", Volume 82. International Journal for Numerical Methods in Fluids 6 289-315
[46] Jungwoo Kim and Dongjoo Kim and Haecheon Choi. (2001) "An Immersed-Boundary Finite-Volume Method for Simulations of Flow in Complex Geometries", Volume 171. Journal of Computational Physics 1 132 - 150
[47] C.S. Peskin. (2002) "The immersed boundary method", Volume 112. Acta Numerica 479 - 517
[48] Lucy Zhang and Axel Gerstenberger and Xiaodong Wang and Wing Kam Liu. (2004) "Immersed finite element method", Volume 193. Computer Methods in Applied Mechanics and Engineering 21 2051 - 2067
[49] Zhang, Zhi-Qian and Liu, G. R. and Khoo, Boo Cheong. (2013) "A three dimensional immersed smoothed finite element method (3D IS-FEM) for fluid–structure interaction problems", Volume 51. Computational Mechanics 2 129–150
[50] Burman, Erik and Claus, Susanne and Hansbo, Peter and Larson, Mats G. and Massing, André. (2015) "CutFEM: Discretizing geometry and partial differential equations", Volume 104. International Journal for Numerical Methods in Engineering 7 472-501
[51] A. Main and G. Scovazzi. (2018) "The shifted boundary method for embedded domain computations. Part I: Poisson and Stokes problems", Volume 372. Journal of Computational Physics 972 - 995
[52] A. Main and G. Scovazzi. (2018) "The shifted boundary method for embedded domain computations. Part II: Linear advection-diffusion and incompressible Navier-Stokes equations", Volume 372. Journal of Computational Physics 996 - 1026
[53] Xu, Fei and Kamensky, David and Varduhn, Vasco and Wang, Chenglong and Wasion, Sean A. and Sotomayor-Rinaldi, Bryann and Darling, Carolyn N. and Schillinger, Dominik and Hsu, Ming-Chen. (2016) "An Immersogeometric Method for the Simulation of Turbulent Flow Around Complex Geometries". Advances in Computational Fluid-Structure Interaction and Flow Simulation: New Methods and Challenging Computations. Springer International Publishing 111–125
[54] J. Wolf and D. Baumgärtner and R. Rossi and P. Dadvand and R. Wüchner. (2015) "Contribution to the Fluid-Structure Interaction Analysis of Ultra-Lightweight Structures using an Embedded Approach". International Center for Numerical Methods in Engineering
[55] J. Nitsche. (1971) "ber ein Variationsprinzip zur Lösung von Dirichlet-Problemen bei Verwendung von Teilräumen, die keinen Randbedingungen unterworfen sind", Volume 36. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 1 9-15
[56] R. Codina and J. Baiges. (2009) "Approximate imposition of boundary conditions in immersed boundary methods", Volume 80. Int. J. Numer. Meth. Engng. 1379-1405
[57] J.M. Urquiza and A. Garon and M.-I. Farinas. (2014) "Weak imposition of the slip boundary condition on curved boundaries for Stokes flow", Volume 256. Journal of Computational Physics 748-767
[58] A. Massing and M.G. Larson and A. Logg and M.E. Rognes. (2014) "A Stabilized Nitsche Fictitious Domain Method for the Stokes Problem", Volume 61. Journal of Scientific Computing 3 604-628
[59] A. Massing and B. Schott and W.A. Wall. (2018) "A stabilized Nitsche cut finite element method for the Oseen problem", Volume 328. Comput. Methods Appl. Mech. Engrg. 262-300
[60] M. Winter and B. Schott and A. Massing and W.A. Wall. (2018) "A Nitsche cut finite element method for the Oseen problem with general Navier boundary conditions", Volume 330. Comput. Methods Appl. Mech. Engrg. 220-252
[61] Baiges, Joan and Codina, Ramon and Henke, Florian and Shahmiri, Shadan and Wall, Wolfgang A. (2012) "A symmetric method for weakly imposing Dirichlet boundary conditions in embedded finite element meshes", Volume 90. International Journal for Numerical Methods in Engineering 5 636-658
[62] Mika Juntunen and Rolf Stenberg. (2009) "Nitsche's method for general boundary conditions", Volume 78. Mathematics of Computation 1353-1374
[63] Glowinski, Roland and Pan, Tsorng-Whay and Periaux, Jacques. (1995) "A Lagrange multiplier/fictitious domain method for the Dirichlet problem –- Generalization to some flow problems", Volume 12. Japan Journal of Industrial and Applied Mathematics 1 87
[64] R. Glowinski and T.W. Pan and J. Periaux. (1998) "Distributed Lagrange multiplier methods for incompressible viscous flow around moving rigid bodies", Volume 151. Computer Methods in Applied Mechanics and Engineering 1 181 - 194
[65] C.S. Peskin. (1977) "Numerical analysis of blood flow in the heart", Volume 25. Journal of Computational Physics 3 220 - 252
[66] C.S. Peskin and D.M. McQueen. (1989) "A three-dimensional computational method for blood flow in the heart I. Immersed elastic fibers in a viscous incompressible fluid", Volume 81. Journal of Computational Physics 2 372 - 405
[67] L. Zhu and C.S. Peskin. (2003) "Interaction of two flapping filaments in a flowing soap film", Volume 15. Physics of Fluids 7 1954-1960
[68] Santiago Badia and Francesc Verdugo and Alberto F. Martín. (2018) "The aggregated unfitted finite element method for elliptic problems", Volume 336. Computer Methods in Applied Mechanics and Engineering 533 - 553
[69] Ramon Codina and Guillaume Houzeaux and Herbert Coppola-Owen and Joan Baiges. (2009) "The fixed-mesh ALE approach for the numerical approximation of flows in moving domains", Volume 228. Journal of Computational Physics 5 1591 - 1611
[70] Baiges, Joan and Codina, Ramon. (2010) "The fixed-mesh ALE approach applied to solid mechanics and fluid-structure interaction problems", Volume 81. International Journal for Numerical Methods in Engineering 12 1529-1557
[71] Baiges, Joan and Codina, Ramon and Coppola-Owen, Herbert. (2011) "The Fixed-Mesh ALE approach for the numerical simulation of floating solids", Volume 67. International Journal for Numerical Methods in Fluids 8 1004-1023
[72] Joan Baiges and Ramon Codina and Arnau Pont and Ernesto Castillo. (2017) "An adaptive Fixed-Mesh ALE method for free surface flows", Volume 313. Computer Methods in Applied Mechanics and Engineering 159 - 188
[73] Mok, DP and Wall, WA and Ramm, E. (2001) "Accelerated iterative substructuring schemes for instationary fluid-structure interaction", Volume 2. Computational fluid and solid mechanics 1325–1328
[74] Gerardo Valdés. (2007) "Nonlinear Analysis of Orthotropic Membrane and Shell Structures Including Fluid-Structure Interaction". Universitat Politecnica de Catalunya
[75] Küttler, Ulrich and Wall, Wolfgang A. (2008) "Fixed-point fluid–structure interaction solvers with dynamic relaxation", Volume 43. Computational Mechanics 1 61–72
[76] R. Rossi and E. Oñate. (2010) "Analysis of some partitioned algorithms for fluid-structure interaction", Volume 27. Emerald Group Publishing Limited. Engineering Computations 1 20-56
[77] Küttler, Ulrich and Förster, Christiane and Wall, Wolfgang A. (2006) "A Solution for the Incompressibility Dilemma in Partitioned Fluid–Structure Interaction with Pure Dirichlet Fluid Domains", Volume 38. Computational Mechanics 4 417-429
[78] Santiago Badia and Fabio Nobile and Christian Vergara. (2008) "Fluid-structure partitioned procedures based on Robin transmission conditions", Volume 227. Journal of Computational Physics 14 7027 - 7051
[79] Luca Gerardo–Giorda and Fabio Nobile and Christian Vergara. (2010) "Analysis and Optimization of Robin–Robin Partitioned Procedures in Fluid–Structure Interaction Problems", Volume 48. SIAM Journal on Numerical Analysis 6 2091–2116
[80] Miguel A. Fernández and Mikel Landajuela and Marina Vidrascu. (2015) "Fully decoupled time-marching schemes for incompressible fluid/thin-walled structure interaction", Volume 297. Journal of Computational Physics 156 - 181
[81] Landajuela, Mikel and Vidrascu, Marina and Chapelle, Dominique and Fernández, Miguel A. (2017) "Coupling schemes for the FSI forward prediction challenge: Comparative study and validation", Volume 33. International Journal for Numerical Methods in Biomedical Engineering 4 e2813
[82] Riccardo Rossi and Pavel B. Ryzhakov and E. Oñate. (2009) "A Monolithic FE Formulation for the Analysis of Membranes in Fluids", Volume 24. International Journal of Space Structures 4 205-210
[83] Joris Degroote and Jan Vierendeels. (2011) "Multi-solver algorithms for the partitioned simulation of fluid-structure interaction", Volume 200. Computer Methods in Applied Mechanics and Engineering 25 2195 - 2210
[84] A.E.J. Bogaers and S. Kok and B.D. Reddy and T. Franz. (2014) "Quasi-Newton methods for implicit black-box FSI coupling", Volume 279. Computer Methods in Applied Mechanics and Engineering 113 - 132
[85] Sicklinger, S. and Belsky, V. and Engelmann, B. and Elmqvist, H. and Olsson, H. and Wüchner, R. and Bletzinger, K.-U. (2014) "Interface Jacobian-based Co-Simulation", Volume 98. International Journal for Numerical Methods in Engineering 6 418-444
[86] Charbel Farhat and Kristoffer G. van der Zee and Philippe Geuzaine. (2006) "Provably second-order time-accurate loosely-coupled solution algorithms for transient nonlinear computational aeroelasticity", Volume 195. Computer Methods in Applied Mechanics and Engineering 17 1973 - 2001
[87] P. Causin and J.F. Gerbeau and F. Nobile. (2005) "Added-mass effect in the design of partitioned algorithms for fluid-structure problems", Volume 194. Computer Methods in Applied Mechanics and Engineering 42 4506 - 4527
[88] Idelsohn, S. R. and Del Pin, F. and Rossi, R. and Oñate, E. (2009) "Fluid-structure interaction problems with strong added-mass effect", Volume 80. International Journal for Numerical Methods in Engineering 10 1261-1294
[89] Van Brummelen, Harald. (2009) "Added Mass Effects of Compressible and Incompressible Flows in Fluid-Structure Interaction", Volume 76. Journal of Applied Mechanics
[90] D.A. Knoll and D.E. Keyes. (2004) "Jacobian-free Newton-Krylov methods: a survey of approaches and applications", Volume 193. Journal of Computational Physics 2 357 - 397
[91] Minami, S. and Yoshimura, S. (2010) "Performance evaluation of nonlinear algorithms with line-search for partitioned coupling techniques for fluid–structure interactions", Volume 64. International Journal for Numerical Methods in Fluids 10–12 1129–1147
[92] Joris Degroote and Robby Haelterman and Sebastiaan Annerel and Peter Bruggeman and Jan Vierendeels. (2010) "Performance of partitioned procedures in fluid-structure interaction", Volume 88. Computers & Structures 7 446 - 457
[93] Joris Degroote and Klaus-Jürgen Bathe and Jan Vierendeels. (2009) "Performance of a new partitioned procedure versus a monolithic procedure in fluid-structure interaction", Volume 87. Computers & Structures 11 793 - 801
[94] Thomas Spenke and Norbert Hosters and Marek Behr. (2020) "A multi-vector interface quasi-Newton method with linear complexity for partitioned fluid-structure interaction", Volume 361. Computer Methods in Applied Mechanics and Engineering 112810
[95] Quarteroni, Alfio. (2017) "Navier-Stokes equations". Numerical Models for Differential Problems. Springer International Publishing 457–510
[96] Bruce M. DeBlois. (1997) "Linearizing convection terms in the Navier-Stokes equations", Volume 143. Computer Methods in Applied Mechanics and Engineering 3 289 - 297
[97] D. Boffi and F. Brezzi and M. Fortin. (2013) "Mixed Finite Element Methods and Applications". Springer
[98] Tobias Gelhard and Gert Lube and Maxim A. Olshanskii and Jan-Hendrik Starcke. (2005) "Stabilized finite element schemes with LBB-stable elements for incompressible flows", Volume 177. Journal of Computational and Applied Mathematics 2 243 - 267
[99] C.A. Felippa. (2001) "Introduction to finite element methods". University of Colorado, USA
[100] A.N. Brooks and T.J.R. Hughes. (1982) "Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations", Volume 32. Comput. Methods Appl. Mech. Engrg. 1 199 - 259
[101] T.J.R. Hughes and L.P. Franca and M. Balestra. (1986) "A new finite element formulation for computational fluid dynamics: V. Circumventing the babuska-brezzi condition: a stable Petrov-Galerkin formulation of the stokes problem accommodating equal-order interpolations", Volume 59. Computer Methods in Applied Mechanics and Engineering 1 85 - 99
[102] Thomas J.R. Hughes and Leopoldo P. Franca and Gregory M. Hulbert. (1989) "A new finite element formulation for computational fluid dynamics: VIII. The galerkin/least-squares method for advective-diffusive equations", Volume 73. Computer Methods in Applied Mechanics and Engineering 2 173 - 189
[103] J. Cotela and R. Rossi and E. Oñate. (2017) "A FIC-based stabilized finite element formulation for turbulent flows", Volume 315. Comput. Methods Appl. Mech. Engrg. 607 - 631
[104] T.J.R. Hughes. (1995) "Multiscale phenomena: Green's function, the dirichlet to Neumann formulation, subgrid scale models, bubbles and the origins of stabilized formulations", Volume 127. Comput. Methods Appl. Mech. Engrg. 1 387-401
[105] T.J.R. Hughes and G.R. Feijóo and L. Mazzei and J.B. Quincy. (1998) "The variational multiscale method-a paradigm for computational mechanics", Volume 166. Comput. Methods Appl. Mech. Engrg. 1 3-24
[106] R. Codina. (2001) "A stabilized finite element method for generalized stationary incompressible flows", Volume 190. Comput. Methods Appl. Mech. Engrg. 20 2681-2706
[107] R. Codina. (2002) "Stabilized finite element approximation of transient incompressible flows using orthogonal subscales", Volume 191. Computer Methods in Applied Mechanics and Engineering 39 4295 - 4321
[108] R. Codina and J. Principe and O. Guasch and S. Badia. (2007) "Time dependent subscales in the stabilized finite element approximation of incompressible flow problems", Volume 196. Computer Methods in Applied Mechanics and Engineering 21 2413 - 2430
[109] A. Meurer and C.P. Smith and M. Paprocki and O. Certík and S.B. Kirpichev and M. Rocklin and AMiT Kumar and S. Ivanov and J.K. Moore and S. Singh and T. Rathnayake and S. Vig and B.E. Granger and R.P. Muller and F. Bonazzi and H. Gupta and S. Vats and F. Johansson and F. Pedregosa and M.J. Curry and A.R. Terrel and S. Roucka and A. Saboo and I. Fernando and S. Kulal and R. Cimrman and A. Scopatz. (2017) "SymPy: symbolic computing in Python", Volume 3. PeerJ Computer Science e103
[110] O.C. Zienkiewicz and R.L. Taylor and P. Nithiarasu and J.Z. Zhu. (1977) "The finite element method", Volume 3. McGraw-hill London
[111] T.J. Chung. (1978) "Finite element analysis in fluid dynamics", Volume 78. NASA STI/Recon Technical Report A
[112] P.J. Roache. (2002) "Code verification by the method of manufactured solutions", Volume 124. J. Fluids Eng. 1 4–10
[113] K. Salari and P. Knupp. (2000) "Code Verification by the Method of Manufactured Solutions"
[114] R.F. Ausas and F.S. Sousa and G.C. Buscaglia. (2010) "An improved finite element space for discontinuous pressures", Volume 199. Comput. Methods Appl. Mech. Engrg. 1019-1031
[115] R.F. Ausas and F.S. Sousa and S.R. Idelsohn. (2011) "A statically condensable enrichment for pressure discontinuities in two-phase flows", Volume 30. Mecánica Computacional 4 175-191
[116] S.R. Idelsohn and J.M. Gimenez and N.M. Nigro. (2018) "Multifluid flows with weak and strong discontinuous interfaces using an elemental enriched space", Volume 86. International Journal for Numerical Methods in Fluids 12 750-769
[117] D. Baumgärtner and J. Wolf and R. Rossi and P. Dadvand and R. Wüchner. (2018) "A robust algorithm for implicit description of immersed geometries within a background mesh", Volume 5. Advanced Modeling and Simulation in Engineering Sciences 1 21
[118] Paula A. Rudenick and Bart H. Bijnens and David García-Dorado and Arturo Evangelista. (2013) "An in vitro phantom study on the influence of tear size and configuration on the hemodynamics of the lumina in chronic type B aortic dissections", Volume 57. Journal of Vascular Surgery 2 464 - 474.e5
[119] E. Soudah and P. Rudenick and M. Bordone and B. Bijnens and D. GarcÃa-Dorado and A. Evangelista and E. Oñate. (2015) "Validation of numerical flow simulations against in vitro phantom measurements in different type B aortic dissection scenarios", Volume 18. Taylor & Francis. Computer Methods in Biomechanics and Biomedical Engineering 8 805-815
[120] T.J.R. Hughes and J.A. Cottrell and Y. Bazilevs. (2005) "Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement", Volume 194. Computer Methods in Applied Mechanics and Engineering 39 4135 - 4195
[121] A. Coll. (2014) "Robust volume mesh generation for non-watertigh geometries". Universitat Politecnica de Catalunya
[122] Dapogny, Charles and Dobrzynski, Cécile and Frey, Pascal. (2014) "Three-dimensional adaptive domain remeshing, implicit domain meshing, and applications to free and moving boundary problems". Elsevier. Journal of Computational Physics
Document information
Published on 08/10/20
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?
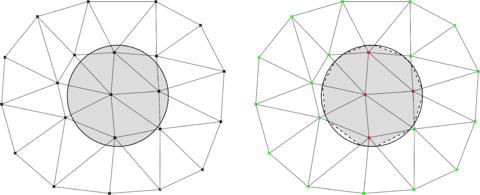
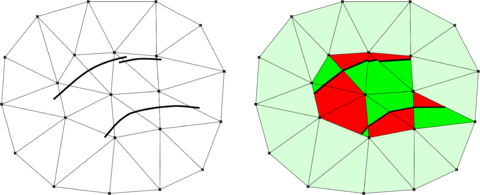
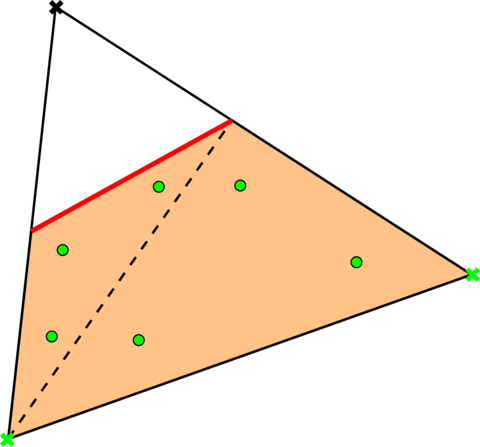
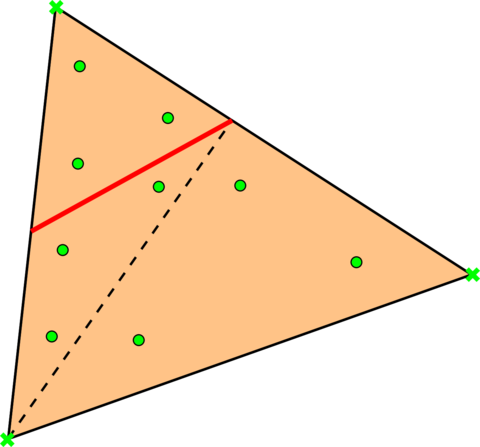
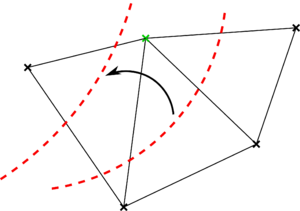






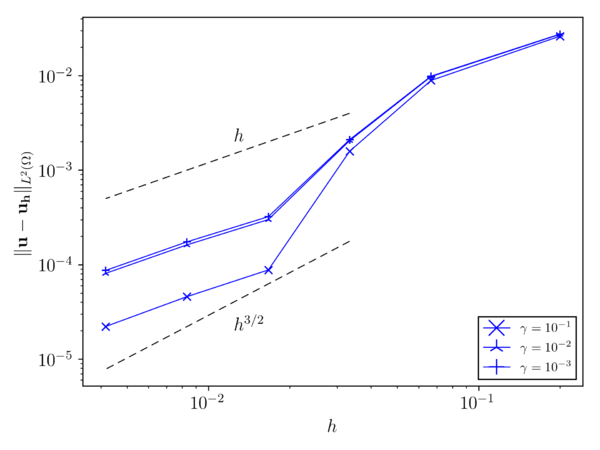
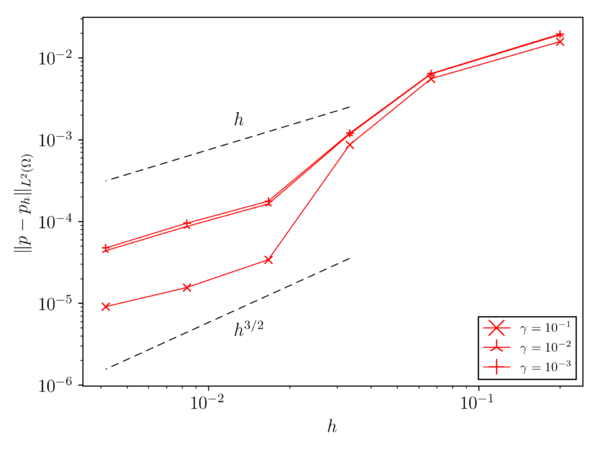
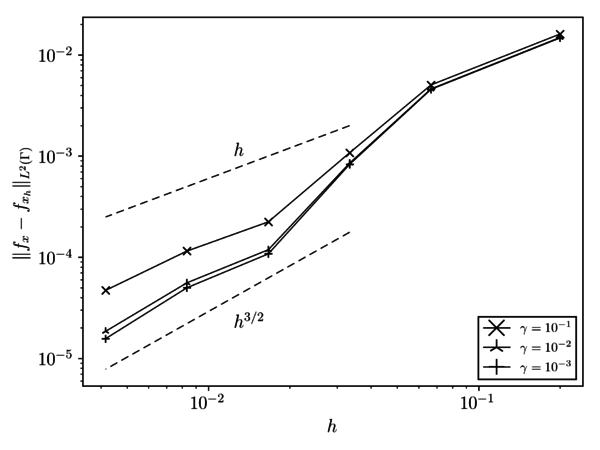
![by [m/s2].](/wd/images/thumb/8/86/Draft_Samper_633963255-test-cylinder_pseudocompressibility_body_force_y-0cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-test-cylinder_pseudocompressibility_body_force_y-0cm-0cm-0cm-0cm.png)
![by zoom [m/s2].](/wd/images/thumb/9/96/Draft_Samper_633963255-test-cylinder_pseudocompressibility_body_force_y_close-22_5cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-test-cylinder_pseudocompressibility_body_force_y_close-22_5cm-0cm-0cm-0cm.png)
![\lVert v\rVert [m/s].](/wd/images/thumb/b/b6/Draft_Samper_633963255-test-cylinder_pseudocompressibility_v-0cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-test-cylinder_pseudocompressibility_v-0cm-0cm-0cm-0cm.png)
![\lVert v\rVert zoom [m/s].](/wd/images/thumb/4/44/Draft_Samper_633963255-test-cylinder_pseudocompressibility_v_close-22_5cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-test-cylinder_pseudocompressibility_v_close-22_5cm-0cm-0cm-0cm.png)
![p [Pa].](/wd/images/thumb/0/0e/Draft_Samper_633963255-test-cylinder_pseudocompressibility_p-0cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-test-cylinder_pseudocompressibility_p-0cm-0cm-0cm-0cm.png)
![p zoom [Pa].](/wd/images/thumb/3/37/Draft_Samper_633963255-test-cylinder_pseudocompressibility_p_close-22_5cm-0cm-0cm-0cm.png/600px-Draft_Samper_633963255-test-cylinder_pseudocompressibility_p_close-22_5cm-0cm-0cm-0cm.png)