La simplificación en ingeniería, ventajas e inconvenientes.
Francisco Zárate a,b , Juan Jose Cuellar c Antonio Emmanuel Regalado d
aCentre Internacional de Mètodes Numèrics en Enginyeria (CIMNE) www.cimne.com
bUniversitat Politècnica de Catalunya (UPC),
Gran Capitan s/n, Campus Nord, 08034 Barcelona, España.
cCalidad Consultoría y Construcción S.A. de C.V.
Arco Iris 110 A, colonia Parque 38010 Celaya Guanajuato México
dFacultad de Ingeniería Civil de la Universidad de Guanajuato.
Av. Juárez No. 77; Zona Centro; C.P. 36000; Guanajuato, Gto.
zarate@cimne.upc.edu; juanjosecuellar@gmail.com; regaladogonzalez@gmail.com
Resumen
Siempre que se realiza una simplificación, se suele cometer un error asociado, la capacidad del ingeniero en cuantificar o poder compensar dicho error con coeficientes de seguridad u otros mecanismos permite adoptar dichas simplificaciones en la mayoría de las situaciones. Sin embargo, no en todos los casos es posible aplicar dichas simplificaciones en los cálculos. Los procedimientos y programas de cálculo son muy diferentes en ambos casos.
El presente trabajo muestra dos ejemplos de cálculo numérico asociado a una misma obra. Mientras que el primero tiene como finalidad el dimensionamiento y verificación de la capacidad estructural, el segundo pone de manifiesto la necesidad de considerar en detalle aspectos que han sido obviados o simplificados a fin de dar una respuesta adecuada. Los códigos usados son muy distintos, en el primer caso, es posible aplicar códigos comerciales, mientras que en el segundo es necesario usar programas diseñados para la investigación.
Keywords. Método de elementos discretos, Método de elementos finitos, Mecánica de fractura, Estrategia FEM-DEM
Introducción
El cálculo estructural siempre ha sido una herramienta de análisis que caracteriza a la ingeniera civil, y en muchos casos es una especialización del ingeniero. La aplicación más directa se centra en el dimensionamiento de los elementos estructurales de una obra, como puede ser el número y diámetro de los elementos de acero de refuerzo, las propiedades mecánicas del hormigón o las dimensiones de una columna. Sin embargo, cuando el cálculo estructural intenta describir de forma más precisa el comportamiento de la estructura para dar respuesta a las causas o consecuencias de dicho comportamiento, estamos ante lo que denomínanos el análisis estructural forense.
Los inicios del cálculo estructural se remontan a los trabajos de Galileo [1], seguido por autores como Bernoulli, Euler, Coulomb, etc. Quienes atacan problemas muy particulares que resuelven con nuevas herramientas matemáticas. Quizás no sea hasta el año de 1742 cuando por motivo de unas grietas aparecidas en la cúpula vaticana [2] se aplican los conceptos desarrollados hasta entonces sobre una simplificación del problema, es decir sobre un modelo abstracto y que daría origen al análisis estructural forense.
El éxito de este análisis conduce a establecer las bases de los métodos de cálculo dando pie al análisis del dimensionamiento estructural mediante obras como la “Mecánica Analítica" de Lagrange [3], los métodos de rigidez y flexibilidad [4] y las ecuaciones de campo de la elasticidad [5] propuestas por Navier, así como el planteamiento riguroso de la elasticidad desarrollado por Cauchy [6]. Mucho camino hubo que recorrer hasta que el cálculo de estructuras se base en el principio de los trabajos virtuales propuesto por Mohr [7] o los métodos energéticos desarrollados por Castigliano [8].
La introducción de las ecuaciones diferenciales en derivadas parciales, análisis funcional y métodos proyectivos de aproximación desarrollados por Ritz [9] y popularizado por Timoshenko [10] sientan las bases de los actuales métodos de cálculo fundamentados en la resolución de dichas ecuaciones utilizando el principio variacional de los trabajos virtuales tales como los volúmenes finitos o elementos finitos [11,12,13]. La introducción del ordenador en la ingeniería sustituye a los engorrosos métodos energéticos para el cálculo estructural y permite popularizar las nuevas metodologías de resolución de ecuaciones diferenciales.
Análisis estructural dimensional
La finalidad del análisis estructural dimensional es la de proporcionar de manera eficiente en tiempo y costo la cantidad y tamaño de los distintos elementos que conforman una estructura. A fin de que el tiempo invertido en el análisis sea aceptable se requiere que se realicen una serie de simplificaciones sobre las características de la estructura, los materiales utilizados y el tipo de solicitaciones a las que se encuentra sujeta.
Sin embargo, el mal uso o abuso de estas simplificaciones puede llegar a comprometer los resultados, subestimado la capacidad resistente y por ello encareciendo la obra, o bien sobreestimando dicha capacidad, lo que puede provocar el colapso estructural.
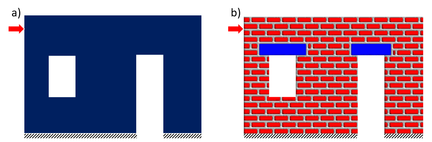
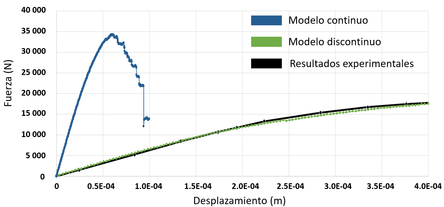
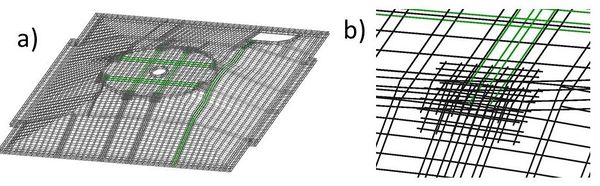
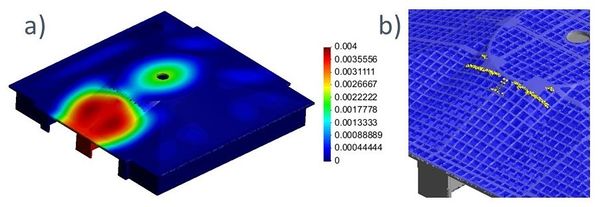
Un ejemplo muy obvio podría ser el considerar que todo el material a utilizar es homogéneo y de propiedades constantes. Nada más fuera de la realidad, sin embargo, esta simplificación permite reducir las variables y los procedimientos de cálculo para evaluar la capacidad resistente de una estructura. En este sentido la Figura 1a muestra una pared homogénea considerando propiedades de un mortero en obra, la Figura 1b representa la misma pared, formada por tabiques, mortero y cerramientos de hormigón. La carga aplicada a dicha pared corresponde a una fuerza de cortante horizontal a nivel de azotea. Sin entrar en más detalles de dimensionamiento o propiedades del material, la Figura 2 muestra los resultados de fuerza aplicada contra el desplazamiento horizontal máximo obtenidos en ambos casos.
Es claro que el resultado es muy diferente, aunque solo se trate de un ejemplo extremo para poner de manifiesto que una mala simplificación puede conducir a errores considerables.
Por lo general este tipo de errores no suelen cometerse en la mayoría de los análisis, sin embargo, la diferencia entre el resultado obtenido y el real puede ser importante. Es aquí donde entran en juego las normativas de cálculo pues podemos diversificar su objetivo en dos aspectos. El primero unificar los procesos de cálculo de manera que el análisis sea lo más homogéneo en las diversas áreas de cálculo y en segundo lugar establecer algoritmos y variables de calculo que minimicen el efecto del error acumulado por las distintas simplificaciones de cálculo, al igual que garantizar un dimensionamiento estructural sobrestimado a fin de soportar acciones no consideradas. Es decir, de proveer a las estructuras con un coeficiente de seguridad que absorba errores de cálculo y cargas no cuantificadas correctamente.
Por ejemplificar, las normas técnicas complementarias para diseño y construcción de estructuras metálicas de la ciudad de México [20] propone considerar el área neta de barras sujetas a tracción considerando que los agujeros para pernos o tornillos sea 1.5 mm mayor que el diámetro nominal del agujero; lo que claramente reduce el área real de la sección resistente.
Muchos de los códigos comerciales enfocados para este tipo de análisis llevan incorporados las normativas de diseño correspondientes de manera que simplifican la labor del diseño. En el caso particular de este trabajo se ha utilizado el código SAP2000 [21].
Análisis estructural forense
En ocasiones es necesario evaluar el comportamiento estructural de una obra de forma más minuciosa y precisa. Las simplificaciones en este caso, deben ser las mínimas pues el resultado se puede ver comprometido. Es el caso del análisis estructural forense, donde se busca el comportamiento estructural de la manera más real posible. El mercado para este tipo de estudios suele ser el peritaje judicial, estudios de rehabilitación estructural o bien el diseño y actualización del conjunto de normativas de evaluación estructural.
Los diseños geométricos utilizados en este tipo de análisis suelen ser exhaustivos y minuciosos lo que lleva a un gran consumo de horas por parte de los delineantes. En cuanto a los modelos numéricos para la caracterización de los materiales en general son no lineales y se definen en régimen plástico o de daño, si se trata de metales o de materiales frágiles.
Es obvio que los códigos utilizados, principalmente basados en elementos finitos, contemplan una serie de características que no están presentes en los códigos comerciales, pues el objetivo es tratar de reproducir la física completa del problema, que, en muchos casos, no solo pasa por un estudio de resistencia de materiales sino también puede incluir efectos térmicos, magnéticos o aerodinámicos acoplados. Adicionalmente, se hace uso omiso de cualquier normativa de construcción pues como se ha mencionado, estas sirven para minimizar los errores que se inducen por las simplificaciones de cálculo.
Al ser capaces de modelar tal cantidad de fenómenos físicos, la velocidad de cálculo se reduce, llegando a tomar varias horas o días incluso, de manera que el uso de ordenadores paralelos y de gran capacidad pueden llegar a ser usados.
El tipo de resultados obtenidos suele indicar zonas de daño, de fisuración, cargas ultimas, o capacidad resistente ultima, deformaciones extremas e incluso el colapso estructural.
Ejemplos
En este apartado se muestran dos ejemplos del análisis estructural de una misma obra, el primer análisis corresponde al dimensionamiento estructural utilizando el código comercial SAP2000 [21], mientras que el segundo corresponde a un análisis forense para determinar el efecto causado por un asentamiento diferencial de la estructura mediante la ayuda del programa FEM2DEM_3D de investigación [22].
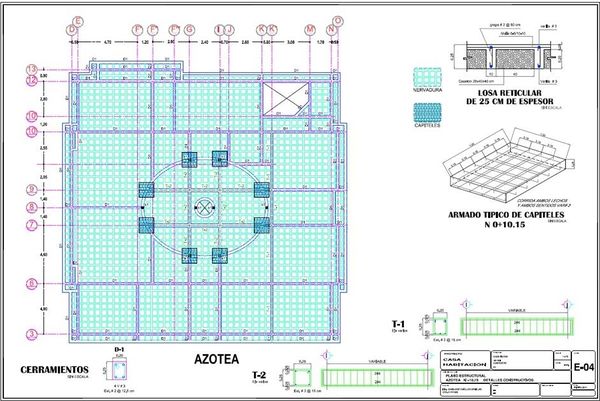
La obra en cuestión corresponde al techo de una casa habitación realizada mediante un forjado reticular. El uso de forjados reticulares como elementos estructurales está ampliamente consensuado y permite construir geometrías arquitectónicas más libres. La planta de la obra es un cuadrado de 22m de lado con una superficie plana ovalada en el centro y los lados en parteaguas con un desnivel de 2m. En la Figura 1 se muestra la planta estructural en donde se puede observar claramente la armadura de acero. Básicamente se trata de un forjado reticular de 0.25m de espesor con una capa de compresión de 0.05m y casetones de 0.40 × 0.40 × 0.20m. A lo largo de las nervaduras se colocan varillas de acero del No. 3 (ϕ = 0.0095m).
Adicionalmente existe una serie de cerramientos (D1) y vigas (T1 y T2) así como cuatro capiteles de columna. Los cerramientos tienen una sección de 0.25 × 0.20m armados con 4 varillas de acero del No. 3. Las vigas T1 y T2 tienen un espesor de 0.25m y un ancho de 0.20m para la viga T1 y de 0.25m para la viga T2. Ambas están armadas con 4 varillas de acero del No. 4 (ϕ = 0.0127m). Finalmente, el armado de los capiteles se realiza con varillas del No. 3 @ 0.15m en ambos lechos y en ambas direcciones. La Figura 2 a) muestra el armado de toda la losa, así como un detalle del armado de los capiteles en la Figura 2 b).
Las propiedades del hormigón son. = 21 × 109 Pa, = 0.20, = 24 × 103 N/m3, = 20 MPa, = 2 MPa y G = 100 × 10-3 J/m2.
Las cargas consideradas son el peso propio de la estructura, las cargas muertas 1620 N/m2 y las cargas vivas 400 N/m2. Dichos valores consideran el peso del plafón, las instalaciones y acabados finales, sin considerar cargas de nieve o viento.
Análisis estructural dimensional: Losa reticular
El modelo geométrico utilizado para este análisis corresponde a una estructura bidimensional en el espacio analizada en el paquete de cómputo denominado SAP2000 [21], el cual satisface lo dispuesto en los reglamentos vigentes en México, permitiendo realizar análisis tridimensionales estáticos y dinámicos.
En el análisis de la superestructura se utilizó el método de elementos finitos, tanto para los marcos formados como para las superficies de las losas definidas por elementos de placa, mediante el programa SAP2000 [21]. Las trabes y vigas se analizaron elásticamente, formando marcos tridimensionales, mediante el método matricial también contenido en el código mencionado. Estas simplificaciones en el proceso de cálculo adolecen más a la capacidad de cómputo y a una reducción en el tiempo de cálculo.
Debido a dichas hipótesis de análisis es necesario garantizar la estabilidad de la estructura mediante coeficientes de seguridad según las especificaciones aplicables en el reglamento del ACI-318-14 [23], el manual de diseño de obras civiles de la C.F.E. [24,25]. Igualmente se considera la mayoración de las solicitaciones a la estructura. En particular éste es el caso se han considerado las solicitaciones como la combinación más desfavorable de cargas vivas, muertas, e instantáneas de acuerdo con las Normas técnicas complementarias del D.F. [20].La Figura 2 muestra la distribución de cargas sobre el lucernario de la losa de azotea aplicadas en el modelo implementado en SAP2000.
Otro ejemplo de simplificación realizada en el cálculo corresponde al diseño sísmico, todas las losas han sido consideradas como diafragmas rígidos para el desplazamiento sísmico modal. Se revisaron también con el auxilio de hojas de cálculo. Es importante señalar que las trabes de grandes claros y las trabes en voladizo, se revisaron por deflexiones según lo indicado en el reglamento de Construcciones para el Distrito Federal y su respectiva Norma Técnica Complementaria [20].
Es obvio que la ocurrencia de la combinación de cargas utilizadas es altamente improbable, sin embargo, el diseñar con estas consideraciones ayudan a minimizar las simplificaciones de cálculo consideradas, tanto en análisis estático como dinámico.
No hay que perder de vista que el objetivo del análisis corresponde a verificar la capacidad resistente de los elementos estructurales, considerando las especificaciones aplicables en el reglamento del ACI-318-14 [23], el Manual de diseño de obras civiles de la C.F.E. [24,25] y las Normas técnicas complementarias del D.F. [20].
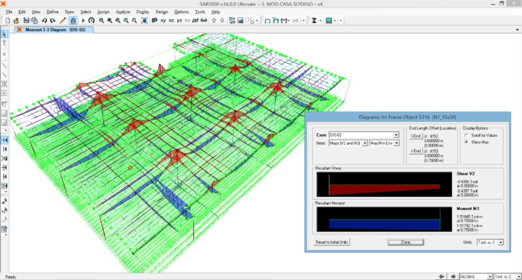
La Figura 3 muestra en paso en el proceso de verificación estructural, donde se revisan los momentos flectores sobre las vigas y trabes de la estructura. Una vez verificadas las capacidades resistentes de los elementos estructurales sus dimensiones quedan reflejadas en el plano estructural (Figura 1) a fin de ser construidas en obra.
El resultado de éste análisis se ve reflejado directamente en la memoria de cálculo.
Análisis estructural forense: Losa reticular
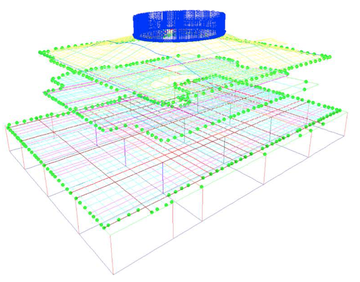
El éxito de este análisis recae en reducir al máximo las simplificaciones de cálculo ya que su objetivo es reproducir de la manera más fiable el comportamiento estructural ante una solicitación muy concreta. Es por ello que el modelo geométrico utilizado para este análisis es lo más apegado a la geometría estructural real. En la Figura 4 se muestra la manera que se han modelado la losa reticular, las vigas el armado de acero, obviando los estribos (simplificación que provoca un mínimo error en los resultados).
Las propiedades del material corresponden a las descritas previamente, utilizando un modelo de daño lineal basado en una superficie de daño de Mohr Coulomb para materiales frágiles en el caso del hormigón y de materiales dúctiles para el acero. A diferencia del análisis anterior, este hecho trata de reproducir fielmente el comportamiento del material.
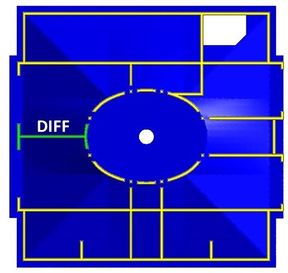
El objetivo es determinar el efecto provocado en la estructura debido a un asentamiento diferencial de 0.0035 m de los puntos de la base del muro como se indica en la Figura 5.
La placa se encuentra apoyada sobre los muros mostrados en la Figura 5. A efectos del análisis dichos muros se consideran lo suficientemente rígidos y empotrados en su base.
En particular este análisis permite observar la formación de grietas que puedan comprometer la estabilidad o funcionalidad de la estructura.
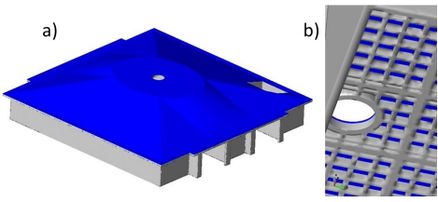
El problema se ha resuelto utilizando una malla de 1,369,192 tetraedros y 368,969 nodos. Por otra parte, se han definido 5,084 elementos lineales para representar las varillas de acero. La Figura 6 a) representa el conjunto del forjado y muros a analizar mientras que la Figura 6 b) corresponde a un detalle cercano al lucernario donde se aprecian las nervaduras de la placa, así como algunas de las vigas T2.
la Figura 7 a) muestra los resultados del desplazamiento de la estructura después de que el asentamiento diferencial de la base sea de 0.0035 m. En la Figura 7 b) se aprecia un corte muy definido en la cubierta superior. Se observa que el desgarro en la cubierta es perpendicular a la dirección del muro, poniendo de manifiesto la gran rigidez que tiene la cubierta superior.
En la Figura 8 a) se puede apreciar la deformada de la estructura vista desde abajo. Es interesante observar que el lucernario sufre los desplazamientos máximos, incluso mayores a los que sufre el muro sujeto al asentamiento diferencial. La Figura 8 b) muestra una vista inferior de la losa donde se aprecia el daño producido en la unión del muro con ésta.
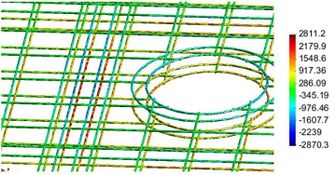
En la Figura 9 se observan los esfuerzos axiales sobre los elementos de acero pertenecientes a la viga T2 en la zona cercana al lucernario. En esta figura se puede observar los elementos en tracción y compresión debido a gran flexión a la que está sujeta esta parte de la estructura.
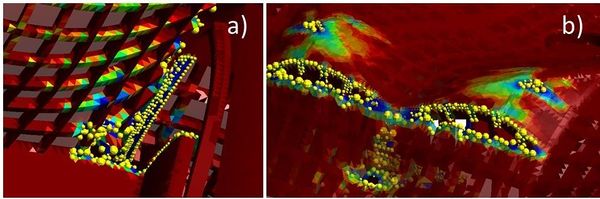
La Figura 10 muestra las zonas dañadas de la estructura utilizando una visualización de la estructura deformada con un factor de escala de 5000. El recuadro a) muestra una vista inferior de la losa en donde se puede observar la separación entre el muro y la losa, mientras que el recuadro b) muestra una vista superior mostrando el desgarro de la cubierta. En vista de los resultados obtenidos es claramente notorio la gran rigidez que posee la losa
Resulta claro que los resultados obtenidos no pueden ser previstos con el análisis dimensional, por lo que ha sido necesario reducir al mínimo las simplificaciones de cálculo en beneficio de la calidad de los resultados. En contrapartida el esfuerzo computacional es muy elevado.
Conclusiones
El objetivo de este trabajo es el de poner de manifiesto el uso adecuado de hipótesis simplificativas en los procesos de cálculo computacional, aunque su aplicación resulta obvia en este trabajo, no siempre lo es así. Por lo que el buen criterio del calculista debe optar por ciertas simplificaciones en aras de una adecuada respuesta de diseño. Por otra parte, el considerar un análisis más realista permite conocer adecuadamente la respuesta estructural, ya sea de forma preventiva o resolutiva. Igualmente, este tipo de análisis permite verificar la idoneidad de las normas y simplificaciones en el proceso de diseño.
Referencias
[l] G. Galilei: ´´Diálogo y demostración matemática sobre dos nuevas ciencias". 1638. Traducción al español de Editora Nacional. 1976
[2] H. Straub: ´´A history of civil engineering". Leonard Hill Ltd. 1960
[3] J. L. Lagrange: "Mecanique Analytique". 1788. Reimpresión A. Blanchard 1965
[4] C. L. MH. Navier: "Resumé des lec;ons donnees á l'Ecóle des Ponts et Chaussées". Carilian-Goeury 1826
[5] C. L. M. H. Navier: "Memoire sur les lois d'equilibre et du mouvement des corps solides elastiques". Bull. Soc. Philomath. 1821
[6] A. L. Cauchy: "Exercises de Mathematiques". 1827
[7] O. Mohr: "Beitrag sur Theorie des Bogenfachwerks". Zeitsh. Des Arch. Und Ing. zu Hannover 1874.
[8] C. A. P. Castigliano: "Theorie de 1 "équilibre des systémes élastiques et ses applications". Negro 1879
[9] W. Ritz: "Über e in e neue Methode ... ". Zeitsch. Reine und Angew. Mathem. 1909
[10] S. P. Timoshenko: "Einige Stabiliüitsprobleme der Elastizitatstheorie". Zeitch. Mathem. und Phys. 1910
[11] Courant, R. 1943. Variational methods for the solution of problems of equilibrium and vibrations. Bulletin of the American Mathematical Society 49, l-23.
[12] Courant, R. 1960. Remarks about the Rayleigh-Ritz Method. In Boundary problems in differential equations, R. Lanqer, ed., pp. 273-277. Madison: Univ. of Wisconsin Press. Courant, R., & Hilbert D. 1924. Methoden der mathematisch
[13] Zienkiewicz & Cheung; The Finite Element Method in Structural and Continuum Mechanics”, 1967
[14] SAP2000
[15] Zárate, F. & Oñate, E. A simple FEM–DEM technique for fracture prediction in materials and structures. Comp. Part. Mech. (2015) 2: 301-314. https://doi.org/10.1007/s40571-015-0067-2
[16] Zárate, F., Cornejo, A. & Oñate, E. A three-dimensional FEM–DEM technique for predicting the evolution of fracture in geomaterials and concrete, Comp. Part. Mech. (2017). https://doi.org/10.1007/s40571-017-0178-z
[17] Oñate E., Zárate F., Celigueta M.A., González J.M., Miquel J., Carbonell J.M., Arrufat F., Latorre S., Santasusana M., Advances in the DEM and Coupled DEM and FEM Techniques in Non Linear Solid Mechanics. In: Oñate E., Peric D., de Souza Neto E., Chiumenti M. (eds) Advances in Computational Plasticity. Computational Methods in Applied Sciences, vol 46. Springer, Cham (2018)
[18] González, J.M., Zárate, F. & Oñate, E. Pulse fracture simulation in shale rock reservoirs: DEM and FEM–DEM approaches. Comp. Part. Mech. (2017). https://doi.org/10.1007/s40571-017-0174-3
[19] Zárate, F., Gonzalez, J.M., Miquel J., Lohner, R., Oñate, E., A coupled FEM-DEM procedure for predicting blasting operations in tunnels. Papers Repository of the International Centre for Numerical Methods in Engineering (CIMNE) (2017)
[20] Secretaria de Obras y Servicio, Normas tecnicas complementarias para diseño y construccion de estructuras metalicas. Gaceta Oficial del Distrito Federal, No 300 Tomo IX (1995)
[21] Wilson E., Habibullah A., Sap 2000 Integrated Finite Element Analysis and Design of Structures Basic Analysis Refence Manual, Computers and Structures, 1998, Berkeley,USA
[22] Zarate, F. FEM2DEM 3D, Finite-Discrete element code, CIMNE (2017) Barcelona.
[23] Requisitos del reglamento para concreto estructural ACI 218-14, (2014) American Concrete Institute. USA.
[24] Manual de diseño de obras civiles, Diseño por sismo. (2008) Comisión Federal de Electricidad. México D.F.
[25] Manual de diseño de obras civiles, Diseño por viento. (2008) Comisión Federal de Electricidad. México D.F.
Document information
Published on 01/10/18
Submitted on 13/09/18
Volume 2, 2018
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?