Regional Allocation of CO2 Intensity Reduction Targets Based on Cluster Analysis

Abstract

To meet China’s CO₂ intensity target of 40%–45% reduction by 2020 based on the 2005 level, a regional allocation method based on cluster analysis is developed. Thirty Chinese provinces are classified into six groups based on economy, emissions, and reduction potential indicators. Under the equity principle, the two most developed groups are assigned the highest reduction targets (55% and 65%, respectively). However, their reduction potential is limited. Under the efficiency principle, the two groups with the highest reduction potential take the highest targets (48% and 61%, respectively), but their economy is relatively backward. When equity and efficiency are equally weighted, the 5th group with a prominent reduction potential takes the highest target (54%), and the 2nd and the 3rd groups with large industry scales take the second highest target (49%). However, under all the three allocation schemes, the targets are not greater than 40% for the 4th and the 6th groups, which have a relatively low economic ability, emissions, and reduction potential. Due to inconsistency between economic and reduction potential, corresponding market mechanisms and policy instruments should be established to ensure equity and efficiency of regional target allocation.

Keywords

CO2 intensity reduction targets allocation ; cluster analysis ; regional difference

1. Introduction

In late 2009, the Chinese Government announced its voluntary CO₂ emissions reduction target: reducing its CO₂ emissions per capita GDP, which is also called CO₂ intensity, by 40%–45% by 2020 based on the 2005 level [ CGOWP , 2010 ]. According to the fulfillment of China’s energy intensity target during the 11th Five-Year Plan, this national CO₂ intensity target will also be allocated to each province. However, there is still no officially published allocation plan.

This issue has been discussed by several researches [ Yi et al ., 2011  ;  Zhang et al ., 2011 ], which set different reduction targets for each province respectively according to regional differences. However, in practice, this highly differential policy may lead to high transaction and implementation costs, and low feasibility. In fact, in the 12th Five-Year Plan both the official regional allocation of the energy intensity target [ SC , 2011 ] and the preliminary allocation of the CO₂ intensity target [ 21CW, 2011 ] take a two-step procedure: they group the provinces into different clusters at first and then assign reduction targets to each cluster. In the allocation plan of the energy intensity target the 31 provinces are divided into 5 clusters, whose reduction targets form 5 levels ranging from 10% to 18%. For the allocation of the CO₂ intensity target, the 31 provinces are divided into 7 clusters, whose reduction targets form 7 levels ranging from 10% to 20%. Therefore, this two-step procedure is applied in this study.

This paper adopts the cluster analysis in multivariate statistical analysis to group the provinces into clusters based on regional similarities in economic, emissions, and reduction potential. Then CO₂ intensity targets are assigned to each cluster according to the equity or efficiency principle, and allocation results and policy implications are also discussed. This allocation method emphasizes the major differences between regional clusters while it ignores the minor differences within each cluster. Compared with existing researches [ Yi et al ., 2011  ;  Zhang et al ., 2011 ], this study adopts the similar two-step procedure with the allocation policy of energy and CO₂ intensity targets in the 12th Five-Year Plan, therefore the results in this paper will be more in accordance with the policy demand.

2. Data and methodology

2.1. Indicator selection and cluster analysis method

Allocation principles in CO₂ emissions reduction efforts are often based on economic ability, emissions levels and reduction potential [ Yi et al ., 2011  ;  Zhang et al ., 2011 ]. In this study, seven indicators are selected to reflect regional differences in these three aspects (Table 1 ). For the economic ability, the per capita GDP and industrial added value are selected to reflect the overall economic level and the industrial scale, respectively. Regional emissions levels can be evaluated by per capita or total emissions criteria. The present situation of CO₂ emissions in China is that per capita emissions and total emissions are spatially mismatched to some degree: some developed provinces (Shanghai, Tianjin, etc.) have high per capita emissions but low total emissions; yet some provinces with large economies and population (Guangdong, Henan, etc.) have high total emissions yet low per capita emissions. Therefore, we use the per capita CO₂ emissions and additionally the accumulated total CO₂ emissions to give a comprehensive evaluation of regional emissions levels. As for the CO₂ reduction potential, the share of industry in total GDP and the share of energy intensive sectors in the industry are selected to reflect the structural reduction potential of the overall economy and industry, respectively. The energy consumption per unit of industrial added value is used to reflect the technical reduction potential. It is worth noting that aside from structural adjustment and technical progress, the improvement in the structure of energy consumption through the development of renewable energy can also contribute to the CO₂ emissions reduction. However, on the one hand, the utilization potential of renewable energy in each province should be evaluated from multiple aspects, including the resource endowments, technical feasibility, costs and benefits, and so on. Thus, the results may vary with different methods and aspects in the evaluating process. There is also no officially published statistics on renewable energy potential. On the other hand, the main use of renewable energy is by on-grid power generation, which can reduce CO₂ emissions for all provinces covered by the power grid. So, it is more meaningful to consider the utilization potential of renewable energy at grid or national level. Therefore, based on the reasoning from these two aspects, this study doesn’t include renewable energy potential within reduction potential indicators, but is mainly based on officially published and widely recognized statistics.

Table 1. Indicators for cluster analysis

Interpretation	Indicator
Economic ability	Per capita GDP Industrial added value
Emissions level	Per capita CO2 emissions Accumulated total CO2 emissions
Reduction potential	Share of industry in GDP Share of energy intensive sectors in industrya Energy consumption per unit of industrial added value

a. This share is in terms of added value. Fifteen energy intensive sectors with the highest energy consumption per unit of industrial added value are selected based on the NBSC [2007]

Based on the seven indicators above, the cluster analysis as a multi-variate statistical analysis is applied to group the similar provinces into clusters. Cluster analysis methods fall into two categories: hierarchical cluster methods and non-hierarchical cluster methods. Following suggestions from related researches [ Punj and Stewart, 1983 ; Soares et al ., 2003  ;  del Campo et al ., 2008 ], this study adopts a two-step procedure: the hierarchical cluster method is first employed to establish the proper number of clusters, then the cluster centroids from the first step are used as the initial condition of a non-hierarchical cluster method, which helps to fine-tune the results from the hierarchical cluster method.

For the first step of hierarchical cluster analysis, the method of Ward [1963] is selected because it outperforms other hierarchical cluster methods when outliers are absent [ Punj and Stewart, 1983 ]. Some researches on regional cluster analysis also suggest that Ward’s method gives the best interpretative solution [ Soares et al ., 2003  ;  del Campo et al ., 2008 ]. In Ward’s method, the union of two clusters occurs when it results in minimum information loss, which is measured by an increase in error sum of squares (S). If there are n clusters, and S_k is the error sum of squares for the kth cluster, then:

$S_{k}=\sum _{i=1}^{n_{k}}\left(x_{i}-{\overline {x}}_{k}\right){'}\left(x_{i}-\right.$$\left.{\overline {x}}_{k}\right){\mbox{,}}$

( 1)

where n_k is the number of provinces in the fcth cluster, x_i   is a column vector comprising the seven indicators of ith province, ${\textstyle {\overline {x}}_{k}}$ is the centroid of the k   th cluster (averages of provinces within this cluster). Total error sum of squares is defined as: ${\textstyle S=\sum _{j=1}^{n}S_{j}}$ . In each step, every possible fusion of two clusters is considered, and the pair of clusters which lead to the least increase in S will be united.

In the second step, the number and centroids of clusters generated from Ward’s method are used as initial conditions for the K-means non-hierarchical method [ Lloyd, 1982 ]. The procedure is as follows: 1) definition of k initial cluster centroids; 2) an observation is assigned to the nearest cluster, followed by a recalculation of the new cluster centroid; 3) repeating step 2 until the results remain unchanged.

2.2. Allocation method

Here, G_i is defined as the reduction target for the ith cluster of province, G_i is computed as follows:

$G_{i}=a\times W_{i}{\mbox{,}}$

( 2)

where a is an adjustment coefficient (a > 0); and W_i (0 < W_i < 1) is the weight for the i th cluster. The relationship between provincial and national CO₂ intensity is calculated as follows:

$I_{20}=\sum _{i=1}{\frac {Y_{i,20}}{Y_{20}}}\times I_{i,20}{\mbox{,}}$

( 3)

where I_{i ,20} and I₂₀ are the CO₂ intensities of the ith cluster and of the whole nation in 2020, respectively. Y_{i ,20} and Y₂₀ are the GDP of the ith cluster and of the whole nation in 2020, respectively.

In Eq. (3) the CO₂ intensity of the ith cluster and of the whole nation in 2020 can be computed from their respective values in 2005 and the reduction targets (this study is based on the 45% national CO₂ intensity reduction target):

$I_{05}\times \left(1-45\%\right)=\sum _{i=1}{\frac {Y_{i,20}}{Y_{20}}}\times I_{i,05}\times \left(1-\right.$$\left.a\times W_{i}\right){\mbox{.}}$

( 4)

This equation indicates that the GDP of the nation and each province should be forecasted first in order to determine the value of a . Then the reduction targets (G_i ) of each cluster can be computed from Eq.  (2) .

Finally, W_i determines the relative value of the reduction target of each cluster, and is calculated as follows:

$W_{i}=\sum _{j=1}^{7}{\alpha }_{j}\times {\frac {X_{i,j}}{X_{j,max}}}{\mbox{,}}$

( 5)

where, X_{j max} (j = 1,2,…,7) represents the maximum value of the j th indicator in all regions; X_i,j (j = 1,2,…,7) represents the mean value of the jth indicator for the ith cluster; α_j   is the weight for each indicator, which approves ${\textstyle \sum _{j=1}^{7}{\alpha }_{j}=1}$ . The value of α_j is based on different allocation principles, which are described in the following section.

2.3. Allocation principles

Equity and efficiency are two important principles in reduction effort sharing [ Marklund and Samakovlis, 2007 ]. The equity principle can be defined from at least two aspects. First, from the aspect of economic ability, the developed regions should take greater burdens in intensity reduction; and second, from the polluter pays view, regions with higher emissions should take greater reduction burdens [ Yi et al., 2011 ]. The efficiency principle aims to minimize the mitigation costs. The mitigation costs are usually lower in regions with greater reduction potential [ Zhang et al., 2011 ].

Following the above definitions of the two principles, we designed two allocation schemes according to equity and efficiency, respectively, and also employed a third comprehensive allocation scheme in which equity and efficiency are weighed equally. Under the equity principle, the weights are averagely assigned to the four indicators related to economic ability and emissions level, i.e., the weight for each indicator is 1/4. Under the efficiency principle, the weights are averagely assigned to the 3 indicators related to the reduction potential, i.e., the weight for each indicator is 1/3. Under the comprehensive allocation scheme, the weight for each of the first 4 indicators in Table 1 is 1/8, which sum up to 1/2; the weight for each of the last 3 indicators in Table 1 is 1/6, which also sum up to 1/2, which means that equity and efficiency are equally weighted. Here we should notice that different choice of weights will directly affect the reduction targets of each cluster. However, there exists no clear guidance for determining those weights, and in related researches these weights are assigned in a relatively simplified and direct way [ Yi et al ., 2011  ;  Ringius et al ., 1998 ]. In addition, this study mainly focuses on the discussion of the reduction targets allocation method based on regional clusters, which will give possible allocation results under the equity and efficiency principles, respectively according to the weights set above. However, because the reduction targets are closely related to the benefits of each region, how to assign the weights of each indicator should be decided through consultations of the decision makers and regional governments.

2.4. Data source and processing

The base year of China’s CO₂ intensity reduction target is 2005, but CO₂ emissions data is not available in any Chinese official sources. Thus, we first need to compute the CO₂ intensity of the whole nation and each province in 2005. Following the IPCC guidelines [ IPCC, 2006 ], national and provincial CO₂ emissions from energy consumption are calculated by Eq. (6) , using the energy balance table in NBSC [2007]  :

$E_{{CO}_{2}}=\sum _{i}A_{i}\times e_{i}\times c_{i}\times o_{i}\times {\frac {44}{12}}{\mbox{,}}$

( 6)

where A_j represents the consumption of fuel i (in t or m³ ), e_i represents the net heat value of fuel i (in kJ (kg)^–1 or kJ m^–3 ), c_i is the carbon emission factor of fuel i (in kg C (GJ)^–1 ), o_i is the carbon oxidation rate of fuel i . Here, 16 types of fossil fuels within the energy balance table are included ( Table 2 ). The net heat values (e_i ) are obtained from the NBSC [2007] . Carbon emissions factors and carbon oxidation rates are obtained from the IPCC [2006] . The carbon oxidation rates of different fuels are set to the default value 1. The fuel consumption A_i is calculated as follows:

$A_{i}=F_{i}+P_{i}+H_{i}-N_{i}{\mbox{,}}$

( 7)

Table 2. Coefficients of various fossil fuels

Fuel type	Net heat value ei		Carbon emissions factor ci (kg C (GJ)–1 )
	Unit	Value
Raw coal	kJ (kg)–1	20,908	25.8
Cleaned coal	kJ (kg)–1	26,344	25.8
Other washed coal	kJ (kg)–1	8,363	25.8
Briquettes	kJ (kg)–1	20,700	26.6
Coke	kJ (kg)–1	28,435	29.2
Coke oven gas	kJ m–3	17,350	12.1
Crude oil	kJ (kg)–1	41,816	20.0
Gasoline	kJ (kg)–1	43,070	18.9
Kerosene	kJ (kg)–1	43,070	19.5
Diesel oil	kJ (kg)–1	42,652	20.2
Fuel oil	kJ (kg)–1	41,816	21.1
LPG	kJ (kg)–1	50,179	17.2
Refinery gas	kJ (kg)-1	46,055	15.7
Natural gas	kJ m–3	38,931	15.3
Other coking products	kJ (kg)–1	40,200	20.0
Other petroleum products	kJ (kg)–1	33,453	22.0

where, F_i is the final consumption of fuel i , P_i and H_i are the energy inputs for the generation of electricity and heat respectively ^① , and N₁ is the energy consumption of fuel i for non-energy use in industry.

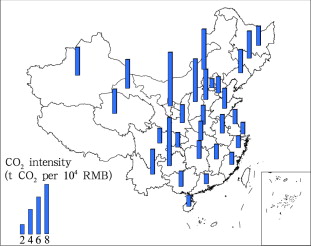
Because data of Tibet is not available, this study only includes 30 provinces (excluding Tibet). Following the above method, the national CO₂ intensity in 2005 is calculated as 3.19 t CO₂ per 10,000 RMB (GDP is based on a constant price since 2005). According to the 45% reduction target, the national CO₂ intensity in 2020 should not be greater than 1.75 t CO₂ per 10,000 RMB. The CO₂ intensity of each province in 2005 is shown in Figure 1 .

Figure 1. Provincial CO2 intensity in 2005

The per capita GDP, the industrial added value, and the energy consumption per unit of industrial added value are based on constant prices of 2005. The accumulated total CO₂ emissions are the sum of the emissions from 2005 to 2009, which can reflect the recent trends in CO₂ emissions for each province. As mentioned above, we need to forecast the GDP of each province. The predicted growth rates according to the 12th Five-Year Plan of each province are used as the average growth rates from 2010 to 2020 (Table 3 ).

Table 3. Projections of annual average growth rates of provincial GDP from 2010 to 2020

Province	GDP growth rate (%)
Beijing	8.0
Tianjin	12.0
Hebei	9.0
Shanxi	13.0
Inner Mongolia	12.0
Liaoning	11.0
Jilin	12.0
Heilongjiang	12.0
Shanghai	8.0
Jiangsu	10.0
Zhejiang	8.0
Anhui	10.0
Fujian	10.0
Jiangxi	11.0
Shandong	9.0
Henan	9.0
Hubei	10.0
Hunan	10.0
Guangdong	8.0
Guangxi	10.0
Hainan	13.0
Chongqing	12.5
Sichuan	12.0
Guizhou	12.0
Yunnan	10.0
Shaanxi	12.0
Gansu	12.0
Qinghai	12.0
Ningxia	12.0
Xinjiang	10.0

3. Results and discussion

3.1. Cluster analysis

In order to eliminate the effects of different scales, the cluster analysis is carried out with standardized variables. First, the dendrogram from Ward’s method (Fig. 2 ) indicates that provinces can be grouped into 4 or 6 clusters. However, in the 4 clusters solution the number of provinces in each cluster is greatly unbalanced, i.e., the lowermost branch in Figure 2 contains 17 provinces. Therefore, we chose to group the provinces into 6 clusters at a distance slightly less than 5. Then, the centroids of the 6 clusters will be used as initial condition for the K -means method, where we still get the same result, which confirms that the result from Ward’s method is reasonable. Table 4 shows the result of the cluster analysis, and Table 5 lists the centroids of each cluster, i.e., the mean values of the indicators in each cluster.

Figure 2. Dendrogram from Ward’s method

Table 4. Results of the cluster analysis

Cluster	Number of province	Provinces included
1	3	Beijing, Tianjin, Shanghai
2	4	Shandong, Zhejiang, Guangdong, Jiangsu
3	3	Henan, Hebei, Liaoning
4	5	Heilongjiang, Shaanxi, Fujian, Xinjiang, Jilin
5	3	Ningxia, Inner Mongolia, Shanxi
6	12	Qinghai, Guizhou, Gansu, Hainan, Yunnan, Chongqing, Guangxi, Jiangxi, Hubei, Sichuan, Hunan, Anhui

Table 5. Mean values of indicators at the cluster centroids

Indicator	Cluster 1	Cluster 2	Cluster 3	Cluster 4	Cluster 5	Cluster 6	National average
Per capita GDP (RMB per person)	44,234	24,199	15,037	13,887	13,022	9,173	14,040
Industrial added value (100 million RMB)	2,574	8,934	4,350	1,884	1,275	1,305	2,481
Per capita CO2 emissions (t CO2 per person)	8.6	5.3	5.9	4.6	9.4	2.9	4.5
Accumulated total CO2 emissions (100 million t CO2 )	7.0	23.9	22.4	8.3	13.2	7.3	11.8
Share of industry in GDP (%)	40	49	45	42	42	33	42
Share of energy intensive sectors in industry (%)	33	32	55	27	76	51	40
Energy consumption per unit of industrial added value (t ce per 10,000 RMB)	1.38	1.60	3.85	2.53	7.09	3.59	2.59

Notes: Apart from accumulated total CO₂ emissions, other data are from the base year 2005. Italics represent values above the national average

Clusters 1 and 2 are regions with a developed economy but with low reduction potential. Cluster 1 includes three municipalities, i.e., Beijing, Shanghai, and Tianjin, and represents the most advanced level of economy, with its per capita GDP over 40,000 RMB, which is much higher than the other five clusters. This high level of living standard also leads to high per capita emissions. However, its economic structure and energy efficiency are relatively optimal, indicating a low reduction potential. Cluster 2 includes four provinces, which are featured by large scale industry and high total CO₂ emissions aside from their developed economies. The total industrial value of these four provinces amounts to 42% of the whole nation in 2005, and their average industrial added value is nearly 900 billion RMB. As a result, the accumulated total CO₂ emissions of this cluster are the highest, because the CO₂ here is mainly generated from industry. In terms of reduction potential, the technical reduction potential of cluster 2 is relatively low since its energy efficiency is close to that of cluster 1; while its high share of industry in the GDP suggests that further decreases in CO₂ intensity can be exploited by accelerating the development of the tertiary industry.

Clusters 3 and 4 are around the national average in terms of their economic level. Provinces in cluster 3 should put their main focus on energy saving and CO₂ reduction due to their high total emissions and significant reduction potential. Three provinces with large industries included in cluster 3 have similar accumulated total emissions with cluster 2, but their economic structure and technical level are much inferior compared to cluster 2. Therefore, there is high reduction potential. Five provinces are included in cluster 4. Their share of industry and energy consumption per unit of industrial added value are near the national average, thus cluster 4 has a moderate reduction potential.

Provinces in cluster 5 and 6 are mainly located in central and western China. They share common features of relatively backward economies and high reduction potential. In cluster 5, Shanxi and Inner Mongolia are rich in coal reserves, resulting in a high ratio of energy intensive sectors and a highly unbalanced industry structure. In addition, due to its relatively low economic and technical level, cluster 5 also has much higher energy consumption per unit of industrial added value than the other clusters. In cluster 6, the majority of provinces belongs to the most undeveloped regions. Their emissions and industry scale are relatively small. However, regions in this cluster are undergoing a rapid industrial process. Thus their energy consumption and CO₂ emissions still have a large increasing potential with the expanding of economy.

3.2. Allocation results and mitigation policies

The allocation results from the equity, efficiency, and comprehensive schemes are shown in Table 6 . According to the equity principle, cluster 1 and 2 with the most developed economies and high emissions levels take the major role in CO₂ reduction, with their reduction targets being 55% and 65%, respectively. The next is cluster 3 with its reduction target being 50%. For the provinces in cluster 1 and 2, since their industrial structure and technical level are already optimal, a further decrease in CO₂ intensity can be achieved by emphasizing the development of high-tech industry and modern service industry, accelerating the innovation of energy saving technology, and promoting the exploitation and utilization of renewable energy, thus reducing the reliance on importing energy. However, these two clusters’ regions have relatively low reduction potential, which leads to significant mitigation costs within these regions. Under the equity principle, a market trading system should be established to allow developed regions achieving their reduction targets in regions with low mitigation costs in order to reduce the overall mitigation costs. Under the three allocation schemes, the reduction target of cluster 3 changes slightly, ranging from 48% to 50%. Provinces in this cluster have large scale industries and high reduction potential. They should strengthen the retrofitting of traditional industry and improve positions in industry chains in order to narrow the gap with cluster 1 and 2.

Table 6. Allocation results of the CO₂ intensity reduction target (%)

Cluster	Equity principle	Efficiency principle	Comprehensive scheme
1	55	32	42
2	65	37	49
3	50	48	49
4	29	35	32
5	43	61	54
6	20	40	32

Under the efficiency principle, cluster 5 has the highest reduction target of 61%, followed by clusters 3 and 6, whose reduction targets are 48% and 40%, respectively. The unique coal reserves of the provinces in cluster 5 are among the main reasons for their heavy industry structure and low energy efficiency. These regions should take measures to lower the ratio of energy intensive industry, to reduce their dependence on coal resources, and to promote the innovation of clean coal technology. Provinces in cluster 6 have undergone a rapid development since the implementation of national strategies like the Central Region Growing Up [ SC , 2012 ] and the Western Region Development [ SC, 2004 ], but the traditional industrial path of high energy consumption, heavy pollution and low output [ NDRC, 2007 ] should be avoided. These regions need to develop a high energy efficient industry, and selectively accept the transfer of high-tech industry from the eastern provinces. In addition, based on local situations, these provinces can develop renewable energy to improve their energy structure, like hydroelectricity in Hubei and Chongqing, and wind and solar power in northwestern China. However, we should note that even though provinces of these clusters have high reduction potentials and low mitigation costs, their economies are also relatively undeveloped. Therefore, high reduction targets for them may risk damaging their economic development and widening the gap between rich and poor regions. Accordingly, under the efficiency principle, a well designed policy for financial aid and transfer payment is needed, and the cooperation between eastern and central-western provinces should be strengthened to help undeveloped regions to adjust their economic structure and to improve their technologies.

Focusing on the comprehensive allocation scheme, cluster 5 with a prominently structural and technical reduction potential has the highest reduction target (54%). Clusters 2 and 3, with large scales of industry and emissions, have the second highest reduction targets (49%). Due to the economic ability, emissions level and reduction potential of clusters 4 and 6 are all under the national average level, with the economy of cluster 6 as the most undeveloped, the reduction targets of these two clusters are only 32%. This allocation scheme considers the integration of regional differences in economic ability, emissions level, and reduction potential.

4. Conclusions

In this study, the CO₂ intensity reduction targets are allocated based on a cluster analysis. Seven indicators are selected to comprehensively reflect regional differences in economic ability, emissions level, and reduction potential. By using a cluster analysis, the 30 provinces are divided into six clusters: the first two clusters have developed economies and low reduction potential; clusters 3, 5 and 6 have high reduction potential, but their economies are around or below the national average.

Under the equity principle, the most developed clusters 1 and 2 take the major burden in CO₂ reduction, with their reduction targets reaching 55% and 65%, respectively. However, the mitigation costs inside these two clusters are high, therefore a market trading system should be established to reduce overall mitigation costs. Under the efficiency principle, clusters 3 and 5, with significant reduction potential, take the major burden in CO₂ reduction, with their reduction targets being 48% and 61%, respectively. However, these high targets may lead undeveloped provinces to undertake heavy economic restructuring, thus policy inclination and financial aid for these provinces should be strengthened. By weighing equity and efficiency equally, the comprehensive allocation scheme gives a comprehensive consideration of regional differences in multiple aspects. Under this scheme, cluster 5, with prominently technical and structural reduction potential, and clusters 2 and 3, with large scale of industry, take the major burden in CO₂ reduction, with their reduction targets being 54%, 49%, and 49%, respectively. The different allocation results under the three schemes mainly originate from the fact that provincial economic ability and reduction potential are spatially mismatched. This fact determines that equity and efficiency can not be achieved simultaneously by the allocation of regional targets alone. Corresponding market mechanisms and policy instruments should be established to optimize the overall mitigation cost and at the same time provide enough development space especially for the developing regions.

Acknowledgements

This study is supported by the Natural Science Foundation (No. 71273153) and National Key Technology Research and Development Program (No. 2009BAC62B01). The authors appreciate the helpful suggestions and comments of anonymous reviewers and the editors.

References

1. 21CW, 2011 21CW (21st Century Website), 2011[2011-09-19]: Preliminary allocation plan of CO₂ intensity target in 12th Five-Year Plan set: Guangdong ranks first with 20% (in Chinese). Accessed http://www.21cbh.com/HTML/2011-4-19/zNMDAwMDIzMzMzNg.html .
2. CGOWP, 2010 CGOWP (Chinese Government’s Official Web Portal), 2010[2012-10-28]: China will reduce its CO₂ emissions per GDP by 40% to 45% (in Chinese). Accessed http://www.gov.cn/wszb/zhibo409/content_1712489.htm .
3. del Campo et al., 2008 C. del Campo, C. Monteiro, J.O. Soares; The European regional policy and the socioeconomic diversity of European regions: A multivariate analysis; European Journal of Operational Research, 187 (2) (2008), pp. 600–612
4. IPCC, 2006 IPCC; IPCC guidelines for national greenhouse gas inventories, Tokyo IGES (2006), pp. 18–24
5. Lloyd, 1982 S.P. Lloyd; Least squares quantization in PCM; IEEE Transactions on Information Theory, 28 (2) (1982), pp. 129–137
6. Marklund and Samakovlis, 2007 P.O. Marklund, E. Samakovlis; What is driving the EU burden-sharing agreement: Efficiency or equity?; Journal of Environmental Management, 85 (2) (2007), pp. 317–329
7. Meng et al., 2011 L. Meng, J.E. Guo, J. Chai, et al.; China’s regional CO₂ emissions: Characteristics, inter-regional transfer and emission reduction policies  ; Energy Policy, 39 (10) (2011), pp. 6136–6144
8. NBSC (National Bureau of Statistics of China), 2007 NBSC (National Bureau of Statistics of China); China Energy Statistical Year Book 2006 (in Chinese), China Statistics Press (2007), pp. 122–238
9. NDRC, 2007 NDRC (National Development and Reform Commission), 2007[2012-10-28]: Pollution reduction is becoming the reinforced constraints and will be accelerating soon (in Chinese). Accessed http://www.ndrc.gov.cn/mtbd/t20070306_119955.htm .
10. Punj and Stewart, 1983 G. Punj, D.W. Stewart; Cluster analysis in marketing research: Review and suggestions for application; Journal of Marketing Research, 20 (2) (1983), pp. 134–148
11. Ringius et al., 1998 L. Ringius, A. Torvanger, B. Holtsmark; Can multi-criteria rules fairly distribute climate burdens? OECD results from three burden sharing rules; Energy Policy, 26 (10) (1998), pp. 777–793
12. SC, 2004 SC (State Council), 2004[2012-10-28]: Guidelines on deepening the western region development (in Chinese). Accessed http://www.gov.cn/gongbao/content/2004/content_62726.htm
13. SC, 2011 SC (State Council), 2011[2011-10-12]: Synergy operational schemes of saving energy and reducing pollution in 12th Five-Year Plan (in Chinese). Accessed http://www.gov.cn/zwgk/2011-09/07/content_1941731.htm .
14. SC, 2012 SC (State Council), 2012[2012-10-28]: Guidelines on promoting the central region growing up (in Chinese). Accessed http://www.gov.cn/gongbao/content/2012/content_2218027.htm .
15. Soares et al., 2003 J.O. Soares, M.M.L. Marques, C.M.F. Monteiro; A multivariate methodology to uncover regional disparities: A contribution to improve European Union and governmental decisions; European Journal of Operational Research, 145 (1) (2003), pp. 121–135
16. Ward, 1963 J.H. Ward; Hierarchical grouping to optimize an objective function; Journal of the American Statistical Association, 58 (301) (1963), pp. 236–244
17. Yang et al., 2011 G. Yang, Z.-H. Tang, H.-X. Shi, et al.; Regional differences of carbon dioxide emission in China and emission-reduction policy recommendations; Advances in Climate Change Research (in Chinese), 7 (1) (2011), pp. 35–40
18. Yi et al., 2011 W.-J. Yi, L.-L. Zou, J. Guo, et al.; How can China reach its CO₂ intensity reduction targets by 2020? A regional allocation based on equity and development  ; Energy Policy, 39 (5) (2011), pp. 2407–2415
19. Zhang et al., 2011 Y.-X. Zhang, J.-F. Li, T.-T. Feng; Research on provincial allocation method of China’s CO₂ intensity reduction in 2020  ; Money China (in Chinese), 2 (2011), pp. 36–40

Notes

①. This means that the CO₂ emissions from heat and power generation are attributed to the production side, which is in line with the majority of recent studies [ Meng et al., 2011  ; Yang et al., 2011 ]