Bayesian estimation of seismic hazards in Iran

Abstract

Seismic hazard assessment is a basic tool for rational planning and designing in areas of different seismic activity. The Bayesian probability estimation was applied in this study to assess seismic hazard. The estimation procedure provides a posterior probability distribution that integrates prior estimates based on the knowledge of the process, and the likelihood of occurrence based on historical data. The Bayesian approach was applied to calculate the probability that a certain cut-off magnitude would be exceeded at certain time intervals in different regions of Iran. The results for the cut-off magnitude of 6.5 indicate that the highest probability of seismic hazard exists in the Alborz, Kopeh-Dagh, Bandar-Abas, Kerman, and Zagros regions. The seismic hazard is lowest for the Esfahan–Sirgan region, the Arabian Platform, the Persian Gulf, and Kavir in Central Iran. The comparison between the Bayesian results and the seismotectonic models of Iran reveals that it is possible to partition the spatially distributed epicenters of earthquake events into different regions. In general, these regional divisions agree with previously proposed seismotectonic provinces of Iran.

Keywords

Bayesian approach ; Prior estimates ; Seismic hazard ; Seismotectonic province ; Iran

1. Introduction

Iran is one of the most seismically active areas in the world. However, the spatial distribution and magnitude of earthquake events in different regions of the Iranian Plateau are not similar. This is primarily a result of Iran’s position in a 1000 km wide zone of compression between the colliding Eurasian and Arabian continents  [1] and its location between the Arabian Plate in the south and southwest and the Indian Plate in the east. Iran does not appear to be a single crustal block, and shortening is thought to be concentrated in the three main active belts of Zagros, Kopeh-Dagh–Alborz–Talesh, and Central Iran (CI) and the Dasht-e-Lut Basin  [2] .

Seismic analyses and the study of seismotectonic structure in Iran have been conducted in several previous studies  [3] , [4] , [5] , [6] , [7] , [8] , [9]  and [10] . The Iranian Plateau is one of the most seismically active areas of the world and frequently suffers destructive and catastrophic earthquakes that cause great loss of human life and widespread damage. In Iran, a destructive earthquake occurs every few years because it is situated over a seismic zone. Many destructive earthquakes in the last century confirm the high seismicity of Iran: Silakhor (${\textstyle M_{s}=7.4}$ , 1909), Kopeh-Dagh (${\textstyle M_{s}=7.3}$ , 1929), Salmas (${\textstyle M_{s}=7.4}$ , 1930), Pasni (${\textstyle M_{s}=7.3}$ , 1947), Mazandaran (${\textstyle M_{s}=7.4}$ , 1957), Sahne (${\textstyle M_{s}=7.2}$ , 1957), Buyin Zahra (${\textstyle M_{s}=7.2}$ , 1962), Dasht-e-Bayaz (${\textstyle M_{s}=7.4}$ , 1968), Fars (${\textstyle M_{s}=7.2}$ , 1972), Tabas (${\textstyle M_{s}=7.7}$ , 1978), Kerman (${\textstyle M_{s}=7.3}$ , 1981), Rudbar–Manjil (${\textstyle M_{s}=7.2}$ , 1990), and Birjand–Qayen (${\textstyle M_{s}=7.3}$ , 1997). In the past three decades, only the Tabas earthquake of 1978, the Rudbar–Manjil earthquake of 1990, and the Bam earthquake of 2003 caused nearly 100,000 deaths  [11] . The sources of all of these seismic events correspond to active reverse or strike-slip faults mainly concentrated in the south and north-west of Iran and eastern Iran.

Bozorgnia and Mohajer-Ashjai  [12] studied the estimated Peak Ground Acceleration (PGA) in major cities of Iran to determine various annual hazards. Nowroozi and Ahmadi  [7] estimated that the provinces that are located southwest of the Zagros Thrust and northeast of the Arabian landmass are the most likely to produce earthquakes with magnitude of six in less than a decade. However, the northern and northeastern provinces are each capable of producing an earthquake with a magnitude of 7.5 per century. The seismic hazard is lowest for Esfahan–Sirgan, the Arabian Platform, the Persian Gulf, Kavir in CI, and the Arvand–Shatt-Al-Arab (ASAA) provinces. The highest seismic hazard exists for Alborz, Kopeh-Dagh (KD), Ferdows, and Fars provinces. Ahmadi et al.  [9] concluded that almost all the regions of Iran, with the exception of Esfahan–Sirjan, CI, and the ASAA region, have a high level of hazard for producing earthquakes with large PGA.

Tavakoli and Ghafory-Ashtiany  [10] developed a seismic hazard map of Iran based on probabilistic seismic hazard computation. They estimated the contour levels of the PGA map range from 0.15 to 0.48 g for a return period of 475 years. The maximum mean acceleration was expected in the vicinity of Tabriz, Tehran and Dasht-e-Bayaz, and the smallest accelerations were expected in two regions of a narrow band, trending NW–SE and extending from Urumiyeh to Esfahan, and the other in the Central Lut zone in Eastern Iran. Mirzaei et al.  [8]  and [13] suggested a maximum possible magnitude of no less than ${\textstyle M_{s}=7.8}$ in the different regions of Iran.

After an important seismic event, decisions are often required irrespective of the state of completeness and quality of information. In seismic hazard computations the uncertainties of the basic input data are considered by making alternative interpretations where significant uncertainties exist  [14] . Therefore, decisions may be taken under conditions of large uncertainty. Bayesian probability theory provides a rigorous means of combining prior information on seismic activity with historical observations of earthquake occurrences. Such information may be used to supplement seismic datasets when they are incomplete, inaccurate or cover too short a period of time  [15] .

By considering the seismic activity of Iran, the effects of earthquakes on human lives and the national economy, it seems reasonable to pay attention to the seismic hazard in a seismogenic area of Iran. In the present study, a time-independent Bayesian method was applied to different zones of Iran to estimate seismic hazard and the probability that certain cut-off magnitudes would be exceeded over specific time intervals. The usefulness of the results in similar regions with similar or different seismological characteristics (i.e., seismotectonic provinces) was assessed.

2. Tectonic and geological background

At the longitude of CI, the overall Arabian–Eurasia convergence is moving roughly N–S at ∼25–35 mm yr⁻¹   [2] . Uncertainty in this direction and rate exist because of ambiguities in the interpretation of seafloor spreading data from the Red Sea and Gulf of Aden  [16] , and because of the poorly determined motion of Arabia with GPS coverage. Since the Arabian–Eurasia Euler pole lies in the Mediterranean region, the convergence rate increases with longitude, with values about 5–10 mm yr⁻¹ higher in eastern Iran than in the west. Shortening is thought to be concentrated in the three main active belts of the Zagros, Kopeh-Dagh–Alborz–Talesh and Central Caspian Sea, with large areas of CI, the Dasht-e-Lut and the South Caspian Basin being relatively flat, aseismic, and un-deformed  [2] .

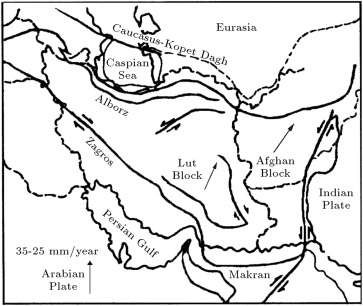
The low elevation and apparent lack of seismicity in the Dasht-e-Lut suggest that the Lut Block is a relatively rigid block within this distributed deforming zone. Some of the roughly N–S right-lateral shear between CI and Afghanistan, which is effectively part of stable Eurasia, occurs on the long N–S strike-slip faults of Sistan near the Iran–Afghan border  [17] . However, some shear is also taken up on right-lateral faults striking N–S to NNW–SSE on the western side of the Lut Block. The data from GPS studies and preliminary results suggest that the Zagros accounts for one-third to one-half of the total Arabia–Eurasia convergence  [18] . The remaining convergence that is taken up within central and northern Iran will require ∼20 mm yr⁻¹ of strike-slip to be accommodated in the faults on either side of the Lut Block  [19] . The Central Iranian Block is being compressed between two plates of greater rigidity, and it is characterized by coherent plate motion with low-level internal deformation of less than 2 mm yr⁻¹   [20] . This block is bordered by the Zagros folded belt in the southwest, the Alborz Mountains in the north, the KD Mountains in the northeast, and several strike-slip faults in the east (Figure 1 ). Several earthquakes are associated with surface faulting in this region. The Central Iranian Block is characterized by discontinuous seismic activity with shallow, large magnitude earthquakes, with apparent long recurrence periods  [17] .

Figure 1. Active tectonic features of Iran demonstrate how the northward motion of the Arabia plate relative to Eurasia is absorbed in Iran.

The Zagros Mountain belt of western Iran is a result of the collision of the Arabian and CI continental blocks (Figure 1 ). At the surface, the Zagros Mountains consist of long, linear, asymmetrical folds that form a 200–300 km wide series of ranges extending about 1200 km from eastern Turkey to the Straits of Hormuz  [21] . Seismicity in the Zagros belt is restricted to the region between the main Zagros Thrust and the Persian Gulf. Most of the larger earthquakes occur on high-angle reverse planes that strike parallel to the trend of the fold axes  [22] . Strong earthquakes are thought to occur on blind active thrust faults that do not reach the surface  [5] . Furthermore, seismicity in the Zagros Belt is restricted to the region between the main Zagros Thrust and the Persian Gulf  [21] . Most of the larger earthquakes occur on high-angle reverse planes striking parallel to the trend of the fold axes  [22] .

The Alborz is a stack of thrust sheets, produced by late Cenozoic compressional deformation  [23] . Exposed thrusts with the greatest throw generally occur in the south of the Alborz. Prominent left-lateral strike-slip faults occur along the length of the Alborz, trending parallel to the thrusts and folds in each region. Structures at both the eastern and western ends of the Alborz change in strike to pass into adjacent fold and thrust belts: the Talesh in the west and the KD in the east  [24] . In the KD, crustal shortening has been taking place in a belt of up to 200–300 km wide as a result of compressional motion of the CI Block against the stable plates of Turkemenistan and Afghanistan. Several active faults affect the Central Alborz[25]  and [26] . Most are parallel to the range and accommodate the present day oblique convergence across the mountain belt. To the north, the Khazar and North Alborz reverse faults dip southward with a slight component of left lateral strike slip motion  [26] .

3. Seismicity and seismogenic sources

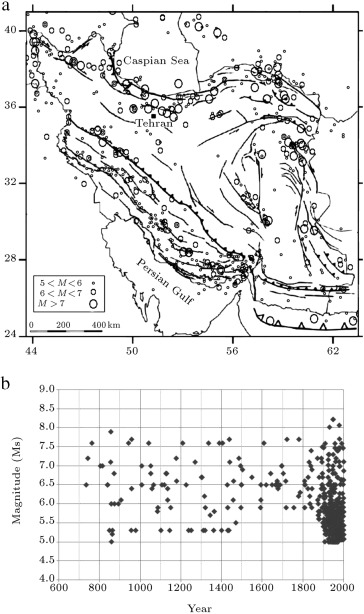
Seismic assessment at the study site rely mainly on the catalogue of earthquakes and potential seismic sources that are compiled from available references containing historical and instrumental events. The seismic catalogue of Iran can be divided into historical (pre-1900) and instrumental (post-1900) components. The comprehensive study of Ambraseys  [27] and other subsequent studies  [25] , [28] , [29]  and [30] noted the destructive historical earthquakes in Iran. Historical earthquakes had ascribed magnitudes that were computed based on a simple linear relationship between intensities and magnitudes  [31] . Early (pre-1964) and recent (post-1964) instrumentally recorded events were collected from Moinfar et al.,  [31] and the global seismological networks  [32] . Many relocation analyses were performed on the instrumental component of the catalogue[1] , [2] , [3] , [4] , [33]  and [34] . Historical magnitude inaccuracies are approximately 0.3–0.5 units  [28]  and [29] , and instrumental magnitude errors are usually considered to be less than 0.3 units  [35] . The final collective catalogue in this study was prepared by eliminating aftershocks, foreshocks  [36]  and [37] and incorrectly reported events from the data. The cleaned and updated catalogue contained earthquake magnitudes given in several scales. The moment magnitude (${\textstyle M_{w}}$ ) and the surface-wave magnitude (${\textstyle M_{s}}$ ) scales are the most reliable and important scales for earthquake magnitude  [38] . However, there are few earthquakes in Iran that have been measured by ${\textstyle M_{w}}$ , and this scale has not been used to determine their magnitudes. Thus, body-wave magnitude (mb) and Richter local-magnitude scales were converted to ${\textstyle M_{s}}$ , according to the relationships proposed by  [39] . The uncertainty of epicenter locations for historical events, early and recent instrumental earthquakes, was assumed to be 20 km, 10 km and 5 km, respectively  [1]  and [5] .

Figure 2 (a) shows the epicenter location of historical and instrumental events with main major faults for Iran, spanning the area between ${\textstyle 24{\mbox{°}}N}$ to ${\textstyle 40{\mbox{°}}N}$ and ${\textstyle 44{\mbox{°}}E}$ to ${\textstyle 61{\mbox{°}}E}$ . Figure 2 (b) shows the available data for earthquakes in Iran with ${\textstyle M_{s}\geq 5.0}$ after the removal of aftershock and foreshock earthquakes. In summary, the database used in this study in the prior estimation contains 140 historical and 495 instrumental events. For studies of seismology and hazard analyses, it is essential to divide the Iranian plateau into different regions with similar seismological characteristics. These regions are called seismotectonic provinces. The seismotectonic structure of Iran had been studied previously. Stocklin  [40] , Takin  [41] , Berberian  [42] and Mirzaei et al.  [13] suggested simplified gross provinces, with a small number of divisions consisting of only nine, four, nine and five regions, respectively. More elaborate divisions, consisting of 23 and 20 seismotectonic provinces, were suggested by Nowroozi  [4] and Tavakoli and Ghafory-Ashtiany  [10] . Identification of the boundaries in these investigations is the drawback of these methods. Zamani and Heshami  [43] and Ansari et al.  [44] provided hierarchical clustering of the geophysical and geological information of Iran, and obtained different results with different tectonic zoning maps. The shortcoming of this approach is that the seismic catalogue is not complete, and it is very difficult to construct a complete model based on incomplete data.

Figure 2. (a) The epicenter location of historical and instrumental events with major faults. (b) The data with ${\textstyle M_{s}\geq 5.0}$ available from Iran after the removal of the aftershock and foreshock earthquakes.

4. The applied method

To estimate probability measures to various possible outcomes is necessary when calculating the probability of an event. The assignment can be based on prior conditions, the results of empirical observations, or both. It is normally preferable to estimate uncertainty by using an adequate number of reliable observations. However, in many situations, there are not enough available data. In this regard, the validity of the a priori basis for calculating probability depends on the reasonableness of the underlying assumptions, whereas the empirical relative frequency basis relies on a large amount of observational data. When data are limited, the relative frequency may have limited usefulness on its own. However, the probability concept can still be used by combining observed data and judgment. The Bayesian approach can be used for this judgment. In this approach, the parameters are considered to be random variables. This allows for the systematic combination of subjective judgment based on intuition and indirect information with observed data to obtain a balanced estimate. The estimate can also be updated as more information becomes available.

When the observed data are limited, as it is often the case in seismicity studies, the statistical estimates should be supplemented with judgmental information. By the classical statistical approach, there is no provision for combining judgmental information with observational data when estimating parameters  [45] . Bayesian probability theory is consistent with the fundamental probability, and its most important aspect is that it allows for the updating of current probabilities when new information becomes available. This aspect is very useful when historical data are incomplete or cover a short period of time that is insufficient to define secular rates of seismicity. Benjamin  [46] was the first to apply the Bayesian updating for investigating earthquake occurrence when using a Poisson model. The Bayesian updating has since been applied to many earthquake engineering problems  [15] , [47] , [48] , [49] , [50] , [51]  and [52] . If the number of earthquakes occurring within a specified period of time, ${\textstyle t}$ , is equal to n, and the distribution follows a Poisson model with the mean rate of earthquake occurrences, ${\textstyle v}$ , the probability distribution is given by the expression:

$P(N=n\vert v,t)=(v\cdot t)^{n}e^{-v\cdot t}/n!\quad {\mbox{for  }}n=0,1,2,\ldots {\mbox{.}}$

( 1)

The Bayesian updating  [53] , which includes both inherent (aleatory) and statistical (epistemic) uncertainty, is expressed as:

$Pr(N=n\vert t)=\int _{0}^{\infty }P(N=n\vert v,t)f^{''}(v)dv{\mbox{,}}$

( 2)

where ${\textstyle f^{''}(v)}$ represents the posterior probability density. This function is updated from the previous distribution of the mean rate of earthquake occurrences. Cornell  [47] and Campbell  [15] showed that the uncertainty in the mean rate of earthquake occurrences (${\textstyle v}$ ) may be represented by a gamma distribution with parameters ${\textstyle n^{''}}$ and ${\textstyle t^{''}}$ , which are unknown parameters. The parameters ${\textstyle n^{''}}$ and ${\textstyle t^{''}}$ represent updated values of the number of earthquakes and the time period of observation, respectively. Campbell  [15] computed these parameters as:

$n^{''}=n_{0}+({\bar {v}}^{'}/\sigma _{v}^{'})^{2}{\mbox{,}}$

( 3a)

where ${\textstyle n_{0}}$ is the number of earthquakes observed within a time period of ${\textstyle t_{0}}$ years, and ${\textstyle v^{'}}$ and ${\textstyle \sigma _{v}^{'}}$ represent the prior estimates of the mean and standard deviation of the mean rate of earthquake occurrence. Esteva  [54] suggested that statistical estimates of seismicity from large geotectonically similar regions could be used as prior estimates of ${\textstyle v}$ for the region of interest. Lomnitz  [55] used the historical record of major earthquakes in Chile to establish an estimate of the mean rate of occurrence for these rare events. In the proposed model by Shedlock et al.  [56] and Campbell  [15] , the prior evaluation of seismicity was obtained using seismotectonic data based on relationships between the seismic moment, slip rate, earthquake recurrence rate and magnitude that Stavrakakis and Drakoploulos  [49] used for the seismotectonic relationships.

Eq. (2) can be evaluated by a weighted average of all possible Poisson probability functions that are associated with different values of ${\textstyle v}$ . By calculating the marginal Bayesian distribution of ${\textstyle n}$ events, the probability of exceeding a lower bound magnitude, ${\textstyle M_{bound}}$ , which is the probability of at least one event of ${\textstyle M\geq M_{bound}}$ occurring in the next ${\textstyle t}$ years, is:

${\tilde {P}}(0,t)=1-Pr(N=0\vert n^{''},t^{''},t)=1-({\frac {t^{''}}{t+t^{''}}})^{n^{''}}{\mbox{.}}$

( 4)

Once the uncertainties of the mean rate of occurrence are considered, this distribution provides the probability of the number of events above a predetermined lower bound magnitude, over time period ${\textstyle t}$ .

5. Results and discussion

The Bayesian extreme value distribution presented above has been used to estimate the seismic hazard in Iran. To study the seismic hazard assessment in Iran and adjacent areas, we determined 40 major Iranian municipalities (Table 1 ). The seismic assessment at the study area depends mainly on the catalogue of earthquakes and potential seismic sources within a radius of 200 km. Consequently, the seismic hazard estimates were obtained from an area with a radius of 200 km around each municipality. In the background seismicity concept, small and moderately sized earthquakes can randomly occur in the defined area. This value is often defined as earthquakes with a magnitude of 6.5 or lower, and is based on the activity level of the region  [13] . In this study, we focused on earthquakes with magnitudes above 6.5, since they account for most of the moment release and are most likely to be recorded accurately because of their size. We used data from a catalogue covering the time period of 1900–2011, because a reliable catalogue of earthquakes with magnitude of 6.5 in Iran was only available for this time period. The database used in the Bayseian updating contains 53 instrumental events after 1900 for ${\textstyle M_{s}\geq 6.5}$ . The catalogue information was updated based on the prior estimation, which may have been based on incomplete data for historical records. Since earthquake magnitudes have always been reported with some uncertainty in Iran, seismic gaps and the uncertainty of earthquake magnitudes were considered in the analysis of the Iranian earthquake data. These considerations are necessary for regions, such as Iran, where few earthquake databases are available. Due to the lack of sufficient seismic data and the low precision of the available data, it was not possible to relate the occurrence of the earthquakes to their causative sources. Additionally, a high number of earthquakes in the highly seismic region of Iran occur on hidden faults  [13] , and it is not possible to calculate the seismic parameters for each source or based on the seismicity information from the sources. As a result, we accepted that statistical estimates of seismicity from historical and instrumental data with ${\textstyle M_{s}\geq 5.0}$ in each area were used as prior estimates of the mean rate of earthquake occurrences for the region. Therefore, prior estimation of the mean rate of earthquake occurrence seismic parameters was obtained in each area. For this purpose, the method proposed by Kijko and Sellevoll,  [57]  and [58] was employed to consider uncertainty by maximum likelihood estimation in the magnitude of recorded earthquakes and in the incomplete earthquake catalogue. The prior estimation of the mean rate of earthquake occurrences for each area is shown in Table 1 . Three values of the Coefficients Of Variation (COV) for the prior estimation of ${\textstyle v}$ were assumed: 0.1, 0.25 and 0.5. These COVs were estimated based on the effect of errors in reported magnitudes (0.1–0.5 units) and epicenter coordinates (5, 10 and 20 km) on the mean rate of earthquake occurrences.

Table 1. Probability of exceeding a magnitude of 6.5 over 50 and 100 years for different areas of Iran.

Major Iranian municipalities	Prior estimates		Probability of exceedance in:		Major Iranian municipalities	Prior estimates		Probability of exceedance in:
	${\textstyle v^{'}}$	COV of ${\textstyle v^{'}}$	50	100		${\textstyle v^{'}}$	COV of ${\textstyle v^{'}}$	50	100
Abadan	0.011	0.10	0.418	0.660	Lar	0.03	0.10	0.773	0.947
		0.25	0.395	0.629			0.25	0.758	0.935
		0.50	0.330	0.535			0.50	0.729	0.910
Ahvaz	0.009	0.10	0.361	0.591	Mashhad	0.028	0.10	0.747	0.935
		0.25	0.358	0.584			0.25	0.720	0.915
		0.50	0.350	0.563			0.50	0.661	0.864
Arak	0.015	0.10	0.524	0.772	Nikshahr	0.013	0.10	0.482	0.730
		0.25	0.507	0.750			0.25	0.501	0.745
		0.50	0.463	0.691			0.50	0.546	0.777
Ardebil	0.026	0.10	0.722	0.921	Orumieh	0.014	0.10	0.500	0.749
		0.25	0.698	0.902			0.25	0.485	0.728
		0.50	0.646	0.854			0.50	0.448	0.675
Bam	0.036	0.10	0.835	0.972	Qazvin	0.026	0.10	0.725	0.923
		0.25	0.836	0.969			0.25	0.718	0.914
		0.50	0.840	0.965			0.50	0.703	0.894
Bandar Abas	0.034	0.10	0.815	0.965	Qom	0.019	0.10	0.604	0.841
		0.25	0.808	0.958			0.25	0.559	0.797
		0.50	0.795	0.945			0.50	0.440	0.662
Bandar Chabahar	0.020	0.10	0.626	0.858	Rasht	0.025	0.10	0.712	0.916
		0.25	0.597	0.830			0.25	0.706	0.907
		0.50	0.526	0.752			0.50	0.695	0.889
Bandar Jask	0.019	0.10	0.604	0.841	Sabzevar	0.028	0.10	0.754	0.938
		0.25	0.559	0.797			0.25	0.757	0.935
		0.50	0.440	0.662			0.50	0.764	0.930
Birjand	0.027	0.10	0.731	0.926	Sanandaj	0.018	0.10	0.588	0.829
		0.25	0.689	0.895			0.25	0.564	0.802
		0.50	0.587	0.805			0.50	0.504	0.731
Bojnurd	0.036	0.10	0.832	0.971	Sari	0.028	0.10	0.747	0.935
		0.25	0.822	0.963			0.25	0.720	0.915
		0.50	0.804	0.949			0.50	0.661	0.864
Bushehr	0.012	0.10	0.446	0.692	Semnan	0.032	0.10	0.790	0.955
		0.25	0.420	0.657			0.25	0.757	0.935
		0.50	0.347	0.556			0.50	0.685	0.880
Esfahan	0.014	0.10	0.497	0.745	Shahrekurd	0.011	0.10	0.424	0.668
		0.25	0.465	0.707			0.25	0.432	0.672
		0.50	0.378	0.594			0.50	0.452	0.683
Ghuchan	0.037	0.10	0.848	0.976	Shiraz	0.012	0.10	0.449	0.695
		0.25	0.868	0.979			0.25	0.439	0.679
		0.50	0.896	0.984			0.50	0.414	0.638
Gorgan	0.025	0.10	0.705	0.911	Sirjan	0.031	0.10	0.780	0.950
		0.25	0.666	0.880			0.25	0.749	0.930
		0.50	0.572	0.793			0.50	0.680	0.877
Hamedan	0.017	0.10	0.571	0.815	Tabas	0.032	0.10	0.787	0.953
		0.25	0.566	0.805			0.25	0.738	0.924
		0.50	0.555	0.782			0.50	0.618	0.830
Ilam	0.012	0.10	0.449	0.695	Tabriz	0.036	0.10	0.823	0.967
		0.25	0.439	0.679			0.25	0.769	0.940
		0.50	0.414	0.638			0.50	0.639	0.845
Iranshahr	0.015	0.10	0.524	0.772	Tehran	0.036	0.10	0.826	0.969
		0.25	0.507	0.750			0.25	0.788	0.949
		0.50	0.463	0.691			0.50	0.705	0.893
Kashan	0.017	0.10	0.568	0.812	Yasuj	0.011	0.10	0.421	0.664
		0.25	0.546	0.786			0.25	0.414	0.651
		0.50	0.491	0.719			0.50	0.394	0.616
Kerman	0.037	0.10	0.845	0.975	Yazd	0.008	0.10	0.326	0.546
		0.25	0.856	0.976			0.25	0.312	0.523
		0.50	0.873	0.977			0.50	0.270	0.455
Kermanshah	0.018	0.10	0.595	0.835	Zahedan	0.022	0.10	0.656	0.880
		0.25	0.604	0.836			0.25	0.604	0.835
		0.50	0.625	0.841			0.50	0.468	0.692
Khoramabad	0.017	0.10	0.571	0.815	Zanjan	0.023	0.10	0.679	0.896
		0.25	0.566	0.805			0.25	0.661	0.878
		0.50	0.555	0.782			0.50	0.622	0.836

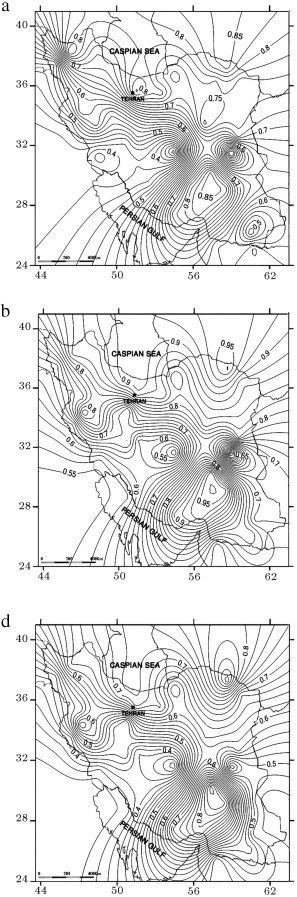
The results of this study are shown in Table 1 , Figure 3  and Figure 4 . Table 1 shows the probability of exceeding the lower bound magnitude over time periods of 50 and 100 years. These time intervals are of engineering interest because they are equal to the lifetime of the structures. Table 1 indicates the probability of occurrences of earthquakes of a magnitude of 6.5 or higher for three COV values of 0.1, 0.25 and 0.5. The calculated probability for earthquake hazard is displayed as an iso-probability contour during the typical lifetime of structures. The Bayesian probabilities are graphically shown in Figure 3  and Figure 4 . These traces indicate that an increase in the COV can cause a slight decrease in the probability of exceeding the lower bound of predicted magnitudes.

Figure 3. Seismic zoning map of Iran (probability of exceeding minimum magnitude bounds) using the Bayesian approach over 50 years: (a) The coefficient of variation of 0.1 for prior information; (b) the coefficient of variation of 0.25 for prior information; and (c) the coefficient of variation of 0.5 for prior information.

Figure 4. Seismic zoning map (probability of exceedance) of Iran using the Bayesian approach for 100 years: (a) The coefficient of variation of 0.1 for prior information; (b) the coefficient of variation of 0.25 for prior information; and (c) the coefficient of variation of 0.5 for prior information.

The probability of occurrence of earthquakes with a magnitude of 6.5 or greater is higher than 0.5 for almost all of Iran. The results indicate that the regions of Alborz, KD, the Arabian landmass, Kerman Province, and Zagros Thrust have high seismic hazard. The seismic hazard is lowest for the Esfahan–Sirjan, CI, and ASAA regions. However, these results may be due to a difference in catalogues or differences in definitions of the considered seismic zones and parameters discussed by other studies. Our results are generally compatible with the results from previous studies  [7] , [9] , [10] , [11]  and [12] .

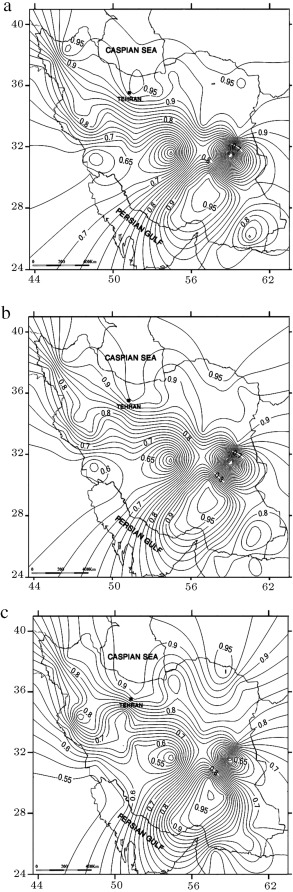
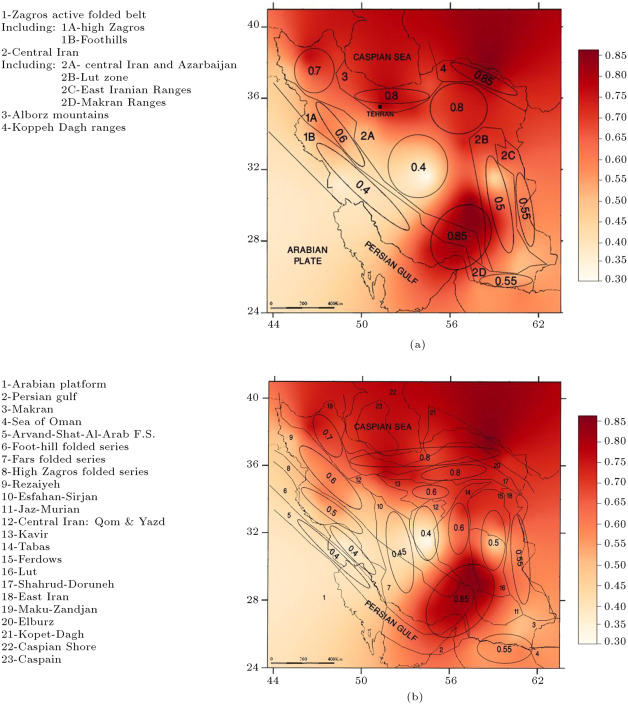
Tectonic zoning maps of different regions, each with their own characteristics, were developed for Iran. In general, these maps should allow for zoning of regions that are similar and close to each other. To separate one seismotectonic province from another, there must be a difference in seismicity or tectonics or, preferably, both  [59] . By accepting that there is correlation between seismotectonic features and spatial distribution of the earthquakes in the region  [60] , the results of this study provide an important basis for the study of partitioning earthquake ground motion data into a number of subgroups, such as seismotectonic provinces. In this study, the seismotectonic model of Nowroozi  [4] and Berberian  [42] was selected for comparison and verification. This comparison was made regarding the correspondence between seismotectonic provinces in Alborz, Zagros, and CI.

Berberian  [42] subdivided the Zagros belt into the “High Zagros” and “Foothills” provinces. Figure 5 (a) shows the consistency of our results with the subdivision of Berberian  [42] . Nowroozi  [4] divided the Zagros belt into four provinces. In comparison with the results of Nowroozi  [4] , our results showed good agreement between the locations of Fars, high Zagros, foothills and the ASAA folded series (Figure 5 (b)). Despite the Nowroozi  [4] and Berberian  [42] models, the existence of a separate region with high seismicity north of the city of Bandar-Abas (${\textstyle 28{\mbox{°}}N,56{\mbox{°}}E}$ ) was detectable in this study. This finding supports the previous results of Regard et al.  [61] .

Figure 5. The hazard map based on the Bayesian result comparison with the (a) Berberian  [42] and (b) Nowroozi  [4] models. The hazard is expressed as the probability of occurrence in 50 years with a COV equal to 0.25. The ellipses show the regions with the same probability of exceedance.

Berberian  [42] subdivided CI into the major provinces of CI, Lut Block, East Iranian Ranges, and Makran Ranges (Figure 5 (a)). Our results agree with the seismotectonic model of Nowroozi  [4] and show regions in the Makran, East Iran, Ferdows, Jaz-Murian, Esfahan–Sirjan, Qom–Yazd and Tabas provinces (Figure 5 (b)). Because of the high seismicity of the Kerman Province over the past three decades, the results from this region differ from the Nowroozi  [4] and Berberian  [42] models.

Figure 5 shows the formation of regions in the KD in the Alborz Region: two in the southeast, southwest of the Caspian Sea, and northeast of Iran. There is agreement between the location of these clusters and corresponding seismo-tectonic provinces proposed by Nowroozi  [4] and Berberian  [42] .

6. Conclusions

Iran does not appear to be a single crustal block, but an assemblage of zones comprising the Alborze Range, the Zagros Mountains and CI. Bayesian probability theory provides more reliable estimates of seismic hazard than conventional methods. This is the first time that the Bayesian updating of earthquake occurrence has been applied to Iran and the surrounding regions. Earthquake datasets are severely incomplete, especially for historical earthquakes. The major limitation of the seismic hazard assessment is that the results rely on seismotectonic provinces and associated statistics. To avoid this limitation, we estimated the non-regionalized approach of hazard assessment based on Bayesian updating. The prior estimate was calculated with consideration of the uncertainty. We have used a tool for seismic hazard assessment, which is promising and comparable with corresponding classical methods. Additionally, we have obtained a set of probabilistic maps with engineering significance.

The comparison of results between the Bayesian method and seismotectonic models revealed the ability of the Bayesian method to identify seismotectonic provinces based on data alone. Identification of different seismotectonic provinces with similar characteristics in a region of intensity is one of the most important goals of seismic hazard studies. This task is usually completed by subjective interpretation, based on geological and seismotectonic information. It should be emphasized that Bayesian updating is a strong tool that can be used for more reliable geological and seismological interpretation.

References

1. [1] E.R. Engdahl, J.A. Jackson, S.C. Myers, E.A. Bergman, K. Priestley; Relocation and assessment of seismicity in the Iran region; Geophys. J. Int., 167 (2006), pp. 761–778
2. [2] M. Talebian, J.A. Jackson; A reappraisal of earthquake local mechanisms and active shortening in the Zagros mountain of Iran; Geophys. J. Int., 156 (2004), pp. 506–526
3. [3] M. Niazi, J.R. Basford; Seismicity of Iranian Plateau and Hindu Kush region; Bull. Seismol. Soc. Am., 58 (1968), pp. 417–426
4. [4] A.A. Nowroozi; Seismotectonic provinces of Iran; Bull. Seismol. Soc. Am., 66 (1976), pp. 1249–1276
5. [5] M. Berberian; Master blind thrust faults hidden under the Zagros folds: active basement tectonics and surface morphotectonics; Tectonophysics, 241 (1995), pp. 193–224
6. [6] G. Ahmadi, A.A. Nowroozi; Earthquake risk analysis of Iran-III, intensity estimates for various return periods and epicentral distance; Bull. Iran. Pet. Inst., 80 (1980), pp. 1–13
7. [7] A.A. Nowroozi, G. Ahmadi; Analysis of earthquake risk I Iran based on seismotectonic provinces; Tectonophysics, 122 (1986), pp. 89–114
8. [8] N. Mirzaei, M. Gao, Y.T. Chen; Seismicity in major seismotectonic provinces of Iran; Earthq. Res. China, 11 (1997), pp. 351–361
9. [9] G. Ahmadi, N. Mostaghel, A.A. Nowroozi; Probabilistic seismic risk for various peak ground accelerations; Iran. J. Sci. Technol., 13 (1989), pp. 115–156
10. [10] B. Tavakoli, M. Ghafory-Ashtiany; Seismic hazard assessment of Iran; Ann. Geofis., 42 (1999), pp. 1013–1021 The Global Seismic Hazard Assessment Program (GSHAP) 1992–1999
11. [11] United States Geological Survey Website (2004). http://earthquake.usgs.gov/ .
12. [12] Y. Bozorgnia, A. Mohajer-Ashjai; Seismic risk investigation of major cities of Iran; J. Earth Space Phys., 11 (1982), pp. 15–38
13. [13] N. Mirzaei, M. Gao, Y.-T. Chen; Delineation of potential seismic sources for seismic zoning of Iran; J. Seismol., 3 (1999), pp. 17–30
14. [14] D. Mayer-Rosa; The assessment of seismic hazard and GSHAP aspects; Sci. Iran., 2 (1995), pp. 137–143
15. [15] K.W. Campbell; Bayesian analysis of extreme earthquake occurrences: part I, probabilistic hazard model; Bull. Seismol. Soc. Am., 72 (1982), pp. 1689–1705
16. [16] D. Chu, R.G. Gordon; Current plate motions across the Red sea; Geophys. J. Int., 135 (1998), pp. 313–328
17. [17] M. Berberian, J.A. Jackson, M. Qorashi, M. Talebian, M.M. Khatib, K. Priestley; The 1994 sefidabeh earthquakes in eastern Iran: blind thrusting and bedding-plane slip on a growing anticline, and active tectonics of the Sistan suture zone; Geophys. J. Int., 142 (2000), pp. 283–299
18. [18] M. Tatar, D. Hatzfeld, J. Martinod, A. Walpersdorf, M. Ghafori-Ashtiany, J. Chery; The present-day deformation of the central Zagros from GPS measurements; Geophys. Res. Lett., 29 (2002)
19. [19] M. Berberian, J.A. Jackson, E. Fielding, B.E. Parsons, K. Priestley, M. Ghorashi, M. Talebian, R. Walker, T.J. Wright, C. Baker; The 1998 March 14 Fandoqa earthquake (${\textstyle M_{w}}$ 6.6) in Kerman province, southeast Iran: re-rupture of the 1981 Sirch earthquake fault, triggering of slip on adjacent thrusts and the active tectonics of the Gowk fault zone  ; Geophys. J. Int., 146 (2001), pp. 371–398
20. [20] P. Vernant, F. Nilforoushan, D. Hatzfeld, M. Abassi, C. Vigny, F. Masson, H. Nankali, J. Martinod, A. Ashtiani, R. Bayer, F. Tavakoli, J. Che’ry; Contemporary crustal deformation and plate kinematics in Middle East constrained by GPS measurements in Iran and northern Oman; Geophys. J. Int., 157 (2004), pp. 381–398
21. [21] D. Hatzfeld, M. Tatar, K. Priestley, M. Ghafory-Ashtiany; Seismological constraints on the crustal structure beneath the Zagros Mountain belt (Iran); Geophys. J. Int., 155 (2003), pp. 403–410
22. [22] J.A. Jackson, D. McKenzie; Active tectonics of the Alpine–Himalayan belt between western Turkey and Pakistan; Geophys. J. Int., 77 (1984), pp. 185–264
23. [23] M. Alavi; Tectonostratigraphic synthesis and structural style of the Alborz mountain system in northern Iran; J. Geodyn., 21 (1996), pp. 1–33
24. [24] M. Berberian; Seismic sources of the Transcaucasian historical earthquakes; D. Giardini, S. Balassanian (Eds.), Historical and Prehistorical Earthquakes in the Caucasus, Kluwer Academic Publishers, Dordrecht (1997), pp. 233–311
25. [25] M. Berberian, R.S. Yeats; Contribution of archaeological data to studies of earthquake history in the Iranian Plateau; J. Struct. Geol., 23 (2001), pp. 563–584
26. [26] M.B. Allen, S.J. Vincent, G.I. Alsopb, A. Ismail-zadeh, R. Flecker; Late Cenozoic deformation in the South Caspian region: effects of a rigid basement block within a collision zone; Tectonophysics, 366 (2003), pp. 223–239
27. [27] N.N. Ambraseys; Historical seismicity of north–central Iran; Geol. Surv. Iran, 29 (1974), pp. 47–96
28. [28] N.N. Ambraseys, C.P. Melville; A History of Persian Earthquakes; Cambridge University Press, UK (1982)
29. [29] M. Berberian; Natural Hazards and the First Earthquake Catalogue of Iran; IIEES, Iran (1994)
30. [30] M. Berberian, R.S. Yeats; Patterns of historical earthquake rupture in the Iranian Plateau; Bull. Seismol. Soc. Am., 89 (1999), pp. 120–139
31. [31] Moinfar, A., Mahdavian, A. and Maleki, E. “Historical and instrumental earthquake data collection of Iran”, Mahab Ghods Consultant Engineers, Iran (in Persian) (1994).
32. [32] ISC, On-line Bulletin, Thatcham, UK (2011). http://www.isc.ac.uk  (accessed: 1.2.11).
33. [33] N.N. Ambraseys; Reassessment of earthquakes 1990–1999 in the eastern Mediterranean and Middle East; Geophys. J. Int., 145 (2001), pp. 471–485
34. [34] E.R. Engdahl, R. Hilst, R. Buland; Global teleseismic earthquake relocation with improved travel times and procedures for depth determination; Bull. Seismol. Soc. Am., 88 (1998), pp. 722–743
35. [35] M. Ashtari; Time independent seismic hazard analysis in Alborz and surrounding area; Nat. Hazards, 42 (2007), pp. 237–252
36. [36] J.K. Gardner, L. Knopof; Is the sequence of earthquake in southern California, with aftershocks removed, Poissonian?; Bull. Seismol. Soc. Am., 64 (1974), pp. 1363–1367
37. [37] L. Jones, P. Molnar; Frequency of foreshocks; Nature, 262 (1976), pp. 677–679
38. [38] M. Shokri-Ghasabeh, A. Bakhshiani, K. Hansen; Seismic risk analysis of Iranian construction projects; Sci. Iran., 17 (2010), pp. 62–73
39. [39] IRCOLD. “Iranian Committee of Large Dams: relationship between MS and mb”, Internal Report (in Persian) (1994).
40. [40] J. Stocklin; Structural history and tectonics of Iran, a review; Bull. Am. Assoc. Petrol. Geol., 52 (1968), pp. 1229–1258
41. [41] M. Takin; Iranian geology and continental drift in the Middle East; Nature, 235 (1972), pp. 147–150
42. [42] Berberian, M. “Contribution to the seismotectonic of Iran, Part II”, Rep. No. 39, Geological Survey of Iran (1976).
43. [43] A. Zamani, N.A. Heshami; Computer-based self-organized tectonic zoning: tentative pattern recognition for Iran; Comput. Geosci., 30 (2004), pp. 705–718
44. [44] A. Ansari, A. Noorzad, H. Zafarani; Clustering analysis of the seismic catalog of Iran; Comput. Geosci., 35 (2009), pp. 705–718
45. [45] A.H. Ang, W.H. Tang; Probability Concepts in Engineering Planning and Design; Basic Principles, 1 (2nd Edn.), Wiley, New York (1975)
46. [46] J.R. Benjamin; Probabilistic models for seismic force design; J. Struct. Div., ASCE, 94 (ST5) (1968), pp. 1175–1196
47. [47] C.A. Cornell; Bayesian statistical decision theory and reliability-based design; A.M. Freundenthal (Ed.), Proceedings of the International Conference on Structural Safety and Reliability, Smithsonian Institute, Washington, DC (1972), pp. 47–66 1969
48. [48] K.W. Campbell; Bayesian analysis of extreme earthquake occurrences: part II probabilistic hazard model; Bull. Seismol. Soc. Am., 73 (1983), pp. 1099–1115
49. [49] G.N. Stavrakakis, J. Drakopoulos; Bayesian probabilities of earthquake occurrence in Greece and surrounding areas; Pure Appl. Geophys., 144 (1995), pp. 307–319
50. [50] T.M. Tsapanos, G.A. Papadopoulos, O. Galanis; Time independent seismic hazard analysis of Greece deduced from Bayesian statistics; Nat. Hazards Earth Syst. Sci., 3 (2003), pp. 129–134
51. [51] M. Wang, T. Takada; A Bayesian framework for prediction of seismic ground motion; Bull. Seismol. Soc. Am., 99 (2009), pp. 2348–2364
52. [52] M. Mahdavi Adeli, A. Deylami, M. Banazadeh, M.M. Alinia; A Bayesian approach to construction of probabilistic seismic demand models for steel moment-resisting frames; Sci. Iran., 18 (2011), pp. 885–894
53. [53] J.R. Benjamin, C.A. Cornell; Probability, Statistics and Decision for Civil Engineers; McGraw-Hill, New York (1970), p. 684
54. [54] Esteva, L. “Seismicity prediction: Bayesian approach”, Proceedings of the 4th World Conference on Earthquake Engineering , Santiago, Chile, pp. 172–184 (1969).
55. [55] Lomnitz, C. “An earthquake risk map of Chile”, Proceedings of the Fourth World Conference on Earthquake Engineering , I, Santiago, Chile, pp. 161–171 (1969).
56. [56] K.M. Shedlock, R.K. McGuire, D.G. Herd; Earthquake Recurrence in the San Francisco Bay Region, California, from Fault Slip and Seismic Moment; US Geol. Surv. (1980) Open-File Rept: 80-999
57. [57] A. Kijko, M.A. Sellevoll; Estimation of earthquake hazard parameters from incomplete data files, part I, utilization of extreme and complete catalogs with different threshold magnitudes; Bull. Seismol. Soc. Am., 79 (1989), pp. 645–654
58. [58] A. Kijko, M.A. Sellevoll; Estimation of earthquake hazard parameters from incomplete data files, part II, incorporation of magnitude heterogeneity; Bull. Seismol. Soc. Am., 82 (1992), pp. 120–134
59. [59] M. Berberian; Evaluation of the instrumental and relocated epicenters of Iranian earthquakes; Geophys. J. R. Astron. Soc., 58 (1979), pp. 625–630
60. [60] K. Aki; Characterization of barriers on an earthquake fault; J. Geophys. Res., 84 (1979), pp. 6140–6148
61. [61] V. Regard, O. Bellier, J.C. Thomas, D. Bourles, S. Bonnet, M.R. Abbassi, R. Braucher, J. Mercier, E. Shabanian, S.H. Soleymani, Kh. Feghhi; Cumulative right-lateral fault slip rate across the Zagros–Makran transfer zone: role of the Minab–Zendan fault system in accommodating Arabia–Eurasia convergence in southeast Iran; Geophys. J. Int., 162 (2005), pp. 177–203