Design and optimization of Halbach magnetic gear

Abstract

This article proposes a new structure to enhance the torque and torque density of permanent magnet gears. The outer magnet is designed with a dual-layer permanent magnet configuration, where the first layer adopts a Halbach array, and the other layer utilizes a conventional radial magnetization structure. With the optimization objectives defined as maximum torque and torque density, and guided by parameter sensitivity, optimization analysis was conducted using response surface method and multi-objective genetic algorithm. The optimized parameters were determined, and finite element simulations were performed to validate the optimization results. The result indicate a 22.22% increase in torque and a 27.42% increase in torque density compared to the previous the traditional magnet gear. The performance of the proposed new structure of magnetic gear has shown significant improvement.

Keywords: Mangentic gear, Halbach, RSM, electromagnetic torque, torque density

1. Introduction

As the demand for energy increases in society, wind energy has gained significant attention as a clean and renewable energy source [1,2]. The wind turbine gearbox is a crucial component in the doubly-fed wind power generation system, playing a vital role in power transmission. However, the mechanical gearbox is constrained by factors such as the continuous impact of wind direction changes, variable loads, and noise vibrations, making it the component with the highest failure rate in wind turbine generators [3]. While direct-drive systems in wind power generation, which eliminate the need for mechanical gearboxes by directly utilizing the wind turbine blades to drive the generator, simplify the structure, the increasing single-machine power leads to a growing weight and volume of these direct-drive systems. Numerous studies indicate that the drive chain of direct-drive systems is limited by factors such as weight, cost, efficiency, resulting in various shortcomings [4]. Considered as a potential alternative to mechanical gears, magnet gears present several advantages, including low noise, minimal vibration, maintenance-free operation, and built-in overload protection. However, early limitations, such as the parallel-axis topology and lower magnetic material performance, curtailed their ability to achieve higher torque densities, impeding widespread development and adoption. Since the inception of the field modulated permanent magnet gear by Howe in 2001 [5], there has been a substantial improvement in the performance and application of magnetic materials in permanent magnet gears. This advancement has resulted in a significant upswing in both output torque and torque density. As a result, scholars have introduced a range of topological structures, use comprehensive depiction of the evolving in a renewed research focus on permanent magnet gear [6-8].

Presently, lots of scholars have contributed noteworthy research findings in the analysis of magnetic gears. In Mafi et al. [9], the incorporation of Halbach arrays into magnetic gears is introduced, resulting in a significant augmentation of their torque capabilities. In Shin and Chang [10], the modulation effect of the demagnetization block is equated to the air gap magnetic conductivity. This model calculates torque and air gap magnetic density using scalar magnetic potential theory, rendering it more amenable to parameterized optimization computations. Additionally, in Chen et al. [11] puts forth magnetic gears with variable transmission ratios, enhancing their suitability for variable-speed electric vehicles and wind turbines, thereby increasing the practicality of magnetic gears. And lots of scholars focus their research on the optimization of magnetic gears. Correspondingly, in Lu et al. [12] conducts a meticulous examination of the material properties of the modulators in magnet gears, aiming to minimize losses and elevate transmission efficiency. In Ruiz-Ponce et al. [13], an optimization design is executed on axial permanent magnet gears utilizing a two-dimensional magnetic equivalent circuit model and a genetic algorithm. This design not only diminishes ineffective harmonics in the air gap, augmenting air gap flux density for heightened torque density but also undergoes optimization through a genetic algorithm. And Jing et al. [14], Gardner et al. [15], Tan et al. [16] and Chen et al. [17], they use different methods to optimize the characteristic of magnetic gears, such as structure, material, algorithm. 

To enhance the output torque and torque density of magnet gears, this article proposes a Halbach Array enhanced Field Modulated Permanent Magnetic Gear (HFMPMG) based on the Field Modulated Permanent Magnetic Gear (FMPMG). The HFMPMG is parametrically modeled using ANSYS software. The Response Surface Method (RSM) is employed to analyze the optimization of structural parameters for the HFMPMG, resulting in a three-dimensional response surface. Subsequently, the Multi-Objective Genetic Algorithm (MOGA) is applied to obtain the optimal solution. Finally, the proposed HFMPMG is validated through confirmation tests.

2. Topology and operation principle

Figure 1 depicts the topological structure of the FMPMG, which is made up of an outer rotor, an inner rotor and modulators which can modulate the inner and outer air-gap.

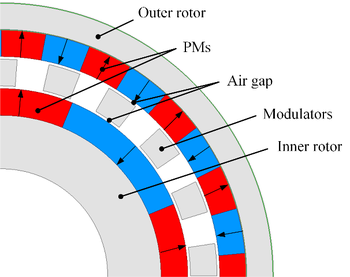
Figure 1. FMPMG topology

In order to efficiently couple the magnetic fields generated by the internal and exterior permanent magnets and achieve torque transfer, the modulators primarily modifies the inner and outer air-gap magnetic fields. The harmonic logarithm of magnetic gear air-gap fields is expressed as

$p_{m,j}=\vert mp+jn\vert {\mbox{ }}$

(1)

where $m=1,3,5...j=0,\pm 1,\pm 2,\pm 3,...$, ${\textstyle p}$ is the number of pole pairs for the inner or outer PMs, and ${\textstyle n}$ is the number of modulators.

If the magnetic pole pair number of the inner rotor permanent magnet in FMPMG is $p_{1}$ and the corresponding rotational speed is ${\textstyle {\omega }_{1}}$, the number of modulator is $n_{2}$, and the corresponding rotational speed is ${\omega }_{2}$, the magnetic pole pair number of the outer rotor permanent magnet is $p_{3}$, and the corresponding rotational speed is ${\omega }_{3}$, the harmonic magnetic field pole pair numbers in the air gap and the corresponding angular velocities of the harmonics are given by:

${\omega }_{m,j}={\frac {mp_{1}}{mp_{1}+jn_{2}}}{\omega }_{1}+{\frac {jn_{2}}{mp_{1}+jn_{2}}}{\omega }_{2}{\mbox{   }}$

(2)

where ${\omega }_{m,j}$ is the angular velocity of the spatial harmonic component.

In coupling the magnetic fields of the inner and outer rotors in the Field Modulated Permanent Magnetic Gear (FMPMG), it becomes imperative to align the radially harmonic component of the modulated air gap flux generated by the outer rotor's permanent magnet with the radial harmonic component produced by the inner rotor's permanent magnet.

According to the theory of magnetic field wave angular velocity, two rotating magnetic fields can only achieve stable speed and torque transmission when the magnetic pole numbers and rotational speeds are equal. Therefore, to couple the magnetic fields of the inner and outer rotors in FMPMG, it is necessary to match the radially harmonic component of the modulated air gap flux produced by the outer rotor permanent magnet with the radial harmonic component produced by the inner rotor permanent magnet. Among all the harmonic magnetic fields, when $m=1,\,j=-1$, the synchronous harmonic generated by the inner and outer rotor permanent magnets at the air gap is the largest. Therefore, this harmonic can be considered as the main working harmonic of FMPMG. Other harmonics have relatively smaller amplitudes, and their impact on the average torque of FMPMG is smaller. To achieve the stable operation of the three rotors in FMPMG, the pole pair number of the outer rotor permanent magnet should be represented as $p_{3}=n_{2}-p_{1}$.

When ${\omega }_{2}{\mbox{=}}0$, the gear ratio $G_{r}$ is given by:

$G_{r}=-{\frac {p_{3}}{p_{1}}}$

(3)

This article proposes a improved Halbach Array Field Modulated Permanent Magnetic Gear (HFMPMG), depicted in Figure 2.

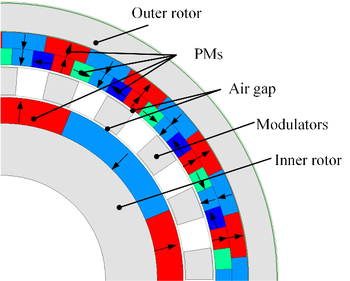
Figure 2. HFMPMG topology

The inner rotor is the same as the conventional FMPMG topology which has one layer of permanent magnets with the arrangement of N-pole-S-pole-N-pole. However, a modification is introduced in the structure of the outer rotor's permanent magnets, employing a double-layer configuration. The first layer adheres to a Halbach array arrangement, while the second layer follows the conventional FMPMG arrangement. This dual-layer design serves dual purposes: it mitigates magnetic flux leakage and adjusts the peak value of radial magnetic density, thereby enhancing the sinusoidal nature of the waveform. Essential structural parameters for the HFMPMG are outlined in Table 1.

Table 1. Design parameters of HFMPMG

Parameter	Description	Values
${\textstyle Ri}$	Inner radius of inner rotor core /mm	40
${\textstyle L1}$	Thickness of inner rotor core /mm	20
${\textstyle L2}$	Thickness of inner PMs /mm	10
${\textstyle L3}$	Thickness of modulator /mm	10
${\textstyle L4}$	Thickness of outer PMs /mm	10
${\textstyle L5}$	Thickness of outer rotor core /mm	10
${\textstyle g1}$	Thickness of the inner air gap/mm	1
${\textstyle g2}$	Thickness of the outer air gap /mm	1
${\textstyle AL}$	Axial length /mm	60

3. Multiobjective optimization of HFMPMG

Given the both structural disparities, the HFMPMG necessitates the consideration of more parameters in the optimization process, because the parameters significantly influence the output torque and torque density. The optimization goal is also increased from single objective to multiobjective. To obtain accurate design parameters for achieving higher torque and torque density, this article advocates a comprehensive approach that integrates parameter sensitivity analysis with response surface method. Based on the sensitivity analysis results, the MOGA algorithm is employed to optimize the modeling parameters of HFMPMG. Finally, finite element analysis is conducted to compare the performance differences between HFMPMG and FMPMG. The whole process of optimization design is shown in Figure 1.

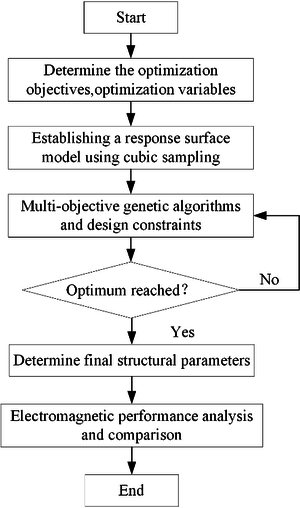
Figure 3. Optimization design process of HFMPMG

3.1 Optimization objectives and optimization parameters

FMPMG is typically used to transmit mechanical torque, so the magnitude of the output torque per unit volume is a crucial criterion for assessing its performance. Additionally, depending on the application scenario, parameters such as torque peak values and fluctuation are standards for evaluating FMPMG performance. In the optimization of HFMPMG in this article, the primary objectives for optimization will be its maximum output torque and torque density.

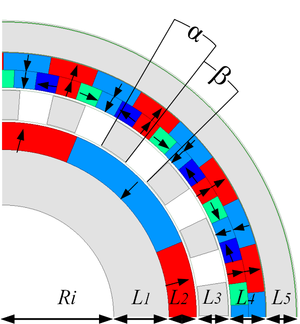
Figure 4. Optimization parameters model

The main optimization parameters of HFMPMG are illustrated in Figure 4. ${\textstyle Ri}$ is the inner radius of inner yoke iron, ${\textstyle L1}$ is the thickness of inner rotor core, ${\textstyle L2}$ is the thickness of inner PMs, ${\textstyle L3}$ is the thickness of modulator, ${\textstyle L4}$ is the thickness of outer PMs, ${\textstyle L5}$ is the thickness of outer rotor core. ${\textstyle \alpha }$ is the central angle corresponding to the modulator, and ${\textstyle \beta }$ is the central angle corresponding to the nonmagnetic epoxy resin. The modulator fill factor ${\textstyle \lambda }$ represents the proportion of the angle occupied by the magnetic silicon steel block and nonmagnetic epoxy resin in the modulator. It can be expressed as:

$\lambda {\mbox{=}}{\frac {\alpha }{\alpha {\mbox{+}}\beta }}$

(4)

The optimization range structural parameters for HFMPMG is shown in Table 2.

Table 2. Parameter optimization range of HFMPMG

Parameter	Description	Values
${\textstyle Ri}$	Inner radius of inner rotor core /mm	[39-41]
${\textstyle L1}$	Thickness of inner rotor core /mm	[19-21]
${\textstyle L2}$	Thickness of inner PMs /mm	[9-11]
${\textstyle L3}$	Thickness of modulator /mm	[8-11]
${\textstyle L4}$	Thickness of outer PMs /mm	[9-11]
${\textstyle L5}$	Thickness of outer rotor core /mm	[9-11]
${\textstyle \lambda }$	Modulator fill factor	[0.4-0.6]

3.2 Parameter sensitivity analysis

The optimization process for HFMPMG encompasses a total of 7 parameters, leading to a geometric expansion in the number of samples. Thus, it becomes imperative to initially scrutinize the influence of optimization parameters on the objectives. Table 3 outlines the impact of each parameter on the optimization objectives. This analysis facilitates the identification of effective ranges for each optimization variable and allows for the prioritization of parameters significantly influencing the optimization objectives. This approach significantly shortens the optimization design time and improves optimization efficiency.

Table 3. Sensitivity analysis of HFMPMG

Parameter	${\textstyle L1}$	${\textstyle L2}$	${\textstyle L3}$	${\textstyle L4}$	${\textstyle L5}$	${\textstyle Ri}$	${\textstyle \lambda }$
Sensitivity	0.02098	0.2351	0.2416	0.1612	0.1485	0.0285	0.1629

3.3 RSM optimization

Utilizing response surface method for the optimization analysis of magnetic gears does not require explicit expressions of the relationship between various structural parameters and optimization objectives. It only involves fitting a surface equation that closely approximates the actual model and establishing the corresponding response surface model. Based on the response surface method, the response model for HFMPMG is given as:

$f(x)={\beta }_{0}+\sum _{i=1}^{3}{\beta }_{i}x_{i}+\sum _{i=1}^{3}{\beta }_{ii}x_{i}^{2}+\sum _{i=1}^{2}\sum _{j\geqslant 1}^{3}{\beta }_{ij}x_{i}y_{i}+\epsilon$

(5)

where $f(x)$ is the predicted value of the outer torque or torque density, ${\beta }_{0}$ is a constant term, ${\beta }_{i}$ is the linear coefficient of the design variable, ${\beta }_{ii}$ is the quadratic coefficient of structural parameters, and ${\beta }_{ij}$ is the product coefficient of different structural parameters. In addition, $x_{i}$ and $x_{j}$ are two different structural parameters, and $\epsilon$ is the statistical error.

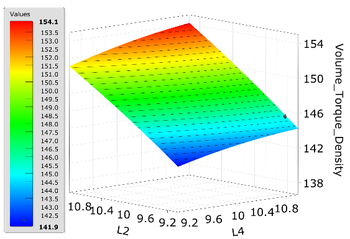
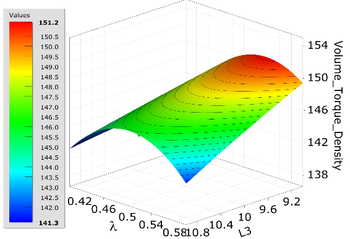
In accordance with Eq. (5), it can obtain the results of RSM, which offering a comprehensive depiction of the evolving relationship between the optimization objective and the chosen structural parameters. The outcomes are depicted in Figure 5. From Figure 5(a), it can be seen that as the ${\textstyle L2}$ and ${\textstyle L4}$ decreases, the torque density also gradually decreases. The decrease in the thickness of the PMs can reduce the volume of HFMPMG, but due to the reduction of the magnetic field coupling strength at the air gap, it will greatly reduce the torque density of HFMPMG. From Figure 5(b), it can be seen that when the thickness of the modulator is constant and the modulator fill factor ${\textstyle \lambda }$ is around 0.5, the torque density also reaches its maximum. When ${\textstyle \lambda }$ increases or decreases, the torque density decreases. Because when ${\textstyle \lambda }$ decreases, the magnetic circuit saturates, the magnetic density of the inner and outer air gaps decreases, and the modulator is not significant. However, as ${\textstyle \lambda }$ increases, the air gap magnetic density gradually increases. When ${\textstyle \lambda }$ is too large, a large amount of magnetic leakage will lead to a decrease in the performance of HFMPMG. Similarly, when ${\textstyle \lambda }$ is fixed, the torque density increases as ${\textstyle L3}$ decreases. From this, it can be seen that the modulation effect of the modulator in the entire HFMPMG is very obvious. After obtaining the appropriate response surface, the MOGA algorithm was selected for intelligent optimization to determine the final optimization value with high sensitivity, as shown in Table 4.

(a) $L_{2}$ and ${\textstyle L_{4}}$ (b) $\lambda$ and ${\textstyle L_{4}}$

Figure 5. Response of structural parameters to optimization objectives

Table 4. Optimization results of structural parameters

Parameter	Description	Values
${\textstyle Ri}$	Inner radius of inner rotor core /mm	39.447
${\textstyle L1}$	Thickness of inner rotor core /mm	19.798
${\textstyle L2}$	Thickness of inner PMs /mm	10.441
${\textstyle L3}$	Thickness of modulator /mm	9
${\textstyle L4}$	Thickness of outer PMs /mm	10.174
${\textstyle L5}$	Thickness of outer rotor core /mm	9
${\textstyle \lambda }$	Modulator fill factor	0.555

4. Performance analysis and comparison

4.1 Magnetic field characteristics

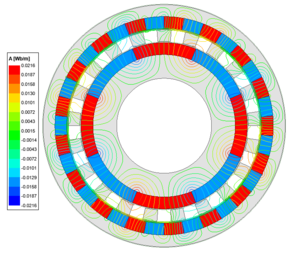
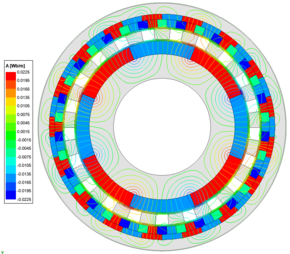
After conducting finite element analysis, the gap magnetic field profiles of the FMPMG and HFMPMG are revealed, as depicted in Figure 6. A careful examination of the magnetic field line comparison diagram elucidates that after modulation both configurations exhibit 8 peaks extending towards the outer rotor and 17 peaks reaching the inner rotor. Notably, these peaks align precisely with the pole pairs of the inner and outer rotors. In comparison to the FMPMG , the HFMPMG used the refined Halbach magnetization method applied to the outer rotor, achieves a heightened ability to guide the radial magnetic permanent magnet's orientation, thereby augmenting the magnetic focusing effect.

(a) FMPMG (b) HFMPMG

Figure 6. Flux line distributions

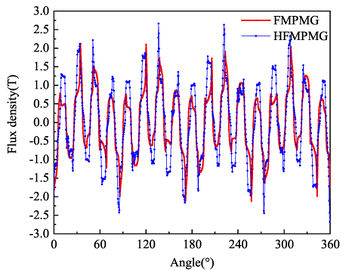
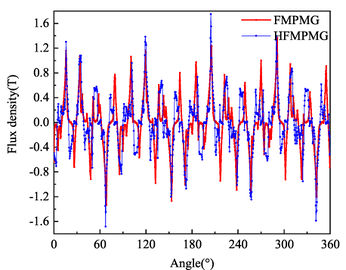
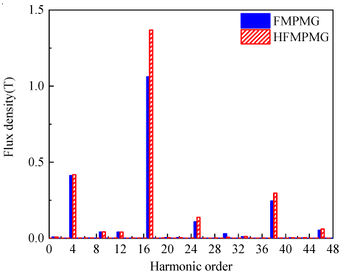
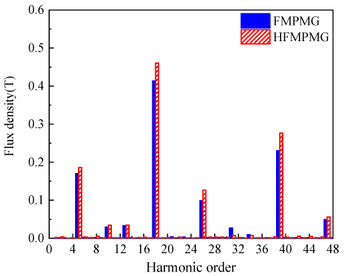
Figure 7 depicts the radial and tangential distribution of magnetic density in the outer air gap for both the FMPMG and HFMPMG, while Figure 8 presents the Fourier harmonic spectrum of magnetic density within the outer air gap. A clear insight gleaned from both Figure 7 and Figure 8 reveals a noteworthy trend: the presence of the double-layer outer permanent magnet in the HFMPMG substantially amplifies the peak values of radial effective harmonics, specifically harmonics 4 and 17. This augmentation holds the promise of fostering an increase in torque, consequently enhancing torque density.

(a) Radial component (b) Tangential component

Figure 7. Flux density in outer air gap

(a) Radial component (b) Tangential component

Figure 8. Harmonic spectra of flux density in outer air gap

4.2 Torque characteristics

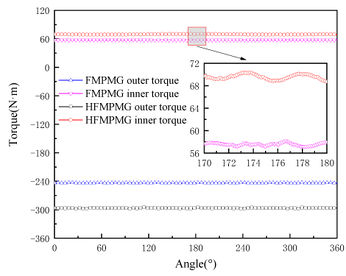
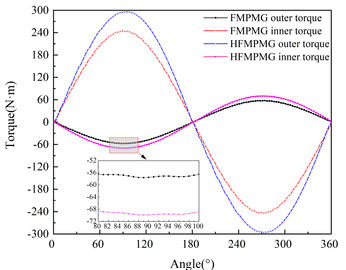
In accordance with Eq. (3) provided above, when the modulator remains stationary, the inner rotor and outer rotor exhibit motion in opposite directions in accordance with the ratio of their pole numbers. In the case of the HFMPMG, specific speeds are assigned to the inner and outer rotors, set at 170rpm and 40rpm, respectively. Employing finite element software simulation facilitates the derivation of stable torque output waveforms for both the inner and outer rotors.

Examining Figure 9(a), it is evident that both the FMPMG and HFMPMG demonstrate the capability to generate nearly linear torque waveforms during motion. However, following structural optimization and refinement, the output torque of the HFMPMG reaches 297N·m , surpassing the output torque of the FMPMG, which stands at 243N·m. This represents a notable increase of 22.22%. Similarly, as illustrated in Figure 9(b), the static torque curves of both the FMPMG and HFMPMG exhibit sine characteristics consistent with a transmission ratio of 4.25. In summation, based on the insights derived from both figures, it becomes apparent that the performance of the HFMPMG outpaces that of the FMPMG.

(a) Dynamic torque curve (b) Static torque curve

Figure 9. Torque characteristics

4.3 Torque density

To elucidate the electromagnetic characteristics of the HFMPMG, we conducted calculations comparing the volume, PM mass, maximum output torque and torque density of both HFMPMG and FMPMG in Table 5. It can be observed that HFMPMG utilizes a smaller volume and less permanent magnet material, yet it achieves an increase in output torque, resulting in a higher torque density.

Table 5. Comparison of the characteristics of HFMPMG and FMPMG

Parameter	HFMPMG	FMPMG
Magnetic gear volume (${\mbox{L}}^{3}$)	1.879	1.961
Magnets Weight (kg)	4.01	4.24
Outer torque (N.m)	297	243
Torque density (${\mbox{N}}\cdot m{\mbox{/L}}^{3}$)	158	124

5. Conclusions

(1) This article introduces an enhanced Halbach Array Field Modulated Permanent Magnetic Gear (HFMPMG). Its outer magnet is designed with a dual-layer permanent magnet configuration, where the first layer adopts a Halbach array, and the other layer utilizes a conventional radial magnetization structure.

(2) An exhaustive optimization analysis of critical structural parameters for the HFMPMG is undertaken employing a methodology encompassing parameter sensitivity analysis, response surface analysis, and a multi-objective genetic algorithm. This systematic approach ensures the swift, efficient, and precise attainment of optimized parameters.

(3) The results of magnetic and torque characteristics between the HFMPMG and FMPMG unequivocally affirm that HFMPMG demonstrates superior output torque and higher torque density. The outer torque increased by 22.22% and torque density increased by 27.42%. respectively. thereby validating the rationale and correctness of the optimized parameter acquisition process.

Acknowledgment

This work was funded by the Natural Science Research Project of Liaoning Province Education Department (Grant No.JDL2020001) and partly funded by the Technological Innovation Research Foundation Project of Dalian (Grant No.2018J12SN071).

References

[1] Kjaer A.B., Korsgaard S., Nielsen S.S., et al. Design, fabrication, test, and benchmark of a magnetically geared permanent magnet generator for wind power generation. IEEE Transactions on Energy Conversion, 35(1):24-32, 2019.

[2] Roga S., Bardhan S., Kumar Y., et al. Recent technology and challenges of wind energy generation: A review. Sustainable Energy Technologies, 52, 102239, 2022.

[3] Ruiz-Ponce G., Arjona M.A., Hernandez C., et al. A Review of magnetic gear technologies used in mechanical power transmission. Energies, 16(4), 1721, 2023.

[4] Padinharu D.K.K., Li G.-J., Zhu Z.-Q., et al. Permanent magnet vernier machines for direct-drive offshore wind power: Benefits and Challenges. IEEE Access, 10:20652-68, 2022.

[5] Atallah K., Howe D. A novel high-performance magnetic gear. IEEE Transactions on Magnetics, 37(4):2844-6, 2001.

[6] Yanjun G., Zhi Y., Peng Z. Modeling and analysis on starting characteristics of CPMGs. China Mechanical Engineering, 29(13):1513, 2018.

[7] Jing L., Gong J., Huang Z., et al. A new structure for the magnetic gear. IEEE Access, 7:75550-75555, 2019.

[8] Gouda E.A. A new design of magnetic gear for wind turbine. MEJ Mansoura Engineering Journal, 39(1):1-6, 2020.

[9] Mafi H., Afjei E., Ghaheri A. Design of coaxial magnetic gear utilising a novel permanent magnet Halbach array structure. IET Electric Power Applications, 15(3):299-309, 2021.

[10] Shin H., Chang J. Analytical magnetic field calculation of coaxial magnetic gear with flux concentrating rotor. IEEE Transactions on Magnetics, 52(7):1-4, 2015.

[11] Chen M., Chau K-.T., Lee C.H., et al. Design and analysis of a new axial-field magnetic variable gear using pole-changing permanent magnets. Progress in Electromagnetics Research, 153:23-32, 2015.

[12] Lu Y., Luo S., Wu S. Influence of material properties of magnetic adjusting ring on the loss of magnetic gear. Journal of Mechanical Engineering, 52(22):269-75, 2023.

[13] Ruiz-Ponce G., Arjona M.A., Hernandez C., et al. Design optimization of an axial flux magnetic gear by using reluctance network modeling and genetic algorithm. Energies, 16(4):1852, 2023.

[14] Jing L., Wang T., Pan Y., et al. Optimization of dual-flux-modulator magnetic gear with HTS bulks and uneven segment based on GA. IEEE Transactions on Applied Superconductivity, 32(6):1-5, 2022.

[15] Gardner M.C., Praslicka B., Johnson M., et al. Optimization of coaxial magnetic gear design and magnet material grade at different temperatures and gear ratios. IEEE Transactions on Energy Conversion, 36(3):2493-501, 2021.

[16] Tan C., Jing L., Liu W., et al. A high torque and low ripple magnetic gear with embedded permanent magnet. Journal of Electrical Engineering & Technology, 18(3):1799-807, 2023.

[17] Chen Y., Zhao X., Ho S., et al. Design and optimization of yokeless magnetic gear with asymmetric Halbach permanent magnet array for electric vehicle powertrain. IET Renewable Power Generation, 16(11):2223-32, 2022.