Responses of the ocean carbon cycle to climate change: Results from an earth system climate model simulation

Abstract

Based on simulations using the University of Victorias Earth System Climate Model, we analyzed the responses of the ocean carbon cycle to increasing atmospheric CO₂ levels and climate change from 1800 to 2500 following the RCP 8.5 scenario and its extension. Compared to simulations without climate change, the simulation with a climate sensitivity of 3.0 K shows that in 2100, due to increased atmospheric CO₂ concentrations, the simulated sea surface temperature increases by 2.7 K, the intensity of the North Atlantic deep water formation reduces by 4.5 Sv, and the oceanic uptake of anthropogenic CO₂ decreases by 0.8 Pg C. Climate change is also found to have a large effect on the North Atlantics ocean column inventory of anthropogenic CO₂ . Between the years 1800 and 2500, compared with the simulation with no climate change, the simulation with climate change causes a reduction in the total anthropogenic CO₂ column inventory over the entire ocean and in North Atlantic by 23.1% and 32.0%, respectively. A set of simulations with climate sensitivity variations from 0.5 K to 4.5 K show that with greater climate sensitivity climate change would have a greater effect in reducing the oceans ability to absorb CO₂ from the atmosphere.

Keywords

Climate change ; Ocean carbon cycle ; Carbon cycle modeling

1. Introduction

According to the Intergovernmental Panel on Climate Change (IPCC) Fifth Assessment Report (IPCC, 2013 ), many currently observed climate changes are unprecedented and the existence of global warming since the 1950s is unequivocal. Due to human activities such as fossil fuel use and land use changes since pre-industrial times, CO₂ concentrations in the atmosphere have increased by about 40%. Also, only about half of the total anthropogenic CO₂ emissions remain in the atmosphere ((240 ± 10) Pg C); the rest is absorbed by land ((160 ± 90) Pg C) and the ocean ((155 ± 90) Pg C) (IPCC, 2013 ). Based on simulations using 11 coupled climate–carbon cycle models, Friedlingstein et al. (2006) concluded that climate change will reduce the efficiency of the land and the ocean in absorbing atmospheric CO₂ . Furthermore, the IPCC reported that CO₂ increases and climate change have different effects on the lands and oceans carbon storage. CO₂ increases will lead to the increased carbon storage by the land and ocean. Climate change will reduce the land and oceans capacity to absorb atmospheric CO₂ due to the increasing temperatures of both the land and ocean and increasing oceanic stratification. The ocean, which has absorbed 27.9% of the anthropogenic CO₂ in the past 200 years (IPCC, 2013 ), plays a crucial role in the global carbon cycle.

The ocean carbon cycle is determined by a series of complex interactions involving the air-sea exchange, inorganic carbon chemistry, ocean general circulation, and marine biological processes (Plattner et al., 2001 ). Recently, many studies have discussed the ocean carbon cycle impact of increased atmospheric CO₂ and climate change. These studies indicate that rising atmospheric CO₂ levels lead to increased radiative forcing produced by greenhouse gases (IPCC, 2013 ), which causes sea surface warming. Warming seawater will decrease the CO₂ solubility of seawater (Plattner et al., 2001 ), resulting in a reduction in oceanic CO₂ uptake. Furthermore, global warming will cause increased ocean stratification (Sarmiento et al., 1998 ), which then will cause a reorganization of the thermohaline circulation and the reduction or even collapse of the North Atlantic deep water formation (Manabe and Stouffer, 1994  and Stocker and Schmittner, 1997 ). These changes will reduce the total transport of oceanic CO₂ from the ocean surface to the deep ocean (Maier-Reimer et al., 1996  and Matebr and Hirst, 1999 ). The reduction in oceanic carbon uptake, caused by the processes mentioned above, will in turn accelerate the increase in atmospheric CO₂ (Joos et al., 1999 ). Ocean carbon cycle studies in China began later than other studies worldwide, but have developed rapidly. The early studies mainly used two-dimensional carbon cycle models. For example, Xu et al. (1997) discussed the inorganic carbon cycle, and the sinks and sources of oceanic carbon uptake. Pu and Wang, 2000  and Pu and Wang, 2001 analyzed the distribution of chemical components related to carbon and the critical factors influencing the distribution of carbon in the Indian Ocean. At present, three-dimensional ocean carbon cycle models are being widely used in climate change research. Xing (2000) and Jin and Shi (2001) pointed out that the biological pump plays an important role in the ocean carbon cycle. Li and Xu (2012) used a perturbation approach to compare the different effects on oceanic CO₂ uptake in the Pacific Ocean and also modeled its biological processes. In addition to discussing the factors that influence oceanic CO₂ uptake, other studies (Xu and Li, 2009  and Bao et al., 2012 ) have analyzed oceanic CO₂ uptake and distribution based on simulations. Moreover, Wei et al., 2012  and Wei et al., 2014 employed an earth system model (BNU-ESM) to investigate the different climate change and ocean warming responses, including oceanic CO₂ uptake, carbon sequestration, and ocean acidification, to various anthropogenic CO₂ emission scenarios.

Based on the previous work noted above, this study uses an earth climate model to simulate the effect of increased atmospheric CO₂ and associated climate changes on oceanic CO₂ uptake and the ocean carbon cycle.

2. Model and methods

2.1. Model description

The University of Victoria Earth System Climate Model (UVic) was used, which consists of an energy-moisture balance atmospheric model (Fanning and Weaver, 1996 ), a dynamic-thermodynamic sea-ice model (Bitz et al., 2001 , Hibler, 1979  and Hunke and Dukowicz, 1997 ), and a primitive equation ocean general circulation model (Pacanowski, 1995 ). This model has a horizontal resolution of 3.6° longitude and 1.8° latitude, and divides the ocean into 19 vertical layers.

In order to guarantee the models computational efficiency, we used a simplified atmospheric model with only one layer, and included only CO₂ forcing, with no other greenhouse gas forcing such as CH₄ or aerosol forcing. The vertically integrated thermodynamic energy balance equations assume that the energy and specific humidity decrease vertically with specified scale heights. Momentum conservation equations are replaced by specified wind data, and the atmospheric heat and moisture transport by diffusion are parameterized for simplification (Weaver et al., 2001 ). The models wind stress data, 1958–1998 daily reanalysis data (Kalnay et al., 1996 ), are used to force the ocean and ice components and to calculate the latent heat and sensible heat fluxes between the atmosphere and ocean or ice components. The coupled models ocean component is Modular Ocean Model (MOM) version 2.2, which is based on Navier Stokes equations that are conditional on Boussinesq and hydrostatic approximations. In the sea-ice component, an elastic-viscous-plastic rheology represents the sea-ice dynamics, and various options for the sea-ice thermodynamics and thickness distribution are included. More information and equations may be found in Weaver et al. (2001) .

In addition, our model simulations of the ocean carbon cycle are based not only on the inorganic carbon cycle, following the protocol of the Ocean Carbon Cycle Model Intercomparison Project (Orr et al., 1999 ), but also take into consideration the ocean ecosystem, including the interactions between nutrients, phytoplankton, zooplankton, and detritus (Schmittner et al., 2008 ). Model simulations of the terrestrial carbon cycle and vegetation are based on the Met Office-Hadley Centre TRIFFID dynamic vegetation model (Meissner et al., 2003 ). The model we used in this paper simulates well the large-scale distribution of key climate variables (Weaver et al., 2001 ) and the ocean carbon cycle (Schmittner et al., 2008 ), and has been widely used in various global climate and carbon cycle studies (Friedlingstein et al., 2006  and Schmittner et al., 2008 ).

2.2. Simulation experiments

Before conducting the sensitivity simulations, we first set the atmospheric CO₂ concentration at the pre-industrial level of 280 × 10⁻⁶ , and set the mean state of the climate from 1960 to 1990 as the initial condition (Weaver et al., 2001 ). Then we spun up the model for 10,000 years to reach a quasi-equilibrium state between the climate and carbon cycle. At this time, the air-sea carbon flux is close to zero. Then we conducted transient simulations based on specified atmospheric CO₂ levels. Starting from the end of the spin-up simulation, the atmospheric CO₂ concentration is based on observations made from 1800 to 2005, and under the RCP 8.5 scenario after 2005. According to the IPCC (2013) , the Representative Concentration Pathways (RCPs) usually refer to the pathways extending to 2100 and their corresponding emission scenarios. Extended Concentration Pathways (ECPs) describe the RCPs' extensions from 2100 to 2500. Specifically, RCP 8.5 is a relatively high CO₂ concentration pathway; the atmospheric CO₂ concentration reaches to 935.9 × 10⁻⁶ by year 2100, then continues to rise over time, and the corresponding ECP maintains a constant concentration after 2250 (Fig. 1 a).

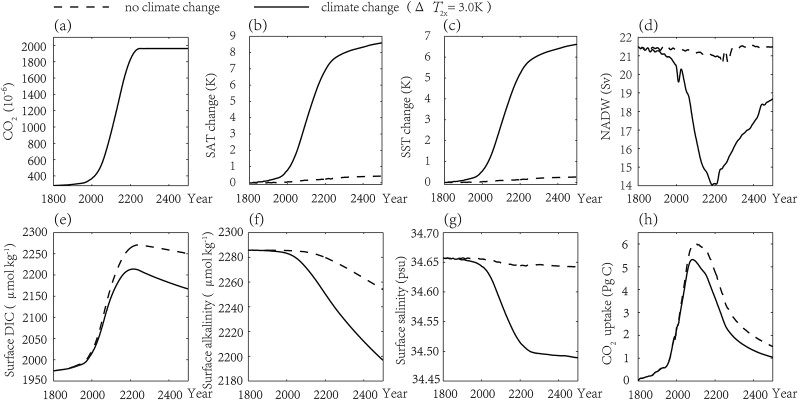
Fig. 1. Time series with (solid lines) and without (dashed lines) climate change, (a) atmospheric CO2 , (b) global mean surface air temperature change (relative to 1800), (c) global mean sea surface temperature change (relative to 1800), (d) intensity of the North Atlantic deep water formation (NADW), (e) global mean surface DIC concentration, (f) global mean surface alkalinity, (g) global mean surface salinity, (h) oceanic uptake of anthropogenic CO2 .

Based on the specified atmospheric CO₂ concentration, two simulations were performed. One simulation considers climate change due to atmospheric CO₂ increase and the impact on the ocean carbon cycle due to climate change. The other simulation does not consider climate change due to the atmospheric CO₂ increase, but assumes that while the change in atmospheric CO₂ has no direct radiation effect on global climate, the atmospheric CO₂ increase has a small effect on global warming due to its influence on terrestrial vegetation. In the first simulation, we specified different climate sensitivity values. The equilibrium climate sensitivity refers to the change in the annual and global mean surface temperature when the climate system reaches a steady state, following a doubling of the atmospheric CO₂ concentration. Empirical equations are adopted in the model to calculate the radiative forcing by the change in the atmospheric CO₂ concentration, and therefore radiative forcing can be modified by changing the empirical equations' coefficient, thus changing the climate sensitivity. In our simulations, the climate sensitivity ΔT_2x varies from 0.5 K to 4.5 K at intervals of 0.5 K (ΔT_2x  = 0.5 K, 1.0 K, 1.5 K, 2.0 K, 2.5 K, 3.0 K, 3.5 K, 4.0 K, and 4.5 K). Current estimates of climate sensitivity are 1.5–4.5 K, according to IPCC Fifth Assessment Report (IPCC, 2013 ). In this study, we focus on the difference between the simulation with a climate sensitivity of 3.0 K and the simulation with no climate change with respect to the ocean carbon cycle and the oceans ability to uptake atmospheric CO₂ . We also analyze the possible responses of the ocean carbon cycle to different climate sensitivities.

3. Results

Given a specified CO₂ concentration (RCP 8.5, Fig. 1 a), the responses of the oceanic CO₂ uptake to increasing atmospheric CO₂ concentrations and/or climate change are as follows. If increased atmospheric CO₂ has no influence on climate change through radiation, the changes in the global mean land surface air and sea surface temperatures are small enough to be ignored (Fig. 1 b and c), and can be regarded as resulting in no climate change (climate sensitivity is 0). When the climate sensitivity is set to 3.0 K, global mean land surface air and sea surface temperatures show a rising trend. Even if the CO₂ concentration remains constant after the year 2250, these temperatures still continue to rise at a relatively slower rate (Fig. 1 b and c). Relative to the year 1800, the global mean land surface air and sea surface temperatures increase by nearly 8.6 K and 6.6 K by the year 2500, respectively. Research has indicated that, under the same salinity, alkalinity, and dissolved inorganic carbon concentrations, a sea surface warming of 1 K will increase the sea surface CO₂ partial pressure about 4% (Takahashi et al., 1993 ). Meanwhile, sea surface warming will reduce seawater CO₂ solubility (Plattner et al., 2001 ), thus decreasing the oceanic CO₂ uptake. As shown in Fig. 1 e–g, compared with the simulations with no climate change, decreases in the global mean surface dissolved inorganic carbon (DIC) concentrations, alkalinity, and salinity by year 2500 are 83.4 μmol kg⁻¹ (3.7%), 57.2 μmol kg⁻¹ (2.5%), and 0.2 psu (0.4%) respectively, all of which reach maximum values. In addition, the changes in DIC concentrations and alkalinity have opposite effects on sea surface CO₂ partial pressure whereby one can nearly offset the other (Plattner et al., 2001 ). Moreover, Zhou et al. (2005) reported that global warming leads to a rise in sea surface temperature and a dilution in sea surface water at the high latitudes of the North Atlantic Ocean. This will reduce the density of seawater and weaken the meridional density gradient between the high and low latitudes, which will result in the weakening of the thermohaline circulation. This weakening will mainly be limited to the North Atlantic rather than the whole conveyor belt. As shown in Fig. 1 d, in our simulation, compared with the no climate change case, the intensity of the North Atlantic deep water formation, represented by the maximum meridional overturning stream function, decreases by about 7 Sv at most (1 Sv = 10⁶  m³  s⁻¹ , year 2185). The weakening of the North Atlantic deep water formation affects the transport of carbon from the sea surface to deep water, thereby influencing the oceanic CO₂ uptake (Friedlingstein et al., 2006 ). Since the rate of oceanic CO₂ uptake depends on CO₂ solubility, the differences between atmospheric and sea surface CO₂ partial pressure, and the ocean dynamic transport of DIC, climate change reduces the oceanic uptake of anthropogenic CO₂ emissions, and the specific tendencies over time are shown in Fig. 1 h. In our simulations, the oceanic uptake of anthropogenic CO₂ (this years total oceanic CO₂ uptake minus that in 1800) reaches a maximum of 6.0 Pg C in 2093 with no climate change, while it reaches a maximum of 5.3 Pg C in 2083 with climate change. And the maximum difference of 1.2 Pg C between the two simulations occurs in 2180.

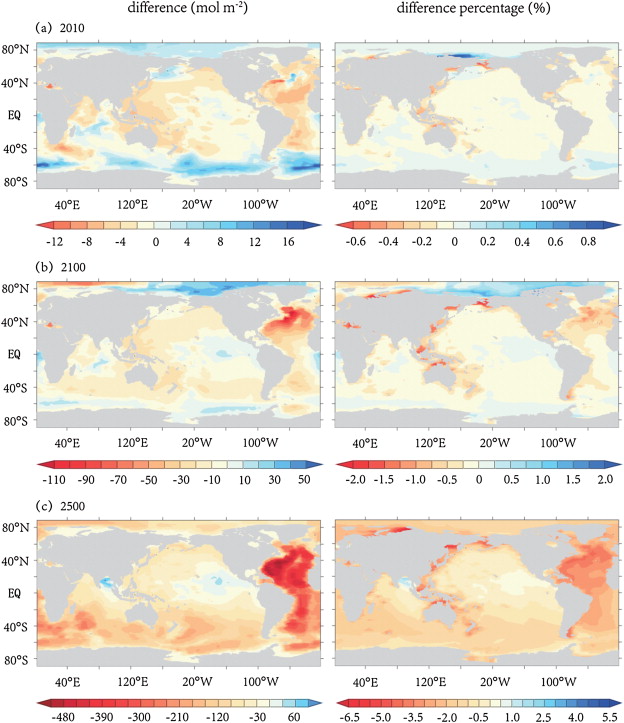
In order to investigate the distribution of anthropogenic CO₂ in the ocean, we vertically integrated the DIC concentration change (DIC concentration in a given year minus that in 1800) in all 19 layers to produce a global distribution map of the anthropogenic CO₂ column inventory with and without climate change, as shown in Fig. 2 . Anthropogenic CO₂ is not uniformly distributed throughout the ocean. Whether or not there is climate change, the maximum vertically integrated anthropogenic CO₂ concentration is always found in the North Atlantic Ocean. Due to the formation of North Atlantic deep water, this basin is a major area where seawater sinks (Stocker et al., 1994  and Sabine et al., 2004 ). As it sinks, this seawater can transport the anthropogenic CO₂ absorbed by the ocean surface to depth more efficiently than in other basins, and thus accumulates a large concentration of anthropogenic CO₂ . According to our model, the North Atlantic (north to the equator) and the Arctic Ocean account for 10% of the global ocean area and 11.9% of the global ocean volume, but they stored 24.0% (without climate change) and 23.5% (with climate change) of the global oceanic uptake of anthropogenic CO₂ in 2010, respectively, and 22.0% and 19.5% in 2500, respectively. In 2010, there were no obvious differences in the vertically integrated anthropogenic CO₂ concentrations between the simulations with and without climate change; the difference in the column inventory of anthropogenic CO₂ is just 4.1 Pg C (Table 1 ). However, as atmospheric CO₂ is absorbed continuously by the ocean and is then transported to the deep ocean, the difference becomes more significant (Fig. 2 b and c). By 2500, compared to the simulation with no climate change, climate change results in a decrease of 23.1% in the column inventory of anthropogenic CO₂ in the entire ocean, and of 32.0% in the North Atlantic-Arctic ocean (Table 1 ).

Fig. 2. Column inventory of anthropogenic CO2 (the difference: with climate change minus without climate change, unit: mol m−2 ; the percentage: the difference in the results between the simulation with and without climate change divided by the result from the simulation without climate change, unit: %).

Table 1. Total anthropogenic CO₂ column inventory (Pg C) in simulations with and without climate change.

Year	Entire ocean			Atlantic-Arctic ocean
	No climate change	ΔT2x  = 3.0 K	Percentage	No climate change	ΔT2x  = 3.0 K	Percentage
2010	144.9	140.8	2.8%	34.8	33.2	4.6%
2100	575.9	535.0	7.1%	147.9	134.8	8.9%
2500	1,974.8	1,518.2	23.1%	434.3	295.3	32.0%

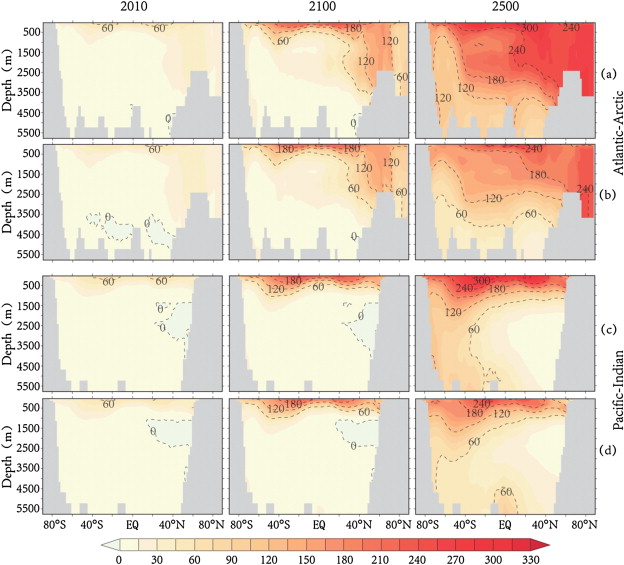
Next, we divided the ocean into the Atlantic-Arctic and the Pacific-Indian basins and analyzed the latitude-depth distribution of anthropogenic CO₂ to gain a better understanding of the distribution and transport of anthropogenic CO₂ .

Anthropogenic CO₂ enters the ocean via the air-sea exchange and the contours of the highest anthropogenic CO₂ concentrations appear in basins shallower than 500 m under each scenario (Fig. 3 ). This means that anthropogenic CO₂ concentrates in the near surface water, and the thermocline is a crucial area for the oceanic uptake of anthropogenic CO₂ . As shown in Fig. 3 , the highest concentration of anthropogenic CO₂ is found in the subtropics where near surface seawater shows convergence and subsidence, thus allowing DIC to be transported to the deep ocean, and benefitting further oceanic uptake of anthropogenic CO₂ (Bao et al., 2012 ).

Fig. 3. Latitude-depth distributions of anthropogenic CO2 (in μmol kg−1 ) in years 2010, 2100, and 2500 for the Atlantic-Arctic (a, b) and Pacific-Indian oceans (c, d) with climate change (a, c) and without climate change (b, d).

The penetration depth of anthropogenic CO₂ in the ocean depends on the rate that the near sea surface anthropogenic CO₂ is transported to the interior (Sabine et al., 2004 ). And the transport rate mainly depends on ocean circulation factors, such as thermocline ventilation, deep water and intermediate water formation, and so on (Friedlingstein et al., 2006 ). As it is affected by these factors, the penetration of anthropogenic CO₂ absorbed by the Pacific-Indian ocean is shallower and slower, and the penetration of anthropogenic CO₂ absorbed by the basins with deep water formation, such as the North Atlantic Ocean, is deeper and faster (Fig. 3 ). One study reports that regardless of whether basins are characterized by deep water formation or not, the time scales of the near surface water being mixed to the deep ocean may be centuries (Sabine et al., 2004 ). Climate change increases sea surface temperature (Fig. 1 b), which causes a decrease in the oceanic CO₂ uptake by reducing the seawaters CO₂ solubility (Plattner et al., 2001 ). This also leads to increased stratification (Sarmiento et al., 1998 ). The increased stratification leads to a decrease in vertical mixing along the isopycnals and overturning circulation, which decreases the carbon vertical transport. The increased stratification also causes a gradual collapse of thermohaline circulation throughout the entire deep ocean — the thermohaline circulation plays the major role in the carbon balance on a century time scale (Sarmiento et al., 1998 ), and its collapse has been verified in related early simulations (Joos et al., 1999 ). As Fig. 3 shows, in the year 2500 the 240 μmol kg⁻¹ contour of the DIC concentration can extend to a depth of 4,000 m in the Atlantic-Arctic ocean without climate change (Fig. 3 a), but in the simulation with ΔT_2x  = 3.0 K, it is confined to the sea surface in most of the world ocean (Fig. 3 b).

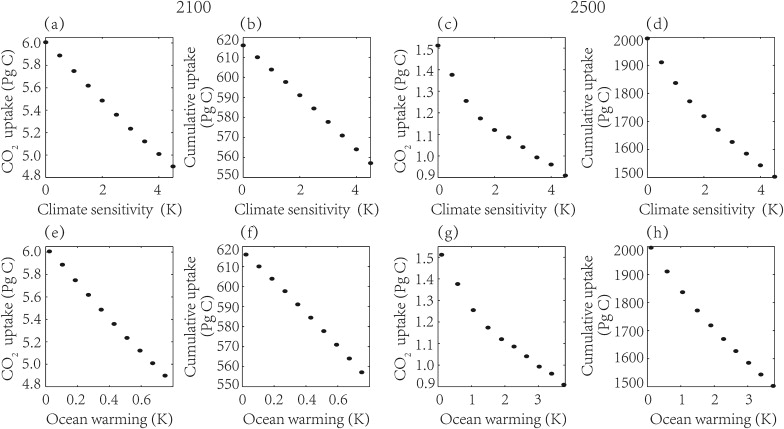
To further analyze the effects of climate change on the ocean carbon cycle, we calculated changes in the global oceanic anthropogenic CO₂ uptake for the years 2100, 2500, and 1800–2100, as well as the 1800–2500 cumulative uptake for different climate sensitivities. The climate sensitivities range from 0.5 K to 4.5 K at intervals of 0.5 K, and with no climate change the climate sensitivity is 0, as shown in Fig. 4 . In 2100, the oceanic uptake of anthropogenic CO₂ shows a linear change along with the climate sensitivity. When climate sensitivity increases by 0.5 K, the annual uptake decreases by about 0.1 Pg C, and cumulative uptake decreases by about 6.5 Pg C. In 2500, the change does not display a linear trend. Without climate change, the oceanic anthropogenic CO₂ uptake is 1.5 Pg C and the cumulative uptake is 1,996.0 Pg C. When the climate sensitivity reaches 4.5 K, the annual uptake is 0.9 Pg C and the cumulative uptake is 1,502.8 Pg C, representing decreases of 39.9% and 24.7%, respectively. As shown in Table 2 , both the global mean surface air warming and global mean ocean warming values become larger as climate sensitivity increases. Regarding the global mean ocean warming, simulated under different climate sensitivities (horizontal axis), the oceanic carbon uptake and cumulative uptake of anthropogenic CO₂ show a similar trend in the Figures whose horizontal axis is climate sensitivity. This series of simulations illustrate that climate warming decreases oceanic carbon uptake, and the higher the climate sensitivity or the greater the ocean warming, the larger is the reduction in the oceanic uptake of anthropogenic CO₂ .

Fig. 4. Oceanic uptake of anthropogenic CO2 for years 2100 and 2500, and the cumulative anthropogenic CO2 uptake (1800–2100 and 1800–2500) as a function of climate sensitivity (a–d) and global mean ocean warming (e–h) (Each dot represents a specified simulation with a specified climate sensitivity ΔT2x  = 0,0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5 K).

Table 2. 1800–2100 and 1800–2500 global mean surface air warming and global mean ocean warming with specified climate sensitivities (K).

Climate sensitivity	2100		2500
	Surface air	Entire ocean	Surface air	Entire ocean
0	0.2	0.0	0.4	0.1
0.5	0.7	0.1	1.7	0.6
1.0	1.3	0.2	3.0	1.1
1.5	2.0	0.3	4.4	1.5
2.0	2.6	0.3	5.8	1.9
2.5	3.2	0.4	7.3	2.3
3.0	3.8	0.5	8.6	2.6
3.5	4.4	0.6	9.9	3.0
4.0	5.0	0.7	11.2	3.4
4.5	5.7	0.8	12.5	3.8

4. Conclusions and discussion

• For the same CO₂ concentrations, relative to simulations without climate change (climate sensitivity is 0), when the climate sensitivity is set as 3.0 K, the changes in global mean surface air temperature and global mean sea surface temperature become larger over time, showing increases of 8.2 K and 6.4 K, respectively, by the year 2500. This warming has direct impacts on the sea surface partial pressure and the solubility of CO₂ . Owing to climate change, the sea surface DIC concentration, alkalinity, and salinity also decrease by 3.7%, 2.5%, and 0.4%, respectively. Moreover, the North Atlantic thermohaline circulation weakens as a result of ocean warming and freshening, and the intensity of the North Atlantic deep water formation decreases by 7 Sv by the year 2185. Due to the net effect of climate change, the oceanic uptake of anthropogenic CO₂ decreases by 1.2 Pg C by the year 2180.
• Anthropogenic CO₂ is not evenly distributed in the ocean, and the maximum vertically integrated values are found in the North Atlantic basin because of the characteristic North Atlantic deep water formation. The largest vertically integrated differences induced by climate change (ΔT_2x  = 3.0 K) are also found in the North Atlantic basin. By the year 2500, the total anthropogenic CO₂ in the entire ocean and in the North Atlantic-Arctic basins decrease by 23.1% and 32.0%, respectively, as a result of climate change, and the reduction in the North Atlantic-Arctic basin accounts for 30.4% of the total reduction, despite the fact that the area accounts for just 16.1% of the total ocean area, the volume accounts for just 11.9% of the total ocean volume.
• Anthropogenic CO₂ is also unevenly distributed with increasing depth in the ocean. Anthropogenic CO₂ mainly concentrates in the thermocline and its highest concentrations are found in subtropical surface waters. In the simulation with a climate sensitivity of 3.0 K, the concentrations of anthropogenic CO₂ in subtropical surface water decreased by about 20% in 2500 relative to the case without climate change. Compared with the Pacific and Indian oceans, the transport rate is faster and the concentration of anthropogenic CO₂ is higher in deep water formation regions such as the North Atlantic basin.
• Different climate sensitivities have different effects on the ocean carbon cycle. The greater the climate sensitivity, the less the annual oceanic and cumulative uptakes.

In this study, we chose a specified atmospheric CO₂ concentration to simulate resultant changes in the oceanic CO₂ uptake and the ocean carbon cycle affected by climate change. The ocean is an important carbon sink. In reality, if the CO₂ uptake by the ocean decreases, the anthropogenic CO₂ accumulating in the atmosphere will increase, which will in turn affect climate change. Therefore, it is necessary to study the impact of climate change on the ocean carbon cycle and the resulting feedback of the ocean carbon cycle to climate change. In future studies, we will use a specified CO₂ emission to investigate the feedback interactions between climate change, atmospheric CO₂ concentrations, and the ocean carbon cycle.

Acknowledgements

This work is supported by National Natural Science Foundation of China (41276073 ) and the Fundamental Research Funds for the Central Universities (2102XZZX012 ).

References

1. Bao et al., 2012 Y. Bao, F.-L. Qiao, Z.-Y. Song; The 3-dimensional numerical simulation of global ocean carbon cycle; Acta Oceanol. Sin., 34 (3) (2012), pp. 19–26 (in Chinese)
2. Bitz et al., 2001 C.M. Bitz, M.M. Holland, A.J. Weaver, et al.; Simulating the ice-thickness distribution in a coupled climate model; J. Geophys. Res. Oceans, 106 (C2) (2001), pp. 2441–2463
3. Fanning and Weaver, 1996 A.F. Fanning, A.J. Weaver; An atmospheric energy-moisture balance model: climatology, interpentadal climate change, and coupling to an ocean general circulation model; J. Geophys. Res. Atmospheres, 101 (D10) (1996), pp. 15111–15128
4. Friedlingstein et al., 2006 P. Friedlingstein, P. Cox, R. Betts, et al.; Climate-carbon cycle feedback analysis: results from the C4MIP model intercomparison; J. Clim., 19 (14) (2006), pp. 3337–3353
5. Hibler, 1979 W.D. Hibler III; A dynamic thermodynamic sea ice model; J. Phys. Oceanography, 9 (4) (1979), pp. 815–846
6. Hunke and Dukowicz, 1997 E.C. Hunke, J.K. Dukowicz; An elastic-viscous-plastic model for sea ice dynamics; J. Phys. Oceanography, 27 (9) (1997), pp. 1849–1867
7. IPCC, 2013 IPCC; Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press, Cambridge (2013) Accessed http://www.climatechange2013.org/images/report/WG1AR5_ALL_FINAL.pdf
8. Jin and Shi, 2001 X. Jin, G.-Y. Shi; The role of biological pump in ocean carbon cycle; Chin. J. Atmos. Sci., 25 (5) (2001), pp. 683–688 (in Chinese)
9. Joos et al., 1999 F. Joos, G.K. Plattner, T.F. Stocker, et al.; Global warming and marine carbon cycle feedbacks on future atmospheric CO₂; Science, 284 (5413) (1999), pp. 464–467
10. Kalnay et al., 1996 E. Kalnay, M. Kanamitsu, R. Kistler, et al.; The NCEP/NCAR 40-year reanalysis project; Bull. Am. Meteorol. Soc., 77 (3) (1996), pp. 437–471
11. Li and Xu, 2012 Y.-C. Li, Y.-F. Xu; Uptake and storage of anthropogenic CO₂ in the Pacific Ocean estimated using two modeling approaches  ; Adv. Atmos. Sci., 29 (4) (2012), pp. 795–809
12. Maier-Reimer et al., 1996 E. Maier-Reimer, U. Mikolajewicz, A. Winguth; Future ocean uptake of CO₂ : interaction between ocean circulation and biology  ; Clim. Dyn., 12 (10) (1996), pp. 711–722
13. Manabe and Stouffer, 1994 S. Manabe, R.J. Stouffer; Multiple-century response of a coupled ocean-atmosphere model to an increase of atmospheric carbon dioxide; J. Clim., 7 (1) (1994), pp. 5–23
14. Matebr and Hirst, 1999 R.J. Matebr, A.C. Hirst; Climate change feedback on the future oceanic CO₂ uptake  ; Tellus B, 51 (3) (1999), pp. 722–733
15. Meissner et al., 2003 K.J. Meissner, A.J. Weaver, H.-D. Matthews, et al.; The role of land surface dynamics in glacial inception: a study with the UVic Earth System Model; Clim. Dyn., 21 (7–8) (2003), pp. 515–537
16. Orr et al., 1999 J.C. Orr, R. Najjar, C.L. Sabine, et al.; Abiotic-howto, Internal OCMIP Report; LSCE/CEA Saclay (1999), p. 25
17. Pacanowski, 1995 R.C. Pacanowski; MOM 2 documentation, users guide and reference manual; GFDL Ocean Group Tech. Rep., 3 (3) (1995), p. 232
18. Plattner et al., 2001 G.K. Plattner, F. Joos, T.F. Stocker, et al.; Feedback mechanisms and sensitivities of ocean carbon uptake under global warming; Tellus B, 53 (5) (2001), pp. 564–592
19. Pu and Wang, 2000 Y.-F. Pu, M.-X. Wang; An ocean carbon cycle model part I: establishing of carbon model including an oceanic dynamic general circulation field, chemical, physical and biological processes occurred in the ocean; Climatic Environ. Res., 5 (2) (2000), pp. 129–140 (in Chinese)
20. Pu and Wang, 2001 Y.-F. Pu, M.-X. Wang; An ocean carbon cycle model part II: simulation analysis on the Indian Ocean; Climatic Environ. Res., 6 (1) (2001), pp. 67–76 (in Chinese)
21. Sabine et al., 2004 C.L. Sabine, R.A. Feely, N. Gruber, et al.; The oceanic sink for anthropogenic CO₂; Science, 305 (5682) (2004), pp. 367–371
22. Sarmiento et al., 1998 J.L. Sarmiento, T.M.C. Hughes, R.J. Stouffer, et al.; Simulated response of the ocean carbon cycle to anthropogenic climate warming; Nature, 393 (6682) (1998), pp. 245–249
23. Schmittner et al., 2008 A. Schmittner, A. Oschlies, H.D. Matthews, et al.; Future changes in climate, ocean circulation, ecosystems, and biogeochemical cycling simulated for a business-as-usual CO₂ emission scenario until year 4000 AD  ; Glob. Biogeochem. Cycles, 22 (2008), p. 1013
24. Stocker and Schmittner, 1997 T.F. Stocker, A. Schmittner; Influence of CO₂ emission rates on the stability of the thermohaline circulation  ; Nature, 388 (6645) (1997), pp. 862–865
25. Stocker et al., 1994 T.F. Stocker, W.S. Broecker, D.G. Wright; Carbon uptake experiments with a zonally-averaged global ocean circulation model; Tellus B, 46 (2) (1994), pp. 103–122
26. Takahashi et al., 1993 T. Takahashi, J. Olafsson, J.G. Goddard, et al.; Seasonal variation of CO₂ and nutrients in the high-latitude surface oceans: a comparative study  ; Glob. Biogeochem. Cycles, 7 (4) (1993), pp. 843–878
27. Weaver et al., 2001 A.J. Weaver, M. Eby, E.C. Wiebe, et al.; The UVic Earth System Climate Model: model description, climatology, and applications to past, present and future climates; Atmos. Ocean, 39 (4) (2001), pp. 361–428
28. Wei et al., 2012 T. Wei, S. Yang, J.C. Moore, et al.; Developed and developing world responsibilities for historical climate change and CO₂ mitigation  ; Proc. Natl. Acad. Sci., 109 (32) (2012), pp. 12911–12915
29. Wei et al., 2014 T. Wei, W. Dong, W. Yuan, et al.; Influence of the carbon cycle on the attribution of responsibility for climate change; Chin. Sci. Bull., 59 (19) (2014), pp. 2356–2362
30. Xing, 2000 R.-N. Xing; A three-dimensional world ocean carbon cycle model with ocean biota; Chin. J. Atmos. Sci., 24 (3) (2000), pp. 333–340 (in Chinese)
31. Xu and Li, 2009 Y.-F. Xu, Y.-C. Li; Estimates of anthropogenic CO₂ uptake in a global ocean model  ; Adv. Atmos. Sci., 26 (2) (2009), pp. 265–274
32. Xu et al., 1997 Y.-F. Xu, M.-X. Wang, X.-Z. Jin; A two-dimensional ocean thermohaline circulation carbon cycle model; Sci. Atmos. Sin., 21 (5) (1997), pp. 573–580 (in Chinese)
33. Zhou et al., 2005 T.-R. Zhou, X. Yu, Y. Liu, et al.; Weak response of the Atlantic thermohaline circulation to an increase of atmospheric carbon dioxide in IAP/LASG Climate System Model; Chin. Sci. Bull., 50 (3) (2005), pp. 269–275 (in Chinese)