Approximation of the scalar convection-diffusion-reaction equation with stabilized finite element formulations of high order

Resumen

En este artículo presentamos formulaciones estabilizadas de elementos finitos para resolver la ecuación de convección-difusión-reacción escalar en el caso de difusión pequeña. Por un lado, resumimos la aplicación de las formulaciones ASGS y OSS basadas en el concepto de métodos variacionales multiescala. Por otro lado, discutimos aspectos de la utilización de elementos de alto orden, centrando nuestros experimentos numéricos en elementos cuadráticos, cúbicos y de cuarto orden. Asimismo, la aplicación del método OSS requiere de la introducción de una proyección, para lo cual introducimos una modificación del elemento simplicial de cuarto orden con una regla de integración numérica asociada.

Palabras clave: Convección-difusión-reacción, métodos de elementos finitos estabilizados, convección dominante, alto orden, cuadraturas nodales

Abstract

In this paper we present stabilized finite element formulations of to solve the scalar convection-diffusion-reaction equation in the case of small diffusion. On the one hand, we summarize the application of the ASGS and OSS formulations based on the concept of variational multiscale methods. On the other hand, we discuss aspects of the use of high order elements, focusing our numerical experiments on quadratic, cubic and fourth order elements. Likewise, the application of the OSS method requires the introduction of a projection, for which we introduce a modification of the fourth order simplicial element with an associated numerical integration rule.

Keywords: Convection-diffusion-reaction, stabilized finite element methods, dominant convection, high order, nodal quadratures

1. Introducción

El contar con equipos computacionales más robustos tanto en memoria RAM como en velocidad de los procesadores ha permitido entre otras cosas incentivar a numerosos investigadores al estudio de métodos numéricos complejos en fluidos que abordan modelos constitutivos cada vez más reales, buscando resolver las ecuaciones sin hacer hipótesis de simplificación por su complejidad. Dentro de este marco, la ecuación de convección-difusión-reacción (CDR) es un modelo matemático de simulación del transporte de una magnitud física que se utiliza entre otras cosas en la simulación del transporte de contaminantes.

Es bien conocido que el método estándar de elementos finitos de Galerkin aplicado a la ecuación de CDR presenta inestabilidades en la solución cuando el término convectivo es dominante frente al término difusivo, motivo por el cual distintos autores han desarrollado formulaciones estabilizadas. Dicha estabilización consiste en añadir términos que dependen de la malla de elementos finitos a los términos de Galerkin. Así, se pueden encontrar en la literatura diferentes métodos, como el método Streamline-upwind/Petrov-Galerkin (SUPG) [1,2,3], el método de Galerkin-mínimos cuadrados (GLS) [4,5,6], el método de las características-Galerkin (CG) [7] y el método de Taylor-Galerkin (TG) [8], entre otros. Una descripción y comparación de estos métodos se puede encontrar en [9], en donde se expone que todos los métodos esencialmente consisten en la adición de un término de estabilización a la formulación original de Galerkin, y que fundamentalmente excepto por menores modificaciones este término se puede escribir como un parámetro numérico, denominado tiempo intrínseco, multiplicado al producto ${\textstyle L^{2}}$ entre el residuo de la ecuación diferencial a ser resuelta y un operador aplicado a la función de prueba.

En el presente trabajo nos centraremos en los métodos llamados variacionales multiescalas (VMS, por Variational Multi-Scale), introducidos por Hughes y otros [10,11] (véase [12] para una revisión de esta teoría). En particular, nos centraremos en la versión más común, a la que nos referiremos como método ASGS (por Algebraic Sub-Grid Scale), y al llamado método OSS (por Orthogonal Subscale Stabilization) [13,14,15,16,17].

Además de describir resumidamente los métodos ASGS y OSS, la contribución fundamental del presente trabajo es analizar su comportamiento con elementos finitos de alto orden, en particular cuadráticos, cúbicos y de cuarto orden, en todos los casos de clase ${\textstyle C^{0}}$. Para estudiar dicho comportamiento, presentaremos resultados de convergencia en malla usando soluciones manufacturadas y analizaremos cómo son de robustos estos métodos en presencia de capas límite de la solución. Asimismo, en el caso del método OSS es necesario llevar a cabo una proyección en el espacio de elementos finitos, para lo cual resulta especialmente conveniente usar reglas de integración numérica con los puntos de integración en los nodos. Para elementos simpliciales de cuarto orden esto nos lleva a proponer una modificación del elemento estándar, que describimos en detalle para el caso del elemento triangular.

El artículo está organizado como sigue. En la siguiente sección se describe el problema a resolver y las aproximaciones y formulaciones de los métodos variacionales estabilizados ASGS y OSS. En la Sección 3 presentamos el elemento finito triangular de cuarto orden modificado. Las pruebas de convergencia en malla con soluciones analíticas conocidas y las pruebas de estabilidad con capas límite, así como un ejemplo práctico, se presentan en la Sección 4. Finalmente, en base a los resultados obtenidos se extraen algunas conclusiones en la Sección 5.

2. Planteamiento del problema, aproximación y estabilización numérica

En esta sección vamos a describir la aproximación y estabilización numérica de la ecuación escalar transitoria de CDR, con condiciones de contorno y condiciones iniciales conocidas.

2.1 Problema de contorno

Sea ${\textstyle \Omega }$ un dominio acotado de ${\textstyle \mathbb {R} ^{d}}$ ${\textstyle (d=1,2,3)}$ y sea ${\textstyle \gamma =\left[0,T\right]}$, con ${\textstyle T>0}$, el dominio temporal. El problema que nos planteamos consiste en encontrar ${\textstyle u:\Omega \times \gamma \rightarrow \mathbb {R} }$ tal que

$\partial _{t}u+{\mathcal {L}}(u)=f,\qquad \left(\mathbf {x} ,t\right)\in \Omega \times \gamma ,$

(1)

con

${\mathcal {L}}(u):=-k\partial _{i}\partial _{i}u+a_{i}\partial _{i}u+su,$

(2)

sujeta a condiciones de contorno de Dirichlet

$u=u_{D},\qquad \left(\mathbf {x} ,t\right)\in \partial \Omega _{D}\times \mathbf {\gamma } ,$

condiciones de contorno de Neumann

$kn_{i}\partial _{i}u=\varphi ,\qquad \left(\mathbf {x} ,t\right)\in \partial \Omega _{N}\times \mathbf {\gamma ,}$

y condiciones iniciales

$u=u_{0},\qquad \mathbf {x} \in \Omega ,\quad {\mbox{ }}t=0.$

En estas ecuaciones, ${\textstyle \partial _{t}}$ denota la derivada temporal y ${\textstyle \partial _{i}}$ la derivada con respecto a la ${\textstyle i}$-ésima coordenada cartesiana ${\textstyle (i=1,\dots ,d)}$. Hemos usado la notación de Eintein, de manera que los índices repetidos indican suma sobre todas las coordenadas espaciales. Los coeficientes en (2) son ${\textstyle k>0}$ la difusión, ${\textstyle a_{i}}$ la componente en la dirección ${\textstyle i}$ del campo convectivo de velocidades ${\textstyle \mathbf {a} \in \mathbb {\mathbb {R} } ^{d}}$ (para flujo incompresible ${\textstyle \nabla \cdot \mathbf {a} =0}$) y ${\textstyle s\geq {0}}$ el coeficiente de reacción. ${\textstyle f}$ es el término fuente conocido y ${\textstyle n_{i}}$ es la componente ${\textstyle i}$-ésima de la normal unitaria a la frontera, denotada por ${\textstyle \partial \Omega }$, la cual está dada por ${\textstyle \partial \Omega =\partial \Omega _{D}\cup \partial \Omega _{N}.}$ Las condiciones de contorno de Dirichlet ${\textstyle u_{D}}$ y las condiciones de contorno de Neumann ${\textstyle \varphi }$ son conocidas en las fronteras ${\textstyle \partial \Omega _{D}}$ y ${\textstyle \partial \Omega _{N}}$, respectivamente. Las condiciones iniciales y de contorno de Dirichlet verifican la siguiente condición de compatibilidad ${\textstyle u_{0}\left(\mathbf {x} \right)|_{\partial \Omega _{D}}=u_{D}\left(\mathbf {x} ,0\right).}$

2.2 Forma variacional o débil del problema

Sea ${\textstyle {\mathcal {W}}}$ el espacio de funciones de ${\textstyle H^{1}(\Omega )}$ (funciones en ${\textstyle L^{2}(\Omega )}$ con derivadas en ${\textstyle L^{2}(\Omega )}$) que sea anulan en ${\textstyle \partial \Omega _{D}}$, y sea ${\textstyle L^{2}\left(0,T;{\mathcal {W}}\right)}$ el espacio de funciones en ${\textstyle \Omega \times \gamma }$ tales que la norma ${\textstyle H^{1}(\Omega )}$ es ${\textstyle L^{2}(\gamma )}$. Para simplificar la exposición, supongamos que ${\textstyle u_{D}=0}$.

Multiplicando (1) por una función ${\textstyle v\in {\mathcal {W}}}$ e integrando el término de difusión por partes, se obtiene la forma débil o variacional del problema, la cual consiste en encontrar ${\textstyle u\in L^{2}\left(0,T;{\mathcal {W}}\right)}$ tal que

$\left(\partial _{t}u,v\right)+B(u,v)=\left\langle f,v\right\rangle +\left\langle \varphi ,v\right\rangle _{\partial \Omega _{N}}\qquad \forall v\in {\mathcal {W}},$

(3)

donde

$B(u,v)=\int _{\Omega }k\partial _{i}v\partial _{i}u+\int _{\Omega }va_{i}\partial _{i}u+\int _{\Omega }vsu,$ $\left(\partial _{t}u,v\right)=\int _{\Omega }v\partial _{t}u,$ $\left\langle f,v\right\rangle =\int _{\Omega }vf,$ $\left\langle \varphi ,v\right\rangle _{\partial \Omega _{N}}=\int _{\partial \Omega _{N}}v\varphi ,$

y cumpliéndose la condición inicial ${\textstyle u=u_{0}}$ en ${\textstyle t=0}$ en ${\textstyle L^{2}(\Omega )}$. En lo que sigue, tomaremos ${\textstyle \varphi =0}$ para simplificar la notación.

2.3 Aproximación numérica con el método estándar de Galerkin

La ecuación ${\textstyle \left(\right.}$3$\left.\right)$ es la que aproximamos numéricamente en el espacio usando una formulación de elementos finitos. La discretización temporal la llevaremos a cabo mediante un método de diferencias finitas. En principio, podríamos discretizar primero en espacio o en tiempo indistintamente, aunque en nuestro caso llevaremos a cabo primero la discretización temporal.

2.3.1 Discretización temporal en diferencias finitas

Consideremos una partición uniforme del intervalo de tiempo ${\textstyle 0=t^{0}<t^{1}<\dots {<}t^{N}=T}$, con ${\textstyle \delta t=t^{n+1}-t^{n}}$, siendo ${\textstyle \delta t}$ es el tamaño del paso de tiempo, considerado constante. Aquí y en adelante, usaremos el superíndice ${\textstyle n}$ para indicar el nivel de tiempo ${\textstyle n}$.

Aunque la discretización en el tiempo puede realizarse mediante cualquier aproximación de la derivada temporal en diferencias finitas o elementos finitos, aquí utilizaremos la regla trapezoidal generalizada. Para una función genérica ${\textstyle f}$, sea

$f^{n+\theta }=\theta f^{n+1}+\left(1-\theta \right)f^{n},\qquad {0}\leq \theta \leq {1.}$

(4)

Aproximaremos

$\delta _{t}^{n}f:={\frac {1}{\delta t}}(f^{n+1}-f^{n})={\frac {1}{\theta \delta t}}(f^{n+\theta }-f^{n})\approx (\partial _{t}f)^{n+\theta }.$

Esta aproximación es de segundo orden en ${\textstyle \delta t}$ en el caso en que ${\textstyle \theta =1/2}$ (método de Crank-Nicolson) y de primer orden si ${\textstyle \theta \not =1/2}$. El caso ${\textstyle \theta =1}$ corresponde al método de Euler implícito o el método de diferencias hacia atrás de primer orden, a menudo abreviado como BDF1. Puesto que nuestro interés en este trabajo se centra en la aproximación espacial, en los ejemplos numéricos hemos usado este último método.

En cada paso de tiempo, el problema ${\textstyle \left(\right.}$3$\left.\right)$ discretizado en el tiempo, consiste en encontrar ${\textstyle u^{n+1}\in {\mathcal {W}}}$ tal que

$\left(\delta _{t}^{n}u,v\right)+B(u^{n+\theta },v)=\left\langle f^{n+\theta },v\right\rangle \qquad \forall v\in {\mathcal {W}}.$

(5)

2.3.2 Discretización de Galerkin en el espacio

Para aproximar numéricamente la ecuación ${\textstyle (}$5$)$ en el espacio por el método de elementos finitos, consideremos una partición del dominio ${\textstyle \Omega }$, de manera que ${\textstyle {\overset {n_{el}}{\underset {e=1}{\cup }}}\Omega ^{e}=\Omega }$ y ${\textstyle \Omega ^{e_{1}}\cap \Omega ^{e_{2}}=\emptyset }$ para cualesquiera ${\textstyle e_{1}}$, ${\textstyle e_{2}}$, ${\textstyle e_{1}\neq e_{2}}$, donde ${\textstyle n_{el}}$ es el número de elementos de la partición y ${\textstyle \Omega ^{e}}$ es el dominio del elemento ${\textstyle e}$.

Si ${\textstyle {\mathcal {W}}_{h}}$ es un espacio conforme de elementos finitos para aproximar ${\textstyle {\mathcal {W}}}$ (${\textstyle {\mathcal {W}}_{h}\subset {\mathcal {W}}}$), entonces el problema discreto que se conoce como el método estándar de Galerkin, que resuelve la ecuación escalar transitoria de CDR ${\textstyle (}$1$)$ con condiciones de Dirichlet y de Neumann homogéneas en la frontera, consiste en: dado ${\textstyle u_{h}^{n}\in {\mathcal {W}}_{h},}$ encontrar ${\textstyle u_{h}^{n+1}\in {\mathcal {W}}_{h}}$ tal que

$\left(\delta _{t}^{n}u_{h},v_{h}\right)+B(u_{h}^{n+\theta },v_{h})=\left\langle f^{n+\theta },v_{h}\right\rangle \qquad \forall v_{h}\in {\mathcal {W}}_{h},$

(6)

para ${\textstyle n=0,1,\dots ,N-1}$, siendo ${\textstyle u_{h}^{0}}$ conocido proyectando la condición inicial en ${\textstyle {\mathcal {W}}_{h}}$ (con el producto escalar de ${\textstyle L^{2}(\Omega )}$).

2.4 Métodos de estabilización numérica

Como se mencionó anteriormente, el método estándar de Galerkin presenta inestabilidades numéricas cuando el término convectivo es dominante con respecto al término difusivo. Los métodos que vamos a utilizar para la estabilización numérica se pueden enmarcar en el método variacional multiescalas (VMS) [10,11]. En particular, veremos dos opciones, correspondientes a dos elecciones del espacio de subescalas (véase también [13,15,16]).

2.4.1 El método variacional mutiescalas (VMS)

Aunque el método VMS puede considerar un número arbitrario de escalas en la solución, en la mayoría de las ocasiones basta con considerar dos escalas para diseñar un método de estabilización. La idea básica es descomponer para cada instante de tiempo la variable continua desconocida ${\textstyle u(\cdot ,t)\in {\mathcal {W}}}$ en una parte resoluble en el espacio de elementos finitos ${\textstyle u_{h}(\cdot ,t)\in {\mathcal {W}}_{h}}$, con ${\textstyle {\mathcal {W}}_{h}\subset {\mathcal {W}}}$, y una parte en la escala de una submalla ${\textstyle {\tilde {u}}(\cdot ,t)\in {\tilde {\mathcal {W}}}}$, con ${\textstyle {\tilde {\mathcal {W}}}\subset {\mathcal {W}}}$, la cual no puede ser capturada por la malla de elementos finitos, siendo ${\textstyle {\mathcal {W}}={\mathcal {W}}_{h}\oplus {\tilde {\mathcal {W}}}}$, donde ${\textstyle {\mathcal {\tilde {W}}}}$ es cualquier espacio para completar ${\textstyle {\mathcal {W}}_{h}}$ en ${\textstyle {\mathcal {W}}}$. Para evitar tecnicismos, podemos pensar en ${\textstyle {\mathcal {W}}}$ y ${\textstyle {\mathcal {\tilde {W}}}}$ como espacios dimensionalmente finitos, con una dimensión grande. Puesto que ${\textstyle {\tilde {\mathcal {W}}}}$ representa la componente de ${\textstyle {\mathcal {W}}}$ que no es reproducida por el espacio de elementos finitos, la llamamos espacio de las subescalas. De este modo, la variable continua desconocida podemos escribirla como ${\textstyle u=u_{h}+{\tilde {u}}}$, donde ${\textstyle u_{h}}$ es la componente de ${\textstyle u}$ en el espacio de elementos finitos y ${\textstyle {\tilde {u}}}$ es su componente en el complemento (con respecto a un cierto producto interno) de ${\textstyle {\mathcal {W}}}$. La misma descomposición es aplicable a las funciones de test.

Aplicando la descomposición mencionada a la ecuación continua ${\textstyle \left(\right.}$3$\left.\right)$ se obtiene:

$\left(\partial _{t}\left(u_{h}+{\tilde {u}}\right),v_{h}+{\tilde {v}}\right)+B\left(u_{h}+{\tilde {u}},v_{h}+{\tilde {v}}\right)=\left\langle f,v_{h}+{\tilde {v}}\right\rangle \qquad \forall v{}_{h}\in {\mathcal {W}}_{h},\;\forall {\tilde {v}}\in {\tilde {\mathcal {W}}}.$

(7)

Utilizando la linealidad de las formas involucradas, la ecuación ${\textstyle \left(\right.}$7$\left.\right)$ se puede descomponer en el siguiente sistema de ecuaciones:

$\left(\partial _{t}u_{h},v_{h}\right)+\left(\partial _{t}{\tilde {u}},v_{h}\right)+B\left(u_{h},v_{h}\right)+B\left({\tilde {u}},v_{h}\right)=\left\langle f,v_{h}\right\rangle \qquad \forall v_{h}\in {\mathcal {W}}_{h},$ (8) $\left(\partial _{t}u_{h},{\tilde {v}}\right)+\left(\partial _{t}{\tilde {u}},{\tilde {v}}\right)+B\left(u_{h},{\tilde {v}}\right)+B\left({\tilde {u}},{\tilde {v}}\right)=\left\langle f,{\tilde {v}}\right\rangle \qquad \forall {\tilde {v}}\in {\tilde {\mathcal {W}}}.$ (9)

Para simplificar el método resultante, vamos a asumir que $\partial _{t}{\tilde {u}}=0$, lo cual implica que la variación temporal de las subescalas en ${\textstyle \left(\right.}$8$\left.\right)$ y ${\textstyle \left(\right.}$9$\left.\right)$ es despreciable comparada con el resto de términos. En [17] las subescalas que satisfacen esta condición son llamadas cuasi-estáticas. La inclusión o no de la derivada temporal de las subescalas se analiza en detalle en [18], donde se muestra que es esencial para evitar las inestabilidades que pueden producirse para pasos de tiempo pequeños, que en este trabajo no consideraremos.

Con esta suposición el sistema de ecuaciones ${\textstyle \left(\right.}$8$\left.\right)$ y ${\textstyle \left(\right.}$9$\left.\right)$ se escribe de la siguiente manera:

$\left(\partial _{t}u_{h},v_{h}\right)+B\left(u_{h},v_{h}\right)+B\left({\tilde {u}},v_{h}\right)=\left\langle f,v_{h}\right\rangle \qquad \forall v_{h}\in {\mathcal {W}}_{h},$ (10) $\left(\partial _{t}u_{h},{\tilde {v}}\right)+B\left(u_{h},{\tilde {v}}\right)+B\left({\tilde {u}},{\tilde {v}}\right)=\left\langle f,{\tilde {v}}\right\rangle \qquad \forall {\tilde {v}}\in {\tilde {\mathcal {W}}}.$ (11)

La ecuación ${\textstyle \left(\right.}$10$\left.\right)$ corresponde a la escala resoluble ${\textstyle u_{h}}$ en el espacio de elementos finitos y tiene tres términos a su lado izquierdo, donde el primero y segundo términos son la contribución temporal y espacial de ${\textstyle u_{h}}$ del método estándar de Galerkin y el tercero toma en cuenta la influencia de la subescala en ${\textstyle u_{h}}$.

De la ecuación ${\textstyle \left(\right.}$11$\left.\right)$ se obtiene ${\textstyle {\tilde {u}}}$, que es la contribución de la subescala sobre la componente en el espacio de elementos finitos. Para evitar aproximar derivadas de ${\textstyle {\tilde {u}}}$, podemos considerar la siguiente integración por partes en cada elemento:

$B\left({\tilde {u}},v_{h}\right)={\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left(-k\partial _{i}\left(\partial _{i}v_{h}\right){\tilde {u}}-\partial _{i}v_{h}a_{i}{\tilde {u}}+v_{h}s{\tilde {u}}\right)$ $+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\partial \Omega ^{e}}k\partial _{i}v_{h}n_{i}{\tilde {u}}+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\partial \Omega ^{e}}v_{h}n_{i}a_{i}{\tilde {u}}.$

(12)

Sea ${\textstyle {\mathcal {L}}^{*}}$ el adjunto del operador ${\textstyle {\mathcal {L}}}$, dado por

${\mathcal {L}}^{*}\left(v_{h}\right)=-k\partial _{i}\left(\partial _{i}v_{h}\right)-a_{i}\partial _{i}v_{h}+sv_{h}.$

(13)

La ecuación ${\textstyle \left(\right.}$12$\left.\right)$ se puede escribir como

$B\left({\tilde {u}},v_{h}\right)={\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}{\mathcal {L}}^{*}\left(v_{h}\right){\tilde {u}}+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\partial \Omega ^{e}}k\partial _{i}v_{h}n_{i}{\tilde {u}}+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\partial \Omega ^{e}}v_{h}n_{i}a_{i}{\tilde {u}}.$

(14)

Reemplazando ${\textstyle \left(\right.}$14$\left.\right)$ en la ecuación ${\textstyle \left(\right.}$10$\left.\right)$, ésta se puede escribir como

$\left(\partial _{t}u_{h},v_{h}\right)+B\left(u_{h},v_{h}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}{\mathcal {L}}^{*}\left(v_{h}\right){\tilde {u}}+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\partial \Omega ^{e}}k\partial _{i}v_{h}n_{i}{\tilde {u}}+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\partial \Omega ^{e}}v_{h}n_{i}a_{i}{\tilde {u}}=\left\langle f,v_{h}\right\rangle$

(15)

para todo ${\textstyle v_{h}\in {\mathcal {W}}_{h}}$. Ahora bien integrando por partes los términos ${\textstyle B\left(u_{h},{\tilde {v}}\right)}$ y ${\textstyle B\left({\tilde {u}},{\tilde {v}}\right)}$ de la ecuación ${\textstyle \left(\right.}$11$\left.\right)$, ésta se puede escribir como

${\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\partial \Omega ^{e}}k{\tilde {v}}n_{i}\partial _{i}\left(u_{h}+{\tilde {u}}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}{\tilde {v}}{\mathcal {L}}\left({\tilde {u}}\right)={\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}{\tilde {v}}\left[f-{\mathcal {L}}\left(u_{h}\right)\right]-{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}{\tilde {v}}\partial _{t}u_{h}\qquad \forall {\tilde {v}}\in {\tilde {\mathcal {W}}}.$

(16)

Observemos que el primer término de la ecuación ${\textstyle \left(\right.}$16$\left.\right)$ se anula, ya que en la frontera de los elementos las componentes normales de los flujos de ${\textstyle u}$ son iguales pero de signo contrario, debido a que los flujos difusivos deben ser continuos a través de los contornos ínter-elementales. Como resultado de esto, la ecuación ${\textstyle \left(\right.}$16$\left.\right)$ es equivalente a encontrar ${\textstyle {\tilde {u}}\in {\tilde {\mathcal {W}}}}$ tal que

${\mathcal {L}}\left({\tilde {u}}\right)=f-{\mathcal {L}}\left(u_{h}\right)-\partial _{t}u_{h}+v_{h,{ort}},\qquad \mathrm {en} \;\Omega ^{e}\quad \forall v_{h,{ort}}\in {\tilde {\mathcal {W}}}^{\perp },$ (17) ${\tilde {u}}={\tilde {u}}_{esq},\qquad \mathrm {en} \;\partial \Omega ^{e},$ (18)

para ${\textstyle e=1,...,n_{el}}$ y para una cierta función ${\textstyle {\tilde {u}}_{esq}}$, que llamamos el esqueleto de ${\textstyle u}$. Es importante observar que la ecuación ${\textstyle \left(\right.}$17$\left.\right)$ se verifica para cualquier elemento ${\textstyle v_{h,{ort}}}$ ortogonal a ${\textstyle {\tilde {\mathcal {W}}}.}$ La presencia del elemento ${\textstyle v_{h,{ort}}}$ en la ecuación ${\textstyle \left(\right.}$17$\left.\right)$ garantiza que ${\textstyle {\mathcal {L}}\left({\tilde {u}}\right)-\left[f-{\mathcal {L}}\left(u_{h}\right)\right]+\partial _{t}u_{h}}$ pertenezca a ${\textstyle {\tilde {\mathcal {W}}}^{\perp }}$, que es lo que implica la ecuación ${\textstyle \left(\right.}$16$\left.\right)$ sin el primer término. En otras palabras, ${\textstyle v_{h,{ort}}}$ garantiza que ${\textstyle {\tilde {u}}}$ pertenezca al espacio de subescalas ${\textstyle {\tilde {\mathcal {W}}}}$ (y no a todo el espacio ${\textstyle {\mathcal {W}}}$).

Las ecuaciones ${\textstyle \left(\right.}$15$\left.\right),$ ${\textstyle \left(\right.}$17$\left.\right)$ y ${\textstyle \left(\right.}$18$\left.\right)$ equivalen exactamente al sistema de ecuaciones ${\textstyle \left(\right.}$10$\left.\right)$ y ${\textstyle \left(\right.}$11$\left.\right),$ en donde hasta ahora no hemos hecho ninguna aproximación. El siguiente paso es hacer una selección de las funciones ${\textstyle {\tilde {u}}_{esq},}$ ${\textstyle v_{h,ort}}$ y una solución aproximada de la ecuación ${\textstyle \left(\right.}$17$\left.\right).$ La manera de escoger dichas funciones da lugar a las formulaciones ASGS y OSS que describimos más adelante. Los pasos comunes los describimos a continuación.

Para seleccionar ${\textstyle {\tilde {u}}_{esq}}$ vamos a usar el siguiente argumento. Para tener una aproximación discreta óptima de ${\textstyle u}$ que dé valores nodales exactos, se podría pedir que las subescalas se anulen en los contornos de los elementos. En problemas unidimensionales esto da condiciones de contorno homogéneas para el problema ${\textstyle \left(\right.}$17$\left.\right)$ y ${\textstyle \left(\right.}$18$\left.\right)$ en los extremos de cada elemento. Para los casos de más de una dimensión espacial, esto no es posible, puesto que la solución del problema continuo ${\textstyle u}$ tendría que ser polinómica en los contornos de los elementos para que pudiera coincidir con ${\textstyle u_{h}}$. Sin embargo, imponer que ${\textstyle {\tilde {u}}_{esq}=0}$ puede pensarse como una aproximación.

Suponer que ${\textstyle {\tilde {u}}_{esq}=0}$ equivale a considerar el espacio de las subescalas ${\textstyle {\tilde {\mathcal {W}}}}$ como un espacio de funciones burbuja, es decir, un espacio de funciones que se anulan en los contornos de los elementos (véase [19,6]). Con esta aproximación, los términos con las integrales en los contornos de los elementos de la ecuación ${\textstyle \left(\right.}$15$\left.\right)$ desaparecen, por lo cual el problema a ser resuelto consiste en encontrar para cada instante de tiempo ${\textstyle t}$ una función ${\textstyle u_{h}(\cdot ,t)\in {\mathcal {W}}_{h}}$ tal que

$\left(\partial _{t}u_{h},v_{h}\right)+B\left(u_{h},v_{h}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}{\mathcal {L}}^{*}\left(v_{h}\right){\tilde {u}}=\left\langle f,v_{h}\right\rangle \qquad \forall v_{h}\in {\mathcal {W}}_{h},$

(19)

en donde todavía hace falta determinar ${\textstyle {\tilde {u}}}$. Para ello, tenemos que resolver de forma aproximada el problema ${\textstyle \left(\right.}$17$\left.\right)$ y ${\textstyle \left(\right.}$18$\left.\right)$ en el espacio de las subescalas ${\textstyle {\tilde {\mathcal {W}}}}$ de funciones burbuja. Formalmente podemos escribir:

${\tilde {u}}={\mathcal {L}}^{-1}\left[f-{\mathcal {L}}\left(u_{h}\right)-\partial _{t}u_{h}+v_{h,ort}\right],$

(20)

en cada elemento, donde ${\textstyle {\mathcal {L}}^{-1}}$ es el operador inverso del operador ${\textstyle {\mathcal {L}}}$ con condiciones de Dirichlet homogéneas.

De la ecuación ${\textstyle \left(\right.}$19$\left.\right)$ vemos que solo se necesita la componente de ${\textstyle {\tilde {u}}}$ sobre el espacio ${\textstyle {\mathcal {L}}\left({\mathcal {W}}_{h}\right)}$, donde ${\textstyle {\mathcal {L}}\left({\mathcal {W}}_{h}\right)}$ es el espacio de funciones de la forma ${\textstyle {\mathcal {L}}\left(v_{h}\right)}$, con ${\textstyle v_{h}\in {\mathcal {W}}_{h}}$. Esto sugiere aproximar ${\textstyle \left(\right.}$20$\left.\right)$ como

${\tilde {u}}\approx \tau ^{e}\left[f-{\mathcal {L}}\left(u_{h}\right)-\partial _{t}u_{h}+v_{h,ort}\right]\quad {\hbox{en}}~\Omega ^{e},$

(21)

donde ${\textstyle \tau ^{e}}$ es el parámetro de estabilización y que se calcula dentro del dominio de cada elemento. Es una aproximación algebraica al operador ${\textstyle {\mathcal {L}}^{-1}}$.

El diseño de ${\textstyle \tau ^{e}}$ es una de las piedras angulares en el desarrollo de los métodos de elementos finitos estabilizados. Algunas formulaciones algebraicas para el diseño del parámetro de estabilización para la ecuación escalar de CDR en 1D, basadas en el principio del máximo discreto, pueden encontrarse en [10,11,9]. Un posible argumento para obtener ${\textstyle \tau ^{e}}$ es el análisis de Fourier que se presenta en [17,20,21]. En este trabajo, para abordar la utilización de elementos finitos de alto orden, el diseño del ${\textstyle \tau }$ que adoptaremos es:

$\tau ^{e}=\left[c_{1}{\frac {k}{\left({\frac {h^{e}}{p^{2}}}\right)^{2}}}+c_{2}{\frac {|{\boldsymbol {a}}|}{\frac {h^{e}}{p}}}+c_{3}s\right]^{-1},$

(22)

donde ${\textstyle c_{1},}$ ${\textstyle c_{2},}$ ${\textstyle c_{3}}$ son constantes algorítmicas, que para los ejemplos numéricos hemos adoptado ${\textstyle c_{1}=12,}$ ${\textstyle c_{2}=2}$ y ${\textstyle c_{3}=1,}$ ${\textstyle k}$ es coeficiente de difusión, ${\textstyle |\mathbf {a} |}$ es la norma de la velocidad, ${\textstyle s}$ es el coeficiente de reacción, ${\textstyle h^{e}}$ es el diámetro del elemento y ${\textstyle p}$ es el orden polinomial de interpolación.

A falta de determinar la función ${\textstyle v_{h,ort}}$, y por consiguiente el espacio de subescalas, el problema para la función ${\textstyle u_{h}}$ se obtiene reemplazando la ecuación (21) en (19) y usando la expresión (22).

2.4.2 El método ASGS (Algebraic Sub-Grid Scales)

La idea del método ASGS es tomar como espacio de subescalas el espacio de funciones que son residuos de funciones de elementos finitos, es decir, el espacio de funciones de la forma ${\textstyle f-{\mathcal {L}}\left(v_{h}\right)-\partial _{t}v_{h}}$, con ${\textstyle v_{h}\in {\mathcal {W}}_{h}}$. Esto nos lleva a que ${\textstyle v_{h,ort}=0}$.

El problema que finalmente obtenemos a partir de (21) y (19) con ${\textstyle v_{h,ort}=0}$ es:

$\left(\partial _{t}u_{h},v_{h}\right)+B\left(u_{h},v_{h}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left(-{\mathcal {L}}^{*}\left(v_{h}\right)\right)\tau ^{e}\left[\partial _{t}u_{h}+{\mathcal {L}}\left(u_{h}\right)-f\right]=\left\langle f,v_{h}\right\rangle \qquad \forall v_{h}\in {\mathcal {W}}_{h}.$

(23)

Esta ecuación variacional discreta, a la cual hay que añadirle las condiciones iniciales, la podemos ahora discretizar en el tiempo usando por ejemplo la regla trapezoidal descrita anteriormente. Para ello, habrá que sustituir ${\textstyle \partial _{t}u_{h}}$ por ${\textstyle \delta _{t}^{n}u_{h}}$ y evaluar el resto de funciones dependientes del tiempo que aparecen en ${\textstyle t^{n+\theta }}$.

El parámetro de estabilización ${\textstyle \tau ^{e}}$ para elementos finitos de alto orden está dado por la ecuación ${\textstyle \left(\right.}$22$\left.\right)$, el operador ${\textstyle {\mathcal {L}}}$ por ${\textstyle \left(\right.}$2$\left.\right)$ y el operador ${\textstyle {\mathcal {L}}^{*}}$ por la ecuación ${\textstyle \left(\right.}$13$\left.\right)$.

2.4.3 El método OSS (Orthogonal Subscales Stabilization)

En este caso, el espacio de subescalas no será el espacio de residuos de elementos finitos como en el caso anterior, sino que se toma como espacio ${\textstyle {\mathcal {\tilde {W}}}}$ el espacio ortogonal en el sentido de ${\textstyle L^{2}}$ al espacio de elementos finitos, es decir,

${\mathcal {{\tilde {W}}={\mathcal {W}}}}_{h}^{\perp },$

(24)

que es una legítima elección que cumple con ${\textstyle {\mathcal {W}}={\mathcal {W}}_{h}\oplus {\mathcal {\tilde {W}}}}$.

Tomando en cuenta (24), de (17) se sigue que

$v_{h,{ort}}\in {\mathcal {W}}_{h},\quad {\tilde {u}}\in {\mathcal {W}}_{h}^{\perp },$

lo que significa que ${\textstyle v_{h,{ort}}}$ es una función del espacio de elementos finitos y por lo tanto numéricamente calculable, mientras que ${\textstyle {\tilde {u}}}$ estará en el espacio ortogonal a ${\textstyle {\mathcal {W}}_{h}}$. A este espacio ${\textstyle {\mathcal {W}}_{h}^{\perp }}$ escogido para las subescalas ${\textstyle {\tilde {u}}}$ lo denominamos espacio de subescalas ortogonales.

Puesto que ${\textstyle {\tilde {u}}\in {\mathcal {W}}_{h}^{\perp }}$, de (21) se tiene que

$0=\int _{\Omega }{\tilde {u}}v_{h}\approx {\overset {n_{el}}{\underset {e=1}{\sum }}}\int _{\Omega ^{e}}\tau ^{e}\left[f-{\mathcal {L}}\left(u_{h}\right)-\partial _{t}u_{h}\right]v_{h}+{\overset {n_{el}}{\underset {e=1}{\sum }}}\int _{\Omega ^{e}}\tau ^{e}\left(v_{h,{ort}}\right)v_{h}\qquad \forall v_{h}\in {\mathcal {W}}_{h}.$

(25)

Si llamamos ${\textstyle {\Pi }_{\tau }}$ la proyección ${\textstyle L^{2}}$ sobre el espacio de elementos finitos pesada con ${\textstyle \tau ^{e}}$ dentro de cada elemento, de (25) se tiene que

$v_{h,{ort}}=-{\Pi }_{\tau }\left[f-{\mathcal {L}}\left(u_{h}\right)-\partial _{t}u_{h}\right].$

(26)

Reemplazando (26) en (21) tenemos

${\tilde {u}}\approx \tau ^{e}\left[f-{\mathcal {L}}\left(u_{h}\right)-\partial _{t}u_{h}-{\Pi }_{\tau }\left[f-{\mathcal {L}}\left(u_{h}\right)-\partial _{t}u_{h}\right]\right].$

(27)

Sea ahora

${\Pi }_{\tau }^{\perp }={I}-{{\Pi }_{\tau }},$

(28)

donde ${\textstyle {I}}$ es la identidad en ${\textstyle {\mathcal {W}}}$ y ${\textstyle {\Pi }_{\tau }^{\perp }}$ es la proyección sobre el espacio ortogonal al espacio de elementos finitos. La ecuación (27) se puede escribir entonces como

${\tilde {u}}\approx \tau ^{e}{\Pi }_{\tau }^{\perp }\left[f-{\mathcal {L}}\left(u_{h}\right)-\partial _{t}u_{h}\right].$

(29)

Podemos reemplazar esta expresión en (15) y usar el hecho de que las integrales sobre los contornos de los elementos son cero, con lo cual obtenemos la formulación estabilizada de elementos finitos OSS que resuelve la ecuación escalar de CDR transitoria, la cual consiste en encontrar ${\textstyle u_{h}(\cdot ,t)\in {\mathcal {W}}_{h}}$ en cada instante de tiempo ${\textstyle t}$ tal que

$\left(\partial _{t}u_{h},v_{h}\right)+B\left(u_{h},v_{h}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left(-{\mathcal {L}}^{*}\left(v_{h}\right)\right)\tau ^{e}{\Pi }_{\tau }^{\perp }\left[\partial _{t}u_{h}+{\mathcal {L}}\left(u_{h}\right)-f\right]=\left\langle f,v_{h}\right\rangle \qquad \forall v_{h}\in {\mathcal {W}}_{h}.$

(30)

Podemos aplicar aquí los mismos comentarios que para ${\textstyle \left(\right.}$23$\left.\right)$. Sin embargo, hay una consideración importante a tener en cuenta, y es que puesto que ${\textstyle \partial _{t}u_{h}}$ es una función que pertenece al espacio de elementos finitos ${\textstyle {\mathcal {W}}_{h}}$, su componente en el espacio ortogonal es nula, esto es, la ecuación variacional discreta anterior se reduce a

$\left(\partial _{t}u_{h},v_{h}\right)+B\left(u_{h},v_{h}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left(-{\mathcal {L}}^{*}\left(v_{h}\right)\right)\tau ^{e}{\Pi }_{\tau }^{\perp }\left[{\mathcal {L}}\left(u_{h}\right)-f\right]=\left\langle f,v_{h}\right\rangle \qquad \forall v_{h}\in {\mathcal {W}}_{h}.$

(31)

2.4.4 Propiedades de estabilidad y convergencia

Aunque los métodos ASGS y OSS difieren en la definición del espacio de subescalas, ambos tienen las mismas propiedades de estabilidad y convergencia. No es nuestro objetivo presentar el análisis numérico de estos métodos, el cual puede encontrarse en [22] (véase también [23,24] y [25] para la teoría general), sino mostrar en qué sentido dichos métodos son estables y convergen, justificar la expresión del parámetro de estabilización (y en particular de su dependencia en ${\textstyle p}$) e indicar cómo debe ser la integración numérica para preservar la convergencia asociada a la integración exacta. Explotaremos este último punto en el apartado siguiente.

Para simplificar la exposición, consideremos el problema estacionario, con coeficientes constantes, ${\textstyle s=0}$ y malla de elementos finitos uniforme, de tamaño ${\textstyle h}$. En este caso, el parámetro de estabilización dado por (22) será el mismo en todos los elementos.

Los métodos ASGS y OSS se puede demostrar que son estables y convergentes en la norma:

${\vert \!\vert \!\vert }v_{h}{\vert \!\vert \!\vert }^{2}:=k\Vert \nabla v_{h}\Vert ^{2}+\tau \Vert \mathbf {a} \cdot \nabla v_{h}\Vert ^{2},$

(32)

donde ${\textstyle \Vert \cdot \Vert }$ es la norma de ${\textstyle L^{2}(\Omega )}$. El punto clave para demostrar esta estabilidad es hacer uso del estimador inverso (ver por ejemplo [25])

${\Vert \nabla v_{h}\Vert \leq C_{inv}{\frac {p^{2}}{h}}\Vert v_{h}\Vert },$

válido para cualquier función de elementos finitos ${\textstyle v_{h}}$, siendo ${\textstyle C_{inv}}$ una constante que depende de la forma de la malla, pero no de su tamaño ${\textstyle h}$ ni del orden de interpolación ${\textstyle p}$ . La potencia 2 de ${\textstyle p^{2}}$ es precisamente quien obliga a dividir ${\textstyle h}$ por ${\textstyle p^{2}}$ en la contribución del término difusivo en el parámetro de estabilización dado por (22). Con ello tenemos garantizada la estabilidad.

Para analizar la convergencia es necesario hacer uso de las propiedades de interpolación. Si ${\textstyle \Vert \cdot \Vert _{H^{r}}}$ es la norma del espacio de Sobolev ${\textstyle H^{r}(\Omega )}$, la solución ${\textstyle u}$ del problema continuo es suficientemente regular y ${\textstyle {\tilde {u}}_{h}}$ es su mejor aproximación en el espacio de elementos finitos, se tiene que

$\Vert u-{\tilde {u}}_{h}\Vert _{H^{r}}\leq C{\frac {h^{p+1-r}}{p^{p+1-r}}}\Vert u\Vert _{H^{p+1}},$

(33)

donde los casos de interés corresponden a ${\textstyle r=0}$ y ${\textstyle r=1}$. Aquí y en lo que sigue, ${\textstyle C}$ es una constante que no depende de la malla. Con este estimador de interpolación, es posible demostrar que la función de error de las formulaciones que consideramos, dada por

$E(h)=k^{1/2}\Vert \nabla u-\nabla {\tilde {u}}_{h}\Vert +\tau ^{1/2}\sum _{K}\Vert -k\Delta (u-{\tilde {u}}_{h})+\mathbf {a} \cdot \nabla (u-{\tilde {u}}_{h})\Vert _{K}+\tau ^{-1/2}\Vert u-{\tilde {u}}_{h}\Vert$

se comporta como

$E(h)=\left[k+{\frac {\vert \mathbf {a} \vert h}{p}}+\min \left(p^{2},{\frac {\vert \mathbf {a} \vert ^{2}h^{2}}{p^{2}k^{2}}}\right)k\right]^{1/2}{\frac {h^{p}}{p^{p}}}\Vert u\Vert _{H^{p+1}}.$

(34)

Que ${\textstyle E(h)}$ sea la función de error de los métodos ASGS y OSS en la norma (32) quiere decir que

${\vert \!\vert \!\vert }u-u_{h}{\vert \!\vert \!\vert }\leq CE(h).$

En virtud de la expresión (32) de la norma de trabajo y de la función de error (34), se observa que el estimador de error presentado es óptimo tanto para advección dominante como para difusión dominante. Hay que notar sin embargo que si se considera la convergencia en ${\textstyle p}$, hay un rango de parámetros en los que se pierde la optimalidad (véase [22]).

El objetivo de haber presentado los resultados de estabilidad y convergencia en este trabajo es doble. Por un lado, justifica la validez de la expresión del parámetro de estabilización (22) para elementos de alto orden, que es el caso que nos ocupa. Por otro lado, nos permite observar que si la integración es numérica y no exacta (como obviamente siempre es el caso), hay un límite de exactitud mínimo para no perder orden de convergencia de la aproximación. En el apartado siguiente presentaremos una modificación del elemento triangular de cuarto orden con una cuadratura numérica asociada. En este caso, ${\textstyle p=4}$, con lo que de acuerdo con (34) la cuadratura debe ser como mínimo de cuarto orden en el caso de difusión dominante y de orden ${\textstyle 9/2}$ para convección dominante. De hecho, en presencia de término reactivo (${\textstyle s>0}$) y con reacción dominante se obtiene que la cuadratura mínima debe ser de quinto orden. Este hecho lo usamos a continuación.

3. Elemento finito triangular modificado de cuarto orden

3.1 Introducción

En el método OSS, para calcular la proyección ortogonal del residuo en la ecuación ${\textstyle \left(\right.}$31$\left.\right)$, lo que hacemos es calcular la proyección del residuo en el espacio de elementos finitos. Suponiendo para simplificar que los parámetros de estabilización son iguales para todos los elementos, debemos resolver el sistema

$\int _{\Omega }v_{h}\Pi _{\tau }=\int _{\Omega }v_{h}\left[{\mathcal {L}}(u_{h})-f\right],\quad \forall v_{h}\in {\mathcal {W}}_{h},$

(35)

siendo ${\textstyle \Pi _{\tau }=\Pi _{\tau }({\mathcal {L}}(u_{h})-f)}$. Cuando expresamos ${\textstyle \Pi _{\tau }}$ en función de los valores nodales ${\textstyle \mathbf {\Pi } }$ y tomamos ${\textstyle v_{h}}$ como las funciones de forma, (35) da lugar al sistema lineal

$\mathbf {M} \mathbf {\Pi } =\mathbf {R} ,$

(36)

donde ${\textstyle \mathbf {R} }$ es conocido y ${\textstyle \mathbf {M} }$ es la matriz de masa de la partición de elementos finitos. Esta matriz de masa es en principio llena, por lo que es necesario resolver el sistema (36). Sin embargo, es bien sabido que ${\textstyle \mathbf {M} }$ se puede aproximar por una matriz diagonal ${\textstyle \mathbf {M} _{d}}$ usando una regla de integración numérica con los puntos de integración en los nodos (cuadratura cerrada) en vez de la integral exacta que aparece en (35). Con ello la resolución del sistema que aproxima a (36) es trivial. El punto clave es que la exactitud de la regla de integración numérica debe preservar la de la aproximación de elementos finitos que se tendría con la integración exacta.

En ocasiones las matrices de masa diagonales obtenidas a través de una cuadratura cerrada presentan en su diagonal valores nulos, lo cual hace que no sean invertibles e imposibilita su uso. En elementos lineales como el ${\textstyle P_{1}}$ (simplicial, es decir, triangular para ${\textstyle d=2}$ y tetraédrico para ${\textstyle d=3}$), esta matriz se obtiene directamente utilizando integración cerrada, con todos sus pesos distintos de cero. Lo mismo sucede para elementos cúbicos, mientras que los elementos cuadráticos tienen que subdividirse en elementos lineales y usar cuadradura nodal para la división resultante; con este procedimiento puede obtenerse una matriz de masa diagonal que, si bien reduciría el orden de convergencia en caso de que se reemplazara por ella la matriz de masa original, puede usarse como precondicionador para resolver el sistema (36).

Atención especial merece el elemento de cuarto orden ${\textstyle P_{4}}$ simplicial. Veremos a continuación que es posible modificar el elemento convencional, en el sentido de alterar la posición de los nodos centrales, y plantear una regla de integración numérica con los puntos de integración en los nodos y los pesos distintos de cero, lo cual nos permitirá aproximar la matriz de masa por una matriz diagonal invertible. Además, dicha regla de integración veremos que es capaz de integrar de manera exacta hasta un polinomio completo de quinto grado, con lo que de acuerdo con la discusión del apartado anterior no se disminuirá el orden de aproximación de la formulación final.

Aunque es posible aplicar la modificación que proponemos tanto para ${\textstyle d=2}$ como para ${\textstyle d=3}$, haremos los desarrollos en el primer caso. Plantearemos el elemento ${\textstyle P_{4}}$ modificado considerando móviles los tres nodos interiores del elemento ${\textstyle P_{4}}$ original y parametrizando la posición de los mismos con una variable cuyo valor será incógnita, al igual que los pesos de la regla de integración nodal asociada; la posición de los 12 nodos restantes es la misma que la del elemento ${\textstyle P_{4}}$ original.

3.2 Descripción del elemento P₄ modificado

En la Figura 1 se representa el elemento en el dominio de referencia, dado por el triángulo ${\textstyle 0\leq x\leq 1}$, ${\textstyle 0\leq y\leq 1}$, ${\textstyle x+y\leq 1}$. Las posiciones de los nodos sobre los lados es la del elemento estándar, pero hemos introducido una variable ${\textstyle z}$ para parametrizar la posición de los tres nodos interiores, obteniéndose así el elemento que llamaremos ${\textstyle P_{4}}$ modificado, con los tres nodos interiores móviles en función del parámetro ${\textstyle z}$. Obsérvese que con ${\textstyle z=1/4}$ tendríamos el elemento ${\textstyle P_{4}}$ original.

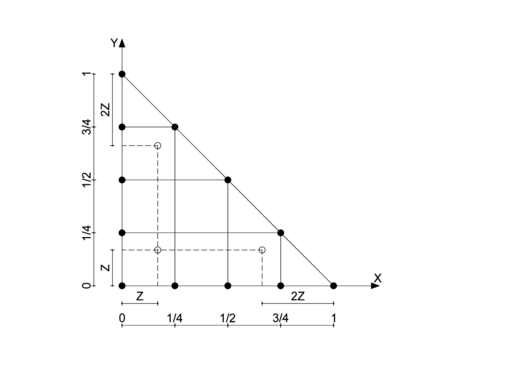
Figura 1. Elemento P4-modificado con los 3 nodos interiores móviles

3.3 Integral exacta

Consideremos un polinomio de grado ${\textstyle n}$ de la forma:

$p\left(x,y\right)={\overset {n+1}{\underset {i=1}{\sum }}}{\overset {i}{\underset {j=1}{\sum }}}a_{ij}x^{i-j}y^{j-1},$

(37)

donde los coeficientes ${\textstyle a_{ij}}$ son constantes. La integral exacta ${\textstyle I_{E}}$ de ${\textstyle p(x,y)}$ sobre la región triangular de la Figura 1 está dada por:

$I_{E}=\sum _{i=1}^{n+1}\sum _{j=1}^{i}a_{ij}\int _{0}^{1}\int _{0}^{1-x}x^{i-j}y^{j-1}{d}y{d}x.$

(38)

Sea

$\alpha _{ij}=\int _{0}^{1}\int _{0}^{1-x}x^{i-j}y^{j-1}{d}y{d}x\quad \,\,\,\,\forall i=1,2,...,n+1,\,\,\forall j=1,2,...,i.\qquad$

(39)

Reemplazando (39) en (38) tenemos:

$I_{E}=\sum _{i=1}^{n{\hbox{+1}}}\sum _{j=1}^{i}a_{ij}\alpha _{ij}.$

(40)

3.4 Integral numérica

La integral exacta ${\textstyle I_{E}}$ vamos a aproximarla mediante una cuadratura cerrada sobre una región triangular con 15 puntos distribuidos de la siguiente manera: 3 puntos (1, 2, 3) en los vértices del triángulo, 9 puntos numerados del 4 al 12 distribuidos simétricamente en los lados del triángulo y los 3 puntos móviles interiores restantes (13, 14, 15) distribuidos simétricamente como se ve en la Figura 2.

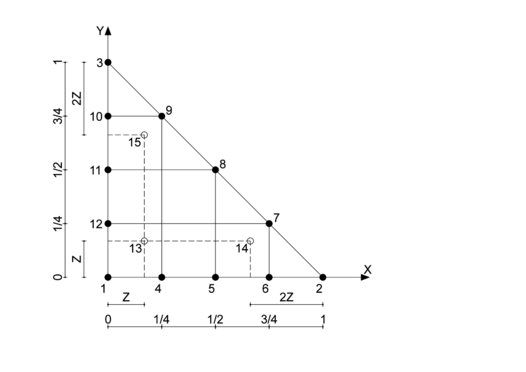
Figura 2. Posición de los 15 puntos de integración numérica

Los pesos ${\textstyle w_{1},w_{2},w_{3}}$ y ${\textstyle w_{4}}$ están asociados a los puntos detallados en la Figura 3 para los 15 puntos de integración. Estos pesos, junto con el parámetro ${\textstyle z}$, son las incógnitas a determinar.

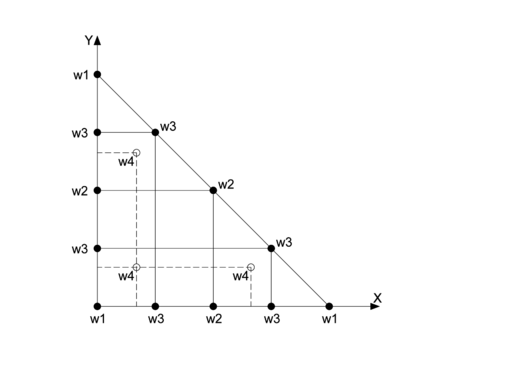
Figura 3. Pesos para los 15 puntos de integración numérica

Con las posiciones y los pesos de los 15 puntos de integración que se detallan en las Figuras 2 y 3, planteamos la integral numérica, ${\textstyle I_{N}}$, como sigue:

$I_{N}=\sum _{k=1}^{3}w_{1}p\left(x_{k},y_{k}\right)+\sum _{k=1}^{3}w_{2}p\left(x_{3k+2},y_{3k+2}\right)+\sum _{k=1}^{3}w_{3}p\left(x_{3k+1},y_{3k+1}\right)$ $+\sum _{k=1}^{3}w_{3}p\left(x_{3k+3},y_{3k+3}\right)+\sum _{k=1}^{3}w_{4}p\left(x_{12+k},y_{12+k}\right)$

(41)

De la ecuación (41), reemplazando ${\textstyle p(x,y)}$ dado en la ecuación (37) y agrupando términos, obtenemos:

$I_{N}=\sum _{k=1}^{3}(\sum _{i=1}^{n+1}\sum _{j=1}^{i}a_{ij}(w_{1}x_{k}^{i-j}y_{k}^{j-1}+w_{2}x_{3k+2}^{i-j}y_{3k+2}^{j-1}+w_{3}x_{3k+1}^{i-j}y_{3k+1}^{j-1}$ $\quad +w_{3}x_{3k+3}^{i-j}y_{3k+3}^{j-1}+w_{4}x_{12+k}^{i-j}y_{12+k}^{j-1}))$ $=\sum _{i=1}^{n+1}\sum _{j=1}^{i}a_{ij}\sum _{k=1}^{3}(w_{1}x_{k}^{i-j}y_{k}^{j-1}+w_{2}x_{3k+2}^{i-j}y_{3k+2}^{j-1}+w_{3}x_{3k+1}^{i-j}y_{3k+1}^{j-1}$ $\quad +w_{3}x_{3k+3}^{i-j}y_{3k+3}^{j-1}+w_{4}x_{12+k}^{i-j}y_{12+k}^{j-1}).$

(42)

Puesto queremos que la integral exacta y la integral numérica sean iguales, esto es ${\textstyle I_{E}=I_{N}}$, de las ecuaciones (40) y (42) se tiene que:

$\alpha _{ij}=\sum _{k=1}^{3}(w_{1}x_{k}^{i-j}y_{k}^{j-1}+w_{2}x_{3k+2}^{i-j}y_{3k+2}^{j-1}+w_{3}x_{3k+1}^{i-j}y_{3k+1}^{j-1}$ $\quad +w_{3}x_{3k+3}^{i-j}y_{3k+3}^{j-1}+w_{4}x_{12+k}^{i-j}y_{12+k}^{j-1}),$

(43)

para todo ${\textstyle i=1,2,...,n+1}$, ${\textstyle j=1,2,...,i}$, donde ${\textstyle n}$ es el grado del polinomio completo cuya integral exacta sobre una región triangular se quiere calcular numéricamente.

Las ecuaciones (39) y (43) nos permiten obtener un sistema de ecuaciones no lineal para determinar ${\textstyle w_{1}}$, ${\textstyle w_{2}}$, ${\textstyle w_{3}}$, ${\textstyle w_{4}}$ y ${\textstyle z}$. Recordemos que los puntos ${\textstyle (x_{k},y_{k}),}$ ${\textstyle (x_{3k+1},y_{3k+1}),}$ ${\textstyle (x_{3k+2},y_{3k+2}),}$ ${\textstyle (x_{3k+3},y_{3k+3})}$, ${\textstyle k=1,2,3}$, son las coordenadas de los 12 puntos ubicados en los vértices y lados del triángulo respectivamente, y los puntos ${\textstyle (x_{12+k},y_{12+k})}$, ${\textstyle k=1,2,3}$, son las coordenadas de los 3 puntos interiores cuya ubicación está parametrizada con la variable ${\textstyle z}$.

3.5 Cuadratura cerrada para integración exacta de un polinomio de cuarto grado

Utilizando las ecuaciones (39) y (43) para ${\textstyle n=4,}$ fácilmente se puede plantear el sistema no lineal de 15 ecuaciones para integrar exactamente un polinomio completo de cuarto grado. De las 15 ecuaciones, obtenemos tres ecuaciones linealmente independientes en términos del parámetro ${\textstyle z}$, que son:

${\frac {w_{2}}{16}}+{\frac {15}{128}}w_{3}+(-9z^{4}+13z^{3}-6z^{2}+z)w_{4}={\frac {1}{120}},$ ${\frac {w_{2}}{16}}+{\frac {9}{128}}w_{3}+(9z^{4}-8z^{3}+2z^{2})w_{4}={\frac {1}{180}},$ ${\frac {w_{2}}{8}}+{\frac {3}{16}}w_{3}+(3z^{3}-3z^{2}+z)w_{4}={\frac {1}{60}}.$

Resolviendo este sistema de ecuaciones en términos del parámetro ${\textstyle z}$, se tiene:

$w_{2}={\frac {72z^{3}-77z^{2}+27z-3}{45z(2z-1)}},$ (44) $w_{3}={\frac {-8(18z^{3}-23z^{2}+9z-1}{135z(2z-1)}},$ (45) $w_{4}={\frac {-1}{360z^{2}(2z-1)}}.$ (46)

Para obtener la ecuación parametrizada para ${\textstyle w_{1}}$, podemos usar la primera ecuación del sistema de 15 ecuaciones mencionado anteriormente. Reemplazando ${\textstyle i=1,}$ ${\textstyle j=1,}$ en las ecuaciones (39) y (43), tenemos respectivamente:

$\alpha _{11}=\int _{0}^{1}\int _{0}^{1-x}{d}y{d}x={\frac {1}{2}},$ (47) $\alpha _{11}=3w_{1}+3w_{2}+6w_{3}+3w_{4}.$ (48)

Igualando las ecuaciones (47) y (48) y reemplazando las ecuaciones (44), (45) y (46), tenemos:

$w_{1}={\frac {288z^{3}-224z^{2}+50z-3}{1080z^{2}}}.$

(49)

Las ecuaciones parametrizadas (44), (45), (46) y (49), verifican las 11 ecuaciones restantes del sistema no lineal de 15 ecuaciones planteadas para ${\textstyle n=4.}$ Por lo tanto, con las ecuaciones parametrizadas para ${\textstyle w_{1},w_{2},w_{3}}$ y ${\textstyle w_{4}}$ hemos obtenido un conjunto infinito de soluciones de parámetro ${\textstyle z}$. Por ejemplo para ${\textstyle z={\frac {1}{6}}}$ tenemos: ${\textstyle w_{1}={\frac {2}{135}},\,w_{2}={\frac {11}{180}},\,w_{3}={\frac {-4}{135}},\,w_{4}={\frac {3}{20}}}$, donde observamos que todos los pesos son distintos de cero. Como observación, notemos que para ${\textstyle z={\frac {1}{4}}}$, nos da, ${\textstyle w_{1}=0,\,w_{2}=-{\frac {1}{90}},\,w_{3}={\frac {2}{45}},\,w_{4}={\frac {4}{45}},}$ que es la cuadratura cerrada con los puntos de integración numérica coincidiendo con los nodos del elemento ${\textstyle P_{4}}$ original, donde no todos los pesos son distintos de cero.

3.6 Cuadratura cerrada para integración exacta de un polinomio de quinto grado

En el apartado anterior hemos obtenido un conjunto infinito de cuadraturas cerradas que integran en forma exacta hasta un polinomio completo de cuarto grado sobre una región triangular con puntos de integración coincidentes con los nodos del elemento ${\textstyle P_{4}}$ modificado, con sus tres nodos interiores móviles dependientes del parámetro ${\textstyle z}$, y con valores de ${\textstyle z}$ para los cuales todos los pesos son distintos de cero. Ahora nos proponemos obtener de este conjunto infinito de cuadraturas, al menos una cuadratura que integre exactamente un polinomio completo de quinto grado, también con todos sus pesos distintos de cero.

Utilizando las ecuaciones (39) y (43) para ${\textstyle n=5,}$ obtenemos 6 ecuaciones no lineales adicionales al sistema no lineal anterior de 15 ecuaciones. De estas 6 ecuaciones adicionales, solo 1 es linealmente independiente con el sistema anterior, la misma que se obtiene reemplazando ${\textstyle i=6}$ y ${\textstyle j=1}$ en las ecuaciones (39) y (43):

$w_{1}+{\frac {w_{2}}{16}}+{\frac {61}{128}}w_{3}+(2z^{5}+(1-2z)^{5}w_{4})={\frac {1}{42}}.$

(50)

Reemplazando en la ecuación (50) las soluciones parametrizadas de ${\textstyle w_{1},w_{2},w_{3}}$ y ${\textstyle w_{4}}$ dadas por las ecuaciones (49), (44), (45) y (46) respectivamente, se obtiene la ecuación:

${\frac {z^{2}}{2}}-{\frac {z}{3}}+{\frac {1}{21}}=0,$

(51)

cuya solución es:

$z={\frac {7+{\sqrt {7}}}{21}},\qquad z={\frac {7-{\sqrt {7}}}{21}}.$

(52)

Reemplazando las soluciones parametrizadas de ${\textstyle w_{1},w_{2},w_{3}}$ y ${\textstyle w_{4}}$ en las 5 ecuaciones restantes, es decir, para ${\textstyle i=6}$ y ${\textstyle j=2,3,4,5,6}$ en la ecuaciones (39) y (43), se obtiene la misma ecuación (51), con lo cual la solución es única para todas las ecuaciones del sistema.

De las dos soluciones de ${\textstyle z}$, vamos a encontrar la cuadratura cerrada para:

$z={\frac {7-{\sqrt {7}}}{21}}.$

(53)

Reemplazando el valor ${\textstyle z}$ de la ecuación (53) en las ecuaciones parametrizadas (49), (44), (45) y (46) se obtienen los pesos ${\textstyle w_{1},w_{2},w_{3}}$ y ${\textstyle w_{4}}$, todos distintos de cero:

$w_{1}={\frac {11{\sqrt {7}}}{15120}}+{\frac {1}{216}},\qquad \qquad \qquad w_{2}={\frac {11{\sqrt {7}}}{630}}-{\frac {1}{30}},$ $w_{3}={\frac {4}{135}}-{\frac {4{\sqrt {7}}}{945}},\qquad \qquad \qquad w_{4}={\frac {49}{360}}-{\frac {7{\sqrt {7}}}{720}}.$

Con todo esto, hemos obtenido un elemento ${\textstyle P_{4}}$ modificado, con las posiciones de los nodos interiores dadas por ${\textstyle z={\frac {7-{\sqrt {7}}}{21}}}$, y cuya cuadratura cerrada sobre una región triangular con puntos de integración coincidentes con los nodos del elemento ${\textstyle P_{4}}$ modificado integra de forma exacta hasta un polinomio completo de quinto grado, siendo todos los pesos distintos de cero.

La matriz de masa aproximada que se obtiene con la cuadratura cerrada sobre el elemento ${\textstyle P_{4}}$ modificado es una matriz diagonal con todos sus elementos distintos de cero. Este elemento ${\textstyle P_{4}}$ modificado es el que utilizamos en todos nuestros ejemplos numéricos para el cálculo de la proyección ortogonal del residuo en el método OSS.

En la Tabla 1 presentamos la cuadratura cerrada del elemento ${\textstyle P_{4}}$ modificado que acabamos de obtener.

$a={\frac {11{\sqrt {7}}}{15120}}+{\frac {1}{216}},\qquad$

$b={\frac {11{\sqrt {7}}}{630}}-{\frac {1}{30}},$

$c={\frac {4}{135}}-{\frac {4{\sqrt {7}}}{945}},\qquad \quad \,d={\frac {49}{360}}-{\frac {7{\sqrt {7}}}{720}}.$

Tabla 1. Cuadratura cerrada del elemento $P_{4}$ modificado

Puntos	$x$	$y$	Pesos
1	0	0	$a$
2	1	0	$a$
3	0	1	$a$
4	1/4	0	$c$
5	1/2	0	$b$
6	3/4	0	$c$
7	3/4	1/4	$c$
8	1/2	1/2	$b$
9	1/4	3/4	$c$
10	0	3/4	$c$
11	0	1/2	$b$
12	0	1/4	$c$
13	${\frac {7-{\sqrt {7}}}{21}}$	${\frac {7-{\sqrt {7}}}{21}}$	$d$
14	${\frac {7+2{\sqrt {7}}}{21}}$	${\frac {7-{\sqrt {7}}}{21}}$	$d$
15	${\frac {7-{\sqrt {7}}}{21}}$	${\frac {7+2{\sqrt {7}}}{21}}$	$d$

4. Resultados de los experimentos numéricos

4.1 Pruebas de convergencia en malla

Las pruebas de convergencia en malla que hemos llevado a cabo consisten en calcular el error en norma ${\textstyle L^{2}}$, es decir, la norma ${\textstyle L^{2}}$ de la diferencia entre entre la solución exacta y su aproximación numérica. Considerando solamente refinamiento en ${\textstyle h}$, si el error del método se comporta como el error de interpolación, situación que puede considerarse óptima, este error debe comportarse como

$e=\left\Vert u-u_{h}\right\Vert _{L^{2}}\leq Ch^{p+1},$

(54)

que corresponde al mismo comportamiento que el error de interpolación (33) con ${\textstyle r=0}$ (y absorbiendo en la constante ${\textstyle C}$ la dependencia con ${\textstyle p}$). Consideraremos los casos ${\textstyle 1\leq p\leq 4}$.

Si graficamos la ecuación (54) (en el caso de la igualdad) en el plano, con ${\textstyle \log(e)}$ en las ordenadas y ${\textstyle \log(h)}$ en las abscisas, tenemos una línea recta en la que ${\textstyle p+1}$ es la pendiente teórica óptima de convergencia. Las pruebas de convergencia en malla consisten entonces en verificar que la pendiente calculada sea precisamente ${\textstyle p+1}$. Para ello, seleccionamos como solución exacta ${\textstyle u}$ a la función polinómica espacio-temporal

$u\left(x,y,t\right)=x^{6}y^{6}\left(1-x\right)^{6}\left(1-y\right)^{6}t,$

e imponemos el término fuente ${\textstyle f}$ en la ecuación escalar de CDR transitoria (1) para que esta sea precisamente la solución exacta del problema:

$f=\partial _{t}u\left(x,y,t\right)-k\partial _{i}\partial _{i}u\left(x,y,t\right)+a_{i}\partial _{i}u\left(x,y,t\right)+su\left(x,y,t\right),$

donde las constantes de difusión ${\textstyle k}$, las componentes de la velocidad de convección ${\textstyle a_{i}}$ y la reacción ${\textstyle s}$ están dadas en cada uno de los ejemplos, tomando ${\textstyle k=10^{-3}}$ para todos los casos. Elegimos también las condiciones de contorno (todas de Dirichlet) e iniciales para que la solución sea la que hemos elegido.

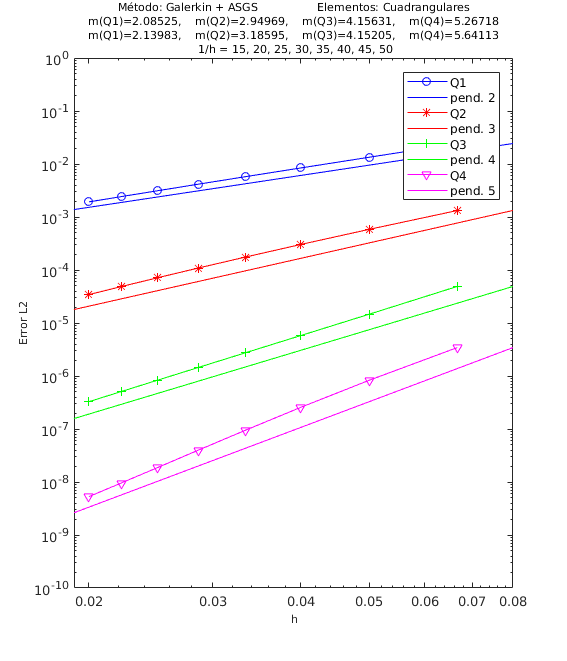
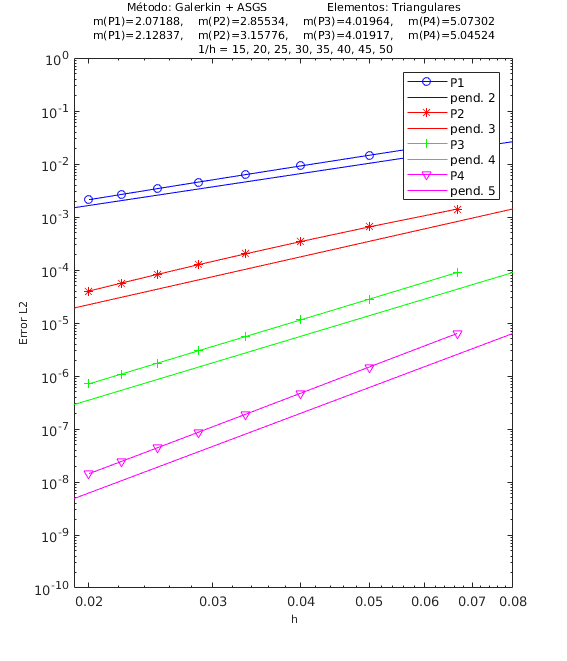
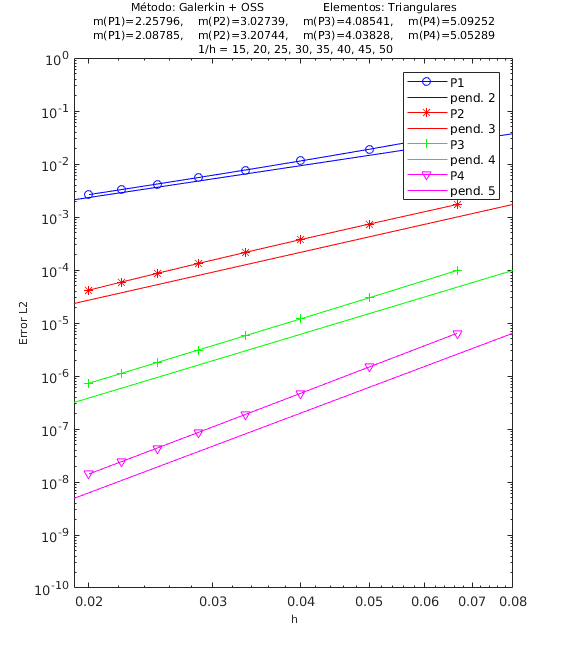
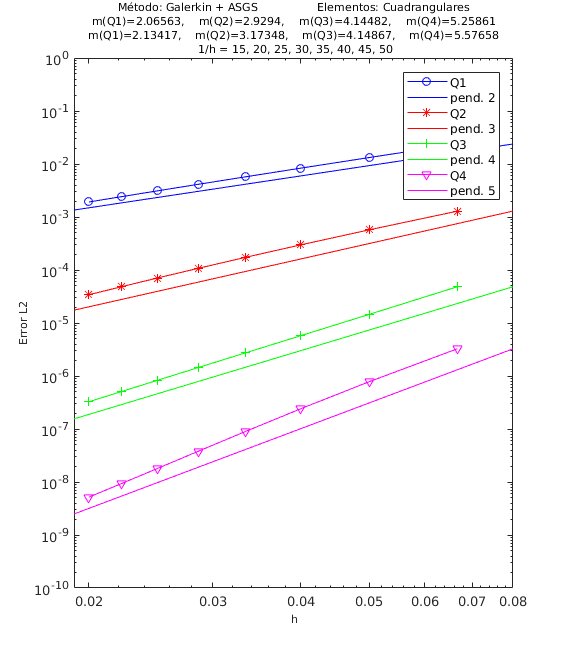
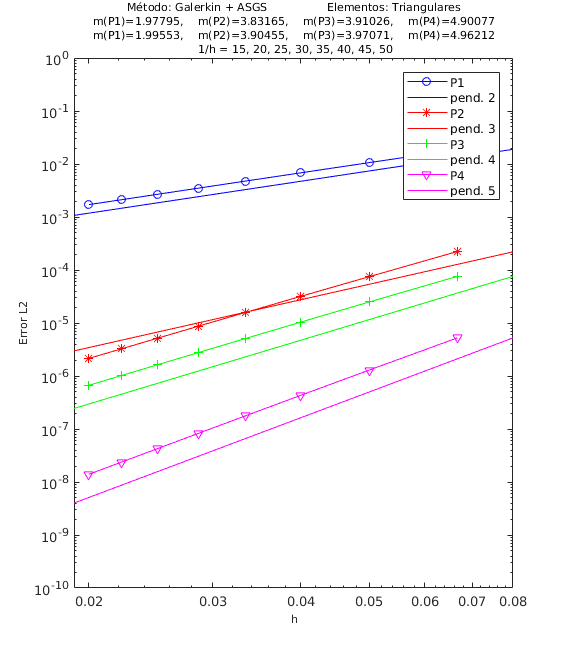
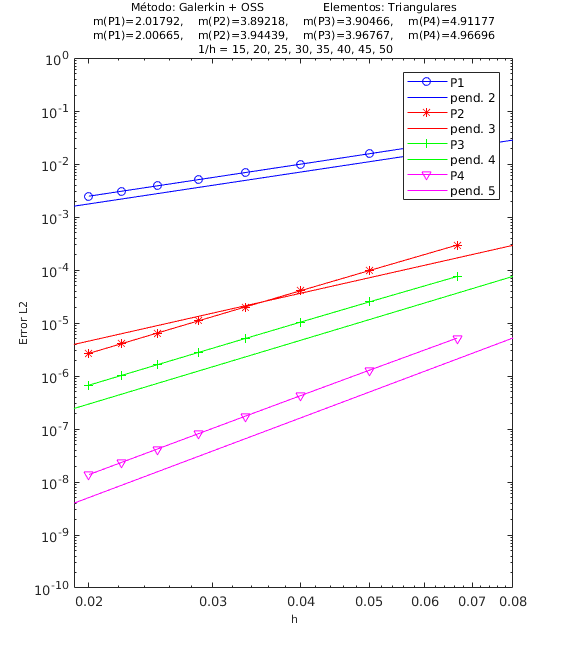
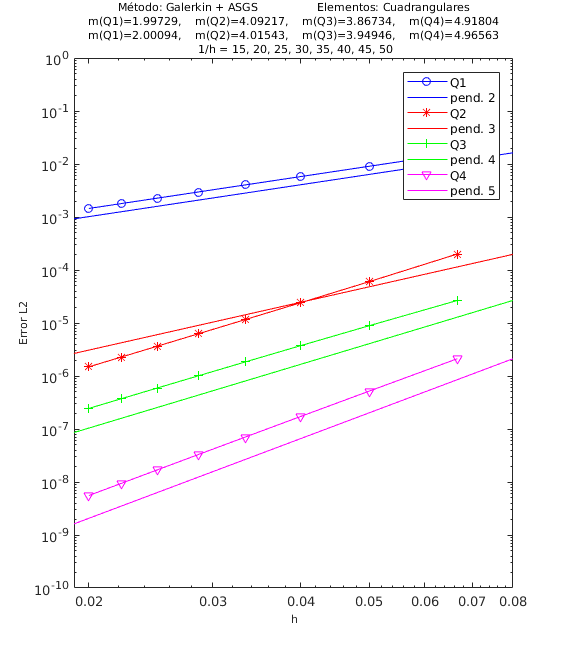
En las Figuras 4, 5 y 6 presentamos los resultados de los experimentos numéricos de las pruebas de convergencia en malla con solución analítica conocida, tanto para el método ASGS como para el OSS. En cada gráfica se puede apreciar con línea continua la pendiente teórica de convergencia y con línea con apéndices sobre ella la pendiente calculada. Presentamos los resultados para los distintos grados polinómicos de las funciones de forma estudiados, es decir, elementos lineales, cuadráticos, cúbicos y de cuarto orden triangulares ${\textstyle P_{1},\;P_{2},\;P_{3},\;P_{4}}$ y elementos cuadrangulares ${\textstyle Q_{1},\;Q_{2},\;Q_{3},\;Q_{4}}$, respectivamente.

El dominio computacional es el cuadrado ${\textstyle \left[0,1\right]\times \left[0,1\right]}$ y el intervalo de tiempo es ${\textstyle \left[0,1\right]}$. El tamaño del paso de tiempo lo hemos tomado como ${\textstyle \delta t=0.2}$. Como se verá a continuación, en este caso el error está dominado por la aproximación espacial, no se ve afectado por la aproximación de la discretización temporal. La malla de elementos finitos consiste en triángulos o cuadrados formando una malla regular. Para cada grado polinómico de las funciones de forma ${\textstyle P_{1},\;P_{2},\;P_{3},\;P_{4}}$ o ${\textstyle Q_{1},\;Q_{2},\;Q_{3},\;Q_{4},}$ hemos calculado los errores en norma ${\textstyle L^{2}}$ para ocho mallas de tamaño ${\textstyle h}$, siendo ${\textstyle {\frac {1}{h}}=15,\;20,\;25,\;30,\;35,\;40,\;45,\;50,}$ el número de partes en que se ha dividido cada lado del cuadrado. En la Tabla 2 se muestra el número de elementos y el número de nodos para cada refinamiento, tanto para elementos triangulares como para elementos cuadrangulares. El integrador temporal utilizado es BDF1.

Tabla 2. Refinamiento para elementos triangulares y cuadrangulares

Triángulos		Número de nodos
${\textstyle 1/h}$	elem.	$P1$	$P2$	$P3$	$P4$
15	450	256	961	2116	3721
20	800	441	1681	3721	6561
25	1250	676	2601	5776	10201
30	1800	961	3721	8281	14641
35	2450	1296	5041	11236	19881
40	3200	1681	6561	14641	25921
45	4050	2116	8281	18496	32761
50	5000	2601	10201	22801	40401

Cuadrados		Número de nodos
${\textstyle 1/h}$	elem.	$Q1$	$Q2$	$Q3$	$Q4$
15	225	256	961	2116	3721
20	400	441	1681	3721	6561
25	625	676	2601	5776	10201
30	900	961	3721	8281	14641
35	1250	1296	5041	11236	19881
40	1600	1681	6561	14641	25921
45	2025	2116	8281	18496	32761
50	2500	2601	10201	22801	40401

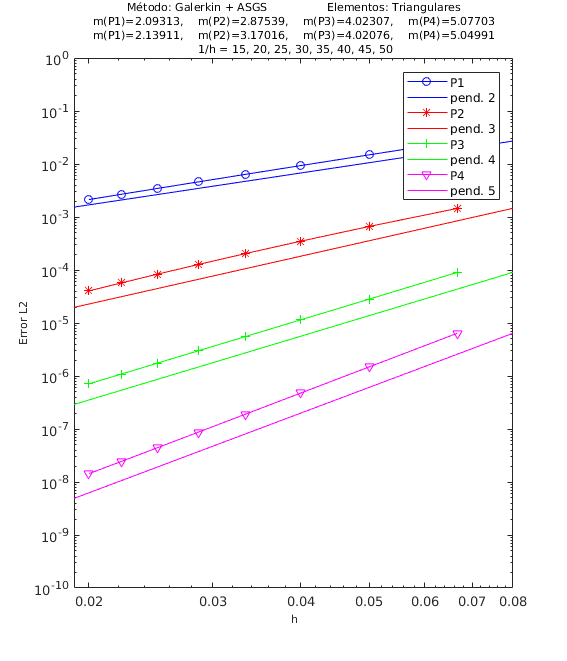
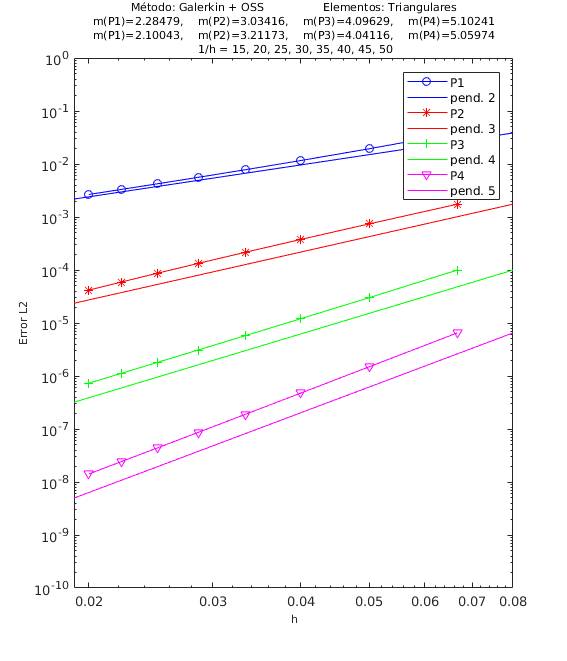
En el encabezado de las gráficas de las pruebas de convergencia en malla se adjuntan dos filas con los valores de las pendientes calculadas; la primera fila corresponde a los valores de las pendientes de las rectas que pasan por los primeros 5 puntos y la segunda fila son las pendientes de las rectas que pasan por los últimos 5 puntos de los 8 puntos del refinamiento de malla evaluados. De esta manera podemos visualizar numéricamente la tendencia de la convergencia de las pendientes calculadas hacia el valor teórico. Para el cálculo de dichas pendientes se ha utilizado el método de los mínimos cuadrados. La simbología ${\textstyle m(P1),}$ ${\textstyle m(P2),}$ ${\textstyle m(P3),}$ ${\textstyle m(P4),}$ corresponde a las pendientes para elementos triangulares lineales, cuadráticos, cúbicos y de cuarto orden, respectivamente, mientras que para elementos cuadrangulares lineales, cuadráticos, cúbicos y de cuarto orden la simbología es ${\textstyle m(Q1),}$ ${\textstyle m(Q2),}$ ${\textstyle m(Q3),}$ ${\textstyle m(Q4)}$. Los valores de las pendientes teóricas se corresponden con ${\textstyle m(P1)=m(Q1)=2}$, ${\textstyle m(P2)=m(Q2)=3}$, ${\textstyle m(P3)=m(Q3)=4}$, ${\textstyle m(P4)=m(Q4)=5}$.

Los experimentos numéricos que presentamos son los siguientes: en la Figura 4 convección dominante ${\textstyle \left|{\boldsymbol {a}}\right|=1}$ y una pequeña reacción ${\textstyle s=10^{-3}}$, en la Figura 5 convección y reacción del mismo orden, con ${\textstyle \left|{\boldsymbol {a}}\right|=1}$ y ${\textstyle s=1}$, y en la Figura 6 una pequeña convección ${\textstyle \left|{\boldsymbol {a}}\right|=10^{-3}}$ y reacción dominante ${\textstyle s=1}$. Para todos los ejemplos tomamos ${\textstyle k=10^{-3}}$, como se ha indicado anteriormente.

Figura 4. Convergencia ASGS-OSS, elementos triangulares y cuadrangulares. $k=10^{-3},$ $\mathbf {a} =\left[\cos {60}^{\circ },\mathrm {sin60^{\circ }} \right]$, $s=10^{-3}$

Figura 5. Convergencia ASGS-OSS, elementos triangulares y cuadrangulares. $k=10^{-3}$, $\mathbf {a} =\left[\cos {60}^{\circ },\mathrm {sin60^{\circ }} \right]$, $s=1$

Figura 6. Convergencia ASGS-OSS, elementos triangulares y cuadrangulares. $k=10^{-3}$, $\mathbf {a} =\left[\cos {60}^{\circ },\mathrm {sin60^{\circ }} \right]\times 10^{-3}$, $s=1$

Para los dos métodos de estabilización ASGS y OSS, los valores de las constantes algorítmicas ${\textstyle c_{i},}$ ${\textstyle i=1,2,3}$ se han calibrado a ${\textstyle c_{1}=12,}$ ${\textstyle c_{2}=2,}$ ${\textstyle c_{3}=1}$. También es necesario indicar que para el método OSS con elementos triangulares de cuarto orden ${\textstyle P_{4}}$, hemos usado en el mallado el elemento ${\textstyle P_{4}}$ modificado mencionado en la Sección 3.

En las gráficas de las figuras de convergencia en malla se observa tanto gráfica como numéricamente que las pendientes calculadas son mayores o tienden al valor de la pendiente teórica ${\textstyle p+1}$. Los resultados muestran claramente que las formulaciones ASGS y OSS son capaces de aproximar correctamente el problema de CDR escalar transitorio con todas las combinaciones de convección y reacción dominantes.

4.2 Pruebas con capas límite

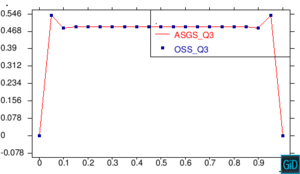
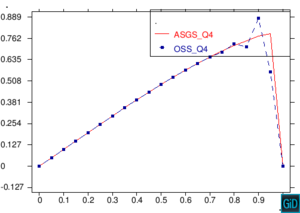
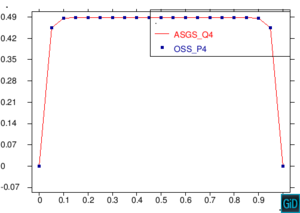
A continuación presentamos un grupo de pruebas cualitativas para observar la estabilidad de los métodos de elementos finitos ASGS y OSS en la ecuación escalar transitoria de CDR. Se analizan cuatro casos en el dominio ${\textstyle \Omega =[0,1]\times [0,1]}$, ${\textstyle \gamma =\left[0,1\right],}$ combinando los valores de término fuente ${\textstyle f=1}$, ${\textstyle f=0}$ y con el coeficiente de reacción ${\textstyle s=0,}$ ${\textstyle s=1}$, y además variando la dirección de la velocidad, considerando un valor de ${\textstyle \left|\mathbf {a} \right|=1}$ para todos los casos. El valor del coeficiente de difusión es ${\textstyle k=10^{-5}}$ para todos los ejemplos, con el fin de tener convección dominante y poder probar la estabilidad de los métodos. El tamaño del paso de tiempo considerado constante es ${\textstyle \delta t=0.2}$ y el tamaño del elemento para todas las figuras es ${\textstyle 1/h=20}$. En todos los casos excepto el caso de la Figura 8, se imponen condiciones de Dirichlet homogéneas, observando inestabilidades locales en el contorno, como era de esperar, pero siendo las soluciones globalmente estables. Para el caso de la Figura 8, las condiciones de Dirichlet en el contorno son: ${\textstyle u(x,0,t)=1\;\mathrm {en\;0\leq x\leq {0.3}} }$, ${\textstyle u(x,0,t)=0\;\mathrm {en} 0.3<x\leq {1}}$, ${\textstyle u(0,y,t)=1,\;u(1,y,t)=0,\;u(1,x,t)=0}$. La condición inicial para todos los casos es ${\textstyle u\left(\mathbf {x} ,0\right)=0}$ en todo ${\textstyle \Omega }$.

En cada figura se presentan ocho gráficos que corresponden a los cuatro grados polinómicos de las funciones de forma analizadas para cada método estabilizado de elementos finitos ASGS y OSS. La solución se presenta en ${\textstyle t=1}$, tiempo en el cual se ha alcanzado el estado estacionario usando el integrador temporal BDF1.

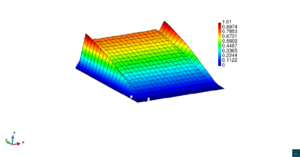
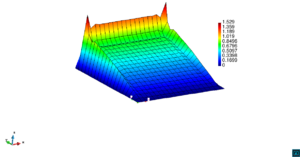
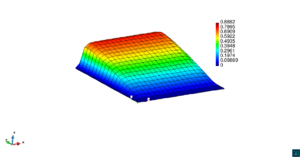
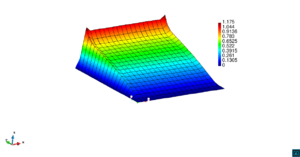
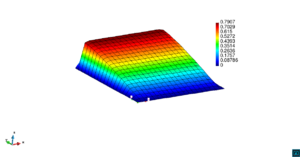
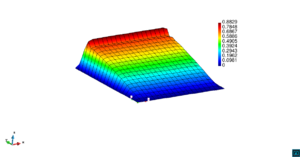
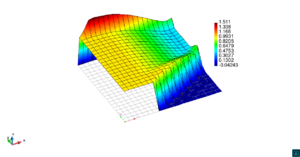
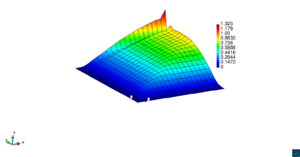
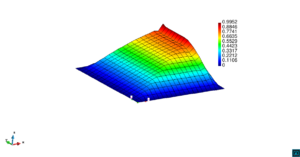
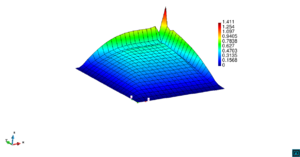
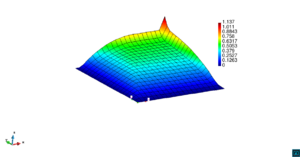
En la Figura 7 presentamos el caso con término fuente ${\textstyle f=1}$, velocidad de convección en la dirección del eje ${\textstyle y}$ ${\textstyle \mathbf {a} =[0,1]}$, coeficiente de reacción ${\textstyle s=0}$ y condiciones de Dirichlet homogéneas. En la Figura 8 se encuentra el caso con término fuente ${\textstyle f=0}$, velocidad de convección inclinada ${\textstyle \mathbf {a} =\left[\sin 60^{\circ },\cos 60^{\circ }\right],}$ coeficiente de reacción ${\textstyle s=0,}$ y las condiciones de Dirichlet en el contorno dadas anteriormente. En la Figura 9 encontramos el caso con término fuente ${\textstyle f=1,}$ velocidad de convección inclinada ${\textstyle \mathbf {a} =\left[\sin 60^{\circ },\cos 60^{\circ }\right],}$ coeficiente de reacción ${\textstyle s=0}$ y condiciones de Dirichlet homogéneas. Y, finalmente, en la Figura 10 tenemos el caso con término fuente ${\textstyle f=1,}$ velocidad de convección inclinada ${\textstyle \mathbf {a} =\left[\sin 30^{\circ },\cos 30^{\circ }\right],}$ coeficiente de reacción ${\textstyle s=1}$ y condiciones de Dirichlet homogéneas.

$ASGS$ $OSS$ $Q1$ $Q2$ $Q3$ $Q4$

Figura 7. Capas límite con ASGS y OSS, elementos cuadrangulares. $k=10^{-5}$, $\mathbf {a} =\left[0,1\right]$, $s=0$, $f=1$ y condiciones de Dirichlet homogéneas en todo el contorno

$ASGS$ $OSS$ $Q1$ $Q2$ $Q3$ $Q4$

Figura 8. Capas límite con ASGS y OSS, elementos cuadrangulares. $k=10^{-5}$, $\mathbf {a} =\left[\sin {60}^{\circ },\cos 60^{\circ }\right]$, $s=0$, $f=0$ y condiciones de Dirichlet homogéneas en todo el contorno

$ASGS$ $OSS$ $Q1$ $Q2$ $Q3$ $Q4$

Figura 9. Capas límite con ASGS y OSS, elementos cuadrangulares. $k=10^{-5}$, $\mathbf {a} =\left[\sin 60^{\circ },\cos {60}^{\circ }\right]$, $s=0,\quad f=1$ y condiciones de Dirichlet homogéneas en todo el contorno

$ASGS$ $OSS$ $Q1$ $Q2$ $Q3$ $Q4$

Figura 10. Capas límite con ASGS y OSS, elementos cuadrangulares. $k=10^{-5}$, $\mathbf {a} =\left[\sin 30^{\circ },\cos 30^{\circ }\right]$, $s=1$, $f=1$ y condiciones de Dirichlet homogéneas en todo el contorno

En todos las figuras se observa que el comportamiento es el esperado en concordancia con los datos de cada figura. Además observamos que en todas la figuras existen inestabilidades en los bordes correspondientes a las capas límite, las cuales es importante notar que se atenúan al incrementar el refinamiento polinómico.

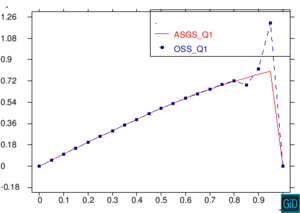
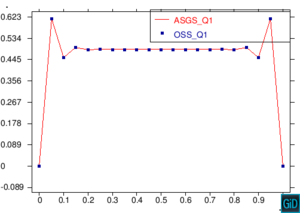
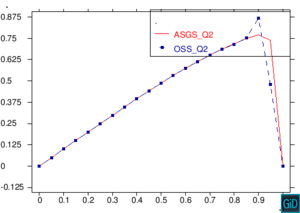
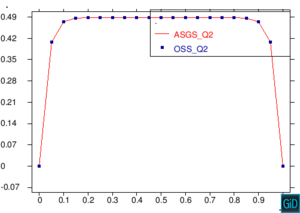
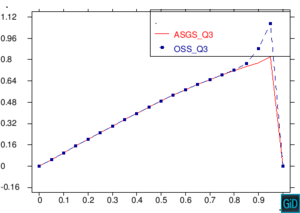
En la Figura 11 encontramos una comparación de los métodos ASGS y OSS, realizando cortes sobre las gráficas de capas límite para los dos métodos ASGS y OSS del ejemplo de la Figura 7, y graficando los dos cortes sobre un mismo plano cartesiano. Los cortes que encontramos en la Figura 11 son cortes longitudinales y cortes trasversales. Como era de esperar, aparecen oscilaciones localizadas en las capas límites que no se propagan al interior del dominio. Para eliminarlas habría que introducir algún método de captura de discontinuidades. Se observa también que los picos espúreos del método OSS son mayores que los del método ASGS. Este comportamiento es conocido, como también lo es la mayor exactitud del método OSS, y los resultados presentados aquí corroboran este hecho para elementos de alto orden.

Cortes longitudinales paralelos al eje ${\textstyle y}$ Cortes transversales paralelos al eje ${\textstyle x}$ $Q1$ $Q2$ $Q3$ $Q4$

Figura 11. Comparación ASGS y OSS, elementos cuadrangulares. Cortes longitudinales y transversales del ejemplo de la Figura 7

4.3 Transporte de una concentración

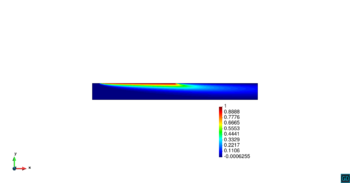
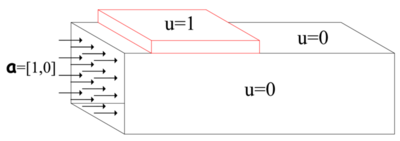
Presentamos a continuación los resultados numéricos para un ejemplo menos académico, consistente en el transporte y difusión de una concentración en parte de la superficie de un ducto de directriz ${\textstyle x}$. Suponemos que tenemos un flujo constante con velocidad unidireccional ${\textstyle \mathbf {a} =\left[100,0,0\right]}$ en un ducto, como se ilustra en la Figura 12. También asumimos que sobre una región de la pared superior del ducto tenemos una concentración constante ${\textstyle u=1}$ de una variable ${\textstyle u}$, y sobre el resto de la periferia del ducto, incluyendo la sección transversal a la entrada del flujo, asumimos el valor ${\textstyle u=0}$. Queremos estudiar como se propaga esta concentración dentro del flujo considerado.

Figura 12. Ducto en 3D

Considerando el ancho mucho mayor que la altura y debido a que el flujo es constante en toda la sección transversal del ducto, podemos simplificar el planteamiento del problema a dos dimensiones como vemos en la Figura 13.

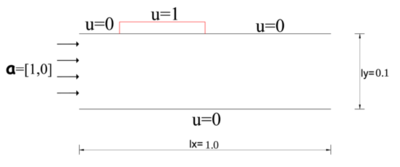
Figura 13. Ducto en 2D

El modelo matemático que resuelve el problema planteado es:

$\partial _{t}u-k\partial _{i}\partial _{i}u+a_{i}\partial _{i}u=f,\quad {\hbox{ en}}~\Omega \times \gamma$ $u=u_{D},\quad {\hbox{ en}}~\partial \Omega _{D}\times \mathbf {\gamma } ,$ ${\frac {\partial {u}}{\partial x}}=0,\quad {\hbox{ en}}~\partial \Omega _{N}\times \mathbf {\gamma } ,$ $u=0,\quad {\hbox{ en}}~\Omega \times \{0\}.$

Para nuestro problema, ${\textstyle k=10^{-3},}$ ${\textstyle \mathbf {a} =\left[1,0\right],}$ ${\textstyle f=0,}$ el dominio ${\textstyle \Omega }$ es el rectángulo de dimensiones ${\textstyle l_{x}=1}$ y ${\textstyle l_{y}=0,1}$ y el intervalo de tiempo es ${\textstyle \gamma =\left[0,1\right]}$.

Las condiciones de Dirichlet en el contorno ${\textstyle \partial \Omega _{D}}$ donde se imponen son:

$u_{D}(x,y,t)={\begin{cases}0&x\in [0,1],~y=0,~t\in [0,1]\\0&x=0,~y\in [0,0.1],~t\in [0,1]\\0&x\in [0,0.05)\cup (0.5,1],~y=0.1,~t\in [0,1]\\1&x\in [0.05,0.5],~y=0.1,~t\in [0,1]\end{cases}}$

(55)

En el extremo derecho (${\textstyle \partial \Omega _{N}}$) no se impone ninguna condición de Dirichlet, sino que se considera libre.

El intervalo de tiempo ${\textstyle [0,1]}$ se discretiza mediante una partición uniforme de tamaño ${\textstyle \delta t=0.2}$. Como en los ejemplos anteriores, el integrador temporal utilizado es BDF1. La malla de elementos finitos utilizada consiste en 850 elementos cuadrangulares formando una malla regular, con 918 nodos para el elemento ${\textstyle Q_{1},}$ 3535 nodos para el ${\textstyle Q_{2},}$ 7852 nodos para el ${\textstyle Q_{3}}$ y 13869 nodos para el ${\textstyle Q_{4}.}$

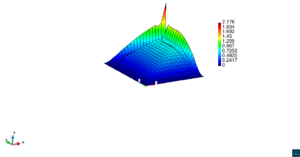
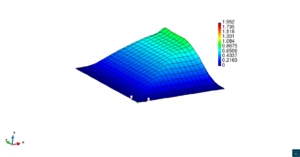
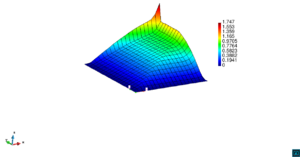
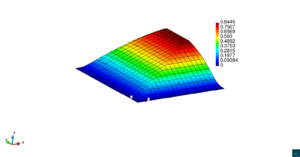
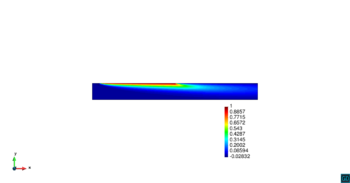
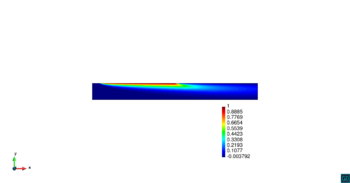
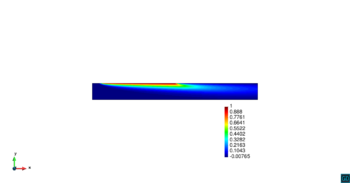
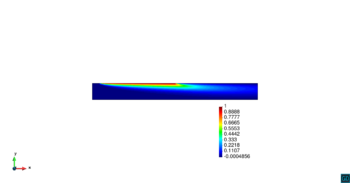
En la Figura 14 se muestran los resultados de la simulación numérica de este problema en ${\textstyle t=1}$ para los dos métodos ASGS y OSS y para los cuatro grados polinómicos de las funciones de forma, ${\textstyle Q_{1},}$ ${\textstyle Q_{2},}$ ${\textstyle Q_{3},}$ y ${\textstyle Q_{4},}$ observando en todos los casos que los resultados son los esperados en concordancia con los datos del problema. Se visualiza el efecto de la convección dominante, ya que se observa que la concentración ${\textstyle u}$ que se prescribe como condición de contorno se transporta al interior de dominio con poca difusión. En ninguno de los casos considerados se aprecian oscilaciones, que es el objetivo de los métodos de estabilización.

$ASGS$ $OSS$ $Q1$ $Q2$ $Q3$ $Q4$

Figura 14. Transporte de una concentración

5. Conclusiones

En este artículo hemos presentado una revisión de los métodos estabilizados ASGS y OSS y su estudio con elementos finitos de alto orden, cuadráticos, cúbicos y de cuarto orden, para resolver la ecuación escalar de CDR en problemas con convección y reacción dominantes. En el cálculo del parámetro de estabilización ${\textstyle \tau }$ hemos incluido el grado del polinomio, para de esta manera poder utilizar elementos finitos de alto orden y mantener el orden de aproximación óptimo tanto en ${\textstyle h}$ como en ${\textstyle p}$. Para poder usar de forma eficiente el método OSS con el elemento simplicial de cuarto orden, hemos presentado el procedimiento para construir un elemento ${\textstyle P_{4}}$ modificado, el cual permite aproximar la matriz de masa por una matriz diagonal con todos sus elementos distintos de cero; hemos usado este elemento modificado en todos los ejemplos con elementos de cuarto orden con el método OSS.

Los experimentos numéricos de las pruebas de convergencia en malla para elementos lineales y de alto orden revelan que la convergencia de los dos métodos estabilizados es óptima, para todos los casos de convección y reacción dominantes, tanto para elementos triangulares como para elementos cuadrangulares, y para todos los grados polinómicos de las funciones de forma que hemos considerado. Hemos observado que las pendientes de convergencia del método OSS son ligeramente mayores que las del método ASGS, lo cual indica mayor precisión del método OSS. Además, también se concluye que para un número de nodos dado, los errores son menores cuando mayor es el grado del polinomio de forma utilizado, lo cual indica que para obtener un menor coste computacional para una precisión dada podría ser conveniente utilizar elementos finitos de alto orden. Sin embargo, no ha sido nuestro objetivo estudiar con detalle el coste computacional de los métodos presentados.

En términos generales, los resultados de las pruebas de capas límite han sido los esperados y están en concordancia con las condiciones impuestas en cada caso. Asimismo, hemos observado que el método OSS produce más oscilaciones localizadas en las capas límites, como ya era conocido para el caso de elementos lineales y cuadráticos.

Finalmente, los resultados del ejemplo de la simulación numérica del transporte de una concentración han sido satisfactorios, de acuerdo con el fenómeno físico planteado. En este caso, las diferencias de los resultados entre los métodos ASGS y OSS son insignificantes.

Agradecimientos

R. Codina agradece la ayuda recibida a través del programa ICREA Academia, del Gobierno de Catalunya.

Referencias

[1] Brooks A.N., Hughes T.J.R. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equation. Computer Methods in Applied Mechanics and Engineering, 32:199-259, 1982.

[2] Kelly D.W., Nakazawa S., Zienkiewicz O.C., Heinrich J.C. A note on upwinding and anisotropic balancing dissipation in finite element approximations to convective diffusion problems. International Journal for Numerical Methods in Engineering, 15:1705-1711, 1980.

[3] Johnson C., Nävert U., Pitkäranta J. Finite element methods for linear hyperbolic equations. Computer Methods in Applied Mechanics and Engineering, 45:285-312, 1984.

[4] Hughes T.J.R., Franca L.P., Hulbert G.M. A new finite element formulation for computational fluid dynamics: VIII. The Galerkin/least-squares method for advective-diffusive equations. Computer Methods in Applied Mechanics and Engineering, 73:173-189, 1989.

[5] Franca L.P., Frey S.L., Hughes T.J.R. Stabilized finite element methods: I. Application to the advective-diffusive model. Computer Methods in Applied Mechanics and Engineering, 95:253-276, 1992.

[6] Brezzi F., Franca L.P., Hughes T.J.R., Russo A. $b=\int g$. Computer Methods in Applied Mechanics and Engineering, 145:329-339, 1997.

[7] Douglas J., Russel T. Numerical methods for convection dominated problems based on combining the method of characteristics with finite elements or finite difference procedures. SIAM Journal on Numerical Analysis, 9:871-885, 1982.

[8] Donea J. A Taylor-Galerkin method for convection transport problems. International Journal for Numerical Methods in Engineering, 20:101-119, 1984.

[9] Codina R. Comparison of some finite element methods for solving the diffusion-convection-reaction equation. Computer Methods in Applied Mechanics and Engineering, 156:185-210, 1998.

[10] Huges T.J.R. Multiscale phenomena: Green's functions, the Dirichlet-to-Neumann formulation, subgrid scale models, bubbles and the origins of stabilized methods. Computer Methods in Applied Mechanics and Engineering, 127:387-401, 1995.

[11] Huges T.J.R., Feijóo G.O., Mazzei L., Quincy J.B. The variational multiscale method-a paradign for computational mechanics. Computer Methods in Applied Mechanics and Engineering, 166:3-24, 1998.

[12] Codina R., Badia S., Baiges J., Principe J. Variational multiscale methods in computational fluid dynamics. In Encyclopedia of Computational Mechanics, Part 1. Fluids, John Wiley & Sons Ltd, 2017.

[13] Codina R. Finite element approximation of the convection-diffusion equation: Subgrid-scale spaces, local instabilities and anisotropic space-time discretizations. In Bail 2010 - Boundary and Interior Layers, Computational and Asymptotic Methods, Part of the Lecture Notes in Computational Science and Engineering, C. Clavero, J.L. Gracia and F.J. Lisbona (Eds.), 81:85-97, Springer, 2011.

[14] Codina R. Stabilization of incompressibility and convection through orthogonal sub-scales in finite element methods. Computer Methods in Applied Mechanics and Engineering, 190:1579-1599, 2000.

[15] Codina R. On stabilized finite element methods for linear systems of convection-diffusion-reaction equations. Computer Methods in Applied Mechanics and Engineering, 188:61-82, 2000.

[16] Codina R. A stabilized finite element method for generalized stationary incompressible flows. Computer Methods in Applied Mechanics and Engineering, 190:2681-2706, 2001.

[17] Codina R. Stabilized finite element approximation of transient incompressible flows using orthogonal subscales. Computer Methods in Applied Mechanics and Engineering, 191:4295-4321, 2002.

[18] Codina R., Principe J., Guasch O., Badia S. Time dependent subscales in the stabilized finite element approximation of incompressible flow problems. Computer Methods in Applied Mechanics and Engineering, 196:2413-2430, 2007.

[19] Baiocchi C., Brezzi F., Franca L.P. Virtual bubbles and Galerkin/least-squares type methods (Ga.L.S). Computer Methods in Applied Mechanics and Engineering, 105:125-141, 1993.

[20] Codina R., Blasco J. Analysis of a stabilized finite element approximation of the transient convection-diffusion-reaction equation using orthogonal subscales. Computing and Visualization in Science, 4:167-174, 2002.

[21] Principe J., Codina R. On the stabilization parameter in the subgrid scale approximation of scalar convection-diffusion-reaction equations on distorted meshes. Computer Methods in Applied Mechanics and Engineering, 199:1386-1402, 2010.

[22] Codina R. On ${\textstyle hp}$ convergence of stabilized finite element methods for the convection-diffusion equation. SeMA Journal, 75:591-606, 2018.

[23] Houston P., Süli E. Stabilised ${\textstyle hp}$-finite element approximation of partial differential equations with nonnegative characteristic form. Computing, 66:99-119, 2001.

[24] Lube G., Rapin G. Residual-based stabilized higher-order FEM for advection-dominated problems. Computer Methods in Applied Mechanics and Engineering, 195:4124-4138, 2006.

[25] Schwab Ch. $p$- and ${\textstyle hp}$-Finite element methods. Theory and application to solid and fluid mechanics. Oxford University Press, 388 pp., 1998.