Approximation of the shallow water equations with higher order finite elements and variational multiscale methods

Resumen

En este artículo presentamos aproximaciones de elementos finitos de alto orden usando métodos variacionales estabilizados de subescalas para aproximar las ecuaciones del movimiento de un fluido en aguas poco profundas (shallow water equations, en inglés). Escribimos estas ecuaciones como un sistema de ecuaciones de tipo convección-difusión-reacción (CDR) no lineal y transitorio, y planteamos los desarrollos en este marco general. Los métodos variacionales de multiescala (VMS) se basan en la descomposición de las incógnitas del problema continuo en una parte resoluble en el espacio de elementos finitos y otra que no puede ser capturada por la malla de elementos finitos y que la denominamos subescala. La subescala se aproxima en términos de la solución de elementos finitos, obteniéndose un esquema numérico robusto, que permite en particular igual interpolación para todas las incógnitas y la posibilidad de tratar con flujos de convección dominante (no consideraremos la posibilidad de tratar con choques). Los métodos VMS que consideraremos son los llamados de subscalas algebraicas (ASGS, por Algebraic SubGrid Scales) y subescalas ortogonales (OSS, por Orthogonal Subgrid Scales).

Palabras clave: Aguas poco profundas, elementos finitos, estabilización, sistemas acoplados, alto orden

Abstract

In this article, we present approximations with finite elements of high order using stabilized variational multiscale methods to approximate the equations of motion of a fluid in shallow waters. We write these equations as a system of non-linear and transient convection-diffusion-reaction (CDR) equations and we perform our developments in this general framework. Variational multiscale methods (VMS) are based on the decomposition of the unknowns of the continuous problem in a resolved component in the finite element space and another component that cannot be captured by the finite element mesh, and that we call subscale. The subscale is approximated in terms of the finite element solution, obtaining a robust numerical scheme, which in particular allows one to use the same interpolation for all unknowns and the possibility to deal with convection dominated flows (we will not consider the possibility of dealing with shocks). The two VMS methodologies that we will consider are called algebraic subscales (ASGS) and orthogonal subscales (OSS).

Keywords: Shallow waters, finite elements, stabilization, coupled systems, high order

1. Introducción

Las ecuaciones del movimiento de un fluido en aguas poco profundas se obtienen a partir de las ecuaciones Euler para fluidos invíscidos o a partir de las ecuaciones de Navier-Stokes para fluidos con viscosidad. Estas ecuaciones describen el movimiento en una capa delgada de fluido de densidad constante en equilibrio hidrostático, limitada en su parte inferior por la topografía del terreno y por arriba por una superficie libre, y promediando las variables a lo largo de la profundidad. Son una buena aproximación del comportamiento de un fluido cuando la profundidad del dominio estudiado es pequeña con respecto al tamaño global de este dominio. Es por esto que dichas ecuaciones describen bien el flujo en canales, ríos, lagos y lagunas, flujos de marea, corrientes marinas, avance de un frente de onda, arrastre de sedimentos, variación de concentración salina, flujo en la rotura de presas, flujos atmosféricos, transporte de contaminantes y tsunamis, entre otros; véase por ejemplo [1,2,3,4].

Se ha realizado una extensa investigación numérica en el área de las ecuaciones del movimiento de un fluido en aguas poco profundas, aplicando métodos de diferencias finitas [5], métodos de volúmenes finitos [6,7,8], métodos de elementos finitos [9,10,11,12,13], métodos tipo Godunov [14,15] y métodos de Boltzmann [16].

Las ecuaciones del movimiento de un fluido en aguas poco profundas que vamos a utilizar son las obtenidas a partir de las ecuaciones de Navier-Stokes para fluidos viscosos, y que se encuentran descritas por ejemplo en [17], entre otras referencias. El problema que se debe resolver puede escribirse en forma conservativa en términos de la profundidad del fluido y de las velocidades promediadas en la plano donde el flujo medio tiene lugar. La presencia del término fuente en la ecuación de momento, la consideración de batimetría variable, fricción en el fondo del lecho, tensión en la superficie libre del agua debida al viento y el efecto de Coriolis son aspectos que se pueden tener en cuenta en el modelo físico.

En este trabajo vamos ha realizar la aproximación de las ecuaciones del movimiento de un fluido en aguas poco profundas con elementos finitos de alto orden y usando los métodos VMS (Variational Multi-Scale) llamados ASGS (Algebraic SubGrid Scale) y OSS (Orthogonal Subgrid Scale). La contribución de este trabajo es tanto aplicar estas técnicas (por otro lado conocidas) al problema de flujo de aguas poco profundas como experimentar con elementos de orden elevado (hasta cuarto orden).

Veremos en primer lugar cómo a través de un cambio de variables adecuado y linearizando las ecuaciones de partida, cada iteración del proceso no lineal puede escribirse como un sistema acoplado de ecuaciones de convección-difusión-reacción (CDR). Plantearemos la aproximación de este sistema general de ecuaciones, particularizándolo después al problema de aguas poco profundas.

La estrategia de discretización que plantearemos consiste en dos pasos. Primero procederemos a discretizar en el tiempo mediante un esquema de integración temporal en diferencias finitas, y luego realizaremos una aproximación de elementos finitos en el espacio. Este procedimiento desacopla los errores provenientes de la discretización temporal de los correspondientes a la discretización espacial. Sin embargo, se tiene que señalar que el enfoque más común es proceder a la inversa, es decir, primero discretizar en el espacio y luego aproximar el sistema resultante de ecuaciones diferenciales en el tiempo. Para el método convencional de Galerkin ambos caminos dan lugar al mismo problema discreto, pero no es así para todos los métodos de estabilización basados en VMS. En lo concerniente a la discretización temporal, usaremos la regla trapezoidal generalizada, que es el método en diferencias finitas más sencillo; sin embargo, podríamos aplicar cualquier otro esquema en diferencias finitas.

En cuanto a la discretización espacial, es bien conocido que el método estándar de Galerkin puede fallar por dos razones: la presencia del término convectivo (no-lineal) dominante con respecto al término viscoso, y la necesidad de usar diferentes interpolaciones de elementos finitos para la profundidad y las velocidades promediadas, similarmente a lo que ocurre para la presión y la velocidad en el clásico problema de Stokes; dicha necesidad se plantea en forma de condición inf-sup. Ambas pueden superarse mediante una formulación estabilizada. Aquí vamos a usar las formulaciones basadas en subescalas y, en particular, el enfoque introducido por Hughes y otros en [18,19] para la ecuación de CDR escalar y generalizado a sistemas lineales en [20,21] y que corresponde al método ASGS para resolver el problema de CDR vectorial estacionario. La idea básica es aproximar el efecto de la componente de la solución continua que no puede ser resuelta por la malla de elementos finitos en términos de la solución en el espacio de elementos finitos. Una importante característica introducida en [22,23] es que la componente no resuelta, denominada subescala, se considera ortogonal respecto del producto escalar de ${\textstyle L^{2}}$ al espacio de elementos finitos, lo cual se explicará más adelante. Esta idea fue primero introducida en [23] como una extensión de un método de estabilización originalmente introducido para el problema de Stokes en [24] y totalmente analizado para la ecuación estacionaria de Navier-Stokes en [25]. Con estas ideas aplicadas al problema de CDR vectorial estacionario se obtiene el método OSS para resolver dicho problema. Finalmente, para el problema de CDR vectorial transitorio, que es el que usamos directamente para resolver las ecuaciones del movimiento de un fluido en aguas poco profundas, la formulación obtenida está basada en lo expuesto en [26,27,22]. Hay que hacer notar que no consideraremos el posible desarrollo de choques en la solución, es decir, discontinuidades que pueden llegar a producirse en el límite invíscido. Para su aproximación hay que recurrir a técnicas de captura de discontinuidades que no consideraremos en este trabajo.

El artículo está organizado como sigue. En la siguiente sección se describe la física del problema que queremos resolver y la obtención de la ecuación vectorial de CDR transitoria que representa el problema del movimiento de un fluido en aguas poco profundas. Las aproximaciones y formulaciones numéricas están descritas en la Sección 3. En la Sección 4 se presentan pruebas numéricas de convergencia en malla con soluciones analíticas conocidas y ejemplos numéricos de referencia en la literatura. Finalmente, en base a los resultados obtenidos se extraen algunas conclusiones en la Sección 5.

2. Planteamiento del problema, linealización y discretización temporal

2.1 Ecuaciones de gobierno

Sea ${\textstyle \Omega }$ un dominio acotado de ${\textstyle \mathbb {R} ^{2}}$ con coordenadas cartesianas ${\textstyle \mathbf {x} =(x_{1},x_{2})}$. Consideremos un fluido que se mueve durante el intervalo de tiempo ${\textstyle [0,T]}$ en el dominio de ${\textstyle \mathbb {R} ^{3}}$ dado por ${\textstyle \Omega \times (-H({\mathbf {x} }),\eta ({\mathbf {x} },t))}$, donde ${\textstyle x_{3}=-H({\mathbf {x} })}$ representa la batimetría del terreno y ${\textstyle x_{3}=\eta ({\mathbf {x} },t)}$ es la superficie libre del fluido, ${\textstyle {\mathbf {x} }\in \Omega }$, ${\textstyle t\in [0,T)}$, que será incógnita del problema. Consideraremos que ${\textstyle h({\mathbf {x} },t):=H({\mathbf {x} })+\eta ({\mathbf {x} },t)}$ es mucho menor que el diámetro de ${\textstyle \Omega }$, por lo que supondremos válida la aproximación de las ecuaciones de movimento en aguas poco profundas, las cuales se obtienen por integración vertical de las ecuaciones generales de movimiento, bien sea de fluidos viscosos (ecuaciones de Navier-Stokes) o invíscidos (ecuaciones de Euler); véase por ejemplo [17,28]. En este trabajo vamos a utilizar las ecuaciones obtenidas a partir de las ecuaciones de Navier-Stokes para un fluido newtoniano incompresible e isotérmico, incluyendo la tensión superficial provocada por los efectos del viento, así como también los efectos de Coriolis. Dichas ecuaciones pueden escribirse en forma indicial como

$\partial _{t}\left(hU_{i}\right)+\partial _{j}\left(hU_{i}U_{j}\right)+\partial _{i}{\frac {1}{2}}g\left(h^{2}-H^{2}\right)-\partial _{j}\left({\frac {h}{\rho }}{\bar {\tau }}_{ji}\right)+Q_{i}=0,\quad i=1,2,$ (1) $\partial _{t}h+\partial _{i}\left(hU_{i}\right)=0,$ (2)

con

${\overline {\tau }}_{ij}=\mu _{H}\left(\partial _{j}U_{i}+\partial _{i}U_{j}-{\frac {2}{3}}\delta _{ij}\partial _{k}U_{k}\right),\quad i,j=1,2,$ (3) $Q_{i}=h{\hat {f}}\left(-\delta _{i1}U_{2}+\delta _{i2}U_{1}\right)-g\left(h-H\right)\partial _{i}H+{\frac {h}{\rho }}\partial _{i}p_{a}-{\frac {1}{\rho }}\tau _{3i}^{s}+gU_{i}U_{0}{\hbox{Ch}}^{-1}h^{-2},\quad i=1,2,$ (4)

y

$U_{0}={\sqrt {U_{1}^{2}+U_{2}^{2}}},$

donde ${\textstyle U_{i}({\mathbf {x} },t)}$ ${\textstyle \left(i=1,2\right)}$ son las componentes de la velocidad promediadas en la profundidad, ${\textstyle \delta _{ij}}$ es la delta de Kronecker, ${\textstyle \partial _{t}}$ denota la derivada temporal y ${\textstyle \partial _{i}}$ la derivada con respecto a la ${\textstyle i}$-ésima coordenada cartesiana ${\textstyle (i=1,2)}$ en ${\textstyle \Omega }$. En las ecuaciones anteriores y en lo que sigue, índices repetidos indican la notación de sumación de Einstein, y los subíndices ${\textstyle i,}$ ${\textstyle j,}$ ${\textstyle k}$ recorren desde 1 hasta 2. En las expresiones anteriores, ${\textstyle g}$ es la aceleración de la gravedad, ${\textstyle \rho }$ la densidad del fluido, ${\textstyle {\bar {\tau }}_{ij}}$ son las tensiones viscosas promediadas, ${\textstyle \mu _{H}}$ es el coeficiente de viscosidad dinámico, ${\textstyle {\hat {f}}}$ es el parámetro de Coriolis, ${\textstyle p_{a}}$ es la presión atmosférica, ${\textstyle \tau _{3i}^{s}}$ ${\textstyle \left(i=1,2\right)}$ son las tensiones en la superficie libre del agua debidas al viento, ${\textstyle {\hbox{Ch}}}$ es el coeficiente de Chézy para el rozamiento en el fondo y ${\textstyle U_{0}}$ es la norma euclídea de ${\textstyle \left(U_{1},U_{2}\right)}$.

Las ecuaciones (1) y (2) representan un sistema de tres ecuaciones, cuyo vector de incógnitas es

$\mathbf {U} ^{T}=\left[U_{1},U_{2},h\right].$

Dichas ecuaciones constituyen las ecuaciones del movimiento de un fluido en aguas poco profundas. Se deben completar con condiciones iniciales y de contorno. Los valores iniciales para la elevación del agua y las velocidades promediadas deben ser conocidos como condiciones iniciales. Con respecto a las condiciones de contorno, es bien conocido que el problema está bien puesto si la velocidad promediada se especifica en el contorno de entrada del dominio computacional ${\textstyle \Omega }$, mientras que en el resto del contorno se prescribe la componente normal de las tensiones viscosas y la elevación del fluido.

Las ecuaciones para aguas poco profundas descritas anteriormente, en su forma conservativa, se presentaron en esta forma en las referencias [29,30]. Debido a su complejidad, en la literatura existen muchas variantes de estas ecuaciones con distintas simplificaciones, tanto para las ecuaciones que parten de las ecuaciones de Euler [28], como para las ecuaciones obtenidas de las ecuaciones de Navier-Stokes [17].

En nuestro trabajo utilizaremos las ecuaciones (1) y (2) sin eliminar o hacer simplificaciones de ninguno de sus términos. Mediante un cambio de variables transformaremos las ecuaciones para poder escribirlas como una ecuación vectorial de convección-difusión-reacción (CDR) transitoria de la forma

$\partial _{t}\mathbf {u} -\partial _{i}\left(\mathbf {K} _{ij}\partial _{j}\mathbf {u} \right)+\partial _{i}\left(\mathbf {A} _{i}\mathbf {u} \right)+\mathbf {Su} =\mathbf {F} ,$

(5)

para la que más adelante, en la Sección 3, presentaremos su aproximación numérica por elementos finitos mediante los métodos variacionales de subescalas ASGS y OSS. En las ecuaciones anteriores, ${\textstyle \mathbf {u} }$ es el vector de incógnitas, ${\textstyle \mathbf {F} }$ el vector de fuerzas conocido y ${\textstyle \mathbf {K} _{ij}}$, ${\textstyle \mathbf {A} _{i}}$, ${\textstyle \mathbf {S} }$ matrices dadas, que pueden depender de ${\textstyle \mathbf {u} }$ en problemas no lineales. Para una descripción general de cómo tratar el problema genérico descrito y sus aplicaciones en mecánica de fluidos, véase [31].

2.2 Cambio de variables

Realizando el cambio de variables ${\textstyle u_{i}:=hU_{i}}$ y ${\textstyle P:={\frac {1}{2}}g\left(h^{2}-H^{2}\right)}$, con ${\textstyle \partial _{t}P=hg\partial _{t}h}$, las ecuaciones (1) y (2) se pueden escribir de la siguiente manera:

$\partial _{t}u_{i}+\partial _{j}\left(U_{j}u_{i}\right)+\partial _{i}P-\partial _{j}{\frac {\mu _{H}}{\rho }}\left[\left(\partial _{i}u_{j}+\partial _{j}u_{i}-{\frac {2}{3}}\delta _{ij}\partial _{k}u_{k}\right)-\left(U_{j}\partial _{i}h+U_{i}\partial _{j}h-{\frac {2}{3}}\delta _{ij}U_{k}\partial _{k}h\right)\right]$ $\qquad +{\hat {f}}\left(-\delta _{i1}u_{2}+\delta _{i2}u_{1}\right)+gU_{0}{\hbox{Ch}}^{-1}h^{-3}u_{i}-g\left(h-H\right)\partial _{i}H+{\frac {h}{\rho }}\partial _{i}p_{a}-{\frac {1}{\rho }}\tau _{3i}^{s}=0,\quad i=1,2,$ (6) ${\frac {1}{hg}}\partial _{t}P+\partial _{i}u_{i}=0.$ (7)

Las ecuaciones (6) y (7) se pueden escribir fácilmente en el formato de la ecuación (5), considerando ésta como una ecuación no lineal, con las matrices de coeficientes dependientes de la incógnita. Sin embargo, detallaremos esta identificación en el caso del problema linealizado y discretizado en el tiempo.

2.3 Discretización en el tiempo y linealización

Para la discretización temporal de las ecuaciones de movimiento, consideremos una partición uniforme del intervalo de tiempo ${\textstyle 0=t^{0}<t^{1}<\dots <t^{N}=T}$, con ${\textstyle \delta t=t^{n+1}-t^{n}}$, donde ${\textstyle \delta t}$ es el tamaño del paso de tiempo, considerado constante. Aquí y en adelante, usaremos el superíndice ${\textstyle n}$ para indicar el nivel de tiempo ${\textstyle n}$.

Aunque la discretización en el tiempo puede realizarse mediante cualquier aproximación de la derivada temporal en diferencias finitas o elementos finitos, aquí utilizaremos la regla trapezoidal generalizada. Para una función genérica ${\textstyle f}$, sea

$f^{n+\theta }=\theta f^{n+1}+\left(1-\theta \right)f^{n},\qquad 0\leq \theta \leq 1.$

(8)

Aproximaremos

$\delta _{t}^{n}f:={\frac {1}{\delta t}}(f^{n+1}-f^{n})={\frac {1}{\theta \delta t}}(f^{n+\theta }-f^{n})\approx (\partial _{t}f)^{n+\theta }$

Esta aproximación es de segundo orden en ${\textstyle \delta t}$ en el caso en que ${\textstyle \theta =1/2}$ (método de Crank-Nicolson) y de primer orden si ${\textstyle \theta \not =1/2}$. Para ${\textstyle \theta =1}$ corresponde al método de Euler implícito o el método de diferencias hacia atrás de primer orden, a menudo abreviado como BDF1.

En cuanto a la linealización, utilizaremos el método de punto fijo de Picard. En cada iteración de cada paso de tiempo, el problema a resolver es de la forma

$\delta _{t}^{n}u_{i}+\partial _{j}\left(a_{j}u_{i}\right)+\partial _{i}p-\partial _{j}{\hat {\tau }}_{ji}+S_{ij}u_{j}+b_{i}=0,\quad i=1,2,$ (9) ${\frac {1}{h_{0}g}}\delta _{t}^{n}p+\partial _{i}u_{i}=0.$ (10)

Usando un superíndice adicional para el contador de iteraciones, las variables introducidas en (9)-(10) para la iteración ${\textstyle i}$-ésima en el paso de tiempo ${\textstyle n}$ son

${3}a_{j}=U_{j}^{n+\theta ,i-1},\quad u_{j}=\left(hU_{j}\right)^{n+\theta ,i},$ $h_{0}=h^{n+\theta ,i-1},\quad p=P^{n+\theta ,i},$ $\delta _{t}^{n}p={\frac {1}{\theta \delta t}}\left(p-P^{n}\right),\quad \delta _{t}^{n}u_{j}={\frac {1}{\theta \delta t}}\left[u_{j}-\left(hU_{j}\right)^{n}\right],$ ${\hat {\tau }}_{ij}={\frac {\mu _{H}}{\rho }}\left(\partial _{i}u_{j}+\partial _{j}u_{i}-{\frac {2}{3}}\delta _{ij}\partial _{k}u_{k}\right),\quad \tau _{ij}^{*}={\frac {\mu _{H}}{\rho }}\left(a_{j}\partial _{i}h_{0}+a_{i}\partial _{j}h_{0}-{\frac {2}{3}}\delta _{ij}a_{k}\partial _{k}h_{0}\right),$ $S_{11}=S_{22}={\hbox{Ch}}^{-1}gU_{0}^{n+\theta ,i-1}h_{0}^{-3},\quad U_{0}^{n+\theta ,i-1}={\sqrt {\left(U_{1}^{n+\theta ,i-1}\right)^{2}+\left(U_{2}^{n+\theta ,i-1}\right)^{2}}},$ $S_{12}=-S_{21}=-{\hat {f}},\quad b_{i}=b_{i}^{*}+\partial _{j}\tau _{ji}^{*},$ $b_{i}^{*}=-g\left(h_{0}-H\right)\partial _{i}H+{\frac {1}{\rho }}h_{0}\partial _{i}p_{a}-{\frac {1}{\rho }}\tau _{3i}^{S}.\quad$

Obsérvese que la forma linealizada de las tensiones viscosas ${\textstyle {\overline {\tau }}_{ij}}$ dada en (3) corresponde a ${\textstyle {\hat {\tau }}_{ij}-\tau _{ij}^{*},}$ donde ${\textstyle {\hat {\tau }}_{ij}}$ está escrito en términos de las variables de la iteración actual, mientras que ${\textstyle \tau _{ij}^{*}}$ se calcula con los valores de las variables correspondientes a la iteración anterior.

2.4 Forma vectorial

Para escribir las ecuaciones (9) y (10) en la forma vectorial (5), aunque discretizada en el tiempo, escribimos las mismas como un sistema de tres ecuaciones con tres incógnitas:

$\delta _{t}^{n}u_{1}-{\frac {\mu _{H}}{\rho }}\left({\frac {4}{3}}\partial _{1}^{2}u_{1}+{\frac {1}{3}}\partial _{1}\partial _{2}u_{2}+\partial _{2}^{2}u_{1}\right)+a_{1}\partial _{1}u_{1}+a_{2}\partial _{2}u_{1}+\partial _{1}p+\left(\partial _{1}a_{1}+\partial _{2}a_{2}+S_{11}\right)u_{1}+S_{12}u_{2}$ $\qquad +b_{1}^{*}+\partial _{1}\tau _{11}^{*}+\partial \tau _{21}^{*}=0,$ (11) $\delta _{t}^{n}u_{2}-{\frac {\mu _{H}}{\rho }}\left(\partial _{1}^{2}u_{2}+{\frac {1}{3}}\partial _{1}\partial _{2}u_{1}+{\frac {4}{3}}\partial _{2}^{2}u_{2}\right)+a_{1}\partial _{1}u_{2}+a_{2}\partial _{2}u_{2}+\partial _{2}p+\left(\partial _{1}a_{1}+\partial _{2}a_{2}+S_{22}\right)u_{2}+S_{21}u_{1}$ $\qquad \,+b_{2}^{*}+\partial _{1}\tau _{12}^{*}+\partial _{2}\tau _{22}^{*}=0,$ (12) ${\frac {1}{h_{0}g}}\delta _{t}^{n}p+\partial _{1}u_{1}+\partial _{2}u_{2}=0.$ (13)

La forma vectorial discreta en el tiempo de (5) del sistema de ecuaciones (11), (12) y (13), linealizada con el método de Picard y escribiendo la divergencia del flujo convectivo como derivada convectiva, está entonces dada por

$\left[{\begin{array}{c}\delta _{t}^{n}u_{1}\\\delta _{t}^{n}u_{2}\\{\frac {1}{h_{0}g}}\delta _{t}^{n}p\end{array}}\right]-{\frac {\mu _{H}}{\rho }}\left[{\begin{array}{ccc}{\frac {4}{3}}&0&0\\0&1&0\\0&0&0\end{array}}\right]\partial _{1}^{2}\left[{\begin{array}{c}u_{1}\\u_{2}\\p\end{array}}\right]-{\frac {\mu _{H}}{\rho }}\left[{\begin{array}{ccc}0&{\frac {1}{6}}&0\\{\frac {1}{6}}&0&0\\0&0&0\end{array}}\right]\partial _{1}\partial _{2}\left[{\begin{array}{c}u_{1}\\u_{2}\\p\end{array}}\right]$ $-{\frac {\mu _{H}}{\rho }}\left[{\begin{array}{ccc}1&0&0\\0&{\frac {4}{3}}&0\\0&0&0\end{array}}\right]\partial _{2}^{2}\left[{\begin{array}{c}u_{1}\\u_{2}\\p\end{array}}\right]-{\frac {\mu _{H}}{\rho }}\left[{\begin{array}{ccc}0&{\frac {1}{6}}&0\\{\frac {1}{6}}&0&0\\0&0&0\end{array}}\right]\partial _{2}\partial _{1}\left[{\begin{array}{c}u_{1}\\u_{2}\\p\end{array}}\right]$ $+\left[{\begin{array}{ccc}a_{1}&0&1\\0&a_{1}&0\\1&0&0\end{array}}\right]\partial _{1}\left[{\begin{array}{c}u_{1}\\u_{2}\\p\end{array}}\,\right]+\left[{\begin{array}{ccc}a_{2}&0&0\\0&a_{2}&1\\0&1&0\end{array}}\right]\partial _{2}\left[{\begin{array}{c}u_{1}\\u_{2}\\p\end{array}}\right]$ $+\left[{\begin{array}{ccc}\partial _{1}a_{1}+\partial _{2}a_{2}+S_{11}&S_{12}&0\\S_{21}&\partial _{1}a_{1}+\partial _{2}a_{2}+S_{22}&0\\0&0&0\end{array}}\right]\left[{\begin{array}{c}u_{1}\\u_{2}\\p\end{array}}\right]=\left[{\begin{array}{c}-Q_{1}\\-Q_{2}\\0\end{array}}\right],$

(46)

con

$Q_{1}=b_{1}^{*}+\partial _{1}\tau _{11}^{*}+\partial _{2}\tau _{21}^{*},$ $Q_{2}=b_{2}^{*}+\partial _{1}\tau _{12}^{*}+\partial _{2}\tau _{22}^{*}.$

La ecuación (46) corresponde a la ecuación vectorial de CDR transitoria (5) del movimiento de un fluido en aguas poco profundas discretizada en el tiempo y linealizada. Las matrices ${\textstyle \mathbf {K} _{ij}}$, ${\textstyle \mathbf {A} _{i},}$ ${\textstyle \mathbf {S} }$ y ${\textstyle \mathbf {F} }$ son

$\mathbf {K} _{11}={\frac {\mu _{H}}{\rho }}\left[{\begin{array}{ccc}{\frac {4}{3}}&0&0\\0&1&0\\0&0&0\end{array}}\right],\quad \mathbf {K} _{12}=\mathbf {K} _{21}={\frac {\mu _{H}}{\rho }}\left[{\begin{array}{ccc}0&{\frac {1}{6}}&0\\{\frac {1}{6}}&0&0\\0&0&0\end{array}}\right],\quad \mathbf {K} _{22}={\frac {\mu _{H}}{\rho }}\left[{\begin{array}{ccc}1&0&0\\0&{\frac {4}{3}}&0\\0&0&0\end{array}}\right],$ $\mathbf {A} _{1}=\left[{\begin{array}{ccc}a_{1}&0&1\\0&a_{1}&0\\1&0&0\end{array}}\right],\quad \mathbf {A} _{2}=\left[{\begin{array}{ccc}a_{2}&0&0\\0&a_{2}&1\\0&1&0\end{array}}\right],$ $\mathbf {S} =\left[{\begin{array}{ccc}\partial _{1}a_{1}+\partial _{2}a_{2}+S_{11}&S_{12}&0\\S_{21}&\partial _{1}a_{1}+\partial _{2}a_{2}+S_{22}&0\\0&0&0\end{array}}\right],\quad \mathbf {F=} \left[{\begin{array}{c}-Q_{1}\\-Q_{2}\\0\end{array}}\right].$

Obsérvese que las matrices ${\textstyle \mathbf {K} _{ij}}$ son simétricas. Los coeficientes de las matrices ${\textstyle \mathbf {A} _{i},}$ ${\textstyle \mathbf {S} }$ y ${\textstyle \mathbf {F} }$ no todos son constantes, pues algunos dependen de las velocidades del flujo, elevación del nivel del agua, su batimetría y sus gradientes, cuyos valores corresponden a la iteración anterior resultado de la linealización. El vector de incógnitas es

$\mathbf {u} ^{T}=\left[u_{1},u_{2},p\right].$

3. Aproximación espacial y estabilización numérica

En esta sección vamos a describir la aproximación espacial mediante el método de los elementos finitos y estabilización numérica de la ecuación vectorial de CDR transitoria (5), considerando que las matrices de coeficientes están evaluadas con las incógnitas de una iteración anterior como resultado de la linealización. Esta aproximación la podremos aplicar directamente a (46), teniendo en cuenta que en este caso hemos discretizado el tiempo mediante un esquema de diferencias finitas y hemos escrito el término convectivo como ${\textstyle \mathbf {A} _{i}\partial _{i}\mathbf {u} }$; las modificaciones necesarias por escribir así este término son obvias.

Es conocido que la aproximación de la ecuación estacionaria escalar de CDR por el método estándar de elementos finitos de Galerkin no es estable cuando el término convectivo es dominante con respecto al término difusivo. Para el caso vectorial sucede exactamente lo mismo, con el agravante de la no linealidad en los términos convectivos y de la compatibilidad en la interpolación de las incógnitas. Para resolver estos problemas, introduciremos los métodos de elementos finitos estabilizados ASGS y OSS basados en la formulación VMS.

3.1 Forma diferencial del problema

La ecuación diferencial que vamos a aproximar numéricamente es la ecuación vectorial transitoria de CDR en 2D, con condiciones de contorno de Dirichlet, Neumann y condiciones iniciales conocidas. Aunque todo lo desarrollado en esta sección es fácilmente aplicable a 3D, hemos preferido restringirnos a 2D por su directa aplicación a las ecuaciones del movimiento de un fluido en aguas poco profundas. El problema consiste en encontrar ${\textstyle \mathbf {u} :\Omega \times \gamma \rightarrow \mathbb {R} ^{n_{inc}}}$, ${\textstyle \Omega \subset \mathbb {R} ^{2}}$, ${\textstyle \gamma =\left[0,T\right]}$, tal que

$\partial _{t}\mathbf {u} +{\mathcal {L\left(\mathbf {u} \right)}}=\mathbf {F} ,\qquad \left(\mathbf {x} ,t\right)\in \Omega \times \gamma ,$

(61)

con

${\mathcal {L\left(\mathbf {u} \right)}}:=-\partial _{i}\left(\mathbf {K} _{ij}\partial _{j}\mathbf {u} \right)+\partial _{i}\left(\mathbf {A} _{i}\mathbf {u} \right)+\mathbf {Su} ,$

(62)

sujeta a condiciones de contorno de Dirichlet

$\mathbf {u} =\mathbf {u} _{D},\qquad \left(\mathbf {x} ,t\right)\in \partial \Omega _{D}\times \mathbf {\gamma } ,$

condiciones de contorno de Neumann

$n_{i}\mathbf {A} _{i}^{f}\mathbf {u} -n_{i}\mathbf {K} _{ij}\partial _{j}\mathbf {u} ={{\boldsymbol {}}\varphi },\qquad \left(\mathbf {x} ,t\right)\in \partial \Omega _{N}\times \mathbf {\gamma } ,$

(63)

y condiciones iniciales

$\mathbf {u} =\mathbf {u} _{0},\qquad \mathbf {x} \in \Omega ,\quad t=0.$

Hemos considerado que la frontera de ${\textstyle \Omega }$ (denotada por ${\textstyle \partial \Omega }$) está dada por ${\textstyle \partial \Omega =\partial \Omega _{D}+\partial \Omega _{N}}$ y las matrices de convección ${\textstyle \mathbf {A} _{i}}$ se pueden descomponer en dos términos, uno propiamente convectivo ${\textstyle \mathbf {A} _{i}^{c}}$ y otro que contribuye al flujo de la incógnita, ${\textstyle \mathbf {A} _{i}^{f}}$, de manera que ${\textstyle \mathbf {A} _{i}=\mathbf {A} _{i}^{c}+\mathbf {A} _{i}^{f}}$.

La ecuación (61) es un sistema de ${\textstyle n_{inc}}$ ecuaciones diferenciales en derivadas parciales, con ${\textstyle n_{inc}=3}$ para las ecuaciones de aguas poco profundas. Las matrices de difusividad ${\textstyle \mathbf {K} _{ij}}$, convección ${\textstyle \mathbf {A} _{i}}$ y de reacción ${\textstyle \mathbf {S} }$ son matrices cuadradas de orden ${\textstyle n_{inc}\times n_{inc}}$, mientras que ${\textstyle \mathbf {u} }$ y ${\textstyle \mathbf {F} }$ son vectores de ${\textstyle n_{inc}}$ componentes.

Suponemos que las condiciones iniciales y de contorno de Dirichlet verifican la condición de compatibilidad ${\textstyle \mathbf {u} _{0}\left(\mathbf {x} \right)|_{\partial \Omega _{D}}=\mathbf {u} _{D}\left(\mathbf {x} ,0\right)}$.

3.2 Forma débil del problema estacionario

Para simplificar la exposición, empecemos considerando el problema estacionario de la ecuación vectorial de CDR, con condiciones de Dirichlet homogéneas en toda su frontera. Dicho problema consiste en hallar ${\textstyle \mathbf {u} :\Omega \rightarrow \mathbb {R} ^{n_{inc}}}$ tal que

${\mathcal {L\left(\mathbf {u} \right)}}:=-\partial _{i}\left(\mathbf {K} _{ij}\partial _{j}\mathbf {u} \right)+\partial _{i}\left(\mathbf {A} _{i}\mathbf {u} \right)+\mathbf {Su} =\mathbf {F} ,\qquad \mathbf {x} \in \Omega ,$ (64) $\qquad \qquad \qquad \qquad \qquad \mathbf {u} =\mathbf {0} ,\mathbf {\qquad x} \in \partial \Omega {.}$ (65)

Para escribir la forma débil del problema (64)-(65), sea ${\textstyle {\mathcal {W}}}$ el espacio donde la ecuación diferencial tiene sentido distribucional. Por ejemplo, si ${\textstyle \mathbf {K} _{ij}}$ define una forma cuadrática definida positiva (que no es el caso en las ecuaciones de aguas poco profundas), dicho espacio es ${\textstyle {\mathcal {W}}:=\left(H_{0}^{1}(\Omega \right))^{n_{inc}}}$, es decir, el espacio de funciones vectoriales cuyas componentes son funciones cuadrado integrable, que tienen primera derivada cuadrado integrable y que se anulan en la frontera ${\textstyle \partial \Omega }$. Suponemos también que ${\textstyle \mathbf {F} }$ multiplicado por funciones de ${\textstyle {\mathcal {W}}}$ es integrable, y que las matrices ${\textstyle \mathbf {K} _{ij},}$ ${\textstyle \mathbf {A} _{i}}$ y ${\textstyle \mathbf {S} }$ tienen coeficientes acotados.

Podemos ahora escribir la forma débil del problema (64)-(65) como sigue: hallar ${\textstyle \mathbf {u} \in {\mathcal {W}}}$ tal que

$\int _{\Omega }\partial _{i}\mathbf {v} ^{T}\mathbf {K} _{ij}\partial _{j}\mathbf {u} {\,d}\Omega {+\int }_{\Omega }\mathbf {v} ^{T}\partial _{i}\left(\mathbf {A} _{i}^{c}\mathbf {u} \right){\,d}\Omega {-\int }_{\Omega }\partial _{i}\mathbf {v} ^{T}\mathbf {A} _{i}^{f}\mathbf {u} {\,d}\Omega {+\int }_{\Omega }\mathbf {v} ^{T}\mathbf {Su} {\,d}\Omega$ $=\int _{\Omega }\mathbf {v} ^{T}\mathbf {F} {\,d}\Omega {+\int }_{\partial \Omega }(\mathbf {v} ^{T}\mathbf {K} _{ij}\partial _{j}\mathbf {u} )n_{i}{\,d}\Gamma {-\int }_{\partial \Omega }(\mathbf {v} ^{T}\mathbf {A} _{i}^{f}\mathbf {u} )n_{i}{\,d}\Gamma ,\qquad \forall \mathbf {v} \in {\mathcal {W}},$

(66)

donde ${\textstyle n_{i}}$ es la componente ${\textstyle i}$-ésima de la normal unitaria a ${\textstyle \partial \Omega }$.

Los dos últimos términos del lado derecho de la ecuación (66) son valores conocidos, pues o bien la función de test ${\textstyle \mathbf {v} }$ es nula en el caso en el que ${\textstyle \partial \Omega _{D}=\partial \Omega }$ o bien usamos la condición de Neumann (63). Nos restringiremos al primer caso, como hemos indicado, con lo cual la forma variacional o débil del problema (64)-(65) consiste en encontrar ${\textstyle \mathbf {u} \in {\mathcal {W}}}$ tal que

$B(\mathbf {u} ,\mathbf {v} )=\left\langle \mathbf {F} ,\mathbf {v} \right\rangle \qquad \forall \mathbf {v} \in {\mathcal {W}},$

(67)

donde la forma ${\textstyle B(\mathbf {u} ,\mathbf {v} )}$ y la forma lineal ${\textstyle \left\langle \mathbf {F} ,\mathbf {v} \right\rangle }$ están dadas por

$B(\mathbf {u} ,\mathbf {v} )=\int _{\Omega }\partial _{i}\mathbf {v} ^{T}\mathbf {K} _{ij}\partial _{j}\mathbf {u} {\,d}\Omega {+\int }_{\Omega }\mathbf {v} ^{T}\partial _{i}\left(\mathbf {A} _{i}^{c}\mathbf {u} \right){\,d}\Omega {-\int }_{\Omega }\partial _{i}\mathbf {v} ^{T}\mathbf {A} _{i}^{f}\mathbf {u} {\,d}\Omega {+\int }_{\Omega }\mathbf {v} ^{T}\mathbf {Su} {\,d}\Omega ,$ (68) $\left\langle \mathbf {F} ,\mathbf {v} \right\rangle =\int _{\Omega }\mathbf {v} ^{T}\mathbf {F} {\,d}\Omega {.}$ (69)

3.3 Método estándar de Galerkin para el problema estacionario

Para aproximar numéricamente la ecuación (67) en el espacio por el método de los elementos finitos, consideremos una partición ${\textstyle \{\Omega ^{e}\}}$ de ${\textstyle \Omega }$, con ${\textstyle e=1,\dots ,n_{el}}$, siendo ${\textstyle n_{el}}$ el número de elementos de la partición. Sea ${\textstyle {\mathcal {W}}_{h}}$ un espacio conforme de elementos finitos para aproximar ${\textstyle {\mathcal {W}}}$ ${\textstyle \left({\mathcal {W}}_{h}\subset {\mathcal {W}}\right)}$. El problema discreto que se conoce como el método estándar de Galerkin, que aproxima la ecuación vectorial de CDR estacionaria (65), consiste en hallar ${\textstyle \mathbf {u} _{h}\in {\mathcal {W}}_{h}}$ tal que

$B(\mathbf {u} _{h},\mathbf {v} _{h})=\left\langle \mathbf {F} ,\mathbf {v} _{h}\right\rangle \qquad \forall \mathbf {v} _{h}\in {\mathcal {W}}_{h}.$

(70)

En general, es necesario que la interpolación de las incógnitas satisfaga ciertas condiciones de compatibilidad (usualmente expresadas en forma de condiciones inf-sup). Sin embargo, con la estabilización que introduciremos más adelante esto no es necesario, por lo que presentamos a continuación algunos aspectos de implementación usando igual interpolación.

Observemos primero que podemos escribir

$B(\mathbf {u} _{h},\mathbf {v} _{h}):={\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left(\partial _{i}\mathbf {v} _{h}^{T}\mathbf {K} _{ij}\partial _{j}\mathbf {u} _{h}+\mathbf {v} _{h}^{T}\partial _{i}\left(\mathbf {A} _{i}^{c}\mathbf {u} _{h}\right)-\partial _{i}\mathbf {v} _{h}^{T}\mathbf {A} _{i}^{f}\mathbf {u} _{h}+\mathbf {v} _{h}^{T}\mathbf {Su} _{h}\right){\,d}\Omega ,$ (71) $\left\langle \mathbf {F} ,\mathbf {v} _{h}\right\rangle ={\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\mathbf {v} _{h}^{T}\mathbf {F} {\,d}\Omega {.}$ (72)

Escribamos ${\textstyle \mathbf {u} _{h}=\left({\hat {u}}^{1},{\hat {u}}^{2},...,{\hat {u}}^{n_{inc}}\right)^{T}}$. Si usamos las mismas funciones de interpolación de clase ${\textstyle C^{0}}$ (lagrangianas) para todos las componentes de la incógnita, podemos escribir

${\hat {u}}^{q}({\mathbf {x} })={\overset {M}{\underset {m=1}{\sum }}}u_{m}^{q}N_{m}\left(\mathbf {x} \right),\qquad q=1,...,n_{inc},$

(73)

donde ${\textstyle M}$ es el número de nodos de la malla de elementos finitos, ${\textstyle N_{m}\left(\mathbf {x} \right)}$ son las funciones de forma y ${\textstyle u_{m}^{q}}$ es el valor nodal de la componente ${\textstyle q}$ de la incógnita en el nodo ${\textstyle m}$ de la malla. Además, utilizando el método de Galerkin tomamos como funciones de prueba ${\textstyle \mathbf {v} _{h}}$ las dadas por:

$\mathbf {v} _{h}^{T}=\mathbf {v} _{h,p}^{T}=\left(\delta _{1p}N_{l},\delta _{2p}N_{l},...,\delta _{n_{inc}p}N_{l}\right),\quad p=1,\dots ,n_{inc},\quad l=1,\dots ,M,$

(74)

donde ${\textstyle \delta _{ip}}$ es la delta de Kronecker. Reemplazando (73) y (74) en (70), (71) y (72) se tiene:

${\underset {e=1}{\overset {n_{el}}{\sum }}}\sum _{q=1}^{n_{inc}}{\overset {M}{\underset {m=1}{\sum }}}\left[\int _{\Omega ^{e}}\partial _{i}N_{l}\left(K_{ij}\right)_{pq}\partial _{j}N_{m}{\,d}\Omega +\int _{\Omega ^{e}}N_{l}\left(A_{i}^{c}\right)_{pq}\partial _{i}N_{m}{\,d}\Omega \right.$ $\left.-\int _{\Omega ^{e}}\partial _{i}N_{l}{\bigl (}A_{i}^{f}{\bigr )}_{pq}N_{m}{\,d}\Omega +\int _{\Omega ^{e}}N_{l}S_{pq}N_{m}{\,d}\Omega \right]u_{m}^{q}={\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}N_{l}f_{p}{\,d}\Omega ,$ $p=1,\dots ,n_{inc},~l=1,\dots ,M.$

(75)

En esta expresión, ${\textstyle (K_{ij})_{pq},}$ ${\textstyle (A_{i}^{c})_{pq}}$, ${\textstyle (A_{i}^{f})_{pq}}$ y ${\textstyle (S)_{pq}}$ son los coeficientes del elemento de fila ${\textstyle p}$-ésima y columna ${\textstyle q}$-ésima de las correspondientes matrices ${\textstyle \mathbf {K} _{ij}}$, ${\textstyle \mathbf {A} _{i}^{c}}$, ${\textstyle \mathbf {A} _{i}^{f}}$ y ${\textstyle \mathbf {S} }$. El ensamblaje de la ecuación (75) da lugar, una vez impuestas las condiciones de contorno, a un sistema lineal de ecuaciones cuya solución proporciona los valores nodales de la aproximación numérica del problema estacionario (64)-(65).

3.4 Método de las subescalas, problema estacionario

Como ya dijimos antes, el método estándar de Galerkin presenta inestabilidades numéricas cuando el término convectivo es dominante con respecto al término difusivo y debido a las condiciones de compatibilidad entre la interpolación de las variables. El método que vamos a utilizar para la estabilización numérica es el método variacional de subescalas (VMS) introducido por Hughes y otros en [18,19] para resolver las inestabilidades numéricas del método de Galerkin en el problema de CDR escalar estacionario y generalizado en [20,21] al problema de CDR vectorial estacionario.

La idea básica es descomponer la variable continua desconocida ${\textstyle \mathbf {u} \in {\mathcal {W}}}$ en una parte resoluble en el espacio de elementos finitos ${\textstyle \mathbf {u} _{h}\in {\mathcal {W}}_{h},}$ con ${\textstyle {\mathcal {W}}_{h}\subset {\mathcal {W}}}$, y una parte en la escala de una submalla ${\textstyle {\tilde {\mathbf {u} }}\in {\tilde {\mathcal {W}}}}$, ${\textstyle {\tilde {\mathcal {W}}}\subset {\mathcal {W}},}$ la cual no puede ser capturada por la malla de elementos finitos, siendo ${\textstyle {\mathcal {W}}={\mathcal {W}}_{h}\oplus {\tilde {\mathcal {W}}}}$, donde ${\textstyle {\mathcal {\tilde {W}}}}$ es cualquier espacio para completar ${\textstyle {\mathcal {W}}_{h}}$ en ${\textstyle {\mathcal {W}}}$. Para evitar tecnicismos, podemos pensar de ${\textstyle {\mathcal {W}}}$ y ${\textstyle {\mathcal {\tilde {W}}}}$ como espacios dimensionalmente finitos, con una dimensión grande. Puesto que ${\textstyle {\tilde {\mathcal {W}}}}$ representa la componente de ${\textstyle {\mathcal {W}}}$ que no puede ser capturada por el espacio de elementos finitos, la llamamos espacio de las subescalas. De este modo, la variable continua desconocida podemos escribirla como ${\textstyle \mathbf {u} =\mathbf {u} _{h}+{\tilde {\mathbf {u} }}}$, donde ${\textstyle \mathbf {u} _{h}}$ es la componente de ${\textstyle \mathbf {u} }$ en el espacio de elementos finitos y ${\textstyle {\tilde {\mathbf {u} }}}$ es su componente en el complemento (con respecto a un cierto producto interno) en ${\textstyle {\mathcal {W}}}$.

Aplicando la descomposición mencionada a la ecuación continua (67) se obtiene:

$B(\mathbf {u} _{h}+{\tilde {\mathbf {u} }},\mathbf {v} _{h}+{\tilde {\mathbf {v} }})=\left\langle \mathbf {F} ,\mathbf {v} _{h}+{\tilde {\mathbf {v} }}\right\rangle \qquad \mathbf {\forall v} _{h}\in {\mathcal {W}}_{h},~\forall {\tilde {\mathbf {v} }}\in {\tilde {\mathcal {W}}}.$

(76)

Hemos considerado el problema linealizado, por lo cual ${\textstyle B}$ es una forma bilineal (para el tratamiento generalizado de problemas no lineales, véase [22,32]). Utilizando este hecho, la ecuación (76) se puede descomponer en el siguiente sistema de ecuaciones:

$B\left(\mathbf {u} _{h},\mathbf {v} _{h}\right)+B\left({\tilde {\mathbf {u} }},\mathbf {v} _{h}\right)=\left\langle \mathbf {F} ,\mathbf {v} _{h}\right\rangle \qquad \mathbf {\forall v} _{h}\in {\mathcal {W}}_{h},$ (77) $B\left(\mathbf {u} _{h},{\tilde {\mathbf {v} }}\right)+B\left({\tilde {\mathbf {u} }},{\tilde {\mathbf {v} }}\right)=\left\langle \mathbf {F} ,{\tilde {\mathbf {v} }}\right\rangle \qquad \forall {\tilde {\mathbf {v} }}\in {\tilde {\mathcal {W}}}.$ (78)

La ecuación (77) corresponde a la escala resoluble ${\textstyle \mathbf {u} _{h}}$ en el espacio de elementos finitos y tiene dos términos a su lado izquierdo, el primero es la contribución del método de Galerkin y el segundo toma en cuenta la influencia de la subescala en ${\textstyle \mathbf {u} _{h}}$. De la ecuación (78) debe obtenerse una aproximación a ${\textstyle {\tilde {\mathbf {u} }}}$.

De forma análoga a la ecuación (71), para el segundo término del lado izquierdo de la ecuación (77) tenemos

$B\left({\tilde {\mathbf {u} }},\mathbf {v} _{h}\right)={\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left(\partial _{i}\mathbf {v} _{h}^{T}\mathbf {K} _{ij}\partial _{j}\mathbf {\tilde {\mathbf {u} }} +\mathbf {v} _{h}^{T}\partial _{i}\left(\mathbf {A} _{i}^{c}\mathbf {\tilde {\mathbf {u} }} \right)-\partial _{i}\mathbf {v} _{h}^{T}\mathbf {A} _{i}^{f}\mathbf {\tilde {\mathbf {u} }} +\mathbf {v} _{h}^{T}\mathbf {S{\tilde {\mathbf {u} }}} \right){\,d}\Omega ,$

(79)

e integrando por partes dentro de cada elemento y recordando que ${\textstyle \mathbf {A} _{i}=\mathbf {A} _{i}^{c}+\mathbf {A} _{i}^{f}}$ tenemos

$B\left({\tilde {\mathbf {u} }},\mathbf {v} _{h}\right)={\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left(-\partial _{j}\left(\partial _{i}\mathbf {v} _{h}^{T}\mathbf {K} _{ij}\right){\tilde {\mathbf {u} }}-\partial _{i}\mathbf {v} _{h}^{T}\mathbf {A} _{i}\mathbf {\tilde {\mathbf {u} }} +\mathbf {v} _{h}^{T}\mathbf {S} \mathbf {\tilde {\mathbf {u} }} \right){\,d}\Omega$ $+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\partial \Omega ^{e}}\partial _{i}\mathbf {v} _{h}^{T}\mathbf {K} _{ij}n_{j}{\tilde {\mathbf {u} }}{\,d}\Gamma +{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\partial \Omega ^{e}}\mathbf {v} _{h}^{T}n_{i}\mathbf {A} _{i}^{c}\mathbf {\tilde {u}} {\,d}\Gamma {.}$

(80)

Sea ${\textstyle {\mathcal {L}}^{*}}$ el adjunto del operador ${\textstyle {\mathcal {L}}}$, dado por

$\left({\mathcal {L}}^{*}\left(\mathbf {v} _{h}\right)\right)^{T}=-\partial _{j}\left(\partial _{i}\mathbf {v} _{h}^{T}\mathbf {K} _{ij}\right)-\partial _{i}\mathbf {v} _{h}^{T}\mathbf {A} _{i}+\mathbf {v} _{h}^{T}\mathbf {S} ,$

(81)

donde hemos usado que en nuestro caso ${\textstyle \mathbf {K} _{ji}^{T}=\mathbf {K} _{ij}}$. La ecuación (80) se puede escribir como

$B\left({\tilde {\mathbf {u} }},\mathbf {v} _{h}\right)={\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left({\mathcal {L}}^{*}\left(\mathbf {v} _{h}\right)\right)^{T}{\tilde {\mathbf {u} }}{\,d}\Omega +{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\partial \Omega ^{e}}\partial _{i}\mathbf {v} _{h}^{T}\mathbf {K} _{ij}n_{j}{\tilde {\mathbf {u} }}{\,d}\Gamma +{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\partial \Omega ^{e}}\mathbf {v} _{h}^{T}n_{i}\mathbf {A} _{i}^{c}\mathbf {\tilde {u}} {\,d}\Gamma {.}$

(82)

Reemplazando (82) en la ecuación (77), ésta se puede escribir como

$B\left(\mathbf {u} _{h},\mathbf {v} _{h}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left({\mathcal {L}}^{*}\left(\mathbf {v} _{h}\right)\right)^{T}{\tilde {\mathbf {u} }}{\,d}\Omega +{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\partial \Omega ^{e}}\left(\partial _{i}\mathbf {v} _{h}^{T}\mathbf {K} _{ij}n_{j}{\tilde {\mathbf {u} }}+\mathbf {v} _{h}^{T}n_{i}\mathbf {A} _{i}^{c}\mathbf {\tilde {u}} \right){\,d}\Gamma =\left\langle \mathbf {F} ,\mathbf {v} _{h}\right\rangle \quad \forall \mathbf {v} _{h}\in {\mathcal {W}}_{h}.$

(83)

Ahora bien, integrando también por partes dentro de cada elemento los dos términos de la ecuación (78), ésta queda

${\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\partial \Omega ^{e}}{\tilde {\mathbf {v} }}^{T}n_{i}\mathbf {K} _{ij}\partial _{j}\left(\mathbf {u} _{h}+{\tilde {\mathbf {u} }}\right){\,d}\Gamma +{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}{\tilde {\mathbf {v} }}^{T}{\mathcal {L}}\left({\tilde {\mathbf {u} }}\right){\,d}\Omega ={\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}{\tilde {\mathbf {v} }}^{T}\left[\mathbf {F} -{\mathcal {L}}\left(\mathbf {u} _{h}\right)\right]{\,d}\Omega \qquad \forall {\tilde {\mathbf {v} }}\in {\tilde {\mathcal {W}}}.$

(84)

Observemos que el primer término de la ecuación (84) se anula, ya que en la frontera de los elementos las componentes normales de los flujos de ${\textstyle \mathbf {u} }$ son iguales pero de signo contrario, debido a que los flujos difusivos deben ser continuos a través de los contornos inter-elementales. Como resultado de esto, la ecuación (84) es equivalente a encontrar ${\textstyle {\tilde {\mathbf {u} }}\in {\tilde {\mathcal {W}}}}$ tal que

${\mathcal {L}}\left({\tilde {\mathbf {u} }}\right)=\mathbf {F} -{\mathcal {L}}\left(\mathbf {u} _{h}\right)+\mathbf {v} _{h,{ort}}~~\mathrm {en} \;\Omega ^{e},~~\forall \mathbf {v} _{h,{ort}}\in {\tilde {\mathcal {W}}}^{\perp },$ (85) ${\tilde {\mathbf {u} }}={\tilde {\mathbf {u} }}_{esq}~~\mathrm {en} \;\partial \Omega ^{e},$ (86)

para ${\textstyle e=1,...,n_{el}}$, donde ${\textstyle {\tilde {\mathbf {u} }}_{esq}}$ es la subescala evaluada en los contornos interelementales. Es importante observar que la ecuación (85) se verifica para cualquier elemento ${\textstyle \mathbf {v} _{h,{ort}}}$ ortogonal a ${\textstyle {\tilde {\mathcal {W}}}.}$ La presencia del elemento ${\textstyle \mathbf {v} _{h,{ort}}}$ en la ecuación (85) garantiza que ${\textstyle {\mathcal {L}}\left({\tilde {\mathbf {u} }}\right)-\left[\mathbf {F} -{\mathcal {L}}\left(\mathbf {u} _{h}\right)\right]}$ pertenece a ${\textstyle {\tilde {\mathcal {W}}}^{\perp }}$, que es lo que implica la ecuación (84) sin el primer término. En otras palabras ${\textstyle \mathbf {v} _{h,{ort}}}$ garantiza que ${\textstyle {\tilde {\mathbf {u} }}}$ pertenezca al espacio de subescalas ${\textstyle {\tilde {\mathcal {W}}}}$ (y no a todo el espacio ${\textstyle {\mathcal {W}}}$).

Las ecuaciones (83), (85) y (86) equivalen exactamente a los problemas (77) y (78), ya que hasta ahora no hemos hecho ninguna aproximación. Veremos ahora posibles aproximaciones para poder calcular de forma efectiva ${\textstyle {\tilde {\mathbf {u} }}}$, las cuales darán lugar a los métodos ASGS y OSS. En esencia, lo que debemos hacer es seleccionar las funciones ${\textstyle {\tilde {\mathbf {u} }}_{esq}}$, ${\textstyle \mathbf {v} _{h,{ort}}}$ y proponer una solución aproximada de la ecuación (85).

3.4.1 El método ASGS para el problema de CDR vectorial estacionario

Un caso particular del método de las subescalas descrito anteriormente es el método denominado ASGS. Para seleccionar ${\textstyle {\tilde {\mathbf {u} }}_{esq}}$ vamos a usar el siguiente argumento. Para tener una aproximación discreta óptima de ${\textstyle \mathbf {u} }$ que diera valores nodales exactos, se podría pedir que las subescalas se anularan en los nodos. En problemas unidimensionales esto da condiciones de contorno homogéneas en (86). Para los casos de más de una dimensión espacial, la elección de ${\textstyle {\tilde {\mathbf {u} }}_{esq}=\mathbf {0} }$ es solo una aproximación. En otras palabras, estamos tomando el espacio de las subescalas ${\textstyle {\tilde {\mathcal {W}}}}$ como un espacio de funciones burbuja, es decir, el espacio de funciones que se anulan en los contornos de los elementos (véase [33,34]). Esta aproximación, que adoptaremos en lo que sigue, no es sin embargo imprescindible (véase [35]).

Con esta aproximación, el término de las integrales en los contornos de los elementos de la ecuación (83) se elimina, por lo cual el problema que debemos resolver es encontrar ${\textstyle \mathbf {u} _{h}\in {\mathcal {W}}_{h}}$ tal que

$B\left(\mathbf {u} _{h},\mathbf {v} _{h}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left({\mathcal {L}}^{*}\left(\mathbf {v} _{h}\right)\right)^{T}{\tilde {\mathbf {u} }}{\,d}\Omega =\left\langle \mathbf {F} ,\mathbf {v} _{h}\right\rangle \qquad \forall \mathbf {v} _{h}\in {\mathcal {W}}_{h},$

(87)

en donde todavía hace falta determinar ${\textstyle {\tilde {\mathbf {u} }}}$.

La siguiente aproximación del método ASGS es tomar ${\textstyle \mathbf {v} _{h,{ort}}=\mathbf {0} }$, lo cual supone considerar que las subescalas están en el espacio de residuos, es decir, éste está compuesto por funciones de la forma ${\textstyle \mathbf {F} -{\mathcal {L}}\left(\mathbf {v} \right)}$, con ${\textstyle \mathbf {v} \in {\mathcal {W}}}$. Podemos entonces escribir simbólicament la solución del problema (85)-(86), asumiendo ${\textstyle \mathbf {\tilde {u}} _{esq}=\mathbf {0} }$ y considerando ${\textstyle \mathbf {v} _{h,{ort}}=\mathbf {0} }$, como

${\tilde {\mathbf {u} }}={\mathcal {L}}^{-1}\left[\mathbf {F} -{\mathcal {L}}\left(\mathbf {u} _{h}\right)\right],$

(88)

donde ${\textstyle {\mathcal {L}}^{-1}}$ es el operador inverso del operador ${\textstyle {\mathcal {L}}}$ con condiciones de Dirichlet homogéneas.

De (87) se observa que solo se necesita la componente de ${\textstyle \mathbf {\tilde {u}} }$ sobre el espacio ${\textstyle {\mathcal {L}}\left({\mathcal {W}}_{h}\right)}$, donde ${\textstyle {\mathcal {L}}\left({\mathcal {W}}_{h}\right)}$ es el espacio de funciones de la forma ${\textstyle {\mathcal {L}}\left(\mathbf {v} _{h}\right)}$, con ${\textstyle \mathbf {v} _{h}\in {\mathcal {W}}_{h}}$; esto sugiere aproximar (88) como

${\tilde {\mathbf {u} }}\approx {\tau }^{e}\left[\mathbf {F} -{\mathcal {L}}\left(\mathbf {u} _{h}\right)\right],$

(89)

donde ${\textstyle {\tau }^{e}}$ es una matriz de ${\textstyle n_{inc}\times n_{inc}}$ componentes a la que denominamos matriz de parámetros de estabilización y que se calcula dentro del dominio de cada elemento. El diseño de la matriz ${\textstyle {\tau }^{e}}$ es una de las piedras angulares en el desarrollo de los métodos de elementos finitos estabilizados. Algunas formulaciones algebraicas para el diseño del parámetro de estabilización para la ecuación escalar de CDR en 1D, basadas en el principio del máximo discreto, pueden encontrarse en [18,19,26]; la extensión a sistemas puede consultarse en [20]. Asimismo, en [27,22] se propone un diseño del parámetro de estabilización basado en un análisis de Fourier, considerando el problema de flujo en aguas poco profundas en [12]. En este trabajo vamos a utilizar precisamente el diseño algorítmico del ${\textstyle {\tau }^{e}}$ desarrollado en [12] y que está dado por

${\tau }^{e}=\mathrm {diag} (\tau ^{e},\tau ^{e},0),$

con el parámetro ${\textstyle \tau ^{e}}$ dado por

$\tau ^{e}=\left[c_{1}{\frac {\nu _{H}}{\left(h^{e}\right)^{2}}}+c_{2}{\frac {|\mathbf {a} |}{h^{e}}}+c_{3}|S_{11}|+c_{4}|S_{12}|\right]^{-1},$

para elementos finitos lineales, siendo ${\textstyle \nu _{H}={\frac {\mu _{H}}{\rho }}}$ el coeficiente de viscosidad cinemática y ${\textstyle |\mathbf {a} |}$ la norma de la velocidad. Se entiende que las funciones que aparecen en esta expresión se calculan dentro de cada elemento ${\textstyle e}$, cuyo diámetro es ${\textstyle h^{e}}$, y ${\textstyle c_{1}}$, ${\textstyle c_{2}}$, ${\textstyle c_{3}}$ y ${\textstyle c_{4}}$ son constantes algorítmicas.

Para elementos de alto orden, la experimentación numérica y también el análisis teórico (que está fuera del objetivo de este artículo) nos han llevado a proponer como matriz de parámetros de estabilización:

${\tau }^{e}=\mathrm {diag} (\tau _{1}^{e},\tau _{1}^{e},\tau _{2}^{e}),$

(90)

con

$\tau _{1}^{e}=\left[c_{1}{\frac {\nu _{H}}{\left({\frac {h^{e}}{d^{2}}}\right)^{2}}}+c_{2}{\frac {|\mathbf {a} |}{\frac {h^{e}}{d}}}+c_{3}|S_{11}|+c_{4}|S_{12}|\right]^{-1},{\mbox{ }}\tau _{2}^{e}={\frac {\left({\frac {h^{e}}{d}}\right)^{2}}{c_{1}\tau _{1}}},$

(91)

donde ${\textstyle c_{1},}$ ${\textstyle c_{2},}$ ${\textstyle c_{3}}$ y ${\textstyle c_{4}}$ son los mismos coeficientes que antes, y que para los ejemplos numéricos hemos adoptado como ${\textstyle c_{1}=12,}$ ${\textstyle c_{2}=2}$ y ${\textstyle c_{3}=c_{4}=1}$ y ${\textstyle d}$ es el orden polinomial de interpolación.

Reemplazando la ecuación (89) en (87), finalmente tenemos la formulación estabilizada ASGS para resolver la ecuación vectorial de CDR estacionaria, la cual consiste en encontrar ${\textstyle \mathbf {u} _{h}\in {\mathcal {W}}_{h}}$ tal que

$B\left(\mathbf {u} _{h},\mathbf {v} _{h}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left(-{\mathcal {L}}^{*}\left(\mathbf {v} _{h}\right)\right)^{T}{\tau }^{e}\left[{\mathcal {L}}\left(\mathbf {u} _{h}\right)-\mathbf {F} \right]{\,d}\Omega =\left\langle \mathbf {F} ,\mathbf {v} _{h}\right\rangle \qquad \forall \mathbf {v} _{h}\in {\mathcal {W}}_{h}.$

(92)

3.4.2 El método OSS para el problema de CDR vectorial estacionario

A continuación vamos a describir el método OSS propuesto en [23]. El punto de partida es la elección del espacio de las subescalas, que ahora no será el espacio de residuos de elementos finitos como en el caso anterior, sino que se toma como espacio ${\textstyle {\mathcal {\tilde {W}}}}$ el espacio ortogonal en el sentido de ${\textstyle L^{2}}$ al espacio de elementos finitos, es decir,

${\mathcal {{\tilde {W}}={\mathcal {W}}}}_{h}^{\perp },$

(93)

que es una legítima elección que cumple con ${\textstyle {\mathcal {W}}={\mathcal {W}}_{h}\oplus {\mathcal {\tilde {W}}}.}$

Tomando en cuenta (93) de (85) se sigue que

$\mathbf {v} _{h,{ort}}\in {\mathcal {W}}_{h},\quad \mathbf {\tilde {u}} \in {\mathcal {W}}_{h}^{\perp },$

lo que significa que ${\textstyle \mathbf {v} _{h,{ort}}}$ es una función del espacio de elementos finitos y por lo tanto numéricamente calculable, mientras que ${\textstyle \mathbf {\tilde {u}} }$ estará en el espacio ortogonal a ${\textstyle {\mathcal {W}}_{h}}$. A este espacio ${\textstyle {\mathcal {W}}_{h}^{\perp }}$ escogido para las subescalas ${\textstyle \mathbf {\tilde {u}} }$ lo denominamos espacio de subescalas ortogonales.

Para resolver (85) y (86), al igual que en el método ASGS, asumimos ${\textstyle \mathbf {\tilde {u}} _{esq}=\mathbf {0} }$ y escribimos

$\mathbf {\tilde {u}} ={\mathcal {L}}^{-1}\left[\mathbf {F} -{\mathcal {L}}\left(\mathbf {u} _{h}\right)\right]+{\mathcal {L}}^{-1}\left(\mathbf {v} _{h,{ort}}\right),$

(94)

donde, como en el método ASGS, ${\textstyle {\mathcal {L}}^{-1}}$ es el inverso del operador ${\textstyle {\mathcal {L}}}$ con condiciones de Dirichlet homogéneas. De (87) se observa que solo se necesita la componente de ${\textstyle \mathbf {\tilde {u}} }$ sobre el espacio ${\textstyle {\mathcal {L}}\left({\mathcal {W}}_{h}\right)}$ y, al igual que en el método ASGS, esto sugiere aproximar (94) como

$\mathbf {\tilde {u}} \approx {\tau }^{e}\left[\mathbf {F} -{\mathcal {L}}\left(\mathbf {u} _{h}\right)\right]+{\tau }^{e}\mathbf {v} _{h,{ort}}.$

(95)

Puesto que ${\textstyle \mathbf {\tilde {u}} \in {\mathcal {W}}_{h}^{\perp }}$, de (95) se tiene

$0=\int _{\Omega }\mathbf {\tilde {u}} ^{T}\mathbf {v} _{h}{\,d}\Omega \approx {\overset {n_{el}}{\underset {e=1}{\sum }}}\int _{\Omega ^{e}}\left({\tau }^{e}\left[\mathbf {F} -{\mathcal {L}}\left(\mathbf {u} _{h}\right)\right]\right)^{T}\mathbf {v} _{h}{\,d}\Omega +{\overset {n_{el}}{\underset {e=1}{\sum }}}\int _{\Omega ^{e}}\left({\tau }^{e}\mathbf {v} _{h,{ort}}\right)^{T}\mathbf {v} _{h}{\,d}\Omega \qquad \forall \mathbf {v} _{h}\in {\mathcal {W}}_{h}.$

(96)

Si llamamos ${\textstyle \mathbf {\Pi } _{\tau }}$ la proyección ${\textstyle L^{2}}$ sobre el espacio de elementos finitos pesada con ${\textstyle {\tau }^{e}}$ dentro de cada elemento, de (96) se tiene que

$\mathbf {v} _{h,{ort}}=-\mathbf {\Pi } _{\tau }\left[\mathbf {F} -{\mathcal {L}}\left(\mathbf {u} _{h}\right)\right].$

(97)

Reemplazando (97) en (95) tenemos

$\mathbf {\tilde {u}} \approx {\tau }^{e}\left[\mathbf {F} -{\mathcal {L}}\left(\mathbf {u} _{h}\right)-\mathbf {\Pi } _{\tau }\left[\mathbf {F} -{\mathcal {L}}\left(\mathbf {u} _{h}\right)\right]\right].$

(98)

Sea ahora

$\mathbf {\Pi } _{\tau }^{\perp }=\mathbf {I} -\mathbf {\mathbf {\Pi } _{\tau }} ,$

(99)

donde ${\textstyle \mathbf {I} }$ es la identidad en ${\textstyle {\mathcal {W}}_{h}}$ y ${\textstyle \mathbf {\Pi } _{\tau }^{\perp }}$ es la proyección sobre el espacio ortogonal al espacio de elementos finitos. La ecuación (98) se puede escribir entonces como

$\mathbf {\tilde {u}} \approx {\tau }^{e}\mathbf {\Pi } _{\tau }^{\perp }\left[\mathbf {F} -{\mathcal {L}}\left(\mathbf {u} _{h}\right)\right].$

(100)

Podemos reemplazar esta expresión en (83) y usar el hecho de que las integrales sobre los contornos de los elementos son cero, con lo cual obtenemos la formulación estabilizada de elementos finitos OSS que resuelve la ecuación vectorial de CDR estacionaria, la cual consiste en encontrar ${\textstyle \mathbf {u} _{h}\in {\mathcal {W}}_{h}}$ tal que

$B\left(\mathbf {u} _{h},\mathbf {v} _{h}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left(-{\mathcal {L}}^{*}\left(\mathbf {v} _{h}\right)\right)^{T}{\tau }^{e}\mathbf {\Pi } _{\tau }^{\perp }\left[{\mathcal {L}}\left(\mathbf {u} _{h}\right)-\mathbf {F} \right]{\,d}\Omega =\left\langle \mathbf {F} ,\mathbf {v} _{h}\right\rangle \qquad \forall \mathbf {v} _{h}\in {\mathcal {W}}_{h}.$

(101)

3.4.3 Generalización

Las ecuaciones (92) y (101), que definen respectivamente los métodos ASGS y OSS, se pueden escribir en forma conjunta de la siguiente manera: encontrar ${\textstyle \mathbf {u} _{h}\in {\mathcal {W}}_{h}}$ tal que

$B\left(\mathbf {u} _{h},\mathbf {v} _{h}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left(-{\mathcal {L}}^{*}\left(\mathbf {v} _{h}\right)\right)^{T}{\tau }^{e}{\mathcal {\mathbf {P} }}\left[{\mathcal {L}}\left(\mathbf {u} _{h}\right)-\mathbf {F} \right]{\,d}\Omega =\left\langle \mathbf {F} ,\mathbf {v} _{h}\right\rangle \qquad \forall \mathbf {v} _{h}\in {\mathcal {W}}_{h},$

(102)

donde

${\mathcal {\mathbf {P} }}=\mathbf {I} {\hbox{ para el metodo ASGS}},$ $\mathbf {\Pi } _{\tau }^{\perp }{\hbox{ para el metodo OSS}}.$

En términos generales, ambas formulaciones, ASGS y OSS, consiguen el objetivo de estabilizar el problema. Aunque como veremos en los ejemplos numéricos su comportamiento en el problema que nos ocupa es parecido, la formulación OSS es habitualmente más precisa, aunque algo más costosa. Asimismo, permite simplificaciones que no consideraremos en este trabajo (véase por ejemplo la discusión en [31]).

3.5 Ecuación de CDR vectorial transitoria

Describimos a continuación la extensión de las formulaciones introducidas al problema transitorio. Como en el caso estacionario, consideramos para simplificar condiciones de contorno de Dirichlet homogéneas.

Las únicas modificacions que debemos tener en cuenta son las originadas por el término ${\textstyle \partial _{t}\mathbf {u} }$ en la ecuación (61). En particular, la forma variacional continua será, en vez de (67): hallar ${\textstyle \mathbf {u} :\gamma \rightarrow {\mathcal {W}}}$ tal que

$(\partial _{t}\mathbf {u} ,\mathbf {v} )+B(\mathbf {u} ,\mathbf {v} )=\langle \mathbf {F} ,\mathbf {v} \rangle \quad \forall \mathbf {v} \in {\mathcal {W}},$

y cumpliendo la condición inicial. Aquí y en lo que sigue, ${\textstyle ({f},{g})=\int _{\Omega }{f}^{T}{g}{\,d}\Omega }$ para cualesquiera funciones vectoriales ${\textstyle {f}}$ y ${\textstyle {g}}$ de ${\textstyle L^{2}(\Omega )^{2}}$.

Como hemos indicado anteriormente, la discretización en el tiempo la llevaremos a cabo usando la regla trapezoidal. Una vez linealizadas las ecuaciones mediante el método de Picard, el problema continuo en el espacio que habrá que resolver en cada paso de tiempo, escrito en forma variacional, será: dado ${\textstyle \mathbf {u} ^{n}\in {\mathcal {W}}}$, encontrar ${\textstyle \mathbf {u} ^{n+1}\in {\mathcal {W}}}$ tal que

$(\delta _{t}^{n}\mathbf {u} ,\mathbf {v} )+B(\mathbf {u} ,\mathbf {v} )=\langle \mathbf {F} ,\mathbf {v} \rangle \quad \forall \mathbf {v} \in {\mathcal {W}},$

para ${\textstyle n=1,2,\dots }$, siendo ${\textstyle \mathbf {u} ^{0}}$ la condición inicial. Recordemos de la notación introducida en (11)-(13) que se sobreentiende en esta ecuación que la incógnita ${\textstyle \mathbf {u} }$ (y el término de fuerzas) está aproximada en el instante de tiempo ${\textstyle t^{n+\theta }=t^{n}+\theta \delta t}$ (y en una iteración determinada).

Al plantear la descomposición ${\textstyle \mathbf {u} =\mathbf {u} _{h}+{\tilde {\mathbf {u} }}}$, igual que hicimos en el caso estacionario, aparecerá el término ${\textstyle \partial _{t}{\tilde {\mathbf {u} }}}$, que en principio no es nulo. Sin embargo, en todo lo que sigue haremos la suposición de que ${\textstyle \partial _{t}{\tilde {\mathbf {u} }}=\mathbf {0} }$, lo cual implica que la variación temporal de las subescalas es despreciable comparada con el resto de términos. En [22] las subescalas que satisfacen esta condición son llamadas cuasi-estáticas, mientras que se denominan dinámicas si no se hace esta hipótesis (véase [22,36,37]).

3.5.1 Formulación ASGS para el problema de CDR vectorial transitorio

Siguiendo los mismos pasos que para llegar a la aproximación (92) del problema estacionario, el caso transitorio aproximado mediante el método ASGS consiste en: dado ${\textstyle \mathbf {u} _{h}^{n}\in {\mathcal {W}}_{h}}$, encontrar ${\textstyle \mathbf {u} _{h}^{n+1}\in {\mathcal {W}}_{h}}$ tal que

$\left(\delta _{t}^{n}\mathbf {u} _{h},\mathbf {v} _{h}\right)+B\left(\mathbf {u} _{h},\mathbf {v} _{h}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left(-{\mathcal {L}}^{*}\left(\mathbf {v} _{h}\right)\right)^{T}{\tau }^{e}\left[\delta _{t}^{n}\mathbf {u} _{h}+{\mathcal {L}}\left(\mathbf {u} _{h}\right)-\mathbf {F} \right]{\,d}\Omega =\left\langle \mathbf {F} ,\mathbf {v} _{h}\right\rangle \quad \forall \mathbf {v} _{h}\in {\mathcal {W}}_{h}.$

(103)

Nótese que no aparece el término ${\textstyle \left(\delta _{t}^{n}{\tilde {\mathbf {u} }},\mathbf {v} _{h}\right)}$, puesto que hemos supuesto subescalas cuasi-estacionarias, pero sí que aparece ${\textstyle \delta _{t}^{n}\mathbf {u} _{h}}$ en el término de estabilización.

La matriz de parámetros de estabilización ${\textstyle {\tau }^{e}}$ para elementos finitos de alto orden está dada por las ecuaciones (90) y (91), el operador ${\textstyle {\mathcal {L}}}$ por (62) y el operador ${\textstyle {\mathcal {L}}^{*}}$ por la ecuación (81).

3.5.2 Formulación OSS para el problema de CDR vectorial transitorio

También podemos seguir los mismos pasos que para el método ASGS en el caso del método OSS. La aproximación numérica a la que llegaremos será la siguiente: dado ${\textstyle \mathbf {u} _{h}^{n}\in {\mathcal {W}}_{h}}$, encontrar ${\textstyle \mathbf {u} _{h}^{n+1}\in {\mathcal {W}}_{h}}$ tal que

$\left(\delta _{t}^{n}\mathbf {u} _{h},\mathbf {v} _{h}\right)+B\left(\mathbf {u} _{h},\mathbf {v} _{h}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left(-{\mathcal {L}}^{*}\left(\mathbf {v} _{h}\right)\right)^{T}{\tau }^{e}\mathbf {\Pi } _{\tau }^{\perp }\left[\delta _{t}^{n}\mathbf {u} _{h}+{\mathcal {L}}\left(\mathbf {u} _{h}\right)-\mathbf {F} \right]{\,d}\Omega =\left\langle \mathbf {F} ,\mathbf {v} _{h}\right\rangle \quad \forall \mathbf {v} _{h}\in {\mathcal {W}}_{h}.$

Podemos aplicar aquí los mismos comentarios que para (103). Sin embargo, hay una consideración importante a tener en cuenta, y es que puesto que ${\textstyle \delta _{t}^{n}\mathbf {u} _{h}}$ es una función que pertenece al espacio de elementos finitos ${\textstyle {\mathcal {W}}_{h}}$, su componente en el espacio ortogonal es nula, esto es, la ecuación variacional discreta anterior se reduce a

$\left(\delta _{t}^{n}\mathbf {u} _{h},\mathbf {v} _{h}\right)+B\left(\mathbf {u} _{h},\mathbf {v} _{h}\right)+{\underset {e=1}{\overset {n_{el}}{\sum }}}\int _{\Omega ^{e}}\left(-{\mathcal {L}}^{*}\left(\mathbf {v} _{h}\right)\right)^{T}{\tau }^{e}\mathbf {\Pi } _{\tau }^{\perp }\left[{\mathcal {L}}\left(\mathbf {u} _{h}\right)-\mathbf {F} \right]{\,d}\Omega =\left\langle \mathbf {F} ,\mathbf {v} _{h}\right\rangle \quad \forall \mathbf {v} _{h}\in {\mathcal {W}}_{h}.$

(104)

4. Resultados de los experimentos numéricos

Con el fin de evaluar las formulaciones de los métodos variacionales de subescalas ASGS y OSS con elementos finitos de alto orden aplicados a las ecuaciones del movimiento de un fluido en aguas poco profundas, hemos realizado diferentes experimentos numéricos, tales como pruebas de convergencia en malla y la aproximación de varios problemas que se encuentran en la literatura. A continuación presentamos los resultados para un test de convergencia y para dos ejemplos que se han convertido en clásicos.

El método de linealización empleado es el de Picard. El criterio de convergencia en no linealidad lo hemos fijado en la norma ${\textstyle L^{2}}$, de manera que el proceso iterativo lo hemos considerado convergido cuando

${\frac {\left\Vert \mathbf {u} _{h}^{i}-\mathbf {u} _{h}^{i-1}\right\Vert _{L^{2}}}{\left\Vert \mathbf {u} _{h}^{i}\right\Vert _{L^{2}}}}<{tol},$

donde ${\textstyle i}$ es el contador de iteraciones en un paso de tiempo dado y tol es la tolerancia de convergencia, fijada en ${\textstyle 10^{-5}}$ en todos los ejemplos. Aquí y en lo que sigue, las normas ${\textstyle L^{2}}$ se extienden a todo el dominio ${\textstyle \Omega }$. Asimismo, todas las unidades se consideran dadas en el SI.

4.1 Pruebas de convergencia en malla

Las pruebas de convergencia en malla que hemos llevado a cabo consisten en calcular el error en norma ${\textstyle L^{2}}$ entre el valor exacto y la aproximación numérica de una incógnita ${\textstyle u}$ (cualquiera de las del problema). Si el error del método se comporta como el error de interpolación, situación que puede considerarse óptima, este error debe comportarse como

$e=\left\Vert u-u_{h}\right\Vert _{L^{2}}\leqslant ch^{d+1},$

(105)

donde ${\textstyle u_{h}}$ es la aproximación de ${\textstyle u}$ en el espacio de elementos finitos, ${\textstyle c}$ es una constante positiva, ${\textstyle h}$ es aquí el diámetro de la partición de elementos finitos (no la altura de la lámina de agua) y ${\textstyle d}$ el grado polinómico de la función de forma correspondiente a la interpolación de la aproximación ${\textstyle u_{h}}$. Aunque consideraremos valores de hasta ${\textstyle d=4}$, no consideraremos convergencia en ${\textstyle d}$, por lo que la constante ${\textstyle c}$ la tomaremos fija (sabemos que decrece con ${\textstyle d}$).

Si graficamos la ecuación (105) (en el caso de igualdad) en el plano ${\textstyle \mathbb {R} ^{2}}$ con ${\textstyle \log e}$ en las ordenadas y ${\textstyle \log h}$ en las abscisas, tenemos una línea recta, donde ${\textstyle d+1}$ es la pendiente teórica óptima de convergencia. Las pruebas de convergencia en malla consisten entonces en verificar que la pendiente calculada sea precisamente ${\textstyle d+1}$. Para ello, seleccionamos como solución exacta tanto para las velocidades ${\textstyle U_{1}}$, ${\textstyle U_{2}}$ como para la elevación de la superficie libre del agua ${\textstyle \eta }$ la función polinómica espacio-temporal

$\eta \left(x,y,t\right)=U_{1}\left(x,y,t\right)=U_{2}\left(x,y,t\right)=x^{6}y^{6}\left(1-x\right)^{6}\left(1-y\right)^{6}t,$

e imponemos el término fuente ${\textstyle \mathbf {F} }$ en la ecuación vectorial de CDR transitoria (5) mediante las siguientes expresiones tomadas de las ecuaciones (1), (2):

$f_{i}=\partial _{t}\left(hU_{i}\right)+\partial _{j}\left(hU_{i}U_{j}\right)+\partial _{i}{\frac {1}{2}}g\left(h^{2}-H^{2}\right)-\partial _{j}\left({\frac {h}{\rho }}{\bar {\tau }}_{ji}\right)+Q_{i}\qquad i=1,2,$ $f_{3}=\partial _{t}h+\partial _{i}\left(hU_{i}\right),$

siendo ${\textstyle \mathbf {F} =[f_{1},f_{2},f_{3}]^{T}}$ y ${\textstyle {\bar {\tau }}_{ji}}$ y ${\textstyle Q_{i}}$ dados por las ecuaciones (3) y (4), respectivamente. Hemos tomado ${\textstyle H=1}$ m, es decir, batimetría constante con profundidad de 1 m, aceleración de la gravedad ${\textstyle g=10}$ m/s${\textstyle ^{2}}$ y viscosidad cinemática ${\textstyle \nu _{H}={\frac {\mu _{H}}{\rho }}=10^{-3}}$ m${\textstyle ^{2}}$/s. El parámetro de Coriolis ${\textstyle {\hat {f}}}$, las tensiones de superficie libre debidas al viento ${\textstyle \tau _{3i}^{s}}$, las variaciones de presión atmosférica ${\textstyle p_{a}}$ y el coeficiente de fricción en el fondo ${\textstyle {\hbox{Ch}}}$ no han sido tomados en cuenta para los ejemplos de las pruebas de convergencia en malla.

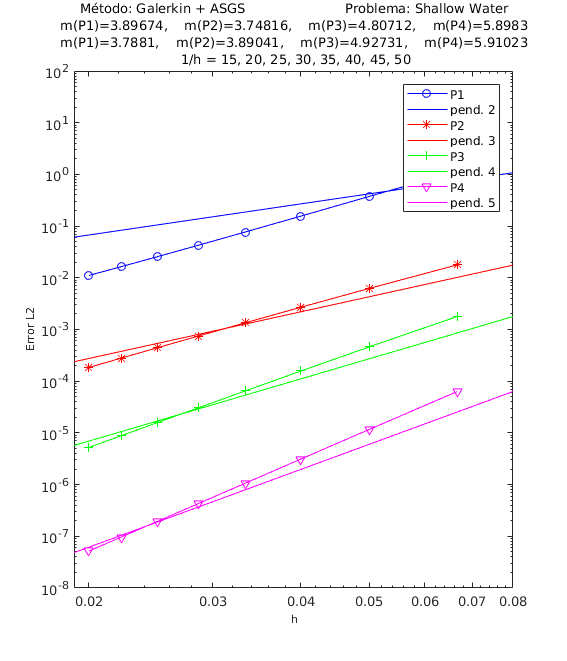
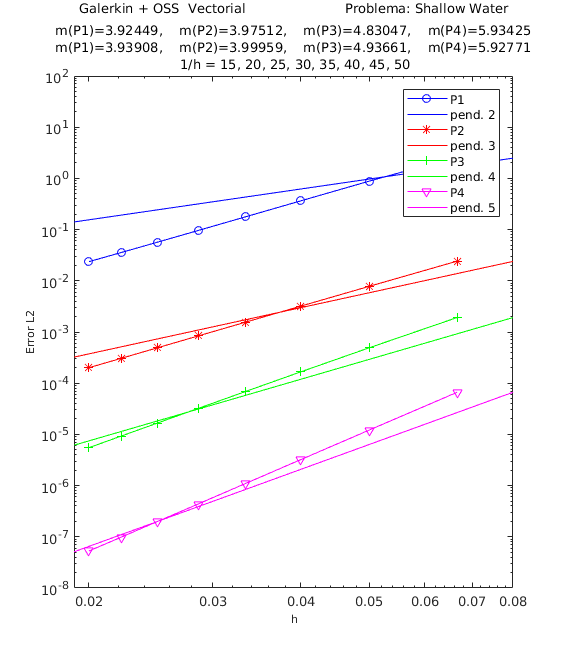
A continuación presentamos los resultados de los experimentos numéricos de las pruebas de convergencia en malla con solución analítica conocida, tanto para el método ASGS como para el OSS. En cada gráfica se puede apreciar con línea continua la pendiente teórica de convergencia y con línea con apéndices sobre ella la pendiente calculada. Presentamos los resultados para los distintos grados polinómicos de las funciones de forma estudiados, es decir, elementos lineales, cuadráticos, cúbicos y de cuarto orden triangulares ${\textstyle P_{1},\;P_{2},\;P_{3},\;P_{4}}$ y cuadrangulares ${\textstyle Q_{1},\;Q_{2},\;Q_{3},\;Q_{4}}$, respectivamente.

El dominio computacional es el cuadrado ${\textstyle \left[0,1\right]\times \left[0,1\right]}$ y el intervalo de tiempo es ${\textstyle \left[0,1\right]}$, con incrementos para cada paso de tiempo ${\textstyle \delta t=0.2}$. La malla de elementos finitos consiste en triángulos o cuadrados formando una malla regular. Para cada grado polinómico de las funciones de forma ${\textstyle P_{1},\;P_{2},\;P_{3},\;P_{4}}$ o ${\textstyle Q_{1},\;Q_{2},\;Q_{3},\;Q_{4},}$ hemos calculado los errores con norma ${\textstyle L^{2}}$ para ocho mallas de tamaño ${\textstyle h}$, siendo ${\textstyle {\frac {1}{h}}=15,\;20,\;25,\;30,\;35,\;40,\;45,\;50,}$ el número de partes en las que se ha dividido cada lado del cuadrado. En la Tabla 1 se muestran el número de elementos y el número de nodos para cada refinamiento, tanto para elementos triangulares como para elementos cuadrangulares. El integrador temporal utilizado es BDF1.

Tabla 1. Refinamiento para elementos triangulares y cuadradangulares

Triángulos		Número de nodos
${\textstyle 1/h}$	elem.	$P_{1}$	$P_{2}$	$P_{3}$	$P_{4}$
15	450	256	961	2116	3721
20	800	441	1681	3721	6561
25	1250	676	2601	5776	10201
30	1800	961	3721	8281	14641
35	2450	1296	5041	11236	19881
40	3200	1681	6561	14641	25921
45	4050	2116	8281	18496	32761
50	5000	2601	10201	22801	40401

 

Cuadrados		Número de nodos
${\textstyle 1/h}$	elem.	$Q_{1}$	$Q_{2}$	$Q_{3}$	$Q_{4}$
15	225	256	961	2116	3721
20	400	441	1681	3721	6561
25	625	676	2601	5776	10201
30	900	961	3721	8281	14641
35	1250	1296	5041	11236	19881
40	1600	1681	6561	14641	25921
45	2025	2116	8281	18496	32761
50	2500	2601	10201	22801	40401

En el encabezado de las gráficas de las pruebas de convergencia en malla se adjuntan dos filas con los valores de las pendientes calculadas; la primera fila corresponde a los valores de las pendientes de las rectas que pasan por los primeros 5 puntos y la segunda fila son las pendientes de las rectas que pasan por los últimos 5 puntos de los 8 puntos del refinamiento de malla evaluados ${\textstyle \left({\frac {1}{h}}=15,\;20,\;25,\;30,\;35,\;40,\;45,\;50\right)}$. De esta manera podemos visualizar numéricamente la tendencia de la convergencia de las pendientes calculadas hacia el valor teórico. Para el cálculo de dichas pendientes se ha utilizado el método de los mínimos cuadrados. La simbología ${\textstyle m(P1),}$ ${\textstyle m(P2),}$ ${\textstyle m(P3),}$ ${\textstyle m(P4),}$ corresponde a las pendientes para elementos triangulares lineales, cuadráticos, cúbicos y de cuarto orden, respectivamente, mientras que para elementos cuadrangulares lineales, cuadráticos, cúbicos y de cuarto orden la simbología es ${\textstyle m(Q1),}$ ${\textstyle m(Q2),}$ ${\textstyle m(Q3),}$ ${\textstyle m(Q4)}$. Los valores de las pendientes teóricas para las variables de velocidad se corresponden con: ${\textstyle m(P1)=m(Q1)=2}$, ${\textstyle m(P2)=m(Q2)=3}$, ${\textstyle m(P3)=m(Q3)=4}$, ${\textstyle m(P4)=m(Q4)=5}$, y las pendientes teóricas para la variable ${\textstyle \eta }$ se corresponden con ${\textstyle m(P1)=m(Q1)=1}$, ${\textstyle m(P2)=m(Q2)=2}$, ${\textstyle m(P3)=m(Q3)=3}$, ${\textstyle m(P4)=m(Q4)=4}$.

En la Figura 1 se muestra la convergencia en malla para la primera componente de la velocidad usando elementos triangulares. Las otras variables muestran igualmente convergencia óptima para todos los elementos considerados. Lo mismo sucede en el caso de elementos cuadrangulares.

Para los dos métodos de estabilización considerados, ASGS y OSS, los valores de las constantes algorítmicas ${\textstyle c_{i},}$ ${\textstyle i=1,2,3,4,}$ se han calibrado a ${\textstyle c_{1}=12,}$ ${\textstyle c_{2}=2,}$ ${\textstyle c_{3}=1,}$ ${\textstyle c_{4}=1}$, como ya se ha mencionado. Para la convergencia del método OSS con elementos cuadráticos cuadrados ${\textstyle Q_{2}}$ fue necesario utilizar ${\textstyle c_{1}=15.}$ Aunque para los elementos lineales ${\textstyle Q_{1}}$ y de alto orden ${\textstyle Q_{3},}$ ${\textstyle Q_{4},}$ es suficiente utilizar ${\textstyle c_{1}=4,}$ hemos preferido usar ${\textstyle c_{1}=15}$ para todos los elementos con el objeto de uniformizar los datos en las gráficas de las pruebas de convergencia en malla. En las figuras de las gráficas de convergencia en malla se observa tanto gráfica como numéricamente que las pendientes calculadas son mayores o tienden al valor de la pendiente teórica ${\textstyle d+1}$.

Figura 1: Convergencia ASGS-OSS, elementos triangulares, velocidad $U_{1}$.

Los resultados de las gráficas de convergencia muestran claramente que las formulaciones generalizadas para los métodos estabilizados ASGS y OSS son capaces de aproximar correctamente el problema de CDR vectorial transitorio con convección dominante que estamos considerando, con igual interpolación para todas las variables e incluyendo no linealidad en los términos convectivo y de reacción.

4.2 Flujo a través de un obstáculo elíptico

Este caso de referencia ha sido ampliamente examinado en la literatura utilizando diferentes métodos, como volúmenes finitos [6,7], método de Godnov [14], método de los mínimos cuadrados con elementos finitos [10,13], o esquemas WENO en diferencias finitas [5]. En el presente trabajo vamos a reexaminar el caso de referencia con el método variacional ASGS y utilizando funciones de forma cuadráticas, cúbicas y de cuarto orden.

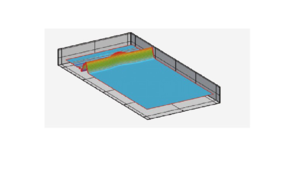
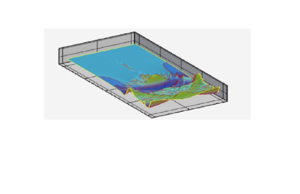
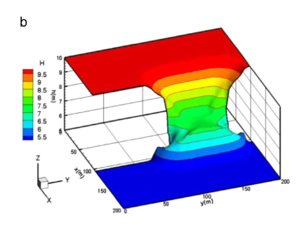
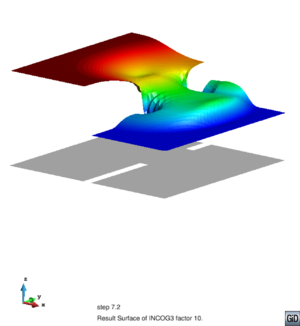
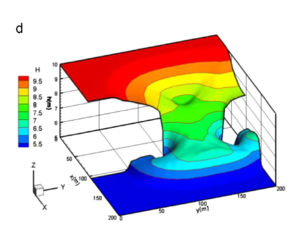
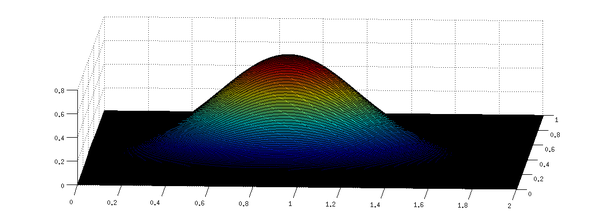
El dominio computacional es ${\textstyle \left[0,\right]\times \left[0,\right]}$ y la batimetría mostrada en la Figura 2 está dada por

$z\left(x,y\right)=0.8\,{\exp }(-5(x-0.9)^{2}-50\left(y-0.5\right)^{2}).$

El movimiento se inicia con la condición inicial de la superficie libre del agua perturbada por un desplazamiento hacia arriba de ${\textstyle 0.01}$ m en la región ${\textstyle 0.05\leq x\leq {0.15}}$:

$\eta (x,y,0)=\left\{{\begin{array}{cc}0.01\;{\hbox{m}}&\qquad {\hbox{ si}}\quad {0.05}\leq x\leq {0.15},\\0\;{\hbox{ m}}&\qquad {\hbox{ de otra manera}}.\end{array}}\right.$

El momento inicial en las direcciones ${\textstyle x,}$ ${\textstyle y}$ es nulo:

$U_{1}(x,y,0)=U_{2}(x,y,0)=0\;{\hbox{m/s}}.$

En cuanto al mallado, con el objeto de comparar los resultados entre elementos lineales y de alto orden, hemos considerado conveniente utilizar refinamientos de malla para elementos ${\textstyle Q_{1},}$ ${\textstyle Q_{2},}$ ${\textstyle Q_{3},}$ y ${\textstyle Q_{4}}$ que den el mismo o aproximadamente el mismo número de nodos entre sí. Tomamos como referencia el refinamiento de malla para ${\textstyle Q_{2}}$, que consta de ${\textstyle 200\times {100}}$ elementos cuadrados uniformes de ${\textstyle 9}$ nodos, es decir, el espaciado en las direcciones ${\textstyle x}$ e ${\textstyle y}$ es ${\textstyle \delta x=\delta y=0.01}$ m, con un total de ${\textstyle 80601}$ nodos. De esta manera, la malla de referencia para elementos ${\textstyle Q_{1}}$ consta de ${\textstyle 400\times {200}}$ elementos cuadrados uniformes de 4 nodos, es decir ${\textstyle \delta x=\delta y=0.005}$ m, con un total de ${\textstyle 80601}$ nodos. La malla de referencia para elementos ${\textstyle Q_{3}}$ consta de ${\textstyle 133\times {67}}$ elementos cuadrados uniformes de 16 nodos, es decir ${\textstyle \delta x=\delta y=0.015}$ m, con un total de ${\textstyle 80800}$ nodos. Finalmente, la malla de referencia para elementos ${\textstyle Q_{4}}$ consta de ${\textstyle 100\times {50}}$ elementos cuadrados uniformes de 25 nodos, es decir ${\textstyle \delta x=\delta y=0.02}$ m, con un total de ${\textstyle 80601}$ nodos.

El tamaño del paso de tiempo es uniforme, con ${\textstyle \delta t=0.001}$ s, y el integrador temporal es BDF1 en todos los casos.

La referencia del nivel del agua en reposo, es decir, con ${\textstyle \eta =0}$ m, es ${\textstyle z=H=1.0}$ m.

Figura 2: Flujo a través de un obstáculo elíptico. Ilustración del dominio computacional y de la batimetría.

$Q_{3}$ $Q_{4}$ 0.12 s 0.24 s 0.36 s 0.48 s 0.60 s

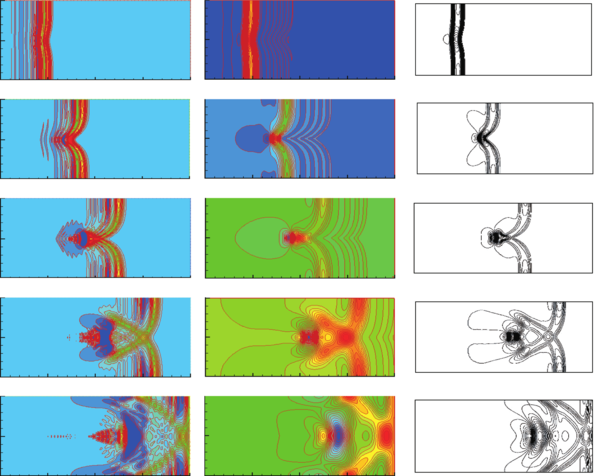
Figura 3: Flujo a través de un obstáculo elíptico. Contornos 2D de la superficie libre del agua $\eta {.}$

La Figura 3 muestra los contornos 2D de la superficie libre del agua ${\textstyle \eta }$ para distintos instantes de tiempo ${\textstyle t=0.12,0.24,0.36,0.48,0.60}$ s. Los contornos 2D calculados se presentan para los elementos ${\textstyle Q_{3}}$ y ${\textstyle Q_{4}}$, con similares resultados para elementos ${\textstyle Q_{1}}$ y ${\textstyle Q_{2}}$. A pesar de ser calculados para todos los elementos con mallas con igual número total de nodos, los resultados conforme se aumenta el orden de los polinomios de interpolación presentan mayor detalle que los de menor orden; esto se aprecia mirando los gráficos horizontalmente para un instante de tiempo, comparando los resultados de elementos ${\textstyle Q_{3}}$ y ${\textstyle Q_{4}}$.

$t=0.12$ s $t=0.24$ s $t=0.36$ s $t=0.48$ s $t=0.60$ s (a) (b)

Figura 4: Flujo a través de un obstáculo elíptico. Contornos de la superficie libre del agua $\eta ,$ con elementos $Q_{2}$. (a) Resultados del presente estudio, (b) resultados de Shin-Jye Liang y Ying-Chih Chen [10].

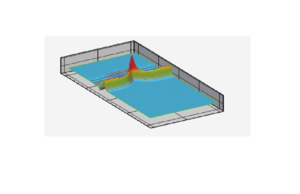
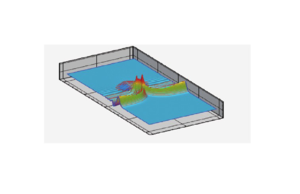
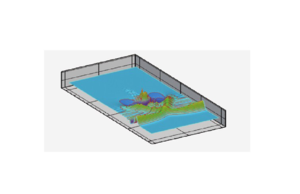
En la Figura 4 mostramos una comparación de los resultados de los contornos 3D de la superficie libre del agua ${\textstyle \eta }$. Los gráficos de la parte izquierda corresponden a los resultados de nuestro trabajo y los gráficos de la parte derecha son los resultados de Shin-Jye Liang y Ying-Chih Chen [10], ambos estudios con iguales características de mallado y paso de tiempo (elementos ${\textstyle Q_{2},}$ ${\textstyle \delta x=\delta y=0.01}$ m y ${\textstyle \delta t=0.001}$ s). Con respecto a los otros resultados 3D para elementos ${\textstyle Q_{1},}$ ${\textstyle Q_{3},}$ y ${\textstyle Q_{4}}$ de nuestro trabajo, las diferencias entre sí y con respecto al elemento ${\textstyle Q_{2}}$ son visualmente imperceptibles, por lo que en la Figura 4(a) presentamos solo los resultados correspondientes al elemento ${\textstyle Q_{2}}$, para poder así compararlos con los resultados de [10]. En ambos trabajos el comportamiento de la onda es bastante similar, aunque en nuestro caso la evolución temporal es más disipativa por haber utilizado un integrador temporal de primer orden (recuérdese que nuestro propósito es el diseño de aproximaciones precisas y robustas en el espacio). Así, la perturbación que inicialmente es plana y se propaga hacia la derecha se ve afectada por el obstáculo elíptico en la parte inferior del lecho. El incremento de la amplitud de onda debido a la disminución de la profundidad del agua es obvio en ${\textstyle t=0.24}$ s, debido a la disminución de la velocidad de onda, siendo la más baja de todo el flujo en el momento en el cual la onda atraviesa el punto más alto del obstáculo elíptico y que aproximadamente se produce en el instante ${\textstyle t=0.24}$ s. Se observan ondas estacionarias de reflexión justo detrás del pico producido por el choque de la onda con el obstáculo elíptico, en ${\textstyle t=0.24,0.36,0.48}$ y ${\textstyle 0.60}$ s.

Tabla 2. Flujo a través de un obstáculo elíptico. Picos de elevación máxima

Tiempo (s)	Elevación de la superficie
	libre del agua, $\eta$ (mm)
	$Q_{1}$	$Q_{2}$	$Q_{3}$	$Q_{4}$
0.12	5.0975	5.0939	5.0716	4.9786
0.24	7.2415	7.2120	7.1718	6.9990
0.36	5.9430	5.8503	5.7924	5.5978
0.48	5.6073	5.6526	5.6161	5.1742
0.60	3.9634	3.9812	3.9523	3.7503

En la Tabla 2 se encuentran tabuladas las elevaciones de la superficie libre del agua ${\textstyle \eta ,}$ correspondientes a los picos más altos de la onda para los instantes de tiempo ${\textstyle t=0.12,0.24,0.36,0.48}$ y ${\textstyle 0.60}$ s. Observamos como en todos los casos la onda alcanza su pico máximo en ${\textstyle t=0.24}$ s, debido precisamente a que alrededor de ${\textstyle t=0.24}$ s la onda atraviesa el punto más alto del obstáculo elíptico. También observamos que para cada instante de tiempo la elevación de la superficie del agua ${\textstyle \eta }$ disminuye conforme se incrementa el orden del elemento, lo que es completamente coincidente con la mejor precisión en elementos de alto orden. Como podemos ver en la Tabla 2, para un instante de tiempo las variaciones de ${\textstyle \eta }$ conforme se aumenta el orden del elemento son del orden de las décimas, centésimas y en algunos casos milésimas de milímetro, por lo que dichas variaciones son visualmente imperceptibles, como se ha mencionado anteriormente, motivo por el cual en la Figura 4(a) se ha presentado solo el contorno 3D correspondiente a elementos ${\textstyle Q_{2}}$.

(a)	(b)	(c)
Figura 5: Flujo a través de un obstáculo elíptico. Contornos 2D de la superficie libre del agua de: (a) resultados de Shin-Jye y Ying-Chih Chen [10] con elementos $Q_{2}$ cuadrado de 9 nodos, (b) resultados de Ying-Chih Chen [13] con elementos $P_{1}$ triángulos de 3 nodos, (c) resultados de Akoh et al. [6] con elementos $P_{1}$.

Finalmente, en la Figura 5 presentamos los resultados de los contornos 2D del nivel de superficie libre del agua ${\textstyle \eta }$ de: (a) Shin-Jye y Ying-Chih Chen [10] (con elementos ${\textstyle Q_{2},}$ ${\textstyle \delta x=\delta y=0.01}$ m y ${\textstyle \delta t=0.001}$ s, (b) Lian y Hsu [13] (con elementos ${\textstyle P_{1}}$, ${\textstyle \delta x=\delta y=0.01}$ m y ${\textstyle \delta t=0.0005}$ s) y (c) Akoh et al.  [6] (con elementos ${\textstyle P_{1}}$, ${\textstyle \delta x=\delta y=0.01}$ m y ${\textstyle \delta t=0.0005}$ s), para ser comparados con nuestros resultados de la Figura 3. En general observamos que los resultados del presente trabajo dan estructuras de ondas y gradientes más nítidos y con mas detalle que los resultados de [10,13] y [6].

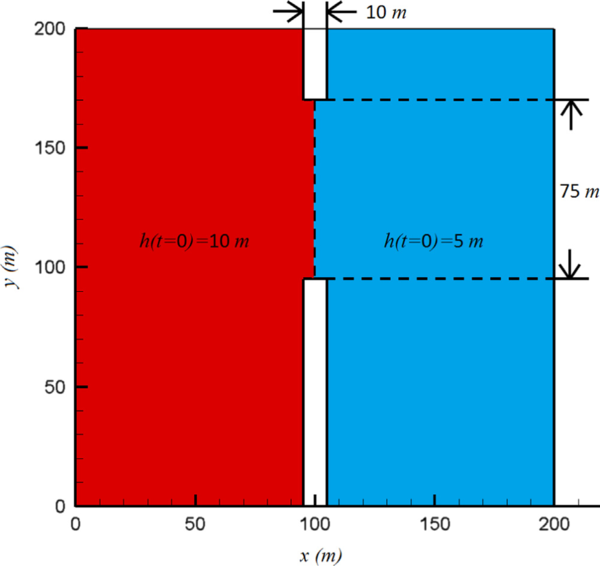
4.3 Flujo de la rotura de una presa a través de una compuerta de esclusa

A continuación consideramos el problema de la rotura de una presa, el cual se puede encontrar por ejemplo en [38,39]. La ilustración del problema se muestra en la Figura 6(a). La geometría del dominio computacional es una región cuadrada de 200 m ${\textstyle \times }$ 200 m con fondo plano sin fricción, y deslizamiento libre en todas las paredes del embalse (aguas arriba) y del desembalse (aguas abajo), excepto en las paredes interiores de separación del embalse y desembalse y de la compuerta de la esclusa. Dicha compuerta de esclusa de 75 m de ancho está localizada en la mitad del dominio. El nivel inicial del agua en el embalse de la presa (aguas arriba) es de 10 m, y el del desembalse (aguas abajo) es de 5 m de alto con el agua en reposo. En el instante en que falla la presa, el embalse de agua se libera a través de la compuerta de esclusa, creando ondas de propagación aguas abajo (desembalse). En cuanto a las condiciones de contorno, las velocidades en la dirección perpendicular a las paredes de la presa, tanto en el embalse como en el desembalse (partes derecha e izquierda correspondientemente de la Figura 6(a)), es necesario prescribirlas a cero; además la velocidad tangencial en las paredes interiores de separación del embalse y desembalse, así como también en las paredes de la compuerta de la esclusa, también se debe prescribir a cero. El borde izquierdo del desembalse es libre, por lo tanto la velocidad perpendicular a este borde la dejamos sin prescribir a cero. La superficie libre del agua ${\textstyle \eta }$ no se prescribe, se deja libre en todo el contorno.

Debido a que la velocidad del flujo en la dirección ${\textstyle x}$ es muy variable, el comportamiento de los parámetros de estabilización también es muy variable, con valores en nada comparables con el paso de tiempo, lo cual genera problemas de convergencia. Para evitar estos problemas, hemos redefinido ${\textstyle \tau _{1}}$ en cada elemento ${\textstyle e}$ como

$\tau _{1}^{e}\gets \min(\tau _{1}^{e},\alpha \delta t),$

(106)

donde ${\textstyle \delta t}$ es el paso de tiempo y ${\textstyle \alpha }$ es un parámetro que es necesario ajustar dependiendo del tamaño de la malla y del grado del polinomio de las funciones de forma. Para este caso estudiado hemos adoptado ${\textstyle \alpha =10}$ para elementos ${\textstyle P_{1}}$ y ${\textstyle P_{2}}$, para elementos ${\textstyle P_{3}}$ se ha usado ${\textstyle \alpha =1}$ y para elementos ${\textstyle P_{4}}$ se ha tomado ${\textstyle \alpha =0.5}$. El valor de ${\textstyle \tau _{2}^{e}}$ se calcula con (91), pero en este caso con el ${\textstyle \tau _{1}^{e}}$ calculado en (106).

(a)	(b)
Figura 6: Flujo de la rotura de una presa. (a) Geometría y condiciones iniciales del problema. (b) Malla con elementos triangulares $P_{1}$ con 3733 nodos.

En la Figura 6(b) se encuentra la malla usada con 7164 elementos triangulares ${\textstyle P_{1}}$, que dan un total de 3733 nodos.

(a) (b) Contorno 2D Corte longitudinal

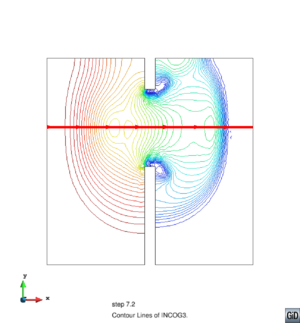
Figura 7: Flujo de la rotura de una presa. Contornos 2D y corte longitudinal de la superficie libre del agua en 7.2 s. Comparación de: (a) Estudio presente, (b) ELRBFCM [38].

(a) (b) Contorno 2D Corte longitudinal

Figura 8: Flujo de la rotura de una presa. Contornos 2D y corte longitudinal de la velocidad en la dirección $x$ en 7.2 s. Comparación de: (a) Estudio presente, (b) ELRBFCM [38].

Tiempo $t=3.5$ s $t=7.2$ s (a) (b)

Figura 9: Flujo de la rotura de una presa. Contornos 3D de la superficie libre del agua, para los instantes de tiempo $t=3.5$ s y $t=7.2$ s. Comparación de: (a) Estudio presente, (b) ELRBFCM [38].

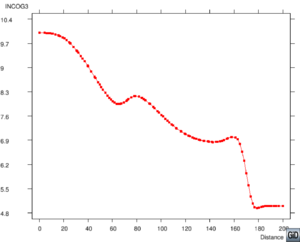
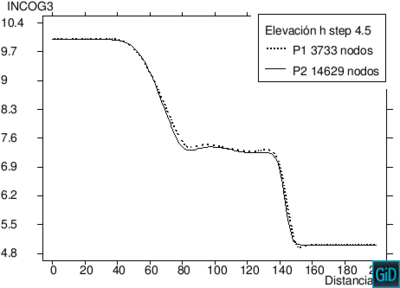
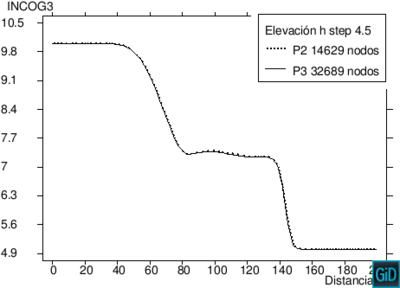
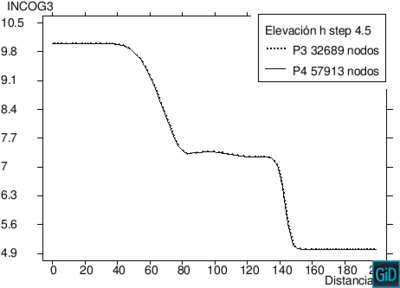
Figura 10: Flujo de la rotura de una presa. Corte longitudinal de la superficie libre del agua en $t=$ 4.5 s. Comparación del refinamiento para elementos $P_{1}$, $P_{2}$, $P_{3}$ y $P_{4}$.

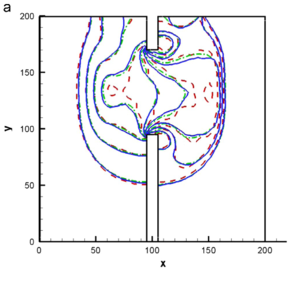
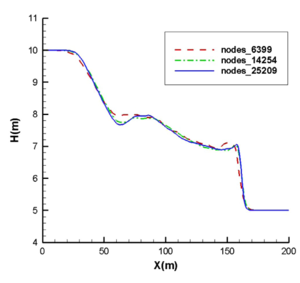
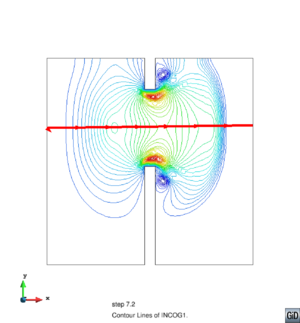
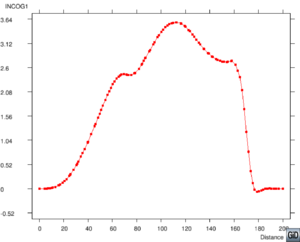
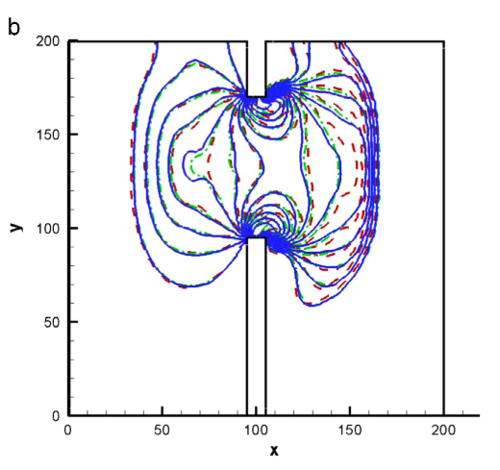
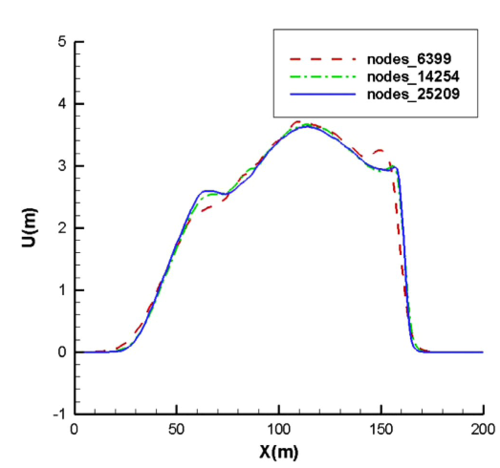
En las Figuras 7 y 8 se presentan los contornos 2D y los cortes longitudinales indicados de la superficie libre del agua y de la velocidad en la dirección ${\textstyle x}$ en ${\textstyle t=}$7.2 s, respectivamente. En las Figuras 7(a) y 8(a) se encuentran los resultados de nuestro trabajo, mientras que en las Figuras 7(b) y 8(b) están los resultados de C.K. Chou et al. con el método ELRBFCM [38]. Observando los cortes longitudinales de las Figuras 7 y 8 vemos que nuestros resultados coinciden con los de C.K. Chou en el perfil de 25209 nodos, pero en nuestro trabajo hemos usado una malla con elementos triangulares ${\textstyle P_{1}}$ con 3733 nodos, lo que incide en un menor costo computacional. También los contornos 2D, tanto de la superficie libre del agua como de la velocidad en la dirección ${\textstyle x}$ en las Figuras 7 y 8, presentan mejores y más nítidos detalles que los resultados de [38].

También presentamos la simulación del proceso de rotura de la presa en ${\textstyle t=3.5}$ s y ${\textstyle t=7.2}$ s, que se muestra en la Figura 9(a) con 3733 nodos en el caso de nuestro trabajo y con 14254 nodos para los resultados de C.K. Chou et al. [38] en la Figura 9(b).

Finalmente presentamos una comparación de los resultados de elementos lineales ${\textstyle P_{1}}$ con elementos de alto orden ${\textstyle P_{2}}$, ${\textstyle P_{3}}$ y ${\textstyle P_{4}}$ de los cortes longitudinales de la superficie libre del agua en el instante de tiempo ${\textstyle t=4.5}$ s en la Figura 10. Tomando como base la malla de 7164 elementos triangulares ${\textstyle P_{1}}$ con 3733 nodos y aumentado el orden de interpolación con el mismo número de elementos, obtenemos mallas con elementos triangulares ${\textstyle P_{2}}$ con un total de 14629 nodos, ${\textstyle P_{3}}$ con 32689 nodos y ${\textstyle P_{4}}$ con 57913 nodos. Observando las gráficas se concluye que al aumentar el orden de interpolación se obtienen mejores resultados tanto de la superficie libre del agua como de la velocidad en la dirección ${\textstyle x}$, como era de esperar.

5. Conclusiones

En este artículo se ha presentado una revisión de los métodos estabilizados ASGS y OSS para una ecuación vectorial de tipo CDR general, estacionaria y transitoria, con aplicación a las ecuaciones del movimiento de un fluido en aguas poco profundas. Asimismo, se ha estudiado la utilización de elementos finitos de alto orden, cuadráticos, cúbicos y de cuarto orden, con elementos tanto triangulares como cuadrangulares.

Las formulaciones variacionales estabilizadas ASGS y OSS nos permiten utilizar igual interpolación en todas las variables, que en nuestro caso son tres, las dos componentes de la velocidad ${\textstyle U_{1},}$ ${\textstyle U_{2}}$ y la elevación ${\textstyle \eta }$ de la superficie libre del agua. Nos permiten también poder tratar con flujos de convección dominante. Estas dos dificultades se unen a la complejidad adicional de la no linealidad tanto en los términos convectivos como en la derivada temporal de la elevación de la superficie libre del agua. Para poder utilizar elementos finitos de alto orden fue necesario cambiar el cálculo del parámetro de estabilización, incluyendo en este cálculo el grado del polinomio.

De los resultados del test de convergencia realizados se puede concluir que puede ser ventajoso utilizar elementos de alto orden para el problema que hemos considerado. En términos generales, los errores para un número de nodos dado son menores cuanto mayor es el orden del polinomio utilizado. También se observó con experimentación numérica que la inclusión del término ${\textstyle \tau _{2}}$ en la matriz ${\textstyle {\tau }}$ es totalmente necesaria para el ejemplo de la rotura de la presa, ya que si se considera ${\textstyle \tau _{2}=0}$ el resultado es que con elementos ${\textstyle P_{1}}$ y ${\textstyle P_{2}}$ se presentan problemas de estabilidad alrededor de los 7 s, y con elementos ${\textstyle P_{3}}$ y ${\textstyle P_{4}}$ estos problemas se presentan desde ${\textstyle t=0.1}$ s. Sin embargo, para las pruebas de convergencia en malla y el ejemplo del flujo a través de un obstáculo elíptico, es indiferente el usar ${\textstyle \tau _{2}=0}$ o ${\textstyle \tau _{2}={\frac {\left(h/d\right)^{2}}{c_{1}\tau _{1}}}}$, ya que las variaciones de los resultados en estos casos son mínimas.

En general, el comportamiento de los métodos estabilizado ASGS y OSS para el problema que hemos estudiado es completamente satisfactorio, mostrando que la comparación de nuestros resultados con los resultados de otros autores es favorable en todos los casos a nuestras formulaciones.

Referencias

[1] P. Brufau and P. García-Navarro. (2000) "Two-dimensional dam break flow simulation", Volume 33. International Journal for Numerical Methods in Fluids 35–37.

[2] J. C. Hsiek and T.Y. Yang. (2003) "Investigation on the suitability of two dimensional depth-averaged models for bend-flow simulation", Volume 129. ASCE Journal of Hydraulic Engineering 433-465.

[3] E. Pena. (2002) "Estudio numérico y experimental del transporte de sedimentos en cauces aluviales". Universidade de A Coruña.

[4] E. Zahibo and N. Pelinovsky. (2006) "Analytical and numerical study of nonlinear effects at tsunami modeling", Volume 174. Applied Mathematics and Computation 795-809.

[5] Y. Xing and C.W. Shu. (2005) "High order finite difference WENO schemes for a class of hyperbolic systems with source terms", Volume 208. Journal of Computational Physics 206–227.

[6] R. Akoh and S. Li and F. Xiao. (2008) "A CIP/multi-moment finite volume method for shallow water equations with source terms", Volume 56. International Journal for Numerical Methods in Fluids 2245–2270.

[7] Y. Xing and C.W. Shu. (2006) "High order well-balanced finite volume WENO schemes and discontinuos Galerkin methods for a class of hyperbolic systems with source terms", Volume 216. Journal of Computational Physics 567–598.

[8] V. Alessandro and V. Caleffi, V. and A. Zanni. (2002) "Case study: Malpasset dam-break simulation using a two-dimensional finite volume method", Volume 128. ASCE Journal of Hydraulic Engineering 460-472.

[9] E. Hanert and V. Legat and E. Deleersnijder. (2002) "A comparison of three finite elements to solve the linear shallow water equations", Volume 5. Ocean Modelling 17–35.

[10] S.-J. Liang and Y.-C. Chen. (2011) "Space-time least-squares finite-element method for shallow-water equations", Volume 19. Journal of Marine Science and Technology 571–578.

[11] S. Takase and K. Kashiyama and S. Tanaka and Tayfun E. Tezduyar. (2010) "Space-time SUPG formulation of the shallow-water equations", Volume 64. International Journal for Numerical Methods in Fluids 1379–1394.

[12] R. Codina. (2001) "Finite element approximation of the shallow water equations using subgrid scale stabilization.". CD Proceedings of the Eccomas CFD 2001, Swansea.

[13] S.J. Liang and T.W. Hsu. (2009) "Least-squares finite-element method for shallow-water equations with source terms", Volume 25. Acta Mechanica Sinica 597–610.

[14] R. Le Veque. (1998) "Balancing source terms and flux gradients in high-resolution Godunov methods: the quasi-steady wave-propagation algorithm", Volume 146. Journal of Computational Physics 346–365.

[15] M. Fujihara and A.G.L. Borthwick. (2000) "Godunov-type solution of curvilinear shallow-water equations", Volume 126. ASCE Journal of Hydraulic Engineering 827-836.

[16] J.G. Zhou. (2002) "A lattice Boltzmann model for the shallow water equations", Volume 191. Computer Methods in Applied Mechanics and Engineering 3527–3539.

[17] O.C. Zienkiewicz and R.L. Taylor. (2000) "The Finite Element Method. Volume 3: Fluid Mechanics", Volume 1. Butterworth-Heinemann, 5 Edition.

[18] T.J.R. Hughes. (1995) "Multiscale phenomena: Green's function, the Dirichlet-to-Neumann formulation, subgrid scale models, bubbles and the origins of stabilized formulations", Volume 127. Computer Methods in Applied Mechanics and Engineering 387–401.

[19] T.J.R. Hughes and G.R. Feijóo and L. Mazzei and J.B. Quincy. (1998) "The variational multiscale method–a paradigm for computational mechanics", Volume 166. Computer Methods in Applied Mechanics and Engineering 3–24.

[20] R. Codina. (2000) "On stabilized finite element methods for linear systems of convection-diffusion-reaction equations", Volume 188. Computer Methods in Applied Mechanics and Engineering 61–82.

[21] R. Codina. (2001) "A stabilized finite element method for generalized stationary incompressible flows", Volume 190. Computer Methods in Applied Mechanics and Engineering 2681–2706.

[22] R. Codina. (2002) "Stabilized finite element approximation of transient incompressible flows using orthogonal subscales", Volume 191. Computer Methods in Applied Mechanics and Engineering 4295–4321.

[23] R. Codina. (2000) "Stabilization of incompressibility and convection through orthogonal sub-scales in finite element methods", Volume 190. Computer Methods in Applied Mechanics and Engineering 1579–1599.

[24] R. Codina and J. Blasco. (1997) "A finite element formulation for the Stokes problem allowing equal velocity-pressure interpolation", Volume 143. Computer Methods in Applied Mechanics and Engineering 373–391.

[25] R. Codina and J. Blasco. (2000) "Analysis of a pressure-stabilized finite element approximation of the stationary Navier-Stokes equations", Volume 87. Numerische Mathematik 59–81.

[26] R. Codina. (1998) "Comparison of some finite element methods for solving the diffusion-convection-reaction equation", Volume 156. Computer Methods in Applied Mechanics and Engineering 185–210.

[27] R. Codina and J. Blasco. (2002) "Analysis of a stabilized finite element approximation of the transient convection-diffusion-reaction equation using orthogonal subscales", Volume 4. Computing and Visualization in Science 167–174.

[28] H. Yamamoto. (2009) "Lecture 8: The Shallow-Water Equations". 2009 Program of Study: Nonlinear waves, pp. 71-79.

[29] J. Peraire and O.C. Zienkiewics and K. Morgan. (1986) "Shallow water problems: a general explicit formulation", Volume 22. International Journal for Numerical Methods in Engineering 547–574.

[30] J. Peraire. (1986) "A finite element method for convection dominated flows". University of South Wales, Swansea.

[31] R. Codina and S. Badia and J. Baiges and J. Principe. (Por aparecer) "Variational Multiscale Methods in Computational Fluid Dynamics, in Encyclopedia of Computational Mechanics". John Wiley & Sons Ltd.

[32] R. Codina and J.M. González-Ondina and G. Díaz-Hernández and J. Principe. (2008) "Finite element approximation of the modified Boussinesq equations using a stabilized formulation", Volume 57. International Journal for Numerical Methods in Fluids 1249–1268.

[33] C. Baiocchi and F. Brezzi and L.P. Franca. (1993) "Virtual bubbles and Galerkin/least-squares type methods (Ga.L.S)", Volume 105. Computer Methods in Applied Mechanics and Engineering 125–141.

[34] F. Brezzi and L.P. Franca and T.J.R. Hughes and A. Russo. (1997) "$b=\int g$", Volume 145. Computer Methods in Applied Mechanics and Engineering 329–339.

[35] R. Codina and J. Principe and J. Baiges. (2009) "Subscales on the element boundaries in the variational two-scale finite element method", Volume 198. Computer Methods in Applied Mechanics and Engineering 838–852.

[36] R. Codina and J. Principe and O. Guasch and S. Badia. (2007) "Time dependent subscales in the stabilized finite element approximation of incompressible flow problems", Volume 196. Computer Methods in Applied Mechanics and Engineering 2413–2430.

[37] R. Codina and J. Principe. (2007) "Dynamic subscales in the finite element approximation of thermally coupled incompressible flows", Volume 54. International Journal for Numerical Methods in Fluids 707-730.

[38] C.K. Chou and C.P. Sun and D.L. Young and V. Sladek. (2015) "Extrapolated local basis function collocation method for shallow water problems", Volume 50. Engineering Analysis with Boundary Elements 275–290.

[39] S.J. Liang and J.H. Tang and M.S. Wu. (2008) "Solution of shallow-water equations using least-squares finite-element method", Volume 24. Acta Mechanica Sinica 523–532.