Abstract
Some residential buildings are irregular, having plants with entrances, fact which can worsen their behavior during potential seismic events. They can present demands that are much higher than their design capacity. The objective of this monograph is to study the seismic performance factors of buildings by applying the FEMA P695 methodology to a set of regular and irregular structural configurations with and without incorporating closure beams in their entrances. The case studies consider low-rise reinforced concrete buildings located in high seismic hazard areas. The structures are analyzed, considering the hypothesis of flexible diaphragm, in the linear range (using the Robot Structural Analysis computer code) and in the nonlinear range (using the SeismoStruct 7.0.3 computer code); both are based on the finite element method. The seismic response of the structures is evaluated by performing nonlinear pseudo-static analysis and incremental dynamic analysis (IDA). It is worth noting that the response of the buildings with entrances by applying the pushover analysis requires specifying certain rules of application, which are proposed herein. The performance point is calculated by applying the extended N2 method, which is especially applicable to buildings with irregularities in plan considering the effect of the higher modes of vibration. This allows obtaining the seismic response of the buildings to earthquakes similar to those of the seismic code. The displacement corresponding to the performance point allows making evaluations by means of the method of the quadrants and the damage index indicates if the structure is fragile or ductile. In addition, an alternative method is proposed to obtain the ductility and factors such as the torsional irregularity index, which is a dimensionless coefficient that characterizes the structural response and relates it to the existing irregularities. Comparisons among structures with different irregularity in plant are also made considering their fragility curves. The R coefficient is adopted according to the current regulations applying FEMA P695 and a new value of R is established by using the IDA curves obtained from the nonlinear analysis.
CAPÍTULO 1. EL PROBLEMA DE LA TORSIÓN EN EDIFICIOS IRREGULARES
Actualmente, es común observar en las edificaciones que nos rodean diseños arquitectónicos llamativos y con formas irregulares, lo que produce excentricidad en planta, todo ello para satisfacer la configuración estructural y no estructural moderna, se observa como esta ubicación, forma y tamaño de los elementos estructurales (columnas, vigas, losas y muros) y los no estructurales (cerramientos), junto a las técnicas constructivas, exponen a la estructura a sufrir mayor daño sísmico, por lo cual es necesario que el diseño sismorresistente pueda garantizar el comportamiento dúctil y con capacidad de disipar energía por parte de los elementos.
Por consiguiente, estas irregularidades propician, por un lado, zonas de concentración de esfuerzos en los ángulos interiores en donde se unen los diferentes cuerpos que se forman y por otro lado, condicionan la vulnerabilidad sísmica, la cual es entendida por el conjunto de parámetros capaz de predecir el tipo de daño estructural, modo de falla y la capacidad resistente de una edificación [1]; dicha vulnerabilidad en estructuras de hormigón armado acarrea la pérdida de capacidad de la estructura a resistir las cargas horizontales originadas por un sismo específico, llegando a un estado de colapso en el cual ya no son capaces de soportar las cargas de gravedad.
En Venezuela, la necesidad de espacios destinados a la circulación, ha llevado a diseñar edificaciones residenciales irregulares con planta con entrantes. Recientemente, investigaciones de Vielma et al. [2] [3], han demostrado que este tipo de irregularidad en edificios existentes, pudiese producir demandas muy superiores a la capacidad de diseño, ya que, según Naeim y Bopana [4], las aberturas propician el comportamiento del diafragma como diafragma flexible.
La norma sismorresistente Covenin 1756 [5] vigente en Venezuela, contempla a los entrantes como una irregularidad que origina el comportamiento global de diafragma flexible. Es de hacer notar que los procedimientos simplificados de análisis que aún se contemplan en las normas de diseño sismorresistente tienen aplicabilidad únicamente si los entrepisos funcionan como diafragmas rígidos. Queda supuesto que si no existen diafragmas rígidos, no se producirá una distribución uniforme de los cortantes sísmicos en los planos resistentes de la estructura.
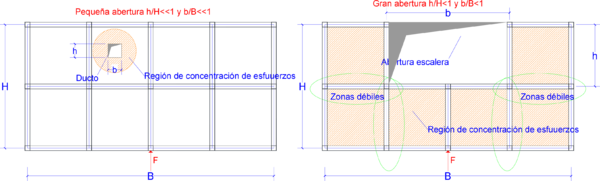
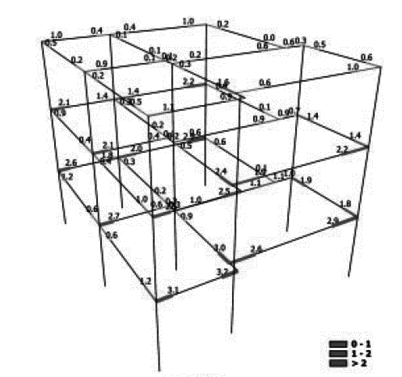
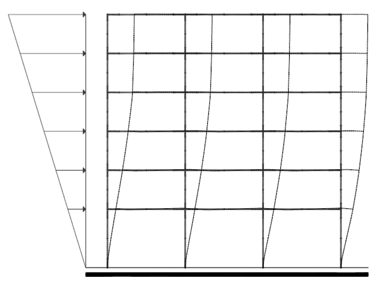
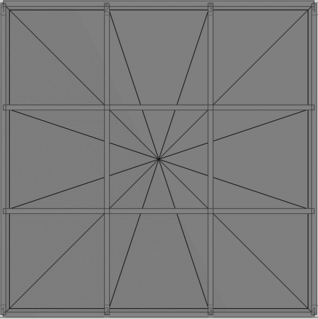
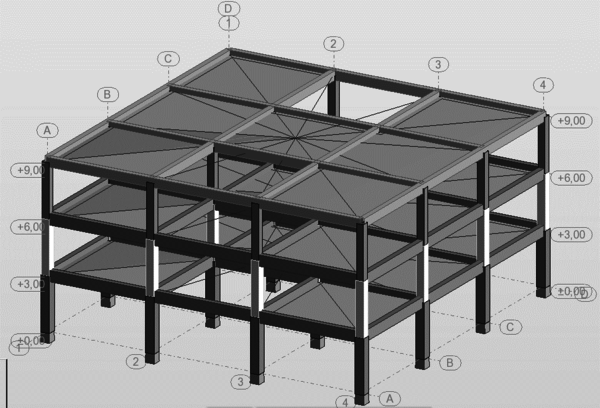
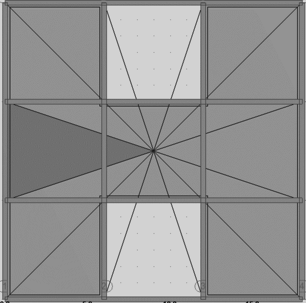
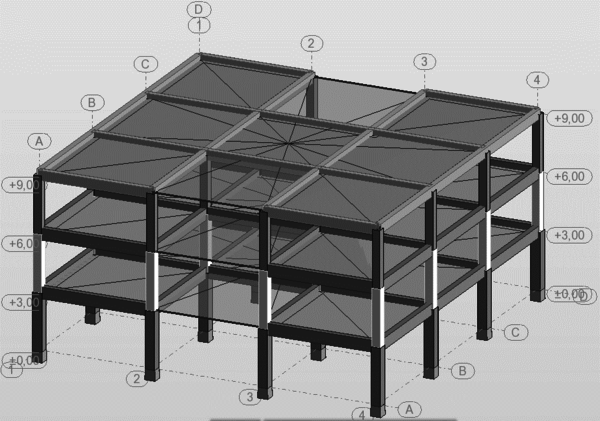
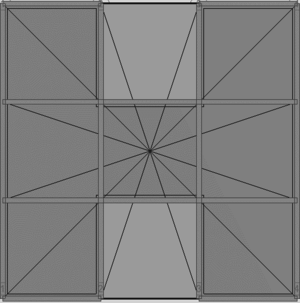
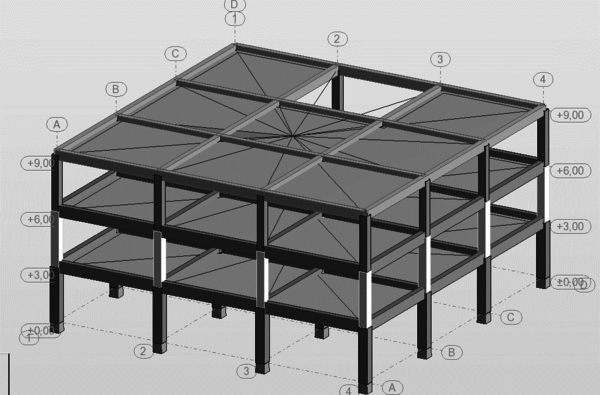
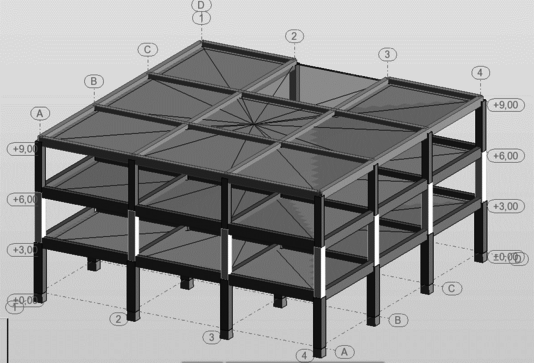
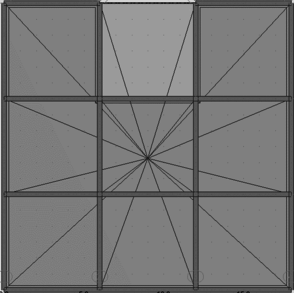
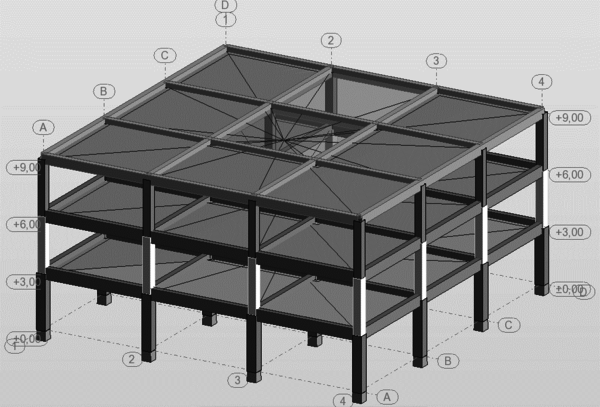
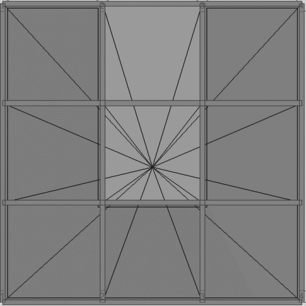
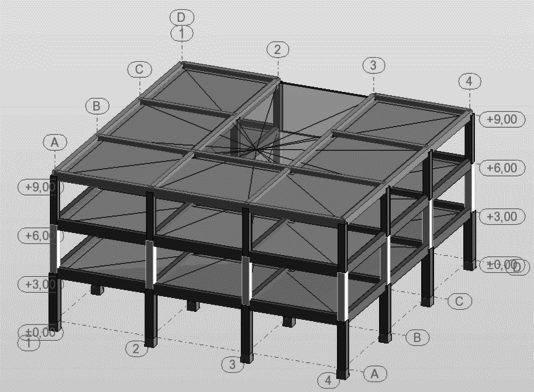
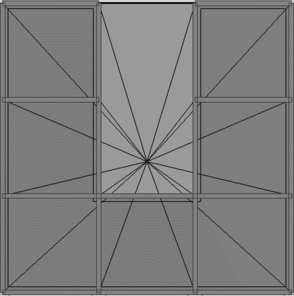
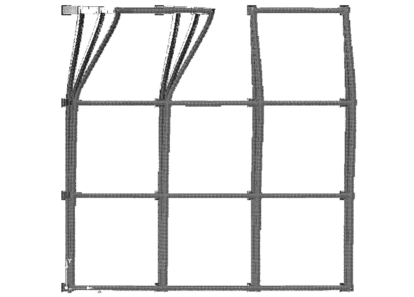
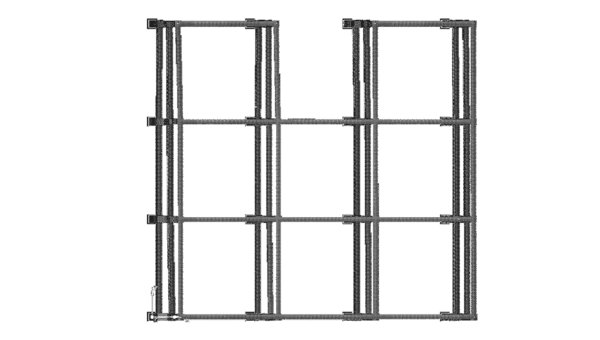
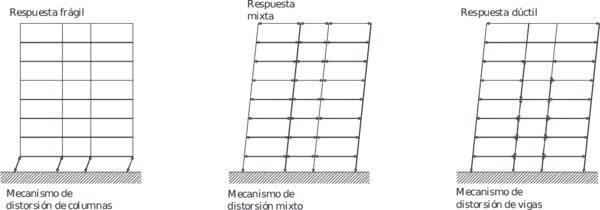
En la Figura 1.1 puede apreciarse el efecto que las aberturas tienen sobre la concentración de esfuerzos y sobre la respuesta de los diferentes elementos de la estructura. Nótese que las pequeñas aberturas tienen un efecto local sobre la concentración de esfuerzos, mientras que las grandes aberturas no solamente afectan el comportamiento global, sino que generan el debilitamiento de las líneas resistentes en diferentes direcciones, [6].
Así mismo, según recientes investigaciones [3] [7], la presencia de estas aberturas influye sobre la amplificación de momentos torsores en las columnas ubicadas en aquellas zonas del perímetro próximas a las aberturas.
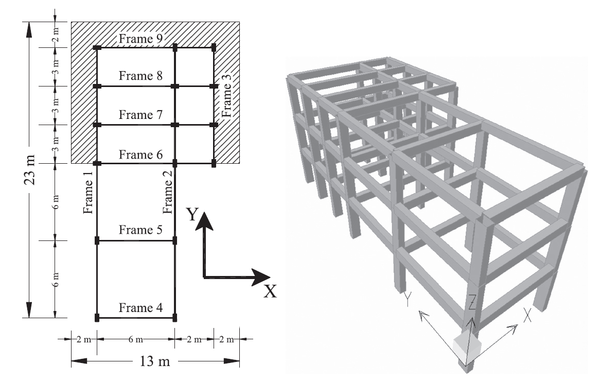
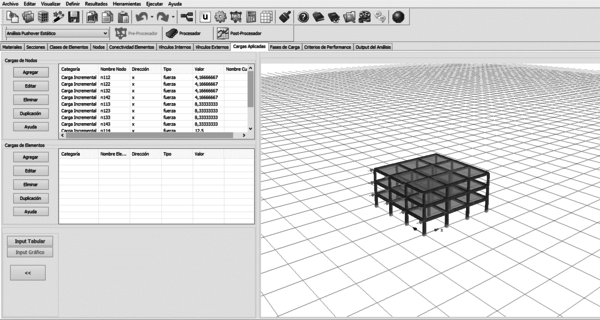
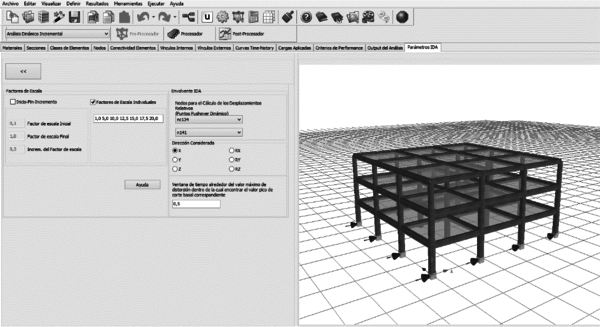
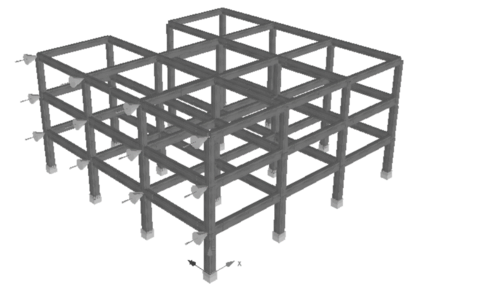
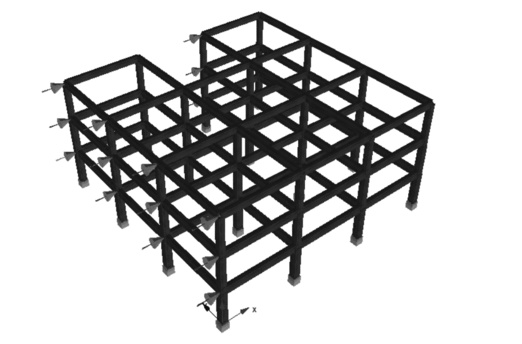
En esta monografía se determinará si la irregularidad en planta con entrantes influye sobre la respuesta sísmica de edificios bajos de hormigón armado, con amenaza sísmica y con características geotécnicas similares a las que corresponden a la mayoría de los edificios de la ciudad de Barquisimeto. Para el análisis y diseño se considera una zona de alta amenaza sísmica, sobre suelos rígidos (perfil S2), diseñados para alcanzar una alta ductilidad, aplicando un factor de reducción de respuesta R=6. Las tipologías a analizar contemplan edificios con planta regular y con plantas irregulares con entrantes y también edificios con plantas con entrantes a los que se les ha incorporado vigas de cierre en los entrantes. Se plantea la utilización de programas basados en el método de elementos finitos; Robot Structural en su versión educativa para el análisis lineal [8] y SeismoStruct en versión educativa 7.0.3 (análisis no lineal) [9], que permiten realizar el diseño y análisis del comportamiento de estas estructuras con irregularidades, para así obtener resultados de la respuesta de la edificación ante un posible evento sísmico y validar los factores de prestaciones sísmicas aplicados en el diseño, así como un índice de daño basado en rotaciones de los elementos y la amplificación de las rotaciones de planta..
1.1 Contexto del tema
La importancia de la investigación se centra en comparar la vulnerabilidad sísmica de edificios irregulares en planta de hormigón armado con la de edificios regulares. El problema permitirá establecer cómo influye la irregularidad en plantas sobre los factores de prestaciones sísmicas de un edificio; para dicha evaluación se emplearán programas especializados de elementos finitos que proporcionan a los profesionales información relevante de su comportamiento estructural que será útil en sus diseños y en la aproximación al comportamiento real de las mismas, aplicando la metodología FEMA P695, que según Vielma y Cando [10] apoyándose en el documento “Quantification of building seismic performance factors” [11],se describe como una metodología que tiene la finalidad de evaluar nuevos sistemas estructurales y proponer sus factores para el diseño. Sin embargo, también es una herramienta práctica y directa para la evaluación de los factores de prestaciones de sistemas estructurales existentes. El procedimiento lineal de diseño contenido en las normas se basa en convertir el complicado comportamiento no lineal de la estructura de un edificio bajo cargas sísmicas en un problema lineal equivalente. Las normas prescriben una serie de requerimientos para estructuras basados en el sistema estructural. Estos requerimientos regulan la configuración, el tamaño. Los materiales de construcción, el detallado y la resistencia y rigidez de la estructura.
Es importante enfatizar buena parte de las edificaciones residenciales en Venezuela tienen como característica configuracional la irregularidad en plantas, lo que representa un factor desfavorable ante un probable evento sísmico y motiva a profundizar más en el tema. Cabe destacar, que las estructuras estudiadas son aporticadas de hormigón armado, ya que es uno de los sistemas constructivos más empleado en los países con demandas sísmicas importantes.
Aunado a esto se tiene que la normativa sismorresistente con la que se cuenta, requiere de mejoras en cuanto a las especificaciones del comportamiento estructural de sistemas irregulares.
1.2 Avances en el problema de la torsión
Seguidamente se muestran algunos trabajos relativos al tema, que han sido desarrollados a nivel numérico, procurando obtener una adecuada comprensión de la manera que las estructuras son afectadas por la excentricidad generada por la irregularidad.
Lucchini et al. [12]. Los autores investigaron la influencia de cinco medidas de intensidad (IM) aplicadas a un edificio tri-dimensional con planta irregular, sujeto a la acción de dos componentes simultáneas de terremoto. Estas medidas de intensidad son muy importantes dentro del contexto del diseño con base en prestaciones, debido a que permiten correlacionarlas con los parámetros de demanda (EDP), que usualmente señalan el daño sísmico en las estructuras.
La selección adecuada de las medidas de intensidad es compleja, ya que se procura que estas posean una sencillez a la hora de aplicarlas, acompañada de una buena precisión en la determinación del daño sísmico. Esto a su vez permite que se reduzca el número acelerogramas empleados en el análisis durante la evaluación de las prestaciones.
Una de las limitaciones importantes que encontraron los autores radica en que la mayoría de las medidas de intensidad han sido determinadas con base en resultados de estructuras bi-direccionales sujetas a la acción de terremotos unidireccionales. Por este motivo, los autores consideran que no es extensible dichas medidas de intensidad al caso de edificios tri-dimensionales con irregularidades.
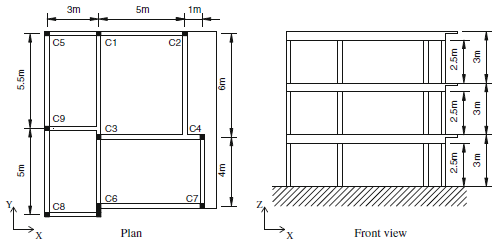
Para realizar los análisis dinámicos, los autores consideraron el registro de Herceg-Novi (Terremoto de Montenegro) escalado para una aceleración pico (PGA) de 0,15g. El análisis empleado fue el IDA (análisis incremental dinámico) utilizando el registro aplicado según: 100% en dirección X y 30% en dirección Y, luego 30% en dirección X y 100% en dirección Y. El edificio objeto de estudio fue el bien documentado SPEAR, ver Figura 1.2.
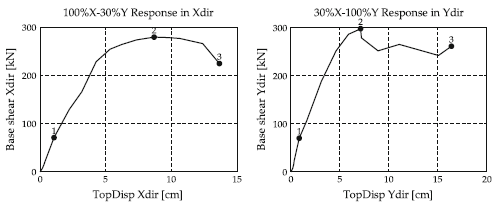
Las curvas pushover dinámicas obtenidas para cada dirección de análisis fueron las que se muestran:
Las demandas de desplazamientos las han graficado de una manera muy interesante, haciendo uso de la forma de trabajar del método N2 extendido. Han graficado las demandas de desplazamientos en cada dirección de análisis, en los tres puntos mostrados en la Figura 1.3 anteriores.
Los autores reportan un decremento del comportamiento torsional de la respuesta, a medida que se incrementa la intensidad sísmica. Esto se puede notar en la Figura 1.4. También al comparar la relación entre los desplazamientos del nivel de cubierta, encontraron que a medida que se incrementa la intensidad sísmica, se reduce el comportamiento torsional del edificio.
Luego el estudio fue conducido usando 120 pares de registros de terremotos superficiales, con magnitudes de momentos superiores a 5,6. Las componentes verticales de los acelerogramas fueron despreciadas al no considerarlas definitivas en el tipo de edificios analizado.
Los parámetros de demanda seleccionados fueron la deriva de entrepiso máxima alcanzada en cualquiera de los niveles del edificio (MIDR), la deriva global que corresponde al máximo desplazamiento lateral ocurrido en el nivel de techo, dividido por la altura total del edificio (RDR). Adicionalmente consideraron las derivas medias en cada nivel y los valores relativos de las derivas de todos los nodos de un nivel con respecto del nodo ubicado en la esquina flexible de la planta (nodo C2) obteniéndose unas cantidades definidas como MIDRM y MIDRC, respectivamente. De igual manera fueron calculadas las cantidades correspondientes a la deriva global, originándose unas cantidades definidas como RDRM y RDRC, respectivamente.
La definición de las medidas de intensidad la llevaron a cabo considerando en primer lugar la pseudo-aceleración alcanzada en el primer período de vibración , quien es la más popular entre los estudiosos del tema. Sin embargo, esta aceleración se considera que no predice adecuadamente la intensidad para la que se alcanzan los daños en estructuras irregulares en las que esta es determinante para que la estructura alcance una respuesta no lineal.
Por todo esto, los autores consideraron cuatro alternativas a la hora de fijar una medida de intensidad, aparte de la señalada anteriormente:
- Un vector de medidas de intensidad, evaluado en periodos altos
- Una medida de intensidad que combina las pseudo-aceleraciones a dos periodos específicos: que es el primer periodo elástico y que es el primer periodo elongado por el daño
- Un vector de medidas de intensidad, mejorado con la adición de un parámetro
- Un vector de medidas de intensidad que combina las pseudo-aceleraciones de las dos componentes ortogonales del terremoto
El procedimiento general aplicado contempló análisis de regresión para la variable dependiente (parámetro de demanda, EDP) en sus diferentes variaciones expuestas anteriormente y la variable independiente (mediad de intensidad IM) para las cinco variantes enumeradas. Los resultados obtenidos con estas medidas de intensidad no son concluyentes para las medidas de intensidad dos y cinco, pero se notan algunas mejoras para la medida de intensidad dos y tres. Los autores proponen que se siga evaluando edificios con diferentes tipos de irregularidades, a fin de obtener una mejor alternativa.
Kilar y Fajfar [13]. Los autores proponen un método para realizar el análisis con empuje incremental de estructuras complejas. La metodología se desarrolla sobre la base de estructuras modeladas en tres dimensiones, paro discretizadas en macro-elementos, consistentes en pórticos planos. A cada pórtico plano se la asocia un comportamiento bi-lineal o multi-lineal. Se propone una metodología que se prueba en un edificio de pórticos con muros configurado regular e irregularmente.
Los autores valoran las dificultades existentes para la época, para el pre-proceso de modelos muy complejos y luego para el post-proceso de los resultados obtenidos del análisis.
El procedimiento computacional comprende los pasos siguientes:
Todos los datos estructurales deben ser conocidos. Adicionalmente a los datos para el análisis elástico, los momentos de plastificación son requeridos, para aquellos puntos en los que se espera se formen rótulas plásticas.
La distribución de las fuerzas sísmicas sobre la altura es escogida (puede ser uniforme, triangular o por forma modal). El paso del incremento de las cargas se realiza de manera arbitraria. En el caso de estructuras irregulares, se debe especificar las coordenadas del centro de masas y también la dirección de las fuerzas aplicadas.
Para cada paso de carga, se realiza un análisis elástico. El incremento del desplazamiento global, al igual que los incrementos en la distribución de las fuerzas, desplazamientos y fuerzas internas se calculan para cada macro-elemento.
Para cada tipo de macro-elemento, se ha definido una relación de cortante basal vs. Desplazamiento en el techo. Usando tales relaciones, se calculan los factores para cada evento anticipado. Este factor de define como la ratio que existe entre el incremento de carga que origina un evento y el incremento de carga seleccionado. Por tanto, el factor de evento es una especie de factor de escala para el incremento de carga externa seleccionado. El factor de evento más pequeño define el evento que ocurrirá a continuación y el incremento de carga actual que deberá ser añadido a la carga total para que el siguiente evento ocurra.
Todas las cantidades descritas en el paso 3, se escalan aplicando el factor de evento mínimo y se adicionan los resultados a los del paso previo.
El modelo matemático y/o la rigidez del macro-elemento que inició el evento, es cambiada de acuerdo con las reglas descritas previamente.
Se repiten los pasos 3 al 6 con el modelo matemático actualizado.
Existen muchas opciones para concluir el análisis por ejemplo la formación de un mecanismo plástico para la estructura completa, la excedencia de un desplazamiento máximo admisible a nivel de cubierta o la detección de un mecanismo de falla frágil.
Los autores reconocen las bondades otorgadas por el análisis pushover, sin embargo, afrontan los nuevos retos de extender este tipo de análisis al ámbito de las estructuras tridimensionales. En ese caso, se deben resolver cuestiones como la existencia de estructuras asimétricas que impongan limitaciones a la aplicación de las dos componentes ortogonales de fuerzas y la posibilidad de demandas de ductilidad en los elementos más flexibles o más rígidos de la estructura, producidas por el efecto de la torsión.
Para el caso preciso de pórticos, los autores declaran que el análisis solo puede ser efectuado a aquellos pórticos regulares (en elevación).
Una de las principales tareas emprendidas es poder responder a las preguntas formuladas por De La Llera y Chopra, en cuanto a la distribución de la rigidez en las plantas, cómo localizar y distribuir el daño entre las plantas, y cuáles serían los macro-elementos que requieren ser reforzados, con la finalidad de obtener un mejor desempeño sísmico de la estructura.
Entre los ejemplos presentan dos edificios, uno regular y otro irregular, los cuales se han analizado aplicando el método propuesto. El primero de los edificios presenta la variante de que se le ha dado una configuración simétrica y luego una asimétrica.
En el caso del edificio irregular mostrado en la Figura 1.5, los autores siguen usando los macro-elementos, aplicando a su vez las cargas laterales en el centro de masa de cada nivel. Sin embargo, no aportan en el artículo mayor información sobre la distribución de estas cargas sobre los macro-elementos empleados en el análisis.
Chandler y Duan [14]. El estudio se basa en la respuesta sísmica de estructuras asimétricas. Estas han sido diseñadas de acuerdo con las normas internacionales más conocidas. Abordan tópicos tales como: la interpretación de la torsión accidental contenida en las normas, la influencia del factor de reducción de respuesta sobre el período lateral desacoplado y la respuesta torsional de este tipo de edificios. Realizaron análisis sobre modelos de un solo nivel, sometiéndolos a la acción de acelerogramas escalados para cumplir con dos estados límite: de servicio y último.
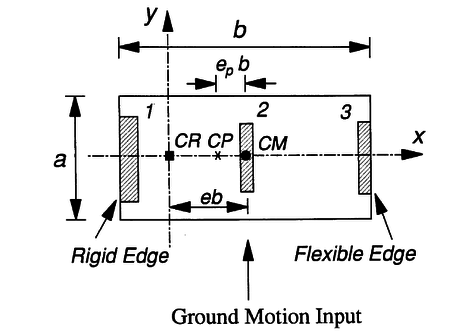
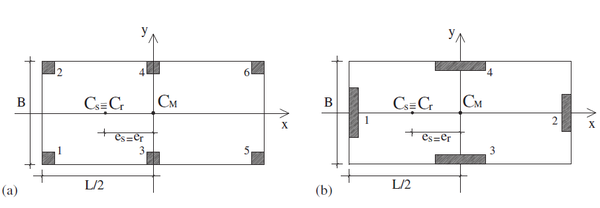
El estudio de las estructuras desbalanceadas torsionalmente se lleva a cabo mediante un modelo muy simple, en el cual el desbalance torsional se alcanza mediante la presencia de un borde rígido, definido mediante un muro estructural con sección transversal mayor que el resto de los muros que sostienen un diafragma rígido.
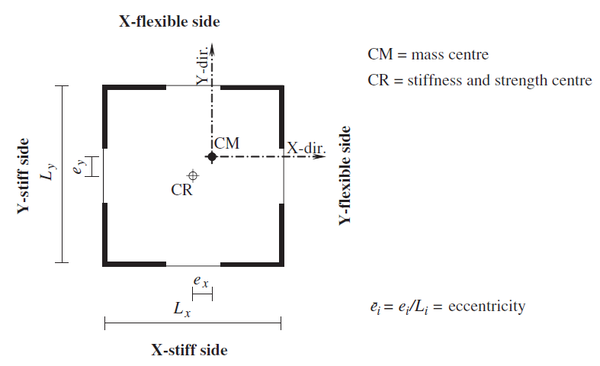
En la Figura 1.6 mostrada se desprenden una serie de características relativas a los problemas de torsión en edificios. En primer lugar, se aprecia el centro de masa ( ) que es definido como el centro geométrico de la losa del edificio, dado que las cargas de la misma son uniformes. En el centro de masa es el lugar en el cual se aplican las cargas laterales. Seguidamente se aprecia el centro de rigidez. Se define al centro de rigidez ( ), como el punto en el cual la aplicación de las fuerzas laterales conduce exclusivamente a que se produzcan traslaciones en la planta.
A la distancia que existe entre el centro de masa y el centro de rigidez se le denomina excentricidad estática , que suele presentarse de manera normalizada contra la dimensión del edificio en la dirección de la excentricidad , resultando un parámetro adimensional que caracteriza la respuesta torsional del edificio .
Adicionalmente se definen otros parámetros tales como: el radio de giro torsional , que no es otra cosa sino el segundo momento de inercia de los soportes verticales con respecto del centro de rigidez ( ). El radio de giro torsional se puede comparar con el radio de giro traslacional en la dirección de análisis, dando origen a un parámetro que se puede normalizar con respecto de la longitud en la dirección del análisis:
|
|
(1.1) |
Este parámetro adimensional, conocido como el radio de giro de rigidez normalizado, da cuenta de la rigidez relativa de los elementos en los bordes de la estructura, comparada con respecto a la rigidez del elemento central.
Finalmente, se determina el centro de resistencia , que se obtiene como el primer momento de las resistencias aportadas por cada uno de los soportes verticales. El segundo momento de resistencia de los elementos verticales respecto del centro de resistencia , define el radio de giro de resistencia normalizado . A la distancia que se genera entre el y se le denomina excentricidad de resistencia, .
Los resultados de los análisis aplicados al sistema torsionalmente desbalanceado, mostrado en la Figura 1.6, se comparan con los resultados obtenidos al analizar una estructura similar, pero considerando un balance torsional, que se logra mediante la modificación de la losa, que es artificialmente desplazada, hasta que su centro de masa coincide con el centro de rigidez . Esto permite que la respuesta estructural sea exclusivamente traslacional, cuando se aplica el análisis lineal y no lineal dinámico. De esta manera, los sistemas estructurales resultantes, son tratados con la torsión accidental prescrita en las normas y sin ella (5% de la excentricidad producida en cada dirección de análisis).
Harasimowicz y Goel [15]. En este trabajo se discuten aspectos controversiales relativos al comportamiento y diseño de edificios con irregularidad en planta. El aspecto fundamentalmente tratado es el que tiene que ver con la definición y determinación de los centros de referencia para la determinación de la torsión.
Comienzan definiendo la excentricidad de diseño como:
|
(1.2) |
donde: es la excentricidad estructural (estática) a un nivel j, es la dimensión en planta del edificio perpendicular a la dirección de análisis. Los coeficientes son especificados de acuerdo a la norma que se aplica.
Estos valores de excentricidad estructural se especifican para prevenir el efecto de la irregularidad en planta de las edificaciones. Representan la distancia que hay entre el centro de masa del nivel y el “centro de referencia”. Los autores usan este término para distinguir entre los diferentes enfoques que más adelante se van a especificar.
Actualmente no existe una definición unánime del “centro de referencia”. Por ejemplo, los autores citan que Poole indica que el centro de referencia es el centro de rigidez, en el que, al aplicarse las fuerzas de piso, produce un movimiento exclusivamente traslacional. Humar, por su parte, se refiere al centro de referencia como centro de resistencia, que se obtiene al aplicar fuerzas en un determinado nivel, sin producir rotaciones en dicho nivel, pero originándolas en otros niveles de la estructura. Otros autores, como Cheung y Tso y Hejal y Chopra consideran que los centros de referencia son un conjunto de puntos ubicados en la estructura, de tal manera que cuando se les aplican las cargas laterales, no llega a producirse rotación en ninguno de los pisos del edificio.
Otras definiciones del centro de referencia incluyen el centro de torsión y el centro de cortante. El primero se define como el punto de una planta que, al aplicarle un conjunto de momentos torsores, permanece estacionario, esto es, solo se produce torsión alrededor de esos puntos. Finalmente, el centro de corte de un nivel, es definido como el punto en el cual la aplicación de fuerzas cortantes de entrepiso no llega a producir efectos de torsión en ninguno de los pisos del edificio.
Es evidente que a menos que se trate de un edificio de un solo nivel, los centros de referencia no tienen por qué coincidir.
Conforme a los diversos puntos que se pueden asumir como centros de referencia, es muy conveniente definir en cuál de ellos las normas deben postular la aplicación de las provisiones torsionales estáticas, similares a las expuestas en la fórmula anterior.
Loa autores encontraron que a pesar de que los centros de referencia fueron definidos de formas muy diferentes, los resultados en cuanto al diseño de elementos no variaron significativamente, así que no es determinante la aplicación de las posibles variantes consideradas.
Paulay [16]. El autor propone un procedimiento para identificar el efecto torsional en edificios, que es completamente diferente al contenido en las normas. Para ello es necesario conocer el mecanismo de plastificación tridimensional de la estructura.
El autor comienza refiriéndose al conocido “diseño por capacidad” establecido en Nueva Zelanda. De acurdo con esta filosofía. Las estructuras y, por ende, los elementos estructurales primarios son proporcionados y detallados para soportar exitosamente importantes desplazamientos inducidos por los sismos. El resto de los elementos estructurales deben mantener suficiente resistencia, para poder disipar energía de manera estable. El objetivo es por tanto claro: obtener un fallo dúctil en el que la demanda de ductilidad en los elementos no sea excesiva. Esta estrategia ha sido incorporada lentamente en la mayoría de las normas de diseño sismorresistente. Sin embargo, su aplicación en el contexto de la torsión no ha sido tan claro aún.
Para comenzar, expone los mecanismos cinemáticamente admisibles de fallo torsional.
El autor comienza definiendo el centro de rigidez, de tal forma que pudiera establecerse una comparativa con el artículo anterior. La definición está basada en la expresión siguiente:
|
|
(1.3) |
donde los términos contenidos en la expresión se refieren a las coordenadas de los elementos resistentes y la rigidez de los mismos calculada de manera convencional. De manera que la rigidez torsional queda definida como sigue:
|
|
(1.4) |
De la relación entre las rigideces rotacional y traslacional, surge el radio de giro de rigidez:
|
(1.5) |
La distancia que separa el centro de masa del centro de rigidez se denomina excentricidad de rigidez y se muestra en la Figura 1.7.
El desplazamiento en una dirección específica, bajo la acción de una fuerza paralela a esa dirección está dado por:
|
|
(1.6) |
Mientras tanto, el ángulo de torsión se obtiene como:
|
|
(1.7) |
La fuerza cortante que es producida en un elemento específico por la rotación se calcula a partir de una expresión que combina parte de los desarrollos obtenidos hasta este punto:
|
|
(1.8) |
En cuanto a la rigidez del sistema, planteada en función del desplazamiento del centro de masa, se calcula como:
|
|
(1.9) |
La expresión anterior sirve de base para determinar las propiedades dinámicas de los edificios.
De igual forma, el autor menciona la manera como las normas de diseño sismorresistente han incorporado la excentricidad en el análisis. Presenta las siguientes expresiones para el cálculo de la excentricidad a ser aplicada a las estructuras:
|
(1.10) |
Estos valores marcan los límites a la excentricidad a ser considerada. Toman en consideración, entre otras cosas, la incertidumbre asociada a la determinación del centro de masa y del centro de rigidez , así como al efecto de resonancia de las vibraciones traslacionales y rotacionales.
De la Colina [17]. El autor aborda el tema de la torsión en edificios desbalanceados torsionalmente. Aplica el análisis no lineal, con acciones sísmicas bi-direccionales definidas mediante un conjunto de registros fuertes. Centra su estudio en los siguientes parámetros:
El factor de reducción de respuesta
Los factores utilizados para determinar la excentricidad
El periodo inicial de la estructura
La excentricidad inicial de rigidez
Los resultados obtenidos sugieren la necesidad de cuestionar la conveniencia de aplicar el diseño de elementos estructurales solo con la acción sísmica en una dirección.
En el estudio se inicia la revisión de los procedimientos normativos usuales, que proponen la determinación de la excentricidad a partir de expresiones del tipo:
|
(1.11) |
Nótese la presencia de los coeficientes y , que afectan los valores de la excentricidad estática determinada como la diferencia de las coordenadas del centro de masa CM y el centro de rigidez CR. El coeficiente toma en cuenta las diferencia en la respuesta sísmica obtenida en los diferentes tipos de análisis: estático y dinámico, asumiendo valores ente 1,0 y 1,5. El coeficiente incluye el efecto del corte negativo que se llega a producir en el borde rígido de la planta, asumiendo valores de 0.0, 0.5 y 1.0. El tercer coeficiente presente en las expresiones es el que proporciona la fracción de la excentricidad accidental, que afecta a la dimensión de la planta en la dirección de análisis. Los valores usualmente encontrados en las normas para son de 0.05 y 0.10.
Una nota interesante se presenta al final de la introducción de este trabajo: el autor justifica la no utilización del coeficiente en el análisis, debido a la adecuada determinación de la posición del centro de masa y del centro de rigidez.
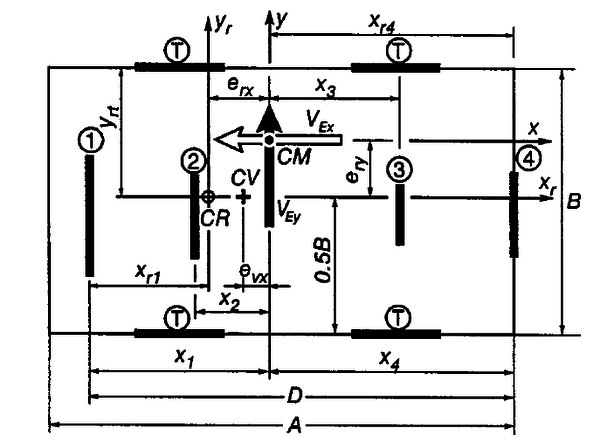
El edificio analizado por el autor es el mismo que analizaron en un estudio previo de Wong y Tso y que ha sido ampliamente referenciado en trabajos similares, ver Figura 1.8.
El concepto de edificio torsionalmente balanceado o desbalanceado, tiene que ver con los valores que alcanza la excentricidad estática. Así, para edificios con se considera que el sistema está torsionalmente balanceado, mientras que para valores de , se considera que el edificio está torsionalmente desbalanceado.
A diferencia de otros autores, este considera la importancia de la excentricidad de resistencia , medida desde la posición inicial del centro de masa . Los valores de la excentricidad de resistencia, resultan ser más bajos que los de la excentricidad estática , como suele presentarse en la mayoría de las estructuras diseñadas según normas.
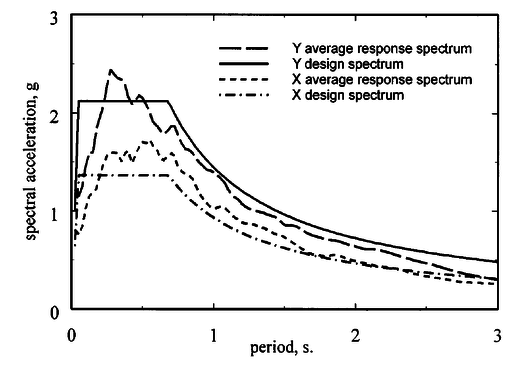
Seleccionó un grupo de diez registros, que aplicó de manera bi-direccional, pero con una componente mayor que la otra. Los acelerogramas fueron modificados para hacerlos compatibles con los espectros de diseño aplicables a cada dirección de análisis, Figura 1.9. Nótese que a la dirección de análisis y le correspondió la mayor componente de aceleración.
El autor utilizó como variable de estudio la distancia transversal entre muros, normalizada con respecto del ancho de la planta: .
El autor concluye que el factor depende del factor de reducción de respuesta , del período inicial y de la excentricidad estática , esto con el objetivo de mantener valores de demanda de ductilidad en el extremo flexible cercanas a la unidad.
Las rotaciones de las losas dependen casi exclusivamente del valor del factor de reducción de respuesta .
La influencia del periodo lateral sobre la demanda de ductilidad en elementos rígidos y flexibles, es prácticamente despreciable.
El incremento de la excentricidad estática origina el incremento en las demandas de ductilidad en los elementos rígidos y flexibles de la planta.
Tso y Smith [18]. Los autores se enfocan en estudiar las disposiciones tradicionales de que, al cambiar la resistencia de elementos resistentes a cargas laterales, no se debe ajustar la rigidez. Estas disposiciones afectan especialmente a las estructuras constituidas por muros. En ese caso, se debería realizar un ajuste de las propiedades de los elementos cuando se apliquen las provisiones normativas referentes a la torsión. Para esto los autores examinaron las que para la fecha constituían las normas más completas y avanzadas en cuanto al tema: el UBC 1997 y el Eurocodigo 8 de 1994.
De manera muy directa, las normas de diseño contemplan que el efecto torsional sea controlado mediante el incremento de la resistencia en el la parte flexible de la estructura (más propensa a sufrir incremento en los desplazamientos) y una reducción en la resistencia de la zona rígida (propensa a sufrir decrementos en los desplazamientos debidos a la torsión).
Los incrementos de desplazamientos en las zonas flexibles originan incrementos en la demanda de ductilidad. Sin embargo, algunas normas de manera tradicional, no proponen medidas de cambio para la resistencia de los elementos ubicados en las zonas flexibles, produciendo diseños similares a los que se obtendrían en un edificio completamente simétrico.
El autor, desde un punto de vista normativo, define dos tipos de elementos resistentes a cargas laterales: loe elementos tipo K y los elementos tipo D.
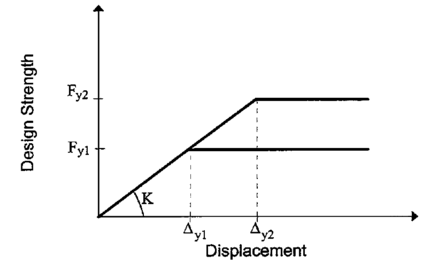
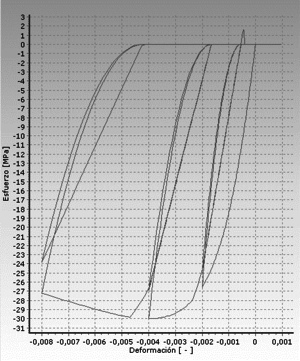
Los elementos tipo K se distinguen por ser de rigidez constante. Un incremento en la resistencia, trae como consecuencia un incremento en el desplazamiento de plastificación, lo que a la larga termina produciendo una reducción en la demanda de ductilidad. Sin embargo, se ha llegado a la conclusión que considerar que una estructura dispone solamente de elementos tipo K es erróneo. Se ha determinado, por el contrario, que la resistencia de plastificación determina la rigidez de los elementos. En la Figura 1.10 se puede apreciar la relación entre resistencia de diseño y desplazamientos de muros del tipo K.
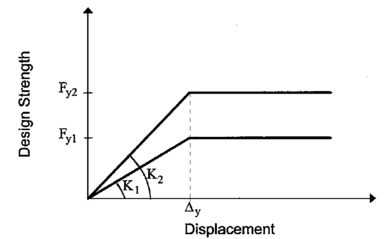
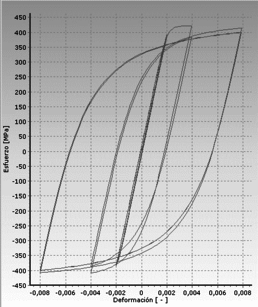
Por otro lado, los muros que cumplen con mantener similares desplazamientos de plastificación, aunque tengan distintas rigideces, se denominan muros de tipo D. La modificación de la resistencia en este tipo de elementos puede afectar las demandas de ductilidad que pueden enfrentar. Ver Figura 1.11.
El enfoque del autor consiste en encontrar las semejanzas en el comportamiento de los elementos tipo K (obtenidos por procedimientos normativos) y los elementos tipo D, que son los deseados por comportamiento.
Los autores realizaron una serie de análisis en rango no lineal del mismo edificio de un solo nivel constituido por muros estructurales. Utilizaron una serie de 10 registros de terremotos fuertes, normalizados para alcanzar una aceleración pico de 0.3g.
Los análisis no lineales de los modelos se efectuaron utilizando doble componente de los registros acelerográficos. Se aplicó un amortiguamiento del 5% del amortiguamiento crítico.
Luego de los análisis, los autores les hicieron seguimiento a las principales variables de la respuesta: los desplazamientos y las ductilidades alcanzadas por los muros de la zona rígida y de la zona flexible.
Entre las conclusiones de este trabajo deben mencionarse los cambios sugeridos en cuanto al enfoque del diseño de los elementos tipo K y D. Sin embargo, advierten que las mejoras se deben aplicar de forma independiente según sea el tipo de elemento en una estructura.
Magliulo et al. [19]. En este trabajo se presentan los resultados obtenidos del análisis de estructuras de hormigón armado, diseñadas conforme al EC-2 y al EC-8. Al tratarse de estructuras irregulares en planta, se ha aplicado el método N2 extendido, que contempla el Eurocódigo para introducir el efecto de la irregularidad a unos resultados obtenidos del análisis pushover clásico. Proponen tres métodos para mejorar el análisis N2, incorporando la excentricidad accidental que contemplan muchas de las normas de diseño sismo-resistente a nivel mundial. También evalúan el valor del factor de reducción de respuesta aplicado por el Eurocódigo 8 a estructuras torsionalmente flexibles.
En el método N2 extendido, se ha pretendido aplicar las correcciones delos desplazamientos en las zonas “rígidas” de los edificios. También se ha pretendido incorporar el efecto de los modos superiores a la vibración de los edificios con irregularidades en elevación. Esencialmente el método consiste en los pasos siguientes:
Obtención de la respuesta no lineal, a través del análisis pushover clásico, en dos direcciones independientes con las fuerzas sísmicas equivalentes aplicadas en los centros de masas y con sentidos opuestos.
Mediante el análisis modal del modelo 3D se obtienen los desplazamientos y derivas de los nodos de los pórticos.
Se aplican unos grupos de factores de corrección tanto en planta como en elevación, para corregir los desplazamientos y las derivas calculadas mediante el método N2.
El problema del método es que no incorpora el efecto de la torsión accidental, que está, sin embargo, en tela de juicio por varios autores importantes, debido a que no justifican el trabajo adicional impuesto a los proyectistas de estructuras. El edificio objeto de estudio se muestra en la Figura 1.12:
Los autores usaron análisis no lineal con rótulas plásticas, ya que definen relaciones de no linealidad entre los momentos y las rotaciones, manteniendo en rango lineal al resto de los desplazamientos.
También aplicaron análisis no lineal dinámico, utilizando para esto acelerogramas provenientes de 8 registros reales ocurridos en Europa y Asia.
Para incorporar la torsión accidental, los autores proponen tres variantes al método N2 de Fajfar.
El primero lo obtienen aplicando cuatro análisis modales a la estructura con las diferentes posiciones del centro de masa. Los resultados de los desplazamientos del nivel de cubierta de los pórticos y de los centros de masa, se combinan aplicando el método SRSS, para las componentes ortogonales consideradas en el estudio. Estos desplazamientos combinados, se normalizan luego con respecto de los desplazamientos del centro de masas. Para las cuatro combinaciones posibles, se selecciona la que proporciona el mayor valor.
Luego aplican ocho análisis no lineales pseudo-estáticos: dos signos de empuje (positivo y negativo) para las cuatro variantes de posiciones del CM aplicado anteriormente. Para cada pórtico se obtienen igualmente desplazamientos que se combina aplicando SRSS. Se normalizan estos desplazamientos de pórticos, dividiendo por el desplazamiento del CM.
Se calculan cuatro factores de corrección para cada uno de los pórticos, dividiendo el valor del resultado normalizado obtenido en el análisis modal, entre el desplazamiento normalizado obtenido en el análisis no lineal. Con estos factores de corrección, se amplifican los desplazamientos, únicamente de los nodos ubicados en la “zona rígida del edificio”.
La segunda variante se realiza como sigue: en primer lugar, se realizan cuatro análisis modales espectrales, para cuatro posiciones diferentes del centro de masas. Seguidamente se calculan los valores normalizados de los desplazamientos de los pórticos con respecto del centro de masa, en cada dirección.
Se llevan a cabo ocho análisis no lineales pseudo estáticos, determinados para las cuatro posiciones del centro de masa y con cambios en el sentido durante el análisis. Se obtienen los factores de corrección para los desplazamientos normalizados de los pórticos, conforme al procedimiento aplicado en el primer método. Se aplican estos factores de corrección a los desplazamientos de los pórticos obtenidos del análisis no lineal. De esta manera, se obtienen cuatro factores de corrección, uno por cada posición del centro de masa.
Se amplifican las cantidades relevantes de la zona rígida de la estructura por los factores de corrección obtenidos. A diferencia del primer método, estas cantidades relevantes se combina entre sí (pares de cantidades ortogonales) aplicando la regla del SRSS. Se termina el procedimiento seleccionando los máximos valores de los parámetros de demanda resultantes.
En el tercer método se repiten los dos primeros pasos expuestos del segundo método. El tercer paso es exactamente igual a los procedimientos anteriores, la diferencia estriba en que en este método se calculan ocho factores de corrección, ya que se considera también el signo del análisis. Seguidamente se amplifican los parámetros relevantes de los nodos de la zona rígida de la estructura. Los parámetros de demanda se obtienen mediante la regla de SRSS, pero esta vez considerando el cambio del signo, lo que genera 16 posibles combinaciones.
Es importante indicar en este punto, que la aplicación de las cargas del análisis no lineal pseudo estático prácticamente conduce a los mismos resultados obtenidos con los métodos anteriores, por tanto, se puede afirmar que independientemente de la irregularidad de la estructura, el signo utilizado en el análisis no lineal pseudo estático, no afectan sensiblemente los resultados.
Los autores también realizaron una serie de análisis no lineales dinámicos, con la finalidad de comparar los resultados con los alcanzados en los análisis no lineales pseudo estáticos. Fijaron un criterio para determinar el colapso, con base al 75% de la rotación última obtenida con las fórmulas empíricas.
Un parámetro importante que evaluaron los autores es el de la ductilidad de rotación. Esta es calculada como la ratio entre la rotación alcanzada en la cuerda de un elemento y la rotación correspondiente al límite de la plastificación, utilizando la siguiente ecuación empírica:
|
|
(1.12) |
Entre las conclusiones, los autores encuentran que el actual factor de reducción de respuesta prescrito por el Eurocódigo 8 es excesivamente penalizado por efecto de la irregularidad, generando un diseño conservador, todo de acuerdo con los resultados alcanzados del análisis dinámico no lineal.
Marino y Rossi [20]. Los autores de este artículo proponen un método para la ubicación exacta del eje de torsión de edificios de múltiples niveles. Lo logran proponiendo expresiones matemáticas rigurosas, sobre la base de un enfoque analítico. Se reportan los resultados, comparándolos con los obtenidos mediante un procedimiento previo.
Comienzan haciendo referencia a la resolución normativa de los problemas de estructuras irregulares. Cuáles son los principales métodos aplicados, dependiendo de los tipos de análisis implementados. Continúan con la definición del centro de masa, centro de rigidez, centro de corte y centro de torsión, en la misma tendencia que se ha encontrado en los trabajos de otros investigadores.
Dada la importancia que tiene el eje de torsión en este trabajo, se analiza especialmente la definición del centro de torsión. Este es definido como el punto en la losa de un nivel, que no sufriría ninguna traslación, si se aplica en la planta un momento torsor.
Algunos autores han reportado que los centros de torsión y de corte, no existen en la realidad en edificios de múltiples niveles. Sin embargo, para determinadas condiciones de cargas, se han logrado identificar tipologías en las que el centro de corte generalizado y el centro de torsión generalizado, coinciden formando un eje único. Adicionalmente, se han definido a edificios en los que los centros de masa se encuentran alineados en un eje y mantienen el mismo radio de giro en todos los niveles, se les denomina sistemas regularmente asimétricos. Desafortunadamente, edificios asimétricos casi nunca cumplen con las condiciones para poder clasificar dentro de este grupo selecto de edificios. Esto trae como consecuencia que, para estos edificios asimétricos reales, no es posible aplicar el método estático equivalente.
La formulación desarrollada por los autores, para determinar de manera analítica la posición óptima del centro de torsión, no es reproducida aquí. Solo se hace referencia de que la misma ha sido aplicada a una serie de edificios asimétricos.
La expresión fundamental en la que se basa este estudio se relaciona con la definición del plano de carga, en la que se logra obtener la minimización de las rotaciones que se producen en las plantas del edificio. Dicha expresión es:
|
|
(1.13) |
Sin embargo, los autores cuestionan la practicidad de esta función, dada la gran variabilidad que existe entre las diferentes estructuras, además de las cargas gravitatorias y sísmicas que pueden llegar a producirse. Sobre los resultados de un estudio paramétrico en el que se han analizado edificios de estructura conformada por muros y pórticos, se ha llegado a la conclusión de que el eje óptimo de torsión coincide con el centro de torsión ubicado en la planta que coincide aproximadamente con el 80% de la altura total del edificio.
Partiendo de estos procedimientos, los autores presentan dos procedimientos con enfoques diferentes. Uno denominado enfoque analítico, tiene que ver con la obtención del eje óptimo de torsión a través de la manipulación de la matriz de rigidez y otro enfoque denominado numérico, que busca la minimización de la función mostrada anteriormente mediante métodos numéricos. Ambos métodos son definidos por sus autores como “exactos” en contraste con el método aproximado de autores previos.
A manera de conclusión, los autores resaltan la validez de los dos métodos exactos aquí planteadas y aconsejan su utilización acompañada de un programa de análisis estructural y de cálculos manuales, dependiendo si se aplica el enfoque analítico o el enfoque numérico, respectivamente.
Chopra y Goel [21]. En este trabajo se introducen los resultados de la respuesta dinámica de las estructuras a la determinación de las fuerzas estáticas aplicadas en el análisis no lineal, manteniendo la simplicidad de este último tipo de análisis. Para esto en el análisis pushover modal se llevan a cabo los análisis utilizando distribuciones de fuerzas laterales que tiene que ver con la distribución que se obtiene en cada modo. Se propone aquí incorporar solamente los modos más relevantes y encontrar la respuesta máxima de la estructura a través de la combinación cuadrática completa ( ). El método propuesto demuestra ser similar en resultados cuando se lo aplica a estructuras con comportamiento elástico. Sin embargo, cuando se trata de estructuras con comportamiento inelástico, con variantes en la distribución del a rigidez, el método presenta resultados muy disímiles.
Es clave en este estudio la aplicación de un procedimiento de análisis desacoplado de historia de respuesta modal, que luce similar en cuanto a resultados se refiere, al análisis de historia tiempo, cuando se trata de respuesta elástica.
Partiendo de la ecuación de equilibrio dinámico, los autores encuentran una distribución espacial de fuerzas del edificio:
|
|
(1.14) |
con siendo el enésimo modo natural de vibración de la estructura, consistente en tres subvectores: y con:
|
|
(1.15) |
en donde:
|
(1.16) |
de aquí se pueden expresar las fuerzas sísmicas efectivas como:
|
|
(1.17) |
Los vectores asociados con las componentes e de los terremotos están dados por la misma ecuación:
|
|
(1.18) |
Cuando se supone que el enfoque puede ser aplicado a sistemas cuya respuesta es inelástica, es necesario tener en cuenta que estos ya no responden desde el punto de vista dinámico como lo hicieron al tener comportamiento elástico. Entonces las ecuaciones formuladas solo pueden ser vistas como aproximadas para los sistemas con respuesta inelástica.
El análisis modal pushover se puede realizar sobre sistemas elásticos e inelásticos. En el caso de sistemas con respuesta elástica, se define el vector de fuerzas equivalentes en cada dirección como:
|
(1.19) |
donde los tres vectores , y están dados por la ecuación anterior. La aceleración y es la deformación pico del enésimo modo de un sistema lineal de un grado de libertad. Lógicamente es la ordenada del espectro de respuesta o del espectro de diseño del enésimo modo del sistema de un grado de libertad. De manera alterna, la respuesta pico modal podrá ser obtenida si se somete a la estructura a las fuerzas y los torques definidos mediante:
|
|
(1.20) |
Las fuerzas laterales se van incrementando hasta que la estructura alcanza los siguientes desplazamientos a nivel de cubierta:
|
|
(1.21) |
|
(1.22)
(1.23) |
Cabe indicar que, bajo la acción de las fuerzas de empuje laterales, se alcanzan de manera simultánea las tres componentes de los desplazamientos a nivel de cubierta. La respuesta modal pico se alcanza mediante la combinación cuadrática completa (CQC) de tosas las componentes modales consideradas en el análisis. Se usa esta combinación, dado que los edificios asimétricos presentan modos de vibración con periodos muy próximos entre sí.
Para el análisis de estructuras inelásticas, se aplica el mismo procedimiento, pero esta vez se determina el desplazamiento como la deformación máxima de un sistema de un grado de libertad inelástico.
A continuación, se resume el procedimiento de análisis modal pushover
- Calcular las frecuencias naturales y modos de vibración mediante análisis dinámico elástico del edificio.
- Para el enésimo modo, obtener la curva de capacidad mediante el análisis no lineal convencional, pero utilizando una distribución de fuerzas dada por el vector . Entre dos curvas pushover obtenidas de dos direcciones laterales, escoger la curva de capacidad en la dirección dominante del modo. Como siempre, las cargas gravitatorias se aplican antes del análisis pushover. Se deberá tomar nota de los valores de los desplazamientos alcanzados al aplicar dichas cargas.
- Idealizar la curva de capacidad como una curva bi-lineal. Si la curva pushover posee una rigidez post-plastificación negativa bajo el efecto P-delta, así lo deberá reflejar la curva idealizada.
- Transformar la curva bilineal idealizada en una relación fuerza-desplazamiento para cada modo de los sistemas de un grado de libertad inelásticos (este es un procedimiento muy parecido al que se aplica en el método N2).
- Calcular la deformación máxima el enésimo modo para el sistema de un grado de libertad inelástico. Obtener el periodo de vibración.
- Calcular el desplazamiento máximo en la dirección de la curva pushover asociado con el enésimo modo inelástico.
- De las curvas pushover originales, extraer los valores de interés bajo los efectos combinados de gravedad y cargas laterales.
- Repetir los pasos del 3 al 7 para tanto modos como sean necesarios.
- Calcular la respuesta dinámica del modo enésimo
- Determinar la respuesta total (demanda) combinando respuesta de gravedad y las respuestas máximas modales usando la combinación cuadrática completa ( ).
Athanatopoulou y Doudoumis [22]. En este artículo se presenta un procedimiento para determinar las direcciones principales bajo cargas laterales de edificios de múltiples niveles que incluyen diafragmas rígidos. El procedimiento se fundamenta en un criterio racional y en una formulación analítica.
Las direcciones principales dependen de las cargas laterales aplicadas, asumiendo que tales cargas pasan por un eje vertical.
El artículo comienza enumerando las principales normas que hacen referencia a la dirección principal de ejes ortogonales, que permite aplicar determinados procedimientos. Sin embargo, indican que no existe una definición formal de esta orientación principal de ejes.
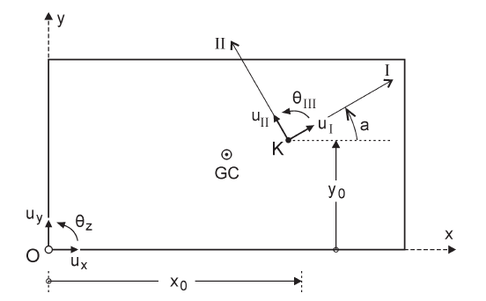
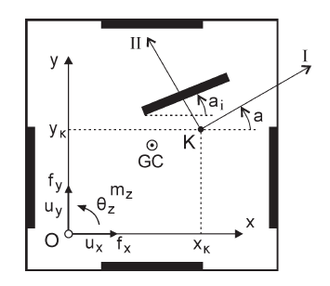
Los autores entonces pasan a definir un sistema conformado por un origen de coordenadas definido como centro elástico, en el que converge un par de ejes I y II, denominados direcciones principales, véase la Figura 1.13. La orientación de estos ejes es tal que, al aplicar en el centro elástico una fuerza paralela a la dirección I o II, solo se produce traslación a lo largo de esos ejes, sin ningún tipo de rotación. La relación entre la orientación de los ejes está determinada por la rigidez que posee la estructura a lo largo de los mismos. En el caso del eje I, este posee la mayor rigidez, llegando a desarrollar los menores desplazamientos, mientras que el eje II es el menos rígido, desarrollando los mayores desplazamientos.
Desarrollo para edificios de un solo nivel
En el caso de edificios de n solo nivel, el diafragma rígido presenta tres grados de libertad: dos traslaciones y una rotación:
|
|
(1.24) |
con una matriz de rigidez lateral:
|
|
(1.25) |
De la matriz de rigidez lateral es posible determinar la ubicación del centro elástico mediante las ecuaciones:
|
(1.26) |
Con el eje principal I determinado conforme a la orientación obtenida de:
|
|
(1.27) |
El otro eje (II) tiene una orientación definida conforme a un ángulo de 90° con respecto a la orientación del eje I.
De acuerdo con el nuevo sistema de centro elástico y ejes principales, queda definido el vector de desplazamientos referido a dicho sistema:
|
|
(1.28) |
con una matriz de rigidez lateral:
|
|
(1.29) |
con las rigideces laterales:
|
(1.30)
(1.31) |
Desarrollo para edificios de múltiples niveles
En el caso de edificios de múltiples niveles, las expresiones anteriores pueden adaptarse, considerando dos clases de edificios: los isótropos y los pertenecientes a un caso general.
Los edificios isótropos son una clase especial que contienen matrices de rigidez lateral proporcionales y que se conectan a nivel de piso mediante diafragmas rígidos. Las matrices de rigidez lateral de los elementos resistentes satisfacen la relación:
|
|
(1.32) |
En donde es el número de elementos y es la matriz de rigidez de orden , siendo el número de pisos y una constante de proporcionalidad.
En el caso del sistema arbitrario de coordenadas mostrado en la Figura 1.14, se puede definir la rigidez lateral de ese sistema como:
|
|
(1.33) |
con los desplazamientos definidos mediante el vector:
|
|
(1.34) |
donde los vectores , y contienen las dos componentes de traslaciones y rotaciones de los niveles del edificio, respectivamente.
Las coordenadas del origen del punto K y la orientación de sus ejes está dada por:
|
|
(1.35) |
|
|
(1.36) |
|
|
(1.37) |
Los ejes I y II definen los planos principales de flexión, mientras que la traza de la intersección de ambos planos termina definiendo el eje elástico del edificio isótropo.
Para el caso general de edificios, se asume que no existe ni un eje elástico, ni unas direcciones principales, rigurosamente definidas. Esto ha llevado a Makarios y Anastassiadis a proponer un eje óptimo de torsión, que queda definido como la línea vertical que conecta los puntos de los diafragmas en los que los cuadrados de las rotaciones de piso son minimizados, lo que se expresa como:
|
|
(1.38) |
Vistas las propuestas realizadas en trabajos que abordan el tema, los autores se decantan por definir las direcciones de los ejes principales como las direcciones que mantienen la siguiente propiedad: cuando el plano vertical de cargas estáticas laterales pasa a través del eje óptimo de torsión, a lo largo de las direcciones principales I o II, entonces la suma de los cuadrados de los desplazamientos resultantes de las trazas del eje óptimo de torsión en cada uno de los niveles, se transforma en máximo o mínimo, respectivamente. Esta propuesta está en concordancia con las definiciones efectuadas para el caso del edificio de un solo nivel.
Implementación de la propuesta
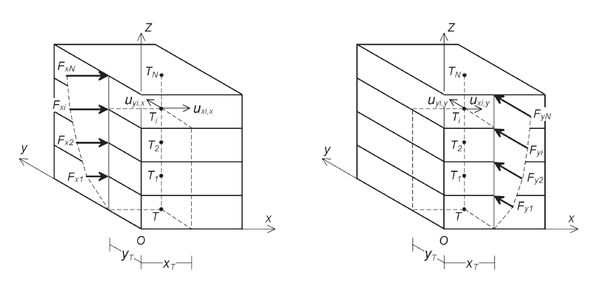
En la Figura 1.15 se puede observar la implementación de la metodología propuesta a un edificio de múltiples niveles. Nótese que el plano que contiene las fuerzas laterales pasa por el punto de ubicación de la traza del eje de torsión en cada uno de los planos de los niveles. Nótese la presencia de dos planos, uno por cada dirección ortogonal de la estructura.
Los desplazamientos, una vez que se aplican las fuerzas laterales en cada nivel quedan:
|
(1.39) |
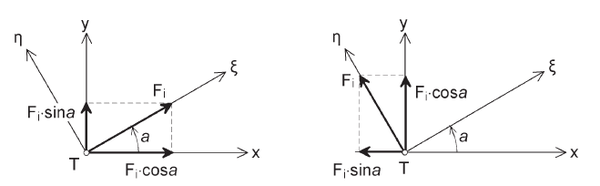
Se propone la siguiente composición del sistema de ejes (Figura 1.16):
La orientación de los ejes principales se consigue a través de:
|
|
(1.40) |
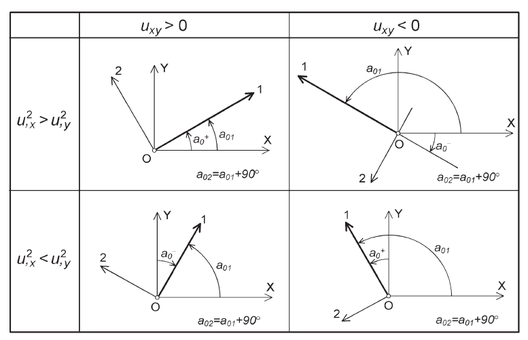
Este ángulo permite obtener la orientación de los ejes principales aplicando el criterio mostrado en la Figura 1.17.
Finalmente, el parámetro alcanza los valores máximos y mínimos a partir de:
|
|
(1.41) |
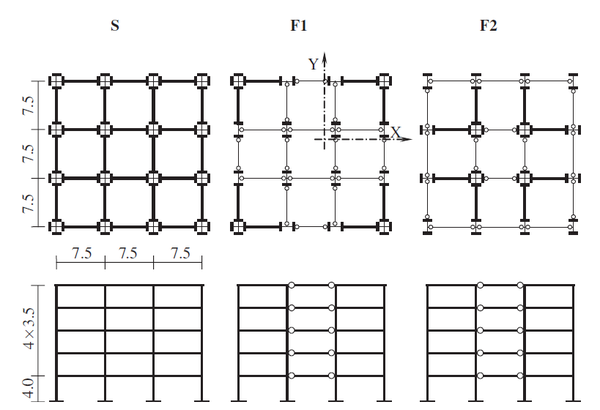
Marusic y Fajfar [23]. Los autores investigaron sobre la respuesta de edificios de acero torsionalmente desbalanceados. Encontraron que la respuesta de estos edificios, tanto en rango elástico como inelástico era cualitativamente semejante, con la excepción del borde rígido en la dirección fuerte de un edificio torsionalmente rígido y en el caso del borde rígido en el sentido débil de un edificio torsionalmente flexible. Adicionalmente determinaron que la respuesta es influenciada por la intensidad del terremoto utilizado, así como también por la magnitud de la deformación plástica. El decremento de la rigidez en una dirección, producto de deformaciones plásticas, puede influenciar el comportamiento en una dirección ortogonal. En general, los efectos torsionales se reducen con el incremento de las deformaciones plásticas, aunque las deformaciones plásticas sean pequeñas.
La investigación se condujo a través de un estudio paramétrico considerando varias configuraciones de edificios diseñados conforme a normas, con un número de 5 niveles. Se adoptó un factor de reducción de respuesta R=6 y una aceleración básica de diseño de 0,35g.
Los edificios mostrados en la Figura 1.18 presentan diferencias en cuanto a la rigidez torsional y de resistencia. Las tres estructuras muestran distintas uniones viga-columna, que se consideran tipo resistente a momento en los nodos de la estructura “S”, mientras que, en las otras dos estructuras, solo los nodos mostrados tienen conexiones resistentes a momento.
La modificación de las secciones transversales de los dos edificios con juntas no resistentes a momentos, permitió obtener valores de rigidez lateral prácticamente iguales para los tres edificios. Puede notarse que el segundo edificio, al tener sus juntas resistentes a momentos en nodos de la periferia, es torsionalmente más resistente que el tercero de los edificios, considerado como torsionalmente flexible.
Adicionalmente, fue introducida la asimetría en los edificios, mediante la modificación de las excentricidades de las masas. Esto generó en las plantas un lado rígido y otro flexible. En la Figura 1.19 puede notarse que el lado flexible se ubica más próximo al centro de masa de la planta, mientras que el lado rígido se encuentra más alejado de este último.
El análisis no lineal fue llevado a acabo usando seis acelerogramas de registros de terremotos fuertes (se tomaron las dos componentes de cada registro) Las componentes de los sismos fueron escaladas, de manera que pudieron reproducir el efecto sobre la dirección fuerte y la dirección débil. Los acelerogramas se aplicaron de forma simultánea en ambas direcciones de análisis.
Los desplazamientos laterales calculados en los edificios para comportamiento elástico e inelástico, mostraron ser cualitativamente similares, ya que presentaron una variación muy baja en cuanto a la deformada.
Los resultados muestran también que la diferencia entre los desplazamientos del lado rígido y del lado flexible, tiende a disminuir a medida que se va alcanzando comportamiento más inelástico. Por el contrario, para el caso elástico, pudo registrarse que los desplazamientos en el lado flexible eran mayores que en el lado rígido.
Con base en los resultados obtenidos, los autores proponen las siguientes recomendaciones de cara al desarrollo y mejora de los métodos simplificados de análisis:
El desplazamiento del centro de masa en un edificio de planta asimétrica es prácticamente el mismo desplazamiento que se obtiene para un edificio de planta simétrica.
La amplificación de los desplazamientos, determinada por el análisis elástico, puede ser utilizada en el rango inelástico.
Cualquier efecto favorable que a nivel de desplazamientos en el lado rígido se puedan presentar en edificios torsionalmente rígidos, puede desaparecer cuando se produce el comportamiento inelástico.
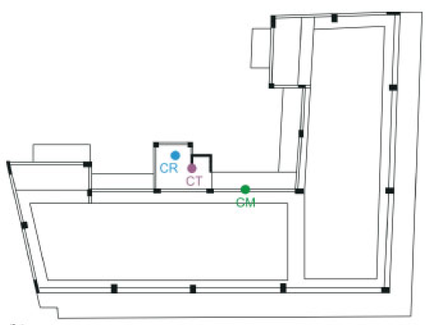
Kosmopoulos y Fardis [24]. Este estudio ha sido efectuado sobre cuatro edificios de hormigón armado, de tres a seis niveles, con fuertes irregularidades y un bajo nivel de ingeniería sismorresistente. Los autores tomaron como elemento de comparación la rotación de la cuerda de la deformada de los edificios sometidos a diferentes tipos de análisis. Como conclusiones presentan que el análisis elástico tiende a sobreestimar los efectos torsionales inelásticos. Por otro lado, el análisis modal espectral tiende a sobre estimare el efecto torsional inelástico en el lado rígido delos edificios torsionalmente rígidos, mientras que tiende a subestimarlos en el lado flexible. Finalmente presentan un análisis de acuerdo al período de las estructuras y como este tiende a afectar los valores de la rotación de la cuerda de la deformada elástica, calculada del análisis estático elástico.
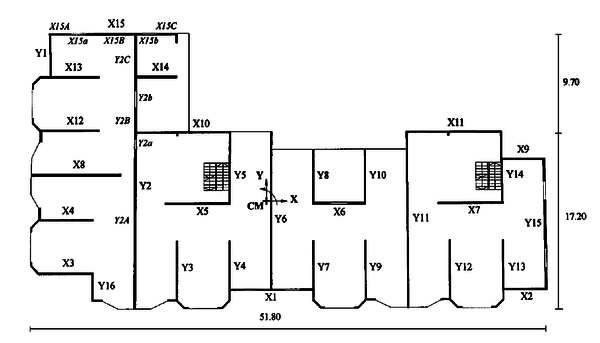
La rotación de las cuerdas de los elementos de los casos estudiados, han sido calculadas mediante el análisis no lineal de respuesta en el tiempo, aplicando 56 acelerogramas producto de registros, en ambas direcciones de análisis. Los valores medios y las desviaciones estándar fueron comparados con los valores obtenidos mediante el análisis elástico aplicando el método estático equivalente con una distribución de fuerzas triangular invertida y con la aplicación del análisis modal-espectral. Entre los casos estudiados, cabe resaltar el del edificio “Atenas”, que presenta una marcada irregularidad en planta, dada su forma de L (Figura 1.20).
Entre los casos estudiados, los autores presentan la desviación de las cuerdas de los miembros de cada nivel, con respecto a la rotación de la cuerda promedio de los miembros de ese mismo nivel, determinando de alguna manera, aquellos miembros en los que el efecto de la torsión afecta el comportamiento de dichos elementos.
Las normas de diseño y rehabilitación de edificios, permiten estimar las demandas de deformación en los extremos de los miembros estructurales a partir de los desplazamientos obtenidos del análisis elástico utilizando el espectro elástico de diseño con un 5% del amortiguamiento, siempre que se cumpla que la relación demanda-capacidad a momentos no supere un valor de 2,0.
|
|
(1.42) |
Los valores calculados para la , proporciona una estimación aproximada del valor de la ductilidad de rotación que se alcanza en los extremos de los miembros estructurales.
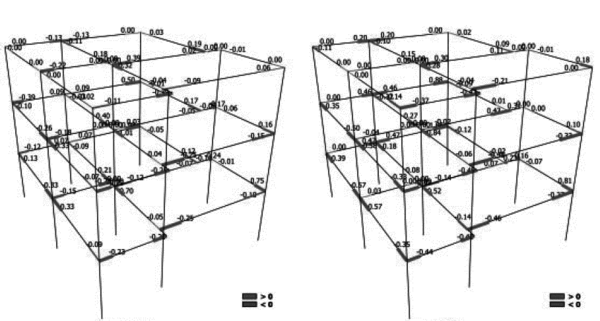
Nótese que en las Figuras 1.21 y 1.22, solo se muestran los valores calculados en los extremos de las vigas.
Como conclusión, los autores muestran que los valores de la ductilidad de rotación en miembros pertenecientes al mismo nivel, son muy uniformes, con excepción de aquellos edificios en los que la respuesta dinámica está influenciada claramente por los modos superiores de vibración.
Los edificios cuya respuesta se ubica en el rango de periodos del espectro dominado por la velocidad, presentan estimaciones adecuadas de las rotaciones inelásticas de las cuerdas.
De Stefano y Pintucchi [25]. Los autores comienzan realzando los méritos del método N2 extendido como una solución en la búsqueda de la extensión de los resultados del análisis no lineal con empuje incremental (pushover). Sin embargo, cuestionan la aplicabilidad de los resultados del análisis modal espectral (necesario para aplicar el método) dado que se debe cumplir con cierto conservadurismo en cuanto a la predicción de los desplazamientos inelásticos a partir del análisis elástico.
Los resultados del estudio muestran que el método N2 extendido es aplicable a estructuras con moderado o gran rigidez torsional, pero que no aportan resultados valederos para aquellas estructuras torsionalmente extremadamente rígidas.
La implementación de procedimientos complementarios al análisis pushover, persigue varios objetivos prácticos: la contribución de los modos superiores de vibración, los efectos de la degradación de la rigidez en la modificación de las propiedades dinámicas del edificio y la incorporación de los efectos torsionales de los edificios irregulares.
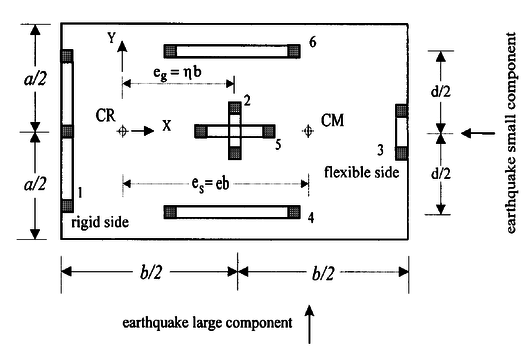
El estudio se basa en la respuesta de un edificio de un solo nivel, asimilable a un sistema de un grado de libertad, como se muestra en la Figura 1.23.
Los autores proponen un estudio paramétrico de la respuesta de ese edificio, con base en un estudio para métrico, en el cual es necesario definir previamente ciertos valores característicos.
Momento polar de inercia de la masa del sistema, referido al eje z que pasa por el centro de masa:
|
|
(1.43) |
El radio de giro del sistema, normalizado con respecto de la dimensión de la planta en dirección :
|
|
(1.44) |
La rigidez lateral total del sistema, asumida igual en ambas direcciones:
|
|
(1.45) |
El periodo lateral desacoplado del sistema estructural, asumido igual en ambas direcciones de análisis:
|
|
(1.46) |
La excentricidad estática, definida como la distancia que hay entre el centro de masa y el centro de rigidez de la planta, normalizada con respecto de la dimensión en la dirección :
|
|
(1.47) |
El momento polar de inercia de la rigidez del sistema, también conocida como la rigidez torsional, calculada respecto del eje z que pasa por el centro de rigidez de la estructura:
|
|
(1.48) |
El radio de giro de rigidez del sistema, normalizado con respecto a la dimensión de la planta en dirección :
|
|
(1.49) |
La resistencia total del sistema en cada una de las direcciones, tomada igual para cada dirección y calculada como:
|
|
(1.50) |
La excentricidad de resistencia, definida como la distancia que hay entre el centro de masa y el centro de resistencia de la planta, normalizada con respecto de la dimensión de la planta en la dirección paralela a :
|
|
(1.51) |
El momento polar de inercia de la resistencia del sistema con respecto del eje z que pasa por el centro de resistencia de la planta:
|
|
(1.52) |
El radio de giro de resistencia del sistema, normalizado con respecto de la dimensión de la planta paralela al eje :
|
|
(1.53) |
En el estudio paramétrico variaron: la rigidez torsional y la resistencia, el periodo estructural, el factor de reducción de respuesta y las excentricidades de rigidez y resistencia.
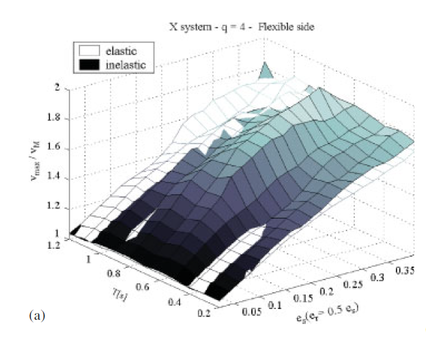
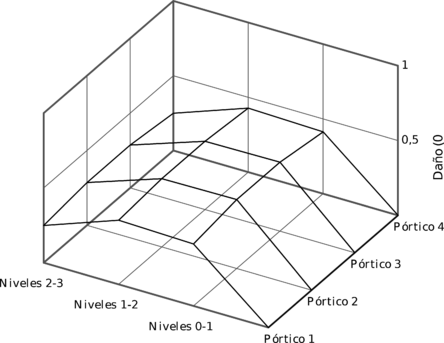
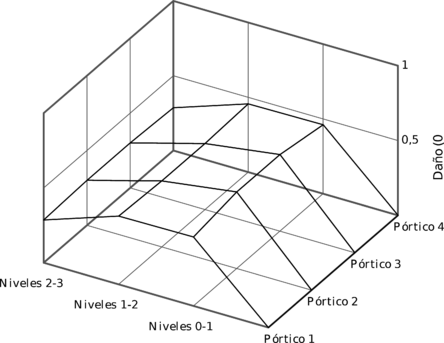
Los resultados los presentan utilizando la relación de desplazamientos entre el lado rígido o flexible de la estructura y el centro de masa. Los resultados del estudio paramétrico son presentados bajo la forma de gráfico en 3D, véase la Figura 1.24.
Los autores cotejan sus resultados para cuestionar la aplicación del método N2 extendido a una amplia gama de edificios. En resumen, desaconsejan su uso para edificios extremadamente rígidos torsionalmente hablando y con valores de ductilidad baja o media.
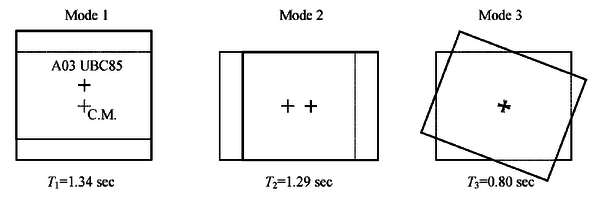
Reyes y Chopra [26]. En este artículo los autores presentan los resultados de un estudio en el cual evaluaron el análisis pushover modal en tres dimensiones, para evaluar las demandas sísmicas en edificios asimétricos en planta. El estudio ha sido realizado sobre ocho edificios con estructura metálica, diseñados conforme a la versión del año 1985 y 2006 del Uniform Building Code. Aplicaron para esto 39 acelerogramas con doble componente, escalados a dos niveles de intensidad, lo que permitió evaluar los resultados obtenidos del análisis no lineal de historia tiempo con los alcanzados a través del método de análisis pushover modal.
Los autores reconocen la importancia de incorporar de forma precisa los efectos de la torsión inducida por la asimetría estructural, a los resultados extendidos del análisis pushover convencional. Cuestionan la validez del procedimiento de análisis no lineal prescrito en el ASCE-SEI 41-06.
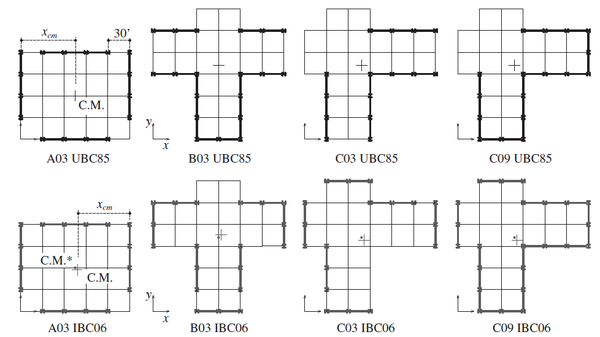
En la Figura 1.25 se pueden apreciar los modelos estudiados con sus particulares configuraciones en planta, lo que genera excentricidades. Los edificios han sido modelados con tres y nueve niveles de altura. Solo los modelos de doble asimetría se han modelado con dos alturas, mientras que el resto solo con tres niveles. Debe notarse que los casos diseñados conforme a la nueva versión del IBC disponen de una rigidez torsional mayor, proporcionada por la disposición de las columnas y su unión mediante vigas a nivel de piso.
Los periodos de vibración de los tres primeros modos del primer edificio estudiado, evidencian el desacoplamiento que hay con los modos traslacionales y rotacionales. Además, se puede notar que los periodos de los modos traslacionales son mayores que el del modo rotacional, lo que representa una característica común de edificios con pórticos en el perímetro, Figura 1.26.
Dos observaciones pueden realizarse sobre los resultados del análisis elástico: la versión nueva del IBC reduce significativamente los desplazamientos originados por la torsión, mientras que de alguna manera permite un acople más fuerte entre los modos de vibración traslacionales y rotacionales.
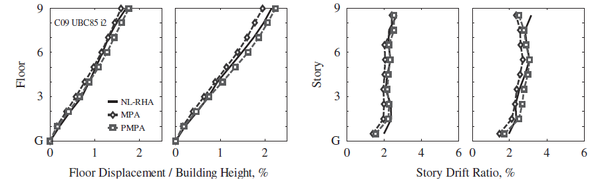
Los resultados muestran un excelente ajuste de las derivas y los desplazamientos de piso, si se compara con los resultados obtenidos del análisis no lineal de historia de respuesta.
Los resultados se han comparado en las columnas correspondientes a los lados rígidos y flexibles de la estructura, definiendo una serie de puntos de interés especial. Estos resultados se han graficado y se muestran en la Figura 1.27.
La comparación de los resultados efectuada con respecto al procedimiento contemplado en el ASCE-SEI 41-06, se ha llevado a cabo aplicando lo establecido en este último, pero introduciendo las variantes siguientes:
El desplazamiento objetivo es igual al establecido en el análisis pushover modal, a fin de poder realizar una comparación significativa.
Para determinar las demandas sísmicas bajo sismos en dirección x o y, se define el período fundamental como aquel que corresponde al modo con mayor masa efectiva.
Solo se aplica la componente x o y de las fuerzas laterales para estimar las demandas sísmicas en cada dirección. Esto significa, que no se consideran las componentes de desplazamiento generadas por acciones sísmicas ortogonales.
Luego los desplazamientos totales se determinan aplicando la regla de la raíz cuadrada de la suma de los cuadrados, para el conjunto de los desplazamientos en cada una de las direcciones.
Entre las conclusiones obtenidas para el análisis de estos edificios irregulares en planta, se tiene que el procedimiento de análisis pushover modal subestima las derivas de entrepiso de los pórticos ubicados en el lado flexible del edificio, mientras que en el lado rígido la estimación es bastante acertada. Se recomienda el procedimiento para la evaluación de edificios nuevos o existentes, bajo la consideración de que este método es conservador.
Finalmente, en cuanto a la evaluación del procedimiento contenido en el ASCE-SEI 41-06, los autores concluyen en que la distribución de fuerzas prescrita en esta norma, subestima gravemente las derivas de entrepiso para edificios con irregularidades en planta, pero sigue siendo adecuado para edificios regulares.
1.3 Trabajos sobre el tema realizados en Venezuela
Vielma [27], realizó la caracterización del comportamiento sísmico de edificios de hormigón armado mediante la respuesta no lineal, para ello empleó edificios porticados en zonas de alta sismicidad y proyectados conforme al [28] y [29]. Para lograr la caracterización de la respuesta sísmica, se incluyen en este estudio: la aplicación de un procedimiento de pre-dimensionamiento sísmico de secciones de los elementos de los edificios proyectados, la propuesta de un procedimiento de análisis estático no lineal con control de fuerzas, la determinación del modo de colapso, el estudio de la influencia de la reserva de resistencia y la redundancia en los factores de reducción de respuesta, el cálculo de la ductilidad máxima de los pórticos, la formulación de un índice de daño sísmico objetivo y la determinación de umbrales objetivos de daño correspondientes a unos Estados Límite específicos.
Luego de analizar los resultados obtenidos se llegan a las siguientes conclusiones: los valores de los factores de reducción de respuesta no son constantes y pueden variar entre los pórticos que conforman un edificio; en los edificios de ductilidad limitada la respuesta será satisfactoria cuando la demanda sísmica mantenga a la estructura en el rango elástico y para demandas sísmicas mayores solo los edificios porticados disponen de suficiente ductilidad y reserva de resistencia.
Vielma y Cando [10], determinaron la vulnerabilidad sísmica de estructuras de acero residenciales proyectadas conforme a las normas vigentes en el Ecuador y las AISC seismic provisions for structural steel buildings, para lograr dicho objetivo, la metodología empleada fue FEMA P695 en la definición de los arquetipos para estudiar el comportamiento sismo-resistente de las estructuras metálicas del Ecuador, se emplean análisis numéricos en rango no lineal, tanto pseudo- estático como dinámico; estos últimos análisis son los que permiten, mediante procedimientos tanto deterministas como probabilistas, calcular los valores del ratio de margen de colapso. Se obtiene al analizar los resultados que el edificio diseñado conforme al enfoque por fuerzas llega a desarrollar una respuesta que resulta insatisfactoria desde el punto de vista sismo-resistente, debido a que en la dirección débil de las columnas su respuesta es frágil, es importante resaltar que las conexiones, en especial las juntas viga-columna, presentan el uso intensivo y en algunos casos indiscriminado de la soldadura, sin tener en consideración las recomendaciones especializadas para obtener uniones rígidas. Se estima conveniente incluir en las futuras versiones de la NEC una relación columna fuerte-viga débil mucho más rigurosa, que permita que las columnas sean privilegiadas sobre las vigas, cosa que no ocurre en la actualidad.
Vielma et al. [30], realizaron la evaluación sísmica de un edificio de hormigón armado de acuerdo con los códigos Venezolanos, la estructura constaba de dos pisos y representa una tipología común de uso residencial, para el diseño se considera una zona de alta amenaza sísmica y es detallada para un alto valor de ductilidad (factor de reducción de respuesta de R=6); el modelado se realiza según su diseño original (OB), un segundo modelo ajustado a los requerimientos sísmicos (RB) teniendo en cuenta la condición "fuerte viga-columna débil" y un tercer modelo con mira al diseño basado en el desplazamiento de Priestley et al. [31] (DBDB).
Vale destacar que estos tres modelos sólo difieren en las dimensiones de sus elementos estructurales. Se emplea análisis estático no lineal (Pushover), generando la curva de capacidad y los resultados obtenidos muestran el exceso del límite establecido para las derivas en el edificio OB, mientras que en el RB se obtuvieron el cumplimiento del rango establecido de derivas, en el edificio DBDB no se examinaron derivas ya que fue diseñado basado en el método señalado en [31], donde las fuerzas sísmicas generadas se limitan para no superar el valor límite de deriva especificada en el código venezolano. Vale acotar que el edificio original (OB) registra valores de ductilidad más baja que el edifico ajustado a los requerimientos sísmicos (RB) y el edificio a base de desplazamiento (DBDB).
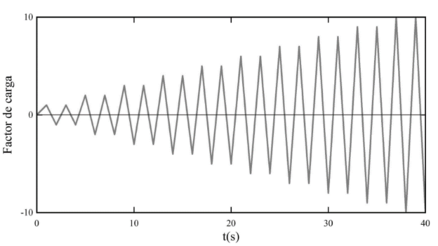
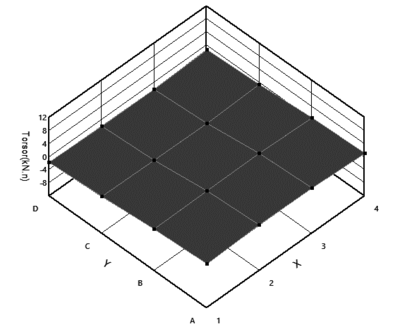
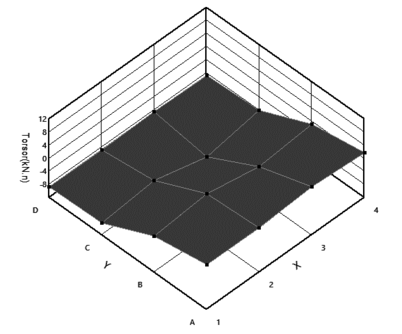
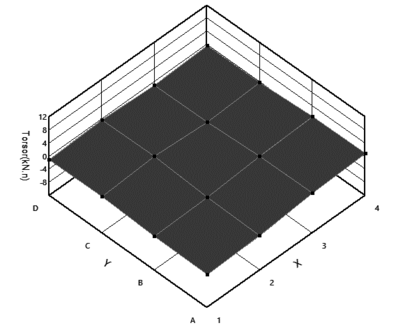
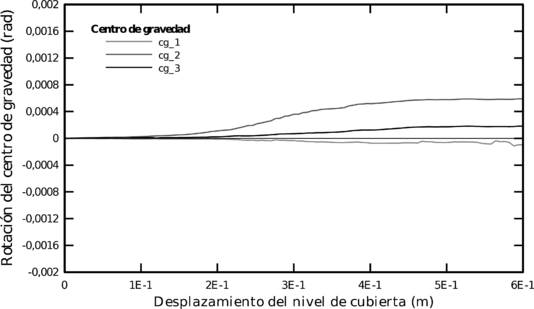
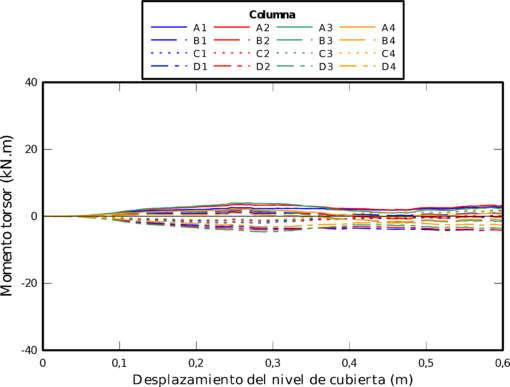
También se determinaron los momentos máximos de torsión en cada columna antes de la aplicación del terremoto, para las cuatro combinaciones generadas se grafica la torsión en función del tiempo, donde se designan los nodos correspondientes a los soportes, mientras que también en otro grafico se muestra el rango máximo de momento de torsión para cada columna del análisis tridimensional; se hace evidente que los momentos de torsión máxima se producen en las columnas extremas y en las columnas situadas en la intersección de la estructura, esto es una característica relevante que confirma el efecto negativo de la irregularidad en planta con la acción sísmica.
Alfaro y Márquez [32] analizaron una estructura de hormigón armado, construida por el Banco Obrero en el año 1968, la cual fue sometida a un análisis elástico a través del programa de cálculo Robot Structural, obteniéndose los desplazamientos elásticos de los diferentes niveles; posteriormente haciendo uso de un factor de reducción de respuesta R = 4,5 y 6, y de los factores de amplificación de 0,80 y 1,5 se determinaron los desplazamientos inelásticos y en consecuencia las derivas de entrepiso, los valores obtenidos para las derivas de entrepiso muestran que la edificación presenta falla por desplazamiento, debido a que sobrepasan el valor indicado por la norma venezolana. Por tal motivo, y con la finalidad de optimizar el comportamiento sismorresistente de la estructura se planteó el redimensionado de las secciones de vigas y columnas.
Seguidamente, haciendo uso del programa Zeus NL v1.9 se llevó a cabo el análisis estático no lineal (Pushover) en dos dimensiones, tanto para los pórticos de carga, como de amarre; de donde se obtuvieron las curvas de capacidad y a partir de ellas los valores de ductilidad y reserva de resistencia. Los pórticos del Edificio original presentan baja ductilidad, a diferencia del edificio redimensionado con R=4,5 y 6, lo que implica que el edificio original es menos dúctil y por consiguiente con menor capacidad de disipar energía que el edificio redimensionado.
A través del análisis dinámico se encontró que los máximos torsores se produjeron en las esquinas de los entrantes de la planta, mientras que las rotaciones en el edificio original con diafragma flexible ocurrieron en las columnas perimetrales duplicándose su valor con respecto a las columnas centrales de la edificación, para las diferentes direcciones de análisis consideradas. Finalmente para el edificio con diafragma rígido se observó que las rotaciones fueron menores en comparación a los resultados obtenidos del edificio original con diafragma flexible.
Barrios [33] estudió la respuesta sísmica del edificio Villa Azul, ubicado en Tucacas, Estado Falcón, para ello se emplearon programas basados en el método de elementos finitos; Robot Structural (análisis lineal) y Zeus NL (análisis no lineal). Como resultado del análisis elástico se determinó, que los valores de deriva de entrepiso alcanzados en el Módulo Lateral Original sobrepasaban al valor límite establecido en la norma para edificaciones sismorresistente, resultando así elementos estructurales con secciones insuficientes para controlar adecuadamente los daños producidos por las fuerzas sísmicas; mientras que para el Módulo Central las derivas de entrepiso obtenidas cumplían con el límite especificado en la norma para ambos factores; debido a esto surgió la necesidad de plantear para el Módulo Lateral un segundo modelo denominado Módulo Lateral Redimensionado, con el fin de comparar con el modelo original y cuyas secciones de vigas y columnas han sido modificadas permitiendo obtener nuevamente las derivas de entrepiso y dar cumplimiento con los valores límites establecidos en la normativa.
Seguidamente se planteó el análisis no lineal de los diferentes módulos aplicando el análisis con empuje incremental convencional, mediante este procedimiento se obtuvieron las curvas de capacidad de cada uno de los pórticos de los módulos definidos, con las curvas de capacidad se determinaron los valores de ductilidad estructural y reserva de resistencia para cada uno de los pórticos, donde se observaron que tanto los pórticos de carga como los pórticos de amarre tienen valores de reserva de resistencia y ductilidad satisfactoria.
CAPÍTULO 2. METODOLOGÍAS DE EVALUACIÓN DEL COMPORTAMIENTO SÍSMICO
2.1. Introducción
En este capítulo se mencionan algunos estudios de investigación que están relacionados con el presente trabajo, además de un breve desarrollo de la Metodología FEMA P695, la cual se utilizará para determinar los factores de prestaciones sísmicas de edificios irregulares en planta, basándose en convertir el complicado comportamiento no lineal de la estructura de un edificio bajo cargas sísmicas en un problema lineal equivalente; así como la descripción de los tipos de análisis a emplear, como lo son el análisis inelástico con empuje incremental y el inelástico dinámico, definición de espectros, estados límites y diafragma. Vale acotar, que se presenta la deducción de fórmulas para determinar la cuerda de la deformada de los elementos y un procedimiento computacional del método N2 extendido, con el cual se estima que la distribución de la demanda a través de la estructura puede lograrse combinando los resultados del análisis con empuje incremental con los resultados normalizados del análisis modal elástico y glosario de términos.
2.2. Tipos de análisis
Seguidamente se muestran algunos de los tipos de análisis empleados en la evaluación sísmica de los edificios en general y de los edificios con irregularidades en particular. Se exponen de manera resumida y general los pasos de los procedimientos.
2.2.1. Análisis inelástico con empuje incremental
Este tipo de análisis se fundamenta en la aplicación pseudo-estática (independiente del tiempo) y monótona de las fuerzas laterales equivalentes a los sismos o de los desplazamientos inducidos por estos. Dependiendo de cómo se aplique el procedimiento, se dice que el análisis es con control de fuerzas o con control de desplazamientos. Para ello es necesario definir un patrón de fuerzas o desplazamientos que simulen la distribución de las fuerzas sísmicas equivalentes. Una de las soluciones mayormente aceptadas consiste en asumir que el patrón de fuerzas o desplazamientos obedece a una distribución creciente con la altura, lo que equivale a una distribución triangular. Esta distribución es aproximadamente la misma que se obtiene para el primer modo de vibración, véase la Figura 2.1
Todas las fuerzas o desplazamientos laterales se inicializan en cero. Se van incrementando de manera secuencial, pasando por una serie de incrementos en los que el comportamiento es elástico, hasta que, llegados a un incremento, se produce la primera plastificación, en la que se pierde tanto la rigidez como la resistencia lateral original. De esta forma, se continuarán plastificando las demás secciones de los elementos de la estructura, hasta que llegado cierto incremento la resistencia lateral global ya no se incrementa más, alcanzándose un comportamiento plástico global, cuyo desarrollo dependerá si la estructura es dúctil o frágil. De esta forma se observarán desplazamientos más o menos grandes sin un incremento sustancial de las acciones laterales. En este punto vale la pena indicar que los métodos de resolución con control de desplazamiento son más efectivos, puesto que alcanzado el punto de plasticidad global se llega a un punto de singularidad a partir del cual el procedimiento con base en fuerzas puede dejar de converger, puesto que para un mismo incremento de fuerzas puede alcanzarse más de un desplazamiento que satisfaga las ecuaciones globales de equilibrio [34].
2.2.2. Análisis inelástico dinámico
El análisis inelástico dinámico es el más completo y que puede proporcionar información sobre las características de la respuesta de una estructura frente a acciones sísmicas, sin embargo, este tipo de análisis es el más costoso computacionalmente hablando. Para realizarlo se requiere del modelizado de la estructura, que puede efectuarse mediante métodos de plasticidad concentrada o distribuida. A la hora de definir la acción dinámica se puede utilizar una función del tiempo o un acelerograma, pudiendo ser éste último un registro de un terremoto o un acelerograma sintético.
El análisis dinámico que se realiza con una función del tiempo como la que se muestra en la Figura 2.2, permite estudiar la forma general de la respuesta histerética indicando la forma cómo la estructura disipa energía. Para llevarlo a cabo se debe definir una función polinómica, de signos alternantes que representa el desplazamiento aplicado en alguno de los nodos de la estructura, que ha sido previamente cargada con las acciones de gravedad transformadas en cargas puntuales nodales.
En la Figura 2.3 se muestran los resultados del análisis, observándose la estabilidad de los ciclos de histéresis, que evidencia que la estructura tiene una capacidad de disipar energía de forma dúctil. Además, en esta Figura se aprecia que el análisis dinámico permite obtener el valor del desplazamiento máximo para el cual ocurre el colapso de la estructura. Este desplazamiento suele obtenerse en el punto en el que la estructura alcanza el máximo cortante en la base. A partir de este desplazamiento el cortante en la base de los ciclos siguientes se reduce.
2.2.3. Rotación de la cuerda de la deformada
Panagiotakos y Fardis presentan una expresión menos general que en publicaciones pasadas, deducida para columnas y vigas usuales:
|
|
(2.1) |
donde: : cociente de vano a corte al final del miembro.
cociente de refuerzos mecánico , de la armadura longitudinal a tracción y compresión, respectivamente.
: cociente de fuerza axial normalizado respecto del ancho b de la zona a compresión, la profundidad de la sección y
: cociente del acero transversal paralelo a la dirección x de la carga. = espaciamiento de estribos, = esfuerzo de plastificación de estribos.
: factor de efectividad del confinamiento.
|
|
(2.2) |
donde:
: dimensiones de los núcleos confinados de hormigón.
distancias de las barras restringidas a lo largo del perímetro.
: coeficiente para el acero de las barras longitudinales, igual a 0,016 para acero dúctil y para acero con tratamiento térmico o 0,0105 para acero frágil.
|
|
(2.3) |
Para estribos rectangulares con ramas paralelas al lado del núcleo con longitud bo y nh ramas paralelas al lado con longitud . [35]
2.2.4. Método N2 extendido
Cuando se intenta extender la aplicabilidad del método pushover, es preciso recordar que el análisis no-lineal con empuje incremental se introdujo como un análisis simple para verificar la debilidad de nuevos proyectos y la capacidad de proyectos existentes [36]. Pensar en refinar este método hasta el punto que no se pueda justificar las asunciones o hasta hacerlo más complicado que el método de análisis de historia-tiempo, no está justificado.
La idea básica que se tiene al aplicar el método N2 extendido, es mantenerlo lo más simple posible. El problema de los modos superiores de vibración se resuelve mediante factores de corrección, basados en el análisis modal elástico.
Los resultados dependen de la intensidad del terremoto, ya que se ha demostrado que los efectos de los modos superiores calculados a partir del análisis de historia de respuesta no lineal dependen considerablemente de las deformaciones plásticas, que a su vez dependen de la intensidad del terremoto.
En el método N2 se estima que la distribución de la demanda a través de la estructura puede lograrse combinando los resultados del análisis con empuje incremental con los resultados normalizados del análisis modal elástico.
Los efectos de los modos superiores en la altura cuando se calculan desplazamientos son despreciables, pero deben ser tomados en cuenta a la hora de calcular las derivas.
Existen dos problemas en los que el método es especialmente aplicable: a los edificios con irregularidad en planta y a los edificios altos. En el método N2 se asume que los modos superiores influyen en el rango inelástico al igual que en el rango elástico.
Procedimiento computacional
Realizar el análisis N2 básico. Si hubiese asimetría en planta, usar 2 modelos bi-dimensionales, uno para cada dirección. Preferiblemente usar un modelo 3D. Se aplican cargas en cada dirección de manera independiente en los centros de masas. Se hace en un sentido (+) y otro (-). El desplazamiento objetivo (demanda de desplazamiento en el CM (centro de masa) del nivel de cubierta) se determina para cada una de las direcciones (como el mayor de los valores obtenidos para cada sentido). Se asume que el efecto de los modos superiores sobre el desplazamiento objetivo es despreciable.
Realizar el análisis modal elástico estándar del modelo 3D independientemente en las dos direcciones horizontales, considerando todos los modos relevantes (usar regla CQC), combinar luego los resultados en ambas direcciones usando la regla SRSS. Determinar los desplazamientos y las derivas de entrepiso en el CM de cada nivel. Normalizar los resultados en cada dirección de forma tal que el desplazamiento en el CM sea igual al desplazamiento objetivo.
Determinar la demanda sísmica mediante los resultados de los pasos 1 y 2. Esto puede ser logrado aplicando dos grupos de factores de corrección, uno para desplazamientos (en planta) y el otro para derivas de entrepiso (a lo largo del alzado). El grupo determinado para los desplazamientos en planta, también aplica para las derivas de entrepiso. Por tanto, el factor correspondiente para la deriva de entrepiso en un nivel determinado y para una posición en planta determinada, es el producto de dos factores. Los factores de corrección se definen para cada dirección de forma separada. Se les aplicará a los resultados relevantes del análisis pushover.
El factor de corrección para desplazamientos por torsión se define como el cociente entre los desplazamientos normalizados del nivel de techo obtenidos del análisis modal elástico (paso 2.2.4.2) y el análisis pushover (paso 2.2.4.1). El desplazamiento normalizado de la cubierta es el desplazamiento de techo en un punto arbitrario, dividido por el desplazamiento del CM del techo. Si el desplazamiento normalizado del nivel de techo obtenido mediante análisis modal elástico es menor que 1.0, entonces un valor de 1.0 será el utilizado. No se considerarán desamplificaciones por torsión. Estos factores de corrección dependerán de la posición en el plano de planta.
El factor de corrección de derivas de entrepiso bajo efecto de los modos superiores en elevación se define como el cociente entre las derivas de entrepiso normalizadas obtenidas del análisis modal elástico (paso 2.2.4.2) y los resultados obtenidos del análisis pushover (paso 2.2.4.1). Igual que en el caso de torsión, no se aplica desamplificación. Si por ejemplo el cociente es menor que 1.0 se usa el valor de 1.0. Se determina un factor de corrección para casa piso en cada dirección.
Los factores de corrección de derivas de piso resultantes (obtenidos como el producto de los dos factores de corrección descritos anteriormente) se aplican a todas las cantidades de deformación (por ejemplo, las rotaciones totales de las juntas, consistente en una parte elástica y otra plástica). También se aplican a las fuerzas internas, haciendo que las fuerzas internas resultantes no excedan la capacidad portante de un elemento estructural. [36].
2.2.5. Método de análisis dinámico espacial con diafragma flexible según la norma COVENIN 1756-2001
Número de Modos
El número de modos de vibración a utilizar en el análisis es aquel que garantice que la suma de las masas participativas de los modos en cada una de las direcciones horizontales del sismo, excede el noventa por ciento (90%) de la masa total del edificio.
Combinación Modal
La combinación de los máximos valores de respuesta en cada modo, se hará según el criterio de la combinación cuadrática completa tal como se indica en a subsección 9.6.2.1, para cada dirección del sismo.
Torsión Adicional
Los efectos de excentricidades accidentales y de la componente rotacional del terreno se incluyen en el diseño considerando los siguientes cuatro casos adicionales de análisis dinámico. En cada caso, se modificará la distribución de masa de cada piso, de manera gradual, tal que el centro de masa se desplace a una distancia en dirección X y una distancia en dirección Y, dada por:
1)
2)
3)
donde:
|
(2.4) |
=la mayor dimensión horizontal en cada nivel en dirección X.
=la mayor dimensión horizontal en cada nivel en dirección Y.
En cada uno de estos casos, los centros de masa para todos los pisos se desplazarán la misma magnitud, dirección y sentido [5].
2.2.6. Metodología FEMA P695
La metodología se encuentra basada en el procedimiento publicado por la FEMA Quantification of building seismic performance factors, (2009) bajo la denominación FEMA P695. Aquí hay que hacer notar que esta metodología ha sido originalmente formulada con la finalidad de evaluar nuevos sistemas estructurales y proponer sus factores para el diseño. Sin embargo, el carácter general de la metodología, su especial y detallado tratamiento en la determinación de los factores y, sobre todo, su carácter puntero en cuanto al estado del arte lo convierten en una herramienta práctica y directa para la evaluación de los factores de prestaciones de sistemas estructurales existentes.
Metodología general de evaluación
La metodología de evaluación de los modelos seleccionados es la que aparece descrita en el documento Quantification of building seismic performance factors, que ha sido publicada por el FEMA (2009) bajo la denominación FEMA P695.
El procedimiento lineal de diseño contenido en las normas se basa en convertir el complicado comportamiento no lineal de la estructura de un edificio bajo cargas sísmicas en un problema lineal equivalente.
Las normas prescriben una serie de requerimientos para estructuras basados en el sistema estructural. Estos requerimientos regulan la configuración, el tamaño. Los materiales de construcción, el detallado y la resistencia y rigidez de la estructura.
Los requerimientos son controlados mediante la asignación de una serie de coeficientes de respuesta del sistema que son el factor de reducción de respuesta, el factor de amplificación de desplazamientos y el factor de reserva de resistencia respectivamente y que representan las propiedades del material y el detallado del sistema.
La metodología que se describe a continuación se sustenta en la revisión de investigaciones relevantes en el área de la respuesta no lineal y la simulación de colapso. Se basa en los siguientes principios:
• Es aplicable a nuevos sistemas estructurales.
•Es compatible con normas de diseño, por ejemplo, provisiones NEHRP y ASCE/SEI 7.
•Es compatible con el objetivo de prestación de seguridad de vida que se expresa de forma tácita en las normativas de diseño sismo-resistente.
• La amenaza se basa en el máximo terremoto esperado.
• Los conceptos son consistentes con las definiciones de factores de prestaciones sísmicas de las normas actuales.
• La seguridad se expresa en términos del cociente de margen de colapso.
• Las prestaciones se cuantifican a través de la simulación del colapso.
• La incertidumbre se considera directamente en la evaluación del colapso.
Los factores de prestaciones sísmicas se aplican en las normas de diseño con la finalidad de estimar las demandas de resistencia y de deformación de sistemas resistentes a sismos que, si bien son diseñados mediante métodos lineales, finalmente responden en rango no lineal.
Los factores de reducción se utilizan en el diseño en la mayoría de las normas a nivel mundial y sus valores se han venido convirtiendo en críticos en la determinación de las fuerzas sísmicas. Los factores se han determinado sobre la base del juicio ingenieril sobre comparaciones cualitativas con la respuesta de sistemas estructurales utilizados a lo largo del tiempo. Algunos sistemas modernos al no haber sido sometidos a terremotos fuertes, no han sido probados o se desconoce su capacidad de alcanzar los objetivos del diseño. En la medida que nuevos sistemas estructurales están siendo introducidos en cada revisión de las normas, se incrementa la incertidumbre sobre la capacidad de las prestaciones del conjunto de edificaciones, haciéndose cada vez más urgente la cuantificación de las prestaciones proporcionadas por las regulaciones símicas actuales.
Los avances en el diseño sísmico con base en prestaciones y el desarrollo de tecnologías ha dado como resultado la posibilidad de aplicar técnicas de simulación no lineal de colapso para relacionar los factores de prestaciones sísmicas con las capacidades de prestaciones sísmicas sobre una base probabilista. El propósito de la metodología es proporcionar una base racional para determinar las prestaciones del sistema que, siendo apropiadamente aplicados en el proceso de diseño sísmico, da como resultado una seguridad equivalente frente al colapso en un terremoto, comparable con la seguridad inherente formulada en las normas sísmicas actuales, para edificaciones con diferentes sistemas sismo-resistentes.
La metodología es recomendada para ser aplicada con normas de diseño y documenta los recursos para establecer criterios mínimos aceptables de diseño para sistemas sismo-resistentes conformes con la aplicación de las normas.
También proporcionan la base para evaluar aquellos sistemas conformes con las normas en su capacidad de alcanzar los objetivos de las prestaciones. Posiblemente trabajos futuros permitan que la metodología sea utilizada para modificar o eliminar aquellos sistemas estructurales o requerimientos que no cumplen de manera confiable con esos objetivos. Véase Figura 2.4.
La metodología requiere que los edificios a ser analizados satisfagan los requisitos de diseño del ASCE/SEI 7-05 [38] , incluyendo los límites en la regularidad estructural, derivas, alturas, entre otros. En la Figura 2.4 se muestra un resumen de las interrelaciones de las diferentes etapas del proceso contempladas en la Metodología.
Consistencia con el objetivo de aseguramiento de vida
La metodología muestra consistencia con el objetivo básico de aseguramiento de vida. No se contemplan estados de prestaciones inferiores a este, como suele ser por ejemplo el estado de ocupación inmediata.
Consistencia con una baja probabilidad de colapso
La metodología alcanza el objetivo primario de aseguramiento de la vida exigiendo una baja probabilidad de colapso de las estructuras analizadas, cuando son sometidas a la acción del sismo máximo considerado (SMC).
Generalmente el riesgo de aseguramiento de vida (probabilidad de muerte o que se produzcan heridos) es difícil de calcular de forma precisa., bajo la incertidumbre que existe en cuanto a la variación de muertes para un modo de colapso específico, más aun con la incertidumbre que se genera de las bajas que se producen bajo fallas locales que suelen ocurrir sin que se produzca el colapso de la estructura.
Consistencia con los factores de prestaciones sísmicas
Es necesario introducir los factores de diseño definidos en el ASCE/SEI 7-05, como son:
: Factor de reducción de respuesta
: Factor de amplificación de desplazamientos
: Factor de reserva de resistencia
En la Figura 2.5 se pueden apreciar las relaciones que permiten definir los tres factores de diseño, que servirán para la evaluación de las prestaciones sísmicas de la estructura. Es necesario aclarar que en la figura aparecen factores que son adimensionales (relacionan fuerzas, desplazamientos o aceleraciones, aquí se expresan como si se tratase de una cantidad relativa (resta) con unas dimensiones que en realidad no posee.
De la Figura 2.5 se comienza definiendo el factor de reducción de respuesta:
|
|
(2.5) |
donde es el valor de la fuerza que debería desarrollar el sistema si este se mantuviese elástico y es el valor del cortante prescrito para el diseño. La reserva de resistencia se define mediante:
|
|
(2.6) |
siendo el valor máximo del cortante en la base alcanzado durante el análisis con empuje incremental o máxima resistencia lateral de la estructura. Finalmente, se define el factor de amplificación de desplazamientos como:
|
|
(2.7) |
En esta última expresión, es el desplazamiento definido de cubierta del sistema cuando se ha producido una plastificación global, correspondiente al sismo de diseño y es el desplazamiento correspondiente al terremoto de diseño si la estructura mantuviese un comportamiento elástico.
Descripción de la metodología
El enfoque técnico incluye una combinación de conceptos básicos normativos, análisis avanzados en rango no lineal y técnicas de evaluación con base en riesgo.
Pasos de la metodología
La metodología general se encuentra resumida en el flujograma de la Figura 2.6.
En la Figura 2.6 se muestra el procedimiento general a aplicar, nótese que en las cuatro ramas se recoge información muy valiosa que luego será utilizada para alimentar los inputs de la metodología, aplicándolos de manera sistemática [10].
2.2.7. Curvas de capacidad
Al someter una estructura a una fuerza cuya aplicación es controlada y gradualmente creciente, se produce sobre esta una deflexión de tal modo que, a partir de cierto nivel de fuerza, se comienzan a producir fallas locales producto de plastificaciones. Las curvas de capacidad grafican dicha deformación lateral medida en el último nivel versus el corte basal acumulado de la estructura. Ver Figura 2.7.
La forma de la curva está definida por la naturaleza de la fuerza incremental, además de la capacidad resistente de los componentes individuales. Afecta también la configuración estructural, ya que de ella depende la adecuada distribución de esfuerzos y la posibilidad de la estructura para redistribuirlos y de esta manera agotar la capacidad de todos los elementos resistentes de ser posible [39].
2.2.8. Ductilidad
Es la capacidad que tienen las estructuras, sus componentes o los materiales que la constituyen, de deformarse más allá del límite elástico sin pérdida de resistencia y de acumular energía durante los ciclos de carga (histeresis).
En la generalidad de las estructuras de edificios compuestos por estructuras aporticadas, con la inclusión o no de muros de corte, cuya caracteristica común es la hiperestaticidad y la redundancia, la economía en el diseño se logra al permitir que algunos elementos incursionen en el rango inelastico, es decir, que sean capaces de disipar la energia del sismo por medio de la friccion interna y la deformación plástica. De esa manera será posible diseñar para fuerzas horizontales sustancialmente menores a las correspondientes a una respuesta elástica.
Cuando mayor sea la ductilidad que desarrolle la estructura, mayor sera la energía disipada y mayor podrá ser la reducción de las fuerzas de diseño. Debe verificarse que los elementos de la estructura columnas, muros y vigas desarrollen ductilidades tales, que permitan a la estructura como un todo, tener un comportamiento ductil compatible con el factor de reducción de ductilidad R, asumido en la determinación de las fuerzas laterales de diseño.
La incursión de los elementos de una determinada estructura, en el rango inelástico, debe ser selectiva y secuencial, de manera de disipar de la estructura, minimizando la posibilidad de daño severo en elementos verticales y eliminando la posibilidad de colapso de la estructura. El diseño debe ir orientado a que sean los elementos horizontales los que ingresen primero en el rango inelástico con la formación de rotulas plásticas en sus extremos, mientras los elementos verticales permaneceran en el rango elástico.
Finalmente, las columnas o muros ingresan en el rango inelástico con la formación probable de rótulas en su base [41].
2.2.9. Estados Límites
El desempeño de una estructura o parte de ella está referido a un conjunto de estados límites, más allá de los cuales la estructura sobrepasa los daños admisibles para su uso previsto. Generalmente estos se suelen agrupar en Estados Límites de Servicio, Daños Reparables y Prevención de Colapso [42].
Estado Límite de Servicio
Son aquellos que puedena afectar el correcto funcionamiento para el cual fue proyectada la edificación, sin perjudicar su capacidad resistente. Típicamente y para cargas gravitacionales, en adición a la capacidad portante, en las normas se establecen límites para: flechas, fisuración visible, deformaciones incluidos los efectos a largo plazo, vibraciones excesivas. En el caso de las acciones sísmicas, si bien no se suele indicar en forma explícita, tal estado límite se asocia a daños menores en elementos no estructurales: fisuras, roturas de vidrios, entre otros.
Estado Límite de daños reparables
Estos daños son aquellos en los cuales los efectos en la acción sísmica están limitados a ciertos niveles de “daños económicamente reparables”; esto es, daños en elementos portantes del sistema resistente a sismos, lo cual puede equipararse al inicio de la cadencia en algunos de sus elementos.
Estado Límite de prevención de colapso
Es aquel asociado a una elevada probabilidad de ruina (ó inestabilidad) de la edificación ó de una parte importante de ella, como consecuencia de pérdida excesiva de resistencia, agotamiento resistente, o demanda excesivas de ductilidad que conducen a daños irreversibles con reducciones significativas de la resistencia [42].
2.2.10. Irregularidades según la norma COVENIN 1756-2001
La norma venezolana COVENIN 1756-2001 [5] establece para el análisis de edificaciones sismorresistentes dos tipos de irregularidades en cuanto a la configuración estructural como son: en planta y elevación. En el presente trabajo se estudió el caso específico de estructuras con irregularidad en planta, las cuales se originan si presentan:
Gran Excentricidad
En algún nivel la excentricidad entre la línea de acción del cortante en alguna dirección, y el centro de rigidez supera el veinte por ciento (20%) del radio de giro inercial de la planta.
Riesgo torsional elevado
Si en algún piso se presenta cualquiera de las siguientes situaciones:
El radio de giro torsional en alguna dirección es inferior al cincuenta por ciento (50%) del radio de giro inercial r.
La excentricidad entre la línea de acción del cortante y el centro de rigidez de la planta supera el treinta por ciento (30%) del valor del radio de giro torsional en alguna dirección.
Sistema no ortogonal
Cuando una porción importante de los planos del sistema sismorresistente no sean paralelos a los ejes principales de dicho sistema.
Diafragma Flexible
-Cuando la rigidez en su plano sea menor a la de una losa equivalente de hormigón armado de 4 cm de espesor y la relación no sea mayor que 4,5.
-Cuando un número significativo de plantas tenga entrantes cuya menor longitud exceda el cuarenta por ciento (40%) de la dimensión del menor rectángulo que inscribe a la planta, medida paralelamente a la dirección del entrante; o cuando el área de dichos entrantes supere el treinta por ciento (30%) del área del citado rectángulo circunscrito.
-Cuando las plantas presenten un área total de aberturas internas que rebasen el veinte por ciento (20%) del área bruta de las plantas.
-Cuando existan aberturas prominentes adyacentes a los planos sismorresistentes importantes o, en general, cuando se carezca de conexiones adecuadas con ellos.
-Cuando en alguna planta el cociente largo/ancho del menor rectángulo que inscriba a dicha planta sea mayor que 5.
2.2.11. Espectro de Diseño
Muchas de las reglamentaciones para diseño sísmico alrededor del mundo especifican la acción sísmica para diseño a través de un espectro de diseño de pseudo-aceleraciones.
En el caso más general este espectro, por simplicidad en su formulación, se ha dividido en tres partes: la zona de periodos bajos, definida a través de una recta que parte de la aceleración máxima esperada en la superficie del suelo y que termina en la aceleración espectral máxima; la zona de periodos intermedios o periodos de amplificación máxima, definida por una constante que representa la aceleración espectral máxima especificada, y la tercera rama, o rama descendente, tradicionalmente se ha especificado proporcional a .
De acuerdo con las formas descritas, el espectro de diseño queda completamente definido en términos de cinco parámetros: la aceleración máxima a nivel de la superficie del suelo, , la aceleración espectral máxima, , el primer periodo de quiebre del espectro, , que define la zona de periodos bajos, el segundo periodo de quiebre del espectro, , que define el final de la meseta de amplificación máxima, y el exponente α, que define la forma de la caída del espectro. Para pasar del espectro elástico al espectro inelástico, la mayor parte de normativas sísmicas lo hacen por medio del factor de reducción [43].
Espectros Elásticos e Inelásticos
Hoy en día, gracias a la obtención de los sismos más fuertes que se tienen registrados en una base de datos, es posible obtener espectros a los que se les denomina elásticos. Para el diseño estructural de edificaciones se trabaja con espectros inelásticos, debido a que al trabajar con espectros elásticos se obtendrían secciones de vigas, columnas y elementos estructurales presentes en la edificación de grandes dimensiones esto tendría una gran resistencia y estabilidad de la estructura ante la presencia de fuerzas sísmicas, sin embargo resultaría demasiado alto su costo de construcción, por tal motivo se introduce un factor de reducción de fuerzas sísmicas el cual reduce la intensidad que presenta el espectro elástico convirtiéndolo en un espectro inelástico y consecuentemente disminuyendo las secciones de los elementos estructurales presentes en la edificación reduciendo sus costos lo que facilita su construcción [43].
Espectro de diseño elástico
Las ordenadas Ad de los espectros de diseño elástico quedan definidas en función del período fundamental de la estructura . Ver Figura 2.8.
|
|
(2.8) |
|
|
(2.9) |
|
|
(2.10) |
Espectro de diseño inelástico
Las fuerzas de diseño obtenidas para los diferentes espectros elásticos son reducidas de acuerdo a la ductilidad de las diferentes tipologías estructurales utilizando los factores de reducción de respuesta ( ).
|
|
(2.11) |
|
|
(2.12) |
|
|
(2.13) |
siendo:
|
|
(2.14) |
Las ordenadas de los espectros de diseño elástico quedan definidas en función del período fundamental de la estructura ( ). Ver Figura 2.9.
CAPÍTULO 3. ESTUDIO DE EDIFICIOS CON PLANTAS CON RE-ENTRANTES
En este capítulo se aplican las metodologías de análisis ya expuestas al análisis de un grupo de edificios irregulares de hormigón armado, caracterizados por tener plantas con re-entrantes. Este tipo de irregularidad es penado en la mayoría de las normas de diseño sismorresistente a nivel mundial, sin embargo, el grado de severidad de la penalización suele variar, produciendo lógicamente resultados variables, que no siempre garantizan un adecuado comportamiento torsional. Para estudiar esto, se ha aplicado análisis incremental dinámico, para conocer si las medidas normativas adoptadas permiten mitigar los efectos de la torsión sobre la estructura.
3.1. Procedimiento de análisis
En este trabajo se estudia la vulnerabilidad sísmica de edificios de hormigón armado con plantas con entrantes, se parte de una geometría regular en planta de hormigón armado y se analizan siete tipologías, basados en la Norma venezolana [5]. Se realiza la modelación, análisis y diseño de los diferentes tipos de edificaciones que se están sometiendo a estudio, con el fin de comprender los criterios y factores que influyen en las mismas.
3.1.1. Descripción de las estructuras
En el presente trabajo se analiza el comportamiento sísmico de siete tipologías de edificios de hormigón armado con plantas con entrantes. Vale acotar, que con esta característica se han construido una gran cantidad de edificios residenciales en el país.
Las configuraciones de los edificios constan de tres (3) niveles. Se parte de una geometría regular en planta que contempla tres vanos en dirección x, equiespaciados cada seis metros por tres vanos en la dirección y, equiespaciados cada seis metros. En elevación los pórticos tienen tres metros de altura. El sistema de losas consiste en losas macizas de 15 cm de espesor total. Las cargas a considerar serán las correspondientes a los materiales que constituyen la estructura y elementos fijos no estructurales, determinadas según la norma Covenin 2002-98 [44] (cargas permanentes). Las cargas variables se definen según el uso previsto de la edificación, en este caso el uso es residencial. Finalmente, las cargas sísmicas corresponden a un emplazamiento sobre suelo rígido (suelo S2) para una aceleración de diseño correspondiente a una zona 5 (0,3g).
El grupo de edificios seleccionados para el análisis consiste en siete tipos caracterizados por diferentes configuraciones. Cada configuración se describe a continuación:
- Configuración 1: Edificio completo
Descripción: Edificio con planta cuadrada sin entrantes. (Figuras 3.1 y 3.2)
- Configuración 2: H con vigas
Descripción: Edificio con planta cuadrada con entrantes en dos costados, con vigas de cierre. (Figuras 3.3 y 3.4)
- Configuración 3: H sin vigas
Descripción: Edificio con planta cuadrada con entrantes en dos costados. (Figuras 3.5 y 3.6)
- Configuración 4: U con viga
Descripción: Edificio con planta cuadrada con entrante en un solo costado, con viga de cierre. (Figuras 3.7 y 3.8)
- Configuración 5: U sin viga
Descripción: Edificio con planta cuadrada con entrante en un solo costado. (Figuras 3.9 y 3.10)
- Configuración 6: UU con viga
Descripción: Edificio con planta cuadrada con entrante doble en un solo costado, con dos vigas de cierre. (Figuras 3.11 y 3.12)
- Configuración 7: UU sin viga
Descripción: Edificio con planta cuadrada con entrante doble en un solo costado. (Figuras 3.13 y 3.14)
Las configuraciones anteriores se pueden apreciar a continuación.
3.1.2. Verificación normativa de la irregularidad
A continuación, se presenta una serie de verificaciones normativas aplicadas a la configuración de los edificios objeto de estudio. Los edificios se someten a una verificación completa de la regularidad, siguiendo el orden que se presenta en la Norma Covenin 1756 [45] [5]. En el numeral 6.4.1 se indica que “para las irregularidades tipificadas como a.4, b.1 y b.2 en la Sección 6.5.2, así como en los sistemas estructurales Tipo I con columnas articuladas en su base, los valores de R serán minorados multiplicando los valores de la Tabla 6.4 por 0.75”, así que se procede a revisar todos estos puntos.
Verificación de gran excentricidad (b.1). Se considerará que un edificio presenta irregularidad en planta si “En algún nivel la excentricidad entre la línea de acción del cortante en alguna dirección, y el centro de rigidez supera el veinte por ciento (20%) del radio de giro inercial de la planta.
La verificación b.2 correspondiente a riesgo torsional elevado ( ) presenta dos componentes. El primero, señalado como b.2.i, considera que hay irregularidad en planta si en alguno de los pisos se presentase “El radio de giro torsional en alguna dirección es inferior al cincuenta por ciento (50%) del radio de giro inercial ”.
La segunda verificación tiene que ver con la excentricidad en planta y se considerará irregular aquel edificio en el que “La excentricidad entre la línea de acción del cortante y el centro de rigidez de la planta supera el treinta por ciento (30%) del valor del radio de giro torsional en alguna dirección”.
Seguidamente corresponde verificar si los edificios se deben modelar con diafragma rígido o si, por el contrario, las aberturas en ellos requieren la incorporación de diafragmas flexibles. Para llevar a cabo esta verificación es necesario cumplir con los cinco puntos siguientes, el primero consiste en que para la losa: “la rigidez en su plano sea menor a la de una losa equivalente de hormigón armado de 4 cm de espesor y la relación no sea mayor que 4,5”.
El segundo punto es verificado a través de dos características: la longitud de los entrantes respecto de la mínima longitud en planta y la relación del área de los entrantes con respecto al área total. El tercer punto tiene que ver con la proporción de aberturas internas, que en todos los edificios estudiados cumplen. El punto cuatro se relaciona con aberturas prominentes cercanas a miembros sismorresistentes y el quinto a la relación de esbeltez del menor rectángulo que inscribe la planta de la edificación.
| Coeficiente de aceleración A0 | 0,30 |
| Zona sísmica | 5,00 |
| Factor de Corrección φ | 1 |
| Tipo de suelo | S2 |
| Factor de Importancia α | 1,00 |
| Grupo según su uso | B2 |
| Nivel de diseño | ND3 |
| Tipo de estructura | I |
| Factor de reducción de respuesta | 6 |
3.1.3. Parámetros sísmicos empleados en el análisis
Los parámetros sísmicos considerados para la modelación estructural tomados de la norma venezolana COVENIN 1756-2001 [5] corresponden a un emplazamiento con una amenaza sísmica alta, sobre un suelo muy rígido (suelo tipo S2). Bajo la exposición de las estructuras, se determina que las mismas deberán ser diseñadas y detalladas para poder desarrollar un nivel alto de ductilidad (correspondiente a un nivel de diseño 3) con una tipología estructural de pórticos, ver Tabla 3.1.
3.1.4. Análisis no lineal
La simulación de las estructuras en el rango lineal se realiza mediante el programa de cálculo Robot Structural Analysis 2015 (versión educativa) [8] (diseño y análisis), se requieren ciertos procedimientos y parámetros normativos que permitan realizar dicho análisis en todos los elementos, los cuales se describen a continuación:
- -Se introducen los parámetros de entrada conforme a las propiedades y características estructurales de la edificación en estudio.
- -Seguidamente se ajusta el diseño de acuerdo a las dimensiones de las secciones de los elementos que conforman el edificio proyectado, para luego realizar el análisis de cargas. Se consideran las cargas de servicio y las fuerzas horizontales producto de la actividad sísmica que actúan en los elementos de hormigón armado que conforman dicha estructura.
- -Es necesario la incorporación del espectro inelástico de diseño, de acuerdo a las características geotécnicas del lugar donde se localiza la edificación, conjuntamente con el factor de reducción y sus posibles aceleraciones, esto en función de las disposiciones normativas. Con base en estos parámetros se realiza el análisis espectral y los diferentes modos de vibración.
- -Una vez modelada la edificación en un rango elástico, se verifican las dimensiones de las secciones para cada elemento estructural de acuerdo con lo establecido en la norma y finalmente se verifican las derivas.
Posteriormente al análisis elástico, se utiliza el programa SeismoStruct 7.0.3 [9] para realizar el análisis no lineal con el cual se evalúa la respuesta global de la estructura más allá de la capacidad elástica-lineal con el fin de identificar la evolución de la degradación de los elementos que la conforman; utilizando análisis basado en elementos finitos, donde cada miembro se discretiza en elementos y esos elementos a su vez en fibras, dependiendo de la sección transversal (método de fibras basados en desplazamientos). Véase las Figuras 3.15 y 3.16. Las propiedades de los materiales utilizados se presentan en la Tabla 3.2, mientras que las características de las leyes de comportamiento empleadas se muestran en las Figuras 3.17 (hormigón) y 3.18 (acero).
| Propiedades del hormigón | |
| Esfuerzo de compresión medio | 25000(kPa) |
| Esfuerzo de tracción medio | 2500(kPa) |
| Módulo de elasticidad | 23500000(kPa) |
| Deformación al valor del máximo pico de esfuerzo | 0,002 (m/m) |
| Peso específico | 24(kN/m3) |
| Propiedades del acero | |
| Módulo de elasticidad | 2,00E+08(kPa) |
| Límite de fluencia | 420000(kPa) |
| Parámetro de endurecimiento por deformación (-) | 0,005 |
| Parámetro de forma inicial de la curva de transición (-) | 20 |
| Coef. de calibración de forma de la curva de transición A1 (-) | 18,5 |
| Coef. de calibración de forma de la curva de transición A2 (-) | 0,15 |
| Coef. de calibración del endurecimiento isotrópico A3 (-) | 0 |
| Coef. de calibración del endurecimiento isotrópico A4 (-) | 1 |
| Deformación de rotura/pandeo (-) | 0,1 |
| Peso específico | 78(kN/m3) |
Vale indicar, que la estructura se someterá a cargas de gravedad actuando en los nodos de los elementos y conjuntamente estará sujeta a las fuerzas laterales equivalentes al sismo que se incrementan a partir del corte basal de diseño, lo que origina grandes desplazamientos hasta llegar al colapso total de la estructura y justo antes de que esto suceda se medirá la rotación en la cuerda de la deformada.
Por consiguiente, la determinación de la respuesta sísmica de los edificios se llevará a cabo mediante procedimientos no lineales de dos tipos. Por un lado se emplea el procedimiento pseudo-estático, conocido como análisis con empuje incremental, que se llevará a cabo mediante la versión modificada conocida como análisis con empuje incremental adaptativo, caracterizado por la modificación del perfil de fuerzas aplicadas a medida que se van produciendo cambios en la rigidez de los elementos producto de la no linealidad [46], [47] y [48]. De este tipo de análisis se obtendrá la curva de capacidad para cada una de las direcciones de los casos a estudiar [49], sobre las que se aplicará el procedimiento N2 modificado, [50] con la finalidad de obtener el punto de capacidad por demanda, que toma en consideración la irregularidad tanto en planta como en elevación. Este punto de capacidad por demanda permitirá evaluar la respuesta de los edificios mediante el procedimiento que combina enfoque deterministas y probabilistas propuesto en [51], que finalmente condice a la determinación de curvas de fragilidad y umbrales de daño con valores procedentes de los análisis dinámicos [52].
El análisis dinámico no lineal se lleva a cabo teniendo las cargas gravitatorias factorizadas. Con este tipo de análisis no lineal se busca obtener los valores de la capacidad media de colapso SCT y el cociente de margen de colapso MR, para cada uno de los modelos de arquetipos. La intensidad del terremoto ðð es definida con base en la intensidad media espectral del conjunto de terremotos de fuente lejana medida en el período T.
La determinación del cociente de margen de colapso para cada modelo de arquetipo índice puede llegar a requerir de hasta 200 análisis de historia tiempo no lineal. En el presente trabajo el número de análisis se amplía al número de acelerogramas empleados. Dentro del grupo de registros seleccionados deberá resaltarse un grupo de acelerogramas que han sido especialmente dañinos, de reciente ocurrencia alrededor del mundo. Como ya se ha indicado, los registros de sismos se tomarán en sus dos componentes horizontales, no se considerará la componente vertical, porque se tiene asumido que la misma no conduce al colapso de las estructuras, que es el fin último del análisis no lineal dinámico [10].
Terremoto de Sumatra, Indonesia (14 de septiembre de 2007)
Este terremoto afectó la costa sudoeste de Sumatra, con una Mw de 8,4. Se caracterizó por la gran cantidad de réplicas y de sismos precursores.
Según reportes de las autoridades locales, se produjo cerca de una veintena de fallecidos y cerca de 100 heridos. Afortunadamente el número de pérdidas fue bajo en comparación con el poder destructivo del terremoto. Ha quedado registrado como uno de los cuatro terremotos de magnitud mayor que 7,9 que afectó esta zona del sudeste asiático. De este terremoto de han seleccionado los registros de las estación de la Isla de Sikuai [10]. Ver Tabla 3. 3
Terremoto de Northridge, Estados Unidos (17 de enero de 1994)
Este terremoto ocurrió cerca de la ciudad de Los Ángeles, teniendo una Mw de 6,7. Tuvo una de las aceleraciones instrumentales más altas registradas en zonas urbanas en Norteamérica.
Su efecto causó 72 fallecidos y alrededor de 12.000 heridos. Las pérdidas materiales fueron cuantiosas, dando origen a la revisión de sistemas constructivos que fallaron por la acción del terremoto.
De este terremoto de han seleccionado los registros de las estaciones Carbon Canyon Dam y Los Angeles Griffith Observatory. Ver Tabla 3. 3
Terremoto del Este de Turquía (23 de octubre de 2011)
Ese terremoto de Mw 7,9 tuvo su epicentro en la localidad de Van ubicada en el este de Turquía. Las autoridades turcas reportaron un número de 138 fallecidos, más de 500 desaparecidos y 350 heridos. Las pérdidas materiales incluyeron más de 500 edificaciones.
De este terremoto de han seleccionado los registros de las estaciones Van Muradiye y Bitlis Merkez [10]. Ver Tabla 3. 3.
| Terremoto | Estación | Componente |
| Sumatra (Indonesia) | Sikuai Island | 090 |
| 360 | ||
| Northridge(EEUU) | Carbon Canyon
Dam
|
131 |
| 041 | ||
| Los Angeles
Griffith Observatory |
360 | |
| 270 | ||
| Este de Turquía | Van Muradiye | N |
| S | ||
| Bitlis Merkez | N-S | |
| E-W |
La intensidad media de colapso puede ser entendida más fácilmente si se le estudia a la luz del concepto de análisis incremental dinámico (IDA por sus siglas del inglés) que se lleva a cabo escalando progresivamente los acelerogramas hasta que la estructura alcanza el punto de colapso. De esta forma, cada análisis dinámico no lineal representa un punto de la curva IDA, que está representando una medida de prestaciones (MP) contra una medida de intensidad (MI). En la Figura 3.19 se puede apreciar un conjunto de curvas IDA correspondientes a la ilustración del procedimiento contenida en el FEMA.
Las diferencias entre las curvas IDA se dan por las diferencias en el contenido frecuencial de los terremotos. Se estima que el colapso se produce cuando ocurren desplazamientos laterales excesivos.
Con los resultados obtenidos del análisis IDA, se puede generar una curva de fragilidad de colapso, mediante una función de distribución cumulativa que relaciona la intensidad de un terremoto con la probabilidad de alcanzar el colapso. En la Figura 3.36 se puede apreciar un ejemplo de función cumulativa obtenida al ajustar la distribución lognormal a los datos obtenidos en el análisis IDA.
La fragilidad lognormal de colapso se define mediante dos parámetros: la intensidad media de colapso y la desviación del logaritmo natural, La capacidad media de colapso corresponde a una probabilidad de colapso de 50%. La pendiente de la distribución lognormal corresponde a la desviación , reflejando así la dispersión de resultados bajo la variabilidad de registro a registro. En la metodología solo se calcula el valor de la intensidad media de colapso mientras que para se asume un valor fijo de 0,4 para sistemas con ductilidad basada en el período mayor o igual a 3.
Esta última decisión se fundamenta en varios motivos. Primero que nada estudios previos han demostrado que la variabilidad entre registros es prácticamente constante [53], En segundo lugar, el cálculo más preciso de la variabilidad entre registros no afectaría de forma significativa el cálculo de la razón media de colapso cuando se combinan varias fuentes de incertidumbre de colapso.
De entre todos los resultados obtenidos al calcular las curvas IDA, la metodología requiere únicamente de la identificación de la intensidad media de colapso . Una forma eficiente de conseguirlo consiste simplemente en escalar todos los acelerogramas escogidos con respecto al máximo terremoto considerado () cuyo valor se ha expresado como SMT, iniciando desde allí los análisis, hasta que la mitad de los terremotos escalados produzcan el colapso.
La intensidad más baja en la que la mitad de los terremotos causa el colapso se considerará como la intensidad media de colapso . De acuerdo con esta selección del ajuste de la intensidad de los terremotos logrará reducirse razonablemente la cantidad de análisis dinámicos en comparación con los requeridos en un procedimiento estándar de IDA.
Seguidamente se calcula el valor de la intensidad del máximo terremoto considerado SMT directamente del espectro de diseño y para un período fundamental T. La razón entre la intensidad media de colapso y la intensidad del máximo terremoto considerado proporciona el valor de la razón de margen de colapso:
|
|
(3.1) |
En la metodología, las intensidades de los registros se definen en términos de la intensidad espectral media del grupo de terremotos de fuente lejana, en lugar de hacerlo con respecto a la intensidad espectral de cada registro individual. Esto conceptualmente significa que el conjunto de sismos de fuente lejana es representativo de un grupo de registros de un terremoto característico para el cual las intensidades espectrales de los registros individuales exhibirán dispersiones alrededor del valor medio. Por tanto, la capacidad media de colapso de la estructura es igual a la capacidad media del conjunto de sismos de fuente lejana en el punto para el cual la mitad de los registros causan el colapso del modelo de arquetipo índice [10].
Una vez realizado los análisis establecidos se podrá conocer el comportamiento de las estructuras con la incorporación de entrantes en sus plantas, cuando son sometidas a acciones sísmicas, así como el índice de daño de las mismas, con el cual se determina si los elementos llegan al colapso, a través del cociente entre la rotación en la cuerda de la deformada y la rotación última de la cuerda.
3.2. Resultados
El estudio se basa en el análisis de edificios porticados bajos de hormigón armado con altura de 3 niveles, emplazados en una zona de alta amenaza sísmica, diseñados para alcanzar una alta ductilidad (R=6). La resistencia del hormigón es de y del acero . Se parte de una geometría regular en planta que contempla tres vanos en dirección , equiespaciados cada seis metros por tres vanos en la dirección , equiespaciados cada seis metros, la altura de entrepiso es de 3 m.
Se trabaja con diversas configuraciones, las cuales contemplan edificios con planta regular y con plantas irregulares con entrantes y también edificios con plantas con entrantes a los que se les ha incorporado vigas de cierre en los entrantes, ya que entre las irregularidades que más comúnmente se encuentran en las edificaciones residenciales de Venezuela está la planta con entrantes.
El sistema de losas consiste en losas macizas de 15 cm de espesor total. Las cargas a considerar serán las correspondientes a los materiales que constituyen la estructura y elementos fijos no estructurales, determinadas según la norma Covenin 2002‐98 (cargas permanentes). Las cargas variables se definen según el uso previsto de la edificación, en este caso el uso es residencial. Finalmente, las cargas sísmicas corresponden a un emplazamiento sobre un suelo rígido (perfil S2).
Las estructuras son modeladas haciendo uso de programas basados en el método de elementos finitos: Robot Structural (diseño y análisis lineal) [8] y SeismoStruct 7.0.3 (análisis no lineal) [9]; los cuales permiten realizar un análisis del comportamiento de las estructuras y así obtener resultados de la respuesta de la edificación ante un posible evento sísmico y validar los factores de prestaciones sísmicas aplicados en el diseño.
La determinación de la respuesta sísmica de los edificios se lleva a cabo mediante procedimientos de análisis no lineal de dos tipos. Por un lado se tiene el procedimiento pseudo-estático, conocido como análisis con empuje incremental, caracterizado por la modificación del perfil de fuerzas aplicadas a medida que se van produciendo cambios en la rigidez de los elementos producto de la no linealidad [28] [29] [30].
El otro tipo de análisis es el análisis dinámico no lineal, que se llevará a cabo mediante la aplicación de un grupo de acelerogramas seleccionados. Se debe resaltar que estos acelerogramas corresponden a terremotos que han sido especialmente dañinos, de reciente ocurrencia alrededor del mundo (Terremoto de Sumatra, Indonesia (14 de septiembre de 2007); Northridge, EEUU (17 de enero de 1994); Terremoto del Este de Turquía (23 de octubre de 2011). Del análisis dinámico se obtienen los resultados necesarios para comparar las componentes de los desplazamientos, con el fin de verificar contra los criterios previamente definidos si el comportamiento de la estructura permite clasificarla como regular o irregular [38], consiguiendo un argumento confiable para evaluar los criterios de diafragma rígido o flexible de [5]. También se determinan los valores de los torsores y rotaciones mediante análisis no lineal.
3.3. Análisis de Cargas
De acuerdo a la Norma COVENIN [44] “Criterios y Acciones Mínimas para Proyectos de Edificaciones 2002-88”, para viviendas multifamiliares, la carga variable es de para la losa de entrepiso y de para losa de techo. Las cargas permanentes se han calculado en las Tablas 3.4 y 3.5.
| Losa de entrepiso (e=15cm) | ||
| Carga permanente | CP (kgf/m2) | |
| Losa Maciza (e=15cm) | 360 | |
| Paredes o tabiques (bloques de arcilla + friso) | 150 | |
| Pavimento (granito o baldosa) | 100 | |
| Friso de yeso e=1,5 cms | 30 | |
| Total | 640 | |
| Losa de techo (e=15cm) | ||
| Carga permanente | CP (kgf/m2) | |
| Losa Maciza (e=15cm) | 360 | |
| Impermeabilización | 100 | |
| Friso de yeso e=1,5 cms | 30 | |
| Total | 490 | |
3.4. Análisis elástico
El estudio de las estructuras en el rango elástico se realizó a través del programa Robot Structural versión educativa del año 2015, en el cual se utiliza el módulo edificio, definido en el cuadro de diálogo del programa. Posteriormente se definen las unidades y la normativa a utilizar, se emplean columnas y vigas para modelar las estructuras con sus respectivas secciones y propiedades de los materiales, trabajando por plantas.
Vale acotar, que las losas son modeladas como losas macizas, permitiendo que sus pesos y las cargas variables y permanentes que soportan, se distribuyan hacia las vigas de piso que las soportan. Esta distribución se realiza de forma automática por el programa de análisis, permitiendo que las cargas sean asignadas conforme a la longitud de los vanos. Cabe indicar que en el caso presente esta distribución se similar tanto para las vigas orientadas según el eje x, como según el eje y, debido a que las luces son iguales.
Una vez modelada la edificación se procedió a realizar el análisis modal, asignándose tres modos de vibración por piso, para un total de nueve modos; los cuales al realizar el análisis de la estructura representan un número acertado ya que el porcentaje de la masa participativa arrojado cumple con los requisitos normativos obteniéndose valores por encima de 90%.
Posteriormente, se realiza el análisis espectral el cual permite obtener las cargas sísmicas a partir del espectro de diseño elástico establecido en la Norma COVENIN 1756-2001, aplicando un factor de reducción R=6, transformándolo en un espectro inelástico. El espectro incorpora las características del edificio tales como el material, uso previsto, características del suelo de fundación y zona sísmica en la cual están emplazados.
Al concluir el análisis modal y espectral, se procede a la verificación detallada del diseño elástico, verificando los resultados obtenidos, en cuanto a la capacidad de las secciones de los elementos estructurales (cuantías de acero), período de la edificación, aceleraciones, desplazamientos para verificar las derivas de entrepiso y chequeo de cortante mínimo según valores normativos.
Es importante destacar que se realizó la verificación del cortante basal a través del método estático equivalente y también a través de los dispuesto en el numeral 7.1 de la Norma.
3.5. Derivas de Entrepiso
Las estructuras al ser sometidas a fuerzas laterales provocadas por sismos, tienden a desplazarse. Al cuantificar estos desplazamientos de manera adimensional, dividiéndolos por la altura de entrepiso, se obtienen las derivas de entrepiso.
Según COVENIN 1756-2001 en el capítulo 10, el valor de deriva máxima es de 0,018 ya que las estructuras estudiadas pertenecen al grupo B2. Para los métodos de análisis el desplazamiento lateral total de un nivel en cada plano resistente (pórticos) se calculará transformando el desplazamiento elástico Δei, por ; este a su vez incluye los efectos traslacionales, de torsión en planta y .
Al verificar las derivas de entrepiso de todas las configuraciones de los edificios considerando un comportamiento inelástico, para un factor de reducción de respuesta de 6 y estableciendo comparación con el valor establecido en la norma COVENIN 1756-2001, se verificó que las mismas cumplen con el valor máximo establecido en dicha norma (0,018) y por ello las secciones poseen capacidad para soportar desplazamientos laterales, ya que cumplen con la deriva máxima permisible en la norma venezolana, lo que indica un diseño adecuado bajo los requisitos de resistencia y desplazamiento, sin que se llegasen a producir daños en componentes no estructurales como producto de desplazamientos excesivos. Ver Tablas de la 3.6 a la 3.12.
| Estructura completa | Elástica (cm) | Inelástica (%) | Inelástica (%) | ||||
| Caso | Niveles | X | Y | X | Y | X | Y |
| 100% X+30%Y | 2 y 3 | 0,115 | 0,034 | 1,006 | 0,298 | 1,006 | 0,298 |
| 1 y 2 | 0,191 | 0,059 | 1,671 | 0,516 | 1,671 | 0,516 | |
| 0 y 1 | 0,131 | 0,039 | 1,146 | 0,341 | 1,146 | 0,341 | |
| 30% X+100%Y | 2 y 3 | 0,034 | 0,115 | 0,298 | 1,006 | 0,298 | 1,006 |
| 1 y 2 | 0,059 | 0,191 | 0,516 | 1,671 | 0,516 | 1,671 | |
| 0 y 1 | 0,039 | 0,131 | 0,341 | 1,146 | 0,341 | 1,146 | |
| H con vigas | Elástica (cm) | Inelástica (%) | Inelástica (%) | ||||
| Caso | Niveles | X | Y | X | Y | X | Y |
| 100% X+30%Y | 2 y 3 | 0,106 | 0,032 | 0,928 | 0,280 | 0,928 | 0,280 |
| 1 y 2 | 0,185 | 0,056 | 1,619 | 0,490 | 1,619 | 0,490 | |
| 0 y 1 | 0,128 | 0,039 | 1,120 | 0,341 | 1,120 | 0,341 | |
| 30% X+100%Y | 2 y 3 | 0,032 | 0,107 | 0,280 | 0,936 | 0,280 | 0,936 |
| 1 y 2 | 0,055 | 0,186 | 0,481 | 1,628 | 0,481 | 1,628 | |
| 0 y 1 | 0,039 | 0,128 | 0,341 | 1,120 | 0,341 | 1,120 | |
| H sin vigas | Elástica (cm) | Inelástica (%) | Inelástica (%) | ||||
| Caso | Niveles | X | Y | X | Y | X | Y |
| 100% X+30%Y | 2 y 3 | 0,108 | 0,031 | 0,945 | 0,271 | 0,945 | 0,271 |
| 1 y 2 | 0,187 | 0,055 | 1,636 | 0,481 | 1,636 | 0,481 | |
| 0 y 1 | 0,128 | 0,038 | 1,120 | 0,333 | 1,120 | 0,333 | |
| 30% X+100%Y | 2 y 3 | 0,033 | 0,105 | 0,289 | 0,919 | 0,289 | 0,919 |
| 1 y 2 | 0,056 | 0,183 | 0,490 | 1,601 | 0,490 | 1,601 | |
| 0 y 1 | 0,039 | 0,126 | 0,341 | 1,103 | 0,341 | 1,103 | |
| U con vigas | Elástica (cm) | Inelástica (%) | Inelástica (%) | ||||
| Caso | Niveles | X | Y | X | Y | X | Y |
| 100% X+30%Y | 2 y 3 | 0,106 | 0,041 | 0,928 | 0,359 | 0,928 | 0,359 |
| 1 y 2 | 0,181 | 0,070 | 1,584 | 0,613 | 1,584 | 0,613 | |
| 0 y 1 | 0,121 | 0,047 | 1,059 | 0,411 | 1,059 | 0,411 | |
| 30% X+100%Y | 2 y 3 | 0,032 | 0,110 | 0,280 | 0,963 | 0,280 | 0,963 |
| 1 y 2 | 0,054 | 0,187 | 0,473 | 1,636 | 0,473 | 1,636 | |
| 0 y 1 | 0,036 | 0,135 | 0,315 | 1,181 | 0,315 | 1,181 | |
| U sin vigas | Elástica (cm) | Inelástica (%) | Inelástica (%) | ||||
| Caso | Niveles | X | Y | X | Y | X | Y |
| 100% X+30%Y | 2 y 3 | 0,109 | 0,037 | 0,954 | 0,324 | 0,954 | 0,324 |
| 1 y 2 | 0,185 | 0,064 | 1,619 | 0,560 | 1,619 | 0,560 | |
| 0 y 1 | 0,123 | 0,043 | 1,076 | 0,376 | 1,076 | 0,376 | |
| 30% X+100%Y | 2 y 3 | 0,033 | 0,107 | 0,289 | 0,936 | 0,289 | 0,936 |
| 1 y 2 | 0,056 | 0,183 | 0,490 | 1,601 | 0,490 | 1,601 | |
| 0 y 1 | 0,037 | 0,122 | 0,324 | 1,068 | 0,324 | 1,068 | |
| UU con vigas | Elástica (cm) | Inelástica (%) | Inelástica (%) | ||||
| Caso | Niveles | X | Y | X | Y | X | Y |
| 100% X+30%Y | 2 y 3 | 0,098 | 0,041 | 0,858 | 0,359 | 0,858 | 0,359 |
| 1 y 2 | 0,167 | 0,070 | 1,461 | 0,613 | 1,461 | 0,613 | |
| 0 y 1 | 0,111 | 0,047 | 0,971 | 0,411 | 0,971 | 0,411 | |
| 30% X+100%Y | 2 y 3 | 0,029 | 0,102 | 0,254 | 0,893 | 0,254 | 0,893 |
| 1 y 2 | 0,050 | 0,174 | 0,438 | 1,523 | 0,438 | 1,523 | |
| 0 y 1 | 0,033 | 0,116 | 0,289 | 1,015 | 0,289 | 1,015 | |
| UU sin vigas | Elástica (cm) | Inelástica (%) | Inelástica (%) | ||||
| Caso | Niveles | X | Y | X | Y | X | Y |
| 100% X+30%Y | 2 y 3 | 0,104 | 0,034 | 0,910 | 0,298 | 0,910 | 0,298 |
| 1 y 2 | 0,174 | 0,059 | 1,523 | 0,516 | 1,523 | 0,516 | |
| 0 y 1 | 0,114 | 0,040 | 0,998 | 0,350 | 0,998 | 0,350 | |
| 30% X+100%Y | 2 y 3 | 0,031 | 0,098 | 0,271 | 0,858 | 0,271 | 0,858 |
| 1 y 2 | 0,052 | 0,167 | 0,455 | 1,461 | 0,455 | 1,461 | |
| 0 y 1 | 0,034 | 0,112 | 0,298 | 0,980 | 0,298 | 0,980 | |
Una vez verificadas las derivas de entrepiso de los edificios, se procede a verificar nuevamente la compatibilidad geométrica de los miembros y la condición de columna fuerte-viga débil. Satisfechos estos requerimientos específicos, se procede a efectuar el detallado de miembros estructurales, garantizando con esto que existirá un comportamiento dúctil. A manera ilustrativa, se presentan unas tablas que resumen el armado de los miembros del edificio completo (Tabla A.1 a la A.6 de los Anexos).
3.6. Análisis no lineal
Una vez culminado el diseño y análisis en el rango lineal y partiendo de los resultados obtenidos en el mismo, como lo son las dimensiones definitivas de los elementos estructurales y su respectivo armado (despiece y detallado) para lo que se utilizó la versión educativa del programa Autocad Structural Detailing, se realizó el análisis en el rango no lineal de las edificaciones; este tipo de análisis resulta muy valioso, ya que permite conocer el comportamiento en el rango inelástico en el que incursionan las estructuras al ser sometidas a acciones sísmicas fuertes; se hace uso del programa SeismoStruct 7.0.3 [9], el cual es capaz de realizar análisis complejos en el rango inelástico a estructuras constituidas por diferentes materiales.
Primeramente, se introducen las características de la estructura en cuanto al número de vanos, pisos y pórticos, así como sus respectivas longitudes, material estructural a emplear, tipo de análisis y condiciones de la carga a utilizar.
Una vez definida la configuración estructural, se presenta un entorno de trabajo en base a pestañas que corresponderán al tipo de análisis a efectuar; la determinación de la respuesta sísmica de los edificios se lleva a cabo mediante procedimientos no lineales de dos tipos, el primero a realizar es el pseudo-estático, conocido como análisis con empuje incremental o también como análisis pushover. Se procede a definir los materiales, secciones de los elementos, clase de elementos, nodos, conectividad de elementos, vínculos internos y externos, cargas aplicadas, fases de carga, criterios de prestaciones y las opciones de salidas del análisis, todo esto en la fase del pre-proceso. Ver Figura 3.20.
Seguidamente se avanza a la etapa del proceso para luego llegar a la del post-proceso, en la cual se visualizan una gran cantidad de resultados de especial interés ya que de este tipo de análisis se obtiene la curva de capacidad para cada una de las direcciones de los casos a estudiar [31], sobre las que se aplica el procedimiento N2 extendido, con la finalidad de obtener el punto de capacidad por demanda, que toma en consideración la irregularidad tanto en planta como en elevación. Este punto de capacidad por demanda permitirá evaluar la respuesta de los edificios mediante el procedimiento que combina enfoque deterministas y probabilistas propuesto en [51], que finalmente conduce a la determinación de curvas de fragilidad y umbrales de daño con valores procedentes de los análisis dinámicos [52].
Por otro lado, al realizar el análisis dinámico incremental, el entorno de trabajo es muy parecido al del pseudo-estático, con la diferencia de que existe en la etapa del pre-procesador una pestaña anexa denominada parámetros IDA. Ver Figura 3.21. En este análisis se utiliza un grupo de diez acelerogramas seleccionados previamente. Ver Tabla 3. 3. Se debe resaltar que estos acelerogramas corresponden a terremotos que han sido especialmente dañinos, de reciente ocurrencia alrededor del mundo como: el terremoto de Sumatra, Indonesia (14 de septiembre de 2007), Northridge, (EEUU) (17 de enero de 1994), terremoto del Este de Turquía (23 de octubre de 2011)); con este tipo de análisis no lineal se busca obtener los valores de la capacidad media de colapso y la razón de margen de colapso CMR, para cada uno de los modelos.
La intensidad media de colapso (IDA) se lleva a cabo escalando progresivamente los acelerogramas hasta que la estructura alcanza el punto de colapso. De esta forma, cada análisis dinámico no lineal representa un punto de la curva IDA, que está representando una medida de prestaciones (MP) contra una medida de intensidad (MI); con los resultados obtenidos del análisis IDA, se puede generar una curva de fragilidad de colapso, mediante una función de distribución cumulativa que relaciona la intensidad de un terremoto con la probabilidad de alcanzar el colapso.
3.7. Procedimiento de análisis con empuje incremental para edificios con entrantes
El estudio de la respuesta de edificios con entrantes aplicando el análisis con empuje incremental (análisis Pushover) no dispone de reglas específicas de aplicación. En la literatura no abundan ejemplos de este tipo de análisis aplicado a estructuras con irregularidad en planta, y menos en el caso de edificios con el tipo particular de irregularidad resultante de la presencia de entrantes.
El principal problema que originan los entrantes en las estructuras es que se produce una interrupción en las líneas resistentes horizontales, al no existir usualmente la continuidad en las vigas o al no existir vigas de cierre y cuando por alguna razón no es posible aplicar otras restricciones laterales como la utilización de diafragmas rígidos o simplemente las características del modelo deben reflejar la condición de diafragma flexible. Esto trae como consecuencia que aplicar las cargas del empuje incremental conforme al patrón lateral usual, no va a conducir a resultados consistentes con la teoría de este tipo de análisis, que pretende obtener la respuesta estructural no lineal tomando en consideración exclusivamente efectos traslacionales.
En la Figura 3.22 se puede apreciar un edificio de 3 niveles con entrante por un costado, que hace que su proyección en planta se asemeje a una “u”. Nótese que sobre los nodos de la unión de vigas y columnas se aplican las cargas incrementales, con una distribución triangular superior en dirección x, con valores iguales para los nodos de cada nivel.
En la Figura 3.23 se muestra la deformada (con desplazamientos amplificados por un factor de 5) una vez que se han aplicado las cargas incrementales, hasta que se alcanza el colapso de la estructura. Nótese que la deformada es asimétrica debido a que el tramo del pórtico de la izquierda, en el cual existe el entrante, tiene una rigidez inferior a la de los pórticos que están completos. Nótese además que el tramo incompleto de la derecha no sufre prácticamente ningún desplazamiento. De esta manera se puede apreciar que el análisis con empuje incremental no logra su objetivo primario, que es el de obtener el colapso de la estructura mediante desplazamientos traslacionales en cada dirección de manera desacoplada.
Para corregir esta situación, se ha realizado la modificación siguiente sobre las cargas incrementales laterales: se ha mantenido los valores iniciales para los pórticos completos, manteniéndose la proporcionalidad entre las mismas. Seguidamente se modifican las cargas laterales que se aplican a los tres nodos del tramo incompleto, re-calculando los valores de las cargas de cada nivel. Para esto es útil obtener la rigidez de cada uno de los pórticos, tanto los completos como los incompletos y obtener la relación de las mismas del pórtico incompleto de la izquierda entre los pórticos completos. Nótese que, en el caso presente, dada la simetría geométrica y de secciones, la rigidez del pórtico incompleto es un tercio de la rigidez de los pórticos completos. De acuerdo con esta relación, para que sobre el pórtico incompleto de la izquierda se produzcan los mismos desplazamientos laterales, se requiere de cargas laterales que sean un tercio de las cargas laterales aplicadas a los pórticos completos. De esta manera se obtienen los valores a ser aplicados sobre los nodos del pórtico incompleto de la izquierda.
Finalmente, y para evitar replicar el problema del pórtico incompleto de la derecha que no se desplaza, se aplican sobre este las mismas cargas que sobre el pórtico incompleto de la izquierda, véase la Figura 3.24. De esta forma se logran traslaciones similares al resto de los pórticos, como se muestra en la Figura 3.25 en la que se aprecia que en el punto de fallo de la estructura, el comportamiento es completamente traslacional.
3.8. Prevención del colapso estructural
La prevención del colapso estructural es el principal objetivo del diseño sismorresistente. La definición del colapso puede realizarse en función de diferentes cantidades de la respuesta estructural, en términos locales (deformaciones, curvaturas, rotaciones) o globales (derivas de pisos, deriva global). El colapso implica que los sistemas horizontales y verticales usados para soportar tanto cargas de gravedad como sísmicas son incapaces de soportar las cargas de gravedad actuantes en el edificio.
Generalmente el colapso estructural sucede si los elementos verticales encargados de soportar cargas fallan a compresión y si se pierde la capacidad de transmitir fuerza cortante entre elementos verticales y horizontales tales como sucede con la falla por cortante entre columnas y losas macizas (sin vigas). El colapso puede ser alcanzado por una inestabilidad global. Se puede dar el caso de que entrepisos presenten desplazamientos laterales excesivos, lo que incrementa el efecto P-Δ, y este a su vez incrementa al momento de vuelco, especialmente en columnas de plantas inferiores.
La prevención del colapso estructural se puede lograr si se controla el modo de fallo. Esto constituye la base del diseño por capacidad de las estructuras. Según este tipo de diseño, el proyectista decide donde ocurrirá el daño en la estructura, imponiendo a su vez un modo de falla dúctil global. En la práctica esto se alcanza haciendo que las partes de la estructura que han de incursionar en comportamiento plástico/daño, sean capaces de absorber mayor energía, gracias a un adecuado detallado.
Las fallas frágiles a evitar en estructuras de hormigón armado son:
- Pandeo de las barras de refuerzo
- Falla por inadecuado anclaje o insuficiente adherencia
- Falla por cortante en miembros estructurales
3.9. Características de la respuesta no lineal
El parámetro más conveniente para cuantificar la ductilidad global de un sistema estructural baso cargas sísmicas es la ductilidad de desplazamiento µδ. Esta ductilidad puede ser expresada como ductilidad de entrepiso en lugar de ductilidad de desplazamiento del nivel de cubierta. La ductilidad traslacional de entrepiso es una medida de la distribución de la ductilidad a lo largo de la altura de edifcios de múltiples niveles y puede ser utilizada para detectar demandas inelásticas localizadas en edificios irregulares.
La ductilidad de desplazamiento se fundamenta en la relación:
|
|
(3.2) |
donde es el desplazamiento último y es el desplazamiento de plastificación. Sin embargo la evaluación de estas características no siempre es sencilla, especialmente en el caso de que no siempre está claramente definido, como consecuencia de la no linealidad de la respuesta que se obtiene luego de un proceso que combina el agrietamiento del hormigón y la plastificación del acero en distintos puntos de la estructura. Según Park [54] existen varias definiciones del punto de plastificación:
La deformación que produce la primera plastifiación de un sistema elasto-plástico equivalente con la misma rigidez inicial y el mismo cortante último del sistema real.
La deformación correspondiente al punto de plastificación de un sistema elastoplástico equivalente con la misma energía absorbida que el sistema real.
La deformación correspondiente al punto de plastificación de un sistema elastoplástico equivalente con una rigidez inicial reducida (75% del valor del cortante último).
La utilización de una rigidez secante toma en consideración la reducción de la rigidez estructural bajo agrietamientos. [6]
De manera similar se tienen las siguientes definiciones para las deformaciones últimas, Park (1988):
a. Deformación hasta un valor límite de deformación.
b. Deformación correspondiente al punto de cortante máximo.
c. Deformación correspondiente a un desplazamiento post-pico en el cual ocurre la pérdida de parte de la resistecia lateral (entre un 10% y un 15%)
d. Deformación correspondiente a la fractura o pandeo.
Las estructuras ususalmente tienen una resistencia post-pico remanente y no sufren una reducción abrupta en resistencia, especialmente para pórticos especiales resistentes a momentos. Las deformaciones calculadas conforme a los cirterios a y b pueden subestimar la respuesta estructural. Por tanto, se considerán más realistas los criterios c y d [6].
3.10. Capacidad dúctil y factores de reducción de fuerzas
Ya es conocida la relación que existe entre la demanda de ductilidad y el factor de reducción de respuesta; de hecho, el análisis sísmico usa dicha relación para obtener las fuerzas de diseño, ver Figura 3.26.
|
|
(3.3) |
La idealización mostrada en la que se igualan los desplazamientos, es inadecuada para estructuras de períodos bajos y altos y también resulta de dudosa validez para estructuras de períodos intermedios cuando las características de la respuesta inelástica se desvía de la respuesta elasto-plástica de manera significativa.
Adicionalmente, no existe consenso en cuanto a la definición apropiada de los desplazamientos de plastificación y último.
- Aunque la resistencia nominal representa otra fuente de incertidumbre.
El desplazamiento de plastificación se suele definir como: la intersección de la línea que va desde el origen con una rigidez inicial y la resistencia nominal.*(Punto también suele definirse mediante el punto de primera plastificación estructural (otra fuente de incertidumbre) lo que permite definir una rigidez secante con el origen y luego se intersecta con la rigidez nominal (originando el punto 3). Los desplazamientos del punto 3 suelen ser entre 1,8 y 4 veces más grandes que los del punto 1.
El desplazamiento del punto último también presenta varias definiciones. Entre las más usadas se encuentra el desplazamiento en el punto de corte máximo (punto 4), el desplazamiento correspondiente a la disminución del 20% a 50% de la resistencia máxima (punto 5) y el desplazamiento para el cual se produce fractura en el refuerzo transversal. Ver Figura 3.27.
Obviamente, con esa gran variedad de valores de desplazamientos límite, es lógico que se presente una variación considerable ante los valores de la ductilidad calculados por diferentes métodos [31].
3.11. Definición de ductilidad según N2
Uno de los métodos utilizados para determinar la capacidad de una estructura frente a un nivel de demanda específico, es el método N2 [49].En este método la capacidad estructural se obtiene a partir del análisis no lineal con empuje incremental, dando como resultado la curva de capacidad del edificio. Esta curva de capacidad se transforma en espectro de capacidad luego de aplicar una serie de operaciones que convierten la respuesta de un sistema de un grado de libertad equivalente.
Llegados a este punto, se tiene el problema recurrente de ¿dónde ocurre la plastificación global de la estructura?. Para resolverlo se procede a idealizar el espectro de capacidad mediante una forma bi-lineal, que se construye mediante un tramo horizontal (que algunos autores definen según el punto máximo de cortante) y un tramo secante, que va desde el origen hasta un punto cuyo cortante iguala al 60% del cortante máximo. La intersección de la rama horizontal con la rama secante da origen al punto de plastificación global.
Luego, se obtiene el punto de capacidad por demanda , aplicando un procedimiento que involucrea al espectro elástico de diseño. Este punto representa la capacidad de la estructura cuando es sometida a una acción equivalente al terremoto de diseño y se interpreta a través de la relación:
|
|
(3.4) |
como la ductilidad que alcanza la estructura [31].
3.12. Proceso de los resultados del análisis no lineal
Como se ha mostrado, existen varios criterios para el cálculo de la ductilidad global o de desplazamiento de una estructura, partiendo del análisis no lineal. Por este motivo, se propone un método alternativo que procura determinar de forma objetiva los valores de la ductilidad de sistemas estructurales con diferentes tipos de fallo. Este método procura alcanzar el balance de la energía disipada obtenida de la curva de capacidad y de la forma idealizada que la representa. Ver Figuras 3.28 y 3.29.
Determinación del punto de fallo de un edificio
Criterios utilizados
De acuerdo con investigaciones que se han llevado a cabo en las dos décadas pasadas, existe una gran variedad de criterios adoptados para definir el punto de fallo de un edificio sometido al análisis con empuje incremental.
Una nueva propuesta para calcular la ductilidad de desplazamiento
Habiendo estudiado los modelos utilizados para determinar la ductilidad de desplazamiento y conocidas las fortalezas y debilidades de cada uno de ellos, cabe preguntarse si es posible formular un nuevo modelo que de alguna manera reduzca las debilidades de los modelos existentes. Obviamente se trata de minimizar estas debilidades, entendiendo que es prácticamente imposible formular un modelo que permita satisfacer toda la casuística que se pueda llegar a producir. En este trabajo se propone un procedimiento que en primer lugar pretende satisfacer el criterio de que la forma idealizada de la curva de capacidad debe satisfacer la cantidad de energía disipada en la curva de capacidad.
Para lograr este equilibrio energético resulta evidente que el modelo propuesto por [54] resulta inconveniente, ya que fijar el desplazamiento último como el punto en el que se produce el cortante en la base máximo usualmente conduce a notables desbalances en las áreas bajo las curvas.
En el caso presente se hace uso del desplazamiento último con base en la rotación última. Este procedimiento combina tanto criterios locales como global de fallo y es una extensión de un procedimiento similar aplicado por [10] la determinación del fallo de edificios de estructura metálica. Para decidir en qué paso de carga se produce el fallo global de la estructura, se toma en consideración los tipos de fallos que han sido considerados en el punto anterior. Nótese que tanto para el fallo por distorsión de columnas, como por distorsión de vigas como el mecanismo mixto, estos se alcanzan cuando todos los extremos inferiores de las columnas alcanzan la rotación última, independientemente de la secuencia de aparición de rotaciones últimas en los extremos del resto de los miembros de la estructura.
En la Figura 3.30 puede apreciarse la deformada del edificio “H” sin vigas de cierre cuando se ha sometido a cargas laterales en dirección x. Nótese que el fallo se obtiene justo en el momento en el cual se ha alcanzado la rotación última en todos los extremos de columnas de planta baja. Este paso de carga permite obtener el valor del desplazamiento correspondiente en la curva de capacidad, en el caso presente el desplazamiento último es igual a 0,355m.
El procedimiento contempla la selección de un punto de comportamiento elástico sobre la curva de capacidad. Este punto corresponde al valor del cortante en la base en el cual se comienza a degradar la rigidez inicial, o sea, en el punto en el que se comienza a reducir la pendiente inicial. Este punto se tomará como punto de “pívot”, para el trazado del segundo tramo de la curva de capacidad idealizada.
Este segundo tramo llega hasta el punto en que se alcanza la plastificación global de la estructura. Para determinarlo, se realiza el ajuste del punto de plastificación hasta lograr que las áreas bajo las curvas de capacidad original e idealizada se igualen. Como se sabe, las áreas bajo ambas curvas se obtienen mediante la integración de las mismas desde el origen hasta el punto del desplazamiento último determinado mediante el procedimiento anterior. En la Figura 3.31 se muestra el resultado de aplica el procedimiento descrito al Edificio H sin viga analizado en dirección x.
Nótese la buena correspondencia entre el punto de intersección de las curvas que representan las integrales y el punto de desplazamiento último.
En las Figuras 3.32 y 3.33 se puede apreciar el tipo de falla frágil con su correspondiente curva de capacidad.
Finalmente, en las Figuras 3.34 y 3.35, se puede apreciar el tipo de falla dúctil con su curva de capacidad.
3.13. Determinación de la rotación de los elementos
La capacidad de rotación de la cuerda de la deformada depende tanto de las propiedades geométricas y mecánicas del elemento considerado como de la acción sísmica presentada; por lo cual, dicha rotación no puede ser definida como una propiedad intrínseca de un elemento. El enfoque correcto, por lo tanto, es calcular la capacidad como una función de la demanda sísmica. Vale destacar que la evaluación sería mucho más simple y rápida si fuera posible eliminar la dependencia de la demanda y reemplazar cálculos teóricos complejos con formulaciones empíricas sencillas, por lo cual se presenta una expresión empírica para la determinación de la rotación última de la cuerda de la deformada, basándose en resultados de carga cíclica con base a métodos estadísticos. Los resultados de los edificios analizados se muestran en las Tablas A.7 a la A.13 de los anexos
3.14. Método N2
N2 se presenta como un método para determinar el punto de demanda por capacidad de una estructura y así caracterizar la respuesta sísmica de la misma frente a un terremoto similar al normativo a través del análisis no lineal con empuje incremental. Se hace uso del desplazamiento correspondiente al punto de demanda por capacidad para luego efectuar evaluaciones a través del método de los cuadrantes y el índice de daño.
Vale acotar que N2 es efectivo en estructuras regulares en planta y elevación; para su aplicación se realiza la superposición del espectro de capacidad con el espectro de demanda de la estructura. Es importante señalar que el espectro de capacidad surge de la curva de capacidad correspondiente a un sistema de un grado de libertad equivalente y con forma bilineal idealizada. Se toma en consideración el efecto del primer modo de vibración de la edificación. Dicho procedimiento se realizó de la siguiente manera:
Transformación de la respuesta no lineal pseudo-estática a un sistema de un grado de libertad equivalente, para lo cual se determinan el factor de participación modal FPM y el coeficiente de masa efectiva CME a través de los desplazamientos del primer modo de vibración en cada nivel (análisis no lineal, autovalores) normalizados respecto al período del primer modo de vibración de la estructura, las masas por niveles y el peso sísmico de cada nivel. Ver Tabla 3.13.
| Desplazamientos del primer modo en cada nivel autovalores | ||
| Fi | Edificio | NODOS EN CADA NIVEL |
| 1,27E-05 | nivel 1 | n112 |
| 3,24E-05 | nivel 2 | n113 |
| 4,85E-05 | nivel 3 | n114 |
| T=0.3893 | ||
| Normalizados | ||
| 2,62E-01 | ||
| 6,68E-01 | ||
| 1 | ||
| Masas por niveles | ||
| Masas | ||
| 34001,37615 | nivel 1 | |
| 33423,3945 | nivel 2 | Peso sísmico |
| 25145,87156 | nivel 3 | 908118 kgf |
| Factor de participación modal | ||
| Numerador | Denominador | |
| 8896,698652 | 2327,883629 | 4,32E-01 |
| 22338,50467 | 14929,92554 | 1,08E+00 |
| 25145,87156 | 25145,87156 | 1,22E+00 |
| 56381,07488 | 42403,68073 | 2,74E+00 |
| FPM | 1,329626908 | |
| Coeficiente de masa efectiva | ||
| Numerador | Denominador 1 | Denominador 2 |
| 3178825605 | 92570,6422 | 42403,68073 |
| CME | 0,809822558 | |
Transformación de la curva de capacidad a espectro de capacidad, para lo cual se hace uso de los factores anteriormente determinados (factor de participación modal FPM y el coeficiente de masa efectiva CME). Ver Figura 3.37.
Se procede a graficar el espectro de demanda superpuesto con el espectro de capacidad; seguido de la determinación del espectro inelástico para lo cual se realiza un procedimiento gráfico en el que se obtiene la curva de capacidad idealizada a través de ciertos puntos como el origen (0,0), las coordenadas del de la curva de capacidad y el 60% de , generando así un tramo horizontal y un tramo secante, que va desde el origen hasta un punto cuyo cortante iguala al 60% del cortante máximo. Se realiza una prolongación de una linea recta que pasa por el origen hasta el espectro elástico calculando asi dicha intersección que sirve para la determinación de la ductilidad (identificando la intersección en la meseta del espectro elástico) que se define como la razón del desplazamiento de plastificación de la curva idealizada y el desplazamiento del punto de capacidad. Finalmente se determina el punto de demanda por capacidad como el punto generado por la intersección del espectro inelástico y la curva de capacidad idealizada. Ver Figura 3.38.
El punto de demanda por capacidad permite evaluar la respuesta sísmica de la estructura a través del método de los cuadrantes y el índice de daño objetivo, en ambos procedimientos se debe re-transformar la respuesta de un sistema de un grado de libertad equivalente a la respuesta de un sistema estructural con múltiples grados de libertad, para lo cual se utiliza nuevamente el factor de participación modal y el coeficiente de masa efectiva .
El método de los cuadrantes es un procedimiento gráfico en el cual se debe disponer de la curva de capacidad normalizada, la cual es generada como la razón de la deriva total entre la altura total de edificio y el cortante en la base entre el peso sísmico. Luego de transformar el desplazamiento del punto de demanda por capacidad en un sistema de 3GDL por nivel, se debe normalizar dicho desplazamiento y se procede a graficar junto a la curva de capacidad normalizada. Es importante señalar que los ejes vertical y horizontal que definirán los cuadrantes en dicho gráfico surgen como los valores de cortante dinámico normalizado ( ) para el eje horizontal y el desplazamiento del centro de gravedad de nivel de cubierta para el desplazamiento del estado límite de daños reparables (ELDR), normalizado para el eje vertical. Si el punto se encuentra en el primer cuadrante es indicativo de un comportamiento adecuado de la estructura. Ver Figura 3.39.
Por otro lado, el índice de daño se determina a través de la curva deriva global normalizada y el índice de daño. Dichos valores de índice de daño provienen de una ecuación que tiene como base datos como: la pendiente que resulta del cociente entre el cortante y deriva normalizada; pendiente máxima y el desplazamiento último normalizado. Se debe graficar el punto de demanda por capacidad normalizado sobre la curva y así obtener para dicho punto el valor del índice de daño y la deriva en la cual se alcanza dicho daño en la estructura. Ver Figura 3.40. Este valor de índice de daño permite caracterizar la respuesta sismorresistente de las estructuras mediante un número único que indica si la misma es dúctil o frágil.
3.15. El método N2 extendido
N2 extendido surge de la necesidad de refinar el método N2 clásico, el cual presenta ciertas limitaciones en estructuras con irregularidades en planta y elevación, ya que para las mismas al considerar un modelo idealizado de un sistema de un grado de libertad con el efecto del periodo del primer modo de vibración es poco cercano a la realidad. Por lo tanto, el método N2 extendido es un procedimiento en el cual se consideran los efectos de modos superiores de vibración en los que se incorpora la respuesta dinámica de las estructuras irregulares, por lo que se aplican unos factores de corrección tanto en planta como en elevación a los resultados obtenidos de N2 clásico. Así mismo, es importante destacar que a través de los resultados obtenidos se determinan factores de prestaciones sísmicas (derivas, índice de daño local, torsores, rotaciones, P-delta) que describen el comportamiento estructural de las edificaciones estudiadas. El desarrollo del método se detalla a continuación:
| Análisis modal-espectral | Deriva de entrepiso (%) | Nivel | |
| Espectro elástico de diseño | 0 | 3 | |
| Nivel | Desplazamiento (mm) | 0,497 | 3 |
| 3 | 57,80 | 0,497 | 2 |
| 2 | 42,90 | 0,850 | 2 |
| 1 | 17,40 | 0,850 | 1 |
| 0 | 0 | 0,580 | 1 |
| 0,580 | 0 | ||
Paso 1. Análisis modal espectral utilizando el espectro elástico de diseño, determinación de las derivas de entrepiso a través de los desplazamientos de los centros de gravedad de cada piso. Ver Tabla 3.14.
Paso 2. Determinación de deriva de entrepiso a través de los desplazamientos obtenidos para los centros de masa cuando se produce el desplazamiento del punto de capacidad por demanda de nivel de cubierta en análisis con empuje incremental (pushover) del método N2 clásico. Ver Tabla 3.15.
| N2 clásico | Deriva de entrepiso (%) | Nivel | |
| Análisis pushover | 0 | 3 | |
| Desplazamiento (mm) | Nivel | 1,151 | 3 |
| 121,59 | 3 | 1,150 | 2 |
| 87,07 | 2 | 1,646 | 2 |
| 37,67 | 1 | 1,647 | 1 |
| 0,00 | 0 | 1,256 | 1 |
| 1,256 | 0 | ||
| 0 | 0 | ||
Paso 3. Determinación de derivas de entrepiso, obtenidas con los desplazamientos del análisis modal espectral afectado por un factor de escala el cual corresponde a la relación entre los desplazamientos del N2 clásico (obtenidos en el Paso 2) y los desplazamientos del modal espectral obtenidos en el Paso 1. Ver Tabla 3.16.
| Valores del análisis modal-espectral escalados | Deriva de entrepiso (%) | Nivel | |
| Desplazamiento (cm) | Nivel | 0,000 | 3 |
| 121,58 | 3 | 1,045 | 3 |
| 90,24 | 2 | 1,045 | 2 |
| 36,60 | 1 | 1,788 | 2 |
| 0,000 | 0 | 1,788 | 1 |
| 1,220 | 1 | ||
| 1,220 | 0 | ||
| Factor de escala | 2,103583045 | 0,000 | 0 |
Paso 4. Cálculo del factor de corrección por elevación tomando en consideración la acción de los modos superiores de vibración. El factor de corrección de desplazamientos surge como el cociente entre el desplazamiento modal espectral escalado y el desplazamiento obtenido del análisis pushover. El factor de corrección de derivas se obtiene como la razón entre las derivas del análisis modal espectral escalado y las derivas del método N2 clásico. Los valores de desplazamiento y derivas corregidos por elevación serán los correspondientes al producto de los desplazamientos del N2 clásico y su respectivo factor de elevación determinado según este Paso. Ver Tabla 3.17.
| Factor de corrección por la acción de modos superiores | |||
| Factor de corrección de desplazamientos | CE | Nivel | |
| Relación | Nivel | 1,000 | 3 |
| 1,000 | 3 | 1,036 | 2 |
| 1,036 | 2 | 1,000 | 1 |
| 0,971 | 1 | 1,000 | 0 |
| 1,000 | 0 | ||
| Factor de corrección de derivas | CE | Nivel | |
| Relación | Nivel | 1,000 | 3 |
| 0,908 | 3 | 1,085 | 2 |
| 1,085 | 2 | 1,000 | 1 |
| 0,971 | 1 | 1,000 | 0 |
| 1,000 | 0 | ||
| Valores modificados de desplazamientos | Valores modificados de derivas | ||
| Desplazamiento (mm) | Nivel | Deriva de entrepiso (%) | Nivel |
| 121,587 | 3 | 0,000 | 3 |
| 90,243 | 2 | 1,150 | 3 |
| 37,674 | 1 | 1,150 | 2 |
| 0,000 | 0 | 1,788 | 2 |
| 1,788 | 1 | ||
| 1,255 | 1 | ||
| 1,255 | 0 | ||
| 0,000 | 0 | ||
Paso 5. Desplazamientos del centro de gravedad de los pórticos del edificio, obtenidos del análisis pushover, correspondientes a los originados por el factor de carga que produce el desplazamiento del punto de demanda por capacidad. Se procede a transformar dichos desplazamientos con respecto al desplazamiento del punto de demanda por capacidad y la normalización del mismo con respecto al CG del nivel de cubierta. Ver Tabla 3.18.
Paso 6. Desplazamiento del centro de gravedad de los pórticos del edificio, obtenidos mediante el análisis modal espectral, los cuales se transforman a desplazamiento del CG de nivel de cubierta y posteriormente se normalizan con respecto al CG del nivel de cubierta. Ver Tabla 3.19.
Paso 7. Cálculo del factor de corrección por planta tomando en consideración la acción de modos superiores de vibración y la ubicación del pórtico. Se realiza una relación de desplazamientos normalizados como los desplazamientos de los pórticos calculados mediante el análisis modal espectral, entre los desplazamientos de los pórticos obtenidos del análisis pushover. Ver Tabla 3.20.
| Factor de corrección por efecto de modos superiores en planta | ||||
| Desplazamiento del punto de demanda por capacidad | 1,22E+02 | |||
| CG nivel 3 | CG pórtico A | CG pórtico B | CG pórtico C | CG pórtico D |
| 121,590 | 119,768 | 120,585 | 120,543 | 119,632 |
| Transformación a desplazamiento del punto de demanda por capacidad | ||||
| CG nivel 3 | CG pórtico A | CG pórtico B | CG pórtico C | CG pórtico D |
| 1,22E+02 | 1,20E+02 | 1,21E+02 | 1,21E+02 | 1,20E+02 |
| Normalización respecto a CG nivel 3 | ||||
| CG nivel 3 | CG pórtico A | CG pórtico B | CG pórtico C | CG pórtico D |
| 1,00E+00 | 9,85E-01 | 9,92E-01 | 0,991 | 0,983 |
| Factor de corrección por efecto de modos superiores en planta | ||||
| Desplazamientos en los pórticos producidos por el análisis modal espectral | ||||
| Desplazamiento del CG nivel de cubierta | 57,800 | mm | Desplazamiento del punto de demanda por capacidad | 121,587 |
| CG nivel 3 | CG pórtico A | CG pórtico B | CG pórtico C | CG pórtico D |
| 57,8 | 80,504 | 80,695 | 80,695 | 80,505 |
| Transformación a desplazamiento del CG3 | ||||
| CG nivel 3 | CG pórtico A | CG pórtico B | CG pórtico C | CG pórtico D |
| 57,8 | 80,504 | 80,695 | 80,695 | 80,505 |
| Normalización respecto a CG nivel 3 | ||||
| CG nivel 3 | CG pórtico A | CG pórtico B | CG pórtico C | CG pórtico D |
| 1 | 1,392 | 1,396 | 1,396 | 1,392 |
Paso 8. Finalmente, se realiza la superposición de la corrección de los desplazamientos en planta y en elevación para determinar las derivas definitivas por el método N2 extendido. Los desplazamientos corregidos por modos superiores en planta surgen como el producto de los desplazamientos corregidos por modos superiores en elevación y el desplazamiento correspondiente en cada pórtico, obtenidos de acuerdo con la irregularidad en planta, ver Tabla 3.21. De la misma manera, las derivas corregidas por modos superiores en planta surgen como el producto de las derivas corregidas por modos superiores en elevación y las derivas correspondientes de cada pórtico. Ver Tabla 3.22.
| Factor de corrección por efecto de modos superiores en planta | ||||
| Factores de corrección según ubicación del pórtico | ||||
| Relación entre desplazamientos normalizados | ||||
| CG nivel 3 | CG pórtico A | CG pórtico B | CG pórtico C | CG pórtico D |
| 1 | 1,413 | 1,407 | 1,408 | 1,415 |
| Factores de corrección | ||||
| CG nivel 3 | CG pórtico A | CG pórtico B | CG pórtico C | CG pórtico D |
| 1 | 1,413 | 1,407 | 1,408 | 1,415 |
| Desplazamientos corregidos por modos superiores en elevación | |||||
| Desplazamiento (mm) | Nivel | ||||
| 121,587 | 3 | ||||
| 90,243 | 2 | ||||
| 37,674 | 1 | ||||
| 0,000 | 0 | ||||
| Desplazamientos corregidos por modos superiores en planta | |||||
| Pórtico A | Pórtico B | ||||
| Desplazamiento (mm) | Nivel | Desplazamiento (mm) | Nivel | ||
| 171,920 | 3 | 171,159 | 3 | ||
| 127,601 | 2 | 127,036 | 2 | ||
| 53,270 | 1 | 53,035 | 1 | ||
| 0,000 | 0 | 0,000 | 0 | ||
| CG 3 | Pórtico C | Pórtico D | |||
| Desplazamiento (mm) | Nivel | Desplazamiento (mm) | Nivel | Desplazamiento (mm) | Nivel |
| 121,587 | 3 | 171,218 | 3 | 172,116 | 3 |
| 90,243 | 2 | 127,080 | 2 | 127,747 | 2 |
| 37,674 | 1 | 53,053 | 1 | 53,331 | 1 |
| 0,000 | 0 | 0,000 | 0 | 0,000 | 0 |
Debe indicarse que tanto los desplazamientos como las derivas corregidas aplicando este procedimiento, no deben ser inferiores en ningún caso a los desplazamientos y derivas calculadas mediante el método N2 clásico, de manera que el efecto de la irregularidad sobre la respuesta sísmica del edificio siempre conduce a una corrección más desfavorable, penalizando de esta manera la irregularidad en planta y elevación.
| Derivas corregidas por modos superiores en elevación | |||||
| Deriva de entrepiso (%) | Nivel | ||||
| 0 | 3 | ||||
| 1,1505 | 3 | ||||
| 1,1505 | 2 | ||||
| 1,7880 | 2 | ||||
| 1,7880 | 1 | ||||
| 1,2558 | 1 | ||||
| 1,2558 | 0 | ||||
| 0,000 | 0 | ||||
| Derivas corregidos por modos superiores en planta | |||||
| Pórtico A | Pórtico B | CG | |||
| Deriva de
entrepiso (%) |
Nivel | Deriva de entrepiso (%) | Nivel | Deriva de
entrepiso (%) |
Nivel |
| 0,000 | 3 | 0,000 | 3 | 0,000 | 3 |
| 1,626 | 3 | 1,619 | 3 | 1,150 | 3 |
| 1,626 | 2 | 1,619 | 2 | 1,150 | 2 |
| 2,528 | 2 | 2,517 | 2 | 1,788 | 2 |
| 2,528 | 1 | 2,517 | 1 | 1,788 | 1 |
| 1,775 | 1 | 1,767 | 1 | 1,255 | 1 |
| 1,775 | 0 | 1,767 | 0 | 1,255 | 0 |
| 0,000 | 0 | 0,000 | 0 | 0,000 | 0 |
| Pórtico C | Pórtico D | ||||
| Deriva de
entrepiso (%) |
Nivel | Deriva de entrepiso (%) | Nivel | ||
| 0,000 | 3 | 0,000 | 3 | ||
| 1,620 | 3 | 1,628 | 3 | ||
| 1,620 | 2 | 1,628 | 2 | ||
| 2,517 | 2 | 2,531 | 2 | ||
| 2,517 | 1 | 2,531 | 1 | ||
| 1,768 | 1 | 1,777 | 1 | ||
| 1,768 | 0 | 1,777 | 0 | ||
| 0,000 | 0 | 0,000 | 0 | ||
3.16. Índice de irregularidad torsional
El índice de irregularidad torsional es un índice que permite cuantificar de manera rápida el grado de susceptibilidad que posee una estructura determinada de sufrir efectos negativos producto de la torsión. Para determinar el índice de irregularidad torsional se parte de valores que se determinan de manera sencilla.
La expresión para determinar el índice de irregularidad torsional está dado por:
|
|
(3.5) |
En donde: y son el perímetro y el área del polígono que define la planta, respectivamente. y son el perímetro y el área de un rectángulo que daría cabida completamente a la panta de la estructura, respectivamente. y son la coordenada del centro de rigidez de la planta rectangular y de la planta irregular, respectivamente. Finalmente, es la longitud total del lado paralelo a la coordenada del centro de rigidez, en la dirección que se está considerando. Ver Figura 3.40 y la Tabla 3.23 con los valores calculados para los edificios objeto de estudio. Estos valores serán retomados al estudiar el efecto sobre los momentos torsores obtenidos del análisis no lineal, lo que permitirá evaluar la pertinencia de la expresión analítica propuesta.
| Estructura | Area (m2) | Perímetro (m) | IEi=Pi/Ai (m-1) | IENi=IEi/IE1 | YCR | eCRi=|yCR1-yCRi| | ri=eCRi/L | pi=1+ri0,25 | IITi=Iei*pi |
| Completa | 324,00 | 72,00 | 0,22 | 1,00 | 9,00 | 0,00 | 0,00 | 1,00 | 1,00 |
| H con viga | 252,00 | 72,00 | 0,29 | 1,29 | 9,00 | 0,00 | 0,00 | 1,00 | 1,29 |
| H sin viga | 252,00 | 96,00 | 0,38 | 1,71 | 9,00 | 0,00 | 0,00 | 1,00 | 1,71 |
| U con viga | 288,00 | 72,00 | 0,25 | 1,13 | 9,00 | 0,00 | 0,00 | 1,00 | 1,13 |
| U sin viga | 288,00 | 84,00 | 0,29 | 1,31 | 8,49 | 0,51 | 0,03 | 1,41 | 1,85 |
| UU con viga | 252,00 | 72,00 | 0,29 | 1,29 | 9,00 | 0,00 | 0,00 | 1,00 | 1,29 |
| UU sin viga | 252,00 | 96,00 | 0,38 | 1,71 | 8,28 | 0,72 | 0,04 | 1,45 | 2,48 |
3.17. Momentos torsores en el punto de capacidad por demanda
Al presentarse irregularidad en las estructuras el centro de rigidez se aleja del centro de gravedad generándose así momentos torsores. En esta investigación se han recogido los resultados de los momentos torsores que se producen en los empotramientos de las columnas una vez que se ha realizado el análisis no lineal con empuje incremental, con la finalidad de compararlos entre sí y comparar los momentos torsores que se producen en las estructuras con diferente irregularidad en planta.
En la Figura 3.41 se muestran los resultados de la estructura completa. En esta figura puede notarse una representación tri-dimensional, en la que en los ejes x e y se han colocado en estas direcciones, lo cual permite localizar las columnas, mientras que en el eje z se ha graficado el valor correspondiente del momento torsor alcanzado en la columna cuando la estructura alcanza el punto de capacidad por demanda. Nótese que los colores indican la variación de los torsores de columna a columna, valores que se han interpolado de los valores registrados para cada columna, dependiendo de la ubicación de estas en planta. Nótese que los colores mostrados denotan una pequeña variación de los momentos torsores en planta cuando se aplica el análisis en dirección x, lo que indica que las solicitaciones por torsión en las columnas de planta baja son bastante uniformes para la estructura completamente regular.
En el caso de la estructura con mayor irregularidad en planta, la UU sin viga de cierre, la Figura 3.42 que contiene los resultados del análisis en la dirección en la que esta estructura presenta irregularidad en planta (dirección x), muestran una notable variación de los momentos torsores. Por ejemplo, para las columnas emplazadas en el eje D, que resulta ser el más alejado del centro de rigidez de la planta, las columnas experimentan momentos torsores de signo negativo muy similares entre las cuatro columnas de dicho eje. Similar comportamiento se aprecia en las columnas del eje C, con la excepción de la columna C-3, en la que se produce un incremento puntual del torsor. Luego, al estar en el eje B, cuya coordenada y es inferior a la coordenada y del centro de rigidez, se produce una natural inversión del signo de los momentos torsores, que afecta a las columnas del eje B, hasta alcanzar las columnas del eje A, que, siendo el eje más alejado del centro de rigidez, presenta los mayores valores positivos de los momentos torsores.
Si en este punto se comparan los valores de los momentos torsores de la Figura 3.42 con los de la Figura 3.42, puede notarse que los máximos torsores de la estructura irregular son prácticamente 12 veces mayores que los de la estructura regular. De esta manera se demuestra lo que siempre se ha resaltado en las normas de diseño sismorresistente y en las publicaciones sobre diseño conceptual: que la irregularidad en planta incrementa la solicitación torsional sobre las columnas de la estructura, pero que se ha tratado de manera intuitiva, sin recibir una valoración comparada como la que se muestra en este apartado.
Finalmente, en la Figura 3.43 se muestran los resultados del análisis aplicado al edificio UU sin viga, pero esta vez obtenidos en el análisis en dirección y. Nótese que, debido a la simetría de la estructura en esta dirección, el centro de rigidez presenta una excentricidad nula con respecto al centro de gravedad, por lo que se reducen los efectos de la torsión, queda claro que existe una pequeña variación de los momentos torsores en las diferentes columnas de la planta baja de este edificio.
3.18. Curvas de fragilidad de colapso
Las curvas de fragilidad de colapso se determinan con la media de las diez curvas IDAS de cada una de las estructuras en cada una de las direcciones. Se toma de la media de las curvas la aceleración correspondiente al punto donde la pendiente se haga menor al 20% de la pendiente inicial, valor que se ha denominado intensidad media de colapso ( ). Además, se debe contar con la desviación estándar de la intensidad media de colapso, el cual es constante en todos los modelos de acuerdo con las recomendaciones de la metodología del FEMA P695, con un valor correspondiente a 0,4. Se obtiene el gráfico de la curva de fragilidad con las coordenadas de la aceleración espectral obtenida de los resultados de las curvas IDAS y la probabilidad de colapso de la estructura que corresponde a una distribución log-normal. Vale indicar que esta es una distribución que está programada en las hojas de cálculo de Excel, por tanto, su generación es inmediata. Ver Figura 3.44.
Estas curvas permiten determinar la probabilidad de excedencia del estado de colapso para un valor dado de aceleración espectral. De esta manera, es posible conocer la probabilidad de que, alcanzado un cierto valor de aceleración espectral, la estructura alcance el colapso. Esta probabilidad de colapso es un indicador directo del porcentaje del costo inicial que se necesitaría invertir en una estructura una vez ocurrido un evento sísmico, caracterizado mediante la aceleración espectral. Por ejemplo, si una estructura es diseñada para una aceleración de 0,3g para su vida útil, que en el caso de los edificios residenciales es de 50 años, al entrar con este valor de aceleración espectral en la curva de fragilidad de colapso se obtiene un valor de probabilidad de excedencia de, por ejemplo, 0,5. Esto significa que existe un 50% de probabilidad de que la estructura bajo ese valor de aceleración, alcance el colapso, lo que requeriría que el propietario disponga de un monto equivalente al 50% de la inversión inicial para asumir la reposición de la edificación. Esto desde un punto de vista práctico se materializa mediante la contratación de un seguro que cubra esa probabilidad de colapso, siendo esa probabilidad de colapso repartida en la prima pura que cobran las aseguradoras, repartida a lo largo de la vida útil del inmueble. El edificio obviamente se asegura por el monto total de su reposición, más costos asociados con la demolición y los costos asociados con los componentes no estructurales y contenidos.
3.19. Evaluación del factor de reducción de respuesta R a través del FEMA P695
FEMA P695 presenta una serie de parámetros que son utilizados para realizar la evaluación del factor de reducción de respuesta empleado en los modelos realizados. Vale acotar que el ratio medio de colapso se determina como factor inicial para realizar la caracterización de la seguridad estructural frente al colapso; dicho valor se debe corregir en base a las incertidumbres establecidas en la metodología. A continuación, se describe el proceso:
Cálculo de la aceleración del máximo terremoto considerado , obtenido del espectro elástico como la aceleración correspondiente del periodo del primer modo de vibración por cada dirección de análisis de cada estructura. Es relevante señalar que el de todas las estructuras es de 0,78.
Determinación de la razón media de colapso como el cociente entre el valor de la aceleración en la curva media obtenida en las IDA estándar y la aceleración del máximo terremoto considerado .
|
|
(3.6) |
Corrección de a través del factor de forma espectral , el cual está determinado por la ductilidad y el periodo del primer modo de vibración de cada estructura. Ver Tabla 3.24 a la 3.28 y la Figura 3.45.
|
|
(3.7) |
| T (s) | Ductilidad con base en el periodo | |||||||
| 1 | 1,1 | 1,5 | 2 | 3 | 4 | 6 | ≥8 | |
| ≤ 0,5 | 1,00 | 1,02 | 1,04 | 1,06 | 1,08 | 0,09 | 1,12 | 1,14 |
| 0,6 | 1,00 | 1,02 | 1,05 | 1,08 | 1,09 | 1,11 | 1,13 | 1,16 |
| 0,7 | 1,00 | 1,03 | 1,06 | 1,08 | 1,10 | 1,12 | 1,15 | 1,18 |
| 0,8 | 1,00 | 1,03 | 1,06 | 1,08 | 1,11 | 1,14 | 1,17 | 1,20 |
| 0,9 | 1,00 | 1,03 | 1,07 | 1,09 | 1,13 | 1,15 | 1,19 | 1,22 |
| 1 | 1,00 | 1,04 | 1,08 | 1,10 | 1,14 | 1,17 | 1,21 | 1,25 |
| 1,1 | 1,00 | 1,04 | 1,08 | 1,11 | 1,15 | 1,18 | 1,23 | 1,27 |
| 1,2 | 1,00 | 1,04 | 1,09 | 1,12 | 1,17 | 1,20 | 1,25 | 1,30 |
| 1,3 | 1,00 | 1,05 | 1,10 | 1,13 | 1,18 | 1,22 | 1,27 | 1,32 |
| 1,4 | 1,00 | 1,05 | 1,10 | 1,14 | 1,19 | 1,23 | 1,30 | 1,35 |
| ≥1,5 | 1,00 | 1,05 | 1,11 | 1,15 | 1,21 | 1,25 | 1,32 | 1,37 |
| x | y | |
| Completa | En T = 0,60293 | En T = 0,60293 |
| Sa = 0,78 | Sa = 0,78 | |
| H con viga | En T = 0,49814 | En T = 0,49968 |
| Sa = 0,78 | Sa = 0,78 | |
| H sin viga | En T = 0,50067 | En T = 0,4928 |
| Sa = 0,78 | Sa = 0,78 | |
| U con viga | En T = 0,57353 | En T = 0,57229 |
| Sa = 0,78 | Sa = 0,78 | |
| U sin viga | En T = 0,578 | En T = 0,56872 |
| Sa = 0,78 | Sa = 0,78 | |
| UU con viga | En T = 0,60018 | En T = 0,58256 |
| Sa = 0,78 | Sa = 0,78 | |
| UU sin viga | En T = 0,60018 | En T = 0,58256 |
| Sa = 0,78 | Sa = 0,78 |
| Estructuras | Sa
SMT | |
| Completa | 0,602 | 0,780 |
| H con viga en x | 0,498 | 0,780 |
| H con viga en y | 0,500 | 0,780 |
| H sin viga en x | 0,501 | 0,780 |
| H sin viga en y | 0,493 | 0,780 |
| U con viga en x | 0,574 | 0,780 |
| U con viga en y | 0,572 | 0,780 |
| U sin viga en x | 0,578 | 0,780 |
| U sin viga en y | 0,569 | 0,780 |
| UU con viga en x | 0,600 | 0,780 |
| UU con viga en y | 0,583 | 0,780 |
| UU sin viga en x | 0,600 | 0,780 |
| UU sin viga en y | 0,583 | 0,780 |
| Estructuras | Periodo del primer modo | Ductilidad idealizada | SSF |
| Completa | 0,602 | 5,568 | 1,125 |
| UU sin viga x | 0,600 | 6,634 | 1,139 |
| UU sin viga y | 0,582 | 5,878 | 1,128 |
| UU con viga en x | 0,551 | 5,196 | 1,117 |
| UU con viga en y | 0,549 | 5,209 | 1,112 |
| U sin viga x | 0,578 | 5,967 | 1,129 |
| U sin viga y | 0,568 | 5,188 | 1,117 |
| U con viga x | 0,573 | 6,740 | 1,137 |
| U con viga y | 0,572 | 5,265 | 1,118 |
| H sin viga x | 0,582 | 5,378 | 1,123 |
| H sin viga y | 0,576 | 5,493 | 1,124 |
| H con viga x | 0,498 | 5,370 | 1,110 |
| H con viga y | 0,499 | 4,895 | 1,103 |
| Estructuras | SCT | CMR (SCT/SMT) | SSF | ACMR |
| Completa | 1,646 | 2,110 | 1,126 | 2,375 |
| H con viga en x | 1,578 | 2,024 | 1,111 | 2,247 |
| H con viga en y | 1,526 | 1,957 | 1,103 | 2,159 |
| H sin viga en x | 1,567 | 2,009 | 1,124 | 2,258 |
| H sin viga en y | 1,498 | 1,920 | 1,125 | 2,160 |
| U con viga en x | 1,474 | 1,890 | 1,137 | 2,150 |
| U con viga en y | 1,399 | 1,794 | 1,119 | 2,007 |
| U sin viga en x | 1,586 | 2,033 | 1,130 | 2,297 |
| U sin viga en y | 1,604 | 2,056 | 1,118 | 2,298 |
| UU con viga en x | 1,431 | 1,835 | 1,118 | 2,051 |
| UU con viga en y | 1,403 | 1,799 | 1,112 | 2,000 |
| UU sin viga en x | 1,410 | 1,808 | 1,140 | 2,060 |
| UU sin viga en y | 1,545 | 1,9801 | 1,129 | 2,236 |
| Incertidumbres FEMA P695 | |
| 0,4 | |
| 0,4 | |
| 0,1 | |
| 0,1 | |
| 0,58 | |
Se establece la incertidumbre total de acuerdo a fórmula establecida en el FEMA P695, la cual contempla una serie de variables que corresponden a la ductilidad de cada estructura, calidad o grado de actualización de la normativa empleada, incertidumbre debido a los datos de ensayos empleados y calidad del análisis o modelado empleado. Dicha incertidumbre es usada en el paso siguiente para la evaluación de R. Ver Tabla 3.29.
| (3.8) |
Evaluación del factor de reducción de respuesta según el de las estructuras en cada dirección de análisis según valores establecidos en FEMA P695 [11]. Ver Tablas 3.31 y 3.32.
|
|
(3.9) |
|
|
(3.10) |
| Incertidumbre total | 5% | 10%(ACMR 10%) | 15% | 20% (ACMR 20%) | 25% |
| 0,275 | 1,570 | 1,420 | 1,330 | 1,260 | 1,200 |
| 0,300 | 1,640 | 1,470 | 1,360 | 1,290 | 1,220 |
| 0,325 | 1,710 | 1,520 | 1,400 | 1,310 | 1,250 |
| 0,350 | 1,780 | 1,570 | 1,440 | 1,340 | 1,270 |
| 0,375 | 1,850 | 1,620 | 1,480 | 1,370 | 1,290 |
| 0,400 | 1,930 | 1,670 | 1,510 | 1,400 | 1,310 |
| 0,425 | 2,010 | 1,720 | 1,550 | 1,430 | 1,330 |
| 0,450 | 2,100 | 1,780 | 1,590 | 1,460 | 1,350 |
| 0,475 | 2,180 | 1,840 | 1,640 | 1,490 | 1,380 |
| 0,500 | 2,280 | 1,900 | 1,680 | 1,520 | 1,400 |
| 0,525 | 2,370 | 1,960 | 1,720 | 1,560 | 1,420 |
| 0,550 | 2,470 | 2,020 | 1,770 | 1,590 | 1,450 |
| 0,575 | 2,570 | 2,090 | 1,810 | 1,620 | 1,470 |
| 0,600 | 2,680 | 2,160 | 1,860 | 1,660 | 1,500 |
| 0,625 | 2,800 | 2,230 | 1,910 | 1,690 | 1,520 |
| 0,650 | 2,910 | 2,300 | 1,960 | 1,730 | 1,550 |
| 0,675 | 3,040 | 2,380 | 2,010 | 1,760 | 1,580 |
| 0,700 | 3,160 | 2,450 | 2,070 | 1,800 | 1,600 |
| 0,725 | 3,300 | 2,530 | 2,120 | 1,840 | 1,630 |
| 0,750 | 3,430 | 2,610 | 2,180 | 1,880 | 1,660 |
| 0,775 | 3,580 | 2,700 | 2,230 | 1,920 | 1,690 |
| 0,800 | 3,730 | 2,790 | 2,290 | 1,960 | 1,720 |
| 0,825 | 3,880 | 2,880 | 2,350 | 2,000 | 1,740 |
| 0,850 | 4,050 | 2,970 | 2,410 | 2,040 | 1,770 |
| 0,875 | 4,220 | 3,070 | 2,480 | 2,090 | 1,800 |
| 0,900 | 4,390 | 3,170 | 2,540 | 2,130 | 1,830 |
| 0,925 | 4,580 | 3,270 | 2,610 | 2,180 | 1,870 |
| 0,950 | 4,770 | 3,380 | 2,680 | 2,220 | 1,900 |
| FEMA P695 | Estructuras | ACMR | ACMR 10% FEMA
(todas las estructuras) |
ACMR 20% FEMA
(c/u de las estructuras) |
ACMRprom ≥ACMR10% ACMR≥ACMR20% |
| Completa | 2,375 | 2,113 | 1,633 | El valor de R normativo es seguro | |
| H con viga en x | 2,247 | El valor de R normativo es seguro | |||
| H con viga en y | 2,159 | El valor de R normativo es seguro | |||
| H sin viga en x | 2,258 | El valor de R normativo es seguro | |||
| H sin viga en y | 2,160 | El valor de R normativo es seguro | |||
| U con viga en x | 2,150 | El valor de R normativo es seguro | |||
| U con viga en y | 2,007 | El valor de R normativo es seguro | |||
| U sin viga en x | 2,297 | El valor de R normativo es seguro | |||
| U sin viga en y | 2,298 | El valor de R normativo es seguro | |||
| UU con viga en x | 2,051 | El valor de R normativo es seguro | |||
| UU con viga en y | 2,000 | El valor de R normativo es seguro | |||
| UU sin viga en x | 2,060 | El valor de R normativo es seguro | |||
| UU sin viga en y | 2,236 | El valor de R normativo es seguro | |||
| Todas las estructuras (promedio) | 2,177 | El valor de R normativo es seguro |
Una vez realizada la corrección en planta y elevación de las estructuras (N2 extendido) se determinan ciertos parámetros que son útiles en la caracterización de la respuesta estructural, como lo son el índice de daño, rotaciones, torsores y el efecto P-delta. El índice de daño se determina en las columnas de acuerdo a la ubicación en los pórticos correspondientes, surge como el cociente entre las derivas corregidas del método N2 extendido (demandas) entre theta U o las rotaciones ultimas (capacidad) que reflejan la máxima rotación del elemento antes de fallar. Los valores del índice de daño oscilan entre 0 y 1, en donde el 1 representa el agotamiento de la capacidad de la estructura o colapso. Ver Figura 3.46 y Figura 3.47.
Estos valores permiten determinar conforme a los resultados del método N2 extendido, la ubicación de las columnas en las que ocurriría el mayor daño. Este procedimiento puede ser útil con la finalidad de determinar algunos componentes débiles en la configuración de estructuras existentes que potencialmente deberían ser reforzados.
Las rotaciones de los centros de gravedad en cada nivel son extraídas del análisis con empuje incremental (pushover) en la fase del post proceso, siguiendo la ruta desplazamientos estructurales, rotación en el eje Z y nodos correspondientes a los centros de gravedad por cada nivel. Ver Figura 3.48.
Las torsores presentados en la base o apoyos de las columnas se obtienen en el análisis con empuje incremental (pushover) en la fase del post proceso, siguiendo la ruta fuerzas y momentos en los apoyos, momento en eje Z y fuerzas/ momentos totales en los apoyos. También se muestran los torsores en cada una de las columnas siguiendo la misma ruta, pero con opción fuerzas/ momentos individuales en los apoyos y selecciono el nodo de cada una de las columnas. Ver Figuras 3.49 y 3.50. Al presentarse irregularidad en las estructuras, el centro de rigidez se aleja del centro de gravedad generándose así momentos torsores.
Para determinar el efecto P-Delta se utiliza el análisis con empuje incremental (pushover) en la fase del post proceso, siguiendo la ruta fuerzas y momentos en los apoyos, momento en eje y, y fuerzas/ momentos totales en los apoyos. Se grafica el cortante en la base vs los momentos totales en apoyos en la dirección ortogonal a la del análisis, que equivale al momento de volcamiento para visualizar dicho efecto, el cual corresponde al punto máximo de cortante en la base a partir del cual el momento de volcamiento se incrementa a pesar de que las fuerzas laterales decrecen. Este efecto es debido a que, llegados a este punto, el aporte al momento de volcamiento por parte de las cargas gravitatorias es notable, dado el incremento de los desplazamientos laterales, que desplazan los puntos de aplicación de dichas cargas gravitatorias de su posición original. Ver Figura 3.52.
3.20. Determinación del factor de reducción de respuesta R mediante curvas IDAS
La determinación de R se realiza con la superposición de la curva media obtenida de las IDAS de cada estructura en cada una de sus direcciones y del espectro de capacidad de las mismas; por lo cual se establece R como la relación entre la aceleración de colapso de la curva media y la aceleración máxima del espectro de capacidad. Ver Tabla 3.32.
| Estructuras | Sa Colapso | Sa máxima | R con IDAS |
| completa | 5,185 | 0,509 | 10,186 |
| UU sin viga x | 4,096 | 0,521 | 7,853 |
| UU sin viga y | 4,688 | 0,598 | 7,836 |
| UU con viga en x | 4,184 | 0,604 | 6,920 |
| UU con viga en y | 4,066 | 0,602 | 6,748 |
| U sin viga x | 4,883 | 0,509 | 9,590 |
| U sin viga y | 4,970 | 0,557 | 8,916 |
| U con viga x | 4,368 | 0,552 | 7,912 |
| U con viga y | 4,051 | 0,549 | 7,372 |
| H sin viga x | 4,793 | 0,537 | 8,924 |
| H sin viga y | 4,470 | 0,608 | 7,347 |
| H con viga x | 4,847 | 0,604 | 8,019 |
| H con viga y | 4,601 | 0,596 | 7,711 |
Los resultados de la Tabla 3.32 muestran que los valores de determinados combinando los resultados del análisis no lineal son menores para los edificios irregulares que para el edificio regular.
Una vez analizadas las estructuras consideradas en esta monografía y calculados los factores de prestaciones sísmicas a través del FEMA P695; se puede establecer la influencia de la irregularidad sobre la amplificación de la respuesta sísmica de los componentes estructurales de los edificios porticados bajos de hormigón armado, además de proponer una serie de recomendaciones para el diseño de los mismos, los cuales presentan irregularidad producida por plantas con entrantes. Vale acotar que se diseñó el conjunto de edificios sin y con entrantes conforme a las normas venezolanas vigentes y se realizó análisis en el rango elástico e inelástico (método de elementos finitos) y dentro de este último, de manera pseudo-estática y dinámica para obtener la respuesta sísmica de las estructuras.
A través del análisis elástico [8] se determinaron las derivas (desplazamientos) y cuantía de acero (resistencia) de los elementos de todas las estructuras, en cada uno de sus niveles y por dirección de análisis, obteniendo valores de derivas que cumplen con los normativos y que son mayores en aquellas estructuras con mayor índice de irregularidad y que no presentan vigas de cierre incorporadas en sus entrantes (edificio U sin viga y UU sin viga). El análisis no lineal [9] se lleva a cabo mediante procedimientos no lineales de dos tipos, el pseudo-estático (pushover) y el análisis dinámico incremental (curvas IDAS), los cuales sirven de apoyo para aplicar ciertas metodologías en la determinación de los factores de prestaciones sísmicas.
El estudio de la respuesta de edificios con entrantes aplicando el análisis con empuje incremental (análisis Pushover) no dispone de reglas específicas de aplicación, la presencia de entrantes originan en las estructuras una interrupción en las líneas resistentes horizontales, lo que trae como consecuencia que al aplicar las cargas del empuje incremental conforme al patrón lateral usual, no va a conducir a resultados consistentes con la teoría de este tipo de análisis que pretende obtener la respuesta estructural no lineal, tomando en consideración exclusivamente efectos traslacionales. Para corregir esta situación, se ha realizado la modificación siguiente sobre las cargas incrementales laterales: se han mantenido los valores iniciales para los pórticos completos, manteniéndose la proporcionalidad entre las mismas. Seguidamente se modifican las cargas laterales que se aplican a los tres nodos del tramo incompleto, re-calculando los valores de las cargas de cada nivel. Para esto es útil obtener la rigidez de cada uno de los pórticos, tanto los completos como los incompletos y obtener la relación de las mismas del pórtico incompleto entre los pórticos completos. Es importante señalar que dada la simetría geométrica y de secciones, la rigidez del pórtico incompleto es un tercio de la rigidez de los pórticos completos. De acuerdo con esta relación, para que sobre el pórtico incompleto se produzcan los mismos desplazamientos laterales, se requiere de cargas laterales que sean un tercio de las cargas laterales aplicadas a los pórticos completos.
Por otro lado, se ha realizado el cálculo de la ductilidad global o de desplazamiento de una estructura, partiendo del análisis no lineal. En esta monografía se ha propuesto un método alternativo que procura determinar de forma objetiva los valores de la ductilidad de sistemas estructurales con el tipo de fallo de los mismos. En este trabajo se propone un procedimiento que en primer lugar pretende satisfacer el criterio de que la forma idealizada de la curva de capacidad debe satisfacer la cantidad de energía disipada en la curva de capacidad. En el caso presente se hace uso del desplazamiento último con base en la rotación última. El procedimiento contempla la selección de un punto de comportamiento elástico sobre la curva de capacidad. Este punto corresponde al valor del cortante en la base en el cual se comienza a degradar la rigidez inicial, o sea, en el punto en el que se comienza a reducir la pendiente inicial.
Este punto se tomará como punto de “pívot”, para el trazado del segundo tramo de la curva de capacidad idealizada. Este segundo tramo llega hasta el punto en que se alcanza la plastificación global de la estructura. Para determinarlo, se realiza el ajuste del punto de plastificación hasta lograr que las áreas bajo las curvas de capacidad original e idealizada se igualen. Como se sabe, las áreas bajo ambas curvas se obtienen mediante la integración de las mismas desde el origen hasta el punto del desplazamiento último determinado mediante el procedimiento anterior. Por otro lado, es relevante señalar la buena correspondencia entre el punto de intersección de las curvas que representan las integrales y el punto de desplazamiento último en todas las estructuras analizadas y el tipo de fallo presente en dichas estructuras es del tipo dúctil. La ductilidad determinada a través del método alternativo representa valores mayores con respecto a los de la metodología propuesta por Park siendo esta relación inversamente proporcional en el caso de la reserva de resistencia. La ductilidad en dirección x es mayor a la de la dirección y en los edificios analizados.
En el mismo orden de ideas, se realizó el cálculo de los valores de la rotación última de la cuerda de la deformada de vigas y columnas los cuales se utilizaron para el cálculo del índice de daño local en las estructuras analizadas, lo que permitió conocer el porcentaje de daño sufrido por la edificación una vez expuesta a terremotos a lo largo de toda su vida útil, dando paso al conocimiento de las áreas afectadas para establecer formas de recuperación y su impacto monetario. Entre los casos de estudio se presentan rotaciones últimas mayores en columnas esquineras, perimetrales y por ultimo las centrales, existiendo mayores rotaciones en pisos superiores. En cuanto a vigas en dirección x y perimetrales, sus rotaciones son mayores a las centrales y en dirección y, aumentando también su valor al incrementar de nivel.
Se ha empleado el método N2 para determinar el punto de demanda por capacidad de las estructuras y así caracterizar la respuesta sísmica de la misma frente a un terremoto similar al normativo; se evaluó la respuesta sísmica de las estructuras a través del método de los cuadrantes y el índice de daño. En el método de los cuadrantes el punto de capacidad por demanda de todas las estructuras se encuentra en el primer cuadrante lo cual es indicativo de un comportamiento adecuado de la estructura y por ello no carecen de rigidez ni resistencia lateral. Por otro lado, el índice de daño y la deriva en la cual se alcanza dicho daño en la estructura se obtuvo graficando el punto de demanda por capacidad normalizado; este valor de índice de daño permite caracterizar la respuesta sismorresistente de las estructuras mediante un número único que indica si la misma es dúctil o frágil, en ninguna de las estructuras en estudio se obtienen valores iguales a uno que indicaría el colapso de la estructura; dicho valor se recomienda sea menor a 80% en estructuras nuevas ya que este porcentaje indica lo que sufriría la estructura al ser sometida a un terremoto en su vida útil y la parte de ella que sería afectada y debe ser recuperada a través de una considerable inversión. El índice de daño en la estructura completa es menor al de las demás estructuras analizadas, en las cuales el índice de daño con la incorporación de la viga de cierre en los entrantes (H con viga, U con viga y UU con viga) disminuye con respecto a las que no poseen vigas de cierre (H sin viga, U sin viga y UU sin viga).
El índice de daño se determina en las columnas de acuerdo a la ubicación en los pórticos correspondientes, se calcula como el cociente entre las derivas corregidas del método N2 extendido (demandas) entre las rotaciones últimas (capacidad) que representan la máxima rotación del elemento antes de fallar. Para los casos de estudio el índice de daño en columnas internas es mayor al de columnas externas de las estructuras y es mayor en las columnas del primer nivel. La estructura completa presenta un índice de daño de 0,55 siendo menor que en estructuras con irregularidad (UU sin viga, U sin viga, H sin viga) en las cuales alcanza un valor de 0,70.
Las rotaciones de los centros de gravedad en cada nivel en las estructuras U sin viga y UU sin viga son elevadas con respecto a las otras estructuras analizadas, lo que indica que la ausencia de las vigas de cierre en las estructuras con entrantes perjudica su comportamiento sismorresistente, al incrementar los momentos torsores en planta. Al presentarse irregularidad en las estructuras, el centro de rigidez se aleja del centro de gravedad generándose así momentos torsores, dichos torsores según la evaluación a las estructuras son mayores en las que no presentan vigas de cierre en los entrantes (H sin viga, U sin viga y UU sin viga) y se incrementan notablemente en las estructuras con mayor irregularidad (U sin viga y UU sin viga). Es importante resaltar que los máximos torsores presentados en la estructura irregular (UU sin viga) son prácticamente 12 veces mayores que los de la estructura regular (completa). De esta manera se demuestra lo que siempre se ha resaltado en las normas de diseño sismorresistente y en las publicaciones sobre diseño conceptual: que la irregularidad en planta incrementa la solicitación torsional sobre las columnas de la estructura, pero que se ha tratado de manera intuitiva, sin recibir una valoración comparada como la que se muestra en este apartado.
El efecto P-Delta se origina cuando el aporte al momento de volcamiento por parte de las cargas gravitatorias es notable, dado el incremento de los desplazamientos laterales, que mueven los puntos de aplicación de dichas cargas gravitatorias de su posición original. Mientras la estructura es más irregular (H sin viga, U sin viga y UU sin viga) el efecto P-Delta aumenta ya que resisten menos momento total en los apoyos, hasta que se produce el efecto P-Delta, con respecto a estructuras con menor irregularidad (H con viga, U con viga y UU con viga).
Vale acotar, que el índice de irregularidad torsional obtenido es un coeficiente adimensional que permite caracterizar la respuesta estructural y la correlaciona con la irregularidad presentada, estableciendo la vulnerabilidad torsional de una estructura sin la necesidad de efectuar análisis computacionalmente más costosos. Los resultados muestran que, el índice de irregularidad torsional es mayor en la estructura UU sin viga, seguido de U sin viga y H sin viga. Es importante señalar que algunas de las estructuras que se analizaron estudiando el riesgo torsional según la norma Covenin, arrojaron valores que no permitían considerarlas como irregulares, sin embargo, al obtener la respuesta no lineal, se pudo verificar que las mismas presentan notable amplificación de los momentos torsores (estructura H sin viga, U sin viga y UU sin viga). El valor de R adoptado en el diseño es seguro. Dicha verificación se realizó a través de la metodología FEMA P695 de acuerdo a la razón de margen de colapso, incertidumbres determinadas para cada una de las estructuras según dirección de análisis y para todas las estructuras en conjunto junto con valores de las curvas de fragilidad de colapso obtenidas, indicando esto que los valores de R propuestos según normativa vigente son apropiados.
De acuerdo con los resultados mostrados, se hace necesario ampliar los estudios en el área d ela respuesta de las estructuras irregulares en los que se incorporen las posibles irregularidades en elevación. Igualmente, llevar a cabo investigaciones con edificios de mayor altura para determinar sus factores de prestaciones sísmicas producto de las irregularidades presentadas e incorporar tipologías mixtas y de acero en el estudio.
BIBLIOGRAFÍA
| [1] | I. Fundación Wikimedia, «Wikipedia,» 24 Noviembre 2014. [En línea]. Available: http://es.wikipedia.org/wiki/Vulnerabilidad_s%C3%ADsmica. [Último acceso: 12 Febrero 2015]. |
| [2] | J. C. Vielma, A. Barbat, R. Ugel y R. Herrera, Analysis of the seismic response of plan-asimmetric RC building, New York: Nova Science Publishers, 2013, pp. 1-23. |
| [3] | J. C. Vielma, A. Barbat y Y. Martínez, «The quadrants method: A procedure to evaluate the seismic performance of existing building,» de XV World Conference on Earthquake Engineering, Lisboa, 2012. |
| [4] | F. Naeim y R. Bopana, «Seismic Design of Floor Diaphragms,» Heilderberg, Springer, 2001, pp. 373-408. |
| [5] | Covenin 1756, «Edificaciones sismorresistentes,» Fondonorma, Caracas, 2001. |
| [6] | L. Di Sarno y A. Elnashai, «Fundamentals of Earthquake Engineering,» Chichester, John Wiley and Sons, 2008. |
| [7] | R. Herrera, J. Vielma, R. Ugel y A. Barbat, «Optimal design and earthquake resistant design evaluation of low rise framed rc building,» Natural Science, Earthquake Special Issue, vol. X, nº no. 2, pp. 20-34, 2012. |
| [8] | Autodesk, Inc, «Robot. Manual de usuario,» 2015. |
| [9] | Seismo Soft, «SeismoStruct v7.0.2. A computer program for static and dynamic nonlinear analysis of framed structures,» 2014. |
| [10] | J. C. Vielma y M. Cando, Evaluación de la vulnerabilidad sísmica de estructuras de acero residenciales proyectadas conforme a las normas vigentes en el Ecuador y las AISC seismic provisions for structural steel buildings, Barcelona: Centro Internacional de Métodos Numéricos en Ingeniería CIMNE, 2014. |
| [11] | FEMA, «Quantification of Building Seismic Performance Factors,» Washington D.C, 2009. |
| [12] | A. Lucchini, F. Mollaioli y G. Monti, «Intensity measures for response prediction of a torsional building subjected to bi-directional earthquake ground motion,» Bull Earthquake Eng, vol. 9, p. 1499–1518, 2011. |
| [13] | V. Kilar y P. Fajfar, «Simple push-over analysis of asymmetric buildings,» Earthquake engineering and structural dynamics, vol. 26, pp. 233-249, 1997. |
| [14] | A. M. Chandler y X. N. Duan, «Performance of asymmetric code-designed buildings for serviceability and ultimate limit states,» Earthquake engineering and structural dynamics, vol. 26, pp. 717-735, 1997. |
| [15] | A. P. Harasimowicz y R. K. Goel, «Seismic code analysis of multi-storey asymmetric buildings,» Earthquake Engineering and Structural Dynamics, vol. 27, pp. 173-185, 1998. |
| [16] | T. Paulay, «Torsional mechanisms in ductile building systems,» Earthquake Engng. Struct. Dyn., vol. 27, pp. 1101-1121 , 1998. |
| [17] | J. De la Colina, «Effects of torsion factors on simple non-linear systems using fully-bidirectional analyses,» Earthquake Engng. Struct. Dyn., vol. 28, pp. 691-706, 1999. |
| [18] | W. K. Tso y S. H. Smith, «Re-evaluation of seismic torsional provisions,» Earthquake Engng. Struct. Dyn., vol. 28, pp. 899-917, 1999. |
| [19] | G. Magliulo, G. Maddaloni y E. Cosenza, «Extension of N2 method to plan irregular buildings considering accidental eccentricity,» Soil Dynamics and Earthquake Engineering, vol. 43, pp. 69-84, 2012. |
| [20] | E. M. Marino y P. Rossi, «Exact evaluation of the location of the optimum torsion axis,» Struct. Design Tall Spec. Build, vol. 13, p. 277–290, 2004. |
| [21] | A. K. Chopra y R. K. Goel, «A modal pushover analysis procedure to estimate seismic demands for unsymmetric-plan buildings,» Earthquake Engng Struct. Dyn, vol. 33, p. 903–927, 2004. |
| [22] | A. M. Athanatopoulou y I. N. Doudoumis, « Principal directions under lateral loading in multistoreyasymmetric buildings.,» Struct. Design Tall Spec. Build., vol. 17, p. 773–794, 2008. |
| [23] | D. Marusic y P. Fajfar, «On the inelastic seismic response of asymmetric buildings under bi-axial excitation.,» Earthquake Engng Struct. Dyn., vol. 34, p. 943–963, 2005. |
| [24] | A. J. Kosmopoulos y M. N. Fardis, «Estimation of inelastic seismic deformations in asymmetric multistorey RC buildings,» Earthquake Engng Struct. Dyn., vol. 36, p. 1209–1234, 2007. |
| [25] | M. De Stefano y B. Pintucchi, « Predicting torsion-induced lateral displacements for pushover analysis: Influence of torsional system characteristics.,» Earthquake Engng Struct. Dyn., vol. 39, p. 1369–1394, 2010. |
| [26] | J. C. Reyes y A. K. Chopra, «Evaluation of three-dimensional modal pushover analysis for unsymmetric-plan buildings subjected to two components of ground motion,» Earthquake Engng Struct. Dyn., vol. 40, p. 1475–1494, 2011. |
| [27] | J. C. Vielma, «Caracterización del comportamiento sísmico de edificios de hormigón armado mediante la respuesta no lineal.,» Universitat Politecnica de Catalunya, Barquisimeto, 2008. |
| [28] | Européen Comité, «Design of structures for earthquake resistance,» Européen Comité, Brussels, 2003. |
| [29] | International Code Council, «International Building Code -2003,» Cincinnati, 2003. |
| [30] | J. Vielma, R. Ugel, R. Herrera y Y. Martínez, «Seismic Evaluation of Low Rise RC Framed Building Designed According to Venezuelan Codes,» 2013, pp. 283-298. |
| [31] | M. Priestley, G. Calvi y M. Kowalski, «Displacement-based seismic design of structures.,» Pavia, 2007. |
| [32] | A. Alfaro y Márquez, «Evaluación del comportamiento sismorresistente de estructuras de concreto armado con irregularidad en planta de tipo: diafragma flexible.,» Barquisimeto, 2012. |
| [33] | A. Barrios, «Estudio de la respuesta sísmica del edificio Villa Azul, ubicado en Tucacas Estado Falcón,» Barquisimeto, 2012. |
| [34] | J. C. Vielma, A. Barbat y S. Oller, Proyecto sismorresistente de estructuras porticadas, Barcelona: Centro Internacional de Métodos Numéricos en Ingeniería CIMNE, 2010. |
| [35] | T. Panagiotakos y N. Fardis, «Seismic performance of R.C frames designed to Eurocode or to the Greek Codes 2000,» 2004, pp. 221-259. |
| [36] | M. Kreslin y P. Fajfar, «The extended N2 method considering higher mode effects in both plan and elevation,» 2011. |
| [37] | N. Newmark, «A method of computations for structural dynamics. Journal of the Engineering Mechanics Division,» Reston, 1959, pp. 67-94. |
| [38] | American Society of Civil Engineers, «Minimum Design Loads for Buildings and Other Structures,» Reston, 2005. |
| [39] | P. Meneses, «Análisis de Edificios de Hormigón Armado en Base a Pórticos Planos Acoplados a Muros de Altura Parcia,» Valdivia, 2006. |
| [40] | G. Quincot, «Propuesta para considerar la irregularidad estructural en la resistencia lateral de las estructuras en Perú,» Lima, 2010. |
| [41] | [En línea]. Available: http://www.biblioteca.udep.edu.pe/BibVirUDEP/tesis/pdf/1_122_180_80_1139.pdf. |
| [42] | [En línea]. Available: http://www.arqhys.com/contenidos/espectros-diseno-resistentes.html. |
| [43] | H. Bernal, «Evaluación del Factor de Redundancia RR y del Factor de Reducción de las Fuerzas Sísmicas.,» 2008. |
| [44] | COVENIN 2002-88, «Criterios y Acciones Mínimas para Proyectos de Edificaciones,» Caracas, 2002. |
| [45] | Fondonorma, «Norma Venezolana COVENIN 1756:2001. Edificaciones sismorresistentes,» Fondonorma, Caracas, 2001. |
| [46] | S. Han y A. Chopra, «Approximate incremental dynamic analysis using the modal pushover analysis procedure,» Earthquake Engineering and Structural Dynamics, vol. XXXV, nº 3, p. 1853‐1873, 2006. |
| [47] | P. Fajfar, D. Marusic y I. Perus, «Torsional effects in the pushover‐based seismic analysis of buildings,» vol. 9, nº 6, p. 831‐854, 2005. |
| [48] | V. Papanikolaou y A. Elnashai, «Evaluation of conventional and adaptive pushover analysis I: methodology,» Journal of Earthquake Engineering, vol. IX, nº 6, p. 923‐941, 2005. |
| [49] | P. Fajfar, «Nonlinear analysis method for performance based seismic design,» Earthquake Spectra, vol. XVI, nº 3, p. 573‐591, 2000. |
| [50] | M. Kreslin y P. Fajfar, «The extended N2 method considering higher mode effects in both plan and elevation,» Bulletin of Earthquake Engineering, vol. X, nº 2, p. 699‐ 715, 2011. |
| [51] | P. Pinto, R. Gianini y P. Franchin, «Seismic reliability analysis of structures,» Pavia, 2006. |
| [52] | D. Vamvatsikos y A. Cornell, «Incremental dynamic analysis,» Earthquake Engineering and Structural Dynamics, vol. XXXI, nº 3, p. 491‐514, 2002. |
| [53] | J. Egozcue, A. Barbat, J. Canas, J. Miquel y E. Banda, «A method to estimate occurrence probabilities in low seismic activity regions,» vol. XX, nº 1, pp. 43-60, 1991. |
| [54] | R. Park, «State-of-the Art Report: Ductility evaluation from laboratory and analytical testing,» de In proceedings 9th WCEE. IAEE, Tokyo-Kyoto, 1988. |
| [55] | J. Moehle, Seismic design of reinforced concrete buildings, New York: McGraw-Hill, 2015. |
| [56] | Y.F. Vargas, L.G. Pujades, A.H. Barbat, J.E. Hurtado, "Capacity, fragility and damage in reinforced concrete buildings: a probabilistic approach", Bulletin of Earthquake Engineering 11 (6), 2007-2032, 2013. |
| [57] | O.D. Cardona, M.G. Ordaz, E. Reinoso, L. Yamín, H.A. Barbat, "CAPRA - Comprehensive Approach to Probabilistic Risk Assessment: International Initiative for Risk Management Effectiveness", 15 WCEE, Lisbon, 2012. |
| [58] | A.H. Barbat, S. Lagomarsino, L.G. Pujades, “Vulnerability assessment of dwelling buildings”, Assessing and managing earthquake risk, 115-134, 2008. |
ANEXOS
Secciones transversales y armadura de refuerzo del edificio completo.
| Nivel planta baja | ||||
| Estructura completa | Columna | Sección | Acero Longitudinal | Acero Transversal |
| A1 | ||||
| D1 | ||||
| A4 | ||||
| D4 | ||||
| A2 | ||||
| A3 | ||||
| D2 | ||||
| D3 | ||||
| B4 | ||||
| C4 | ||||
| B1 | ||||
| C1 | ||||
| B2 | ||||
| B3 | ||||
| C2 | ||||
| C3 | ||||
| Primer nivel | ||||
| Estructura completa | Columna | Sección | Acero Longitudinal | Acero Transversal |
| A1 | ||||
| D1 | ||||
| A4 | ||||
| D4 | ||||
| A2 | ||||
| A3 | ||||
| D2 | ||||
| D3 | ||||
| B4 | ||||
| C4 | ||||
| B1 | ||||
| C1 | ||||
| B2 | ||||
| B3 | ||||
| C2 | ||||
| C3 | ||||
| Nivel de cubierta | ||||
| Estructura completa | Columna | Sección | Acero Longitudinal | Acero Transversal |
| A1 | ||||
| D1 | ||||
| A4 | ||||
| D4 | ||||
| A2 | ||||
| A3 | ||||
| D2 | ||||
| D3 | ||||
| B4 | ||||
| C4 | ||||
| B1 | ||||
| C1 | ||||
| B2 | ||||
| B3 | ||||
| C2 | ||||
| C3 | ||||
| Estructura completa | Nivel planta baja | ||||
| dirección x | Viga | Sección | Acero Longitudinal | Acero Transversal | |
| VA |
| ||||
| VD |
| ||||
| VB |
| ||||
| VC |
| ||||
| dirección y | V1 |
| |||
| V4 |
| ||||
| V2 |
| ||||
| V3 |
| ||||
| Estructura completa | Primer nivel | ||||
| dirección x | Viga | Sección | Acero Longitudinal | Acero Transversal | |
| VA |
| ||||
| VD |
| ||||
| VB |
| ||||
| VC |
| ||||
| dirección y | V1 |
| |||
| V4 |
| ||||
| V2 |
| ||||
| V3 |
| ||||
| Estructura completa | Nivel de cubierta | ||||
| dirección x | Viga | Sección | Acero Longitudinal | Acero Transversal | |
| VA |
| ||||
| VD |
| ||||
| VB |
| ||||
| VC |
| ||||
| dirección y | V1 |
| |||
| V4 |
| ||||
| V2 |
| ||||
| V3 |
| ||||
A continuación se muestra el proceso para determinar la rotación última de la cuerda de la deformada de los elementos en base a lo propuesto por Panagiotakos y Fardis [35].
Código para la determinación de la rotación de los elementos
Con la finalidad de hacer más eficiente el cálculo de las rotaciones últimas en los diferentes miembros de los edificios de esta monografía, se ha preparado un programa en Matlab, que se muestra a continuación.
%%%%%%%%%%%%%%%%%%%%%%%% UCLA-DIC-VEN%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%PROGRAMA PARA DETERMINAR LA ROTACIÓN ÚLTIMA DE LA CUERDA DE LA DEFORMADA%
%%%%%%%%%%%%% ELABORADO POR: MULDER MARÍA MANUELA%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%AULA UCLA-CIMNE%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Comentario: este programa permite el cálculo de la rotación última de la
%cuerda de la deformada, con base en los siguientes datos: acciones internas
%obtenidas del análisis, corte y axial, propiedades geométricas y
% mecánicas de la sección transversal de la viga o la columna,
% distribución del acero longitudinal y transversal, entre otros.
% El programa se ha desarrollado en función al algoritmo del EC-8,
%deducido para columnas y vigas usuales.
%Entrada de datos básicos
disp('Ratio de fuerza axial normalizado respecto del ancho b de la zona a compresión, profundidad de la sección h y fc')
N=input('Ingrese la Fuerza Axial en MN')
b=input('Ingrese el ancho de la sección en m')
hc=input('Ingrese la altura de la sección en m')
fc=input('Ingrese la resistencia del hormigón en MPA')
v=N/(b*hc*fc);
disp('El Ratio de fuerza axial normalizado respecto del ancho b de la zona a compresión, profundidad de la sección h y fc es=')
v
pause
%Cálculo del ratio de vano a corte al final del miembro
disp('Ratio de vano a corte al final del miembro ')
M=input('Ingrese el Momento en MN*m')
Vh=input('Ingrese el cortante en MN')
Ls=M/Vh;
x=(Ls/hc);
disp('El Ratio de vano a corte al final del miembro es=')
x
pause
%Entrada de propiedades mecánicas de la sección
fyw=input('Ingrese el esfuerzo de plastificación de estribos, en MPA')
disp('Ratio del acero transversal paralelo a la dirección X de la carga')
Sh=input('Ingrese el espaciamiento de estribos en m')
Ram=input('Ingrese el número de ramas en la dirección X de análisis')
diam=input('Ingrese el diámetro de estribos en m')
Area=((3.1416*(diam^2))/4)
Asx= (Ram*Area)
ROsx= (Asx/(b*Sh));
ROsx
ROsxporc=ROsx*100;
ROsxporc;
sprintf('El ratio del acero transversal paralelo a la dirección de la carga es en porcentaje> %d%%',ROsxporc)
pause
%Determinación del factor de efectividad del confinamiento
disp('Factor de efectividad del confinamiento')
r=input('Ingrese el recubrimiento de la sección en m')
bo=(b-(2*r));
ho=(hc-(2*r));
d=(hc-r);
bi=input('Ingrese la distancia de las barras restringidas a lo largo del perímetro en m')
n=input('Ingrese el número de distancias de las barras restringidas a lo largo del perímetro')
a=0
B=0
for i=1:n
c=(bi^2)
B=a+c
a=B
end
alfa=((1-Sh)/(2*bo))*((1-Sh)/(2*ho))* ((1)-(a/(6*ho*bo)))
pause
%Cálculo de los Ratios de refuerzos mecánicos, de la armadura longitudinal a
%tracción y compresión
disp('Ratios de refuerzos mecánicos, de la armadura longitudinal a tracción y compresión')
diamt=input('Ingrese el diámetro de las varillas a tracción en m')
nbt=input('Ingrese el número de varillas a tracción')
Ast=((3.1416*(diamt^2))/4)*nbt
Rot=(Ast/(b*d))
w=((Rot*fyw)/fc)
if w>0.01
w=w
disp('El ratio de refuerzo mecánico de la armadura longitudinal a tracción es=')
w
wporc=w*100;
wporc;
sprintf('El ratio de refuerzo mecánico de la armadura longitudinal a tracción es en porcentaje> %d%%',wporc)
else
w=0.01
wporc=w*100;
wporc;
sprintf('El ratio de refuerzo mecánico de la armadura longitudinal a tracción es en porcentaje> %d%%',wporc)
end
diamc=input('Ingrese el diámetro de las varillas a compresión en m')
nbc=input('Ingrese el número de varillas a compresión')
Asc=((3.1416*(diamc^2))/4)*nbc
Roc=(Asc/(b*d))
wprima=((Roc*fyw)/fc)
if wprima>0.01
wprima=wprima
disp('El ratio de refuerzo mecánico de la armadura longitudinal a compresión es=')
wprima
wprimaporc=wprima*100;
wprimaporc;
sprintf('El ratio de refuerzo mecánico de la armadura longitudinal a compresión es en porcentaje> %d%%',wprimaporc)
else
wprima=0.01
wprimaporc=wprima*100;
wprimaporc;
sprintf('El ratio de refuerzo mecánico de la armadura longitudinal a compresión es en porcentaje> %d%%',wprimaporc)
end
%Cálculo de la rotación última de la cuerda de la deformada
thetau=(0.0172/1.5*(0.3^v)*(((wprima/w)*fc)^0.175)*((x)^0.4)*(25^((alfa*fyw*ROsx)/fc)))
Al aplicar este código se han calculado los valores de la rotación última de la cuerda de la deformada de vigas y columnas que se muestran resumidamente en la Tabla A.7 a la A.13, los cuales son utilizados para el cálculo del índice de daño en las estructuras analizadas, lo que permitirá conocer el porcentaje de daño sufrido por la edificación una vez expuesta a terremotos a lo largo de toda su vida útil, dando paso al conocimiento de las áreas afectadas para establecer formas de recuperación y su impacto monetario.
| Niveles | |||||
| Estructura completa | Ubicación | Planta baja | Primer nivel | Nivel de cubierta | |
| columnas | A1 D1 A4 D4 | 0,027 | 0,039 | 0,044 | |
| A2 A3 D2 D3 B4 C4 B1 C1 | 0,025 | 0,037 | 0,038 | ||
| B2 B3 C2 C3 | 0,022 | 0,038 | 0,036 | ||
| vigas x | VA VD | 0,029 | 0,029 | 0,031 | |
| VB VC | 0,028 | 0,028 | 0,031 | ||
| Vigas y | V1 V4 | 0,029 | 0,029 | 0,032 | |
| V2 V3 | 0,030 | 0,028 | 0,033 | ||
| Niveles | |||||
| h con viga | Ubicación | Planta baja | Primer nivel | Nivel de cubierta | |
| columnas | A1 D1 A4 D4 | 0,028 | 0,039 | 0,044 | |
| A2 A3 D2 D3 B4 C4 B1 C1 | 0,026 | 0,037 | 0,042 | ||
| B2 B3 C2 C3 | 0,024 | 0,034 | 0,040 | ||
| vigas x | VA VD | 0,028 | 0,029 | 0,031 | |
| VB VC | 0,028 | 0,028 | 0,031 | ||
| Vigas y | V1 V4 | 0,029 | 0,027 | 0,031 | |
| V2 V3 | 0,027 | 0,029 | 0,031 | ||
| Niveles | |||||
| h sin viga ( | Ubicación | Planta baja | Primer nivel | Nivel de cubierta | |
| columnas | A1 D1 A4 D4 | 0,027 | 0,039 | 0,043 | |
| A2 A3 D2 D3 B4 C4 B1 C1 | 0,026 | 0,037 | 0,042 | ||
| B2 B3 C2 C3 | 0,024 | 0,034 | 0,040 | ||
| vigas x | VA VD | 0,030 | 0,030 | 0,033 | |
| VB VC | 0,028 | 0,028 | 0,031 | ||
| Vigas y | V1 V4 | 0,029 | 0,027 | 0,031 | |
| V2 V3 | 0,029 | 0,029 | 0,031 | ||
| Niveles | |||||
| u con viga ( | Ubicación | Planta baja | Primer nivel | Nivel de cubierta | |
| columnas | A1 D1 A4 D4 | 0,028 | 0,039 | 0,044 | |
| A2 A3 D2 D3 B4 C4 B1 C1 | 0,025 | 0,037 | 0,038 | ||
| B2 B3 C2 C3 | 0,023 | 0,034 | 0,037 | ||
| vigas x | VA VD | 0,028 | 0,029 | 0,031 | |
| VB VC | 0,030 | 0,028 | 0,028 | ||
| Vigas y | V1 V4 | 0,028 | 0,029 | 0,031 | |
| V2 V3 | 0,030 | 0,028 | 0,028 | ||
| Niveles | |||||
| u sin viga ( | Ubicación | Planta baja | Primer nivel | Nivel de cubierta | |
| columnas | A1 D1 A4 D4 | 0,028 | 0,039 | 0,043 | |
| A2 A3 D2 D3 B4 C4 B1 C1 | 0,025 | 0,037 | 0,038 | ||
| B2 B3 C2 C3 | 0,022 | 0,034 | 0,037 | ||
| vigas x | VA VD | 0,029 | 0,029 | 0,031 | |
| VB VC | 0,030 | 0,028 | 0,033 | ||
| Vigas y | V1 V4 | 0,029 | 0,029 | 0,031 | |
| V2 V3 | 0,028 | 0,028 | 0,033 | ||
| Niveles | |||||
| UU con viga ( | Ubicación | Planta baja | Primer nivel | Nivel de cubierta | |
| columnas | A1 D1 A4 D4 | 0,028 | 0,039 | 0,044 | |
| A2 A3 D2 D3 B4 C4 B1 C1 | 0,026 | 0,037 | 0,040 | ||
| B2 B3 C2 C3 | 0,024 | 0,034 | 0,040 | ||
| vigas x | VA VD | 0,028 | 0,029 | 0,031 | |
| VB VC | 0,028 | 0,028 | 0,031 | ||
| Vigas y | V1 V4 | 0,028 | 0,029 | 0,031 | |
| V2 V3 | 0,028 | 0,028 | 0,031 | ||
| Niveles | |||||
| UU sin viga ( | Ubicación | Planta baja | Primer nivel | Nivel de cubierta | |
| columnas | A1 D1 A4 D4 | 0,027 | 0,039 | 0,043 | |
| A2 A3 D2 D3 B4 C4 B1 C1 | 0,025 | 0,037 | 0,039 | ||
| B2 B3 C2 C3 | 0,024 | 0,034 | 0,040 | ||
| vigas x | VA VD | 0,029 | 0,029 | 0,031 | |
| VB VC | 0,028 | 0,028 | 0,031 | ||
| Vigas y | V1 V4 | 0,029 | 0,027 | 0,031 | |
| V2 V3 | 0,028 | 0,028 | 0,031 | ||
Document information
Published on 17/04/18
Submitted on 17/04/18
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?