Chaos control via Mathieu-Van der Pol system and Linear Optimal Control design with a non-ideal excitation and parametric uncertainties

Abstract

The hyper-chaotic Mathieu-Van der Pol system is an important autonomous system model, with four state variables and four Lyapunov exponents, three of which are positive. Also called the Tri-Chaos, the Mathieu-Van der Pol system was mathematically modeled via linear coupling of Mathieu and Van der Pol non-linear and non-autonomous systems. In this work, a non-ideal system based on the Mathieu-Van der Pol System is modeled considering its parameters as uncertain, which makes it closer to reality. Numerical simulations are presented demonstrating that the system has a chaotic behavior with three positive Lyapunov exponents. Given such unstable and unpredictable behavior, the linear optimal control design is proposed to reduce the chaotic movement of this system to a fixed point. The simulation results show that the identification by Linear Optimal Control is very effective.

Keywords: Non-ideal system, uncertain parameters, optimal linear control

1. Introduction

Humanity is going through a very fast technological revolution, which makes well established companies and start-ups strive daily to invest in the search for introducing new, customizable, autonomous and more efficient products in the work market. For such purposes, mechanical engineering contributes with projects of advanced technological products, such as the manufacturing of electric and autonomous vehicles in the automotive sector. Therefore, with a simple software update, costs related to maintenance for changing oil, filters and other parts of cars powered by internal combustion engines, will be replaced.

The challenge of creating a new product requires developing projects that are straightforward concerning the objectives to be achieved and all stages to be completed, from their beginning, development, until their end. During the execution phase of a mechanical project, the probability of mistakes happening is high, leading to undesirable effects, that is, negative effects, or even chaotic ones. Considering this, managing the risks effectively may decrease the occurrence of a chaotic event that hinders the development of a project. Formally speaking, a chaotic event, or simply chaos, represents the irregularity of a dynamical system. Its essential characteristics are: sensitivity to initial conditions, which means that its evolution in time may be altered by small perturbations, and unpredictability, which implies that it is impossible to predict the posterior evolution of the system, even knowing its state during a long-time interval.

A priori, it is possible to state that a chaotic response can be understood based on a series of contraction-expansion-bending transformations, and among the tools applied to characterize chaos, the Lyapunov exponents stand out, which are one of the invariants of the system, and may be used even for evaluating other invariants [1].

Due to the possibility of a chaotic event happening during the development of projects, the alternative is to seek to mitigate this disorder state, that is, to manage the chaos that is inherent to the system, checking the weaknesses that unexpectedly arise, so as not to harm the production stage. Nowadays, Chaos Engineering contributes to carrying out experiments in the infrastructure and pointing out the weaknesses related to the system before they arise. This empirical verification process leads to invulnerable systems, and provides reliability for a complex system to operate under turbulent situations during the operational process of production. In 1990, Grebogi, Edward Ott and James Yorke demonstrated the possibility of controlling chaos [2]. Ever since then, controlling chaotic systems has been of great interest in mechanical engineering, and implies in designing state feedback control laws which stabilize the chaotic system around the instable equilibrium points. Many control techniques may be used to control a system, and each of them presents peculiarities and different results, especially in practice. To stabilize chaotic systems, in many works feedback linear control was used [10,11,18]. In the present paper, we apply the Optimal Linear Control (OLC) methodology, proposed by Rafikov and Balthazar [18], which ensures the application of linear control to nonlinear systems. Among the main characteristics of Optimal Linear Control, we highlight the use of the state-space representation model, the obtaining of optimal control signals through the Algebraic Ricatti Equation (ARE), and the objective function, parameterized by the matrices Q and R to weigh the state and control vectors, respectively [18].

This work aims at proposing a new numerical model for the Mathieu-Van der Pol system coupled to a source with a rotative unbalance [4,5,6,7] and considering uncertain parameters; afterwards, a control technique is applied to stabilize the whole proposed system.

Nowadays, the applications in mechanical engineering require that the systems operate with optimal parameters under certain operation conditions, which demonstrates the need for developing realistic numerical models which consider uncertainties in the parameters and inputs of the system properly. In mechanical engineering, the uncertainties have been considered in several areas, such as structure dynamics [13], rotor dynamics [14], robot manipulators [15], among others. In the process of modeling dynamical systems, uncertainties may be considered based on a probabilistic approach, through predefined intervals, or even the possibility theory [16].

2. Mathematical model

The Mathieu-Van der Pol autonomous system is a model with four state variables and three positive Lyaponuv exponents, proposed by Shih-Yu et al. [3]. It is a hyper-chaotic system that was modeled via linear coupling of the non-linear and non-autonomous systems of Mathieu and Van der Pol [3], whose equations of motion are as follows:

${\dot {x}}_{1}=x_{2}$ ${\dot {x}}_{2}=-(a+bx_{3})x_{1}-(a+bx_{3})x_{1}^{3}-cx_{2}+dx_{3}$ ${\dot {x}}_{3}=x_{4}$ ${\dot {x}}_{4}=-ex_{3}+f(1-x_{3}^{2})x_{4}+gx_{1}$

(1)

where ${\textstyle x_{1}}$, ${\textstyle x_{2}}$, ${\textstyle x_{3}}$ and ${\textstyle x_{4}}$ are the four states of the system and ${\textstyle a,b,c,d,e,f}$ and ${\textstyle g}$ are the parameters of the Mathieu-Van der Pol System [3,24].

The next section deals with non-ideal excitations, as well as presents a proposal for a new model called Non-Ideal Mathieu-Van der Pol System.

2.1 Non-ideal system

A system is said to be ideal when the excitation does not influence the response of the system, ie, the ideal excitation has an ideal power source [8,9,10,11,12]. On the other hand, when the excitation is influenced by the response of the system, the excitation is said to be non-ideal [19]. A non-ideal excitation can be modeled as shown in Figure 1 [4,11].

Figure 1. Non-ideal power source [11]

This representation on the based in Kononenko model and can be mathematically modeled according to equations (2), where ${\textstyle m_{1}}$ is a DC motor mass, ${\textstyle m_{0}}$ is unbalanced mass, ${\textstyle l}$ is the dumping, ${\textstyle k}$ is the rigidity, ${\textstyle r}$ is the eccentricity distance from the unbalanced mass to the torque source, ${\textstyle (I+m_{0}r^{2})}$ is the moment of inertia of the unbalanced mass, and the state variables are ${\textstyle X}$ representation for the beam tip position and ${\textstyle \varphi }$ for the unbalanced mass angular position. The net torque is a function of the angular velocity ${\textstyle {\dot {\varphi }}}$ and described as for ${\textstyle S({\dot {\varphi }})=a-b{\dot {\varphi }}}$ [6,11,17], where a is the net torque applied by the DC motor and b is the resistive net torque constant

${}(m_{1}+m_{0}){\ddot {X}}+l{\dot {X}}+kX=m_{0}r({\dot {\varphi }}^{2}cos\varphi +{\ddot {\varphi }}sen\varphi ))$ $(I+m_{0}r^{2}){\ddot {\varphi }}-m_{0}r{\ddot {X}}sen\varphi =s({\dot {\varphi }})$

(2)

The first characteristic of a non-ideal system is that it presents an equation that describes the interaction of the energy source with the ideal dynamic system, and the second characteristic is that the dynamics of a non-ideal system approaches the ideal case as the supplied power increases. For the present work the adimensional non-ideal mathematical model configuration [6,9] of the non-ideal power source is given by equations (3)

${}{\ddot {x}}_{1}=-(a+bx_{2})x_{1}-(a+bx_{2})x_{1}^{3}-c{\dot {x}}_{1}+dx_{2}+\mu ({\dot {z}}^{2}cosz+{\ddot {z}}senz)$ ${\ddot {x}}_{2}=ex_{2}+f(1-x_{2}^{2}){\dot {x}}_{2}+gx_{1}$ ${\ddot {z}}=\varepsilon {\ddot {x}}_{1}senz+\alpha -\beta {\dot {z}}$

(3)

The angular position ${\textstyle z}$ is the non-ideal excitation response, ${\textstyle \alpha }$, ${\textstyle \beta }$ are motor torque constants, ${\textstyle \epsilon }$ is the distance from the unbalanced mass to the rotation center of the DC motor and ${\textstyle \mu }$ is related to the moment of inertia of the system. All parameters are dimensionless positive constants. The term ${\textstyle \mu ({\dot {z}}^{2}cosz+{\ddot {z}}senz)}$ is due to the interaction between the dynamical system and an energy source, for example, a DC motor with limited power supply. ${\textstyle \mu ({\dot {z}}^{2}cosz+{\ddot {z}}senz)}$ is responsible for the Non-idealization of the system. The parameter ${\textstyle \alpha }$ is the applied torque constant and depends on the initial conditions, and ${\textstyle \beta }$ is the resistive net torque and has no influence of initial conditions and is considered as internal damping of the DC Motor.

Making ${\textstyle y_{1}=x_{1}}$, ${\textstyle y_{2}={\dot {x_{1}}}}$,${\textstyle y_{3}=z}$,${\textstyle y_{4}={\dot {z}}}$, ${\textstyle y_{5}=x_{2}}$ and ${\textstyle y_{6}={\dot {x_{2}}}}$, ${\textstyle y_{5}=z}$ and, has

${}{\dot {y}}_{1}=y_{2},$ ${\dot {y}}_{2}=-{\frac {-(a+by_{3})y_{1}-(a+by_{3})y_{1}^{3}-cy_{2}+dy_{3}+\mu y_{4}^{2}cosy_{3}+(\alpha {-\beta }y_{4})\mu seny_{3}}{1-\mu \epsilon (seny_{3})^{2}}},$ ${\dot {y}}_{3}=y_{4},$ ${\dot {y}}_{4}=-{\frac {\epsilon (-(a+by_{3})y_{1}-(a+by_{3})y_{1}^{3}-cy_{2}+dy_{3})seny_{3}+\mu \epsilon y_{4}^{2}cosy_{3}seny_{3}+\alpha -\beta y_{4}}{1-\mu \epsilon (seny_{3})^{2}}},$ ${\dot {y}}_{5}=y_{6},$ ${\dot {y}}_{6}=-ey_{5}+f(1-y_{5}^{2})y_{6}+gy_{1}.$

(4)

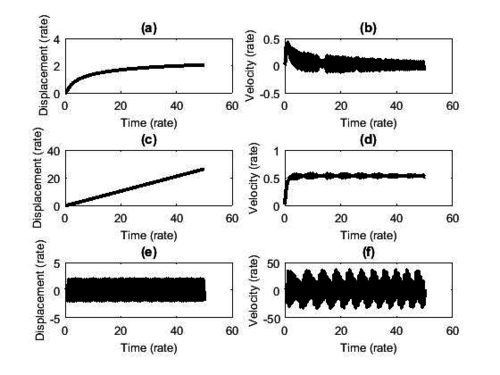
Figures  2 and  3 illustrate the behavior of the adopted dynamical model, using numerical values ${\textstyle a=91.7,b=5.023,c=0.01}$, $d=91,e=87.001,f=18$ and ${\textstyle g=9.5072}$ [24] for the Mathieu-Van der Pol System and ${\textstyle \alpha =0.8}$, ${\textstyle \beta =1.5}$, ${\textstyle \epsilon =0.3}$ and ${\textstyle \mu =0.2}$ for the non-ideal excitation [6].

Figure 2. Time History. (a) displacement for the Mathieu system. (b) Velocity for the Mathieu system. (c) Displacement for the non-ideal excitation. (d) Velocity for the non-ideal excitation. (e) Displacement for Van der Pol system. (f) Velocity for the Van der Pol system

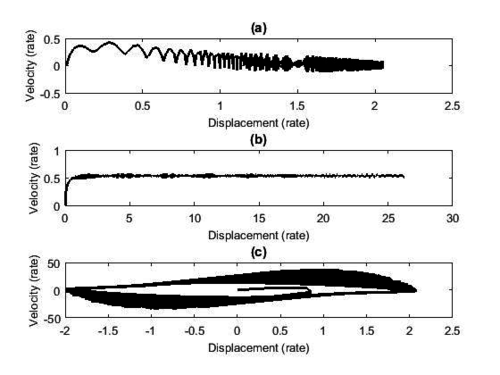
Figure 3. Phase Portrait. (a) Mathieu system. (b) Non-ideal excitation. (c) Van der Pol system

Figure 4 illustrates the six Lyapunov exponents, ${\textstyle \lambda _{1}=8.9985}$; ${\textstyle \lambda _{2}=8.9539}$; ${\textstyle \lambda _{3}=-6.4645}$; ${\textstyle \lambda _{4}=-1.4999}$ and ${\textstyle \lambda _{5}=-3.203}$, ${\textstyle \lambda _{6}=-3.2329}$, demonstrating the presence of chaos with one positive Lyapunov exponent. The total time for computing the Lyapunov exponents was ${\textstyle \Delta \tau =100.000}$ with a time-step of ${\textstyle \tau =1}$ [25].

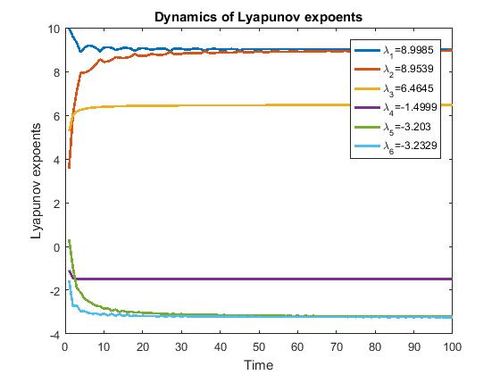
Figure 4. Dynamics of Lyapunov expoents

Aiming to minimize vibrations and reduce the oscillatory motion caused in the system , in the following section we propose the application of Linear Optimal Control to reduce this chaotic behavior to a fixed point.

To consider the effect of the parameter uncertainties on the performance of the controller  they are added to the state and will be associated with the difference between real values and the parameters of the mathematical model with a random error of 20%, where will be the normally distributed random functions [20]. The nominal values of the parameters are given below.

The real unknown parameters of system are supposed to be as follows: ${\textstyle {\bar {a}}=73.36+36.68r(t)}$, ${\textstyle {\bar {b}}=4.024+2.012(t)}$, ${\textstyle {\bar {c}}=0.008+0.002(t)}$, ${\textstyle {\bar {d}}=72.8+36.4r(t)}$, ${\textstyle {\bar {e}}=69.6008+34.8004r(t)}$, ${\textstyle {\bar {f}}=14.4+7.2r(t)}$, ${\textstyle {\bar {g}}=7.5928+3.8288r(t)}$, ${\textstyle {\bar {\alpha }}=0.64+0.32r(t)}$, ${\textstyle {\bar {\mu }}=0.16+0.08r(t)}$, ${\textstyle {\bar {\beta }}=1.2+0.6r(t)}$ and ${\textstyle {\bar {eta}}=0.24+0.12r(t)}$, where ${\textstyle r(t)}$ are normally distributed random functions [20]. Numerical simulation results are shown in the next section, where the robustness of the methods is assessed considering that the system parameters present uncertainties.

3. Control design

The Optimal Linear Control design for the Non-ideal Mathieu-Van der Pol system reduces the oscillatory movement to a small stable orbit. Due to its simplicity in terms of configuration and implementation, the linear state feedback control is especially attractive [18].

It should be stressed that this approach is analytical and it can be used without dropping any non-linear term. Rewriting the equations of motion (4), in a state form:

${}{\dot {x}}=A{x}+g({x})$

(5)

Considering a vector function ${\textstyle {\tilde {x}}}$, witch characterizes the desired trajectory, and the control vector ${\textstyle U}$, consisting of two parts: ${\textstyle {\tilde {u}}}$ for the feedforward and ${\textstyle u_{f}}$ for a linear feedback, in such way that,

${}u_{f}=Bu$

(6)

where ${\textstyle B}$ is a constant matrix, and driving the deviation of the trajectory of system (6) to the desired one ${\textstyle y=x-{\tilde {x}}}$.

The control is optimal, in order to transfer the non-linear system (4) from any initial to final state ${\textstyle y(t_{f})=0}$, minimizing the functional${\textstyle {\tilde {J}}={\frac {1}{2}}\int _{0}^{\infty }(y^{T}{\tilde {Q}}y+u^{t}Ru)dt}$, where the symmetric matrix ${\textstyle P(t)}$ is evaluated through the solution of the matrix Ricatti differential equation [19,20,21,22]

${}PA+A^{T}P-PBR^{-1}B^{T}P+Q=0$

(7)

satisfying the final condition ${\textstyle P(t_{f})=0}$.

In addition, with the feedback control (4), there exists a neighborhood ${\textstyle \Gamma _{0}\subset \Gamma }$,${\textstyle \Gamma \subset \Re ^{n}}$, of the origin such that if ${\textstyle x_{0}\in \Gamma _{0}}$, the solution ${\textstyle x(t)=0}$,${\textstyle t\geq {0}}$ of the controlled system (7) is locally asymptotically stable, and ${\textstyle J_{min}=x_{0}^{T}P(0)x_{0}}$. Finally, if ${\textstyle \Gamma =\Re ^{n}}$ then the solution ${\textstyle y(t)=0}$,${\textstyle t>0}$ of the controlled system (7) is globally asymptotically stable.

Using the theorem [20] the dynamic error y can be minimized (${\textstyle y\rightarrow 0}$).

3.1 Application of the optimal linear control to the system

From equation (4):

${}{\dot {y}}_{1}=y_{2}+U,$ ${\dot {y}}_{2}=-{\frac {-(a+by_{3})y_{1}-(a+by_{3})y_{1}^{3}-cy_{2}+dy_{3}+\mu y_{4}^{2}cosy_{3}+(\alpha {-\beta }y_{4})\mu seny_{3}}{1-\mu \epsilon (seny_{3})^{2}}},$ ${\dot {y}}_{3}=y_{4},$ ${\dot {y}}_{4}=-{\frac {\epsilon (-(a+by_{3})y_{1}-(a+by_{3})y_{1}^{3}-cy_{2}+dy_{3})seny_{3}+\mu \epsilon y_{4}^{2}cosy_{3}seny_{3}+\alpha -\beta y_{4}}{1-\mu \epsilon (seny_{3})^{2}}},$ ${\dot {y}}_{5}=y_{6},$ ${\dot {y}}_{6}=-ey_{5}+f(1-y_{5}^{2})y_{6}+gy_{1}.$

(8)

where the function of control ${\textstyle U}$ is defined in equation (5).

We will obtain

${\textstyle B={\begin{pmatrix}1\\1\\1\\1\\1\\1\end{pmatrix}}}$, ${\textstyle y={\begin{pmatrix}x_{1}-{\tilde {x}}_{1}\\x_{2}-{\tilde {x}}_{2}\\x_{3}-{\tilde {x}}_{3}\\x_{4}-{\tilde {x}}_{4}\\x_{5}-{\tilde {x}}_{5}\\x_{6}-{\tilde {x}}_{6}\end{pmatrix}}}$, ${\textstyle {\tilde {x}}={\begin{pmatrix}0\\0\\0\\0\\0\\0\end{pmatrix}}}$,${\textstyle Q=I_{6}}$, ${\textstyle A={\begin{pmatrix}0&1&0&0&0&0\\-91.77&-0.01&91.10&0&0&0\\9.50&0&0&1&0&0\\-0.09&0&0.09&-1.49&0&0\\0&0&0&1&0&1\\9.50&0&0&0&-87.00&17.99\end{pmatrix}}}$

where the controllability matrix ${\textstyle R}$ of the system for the pair [${\textstyle A,B}$] is obtained by ${\textstyle R=[B|AB|A^{2}B|A^{3}B|A^{4}B|A^{5}B]}$.

Thus, ${\textstyle R={\begin{pmatrix}1\end{pmatrix}}}$. Then the Matrix

${\textstyle P(t)}$ is given by ${\textstyle P=10^{4}{\begin{pmatrix}0.216&0.031&0.406&-0.030&-0.647&0.040\\0.031&0.004&0.058&-0.004&-0.093&0.005\\0.406&0.058&0.767&-0.058&-1.218&0.071\\-0.030&-0.004&-0.058&0.004&0.092&-0.005\\-0.647&-0.093&-1.218&0.092&1.944&-0.123\\0.040&0.005&0.076&-0.005&-0.123&0.008\end{pmatrix}}}$

and (an optimal control)

${\textstyle u=10^{2}(1.6765x_{1}+0.2493x_{2}+3.2667x_{3}-0.2353x_{4}-4.6331x_{5}+0.2116x_{6}}$).

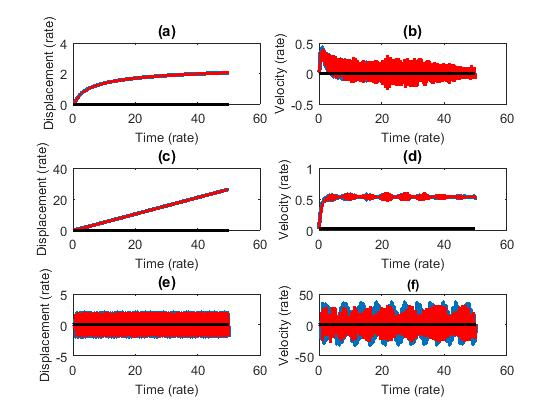
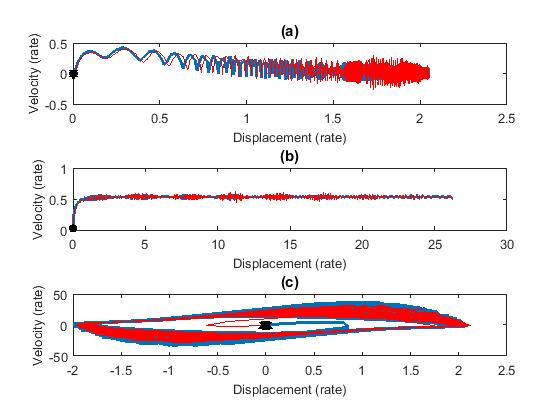
The trajectories of the system with control can be seen in Figures 5 and 6. According to the optimal control verification [23], the function is numerically calculated by ${\textstyle L(t)=y^{T}{\tilde {Q}}y}$, where ${\textstyle L(t)}$ is positive definite.

Figure 5. Time History - the blue line is related to the system with uncertain parameters; the red line, with fixed parameters; the black line, in turn, is related to the controlled system. (a) Displacement for the Mathieu system. (b) Velocity for the Mathieu system. (c) Displacement for the non-ideal excitation. (d) Velocity for the non-ideal excitation. (e) Displacement for Van der Pol system. (f) Velocity for the Van der Pol system

Figure 6. Phase Portrait - the blue line is related to the system with uncertain parameters; the red line, with fixed parameters; the black line, in turn, is related to the controlled system. (a) Mathieu system. (b) Non-ideal excitation. (c) Van der Pol system

4. Conclusions

In this work, the dynamics of a new model called the Non-Ideal Mathieu-Van Der Pol System with chaotic behavior is analyzed through the Lyapunov exponents. Three positives exponentes was found, which demonstrates the existence of a chaotic behavior and characterizes an hyper chaotic behavior. The chaotic behavior detected in the system indicates that the system is unstable and its construction, development and efficiency are not possible, and this behavior is not desired To stabilize such chaotic behavior, a control method based on the Linear Optimal Control was implemented as a strategy for reducing the chaotic motion of the system to a desired fixed point applied to any initial condition imposed on the system.

Figures 5 and 6 illustrated the effectiveness of the control strategy applied to solve these problems. The potential results of this work may be used, in future research in projects of advanced technological products, such as the manufacturing of electric and autonomous vehicles in the automotive sector. 

Acknowledgements

The authors would like to thank Universidade Estadual Paulista ”Júlio de Mesquita Filho”, especially the Faculty of Engineering of Ilha Solteira, for the space provided to carry out the work, as well as the Laboratory of Complex Systems. We would also like to thank the Universidade Federal do Estado de Mato Grosso for the support given to the work.

References

[1] Nayfeh, A.H., Mook, D.T. Non-linear oscillations. John Wiley & Sons, New York, 1979.

[2] Ott, E., Grebogi, C., Yorque, J.A. Controlling chaos. Phys. Rev. Lett., 66:1196-1199, 1990.

[3] Shih-Yu, L., Sheng-Chieh, H., Cheng-Hsiung, Y., Zheng-Ming, G. Generating tri-chaos attractors with three positive Lyapunov exponents in new four order system via linear coupling. Nonlinear Dyn., 69:805-816, 2012.

[4] Balthazar, J.M., Mook, D.T., Weber, H.I., Brasil, R.M.L.R.F., Fenili, A., Belato, D., Felix, J.L.P. An overview on non-ideal vibrations. Meccanica, 38(6):613-621, 2003.

[5] Dantas, M.J.H., Balthazar, J.M. On local analysis of oscillations of a non-ideal and non-linear mechanical model. Meccanica, 39:313-330, 2004.

[6] Chavarette, F.R. On an optimal linear control of a chaotic non-ideal duffing system. Applied Mechanics and Materials, 138-139:50-55, 2012.

[7] Souza, S.L.T., Caldas, I.L., Viana, R.L., Balthazar, J.M. Control and chaos for vibro-impact and non-ideal oscillators. Journal of Theoretical and Applied Mechanics, 46-3:641-664, 2008.

[8] Belato, D., Weber, H.I., Balthazar, J.M., Mook, D.T. Chaotic vibrations of a nonideal electro-mechanical system. International Journal of Solids and Structures, 38:1699-1706, 2001.

[9] Piccirillo, V., Balthazar, J. M., Pontes JR, B.R., Felix, J.L.P. On a nonlinear and chaotic non-ideal vibrating system with shape memory alloy (SMA). Journal of Theoretical and Applied Mechanics, 46-3:597-620, 2008.

[10] Chavarette, F.R., Balthazar, J.M., Felix, J.L.P. Remarks on an optimal linear control design applied to a nonideal and an ideal structure coupled to an essentially nonlinear oscillator. Journal of Computational and Nonlinear Dynamics, 5:1-9, 2010.

[11] Chavarette, F.R. Control design applied to a non-ideal structural system with behavior chaotic. International Journal of Pure and Applied Mathematics, 86-3:487-500, 2013.

[12] Tsuchida, M., Guilherme, K.L., Balthazar, J.M. On chaotic vibrations of a non-ideal system with two degrees of freedom: 1:2 resonance and sommerfeld effect. Journal of Sound and Vibration, 282:1201-1207, 2005.

[13] Ghanem, R.G., Spanos, P.D. Stochastic finite elements: A spectral approach. Courier Dover Publications, 1991.

[14] Koroishi, E.H., Cavalini Jr, A.A., de Lima, A.M.G. , Stefen Jr, V. Stochastics modeling of exible rotors. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 34:597-603, 2012.

[15] Lara-Molina, F.A., Rosario, J.M., Dumur, D., Wenger, P. Generalized predictive control of parallel robots. Proceeding of Robot Motion and Control, 422, Lecture Notes in Control and Information Sciences, 159-169, 2012.

[16] Moller, B., Beer, M. Fuzzy randomness, uncertainty in civil engineering and computational mechanics. Springer-Verlag, 2004.

[17] Tusset, A.M., Balthazar, J.M., Chavarette, F.R., Felix, J.L.P. On energy transfer phenomena, in a nonlinear ideal and nonideal essential vibrating systems, coupled to a (MR) magneto-rheological damper. Nonlinear Dyn., 69-4:1-22, 2012.

[18] Rafikov, M., Balthazar, J.M. On control and synchronization in chaotic and hyperchaotic system via linear control feedback. Communications in Nonlinear Science and Numerical Simulation, 13:1246-1255, 2008.

[19] Chavarette, F.R., Peruzzi, N.J., Balthazar, J.M., Barbanti, L., Damasceno, B.C. On an optimal linear control applied to a non-ideal load transportation system, modeled whit periodic coefficients. Applied Mechanics and Materials, 52-54:13-18, 2011.

[20] Chavarette, F.R. Optimal linear control to parametric uncertainties in a micro electro mechanical system. International Journal of Pure and Applied Mathematics, 83-4:539-548, 2013.

[21] Frahm, H. Adevice for damping vibrations of bodies. US Patent 989958, 1911.

[22] Viquié, R., Kerschen, G. Nonlinear vibration absorber coupled to a nonlinear primary system: A tuning methodology. Journal of Sound and Vibration, 326:780-793, 2009.

[23] Cveti-anin, L. Dynamics of the non-ideal mechanical systems: a review. Journal of the Serbian Society for Computational Mechanics, 4-2:75-86, 2010.

[24] Chavarette, F.R., Peruzzi, N. J., Lopes, M.L.M., Cossi, A.M. A note of optimal linear control technical applied in the chaos stabilization in the Mathieu-van der Pol autonomous oscillator. International Journal of Applied Mathematics, 25:861-869, 2012.

[25] Wolf, A., Swift, J.B., Swinney, H.L., Vastano, J.A. Determining Lyapunov exponents from a time series. Physica D: Nonlinear Phenomena, 16(3):285-317, 1985.