Resumen
En este documento se presenta una propuesta novedosa de un algoritmo híbrido modular, como herramienta para resolver problemas de ingeniería del mundo real. Se implementa y aplica un algoritmo memético, MemMABC, para la solución de dos casos de diseño de mecanismos, con el fin de evaluar su eficiencia y rendimiento. El algoritmo propuesto es simple y flexible debido a su modularidad; estas características lo vuelven altamente reutilizable para ser aplicado en una amplia gama de problemas de optimización. Las soluciones de los casos de estudio también son modulares, siguiendo un esquema de programación estructurada que incluye el uso de variables globales para la configuración, y de subrutinas para la función objetivo y el manejo de las restricciones. Los algoritmos meméticos son una buena opción para resolver problemas duros de optimización, debido a la sinergia derivada de la combinación de sus componentes: una metaheurística poblacional para búsqueda global y un método de refinamiento local. La calidad en los resultados de las simulaciones sugiere que el MemMABC puede aplicarse con éxito para la solución de problemas duros de diseño en ingeniería.
Palabras clave: ABC, síntesis dimensional, algoritmos meméticos, metaheurísticas, optimización.
Abstract
In this paper a novel proposal of a modular hybrid algorithm as a tool for solving real-world engineering problems is presented. A memetic algorithm, MemMABC, is implemented with this approach and applied to solve two case studies of mechanism design, in order to evaluate its efficiency and performance. Because of its modularity, the proposed algorithm is simple and flexible; these features make it quite reusable to be applied on different optimization problems, with a wide scope. The solutions of the optimization problems are also modular, following a scheme of structured programming that includes the use of global variables for configuration, and subroutines for the objective function and the restrictions. Memetic algorithms are a good option to solve hard optimization problems, because of the synergy derived from the combination of their components: a global search population-based metaheuristic and a local refinement method. The quality of simulation results suggests that MemMABC can be successfully applied to solve hard problems in engineering design.
1 Introducción
Actualmente, la solución de casos de ingeniería del mundo real mediante su planteamiento como problemas de optimización es una práctica de uso extendido en el campo de la ingeniería [1], dado que existe una amplia base de métodos para resolver dichos problemas matemáticos. Entre las ventajas derivadas de esta abstracción destacan la alta reconfigurabilidad tanto en la definición de los casos de estudio como en su implementación física, la posibilidad de encontrar más de una solución si el problema es multimodal (cuya prueba representa en sí todo un problema teórico), y la facilidad de evaluación del rendimiento de los sistemas propuestos, entre otras. Existen diversas opciones para resolver estos problemas de optimización, siendo las más empleadas los métodos clásicos y las metaheurísticas.
Los métodos clásicos de optimización son técnicas analíticas que hacen uso del cálculo diferencial para localizar los valores óptimos [2]. Estos métodos tienen un alcance limitado en las aplicaciones prácticas, ya que la mayoría de los problemas de ese tipo están fuertemente restringidos o involucran funciones que no son continuas y/o diferenciables; sin embargo, por su carácter de métodos exactos deben considerarse como la primera opción al resolver problemas de optimización. Por su parte, las metaheurísticas resuelven de forma aproximada los problemas de optimización por medio de técnicas de prueba y error, siendo una de las áreas de la inteligencia artificial con mayor actividad; frecuentemente aparecen mejoras a los algoritmos existentes e incluso nuevos algoritmos, basados en diferentes filosofías [3]. La metodología de diseño de las metaheurísticas generalmente es la misma: se estudia un fenómeno de la naturaleza, se abstrae un modelo descriptivo y se simula con un algoritmo [4]; después se evalúa el desempeño de dicho algoritmo usando bancos de pruebas con funciones conocidas [5,6]. Sin embargo, la mayoría de los casos se quedan en esa etapa experimental, y no se aplican para resolver problemas del mundo real.
La complejidad ya citada de los problemas en ingeniería hace que por lo general sea impráctico o imposible el usar métodos tradicionales para resolverlos usando recursos de cómputo convencionales. Sin embargo, muchos de estos casos sólo requieren una solución fácilmente alcanzable y suficientemente buena para ser fabricada; así, las metaheurísticas son una opción factible para dichos problemas, con soluciones de calidad tanto desde el punto de vista algorítmico como del diseño.
La hibridación potencia el desempeño de las metaheurísticas, mediante la combinación sinérgica de algoritmos de población para búsqueda global (GS) con técnicas de búsqueda local (LS) [7]. Existe toda una taxonomía para clasificar a las metaheurísticas híbridas (HM), dependiendo de la manera en que se combinen sus elementos básicos [8]. Destacan por su diseño simple las HM de tipo integrativo y trabajo en equipo, donde el algoritmo de búsqueda local (subordinado) se convierte en un componente del método de población (maestro); los algoritmos meméticos (MA) son los ejemplos más representativos de esta categoría [9,10].
La aplicación de los MA [11] se ha enfocado mayormente a la optimización combinatoria, en casos tales como el del agente viajero (TSP) [12], la programación de enfermeras [13] y el problema de la mochila (KP) [14]. El uso de estos métodos en diseño en ingeniería del mundo real es un campo poco explorado; entre los desarrollos destacan la cinemática inversa de un manipulador robótico [15], el diseño de filtros para comunicaciones [16], el manejo de redundancia [17] y la planificación de tareas en mallas de cómputo [18].
En optimización son bien conocidos los teoremas de No Free Lunch [19], estableciendo que si un algoritmo se desempeña particularmente bien para una clase determinada de problemas entonces su rendimiento es inferior al promedio en los casos restantes. Esto es, no hay un algoritmo que resuelva eficientemente cualquier problema; sin embargo, si se considera la estructura de los problemas y su modelado se pueden diseñar métodos suficientemente generales para que el conjunto de sus aplicaciones sea muy amplio. Adicionalmente, los algoritmos serán altamente reutilizables si se programan de manera modular [20].
En este trabajo se presenta la implementación de un algoritmo memético, desarrollado a partir de los algoritmos de colonia artificial de abejas modificado (MABC) y de caminata aleatoria (RW), aplicado a dos casos de síntesis de mecanismos. El objetivo es mostrar la utilidad de estos métodos para resolver problemas de optimización en ingeniería, si dichos casos se plantean correctamente desde el punto de vista matemático y la programación de los algoritmos se realiza de manera estructurada. La organización del escrito es la siguiente: en la Sección 2 se incluye una introducción a las metaheurísticas y dentro de ésta a los algoritmos meméticos; en la Sección 3 se explica el MA propuesto y sus componentes; la Sección 4 describe los casos de estudio; la Sección 5 corresponde a la implementación computacional del algoritmo; en la Sección 6 se analizan los resultados obtenidos, y en la Sección 7 se presenta la discusión final.
2 Algoritmos meméticos
2.1 Metaheurísticas de población
Las metaheurísticas basadas en población toman un conjunto inicial de soluciones (individuos) para buscar los valores óptimos, y tratan de ajustar dichas soluciones dentro del área de búsqueda conforme transcurren las generaciones; existen dos grupos generales en estos algoritmos: computación evolutiva e inteligencia de cúmulos. Una metaheurística efectúa su búsqueda mediante dos tareas: la exploración (diversificación) y la explotación (intensificación); generalmente, las técnicas de población son buenas diversificando pero realizan una intensificación deficiente [3].
2.2 Algoritmo de colonia artificial de abejas
Los algoritmos de inteligencia de cúmulos son metaheurísticas del campo de la inteligencia artificial, basadas en modelos sobre la manera en que se organizan diferentes sociedades de organismos vivos. La colonia artificial de abejas (Artificial Bee Colony, ABC) es un algoritmo de inteligencia de cúmulos, propuesto por Karaboga en 2005 [21], que se basa en la conducta de los enjambres durante dos procesos naturales: el reclutamiento de abejas para la explotación de fuentes de alimento y el abandono de las fuentes agotadas.
En el algoritmo ABC, las abejas en una colonia se dividen en tres grupos: empleadas, observadoras y exploradoras. El número de empleadas es igual al número de fuentes y cada empleada está asignada a una de ellas; después de alcanzar su fuente, cada abeja calcula una nueva solución a partir de ahí y conserva la mejor entre ambas. El número de observadoras es igual al de las empleadas y su asignación a las fuentes se determina con base en el rendimiento de las mismas; las observadoras también calculan nuevas soluciones a partir de su fuente asignada. Finalmente, cuando una fuente no mejora después de un determinado número de ciclos, se abandona y es remplazada por otra encontrada por una exploradora. Las tres etapas de evaluación de fuentes del ABC se muestran en la Figura 1.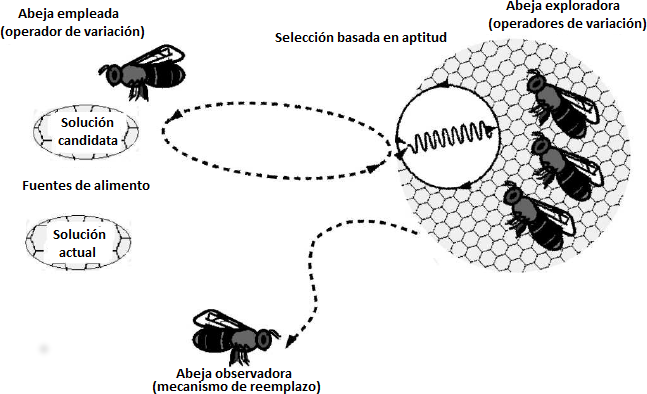
|
| Figura 1: Proceso de generación y sustitución de fuentes en el algoritmo Artificial Bee Colony (ABC) [22] |
Se han desarrollado diferentes versiones del algoritmo ABC; la modificación propuesta por Mezura y Cetina [22] maneja problemas de optimización numérica con restricciones, con una selección de individuos tipo torneo basada en los criterios propuestos por Deb [23]. Dicho algoritmo, denominado Modified Artificial Bee Colony (MABC), usa tres parámetros definidos por el usuario: el número de fuentes (soluciones posibles) SN, el número total de ciclos MCN, y el número de intentos sucesivos de mejora en una fuente antes de remplazarla.
2.3 Búsqueda Local
Los algoritmos de búsqueda local parten de un conjunto inicial de soluciones (normalmente con un individuo), iterando para realizar transiciones con los vecinos de la configuración actual; la idea es encontrar mejores poblaciones dentro del vecindario y convertirlas en la siguiente configuración, o en caso contrario conservar la solución inicial [24]. En la Figura 2 se muestra un ejemplo de LS, indicada para el primer individuo de la población, .
En los casos de optimización combinatoria el vecindario es el conjunto de soluciones a las que se accede por medio de un cambio unitario en el individuo actual, mientras que en los problemas de tipo continuo es un conjunto compuesto por un número infinito de puntos, por lo que se requiere de una estrategia de modificación para encontrar aquellos que se consideren como vecinos [25]. La búsqueda de vecinos puede ser estocástica o determinística, enfocada a encontrar sólo uno o todo un conjunto de ellos.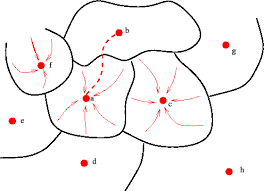
|
| Figura 2: Búsqueda local basada en vecindarios. |
2.4 Caminata aleatoria
Existen diversos algoritmos que pueden emplearse para implementar una búsqueda local. Entre ellos, la caminata aleatoria (Random Walk, RW) es un método directo de fácil implementación ya que no necesita el gradiente ni el hessiano de la función objetivo; el Algoritmo 1 muestra este método. RW se basa en aproximaciones hacia el óptimo local a partir de un punto inicial , donde el vecino siguiente se genera por (1):
|
|
(1) |
donde es una longitud preestablecida y es un vector unitario que requiere de un conjunto con números aleatorios en el intervalo [-1,1], cuya cardinalidad corresponde al total de variables del vector de diseño. Los valores del conjunto se transforman en direcciones de búsqueda, y se debe evitar que ésta se dirija hacia las diagonales del hipercubo unitario que rodea al punto inicial [2]; por ello, los números aleatorios generados se aceptan solamente si , calculando a por (2),
|
|
(2) |
|
2.5 Definición de algoritmo memético
Los algoritmos meméticos son métodos híbridos, que combinan sinérgicamente una metaheurística de población como buscador global con el refinamiento de otro algoritmo utilizado como buscador local. La finalidad es compensar la debilidad del algoritmo basado en población para explotar el espacio de soluciones factibles; el buscador local puede ser determinístico o metaheurístico [10,26]. El Algoritmo 2 corresponde a un MA básico, considerando métodos generales para las búsquedas global (línea 8) y local (líneas 6 y 10).
|
3 Desarrollo del algoritmo propuesto
En este trabajo se implementa el algoritmo MemMABC, que combina al MABC como buscador global y a RW como búsqueda local activada por tiempo; el Algoritmo 3 corresponde al MemMABC. La activación de las etapas de refinamiento se controla con la variable , que es el número de generaciones entre cada LS, mientras que su profundidad depende de la variable Intensidad.
El algoritmo RW fue modificado en MemMABC para reducir tanto el esfuerzo computacional requerido como para permitir el manejo de restricciones, esto último empleando las reglas de Deb. Para la condición de paro se estableció un máximo de evaluaciones de la función objetivo (); esto permite una comparación justa entre el algoritmo y otros métodos de optimización [27]. El MemMABC se implementó de manera modular con programación estructurada, aumentando su reutilizabilidad mediante un diseño simple y flexible; para ello se diseñaron las siguientes funciones:
- : configuración de parámetros del algoritmo, contadores y cotas.
- : entrada: individuo ; salida: valor de función objetivo en .
- : entrada: individuo ; salida: suma de violación de restricciones de .
- : entrada: individuos y ; salida: mejor solución aplicando las reglas de Deb.
- : entrada: población total; salida: mejor individuo por función objetivo.
- : entrada: mejor individuo; salida: mejor individuo en el vecindario.
|
4 Casos de estudio
Para la prueba de los algoritmos se usaron dos problemas reales de síntesis de mecanismos, los cuales se seleccionaron por su alta complejidad. La medida de dicha complejidad es el parámetro [6], que corresponde a la relación entre la zona factible y el espacio de búsqueda del problema, vista como el porcentaje de soluciones factibles encontradas en un número arbitrariamente grande de soluciones generadas al azar. En cada caso de estudio se tomó un millón de valores, generando =0.0043% y =0002%, respectivamente. Los casos se plantearon como optimización mono-objetivo, definiéndose tanto su función objetivo () como las cotas y las restricciones asociadas.
Si bien en el enfoque del diseño mecatrónico normalmente se consideran aspectos tanto cinemáticos como dinámicos para el planteamiento de problemas de optimización (MODOP, Multiobjective Dynamic Optimization Problem) [1], para estos casos de estudio el análisis se centró en el comportamiento cinemático de los sistemas porque unicamente se necesita determinar el diseño estructural de los mismos. En etapas posteriores se considerarán otros aspectos, tales como el peso, resistencia de los materiales empleados, estética, diseño del controlador, etc., que convertirán a estos problemas en casos MODOP.
4.1 Caso 1: Mecanismo de cuatro barras para seguimiento de una trayectoria lineal (CE1)
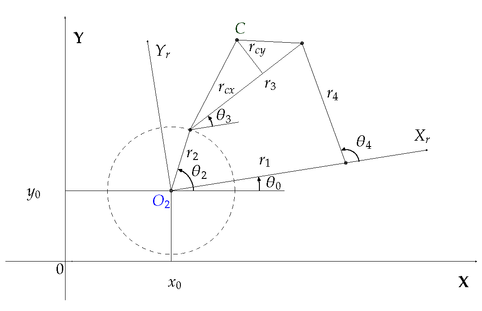
El mecanismo de cuatro barras es uno de los más utilizados en el diseño de maquinaria, debido a su simplicidad para movimientos controlados de un grado de libertad [28,29]. La Figura 3 muestra un mecanismo de cuatro barras cuyos elementos son: barra de referencia (), manivela (), biela () y balancín (); para realizar el análisis de posición se parte de la ecuación de cierre de circuito, indicada en (3):
|
|
(3) |
|
| Figura 3: Mecanismo de cuatro barras |
El giro de , dado por el ángulo , provoca que oscile, desplazando a su vez a . Cada punto que cruza el mecanismo se determina por el acoplador , cuya coordenada de posición se indica en (4),
|
|
(4) |
Para este caso el acoplador debe pasar sin sincronización previa por seis puntos alineados verticalmente, cuyas coordenadas están dadas en (5); el desarrollo detallado de este problema específico se encuentra en [30]
|
|
(5) |
Se desea minimizar la distancia entre los puntos ideales y los puntos calculados , por lo que se propone la función objetivo en (6), correspondiente al error cuadrático entre dichos puntos:
|
|
(6) |
El vector de diseño correspondiente está dado por (7); para completar la caracterización del problema de optimización numérica se requiere considerar las cotas de las variables de diseño, mismas que se expresan en (8)
|
|
4.2 Caso 2: Efector final tipo pinza de dos dedos (CE2)
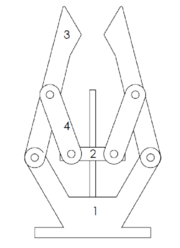
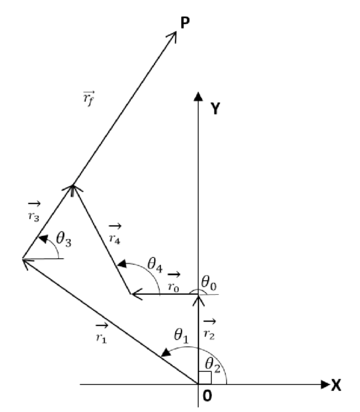
Los robots son sistemas mecatrónicos programados para tareas específicas tales como soldar o perforar, cuya realización requiere de efectores finales [31]; dichos efectores se clasifican en herramientas y manipuladores. Los manipuladores emulan manos humanas; el tipo más común tiene dos dedos y un grado de libertad (Figura 4). Sus elementos son: 1) base, 2) tornillo de potencia y tuerca, 3) eslabón de agarre y, 4) eslabón de acoplamiento; la Figura 5 muestra su diagrama esquemático, donde cada vector se relaciona con el -ésimo eslabón del mecanismo. La ecuación de cierre de circuito está dada por (9), mientras que las expresiones en (10) corresponden a la posición de los extremos del efector:
|
|
(9) |
|
|
| Figura 4: Efector final |
Uno de los aspectos más importantes en este diseño corresponde a la fuerza de agarre o a su transmisión; así, es la fuerza de agarre ejercida por el efector sobre el objeto de interés, y está dada por (11),
|
|
(11) |
El criterio para evaluar el desempeño de este manipulador es que la fuerza de sujeción sea constante en toda la apertura o espacio de trabajo; una explicación detallada de este problema se encuentra en [32]. Como se observa en la Figura 4, la posición del extremo del efector depende de la altura de la tuerca en el tornillo de potencia; así, se requiere minimizar la función objetivo, la cual debe tender a cero para mantener la fuerza constante como se indica en (12):
|
|
(12) |
|
| Figura 5: Diagrama esquemático del efector final |
El espacio de trabajo del efector está definido por
- : Dimensiones mínima y máxima del objeto de interés.
- : Rango de apertura de los extremos del efector.
- : Valores extremos de la posición de la tuerca.
- : Rango de variación de la posición de la tuerca.
El vector de diseño se expresa en (13), con las cotas de (14),
|
|
5 Implementación computacional
La implementación de algoritmos se programó en MATLAB R2013a, sobre una plataforma computacional con procesador Intel Core i7 @1.75 GHz, 8Gb de memoria RAM y sistema operativo Windows 8. Para la evaluación del desempeño los casos de estudio se resolvieron usando tanto el algoritmo MABC como el MemMABC, con 30 simulaciones por algoritmo en cada caso. Se usó una condición de paro adicional, con detención anticipada al alcanzar el valor óptimo =0; también se consideró =1000 si en una corrida específica no se generaba alguna solución factible.
La configuración del MemMABC requiere de seis parámetros: , número de variables de diseño; , número de fuentes de alimento; , número máximo de evaluaciones de la función objetivo; , número de generaciones para la activación de la LS; , número máximo de evaluaciones de la función objetivo en la LS, y , número máximo de intentos consecutivos de mejora de una fuente. En el CE1 se consideró =1,000,000, =50, =2,800, =750, e =10,000, mientras que para el CE2 se tomó =35,000, =5, =1,650, =8,500, y =40.
6 Resultados
Para la solución de ambos casos de estudio primeramente se utilizó la programación cuadrática secuencial (Sequential Quadratic Programming, SQP) reconocida como uno de los métodos más eficientes de optimización clásica. La implementación se realizó con la función fmincon de MATLAB, ejecutándose 30 simulaciones para cada caso de estudio y tomando puntos de inicio aleatorios dentro del espacio de búsqueda. Sin embargo, SQP presentó un rendimiento deficiente, ya que en el CE1 se obtuvo solamente una solución factible, con =2.34567 en 1,000,000 de evaluaciones, mientras que para el CE2 solo dos de sus simulaciones generaron resultados factibles, siendo su mejor valor =9.83E-17, con 35,000 evaluaciones; por ello sus resultados no se consideraron para el análisis de desempeño mostrado en las tablas siguientes. La razón de este pobre rendimiento es la alta sensibilidad de SQP al punto de inicio, especialmente cuando la dimensionalidad o las restricciones del problema aumentan.
6.1 Caso de estudio CE1
La Tabla 1 contiene los resultados de las treinta simulaciones para el CE1, resaltando el mejor valor generado por cada algoritmo. El análisis estadístico de los resultados obtenidos se presenta en la Tabla 2. Como se observa, el valor mínimo de la función objetivo se obtuvo con MemMABC (=0.01466775), con una varianza de =0.0704462, significativamente menor que la correspondiente a MABC y que indica un desempeño estable del algoritmo. Adicionalmente, MemMABC requirió un 10% menos evaluaciones e incluso alcanzó su mejor valor antes del límite .
La Tabla 3 contiene la mejor solución para cada algoritmo implementado, representada por el vector de variables de diseño. Como se mencionó anteriormente, MemMABC produjo la mejor solución. La Figura 6 muestra el mecanismo correspondiente a dicha solución y su trayectoria sobre los puntos de precisión, marcados como en una simulación del movimiento realizada con GeoGebra; se puede observar en la figura que el mecanismo pasa sobre todos los puntos en su recorrido ascendente y presenta un lazo de retorno muy pequeño, lo cual implica un tiempo de recuperación corto que puede representar una ventaja si el dispositivo se analiza desde el punto de vista de ingeniería.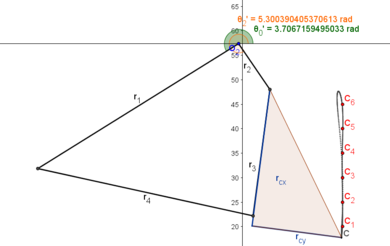
|
| Figura 6: Simulación de la mejor solución del MemMABC - CE1 |
6.2 Caso de estudio CE2
La Tabla 4 muestra los resultados obtenidos en las treinta corridas para el CE2, resaltando el mejor valor generado por cada método; cuando un algoritmo obtuvo el valor óptimo en más de una corrida se consideró como segundo parámetro el menor número de evaluaciones de la función objetivo. Por su parte, en la Tabla 5 se presenta el análisis estadístico de los resultados; si bien ambos algoritmos presentan un comportamiento similar, MemMABC tuvo mejores valores y generó el valor óptimo después de 15,839 evaluaciones de la función objetivo, aproximadamente 12% menos que las 17,813 evaluaciones requeridas por el MABC.
En la Tabla 6 se muestran los vectores de diseño correspondientes a la mejor solución obtenida por cada algoritmo implementado. La variedad de soluciones muestra que el problema es multimodal; por su naturaleza poblacional los algoritmos empleados tienen un mejor comportamiento en los casos en que se tiene más de un valor óptimo. Este aspecto se refuerza por el uso de más de un algoritmo para resolver el problema, ya que la gama de soluciones permite al diseñador no sólo escoger un valor óptimo, sino además elegir el que mejor se adapte a aspectos tales como la fabricación o la instalación del mecanismo o sistema real.
| MemMABC | MABC | ||||
| 2-5 | FO | Evals | FO | Evals | |
| x1000 | x1000 | ||||
| Sim | |||||
| 1-1 1 | 0.301461 | 1000 | 0.208516 | 990 | |
| 2 | 0.500330 | 900 | 0.107299 | 1000 | |
| 3 | 0.074992 | 910 | 1.107299 | 1000 | |
| 4 | 0.044517 | 910 | 0.067285 | 1000 | |
| 5 | 0.140069 | 910 | 0.626309 | 960 | |
| 6 | 0.083722 | 910 | 0.062770 | 1000 | |
| 7 | 0.094170 | 910 | 0.118344 | 990 | |
| 8 | 0.301364 | 910 | 1.987648 | 1000 | |
| 9 | 0.130068 | 910 | 0.696017 | 980 | |
| 10 | 0.123883 | 910 | 0.521547 | 980 | |
| 11 | 0.171383 | 910 | 0.330611 | 970 | |
| 12 | 0.029678 | 910 | 1.071400 | 990 | |
| 13 | 0.102760 | 910 | 0.046103 | 1000 | |
| 14 | 0.036344 | 910 | 0.841517 | 1000 | |
| 15 | 1.324383 | 910 | 0.055782 | 1000 | |
| 16 | 0.111527 | 910 | 0.480897 | 980 | |
| 17 | 0.096556 | 910 | 0.690968 | 1000 | |
| 18 | 0.014667 | 900 | 0.047740 | 1000 | |
| 19 | 0.026348 | 910 | 1.191474 | 980 | |
| 20 | 0.039964 | 910 | 0.063390 | 1000 | |
| 21 | 0.150369 | 910 | 0.029598 | 1000 | |
| 22 | 0.224345 | 910 | 0.135714 | 1000 | |
| 23 | 0.281801 | 910 | 6.047393 | 970 | |
| 24 | 0.539555 | 910 | 0.182488 | 960 | |
| 25 | 0.143620 | 910 | 0.308238 | 1000 | |
| 26 | 0.052217 | 910 | 0.238166 | 920 | |
| 27 | 0.321617 | 910 | 0.126951 | 1000 | |
| 28 | 0.505811 | 910 | 0.490899 | 1000 | |
| 29 | 0.686442 | 910 | 0.072311 | 900 | |
| 30 | 0.104808 | 910 | 0.116885 | 1000 | |
| MemMABC | MABC | |||
| 3-5 Parámetro | ||||
| 1-1 Min | 0.014667 | 0.029598 | ||
| Max | 1.324383 | 6.047393 | ||
| Mediana | 0.126975 | 0.223341 | ||
| Promedio | 0.225292 | 0.602385 | ||
| Varianza | 0.070446 | 1.222448 | ||
| Desviación Est. | 0.265417 | 1.105644 | ||
| Evs/Min | 900000 | 1000000 | ||
| Promedio de Evs | 924333 | 985300 |
| MemMABC | MABC | ||||
| 3-5 Variable | |||||
| 1-1 | 47.61022 | 48.51296 | |||
| 11.29351 | 10.44436 | ||||
| 26.05979 | 23.76895 | ||||
| 44.17324 | 44.73566 | ||||
| 28.09277 | 24.56259 | ||||
| 18.09717 | 15.23919 | ||||
| 3.70672 | 3.64450 | ||||
| -0.72692 | 3.79430 | ||||
| 57.39457 | 55.81364 | ||||
| 2.03045 | 1.57201 | ||||
| 2.54567 | 2.38873 | ||||
| 2.97677 | 2.87644 | ||||
| 3.40864 | 3.35841 | ||||
| 3.87709 | 3.89958 | ||||
| 4.45365 | 4.65024 |
| MemMABC | MABC | ||||
| 2-5 | FO | Evals | FO | Evals | |
| Sim | |||||
| 1-1 1 | 0 | 27787 | 0 | 19589 | |
| 2 | 0 | 23058 | 0 | 25554 | |
| 3 | 0 | 23224 | 0 | 18812 | |
| 4 | 0.002451 | 34424 | 0 | 26722 | |
| 5 | 0.000756 | 34228 | 0 | 34542 | |
| 6 | 0 | 23177 | 0 | 29303 | |
| 7 | 0.000664 | 32302 | 0 | 25965 | |
| 8 | 0.002046 | 34167 | 0.005760 | 35000 | |
| 9 | 0 | 23471 | 0 | 25658 | |
| 10 | 0 | 23288 | 0 | 31758 | |
| 11 | 0 | 23398 | 0 | 20144 | |
| 12 | 7.70E-34 | 31999 | 6.95E-30 | 35000 | |
| 13 | 0 | 15839 | 0 | 26860 | |
| 14 | 7.70E-34 | 34230 | 4.64E-07 | 35000 | |
| 15 | 0.001725 | 31810 | 0 | 31983 | |
| 16 | 0.000432 | 31672 | 0.001345 | 35000 | |
| 17 | 0.005217 | 33034 | 0 | 25001 | |
| 18 | 0 | 23294 | 0 | 26876 | |
| 19 | 0 | 22961 | 0 | 34107 | |
| 20 | 0.001381 | 35000 | 0.001704 | 35000 | |
| 21 | 0 | 23413 | 0.000262 | 35000 | |
| 22 | 0 | 23068 | 0 | 17813 | |
| 23 | 7.70E-34 | 31850 | 0.001315 | 35000 | |
| 24 | 0 | 23385 | 5.12E-05 | 35000 | |
| 25 | 3.08E-33 | 33036 | 0.000553 | 35000 | |
| 26 | 0.002821 | 31974 | 0.005916 | 35000 | |
| 27 | 0 | 23350 | 0 | 27485 | |
| 28 | 0 | 23229 | 0.006262 | 35000 | |
| 29 | 0 | 23504 | 0 | 27970 | |
| 30 | 7.70E-34 | 32682 | 0 | 28406 | |
| MemMABC | MABC | |||
| 3-5 Parámetro | ||||
| 1-1 Min | 0 | 0 | ||
| Max | 0.0052177 | 0.0062623 | ||
| Mediana | 0 | 0 | ||
| Promedio | 0.0005832 | 0.0007724 | ||
| Varianza | 1.375E-06 | 3.211E-06 | ||
| Desviación Est. | 0.0011728 | 0.0017919 | ||
| Evs/Min | 15839 | 17813 | ||
| Promedio de Evs | 27731 | 29748 |
| MemMABC | MABC | |||
| 3-5 Variable | ||||
| 1-1 | 123.7098 | 115.4636 | ||
| 1.2633 | 20.1385 | |||
| 44.5135 | 49.0498 | |||
| 59.2174 | 31.5840 | |||
| 131.7432 | 112.0447 | |||
| 18.2780 | 5.3617 | |||
| 149.1273 | 149.3967 | |||
| 2.5777 | 2.4109 |
|
|
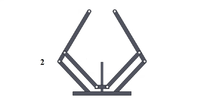
|
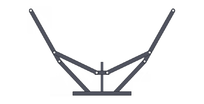
|
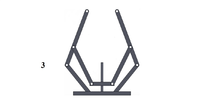
|
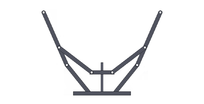
|
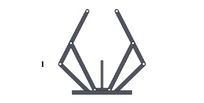
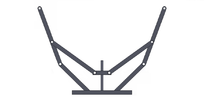
| Figura 7: Simulación de mecanismos con los mejores resultados del MemMABC - CE2 | ||
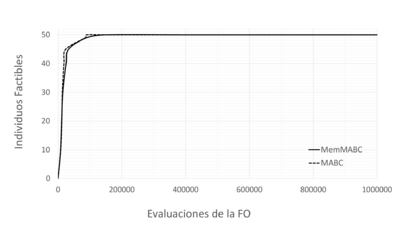
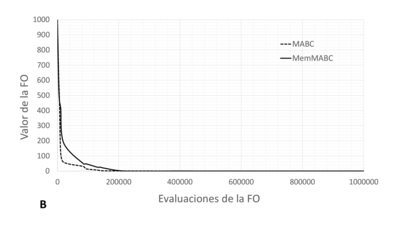
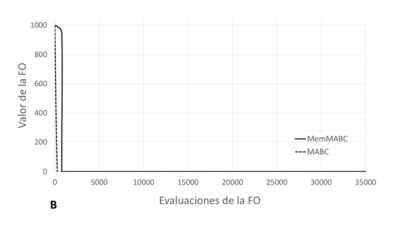
Las Figuras 8 y 9 muestran la convergencia de los algoritmos implementados para el CE1 y el CE2, respectivamente, considerando la mejor solución de cada método; se incluye tanto el comportamiento de los conjuntos de individuos respecto a la factibilidad como la evolución del mejor valor. Como puede observarse, ambos algoritmos presentan un alto rendimiento; sin embargo, MemMABC tuvo tanto mayor eficacia, reflejada en los valores mínimos y en la varianza, como mayor eficiencia si se considera que el número de evaluaciones de la función objetivo requeridas para alcanzar las soluciones fue en promedio un 10% menor con respecto a MABC.
|
|
| Figura 8: Convergencia de la mejor solución (CE1): A) Número de individuos factibles, B) Valor de la función objetivo | |

|
|
| Figura 9: Convergencia de la mejor solución - CE2: A) Número de individuos factibles, B) Valor de la función objetivo | |
7 Discusión final
Si bien las metaheurísticas han sido ampliamente desarrolladas y estudiadas para optimización, su aplicación para resolver problemas del mundo real aún es muy limitada. Dada su condición de métodos de solución aproximados pueden convertirse en excelentes herramientas para el diseño en ingeniería, donde se buscan buenas soluciones que puedan ser llevadas a la práctica con el menor gasto posible de recursos. Considerando esto, la mejora ofrecida por la hibridación en los algoritmos meméticos satisface no solo dicha necesidad, sino además cumple con los requerimientos derivados de la visión de estos algoritmos como buscadores de soluciones óptimas, ya que la calidad de sus resultados los hace sumamente competitivos ante los métodos clásicos.
El algoritmo MemMABC produce resultados de alta calidad, tanto desde el punto de vista de la algoritmia como desde el de la ingeniería. El uso de algoritmos meméticos implementados en forma modular ofrece una gama amplia de posibilidades de aplicación debido a la reutilizabilidad. Aunque en este trabajo se presentan dos casos de estudio sobre síntesis de mecanismos, la simplicidad y modularidad del MemMABC facilita su uso para resolver otros problemas de ingeniería del mundo real; en este sentido, el principal requerimiento es una adecuada interpretación y formulación matemática del caso particular y de sus restricciones.
Agradecimientos
Los autores agradecen el apoyo recibido del Instituto Politécnico Nacional de México, por su Secretaría de Investigación y Posgrado vía el proyecto SIP-20161615.
Referencias
[1] Alvarez-Gallegos J., Cruz-Villar C.A., Portilla-Flores E.A. Evolutionary dynamic optimization of a continuously variable transmission for mechanical efficiency maximization. In Gelbukh A., de Albornoz Á., Terashima-Marín H. (Eds) MICAI 2005: Advances in Artificial Intelligence. Lecture Notes in Computer Science, Vol. 3789:1093-1102, Springer Verlag, 2005.
[2] Rao S. Engineering optimization: theory and practice. John Wiley & Sons, 4th Edition, 2009.
[3] Boussaid I., Lepagnot J., Siarry P. A Survey on optimization metaheuristics. Information Sciences, 237:82-117, 2013.
[4] Eiben A.E., Smith J.E. Introduction to evolutionary computing. Springer Verlag, 2007.
[5] Suganthan P.N., Hansen N., Liang J.J., Deb K., Chen Y.P., Auger A., Tiwari S. Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization. Technical Report 2005005, Nanyang Technological University, 2005.
[6] Liang J., Runarsson T., Mezura Montes E., Clerc M., Suganthan P., Coello C., Deb K. Problem definitions and evaluation criteria for the cec 2006. Technical report, Nanyang Technological University, 2006.
[7] Rodríguez F.J., García C., Lozano M. Hybrid metaheuristics based on evolutionary algorithms and simulated annealing: Taxonomy, comparison and sinergy test. IEEE Transactions on Evolutionary Computation, 16:787-800, 2012.
[8] Krasnogor K., Smith J. (2005) A tutorial for competent memetic algorithms: Model, taxonomy, and design issues. IEEE Transactions on Evolutionary Computation, 9(5):474-488, 2005.
[9] Kumar S., Sharma V.K., Kumari R. Memetic search in differential evolution algorithm. Int. J. Comput. Appli., 90(6):40-47, 2014.
[10] Krasnogor N., Aragón A., Pacheco J. Memetic algorithms. Vol. 2, Chap. 12:905-936, Springer Berlin, 2012.
[11] Ong Y., Lim M., Chen X. Memetic computation: Past, present and future. IEEE Computational Inteligence Magazine, 5(2):24-31, 2010.
[12] Arango M.D., Serna C.A. A memetic algorithm for the traveling salesman problem. IEEE Latin America Transactions, 13(8):2674-2679, 2015.
[13] Gonsalves T., Kuwata K. Memetic algorithm for the nurse scheduling problem. Int. J. Artif. Intell. Applic. (IJAIA), 6(4):43-52, 2015.
[14] Ozcan E., Basaran C. A case study of memetic algorithms for constraint optimization. Soft Computing, 13:871-882, 2009.
[15] González C., Blanco D., Moreno L. A memetic approach to the inverse kinematics problem. In Proceedings of 2012 IEEE International Conference on Mechatronics and Automation, 180-185, 2012.
[16] Tagawa K., Masuoka M., Tsukamoto M. Robust optimum design of saw filters with the taguchi method and a memetic algorithm. In 2005 IEEE Congress on Evolutionary Computation, 3:2146-2153, 2005.
[17] Wang Z., Tang K., Yao X. A memetic algorithm for multi-level redundancy allocation. IEEE Transactions on Reliability, 59 (4):754-765, 2010.
[18] Zhong L., Long Z., Zhang J., Song H. An efficient memetic algorithm for job scheduling in computing grid. Commun. Comput. Inform. Science Series, 86:650-656, Springer Verlag, 2010.
[19] Wolpert D., Macready W. No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1(1):67-82, 1997.
[20] Adriaensen S., Brys T., Nowé A. Designing reusable metaheuristic methods: A Semi-automated approach. In IEEE Congress on Evolutionary Computation, 2969-2976, 2014.
[21] Karaboga D. An idea based on honey bee swarm for numerical optimization. Technical Report TR06, Erciyes University, 2005.
[22] Mezura Montes E., Cetina Domínguez O. Empirical analysis of a modified artificial bee colony for constrained numerical optimization. Applied Mathematics and Computation, 218:10943–10973, 2012.
[23] Deb K. An effcient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Engrg., 186:311-338, 2000.
[24] Moscato P., Cotta C. A Gentle introduction to memetic algorithms. Kluwer Academic Publishers, 105-144, 2003.
[25] Montes de Oca M.A., Cotta C., Neri F. Local search. Springer Verlag, Vol. 379, 29-42, 2012.
[26] Domínguez Isidro S., Mezura Montes E., Leguizamón G. Memetic differential evolution for constrained numerical optimization problems. In Proceedings of 2013 IEEE Congress on Evolutionary Computation, 2996-3003, 2013.
[27] Mernik M., Liu S., Karaboga D., Crepinsek M. On clarifying misconceptions when comparing variants of the artificial bee colony algorithm by offering a new implementation. Information Sciences, 291:115–127, 2015.
[28] Norton R. Diseño de maquinaria: una introducción a la síntesis y análisis de mecanismos y máquinas. McGraw Hill, México, 1995.
[29] Pérez R. Análisis de mecanismos y problemas resueltos. Alfaomega, México, 2007.
[30] Vega-Alvarado E., Santiago-Valentín E., Sánchez-Márquez A., Solano-Palma A., Portilla-Flores E.A., Flores-Pulido L. Síntesis óptima de un mecanismo plano para seguimiento de trayectoria utilizando evolución diferencial. Research in Computing Science, 72:85-89, 2014.
[31] De Silva C.W. Mechatronics: an integrated approach. CRC Press, 2005.
[32] Santiago-Valentín E., Solano-Palma A., Bautista-Camino P., Rueda-Meléndez J., Portilla-Flores E.A. Diseño óptimo para transmisión de fuerza en un efector final. Research in Computing Science, 91:117-130, 2015.
Document information
Published on 03/01/18
Accepted on 27/09/16
Submitted on 04/05/16
Volume 34, Issue 1, 2018
DOI: 10.23967/j.rimni.2017.5.002
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?