Finite element formulation for thin-walled open composite beams including the effect of flexural and torsional shear deformation

Resumen

En esta investigación se obtiene el campo de desplazamientos y deformaciones para una viga de sección abierta y pared delgada formada por laminados compuestos incluyendo en su cinemática las deformaciones tangenciales por cortante por flexión y torsión. La ecuación de equilibrio del sistema se define a través de una formulación variacional, mostrando que incluir las deformaciones de corte por torsión hace posible formular elementos finitos de clase C_o . Las relaciones tensión-deformación se obtienen en la sección transversal de una viga de sección abierta formada por laminados compuestos extendiendo la teoría de laminados de primer orden - FSDT: first-order shear deformation ) y usando una «condición de esfuerzos nulos en el contorno». Se formulan 3 elementos finitos unidimensionales BSW (beam with shear and warping) con grado de continuidad C_o para el estudio de vigas de sección abierta formadas por laminados compuestos. Mediante el uso de los elementos BSW se evalúa la influencia de la estrategia de integración ante el fenómeno de bloqueo por tensiones tangenciales y la velocidad de convergencia para los desplazamientos y giros. Se compara la integración de la matriz de rigidez cuando se aplican técnicas de integración exacta y reducida. Finalmente, se realizan 2 ejemplos donde se estudia el comportamiento a torsión pura y flexotorsión de una viga con sección en C empotrada en un extremo y se comparan los resultados obtenidos con otros de la literatura.

Abstract

In this paper we derive the field of displacements and strains for thin-walled open composite beams with composite laminated material including in their kinematics flexural and torsional shear deformations effects. The equilibrium equations are defined through the variational formulation and show that is possible to formulate C_o finite elements taking into account the torsional shear deformation. Stress-strain relationships for the cross-section of thin-walled composite beams are obtained by extending first-order laminate (FSDT: first-order shear deformation) theory and using a «free stress resultant condition at the boundary». Three different one-dimensional finite elements with C_o continuity are formulated for the study of thin-walled open composite beams and they are labelled as BSW (beam with shear and warping). The influence of the integration strategy in the BSW elements is evaluated via the shear-locking phenomenon and the rate of convergence for displacements and rotations. The stiffness matrix integration is compared using exact and reduced integration methods. Examples of pure torsion and flexo-torsion in a cantilever composite beam are performed. Numerical results are compared to those reported by other authors.

Palabras clave

Vigas ; Pared delgada ; Sección abierta ; Compuestos ; Flexión ; Torsión ; Alabeo ; Deformaciones tangenciales ; Elementos finitos

Keywords

Beams ; Thin-walled ; Open section ; Composite ; Flexion ; Torsion ; Warping ; Shear deformation ; Finite elements

1. Introducción

El uso de vigas de sección abierta formadas por laminados compuestos experimentó un aumento importante en ingeniería civil, naval y mecánica desde comienzos de la década de 1990 gracias a las propiedades específicas que exhiben: alta relación rigidez/peso y resistencia mecánica/peso, alta resistencia a la degradación ambiental y baja conductividad térmica. Además, por su ligereza, estas vigas son muy adecuadas para estructuras donde el peso constituye una variable fundamental en el proceso de diseño [1] ; [2]  ;  [3] .

Desde la teoría de Vlasov [4] , aplicable a vigas de pared delgada en materiales isótropos, se han realizado numerosas investigaciones, entre las que destacan los estudios realizados por Bauld y Tzeng [5] , quienes extendieron la teoría de Vlasov a laminados compuestos, aunque no consideraron las deformaciones transversales en sus análisis; Bank y Bednarczyk [6] y Barbero et al. [7] desarrollaron expresiones simples para el análisis a flexión, torsión y alabeo de vigas en compuestos; Wu y Sun [8] incluyeron en su cinemática las deformaciones tangenciales por flexión y torsión mostrando la utilidad de tenerlas en cuenta durante los análisis; Massa y Barbero [9] consideraron las deformaciones transversales por flexión en sus análisis; Kollar y Pluzsik [10] y Pluzsik y Kollar [11] mostraron la importancia de incluir las deformaciones tangenciales por flexión en los análisis de vigas con alabeo restringido; Lee y Lee [12] desarrollaron un modelo analítico para el estudio de vigas a flexión y torsión que incluye alabeo, pero no consideraron las deformaciones tangenciales, lo que los llevó a utilizar una combinación de elementos lagrangianos y hermíticos en sus análisis. Posteriormente, Lee [13] presentó un modelo general para el estudio de vigas sometidas a flexión incluyendo en su formulación deformaciones tangenciales por flexión y «deformaciones de corte por alabeo», lo que le permitió desarrollar elementos finitos lagrangianos. Sin embargo, Lee utilizó una fórmula para el cálculo del alabeo que solo es aplicable a secciones transversales doblemente simétricas y no contempló la torsión en sus estudios. Kim et al. [14] presentaron soluciones exactas para el estudio a torsión de vigas de sección abierta sin considerar las deformaciones tangenciales dentro de su formulación, lo que les llevó a usar elementos hermíticos de tercer orden en sus análisis. Back y Will [15] extendieron el modelo general de Lee [13] mejorando la fórmula para el cálculo del alabeo haciéndola válida también para secciones con una sola simetría, pero tampoco estudiaron la torsión. Finalmente, Feo y Mancusi [16] sugirieron una aproximación al estudio de vigas en materiales compuestos mediante el uso de elementos finitos hermíticos, contemplaron en su análisis las deformaciones tangenciales por flexión y resolvieron la función de alabeo a través de funciones de aproximación dependientes de la coordenada curvilínea de la línea media de la sección transversal.

En este trabajo se compatibilizan de forma adecuada los campos de deformaciones de los laminados con la sección transversal de viga partiendo de las investigaciones de Lee [13] y Back y Will [15] , y extendiendo la hipótesis de « condición de esfuerzos nulos en el contorno » [7]  ;  [14] a laminados de primer orden - FSDT [17] . Se formulan elementos finitos tipo BSW que incluyen las deformaciones tangenciales debidas al cortante por flexión y torsión para el análisis a flexión y torsión de vigas de sección abierta y laminados compuestos. A diferencia de Lee [13] y Back y Will [15] , el valor de la función de alabeo se obtiene a través de un algoritmo de búsqueda por grafos [18] , generalizando la formulación a cualquier configuración de sección abierta. Los elementos se han formulado para funciones de aproximación lineal (L-BSW) , cuadrática (Q-BSW) y cúbica (C-BSW) , comprobándose la validez de los resultados frente a los obtenidos usando elementos cuadriláteros S9R5 [19] .

En este trabajo también se estudia la influencia del método de integración numérica (exacta y reducida) en el bloqueo producido por tensiones tangenciales y sus consecuencias en la convergencia de la solución. Se modeliza una viga en voladizo con sección C y se comparan los resultados obtenidos a flexión y torsión con otros de la literatura [14] .

2. Teoría general de vigas

2.1. Cinemática

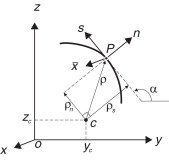
El desarrollo del modelo de viga requiere 2 sistemas ortogonales de coordenadas (fig. 1 ), el sistema cartesiano (x , y , z ) donde el eje x   corresponde al eje longitudinal de la viga, y el sistema local ${\textstyle ({\overline {x}},n,s)}$ para un punto P sobre la línea media de la sección transversal.

Figura 1. Sistemas de coordenadas en una sección abierta de pared delgada.

En el sistema local el eje ${\textstyle {\overline {x}}}$ es paralelo al eje x , por lo que en adelante se usarán indistintamente. El eje n es normal a la línea media de la sección en el punto P . Los 2 sistemas están relacionados por el ángulo α medido desde el eje y hasta el eje s en el sentido contrario a las agujas del reloj. La distancia entre el punto P y el centro de giro c de la sección transversal se evalúa como la suma de los vectores ρ_n y ρ_s , paralelos a los ejes s y n , respectivamente.

El campo de desplazamientos se obtiene suponiendo que el ángulo de giro por torsión es pequeño, el contorno de la sección transversal no se deforma en su plano, y las líneas rectas normales al eje longitudinal de la viga permanecen rectas antes de la deformación pero no necesariamente normales al eje después. Así, para un punto P con coordenadas (y , z , n ) se tiene:

$u=u_{o}-(y+nsin\alpha ){\theta }_{z}+(z-ncos\alpha ){\theta }_{y}-$$({\omega }_{s}-{\omega }_{n}){\phi }_{\omega }$ $v=v_{c}-\left[(z-z_{c})-ncos\alpha \right]{\theta }_{x}$ $w=w_{c}+\left[(y-y_{c})+nsin\alpha \right]{\theta }_{x}$

( 1)

donde u_o , ${\textstyle v_{c}}$ y ${\textstyle w_{c}}$ son los desplazamientos de sólido rígido en los ejes x , y y z , respectivamente; θ_x , θ_y y θ_z son las rotaciones alrededor de los ejes x , y y z ; ϕ_ω es la intensidad de alabeo por torsión a la que está sometida la sección; ω_s es la función de alabeo primario definida desde el centro de esfuerzos cortantes c y evaluada sobre la línea media de la sección transversal; y ω_n es la componente de alabeo secundario o alabeo en el espesor.

De acuerdo con Wu y Sun [8] , las rotaciones θ_y y θ_z se definen en función de las deformaciones tangenciales debidas a flexión ${\textstyle {\gamma }_{xz}^{o}}$ y ${\textstyle {\gamma }_{xy}^{o}}$ , la intensidad de alabeo ϕ_ω , en función de la variación en el ángulo de giro por torsión ∂_xθ_x , y las deformaciones tangenciales generadas por la torsión γ_t :

${\theta }_{y}=-{\partial }_{x}w_{c}+{\gamma }_{xz}^{o};{\theta }_{z}=$${\partial }_{x}v_{c}-{\gamma }_{xy}^{o}$ ${\phi }_{\omega }={\partial }_{x}{\theta }_{x}-{\gamma }_{t}$

( 2)

De la expresión (2) se deduce que cuando no hay deformaciones tangenciales por torsión, o estas son despreciables (γ_t  ≈ 0), la intensidad del alabeo equivale a la variación del ángulo de torsión por unidad de longitud (ϕ_ω  = ∂_xθ_x ) y se recupera la teoría de Vlasov [4] .

La función normalizada de alabeo primario por torsión ω_s y la función de alabeo secundario ω_n se definen como:

${\omega }_{s}={\int }_{s}{\rho }_{s}\quad ds\quad ;\quad {\omega }_{n}=$${\rho }_{n}n$

( 3)

La función de alabeo ω_s se evalúa de forma automática para cada punto de la línea media de la sección transversal utilizando algoritmos de búsqueda por grafos [18]  ;  [20] .

2.2. Deformaciones

Siguiendo la teoría de pequeños desplazamientos, se define el campo de deformaciones como:

${\varepsilon }_{x}={\varepsilon }_{x}^{o}-\left(y+nsin\alpha \right){\kappa }_{z}+$$\left(z-ncos\alpha \right){\kappa }_{y}-\left({\omega }_{s}-\right.$$\left.{\rho }_{n}n\right){\kappa }_{\omega }$ ${\gamma }_{xs}={\gamma }_{xy}^{o}cos\alpha +{\gamma }_{xz}^{o}sin\alpha +$${\rho }_{s}{\gamma }_{t}+n{\kappa }_{xs}$ ${\gamma }_{xn}={\gamma }_{xy}^{o}sin\alpha -{\gamma }_{xz}^{o}cos\alpha -$${\rho }_{n}{\gamma }_{t}$

( 4)

donde ${\textstyle {\varepsilon }_{x}^{o}}$ es la deformación axial; ${\textstyle {\gamma }_{xy}^{o}}$ y ${\textstyle {\gamma }_{xz}^{o}}$ son las deformaciones tangenciales por flexión; γ_t es la deformación angular por torsión; κ son las curvaturas debido a flexión (κ_y , κ_z ), torsión (κ_xs ) y alabeo (κ_ω ). De las ecuaciones (1) y (4) se deducen las siguientes deformaciones y curvaturas [20] :

${\varepsilon }_{x}^{o}={\partial }_{x}u_{o}$

( 5a)

${\gamma }_{xy}^{o}={\partial }_{x}v_{c}-{\theta }_{z}\quad {\gamma }_{xz}^{o}=$${\partial }_{x}w_{c}+{\theta }_{y}$

( 5b)

${\gamma }_{t}={\partial }_{x}{\theta }_{x}-{\phi }_{\omega }$

( 5c)

${\kappa }_{y}={\partial }_{x}{\theta }_{y}\quad {\kappa }_{z}=$${\partial }_{x}{\theta }_{z}$

( 5d)

${\kappa }_{xs}={\partial }_{x}{\theta }_{x}+{\phi }_{\omega }\quad {\kappa }_{\omega }=$${\partial }_{x}{\phi }_{\omega }$

( 5e)

Para el caso en que se supone despreciable la contribución de las deformaciones angulares por torsión (γ_t  ≈ 0 y ϕ_ω  = ∂_xθ_x ), el valor de la curvatura por torsión será κ_xs  = 2∂_xθ_x , recuperándose las expresiones empleadas por Lee y Lee [12] , Back y Will [15] , Sheikh y Thomsen [21] .

Agrupando los términos del campo de deformaciones 4 y aplicando un cambio de variables, resulta:

${\varepsilon }_{x}={\overline {\varepsilon }}_{x}^{o}+n{\overline {\kappa }}_{x}\quad ;\quad {\gamma }_{xs}=$${\overline {\gamma }}_{xs}^{o}+n{\overline {\kappa }}_{xs}\quad ;\quad {\gamma }_{xn}=$${\overline {\gamma }}_{xn}^{o}$

( 6)

donde ${\textstyle {\overline {\varepsilon }}_{x}^{o}}$ es una deformación axial, ${\textstyle {\overline {\gamma }}_{xs}^{o}}$ y ${\textstyle {\overline {\gamma }}_{xn}^{o}}$ son deformaciones tangenciales, y ${\textstyle {\overline {\kappa }}_{x}}$ y ${\textstyle {\overline {\kappa }}_{xs}}$ son curvaturas de flexión y torsión en la línea media de la sección.

2.3. Equilibrio seccional mediante una formulación variacional

La energía potencial de deformación se define como:

$U={\frac {1}{2}}\int \int {\int }_{V}\left({\sigma }_{x}{\varepsilon }_{x}+\right.$$\left.{\tau }_{xs}{\gamma }_{xs}+{\tau }_{xn}{\gamma }_{xn}\right)dV$

( 7)

Al reemplazar las deformaciones de la ecuación (4) se obtiene:

$U={\frac {1}{2}}\int \int {\int }_{V}\left\{{\sigma }_{x}\left[{\varepsilon }_{x}^{o}-\right.\right.$$\left.\left.\left(y+nsin\alpha \right){\kappa }_{z}+\right.\right.$$\left.\left.\left(z-ncos\alpha \right){\kappa }_{y}-\right.\right.$$\left.\left.\left({\omega }_{s}-{\rho }_{n}n\right){\kappa }_{\omega }\right]+\right.$$\left.{\tau }_{xs}\left[{\gamma }_{xy}^{o}cos\alpha +\right.\right.$$\left.\left.{\gamma }_{xz}^{o}sin\alpha +{\rho }_{s}{\gamma }_{t}+\right.\right.$$\left.\left.n{\kappa }_{xs}\right]+{\tau }_{xn}\left[{\gamma }_{xy}^{o}sin\alpha -\right.\right.$$\left.\left.{\gamma }_{xz}^{o}cos\alpha -{\rho }_{n}{\gamma }_{t}\right]\right\}dV$

( 8)

Así, la variación de la energía potencial de deformación del sistema se evalúa a partir de la ecuación (8), resultando la expresión en función de los esfuerzos seccionales [20] :

$\delta U={\int }_{l}\left\{N_{x}\delta {\varepsilon }_{x}^{o}+\right.$$\left.M_{z}\delta {\kappa }_{z}+M_{y}\delta {\kappa }_{y}+\right.$$\left.B_{\omega }\delta {\kappa }_{\omega }+M_{t}\delta {\kappa }_{xs}+\right.$$\left.Q_{y}\delta {\gamma }_{xy}^{o}+Q_{z}\delta {\gamma }_{xz}^{o}+\right.$$\left.T\delta {\gamma }_{t}\right\}dx$

( 9)

donde N_x es el esfuerzo axial, M_z y M_y son los momentos flectores en los ejes z e y , M_t es el momento torsor en el espesor de la pared de la sección, B_ω es el momento de alabeo (bimomento), Q_y y Q_z son las fuerzas de corte en las direcciones y y z , y T es el torsor asociado a las deformaciones angulares, definidas en el área de la sección transversal. Las expresiones de estos esfuerzos son [20] :

$N_{x}=\int {\int }_{A}{\sigma }_{x}dA$

( 10a)

$M_{z}=-\int {\int }_{A}\left[{\sigma }_{x}\left(y+nsin\alpha \right)\right]dA$

( 10b)

$M_{y}=\int {\int }_{A}\left[{\sigma }_{x}\left(z-ncos\alpha \right)\right]dA$

( 10c)

$B_{\omega }=-\int {\int }_{A}\left[{\sigma }_{x}\left({\omega }_{s}-\right.\right.$$\left.\left.{\rho }_{n}n\right)\right]dA$

( 10d)

$M_{t}=\int {\int }_{A}{\tau }_{xs}ndA$

( 10e)

$Q_{y}=\int {\int }_{A}\left({\tau }_{xs}cos\alpha +{\tau }_{xn}sin\alpha \right)dA$

( 10f)

$Q_{z}=\int {\int }_{A}\left({\tau }_{xs}sin\alpha -{\tau }_{xn}cos\alpha \right)dA$

( 10g)

$T=\int {\int }_{A}\left({\tau }_{xs}{\rho }_{s}-{\tau }_{xn}{\rho }_{n}\right)dA$

( 10h)

2.4. Ecuaciones constitutivas para el laminado compuesto

La ecuación constitutiva para un laminado de material compuesto en su sistema de coordenadas local ${\textstyle ({\overset {\mbox{ˆ}}{x}},{\overset {\mbox{ˆ}}{y}},{\overset {\mbox{ˆ}}{n}})}$ , siguiendo la teoría FSDT (first-order shear deformation)[17] se escribe como [20] :

$\left\{{\begin{array}{c}N_{\overset {\mbox{ˆ}}{x}}\\N_{\overset {\mbox{ˆ}}{y}}\\N_{{\overset {\mbox{ˆ}}{x}}\quad {\overset {\mbox{ˆ}}{y}}}\\M_{\overset {\mbox{ˆ}}{x}}\\M_{\overset {\mbox{ˆ}}{y}}\\M_{{\overset {\mbox{ˆ}}{x}}\quad {\overset {\mbox{ˆ}}{y}}}\\Q_{\overset {\mbox{ˆ}}{y}}\\Q_{\overset {\mbox{ˆ}}{x}}\end{array}}\right\}=\left[{\begin{array}{cccccccc}A_{11}&A_{12}&A_{16}&B_{11}&B_{12}&B_{16}&0&0\\A_{12}&A_{22}&A_{26}&B_{12}&B_{22}&B_{26}&0&0\\A_{16}&A_{26}&A_{66}&B_{16}&B_{26}&B_{66}&0&0\\B_{11}&B_{12}&B_{16}&D_{11}&D_{12}&D_{16}&0&0\\B_{12}&B_{22}&B_{26}&D_{12}&D_{22}&D_{26}&0&0\\B_{16}&B_{26}&B_{66}&D_{16}&D_{26}&D_{66}&0&0\\0&0&0&0&0&0&H_{44}&H_{45}\\0&0&0&0&0&0&H_{45}&H_{55}\end{array}}\right]\left\{{\begin{array}{c}{\varepsilon }_{\overset {\mbox{ˆ}}{x}}^{o}\\{\varepsilon }_{\overset {\mbox{ˆ}}{y}}^{o}\\{\gamma }_{{\overset {\mbox{ˆ}}{x}}\quad {\overset {\mbox{ˆ}}{y}}}^{o}\\{\kappa }_{\overset {\mbox{ˆ}}{x}}\\{\kappa }_{\overset {\mbox{ˆ}}{y}}\\{\kappa }_{{\overset {\mbox{ˆ}}{x}}\quad {\overset {\mbox{ˆ}}{y}}}\\{\gamma }_{{\overset {\mbox{ˆ}}{y}}\quad {\overset {\mbox{ˆ}}{n}}}^{o}\\{\gamma }_{{\overset {\mbox{ˆ}}{x}}\quad {\overset {\mbox{ˆ}}{n}}}^{o}\end{array}}\right\}$

( 11)

donde A_ij , B_ij , D_ij y H_ij son los coeficientes de las matrices de rigidez membranal, de acoplamiento, de flexión y de tensiones tangenciales, definidas por [17]  ;  [20] :

$\left(A_{ij},B_{ij},D_{ij},H_{ij}\right)={\int }_{-{\frac {h}{2}}}^{\frac {h}{2}}Q_{ij}\left(1,{\overset {\mbox{ˆ}}{n}},{\overset {\mbox{ˆ}}{n}}^{2},f({\overset {\mbox{ˆ}}{n}})\right)d{\overset {\mbox{ˆ}}{n}}$

La función de ponderación ${\textstyle f({\overset {\mbox{ˆ}}{n}})}$ permite considerar la distribución parabólica de las tensiones en el espesor del laminado.

Los ejes ${\textstyle {\overset {\mbox{ˆ}}{x}}}$ y ${\textstyle {\overset {\mbox{ˆ}}{n}}}$ del sistema de coordenadas local del laminado ${\textstyle ({\overset {\mbox{ˆ}}{x}},{\overset {\mbox{ˆ}}{y}},{\overset {\mbox{ˆ}}{n}})}$ son paralelos y tienen el mismo sentido que los ejes ${\textstyle {\overline {x}}}$ y n   del sistema de coordenadas local en la línea media de la sección transversal (${\textstyle {\overline {x}},n,s}$ ). De esta forma:

${\varepsilon }_{\overset {\mbox{ˆ}}{x}}^{o}={\overline {\varepsilon }}_{x}^{o}\quad ;\quad {\kappa }_{\overset {\mbox{ˆ}}{x}}=$${\overline {\kappa }}_{x}\quad ;\quad {\gamma }_{{\overset {\mbox{ˆ}}{x}}\quad {\overset {\mbox{ˆ}}{n}}}^{o}=$${\overline {\gamma }}_{xn}^{o}$ ${\gamma }_{{\overset {\mbox{ˆ}}{x}}\quad {\overset {\mbox{ˆ}}{y}}}^{o}=$$-{\overline {\gamma }}_{xs}^{o}\quad ;\quad {\kappa }_{{\overset {\mbox{ˆ}}{x}}\quad {\overset {\mbox{ˆ}}{y}}}=$$-{\overline {\kappa }}_{xs}$

( 12)

Las relaciones tensión-deformación (11) deben simplificarse con el fin de hacerlas compatibles con las componentes del vector de deformaciones a nivel de la sección transversal de las vigas de pared delgada en laminados compuestos (6) .

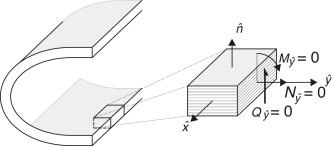
Lee y Lee [12] , Sheikh y Thomsen [21] y Back y Will [15] sugieren una «condición de tensiones nulas en el contorno», donde simplifican las componentes de tensión a nivel de las capas del laminado suponiendo que las tensiones laterales (normal y de corte) son nulas. Esta condición, sin embargo, tiene la desventaja de no contemplar la interrelación entre las diferentes capas que conforman el laminado. Por otra parte, Barbero et al. [7] y Kim et al. [14] proponen una «condición de esfuerzos nulos en el contorno» para vigas laminadas esbeltas CLT en la que simplifican las componentes de los esfuerzos a nivel de laminado considerando que ${\textstyle N_{\overset {\mbox{ˆ}}{y}}=M_{\overset {\mbox{ˆ}}{y}}=}$$0$ en el contorno, lo que permite considerar la interrelación de las capas del laminado. Sin embargo, por tratarse de laminados esbeltos, no se captura de forma precisa el comportamiento a torsión. En este trabajo se usa la propuesta de Barbero et al. [7] y Kim et al. [14] y de forma adicional se impone que ${\textstyle Q_{\overset {\mbox{ˆ}}{y}}=0}$ en el borde (fig. 2 ), con el fin de incluir la interrelación entre las capas del laminado.

Figura 2. Fuerzas y momentos en el borde longitudinal de una viga de sección abierta y pared delgada en laminados compuestos.

Al imponer esta nueva condición de esfuerzo cortante nulo en el contorno, es posible evaluar las deformaciones ${\textstyle {\varepsilon }_{\overset {\mbox{ˆ}}{y}}^{o}}$ , ${\textstyle {\kappa }_{\overset {\mbox{ˆ}}{y}}}$ y ${\textstyle {\gamma }_{{\overset {\mbox{ˆ}}{y}}{\overset {\mbox{ˆ}}{n}}}^{o}}$ como una combinación lineal de las componentes de deformación conocidas (${\textstyle {\varepsilon }_{\overset {\mbox{ˆ}}{x}}^{o}}$ , ${\textstyle {\gamma }_{{\overset {\mbox{ˆ}}{x}}{\overset {\mbox{ˆ}}{y}}}^{o}}$ , ${\textstyle {\kappa }_{\overset {\mbox{ˆ}}{x}}}$ , ${\textstyle {\kappa }_{{\overset {\mbox{ˆ}}{x}}{\overset {\mbox{ˆ}}{y}}}}$ y ${\textstyle {\gamma }_{{\overset {\mbox{ˆ}}{x}}{\overset {\mbox{ˆ}}{n}}}^{o}}$ ).

Imponiendo que ${\textstyle N_{\overset {\mbox{ˆ}}{y}}=M_{\overset {\mbox{ˆ}}{y}}=}$$Q_{\overset {\mbox{ˆ}}{y}}=0$ en el borde del laminado en las relaciones tensión-deformación para un laminado, se obtiene la siguiente relación entre las fuerzas internas y las deformaciones generalizadas de la sección transversal de la viga de laminados compuestos:

$\left\{{\begin{array}{c}N_{x}\\M_{z}\\M_{y}\\B_{\omega }\\M_{t}\\Q_{y}\\Q_{z}\\T\end{array}}\right\}=\left[{\begin{array}{cccccccc}E_{11}&E_{12}&E_{13}&E_{14}&E_{15}&E_{16}&E_{17}&E_{18}\\&E_{22}&E_{23}&E_{24}&E_{25}&E_{26}&E_{27}&E_{28}\\&&E_{33}&E_{34}&E_{35}&E_{36}&E_{37}&E_{38}\\&&&E_{44}&E_{45}&E_{46}&E_{47}&E_{48}\\&&&&E_{55}&E_{56}&E_{57}&E_{58}\\&&&&&E_{66}&E_{67}&E_{68}\\&sim.&&&&&E_{77}&E_{78}\\&&&&&&&E_{88}\end{array}}\right]\left\{{\begin{array}{c}{\varepsilon }_{x}^{o}\\{\kappa }_{z}\\{\kappa }_{y}\\{\kappa }_{\omega }\\{\kappa }_{xs}\\{\gamma }_{xy}^{o}\\{\gamma }_{xz}^{o}\\{\gamma }_{t}\end{array}}\right\}$

( 13a)

En forma compacta:

${\overset {\mbox{ˆ}}{\boldsymbol {\sigma }}}={\boldsymbol {\mbox{E}}}{\overset {\mbox{ˆ}}{\boldsymbol {\varepsilon }}}$

( 13b)

Los coeficientes de esta matriz de rigidez dependen de la geometría y de las propiedades de la sección transversal del elemento, tal como se muestra en el Apéndice 1.1.

3. Formulación de elementos finitos BSW

Los elementos finitos formulados (denominados BSW por beam with shear and warping ) para el estudio de vigas de sección abierta en laminados compuestos son unidimensionales con grado de continuidad C_o . Tienen 7 grados de libertad por nodo y consideran dentro de su cinemática los desplazamientos debidos a las deformaciones por corte inducidas por flexión y por torsión, así como los desplazamientos longitudinales generados por el alabeo restringido.

En esta investigación se han desarrollado 3 elementos: L-BSW (lineal de 2 nodos), Q-BSW (cuadrático de 3 nodos) y C-BSW (cúbico de 4 nodos). La formulación que se presenta sigue la metodología empleada por Oñate [22] para elementos de viga en 3 dimensiones, por Lee [13] para análisis a flexión de vigas de materiales compuestos, y por Back y Will [15] para vigas de materiales compuestos con sección T .

3.1. Desplazamientos

El vector de movimientos de un punto u :

${\boldsymbol {\mbox{u}}}=\sum _{i=1}^{n}N_{i}{\boldsymbol {\mbox{a}}}_{i}^{\left(e\right)}=$${\boldsymbol {\mbox{N}}}{\boldsymbol {\mbox{a}}}^{\left(e\right)}$

( 14)

donde

${\boldsymbol {\mbox{N}}}=\left[N_{1}I_{7},N_{2}I_{7},\ldots ,N_{n}I_{7}\right]$

( 15)

y

${\boldsymbol {\mbox{u}}}=\left\{{\begin{array}{c}u_{0}\\v_{c}\\w_{c}\\{\theta }_{x}\\{\theta }_{y}\\{\theta }_{z}\\{\phi }_{w}\end{array}}\right\};\quad {\boldsymbol {\mbox{a}}}^{\left(e\right)}=$$\left\{{\begin{array}{c}{\boldsymbol {\mbox{a}}}_{1}^{\left(e\right)}\\{\boldsymbol {\mbox{a}}}_{2}^{\left(e\right)}\\\vdots \\{\boldsymbol {\mbox{a}}}_{n}^{\left(e\right)}\end{array}}\right\};\quad {\boldsymbol {\mbox{a}}}_{i}^{\left(e\right)}=$$\left\{{\begin{array}{c}u_{oi}\\v_{ci}\\w_{c}i\\{\theta }_{x}i\\{\theta }_{yi}\\{\theta }_{zi}\\{\phi }_{\omega i}\end{array}}\right\}$

( 16)

son, respectivamente, la matriz de funciones de forma (N ), la matriz identidad de 7 × 7 (${\textstyle I_{7}}$ ), el número de nodos del elemento (n ), el vector de movimientos de un punto del elemento (a^{(e )} ) y de un nodo (${\textstyle {\boldsymbol {\mbox{a}}}_{i}^{\left(e\right)}}$ ).

3.2. Matriz de deformación del elemento

La matriz de deformación B relaciona las deformaciones generalizadas de la sección transversal de la viga ${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\varepsilon }}}}$ con el vector de movimientos nodales a^{(e )} o con los siguientes movimientos:

${\overset {\mbox{ˆ}}{\boldsymbol {\varepsilon }}}={\boldsymbol {\mbox{D}}}{\boldsymbol {\mbox{u}}}=$${\boldsymbol {\mbox{D}}}{\boldsymbol {\mbox{Na}}}^{e}={\boldsymbol {\mbox{Ba}}}^{e}$

( 17)

Es importante destacar que las deformaciones de la sección transversal de la viga (ecuaciones 4 y 5) se definen en términos de las primeras derivadas del campo de desplazamientos, permitiendo formular elementos finitos con un grado de continuidad C_o .

La expresión del operador D se deduce de las ecuaciones (4) y (5). La matriz de deformación B se obtiene por:

${\boldsymbol {\mbox{B}}}={\boldsymbol {\mbox{D}}}{\boldsymbol {\mbox{N}}}$

( 18)

Para un nodo i :

${\boldsymbol {\mbox{B}}}_{i}=\left[{\begin{array}{ccccccc}{\partial }_{x}N_{i}&0&0&0&0&0&0\\0&0&0&0&0&{\partial }_{x}N_{i}&0\\0&0&0&0&{\partial }_{x}N_{i}&0&0\\0&0&0&0&0&0&{\partial }_{x}N_{i}\\0&0&0&{\partial }_{x}N_{i}&0&0&N_{i}\\0&{\partial }_{x}N_{i}&0&0&0&-N_{i}&0\\0&0&{\partial }_{x}N_{i}&0&N_{i}&0&0\\0&0&0&{\partial }_{x}N_{i}&0&0&-N_{i}\end{array}}\right]$

( 19)

3.3. Matriz de rigidez del elemento

La matriz de rigidez se obtiene del equilibrio del elemento. Su expresión tiene la forma usual [22]  ;  [20] :

${\boldsymbol {\mbox{K}}}^{\left(e\right)}={\int }_{l(e)}{\boldsymbol {\mbox{B}}}^{T}\quad {\tilde {\boldsymbol {\mbox{E}}}}\quad {\boldsymbol {\mbox{B}}}\quad dx$

( 20)

donde ${\textstyle {\tilde {\boldsymbol {\mbox{E}}}}}$ es la matriz constitutiva que relaciona las fuerzas internas y las deformaciones generalizadas de la sección transversal de la viga de laminados compuestos (13a) . Los componentes de ${\textstyle {\tilde {\boldsymbol {\mbox{E}}}}}$ se incluyen en el Apéndice 1.1. El tamaño de la matriz K^{(e )} es (7 × n ) × (7 × n ), siendo n el número de nodos del elemento.

4. Integración numérica de la matriz de rigidez

En este apartado se comparan los resultados obtenidos al aplicar 2 métodos diferentes de integración numérica (exacta y reducida) en las componentes a flexión y torsión de la matriz de rigidez de los elementos formulados (L-BSW , Q-BSW y C-BSW ).

El estudio que se presenta incluye 2 tipos de análisis de una viga en voladizo con sección en doble T . El primer análisis evalúa el bloqueo por tensiones tangenciales de los elementos mediante la variación de la relación de esbeltez de viga. El segundo análisis estudia la convergencia de la solución numérica al variar el número de elementos usados en la discretización.

En este trabajo se adoptan la geometría y las propiedades usadas por Lee [13] , Kim et al. [14] , Back y Will [15] y Sheikh y Thomsen [21] en sus análisis.

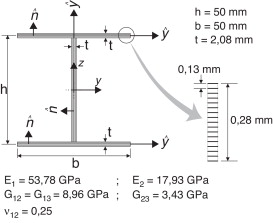
La figura 3 muestra la sección y las propiedades de la viga de laminados compuestos usada en los análisis. Los laminados de la sección transversal son unidireccionales con 16 capas ([φ ]₁₆ ) de láminas en fibra de vidrio embebida en matriz epóxica (Gl.-Ep, Reddy [17] ) de 0,13 mm de espesor cada una [20] .

Figura 3. Geometría de la viga con sección I y propiedades de las láminas que la conforman.

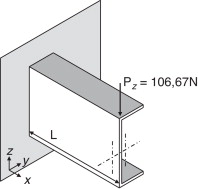
Los resultados obtenidos con los elementos desarrollados se comparan con los resultados de modelos en Abaqus utilizando elementos cuadriláteros tipo S9R5 [19] con mallas de entre 648 y 960 elementos, dependiendo de la esbeltez de la viga analizada. En la figura 4 se muestra el modelo de 960 elementos S9R5 utilizado para verificar los resultados del análisis de torsión de una viga de 1 m de longitud (esbeltez λ  = L /20).

Figura 4. Modelo de 960 elementos cuadriláteros S9R5 [19] , usado para simular una viga I de 1.000 mm de longitud sometida a torsión.

El análisis a flexión se realiza calculando el desplazamiento vertical ${\textstyle w}$ del extremo libre de la viga en voladizo donde se aplica una carga vertical de 2 kN. En el análisis a torsión (fig. 4 ) se aplica un momento torsor de 1 kN mm en el extremo libre y se obtiene el giro por torsión θ de la sección transversal en el punto de aplicación del momento.

4.1. Análisis de bloqueo por tensiones tangenciales

Se entiende por bloqueo la incapacidad intrínseca que tiene un elemento de satisfacer la condición de deformación transversal nula cuando su longitud tiende al infinito [22] . Esto conduce a una sobrerrigidez numérica a medida que la longitud del elemento aumenta. Una alternativa para sortear este problema es subintegrar los términos de la matriz de rigidez que incluyen las deformaciones transversales (debidas a la flexión y a la torsión) utilizando un número de puntos de integración inferior al necesario para su cálculo exacto [22] .

Concretamente, el número de puntos de integración para las integraciones exacta (E ) y reducida (R ) para los diferentes elementos estudiados es el siguiente: L-BSW : 2 (E ), 1 (R ), Q-BSW : 3 (E ), 2 (R ), C-BSW : 4 (E ), 3 (R ), donde el numero indica la cantidad de puntos de integración para el cálculo de los términos de la matriz de rigidez que contienen las deformaciones transversales. Es destacable que el resto de términos de la matriz de rigidez se calcula de manera exacta, utilizando un número de puntos de integración igual al de la integración reducida [22] .

Con el ánimo de estudiar la capacidad para satisfacer la condición de deformaciones transversales nulas de los elementos implementados, se analizan modelos de un solo elemento finito BSW y se varía su longitud (manteniendo su altura constante) alcanzando relaciones de esbeltez λ entre 1 y 20.

Los resultados obtenidos aplicando integración numérica exacta y reducida en las componentes de flexión y torsión de la matriz de rigidez se normalizan respecto a los obtenidos usando los modelos con elementos cuadriláteros S9R5 [19] , que se comparan en las tablas 1 y 2 . La primera tabla corresponde al análisis a flexión y la segunda al análisis a torsión. Los datos incluidos corresponden a las vigas modelizadas con secuencia de apilado unidireccional [0]₁₆ .

Tabla 1. Viga I de laminados [0]₁₆ sometida a flexión. Comparación de resultados en análisis de bloqueo entre integración exacta e integración reducida.

λ  = L /h	${\textstyle w_{BSW}/w_{S9R5}}$
	L-BSW	Q-BSW	Q-BSW	C-BSW
	(Int. red)	(Int. exac)	(Int. red)	(Int. exac)
1	0,5520	0,5711	0,5713	0,5713
2	0,5706	0,6294	0,6312	0,6312
3	0,6180	0,7168	0,7237	0,7237
4	0,6536	0,7799	0,7957	0,7957
5	0,6783	0,8193	0,8468	0,8468
6	0,6952	0,8417	0,8828	0,8828
7	0,7073	0,8528	0,9083	0,9083
10	0,7272	0,8527	0,9510	0,9510
15	0,7397	0,8258	0,9771	0,9771
20	0,7442	0,8031	0,9870	0,9870

Tabla 2. Viga I de laminados [0]₁₆ sometida a torsión. Comparación de resultados en análisis de bloqueo entre integración exacta e integración reducida

λ  = L /h	θBSW /θS 9R 5
	L-BSW	Q-BSW	Q-BSW	C-BSW
	(Int. red)	(Int. exac)	(Int. red)	(Int. exac)
1	3,0683	3,4272	3,4411	3,4410
2	1,2825	1,5362	1,5756	1,5755
3	1,0575	1,2677	1,3420	1,3417
4	0,9747	1,1418	1,2491	1,2486
5	0,9314	1,0599	1,1937	1,1930
6	0,9078	1,0039	1,1578	1,1567
7	0,8937	0,9629	1,1309	1,1295
10	0,8849	0,8953	1,0830	1,0806
15	0,9118	0,8585	1,0457	1,0412
20	0,9535	0,8528	1,0302	1,0237

Las tablas 1 y 2 muestran que los resultados que más se aproximan a los obtenidos con las modelizaciones con elementos cuadriláteros S9R5[19] para flexión y torsión son los de los elementos C-BSW con integración exacta y Q-BSW con integración reducida, y cabe señalar que entre ellos no hay diferencias apreciables. Después destacan los resultados del elemento Q-BSW con integración exacta y, por último, los resultados de L-BSW con integración reducida. Los resultados para el elemento C-BSW con integración reducida fueron coincidentes con los de integración exacta.

Vale la pena remarcar que en ninguno de los casos estudiados se obtuvo el bloqueo de la solución.

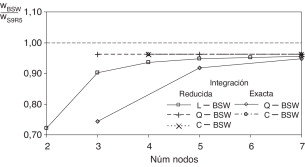
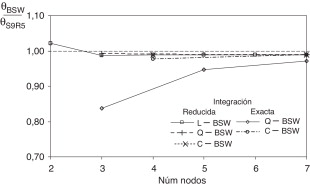
4.2. Análisis de convergencia

Se estudia la convergencia de los elementos formulados (L-BSW , Q-BSW y C-BSW ) para los casos en que se utiliza integración numérica exacta y reducida de las componentes a flexión y torsión de la matriz de rigidez del elemento. El análisis se realiza en vigas de longitud y altura constante (esbeltez λ  = 20) variando el número de elementos BSW usados en cada modelización y se comparan con los resultados obtenidos usando un modelo de 960 elementos cuadriláteros S9R5[19] .

Aunque el análisis de convergencia se ha realizado en vigas con secuencias de apilado [φ ]₁₆ (φ  ∈ [0 15, 30, 45, 75, 90]), en este apartado solamente se muestran los resultados obtenidos para la secuencia [45]₁₆ , por ser la que presenta mayores diferencias porcentuales con respecto a los resultados obtenidos en modelos con elementos cuadriláteros S9R5[19] . En [20] se puede encontrar más información sobre el resto de resultados.

Los resultados de la integración numérica exacta y reducida se comparan en las tablas 3 y 4 . La primera tabla corresponde al análisis a flexión y la segunda al análisis a torsión.

Tabla 3. Viga de laminados [45]₁₆ sometida a flexión. Convergencia de resultados utilizando integración exacta y reducida

Núm. elementos	${\textstyle w_{BSW}/w_{S9R5}}$
	L-BSW	Q-BSW	Q-BSW	C-BSW
	(Int. red)	(Int. exac)	(Int. red)	(Int. exac)
1	0,7224	0,7426	0,9613	0,9613
2	0,9016	0,9178	0,9613	0,9613
3	0,9350	0,9471	0,9613	0,9613
4	0,9466	0,9552	0,9613	0,9613
5	0,9517	0,9583	0,9613	0,9613
6	0,9547	0,9598	0,9613	0,9613
7	0,9563	0,9603	0,9613	0,9613
8	0,9578	0,9608	0,9613	0,9613

Tabla 4. Viga de laminados [45]₁₆ sometida a torsión. Convergencia de resultados utilizando integración exacta y reducida

Núm. elementos	θBSW /θS 9R 5
	L-BSW	Q-BSW	Q-BSW	C-BSW
	(Int. red)	(Int. exac)	(Int. red)	(Int. exac)
1	1,0224	0,8370	0,9924	0,9766
2	0,9862	0,9475	0,9889	0,9880
3	0,9880	0,9713	0,9889	0,9889
4	0,9880	0,9801	0,9889	0,9889
5	0,9880	0,9836	0,9889	0,9889
6	0,9889	0,9862	0,9889	0,9889
7	0,9889	0,9871	0,9889	0,9889
8	0,9889	0,9871	0,9889	0,9889

En líneas generales, todos los elementos estudiados convergen a la solución obtenida con la malla de elementos cuadriláteros S9R5.

En los análisis a flexión, los resultados del elemento Q-BSW con integración exacta se aproximan más a los de elementos C-BSW que los resultados de L-BSW con integración reducida, mientras que en los análisis a torsión sucede lo contrario.

En las figuras 5 y 6 se comparan los resultados obtenidos con los elementos L-BSW , Q-BSW y C-BSW ; el parámetro de comparación es el número de nodos. No se incluyen los resultados de los modelos con elementos lineales L-BSW e integración exacta por presentar bloqueo de la solución.

Figura 5. Comparación de resultados en análisis de convergencia según el número de nodos para una viga sometida a flexión.

Figura 6. Comparación de resultados en análisis de convergencia según el número de nodos para una viga sometida a torsión.

Las figuras 5 y 6 muestran que los modelos con elementos L-BSW e integración reducida tienen un mejor comportamiento que los elementos Q-BSW con integración exacta para el mismo número de nodos.

También se observa que no hay diferencias importantes entre los resultados obtenidos con los elementos Q-BSW con integración reducida y con los elementos C-BSW .

5. Análisis de una viga en voladizo con sección en C

Se estudia el comportamiento a flexión y torsión de una viga con sección C formando laminados compuestos (fig. 7 ), empotrada en un extremo y sometida a carga vertical excéntrica que genera un momento torsor negativo de 1 kN mm.

Figura 7. Viga con sección C sometida a carga vertical excéntrica.

Las propiedades de la sección se muestran en la figura 8 .

Figura 8. Geometría de la viga con sección en C y propiedades de las láminas que la conforman.

El análisis se realiza con 10 elementos de 2 nodos (lineales) e integración reducida L-BSW .

Al igual que en el apartado 4, los laminados que conforman la viga tienen 16 capas de láminas en fibra de vidrio embebida en matriz epóxica (Gl.-Ep, Reddy [17] ) de 0,13 mm de espesor cada una (Vargas [20] ).

Los resultados obtenidos usando 10 elementos L-BSW se comparan con los resultados obtenidos con 400 elementos cuadriláteros S9R5 (tipo DK, 9 nodos, 5 grados de libertad e integración reducida [19] ).

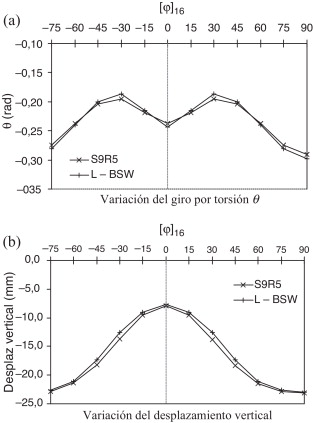
Se analiza la variación del giro por torsión para laminados unidireccionales [φ ]₁₆ y bidireccionales [± φ ]_4s cuando cambia el ángulo de orientación de las fibras que componen la sección transversal de la viga.

• Laminados unidireccionales [φ ]₁₆ . La figura 9 muestra los resultados cuando se aplica la carga puntual excéntrica. Se observan diferencias entre los modelos comparados de un 4,3% en el giro por torsión y de un 8,5% en el desplazamiento vertical.

Figura 9. Variación de los resultados en el extremo libre de la viga C en voladizo para diferentes orientaciones de las fibras en laminados unidireccionales (carga vertical excéntrica).

• Laminados [± φ ]_4s . La figura 10 muestra los resultados cuando se aplica la carga puntual excéntrica. Se observa que las modelizaciones con elementos unidimensionales (L-BSW ) presentan diferencias de un 2,7% en el giro por torsión y de un 2,3% en el desplazamiento vertical con respecto a las modelizaciones con elementos cuadriláteros S9R5 [19] .

Figura 10. Variación de los resultados en el extremo libre de la viga C en voladizo para diferentes orientaciones de las fibras en laminados [± φ ]4s (carga vertical excéntrica).

En las referencias [22]  ;  [20] se muestran otros ejemplos de aplicación del elemento L-BSW al cálculo de vigas de sección abierta con materiales compuestos.

6. Conclusiones

Se han formulado, implementado y validado elementos finitos tipo BSW para el análisis a flexión y torsión en vigas de sección abierta y constituidas por laminados compuestos. La cinemática de la viga incluye las deformaciones de corte por flexión y torsión. Los elementos usan algoritmos de búsqueda por grafos [18] para el cálculo de la función de alabeo primario de tal manera que son independientes de la sección de la viga. Los elementos desarrollados en esta investigación son de 3 tipos, según las funciones de interpolación de los movimientos: lineal L-BSW , cuadrático Q-BSW y cúbico C-BSW . Los resultados se han comparado con los obtenidos con elementos cuadriláteros S9R5 [19] y con resultados de la literatura.

El estudio de la influencia entre aplicar integración numérica exacta y reducida de las componentes a flexión y torsión de la matriz de rigidez del elemento ha mostrado que los elementos L-BSW presentan bloqueo con integración exacta, mientras que los de aproximación Q-BSW y C-BSW no. También se observa que se requieren al menos 5 elementos de aproximación cuadrática Q-BSW con integración exacta para obtener los mismos resultados que utilizando elementos de aproximación cúbica C-BSW .

El fenómeno de bloqueo se eliminó en los elementos de aproximación lineal L-BSW utilizando integración reducida. En este caso, esto equivale a calcular todos los términos de la matriz de rigidez con un solo punto de integración.

Los elementos de aproximación cuadrática mejoran sus resultados al aplicar integración reducida y se aproximan a los resultados obtenidos con elementos de aproximación cúbica C-BSW .

Los elementos C-BSW no presentan variaciones apreciables en sus resultados cuando cambia el tipo de integración numérica (reducida o exacta).

Los elementos de aproximación cuadrática Q-BSW convergen con 2 elementos a los resultados obtenidos con modelos de elementos de aproximación cúbica. Estos últimos proporcionan buenos resultados utilizando un solo elemento.

El elemento que mejor convergencia presenta a un menor número de nodos es el de aproximación cuadrática Q-BSW con integración reducida. Sus resultados no presentan diferencias apreciables con respecto a los obtenidos con elementos con aproximación cúbica C-BSW .

En el estudio de una viga con sección en C, la diferencia en los resultados utilizando los elementos de aproximación lineal L-BSW e integración reducida (10 elementos en cada modelo de viga) frente a los modelos de 400 elementos cuadriláteros S9R5 fue inferior al 10% en los casos de torsión pura y flexotorsión.

Agradecimientos

Se agradece al Ministerio de Fomento de España por subvencionar parte de este trabajo a través de las ayudas del Programa del Plan Nacional I+D en la Construcción: 2004/32 y C9/2006. Este trabajo fue también parcialmente financiado por el proyecto SAFECON del European Research Council.

A.1. Coeficientes matriz de la sección transversal ${\textstyle {\tilde {\boldsymbol {\mbox{E}}}}}$A.1. Coeficientes matriz de la sección transversal E ~ {\textstyle {\tilde {\boldsymbol {\mbox{E}}}}}

Los coeficientes de la matriz de rigidez de la sección transversal de la viga son:

$E_{11}={\int }_{s}A_{11}ds$ $E_{12}=-{\int }_{s}\left(A_{11}y+B_{11}sin\alpha \right)ds$ $E_{13}={\int }_{s}\left(A_{11}z-B_{11}cos\alpha \right)\quad ds$ $E_{14}=-{\int }_{s}\left(A_{11}{\omega }_{s}-B_{11}{\rho }_{n}\right)\quad ds$ $E_{15}={\int }_{s}B_{16}\quad ds$ $E_{16}={\int }_{s}A_{16}cos\alpha \quad ds$ $E_{17}={\int }_{s}A_{16}sin\alpha \quad ds$ $E_{18}={\int }_{s}A_{16}{\rho }_{s}\quad ds$ $E_{22}={\int }_{s}\left(A_{11}y^{2}+2B_{11}ysin\alpha +\right.$$\left.A_{11}{sin}^{2}\alpha \right)\quad ds$ $E_{23}=-{\int }_{s}\left(A_{11}yz+B_{11}\left(zsin\alpha -\right.\right.$$\left.\left.ycos\alpha \right)-D_{11}sin\alpha cos\alpha \right)\quad ds$ $E_{24}={\int }_{s}\left(A_{11}y{\omega }_{s}+B_{11}\left({\omega }_{s}sin\alpha -\right.\right.$$\left.\left.y{\rho }_{n}\right)-D_{11}{\rho }_{n}sin\alpha \right)\quad ds$ $E_{25}=-{\int }_{s}\left(B_{16}y+D_{16}sin\alpha \right)\quad ds$ $E_{26}=-{\int }_{s}\left(A_{16}y+B_{16}sin\alpha \right)cos\alpha \quad ds$ $E_{27}=-{\int }_{s}\left(A_{16}y+B_{16}sin\alpha \right)sin\alpha \quad ds$ $E_{28}=-{\int }_{s}\left(A_{16}y+B_{16}sin\alpha \right){\rho }_{s}\quad ds$ $E_{33}={\int }_{s}\left(A_{11}z^{2}-2B_{11}zcos\alpha +\right.$$\left.D_{11}{cos}^{2}\alpha \right)\quad ds$ $E_{34}=-{\int }_{s}\left(A_{11}z{\omega }_{s}-B_{11}\left({\omega }_{s}cos\alpha +\right.\right.$$\left.\left.z{\rho }_{n}\right)+D_{11}{\rho }_{n}cos\alpha \right)\quad ds$ $E_{35}={\int }_{s}\left(B_{16}z-D_{16}cos\alpha \right)\quad ds$ $E_{36}={\int }_{s}\left(A_{16}z-B_{16}cos\alpha \right)cos\alpha \quad ds$ $E_{37}={\int }_{s}\left(A_{16}z-B_{16}cos\alpha \right)sin\alpha \quad ds$ $E_{38}={\int }_{s}\left(A_{16}z-B_{16}cos\alpha \right){\rho }_{s}\quad ds$ $E_{44}={\int }_{s}\left(A_{11}{{\omega }_{s}}^{2}-2B_{11}{\omega }_{s}{\rho }_{n}+\right.$$\left.D_{11}{{\rho }_{n}}^{2}\right)\quad ds$ $E_{45}=-{\int }_{s}\left(B_{16}{\omega }_{s}-D_{16}{\rho }_{n}\right)\quad ds$ $E_{46}=-{\int }_{s}\left(A_{16}{\omega }_{s}-B_{16}{\rho }_{n}\right)cos\alpha \quad ds$ $E_{47}=-{\int }_{s}\left(A_{16}{\omega }_{s}-B_{16}{\rho }_{n}\right)sin\alpha \quad ds$ $E_{48}=-{\int }_{s}\left(A_{16}{\omega }_{s}-B_{16}{\rho }_{n}\right){\rho }_{s}\quad ds$ $E_{55}={\int }_{s}D_{66}\quad ds$ $E_{56}={\int }_{s}B_{66}cos\alpha \quad ds$ $E_{57}={\int }_{s}B_{66}sin\alpha \quad ds$ $E_{58}={\int }_{s}B_{66}{\rho }_{s}\quad ds$ $E_{66}={\int }_{s}\left(A_{66}{cos}^{2}\alpha +{\mathbb {H} }_{55}{sin}^{2}\alpha \right)\quad ds$ $E_{67}={\int }_{s}\left(A_{66}-{\mathbb {H} }_{55}\right)cos\alpha sin\alpha \quad ds$ $E_{68}={\int }_{s}\left(A_{66}{\rho }_{s}cos\alpha -{\mathbb {H} }_{55}{\rho }_{n}sin\alpha \right)\quad ds$ $E_{77}={\int }_{s}\left(A_{66}{sin}^{2}\alpha +{\mathbb {H} }_{55}{cos}^{2}\alpha \right)\quad ds$ $E_{78}={\int }_{s}\left(A_{66}{\rho }_{s}sin\alpha +{\mathbb {H} }_{55}{\rho }_{n}cos\alpha \right)\quad ds$ $E_{88}={\int }_{s}\left(A_{66}{{\rho }_{s}}^{2}+{\mathbb {H} }_{55}{{\rho }_{n}}^{2}\right)\quad ds$

( 21)

Los términos ${\textstyle A_{ij}}$ , ${\textstyle B_{ij}}$ , ${\textstyle D_{ij}}$ y ${\textstyle {\mathbb {H} }_{ij}}$ se obtienen incluyendo la nueva «condición de esfuerzos nulos en el contorno» en las relaciones tensión-deformación para un laminado.

A.2. Coeficientes de la matriz del elemento de viga

Los coeficientes de la matriz de rigidez del elemento de viga son:

${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{11}=$${\int }_{l(e)}E_{11}N_{i}^{'}N_{j}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{12}=$${\int }_{l(e)}E_{16}N_{i}^{'}N_{j}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{13}=$${\int }_{l(e)}E_{17}N_{i}^{'}N_{j}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{14}=$${\int }_{l(e)}\left(E_{15}+E_{18}\right)N_{i}^{'}N_{j}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{15}=$${\int }_{l(e)}\left(E_{13}N_{j}^{'}+E_{17}N_{j}\right)N_{i}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{16}=$${\int }_{l(e)}\left(E_{12}N_{j}^{'}-E_{16}N_{j}\right)N_{i}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{17}=$${\int }_{l(e)}\left[E_{14}N_{i}^{'}N_{j}^{'}+\left(E_{15}-\right.\right.$$\left.\left.E_{18}\right)N_{i}^{'}N_{j}\right]dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{22}=$${\int }_{l(e)}E_{66}N_{i}^{'}N_{j}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{23}=$${\int }_{l(e)}E_{67}N_{i}^{'}N_{j}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{24}=$${\int }_{l(e)}\left(E_{56}+E_{68}\right)N_{i}^{'}N_{j}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{25}=$${\int }_{l(e)}\left(E_{36}N_{j}^{'}+E_{67}N_{j}\right)N_{i}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{26}=$${\int }_{l(e)}\left(E_{26}N_{j}^{'}-E_{66}N_{j}\right)N_{i}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{27}=$${\int }_{l(e)}\left[E_{46}N_{i}^{'}N_{j}^{'}+\left(E_{56}-\right.\right.$$\left.\left.E_{68}\right)N_{i}^{'}N_{j}\right]dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{33}=$${\int }_{l(e)}E_{77}N_{i}^{'}N_{j}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{34}=$${\int }_{l(e)}\left(E_{57}+E_{78}\right)N_{i}^{'}N_{j}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{35}=$${\int }_{l(e)}\left(E_{37}N_{j}^{'}+E_{77}N_{j}\right)N_{i}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{36}=$${\int }_{l(e)}\left(E_{27}N_{j}^{'}-E_{67}N_{j}\right)N_{i}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{37}=$${\int }_{l(e)}\left[E_{47}N_{i}^{'}N_{j}^{'}+\left(E_{57}-\right.\right.$$\left.\left.E_{78}\right)N_{i}^{'}N_{j}\right]dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{44}=$${\int }_{l(e)}\left(E_{55}+2E_{58}+E_{88}\right)N_{i}^{'}N_{j}^{'}dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{45}=$${\int }_{l(e)}\left[\left(E_{35}+E_{38}\right)N_{i}^{'}N_{j}^{'}+\right.$$\left.\left(E_{57}+E_{78}\right)N_{i}^{'}N_{j}\right]dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{46}=$${\int }_{l(e)}\left[\left(E_{25}+E_{28}\right)N_{i}^{'}N_{j}^{'}-\right.$$\left.\left(E_{56}+E_{68}\right)N_{i}^{'}N_{j}\right]dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{47}=$${\int }_{l(e)}\left[\left(E_{45}+E_{48}\right)N_{i}^{'}N_{j}^{'}+\right.$$\left.\left(E_{55}-E_{88}\right)N_{i}^{'}N_{j}\right]dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{55}=$${\int }_{l(e)}\left[E_{33}N_{i}^{'}N_{j}^{'}+E_{37}\left(N_{i}^{'}N_{j}+\right.\right.$$\left.\left.N_{i}N_{j}^{'}\right)+E_{77}N_{i}N_{j}\right]dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{56}=$${\int }_{l(e)}\left[E_{23}N_{i}^{'}N_{j}^{'}+E_{27}N_{i}N_{j}^{'}-\right.$$\left.E_{36}N_{i}^{'}N_{j}-E_{67}N_{i}N_{j}\right]dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{57}=$${\int }_{l(e)}\left[E_{34}N_{i}^{'}N_{j}^{'}+\left(E_{35}-\right.\right.$$\left.\left.E_{38}\right)N_{i}^{'}N_{j}+E_{47}N_{i}N_{j}^{'}+\right.$$\left.\left(E_{57}-E_{78}\right)N_{i}N_{j}\right]dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{66}=$${\int }_{l(e)}\left[E_{22}N_{i}^{'}N_{j}^{'}-E_{26}\left(N_{i}^{'}N_{j}+\right.\right.$$\left.\left.N_{i}N_{j}^{'}\right)+E_{66}N_{i}N_{j}\right]dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{67}=$${\int }_{l(e)}\left[E_{24}N_{i}^{'}N_{j}^{'}+\left(E_{25}-\right.\right.$$\left.\left.E_{28}\right)N_{i}^{'}N_{j}-E_{46}N_{i}N_{j}^{'}-\right.$$\left.\left(E_{56}+E_{68}\right)N_{i}N_{j}\right]dx$ ${\left[{\boldsymbol {\mbox{K}}}_{ij}^{\left(e\right)}\right]}_{77}=$${\int }_{l(e)}\left[E_{44}N_{i}^{'}N_{j}^{'}+\left(E_{45}-\right.\right.$$\left.\left.E_{48}\right)\left(N_{i}N_{j}^{'}+N_{i}^{'}N_{j}\right)+\right.$$\left.\left(E_{55}-2E_{58}+E_{88}\right)N_{i}N_{j}\right]dx$

( 22)

donde ${\textstyle N_{i}^{'}={\partial }_{x}N_{i}}$ , y los coeficientes E_ij se definen de acuerdo a las ecuaciones (21).

References

1. [1] M.D.G. Pulido, J.A. Sobrino; Hacia la aplicación de los materiales compuestos en el diseño de pasarelas; S. Oller (Ed.), Análisis y cálculo de estructuras de materiales compuesos, Centre Internacional de Mètodes Numèrics en Enginyeria (CIMNE) (2002), pp. 547–576
2. [2] S. Oller Simulación numérica del comportamiento mecánico de los materiales compuestos. Centre Internacional de Mètodes Numèrics en Enginyeria (CIMNE), 2003.
3. [3] F. G. Rastellini Modelización numérica de la no-linealidad constitutiva de laminados compuestos. PhD thesis, Universidad Politécnica de Cataluña, 2006.
4. [4] V. Z. Vlasov. Thin-walled Elastic Beams. Israel Program for Scientific Translations, 1961.
5. [5] N.R. Bauld, L.-S. Tzeng; A Vlasov theory for fiber-reinforced beams with thin-walled open cross sections; Int. J. Solids Struct., 20 (3) (1984), pp. 277–297
6. [6] L.C. Bank, P.J. Bednarczyk; A beam theory for thin-walled composite beams; Compos. Sci. Technol., 32 (4) (1988), pp. 265–277
7. [7] E.J. Barbero, R. Lopez-Anido, J.F. Davalos; On the Mechanics of Thin-Walled Laminated Composite Beams; J. Compos. Mater., 27 (8) (1993), pp. 806–829
8. [8] X.-X. Wu, C.T. Sun; Simplified theory for composite thin-walled beams; AIAA Journal, 30 (1992), pp. 2945–2951
9. [9] J.C. Massa, E.J. Barbero; A Strength of Materials Formulation for Thin Walled Composite Beams with Torsion; J. Compos. Mater., 32 (17) (1998), pp. 1560–1594
10. [10] L.P. Kollar, A. Pluzsik; Analysis of Thin-Walled Composite Beams with Arbitrary Layup; J. Reinf. Plast. Compos., 21 (16) (2002), pp. 1423–1465
11. [11] A. Pluzsik, L.P. Kollar; Effects of Shear Deformation and Restrained Warping on the Displacements of Composite Beams; J. Reinf. Plast. Compos., 21 (17) (2002), pp. 1517–1541
12. [12] J. Lee, S. Lee; Flexural-torsional behavior of thin-walled composite beams; Thin Walled Struct., 42 (2004), pp. 1293–1305
13. [13] J. Lee; Flexural analysis of thin-walled composite beams using shear-deformable beam theory; Compos. Struct., 70 (2) (2005), pp. 212–222
14. [14] N.-I. Kim, D.K. Shin, M.-Y. Kim; Exact solutions for thin-walled open-section composite beams with arbitrary lamination subjected to torsional moment; Thin Walled Struct., 44 (6) (2006), pp. 638–654
15. [15] S.Y. Back, K.M. Will; Shear-flexible thin-walled element for composite i-beams; Eng. Struct., 30 (5) (2008), pp. 1447–1458
16. [16] L. Feo, G. Mancusi; Modeling shear deformability of thin-walled composite beams with open cross-section; Mech. Res. Commun., 37 (3) (2010), pp. 320–325
17. [17] J. Reddy; Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; (second edition)CRC Press (2004)
18. [18] G. Alfano, F. Marotti de Sciarra, L. Rosati; Automatic analysis of multicell thin-walled sections; Comput. Struct., 59 (4) (1996), pp. 641–655
19. [19] ABAQUS. Users manual: version 6.6. Hibbit, Karlsson & Sorensen, Inc., 2007.
20. [20] P.E. Vargas, Formulación de elementos finitos para vigas de sección abierta en laminados compuestos. PhD thesis, Universitat Politècnica de Catalunya, 2012.
21. [21] A.H. Sheikh, O.T. Thomsen; An efficient beam element for the analysis of laminated composite beams of thin-walled open and closed cross sections; Compos. Sci. Technol., 68 (2008), pp. 2273–2281
22. [22] E. Oñate; Structural analysis with the finite element method. Linear statics. Vol. 2 Beams, plates and shells; CIMNE (2013)