Agradecimientos
Los autores desean agradecer sinceramente al Dr. Lluis Pujades B por sus aportes y desinteresada ayuda en la revisión y sugerencias de los capítulos 4 y 7 de esta obra. Además se agradecen las innumerables sugerencias y ayuda en la revisión y corrección de los textos a la arquitecto Virginia Vásquez F., quien destinó muchas horas de su tiempo en pro del mejor resultado de esta publicación.
Los puentes son obras civiles de las que se requiere su integridad estructural y accesibilidad después de la ocurrencia de un sismo. Sin embargo, a través de los años se ha demostrado que estos sistemas son muy vulnerables, lo cual quedó de manifiesto tras la ocurrencia los grandes sismos de San Fernando (1971), Loma Prieta (1989), Northridge (1994), Kobe (1995) y Taiwán (1999). En todos ellos quedó claro que los puentes, por su importancia estratégica de comunicación inter e intra-urbana, son sistemas para los que se debe garantizar su uso para las comunicaciones de emergencia. Las tristes lecciones de los sismos recientes muestran que las subestimaciones en la demanda sísmica han jugado un rol fundamental, así como las malas concepciones estructurales y un detallado insuficiente. Es sin embargo gracias a estas lecciones que se ha podido avanzar en la consolidación de propuestas de diseño y normativas más racionales acordes a nuestros tiempos. En este sentido, los conceptos de ductilidad y disipación de energía juegan hoy un rol importantísimo en las propuestas de diseño.
De entre las tipologías de puentes existentes, los puentes de tirantes son sin duda una alternativa muy importante, puesto que permiten salvar grandes luces y ser, junto a los puentes suspendidos, las obras de ingeniería más impresionantes por su envergadura, impacto y belleza estética. Hoy en día, la tecnología permite alcanzar luces en puentes de tirantes de más de 1000 m, todo un récord, y alcanzar alturas impresionantes. Pese a su aparente sencillez, el diseño y construcción de obras de este tipo resultan un gran desafío en todas sus etapas; siendo sin duda la consolidación de la técnica de la construcción en voladizo la que ha permitido el desarrollo de las mega-estructuras que podemos apreciar hoy en día. El rápido progreso que ha experimentado la técnica constructiva en relación a puentes de tirantes ha sido muy marcada en los últimos veinte años debido al uso de ordenadores más potentes, programas de cálculo más sofisticados y completos, el desarrollo de vigas en cajón con tableros ortótropos y las mejoras en la técnica de fabricación y montaje de tirantes de alta resistencia. Este progreso se ha traducido en una competencia entre los ingenieros de puentes de Europa, Japón, USA y más recientemente China. Los puentes de tirantes están ingresando a una nueva era, con luces que bordean los 1000 m y con la incorporación de dispositivos de control inteligentes.
Los puentes de tirantes han crecido mucho en popularidad. Su efecto estético hace que sean la tipología estructural preferida por los proyectistas. Por ello es importante que para grandes luces, estas estructuras sean lo más simétricas y sencillas posible, ya que de ello dependerá en gran parte su desempeño sísmico. De los análisis de varias observaciones, incluyendo pruebas de vibración ambiental y forzada, es sabido que los puentes de tirantes tienen muy poco amortiguamiento estructural (0.3% al 2%). Esto es muy importante a tener en cuenta, ya que estas estructuras ocasionalmente experimentan cargas extremas, como en sismos severos o con mucho viento ambiental. Por tales circunstancias, la respuesta debe ser controlada dentro de ciertos límites de serviciabilidad y seguridad.
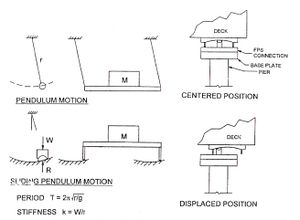
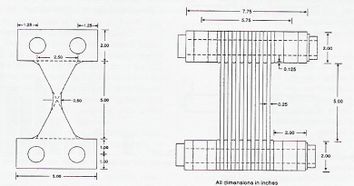
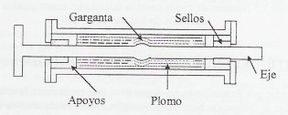
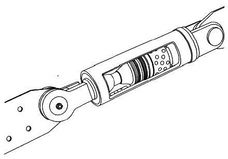
Debido a su importancia, es deseable que los grandes puentes con luces superiores a los 200 m sean diseñados de forma conservadora; como ocurrencia, es común requerir una respuesta estructural elástica o casi elástica para un sismo de diseño de muy baja probabilidad de ocurrencia. Por ello, a fin de mantener una respuesta elástica en los elementos estructurales y, a su vez, tener una estructura capaz de disipar energía, se puede recurrir al uso de dispositivos activos o pasivos de control sísmico. Originados como elementos de uso militar, los dispositivos de disipación de energía y aislamiento de base rápidamente comenzaron su incursión en el mundo civil, para mejorar el desempeño sísmico de las construcciones. Muchos edificios se han construido empleando estos sistemas, los que rápidamente han sido incorporados a los puentes. De entre los dispositivos de aislamiento de base, los aisladores basales de goma con núcleo de plomo y más recientemente los sistemas de péndulo de fricción, son los que más se están utilizando por su sencillez, eficacia y comportamiento. Como dispositivos de disipación de energía, son los amortiguadores hidráulicos o de fluidos viscosos los que han tenido un mayor desarrollo y aplicación durante las últimas dos décadas, empleándose hoy en día en puentes nuevos y como refuerzo en puentes existentes. Aunque en forma mucho más incipiente y a menor escala, los sistemas activos de control comienzan a aplicarse a los puentes en general y, en el caso de los puentes de tirantes, su empleo se comienza a orientar hacia el control de tendones activos y al aislamiento de la superestructura a través de sistemas semi-activos e híbridos principalmente, aunque eso sí, actualmente en una fase experimental y analítica.
Resulta muy importante en puentes de tirantes un adecuado diseño conceptual que tome en cuenta seriamente los aspectos del diseño sísmico, sobre todo en zonas de sismicidad moderada a alta. En este sentido, es importante resaltar que el mejor desempeño sísmico será aquel que esté relacionado con la estructura que tenga mayor uniformidad, sencillez y simetría. Es sabido que cuando se cumplen estos requisitos, el desempeño será satisfactorio. El problema del buen comportamiento sísmico no se resuelve con métodos complejos o procesos engorrosos y tediosos de cálculo, sino evitando los problemas, siendo la simpleza y armonía sinónimos de buen desempeño.
Las siguientes páginas corresponden a la presentación de los últimos avances y novedades en materia de comportamiento sísmico de puentes de tirantes de gran luz. La idea ha surgido de la necesidad de unificar experiencias y criterios, y tiene como objetivo presentar al lector una visión actualizada acerca del comportamiento de estos sistemas y la reciente introducción y uso de sistemas avanzados adicionales de protección pasiva y activa. A modo introductorio, se presentan los aspectos generales del comportamiento de puentes de tirantes frente a cargas estáticas. Se exponen los resultados de las investigaciones más recientes acerca del comportamiento sísmico general de puentes de tirantes de gran luz, se analiza la problemática de la caracterización de la acción sísmica de entrada, se presentan los desarrollos y resultados de investigaciones recientes en materia de dispositivos de control de vibraciones aplicado a puentes, se analiza la temática del comportamiento sísmico de puentes de tirantes con incorporación de sistemas pasivos y activos y finalmente se presentan algunos aspectos básicos y actualizados relacionados con el análisis y diseño estructural.
Capítulo 1. Introducción General
Construcción Puente Centenario Panamá
Los puentes son sin duda las obras de Ingeniería Civil más atractivas desde el punto de vista estructural. Su relativa simplicidad conceptual los hace fácilmente comprensibles, sin embargo es esta aparente sencillez la que debe preocuparnos, sobre todo cuando tratamos de comprender su comportamiento sísmico. Pero no sólo desde el punto de vista estructural son apasionantes estas obras: el proyecto, construcción, conservación, explotación, así como los aspectos funcionales, estéticos, económicos y políticos los hacen sumamente interesantes, pues constituyen un acontecimiento social a toda escala (Maldonado et al, 1998).
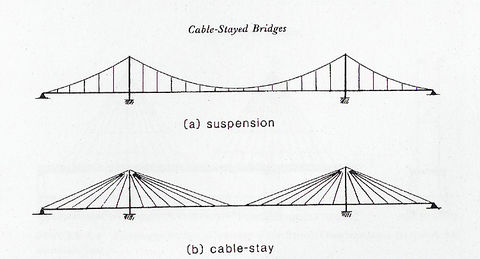
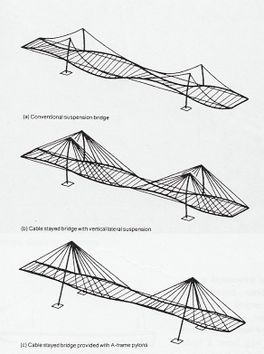
De entre ellos, son los puentes soportados por cables los que más interés han despertado debido a que permiten alcanzar actualmente las mayores luces, resolviendo así muchos problemas prácticos en los que es necesario atravesar grandes extensiones sin disponer de ningún tipo de apoyo intermedio. Estos puentes son hoy en día un desafío desde todo punto de vista, debido a las exigencias cada vez mayores de alcanzar claros más grandes, y así como en los grandes rascacielos, constituyen muchas veces más bien un capricho humano o ese deseo competitivo e insaciable de romper récords y vencer los obstáculos a cualquier costo. Los esquemas soportados por cables que hoy en día más se emplean son sin duda los puentes suspendidos y los puentes de tirantes o atirantados, tal como se aprecia en la Fig.1-1 (Podolny y Scalzi, 1986).
Desde el punto de vista estructural, ambas tipologías son totalmente diferentes, ya que a diferencia de la primera, en los puentes de tirantes los cables son pretensados. Teniendo en cuenta aspectos económicos y funcionales, los puentes suspendidos permiten alcanzar mayores claros con una mayor economía respecto de los puentes atirantados (Podolny y Scalzi, 1986). Las mayores luces para puentes de tirantes son del orden de los 900 m, aunque existen estudios recientes que muestran la factibilidad y posibilidad de construir puentes de tirantes con claros superiores a 1000 m, basado en el alto estándar actual de los métodos de cálculo y en el alivianamiento de la superestructura mediante tableros ortótropos (Aschrafi, 1998; Nagai et al, 1998).
A modo de ejemplo, a continuación se presenta un ranking de los mayores puentes actuales del mundo, algunos de los cuales aún no han finalizado su fase constructiva o que se encuentran en etapa de proyecto (tabla 1-1).
| PUENTE | TIPO | PAIS | LUZ PRINCIPAL (m) | AÑO FINALIZACION |
| 1.- Messina | Suspendido | Italia | 3300 | 2011 ???? |
| 2.- Kitan Straight | Suspendido | Japón | 2500 | ?????? |
| 3.- Qiongzhou Haixia | Suspendido | China | 2500 | ?????? |
| 4.- Akashi Kaikyo | Suspendido | Japón | 1991 | 1998 |
| 5.- Suzhou – Nantong | Atirantado | China | 1088 | 2008 ?????? |
| 6.- Stonecutters | Atirantado | China | 1018 | 2007 ?????? |
| 7.- Dongfang | Atirantado | China | 900 | ??????? |
| 8.- Lingding | Atirantado | China | 900 | ?????? |
| 9.- Tatara | Atirantado | Japón | 890 | 1999 |
| 10.- Hu – Pu | Arco | China | 550 | 2003 |
| 11.- New River George | Arco | USA | 518 | 1978 |
| 12.- Pont de Québec | Celosía metálica | Canadá | 549 | 1917 |
A pesar de la relativa sencillez de los puentes en general, los sismos recientes de San Fernando (1971), Loma Prieta (1989), Northridge (1994), Kobe (1995) y Taiwán (1999) han mostrado que estos sistemas son bastante vulnerables, sobre todo los de hormigón armado, por lo que resulta prioritario mejorar la comprensión de este fenómeno y aprender las lecciones de los sismos más recientes (Priestley et al, 1996). Estos sistemas estructurales tienen pocos grados de redundancia, por lo que los mecanismos de colapso deben ser conocidos con detalle para alcanzar un adecuado desempeño. Aspectos que deben ser considerados: grado de redundancia del sistema, interacción suelo – estructura, variabilidad espacial, efectos torsionales, cercanía de la fuente, fallas geológicas en el emplazamiento y aspectos geotécnicos, efectos debidos a la longitud del puente, componente vertical del movimiento, amortiguamiento del sistema (Valdebenito, 2005). Todos estos aspectos a considerar son generales, y se pueden encontrar explicados en las referencias de Kawashima (2000); Cheung et al (2000), Calvi (2004) y Ghasemi (1999).
La búsqueda de medios para proporcionar resistencia adecuada a los puentes y asegurar un comportamiento satisfactorio para diferentes niveles de intensidad ha propiciado el desarrollo de dispositivos especiales de control de vibraciones. En términos generales, en vez de dar mayor resistencia como en un esquema tradicional de protección sísmica, lo que acá se busca es reducir los esfuerzos internos y los desplazamientos a través de sistemas especiales que aíslen de vibraciones y/o disipen energía. De los sistemas de control empleados en puentes, los pasivos son los más usados por su menor costo de adquisición, instalación y manutención, así como por su gran fiabilidad y mayor desarrollo teórico y tecnológico (Jara y Casas, 2002). Se puede decir en cierto sentido que han sido justamente los puentes los primeros sistemas estructurales que incorporaron, en forma moderna y un tanto casual, a los sistemas de aislamiento de base, al reemplazar los antiguos sistemas de apoyos en base a rodillos por los apoyos de goma de neopreno zunchado. Por otro lado, los sistemas activos, semiactivos e híbridos han comenzado tímidamente a emplearse en puentes actuales. Sin duda les espera un futuro muy prometedor, sobre todo los sistemas semiactivos, dada sus incomparables ventajas, aunque de momento su uso es muy limitado y peor aún, no han sido debidamente probados en estructuras reales frente a sismos reales. En definitiva, el criterio general de reducir la demanda sísmica en la estructura, más que en tratar de incrementar su capacidad resistente o de deformación mediante sistemas especiales y criterios adecuados, es sin duda un esquema de protección sísmica indiscutiblemente ventajoso (Jara y Casas, 2002).
En el caso de los puentes atirantados, el desempeño sísmico de éstos ha sido en general muy satisfactorio, tal vez debido a su gran flexibilidad. A pesar de lo anterior, la comprensión de su desempeño es muy compleja, por lo que resulta muy adecuado y prometedor disponer de sistemas especiales de protección sísmica adicional. Los sistemas de control de vibraciones en ésta área también han experimentado un gran desarrollo, sobre todo en los últimos 10 años, enfocándose su uso más que nada en incorporar sistemas pasivos de distinto tipo, aunque más recientemente se comienzan a probar y usar sistemas híbridos y semiactivos, eso sí, en una fase muy experimental y teórica. En puentes de tirantes, estos sistemas se han empleado básicamente para controlar las vibraciones en los cables debido al efecto del viento y la lluvia (rain – wind vibration) o para resolver problemas en puentes aerodinámicamente complejos o inestables, más que en mitigar los efectos sísmicos. A pesar de ello, el uso de estos dispositivos para el control de la acción sísmica comienza a emplearse con mayor fuerza; y no solo en los cables para mitigar los efectos de la interacción cable – tablero (Macdonald y Georgakis, 2002), sino que también para aislar la superestructura, como ocurre en el recientemente inaugurado puente Rion – Antirión, en el Golfo de Corintio, Grecia (Infanti et al, 2004).
Otro aspecto a considerar, y que de algún modo privilegia la selección de los puentes atirantados, es sin duda su forma estética. Esto los hace ser preferidos por los diseñadores quienes muchas veces priman la forma y la estética por sobre temas estructurales, para así ganar originalidad y el reconocimiento público, so pena de perjudicar muchas veces aspectos económicos o puramente técnicos (Walter, 1999). En este sentido, existe una amplia literatura, como la propuesta por Billington y Deodatis (1991).
El desarrollo histórico de los puentes de tirantes ocupa un lugar importante en muchas publicaciones recientes, por lo que a continuación se resumirán brevemente los hechos más significativos, de acuerdo a los antecedentes proporcionados por Gimsing (1983); Podolny y Scalzi (1986); Troitsky (1988); Walter (1999) y Virlogeux (1999).
El primer intento de puente atirantado data de 1784, cuando el carpintero alemán C.T. Loescher diseñó una estructura completa en madera con atirantamiento. Este tenía una luz de 32 m. Estos primeros puentes de tirantes eran en realidad un híbrido entre puente suspendido y atirantado, y fueron construidos a finales del siglo XVIII principalmente en Inglaterra y USA. Dos importantes accidentes en esta tipología hicieron que se cuestionara seriamente su desempeño: el fallo del puente sobre el Tweed River, en Dryburgh – Abbey, Inglaterra (1818) y el fallo del puente sobre el río Saale, en Nienburg, Alemania (1824). El primero falló debido al viento, mientras que el fallo del segundo se debió a una subestimación en la sobrecarga. A raíz de ello, el propio Navier en 1830 en su texto Memoire Sur Les Ponts Suspendeé hace una severa crítica a las tipologías de puentes soportados por cables, en el cual planteaba el hecho de que la excesiva flexibilidad de éstos hacía que tuvieran un mal desempeño estructural. Sin duda con los primeros trabajos de Roebling (Brooklyn Bridge, Niagara Falls) se devuelve la confianza en estas estructuras, las que comienzan a tener un rol protagónico en la historia de la ingeniería estructural.
Los primeros puentes modernos atirantados de hormigón fueron construidos por Eduardo Torroja hacia 1926 (acueducto Tempul, España) y por Albert Caquot en 1952 (Puente sobre el canal Donzère, Francia). Sin embargo el desarrollo real comenzó con los trabajos de Franz Dischinger y sus famosos puentes sobre el Rhin de Düsseldorf y Colonia (Alemania), como se aprecia en la Fig. 1-2.
Hacia finales de los 50, Morandi construye el primer puente atirantado multiclaro con tirantes de hormigón monocable en el Lago Maracaibo, Venezuela (Fig. 1-3). En él llama la atención la gran rigidez de las torres, para poder controlar la gran flexibilidad longitudinal del sistema.
Hacia 1965 Polcevera construye los primeros puentes en Italia utilizando la técnica de los voladizos sucesivos. Así como Wadi – Kuf (Libia, 1972) y el puente Magdalena en Colombia (1975), todos ellos contaban con claros principales que superaban los 140 m, usando el esquema de atirantamiento provisional en su construcción. Sin embargo, es hacia 1967 (Puente Friedrich Ebert, Bonn, Alemania) que comienzan a construirse los primeros puentes multicables modernos. En la década de los 80 y durante los 90 comienza una verdadera explosión en la construcción de puentes de tirantes, entre los que destacan el puente Barrios de Luna, de Fernández Casado (España); el puente de Annacis (Canadá), el puente Ikuchi (Japón), el puente Skarnsund (Noruega), el puente Yang Pu (China), el puente de Normandía (Francia), el puente Öresund (Suecia), el puente Higashi – Kobe (Japón) y el reciente puente Tatara (Japón) que ostenta ser actualmente el que posee el claro más largo del mundo (890 m). Algunos de estos puentes se aprecian en las Figs. 1-4 y 1-5.
|
Fig.1-4 Puente Normandía, Francia
|
Fig.1-5 Puente Tatara, Japón |
La evolución de los récords de claros más largos se puede apreciar en la Fig. 1-6, tomada de Virlogeaux (1999).
Sin duda el nuevo viaducto francés de Millau (inaugurado en 2004), sobre el valle del Tarn, en la autopista que une Montpellier con París y diseñado por Michel Virlogeaux y Sir Norman Foster, resulta todo un desafío de la ingeniería de puentes debido a la gran altura de sus pilas, la rigidez elegida para las mismas y por tener un atirantamiento central. Para Francia resulta ser uno de sus proyectos emblemáticos, y pese a sus muchos detractores, se ha logrado imponer como uno de los íconos de la ingeniería moderna (Fig. 1-7).
| Fig.1-7 Viaducto de Millau, Francia |
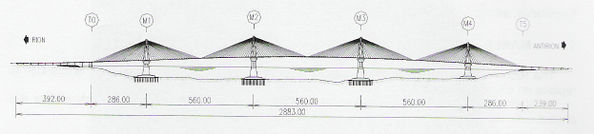
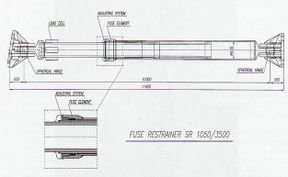
De entre los puentes modernos que incorporan dispositivos especiales de disipación de energía, destaca el recientemente inaugurado puente Rion – Antirión, en el golfo de Corinto, Grecia (Fig. 1-8). Este puente cuenta con una serie de amortiguadores de fluido viscoso para controlar las vibraciones y desplazamientos del tablero, además de fusibles estructurales que permiten dar una rigidez adecuada a la superestructura, pero que frente a un sismo severo, fallan para permitir el libre trabajo y operación de los amortiguadores (Teyssandier, 2002).
Capítulo 2. Comportamiento Frente a Cargas Estáticas
El comportamiento estructural de los puentes de tirantes viene dado, en términos generales, por la interacción de las diferentes partes que constituyen el puente. Así, la contribución de cada uno de sus elementos afectará, en razón de su medida, en el comportamiento global de la estructura (Walter, 1999).
Por otro lado, las múltiples posibilidades de seleccionar los elementos constituyentes, y la variabilidad en las tipologías disponibles, hacen que existan muy amplias posibilidades, y con ello, múltiples alternativas de comportamiento. En el caso de los puentes de tirantes, los aspectos más influyentes en el comportamiento son el layout de los cables, el tipo de tablero y el tipo de torre (Walter, 1999). Podemos dar algunas características generales de comportamiento que se cumplen en aquellos sistemas que tengan una cierta regularidad. La importancia de caracterizar estructuralmente estos sistemas, radica en el hecho de que nos permitirá de algún modo tener algunas ideas básicas del comportamiento cuando analicemos su respuesta frente a solicitaciones sísmicas, por lo que estos aspectos básicos se analizan a continuación.
2.1. Disposición de los Tirantes
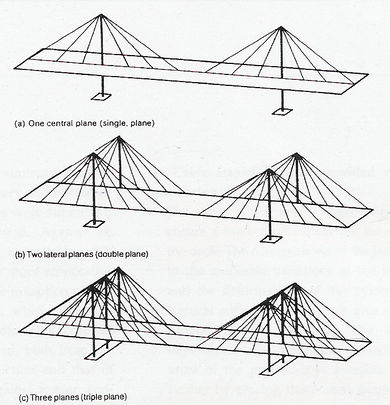
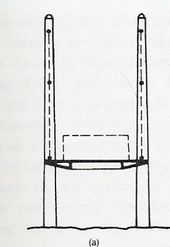
Este es uno de los ítems fundamentales en el diseño y concepción de puentes de tirantes. Lo primero que se debe seleccionar en el proceso de diseño es el número de planos de cables. En este sentido podemos diferenciar los sistemas con suspensión central y aquellos con suspensión lateral, como se muestra en Fig. 2-1.
La selección del número de planos de cables dependerá de aspectos como la estética del puente y de las características estructurales particulares del mismo, dado que bajo la acción de cargas vivas, la deformación de la estructura es gobernada esencialmente por la rigidez de las pilas y el sistema de suspensión. En general, el sistema de atirantamiento con planos laterales es más eficiente ya que aumenta la rigidez torsional y de flexión transversal del sistema, lo que lo hace adecuado para combatir efectos aerodinámicos sobre todo en sistemas en donde el tablero tenga muy poco canto. Sistemas de tres planos de cables han sido muy poco utilizados, aunque parecen ser una buena solución sobre todo para tableros muy anchos y/o puentes de claros muy largos, donde la flexión transversal pueda gobernar el diseño del tablero (Walter, 1999).
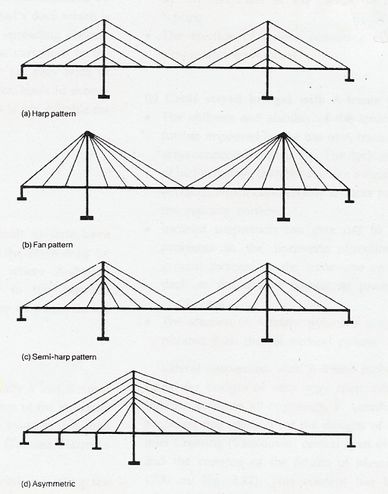
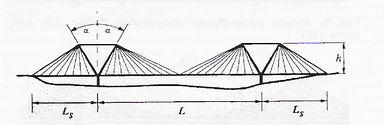
En cuanto al layout longitudinal, podemos categorizar los puentes básicamente en los mostrados en la Fig. 2-2.
|
Fig.2-2 Layout longitudinal (Walter, 1999) |
El sistema en arpa parece no ser el mejor esquema desde el punto de vista estático. En efecto, estudios paramétricos (Walter, 1999) muestran que en general los axiles son marcadamente mayores en la configuración tipo arpa que en la abanico. Aunque los momentos flectores en el tablero no son apreciablemente diferentes en uno u otro tipo, los momentos flectores en la pila son mayores en la configuración en arpa, para la zona bajo el tablero. En cuanto a las deformaciones, no hay diferencias apreciables, excepto para condiciones de carga asimétrica, en donde éstas aumentan para la configuración en arpa. El gran problema de la configuración en abanico es la dificultad que se presenta para un adecuado sistema de anclaje de los cables en las torres, ya que se generan concentraciones de esfuerzos, a veces excesivos, y dificultades en la materialización de éstos. Parece ser entonces que una solución intermedia, como la semi-arpa puede ser muy ventajosa.
En el caso de puentes de vanos múltiples, el mayor problema resulta ser el obtener una adecuada estabilidad longitudinal bajo la acción de cargas asimétricas de tráfico. En este caso, se deben proveer de pilas con la rigidez necesaria para garantizar la estabilidad del sistema, dado que la ausencia de puntos fijos intermedios excluye la posibilidad de usar cables de retención. Puentes como el Great Belt (Dinamarca), Maracaibo (Venezuela) o el reciente viaducto Millau (Francia) disponen de pilas rígidas para lograr una adecuada estabilidad (Virlogeux, 1999).
2.2. Tablero
El tipo de tablero a usar resulta esencial en la concepción de un puente atirantado. Tableros muy pesados no resultan prácticos por el costo económico y estructural. Es sabido que los momentos flectores aumentan en el tablero conforme éste es más rígido, lo que sugiere entonces usar tableros más bien flexibles, para así disminuir la flexión. En todo caso, no se puede dar toda la flexibilidad que uno quisiera, ya que los efectos aerodinámicos empiezan a jugar un rol decisivo. Así, la rigidez óptima no solo depende del espaciamiento de los tirantes, sino también del método de suspensión y del ancho del tablero. En el caso de puentes con atirantamiento central, resulta necesario disponer de tableros con alta rigidez torsional. Para puentes de atirantamiento lateral, es posible conseguir secciones más delgadas, dado que los momentos flectores son en general más bajos. En este caso las dimensiones mínimas estarán dadas por la flexión transversal (Walter, 1999).
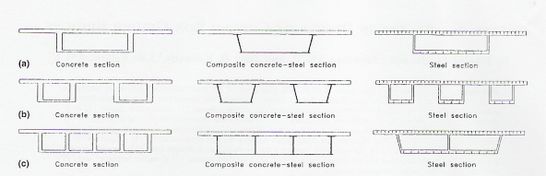
La elección de los materiales del tablero es uno de los criterios que gobierna el costo completo del sistema, siendo los más livianos aquellos metálicos con tablero ortótropo. A pesar de ello, el costo de fabricación hace que sean muy caros, por lo que se prefiere, a pesar de su mayor peso, el uso de tableros de hormigón o mixtos. Los tableros ortótropos se reservan entonces para puentes de claros muy largos, donde el tema del peso se vuelve crítico, y por tanto, que gobierna el diseño. En la Fig. 2-3 se pueden apreciar algunos tableros típicos (Sennah y Kennedy, 2001).
Debido a los fuertes axiles que se generan en los tableros, sobre todo en puentes con configuración de los cables en arpa, resulta necesario considerar las características de estabilidad del tablero y las vigas longitudinales, sobre todo si el sistema es metálico. Por ello, para puentes de gran luz resulta imperioso hacer análisis de estabilidad por elementos finitos. Se ha demostrado que la carga crítica que genera inestabilidad es alta cuando la razón entre la longitud del claro principal y la longitud total es pequeña. Así mismo, si la razón entre la inercia de la pila y la inercia del tablero aumenta, la carga crítica disminuye. Además, la configuración tipo arpa es ventajosa en este sentido, mientras que el tipo de pila no es significativo (Shu y Wang, 2001).
En cuanto a las tipologías, se puede decir que existe una amplia variedad en todas las materialidades, algunas de las cuales parecen desafiar toda lógica, como se aprecia en las Figs. 2-4, 2-5, 2-6, 2-7 y 2-8 (Walter, 1999; Reis y Oliveira, 2004).
|
Fig. 2-6 Sección para puente East Huntingdon (Walter, 1999) |
Fig. 2-7 Sección tipo Vierendeel (Walter, 1999) |
2.3. Pilas
Los estudios paramétricos hechos por Walter (1999), muestran que el incremento en la rigidez de las pilas induce una disminución en los momentos flectores en el tablero, y de forma análoga, un aumento en la rigidez del tablero induce una disminución en los momentos de las pilas. Algo similar ocurre con las deformaciones en el tablero, es decir, conforme aumenta la inercia de las pilas disminuyen las deformaciones en el tablero.
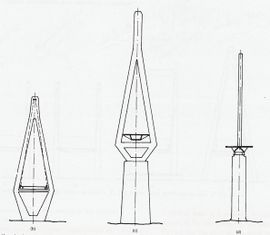
Indudablemente el tipo de pila es fundamental en el desempeño del sistema completo. Su elección estará en función de aspectos estructurales como el tipo de atirantamiento y longitud del claro principal, como así mismo de aspectos estéticos. De este modo, los planos de cables pueden ser verticales o inclinados, lo que necesariamente condicionará el tipo de pila, como se muestra en la Fig. 2-9.
|
Fig. 2-9 Condicionamiento del tipo de torre según suspensión empleada (Walter, 1999) |
Las figuras muestran como influye el tipo de pila y el esquema de atirantamiento empleado en el comportamiento (en este caso las deformaciones). Es claro que el atirantamiento en abanico con planos laterales inclinados es más eficiente que los otros por la gran estabilidad geométrica que induce la pila tipo “A”. Ello hace que esta tipología sea adecuada para puentes de gran luz (Walter, 1999). A la luz de lo anterior resulta claro entonces que el tipo de pila irá en directa relación con el sistema estructural que se tenga. La variedad de formas de las pilas es tan rica como tipos de puentes existen, siendo las más usadas los tipos “H”, “A”, diamante y la pila simple en voladizo, tal como se muestra en la Fig. 2-10.
En cuanto a puentes de claros muy largos, es indudable que esto afecta directamente al tipo de pila y su tamaño. Se han propuesto algunas alternativas, tales como pilas inclinadas, para salvar tales luces, como se muestra en la Fig. 2-11 (Starossek, 1996).
Indudablemente, estructuras de grandes luces llevan asociados problemas mucho mayores, básicamente por los grandes esfuerzos generados en todo el conjunto. Por ello, el conocimiento y cuantificación de las no linealidades es fundamental. En este sentido, trabajos recientes como el de Ren (1999), indican que las no linealidades últimas en puentes de tirantes de gran luz tienen efectos perjudiciales, sobre todo la no linealidad del material, que resulta ser de mayor importancia frente a la no linealidad geométrica.
Capítulo 3. Comportamiento Sísmico de Puentes Atirantados
La mayoría de los daños por efecto de sismos, son la interrupción de las redes de comunicación y de otras líneas vitales. Por ello resulta de vital importancia que su seguridad sea convenientemente alta. Los puentes son estructuras muy vulnerables en ese sentido, y esenciales en las redes viales, por lo que la comprensión de su comportamiento sísmico resulta fundamental (Maldonado et al, 1998). A partir del sismo de San Fernando, en 1971, la sociedad científica tomó consciencia de la importancia del efecto sísmico en el diseño y construcción de puentes, experiencia que permitió revisar, modificar y actualizar los códigos de diseño a partir de sismos más recientes. Muchas de las normativas tienen su origen en estudios de edificaciones, y es importante destacar las grandes diferencias que presentan los puentes en comparación con los edificios en relación a la respuesta sísmica (Barenberg y Foutch, 1988).
Los puentes atirantados de gran luz, producto de sus grandes dimensiones y flexibilidad, usualmente tiene períodos fundamentales muy largos, aspecto que los distingue de otras estructuras, y que por supuesto, afecta enormemente su comportamiento dinámico. Sin embargo, la flexibilidad y las características dinámicas de este tipo de puentes dependen de varios parámetros tales como el tamaño del claro o claros, el sistema de atirantamiento usado y su layout, las condiciones de soporte y muchos otros aspectos que discutiremos en las páginas siguientes. En general, esta tipología estructural es compleja, consistiendo en varios componentes estructurales con diferentes propiedades individuales de rigidez y amortiguamiento. Son estructuras más flexibles que los puentes normales de vigas, por lo que precisan de un adecuado análisis dinámico para su diseño sísmico. Por ello, en los puentes de tirantes es muy importante determinar en forma precisa sus períodos, formas modales y características de amortiguamiento. Así, las pruebas de carga dinámica que se realizan en ellos resultan clave para validar las hipótesis iniciales y los esquemas y modelos usados en la concepción de los mismos.
El comportamiento sísmico de los puentes de tirantes ha sido en términos generales muy satisfactorio, no reportándose casos de colapsos o daños muy severos en los últimos años. La mayor causa de daño han sido los movimientos diferenciales en los apoyos, sobre todo cuando el sismo actúa en la dirección longitudinal o transversal, en lo que hoy forma parte de los llamados problemas de variabilidad espacial (Walter, 1999).
En lo que sigue, se analizarán los trabajos más recientes sobre los aspectos generales del comportamiento sísmico de puentes atirantados, en términos de sus propiedades dinámicas, esquemas de modelación y análisis, comportamiento no lineal, efecto de la vibración de los cables, influencia del tipo de apoyo, respuesta de las torres, interacción suelo-estructura, respuesta sísmica vertical y variabilidad espacial. Además se expondrán y discutirán los aspectos más actuales acerca de la respuesta de puentes multi-vano y puentes curvos. Finalmente se revisarán algunas consideraciones sobre la respuesta de puentes extra-largos y se discutirán los pocos reportes de fallas que han experimentado estas estructuras durante sismos severos recientes
3.1. Caracterización Dinámica General
3.1.1. Frecuencias naturales y modos de vibración
Los puentes de tirantes tienen en general poca sensitividad frente a excitaciones sísmicas. Sin embargo, es claro que los principales problemas provienen a nivel del tablero frente a movimientos horizontales (Walter, 1999). La componente vertical tiene mayor importancia en el análisis y diseño de las pilas y cables, y no así en el tablero, ya que en general en los puentes modernos éste se encuentra soportado por los cables, que constituyen en definitiva una infinidad de soportes elásticos equiespaciados, como discutiremos más adelante.
Los resultados del análisis modal en puentes de tirantes se encuentran en muchos papers de investigadores, con énfasis en el comportamiento sísmico de los mismos. Los primeros modos de vibración son de período muy largo, del orden de varios segundos, y son fundamentalmente modos asociados al tablero. Ellos son seguidos por modos de vibración de los cables, los que se encuentran acoplados con los del tablero. Los modos de las torres usualmente son modos de vibración superiores, los que se pueden acoplar al tablero dependiendo de las condiciones de soporte, como se explicará más adelante. Los modos obtenidos son clasificados en sus direcciones de acción, esto es, en dirección longitudinal, transversal y torsional, pensando en que uno de ellos es el predominante. Indudablemente esto es más difícil de separar cuando los modos se presentan marcadamente acoplados (Morgenthal, 1999). Para puentes atirantados típicos existen fuertes acoplamientos (como el de flexión y torsión) en las tres direcciones ortogonales. Este movimiento acoplado diferencia la respuesta respecto de los puentes suspendidos para los cuales existe movimiento vertical, lateral y torsional puro, muy fáciles de distinguir. Ello implica la absoluta necesidad de realizar modelación tridimensional del sistema (Wethyavivorn y Fleming, 1987).
Un análisis exacto de las frecuencias naturales y formas modales en puentes atirantados es fundamental no sólo para el estudio de la respuesta sísmica, sino también para el estudio de la acción del viento y las cargas de tráfico. En general, los cables son modelados como elementos de enrejado en un análisis por elementos finitos tradicional. Este método es simple pero inadecuado para un análisis dinámico más exacto de un puente de tirantes, debido a que no considera la vibración transversal de los cables. Resultados numéricos y experimentales indican que la forma de modelar los cables tiene un significativo efecto en la predicción de las características dinámicas de puentes atirantados. La discretización de cada cable en series de elementos ayuda a predecir las vibraciones de éstos, tal como se explica en el trabajo de Au (2001). Por otro lado, hay estudios analíticos sobre el cálculo de las frecuencias naturales de puentes atirantados de gran luz, con torres tipo “H” y tipo “A”, y considerando distintos esquemas de modelación de los cables (Bruno y Leonardi, 1997). En todos estos trabajos se deja en claro la fuerte dependencia de las frecuencias naturales con los parámetros geométricos.
Existen muchos estudios analíticos y experimentales que presentan resultados de observaciones y mediciones en puentes existentes, como por ejemplo en el puente Indiano, Florencia, Italia (Clemente et al, 2004); puente Garigliano, Italia (Clemente et al, 1998), puente Higashi-Kobe, Japón (Ganev et al, 1998; Kitazawa et al, 1989, 1992), puente Quincy Bayview, USA (Wilson y Liu, 1991, Pridham y Wilson, 2005), puente Vasco Da Gama, Lisboa, Portugal (Branco et al, 2000; Cunha et al, 2001), puente Tampico, México (Muriavila et al, 1991).
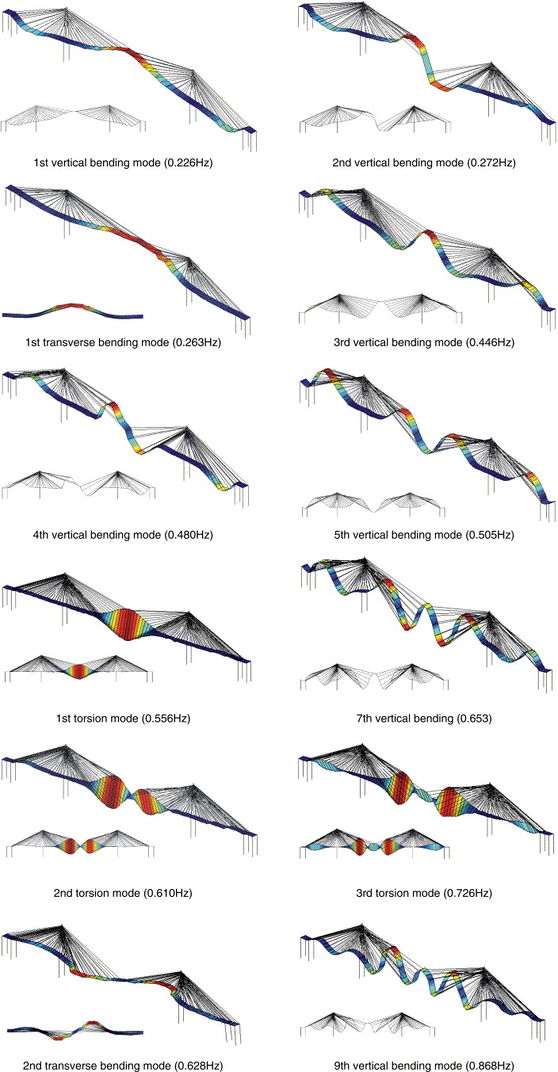
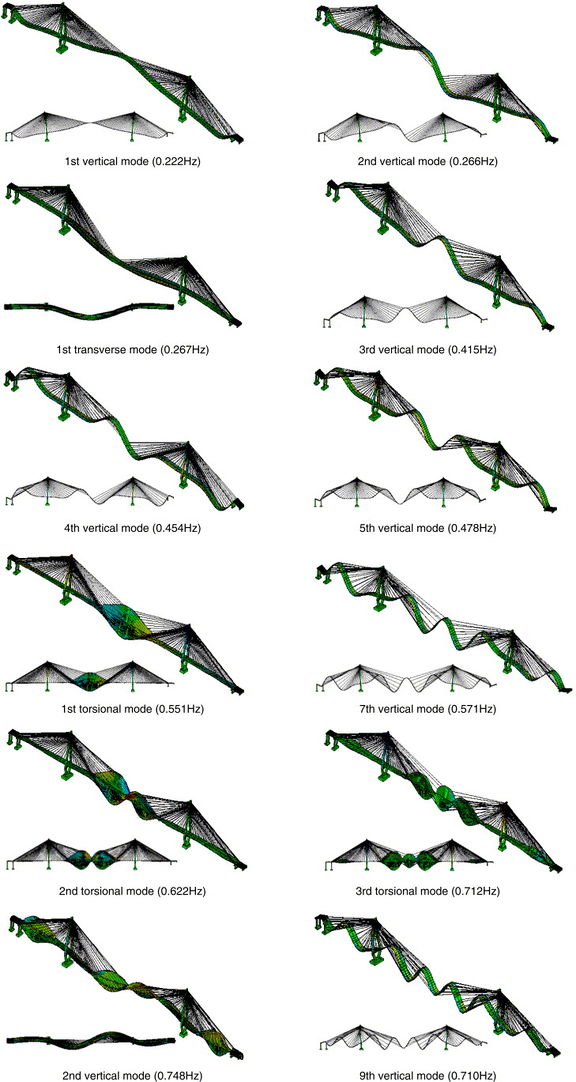
A continuación se presentan resultados típicos de estudios analíticos y experimentales de las características dinámicas, en este caso, del puente Quingzhou, China.
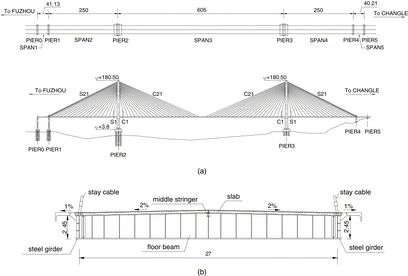
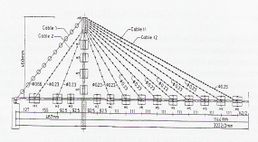
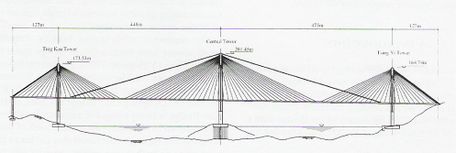
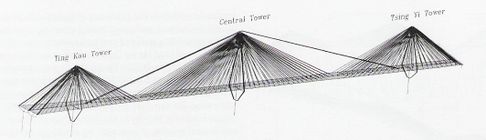
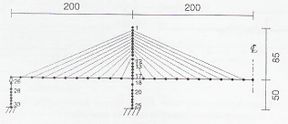
Se ha elegido este puente debido a que es representativo de los puentes de tirantes de gran luz, con un claro principal de 605 m, y siendo actualmente el claro más largo de tablero compuesto del mundo. El puente ha sido estudiado extensivamente en los trabajos de Ren et al (2005) y Ren y Peng (2005). La Fig. 3-1 muestra una fotografía del puente, y la geometría general es la que se muestra en la Fig. 3-2.
Se aprecia una muy buena correlación entre los resultados medidos experimentales y los resultados numéricos mediante elementos finitos. El análisis experimental se hizo empleando un sistema de identificación estocástico (Fig. 3-3). La Fig. 3-4 muestra los resultados del estudio numérico.
Los resultados muestran la conveniencia de realizar estudios experimentales en puentes de gran envergadura. Ellos son suficientes para identificar los modos más significativos. Se muestra que el rango bajo de frecuencias naturales (0 – 1.0 Hz) es de interés, debido a que muchos modos se enmarcan en este rango, característicos de este tipo de puentes. El mecanismo de amortiguamiento es complicado, como se discutirá en la próxima sección. En efecto, una evaluación analítica del amortiguamiento del puente es difícil, y no es comprendida adecuadamente todavía. Para este puente, las frecuencias fundamentales de los cables resultan relativamente bajas, siendo en promedio de 0.36 Hz para los cables más largos, y de 1.97 Hz. para los más cortos.
Pruebas similares efectuadas en otros puentes, han permitido realizar correlaciones de las frecuencias naturales en función de la longitud del claro principal L, tanto para oscilaciones flexurales verticales (f1 BV), como para las oscilaciones flexurales transversales (f1 BH) y torsionales (f1 T) (Kawashima et al, 1993):
f1 BV=33.8L-0.763
f1 BH=482L-1.262
f1 T=17.5L-0.453
3.1.2. Amortiguamiento
En general, el amortiguamiento en puentes atirantados es bastante bajo, por lo que la tradicional consideración del 5% del amortiguamiento crítico no es real, y peor aún, no va por el lado de la seguridad. Las investigaciones en esta área han mostrado que la generalización de los valores del amortiguamiento son difíciles de determinar debido a que varían significativamente dependiendo de la configuración del puente (Morgenthal, 1999). Las fuentes de disipación de energía son básicamente: no linealidad de los materiales, fricción en los apoyos móviles, fricción con el aire, radiación de la energía desde las fundaciones al suelo, etc.
Esencialmente hay dos formas en las cuales es considerado el amortiguamiento en casi todas las investigaciones. Primero, disipación por pérdida histerética elasto-plástica, que requiere de un análisis no lineal con la aplicación de las características no lineales de los materiales, la cual es más importante cuando el sistema considera sistemas especiales de disipación de energía. En segundo lugar, y el más común, se considera un amortiguamiento equivalente, no viscoso, de tipo Rayleigh (Clough y Penzien, 1993). En todo caso, las razones de amortiguamiento suelen ser del orden del 2% del crítico en puentes atirantados (Morgenthal, 1999). De acuerdo a Abdel-Ghaffar (1991), valores de este nivel se han encontrado en muchas medidas reales, aunque en el pasado, los investigadores empleaban razones de amortiguamiento que variaban entre un 2% a un 3%.
Yamaguchi y Jayawardena (1991), han propuesto una estimación analítica del amortiguamiento en cables suspendidos y sistemas de cables, a través de un análisis por elementos finitos. Encontraron que la amplitud de la deformación dinámica definida sobre la base de la deformación no lineal, tiene una buena correlación con el amortiguamiento modal.
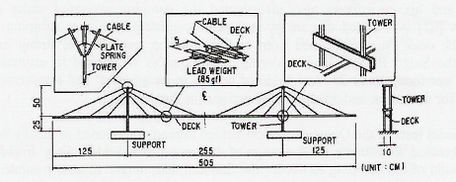
Por otro lado, Kawashima et al (1988, 1990, 1993) y Kawashima y Unjoh (1989, 1991, 1992), han hecho varias investigaciones sobre la determinación del amortiguamiento en puentes atirantados. Se realizaron modelos a escala en los cuales la razón de amortiguamiento fue obtenida del decaimiento medio en 13 ciclos. La Fig. 3-5 muestra al puente Meiko – Nishi (Japón) al que se le aplicaron las pruebas en el modelo a escala.
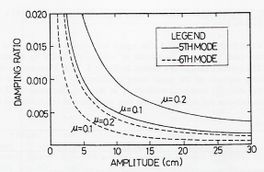
En las pruebas anteriores, se encontró que la razón de amortiguamiento crítica era dependiente con la amplitud de la excitación y la forma modal (Fig. 3-6), así como el tipo de cable. Las razones de amortiguamiento para la configuración del puente en abanico presentaron amortiguamientos entre un 1.2 y un 1.5%, siendo los mayores para las máximas amplitudes de oscilación. Valores más altos para la configuración en arpa pueden ser atribuidos a grandes deformaciones flexurales del tablero en la dirección vertical.
Es indudable que la razón de amortiguamiento varía con el tipo estructural, por lo que Kawashima sugiere una aproximación en la que la capacidad de disipación de energía sea evaluada para cada segmento estructural en el que es dividido el puente, y a partir de ahí se determine el amortiguamiento. En estas subestructuras la disipación de energía se considera constante: tablero, torres, cables y elementos de soporte. La no linealidad de los materiales es considerada como mecanismo prevaleciente para disipación de energía. Kawashima reduce el problema aplicando funciones de disipación de energía para las subestructuras, que pueden determinarse experimentalmente o de los trabajos antes citados.
Kawashima y sus colaboradores han investigado el tema del amortiguamiento en puentes de tirantes para la condición sísmica, encontrándose que éstos son marcadamente mayores que los resultados de pruebas dinámicas. Los registros de movimiento fuerte para el puente Suigo (Japón), aplicando tres sismos, fueron empleados para estimar el amortiguamiento. Se determinaron valores para la torre del 2% en la dirección longitudinal, 0 - 1% en la dirección transversal; y para el tablero un 5%. Similares pruebas para este puente fueron hechas por Atkins y Wilson (2000), encontrándose valores para el amortiguamiento que variaron entre un 0.5% y un 2%.
Pruebas dinámicas de dos modelos de puentes de 3.22 m de largo fueron hechas por Garevski y Savern (1992, 1993). Estas confirmaron el hecho que la razón de amortiguamiento depende fuertemente del modo considerado. Esto se debe a las diferentes formas modales y a la contribución no uniforme de sus miembros. La tabla 3-1 muestra lo anterior.
| MODELO A | MODELO B | ||||||||
| Mesa vibratoria | Vibradores portátiles | Mesa vibratoria | Vibradores portátiles | ||||||
| Modo | Tipo | Frecuencia (Hz) | Amortig. (%) | Frecuencia (Hz) | Amortig. (%) | Frecuencia (Hz) | Amortig. (%) | Frecuencia (Hz) | Amortig. (%) |
| 1 | Lateral | 4.28 | 0.45 | 4.24 | 0.42 | 4.16 | 0.43 | 4.17 | 0.34 |
| 2 | Vertical | 6.19 | 0.38 | 6.19 | 0.37 | 5.86 | 0.33 | 5.81 | 0.56 |
| 3 | Vertical | 8.93 | 0.42 | 9.03 | 0.38 | 8.83 | 0.72 | 8.66 | 0.83 |
| 4 | Lateral | 11.88 | 0.29 | 11.88 | 0.26 | 11.39 | 2.01 | 11.58 | 1 |
| 5 | vertical | 13.65 | 0.44 | 13.65 | 0.42 | 13.75 | 0.56 | 13.81 | 1.23 |
Estudios similares, donde se muestra la influencia modal y la alta dependencia con el acoplamiento modal, para estudios de vibración de puentes en Japón, se pueden revisar en el trabajo de Yamaguchi y Manabu (1997).
Se han propuesto otros métodos para determinar el amortiguamiento modal, basado en pruebas de vibración forzada, como el planteado por Nakamura et al (2000).
Se han establecido algunas relaciones empíricas entre el amortiguamiento modal y la frecuencia natural (Takeda et al, 2000). Las pruebas obtenidas de excitaciones forzadas, muestran como las razones de amortiguamiento crítico dependen del número de modos y sus direcciones, así como de las formas modales. Así, podemos relacionar los amortiguamientos con la longitud de la luz principal del puente L. Las razones de amortiguamiento crítico desminuyen conforme aumenta el largo principal (Kawashima et al, 1988; Kawashima y Unjoh, 1991).
Podemos escribir:
ξBV = 0.237L-0.645
ξBH = 1.751L-0.990
ξT = 0.190L-0.638
donde ξBV, ξBH y ξT son las razones de amortiguamiento crítico para oscilaciones flexurales verticales, flexurales transversales y torsionales respectivamente.
Del mismo modo, podemos relacionarlo con las frecuencias naturales de vibración definidas en 3.1.1:
ξBV = 0.0053 + 0.0060f1BV
ξBH = 0.0153 + 0.0037f1BH
ξT = -0.0016 + 0.0057f1T
3.2. Modelación y Análisis Dinámico
3.2.1. Modelación estructural
Muchos de los grandes puentes atirantados modernos se encuentran en zonas de alta sismicidad, sin embargo muy pocos de ellos han experimentado movimientos sísmicos severos que hayan podido registrarse. Por lo anterior, surge la necesidad de contar con adecuadas técnicas de modelación y análisis. En la actualidad existen tres formas de estudiar la respuesta dinámica de estas estructuras: usando pruebas de carga dinámica en puentes reales, usando modelos a escala y a través de modelos computacionales (Morgenthal, 1999).
Recientemente, modelos estructurales analíticos y métodos numéricos han sido desarrollados con el fin de realizar análisis dinámicos. La utilidad de tales soluciones analíticas queda limitada por lo realista que sea la representación del modelo matemático empleado (Maldonado et al, 1998).
La problemática de determinar modelos lineales de estructuras con base en datos de sismos reales, puede ser analizada usando “Sistemas de Identificación”. Evidentemente, la exactitud estará en el determinar los estimativos óptimos de los parámetros del modelo mediante la minimización de los resultados entre las respuestas reales de la estructura y el modelo. En el caso de puentes de gran luz, Tan y Liu (1996) plantean un algoritmo práctico basado en sistemas de identificación con la finalidad de determinar sistemáticamente la mejor estimación de los parámetros dinámicos en un puente de gran luz. El método ha sido realizado con un esquema de trabajo bajo la producción de un error aproximado en el cual los valores paramétricos son calculados mediante la minimización del ajuste entre la respuesta de la estructura filtrada y la respuesta del modelo (Maldonado et al, 1998).
En la actualidad, la modelación estructural de puentes de tirantes se realiza casi exclusivamente en forma tridimensional. Con el advenimiento y desarrollo vertiginoso de los ordenadores, han aparecido programas y herramientas numéricas cada vez más completas para el análisis de puentes, desplazando definitivamente a los modelos planos, que aunque muy prácticos, a veces pueden incurrir en errores severos cuando el puente es complejo en su geometría o materialidad, dado que se desprecian ciertos efectos que bajo determinadas circunstancias pueden ser importantes. La modelación espacial en cambio, considera a la estructura como un todo, no dependiendo la modelación de la dirección considerada. Para puentes con curvatura o geometría compleja, la modelación tridimensional es más que necesaria, ya que la respuesta no dependerá solamente del acoplamiento entre la respuesta longitudinal y transversal, sino que será el resultado de un acoplamiento del comportamiento del puente en todas las direcciones (Maldonado et al, 1998).
La modelación a través de elementos finitos resulta una herramienta muy poderosa, aunque a veces no muy práctica, sobre todo si se desean realizar estudios paramétricos y donde no importa determinar tensiones y deformaciones punto a punto. El empleo del método de elementos finitos necesariamente implica un conocimiento teórico del método para un adecuado modelado estructural, y por su naturaleza, requiere un tiempo computacional mayor. Esto toma especial importancia cuando se modelan puentes de gran luz, en donde la gran cantidad de elementos hace que el procesado numérico sea más extenso. Herramientas computacionales como SAP2000 (2005), ANSYS (2005) o ABAQUS (2005) permiten enfrentar exitosamente el análisis de un puente de gran luz por medio de elementos finitos. Todos ellos, en mayor o menor grado, incluyen la posibilidad de realizar análisis no lineal y modelado de elementos especiales only tension, que permiten simular adecuadamente los cables e incluir el pretensado de éstos. Estos paquetes computacionales han tenido un desarrollo muy amplio en los últimos años, que permiten sacar el máximo provecho a las nuevas tecnologías informáticas, con interfaces gráficas cada vez mejores, y con la posibilidad de introducir modelos propios de comportamiento de materiales para análisis no lineal y modelado de sistemas sencillos de disipación de energía.
|
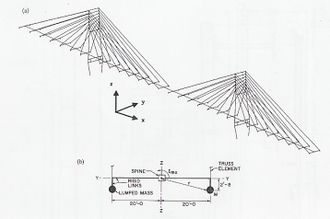
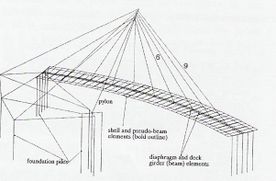
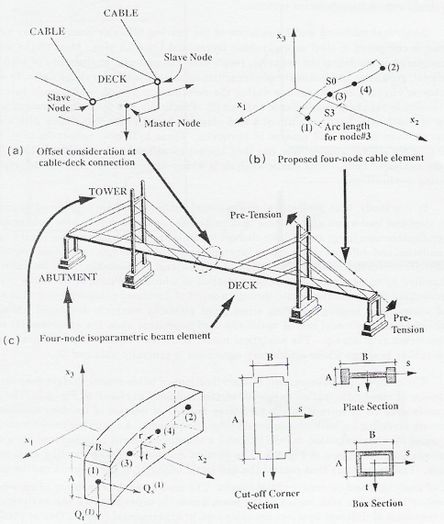
Fig. 3-7 Modelo de elemento finito empleado: (a) Diagrama de los elementos; (b) Detalle de la modelación de la sección transversal del tablero (Wilson y Gravelle, 1991) |
Wilson y Gravelle (1991) proveen una detallada descripción del desarrollo de una clase de elemento finito lineal para el análisis dinámico de puentes atirantados. A continuación, en Figs. 3-7, 3-8, 3-9, 3-10 y 3-11 se muestran los modelos empleados.
| |
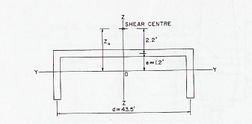
|
Fig. 3-8 Sección C para determinación de la torsión en el tablero (Wilson y Gravelle, 1991) |
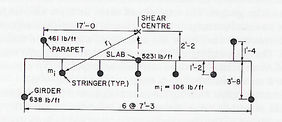
Fig. 3-9 Distribución de masas para modelación de la sección transversal del tablero (Wilson y Gravelle, 1991) | |
|
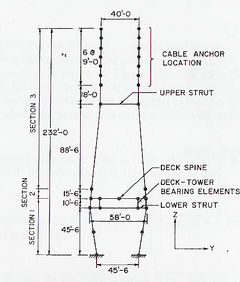
Fig. 3-10 Modelación de las torres (Wilson y Gravelle, 1991) |
Fig. 3-11 Modelación de apoyos en conexión tablero-torre (Wilson y Gravelle, 1991)
|
Caicedo et al (2000), presentan un estudio comparativo de modelación por elementos finitos para el análisis dinámico de puentes de tirantes, basado en el puente Cape Girardeau, Missouri, USA. Este presenta un tablero mixto compuesto de dos vigas maestras de acero a lo largo del puente, en los costados del tablero, el cual es una losa de hormigón armado. Un modelo del tablero asume una sección rectangular, y el segundo modelo incluye masas concentradas adicionales para tener en cuenta los efectos torsionales. Los resultados muestran que el segundo modelo refleja en forma más real el comportamiento del tablero frente a torsiones, lo cual es especialmente importante en cuestiones aerodinámicas.
|
Fig. 3-12 Modelación de la sección transversal del puente Cape Girardeau (Caicedo et al, 2000) |
La Fig. 3-12 muestra la modelación estructural de la sección transversal del puente.
Por otra parte, Zhu et al (2000), han propuesto un modelo de tres vigas maestras longitudinales para representar estructuralmente al tablero frente a efectos torsionales.
|
Fig. 3-13 Diagrama esquemático del modelo: (a) Tablero; (b) Modelo (Zhu et al, 2000) |
El modelo consiste en conectar las dos vigas laterales, dispuestas simétricamente, con una viga central a través de conexiones rígidas transversales. El modelo fue probado para los datos experimentales medidos en el puente Nampu (China), encontrándose que las propiedades modales del puente son razonablemente más precisas frente a los modelos tradicionales con una o dos vigas longitudinales. En la Fig. 3-13 se muestra la modelación usada.
3.2.2. Análisis dinámico
Existen diferentes metodologías de análisis dinámico, dependiendo de la complejidad de la estructura y del grado de exactitud de la respuesta esperada. El análisis mediante fuerzas estáticas equivalentes, como el planteado por Walter (1999), no es recomendable para puentes de gran luz, y casi se ha dejado de usar con el advenimiento de los nuevos programas comerciales de análisis y diseño estructural, en donde casi todos, permiten realizar análisis sísmico-dinámico tridimensional de estructuras. En todo caso, el método estático equivalente entrega una buena aproximación al problema, y por su simplicidad de aplicación y uso, ha sido ampliamente utilizado. Además, es un procedimiento que se encuentra presente en casi todos los códigos de diseño.
Por otra parte, los métodos dinámicos agrupan al método de análisis modal espectral, el método de análisis paso a paso y los métodos de análisis no lineal.
- El análisis modal espectral se fundamenta en el uso de espectros de respuesta, y permite determinar las respuestas máximas en las masas concentradas del modelo dinámico para estructuras complejas en el rango elástico lineal, es decir, para sismos de intensidad media. Su uso está muy generalizado, aunque presenta ciertas dificultades. Además en la determinación de la respuesta máxima es necesario combinar las respuestas modales de acuerdo a reglas de combinación modal, tales como la regla de la raíz cuadrática de la suma de los cuadrados máximos (SRSS) o la combinación cuadrática completa (CQC).
- El análisis paso a paso entrega la respuesta en el tiempo de la estructura para cada modo. Para ello es necesario el empleo de registros sísmicos de aceleraciones, reales o sintéticos, en donde la respuesta es determinada a partir de conocer las formas modales, las frecuencias de vibración y los correspondientes coeficientes de amortiguamiento crítico. La solución numérica de este problema es la clásica de la dinámica estructural, ya sea a partir de la Integral de Duhamel o por integración directa de la ecuación de movimiento.
Wethyavivorn y Fleming (1987), presentaron un estudio comparativo entre el uso de espectros de respuesta y el análisis paso a paso para puentes de tirantes, con énfasis en los métodos de combinación modal. Así mismo, Abdel-Ghaffar (1991), en su estado del arte sobre la respuesta sísmica de puentes de tirantes, presenta una descripción detallada de los métodos de análisis sísmico empleados hasta 1991. Otro estudio comparativo es presentado por Simoes y Negrão (1996). En éste, una optimización integrada por elementos finitos es presentada, mostrando que el método de análisis paso a paso resulta más adecuado para estudios de comportamiento no lineal (de material o geométrico), como se presenta frecuentemente en puentes de gran luz.
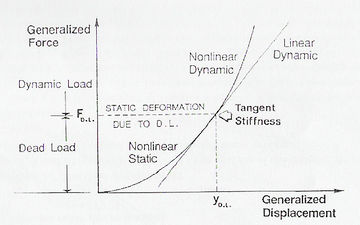
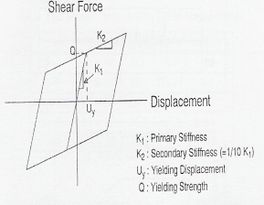
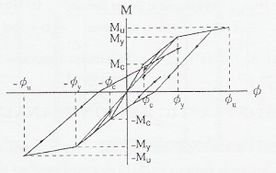
- El análisis no lineal resulta ser la herramienta de análisis más adecuada para estructuras muy largas o que puedan ser excitadas por movimientos sísmicos intensos. En efecto, ante la ocurrencia de un sismo severo, es esperable que la estructura incurra en régimen no lineal, disipando así parte de la energía suministrada. Los métodos anteriores no reflejan adecuadamente este problema, por lo que muchas veces la respuesta no se aproxima bien a la realidad (Maldonado et al, 1998). Por otra parte, la presencia de apoyos, juntas de dilatación y dispositivos adicionales de disipación de energía introducen efectos no lineales importantes, por lo que su consideración en el análisis de puentes de gran luz es un requisito. La no linealidad en puentes de tirantes es principalmente de tipo geométrico, debido a las grandes deformaciones que experimentan. Los análisis no lineales en puentes de tirantes pueden resolverse a través de las metodologías paso a paso, usando procedimientos de integración en el cual se considere la rigidez tangente, como se muestra en la Fig. 3-14 (Abdel-Ghaffar, 1991).
Conviene señalar finalmente, que el análisis sísmico de puentes de tirantes mediante el uso de espectros de respuesta es más que cuestionable, aunque los primeros trabajos de los investigadores lo recomendaban. En primer lugar, la superposición modal sólo es posible para estructuras con comportamiento lineal, lo cual no es usual en puentes atirantados de gran luz. En segundo lugar, los procedimientos de superposición modal deben ser adecuadamente razonables y empleados con cuidado, ya que métodos de combinación, como la regla SRSS, son válidos sólo si no existe acoplamiento modal (Morgenthal, 1999).
3.3. Respuesta Sísmica de Puentes de Gran Luz
3.3.1. Comportamiento sísmico no lineal
Los puentes atirantados tienen por su naturaleza un comportamiento no lineal. El análisis no lineal estático bajo cargas muertas es esencial como punto de partida para el análisis sísmico no lineal, tomando como base el estado deformado para carga muerta en el puente a analizar (Abdel Ghaffar, 1991). Para puentes de luces principales mayores a 600 m, los análisis no lineales geométricos y de material son muy necesarios cuando las estructuras son sometidas a movimientos fuertes.
Las no linealidades de material dependen de la estructura específica, en tanto que las no linealidades geométricas están presentes en todo puente atirantado, y se originan fundamentalmente en el combamiento de los cables, la acción compresiva en el tablero y torres, y el efecto de las grandes deflexiones debido a la flexibilidad de este tipo de estructuras (Morgenthal, 1999). En este sentido, el trabajo desarrollado por Ren (1999) entrega un buen análisis de los efectos e importancias de ambas formas de no linealidad en puentes atirantados.
En la actualidad existen muchos programas de elementos finitos que toman en cuenta las no linealidades en este tipo de estructuras. Así, es posible considerar el comportamiento no lineal de los cables usando la fórmula de Ernst o aplicando formulaciones de elementos multicable. El comportamiento no lineal de las torres y vigas principales debido a la flexocompresión, también puede ser considerada teniendo en cuenta la rigidez axial y flexional. El cambio completo en la geometría del puente como tercera fuente de no linealidad geométrica puede ser considerada a través de un proceso incremental, en el cual se recalcula la rigidez de la estructura a partir de las coordenadas nodales previas (Morgenthal, 1999).
La no linealidad de los materiales, fundamental en un análisis push-over, hoy en día puede ser considerada a partir del conocimiento de las leyes constitutivas de los materiales y a partir del conocimiento de los comportamientos histeréticos de las zonas de disipación de energía, para lo cual continuamente se proponen nuevos modelos de comportamiento en base a pruebas de carga en laboratorio. Muchos programas actuales de elementos finitos incluyen la posibilidad de considerar tales análisis.
Abdel – Ghaffar y Nazmy (1990, 1991) realizaron diferentes análisis considerando no linealidades geométricas y comparando la respuesta para el caso de excitación uniforme y asíncrona. Estos trabajos serán discutidos cuando se analice el tema de la variabilidad espacial. Otros estudios parecidos a los anteriores han sido realizados por Fan et al (1992).
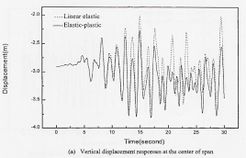
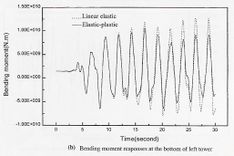
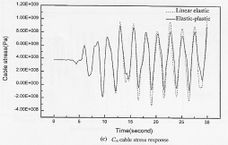
Ren y Obata (1999) han investigado el comportamiento sísmico elasto-plástico de puentes atirantados de gran luz a través de modelos de elementos finitos. Han considerado las no linealidades geométricas en términos del combamiento de los cables, interacción flexión-compresión y grandes desplazamientos. Las no linealidades del material las han considerado cuando fluye el acero de las vigas principales. Para lo anterior han tomado un puente existente de 605 m de claro principal, y lo han sometido a tres registros sísmicos severos. La evaluación de la respuesta residual elasto-plástica la han considerado definiendo un nuevo tipo de índice de daño sísmico llamado Razón de Deformación Plástica Máxima Equivalente. Los resultados muestran que el efecto elasto-plástico tiende a reducir la respuesta sísmica de puentes de gran luz. La respuesta sísmica elástica y elasto-plástica depende fuertemente de las características del sismo de entrada. Además, se muestra que la no linealidad geométrica tiene poca influencia en la respuesta sísmica para eventos extremos. La Fig. 3-15 muestra una comparación de la respuesta bajo el sismo de Higashi – Kobe.
Otros trabajos más recientes, como el de Aso et al (2000), analiza el problema del comportamiento no lineal de puentes atirantados considerando la acción fluctuante de la fuerza axial, dejando en claro la importancia que tiene considerar tal efecto en los análisis.
3.3.2. Efecto de la vibración de los cables en la respuesta
La importancia de la vibración de los cables en la respuesta sísmica de puentes atirantados de gran luz se encuentra bien documentada en la literatura mundial. En los trabajos de Abdel – Ghaffar (1991) y Abdel-Ghaffar y Khalifa (1991) se concluye la conveniencia de una adecuada modelación de la vibración de los cables. Ellos sugieren el uso de una formulación a través de multi-elementos de cable. Solo si la distribución de la masa a lo largo del cable es modelada y asociada con grados de libertad adicionales, la respuesta de los cables puede ser adecuadamente obtenida. En estos estudios se demuestra el fuerte acoplamiento que existe entre los cables, el tablero y las torres. La discretización en pequeños elementos de cable da como resultado la aparición de nuevos y numerosos modos de vibración, muy complejos, así como nuevos modos tablero – torre. Sería imposible predecir tales movimientos usando los procedimientos usuales con las expresiones existentes para determinar frecuencias naturales de cables aislados inclinados. El elemento de cable múltiple provee los movimientos acoplados cable – tablero, incluyendo la flexión lateral y torsional del tablero. Tales movimientos no pueden ser predichos con la modelación de un solo cable. Lo más importante es que además estos nuevos modos tienen factores de participación altos, lo que hace que sean importantes en la respuesta sísmica.
Un estudio similar, hecho por Tuladhar et al (1995) muestra básicamente los mismos resultados, en base a estudios paramétricos para tres ejemplos de puentes, e incluye el efecto del módulo de elasticidad de los cables y la respuesta, para diferentes sismos de entrada. En forma similar, tal vez con algo más de precisión, Cheng y Lau (2002) proponen un nuevo modelo de elemento de cable de 3 nodos, para permitir la modelación de los movimientos transversales de los cables. Este procedimiento permite además incluir el efecto no lineal de los cables causado por su peso propio. Otro estudio, similar a los anteriores, desarrollado por Macdonald y Georgakis (2002), hace un estudio de la interacción cable – tablero considerando la respuesta de un modelo cable – tablero simplificado, para análisis de historias temporales no lineales.
Sin embargo, Caetano et al (1996, 2000) realizan un completo trabajo teórico – experimental para cuantificar los movimientos acoplados cable – tablero en puentes atirantados. Ellos presentan un modelo físico para el estudio dinámico de la interacción entre los cables y el sistema tablero/torres, mostrando un claro acoplamiento en tal sistema. Para lo anterior, realizan un modelo físico a escala del puente Jindo, Corea del Sur; cuyas características de masa y rigidez son convenientemente escaladas, tal como se aprecia en las Figs. 3-16 y 3-17.
|
Fig. 3-16 Características generales puente Jindo (Caetano et al, 2000) |
Fig. 3-17 Modelo físico del puente Jindo (Caetano et al, 2000) |
Se realizaron pruebas estándar de análisis modal usando un vibrador electrodinámico y una mesa vibradora. Los estudios modales mostraron la existencia de una clara interacción dinámica entre los cables y el sistema tablero/torres, asociado con la aparición de varios grupos de formas modales, muy cercanas frecuencialmente, como se puede apreciar en la tabla 3-2.
| Modo | Frec. natural sistema multicable (Hz) | Frecuencia asociada sistema un elemento cable (Hz) | Razón de factor de particip. modal | Tipo de modo |
| 1 | 4.26 | 4.28 | <1 | 1º transv., simétrico |
| 2 | 6.14 | 6.21 | >1 | 1º vert., simétrico |
| 3 | 6.94 | 6.21 | >1 | 1º vert., simétrico |
| 4 | 6.94 | 6.21 | >1 | 1º vert., simétrico |
| 5 | 7.15 | 11.71 | <1 | 1º transv., asimétrico |
| 6 | 7.16 | 4.28 | <1 | 1º transv., simétrico |
| 7 | 7.93 | 9.12 | >1 | 1º vert., asimétrico |
| 8 | 7.93 | 9.12 | >1 | 1º vert., asimétrico |
| 9 | 8.11 | 11.71 | <1 | 1º transv., asimétrico |
| 10 | 8.11 | 11.71 | <1 | 1º transv., asimtétrico |
| 11 | 8.42 | 9.12 | >1 | 1º vert., asimétrico |
| 12 | 8.42 | 9.12 | >1 | 1º vert., asimétrico |
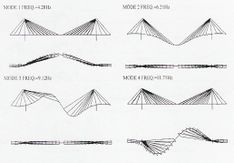
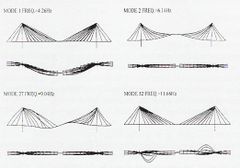
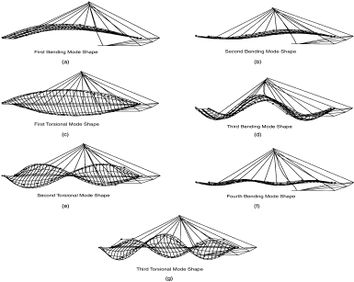
Algunas de las frecuencias y formas modales calculadas, para el modelo con un solo elemento cable y el modelo multi-cable, se pueden apreciar en las Figs. 3-18 y 3-19.
|
Fig. 3-18 Frec. y formas modales para sistema con un solo elemento cable (Caetano et al, 2000) |
Fig. 3-19 Frecuencias y formas modales para sistema multi-cable (Caetano et al, 2000) |
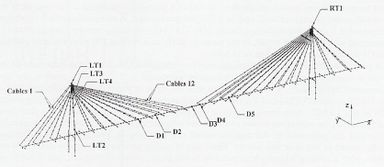
En una segunda etapa de la investigación, se calculó y correlacionó con los datos medidos, la respuesta del sistema frente a acelerogramas artificiales. En esta nueva fase, se encontró que la interferencia de los cables con respecto a las oscilaciones globales podrían causar una disminución en la respuesta del puente. Sin embargo, el sistema de amortiguamiento podría no ser desarrollado en el caso de tener un estrecho ancho de banda en la excitación, causando grandes amplitudes de vibración en algunos cables, con una no linealidad significativa e introduciendo modos de vibración superiores. La Fig. 3-20 muestra la discretización realizada al modelo numérico multi-cable.
|
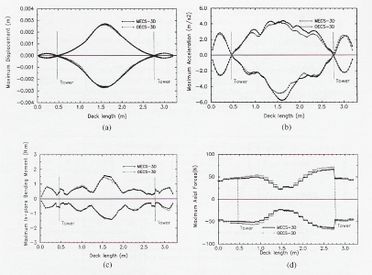
Fig.3-21 Valores pico para la respuesta calculada en vigas principales (Caetano et al, 2000) |
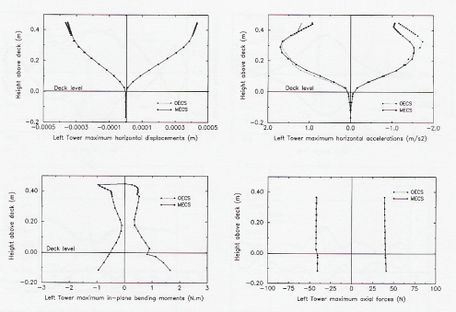
Las Figs. 3-21 y 3-22 muestran la respuesta (valores pico) para las vigas principales y una de las torres del puente, considerando el modelo OECS (elemento de cable singular) y modelo MECS (elemento de cable múltiple).
La comparación de la respuesta pico, para los modelos MECS y OECS, muestran diferencias para el tablero de un 10% en desplazamiento, 16% en aceleración, 15% en momento de flexión y 14% en el esfuerzo axial. Para las torres, estas diferencias llegan a ser del 3% para desplazamientos, 13% en aceleración, 1.5% en momento flector y 4% en esfuerzo axial. A la luz de lo antes expuesto, y en base a los estudios realizados, se tiene que para niveles pequeños de vibración, los cables podrían actuar favorablemente reduciendo la respuesta global. Este efecto amortiguador es más importante si las frecuencias naturales de los modos fundamentales de vibración se encuentran en el rango de las primeras frecuencias naturales de los cables. En cambio, para vibraciones elevadas que contengan la primera frecuencia fundamental de los cables, el sistema experimenta significantes no linealidades. Estas vibraciones asociadas con modos superiores de los cables, pueden inducir contribuciones de los modos superiores de la estructura, lo cual es evidentemente desfavorable.
El efecto de los cables en la respuesta global, hace que la mitigación de las vibraciones en estos sea estudiada desde un punto de vista sísmico. Si bien es cierto que la mitigación de la vibración de los cables con la incorporación de dispositivos adiciones de disipación de energía se asocia más bien al fenómeno aerodinámico del Rain-Wind Vibration, la incorporación de tales dispositivos también puede ejercer un efecto favorable frente a acciones sísmicas, sobre todo en puentes de gran luz. Los cables en general tienen muy poco amortiguamiento, por lo que aumentar adicionalmente este parámetro, tiene un efecto positivo desde el punto de de vista sísmico. En este sentido, el trabajo presentado por Forars et al (2000) apunta en esta dirección, mostrando que la modelación apropiada de los cables puede aumentar o reducir la respuesta global de un puente atirantado, dependiendo de la frecuencia de excitación. Así mismo, la incorporación de amortiguamiento adicional en los cables pueden atenuar la respuesta global bajo ciertas circunstancias, en las que la consideración de la flexibilidad de los soportes en el análisis puede tener un significativo efecto en los resultados.
3.3.3. Influencia de las condiciones de apoyo
La respuesta de un puente atirantado a las cargas aplicadas depende fuertemente de la forma en la que el tablero se conecta a las torres y estribos. Si el tablero está suspendido libremente por las torres, las fuerzas sísmicas inducidas serán mínimas, pero mantendrán al puente en una condición de excesiva flexibilidad bajo condiciones de servicio. Por otro lado, una conexión rígida entre el tablero y las torres reducirá los desplazamientos en condiciones de servicio pero incrementará en forma notable los esfuerzos en caso de sismo (Abdel – Ghaffar, 1991).
La influencia de diferentes condiciones de apoyo en puentes de tirantes, referido a la distribución modal, ha sido investigada por Abdel – Ghaffar (1991). La Fig. 3-23 muestra que los apoyos móviles convierten a la estructura en una más flexible, transformando la estructura en una de período más largo. Lo anterior puede ser beneficioso desde el punto de vista sísmico, ya que el aumento de período hace disminuir las amplificaciones espectrales.
A modo de ejemplo, Ganev et al (1998), mencionan que el puente Higashi – Kobe fue deliberadamente diseñado con tablero móvil longitudinal a modo de aumentar su período fundamental y así disminuir los valores máximos espectrales. Sin embargo, la decisión sobre las condiciones de apoyo del tablero, está gobernada por una condición de serviciabilidad, así como por consideraciones sísmicas (Morgenthal, 1999). Lo anterior obliga a adoptar una solución intermedia que puede lograrse con apoyos especiales y/o dispositivos especiales de absorción de energía localizados en los puntos de apoyo para así disipar la energía sísmica, manteniendo la serviciabilidad.
Estudios muy similares a los anteriores, fueron hechos por Tuladhar y Dilger (1999). En ellos, se estudiaron dos puentes de tirantes con diferentes condiciones de apoyo. El primer puente tenía torres de hormigón y tablero metálico, en tanto que el segundo tenía torres de hormigón y tablero compuesto, con claros de 371 y 465 m respectivamente. Los estudios mostraron que la colocación de apoyos elásticos para el tablero a las torres generan muy bajos desplazamientos y momentos de flexión del tablero, en comparación con apoyos en base a rodillos o fijos. El apoyo de rodillo genera bajo esfuerzo de corte y momento en la base de las torres, pero no necesariamente una baja respuesta del sistema como un todo. Este tipo de apoyo provoca muy bajas frecuencias naturales en la dirección longitudinal, confirmando la mayor flexibilidad en esa dirección. Así mismo, se estudió el efecto de la variación de la rigidez longitudinal de los apoyos elásticos del tablero, mostrando que influyen notablemente en los primeros modos longitudinales, pero no así en los modos simétricos ni en los superiores. Por otro lado, se estudio el modo en que los efectos de propagación de las ondas sísmicas afectan la respuesta, para diferentes condiciones de soporte, observándose que la respuesta sísmica muestra una gran variabilidad con los cambios de velocidad de propagación cuando el puente está fijo a los apoyos, no siendo tan pronunciada esa diferencia cuando el puente tiene apoyos tipo rodillo o apoyos elásticos.
3.3.4. Respuesta sísmica de las torres
La función de las torres es soportar el sistema de cables y transferir sus esfuerzos a las fundaciones. Ellas están sometidas a grandes compresiones, y a momentos de flexión que dependerán del layout de los cables y condiciones de soporte tablero – torre. Las torres pueden ser metálicas o de hormigón, siendo estas últimas generalmente más económicas para condiciones similares de rigidez. Sin embargo, su peso es generalmente mayor que las de acero, por lo que en su elección habrá que tener en cuenta las condiciones locales del suelo y la rapidez de construcción (Morgenthal, 1999). Resulta indudable entonces que la respuesta sísmica de las torres estará condicionada por varios aspectos, que a los anteriores, debemos agregar la forma geométrica de la torre, la que dependerá de las cargas aplicadas, el esquema de atirantamiento empleado y condiciones estéticas. Se debe enfatizar en el hecho que el diseño en hormigón es indudablemente más pesado, lo que induce mayores esfuerzos sísmicos que en el caso de torres de acero.
Estudios como el de Hodhod y Wilson (1995) presentan resultados generales en cuanto a la respuesta sísmica de las torres, centrándose en el efecto de las características frecuenciales del movimiento del suelo en la respuesta, para un puente atirantado de ejemplo. Del estudio, se concluye que la respuesta sísmica de las torres depende del contenido frecuencial del movimiento del suelo, siendo una buena medida de ésta, la razón PGA / PGV1. Las deflexiones resultan ser dependientes de la frecuencia en este caso, en tanto que los esfuerzos de corte en la base y los momentos flectores son menos sensibles.
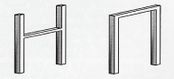
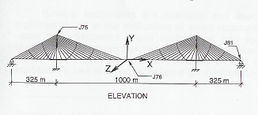
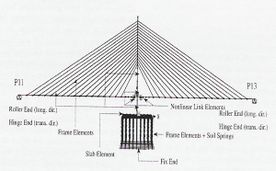
Hayashikawa et al (2000) han estudiado el comportamiento sísmico no lineal de torres de acero de puentes de tirantes sometidos a sismos tridimensionales intensos. Se han considerado las no linealidades debidas a cambios geométricos y por fuentes materiales, empleándose el procedimiento iterativo de la rigidez tangente para obtener la respuesta sísmica no lineal. Se realizaron ejemplos numéricos para tres formas diferentes de torres: tipo A, tipo H y tipo pórtico. La Fig. 3-24 muestra la vista general del modelo elegido y las tipologías de torres empleadas.
Los períodos naturales, desplazamientos máximos en la cúspide de las torres en dirección longitudinal, y las curvaturas máximas tienden a disminuir conforme aumenta la rigidez longitudinal proveída por los cables, tal como se aprecia en la Fig. 3-25.
|
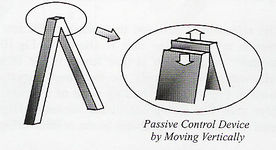
Fig. 3-26 Torre con sistema pasivo (Hayashikawa et al, 2000) |
Posteriormente se estudió el efecto de incorporar control pasivo en los puentes, en base a movimiento vertical con fricción (Fig. 3-26). Los períodos naturales evidentemente aumentaron, sobre todo en las tipologías H y aporticada. Definiendo por L1 la dirección longitudinal y H1 la dirección transversal, en la tabla 3-3 se aprecia la comparación de los períodos naturales para los sistemas con y sin disipación.
| Sistema sin disipación | Sistema con disipación | ||||||
| Modo | Tipo A | Tipo H | Pórtico | Tipo A | Tipo H | Pórtico | |
| L1 | 0.3229 | 0.3228 | 0.3719 | 0.3196 | 0.3806 | 0.4820 | |
| H1 | 1.0355 | 1.2535 | 1.7832 | 2.6191 | 2.5192 | 2.9818 | |
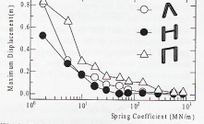
Los resultados de las investigaciones con incorporación de aislamiento pasivo friccionante, mostraron la efectividad en la reducción de las fuerzas de reacción en las bases de las torres. La adopción de control pasivo en las torres va acompañada de una significativa reducción de las fuerzas inducidas, si se compara con el caso no aislado.
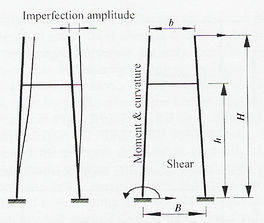
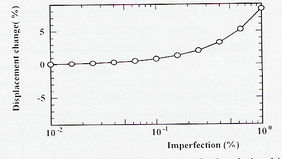
Estudios similares, sin aislamiento sísmico, en base a investigaciones paramétricas sobre el comportamiento dinámico de torres de acero tipo H en puentes de tirantes, realizados por el mismo investigador, han mostrado la influencia individual de diferentes aspectos del diseño, tales como el mecanismo de amortiguamiento, movimiento sísmico de entrada, formas modales e incidencia de las imperfecciones iniciales. Los resultados mostraron que la altura, longitud y baja disipación de energía por fluencia en la viga puntal horizontal de la torre afecta significativamente el comportamiento estructural. Las imperfecciones iniciales dentro del rango de diseño tienen un efecto perjudicial en la respuesta sísmica de las torres, que crecen rápidamente más allá del rango de diseño, como se muestra en la Fig. 3-27.
Aunque la construcción de torres de acero en puentes atirantados no se utiliza en forma masiva en la actualidad, la elección de ésta materialidad estará en función de aspectos no sólo estructurales, sino también estéticos. Estudios detallados efectuados durante la fase constructiva han mostrado que las torres de acero son económicamente más costosas que las de hormigón. A pesar de las buenas bondades del acero, si agregamos la variable manutención, entonces rápidamente nos daremos cuenta de porqué la construcción de torres de acero es más limitada. La solución metálica parece ser la respuesta sólo en estructuras con suspensión central, cuando el mínimo ancho del tablero requerido es el factor que gobierna la economía del puente (Walter, 1999).
Finalmente se puede decir que se observa una falta de estudios en esta materia. Hasta la fecha existen pocos trabajos referentes al análisis de la respuesta sísmica de las torres en puentes de tirantes. La respuesta sísmica de las torres dependerá entre otras cosas de la geometría de estas (que como se ha visto resulta ser muy variable, dependiendo de la tipología de puente usada) y su materialidad. Estudios paramétricos en este sentido serían muy interesantes y bien aceptados por la comunidad científica, así como estudios comparativos más profundos entre las tipologías en acero y hormigón.
3.3.5. Influencia de las condiciones del suelo e interacción suelo – estructura
Es bien sabido que el suelo juega un rol central en la respuesta sísmica de estructuras en general, por lo que la consideración de la interacción suelo – estructura en puentes de tirantes reviste una gran importancia. La importancia del suelo en la respuesta dinámica se debe básicamente a tres efectos: la amplificación dinámica, la interacción cinemática y la interacción inercial (Morgenthal, 1999). Todos estos efectos dependerán de las condiciones particulares del suelo en la zona de emplazamiento de la estructura, los que en definitiva modifican la señal sísmica en su contenido frecuencial, amplitud y duración.
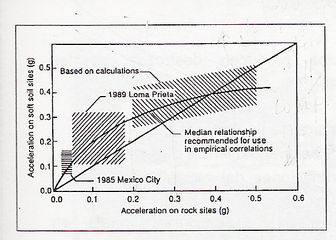
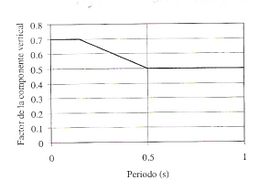
En la actualidad es admitida una amplificación de la aceleración (amplificación dinámica) en presencia de depósitos blandos o no consolidados, hasta niveles de aceleración en roca de 0,40g, invirtiéndose la relación para valores superiores, dando lugar a comportamientos no lineales del suelo (Figueras, 2004). La Fig. 3-28 grafica la situación.
Además del efecto local antes citado, pueden tener mayor o menor importancia, dependiendo de las condiciones particulares del suelo y la estructura, efectos como la amplificación topográfica y la posibilidad de licuación de suelos.
La interacción cinemática significa la influencia que el suelo podría ejercer en el movimiento de una fundación rígida embebida en el suelo circundante. Una condición necesaria para que este efecto sea importante, es que las dimensiones de las fundaciones sean del mismo orden de magnitud que las principales longitudes de ondas sísmicas del movimiento (Calvi y Pinto, 1996).
Finalmente, la interacción inercial describe el efecto que la inercia de la estructura en movimiento tiene sobre la deformación del suelo (Morgenthal, 1999).
Betti et al (1993), entregan pautas útiles para la modelación de sistemas de puentes soportados por cables considerando interacción suelo – estructura. Proponen separar cada parte del sistema (suelo, fundaciones, estructura) y analizar por separado cada una, con la ventaja de que la técnica numérica o analítica puede ser elegida de acuerdo a las conveniencias particulares. Evidentemente, las respuestas individuales combinadas deberán satisfacer las condiciones de equilibrio y continuidad. Además estudiaron la influencia de diferentes ondas sísmicas en la respuesta de puentes atirantados. Todos los análisis realizados fueron hechos usando una estructura fija y otra considerando la modelación de la interacción suelo – estructura. Encontraron que ondas incidentes con inclinación causan un movimiento de balanceo de las fundaciones, que como se verá más adelante, tiene un efecto positivo de aislamiento de vibraciones en la respuesta sísmica.
Otra forma de modelación, en los llamados métodos directos, consiste en modelar el suelo conjuntamente con la estructura, o sea, el suelo es incluido en el modelo analítico global. Aquí se pueden emplear diferentes formulaciones de elementos y propiedades para la estructura y el suelo, pero el problema se resuelve como uno. Esto impone gran importancia a las condiciones de contorno del problema (Wolf, 1985, 1988).
Zheng y Takeda (1995), estudiaron la aplicabilidad de usar modelos mecánicos en base a resortes (soil – spring) para las fundaciones. Compararon análisis bidimensionales de elementos finitos con modelos simplificados. Encontraron que los modelos simplificados son adecuados y reflejan bien la realidad para movimientos del suelo de bajas frecuencias, sin embargo, para altas frecuencias la precisión en los resultados empeora. La Fig. 3-29 muestra las funciones de transferencia para movimiento horizontal y vertical respectivamente. Estos resultados sugieren que el modelo masa – resorte es una buena aproximación para el análisis de estructuras de período largo, como los puentes de tirantes de gran luz. Sin embargo, la contribución de los modos superiores podría ser subestimada.
|
Fig. 3-30 Modelaciones pila – fundación considerando interacción suelo – estructura: arriba, modelo masa – resorte; abajo, modelo de elementos finitos (Elassaly, et al, 1995) |
Por otra parte, Elassaly et al (1995), presentaron resultados de la investigación de dos casos de puentes de tirantes, en referencia a los efectos de diferentes métodos de idealización para el sistema pila – fundación. Primeramente se emplearon resortes y amortiguadores en la modelación; y en segundo lugar, se realizó una discretización del suelo circundante con elementos de deformaciones planas, como las mostradas en la Fig. 3-30.
Calvi y Pinto (1996) entregaron recomendaciones para los códigos de diseño sobre la base de estudios numéricos y experimentales, en cuanto a la consideración de la interacción suelo – estructura en el análisis sísmico de puentes. En los análisis numéricos, consideraron un modelo mecánico de una pila con resortes que representan la rigidez del suelo; y una relación momento – curvatura en la rótula plástica según el modelo de Takeda (Fig. 3-31).
En los análisis, se consideró un amortiguamiento equivalente efectivo del sistema a través de la suma ponderada de los amortiguamientos de sus partes. Los resultados mostraron que mientras en la mayoría de los casos la interacción suelo – estructura produce un aumento en los desplazamientos máximos, este efecto no es muy significativo. Además, las demandas inelásticas en términos de curvatura no son especialmente afectadas por la interacción suelo – estructura, mostrando una tendencia a decrecer.
Ganev et al (1998), realizaron algunas investigaciones en el puente Higashi – Kobe (Japón), en el cual mostraron claras evidencias de licuefacción. Las aceleraciones en superficie eran menores que las encontradas a 34 m de profundidad, con períodos marcadamente mayores. Las medidas de campo tomadas en el puente fueron empleadas para validar las aproximaciones numéricas para el análisis de la interacción suelo – estructura. Uno de los aspectos más interesantes asociados con la interacción, era la degradación de la rigidez del suelo. Tres factores fueron considerados para tener en cuenta este efecto: dependencia no lineal tensión – deformación del suelo, separación del suelo de la estructura y aumento de la presión de poros.
En su Tesis de Master, Morgenthal (1999) plantea que al no considerarse los efectos de las condiciones locales del suelo y la interacción suelo – estructura, se produce una subestimación de los desplazamientos de la superestructura, sobre todo frente a suelos blandos. Sin embargo, tal subestimación se produce principalmente si el suelo tiene una frecuencia fundamental cercana a alguna de las de la estructura. En términos de aproximaciones simplificadas, plantea que las modelaciones de base fija sólo pueden justificarse para estructuras fundadas en roca, como suele ocurrir en puentes de gran luz.
3.3.6. Comportamiento sísmico frente a aceleraciones verticales. Sismos de campo cercano
El diseño de puentes para carga sísmica rara vez incluye los efectos de las aceleraciones verticales, debido en parte a una falta de conocimiento sobre su ocurrencia y en la amplitud del movimiento vertical del suelo. En este sentido, los datos actualmente disponibles sobre sismos de campo cercano indican que los movimientos sísmicos verticales pueden ser mayores que los horizontales, y ambos pueden en conjunto llegar a ser hasta 3 ó más veces mayor que los valores de diseño, lo que refuta la recomendación general de tomar como aceleración efectiva máxima vertical los 2/3 de la aceleración efectiva máxima horizontal, como plantea el Eurocódigo 8 (Foutch, 1997). De este modo, las medidas en la respuesta estructural muestran la posibilidad de amplificaciones significativas en la dirección vertical, atribuibles a la componente vertical de movimiento del suelo. El movimiento vertical genera esfuerzos axiales fluctuantes en las pilas, lo que podría causar inestabilidad en los lazos de histéresis e incrementar la demanda de ductilidad, generando de paso esfuerzos de gran magnitud en estribos y fundaciones, no cubiertos por los actuales códigos de diseño (Saadeghvaziri y Foutch, 1991). La Fig. 3-32 deja en claro lo antes explicado para el caso de un puente estándar simétrico con una única pila central.
|
Fig. 3-32 Historias temporales de esfuerzo axial en pila central para excitación horizontal y horizontal + vertical ( Saadeghvaziri y Foutch, 1991). |
El estudio de Saadeghvaziri y Foutch mostró que el esfuerzo axial fluctuante en las pilas genera mayores desplazamientos horizontales y fluctuaciones en la capacidad a cortante de las mismas. El estudio concluye que para sismos con aceleraciones efectivas máximas del suelo de 0.40g ó menos, el daño adicional causado por la componente vertical es mínimo; mientras que para movimientos sísmicos con aceleraciones efectivas máximas del suelo de 0.70g la adición de la componente vertical genera un notable mayor daño. De allí, la importancia de considerar la componente vertical en el análisis y diseño de puentes ubicados en zonas cercanas a la falla, que pudieran experimentar picos de aceleración vertical mayores a los horizontales.
Un estudio similar al anteriormente expuesto fue presentado por Papazoglou y Elnashai (1996), en donde se conjugan evidencias de campo y de resultados dinámicos para el estudio de la respuesta de edificios y puentes frente a la acción de aceleraciones verticales en sismos fuertes.
Broekhuinzen (1996), Yu (1996) y Yu et al (1997) realizaron estudios paramétricos referentes a los efectos de las aceleraciones verticales en puentes, centrándose en tres pasos a nivel ubicados a 15 km de la falla del sismo de Northridge (1994). Broekhuinzen (1996) investigó los efectos de las aceleraciones verticales en puentes con tablero de hormigón pretensado. Para aceleraciones verticales de 1.0g encontró que los esfuerzos admisibles en el tablero pueden ser excedidos. Por otra parte, los estudios de Yu (1996) y Yu et al (1997) encontraron incrementos de hasta un 21% en los esfuerzos axiales y de un 7% en los momentos longitudinales debido a la adición de la componente vertical de aceleración.
Por otra parte, Silva (1997) explica las características generales que presentan los movimientos sísmicos verticales, en un estudio realizado en USA. En el trabajo se muestran los efectos generales sobre estructuras, para sismos de campo cercano, con distancias epicentrales de 10 a 15 km. En el caso de campo cercano, las duraciones son más cortas en tanto que las historias temporales de desplazamiento y velocidad pueden incrementar significativamente su amplitud, y presentar características de pulso, dependiendo de las características de directividad de la ruptura, con movimientos verticales de corto período que exceden significativamente los horizontales. Los resultados de la investigación arrojan la conveniencia de no considerar el factor 2/3 de la razón entre aceleración efectiva máxima vertical a horizontal para la zona central de USA, siendo apropiado sólo en la zona oeste, para estructuras de períodos de alrededor de 0.3 seg y distancias mayores a 50 km.
Gloyd (1997) presentó criterios usados en el diseño de 60 puentes de sección cajón pretensados, con la consideración de los efectos de la aceleración vertical. En el diseño se usaron amplitudes espectrales iguales a 2/3 del espectro horizontal, mostrando que los valores de diseño para el cortante en el tablero y los momentos flectores para dos puentes de vano continuo tenían una respuesta dinámica para aceleraciones verticales mucho mayor que para sólo los efectos de carga muerta, con una inversión importante de momentos en el tablero, tanto en la zona de momento positivo como negativo.
Más recientemente Button et al (2002) presentaron los resultados de un estudio paramétrico de los efectos de los movimientos verticales en la respuesta sísmica de puentes tipo. Para lo anterior se plantearon seis puentes diferentes a modo de cubrir una variedad representativa en cuanto a tipo y geometría, para magnitudes sísmicas de 6.5 a 7.5, tanto en roca como suelo y para distancias epicentrales de 1, 5, 10, 20 y 40 km. Se analizaron las respuestas de los diferentes puentes incluyendo y excluyendo los movimientos verticales, concluyendo que tanto en suelo como roca y para magnitudes mayores a 5.5 y distancias epicentrales menores a 40 km, para períodos comprendidos entre 0.2 y 3.0 seg, el radio espectral V/H es menor a 2/3; mientras que para períodos menores a 0.2 seg, la razón espectral era mayor a 2/3. El tradicional uso de la razón espectral V/H de 2/3 empleada en los códigos es conservadora para la respuesta vertical del tablero, pero no lo es para los esfuerzos axiales en las pilas. La Fig. 3-33 muestra los resultados de las aceleraciones espectrales horizontal y vertical respectivamente, para M = 7.5, y distancias epicentrales de 1, 5, 10, 20 y 40 km.
|
Fig. 3-33 Aceleraciones espectrales horizontal (punteado) y vertical (continuo) (Button et al, 2002) |
Prácticamente todas las investigaciones han sido realizadas en puentes estándar de vigas, y no existen a la fecha estudios concretos en puentes de tirantes. El hecho de tener un sistema de tirantes en esta tipología provee de un sistema continuo de apoyos elásticos al tablero, con espaciamientos que actualmente oscilan entre 8 y 12 m en puentes de hormigón. Lo anterior hace que el efecto de las aceleraciones verticales no sea tan importante en el análisis del tablero, sin embargo los esfuerzos axiales en las pilas podrían verse notablemente comprometidos a la luz de los resultados de las investigaciones anteriores.
3.3.7. Variabilidad espacial en puentes atirantados de gran luz
La variabilidad espacial del movimiento del suelo es un fenómeno bien conocido, y del cual existe actualmente una extensa literatura. El fenómeno reviste especial importancia en ciertas estructuras especialmente alargadas, tales como tuberías, puentes y túneles; y consiste básicamente en una condición de movimiento no sincrónico o diferencial de los soportes, el que es normalmente ignorado en los análisis, limitándose al uso de registros o espectros que son idénticos en todos los puntos de apoyo, situación que evidentemente puede variar notablemente, sobre todo si los soportes se encuentran a distancias considerables como ocurre en puentes de gran luz.
Sin duda, el Eurocódigo 8 (CEN, 1998b) es quizá uno de los pocos códigos que toma en consideración este fenómeno, y le reviste especial importancia en puentes con extensiones sobre los 600 m y en aquellos casos en que las condiciones del suelo son marcadamente diferentes entre un apoyo y otro. La norma plantea tres métodos de análisis para tener en cuenta este efecto: descripción del movimiento del suelo en diferentes puntos como componentes de un campo aleatorio, homogéneo en el espacio y estacionario en el tiempo y completamente definido a través de su matriz de covarianza; como componentes de un modelo aleatorio simplificado o a través de un modelo cinemático puro, consistente en un conjunto de desplazamiento estáticos relativos (Calvi y Pinto, 1996).
La respuesta estructural frente al fenómeno de excitación en múltiples soportes ha sido investigada por Clough y Penzien (1993), y es conocido desde hace más de 3 décadas.
El fenómeno de la variabilidad espacial involucra varios mecanismos que hoy en día han sido identificados, los que a continuación se señalan:
- Efecto del paso de onda
- Fenómeno de incoherencia
- Efecto de las condiciones locales del suelo
- Efecto de la atenuación anelástica y expansión geométrica de ondas
- Extensión de la fuente sísmica
El efecto del paso de onda se refiere al desfase generado en los tiempos de llegada de ondas S a los diferentes puntos (apoyos) de una estructura, la que queda caracterizada por las condiciones locales del suelo y la velocidad de propagación de tales ondas. La falta de coherencia de las ondas sísmicas se provoca por las refracciones y reflexiones de las mismas en semi-espacios no homogéneos, en tanto que las condiciones locales del suelo variables afectan los contenidos frecuenciales y las amplitudes de las ondas sísmicas. El efecto de atenuación anelástica y expansión geométrica de ondas corresponde al decaimiento de las amplitudes de las mismas con la distancia al foco, debido a la disipación de la energía y filtrado de altas frecuencias, mientras que la extensión de la fuente sísmica se refiere al tamaño de la zona de ruptura en la falla. De todos estos fenómenos, son los primeros tres los que más nos interesan, dado que es sabido que el efecto de la atenuación anelástica y la expansión geométrica, así como la extensión de la fuente sísmica no tienen una mayor incidencia en la variabilidad espacial de puentes de gran luz (Bayrak, 1996; Ettouney et al, 2001).
Existen varios trabajos de investigación referentes al fenómeno de la variabilidad espacial en estructuras en general, entre los que podemos citar a Loh y Ku (1995), que propusieron una metodología de análisis basada en espectros de respuesta; Kahan et al (1995), que estudiaron la influencia del paso de onda en la respuesta; Shinozuka y Deodatis (1996), que presentaron una metodología para generar historias temporales de movimientos sísmicos teniendo en cuenta la variabilidad espacial, compatibles con espectros de respuesta y duración prescrita y teniendo en cuenta la propagación de ondas y la falta de coherencia; Petrov (1996), que estudió la respuesta general considerando excitación en múltiples soportes para sistemas extensos de varios grados de libertad sujetos a varios componentes de excitación sísmica aleatoria no estacionaria; Bayrak (1996), que estudió el efecto del paso de onda en la respuesta de puentes de gran luz; Ramírez y Ayala (1997), que estudiaron el efecto de la variabilidad espacial de ondas sísmicas sobre la respuesta no lineal de puentes, tomando en cuenta el efecto del paso de onda y la incoherencia; Tzanetos et al (2000), que estudiaron la respuesta dinámica inelástica de puentes de hormigón armado sujetos a movimiento no sincrónico considerando registros naturales y artificiales y tomando en cuenta el efecto del paso de onda y la incoherencia.; Saxena et al (2000), que analizaron el efecto de la variabilidad espacial en la respuesta dinámica no lineal de puentes multi-claro considerando el efecto del paso de onda, la incoherencia y las condiciones locales del suelo, Ettouney et al (2001), que presentaron una metodología de análisis sísmico de puentes de gran luz con movimiento no uniforme empleando análisis en el dominio de frecuencias; Qingshan et al (2002), que estudiaron el efecto de la incoherencia en la respuesta sísmica de estructuras con múltiples soportes; Petronijevic et al (2002), que estudiaron la respuesta sísmica de puentes frente a excitación de múltiples soportes teniendo en cuenta la interacción suelo – estructura; Tubino et al (2003), que propusieron una nueva estrategia de análisis sísmico de estructuras sometidas a excitación de múltiples soportes usando descomposición ortogonal para el desacoplamiento de las contribuciones pseudo-estáticas y dinámicas del movimiento; Sextos et al (2003), que estudiaron el efecto de la variabilidad del movimiento del suelo acoplado y la interacción fundación – suelo en la respuesta sísmica de puentes de hormigón largos; Sextos et al (2004), que estudiaron los efectos de la interacción suelo – estructura y la variabilidad espacial en puentes irregulares, con aplicación al puente Krystallopigi; Li y Li (2004), que presentaron una nueva metodología basada en espectros de respuesta para el análisis de estructuras con excitación de múltiples soportes; Jiahao et al (2004), que presentaron una estrategia de análisis sísmico de puentes de gran luz con la consideración de la variabilidad espacial usando un método de vibraciones estocásticas llamado Método de la Pseudo Excitación; Soyluk (2004), que presentó una comparación de varias estrategias de análisis dinámico en base a métodos estocásticos en puentes de gran luz sujetos a excitación de múltiples soportes; y finalmente Lupoi et al (2005), que estudiaron el fenómeno de la variabilidad espacial en puentes teniendo en cuenta el efecto del paso de onda, la incoherencia y las condiciones locales del suelo, con una clara orientación al diseño.
Por otra parte, se han realizado algunas investigaciones tendientes a estudiar el comportamiento de puentes frente a excitación de múltiples soportes con la incorporación de sistemas de control activo y pasivo, como en los trabajos desarrollados por Betti y Testa (1995) y Betti et al (1996).
En cuanto a puentes atirantados de gran luz, también se han realizado varias investigaciones, las que fueron comenzadas por Abdel – Ghaffar a comienzo de los años 80. En puentes de gran luz el problema se suscita cuando éste es largo en comparación con las longitudes de onda sísmica en el rango de frecuencias de importancia en la respuesta sísmica, siendo muy complicada la correlación del movimiento en los soportes (Abdel – Ghaffar, 1991). Así por ejemplo, en el caso de un puente con dos apoyos, se tendrán 12 componentes diferentes de movimiento del suelo si consideramos la variabilidad espacial, en tanto que si el análisis es hecho considerando movimiento uniforme se tendrán solo 3 componentes de movimiento.
Abdel – Ghaffar y Nazmy (1990, 1991, 1992) realizaron estudios en puentes de tirantes de gran luz, en hormigón y acero, con registros reales y considerando movimiento uniforme y excitación en múltiples soportes a modo de poder realizar comparaciones. Los resultados de los análisis mostraron que la excitación de múltiples soportes tiene un significativo efecto, por lo que debe ser considerado en el análisis de la respuesta sísmica. Este efecto resulta ser especialmente importante en los puentes más rígido y en aquellos asentados sobre suelos con diferentes propiedades dinámicas locales en los puntos de apoyo, induciéndose en general mayores esfuerzos que en el caso de tener movimiento uniforme. Sin embargo, el grado de incremento en los esfuerzos dependerá del problema específico, y en particular, de aspectos tales como la longitud del claro, la rigidez estructural y el grado de redundancia. Es importante destacar que la distribución espacial de los esfuerzos máximos no ocurre al mismo tiempo; los valores representan los máximos en una sección estructural en particular, sin embargo, queda de manifiesto la importancia de considerar en los análisis de puentes de gran luz la consideración de la excitación en múltiples soportes. En cuanto al efecto del paso de onda, dependiendo de las propiedades dinámicas de los suelos locales en los puntos de apoyo, para efectos de análisis, Abdel – Ghaffar y Nazmy recomiendan considerar un desfase dado por la velocidad de propagación de las ondas S entre los puntos de apoyo, sin considerar el efecto dispersivo que para efectos prácticos es despreciable en estos casos. Los resultados de los análisis muestran además que las diferencias decrecen conforme aumentan las velocidades de propagación de onda, aproximándose los valores a los del movimiento uniforme.
La Fig. 3-34 muestra la configuración geométrica de los puentes analizados, en tanto que la Fig. 3-35 muestra los esfuerzos en el tablero para el modelo 1, considerando el sismo de El Centro (1940).
|
Fig. 3-34 Modelo 3D de los puentes analizados (Abdel-Ghaffar y Nazmy, 1992) |
Allam y Datta (1999, 2000, 2004) estudiaron el comportamiento sísmico de puentes atirantados considerando movimiento del suelo aleatorio multi-componente. Los análisis toman en cuenta la variabilidad espacial y el efecto del ángulo de incidencia del sismo. Los resultados de las investigaciones mostraron que la respuesta del puente está influenciada por la razón de la inercia torre/tablero. Así mismo, el ángulo de incidencia del sismo tiene un importante efecto en la respuesta, así como también la razón entre las componentes vertical y horizontal (en la dirección del puente), en donde queda claro que la componente longitudinal del movimiento del suelo significativamente influye en la vibración vertical del puente.
Soyluk y Dumanoglu (2000, 2003, 2004) estudiaron los efectos de la variabilidad espacial del movimiento del suelo en puentes de tirantes a partir de análisis estocásticos. El movimiento del suelo fue descrito por la función de densidad de poder espectral, mientras que la variabilidad espacial fue considerada teniendo en cuenta el efecto del paso de onda, las condiciones locales del suelo y la incoherencia. Los resultados de la investigación confirman, una vez más, que la variabilidad espacial y los efectos de propagación del movimiento del suelo tienen importantes efectos en el comportamiento dinámico de puentes de tirantes, siendo posible que la variabilidad sea incluida en el análisis estocástico de éstos. Se observó también que la velocidad del movimiento del suelo influye notablemente en la respuesta. Por otro lado, los desplazamientos totales del puente son dominados por la componente dinámica, en tanto que la componente seudo-estática tiene una notable influencia en la variabilidad espacial del movimiento del suelo. Las Figs. 3-36 y 3-37 muestran los momentos flectores en el tablero, considerando excitación general y movimiento uniforme.
|
Fig. 3-36 Momentos normalizados en el tablero: (a) excitación general; (b) movimiento uniforme (Soyluk y Dumanoglu, 2004) |
Fig. 3-37 Momentos flectores medios máximos del tablero para diferentes velocidades de propagación de ondas (caso de excitación general) (Soyluk y Dumanoglu, 2004) |
Li et al (2004), estudiaron las bondades de emplear el llamado Método de la Pseudo Excitación en el análisis dinámico de puentes de tirantes considerando la variabilidad espacial a través del efecto del paso de onda y la incoherencia, mostrando que en particular el efecto del paso de onda tiene una singular importancia.
Recientemente, Soyluk et al (2004) realizaron un estudio comparativo de varias estrategias de análisis considerando movimiento asíncrono de los soportes. Fueron considerados tanto métodos determinísticos como métodos estocásticos en los análisis, para varias velocidades de onda. Los resultados confirmaron que la respuesta estructural usualmente presenta importantes amplificaciones dependiendo del decrecimiento de la velocidad de propagación de las ondas sísmicas.
3.4. Respuesta Sísmica de Puentes Multi-vano
Hoy en día existe una tendencia a diseñar puentes de gran luz con múltiples claros, es decir, con tres o más torres. Estas estructuras, a diferencia de los puentes normales, requieren de una adecuada rigidez longitudinal para asegurar la estabilidad global del sistema, y en particular, de las torres centrales. Por lo general, esto se logra empleando pilas rígidas, ya que la ausencia de puntos fijos intermedios no permite el uso de cables de retención (Walter, 1999).
A la fecha, existen muy pocos trabajos que enfoquen directamente el problema del comportamiento sísmico de puentes de tirantes de múltiples vanos. En este sentido, hacen falta estudios comparativos y análisis paramétricos para optimizar los diseños.
Ni et al (2005), presentaron un trabajo relacionado con el comportamiento sísmico en puentes multi-claro, con la presencia de cables estabilizadores. El estudio fue hecho en el puente Ting Kau (Hong Kong), uno de los puentes atirantados multi-claro que emplea cables estabilizadores. Para realizar los análisis dinámicos se empleo un modelo 3D de elementos finitos, que mostró que la estabilización longitudinal a través de cables estabilizadores presenta modos globales con una fuerte interacción entre el tablero, torres y cables. Las Figs. 3-38 y 3-39 muestran una vista general del puente y el modelo de elementos finitos empleado respectivamente.
Se encontró que la respuesta sísmica y los esfuerzos internos en la torre central eran mucho mayores que en las otras torres. El empleo de cables estabilizadores resultó muy efectivo en reducir los esfuerzos internos en la torre central, generados por la excitación sísmica longitudinal, pero afecta en forma insignificante la respuesta sísmica del tablero y torres laterales. Lo anteriormente explicado se ilustra mejor en las tablas 3-4 y 3-5, y en las Figs. 3-40 y 3-41.
| Modo | Sin cable estabilizador (LSC) | Con cable estabilizador |
| 1 | 0.1634 | 0.1421 |
| 2 | 0.1653 | 0.1659 |
| 3 | 0.1812 | 0.1838 |
| 4 | 0.2244 | 0.2216 |
| 5 | 0.2455 | 0.2455 |
| 6 | 0.2484 | 0.2484 |
| 7 | 0.3008 | 0.2942 |
| 8 | 0.3446 | 0.3442 |
| 9 | 0.3707 | 0.3679 |
| 10 | 0.4590 | 0.4587 |
|
Fig. 3-40 Respuesta de la torre central en la cúpula para sismo de El Centro: (a) longitudinal (b) lateral (Ni et al, 2005) |
Fig. 3-41Envolvente de la respuesta de la torre central para sismo de El Centro (Ni et al, 2005) |
| Sin LSC | Con LSC | |||
| Ubicación | Qx (MN) | Mz (MNm) | Qx (MN) | Mz (MNm) |
| Torre Ting Kau | 3.02 | 239 | 3.08 | 248 |
| Torre central | 26.70 | 1424 | 29.81 | 1588 |
| Torre Tsing Yi | 2.90 | 218 | 2.87 | 219 |
3.5. Respuesta Sísmica de Puentes Atirantados Curvos
En la actualidad son pocos los ejemplos en el mundo de puentes atirantados curvos. Estos en general son de luces pequeñas y medianas, y aparecen más bien como una novedad estética o arquitectónica para salvar luces. Por lo anterior, el estudio de la respuesta sísmica de este tipo de estructuras es escaso, lo que implica una urgente necesidad de profundizar en la investigación en esta tipología de puentes de tirantes.
Los primeros trabajos fueron desarrollados por Brownjohn et al (1999) y Brownjohn y Xia (2000), para el puente Safti Link (Singapur). El puente tiene un claro principal de 100 m, y fue estudiado a través de modelos analíticos y con ensayos dinámicos ambientales. En la Fig. 3-42 se aprecia una vista del puente construido, y en la Fig. 3-43 se muestra el modelo de elementos finitos empleado. Para esta tipología especial de puentes de tirantes queda clara la importancia de un adecuado modelado, el que debe ser necesariamente tridimensional.
|
Fig. 3-42 Puente Safti Link (Brownjohn y Xia, 2000) |
Fig. 3-43 FEM para puente Safti Link (Brownjohn et al, 1999) |
La comparación de los resultados y el análisis de vibraciones libres mostraron que la modelación del tablero fija en los extremos es un factor importante en el comportamiento, en tanto que una correcta modelación de los cables no lo es tanto, excepto para la identificación de las formas modales de los cables con interacción con la superestructura débil. La estimación de las tensiones en los cables obtenidas de las pruebas dinámicas puede resultar no muy exacta a menos que la rigidez de los anclajes y la distribución de la masa se conozcan bien. Así mismo, se concluyó que el modelo de elementos finitos predice muy bien la respuesta dinámica del puente, mostrando adecuadamente los modos torsionales. Se observó además que los modos verticales y laterales en el prototipo son ligeramente más bajos en frecuencia que los predichos, mientras que lo contrario ocurrió para los modos torsionales. Evidentemente, debido a la asimetría, los modos verticales y laterales tienen una componente torsional importante.
El trabajo de Brownjohn y Xia, publicado en 2000, investiga las propiedades dinámicas del mismo puente, mediante el empleo de modelos basados en sensibilidad. Con los datos modales medidos con anterioridad, las propiedades dinámicas simuladas obtenidas mediante el modelo de elementos finitos tuvieron una significativa mejora debido a la modificación de ciertos parámetros estructurales como el módulo de Young del hormigón y la geometría de la estructura. Las formas modales obtenidas son las mostradas en la Fig. 3-44. Al comparar los resultados teórico (FEM) y experimental (EMA) para el análisis dinámico, se obtuvo la tabla 3-6. Los resultados muestran que no existe una buena consistencia entre las pruebas experimentales y teóricas, debido a errores en la modelación y a incertezas en la estructura, lo que sugiere mejorar el modelo de elementos finitos usado
|
Fig. 3-44 Formas modales obtenidas (Brownjohn y Xia, 2000) |
| Modo | Frec (FEM) | Frec (EMA) | Diferencia (%) | Forma modal | ||
| 1 | 1.26 | 1.18 | Primera flexión | |||
| 2 | 1.61 | 2.76 | -41.58 | Segunda flexión | ||
| 3 | 2.62 | 3.59 | -27.09 | Primera torsión | ||
| 4 | 3.71 | 4.61 | -19.50 | Tercera flexión | ||
| 5 | 4.88 | 6.10 | -19.96 | Segunda torsión | ||
| 6 | 6.16 | 7.00 | -11.94 | Cuarta flexión | ||
| 7 | 7.00 | 9.10 | -23.11 | Tercera torsión | ||
Astaneh – Asl y Black (2001) realizaron algunos estudios sísmicos para una propuesta de puente atirantado curvo en la Bahía San Francisco – Oakland, cuyo puente original resultó seriamente dañado durante el sismo de Loma Prieta (1989). Hicieron análisis temporales inelásticos para completar el diseño sísmico del puente, mostrando que la estructura propuesta en particular no tenía modos torsionales predominantes, debido a que el tablero era una estructura 3D soportada en tres puntos: la torre principal y los estribos.
Gentile y Martinez y Cabrera (2004), analizaron el comportamiento dinámico de dos puentes atirantados curvos ubicados en el aeropuerto Malpensa (Milán). Investigaron los parámetros dinámicos de los puentes en base a modelos teóricos y pruebas de carga dinámica, mostrando en los resultados una buena correlación. Determinaron para ambos puentes 11 modos de vibración con frecuencias entre 0 y 10 Hz, con una correspondencia uno a uno en ambos puentes. Los resultados mostraron la inexistencia de evidencia que sugiriera un comportamiento no lineal.
3.6. Aspectos a Considerar en Puentes Atirantados Extra – largos
La tecnología actual permite alcanzar grandes luces a través de puentes atirantados. En la actualidad es posible el diseño y construcción de puentes atirantados extra largos, es decir, con luces que superen los 1000 m, pudiendo competir con los puentes suspendidos.
Nazmy (1995), estudió la factibilidad sísmica de un puente atirantado extra-largo, con un claro principal de 1000 m, como se muestra en la Fig. 3-45.
Para la modelación y análisis de un puente de estas características, necesariamente se debe considerar en la formulación la aplicación de modelos tridimensionales y el análisis no lineal, debido al alto grado de no linealidad geométrica y del material que presenta. Las principales fuentes de no linealidad provienen en este caso de los cambios en la geometría del puente debido a deformaciones finitas, cambios en el combamiento de los cables debido a cambios en las tensiones e interacción entre los momentos flectores y los grandes esfuerzos axiales de compresión en la torre y vigas cajón principales.
En el caso de un puente extra largo como el presentado, Nazmy plantea la necesidad de conectar la torre y el tablero a través de apoyos elásticos. En efecto, un apoyo rígido induciría excesiva flexión y cortante en la torre durante un sismo, en tanto que si se permite el desplazamiento libremente, la flexibilidad resulta excesiva, con desplazamientos laterales del tablero inconcebibles. Estos soportes elásticos permitirían el control del período natural del puente en la dirección longitudinal. Por otra parte, la configuración de la torre y viga principal cajón deben ser capaces de proveer suficiente rigidez torsional para evitar problemas de inestabilidad aerodinámica y soportar excitación sísmica transversal. Nazmy recomienda el empleo de geometrías tipo “A”, diamante, delta o “Y” invertida para mejorar las condiciones de estabilidad global del sistema. Con respecto al arreglo de los cables, el autor plantea que el hecho de tener un sistema multi-cable, y frente a excitación de múltiples soportes, hace que aparezcan grandes esfuerzos pseudos-estáticos, los cuales tienden a disminuir conforme aumenta el claro del puente. Así mismo recomienda anclar los cables al tablero a través de dispositivos de amortiguamiento para evitar la transmisión de vibraciones del tablero a los cables, y mitigar el efecto del rain-wind vibration. La tabla 3-7 resume los resultados de la respuesta sísmica (en este caso desplazamientos) para los nudos seleccionados y que se explicitan en la Fig. 3-45. L Indica lineal y NL indica no lineal. Los cinco casos analizados se explicitan a continuación:
Caso 1 : Tablero flotante en la dirección longitudinal con cables convencionales de acero.
Caso 2 : Tablero restringido longitudinalmente entre la viga cajón y las torres a través de soportes elásticos, con una rigidez de 120 MN/m.
Caso 3 : Similar al caso anterior, con una rigidez del resorte de 40 MN/m.
Caso 4 : Similar al caso 1, pero usando cables con fibra de carbono. Esto implica una notable disminución del peso de los cables.
Caso 5 : Similar al caso 1, con la adición de amarras entre los cables, como se aprecia en la Fig. 3-45.
| Respuesta | J75 dir-X | J76 dir-Y | J76 dir-Z | J81 dir-X | Torre S.F. | Torre B.M. | ||||||
| Análisis | L | NL | L | NL | L | NL | L | NL | L | NL | L | NL |
| Caso 1 | 33.7 | 45.1 | 65.9 | 54.6 | 153 | 155 | 26.5 | 50.1 | 2.19 | 2.25 | 216 | 274 |
| Caso 2 | 57.3 | 56.2 | 81.8 | 60.4 | 162 | 163 | 48.1 | 47.8 | 30.7 | 30.1 | 1504 | 1450 |
| Caso 3 | 69.6 | 72.8 | 85.4 | 62.5 | 153 | 157 | 60.5 | 60.8 | 18.3 | 19.6 | 1065 | 1170 |
| Caso 4 | 45.3 | 59.5 | 74.2 | 72.9 | 174 | 174 | 27.8 | 33.1 | 2.62 | 2.91 | 316 | 375 |
| Caso 5 | 41.3 | 43.3 | 65.7 | 60.6 | 155 | 157 | 30.4 | 34.6 | 2.32 | 2.79 | 293 | 321 |
La tabla anterior deja bastante claro el alto grado de no linealidad en un puente extra largo, sobre todo cuando el tablero se encuentra totalmente suspendido. Además se aprecia que el uso de cables de fibra de carbono o de amarras entre los tirantes disminuye la no linealidad a costa de un aumento en los esfuerzos.
3.7. Fallo en Puentes de Tirantes Durante Sismos Recientes
Debido a su gran flexibilidad, los puentes de tirantes han presentado en general un adecuado desempeño frente a terremotos, pese a la complejidad de su comportamiento sísmico. No obstante, ello no ha significado la ausencia de daños durante sismos recientes, sin embargo, la evidente falta de reportes de daños en este tipo de puentes deja en claro su buen comportamiento.
Entre los recientes reportes de fallas en puentes de tirantes, Filiatrault et al (1993) detallan los daños y las circunstancias para el puente Shipshaw, el cual cruza el río Saguenay, cerca de Jonquiere, Québec, Canadá. Este sufrió algunos daños debidos al terremoto de Saguenay, el 25 de noviembre de 1988 (ML = 6.0). Durante el evento, una de las cuatro placas de anclaje que conectan la viga en cajón de acero a uno de los estribos falló, lo cual fue confirmado por los análisis numéricos y medidas de vibraciones libres en la estructura. Los resultados de análisis por elementos finitos mostraron que las placas de anclaje estaban sometidas a fuertes concentraciones de tensiones para carga muerta, y que el incremento de tensiones debido al sismo fue suficiente para generar la falla.
Recientemente, Chang et al (2004) detallaron los daños y las causas en el puente Chi-Lu, que conecta Chi-Chi con el poblado de Lu-Ku, sobre el río Juoshuei, Taiwán (Fig. 3-46 y 3-47). La estructura fue sometida al sismo de Chi-Chi, Taiwán (1999), con una magnitud ML = 7.3. Al momento del sismo, la estructura estaba en su etapa constructiva final, y sufrió daño severo en el tablero, en el lado sur del puente (Fig. 3-48). Daños adicionales se observaron en la pila central, que mostró evidencia de agrietamiento menor bajo el nivel del tablero, y agrietamiento severo que se extendía hasta el nivel de los cables inferiores (Fig. 3-49).
|
|
|
|
|
|
Los resultados de los análisis numéricos posteriores mostraron que era predecible la falla por flexión biaxial en la viga principal, usando seis registros reales similares al del puente Chi-Lu. Así mismo, los resultados del análisis no lineal reflejaron adecuadamente el daño en la base de la pila, debido a flexión con respecto al eje débil. El hecho de que el puente aún no estuviera finalizado al momento del sismo, hizo que los análisis y diseño previo perdieran algo de valor, ya que la estructura se debió comportar de forma asimétrica.
El sismo de Taiwán (1999) entregó muchas lecciones, e hizo que muchos puentes en general fueran reforzados y/o reparados, y en particular el puente Chi-Lu. Sin embargo, en el caso de puentes de tirantes es impráctica la reparación de miembros estructurales, siendo más simple y eficiente el empleo de sistemas de aislamiento sísmico y disipación de energía como estrategia de reparación y/o mejoramiento del desempeño sísmico (Lai et al, 2004).
Capítulo 4. Caracterización Sísmica de Entrada
La caracterización sísmica de entrada es un tema fundamental en el estudio de la respuesta sísmica de estructuras en general, y en especial, en puentes atirantados de gran luz. Las grandes luces alcanzadas por algunas de estas estructuras hacen que sean seriamente tomados en cuenta aspectos como la variabilidad espacial y la interacción suelo-estructura. Del mismo modo, la condición de cercanía de la fuente sísmica resulta fundamental en la comprensión del fenómeno y la predicción del comportamiento, dado que los contenidos frecuenciales, duración y amplitudes varían mucho; y resultan de especial interés cuando se adicionan sistemas especiales de disipación de energía que tengan un marcado comportamiento no lineal.
La acción sísmica ha sido tradicionalmente expresada en términos de la aceleración efectiva máxima del suelo, aunque la experiencia ha mostrado que a veces no es un buen indicador, dado que se han observado daños moderados en estructuras sometidas a acciones con aceleraciones efectivas importantes y viceversa. Ello se debe a que además de la aceleración del suelo, aspectos como la intensidad, contenido frecuencial y duración tienen un efecto decisivo (Maldonado et al, 1998).
De acuerdo a Abdel – Ghaffar (1991), el movimiento sísmico de entrada, independiente de la problemática de la excitación en múltiples soportes, debe satisfacer dos requisitos:
1.- Tres o más conjuntos de registros sísmicos apropiados deben ser usados, con duraciones de movimiento fuerte de al menos 20 seg ó 6 veces el período fundamental del puente.
2.- Las ordenadas del espectro de entrada del suelo deben no ser menores que el 90% de los espectros de diseño sobre el rango de los primeros cinco períodos de vibración del puente en la dirección considerada
La elección de registros sísmicos adecuados a la problemática a analizar, resulta entonces de mucha importancia, siendo factible el uso de registros sintéticos compatibles con espectros una buena alternativa, así como el uso de espectros de velocidad y desplazamiento en puentes de largo período. En lo que sigue, se analizará y discutirá el uso de registros sísmicos reales y sintéticos, los efectos de fuente cercana, el uso de espectros de respuesta y la aplicabilidad y conveniencia de uso de espectros de velocidad y desplazamiento en puentes de período largo.
4.1. Registros Sísmicos Temporales Reales
En el empleo de registros temporales es muy importante el uso de una familia de acelerogramas que representen de la mejor forma posible la actividad sísmica del lugar donde se ubicará el puente. El problema central reside en que al intentar estudiar la respuesta de un puente usando registros reales, a veces no es posible contar con la información en el lugar preciso, y por lo general, se termina utilizando los acelerogramas disponibles, los que corresponden a registros con características diferentes a los del lugar de estudio (Maldonado et al, 1998). De aquí la importancia que reviste a nivel de país, el hecho de contar con una buena y contundente instrumentación sísmica.
Los puentes atirantados de gran luz por lo general incurren en el rango no lineal, por lo que la adecuada selección de registros sísmicos para análisis no lineal de estructuras resulta de sumo interés. En este sentido, recientemente Lestuzzi et al (2004), realizaron una investigación en la cual se desarrollaron criterios para la selección de registros sísmicos para ser usados en análisis no lineal de estructuras con comportamiento dúctil. La metodología adoptada consistió en realizar investigaciones sistemáticas de la respuesta no lineal de estructuras de un grado de libertad sometidas a diferentes tipos de registros sísmicos. El desempeño estructural fue descrito por seis diferentes modelos histeréticos de comportamiento; mientras que para los sismos se empleó una base de datos de 164 registros obtenidos de la Base de Datos Europea de Movimiento Fuerte. Fueron investigados distintos parámetros sísmicos, como aceleración efectiva máxima del suelo, aceleración espectral, pendiente del espectro de respuesta, intensidad espectral, etc. A raíz de las observaciones y análisis, se propuso una intensidad espectral modificada para la predicción del impacto sísmico en estructuras, la que tomó en cuenta la frecuencia natural de la estructura y la ductilidad de diseño (Fig. 4-1). La nueva definición de intensidad espectral viene dada por:
Los resultados de la investigación arrojaron que la aceleración espectral Sa del registro temporal de aceleración debe ser igual o cercana a la aceleración espectral del espectro de diseño dado, para el período fundamental T0 de la estructura en estudio, y lo más alejado posible dentro del rango comprendido entre T0 y TS, donde TS corresponde al período fundamental asociado a la rigidez secante para la ductilidad de diseño. Además la elegibilidad de varios registros temporales candidatos puede ser rankeada de acuerdo a la nueva intensidad espectral definida.
4.2. Registros Sísmicos Temporales Sintéticos
Una buena alternativa de realizar análisis sísmico de estructuras es mediante el empleo de registros temporales sintéticos. Con ellos, es posible generar señales artificiales de corta duración que se espera tengan el mismo efecto sobre las estructuras que el del terremoto real que se quiere simular. Los registros artificiales más empleados son los generados a partir de espectros de diseño, los que consideran en forma aproximada, las condiciones locales del suelo, además de la posibilidad de considerar aspectos como la magnitud, distancia focal, ley de atenuación y contenido frecuencial (Maldonado et al, 1998).
La característica principal de los registros sintéticos es que permiten obtener historias temporales ricas en contenido para una banda amplia de frecuencias. Por lo anterior, el uso de registros artificiales ha sido fuente de varias investigaciones, sobre todo por su utilidad en zonas donde no existen registros sísmicos o donde éstos son escasos (Haarala, 2003).
Recientemente, Ólafsson y Sigbjörnsson (2004) presentaron una nueva metodología de generación de acelerogramas sintéticos basada en el uso de modelos de tiempo discreto. En su estudio presentaron el modelo de fuente sísmica para simulación de movimiento del suelo de Brune en forma discreta, así como el modelo de Savage-Haskell que incluye el efecto de la directividad. Los modelos de tiempo discreto fueron presentados como series de filtros recursivos (modelos ARMA) que simplifican el proceso de simulación y no involucran la transformada numérica de Fourier. Las correspondientes funciones de transferencia discreta fueron formuladas a través de la transformada Z, y luego derivadas para obtener una respuesta similar a la función de transferencia original en tiempo continuo. Los resultados de la investigación dieron cuenta de que el modelo se ajustaba bien al problema físico, representaban bien los efectos de amplificación dinámica y permitían una representación adecuada del movimiento fuerte del suelo.
4.3. Sismos de Fuente Cercana
En la selección de los registros sísmicos para el análisis es muy importante la consideración de la cercanía de la fuente sísmica, si es que es el caso. Las características de proximidad a la fuente son muy diferentes a las de campo lejano, ya que vienen caracterizadas por presentar, en la mayoría de los casos, picos de amplitud y contenidos frecuenciales altos. Somerville (1997), explica los efectos de la directividad de la ruptura para movimientos de campo cercano y describe un modelo empírico de estos efectos. Propone algunas guías para la especificación y selección de los espectros de respuesta e historias temporales que representen los movimientos de campo cercano y concluye que los efectos de la directividad afectan significativamente en la respuesta sísmica de estructuras, dado que la superficie de fractura se inicia en algún punto de la falla y se propaga en una o ambas direcciones de ésta. Concluye que al desarrollarse la falla en una dirección predominante, el movimiento del suelo en un lugar específico puede verse notablemente influenciado por su ubicación respecto de la dirección de propagación de la ruptura. En general, un punto situado hacia “aguas abajo” en la dirección de propagación de la ruptura experimentará un aumento de las aceleraciones efectivas máximas del suelo, un predominio de altas frecuencias y una menor duración del movimiento fuerte.
Chopra y Chintanapakdee (2001), presentaron un estudio comparativo para sistemas de 1 grado de libertad entre la respuesta sísmica frente a movimientos de campo cercano y campo lejano. Concluyeron que para un mismo factor de ductilidad, los movimientos de campo cercano imponen una mayor demanda de resistencia frente a un sismo de campo lejano.
Loh et al (2002), describieron las lecciones aprendidas del comportamiento sísmico de puentes para el terremoto de Chi-Chi, Taiwán (1999), debido a que pudo recolectarse mucha información y registros de campo cercano, permitiendo así un estudio detallado y cuidadoso del fenómeno en puentes.
Akkar y Gülkan (2002), describieron algunos rasgos prominentes de los movimientos del suelo de campo cercano a través de espectros de desplazamiento y pseudo-velocidad, encontrando que éstos permiten una descripción más racional de la demanda sísmica de campo cercano.
Li y Zhu (2003), presentaron un estudio comparativo sobre espectros de diseño considerando sismos de campo cercano. Para ello recolectaron y discutieron movimientos sísmicos de campo cercano, clasificándolos por su magnitud y condición de sitio. Algunos parámetros del movimiento sísmico del suelo, como la aceleración del suelo máxima horizontal y vertical (PGA), el período esquina del espectro de respuesta de aceleración elástico y la demanda de aceleración espectral para períodos moderados y largos fueron analizados. Basados en el concepto de diseño considerado en el código UBC 97 (International Code Council, 1997) y la curva de diseño espectral representativa, establecieron expresiones para los factores de campo cercano. Del espectro de diseño para campo cercano obtenido, y comparándolo con los códigos americano y chino, concluyeron que el código UBC 97 subestima los factores de campo cercano para eventos pequeños a moderados, y es conservador para sismos de gran magnitud. Asimismo, los factores de campo cercano propuestos resultaron mayores con respecto de los propuestos en el código chino.
4.4. Espectros de Respuesta. Uso de Espectros de Velocidad y Desplazamiento en Estructuras de Período Largo
Los Espectros de respuesta corresponden a la máxima respuesta (en desplazamiento, velocidad o aceleración) a las que pueden llegar distintos osciladores de 1 grado de libertad con características distintas de amortiguamiento (ξ) y período fundamental (Tn). Estas curvas de espectros muchas veces no pueden utilizarse como espectros de diseño, debido a las fuertes discontinuidades que presentan. Por ello se emplean espectros medios que son obtenidos a partir de varios registros reales de terremotos ocurridos en una zona determinada, y posterior suavizado y superposición. A partir del análisis estadístico de varios espectros medios, se obtiene los espectros de diseño, empleados en las normas sísmicas (Valdebenito, 2005).
La mayoría de los códigos de diseño proponen espectros de diseño específicos, los que evidentemente están en función de la tipología y materialidad estructural, tipo de suelo (para tener en cuenta los efectos locales) y algunos parámetros sísmicos, siendo el más utilizado la aceleración efectiva máxima del suelo, la que se obtiene de cartas o listados de zonificación sísmica. Además, muchos códigos incluyen en su formulación de espectros de diseño coeficientes de importancia, que aumentan la aceleración espectral o la disminuyen dependiendo de la importancia que tenga la estructura a diseñar. En su formulación, los espectros de diseño incorporan el factor de reducción R del cual ya se ha hablado, y en general quedan expresados en función del amortiguamiento y el período fundamental. Algunos códigos incluyen en la formulación de sus espectros, la consideración de la cercanía de la fuente sísmica, a través de factores de campo cercano, como fue discutido en el punto anterior. En el análisis dinámico modal espectral (que utiliza espectros de respuesta para determinar la respuesta sísmica de estructuras) se acostumbra a hablar de pseudoespectros, a raíz de ciertas simplificaciones numéricas y dado que en general los amortiguamientos estructurales son bajos. Así, los pseudoespectros de desplazamiento, velocidad y aceleración quedan definidos y relacionados por:
- Pseudoespectro de desplazamiento: Sd(Tn, ξ) = MVA{u(t)}
- Pseudoespectro de velocidad: Sv(Tn, ξ) = MVA{u´(t)}
- Pseudoespectro de aceleración: Sa(Tn, ξ) = MVA{u´´(t)}
Se verifica además la relación:Sa = ωSv = ω2Sd
Los espectros de respuesta permiten tener una primera visión de la respuesta lineal esperada. Dado que las estructuras de largo período, como los puentes de gran luz, es normal que incurran en el rango no lineal, resulta preferible el uso de registros reales o sintéticos frente a espectros elásticos, o alternativamente, el uso de espectros inelásticos con los factores de ductilidad adecuados.
Por otro lado, los puentes atirantados de gran luz quedan caracterizados dinámicamente por tener períodos fundamentales largos, los que en su respuesta pueden verse afectados por la velocidad o el desplazamiento más que por la aceleración. En efecto, el espectro elástico de respuesta del Eurocódigo 8 (CEN, 1998b), se puede dividir en tres regiones: la zona sensible a aceleración (períodos menores a 0.4 seg para suelo duro o roca), la zona sensible a la velocidad (períodos comprendidos entre 0.4 y 3 seg) y la zona sensible a desplazamientos (períodos mayores a 3 seg). Por lo anterior, el diseño de estructuras alargadas o con apoyos distantes requiere el conocimiento de los movimientos del suelo para períodos más allá de 1 a 10 seg. En este sentido, Trifunac (1995) analiza el proceso que gobierna la respuesta de estructuras de período largo, empleando observaciones de movimiento fuerte para proponer extrapolaciones cuantitativas de amplitudes espectrales de pseudos velocidad. Las extensiones a largo período las plantea para campo lejano, campo cercano y para una transición entre ambas. Concluye y plantea la forma de extrapolar el pseudoespectro de velocidad para movimiento fuerte a bandas frecuenciales más allá de las que pudiesen registrarse en acelerogramas reales. Los resultados más reales son aquellos asociados a magnitudes comprendidas entre 3.5 y 7 para movimiento horizontal, no siendo muy real para movimientos verticales con magnitudes mayores a 6.5.
Tolis (1999), Bommer (1999) y Bommer et al (2000) estudiaron el uso de espectros de desplazamientos para estructuras de período largo, con orientación hacia el diseño basado en desempeño. Plantearon que el espectro de desplazamiento derivado del espectro de aceleración no es conveniente, ya que no existen relaciones de atenuación dependientes de la frecuencia derivadas específicamente para este propósito, además de que el crecimiento sostenido de la amplitud de desplazamiento con el período no es cierta en todo el rango de frecuencias. Usando una base extensa de registros sísmicos fuertes europeos, obtuvieron relaciones de atenuación para ordenadas espectrales horizontales en desplazamiento. Con ello, obtuvieron espectros de diseño en desplazamiento para roca, suelo blando y suelo rígido, para sismos con distancias epicentrales superiores a 50 km y magnitudes comprendidas entre 5.5 y 7.5, para seis niveles de amortiguamiento y períodos de hasta 3 seg.
Recientemente, Faccioli et al (2004) presentaron los rasgos más sobresalientes para espectros de desplazamiento de período largo (hasta 10 seg) a partir de datos de registros sísmicos de movimiento fuerte en Taiwán, Japón, Italia y Grecia. Los espectros de desplazamiento fueron expresados como función de la magnitud, distancia a la fuente y condiciones de sitio, demostrando que la magnitud de momento sísmico (MW) y la distancia epicentral controlan la forma del espectro. A partir de consideraciones físicas simples, obtuvieron una expresión analítica para la variación del desplazamiento máximo del suelo (PGD) en función de la magnitud y distancia epicentral. Encontraron además que no existe mucha influencia de la razón de amortiguamiento crítico para largos períodos. La Fig. 4-2 muestra la dependencia del espectro de desplazamiento con las condiciones de sitio y distancia a la falla, para un amortiguamiento del 5% y registros sísmicos de Taiwán, para rangos de magnitud 5.4<M<6.0 y 6.0<M<6.5. La Fig. 4-3 muestra la dependencia del espectro de desplazamiento para campo cercano (línea gruesa) y distancia intermedia (línea delgada) para los registros de Kobe (Japón).
Capítulo 5. Sistemas de Control de Vibraciones y Disipación de Energía en Puentes
Si bien es cierto que las medidas de protección sísmica tradicional en puentes han progresado mucho en los últimos años, las nuevas tendencias de diseño sísmico con la incorporación de sistemas adicionales de aislamiento sísmico y disipación de energía tienen un futuro muy prometedor del que apenas se tiene conciencia. Los esquemas tradicionales recurren a la modificación de las propiedades de rigidez, masa o geometría de la estructura para intentar reducir las fuerzas de inercia y los desplazamientos generados por un sismo. Así, en el diseño tradicional actual se busca tratar de permitir cierto daño en la estructura a través de la ductilidad proveída al sistema con el ánimo de evitar diseños demasiado conservadores y por ende, de alto coste económico. En otras palabras, en la filosofía actual, se pretende otorgar a la estructura de una cierta capacidad de disipación de energía, más que en dar resistencia contra todo evento (Jara y Casas, 2002).
Las nuevas tendencias, intentan conseguir estructuras más esbeltas y económicas en zonas de alto riesgo sísmico, a partir de la incorporación de dispositivos especiales que en vez de dar más resistencia a la estructura, desvían la energía que impone el sismo. En otras palabras, estas nuevas estrategias de control sísmico se orientan en la reducción de la demanda sísmica, más que en tratar de aumentar la resistencia de la estructura o su capacidad de deformación. La adecuada aplicación de este criterio conduce a sistemas que se comportan elásticamente durante grandes sismos, al contrario del diseño tradicional, en donde se pretende mejorar la capacidad de disipación de energía a través del daño controlado. La Fig. 5-1 (a) presenta el caso de un puente diseñado tradicionalmente, en el cual la energía sísmica es disipada a través del daño en las zonas de plastificación (rótulas plásticas). Por lo anterior, se exige a la estructura una ductilidad adecuada para disipar esa energía entregada, lo que se traduce en daño y deformaciones que a veces son bastante considerables. La Fig. 5-1(b) presenta el caso de un puente con sistema de control en base a apoyos de goma laminada. En este caso se reducen las fuerzas inerciales en las pilas del puente, y con ello, la demanda de resistencia. La disipación de energía inelástica que se demanda en un sismo extremo, se logra a través de la deformación histerética de los apoyos, en vez del daño en las pilas (Jara y Casas, 2002).
Otra forma de controlar vibraciones en puentes, sin la necesidad de instalar dispositivos especiales, es a través del concepto de aislamiento oscilante de pilas de puentes sobre fundación directa. En este caso, el efecto de aislamiento sísmico se logra a través del balanceo inelástico de las fundaciones.
|
Fig. 5-2 Aislación sísmica en un puente por balanceo de las fundaciones (Kawashima y Hosoiri, 2003) |
En el trabajo presentado por Kawashima y Hosoiri (2003), se explica este concepto: al ocurrir separación de la fundación del suelo de soporte debido a la respuesta oscilante, la deformación plástica de la pila en la rótula plástica disminuye como resultado del ablandamiento de la histéresis momento-rotación de la fundación. Como consecuencia, el balanceo inelástico de la fundación se convierte en un efecto aislador de la respuesta del puente. Dicho efecto aislador aumenta al disminuir el largo de la fundación. Lo anterior queda ilustrado en la Fig. 5-2.
El desarrollo formal de los sistemas de control de vibraciones comienza a finales de la década de los 60. En este sentido, se puede decir que fueron justamente los puentes las primeras estructuras en ser “aisladas” al incorporarse los sistemas de apoyo de neopreno zunchado como aparatos de apoyo, que en un comienzo tenían un propósito radicalmente diferente.
El control de vibraciones es un campo relativamente reciente, y a pesar de ello, es fuente de muchos trabajos de investigación teórico, experimental y aplicado; sobre todo, en zonas de alta sismicidad. Por ello, hoy en día se reconoce a ésta estrategia como innovadora, y de amplia aplicación en estructuras nuevas y en refuerzos y reparaciones de estructuras existentes (Jara y Casas, 2002). En lo que sigue, se hará una descripción general de los diversos dispositivos de control de vibraciones de más interés en ingeniería sísmica de puentes. No se profundizará en los diversos temas, dado que a la fecha existe una nutrida bibliografía que ha sido anexada en las referencias de este trabajo. Un buen estado del conocimiento en relación a la disipación de energía suplementaria se puede encontrar en el trabajo de Soong y Spencer (2002).
5.1. Sistemas de Control Pasivo
Los sistemas de control pasivo transforman la energía cinética del sistema en calor, transfiriendo la energía entre los distintos modos de vibración. Su característica principal es que no requieren de energía adicional externa para su operación (Jara y Casas, 2002). Estos sistemas en general actúan elásticamente durante grandes sismos, permitiendo que la estructura permanezca en condiciones de funcionalidad después del evento. Debido a su menor costo, alta eficiencia y baja manutención, son los sistemas de protección sísmica adicional más utilizados en el mundo. Los sistemas de control pasivo pueden ser clasificados como sigue (tabla 5-1):
| Aislamiento de base | Disipadores de energía | Conectores sísmicos | Amortiguadores resonantes |
| Apoyos laminados (RB) | Amortiguadores por plastificación de metales (MD) | Unidades de transmisión de choque (STU) | Amortiguadores de masa sintonizada (TMD) |
| Apoyos laminados de alto amortiguamiento (HDR) | Amortiguadores de fricción (FD) | Dispositivos de control de desplazamientos (DCD) | Amortiguadores de líquido sintonizado (TLD) |
| Apoyos laminados con núcleo de plomo (LRB) | Amortiguadores visco elásticos (VE) | Dispositivos de conexión rígida (RCD) | |
| Apoyos laminados con disipadores de energía | Amortiguadores de fluidos viscosos (VF) | ||
| Apoyos deslizantes lubricados (SB) | Amortiguadores por extrusión de plomo (LED) | ||
| Aleaciones con memoria de forma (SMA) |
5.1.1. Sistemas de aislamiento de base
Estos sistemas incrementan el período fundamental de vibración de una estructura, para así alejarla de las zonas del espectro de respuesta con mayor amplitud espectral. Muchas veces se combinan con otros dispositivos, como por ejemplo conectores sísmicos, para así limitar los desplazamientos que a veces pueden resultar excesivos (Jara y Casas, 2002).
- * Apoyos laminados (RB):
Los apoyos laminados o elastoméricos son sin duda los antecesores de los sistemas actuales de aislamiento sísmico. Son fabricados mediante vulcanización de láminas de neopreno con placas de acero, siendo empleados como aparatos de apoyo en puentes para permitir los movimientos horizontales del tablero producidos por temperatura, reología y frenado. La inclusión de láminas de acero les permite mejorar la rigidez vertical, en tanto que su baja rigidez lateral proporciona un efecto aislador en el sistema, aunque en el marco general, no tienen una gran capacidad de disipación de energía.. Por otra parte, el elastómero proporciona la fuerza de recuperación necesaria para regresar al apoyo a su posición original (Jara y Casas, 2002). Estos apoyos son los más estudiados a la fecha, cuyas propiedades han sido verificadas en pruebas de laboratorio y por análisis a través de elementos finitos. Las Figs. 5-3 y 5-4 muestran apoyos elastoméricos típicos.
|
Fig. 5-3 Apoyo elastomérico (Valdebenito, 2005) |
Fig. 5-4 Corte seccional de un apoyo elastomérico (Valdebenito, 2005) |
- * Apoyos laminados de alto amortiguamiento (HDR):
Corresponden a apoyos de neopreno a los que se adicionan aditivos durante la fabricación para así aumentar el amortiguamiento intrínseco, de modo que de un sistema de apoyo de neopreno tradicional (con amortiguamiento del orden del 5%), se pasa a un sistema con mayor capacidad de disipación de energía, debido a que su amortiguamiento aumenta a valores del 15 a 20%, reduciendo de paso los desplazamientos del aislador. Para aumentar el amortiguamiento, se adicionan partículas de carbón, resinas o aceites en el proceso de fabricación del elastómero. Otra de las características de este tipo de dispositivos es que presentan un comportamiento no lineal para deformaciones de cortante menores al 20%, y presentan una elevada rigidez inicial de mucha utilidad para restringir los desplazamientos por viento, tráfico o sismos ligeros. Lamentablemente estos apoyos son dependientes de la amplitud de los desplazamientos y de la historia de carga (Jara y Casas, 2002). La disipación de energía de estos dispositivos es intermedia entre un amortiguamiento viscoso y uno histerético. La Fig. 5-5 muestra a un HDR en pleno ensayo de carga.
|
Fig. 5-5 Ensayo de carga cíclica para un HDR (Valdebenito, 2005) |
- Apoyos laminados con núcleo de plomo (LRB):
Estos apoyos son similares a los RB, pero se les inserta un elemento de plomo en perforaciones hechas previamente en el elastómero, con el objeto de permitir una disipación adicional de energía histerética por fluencia del plomo. Estos dispositivos han sido ampliamente utilizados en la protección sísmica de puentes, ya que cumplen con los requisitos necesarios: soportar eficientemente carga vertical, incrementar la flexibilidad horizontal, tener una rigidez inicial suficiente, proporcionar amortiguamiento histerético.
El empleo del plomo como material histerético se debe a que posee una baja resistencia a fluencia para esfuerzos cortantes además de poseer una rigidez inicial elevada, entre otras características. Las Figs. 5-6 muestra un corte seccional típico de un LRB.
|
Fig. 5-6 Corte seccional típìco de un LRB (Cortesía de DIS Seismic Isolator TM) |
Un buen estado del arte referente al comportamiento sísmico de puentes aislados con estos dispositivos se puede encontrar en el trabajo de Kunde y Jangid (2003). Otros trabajos recientes en este tema se refieren al comportamiento de puentes aislados con dispositivos LRB frente a sismos de campo cercano (Shen et al, 2004); a la respuesta sísmica de puentes aislados con dispositivos LRB considerando la interacción suelo-estructura (Tongaonkar y Jangid, 2003) y sobre la respuesta sísmica de puentes con dispositivos LRB frente a sismos bidireccionales (Jangid, 2004).
- Apoyos deslizantes (SB)
Estos dispositivos corresponden a placas de acero que disipan energía por fricción. De entre estos dispositivos, el que mayor éxito, desarrollo y uso en puentes ha tenido es el llamado Péndulo de Fricción (FPS). En este sistema, se adiciona un mecanismo en base a placas de acero curvas para restituir la posición original de la estructura después de la deformación, combinando de esta forma la acción del deslizamiento con la fuerza recuperadora que provee la gravedad. Así, el movimiento de la superficie cóncava produce un movimiento pendular en la estructura que soporta ya que cualquier movimiento horizontal produce un levantamiento de la masa que soporta el apoyo. El amortiguamiento es generado por la fricción entre las superficies en contacto (Jara y Casas, 2002). Las Figs. 5-7 y 5-8 muestran un péndulo de fricción típico y un corte esquemático del mismo, en tanto que la Fig. 5-9 muestra los principios básicos de su funcionamiento y mecanismo de acción.
|
Fig. 5-7 Péndulo de Fricción (Gentileza de Earhquake Protection Systems Inc, 2000) |
Fig. 5-8 Sección típica de un FPS(Gentileza de Earhquake Protection Systems Inc, 2000) |
Los dispositivos de fricción, como el FPS, poseen un marcado comportamiento no lineal, por ello se debe tener especial cuidado en su empleo para sismos de campo cercano ya que los picos de aceleración que pudiesen presentarse pueden introducir paquetes de energía considerables en los modos superiores. En el trabajo de Tsopelas et al (1996), se presentó un estudio experimental sobre sistemas de aislamiento deslizante en puentes, y más recientemente, Kunde y Jangid (2003) presentaron en su estado del arte, un panorama global referente al comportamiento de estos dispositivos.
5.1.2. Sistemas disipadores de energía
Los disipadores de energía transforman en calor la energía cinética que transmite el sismo a la estructura. De esta forma, proporcionan un amortiguamiento adicional, pudiendo emplearse hoy en día como sistemas alternativos de aislamiento de vibraciones. En términos generales, estos dispositivos pueden dividirse entre los que disipan energía histerética y los de carácter viscoso. Los primeros dependen del desplazamiento y disipan energía mediante plastificación de algún metal, por extrusión (de plomo o acero) o a través de fricción entre dos superficies de deslizamiento. Los amortiguadores viscosos en cambio, son dependientes de la velocidad y la frecuencia, trabajando mediante la deformación por cortante entre capas de materiales viscoelásticos o por flujo de fluidos viscosos (Jara y Casas, 2002). En relación a lo anterior, Yang et al (2002) presentaron un procedimiento de diseño óptimo para sistemas de disipación de energía, que envuelve la determinación de sus ubicaciones óptimas y sus correspondientes capacidades.
- Amortiguadores por fluencia de metales (MD)
Estos amortiguadores son los dispositivos de disipación de energía que más se han utilizado, ya sea solos o en combinación con otros sistemas de control. Su principio básico de disipación es a través de la deformación histerética de un metal, generalmente acero. Por lo general estos dispositivos funcionan disipando energía por flexión o torsión, por lo que casi siempre estos elementos son de inercia variable para favorecer la fluencia en todo el miembro y no se concentre sólo en una sección del dispositivo. Para el caso de puentes, es importante que el dispositivo permita grandes desplazamientos y disipe energía en todas las direcciones (Jara y Casas, 2002).
Las Figs. 5-10 muestra un dispositivo ADAS de fluencia.
- Amortiguadores de extrusión de plomo (LED)
El amortiguador de extrusión es un dispositivo que transforma la energía mecánica en calor mediante la disipación histerética de algún metal, generalmente plomo. La extrusión consiste en forzar el material a través de un orificio, con lo cual el área inicial de la sección transversal se reduce por deformación plástica. Estos dispositivos trabajan como conectores sísmicos STU, al impedir el desplazamiento ante la acción del viento o las fuerzas de tráfico longitudinales. La Fig. 5-11 muestra el esquema típico de un amortiguador de extrusión de plomo (Jara y Casas, 2002).
En el caso de los amortiguadores de extrusión de plomo, la recuperación es rápida a temperatura ambiente, y la fuerza necesaria para su extrusión es casi la misma en cada ciclo. Según Skinner et al (1993), los amortiguadores de extrusión presentan ciclos histeréticos de tipo Coulomb (rectangulares), son independientes de la amplitud y frecuencia típica de sismos; además de que no se ven afectados por la fatiga y endurecimiento. Además tienen una vida útil prolongada y no necesitan ser reemplazados después de un sismo, ya que recuperan su forma original luego de la extrusión. Al aumentar la temperatura en el proceso, la fuerza de extrusión disminuye lo mismo que la energía absorbida y el calor generado.
- Amortiguadores de fricción (FD)
Este tipo de dispositivos presentan un buen comportamiento ya que no son afectados por la amplitud de carga., la frecuencia del movimiento o el número de ciclos de carga. La mayor parte de estos sistemas utilizan dos superficies de deslizamiento fabricadas con: acero – acero, latón –acero o bronce impregnado con grafito – acero inoxidable. Por lo anterior, la composición y buena calidad de los materiales es fundamental para asegurar una adecuada vida útil. Estos dispositivos muchas veces se combinan con otros para mejorar la eficiencia, como por ejemplo con amortiguadores viscoelásticos: la acción friccionante para sismos y el amortiguador viscoelástico para excitaciones de baja energía.
|
Fig. 5-12 Dispositivo de fricción “Sumitomo” (Adaptado de López Almansa y Bozzo, 2003) |
A falta de mayores investigaciones en ésta área, como modelo de comportamiento se emplea la teoría clásica de la fricción de Coulomb, que aunque muy simplificada, produce buenos resultados. Bajo un comportamiento histerético, se acepta el amortiguamiento de fricción de Coulomb con coeficiente de fricción μ constante. Entre los inconvenientes de estos dispositivos se destacan los problemas de mantenimiento, la relajación en el tiempo y la durabilidad y comportamiento a largo plazo (Jara y Casas, 2002). La Fig. 5-12 muestra un dispositivo de fricción “Sumitomo”.
- Amortiguadores viscoelásticos (VE)
Corresponden a materiales copolímeros o vidriados que se emplean a través de capas intercaladas con placas de acero. Estos dispositivos disipan la energía al producirse cierta deformación por cortante en las capas viscoelásticas. Su comportamiento depende de la frecuencia de vibración, nivel de deformación y temperatura. A diferencia de los dispositivos de fricción y fluencia, éstos no afectan el comportamiento lineal del sistema, incrementando el amortiguamiento viscoso y la rigidez lateral (Jara y Casas, 2002). Los dispositivos viscoelásticos son bastante eficientes para sismos frecuentes de pequeña intensidad, como también en eventos de gran magnitud. Las Figs. 5-13 muestra un amortiguador viscoelástico típico.
El uso de dispositivos viscoelásticos en puentes ha sido muy escaso. Sin embargo, ha habido algunos trabajos que muestran la factibilidad de su empleo. Grenier (1992), discute el uso de fluidos viscoelásticos, concluyendo que son dispositivos que presentan muchas bondades estructurales frente a sismos severos. En tiempo normal, permiten expansiones termales del tablero y en caso de sismos permiten el aislamiento del puente.
|
Fig. 5-13 Amortiguador VE (adaptado de Soong y Spencer, 2002) |
Un trabajo más reciente, presentado por Feng et al (2000), muestra la factibilidad de emplear amortiguadores viscoelásticos en las juntas de expansión de puentes como dispositivos de protección sísmica. El trabajo plantea el uso de estos dispositivos con el objeto de evitar el choque entre subestructuras y/o evitar el desanclaje de los apoyos durante sismos severos. Demostró que los dispositivos VE son eficientes para evitar desplazamientos relativos en las juntas de expansión sin la introducción de un aumento excesivo en la demanda de ductilidad para las subestructuras.
- Aleaciones con memoria de forma (SMA)
Las aleaciones con memoria de forma son cierta clase de aleaciones que tienen la característica de transformarse de fase con un incremento de temperatura específico, según el tipo de aleación. Transforman sus propiedades desde la fase austerita (temperaturas elevadas) hasta la fase martensita (temperaturas bajas). Las aleaciones más interesantes en ingeniería de puentes son: Nitinol (níquel – titanio); aleación de hierro, manganeso y silicio (FeMnSi), dos familias que tienen como base el cobre, y algunas formulaciones especiales con acero inoxidable. En este tipo de materiales, la estructura cristalina cambia por efecto del calentamiento del material, alterando sus propiedades elásticas y de capacidad de disipación de energía interna, haciendo que se pueda modificar la rigidez, las fuerzas inducidas o el amortiguamiento, como se aprecia en las Fig. 5-14 y 5-15 (Jara y Casas, 2002).
|
Fig. 5-14 Ciclo de histéresis de un SMA en fase martensítica (Jara y Casas, 2002) |
Fig. 5-15 Ciclo histerético superelásticos de un SMA en fase austenítica (Jara y Casas, 2002) |
Cuando la temperatura ambiente corresponde a la de la fase martensítica los ciclos de histéresis son semejantes a los del acero convencional (Fig. 5-14). Si la temperatura en el material aumenta más allá de la transición a la fase austenítica, los ciclos que se producen bajo carga dinámica proporcionan un efecto histerético que no muestra deformaciones residuales, efecto que se conoce como súper elasticidad. A mayores temperaturas, el material se comporta elásticamente, sin características histeréticas. Independientemente del nivel de deformaciones, la fluencia, amortiguamiento y resistividad eléctrica cambian notablemente durante los cambios de fase de la aleación. Los inconvenientes más notables en estos materiales son la fatiga ante pocos ciclos de histéresis, bandas de frecuencia limitada, disipación de calor y elevado costo (Jara y Casas, 2002). El empleo de estas aleaciones en puentes es muy reciente, limitándose sólo a estudios teóricos y experimentales, pero no en estructuras reales. DesRoches (2000) y Adachi et al (2000) estudiaron el comportamiento de puentes usando SMA, siendo atractivo su uso en las juntas. La Fig. 5-16 muestra un esquema del empleo de los SMA en puentes simples.
Otros trabajos más recientes como el de Matsuzaki et al (2005), muestran el comportamiento de los SMA usados como elementos de amortiguamiento controlados activamente en conjunto con elementos pasivos.
- Amortiguadores de fluidos viscosos (VF)
Durante los últimos años se ha desarrollado otro planteamiento para reducir la respuesta sísmica de las estructuras: se trata del uso de sistemas amortiguantes. El objetivo de agregar dispositivos amortiguantes es disipar preferentemente la energía inducida por la excitación sísmica en dichos elementos diseñados específicamente con esta finalidad, y que no forman parte del sistema estructural que soporta la carga gravitacional. La clave de esta filosofía de diseño es limitar o eliminar el daño al sistema resistente de la carga gravitacional. En caso necesario dichos dispositivos pueden ser fácilmente remplazados después de un sismo severo, el inmueble no quedaría fuera de servicio ni se vería comprometida la estabilidad del mismo, y el costo total del reemplazo podría ser bastante menor que los costos de reparación e interrupción del funcionamiento en una construcción convencional. Las Figs. 5-17 y 5-18 muestran la disposición de los amortiguadores viscosos en el puente Coronado (USA) y la envergadura de tales dispositivos para un puente de autopista de capacidad 680 T respectivamente (Álvarez, 2004).
|
Fig. 5-17 Amortiguadores del puente Coronado, San Diego, USA (Gentileza de Taylor Devices Inc.) |
Fig. 5-18 Amortiguadores para puente de autopista de capacidad 680 T (Gentileza de Taylor Devices, Inc.) |
Los amortiguadores de fluidos viscosos (o también llamados amortiguadores hidráulicos) son dispositivos capaces de limitar el desplazamiento y/o la fuerza a la que se verá sometida una estructura durante un terremoto, disipando energía por pérdidas internas en la cabeza del pistón cuando ocurren movimientos rápidos. Así, el fluido (generalmente gel de silicona) es forzado a pasar de un compartimiento al otro a través de orificios, a muy alta velocidad, disipando la energía por rozamiento viscoso y transferencias de calor (Álvarez, 2002). Las Figs. 5-19 y 5-20 muestran un esquema seccional típico de un amortiguador viscoso y una vista 3D respectivamente.
Los amortiguadores de fluidos viscosos conectan dos elementos de una estructura, de los cuales uno se puede desplazar con respecto del otro, como por ejemplo un estribo o una pila en un extremo, y el tablero en el otro. La Fig. 5-21 muestra un caso típico.
La relación fuerza (F) – velocidad (V) para los amortiguadores viscosos está dada por la ley constitutiva:
donde Cn es el coeficiente de amortiguamiento con unidades de fuerza por velocidad elevada a la potencia n, que es a su vez un exponente positivo real y sgn( ) es la función signo. La ecuación anterior se transforma en F=C1V para n=1, que representa un amortiguador con comportamiento lineal, y en F=C0 sgn(V) para n=0, que representa un amortiguador de fricción; de este modo, n caracteriza la no linealidad de los amortiguadores. Los valores típicos del exponente n están comprendidos en el intervalo de 0.1 a 2 (Constantinou, 2003). La Fig. 5-22 muestra un diagrama fuerza – velocidad para un amortiguador viscoso con Cn = 1MN/(m/s) para distintos valores de n.
El tipo de relación fuerza – velocidad proporcionada por los dispositivos depende principalmente del tipo de fluido empleado (Virtuoso et al, 2000). Estos aparatos pueden fabricarse para un amplio intervalo de combinaciones de valores de Cn y n.; y su costo es por lo general proporcional a la máxima fuerza de amortiguamiento requerida (Murphy y Collins, 2000). Lee y Taylor (2001), presentaron un actualizado estado del conocimiento en materia de amortiguadores de fluidos viscosos y sus tendencias futuras.
En cuanto al diseño y comportamiento de los amortiguadores de fluidos viscosos, los últimos trabajos presentados corresponden a Kim et al (2003), que mostraron un procedimiento novedoso de diseño de amortiguadores de fluidos viscosos en base al método del espectro de capacidad, en el contexto de la filosofía de diseño sísmico basado en desempeño. Por otro lado, Singh et al (2003) presentaron una formulación para el diseño óptimo de amortiguadores viscosos representados por el modelo de Maxwell. La importancia de este trabajo reside en el hecho de que la formulación de Maxwell captura la dependencia de la frecuencia para el amortiguamiento y los coeficientes de rigidez observados en el orificio para el fluido, especialmente a altos niveles de deformación. En cuanto a amortiguadores de fluidos viscosos con comportamiento no lineal, se pueden encontrar algunas recomendaciones y consideraciones para el diseño y comportamiento en los trabajos de Pekcan et al (1999) y Lin y Chopra (2002).
El uso de los amortiguadores de fluidos viscosos se ha generalizado mucho en los últimos años tanto en puentes como en edificaciones, debido a sus múltiples ventajas, tanto para fines sísmicos como eólicos. Los estudios hechos en puentes muestran la conveniencia del uso de estos dispositivos para reducir las fuerzas sísmicas en la superestructura y permitir los desplazamientos del tablero debido a efectos térmicos, por frenado, etc. En este sentido, el trabajo presentado por Jerónimo y Guerreiro (2002) evalúa paramétricamente el comportamiento sísmico no lineal de puentes con la introducción de dispositivos de disipación de energía en base a fluidos viscosos. Las aplicaciones en puentes de tirantes se discutirán en el próximo capítulo.
- Otros sistemas de disipación de energía
Además de los dispositivos descritos anteriormente, existen varias otras propuestas de disipación de energía, muchas de las cuales se encuentran actualmente en fase experimental. Parvin y Ma (2001) propusieron una combinación de resortes helicoidales y amortiguadores viscosos como sistema de aislamiento y disipación de energía en puentes a modo de mitigar los efectos de las aceleraciones verticales. Los resortes fueron colocados entre la superestructura y la subestructura a modo de apoyos. Además se colocaron resortes horizontales entre el tablero y los estribos, y los amortiguadores viscosos (no lineales) fueron colocados con el objeto de reducir los desplazamientos sísmicos. Los resultados de la investigación mostraron que el sistema era lo suficientemente flexible como para reducir la respuesta en aceleración, en tanto que la respuesta en desplazamiento era bien controlada por los amortiguadores. La Fig. 5-23 muestra la disposición de los dispositivos en el puente, en tanto que las Figs. 5-24 muestra las deflexiones verticales a lo largo del claro para diferentes condiciones.
Fig. 5-23 Prototipo del puente y disposición de los dispositivos (Parvin y Ma, 2001)
Más recientemente, Buckle et al (2005) propusieron el uso de dispositivos tipo shear link como sistemas adicionales de protección sísmica para el puente San Francisco – Bahía Oakland. La propuesta consistió en colocar estos dispositivos en la pila principal del puente, como se muestra en las Figs. 5-25, 5-26 y 5-27.
|
Fig. 5-26 Sección transversal de la torre y disposición del dispositivo (Buckle et al, 2005) |
Fig. 5-27 Diagrama esquemático del dispositivo Shear Link (Buckle et al, 2005) |
Si bien es cierto que el uso de estos dispositivos ha sido preferentemente en edificación, su uso en puentes es prácticamente inexistente. Por lo anterior, se debió realizar una serie de pruebas y ensayos en laboratorio para probar la eficacia del dispositivo, como se muestra en la Fig. 5-28.
Los test mostraron que los dispositivos eran adecuados como sistemas de disipación de energía, pudiendo ser diseñados para tener una gran tolerancia para deformaciones inelásticas. Su uso se ve como algo novedoso y atractivo en puentes de gran luz debido a su bajo costo y poca manutención requerida.
5.1.3. Conectores sísmicos
Los conectores sísmicos son la designación genérica para varias denominaciones encontradas en la literatura especializada: STU para Shock Transmisión Unit, DCD para Displacement Control Device, RCD para Rigid Conection Device, LUD para Lock – Up Device, etc. Estos dispositivos pueden conectar rígidamente algunos elementos de la estructura cuando ésta es solicitada dinámicamente, favoreciendo la distribución de la acción sísmica entre un mayor número de elementos estructurales, mientras que por otro lado, prácticamente no oponen resistencia ante cargas de servicio (Álvarez, 2002).
Los conectores sísmicos (también llamados transmisores de impacto) se pueden clasificar en mecánicos e hidráulicos.
Los conectores mecánicos se basan en el anclaje de una barra de acero por medio de cuñas cónicas, como por ejemplo el conector Transpec ® que se muestra en la Fig. 5-29.
El dispositivo consiste en un bloque metálico de anclaje perforado por dos agujeros cónicos opuestos a través de los cuales se puede deslizar una barra de acero. Se coloca una cuña alrededor de la barra en cada agujero, manteniendo abiertas y centradas las dos cuñas para que la barra pueda deslizar libremente a bajas velocidades. Además el sistema lleva dos pequeños gatos hidráulicos a cada lado del bloque de anclaje, tal que cuando ocurre un sismo, los gatos hacen las veces de detonador empujando la mordaza correspondiente a la dirección del movimiento, lo que ancla la barra, mientras que la otra mordaza es empujada en la misma dirección, sin bloquear la barra. Cuando se invierte la dirección del desplazamiento, el dispositivo actúa sobre el otro lado, y así los dos elementos de la estructura quedan conectados. Los conectores Transpec ® se han empleado en el puente Vasco de Gama, en Lisboa, en combinación con aparatos POT (Álvarez, 2002).
Los conectores hidráulicos consisten en un cilindro de acero que contiene un émbolo y dos compartimientos separados por la cabeza de éste. El interior del cilindro se encuentra relleno con un gel de silicona que ofrece propiedades tixotrópicas especiales, que la hacen muy deformable bajo carga lenta, pero actúa como un sólido rígido ante cargas rápidas. Ante movimientos lentos del pistón, el fluido pasa a través de los agujeros de éste y es desplazado de un compartimiento a otro, generándose solamente fuerzas de rozamiento pequeñas. Cuando se aplica al sistema una carga dinámica, el movimiento del pistón es despreciable, permitiendo la rigidización del sistema. En este sentido, son muy similares a los amortiguadores viscosos. En su Tesina de Especialidad, Forment (2000) explica detalladamente el funcionamiento y aplicaciones de estos dispositivos. La Fig. 5-30 muestra un conector hidráulico.
Otro tipo de conectores sísmicos lo constituyen los llamados fusibles estructurales, que corresponden a dispositivos usados para restringir el desplazamiento en estructuras bajo ciertas condiciones de acción. Pueden ser usados para suprimir los desplazamientos bajo condiciones de serviciabilidad y para limitar las fuerzas durante un sismo. El fusible estructural actúa como una llave de cortante bajo cargas de viento o impacto, pero excediendo un cierto valor umbral, activado por ejemplo por un sismo severo, el fusible falla permitiendo el libre desplazamiento del tablero de un puente (Morgenthal, 1999). La Fig. 5-31 muestra la curva de comportamiento típica de un fusible estructural.
Los fusibles estructurales pueden combinarse con otros dispositivos de control de vibraciones para mejorar las condiciones de desempeño sísmico de un puente. El nuevo puente Rion – Antirión, en el Golfo de Corinto, Grecia, contiene un conjunto de fusibles estructurales combinados con amortiguadores de fluidos viscosos, como será discutido en el próximo capítulo. La Fig. 5-32 muestra una vista digital general de la disposición de tales dispositivos.
|
Fig. 5-31 Comportamiento de un fusible estructural (Morgenthal, 1999) |
5.1.4. Amortiguadores resonantes
Los amortiguadores resonantes son en general cualquier dispositivo de gran masa (o momento de inercia) incorporado a una estructura para reducir oscilaciones al ejercer sobre ésta importantes fuerzas de inercia que tienden a compensar el efecto de la excitación; es decir, en vez de disipar la energía la “desvían” para que afecte a modos de vibración que involucren básicamente desplazamientos relativos entre la masa auxiliar y la estructura principal y por tanto no dañen a ésta. Entre los dispositivos amortiguadores resonantes destacan los amortiguadores de masa sintonizada (TMD) y los amortiguadores de líquido sintonizado (TLD).
Los amortiguadores de masa sintonizada (TMD) trabajan bajo el concepto de péndulo simple, cuyo período se trata de sintonizar con el primer modo natural de la estructura que se quiere amortiguar. Existen dos tipos: los que aplican fuerzas a la estructura (tiene una gran masa) y los que aplican momentos (tienen elevados momentos de inercia, ejerciendo un efecto estabilizador de tipo giroscópico). El principio físico general de los TMD es muy simple, y consiste en que si el sistema es excitado armónicamente con una frecuencia igual a la natural del sistema auxiliar, toda la energía de la excitación se emplea en acelerar la masa auxiliar, y la estructura principal no oscila. Obviamente que en el caso real la excitación no es armónica, sin embargo si se seleccionan adecuadamente los parámetros, la respuesta se reduce significativamente. Estos dispositivos se instalan normalmente en la parte más alta de edificaciones, y en torres de puentes, por lo que su uso en éstos últimos está más indicado para proteger torres de puentes atirantados y colgantes. La Fig. 5-33 muestra un TMD típico.
Los amortiguadores de masa son elementos costosos y sofisticados, y por lo general se diseñan en conjunto con un sistema de actuadores y algoritmo de control para optimizar su desempeño, convirtiéndose así en sistemas activos. Por lo anterior, la eficacia de los TMD es cuestionable como dispositivos de control sísmico intenso, y suelen proyectarse para reducir vibraciones de terremotos pequeños a medianos y para la acción del viento (López Almansa y Bozzo, 2003). Los TMD se emplean para mitigar el efecto de las vibraciones asociadas al modo fundamental de vibración de una estructura, por lo que no son eficientes cuando existen modos acoplados de vibración; sin embargo, se han propuesto algunas alternativas para esto en base a varias masas pendulares, y controlar así varios modos de vibración. Evidentemente que los requisitos de diseño y las condiciones de espacio necesarias se vuelven más complejas en éste caso.
En el caso de puentes, Japón es el país que lleva el liderazgo en esta materia. Se han instalado principalmente en las torres para protegerlos de los efectos del viento durante su construcción, y en algunos casos, para mejorar el comportamiento del puente una vez finalizada la construcción (Jara y Casas, 2002). Algunos puentes que cuentan con estos dispositivos son el puente Meiko Nishi, el puente Funade y el puente Trans – Tokio Bay, todos en Japón. También se han instalado amortiguadores de masa en las torres principales del puente Akashi – Kaikyo (Japón), el mayor puente del mundo actualmente (Fig. 5-34).
|
Fig. 5-34 Puente Akashi – Kaikyo; Japón (Valdebenito, 2005) |
El empleo de los TMD en el puente Akashi-Kaikyo, fue para reducir el efecto de las vibraciones producidas por el viento durante y después de su construcción (Tatsumi y Hata, 1998). Las torres tienen 293 m de altura y una frecuencia natural muy baja, lo que las hace susceptibles a las vibraciones del viento. Los TMD utilizados son una masa colgante pendular, un resorte y un amortiguador de aceite. Se instaló un TMD de 84 T de peso para reducir las vibraciones del primer modo debidas a flexión y un segundo TMD de 114 T para reducir las vibraciones del primer modo en torsión del puente terminado. Como antecedente anecdótico, durante la etapa constructiva del puente aconteció el sismo de Kobe, cuya falla Nojima se ubica entre las torres del puente. El evento provocó un aumento del vano principal de 80 cm y un incremento en la longitud total del puente de 110 cm, sin embargo, aún cuando las torres del puente ya estaban terminadas, no presentaron ningún daño, debido en parte posiblemente a la presencia de los TMD (Jara y Casas, 2002).
En los amortiguadores de líquido sintonizado (TLD) la masa se sustituye por un líquido (agua, soluciones coloidales, barro pesado, etc.) cuyas oscilaciones producen el efecto amortiguador deseado. Estos dispositivos son más simples, fiables y económicos que los TMD, sin embargo su eficacia es menor (López Almansa y Bozzo, 2003). Al igual que en los TMD, los TLD se han instalado con el objeto de reducir las vibraciones producidas por el viento en estructuras esbeltas. A diferencia de los TMD, estos dispositivos no necesitan de un umbral de disparo, ya que siempre están activos, además de prácticamente no requerir manutención (Jara y Casas, 2002). La altura de la columna es el parámetro que define la frecuencia del amortiguador, sin embargo, variaciones pequeñas en la altura no modifican en forma significativa la respuesta durantes movimientos sísmicos fuertes. Para estructuras con frecuencias fundamentales diferentes en ambas direcciones principales, se pueden usar tanques rectangulares para así disipar energía en ambas direcciones. Su aplicación en puentes es liderada, al igual que con los TMD, por Japón, quienes han instalado estos dispositivos en el puente Higashi – Kobe, el puente Toda y el puente Ikushi.
Xue et al (2000), realizaron estudios analíticos para determinar la posible reducción de los efectos torsionales en puentes colgantes sujetos a viento cuando se incorpora un TLD. Los resultados demuestran que este tipo de sistemas puede reducir en forma efectiva las vibraciones por torsión en puentes de gran luz.
5.2. Sistemas de Control Activo
Los sistemas de control activo consisten en una fuente de energía externa que aplica fuerzas a la estructura mediante una serie de actuadores con el propósito de disipar la energía cinética del sistema estructural. La respuesta se mide con sensores físicos que se encargan de enviar las señales a un ordenador para que mediante un algoritmo de control envíe la señal a los actuadotes. En el control activo, la excitación es captada normalmente por un sensor piezoeléctrico o similar, el cual envía la señal a un controlador, compuesto básicamente por un ordenador, el que a través de un algoritmo de control, envía la orden al actuador para modificar las condiciones de estabilidad global del sistema, es decir, el sistema de control debe ser lo suficientemente confiable como para dar órdenes razonables a los actuadores, y éstos deben ser lo suficientemente robustos como para imponer fuerzas (o momentos) que permitan corregir las condiciones del sistema. De allí que las necesidades de energía sean considerables. Las Figs. 5-35 y 5-36 muestran un esquema de control activo (semi-activo) y distintos tipos de actuadotes para el control.
|
Fig. 5-35 Sistema de control activo (Valdebenito, 2005) |
Fig. 5-36 Distintos actuadotes para control activo (Valdebenito, 2005) |
El control activo presenta varias ventajas comparativas respecto de los sistemas pasivos: mayor efectividad en el control de vibraciones de la estructura, son relativamente insensibles a las condiciones del terreno y a las características dinámicas del movimiento, son útiles para mitigar diferentes tipos de riesgo, permiten seleccionar el tipo de acciones sobre las que orientar la protección de la estructura (Jara y Casas, 2002). Los principales inconvenientes en la aplicación de estos sistemas son su elevado costo, manutención y la necesidad de una fuente externa de energía, la que muchas veces puede fallar en caso de un evento extremo. Por lo anterior, se han ideado estrategias inteligentes de control semi-activo e híbrido, como se discutirá más adelante.
Entre los sistemas de control activo se puede incluir el aislamiento de base activo (ABI), amortiguadores de masa activos (AMD), cables activos (AC), materiales inteligentes, fluidos controlables, etc. Todos estos sistemas pueden ser empleados tanto en los sistemas de protección semi-activo e híbrido. De este modo, en el control activo se hace uso de una gran cantidad de actuadores que incluyen amortiguadores de masa activos, amortiguadores de masa híbridos y tendones de control, que pueden emplear actuadores hidráulicos, neumáticos, electromagnéticos, etc. (Jara y Casas, 2002). El inevitable grado de complejidad e incertidumbre que generan estos sistemas, hacen que los dispositivos pasivos sigan siendo universalmente más empleados. En todo caso, hoy en día los sistemas de control activo (así como los sistemas semi-activo e híbridos) son fuente de mucha investigación, sobre todo analítica y experimental. Las principales investigaciones en este campo apuntan hacia la búsqueda de algoritmos eficientes y confiables de control más que en desarrollar nuevos dispositivos. En todo caso, aún existen muchas barreras y retos por resolver: es necesario fortalecer el desarrollo de actuadores para el caso de sismos fuertes, la reducción del coste de implementación y mantenimiento, la eliminación de los problemas inherentes a la fuente externa de energía, el aumento de la confianza y robustez del sistema (Jara y Casas, 2002).
En el caso de puentes, el control de vibración activa está orientado a evitar problemas de resistencia última y fatiga. También han sido instalados temporalmente durante la construcción de torres y tableros en aquellos casos en que no existe otro mecanismo de protección adecuado contra viento o sismo (Jara y Casas, 2002). La primera aplicación práctica en puentes corresponde al puente colgante Rainbow (Tokio, Japón). Otras aplicaciones han sido el puente Akashi – Kaikyo (Japón), el puente de la autopista I35 en EEUU y el viaducto del tren metropolitano de Tokio, al que se instalaron por primera vez tendones activos (Active Tendon System, ATS). Por otra parte, el Instituto de Investigaciones del Departamento de Obras Públicas de Japón, desarrolló un sistema activo de amortiguamiento variable para puentes (Active variable Damper, AVD). La fuerza activa en este amortiguador se modifica en función de la respuesta del puente., presentando amortiguamientos altos para movimientos de pequeña amplitud (como los producidos por el tráfico o el viento), y amortiguamientos bajos para excitaciones de gran amplitud, como en un sismo. Para sismos severos, el amortiguamiento crece nuevamente para eliminar vibraciones y evitar daño (Jara y Casas, 2002).
5.3. Sistemas de Control Híbrido
Los sistemas híbridos son una combinación de control pasivo y control activo (o semi-activo), como por ejemplo una estructura equipada con una masa amortiguadora activa (AMD) en su parte superior, junto con una serie de amortiguadores viscoelásticos en otras zonas de la estructura (Jara y Casas, 2002). En este caso, una parte de la disipación de la energía está encomendada a los amortiguadores pasivos, por lo que las necesidades de energía del sistema activo se reducen. Además cuentan con el beneficio de un sistema de disipación, en el supuesto de una falla de energía del sistema activo durante un sismo. La Fig. 5-37 muestra un esquema híbrido típico.
La mayor parte de las aplicaciones de sistemas de control activo en estructuras reales son realmente sistemas híbridos. Así, un sistema híbrido puede verse como un sistema pasivo que utiliza un control activo complementario. Alternativamente, el control pasivo puede adicionarse al control activo para reducir los requerimientos de energía, y por ello, generalmente los requisitos de energía necesarios en un sistema híbrido son marcadamente menores que en un sistema activo. Por tanto, una ventaja paralela es que en caso de falta de energía, el sistema cuenta con el control pasivo.
|
Fig. 5-37 Sistema de control híbrido (Valdebenito, 2005) |
De los sistemas de control híbrido, el más empleado ha sido el amortiguador de masa híbrida (HMD), consistente en una combinación de un TMD pasivo y un actuador. Su gran eficiencia se debe básicamente al TMD, en tanto que el actuador se emplea para aumentar la eficiencia del HMD y elevar la robustez del sistema frente a cambios en las características dinámicas de la estructura (Soong y Spencer, 2002).
La aplicación de estos sistemas en puentes ha aumentado mucho en los últimos años, sobre todo en puentes de tirantes y puentes colgantes, como se discutirá en el próximo capítulo. Un estudio interesante en esta temática fue presentado por Yang et al (1995), en el cual se analizó el comportamiento de dos sistemas híbridos: apoyos de goma y amortiguadores variables (actuadores), y apoyos deslizantes y actuadores. Como algoritmos de control se emplearon los esquemas VSS (Variable Structure System) y SMC (Sliding Mode Control). Las simulaciones mostraron que los métodos de control eran robustos con respecto a las incertidumbres paramétricas del sistema, y que por lo tanto los sistemas eran eficientes. Otro sistema que ha sido aplicado en torres de puentes, es un amortiguador de masa híbrido que trabaja en dos direcciones, en el cual el sistema consiste en una masa deslizante en forma de arco, combinado con un sistema activo controlado por un motor (Jara y Casas, 2002).
5.4. Sistemas de Control Semi-activo
Los sistemas semi-activos corresponden a un sistema activo con requerimientos de energía varios órdenes de magnitud inferior que los necesarios para un sistema activo típico, de aquí su reciente gran desarrollo y prometedor futuro. Estos sistemas no adicionan energía suplementaria al sistema, por lo que la estabilidad de la estructura queda garantizada, convirtiéndolos en sistemas más eficientes y confiables ante un sismo, en los cuales es común la interrupción del suministro de energía durante el evento. En este caso, los actuadores no se diseñan para producir movimiento en la estructura en sentido opuesto, sino que intentan detenerla. Por ello tal vez sería mejor hablar de sistemas pasivos controlados. Muchos de estos sistemas operan solo con baterías, lo que resulta vital durante un terremoto (Jara y Casas, 2002). Además, en contraste con el control activo, el semi-activo no tiene el potencial de desestabilizar al sistema estructural. Entre los sistemas semi-activos más utilizados, encontramos los Amortiguadores Hidráulicos Semi-Activos (SAHD), Los Fluidos controlables (Amortiguadores Electroreológicos (ERD) y Amortiguadores Magnetoreológicos (MRD)), los amortiguadores de orificio variable, los amortiguadores de masa sintonizada inteligentes (STMD), los amortiguadores de fricción variable y los amortiguadores de rigidez variable. Evidentemente, todos los dispositivos anteriores necesitan electricidad para controlar los mecanismos y dispositivos especiales, por lo que son menos confiables que los sistemas pasivos y les exige mayor mantenimiento (Jara y Casas, 2002).
Soong y Spencer (2000), estudiaron la aplicación en una estructura real de un sistema semi-activo en EEUU, para el puente Walnut Creek. Esta fue la primera aplicación real de un sistema semi-activo a un puente, para lo cual se instaló un amortiguador hidráulico convencional con una válvula de orificio variable que controla la resistencia del flujo (SAHD).
Los amortiguadores de orificio variable consisten en un dispositivo electromecánico que contiene una válvula de orificio variable para alterar la resistencia al flujo de un amortiguador hidráulico convencional. La Fig. 5-38 muestra un esquema tipo.
Los estudios concernientes a estos dispositivos aplicados a puentes datan de 1990, y desde entonces han sido objeto de muchas investigaciones, como se puede ver en el estado del arte sobre sistemas de control estructural presentado por Spencer y Nagarajaiah (2003).
Los dispositivos de rigidez variable se emplean desde 1993, y aunque los amortiguadores de orificio variable pueden emplearse para modificar la rigidez, ellos no pueden variar la rigidez continuamente entre diferentes estados. Nagarajaiah desarrolló un dispositivo de rigidez variable semi-activo, como se aprecia en la Fig. 5-39.
|
Fig. 5-38 Esquema de un amortiguador de orificio variable (Spencer y Nagarajaiah, 2003) |
|
Fig. 5-39 Dispositivo de rigidez variable: (a) implementación; (b) modelo a escala del dispositivo (Spencer y Nagarajaiah, 2003)
|
Las curvas histeréticas fuerza-desplazamiento dejan en claro que el dispositivo puede variar significativamente la rigidez, en forma suave y continua, como se ve en la Fig. 5-40 (Spencer y Nagarajaiah, 2003).
Los amortiguadores de masa sintonizada inteligentes o semi-activos ( STMD) corresponden a una interesante alternativa a los TMD convencionales. Como es sabido, los TMD son muy sensibles a las frecuencias de sintonización de la masa principal, incluso al ser óptimamente diseñados. Por lo anterior, los TMD múltiples (con múltiples masas) pueden salvar esta importante limitación; sin embargo, los TMD múltiples no pueden actuar eficientemente en tiempo real. Por ello, los amortiguadores de masa sintonizada semi-activos son una alternativa atractiva, ya que al tener rigidez variable, constituyen un sistema robusto a cambios en la rigidez y amortiguamiento de la estructura (Spencer y Nagarajaiah, 2003). La variación de la rigidez de los STMD está basada en la estimación de la frecuencia instantánea y en un controlador de tiempo frecuencial desarrollado por Nagarajaiah y Varadarajan (2000). Los estudios más recientes en ésta área corresponden a investigaciones experimentales en edificios altos benchmark, con reducción de respuesta comparable con amortiguadores de masa sintonizados activos, pero con consumos de energía mucho menores (Varadarajan y Nagarajaiah, 2003). Además existen algunos estudios acerca de amortiguadores de líquido sintonizado semi-activo, basados en amortiguadores de líquido sintonizado con orificio variable (Yalla et al, 2001).
Otro tipo de dispositivo semi-activo lo constituyen los llamados amortiguadores de fricción variable, propuestos desde 1991. Estos dispositivos, de los cuales existe una amplia variedad, emplean las fuerzas generadas por una superficie de fricción para disipar energía en sistemas estructurales. Recientemente, sistemas de fricción variables han sido estudiados por Yang y Agrawal (2002) para la reducción de la respuesta sísmica en edificios.
De todos los dispositivos semi-activos que hoy en día existen, son los amortiguadores de fluidos controlables los que han tenido mayor impacto y que han sido objeto de mayor cantidad de investigación analítica y experimental. La característica esencial de los fluidos controlables es su habilidad para transformarse en forma casi instantánea, de un fluido viscoso lineal a un semisólido con resistencia a la fluencia controlable cuando se le expone a un campo eléctrico o magnético (Jara y Casas, 2002). En general, estos dispositivos emplean algunas válvulas o mecanismos activados electrónicamente para realizar los cambios en las características del amortiguador, por lo que pueden resultar poco eficientes en términos de su mantenimiento. De entre los dispositivos de fluidos controlables, destacan dos: los amortiguadores electroreológicos (ERD) y los amortiguadores magnetoreológicos (MRD) (Spencer y Nagarajaiah, 2003), los que a continuación se describen:
Amortiguadores electroreológicos (ERD): Son dispositivos de amortiguamiento variable, capaces de modificar en forma dramática su resistencia al verse sometidos a un campo eléctrico. Los ERD consisten en una base fluida, usualmente un líquido aislante de baja viscosidad, mezclado con partículas no conductoras, que al aplicárseles un campo eléctrico, las partículas polarizan y solidifican la mezcla con un cambio drástico en su comportamiento reológico. El gran interés en este tipo de fluidos radica en su habilidad para proporcionar en forma simple y rápida una interfase entre el control electrónico y el sistema mecánico. Además, su capacidad para trabajar como válvulas rápidas, sin la necesidad del uso de partes móviles que pongan en riesgo la confiabilidad del sistema, representa una gran ventaja. Ofrecen además gran capacidad y flexibilidad para alterar la respuesta de una estructura cuando se enfrenta a condiciones cambiantes o inesperadas. En la actualidad se patentan alrededor de 20 nuevos materiales electroreológicos al año (Jara y Casas, 2002), de entre los cuales los más interesantes (Anhydrous) pueden operar a altas y bajas temperaturas, con resistencia al cortante elevadas y bajos requerimientos de potencia. La modelación de los materiales electroreológicos responde razonablemente bien como fluido plástico de Bingham (Fig. 5-41), dado que una vez que se alcanza la tensión de fluencia máxima se observa una relación newtoniana entre la tensión cortante y la tasa de deformación por cortante. En todo caso, los intentos de modelación de estos materiales ha sido dificultoso por el hecho de que el material se comporta como diferentes modelos idealizados dependiendo del campo eléctrico y la amplitud de deformación. Para niveles de deformación previa a la fluencia, su comportamiento es esencialmente viscoelástico lineal. La deformación de fluencia decrece con el campo eléctrico y la tensión de fluencia aumenta con el cuadrado del campo eléctrico (Jara y Casas, 2002). Kawashima et al (1994) diseñaron un dispositivo electroreológico con fluido tipo anhydrous para determinar la efectividad y aplicabilidad de estos amortiguadores. El dispositivo era capaz de desarrollar una fuerza de hasta 400 T, suficiente como para ser empleada en control estructural. Posteriormente, se desarrollaron otras pruebas en amortiguadores electroreológicos, con aplicación a puentes, como en los trabajos desarrollados por Makris y McMahon (1996, 1997). Un buen estado del arte sobre amortiguadores electroreológicos se puede encontrar en el trabajo desarrollado por Symans y Constantinou (1999). La revisión de la literatura técnica no entrega resultados novedosos posteriores a 1999. A juicio de Spencer y Nagarajaiah (2003), lo anterior se debe a que con el advenimiento de los amortiguadores magnetoreológicos (MRD), los dispositivos electroreológicos prácticamente quedaron obsoletos, principalmente debido a que los MRD han mostrado tener mejores aplicaciones en Ingeniería Civil. La Fig. 5-42 muestra un esquema del dispositivo empleado, y la Fig. 5-43 muestra las fuerzas desarrolladas por el amortiguador.
|
Fig. 5-41 Comportamiento del material ER según modelo de Bingham: (a) tensión cortante-def. plana, (b) fuerza-despl. plano (Symans y Constantinou, 1999) |
Fig. 5-42 Amortiguador electroreológico (Kawashima et al, 1994)
Fig. 5-43 Fuerzas de amort. en el ERD: (a) fuerzas debidas a la viscosidad del fluido, (b) fuerzas debidas a los efectos ER (Kawashima et al, 1994) |
- Amortiguadores magnetoreológicos (MRD): Estos sistemas se caracterizan por su habilidad de modificar en forma dramática su resistencia cuando se les somete a un campo magnético. Los fluidos MRD son suspensiones no coloidales de partículas paramagnéticas, de tamaño micrométrico, magnéticamente polarizables, dispersas en un medio como aceite de mineral o silicona. Al aplicar un campo magnético al fluido, se forman cadenas de partículas y el fluido se transforma en un semisólido, mostrando un comportamiento viscoplástico (Jara y Casas, 2002). Los dispositivos magnetoreológicos, a diferencia de los electroreológicos que funcionan en presencia de un campo eléctrico, son poco conocidos, pero presentan enormes ventajas respecto de los anteriores, ya que tienen una elevada resistencia a la fluencia y un comportamiento histerético estable en un intervalo amplio de temperaturas, además de que la energía que necesitan para operar es menor. La transición al equilibrio reológico se alcanza en pocos milisegundos, permitiendo la construcción de dispositivos de gran ancho de banda. Una de las grandes ventajas de los dispositivos magnetoreológicos es que operan con requerimientos muy bajos de energía: 12 a 24 Voltios, y una fuente de energía de sólo 1 ó 2 Amp. Además, este medio de control puede funcionar como un sistema pasivo aún cuando la fuente de poder no esté activa. Según Jara y Casas (2002), las diferencias más importantes entre los ERD y los MRD son que los MRD tienen una resistencia de fluencia inducida que es de 20 a 50 veces mayor que en los ERD; además los MRD son menos sensibles a los contaminantes y temperaturas extremas; la corriente requerida en los ERD es en mA, mientras que en los MRD es en Amp, para una misma potencia; los dispositivos MRD son en general de menores dimensiones que los ERD, para una misma capacidad; y finalmente, los MRD no son sensibles a los procesos de manufactura o uso.
La Fig. 5-44 muestra un esquema de un dispositivo magnetoreológico para 20 T. Recientemente se han publicado varios trabajos referentes a la modelación fenomenológica de amortiguadores MRD.
|
Fig. 5-44 Diagrama esquemático de un MRD (Gentileza de Lord Corporation Inc.) Fig. 5-45 Modelo mecánico para un MRD (Yang et al, 2004) |
La Fig. 5-45, por ejemplo, propone un modelo de comportamiento basado en el modelo histerético de Bouc y Wen. Este modelo es el que más universalmente se ha adoptado para representar el comportamiento de los MRD. Los recientes trabajos de Yang et al (2004) y Domínguez et al (2004) apuntan en éste sentido. Muy recientemente, Song y Ahmadian (2005) publicaron un trabajo donde estudiaron la aplicación de modelos no paramétricos aproximados para modelar amortiguadores magnetoreológicos. En este trabajo criticaron el uso del modelo de Bouc y Wen por no ser adecuado para estudios de simulación e implementación en tiempo real de los algoritmos de control más avanzados; y concluyeron que los modelos no paramétricos se ajustan mejor en la predicción de las características de la fuerza amortiguadora, comportamiento bilineal del amortiguador, histéresis y saturación electromagnética. El desempeño de los MRD es en general muy estable, tanto en presencia o no del campo magnético. La Fig. 5-46 muestra el desempeño para un dispositivo magnetoreológico de 20 T de capacidad. Del mismo modo, resultados experimentales hechos en prototipos frente a excitaciones sísmicas, han mostrado que en general estos dispositivos reducen considerablemente la respuesta, como se aprecia en la Fig. 5-47, para un MRD excitado con el sismo de El Centro (1940) y controlado con un algoritmo Clipped-Optimal (Spencer et al, 1997).
|
Fig. 5-46 Desempeño de un MRD de 20 T de capacidad (Spencer et al, 1997) |
Fig. 5-47 Respuesta sísmica para un MRD usando algoritmo de control “Clipped-Optimal”. En línea gruesa respuesta con control, y en línea delgada respuesta sin control (Spencer et al, 1997) |
Aún cuando falta bastante desarrollo teórico y experimental, los estudios de simulación realizados muestran que los MRD son capaces de reducir eficientemente la respuesta sísmica, como quedó demostrado en la Fig. 5-47. Muchos autores consideran que en un futuro muy próximo, los fluidos controlables serán una alternativa importante para la protección sísmica de estructuras (Jara y Casas, 2002). En este sentido, se ha desarrollado una extensiva investigación de tipo experimental con estos dispositivos, como por ejemplo en los trabajos de Dyke et al (1996, 1997, 1999) y Yi et al (1998). En un trabajo más reciente, Koo et al (2004) investigaron el tiempo de respuesta de amortiguadores magnetoreológicos y su efecto en los parámetros de operación, mostrando que para una velocidad dada, el tiempo de respuesta permanece constante y no es función de la corriente aplicada. Además se concluyó que el tiempo de respuesta disminuye exponencialmente conforme aumenta la velocidad.
Otra cantidad importante de investigaciones se ha realizado en la búsqueda de algoritmos de control eficientes. Los primeros algoritmos empleados fueron los basados en la Teoría de la Estabilidad de Lyapunov, el Control Descentralizado Bang – Bang y el control Clipped Optimal (Dyke y Spencer, 1997). Posteriormente, Jansen y Dyke (2000) presentaron un trabajo en el cual comparaban distintas estrategias de control: Lyapunov, Control Descentralizado Bang – Bang, Disipación Máxima de Energía, Control Clipped-Optimal y Fricción Homogénea Modulada, encontrando que los más adecuados para los MRD son el Lyapunov, el Clipped-Optimal y el de Fricción. Recientemente, se han propuesto nuevas e interesantes estrategias de control para los dispositivos magnetoreológicos, basadas en Redes Neuronales, Conjuntos Difusos y Control Modal ( Jung et al, 2004a, 2004b; Choi et al, 2004; Cho et al, 2005 y Wang y Liao, 2005).
En cuanto a las aplicaciones de los dispositivos magnetoreológicos, parece ser que tienen un futuro muy prometedor. Un actualizado estado del arte en cuanto a sistemas de control semi-activo usando amortiguadores magnetoreológicos con un claro enfoque hacia las aplicaciones en ingeniería civil puede encontrarse en el trabajo de Jung et al (2004b). En este sentido, existe una abundante cantidad de trabajos referentes a la aplicación de este tipo de dispositivos en puentes, desde el año 2000 en adelante, como en los trabajos de Abe et al (2000); Liu et al (2000, 2001) y Gordaninejad et al (2002). Lee y Kawashima (2004), presentaron una investigación para determinar la eficiencia de amortiguadores suplementarios magnetoreológicos en puentes con sistema de aislamiento, para sismos de campo cercano. Mostraron la eficiencia de los amortiguadores suplementarios para mitigar los grandes desplazamientos del tablero y el comportamiento histerético de las pilas para sismos cercanos a la fuente. Más recientemente, Liu et al (2005), presentaron un estudio comparativo sobre el control de vibraciones de un puente a escala, usando amortiguadores magnetoreológicos. Sahasrabudhe y Nagarajaiah (2005) recientemente publicaron los resultados de una investigación sobre el control semi-activo en puentes con sistema de aislamiento en base a aisladores deslizantes usando amortiguadores magnetoreológicos como sistema de control de desplazamientos. Los resultados numéricos y experimentales mostraron la eficiencia de tales dispositivos frente a sismos de campo cercano. En cuanto a puentes de tirantes, existen varios estudios, sobre todo para la mitigación de las vibraciones de los cables, como será expuesto en el próximo capítulo.
Capítulo 6. Comportamiento Sísmico de Puentes Atirantados con Incorporación de Sistemas Adicionales de Protección Sísmica
El gran desarrollo de los sistemas de control de vibraciones durante los últimos años ha permitido la protección sísmica de una infinidad de tipologías estructurales. Los puentes de tirantes no han quedado ajenos a estas relativamente nuevas tecnologías, y dado que todas las nuevas tendencias de diseño apuntan en esta dirección, merece un estudio aparte el comportamiento sísmico de estas estructuras cuando incorporan estos dispositivos. Los puentes de tirantes experimentan muy bajo amortiguamiento, por lo que la disposición de sistemas adicionales que disipen la energía que entrega un sismo a la estructura, resulta muy beneficioso.
La aplicación del Control de Vibraciones en puentes de tirantes comenzó hace algo más de 20 años, con la incorporación de los primeros dispositivos pasivos de aislación sísmica. Desde ese entonces, el desarrollo no se ha detenido, y pese a ser una tecnología que bastante se ha desarrollado, su incorporación en puentes atirantados ha sido lenta. Muchos de los dispositivos de control han sido probados en forma analítica y experimental, pero desde el punto de vista sísmico, no son muchos puentes los que cuentan con sistemas de protección más avanzados, tal vez por las buenas lecciones que han dejado los sismos fuertes más recientes y por la falta de normativas específicas que regulen los procesos de diseño en todas sus etapas. Los principales usos de estos sistemas en puentes atirantados han estado más bien enfocados a la mitigación de vibraciones en los cables debido a la acción del viento, que en disipar energía sísmica. Así, las nuevas tecnologías de protección pasiva, a través de dispositivos de aislación y disipación de energía, comienzan a utilizarse con fines antisísmicos en puentes recientemente, como en los puentes Cape Girardeau (USA) y Rion – Antirión (Grecia). Así mismo, la constante investigación y experimentación en Control de Vibraciones, ha permitido el desarrollo de nuevos y mejores dispositivos, cuyas características de comportamiento son mejor conocidas, y con mayores capacidades para poder ser empleadas en estructuras más grandes, de acuerdo al desarrollo actual y las nuevas tendencias. Por otra parte, la aplicación de las nuevas tecnologías de protección semi-activa e híbrida en puentes ha comenzado hace muy poco, y tímidamente se comienza a experimentar y probar en puentes de tirantes, sobre todo para la mitigación de las vibraciones en los cables debido al fenómeno del Rain-Wind Vibration.
El desarrollo del Control de Vibraciones ha sido grande los últimos años, y se espera que siga creciendo a futuro. Con la mejora de las tecnologías computacionales y el desarrollo de mejores programas para la modelación y análisis estructural, el análisis numérico y experimental permite hoy predecir de forma mucho más precisa el comportamiento de estructuras más grandes, y por ende, más complejas. En lo que sigue, se presenta un estado del conocimiento actualizado referente a la protección pasiva y activa de puentes de tirantes. Se exponen las más recientes investigaciones, se analiza el caso del recientemente inaugurado puente Rion-Antirión (Grecia) y se presentan algunos resultados de las pruebas analíticas hechas en el modelo benchmark del puente Memorial Bill Emerson (USA).
6.1. Comportamiento de Puentes con Sistemas Pasivos. El Puente Rion-Antirión, Grecia
6.1.1. Investigaciones recientes
El control pasivo está basado en la disipación de energía a través de dispositivos especiales. Estos elementos se sitúan en zonas críticas tales como la unión estribo-tablero y la unión torre-tablero, para concentrar comportamiento histerético en estos absorbedores de energía especialmente diseñados. El comportamiento inelástico en los elementos estructurales principales debe evitarse, asegurando la serviciabilidad después de un sismo (Morgenthal, 1999).
Los primeros trabajos acerca del control pasivo en puentes atirantados corresponden a Ali y Abdel-Ghaffar (1991a, 1991b). En estas primeras incursiones, propusieron el uso de apoyos de goma elastoméricos (dispositivos LRB) como sistemas de control pasivo en puentes de tirantes. Las Figs. 6-1, 6-2 y 6-3 muestran la modelación, elaboración del modelo de comportamiento y localización de los dispositivos respectivamente.
|
Fig. 6-2 Modelo de comportamiento (Ali y Abdel-Ghaffar, 1991a) |
Fig. 6-3 Conexiones torre-tablero con los LRB (Ali y Abdel-Ghaffar, 1991a) |
Los resultados de la investigación arrojaron la conveniencia de utilizar dispositivos de control pasivo como los propuestos, sin embargo, el aumento en la flexibilidad de la estructura hace que aumenten notablemente los desplazamientos. El efecto de tener un corazón de plomo en los apoyos de goma (LRB), es análogo a proveer amortiguamiento adicional. Así mismo, se concluyó que la distribución de las fuerzas transmitidas a las torres, tablero y cables depende de la ubicación de los dispositivos. Del mismo modo, la disposición de estos apoyos en los estribos redujeron las fuerzas en las torres.
Un estudio posterior, realizado por Niihara et al (1994), investigó la mejora en la resistencia sísmica de puentes atirantados de gran luz de hormigón pretensado con la incorporación de amortiguadores pasivos histeréticos, usando historias temporales como caracterización sísmica. En la investigación se discutió la reducción de los desplazamientos del tablero y los momentos de flexión en las torres desde el punto de vista del layout de los cables y la longitud del claro principal. Los modelos analíticos, para puentes de 400 m de largo, se muestran en la Fig. 6-4.
Las características histeréticas del amortiguador y la caracterización sísmica de entrada se muestran en las Figs. 6-5 y 6-6.
|
Fig. 6-5 Características histeréticas del amortiguador (Niihara et al, 1994) |
Fig. 6-6 Registro de aceleración (arriba) y espectro de aceleración (abajo) (Niihara et al, 1994) |
Los resultados de la investigación de Niihara y sus colaboradores, mostraron que la configuración de cables en semi-arpa es más efectiva que la configuración tipo arpa en puentes de gran luz. Los amortiguadores histeréticos incrementan la resistencia sísmica independientemente de la longitud del claro principal. La Fig. 6-7 muestra los resultados comparativos de la respuesta en desplazamiento para las configuraciones en semi-arpa y arpa, y para las tres condiciones de apoyo al tablero: flotante, fija y amortiguada. De ellos resulta evidente la disminución de la respuesta cuando el sistema incorpora amortiguamiento histerético adicional.
Del mismo modo, para el puente de 400 m de largo se estudiaron los efectos de los amortiguadores histeréticos cuando los miembros estructurales plastifican, mostrando que son benéficos justamente en puentes de gran luz.
|
Fig. 6-8 Modelo elasto-plástico (Niihara et al, 1994) |
Fig. 6-9 Relación momento – curvatura según modelo de Muto (Niihara et al, 1994) |
La Fig. 6-8 muestra el modelo elasto-plástico elegido para el puente, en tanto que la Fig. 6-9 muestra la relación momento – curvatura en las zonas de plastificación de acuerdo al modelo de Muto. La Fig. 6-10 señala la respuesta en desplazamiento del tablero para el análisis elasto-plástico, mostrando el claro efecto benéfico de los amortiguadores. En el tablero flotante, las grandes amplitudes continúan después del shock principal, en tanto que en presencia del amortiguador las amplitudes decrecen rápidamente.
|
Fig. 6-10 Respuesta en desplazamiento del tablero según análisis elasto-plástico (Niihara et al, 1994) |
En 1995, Ali y Abdel-Ghaffar realizaron un estudio similar al realizado en 1991, en el cual propusieron un puente en configuración tipo arpa con la incorporación de dispositivos pasivos de control de vibraciones, consistentes en apoyos de goma con núcleo de plomo.
Kitazawa et al (1994), desarrollaron un tipo especial de amortiguador viscoso para puentes atirantados de gran luz en Japón. Propusieron un amortiguador tipo veleta para el cual obtuvieron sus características dinámicas a través de pruebas de carga, encontrando que el desempeño del amortiguador era bueno, sobre todo cuando era aplicado en estructuras de largo período, como en puentes de tirantes de gran luz. La propuesta del amortiguador se aprecia en la Fig. 6-11.
|
Fig. 6-11 Amortiguador tipo veleta (Kitazawa et al, 1994) |
En esta oportunidad se mejoró el modelo de análisis del puente, al incluir una modelación por elementos finitos basada en la formulación Lagrangiana total. Además se incluyó una modelación isoparamétrica de 4 nodos para los cables, a modo de tener en cuenta las vibraciones de éstos en su plano y fuera de él. Se estudiaron además varias propuestas de dispositivos, tales como los apoyos de goma con núcleo de plomo y los dispositivos de extrusión. La conclusión general fue que el uso de dispositivos de disipación de energía ofrece ventajas potenciales para el diseño sismo-resistente de puentes. Concluyeron además que los puentes de tramos más cortos son mejores candidatos para una mayor efectividad de los dispositivos.
Otra propuesta de protección sísmica pasiva fue estudiada por Villaverde y Martin (1995). En su estudio, investigaron la efectividad de agregar a los puentes de tirantes accesorios de relativa poca masa, alto amortiguamiento y frecuencia natural igual a una de las frecuencias naturales del puente, a modo de reducir la respuesta global frente a excitaciones sísmicas. El estudio se basó en la formulación hecha en edificios, en donde se mostró que su inclusión aumentaba el amortiguamiento estructural. La investigación incluyó pruebas numéricas y experimentales. Para el estudio numérico, se modeló un puente atirantado a través de elementos finitos y se analizó con y sin los accesorios de amortiguamiento adicional. En las pruebas experimentales, un puente de tirantes de 3.7 m de largo y un sistema de accesorios consistente en pequeñas masas, un pequeño resorte y un pequeño amortiguador viscoso fueron construidos. Las pruebas numéricas arrojaron una reducción de la respuesta longitudinal en más de un 88%, en tanto que las pruebas experimentales entregaron una reducción longitudinal de la respuesta de un 41%.
Un estudio más reciente hecho por Vader y McDaniel (2004), investigó el uso de amortiguadores viscosos y de fricción insertados entre los shaft verticales de la torre para el nuevo puente San Francisco – Oakland. El estudio se centró en comparar la respuesta sísmica al colocar tales dispositivos para las dos propuestas de puentes: atirantado y suspendido. El comportamiento de los dispositivos fue comparado con un nuevo dispositivo shear link anteriormente propuesto. Además fueron considerados los efectos de la directividad de la ruptura de falla, para averiguar si los movimientos de pulso generados reducían la funcionalidad de los amortiguadores. Los resultaron mostraron que efectivamente los efectos de la directividad de la ruptura de la falla reducen el desempeño sísmico de los amortiguadores. La Fig. 6-12 muestra los resultados de la respuesta en la torre para la propuesta de puente atirantado considerando los dos dispositivos propuestos (amortiguador viscoso y amortiguador de fricción) comparados con el dispositivo Shear Link, considerando dos posibles configuraciones de los dispositivos: en diagonal y atravesado.
Los resultados muestran que la disposición de amortiguadores de fricción en diagonal trabaja bien en el modelo de puente atirantado, sin embargo, generan muy altos valores del esfuerzo cortante, y por tanto, los amortiguadores viscosos son la mejor opción en este caso. Estos últimos reducen los momentos en la torre y los desplazamientos relativos, al mismo tiempo que mantienen los esfuerzos de corte basal a niveles cercanos a los determinados para el puente considerando la incorporación de dispositivos shear link.
En otro estudio, Xu et al (2004), investigaron el comportamiento del puente atirantado Canal Norte, en la Bahía Hang Zhou (China). En su trabajo, propusieron el uso de amortiguadores de fluidos viscosos dispuestos longitudinal y transversalmente para mejorar las condiciones de respuesta frente a vibraciones en general, en ambas direcciones principales. Discutieron además sobre cómo combinar el sistema estructural general con el sistema de reducción de vibraciones a modo de satisfacer las necesidades de uso normal y las condiciones sísmicas.
6.1.2. El puente Rion-Antirión, Grecia
De entre los puentes atirantados de gran luz que incorporan dispositivos adicionales de protección sísmica pasiva, se encuentra el recientemente inaugurado Puente Rion – Antirión, en el Golfo de Corinto, Grecia. El puente, localizado en una zona de alta sismicidad generado por fallas locales activas, consiste en un sistema atirantado de varios claros, con tablero continuo y totalmente suspendido, como se aprecia en la Fig. 6-13. La longitud total del puente es de 2252 m, dividido en tres claros de 560 m y dos de aproximación de 286 m cada uno. La Fig. 6-14 muestra una vista en elevación del puente. La descripción general del puente, y sus aspectos básicos relativos al diseño y construcción se pueden encontrar en los trabajos de Combault et al (2000), Teyssandier (2002) y Teyssandier et al (2003).
El puente fue diseñado para soportar eventos sísmicos con una aceleración efectiva máxima del suelo de 0.48g, y movimientos tectónicos entre dos pilas consecutivas de hasta 2 m en cualquier dirección. Esto fue posible gracias al empleo de un sistema de disipación de energía que conecta el tablero con cada pila y limita su movimiento durante la ocurrencia de un sismo intenso, mientras que disipa energía (Álvarez, 2004).
|
Fig. 6-15 Espectro de diseño (Combault et al, 2000) |
Los aspectos básicos del diseño sísmico del puente incluyen un espectro de respuesta para un período de retorno de 2000 años (Fig. 6-15) y una aceleración espectral máxima de 1.20g. Para el análisis dinámico, se utilizó un modelo de elementos finitos 3D de toda la estructura, tomándose en cuanta una serie de aspectos muy importantes, de entre los que se destacan (Combault et al, 2000):
- Comportamiento histerético no lineal del suelo reforzado
- Posibles deslizamientos de la base de la pila en el lecho de grava
- Comportamiento no lineal de las pilas
- Comportamiento no lineal de los tirantes
- Comportamiento no lineal del tablero compuesto
- Efectos de segundo orden
El sistema amortiguante está formado por fusibles y amortiguadores viscosos actuando en paralelo, conectando el tablero con las pilas en dirección transversal. Los fusibles se encuentran diseñados para trabajar como conexiones rígidas para soportar sismos moderados y las altas cargas de viento. Ante la ocurrencia del sismo de diseño, los fusibles están calculados para fallar, dejando libres a los amortiguadores viscosos para disipar la energía inducida (Álvarez, 2004). La Fig. 6-16 muestra la disposición del sistema de aislación y disipación en el puente, mientras que la Fig. 6-17 muestra un esquema de los fusibles empleados.
|
Fig. 6-16 Disposición del sistema de aislamiento eastomérico y disipación de energía longitudinal y transversal (Infanti et al, 2004) |
Fig. 6-17 Configuración de los fusibles estructurales (Infanti et al, 2003) |
En cada pilono se instalaron 4 amortiguadores viscosos, con una capacidad de 3500 kN de reacción cada uno y una constante de amortiguamiento C = 3000 kN/(m/s)0.15. Los fusibles son de una capacidad de 10500 kN. Para las pilas de transición se emplearon los mismos amortiguadores anteriores pero fusibles estructurales de 3400 kN de capacidad.
El comportamiento y los requerimientos del sistema de disipación fueron evaluados mediante un análisis temporal no lineal de un modelo 3D de la estructura. Sin embargo, las hipótesis de diseño y el comportamiento real de los dispositivos debían ser verificados en prototipos a escala natural. Los amortiguadores y fusibles fueron ensayados en el Laboratorio de la Universidad de California en San Diego (USA). En esta temática, Infanti et al (2003, 2004) muestran en sus trabajos la metodología, implementación y resultados de los ensayos realizados a los dispositivos en el laboratorio a escala natural. Las Figs. 6-18 y 6-19 muestran el prototipo de los amortiguadores montado en el marco de pruebas y el ensayo de fatiga para los fusibles respectivamente.
|
Fig. 6-18 Prototipo del amortiguador viscoso montado en marco de pruebas (Infanti et al, 2004) Fig. 6-19 Fusible estructural en una prueba de fatiga (Infanti et al, 2004) |
Otra novedad que incluye el puente Rion-Antirión, es la adición de desviadores antisísmicos, que actúan como verdaderos amortiguadores para mitigación de vibraciones en los cables. Aunque en general también se emplean amortiguadores hidráulicos en puentes de tirantes y colgantes para disminuir el efecto del Rain Vibration y mejorar así las condiciones aerodinámicas, lo cierto es que además tienen un propósito anti-sísmico, ya que como fue comentado en los capítulos anteriores, bajo ciertas circunstancias las vibraciones de los cables pueden modificar la respuesta sísmica global del puente e introducir paquetes de energía no despreciable en modos de vibración superiores. En este sentido, Lecinq et al (2003) entregan una descripción de las medidas de mitigación que existen hoy en día para aumentar el amortiguamiento de los cables y describe los desviadores antisísmicos empleados en el puente Rion-Antirión. La Fig. 6-20 muestra una vista renderizada de un amortiguador hidráulico interno empleado para mitigación de vibraciones en los tirantes.
La Fig. 6-21 muestra un amortiguador externo para vibración de cables, en este caso, utilizado en el puente Normandía (Francia). La Fig. 6-22 muestra la disposición de la sección de los desviadores antisísmicos utilizados en el puente Rion-Antirión.
|
Fig. 6-20 Amortiguador hidráulico interno (Lecinq et al, 2003) |
Fig. 6-21 Amortiguador hidráulico externo (Lecinq et al, 2003) |
En su Tesis de Master, Morgenthal (1999) realizó un estudio detallado sobre el comportamiento sísmico del puente Rion-Antirión. En él, describió el puente y planteó un modelo de análisis a través de elementos finitos, para posteriormente estudiar medidas de control de la respuesta sísmica a través de la incorporación y prueba de distintos dispositivos, entre los que se encuentran fusibles estructurales, transmisores de choque, amortiguadores hidráulicos y aisladores elasto-plásticos. Realizó finalmente un estudio paramétrico del comportamiento de distintos dispositivos de aislación del tablero.
6.2. Comportamiento de Puentes con Sistemas Activos, Semi-activos e Híbridos
6.2.1. Investigaciones y aplicaciones recientes
El campo del Control de Vibraciones ha experimentado una inmensa evolución en los últimos años. Diferentes técnicas han sido desarrolladas y muchos dispositivos distintos se encuentran disponibles hoy en día. De entre las estrategias, el control activo se basa esencialmente en evitar el impacto de las fuerzas externas (no solo de origen sísmico) a través de modificaciones favorables de las vibraciones (Morgenthal, 1999). Aunque en estricto rigor los sistemas activos, semi-activos e híbridos son diferentes, en este trabajo hemos decidido incluirlos dentro de un solo gran grupo, para diferenciarlo de los sistemas pasivos que no necesitan energía externa para funcionar. Esta forma de presentar esta parte del trabajo es más cómoda, dado que el tema a tratar se refiere a estrategias que necesitan de energía para actuar, de un controlador para ejecutar el algoritmo de control y de actuadores en mayor o menor grado.
Aunque el control activo en puentes de tirantes fue propuesto por primera vez a fines de los años 70, los estudios y aplicaciones no comenzaron sino hasta hace algo más de una década, enfocándose principalmente en el empleo de estrategias para mitigar el efecto de las vibraciones en los cables, ya sea por efectos aerodinámicos, por sismo o inducidos por las cargas de tráfico. En este sentido, algunas soluciones especiales como el Control de Tendones Activos (Active Tendon Control) han sido desarrolladas desde comienzo de los años 90. En esta estrategia, se instalan sensores en los cables, muy cerca de la zona de anclaje al tablero, para detectar los movimientos de éste. Los movimientos detectados son procesados a través de un algoritmo de control que envía la orden a los actuadores servo hidráulicos o de otro tipo, fijos en los extremos de los cables, para así realizar las correcciones correspondientes. Estos actuadores cambian la tensión de los cables en tiempo real, lo cual puede ser muy ventajoso. Aunque esta estrategia es muy efectiva, los costos en general son muy elevados, la manutención debe realizarse con cuidado y por personal especializado, y la dependencia del suministro eléctrico puede ser crítica durante un evento sísmico de magnitud. Warnitchai et al (1993) han estudiado experimentalmente el uso de tendones activos en puentes de tirantes, tal como se aprecia en la Fig. 6-23.
|
Fig. 6-23 Control de Tendones Activos (Warnitchai et al,1993) |
Magana et al (1994) propusieron un controlador no lineal activo para reducir las deformaciones del tablero de puentes atirantados excitados verticalmente. La principal característica del nuevo controlador era que no empleaba información acerca de la estadística del movimiento del suelo ni las variaciones en los parámetros del modelo, empleando sólo los valores máximos de las distribuciones. El desempeño del controlador fue verificado a través de simulaciones computacionales en las que se empleó un sistema de control de lazo cerrado, resultando un buen sistema para el control de las vibraciones verticales.
Los primeros estudios analíticos y experimentales sobre la aplicación de sistemas activos en puentes de tirantes fueron desarrollados por Schemmann y Smith (1996, 1998). El primer trabajo consistió en la realización de un modelo analítico experimental de un puente atirantado controlado activamente, y desarrollado como parte de un proyecto de investigación interdisciplinario e inter-institucional para analizar los efectos del control de vibraciones activo en puentes atirantados sujetos a acciones sísmicas. El segundo trabajo presentado, se basó en el puente Jindo, Korea del Sur. El objetivo de la investigación era mejorar la comprensión de cómo las complejidades asociadas a la modelación de puentes atirantados, tales como el comportamiento no lineal y la participación de modos superiores acoplados en la respuesta sísmica, afectan la efectividad de los esquemas de control activo. La investigación se dividió en dos partes: la primera, que estudió aspectos vinculados a la modelación, y la segunda parte, que estudió aspectos relacionados al análisis. Los resultados del trabajo mostraron significativas reducciones en los esfuerzos internos máximos, y de probar varias configuraciones posibles de los actuadores, se concluyó que la disposición más efectiva es aquella en la cual los actuadores de localizan cerca del centro del claro principal del puente.
|
Fig. 6-24 Historias temporales de desplazamientos controlados (línea continua) y no controlados (línea segmentada): (a) Modo 1 controlado; (b) modos 1, 9, 26 y 35 controlados (Schemmann y Smith, 1998) |
El estudio mostró que sólo necesitan ser controlados los modos de primer orden para reducir la respuesta en desplazamiento; sin embargo, el control de modos superiores es esencial para reducir las fuerzas. Por otro lado, el control de modos acoplados puede aumentar la respuesta de la estructura en términos de fuerzas.
La Fig. 6-24 muestra parte de los resultados obtenidos, en términos de desplazamientos laterales en la mitad del claro, sujeto a excitación sísmica uniforme.
Otro trabajo muy interesante, desarrollado por Goto e Higuchi (1996), se refiere a la aplicación de sistemas activos en puentes de tirantes en construcción. En su estudio, investigaron la aplicabilidad de usar sistemas activos de rigidez variable para mejorar el comportamiento sísmico de puentes atirantados de hormigón pretensado en construcción, a través de simulaciones numéricas en un puente modelo. Los resultados mostraron una significativa reducción de la respuesta en aceleración.
Shoureshi et al (1999), presentaron una estrategia de control híbrida adaptativa en base a técnicas de retroalimentación, para lo cual ensayaron un modelo físico a escala de un puente atirantado existente. Emplearon un método analítico para localizar los sensores y actuadores en la estructura en base a datos de formas de deflexión operacional (ODS) dentro de los rangos frecuenciales de interés. Los resultados mostraron que el control híbrido de vibraciones era eficiente para controlar vibraciones aleatorias (como las de origen sísmico), siempre y cuando se haga una óptima localización de los sensores y actuadores.
Otras estrategias recientes acerca del control activo en puentes de tirantes han sido propuestas en los trabajos de Li et al (2001) y Helduser y Bonefeld (2001). El primero investiga la aplicación de amortiguadores de masa activa (AMD) en puentes atirantados de gran luz, empleando el clásico algoritmo de control óptimo lineal y aplicado al segundo puente Nanjing Yangtze, China; mostrando que el empleo de tal estrategia es factible y beneficiosa en la reducción de la respuesta sísmica, sobre todo por el hecho de que basta con controlar el primer modo para reducir significativamente los desplazamientos laterales. El segundo trabajo, introduce el uso de actuadores electro-hidráulicos como estrategia de protección activa en puentes de tirantes.
Varios de los trabajos más recientes sobre protección sísmica activa/semi-activa en puentes atirantados, se refieren al estudio de los algoritmos de control y su aplicación en sistemas activos. Las estrategias de control activo son inútiles si el algoritmo de control no es lo adecuadamente fiable, robusto y eficiente. Algunos trabajos recientes en este sentido, comienzan a desplazar a los clásicos algoritmos de control cerrado, lineal, Lyapunov o Bang-Bang, por mencionar algunos; como en la propuesta de control en base a Conjuntos Difusos de Magana y Rodellar (2000), o la reducción de la respuesta sísmica basada en algoritmos de Control Modal que proponen Wang et al (2004). En este sentido, Iemura y Pradono (2002, 2004 y 2005) han realizado varias investigaciones acerca del control de la respuesta sísmica semi-activa en puentes atirantados. En los primeros dos trabajos, estudiaron la efectividad del control de la respuesta sísmica pasiva y semi-activa a través de análisis numéricos en un puente existente en Japón y en un puente benchmark en USA, los que contaban con apoyos fijos entre el tablero y las torres, y reemplazando estas conexiones por amortiguadores y aisladores. Estos últimos eran de tipo elástico e histerético, en tanto que los amortiguadores eran de tipo lineal y variable, que usaban control semi-activo que incorporaban un algoritmo de control en base a rigidez pseudo-negativa. La principal ventaja de esta estrategia, es que los loops histeréticos de rigidez pseudo-negativa producidos por el amortiguador variable, combinado con una curva de rigidez positiva de la conexión torre-tablero, crean características de comportamiento fuerza-deformación muy cercanas a la elasto-plástica perfecta, con una gran razón de amortiguamiento. Además de ello, el algoritmo de control es simple y los sensores son requeridos sólo en los amortiguadores para medir los desplazamientos y velocidades relativas. La Fig. 6-25 muestra el puente elegido para su análisis en Japón (puente Tempozan, Kobe), mientras que la Fig. 6-26 muestra los modelos estructurales para el puente original (izquierda) y modificado (derecha).
|
Fig. 6-26 Modelos estructurales del puente original (izquierda) y modificado con el sistema de aislamiento y amortiguamiento adicional (derecha) (Iemura y Pradono, 2004)
|
La estrategia era crear loops histeréticos de rigidez pseudo-negativa a través de amortiguadores de orificio variable (Fig. 6-27). El amortiguador variable que produce este tipo de histéresis es entonces llamado Amortiguador de Rigidez Pseudo negativa (PNS). El punto es que, por ejemplo, los amortiguadores viscosos generan curvas de histéresis elípticas (Fig. 6-28b) al ser excitados por movimientos sinusoidales. Puesto que la fuerza transmitida a los otros miembros es la suma de las fuerzas del amortiguador y las fuerzas de rigidez de los otros apoyos existentes (Fig. 6-28a), obtenemos la curva de histéresis de la Fig. 6-28c. Por otro lado, al producir curvas de histéresis de rigidez pseudo-negativa (Fig. 6-28e), la suma con las fuerzas de rigidez de los apoyos (Fig. 6-28d) produce la curva de histéresis de la Fig. 6-28f. Aquí, las fuerzas máximas son controladas por las fuerzas de los otros apoyos, pero con un área encerrada mucho mayor, lo que implica una mayor disipación de energía.
En los análisis, se consideraron los efectos de la interacción suelo-estructura y efectos tridimensionales, demostrando que los PND reducen la respuesta sísmica mejor que los amortiguadores de fluido viscoso pasivo. Finalmente, en su más reciente trabajo, Iemura y Pradono (2005), se refieren a la aplicación del algoritmo LQR (Linear Quadratic Regulador) de control semi-activo para la respuesta sísmica en puentes de tirantes. Aunque este algoritmo aplicado al control sísmico ha sido estudiado con profundidad, en esta nueva investigación se discuten los loops histeréticos producidos por el control LQR y se muestra la importancia de investigar tales loops para la respuesta sísmica. Se propone además un método para reproducirlos, cuando trabajan en conjunto con dispositivos de orificio variable.
Una de las estrategias de control semi-activo en puentes de tirantes que empieza a imponerse, es sin duda el empleo de los fluidos controlables. Entre ellos, el uso de los amortiguadores magnetoreológicos es que mejor futuro tiene, por sus múltiples bondades, entre las que se destacan la poca energía que requieren para operar y su buen desempeño. En este sentido, el trabajo presentado por Chen et al (2003) muestra el único caso de aplicación práctica conocida de estos dispositivos en puentes atirantados que actualmente se tiene. La aplicación de los dispositivos fue hecha al puente Dongting Lake, que cruza el lago Dongting en su encuentro con el río Yangtze, en el sur de China. Después de que el puente fue completado en 1999, se apreció que los cables sufrían los efectos de vibración debidos a la lluvia y viento (rain-wind-induced vibration). Para investigar la factibilidad de emplear dispositivos magnetoreológicos como solución al problema, se desarrolló un proyecto de investigación conjunto entre la Universidad de China Sur Central y la Universidad Politécnica de Hong Kong.
|
Fig. 6-29 Amortiguadores MR en puente Dongting Lake (Spencer y Nagarajaiah, 2003) |
A la luz de los buenos resultados de las investigaciones, se decidió implementar estos dispositivos como solución al problema, aplicándolos a los 156 cables más largos. La instalación finalizó en junio del 2002, constituyendo la primera aplicación en el mundo de estos dispositivos en puentes de tirantes. El trabajo de estos investigadores, describe la implementación de los dispositivos para la reducción de las vibraciones de los cables. La Fig. 6-29 muestra un par de fotografías con los dispositivos instalados en el puente.
Un estado del arte sobre control de la respuesta sísmica activa y semi-activa se puede encontrar en el trabajo de Ni et al (2001).
6.2.2. Problema benchmark del puente Memorial Bill Emerson, USA
El puente memorial Bill Emerson se ubica en Cape Girardeau, Missouri, USA, y fue inaugurado al uso público en diciembre del 2003 para reemplazar al antiguo puente Cape Girardeau, sobre el río Mississippi. La estructura es un puente atirantado con una configuración de doble plano de tirantes dispuestos en semi-arpa, con un vano principal de 345 m, como se aprecia en las Figs. 6-30 y 6-31.
|
Fig. 6-30 Vista general del puente Memorial Bill Emerson |
Fig. 6-31 Vista general del puente Memorial Bill Emerson |
Para el puente en cuestión, se planteó un problema benchmark con el propósito de proveer un marco de pruebas y ensayos para el desarrollo de estrategias de control en puentes de tirantes sometidos a acciones sísmicas. Cada participante de este estudio benchmark debía plantear la definición del problema y evaluar y reportar los resultados de la estrategia propuesta. La definición del problema y los modelos dinámicos en MATLAB® (1997), aún se encuentran disponibles en la página web http://wusceel.cive.wustl.edu/ (Dyke et al, 2002). La Fig. 6-32 muestra la definición del puente a considerar en todas las propuestas.
Basado en dibujos detallados del puente, se desarrolló un modelo de evaluación tridimensional a partir de las ecuaciones de equilibrio generadas para la posición deformada de la estructura. Los criterios de evaluación presentados para el problema de diseño eran consistentes con las metas del control de la respuesta sísmica del puente. Cada participante en este estudio de control del puente de referencia, tenía la tarea de definir (incluso los dispositivos, sensores y algoritmos), evaluar e informar acerca de las estrategias de control propuestas. Estas estrategias o pueden ser pasivas, activas, semi-activas o una combinación de ellas. Un programa de simulación fue proporcionado para facilitar la comparación directa de las capacidades y eficacia de las estrategias de control, proporcionándose además una muestra de estrategia de control a modo de ejemplo.
El problema benchmark en Cape Girardeau se dividió en dos etapas:
- Fase 1: Control del movimiento longitudinal
- Fase 2: Control del movimiento bi-direccional, con consideración de efectos de la variabilidad espacial.
Un resumen del problema benchmark del puente Memorial Bill Emerson se puede encontrar en el artículo presentado por Dyke et al (2000).A raíz de esta propuesta, se recibieron y se continúan aceptando muchas estrategias de control, fundamentalmente en base a control híbrido y semi-activo.
De entre las estrategias de control híbrido que se han recibido, se destacan las propuestas de Park et al (2003a, 2003b, 2003c), acerca del control híbrido para la fase II del problema mediante el empleo de dispositivos LRB como sistema pasivo y amortiguadores magnetoreológicos como sistema activo, usándose algoritmos de control LQG, Bang-Bang, H2 y H∞; Jung et al (2004c), que proponen una estrategia de control para la fase I del problema en base a dispositivos LRB y semi-activos (como amortiguadores de fluido controlable o de orificio variable) empleando algoritmos de control Clipped Optimal; Park et al (2005), que proponen una estrategia de control difusa; Kim y Adeli (2005), que proponen un algoritmo de control en base a cuadrados mínimos lineales retroalimentados.
En cuanto a las estrategias de control semi-activo, se destacan los trabajos de He et al (2001), acerca del control semi-activo a través de amortiguadores de rigidez; Bakule et al (2002), que propusieron un esquema de control descentralizado; Ruangrassamee y Kawashima (2002), que propusieron el empleo de amortiguadores magnetoreológicos; Moon et al (2003), que propusieron para la fase I el empleo de amortiguadores magnetoreológicos con un esquema de control de modo deslizante (SMC); Iemura y Pradono (2003), que plantearon el uso de amortiguadores de orificio variable con control de la rigidez pseudo-negativa; Agrawal et al (2003), que estudiaron la efectividad y desempeño de algunos sistemas de control pasivo (amortiguadores de fluido viscoso lineales y no lineales) y semi-activo (amortiguadores de rigidez semi-activa y amortiguadores de fricción semi-activa); Jung et al (2003), que propusieron para la fase I del problema, el uso de amortiguadores magnetoreológicos con énfasis en el estudio de varios modelos dinámicos de comportamiento para los dispositivos; Dai et al (2004), que propusieron una estrategia de control semi-activa sobre la base del uso de amortiguadores magnetoreológicos controlados por un algoritmo clipped optimal y considerando el problema de la excitación de múltiples soportes; Loh y Chang (2005), que propusieron el uso de amortiguadores magnetoreológicos y compararon la respuesta empleando varios algoritmos de control.
Capítulo 7. Aspectos del Análisis y Diseño
El análisis estructural de un puente dependerá indudablemente del modelado de la estructura, que se reflejará en el grado de precisión en los resultados. El desarrollo vertiginoso de ordenadores cada vez más potentes y capaces, permite hoy en día resolver estructuras de gran tamaño, más complejas, y probarlas para una infinidad de casos en relativamente poco tiempo. Por ello, el tiempo de computación necesario dependerá de la modelación elegida y de la precisión deseada en los resultados. De aquí la evidente necesidad de contar con una buena modelación de la estructura, ya que en definitiva, de ello dependerá directamente lo que obtengamos como resultado. Dado que la mayor parte de los aisladores y disipadores de energía trabajan en régimen no lineal, es recomendable que el análisis del sistema puente – aislador, considere los aspectos no lineales, de preferencia mediante el uso de acelerogramas naturales propios de la zona de interés. A pesar de la actual capacidad de los ordenadores y de la disponibilidad de más y mejores programas de análisis de puentes y estructuras en general que permiten el análisis no lineal, se reconoce que el tiempo y nivel de conocimiento que debe tener el proyectista responsable, son dos limitaciones serias del uso extensivo de éstos métodos en la práctica (Jara y Casas, 2002). Por ello, muchas veces es preferible el uso de métodos simplificados que conducen a resultados más o menos precisos. El caso de los puentes de tirantes de gran luz es, en este sentido, un problema bastante más complejo, debido al marcado comportamiento no lineal que presentan estas estructuras, lo que obliga a realizar los análisis teniendo en cuanta dicha condición, y escapando a los métodos más sencillos de análisis modal y estático equivalente que a través de la definición iterativa de la rigidez y amortiguamiento equivalente permiten la resolución de estructuras relativamente complejas.
El diseño de la mayoría de los puentes atirantados en zonas de moderada y alta sismicidad es por lo general bastante más complejo que el diseño de puentes convencionales. Los códigos de diseño de puentes y las previsiones más modernas han sido desarrollados en términos generales y para puentes estándar, con el objeto de tener estructuras seguras y económicas. Como filosofía general de diseño, se establece la imperiosa necesidad de que frente a un sismo extraordinariamente severo, y por ende poco frecuente, se acepte daño estructural, pero permitiendo las comunicaciones de emergencia. Para los nuevos puentes de tirantes, las previsiones de los códigos de diseño pueden no ser aplicables, por lo que es necesario el urgente desarrollo de guías y recomendaciones generales de diseño sísmico para estas estructuras, basado en investigación numérica, experimental y a través de modelos a escala. Además, la falta de información referente al verdadero desempeño de estos puentes durante terremotos severos, aumenta la incertidumbre no solamente en términos de un adecuado diseño, sino también debido al aumento gradual en las mayores luces. (Abdel-Ghaffar, 1991).
A la fecha, las normas existentes se limitan a los sistemas de aislamiento y disipación de energía, sin incluir aspectos relacionados con sistemas híbridos, activos o semi-activos. Las especificaciones para el diseño de puentes con apoyos de neopreno con núcleo de plomo, editadas por el Ministerio de Obras y Desarrollo de Nueva Zelanda en 1983, constituyen las primeras normas de diseño de puentes con sistemas adicionales de protección sísmica basada en aislamiento y disipación de energía. Posteriormente, en los años 90 se publican por primera vez recomendaciones oficiales en USA (1991, 1999), Japón (1996), Italia (1991) y en general en Europa a través del Eurocódigo 8 (CEN, 1998a, 1998b).
En las siguientes páginas se presentan algunos aspectos generales relacionados con el análisis y diseño de puentes que incorporan dispositivos adicionales de disipación de energía. La primera parte se refiere a aspectos relacionados con el análisis estructural, en segundo lugar se presentan aspectos vinculados a la filosofía general de diseño, consideraciones sobre la entrada sísmica y la incorporación de sistemas pasivos de protección, con una orientación hacia los planteamientos y sugerencias de las normativas existentes. La última parte se refiere a las consideraciones generales del Eurocódigo 8 parte 2.
7.1 Consideraciones Sobre los Métodos de Análisis
Existen diversas condiciones que se deben satisfacer para que los resultados de un modelo simplificado sean representativos de la realidad, por lo que deben conocerse detalladamente las limitaciones del modelo estructural y saber cuales son los requisitos bajo los cuales puede aplicarse. El método de análisis más conveniente depende de muchos factores como son: el tipo de terreno, la presencia de fallas activas cercanas, el tipo de dispositivo de control, las características estructurales del puente, la variabilidad espacial, el amortiguamiento, etc. En el caso de los puentes de tirantes el panorama es más complejo aún debido al comportamiento marcadamente no lineal que presentan las estructuras de gran luz. Además, el efecto de los cables, la interacción suelo-estructura, el tipo de apoyo tablero-torre y el tipo de atirantamiento entre otros, son aspectos decisivos en la modelación y el análisis. Por esta razón, en el caso de puentes de tirantes no es recomendable el uso de modelos estructurales planos ni el análisis mediante métodos lineales equivalentes, a pesar de estar permitido por casi todos los códigos de diseño.
En cuanto al análisis dinámico de los puentes de tirantes, tampoco es recomendado el método estático por su excesiva simplificación en este caso. El análisis mediante espectros de diseño y el método de análisis a través de historias temporales son los más usados y que mejores resultados entregan. Para el caso del análisis en el tiempo para puentes con dispositivos pasivos, el procedimiento es el mismo que se establece en puentes convencionales, con el cuidado de que las historias de aceleración que se utilicen se ajusten lo más posible a los espectros del sitio que proponen las normas para mantener el mismo nivel de riesgo, y que el modelo inelástico de la estructura y de los aisladores sea representativo de su comportamiento. En este mismo sentido, Jara y Casas (2002) recomiendan que:
- Se utilicen al menos tres pares de acelerogramas horizontales de eventos registrados. Se pueden usar acelerogramas sintéticos pero se da preferencia al uso de acelerogramas naturales. Los acelerogramas deben ser escalados para los distintos niveles de intensidad recomendados por las normas.
- La duración de los acelerogramas debe ser congruente con las características del foco del sismo de proyecto y, en el caso de emplazamientos inferiores a 15 km de una falla activa importante, deberán incorporarse los fenómenos de campo cercano.
- La revisión de las deformaciones, desplazamientos y tensiones se hará en base a la media de los valores máximos del conjunto de acelerogramas que se emplean para cada nivel de intensidad.
- Deben considerarse los efectos de fricción, carga vertical, bilateral y/o velocidad de carga, en los casos en que el sistema aislante se vea afectado por estos parámetros.
- Las características de deformación de los elementos en los que se admite cierta plastificación, se aproximarán lo más fielmente posible al comportamiento post-elástico real.
El método de análisis en el tiempo realizado con registros reales y considerando los aspectos no lineales, es considerado el método más preciso y aplicable en todos los casos de puentes atirantados que incorporen o no dispositivos adicionales de disipación de energía. Los métodos alternativos simplificados son útiles utilizarlos en las etapas de prediseño, ya que significan un ahorro importante de tiempo, pero nunca para ser empleados en un diseño definitivo.
Kawashima (2000), plantea una serie de recomendaciones referentes al análisis sísmico de puentes en general. Establece que en las recomendaciones provisionales de 1996 del ATC-32 para los puentes de California, los métodos se clasifican en Análisis Estático Elástico (AEE), Análisis Dinámico Elástico (ADE), Análisis Estático Inelástico (AEI) y Análisis Dinámico Inelástico (ADI). En el AEE, la respuesta elástica del puente se divide entre el factor de comportamiento y los elementos estructurales se dimensionan con el enfoque de diseño por capacidad. Por otro lado, en el AEI se emplea un análisis push-over; que es muy útil para evaluar el comportamiento estructural y las demandas sísmicas, aunque no puede reproducir fielmente la respuesta dinámica (Krawinkler y Seneviratna, 1998). Los requerimientos mínimos de análisis se presentan en la tabla 7-1; dichos requerimientos varían con la categoría del puente, el tipo de configuración y el nivel de evaluación. La configuración tipo I considera puentes con comportamiento simple, incluyendo puentes con superestructura continua, vanos bien balanceados, pilas con rigidez similar y respuesta vertical despreciable. La configuración tipo II considera puentes con respuesta más compleja, que no pueden representarse adecuadamente mediante un AEE, incluyendo puentes con articulaciones intermedias en la superestructura, configuración irregular, pilas de rigidez no uniforme, tableros muy esviados o que puedan ser excitados por aceleraciones verticales del suelo. En las especificaciones CALTRANS (1999), se emplean los métodos AEE, ADE y AEI (Kawashima, 2000).
| Importancia | Configuración | Evaluación de la funcionalidad | Evaluación de la seguridad |
| Puente ordinario | Tipo I | No se requiere | AEE o ADE |
| Tipo II | No se requiere | ADE | |
| Puente importante | Tipo I | AEE o ADE | AEE o ADE |
| Tipo II | ADE | ADE, AEI y ADI |
Si se sigue la clasificación de la tabla 7-1, el AEE y el ADE se utilizan en el Eurocódigo 8 (CEN, 1998b) y en la instrucción española IAP (Ministerio de Fomento, 1998). En ellos se proporciona una descripción detallada para tres métodos de AEE: modelo de tablero rígido, modelo de tablero flexible y modelo de pila única. El método se selecciona dependiendo de la deformación relativa del tablero y de la interrelación de la respuesta de las pilas adyacentes. En ambas normas se prevé el análisis no lineal en el dominio del tiempo, estableciéndose según el Eurocódigo 8 (CEN, 1998b), que este método debe emplearse en combinación con un análisis con espectros de respuesta.
En Nueva Zelanda se usan el AEE, el ADE y el ADI (Kawashima, 2000). Los análisis dinámicos (ADE y ADI) se recomiendan cuando no resulta apropiado representar el puente mediante un sistema de un grado de libertad.
En Japón, los métodos analíticos también se escogen dependiendo de la configuración estructural, como se muestra en la tabla 7-2. El análisis push over se usa para casi todos los puentes, en particular para el diseño de los puentes tipo pórtico. El ADI es ampliamente usado; como los datos de entrada requeridos para un análisis push over y un ADE son casi los mismos que para un ADI, este último se puede efectuar fácilmente una vez que los datos han sido preparados. Dado el avance tecnológico en cuanto a informática, se prevé una clara tendencia hacia el uso más frecuente del ADI.
| Categoría | Evaluación de la funcionalidad | Evaluación de la seguridad | |
| Puentes con respuesta estructural simple | AEE | AEI | |
| Puentes con respuesta estructural compleja | Es aplicable el análisis estático equivalente | AEE y ADE | AEI y ADI |
| No es aplicable el análisis estático equivalente | ADE | ADI | |
7.2. Consideraciones Para el Diseño
7.2.1. Filosofía general de diseño
La filosofía actual de diseño de puentes es la misma que ha sido aceptada prácticamente por todos los reglamentos desde la década de 1970: se pretende que los puentes sean funcionales y que los componentes estructurales permanezcan dentro del régimen elástico, después de ocurrido un evento moderado o pequeño; por otra parte, en el caso de ocurrencia de un sismo severo, se acepta cierto nivel de daño, sin poner en riesgo la estabilidad de la estructura (Jara y Casas, 2002). En este sentido, casi todos los códigos adoptan como filosofía general de diseño el hecho de que un puente debe ser diseñado para que, ocurrido un evento extremo, se mantengan las comunicaciones de emergencia.
Dentro de la filosofía de diseño se reconoce la importancia de cada puente desde el punto de vista del impacto económico y social que pueda ocasionar su derrumbe o la suspensión del tránsito. Este aspecto se incluye en la mayor parte de las normas mediante un factor que incrementa la intensidad sísmica, sin embargo, en la última versión del Manual japonés Menshin (Japan Road Association, 1996), la importancia del puente se incluye en el factor de ductilidad admisible, en el que también se incluye el desplazamiento último del elemento y la duración del movimiento sísmico. De este modo, en los sismos de campo cercano, los elementos estructurales no experimentan muchos ciclos repetidos de carga y el factor de reducción puede alcanzar valores de 3.6 en un puente ordinario y de 3.2 en puentes importantes. Para un puente ordinario expuesto a un sismo de larga duración, que puede llevar los elementos a varios ciclos de carga y descarga en el rango inelástico, el factor de reducción máximo es de 2.6; mientras que en un puente importante es de 2.4, o sea, un 8% menor. La diferencia se fundamente en el hecho del deterioro que sufre un elemento cuando se somete a ciclos repetidos de carga y descarga. En el caso de puentes con disipadores de energía, los sismos de campo cercano no favorecen la disipación histerética de los dispositivos, por lo que su inclusión es más delicada. Es indudable que el fallo de un puente especialmente importante es inconcebible, por lo que parece razonable proporcionar mayor capacidad a este tipo de estructuras (Jara y Casas, 2002).
A pesar de que algunos puentes han cumplido con los criterios de diseño especificados en la actual normativa, su comportamiento sísmico no ha sido satisfactorio, aún en sismos considerados moderados. Los daños que han experimentado y las cuantiosas pérdidas derivadas de las limitaciones en su uso, han mostrado la necesidad de modificar algunos aspectos del diseño tradicional. En base a esto, los criterios de diseño sísmico están sufriendo un cambio en su filosofía, que está dando origen a una nueva generación de códigos.
Las bases de la filosofía de diseño y los criterios de desempeño sísmico son más o menos los mismos entre los diferentes códigos; por ejemplo, para sismos de pequeños a moderados los puentes deberían exhibir un comportamiento básicamente elástico, sin daño significativo, mientras que para sismos de gran magnitud los puentes no debieran colapsar, siguiendo en gran medida los criterios empleados en los edificios. Sin embargo, las tendencias parecen estar cambiando: los puentes ubicados en las vías de comunicación importantes deberían tener un desempeño sísmico más alto que los edificios, ya que la atención de los inmuebles dañados no podría llevarse a cabo si los puentes, teniendo el mismo nivel de desempeño sísmico que los edificios, sufren daño severo y no permiten el tráfico vehicular inmediatamente después de la inspección preventiva (Kawashima, 2000). En un trabajo de reciente publicación, Calvi (2004), describe la experiencia y las innovaciones en materia de diseño sísmico de puentes. Realiza una descripción de las actuales filosofías de diseño, que a continuación se resumen:
Diseño por resistencia (diseño elástico): Los puentes han sido diseñados con referencia a los espectros de respuesta en aceleración por más de 40 años por razones más bien históricas, ya que, en efecto, resulta más cómodo el diseño considerando que las acciones son fuerzas en vez de desplazamientos, temperatura o acciones de origen sísmico. La concepción primitiva de diseño sísmico era mantener a las estructuras en el rango elástico a través de la consideración de que la carga sísmica era un porcentaje del peso de la estructura, aplicado como carga lateral uniforme. Las consecuencias de esta aproximación se resumían en severas subestimaciones de las deformaciones sísmicas, combinaciones inadecuadas de los patrones de acción producidos por la gravedad y el sismo y con ello un detallado generalmente insuficiente.
Diseño por ductilidad: A medida que fueron comprendidas las características dinámicas de la respuesta sísmica, y que se entendió que las estructuras sobrevivían a respuestas de aceleración que aparentemente excedían los valores de resistencia última, se adoptó el concepto de ductilidad. Este fue entonces, una forma de reconciliar las inconsistencias en el fundamento del diseño por resistencia, en la cual se atribuía a la estructura una capacidad de deformarse inelásticamente sin pérdida significativa de resistencia. La mayoría de los códigos se basan todavía en estos conceptos. El espectro de aceleración elástico es reducido como una función de una ductilidad asumida, de modo que los llamados métodos de diseño por capacidad fueron aplicados para asegurar que los mecanismos post-elásticos se desarrollarían. En otras palabras, se concibe el diseño por ductilidad tal que las estructuras disipan la energía a través del daño, para lo cual la fuerza elástica es obtenida a partir del espectro de diseño elástico, y reducida por un factor de comportamiento que es función de la ductilidad admisible.
Diseño por desplazamiento: diseño basado en desempeño: El enfoque general del diseño sísmico, tanto en edificios como en puentes, es el de preservar la vida humana, sin tener la posibilidad de predecir el desempeño estructural ante un evento sísmico determinado. Aunque el colapso está prevenido para el sismo de diseño, no hay garantía de que la estructura pueda seguir usándose ante la ocurrencia de dicho evento. Luego, aunque se evite la pérdida de vidas, el costo económico puede ser muy alto. Como consecuencia, el desarrollo del diseño basado en desempeño ha surgido como una metodología más completa y racional para predecir, bajo cierto nivel de confianza, la respuesta sísmica de las estructuras basado en el nivel de diseño impuesto (adaptado de Álvarez, 2002). En este sentido, las pérdidas económicas sufridas por un cierto evento sísmico pueden ser limitadas, y la pérdida de vidas y de los servicios de emergencia necesarios en las operaciones posteriores al sismo, pueden ser reducidas. Así, en el caso de puentes se considera que es suficiente con tres niveles de desempeño:
- Operacional sin interrupción del tráfico
- Operacional con daños menores
- Nivel cercano al colapso
La importancia del puente también debe ser considerada en los objetivos de diseño. Los criterios para un diseño basado en desempeño aún están por ser definidos (Lobo, 2000; Floren y Mohammadi, 2001). La barrera más inmediata en la implementación del diseño basado en desempeño es el desarrollo de procedimientos necesarios para predecir adecuadamente el desempeño estructural de un puente ante un evento dado. Actualmente la investigación está en proceso de desarrollo de métodos para analizar puentes y sus componentes, que permitirán una evolución cuantificable del desempeño, por lo que aún queda mucho trabajo para alcanzar el nivel de certeza necesario para implementar un programa de diseño basado en desempeño (Álvarez, 2002). De acuerdo a Calvi (2004), existen fundadas razones que aconsejan la poca conveniencia de continuar con el uso de la metodología de diseño basado en fuerzas. Entre otras razones se destaca:
- Suposiciones no válidas para las relaciones entre los desplazamientos elástico e inelástico;
- Interdependencia entre la resistencia y la rigidez, lo que implica que la rigidez no puede conocerse exactamente a menos que la estructura esté completamente diseñada;
- Inadecuada representación de las variaciones de las características histeréticas de distintos sistemas estructurales;
- Definición simplista e inapropiada de los factores de comportamiento para todas las categorías estructurales, así como una falta de apreciación de que la capacidad dúctil puede variar mucho dentro de una clase estructural. En el caso de puentes se ha mostrado en este sentido, que el procedimiento de diseño estándar basado en una reducción de las fuerzas no garantiza un nivel uniforme de protección;
- Una inadecuada representación de la influencia de la flexibilidad de las fundaciones en la respuesta sísmica;
- Una inadecuada representación del desempeño estructural de sistemas donde la acción inelástica es desarrollada en diferentes miembros a diferentes niveles de respuesta estructural.
7.2.2. Consideraciones sobre la entrada sísmica
La Fig. 7-1 muestra los espectros de diseño elástico propuestos en las diferentes normas de puentes. Para fines de comparación se ilustran los espectros correspondientes a terreno firme, para un amortiguamiento del 5% sin ningún aumento por efecto de la importancia o reducciones por comportamiento inelástico. La tendencia general es muy similar entre las normas AASHTO (American Association of State Highway and Transportation Officials, 1991), Eurocódigo 8 (CEN, 1998b) y AUTOSTRADE (1991). El reglamento japonés presenta pocas variaciones en todo el intervalo de períodos y el espectro de menor intensidad corresponde al diseño elástico con el que se diseña inicialmente la estructura de acuerdo al manual Menshin (Japan Road Association, 1996). La aceleración espectral es la forma básica de representación de la entrada sísmica cuando los parámetros fundamentales de diseño son la resistencia y la ductilidad. Sin embargo tal enfoque parece ser no el más adecuado cuando se analizan estructuras de largo período, como los puentes atirantados de gran luz. Así mismo, la posibilidad de la presencia de pulsos fuertes, característicos de los sismos cercanos a la fuente, podrían tener un impacto moderado en la forma estructural.
|
Fig. 7-1 Comparación de los espectros elásticos para terreno firme y 5% de amortiguamiento para varios códigos de diseño (Jara y Casas, 2002) |
Por otra parte, se reconoce hoy las grandes demandas de desplazamiento típicas de estructuras de período largo, que en presencia de los efectos de cercanía de la fuente sísmica tienen un fuerte impacto en este parámetro (Calvi, 2004).
Del mismo modo, podemos operar con espectros de desplazamiento, tal como se aprecia en la Fig. 7-2, en la cual se han representado los valores espectrales de desplazamiento para diferentes magnitudes y distancias a la falla (Calvi, 2004)
En cuanto a los efectos de la variabilidad espacial, es conocido que este fenómeno puede incrementar la respuesta sísmica de puentes de gran luz. De entre los aspectos que inciden en el fenómeno de la variabilidad espacial, son el problema de la falta de coherencia, el efecto del paso de onda y las condiciones locales, los que mayor afectan a una estructura de gran luz. En este sentido, el EC8-2 (CEN, 1998b) recomienda tomar en cuenta este efecto si existen discontinuidades geológicas o marcadas características topográficas capaces de introducir variaciones importantes en las características del movimiento del suelo, o si la longitud del puente supera los 600 m.
En cuanto a los efectos de la cercanía de la fuente sísmica, es importante la consideración de este aspecto cuando las estructuras se localizan cercanas a las zonas de falla. En efecto, los sismos de Northridge y Kobe dejaron de manifiesto que este efecto es muy importante por las altas aceleraciones alcanzadas, caracterizadas por pulsos de período largo (Kawashima, 2000). Para representar este efecto, en adición a los movimientos de terreno Tipo I, se han incluido movimientos Tipo II en el código japonés de diseño sísmico de puentes carreteros (Japan Road Association, 1996), para aquellos sismos de baja probabilidad de ocurrencia. Los movimientos de terreno tipo II corresponden a sismos de campo cercano, para magnitudes de 7 a 7.2, como se muestra en la tabla 7-3.
| Tipo de movimiento del suelo de diseño | Importancia del puente | Método de diseño | |||
| Tipo A (Puente estándar) | Tipo B (Puente importante) | Fuerza lateral estática equivalente | Análisis dinámico | ||
| Movimiento del suelo con alta probabilidad de ocurrencia | Prevención de daño | Método del coeficiente sísmico | Análisis paso a paso o análisis modal espectral | ||
| Movimiento del suelo con baja probabilidad de ocurrencia | Tipo I (sismo interplaca - campo lejano) | Prevenir daño crítico | Daño limitado | Método de diseño por ductilidad | |
| Tipo II (sismo intraplaca – campo cercano) | |||||
El espectro de diseño para movimientos Tipo II se determinó con base en los espectros de respuesta en aceleraciones obtenidos de los registros del sismo de Hyogo-ken Nambu. Además, el EC8-2 (CEN, 1998b) señala la necesidad de contar con espectros para el proyecto de puentes con dispositivos aislantes que se ubiquen a menos de 15 km de la falla activa (Álvarez, 2002). En efecto, en campo cercano, la influencia de los pulsos de velocidad puede reducir la efectividad del amortiguamiento adicional (y de la absorción histerética de energía). Para el movimiento del suelo de tipo pulso de velocidad, la influencia del amortiguamiento en la reducción del desplazamiento es mucho menos pronunciada que en un movimiento del suelo “normal” (Calvi, 2004).
7.2.3. Consideraciones en puentes con sistemas pasivos de protección
En el caso de sistemas con dispositivos pasivos de protección sísmica, se admiten dos criterios. El criterio denominado en algunos códigos como aislamiento total, pretende evitar daños en los elementos estructurales durante el sismo de diseño, a diferencia de un puente convencional en el que se espera que la deformación inelástica de algunos de sus elementos contribuya a disipar la energía que introduce el sismo en la estructura; se mejora así el comportamiento del puente pero no se puede asegurar un beneficio económico derivado de la instalación del sistema de aislamiento. El otro criterio, conocido como de aislamiento parcial, tiene como objetivo reducir los costes del proyecto aprovechando la disminución de las fuerzas sísmicas en los elementos estructurales, manteniendo el mismo nivel de comportamiento que en el caso de los puentes convencionales. Si se adopta la alternativa de aislamiento total, se alcanzan reducciones en los costos del orden del 10% (Mayes et al, 1992). Si se opta por el aislamiento parcial, el coste es semejante o incluso ligeramente menor que en el de un diseño tradicional. Puesto que no existe experiencia suficiente en puentes con aislamiento sísmico que hayan experimentado terremotos severos, en el código japonés Menshin (Japan Road Association, 1996) la fuerza sísmica que debe aplicarse a una estructura como resultado del uso de un sistema de control pasivo, se limita a una pequeña reducción de los espectros que se proponen para puentes convencionales. Así, el beneficio de los disipadores se limita únicamente a la dirección longitudinal, debido a la especificación que restringe los desplazamientos transversales de los apoyos. En la medida que se acumule mayor información sobre puentes reales sometidos a sismos grandes, se espera que esta limitación sea eliminada (Jara y Casas, 2002).
Los sistemas sismorresistentes se seguirán empleando dada su difundida práctica, sin embargo, lentamente comienzan a ceder terreno a los sistemas de aislamiento y disipación de energía. El uso de amortiguadores o de conectores sísmicos (aunque estos últimos no disipan energía) posibilita la construcción de puentes con tableros continuos de varios tramos apoyados sobre aparatos POT, eliminando juntas que hacen al puente poco confortable al usuario y proporcionando a la superestructura un mejor desempeño sísmico al tener una estructura más monolítica (Álvarez, 2002). Desde el punto de vista del EC8-2 (CEN, 1998b), la protección sísmica total mantendría a la estructura completa en el rango elástico (con la excepción del dispositivo disipador) para la acción sísmica de proyecto, en tanto que la protección sísmica parcial permitiría al tablero del puente operar en el rango elástico, pero no así las pilas ante la acción sísmica de diseño.
Un aspecto importante a considerar es el amortiguamiento del sistema puente – disipador. Una vez determinado el amortiguamiento equivalente de los dispositivos, resulta de mucha importancia estimar el amortiguamiento estructural del sistema completo. Este punto no está definido claramente en las normas, constituyendo una de las debilidades del llamado método de la estructura equivalente (Jara y Casas, 2002). Con excepción del manual japonés Menshin (Japan Road Association, 1996), no se menciona explícitamente la forma en que interviene el amortiguamiento de los otros componentes del puente. La Fig. 7-3 muestra la reducción espectral de la respuesta sísmica por efecto del nivel de amortiguamiento para distintos códigos de diseño.
|
Fig. 7-3 Reducción espectral de la respuesta por efecto del amortiguamiento para distinto códigos (Jara y Casas, 2002) |
A pesar de los requisitos que se imponen a los ensayos para la determinación de las características de los aisladores y disipadores, y de los programas de inspección y mantenimiento que se exigen a las estructuras con dispositivos de control sísmico, existe una clara tendencia que ha dado origen a que las especificaciones sobre el uso de aisladores sean más conservadoras que en los sistemas tradicionales, con el consecuente incremento de los costos (Jara y Casas, 2002). En este sentido, en 1994 la Federal Highway Administration (FHWA), California Department of Transportation (CALTRANS) y la Highway Innovative Technology Evaluation Center (HITEC) realizaron en Estados Unidos un programa de evaluación y pruebas para sistemas de aislamiento sísmico y disipación de energía. Como organización establecida bajo acuerdo entre FHWA y la Fundación de Investigación en Ingeniería Civil, subsidiaria de la American Society of Civil Engineering (ASCE), tuvieron la misión de evaluar nuevos productos, materiales y equipos para el cual no existían estándares de fabricación. Con ello, se buscaba mejorar el impacto y las expectativas de los sistemas de aislación sísmica y disipación de energía, con un aumento en la confianza en estas nuevas tecnologías, además de proveer una fuente rica de datos para académicos e investigadores. El programa finalizó en 1999, y permitió el reporte de 14 publicaciones como resultado de las investigaciones (Ghasemi, 1999).
7.3. Normativa Para Puentes con Aisladores y Disipadores. Generalidades del Eurocódigo 8-parte 2
A la fecha existe una clara ausencia en cuanto a regulaciones específicas respecto de la aplicación práctica en estructuras reales de dispositivos de control pasivo, y con mayor razón para el control activo en donde sencillamente no existe nada. Hoy en día sólo unas pocas recomendaciones y normas sobre sistemas de aislamiento y disipación de energía para puentes, permiten contar con reglamentaciones y unificación de criterios. En este sentido, la monografía desarrollada por Jara y Casas (2002) respecto al estado del arte sobre el control de vibraciones en puentes incluye, en su último capítulo, una descripción general actualizada acerca de las distintas normativas para puentes con aisladores y disipadores de energía, por lo que aquí no se insistirá nuevamente en ello.
De entre los códigos de diseño que incluyen recomendaciones específicas para el análisis y diseño de puentes con dispositivos pasivos, se destacan el código norteamericano AASHTO (American Association of State Highway and Transportation Officials, 1991, 1999); el código italiano AUTOSTRADE (1991), el manual japonés MENSHIN (Japan Road Association, 1996) y el EUROCODIGO 8 parte 2 (CEN, 1998b).
El código AASHTO incorpora un suplemento editado en 1991 que se titula “Guide Specifications for Seismic Isolation Design”, el que presenta las especificaciones para el diseño sísmico de puentes con aislación basal, para su aplicación en USA. Las normas están orientadas a proyectos de puentes nuevos, sin recomendaciones para puentes existentes, a pesar de que en USA aproximadamente el 50% de los proyectos de puentes que incorporan aislamiento sísmico, corresponden al refuerzo de puentes. La nueva revisión de 1999 incorpora recomendaciones para dispositivos deslizantes y disipadores de energía viscosos, además de modificar algunos aspectos relativos a los métodos de análisis y disminuir los factores de reducción de fuerzas sísmicas.
Las “Instrucciones para la Protección Sísmica de Puentes con Dispositivos Aisladores – Disipadores” (AUTOSTRADE, 1991), se aplican a puentes con tableros simplemente apoyados o continuos que cuenten con dispositivos aisladores y disipadores de energía, con base en los principios generales contenidos en la parte I de las “Especificaciones Técnicas para Construcciones en Zonas Sísmicas”, para lo cual diferencia los dispositivos de control entre los dispositivos con carácter predominantemente elástico (aquellos cuya función es solo aumentar el período fundamental de la estructura); los dispositivos de comportamiento viscoelástico (cuya respuesta está en función de la velocidad de aplicación de la fuerza) y los dispositivos de comportamiento elasto-plástico (cuya capacidad de disipación está definida por el comportamiento histerético del material).
El Manual de diseño MENSHIN (1989), corresponde a la primera guía de diseño de puentes con aislamiento sísmico en Japón. Tres años después, un equipo formado por el Instituto de Investigación de Obras Públicas y 28 empresas privadas, editaron el Manual para el Diseño de Puentes con el Sistema Menshin, que se incorporan a las Especificaciones de Diseño de Puentes de Autopista de la Asociación Japonesa de Carreteras, en 1996.
El EUROCODIGO 8- parte 2 propone tres grados de importancia para los puentes: superior a la media, media e inferior a la media, para lo cual asigna factores de importancia de 1.3, 1.0 y 0.70 respectivamente. Así mismo, define dos estados límites de diseño: un estado límite último y un estado límite de servicio. El primero plantea que, tras la ocurrencia del sismo de proyecto, el puente debe mantener su integridad estructural aunque ciertas partes queden muy dañadas. Así mismo, el puente debe ser capaz de admitir daños (disipación de energía) y para lograr la disipación de energía, se permite la formación de articulaciones plásticas a flexión en ciertas secciones de las pilas. El tablero debe mantenerse sin daño (intervalo elástico) y debe protegerse del descalce en apoyos. El estado límite de servicio plantea que tras la ocurrencia de sismos de elevada probabilidad de ocurrencia durante la vida útil del puente, las zonas dedicadas a contribuir con la disipación de energía pueden sufrir sólo daños ligeros.
Los niveles de ductilidad se introducen a través de los llamados “factores de comportamiento q”, como quedan graficados en la Fig. 7-4. El comportamiento dúctil se logra a través de la formación de las rótulas plásticas o a través del aislamiento sísmico. En cuanto a las condiciones de sitio, el EC8-2 define tres tipos de suelo, dependiendo de la rigidez de éste, cuantificado a través de la velocidad de propagación de ondas “S”, como lo establece la mayoría de los códigos.
|
Fig. 7-4 Comportamiento sísmico previsto y factores de comportamiento según EC8-2 | |
|
Fig. 7-5 Espectros de diseño dúctil de aceleraciones para puentes de hormigón armado según EC8-2 |
Fig. 7-6 Factores para calcular la componente vertical de la acción sísmica según EC8-2 |
Los espectros de diseño, se encuentran divididos por los correspondientes factores de comportamiento q, para el diseño por ductilidad, tal como se aprecia en la Fig. 7-5. El cálculo de la componente vertical de la aceleración es introducido como una función de la aceleración horizontal, tal como se muestra en la Fig. 7-6.
Los factores de comportamiento q quedan definidos de acuerdo a la tabla 7-4.
| Elementos dúctiles | Comportamiento sísmico | |
| Ductilidad limitada | dúctiles | |
| Pilas de hormigón armado | ||
| Pilas verticales a flexión, a ≥ 3.5 | 1.5 | 3.5 |
| Pilas cortas, a = 1 | 1.0 | 1.0 |
| Tornapuntas inclinados a flexión | 1.2 | 2.0 |
| Pilas de acero | ||
| Pilas verticales a flexión | 1.5 | 3.5 |
| Tornapuntas inclinados a flexión | 1.2 | 2.0 |
| Pilas con arriostrado normal | 1.5 | 2.5 |
| Pilas con arriostrado excéntrico | 3.5 | |
| Estribos | 1.0 | 1.0 |
| Arcos | 1.2 | 2.0 |
| a = H/L es la esbeltez del elemento.
Para 1.0 < a < 3.5 los factores q se obtienen por interpolación lineal | ||
En cuanto a la incorporación de sistemas pasivos, el EC8 - 2 propone dos criterios de diseño denominados aislamiento total y aislamiento parcial, como ya fue explicado anteriormente. Si se consigue un aislamiento total, se evitará el daño en los elementos estructurales durante el sismo de diseño, a diferencia de un puente convencional, en que se espera que la deformación inelástica de algunos de sus elementos contribuya en la disipación de energía; de esta forma se mejora el comportamiento del puente pero no se asegura un beneficio económico derivado de la instalación de los dispositivos pasivos. El aislamiento parcial tiene como objeto reducir los costes del proyecto, aprovechando la reducción de las fuerzas sísmicas en los elementos estructurales, manteniendo el mismo nivel de comportamiento que en el caso de los puentes convencionales.
En cuanto al diseño específico de puentes de tirantes, el Eurocódigo 8 – 2, escuetamente clasifica a esta tipología como de puentes especiales, para lo cual plantea en forma muy resumida algunas recomendaciones en cuanto a la selección del comportamiento sísmico deseado y la evitación de modos de falla frágil.
Referencias
ABAQUS (2005), Finite Element Analysis Program V. 6.5, Abaqus Inc., Providence, RI, USA
Abdel – Ghaffar, A.M., Nazmy, A.S. (1990), Non-Linear Earthquake Response Analysis of Long-Span Cable-Stayed Bridges: Theory, Earthquake Engineering and Structural Dynamics, Vol. 19, 45 – 62 (1990), John Wiley & Sons Ltd.
Abdel – Ghaffar, A.M., Nazmy, A.S. (1990), Non-Linear Earthquake Response Analysis of Long-Span Cable-Stayed Bridges: Applications, Earthquake Engineering and Structural Dynamics, Vol. 19, 63 – 76 (1990), John Wiley & Sons Ltd.
Abdel – Ghaffar, A.M., Nazmy, A.S. (1991), 3-D Nonlinear Seismic Behaviour of Cable-Stayed Bridges, Journal of Structural Engineering, Vol. 117, No. 11, ASCE.
Abdel – Ghaffar, A.M. (1991), Cable-Stayed Bridges Under Seismic Action, Cable – Stayed Bridges: Recent Development and their Future, Proceedings of the Seminar, Yokohama, Japan, 10 – 12 December 1991, Elsevier Science Pub.
Abdel – Ghaffar, A.M., Khalifa, M.A. (1991), Importance of Cable Vibration in Dynamics of Cable – Stayed Bridges, Journal of Engineering Mechanics, Vol. 117 (11), ASCE, pp 2571 – 2589.
Abdel – Ghaffar, A.M., Nazmy, A.S. (1992), Effects of Ground Motion Spatial Variability on the Response of Cable – Stayed Bridges, Earthquake Engineering and Structural Dynamics, Vol. 21 (1992), John Wiley & Sons, pp 1 – 20.
Abe, M., Erkus, B., Fujino, Y., Park, K.S. (2000), Applicability of Semi-Active Control for Seismic Protection of Bridges, Proceedings of the International Conference on Advances in Structural Dynamics, Hong Kong, Peoples R. China.
Adachi, Y., Unjoh, S., Kondoh, M. (2000), Development of a Shape Memory Alloy Damper for Intelligent Bridge Systems, Proceedings of the 1999 International Symposium and Exhibition on Shape Memory Alloy Materials, Kanazawa, Japan, Trans Tech Publ. Ltd.
Agrawal, A.K., Yang, J.N., He, W.L. (2003), Applications of Some Semiactive Control Systems to Benchmark Cable-Stayed Bridge, Journal of Structural Engineering, ASCE, pp 884 – 894.
Akkar, S., Gülkan, P. (2002), Spectral Velocity and Displacement in Performance Based Earthquake Resistant Design, 12th European Conference on earthquake Engineering, London, U.K., Elsevier Science Ltd., Paper No. 137.
Ali, H-E., Abdel Ghaffar, A.M. (1991a), Passive Seismic Control of Cable-Stayed Bridges, Proceedings from the First U.S. – Japan Workshop on Earthquake Protective Systems for Bridges, Buffalo, USA, National Center for Earthquake Engineering Research, pp 543 – 556.
Ali, H-E., Abdel Ghaffar, A.M. (1991b), Seismic Energy Dissipation for Cable-Stayed Bridges Using Passive Devices, Earthquake Engineering and Structural Dynamics, Vol. 23, John Wiley & Sons Ltd., pp 877 – 893.
Ali, H.M., Abdel-Ghaffar, A.M. (1995), Modelling the Nonlinear Seismic Behaviour of Cable-Stayed Bridges with Passive Control Bearings, Computers & Structures, Vol. 54, No. 3, Pergamon, pp 461 – 492.
Álvarez, J. (2002), Respuesta Sísmica de Puentes Arco Empleando Amortiguamiento Viscoso Suplementario, Proyecto de Tesis Doctoral, Departamento de Ingeniería del Terreno, Cartográfica y Geofísica, ETSCCPB, Universidad Politécnica de Catalunya, Barcelona, España.
Álvarez, J. (2004), Respuesta Sísmica de Puentes Arco Empleando Amortiguamiento Viscoso Suplementario, Tesis Doctoral, Departamento de Ingeniería del Terreno, Cartográfica y Geofísica, ETSCCPB, Universidad Politécnica de Catalunya, Barcelona, España.
Allam, S., Datta, T.K. (1999), Seismic Behaviour of Cable – Stayed Bridges Under Multi – Component Random Ground Motion, Engineering Structures, Vol. 21 (1999), Elsevier Science Ltd., pp 62 – 74.
Allam, S., Datta, T.K. (2000), Analysis of Cable – Stayed Bridges Under Multi – Component Random Ground Motion by Response Spectrum Method, Engineering Structures, Vol. 22 (2000), Elsevier Science Ltd., pp 1367 – 1377.
Allam, S., Datta, T.K. (2004), Seismic Response of Cable – Stayed Bridge Deck Under Multi – Component Non-Stationary Random Ground Motion, Earthquake Engineering and Structural Dynamics, Vol. 33 (2004), John Wiley & Sons, pp 375 – 393.
American Association of State Highway and Transportation Officials (1991), Guide Specifications for Seismic Isolation Design, Washington, D.C., USA.
American Association of State Highway and Transportation Officials (1999), Guide Specifications for Seismic Isolation Design, 2nd edition, Washington, D.C., USA.
ANSYS (2005), Finite Element Analysis Software V. 7.0, Ansys Inc., Canonsburg, Pa, USA
Aschrafi, M. (1998), Comparative Investigations of Suspension Bridges and Cable-Stayed Bridges for Spans Exceeding 1000 m, IABSE Symposium Japan 1998 Long – Span and High Rise Structures, Kobe, Japan. Edit Zurich IABSE, pp 447 – 452.
Aso, T., Mizutori, K., Shuto, M., Arikado, A., Momota, K., Otsuka, H. (2000), Non-Linear Earthquake Response Analysis of PC Cable-Stayed Bridges Considering the Fluctuant Axial Force, 12th World Conference On Earthquake Engineering, Auckland, NZ, Paper No. 1360.
Astaneh – Asl, A.., Black, R.G. (2001), Seismic and Structural Engineering of a Curved Cable-Stayed Bridge, Journal of Bridge Engineering, Vol. 6, No. 6, ASCE.
ATC-32, (1996), Improved Seismic Design Criteria for California Bridges: Provisional Recommendations, Applied Technology Council, Redwood City, California, USA.
Atkins, J.C., Wilson, J. (2000), Analysis of Damping in Earthquake Response of Cable-Stayed Bridges, 12th World Conference on Earthquake Engineering, Auckland, NZ, Paper no. 1468.
Au, F.T.K., Cheng, Y.S., Cheung, Y.K., Zheng, D.Y. (2001), On the Determination of Natural Frequencies and Mode Shapes of Cable-Stayed Bridges, Applied Mathematical Modelling, Vol. 25 (2001), Elsevier Science Ltd, pp 1099 – 1115.
Autostrade, (1991), Istruzioni per la Progettazione Antisísmica dei Ponti con Limpiego di Dispositivi Isolatori/Dissipatori, Prevenzione Antisísmica di Manufatti della Rete Autostrade S.P.A.
Bakule, L., Paulet-Crainiceanu, F., Rodellar, J. (2002), Decentralized Control Design for a Cable-Stayed Bridge Benchmark, Proceedings of the American Control Conference, Anchorage, Alaska, pp 3046 – 3051.
Barenberg, M.E., Foutch, D.A. (1988), Evaluation of Seismic Design Procedures for Highway Bridges, Journal of Structural Division, ASCE, 114 (7), pp 1588 – 1605.
Bayrak, O. (1996), Effect of Multiple Seismic Input on the Response of Long Multi – Span Bridges, 11th World Conference on Earthquake Engineering, Acapulco, Mexico, Elsevier Science Ltd., Paper No. 523.
Betti, R., Abdel – Ghaffar, A.M., Niazy, A.S. (1993), Kinematic Soil – Structure Interaction for Long – Span Cable – Supported Bridges, Earthquake Engineering and Structural Dynamics, Vol. 22, John Wiley & Sons Ltd, , pp 415 – 430.
Betti, R., Testa, R.B. (1995), Vibration and Damage Control for Long – Span Bridges, Smart Materials and Structures, Vol. 4 (1995), IoP Publ., pp. A91 – A100.
Betti, R., Panariello, G.F., Poulin, K. (1996), Vibration Control of Structures with Multiple Support Excitation, 11th World Conference on Earthquake Engineering, Acapulco, Mexico, Elsevier Science Ltd., Paper No. 555.
Billington, D.P., Deodatis, G. (1991), Form and Aesthetics in Cable – Stayed Bridges, Cable – Stayed Bridges: Recent Development and their Future, Proceedings of the Seminar, Yokohama, Japan, 10 – 12 December 1991, Elsevier Science Pub.
Bommer, J.J. (1999), Displacement Spectra for Seismic Design, Journal of Earthquake Engineering, Vol. 3, No. 1 (1999), World Scientific Publ., pp 1 – 32.
Bommer, J.J., Elnashai, A.M., Weir, A.G. (2000), Compatible Acceleration and Displacement Spectra for Seismic Design Codes, 12th World Conference on Earthquake Engineering, Auckland, New Zealand, Elsevier Science Ltd., Paper No. 207.
Branco, F.A., Mendes, P.M., Guerreiro, L.M.C. (2000), Special Studies for Vasco da Gama Bridge, Journal of Bridge Engineering, Vol. 5, No.3, ASCE.
Broekhuinzen, D.S. (1996), Effects of Vertical Acceleration on Presstressed Concrete Bridges, MS Thesis, Univ. of Texas, Austin, Texas, USA.
Brownjohn, J.M.W., Lee, J., Cheong, B. (1999), Dynamic Performance of a Curved Cable – Stayed Bridge, Engineering Structures, Vol. 21 (1999), Elsevier Science Ltd, pp 1015 – 1027.
Brownjohn, J.M.W., Xia, P. (2000), Dynamic Assessment of Curved Cable-Stayed Bridge by Model Updating, Journal of Structural Engineering, Vol. 126, No. 2, ASCE.
Bruno, D., Leonardi, A. (1997), Natural Periods of Long-Span Cable-Stayed Bridges, Journal Of Bridge Engineering, Vol.2, No.3, ASCE.
Buckle, I., Dusicka, P., Itani, A. (2005), Development of Built-Up Shear Links as Energy Dissipators for the Seismic Protection of Long Span Bridges, Bridge Structures, Vol. 1, No. 1, Taylor & Francis Ltd., pp 19 – 27.
Button, M.R., Cronin, C.J., Mayes, R.L. (2002), Effect of Vertical Motions on Seismic Response of Highway Bridges, Journal of Structural Engineering, Vol. 128, No. 12, ASCE, pp 1551 – 1564.
Caetano, E., Cunha, A., Taylor, C. (1996), Experimental Analysis of Coupled Cable – Deck Motions in Cable – Stayed Bridges, Proceedings of 11th World Conference on Earthquake Engineering, Acapulco, México, Paper No. 913, Elsevier Science Ltd.
Caetano, E., Cunha, A., Taylor, C. (2000), Investigation of Dynamic Cable – Deck Interaction in a Physical Model of a Cable – Stayed Bridge. Part I: Modal Analysis, Earthquake Engineering and Structural Dynamics, Vol. 29 (2000), John Wiley & Sons Ltd, pp 481 – 498.
Caetano, E., Cunha, A., Taylor, C. (2000), Investigation of Dynamic Cable – Deck Interaction in a Physical Model of a Cable – Stayed Bridge. Part II: Seismic Response, Earthquake Engineering and Structural Dynamics, Vol. 29 (2000), John Wiley & Sons Ltd, pp 499 – 521.
Caicedo, J.M., Turan, G., Dyke, S.J., Bergman, L.A. (2000), Comparison of Modelling Techniques for Dynamic Analysis of a Cable-Stayed Bridge, Proceedings of the Engineering Mechanics Specialty Conference, Austin, Texas, May. 21 -24, 2000.
Caltrans, (1999), Seismic Design Criteria, Version 1.1, California Department of Transportation, Sacramento, California, USA.
Calvi, G.M., Pinto, P.E. (1996), Experimental and Numerical Investigations on the Seismic Response of Bridges and recommendations for Code Provisions, Lisboa Laboratorio Nacional de Engenharia Civil.
Calvi, G.M. (2004), Recent Experience and Innovative Approaches in Design and Assessment of Bridges, 13th World Conference on Earthquake Engineering, Vancouver, B.C., Canada, August 1 – 6, 2004, Paper No. 5009.
Chang, K.C., Mo, Y.L., Chen, C.C., Lai, L.C., Chou, C.C. (2004), Lessons Learned From the Damaged Chi-Lu Cable – Stayed Bridge, Journal of Bridge Engineering, Vol. 9, No. 4 (2004), ASCE, pp 343 – 352.
Chen, Z-Q., Wang, X-Y., Ko, J-M., Ni, Y-Q., Spencer, B.F., Yang, G. (2003), MR Damping System on Dongting Lake Cable-Stayed Bridge, Proceedings of the 2003 Smart Structures and Materials Conference, San Diego, USA, SPIE Intl., pp 229 – 235.
Cheng, S.H., Lau, D.T. (2002), Modelling of Cable Vibration Effects of Cable-Stayed Bridges, Journal of Earthquake Engineering and Engineering Vibration, Vol.1, No.1, Institute of Engineering Mechanics, China.
Cheung, M.S., Lau, D.T., Li, W.C. (2000), Recent Development on Computer Bridge Analysis and Design, Progress in Structural Engineering and Materials, Vol. 2, John Wiley & Sons, Ltd, USA, pp. 376 – 385.
Cho, S-W., Kim, B-W., Jung, H-J., Lee, I-W. (2005), Implementation of Modal Control for Seismically Excited Structures Using Magnetorheological Dampers, Journal of Engineering Mechanics, Vol. 131, No. 2, ASCE, pp 177 – 184.
Choi, K-M., Cho, S-W., Jung, H-J., Lee, I-W. (2004), Semi-Active Fuzzy Control for Seismic Response Reduction Using Magnetorheological Dampers, Earthquake Engineering and Structural Dynamics, Vol. 33 (2004), John Wiley & Sons, pp 723 – 736.
Chopra, A.K., Chintanapakdee, Ch. (2001), Comparing Response of SDF Systems to Near-Fault and Far-Fault Earthquake Motions in the Context of Spectral Regions, Earthquake Engineering and structural Dynamics, Vol. 30 (2001), John Wiley & Sons Ltd., pp 1769 – 1789.
Clemente, P., Marulo, F., Lecce, L., Bifulco, A. (1998), Experimental Modal Analysis of the Garigliano Cable-Stayed Bridge, Soil Dynamics and Earthquake Engineering, Vol. 17 (1998), Elsevier Science Ltd, pp 485 – 493.
Clemente, P., Celebi, M., Bongiovanni, G., Rinaldis, D. (2004), Seismic Analysis of the Indiano Cable-Stayed Bridge, 13th World Conference on Earthquake Engineering, Vancouver, B.C., Canada, August 1 – 6, 2004, Paper No. 3296.
Clough, R.W., Penzien, J. (1993), Dynamics of Structures, 2th edition, McGraw Hill.
Combault, J., Morand, P., Pecker, A. (2000), Structural Response of the Rion-Antirion Bridge, 12th World Conference on Earthquake Engineering, Auckland, New Zealand, Elsevier Science Ltd., Paper No. 1609.
Comité Europeo de Normalización (CEN), (1998a), Eurocódigo 8: Disposiciones Para el Proyecto de Estructuras Sismorresistentes. Parte 1 – 1: Reglas Generales. Acciones Sísmicas y Requisitos Generales de las Estructuras, ENV 1998 -1 -1, Edición de la Asociación Española de Normalización y certificación.
Comité Europeo de Normalización (CEN), (1998b), Eurocódigo 8: Disposiciones Para el Proyecto de Estructuras Sismorresistentes. Parte 2: Puentes, ENV 1998 -2, Edición de la Asociación Española de Normalización y certificación.
Constantinou, M.C. (2003), Damping Systems for New and Retrofit Construction, FIB Symposium: Concrete Structures in Seismic Regions, Athens, Greece.
Cunha, A., Caetano, E., Delgado, R. (2001), Dynamic Tests on Large Cable-Stayed Bridge, Journal of Bridge Engineering, Vol.6, No.1, ASCE.
Dai, Z-B., Huang, J-Z., Wang, H-X. (2004), Semi-Active Control of a Cable-Stayed Bridge Under Multiple-Support Excitations, Journal of Zhejiang University SCIENCE, 2004 5 (3), pp 317 – 325.
DesRoches, R. (2000), Shape Memory Alloy – Based Response Modification of Simply Supported Bridges, Advances in Structural Dynamics, Vol. 1, Elsevier Science Ltd.
Dominguez, A., Sedaghati, R., Stiharu, I. (2004), Modelling the Hysteresis Phenomenon of Magnetorheological Dampers, Smart Materials and Structures, Vol. 13 (2004), IoP Publ., pp 1351 – 1361.
Dyke, S.J., Spencer, B.F., Sain, M.K., Carlson, J.D. (1996), Experimental Verification of Semi-Active Structural Control Strategies Using Acceleration Feedback, Proceedings of the 3rd International Conference on Motion and Vibration Control, Chiba, Japan, Vol. III, pp 291 – 296.
Dyke, S.J., Spencer, B.F. (1997), A Comparison of Semi-Active Control Strategies for the MR Damper, Proceedings of the IASTED International Conference on Intelligent Information Systems, the Bahamas.
Dyke, S.J., Spencer, B.F., Sain, M.K., Carlson, J.D. (1997), On the Efficacy of Magnetorheological Dampers for Seismic Response Reduction, 1997 ASME Design Engineering Technical Conference, Sacramento, USA.
Dyke, S.J., Yi, F., French, S., Carlson, J.D. (1999), Application of Magnetorheological Dampers to Seismically Excited Structures, 17th International Modal Analysis Conference, Kissimmee, Fl., USA.
Dyke, S.J., Caicedo, J.M., Turan, G., Bergman, L.A., Hague, S. (2000), Summary of the Benchmark Control Problem for Seismic Response of Cable-Stayed Bridges, Proceedings from the Second European Conference on Structural Control, Paris, France.
Dyke, S.J., Caicedo, J.M., Turan, G., Bergman, L.A., Hague, S. (2002), Introducing Phase I of the Benchmark Problem on the Seismic Response Control of Cable-Stayed Bridges, 7th US National Conference on Earthquake Engineering, Boston, MA, USA.
Elassaly, M., Ghali, M., Elbandry, M. (1995), Influence of Soil Conditions on the Seismic Behaviour of Two Cable – Stayed Bridges, Canadian Journal of Civil Engineering, Vol. 22, National Research Canada, pp 1021 – 1040.
Ettouney, M., Hapij, A., Gajer, R. (2001), Frequency – Domain Analysis of Long – Span Bridges Subjected to Non-uniform Seismic Motions, Journal of Bridge Engineering, Vol. 6, No. 6, ASCE, pp 577 – 586.
Faccioli, E., Paolucci, R., Rey, J. (2004), Displacement Spectra for Long Periods, Earthquake Spectra, Vol. 20, No. 2, Earthquake Engineering Research Institute, pp 347 – 376.
Fan, L., Hu, S., Yuan, W. (1992), Nonlinear Seismic Response Analysis of Long-Span Cable-Stayed Bridge, 10th World Conference on Earthquake Engineering, Madrid, Spain, pp 4815 – 4820.
Feng, M.Q., Kim, J-M., Shinozuka, M., Purasinghe, R. (2000), Viscoelastic Dampers at Expansion Joints for Seismic Protection of Bridges, Journal of Bridge Engineering, Vol. 5, No. 1, ASCE, pp 67 – 74.
Figueras, S. (2004), Evaluación de la Peligrosidad Sísmica, Apuntes del Curso de Doctorado en Ingeniería Sísmica y Dinámica Estructural, Departamento de Ingeniería del Terreno, Cartográfica y Geofísica, Universidad Politécnica de Catalunya, Barcelona, España.
Filiatrault, A., Tinawi, R., Massicotte, B. (1993), Damage to Cable – Stayed Bridge During 1988 Saguenay Earthquake. I: Pseudo static Analysis, Journal of Structural Engineering, Vol. 119, No. 5, ASCE, pp 1432 – 1449.
Filiatrault, A., Tinawi, R., Massicotte, B. (1993), Damage to Cable – Stayed Bridge During 1988 Saguenay Earthquake. II: Dynamic Analysis, Journal of Structural Engineering, Vol. 119, No. 5, ASCE, pp 1450 – 1463.
Floren, A., Mohammadi, J. (2001), Performance-Based Design Approach in Seismic Analysis of Bridges, Journal of Bridge Engineering, ASCE, Vol. 6, No. 1, pp 37 - 45
Forars, K., Brownjohn, J.M.W., Warnitchai, P. (2000), Effects of Cable Dynamics on the Seismic Performance of Cable – Stayed Bridges, International Conference on Advances in Structural Dynamics (ASD 2000), Hong Kong, Peoples Rep. China, Dec. 13 – 15, 2000.
Forment, J. (2000), Utilización de Amortiguadores y Conectores Sísmicos en Puentes, Tesina de Especialidad, Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos de Barcelona, Universidad Politécnica de Catalunya, Barcelona, España.
Foutch, D.A. (1997), A Note on the Occurrence and Effects of Vertical Earthquake Ground Motion, FHWA / NCEER Workshop on the National Representation of Seismic Ground Motion for New and Existing Highway Facilities, Burlingame, USA, National Center for Earthquake Engineering Research, State University of New York at Buffalo, N.Y., USA, pp 253 – 275.
Ganev, T., Yamazaki, F., Ishizaki, H., Kitazawa, M. (1998), Response Analysis of the Higashi-Kobe Bridge and Sorrounding Soil in the 1995Hyogoken – Nambu Earthquake, Earthquake Engineering and Structural Dynamics, Vol. 27 (1998), John Wiley & Sons Ltd, pp 557 – 576.
Garevski, M.A., Severn, R.T. (1992), Dynamic Analysis of Cable-Stayed Bridges by Means of 3D Analytical and Physical Modelling, 10th World Conference on Earthquake Engineering, Madrid, Spain, pp 4809 – 4814.
Garevski, M.A., Severn, R.T. (1993), Damping and Response Measurement on a Small – Scale Model of a Cable-Stayed Bridge, Earthquake Engineering and Structural Dynamics, Vol. 22, 13 – 29 (1993), John Wiley & Sons Ltd.
Gentile, C., Martinez y Cabrera, F. (2004), Dynamic Performance of Twin Curved Cable-Stayed Bridges, Earthquake Engineering and Structural Dynamics, Vol. 33 (2004), John Wiley & Sons Ltd, pp 15 – 34.
Ghasemi, H. (1999), Seismic Protection of Bridges, Public Roads: Mar/Apr 1999, ProQuest Science Journals, Ann Arbor, USA.
Gimsing, N.J. (1983), Cable – Supported Bridges, John Wiley & Sons, Ltd, USA.
Gloyd, S. (1997), Design of Ordinary Bridges for Vertical Seismic Acceleration, FHWA / NCEER Workshop on the National Representation of Seismic Ground Motion for New and Existing Highway Facilities, Burlingame, USA, National Center for Earthquake Engineering Research, State University of New York at Buffalo, N.Y., USA, pp 277 – 290.
Gordaninejad, F., Saiidi, M., Hansen, B.C., Ericksen, E.O., Chang, F-K. (2002), Magneto-rheological Fluid Dampers for Control of Bridges, Journal of Intelligent Material Systems and Structures, Vol. 13, SAGE Publ., pp 167 – 180.
Goto, Y., Higuchi, S-I. (1996), Active Variable Stiffness Control System for PC Cable-Stayed Bridge Under Construction, 11th World Conference on Earthquake Engineering, Acapulco, México, Elsevier Science Ltd., Paper No. 1323.
Grenier, A. (1992), Seismic Protection of Bridges by the Viscoelastic Technique, 10th World Conference on Earthquake Engineering, Madrid, Spain, AA Balkema Publ.
Haarala, L. (2003), Simulación de Movimientos Sísmicos Intensos para Zonas con Pocos Registros y su Aplicación a la Evaluación del Comportamiento de Estructuras, Tesis Doctoral, Departamento de Ingeniería del Terreno, Cartográfica y Geofísica, Universidad Politécnica de Catalunya, Barcelona, España.
Hayashikawa, T., Matsui, Y., Kaneko, T. (2000), Nonlinear Dynamic Behaviour and Seismic Isolation of Steel Towers of Cable-Stayed Bridges Under Great Earthquake Ground Motion, 12th World Conference on Earthquake Engineering, Auckland, NZ, Paper no. 0469.
He, W.L., Agrawal, A.K., Mahmoud, K. (2001), Control of Seismically Excited Cable-Stayed Bridge Using Resetting Semiactive Stiffness Dampers, Journal of Bridge Engineering, ASCE, pp 376 – 384.
Helduser, S., Bonefeld, R. (2001), Active Damping in Civil Engineering Using Hydraulic Actuators, Proceedings of the 5th International Conference on Fluid Power Transmission and Control, Zhejiang University, Hangzhou, Peoples Rep. China, Int. Academic Publ., pp 259 – 263.
Hodhod, O.A., Wilson, J.C. (1995), Characteristics of the Seismic Response of a Cable-Stayed Bridge Tower, 10th European Conference on Earthquake Engineering, Vienna, Austria, AA Balkema Publ, pp 2069 – 2074.
Iemura, H., Pradono, M.H. (2002), Passive and Semi-Active Seismic Response Control of a Cable-Stayed Bridge, Journal of Structural Control, Vol. 9, John Wiley & Sons Ltd., pp 189 – 204.
Iemura, H., Pradono, M.H. (2003), Application of Pseudo-Negative Stiffness Control to the Benchmark Cable-Stayed Bridge, Journal of Structural Control, Vol. 10 (2003), John Wiley & Sons Ltd., pp 187 - 203
Iemura, H., Pradono, M.H. (2004), Pseudo Negative Stiffness Dampers for Earthquake Response Control of Cable-Stayed Bridges, 13th World Conference on Earthquake Engineering, Vancouver, Canada, Elsevier Science Ltd., Paper No. 664.
Iemura, H., Pradono, M.H. (2005), Simple Algorithm for Semi-Active Seismic Response Control of Cable-Stayed Bridges, Earthquake Engineering and Structural Dynamics, Vol. 34 (2005), John Wiley & Sons Ltd., pp 409 – 423.
Infanti, S., Papanikolas, P., Theodossopoulos, G. (2003), Rion-Antirion Bridge: Full-Scale Testing of Seismic Devices, Proceedings from the FIB Symposium: Concrete Structures in Seismic Regions, Athens, Greece.
Infanti, S., Papanikolas, P., Benzoni, G., Castellano, M.G. (2004), Rion – Antirion Bridge: Design and Full – Scale Testing of the Seismic Protection Devices, 13th World Conference on Earthquake Engineering, Vancouver, B.C., Canada, August 1 – 6, 2004, Paper No. 2174.
International Code Council (1997), Uniform Building Code 1997, Prentice Hall
Jangid, R.S. (2004), Seismic Response of Isolated Bridges, Journal of Bridge Engineering, Vol. 9, No. 2, ASCE, pp 156 – 166.
Jansen, L.M., Dyke, S.J. (2000), Semi-Active Control Strategies for MR Dampers: A Comparative Study, Journal of Engineering Mechanics, Vol. 126, No. 8, ASCE, pp 795 – 803.
Japan Road Association (1996), 1996 Seismic Design Specifications of Highway Bridges, Japan.
Jara, M., Casas, J.R. (2002), Criterios de Diseño de Puentes con Aisladores y Disipadores de Energía, Monografía CIMNE IS – 49, Universidad Politécnica de Catalunya, Barcelona, España.
Jara, M., Casas, J.R. (2002), Control de Vibraciones en Puentes. Un Estado del Arte y de la Práctica, Monografía CIMNE IS – 48, Universidad Politécnica de Catalunya, Barcelona, España.
Jerónimo, E., Guerreiro, L. (2002), Seismic Displacement Analysis of Bridges With Viscous Dampers, 12th European Conference on Earthquake Engineering, London, U.K., Elsevier Science Ltd., Paper No. 373.
Jiahao, L., Yahui, Z., Yan, Z. (2004), Seismic Spatial Effects on Dynamic Response of Long – Span Bridges in Stationary Inhomogeneous Random Fields, Journal of Earthquake Engineering and Engineering Vibration, Vol. 3, No. 2, IEM.
Jung, H-J., Spencer, B.F., Lee, I-W. (2003), Control of Seismically Excited Cable-Stayed Bridge Employing Magnetorheological Fluid Dampers, Journal of Structural Engineering, ASCE, pp 873 – 883.
Jung, H-J., Lee, H-J., Yoong, W-H., Oh, J-W., Lee, I-W. (2004a), Technical Note: Semiactive Neurocontrol for Seismic Response Reduction Using Smart Damping Strategy, Journal of Computing in Civil Engineering, Vol. 18, No. 3, ASCE, pp 277 – 280.
Jung, H-J., Spencer, B.F., Ni, Y.Q., Lee, I-W. (2004b), State-of-the-Art of Semiactive Control Systems Using MR Fluid Dampers in Civil Engineering Applications, Structural Engineering and Mechanics, Vol. 17 (3-4), Techno Press, Ltd., pp 493 – 526.
Jung, H-J., Park, K-S., Spencer, B.F., Lee, I-W. (2004c), Hybrid Seismic Protection of Cable-Stayed Bridges, Earthquake Engineering and Structural Dynamics, Vol. 33 (2004), John Wiley & Sons Ltd., pp 795 – 820.
Kahan, M.; Gibert, R-J., Bard, P-Y. (1995), Influence of Seismic Waves Spatial Variability on Bridges: A Sensitivity Analysis, 10th European Conference on Earthquake Engineering, Vienna, Austria, AA Balkema Publ., pp 2145 – 2150.
Kawashima, K., Unjoh, S., Azuta, I. (1988), Damping Characteristics of Cable-Stayed Bridges, Proceedings of 9th World Conference on Earthquake Engineering, Tokyo, Japan, Vol.6, pp 471 – 476.
Kawashima, K., Unjoh, S. (1989), Damping Characteristics of Cable-Stayed Bridges Associated with Energy Dissipation at Movable Supports, Structural Engineering/Earthquake Engineering, Vol.6, No.1, Japan Society of Civil Engineering, pp 123 – 130.
Kawashima, K., Unjoh, S., Azuta, I. (1990), Analysis of Damping Characteristics of a Cable-Stayed Bridge Based on Strong Motion Records, Structural Engineering/Earthquake Engineering, Vol.7, No.1, Japan Society Of Civil Engineering, pp 169 – 178.
Kawashima, K., Unjoh, S. (1991), Seismic Behaviour of Cable-Stayed Bridges, Cable – Stayed Bridges: Recent Development and their Future, Proceedings of the Seminar, Yokohama, Japan, 10 – 12 December 1991, Elsevier Science Pub.
Kawashima, K., Unjoh, S. (1992), Damping Characteristics of Cable-Stayed Bridges, 10th World Conference on Earthquake Engineering, Madrid, Spain, pp 4803 – 4808.
Kawashima, K., Unjoh, S., Tsunomono, M. (1993), Estimation of Damping Ratio of Cable-Stayed Bridges for Seismic Design, Journal of Structural Engineering, Vol. 119 (4), pp 1015 – 1031, ASCE.
Kawashima, K., Unjoh, S., Suzuki, S., Endoh, S. (1994), Application of Electro-Rheological Fluid for Variable Damper, Proceedings from the 3rd U.S. – Japan Workshop on Earthquake Protective Systems for Bridges, Berkeley, USA, National Center for Earthquake Engineering Research, pp 3-31 – 3-38.
Kawashima, K. (2000), Seismic Design and Retrofit of Bridges, 12th World Conference on Earthquake Engineering, Auckland, NZ, Paper No. 2828.
Kawashima, K., Hosoiri, K. (2003), Rocking Isolation of Bridge Columns on Direct Foundations, FIB Symposium: Concrete Structures in Seismic Regions, Athens, Greece.
Kim, J., Choi, H., Min, K.W. (2003), Performance-Based Design of Added Viscous Dampers Using Capacity Spectrum Method, Journal of Earthquake Engineering, Vol. 7 (1), World Scientific Publ., pp 1 – 24.
Kim, H., Adeli, H. (2005), Wavelet-Hybrid Feedback Linear Mean Squared Algorithm for Robust Control of Cable-Stayed Bridges, Journal of Bridge Engineering, ASCE, pp 116 – 123.
Kitazawa, M., Yamagami, T., Fukuzawa, K., Fujita, K. (1989), Seismic Test on Higashi – Kobe Bridge. Cable-Stayed Bridge – Using Scale Models, Conference on Earthquake Behaviour of Buried Pipelines, Storage, Telecommunication and Transportation Facilities, Jul. 23 – 27, Honolulu, Hi, USA.
Kitazawa, M., Nishimori, K., Noguchi, J., Shimoda, I. (1992), Earthquake Resistant Design of a Long – Period Cable-Stayed Bridge, 10th World Conference on Earthquake Engineering, Madrid, Spain, pp 4797 – 4802.
Kitazawa, M., Iseki, J., Shimoda, I. (1994), Development of New Type Damper for Cable-Stayed Bridge, Proceedings from the Third U.S. – Japan Workshop on Earthquake Protective Systems for Bridges, Berkeley, USA, National Center for Earthquake Engineering Research, pp 2-39 – 2-46.
Koo, J.H., Gonçalves, F.D., Ahmadian, M. (2004), Investigation of the Response Time of Magnetorheological Fluid Dampers, Proceedings of the Smart Structures and Materials 2004 Conference, San Diego, CA, USA, Society of Photo-Optical Instrumentation Engineers.
Krawinkler, H., Seneviratna, G.D.P.K. (1998), Pros and Cons of a Pushover Analysis for Seismic Performance Evaluation, Journal of Engineering Structures, Vol. 20, No. 4 – 6, pp 452 – 464.
Kunde, M.C., Jangid, R.S. (2003), Seismic Behaviour of Isolated Bridges: A-State of-the-Art Review, Electronic Journal of Structural Engineering, Vol. 3 (2003), EJSE International.
Lai, G., Chen, Ch-Ch., Hsu, M.Ch. (2004), Cable – Stayed Bridge Retrofit Using Isolation System, 13th World Conference on Earthquake Engineering, Vancouver, Canada, Elsevier Science Ltd., Paper No. 3253.
Lecinq, B., Messein, J.P., Boutillon, L. (2003), The Rion-Antirion Bridge Stay Cables: A Seismic Approach, Proceedings from the FIB Symposium: Concrete Structures in Seismic Regions, Athens, Greece.
Lee, D., Taylor, D.P. (2001), Viscous Damper Development and Future Trends, The Structural Design of Tall Buildings, Vol. 10 (2001), John Wiley & Sons Ltd., pp 311 – 320
Lee, T.Y., Kawashima, K. (2004), Effectiveness of Supplementary Dampers for Isolated Bridges Under Strong Near-Field Ground Motions, 13th World Conference on Earthquake Engineering, Vancouver, Canada, Elsevier Science Ltd., Paper No. 138.
Lestuzzi, P., Schwab, P., Koller, M., Lacave, C. (2004), How to Choose Earthquake Recordings for Non-Linear Seismic Analysis of Structures, 13th World Conference on Earthquake Engineering, Vancouver, Canada, Elsevier Science Ltd., Paper No. 1241.
Li, X-Z., Cai, J., Qiang, S-H. (2001), Active Control of Long Span Cable-Stayed Bridges Under Seismic Loads, International Symposium on Traffic Induced Vibrations and Controls, Beijing, Peoples Rep. China, pp 39 – 46.
Li, X., Zhu, X. (2003), Study on Near-Fault Design Spectra of Seismic Design Code, 3rd International Conference on Earthquake Engineering, Nanjing, China, China Waterpower Press.
Li, J., Li, J. (2004), An Efficient Response Spectrum Analysis of Structures Under Multi – Support Seismic Excitations, 13th World Conference on Earthquake Engineering, Vancouver, Canada, Elsevier Science Ltd., Paper No. 3018.
Li, J.H., Zhang, Y.H., Li, Q.S., Williams, F.W. (2004), Seismic Spatial Effects for Long – Span Bridges, Using the Pseudo Excitation Method, Engineering Structures, Vol. 26 (2004), Elsevier Science Ltd., pp 1207 – 1216.
Lin, W-H., Chopra, A.K. (2002), Earthquake Response of Elastic SDF Systems with Non-Linear Fluid Viscous Dampers, Earthquake Engineering and Structural Dynamics, Vol. 31 (2002), John Wiley & Sons Ltd., pp 1623 – 1642.
Liu, Y., Gordaninejad, F., Evrensel, C.A., Wang, X., Hitchcock, G. (2000), Semi-Active Control of a Two-Span Bridge Using Field-Controllable Magneto-rheological Dampers, Proceedings of the Smart Structures and Materials 2000 Conference: Smart Systems fro Bridges, Structures and Highways, Newport Beach, CA, USA, SPIE.
Liu, Y.M., Gordaninejad, F., Evrensel, C.A., Hitchcock, G. (2001), An Experimental Study on Fuzzy Logic Vibration Control of a Bridge Using Fail-Safe Magneto-rheological Fluid Dampers, Proceedings of the Smart Structures and Materials 2001 Conference: Smart Systems for Bridges, Structures and Highways, Newport Beach, CA, USA, SPIE.
Liu, Y., Gordaninejad, F., Evrensel, C.A., Wang, X., Hitchcock, G. (2005), Comparative Study on Vibration Control of a Scaled Bridge Using Fail-Safe Magneto-Rheological Fluid Dampers, Journal of Structural Engineering, Vol. 131, No. 5, ASCE, pp 743 – 751.
Lobo, W. (2000), Diseño Sísmico de Puentes: Estado del Arte, Revista de Ingeniería Sísmica, No. 63, SMIS, México, pp. 55 – 71.
Loh, C-H.; Ku, B-D. (1995), An Efficient Analysis of Structural Response for Multiple – Support Seismic Excitations, Engineering Structures, Vol. 17, No. 1, Elsevier Science Ltd., pp 15 – 26.
Loh, C-H., Liao, W-I., Chai, J-F. (2002), Effect of Near-Fault Earthquake on Bridges: Lessons Learned From Chi-Chi Earthquake, Journal of Earthquake Engineering and engineering Vibration, Vol. 1, No. 2, IEM.
Loh, C-H., Chang, C-M. (2005), Vibration Control Assessment of ASCE Benchmark Model of Cable-Stayed Bridge, Structural Control and Health Monitoring, In Press, John Wiley & Sons Ltd.
López Almansa, F., Bozzo, L.M. (2003), Aplicación del Control de Estructuras al Diseño Antisísmico, Apuntes del Curso de Master en Ingeniería Sísmica y Dinámica Estructural, Departamento de Ingeniería del Terreno, Cartográfica y Geofísica, Universidad Politécnica de Catalunya, Barcelona, España.
Lupoi, A., Franchin, P., Pinto, P.E., Monti, G. (2005), Seismic Design of Bridges Accounting for Spatial Variability of Ground Motion, Earthquake Engineering and Structural Dynamics, Vol. 34 (2005), John Wiley & Sons Ltd., pp 327 – 348.
Macdonald, J.H.G., Georgakis, C.T. (2002), The Influence of Cable – Deck Interaction on the Seismic Response of Cable – Stayed Bridges, 12th European Conference on Earthquake Engineering, Paper No. 441, London, UK.
Magana, M.E., Hernried, A.G., Scheer, D. (1994), Robust Active Control of Cable-Stayed Bridge Subjected to Earthquake Ground Motion, Proceedings of the 11th Conference on Analysis and Computation, Atlanta, USA, ASCE, pp 317 – 326.
Magana, M.E., Rodellar, J.J. (2000), Fuzzy Logic Control of Cable-Stayed Bridges in the Presence of Seismic Excitation, Shock and Vibration Digest, Vol. 32, No. 1, SAGE Publ.
Makris, N., McMahon, S. (1996), Structural Control with Controllable Fluid Dampers: Design and Implementation Issues, Proceedings of 2th International Workshop on Structural Control, Hong Kong.
Makris, N., McMahon, S. (1997), Large-Scale ER-Damper for Seismic Protection of Bridges, Proceedings of the 1997 15th Structures Congress, Portland, USA, Part 2, ASCE, pp 1451 – 1455.
Maldonado, E., Canas, J.A., Casas, J.R., Pujades, L.G. (1998), Respuesta de Puentes Frente a Acciones Sísmicas, Monografía CIMNE IS – 27, Universidad Politécnica de Cataluña, Barcelona, España.
MATLAB® (1997), The Math Works, Inc., Natick Massachusetts.
Matsuzaki, Y., Ikeda, T., Boller, Ch. (2005), New Technological Development of Passive and Active Vibration Control: Analysis and Test, Smart Materials and Structures, Vol. 14, No. 2, IoP Publ.
Mayes, R.L., Buckle, I.G., Kelly, T.E., Jones, L.R. (1992), AASHTO Seismic Isolation Design Requirements for Highway Bridges, Journal of Structural Engineering, Vol. 118, No. 1, ASCE, pp 284 – 304.
Ministerio de Fomento (1998), IAP, Instrucción sobre las Acciones a Considerar en el Proyecto de Puentes de Carretera, Dirección General de Carreteras, España.
Moon, S.J., Bergman, L.A., Voulgaris, P.G. (2003), Sliding Mode Control of Cable-Stayed Bridge Subjected to Seismic Excitation, Journal of Engineering Mechanics, ASCE, pp 71 – 78.
Morgenthal, G. (1999), Cable-Stayed Bridges – Earthquake Response and Passive Control, Msc Dissertation, Civil Engineering Department, Imperial College of Science, Technology and Medicine, London, UK.
Muriavila, D., Gomez, R., King, C. (1991), Dynamic Structural-Properties of Cable-Stayed Tampico Bridge, Journal of Structural Engineering, Vol. 117 (11), ASCE, pp 3396 – 3416.
Murphy, T.P., Collins, K.R. (2000), Retrofit of Suspension Bridges Subjected to Long Period Earthquake Motion, 12th World Conference on Earthquake Engineering, Auckland, New Zealand, Paper No. 2310.
Nagai, M., Xie, X., Yamaguchi, H., Fujino, Y. (1998), Economical Comparison Between Cable-Stayed and Suspension Systems with a Span Exceeding 1000 meters, Journal of Constructional Steel Research, Vol. 46, Nos. 1 – 3, paper number 49, Elsevier Science Ltd., Great Britain.
Nagarajaiah, S., Varadarajan, N. (2000), Novel Semiactive Variable Stiffness Tuned Mass Damper with Real Time Tuning Capability, Proceedings of the 13th Engineering mechanics Conference, Reston, Va.
Nakamura, M., Ueda, S., Sukumura, J., Hanada, K., Nakai, M., Yoshida, M. (2000), An Evaluation Method of Modal Damping and its Application Based on a FVT of Cable Stayed Bridge, 12th World Conference on Earthquake Engineering, Auckland, NZ, Paper no. 0699.
Nazmy, A.S. (1995), Solutions for the Seismic Problems of Superlong Cable-Stayed Bridges, Proceedings from the 13th Structures Congress: Restructuring: America and Beyond, Boston, USA, ASCE, pp 465 – 468.
New Zealand Ministry of Works and Development, (1983), Design of Lead-Rubber Bridge Bearings, Civil Division Publication 818/A, Wellington, New Zealand.
Ni, Y.Q., Spencer, B.F., Ko, J.M. (2001), Active/Semiactive Seismic Response Control of Cable-Supported Bridges: Current Research Status and Key Issues, China – U.S. Millennium Symposium on Earthquake Engineering, Beijing, Peoples Rep. China, AA Balkema Publ., pp 299 – 304
Ni, Y.Q., Wang, J.Y., Lo, L.C. (2005), Influence of Stabilizing Cables on Seismic Response of a Multispan Cable – Stayed Bridge, Computer – Aided Civil and Infrastructure Engineering, Vol. 20 (2005), Blackwell Publ, pp 142 – 153.
Niihara, Y., Takeda, T., Ichinomiya, T., Suzuki, R. (1994), Improvements in Earthquake Resistance of PC Cable-Stayed Bridges by Hysteresis Dampers, Proceedings from the Third U.S. – Japan Workshop on Earthquake Protective Systems for Bridges, Berkeley, USA, National Center for Earthquake Engineering Research, pp 4-163 – 4-178.
Ólafsson, S., Sigbjörnsson, R. (2004), Generation of Synthetic Accelerograms and Structural Response Using Discrete Time Models, 13th World Conference on Earthquake Engineering, Vancouver, Canada, Elsevier Science Ltd., Paper No. 1624.
Papazoglou, A.J., Elnashai, A.S. (1996), Analytical and Field Evidence of the Damaging Effect of Vertical Earthquake Ground Motion, Earthquake Engineering and Structural Dynamics, Vol. 25, Issue 10, John Wiley & Sons Ltd, pp 1109 – 1137.
Park, K-S., Jung, H-J., Spencer, B.F., Lee, I-W. (2003a), Hybrid Control Systems for Seismic Protection of a Phase II Benchmark Cable-Stayed Bridge, Journal of Structural Control, Vol. 10 (2003), John Wiley & Sons Ltd., pp 231 – 247.
Park, K-S., Jung, H-J., Lee, I-W., Park, J-G. (2003b), Integrated Passive-Active System for Seismic Protection of a Cable-Stayed Bridge, Journal of Earthquake Engineering, Vol. 7, No. 4, Imperial College Press, pp 615 – 633.
Park, K-S., Jung, H-J., Lee, I-W. (2003c), Hybrid Control Strategy for Seismic Protection of a Benchmark Cable-Stayed Bridge, Engineering Structures, Vol. 25 (2003), Elsevier Science Ltd., pp 405 – 417.
Park, K-S., Koh, H-M., Ok, S-Y., Seo, C-W. (2005), Fuzzy Supervisory Control of Earthquake-Excited Cable-Stayed Bridges, Engineering Structures, Article in Press, Elsevier Science Ltd.
Parvin, A., Ma, Z. (2001), The Use of Helical Spring and Fluid Damper Isolation Systems for Bridge Structures Subjected to Vertical Ground Acceleration, Electronic Journal of Structural Engineering, Vol. 2 (2001), EJSE International.
Pekcan, G., Mander, J.B., Chen, S.S. (1999), Fundamental Considerations for the Design of Non-Linear Viscous Dampers, Earthquake Engineering and Structural Dynamics, Vol. 28 (1999), John Wiley & Sons Ltd., pp 1405 – 1425.
Petronijevic, M., Nefovska, M., Brcić, S. (2002), Multiple – Support Seismic Analysis of Bridges Including Soil – Structure Interaction, 12th European Conference on Earthquake Engineering, London, U.K., Elsevier Science Ltd., Paper No. 180.
Petrov, A.A. (1996), Seismic Response of Extended Systems to Multiple Support Excitations, 11th World Conference on Earthquake Engineering, Acapulco, Mexico, Elsevier Science Ltd., Paper No. 1451.
Podolny, W., Scalzi, J.B. (1986), Construction and Design of Cable – Stayed Bridges, 2ª edition, John Wiley & Sons, Inc, USA.
Pridham, B.A., Wilson, J.C. (2005), A Reassessment of Dynamic Characteristics of the Quincy Bayview Bridge Using Output – Only Identification Techniques, Earthquake Engineering and Structural Dynamics, Vol. 34 (2005), John Wiley & Sons Ltd, pp 787 – 805.
Priestley, M.J.N., Seible, F., Calvi, G.M. (1996), Seismic Design and Retrofit of Bridges, John Wiley & Sons, Inc., USA.
Qingshan, Y., Saiidi, M., Hang, W. (2002), Influence of Earthquake Ground Motion Incoherency on Multi – Support Structures, Journal of Earthquake Engineering and Engineering Vibration, Vol. 1, No. 2, IEM.
Ramirez, O., Ayala, A.G. (1997), Efecto de la Variabilidad Espacial de las Ondas Sísmicas en la Respuesta no Lineal de Puentes, Memoria del XI Congreso Nacional de Ingeniería Sísmica, Veracruz, México, pp 1017 – 1026.
Reis, A.J., Oliveira, J.J. (2004), The Europe Bridge in Portugal: concept and structural design, Journal of Constructional Steel Research, Vol.60, Elsevier Science Ltd, pp 363 – 372.
Ren, W.X. (1999), Ultimate Behaviour of Long-Span Cable-Stayed Bridges, Journal of Bridge Engineering, Vol.4, No.1, ASCE, USA.
Ren, W.X., Obata, M. (1999), Elastic-Plastic Seismic Behaviour of Long-Span Cable-Stayed Bridges, Journal of Bridge Engineering, Vol.4, No.3, ASCE.
Ren, W.X., Peng, X.L., Lin, Y.Q. (2005), Experimental and Analytical Studies on Dynamic Characteristics of a Large Span Cable-Stayed Bridge, Engineering Structures, Vol. 27 (2005), Elsevier Science Ltd, pp 535 – 548.
Ren, W.X., Peng, X.L. (2005), Baseline Finite Element Modeling of a Large Span Cable-Stayed Bridge Through Ambient Vibration Tests, Computers & Structures, Vol. 83 (2005), Elsevier Science Ltd, pp 536 – 550.
Ruangrassamee, A., Kawashima, K. (2002), Seismic Response Control of a Benchmark Cable-Stayed Bridge by Variable Dampers, Proceedings of the American Control Conference, Anchorage, Alaska.
Saadeghvaziri, M.A., Foutch, D.A. (1991), Dynamic Behaviour of R/C Highway Bridges Under the Combined Effect of Vertical and Horizontal Earthquake Motions, Earthquake Engineering and Structural Dynamics, Vol. 20 (1991), John Wiley & Sons Ltd, pp 535 – 549.
Sahasrabudhe, S.S., Nagarajaiah, S. (2005), Semi-Active Control of Sliding Isolated Bridges Using MR Dampers: An Experimental and Numerical Study, Earthquake Engineering and Structural Dynamics (in press).
SAP 2000 (2005), Integrated Software for Structural Analysis and Design V. 9.0, Computers & Structures, Berkeley, CA, USA
Saxena, V., Deodatis, G., Shinozuka, M. (2000), Effect of Spatial Variation of Earthquake Ground Motion on the Nonlinear Dynamic Response of Highway Bridges, 12th World Conference on Earthquake Engineering, Auckland, New Zealand, Elsevier Science Ltd., Paper No. 2227.
Schemmann, A.G., Smith, H.A. (1996), Vibration Control of Cable-Stayed Bridges: Analytical Development, Proceedings of the 11th Conference on Engineering Mechanics, Part 2, Fort Laudardale, USA, ASCE, pp 898 – 901.
Schemmann, A.G., Smith, H.A. (1998), Vibration Control of Cable-Stayed Bridges, Part 1 and 2, Earthquake Engineering and Structural Dynamics, Vol. 27, John Wiley & Sons, pp 811 – 824, pp 825 – 843.
Sennah, K., Kennedy, J. (2001), State-of-the-Art in Design of Curved Box – Girder Bridges, Journal of Bridge Engineering, Vol.6, No.3, ASCE, USA.
Sextos, A., Kappos, A., Pitilakis, K (2003), Seismic Response of Long Concrete Bridges: Effect of Coupled Ground Motion Variability and Soil – Foundation Interaction, FIB Symposium: Concrete Structures in Seismic Regions, Athens, Greece.
Sextos, A., Kappos, A., Mergos, P. (2004), Effect of Soil -Structure Interaction and Spatial Variability of Ground Motion on Irregular Bridges: The Case of the Krystallopigi Bridge, 13th World Conference on Earthquake Engineering, Vancouver, Canada, Elsevier Science Ltd., Paper No. 2298.
Shen, J., Tsai, M-H., Chang, K-Ch., Lee, G.C. (2004), Performance of a Seismically Isolated Bridge under Near-Fault Earthquake Ground Motion, Journal of Structural Engineering, Vol. 130, No. 6, ASCE, pp 861 – 868.
Shinozuka, M., Deodatis, G. (1996), Effect of Spatial Variation of Earthquake Ground Motion on Seismic Response of Bridges, FHWA / NCEER Workshop on the National Representation of Seismic Ground Motion for New and Existing Highway Facilities, Burlingame, USA, National Center for Earthquake Engineering Research, pp 343 – 358.
Shoureshi, R.A., Chaghajerdi, A.H., Bell, M.J. (1999), Hybrid Adaptative Robust Structural Vibration Control, Proceedings of the American Control Conference, San Diego, USA, pp 1012 – 1016.
Shu, H.S., Wang, Y.Ch. (2001), Stability Analysis of Box-Girder Cable-Stayed Bridges, Journal of Bridge Engineering, Vol.6, No.1, ASCE, USA.
Silva, W. (1997), Characteristics of Vertical Strong Ground Motions for Applications to Engineering Design, FHWA / NCEER Workshop on the National Representation of Seismic Ground Motion for New and Existing Highway Facilities, Burlingame, USA, National Center for Earthquake Engineering Research, pp 205 – 219.
Simoes, L.M.C., Negrão, J.H.J.O. (1996), Comparison Between Modal and Step-by Step Approaches in the Optimization of Cable-Stayed Bridges Subjected to Seismic Loads, Proceedings of 11th World Conference on Earthquake Engineering, Acapulco, México, Paper no. 1881, Elsevier Science Ltd.
Singh, M.P., Verma, N.P., Moreschi, L.M. (2003), Seismic Analysis and Design with Maxwell Dampers, Journal of Engineering Mechanics, Vol. 129, No. 3, ASCE, pp 273 – 282.
Skinner, R.I., Robinson, W.H., Mc Verry, G.H. (1993), An Introduction to Seismic Isolation, John Wiley & Sons Ltd.
Somerville, P. (1997), The Characteristics and Quantification of Near Fault Ground Motion, FHWA / NCEER Workshop on the National Representation of Seismic Ground Motion for New and Existing Highway Facilities, Burlingame, USA, National Center for Earthquake Engineering Research, pp 293 – 318.
Song, X., Ahmadian, M. (2005), Modelling Magnetorheological Dampers with Application of Nonparametric Approach, Journal of Intelligent Material Systems and Structures, Vol. 16, No. 5, SAGE Publ., pp 421 – 432.
Soong, T.T., Spencer, B.F. (2000), Active, Semi-Active and Hybrid Control of Structures, Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, Elsevier Science Ltd.
Soong, T.T., Spencer, B.F. (2002), Supplemental Energy Dissipation: State-of-the-Art and State-of-the-Practice, Engineering Structures, Vol. 24 (2002), Elsevier Science Ltd., pp 243 – 259.
Soyluk, K., Dumanoglu, A.A. (2000), Comparison of Asynchronous and Stochastic Dynamic Responses of a Cable – Stayed Bridge, Engineering Structures, Vol. 22 (2000), Elsevier Science Ltd., pp 435 – 445.
Soyluk, K., Dumanoglu, A.A. (2003), A Stochastic Analysis of Long Span Structures Subjected to Spatially Varying Ground Motions Including the Site – Response Effect, Engineering Structures, Vol. 25 (2003), Elsevier Science Ltd., pp 1301 – 1310.
Soyluk, K. (2004), Comparison of Random Vibration Methods for Multi – Support Seismic Excitation Analysis of Long – Span Bridges, Engineering Structures, Vol. 26 (2004), Elsevier Science Ltd., pp 1573 – 1583.
Soyluk, K., Dumanoglu, A.A. (2004), Spatial Variability Effects of Ground Motions on Cable – Stayed Bridges, Soil Dynamics and Earthquake Engineering, Vol. 24 (2004), Elsevier Science Ltd., pp 241 – 250.
Soyluk, K., Domanoglu, A.A., Tuna, M.E. (2004), Random Vibration and Deterministic Analysis of Cable – Stayed Bridges to Asynchronous Ground Motion, Structural Engineering and mechanics, Vol. 18, No. 2, Techno-Press Ltd.
Spencer, B.F., Carlson, J.D., Sain, M.K., Yang, G. (1997), On the Current Status of Magnetorheological Dampers: Seismic Protection of Full-Scale Structures, Proceedings of the American Control Conference, Albuquerque, New México, USA, pp 458 – 462.
Spencer, B.F., Nagarajaiah, S. (2003), State of the Art of Structural Control (Forum), Journal of Structural Engineering, July 2003, ASCE, pp 845 – 856.
Starossek, U. (1996), Cable-Stayed Bridges Concept for Longer Spans, Journal of Bridge Engineering, Vol. 1, No. 3, ASCE, USA.
Symans, M.D., Constantinou, M.C. (1999), Semi-active Control Systems for Seismic Protection of Structures: A State-of-the-Art Review, Engineering Structures, Vol. 21 (1999), Elsevier Science Ltd., pp 469 – 487.
Takeda, T., Yamanobe, S., Niihara, Y. (2000), Damping Property of Prestressed Concrete Cable-Stayed Bridges Based on Measured Data, Structural Engineering/Earthquake Engineering, Vol. 17, No.1, Japan Society of Civil Engineering, pp 87 – 103.
Tan, R.Y., Liu, H. (1996), System Identification of a Long-Span Bridge, Proceedings of 11th World Conference on Earthquake Engineering, Acapulco, México, Elsevier Science Ltd.
Tatsumi, M.Y., Hata, K. (1998), Vibration Control of the Main Towers of the Akashi-Kaikyo Bridge’s Superstructure, IABSE Symposium: Long – Span and High – Rise Structures, Kobe, Japan.
Teyssandier, J.P. (2002), Corinthian Crossing, Civil Engineering, Oct. 2002, ProQuest Science Journals.
Teyssandier, J.P., Maublanc, G., Morand, P., Papanikolas, P. (2003), The Rion-Antirion Bridge, Proceedings from the FIB Symposium: Concrete Structures in Seismic Regions, Athens, Greece.
Tolis, S.V. (1999), Displacement Design Spectra, Journal of Earthquake Engineering, Vol. 3, No. 1 (1999), World Scientific Publ., pp 107 – 125.
Tongaonkar, N.P., Jangid, R.S. (2003), Seismic Response of Isolated Bridges with Soil – Structure Interaction, Soil Dynamics and Earthquake Engineering, Vol. 23 (2003), Elsevier Science Ltd., pp 287 – 302.
Trifunac, M.D. (1995), Pseudo Relative Velocity Spectra of Earthquake Ground Motion at Long Periods, Soil Dynamics and Earthquake Engineering, Vol. 14 (1995), Elsevier Science Ltd., pp 331 – 346.
Troitsky, M.S. (1988), Cable – Stayed Bridges, Oxford: BSP professional Books, London, U.K.
Tsopelas, P., Constantinou, M.C., Okamoto, S., Ozaki, D. (1996), Experimental Study of Bridge Seismic Sliding Isolation Systems, Engineering Structures, Vol. 18, No. 4, Elsevier Science Ltd., pp 301 – 310.
Tubino, F., Carassale, L., Solari, G. (2003), Seismic Response of Multi – Supported Structures by Proper Orthogonal Decomposition, Earthquake Engineering and Structural Dynamics, Vol. 32 (2003), John Wiley & Sons Ltd., pp 1639 – 1654.
Tuladhar, R., Dilger, W.H., Elbadry, M.M. (1995), Influence of Cable Vibration on Seismic Response of Cable-Stayed Bridges, Canadian Journal of Civil Engineering, Vol. 22 (5), National Research Council Canada, pp 1001 – 1020.
Tuladhar, R., Dilger, W. (1999), Effect of Support Conditions on Seismic Response of Cable – Stayed Bridges, Canadian Journal of civil Engineering, Vol. 26, No.5 (Oct. 1999), National Research Council Canada, pp 631 – 645.
Tzanetos, N., Elnashai, A.S., Hamdan, F.H., Antoniou, S. (2000), Inelastic Dynamic Response of RC Bridges Subjected to Spatial Non – Synchronous Earthquake Motion, Advances in Structural Engineering, Vol. 3, No. 3, Multi – Science Publ. Co. Ltd., pp 191 – 214.
Vader, T., Mc Daniel, C.C. (2004), Influence of Energy Dissipating Systems on the Seismic Response of Cable Supported Bridges, 13th World Conference on Earthquake Engineering, Vancouver, Canada, Elsevier Science Ltd., Paper No. 1046.
Valdebenito, G. (2005), Comportamiento Sísmico de Puentes, apuntes de clases del curso de Master en Ingeniería Sísmica y Dinámica Estructural, Departamento de Ingeniería del Terreno, Cartográfica y Geofísica, Universidad Politécnica de Catalunya, Barcelona, España.
Varadarajan, N., Nagarajaiah, S. (2003), Wind Response Control of Building with Variable Stiffness TMD: EMD/HT, Journal of Engineering Mechanics, ASCE.
Villaverde, R., Martin, S.C. (1995), Use of Damped Resonant Appendages to Augment Inherent Damping in Cable-Stayed Bridges, 10th European Conference on Earthquake Engineering, Madrid, Spain, AA Balkema Publ., pp 1803 – 1808.
Virlogeux, M. (1999), Recent Evolution of Cable – Stayed Bridges, Engineering Structures, Vol. 21, Elsevier Science Ltd, pp. 737 – 755.
Virtuoso, F., Guerreiro, L., Azevedo, J. (2000), Modelling the Seismic Behaviour of Bridges with Viscous Dampers, 12th World Conference on Earthquake Engineering, Auckland, New Zealand, Paper No. 0782.
Walter, R. (1999), Cable – Stayed Bridges, 2th edition, Thomas Telford Ltd., London, UK.
Wang, K., Lin, X., Zhu, X. (2004), Study on Control of Reducing Seismic Response for Cable-Stayed Bridge Based on Mode Analysis, 13th World Conference on Earthquake Engineering, Vancouver, Canada, Elsevier Science Ltd., Paper No. 3255.
Wang, D.W., Liao, W.H. (2005), Modeling and Control of Magnetorheological Fluid Dampers Using Neural Networks, Smart Materials and Structures, Vol. 14, IoP Publ.
Warnitchai, P., Jujino, Y., Pacheco, B.M., Agret, R. (1993), An Experimental Study on Active Tendon Control of Cable-Stayed Bridges, Earthquake Engineering and Structural Dynamics, Vol. 22, John Wiley & Sons Ltd., pp 93 – 111.
Wethyavivorn, B., Fleming, J. (1987), Three Dimensional Seismic Response of a Cable Stayed Bridge, International Conference on Cable – Stayed Bridges, Bangkok, Thailand, November 18-20, 1987.
Wilson, J.C., Liu, T. (1991), Ambient Vibration Measurements on a Cable-Stayed Bridge, Earthquake Engineering and Structural Dynamics, Vol.20 (1991), John Wiley & Sons, Ltd., pp 723 – 747.
Wilson, J.C., Gravelle, W. (1991), Modelling of a Cable-Stayed Bridge for Dynamic Analysis, Earthquake Engineering and Structural Dynamics, Vol. 20, John Wiley & Sons, Ltd, pp 707 – 721.
Wolf, J.P. (1985), Dynamic Soil – Structure Interaction, Prentice Hall Publ.
Wolf, J.P. (1988), Soil – Structure Interaction Analysis in the Time Domain, Prentice Hall Publ.
Xu, X-L., Liu, W-Q., Wang, R-G., Wang, Z-F., Wu., W-S., Wu, X-L. (2004), A Study of Vibration Reduction Structural System of Long-Span Cable-Stayed Bridges, Proceedings of the Third International Conference on Earthquake Engineering – New Frontier and Research Transformation, Nanjing, Peoples R. China, pp 529 – 534.
Xue, S.D., Ko, J.M., Xu, Y.L. (2000), Control of Torsional Flutter and Buffeting of Long-Span Bridges Using Liquid Column Damper, Advances in Structural Dynamics, Vol. 1, pp 113 – 122.
Yalla, S., Kareem, A., Kantor, C. (2001), Semiactive Tuned Liquid Dampers for Vibration Control of Structures, Engineering Structures, Vol. 23, Elsevier Science Ltd., pp 1469 – 1479.
Yamaguchi, H., Jayawardena, L. (1991), Analytical Estimation of Structural Damping in Cable Structures, Journal of Wind Engineering and Industrial Aerodynamics, Vol. 43 (1 – 3), Elsevier Science Ltd, pp 1961 – 1972.
Yamaguchi, H., Manabu, I. (1997), Mode – Dependence of Structural Damping in Cable-Stayed Bridges, Journal of Wind Engineering and Industrial Aerodynamics, Vol. 72 (1997), Elsevier Science Ltd, pp 289 - 300.
Yang, J.N., Kawashima, K., Unjoh, S. (1995), Hybrid Control of Seismic-Excited Bridge Structures, Earthquake Engineering and Structural Dynamics, Vol. 24, No. 11, John Wiley & Sons Ltd., pp 1437 – 1451.
Yang, J.N., Agrawal , A.K. (2002), Semi-active Hybrid Control Systems for Nonlinear Buildings against Near-Field Earthquakes, Engineering Structures, Vol. 24 (3), Elsevier Science Ltd., pp 271 – 280.
Yang, J.N., Lin, S., Kim, J-H., Agrawal, A.K. (2002), Optimal Design of Passive Energy Dissipation Systems Based on H∞ and H2 Performances, Earthquake Engineering and Structural Dynamics, Vol. 31 (2002), John Wiley & Sons Ltd., pp 921 – 936.
Yang, G., Spencer, B.F., Jung, H-J., Carlson, J.D. (2004), Dynamic Modelling of Large-Scale Magnetorheological Damper Systems for Civil Engineering Applications, Journal of Engineering Mechanics, Vol. 130, No. 9, ASCE, pp 1107 – 1114.
Yi, F., Dyke, S.J., Frech, S., Carlson, J.D. (1998), Investigation of Magnetorheological Dampers for Earthquake Hazard Mitigation, Proceedings of the 2nd World Conference on Structural Control, Kyoto, Japan.
Yu, C-P., (1996), Effect of Vertical Earthquake Components on Bridge Responses, PhD Thesis, Univ. of Texas, Austin, Texas, USA.
Yu, C-P., Broekhuinzen, D.S., Roesset, J.M., Breen, J.E., Kreger, M. (1997), Effect of Vertical Ground Motion on Bridge Deck Response, Workshop on Earthquake Engineering Frontiers in Transportation Facilities, Tech. Rep. No. NCEER – 97 – 0005, National Center of Earthquake Engineering Research, State University of New York at Buffalo, N.Y., USA.
Zheng, J., Takeda, T. (1995), Effects of Soil – Structure Interaction on Seismic Response of PC Cable – Stayed Bridge, Soil Dynamics and Earthquake Engineering, Vol. 14, Elsevier Science Ltd, pp 427 – 437.
Zhu, L.D., Xiang, H.F., Xu, Y.L. (2000), Triple-Girder Model for Modal Analysis of Cable-Stayed Bridges with Zarping Effect, Engineering Structures, Vol. 22 (2000), Elsevier Science Ltd, pp 1313 – 1323.
Document information
Published on 01/01/2005
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?