An appropriate relationship between flexural strength and compressive strength of palm kernel shell concrete

Abstract

This paper presents the determination of an appropriate compressive–flexural strength model of palm kernel shell concrete (PKSC). The direct and indirect Ultrasonic Pulse Velocity (UPV) measurements, with respective to mechanical properties of compression (cube) and flexural (slab) elements, of concrete at various mixes and water/cement (w/c) ratios were made. A total of 225 cubes and 15 slabs of the PKSC were casted for nominal mixes of 1:1:1, 1:1:2 and 1:11/2:3, and varying (w/c) ratios of 0.3–0.7 at interval of 0.1. The test elements were cured for 3, 7, 14, 28, 56 and 91 days in water at laboratory temperature. The elements were then subjected to nondestructive testing using the Pundit apparatus for determination of direct ultrasonic wave velocity and the elastic modulus at the various ages. The cubes were subsequently subjected to destructive compressive test. The 28-day compressive strength–UPV and strength–age statistical relationships at w/c ratio of 0.5 determined from the velocity–strength data set in linear, power, logarithm, exponential and polynomial trend forms. The polynomial trend line in the form y = aln(x) at R² value of 0.989, found appropriate, among others, was proposed for the formulation of the compressive strength–flexural strength model of PKSC at w/c ratio of 0.5.

Keywords

Compressive strength; Palm kernel shell concrete; Nondestructive technique; Rigid pavement maintenance; Direct and indirect ultrasonic pulse velocity

1. Introduction

The static modulus of elastic modulus of elasticity, modulus of rupture (flexural strength) and compressive strength are important properties of concrete. These are the basic parameters for computing deflection in reinforced concrete structures [1]. Maintenance of rigid pavements is more effective if the prevailing condition and residual strength and/or deterioration rate of the strength could be monitored as the pavement is being affected by traffic and weather. Nondestructive Test (NDT) methods offer the advantage of providing information on the in-place properties of hardened concrete, such as the elastic constants, density, resistivity, moisture content, and hardness characteristics. Unlike coring, a destructive testing (DT) approach introduces weak spots while obtaining the test specimens, with the attendant threats to the integrity and safety of the entire structure. Beside, the approach limits what can be detected as information at the core location and, additionally implies the need for the core holes to be repaired. The assessment of in situ compression strength of a rigid pavement structure plays a key role in the evaluation of its adequacy in strength at the time of production (Quality control and assurance, QC/QA) and or even later at service, which is very desirable in the maintenance practice of infrastructural facilities. The knowledge that the critical properties of the concrete and its state are within the expected values and presumptions would restore the confidence of the user of the facility.

Different countries have established various design codes based on empirical relationships between any two of elastic modulus of elasticity, modulus of rupture (flexural strength) and compressive strength of plain concrete at 28 days of curing. Table 1 and Table 2 show some of the countries codes and the empirical relationships proposed for the concrete properties [2].

Table 1. Recommended empirical relationships between elastic modulus of elasticity and flexural strength of plain concrete.

Code	Country	Relationship
IS: 456-2000	India	Ec = 5000fc
ACI	USA	Ec = 4734 ${\textstyle {\sqrt {f_{c}^{'}}}}$
NZS-3101	New Zealand	Ec = 4734 (${\textstyle f_{c}^{'}+6900}$)
EC-02	Europe	Ec = 9500 ${\textstyle \left({\sqrt {f_{c}^{'}}}+8\right)}$)0.33
BS-8110	Britain	Ec = 20,000 + 0.2fc

where E_c = the static modulus of elasticity at 28 days in N/mm².

f_c = cube compressive strength at 28 days in N/mm², and

${\textstyle f_{c}^{'}}$ = cylinder compressive strength at 28 days in N/mm².

Source: Beeby and Narayanan [4].

Table 2. Recommended empirical relationships between flexural strength and compressive strength of plain concrete.

Code	Country	Relationship
IS: 456-2000	India	fr = ${\textstyle 0.7{\sqrt {f_{c}}}}$
ACI	USA	fr = 0.62 ${\textstyle {\sqrt {f_{c}^{'}}}}$
NZS-3101	New Zealand	fr = 0.60 ${\textstyle {\sqrt {f_{c}^{'}}}}$
EC-02	Europe	fr = 0.201fc
BS-8110	Britain	fr = 0.60 ${\textstyle {\sqrt {f_{c}^{'}}}}$

where f_r = modulus of rupture (flexural strength) at 28 days in N/mm².

f_c = cube compressive strength at 28 days in N/mm², and

${\textstyle f_{c}^{'}}$ = cylinder compressive strength at 28 days in N/mm².

Source: Beeby and Narayanan [4].

The NDT methods are the most used to determine the properties of hardened concrete as well as to indirectly evaluate the condition of concrete structures and pavements without the direct loading or the need for direct access to testing position or location. The significance of the methods in virgin concrete construction based on mechanical (strength) property has been much demonstrated for quality control of the new construction or troubleshooting of problems, and/or condition evaluation of older concrete for rehabilitation purposes, quality assurance of concrete repairs and detection of flaws or discontinuities [3]. Thus the NDT can be divided into two groups: (i) those whose main purpose was to estimate strength for design and (ii) those whose main purpose was to evaluate conditions other than strength or integrity evaluation, as usually desirable in pavement maintenance. It is, therefore, clear that the most reliable tests for residual strength are the real time integrity and nondestructive that do not result in either local damage or superficial, which had been mostly based on visual inspections. However, modern day analysis and design of pavement desire that elastic properties of material be accurately determined in place and at appropriate time because routine maintenance should be really linked with the actual and prevailing status of the structure, in this case the residual strength of the concrete pavement. The knowledge that the critical properties of the concrete and its state are within expected values and presumptions would restore the confidence of the user of the facility.

Ultrasonic Pulse Velocity (UPV) is a nondestructive technique that involves measuring the speed of sound waves through materials in order to predict material strength, to calculate low-strain elastic modulus and/or to detect the presence of internal flaws such as cracking, voids, honeycomb, decay and other damages. The technique is applicable where intrusive (destructive) testing is not desirable and has been much applied to concrete, mainly in finding general changes to condition such as areas of weak concrete in a sound structure, but less commonly in ceramics, stone and timber. Also, absolute measurements should be treated with caution because the UPV technique is not always practicable in testing sound concrete, in the investigation of water filled crack depth and very rough surfaces [4], thereby requiring the use of a coupling gel between the transducers and the structure to provide the smoothness in contact. The leading portable UPV test instrument is the Pundit Ultrasonic Testing Machine, which is used to transmit an irrational pulse to travel through a known distance in concrete. The generated Ultrasonic Pulse Velocity (UPV) is correlated with prevailing compressive strength or other properties for in situ and timely decision making in material quality/integrity evaluation. Indeed, the UPV has been adopted to describe the quality of concrete in accordance with the BS 1881 [5] as presented in Table 3. Pulse velocity is influenced by many variables such as mix proportions, aggregate type, age of concrete, moisture content, and other factors [6], which might make strength estimation with the pulse velocity suspect and inaccurate. Therefore, for the UPV–strength relations derived for structures to be reliable, at any time during its service period, the risk level involved must be defined quantitatively, especially with the statistical coefficient of correlation, R² values.

Table 3. Suggested quality criteria for concrete.

Pulse velocity (km/s)	Concrete quality (grading)
Above 4.0	Very good
3.5–4.0	Good
3.0–3.5	Medium
Below 3.0	Poor

Source: IS Code, BS, 1881, 1983.

Some previous studies have concluded that, for normal concrete with a particular mix proportion, there is a good correlation between UPV and the compressive strength [7] and [8] but no clear rules or much explicit quantification on the effect as the mix varies nor for lightweight concrete specifically, such as a vegetative lightweight. Also [1], proposed correlations between flexural tensile strength and compressive strength of cube and cylinder for plain and metakaolin based concrete. Palm kernel shell (PKS) concrete, is an emerging vegetative lightweight concrete derived from recycling the biomass waste of palm kernel shells as substitutes completely for the conventional natural/traditional coarse aggregates. The PKS concrete at certain nominal mix and water cement ratio has been characterized to possess tangible benefits when used in rigid pavement construction [9], such as protection of the environment by conserving the natural resources for coarse aggregates, the lands for mining and landfills, serving as a new and alternate source of concreting aggregates, thus extending the life of sand and gravel mines, economic development opportunities and reduced pollution hazards as either waste dump from palm oil extracting processes or improved human health from the burning of the kernels.

This paper is, therefore aimed at establishing an appropriate relationship between flexural strength and compressive strength from the mechanical properties of a PKS concrete slab determined indirectly through the direct characterization of shear wave velocity at various mixes and water/cement ratios, that is nondestructive, and thereby presents the condition and prevailing condition and strength of a rigid pavement on being subjected to traffic and weather effects when opened for use. The specific objectives, therefore, are to do the following: (i) determine the physical properties of palm kernel shells, (ii) determine the Ultrasonic Pulse Velocity (UPV) and corresponding compressive strength of PKS concrete cubes with both direct and indirect methods at varying nominal mixes, 28-day curing age and water/cement ratio of 0.5, (iii) determine the relationship between the direct UPV and compressive strength of PKSC with various trend lines, (iv) select the most appropriate statistical relationship in (iv) develop the direct UPV–indirect UPV relationship for the PKSC slab, (v) determine the UPV–compressive strength model for the concrete mixes at 28-day curing w/c ratio of 0.5, and hence, (vi) propose the appropriate flexural strength–compressive compressive strength relationship of PKS concrete at 28 days and w/c ratio of 0.5.

2. Materials and methods

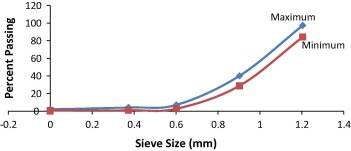
Palm kernel shells (PKS) wastes were obtained from small scale palm oil milling processes and evaluated for nominal lightweight concrete works. The relevant physical and strength properties are presented in Table 4 while the particle size gradation envelope is displayed in Fig. 1. The PKS were washed, dried and employed as coarse aggregate for production of nominal lightweight concrete. Nominal concrete mixes of 1:1:1, 1:1:2 and 1:1½:3 and water/cement ratios of 0.3, 0.4, 0.5, 0.6 and 0.7 were produced with the PKS as the light weight coarse aggregates and the other conventional components of fine aggregates (sand), ordinary Portland cement (OPC) and portable water (WHO Standard). The workability of the various mixes for rigid pavement was also evaluated with the standard slump test apparatus at the time of fresh concrete production. A total number of 225 cubes (150 × 150 × 150 mm) were batched, cured and tested for compressive strength at 7, 14, 28, 56 and 91 days according to the standard Destructive Test (DT) and Nondestructive Test (NDT) procedures. Also fifteen (15) PKS concrete slabs of dimensions 300 mm × 200 mm × 75 mm were produced at w/c ratio of 0.5 from the nominal mixes. But prior to the DT crushing, the PKS concrete cubes were subjected to NDT with the Pundit Apparatus (Model PC 1006) [10] to determine respective transit time, velocity of the pulse and elastic modulus in accordance with the specification of the British standard [11]. The NDT exercise with the indirect approach of the PUNDIT Apparatus was performed on the PKS concrete slabs.

Table 4. Physical properties of PKS.

Property	Average value
Water absorption capacity – 24 h (%)	13.7
Specific gravity	1.26
Bulk density (kg/m3)	640
Moisture content (%)	14.49
Aggregate impact value	5.02
Aggregate crushing value	6.5
Fineness modulus	6.24
Thickness (mm)	1.85

Figure 1. Particle size gradation envelope for palm kernel shell.

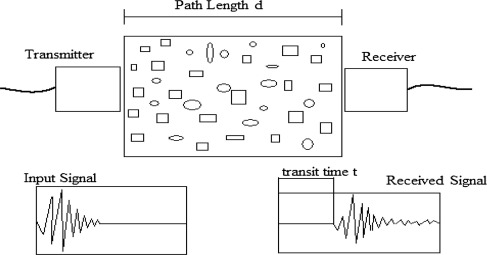
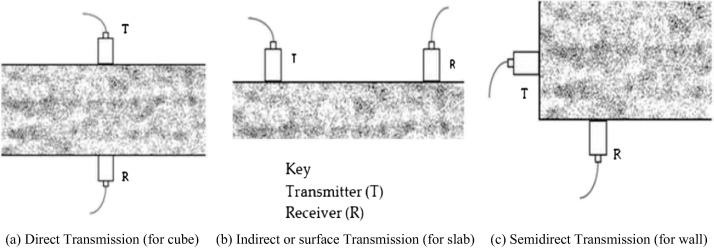
The NDT experimental setup shown schematically in Fig. 2 was performed in order to generate data for development of the fatigue model for a PKSC pavement. Fig. 3 shows the Portable Ultrasonic Non-Destructive Digital Indicating Tester (PUNDIT, Model PC 1006), which was used to measure the velocity of propagation of a compression wave through a testing specimen, while Fig. 4 shows the three methods of the wave propagation and receiving of ultrasonic pulses. Figure 5 and Figure 6 also shows the experimental setup and the testing procedure.

Figure 2. Ultrasonic pulse velocity testing.

Figure 3. The PUNDIT plus set. Source: Pundit (1993).

Figure 4. Methods of propagation and receiving ultrasonic pulses. Source: BS 12504-4, 2004.

Figure 5. Graph of 7-Day compressive strength against water/cement ratio.

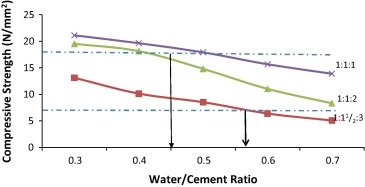
Figure 6. Graph of 28-Day compressive strength against water/cement ratio.

Various forms of the UPV–compressive strength relationship of hardened PKS concrete were tried for the concrete cubes, while the indirect derivation of the flexural strength of the slab was also accomplished using Microsoft Excel Software. The scatter diagram for the development of the relationships between ultrasonic pulse velocity and compressive strength drawn for PKS concrete with the corresponding w/c ratios was plotted with linear, power, logarithm, exponential and polynomial trend lines. The logarithm and polynomial trend lines show greater correlations, with R² values in the range of 0.949–0.993. However, the logarithm trend line was adopted for proposing the flexural strength–compressive strength relationship as the polynomial trend line was so exaggerative.

3. Results and discussion

3.1. Results

Table 5 presents the results of the workability of fresh PKS concrete in evaluation of rolled concrete used as rigid pavement. Table 6, Table 7 and Table 8 show the trend with respect to age of the compressive strength and UPV at the various water cement/ratios and nominal mixes. The resulting trend line equations relating compressive strength to ultrasonic pulse velocity of PKS concrete are shown in Table 9, Table 10 and Table 11. Table 12 shows the logarithm models relating compressive strength to UPV for w/c ratios of 0.3–0.7. The results of the direct UPV (cube specimens) and indirect UPV data (slab specimens) at w/c ratio of 0.5 for the considered nominal mixes are shown in Table 13, Table 14 and Table 15[12] and [13] while Table 16 presents the logarithm models relating the direct to indirect UPV of PKS concrete slab.

Table 5. Slump (cm) of PKS concrete mixes in comparison with rolled compacted concrete.

Mix	bSlump (cm) at various w/c ratio 0.3 0.4 0.5 0.6 0.7					aStandard slump for rolled compacted concrete (cm)	Remarks
1:11/2:3	1.85	2.00	2.10	2.25	2.40	2.15	Slump at w/c = 0.5
1:1:2	1.20	1.35	1.40	1.65	1.90	1.25	Satisfactory for the 3
1:1:1	1.05	1.15	1.20	1.35	1.45	1.00	Nominal mixes

a. ASTM C1170/c1170M and ACI 228.2R [12] and [13].

b. Yusuf [14].

Table 6. Compressive strength (N/mm²) versus ultrasonic pulse velocity (m/s) of PKS concrete (1:1¹/₂:3 mix ratio); Yusuf [14].

Age (days)	w/c = 0.3		w/c = 0.4		w/c = 0.5		w/c = 0.6		w/c = 0.7
	Compressive strength (N/mm2)	UPV (km/s)	Compressive strength (N/mm2)	UPV (km/s)	Compressive strength (N/mm2)	UPV (km/s)	Compressive strength (N/mm2)	UPV (km/s)	Compressive strength (N/mm2)	UPV (km/s)
7	5.20	4.761	4.61	4.451	4.12	4.075	2.75	3.890	2.07	3.270
14	9.21	4.978	8.04	4.777	6.21	4.369	4.81	4.139	3.96	3.642
28	13.12	5.828	10.12	5.686	8.52	5.321	6.37	5.046	5.06	4.302
56	15.80	6.560	13.18	6.163	10.29	5.649	8.63	5.383	7.15	4.838
91	15.81	6.465	13.20	6.275	10.33	5.787	8.65	5.492	7.18	5.056

Table 7. Compressive strength (N/mm²) versus ultrasonic pulse velocity (m/s) of PKS concrete (1:1:2 mix ratio); Yusuf [14].

Age (days)	w/c = 0.3		w/c = 0.4		w/c = 0.5		w/c = 0.6		w/c = 0.7
	Compressive strength (N/mm2)	UPV (km/s)	Compressive strength (N/mm2)	UPV (km/s)	Compressive strength (N/mm2)	UPV (km/s)	Compressive strength (N/mm2)	UPV (km/s)	Compressive strength (N/mm2)	UPV (km/s)
7	8.12	5.059	7.63	4.658	5.18	4.466	4.53	4.042	3.89	3.551
14	13.13	5.333	11.98	4.986	9.58	4.662	7.64	4.322	5.75	3.974
28	19.52	6.045	18.16	5.886	14.80	5.732	11.02	5.441	8.32	4.902
56	21.49	6.685	19.25	6.450	16.47	5.975	12.22	5.699	9.13	5.288
91	21.50	6.793	19.27	6.584	16.51	6.254	12.25	5.806	9.16	5.435

Table 8. Compressive strength (N/mm²) versus ultrasonic pulse velocity (m/s) of PKS concrete (1:1:1 mix ratio); Yusuf [14].

Age (days)	w/c = 0.3		w/c = 0.4		w/c = 0.5		w/c = 0.6		w/c = 0.7
	Compressive strength	UPV (km/s)	Compressive strength	UPV (km/s)	Compressive strength	UPV (km/s)	Compressive strength	UPV (km/s)	Compressive strength	UPV (km/s)
7	10.20	5.157	8.67	4.891	6.64	4.520	5.84	4.220	4.26	3.830
14	15.22	5.498	13.43	5.117	11.27	4.870	9.74	4.560	7.55	4.109
28	21.12	6.216	19.64	6.017	17.92	5.823	15.66	5.672	13.88	5.278
56	22.56	6.813	20.72	6.662	19.61	6.273	17.53	5.950	15.12	5.587
91	22.60	6.925	20.78	6.747	19.64	6.445	17.57	6.175	15.18	5.626

Table 9. Resulting mechanical properties of PKSC using various trend line options (1:1¹/₂:3 mix).

UPVd	Linear			Exponential			Logarithm			Power			Polynomial (order 5)
	UPVi	fcu	fr	UPVi	fcu	fr	UPVi	fcu	fr	UPVi	fcu	fr	UPVi	fcu	fr
3.785	3.649	6.086	1.160	3.125	3.589	0.849	4.288	7.988	1.362	3.762	6.351	1.190	5.937	8.704	1.433
4.075	3.928	6.552	1.212	3.410	4.033	0.910	4.492	8.215	1.385	4.069	6.935	1.253	6.870	7.592	1.322
4.369	4.212	7.025	1.263	3.725	4.588	0.982	4.685	8.421	1.406	4.382	7.535	1.316	8.013	−4.866	#NUM
4.922	4.745	7.914	1.355	4.400	6.046	1.156	5.015	8.754	1.438	4.974	8.685	1.431	10.912	−264.9	#NUM
5.321	5.129	8.556	1.419	4.961	7.607	1.323	5.231	8.960	1.458	5.404	9.530	1.512	13.831	−1625	#NUM
5.649	5.445	9.083	1.470	5.476	9.390	1.499	5.396	9.112	1.473	5.758	10.234	1.577	16.916	−6359	#NUM
5.787	5.579	9.305	1.491	5.708	10.325	1.586	5.463	9.172	1.478	5.908	10.533	1.604	18.434	−11041	#NUM
R2	0.931–0.983			0.522–0.813			0.949–0.989			0.931–0.965			0.986–1.0

where UPV_d = direct UPV reading (cube) in km/s, UPV_i = indirect UPV (slab) in km/s, f_cu – compressive strength in N/mm².

f_r = flexural strength in N/mm².

Table 10. Resulting mechanical properties of PKSC using various trend line options (1:1:2 mix).

UPVd	Linear			Exponential			Logarithm			Power			Polynomial (order 5)
	UPVi	fcu	fr	UPVi	fcu	fr	UPVi	fcu	fr	UPVi	fcu	fr	UPVi	fcu	fr
4.159	3.585	9.762	1.534	3.768	6.682	1.226	4.973	14.286	1.921	4.584	12.772	1.798	−9.674	2379	39.49
4.466	3.850	10.483	1.600	4.156	8.124	1.376	5.179	14.629	1.948	4.920	13.979	1.896	−15.93	14,262	115.5
4.662	4.019	10.943	1.641	4.425	9.300	1.491	5.303	14.830	1.964	5.135	14.761	1.958	−20.98	42,990	218.4
5.230	4.508	12.276	1.756	5.306	14.483	1.937	5.634	15.344	2.004	5.757	17.077	2.135	−41.42	67,453	1184
5.732	4.941	13.454	1.854	6.225	23.039	2.548	5.899	15.734	2.034	6.307	19.181	2.286	−68.71	75,084	4533
5.975	5.150	14.025	1.900	6.726	29.668	2.959	6.018	15.905	2.047	6.573	20.217	2.359	−85.84	72,776	8326
6.254	5.391	14.680	1.952	7.352	40.675	3.565	6.150	16.089	2.061	6.879	21.421	2.441	−109.3	90,360	16,248
R2	0.892–0.919			0.286–0.668			0.980–0.0.993			0.913–0.941			0.997–0.999

where UPV_d = direct UPV reading (cube) in km/s, UPV_i = indirect UPV (slab) in km/s, f_cu – compressive strength in N/mm².

f_r = flexural strength in N/mm².

Table 11. Resulting mechanical properties of PKSC using various trend line options (1:1:1 mix).

UPVd	Linear			Exponential			Logarithm			Power			Polynomial (order 5)
	UPVi	fcu	fr	UPVi	fcu	fr	UPVi	fcu	fr	UPVi	fcu	fr	UPVi	fcu	fr
4.520	4.882	15.890	2.046	4.424	10.95	1.642	5.389	17.863	2.192	5.242	18.096	2.209	17.166	1651	31.82
4.870	5.260	17.120	2.138	4.964	114.66	1.951	5.582	18.212	2.218	5.656	19.485	2.308	22.609	3091	740.09
5.823	6.289	20.470	2.376	6.792	739.43	3.500	6.049	19.021	2.275	6.424	23.634	2.563	47.732	−45,267	9#NUM
6.273	6.775	22.052	2.483	7.876	170.87	4.950	6.243	19.338	2.297	6.820	25.046	2.677	66.810	−67,214	#NUM
6.445	6.691	22.657	2.523	8.335	490.828	5.732	6.313	19.450	2.305	6.970	25.727	2.720	75.667	−97,112	#NUM
R2	0.831–0.937			0.170–0.733			0.966–0.989			0.907–0.953			0.998–0.999

where UPV_d = direct UPV reading (cube) in km/s, UPV_i = indirect UPV (slab) in km/s, f_cu – compressive strength in N/mm².

f_r = flexural strength in N/mm².

Table 12. Equations relating to compressive strength, y (N/mm²) and UPV, x (km/s) of PKSC.

1:11/2:3 Mix
y = 7.712ln(x) + 1.014	R2 = 0.981	w/c = 0.3
y = 6.211ln(x) + 1.006	R2 = 0.975	w/c = 0.4
y = 4.890ln(x) + 0.869	R2 = 0.989	w/c = 0.5
y = 4.125ln(x) + 0.379	R2 = 0.962	w/c = 0.6
y = 3.437ln(x) + 0.211	R2 = 0.949	w/c = 0.7
1:1:2 Mix
y = 10.691ln(x) + 1.698	R2 = 0.989	w/c = 0.3
y = 9.621ln(x) + 1.591	R2 = 0.988	w/c = 0.4
y = 8.491ln(x) + 0.665	R2 = 0.980	w/c = 0.5
y = 6.115ln(x) + 0.819	R2 = 0.991	w/c = 0.6
y = 4.426ln(x) + 0.895	R2 = 0.993	w/c = 0.7
1:1:1 Mix
y = 10.740ln(x) + 3.112	R2 = 0.989	w/c = 0.3
y = 10.260ln(x) + 2.097	R2 = 0.988	for w/c = 0.4
y = 10.010ln(x) + 1.005	R2 = 0.982	w/c = 0.5
y = 8.974ln(x) + 0.637	R2 = 0.984	w/c = 0.6
y = 8.046ln(x) + 0.009	R2 = 0.966	w/c = 0.7

Table 13. Direct and indirect UPV of PKS concrete slab (1:1¹/₂:3 mix); Yusuf [14].

UPV (km/s)	Age (days)
	7	14	28	56	91
Direct	4.075	4.369	5.321	5.649	5.787
Indirect	2.271	3.472	5.226	5.631	5.781

Table 14. Direct and indirect UPV of PKS concrete slab (1:1:2 mix); Yusuf [14].

UPV (km/s)	Age (days)
	7	14	28	56	91
Direct	4.466	4.662	5.732	5.975	6.254
Indirect	2.325	4.484	5.634	5.960	6.145

Table 15. Direct and indirect UPV of PKS concrete slab (1:1:1 Mix); Yusuf [14].

UPV (km/s)	Age (days)
	7	14	28	56	91
Direct	4.520	4.870	5.823	6.273	6.445
Indirect	3.425	4.434	5.625	6.078	6.277

Table 16. Logarithm models for direct and indirect UPV at water/cement ratio of 0.5.

Model	Mix ratio	R2 value
UPVi = 2.769ln(UPVd)	1:11/2:3 Mix	R2 = 0.987
UPVi = 2.884ln(UPVd)	1:1:2 Mix	R2 = 0.969
UPVi = 2.968ln(UPVd)	1:1:1 Mix	R2 = 0.987

where UPV_i is the indirect UPV (cube) and UPV_d is the direct UPV (slab), both in km/s.

3.2. Discussions

The Ultrasonic Pulse Velocity (UPV) is the measure of the quality of concrete. The UPV values of the PKS concrete for all w/c ratios, ages and mix proportions fall within 2.0 and 7.0 km/s. Compared with UPV values in Table 3, the PKS concrete produced for all the mix proportions and w/c ratios of 0.3, 0.4 and 0.5 is good while the ones for w/c ratio of 0.6 and 0.7 are fairly good. This implies that PKS concrete at lower w/c ratios has low workability but high strength, which is adequate for structural works. However, the higher w/c ratios with lower strength are not good enough for rigid pavement. Table 6, Table 7 and Table 8 show the compressive strength variation versus ultrasonic pulse velocity of PKS concrete for the nominal mixes and water/cement ratios.

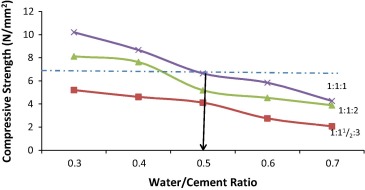
Figure 2 and Figure 3 show the plots of 7-day and 28-day compressive strengths, respectively, against w/c ratio. Based on the two properties, PKS concrete can be produced at w/c ratio of 0.45–0.5 and 0.42–0.57 for 7 and 28 days respectively for mix proportions of 1:1¹/₂:3 and richer. PKS concrete slabs (300 mm × 200 mm × 75 mm) were cast at mix proportions of 1:2:4, 1:1¹/₂:3, 1:1:2 and 1:1:1 and w/c of 0.50, in line with the critical value as depicted in Figure 2 and Figure 3.

Result of Table 6, Table 7 and Table 8 shows that compressive strength and UPV increase with advancement of age but decrease with increase in water/cement ratio. At the same age, both UPV and compressive strength of PKS concrete with low w/c ratio are higher than those with high w/c ratio mainly because of the denser structure of the concrete with lower w/c ratio. Also, a further inspection of the data in the tables and some computations show that for all the nominal mixes studied, the PKS concrete with high w/c ratio (w/c = 0.7) at the age of 7 days has UPV values of between 70% and 75% of that of 28 days, but the corresponding compressive strengths are between 50% and 55%. Similarly, at the age of 7 days, PKS concrete with low w/c ratios (w/c = 0.3) has UPV values that fall in the range of 80–85% of that at 28 days while the corresponding compressive strengths are in the range 55–60%. These imply that, the UPV and compressive strength growth rates of high and low w/c ratio concrete are significantly different at an early age. As a result, the relationship between UPV and compressive strength of PKS concrete becomes unclear when age and mix proportion are taken into consideration simultaneously. This observation suggests that it is better to separately consider the effect of age and mix proportion on UPV and compressive strength relationship. However, the 7-day to 28-day strength ratio of 60–75% normally reported for conventional concrete for QC/QA is equally satisfied with the palm kernel vegetative lightweight concrete, as equally related to the UPV. Thus, it is reasonable and appropriate to consider the parameter as the criteria to evaluate the quality of the palm kernel shell concrete.

The determination of the UPV without the destructive procedure of the structural setup of the element makes it suitable for assessment of the status or prevailing strength of the rigid slab as the deteriorating traffic and or weather induced stresses are imposed.

The scatter diagram and the resulting statistical relationship between ultrasonic pulse velocity and compressive strength for the PKS concrete with the corresponding w/c ratios yielded the equations as presented in Table 12. For the five w/c ratios, the relationship between UPV and compressive strength of PKS concrete is good for the mix proportions with a very high coefficient of correlation, R² in the range 0.949–0.993.

Indirect UPV can be related to direct UPV as presented in Eq. (1)[12]:

${\mbox{UPV}}_{\mbox{i}}=\alpha {\mbox{UPV}}_{\mbox{d}}$

(1)

where UPV_i = indirect UPV (UPV reading of the concrete slab in km/s), UPV_d = direct UPV (UPV reading of the concrete cube in km/s), α = constant

The compressive strength of the PKS concrete slab is expressed as a function of indirect UPV (since the basic pavement design principle is that, the wheel load imposes bending stresses on a slab) in the form given in Eq. (2)[12]:

Table 17 shows the compressive strength of the PKS concrete slab at w/c of 0.5 for the nominal mixes determined from equations in Table 12 and Table 16, and Eqs. (1) and (2):

$f_{\mbox{cu}}=\beta {\mbox{f}}({\mbox{UPV}}_{\mbox{d}})$

(2)

where f_cu = compressive strength, UPV_d = direct ultrasonic pulse velocity, β = constant

Table 17. Indirect UPV (km/s) and compressive strength (N/mm²) of PKSC slab at w/c of 0.5.

Age (days)	1:11/2:3		1:1:2		1:1:1
	UPVi	fcu	UPVi	fcu	UPVi	fcu
7	4.492	8.22	5.179	14.63	5.388	17.86
14	4.685	8.42	5.303	14.83	5.582	18.22
28	5.231	8.96	5.899	15.73	6.049	19.02
56	5.396	9.11	6.018	15.90	6.243	19.34
91	5.463	9.17	6.150	16.09	6.313	19.45

Pavements fail in flexure, and that the true measure of strength is the flexural strength. Eq. (3), derived by [12], relating flexural strength to compressive strength of concrete at w/c ratio of 0.5, and at R² value of 0.980 was employed in calculating the flexural strength of

$f_{\mbox{r}}=0.399f_{\mbox{c}}^{{'}^{0.591}}$

(3)

where ${\textstyle f_{\mbox{c}}^{'}}$ = compressive strength (N/mm²), and f_r = flexural strength (N/mm²)

The data of this study and values obtained from Table 17 and Table 18 were employed to propose relationships between flexural strength (f_r) and compressive strength (f_c) as in Eqs. (4), (5) and (6) for 1:1¹/₂:3, 1:1:2 and 1:1:1 nominal mixes, respectively at 28 days, all at R² > 98%.

$f_{\mbox{r}}=10.82{\mbox{ln}}(f_{\mbox{c}})+1.458$

(4)

$f_{\mbox{r}}=19.75{\mbox{ln}}(f_{\mbox{c}})+2.034$

(5)

$f_{\mbox{r}}=24.15{\mbox{ln}}(f_{\mbox{c}})+2.275$

(6)

Table 18. Flexural strength (N/mm²) of PKS concrete slab at w/c = 0.5.

Age (days)	Concrete mix
	1:11/2:3	1:1:2	1:1:1
7	1.385	1.948	2.192
14	1.406	1.964	2.218
28	1.458	2.034	2.275
56	1.473	2.047	2.297
91	1.478	2.061	2.305

4. Conclusions and recommendations

This paper aimed at proposing an appropriate empirical relationship between flexural strength and compressive strength of palm kernel shell concrete at different mix proportions using ultrasonic pulse velocity.

Consequently the following conclusions can be drawn:

• PKS concrete produced at each nominal mixes and water/cement ratios of 0.3–0.7 is fairly good to good, with compressive strength and UPV increase at advancement of age but decrease with increase in water/cement ratio.
• The appropriate water/cement ratio for production of PKS concrete slab was found as 0.5.
• The logarithm, power and polynomial models described the relationship between compressive strength and UPV of the PKS concrete at over 90% reliability for transforming the nondestructive test data to destructive, more common and conventional strength monitoring quality of lightweight vegetative concrete.
• The logarithm model was found appropriate for proposing relationship between flexural strength and compressive strength of PKS concrete, as the power and polynomial models were exaggerative.
• The direct UPV–indirect UPV logarithm relationship was at R² in the range 96.9–98.7%.
• The logarithm relationship was between flexural strength and compressive strength in the form.
• f_r = aln(f_c) at R² > 98% at 28 days were proposed for 1:1¹/₂:3, 1:1:2 and 1:1:1 nominal mixes.

The application of Research Findings in engineering can be in (i) the use of PKS as full replacement for coarse aggregates in regions, where they are scarce or unavailable for the production of PKS concrete in rigid pavements, but achievable at 1:1¹/₂:3 and richer nominal mixes, (ii) the transformation of other mechanical properties with the compressive strength of PKSC determined, can be used for the design and analysis of rigid pavements for traffic loading pattern and flexural form, while the reliable UPV-strength models (at R² > 95%) are appropriate for mechanistic analysis and design data of PKS rigid pavement, (iii) deriving the elastic dynamic modulus and flexural strength values with which to analyze the rigid pavement from the PKS vegetative slab and the ultrasonic test data set, (iii) inferring the flexural strength for bending influence from traffic from the compressive strength–UPV and the indirect UPV–direct UPV models developed to obtain the prevailing flexural strength of a rigid pavement slab, (iv) the establishment of strength deterioration properties of the pavement layers as being transferred by traffic, desirable as effective pavement maintenance practice with the indirect measurement of UPV through the pavement slab and the development of the NDT quality assurance of concrete construction and condition assessment for structural adequacy, and (v) assessing scheme of in situ compression strength of a rigid pavement structure for pavement maintenance in the evaluation of safety and feasibility in terms of strength at the time of need for effective maintenance of rigid pavements as being affected by traffic and weather conditions.

The following recommendations were also proposed:

• The recycle of PKS biomass waste from palm oil farming as light weight coarse aggregates should be encouraged as lightweight concrete production for rigid pavement works because of its demonstrated potential as a sustainable plant material and maintenance of ecological balances, and effective strategy to address the environmental pollution caused by indiscriminate dumping of PKS at palm oil processing areas.
• The NDT characterization with the UPV measurements for effective pavement maintenance, which deserves the establishment of the in situ strength deterioration properties of the pavement layers as being impacted from repeated traffic induced stresses, should be adopted as both the QC/QA and routine procedure for the PKS concrete pavement. The direct UPV–indirect UPV relationship determined at 95 and more percentage of reliability justifies the adoption.
• The flexural strength model developed from direct measurement of UPV in the logarithmic form with characteristics parameter of constant of 0.399 and index of 0.591 is recommended for routine monitoring or determination of PKS concrete slab as a rigid pavement.
• For further studies, the effect of changes in the volume fraction of cement paste, the source of PKS coarse aggregate (hinterland and coastal), the weather combined with traffic, the UPV–strength relationship should be examined for development of fatigue and other performance-based characteristics of PKS concrete pavement.
• The cost-effective analysis of recycling biomass for pavement rehabilitation should be further explored in order to demonstrate the economic viability, energy conservation, efficiency in transportation facility in poor soil conditions and protection of the environment from health hazard.

Acknowledgments

This paper cannot be put together without the tremendous background information made available by Babatunde Y.A, Odedina M.J. and Aroyehun, K.A., research undergraduate students of the Civil Engineering Department, University of Ilorin, Ilorin, who graduated in July, 2013, authors of excellent books and articles which have been referred to and listed in my references. I thank them. My special thanks to Prof. Y.A. Jimoh, my supervisor and the Dean, Faculty of Engineering and Technology, University of Ilorin, Ilorin, Nigeria, for his immense contribution to this paper. I also extended my appreciation to Dr. A.W. Salami, the Head of Civil Engineering Department, for his immense contribution to the research work.

References

1. [1] K. Anbuvelan, K. Subramanian; An empirical relationship between modulus of elasticity, modulus of rupture and compressive strength of M60 concrete containing metakaolin; Res. J. Appl. Sci. Eng. Technol., 8 (11) (2014), pp. 1294–1298
2. [2] A.W. Beeby, R.S. Naranayan; Designers Handbook to Euro-code 2 Part I: Design of Concrete Structures; Thomas Telford Services Ltd., London (1995)
3. [3] H.N. Tomsett; The practical use of ultrasonic pulse velocity measurements in the assessment of concrete quality; Mag. Concr. Res., 32 (110) (1980), pp. 7–16
4. [4] M. Colombo, R. Felicetti; New NDT techniques for the assessment of fire-damaged concrete structures; Fire Saf. J., 42 (2007), pp. 461–472
5. [5] BSI; Method for Determination of Compressive Strength of Concrete Cubes,; British Standards Institution, London, BS 1881 (1983) Part116
6. [6] Y. Lin, C.P. Lai, T. Yen; Prediction of ultrasonic pulse velocity (UPV) in concrete; ACI Mater. J., 100 (1) (2003), pp. 21–28
7. [7] I. Lawson, K.A. Danso, H.C. Odoi, C.A. Adjei, F.K. Quashie, I.I. Mumuni, I.S. Ibrahim; Non-destructive evaluation of concrete using ultrasonic pulse velocity; Res. J. Appl. Sci. Eng. Technol., 3 (6) (2011), pp. 499–504
8. [8] N.V. Mahure, G.K. Vijh, P. Sharma, N. Sivakumar, M. Ratnam; Correlation between pulse velocity and compressive strength of concrete; Int. J. Earth Sci. Eng., 4 (6) (2011), pp. 871–874
9. [9] I.T. Yusuf, Y.A. Jimoh; The transfer models of compressive to tensile, flexural and elastic properties of Palm Kernel shell concrete; Int. J. Eng. IJE, 11 (2) (2013), pp. 195–200
10. [10] N. Pundit; Manual of Portable Ultrasonic Non Destructive Digital Indicating Tester; C. N. S Instruments, London (1993) 98 pp
11. [11] BSI; Testing Concrete: Determination of Ultrasonic Pulse Velocity; British Standard BS EN 12504-4 (2004)
12. [12] ASTM C1170/c1170M, Standard Test Method for Determining Consistency and Density of Rolled Compacted Concrete Using a Vibrating Table, October 2008.
13. [13] ACI 228.2R; Guide for Selecting Proportions for No-Slump Concrete; American Concrete Institute Committee 211.3R-02, Farmington Hills, MI (1998)
14. [14] I.T. Yusuf, A study of Palm Kernel shell concrete characteristics with destructive and non-destructive methods, Ph.D. Thesis, University of Ilorin, Ilorin, Nigeria, 2013, 240 pp.