Using Fuzzy Clustering Chaotic-based Differential Evolution to solve multiple resources leveling in the multiple projects scheduling problem

Highlights

• This study presents a novel optimization algorithm FCDE.
• Chaotic mapping is used to prevent the algorithm from premature convergence.
• Clustering is utilized to enhance the convergence.
• FCDE is applied to handle multi resource leveling problem effectively.
• Statistical results found FCDE to provide better solutions compared to other methods.

Abstract

Project scheduling is an important part of construction project planning. Resource leveling is the process used within project scheduling to reduce fluctuations in resource usage over the period of project implementation. These fluctuations frequently create the untenable requirement of regularly hiring and firing temporary staff resources to meet short-term project needs. Construction project decision makers currently rely on experience-based methods to manage fluctuations. However, these methods lack consistency and may result in unnecessary wastage of resources or costly schedule overruns. This research introduces a novel optimization model called the Fuzzy Clustering Chaotic-based Differential Evolution for solving multiple resources leveling in the multiple projects scheduling problem (FCDE-MRLMP). The novel Fuzzy Clustering Chaotic-based Differential Evolution (FCDE) algorithm integrates fuzzy c-means clustering and chaotic techniques into the original Differential Evolution (DE) algorithm to handle complex optimization problems. The chaotic technique prevents the optimization algorithm from converging prematurely. The fuzzy c-means clustering technique acts as several multi-parent crossover operators in order to utilize population information efficiently and enhance convergence efficiency. Experiments run indicate that the proposed model obtains optimal results more reliably and efficiently than the benchmark algorithms considered. The proposed optimization model is a promising alternative approach to assist project managers to handle resource-leveling project scheduling problems effectively.

Keywords

Multiple resources leveling; Fuzzy clustering; Chaotic; Differential Evolution; Construction management

Nomenclature

Abbreviations and symbols

FCDE- Fuzzy Clustering Chaotic-based Differential Evolution

MRLMP- multiple resources leveling in the multiple projects

DE- Differential Evolution

PSO- Particle Swarm Optimization

GA- Genetic Algorithm

CLS- chaotic local search

AHP- analytical hierarchy process

FCM- fuzzy c-means

CDE- Chaos Differential Evolution

NFE- number of function evaluations

RI- resource intensity

w_m- weight score

λ- amplifying coefficient

LB- lower bound

UB- upper bound

F- mutation scale factor

CR- crossover probability

NP- population size

G- current generation

${\textstyle G_{\mbox{max}}}$- maximum of generation

${\textstyle D}$- dimension of solution vector

${\textstyle m}$- clustering period

CF- percentage of population to chaos

${\textstyle \mu }$- control parameter in chaos algorithm

1. Introduction

Managing corporate resources efficiently is critical to the long-term success and sustainability development of a construction company [1]. The efficient management helps on keeping operational expenses within planned budget and schedules on time. Time overruns often cause financial loss to the owner due to delays in facility availability [2] and may spark contract disputes that raise operational costs, degrade the company’s reputation, and occasionally lead to project failure [3] and [4].

Construction resources primarily consist of manpower, equipment, materials, funds, and expertise. Construction schedules generated by using network scheduling techniques that often cause resource fluctuations are impractical, inefficient, and costly to implement [5] and [6]. Therefore, construction managers must adjust construction schedules manually to eliminate these fluctuations.

Resource fluctuations are a troublesome issue for contractors [7] because hiring and firing workers to harmonize with fluctuating resource profiles are impractical. However, resources must be managed efficiently in order to maximize resource expenditures and meet contracted schedules. Contractors are thus inevitably burdened by a certain percentage of idle resources during periods of low demand, which detracts from project profits.

The process of smoothing out resources, known as resource leveling, has been studied extensively [8], [9], [10] and [11]. Resource leveling attempts to minimize both the demand peak and the fluctuations in the pattern of resource usage [12] and [13] by optimizing noncritical activities within their available floats while keeping the project duration unchanged. The application of Evolutionary Algorithms (EAs) to resource leveling has attracted increasing attention in recent years [14], [15] and [16]. Based on the principles of natural evolution, EAs are stochastic optimization techniques that have successfully resolved optimization problems in diverse fields [17]. However, EAs suffer from certain weaknesses. Geng et al. [14] identified premature convergence and poor exploitation as the main obstacles preventing EAs from coping effectively with complex optimization problems.

Research on resource leveling has focused mainly on three aspects: (1) single-resource leveling in single-project scheduling, (2) multiple-resource leveling in single-project scheduling, and (3) single-resource leveling in multiple-project scheduling. However, multiple-resource leveling in multiple-project scheduling is the most typical scenario in the construction and manufacturing industries, a situation that is relatively more complex and difficult due to the lack of a standard handling procedure [16]. Thus, developing a methodology for multiple-resource leveling in multiple-project problems and a more efficient algorithm to attain better resource-leveling-problem solutions are essential to improve the management of construction project resources.

The Differential Evolution (DE) [18] algorithm is an evolutionary computation technique. DE has drawn increasing interest from researchers, who have explored the capabilities of this algorithm in a wide range of problems. DE is a population-based stochastic search engine that is efficient and effective for global optimization in the continuous domain. DE uses mutation, crossover, and selection operators at each generation to move a population toward the global optimum. The superior performance of DE over competing algorithms has been verified in multiple published research works [19], [20] and [21].

Despite these advantages, the original DE and its numerous variants have some drawbacks. DE does not guarantee convergence to the global optimum and is easily trapped in local optima, resulting in low optimization precision or even optimization failure [22]. Further, populations may not be distributed over the search space, potentially trapping individuals in a local solution. DE may also require more generations than competing algorithms to converge on the optimal or near-optimal solution [23]. DE is particularly weak in situations in which the global optimum must be located using a limited number of fitness function evaluations. Finally, although DE is good at exploring the search space and locating the region of global minimum, it is slow to exploit the solution [24].

The inherent characteristics of chaotic systems provide an efficient approach maintaining population diversity in search algorithms. Chaos is the irregular motion of a deterministic nonlinear system under deterministic conditions. Because chaotic systems are sensitive to small differences in initial conditions, they may widely generate variant outcomes. This extreme sensitivity to initial conditions reflects the so-called butterfly effect or Liapunove’s sense [25]. Some studies have hybridized DE with the chaotic algorithm. Jia et al. [22] combined chaotic local search (CLS) with a “shrinking” strategy. The CLS helps improve the optimizing performance of the canonical DE by exploring a huge search space in the early run phase to avoid premature convergence and exploiting a small region in the later run phase to refine the final solutions. Bedri Ozer [23] embedded seven chaotic maps to create the initial DE population. It was found that coupling emergent results in different areas, like those of DE and complex dynamics, improving the quality of results in some optimization problems.

Fuzzy c-means clustering is the process of dividing a set of objects into groups or clusters of similarities in order to increase the speed of optimization search in DE. Successful clustering identifies true natural groupings in the dataset. Fuzzy c-means clustering, a soft clustering approach, was introduced to DE to help track the evolution of the search algorithm. In fuzzy clustering, data elements belong to more than one cluster and are associated with each element via a set of membership levels that indicate the strength of association between a particular data element and a particular cluster. Kwedlo [26] proposed a new version of DE, which uses k-means clustering to fine-tune each candidate solution obtained by the mutation and crossover operators of DE. Wang et al. [27] utilized a clustering technique to improve solution accuracy with less computational effort. Experiments demonstrated that the new method efficiently identifies near-optimal solutions.

Hybridization with other different algorithms is an interesting direction for the further improvement of DE [28]. Although there have been many proposals to improve DE, few have studied the hybridization of the clustering and chaotic techniques with the DE method [28]. To the best of our knowledge, fuzzy c-means clustering and chaotic have not previously been used to enhance the performance of DE.

Therefore, the objective of this research was to use fuzzy c-means clustering and chaotic techniques to overcome the aforementioned shortcomings of the original DE. Chaotic sequences rather than random sequences are adopted. Further, very interesting and good results are exploited to prevent the new approach from premature convergence. Meanwhile, fuzzy c-means clustering acts as several multi-parent crossover operators that use population information efficiently to facilitate faster algorithm convergence. The remainder of this paper is organized as follows: Section 2 briefly reviews literature relating to the establishment of the new optimization model. Section 3 provides a detailed description of the proposed optimization model for the resource-leveling problem. Section 4 uses two numerical experiments to demonstrate model performance. The final section presents conclusions and suggests directions for future work.

2. Literature review

2.1. Multiple resources leveling in the multiple projects problem

A total of n projects must be started simultaneously in an enterprise. Each project includes multiple activities and each activity uses p resources. Symbols used in related formulas include the following: the set of activities in the project k is {(i_k, j_k)} = {A_k, …, Z_k}; R_m(t) is the demand for resource m by all n projects on day t; R_mt(i_k, j_k) is the demand for resource m by activity (i_k, j_k) on day t; R_m(i_k, j_k) is the demand for resource m by activity (i_k, j_k) on one day. T_E(i_k, j_k), T_L(i_k, j_k), T_s(i_k, j_k), T_f(i_k, j_k), T(i_k, j_k), S(i_k, j_k) represent early start time, late start time, actual start time, actual finish time, duration, and slack time of (i_k, j_k), respectively. The precedence set of activity (i_k, j_k) is {(pset_k, i_k)}.

Multiple-resource leveling in multiple-project scheduling differs from conventional resource leveling techniques primarily as follows [16]:

Firstly, due to differing levels of resource demand, assimilation must transform absolute demand into relative demand in order to enable all the p resources to be comparable in terms of quantity. The relative demand of resource m in all n projects on day t may be expressed as follows:

${SR}_{m}(t)=\lambda R_{m}(t)/R_{{\mbox{max}}_{m}}$

(1)

where ${\textstyle R_{{\mbox{max}}_{m}}=max}$ {R_m(t)} denotes the maximum demand for resource m in total n projects on one day and λ is an amplifying coefficient within [1100] used to increase simulation accuracy. The above formula limits the relative demand for each resource in a total of n projects on every single day to between 0 and λ.

Secondly, the weight score w_m measures degree of importance for each resource. This paper uses the analytical hierarchy process (AHP) to set the weights of different resources. Larger weight scores correlate to greater priority.

The mathematical formulation objective function for multiple-resource leveling in multiple-projects scheduling is as follows:

$MinRI={\frac {1}{T}}\sum _{t=1}^{T}\sum _{m=1}^{p}\left[w_{m}{\left({SR}_{m}(t)-{\overline {{SR}_{m}}}\right)}^{2}\right]$

(2)

subject to:

$T_{E}(i_{k}{\mbox{,}}\quad j_{k})\leqslant T_{s}(i_{k}{\mbox{,}}\quad j_{k})\leqslant T_{L}(i_{k}{\mbox{,}}\quad j_{k})$

(3)

$max\lbrace T_{s}({pset}_{k}{\mbox{,}}\quad i_{k})+T_{s}({pset}_{k}{\mbox{,}}\quad i_{k})\rbrace \leqslant T_{s}(i_{k}{\mbox{,}}\quad j_{k})\leqslant T_{L}(i_{k}{\mbox{,}}\quad j_{k})$

(4)

$R_{m}(t)=\sum _{k=1}^{n}\sum _{i_{k}{\mbox{,}}\quad j_{k}}R_{mt}(i_{k}{\mbox{,}}\quad j_{k}){\mbox{;}}{\overline {{SR}_{m}}}=$${\frac {1}{T}}\sum _{t=1}^{T}{SR}_{m}(t)$

(5)

$R_{m}(i_{k}{\mbox{,}}\quad j_{k})={\begin{array}{l}R_{m}(i_{k}{\mbox{,}}\quad j_{k})\quad if:\quad T_{s}(i_{k}{\mbox{,}}\quad j_{k})<t\leqslant T_{f}(i_{k}{\mbox{,}}\quad j_{k})\\0\quad {\mbox{if}}:\quad t\leqslant T_{s}(i_{k}{\mbox{,}}\quad j_{k}){\mbox{or}}t>T_{f}(i_{k}{\mbox{,}}\quad j_{k})\end{array}}$

(6)

$S(i_{k}{\mbox{,}}\quad j_{k})=T_{L}(i_{k}{\mbox{,}}\quad j_{k})-$$T_{E}(i_{k}{\mbox{,}}\quad j_{k})$

(7)

where T is equal to the difference between the maximum of the latest finish time and the minimum of the earliest start time for all n projects.

2.2. Related works

In construction projects, many researchers have done numerous studies of modeling resource leveling problem in the literature. A variety of models, ranging from mathematical methods, heuristics to evolutionary, meta-heuristic approaches (e.g. Genetic Algorithm, Particle Swarm Optimization, Differential Evolution, Ant Colony Optimization) were proposed to solve the resource leveling problems [29]. Initially, the mathematical approaches were used to solve the resource leveling problems because they can provide optimal solutions to the problem at hand. However, these methods become impractical when the size of project network reaches a considerably large number. Hence, the increasing number of decision variables causes the problem solving to become infeasible [8]. As a result, mathematical approaches are not computationally manageable for real-world construction projects [12].

Other researchers attempted to utilize heuristic methods in solving the resource leveling problem [9] and [30]. However, using heuristic methods frequently is not sufficiently enough to satisfy project managers despite their simplicity and wide implementation on commercial project management software (e.g. Microsoft Project). The reason is because the methods operate on the basis of pre-defined rules. Consequently, their performance relies on specific types of problem and on which rules are implemented. For this reason, only a decent feasible solution can be produced without any guarantee on finding an optimum solution [31].

Due to the limitations of mathematical and heuristic methods, the application of Evolutionary Algorithms (EAs) for resource leveling has attracted more attention in recent years [14], [15], [32], [33] and [34]. Metaheuristic is recognized as a stochastic optimization method that is inspired by the phenomena seen in nature. They have been successfully used to solve optimization problems in diverse fields [17]. Some widely known metaheuristic algorithms, such as Genetic Algorithm, Particle Swarm Optimization, Ant Colony Optimization, and Differential Evolution, remain an active research area in the scientific community. However, these algorithms are not free from certain limitations. Geng et al. [14] point out that premature convergence and poor exploitation are the major drawbacks for the metaheuristic when facing more complex problems. Thus, more advanced algorithms are continuously needed to achieve satisfactory solutions for resource leveling problem in modern construction projects.

2.3. Differential Evolution optimization algorithm

Differential Evolution (DE) is a simple population-based, direct-search approach to solving global optimization problems [18] and [35]. The original DE algorithm is described briefly as follows:

Let ${\textstyle S\subset R^{n}}$ be the search space of the problem under consideration. DE utilizes NP  , D-dimensional parameter vectors: ${\textstyle X_{i{\mbox{,}}G}=\lbrace x_{i{\mbox{,}}G}^{1}{\mbox{,}}x_{i{\mbox{,}}G}^{2}{\mbox{,}}\ldots {\mbox{,}}x_{i{\mbox{,}}G}^{D}\rbrace {\mbox{,}}i=}$$1{\mbox{,}}2{\mbox{,}}\ldots {\mbox{,}}NP$ as a population for each algorithm generation. The initial population is generated randomly and should cover the entire parameter space. At each generation, DE applies two operators, mutation and crossover (recombination), to yield one trial vector ${\textstyle U_{i{\mbox{,}}G+1}}$ for each target vector ${\textstyle X_{i{\mbox{,}}G}}$. Next, a selection phase determines whether or not the trial vector enters the population in the next generation. For each target vector ${\textstyle X_{i{\mbox{,}}G}}$, the following equation is used to determine the mutant vector:

$V_{i{\mbox{,}}G+1}=X_{r1{\mbox{,}}G}+F(X_{r2{\mbox{,}}G}-$$X_{r3{\mbox{,}}G})$

(8)

where ${\textstyle r_{1}{\mbox{,}}r_{2}{\mbox{,}}r_{3}\in \lbrace 1{\mbox{,}}2{\mbox{,}}\ldots {\mbox{,}}NP\rbrace }$ are randomly selected such that ${\textstyle r_{1}\not =r_{2}\not =r_{3}\not =i}$ and F   is a scaling factor such that ${\textstyle F\in [0{\mbox{,}}1]}$.

Following the mutation phase, the crossover operator is applied to increase diversity. For each mutant vector ${\textstyle V_{i{\mbox{,}}G+1}}$, the following formula is used to generate a trial vector ${\textstyle U_{i{\mbox{,}}G+1}=\left\{u_{i{\mbox{,}}G+1}^{1}{\mbox{,}}u_{i{\mbox{,}}G+1}^{2}{\mbox{,}}\ldots {\mbox{,}}u_{i{\mbox{,}}G+1}^{D}\right\}}$.

$u_{i{\mbox{,}}G+1}^{j}={\begin{array}{cc}v_{i{\mbox{,}}G+1}^{j}&if\quad ({rand}_{j}[0{\mbox{,}}1)\leqslant CRorj=j_{rand}\\x_{i{\mbox{,}}G}^{j}&otherwise\end{array}}\quad j=1{\mbox{,}}2{\mbox{,}}\ldots {\mbox{,}}D$

(9)

CR ⊂ [0, 1] is a user-defined crossover constant and ${\textstyle j_{rand}}$ is a randomly chosen index from ${\textstyle \left\{1{\mbox{,}}2{\mbox{,}}\quad ldots{\mbox{,}}D\right\}}$ that ensures trial vector U_i,G+1 differs from its target X_i,G by at least one parameter.

Trial vector ${\textstyle U_{i{\mbox{,}}G+1}}$ is next compared to the corresponding target vector X_i,G using the greedy criterion to determine whether the former should remain a member of the population in the next generation. The selection operator is expressed as follows:

$X_{i{\mbox{,}}G+1}={\begin{array}{ll}U_{i{\mbox{,}}G+1}&if\quad f(U_{i{\mbox{,}}G+1})<f(X_{i{\mbox{,}}G})\\X_{i{\mbox{,}}G}&otherwise\end{array}}$

(10)

With memberships in the next generation now determined, the DE evolutionary cycle iterates until attaining the stopping condition.

2.4. Chaos sequences

Chaos theory is a scientific theory that describes erratic behavior in certain nonlinear dynamic systems. Chaotic mappings may be visualized as particles traveling within a limited range in a deterministic, nonlinear and dynamic system with no definite regularity associated with the path of travel of these particles. Although particle movement is randomized, movement is extremely sensitive to the initial conditions [36]. Because chaotic sequences may be generated and stored quickly and easily, there is no need for storage over long sequences [23]. Moreover, these sequences are deterministic and reproducible. Thus, many researchers have adopted chaotic sequences instead of random sequences [37] and [38].

The one-dimensional logistic map is one of the simplest systems with a density of periodic orbits:

$X_{n+1}=\mu X_{n}(1-X_{n})$

(11)

In this equation, ${\textstyle X_{n}}$ is the ${\textstyle n^{th}}$ chaotic number, where n   denotes the iteration number. Obviously, ${\textstyle X_{n}\in (0{\mbox{,}}\quad 1)}$ under conditions that initial ${\textstyle X_{0}\in (0{\mbox{,}}\quad 1)}$ and that ${\textstyle X_{0}\not \in \lbrace 0.0{\mbox{,}}\quad 0.25{\mbox{,}}\quad 0.5{\mbox{,}}\quad 0.75{\mbox{,}}\quad 1.0\rbrace }$. The variance of control parameter ${\textstyle \mu }$ in Eq. (11) directly and significantly impacts the behavior of X  . The domain area of control parameter ${\textstyle \mu }$ has often been defined as ${\textstyle \left[0{\mbox{,}}4\right]}$. ${\textstyle \mu =4}$ has been used in several previously published research experiments [39] and [40].

2.5. Fuzzy c-means clustering

Clustering decomposes a set of objects into subgroups or clusters based on similarity so that objects within a cluster are as similar as possible to one another and as dissimilar as possible from objects in other clusters. Principal clustering algorithm categories are as follows: (1) crisp (or hard) clustering procedures in which each data point is assigned to exactly one cluster and (2) fuzzy clustering techniques in which each data point belongs to every cluster according to a specific algorithm degree of membership [41]. Many clustering algorithms have been introduced in the literature. Fuzzy clustering presents the advantage of dealing efficiently with overlapping clusters, delivering better, more stable results than other clustering techniques [42] and [43]. This study employs fuzzy c-means (FCM) clustering [44].

3. Fuzzy c-means Clustering Chaotic-based Differential Evolution for Multiple Resources Leveling in Multiple Projects (FCDE-MRLMP)

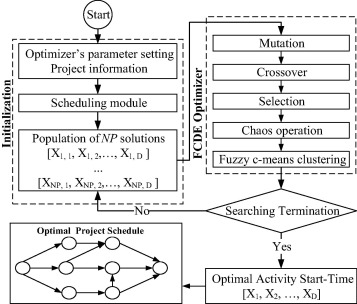
This section describes the newly proposed FCDE-MRLMP model in detail. The FCDE, the core optimizer in the FCDE-MRLMP model, integrates original DE [18] and [35] with fuzzy c-means clustering and chaotic techniques. The chaos approach effectively exploits the whole search space and provides the diversity necessary in the DE population. This operation incurs additional time and iterations to search for the global optimum. The fuzzy c-means clustering technique introduces cluster centers that provide direction to the global optimum search, which improves overall search algorithm efficiency and enhances algorithm convergence speed. Fig. 1 illustrates the proposed model. The objective of the FCDE-MRLMP was to minimize daily fluctuations in resource utilization without changing total project duration.

Figure 1. Flowchart for the FCDE-MRLMP.

3.1. Initialization

Inputs required by the FCDE-MRLMP optimization model include activity relationship, activity duration, and resource demand. In addition, the user must provide search engine parameter settings such as maximum number of search generations ${\textstyle G_{\mbox{max}}}$ and population size (NP). The scheduling procedure uses these inputs in the calculation process to obtain the project duration and resource amount required for each activity. The model operates automatically.

Prior to beginning of the search process, a uniform random generator creates an initial population of feasible solutions. A solution for the resource-leveling problem is represented as a vector with D elements as follows:

$X=[X_{i{\mbox{,}}1}{\mbox{,}}X_{i{\mbox{,}}2}{\mbox{,}}\ldots {\mbox{,}}X_{i{\mbox{,}}D}]$

(12)

where D is the number of decision variables in the problem at hand. D is also the number of non-critical activities in the project network. The index i denotes the ith individual in the population. The vector X represents the start time of D non-critical activities in the network. Because the original DE operates with real-value variables, a function is employed to convert the start times of those activities from real values to integer values that are constrained within the feasible domain.

$X_{i{\mbox{,}}j}=Round(LB(j)+rand[0{\mbox{,}}\quad 1]\times (UB(j)-$$LB(j)))$

(13)

where ${\textstyle X_{i{\mbox{,}}j}}$ is the start time of activity j   at the individual ${\textstyle i{\mbox{th}}}$. ${\textstyle rand[0{\mbox{,}}\quad 1]}$ denotes a uniformly distributed random number between 0 and 1. LB(j) and UB(j) are the early start time and late start time for activity j. In multiple resources leveling in the multiple projects scheduling problem, two constraint conditions limit the actual start time of all activities: (1) actual start time must be between the early and late start times and (2) actual start time is limited by the actual start time of its predecessor activities. The first constraint is simple to handle because limits are fixed prior to calculation. However, the minimum limit of the second constraint is unknown prior to calculation and thus more difficult to elicit. For the decision variables of FCDE on each dimension is determined in turn, when calculating the actual start time of one activity, actual start time of all activities in its predecessor set Ts(pset_k, i_k) has been computed, and the max{Ts(pset_k, i_k) + T(pset_k, i_k)} has been confirmed simultaneously.

3.2. Mutation

Once initialized, DE mutates the population to produce a set of mutant vectors. A mutated vector V_i,G+1 is generated that corresponds to the target vector X_i,G, as in Eq. (8).

3.3. Crossover

The crossover operation exchanges components of the target vector and the mutant vector to diversify the current population. In this stage, a new vector, named the trial vector, is created using Eq. (9).

3.4. Selection

In this stage, the trial vector is compared to the target vector (or the parent) using the greedy criterion. The trial vector replaces the position of the target vector if the trial vector yields a lower objective function value than its parent. Otherwise, the target vector retains its place in the population for another generation. The selection operator is expressed as Eq. (10).

3.5. Chaotic operation

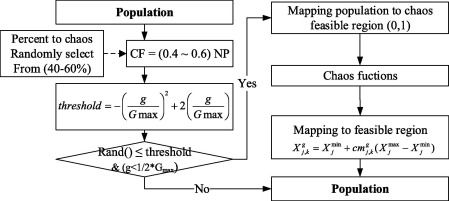
The Chaos Differential Evolution (CDE) algorithm generates chaotic sequences in DE that ensure individuals in the population are distributed as evenly as possible throughout the search space. Integrating CDE into DE enhances global convergence by escaping suboptimal solutions. Fig. 2 shows the main steps used to generate a chaotic population.

Figure 2. Chaotic approach.

In this figure, g   and ${\textstyle G_{\mbox{max}}}$ are the current generation and the maximum generation, respectively. If the probability condition is satisfied, a percentage of the population (CF) is selected for chaos. CF   is then mapped to the chaotic feasible region in range ${\textstyle \left(0{\mbox{,}}\quad 1\right)}$ according to chaotic conditions and performs the logistic map according to Eq. (11) in order to yield chaotic values ${\textstyle {cm}_{j{\mbox{,}}k}^{g}}$. Afterward, Eq. (14) is used to map the chaotic values to the feasible region:

$X_{j{\mbox{,}}k}^{g}=X_{j}^{\mbox{min}}+{cm}_{j{\mbox{,}}k}^{g}(X_{j}^{\mbox{max}}-$$X_{j}^{\mbox{min}})\quad j=1{\mbox{,}}2{\mbox{,}}\ldots {\mbox{,}}D{\mbox{;}}\quad k=$$1{\mbox{,}}2{\mbox{,}}\ldots {\mbox{,}}CF$

(14)

where ${\textstyle X_{j{\mbox{,}}k}^{g}}$ is the ${\textstyle j{\mbox{th}}}$ decision variable of the ${\textstyle k{\mbox{th}}}$ individual in the CF-population at generation g  ; ${\textstyle X_{j}^{\mbox{max}}}$ and ${\textstyle X_{j}^{\mbox{min}}}$ are, respectively, the upper and lower bounds of the jth decision variable.

3.6. Fuzzy clustering operation

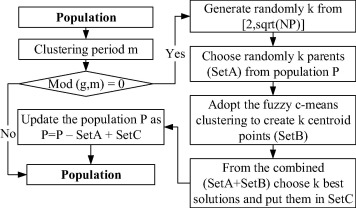
The FCM clustering technique adopted in DE, named FDE, easily conducts an efficient convergence of DE. The FCM was introduced in this study to track the main stream of population movement during DE evolution. Each cluster center may thus be treated approximately as one of the items in the main stream of evolution and replaced in population as candidate individuals. Fig. 3 illustrates the FDE algorithm. m is the clustering period, NP is the population size, and k is the number of centroids [28] and an integer number from ${\textstyle \left[2{\mbox{,}}{\sqrt {NP}}\right]}$.

Figure 3. Fuzzy c-means clustering approach.

Clustering is performed periodically in the FDE to exploit the search space efficiently and to give the DE time to explore the search place and form clusters. This is similar to the method used in [28] and [45]. An attempt to perform the clustering overly early will lead to false cluster identification. Consequently, it is important to choose a clustering period that is large enough so that DE has time to fully form stable clusters. In this approach, parameter m is adopted to control the clustering period.

Initially, the period of the clustering operator specified in the algorithm is set as 10. When the clustering condition is satisfied, fuzzy c-means clustering will create k offspring, which will be used to update the population. Deb [46] proposed a generic population-based algorithm generator for real-parameter optimization, where the optimization task is divided into four independent plans: (i) selection plan, (ii) generation plan, (iii) replacement plan, and (iv) update plan. The flowchart for the above algorithm may also be described using Deb’s population-update algorithm.

• Selection plan: Choose k individuals from current population randomly (set A).
• Generation plan: Create k offspring (set B) using fuzzy c-means clustering.
• Replacement plan: Choose k best solutions (set C) from the combined set (set A + set B) for replacement.
• Update plan: Update the population as P = P-set A + set C.

In the update plan, the k best solutions are chosen from the combined set, which ensures that elites are preserved.

3.7. Stopping condition

The optimization process terminates when a user-set stopping criterion is met. This stopping criterion is often set as the maximum generation ${\textstyle G_{\mbox{max}}}$ or the maximum number of function evaluations (NFE). Search process termination identifies the optimal solution. The project schedule and its corresponding resource histogram may then be constructed based on the optimal start time for activities.

4. Case study

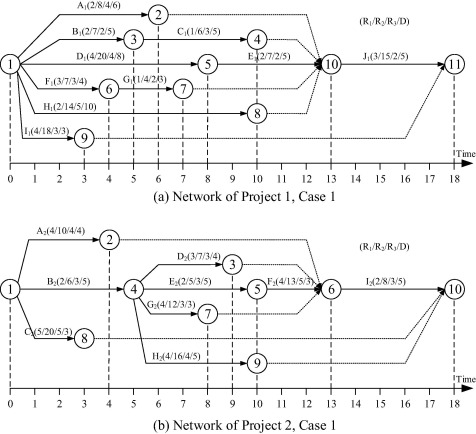
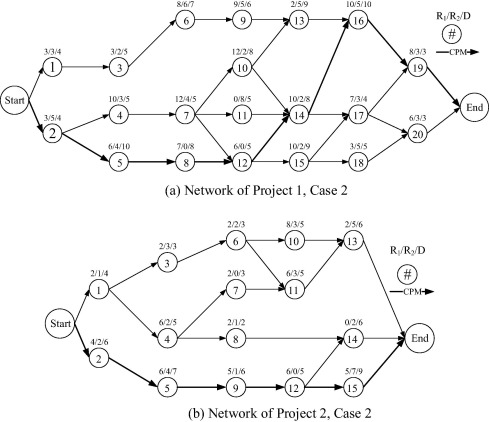
Two construction case studies were used to demonstrate the capability of the newly developed FCDE-MRLMP model. The first case study was adapted from Yan et al. [16]. In the first case study, an enterprise must start two projects with same total project duration. Fig. 4 shows the precedence relationships of the network projects. Each activity in both projects uses three resources (R₁ human, R₂ fund, and R₃ equipment) and has a certain duration D that is indicated above the arrow line.

Figure 4. Networks of two projects – case 1.

Based on the importance of each resource, the AHP method makes pairwise comparison of each resource. The comparison matrix is obtained as follows:

${\begin{array}{c}R_{1}\\R_{2}\\R_{3}\end{array}}\left[{\begin{array}{ccc}1&3&5\\3^{-1}&1&3\\5^{-1}&3^{-1}&1\end{array}}\right]$

Consistency inspection demonstrates that this comparison matrix is acceptable. Weights for each resource are set as follows: ${\textstyle w_{1}=0.637{\mbox{,}}\quad w_{2}=0.258{\mbox{,}}\quad w_{3}=}$$0.105$. Consequently, the objective function for the case study 1 is calculated as follows:

$minRI={\frac {1}{18}}\sum _{t=1}^{18}\left[0.637{\left({SR}_{1}(t)-{\overline {{SR}_{1}(t)}}\right)}^{2}+\right.$$\left.0.258{\left({SR}_{2}(t)-{\overline {{SR}_{2}(t)}}\right)}^{2}+\right.$$\left.0.105{\left({SR}_{3}(t)-{\overline {{SR}_{3}(t)}}\right)}^{2}\right]$

$s.t{\begin{array}{ll}0\leqslant T_{s}(A_{1})\leqslant 7&0\leqslant T_{s}(I_{1})\leqslant 15\\0\leqslant T_{s}(B_{1})\leqslant 3&0\leqslant T_{s}(A_{2})\leqslant 9\\T_{s}(B_{1})+5\leqslant T_{s}(C_{1})\leqslant 8&0\leqslant T_{s}(C_{2})\leqslant 15\\0\leqslant T_{s}(F_{1})\leqslant 6&5\leqslant T_{s}(D_{2})\leqslant 9\\T_{s}(B_{1})+4\leqslant T_{s}(G_{1})\leqslant 10&5\leqslant T_{s}(G_{2})\leqslant 7\\0\leqslant T_{s}(H_{1})\leqslant 3&5\leqslant T_{s}(H_{2})\leqslant 13\end{array}}$

The second case study is a real construction project named Sky Park Residence Project in Viet Nam. All the detailed data of the project were obtained from the Licogi 16 Joint Stock Co. The project is located at the northwest gate of the capital of Hanoi. The total land area of the project is 9262 m², of which construction area is 3342 m², accounting for 36%. Scale of the project includes two blocks, office blocks which are 25 stories tall, tall apartment blocks have 35 floors, 3 basements for car, five floors are used as commercial centers. All the activities considered are extracted from the foundation and basement construction phase. The data for the activities are obtained based on previous data and experts’ experience. Test network was slightly modified to adapt to model requirements. Fig. 5 shows the precedence relationships of the network projects of the second case study. Each activity in both projects uses two resources (R₁ human and R₂ equipment) and has a certain duration D   that is indicated above the activity’s node. In the second case, each recourse has the same importance weights ${\textstyle w_{1}=w_{2}=0.5}$.

Figure 5. Networks of two projects – case 2.

4.1. Optimization result for the FCDE-MRLMP

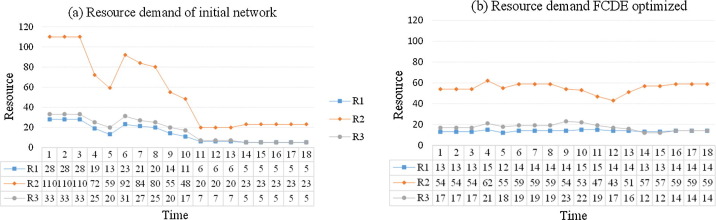
Application of the FCDE-MRLMP model reduces significant fluctuations in resource usage. This study set parameters for the FCDE optimizer are based on proposed values from the literature and several experiments as shown in Table 1. Fig. 6 shows the network resource profile for the projects at initialization and after FCDE-MRLMP optimization process of the first case. It can be seen in Fig. 6 that the proposed algorithm significantly reduces undesirable resource fluctuations. Example on the resource R2, at initial schedule the maximum daily resource usage and maximum deviation in daily resource usage are 110 and 38, respectively. However, after being optimized by proposed algorithm, the maximum daily resource usage and maximum deviation in daily resource usage reduce considerably to 62 and 8, respectively.

Table 1. Settings for FCDE-MRLMP parameters.

Input parameters	Notation	Setting
		Case 1	Case 2
Number of decision variables	D	12	23
Population size	NP	100	200
Mutant factor	F	0.5–0.8	0.5–0.8
Crossover probability	CR	0.8	0.8
Percentage of population to chaos	CF	0.4–0.6	0.4–0.6
Period clustering	m	10	15
Number of centroids in cluster	k	[2, sqrt(NP)]	[2, sqrt(NP)]
Amplification coefficient	${\textstyle \lambda }$	30	30
Maximum generation	Gmax	200	400

Figure 6. Resource profile of projects in case 1.

4.2. Result comparisons

Three different algorithms were used to verify the comparative performance of the proposed model (FCDE-MRLMP). These algorithms were as follows: original DE (DE) [35], Genetic Algorithm (GA) [47], and Particle Swarm Optimization (PSO) [48]. For comparison purposes, all four algorithms used an equal number of function evaluations. In GA, the constant mutant and crossover probability factors were set at 0.5 and 0.9, respectively. In PSO, the two learning factors, c₁, c₂, were both chosen at 2.05, and the inertia factor w is set in the range of 0.3–0.7. DE and FCDE control parameters remained the same, as stated previously in Table 1. Twenty-five independent runs were carried out for all experiments.

Table 2 lists the optimal results, optimal non-critical-activity start times obtained from the new proposed model, and other benchmark algorithms for the first case. RI_m in Table 2 is the resource intensity for single resource m:

$minRI={\frac {1}{18}}\sum _{t=1}^{18}{\left(R_{m}(t)-{\overline {R_{m}(t)}}\right)}^{2}{\mbox{,}}\quad {\overline {R_{m}}}=$${\frac {1}{18}}\sum _{t=1}^{T}R_{m}(t)$

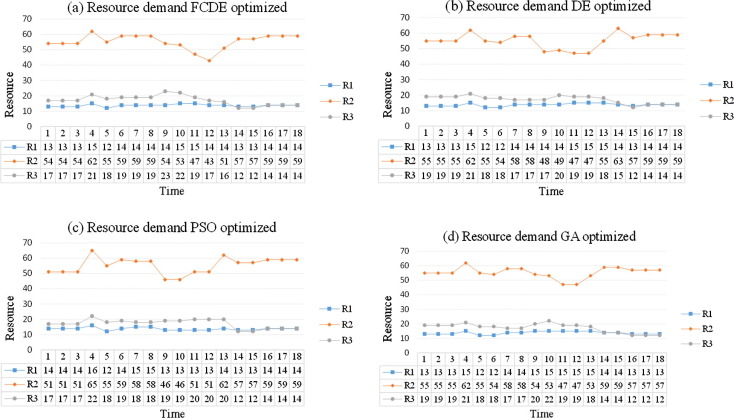
As shown in Table 2, the optimal resource intensity (RI) obtained by FCDE was, respectively, 94.9%, 2.1%, 6.9%, and 8.6% less than the initial schedule, DE, PSO, and GA. Fig. 7 presents the resource profile after being optimized by each algorithm. It can be seen from these figures that the FCDE leveled projects shows a more promising distribution of resources compared to those of benchmark algorithms.

Table 2. Comparison of optimal performance for algorithms on Case 1.

Item	RI	RI1	RI2	RI3	Actual start time of non-critical activities
					A1	B1	C1	F1	G1	H1	I1	A2	C2	D2	G2	H2
Initial	89.46	76.95	1169	123.8	0	0	5	0	4	0	0	0	0	5	5	5
GA	5.327	1.06	13.76	9.17	0	3	8	0	9	0	15	8	12	9	6	13
PSO	4.897	0.84	26.65	7.95	0	0	8	6	10	3	12	0	15	8	5	13
DE	4.652	0.84	21.97	5.73	0	3	9	0	10	0	12	8	15	9	6	13
FCDE	4.558	0.62	21.31	9.51	3	0	8	0	8	0	12	8	15	9	5	13

Figure 7. Resource profile of projects by different algorithms – case 1.

To evaluate the stability and accuracy of each algorithm, optimization performance was expressed in terms of best result found (best), average result (avg), standard deviation (std), and worst result (worst) after 25 runs (Table 3). The best and worst results demonstrate the capacity of each algorithm to find the optimal solution for all of the performance measurement metrics. Average and standard deviation are two additional characteristics that describe solution quality. Standard deviation occurs in cases when algorithms are not able to generate optimal solutions in all executions.

Table 3. Comparison of results for the FCDE-MRLMP and benchmarked algorithms.

Performance measurement			GA	PSO	DE	FCDE
Case 1	Fitness value	Best	5.327	4.897	4.652	4.558
		Avg.	6.907	6.327	5.400	4.760
		Std.	2.112	0.742	0.424	0.300
		Worst	13.385	7.968	6.237	5.339
Case 2		Best	25.329	24.479	24.469	24.469
		Avg.	26.240	25.652	24.520	24.472
		Std.	0.616	1.051	0.123	0.025
		Worst	26.860	26.569	24.861	24.479

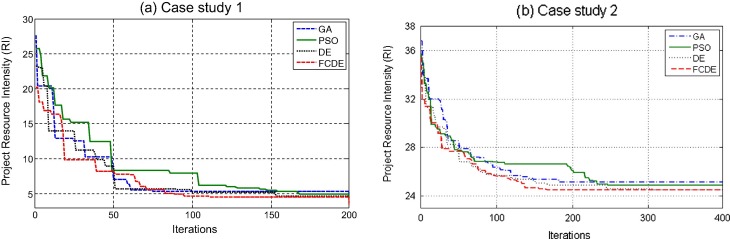
As shown in Table 3, the performance of the FCDE-MRLMP is competitive in terms of accuracy and stability. The highlighted row in Table 3 shows the proposed algorithm with best performance in both case studies. It is clearly shown that the FCDE-MRLMP is only able to find optimal solutions in fitness function in the first case. Further, in terms of average results, FCDE-MRLMP performed the best of the considered algorithms because it generated the lowest average fitness solution, with a value of 4.760 and deviation value of 0.300 for the first case, and in the second case, the value of 24.472 for average fitness and deviation value of 0.025. Fig. 8 illustrates the best fitness value results of different approaches by number of iterations. As can be seen in Fig. 8 the proposed algorithm outperformed the other approaches in terms of convergence since the proposed model found the best solution in fewer iterations than the original DE and other benchmark algorithms.

Figure 8. Best project resource intensity curves for algorithms.

4.3. Hypothesis test

A hypothesis test was performed to further demonstrate the superiority of the FCDE performance over that of benchmark algorithms. Because all indicator comparisons demonstrated that the DE performed better on average than either PSO or GA, the hypothesis tests only considered FCDE and DE. A one-tailed t-test with equal sample sizes and unequal and unknown variances analyzed the following hypothesis tests:

• Hypothesis: FCDE versus standard DE in terms of resource intensity (RI) ( Table 3).
• H₀: There is no difference in RI of the FCDE algorithm and that of the standard DE algorithm.
• H₁: The FCDE algorithm is significantly better than the standard DE algorithm.
• For the first case: FCDE ${\textstyle s_{1}=0.300}$; DE: ${\textstyle s_{2}=0.424}$; n₁ = n₂ = n = 25;

$\nu ={\frac {{\left(s_{1}^{2}/n_{1}+s_{2}^{2}/n_{2}\right)}^{2}}{{\frac {{\left(s_{1}^{2}/n_{1}\right)}^{2}}{n_{1}-1}}+{\frac {{\left(s_{2}^{2}/n_{2}\right)}^{2}}{n_{2}-1}}}}=$${\frac {{\left({0.300}^{2}/25+{0.424}^{2}/25\right)}^{2}}{{\frac {{\left({0.300}^{2}/25\right)}^{2}}{25-1}}+{\frac {{\left({0.424}^{2}/25\right)}^{2}}{25-1}}}}=$$43.2\quad \quad ({\mbox{closest to}}\quad 43)$

• Critical value: with significant level of t-test α = 0.05; ${\textstyle \nu =43}$; we have ${\textstyle t_{\alpha {\mbox{;}}\nu }=t_{0.05{\mbox{;}}43}=1.681}$.
• Statistical test: ${\textstyle t={\frac {\left({\overline {x}}_{1}-{\overline {x}}_{2}\right)}{\sqrt {s_{1}^{2}/n_{1}+s_{2}^{2}/n_{2}}}}=}$${\frac {\left(4.760-5.400\right)}{\sqrt {{0.300}^{2}/25+{0.424}^{2}/25}}}=$$-6.161<-1.681=-t_{0.05{\mbox{;}}43}$.where n   is the sample size (number of experimental runs), ${\textstyle \nu }$ is the degrees of freedom used in the test, and ${\textstyle s_{1}^{2}}$ and ${\textstyle s_{2}^{2}}$ are the unbiased estimators of the variances of the two samples (FCDE and DE). The denominator of t   is the standard error of the difference between two means ${\textstyle {\overline {x}}_{1}}$, ${\textstyle {\overline {x}}_{2}}$ (average).
• For the second case: FCDE ${\textstyle s_{1}=0.025}$; DE: ${\textstyle s_{2}=0.123}$; n₁ = n₂ = n = 25;

$v={\frac {{\left(s_{1}^{2}/n_{1}+s_{2}^{2}/n_{2}\right)}^{2}}{{\frac {{\left(s_{1}^{2}/n_{1}\right)}^{2}}{n_{1}-1}}+{\frac {{\left(s_{2}^{2}/n_{2}\right)}^{2}}{n_{2}-1}}}}=$${\frac {{\left({0.025}^{2}/25+{0.123}^{2}/25\right)}^{2}}{{\frac {{\left({0.025}^{2}/25\right)}^{2}}{25-1}}+{\frac {{\left({0.123}^{2}/25\right)}^{2}}{25-1}}}}=$$25.98\quad \quad ({\mbox{closest to}}\quad 26)$

• Critical value: with significant level of t-test α = 0.05; ${\textstyle \nu =26}$; we have t_α;ν = t_0.05;26 = 1.706

$t={\frac {\left({\overline {x}}_{1}-{\overline {x}}_{2}\right)}{\sqrt {s_{1}^{2}/n_{1}+s_{2}^{2}/n_{2}}}}=$${\frac {\left(24.472-24.580\right)}{\sqrt {{0.025}^{2}/25+{0.123}^{2}/25}}}=$$-1.912<-1.706=-t_{0.05{\mbox{;}}26}$

The statistical test value above is smaller than critical value in both case studies. Therefore, H₀ is rejected. The proposed FCDE is thus demonstrated to be statistically superior to the standard DE in terms of resource intensity.

5. Conclusions

This paper presents FCDE to solve the problem of multiple-resource leveling in the context of multiple-projects scheduling. Integrating fuzzy clustering and chaos algorithms into the DE effectively eliminates the drawbacks of the original DE. The inherent randomness in a chaos algorithm enhances population diversity and avoids entrapment in the local optima, while fuzzy c-means clustering uses moving cluster centers to improve the convergence speed of the search algorithm. Two application case studies were analyzed to illustrate the effectiveness of the proposed model and to demonstrate the capabilities of the model in generating an optimal schedule by eliminating undesirable resource fluctuations and resource idle times. Experimental results and a comparison of results indicate that the FCDE-MRLMP effectively improves the performance of the original DE beyond the levels of performance attained by other benchmark algorithms. The proposed model obtained the optimal values with fewer iteration, the lowest average resource intensity value and the smallest standard deviation values.

The FCDE has a potential application in broad cases because the model is easily modified to solve many other classes of single-objective optimization problems in the construction management field such as resource-allocation and resource-constrained problems. Moreover, resource-leveling problems in the realm of total-project-cost minimization are frequently encountered in construction management. Trade-offs between time and cost are necessary to improve overall construction project benefits. Further work is necessary to address these issues in order to apply FCDE to the resolution of complicated resource-leveling problems that consider multi-objective optimizations. Extending the current FCDE from a single-objective to a multi-objective format using multiple objective Differential Evolution theory is an interesting direction for further research.

Acknowledgments

The authors wish to acknowledge the University of Science and Technology-The University of Da Nang (DUT) for financially supporting this work. Appreciation is also expressed to Faculty of Project Management’s research group at DUT for assistance provided during this investigation. Finally, the authors would like to thank anonymous referees for their valuable comments.

References

1. [1] F.A. Karaa, A.Y. Nasr; Resource management in construction; J. Constr. Eng. Manage., 112 (3) (1986), pp. 346–357
2. [2] M.E. Georgy; Evolutionary resource scheduler for linear projects; Autom. Constr., 17 (5) (2008), pp. 573–583
3. [3] S.A. Assaf, S. Al-Hejji; Causes of delay in large construction projects; Int. J. Project Manage., 24 (4) (2006), pp. 349–357
4. [4] D. Arditi, T. Pattanakitchamroon; Selecting a delay analysis method in resolving construction claims; Int. J. Project Manage., 24 (2) (2006), pp. 145–155
5. [5] J. Martinez, P. Ioannou; Resource leveling based on the modified minimum moment heuristic; Computing in Civil and Building Engineering, ASCE, New York (1993), pp. 287–294
6. [6] R.F. Aziz; Optimizing strategy for repetitive construction projects within multi-mode resources; Alex. Eng. J., 52 (1) (2013), pp. 67–81
7. [7] S. Christodoulou, G. Ellinas, A. Michaelidou-Kamenou; Minimum moment method for resource leveling using entropy maximization; J. Constr. Eng. Manage., 136 (5) (2010), pp. 518–527
8. [8] D. Savin, S. Alkass, P. Fazio; Construction resource leveling based using neural networks; Can. J. Civ. Eng., 23 (3) (1996), pp. 917–925
9. [9] J. Son, M.J. Skibniewski; Multiheuristic Approach for Resource Leveling Problem in Construction Engineering: Hybrid Approachvol. 125, , ASCE (1999), pp. 23–31
10. [10] S.H.H. Doulabi, A. Seifi, S.Y. Shariat; Efficient Hybrid Genetic Algorithm for Resource Leveling via Activity Splittingvol. 137, , ASCE (2011), pp. 137–146
11. [11] T. Gather, J. Zimmermann, J.-H. Bartels; Exact methods for the resource levelling problem; J. Sched., 14 (6) (2011), pp. 557–569
12. [12] L. Yan et al., Optimization of resource allocation in construction using genetic algorithms. in Machine Learning and Cybernetics, in: Proceedings of 2005 International Conference on, 2005.
13. [13] D.F. Dunham; Robustness of genetic algorithm solutions in resource leveling; Syst. Inf. Eng. Des. Symp. (SIEDS) (2015)
14. [14] J.-Q. Geng, L.-P. Weng, S.-H. Liu; An improved ant colony optimization algorithm for nonlinear resource-leveling problems; Comput. Math. Appl., 61 (8) (2011), pp. 2300–2305
15. [15] S.-S. Leu, C.-H. Yang, J.-C. Huang; Resource leveling in construction by genetic algorithm-based optimization and its decision support system application; Autom. Constr., 10 (1) (2000), pp. 27–41
16. [16] G. Yan, L. Nan, Y. Tingting. Multiple resources leveling in multiple projects scheduling problem using particle swarm optimization, in: Natural Computation, 2009. ICNC ’09. Fifth International Conference on, 2009.
17. [17] S. Das, P.N. Suganthan; Differential evolution: a survey of the State-of-the-Art; IEEE Trans. Evol. Comput., 15 (1) (2011), pp. 4–31
18. [18] R.M. Storn, K. Price; Differential evolution – a simple and efficient heuristic for global optimization over continuous spaces; J. Global Optim., 11 (1997), pp. 341–359
19. [19] R.L. Becerra, C.A.C. Coello; Cultured differential evolution for constrained optimization; Comput. Methods Appl. Mech. Eng., 195 (2006) (2006), pp. 4303–4322
20. [20] J. Zhang, A.C. Sanderson; JADE: adaptive differential evolution with optional external archive; IEEE Trans. Evol. Comput, 13 (5) (2009), pp. 945–958
21. [21] B. Mohanty, S. Panda, P.K. Hota; Differential evolution algorithm based automatic generation control for interconnected power systems with non-linearity; Alex. Eng. J., 53 (3) (2014), pp. 537–552
22. [22] D. Jia, G. Zheng, M. Khurram Khan; An effective memetic differential evolution algorithm based on chaotic local search; Inf. Sci., 181 (15) (2011), pp. 3175–3187
23. [23] A. Bedri Ozer; CIDE: chaotically initialized differential evolution; Expert Syst. Appl., 37 (6) (2010), pp. 4632–4641
24. [24] N. Noman, H. Iba; Accelerating differential evolution using an adaptive local search; IEEE Trans. Evol. Comput., 12 (1) (2008), pp. 107–125
25. [25] J.H. Kim, J. Stringer; Applied Chaos; Electric Power Research Institute, Palo Alto, California (1992)
26. [26] W. Kwedlo; A clustering method combining differential evolution with the K-means algorithm; Pattern Recogn. Lett., 32 (12) (2011), pp. 1613–1621
27. [27] Y.-J. Wang, J.-S. Zhang, G.-Y. Zhang; A dynamic clustering based differential evolution algorithm for global optimization; Eur. J. Oper. Res., 183 (1) (2007), pp. 56–73
28. [28] Z. Cai, et al.; A clustering-based differential evolution for global optimization; Appl. Soft Comput., 11 (1) (2011), pp. 1363–1379
29. [29] P. Iyer, et al.; A fuzzy-logic based resource levelling optimisation tool; IFAC-Papers OnLine, 48 (3) (2015), pp. 1942–1947
30. [30] R.B. Harris; Packing Method for Resource Leveling (Pack); J. Constr. Eng. Manage., 116 (2) (1990), pp. 331–350
31. [31] T. Hegazy; Optimization of resource allocation and leveling using genetic algorithms; J. Constr. Eng. Manage., 125 (3) (1999), pp. 167–175
32. [32] S. Hossein Hashemi Doulabi, A. Seifi, S. Shariat; Efficient hybrid genetic algorithm for resource leveling via activity splitting; J. Constr. Eng. Manage., 137 (2) (2011), pp. 137–146
33. [33] K. El-Rayes, D.H. Jun; Optimizing resource leveling in construction projects; J. Constr. Eng. Manage. -Asce, 135 (11) (2009), pp. 1172–1180
34. [34] H. Li, Z. Xu, E. Demeulemeester; Scheduling policies for the stochastic resource leveling problem; J. Constr. Eng. Manage., 141 (2) (2014), p. 04014072
35. [35] K.V. Price, R.M. Storn, J.A. Lampinen; Differential Evolution A Practical Approach to Global Optimization; Springer-Verlag, Berlin Heidelberg (2005)
36. [36] M.-Y. Cheng, K.-Y. Huang, H.-M. Chen; Dynamic guiding particle swarm optimization with embedded chaotic search for solving multidimensional problems; Optim. Lett., 6 (4) (2012), pp. 719–729
37. [37] R. Caponetto, et al.; Chaotic sequences to improve the performance of evolutionary algorithms; IEEE Trans. Evol. Comput., 7 (3) (2003), pp. 289–304
38. [38] C. Yibao, X. Hongmei, M. Tiezhu. Chaos-ant colony algorithm and its application in continuous space optimization, in: Control and Decision Conference, 2008, CCDC 2008, Chinese, 2008.
39. [39] M. Ohya; Complexities and their applications to characterization of chaos; Int. J. Theor. Phys., 37 (1) (1998), pp. 495–505
40. [40] B.L.W. Jiang; Optimizing complex functions by chaos search; Cybern. Syst., 29 (4) (1998), pp. 409–419
41. [41] A.K. Jain, M.N. Murty, P.J. Flynn; Data clustering: a review; ACM Comput. Surv., 31 (3) (1999), pp. 264–323
42. [42] A. El Imrani, et al.; A fuzzy clustering-based niching approach to multimodal function optimization; Cognit. Syst. Res., 1 (2) (2000), pp. 119–133
43. [43] J. Alami, A.E. Imrani, A. Bouroumi; A multipopulation cultural algorithm using fuzzy clustering; Appl. Soft Comput., 7 (2) (2007), pp. 506–519
44. [44] J.C. Bezdek, R. Ehrlich, W. Full; FCM: the fuzzy c-means clustering algorithm; Comput. Geosci., 10 (2–3) (1984), pp. 191–203
45. [45] S. Weiguo, et al.; A weighted sum validity function for clustering with a hybrid niching genetic algorithm; IEEE Trans. Syst. Man Cybern. Part B: Cybern., 35 (6) (2005), pp. 1156–1167
46. [46] K. Deb; A population-based algorithm-generator for real-parameter optimization; Soft Comput., 9 (4) (2005), pp. 236–253
47. [47] R.L. Haupt, S.E. Haupt; Practical Genetic Algorithms; John Wiley & Sons, Inc., NJ (2004)
48. [48] M. Clerc; Particle Swarm Optimization; ISTE Ltd, London (2006)