Efficient calculation of formation energies of kink-pairs in BCC crystals

Resumen

En materiales con estructura cristalina BCC el movimiento de dislocaciones de tipo tornillo a baja temperatura está asociado con la formación y el crecimiento de escalones en la línea de la dislocación. Para entender la movilidad de dislocaciones de tipo tornillo en estos materiales es muy importante la correcta predicción de las energías de nucleación de estos escalones. El cálculo a nivel atomístico de la mecánica de dislocaciones constituye un problema complicado desde el punto de vista tanto numérico como computacional. Este trabajo se centra en el cálculo de las energías de formación de distintas configuraciones de escalones dobles en cristales BCC y en ausencia de cargas exteriores. En nuestro modelo, basado en la teoría discreta de dislocaciones desarrollada por Ariza y Ortiz, la energía almacenada se calcula de forma eficiente mediante un algoritmo de programación basado en NVIDIA Compute Unified Device Architecture (CUDA). Los resultados obtenidos presentan un buen acuerdo con los calculados utilizando primeros principios y potenciales atomísticos, y los correspondientes a la teoría elástica de dislocaciones.

Abstract

Motion of screw dislocations in BCC materials at low temperature is believed to be related to the formation of mobile kinks on the dislocation line. Therefore, the accurate prediction of kink nucleation energies is required to fully describe mobility of screw dislocations in these materials. Studies of fundamental dislocation processes at atomic length scale are numerically and computationally intensive problems. This work studies the calculation of zero-stress formation energies of kink-pair configurations for BCC crystals. Our model for stored energy associated to a dislocation line configuration is based on the theory of discrete dislocations of Ariza and Ortiz. Its value is computed efficiently using an algorithm developed on the NVIDIA Compute Unified Device Architecture (CUDA). Results confirm those obtained using atomistic potentials and first principles calculations, and those based on the continuum theory of dislocations.

Palabras clave

Dislocaciones ; Plasticidad ; Escalones dobles ; Metales BCC

Keywords

Dislocations ; Plasticity ; Double-kinks ; BCC metals

1. Introducción

Durante la última década, la modelización multiescala de materiales desde el nivel atómico hasta el nivel macroscópico, para conseguir describir mecanismos de deformación tales como la plasticidad en cristales, ha atraído la atención de numerosos investigadores. El conocimiento profundo de procesos de deformación y de defectos en la escala de longitud atómica constituye el punto de partida básico para el estudio tridimensional de la dinámica de dislocaciones a microescala [1] y otras simulaciones a mayores escalas de longitud [2] . Esto requiere modelos precisos de la estructura atomística, del movimiento e interacción de puntos relevantes y de los defectos, incluyendo vacantes, huecos intersticiales, impurezas, dislocaciones y límites de grano. Para ello es preciso no solo entender los mecanismos cualitativos subyacentes que controlan la deformación plástica, sino también ser capaces de determinar los parámetros cuantitativos que permitan una descripción predictiva de las propiedades plásticas y resistentes en materiales reales bajo distintas condiciones de servicio.

Los modelos discretos de dislocaciones se utilizan ampliamente como método computacional para estudiar el comportamiento mecánico de materiales con estructura cristalina. La mayoría de estos métodos se basan en la teoría elástica lineal de dislocaciones [3] . A pesar de su sencillez se ha conseguido conocer bastante sobre los mecanismos de deformación y endurecimiento en cristales gracias a estos métodos. Los modelos discretos de dislocaciones son capaces de considerar aspectos que son inaccesibles tanto para la teoría plástica de medios continuos aplicable a escalas de longitud mayores, como para los cálculos atomísticos, debido a las limitaciones de cálculo. En general, algunas de las limitaciones que presentan estos modelos se deben principalmente a que están basados en la teoría elástica lineal de dislocaciones [4] , [5] , [6]  and [7] . La teoría desarrollada por Ariza y Ortiz [8] , en la que se basa este trabajo, pretende en gran parte corregir algunas de dichas limitaciones. Tener en cuenta desde el principio el carácter discreto de las redes es un primer paso para dotar a esta teoría de algunas características deseables. El modelo tiene de manera natural resolución atomística, que elimina de forma automática las divergencias asociadas con los radios de corte en los núcleos de las dislocaciones y por lo tanto la necesidad de introducir parámetros sin significado físico. La elasticidad de las redes se incluye en la teoría discreta utilizando potenciales empíricos, que añaden una importante mejora respecto a la teoría elástica isótropa y preservan el carácter anisótropo del material. En nuestro modelo, cada línea de dislocación posee su propia estructura del núcleo, que depende del potencial interatómico, y las transiciones topológicas aparecen de forma natural sin necesidad de establecer reglas de interacción de manera explícita. Los aspectos teóricos relativos a la mecánica discreta de redes cristalinas pueden verse en detalle en Ariza y Ortiz [8] . Otro elemento importante en nuestro modelo es el uso de la teoría de autodeformaciones de Mura [9] para calcular la energía almacenada en el cristal, dado un conjunto de dislocaciones. La aproximación discreta en combinación con el formalismo de la transformada de Fourier nos ha permitido el cálculo a gran escala de una distribución de deslizamientos en un cristal de forma eficiente [10] . Para materiales con estructura BCC, el movimiento de dislocaciones de tipo tornillo a baja temperatura está controlado por la nucleación y dinámica de escalones y escalones dobles. Dadas las restricciones cristalográficas del material, y gracias al complejo de red definido en el modelo discreto, la geometría de los defectos de tipo escalón puede definirse de forma clara y sencilla.

Con independencia del modelo empleado, el cálculo a nivel atomístico de la mecánica de dislocaciones constituye un problema complicado desde el punto de vista tanto numérico como computacional. En relación con este último aspecto, una forma de agilizar los cálculos y ganar al mismo tiempo capacidad de cálculo computacional es mediante la paralelización en arquitecturas multiprocesador en unidades de procesado gráfico (Graphical Processing Units , GPU). Los beneficios del uso de GPU para acelerar algoritmos en paralelo se han aplicado a variedad de áreas, desde la química y la biología computacional, hasta los video-aceleradores. El desarrollo de aplicaciones en GPU requiere el uso de lenguajes de programación de alto nivel.

En este trabajo hemos utilizado el entorno de trabajo CUDA (Compute Unified Device Architecture) , introducido por NVIDIA en 2006 [11]  and [12] . Se han obtenido las energías de formación de escalones dobles en dislocaciones de tipo tornillo y las correspondientes al crecimiento de estos escalones en materiales BCC. Estos cálculos nos han permitido establecer las longitudes críticas en las que la energía de interacción entre escalones definidos sobre la misma línea de dislocación tiende a cero. En el apartado 2 se describe brevemente el complejo simplicial para materiales BCC, y en el apartado 3 , algunos elementos de la teoría discreta de redes necesarios para ilustrar el modelo de cálculo. Por último, en el apartado 4 hemos obtenido de forma efectiva las energías asociadas a la nucleación y crecimiento de escalones dobles y las hemos comparado con resultados previos, tanto los basados en la teoría elástica lineal de dislocaciones [3] , como los obtenidos mediante simulaciones atomísticas [13] .

2. Complejos de redes para cristales cúbicos centrados en el cuerpo (BCC)

En este apartado presentamos de forma resumida el complejo de red para materiales con estructura cúbica centrada en las caras (BCC) que hemos publicado anteriormente [8]  and [10] y que nos va a permitir introducir con mayor claridad la red dual correspondiente a esta estructura cristalina. Los mecanismos de dislocaciones en redes cristalinas pueden expresarse en términos de campos definidos en la propia red (esto es, el campo de desplazamientos y la densidad de energía) y campos que se definen en redes auxiliares, como los de autodeformaciones que describen las dislocaciones y los campos de densidad de dislocaciones, que son una medida del grado de las autodeformaciones.

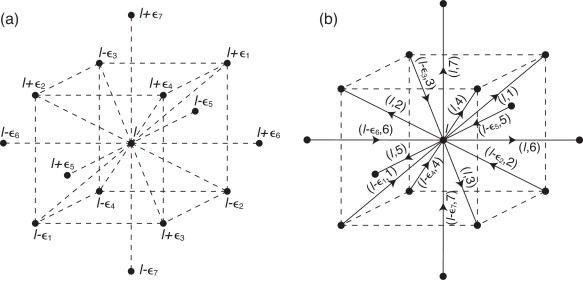
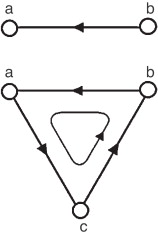
La red de Bravais para un cristal con estructura BCC se genera a partir de la base (-a/2,a/2,a/2), (a/2,-a/2,a/2), (a/2,a/2,-a/2). En nuestro modelo, consideramos la red BCC como una colección de celdas ${\textstyle C}$ de distintas dimensiones, dotadas con operadores diferenciales discretos y una integral discreta. El complejo simplicial CW para esta red (figs. 1 -3 ) consta de: átomos o celdas-0, enlaces atómicos o celdas-1, caras elementales o celdas-2 y volúmenes elementales o celdas-3. Todas las celdas deben tener una orientación que nos permita definir los operadores diferenciales discretos de la red. Supongamos que ω es una forma-0 definida en los átomos de la red y e_ab es un enlace atómico definido entre los átomos a y b ( fig. 4 ). Además, supongamos que e_ab está orientado desde a hasta b . De esta forma, el diferencial dω (e_ab ) de ω en e_ab es:

$d\omega (e_{ab})=\omega (e_{a})-\omega (e_{b}).$

( 1)

Supongamos también que ω es una forma-1 definida en los enlaces atómicos y e_abc una celda triangular con los enlaces atómicos e_ab , e_bc , e_ca a lo largo de su contorno (fig. 4 ). Entonces, el diferencial dω (e_ab ) de ω en e_abc es:

$d\omega (e_{abc})=\omega (e_{ab})+\omega (e_{bc})+$$\omega (e_{ca})$

( 2)

Por último, si ω es una forma-2 definida en las celdas triangulares, entonces su diferencial es el vector:

$d\omega =\sum _{e_{2}\in E_{2}(C)}\omega (e_{2})$

( 3)

Figura 1. Representación del complejo de red cúbica centrada en el cuerpo. a) Vértices. b) Grupo de aristas elementales.

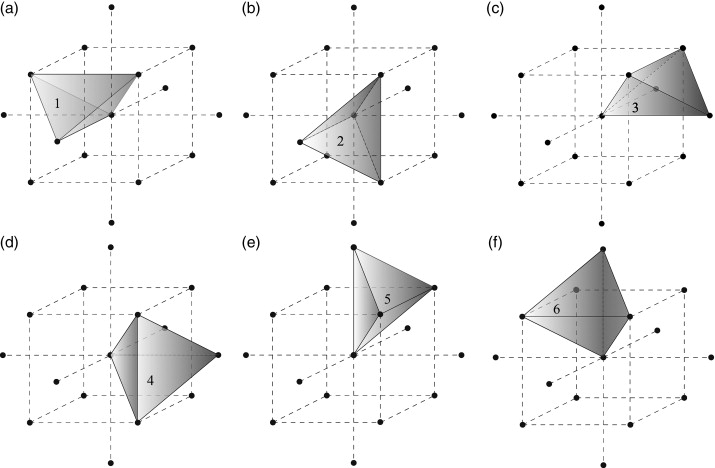
Figura 3. Representación del complejo de red cúbica centrada en el cuerpo. Grupo de volúmenes elementales.

Figura 4. Diagrama para la definición de los operadores diferenciales discretos en aristas y caras del complejo de red.

Por lo tanto, el operador diferencial extiende: formas-0, definidas en los átomos, a formas-1, definidas en los enlaces atómicos; formas-1, definidas en los enlaces atómicos, a formas-2, definidas en las celdas triangulares; y formas-2, definidas en las celdas triangulares, a vectores. Los operadores diferenciales discretos pueden entenderse como los equivalentes discretos del grad , rot y div del cálculo vectorial. En concreto, el diferencial de formas-0 es el equivalente discreto del operador grad , el diferencial de formas-1 es el equivalente discreto del operador rot y el diferencial de formas-2 es el equivalente discreto del operador div del cálculo vectorial. Puede comprobarse a partir de la definición de los operadores discretos [14] que:

$d^{2}=0$

( 4)

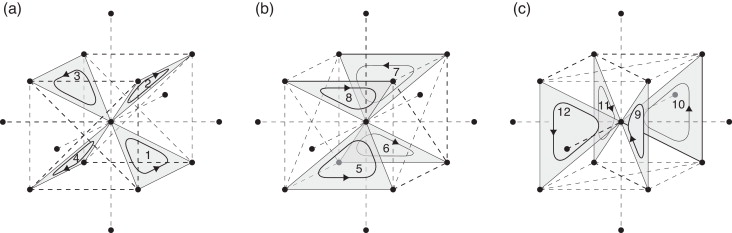
que representa el equivalente discreto de las identidades rot  ∘ grad  = 0 y div  ∘ rot  = 0. Agrupando por tipos las celdas ${\textstyle C}$ de la red BCC, podemos ver que dentro de un mismo tipo las celdas son traslaciones unas de otras y tienen los mismos vecinos, por lo tanto forman redes de Bravais simples [8] . Los materiales BCC tienen un tipo de átomos y 7 tipos de enlaces atómicos (fig. 1 ), 12 tipos de celdas triangulares (fig. 2 ) y 6 tipos de celdas tetraédricas (fig. 3 ), siendo ϵ₁  = (1, 0, 0), ϵ₂  = (0, 1, 0), ϵ₃  = (0, 0, 1), ϵ₄  = (1, 1, 1), ϵ₅  = (0, 1, 1), ϵ₆  = (1, 0, 1) y ϵ₇  = (1, 1, 0). Consecuentemente, es posible aplicar al estudio de las formas discretas que hemos descrito anteriormente la transformada discreta de Fourier (TDF) y sus propiedades, que incluyen la identidad de Parseval discreta y un teorema de convolución discreto (véanse para más detalles [8]  and [15] ). La estructura diferencial para la red BCC definida en las ecuaciones (1) y (2) puede verse en detalle en Ramasubramaniam et al. [10] .

Figura 2. Representación del complejo de red cúbica centrada en el cuerpo. Grupo de áreas elementales.

El complejo se escoge de forma que contiene las direcciones de deslizamiento ${\textstyle {\frac {1}{2}}\left\langle 111\right\rangle }$ y los planos de deslizamiento {110}. Como referencia, en la tabla 1 se presentan los principales sistemas de deslizamiento de las redes BCC. Puede verse fácilmente que los conjuntos elementales de aristas y caras tienen en cuenta estos sistemas.

Tabla 1. Sistemas de deslizamiento en cristales BCC en notación de Schmid y Boas. m es la normal unitaria al plano de deslizamiento y s el vector unitario en la dirección del vector Burgers. Nótese que los vectores se expresan en coordenadas cartesianas y no en la base del cristal

S. D.	A2	A3	A6	B2	B4	B5
${\textstyle {\sqrt {3}}s}$	[${\textstyle {\overline {1}}}$ 11]	[${\textstyle {\overline {1}}}$ 11]	[${\textstyle {\overline {1}}}$ 11]	[111]	[111]	[111]
${\textstyle {\sqrt {2}}m}$	(0${\textstyle {\overline {1}}}$ 1)	(101)	(110)	(0${\textstyle {\overline {1}}}$ 1)	(${\textstyle {\overline {1}}}$ 01)	(${\textstyle {\overline {1}}}$ 10)

S. D.	C1	C3	C5	D1	D4	D6
S. D.	C1	C3	C5	D1	D4	D6
${\textstyle {\sqrt {3}}s}$	[11${\textstyle {\overline {1}}}$ ]	[11${\textstyle {\overline {1}}}$ ]	[11${\textstyle {\overline {1}}}$ ]	[1${\textstyle {\overline {1}}}$ 1]	[1${\textstyle {\overline {1}}}$ 1]	[1${\textstyle {\overline {1}}}$ 1]
${\textstyle {\sqrt {2}}m}$	(011)	(101)	(${\textstyle {\overline {1}}}$ 10)	(011)	(${\textstyle {\overline {1}}}$ 01)	(110)

2.1. Red dual de redes BCC primarias

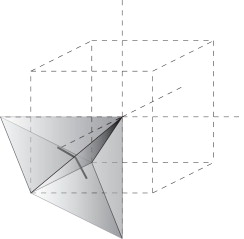
La geometría de las dislocaciones se comprende con más claridad cuando definimos el conjunto dual   de nuestro grupo de celdas primarias ${\textstyle C}$[14] . Dado un complejo tridimensional, el dual de cada celda-3 de ${\textstyle C}$ va a ser su baricentro, es decir, elementos de orden-0. El conjunto dual de las celdas-2 de ${\textstyle C}$ va a estar formado por segmentos o elementos de orden-1 y consiste, para cada celda triangular, en un par de segmentos que unen el baricentro de la cara elemental con los baricentros de los tetraedros que tienen en común (figs. 5 y 6 ). El conjunto dual de las celdas-1 de ${\textstyle C}$ va a ser en general una superficie en su conjunto no plana y de contorno recto. Nuestro interés recae en el segundo de estos conjuntos, ya que nos va a permitir definir las líneas de dislocación a nivel atomístico con total precisión, concatenando segmentos duales elementales. Estos pares de segmentos duales forman también redes de Bravais simples. Hay 12 tipos en total.

Figura 5. Par de segmentos elementales duales a la celda-2 tipo 4 del complejo primario BCC.

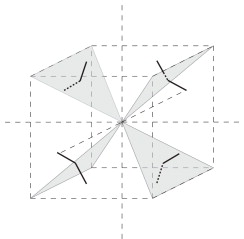
Figura 6. Representación de segmentos elementales de la red dual para algunas celdas de orden 2.

3. Energía almacenada en dislocaciones discretas

Vamos a comenzar este apartado exponiendo algunos elementos de la teoría discreta [8] que necesitaremos para obtener más adelante la expresión de la energía de formación de defectos tipo escalón en una línea de dislocación. Discutiremos brevemente la obtención del modelo de constantes de fuerza a partir de potenciales interatómicos [16]  and [17] y, por último, presentaremos algunos detalles de la implementación del cálculo de la energía en CUDA.

En el contexto de los operadores discretos y dada la invariancia de la energía de un cristal frente a traslaciones, la energía de una red perfecta puede escribirse desde el punto de vista del diferencial del campo de desplazamientos d''u y unas constantes de fuerza entre enlaces atómicos B , en lugar de la representación clásica en términos del campo de desplazamientos u y unas constantes de fuerzas entre átomos A . De esta forma tenemos:

$E({\boldsymbol {\mbox{u}}})=\sum _{e_{1}\in E_{1}}\sum _{e_{1}^{'}\in E_{1}}{\frac {1}{2}}B_{ij}(e_{1},e_{1}^{'}){du}_{i}(e_{1}){du}_{j}(e_{1}^{'})$ $\equiv {\frac {1}{2}}\left\langle {\boldsymbol {\mbox{B}}}d{\boldsymbol {\mbox{u}}},d{\boldsymbol {\mbox{u}}}\right\rangle$

( 5)

donde ${\textstyle B_{ij}(e_{1},e_{1}^{'})}$ representa la energía de interacción dado un diferencial de desplazamiento unidad en la dirección de la coordenada j   en el enlace ${\textstyle e_{1}^{'}}$ y un diferencial de desplazamiento unidad en la dirección de la coordenada i en el enlace e₁ . Dado que el operador diferencial es lineal, la energía (5) puede escribirse alternativamente como:

$E({\boldsymbol {\mbox{u}}})=\sum _{e_{0}\in E_{0}}\sum _{e_{0}^{'}\in E_{0}}{\frac {1}{2}}A_{ij}(e_{0},e_{0}^{'})u_{i}(e_{0})u_{j}(e_{0}^{'})$ $\equiv {\frac {1}{2}}\left\langle {\boldsymbol {\mbox{A}}}{\boldsymbol {\mbox{u}}},{\boldsymbol {\mbox{u}}}\right\rangle$

( 6)

donde ${\textstyle A_{ij}(e_{0},e_{0}^{'})}$ representa la energía de interacción dado un desplazamiento unidad en la dirección de la coordenada j   en el átomo ${\textstyle e_{0}^{'}}$ y un desplazamiento unidad en la dirección de la coordenada i en el átomo e₀ .

Además, por la invariancia ante traslaciones de la red, podemos escribir B''d''u y Au en forma de convolució y tras aplicar la indentidad de Parseval podemos obtener la representación de la TDF de la energía armónica como:

$E(u)={\frac {1}{{\left(2\pi \right)}^{2}}}{\int }_{{\left[-\pi ,\pi \right]}^{2}}{\frac {1}{2}}\left\langle {\overset {\mbox{ˆ}}{\boldsymbol {\Psi }}}(\theta ){\overset {\mbox{ˆ}}{d{\boldsymbol {u}}}}(\theta ),{\overset {\mbox{ˆ}}{d{\boldsymbol {u}}}}^{\ast }(\theta )\right\rangle \quad d^{2}\theta$

( 7a)

$E(u)={\frac {1}{{\left(2\pi \right)}^{2}}}{\int }_{{\left[-\pi ,\pi \right]}^{2}}{\frac {1}{2}}\left\langle {\overset {\mbox{ˆ}}{\boldsymbol {\Phi }}}(\theta ){\overset {\mbox{ˆ}}{\boldsymbol {u}}}(\theta ),{\overset {\mbox{ˆ}}{\boldsymbol {u}}}{}^{\ast }(\theta )\right\rangle \quad d^{2}\theta$

( 7b)

Las representaciones anteriores indican que los campos de constantes de fuerzas entre enlaces atómicos, Ψ , y entre átomos, Φ , están relacionados por:

${\overset {\mbox{ˆ}}{\Phi }}_{ij}=Q_{1}^{T}{\overset {\mbox{ˆ}}{\Psi }}_{ij}Q_{1}^{\ast }$

( 8)

donde Q₁ representa el operador diferencial entre celdas-0 y celdas-1 expresado en el dominio de Fourier [10] . En este punto, es fácil disponer de la energía de un cristal con dislocaciones solo con incluir en la expresión (5) las autodeformaciones correspondientes a deslizamientos en el cristal [9] .

Dada una deformación homogénea invariante de la red de la forma:

${\boldsymbol {\mbox{F}}}={\boldsymbol {\mbox{I}}}+{\frac {\xi }{d}}{\boldsymbol {\mbox{b}}}\otimes {\boldsymbol {\mbox{m}}}$

( 9)

donde m es la normal unitaria al plano de deslizamiento, b el vector de Burgers, d   la distancia entre planos y ${\textstyle \xi \in \mathbb {Z} }$ la magnitud del deslizamiento, las autodeformaciones β son:

${\boldsymbol {\beta }}=({\boldsymbol {\mbox{F}}}-{\boldsymbol {\mbox{I}}})d{\boldsymbol {\mbox{x}}}(e_{1})=$$(d{\boldsymbol {\mbox{x}}}(e_{1})\cdot {\boldsymbol {\mbox{m}}}){\frac {\xi }{d}}{\boldsymbol {\mbox{b}}}.$

( 10)

El producto (dx (e₁ ) · m ) es cero cuando la arista correspondiente está contenida en el plano de deslizamiento y es igual a la distancia entre planos d en caso contrario. Podemos suponer que las autodeformaciones exactas o compatibles de este tipo no cuestan energía al cristal. Por lo tanto, la energía elástica puede escribirse como:

$E({\boldsymbol {\mbox{u}}},{\boldsymbol {\xi }})={\frac {1}{2}}\left\langle {\boldsymbol {\mbox{B}}}(d{\boldsymbol {\mbox{u}}}-\right.$${\boldsymbol {\beta }}),\quad d{\boldsymbol {\mbox{u}}}-$$\left.{\boldsymbol {\beta }}\right\rangle$

( 11)

que sustituye la ecuación (5) cuando existe deslizamiento cristalográfico.

Suponiendo una distribución de fuerzas ${\textstyle {\boldsymbol {\mbox{f}}}:E_{0}\rightarrow {\mathbb {R} }^{n}}$ actuando sobre el cristal, la energía potencial total de la red viene dada por:

$F({\boldsymbol {\mbox{u}}},{\boldsymbol {\xi }})=E({\boldsymbol {\mbox{u}}},{\boldsymbol {\xi }})-$$\left\langle {\boldsymbol {\mbox{f}}},{\boldsymbol {\mbox{u}}}\right\rangle$

( 12)

Minimizando F (u , ξ ) con respecto a u , obtenemos la ecuación de equilibrio:

${\boldsymbol {\mbox{A}}}{\boldsymbol {\mbox{u}}}={\boldsymbol {\mbox{f}}}+$$\delta {\boldsymbol {\mbox{B}}}{\boldsymbol {\beta }}$

( 13)

donde δBβ puede considerarse la distribución de autofuerzas correspondiente a la autodeformación β . La energía almacenada en el cristal en término del campo de deslizamiento se escribe como:

$E({\boldsymbol {\xi }})={\frac {1}{2}}\left\langle {\boldsymbol {\mbox{H}}}{\boldsymbol {\xi }},{\boldsymbol {\xi }}\right\rangle$

( 14)

donde el operador H se define por

$\left\langle {\boldsymbol {\mbox{H}}}{\boldsymbol {\xi }},{\boldsymbol {\xi }}\right\rangle =$$\left\langle {\boldsymbol {\mbox{B}}}{\boldsymbol {\beta }},{\boldsymbol {\beta }}\right\rangle -$$\left\langle {\boldsymbol {\mbox{A}}}^{-1}\delta {\boldsymbol {\mbox{B}}}{\boldsymbol {\beta }},\quad \delta {\boldsymbol {\mbox{B}}}{\boldsymbol {\beta }}\right\rangle$

( 15)

en la que β y ξ se relacionan mediante

${\boldsymbol {\beta }}=\sum _{s=1}^{M}\sum _{e_{1}\in E_{1}({\boldsymbol {\mbox{m}}}^{s})}{\xi }^{s}(e_{1}){\boldsymbol {\mbox{b}}}^{s}\quad e^{1}.$

( 16)

Por invariancia frente a traslaciones debemos tener

${\boldsymbol {\mbox{H}}}{\boldsymbol {\xi }}={\boldsymbol {\Upsilon }}\ast {\boldsymbol {\xi }}$

( 17)

para un módulo de endurecimiento discreto ϒ , el cual queda totalmente definido a partir de las constantes de fuerza del material.

En la teoría elástica de dislocaciones [9] se demuestra que la energía (14) puede expresarse en función de la densidad de dislocaciones α y que dicha energía, E (α ), es independiente de la distribución de dislocaciones utilizada para inducir α . Por lo tanto, 2 distribuciones que difieren de forma exacta y que, en consecuencia, representan la misma densidad de dislocaciones son energéticamente iguales. El análogo discreto se puede obtener usando la descomposición de Hodge-Helmholtz para redes perfectas:

${\boldsymbol {\beta }}=d{\boldsymbol {\mbox{v}}}+\delta {\boldsymbol {\Delta }}^{-1}{\boldsymbol {\alpha }}$

( 18)

donde v  = Δ⁻¹δ''β . Sustituyendo esta expresión por (11) y minimizando la energía potencial F (u , α ) con respecto a u , se obtiene:

$F({\boldsymbol {\alpha }})=E({\boldsymbol {\alpha }})-\left\langle {\boldsymbol {\mbox{B}}}\delta {\boldsymbol {\Delta }}^{-1}{\boldsymbol {\alpha }},d{\boldsymbol {\mbox{A}}}^{-1}{\boldsymbol {\mbox{f}}}\right\rangle -$${\frac {1}{2}}\left\langle {\boldsymbol {\mbox{f}}},{\boldsymbol {\mbox{A}}}^{-1}{\boldsymbol {\mbox{f}}}\right\rangle$

( 19)

Por lo tanto, de forma análoga a la teoría continua, hemos derivado la expresión de la energía almacenada en términos de densidad de dislocaciones a partir de la energía correspondiente a una distribución de dislocaciones. Vemos a continuación la forma detallada de la energía almacenada E (α ).

3.1. Energía asociada a la nucleación y movimiento de escalones

En la mayoría de los materiales con estructura cristalina no existen las dislocaciones rectas. En general, las dislocaciones contienen escalones y quiebros; los segmentos correspondientes a los primeros están contenidos en el plano de deslizamiento de la dislocación madre , mientras que los segmentos correspondientes a los segundos son perpendiculares a este plano de deslizamiento. Los escalones son bastante móviles en comparación con los quiebros, que son incapaces de deslizar en los planos cristalográficos del material y requieren para moverse la difusión de defectos en la red, tales como vacantes o átomos intersticiales.

Aquí nos centramos en la determinación de las energías asociadas a la nucleación y al crecimiento de escalones en dislocaciones de tipo tornillo. A baja temperatura, cuando la densidad de dislocaciones es baja y puede por tanto calificarse como diluida, el comportamiento plástico de materiales BCC es función de la movilidad de estos escalones. Hay 2 tipos de escalones: los aislados, o escalones geométricos , y los escalones dobles. Estos últimos tienen una energía de formación relativamente baja, se forman y desaparecen espontáneamente si hay energía térmica suficiente y su concentración responde a una distribución de Boltzmann. Una vez formado el doble escalón, cada escalón puede alejarse del otro dando lugar a una nueva línea de dislocación y 2 escalones aislados. La repetición del proceso descrito no es sino el movimiento de dislocaciones de tipo tornillo.

En virtud de la descomposición discreta de Hodge-Helmholtz para redes perfectas [8] , la energía almacenada en función de la densidad de dislocaciones α se escribe como:

$E({\boldsymbol {\alpha }})={\frac {1}{2}}\left\langle {\boldsymbol {\mbox{B}}}\delta {\boldsymbol {\Delta }}^{-1}\alpha ,\delta {\boldsymbol {\Delta }}^{-1}\alpha \right\rangle -$${\frac {1}{2}}\left\langle {\boldsymbol {\mbox{A}}}^{-1}\delta {\boldsymbol {\mbox{B}}}\delta {\boldsymbol {\Delta }}^{-1}\alpha ,\delta {\boldsymbol {\mbox{B}}}\delta {\boldsymbol {\Delta }}^{-1}\alpha \right\rangle \equiv {\frac {1}{2}}\left\langle {\boldsymbol {\Gamma }}\ast \alpha ,\alpha \right\rangle$

( 20)

donde Γ representa la energía de interacción entre 2 segmentos de dislocación unitarios. En las aplicaciones que vamos a ver en este trabajo utilizaremos la representación de la TDF para la expresión anterior:

$E({\boldsymbol {\alpha }})={\frac {1}{{\left(2\pi \right)}^{3}}}{\int }_{{\left[-\pi ,\pi \right]}^{3}}{\frac {1}{2}}\left\langle {\overset {\mbox{ˆ}}{\Gamma }}(\theta ){\overset {\mbox{ˆ}}{\boldsymbol {\alpha }}}(\theta ),{\overset {\mbox{ˆ}}{\boldsymbol {\alpha }}}^{\ast }(\theta )\right\rangle d{\theta }_{1}d{\theta }_{2}d{\theta }_{3}$

( 21)

donde

${\overset {\mbox{ˆ}}{\Gamma }}={\overset {\mbox{ˆ}}{\Delta }}_{2}^{-T}Q_{2}^{\ast }({\overset {\mbox{ˆ}}{\Psi }}-$${\overset {\mbox{ˆ}}{\Psi }}Q_{1}^{\ast }{\overset {\mbox{ˆ}}{\Phi }}^{-1}Q_{1}^{T}{\overset {\mbox{ˆ}}{\Psi }})Q_{2}^{T}{\overset {\mbox{ˆ}}{\Delta }}_{2}^{-1}$

( 22)

y Δ₂ representa el operador laplaciano discreto y se obtiene a partir de los operadores diferenciales Q_i[8] .

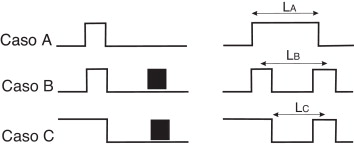
Vamos a estudiar las siguientes configuraciones (fig. 7 ):

• Caso A: nucleación de un escalón doble en un punto arbitrario sobre una línea de dislocación infinita y posterior separación de los escalones en la dirección de la línea infinita.
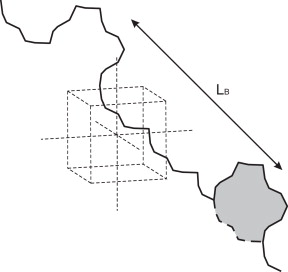
• Caso B: nucleación de un escalón doble en un punto arbitrario sobre una línea infinita en la que existe un escalón doble a una distancia L_B .
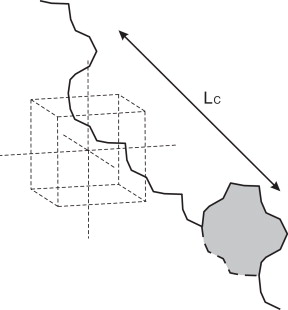
• Caso C: nucleación de un escalón doble en un punto arbitrario sobre una línea infinita en la que existe un escalón aislado a una distancia L_C .

Figura 7. Esquema de las 3 configuraciones que estudiamos en este trabajo.

En todos los casos, el incremento de energía asociado al cambio de configuración viene dado por

$\Delta E=E_{k+1}-E_{k}$ $={\frac {1}{{\left(2\pi \right)}^{3}}}{\int }_{{\left[-\pi ,\pi \right]}^{3}}{\frac {1}{2}}\left\langle {\overset {\mbox{ˆ}}{\Gamma }}(\theta ){\overset {\mbox{ˆ}}{\alpha }}_{k+1}(\theta ),{\overset {\mbox{ˆ}}{\alpha }}_{k+1}^{\ast }(\theta )\right\rangle d{\theta }_{1}d{\theta }_{2}d{\theta }_{3}$ $-{\frac {1}{{\left(2\pi \right)}^{3}}}{\int }_{{\left[-\pi ,\pi \right]}^{3}}{\frac {1}{2}}\left\langle {\overset {\mbox{ˆ}}{\Gamma }}(\theta ){\overset {\mbox{ˆ}}{\alpha }}_{k}(\theta ),{\overset {\mbox{ˆ}}{\alpha }}_{k}^{\ast }(\theta )\right\rangle d{\theta }_{1}d{\theta }_{2}d{\theta }_{3}$ $={\frac {1}{{\left(2\pi \right)}^{3}}}{\int }_{{\left[-\pi ,\pi \right]}^{3}}\left\langle {\overset {\mbox{ˆ}}{\Gamma }}(\theta ){\overset {\mbox{ˆ}}{\alpha }}_{k}(\theta ),\Delta {\overset {\mbox{ˆ}}{\alpha }}^{\ast }(\theta )\right\rangle d{\theta }_{1}d{\theta }_{2}d{\theta }_{3}$ $+{\frac {1}{{\left(2\pi \right)}^{3}}}{\int }_{{\left[-\pi ,\pi \right]}^{3}}{\frac {1}{2}}\left\langle {\overset {\mbox{ˆ}}{\Gamma }}(\theta )\Delta {\overset {\mbox{ˆ}}{\alpha }}(\theta ),\Delta {\overset {\mbox{ˆ}}{\alpha }}^{\ast }(\theta )\right\rangle d{\theta }_{1}d{\theta }_{2}d{\theta }_{3}$

( 23)

y puede escribirse también como

$\Delta E=E_{interacci{\acute {o}}n}+E_{bucle}$

( 24)

siendo

$\Delta \alpha ={\alpha }_{k+1}-{\alpha }_{k}$

( 25)

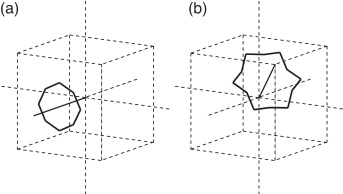
la diferencia de la densidad de dislocación de las configuraciones k  + 1 y k . En particular, la mínima diferencia entre 2 configuraciones consiste en aplicar un deslizamiento ξ en una arista elemental. Cada deslizamiento unitario en una arista da lugar a una densidad de dislocación unitaria en las caras que tienen esa arista en común y se corresponde en la red dual con un grupo de segmentos elementales ( fig. 6 ) que forman bucles elementales o líneas de dislocación elementales. Cuando la arista elemental es de tipo cartesiano, el bucle está formado por cuatro pares de segmentos elementales (fig. 8 a), mientras que si el bucle es de tipo diagonal, el bucle está formado por 6 pares de segmentos elementales (fig. 8 b).

Figura 8. Bucles de dislocación elementales en materiales BCC. a) Bucle tipo cartesiano. b) Bucle tipo diagonal.

Los deslizamientos ξ en aristas contiguas originan líneas de dislocación que se forman por superposición de bucles de dislocación elementales. En la figura 9 puede verse un ejemplo correspondiente a la línea de dislocación para un deslizamiento unitario en 2 aristas contiguas, una cartesiana y otra diagonal.

Figura 9. Línea de dislocación para un deslizamiento unitario en 2 aristas contiguas.

En nuestro modelo discreto podemos definir una línea de dislocación infinita a partir de segmentos de dislocación elementales, solo con elegir adecuadamente las caras o celdas-2 que tienen un campo de densidad de dislocación α   distinto de cero. A modo de ejemplo, la línea de dislocación infinita en la dirección ${\textstyle (11{\overline {1}})}$ que se muestra en la figura 10 representa densidades de dislocación distintas de cero en la caras e₂ (i , l ) que siguen la secuencia {e₂ (6, l ), e₂ (12, l ), e₂ (2, l )} (utilizamos la numeración de las caras mostrada en la fig. 2 ), siendo l el índice de la red de Bravais [8] . Su definición en el espacio real viene dada por

$\alpha (e_{2}(2,l))=\delta ({\boldsymbol {x}}-\nu {\boldsymbol {a}}_{3}),-$$\infty \leq \nu \leq +\infty \alpha (e_{2}(6,l))=\delta ({\boldsymbol {x}}-$$\nu {\boldsymbol {a}}_{3}-\nu {\boldsymbol {a}}_{1}-\nu {\boldsymbol {a}}_{2}),-$$\infty \leq \nu \leq +\infty \alpha (e_{2}(12,l))=-\delta ({\boldsymbol {x}}-$$\nu {\boldsymbol {a}}_{3}-\nu {\boldsymbol {a}}_{1}),-\infty \leq \nu \leq +$$\infty$

( 26)

y aplicando la TDF [18] , los ${\textstyle {\overset {\mbox{ˆ}}{\alpha }}(\theta )}$ se definen de la siguiente forma

${\overset {\mbox{ˆ}}{\alpha }}(2,{\boldsymbol {\theta }})=$$2\pi \delta ({\boldsymbol {\theta }}-{\boldsymbol {\Theta }})$ ${\overset {\mbox{ˆ}}{\alpha }}(6,{\boldsymbol {\theta }})=$$2\pi \delta ({\boldsymbol {\theta }}-{\boldsymbol {\Theta }})e^{-i{\theta }_{1}}e^{-i{\theta }_{2}}$ ${\overset {\mbox{ˆ}}{\alpha }}(12,{\boldsymbol {\theta }})=$$-2\pi \delta ({\boldsymbol {\theta }}-{\boldsymbol {\Theta }})e^{-i{\theta }_{1}}$

( 27)

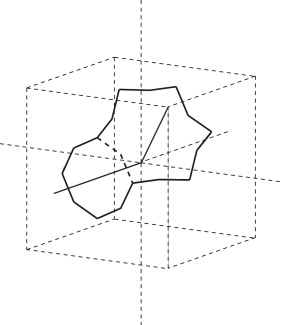
Figura 10. Geometría de una línea de dislocación infinita en la que se nuclea y crece un escalón doble.

Cuando sobre esta línea se nuclea un escalón doble y este aumenta su longitud inicial, se genera una nueva línea de dislocación de longitud finita y paralela a la línea infinita original (fig. 10 ). Podemos obtener fácilmente los nuevos valores de ${\textstyle {\overset {\mbox{ˆ}}{\alpha }}(\theta )}$ para los 2 escalones, las 2 líneas semi-infinitas y la línea finita. Por ejemplo, para el nuevo segmento que sigue la secuencia de celdas elementales {e₂ (4, l ), e₂ (8, l ), e₂ (10, l )}, obtenemos

${\overset {\mbox{ˆ}}{\alpha }}(4,{\boldsymbol {\theta }})=$$e^{-i(2{\theta }_{1}+{\theta }_{2})}\sum _{k=1}^{N}e^{-ik{\theta }_{3}}$ ${\overset {\mbox{ˆ}}{\alpha }}(8,{\boldsymbol {\theta }})=$$e^{-i{\theta }_{1}}\sum _{k=1}^{N}e^{-ik{\theta }_{3}}$ ${\overset {\mbox{ˆ}}{\alpha }}(10,{\boldsymbol {\theta }})=$$-e^{-i({\theta }_{1}+{\theta }_{2})}\sum _{k=1}^{N}e^{-ik{\theta }_{3}}$

( 28)

Dado el carácter oscilatorio de los integrandos en la ecuación (23) y las funciones δ   que aparecen en ${\textstyle \Delta {\overset {\mbox{ˆ}}{\alpha }}(\theta )}$ , el cálculo de los incrementos de energía ΔE tiene un coste computacional elevado.

3.2. Potenciales interatómicos

La modelización a nivel atomístico de defectos en materiales normalmente implica el uso de potenciales empíricos o semiempíricos. Existe una gran variedad de dichos potenciales, por ejemplo, entre pares de átomos como el clásico de Lennard-Jones, o potenciales que hacen uso de funciones definidas entre átomos como el método de los átomos embebidos (EAM) para metales FCC, el método de los átomos embebidos modificados (MEAM) para metales BCC, el potencial de Finnis-Sinclair (FS) [16] o el más reciente potencial de Finnis-Sinclair extendido [17] para materiales de transición. Este último, basado en el potencial de Finnis-Sinclair, pero incluyendo polinomios de mayor grado, evalúa más adecuadamente la energía del cristal en condiciones lejanas al equilibrio para materiales BCC y extiende el potencial a materiales con estructura FCC.

La energía de un cristal, según el potencial de Finnis-Sinclair, puede expresarse como

$E={\frac {1}{2}}\sum _{i,j}V_{ij}(r_{ij})+\sum _{i}F_{i}({\rho }_{i})$

( 29)

$\rho =\sum _{j}{\Phi }_{ij}(r_{ij})$

donde r_ij son las distancias interatómicas, V y Φ los potenciales entre pares de átomos, ρ la densidad electrónica y F la función de embebido. El potencial extendido de Finnis-Sinclair [17] se diferencia del clásico [16] en el término V (r ), que incluye un polinomio de sexto grado, esto es

$V(r)={\begin{array}{cc}{\left(r-c\right)}^{2}(c_{0}+c_{1}r+c_{2}r^{2}+c_{3}r^{3}+c_{4}r^{4})&,r\leq c\\0&,r>c\end{array}}$

donde c es el parámetro de corte considerado entre segundos y terceros vecinos. Los parámetros c₀ , c₁ , c₂ , c₃ y c₄ se ajustan para cada material. Además, este potencial extendido añade un segundo término en la función de densidad electrónica ρ , que toma un valor nulo para estructuras cristalinas tipo BCC.

Adaptando este potencial a nuestro modelo discreto de redes, la energía puede escribirse como

$E={\frac {1}{2}}{\int }_{E_{1}}V(\vert d{\boldsymbol {\mbox{x}}}(e_{1})\vert )+$${\int }_{E_{0}}F(\rho )$

( 30)

$\rho ={\int }_{E_{1}\bigcap St(e_{0})}\Phi (\vert d{\boldsymbol {\mbox{x}}}(e_{1})\vert )$

Si se linealiza la energía, las constantes de fuerza entre aristas se obtienen como

$B(e_{1},e_{1})=PI+Q{\frac {d{\boldsymbol {\mbox{x}}}(e_{1})\otimes d{\boldsymbol {\mbox{x}}}(e_{1})}{\vert d{\boldsymbol {\mbox{x}}}(e_{1})\vert ^{2}}}$ $B(e_{1},e_{1}^{'})=R{\frac {d{\boldsymbol {\mbox{x}}}(e_{1})\otimes d{\boldsymbol {\mbox{x}}}(e_{1}^{'})}{\vert d{\boldsymbol {\mbox{x}}}(e_{1})\vert \vert d{\boldsymbol {\mbox{x}}}(e_{1}^{'})\vert }}$

( 31)

si ${\textstyle \lbrace e_{1},e_{1}^{'}\rbrace }$ tienen un vértice en común

$B(e_{1},e_{1}^{'})=0\quad otro{\mbox{ }}caso$

donde P , Q y R son combinaciones de las derivadas de V , F y Φ.

Para comparar las diferencias, al usar los potenciales de Finnis-Sinclair y Finnis-Sinclair extendido en nuestro modelo discreto se han calculado las constantes elásticas, c₁₁ , c₁₂ y c₄₄ , a partir de dichos potenciales mediante la matriz dinámica de la red

$c_{ijkl}+c_{ilkj}={\frac {{\delta }^{2}D_{ik}}{\delta k_{j}\delta k_{l}}}(0)$

( 32)

donde D_ik es la matriz dinámica obtenida a partir de las constantes de fuerza interatómicas (31) . El valor de las constantes elásticas para diferentes materiales, calculadas a partir de ambos potenciales y su valor experimental, puede verse en la tabla 2 .

Tabla 2. Constantes elásticas (Mbar) para distintos materiales

	Experimental			Finnis-Sinclair			Finnis-Sinclair extendido
	c11	c12	c44	c11	c12	c44	c11	c12	c44
Mo	4,637	1,578	1,092	4,641	1,613	1,088	-	-	-
Ta	2,663	1,582	0,874	2,656	1,610	0,823	2,522	1,629	0,857
V	2,29	1,21	0,444	2,276	1,185	0,425	2,240	1,177	0,446
W	5,32	2,049	1,631	5,218	2,044	1,602	5,301	2,056	1,624

3.3. Implementación en CUDA

En este apartado describimos brevemente cómo hemos utilizado la tecnología CUDA de NVIDIA para integrar el modelo de programación GPGPU en el cálculo de las integrales en la ecuación (23) . Esta tecnología se basa en aprovechar la paralelización en la ejecución de los procesos en la GPU y, además, se beneficia del hecho de que las tarjetas gráficas, usadas como dispositivos de cálculo, son a su vez compatibles con equipos informáticos convencionales. Para calcular el incremento de energía (23) hemos codificado en lenguaje C el método de Simpson para la integración numérica. El dominio de integración es en general tridimensional, por lo tanto tenemos un bucle triple anidado que, codificado en C, adopta la forma básica:

$for(i=0;i<puntos;i++)$ $for(j=0;j<puntos;j++)$ $for(k=0;k<puntos;k++)$

( 33)

La manifiesta paralelización de este código hace que su adaptación a CUDA C sea muy intuitiva y por consiguiente inmediata. Se observa que si tomamos como índice principal i , las operaciones restantes que se realizan mediante el bucle doble son independientes entre sí. Esto permite trasladar el problema de una ejecución secuencial en CPU a una ejecución en paralelo en la GPU, estableciendo una correspondencia entre los términos del índice i y los hilos de ejecución. De esta forma, se logran lanzar en paralelo tantos bucles dobles en la GPU como sean necesarios.

La ventaja que ofrece este algoritmo es su inmediata adaptación a CUDA, que resulta muy intuitiva y por consiguiente sencilla. Sin embargo, no debe olvidarse la limitación de la capacidad de almacenamiento del dispositivo. En el caso que hemos analizado, las estructuras de memoria voluminosas se han creado y almacenado en la memoria global, asignando a cada hilo unas posiciones para almacenar los resultados reservadas a priori. Con ello hemos evitado posibles problemas de colisión entre hilos. Una vez concluido el proceso de evaluación y terminada la ejecución de todos los hilos, se han sumado los resultados en la CPU, de manera rápida y eficiente. Otro aspecto diferenciador entre ambos algoritmos que conviene destacar es la estructura de almacenamiento de datos. En general, en el algoritmo original los datos están almacenados en tensores de orden n , mientras que en su versión en CUDA se almacenan en forma de vectores ubicados tanto en la memoria global de la GPU, para los datos de entrada, como en los registros, para los datos auxiliares propios de los hilos que no comparten información entre ellos.

El código CUDA C emplea precisión float sencilla. Sin embargo, es importante tener presente que los términos de los integrandos son complejos y, por tanto, cada dato ocupa 8 Bytes de memoria en total. Los cálculos se han realizado en un equipo convencional Intel Quadcore @2.33 GHz con 4 GB de memoria RAM. El dispositivo GPU es una tarjeta NVIDIA 265GTX con 1 GB de memoria global, 16 kB de memoria local, 64 kB de memoria compartida y 96 núcleos. Hemos utilizado las bibliotecas y los pilotos para el sistema operativo OpenSuse 10.4 y el compilador nvcc que incorpora NVIDIA. Para la compilación del código en CUDA, hemos usado las banderas

$nvcc\quad -lcublas\quad \ast .cu\quad -o\quad file$

( 34)

La ejecución del código implica la definición de 2 parámetros, esto es, el número de bloques y el número de hilos por bloque. Hemos podido comprobar que la velocidad de ejecución en GPU es sensible al número de bloques N_b , y que se obtienen las máximas velocidades cuando se utiliza un número de bloques múltiplo de 64. Este hecho es independiente del número de hilos N_h que definamos en cada bloque y de la utilización completa o no del total de hilos que resulta del producto N_b  × N_h . En segundo lugar, hemos puesto a punto la herramienta de cálculo mediante un estudio de sensibilidad respecto del número de puntos de integración necesarios para alcanzar una convergencia aceptable en los resultados para el problema que queremos abordar. En la tabla 3 incluimos los tiempos de ejecución y valores de energía para una configuración concreta (fig. 11 ), en función del número de puntos de integración en cada dimensión, N , y del entorno de ejecución: GPU, CPU sistema operativo Windows y CPU sistema operativo Linux. Dado que la mejora alcanzable en los tiempos de ejecución en la CPU es una cuestión extensamente estudiada para algoritmos tan sencillos en su estructura como el utilizado en este trabajo, haciendo o no uso de librerías OpenMP y MPI, nuestro objetivo ha sido comparar los tiempos de ejecución en CPU, sin gestión eficiente de los microprocesadores, y en GPU. Los tiempos de ejecución en GPU tienen un comportamiento del tipo N² , consistente con la utilización de un bucle doble en lugar del bucle triple anidado inicial, gracias a la paralelización de uno de los bucles anidados.

Tabla 3. Comparación de los valores de la energía de interacción para el caso 0 cuando L_A  = 20a , para distinto número de puntos de integración N . La columnas CPU/GPU representan la aceleración del tiempo de ejecución GPU respecto CPU.

	GPU		CPUwindows		CPU/GPU	CPUlinux		CPU/GPU
N	Tiempo (s )	Energía (eV )	Tiempo (s )	Energía (eV )		Tiempo (s )	Energía (eV )
20	111	−6.236E+00	140	−6.236E+00	1,26	100	−6.236E+00	0,90
50	703	−8.052E-01	3100	−8.052E-01	4,41	1250	−8.052E-01	1,78
60	1026	−8.059E-01	5340	−8.059E-01	5,20	2160	−8.059E-01	2,10
64	1175	−8.060E-01	6463	−8.060E-01	5,49	3008	−8.060E-01	2,56
100	2905	−8.061E-01	16400	−8.061E-01	5,64	11400	−8.061E-01	3,92
200	12180	−8.061E-01	130800	−8.061E-01	10,73	103400	−8.061E-01	8,48
300	30170	−8.061E-01	–	–	–	–	–	–
400	61690	−8.061E-01	–	–	–	–	–	–

Figura 11. Geometría de un bucle de dislocación básico nucleado en una línea de dislocación infinita de dirección ${\textstyle (11{\overline {1}})}$ .

A la vista de los resultados presentados en la tabla 3 podemos concluir que para N  = 100 se alcanza la máxima convergencia. Sin embargo, la utilización de 64 puntos de integración implica una reducción de tiempo considerable, con una diferencia en el valor de la energía totalmente aceptable. Por otro lado, es interesante destacar que, cuando el número de puntos de integración N requerido para alcanzar la convergencia es mayor de 100, el tiempo de cálculo en CPU se dispara, mientras que para valores mayores de 200 resulta simplemente inabordable.

4. Resultados numéricos

Como hemos descrito en el apartado 3 , estamos interesados en el cálculo de la energía de formación de defectos en 3 situaciones distintas (fig. 7 ), que se corresponden con algunos de los mecanismos de movimiento de dislocaciones de tipo tornillo en materiales BCC a baja temperatura. En particular, vamos a obtener estas energías para 3 materiales: molibdeno (Mo), wolframio (W) y tántalo (Ta), gracias al modelo de constantes de fuerza obtenido mediante la linealización del potencial tipo Finnis-Sinclair [17] , validado en el apartado 3.2 .

4.1. Caso A

Para calcular la energía de nucleación de un escalón doble, partimos de una configuración con un defecto definido por α_k , esto es, una línea de dislocación infinita, y añadimos un defecto definido por Δα , el menor bucle de dislocación que se pueda generar espontáneamente sobre la dislocación inicial. La altura del escalón doble de menor tamaño es la distancia entre dos mínimos del potencial de Peierls [3] y se corresponde con el módulo del vector de Burgers del material. En nuestro modelo, este bucle, que denominaremos en adelante bucle básico , resulta de la superposición de 4 bucles elementales: dos de tipo cartesiano y 2 de tipo diagonal ( fig. 11 ).

Hemos considerado una línea de dislocación infinita inicial (fig. 11 ) con actividad en el sistema de deslizamiento C5 (tabla 1 ) y definida por la secuencia {e₂ (4, l ), e₂ (8, l ), e₂ (10, l   )}, con vector de Burgers ${\textstyle {\frac {1}{2}}a_{0}\left\langle 11{\overline {1}}\right\rangle }$ . En el espacio de Fourier ${\textstyle {\overset {\mbox{ˆ}}{\alpha }}(\theta )}$ se define como

${\overset {\mbox{ˆ}}{\alpha }}(8,{\boldsymbol {\theta }})=$$2\pi \delta ({\boldsymbol {\theta }}-{\boldsymbol {\Theta }})e^{i{\theta }_{2}}$ ${\overset {\mbox{ˆ}}{\alpha }}(4,{\boldsymbol {\theta }})=$$-2\pi \delta ({\boldsymbol {\theta }}-{\boldsymbol {\Theta }})e^{-i{\theta }_{1}}$ ${\overset {\mbox{ˆ}}{\alpha }}(10,{\boldsymbol {\theta }})=$$2\pi \delta ({\boldsymbol {\theta }}-{\boldsymbol {\Theta }})$

( 35)

Mientras que ${\textstyle \Delta {\overset {\mbox{ˆ}}{\alpha }}(\theta )}$ para el bucle básico viene dado por

${\overset {\mbox{ˆ}}{\alpha }}(3,{\boldsymbol {\theta }})=$$e^{-i({\theta }_{1}+{\theta }_{3})}-e^{-i({\theta }_{1}+2{\theta }_{3})}$ ${\overset {\mbox{ˆ}}{\alpha }}(4,{\boldsymbol {\theta }})=$$e^{-i(2{\theta }_{1}+{\theta }_{2}+2{\theta }_{3})}-e^{-i({\theta }_{1}+{\theta }_{3})}$ ${\overset {\mbox{ˆ}}{\alpha }}(5,{\boldsymbol {\theta }})=$$e^{-i{\theta }_{1}}-e^{-i({\theta }_{1}+{\theta }_{3})}$

( 36)

${\overset {\mbox{ˆ}}{\alpha }}(8,{\boldsymbol {\theta }})=$$e^{-i({\theta }_{1}+{\theta }_{3})}-e^{i{\theta }_{2}}$ ${\overset {\mbox{ˆ}}{\alpha }}(10,{\boldsymbol {\theta }})=$$e^{-i({\theta }_{1}+{\theta }_{2}+{\theta }_{3})}-e^{-i{\theta }_{3}}$

( 37)

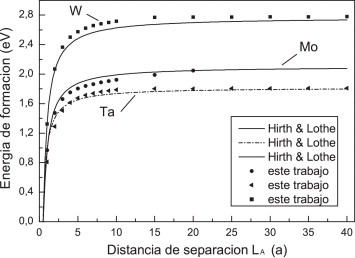
La energía de formación de un escalón doble de longitud L_A , según la teoría clásica de dislocaciones [3] , puede expresarse como

$E_{tot}=2E_{for}+E_{int}$

( 38)

donde E_for es la autoenergía asociada a un escalón aislado y el término E_int corresponde a la energía de interacción entre escalones. Dado que este término es inversamente proporcional a la longitud de separación entre escalones L_A , su valor tiende a cero cuando los escalones están suficientemente alejados. Cuando esto sucede, podemos decir que estamos en la condición de escalones simples aislados. Los resultados obtenidos para los 3 materiales estudiados se han representado en la figura 12 junto con los valores de la energía de formación correspondientes a la teoría elástica lineal de dislocaciones. La comparación es buena, pero dado que la energía (38) se expresa en términos de un parámetro ρ sin significado físico, su validez es más cualitativa que cuantitativa. Nuestros resultados para la energía de formación de un escalón aislado en Ta concuerdan con los obtenidos por Moriarty et al. [13] para 16 posibles configuraciones de escalones. En la figura 12 puede verse que para tántalo obtenemos una energía por escalón de aproximadamente 0.9 eV, mientras que los valores calculados en Moriarty et al. [13] oscilan entre 0.67 y 1.84 eV, dependiendo de la configuración. La energía de nucleación del escalón doble se corresponde con el primer valor en las curvas (L_A  = b ) en la figura 12 .

Figura 12. Energía de formación correspondiente al crecimiento de un escalón doble para diversos materiales BCC.

4.2. Caso B

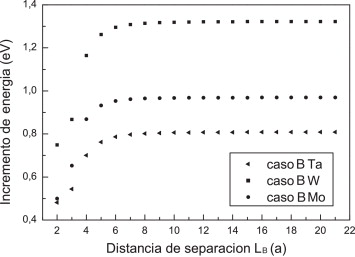
Queremos determinar en este caso la posición en la que la energía de nucleación de un escalón doble es independiente de la existencia de otro escalón doble en la línea de dislocación infinita (fig. 13 ). Para tántalo, hemos obtenido que la distancia L_A entre el escalón doble inicial y el nuevo es aproximadamente 10a , siendo a el parámetro de red del material. El incremento de energía necesario para nuclear el doble escalón a distancias mayores es igual al calculado en el caso anterior ( fig. 14 ).

Figura 13. Modelo de caso B en el complejo simplicial del BCC.

Figura 14. Energía de nucleación de un escalón doble en una línea infinita en la que ya existe otro escalón doble.

4.3. Caso C

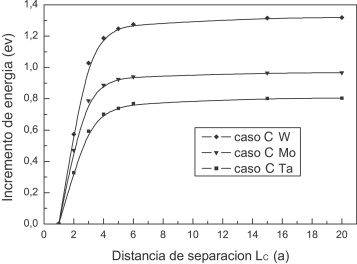
Por último, hemos determinado la distancia L_C en la que la nucleación de un nuevo escalón doble en una línea de dislocación en la que existe inicialmente un escalón aislado (fig. 15 ) podría asemejarse al caso 0, esto es, a la nucleación de un escalón doble en una línea de dislocación recta infinita. Los resultados obtenidos indican (fig. 16 ) que cuando la distancia de separación L_C en tántalo es ≈10a , el incremento de energía necesario para nuclear un doble escalón en una línea de dislocación infinita con un escalón aislado tiende a 0.8 eV, el mismo que obtuvimos en el caso 0 para este material. A esta distancia, la interacción entre el nuevo escalón doble y el escalón aislado se atenúa o desaparece por completo. Podemos concluir que la energía de interacción E_int entre el escalón aislado y el nuevo escalón doble debe tenerse en cuenta cuando L_C  < 6a .

Figura 15. Modelo de caso C en el complejo simplicial del BCC.

Figura 16. Energía de nucleación de un doble escalón en una línea infinita con un escalón aislado.

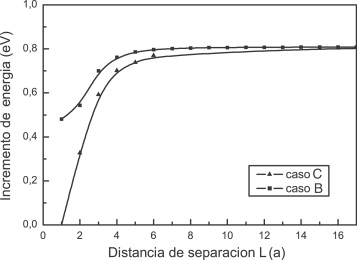
Podemos asimismo observar que la evolución de la energía con respecto a la distancia L_C (fig. 16 ) es análoga a la obtenida para el caso A (fig. 14 ) cuando L es mayor que unas pocas distancias interatómicas a . En la figura 17 puede verse la comparación de ambos casos para el tántalo: las energías de nucleación difieren considerablemente cuando la separación entre el escalón inicial y el nuevo escalón doble es menor de 4a .

Figura 17. Comparación de las energías de nucleación de un doble escalón en una línea infinita con un escalón aislado (caso C) y un doble escalón (caso B) para tántalo.

5. Conclusiones

El movimiento de dislocaciones diluidas de tipo tornillo en materiales BCC y, en consecuencia, el comportamiento plástico de estos materiales a baja temperatura y para niveles de deformación relativamente bajos viene controlado por la nucleación y el crecimiento de escalones dobles. En este trabajo se ha extendido la teoría discreta desarrollada por Ariza y Ortiz [8] al estudio de la energía asociada a estos mecanismos de deformación. En nuestro modelo, el cálculo de la energía implica la evaluación de un integrando que, expresado en el dominio de Fourier, tiene un carácter oscilatorio alto y precisa un número de puntos de integración elevado. En este trabajo hemos aplicado la tecnología CUDA de NVIDIA para integrar el modelo de programación GPGPU en el cálculo de estas integrales, y hemos evaluado la aceleración de tiempo de ejecución que conseguimos respecto al cálculo en CPU. La rebaja en los tiempos de ejecución que se consigue nos permite abordar de forma eficiente el estudio del comportamiento de configuraciones de defectos como las analizadas aquí u otras similares.

Agradecimientos

Los autores desean expresar su agradecimiento por el apoyo recibido al Ministerio de Ciencia e Innovación a través del proyecto DPI2009-14305-C02-01 y a la Consejería de Innovación, Ciencia y Empresa de la Junta de Andalucía a través del proyecto P09-TEP-4493.

References

1. [1] V.V. Bulatov; Current Developments and Trends in Dislocation Dynamics; J. Computer-Aided Mater. Design, 9 (2) (2002), pp. 133–144
2. [2] R. Becker; Developments and Trends in Continuum Plasticity; J. Computer-Aided Mater. Design, 9 (2) (2002), pp. 145–163
3. [3] J.P. Hirth, J. Lothe; Theory of Dislocations; Wiley, Florida (1982)
4. [4] L.P. Kubin, G. Canova; The modelling of dislocation patterns; Scripta Metallurgica et Materialia, 27 (8) (1992), pp. 957–962
5. [5] R. Madec, B. Devincre, L.P. Kubin; Simulation of dislocation patterns in multislip; Scripta Materialia, 47 (10) (2002), pp. 689–695
6. [6] Y.U. Wang, Y.M. Jin, A.M. Cuitino, A.G. Khatachuryan; Nanoscale phase field microelasticity theory of dislocations: model and 3D simulations; Acta Materialia, 49 (10) (2001), pp. 1847–1857
7. [7] Y. Xiang, L.T. Cheng, D.J.E.W. Srolovitz; A level set method for dislocation dynamics; Acta Materialia, 51 (18) (2003), pp. 5499–5518
8. [8] M.P. Ariza, M. Ortiz; Discrete Crystal Elasticity and Discrete Dislocations in Crystals; Archive for Rational Mechanics and Analysis, 178 (2005), pp. 149–226
9. [9] T. Mura; Micromechanics of defects in solids; Kluwer Academic Publishers, Boston (1987)
10. [10] A. Ramasubramaniam, M.P. Ariza, M. Ortiz; A discrete mechanics approach to dislocation dynamics in BCC crystals; Journal of the Mechanics and Physics of Solids, 55 (3) (2007), pp. 615–647
11. [11] NVIDIA CUDA C Programming Guide, 2010.
12. [12] http://www.nvidia.com/page/hote.html
13. [13] L.H. Yang, J.A. Moriarty; Kink-pair mechanisms for a/2lessthan 111greatherthan screw dislocation motion in BCC tantalum  ; Mat Sc. and Eng., A319-321 (2008), pp. 124–129
14. [14] J.R. Munkres; Elements of Algebraic Topology; Perseus Publishing (1984)
15. [15] I. Babuska, E. Vitasek, F. Kroupa; Some applications of the discrete fourier transform to problems of crystal lattice deformation, PARTS I and II; Czech J Phys B (1960), p. 10
16. [16] M.W. Finnis, J.E. Sinclair; A simple empirical N-body potential for transition-metals; Philosophical Magazine A-Physics of Condensed Matter Structure Defects and Mechanical Properties, 50 (1) (1984), pp. 45–55
17. [17] X.D. Dai, Y. Kong, J.H. Li, B.X. Liu; Extended Finnis-Sinclair potential for BCC and FCC metals and alloys; Journal of Physics: Condensed Matter, 18 (2006), pp. 4527–4542
18. [18] D.C. Champeney; Fourier Transforms and their physical applications; (2nd ed.)Academic Press Inc, London (1973)