Magnetohydrodynamic double diffusive natural convection in trapezoidal cavities

Abstract

A numerical work has been carried out to study the effects of magnetic field on double diffusive natural convection in a trapezoidal enclosure. Both inclined walls and bottom wall were kept at constant temperature and concentration where the bottom wall temperature and concentration are higher than those of the inclined walls. Top wall of the cavity is adiabatic and impermeable. The trapezoidal enclosure is subjected to a horizontal magnetic field. To investigate the effects, finite volume method is used to solve the governing equations for different parameters such as Grashof number, inclination angle of inclined wall of the enclosure, Hartmann number and buoyancy ratio. The numerical results are reported for the effect of studied parameters on the contours of streamline, temperature, and concentration. In addition, results for both local and average Nusselt and Sherwood numbers are presented and discussed for various parametric conditions. This study is done for constant Prandtl number, Pr = 0.7; aspect ratio = 1 and Lewis number, Le = 2. The studied range of Grashof number is from Gr = 10³ to 10⁶, inclination angle from 0° to 75°, Hartmann number from 0 to 15 and buoyancy ratio from −2 to 2 which covers the double diffusive range in the cases of aiding and opposing flows. It is found that heat and mass transfer decreased as φ increases from 0° to 75°. Also heat and mass transfer decreased as Hartman number increased from 0 to 15. Finally, the predicted results for both average Nusselt and Sherwood numbers were correlated in terms of the studied parameters.

Keywords

Trapezoidal enclosure; Natural convection; Double diffusive; Magnetic field

Nomenclature

B- magnetic induction, ${\textstyle {\mbox{Tesla}}={\mbox{N}}/{\mbox{Am}}^{2}}$

c_h- high concentrations at the bottom wall of the cavity

c_c- low concentrations at the left and right walls of the cavity

C- dimensionless concentration, C = (c – c_c)/(c_h – c_c)

C_p- specific heat at constant pressure

D- mass diffusivity

g- acceleration of gravity

Gr_s- solutal Grashof number

Gr- thermal Grashof number

h- heat transfer coefficient

h_s- solutal heat transfer coefficient

H- cavity height

k- fluid thermal conductivity

L- bottom wall of the cavity length

Le- Lewis number, Le = α/D

N- buoyancy ratio

Nu- average Nusselt number, Nu = hL/k

p- pressure

P- dimensionless pressure, ${\textstyle P={pL}^{2}/{\rho }^{_{\ast }}{\alpha }^{2}}$

Pr- Prandtl number, Pr = ν/α

Ra_s- solutal Rayleigh number

Ra- thermal Rayleigh number

Sh- average Sherwood number, Sh = h_s L/D

Sh_i- local Sherwood number

T- local temperature

T_c- cold wall temperature

T_h- hot wall temperature

ΔT- temperature difference

u- velocity components in x direction

v- velocity components in y direction

U- dimensionless velocity component in X direction

V- dimensionless velocity component in Y direction

x, y- dimensional coordinates

X, Y- dimensionless coordinates

Greek symbols

α- thermal diffusivity

β_T- coefficient of thermal expansion

β_S- coefficient of solutal expansion

θ- dimensionless temperature, (T − T_c)/(T_h − T_c)

ϕ- trapezoidal inclination angle

μ- dynamic viscosity

ν- kinematics viscosity

ρ- local fluid density

ρ^∗- dimensionless density, NC- θ

1. Introduction

Double diffusive natural convection heat transfer has an essential role in modern life. Application of double diffusive natural convection heat transfer is common in many engineering fields such as, drying processes, printing, building heating and cooling, solar collector, and heat exchangers. In most of these applications, convective heat and mass transfer are investigated, and the cavities are of various shapes including triangular, rectangular, trapezoidal, sinusoidal or ellipsoidal. Magnetic field is also an important control parameter for convective heat and mass transfer in pipes, ducts and cavities.

Basak et al. [1] and [2] investigated the natural convection in a trapezoidal enclosure filled with porous matrix by applying finite element method. In their investigation, they studied the effect of uniform and non-uniform heating of bottom wall where the two vertical walls were maintained at constant cold temperature and top wall is well insulated. They also investigated natural convection in trapezoidal enclosures for uniformly heated bottom wall, and linearly heated vertical wall(s) with insulated top wall by using finite element method. Basak et al. [3] extended their work to various inclination angle for the trapezoidal. A study on natural convection on a trapezoidal porous enclosure has been carried out by Baytas and Pop [4]. They solved the problem by finite-difference method with boundary conditions as top enclosure being cooled, bottom cylindrical surfaces being heated and the remaining two non-parallel plane sidewalls of enclosure being adiabatic. In trapezoidal geometries, numerical studies are widely available, such as those by Dong and Ebadian [5] and Boussaid et al. [6] and [7] in the laminar-flow regime and by Van der Eyden et al. [8] in the turbulent flow regime. Kumar and Kumar [9] studied the coupled non-linear partial differential equations governing the natural convection from an isothermal wall of a trapezoidal porous enclosure by using finite element method. Kumar [10] studied thermal analysis to investigate the natural convection for a trapezoidal absorber plate and compared the results with the rectangular enclosure. Authors found that the convective heat transfer coefficient for rectangular enclosure is 31–35% lower. Iyican and Bayazitoglu [11] investigated natural convective flow and heat transfer within a trapezoidal enclosure with parallel cylindrical top and bottom walls at different temperatures and plane adiabatic side walls. Karyakin [12] reported two-dimensional laminar natural convection in enclosures of arbitrary cross-section. This study reported on transient natural convection in an isosceles trapezoidal cavity. Fundamental studies on natural convection in trapezoidal enclosures of various forms (including triangular ones as a special case) have been presented by Perić [13], Hasanuzzaman [14] and Hoogendoorn [15] and Varol et al. [16] analyzed numerically the entropy in a right-angle trapezoidal enclosure filled with a porous medium bounded by a solid vertical wall. Authors used finite difference technique in their work at different values of thermal conductivity and solid wall thickness. Kimura and Bejan [17] proposed heatlines for visualization of convective heat transfer through an extension of heat flux line concept to include the advection terms. A smaller number of studies have considered the trapezoidal geometry, which is encountered in several practical applications, such as attic spaces in buildings [18]. Other related works with trapezoidal enclosure can be found in the literature as [19], [20] and [21]. Teamah [22] studied double diffusive in symmetrical trapezoidal enclosure, and the work is extended for different values of Grashof number and aspect ratio as further reported in [23].

Basak et al. [24] studied numerically the natural convection flows in a square cavity filled with a porous matrix for various boundary conditions and wide range of parameters. The stability of the flow in confined rectangular enclosures has also received considerable attention in recent years [25]. Teamah [26] and [27] studied double diffusive flow in a rectangular cavity in the presence of magnetic field and inner heat source. Teamah et al. [28], [29] and [30] extended the previous work by studying the inclined cavity. Recently Teamah and El-Maghlany [31] studied the effect of magnetic field on heat transfer in a rectangular cavity filled with nano-fluid. Further work is done by Khairat and Teamah [32], and they studied the hydro-magnetic mixed convection double diffusive in a lid driven square cavity numerically. Oztop et al. [33] numerically investigated magnetic field effects on natural convection in a square enclosure with a non-isothermal heater. Sivasankaran and Ho [34] studied natural convection of water in the presence of magnetic field with temperature dependent properties in a cavity and deduced that the external magnetic field direction is an important parameter for fluid flow as well as heat transfer. Singh and Sharif [35] extended their works by considering six placement configurations of the inlet and exit ports of a differentially heated rectangular enclosure. A recent investigation indicates the effect of viscous dissipation for Darcy model as studied by Saeid and Pop [36]. Their study shows that the increase in viscous dissipation parameter reduces the heat transfer rate and the average Nusselt number in porous cavities. Tong and Subramanian [37] further utilized extended Darcy model to examine the buoyancy effects on free convection in vertical cavity. A model that bridges the gap between the Darcy and Navier Stokes equations is the Darcy–Forchheimer model which was imposed by [38] to study boundary and inertia effect on flow and heat transfer in porous media.

The present study examined double diffusive effects of magnetic field on natural convection heat transfer in trapezoidal enclosure with different inclination angles. The study also extends the problem of natural convection in trapezoidal enclosure by taking into account magneto-hydrodynamic effect.

2. Mathematical model

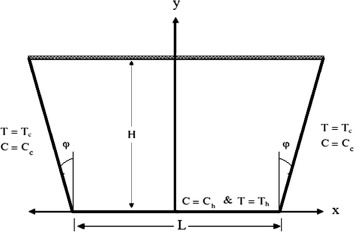
Physical model is plotted in Fig. 1. In this Figure, the cavity is heated from bottom wall and temperature and species concentration of inclined walls are lower than those of bottom wall. The top wall is adiabatic. The length of bottom heated wall is shown by L and the height is H. The cavity is filled with pure fluid and magnetic field affects the system laterally. Inclination angle of the inclined wall is changed as an effective parameter on heat and mass transfer.

Figure 1. Studied model for the problem.

The fluid is assumed to be incompressible, Newtonian and viscous. Both the viscous dissipation and magnetic dissipation are assumed to be negligible. The magnetic Reynolds number is assumed to be so small that the induced magnetic field is neglected. These assumptions lead to the Boussinesq approximation, Eq. (1), with opposite and compositional buoyancy forces which is used for the body force terms in the momentum equations.

$\rho ={\rho }_{\mbox{°}}[1-{\beta }_{T}(T-T_{c})-{\beta }_{S}(c-$$c_{l})]$

(1)

The governing equations for the problem under consideration are based on the balance laws of mass, linear momentum, concentration and thermal energy in two dimensions steady state. In light of assumptions mentioned above, the continuity, momentum, energy and concentration in two dimensional equations can be written as follows:

${\frac {\partial u}{\partial x}}+{\frac {\partial v}{\partial y}}=$$0$

(2)

$u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}=$$-{\frac {1}{\rho }}{\frac {\partial p}{\partial x}}+\nu \left[{\frac {{\partial }^{2}u}{\partial x^{2}}}+\right.$$\left.{\frac {{\partial }^{2}u}{\partial y^{2}}}\right]$

(3)

$u{\frac {\partial v}{\partial x}}+v{\frac {\partial v}{\partial y}}=$$-{\frac {1}{\rho }}{\frac {\partial p}{\partial y}}+\nu \left[{\frac {{\partial }^{2}v}{\partial x^{2}}}+\right.$$\left.{\frac {{\partial }^{2}v}{\partial y^{2}}}\right]+$$[g{\beta }_{T}(T-T_{c})-g{\beta }_{s}(c-c_{l})]+{\frac {\sigma B^{2}}{\rho }}v$

(4)

$u{\frac {\partial T}{\partial x}}+v{\frac {\partial T}{\partial y}}=$$\alpha \left[{\frac {{\partial }^{2}T}{\partial x^{2}}}+{\frac {{\partial }^{2}T}{\partial y^{2}}}\right]$

(5)

$u{\frac {\partial c}{\partial x}}+v{\frac {\partial c}{\partial y}}=$$D\left[{\frac {{\partial }^{2}c}{\partial x^{2}}}+{\frac {{\partial }^{2}c}{\partial y^{2}}}\right]$

(6)

Dimensionless variables are as follows:

$X={\frac {x}{L}}{\mbox{,}}\quad Y={\frac {y}{L}}{\mbox{,}}\quad U=$${\frac {uL}{\alpha }}{\mbox{,}}\quad V={\frac {vL}{\alpha }}{\mbox{,}}\quad P=$${\frac {{pL}^{2}}{{\rho }^{_{\ast }}{\alpha }^{2}}}{\mbox{,}}\quad \theta =$${\frac {T-T_{c}}{T_{h}-T_{c}}}\quad {\mbox{and}}\quad C={\frac {c-c_{c}}{c_{h}-c_{c}}}$

(7)

After employing the dimensionless variables mentioned above, the resulting dimensionless governing equations can be written as

${\frac {\partial U}{\partial X}}+{\frac {\partial V}{\partial Y}}=$$0$

(8)

$U{\frac {\partial U}{\partial X}}+V{\frac {\partial U}{\partial Y}}=$$-{\frac {\partial P}{\partial X}}+Pr\left[{\frac {{\partial }^{2}U}{\partial X^{2}}}+\right.$$\left.{\frac {{\partial }^{2}U}{\partial X^{2}}}\right]$

(9)

$U{\frac {\partial V}{\partial X}}+V{\frac {\partial V}{\partial X}}=$$-{\frac {\partial P}{\partial Y}}+Pr\left[{\frac {{\partial }^{2}V}{\partial X^{2}}}+\right.$$\left.{\frac {{\partial }^{2}V}{\partial Y^{2}}}\right]+$$[Gr(\theta -NC)]-{Ha}^{2}{\mbox{Pr}}\times V$

(10)

$U{\frac {\partial \theta }{\partial X}}+V{\frac {\partial \theta }{\partial Y}}=$$\left[{\frac {{\partial }^{2}\theta }{\partial Y^{2}}}+{\frac {{\partial }^{2}\theta }{\partial Y^{2}}}\right]$

(11)

$U{\frac {\partial C}{\partial X}}+V{\frac {\partial C}{\partial Y}}=$${\frac {1}{Le}}\left[{\frac {{\partial }^{2}C}{\partial X^{2}}}+\right.$$\left.{\frac {{\partial }^{2}C}{\partial Y^{2}}}\right]$

(12)

where Pr is the Prandtl number, Ra is the thermal Rayleigh number, N is the buoyancy ratio = ${\textstyle {\beta }_{S}[(c_{h}-c_{l})]/{\beta }_{T}[(T_{h}-T_{c})]}$, Ha is the Hartmann number = ${\textstyle BL{\sqrt {\sigma /\mu }}}$, Le = α/D.

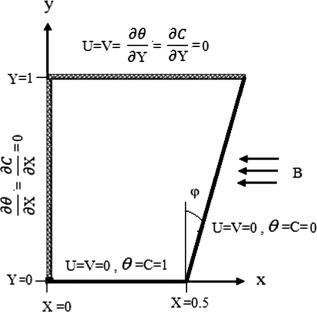
From the symmetry of the problem, half the problem domain is solved as shown in Fig. 2.

Figure 2. The domain studied.

The corresponding boundary conditions in dimensionless form are as follows:

• At right wall: ${\textstyle U=0{\mbox{,}}\quad V=0{\mbox{,}}\quad \theta =0{\mbox{,}}\quad C=}$$0$
• At top wall: ${\textstyle U=0{\mbox{,}}\quad V=0{\mbox{,}}\quad {\frac {\partial \theta }{\partial Y}}=}$$0{\mbox{,}}\quad {\frac {\partial C}{\partial Y}}=0$
• At left symmetry walls: ${\textstyle {\frac {\partial U}{\partial X}}=0{\mbox{,}}{\frac {\partial V}{\partial X}}=}$$0{\mbox{,}}\quad {\frac {\partial \theta }{\partial X}}=$$0{\mbox{,}}{\frac {\partial C}{\partial X}}=0$
• At bottom wall: ${\textstyle U=V=0{\mbox{,}}\quad \theta =1{\mbox{,}}\quad C=1}$

The Nusselt and Sherwood numbers calculated as average values and evaluated along the isothermal walls of the cavity are given by

$Nu=-{\frac {1}{A}}{\int }_{0}^{A}{\left({\frac {\partial \theta }{\partial X}}\right)}_{X=0.5}dY$

(13)

$Sh=-{\frac {1}{A}}{\int }_{0}^{A}{\left({\frac {\partial C}{\partial X}}\right)}_{X=0.5}dY$

(14)

3. Numerical solution

Numerical solutions of the full conservation equations are obtained using the finite volume technique developed by Patankar [39]. This technique is based on the discretization of the governing equations using the central difference in space. Firstly, the number of nodes used was checked. During the program tests (32 ∗32), (52 ∗ 52), (82 ∗ 82) and (122 ∗ 122) grids were checked. The maximum differences between (32 ∗ 32) grids and (122 ∗ 122) are within 0.12%. To save computational time, through this study (52 ∗ 52) grids are used.

The 52 grid points in X and Y   directions were enough to resolve the thin boundary layer near the cavity walls. To calculate both Nusselt and Sherwood numbers, the following numerical differentiations are used, ${\textstyle {\frac {\partial \theta }{\partial Y}}_{Y=0}={lim}_{\Delta Y\rightarrow 0}{\left({\frac {\Delta \theta }{\Delta Y}}\right)}_{Y=0}}$ and ${\textstyle {\frac {\partial C}{\partial Y}}_{Y=0}={lim}_{\Delta Y\rightarrow 0}{\left({\frac {\Delta C}{\Delta Y}}\right)}_{Y=0}}$. Therefore, at the isothermal walls, insulated and impermeable wall and symmetrical side very fine grids are needed to obtain accurate results. In X-direction, the width of 5 control volumes close to both boundaries was 1/4 the width of the central control volumes. Also, in Y-direction, the height of 5 control volumes close to both the horizontal boundaries was 1/4 the height of the central control volumes. The discretization equations were then solved by the Gauss–Seidel method. The iteration method used in this program is a line-by-line procedure, which is a combination of the direct method and the resulting Tri Diagonal Matrix Algorithm (TDMA).

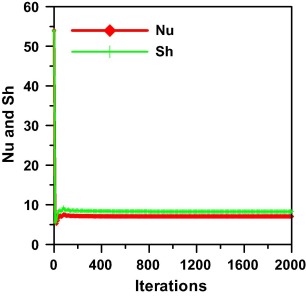
In order to check the convergence of the iteration, local iterative convergence was assessed by monitoring the magnitude of the total heat and mass fluxes across the active walls by setting its variation to less than 10⁻⁵, whereas global iterative convergence was guaranteed by controlling the residuals of the conservation equations by setting its variations to less than 10⁻⁶. Also, the change in the average Nusselt and Sherwood numbers as well as other dependent variables through one hundred iterations was checked. Fig. 3 shows that the change in the average Nusselt and Sherwood numbers is less than 0.01% from their initial values which is an indication for the convergence and stability of the solution.

Figure 3. Stability of the solution.

4. Validation with previous work

Prior to calculations, checks were conducted to validate the calculation procedure by performing simulation for convective heat transfer flow only in a trapezoidal enclosure in the presence of magnetic field with the same configuration as reported by Hasanuzzaman et al. [14]. This is done in the present code by putting the buoyancy ratio equals to zero and this infers neglecting the concentration buoyancy effect. The average values for Nusselt number of the present code are compared to their published results as shown in Fig. 4 taking the studied parameters Ha = 10 and Pr = 0.7. The comparison reflected a good agreement. Most of the results coincide with the maximum deviation of less than 5%.

Figure 4. Comparison of present results published by Hasanuzzaman et al. [14].

5. Results and discussion

5.1. The combined effect of thermal Grashof number (Gr) and trapezoidal inclination angle

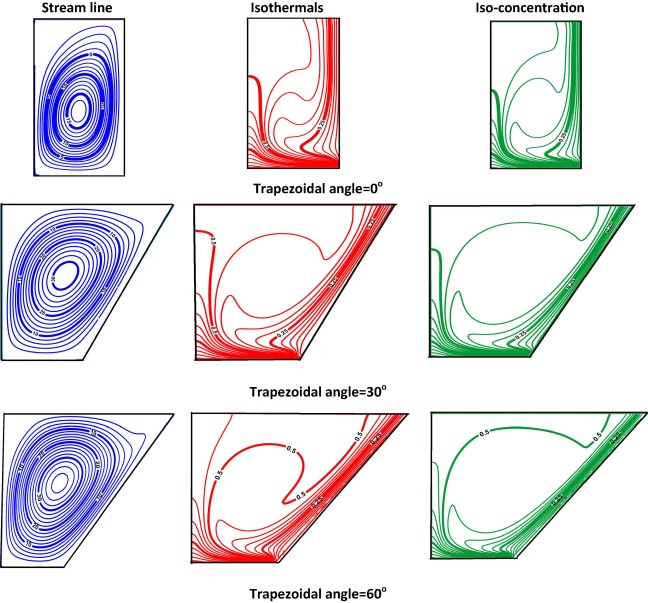
Double diffusive natural convective heat transfer inside a trapezoidal enclosure is studied for different Grashof number, Gr, and trapezoidal angle, ϕ, of enclosure, Hartmann number, Ha and buoyancy ratio. Fig. 5 shows the effects of trapezoidal angle of the cavity on streamline, temperature and concentration distribution. The figure is plotted for different trapezoidal inclination angles at Gr = 10⁵, Ha = 10 and N = 1. They are shown by streamline (on the left column), isotherms (on the middle column) and iso-concentrations (on the right column). In this figure for ϕ = 0°, the cavity is similar to rectangular cavity. The streamlines are uni-cells that revolve in the clockwise direction with strength increasing toward the center, same behavior as reported in [14], [20] and [21]. Isotherms show that temperature contours are accumulated near the corners due to high temperature difference between walls. Flow strength increases with increasing inclination angle of the walls of cavity. At (ϕ = 30°) streamlines fitted the cavity but the circulation cells are elongated diagonally revolving freely in the upper vast area between the walls. Isotherms also show that temperature is increased at the center of the cavity because of the increasing distance between cold walls. By examining the iso-concentrations, their values are also increased due to the increasing distance between the low concentration walls. These effects are more pronounced for (ϕ = 60°) and the streamlines are elongated more in the diagonal direction, the temperature increases in the center of the cavity and so do the iso-concentration values.

Figure 5. Effect of trapezoidal inclination angle on iso-contours Gr = 105, Le = 2.0, Pr = 0.7, Ha = 10 and N = 1.

Fig. 6 shows the effect of trapezoidal angle on local Nusselt number. It is noted that the value of local Nusselt number is the least in the center and then increases same as reported in [14]. The increment is moderate till near the right wall its value jumps steeply which is explained from the fact that circulation cell is cold and when it passes beyond the bottom right corner there is the maximum temperature difference which accounts for crowded isotherms on the corner; then this cell moves clockwise toward the center but its temperature is higher and the temperature gradient is lower near the center; and this is depicted in Fig. 5.

Figure 6. Effect of trapezoidal inclination angle on local Nusselt number at Gr = 105, Le = 2.0, Pr = 0.7, Ha = 10 and N = 1.

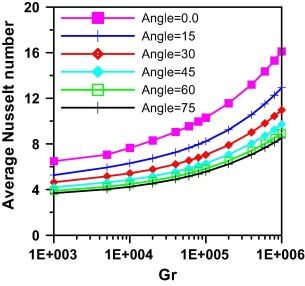
The effect of trapezoidal angle on average Nusselt number is shown in Fig. 7. It is found to decrease in value as the angle increases. This agrees with the discussion of isotherms and iso-concentrations anticipated in Fig. 5 where a greater wall gradient in Isotherms is manifested for lower trapezoidal angles. Severe gradients exist for φ = 0°, moderate gradients exist for φ = 30° and the least ones are for φ = 60°.

Figure 7. Effect of Grashof number and trapezoidal inclination angle on average Nusselt number at N = 1.0 and Ha = 10.

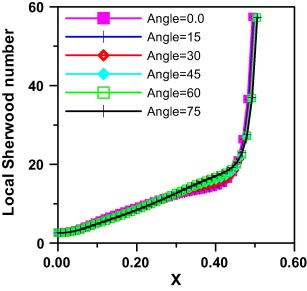
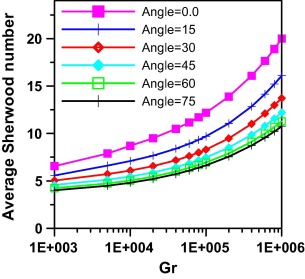
The effect of trapezoidal angle on local Sherwood number is demonstrated in Fig. 8. It shows the same trend as that of local Nusselt explained in Fig. 6 with the high gradient of iso-concentration that is accumulated on the corner causing the steep increase of its values near the inclined walls.

Figure 8. Effect of trapezoidal inclination angle on local Sherwood number at Gr = 105, Le = 2.0, Pr = 0.7, Ha = 10 and N = 1.

Fig. 9 shows the effect of trapezoidal angle on average Sherwood number. It reflects the same trend as that of the average Nusselt number with higher values for lower trapezoidal angles.

Figure 9. Effect of Grashof number and trapezoidal inclination angle on average Sherwood number at N = 1.0 and Ha = 10.

5.2. The combined effect of thermal Grashof number (Gr) and Hartmann number

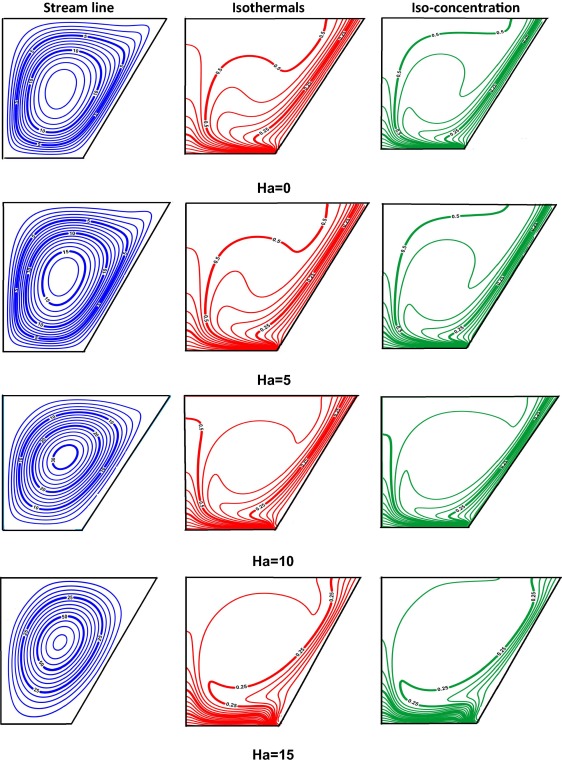
Fig. 10 illustrates the effects of magnetic field on streamlines, isotherms and iso-concentration for ϕ = 30° and Ra = 10⁵. In this figure, Hartmann number changes from Ha = 0–15. As seen from the figure, the flow strength increases as Ha increases as shown from streamlines. Hartmann number affects both isotherms and iso-concentrations, temperature inside the cavity and concentration decreases with increasing Hartmann number. Isotherms and iso-concentrations become steeper near the inclined walls. It means that conduction mode of heat transfer becomes dominant to convection with these increasing effects of magnetic field. This effect is shown slightly when Ha = 5, moderately at Ha = 10 and sharply at Ha = 15.

Figure 10. Effect of Ha on iso-contours Gr = 105, Le = 2.0, Pr = 0.7, angle = 30° and N = 1.

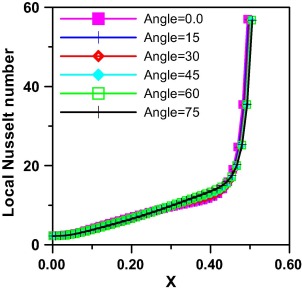
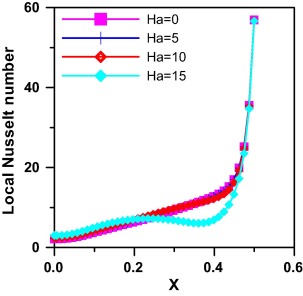
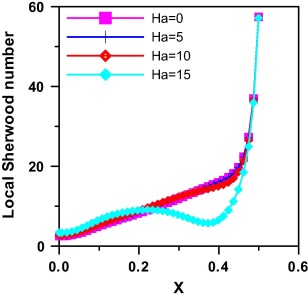
The effect of Ha on local Nusselt number and local Sherwood number is plotted in Figure 11 and Figure 13 respectively, and it is seen that they increase moderately till beyond the inclined wall they increase sharply. It is observed that the increase of magnetic field suppresses both local Nusselt and local Sherwood values and this is due to the force direction exerted by the magnetic field opposing the buoyancy force. For Ha = 15 the behavior differs slightly, the local Nusselt and local Sherwood increase till at position (X = 0.2), they decrease slightly till the position (X = 0.4) then increase steeply till the inclined wall.

Figure 11. Effect of Ha on local Nusselt number Gr = 105, Le = 2.0, Pr = 0.7, angle = 30° and N = 1.

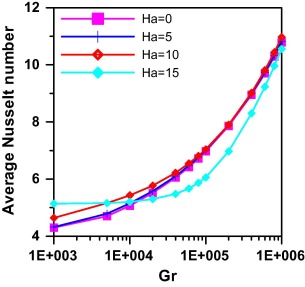
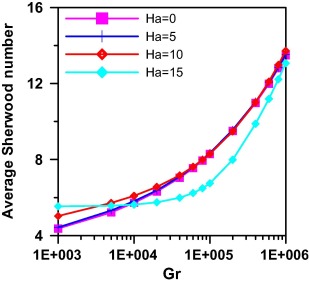
At θ = 30° the effect of Hartman number on Average Nusselt and Sherwood is investigated in Figure 12 and Figure 14 respectively. For the starting value of Grashof 10³ it is noted that average Nusselt and Sherwood values are greater for higher values of Hartman number. For Ha = 0, 5 & 10 as Grashof number exceeds 10³ both average Nusselt and average Sherwood increase monotonically till all reach a same approximate value at Gr = 10⁶. However, for Ha = 15 average Nusselt and Sherwood values increase slightly till Gr = 10⁵ manifesting the dominant conduction regime mode and then increase steeply to reach the same approximate value of the other curves at Gr = 10⁶.

Figure 12. Effect of Grashof and Hartman numbers on average Nusselt number at N = 1.0 and angle = 30°.

Figure 13. Effect of Ha on local Sherwood number Gr = 105, Le = 2.0, Pr = 0.7, angle = 30° and N = 1.

Figure 14. Effect of Grashof and Hartman numbers on average Sherwood number at N = 1.0 and angle = 30°.

5.3. The combined effect of thermal Grashof number (Gr) and buoyancy ratio

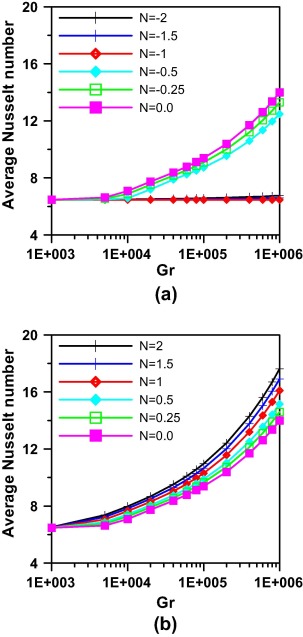
The effect of buoyancy ratio on average Nusselt number is shown in Fig. 15, and it is seen that the average Nusselt number increases with Grashof number as expected and for negative values of buoyancy ratio as in (a) the average Nusselt values increase as N increases and for N = −1 the average Nusselt value is constant as for the two buoyancy forces due to thermal and concentration differences canceling the effect of each other. For positive values of N as in (b) average Nusselt value also increases as N increases.

Figure 15. Effect of Grashof number and Buoyancy ratio on average Nusselt number at θ = 0.0 and Ha = 10 (a for N ⩽ 0 and b for N ⩾ 0).

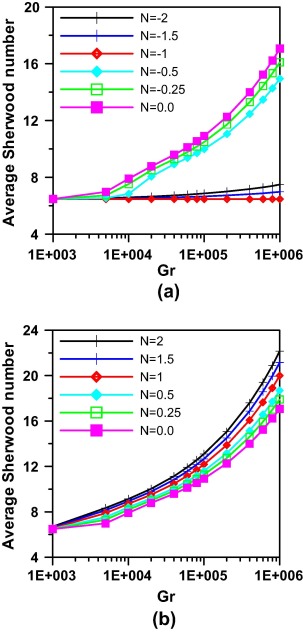
As for the Sherwood number, the effect of buoyancy ratio on average Sherwood number is depicted in Fig. 16, and it is seen that the average Sherwood number increases with Grashof number as expected and for negative values of buoyancy ratio as in (a) the average Sherwood values increase as N increases and for N = −1 the average Sherwood number value is constant as for the two buoyancy forces due to thermal and concentration differences canceling the effect of each other. For positive values of N as in (b) average Sherwood value also increases as N increases.

Figure 16. Effect of Grashof Number and Buoyancy ratio on average Sherwood number at θ = 0.0 and Ha = 10 (a for N ⩽ 0 and b for N ⩾ 0).

5.4. Correlating the results

Correlations are made to relate the studied parameters to calculate both average Nusselt and Sherwood numbers. The results are correlated in terms of buoyancy ratio, Grashof number and trapezoidal angle with maximum error 6.2% for average Nusselt number and 5.4% for average Sherwood number.

${\begin{array}{rl}&Nu=7.442+0.978{_{\ast }}N+6.58{_{\ast }}{10}^{-6}{_{\ast }}Gr-0.07{_{\ast }}\theta \\&Sh=8.42+1.58{_{\ast }}N+8.66{_{\ast }}{10}^{-6}{_{\ast }}Gr-0.0898{_{\ast }}\theta \end{array}}$

6. Conclusion

Steady heat and mass transfer by natural convection flow of a fluid inside a trapezoidal enclosure in the presence of magnetic field was studied numerically. The finite-difference method was employed for the solution of the present problem. Comparisons with previously published work on special cases of the problem were performed and found to be in good agreement. Graphical results for various parametric conditions were presented and discussed. It was found that the heat and mass transfer mechanisms and the flow characteristics inside the enclosure depended strongly on the thermal Grashof number. Increasing the trapezoidal angle always leads to decrease on the heat and mass transfer performance of the enclosure. This is made clarified by plotting the average Nusselt and Sherwood numbers with different values of thermal Rayleigh number and for different inclination angles. Also, it is noted that the increase of buoyancy ratio leads to better heat and mass transfer. Besides the effect of Hartman number increase was not in favor of double diffusive characteristics. Correlations are made to obtain average values of both average Nusselt and Sherwood numbers in terms of studied parameters with acceptable error.

References

1. [1] T. Basak, S. Roy, A. Singh, I. Pop; Finite element simulation of natural convection flow in a trapezoidal enclosure filled with porous medium due to uniform and non-uniform heating; Int. J. Heat Mass Transf., 52 (2009), pp. 70–78
2. [2] T. Basak, S. Roy, S.K. Singh, I. Pop; Finite element simulation of natural convection within porous trapezoidal enclosures for various inclination angles: effect of various wall heating; Int. J. Heat Mass Transf., 52 (2009), pp. 4135–4150
3. [3] T. Basak, S. Roy, S.K. Singh, A.R. Balakrishnan; Natural convection flows in porous trapezoidal enclosures with various inclination angles; Int. J. Heat Mass Transf., 52 (2009), pp. 4612–4623
4. [4] A.C. Baytas, I. Pop; Natural convection in a trapezoidal enclosure filled with a porous medium; Int. J. Eng. Sci., 39 (2001), pp. 125–134
5. [5] Z.F. Dong, M.A. Ebadian; Investigation of double-diffusive natural convection in a trapezoidal enclosure; ASME J. Heat Transf., 116 (2) (1994), pp. 492–495
6. [6] M. Boussaid, A. Mezenner, M. Bouhadef; Convection naturelle de chaleur et de masse dans une cavité trapézoıdale; Int. J. Therm. Sci., 38 (4) (1999), pp. 363–371
7. [7] M. Boussaid, A. Djerrada, M. Bouhadef; Thermosolutal transfer within trapezoidal cavity; Num. Heat Transf., Part A, 43 (4) (2003), pp. 431–448
8. [8] J.T. van der Eyden, Th.H. van der Meer, K. Hanjalić, E. Biezen, J. Bruining; Double-diffusive natural convection in trapezoidal enclosures; Int. J. Heat Mass Transf., 41 (13) (1998), pp. 1885–1898
9. [9] B.V.R. Kumar, B. Kumar; Parallel computation of natural convection in trapezoidal porous enclosure; Math. Comput. Simul., 65 (2004), pp. 221–229
10. [10] S. Kumar; Natural convective heat transfer in trapezoidal enclosure of box-type solar cooker; Renew. Energy, 29 (2004), pp. 211–222
11. [11] L. Iyican, Y. Bayazitoglu; An analytical study of natural convective heat transfer within trapezoidal enclosure; ASME Trans. J. Heat Transf., 102 (1980), pp. 640–647
12. [12] Y.E. Karyakin; Transient natural convection in prismatic enclosures of arbitrary cross-section; Int. J. Heat Mass Transf., 32 (1989), pp. 1095–1103
13. [13] M. Perić; Natural convection in trapezoidal enclosures; Num. Heat Transf., Part A, 24 (2) (1993), pp. 213–219
14. [14] M. Hasanuzzaman, Hakan F. Öztop, M.M. Rahman, N.A. Rahim, R. Saidur, Y. Varol; Magnetohydrodynamic natural convection in trapezoidal cavities; Int. Commun. Heat Mass Transf., 39 (2012), pp. 1384–1394
15. [15] R.A. Kuyper, C.J. Hoogendoorn; Laminar natural convection flow in trapezoidal enclosures; Num. Heat Transf., Part A, 28 (1) (1995), pp. 55–67
16. [16] Y. Varol, H.F. Oztop, I. Pop; Entropy analysis due to conjugate-buoyant flow in a right-angle trapezoidal enclosure filled with a porous medium bounded by a solid vertical wall; Int. J. Therm. Sci., 48 (2009), pp. 1161–1175
17. [17] S. Kimura, A. Bejan; The heatline visualization of convective heat-transfer; J. Heat Transf. – Trans. ASME, 105 (4) (1983), pp. 916–919
18. [18] F. Moukalled, S. Acharya; Natural convection in trapezoidal cavities with baffles mounted on the upper inclined surfaces; Num. Heat Trans., Part A, 37 (6) (2000), pp. 545–565
19. [19] E. Papanicolaou, V. Belessiotis; Double-diffusive natural convection in an asymmetric trapezoidal enclosure: unsteady behavior in the laminar and the turbulent flow regime; Int. J. Heat Mass Transf., 48 (2005), pp. 191–209
20. [20] Y. Varol, H.F. Oztop, I. Pop; Maximum density effects on buoyancy-driven convection in a porous trapezoidal cavity; Int. Commun. Heat Mass Transf., 37 (2010), pp. 401–409
21. [21] Y. Varol, H.F. Oztop, I. Pop; Numerical analysis of natural convection in an inclined trapezoidal enclosure filled with a porous medium; Int. J. Therm. Sci., 47 (2008), pp. 1316–1331
22. [22] M.A. Teamah; Double-diffusive laminar natural convection in a symmetrical trapezoidal enclosure; AEJ – Alexand. Eng. J., 45 (2006), pp. 251–263
23. [23] M.A. Teamah, S.M. El Sherbiny, R.A. Saleh; Effect of Grashof number and aspect ratio on double-diffusive laminar natural convection in a symmetrical trapezoidal enclosure; AEJ – Alexand. Eng. J., 49 (2010), pp. 89–100
24. [24] T. Basak, S. Roy, T. Paul, I. Pop; Natural convection in a square cavity filled with a porous medium: effects of various thermal boundary conditions; Int. J. Heat Mass Transf., 49 (2006), pp. 1430–1441
25. [25] Yang; Transitions and bifurcations in laminar buoyant flows in confined enclosures; ASME J. Heat Transf., 110 (1988), pp. 1191–1204
26. [26] M.A. Teamah; Numerical simulation of double diffusive natural convection in rectangular enclosure in the presences of magnetic field and heat source; Int. J. Therm. Sci., 47 (2008), pp. 237–248
27. [27] M.A. Teamah, A.F. Elsafty, M.Z. Elfeky, E.Z. El-Gazzar; Numerical simulation of double-diffusive natural convective flow in an inclined rectangular enclosure in the presence of magnetic field and heat source, part A: effect of Rayleigh number and inclination angle; Alexand. Eng. J., 50 (2011), pp. 269–282
28. [28] M.A. Teamah, W.M. El-Maghlany; Numerical simulation of double-diffusive mixed convective flow in rectangular enclosure with insulated moving lid; Int. J. Therm. Sci., 49 (2010), pp. 1625–1638
29. [29] M.A. Teamah, A.F. Elsafty, E.Z. Massoud; Numerical simulation of double-diffusive natural convective flow in an inclined rectangular enclosure in the presence of magnetic field and heat source; Int. J. Therm. Sci., 52 (2012), pp. 161–175
30. [30] Mohamed A. Teamah, Medhat M. Sorour, Wael M. El-Maghlany, Amr. Afifi; Numerical simulation of double diffusive laminar mixed convection in shallow inclined cavities with moving lid; Alexand. Eng. J., 52 (3) (2013), pp. 227–239
31. [31] M.A. Teamah, W.M. El-Maghlany; Augmentation of natural convective heat transfer in square cavity by utilizing nanofluids in the presence of magnetic field and uniform heat generation/absorption; Int. J. Therm. Sci., 58 (2012), pp. 130–142
32. [32] M.M. Khairat Dawood, M.A. Teamah; Hydro-magnetic mixed convection double diffusive in a lid driven square cavity; Euro. J. Sci. Res., 85 (3) (2012), pp. 336–355
33. [33] Y. Varol, H.F. Oztop, I. Pop; Natural convection in right-angle porous trapezoidal enclosure with partially cooled from inclined wall; Int. Commun. Heat Mass Transf., 36 (1) (2009), pp. 6–15
34. [34] S. Sivasankaran, C.J. Ho; Effect of temperature dependent properties on MHD convection of water near its density maximum in a square cavity; Int. J. Therm. Sci., 47 (2008), pp. 1184–1194
35. [35] S. Singh, M.A.R. Sharif; Mixed convection cooling of a rectangular cavity with inlet and exit openings on differentially heated side walls; Num. Heat Transf. Part A, 44 (2003), pp. 233–253
36. [36] N.H. Saeid, I. Pop; Viscous dissipation effects on free convection in a porous cavity; Int. Commun. Heat Mass Transf., 31 (2004), pp. 723–732
37. [37] T.W. Tong, E. Subramanian; Boundary layer analysis for natural convection in porous enclosure: use of Brinkman-extended Darcy formulation; Int. J. Heat Mass Transf., 28 (1985), pp. 563–571
38. [38] K. Vafai, C.L. Tien; Boundary and inertia effects on flow and heat transfer in porous media; Int. J. Heat Mass Transf., 24 (1981), pp. 195–203
39. [39] S.V. Patankar; Numerical Heat Transfer and Fluid Flow; McGraw-Hill, New York (1980)