Revisiting the approximate analytical solution of fractional-order gas dynamics equation

Abstract

In this paper, an approximate analytical solution of the time fractional gas dynamics equation arising in the shock fronts, is obtained using a recent semi-analytical method referred as fractional reduced differential transform method. The fractional derivatives are considered in the Caputo sense. To validate the efficiency and reliability of the method, four numerical examples of the linear and nonlinear gas dynamics equations are considered. Computed results are compared with results available in the literature. It is found that obtained results agree excellently with DTM, and FHATM. The solutions behavior and its effects for different values of the fractional order are shown graphically. The main advantage of the method is easiness to implement and requires small size of computation. Hence, it is a very effective and efficient semi-analytical method for solving the fractional order gas dynamics equation.

Keywords

Gas dynamics equation; Caputo time fractional derivatives; Mittag–Leffler function; Fractional reduced differential transform method; Analytical solution

1. Introduction

Gas dynamics equations are mathematical expressions based on the physical laws of conservation of mass, conservation of momentum, conservation of energy, etc. The nonlinear fractional gas dynamics equations are applicable in the shock fronts, rare factions, and contact discontinuities.

Consider the time fractional nonlinear gas dynamics equations

${\frac {{\partial }^{\alpha }u}{\partial t^{\alpha }}}+$$u{\frac {\partial u}{\partial x}}-u(1-u)=0{\mbox{,}}\quad x\in R{\mbox{,}}\quad 0<\alpha \leqslant 1{\mbox{,}}$

(1)

subject to the initial condition ${\textstyle u(x{\mbox{,}}0)=f(x)}$, where ${\textstyle \alpha }$ is a parameter describing the order of the time fractional derivatives. When ${\textstyle \alpha =1}$, Eq. (1) reduces into the classical gas dynamics equation.

Since several physical phenomena arising in engineering as well as in allied sciences can be explained successfully by developing models with the help of the fractional calculus theory. The fractional order equations response ultimately converges to the integer order equations, achieving a special attention nowadays. The fractional differentiations are very effective due to wide range of applications for mathematical modeling of the real world problems e.g. earthquake modeling, traffic flow models, diffusion model, control, and relaxation processes [1], [2], [3], [4], [5], [6], [7], [8], [9], [10] and [11]. Before the nineteenth century, there was no scheme available for the analytical solutions. In the beginning of twentieth century, researchers started to pay attention to find the robust and stable analytical approaches for the exact (approximate) solution of the fractional differential equations. However, several analytical schemes, e.g., Adomian decomposition methods [12] and [13], differential transform methods [14], [15] and [16], Homotopy Perturbation Methods [17], [18], [19] and [20], and homotopy analysis methods [21] and [22] are developed for the approximate analytical solutions of the fractional differential equations. However, the major disadvantage of these analytical methods is that they involve complicated and huge computation. To overcome that, a semi-analytical approach referred as fractional reduced differential transform method (FRDTM) is developed by Keskin and Oturanc [23]. The method is a very effective, reliable, efficient, and very powerful analytical scheme (see [24], [25], [26], [27] and [28]).

In recent years, the approximate analytical solutions of some different varieties of gas dynamics equations, are obtained using several analytical and numerical approaches [29], [30], [31], [32], [33], [34], [35] and [36]. The homogenous and non-homogenous nonlinear gas dynamics equations were solved by implementing the differential transform method [37] and [38] and Fractional homotopy analysis transform method [39]. Yang et al. [41] proposed integral transforms method via local fractional calculus to solve various local fractional ordinary and partial differential equations while Yang and Baleanu [42] proposed local fractional variation iteration method to solve fractional heat conduction equation. In [43], Yang et al. obtained approximate solutions for diffusion equations. The Homotopy Perturbation Method was extended to solve the wave equation via local fractional derivative [44]. Hajmohammadi and Nourazar [45] examined differential transform method and Adomian decomposition method for solving a characteristic value problem while a conjugate forced convection heat transfer from a good conducting plate with temperature-dependent thermal conductivity is studied analytically and numerically in [46]. In [47], they considered fluid flow and heat transfer repercussions to introduce a micro gas layer into a cylindrical Couette flow assembly dealing with a power law liquid, while Hajmohammadi et al. [48] studied the effects of thin gas layer exerts on the hydrodynamic aspects of power law liquid in a radial Couette flow between two cylinders. Authors of [49] proposed a new algorithm based on semi-analytical methods to solve the conjugate heat transfer problems. İbiş and Bayram [50] used fractional variational iteration method to obtain analytical approximate solution of time fractional Fornberg–Whitham equation. Prakash et al. [51] proposed a numerical algorithm based on a modified He-Laplace to solve space and time nonlinear fractional differential difference equations. The method is a combined form of the fractional homotopy perturbation and Laplace transforms method. Kumar [52] introduced homotopy perturbation transform method to provide an analytical solution to time fractional cauchy-reaction diffusion equation.

In this paper, we reconsider the approximate analytical solution of the time-fractional gas dynamics equations of order ${\textstyle \alpha \quad (0<\alpha \leqslant 1)}$ using the fractional order reduced differential transform method. The results obtained by the present method are much better approximations and converge rapidly than DTM and FHATM [38] and [39]. The paper is organized as follows. In Section 2, some basic preliminaries and notations of the fractional calculus theory are reviewed which will be useful for the ongoing study. Section 3 describes the method. In Section 4, exact solutions of four numerical problems of the time-fractional homogenous and non-homogeneous gas dynamics equations are demonstrated while Section 5 concludes our study.

2. Fractional calculus theory

Fractional calculus theory is more than twenty decades years’ old theory present in the literature. In the fractional integrals and derivatives, several definitions are proposed but the first major contribution to give a proper and most meaningful definition goes to Liouville [2] as given in Definition 2.1.

Definition 2.1.

For any given function ${\textstyle f\in R}$, the Riemann–Liouville fractional integral operator [3] of order ${\textstyle \alpha \geqslant 0}$, is defined by

$J^{\alpha }f(x)={\frac {1}{\Gamma (\alpha )}}{\int }_{0}^{x}{\left(x-t\right)}^{\alpha -1}f(t)dt{\mbox{,}}\quad \alpha >0{\mbox{,}}\quad x>0{\mbox{,}}$ $J^{0}f(x)=f(x){\mbox{.}}$

(2)

Caputo and Mainardi [3] proposed a modified fractional differentiation operator ${\textstyle D^{\alpha }}$ on the theory of visco-elasticity to overcome the discrepancy of Riemann–Liouville derivative [2] while modeling the real world problems using the fractional differential equations. Further, they demonstrated that their proposed Caputo fractional derivative allows the utilization of initial and boundary conditions involving integer order derivatives having straightforward physical interpretations.

Definition 2.2.

The fractional derivative of ${\textstyle f(x)\in R}$, in the Caputo sense [3] is defined as

$D^{\alpha }f(x)=J^{m-\alpha }D^{m}f(x)={\frac {1}{\Gamma (m-\alpha )}}{\int }_{0}^{x}{\left(x-t\right)}^{m-\alpha -1}f^{\left(m\right)}(t)dt{\mbox{,}}$

(3)

for ${\textstyle m-1<\alpha \leqslant m{\mbox{,}}\quad m\in N{\mbox{,}}\quad x>0{\mbox{,}}\quad f\in C_{-1}^{m}}$.

The basic properties of the Caputo fractional derivative can be given as follows:

Lemma 2.1.

If  ${\textstyle m-1<\alpha \leqslant m{\mbox{,}}\quad m\in N}$and  ${\textstyle f\in C_{\mu }^{m}{\mbox{,}}\quad \mu \geqslant -1}$, then we have

$D^{\alpha }J^{\alpha }f(x)=f(x){\mbox{,}}\quad x>0{\mbox{,}}$ $J^{\alpha }D^{\alpha }f(x)=f(x)-\sum _{k=0}^{m}f^{\left(k\right)}(0^{+}){\frac {x^{k}}{k!}}{\mbox{,}}\quad x>0{\mbox{,}}$

(4)

In this paper, the Caputo fractional derivative is considered since it allows the traditional initial and boundary conditions to be included in the formulation of the physical problems. One can refer[1], [2], [3], [4], [5], [6], [7], [8], [9], [10] and [11]for the important characteristics of the fractional derivatives.

3. Fractional reduced differential transform method

In this section, the basic properties of the fractional reduced differential transform method are described. Let ${\textstyle w(x{\mbox{,}}t)}$ be a function of two variables, which can be represented as a product of two single-variable functions, i.e., ${\textstyle w(x{\mbox{,}}t)=F(x)G(t)}$. Using the properties of the one-dimensional differential transform method, ${\textstyle w(x{\mbox{,}}t)}$ can be written as

$w(x{\mbox{,}}t)=\sum _{i=0}^{\infty }F(i)x^{i}\sum _{j=0}^{\infty }G(j)t^{j}=$$\sum _{i=0}^{\infty }\quad \sum _{j=0}^{\infty }W(i{\mbox{,}}j)x^{i}t^{j}{\mbox{,}}$

(5)

where ${\textstyle W(i{\mbox{,}}j)=F(i)G(j)}$ is referred as the spectrum of ${\textstyle w(x{\mbox{,}}t)}$.

Assume ${\textstyle R_{D}}$ and ${\textstyle R_{D}^{-1}}$ denote the fractional reduced differential transform (FRDT) operator and inverse FRDT operator, respectively. The basic definition and properties of FRDTM are described below.

Definition 3.1.

If ${\textstyle w(x{\mbox{,}}t)}$ is analytic and continuously differentiable with respect to the space variable ${\textstyle x}$ and time variable ${\textstyle t}$ in the domain of interest, then the t-dimensional spectrum function

$W_{k}(x)={\frac {1}{\Gamma (k\alpha +1)}}{\left[D_{t}^{k}(w(x{\mbox{,}}t))\right]}_{t=t_{0}}$

(6)

is referred as the fractional reduced differential transform function of ${\textstyle w(x{\mbox{,}}t)}$, where ${\textstyle \alpha }$ is a parameter which describes the order of the time-fractional derivative. In this paper, ${\textstyle w(x{\mbox{,}}t)}$ (lowercase) is used for the original function and ${\textstyle W_{k}(x)}$ (uppercase) is used for the fractional reduced transformed function for clarity.

Now the inverse fractional reduced differential transform of ${\textstyle W_{k}(x)}$ is defined as

$w(x{\mbox{,}}t)=\sum _{k=0}^{\infty }W_{k}(x){\left(t-t_{0}\right)}^{k\alpha }{\mbox{.}}$

(7)

From Eqs. (6) and (7), it can be found that

$w(x{\mbox{,}}t)=\sum _{k=0}^{\infty }{\frac {1}{\Gamma (k\alpha +1)}}{\left[D_{t}^{k}(w(x{\mbox{,}}t))\right]}_{t=t_{0}}{\left(t-t_{0}\right)}^{k\alpha }{\mbox{.}}$

(8)

In particular, for ${\textstyle t_{0}=0}$, Eq. (8) becomes

$w(x{\mbox{,}}t)=\sum _{k=0}^{\infty }{\frac {1}{\Gamma (k\alpha +1)}}{\left[D_{t}^{k}(w(x{\mbox{,}}t))\right]}_{t=0}t^{k\alpha }{\mbox{,}}$

(9)

showing that the fractional reduced differential transform method is a special case of the power series expansion of a function.

Assume ${\textstyle u(x{\mbox{,}}t)=R_{D}^{-1}[U_{k}(x)]{\mbox{,}}\quad v(x{\mbox{,}}t)=}$$R_{D}^{-1}[V_{k}(x)]$, and the convolution ${\textstyle \otimes }$ denotes the fractional reduced differential transform of the multiplication, the fundamental operations of the fractional reduced differential transform are given in Table 1, where ${\textstyle \Gamma }$ denotes the Gama function.

Table 1. Basic properties of the fractional reduced differential transform method.

Original Function	FRDTM Function
${\textstyle w(x{\mbox{,}}t)}$	${\textstyle R_{D}\lbrace w(x{\mbox{,}}t)\rbrace =W_{k}(x)}$
${\textstyle u(x{\mbox{,}}t)v(x{\mbox{,}}t)}$	${\textstyle U_{k}(x)\otimes V_{k}(x)={\sum }_{r=0}^{k}U_{r}(x)V_{k-r}(x)}$
${\textstyle a_{1}u(x{\mbox{,}}t)\pm a_{2}v(x{\mbox{,}}t)}$	${\textstyle a_{1}U_{k}(x)\pm a_{2}V_{k}(x)}$
${\textstyle x^{m}t^{n}u(x{\mbox{,}}t)}$	${\textstyle {\begin{array}{ll}x^{m}U_{k-n}(x){\mbox{,}}&\forall \quad k\geqslant n{\mbox{;}}\\0{\mbox{,}}&else{\mbox{.}}\end{array}}}$
${\textstyle D_{x}^{l}u(x{\mbox{,}}t)}$	${\textstyle D_{x}^{l}U_{k}(x)}$
${\textstyle D_{t}^{N\alpha }(u(x{\mbox{,}}t))}$	${\textstyle {\frac {\Gamma (1+(k+N)\alpha )}{\Gamma (1+k\alpha )}}U_{k+N}(x)}$
${\textstyle x^{m}}$	${\textstyle x^{m}\delta (k)}$
${\textstyle e^{\lambda t}}$	${\textstyle {\frac {{\lambda }^{k}}{k!}}}$
${\textstyle sin(wt+c)}$	${\textstyle {\frac {w^{k}}{k!}}sin\left({\frac {\pi k}{2!}}+c\right)}$
${\textstyle cos(wt+c)}$	${\textstyle {\frac {w^{k}}{k!}}cos\left({\frac {\pi k}{2!}}+c\right)}$

Definition 3.1.

The Mittag–Leffler function ${\textstyle E_{\alpha }(z)}$ with ${\textstyle \alpha >0}$ is defined by the following series representation, valid in the whole complex plane [40]:

$E_{\alpha }(z):=\sum _{k=0}^{\infty }{\frac {z^{k}}{\Gamma (1+k\alpha )}}$

(10)

4. Numerical experiments and discussions

In this section, we describe the fractional reduced differential transform method by taking three numerical examples of the fractional order gas dynamics equation to validate its efficiency and reliability.

Example 4.1.

Consider the following homogenous nonlinear time-fractional gas dynamics equation as

${\frac {{\partial }^{\alpha }u}{\partial t^{\alpha }}}+$$u{\frac {\partial u}{\partial x}}-u(1-u)=0{\mbox{,}}\quad 0<\alpha \leqslant 1{\mbox{,}}$

(11)

subject to the initial condition

$u(x{\mbox{,}}0)=e^{-x}{\mbox{.}}$

(12)

Applying FRDTM on Eq. (11), we find the following recurrence relation:

${\frac {\Gamma (k\alpha +\alpha +1)}{\Gamma (k\alpha +1)}}U_{k+1}(x)=$$-\sum _{r=0}^{k}\quad U_{r}(x){\frac {\partial }{\partial x}}U_{k-r}(x)+$$U_{k}(x)-\sum _{r=0}^{k}U_{r}(x)U_{k-r}(x){\mbox{.}}$

(13)

Applying FRDTM to the initial condition (12), we get

$U_{0}(x)=-e^{-x}{\mbox{.}}$

(14)

Using the recurrence relation (13) and the transformed initial condition (14), the first few components of ${\textstyle U_{k}(x)}$ are given as

$U_{1}(x)={\frac {1}{\Gamma (1+\alpha )}}e^{-x}{\mbox{,}}\quad U_{2}(x)=$${\frac {1}{\Gamma (1+2\alpha )}}e^{-x}{\mbox{,}}\quad U_{3}(x)=$${\frac {1}{\Gamma (1+3\alpha )}}e^{-x}{\mbox{,}}\quad U_{4}(x)=$${\frac {1}{\Gamma (1+4\alpha )}}e^{-x}{\mbox{,}}\quad \ldots \quad {\mbox{,}}\quad U_{k}(x)=$${\frac {1}{\Gamma (1+k\alpha )}}e^{-x}{\mbox{,}}\quad \ldots$

(15)

Therefore, from Eq. (7) the analytical approximate solution of Eq. (11) can be obtained as

$u(x{\mbox{,}}t)=\sum _{k=0}^{\infty }U_{k}(x)t^{k\alpha }=$$U_{0}(x)+U_{1}(x)t^{\alpha }+U_{2}(x)t^{2\alpha }+U_{3}(x)t^{3\alpha }+$$\cdots$ $\quad =e^{-x}\left(1+{\frac {t^{\alpha }}{\Gamma (1+\alpha )}}+\right.$$\left.{\frac {t^{2\alpha }}{\Gamma (1+2\alpha )}}+{\frac {t^{3\alpha }}{\Gamma (1+3\alpha )}}+\right.$$\left.\cdots +{\frac {t^{k\alpha }}{\Gamma (1+k\alpha )}}+\right.$$\left.\cdots \right)$ $\quad =e^{-x}\sum _{k=0}^{\infty }{\frac {{\left(t^{\alpha }\right)}^{k}}{\Gamma (1+k\alpha )}}=$$e^{-x}E_{\alpha }(t^{\alpha }){\mbox{,}}$

(16)

where ${\textstyle E_{\alpha }(t)}$ is well known Mittag–Leffler function defined by Eq. (10). When ${\textstyle \alpha =1}$, the exact solution (16) has the closed form ${\textstyle u(x{\mbox{,}}t)=e^{-x+t}}$ , an exact solution of the classical gas dynamics Eq. (11) with ${\textstyle \alpha =1}$. The same solution was obtained by Kumar et al. [39] using FFHATM, a combined form of HAM and Laplace transform method. It can be noticed that the solution ${\textstyle u(x{\mbox{,}}t)=e^{t-x}}$ grows exponentially with time t.

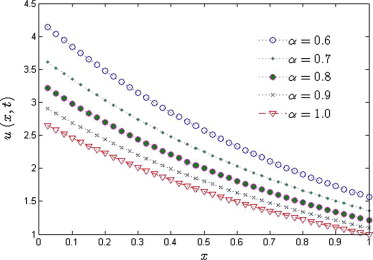
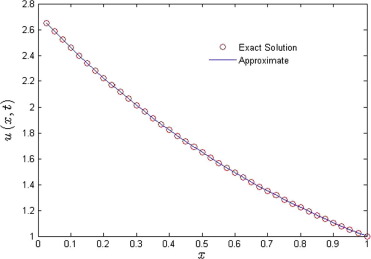
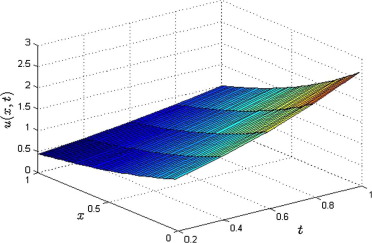
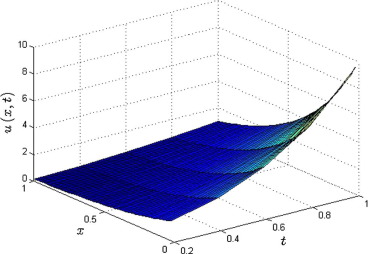
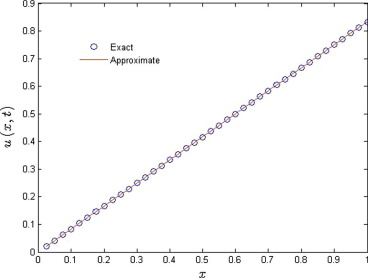
Fig. 1 shows the solution behavior of Example 4.1 for the different fraction Brownian motion ${\textstyle \alpha =0.6}$, 0.7, 0.8, 0.9 while Fig. 2 shows the comparison between the well-known exact solution (square) and solution (line) obtained by the method for the classical case. Fig. 3 depicts the obtained physical solution profile for ${\textstyle \alpha =1\quad and\quad t=1}$.

Figure 1. Approximate solutions ${\textstyle u(x{\mbox{,}}t)}$ obtained by FRDTM for ${\textstyle t=1}$ at different ${\textstyle \alpha }$.

Figure 2. Comparison between the exact solution and the solution obtained by FRDTM for ${\textstyle \alpha =1\quad and\quad t=1}$.

Figure 3. Physical solution profile of Example 4.1 for ${\textstyle \alpha =1}$.

Example 4.2.

In this example, consider the following homogenous nonlinear time fractional gas dynamics equation given as follows:

${\frac {{\partial }^{\alpha }u}{\partial t^{\alpha }}}+$$u{\frac {\partial u}{\partial x}}-u(1-u)loga=0{\mbox{,}}\quad a>0{\mbox{,}}\quad 0<\alpha \leqslant 1{\mbox{,}}$

(17)

subject to the initial condition

$u(x{\mbox{,}}0)=a^{-x}{\mbox{.}}$

(18)

Applying the method to Eq. (17), we obtain the following recurrence relation:

${\frac {\Gamma (k\alpha +\alpha +1)}{\Gamma (k\alpha +1)}}U_{k+1}(x)=$$-\sum _{r=0}^{k}U_{r}(x){\frac {\partial }{\partial x}}U_{k-r}(x)+$$(loga)U_{k}(x)-(loga)\sum _{r=0}^{k}U_{r}(x)U_{k-r}(x){\mbox{.}}$

(19)

Using the method to the initial condition (18), we obtain

$U_{0}(x)=a^{-x}{\mbox{.}}$

(20)

Using the recurrence relation (19) and the transformed initial condition (20), the first few components of ${\textstyle U_{k}(x)}$ are given by

$U_{1}(x)={\frac {loga}{\Gamma (1+\alpha )}}a^{-x}{\mbox{,}}\quad U_{2}(x)=$${\frac {{\left(loga\right)}^{2}}{\Gamma (1+2\alpha )}}a^{-x}{\mbox{,}}\quad U_{3}(x)=$${\frac {{\left(loga\right)}^{3}}{\Gamma (1+3\alpha )}}a^{-x}{\mbox{,}}\quad U_{4}(x)=$${\frac {{\left(loga\right)}^{4}}{\Gamma (1+4\alpha )}}a^{-x}{\mbox{,}}\quad \ldots \quad {\mbox{,}}\quad U_{k}(x)=$${\frac {{\left(loga\right)}^{k}}{\Gamma (1+k\alpha )}}a^{-x}{\mbox{,}}\quad \ldots$

(21)

Using the differential inverse reduced transform of ${\textstyle U_{k}(x)}$, we have

$u(x{\mbox{,}}t)=\sum _{k=0}^{\infty }U_{k}(x)t^{k\alpha }=$$U_{0}(x)+U_{1}(x)t^{\alpha }+U_{2}(x)t^{2\alpha }+U_{3}(x)t^{3\alpha }+$$\cdots$ $\quad =e^{-x}\left(1+{\frac {\left(t^{\alpha }loga\right)}{\Gamma (1+\alpha )}}+\right.$$\left.{\frac {{\left(t^{\alpha }loga\right)}^{2}}{\Gamma (1+2\alpha )}}+\right.$$\left.{\frac {{\left(t^{\alpha }loga\right)}^{3}}{\Gamma (1+3\alpha )}}+\right.$$\left.\cdots +{\frac {{\left(t^{\alpha }loga\right)}^{k}}{\Gamma (1+k\alpha )}}+\right.$$\left.\cdots \right)$ $\quad =e^{-x}\sum _{k=0}^{\infty }{\frac {{\left(t^{\alpha }loga\right)}^{k}}{\Gamma (1+k\alpha )}}=$$e^{-x}E_{\alpha }(t^{\alpha }loga){\mbox{.}}$

(22)

The same solution was obtained by Kumar et al. [39] using FHATM. When ${\textstyle \alpha \rightarrow 1}$ in Eq. (22), we get

$u(x{\mbox{,}}t)=a^{-x}\sum _{k=0}^{\infty }{\frac {{\left(tloga\right)}^{k}}{\Gamma (1+k)}}=$$a^{-x+t}{\mbox{.}}$

(23)

as the same exact solution for the classical gas dynamics Eq. (17). The above result completely agrees with Kumar et al. [39].

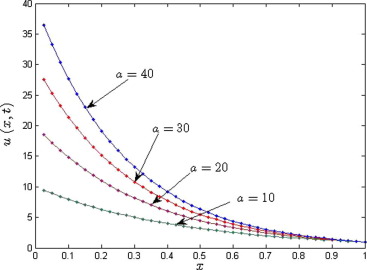
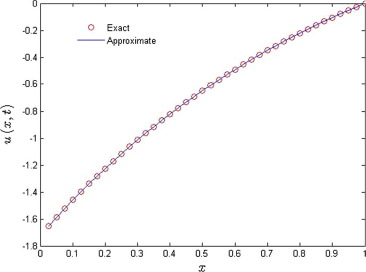
Fig. 4 shows the comparison of the exact solution and the approximate solution obtained by FRDTM for different values of ${\textstyle a=10}$, 20, 30, 40 and also for the standard Brownian motion, ${\textstyle \alpha =1}$ for Example 4.2. Fig. 4 clearly shows that exact and approximate solutions are in good agreement for different ${\textstyle a}$. Fig. 5 shows the physical solution profile obtained by FRDTM at ${\textstyle a=10{\mbox{,}}\quad \alpha =1\quad and\quad t=1}$.

Figure 4. Comparison between the exact solution (squares) and the solution (lines) obtained by the fractional reduced differential transform method for ${\textstyle t=1}$.

Figure 5. Physical solution profile obtained by FRDTM at ${\textstyle a=10{\mbox{,}}\quad \alpha =1\quad and\quad t=1}$.

Example 4.3.

Consider the following non-homogeneous time fractional order gas dynamics equation:

${\frac {{\partial }^{\alpha }u}{\partial t^{\alpha }}}+$$u{\frac {\partial u}{\partial x}}+{\left(1+t\right)}^{2}u^{2}=$$x^{2}{\mbox{,}}\quad 0<\alpha \leqslant 1{\mbox{,}}$

(24)

subject to the initial condition

$u(x{\mbox{,}}0)=x{\mbox{.}}$

(25)

Applying the method to Eq. (24), we obtain the following iteration formula:

${\frac {\Gamma (k\alpha +\alpha +1)}{\Gamma (k\alpha +1)}}U_{k+1}(x)=$$-\sum _{r=0}^{k}U_{r}(x){\frac {\partial }{\partial x}}U_{k-r}(x)-$$R_{D}[{\left(1+t\right)}^{2}u^{2}]+x^{2}\delta (k){\mbox{.}}$

(26)

We treat the nonlinear term ${\textstyle R_{D}[{\left(1+t\right)}^{2}u^{2}]}$ as

$R_{D}[{\left(1+t\right)}^{2}u^{2}]=R_{D}[(1+2t+t^{2})v]=R_{D}[v+$$2tv+t^{2}v]=V_{k}+2V_{k-1}+V_{k-2}{\mbox{,}}$

(27)

where ${\textstyle v(x{\mbox{,}}t)=u(x{\mbox{,}}t)u(x{\mbox{,}}t)}$, and ${\textstyle V_{k}(x)={\sum }_{r=0}^{k}U_{r}(x)U_{k-r}(x)}$.

Using the method to the initial condition (28), we get

$U_{0}(x)=x{\mbox{.}}$

(28)

Using Eq. (28) in Eqs. (26) and (27), the following ${\textstyle U_{k}(x)}$ values are obtained successively:

$U_{1}(x)={\frac {-x}{\Gamma (1+\alpha )}}{\mbox{,}}U_{2}(x)=$${\frac {2x}{\Gamma (1+2\alpha )}}+2x^{2}\left({\frac {1}{\Gamma (1+2\alpha )}}-\right.$$\left.{\frac {\Gamma (1+\alpha )}{\Gamma (1+2\alpha )}}\right){\mbox{,}}$

$U_{3}(x)=-x\left({\frac {4}{\Gamma (1+3\alpha )}}+{\frac {\Gamma (1+2\alpha )}{\Gamma (1+3\alpha ){\left(\Gamma (1+\alpha )\right)}^{2}}}\right)-$$x^{2}\left({\frac {10}{\Gamma (1+3\alpha )}}-{\frac {6\Gamma (1+\alpha )}{\Gamma (1+3\alpha )}}+\right.$$\left.{\frac {\Gamma (1+2\alpha )}{\Gamma (1+3\alpha ){\left(\Gamma (1+\alpha )\right)}^{2}}}-\right.$$\left.{\frac {4\Gamma (1+2\alpha )}{\Gamma (1+3\alpha )\Gamma (1+\alpha )}}+\right.$$\left.{\frac {\Gamma (1+2\alpha )}{\Gamma (1+3\alpha )}}\right)-$$4x^{3}\left({\frac {1}{\Gamma (1+3\alpha )}}-{\frac {\Gamma (1+\alpha )}{\Gamma (1+3\alpha )}}\right){\mbox{,}}\quad \ldots$

(29)

$U_{4}(x)=x\left({\frac {4\Gamma (1+3\alpha )}{\Gamma (1+\alpha )\Gamma (1+2\alpha )\Gamma (1+4\alpha )}}+\right.$$\left.{\frac {8}{\Gamma (1+4\alpha )}}+{\frac {2\Gamma (1+2\alpha )}{\Gamma (1+4\alpha ){\left(\Gamma (1+\alpha )\right)}^{2}}}\right)+$$x^{2}\left[3\left({\frac {10}{\Gamma (1+4\alpha )}}-{\frac {6\Gamma (1+\alpha )}{\Gamma (1+4\alpha )}}+\right.\right.$$\left.\left.{\frac {\Gamma (1+2\alpha )}{\Gamma (1+4\alpha ){\left(\Gamma (1+\alpha )\right)}^{2}}}-\right.\right.$$\left.\left.{\frac {4\Gamma (1+2\alpha )}{\Gamma (1+4\alpha )\Gamma (1+\alpha )}}+\right.\right.$$\left.\left.{\frac {\Gamma (1+2\alpha )}{\Gamma (1+4\alpha )}}\right)+\right.$$\left.2\left({\frac {4}{\Gamma (1+4\alpha )}}+{\frac {\Gamma (1+2\alpha )}{\Gamma (1+4\alpha ){\left(\Gamma (1+\alpha )\right)}^{2}}}\right)+\right.$$\left.{\frac {6}{\Gamma (1+\alpha )}}\left({\frac {1}{\Gamma (1+4\alpha )}}-\right.\right.$$\left.\left.{\frac {\Gamma (1+\alpha )}{\Gamma (1+4\alpha )}}\right)+\right.$$\left.{\frac {4\Gamma (1+3\alpha )}{\Gamma (1+4\alpha )\Gamma (1+2\alpha )\Gamma (1+\alpha )}}-\right.$$\left.{\frac {8\Gamma (1+3\alpha )}{\Gamma (1+4\alpha )\Gamma (1+2\alpha )}}-\right.$$\left.{\frac {2\Gamma (1+3\alpha )}{\Gamma (1+4\alpha ){\left(\Gamma (1+\alpha )\right)}^{2}}}+\right.$$\left.{\frac {2\Gamma (1+3\alpha )}{\Gamma (1+4\alpha )\Gamma (1+\alpha )}}\right]+$$x^{3}{\frac {16}{\Gamma (1+4\alpha )}}-{\frac {16\Gamma (1+\alpha )}{\Gamma (1+4\alpha )}}+$$2\left({\frac {10}{\Gamma (1+4\alpha )}}-{\frac {6\Gamma (1+\alpha )}{\Gamma (1+4\alpha )}}+\right.$$\left.{\frac {\Gamma (1+2\alpha )}{\Gamma (1+4\alpha ){\left(\Gamma (1+\alpha )\right)}^{2}}}-\right.$$\left.{\frac {4\Gamma (1+2\alpha )}{\Gamma (1+4\alpha )\Gamma (1+\alpha )}}+\right.$$\left.{\frac {\Gamma (1+2\alpha )}{\Gamma (1+4\alpha )}}\right)+$$\left({\frac {4-8\Gamma (1+\alpha )}{\Gamma (1+\alpha )}}\right)\left({\frac {1}{\Gamma (1+2\alpha )}}+\right.$$\left.{\frac {\Gamma (1+\alpha )}{\Gamma (1+2\alpha )}}\right)\left({\frac {\Gamma (1+3\alpha )}{\Gamma (1+4\alpha )}}\right)+$$x^{4}\left[8\left({\frac {1}{\Gamma (1+4\alpha )}}-{\frac {\Gamma (1+\alpha )}{\Gamma (1+4\alpha )}}\right)\right]{\mbox{;}}$

Continuing this process, ${\textstyle U_{k}(x)\quad for\quad k\geqslant 5}$ can be obtained and hence, by using the differential inverse reduced transform of ${\textstyle U_{k}(x)}$, we get

$u(x{\mbox{,}}t)=\sum _{k=0}^{\infty }U_{k}(x)t^{k\alpha }=$$U_{0}(x)+U_{1}(x)t^{\alpha }+U_{2}(x)t^{2\alpha }+U_{3}(x)t^{3\alpha }+$$\cdots$

(30)

$u(x{\mbox{,}}t)=x-{\frac {x}{\Gamma (1+\alpha )}}t^{\alpha }+$$\left\{{\frac {2x}{\Gamma (1+2\alpha )}}+2x^{2}\left({\frac {1}{\Gamma (1+2\alpha )}}-\right.\right.$$\left.\left.{\frac {\Gamma (1+\alpha )}{\Gamma (1+2\alpha )}}\right)\right\}t^{2\alpha }-$$\left\{x\left({\frac {4}{\Gamma (1+3\alpha )}}+{\frac {\Gamma (1+2\alpha )}{\Gamma (1+3\alpha ){\left(\Gamma (1+\alpha )\right)}^{2}}}\right)-\right.$$\left.x^{2}\left({\frac {10}{\Gamma (1+3\alpha )}}-{\frac {6\Gamma (1+\alpha )}{\Gamma (1+3\alpha )}}+\right.\right.$$\left.\left.{\frac {\Gamma (1+2\alpha )}{\Gamma (1+3\alpha ){\left(\Gamma (1+\alpha )\right)}^{2}}}-\right.\right.$$\left.\left.{\frac {4\Gamma (1+2\alpha )}{\Gamma (1+3\alpha )\Gamma (1+\alpha )}}+\right.\right.$$\left.\left.{\frac {\Gamma (1+2\alpha )}{\Gamma (1+3\alpha )}}\right)-\right.$$\left.4x^{3}\left({\frac {1}{\Gamma (1+3\alpha )}}-{\frac {\Gamma (1+\alpha )}{\Gamma (1+3\alpha )}}\right)\right\}+$$\cdots$

(31)

As ${\textstyle \alpha \rightarrow 1}$ in Eq. (31), we have

$u(x{\mbox{,}}t)=\sum _{k=0}^{\infty }U_{k}(x)t^{k\alpha }=$$x-xt+{xt}^{2}-{xt}^{3}+\cdots =x(1-t+t^{2}-t^{3}+\cdots )$

$or\quad u(x{\mbox{,}}t)={\frac {x}{1+t}}{\mbox{,}}$

(32)

which is the same exact solution obtained by Das and Kumar [38].

Fig. 6 shows the comparison of the exact solution ${\textstyle u(x{\mbox{,}}t)}$ and the approximate solution ${\textstyle {\tilde {u}}_{4}(x{\mbox{,}}t)}$ obtained by FRDTM for the standard Brownian motion, ${\textstyle \alpha =1}$ of the Example 4.3, depicting the good agreement between the exact and approximate solutions. The absolute error ${\textstyle w(x{\mbox{,}}t)=\vert u(x{\mbox{,}}t)-{\tilde {u}}_{4}(x{\mbox{,}}t)\vert }$ is given in Table 2. From Table 2, it is observed that at a fixed value of ${\textstyle \alpha }$, as ${\textstyle t}$ increases, the absolute error also increases.

Figure 6. Comparison between the exact solution and the solution obtained by FRDTM at ${\textstyle \alpha =1\quad and\quad t=0.2}$.

Table 2. Absolute error between exact and approximate solution at different x and t for Example 4.3.

x  ⧹${\textstyle w(x{\mbox{,}}t)}$	${\textstyle t=0.2{\mbox{,}}\quad \alpha =1}$	${\textstyle t=0.4{\mbox{,}}\quad \alpha =1}$	${\textstyle t=0.8{\mbox{,}}\quad \alpha =1}$
0.2	0.0533e−003	0.0015	0.0364
0.4	0.1067e−003	0.0029	0.0728
0.6	0.1600e−003	0.0044	0.1092
0.8	0.2133e−003	0.0059	0.1456
1.0	0.2667e−003	0.0073	0.1820

Example 4.4.

Consider the following homogenous non-linear time fractional-order gas dynamics equation:

${\frac {{\partial }^{\alpha }u}{\partial t^{\alpha }}}+$$u{\frac {\partial u}{\partial x}}-u(1-u)=-e^{-x+t}{\mbox{,}}\quad 0<\alpha \leqslant 1{\mbox{,}}$

(33)

subject to the initial condition

$u(x{\mbox{,}}0)=1-e^{-x}{\mbox{.}}$

(34)

Applying the described method to Eq. (33), we obtain the following iteration formula:

${\frac {\Gamma (k\alpha +\alpha +1)}{\Gamma (k\alpha +1)}}U_{k+1}(x)=$$-\sum _{r=0}^{k}U_{r}(x){\frac {\partial }{\partial x}}U_{k-r}(x)+$$U_{k}(x)-\sum _{r=0}^{k}U_{r}(x)U_{k-r}(x)-{\frac {e^{-x}}{k!}}{\mbox{.}}$

(35)

Using the method to the initial condition (34), we get

$U_{0}=1-e^{-x}{\mbox{.}}$

(36)

Using Eq. (38) in Eq. (37), the following ${\textstyle U_{k}(x)}$ are obtained successively:

$U_{1}(x)=-{\frac {e^{-x}}{0!}}{\frac {1}{\Gamma (1+\alpha )}}{\mbox{;}}$ $U_{2}(x)=-{\frac {e^{-x}}{1!}}{\frac {\Gamma (1+\alpha )}{\Gamma (1+2\alpha )}}{\mbox{;}}$ $U_{3}(x)=-{\frac {e^{-x}}{2!}}{\frac {\Gamma (1+2\alpha )}{\Gamma (1+3\alpha )}}$ $\vdots$ $U_{k}(x)=-{\frac {e^{-x}}{(k-1)!}}{\frac {\Gamma (1+(k-1)\alpha )}{\Gamma (1+k\alpha )}}{\mbox{,}}\quad for\quad k\geqslant 1$

(37)

Using the differential inverse reduced transform of ${\textstyle U_{k}(x)}$, we get

$u(x{\mbox{,}}t)=\sum _{k=0}^{\infty }U_{k}(x)t^{k\alpha }=$$U_{0}(x)+U_{1}(x)t^{\alpha }+U_{2}(x)t^{2\alpha }+U_{3}(x)t^{3\alpha }+$$\cdots =1-e^{-x}-{\frac {e^{-x}}{0!}}{\frac {t^{\alpha }}{\Gamma (1+\alpha )}}-$${\frac {e^{-x}}{1!}}{\frac {\Gamma (1+\alpha )t^{2\alpha }}{\Gamma (1+2\alpha )}}-$${\frac {e^{-x}}{2!}}{\frac {\Gamma (1+2\alpha )t^{3\alpha }}{\Gamma (1+3\alpha )}}-$$\cdots -{\frac {e^{-x}}{(k-1)!}}{\frac {\Gamma (1+(k-1)\alpha )t^{k\alpha }}{\Gamma (1+k\alpha )}}-$$\cdots =1-e^{-x}\left(1+\sum _{k=1}^{\infty }{\frac {\Gamma (1+(k-1)\alpha )t^{k\alpha }}{\left(k-1)!\Gamma (1+k\alpha \right)}}\right)=$$1-e^{-x}E_{\alpha }({Kt}^{\alpha }){\mbox{,}}$

(38)

where ${\textstyle K^{n}={\begin{array}{ll}1{\mbox{,}}&n=0{\mbox{,}}\\{\frac {\Gamma ((n-1)\alpha +1)}{(n-1)!}}&n>0{\mbox{.}}\end{array}}}$

When ${\textstyle \alpha \rightarrow 1}$ in Eq. (38), we obtain

$u(x{\mbox{,}}t)=1-e^{-x}\sum _{k=0}^{\infty }{\frac {t^{k}}{k!}}=$$1-e^{-x+t}{\mbox{,}}$

which is an exact solution of the given classical gas dynamics Eq. (3.1) for ${\textstyle \alpha =1}$ and this result is in complete agreement with Das and Kumar [38].

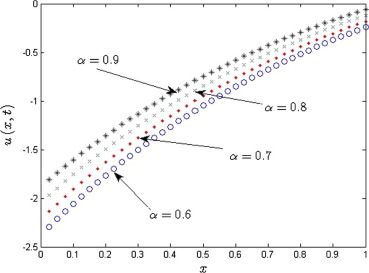
Fig. 7 shows the comparison of the exact solution and approximate solution obtained by described method for the standard Brownian motion, ${\textstyle \alpha =1}$ of the Example 4.4, while Fig. 8 shows the approximate solution behavior for different fraction Brownian motion ${\textstyle \alpha =0.6}$, 0.7, 0.8, 0.9.

Figure 7. Comparison between exact solution and solution obtained by FRDTM for ${\textstyle \alpha =1}$ and ${\textstyle t=1}$.

Figure 8. Approximate solutions obtained by FRDTM for ${\textstyle t=1}$ at different ${\textstyle \alpha }$.

5. Conclusions

In this paper, the fractional order reduced differential transform method is applied for the Caputo time-fractional order gas dynamics equation arising in the shock fronts. The proposed approximated solutions of the gas dynamics equations with an appropriate initial condition are obtained in terms of a power series, without involving the discretization, perturbation, or any other restrictive conditions. Four examples are carried out in order to study the reliability and accuracy of the described method. Solutions obtained by the method agree excellently with DTM, and FHATM. Here, one important point is that the performed computation shows the described method is very easy to implement and needs small size of computation contrary to DTM, and FHATM. Hence, it is a very effective and efficient semi-analytical method for solving the fractional order gas dynamics equation.

Future works

Readers are suggested to consider Power-law non-Newtonian fluid flow for future works. For this, Gas dynamics equation can be solved under study for generalized power-law fluids (refer [47] and [48]). Also, readers can use some other semi-analytical methods such as homotopy, ADM, and VIM (see [45], [46] and [49]).

References

1. [1] F. Mainardi Carpinteri; Fractals and fractional calculus in continuum mechanics; A. Carpinteri, F. Mainardi (Eds.)Springer Verlag, Wien, New York (1997), pp. 277–290
2. [2] K.S. Miller, B. Ross; An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley, New York (1993)
3. [3] M. Caputo, F. Mainardi; Linear models of dissipation in anelastic solids; Rivista Del Nuovo Cimento, 1 (1971), pp. 161–198
4. [4] K.B. Oldham, J. Spanier; The Fractional Calculus. Integrations and Differentiations of Arbitrary Order; Academic Press, New York (1974)
5. [5] S.G. Samko, A.A. Kilbas, O.I. Marichev; Fractional Integrals and Derivatives Theory and Applications; Gordon and Breach, New York (1993)
6. [6] I. Podlubny; Fractional Differential Equations; Academic Press, San Diego (1999)
7. [7] A.A. Kilbas, H.M. Srivastava, J.J. Trujillo; Theory and Applications of Fractional Differential Equations; Elsevier, The Netherlands (2006)
8. [8] R. Hilfer; Application of Fractional Calculus in Physics; World Scientific (2000)
9. [9] G.M. Zaslavsky; Hamiltonian Chaos and Fractional Dynamics; Oxford University Press (2005)
10. [10] R.L. Magin; Fractional Calculus in Bio-engineering; Begell House Publisher, Inc., Connecticut (2006)
11. [11] R. Gorenflo, F. Mainardi; Fractional calculus: integral and differential equations of fractional order; A. Carpinteri, F. Mainardi (Eds.), Fractals and Fractional Calculus, Springer-Verlag, New York (1997)
12. [12] Shaher Momani; Analytical approximate solution for fractional heat-like and wave-like equations with variable coefficients using the decomposition method; Appl. Math. Comput., 165 (2005), pp. 459–472
13. [13] Zaid Odibat, Shaher Momani; Numerical solution of Fokker–Planck equation with space- and time-fractional derivatives; Phys. Lett. A, 369 (2007), pp. 349–358
14. [14] A.S.V. RaviKanth, K. Aruna; Differential transform method for solving the linear and nonlinear Klein–Gordon equation; Comput. Phys. Commun., 180 (5) (2009), pp. 708–711
15. [15] A.S.V. RaviKanth, K. Aruna; Differential transform method for solving linear and non-linear systems of partial differential equations; Phys. Lett. A, 372 (46) (2008), pp. 6896–6898 (17)
16. [16] A.S.V. RaviKanth, K. Aruna; Two-dimensional differential transform method for solving linear and non-linear Schrödinger equations; Chaos, Solitons Fract., 41 (5) (2009), pp. 2277–2281
17. [17] S. Kumar, Om P. Singh; Numerical inversion of the abel integral equation using homotopy perturbation method; Z Naturforsch, 65a (2010), pp. 677–682
18. [18] S. Kumar, H. Kocak, A. Yildirim; A fractional model of gas dynamics equation by using laplace transform; Z Naturforsch, 67a (2012), pp. 389–396
19. [19] S. Kumar; A numerical study for solution of time fractional nonlinear shallow-water equation in oceans; Z Naturforsch A, 68a (2013), pp. 1–7
20. [20] S. Kumar; Numerical computation of time-fractional Fokker–Planck equation arising in solid state physics and circuit theory; Z Naturforsch, 68a (2013), pp. 1–8
21. [21] S. Kumar, A new analytical modelling for telegraph equation via Laplace transform, Appl. Math. Modell. http://dx.doi.org/10.1016/j.apm.2013.11.035.
22. [22] M.M. Khader, S. Kumar, S. Abbasbandy; New homotopy analysis transform method for solving the discontinued problems arising in nanotechnology; Chinese Phys. B, 22 (11) (2013)
23. [23] Y. Keskin, G. Oturanc; Reduced differential transform method: a new approach to factional partial differential equations; Nonlinear Sci. Lett. A, 1 (2010), pp. 61–72
24. [24] P.K. Gupta; Approximate analytical solutions of fractional Benney–Lin equation by reduced differential transform method and the homotopy perturbation method; Comput. Math. Appl., 58 (2011), pp. 2829–2842
25. [25] Mohammed O. Al-Amr; New applications of reduced differential transform method; Alexandria Eng. J., 53 (2014), pp. 243–247
26. [26] V.K. Srivastava, M.K. Awasthi, M. Tamsir; RDTM solution of Caputo time fractional-order hyperbolic telegraph equation; AIP Adv., 3 (2013), p. 032142
27. [27] V.K. Srivastava, M.K. Awasthi, S. Kumar; Analytical approximations of two and three dimensional time-fractional telegraphic equation by reduced differential transform method; Egypt. J. Basic Appl. Sci., 1 (1) (2014), pp. 60–66
28. [28] V.K. Srivastava, S. Kumar, M.K. Awasthi, B.K. Singh; Two-dimensional time fractional-order biological population model and its solution by fractional RDTM; Egypt. J. Basic Appl. Sci., 1 (1) (2014), pp. 71–76
29. [29] H. Jafari, C. Chun, S. Seifi, M. Saeidy; Analytical solution for nonlinear gas dynamics equation by homotopy analysis method; Appl. Appl. Math., 4 (1) (2009), pp. 149–154
30. [30] A.J.M. Jawad, M.D. Petkovic, A. Biswas; Applications of He’s principles to partial differential equations; Appl. Math. Comput., 217 (2011), pp. 7039–7047
31. [31] T.G. Elizarova; Quasi gas dynamics equations; Comput. Fluid Solid Mech., 978-3-642-00291-5Springer Verlag (2009)
32. [32] D.J. Evans, H. Bulut; A new approach to the gas dynamics equation: an application of the decomposition method; Int. J. Comput. Math., 79 (7) (2002), pp. 817–822
33. [33] J.L. Steger, R.F. Warming; Flux vector splitting of the inviscid gas dynamic equations with application to finite-difference methods; J. Comput. Phys., 40 (2) (1981), pp. 263–293
34. [34] A. Aziz, D. Anderson; The use of pocket computer in gas dynamics; Comput. Educat., 9 (1) (1985), pp. 41–56
35. [35] M. Rasulov, T. Karaguler; Finite difference scheme for solving system equation of gas dynamics in a class of discontinuous function; Appl. Math. Comput., 143 (1) (2003), pp. 145–164
36. [36] T.P. Liu, Nonlinear Waves in Mechanics and Gas Dynamics. Defense Technical Information Center, 1990, Accession Number: ADA 238340.
37. [37] J. Biazar, M. Eslami; Differential transform method for nonlinear fractional gas dynamics equation; Inter. J. Phys. Sci., 6 (5) (2011), p. 1203
38. [38] S. Das, R. Kumar; Approximate analytical solutions of fractional gas dynamics; Appl. Math. Comput., 217 (24) (2011), pp. 9905–9915
39. [39] S. Kumar, M.M. Rashidi; New analytical method for gas dynamics equation arising in shock fronts; Comput. Phys. Commun., 185 (7) (2014), pp. 1947–1954
40. [40] F. Mainardi; On the initial value problem for the fractional diffusion-wave equation; S. Rionero, T. Ruggeeri (Eds.), Waves and Stability in Continuous Media, World Scientific, Singapore (1994), pp. 246–256
41. [41] X.J. Yang, D. Baleanu, H.M. Srivastava; Local Fractional Integral Transforms and their Applications; Elsevier (2015)
42. [42] X.J. Yang, D. Baleanu; Fractal heat conduction problem solved by local fractional variation iteration method; Therm. Sci., 17 (2) (2013), pp. 625–628
43. [43] X.J. Yang, D. Baleanu, W.P. Zhong; Approximate solutions for diffusion equations on Cantor space-time; Proc. Romanian Acad., Ser. A, 14 (2) (2013), pp. 127–133
44. [44] X.J. Yang, X.H.M. Srivastava, C. Cattani; Local fractional homotopy perturbation method for solving fractal partial differential equations arising in mathematical physics; Romanian Rep. Phys., 67 (3) (2015), pp. 752–761
45. [45] M.R. Hajmohammadi, S.S. Nourazar; On the solution of characteristic value problems arising in linear stability analysis; semi analytical approach; Appl. Math. Comput., 239 (2014), pp. 126–132
46. [46] M.R. Hajmohammadi, S.S. Nourazar, A.H. Manesh; Semi-analytical treatments of conjugate heat transfer; J. Mech. Eng. Sci., 227 (2012), pp. 492–503
47. [47] M.R. Hajmohammadi, S.S. Nourazar; On the insertion of a thin gas layer in micro cylindrical Couette flows involving power-law liquids; Int. J. Heat Mass Transfer, 75 (2014), pp. 97–108
48. [48] M.R. Hajmohammadi, S.S. Nourazar, A. Campo; Analytical solution for two-phase flow between two rotating cylinders filled with power law liquid and a micro layer of gas; J. Mech. Sci.Technol., 28 (5) (2014), pp. 1849–1854 http://dx.doi.org/10.1007/s12206-013-0913-y
49. [49] M.R. Hajmohammadi, S.S. Nourazar; Conjugate forced convection heat transfer from a heated flat plate of finite thickness and temperature-dependent thermal conductivity; Heat Transfer Eng., 35 (2014), pp. 863–874
50. [50] B. İbiş, M. Bayram; Analytical approximate solution of time-fractional Fornberg–Whitham equation by the fractional variational iteration method; Alexandria Eng. J., 53 (4) (2014), pp. 911–915
51. [51] J. Prakash, M. Kothandapani, V. Bharathi, Numerical approximations of nonlinear fractional differential difference equations by using modified He-Laplace method, Alexandria Eng. J. 55 (1) (2016) 645–651.
52. [52] Sunil Kumar; A new fractional modeling arising in engineering sciences and its analytical approximate solution; Alexandria Eng. J., 52 (4) (2013), pp. 813–819