Abstract
Three-dimensional (3-D) computational code was implemented to solve conservation equations based on finite volume method as to simulate 1.8 L Ford diesel engine. Velocity and pressure of each computational cell is achieved by SIMPLE (semi-implicit method for pressure-linked equations) algorithm. For the exergetic aspect, the initial condition is set at 0.1 MPa and 300 K. The engine modeling is performed with 130 °, 140 °, and 150 ° with respect to x-axis under 1500 and 2500 rpm engine speeds. The results, however, indicate better air/fuel mixture (near stoichiometric equivalence ratio) for 130 ° of injection angle, albeit smaller spray droplets (lower sauter mean diameter) were introduced with 140 °. It is seen that higher soot and NOx mass fraction is attributed to 1500 rpm engine speed. The highest NOx and soot are exhausted at 130 ° and 150 ° of injection, respectively. Second law efficiency was calculated for different spray angle and engine speed schemes such that 36.62%, 30.2%, and 32.07% are associated with 130 °, 140 °, and 150 ° of injection angle under 1500 rpm, respectively. In terms of engine performance, that is, indicated mean effective pressure, indicated specific fuel consumption, and temperature, the best performance metrics are of 130 ° equal to 15.4 bar, 0.3856 kg/kW-h, and 2074.97 K under 1500 rpm, respectively. Instant irreversibility rate is the highest amount with peak value of 17.48 J/deg for 130 deg-1500 rpm, while 140 ° shows higher mean irreversibility rate over crank angle (CA) period.
Introduction
Energy utilization is a vital issue; hence, presentation of a framework to serve the purpose of both frugality and high efficiency seems inevitable. Energy evaluation of internal combustion engines (ICEs) alone, fails to determine the key reasons governing the inefficiency and combustion deficiency since energy balance equation gives the amount of energy either as work delivery or heat generation/dissipation. The study in quality of energy (exergy) sheds light on the sources, which can assist to reduce the losses from a defined control volume. Nowadays special attention is paid for the estimation of operational parameters in energy-related devices through numerical methods. Several studies were devoted to the case-sensitive investigation of the engines and their performance with various operational conditions [1-5]. The effect of spray injection angle on combustion and exhaust emissions were conducted experimentally [6]. The tests were performed by 60 ° and 70 ° injection angle and compared with conventional angle of 156 °. The results, however, showed that the pressure for narrow-angle injection (60 ° or 70 °) is increasing compared to wide-angle strategy (156 °). Park and Reitz [7] applied 2-spray-angle of group-hole nozzle aimed at squish zone (150 ° and 170 °) and bowl (80 ° spray angle). Their work revealed better air/fuel mixture, higher in-cylinder pressure, and reduced emissions with spray-guided injection compared to the baseline conventional case. The authors' previous work covers availability and irreversibility analysis with engine and combustion process based on different operative parameters such as various fuels, inlet charge temperature, and equivalence ratio [8-11].
Literature survey revealed the following results for the consideration of the first and second law in the ICEs; Ghazikhani et al. [12] performed an experimental investigation of exhaust gas recirculation (EGR) impact on irreversibility and brake-specific fuel consumption of diesel engine. They concluded that with EGR introduction, the total in-cylinder irreversibility increases due to the extension of flame region. The effect of n-heptane and natural gas blends were surveyed in homogeneous charge compression ignition (HCCI) engines from the second thermodynamic law viewpoint [13]. A complete chemical kinetic mechanism was utilized in order to analyze the availability of system for varied EGR and natural gas percentage addition. They proved that the natural gas addition accounts for lowering exergy destruction accompanied by the second law efficiency rise. Ozkan et al. [14] discussed the effect of pre-injection timing on diesel engines exergetic and energetic performance elaborately. Their results divulged that with adopting appropriate pre-injection strategy, no perceptible influence could be noticed on thermal and exergetic efficiency; however, NOx emissions were reduced significantly by 7.4%. A new study has been dedicated to determine the optimal operating condition of HCCI engine that is based on crank-angle resolved method [15]. It was observed that the equivalence ratio should be maintained at high values for majority of engine conditions while pressure was used to regulate engine load. Moreover, it was indicated that combustion timing has to be adjusted just before the sharp increase in unburned species losses. Jafarmadar and Zehni [16] carried out exergy analysis in combustion chamber of the IDI diesel engine by three-dimentional modeling. They investigated dwell time duration effect on exergy terms, which resulted in work exergy and exergy efficiency decrease when dwell time increased from 5 ° to 30 °CA.
This work deals with different spray injection angle into the bowl section of CI diesel engine while 1500 and 2500 rpm engine speeds were employed. Spray structure, combustion, and emissions were inspected from the first law perspective. Then the second law analyses were conducted in various forms such as the indicated work, heat release, and chemical exergy as well as the irreversibility term. Finally, regression analysis was performed to develop a fourth order polynomial at six specified cases. Finally, among six cases with different speed and injection angle, 130 deg-1500 rpm shows optimal exergetic efficiency, although, higher emission was issued.
Geometrical Definition and Numerical Simulation
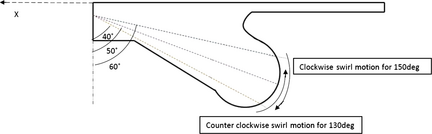
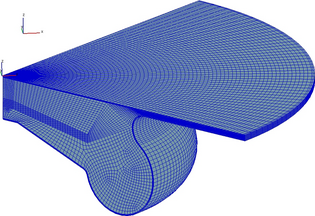
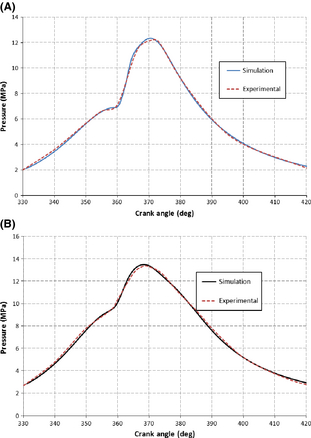
The simulation is according to 1.8-L Ford diesel engine. The numerical modeling in the simulation is detailed in ref. [17]. AVL FIRE code was employed for multidimensional simulation of the respective diesel engine. The swirl/tumble motion in combustion chamber of diesel engine has positive characteristics such as low-NOx emission, low noise, and high engine speed [18-20]. The schematic of combustion chamber with guided spray injection is illustrated in Figure 1. Three sprays of 130 °, 140 °, and 150 ° with respect to x-axis are shown. As seen, 140 ° spray angle collides at central spot of the bowl, 130 ° at near pedestal section inducing the counter clockwise spray diffusion, and 150 ° at near squish zone with clockwise swirl motion of the spray. Boundary conditions, dead state condition, flow and emission simulation sub-models are listed in Table 1. The engine specifications are summarized in Table 2 (for the sake of brevity further explanation on numerical implementation was omitted, more information are detailed in [8]). 3-dimensional gridding of the chamber with sufficient 168,421 mostly unstructured cells was constructed (Fig. 2). The veracity of simulated results is validated according to pressure courses of 1500 and 2500 rpm engine speeds. Figure 3 shows excellent agreement between the modeling and experimental results. The obtained results by computational fluid dynamics (CFD) numerical method were compared with experimental results in terms of the in-cylinder pressure at 1500 and 2500 rpm engine speeds [21]. The highest discrepancies at peak values for 1500 and 2500 engine speeds are lower than 0.1% between experimental and modeling curves.
| Head temperature | 550.15 K |
| Piston temperature | 575.15 K |
| Cylinder temperature | 475.15 K |
| Dead state pressure | 1.01325 bar |
| Dead state temperature | 290.15 K |
| Spray breakup | Modified KH-RT |
| Combustion model | Eddy Break-Up |
| Turbulence model | k-ζ-f |
| Evaporation | Dukowicz |
| NO | Extended Zeldovich |
| Soot | Kennedy-Hiroyasu-Magnussen |
| Wall treatment | Hybridized wall |
| Heat transfer wall mode | Standard wall function |
| Residual gas ratio | 0.5 |
| Fuel injection quantity (mg/cycle) | 31.3 |
| Bore× stroke | 82.5 × 82 mm |
| Displacement | 438 cm3/cylinder |
| Compression ratio | 19.5:1 |
| Swirl ratio @ IVC | 3 |
| Rail pressure | 540–1255 bar (based on engine speed) |
| Nozzle geometry | 5 × 0.15 mm |
| Bowl diameter | 0.0483 m |
| Bowl depth | 0.0144 m |
| Clearance | 0.86 mm |
| Number of nozzle holes | 4 |
| Injection start timing | 3 °CA BTDC |
| Injection spray angle | 130 °, 140 °, 150 ° |
|
|
|
Figure 1. Schematic illustration of guided spray scheme. |
|
|
|
Figure 2. CFD meshing model of combustion chamber at TDC. |
|
|
|
Figure 3. Pressure history for experimental and simulation for (A) 1500 rpm, (B) 2500 rpm [20]. |
Computational Implementation of the Second Law
Exergy is defined as a feature representing the capability of a system in transforming a given amount of energy at prescribed condition to useful work. In other words, exergy characterizes the maximum useful work attained from a system, which is plausible when a reversible process can be established between the initial and final point. The maximum extractable work depends on both ambient condition and the characteristics of the system. In general, total exergy is classified to thermo mechanical exergy and chemical exergy. The former governs the case when no chemical reaction tendency between the working fluid and the environment exists, whereas the latter is related to thermal and physical equilibrium with environment. In the engine applications, all the components of the working medium have to be either oxidized (e.g. fuel, CO, H), or reduced (e.g. NO, OH) in a reversible manner as the system approaches the dead state. The only components of the system, which cannot react chemically with the atmosphere are O2, N2, CO2 and H2O [22, 23]. The thermo mechanical (Extm) and chemical (Exch) exergies are formulated as follows:
|
|
(1) |
|
|
(2) |
where mi, xi, and μi0 are the mass flow, mass fraction, and chemical potential of species i obtained at restricted dead state. Here, μi0 is chemical potential associated with restricted dead state, whereas superscript 0 as in, μi0 and xi0 denote chemical potential and mass fraction associated with actual dead state condition for the species i. At the restricted dead state, there are thermal and mechanical equilibrium, but a chemical potential exists due to chemical reaction tendency with environment. At the actual dead state, this chemical potential is obviated. P0, T0 are the pressure and temperature at dead state conditions, accordingly. The total exergy (Ex) is the sum of chemical and thermo-mechanical exergies:
|
|
(3) |
The rate of indicated work exergy is quantified as given:
|
|
(4) |
dV/dθ denotes volume change of cylinder volume with crank angle (CA) and P is the instantaneous pressure of the cylinder obtained by first law analyzed data. Exq represents the exergy of heat release within cylinder. The exergy of heat release rate (HRR) can be presented by (dQ/dθ is HRR):
|
|
(5) |
Irreversibility is denoted by I term that is the availability destruction concerning the combustion process in the chamber given as:
|
|
(6) |
The chemical availability of the CxHyOz liquid fuel is calculated by the following formula [24]:
|
|
(7) |
where x, y, and z are the number of C, H, and O atoms in a general hydrocarbon fuel. LHV in the equation (7) defines the low heat value of the fuel. Note that w is the water content of the fuel. Af,ch expresses the chemical availability (exergy) of a specific fuel.
|
|
(8) |
In order to quantify the second law efficiency of the engine the following formula is applicable, where Aw is the work transfer availability (exergy):
|
|
(9) |
Results and Discussions
Injection angle impact on spray structure
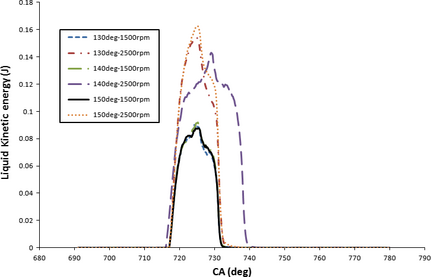
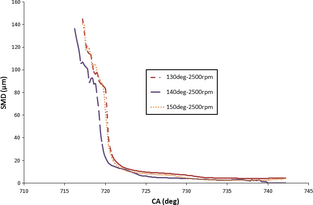
Injection angle variation can influence the fuel flow behavior in the nozzle section due to the pressure and velocity field alteration. Subsequently, spray structure in terms of sauter mean diameter (SMD) and penetration was influenced; thereby air/fuel mixture uniformity can undergo drastic changes. SMD and liquid kinetic energy (injected spray jet energy) of the spray were taken into account as to evaluate the spray characteristics injected into the bowl of the combustion chamber. Figure 4 shows the liquid energy of injected spray at different injection angles with respect to crank-angle under 1500 and 2500 rpm engine speeds. It is apparent that at 2500 rpm engine speed, higher liquid kinetic energy was accomplished. In fact, in most light duty diesel engines, smaller jet penetration is anticipated at higher speed since both swirl and tumble flows are stronger so that the axial momentum of the jet is lower while the radial one is larger. This phenomenon leads to a better atomization of sprays at higher engine speeds. No significant change in liquid energy can be noticed at 1500 rpm engine speed with injection angle variation, however, considering 2500 rpm, the spray direction of 150 ° shows the highest liquid energy with peak value of 0.1627 J. Although spray energy in the case of 140 ° is lower compared to the other injection angles, the prolonged liquid energy duration together with higher liquid energy after 7 °CA ATDC contributes to the highest spray penetration. Figure 5 demonstrates SMD of different sprays injected from different angles against crank-angle. As shown in Figure 5, deviation of spray injection angle from bowl center towards squish and piston bottom wall (130 ° or 150 °) would increase spray droplet diameter. The overall higher liquid jet energy at 140 ° brings about intensified liquid jet disintegration.
|
|
|
Figure 4. Liquid kinetic energy as a function of CA (crank angle) for various injection angles under 1500, 2500 rpm speeds. |
|
|
|
Figure 5. SMD (sauter mean diameter) evolution over CA (crank angle) for various injection angles under 2500 rpm speed. |
Injection angle impact on combustion and emissions
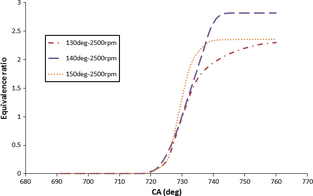
Figure 6 illustrates equivalence ratio of air/fuel mixture as a function of crank-angle for different spray injection angles at 1500 rpm engine speed. As fuel injection starts, fuel to air proportion and equivalence ratio starts to increase. According to Figure 6, lower equivalence ratio variance from stoichiometric ratio (~1) was achieved using 130 ° injection angle that signifies better mixing process, fuel evaporation, and more complete combustion. There are two reasons to explain this trend: first, it goes to the spray flow motion, which induces counter clockwise recirculation, therefore diffusing fuel into squish and top chamber wall. This makes better use of oxygen content in squish area. Another reason is attributed to reduced injection-wall distance and wall wetting for 150 ° spray angle. The uniform mixture distribution yields more obtainable work and heat generation, which will be addressed in subsequent sections.
|
|
|
Figure 6. Equivalence ratio as a function of CA (crank angle) for various injection angles at 2500 rpm speed. |
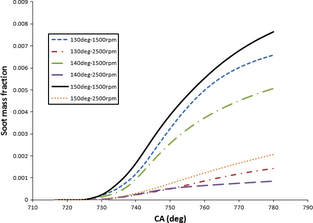
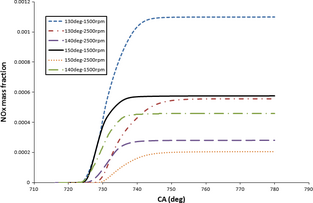
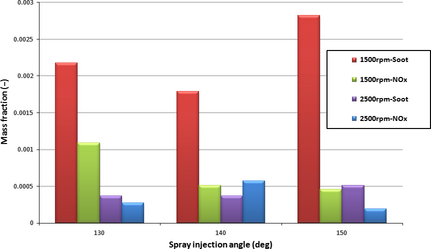
Figure 7 depicts soot mass fraction distribution with crank-angle for injection angles of 130 °, 140 °, and 150 ° at engine speeds of 1500 and 2500 rpm. Figure 7 indicates that higher soot concentration in combustion chamber is associated with low engine speed since higher engine speed increases the tumble flow motion and gas resistance in the chamber. Moreover, deflecting spray direction towards squish or pedestal edge demonstrates bigger droplet diameter and higher probability of spray-wall impingement (see Fig. 5) that can increase soot substantially. The results of soot curves confirms the results of Figure 6 denoting that the highest soot mass fraction is attributed to the highest equivalence ratio for 140 ° case. According to Figure 8, the high intensity NOx concentration is produced with nozzle angle of 130 °, corresponding to the uniform air/fuel mixture within the piston volume (counter clockwise spray motion contributes in well mixing). The homogeneity of fuel-air mixing is conducive to higher burning rate of fuel that can increase the in-cylinder temperature and pressure. NOx emission is expected to rise when the temperature increases. With engine speed increase, NOx emission decreases due to lesser air/fuel mixing time, thus lower evaporation, heat generation, and temperature is expected. Note that the lowest NOx for 1500 and 2500 rpm speeds attributes to 140 ° and 150 ° of the injection angles, respectively (according to maximum temperature presented in Table 3). Figure 9 clearly shows that in order to have the lowest NOx and soot emissions 140 ° and 150 ° of spray angle have to be adopted at 2500 rpm, respectively. This is mainly originated from the role of wall-spray impingement and swirl motion of the flow in the swirl chamber. Irrespective of the spray injection angle, in all cases, 2500 rpm produced lesser emission magnitude.
| deg | 1500 rpm | 2500 rpm | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tmax (K) | IMEP (bar) | ISFC (kg/kW-h) | Af,ch (J) | ηII (%) | Average (dI/dθ) (J/deg) | Tmax (K) | IMEP (bar) | ISFC (kg/kW-h) | ηII (%) | Average (dI/dθ) (J/deg) | |
| |||||||||||
| 130 | 2074.97 | 15.4 | 0.385 | 1381.7 | 36.62 | 2.642 | 1951.18 | 12.5 | 0.540 | 34.03 | 4.166 |
| 140 | 1815.57 | 12.1 | 0.574 | 1368.7 | 30.2 | 2.708 | 1695.98 | 10.4 | 0.721 | 28.12 | 2.887 |
| 150 | 1911.72 | 13.3 | 0.491 | 1376.6 | 32.07 | 2.481 | 1822.77 | 11.2 | 0.639 | 31.12 | 2.746 |
|
|
|
Figure 7. Soot mass fraction as a function of CA (crank angle) for various injection angles under 1500, 2500 rpm speeds. |
|
|
|
Figure 8. NOx mass fraction as a function of CA (crank angle) for various injection angles under 1500, 2500 rpm speeds. |
|
|
|
Figure 9. Emission comparison at different injection angles under 1500, 2500 rpm speeds. |
Injection angle impact on exergy and irreversibility terms
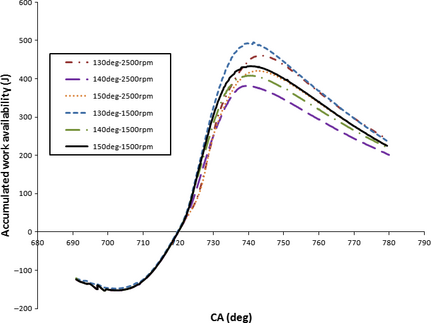
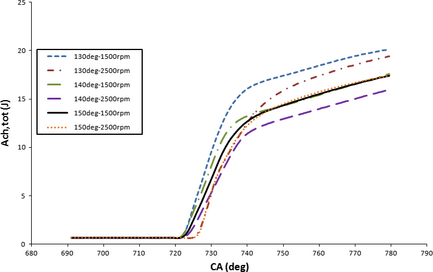
Figure 10 shows accumulated work exergy as a function of CA (time) for various spray injection angles at specified 1500 and 2500 rpm speeds. The compression stroke up to 720 °CA demonstrates negative work exergy values and no perceptible difference in terms of work exergy can be observed between spraying orientation schemes. The accumulated work exergy for expansion and combustion period produce work and starts to increase up to 20 °ATDC, thereafter decreases accordingly. The increase in work exergy in lower engine speed (1500 rpm) is higher than that of higher engine speed. It was also demonstrated that 130 ° of spray injection angle generates higher work exergy amount due to higher uniformity of air/fuel mixture and air entrainment (closer equivalence ratio to 1), therefore higher evaporation and stronger in-cylinder pressure was achieved. Note that 130 ° injection has longer injector – wall distance that prevents fuel deposit on the bowl wall and availability destruction as a result of flame quenching and combustion deterioration. Although higher engine speed expedites spray breakup process as stronger tumble occurs in the chamber, due to irreversibility nature of higher speed and less mixing time the work availability content tends to decrease at high engine speed. The peak values of accumulative work exergy equals 495.1, 460.1 J corresponding to 130 ° of spray angle at 1500 and 2500 rpm, respectively. Higher engine speed reduces the systems capability to fully exploit the provided energy resulted in combustion process, thereby exergy destruction occurs. The results of Table 3 regarding IMEP (indicated mean effective pressure) are in accordance with the work exergy. The highest mean effective pressure is at 130 ° reaching to 15.4 and 12.5 bar at 1500 and 2500 rpm, respectively. With increasing engine speed from 1500 to 2500 rpm, 18.8%, 14.04%, and 15.78% IMEP reduction occurs while 69.8%, 63.1%, and 29.5% peak work exergy reduction happens for 130 °, 140 °, and 150 °, respectively. Capturing heat potential of combustion with increasing engine speed is dropped since increasing speed as a source of irreversibility decreases the heat-work transformation.
|
|
|
Figure 10. Accumulated work availability as a function of CA (crank angle) for various injection angles under 1500, 2500 rpm speeds. |
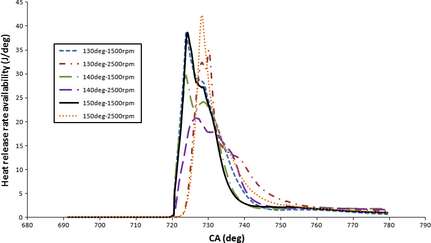
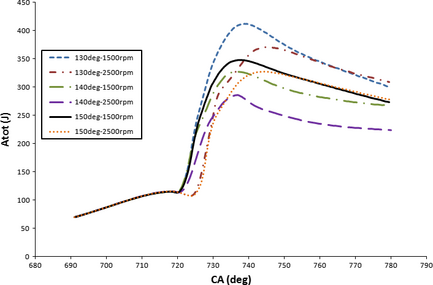
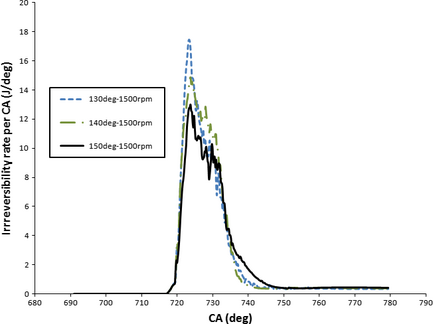
Rate of heat release exergy was depicted in Figure 11 as a function of CA for various spray angles under 1500 and 2500 rpm engine speeds. As shown in Figure 11, longer heat release exergy pertains to low engine speed, meanwhile, heat exergy is delayed in the case of 2500 rpm. The highest and lowest peak values of heat release exergy are associated with 150 ° and 140 ° that happens at 2500 rpm engine speeds. Considering the highest second law efficiency and maximum temperature for the case of 130 °, it can be concluded that 150 ° is incapable of converting useful heat potential into work production, denoting much higher rate of the heat transfer from the chamber wall boundary. Nonetheless, 140 ° possesses the lowest temperature and HRR exergy due to high equivalence ratio and ISFC (indicated specific fuel consumption) and shortage of sufficient oxygen content for mixture evaporation and fuel burning. Increasing engine speed is a source of exergy destruction, therefore lower exergy content is found under higher engine speeds in all exergy forms. Applying 130 ° spray injection is an effective method for creating strong squish since it can induce upward spray flow motion and tumble along the compression stroke, hence powerful pressure was resulted. Higher pressure before combustion initiation makes stronger turbulence and homogeneously distributed fuel air mixture. With upward movement of the spray injection angle, combustion site gets closer to squish zone, hence the majority of the released heat is trapped within the squish zone giving rise to deficient combustion. Increasing temperature and pressure resulted from high quality of spray structure (in-depth penetration of spray and near stoichiometric equivalence ratio) and combustion process of 130 ° spray injection into the bowl section of piston. Higher temperature and pressure amplitude of the combustion chamber for the case of 130 ° of injection angle explains higher overall availability, according to Figure 12. One can find that the total availability rise was delayed a few CAs for 130 ° and 150 ° which implies more opportunity for effective air/fuel mixing before combustion initiates. Consequently, exergy peak values of 130 ° and 150 ° injection angle are 29.8%, 14.6% higher than 140 ° under 1500 rpm, respectively. Table 3 reveals higher maximum temperature and effective pressure (IMEP) when 130 ° of injection angle was applied. As a result, higher total availability for the case of 130 ° once again was proved since availability is correlated with temperature and pressure of a system. Total chemical availability is depicted in Figure 13 with respect to CA for various injection angle and engine speed schemes. Total chemical availability is consisted of fuel chemical availability (reduction or oxidation) and diffusivity availability. As offered by Figure 13, a monotonous trend is presented during compression stroke for chemical availability since no fuel was injected and chemical reaction would not happen. The mole fraction increase and dramatic pressure and temperature rise with combustion initiation induce exergy increase. With regard to 130 °, more fuel was involved in chemical reaction due to fuel diffusion in squish area and higher oxygen content accessibility. However, the rate of chemical exergy increase was reduced after 740 °CA due to combustion chamber expansion and reduced diffusivity as mole concentration of combustion products is stabilized. 130 ° of injection angle prevails in total chemical availability than those of other cases that stems from better combustion implementation and effectual fuel burning reaction, together with higher fuel diffusion with residual gas. Second law efficiency is represented in detail in Table 3, where 130 ° showed superior amount equal to 36.62%, 34.03% under 1500, and 2500 rpm speeds, respectively. On the other hand, the lowest second law efficiency is associated with 140 ° such that 30.2%, 28.12% was achieved regarding 1500 and 2500 rpm, respectively. The results of second law efficiency are consistent with IMEP, ISFC, and Tmax of each case. Irreversibility rate as a function of CA for different spray aiming scheme was depicted in Figure 14 under 1500 rpm engine speed. Based on Table 3 and Figure 14, mean irreversibility rate per CA for 140 ° is dominant (2.708 J/deg over CA domain) while instantaneous peak irreversibility is dominant for 130 ° at 724 °CA (17.48 J/deg). This is because the system cannot seize the whole heat generated over crank-angle period. The mean irreversibility shows the highest amount for the case of 140 ° under both 1500 and 2500 rpm.
|
|
|
Figure 11. HRR (heat release rate) availability as a function of CA (crank angle) for various injection angles under 1500, 2500 rpm speeds. |
|
|
|
Figure 12. Total availability as a function of CA (crank angle) for various injection angles under 1500, 2500 rpm speeds. |
|
|
|
Figure 13. Chemical availability as a function of CA (crank angle) for various injection angles under 1500 and 2500 rpm speeds. |
|
|
|
Figure 14. Irreversibility rate as a function of CA (crank angle) for various injection angles at 1500 rpm. |
A correlation between total availability (A) and CA was developed based on the presented equation (10) (see Table 4). The best curve that data points can map onto is attained with fourth order polynomial. A linear regression analysis for 130 °, 140 °, and 150 ° injection orientation was performed for 1500 and 2500 rpm speed scenarios. Based on the obtained data for a0, a1, a2, a3, and a4 coefficients for the best curve fitting, the most precise formula according to correlation coefficient is presented for 130 deg-1500 rpm case with R2 = 91.93%. However, the lowest RMSE (root mean square error) is the lowest for 140 ° of injection angle to the bowl segment. The formula is presented as follows:
|
|
(10) |
| 1500 rpm | 2500 rpm | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a0 ×(107) | a1 (105) | a2 ×(102) | a3 ×(10−1) | a4 ×(10−4) | RMSE – | R2 (%) | a0 ×(107) | a1 ×(105) | a2 ×(102) | a3 ×(10−1) | a4 ×(10−5) | RMSE – | R2 (%) | |
| ||||||||||||||
| 130 | 4.06 | −2.2 | 4.46 | −4.02 | 1.35 | 3.43 | 91.93 | 1.94 | −1.04 | 2.09 | −1.86 | 6.21 | 3.25 | 91.78 |
| 140 | 3.05 | −1.65 | 3.36 | −3.03 | 1.02 | 2.5 | 91.86 | 2.37 | −1.28 | 2.61 | −2.36 | 7.98 | 2.2 | 89.38 |
| 150 | 3.19 | −1.73 | 3.51 | −3.51 | 1.06 | 2.79 | 91.87 | 1.67 | −2.33 | 1.8 | −1.61 | 5.39 | 2.87 | 91.1 |
The performance and accuracy of developed correlation is gauged by statistical factors such as coefficient of determination (R2), RMSE, defined as:
|
|
(11) |
|
|
(12) |
|
|
(13) |
where Yactual and Ypredicted are computed and predicted values of objective parameters by the developed models, respectively.
Concluding Remarks
Energy analysis was performed along exergy assessment for different injection strategy under different engine speeds. A correlation was observed between the fluid flow and the combustion process with exergy terms. The results can be classified as follows:
- Increasing engine speed results in considerable radial droplet diffusion and spray atomization, this stems from stronger jet energy. Hence, lower soot mass fraction was observed at higher engine speeds.
- 140 ° injection angle produces the lowest SMD that explains lower soot concentration at this spray angle. Lower equivalence ratio (attributed to 130 °) along with more elongated combustion period and combustion heat creation (attributed to 1500 rpm) for the case of 130 deg-1500 rpm caused stoichiometric combustion and the highest NOx generation. The case of 130 deg-1500 rpm was recognized as the optimum condition that yields the maximum energy delivery. It was found that the highest heat, work, chemical, and total exergy was associated with 130 deg-1500 rpm.
- Increasing engine speed from 1500 to 2500 rpm caused second law efficiency reduction by 7.07%, 6.88%, 2.96% and mean irreversibility rate augmentation by 36.5%, 6.2%, and 9.6% for 130 °, 140 °, and 150 ° of injection angle, respectively.
- Second law efficiency of 130 ° spray injection offers the highest values for both engine speeds due the most uniform air-fuel distribution in the combustion chamber. Increasing engine speed reduces second law efficiency irrespective of spray injection angle.
Conflict of Interest
None declared.
References
- Park, C., S. Kim, H. Kim, and Y. Moriyoshi. 2012. Stratified lean combustion characteristics of a spray-guided combustion system in a gasoline direct injection engine. Energy41:401–407.
- Soid, S. N., and Z. A. Zainal. 2011. Spray and combustion characterization for internal combustion engines using optical measuring techniques – a review. Energy36:724–741.
- Kiplomo, R., E. Tomita, N. Kawahara, and S. Yokobe. 2012. Effects of spray impingement, injection parameters, and EGR on the combustion and emission characteristics of a PCCI diesel engine. Appl. Therm. Eng.37:165–175.
- Abagnale, C., M. C. Cameretti, L. De Simio, M. Gambino, S. Iannaccone, and R. Tuccillo. 2014. Numerical simulation and experimental test of dual fuel operated diesel engines. Appl. Therm. Eng.65:403–417.
- Mohan, B., W. Yang, and S. K. Chao. 2014. Development of an accurate cavitation coupled spray model for diesel engine simulation. Energy Convers. Manage.77:269–277.
- Yoon, S. H., J. P. Cha, and C. S. Lee. 2010. An investigation of the effects of spray angle and injection strategy on dimethyl ether (DME) combustion and exhaust emission characteristics in a common-rail diesel engine. Fuel Process. Technol.91:1364–1372.
- Park, S. W., and R. D. Reitz. 2009. Optimization of fuel/air mixture formation for stoichiometric diesel combustion using a 2-spray-angle group-hole nozzle. Fuel88:843–852.
- Taghavifar, H., S. Khalilarya, S. Mirhasani, and S. Jafarmadar. 2014. Numerical energetic and exergetic analysis of CI diesel engine performance for different fuels of hydrogen, dimethyl ether, and diesel under various engine speeds. Int. J. Hydrogen Energy39:9515–9526. doi: 10.1016/j.ijhydene.2014.03.256
- Abassi, A., S. Khalilarya, and S. Jafarmadar. 2011. The influence of the inlet charge temperature on the second law balance under the various operating engine speeds in DI diesel engine. Fuel89:2425–2432.
- Fathi, V., A. Nemati, S. Khalilarya, and S. Jafarmadar. 2011. The effect of the initial charge temperature under various injection timings on the second law terms in a direct injection SI hydrogen engine. Int. J. Hydrogen Energy36:1–8.
- Nemati, A., A. Fathi, R. Barzgar, and S. Khalilarya. 2013. Numerical investigation of the effect of injection timing under various equivalence ratios on energy and exergy terms in a direct injection SI hydrogen fueled engine. Int. J. Hydrogen Energy38:1189–1199.
- Ghazikhani, M., M. E. Feiz, and A. Joharchi. 2010. Experimental investigation of the exhaust gas recirculation effects on irreversibility and brake specific fuel consumption of indirect injection diesel engines. Appl. Therm. Eng.30:1711–1718.
- Amjad, A. K., R. Khoshbakhti Saray, S. M. S. Mahmoudi, and A. Rahimi. 2011. Availability analysis of n-heptane and natural gas blends combustion in HCCI engines. Energy36:6900–6909.
- Ozkan, M., D. B. Ozkan, O. Ozener, and H. Yilmaz. 2013. Experimental study on energy and exergy analyses of a diesel engine performed with multiple injection strategies: effect of pre-injection timing. Appl. Math. Eng.53:21–30.
- Saxena, S., N. Shah, I. Bedoya, and A. Phadke. 2014. Understanding optimal engine operating strategies for gasoline-fueled HCCI engines using crank-angle resolved exergy analysis. Appl. Energy114:155–163.
- Jafarmadar, S., and A. Zehni. 2014. Numerical investigation of the effects of dwell time duration in a two-stage injection scheme on exergy terms in an IDI diesel engine by three-dimensional modeling. Energy Sci. Eng.2:1–13.
- Taghavifar, H., S. Khalilarya, and S. Jafarmadar. 2014. Engine structure modifications effect on the flow behavior, combustion, and performance characteristics of DI diesel engine. Energy Convers. Manage.85:20–32.
- Li, D. T.2000. Combustion process and combustion system of swirl chamber diesel engine. Science Book, Concern, Jiangsu University, Zhenjiang, RP China.
- Li, D. T.2008. Investigation of power machinery: its working processes and measurement techniques, selected papers of Professor Li Detao. Jiangsu University Book Concern, Jiangsu University, Zhenjiang, RP China.
- Wei, S., F. Wang, X. Leng, X. Liu, and K. Ji. 2013. Numerical analysis on the effect of swirl ratios on swirl chamber combustion system of DI diesel engines. Energy Convers. Manage.75:184–190.
- Hawley, J. G., F. J. Wallace, and S. Khalil Arya. 2003. A fully analytical treatment of heat release in diesel engines. Proc. Inst. Mech. Eng. Part D J. Automobile Eng.217:701–717. ISSN 0954–4070.
- Van Gerpen, J. H., and H. N. Shapiro. 1990. Second-law analysis of diesel engine combustion. Trans. ASME J. Eng. Gas Turbine Power112:129–137.
- Rakopoulos, C. D., and E. G. Giakoumis. 2006. Second-law analyses applied to internal combustion engines operation. Prog. Energy Combust. Sci.32:2–47.
- Kotas, T. J.1995. The exergy method of thermal plant analysis. Krieger Publishing, Malabar, FL. ISBN: 0894649469.
Document information
Published on 01/06/17
Submitted on 01/06/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?