Analytical solution for peristaltic flow of conducting nanofluids in an asymmetric channel with slip effect of velocity, temperature and concentration

Abstract

The Peristaltic transport of conducting nanofluids under the effect of slip condition in an asymmetric channel is reported in the present work. The mathematical modelling has been carried out under long wavelength and low Reynolds number approximations. The analytical solutions are obtained for pressure rise, nanoparticle concentration, temperature distribution, velocity profiles and stream function. Influence of various parameters on the flow characteristics has been discussed with the help of graphs. The results showed that the pressure rise increases with increasing magnetic effect and decreases with increasing slip parameter. The effects of thermophoresis parameter and Brownian motion parameter on the nanoparticle concentration and temperature distribution are studied. It is observed that the pressure gradient increases with increasing slip parameter and magnetic effect. The trapping phenomenon for different parameters is presented.

Keywords

Peristaltic transport; Nanofluids; Magnetic effect; Slip parameter; Asymmetric channel

Nomenclature

${\textstyle a_{1}{\mbox{,}}\quad b_{1}}$- amplitudes of the waves

${\textstyle d_{1}+d_{2}}$- channel width

${\textstyle \lambda }$- wavelength of the peristaltic wave

c- wave speed

p- pressure

${\textstyle \phi }$- phase difference

${\textstyle \mu }$- viscosity

M- Hartmann number

${\textstyle B_{0}}$- uniform magnetic field

${\textstyle \psi }$- steam function

${\textstyle \theta }$- temperature distribution

${\textstyle \beta }$- the slip parameter

${\textstyle \gamma }$- thermal slip parameter

${\textstyle {\gamma }_{1}}$- concentration slip parameter

${\textstyle N_{t}}$- Brownian motion parameter

${\textstyle N_{b}}$- thermophoresis parameter

${\textstyle G_{r}}$- local temperature Grashof number

${\textstyle B_{r}}$- nanoparticle Grashof number

${\textstyle \sigma }$- nanoparticle concentration

1. Introduction

In recent times, Peristalsis has attracted much attention due to its important in engineering and medical applications such as chyme movement in the intestine, movement of ovum in the fallopian tube, flow from kidney to bladder, capillaries, arterioles and roller pumps. In view of such industrial and physiological applications, the peristalsis mechanism has been studied in nature by various researchers for different fluids under different conditions [1], [2], [3], [4], [5], [6], [7] and [8]. Nanoparticle research is currently an area of intense scientific interest due to a wide variety of potential applications in medical and electronic field. The nanofluids are a new class of fluids designed by dispersing nano-meter sized materials (nanoparticles, nanofibers, nanotubes, nanorods, nanosheet and nanowires) in base fluids. Choi and Eastman [9] was reported that an innovative technique to improve heat transfer is by using nanoscale particles in base fluid. In the other work by Choi et al. [10] it was also shown that the addition of small amount (less than 1% by volume) of nanoparticles to conventional heat transfer liquids increases the thermal conductivity of the fluid approximately two times.

A detailed analysis of nanofluids was discussed by Buongiorno [11] reveals that this massive increase in the thermal conductivity occurs due to the presence of two main effects namely the Brownian diffusion and thermophoretic diffusion of nanoparticles. Mekheimer and Abd elmaboud [12] pointed out that the cancer tissues may be destroyed when the temperature reaches 40–45 °C. The influence of slip conditions, wall properties and heat transfer on MHD peristaltic transport was studied by Srinivas et al. [13]. Peristaltic transport of a Jeffrey fluid under the effect of slip in an inclined asymmetric channel was studied by Srinivas and Muthuraj [14]. Endoscopic effects on peristaltic flow of nanofluids are studied by Akbar and Nadeem [15]. Ramana Kumari and Radhakrishnamacharya [16] have investigated effect of slip on heat transfer to peristaltic transport in the presence of magnetic field with wall effects. Further the study of Peristaltic flow of a nanofluid in non-uniform tube is done by Akbar et al. [17] using Homotopy Perturbation method. Akbar and Nadeem [18] have investigated the peristaltic flow of a Phan-Thien–Tanner nanofluid in a diverging tube. The analytical and numerical solutions for influence of wall properties on the peristaltic flow of a nanofluid were studied by Mustafa et al. [19]. Further Akbar et al. [20] have studied peristaltic flow of a nanofluid with slip effects. A note on the influence of heat and mass transfer on a peristaltic flow of a viscous fluid in a vertical asymmetric channel with wall slip was studied by Srinivas et al. [21].

Akram et al. [22] have studied consequences of nanofluids on peristaltic flow in an asymmetric channel. Numerical study of Williamson nanofluid in an asymmetric channel is investigated by Akbar et al. [23]. Exact analytical solution of the peristaltic nanofluids flow in an asymmetric channel with flexible walls and slip condition: Application to cancer treatment was discussed by Ebaid et al. [24]. Slip effects on the Peristaltic motion of nanofluids in a channel with wall properties were studied by Mustafa et al. [25].

Recently exact analytical solution for the peristaltic flow of nanofluids in an asymmetric channel with slip effect of the velocity, temperature and concentration was studied by Aly et al. [26]. The study on consequence of nanofluids on peristaltic transport of a hyperbolic tangent fluid model in the occurrence of apt (tending) magnetic field was discussed by Akram and Nadeem [27].

Mustafa et al. [28] studied the influence of induced magnetic field on the peristaltic flow of nanofluids. Peristaltic motion of nanofluids in curved channel was analysed by Hina et al. [29]. Sharidan Shafie et al. [30] studied Partial slip effect on heat and mass transfer of MHD peristaltic transport in a porous medium. Hayat et al. [31] studied Peristaltic transport of Carreau-Yasuda fluid in a curved channel with slip effects.

The nanofluids in peristaltic flow problem under the effect of magnetic field and radiation in the tapered asymmetric channel through porus space was described by Kothandapani and Prakash [32]. The peristaltic transport of Carreau nanofluids under the effect of magnetic field in a tapered asymmetric channel was studied by Kothandapani and Prakash [33]. Effect of thermal radiation parameter and magnetic field on the peristaltic motion of Williamson nanofluids in a tapered asymmetric channel was studied by Kothandapani and Prakash [34]. Nirmala et al. [35] studied combined effects of hall current, wall slip, viscous dissipation and soret effect on MHD Jeffrey fluid flow in a vertical channel with Peristalsis.

The Present work was to discuss the peristaltic flow of nanofluids in an asymmetric channel under the effect of both magnetic field and slip parameters. The governing equations are carried out under the assumption of long wavelength and low Reynolds number. The reduced equations are solved exactly.

The result of the present study finds applications in peristaltic pumping through corrogative and non-corrogative pipes. In the case of corrogative pipe flow the slip effect is important, whereas in the other case slip may not exist.

2. The mathematical model

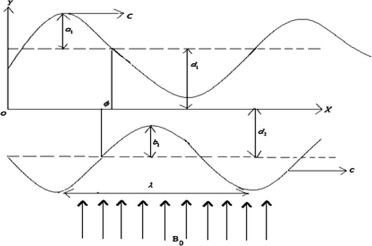
Consider peristaltic transport of an incompressible Newtonian conducting nanofluid in an asymmetric channel with flexible walls. The channel asymmetry is generated by propagation of waves on the channel walls travelling with different amplitudes and phases but with same constant speed c.

In the Cartesian coordinates system ${\textstyle \left({\overline {X}}{\mbox{,}}{\overline {Y}}\right)}$ of the fixed frame, the upper wall ${\textstyle {\overline {h}}_{1}}$ and lower wall ${\textstyle {\overline {h}}_{2}}$ are given by Fig. 1

$\left\{{\begin{array}{l}{\overline {h}}_{1}=d_{1}+a_{1}cos\left({\frac {2\pi }{\lambda }}\left[{\overline {X}}-c{\overline {t}}\right]\right){\mbox{,}}\\{\overline {h}}_{2}=-d_{2}-b_{1}cos\left({\frac {2\pi }{\lambda }}\left[{\overline {X}}-c{\overline {t}}\right]+\varphi \right)\end{array}}\right\}$

where ${\textstyle a_{1}}$ and ${\textstyle b_{1}}$ are amplitude of the waves, ${\textstyle \lambda }$ is the wavelength, ${\textstyle d_{1}+d_{2}}$ is the width of the channel, and the phase difference ${\textstyle \phi }$ varies in the range ${\textstyle 0\leqslant \phi \leqslant \pi }$ where ${\textstyle \phi =0}$ and ${\textstyle \phi =\pi }$ correspond to symmetric cannel with waves out of the phase and in the phase, respectively. Further, ${\textstyle a_{1}{\mbox{,}}\quad b_{1}{\mbox{,}}\quad d_{1}{\mbox{,}}\quad d_{2}}$ and ${\textstyle \phi }$ satisfy the following condition [32].

$a_{1}^{2}+b_{1}^{2}+2a_{1}b_{1}cos\varphi \leqslant {\left(d_{1}+d_{2}\right)}^{2}$

With the following non-dimensional phenomena

$a={\frac {a_{1}}{d_{1}}}{\mbox{,}}b={\frac {a_{2}}{d_{1}}}{\mbox{,}}d=$${\frac {d_{2}}{d_{1}}}$

In the moving frame of reference ${\textstyle \left({\overline {X}}{\mbox{,}}{\overline {Y}}\right)}$, we have

${\overline {x}}={\overline {X}}-c{\overline {t}}{\mbox{,}}{\overline {y}}=$${\overline {Y}}$

The non-dimensional quantities are

$x={\frac {2\pi {\overline {x}}}{\lambda }}{\mbox{,}}\quad y=$${\frac {\overline {Y}}{d_{1}}}{\mbox{,}}\quad t={\frac {2\pi {\overline {t}}}{\lambda }}{\mbox{,}}\quad h_{1}=$${\frac {{\overline {h}}_{1}}{d_{1}}}{\mbox{,}}\quad h_{2}={\frac {{\overline {h}}_{2}}{d_{2}}}{\mbox{,}}M=$${\sqrt {\frac {\sigma }{\mu }}}{dB}_{0}$

Under the assumptions of long wavelength and low Reynolds number approximation, Kothandapani and Prakash [32] found that the flow is governed by the following system of partial differential equations in non-dimensional form

${\frac {{\partial }^{2}}{\partial y^{2}}}\left[{\frac {{\partial }^{2}\psi }{\partial y^{2}}}-\right.$$\left.M^{2}\psi \right]+G_{r}{\frac {\partial \theta }{\partial y}}+$$B_{r}{\frac {\partial \sigma }{\partial y}}=0$

(1)

${\frac {dp}{dx}}={\frac {\partial }{\partial y}}\left[{\frac {{\partial }^{2}\psi }{\partial y^{2}}}-\right.$$\left.M^{2}\psi \right]+G_{r}\theta +B_{r}\sigma$

(2)

${\frac {{\partial }^{2}\theta }{\partial y^{2}}}+N_{b}{\frac {\partial \theta }{\partial y}}{\frac {\partial \sigma }{\partial y}}+$$N_{t}{\left({\frac {\partial \theta }{\partial y}}\right)}^{2}=$$0$

(3)

${\frac {{\partial }^{2}\sigma }{\partial y^{2}}}+{\frac {N_{t}}{N_{b}}}\left({\frac {{\partial }^{2}\theta }{\partial y^{2}}}\right)=$$0$

(4)

where ${\textstyle \psi {\mbox{,}}\quad \theta {\mbox{,}}\quad \sigma }$ and P   are the stream function, temperature distribution, nanoparticle concentration and pressure gradient respectively. Further ${\textstyle N_{t}{\mbox{,}}\quad N_{b}{\mbox{,}}\quad G_{r}{\mbox{,}}\quad B_{r}}$ and M are Brownian motion parameter, thermophoresis parameter, local temperature Grashof number, nanoparticle Grashof number and Hartmann number respectively.

Figure 1. Physical model.

The corresponding boundary conditions are

$\psi ={\frac {F}{2}}{\mbox{,}}{\frac {\partial \psi }{\partial y}}=$$-\beta {\frac {{\partial }^{2}\psi }{\partial y^{2}}}-1\quad {\mbox{at}}\quad h_{1}=$$1+acos(x)$

(5)

$\psi =-{\frac {F}{2}}{\mbox{,}}{\frac {\partial \psi }{\partial y}}=$$\beta {\frac {{\partial }^{2}\psi }{\partial y^{2}}}-1\quad {\mbox{at}}\quad h_{2}=$$-d-bcos(x+\varphi )$

(6)

$\theta +\gamma {\frac {\partial \theta }{\partial y}}=$$0\quad {\mbox{at}}\quad y=h_{1}$

(7)

$\theta -\gamma {\frac {\partial \theta }{\partial y}}=$$1\quad {\mbox{at}}\quad y=h_{2}$

(8)

$\sigma +{\gamma }_{1}{\frac {\partial \sigma }{\partial y}}=$$0\quad {\mbox{at}}\quad y=h_{1}$

(9)

$\sigma -{\gamma }_{1}{\frac {\partial \sigma }{\partial y}}=$$1\quad {\mbox{at}}\quad y=h_{2}$

(10)

where ${\textstyle \beta {\mbox{,}}\quad \gamma }$ and ${\textstyle {\gamma }_{1}}$ represent the slip parameter, thermal slip parameter and concentration slip parameter respectively.

3. The general closed form solution

Now from Eq. (4) we obtain,

$\sigma =-{\frac {N_{t}}{N_{b}}}\theta +c_{1}(x)y+c_{2}(x)$

(11)

where ${\textstyle c_{1}(x)}$ and ${\textstyle c_{2}(x)}$ are two unknown functions. By substituting Eq. (11) into (3) gives

${\frac {{\partial }^{2}\theta }{\partial y^{2}}}+N_{b}c_{1}(x){\frac {\partial \theta }{\partial y}}=$$0$

(12)

The above equation can be solved exactly to get the temperature distribution as

$\theta (x{\mbox{,}}y)=c_{4}(x)e^{-N_{b}f_{1}(x)y}+{\frac {1}{N_{b}}}{\frac {c_{3}(x)}{c_{1}(x)}}$

(13)

The nanoparticle concentration is given by

$\sigma (x{\mbox{,}}y)=-{\frac {N_{t}}{N_{b}}}c_{4}(x)e^{-N_{b}c_{1}(x)y}+$$c_{1}(x)y+c_{2}(x)-{\frac {N_{t}}{N_{b}^{2}}}{\frac {c_{3}(x)}{c_{1}(x)}}$

(14)

where ${\textstyle c_{3}(x)}$ and ${\textstyle c_{4}(x)}$ are two unknown functions. By substituting boundary conditions (7) and (8) in Eq. (13) gives

$c_{4}(x)e^{-N_{b}c_{1}(x)h_{1}}\left[1-\gamma N_{b}c_{1}\right]=$$-{\frac {1}{N_{b}}}{\frac {c_{3}(x)}{c_{1}(x)}}$

(15)

$c_{4}(x)e^{-N_{b}c_{1}(x)h_{2}}\left[1+\gamma N_{b}c_{1}\right]=$$1-{\frac {1}{N_{b}}}{\frac {c_{3}(x)}{c_{1}(x)}}$

(16)

By solving Eqs. (15) and (16) for ${\textstyle c_{3}(x)}$ and ${\textstyle c_{4}(x)}$ we have

$c_{4}={\frac {1}{(1+\gamma N_{b}c_{1})r_{2}^{c_{1}}-(1-\gamma N_{b}c_{1})r_{1}^{c_{1}}}}$

(17)

and

$c_{3}={\frac {-N_{b}c_{1}(1-\gamma N_{b}c_{1})r_{1}^{c_{1}}}{(1+\gamma N_{b}c_{1})r_{2}^{c_{1}}-(1-\gamma N_{b}c_{1})r_{1}^{c_{1}}}}$

(18)

${\mbox{Where}}\quad r_{1}=e^{-N_{b}h_{1}}\quad {\mbox{and}}\quad r_{2}=$$e^{-N_{b}h_{2}}$

(19)

Applying boundary conditions (9) and (10) in Eq. (14) gives

$\left({\gamma }_{1}c_{1}-{\frac {1}{N_{b}}}\right)N_{t}c_{4}r_{1}^{c_{1}}+$$({\gamma }_{1}+h_{1})c_{1}+\left(c_{2}-{\frac {N_{t}}{N_{b}^{2}}}{\frac {c_{3}}{c_{1}}}\right)=$$0$

(20)

$\left({\gamma }_{1}c_{1}+{\frac {1}{N_{b}}}\right)N_{t}c_{4}r_{2}^{c_{1}}+$$({\gamma }_{1}-h_{2})c_{1}-\left(c_{2}-{\frac {N_{t}}{N_{b}^{2}}}{\frac {c_{3}}{c_{1}}}\right)=$$-1$

(21)

Therefore ${\textstyle c_{2}(x)}$ is given from Eq. (20) is

$c_{2}={\frac {N_{t}}{N_{b}^{2}}}{\frac {c_{3}}{c_{1}}}-\left({\gamma }_{1}c_{1}-\right.$$\left.{\frac {1}{N_{b}}}\right)N_{t}c_{4}r_{1}^{c_{1}}-({\gamma }_{1}+$$h_{1})c_{1}$

(22)

By eliminating ${\textstyle c_{2}(x)}$ from Eqs. (22) and (23) to obtain we get,

$N_{t}c_{4}\left[\left({\gamma }_{1}c_{1}-{\frac {1}{N_{b}}}\right)r_{1}^{c_{1}}+\right.$$\left.\left({\gamma }_{1}c_{1}+{\frac {1}{N_{b}}}\right)r_{2}^{c_{1}}\right]+$$(2{\gamma }_{1}+h_{1}-h_{2})c_{1}=-1$

(23)

This can be written as

${\frac {N_{t}}{N_{b}}}\left[{\frac {({\gamma }_{1}N_{b}c_{1}-1)r_{1}^{c_{1}}+({\gamma }_{1}N_{b}c_{1}+1)r_{2}^{c_{1}}}{(\gamma N_{b}c_{1}-1)r_{1}^{c_{1}}+(\gamma N_{b}c_{1}+1)r_{2}^{c_{1}}}}\right]+$$(2{\gamma }_{1}+h_{1}-h_{2})c_{1}=-1$

(24)

which leads to an implicit algebraic equation in ${\textstyle c_{1}(x)}$ and exact solution is difficult to obtain; however, such exact solution is possible when ${\textstyle \gamma ={\gamma }_{1}}$.

Substituting ${\textstyle \gamma ={\gamma }_{1}}$ in Eq. (24), we obtain the exact value of ${\textstyle c_{1}(x)}$

$c_{1}(x)={\frac {1+{\frac {N_{t}}{N_{b}}}}{h_{2}-h_{1}-2{\gamma }_{1}}}$

(24a)

Therefore,

$\left\{{\begin{array}{l}c_{2}={\frac {N_{t}}{N_{b}^{2}}}{\frac {c_{3}}{c_{1}}}-\left({\gamma }_{1}c_{1}-{\frac {1}{N_{b}}}\right)N_{t}c_{4}r_{1}^{c_{1}}-({\gamma }_{1}+h_{1})c_{1}\\c_{3}={\frac {-N_{b}c_{1}(1-\gamma N_{b}c_{1})r_{1}^{c_{1}}}{(1+\gamma N_{b}c_{1})r_{2}^{c_{1}}-(1-\gamma N_{b}c_{1})r_{1}^{c_{1}}}}\\c_{4}={\frac {1}{(1+\gamma N_{b}c_{1})r_{2}^{c_{1}}-(1-\gamma N_{b}c_{1})r_{1}^{c_{1}}}}\end{array}}\right\}$

(24b)

To obtain the stream function ${\textstyle \psi (x{\mbox{,}}y)}$,

Consider Eq. (1)

${\frac {\partial }{\partial y}}\left[{\frac {{\partial }^{2}\psi }{\partial y^{2}}}-\right.$$\left.M^{2}\psi \right]=-G_{r}\theta -B_{r}\sigma +c_{5}$

(25)

$={\Omega }_{1}(x)+{\Omega }_{2}(x)e^{-N_{b}c_{1}y}-B_{r}c_{1}y+$$c_{5}$

(26)

Where

$\left\{{\begin{array}{l}{\Omega }_{1}(x)=\left({\frac {B_{r}N_{t}}{N_{b}}}-G_{r}\right){\frac {1}{N_{b}}}{\frac {c_{3}}{c_{1}}}-B_{r}c_{2}\\{\Omega }_{2}(x)=\left({\frac {B_{r}N_{t}}{N_{b}}}-G_{r}\right)c_{4}\end{array}}\right\}$

(27)

Now the stream function is given by

$\psi (x{\mbox{,}}y)=c_{8}e^{My}+c_{7}e^{-My}-{\frac {1}{M^{2}}}c_{6}-$${\frac {1}{M^{2}}}c_{5}y+g(y)$

(28)

Where

$g(y)=-{\frac {1}{M^{2}}}{\Omega }_{1}y-{\frac {1}{N_{b}c_{1}\left(N_{b}^{2}c_{1}^{2}-M^{2}\right)}}{\Omega }_{2}e^{-N_{b}c_{1}y}+$${\frac {B_{r}c_{1}}{2M^{2}}}\left(y^{2}+{\frac {2}{M^{2}}}\right)$

(29)

Applying the boundary conditions (5) and (6) in Eqs. (28) and (29),

We obtain the following system of equations

${\begin{array}{rl}&c_{8}e^{{Mh}_{1}}+c_{7}e^{-{Mh}_{1}}-c_{6}{\frac {1}{M^{2}}}-c_{5}{\frac {h_{1}}{M^{2}}}=R_{1}(x)\\&c_{8}e^{{Mh}_{2}}+c_{7}e^{-{Mh}_{2}}-c_{6}{\frac {1}{M^{2}}}-c_{5}{\frac {h_{2}}{M^{2}}}=R_{2}(x)\\&c_{8}e^{{Mh}_{1}}(M+M^{2}\beta )+c_{7}e^{-{Mh}_{1}}(-M+M^{2}\beta )-c_{5}{\frac {1}{M^{2}}}=S_{1}(x)\\&c_{8}e^{{Mh}_{2}}(M-M^{2}\beta )+c_{7}e^{-{Mh}_{2}}(-M-M^{2}\beta )-c_{5}{\frac {1}{M^{2}}}=S_{2}(x)\end{array}}$

(30)

Where

${\begin{array}{rl}&R_{1}(x)={\frac {F}{2}}-g(h_{1})\\&R_{2}(x)=-{\frac {F}{2}}-g(h_{2})\\&S_{1}(x)=-1-g^{'}(h_{1})-\beta g^{''}(h_{1})\\&S_{2}(x)=-1-g^{'}(h_{2})+\beta g^{''}(h_{2})\end{array}}$

(31)

The pressure gradient from Eqs. (2) and (25) is given by,

${\frac {dp}{dx}}=c_{5}(x)$

(32)

By solving linear system of Eq. (30) for constants,

${\begin{array}{rl}&c_{5}={\frac {\left\{{\begin{array}{l}\left[\left(a_{11}\right)\left(M^{2}-M^{4}{\beta }^{2}\right)\right]+\left[s_{1}\left(a_{12}\right){\left(M-M^{2}\beta \right)}^{2}\right]\\-\left[\left(R_{1}-R_{2}\right)\left(a_{13}\right){\left(M+M^{2}\beta \right)}^{3}\right]+\left[\left(R_{1}-R_{2}\right)e^{{Mh}_{2}}\left(M+M^{2}\beta \right)(M-M^{2}\beta \right]+\left[s_{1}(a_{14}){\left(M+M^{2}\beta \right)}^{2}\right]\end{array}}\right\}}{{\frac {1}{M^{2}}}\left\{{\begin{array}{l}\left[2a_{15}{\left(M+M^{2}\beta \right)}^{2}\right]+\left[a_{16}\left(M^{2}-M^{4}{\beta }^{2}\right)\right]\\+\left[a_{17}{\left(M-M^{2}\beta \right)}^{2}\right]+\left[a_{18}\left(M+M^{2}\beta \right){\left(M-M^{2}\beta \right)}^{2}\right]+\left[a_{19}{\left(M+M^{2}\beta \right)}^{3}\right]\end{array}}\right\}}}c_{5}={\frac {a_{34}}{a_{35}}}\\&c_{7}={\frac {\left\{{\frac {1}{M^{2}}}\left[a_{20}-a_{21}\right]\left[\left(a_{22}\right)\left(a_{23}\right)-\left(a_{24}\right)\left(a_{25}\right)\right]-\left[\left(a_{26}\right)\left(a_{23}\right)-\left(a_{27}(M+M^{2}\beta )-s_{1}a_{14}\right)a_{28}\right]\left[a_{29}\right]\right\}}{\left\{\left[a_{30}-a_{31}\right]{\frac {1}{M^{2}}}\left[\left(a_{22}\right)\left(a_{23}\right)-a_{32}\left(a_{33}\right)\right]\right\}}}c_{7}={\frac {a_{36}}{a_{37}}}\\&c_{8}={\frac {a_{35}\left\{\left[(R_{1}-R_{2})a_{37}-(e^{-{Mh}_{1}}-e^{-{Mh}_{2}})a_{36}\right]-\left[\left({\frac {h_{2}-h_{1}}{M^{2}}}\right)\left(a_{34}\right)\left(a_{37}\right)\right]\right\}}{\left(a_{14}\right)\left(a_{35}\right)\left(a_{37}\right)}}\\&C_{8}={\frac {a_{38}}{a_{39}}}\\&C_{6}={\frac {\left\{\left[\left(a_{35}\right)\left(a_{37}\right)\right]\left[e^{{Mh}_{1}}\left(a_{35}\right)-\left(a_{34}\right)\right]\right\}+\left\{\left[\left(a_{35}\right)\left(a_{39}\right)\right]\left[a_{36}-R_{1}M^{2}\left(a_{37}\right)\right]\right\}}{\left(a_{35}\right)\left(a_{37}\right)\left(a_{39}\right)}}\end{array}}$

The Pressure rise ${\textstyle \Delta p}$ in terms of the flow rate Q is given as

$\Delta p={\int }_{0}^{1}\left({\frac {dp}{dx}}\right)dx={\int }_{0}^{1}\left[c_{5}\left(x\right)\right]dx=$${\int }_{0}^{1}\left[{\frac {\left\{{\begin{array}{l}\left[\left(a_{11}\right)\left(M^{2}-M^{4}{\beta }^{2}\right)\right]+\left[s_{1}\left(a_{12}\right){\left(M-M^{2}\beta \right)}^{2}\right]\\-\left[\left(R_{1}-R_{2}\right)\left(a_{13}\right){\left(M+M^{2}\beta \right)}^{3}\right]+\left[\left(R_{1}-R_{2}\right)e^{{Mh}_{2}}\left(M+M^{2}\beta \right)(M-M^{2}\beta \right]+\left[s_{1}(a_{14}){\left(M+M^{2}\beta \right)}^{2}\right]\end{array}}\right\}}{{\frac {1}{M^{2}}}\left\{{\begin{array}{l}\left[2a_{15}{\left(M+M^{2}\beta \right)}^{2}\right]+\left[a_{16}\left(M^{2}-M^{4}{\beta }^{2}\right)\right]\\+\left[a_{17}{\left(M-M^{2}\beta \right)}^{2}\right]+\left[a_{18}\left(M+M^{2}\beta \right){\left(M-M^{2}\beta \right)}^{2}\right]+\left[a_{19}{\left(M+M^{2}\beta \right)}^{3}\right]\end{array}}\right\}}}\right]dx={\int }_{0}^{1}\left[{\frac {\left\{{\begin{array}{l}\left[\left(a_{11}\right)\left(M^{2}-M^{4}{\beta }^{2}\right)\right]+\left[s_{1}\left(a_{12}\right){\left(M-M^{2}\beta \right)}^{2}\right]\\-\left[\left(g(h_{2})-g(h_{1})\right)\left(a_{13}\right){\left(M+M^{2}\beta \right)}^{3}\right]+\left[\left(g(h_{2})-g(h_{1})\right)e^{{Mh}_{2}}\left(M+M^{2}\beta \right)(M-M^{2}\beta \right]+\\\left[s_{1}(a_{14}){\left(M+M^{2}\beta \right)}^{2}\right]\end{array}}\right\}}{{\frac {1}{M^{2}}}\left\{{\begin{array}{l}\left[2a_{15}{\left(M+M^{2}\beta \right)}^{2}\right]+\left[a_{16}\left(M^{2}-M^{4}{\beta }^{2}\right)\right]\\+\left[a_{17}{\left(M-M^{2}\beta \right)}^{2}\right]+\left[a_{18}\left(M+M^{2}\beta \right){\left(M-M^{2}\beta \right)}^{2}\right]+\left[a_{19}{\left(M+M^{2}\beta \right)}^{3}\right]\end{array}}\right\}}}\right]dx+{\int }_{0}^{1}\left[{\frac {\left(Q-1-d\right)\left[e^{{Mh}_{2}}\left(M+M^{2}\beta \right){\left(M-M^{2}\beta \right)}^{2}-\left(a_{13}\right){\left(M+M^{2}\beta \right)}^{3}\right]}{{\frac {1}{M^{2}}}\left\{{\begin{array}{l}\left[2a_{15}{\left(M+M^{2}\beta \right)}^{2}\right]+\left[a_{16}\left(M^{2}-M^{4}{\beta }^{2}\right)\right]\\+\left[a_{17}{\left(M-M^{2}\beta \right)}^{2}\right]+\left[a_{18}\left(M+M^{2}\beta \right){\left(M-M^{2}\beta \right)}^{2}\right]+\left[a_{19}{\left(M+M^{2}\beta \right)}^{3}\right]\end{array}}\right\}}}\right]dx$

(33)

where ${\textstyle F=Q-1-d}$.

4. Results and discussion

4.1. Pressure rise

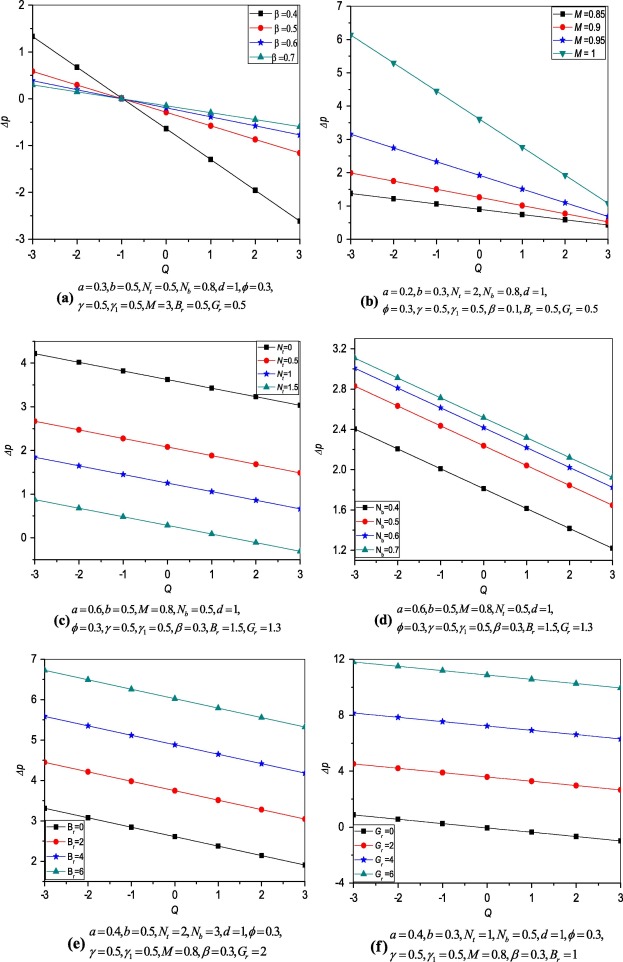
The exact expression for the pressure rise is given by Eq. (33). It is observed that from Eq. (33) the pressure rise is always a decreasing function in terms of flow rate. The variation of pressure rise with flow rate for different values of slip parameter is presented in Fig. 2(a) and it is noticed that the pressure decreases with increasing slip parameter in the pumping region ${\textstyle -1<Q<-3}$ and converse behaviour occurs for the co pumping region ${\textstyle Q>-1}$. The effect of increase in Hartmann number M on pressure rise is shown in Fig. 2(b). It is noticed that the pressure rise decreases with increasing Hartmann number M. From Fig. 2(c) it is observed that ${\textstyle \Delta p}$ decreases with increase in the values of thermophoresis parameter ${\textstyle N_{t}}$. Fig. 2(d) reveals that the pressure rise increases with increase in ${\textstyle N_{b}}$. Fig. 2(e) and (f) shows the increase in pressure rise when increase in local nanoparticle Grashof number ${\textstyle B_{r}}$ and local temperature Grashof number ${\textstyle G_{r}}$. These behaviours are similar to Kothandapani and Prakash [32].

Figure 2. Variation of pressure rise versus flow rate.

4.2. Temperature distribution

4.2.1. Temperature distribution (With slip parameters)

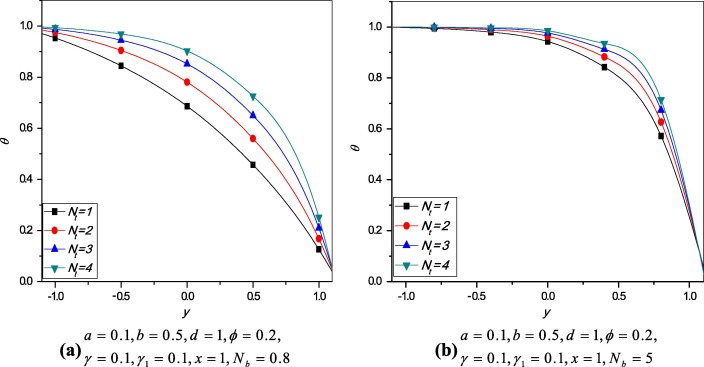
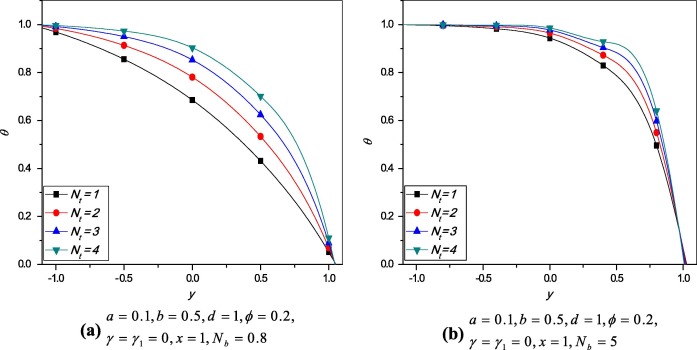
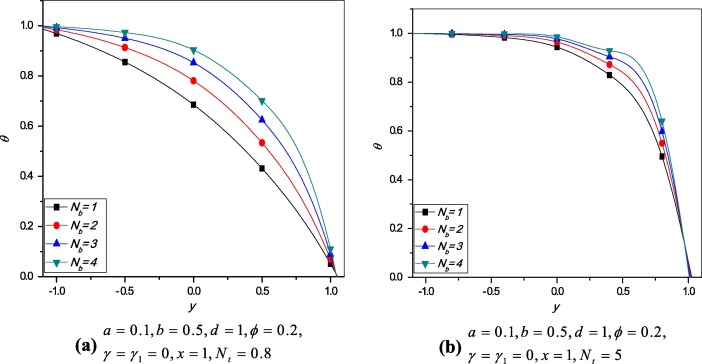
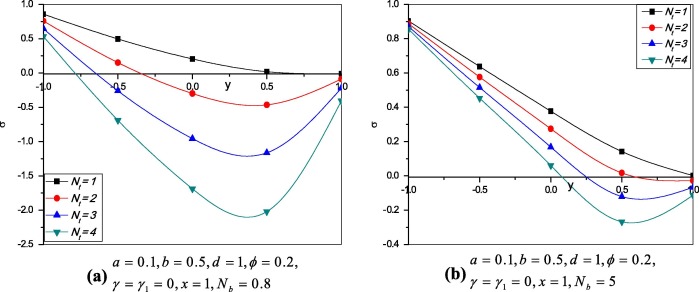
Variation of temperature profile ${\textstyle \theta }$ for different values of thermophoresis parameter ${\textstyle N_{t}}$ and Brownian motion parameter ${\textstyle N_{b}}$ is plotted. It is observed that from Figure 3 and Figure 4 the temperature profile increases when thermophoresis parameter ${\textstyle N_{t}}$ and Brownian motion parameter ${\textstyle N_{b}}$ increase.

Figure 3. Variation of temperature profile ${\textstyle \theta }$ for different values of ${\textstyle N_{t}}$.

Figure 4. Variation of temperature profile ${\textstyle \theta }$ for different values of ${\textstyle N_{b}}$.

4.2.2. Temperature distribution (without slip parameter)

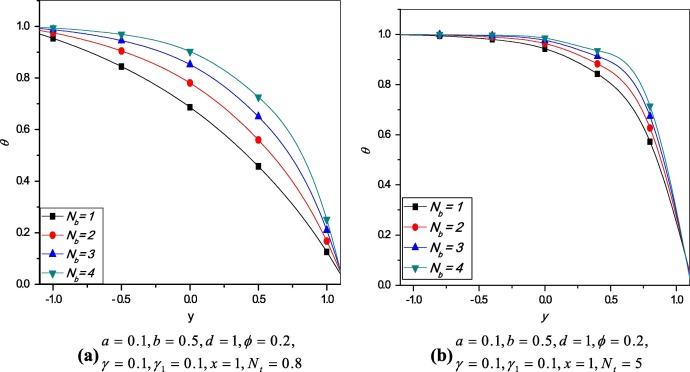
Variation of temperature profile ${\textstyle \theta }$ for different values of thermophoresis parameter ${\textstyle N_{t}}$ and Brownian motion parameter ${\textstyle N_{b}}$ is plotted for ${\textstyle \gamma ={\gamma }_{1}=0}$. The temperature distribution without thermal and concentration slip parameters is presented in Figure 5 and Figure 6. Comparing the results with previous Section 4.2.1, there are no remarkable differences observed for the effects of ${\textstyle N_{t}}$ and ${\textstyle N_{b}}$.

Figure 5. Temperature distribution ${\textstyle \theta }$ for different values of ${\textstyle N_{t}}$ (without slip parameters).

Figure 6. Variation of temperature profile ${\textstyle \theta }$ for different values of ${\textstyle N_{b}}$ (without slip parameter).

4.3. Nanoparticle concentration

4.3.1. Nanoparticle concentration (with slip parameter)

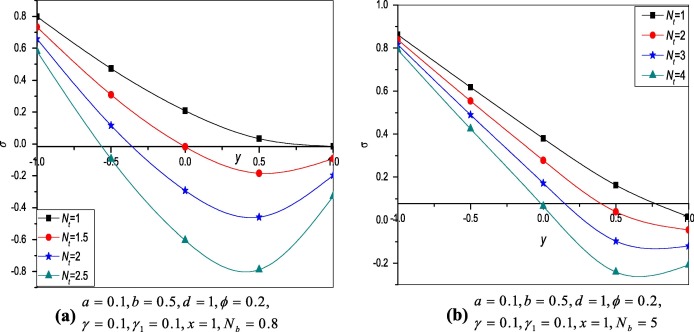
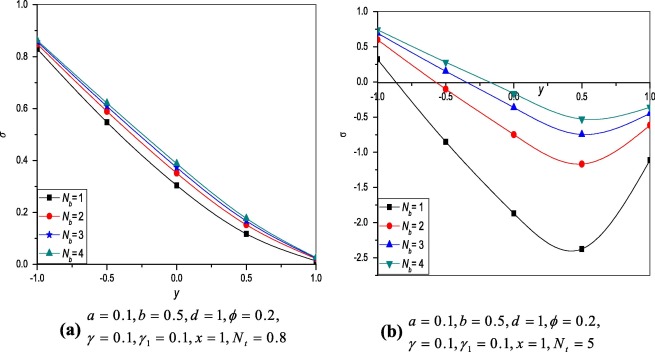
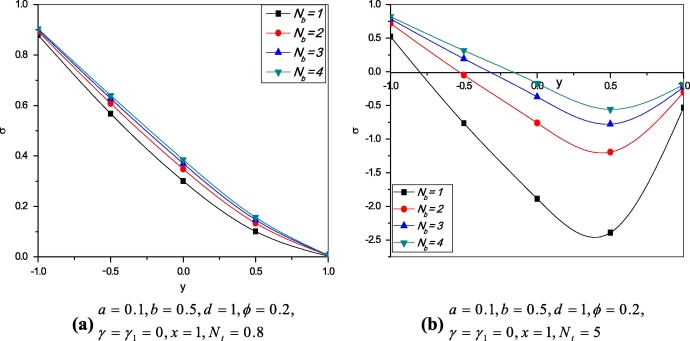
Figure 7 and Figure 8 show the effects of thermophoresis parameter ${\textstyle N_{t}}$ and Brownian motion parameter ${\textstyle N_{b}}$ on the nanoparticle concentration ${\textstyle \sigma }$. From Fig. 7 it is observed that ${\textstyle \sigma }$ decreases with increase in values of ${\textstyle N_{t}}$ and Fig. 8 shows the increase in ${\textstyle \sigma }$ as ${\textstyle N_{b}}$ increases and the results are similar to [26].

Figure 7. Variation of nanoparticle profile ${\textstyle \sigma }$ at different values of ${\textstyle N_{t}}$.

Figure 8. Variation of nanoparticle profile ${\textstyle \sigma }$ at different values of ${\textstyle N_{b}}$.

4.3.2. Nanoparticle concentration (without slip parameter)

The effects of thermophoresis parameter ${\textstyle N_{t}}$ and Brownian motion parameter ${\textstyle N_{b}}$ on the nanoparticle concentration ${\textstyle \sigma }$ are plotted for ${\textstyle \gamma ={\gamma }_{1}=0}$. The nanoparticle concentration without thermal and concentration slip parameters is presented in Figure 9 and Figure 10. The results are similar as the Section 4.3.1.

Figure 9. Variation of nanoparticle profile ${\textstyle \sigma }$ at different values of ${\textstyle N_{t}}$ (without slip parameter).

Figure 10. Variation of nanoparticle profile ${\textstyle \sigma }$ at different values of ${\textstyle N_{b}}$ (without slip parameter).

4.4. Pressure gradient

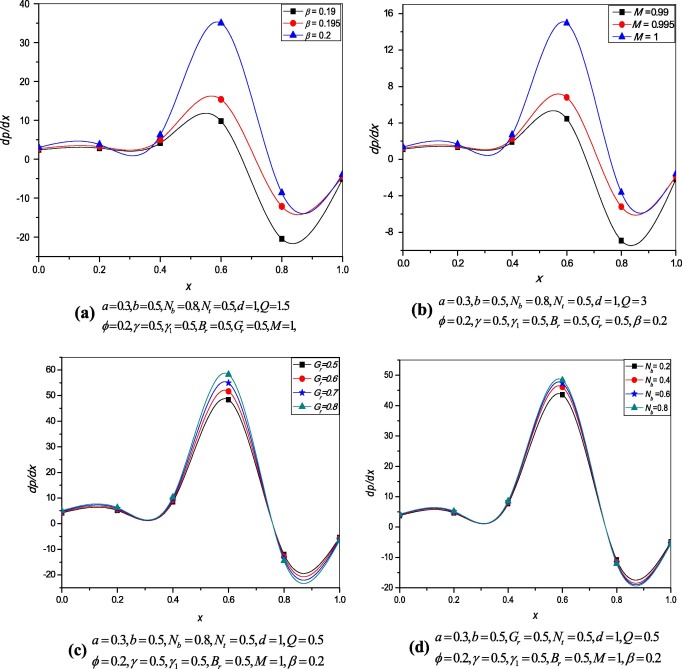
Fig. 11(a)–(d) shows the variation of pressure gradient for different values of slip parameter, Hartmann number, Grashof number and thermophoresis parameters respectively. From these figures it is observed that the pressure gradient increases with increase in ${\textstyle \beta {\mbox{,}}\quad M{\mbox{,}}\quad G_{r}}$ and ${\textstyle N_{b}}$ The small increase in ${\textstyle \beta {\mbox{,}}\quad M}$ effects the large differences in pressure gradient can be observed from Fig. 11(a) and (b) respectively and maximum pressure gradient occurs at ${\textstyle x=0.6}$ where it was ${\textstyle x=0.45}$ in [26].

Figure 11. Variation of the pressure gradient.

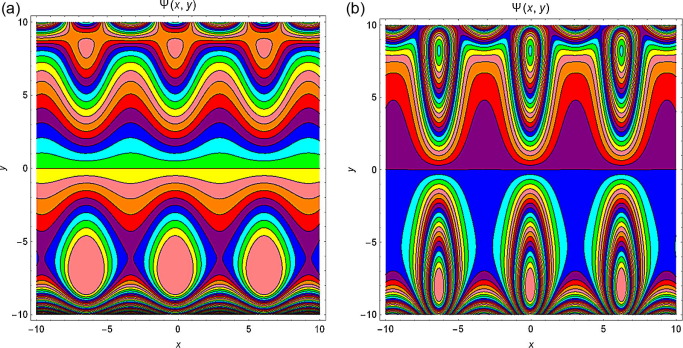
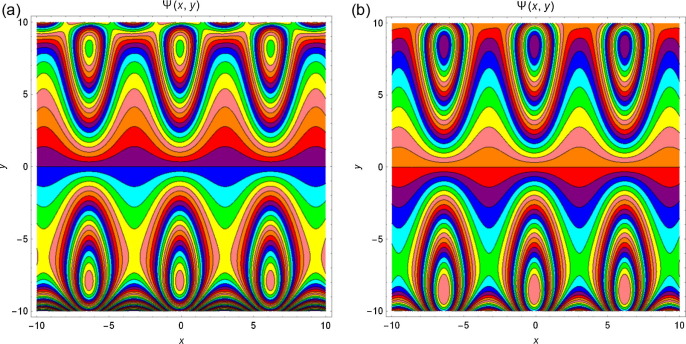
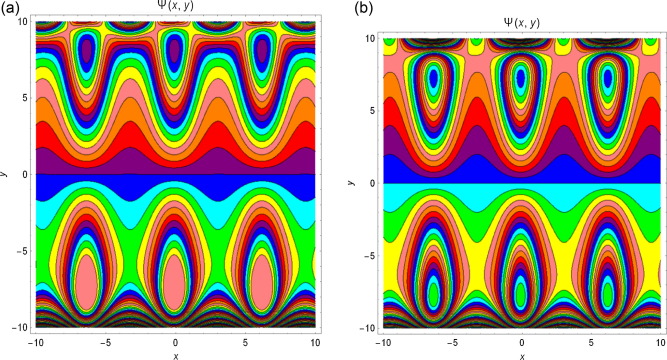
4.5. Streamlines

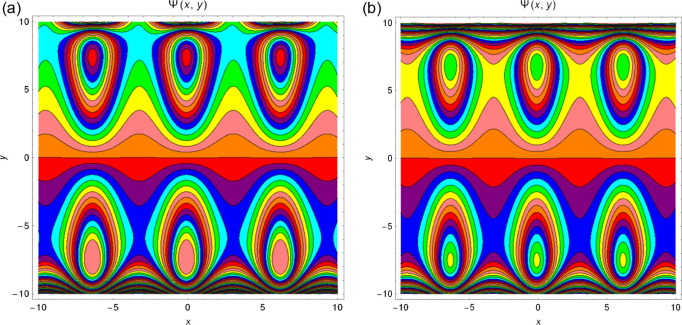
The streamlines for different values of ${\textstyle Q{\mbox{,}}\quad a{\mbox{,}}\quad \beta }$ and M are presented from Figure 12, Figure 13, Figure 14 and Figure 15. It is noticed from Fig. 12 that with increase in Q, the trapping bolus increases in the upper wall. Fig. 13 displays the influence of amplitude on both lower and upper walls, and the trapping bolus decreases with increasing amplitude. Fig. 14 reveals that the bolus increases at both walls of the channel when ${\textstyle \beta }$ increases and from Fig. 15 it is examined that the trapped bolus decreases as M increases at lower and upper walls.

Figure 12. Streamlines for ${\textstyle a=0.1{\mbox{,}}\quad d=1{\mbox{,}}\quad b=0.1{\mbox{,}}\quad \phi =}$$0.2{\mbox{,}}\quad \gamma =0.5{\mbox{,}}\quad {\gamma }_{1}=$$0.5{\mbox{,}}\quad B_{r}=2{\mbox{,}}\quad M=1{\mbox{,}}\quad G_{r}=$$0.5{\mbox{,}}\quad N_{b}=2{\mbox{,}}\quad N_{t}=2{\mbox{,}}\quad \beta =$$0.3$ and for different values of (a) ${\textstyle Q=2.5}$ and (b) ${\textstyle Q=3}$.

Figure 13. Streamlines for ${\textstyle Q=2{\mbox{,}}\quad d=1{\mbox{,}}\quad b=0.1{\mbox{,}}\quad \phi =}$$0.2{\mbox{,}}\quad \gamma =0.5{\mbox{,}}\quad {\gamma }_{1}=$$0.5{\mbox{,}}\quad B_{r}=2{\mbox{,}}\quad M=1{\mbox{,}}\quad G_{r}=$$0.5{\mbox{,}}\quad N_{b}=2{\mbox{,}}\quad N_{t}=2{\mbox{,}}\quad \beta =$$0.3$ and for different values of (a) ${\textstyle a=0}$ and (b) ${\textstyle a=0.3}$.

Figure 14. Streamlines for ${\textstyle a=0.1{\mbox{,}}\quad Q=2{\mbox{,}}\quad d=1{\mbox{,}}\quad b=}$$0.1{\mbox{,}}\quad \phi =0.2{\mbox{,}}\quad \gamma =0.5{\mbox{,}}\quad {\gamma }_{1}=$$0.5{\mbox{,}}\quad B_{r}=2{\mbox{,}}\quad M=1{\mbox{,}}\quad G_{r}=$$0.5{\mbox{,}}\quad N_{b}=2{\mbox{,}}\quad N_{t}=2$ and for different values of (a) ${\textstyle \beta =0.4}$ and (b) ${\textstyle \beta =0.6}$.

Figure 15. Streamlines for ${\textstyle a=0.1{\mbox{,}}\quad Q=2{\mbox{,}}\quad d=1{\mbox{,}}\quad b=}$$0.1{\mbox{,}}\quad \phi =0.2{\mbox{,}}\quad \gamma =0.5{\mbox{,}}\quad {\gamma }_{1}=$$0.5{\mbox{,}}\quad B_{r}=2{\mbox{,}}\quad G_{r}=0.5{\mbox{,}}\quad N_{b}=$$2{\mbox{,}}\quad N_{t}=2{\mbox{,}}\quad \beta =0.3$ and for different values of (a) ${\textstyle M=1}$ and (b) ${\textstyle M=1.1}$.

5. Conclusions

The Peristaltic transport of conducting nanofluids under the effect of slip condition in an asymmetric channel is reported in the present work. The solution of the problem is solved exactly. Both slip effect and Magnetic effect on peristaltic transport of nanofluids are examined.

• The pumping characteristics for different parameters are studied. The pressure rise decreases with increasing the parameters ${\textstyle \beta {\mbox{,}}\quad M{\mbox{,}}\quad N_{t}}$ and increases with increasing the parameters ${\textstyle N_{b}{\mbox{,}}\quad B_{r}{\mbox{,}}\quad G_{r}}$ respectively.
• It is observed the large variations in pressure gradient by small increase in slip parameter and magnetic effects.
• The temperature profile ${\textstyle \theta }$ increases with increase in ${\textstyle N_{t}}$ and ${\textstyle N_{b}}$ and similar behaviour is observed without thermal and concentration slip parameters.
• Nanoparticle concentration decreases with increasing ${\textstyle N_{t}}$ and increases with increasing ${\textstyle N_{b}}$ and the behaviour is the same when there are no thermal and concentration slip parameters.
• It is observed that the pressure gradient increases with increasing parameters ${\textstyle \beta {\mbox{,}}\quad M{\mbox{,}}\quad G_{r}}$ and ${\textstyle N_{b}^{'}}$.
• It is noticed that the size of the bolus increases with increasing parameters ${\textstyle Q{\mbox{,}}\quad \beta }$ and decreases with increasing ${\textstyle a{\mbox{,}}\quad M}$ respectively.

Acknowledgements

The authors thank the referees for their constructive comments which lead to betterment of the article.

Appendix A. 

$a_{11}=\left(s_{1}e^{{Mh}_{2}}-2s_{2}e^{{Mh}_{1}}+s_{2}e^{{Mh}_{1}}e^{2{Mh}_{2}}\right)$

$a_{12}=\left(e^{{Mh}_{2}}-e^{{Mh}_{1}}e^{2{Mh}_{2}}+{\frac {e^{2{Mh}_{2}}}{e^{{Mh}_{1}}}}\right)$

$a_{13}=\left({\frac {e^{2{mh}_{1}}}{2}}\right)$

$a_{14}=(e^{{Mh}_{1}}-e^{{Mh}_{2}})$

$a_{15}=\left(e^{{Mh}_{1}}-{\frac {e^{2{Mh}_{1}}}{e^{{Mh}_{2}}}}\right)$

$a_{16}=\left(2e^{{Mh}_{1}}-e^{2{Mh}_{1}}e^{{Mh}_{2}}-e^{{Mh}_{2}}\right)$

$a_{17}=\left(e^{{Mh}_{1}}e^{2{Mh}_{2}}-{\frac {e^{2{Mh}_{2}}}{e^{{Mh}_{1}}}}\right)$

$a_{18}=e^{{Mh}_{2}}\left(h_{2}-h_{1}\right)$

$a_{19}=\left(h_{2}-h_{1}\right){\frac {e^{2{Mh}_{1}}}{e^{{Mh}_{2}}}}$

${\begin{array}{l}a_{20}=\left(R_{1}-R_{2}\right)e^{{Mh}_{1}}(M+M^{2}\beta )\\a_{21}=s_{1}(e^{{Mh}_{1}}-e^{{Mh}_{2}})\\a_{22}=\left(e^{{Mh}_{1}}\right)(M+M^{2}\beta )-\left(e^{{Mh}_{2}}\right)(M-M^{2}\beta )\\a_{23}=\left(1-{\frac {e^{{Mh}_{1}}}{e^{{Mh}_{2}}}}\right)(M+M^{2}\beta )+\left(1-{\frac {e^{{Mh}_{2}}}{e^{{Mh}_{1}}}}\right)(M-M^{2}\beta )\\a_{24}=\left(h_{2}-h_{1}\right)e^{{Mh}_{1}}(M+M^{2}\beta )+(e^{{Mh}_{1}}-e^{{Mh}_{2}})\\a_{25}=\left({\frac {e^{{Mh}_{1}}}{e^{{Mh}_{2}}}}{\left(M+M^{2}\beta \right)}^{2}-{\frac {e^{{Mh}_{2}}}{e^{{Mh}_{1}}}}{\left(M-M^{2}\beta \right)}^{2}\right)\\a_{26}=\left(s_{1}e^{{Mh}_{1}}(M-M^{2}\beta )-s_{2}e^{{Mh}_{1}}(M+M^{2}\beta )\right)\\a_{27}=\left(R_{1}-R_{2}\right)e^{{Mh}_{1}}\\a_{28}=\left({\frac {e^{{Mh}_{1}}}{e^{{Mh}_{2}}}}{\left(M+M^{2}\beta \right)}^{2}-{\frac {e^{{Mh}_{2}}}{e^{{Mh}_{1}}}}(M-M^{2}\beta )\right)\end{array}}$

${\begin{array}{l}a_{29}=\left[\left({\frac {h_{2}-h_{1}}{M^{2}}}\right)e^{{Mh}_{1}}(M+M^{2}\beta )+{\frac {1}{M^{2}}}(e^{{Mh}_{1}}-e^{{Mh}_{2}})\right]\\a_{30}=e^{{Mh}_{1}}\left(e^{-{Mh}_{1}}-e^{-{Mh}_{2}}\right)(M+M^{2}\beta )\\a_{31}=e^{-{Mh}_{1}}\left(e^{{Mh}_{1}}-e^{{Mh}_{2}}\right)(-M+M^{2}\beta )\end{array}}$

${\begin{array}{l}a_{32}=\left(\left(h_{2}-h_{1}\right)e^{{Mh}_{1}}(M+M^{2}\beta )+(e^{{Mh}_{1}}-e^{{Mh}_{2}})\right)\\a_{33}=\left({\frac {e^{{Mh}_{1}}}{e^{{Mh}_{2}}}}{\left(M+M^{2}\beta \right)}^{2}-{\frac {e^{{Mh}_{2}}}{e^{{Mh}_{1}}}}{\left(M-M^{2}\beta \right)}^{2}\right)\end{array}}$

$a_{34}=\left\{{\begin{array}{l}\left[\left(a_{11}\right)\left(M^{2}-M^{4}{\beta }^{2}\right)\right]+\left[s_{1}\left(a_{12}\right){\left(M-M^{2}\beta \right)}^{2}\right]-\left[\left(R_{1}-R_{2}\right)\left(a_{13}\right){\left(M+M^{2}\beta \right)}^{3}\right]+\left[\left(R_{1}-R_{2}\right)e^{{Mh}_{2}}\left(M+M^{2}\beta \right)(M-M^{2}\beta \right]+\left[s_{1}(a_{14}){\left(M+M^{2}\beta \right)}^{2}\right]\end{array}}\right\}$

$a_{35}={\frac {1}{M^{2}}}\left\{{\begin{array}{l}\left[2a_{15}{\left(M+M^{2}\beta \right)}^{2}\right]+\left[a_{16}\left(M^{2}-M^{4}{\beta }^{2}\right)\right]+\left[a_{17}{\left(M-M^{2}\beta \right)}^{2}\right]+\left[a_{18}\left(M+M^{2}\beta \right){\left(M-M^{2}\beta \right)}^{2}\right]+\left[a_{19}{\left(M+M^{2}\beta \right)}^{3}\right]\end{array}}\right\}$

$a_{36}=\left\{{\frac {1}{M^{2}}}\left[a_{20}-a_{21}\right]\left[\left(a_{22}\right)\left(a_{23}\right)-\right.\right.$$\left.\left.\left(a_{24}\right)\left(a_{25}\right)\right]-\right.$$\left.\left[\left(a_{26}\right)\left(a_{23}\right)-\right.\right.$$\left.\left.\left(a_{27}(M+M^{2}\beta )-s_{1}a_{14}\right)a_{28}\right]\left[a_{29}\right]\right\}$

$a_{37}=\left\{\left[a_{30}-a_{31}\right]{\frac {1}{M^{2}}}\left[\left(a_{22}\right)\left(a_{23}\right)-\right.\right.$$\left.\left.a_{32}\left(a_{33}\right)\right]\right\}$

$a_{38}=a_{35}\left\{\left[(R_{1}-R_{2})a_{37}-(e^{-{Mh}_{1}}-\right.\right.$$\left.\left.e^{-{Mh}_{2}})a_{36}\right]-\left[\left({\frac {h_{2}-h_{1}}{M^{2}}}\right)\left(a_{34}\right)\left(a_{37}\right)\right]\right\}$

$a_{39}=\left(a_{14}\right)\left(a_{35}\right)\left(a_{37}\right)$

References

1. [1] T.W. Latham; Fluid Motion in a Peristaltic Pump; M.Sc. Thesis Massachusetts Institute of Technology, Cambridge (1966)
2. [2] A.H. Shapiro, M.Y. Jaffrin, S.L. Weinberg; Peristaltic pumping with long Wavelengths and low Reynolds number; J. Fluid Mech., 37 (1969), pp. 799–825
3. [3] T.F. Zien, S.A. Ostrach; A long wave approximation to Peristaltic motion; J. Biomech., 3 (1970), pp. 63–75
4. [4] L.M. Srivastava, V.P. Srivastava, S.N. Sinha; Peristaltic transport of a physiological fluid: PartI: Flow in non-uniform geometry; Biorheology, 20 (1983), pp. 153–166
5. [5] R.A. Ramachandra, S. Usha; Peristaltic transport of two immiscible viscous fluids in a circular tube; J. Fluid Mech., 298 (1995), pp. 271–285
6. [6] K. Vajravelu, S. Sreenadh, V.R. Babu; Peristaltic transport of Herschel–Bulkley fluid in an inclined tube; Int. J. Non-Linear Mech., 40 (2005), pp. 83–90
7. [7] K. Vajravelu, S. Sreenadh, P. Lakshminarayana; The influence of heat transfer on Peristaltic transport of Jeffrey fluid in a vertical porous stratum; Commun. Nonlinear Sci. Numer. Simul., 16 (2011), pp. 3107–3125
8. [8] K. Vajravelu, S. Sreenadh, K. Rajinikanth, Changhoon Lee; Peristaltic transport of a Williamson fluid in asymmetric channel with permeable walls; Nonlinear Anal. Real World Appl., 13 (2012), pp. 2804–2822
9. [9] S.U.S. Choi, Jeffrey A. Eastman; Enhancing Thermal Conductivity of Fluids with Nanoparticles; ASME Publications (1995)
10. [10] S.U.S. Choi, Z.G. Zhang, W. Yu, F.E. Lockwood, E.A. Grulke; Anomalous thermal conductivity enhancement in nanotubes suspensions; Appl. Phys. Lett., 79 (2001), pp. 2252–2254
11. [11] J. Buongiorno; Connective transport in nanofluids; ASME, J. Heat Transfer, 128 (2005), pp. 240–250
12. [12] K.S. Mekheimer, Y. Abd elmaboud; The influence of heat transfer and magnetic field on Peristaltic transport of Newtonian fluid in a vertical annulus: application of an endoscope; Phys. Lett. A, 372 (2008), pp. 1657–1665
13. [13] S. Srinivas, R. Gayathri, M. Kothandapani; The influence of slip conditions, wall properties and heat transfer and on MHD peristaltic transport; Comput. Phys. Commun., 180 (2009), pp. 2115–2122
14. [14] S. Srinivas, R. Muthuraj; Peristaltic transport of a Jeffrey fluid under the effect of slip in an inclined asymmetric; Int. J. Appl. Mech., 2 (2) (2010), pp. 437–455
15. [15] N.S. Akbar, S. Nadeem; Endoscopic effects on peristaltic flow of a nanofluid; Commun. Theor. Phys., 56 (2011), pp. 761–768
16. [16] A.V. Ramana Kumari, G. Radhakrishnamacharya; Effect of slip on heat transfer to Peristaltic transport in the presence of magnetic field with wall effects; ARPN J. Eng. Appl. Sci., 6 (7) (2011), pp. 119–131
17. [17] N.S. Akbar, S. Nadeem, T. Hayat, A.A. Hendi; Peristaltic transport of a nanofluid in non-uniform tube; Heat Mass Transfer, 48 (2012), pp. 451–459
18. [18] N.S. Akbar, S. Nadeem; Peristaltic flow of a Phan-Thien–Tanner nanofluid in a diverging tube; Heat Transfer, 41 (2012), pp. 10–22
19. [19] M. Mustafa, S. Hina, T. Hayat, A. Alsaedi; Influence of wall properties on the Peristaltic flow of a nanofluid: analytic and numerical solutions; Int. J. Heat Mass Transfer, 55 (2012), pp. 4871–4877
20. [20] N.S. Akbar, S. Nadeem, T. Hayat, A.A. Hendi; Peristaltic transport of a nanofluid with slip Effects; Maccanica, 47 (2012), pp. 1283–1294
21. [21] S. Srinivas, R. Muthuraj, J. Sakina; A note on the influence of heat and mass transfer on a Peristaltic flow of a viscous fluid in a vertical asymmetric channel with wall slip; Chem. Ind. Chem. Eng. Quart., 18 (3) (2012), pp. 483–493
22. [22] S. Akram, S. Nadeem, A. Ghafoor, C. Lee; consequences of nanofluid on Peristaltic flow in an asymmetric Channel; Int. J. Basic Appl. Sci., 12 (2013), pp. 75–96
23. [23] N.S. Akbar, S. Nadeem, Changhoon Lee, Zafar Hayat Khan, Rizwan UI Haq; Numerical study of Williamson nanofluid in an asymmetric channel; Results Phys., 3 (2013), pp. 161–166
24. [24] A. Ebaid, E.H. Aly; Exact Analytical Solution of the Peristaltic Nanofluids Flow in an Asymmetric Channel with Flexible Walls and Slip Condition: Application to Cancer Treatment; Hindawi Publishing Corporation (2013)
25. [25] M. Mustafa, S. Hina, T. Hayat, A. Alsaedi; Slip effects on the Peristaltic motion of nano fluid in a channel with wall properties; ASME J. Heat Transfer, 135 (2013)
26. [26] E.H. Aly, A. Ebaid; Exact analytical solution for the peristaltic flow of nanofluids in an asymmetric channel with slip effect of the velocity, temperature and concentration; J. Mech., 30 (2014), pp. 411–422
27. [27] S. Akram, S. Nadeem; Consequence of nanofluid on peristaltic transport of a hyperbolic Tangent fluid model in the occurrence of apt (tending) magnetic field; J. Magnet. Magnet. Mater., 358 (2014), pp. 183–191
28. [28] M. Mustafa, S. Hina, T. Hayat, B. Ahmad; Influence of induced magnetic field on the Peristaltic flow of nanofluid; Maccanica, 49 (2014), pp. 521–534
29. [29] S. Hina, M. Mustafa, S. Abbasbandy, T. Hayat, A. Alsaedi; Peristaltic motion of nanofluid in a curved channel; J. Heat Transfer ASME, 136 (2014)
30. [30] Obaid Ullah Mehmood, Norzieha Mustapha, Sharidan Shafie, T. Hayat; Partial slip effect on heat and mass transfer of MHD peristaltic transport in a porous medium; Sains Malaysiana, 43 (7) (2014), pp. 1109–1118
31. [31] Tasawar Hayat, Fahad Munir Abbasi, Bashir Ahmadz, Ahmed Alsaedi; Peristaltic transport of Carreau-Yasuda fluid in a curved channel with slip effects; Plos One, 9 (4) (2014) e95070
32. [32] M. Kothandapani, J. Prakash; Effect of radiation and magnetic field on peristaltic transport of nanofluids through a porus space in a tapered asymmetric channel; J. Magnet. Magnet. Mater., 378 (2015), pp. 152–163
33. [33] M. Kothandapani, J. Prakash; The peristaltic transport of Carreau nanofluid under effect of a magnetic field in a tapered asymmetric channel: application to cancer therapy; J. Mech. Med. Biol., 15 (2015), pp. 1550030–1550062
34. [34] M. Kothandapani, J. Prakash; Effects of thermal radiation parameter and magnetic field on the peristaltic motion of Williamson nanofluids in a tapered asymmetric channel; Int. J. Heat Mass Transfer, 51 (2015), pp. 234–245
35. [35] K. Nirmala, R. Muthuraj, S. Srinivas, D. Lourdu Immaculate; Combined effects of hall current, wall slip, viscous dissipation and soret effect on MHD Jeffrey fluid flow in a vertical channel with Peristalsis; JP J. Heat Mass Transfer, 12 (2) (2015), pp. 131–165