Hemodynamic on abdominal aortic aneurysm: Parametric study

Resumen

El objetivo del presente estudio es determinar qué influencia tienen los parámetros geométricos con las tensiones hemodinámicas en aneurismas abdominales aórticos. Para ello los autores han creado varios modelos geométricos de aneurismas abdominales basándose en sus principales características geométricas (diámetro máximo, diámetro mínimo, longitud aneurisma y asimetría) y técnicas computacionales para calcular la presión y la tensión de corte en el saco aneurismático. Los resultados obtenidos constatan que la presión hemodinámica es la principal carga mecánica que actúa sobre la pared arterial y que la morfometría de los aneurismas podría ser utilizada como buen predictor del riesgo de rotura. Posteriormente, con el objetivo de determinar si los modelos geométricos se podrían usar como aproximación de modelos reales, se compararon varios modelos reales (patient-specific) con sus respectivos modelos geométricos obteniendo una buena aproximación.

Abstract

The aim of this study is to assess how the shape of the abdominal aortic aneurysms (AAA) affects the hemodynamic wall stresses. With this purpose, different AAAs are studied through simplified models based on geometrical parameters of the aneurism such as its maximum and minimum diameter, length and asymmetry. Then, a computational fluid dynamics analysis is performed on the simplified models in order to compute pressure and wall shear stresses on the aneurysm sac. The results obtained show that blood pressure is the main dynamic load acting on the artery wall, and that the morphology of the aneurysm could be a good indicator of risk of failure. Furthermore, the computational results are compared with patient-specific real models with the objective to assess the reliability of the proposed simplified approach.

Palabras clave

Aneurisma aórtico abdominal ; Tensión hemodinámica ; Tensión cortante ; Biomarcador

Keywords

Abdominal aortic aneurysm ; Hemodynamics ; Wall shear stress ; Predictors

1. Introducción

En su definición más aceptada, el aneurisma de aorta abdominal (AAA) se puede considerar como un ensanchamiento localizado, permanente y degenerativo de la pared aórtica, en la zona abdominal. En los AAA, el comportamiento del flujo sanguíneo en el saco aneurismático es un fenómeno complejo debido a la simultaneidad de los procesos que ocurren en su interior desde las escalas moleculares hasta las escalas anatómicas (geométricas). Estos fenómenos provocan modificaciones en las propiedades mecánicas de la pared arterial induciendo variaciones de la forma del aneurisma a lo largo del tiempo, lo que origina modificaciones en los patrones de flujo sanguíneo en su interior y, consecuentemente, alteraciones en la distribución de las tensiones hemodinámicas sobre la capa íntima de la pared arterial [1] , que bajo determinadas condiciones patológicas podría producir el colapso estructural de la pared, provocando su rotura [2]  and [3] .

Hoy en día se reconoce que los actuales criterios clínicos para la evaluación del riesgo de rotura de los AAA son insuficientes y a pesar de que se basan en numerosas pruebas empíricas con frecuencia suelen fallar [1]  and [4] . Debido a ello, en los últimos años investigadores y clínicos han tenido el reto de identificar nuevos criterios que permitan la predicción, con un alto grado de fiabilidad, del riesgo de rotura sobre bases personalizadas. Algunos estudios recientes [5] , [6] , [7] , [8] , [9]  and [10] han propuesto que la predicción del riesgo de rotura de AAA podría ser más objetiva a partir del enfoque biomecánico. Este enfoque establece que, a medida que el AAA crece, se produce un aumento de enzimas que van degradando la pared vascular y las células inflamatorias se van infiltrando, lo que provoca la destrucción de la capa de colágeno y elastina presente en la pared del aneurisma [14] . Este enfoque biomecánico permite, además, integrar diferentes características geométricas, estructurales y biológicas del AAA a lo largo del tiempo, lo cual permite describir cualitativamente posibles zonas de colapso del AAA. Dentro de este enfoque, se ha identificado la tensión de pared como uno de los principales factores que pueden definir y predisponer la rotura de la pared aneurismática. Las primeras predicciones para el cálculo de las tensiones de pared en aneurismas se realizaron mediante el empleo de la ley de Laplace [11] , asumiendo que la geometría del aneurisma se podría considerar como un cilindro o una esfera con un radio de curvatura único equivalente al diámetro máximo del aneurisma. Sin embargo, es bien sabido que la morfología aneurismática es muy compleja, con diferentes radios de curvaturas y formas. Algunos resultados recientes [5] , [12]  and [13] demuestran que la tensión que actúa sobre la pared íntima del aneurisma no está distribuida de forma igualitaria y no se puede calcular de modo satisfactorio mediante el uso de esta ley. Por lo tanto, realizar la predicción de la tensión de pared considerando solo el diámetro mayor del aneurisma no tiene en cuenta factores importantes de la forma superficial del aneurisma. Debido a ello, se plantean nuevos modelos de cálculo tales como los propuestos por [3] , [15] , [9] , [16]  and [17] . Sin embargo, aunque estos modelos proporcionan información sobre los factores que influyen en la distribución de la tensión sobre la pared aneurismática, muchos clínicos cuestionan su utilidad práctica por la dificultad computacional del software de dinámica de fluidos que es necesario utilizar. Por eso, el interés de las nuevas investigaciones se centra en determinar los parámetros geométricos fácilmente identificables que sean capaces de caracterizar la geometría específica del aneurisma del paciente y que a la vez se puedan usar como predictores de la tensión de pared y, por tanto, del riesgo de rotura [7] , [18] , [19]  and [20] .

El presente estudio se enmarca en el enfoque biomecánico como método más preciso para evaluar el riesgo de rotura del AAA. Su objetivo es investigar, mediante el empleo de geometrías virtuales, la influencia de la morfometría del AAA sobre las tensiones hemodinámicas en la región del saco aneurismático. Para ello se han creado 28 geometrías virtuales del AAA basadas en la combinación lineal de los principales parámetros geométricos que la caracterizan y se han determinado las correlaciones entre dichos parámetros con las tensiones de pared y la presión intraluminal. Esto nos permitirá estudiar la distribución de las tensiones hemodinámicas para diferentes tipos de aneurisma y reproducir cualquier estadio de desarrollo de esta patología. Posteriormente, se comprarán modelos reales del AAA en diferentes estadios con modelos virtuales, con el objetivo de determinar si estos modelos se podrían usar como aproximación de los modelos reales. Esto permitirá al clínico identificar rápidamente el tipo de aneurisma de un paciente y localizar las zonas de riesgo de rotura. Los resultados constituirán la base para un estudio más profundo con geometrías reales y parámetros geométricos basados en la forma de la línea media de la luz.

2. Métodos

2.1. Geometría del aneurisma de aorta abdominal

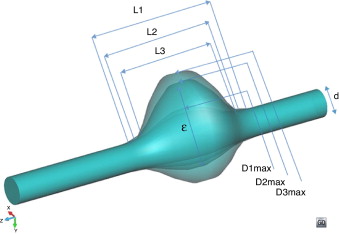
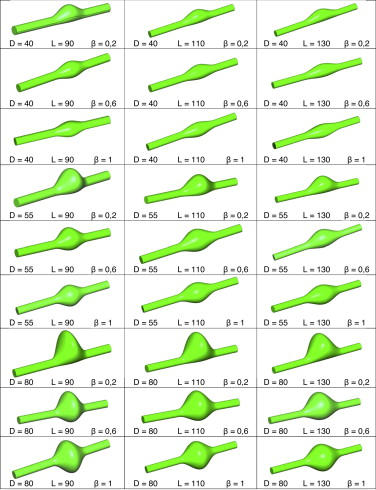
En base a la parametrización descrita en [19] se crearon 28 modelos virtuales basados en la combinación lineal de los 3 parámetros geométricos más representativos que definen un aneurisma (diámetro máximo del aneurisma [D ], longitud del aneurisma [L ], asimetría [β ]), donde D toma los valores de 40, 55 y 80 mm, L los valores de 90, 110 y 130 mm, y β 1, 0,6 y 0,2. La combinación de estos parámetros geométricos permite representar las principales etapas evolutivas de un aneurisma y, consecuentemente, su posible fallo material. En el anexo 1 se muestra una representación gráfica de todos los modelos utilizados para el análisis ( fig. 11 ).

Los modelos geométricos virtuales de AAA creados (fig. 1 ) se dividen en 3 regiones distintas: la entrada, o región proximal que mide 6 cm de longitud con un diámetro constante de 2 cm; la parte central del modelo o saco aneurismático; y la parte distal (salida) que mantiene el mismo diámetro de sección (2 cm) y su longitud es de 10 cm, lo que garantiza que las condiciones de contorno aplicadas a la salida no van a ejercer influencia en los patrones de flujo en el interior del saco aneurismático. Todas las secciones de cada una de las regiones son circulares y perpendiculares al eje Z de la geometría.

Figura 1. Representación esquemática de las geometrías virtuales variando el diámetro (D ), la longitud (L ) y la excentricidad del AAA.

El saco aneurismático se ha caracterizado por su longitud (L ) y un diámetro variable entre un mínimo d (arteria sana) y un diámetro máximo (D ) variable. La asimetría del modelo se describe a través del parámetro excentricidad del aneurisma, a partir de la línea central de la luz (β ) (ecuación 1a). De esta manera, β  = 1,0 indica una completa simetría del aneurisma. El factor que determina la relación entre la longitud (L ) y el diámetro (D ) del saco del AAA se define como índice de dilatación (γ ) (ecuación 1b). Algunos estudios clínicos indican que cuanto menor es el índice de dilatación tanto mayor es la posibilidad de rotura del AAA. Si el índice de dilatación es aproximadamente 1, el aneurisma es esférico, mientras que si es aproximadamente 0 el aneurisma se conoce como fusiforme.

La tasa de deformación (χ ) (ecuación 1 c) es el ratio entre el valor del diámetro sano no deformado (d ) y el valor máximo del diámetro deformado del aneurisma D .

$\beta ={\frac {d}{D}},{\mbox{ }}\gamma ={\frac {D}{L}},{\mbox{ }}\chi ={\frac {D}{d}}$

( 1a,b,c)

En los modelos parametrizados se han variado los valores del diámetro del saco del aneurisma (D ), su longitud (L ) y su simetría (β), mientras que el valor del diámetro de la aorta no deformada se ha mantenido constante (d  = 20 mm), siendo este un valor típico de una aorta abdominal sana. Los clínicos [18] describieron el criterio utilizado para seleccionar el rango de valores para generar los diferentes modelos considerando valores fisiológicos y patológicos comunes en esta enfermedad. El diámetro máximo varía entre 40 mm (considerado como pequeño AAA) y 80 mm (valor superior al umbral utilizado como criterio de intervención quirúrgica y poco frecuente para la práctica clínica). Considerando las estadísticas clínicas, la longitud de los segmentos que representan el AAA se establecieron entre 90-130 mm. Los grados de asimetría varían entre 0,2 (asimetría elevada) y 1,0 (simetría). Se definió un caso de control teniendo en cuenta la geometría y las propiedades de una arteria humana sana (L  = 130 mm, β  = 1 y D  = d  = 20 mm).

2.2. Mallado, ecuaciones de gobierno y condiciones al contorno

Los modelos geométricos se generaron usando CATIA V.5R19 (Dessault Systèmes, París) y se importaron en GiD [21] . GiD es un pre y posprocesador gráfico optimizado para generar mallas computacionales, simulaciones y análisis. Para estudiar la calidad de las mallas generadas y su influencia sobre la presión y la tensión de pared (tensión cortante) se realizó un análisis de sensibilidad. Para ello se escogió el modelo con características geométricas D  = 80, L  = 90 y β  = 1, y se crearon mallas de 250.000, 500.000, 750.000, 1.000.000 y 1.250.000 elementos. Los resultados mostraron que para las simulaciones con mallas de 250.000, 500.000 y 750.000 elementos los valores medios de presión y tensión de pared tuvieron una variabilidad de 2,6 y de 12%, respectivamente. Sin embargo, para las mallas con más de 750.000 elementos, los valores obtenidos para las 2 variables en estudio no tuvieron variaciones significativas. Por lo tanto, para todos los modelos se utilizaron mallas de alrededor de un millón (± 10%) de elementos tetraédricos tridimensionales. El método utilizado de mallado fue el de Advancing Front Method [22] , que se basa en la geometría de superficie obtenida de los modelos parametrizados. Este procedimiento es ideal para estos tipos de simulaciones, ya que garantiza la formación de volúmenes tetraédricos de alta calidad para el cálculo computacional de problemas de fluido (CFD, por sus siglas en inglés).

Para resolver los cálculos CFD se utilizó Kratos [23] . Kratos es un código de elementos finitos que resuelve las ecuaciones de Navier-Stokes. En este trabajo se considera la sangre como fluido homogéneo e incompresible y newtoniano con una densidad constante de 1.060 kg/m³ a 37 °C y una viscosidad dinámica constante de 0,004 kg/(m·s) sin fuerzas externas aplicadas sobre él. Esta consideración para la sangre, cuando fluye por grandes vasos como la aorta, es aceptada en la comunidad científica. Las condiciones de contorno para la velocidad (V ) y la presión (P ) se dan a través del conjunto de ecuaciones (2). Estas son: condición de no deslizamiento en las paredes (2a), perfil de flujo con forma de paraboloide (flujo de Poiseuille) (2b), y tracción dependiente del tiempo debido a la presión intraluminal a la salida (2c).

$u=0\vert _{wall}$

( 2a)

$u_{z}=2(u(t))\left(1-\left({\frac {2r}{dr}}\right)^{2}\right);{\mbox{ }}ur=0\vert _{z=0}$

( 2b)

$\tau _{nn}={\overset {\mbox{ˆ}}{n}}\cdot p(t)l\cdot {\overset {\mbox{ˆ}}{n}}$

( 2c)

donde d_r es el radio interno de la aorta abdominal, u_r es la componente cartesiana del vector de la velocidad en la dirección Z (normal), u(t) y p(t) son las formas de onda (dependientes del tiempo) para la velocidad y la presión, τ_nn es la tracción normal respecto a la superficie, y I es la matriz identidad. Los perfiles de velocidad y de presión utilizados pertenecen a estudios anteriores. Estos perfiles reproducen fiablemente el pulso de velocidad humano en una aorta abdominal sana [24] y los valores de presión prescritos a la salida de la aorta abdominal [17] .

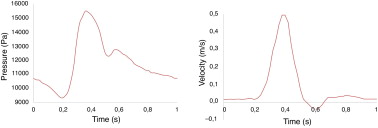
La figura 2 muestra los perfiles pulsátiles utilizados como condiciones de contorno. El número de Womersley que caracteriza este experimento en baja frecuencia, en función de la geometría y de las propiedades viscosas del fluido, es de 16,1, valor típico para el segmento aórtico. El valor del número adimensional de Reynolds es del orden de 355 (flujo no turbulento), basado en el valor medio de la velocidad y el diámetro en la sección de entrada. La onda de presión es de tipo trifásico y pulsátil, así como apropiada para el segmento en estudio, y el pico de presión máxima (sístole) se produce a 0,5 s. Para los cálculos CFD la pared se considera como una superficie impermeable y rígida (ecuación 2a) debido a que el movimiento provocado por el impacto del flujo sobre la pared podría ser despreciable, como se indica en [17] . Es importante destacar que las condiciones de contorno utilizadas en este estudio se han utilizado previamente [7]  and [19] , obteniéndose soluciones estables para simulaciones CFD. El tiempo total de CPU en un ordenador convencional (Microsoft Windows XP 32-bit PC con 4 GB-RAM, dual-core 2.83 GHz) fue aproximadamente de 5 horas para la simulación de 3 ciclos cardíacos (3 s).

Figura 2. Condiciones al contorno para las simulaciones CFD. Izquierda: pulso de velocidad a la entrada. Derecha: pulso de presión a la salida.

3. Resultados

Para cada modelo se calcularon la velocidad y la presión intraluminal en el interior del saco aneurismático, así como la tensión de corte sobre la pared del aneurisma abdominal para 3 ciclos cardíacos completos. El análisis de resultados se realizó para el tercer ciclo cardíaco, comprendido entre instantes de 2-3 s, comprobándose que los resultados eran independientes de las condiciones de contorno impuestas.

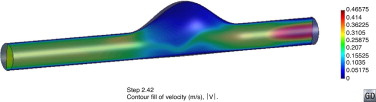
La figura 3 representa la velocidad en el momento de máxima sístole en el tercer ciclo cardíaco para un corte transversal de un modelo de AAA. Se observa el perfil parabólico (ecuación 2b) impuesto como condición de contorno y cómo el flujo está totalmente desarrollado en la parte proximal del aneurisma. Del mismo modo, la presión impuesta en la parte distal del aneurisma (ecuación 2c) está lo suficientemente alejada del saco aneurismático con el objetivo de evitar los efectos de reflexión de ondas de presión.

Figura 3. Visualización del campo de velocidades de una sección transversal de un modelo de AAA.

Los valores de la tensión cortante y de la presión intraluminal se normalizaron en relación con el caso de control, que se corresponde con el modelo de la arteria sana para, posteriormente, correlacionarlas con los parámetros geométricos (longitud y diámetro del aneurisma) y los factores biomecánicos geométricos (FBG) (asimetría, índice de deformación, tasa de deformación) del AAA con el objetivo de definir la relación existente entre ellos.

Con el fin de obtener la correlación entre las tensiones hemodinámicas y las variables geométricas en los 28 modelos de AAA, se llevó a cabo un análisis de correlación entre las variables. Los resultados indicaron que los máximos valores de tensión cortante varían entre 1,355 y 0,926 Pa (1,118 ± 0,18 Pa) y los picos de presión varían desde 15.698 hasta 15.607 Pa (15.615,3 ± 12,7 Pa). El estudio estadístico fue realizado con el código comercial Minitab 15.0 (Minitab Inc).

3.1. Tensión cortante versus diámetro y longitud

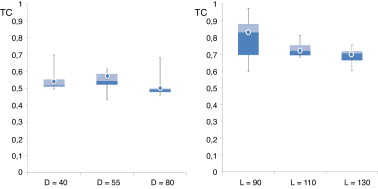
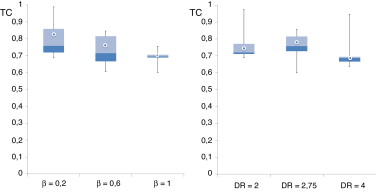
A continuación se muestran los resultados obtenidos para el valor máximo de tensión de cortante (TC) –normalizado respecto al caso de referencia– alcanzado en cada AAA en relación con el diámetro máximo y la longitud del aneurisma para el momento sistólico máximo. Las siguientes gráficas (fig. 4 ) muestran la relación entre los valores de tensión de corte de pared (normalizados respecto al caso de referencia), respecto al diámetro máximo del aneurisma (fig. 4 , izquierda) y a la longitud del aneurisma (fig. 4 , derecha). Se observa que tanto para el diámetro como para la longitud analizadas las muestras son simétricas. También es posible observar cómo a medida que aumentan la longitud y el diámetro del AAA, el rango intercuartílico se reduce, lo que equivale a decir que los valores de la tensión cortante se encuentran muy cercanos a la media, indicando una menor variabilidad de los valores de TC.

Figura 4. Relación entre el valor máximo de TC y el diámetro máximo para D  = 40, D  = 55 y D  = 80 (izquierda). Relación entre el valor máximo de TC y la longitud máxima L  = 90, L  = 110 y L  = 130 (derecha). Todos los valores están normalizados respecto al caso de referencia y expresados sobre la misma escala.

Basándonos en los resultados alcanzados, se observa que existe una correlación negativa significativa a menos del 10% entre la tensión cortante y la longitud del AAA (L ), indicando una ligera tendencia a que los aumentos en el valor de L están asociados a una disminución de la TC.

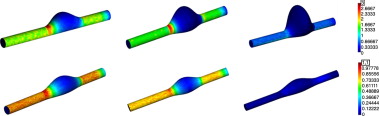
La figura 5 muestra la distribución espacial de la tensión cortante para diferentes modelos de AAA en el momento sistólico máximo. La primera fila muestra la relación entre el máximo valor de TC, para una longitud constante de aneurisma de L  = 90 mm, y diámetro máximo del aneurisma variable de entre D  = 40 mm, D  = 55 mm, D  = 80 mm (de izquierda a derecha). La segunda fila muestra la relación entre el máximo valor de TC, para un diámetro constante de aneurisma de D  = 40 mm, y longitud variable del aneurisma de entre L  = 90 mm, L  = 110 mm, L  = 130 mm (de izquierda a derecha). Se observa cómo los máximos valores de TC se acumulan en la zona distal del aneurisma. Estas zonas clínicamente son una de las más propensas a la rotura.

Figura 5. Distribución superficial del valor máximo de la TC para una longitud constante de L =90 mm y diámetro variable (fila superior), y longitud del AAA variable y diámetro máximo constante de D  = 40 mm (fila inferior). Todos los valores están normalizados respecto al caso de referencia y expresados en la misma escala.

3.2. Tensión cortante versus factores biomecánicos geométricos

La figura 6 muestra los valores de la tensión de corte de pared máxima (normalizada respecto al caso de referencia) para los diferentes casos de AAA estudiados en relación con la asimetría (β ) y la tasa de deformación (χ ) para el momento sistólico máximo. La figura 6 (izquierda) muestra la relación entre los valores de tensión de pared respecto a la asimetría del aneurisma y la figura 6 (derecha) respecto a la tasa de deformación del aneurisma. Se observa que las muestras son simétricas tanto para la asimetría como para la tasa de deformación, lo que demuestra la tendencia de que a medida que aumenta la asimetría y la tasa de deformación del AAA el rango intercuartílico se reduce, lo que es equivalente a plantear que los valores de TC se concentran sobre una zona del AAA con menor variabilidad.

Figura 6. Relación entre el valor máximo de TC y la asimetría β  = 0,2, β  = 0,6 y β  = 1 (izquierda). Relación entre el valor máximo de TC y la tasa de deformación χ  = 90, χ  = 110 y χ  = 130 (derecha). Todos los valores están normalizados respecto al caso de referencia y expresados sobre la misma escala.

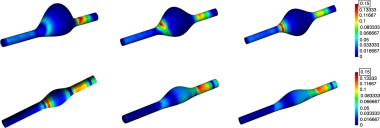
La figura 7 muestra la distribución espacial de la tensión cortante para diferentes modelos de AAA en el momento sistólico máximo. La fila superior muestra la relación entre el máximo valor de TC, para una longitud constante de aneurisma de L  = 130 mm y diámetro máximo del aneurisma de D  = 80 mm, y la asimetría del aneurisma de β  = 0,2, β  = 0,6 y β  = 1 (de izquierda a derecha). La segunda inferior muestra la relación entre el máximo valor de TC y diferentes índices de deformación: χ  = 0,44 (L  = 40 mm, D  = 90 mm), χ  = 0,36 (L  = 40 mm, D  = 110 mm) y χ  = 0,31 (L  = 40 mm, D  = 130 mm).

Figura 7. Distribución superficial del valor máximo de la TC para una longitud constante de L  = 130 mm y D  = 80 mm y asimetría variable (fila superior), y para diferentes tasas de deformación (fila inferior). Todos los valores están normalizados respecto al caso de referencia y expresados en la misma escala.

Las Figura 5  and Figura 6 muestran, además, que las paredes del aneurisma están expuestas a TC de baja intensidad durante el ciclo cardíaco excepto por las zonas proximal y distal, donde las tensiones cortantes alcanzan valores elevados durante la fase de sístole. Estos resultados concuerdan con los valores registrados en los patrones de flujo de las mismas regiones. Los cambios en las distribuciones de TC son igualmente dependientes del tiempo. En general, este comportamiento de las TC puede causar lesiones degenerativas en las paredes del aneurisma, alterando el espesor de la pared del vaso así como sus propiedades mecánicas, provocando el aumento del riesgo de rotura. Se puede notar cómo la longitud, justo por delante de la asimetría, resulta ser el factor que de manera más importante influye sobre la TC en los casos estudiados.

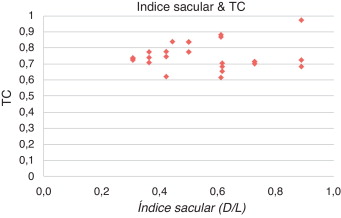
La figura 8 muestra la relación entre el índice de dilatación del AAA y el máximo valor de la tensión cortante alcanzada en el AAA. Los valores han sido normalizados respecto al caso de referencia y los resultados muestran que no existe correlación entre estas 2 variables.

Figura 8. Relación entre el valor máximo de TC y el índice de dilatación (γ = D /L ).

3.3. Presión versus parámetros geométricos del aneurisma

Con el objetivo de estudiar cómo los factores geométricos afectan a la presión, se define la presión media para cada i-nodo de todo el dominio analizado (ecuación 3).

${\overline {P_{i}}}={\frac {1}{T}}\sum _{t=2s}^{t=3s}P_{i,t}{\mbox{ }}para{\mbox{ }}cada{\mbox{ }}i{\mbox{ }}nodo$

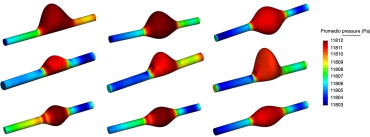
Esta presión nos indica la presión arterial media a la que está sometida la capa íntima del aneurisma. La figura 9 muestra los valores de la presión media (normalizada respecto al caso de referencia) para los diferentes modelos de AAA. La fila superior muestra la relación entre el promedio de presión calculado a lo largo del último ciclo de simulación, para una longitud constante de aneurisma de L  = 130 mm, un diámetro máximo de D  = 80 mm y una asimetría de β  = 0,2, β  = 0,6 y β  = 1 (de izquierda a derecha). La fila central muestra la relación entre la presión media y diferentes diámetros del aneurisma considerando una longitud constante del vaso de L  = 90 mm, una asimetría de β  = 0,2 y una variación del diámetro de izquierda a derecha de D  = 40 mm, D  = 55 mm y D  = 80 mm. La fila inferior muestra la relación de presión media y diferentes longitudes considerando el diámetro constante D = 55 mm, β  = 1 y una variación de la longitud de izquierda a derecha de L  = 90 mm, L  = 110 mm y L  = 130 mm.

Figura 9. Distribución superficial del valor medio de presión respecto a la asimetría para una longitud constante de L  = 130 mm y D  = 80 mm (fila superior), respecto al diámetro considerando L = 90 mm y β  = 0,2 (fila central) y respecto a la longitud considerando D  = 55 mm y β  = 1 (fila inferior). Todos los valores están normalizados respecto al caso de referencia y expresados en la misma escala.

Se puede observar cómo la distribución de las presiones medias en el saco aneurismático permanece casi constante, alrededor de 11,8 kPa para todos los casos. En la zona del cuello distal de los aneurismas se observa un incremento de los valores característicos de la presión media de pared, en los modelos en los que la tasa de deformación es alta, mientras que en el caso contrario las presiones se muestran más uniformes en todo el aneurisma. Los aneurismas que tienen forma esférica (el índice de dilatación es 1 aproximadamente y la asimetría es igual a 1) las máximas presiones se localizan en el anillo o en la parte central del aneurisma. Los cambios en la distribución de la presión de pared son también dependientes del tiempo con patrones similares en diferentes puntos de la pared y con una distribución que tiende a seguir la onda pulsátil. Los mayores gradientes de presión se obtienen durante la aceleración sistólica. Debido a esto, el flujo permanece laminar sin separarse de la pared del saco aneurismático y los mayores gradientes adversos de presión de pared se obtienen durante la desaceleración sistólica tardía casi al inicio del periodo de flujo reverso.

3.4. Comparación del modelo virtual y el caso real

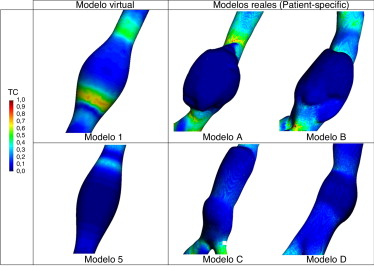
La figura 10 compara la distribución de tensiones de corte sobre la pared aneurismática obtenida en 4 modelos reales (patient-specific ) de aneurismas abdominales con sus modelos virtuales equivalentes. Aunque, las condiciones de contorno utilizadas para los modelos reales [25]  and [26] y el virtual fueron diferentes, los valores de tensión de corte se normalizaron entre 1 (máximo) y 0 (mínimo) para poder comparar las áreas de máxima y mínima influencia. Se observa cómo las zonas en las que se producen los máximos relativos de tensión de corte de los modelos virtuales coinciden de manera cualitativa con los modelos reales. Las características de los modelos virtuales y de los modelos reconstruidos a partir de imágenes médicas de pacientes reales con aneurismas se indican a continuación: fila superior: modelo 1 (virtual) D  = 40, d  = 20 y β  = 0,2; modelo A (real) (D  = 42,96, d  = 20,9 y β  = 0,22) y modelo B (real) (D  = 41,39 d  = 24,53 β  = 0,232). Fila inferior: modelo 5 (virtual) D  = 40, d  = 20 y β  = 0,2; modelo C (real) (D  = 34,82, d  = 20,88 y β  = 0,38); modelo D (real) (D  = 33,51, d  = 20,53, β  = 0,27).

Figura 10. Distribución superficial de la tensión de cortes para AAA virtuales y reconstruidos.

4. Conclusión

El presente trabajo constituye un estudio numérico de 28 AAA virtuales cuyo objetivo es obtener información que permita una mejor comprensión de cómo los aspectos hemodinámicos en el interior del saco aneurismático y la morfometría de los AAA están asociados al riesgo de rotura. También se han comparado los resultados obtenidos entre modelos reales de AAA con su modelo virtual equivalente con el objetivo de determinar si las áreas de máximas tensiones son coincidentes.

De acuerdo con los resultados obtenidos, se han podido confirmar estudios previos que destacan que la morfometría del aneurisma es un factor clave en su evolución y comportamiento. Dependiendo de la forma del aneurisma se desarrollan regiones de recirculación que causan distribuciones locales y temporales de las tensiones hemodinámicas (presión intraluminal y tensión cortante de pared) sobre la pared del aneurisma; estas, a su vez, pueden desencadenar la rotura del aneurisma en función de dónde se produzcan. En aneurismas simétricos se observó que las zonas de máxima tensión de corte eran las zonas proximales y distales del saco aneurismático. Del mismo modo, se observa que existe una relación directa entre la presión intraluminal y los índices de dilatación y la tasa de deformación; además, se comprueba que dicha presión es la tensión mecánica predominante y la primera causa de rotura del aneurisma, por encima de la tensión de corte que actúa sobre la pared. Estos resultados demuestran cómo las cargas hemodinámicas obtenidas se ven afectadas por los diferentes factores geométricos del aneurisma. Por lo tanto la zona de riesgo de colapso del aneurisma no solamente está relacionada con el diámetro máximo del aneurisma, sino que depende de otros factores, tales como la simetría, la tasa de deformación o la presión interna, entre otros. Los resultados obtenidos están en concordancia con estudios previos [8] , [9] , [27]  and [28] .

También se ha realizado un análisis comparativo de diferentes AAA reales y de sus modelos virtuales equivalentes, pudiendo identificar que las áreas donde se producen las máximas tensiones de corte de la pared coinciden de manera cualitativa entre ambos. Este resultado nos indica que los cínicos podrían utilizar los modelos virtuales para identificar las zonas de máximo riesgo de rotura de un aneurisma. Estos podrían obtener los principales parámetros geométricos de un AAA (diámetro, longitud y asimetría) con base en una imagen médica, y con ayuda de su modelo virtual equivalente determinarían de manera cualitativa las áreas críticas de dicho aneurisma. Esta información la podrían utilizar a la hora de predecir cómo va a evolucionar el aneurisma y cómo ayuda a la hora de tomar una mejor decisión clínica. Con el objetivo de tener una morfología de AAA más amplia, en futuros estudios se incluirán nuevos factores geométricos basados en la línea media de la luz tales como la tortuosidad, la curvatura y la torsión del aneurisma.

Anexo 1. 

Figura 11. Representación esquemática de todos los modelos de AAA analizados. Diámetro máximo del aneurisma (D ), longitud del aneurisma (L ) y asimetría (β ).

Bibliografía

1. [1] D.A. Vorp; Biomechanics of abdominal aortic aneurysm; J Biomech., 40 (2007), pp. 1887–1902
2. [2] A.V. Salsac, S.R. Sparks, J.M. Chomaz, J.C. Lasheras; Evolution of the wall shear stresses during the progressive enlargement of symmetric abdominal aortic aneurysms; J. Fluid Mech, 560 (2006), pp. 19–51
3. [3] C.M. Scotti, E.A. Finol; Compliant biomechanics of abdominal aortic aneurysm: A fluid-structural interaction study; Computer and Structures, 85 (2007), pp. 1097–1113
4. [4] S.C. Nicholls, J.B. Gardner, M.H. Meissner, H.K. Johansen; Rupture in small abdominal aortic aneurysms; J Vasc Surg, 28 (5) (1998), p. 884
5. [5] F. Inzoli, F. Boschetti, M. Zappa, T. Longo, R. Fumero; Biomechanical factors in abdominal aortic aneurysm rupture; Eur J Vasc Surg., 7 (1993), pp. 667–674
6. [6] D.H.J. Wang, M.S. Makaroun, M.W. Webster, D.A. Vorp; Effect of intraluminal thrombus on wall stress in patient specific models of abdominal aortic aneurysm; J Vasc Surg., I36 (2002), pp. 598–604
7. [7] G. Guillermo, F. Nieto, E. San Norberto et al. “Biomechanical approach to improve the abdominal aortic aneurysm rupture risk prediction” Aneurysm. Edited by Yasuo Murai. http://dx.doi.org/10.5772.312
8. [8] D.A. Vorp, M.L. Raghavan, M.W. Webster; Mechanical wall stress in abdominal aortic aneurysm: Influence of diameter and asymmetry; J Vasc Surg, 27 (4) (1998), pp. 632–639 doi: 10.1016/S0741-5214(98)70227-7
9. [9] T.C. Gasser, M. Auer, F. Labruto, J. Swedenborg, J. Roy; Biomechanical rupture risk assessment of abdominal aortic aneurysms: Model complexity versus predictability of finite element simulations; Eur J Vasc Endovasc Surg., 40 (2010), pp. 176–185
10. [10] J.M. Goicolea; Factores biomecánicos y su influencia en la función cardiovascular; Rev Esp Cardiol., 58 (2) (2005), pp. 121–125
11. [11] J.D. Humphrey; Cardiovascular solid mechanics. Cells, tissues and organs; Springer-Verlag, New York, NY (2002)
12. [12] M.L. Raghavan, D.A. Vorp, M.P. Federle, M.S. Makaroun, M.W. Webster; Wall stress distribution on three-dimensionally reconstructed models of human abdominal aortic aneurysm; J Vasc Surg., 31 (2000), pp. 760–769
13. [13] D.A. Vorp, M.L. Raghavan, M.W. Webster; Mechanical wall stress in abdominal aortic aneurysm: Influence of diameter and asymmetry; J Vasc Surg., 27 (1998), p. 27
14. [14] W.R. Mower, W.J. Quinones, S.S. Gambhir; Effect of intraluminal thrombus on abdominal aortic aneurysm wall stress; J Vasc Surg., 26 (1997), pp. 602–608
15. [15] K. Ouriel, R.M. Green, C. Donayre, C.K. Shortell, J. Elliott, J.A. Deweese; An evaluation of new methods of expressing aortic aneurysm size: Relationship to rupture; J Vasc Surg, 15 (1992), pp. 12–20
16. [16] C.M. Scotti, A.D. Shkolnik, S.C. Muluk, E.A. Finol; Fluid-structure interaction in abdominal aortic aneurysms: Effects of asymmetry and wall thickness; BioMedical Engineering OnLine, 4 (2005), p. 64 doi:10.1186/1475-925X-4-64
17. [17] Y. Papaharilaou, J.A. Ekaterinaris, E. Manousaki, A.N. Katsamouris; A decoupled fluid structure approach for estimating wall stress in abdominal aortic aneurysm; J. Biomech., 40 (2) (2007), pp. 367–377
18. [18] C. Vaquero; Factores geométricos y su incidencia en Aneurismas de Aorta Abdominal; Estudio preliminar. Reporte interno 33/09 del Hospital Clínico de Valladolid (2009)
19. [19] E. Georgakarakos, C.V. Ioannou, Y. Kamarianakis, Y. Papaharilaou, T. Kostas, E. Manousaki, et al.; The role of geometric parameters in the prediction of abdominal aortic aneurysm Wall stress; Eur. J. Vasc. Endovasc. Surg., 39 (1) (2010), pp. 42–48
20. [20] J. Shum, G. Martufi, E. Martino, C.B. Washington, J. Grisafi, S.C. Muluk, et al.; Quantitative assessment of abdominal aortic aneurysm geometry; Ann Biomed Eng., 39 (1) (2011), pp. 277–286
21. [21] GiD. The personal pre and postprocessor. CIMNE.
22. [22] R. Löhner. A Parallel Advancing Front Grid Generation Scheme; AIAA -00-1005 (2000).
23. [23] P. Dadvand; R. Rossi, E. Oñate. “An object-oriented environment for developing finite element codes for multi-disciplinary applications. Archives of computational methods in engineering. 17-3, pp. 253.297.09/201. ISSN 1134-3060
24. [24] H.L. Goldsmith, G.R. Cokelet, P. Gaehtgens, Robin Fåhraeus: evolution of his concepts in cardiovascular physiology, Am. J. Physiol, 257 (3 Pt 2) (1989) H1005-H1015.
25. [25] E. Soudah, E.Y.K. Ng, T.H. Loong, M. Bordone, U. Pua, S. Narayanan; CFD modelling of abdominal aortic aneurysm on hemodynamic loads using a realistic geometry with CT; Computational and Mathematical Methods in Medicine, 9 (2013), p. 472564 http://dx.doi.org/10.1155/2013/472564
26. [26] G. Vilalta, E. Soudah, J.A. Vilalta, L. Lipsa, M. Bodorne, C. Vaquero, Predicción de las tensiones hemodinámicas de Aneurisma de Aorta Abdominal en función de su morfología, Proceedings of XI Congreso Iberoamericano de Ingeniería Mecánica (2013).
27. [27] J.F. Rodríguez, C. Ruíz, M. Doblaré, G.A. Holzapfel; Mechanical stresses in abdominal aortic aneurysm: Influence of diameter, asymmetry and material anisotropy, J; Biomech. Eng., 130 (2) (2008), p. 021023
28. [28] S.S. Raut, S. Chandra, J. Shum, E.A. Finol; The role of geometric and biomechanical factors in abdominal aortic aneurysm rupture risk assessment; Department of Mechanical Engineering, Carnegie Mellon University, Pittsburgh, PA, USA (2013) Annals of biomedical engineering 03/2013. DOI: 10.1007/s10439-013-0786-6