A study of the annual performance of bifacial photovoltaic modules in the case of vertical facade integration

Abstract

Despite the apparent benefits of bifacial modules, their application still suffers from a lack of visibility on the performance gain that they can actually provide. In this work, we consider the specific application of vertically oriented bifacial modules, notably for facade integration. We have developed a methodology to evaluate the annual electrical performance of bifacial modules based on three tools. First, a double illumination characterization setup is used in a solar simulator for comparing module architectures. Then, a reduced scale outdoor test bench allows us to evaluate bifacial module performance in a variety of configurations. Finally, a ray-tracing model validated with short-term outdoor data leads to the determination of the annual performance gain. This methodology allowed us to find optimal performance according to the most important parameters of application and module. Specifically, a module architecture using half-cut cells, a parallel cell interconnection, and textured glasses have been analyzed with respect to their influence on the resistive losses which increase in dual side illumination as well as to their influence on the effect of non- uniform and diffuse irradiance on the backside of the module. This work enabled us to give directions for innovative full-size module architectures.

Context and Aim of the Study

Bifacial photovoltaic (PV) cells which are able to convert solar radiation from both sides have been developed since the 1960s, but their terrestrial application only started around the 1980s [1, 2]. Even though some modeling work is performed at the megawatt scale [3], only few large bifacial plants have been set up so far, probably due to a lack of confidence from investors in the actual gain of bifacial technology. Indeed, actual commercial energy prediction softwares do not take into account the complex opto-geometrical environment of the modules (generating non-uniform and diffuse backside albedo for instance), and the experimental tests performed so far have often been short term, at small scale or in specific configurations only. New methodologies which consider the complex opto-geometrical environment of bifacial modules are however in development in the research community [4, 5].

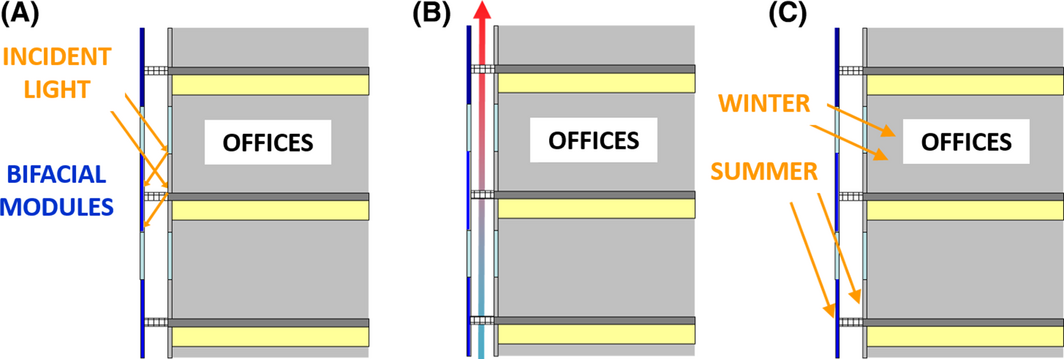
Vertical facade integration of PV modules attracts interest in the building integrated photovoltaics (BIPV) community because PV facades have a large collection area without additional footprint and their vertical installation makes them less sensitive to snow, dust, bird droppings, or tree leaves. However, they suffer from non-optimal orientation and module heating due to integration onto a wall. Using bifacial modules in a double skin configuration can minimize these drawbacks. Figure 1 shows how the gap between module and inner wall allows backside albedo and natural or forced ventilation to give additional power to the module. Additionally, there are seasonal advantages like a higher PV production and heating inside the building during winter as well as vertical sun shading during summer.

Figure 1. Advantages of using bifacial modules on a vertical facade in a double skin configuration: a backside albedo (A), natural or forced ventilation (B), and seasonal advantages (C).

The aim of this article is to evaluate and to maximize the annual performance of a bifacial module in a double skin configuration compared to a monofacial one. For this purpose, we developed a methodology based on indoor characterization with a double illumination setup in solar simulator, on outdoor characterization with an adjustable test bench of the application, and on ray-tracing simulation with an optical model of the application. The study has been performed on a reduced scale application using mini-modules. The bifacial gain is dependent on the opto-geometrical parameters of the application (double skin distance, reflective properties of the inner wall) and on the module architecture (electrical and optical parameters). Therefore, these two categories of parameters have been studied separately. The results enabled us to propose some design rules of the application and perspectives for the optimal bifacial module architecture.

Methodology of the Study

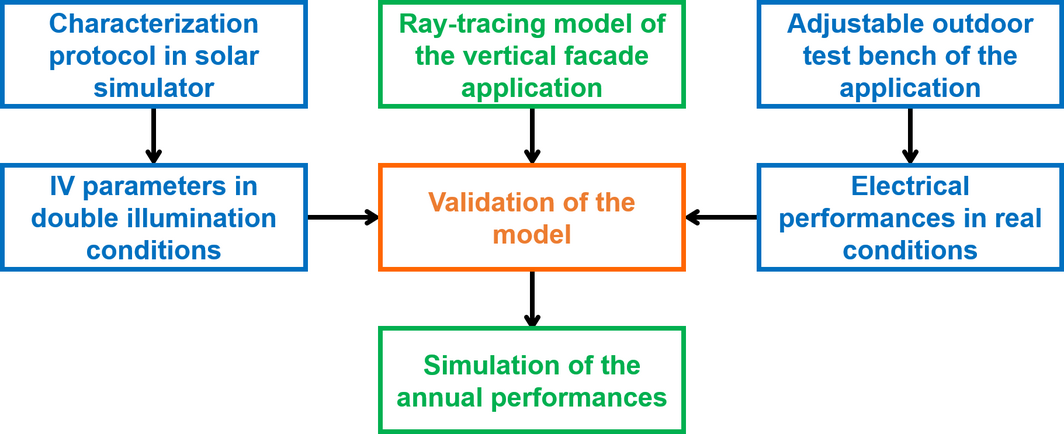
We used mini-modules with four N-type bifacial cells connected in series, encapsulated between two glasses in EVA-HLT (ethylene vinyl acetate - high-light transmission from STR). The type of cells used in this study has a back to front power ratio of 0.9 and has been reported in detail in [6]. Figure 2 shows the different steps implemented for the simulation of the annual performance and the following subsections will describe the three tools used in this methodology.

Figure 2. Schematics of the methodology used for evaluating the annual performance of bifacial modules in a vertical facade application (experimental part in blue, simulation part in green, and validation in orange).

Double illumination characterization setup

Standard characterization protocols for bifacial modules in solar simulators usually consist in measuring each side of the module independently using a black mask on the opposite side. Here, we adapted a double illumination setup existing at the cell level [7-9] for our mini-modules. Figure 3 shows the setup we designed. The bifacial module is placed between two aluminum mirrors (Alanod MIRO^® 4200GP, Ennepetal, Germany) with an angle between mirror and module of ψ = 44.1° optimized with a ray-tracing model of our PASAN solar simulator performed with TracePro^® [10]. Metallic grid filters with several pitches are used for attenuating light on the backside of the module in order to mimic different albedo conditions.

Figure 3. Picture of the double illumination setup positioned in our PASAN solar simulator.

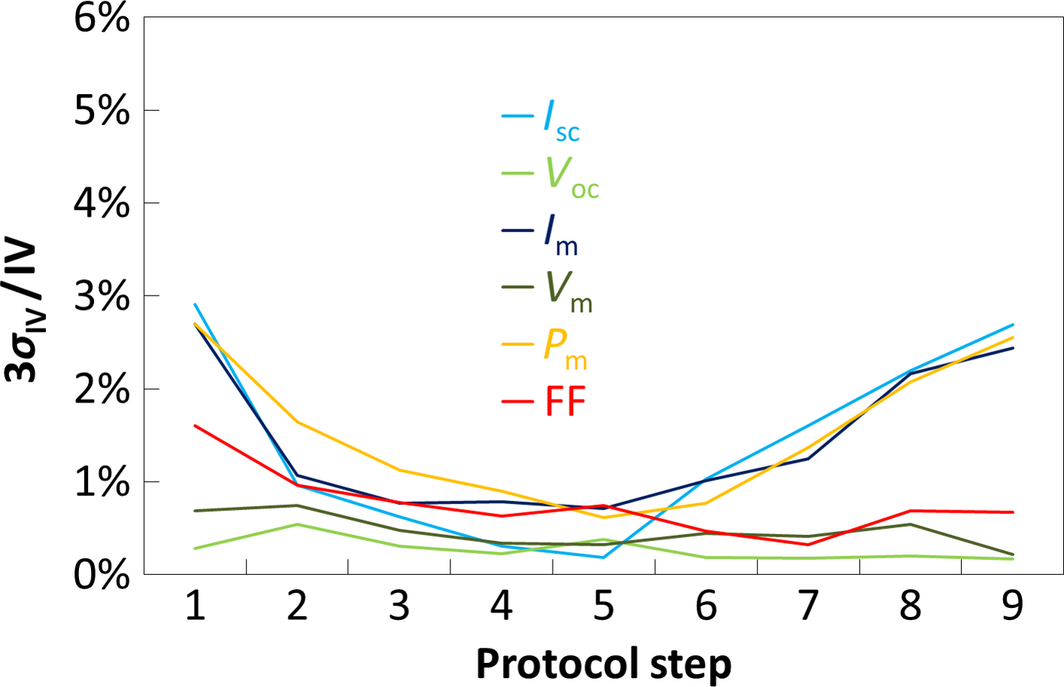
With this setup, we used a protocol with nine main steps depending on the PASAN intensity filters and on our metallic filters (see Table 1). We performed a reproducibility study in order to quantify the 3σ relative uncertainty of every current–voltage (IV) parameter for each step. Figure 4 shows that this uncertainty is comprised in the ±3% range as in Ohtsukas study [7]. The uncertainty is high at step 1 probably because the voltage range of the IV sweeping (kept equal for each step of our protocol) is not fully adapted for low irradiance measurements. It is also high at steps 7, 8, and 9 because the manual change of filters can slightly modify the alignment between the PASAN source and the module. Finally, step 5 shows the lowest uncertainty as this is the calibration step: here, the front short circuit current measured with our setup (I_sc-front) is compared to the I_sc measured in standard test conditions (STC) with a black mask on the back (I_sc-front-STC) and the PASAN light source intensity is adjusted in order to compensate mirrors absorption (about 5%).

Table 1. The nine main steps of our protocol. Additional steps consist in measuring the backside of the module (black mask on the frontside) in order to measure the optical transmission of the metallic filters

Protocol step number	Irradiance on the reference cell (below our setup)	Percentage of light on the back of the module
1	100 W/m2	0% (mask)
2	200 W/m2	0% (mask)
3	400 W/m2	0% (mask)
4	700 W/m2	0% (mask)
5	1000 W/m2	0% (mask)
6	1000 W/m2	23% (filter)
7	1000 W/m2	47% (filter)
8	1000 W/m2	78% (filter)
9	1000 W/m2	100% (no filter)

Figure 4. 3σ relative uncertainty measured for each step of the protocol as well as each IV parameter (σ being the standard deviation).

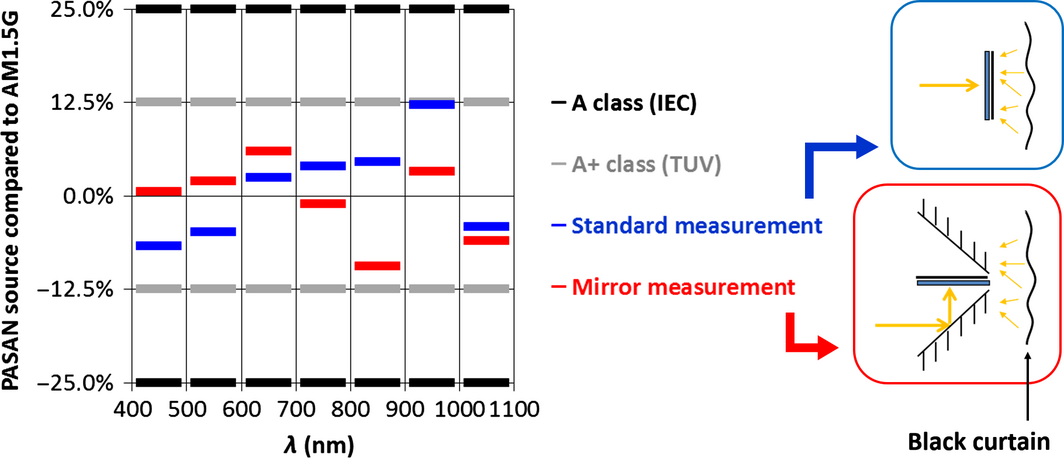
Figure 5 shows the spectral intensity measured with a spectrometer in the standard STC measurement case (in blue) and pondered with the spectral reflectivity of the aluminum mirror with our calibrated setup (in red). This shows that the spectral intensity of the PASAN source belongs to the A+ class (deviation compared to AM1.5G below ±12.5%) as long as the calibration step which compensates the mirror absorption is performed.

Figure 5. Spectral repartition of the PASAN source intensity compared to AM1.5G reference. The blue schematics shows a standard STC measurement and the red one shows a measurement with our double illumination setup. Black curtain reflections are also shown behind the setup.

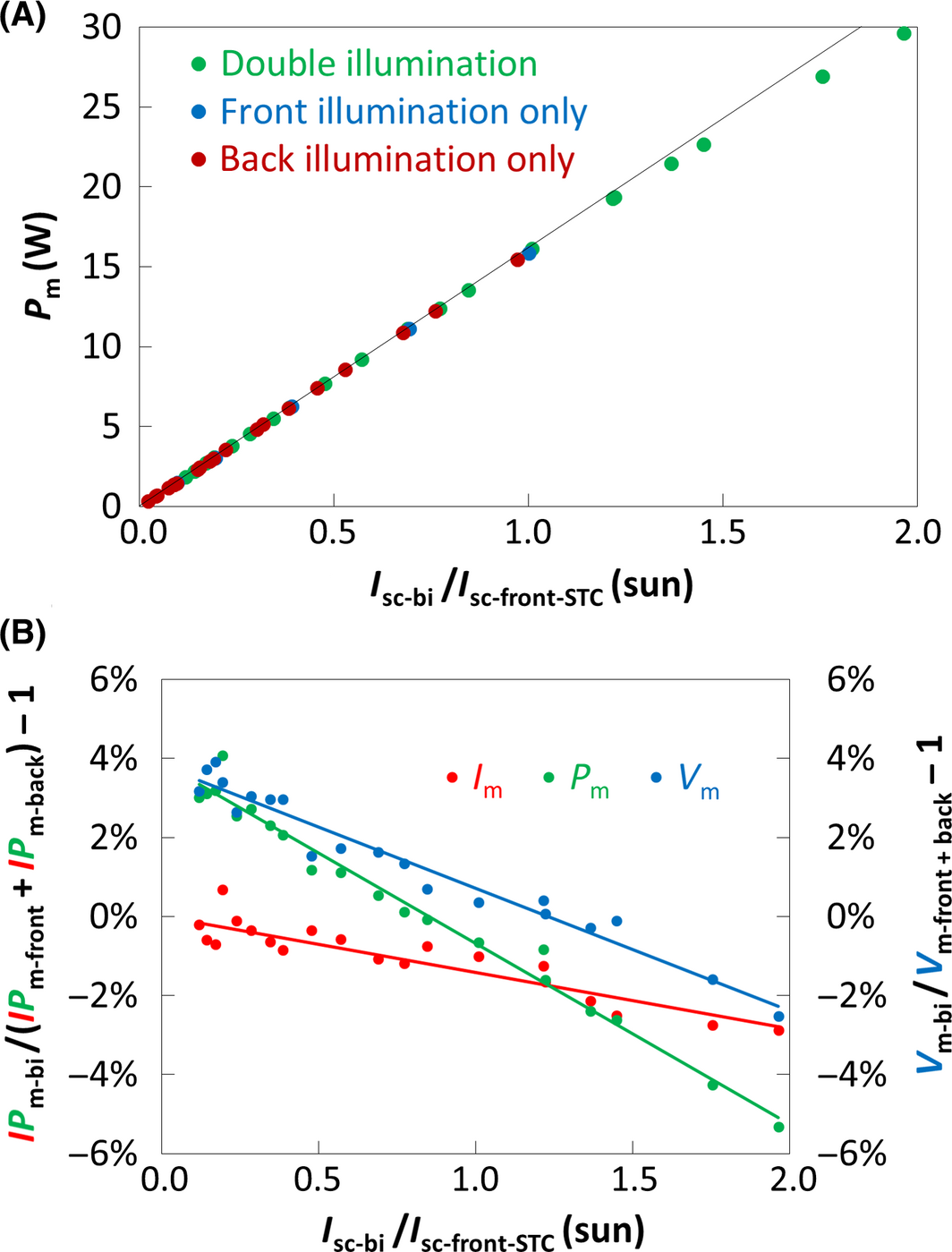
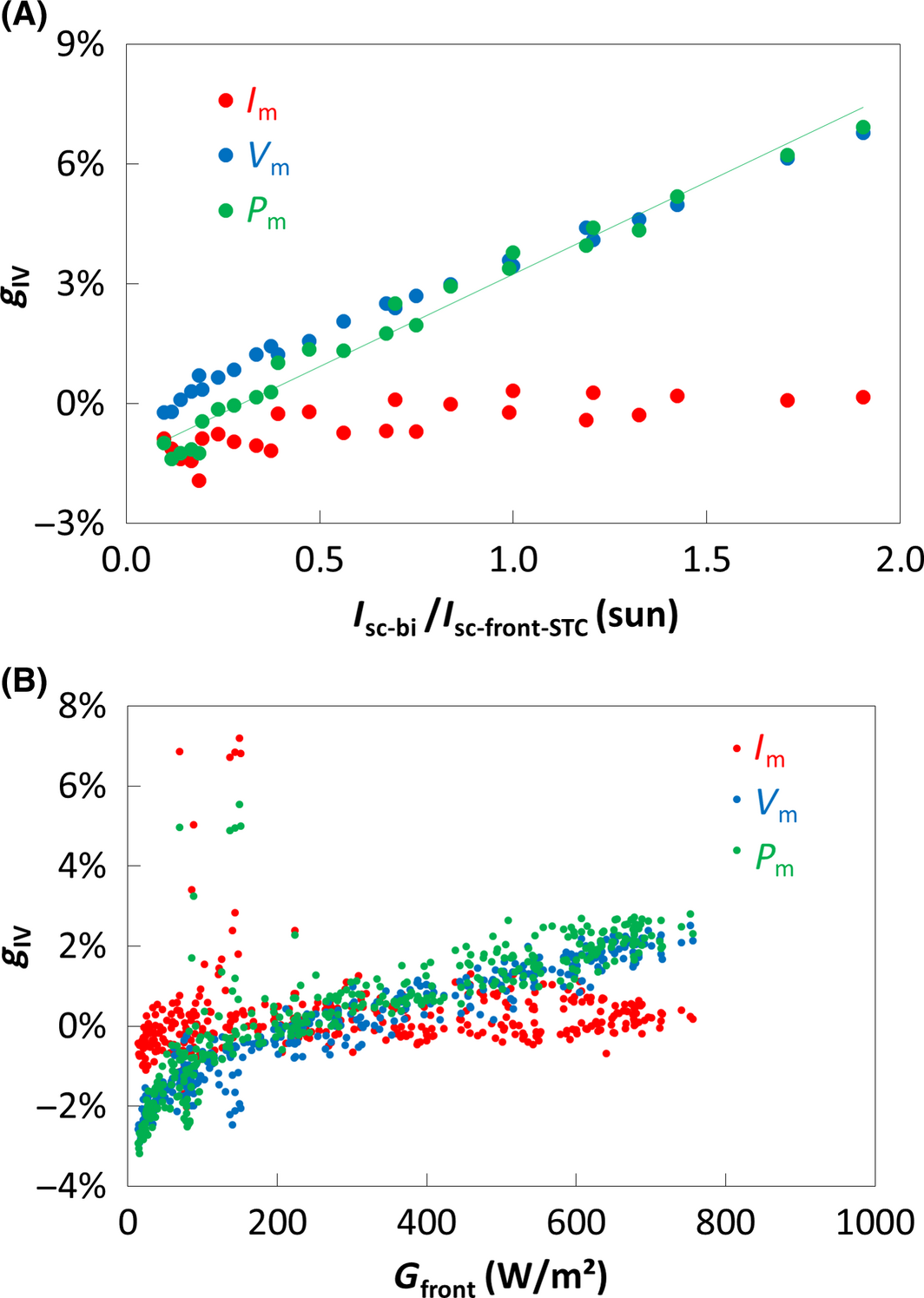
Using our setup, we ensured that all the IV parameters follow the same tendency independently of the illumination mode (frontside only, backside only, double side) and identified the resistive losses which increase when the module receives higher irradiance. Figure 6A shows that the power in double illumination (P_m-bi) gets lower than the linear tendency, which is the sum of frontside and backside powers (P_m-front + P_m-back) as the total irradiance on the module I_sc-bi/I_sc-front-STC increases. Figure 6B details this behavior plotting the gain between P_m-bi and (P_m-front + P_m-back). This shows that the resistive losses reach −5% at 2 sun. Note that for front characterization at low irradiances, the gain is actually positive because of the logarithmic behavior of the voltage (see the V_m parameter evolution in blue).

Figure 6. (A) Power Pm measured for different illumination modes and linear tendency showing the sum of frontside and backside powers (Pm-front and Pm-back). (B) Gain between the double illumination power Pm-bi and (Pm-front + Pm-back) and its separation into the current contribution Im and the voltage contribution Vm.

Outdoor test bench

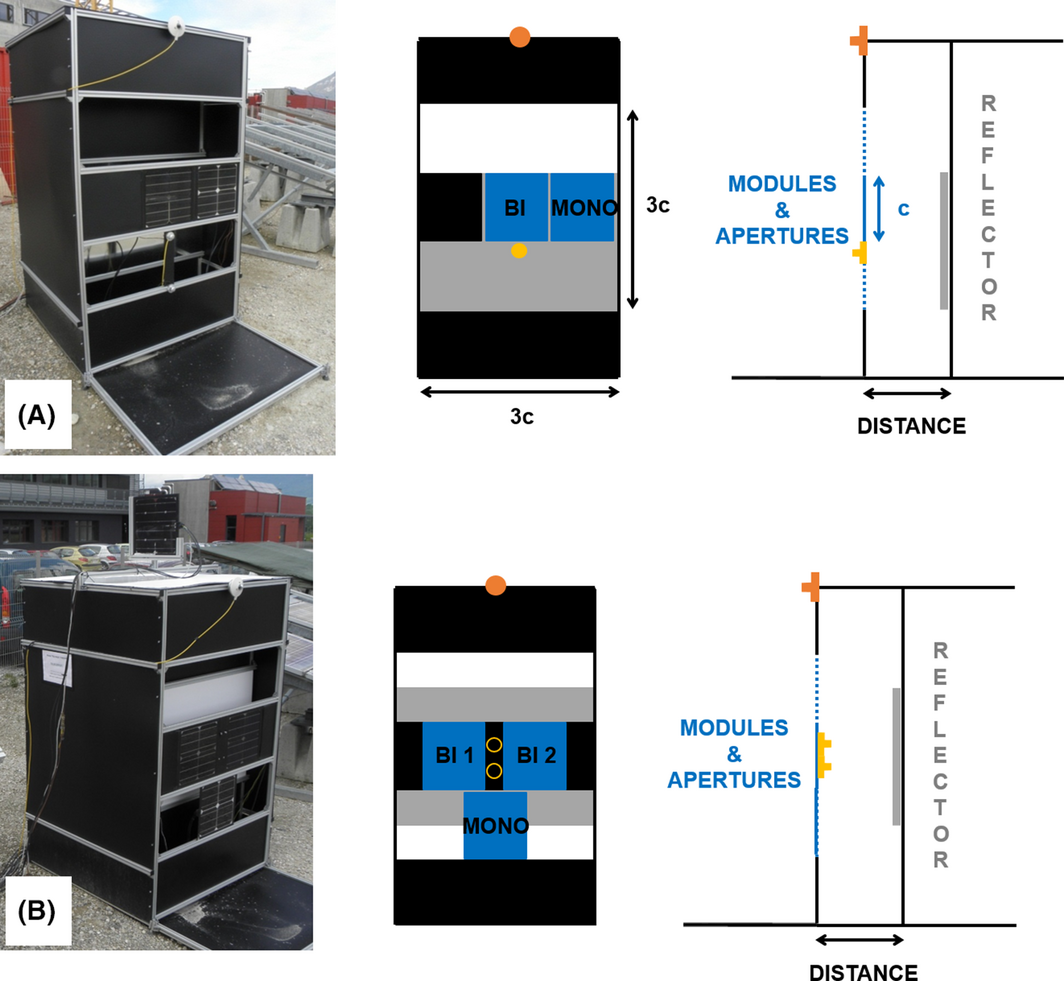
Our outdoor study has been performed on an adjustable reduced scale test bench inspired by a real building facade. From November 2012 until March 2013, we studied the influence of the opto-geometrical parameters of the application, namely the diffuse reflector on the inner wall and its distance to the module. Figure 7A shows the bifacial module in the middle, a monofacial reference on the right (bifacial cells from the same batch encapsulated with EVA-HLT between a glass and a white backsheet), and a reflector behind. In this article, the measure for length will be quantified in terms of number of c: c = 36 cm being the length of our modules, 3c × 2c the area of the reflector, and 3c × 3c the aperture of the opto-geometrical environment. From April 2013 until December 2013, we studied the influence of different module architectures. Figure 7B shows two bifacial modules (a standard architecture on the left and novel one on the right), the monofacial reference below, and a reflector behind. The whole setup is equipped with frontside and backside irradiance sensors (in yellow and orange) as well as calibrated temperature sensors on the back of the modules. These are T-type sensors glued with epoxy and protected from light using aluminum adhesive. The IV parameters have been followed over the year with a Daystar MT5 multi-tracer. These data have been used to compare the temperatures measured with thermocouples and the ones calculated using outdoor and indoor IV parameters. Equation (1) shows the calculation of the temperature T as a function of the open circuit voltage V_oc and the voltage temperature coefficient β (−0.31%/°C, assumed independent of the irradiance G [11]). V_oc(T, G) is directly measured outdoor and V_oc(25, G) is calculated from I_sc(T, G) also measured outdoor. Note that we assume I_sc(25, G) = I_sc(T, G), that is to say a zero current temperature coefficient, otherwise the equation would become non-linear.

Figure 7. Picture and schematics of our reduced scale test bench for studying the opto-geometrical parameters (A) and the module parameters (B). Filled orange circle denotes the front pyranometer CMP3, while the filled and empty yellow circles denote the SPlite pyranometers for front and rear, respectively. All pyranometers are installed vertically and front pyranometers face south.

$T=25\quad +\quad {\frac {V_{OC}\left({\mbox{T,}}\quad G\right)\quad -\quad V_{OC}\left(25,\quad G\right)}{\beta \quad \cdot V_{OC}\left(25,\quad 1000\right)}}$

(1)

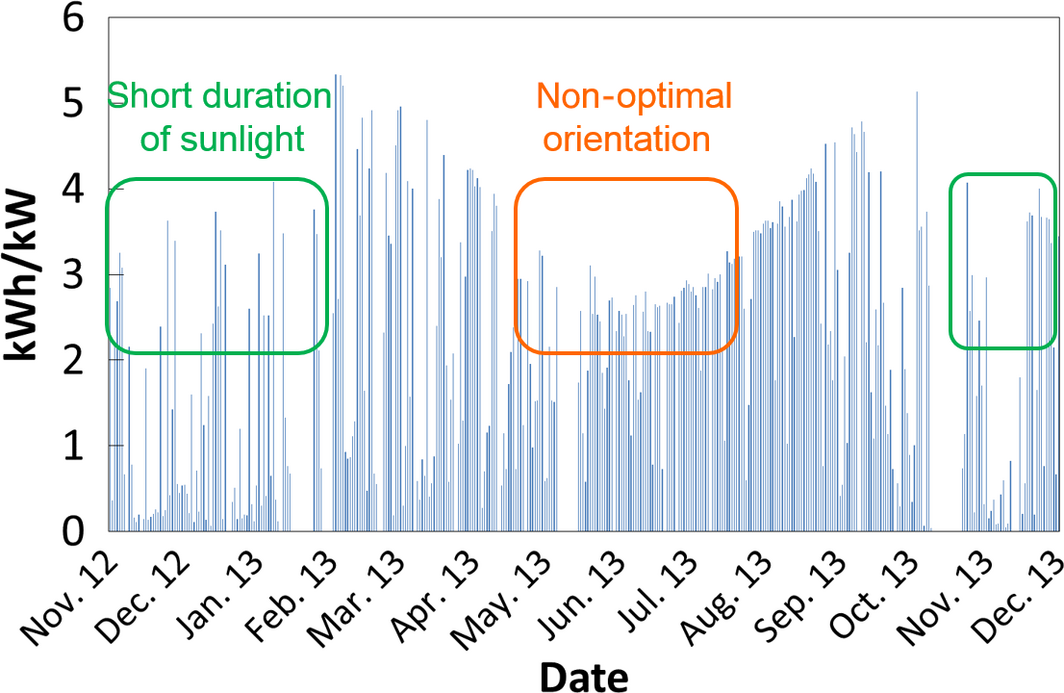
Figure 8 shows the energy yield of the monofacial module in terms of kilowatt-hour per kilowatt-peak over the period of test. Minimum production appears near summer solstice due to non-optimal orientation of the module with respect to solar positions (high azimuth angles on the morning and evening and high elevation angles around noon), and near winter solstice due to short duration of irradiation over the day. This results in a maximum production achieved around spring and autumn solstices.

Figure 8. Daily performance of the monofacial reference module over the whole period of experimental tests.

Annual performance simulation

Ray-tracing model

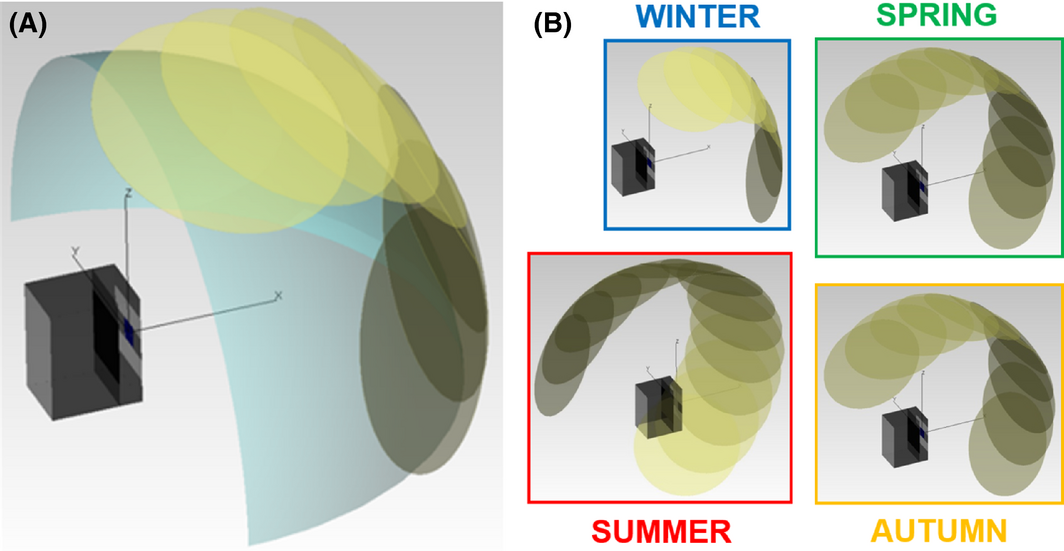
We used the ray-tracing software TracePro^® to create a simple optical model of our test bench (see Figure 9A). The solar disk sources can be set for any position in the sky with solid angle of the sun not being taken into account. Moreover, an isotropic semi-hemispherical background source is defined with an importance sampling applied on the aperture area 3c × 3c. We limit the model to the opto-geometry of the system and do not take into account spectral effects. Additionally, we did not take into account the ground albedo in front of our test bench in order to be able to use the importance sampling tool. Also, the reflective losses, semi-transparency of the module as well as global irradiances below 10 W/m² have not been integrated in the model. Note that Reich went down to 8 W/m² [12] and Sprenger to 5 W/m² [13]. With this model, we can set any diffuse to global ratio and any sun position in order to simulate the spatial and angular distribution of hourly irradiance on the backside of the bifacial module. We defined a typical day for each season of the year as shown on Figure 9B. The input data is taken from PVsyst database [14] and averaged over ±1.5 month around each solstice. Note that the number of rays have been chosen in order to ensure sufficient uniformity of the irradiance as well as limited time of simulation.

Figure 9. (A) Optical model of the test bench with direct (solar disks) and diffuse (isotropic sky) sources irradiating the test bench. (B) Solar positions for each typical day.

Optical to electrical conversion at 25°C

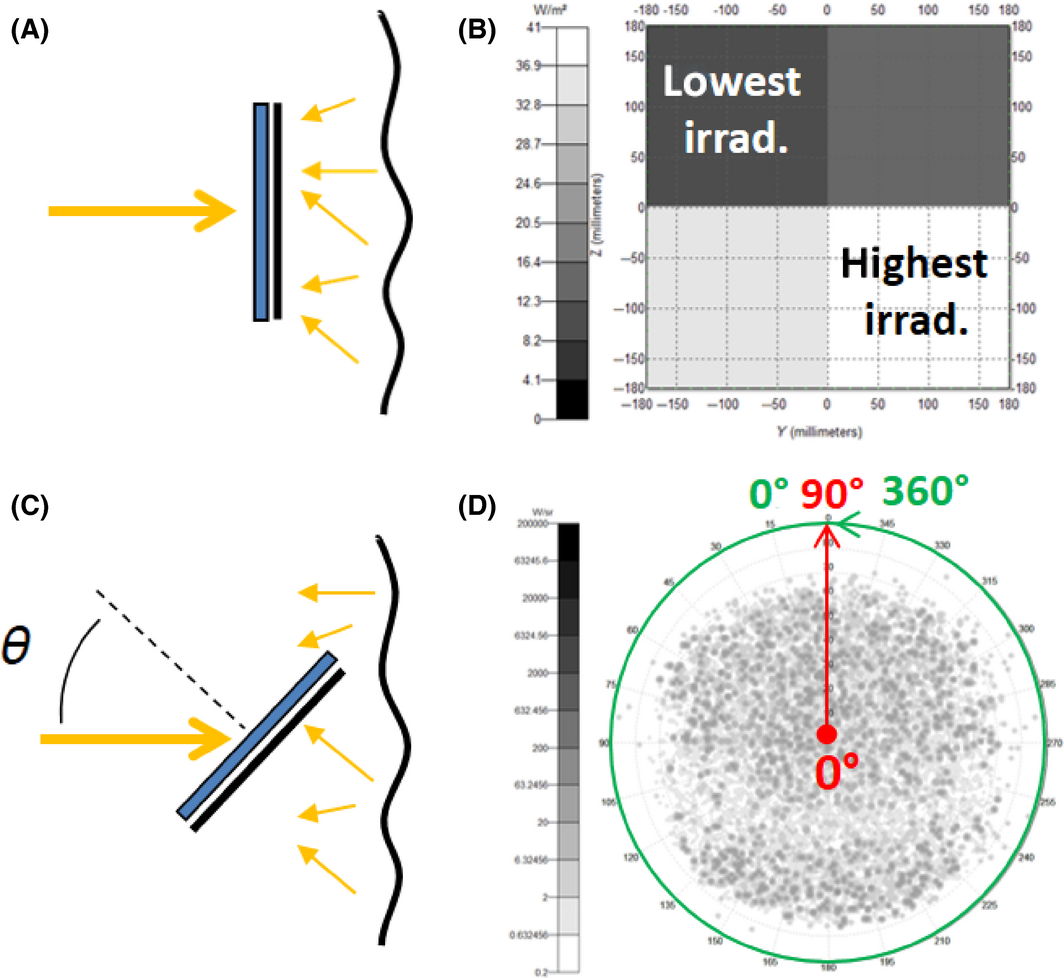
Once the model is designed, we use indoor flash test measurements (front and back independently measured) for converting irradiance data into electrical power data at 25°C. The spatial distribution of the irradiance is taken into account associating indoor STC measurements (Fig. 10A) with the least irradiated cell in the outdoor test bench simulations (Fig. 10B). The conversion is done using a logarithmic relationship between efficiency and irradiance (η = a₁ ln(G) + b₁). The angular distribution is taken into account associating indoor angle measurements (Fig. 10C) with the incidence angles of light rays in the outdoor test bench simulations (Fig. 10D). The conversion is done using a cosinus relationship between power and angle (P_m = c₁ cos(θ)). These conversions are critical hypothesis as we associate irradiance data from input meteorological data based on the measurement device spectral and angular responses with irradiance data based on the monitor cell spectral response at normal incidence and AM1.5G indoor spectrum.

Figure 10. Standard indoor measurement (A) correlated with an example of spatial distribution of outdoor irradiance data (B) each of the four pixels corresponds to a cell, the darker the less irradiated. Indoor angle measurements (C) correlated with an example of angular distribution of outdoor irradiance data (D): red straight axis from 0° to 90° shows the incidence angle of a ray and green circular axis from 0° to 360° maps the direction of incidence of a ray, the darker the more irradiated in this case.

Bifacial power at real temperature

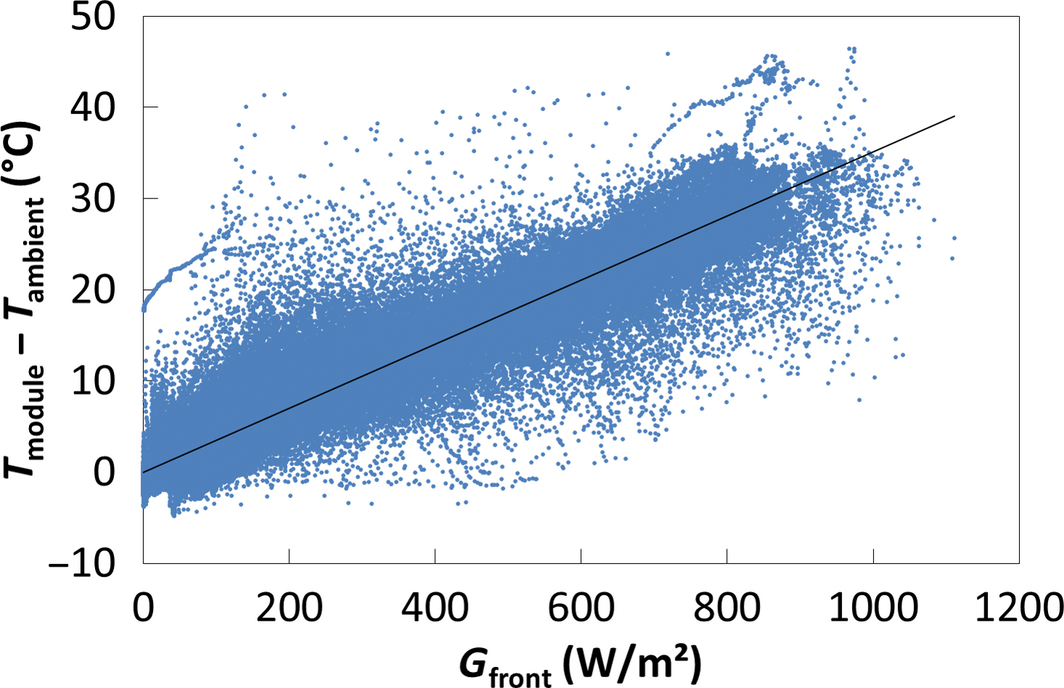
In order to get the electrical power at real operating temperatures, we use a linear model based on outdoor data obtained for the monofacial module. Figure 11 shows the temperature difference T_module–T_ambient as a function of irradiance G_front over the whole year in minute data. The linear approximation lead to a coefficient κ_mono = 0.035°C/(W/m²) in Equation (2). Therefore, the module temperature can be evaluated using the ambient temperature and irradiance measured on site, and the real powers can be calculated. These front and back powers are summed to give the bifacial power. We ensured with double illumination indoor measurements that this hypothesis is valid for the level of total irradiance involved in our application (<1.04 sun).

Figure 11. Temperature difference between monofacial module and ambient as a function of the front irradiance in minute data over the year of test, and its linear approximation.

$T_{module}=T_{ambient}+\kappa \cdot G_{front}$

(2)

Influence of Opto-geometrical Parameters

Experimental data

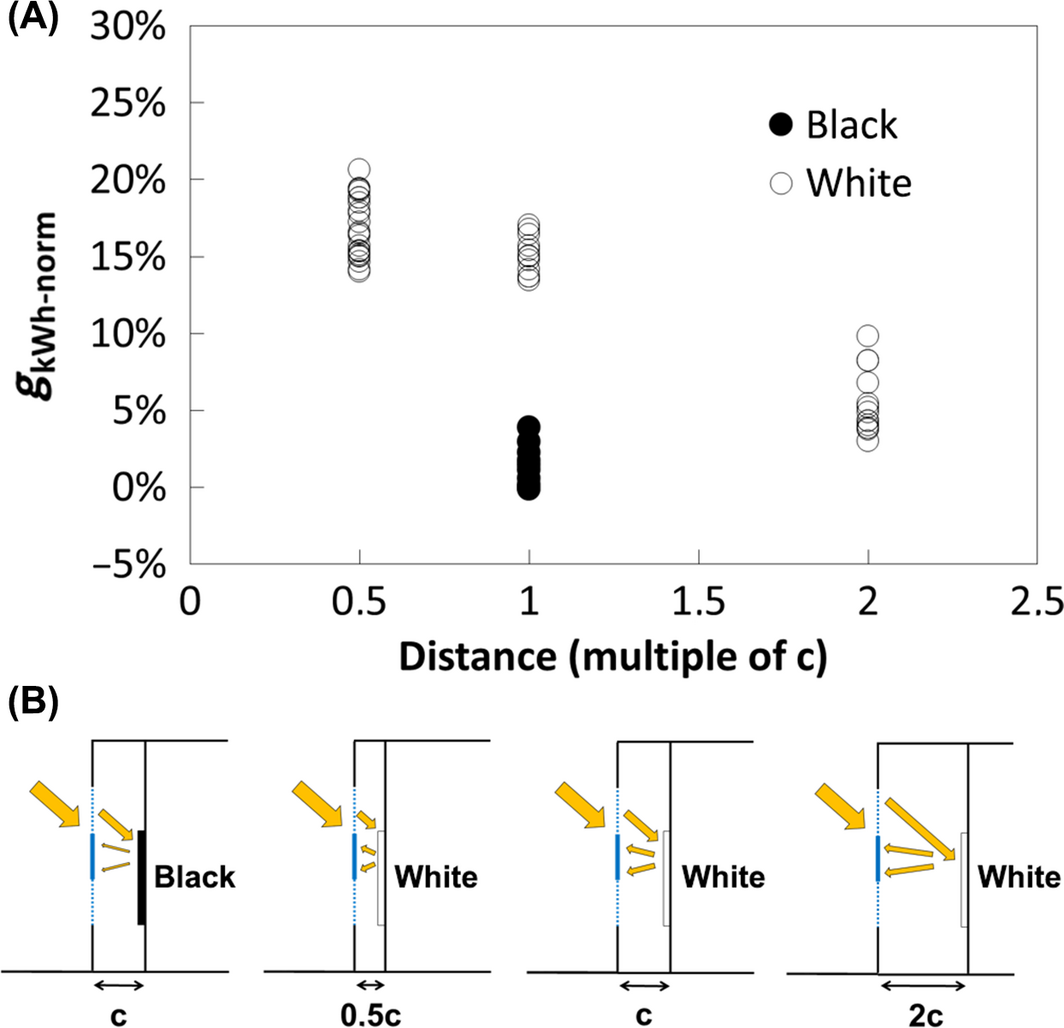
Between November 2012 and March 2013, several opto-geometrical configurations have been tested one after each other varying the module–reflector distance (0.5c, c and 2c; with the module height c = 36 cm) and the inner reflector (black or white). In this test, we used a module of standard architecture (glass–glass structure, full-size cells in series) with the configuration of the test bench shown on Figure 7A. Figure 12 shows the daily electrical energy gain brought by the use of a bifacial module instead of a monofacial one for four configurations. The variability in the data points is due to the period of test and the meteorological conditions, which were more or less cloudy. At a distance c, the use of a white reflector (weighted reflectivity with respect to the solar spectrum, R ~80.4%) gives an energy gain compared to monofacial module (g_kWh-norm) 13% higher than the one obtained with a black reflector (R ~4.9%). At a smaller distance (0.5c), maximal gains appear to be comprised between 15% and 20%.

Figure 12. Daily bifacial electrical energy gain compared to monofacial (powers normalized to the front STC for each module) for different opto-geometrical configurations. The module reflector distance is shown in terms of module height, c = 36 cm.

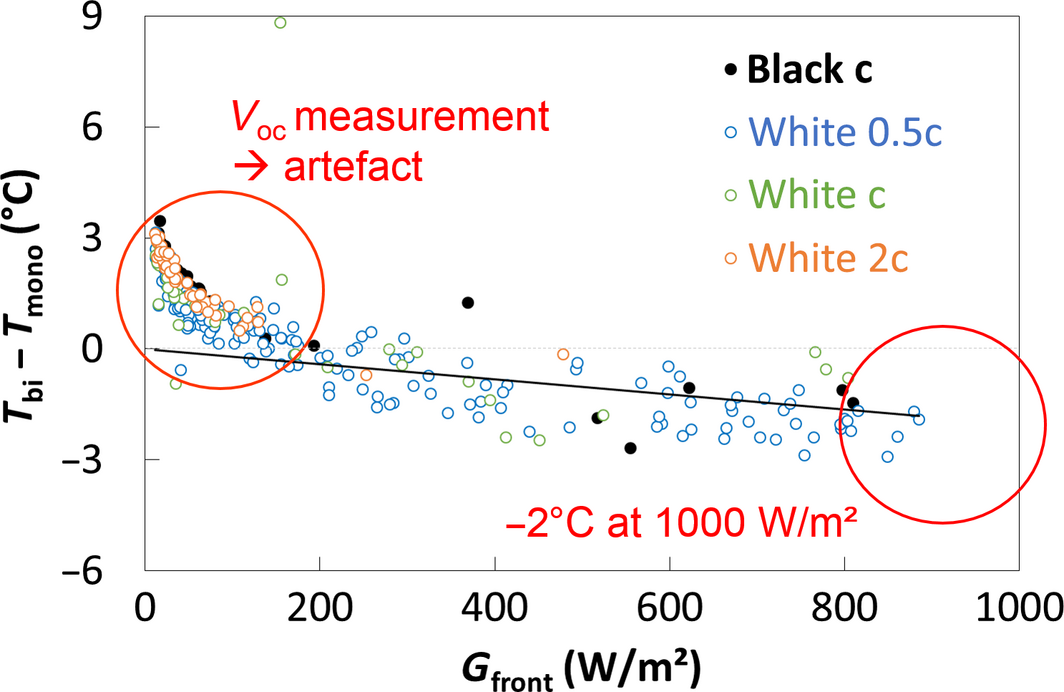
Additionally, the temperature difference between bifacial and monofacial modules is shown in Figure 13 for the four configurations. At low irradiances, a measurement artefact due to the combination of data measured with different IV tracers is visible (temperatures calculated with Equation (1)). For higher irradiances, all the configurations follow the same linear tendency, which reaches −2°C at a front irradiance of 1000 W/m². The main reason is that the bifacial module has twice as much surface compared to the monofacial one to release heat by thermal radiation. Using these data, we define a new coefficient κ_bi = 0.033°C/(W/m²) for the bifacial module, which will be used for simulating its thermal advantage over the year. It must be noticed that both the temperatures measured with thermocouples and calculated with V_oc gave the same linear trend (except at low irradiances) after removing thermal conduction contributions, which are different for a thermocouple glued on a 0.17 mm backsheet compared to a 3 mm backside glass [15].

Figure 13. Temperature difference between bifacial and monofacial module as a function of front irradiance for the four configurations shown in Figure 12 (hourly data points). The linear tendency without taking into account the low irradiance artefact concerns the four configurations all together.

Validation of the model

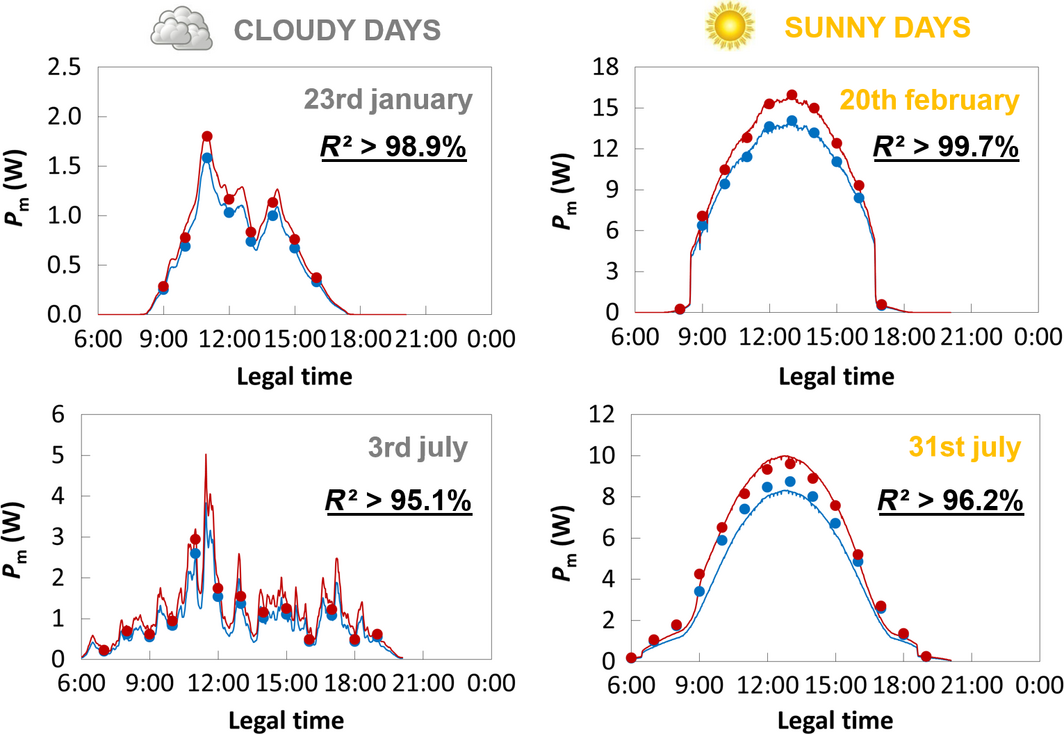
A sunny and a cloudy day have been used to compare the simulation and experimental results for winter period as well as for summer period. The model sources (see Fig. 9) are defined using direct irradiance measured with a sun tracker on our site and diffuse irradiance on the module plane calculated using global irradiance measured with the front pyranometer (filled orange circle on Fig. 7). The backside irradiance is simulated and converted in electrical power data as explained in section 'Optical to electrical conversion at 25°C'. These data are temperature corrected using experimental temperature monitoring. Figure 14 shows the comparison for these 4 days. We use the determination coefficient R² and the Student test (see Equation (3) and Equation (4) – N being the number of data points over the day) to compare the experimental and simulated temporal series (${\textstyle x_{exp}^{i}\quad {\mbox{and}}\quad x_{sim}^{i}}$). Each R² is above 95.1% and the Student test allows us to say that simulations estimate measurements with a confidence interval of 99.9% [16].

Figure 14. Comparison of simulated (dots) and experimental (curves) data for bifacial (red) and monofacial (blue) modules against legal time, with associated R2. Cloudy days on the left, sunny days on the right, winter days on the top, and summer days on the bottom.

$R^{2}=1-{\frac {{{\sum }_{i\quad =\quad 1}^{N}\left(x_{sim}^{i}\quad -\quad x_{\mbox{exp}}^{i}\right)}^{2}}{{{\sum }_{i\quad =\quad 1}^{N}\left(x_{\mbox{exp}}^{i}\quad -\quad x_{\mbox{exp}}^{ave}\right)}^{2}}}$

(3)

$t_{s}={\sqrt {\frac {\left(N-2\right)\cdot R^{2}}{1-R^{2}}}}$

(4)

Annual performance

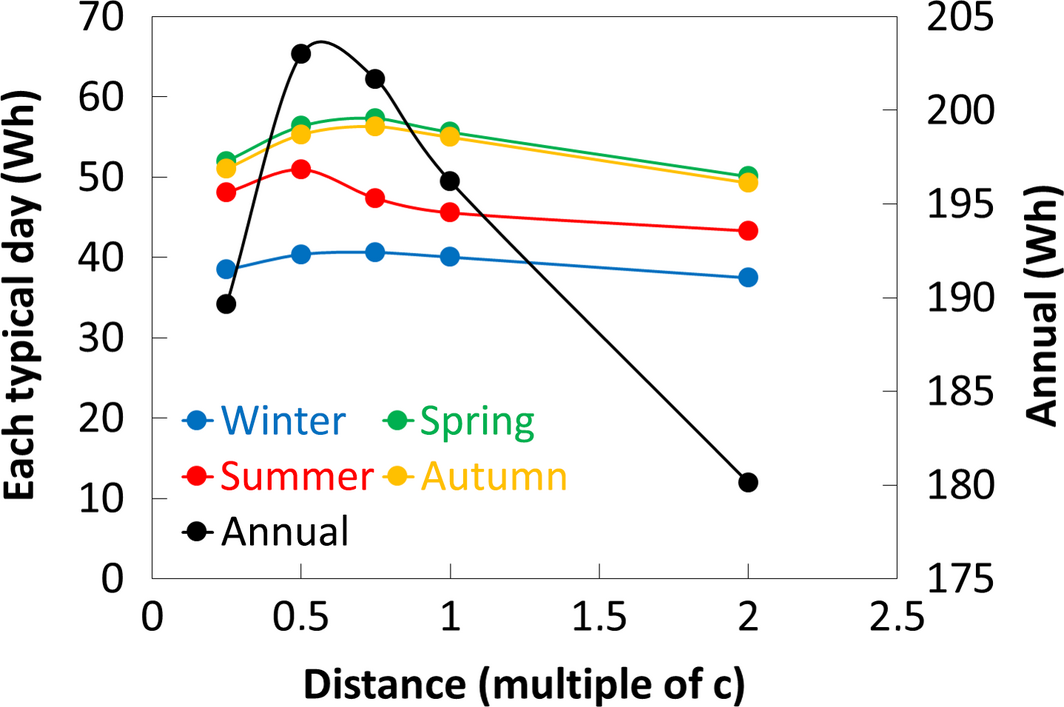
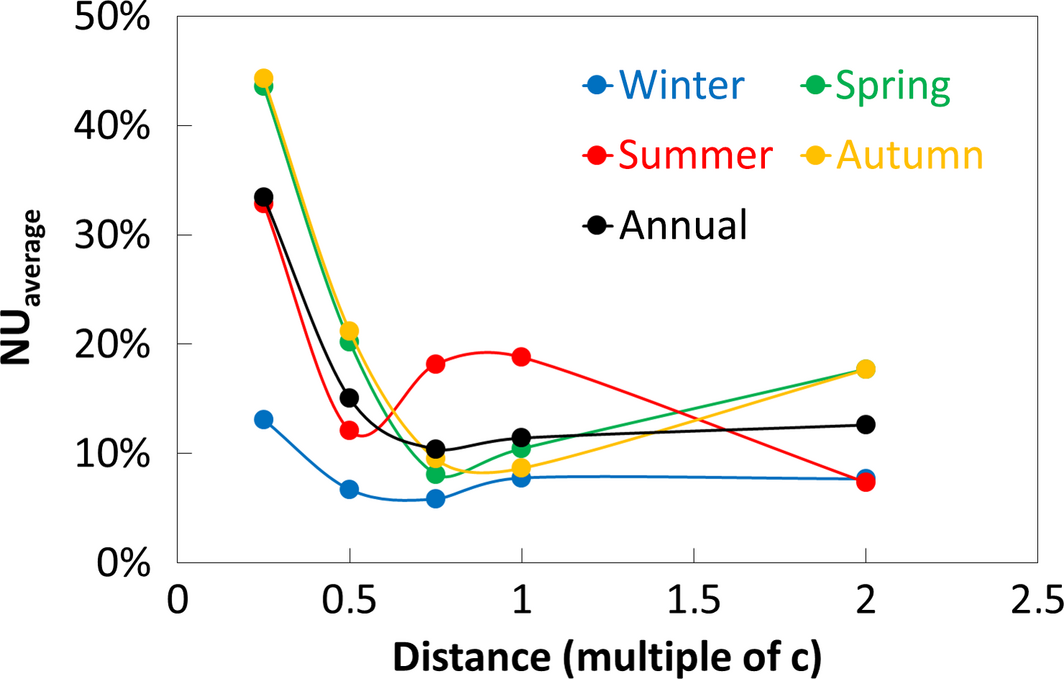
In the previous sections, we obtained experimental data in different configurations of our test bench at specific periods of the year. The model being validated, we can now extrapolate our results over the whole year. Figure 15 shows the bifacial module energy production simulated in watt-hour for each typical day as well as over the year (cumulating each typical day) according to the distance between module and reflector in the white reflector case. As in the monofacial case, we can see that the energy production is maximum near spring and autumn solstices independently of the distance (see Fig. 8). The annual energy production (black curve) clearly shows a maximum between distance 0.5c and 0.75c. Above these distances, the decrease is due to side effects of our test bench, namely the black side walls between the module and the reflector, which absorb the light diffused by the white reflector and prevent the ambient diffuse light from reaching the backside of the module. Below these distances, the decrease is due to current limitation by the least irradiated cell in the module. Indeed, Figure 16 shows the non-uniformity of backside irradiance (daily average of hourly data points calculated with Equation (5)) according to the distance for each typical day as well as over the year. The black curve on the chart shows a strong increase in non-uniformity at short distances. This is mainly due to the module shade as well as the black side walls shade both projected onto the reflector (depending on the position of the sun).

Figure 15. Simulated daily energy production for each typical day (winter in blue, spring in green, summer in red, and autumn in yellow) and over the year (black) as a function of the distance between module and reflector.

Figure 16. Simulated daily averaged non-uniformity of backside irradiance for each typical day (winter in blue, spring in green, summer in red, and autumn in yellow) and over the year (black) as a function of the distance between module and reflector.

$NU={\frac {G_{max}-G_{min}}{G_{max}+G_{min}}}$

(5)

Influence of Module Architecture

Experimental data

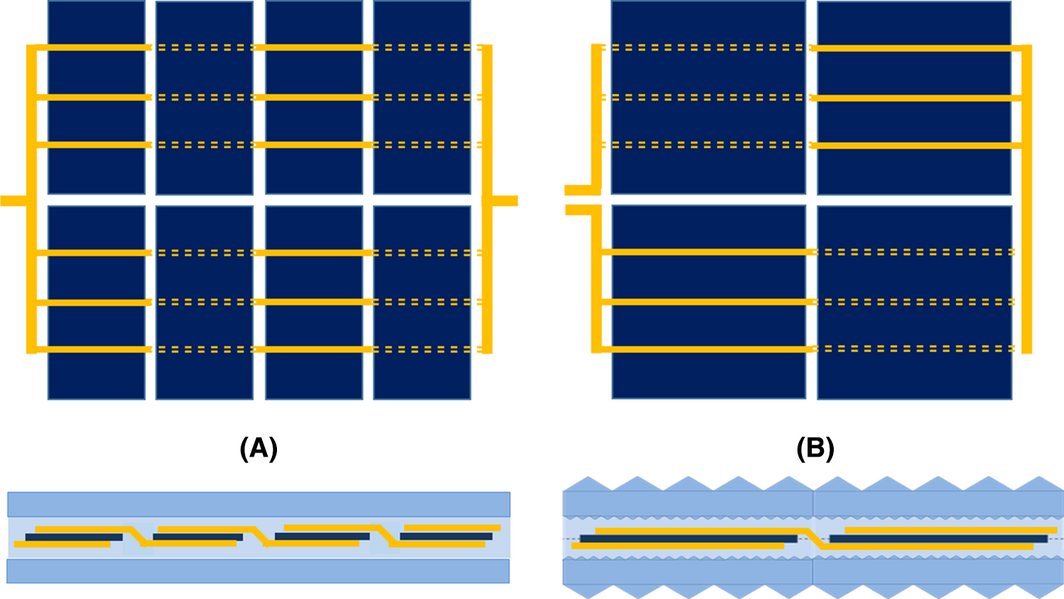
Between April 2013 and December 2013, innovative module architectures have been tested one after each other with the configuration of the test bench shown on Figure 7B. We saw before that bifacial modules suffer from resistive losses due to higher currents, and the backside irradiance is often non-uniform and diffuse. In order to address these issues, we tested two different architectures. On the one hand, a module has been made with two series of half-cut cells connected in parallel in order to reduce the resistive losses and to be less sensitive to non-uniform irradiance (Fig. 17A). We ensured that this architecture has the same I_sc-front-STC and V_oc-front-STC as a standard architecture (four full size cells in series). On the other hand, we used a textured glass on both sides for collecting high incidence angles of diffuse radiation (Fig. 17B). The following subsections describe the experimental tests (indoor and outdoor) performed for finding empirical models, which will allow us later to identify the potential of these novel module architectures at the annual scale.

Figure 17. Schematics of the two different architectures tested: half-cells and parallel strings with flat glasses (A), and four full-size cells in series with textured glasses (B). The modules have been made with cells from the same batch and will be compared to a reference module made of four full-size cells in series encapsulated between flat glasses.

Influence of using half-cells

In order to separate the influence of half-cells from the influence of parallel interconnection, we had to measure the module under uniform illumination. This was possible with our indoor double illumination setup (Fig. 18A) and with our outdoor test bench masking the backside of the module (Fig. 18B). Both charts show the gain brought by the novel architecture compared to the standard one for parameters I_m, V_m, and P_m. The indoor and outdoor measurements are in agreement showing a linear increase in P_m and V_m with total irradiance on the module: we observe a negative gain below 0.25 sun and ~3% at 1 sun. The indoor bifacial characterization shows up to 7% gain at 2 sun. Indeed, as the total irradiance increases on the module, the resistive losses increase on the standard architecture and the use of half-cells brings more and more advantage (higher power due to higher voltage). Note that the negative gain at low irradiances might be due to shunt currents induced by laser cutting of our N-type cells.

Figure 18. Gain of the novel architecture compared to a standard module for the parameters Im, Vm, and Pm obtained with indoor measurements (A – bifacial illumination characterization) and outdoor measurement (B – front characterization only in hourly data).

From the indoor experimental data, we used a linear relationship (green line shown on Fig. 18A) between the power gain g_Pm and the total irradiance incident on the module I_sc-bi/I_sc-front-STC shown in Equation (6) for simulating the contribution of half-cells at the annual scale.

$g_{Pm}=4.6\%\quad \cdot \quad I_{sc-bi}/I_{sc\quad -\quad front-STC}\quad -$$\quad 1.4\%$

(6)

Influence of parallel interconnection

The bifacial gain is critically dependent on the uniformity of irradiance on the module backside (examples in [4, 17]). For vertical facades, the section 'Annual performance' showed that the backside irradiance can be strongly non-uniform if the module–reflector distance is very small. In this case, the upper and lower cells do not receive the same amount of radiation due to the module shade projection onto the back reflector. Therefore, we investigated the advantage of using two strings of cells connected in parallel in the module architecture in order to be less sensitive to non-uniform irradiance.

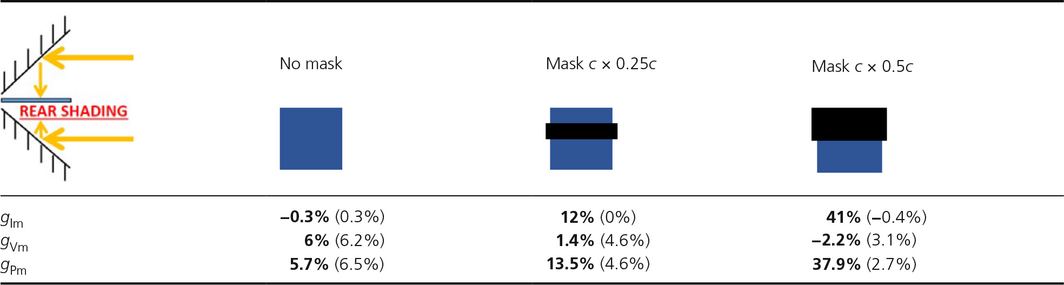
First, we artificially created strong non-uniformities on the backside of the module placed in the double illumination setup. Table 2 shows the gain between the novel architecture and the standard one for parameters I_m, V_m, and P_m in three different backside configurations: no mask, a c × 0.25c mask, and a c × 0.5c mask (no mask on the frontside). For comparison, the gain taking into account resistive losses only (calculation with eq. (6)) is written between brackets. The configuration c × 0.25c shows a strong current gain (12%) due to the interconnection in parallel since the shaded string does not limit the unshaded string in the novel architecture. In terms of voltage, the shaded string slightly limits the unshaded string: a 6% gain due to resistive losses becomes only a 1.4% gain with the parallel interconnection in addition. This still results in a positive effect on the power (13.5% gain). If one of the two strings is fully masked (configuration c × 0.5c), this phenomenon is increased with a higher current gain (+41%) and a voltage loss (−2.2%).

Table 2. Gains of the novel architecture compared to standard one for parameters I_m, V_m and P_m for different shading configurations on the backside of the modules placed in our double illumination setup (see the image on the left corner). The measured gains (in bold) are compared with calculated gains taking into account resistive losses only (between brackets)

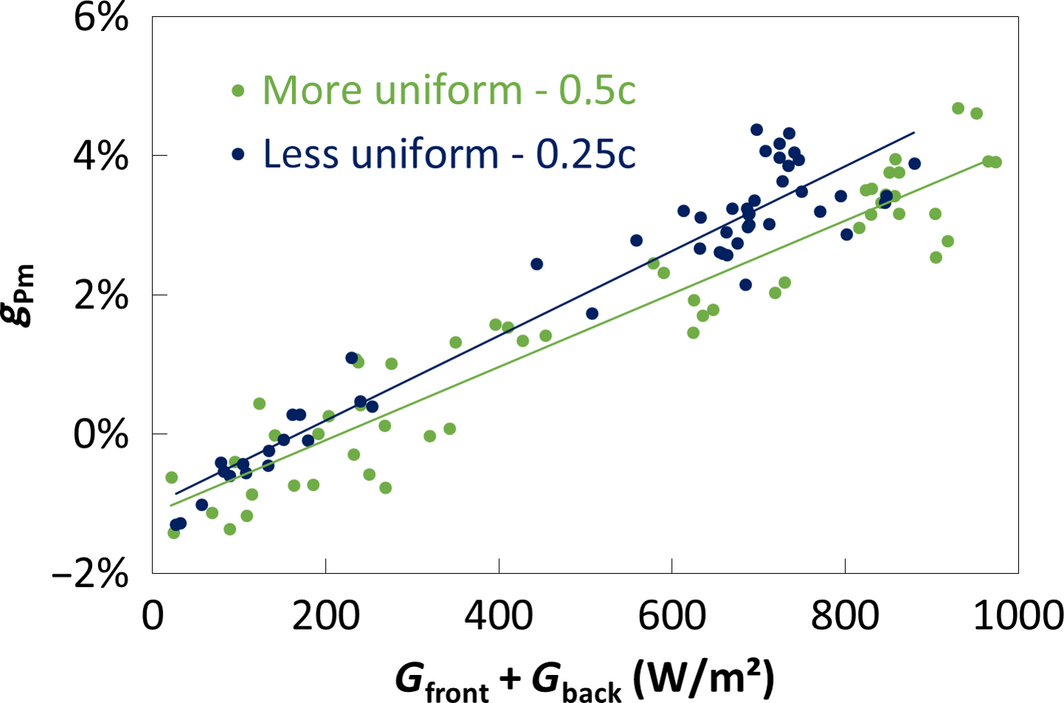
Then, we compared two different configurations of our outdoor test bench by varying the distance between module and reflector: a more uniform irradiance and a less uniform irradiance on the backside of the module as shown on Figure 16. Figure 19 shows that the power gain is about 0.5% higher for the less uniform configuration. This confirms the slight advantage of using a parallel interconnection in outdoor conditions for our specific case. This is the result of about 1% gain for I_m (no current limitation by the least irradiated string) and about 0.5% loss for V_m (voltage limitation by the least irradiated string). Note that both curves have a similar slope due to the resistive loss effect as explained previously.

Figure 19. Hourly data point of the power gain gPm of the novel architecture compared to standard one plotted against the total irradiance on the module Gfront + Gback for two different configurations of the test bench: smaller distance (less uniform irradiance on the backside of the module) and larger distance (more uniform irradiance).

In order to be able to simulate the maximal contribution brought by the parallel interconnection on the annual scale, we expressed the I_sc gain using the spatial distribution of irradiance on each side. The following equations have been used to get Equation (7):

1. I_sc-bi = I_sc-front + I_sc-back for both modules. This is verified at −0.5% in average, while Ohtsuka had +0.4% [7] and Ezquer −1.8% [8].
2. I_sc-front = I_sc-front-STC × G_front for both modules (uniform irradiance on their frontside). G is the global irradiance incident on one face in terms of number of sun.
3. I_sc-back = min (I_{sc-back-string1}, I_{sc-back-string2}) = I_sc-back-STC × min (G_back-string1, G_back-string2) for the standard architecture.
4. I_sc-back = I_{sc-back-string1} + I_{sc-back-string2} = 0.5 × I_sc-back-STC × (G_back-string1 + G_back-string2) for the novel architecture.
5. I_sc-back-STC = r × I_sc-front-STC for both modules, which have the same I_sc in STC conditions. r is the bifacial ratio.
6. the numbers of sun G_front, G_back-string1 and G_back-string2 are linked through the non-uniformity of irradiance NU between the upper string and the lower string of the backside (see eq. (5)), and through the effective albedos A_min = min (G_back-string1, G_back-string2)/G_front and A_ave = 0.5 × (G_back-string1 + G_back-string2)/G_front.

$g_{Isc}=NU\cdot {\frac {r\cdot A_{ave}}{1+r\cdot A_{min}}}$

(7)

Table 3 shows the comparison between calculation and measurements with our indoor setup. Our calculations are validated experimentally in this case of strong non-uniformities artificially created (masks c × 0.25c and c × 0.5c), so we applied this model using outdoor I_sc data. We observed that the measurement values were lower than the calculated values for unknown reasons (chart not represented). Therefore, we decided to add an empirical coefficient of 0.4 in Equation (7) in order to fit outdoor observations. Finally, we associate the resulting I_sc gain to the upper limit of the P_m gain in Equation (8), since the shaded string can suffer from reverse currents. Equation (8) will therefore allow us to evaluate the maximum power gain due to non-uniform irradiance even though the real power gain will be always lower.

Table 3. Comparison between calculated and measured g_Isc in the case of indoor artificially created non-uniformities on the backside of both modules (masks c × 0.25c and c × 0.5c)

Mask on backside	NU	Amin	Aave	gIsc calc.	gIsc meas.
c × 0.25c	33.3%	0.5	0.75	15.2%	13.1%
c × 0.5c	100%	0	0.5	43.6%	44.3%

$g_{Pm-max}\quad =\quad 0.4\quad \cdot \quad NU\quad \cdot \quad {\frac {r\quad \cdot \quad A_{ave}}{1\quad +\quad r\quad \cdot \quad A_{min}}}$

(8)

Influence of linear textured glasses

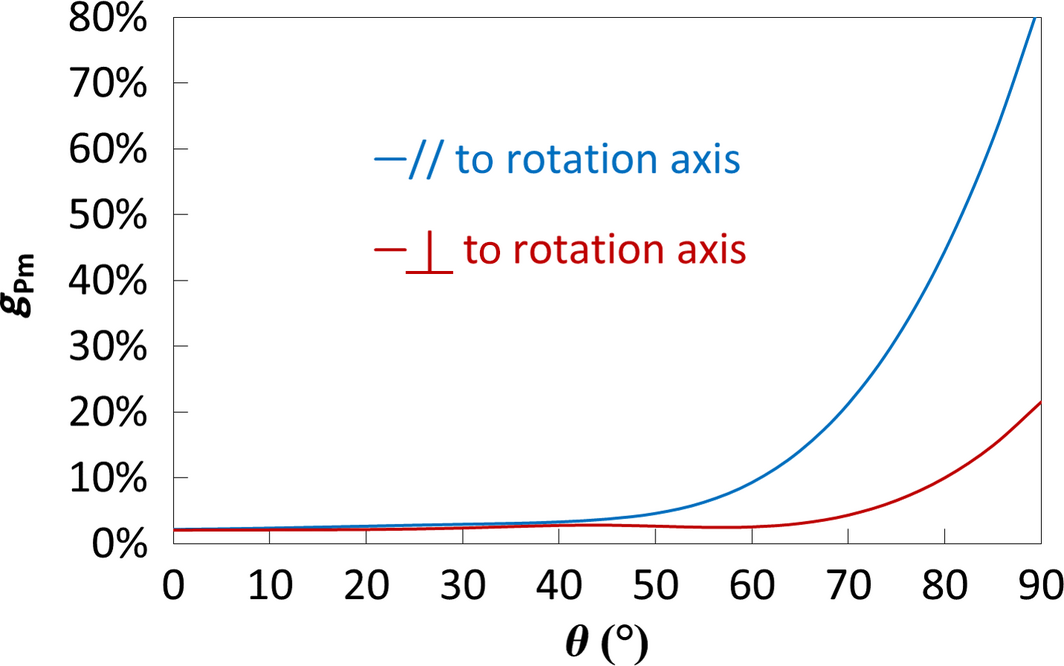
Diffuse radiation plays an important role in bifacial applications particularly on the backside of the module. We compared a bifacial module with a unidirectional textured glass from the company AGC on both sides, to a bifacial module with standard flat glasses. Such a unidirectional texturation can have the advantage of self-cleaning with rain. In order to identify the effect of the glass only, we measured the gain between a monofacial module with the front linear textured glass and a monofacial module with the front flat glass as a function of the incidence angle of light θ (see Fig. 10C). Figure 20 shows the results for two orientations of the texturation: parallel and orthogonal to the rotation axis. For angles below 40°, the gain is about 2–3% due to a light trapping effect. Above 60°, the orthogonal orientation shows a gain increase due to the divergence of the PASAN source as well as parasitic reflections on the black curtain behind the module. For this range of angles, a clear increase in the gain confirms the positive effect of textured glass for the parallel orientation.

Figure 20. Power gain for a monofacial module with a unidirectional textured glass compared to flat glass as a function of the incidence angle of light (0° corresponds to normal incidence) for two different orientations of the textured glass.

In order to be able to simulate the influence of textured glasses at the annual scale on our application, the angular distribution of light on each face of the module has been simulated hourly for each typical day (see Fig. 10D as an example). For each side of the module, the optical flux is integrated over ±45° around the horizontal direction on the one hand, and around the vertical direction on the other hand. We associated this simulated data (normalized with the total flux incident on the surface) with the indoor characterization data shown in Figure 20 in order to obtain the power gain brought by the use of a textured glass for each hourly data point and each side of the module in two different orientations.

Validation of the model

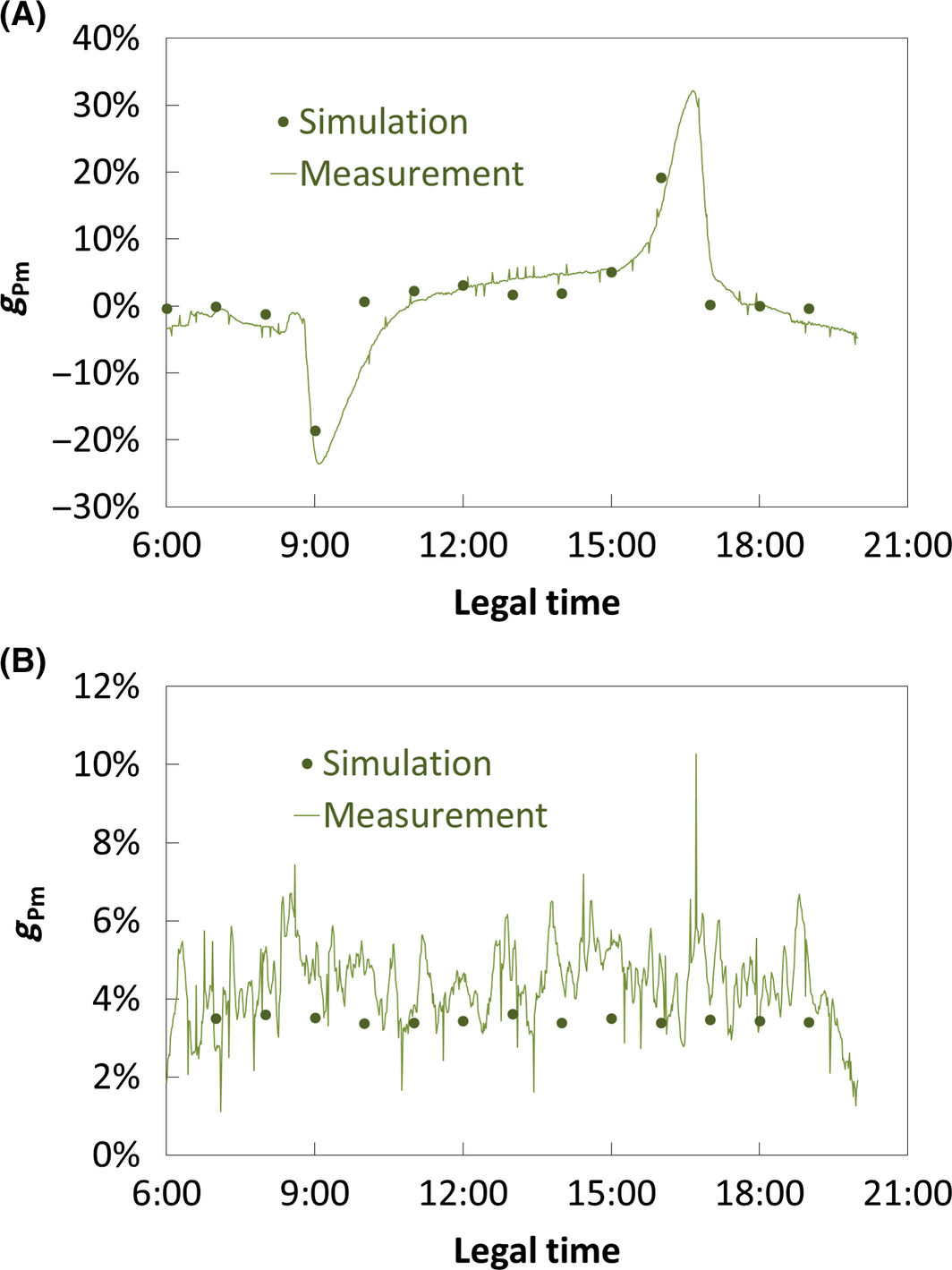
The empirical correlations obtained in section 'Experimental data' have been used to simulate the evolution of P_m over two summer days. We chose a sunny day giving non-uniform irradiance on the backside of the module (NU comprised between 31% and 60%) for the half-cells and parallel interconnection architecture, and a cloudy day giving diffuse irradiance on both sides (diffuse to global ratio above 99.7%) for the linear textured glasses architecture. The comparison of temporal series (simulated and measured) gives R² above 98.8% for the half-cells and parallel interconnection architecture and R² above 94.3% for textured glasses architecture (see eq. (3)). Knowing the number of hourly data points for each day, the Student test allows us to say that the model estimate the reality with a confidence interval of 99.9% (see eq. (4) and [16]).

Figure 21 shows the resulting gain from experimental and simulated data for these two days. The upper chart (sunny day) shows a strong loss for the novel architecture compared to standard one (four full size cells in series) around 9:00 am and a strong gain around 4:30 pm. Indeed, in this configuration, the standard module is on the west side meaning that its backside receive more radiation when the sun rises, and the novel module is on the east side meaning that its backside receives more radiation when the sun goes down. By contrast, the lower chart (cloudy day) does not show this asymmetrical production as the optical flux is completely diffuse on the backside of the module.

Figure 21. (A) Simulated and measured power gain of the half-cells and parallel interconnection architecture compared to standard one on the 31/07/13. (B) Simulated and measured power gain of the textured glasses architecture compared to standard one on the 03/07/13.

Annual performance

Half-cells and parallel interconnection architecture

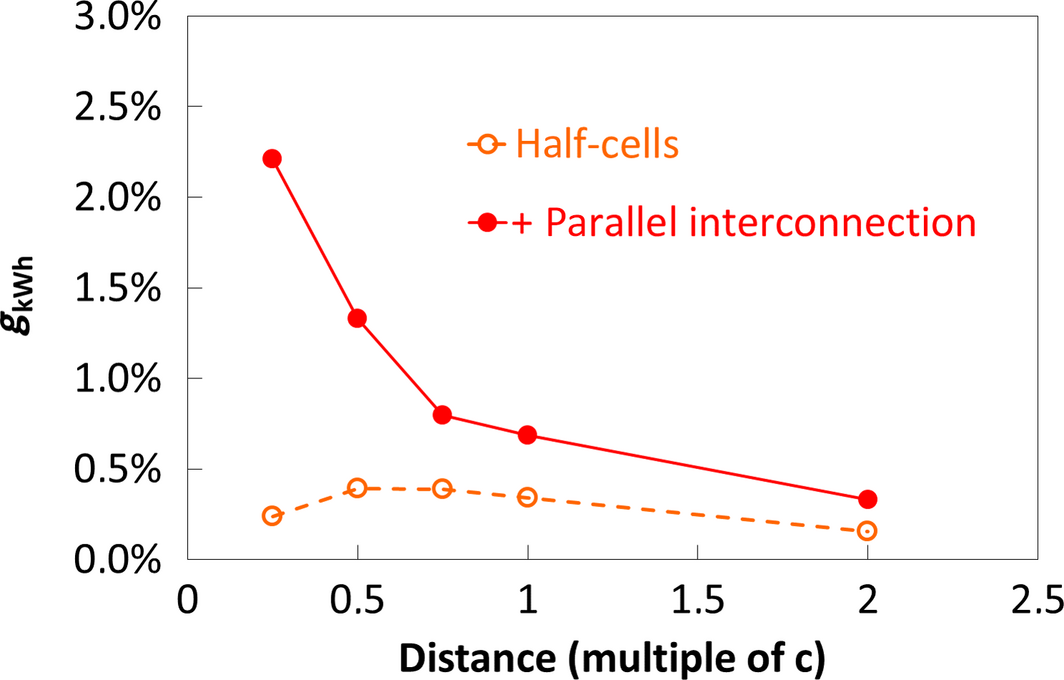
Figure 22 shows the annual simulation of the gain brought by the novel architecture compared to standard one with the influence of half-cells only and with the influence of the parallel interconnection in addition. We observe that the gain due to less resistive losses (half-cells influence) is limited independently of the distance (below 0.4%) as the total irradiance on our south-oriented vertical bifacial module is not very high (1.04 sun maximum, 0.32 sun in average). This type of architecture could be suitable in applications where the module receives more radiation, which implies more resistive losses. We also observe that the maximal gain due to non-uniform irradiance (parallel interconnection influence) is obviously higher for short distances when the non-uniformity of backside irradiance increases. Therefore, this architecture could be suitable for applications which suffer from high non-uniform irradiance on the module like in compact bifacial solar plants for example. Note that the real annual gain considering both effects would be comprised between the dotted and plain curve since the plain red curve describes the maximal g_Pm (see eq. (8)). However, we cannot quantify this with our simple model.

Figure 22. Simulation of the annual gain of the novel architecture compared to standard one varying the distance between module and reflector. The red plain curve shows the parallel interconnection influence in addition to the half-cells influence shown by the orange dotted curve.

Textured glasses architecture

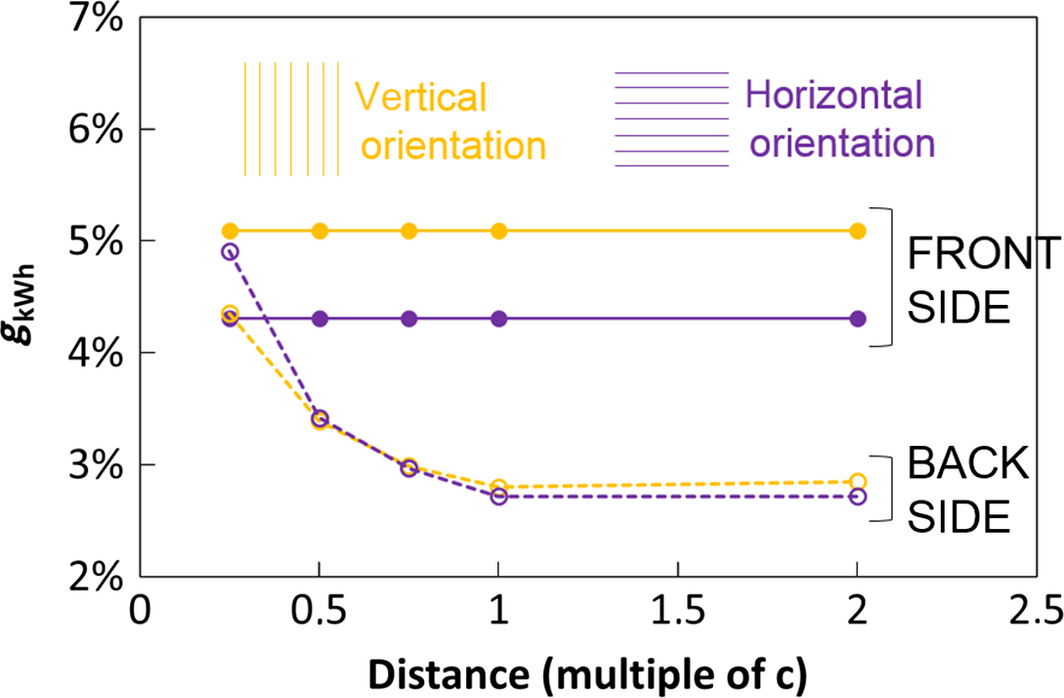
Figure 23 shows the annual simulation of the gain brought by the novel architecture compared to standard one in different orientation of the linear textured glass and for each side of the module. We observe that the backside gain does not depend a lot on the texturation orientation as the white backside reflector is quasi-lambertian, and it increases for shorter distances as the proportion of high incidence angles increases. In a real facade application, the backside gain would be certainly higher since the black inner side walls of our test bench absorb a part of radiations. We also observe that the frontside gain is independent of the distance and lower for the horizontal orientation. This gain would be certainly higher if the ground albedo had been taken into account in our model since more radiation would be incident from the ground.

Figure 23. Simulation of the annual gain of the novel architecture compared to standard one varying the distance between module and reflector.

Bifacial gain considering all contributions

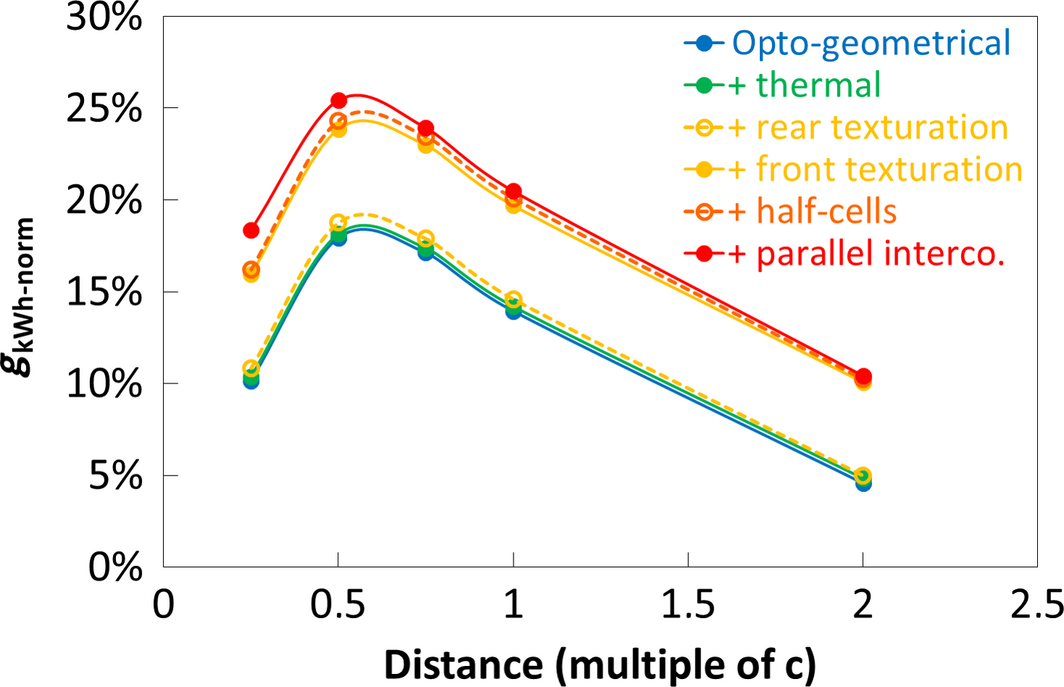
Finally, Figure 24 shows the annual gain of a bifacial module compared to a monofacial one in our reduced scale vertical facade. First, the largest part of the gain is due to the opto-geometrical environment (18.1% for the optimal distance – see section 'Annual performance'). Then, a slight gain is due to the thermal advantage of the bifacial module (0.3% maximum – see section Experimental data). The use of textured glasses in their vertical orientation adds a large gain (up to 5.8%) mainly due to the front glass (up to 5.1%). In comparison, the gain brought by the half-cells and parallel interconnection architecture appears to be limited in our vertical facade application.

Figure 24. Simulation of the annual gain of a bifacial module compared to a monofacial one as a function of the distance between module and reflector. From the bottom to the top, each curve shows an additional contribution to the gain.

Perspective at Real Scale

Full-size module architecture

The electrical and optical architecture of bifacial modules need to be optimized regarding the issues of resistive losses, non-uniform and diffuse backside irradiance. Based on the work described here, we propose the module architectures shown in Figure 25.

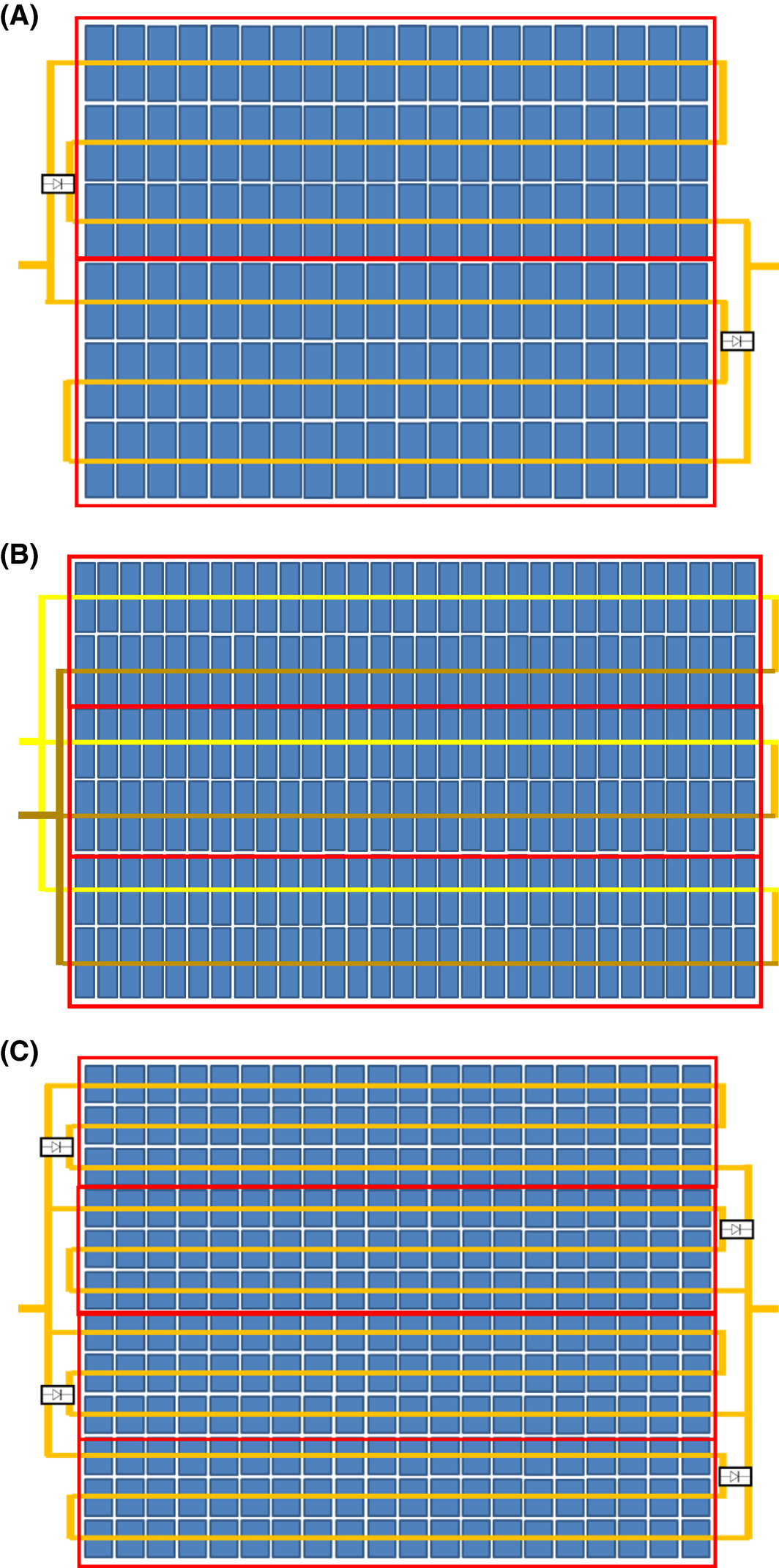
Figure 25. Module electrical architectures equivalent to a 6 × 10 full-size cells module. The division factor of a cell is equal to the number of blocks in parallel shown with red rectangles: factor two (A), factor three (B), and factor four (C).

On the electrical part, the module has two parallel blocks of 60 half-cut cells (Fig. 25A), three parallel blocks of 60 cells cut in three (Fig. 25B), or four parallel blocks of 60 cells cut in four (Fig. 25C). Possible positions of bypass diodes are shown on the images. The two blocks module seems to be the most suitable in practice, since the three blocks module requires electrical insulation between the yellow and brown busbars, and the four blocks module could imply complex soldering process due to the small size of the cells. However, with three or four parallel blocks (smaller cells), the robustness to non-uniform irradiance would be higher and the resistive losses would be lower compared with the two blocks module. Finally, the two and four parallel blocks modules seem to be suitable for vertical facade applications as their positive and negative outputs are positioned on both sides of the module. Therefore, the neighboring modules can be more easily connected in series and resistive losses are minimized at the system level.

On the optical part, the textured glasses can be used on both sides knowing that most part of the gain will be due to the front glass. Ideally, the texturation of glasses would be optimized for several types of bifacial applications: tilted face to the equator or vertical face to east–west on a horizontal white ground or white roof, and vertically integrated onto a white facade.

Further experimental tests

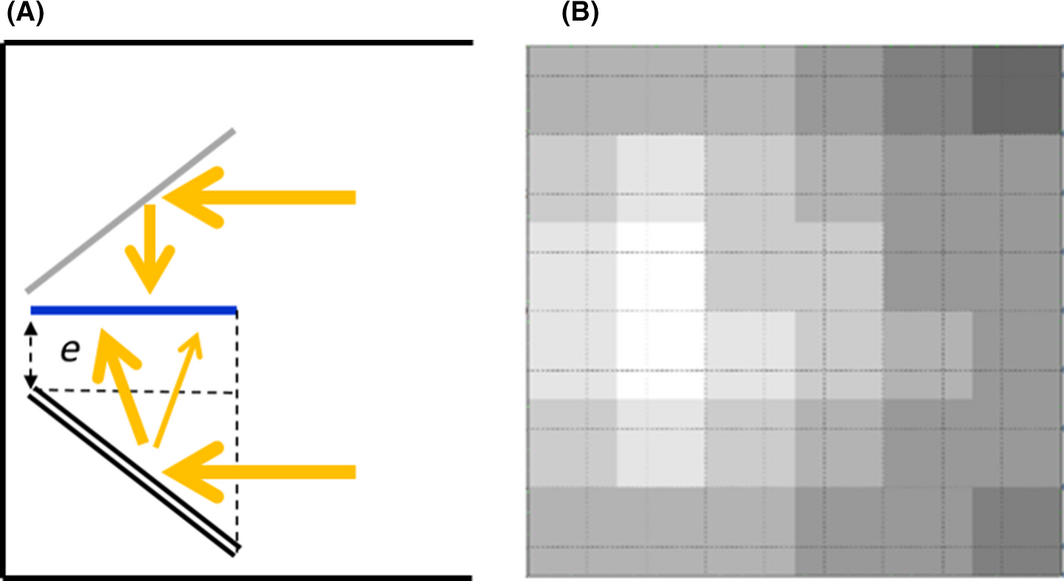
The potential of the module architectures proposed in the previous section must be evaluated experimentally. This must be performed with both an outdoor and an indoor setup. On the one hand, a real size adjustable facade would allow evaluating the optimal module–reflector distance in order to compare it to the 0.5c–0.75c found on our reduced scale test bench. On the other hand, a real size double illumination setup could be designed in order to simulate real outdoor environment conditions. Figure 26A shows that a white reflector (the one used outdoor on a flat roof or vertical facade for example) can be used instead of the back mirror in the double illumination setup. In this case, the radiation incident on the backside of the module would be non-uniform (Fig. 26B), diffuse, and would overall take into account the spectral reflectivity of the reflector as in a real outdoor environment.

Figure 26. (A) Schematics of the adapted double illumination setup (aluminum mirror on the front, white outdoor reflector on the back). (B) Ray-tracing simulation of the distribution of irradiance on the backside of a 6 × 6 cells module (instead of a 6 × 10 cells in portrait orientation) with the adapted double illumination setup (white pixels show the most irradiated cells).

Finally, we designed an optimal real-size standard double illumination setup (mirrors on both sides of the module) with our ray-tracing model of the PASAN solar simulator. We found that a portrait orientation of the module is suitable otherwise the mirrors length would not fit inside the PASAN. We also found an optimal angle between mirror and module of 43° ± 1°. That leads to a similar uniformity of irradiance, a similar global irradiance and a normal incidence in average for our setup and for a standard STC test (considering a perfect mirror and for a distance e = 5 cm – see parameter e on Fig. 26A). For this angle, increasing parameter e does not improve the uniformity of irradiance. Note that an experimental validation of this setup is required since the use of real mirrors (with a part of diffuse reflection, dust, micro-scratches, and less clean areas) could make the non-uniformity of irradiance too high for the characterization standards (NU < 2% for class A [18]). The protocol described in section Double illumination characterization setup must be used and the uncertainties must be evaluated again in the real size case. Such a study could provide additional information to the actual discussions about defining a standard for indoor characterization of bifacial modules in solar simulators.

Conclusion

In this article, we developed a methodology for evaluating the annual performance of bifacial modules integrated on a vertical facade at a reduced scale. First, a protocol using a double illumination setup in a solar simulator has been used. We found that the use of aluminum mirrors does not impact the spectral class of measurement as long as the PASAN source intensity is adjusted. Also, the uncertainty of measurement has been quantified and does not exceed ±3%. Additionally, we performed outdoor tests in real conditions, which allowed us to validate our ray-tracing simulations for both sunny and cloudy days in winter as well as in summer: we found R² > 94.3% with Student test giving a high confidence interval. With these three tools, we were able to quantify the resistive losses which are due to high total irradiance on both sides of the module, the non-uniformity of irradiance on the backside which is due to the module shade projected onto the back reflector, and its diffuse character which is due to the use of quasi-lambertian reflectors.

Regarding the issues above mentioned and using our methodology, we varied opto-geometrical parameters of the application (particularly the distance between module and reflector and the type of reflector) as well as electrical and optical aspects of the module architecture (particularly the cell interconnection and the glasses) in order to maximize the annual performance. The annual electrical energy gain of a bifacial module compared to monofacial could reach 25% with all the cumulated contributions for a module–reflector distance ranging between 0.5c and 0.75c, c being the module height. The highest contribution comes from the opto-geometrical environment of the module namely the irradiance incident on its back, which gives a 18% maximum gain. Another large contribution comes from the use of a linear textured glass vertically oriented on the frontside, which gives a 5% maximum gain.

Based on our tests and simulations for a reduced scale application, we proposed a full-size module architecture which could be more robust to non-uniform irradiance on the backside with less resistive losses and more harnessing of high incidence angles. The next research step will be to evaluate the optimal module–reflector distance in the case of a real-size vertical facade, and to quantify the advantage of the proposed module architecture in several kinds of bifacial applications. This could be achieved with more general simulation tools taking into account the complex opto-geometrical environment of the bifacial module. Finally, the optimized applications will have to be long term tested at the real size power plant scale in order to give confidence to investors.

Acknowledgments

We thank AGC Glass Europe for providing the textured glass samples and for technical discussions. Bruno Sorias work has been supported by a PhD grant from the Commissariat à l'Energie Atomique et aux Energies Alternatives (CEA). The resulting thesis is available online in French [19]. This article is dedicated to the memory of Yves Delesse who actively participated to the instrumentation of the test bench applied in this study.

Conflict of Interest

None declared.

References

1. Cuevas, A.2005. The early history of bifacial solar cells. Pp. 801–805inProceedings 20th European PV solar energy conference, Barcelona.
2. Luque, A., and S. Hegedus. 2003. Handbook of photovoltaic science and engineering. Wiley & Sons, UK.
3. Obara, S., D. Konno, Y. Utsugi, and J. Morel. 2014. Analysis of output power and capacity reduction in electrical storage facilities by peak shift control of PV system with bifacial modules. Appl. Energy128:35–48.
4. Yusufoglu, U. A., T. M. Pletzer, L. J. Koduvelikulathu, C. Comparotto, R. Kopecek, and H. Kurz. 2015. Analysis of the annual performance of bifacial modules and optimization methods. IEEE J. Photovolt.5:320–328.
5. Lo, C. K., Y. S. Lim, and F. A. Rahman. 2015. New integrated simulation tool for the optimum design of bifacial solar panel with reflectors on a specific site. Renew. Energy81:293–307.
6. Cabal, R., Y. Veschetti, V. Sanzone, S. Manuel, S. Gall, F. Barbier, et al. 2013. Industrial process leading to 19.8% on N-Type Cz silicon. Energy Procedia.33:11–17.
7. Ohtsuka, H., M. Sakamoto, M. Koyama, K. Tsutsui, T. Uematsu, and Y. Yazawa. 2001. Characteristics of bifacial solar cells under bifacial illumination with various intensity levels. Prog. Photovolt. Res. Appl.9:1–13.
8. Ezquer, M., I. Petrina, J. M. Cuadra, A. R. Lagunas, and F. Cener-Ciemat. 2009. Design of a special set-up for the IV characterization of bifacial photovoltaic solar cells. Presented at 24th European Photovoltaic Solar Energy Conference and Exhibition, Hamburg.
9. Edler, A.2012. Flasher setup for bifacial measurements. Presented at BIFIPV workshop, Konstanz.
10. Lambda Research Corporation. TracePro: Software for designing optical systems. Available at http://www.lambdares.com/.
11. King, D. L., J. A. Kratochvil, and W. E. Boyson. 1997. Temperature coefficients for PV modules and arrays: measurement methods, difficulties, and results. Photovoltaic Specialists Conference, 1997., Conference Record of the Twenty-Sixth IEEE:1183–1186.
12. Reich, N. H., W. G. J. H. M. van Sark, W. C. Turkenburg, and W. C. Sinke. 2010. Using CAD software to simulate PV energy yield – The case of product integrated photovoltaic operated under indoor solar irradiation. Sol. Energy84:1526–1537.
13. Sprenger, W.2013. Electricity yield simulation of complex BIPV systems. Delft University of Technology, Fraunhofer-Verlag. ISBN 978-3-8396-0606-3, 158 pages.
14. PVsyst. Software for designing PV plants. Available at www.pvsyst.com.
15. Soria, B., and E. Gerritsen. 2013. Vertical Facade Integration of Bifacial PV Modules: Outdoor Testing and Optical Modelling. Presented at 28th European Photovoltaic Solar Energy Conference and Exhibition, Paris.
16. Muneer, T.2004. Solar radiation and daylight models: (with software available from companion web site), 2nd ed. Elsevier Butterworth Heinemann, Oxford; Burlington, MA.
17. Kreinin, L., N. Bordin, A. Karsenty, A. Drori, D. Grobgeld, and N. Eisenberg. 2010. PV module power gain due to bifacial design. Photovoltaic Specialists Conference (PVSC), 2010 35th IEEE:002171–002175.
18. International Electrotechnical Commission. 2007. Norme IEC 60904-9 Ed 2.0 Photovoltaic devices - Part 9: Solar simulator performance requirements. October, 2007.
19. Soria, B.2014. Etude des performances électriques annuelles de modules photovoltaïques bifaces. Cas particulier? Modules bifaces intégrés en façade verticale. Université de Grenoble, https://tel.archives-ouvertes.fr/tel-01126959/document.