Numerical solution of time- and space-fractional coupled Burgers’ equations via homotopy algorithm

Abstract

In this paper, we constitute a homotopy algorithm basically extension of homotopy analysis method with Laplace transform, namely q-homotopy analysis transform method to solve time- and space-fractional coupled Burgers’ equations. The suggested technique produces many more opportunities by appropriate selection of auxiliary parameters ${\textstyle \hslash }$ and ${\textstyle n\quad (n\geqslant 1)}$ to solve strongly nonlinear differential equations. The proposed technique provides ${\textstyle \hslash }$ and ${\textstyle n}$-curves, which describe that the convergence range is not a local point effects and finds elucidated series solution that makes it superior than HAM and other analytical techniques.

Keywords

Laplace transform method; q-Homotopy analysis transform method; Fractional coupled Burgers’ equations; ℏℏ and nn-curves

1. Introduction

Fractional calculus was utilized as an excellent instrument to discover the hidden aspects of various material and physical processes that deal with derivatives and integrals of arbitrary orders [1], [2], [3], [4] and [5]. The theory of fractional differential equations translates the reality of nature excellently in a better and systematic manner [6], [7], [8], [9], [10] and [11]. In recent years, many authors have investigated partial differential equations of fractional order by various techniques such as homotopy analysis technique [12], [13] and [14], operational matrix based method [15], and tau method [16].

This article considers the efficiency of q-homotopy analysis transform method (q-HATM) to solve time- and space- fractional coupled Burgers’ equations. The q-HATM is a graceful coupling of two powerful techniques namely q-HAM and Laplace transform algorithms and gives more refined convergent series solution. The q-HAM was initially introduced and nurtured by El-Tavil and Huseen [17] and [18]. The q-HAM is an extension of the embedding parameter ${\textstyle q\in [0{\mbox{,}}1]}$ arising in the study by Liao HAM [19], [20] and [21] to ${\textstyle q\in \left[0{\mbox{,}}{\frac {1}{n}}\right]}$ that appears in q-HAM. The homotopy analysis method (HAM) is based on homotopy, a rudimentary concept in topology and differential geometry that has been notably applied for solving nonlinear problems occurring in different directions of scientific fields [22], [23], [24], [25], [26], [27] and [28]. The HAM has also been united with Laplace transform to bringing out highly effective technique to investigate nonlinear problems of physical importance [29], [30] and [31]. It is well-known fact the coupling of semi-analytical methods with Laplace transform giving time-consuming consequences and less C.P.U time to investigating nonlinear problems describing engineering applications.

In this letter, we consider the following system of fractional coupled Burgers’ equations

${\frac {{\partial }^{{\alpha }_{1}}u}{\partial t^{{\alpha }_{1}}}}=$${\frac {{\partial }^{2}u}{\partial x^{2}}}+2u{\frac {{\partial }^{{\alpha }_{2}}u}{\partial x^{{\alpha }_{2}}}}-$${\frac {\partial (uv)}{\partial x}}{\mbox{,}}\quad 0<{\alpha }_{i}\leqslant 1{\mbox{,}}$ ${\frac {{\partial }^{{\beta }_{1}}v}{\partial t^{{\beta }_{1}}}}=$${\frac {{\partial }^{2}v}{\partial x^{2}}}+2v{\frac {{\partial }^{{\beta }_{2}}v}{\partial x^{{\beta }_{2}}}}-$${\frac {\partial (uv)}{\partial x}}{\mbox{,}}\quad 0<{\beta }_{i}\leqslant 1$

(1)

subject to the initial conditions

$u(x{\mbox{,}}0)=u_{0}=F(x){\mbox{,}}\quad v(x{\mbox{,}}0)=$$v_{0}=G(x){\mbox{,}}$

(2)

where ${\textstyle \left({\alpha }_{i}{\mbox{,}}{\beta }_{i}{\mbox{,}}\quad i=\right.}$$\left.1{\mbox{,}}2\right)$ are parameters describing the order of the time ${\textstyle \left(i=1\right)}$ and space ${\textstyle \left(i=2\right)}$ fractional derivatives, ${\textstyle x}$ is the space domain and ${\textstyle t}$ is time. When ${\textstyle {\alpha }_{i}={\beta }_{i}=1}$, then the system of Eq. (1) turns down to the classical coupled Burgers’ equations. The most important advantages of using fractional order derivative and integrals over the integer order derivatives and integrals are that they provide a powerful instrument for the description of memory and hereditary properties of different substances.

An excellent literature can be found to study the coupled Burgers’ equations, which are very significant for that the system of Eq. (1) forming a simple model of sedimentations or evolution of scaled volume concentrations of two kinds of gravity [32]. A logistic and remarkable study has been done by number of researchers pertaining to coupled Burgers’ equations [33], [34], [35], [36] and [37]. Recently, Prakash et al. [38] numerically solve the system of Eq. (1) by making use of variational iteration method (VIM) and a systematic comparison has also been made with ADM, GDTM and HPM. In the present article, we observe a highly effective general approach say q-HATM to solve the system of fractional Eq. (1) with concept of fractional Laplace transform of the Caputo derivative [39] at large admissible domain.

2. Basic idea of q-HATM

In this section, we present the basic theory and solution procedure of proposed technique. We take a general fractional nonlinear non-homogeneous partial differential equation of the form:

$D_{t}^{\alpha }u(x{\mbox{,}}t)+Ru(x{\mbox{,}}t)+Nu(x{\mbox{,}}t)=$$g(x{\mbox{,}}t){\mbox{,}}\quad n-1<\alpha \leqslant n$

(3)

where is ${\textstyle D_{t}^{\alpha }u(x{\mbox{,}}t)}$ represents the fractional derivative of the function ${\textstyle u(x{\mbox{,}}t)}$ in terms of Caputo, ${\textstyle R}$ indicates the linear differential operator, ${\textstyle N}$ represents the general nonlinear differential operator and ${\textstyle g(x{\mbox{,}}t)}$ is the source term.

By applying the Laplace transform operator on both sides of Eq. (3), we get the following equation:

$L\left[D_{t}^{\alpha }u\right]+L[Ru]+L[Nu]=L[g(x{\mbox{,}}t)]{\mbox{.}}$

(4)

Making use of the differentiation property of the Laplace transform, it yields

$s^{\alpha }L[u]-\sum _{k=0}^{n-1}s^{\alpha -k-1}u^{\left(k\right)}(x{\mbox{,}}0)+$$L[Ru]+L[Nu]=L[g(x{\mbox{,}}t)]{\mbox{.}}$

(5)

On simplifying, the above equation reduces to

$L[u]-{\frac {1}{s^{\alpha }}}\sum _{k=0}^{n-1}s^{\alpha -k-1}u^{\left(k\right)}(x{\mbox{,}}0)+$${\frac {1}{s^{\alpha }}}[L[Ru]+L[Nu]-L[g(x{\mbox{,}}t)]]=$$0{\mbox{.}}$

(6)

We define the nonlinear operator as

$N[\phi (x{\mbox{,}}t{\mbox{;}}q)]=L[\phi (x{\mbox{,}}t{\mbox{;}}q)]-$${\frac {1}{s^{\alpha }}}\sum _{k=0}^{n-1}s^{\alpha -k-1}{\phi }^{\left(k\right)}(x{\mbox{,}}t{\mbox{;}}q)(0^{+})+$${\frac {1}{s^{\alpha }}}[L[R\phi (x{\mbox{,}}t{\mbox{;}}q)]+$$L[N\phi (x{\mbox{,}}t{\mbox{;}}q)]-L[g(x{\mbox{,}}t)]]{\mbox{,}}$

(7)

where ${\textstyle q\in [0{\mbox{,}}1/n]}$ and ${\textstyle \phi (x{\mbox{,}}t{\mbox{;}}q)}$ are real functions of x, t and q. We construct a homotopy as follows:

$(1-nq)L[\phi (x{\mbox{,}}t{\mbox{;}}q)-u_{0}(x{\mbox{,}}t)]=$$\hslash qH(x{\mbox{,}}t)N[\phi (x{\mbox{,}}t{\mbox{;}}q)]{\mbox{,}}$

(8)

where L   denotes the Laplace transform, ${\textstyle n\geqslant 1}$, ${\textstyle q\in \left[0{\mbox{,}}{\frac {1}{n}}\right]}$ is the embedding parameter, ${\textstyle H(x{\mbox{,}}t)}$ denotes a nonzero auxiliary function, ${\textstyle \hslash \not =0}$ is an auxiliary parameter, ${\textstyle u_{0}(x{\mbox{,}}t)}$ is an initial guess of ${\textstyle u(x{\mbox{,}}t)}$ and ${\textstyle \phi (x{\mbox{,}}t{\mbox{;}}q)}$ is an unknown function. It is obvious that, when the embedding parameter ${\textstyle q=0}$ and ${\textstyle q={\frac {1}{n}}}$, it holds the result

$\phi (x{\mbox{,}}t{\mbox{;}}0)=u_{0}(x{\mbox{,}}t){\mbox{,}}\quad \phi \left(x{\mbox{,}}t{\mbox{;}}{\frac {1}{n}}\right)=$$u(x{\mbox{,}}t){\mbox{,}}$

(9)

respectively. Thus, as q   increases from 0 to ${\textstyle {\frac {1}{n}}}$, the solution ${\textstyle \phi (x{\mbox{,}}t{\mbox{;}}q)}$ varies from the initial guess ${\textstyle u_{0}(x{\mbox{,}}t)}$ to the solution ${\textstyle u(x{\mbox{,}}t)}$. Expanding the function ${\textstyle \phi (x{\mbox{,}}t{\mbox{;}}q)}$ in series form by employing Taylor theorem about q, we have

$\phi (x{\mbox{,}}t{\mbox{;}}q)=u_{0}(x{\mbox{,}}t)+\sum _{m=1}^{\infty }u_{m}(x{\mbox{,}}t)q^{m}{\mbox{,}}$

(10)

where

$u_{m}(x{\mbox{,}}t)={\frac {1}{m!}}{\frac {{\partial }^{m}\phi (x{\mbox{,}}t{\mbox{;}}q)}{\partial q^{m}}}_{q=0}{\mbox{.}}$

(11)

If the auxiliary linear operator, the initial guess, the auxiliary parameter ${\textstyle n{\mbox{,}}\hslash }$ and the auxiliary function are properly chosen, the series (10) converges at ${\textstyle q={\frac {1}{n}}{\mbox{,}}}$ and then we have

$u(x{\mbox{,}}t)=u_{0}(x{\mbox{,}}t)+\sum _{m=1}^{\infty }u_{m}(x{\mbox{,}}t){\left({\frac {1}{n}}\right)}^{m}{\mbox{,}}$

(12)

which must be one of the solutions of the original nonlinear equations. According to the definition (12), the governing equation can be deduced from the zero-order deformation (8).

Define the vectors in the following manner

${\overset {\rightarrow }{u}}_{m}=\lbrace u_{0}(x{\mbox{,}}t){\mbox{,}}u_{1}(x{\mbox{,}}t){\mbox{,}}\ldots {\mbox{,}}u_{m}(x{\mbox{,}}t)\rbrace {\mbox{.}}$

(13)

Now, differentiating the zeroth-order deformation Eq. (8)m-times with respect to q and then dividing them by m  ! and finally setting ${\textstyle q=0{\mbox{,}}}$ we get the following mth-order deformation equation:

$L[u_{m}(x{\mbox{,}}t)-k_{m}u_{m-1}(x{\mbox{,}}t)]=\hslash H(x{\mbox{,}}t)R_{m}({\overset {\rightarrow }{u}}_{m-1}){\mbox{.}}$

(14)

Finally applying the inverse Laplace transform, we have

$u_{m}(x{\mbox{,}}t)=k_{m}u_{m-1}(x{\mbox{,}}t)+\hslash L^{-1}[H(x{\mbox{,}}t)R_{m}({\overset {\rightarrow }{u}}_{m-1})]{\mbox{,}}$

(15)

where the value of ${\textstyle R_{m}({\overset {\rightarrow }{u}}_{m-1})}$ is given as

$R_{m}({\overset {\rightarrow }{u}}_{m-1})={\frac {1}{(m-1)!}}{\frac {{\partial }^{m-1}N[\phi (x{\mbox{,}}t{\mbox{;}}q)]}{\partial q^{m-1}}}_{q=0}{\mbox{,}}$

(16)

and ${\textstyle k_{m}}$ is defined as

$k_{m}={\begin{array}{ll}0{\mbox{,}}&m\leqslant 1{\mbox{,}}\\n{\mbox{,}}&m>1{\mbox{.}}\end{array}}$

(17)

From study it should be analyzed that in special case ${\textstyle n=1}$, q-HATM reduces to the homotopy analysis transform method (HATM).

Example 1.

We consider the time-fractional coupled Burgers’ equation [34] and [36]

${\frac {{\partial }^{\alpha }u}{\partial t^{\alpha }}}=$${\frac {{\partial }^{2}u}{\partial x^{2}}}+2u{\frac {\partial u}{\partial x}}-$${\frac {\partial (uv)}{\partial x}}{\mbox{,}}\quad 0<\alpha \leqslant 1{\mbox{,}}$ ${\frac {{\partial }^{\beta }v}{\partial t^{\beta }}}=$${\frac {{\partial }^{2}v}{\partial x^{2}}}+2v{\frac {\partial v}{\partial x}}-$${\frac {\partial (uv)}{\partial x}}{\mbox{,}}\quad 0<\beta \leqslant 1{\mbox{,}}$

(18)

subject to the initial conditions

$u(x{\mbox{,}}0)=u_{0}=F(x)=sinx{\mbox{,}}\quad v(x{\mbox{,}}0)=$$v_{0}=G(x)=sinx{\mbox{,}}$

(19)

Eqs. (18) and (19) advise that we define the nonlinear operator as

$N^{1}[{\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q){\mbox{,}}{\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q)]=$$L[{\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q)]-\left(1-{\frac {k_{m}}{n}}\right){\frac {1}{s}}F(x)-$${\frac {1}{S^{\alpha }}}L\left[{\frac {{\partial }^{2}{\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q)}{\partial x^{2}}}+\right.$$\left.2{\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q){\frac {\partial {\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q)}{\partial x}}-\right.$$\left.{\frac {\partial ({\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q){\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q))}{\partial x}}\right]{\mbox{,}}$

(20)

$N^{2}[{\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q){\mbox{,}}{\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q)]=$$L[{\psi }_{2}(X{\mbox{,}}t{\mbox{;}}q)]-\left(1-{\frac {k_{m}}{n}}\right){\frac {1}{s}}G(x)-$${\frac {1}{S^{\beta }}}L\left[{\frac {{\partial }^{2}{\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q)}{\partial x^{2}}}+\right.$$\left.2{\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q){\frac {\partial {\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q)}{\partial x}}-\right.$$\left.{\frac {\partial ({\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q){\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q))}{\partial x}}\right]{\mbox{,}}$

(21)

and the Laplace operator as

$L[u_{m}(x{\mbox{,}}t)-k_{m}u_{m-1}(x{\mbox{,}}t)]=\hslash R_{1{\mbox{,}}m}\left[{\overset {\rightarrow }{u}}_{m-1}{\mbox{,}}{\overset {\rightarrow }{v}}_{m-1}\right]{\mbox{,}}$

(22)

$L[v_{m}(x{\mbox{,}}t)-k_{m}v_{m-1}(x{\mbox{,}}t)]=\hslash R_{2{\mbox{,}}m}\left[{\overset {\rightarrow }{u}}_{m-1}{\mbox{,}}{\overset {\rightarrow }{v}}_{m-1}\right]{\mbox{,}}$

(23)

where

$R_{1{\mbox{,}}m}\left[{\overset {\rightarrow }{u}}_{m-1}{\mbox{,}}{\overset {\rightarrow }{v}}_{m-1}\right]=$$L\lbrace u_{m-1}(x{\mbox{,}}t)\rbrace -\left(1-{\frac {k_{m}}{n}}\right){\frac {1}{s}}sinx-$${\frac {1}{s^{\alpha }}}L\left\{{\frac {{\partial }^{2}u}{\partial x^{2}}}+\right.$$\left.2\sum _{i=0}^{m-1}u_{i}{\frac {\partial u_{m-i}}{\partial x}}-\right.$$\left.{\frac {\partial }{\partial x}}\left(\sum _{i=0}^{m-1}u_{i}v_{m-1-i}\right)\right\}{\mbox{.}}$

(24)

$R_{2{\mbox{,}}m}\left[{\overset {\rightarrow }{u}}_{m-1}{\mbox{,}}{\overset {\rightarrow }{v}}_{m-1}\right]=$$L\lbrace v_{m-1}(x{\mbox{,}}t)\rbrace -\left(1-{\frac {k_{m}}{n}}\right){\frac {1}{s}}sinx-$${\frac {1}{s^{\beta }}}L\left\{{\frac {{\partial }^{2}v}{\partial x^{2}}}+\right.$$\left.2\sum _{i=0}^{m-1}v_{i}{\frac {\partial v_{m-i}}{\partial x}}-\right.$$\left.{\frac {\partial }{\partial x}}\left(\sum _{i=0}^{m-1}u_{i}v_{m-1-i}\right)\right\}{\mbox{.}}$

(25)

Appling the inverse of Laplace transform on Eqs. (22) and (23), we get

$u_{m}(x{\mbox{,}}t)=k_{m}u_{m-1}(x{\mbox{,}}t)+\hslash L^{-1}\left\{R_{1{\mbox{,}}m}\left[{\overset {\rightarrow }{u}}_{m-1}{\mbox{,}}{\overset {\rightarrow }{v}}_{m-1}\right]\right\}{\mbox{,}}$

(26)

$v_{m}(x{\mbox{,}}t)=k_{m}v_{m-1}(x{\mbox{,}}t)+\hslash L^{-1}\left\{R_{2{\mbox{,}}m}\left[{\overset {\rightarrow }{u}}_{m-1}{\mbox{,}}{\overset {\rightarrow }{v}}_{m-1}\right]\right\}{\mbox{.}}$

(27)

On solving the above equations, we have

$u_{0}=sinx{\mbox{,}}\quad v_{0}=sinx{\mbox{,}}$

$u_{1}={\frac {\hslash sin{xt}^{\alpha }}{\Gamma (\alpha +1)}}{\mbox{,}}\quad v_{1}=$${\frac {\hslash sin{xt}^{\beta }}{\Gamma (\beta +1)}}{\mbox{,}}$

$u_{2}={\frac {\hslash (\hslash +n)sin{xt}^{\alpha }}{\Gamma (\alpha +1)}}+$${\hslash }^{2}sinx(1-2cosx){\frac {t^{2\alpha }}{\Gamma (2\alpha +1)}}+$$2{\hslash }^{2}sinxcosx{\frac {t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)}}{\mbox{,}}$

$v_{2}={\frac {\hslash (\hslash +n)sin{xt}^{\beta }}{\Gamma (\beta +1)}}+$${\hslash }^{2}sinx(1-2cosx){\frac {t^{2\beta }}{\Gamma (2\beta +1)}}+$$2{\hslash }^{2}sinxcosx{\frac {t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)}}{\mbox{,}}$

(28)

and so on.

In this manner the rest of the iterative components can be obtained. Therefore, the family of q-HATM series solutions of the system of Eq. (18) is given by

$u(x{\mbox{,}}t)=u_{0}(x{\mbox{,}}t)+\sum _{m=1}^{\infty }u_{m}(x{\mbox{,}}t){\left({\frac {1}{n}}\right)}^{m}{\mbox{,}}$ $v(x{\mbox{,}}t)=v_{0}(x{\mbox{,}}t)+\sum _{m=1}^{\infty }v_{m}(x{\mbox{,}}t){\left({\frac {1}{n}}\right)}^{m}{\mbox{.}}$

(29)

If we set ${\textstyle n=1}$ in Eq. (29), we have the solutions derived by making use of HAM as a special case of q-HATM solution. On the other hand, if we take ${\textstyle n=1}$ and ${\textstyle \hslash =-1}$, then we arrive at the results found by using HPM [36], DTM [37] and VIM [38] as a particular case of q-HATM solution. Thus, we can conclude that the results obtained by using q-HATM contain the results obtained with the help of HAM, HPM, DTM and VIM. If we set ${\textstyle \alpha =\beta =1}$ and ${\textstyle \hslash =-1{\mbox{,}}\quad n=1}$ then clearly we can observe that the solution ${\textstyle {\sum }_{m=0}^{N}u_{m}(x{\mbox{,}}t){\left({\frac {1}{n}}\right)}^{m}}$ when ${\textstyle N\rightarrow \infty }$ converges to the exact solution of classical coupled Burgers’ equations, which is the special case of the system of Eq. (18) and is given by

$u=v=sinx\left(1-t+{\frac {t^{2}}{\Gamma (2+1)}}-{\frac {t^{3}}{\Gamma (3+1)}}+\right.$$\left.\cdots +{\left(-1\right)}^{r}{\frac {t^{r}}{\Gamma (r+1)}}+\right.$$\left.\cdots \right)=e^{-t}sinx{\mbox{.}}$

(30)

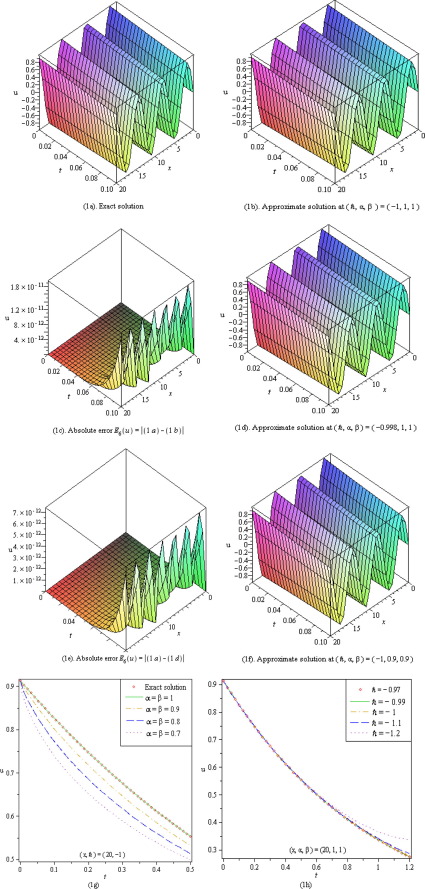
For simplicity, here we consider ${\textstyle u=u(x{\mbox{,}}t)=v(x{\mbox{,}}t)}$ and ${\textstyle \alpha =\beta }$ for every case. The efficiency of purpose method is noticed through the absolute error between exact solution and second order approximation shown in Fig. 1c and e.

Figure 1. (a)–(h) Represent six order approximations HAM (q-HATM, ${\textstyle n=1}$) solution ${\textstyle u(x{\mbox{,}}t)=v(x{\mbox{,}}t)}$ of system of Eq. (18).

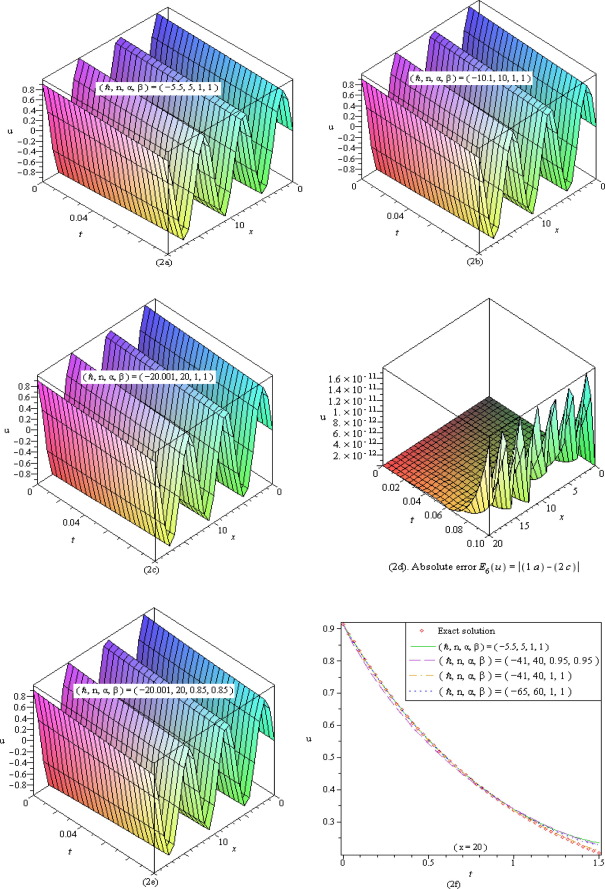
Table 1 shows that q-HATM, can provide many more acceptable solutions compared to all other analytical techniques for same grid point and order of solution series. A proper selection of auxiliary parameters ${\textstyle \hslash }$ and ${\textstyle n}$ gives more correct approximate solution which is identical to exact solution. A horizontal line segment represents the absolute convergence range for q-HATM solution series in ${\textstyle \hslash }$-curve corresponding to ${\textstyle n\quad (n\geqslant 1)}$ (see Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7).

Example 2.

Finally, we consider the following space-fractional coupled Burgers’ equation [34] and [36]

${\frac {\partial u}{\partial t}}={\frac {{\partial }^{2}u}{\partial x^{2}}}+$$2u{\frac {{\partial }^{\alpha }u}{\partial x^{\alpha }}}-$${\frac {\partial (uv)}{\partial x}}{\mbox{,}}\quad 0<\alpha \leqslant 1{\mbox{,}}$ ${\frac {\partial v}{\partial t}}={\frac {{\partial }^{2}v}{\partial x^{2}}}+$$2v{\frac {{\partial }^{\beta }v}{\partial x^{\beta }}}-$${\frac {\partial (uv)}{\partial x}}{\mbox{,}}\quad 0<\beta \leqslant 1$

(31)

subject to the initial conditions

$u(x{\mbox{,}}0)=u_{0}=F(x)=x^{2}{\mbox{,}}\quad v(x{\mbox{,}}0)=$$v_{0}=G(x)=x^{3}{\mbox{,}}$

(32)

Table 1. Comparative study between HPM [36] and q-HATM.

Absolute error ${\textstyle E_{4}(u)=\vert u_{exa.}-u_{app.}\vert }$
${\textstyle x}$	${\textstyle t}$	HPM [36], ${\textstyle \vert u_{exa.}-u_{app.}\vert }$	q-HATM, ${\textstyle \vert u_{exa.}-u_{app.}\vert {\mbox{,}}\quad \quad (\hslash {\mbox{,}}n)}$
−10	0.07	7.5 × 10−9	7.5 × 10−9,    (−1, 1)
			4 × 10−10,    (−0.99, 1)
			2.0 × 10−9,    (−0.98, 1)
			1.5 × 10−9,    (−4.98, 5)
			1.0 × 10−9,    (−58.5, 60)
15	0.2	0.0000016779	0.0000016779,    (−1, 1)
			4.326 × 10−7,    (−0.99, 1)
			5.09 × 10−8,    (−9.8, 10)
			3.470 × 10−7,    (−44.5, 45)

Figure 2. (a)–(f) Show the six order approximate q-HATM solution ${\textstyle u(x{\mbox{,}}t)=v(x{\mbox{,}}t)}$ of system of Eq. (18).

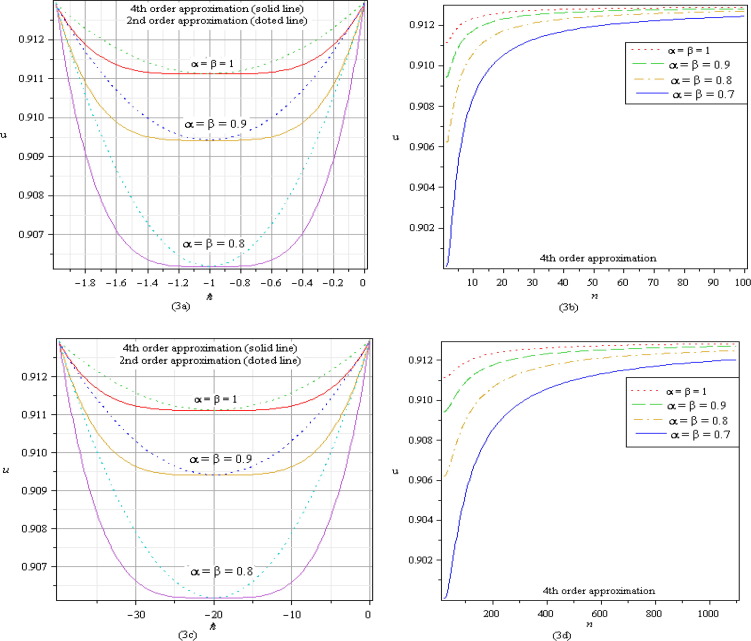
Figure 3. (a)–(d) ${\textstyle \hslash }$ and ${\textstyle n}$-curves at ${\textstyle x=20{\mbox{,}}\quad t=0.002}$ of system of Eq. (18) and show the valid convergence range of ${\textstyle \hslash }$ and asymptotic behaviour of ${\textstyle u(x{\mbox{,}}t)=v(x{\mbox{,}}t)}$ respectively with different values of ${\textstyle \alpha =\beta }$: (3a) for HAM, convergence range is ${\textstyle -1.99\leqslant \hslash <0}$; (3c) for q-HATM, ${\textstyle n=20}$ convergence range is ${\textstyle -39.81\leqslant \hslash <0}$; (3b) at ${\textstyle \hslash =-1}$ and (3d) at ${\textstyle \hslash =-19.8}$, show the validity of corresponding ${\textstyle \hslash }$-curves.

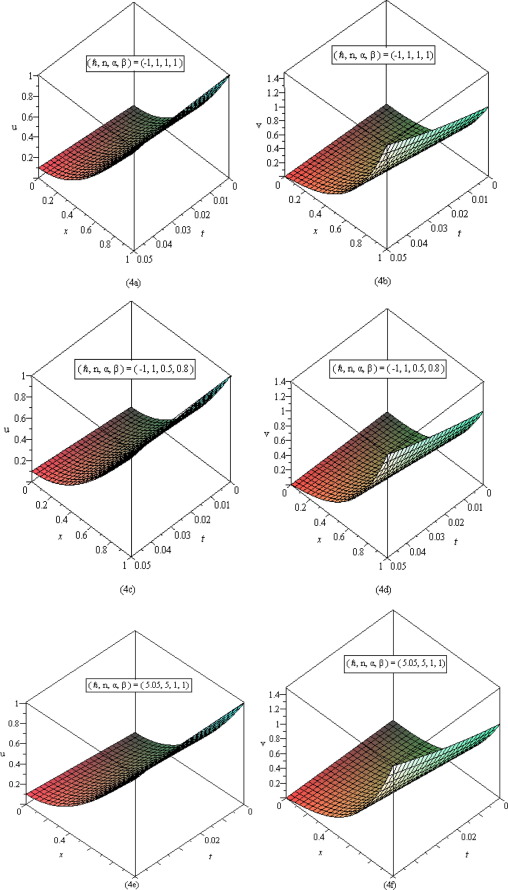
Figure 4. (a)–(f) Show the second order approximate q-HATM surface solution ${\textstyle u(x{\mbox{,}}t)}$ and ${\textstyle v(x{\mbox{,}}t)}$ of system (31) with different values of ${\textstyle \left(\hslash {\mbox{,}}n{\mbox{,}}\alpha {\mbox{,}}\beta \right)}$ versus time variable t   and space variable ${\textstyle x}$.

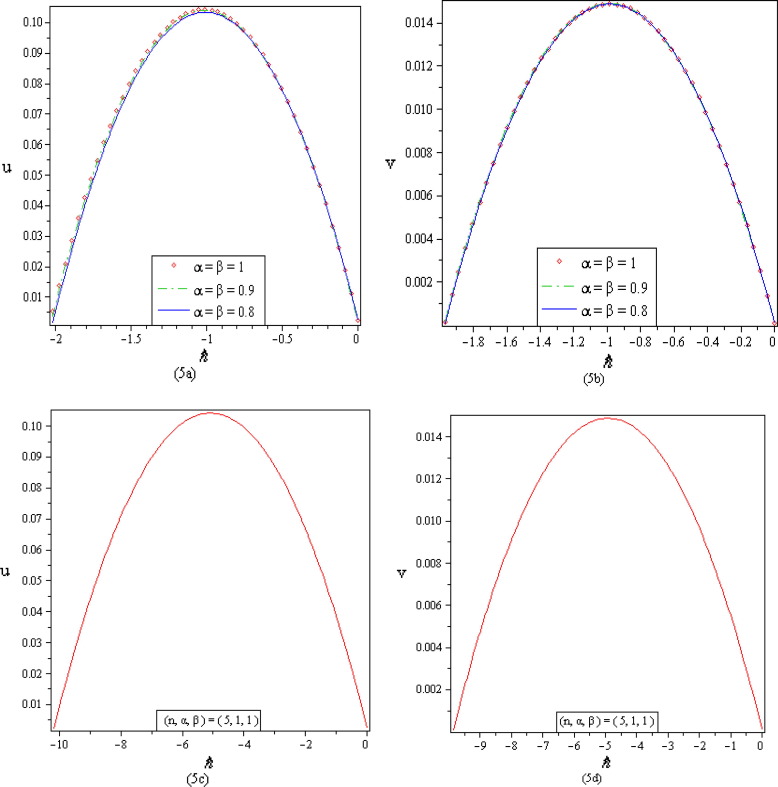
Figure 5. (a)–(d) ${\textstyle \hslash }$-curves at ${\textstyle x=t=0.05}$ for second order approximation of system of fractional Eq. (31) and show the valid convergence range of ${\textstyle u(x{\mbox{,}}t)}$ and ${\textstyle v(x{\mbox{,}}t)}$: (5a) ${\textstyle -2.021\leqslant \hslash <0}$ and (5b) ${\textstyle -1.968\leqslant \hslash <0}$ for HAM; (5c) ${\textstyle -10.18\leqslant \hslash <0}$ and (5d) ${\textstyle -9.85\leqslant \hslash <0}$ for q-HATM, ${\textstyle n=5}$.

Figure 6. (a)–(b) ${\textstyle n}$-curves at ${\textstyle x=t=0.05}$ for second order approximation of system (31) and show the asymptotic behavior of ${\textstyle u(x{\mbox{,}}t)}$ and ${\textstyle v(x{\mbox{,}}t)}$ also describe the validity of ${\textstyle \hslash }$-curve.

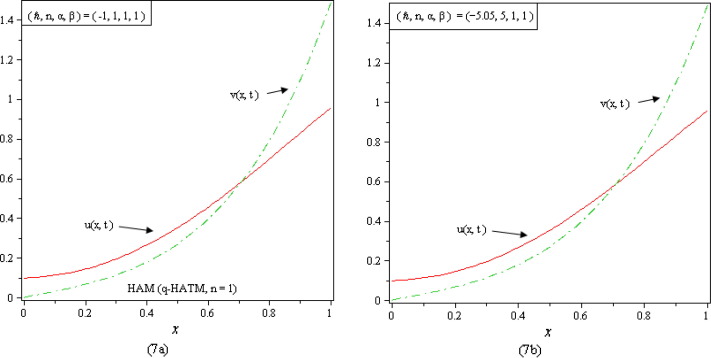
Figure 7. (a)–(b) Show the comparative behaviors of ${\textstyle u(x{\mbox{,}}t)}$ and ${\textstyle v(x{\mbox{,}}t)}$ at ${\textstyle t=0.05}$ versus space variable ${\textstyle x}$. It’s clear to see that both the functions are continuously increasing functions.

Eqs. (31) and (32) advise that we define the nonlinear operator as

$N^{1}[{\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q){\mbox{,}}{\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q)]=$$L[{\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q)]-\left(1-{\frac {k_{m}}{n}}\right){\frac {1}{s}}F(x)-$${\frac {1}{s}}L\left[{\frac {{\partial }^{2}{\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q)}{\partial x^{2}}}+\right.$$\left.2{\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q){\frac {{\partial }^{\alpha }{\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q)}{\partial x^{\alpha }}}-\right.$$\left.{\frac {\partial ({\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q){\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q))}{\partial x}}\right]{\mbox{,}}$

(33)

$N^{2}[{\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q){\mbox{,}}{\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q)]=$$L[{\psi }_{2}(X{\mbox{,}}t{\mbox{;}}q)]-\left(1-{\frac {k_{m}}{n}}\right){\frac {1}{s}}G(x)-$${\frac {1}{s}}L\left[{\frac {{\partial }^{2}{\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q)}{\partial x^{2}}}+\right.$$\left.2{\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q){\frac {{\partial }^{\beta }{\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q)}{\partial x^{\beta }}}-\right.$$\left.{\frac {\partial ({\psi }_{1}(x{\mbox{,}}t{\mbox{;}}q){\psi }_{2}(x{\mbox{,}}t{\mbox{;}}q))}{\partial x}}\right]{\mbox{,}}$

(34)

and the Laplace operator as

$L[u_{m}(x{\mbox{,}}t)-k_{m}u_{m-1}(x{\mbox{,}}t)]=\hslash R_{1{\mbox{,}}m}\left[{\overset {\rightarrow }{u}}_{m-1}{\mbox{,}}{\overset {\rightarrow }{v}}_{m-1}\right]{\mbox{,}}$

(35)

$L[v_{m}(x{\mbox{,}}t)-k_{m}v_{m-1}(x{\mbox{,}}t)]=\hslash R_{2{\mbox{,}}m}\left[{\overset {\rightarrow }{u}}_{m-1}{\mbox{,}}{\overset {\rightarrow }{v}}_{m-1}\right]{\mbox{,}}$

(36)

where

$R_{1{\mbox{,}}m}\left[{\overset {\rightarrow }{u}}_{m-1}{\mbox{,}}{\overset {\rightarrow }{v}}_{m-1}\right]=$$L\lbrace u_{m-1}(x{\mbox{,}}t)\rbrace -\left(1-{\frac {k_{m}}{n}}\right){\frac {1}{s}}x^{2}-$${\frac {1}{s}}L\left\{{\frac {{\partial }^{2}u}{\partial x^{2}}}+\right.$$\left.2\sum _{i=0}^{m-1}u_{i}{\frac {{\partial }^{\alpha }u_{m-i}}{\partial x^{\alpha }}}-\right.$$\left.{\frac {\partial }{\partial x}}\left(\sum _{i=0}^{m-1}u_{i}v_{m-1-i}\right)\right\}{\mbox{.}}$

(37)

$R_{2{\mbox{,}}m}\left[{\overset {\rightarrow }{u}}_{m-1}{\mbox{,}}{\overset {\rightarrow }{v}}_{m-1}\right]=$$L\lbrace v_{m-1}(x{\mbox{,}}t)\rbrace -\left(1-{\frac {k_{m}}{n}}\right){\frac {1}{s}}x^{3}-$${\frac {1}{s}}L\left\{{\frac {{\partial }^{2}v}{\partial x^{2}}}+\right.$$\left.2\sum _{i=0}^{m-1}v_{i}{\frac {{\partial }^{\beta }v_{m-i}}{\partial x^{\beta }}}-\right.$$\left.{\frac {\partial }{\partial x}}\left(\sum _{i=0}^{m-1}u_{i}v_{m-1-i}\right)\right\}{\mbox{.}}$

Obviously, the solution of the mth-order deformation Eqs. (35) and (36) for ${\textstyle m\geqslant 1}$ becomes

$u_{m}(x{\mbox{,}}t)=k_{m}u_{m-1}(x{\mbox{,}}t)+\hslash L^{-1}\left\{R_{1{\mbox{,}}m}\left[{\overset {\rightarrow }{u}}_{m-1}{\mbox{,}}{\overset {\rightarrow }{v}}_{m-1}\right]\right\}{\mbox{,}}$

(38)

$v_{m}(x{\mbox{,}}t)=k_{m}v_{m-1}(x{\mbox{,}}t)+\hslash L^{-1}\left\{R_{2{\mbox{,}}m}\left[{\overset {\rightarrow }{u}}_{m-1}{\mbox{,}}{\overset {\rightarrow }{v}}_{m-1}\right]\right\}{\mbox{,}}$

(39)

On solving the above equations, it gives the following results

$u_{0}=x^{2}{\mbox{,}}\quad v_{0}=x^{3}{\mbox{,}}$

$u_{1}=-\hslash \left(2-5x^{4}+4{\frac {x^{4-\alpha }}{\Gamma (3-\alpha )}}\right)t{\mbox{,}}$

$v_{1}=-\hslash \left(6x-5x^{4}+12{\frac {x^{6-\beta }}{\Gamma (4-\beta )}}\right)t{\mbox{,}}$

$u_{2}=(\hslash +n)u_{1}+{\hslash }^{2}(-84x^{2}+30x^{5}+35x^{6}+$$4(4-\alpha )(3-\alpha )+8){\frac {x^{2-\alpha }}{\Gamma (3-\alpha )}}-$$\left({\frac {4(7-\alpha )}{\Gamma (3-\alpha )}}+{\frac {240}{\Gamma (5-\alpha )}}+\right.$$\left.{\frac {20}{\Gamma (3-\alpha )}}\right)x^{6-\alpha }+$$\left({\frac {8\Gamma (5-\alpha )}{\Gamma (5-2\alpha )}}+\right.$$\left.{\frac {16}{\Gamma (3-\alpha )}}\right){\frac {x^{6-2\alpha }}{\Gamma (3-\alpha )}}-$$12(8-\beta ){\frac {x^{7-\beta }}{\Gamma (4-\beta )}}){\frac {t^{2}}{\Gamma (3-1)}}{\mbox{,}}$

$v_{2}=(\hslash +n)v_{1}+{\hslash }^{2}\left(-84x^{2}+30x^{5}+\right.$$\left.35x^{6}+\left({\frac {12(6-\beta )(5-\beta )}{\Gamma (4-\beta )}}+\right.\right.$$\left.\left.{\frac {12}{\Gamma (2-\beta )}}+{\frac {72}{\Gamma (4-\beta )}}\right)x^{4-\beta }-\right.$$\left.\left({\frac {12(8-\beta )}{\Gamma (4-\beta )}}+\right.\right.$$\left.\left.{\frac {240}{\Gamma (5-\beta )}}+{\frac {60}{\Gamma (4-\beta )}}\right)x^{7-\beta }+\right.$$\left.\left({\frac {24\Gamma (7-\beta )}{\Gamma (7-2\beta )}}+\right.\right.$$\left.\left.{\frac {144}{\Gamma (4-\beta )}}\right){\frac {x^{9-2\beta }}{\Gamma (4-\beta )}}-\right.$$\left.4(7-\alpha ){\frac {x^{6-\alpha }}{\Gamma (3-\alpha )}}\right){\frac {t^{2}}{\Gamma (3-1)}}{\mbox{,}}$

(40)

and so on.

In this manner the rest of the iterative components can be found. Therefore, the q-HATM approximate series solutions of system of Eq. (31) are presented as

$u(x{\mbox{,}}t)=u_{0}(x{\mbox{,}}t)+\sum _{m=1}^{\infty }u_{m}(x{\mbox{,}}t){\left({\frac {1}{n}}\right)}^{m}$ $v(x{\mbox{,}}t)=v_{0}(x{\mbox{,}}t)+\sum _{m=1}^{\infty }v_{m}(x{\mbox{,}}t){\left({\frac {1}{n}}\right)}^{m}$

(41)

Eq. (41) represents the family of q-HATM solutions of system of Eq. (31), which converges rapidly. Although exact solution of system of Eq. (31) is not available so diagrammatical representations to elucidate proposed method. If we set ${\textstyle n=1}$ in Eq. (41), we get the solutions obtained by using HAM as a special case of q-HATM solution. On the other hand, if we let ${\textstyle n=1}$ and ${\textstyle \hslash =-1}$, then we arrive at the results obtained by HPM [36], DTM [37] and VIM [38] as a particular case of q-HATM solution. Thus, we can conclude that the results obtained by using q-HATM contain the results obtained with the help of HAM, HPM, DTM and VIM.

4. Conclusions

In this paper, the q-homotopy analysis transform method (q-HATM) has been successfully employed to time- and space- fractional coupled Burgers’ equations with entice solution procedures. The validity of family of purposed solution in large admissible convergent region, is noticed by ${\textstyle \hslash }$ and ${\textstyle n}$-curves. Positivisms of proposed method is that it provides nonlocal effect, promising large convergence region, straight forward solution procedure and free from any assumption, calculating complicated polynomials and integrations, small/large physical parameters. Thus, it can be winded up that the scheme is highly systematic and can be applied to investigate nonlinear mathematical models describing realistic problems.

Acknowledgments

The authors are highly grateful to the anonymous referee for carefully reading the paper and for his constructive comments and suggestions which have improved the paper.

References

1. [1] K.B. Oldham, J. Spanier; The Fractional Calculus; Acad. Press, New York, NY, USA (1974)
2. [2] K.S. Miller, B. Ross; An Introduction to the Fractional Calculus and Fractional Differential Equations; Willey, New York, NY, USA (1993)
3. [3] I. Podlubny; Fractional Differential Equations, vol. 198, Academic Press, San Diego, Calif, USA (1999) 340p
4. [4] A.A. Kilbas, H.M. Srivastava, J.J. Trujillo; Theory and Applications of Fractional Differential Equations, vol. 204, Elsevier, Amsterdam (2006) 540p
5. [5] D. Baleanu, K. Diethelm, E. Scalas, J.J. Trujillo; Fractional Calculus Models and Numerical Methods; Worl. Scie, Singap. (2012)
6. [6] S. Kumar; A numerical study for solution of time fractional nonlinear shallow-water equation in oceans; Z. Naturforsch. A, 68 (2013), pp. 547–553
7. [7] S. Kumar, H. Kocak, A. Yildirim; A fractional model of gas dynamics equation and its approximate solution by using Laplace transform; Z. Naturforsch. A, 67 (2012), pp. 389–396
8. [8] R.P. Agarwal, M. Benchohra, S. Hamani; A survey on existence results for boundary value problems of nonlinear fractional differential equations and inclusions; Acta Appl. Math., 109 (2010), pp. 973–1033
9. [9] D.H. Shou, J.H. He; Beyond Adomain method: the variational iteration method for solving heat like and wave-like equation with variable coefficients; Phys. Lett. A, 372 (2008), pp. 233–237
10. [10] D. Kumar, J. Singh, S. Kumar; Analytical modeling for fractional multi-dimensional diffusion equations by using Laplace transform; Commun. Numer. Anal., 2015 (1) (2015), pp. 16–29
11. [11] D. Baleanu; About fractional quantization and fractional variational principles; Commun. Nonl. Sci. Numer. Simul., 14 (2009), pp. 2520–2523
12. [12] M. Dehghan, J. Manafian, A. Saadatmandi; Solving nonlinear fractional partial differential equations using the homotopy analysis method; Numer. Methods Part. Diff. Eq., 26 (2) (2010), pp. 448–479
13. [13] M. Dehghan, J. Manafian, A. Saadatmandi; The solution of the linear fractional partial differential equations using the homotopy analysis method; Z. Naturforsch. A, 65a (11) (2010), pp. 549–935
14. [14] M. Dehghan, F. Shakeri; A semi-numerical technique for solving the multi-point boundary value problems and engineering applications; Int. J. Numer. Methods Heat Fluid Flow, 21 (7) (2011), pp. 794–809
15. [15] A. Saadatmandi, M. Dehghan; A new operational matrix for solving fractional-order differential equations; Comput. Math. Appl., 59 (3) (2010), pp. 1326–1336
16. [16] A. Saadatmandi, M. Dehghan; A tau approach for solution of the space fractional diffusion equation; Comput. Math. Appl., 62 (3) (2011), pp. 1135–1142
17. [17] M.A. El-Tawil, S.N. Huseen; The q-homotopy analysis method (q-HAM); Int. J. Appl. Math. Mech., 8 (2012), pp. 51–75
18. [18] M.A. El-Tawil, S.N. Huseen; On convergence of the q-homotopy analysis method; Int. J. Contemp. Math. Sci., 8 (2013), pp. 481–497
19. [19] S.J. Liao, The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems, Ph.D. Thesis, Shanghai Jiao Tong Uni., 1992.
20. [20] S.J. Liao; Homotopy analysis method a new analytical technique for nonlinear problems; Commun. Nonl. Sci. Numer. Simul., 2 (1997), pp. 95–100
21. [21] S.J. Liao; Beyond Perturbation: Introduction to the Homotopy Analysis Method; Chapman and Hall/CRC Press, Boca Raton (2003)
22. [22] D.L. Xu, Z.L. Lin, S.J. Liao, M. Stiassnie; On the steady-state fully resonant progressive waves in water of finite depth; J. Fluid. Mech., 710 (2012), pp. 379–418
23. [23] S.J. Liao; On the homotopy analysis method for nonlinear problems; Appl. Math. Comput., 147 (2004), pp. 499–513
24. [24] H. Jafari, A. Golbabai, S. Seifi, K. Sayevand; Homotopy analysis method for solving multi-term linear and nonlinear diffusion wave equations of fractional order; Comput. Math. Appl., 66 (2010), pp. 838–843
25. [25] H. Xu, J. Cang; Analysis of a time fractional wave-like equation with homotopy analysis method; Phys. Lett. A, 372 (2008), pp. 1250–1255
26. [26] M.M. Rashidi, M.T. Rastegar, M. Asadi, O. Anwar Bég; A study of non-newtonian flow and heat transfer over a non-isothermal wedge using the homotopy analysis method; Chem. Eng. Commun., 199 (2012), pp. 231–256
27. [27] S. Nadeem, A. Hussain, M. Khan; HAM solutions for boundary layer flow in the region of the stagnation point towards stretching sheet; Commun. Nonl. Sci. Numer. Simul., 15 (2010), pp. 475–481
28. [28] S. Nadeem, A. Hussain, M. Khan; Stagnation point of a Jeffrey fluid towards shrinking sheet; Z. Naturforsch., 65 (2010), pp. 540–548
29. [29] M. Khan, M.A. Gondal, I. Hussain, S. Karimi Vanani; A new comparative study between homotopy analysis transform method and homotopy perturbation transform method on semi-infinite domain; Math. Comput. Modell., 55 (2012), pp. 1143–1150
30. [30] D. Kumar, J. Singh, Sushila; Application of homotopy analysis transform method to fractional biological population model; Romanian Rep. Phys., 65 (1) (2013), pp. 63–75
31. [31] D. Kumar, J. Singh, S. Kumar, Sushila; Numerical computation of Klein–Gordon equations arising in quantum field theory by using homotopy analysis transform method; Alexandria Eng. J., 53 (2) (2014), pp. 469–474
32. [32] J. Nee, J. Duan; Limit set of trajectories of the coupled viscous Burger’s equations; Appl. Math. Lett., 11 (1998), pp. 57–61
33. [33] S.E. Esipov; Coupled Burgers equations: a model of polydispersive sedimentation; Phys. Rev. E, 52 (1995), pp. 3711–3718
34. [34] M.A. Abdoua, A.A. Solimanb; Variational iteration method for solving Burger’s and coupled Burger’s equations; J. Comput. Appl. Math., 181 (2005), pp. 245–251
35. [35] M. Dehghan, A. Hamidi, M. Shakourifar; The solution of coupled Burger’s equations using Adomian-Pade technique; Appl. Math. Comput., 189 (2007), pp. 1034–1047
36. [36] A. Yildirim, A. Kelleci; Homotopy perturbation method for numerical solutions of coupled Burgers equations with time- and space-fractional derivatives; Int. J. Numer. Methods Heat Fluid Flow, 20 (2010), pp. 897–909
37. [37] J. Liu, G. Hou; Numerical solutions of the space- and time-fractional coupled Burgers equations by generalized differential transform method; Appl. Math. Comput., 217 (2011), pp. 7001–7008
38. [38] A. Prakash, M. Kumar, K.K. Sharma; Numerical method for solving fractional coupled Burgers equations; Appl. Math. Comput., 260 (2015), pp. 314–320
39. [39] M. Caputo; Elasticita e dissipazione; Zani-Chelli, Bologna (1969)