Study on dynamic response characteristics of radial steel gate under rare earthquake considering fluid structure coupling effect

Abstract

The water resources in southwest China is abundant and the seismicity is strong, so it is necessary to study the dynamic response and safety of hydraulic structures under rare earthquake. Taking a typical radial steel gate as an example, a three-dimensional numerical model considering the interaction between water and gate during the earthquake is established. The accuracy and applicability of the model are verified by comparing with the measured results of the dynamic response of Zipingpu dam during the Wenchuan earthquake. Thereafter, the dynamic displacement and stress, and resonance frequency of the radial gate under the rare earthquake of two wave types are analyzed. The water-structure coupling effect has a great influence on the seismic dynamic response of the radial steel gate. The calculated result of the dynamic response of the gate considering the fluid-structure coupling effect is significantly larger than that of the specification, and the maximum ratio of the two is more than 2.27 times. Under the action of EI wave, the peak value of dynamic stress response is at the bottom of the panel, and the maximum value of resonance frequency (about 49.13 Hz) is located in the middle and lower part of the panel. Under the action of far-field wave, the peak area of dynamic displacement response of the gate is basically the same as that under the action of EI wave, while the maximum value of some measuring points is only half of the maximum value under the action of EI wave. However, the resonance frequency is significantly greater than that of EI wave, the maximum value reaches 65.24 Hz, which appears at the top of the gate. The dynamic response of the gate structure caused by two different wave types of earthquakes is not completely consistent. The comprehensive consideration of different wave types is of significance for the structural design and safety evaluation of the radial steel gate in the earthquake-prone areas.

Keywords: Radial steel gate, rare earthquake, fluid-structure coupling, seismic dynamic response

1. Introduction

Southwest China is located at the junction of the first and second steps of the terrain, with large river drop, so it is rich in hydropower resources. A large number of high dam hydropower stations, such as Ertan Hydropower Station and Jinping Hydropower Station, have been built here [1-4]. Radial steel gates are widely used in these projects due to their large orifice area, simple pier structure, good drainage conditions, convenient opening and closing, and few embedded parts [5]. However, as the regulating throat of hydraulic hub, its structural response characteristics under dynamic load need to be further studied [6]. Southwest China is an earthquake prone area, many gates of hydraulic structures were seriously damaged during the M_s8.0 Wenchuan earthquake in 2008 [7]. The damage and deformation of the gate structure not only affect the normal use function of the gate, but also lead to the loss of the function of regulating and storing water flow of the dam in serious cases, leading to dam break and other secondary disasters. Therefore, it is urgent to study the dynamic response of the radial steel gate under the action of rare earthquake.

Generally, the dynamic response analysis of radial steel gates can be carried out by means of filed monitoring, model test and numerical simulation. Field monitoring can directly record the deformation and stress of the gate structure, but it is difficult to predict the safety of the structure under earthquake. In the aspect of model test, its manufacturing process is complex and costly, and it has obvious size effect. With the breakthrough of computer in the bottleneck of numerical calculation rate, numerical simulation has become the main method to analyze the dynamic stress response of radial steel gate. Zhang et al. [5] used the finite element ANSYS to improve the structure of radial steel gate. The stress and displacement of each component of the improved radial steel gate are significantly lower than those of the traditional gate. Liu et al. [8] carried out a three-dimensional nonlinear analysis of a radial steel gate of a reservoir and investigated the influence of stiffeners on the panel. Wu and Xie [9] used the Galerkin method to derive the system finite element equations of fluid and structure, and analyzed the dynamic characteristics of a radial gate.

Currently, there are mainly three methods can be used to simulate the dynamic response of the gate under earthquake load: (1) the mode-superposition response spectrum method [10], in which only the vibration of the gate is considered, (2) the additional mass method considering the superposition of fluid and vibration [11], and (3) the fluid-solid coupling method considering the coupling effect of fluid and structure [12]. In the earthquake, the vibration movement of the gate structure acts on the water body, making its flow field change. The water body after the change of the flow field also affects the dynamic characteristics of the gate structure, such as damping force, elastic force, inertial force, etc., thus affecting the dynamic response characteristics of the gate structure. Therefore, many studies have pointed out that the coupling process of the water body on the upstream of the gate in the gate movement under earthquake cannot be ignored. Faridmehr et al. [12] established a three-dimensional radial gate model in ABAQUS/Explicit, and found that the results of structural dynamic responses considering fluid-solid coupling are quite different from those of static analysis. Buldgen et al. [11] investigated the classical Westergaard seismic hydrodynamic pressure solution formula through numerical simulation and model test. The results show that the calculated value is conservative than considering the fluid-solid coupling numerical solution because the formula assumes that the structure is completely rigid.

The studies mentioned above have demonstrated that the fluid-structure coupling method is more suitable for simulating the dynamic response of radial steel gates under earthquake. However, most of the previous studies were carried out under the conditions of frequent earthquakes, and the input seismic waves are mostly single EI waves. Hence, study on the dynamic response of the radial steel gates under different seismic waves of rare earthquakes is insufficient. The answer to this question is of special significance for the safety evaluation of radial steel gates under earthquake. Based on the three-dimensional coupled numerical model of gate and water, this paper revises the seismic acceleration curve according to the characteristics of rare earthquakes, and the dynamic response and spatial-temporal distribution characteristics of arc steel gate are studied by using the external excitation of EI wave and far-field seismic wave. The significance of considering water-gate interaction under earthquake has been revealed.

2. Simulation method

2.1 Governing equations considering fluid-structure coupling

In the finite element analysis of fluid-solid coupling under linear small deformation, the fluid is assumed to be a uniform, inviscid and vortex-free ideal fluid [13-14]. According to Euler equation, the dynamic balance equations of fluid can be deduced as follows:

$\rho {\frac {\delta v_{x}}{\delta t}}=-{\frac {\partial p}{\partial x}},\rho {\frac {\delta v_{y}}{\delta t}}=$$-{\frac {\partial p}{\partial y}},\rho {\frac {\delta v_{z}}{\delta t}}=$$-{\frac {\partial p}{\partial z}}$

(1)

or

$\rho {\frac {{\partial }^{2}u}{\partial t^{2}}}=-{\frac {\partial p}{\partial x}},\rho {\frac {{\partial }^{2}v}{\partial t^{2}}}=$$-{\frac {\partial p}{\partial y}},\rho {\frac {{\partial }^{2}w}{\partial t^{2}}}=$$-{\frac {\partial p}{\partial z}}$

(2)

where, $\rho$ is the density of the fluid, $p$ is the pressure of fluid particle, $u$, $v$ and $w$ are the displacement components of the fluid particle in the $x$, $y$ and $z$ directions, and $v_{x}$, $v_{y}$ and $v_{z}$ are the velocity components of the fluid particle in the $x$, $y$ and $z$ directions, $t$ is time. respectively. And the continuity equation of compressible fluid is

$-\left({\frac {\partial v_{x}}{\partial x}}+{\frac {\partial v_{y}}{\partial y}}+{\frac {\partial v_{z}}{\partial z}}\right)={\frac {1}{k}}{\frac {\partial p}{\partial t}}$

(3)

where $k$ is the compressive modulus of fluid.

Using Eqs. (1)-(3), the governing equations of fluid motion can be obtained the following equation:

${\nabla }^{2}p={\frac {\rho }{k}}{\frac {{\partial }^{2}p}{\partial t^{2}}}$

(4)

where ${\nabla }^{2}={\frac {\partial }{\partial x^{2}}}+{\frac {\partial }{\partial y^{2}}}+$${\frac {\partial }{\partial z^{2}}}$ is the Laplace operator.

Obviously, it is difficult to solve Eq. (4) under three-dimensional conditions using conventional finite element methods such as Galerkin's method [15], especially for the fluid-solid coupling interface. Therefore, it is necessary to divide the fluid domain into fluid elements, and then aggregate the discrete motion equations of the whole fluid domain. The Gauss numerical integration of the solution results of each fluid element is weighted and aggregated to obtain the coefficient matrix of the governing equation, and then the motion equation of the whole fluid domain can be expressed as:

$Hp+A{\dot {p}}+E{\ddot {p}}+\rho B{\ddot {r}}+q_{0}=0$

(5)

where $H$, $A$, $E$ and $B$ are the coefficients, $r$ is the displacement (unit: m), $q_{0}$ is the excitation vector (unit: N). It is also necessary to discretize the solid structure by finite element method, and the motion equation:

$M_{\mbox{s}}{\ddot {r}}+C_{s}{\dot {r}}+K_{s}r+f_{p}+f_{0}=0$

(6)

where, $M_{s}$, $C_{s}$ and $K_{s}$ are the mass matrix, damping matrix and stiffness matrix of the structure, respectively; $f_{p}$ is the fluid force at the interface (unit: N), and $f_{p}=-B^{T}p$ by weighted aggregation through Gauss numerical integration; and $f_{0}$ is the external excitation vector other than the fluid force at the interface (unit: N). Then Eqs. (5) and (6) can be combined as:

$\left[{\begin{array}{cc}M_{\mbox{s}}&0\\\rho B&E\end{array}}\right]\left[{\begin{array}{c}{\ddot {r}}\\{\ddot {p}}\end{array}}\right]+\left[{\begin{array}{cc}C_{s}&0\\0&A\end{array}}\right]\left[{\begin{array}{c}{\dot {r}}\\{\dot {p}}\end{array}}\right]+\left[{\begin{array}{cc}K_{s}&-B^{T}\\0&H\end{array}}\right]\left[{\begin{array}{c}r\\p\end{array}}\right]=\left[{\begin{array}{c}\\\end{array}}-f_{0}q_{0}\right]$

(7)

Based on Eq. (7), the structural model and flow field model are first generated in the geometric model software. The external flow field is generated in Workbench, and the finite element model is generated by importing the calculation platform. Then the contact surface between the structure and the fluid is set as the fluid-structure coupling interface, and the external excitation load is input to drive the coupling iteration of the model. In FLUENT, the fluid domain generates pressure under the action of external excitation and transmits it to the structure. The structure then reacts the pressure on the fluid domain with boundary deformation. Such iterative process until the convergence condition is reached. This dynamic mesh technology updates and modifies the fluid domain mesh to ensure that the model mesh does not distort.

2.2 Verification

The accuracy of the above method is analyzed by analyzing the interaction characteristics of Zipingpu dam and reservoir water under the Wenchuan earthquake. Zipingpu Water Control Project [16] is located in the upper reaches of the Minjiang River, more than 60 kilometers northwest of Chengdu, Sichuan Province, and 9 kilometers away from Dujiangyan City. On May 12, 2008, a strong earthquake of magnitude 8.0 occurred in Wenchuan, about 17 km west of Zipingpu Dam, with the maximum intensity of the epicenter as high as XI. This earthquake is characterized by large magnitude, shallow focus (about 14 km), long fault (nearly 300 km) and long duration (about 90 s of main shock) [17]. The strong earthquake caused obvious damage to Zipingpu Dam as shown in Figura 1.

Figure 1. Damage of the dam caused by the Wenchuan earthquake [17]

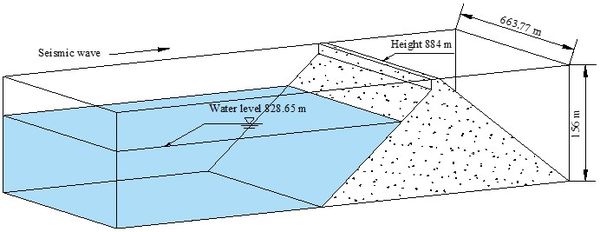
The dam is a concrete face rockfill dam. The length and elevation of the dam crest are 663.77 m and 884 m, respectively. The normal and dead water level are 877 m and 817 m, respectively. The slope ratio of the upstream dam is 1:1.4, the lowest foundation elevation is 728 m, and the dam is constructed in three phases, of which the top elevation in the first and second phases are 796 m and 845 m, respectively, and the reservoir water level during the earthquake is 828.65 m. Based on this, the established three-dimensional model is shown in Figure 2. For the boundary conditions, the upper surface of the fluid is free and incompressible. The contact surface between the dam body and the water body is set as the fluid-solid coupling boundary, and the rest of the fluid surfaces are fixed.

Figure 2. Model of Zipingpu Dam and water

Considering that hydraulic structures are mainly affected by horizontal earthquakes, seismic load input is only considered along the river. The central station of the National Strong Motion Network of China has obtained a large number of main earthquake records with complete seismic phases. Table 1 shows the information collected by the regional station at Zipingpu dam site during the Wenchuan earthquake. Although 7 stations have been set up in this area, the difference of peak acceleration of each station is relatively large, so the measured ground motion cannot be directly used for the simulation calculation of ground motion input. Chen et al. [17] estimated that the peak ground motion of the dam bedrock in the Wenchuan earthquake was more than 0.5 g (g is the acceleration of gravity) according to the measured peak acceleration at the dam crest of Zipingpu Dam. According to the method proposed by Yu et al. [18], the attenuation relationship between the bedrock acceleration and the distance from the fault zone is calculated, and the horizontal peak value of the bedrock of Zipingpu Dam during the Wenchuan earthquake is 0.52 g. Based on these research results and station monitoring data, the peak acceleration used in the final simulation is 0.56 g. In view of this, the seismic wave in the simulation calculation adopts the EI wave as shown in Figure 3, which is generated manually according to the Chinese relevant provisions of the Standard for seismic design of hydraulic structures [19]. The sub-step of seismic wave action time is 0.02 s, and the total action time is 10 s, and the peak acceleration is 0.56 g. And according to the test results [16], the density and friction angle of the dam material are 21.6 g/cm² and 30°, respectively.

Table 1. Basic information of stations

Station	Latitude (°)	Longitude (°)	Site type	Peak acceleration along the river (g)
Wolong, Wenchuan	31.0N	103.2E	Soil	0.96
Bajiao, Shifang	33.3N	104.0E	Soil	0.56
Qingping, Mianzhu	31.5N	104.1E	Soil	0.82
Nanxin, Maoxian	31.6N	103.7E	Soil	0.42
Diban, Maoxian	31.7N	103.9E	Rock	0.31
Zoushixian, Pixian	30.9N	103.8E	Rock	0.12
Zhonghe, Chengdu	30.6N	104.1E	Rock	0.0

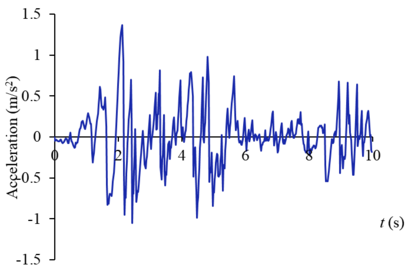
Figure 3. EI seismic wave acceleration curve

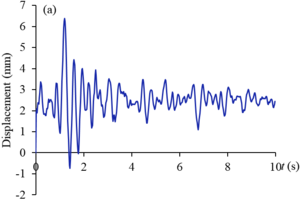
The calculated displacement of the dam considering the coupling effect of water and dam is shown in Figure 4. The dam displacement gradually increases with the elevation, which is the same as the actual damage of Zipingpu dam. The maximum displacement occurring at the dam crest is 273.4 mm. According to the measured data of Chen et al. [17], the measured value of the maximum displacement of the dam is 270.8 mm. The calculated value is close to the measured value, and the error is only 0.9%, indicating that the calculation method in this paper has high accuracy. Meanwhile, calculations were also conducted without considering the coupling effect of water and dam, which showed that the maximum displacement of the dam (198.4 mm) is far less than the actual displacement.

Figure 4. Contour of displacement of the dam

3. Seismic response of radial steel gate

3.1 Numerical Model and parameters

Radial steel gate shown in Figure 5 is selected for the seismic dynamic response analysis considering the fluid-structure coupling effect. The radius of the gate is 12 m, the vertical distance between the support hinge and the gate bottom is 10.9 m, and the panel width is 12 m. Radial gate is a spatial thin-walled structure system mainly composed of gate leaf and arm. The gate leaf structure adopts shell element shell93 which can reflect the spatial stress, and the material is Q235B. The steel material of the support arm is Q345B, and the section is rectangular. In total, there are 14,922 elements of the radial steel gate model. Figure 6 shows the gate - water coupling model. According to the design conditions, the design water level ${\textstyle H}$ is 8.5 m, and the calculated water length ${\textstyle L}$ is selected to be more than 3 times the height of the water, which is 30 m. The water-gate interface is set as the fluid-solid coupling surface, the top of the water is free, and the rest of the surfaces are fixed. Six key parts of the gate are selected for monitoring, including ${\textstyle M_{1}}$ at the top of the gate leaf, ${\textstyle M_{2}}$ at the middle and upper part of the gate leaf, ${\textstyle M_{3}}$ at the middle and lower part of the gate leaf, ${\textstyle M_{4}}$ at the bottom of the gate leaf, ${\textstyle M_{5}}$ at the, and ${\textstyle M_{6}}$ at the lower part of the arm.

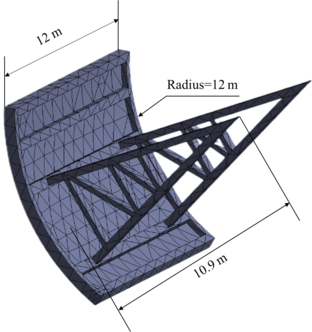
Figure 5. Model of radial steel gate

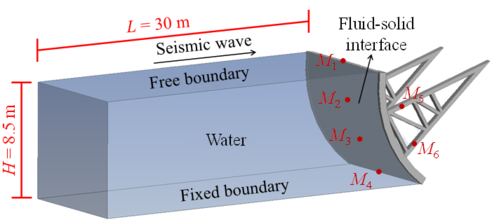
Figure 6. Water-gate coupling model

According to the relevant regulations of the basic acceleration value of rare earthquake of the Standard for seismic design of hydraulic structures [19], the seismic acceleration value in this simulation is 0.30 g, and the corresponding seismic fortification intensity is 8 degrees. The sub-step length of seismic wave action time is 0.02 s, the action time is 10 s in total, and the seismic action load direction is downstream. In addition, EI wave (Figure 3) and far-field seismic wave T1-Ⅱ-1 (Figure 7) are respectively considered for analysis.

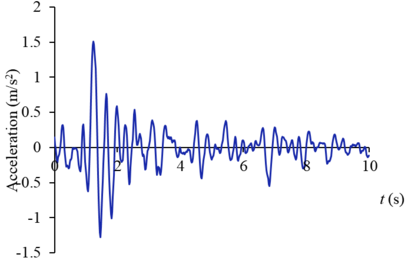
Figure 7. Far field seismic wave T1-Ⅱ-1 acceleration curve

3.2 Dynamic displacement response

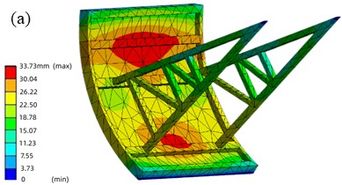
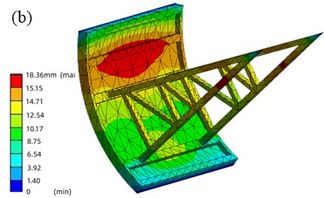
According to the Design specification for steel gates of water and hydropower projects [20], the maximum allowable displacement of the gate is 20 mm. Figure 8 shows the displacement of the gate considering the fluid-structure coupling effect after earthquake. The displacement distribution of EI wave and far-field seismic wave is quite different. Under the action of EI wave, the maximum displacement of the radial gate is 33.7 mm, which exceeds the allowable displacement of the specification. The displacement mainly occurs in the middle of the gate leaf and the middle of the support arm. The maximum displacement is concentrated in the middle and upper part of the gate leaf, and the constrained support hinge and the upper and lower end of the panel have the minimum displacement. Under the action of far-field seismic wave, the maximum displacement of the gate is 18.3 mm, which meets the rigidity requirements of the specification. The displacement mainly occurs in the upper part of the gate leaf, the maximum displacement is concentrated in the upper part of the gate leaf, and the displacement at the connection between the arm and the panel and the arm is small.

Figure 8. Dynamic displacement of gate after earthquake. (a) EI wave. (b) Far-field wave

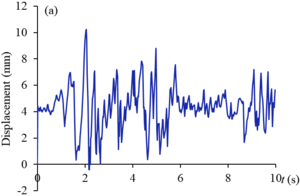
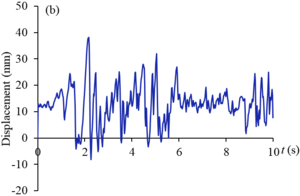
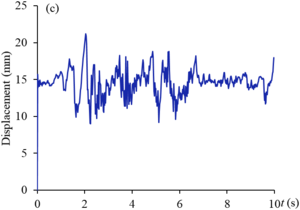
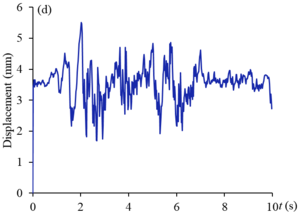
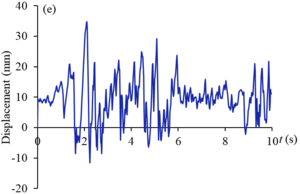
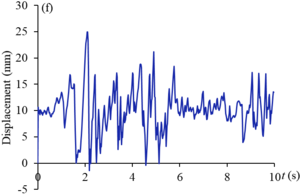
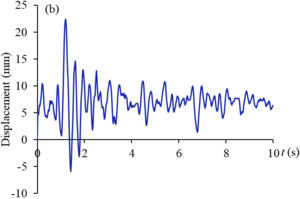
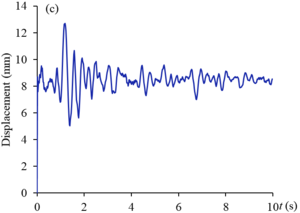
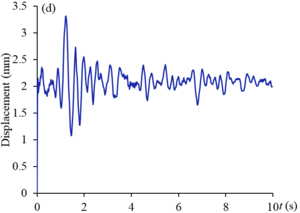
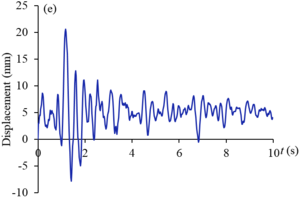
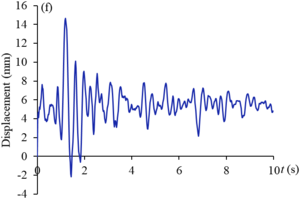
Figures 9 and 10 show the displacement curves of monitoring points ${\textstyle M_{1}}$-${\textstyle M_{6}}$ of gate structure under the action of EI wave and far-field wave, respectively. Under the action of EI wave, the maximum displacements of monitoring points ${\textstyle M_{1}}$ to ${\textstyle M_{6}}$ are 10.2 mm, 38.2 mm, 21.2 mm, 5.5 mm, 34.8 mm and 25.0 mm, respectively. The displacements of monitoring points ${\textstyle M_{2}}$, ${\textstyle M_{3}}$, ${\textstyle M_{5}}$ and ${\textstyle M_{6}}$ exceed the allowable value. The maximum dynamic displacement occurs in the middle and upper part of the panel (${\textstyle M_{2}}$), and the occurrence time is within the sub-step time range of 0.02s before and after 2s. Under the action of far-field wave, the maximum displacements of ${\textstyle M_{1}}$ to ${\textstyle M_{6}}$ monitoring points are 6.4 mm, 22.4 mm, 12.7 mm, 3.3 mm, 20.6 mm and 14.7 mm respectively, which are less than the displacement values of corresponding monitoring points under the action of EI wave, and only the displacements of ${\textstyle M_{2}}$ and ${\textstyle M_{5}}$ monitoring points exceed the allowable values. The maximum displacement value also occurs in the middle and upper part of the panel (${\textstyle M_{2}}$), and the occurrence time is within the sub-step time range of 0.02s before and after 1.3s. It can be seen that the dynamic displacement counter of the structure after the earthquake shown in Figure 8 can reflect the deformation of the gate to a certain extent, but it cannot fully show the true deformation of the structure during the dynamic response duration. The extreme deformation of the structure may occur at a certain time during the response duration.

Figure 9. Displacement curves of monitoring points gate structure under the action of EI wave. (a) ${\textstyle M_{1}}$ point. (b) ${\textstyle M_{2}}$ point. (c) ${\textstyle M_{3}}$ point. (d) ${\textstyle M_{4}}$ point. (e) ${\textstyle M_{5}}$ point. (f) ${\textstyle M_{6}}$ point

Figure 10. Displacement curves of monitoring points gate structure under the action of far field wave. (a) ${\textstyle M_{1}}$ point. (b) ${\textstyle M_{2}}$ point. (c) ${\textstyle M_{3}}$ point. (d) ${\textstyle M_{4}}$ point. (e) ${\textstyle M_{5}}$ point. (f) ${\textstyle M_{6}}$ point

3.3 Dynamic stress response

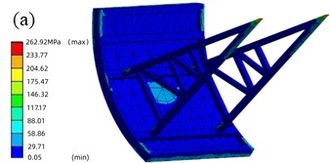
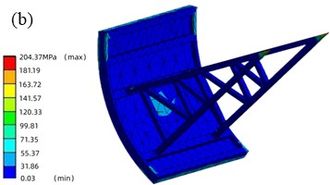
Figure 11 shows the stress distribution of the gate after the earthquake. The maximum stress of the gate structure under the action of EI wave and far-field wave is 262.92 MPa and 204.37 MPa, respectively, which are located in the arm hinge area, exceeding the allowable stress value of the arm material by 156 MPa.

Table 2 shows the stress values of ${\textstyle M_{1}}$-${\textstyle M_{6}}$ monitoring points under earthquake. Based on the difference between the displacement values of the monitoring points after and during the earthquake, the stress values of the monitoring points after the earthquake and the maximum stress values during the earthquake are given. Consistent with the characteristics of displacement distribution, the maximum stress values of the structure during the earthquake are far greater than the stress values of the structure stability after the earthquake. The difference is that the maximum stress values of the structure under the action of EI wave is not all greater than the maximum stresses of the corresponding position under the action of far-field wave, for example, the maximum stresses of ${\textstyle M_{1}}$ and ${\textstyle M_{3}}$ are higher than that under the action of far-field wave. Under the action of EI wave, the stress at the bottom of the gate (${\textstyle M_{4}}$) is the largest. The maximum stress during the earthquake and the stress after the earthquake are 243.0 and 603.3 MPa, respectively, which are far greater than the stresses at other monitoring points. Under the action of far-field waves, the stresses at the middle and lower parts of the gate (${\textstyle M_{3}}$) and the bottom (${\textstyle M_{4}}$) are the largest, and their maximum values during the earthquake are 501.3 MPa and 502.0 MPa, respectively, which are far greater than the stresses at other positions.

According to the Design specification for steel gates of water and hydropower projects [20], if the long side of the gate panel is less than 3 times the short side, the safety factor should be taken as 1.5. Therefore, a safety factor of 1.5 is selected to check the strength of the main position of the gate, that is, when the stress of 1.5 times exceeds the allowable stress, the structure is considered unsafe. Under the action of EI wave, the upper and middle of the gate leaf ${\textstyle M_{2}}$ and the upper of the arm ${\textstyle M_{5}}$ are in an unsafe state when the stress reaches the maximum value, and are in a safe state after stabilization; the bottom of the gate leaf ${\textstyle M_{2}}$ and the lower part of the arm ${\textstyle M_{6}}$ are still in an unsafe state after the stress is stable. Other positions are always in a safe state. Under the action of far-field wave, all positions of ${\textstyle M_{1}}$-${\textstyle M_{6}}$ are in a safe state after the stress is stable, but other positions except ${\textstyle M_{1}}$ are in an unsafe state when the stress reaches the maximum value. From the above stress distribution and strength check of various parts of the structure, under the rare earthquake action, the lower part of the gate leaf and the support arm are the areas with weak dynamic response, and effective structural measures should be taken for reinforcement to enhance local strength.

Table 2. Stress of different parts of gate structure under earthquake

Monitoring points	Position	Stress after earthquake (MPa)		Maximum stress during earthquake (MPa)		Allowable stress (MPa)
		EI wave	Far-filed wave	EI wave	Far-filed wave
${\textstyle M_{1}}$	Top of gate leaf	40.3	89.9	103.3	118.5	337.5
${\textstyle M_{2}}$	Middle and upper part of gate leaf	76.5	72.3	306.5	253.8
${\textstyle M_{3}}$	Middle and lower part of gate leaf	114.4	221.0	152.6	501.3
${\textstyle M_{4}}$	Bottom of the gate leaf	243.0	200.5	603.3	502.0
${\textstyle M_{5}}$	Upper part of arm	96.7	78.5	172.5	143.2
${\textstyle M_{6}}$	Lower part of arm	136.1	59.4	279.4	117.5	156.0

Figure 11. Dynamic stress of gate after earthquake. (a) EI wave. (b) Far-field wave

3.4 Resonance frequency

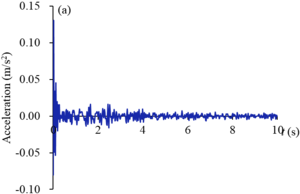
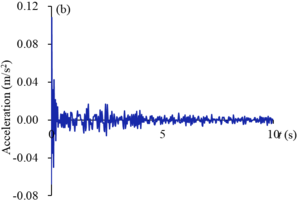
Analyze the acceleration of ${\textstyle M_{1}}$-${\textstyle M_{6}}$ monitoring points under the action of earthquake. Figure 12 shows the acceleration-time curve of ${\textstyle M_{2}}$ point under the action of EI wave and far-field wave, respectively. Under the action of EI wave, the acceleration amplitude of all components fluctuates greatly at first, and then becomes stable after 0.4 s. The maximum acceleration occurs around 0.04 s, and the maximum acceleration of the whole gate occurs in the ${\textstyle M_{2}}$ point, with a maximum value of 0.1308 m/s². The acceleration of ${\textstyle M_{3}}$ point is also large, reaching 0.1018 m/s². The acceleration at other points is relatively small, between 0.01-0.02 m/s². The overall performance of the curve under the action of far-field wave is similar to that of EI wave, and the peak value also appears at about 0.04 s. And then the amplitude of vibration decreases with time, and the amplitude drops sharply after 0.4 s. The maximum acceleration of the gate occurs at ${\textstyle M_{2}}$ and ${\textstyle M_{3}}$ points, which are 0.1081 m/s² and 0.1049 m/s², respectively. The acceleration of ${\textstyle M_{5}}$ and ${\textstyle M_{6}}$ points is also large, reaching above 0.08 m/s².

Figure 12. Acceleration of ${\textstyle M_{2}}$ monitoring point during earthquake. (a) EI wave. (b) Far-field wave

In practical engineering, the maximum acceleration $D$ cannot clearly reflect the dynamic response characteristics of the gate, so the maximum acceleration $D$ and resonance frequency $f$ can be mutually transformed by the following equation:

$a=0.002\times f^{2}\times D$

(8)

where $a$ is the maximum acceleration. The maximum amplitude is numerically equal to the maximum displacement, and the resonant frequency of the gate under the action of two seismic waves can be obtained by substituting Eq. (8) as shown in Table 3. Under the action of far-field wave, the resonance frequency of the gate is large because the maximum displacement value is small. The maximum frequency occurs at ${\textstyle M_{1}}$ point, reaching 65.24 Hz. The frequency of ${\textstyle M_{3}}$ point is also large, reaching 64.26 Hz. This is also the maximum dynamic stress response point of the gate, which indicates that the middle and lower part of the gate leaf is the weak point under the action of far-field seismic waves. However, the resonance frequency of EI wave is generally small, and the maximum frequency occurs at ${\textstyle M_{3}}$ point, reaching 49.13 Hz. The resonance frequency of all points is less than the resonance frequency under the action of far-field seismic wave.

Table 3. Acceleration and resonance frequency at different positions of gate under different wave patterns

Monitoring points	Position	Maximum acceleration (m/s2)		Resonance frequency (Hz)
		EI wave	Far-filed wave	EI wave	Far-filed wave
${\textstyle M_{1}}$	Top of gate leaf	0.0138	0.0528	25.76	65.24
${\textstyle M_{2}}$	Middle and upper part of gate leaf	0.1308	0.1081	40.44	48.49
${\textstyle M_{3}}$	Middle and lower part of gate leaf	0.1018	0.1049	49.13	64.26
${\textstyle M_{4}}$	Bottom of the gate leaf	0.0159	0.0167	38.73	49.60
${\textstyle M_{5}}$	Upper part of arm	0.0913	0.0820	35.56	44.30
${\textstyle M_{6}}$	Lower part of arm	0.0938	0.0919	42.07	56.70

3.5 Comparison with mode-superposition response spectrum method

The mode decomposition response spectrum method is a conventional method specified in the current code for seismic design of hydraulic structures in China. The characteristics of ground motion are described by the maximum seismic response of the ideal simplified single particle system, which takes into account the relationship between the ground motion characteristics and the dynamic characteristics of the structure during the earthquake, and calculates the resonance effect generated by the dynamic characteristics of the structure (natural vibration period, vibration mode) through the response spectrum. That is, the modal analysis results are coupled with a known seismic response spectrum, and then the dynamic response of the structure under seismic load is determined. After the steel gate structure system is discretized, the dynamic balance differential equation of each node in the state of motion is as follows:

$M{\ddot {y}}\left(t\right)+C{\dot {y}}\left(t\right)+Ky\left(t\right)=$$-MI{\ddot {y}}_{g}\left(t\right)$

(9)

where $M$ is the mass matrix, $K$ is the stiffness matrix, $C$ is the damping matrix, $y(t)$, ${\dot {y}}\left(t\right)$ and ${\ddot {y}}\left(t\right)$ are the column vectors of the displacement, velocity and acceleration of the particle relative to the foundation, respectively, ${\ddot {y}}_{g}\left(t\right)$ is the horizontal movement acceleration of the foundation and $I$ is the identity matrix.

When the mode decomposition response spectrum method is used to solve the seismic response, it is necessary to use the maximum seismic action effect of each mode to synthesize the total seismic action effect of the structure, which is to combine the vibration modes to determine the reasonable seismic action effect. Assuming that the ground motion during the earthquake is a stationary random process, the seismic action effect generated by each translational vibration mode can be determined approximately by the following method of "square root sum":

$S={\sqrt {\sum S_{j}^{2}}}$

(10)

where $S$ is horizontal seismic effect, and $S_{j}$ is the effect of horizontal seismic action of $j$ mode, including internal force and deformation.

Table 4 shows the maximum values of dynamic displacement and stress of each monitoring point of the gate under EI wave and far-field seismic wave calculated by the mode decomposition response spectrum method. And the ratio of these values to the maximum values of corresponding monitoring points under the consideration of fluid-structure coupling method in this paper is also given. Since the coupling between the water and gate is not considered by the mode decomposition response spectrum method, both the maximum displacement and the maximum stress are less than those calculated by the fluid-structure coupling method. The maximum displacement and stress of the monitoring points under EI wave are only 0.64 and 0.83 of those under the consideration of fluid-structure coupling, and the maximum displacement and stress under far-field wave are 0.79 and 0.68 of those under the consideration of fluid-structure coupling. Especially for ${\textstyle M_{2}}$ monitoring point, the maximum stress under far-field wave is only 0.44 of that considering the coupling effect.

Table 4. Displacement and stress of gate structure under mode-superposition response spectrum method

Monitoring points	Position	Maximum displacement during earthquake (mm)				Maximum stress during earthquake (MPa)
		EI wave		Far field wave		EI wave		Far field wave
		Value	Ratio	Value	Ratio	Value	Ratio	Value	Ratio
${\textstyle M_{1}}$	Top of gate leaf	6.6	0.63	4.2	0.68	89.4	0.87	77.4	0.65
${\textstyle M_{2}}$	Middle and upper part of gate leaf	25.9	0.65	17.6	0.77	275.9	0.90	112	0.44
${\textstyle M_{3}}$	Middle and lower part of gate leaf	13.1	0.62	10.5	0.83	113.6	0.74	417.5	0.83
${\textstyle M_{4}}$	Bottom of the gate leaf	4.2	0.79	3.1	0.91	440.5	0.73	421.7	0.84
${\textstyle M_{5}}$	Upper part of arm	20.1	0.56	15.4	0.74	141.7	0.82	98.2	0.69
${\textstyle M_{6}}$	Lower part of arm	15.4	0.58	11.7	0.82	255.1	0.91	75.8	0.65

4. Conclusions

(1) The difference between the maximum displacement of Zipingpu dam calculated by the established fluid-structure coupling model and the measured results is not more than 0.9%, which shows that the fluid-structure coupling model in this paper can achieve high accuracy and can be applied to the dynamic response study of radial gate structure.

(2) The maximum dynamic displacement of the gate structure under EI wave occurs at the center of the middle and upper part of the gate leaf, which is 40 mm, which is far more than the allowable value of 20 mm in the current code, and is in danger of damage. The maximum dynamic displacement calculated by far-field seismic wave is also located at the center of the middle and upper part of the gate panel, which is 23 mm, which exceeds the allowable value of the specification, but is significantly less than the displacement under the action of EI wave.

(3) Lower part of the gate leaf and the support arm are the areas with weak dynamic response under the rare earthquake, and effective structural measures should be taken for reinforcement to enhance local strength.

(4) The resonance frequency of the gate under the action of far-field wave is significantly larger, with the maximum frequency of 65.24 Hz, which is located at the top of the gate leaf. The resonance frequency under the action of EI wave is small, with the maximum value of 49.13 Hz, which is located in the middle and lower part of the gate leaf. Under the same basic acceleration value of rare earthquake, different seismic wave modes have great differences in the damage area and damage situation of the gate structure, indicating that the impact of different seismic wave modes on the structure should be considered during the gate design.

(5) The coupling action has obvious influence on the structure. The calculated displacement and stress of the gate ignoring the coupling effect is far less than those considering, which may lead to insecurity. The model proposed in this paper can also be used for seismic response analysis under other liquid solid interactions. However, in some special cases, seismic effects may cause large swells in the liquid. Further research will be conducted on the interaction between large swells caused by earthquakes and existing structures.

References

[1] Lan J.J., Yang Y., Hu S.W., Chang X.L., Weng Y.H., Yao Y. Research progresses and frontiers on control and safety operation of super-large hydraulic complex. Advanced Engineering Sciences, 49(1):27–32, 2017.

[2] Gu X.M., Xiao Y., Yin S.Y., Hao Q. C., Liu H.L., Hao Z.Y., Meng G.P., Pei Q.M., Yan H.J. Hydrogeochemical characterization and quality assessment of groundwater in a long-term reclaimed water irrigation area, North China Plain. Water, 10(9):1209, 2018.

[3] Xiao Y., Xiao D., Hao Q., Liu K., Wang R., Huang X., Liao X., Zhang Y. Accessible phreatic groundwater resources in the central Shijiazhuang of North China Plain: Perspective from the hydrogeochemical constraints. Frontiers in Environmental Science, 9, 2021.

[4] Yin S.Y., Xiao Y., Gu X.M., Hao Q.C., Liu H.L., Hao Z.Y., Meng G.P., Pan X.Y., Pei Q.M. Geostatistical analysis of hydrochemical variations and nitrate pollution causes of groundwater in an alluvial fan plain. Acta Geophysica, 67(4):1191-1203, 2019.

[5] Zhang Z.H., Lan J.X., Fan F. Selection of new type radial steel gate and analysis of static and dynamic characteristics. International Journal of Steel Structures, 21(5):1–14, 2021.

[6] Wang Z.Z., Zhang X.C., Liu J.L. Advances and developing trends in research of large hydraulic steel gates (in Chinese). Journal of Hydroelectric Engineering, 36(10):1–18, 2017.

[7] Li F.Y., Yang Z.Y. Seismic damage analysis on large and medium-sized hydropower project in wenchuan earthquake-stricken area (in Chinese). Water Power, 36(03):47–50, 2010.

[8] Liu Y.X., Guo H., Wang J.L., Sun J.H. Nonlinear finite element static and corrosion sensitive analysis of radial steel gate. International Conference on Green Materials and Environmental Engineering (GMEE2014), 2014.

[9] Wu Y.H., Xie S.Z. Dynamic characteristic analysis of interaction of fluid and hydraulic structures (in Chinese). Journal of Hydraulic Engineering, 1(1):27–34, 1995.

[10] He Y., Zhou X., Liu, J. Dynamic property and seismic performance of square-based membranous latticed shells. Soil Dynamics and Earthquake Engineering, 43:25–32, 2012.

[11] Buldgen L., Caprace J.D., Rigo P., Le Sourne H. Investigation of the added mass method for seismic design of lock gates. Engineering Structures, 131(15):380－393, 2016.

[12] Faridmehr I., Nejad A.F., Baghban M.H., Ghorbani R. Numerical and physical analysis on the response of a dam’s radial gate to extreme loading performance. Water, 12(9):24-25, 2020.

[13] Zhang A.M., Ni B.Y. Three-dimensional boundary integral simulations of motion and deformation of bubbles with viscous effects. Computers ＆ Fluids, 92:22–33, 2014.

[14] Li Y.F., Su H.L., Wang Y.W., Jiang W., Zhu Q.P. Dynamic characteristic analysis of centrifugal pump impeller based on fluid-solid coupling. Journal of Marine Science and Engineering, 10(7):880-880, 2022.

[15] Higdon R.L. An automatically well-balanced formulation of pressure forcing for discontinuous Galerkin methods for the shallow water equations. Journal of Computational Physics, 458:111102, 2022.

[16] Kong X.J., Zhou Y., Zou D.G., Xu B. Study of seismic wave input of Zipingpu concrete face rockfill dam during Wenchuan earthquake (in Chinese). Rock and Soil Mechanics, 33(07):2110-2116, 2012.

[17] Chen H.Q., Xu Z.P., Lee M. Wenchuan earthquake and seismic safety of large dams (in Chinese). Journal of Hydraulic Engineering, 39(10):1158－1167, 2008.

[18] Yu H.Y., Wang D., Yang Y.Q., Xie Q.C., Jiang W.X., Zhou B.F. The preliminary analysis of strong ground motion records from the Ms 8.0 Wenchuan earthquake (in Chinese). Earthquake Engineering and Engineering Vibration, 29(1):1-13, 2009.

[19] Code of China. Standard for seismic design of hydraulic structures. GB 51247–2018, (in Chinese,) China Planning Press, 2018.

[20] Code of China. Design specification for steel gates of water and hydropower projects. SL 74–2019, (in Chinese,) China Water & Power Press, 2019.