Non-linear thermal convection in a Casson fluid flow over a horizontal plate with convective boundary condition

Abstract

Casson fluid flow has many practical applications such as food processing, metallurgy, drilling operations and bio-engineering operations. In this paper, we study Casson fluid flow through a plate with a convective boundary condition at the surface and quantify the effects of suction/injection, velocity ratio, and Soret and Dufour effects. Firstly we used a similarity transformation to change the governing equations to ordinary differential equations which were then solved numerically. The effect of the rheological parameters on the velocity, temperature, and concentration with skin friction, and heat and mass transfer are shown graphically and discussed briefly. It is observed that the velocity of the fluid at the surface decreases with increase of the velocity ratio while the nature of the flow is in opposite characteristics. The local Nusselt number decreases with increase in the velocity ratio. Skin friction at the surface is enhanced by buoyancy ratio and Casson number. Due to injection of the fluid in the system, the mass transfer rate at the surface increases while it decreases with the velocity ratio parameter.

Keywords

Casson fluid; Non-linear thermal convection; Soret and Dufour effect; Viscous dissipation; Suction

1. Introduction

Heat and mass transfer characteristics and convection in a non-Newtonian fluid have practical applications in many engineering and medical sciences [1]. Casson fluid is classified as a most popular non-Newtonian fluid due to its rheological characteristics [2], [3], [4], [5] and [6]. Kameswaran et al. [7] have discussed the Casson fluid flow over a stretching or shrinking sheet. Mahanta and Shaw [8] have studied a three dimensional Casson fluid flow past a porous linearly stretching sheet in the presence of convective boundary condition. The influence of the viscous dissipation on the MHD Casson fluid flow over a non-Darcy porous medium has been discussed by Makanda et al. [9]. Casson fluid flow and heat transfer past an exponentially porous stretching surface have been discussed by Pramanik [10]. Convective boundary condition effect on the stagnation point flow of nanofluid has been discussed by Akbar et al. [11].

The processes of suction and injection find application in many industries such as in the design of thrust bearing and radial diffusers, and thermal oil recovery. Hartnett [12] analyzed the significance of suction or injection on boundary layer flow and noted that suction or injection through the surface can significantly modify the flow field. The effect of the suction or injection on the boundary layer flow and heat transfer has been studied by Pantokratoras [13]. The influence of the thermophoretic and non-linear convection has been studied by Kameswaran et al. [14]. The non-linear convection in nano-fluid flow on stretching sheet has been studied by Shaw et al. [15].

When heat and mass transfer occurs simultaneously in a moving fluid, the relation between the fluxes and the driving potential becomes complex [16], [17] and [18]. The Soret effect (or thermal diffusion) is mainly the occurrence of a diffusion flux due to a temperature gradient, whereas the Dufour effect is due to a heat flux as a result of chemical potential gradients. Such effects are significant in the fields of geosciences and chemical engineering. Hayat et al. [19] studied the magnetohydrodynamics flow of a Casson fluid over a stretching surface with Soret and Dufour effects. Convective boundary conditions are applicable in industries with high temperatures such as in gas turbines, nuclear plants, and thermal energy storage. Non-Newtonian fluids are used in place of Newtonian fluids in these industries [20], [21], [22], [23], [24], [25], [26] and [27].

Heat transfer at the surface of the microvessels is followed by convective heat because of the connective tissue which covers the outer wall of the microvessel. Diffusion and heat flux play a vital role during atherosclerosis, hyperthermia and other diseases. The aim of the present problem is to study the influence of suction or injection due to the permeable surface, Soret and Dufour effects due to mass and heat flux on Casson fluid flow through a plate with a convective boundary condition at the surface. We transformed the governing equations to a system of ordinary differential equation using similarity variables. The transformed equations were solved numerically for different values of the velocity ratio, suction/injection parameter, and the Soret and Dufour parameters. This paper is very useful in medical science to know the flow nature of the blood in the vessel.

2. Mathematical formulation

We consider steady, incompressible Casson fluid flow over a heated flat plate. It is assumed that the free stream moves with a constant velocity ${\textstyle U_{\infty }}$ over the top of the surface and the plate moving opposite or same direction of the free stream with velocity ${\textstyle U_{w}}$.

By assuming homogeneity and thermal equilibrium, the governing equations are written as follows:

${\frac {\partial u}{\partial x}}+{\frac {\partial v}{\partial y}}=$$0{\mbox{,}}$

(1)

$u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}=$$\nu \left(1+{\frac {1}{\beta }}\right){\frac {{\partial }^{2}u}{\partial y^{2}}}+$$g{\beta }_{c}(C-C_{\infty })+g[{\beta }_{0}(T-T_{\infty })+$${\beta }_{1}{\left(T-T_{\infty }\right)}^{2}]{\mbox{,}}$

(2)

$u{\frac {\partial T}{\partial x}}+v{\frac {\partial T}{\partial y}}=$${\alpha }_{m}{\frac {{\partial }^{2}T}{\partial y^{2}}}+{\frac {D_{m}K_{T}}{C_{s}C_{p}}}{\frac {{\partial }^{2}C}{\partial y^{2}}}+$${\frac {\mu }{\rho C_{p}}}\left(1+{\frac {1}{\beta }}\right){\left({\frac {\partial u}{\partial y}}\right)}^{2}{\mbox{,}}$

(3)

$u{\frac {\partial C}{\partial x}}+v{\frac {\partial C}{\partial y}}=$$D_{m}{\frac {{\partial }^{2}C}{\partial y^{2}}}+{\frac {D_{m}K_{T}}{T_{m}}}{\frac {{\partial }^{2}T}{\partial y^{2}}}{\mbox{,}}$

(4)

The corresponding boundary conditions at the surface and far away from the surface are written as follows:

${\begin{array}{lc}u=U_{w}{\mbox{,}}v=V_{w}(x){\mbox{,}}-k{\frac {\partial T}{\partial y}}=h_{f}(T_{f}-T){\mbox{,}}C=C_{w}&{\mbox{at}}\quad y=0{\mbox{,}}\\u\rightarrow U_{\infty }{\mbox{,}}T\rightarrow T_{\infty }{\mbox{,}}C\rightarrow C_{\infty }&{\mbox{as}}\quad y\rightarrow \infty {\mbox{,}}\end{array}}$

(5)

where the velocities of the fluid ${\textstyle u}$ and ${\textstyle v}$ are along the ${\textstyle x}$ and ${\textstyle y}$-axis, respectively, ${\textstyle \nu }$ is the apparent viscosity of the Casson fluid, ${\textstyle g}$ is the acceleration due to gravity, ${\textstyle {\beta }_{0}}$ and ${\textstyle {\beta }_{1}}$ are the linear and non-linear volumetric thermal expansion coefficient, ${\textstyle {\beta }_{c}}$ is the volumetric solute expansion coefficient, ${\textstyle T}$ is the temperature of the fluid, ${\textstyle T_{\infty }}$ is uniform ambient temperature, ${\textstyle C}$ is the concentration of the fluid, ${\textstyle {\alpha }_{m}}$ is the thermal diffusivity, ${\textstyle D_{m}}$ is the effective solutal diffusivity of the medium, ${\textstyle K_{T}}$ is the thermal diffusion ratio, ${\textstyle C_{s}}$ is the concentration susceptibility, and ${\textstyle C_{p}}$ is the specific heat capacity. Convective boundary condition is introduced at the surface of the plate. It is assumed that the bottom surface of the plate is heated by convection from a hot fluid of temperature ${\textstyle T_{f}}$ which is related with the heat transfer coefficient ${\textstyle h_{f}}$ where ${\textstyle k}$ and ${\textstyle T_{w}}$ are the thermal conductivity and the uniform temperature at the wall, respectively. It is noted that ${\textstyle T_{f}>T_{w}>T_{\infty }}$. Following the work of Ishak [28], we define the heat transfer coefficient as ${\textstyle h_{f}={cx}^{-1/2}}$ with constant c   and corresponding Biot number written as ${\textstyle {\mbox{Bi}}={\frac {c}{k}}{\sqrt {U/{\alpha }_{m}}}}$. The variable plate surface permeability function is given as

$V_{w}(x)=-{\frac {f_{w}}{2}}{\sqrt {\frac {U{\nu }_{f}}{x}}}$

(6)

where ${\textstyle U=U_{w}+U_{\infty }}$. ${\textstyle f_{w}}$ is a constant with ${\textstyle f_{w}>0}$ representing the transpiration (suction) rate at the plate surface, ${\textstyle f_{w}<0}$ corresponds to injection and ${\textstyle f_{w}=0}$ for an impermeable surface. We introduce the following similarity transformation to convert the partial governing differential equation to system of ordinary differential equation, written as [29] and [30]

$\eta =y{\sqrt {\frac {U}{\nu x}}}{\mbox{,}}\psi ={\sqrt {\nu xU}}f(\eta ){\mbox{,}}\theta (\eta )=$${\frac {T-T_{\infty }}{T_{w}-T_{\infty }}}{\mbox{,}}\phi (\eta )=$${\frac {C-C_{\infty }}{C_{w}-C_{\infty }}}{\mbox{,}}$

(7)

where ${\textstyle \psi }$ is the stream function which is defined as usual way ${\textstyle u=\partial \psi /\partial y}$ and ${\textstyle v=-\partial \psi /\partial x}$, which by default satisfied the continuity equation. So the remaining governing (2), (3) and (4) are written as

$\left(1+{\frac {1}{\beta }}\right)f^{'''}+{\frac {1}{2}}{ff}^{''}+$$\lambda (\theta +\alpha {\theta }^{2}+N\phi )=0{\mbox{,}}$

(8)

${\theta }^{''}+D_{f}{\mbox{Pr}}{\phi }^{''}+{\frac {1}{2}}Prf{\theta }^{'}+$${\mbox{Br}}\left(1+{\frac {1}{\beta }}\right)f^{{''}2}=$$0{\mbox{,}}$

(9)

${\phi }^{''}+{\mbox{SrSc}}{\theta }^{''}+{\frac {1}{2}}{\mbox{Sc}}\quad f\quad {\phi }^{'}=$$0{\mbox{,}}$

(10)

and the corresponding boundary conditions are written as

${\begin{array}{ll}f=f_{w}{\mbox{,}}f^{'}=1-r{\mbox{,}}{\theta }^{'}=-{\mbox{Bi}}(1-\theta (0)){\mbox{,}}\phi =1{\mbox{,}}&{\mbox{at}}\quad y=0{\mbox{,}}\\f^{'}\rightarrow r{\mbox{,}}\theta \rightarrow 0{\mbox{,}}\phi \rightarrow 0{\mbox{,}}&{\mbox{as}}\quad y\rightarrow \infty {\mbox{.}}\end{array}}$

(11)

The parameters used in the above equations are written as

${\begin{array}{l}\lambda ={\frac {{\mbox{Gr}}_{x}}{{\mbox{Re}}_{x}^{2}}}{\mbox{,}}\quad {\mbox{Gr}}_{x}={\frac {g{\beta }_{0}(T_{w}-T_{\infty })x^{3}}{{\nu }^{2}}}{\mbox{,}}\quad {\mbox{Re}}_{x}={\frac {Ux}{\nu }}{\mbox{,}}\quad \alpha ={\frac {{\beta }_{1}(T_{w}-T_{\infty })}{{\beta }_{0}}}{\mbox{,}}\quad N={\frac {{\beta }_{c}(C_{w}-C_{\infty })}{{\beta }_{0}(T_{w}-T_{\infty })}}{\mbox{,}}\quad {\mbox{Bi}}={\frac {c}{k}}{\sqrt {\frac {\nu }{U}}}{\mbox{,}}\\Pr={\frac {\nu }{\epsilon {\alpha }_{m}}}{\mbox{,}}\quad D_{f}={\frac {\epsilon D_{m}K_{T}(C_{w}-C_{\infty })}{\nu C_{s}C_{p}(T_{w}-T_{\infty })}}{\mbox{,}}\quad {\mbox{Sc}}={\frac {\nu }{\epsilon D_{m}}}{\mbox{,}}\quad {\mbox{Br}}={\frac {\epsilon U^{2}}{C_{p}(T_{w}-T_{\infty })}}{\mbox{,}}\quad {\mbox{Sr}}={\frac {\epsilon D_{m}K_{T}(T_{w}-T_{\infty })}{\nu T_{m}(C_{w}-C_{\infty })}}{\mbox{,}}r={\frac {U_{\infty }}{U_{w}}}{\mbox{,}}\end{array}}$

(12)

where ${\textstyle \lambda }$ is the mixed convection parameter, ${\textstyle {\mbox{Gr}}_{x}}$ is the Grashof number, ${\textstyle {\mbox{Re}}_{x}}$ is the Reynolds number, ${\textstyle \alpha }$ is the nonlinear convection parameter, ${\textstyle N}$ is the buoyancy force, Bi is the Biot number, Pr is the Prandtl number, ${\textstyle D_{f}}$ is the Dufour effect, Br is the Brinkman number, Sc is the Schmidt number, Sr is the Soret number, and r is the velocity ratio.

It is interesting to note that the assisting flow and opposing flow depend on sign of the mixed convection parameter λ. For assisting flow (when λ > 0 i.e., T_w > T_∞), the buoyancy force acts directly in the direction of the main stream flow which accelerates the fluid thus acting as a favorable pressure gradient. For the opposing flow (when λ < 0 i.e., T_w < T_∞), the buoyancy force opposes the fluid flow, impeding the fluid flow and thus behaving as an adverse pressure gradient. This directly affects the Brinkman number as it depends on the temperature difference. The Brinkman number Br > 0 for the case of assisting flow while Br < 0 for the case of opposing flow.

2.1. Skin friction, heat and mass transfer coefficients

The quantities of practical interest in this study are the skin friction coefficient, heat transfer rate and mass transfer rate, which is respectively defined as

$C_{f}={\frac {{\tau }_{w}}{\rho U_{\infty }^{2}}}{\mbox{,}}\quad {\mbox{Nu}}_{x}=$${\frac {{xq}_{w}}{k(T_{f}-T_{\infty })}}{\mbox{,}}\quad {\mbox{Sh}}_{x}=$${\frac {x\quad q_{m}}{D_{s}(C_{w}-C_{\infty })}}{\mbox{.}}$

(13)

The shear stress at the surface of the wall ${\textstyle {\tau }_{w}}$ is defined as

${\tau }_{w}=\left({\mu }_{B}+{\frac {{\tau }_{y}}{\sqrt {2{\pi }_{c}}}}\right){\frac {\partial u}{\partial y}}_{y=0}=$$\left({\mu }_{B}+{\frac {{\tau }_{y}}{\sqrt {2{\pi }_{c}}}}\right){\left({\frac {U^{3}}{\nu x}}\right)}^{1/2}f^{''}(0){\mbox{.}}$

(14)

The surface flux at the wall is defined as

$q_{w}=-k{\frac {\partial T}{\partial y}}_{y=0}=-k(T_{w}-$$T_{\infty }){\left({\frac {U}{\nu x}}\right)}^{1/2}{\theta }^{'}(0){\mbox{.}}$

(15)

Using the above equation, the local Nusselt number ${\textstyle {\mbox{Nu}}_{x}}$ is written as

${\mbox{Re}}_{x}^{1/2}{\mbox{Nu}}_{x}=-{\theta }^{'}(0){\mbox{.}}$

(16)

The mass flux at the surface is written as

$q_{m}=-D_{s}{\frac {\partial C}{\partial y}}_{y=0}=-D_{s}(C_{w}-$$C_{\infty }){\left({\frac {U}{\nu x}}\right)}^{1/2}{\phi }^{'}(0){\mbox{.}}$

(17)

Using the above equation, the local Sherwood number ${\textstyle {\mbox{Sh}}_{x}}$ is written as

${\mbox{Re}}_{x}^{-1/2}{\mbox{Sh}}_{x}=-{\phi }^{'}(0){\mbox{.}}$

(18)

3. Results and discussions

In the present study, we solved the system of differential (8), (9) and (10) with boundary condition Eq. (11) to quantify the effects of various physical parameters. We used similarity variables to transform the governing partial differential equations into ordinary differential equations and then solved the later using the ‘bvp4c’ Matlab package. The effect of the different parameters e.g., suction/injection parameter, Casson parameter, Biot number, Dufour and Soret effect, velocity ratio parameter, Buoyancy ratio, Schmidt Number on the velocity, temperature and concentration on the fluid skin friction, local Nusselt number and local Sherwood number is shown by graphs. In general, the values of the parameters are as follows: ${\textstyle \lambda =0.1{\mbox{,}}\quad \beta =1{\mbox{,}}\quad \alpha =}$$0.1{\mbox{,}}\quad N=0.1{\mbox{,}}\quad D_{f}=0.1{\mbox{,}}\quad {\mbox{Br}}=$$0.1{\mbox{,}}\quad {\mbox{Sr}}=0.1{\mbox{,}}\quad {\mbox{Sc}}=$$5{\mbox{,}}\quad f_{w}=0.1{\mbox{, Bi}}=10{\mbox{,}}\quad r=$$0.5$.

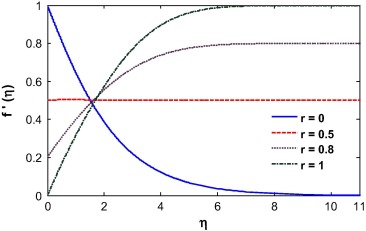
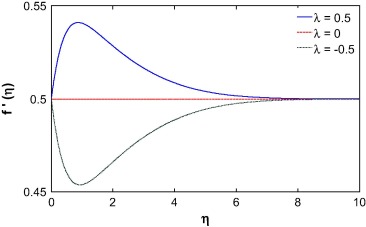
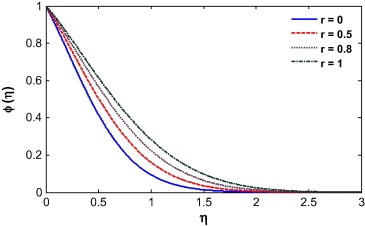
The influence of the different velocity ratio parameter on the velocity profile is depicted in Fig. 1. We observed that the velocity ratio plays a vital role in the behavior of the fluid. The structure of the velocity profiles changes dramatically with the value of velocity ratio. From the boundary condition, it is clear that when r < 0, the velocity at the wall is greater than the velocity away from the wall. The velocity at the wall increases with a decrease in the value of the velocity ratio parameter r. Similarly, for the case r > 0.5, the velocity at the wall is lower than the velocity near the wall and concurrently with an increase in r, the velocity at the wall decreases. The velocity at the wall is unaltered when r = 0.5 and it is parallel to the η-axis as the velocity. To satisfy the boundary condition, the momentum boundary layer converges at r and the boundary layer thickness increases with the velocity ratio parameter and it is observed that the fluid velocity for both assisting and opposing flow is shown in Figure 2 and Figure 3 for different r. For r = 0.5, the momentum boundary layer thickness increases for the case of assisting flow while it decreases for the case of opposing flow. We noted that the velocity is maximum near the wall, although the velocity at the wall is unaltered in line with the boundary condition. It is observed that the boundary layer thickness decreases with decrease in mixed convection parameter λ. For the assisting flow, the favorable pressure gradient pushes the fluid away from the surface which increases the boundary layer thickness. However for opposing flow, the adverse pressure gradients pull the fluid toward the surface which decreases the boundary layer thickness for r > 0.5. An opposite phenomenon is observed for the case of r < 0.5.

Figure 1. Velocity profile for different velocity ratio.

Figure 2. Velocity profile for different mixed convection parameter.

Figure 3. Velocity profile for different mixed convection parameter for r = 0.5.

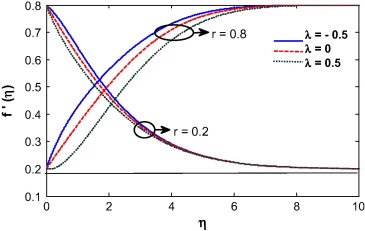
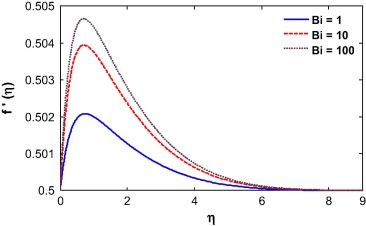
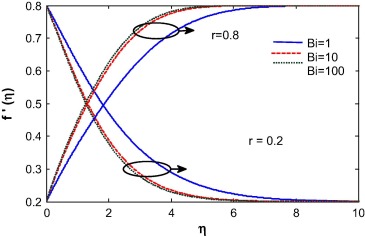
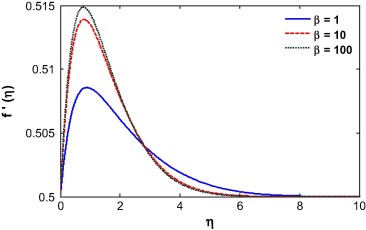
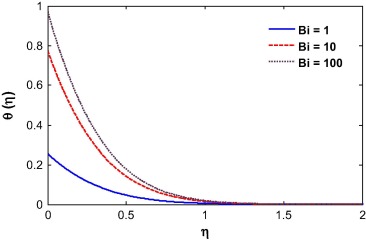
The convective boundary condition is related with the thermal condition on the surface. It is transformed to normal boundary condition when Bi → ∞ and so it has no significant effects on the governing system for higher value of Biot number. The Biot number influences the velocity due to convection which is clearly shown in Figure 4 and Figure 5. The momentum boundary layer thickness decreases with increase in the Biot number when r = 0.5. A similar phenomena was observed for r = 0.8 while the opposite is true when r = 0.2. Basically, with the increase of Biot number, the thermal boundary layer thickness decreases and as a result, the heat transfer rate increases. For r = 0.5 and 0.8, the fluid velocity at the wall is equal or less than the velocity away from the surface (i.e., at infinity), which helps to enhance the boundary layer thickness. For r < 0.5, it observed that the velocity at the wall is higher than the velocity away from the wall. Opposite is true for the case of r > 0.5. When r = 0.5, the velocity of the fluid at the surface and velocity of the fluid far away from the surface (i.e., at infinity) is same and so the velocity is unaltered for this case. The Casson fluid is subject to a yield stress at the surface which enhanced the shear stress at the wall and as a result the velocity is smaller for the case of Casson fluid than for Newtonian fluid. The Casson parameter is inversely proportional to the yield stress. So with an increase in the Casson parameter, the momentum boundary layer thickness decreases (see Fig. 6).

Figure 4. Velocity profile for different Biot number for r = 0.5.

Figure 5. Velocity profile for different Biot number.

Figure 6. Velocity profile for different Casson parameter.

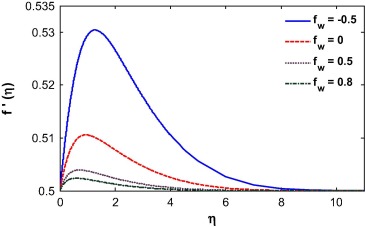
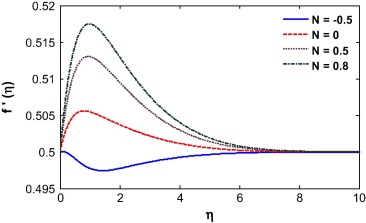
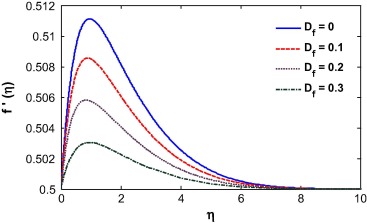
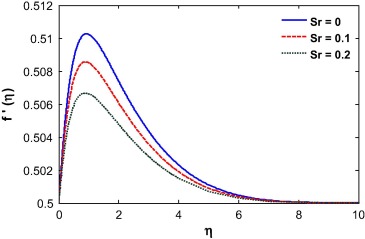
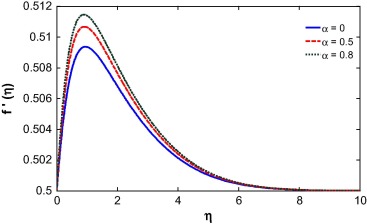
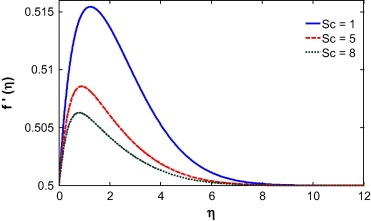
Suction/injection, Soret and Dufour number, Buoyancy ratio and Schmidt number play a vital role in the behavior of the velocity profile as shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12. A similar result was observed by Mustafa et al. [31]. The fluid velocity decreases during suction and increases during injection (see Fig. 7). This can be attributed to an increase in the momentum boundary layer thickness during suction and decrease during injection as shown in earlier work by Motsumi and Makinde [32]. The Soret number enhances mass diffusion near the surface and as a result the boundary layer thickness reduces (see Fig. 8). The nonlinear convection parameter increases the momentum boundary layer thickness (see Fig. 9). This is because the nonlinear part of the thermal convection increases the temperature gradient at the wall which forces the fluid to move away from the surface. The momentum boundary layer thickness increases for the case of increasing buoyancy and it appears much larger for higher values of buoyancy parameter (see Fig. 10). It is observed that the momentum boundary layer thickness decreases by introducing Dufour effect and it decreases with increase of Dufour number (see Fig. 11). In the case of opposing buoyancy, the boundary layer thickness decreases. The momentum boundary layer thickness decreases with an increase in the Schmidt number (see Fig. 12).

Figure 7. Velocity profile for different suction/injection parameter.

Figure 8. Velocity profile for different buoyancy parameter.

Figure 9. Velocity profile for different the Dufour number.

Figure 10. Velocity profile for different Soret number.

Figure 11. Velocity profile for different nonlinear convection parameter.

Figure 12. Velocity profile for different Schmidt number.

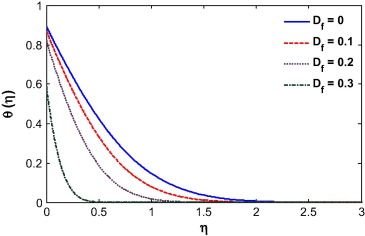
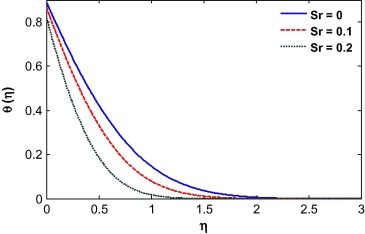
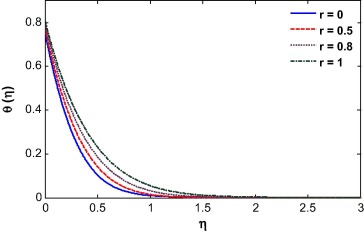
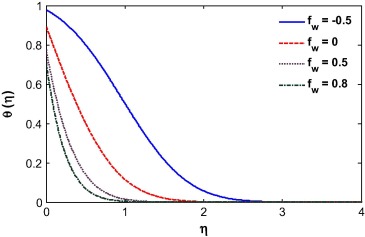
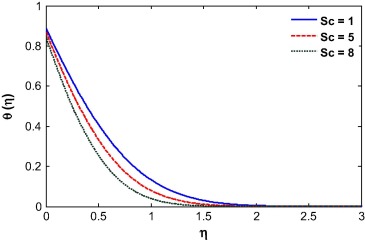
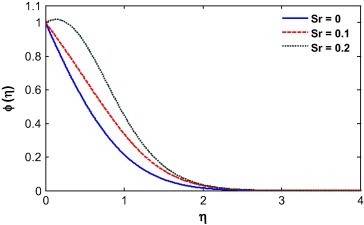
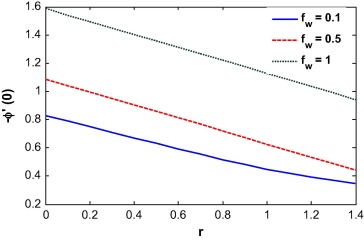
The fluid temperature is highly influenced by the Biot number, Dufour effect, suction/injection, velocity ratio and Schmidt number as shown in Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18. The Biot number is related to the convective boundary condition and it increases the temperature near the surface. As a result the thermal boundary layer increases with an increase in the Biot number (see Fig. 13). The Dufour effect appears mainly due to a mass concentration gradient which is an energy flux and increases the thermal boundary layer thickness (see Fig. 14). An opposite phenomena is observed for the case of Soret parameter (see Fig. 15). Due to suction, the fluid is removed from the system and as a result the thermal boundary layer thickness increases as shown in Fig. 15. For injection, the fluid injects in the system and helps to reduce the thermal boundary layer which is clearly shown in Fig. 16. With an increase in the velocity ratio, the thickness of the thermal boundary layer increases as the fluid velocity at the wall decreases with respect to the velocity at the wall (see Fig. 17). The viscous diffusion rate increases with increase of the Schmidt number that restricts the fluid to flow further and reduces the thickness of thermal boundary layer (see Fig. 18).

Figure 13. Temperature profile for different Biot number.

Figure 14. Temperature profile for different Dufour number.

Figure 15. Temperature profile for different Soret number.

Figure 16. Temperature profile for different velocity ratio.

Figure 17. Temperature profile for different suction/injection parameter.

Figure 18. Temperature profile for different Schmidt number.

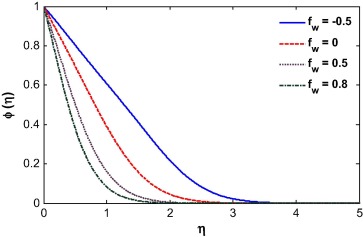
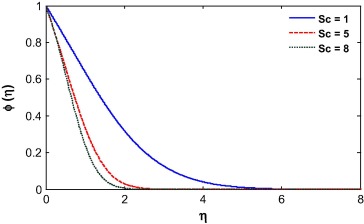
The fluid concentration depends highly on the suction/injection, velocity ratio, Soret and Schmidt number as shown in Figure 19, Figure 20, Figure 21 and Figure 22. Fluid injection increases the amount of fluid available and so reduces the concentration boundary layer thickness. The opposite phenomena is true for the suction parameter as shown in Fig. 19. For velocity ratio r > 0.5, the velocity at the wall is less than the velocity at large distances away and so the fluid moves away from the surface. As a result the concentration layer thickness increases with r. For r > 0.5, the fluid velocity at the surface is more than the velocity at further from the plate which helps to reduce the concentration boundary layer thickness as depicted in Fig. 20. The Soret and Schmidt numbers appear directly in the concentration equation. The concentration boundary thickness decreases with increase in Schmidt number as the Schmidt number reduces the mass diffusion rate at the surface (see Fig. 21). The particles were ejected from the surface due to the Soret effect and as a result the concentration boundary layer thickness increases which is visible in Fig. 22.

Figure 19. Concentration profile for different suction/injection parameter.

Figure 20. Concentration profile for different Schmidt number.

Figure 21. Skin Friction vs. Brinkman number for different Casson parameter.

Figure 22. Concentration profile for different velocity ratio.

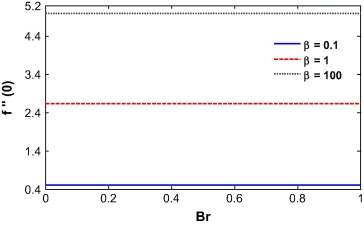
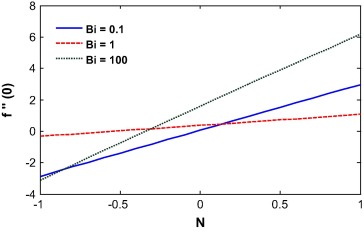
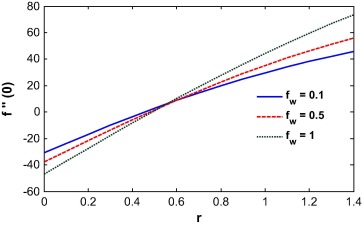
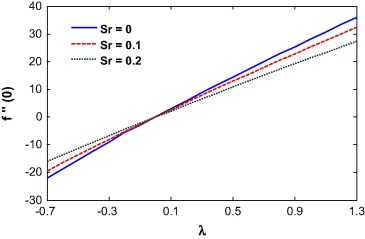
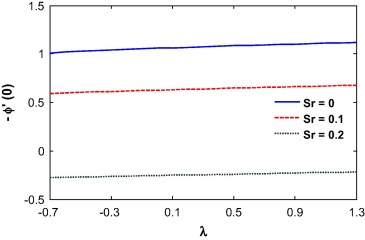
From Eq. (16), it is evident that the skin friction is proportional to the Casson parameter β. So with an increase in β, the skin friction at the wall increases as clearly show in Fig. 23. The Brinkman number has no effect on the skin friction. The skin friction increases with the opposing flow. This is because the rising flow increases the shear stress at the wall which increases the skin friction. For totally opposing flow, the skin friction at the wall increases with the Biot number while a different phenomenon was observed for higher buoyancy parameter (see Fig. 24). The skin friction at the wall decreases with the injection parameter for r < 0.5, while it increases when r > 0.5. This is because for r < 0.5, the velocity at the wall is less than the velocity at infinity which pushes the fluid away from the surface. It is also noted that the skin friction value is negative until r = 0.5 and then becomes positive as shown in Fig. 25. The skin friction is negative for negative values of the mixed convection parameter and is positive for positive λ. It is evident from Fig. 26 that the Soret number reduces the skin friction at the wall for positive mixed convection parameter. The skin friction value is 0.33205734 for λ = D_f = Br = Sr = Sc = 0 and β → ∞ which may compare with the result of Motsumi and Makinde [32] which was 0.3321 for their cases. It shows a good agreement with our present methodology and outcomes of the problem.

Figure 23. Concentration profile for different Soret number.

Figure 24. Skin Friction vs. buoyancy ratio for different Biot number.

Figure 25. Skin Friction vs. velocity ratio for different injection parameter.

Figure 26. Skin Friction vs. mixed convection parameter for different of Soret number.

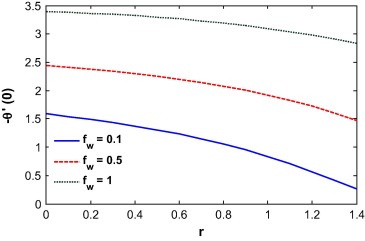
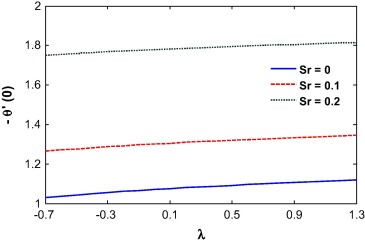
The local Nusselt number is an increasing function of the injection parameter. This is because, fluid injection increases the heat transfer rate at the wall. It nonlinearly decreases with an increase in the velocity ratio. Lower velocity ratio values increase the velocity at the wall which enhances the heat transfer rate near the wall. The mixed convection parameter increases the local Nusselt number at the surface. The Soret number increases the temperature gradient at the surface as shown in Figure 27 and Figure 28.

Figure 27. Local Nusselt number vs. velocity ratio for different injection parameter.

Figure 28. Local Nusselt number vs. velocity ratio for different Soret number.

The effect of the velocity ratio, injection parameter, mixed convection parameter and Soret number on local Sherwood number is shown in Figure 29 and Figure 30. We observe that the local Sherwood number is a decreasing function of the velocity ratio. Injection reduces the mass transfer rate at the wall which increases the local Sherwood number. The local Sherwood number increases due to the Soret effect.

Figure 29. Local Sherwood number vs. velocity ratio for different injection parameter.

Figure 30. Local Sherwood number vs. mixed convection parameter for different Soret number.

4. Conclusion

In the present problem we investigated Casson fluid flow through a permeable plate and the effect of the velocity ratio, suction or injection, Sore and Dufour number. We have considered a convective boundary condition at the surface. The nonlinear governing equations were written as a system of ordinary differential equations by using similarity transformations and then solved numerically. The velocity of the fluid decreased for velocity ratio parameter less than 0.5 and increased with r for velocity ratio parameters greater than 0.5. The momentum boundary layer thickness decreased with an increase in the Casson parameter. The Brinkmann number enhanced the boundary layer thickness for velocity ratio parameter equal to and greater than 0.5 but the opposite is true for velocity ratio parameter less than 0.5. The results of this work may find application in different industrial and medical applications where a Casson fluid is an important medium for heat and mass transfer.

References

1. [1] Y. Khan, Q. Wu, N. Faraz, A. Yildirim, S.T. Mohyud-Din; Heat transfer analysis on the magnetohydrodynamic flow of a non-Newtonian fluid in the presence of thermal radiation: an analytic solution; Z. Naturforsch. A: J. Phys. Sci., 67 (3–4) (2012), pp. 147–152
2. [2] N.S. Akbar; Influence of magnetic field on peristaltic flow of a Casson fluid in an asymmetric channel: application in crude oil refinement; J. Magn. Magn. Mater., 378 (2015), pp. 320–326
3. [3] N.S. Akbar, A.W. Butt; Physiological transportation of Casson fluid in a plumb duct; Commun. Theor. Phys., 63 (2015), pp. 347–352
4. [4] S. Nadeem, R. Mehmood, A.N. Sher; Oblique stagnation point flow of a Casson-nano fluid towards a stretching surface with heat transfer; J. Comput. Theor. Nanosci., 11 (2014), pp. 1422–1432
5. [5] S. Nadeem, R. Ul-Haq, N.S. Akbar, Z.H. Khan; MHD three dimensional flow of Casson fluid past a porous linearly stretching sheet; Alexandria Eng. J., 52 (2013), pp. 577–582
6. [6] S. Nadeem, R. Mehmood, N.S. Akbar; Optimized analytical solution for oblique flow of a Casson-nano fluid with convective boundary conditions; Int. J. Therm. Sci., 78 (2014), pp. 90–100
7. [7] P.K. Kameswaran, S. Shaw, P. Sibanda; Dual solution of Casson fluid flow over a stretching or shrinking sheet; Sadhana, 39 (6) (2014), pp. 1573–1583
8. [8] G. Mahanta, S. Shaw; 3D Casson fluid flow past a porous linearly stretching sheet with convective boundary condition; Alexandria Eng. J., 54 (2015), pp. 653–659
9. [9] G. Makanda, S. Shaw, P. Sibanda; Effects on MHD free convection of a Casson fluis from a horizontal circular cylinder with partial slip in non-Darcy porous medium with viscous dissipation; Boundary Value Problem, 2015 (1) (2015), pp. 1–14
10. [10] S. Pramanik; Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation; Ain Shams Eng. J., 5 (1) (2014), pp. 205–212
11. [11] N.S. Akbar, S. Nadeem, R. Ul Haq, Z.H. Khan; Radiation effects on MHD stagnation point flow of nano fluid towards a stretching surface with convective boundary condition; Chin. J. Aeronaut., 26 (6) (2013), pp. 1389–1397
12. [12] J.P. Hartnett; Mass transfer cooling; W.M. Rohenow, J.P. Hartnett, E.N. Ganic (Eds.), Handbook of Heat Transfer, Hemisphere, Washington (1985), pp. 1–11
13. [13] A. Pantokratoras, Comment on “Forced and free mixed convection boundary layer flow with uniform suction or injection on a vertical flat plate” by T. Watanabe (Acta Mech. 89, 123–132, 1991); Acta Mecha, 186 (2006), pp. 239–240
14. [14] P.K. Kameswaran, P. Sibanda, M.K. Partha, P.V.S.N. Murthy; Thermophoretic and non-linear convection in non-Darcy porous medium; J. Heat Transfer – Trans. ASME, 136 (4) (2014), p. 042601
15. [15] S. Shaw, P.K. Kameswaran, P. Sibanda; Effects of slip on nonlinear convection in nanofluid flow on stretching surfaces; Boundary Value Problem, 2016 (1) (2016), pp. 1–11
16. [16] S.T. Mohyud-Din, Z.A. Zaidi, U. Khan, N. Ahmed; On heat and mass transfer analysis for the flow of a nanofluid between rotating parallel plates; Aerospace Science and Technology, 46 (2015), pp. 514–522
17. [17] N. Ahmed, S.T. Mohyud-Din, S.M. Hassan; Flow and heat transfer of nanofluid in an asymmetric channel with expanding and contracting walls suspended by carbon nanotubes: a numerical investigation; Aerospace Sci. Technol., 48 (2016), pp. 53–60
18. [18] M. Sheikh, Z. Abbas, Homogeneous-heterogeneous reactions in stagnation point flow of Casson fluid due to a stretching/shrinking sheet with uniform suction and slip effects, Ain Shams Eng. J., in press.
19. [19] T. Hayat, S.A. Shehzad, A. Alsaedi; Soret and dufour effects on magnetohydrodynamic (MHD) flow of Casson fluid; Appl. Math. Mech., 33 (2012), pp. 1301–1312
20. [20] A. Hussain, S.T. Mohyud-Din, T.A. Cheema; Analytical and numerical approaches to squeezing flow and heat transfer between two parallel disks with velocity slip and temperature jump; Chin. Phys. Lett., 29 (11) (2012) 114705
21. [21] U. Khan, N. Ahmed, S.T. Mohyud-Din; Thermo-diffusion, diffusion-thermo and chemical reaction effects on MHD flow of viscous fluid in divergent and convergent channels; Chem. Eng. Sci., 141 (2015), pp. 17–27 Elsevier
22. [22] S.T. Mohyud-Din, A. Yildirim, S.A. Sezer; Analytical solution for flow in a slowly deforming channel with weak permeability; Z. Naturforsch. A: J. Phys. Sci., 65a (2010), pp. 1033–1038
23. [23] Y. Khan, S.T. Mohyud-Din; Coupling of he’s polynomials & laplace transformation for MDH viscous flow over a stretching sheet; Int. J. Nonlinear Sci. Numer. Simul., 11 (12) (2010), pp. 1103–1107
24. [24] M.A. Noor, S.T. Mohyud-Din; Variational iteration method for unsteady flow of gas through a porous medium using he’s polynomials and Padé approximants; Comput. Math. Appl., 58 (2009), pp. 2182–2189
25. [25] S.T. Mohyud-Din, M.A. Noor, K.I. Noor; Some relatively new techniques for nonlinear problems; Math. Probl. Eng., Hindawi, 2009 (2009), Article 234849 http://dx.doi.org/10.1155/2009/234849 25
26. [26] S.Z.A. Zaidi, S.T. Mohyud-Din; Convective heat transfer and MHD effects on two dimensional wall jet flow of a nanofluid with passive control mode; Aerospace Sci. Technol., Aerospace Sci. Technol., 49 (2016), pp. 225–230
27. [27] Y. Khan, Q. Wu, N. Faraz, S.T. Mohyud-Din; Three-dimensional flow arising in the long porous slider: an analytic solution; Z. Naturforsch. A: J. Phys. Sci., 66a (2011), pp. 507–511
28. [28] A. Ishak; Similarity solutions for flow and heat transfer over a permeable surface with convective boundary condition; Appl. Math. Comput., 217 (2010), pp. 837–842
29. [29] T. Hayat, S.A. Shehzad, A. Alsaedi, M.S. Alhothuali; Mixed convection stagnation point flow of casson fluid with convective boundary conditions; Chin. Phys. Lett., 29 (11) (2012), p. 114704 (4 Pages)
30. [30] F.M. Abbasi, S.A. Shehzad, T. Hayat, B. Ahmad; Doubly stratified mixed convection flow of maxwell nanofluid with heat generation/absorption; J. Magn. Magn. Mater., 404 (2016), pp. 159–165
31. [31] M. Mustafa, T. Hayat, I. Pop, A. Aziz; Unstaedt boundary layer flow of a Casson fluid due to an impulsevely started moving flat plate; Heat Transfer – Asian Res., 40 (6) (2011), pp. 563–576
32. [32] T.G. Motsumi, O.D. Makinde; Effects of thermal radiation and viscous dissipation on boundary layer flow of nanofluids over a permeable moving flat plate; Phys. Scr., 86 (2012), p. 045003 (8 Pages)