Resumen
En este trabajo se describe el proceso llevado a cabo para analizar numéricamente mediante el método de los elementos finitos (MEF) el comportamiento vibratorio del conjunto móvil de un altavoz dinámico de bobina con doble suspensión inferior y en ausencia de la superior. El estudio se centra en el rango de baja frecuencia. El calibrado del modelo se realiza en base a medidas experimentales de la frecuencia de resonancia y desplazamiento del diafragma. Se hace énfasis en la importancia de los factores de participación asociados a la fuerza de excitación y en los cambios que se producen en estos al introducir fuerzas no equilibradas. Así mismo, el análisis proporciona datos para decidir sobre la distancia entre suspensiones, su número óptimo de pliegues y la ubicación de las trencillas, siendo estos parámetros de gran interés en el diseño de este tipo de altavoces.
Abstract
This paper describes the process undertaken to analyze numerically the vibrational behavior of the moving assembly of a dynamic loudspeaker with double bottom suspension and in the absence of the above one using the finite element method (FEM). The study focuses on the low frequency range. Model calibration was performed based on experimental measurements of the resonance frequency and diaphragm displacement. The importance of the participation factors associated to the excitation force and the changes produced in these when unbalanced forces are introduced are emphasized. The analysis also provides data to decide on the distance between suspensions, their optimal number of folds and the placement of the lead wires, parameters of great interest on the design of this type of loudspeakers.
Palabras clave
Elementos finitos ; Conjunto móvil ; Altavoces dinámicos
Keywords
Finite elements ; Moving assembly ; Dynamic loudspeakers
1. Introducción
Una tendencia actual en el diseño de sistemas de audio profesional es la de minimizar sus dimensiones físicas. Esto implica construir cajas cada vez más pequeñas y, consecuentemente, reducir el tamaño de los transductores. La potencia acústica radiada por estos sistemas vibrantes depende de la velocidad del diafragma o cono (relacionada con el caudal de aire que este desaloja) y de la resistencia mecánica de radiación (parte real de la impedancia acústica) [1] . Este último parámetro es función de la geometría o del perfil del diafragma, que condicionan la radiación acústica del altavoz [2] and [3] , mientras que el primero está directamente relacionado con su vibración. Los altavoces dinámicos de radiación directa presentan una serie de factores limitantes de su rendimiento cuando trabajan en régimen de gran señal [4] . El margen de variación de la geometría del diafragma es uno de estos. En este contexto, la optimización del comportamiento dinámico del conjunto móvil es de vital importancia. Por este motivo surge la necesidad de conseguir desplazamientos mayores modificando otros elementos del sistema.
Frankort [5] fue uno de los primeros autores en realizar un estudio analítico completo de la vibración del diafragma de un altavoz, discretizando la estructura y aplicando un planteamiento en forma de ecuaciones diferenciales. Barlow et al. [6] realizaron un estudio similar de las frecuencias de resonancia para varios perfiles de diafragma usando herramientas de diferencias finitas. Sin embargo, en esos trabajos no se tiene en cuenta el acoplamiento diafragma-aire. Posteriormente, Kagawa et al. [7] y Suzuki y Nomoto [8] contemplaron dicho acoplamiento empleando el método de los elementos finitos (MEF), determinando las frecuencias y los modos de vibración del cono del altavoz y llegando a la conclusión de que por debajo de 500 Hz el cono se comporta como un pistón. Skrodzka [9] estudió dicho comportamiento mediante análisis modal, verificando experimentalmente que las formas nodales del altavoz quedan inalteradas cuando el altavoz se monta en una caja.
Un componente determinante en la vibración del diafragma de un altavoz son sus suspensiones, que establecen en gran parte sus condiciones de contorno. Aunque la suspensión inferior (también denominada araña o spider ) es un factor limitante para el desplazamiento del diafragma, no lo es tanto como la superior. Por tanto, parece lógico estudiar los efectos de no emplear una suspensión superior y así maximizar los desplazamientos del mismo. Esto a su vez conduce a la necesidad de incorporar al menos una doble suspensión inferior ya que, de otra forma, los posibles cabeceos y desplazamientos laterales del conjunto móvil provocarían el rozamiento de la bobina en el entrehierro. Este fenómeno y sus efectos en el rendimiento del altavoz dependerán en parte del tipo de configuración de la bobina en el entrehierro [10] and [11] . De lo anterior se deduce que el conjunto móvil debería diseñarse para maximizar los desplazamientos en la dirección axial o normal a la superficie del diafragma (para aumentar la potencia sonora radiada) y minimizar los desplazamientos radiales o laterales (para evitar que la bobina roce en el entrehierro y se estropee el altavoz).
En este trabajo se realiza un análisis del comportamiento vibratorio del conjunto móvil de un altavoz dinámico de doble suspensión inferior en la zona de baja frecuencia, concretamente hasta 400 Hz. Uno de los objetivos perseguidos es, entre otros, contemplar la posibilidad de prescindir de la suspensión superior del diafragma con el objeto de conseguir mayores desplazamientos. Para ello se han implementado una serie de modelos numéricos empleando el MEF. El modelo numérico implementado no incorpora, por tanto, esta suspensión. Dicho análisis proporciona datos para decidir sobre la distancia entre suspensiones, su número óptimo de pliegues y la ubicación de las trencillas en base a los desplazamientos radiales del altavoz. Dada la importancia de los datos de entrada en el desarrollo del modelo numérico, se hará especial énfasis en el proceso de caracterización del material que conforma la doble suspensión y que ha consistido en un ajuste inverso a partir de datos experimentales.
2. El altavoz de bobina móvil. Parámetros relevantes
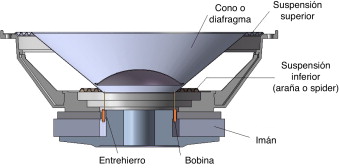
No constituye un objetivo de este trabajo llevar a cabo un estudio exhaustivo sobre los altavoces dinámicos, aunque sí es necesario realizar unos comentarios previos sobre su funcionamiento. Un altavoz de bobina móvil o electrodinámico de radiación directa (fig. 1 ) utiliza el acoplo existente entre el movimiento de una superficie vibrante (cono o diafragma) y la corriente eléctrica i que recorre una bobina circular ubicada en el seno del campo magnético producido por un imán. La fuerza F aplicada al cono del altavoz viene dada según:
|
|
( 1) |
donde B es la densidad de flujo del campo magnético y l es la longitud de la bobina.
|
|
|
Figura 1. Altavoz electrodinámico de radiación directa.
|
Si se asume una corriente compleja i = Iejωt dependiente del tiempo t , de amplitud I y de frecuencia angular ω , la velocidad del diagrama en el estado estacionario vendrá dada por:
|
|
( 2) |
donde ZM es la impedancia mecánica del altavoz, que depende tanto del sistema mecánico, ZMD , como del medio sobre el que se radia, ZMR :
|
|
( 3) |
Sea e = Eejωt la tensión compleja de amplitud E proporcionada por los terminales de la bobina y ZE = RE + jωLE su impedancia eléctrica, donde RE es la resistencia óhmica y LE es la autoinducción de la bobina. El movimiento de esta en el seno de un campo magnético provoca la aparición de una fuerza contraelectromotriz inducida, em , cuya expresión sería:
|
|
( 4) |
La corriente que circule por la bobina vendría dada entonces según:
|
|
( 5) |
Combinando las ecuaciones (2), (4) y (5) se llega a:
|
|
( 6) |
siendo ZMOV = (Bl2 /ZM ) la impedancia de movimiento, que depende de los parámetros mecánicos del sistema, y ZET la impedancia eléctrica total. Como se puede apreciar, ZET presentará un máximo cuando la impedancia mecánica sea mínima, es decir, a la frecuencia de resonancia mecánica. Por esta razón, para determinar experimentalmente la frecuencia de resonancia mecánica se recurre a medidas eléctricas.
Las anteriores ecuaciones son las básicas para describir el funcionamiento del altavoz en el rango lineal y se usan mucho por su simplicidad de representación en forma de circuito equivalente [12] and [13] . Por otra parte, la problemática del diseño de sistemas radiantes se focaliza en la zona de baja frecuencia, donde los desplazamientos del diafragma son mayores. Anteriormente se definió la denominada impedancia mecánica de radiación ZMR , que tiene su origen en la fuerza de reacción que el medio ejerce al ser sometido a una fuerza por el diafragma. En general, está formada por una parte real RMR y una parte imaginaria XMR , que en baja frecuencia y considerando el modelo del pistón en pantalla infinita [12] , para ka ≪ 1 puede aproximarse por:
|
|
( 7) |
siendo k el número de onda, a el radio del pistón, ρ0 la densidad del aire, c la velocidad de propagación del sonido en aire y MMR la masa mecánica de radiación.
Uno de los parámetros de mayor relevancia en este tipo de sistemas radiantes es la frecuencia de resonancia mecánica del conjunto móvil fs , ya que determina el inicio de la curva de respuesta en frecuencia útil y que se produce para:
|
|
( 8) |
siendo MMS = MMD + MMR la masa mecánica del sistema, MMD la masa mecánica del diafragma y CMS la compliancia mecánica de la suspensión, que es la inversa de la constante elástica o módulo de Young del material que la conforma.
Otro parámetro de interés es el desplazamiento máximo del diafragma en función de la frecuencia en la dirección axial, que está relacionado con la potencia acústica que está en condiciones de radiar el sistema. En altavoces de radiación directa la respuesta de presión en frecuencia típica es de tipo filtro paso banda, con una frecuencia de corte inferior que comienza alrededor de la frecuencia de resonancia mecánica. Esta frecuencia de corte inferior y la superior del sistema paso banda son función de las características eléctricas y mecánicas del altavoz, en especial de su conjunto móvil.
3. Descripción del modelo numérico
Aunque la anterior metodología de análisis mediante constantes localizadas permite afrontar muchos de los problemas que se plantean en el estudio de altavoces dinámicos, esta presenta sus limitaciones. Por ejemplo, no permite evaluar riesgos de cabeceo del conjunto móvil al no contemplar desplazamientos en otra dirección que no sea la de vibración principal, como los radiales. Para esos casos es común recurrir a herramientas o métodos numéricos de modelado como el MEF, que es un método muy generalizado para la resolución de diversos problemas de física gobernados por ecuaciones diferenciales y cuyas bases pueden consultarse en [14] . Para el presente trabajo se ha empleado el software de simulación en elementos finitos ANSYS®[15] . La ecuación diferencial de movimiento que gobierna el caso bajo estudio se puede escribir de la siguiente forma:
|
|
( 9) |
donde es el vector de desplazamientos, , y son las matrices de masa, amortiguamiento y rigidez, respectivamente, y es el vector de fuerzas externas aplicadas en los nodos. El programa mencionado anteriormente contempla una matriz de amortiguamiento global, , obtenida como combinación lineal de la matriz de masa y rigidez en la forma , donde α y β son 2 constantes.
Considerando el sistema en vibración libre sin amortiguar y fijando unas condiciones de contorno, se pueden determinar las frecuencias propias y sus respectivas formas modales a partir de:
|
|
( 10) |
Haciendo el cambio de base , operando se llega a (para cada modo considerado):
|
|
( 11) |
donde cada modo se normaliza con Mi = 1, siendo . Por tanto, para un análisis armónico podemos definir el factor de participación del modo i-ésimo como , donde FMAX es el vector de amplitudes de la fuerza armónica aplicada. Los valores de los factores de participación serán mayores para los modos significativamente importantes desde el punto de vista dinámico.
Los diferentes modelos numéricos en elementos finitos implementados corresponden al conjunto móvil de un altavoz de radiación directa con doble suspensión. Se ha utilizado un mallado regular (mapped meshing) y elementos tipo Shell 181[15] . La masa de la bobina se ha simulado como una masa añadida. Se han tomado las precauciones básicas de la técnica de elementos finitos, incorporando más de 10 elementos por longitud de onda para la máxima frecuencia por analizar. A continuación se describe el proceso seguido para el calibrado de los modelos cuyo comportamiento vibratorio se pormenorizará más adelante.
3.1. Calibrado de los modelos
Los datos más comprometidos para calibrar los modelos numéricos son el módulo de Young del material de la doble suspensión inferior y el factor de pérdidas total del sistema. Para determinar el módulo de Young se ha construido un conjunto móvil sin diafragma (para evitar posibles interferencias con este) con doble suspensión inferior, como el que se muestra en la figura 2 .
|
|
|
Figura 2. Conjunto móvil sin diafragma construido para la determinación del módulo de Young del material de la doble suspensión inferior.
|
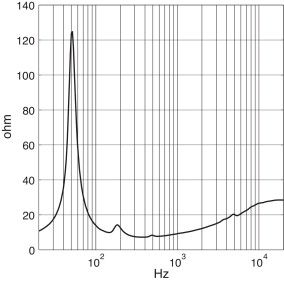
Se ha procedido a medir la impedancia eléctrica según el procedimiento habitual en altavoces [16] . El montaje experimental para llevar a cabo esta medida consiste en un circuito eléctrico en el que el altavoz se monta en serie con una resistencia eléctrica R mucho mayor que el valor esperado de la impedancia del altavoz. En este caso la resistencia era de 1 kΩ. Con ayuda de un generador se lleva a cabo un barrido frecuencial y para cada frecuencia se mide la caída de tensión en la resistencia, eR , y en el altavoz, eA . La primera nos proporciona información sobre las variaciones de intensidad (I = eR /R ), y la caída de tensión en el altavoz nos permite determinar la impedancia eléctrica aplicando la ecuación ZET = eA /I . El resultado obtenido se muestra en la figura 3 .
|
|
|
Figura 3. Impedancia eléctrica medida del conjunto móvil sin diafragma.
|
Anteriormente se mencionó que la frecuencia a la cual se produce el máximo de la impedancia eléctrica corresponde a la frecuencia de resonancia mecánica (en este caso alrededor de 50 Hz). Dado que la masa del sistema es conocida, solo queda ajustar el valor del módulo de Young que hace que el desplazamiento sea máximo a esa frecuencia.
Para completar el calibrado es necesario determinar el factor de pérdidas global del conjunto móvil. Para ello se midieron los desplazamientos del diafragma en función de la frecuencia en la dirección axial del conjunto móvil completo (esta vez con diafragma) y para diferentes tensiones de alimentación siguiendo el procedimiento descrito en [17] .
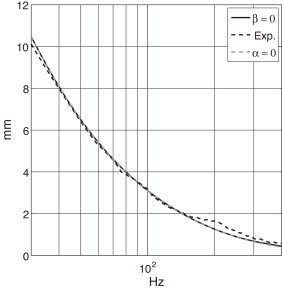
Por otra parte, para disminuir el tiempo dedicado a las simulaciones, los resultados numéricos se ajustaron previamente a los correspondientes a un sistema de un grado de libertad. El factor de pérdidas se obtiene de la minimización de la diferencia entre los resultados medidos experimentalmente cuando se excita el sistema con 55,1 N y los obtenidos numéricamente. De esta manera es posible fijar los parámetros α o β de la matriz . En la figura 4 se presenta una comparativa del desplazamiento para 3 situaciones diferentes: medidas experimentales, simulación en elementos finitos para β = 0 y Fmin y para β ≠ 0 y α = 0. Las 2 simulaciones conducen a resultados similares, lo cual era de esperar pues la estructura se comporta, en la práctica, como un sistema de un solo grado de libertad en ese rango frecuencia. Esto se debe a que los factores de participación de otros modos superiores son despreciables frente al del modo correspondiente a la frecuencia de resonancia mecánica. En los modelos implementados se ha optado por la segunda opción (β = 0 y α ≠ 0), que es la más desfavorable, ya que no se amortiguarían los modos superiores del conjunto móvil que aparecen cuando la fuerza es desequilibrada, como se verá más adelante.
|
|
|
Figura 4. Desplazamiento del conjunto móvil con diafragma: elementos finitos (β = 0 y α ≠ 0), medidas experimentales (Exp.) y elementos finitos (β ≠ 0 y α = 0).
|
3.2. Modelos implementados
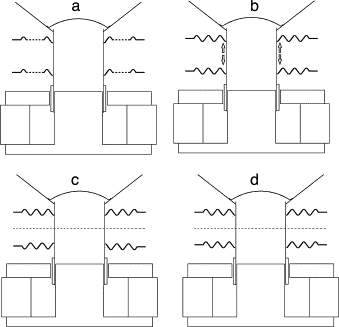
En la figura 5 se presentan los diferentes modelos implementados para estudiar la influencia de la distancia entre suspensiones y el número de pliegues en el desplazamiento del conjunto móvil (aunque se muestran los imanes y el entrehierro, estos no forman parte del conjunto móvil modelado). Aunque no aparece explícitamente en las figuras, también se ha estudiado el efecto de la ubicación de las trencillas. Adicionalmente, se ha analizado el efecto de considerar una configuración simétrica de las suspensiones frente a una asimétrica.
|
|
|
Figura 5. Modelos implementados en función de: a) número de pliegues; b) distancia entre suspensiones; c) configuración simétrica; d) configuración asimétrica.
|
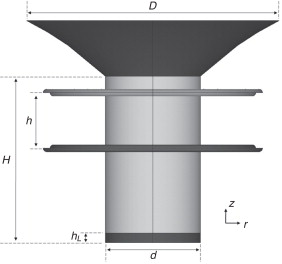
Las dimensiones del modelo de partida se presentan en la figura 6 , donde D = 130 mm es el diámetro del diafragma, H = 85 mm es la altura del cilindro de diámetro interior d = 51,7 mm que está unido al diafragma y en cuya parte inferior se adhiere la bobina de altura hL = 5 mm, y h = 30 mm es la distancia entre suspensiones. La masa total del conjunto móvil es de 24 g (incluyendo la masa de radiación MMR y la de la bobina). La región de referencia de la que posteriormente se compararán los desplazamientos en la coordenada radial r es la de la circunferencia inferior del cilindro.
|
|
|
Figura 6. Geometría del modelo numérico genérico.
|
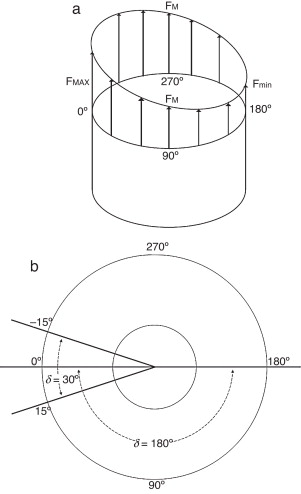
La fuerza se ha aplicado a lo largo de los nodos de la bobina y en la dirección axial z . Para cada uno de los modelos implementados se han aplicado 2 tipos de fuerzas: la equilibrada y la desequilibrada. La opción de fuerza equilibrada ha permitido ajustar el modelo y serviría para evaluar el desplazamiento en el eje z , mientras que la fuerza desequilibrada hace posible analizar los riesgos de las configuraciones estudiadas evaluando el desplazamiento en el eje r . En una situación ideal la fuerza es idéntica en todos los nodos de la bobina; sin embargo, esto no es así en la práctica. La fuerza desequilibrada trata de responder a estas posibles irregularidades, cuyo origen puede estar en la no uniformidad del campo magnético debida a imperfecciones geométricas en el entrehierro. La fuerza desequilibrada empleada en este trabajo tiene la forma de la figura 7 a, donde puede apreciarse una variación sinusoidal a lo largo del perímetro de la circunferencia. La posición del valor máximo de esta fuerza viene representada por la variable angular θ , y sus posibles valores son 0°, 90° y 180°, cubriendo de esta forma una gran cantidad de posibles combinaciones de ubicación fuerza-trencillas. El valor de la fuerza máxima desequilibrada FMAX toma un valor un 5% mayor que el de la fuerza media FM = 55, 1N , y el de la fuerza mínima Fmin , un 5% menor.
|
|
|
Figura 7. a) Distribución angular de la fuerza desequilibrada; b) disposición de las trencillas.
|
En lo que a la disposición de las trencillas se refiere, se han estudiado 2 configuraciones: formando un ángulo δ de 30° (± 15°) y de 180°, como también se aprecia en la figura 7 b. Todo indica que la segunda opción es la óptima, al tratarse de la más equilibrada desde un punto de vista estructural.
4. Resultados
A partir de los análisis modal y armónico, se obtienen los factores de participación de cada modo para la fuerza considerada así como los desplazamientos de cada uno de los nodos, siendo crítico el de algunos puntos concretos. En efecto, un desplazamiento excesivo en la dirección radial de un punto situado en la parte inferior del cilindro provocaría una fricción en el entrehierro. Aunque los resultados que se mostrarán corresponden a desplazamientos radiales, es evidente que las soluciones que conduzcan a mayores desplazamientos axiales implican un mayor caudal de aire desalojado y, por tanto, una mayor potencia sonora radiada.
4.1. Factores de participación
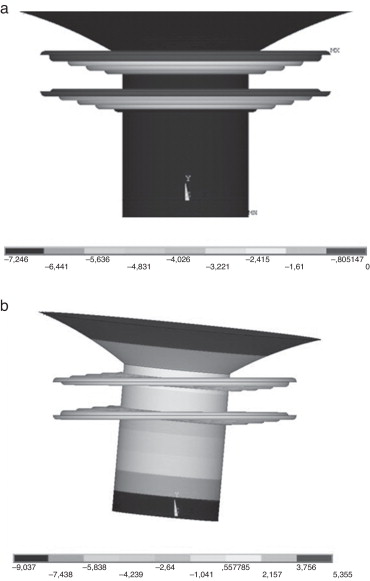
Una vez definido el modelo geométrico genérico del altavoz y realizado su mallado, el primer paso es la realización de un análisis modal y la obtención de los factores de participación para cada una de las fuerzas consideradas. Así, por ejemplo, la simple observación de las formas modales proporciona información relevante. Para ilustrar esta afirmación considérense las 2 formas modales de la figura 8 .
|
|
|
Figura 8. Patrones modales del conjunto móvil: a) modo principal; b) modo con balanceo.
|
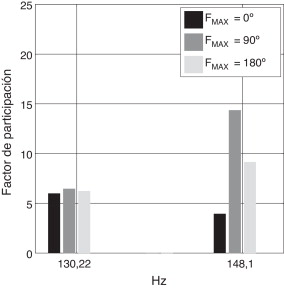
El modo principal presenta un movimiento significativamente predominante en la dirección axial, pero no es así para el caso del modo con balanceo. Una fuerza que conduzca a ese último tipo de situaciones es desfavorable para el correcto funcionamiento del altavoz, como se señaló anteriormente. Para prevenir esto es necesario calcular los factores de participación asociados a los modos para la fuerza considerada. Una fuerza totalmente equilibrada solo activaría el modo principal, que es el responsable de la frecuencia de resonancia mecánica obtenida a partir de la impedancia eléctrica en la sección anterior. Cualquier fuerza no equilibrada completamente provocaría que los factores de participación asociados a los modos cambiasen. En la figura 9 se presenta esta variación para los modos de 130 y 148 Hz para distintas fuerzas desequilibradas. Los valores se han obtenido para un ángulo entre trencillas δ = 30°. Cuando la fuerza presenta un desequilibrio, los factores de participación cambian y adquieren más importancia otros modos. La fuerza aplicada en los siguientes casos corresponderá a un θ = 90°.
|
|
|
Figura 9. Factores de participación para distintas fuerzas desequilibradas en los modos de 130 y 148 Hz.
|
4.2. Ubicación de las trencillas
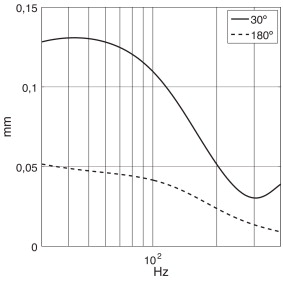
La figura 10 compara los desplazamientos máximos en la dirección radial r , , para 2 configuraciones de trencillas, δ = 30° y δ = 180°. Los desplazamientos máximos son menores para la segunda opción, y se puede afirmar que es mucho más estable que la primera.
|
|
|
Figura 10. Variación del para 2 configuraciones de trencillas.
|
4.3. Configuración simétrica y asimétrica de la doble suspensión
En la figura 11 se muestran los desplazamientos máximos en la dirección radial r , , para 2 disposiciones de suspensiones: simétrica y asimétrica, y los valores δ = 30° y 180°. Como se puede observar, la configuración simétrica presenta una mayor estabilidad, siendo esa diferencia inapreciable en el caso de que las trencillas se dispongan con δ = 180°. Los resultados mostrados en adelante corresponderán a esta última configuración.
|
|
|
Figura 11. Variación del para 2 disposiciones de las suspensiones (simétrica [S] y asimétrica [A]) con δ = 30° y 180°.
|
4.4. Número de pliegues
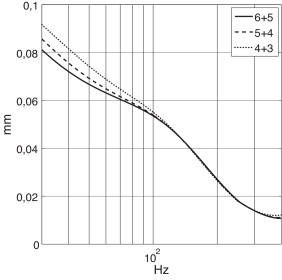
A continuación se presenta el efecto que tiene modificar el número de pliegues de las suspensiones en los desplazamientos en la dirección radial r . La notación empleada para indicar el número de pliegues es del tipo n/m , donde n es el número de pliegues orientados en el sentido positivo del eje z y m en el negativo. La figura 12 muestra el desplazamiento máximo en el eje r , para distintas configuraciones de número de pliegues. En este caso los resultados indican que la situación más favorable se produce cuanto mayor sea este número, ya que los desplazamientos son menores, reduciendo así los riesgos anteriormente comentados.
|
|
|
Figura 12. Influencia del número de pliegues en .
|
4.5. Distancia entre suspensiones
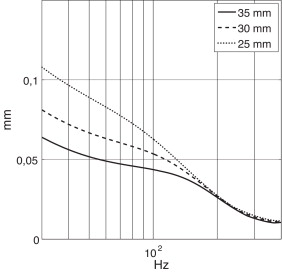
En la figura 13 se muestra el desplazamiento máximo en la dirección r , , para diferentes distancias entre suspensiones. Se puede apreciar que para una mayor distancia entre suspensiones se produce un menor desplazamiento. Este es un resultado esperado. No obstante, en la práctica existen una serie de limitaciones de tipo constructivo que pueden forzar que la distancia escogida sea menor.
|
|
|
Figura 13. Variación del para diferentes distancias entre suspensiones.
|
5. Conclusiones
En este trabajo se ha descrito el proceso seguido para analizar numéricamente el comportamiento vibratorio del conjunto móvil de un altavoz dinámico con doble suspensión inferior y en ausencia de la superior. El estudio se ha desarrollado en el contexto de un proyecto en el que se consideraba la posibilidad de eliminar la suspensión superior para facilitar desplazamientos mayores en altavoces de pequeño tamaño. Para ello se han implementado diversos modelos numéricos en elementos finitos y analizado el efecto de realizar ligeras modificaciones en su estructura.
El calibrado del modelo numérico básico se ha realizado a partir de medidas experimentales de impedancia eléctrica (para determinar la frecuencia de resonancia mecánica) y de desplazamiento del diafragma de un prototipo fabricado al efecto. El dato de la frecuencia de resonancia ha posibilitado determinar el módulo de Young del material de la suspensión, mientras que el factor de pérdidas global del conjunto móvil se ha obtenido de la minimización de la diferencia entre el desplazamiento del diafragma medido experimentalmente y el obtenido a partir de dicho modelo numérico básico.
Dicho procedimiento de calibrado puede ser útil también para problemas análogos y ha permitido analizar otros modelos en los que se ha realizado algún ligero cambio respecto al modelo base y así poder decidir qué configuración es más favorable para el correcto funcionamiento del altavoz.
A la vista de los resultados numéricos cabe destacar, en primer lugar, la importancia del uso de los factores de participación como parámetro para evaluar los riesgos de balanceo cuando se aplican distintas fuerzas de desequilibrio al conjunto móvil. El estudio de distintos tipos de fuerzas no equilibradas permite contemplar situaciones no deseadas y de diverso origen que se dan en la práctica. También se ha analizado el efecto de la ubicación de las trencillas y de la disposición de la doble suspensión, siendo preferible una configuración simétrica con las trencillas formando un ángulo δ = 180°, dado que los desplazamientos radiales son menores, minimizándose así el efecto del balanceo. En cuanto al número de pliegues y la distancia entre suspensiones, un mayor número de estos y una mayor separación entre suspensiones reduce considerablemente los riesgos anteriormente comentados, además de hacer que el conjunto móvil presente una mayor estabilidad. El análisis de dichos resultados permite iniciar una toma de decisiones para el desarrollo de un altavoz de estas características y justifica el empleo de este tipo de metodologías en el proceso de diseño.
Agradecimientos
Los autores quieren agradecer especialmente a José Martínez de Acústica Beyma S.L. sus fructíferas aportaciones durante el desarrollo de este trabajo.
Bibliografía
- [1] L. Kinsler, A. Frey, A. Coppens, J. Sanders; Fundamentals of Acoustics; John Wiley and Sons, New York (1999)
- [2] J. Alba, J. Ramis; Efecto de la modificación del perfil en el rendimiento de altavoces dinámicos de radiación directa; Rev. Int. Métodos Numér. Cálc. Diseño Ing., 18 (2002), pp. 243–254
- [3] A. Chaigne, N. Quaegebeur, On the Influence of the Geometry on Radiation Electrodynamic Loudspeakers. Presented at the 120th Convention of the Audio Engineering Society, Paris, May 2006, paper n°. 6775.
- [4] R. H. Small, Loudspeaker Large-Signal Limitations. Presented at the 1st Convention of the Audio Engineering Society, August 1984, paper n°. 2102.
- [5] F.J.M. Frankort; Vibration Patterns and Radiation Behavior of Loudspeaker Cones; J. Audio Eng. Soc., 26 (1978), pp. 609–622
- [6] D. A. Barlow, G.D. Galletly, J. Mistry, The Resonances of Loudspeaker Diaphragms. Presented at the 65th Convention of the Audio Engineering Society, London, February 1980, paper n°. 1590.
- [7] Y. Kagawa, T. Yamabuchi, K. Sugihara, T. Shindou; A finite element approach to a coupled structural-acoustic radiation system with application to loudspeaker characteristic calculation; J. Sound Vib., 69 (1980), pp. 229–243
- [8] K. Suzuki, I. Nomoto; Computerized analysis and observation of the vibration modes of a loudspeaker; J. Audio Eng. Soc., 30 (1982), pp. 96–106
- [9] E.B. Skrodzka; An influence of an enclosure of modal behavior of loudspeakers; J. Acoust. Soc. Jpn., 20 (1999), pp. 261–270
- [10] M.R. Gander, Moving-Coil Loudspeaker Topology as an Indicator of Linear Excursion Capability. Presented at the 64th Convention of the Audio Engineering Society, New York, November 1979, paper no . 1554.
- [11] W. Klippel, Diagnosis and Remedy of Nonlinearities in Electrodynamical Transducers. Presented at the 109th Convention of the Audio Engineering Society, Los Angeles, September 2000, paper no . 5261.
- [12] L.L. Beranek, T. Mellow; Sound Fields and Transducers; Academic Press, New York (2012)
- [13] M. Colloms, P. Darlington; High Performance Loudspeakers; John Wiley & Sons, New York (2007)
- [14] O.C. Zienkiewicz, R.L. Taylor, J.Z. Zhu; The Finite Element Method: Its Basis and Fundamentals; Elsevier (2013)
- [15] ANSYS theory reference 8.1, ANSYS Inc. (2003).
- [16] AES2-1984 AES Recommended Practice Specification of Loudspeaker Components Used in Professional Audio and Sound Reinforcement.
- [17] W. Klippel; Assessment of Voice-Coil Peak Displacement Xmax; J. Audio Eng. Soc., 51 (2003), pp. 307–323
Document information
Published on 01/09/15
Accepted on 25/04/14
Submitted on 11/03/13
Volume 31, Issue 3, 2015
DOI: 10.1016/j.rimni.2014.04.003
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?


![Variación del urMAX para 2 disposiciones de las suspensiones (simétrica [S] y ...](/wd/images/d/d9/Draft_Content_467132611-1-s2.0-S0213131514000418-gr11.jpg)