Hierarchical boundary element method based on the Barnes-Hut tree applied to exterior creeping flow

Resumen

En este trabajo se exponen un método de elementos de borde en una variante jerárquica y su empleo en flujo de Stokes alrededor de cuerpos rígidos tridimensionales en régimen estacionario. La propuesta se basa en el algoritmo jerárquico de bajo orden descendente y autoadaptativo de Barnes-Hut, que se emplea junto con una formulación integral de contorno indirecta y de segunda clase cuyo término fuente es función de la velocidad no perturbada. El campo solución es la densidad superficial de capa doble modificada para completar el espectro de autovalores del operador integral. De esta manera, los modos rígidos son eliminados y se pueden representar una fuerza y una cupla no nulas sobre el cuerpo. Los elementos son triángulos planos de bajo orden y se emplea una resolución iterativa mediante residuo mínimo generalizado (GMRES) sin precondicionamiento. Los ejemplos numéricos incluyen casos con soluciones analíticas, cuerpos con aristas y vértices o con formas intrincadas. La ventaja principal de la técnica desarrollada se halla en la posibilidad de considerar un número de grados de libertad mayor respecto a los que pueden emplearse con los métodos de colocación al centroide más tradicionales, debido a la disminución de la demanda de memoria primaria y de los tiempos de cómputo.

Abstract

In this work, a hierarchical variant of a boundary element method and its use in Stokes flow around three-dimensional rigid bodies in steady regime is presented. The proposal is based on the descending hierarchical low-order and self-adaptive algorithm of Barnes-Hut, and it is used in conjunction with an indirect boundary integral formulation of second class, whose source term is a function of the undisturbed velocity. The solution field is the double layer surface density, which is modified in order to complete the eigenvalue spectrum of the integral operator. In this way, the rigid modes are eliminated and both a non-zero force and a non-null torque on the body could be calculated. The elements are low order flat triangles, and an iterative solution by generalized minimal residual (GMRES) is used. Numerical examples include cases with analytical solutions, bodies with edges and vertices, or with intricate shapes. The main advantage of the presented technique is the possibility of considering a greater number of degrees of freedom regarding traditional collocation methods, due to the decreased demand of main memory and the reduction in the computation times.

Palabras clave

Método de elementos de borde ; Métodos jerárquicos de bajo orden ; Árbol descendente de Barnes-Hut ; Flujo reptante estacionario ; Colocación ; Formulación indirecta completada

Keywords

Boundary element method ; Low order hierarchical methods ; Descending Barnes-Hut tree ; Stationary creeping flow ; Collocation ; Completed indirect velocity formulation

1. Introducción

Es conocido que en el método de elementos de borde (BEM, por Boundary Element Method[1] ) o de paneles [2]  ;  [3] , en sus formas más clásicas, los elementos interactúan todos contra todos. Por otra parte, en los métodos numéricos relacionados con interacciones entre n partículas [4] , todas contra todas, cada interacción involucra típicamente alguna función de Green proporcional a una potencia inversa de la distancia, así como cada partícula tiene asociado un número constante de atributos geométricos y físicos. La forma de computar las interacciones da lugar a diferentes posibilidades, entre ellas los métodos directos y los jerárquicos.

Los métodos directos son los procedimientos clásicos de sumar por separado las influencias de cada partícula en un punto de observación dado, por lo cual se los denomina también interacciones partícula-partícula (PP). En el caso del BEM clásico, asumiendo que las partículas representan los elementos o paneles de la malla, las interacciones PP conducen al cálculo de matrices de influencia llenas (o densas) involucrando un costo computacional O (M² ), donde M es el número de grados de libertad del problema BEM [5]  ;  [6] .

En cambio, en los métodos jerárquicos, o en árbol, las interacciones entre las partículas se organizan en una jerarquía de cúmulos de partículas, comenzando por un dominio (o celda espacial) que las contiene a todas hasta llegar a celdas con una única partícula. Esto es, emplean una estrategia de «dividir para vencer»  con el fin de reducir el número de operaciones en base a la idea intuitiva de que la contribución de un cúmulo de partículas que está suficientemente lejos de un punto de observación x puede ser aproximada mediante valores representativos al centroide del cúmulo. Por ejemplo, en el caso del BEM de bajo orden que se expone en este trabajo, dichos valores representativos incluirán el promedio 〈ψ 〉 de la densidad superficial de capa doble, el promedio 〈n 〉 de las normales, así como también la suma acumulada de las áreas A^{(e )} de todos los elementos e ubicados dentro de un cúmulo dado.

Entre las variantes más difundidas se cuentan los métodos jerárquicos de bajo orden tipo Barnes-Hut (BH) [7]  ;  [8] , y los métodos jerárquicos de alto orden o, simplemente, métodos multipolares rápidos (FMM, por Fast Multipole Method ) [9]  ;  [10] . Ambas variantes construyen una estructura de datos obtenida mediante una subdivisión recursiva del espacio en celdas usualmente cúbicas, generada en forma jerárquica o recursiva, cuya estructura final dependerá de la distribución espacial de las partículas y de los algoritmos de subdivisión empleados [11] . Mientras que en las variantes de bajo orden se logra la precisión deseada restringiendo los cúmulos que pueden interactuar con una dada partícula, en las variantes FMM, en cambio, se emplean expansiones multipolares a una dada precisión y, en general, aseguran un mejor control en el error de aproximación, al costo de una programación bastante más elaborada cuando los dominios son tridimensionales (3D) [12]  ;  [13] .

En las alternativas tipo FMM se calculan interacciones Celda-Celda (CC), mientras que en las variantes de BH son interacciones Partícula-Celda (PC) y, en algunos casos, interacciones PP. Esto último puede suceder cuando la partícula está tan próxima de una celda que, al subdividirse esta recursivamente, se llega a las celdas más pequeñas posibles, que son aquellas que contienen una única partícula. En general, las aproximaciones PC son gradualmente mejores a medida que la distancia de interacción es mayor, así como también cuando el diámetro de la celda espacial es menor.

La utilidad práctica de las formulaciones rápidas, esto es, con un costo computacional significativamente menor que O (M² ), se evidencia cuando se las entrelaza con los métodos iterativos para resolver de manera aproximada el sistema de ecuaciones relacionado con la formulación integral asociada al BEM. Una comparación entre los métodos jerárquicos de bajo orden, tipo BH [7]  ;  [8] , y los de alto orden, tipo FMM, se realiza en [14] (Sec. 5.2.4).

En [15] se consideró una variante del FMM aplicada a interacciones de partículas esféricas inmersas en flujos estacionarios de fluidos gobernados por las ecuaciones de Laplace o de Stokes, cuyo desempeño se presentó en simulaciones computacionales empleando entre 512 y 8.192 partículas, mientras que en [16] se propuso un FMM para problemas gobernados por las ecuaciones de Helmholtz y de Maxwell en electromagnetismo. Asimismo, en [17] se propuso una variante basada en FMM para el cómputo del Stokeslet y del stresslet involucrados en los métodos que emplean singularidades de ese tipo para modelar flujo de Stokes en un dominio tridimensional, aunque los ejemplos numéricos se restringieron a tests de tiempos de CPU.

Otras veces, los FMM se entrelazan con otros recursos tales como las sumatorias rápidas en las variantes de Ewald o de Wolf, diseñadas en electrostática para sumandos con decaimientos proporcionales a 1/r , donde r es la distancia de separación entre las singularidades, y que son empleadas en dinámica molecular [18]  ;  [19] . Por ejemplo, en [20] se la utiliza en integrales de borde aceleradas para modelar flujo multifase en geometrías no periódicas, mientras que en [18] es parte de una técnica espectral para la evaluación rápida de sumas de n singularidades de tipo Stokeslet en arreglos periódicos.

Un algoritmo jerárquico tipo BH involucra, primero, la construcción de una estructura de datos en la forma de un árbol de octantes (u octree ) en el caso específico de un dominio 3D [12] ; [13]  ;  [7] . Luego, construye aproximaciones de la influencia en un punto de observación x y, toda vez que se pueda, las utiliza para reemplazar la influencia ocasionada por las partículas ubicadas dentro de una celda cúbica, las cuales definen un cúmulo, por su efecto concentrado en su centroide. De este modo, las n partículas quedan organizadas en una jerarquía de celdas (o cubos) anidadas, dando lugar a un árbol de octantes en 3D. A medida que el número de nivel aumenta, cada cubo de lado L asociado a la celda cúbica es dividido en 8 cubos de tamaño L /2, que representan las escalas espaciales de menor tamaño [11] . Si una celda no puede aproximar con suficiente exactitud la influencia en el punto de observación x , entonces su contribución es reemplazada por la suma de las contribuciones de sus celdas hijas. Esta construcción tiene un costo computacional O (M  log(M )), que es significativamente menor con respecto al O (M² ) del algoritmo estándar «todos contra todos».

Los algoritmos jerárquicos de bajo orden de tipo BH son actualmente motivo de atención. Por ejemplo, para simulaciones computacionales en diversas aplicaciones, entre ellas, electromagnetismo [21] , apantallamiento electrostático [22] , ecuación de Helmholtz [23] , fractura en elasticidad tridimensional [24] , dislocaciones dinámicas en deformaciones plásticas [25] , interacción de vórtices en fluidos [26] , así como también astrofísica [27] . En particular, en [28] se extiende el algoritmo de árbol jerárquico de BH para el cálculo del potencial multicuerpo de orden n debido a las interacciones entre n -uplas de partículas, de un modo similar al potencial de 3 cuerpos que se emplea para describir la interacción simultánea de 3 partículas, que no es capturado usando el potencial de interacción de a 2 partículas. Cabe notar también que el uso de los octrees en simulaciones computacionales con n partículas es de creciente interés cuando se los emplea en las GP-GPU (General-Purpose computing on Graphics Processing Units ), como en [29] , [30] y [31] .

En este trabajo se propone un método de elementos de borde jerárquico (HBEM, por Hierarchical BEM) y de bajo orden, basado en una variante descendente del árbol de octantes autoadaptativo de BH [8] . En los ejemplos se considera flujo de Stokes en régimen estacionario alrededor de cuerpos rígidos tridimensionales, el cual será modelado mediante una ecuación integral de borde (BIE, Boundary Integral Equation ) en la alternativa CIV (Completed Indirect Velocity) , según la taxonomía que se da en Ingber-Mammoli [32] . Esta alternativa es de tipo indirecto y de segunda clase, cuyo término fuente es función de la velocidad no perturbada, mientras que el operador integral se modifica para completar su espectro de autovalores. De esa manera, los modos rígidos son eliminados y se pueden representar una fuerza y una cupla no nulas sobre el cuerpo [33]  ;  [34] . El campo solución en la Completed Indirect Velocity-Boundary Integral Equation (CIV-BIE) es la densidad superficial de capa doble ψ , que no cuenta con un significado físico directo. El modelo BEM empleado es de bajo orden para elementos triangulares planos, cuyo sistema de ecuaciones lineales se resuelve numéricamente mediante el método del residuo mínimo generalizado (GMRES) [35] sin precondicionamiento.

2. Formulación integral

2.1. Ecuación integral de borde en la alternativa CIV-BIE

Dado un cuerpo rígido, cerrado y de superficie suave a trozos A , puede calcularse el flujo reptante a su alrededor mediante la alternativa de Hebeker [36] , que constituye una extensión de la propuesta de Power y Miranda [34] , ambas analizadas en Pozrikidis [33] . Esta puede escribirse de la siguiente manera:

${\int }_{A}{\tilde {K}}_{ij}{\psi }_{j}({\boldsymbol {x}})dA_{\boldsymbol {y}}-$${\int }_{A}{\tilde {H}}_{ij}{\psi }_{j}({\boldsymbol {y}})dA_{\boldsymbol {y}}=$$u_{i}({\boldsymbol {x}})\quad \forall {\boldsymbol {x}}\in A$

( 1)

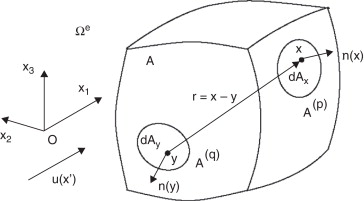
donde el campo solución es la densidad superficial de capa doble ψ (x ), mientras que u_i (x ) son las componentes de la velocidad del flujo sin perturbar. Los elementos diferenciales de superficie se denotan por dA_x  = dA (x ) y dA_y  = dA (y ), y los puntos de integración y de observación son y  = (y₁ , y₂ , y₃ ) y x  = (x₁ , x₂ , x₃ ), respectivamente (ver fig. 1 ).

Figura 1. Esquema de un cuerpo rígido, cerrado y de superficie suave a trozos A ; dominio exterior de flujo Ωe , punto de observación x , punto fuente y , posición relativa r  = x  − y , versores normales n (x ), n (y ), y diferenciales de área dAx , dAy .

El núcleo de capa doble ${\textstyle {\tilde {K}}_{ij}={\tilde {K}}_{ij}({\boldsymbol {x}},{\boldsymbol {y}})}$ es un tensor de rango 2 producido por una densidad de stresslets distribuidos sobre la superficie del cuerpo [37] ; [38]  ;  [33] , y está dado por:

${\tilde {K}}_{ij}({\boldsymbol {x}},{\boldsymbol {y}})=-{\frac {3}{4\pi \mu }}{\frac {r_{i}r_{j}r_{k}}{r^{5}}}n_{k}({\boldsymbol {y}})\quad con\quad {\boldsymbol {r}}=$${\boldsymbol {x}}-{\boldsymbol {y}},y\quad r=\parallel {\boldsymbol {r}}{\parallel }_{2}$

( 2)

siendo n_k  = n_k (y ) la normal unitaria a la superficie en el punto de integración y , y μ la viscosidad dinámica del fluido. Para superficies suaves, este núcleo verifica la siguiente propiedad:

${\int }_{A}{\tilde {K}}_{ij}({\boldsymbol {x}},{\boldsymbol {y}})dA_{\boldsymbol {y}}=$${\frac {1}{2\mu }}{\delta }_{ij}\quad para\quad {\boldsymbol {x}}\in A$

( 3)

donde δ_ij es la delta de Kronecker. Por otra parte, el núcleo ${\textstyle {\tilde {H}}_{ij}={\tilde {H}}_{ij}({\boldsymbol {x}},{\boldsymbol {y}})}$ es la siguiente suma:

${\tilde {H}}_{ij}={\tilde {K}}_{ij}+{\tilde {S}}_{ij}{\mbox{   }}$

( 4)

en la cual ${\textstyle {\tilde {K}}_{ij}({\boldsymbol {x}},{\boldsymbol {y}})}$ está definido por la ecuación (2) , mientras que ${\textstyle {\tilde {S}}_{ij}({\boldsymbol {x}},{\boldsymbol {y}})}$ es el núcleo sourcelet dado por:

${\tilde {S}}_{ij}({\boldsymbol {x}},{\boldsymbol {y}})=-{\frac {{\chi }_{H}}{8\pi \mu }}\left[{\frac {{\delta }_{ij}}{r}}+\right.$$\left.{\frac {r_{i}r_{j}}{r^{3}}}\right]$

( 5)

donde χ_H es un parámetro positivo arbitrario que acopla la densidad de capa simple ϕ con la densidad de capa doble ψ , es decir:

${\boldsymbol {\phi }}({\boldsymbol {x}};{\boldsymbol {\psi }})=$${\chi }_{H}{\boldsymbol {\psi }}({\boldsymbol {x}}){\mbox{   }}$

( 6)

En el trabajo de Hebeker se concluye que χ_H  = 1 es una buena elección, motivo por el cual en este trabajo se adoptará dicho valor. El núcleo ${\textstyle {\tilde {S}}_{ij}({\boldsymbol {x}},{\boldsymbol {y}})}$ es un campo auxiliar ad hoc que permite eliminar los modos rígidos y que da cuenta de la fuerza y el torque global sobre el cuerpo [38] .

2.2. Aproximación de la CIV-BIE mediante una técnica de colocación

Una solución aproximada de la ecuación (1) puede obtenerse mediante una técnica por colocación, en la cual la densidad superficial de capa doble se asume constante en cada elemento, resultando el sistema discreto:

$\sum _{q=1}^{E}\left[{\int }_{A^{\left(q\right)}}{\tilde {\boldsymbol {K}}}^{\left(p,q\right)}dA_{\boldsymbol {y}}{\boldsymbol {\psi }}^{\left(p\right)}-\right.$$\left.{\int }_{A^{\left(q\right)}}{\tilde {\boldsymbol {H}}}^{\left(p,q\right)}dA_{\boldsymbol {y}}{\boldsymbol {\psi }}^{\left(q\right)}\right]=$${\boldsymbol {u}}^{\left(p\right)}$

( 7)

para p  = 1, 2, …, E   , donde ${\textstyle {\tilde {\boldsymbol {H}}}^{\left(p,q\right)}={\tilde {\boldsymbol {H}}}({\boldsymbol {x}}^{\left(p\right)},{\boldsymbol {y}}^{\left(q\right)})}$ y ${\textstyle {\tilde {\boldsymbol {K}}}^{\left(p,q\right)}={\tilde {\boldsymbol {K}}}({\boldsymbol {x}}^{\left(p\right)},{\boldsymbol {y}}^{\left(q\right)})}$ así como los vectores u^{(p )}  = u (x^{(p )} ) y ψ^{(p )}  = ψ (x^{(p )} ), son evaluados en los centroides de los elementos x^{(p )} mediante el doble lazo p , q  = 1, 2, …, E , siendo E el número de elementos en la malla BEM. A nivel discreto, los valores por elemento y nodales son denotados con supra y subíndices, respectivamente. Usando notación matricial y reordenando:

$({\boldsymbol {Q}}-{\boldsymbol {S}}){\boldsymbol {\psi }}=$${\boldsymbol {u}}$

( 8)

donde:

${\boldsymbol {\psi }}={\left[{\begin{array}{llll}{\boldsymbol {\psi }}^{\left(1\right)}&{\boldsymbol {\psi }}^{\left(2\right)}&\ldots &{\boldsymbol {\psi }}^{\left(E\right)}\end{array}}\right]}^{T}\in {\mathbb {R} }^{3E\times 1}$ ${\boldsymbol {u}}={\left[{\begin{array}{llll}{\boldsymbol {u}}^{\left(1\right)}&{\boldsymbol {u}}^{\left(2\right)}&\ldots &{\boldsymbol {u}}^{\left(E\right)}\end{array}}\right]}^{T}\in {\mathbb {R} }^{3E\times 1}$

( 9)

son vectores globales, y […]^T denota la traspuesta. Las matrices globales Q y S están dadas por las sumas:

${\boldsymbol {Q}}=\sum _{q=1}^{E}{\boldsymbol {Q}}^{\left(p,q\right)}$ ${\boldsymbol {S}}=\sum _{q=1}^{E}{\boldsymbol {S}}^{\left(p,q\right)}$

( 10)

respectivamente, con p  = 1, 2, …, E , donde:

${\boldsymbol {Q}}^{\left(p,q\right)}={\begin{array}{cc}\sum _{e=1,e\not =p}^{E}{\boldsymbol {K}}^{\left(p,e\right)}&si\quad q=p;\\-{\boldsymbol {K}}^{\left(p,q\right)}&en\quad otro\quad caso;\end{array}}$

( 11)

cuyas matrices elementales están dadas por:

${\boldsymbol {K}}^{\left(p,q\right)}={\int }_{A}{\tilde {\boldsymbol {K}}}^{\left(p,q\right)}dA_{\boldsymbol {y}}$ ${\boldsymbol {S}}^{\left(p,q\right)}={\int }_{A}{\tilde {\boldsymbol {S}}}^{\left(p,q\right)}dA_{\boldsymbol {y}}$

( 12)

3. Árbol descendente de Barnes-Hut autoadaptativo

Un algoritmo jerárquico construye primero una estructura de datos de tipo árbol con raíz [39] para la representación jerárquica del espacio tridimensional ${\textstyle {\mathbb {R} }^{3}}$ en octantes, y luego calcula las interacciones efectuando un recorrido por el árbol, posiblemente en forma parcial.

Cada vértice ${\textstyle v}$ en un árbol con raíz tiene asociado un número de nivel, que es igual a la longitud del único camino que lo une con el vértice raíz. En consecuencia, el vértice raíz tiene el número de nivel cero, mientras que a medida que los vértices quedan más alejados de la raíz, el número de nivel aumenta. La altura de un árbol es el máximo número de nivel. Por otra parte, 2 vértices cualesquiera en un árbol son adyacentes cuando están unidos por una arista. Los hijos de un vértice ${\textstyle v}$ en un árbol son los vértices adyacentes ubicados en el siguiente número de nivel, o «hacia abajo»  cuando la raíz del árbol se dibuja arriba. Los vértices sin hijos son las hojas del árbol y tienen los números de nivel más elevados. Los antecesores de un vértice diferente de la raíz son todos los vértices que aparecen en el único camino desde la raíz hasta ese vértice, excluyendo a este último e incluyendo a la raíz.

Cada partícula interactúa con una parte del árbol, pues aquellas partes de la nube de puntos que queden más alejadas de la partícula considerada interactúan con ella a través de los niveles más bajos del árbol, i.e., más cerca del vértice raíz, mientras que las partes de la nube más cercanas a la partícula considerada influyen en los niveles más altos del árbol, es decir, más cerca de las hojas.

En la sección 3.1 se resume la construcción de un árbol de BH, donde las partículas contenidas en las hojas representan los paneles de la malla de elementos de borde. Por este motivo, se utilizará indistintamente la denominación de elemento, panel o partícula para los elementos de la malla BEM.

3.1. Ingreso secuencial de los paneles de la malla

La construcción del árbol, naturalmente recursiva, se puede hacer ya sea en forma ascendente, desde las hojas hasta la raíz [40] , o bien en forma descendente, desde la raíz hacia las hojas, como en la versión original de Barnes-Hut [8] , propuesta como una mejora al método de Appel [41] .

El algoritmo recursivo de BH es inherentemente adaptativo, pues no hace ninguna suposición sobre la distribución espacial de las partículas en el octante raíz. En particular, en este trabajo se propone una implementación de dicho algoritmo en una variante mejorada propuesta por Amor López [14] , en el cual las partículas son ingresadas de una en una. La construcción del árbol T se resume con el algoritmo 1 , que es una adaptación del dado por Demmel [42] .

Algoritmo 1.

Construcción del árbol T de BH a partir del arreglo XE con los valores por centroide de la malla BEM.

	Input: arreglo XE con la malla BEM.
	Output: árbol T de BH.
1	procedurehacer_el_arbol (XE, T)
2	E:= size (XE)
3	iniciar_arbol (XE, T)
4	root:= raíz_arbol (T)
5	fore:= 1to E do
6	ingresa_panel (XE, T, root, e)
7	end

donde XE${\textstyle \in {\mathbb {R} }^{E\times n_{c}}}$ es un arreglo de dimensión E y n_c registros, con los datos de los paneles (o elementos), y que incluyen, entre otros, las coordenadas, las áreas, las normales y las densidades por elemento. En los algoritmos se denotará, por ejemplo, con A(I).B el registro B de la componente I del arreglo A .

Cada partícula añadida recorre la línea de antecesores del vértice destino, esto es, visita aquellos vértices ubicados a lo largo del único camino que une la raíz del árbol actual con el vértice destino. El vértice destino es aquel ubicado en el nivel más bajo que podrá contenerla (fig. 2 ). Al hacerlo, se actualizan el área acumulada, la normal promedio y el centroide del cúmulo en cada vértice de la línea de antecesores por los cuales pasa. Esto puede hacerse o bien después de terminar de construir el árbol para entonces calcular los centroides y las áreas de todos los vértices, o bien durante el ingreso de cada partícula. La segunda alternativa, que tiene la ventaja de involucrar un menor número de operaciones, es la que se adopta en este trabajo, y se detalla en la sección 3.2 .

Figura 2. Esquema simplificado de un árbol T de BH. Los paneles de la malla están en sus hojas y los simbolizan los triángulos. Los números de los vértices se indican sin corchetes y los de los paneles, entre corchetes, siendo 0 cuando el vértice posee más de un panel. En línea punteada se marca el único camino a la raíz para el vértice 6, cuyos antecesores son los vértices 5, 2 y 1.

Cada vértice tiene asociada una celda espacial en la forma de un cubo de tamaño variable, donde cada vez que el número de nivel se incrementa en una unidad, la longitud de la arista del cubo se reduce a la mitad. Al inicio solo está el vértice raíz, cuya celda asociada está vacía. La celda es un cubo en ${\textstyle {\mathbb {R} }^{3}}$ cuya longitud del lado y posición es tal que puede contener a toda la malla BEM. Luego se ingresan los paneles de la malla, de uno en uno, que en esta instancia se asimilan a partículas con propiedades geométricas y físicas (en el presente caso: centroide, área, normal y densidad superficial de capa doble ψ ). Para cada panel e añadido, con e  = 1, 2, …, E , se realizan los pasos indicados en el algoritmo 2 , adaptado de Demmel [42] .

Algoritmo 2.

Ingreso del panel genérico e dentro del árbol T de BH.

	Input: arreglo XE , árbol T , un vértice k de T , y panel e .
	Output: árbol T con el panel e ingresado.
1	procedureingresa_panel (XE, T, k, e)
2	z:= T (k).nro_de_partículas
3	switch(z)do
4	case(0)   // vértice sin ocupar
5	almacenar el panel e en el vértice k .
6	case(1) //  vértice ocupado por un único panel i
7	i:= T (k).panel
8	dividir el cubo del vértice k en 8 octantes
9	mover el panel i a su nuevo octante
10	actualizar el centroide asociado al vértice k
11	identificar el hijo h donde irá el panel e
12	ingresa_panel (XE, T, h, e)
13	case(2:)
14	identificar el hijo h donde poner e
15	ingresa_panel (XE, T, h, e)
16	endsw

La construcción recursiva de BH descendente dada por el algoritmo 2 da lugar a un árbol de octantes, una estructura de datos bien conocida para representar datos irregulares en ${\textstyle {\mathbb {R} }^{3}}$ . En la versión descendente del algoritmo de BH, la construcción del árbol finaliza cuando se ingresan las n partículas, y cada hoja tiene 0 o 1 partícula.

Por otra parte, en el algoritmo de BH es necesario un test para decidir cuándo la celda del vértice k está lo suficientemente lejos de una partícula dada i . Existen diversas propuestas, todas basadas en consideraciones geométricas vinculadas con el diámetro de la celda y las distancias relativas. En el algoritmo de BH se considera que una celda c está alejada de la partícula i si la separación relativa verifica:

${\theta }^{\left(i,c\right)}=D_{c}/L_{ic}<\theta {\mbox{   }}$

( 13)

donde D_c es el diámetro de la celda, L_ic  = ∥ x_i  − y_c  ∥ ₂ es la distancia euclídea entre la posición x_i de la partícula i y el centroide y_c de la celda c , mientras que θ es un cierto valor umbral prefijado. Un valor umbral θ relativamente bajo implica que una partícula tiene que estar muy distante de la celda antes de aceptar una expansión multipolar, por lo que tanto el costo computacional como la exactitud aumentan cuando θ disminuye, pues el árbol tiene que ser atravesado hasta sus niveles más profundos, haciendo que se calcule un mayor número de interacciones directas entre partículas. En el límite θ  → 0 se recupera el caso todas contra todas, con un costo computacional O (M² ), mientras que cuando 0 ≪ θ  ≤ 1 hay menos interacciones directas.

3.2. Actualización diferencial en el árbol por el ingreso de un vértice

La actualización diferencial en el árbol de los datos geométricos por el ingreso de un nuevo vértice es un recurso conveniente, siempre que la geometría del problema permanezca invariable. La actualización diferencial se realiza únicamente en los vértices ubicados en la línea de antecesores del vértice destino, por lo que el costo computacional es relativamente bajo. Se puede realizar de la siguiente forma: suponiendo que en una etapa dada en el árbol hay P partículas, entonces en cada vértice k se tienen las áreas:

$A_{k;P}={\begin{array}{ll}A^{\left(e\right)}&si\quad k\quad es\quad hoja;\\\sum _{i\in hijos(k)}A_{i;P}&en\quad otro\quad caso;\end{array}}$

( 14)

y los centroides

${\boldsymbol {x}}_{k;P}={\begin{array}{ll}{\boldsymbol {x}}^{\left(e\right)}&si\quad k\quad es\quad hoja;\\{\frac {1}{Z_{k;P}}}\sum _{i\in hijos(k)}{\boldsymbol {x}}_{i;P}&en\quad otro\quad caso;\end{array}}$

( 15)

respectivamente, donde e es un elemento de la malla BEM, de área A^{(e )} , y Z_k ;P es el número de hijos del vértice k .

Al añadir un nuevo elemento q de la malla de paneles, con centroide x^{(q )} y área A^{(q )} , se tendrán P  + 1 partículas, y los nuevos valores para el área acumulada A_{k ;P +1} y del centroide x_{k ;P +1} en cada vértice k por donde pasa la partícula añadida, es decir, la línea de antecesores del vértice destino, se actualizan con:

$A_{k;P+1}=A_{k;P}+A^{\left(q\right)}$ ${\boldsymbol {x}}_{k;P+1}={\frac {1}{P+1}}\left(P{\boldsymbol {x}}_{k;P}+\right.$$\left.{\boldsymbol {x}}^{\left(q\right)}\right)$

( 16)

dados en [14] (sección 5.3.4, p. 186). Por ejemplo, en la figura 2 se muestra un esquema simplificado de un árbol de BH para el caso de 5 paneles, simbolizados por los triángulos y con centroides x⁽¹⁾ a x⁽⁵⁾ , donde los números sin corchetes indican el número de vértice, mientras que los números entre corchetes indican el identificador del panel, siendo 0 cuando hay más de uno. Solo se muestran el vértice raíz, los vértices internos activos (es decir, que contienen partículas) y las hojas. En dicha figura se ha marcado la línea de antecesores del vértice 6, es decir, los vértices 1, 2 y 5, los únicos que se modificaron cuando se ingresó el panel 3.

3.3. Actualización en el árbol promediando «hacia arriba»

En cada etapa de una resolución iterativa por GMRES del sistema de ecuaciones discreto dado por la ecuación (7) hay que evaluar el producto matriz-vector w  = L  v , donde el vector v representa vectores relacionados con la iteración m , mientras que L es la matriz del sistema. En el caso particular en que v  = ψ^{(m )} , la evaluación rápida del producto matriz-vector dentro del algoritmo de BH implicará, además, calcular la densidad dipolar ψ en todos los vértices del árbol. Por ejemplo, en el caso de la figura 2 , la densidad ψ en cada vértice del árbol T se puede calcular haciendo los promedios «hacia arriba», en el siguiente orden:

$paneles:\quad {\psi }_{3}={\psi }^{\left(2\right)},\quad {\psi }_{4}=$${\psi }^{\left(1\right)},\quad {\psi }_{6}={\psi }^{\left(3\right)};$ $paneles:\quad {\psi }_{7}={\psi }^{\left(4\right)},\quad {\psi }_{8}=$${\psi }^{\left(5\right)};$ ${\psi }_{5}=({\psi }_{6}+{\psi }_{7}+{\psi }_{8})/3;$ ${\psi }_{2}=({\psi }_{4}+{\psi }_{5})/2;$ ${\psi }_{1}=({\psi }_{2}+{\psi }_{3})/2.$

( 17)

Esta tarea se puede hacer de forma sistemática recorriendo recursivamente el árbol de forma ascendente, desde sus hojas hacia la raíz mediante un recorrido en postorden [39] , lo cual da lugar al algoritmo 3 .

Algoritmo 3.

Promedio T.field${\textstyle \in {\mathbb {R} }^{3P\times 1}}$ a partir del campo centroidal v${\textstyle \in {\mathbb {R} }^{3E\times 1}}$ .

	Input: árbol T y vector v .
	Output: promedio en T.field .
1	procedurepromedia_field (T, v)
2	root:= raíz_arbol (T)
3	promedio_up (T, root, v)

El procedimiento promedio  _ up está dado por el algoritmo 4 , donde λ  =∅ representa el vértice vacío.

Algoritmo 4.

Procedimiento auxiliar para el cálculo del promedio T.field${\textstyle \in {\mathbb {R} }^{3P\times 1}}$ con un recorrido en postorden.

	Input: árbol T , vértice k de T , y vector v .
	Output: promedio en el vértice k de T .
1	procedurepromedio_up (T, k, v)
2	if (k = λ ) then return
3
4	c:= hijo_mas_izquierdo (T, k)
5	if (c = λ ) then    //k es hoja
6	T (k).field:= v (k)
7	else
8	s:= 0
9	z:= 0
10	while (c ≠λ ) do
11	promedio_up (T, c, v)
12	e:= T (c).panel
13	s:= s + T (e).field
14	z:= z + 1
15	c:= hermano_derecho (T, c)
16	T (k).field:= s / z

3.4. El algoritmo de BH, la técnica de colocación en la CIV-BIE y el método GMRES

Cuando se emplea el método GMRES [35] para obtener una solución aproximada del sistema discreto dado por la ecuación (7) , basta considerar el producto genérico matriz-vector w  = L  v , donde v y w son los vectores de entrada y salida, respectivamente, relacionados con las diversas etapas en GMRES. En lugar de evaluarlo de forma explícita, es decir, cuando L  = Q  − S es la matriz explícita y densa del sistema de ecuaciones dada por la ecuación (7) , se calcula con la siguiente forma implícita:

• Cálculo de ${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\mbox{v}}}}}$ en los P vértices del árbol T usando los «promedios hacia arriba»:

${\overset {\mbox{ˆ}}{\boldsymbol {\mbox{v}}}}=promedio\_up\quad ({\boldsymbol {\mbox{v}}})$

( 18)

donde:

${\boldsymbol {\mbox{v}}}={\left[{\begin{array}{cccc}{\boldsymbol {\mbox{v}}}^{\left(1\right)}&{\boldsymbol {\mbox{v}}}^{\left(2\right)}&\ldots &{\boldsymbol {\mbox{v}}}^{\left(E\right)}\end{array}}\right]}^{T}\in {\mathbb {R} }^{3E\times 1}$

( 19)

es el vector con los valores de los campos iterados en los centroides de los E paneles, mientras que:

${\overset {\mbox{ˆ}}{\boldsymbol {\mbox{v}}}}={\left[{\begin{array}{cccc}{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{v}}}}_{1}&{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{v}}}}_{2}&\ldots &{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{v}}}}_{P}\end{array}}\right]}^{T}\in {\mathbb {R} }^{3P\times 1}$

( 20)

es el vector con los valores de los campos iterados en los centroides de las P partículas.

• Cálculo secuencial de w en los centroides de los E paneles:

${\boldsymbol {\mbox{w}}}=\sum _{p=1}^{E}{\boldsymbol {\mbox{w}}}^{\left(p,\alpha \right)}\quad con\quad {\boldsymbol {\mbox{w}}},{\boldsymbol {\mbox{w}}}^{\left(p,\alpha \right)}\in {\mathbb {R} }^{3E\times 1}$

( 21)

donde α  = raíz(T ) es el valor inicial del índice α , mientras que el vector w^{(p ,α )} es el valor en los centroides de los paneles e involucra a su vez el cálculo recursivo:

${\boldsymbol {\mbox{w}}}^{\left(p,\alpha \right)}={\begin{array}{ll}{\boldsymbol {S}}^{\left(p,p\right)}{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{v}}}}^{\left(p\right)}&si\quad z=1\quad y\quad q=p\\{\boldsymbol {A}}^{\left(p,p\right)}{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{v}}}}^{\left(p\right)}+{\boldsymbol {B}}^{\left(p,q\right)}{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{v}}}}^{\left(q\right)}&si\quad z=1\quad y\quad q\not =p\\{\boldsymbol {A}}^{\left(p,\alpha \right)}{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{v}}}}^{\left(\alpha \right)}+{\boldsymbol {B}}^{\left(p,\alpha \right)}{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{v}}}}^{\left(\alpha \right)}&si\quad z>1\quad y\quad {\theta }^{\left(p,\alpha \right)}<\theta \\\sum _{\forall \beta \in hijos(\alpha )}{\boldsymbol {\mbox{w}}}^{\left(p,\beta \right)}&en\quad otro\quad caso\end{array}}$

( 22)

correspondiendo cada caso a: autoinfluencia, influencia cercana, influencia lejana e influencia intermedia, respectivamente. El número de partículas alojadas en el vértice α se indica con z  = Z^{(α )} , mientras que:

$q={\begin{array}{ll}I^{\left(\alpha \right)}&si\quad \alpha \quad es\quad una\quad hoja\\0&en\quad otro\quad caso\end{array}}$

( 23)

siendo I^{(α )} el índice del panel alojado en el vértice α .

Algoritmo 5.

Producto matriz-vector w = T(v) .

	Input: arreglo XE , árbol T y vector global v${\textstyle \in {\mathbb {R} }^{3E\times 1}}$ .
	Result: vector global w${\textstyle \in {\mathbb {R} }^{3E\times 1}}$ .
1	functionmatvec (XE, T, v)
2	promedia_field (T,v)    // promedio de v en T
3	E:= size (XE)
4	fore := 1 toEdo
5	root:= raíz_arbol (T)
6	w(e):= influencia (XE,T,root,e)
7	end
8	returnw

En la ecuación (22) , el índice β recorre todos los hijos del vértice genérico α y, además, se tiene en cuenta la condición sobre la separación relativa dada por la ecuación (13) a través de θ . Las matrices de influencia cercana en la ecuación (22) son las siguientes:

${\boldsymbol {A}}^{\left(p,p\right)}={\boldsymbol {K}}^{\left(p,q\right)}$ ${\boldsymbol {B}}^{\left(p,q\right)}={\boldsymbol {S}}^{\left(p,q\right)}-$${\boldsymbol {K}}^{\left(p,q\right)}\quad con\quad q\not =$$p\quad y\quad q>0$

( 24)

mientras que las matrices de influencia lejana son:

${\boldsymbol {A}}^{\left(p,\alpha \right)}={\boldsymbol {K}}^{\left(p,\alpha \right)}$ ${\boldsymbol {B}}^{\left(p,\alpha \right)}={\boldsymbol {S}}^{\left(p,\alpha \right)}-$${\boldsymbol {K}}^{\left(p,\alpha \right)}.$

( 25)

Nótese que la matriz K^{(p ,q )} en la ecuación (24) incide tanto en el bloque diagonal A^{(p ,p )} como fuera de este, es decir, en B^{(p ,q )} , y algo equivalente sucede con la matriz K^{(p ,α )} en la ecuación (25) , lo cual es una consecuencia de la técnica de colocación dada por la ecuación (11) . Además, los índices α , β recorren los vértices del árbol, mientras que los índices p , q recorren los paneles, en los siguientes rangos: 1 ≤ α , β  ≤ P , 1 ≤ p  ≤ E , y 0 ≤ q  ≤ E , donde 0 < E  < P .

Algoritmo 6.

Función auxiliar para el cálculo del producto matriz-vector w = T(v) usando el árbol T .

	Input: arreglo XE , árbol T , vértice k de T y panel e .
	Result: vector elemental w${\textstyle \in {\mathbb {R} }^{3\times 1}}$ .
1	functioninfluencia (XE, T, k, e)
2	z:= T (k).nro_de_partículas
3	switch(z)do
4	case(1)    //se hace BEM clásico
5	j:= T (e).panel
6	if(j = e)then    //panel e = panel j
7	w:= autoinfl_bem (XE, e)
8	else    //panel e ≠ panel j
9	w:= infl_cercana (XE, e, j)
10	end
11	case(2:)
12	x:= XE (e).centroide
13	y:= T (k).centroide
14	D:= T (k).diámetro
15	L:= | x - y |2
16	if(D/L <θ)then
17	w = infl_lejana (XE, x, y)
18	else
19	w:= 0
20	foreach (hijo c de k ) do
21	d:= influencia (XE,T,c,e)
22	w:= w + d
23	end
24	end
25	endsw
26	return  w

En resumen, en la autoinfluencia y en la influencia cercana se emplean las expresiones usuales de la técnica por colocación, es decir, se consideran interacciones tipo PP. En cambio, en la influencia lejana la celda α está lo suficientemente lejos como para aceptar que la malla BEM contenida en la misma se pueda aproximar por los valores promedio almacenados en el vértice α , es decir, se consideran interacciones tipo PC. Por último, en la influencia intermedia, la celda α está tan cerca del centroide p que hay que subdividir recursivamente y volver a analizar.

La ecuación (21) se calcula con el algoritmo 5 , donde se empieza desde la raíz en cada iteración, mientras que la función auxiliar influencia está dada en el algoritmo 6 . Las funciones autoinfl_bem , infl_cercana e infl_lejana en el algoritmo 6 calculan las ecuaciones (22 a-c), respectivamente. Cabe notar que es también un algoritmo recursivo que recorre el árbol, posiblemente de forma parcial, pues no necesariamente tiene que llegar hasta todas las hojas; es decir, si un vértice α está lo suficientemente lejos como para calcular su aporte como vértice lejano, entonces no se recorre el subárbol de vértice α .

4. Cómputo de las tracciones

La fuerza F  = (F₁ , F₂ , F₃ ) y el torque C  = (C₁ , C₂ , C₃ ) con respecto al origen O (x , y , z ) del sistema de coordenadas cartesianas que actúan sobre el cuerpo son computados como un posprocesamiento mediante las integrales de superficie [34] :

${\boldsymbol {F}}={\int }_{A}{\boldsymbol {\phi }}({\boldsymbol {y}})dA_{\boldsymbol {y}};$ ${\boldsymbol {C}}={\int }_{A}[{\boldsymbol {y}}\times {\boldsymbol {\phi }}({\boldsymbol {y}})]dA_{\boldsymbol {y}}.$

( 26)

El campo de tracción en la superficie del cuerpo es la superposición de las tracciones causadas por los potenciales de simple y doble capa. El valor directo de estas tracciones (sobre la superficie del cuerpo) se puede obtener mediante el cálculo de una integral de borde que es débilmente singular en el primer caso, e hipersingular en el segundo [43] . Dado que este trabajo está orientado principalmente a un esquema numérico para el primer caso, como una primera aproximación solo se calcula la contribución del potencial de una sola capa. Entonces, el campo de tracción t_i (x ) = σ_ij (x )n_j (x ) en el punto de observación x , donde σ_ij (x ) es el tensor de tensiones, se obtiene usando [37, sección 3.2, p. 58] ,

$t_{i}{\left({\boldsymbol {x}}\right)}_{\left(e\right)}=$$-{\frac {1}{2}}{\phi }_{i}({\boldsymbol {x}})-{\frac {3}{4\pi }}{\int }_{A}{\tilde {K}}_{ji}({\boldsymbol {y}},{\boldsymbol {x}}){\phi }_{j}({\boldsymbol {y}})dA_{\boldsymbol {y}}\quad con\quad {\boldsymbol {x}}\in A;\quad$

( 27)

donde ${\textstyle {\tilde {K}}_{ji}({\boldsymbol {y}},{\boldsymbol {x}})}$ es el núcleo traspuesto de la ecuación (2) , y ϕ_j (y ) es la densidad superficial de capa simple dada por la ecuación (6) . Nótese que en la ecuación (27) se asume que el versor normal n (x ) está bien definido en el punto de observación x . Esto impide su uso en lugares con discontinuidades geométricas, tales como nodos, aristas o vértices de la malla de superficie poliédrica, al menos en un sentido clásico. Este impedimento se salva, simplemente, haciendo el cómputo de las tracciones en los centroides de los paneles, que siempre son puntos regulares.

La fuerza ${\textstyle {\overset {\mbox{ˆ}}{F}}}$ y el torque ${\textstyle {\overset {\mbox{ˆ}}{C}}}$ adimensionales sobre el cuerpo, y la tracción adimensional en la superficie τ se definen como:

${\overset {\mbox{ˆ}}{F}}_{i}={\frac {F_{i}}{\mu U_{\infty }L}}\quad y\quad {\overset {\mbox{ˆ}}{F}}=$${\frac {F}{\mu U_{\infty }L}};$ ${\overset {\mbox{ˆ}}{C}}_{i}={\frac {C_{i}}{\mu U_{\infty }L^{2}}}\quad y\quad {\overset {\mbox{ˆ}}{C}}=$${\frac {C}{\mu U_{\infty }L^{2}}};$ ${\tau }_{i}({\boldsymbol {x}})={\frac {t_{i}({\boldsymbol {x}})}{\mu U_{\infty }L^{-1}}}\quad y\quad \tau ({\boldsymbol {x}})=$${\frac {t({\boldsymbol {x}})}{\mu U_{\infty }L^{-1}}};$

( 28)

donde U_∞ es la rapidez de la corriente no perturbada, L es una longitud característica, F  = ∥ F  ∥ ₂ , C  = ∥ C  ∥ ₂ , y t (x ) = ∥ t (x ) ∥ ₂ . Los subíndices i  = 1, 2, 3 indican la componente cartesiana x_i correspondiente.

5. Ejemplos numéricos

Se considera el flujo reptante y estacionario alrededor de una esfera y de otros cuerpos rígidos, donde los centroides de cada cuerpo coinciden con el origen de coordenadas cartesiano. En el caso de la esfera, los resultados son comparados con las soluciones analíticas para tres tipos de flujo entrante. En las simulaciones numéricas se adoptaron los siguientes valores: densidad del fluido ρ  = 1 kg/m³ , viscosidad cinemática ν  = 1 m² /s, rapidez no perturbada U_∞  = 10⁻³ m/s.

El número de grados de libertad en el esquema de colocación jerárquico es M  = 3E , mientras que el valor umbral adoptado es θ  = 0, 20, con lo que el porcentaje de coeficientes que se han calculado con expresiones de campo lejano ha fluctuado entre el 50 y el 70 %. Las soluciones numéricas aproximadas se han obtenido utilizando residuo mínimo generalizado (GMRES) sin precondicionamiento [35] .

En todos los casos, se aplica la regla de integración Q₂₁ , lo que significa que se usan 2 puntos de Gauss-Legendre en cada coordenada de integración en la autointegral y en las interacciones cercanas, y 1 punto en las interacciones lejanas [44] . La orientación de los ejes cartesianos en todas las figuras que muestran las distribuciones de las tracciones corresponde a la indicada en el esquema de la figura 1 . En los ejemplos, el valor absoluto del error relativo |e_r | de la fuerza ${\textstyle {\overset {\mbox{ˆ}}{F}}}$ adimensional es computado como ${\textstyle \vert e_{r}\vert =\vert {\overset {\mbox{ˆ}}{F}}_{num}/{\overset {\mbox{ˆ}}{F}}_{(semi)anal{\acute {\imath }}tica}-}$$1\vert$ , y se muestra gráficamente en función del tipo de flujo incidente y del número de grados de libertad M .

5.1. Esfera unitaria

En el caso de la esfera se conocen soluciones analíticas para diversos tipos de flujos incidentes. En particular, se consideran 3 de estos: uniforme, cortante y paraboloidal [34] . Las expresiones analíticas [45]  ;  [46] para la velocidad no perturbada, la fuerza y el torque, en cada caso, se resumen en la tabla 1 . En las simulaciones numéricas se considera una esfera de radio ${\textstyle R=1}$ m. Se utilizaron 24 mallas con refinamiento creciente. Los números de nodos N (×10³ ) y de elementos E (×10³ ) en cada malla se resumen en la tabla 2 . Para comprobar la estabilidad numérica de la solución, se hizo primero el cómputo con las mallas 21, 23 y 24, estructuradas y refinadas de manera uniforme, y luego se repitió el análisis con mallas perturbadas. Las mismas se obtuvieron de cada una de las anteriores introduciendo un desplazamiento nodal pseudoaleatorio tal que mantiene los nodos sobre la superficie de la esfera.

Tabla 1. Flujo reptante estacionario alrededor de una esfera de radio ${\textstyle R}$ . Expresiones analíticas de la fuerza y torque para 3 tipos de flujo incidente [45]  ;  [46] .

Flujo incidente	Velocidad no perturbada u	Fuerza F	Torque C
Uniforme	(U∞ , 0, 0)	${\textstyle (6\pi \mu U_{\infty }R,0,0)}$	0
Cortante	${\textstyle U_{\infty }(x_{2},-x_{1},0)/R}$	0	${\textstyle (0,0,8\pi \mu U_{\infty }R^{2})}$
Paraboloidal	${\textstyle U_{\infty }(x_{1}^{2}+x_{2}^{2},0,0)/R^{2}}$	${\textstyle (4\pi \mu U_{\infty }R,0,0)}$	0

Tabla 2. Flujo reptante estacionario alrededor de una esfera de radio unitario. Números de nodos N (×10³ ) y de paneles E (×10³ ) en cada malla.

z	N	E	z	N	E
1	0,098	0,192	13	6,938	13,872
2	0,218	0,432	14	7,778	15,552
3	0,386	0,768	15	8,666	17,328
4	0,602	1,200	16	9,602	19,200
5	0,866	1,728	17	10,586	21,168
6	1,178	2,352	18	15,002	30,000
7	1,538	3,072	19	20,186	40,368
8	2,402	4,800	20	26,138	52,272
9	3,458	6,912	21	31,106	62,208
10	4,706	9,408	22	36,506	73,008
11	5,402	10,800	23	40,346	80,688
12	6,146	12,288	24	50,786	101,568

Como longitud típica en el cálculo de la fuerza, del torque y de la tracción adimensionales se emplea el diámetro de la esfera, es decir, ${\textstyle L=2R=2}$ m. El valor exacto de la tracción sobre la superficie de una esfera bajo el efecto de un flujo uniforme es igual a la constante ${\textstyle {\boldsymbol {t}}=(3/2)\mu U_{\infty }/R\quad {\boldsymbol {e}}_{1}^{0}}$ , donde ${\textstyle {\boldsymbol {e}}_{1}^{0}}$ es el versor cartesiano en la dirección x₁ . La tracción adimensional τ₁  = t₁ /(μU_∞L⁻¹ ) se muestra en la figura 3 para el caso de las mallas perturbadas 20, 22 y 24, sin que se evidencien cambios de importancia con respecto a las mallas con refinamiento uniforme.

Figura 3. Tracción adimensional τ1 sobre la superficie de la esfera unitaria usando HBEM, con las mallas 20, 22 y 24, de izquierda a derecha, perturbadas con un desplazamiento nodal pseudoaleatorio sin abandonar la superficie de la esfera. El valor analítico de esta tracción adimiensional es 3.

5.2. Geometrías intrincadas o con aristas

Se consideran diversas geometrías intrincadas o con aristas. El primer ejemplo es un cubo de lado L  = 1 m, los 2 siguientes están disponibles en la distribución del mallador NETGEN [47] , mientras que los restantes se seleccionaron del repositorio «180 wrapped tubes » [48] . Algunos de estos últimos pueden considerarse aproximaciones a fibras retorcidas u organismos microscópicos. Las geometrías fueron generadas usando el mallador NETGEN [47] . En ninguno de los casos las surperficies se tocan entre sí, y encierran un volumen finito positivo. Las coordenadas nodales mínimas y máximas son −1/2 y +1/2, respectivamente, mientras que la velocidad no perturbada es ${\textstyle U_{\infty }{\boldsymbol {e}}_{1}^{0}}$ .

En la tabla 3 se listan los ejemplos considerados, incluyendo la cantidad de nodos N y de elementos E de las mallas respectivas siguiendo la nomenclatura dada tanto en Schöberl [47] como en Edelsbrunner [48] , así como la cantidad de vértices V empleados en cada árbol de BH. La altura de cada árbol es de 7 excepto para z ′ = 9, que es de 8.

Tabla 3. Geometrías intrincadas o con aristas. Nomenclatura siguiendo a Schöberl [47] y Edelsbrunner [48] . Números de: nodos N (×10³ ), paneles E (×10³ ) y vértices V (×10³ ) del árbol de BH. La altura de cada árbol de BH es de 7, excepto para z ′ = 9, que es de 8.

z’	Geometría	Caso	N	E	V
1	Cubo unitario		8,67	17,33	26,51
2	Hollow cube		6,01	12,04	17,94
3	Sculpted sphere		6,38	12,76	18,49
4	Speed	(3,3/3)	6,47	12,94	18,97
5	Torsion	(1,6)	5,05	10,10	14,88
6	Curvature	(3, 6/3)	6,59	13,18	19,34
7	Hexagon knots	(1, 3, -24/6)	5,88	11,76	17,14
8	Square knots	(4, 3/4, 0)	6,25	12,49	18,22
9	Triangle knots	(1, 3, -15/3)	5,79	11,59	16,90
10	Circle knots	(3, 4/3)	5,45	10,91	16,03
11	Triangle tori	7/4 time	6,24	12,47	18,36
12	Square tori	−8/4 time	6,00	11,99	17,68

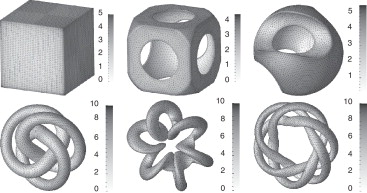
Los campos de la tracción adimensional τ₁ obtenidos con HBEM se muestran en las figuras 4 y 5 . La tracción adimensional τ₁ exhibe el comportamiento esperado en la distribución y en el máximo valor en cada caso, con un incremento en la intensidad cerca de las aristas, y en magnitudes que no difieren significativamente de los correspondientes a la esfera. El caso del cubo ha sido validado anteriormente mediante un cálculo independiente, usando el software libre PETSc-FEM [49] . Este último es un código de cómputo distribuido basado en el método de elementos finitos y orientado a multifísica [50] ; [51]  ;  [52] .

Figura 4. Geometrías intrincadas o con aristas. Arriba: cubo unitario (izq.), hollow cube (cen.) y sculpted sphere (der.) [47] . Abajo: speed (izq.), torsion (cen.) y curvature (der.) [48] . Tracción adimensional τ1 bajo flujo paralelo U∞  = (10−3 , 0, 0) m/s, usando HBEM.

Figura 5. Geometrías intrincadas [48] . Arriba: hexagon knots (izq.), square knots (cen.) y triangle knots (der.). Abajo: circle knots (izq.), triangle tori (cen.) y square tori (der.). Tracción adimensional τ1 bajo flujo paralelo U∞  = (10−3 , 0, 0) m/s, usando HBEM.

5.3. Convergencia en malla y costo computacional

En la figura 6 se muestra el valor absoluto del error relativo |e_r | (en porcentaje) para la fuerza adimensional ${\textstyle {\overset {\mbox{ˆ}}{F}}_{1}}$ y el torque ${\textstyle {\overset {\mbox{ˆ}}{C}}_{3}}$ sobre la esfera unitaria para mallas con refinamiento uniforme, y los flujos incidentes: ${\textstyle e_{r}({\overset {\mbox{ˆ}}{F}}_{1})}$ flujo uniforme (izquierda), ${\textstyle e_{r}({\overset {\mbox{ˆ}}{C}}_{3})}$ flujo cortante (centro) y ${\textstyle e_{r}({\overset {\mbox{ˆ}}{F}}_{1})}$ flujo paraboloidal (derecha), exhibiendo en todos los casos una convergencia monótona.

Figura 6. Valor absoluto del error relativo |er  % | de la fuerza ${\textstyle {\overset {\mbox{ˆ}}{F}}_{1}}$ y el torque ${\textstyle {\overset {\mbox{ˆ}}{C}}_{3}}$ adimensionales sobre la esfera unitaria en función del número de grados libertad M   : ${\textstyle {\overset {\mbox{ˆ}}{F}}_{1}}$ flujo uniforme (izquierda), ${\textstyle {\overset {\mbox{ˆ}}{C}}_{3}}$ flujo cortante (centro) y ${\textstyle {\overset {\mbox{ˆ}}{F}}_{1}}$ flujo paraboloidal (derecha) obtenidos con HBEM.

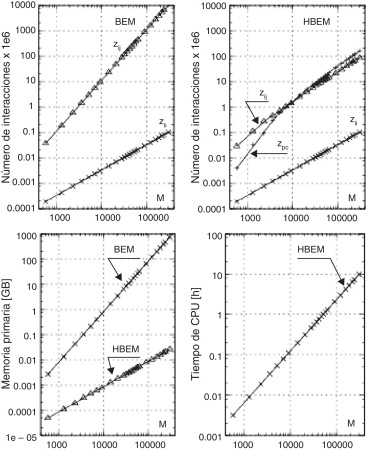
En la figura 7 se muestran curvas indicativas del costo computacional del HBEM comparadas con las correspondientes al BEM clásico, en el caso de la esfera unitaria con refinamiento uniforme y en función del número de grados de libertad M . En dicha figura se trazan las curvas para: el número z_ij de interacciones propias entre los paneles i  − j (cuando i  ≠ j ), el número z_ii de autointeracciones y el número z_pc de interacciones tipo PC, tanto para BEM (arriba a la izquierda) como para HBEM (arriba a la derecha). Por otra parte, la demanda de memoria primaria requerida con BEM se muestra en la citada figura, abajo a la izquierda, y la correspondiente a HBEM se muestra abajo a la derecha. Nótese que, como la matriz del sistema con BEM es densa y no simétrica, el BEM clásico rápidamente se vuelve impracticable, mientras que con HBEM se pueden considerar valores de M relativamente más elevados, dado que sólo se almacena el árbol de BH. Finalmente, el tiempo de CPU usando GMRES con HBEM se muestra abajo a la derecha en la misma figura, usando 4 núcleos de un procesador Xeon W3690.

Figura 7. Costo computacional en función del número de grados de libertad M , en la esfera unitaria con refinamientos uniformes. Números de interacciones propias zij (con i  ≠ j ), autointeracciones zii , y de partícula-celda zpc : con BEM (arriba a la izquierda) versus HBEM (arriba a la derecha). Memoria primaria con BEM versus HBEM (abajo a la izquierda), y tiempo de CPU con HBEM usando GMRES (abajo a la derecha).

6. Conclusiones

En este trabajo se ha expuesto un método de elementos de borde jerárquico HBEM aplicado a la alternativa CIV-BIE, basado en una combinación del esquema de colocación estándar y del árbol jerárquico de bajo orden, autoadaptativo y descendente de Barnes-Hut. Las influencias entre los elementos que resultan de la propuesta son del tipo mixto, e incluyen interacciones tipo partícula-cúmulo, cuando la separación relativa es relativamente grande, así como interacciones partícula-partícula, cuando las partículas están relativamente próximas entre sí. La propuesta equivale a un método tipo matrix free y se ha empleado junto con resolución iterativa mediante residuo mínimo generalizado (GMRES) sin precondicionamiento. También ha sido pensada como complemento a los métodos directos en caso de mallas con elevado número M de grados de libertad. El costo computacional en memoria primaria ha sido significativamente menor al O (M² ) asociado con el BEM clásico mediante colocación al centroide. El método se aplicó al caso de flujo de Stokes en régimen estacionario alrededor de cuerpos tridimensionales cerrados y rígidos, ya sea suaves, con aristas y vértices, o bien de forma intrincada. En las mallas se han empleado triángulos planos de bajo orden. La principal ventaja de la propuesta HBEM presentada se encuentra en que permite considerar un número de grados de libertad mayor comparado con los que pueden emplearse con los métodos más tradicionales de colocación al centroide. Esto se debe principalmente a la reducción en la demanda de memoria primaria para el cómputo y la consecuente disminución de los tiempos de cálculo.

Agradecimientos

Este trabajo ha sido financiado por el Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET, Argentina, proyecto PIP 112-20111-00978), la Universidad Nacional del Litoral (UNL, Argentina, proyecto CAI+D 2009–III-4–2), la Agencia Nacional de Promoción Científica y Tecnológica (ANPCyT, Argentina, proyectos PICT 2010-2492/16, PICT 2009-1141/07, PICT-PRH 2009-0147), EU-IRSES (PIRSES-GA-2009-246977), y ha sido parcialmente realizado con los recursos del Free Software Foundation/GNU-Project , tales como GNU–Linux-OS, GNU–GFortran, GNU–Octave, GNU–Git, GNU–Doxygen y GNU–GIMP, así como otros recursos de código abierto, tales como NETGEN, ParaView, OpenDX, Xfig y LaTeX. L. Dalcín ha hecho diversas sugerencias para mejorar la claridad en la presentación de los algoritmos.

References

1. [1] S.A. Sauter, C. Schwab; Boundary element methods; Springer (2011)
2. [2] J. D’Elía, L. Battaglia, M. Storti; A semi-analytical computation of the Kelvin kernel for potential flows with a free surface; Comp. Appl. Math., 30 (2) (2011), pp. 267–287
3. [3] J. D’Elía, M.A. Storti, E. Oñate, S.R. Idelsohn; A nonlinear panel method in the time domain for seakeeping flow problems; Int. J. Comput. Fluid Dyn., 16 (4) (2002), pp. 263–275
4. [4] K.J. Bowers, R.O. Dror, D.E. Shaw; Zonal methods for the parallel execution of range-limited n-body simulations; J. Comp. Physics, 221 (2007), pp. 303–329
5. [5] J. D’Elía, M. Storti, S. Idelsohn; Un método de paneles para el cálculo de la resistencia de ola en barcos; Rev. Int. Métodos Numér. Cálc. Diseño Ing, 13 (4) (1997), pp. 515–530
6. [6] J. D’Elía, M.A. Storti, S.R. Idelsohn; A panel-Fourier method for free surface methods; J Fluids Eng- Trans ASME, 122 (2) (2000), pp. 309–317
7. [7] S. Aluru, G. M. Prabhu, J. Gustafson, Truly distribution-independent algorithms for the n-body problem, en: Supercomputing ’94 Proceedings, pages 420-428. IEEE, 14-18 Nov 1994.
8. [8] J. Barnes, P. Hut; A hierarchical O (n log n) force-calculation algorithm; Nature, 324 (1986), pp. 446–449
9. [9] L. Greengard, V. Rokhlin; A fast algorithm for particle simulations; J. Comp. Physics, 73 (2) (1987), pp. 325–348
10. [10] L. Greengard; The rapid evaluation of potential fields in particle systems; MIT Press (1988)
11. [11] Y.M. Marzouk, A.F. Ghoniem; K-means clustering for optimal partitioning and dynamic load balancing of parallel hierarchical N-body simulations; J. Comp. Physics, 207 (2005), pp. 493–528
12. [12] M.S. Warren, J.K. Salmon; A parallel hashed oct-tree n-body algorithm; Proceedings of the 1993 ACM/IEEE conference on Supercomputing, ACM (1993), pp. 12–21
13. [13] R.J. Anderson; Tree data structures for N-body simulation; Proceedings of the 37th Annual Symposium on Foundations of Computer Science, IEEE Computer Society, Washington, DC, USA (1996), pp. 224–233
14. [14] M. Amor López, Divide and Conquer Algorithms on Processor Meshes. PhD thesis, Dpto. de Electrónica y Sistemas, Univ. de Santiago de Compostela, 1997.
15. [15] A.S. Sangani, G. Mo; An O(N) algorithm for Stokes and Laplace interactions of particles; Phys. Fluids, 199 (8) (1996), pp. 1990–2010
16. [16] E. Darve, P. Havé; Efficient fast multipole method for low-frequency scattering; J. Comp. Physics, 197 (1) (2004), pp. 341–363
17. [17] A.-K. Tornberg, L. Greengard; A fast multipole method for the three-dimensional Stokes equations; J. Comp. Physics, 227 (3) (2008), pp. 1613–1619
18. [18] D. Lindbo, A.-K. Tornberg; Spectrally accurate fast summation for periodic Stokes potentials; J. Comp. Physics, 229 (23) (2010), pp. 8994–9010
19. [19] E.E. Gdoutos, R. Agrawal, H.D. Espinosa; Comparison of the Ewald and Wolf methods for modeling electrostatic interactions in nanowires; Int. J. Num. Meth. Fluids, 84 (13) (2010), pp. 1541–1551
20. [20] A. Kumar, M.D. Graham; Accelerated boundary integral method for multiphase flow in non-periodic geometries; J. Comp. Physics, 231 (20) (2012), pp. 6682–6713
21. [21] J. Aronsson, I. Jeffrey, V. Okhmatovski; Generalization of the Barnes-Hut algorithm for the Helmholtz equation in three-dimensions; IEEE Antenn. Wireless Propag. Lett., 8 (2009), pp. 425–428
22. [22] P. Li, H. Johnston, R. Krasny; A Cartesian treecode for screened Coulomb interactions; J. Comp. Physics, 228 (10) (2009), pp. 3858–3868
23. [23] J. Aronsson, K. Butt, I. Jeffrey, V. Okhmatovski; The Barnes-Hut hierarchical center-of-charge approximation for fast capacitance extraction in multilayered media; IEEE Trans. Microw. Theory Tech., 58 (5) (2010), pp. 1175–1178
24. [24] I. Benedetti, M.H. Aliabadi; A fast hierarchical dual boundary element method for three-dimensional elastodynamic crack problems; Int. J. for Num. Meth. in Engng., 84 (9) (2010), pp. 1038–1067
25. [25] Z. Wang, N. Ghoniem, S. Swaminarayan, R. LeSar; A parallel algorithm for 3D dislocation dynamics; J. Comp. Physics, 219 (2) (2006), pp. 608–621
26. [26] M. Winkel, R. Speck, H. Hübner, L. Arnold, R. Krause, P. Gibbon; A massively parallel, multi-disciplinary Barnes-Hut tree code for extreme-scale N-body simulations; Comput. Phys. Commun., 183 (4) (2012), pp. 880–889
27. [27] C.O. Ahn, S.H. Lee; A new treecode for long-range force calculation; Comput. Phys. Commun., 178 (2) (2008), pp. 121–127
28. [28] D. Lee, A. Ozakin, A.G. Gray; Multibody multipole methods; J. Comp. Physics, 231 (20) (2012), pp. 6827–6845
29. [29] J. Bédorf, E. Gaburov, S.P. Zwart; A sparse octree gravitational N-body code that runs entirely on the GPU processor; J. Comp. Physics, 231 (7) (2012), pp. 2825–2839
30. [30] A. Yaseen, Y. Yaohang Li; Accelerating knowledge-based energy evaluation in protein structure modeling with Graphics Processing Units; J. Parallel Distrib. Comput., 72 (2) (2012), pp. 297–307
31. [31] E. Gaburov, J. Bédorf, S.P. Zwart; Gravitational tree-code on graphics processing units: implementation in CUDA; Procedia Comput. Sci, 1 (1) (2010), pp. 1119–1127
32. [32] M.S. Ingber, A.A. Mammoli; A comparison of integral formulations for the analysis of low Reynolds number flows; Eng. Anal. Bound. Elem., 23 (1999), pp. 307–315
33. [33] C. Pozrikidis; Boundary Integral and Singularity Methods for Linearized Viscous Flow; Cambridge University Press (1997)
34. [34] H. Power, G. Miranda; Second kind integral equation formulation of Stokes flows past a particle of arbitrary shape; SIAM J. Appl. Math., 47 (4) (1987), pp. 689–698
35. [35] Y. Saad, M. Schultz; Generalized minimum residual method (GMRES); SIAM J. Sci. Statist. Comput., 7 (1986), pp. 856–869
36. [36] F.K. Hebeker; Efficient boundary element methods for three-dimensional exterior viscous flow; Num. Meth. PDE, 2 (4) (1986), pp. 273–297
37. [37] O.A. Ladyzhenskaya; The Mathematical Theory of Viscous Incompressible Flow; (2nd edition)Gordon and Breach Science Publishers (1969)
38. [38] C. Pozrikidis; Introduction to Theoretical and Computational Fluid Dynamics; Oxford (1996)
39. [39] M. Storti, J. d’Elía, R. Paz, L. Dalcín, M. Pucheta, Algoritmos y Estructuras de Datos (notas del curso, disponible en: http://www.cimec.org.ar/mstorti/aed/aednotes.pdf ), 2012.
40. [40] G. Xue; A cost optimal parallel algorithm for computing force field in n-body simulations; Hsu, Kao (Eds.), COCOON 98, LNCS 1949, Springer Verlag, Berlin (1998), pp. 95–104
41. [41] A.W. Appel; An efficient program for many-body simulations; SIAM J. Sci. Stat. Comput., 6 (1) (1985), pp. 85–103
42. [42] D. Demmel, Fast hierarchical methods for the n-body problem. Parts 1 and 2. Course CS267, lecture 24, 1996. Disponible en: http://www.cs.berkeley.edu/demmel/cs267/lecture26/lecture26.html/ .
43. [43] O. Gonzalez; On stable, complete, and singularity-free boundary integral formulations of exterior Stokes flow; SIAM J. Appl. Math., 69 (2009), pp. 933–958
44. [44] J. D’Elía, L. Battaglia, A. Cardona, M. Storti; Full numerical quadrature of weakly singular double surface integrals in Galerkin boundary element methods; Int. J. for Num. Meth. in Biomedical Engng., 27 (2) (2011), pp. 314–334
45. [45] E. Guazzelli, Microhydrodynamique. Cours de base sur les suspensions. Course notes, Groupe Ecoulements de Particules (GEP), IUSTI, Polytech Marseille, 2003.
46. [46] J.K.G. Dhont; An Introduction to Dynamics of Colloids; Elsevier (1996)
47. [47] J. Schöberl, NETGEN 4.3 mesher. Technical report, University of Linz, Austria. Disponible en: http://sourceforge.net/projects/netgen-mesher/ , 2012.
48. [48] H. Edelsbrunner, 180 wrapped tubes. Technical report, Department of Computer Science, Duke University, Durham, Disponible en: http://www.cs.duke.edu/edels/Tubes/ , 2012.
49. [49] PETSc-FEM. A general purpose, parallel, multi-physics FEM program, GNU General Public License. Disponible en: http://www.cimec.org.ar/petscfem , 2012.
50. [50] M.A. Storti, N.M. Nigro, R.R. Paz, L.D. Dalcín; Dynamic boundary conditions in computational fluid dynamics; Comp. Meth. in Appl. Mech. and Engr., 197 (13-16) (2008), pp. 1219–1232
51. [51] L. Battaglia, J. D’Elía, M. Storti; Simulación numérica de la agitación en tanques de almacenamiento de líquidos mediante una estrategia lagrangiana euleriana arbitraria; Rev. Int. Métodos Numér. Cálc. Diseño Ing, 28 (1) (2012), pp. 124–134
52. [52] G. Franck, N. Nigro, M. Storti, J. D’Elía; Numerical simulation of the Ahmed vehicle model near-wake; Lat. Am. Appl. Res., 39 (4) (2009), pp. 295–306