ABSTRACT
The availability of machine learning techniques opens up possibilities in different fields of civil engineering. Their application in conjunction with numerical simulations overcomes the limitations in traditional approaches and pave the road for some new horizons. This communication presents several applications of such a hybrid tool in design and safety assessment of dams and hydraulic structures. They include the generation of behavior prediction models from monitoring data, the identification of behavior patterns with classification models, the analysis of the seismic response of gravity dams with heterogeneous concrete in a probabilistic framework, the investigation of the performance of arch dams, and the estimation of the discharge capacity of arched labyrinth spillways.
Keywords: Dam safety, monitoring, machine learning, numerical methods, uncertainty quantification
1 INTRODUCTION
The advent of the era of big data, with an enormous proliferation of sensors of all kinds, highlighted the value of data and opened up possibilities for its use. There are many fields of application, from social sciences to medicine or marketing. This generated great interest in the development of techniques capable of extracting useful information from databases that in many cases are large and very heterogeneous. As a result, a huge scientific community of developers and users of machine learning (ML) techniques arose. The availability of these methodologies opens up the possibility of tackling complex problems with new approaches also in civil engineering, and specifically in the field of dam safety.
CIMNE is a research center specializing in the development and application of advanced numerical methods. In recent years, a very active line of research was initiated on the combination of these numerical models with ML techniques to tackle practical problems related to dam safety from new perspectives.
This communication includes a review of the most relevant work carried out in this field, which can be classified into the following areas:
- 1. Predictive models based on monitoring data. In this field, machine learning models can be used two ways:
- 1. To predict dam response and compare the result to actual measurements and detect anomalies
- 2. To interpret dam behavior by identifying the strength and nature of the effect of different loads on the response variables
- 2. Classification models to identify behavior patterns. This is an alternative approach to detect anomalies associated to potential failure modes
- 3. Reduced-order-models in combination with complex numerical simulation for uncertainty quantification.
- 4. Curve fitting in and pattern recognition in high-dimensional problems.
In the following sections, the applications are summarized including the motivation, methodology and results.
2 CURVE FITTING IN HYDRAULIC STRUCTURES
2.1 Motivation
Discharge curves are essential in the design and operation of hydraulic structures. This is more acute when dealing with complex geometries, when the involved parameters have combined effects on the hydraulic behavior. The determination of such curves is typically done by means of laboratory testing for different discharge rates and subsequent polynomial curve fitting.
This procedure is cumbersome when a high number of parameters are involved, whose effect is not well known or vary for different values of the hydraulic head over crest. Examples of such structures include gated spillways (Salazar et al 2013) and labyrinth weirs, among others.
In such settings, the resulting polynomials are often complex and therefore hard to use for design optimization. ML models can be an alternative to obtain a unique expression to compute the discharge flow for some particular value of the head over crest, as well as for better understanding of the hydraulic behavior.
This approach was applied to the evaluation of the hydraulic performance of arched labyrinth weirs, including two different ML algorithms for comparison purposes: neural networks (NN) and Random forests (RF).
2.2 Methodology and results
Labyrinth weirs are appropriate for increasing the discharge capacity of spillways when space is limited by site conditions (Salazar and Crookston, 2019). They provide higher discharge rate than a conventional linear weir for a given combination of area occupied and hydraulic head on crest. However, this higher efficiency doesn’t occur for all range of hydraulic head. In particular, most of the additional capacity is lost for high heads because of negative effects such as nappe interference (Salazar et al., 2015). As a result, the optimal design of such structures depends on the particular conditions of each case, both the geometry and the design flow.
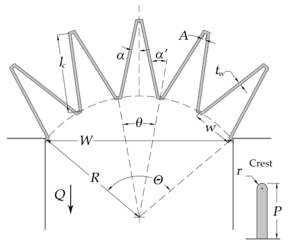
An additional improvement to this typology comprises the use of a curved alignment for the cycles to reduce cost by narrowing the spillway chute (Fig. 1), at the cost of increasing complexity of hydraulic behavior. More parameters are required to define the geometry, and the optimization problem is more complex (Crookston, 2010).
The discharge can be computed as a function of a discharge coefficient Cd:
|
|
(1) |
where Q is the discharge over weir, Lc-cycle is the centerline length of each cycle, N is the number of cycles, g is the gravity acceleration, and H is the total upstream head on weir. In turn, the discharge coefficient is dependent on a set of geometrical parameters (Fig. 1):
Figure 1. Arced labyrinth spillway as proposed by Crookston (2010)
An experimental campaign conducted by Crookston (2010) provided results as for the relationship between hydraulic head over crest and discharge flow rate for different geometrical configurations, showing the above mentioned complexity. In such setting, a separated polynomial expression is required to approximate the experimental results (Crookston and Tullis, 2012).
On the contrary, the NN and RF models generated allowed obtaining a unique expression providing accurate results for all configurations tested, with a predictive error in the same range as that of the uncertainty of the experimental measurements.
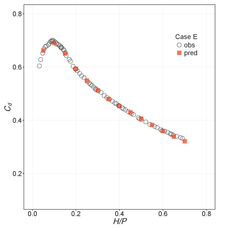
In addition, NN models offered a good estimate of the performance of different geometries, non-tested in laboratory. Although this results cannot be evaluated due to the lack of information on the true behavior, they clearly respond to engineering intuition (Fig. 2).
Figure 2. Discharge curves for arched labyrinth weirs. Left: measured values vs predictions of the NN model for one of the configurations considered. Right: Predictions of the NN model for different values of α. The results of the experiments are depicted with circles, while the predictions of the NN model for intermediate values of α are shown with lines. It can be verified that the predictions are good interpolations between tested geometries.
2.3 Conclusions
ML models offered accurate predictions of the discharge coefficient for different configurations of arched labyrinth weirs. Both NN and RF resulted in unique expressions that were accurate for different geometries. Such models can thus be useful in practice to predict the discharge rate during flood management.
In addition, although RF models failed to compute accurate values of Cd for intermediate geometries, NN provided reasonable results. This can be helpful for design optimization, since the number of configurations tested in laboratory can be reduced, with the corresponding lower cost.
Finally, both models were analyzed as regards the effect of each geometrical parameter on the discharge capacity. Although ML models are often considered as hard to interpret, existing tools allowed extracting the average effect of the more relevant input parameters, which can also be beneficial in the design.
3 PREDICTIVE MODELS BASED ON MONITORING DATA
3.1 Motivation
The first and most frequent field of application of ML in dam engineering is for the analysis of monitoring data. Since the middle of 20th century, statistical models were used to predict dam behavior and isolate the effect of the loads acting on the structure, as well as that of time. During that time, the Hydrostatic-Season-Time model was proposed (Willm and Beaujoint, 1967), which was extensively used from then on. It was first developed to estimate the deformation of arch dams, and the ground hypothesis is that such deformation is due to the superposition of three effects: the reversible action of the hydrostatic load and the temperature, and some irreversible effect of time. This model has shown to be useful in many settings, but also presents certain limitations. It is not that appropriate for other dam typologies and response variables which present different response to the loads. Other limitations include the inability to consider correlated inputs, or the rigidity as for the shape of the relation between inputs and response. ML based models present interesting features that allow overcoming some of the mentioned drawbacks (Salazar et al., 2017a):
- Different kinds of variables can be considered.
- Nonlinear or threshold effects can be captured automatically, without the need for defining a priori the kind of response (linear, exponential, or other).
- Correlated inputs can be considered without loss of accuracy.
3.2 Methodology and results
Predictive models can be used in practice two ways. On the one hand, they can predict dam response in normal operation, given a certain combination of loads. Actual behavior measured by monitoring devices can be compared to the predictions of the model to make decisions regarding dam safety. In addition to the most probable value, warning or safety thresholds can also be computed and used to detect anomalies.
On the other hand, ML models can be analyzed to identify the effect of each load acting on the dam. The paradigmatic example is the separation of the deformation due to the hydrostatic load from that of the temperature in double-curvature arch dams. Although it is well known that both loads are coupled (reservoir level affects to the thermal response because the water temperature is typically different from that of the surrounding air), the both effects are often quantified and isolated from the irreversible effect to better understand the dam behavior.
A set of ML algorithms can be used to tackle this problem. Neural networks (NN) are better known and more frequently used (Mata, 2011), but other techniques have also shown to be useful for such prediction task. In particular, boosted regression trees (BRT) resulted as the most appropriate overall in a comparative study (Salazar et al., 2015) including NN, random forests (RF), support vector machines (SVM) and multi-adaptive regression splines (MARS). Although such result cannot be considered generalizable, it motivated further analysis of BRT models and its implementation in a software application (Salazar et al., 2019b). In addition to the abovementioned features, BRT present other interesting properties:
- Pre-process is not required for the input variables (in contrast for instance with NN, which require normalization of the numerical variables and transformation of the categorical ones).
- Variable selection is performed automatically during model training, which eliminates the need for a preliminary variable selection process, which is hard to optimize.
- Input variables are classified as a function of their importance, or strength of their association to the response under consideration. In addition, the average effect of each input on the response can be analyzed easily through the partial dependence plots.
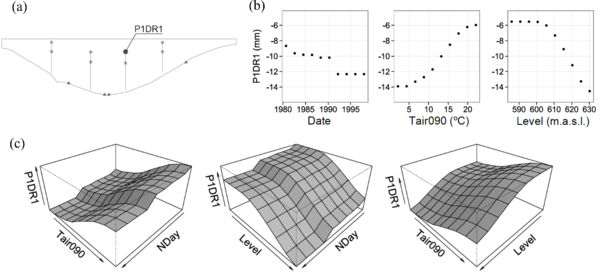
The application of BRT models to the analysis of the monitoring data in an arch dam allowed identification of a small and sudden variation in the response to the hydrostatic load that indeed took place, according to the reports (Fig. 3).
Such change would have been hard to identify with conventional statistical tools (Salazar et al., 2016). In the same analysis, the model was applied to the study of leakage flows with the same set of inputs. Although in this case many of those inputs were obviously not affecting (e.g. temperature), model accuracy was useful, and the evolution of leakage over time, different among locations in the dam body, was captured.
By contrast, there was indeed some inertia with regard to the variation of the external temperature, also different in different areas of the dam, which was also identified by the BRT model.
The same algorithm was implemented in a methodology for generating predictive models that allows its application in real time to detect anomalies. For that, a criterion to define warning thresholds was proposed, which pays attention to control overfitting while making full use of the information available (Salazar et al., 2017b).
This methodology was integrated in a software tool in cooperation with Verbund, which was successfully employed for the assessment of the behavior of an embankment dam (Salazar et al. 2019b). In addition to the options required for model fitting (training and testing periods, training parameters), additional functionalities were included to perform some of the steps involved in the analysis of the monitoring data, such as options for interactive exploration of data and for fixing measurement errors.
Figure 3. Interpretation of the deformation of an arch dam and the contribution of the temperature, the reservoir level, and the irreversible time effects. P1DR1 is the radial deformation at the top of the highest cantilever (a), NDay represents time, Tair090 is the moving average of 90 days of the air temperature, and Level stands for the hydrostatic load. Partial dependence plots (b) can be generated to observe the average effect of each input on the response variable considered. The same plots in 3D (c) show the combined effect of couples of inputs. Soon after 1990 some sudden small change occurred in the response of this device to changes of level and temperature (Salazar et al., 2016).
4 IDENTIFICATION OF BEHAVIOR PATTERNS
4.1 Motivation
The analysis of dam monitoring data for safety assessment and anomaly detection is typically performed by considering a set of relevant response variables. Some behavior model is created, be it a FEM model or some data-based (statistical or ML). These models provide an estimate on the expected response of the dam in front of a certain combination of loads. Such predictions are compared to the actual measurements, and decisions are made on the basis of the result of this comparison. This is a sound approach, which nonetheless requires as many model evaluations as relevant variables are selected. In the case of data-based approaches, a separated model needs to be built and assessed for each output. Then, an additional analysis is required to associate the result of the comparison to some behavior pattern, whether safe or anomalous.
This procedure can be improved by jointly analyzing both the response variables and the loads by means of some ML-based classification model.
4.2 Methodology and results
The proposed methodology includes the following steps:
- 1. Creation and validation of a FEM model of the dam.
- 2. Application of the model to some control period to obtain the reference response, or behavior in normal conditions.
- 3. Determination of the potential anomalies or failure modes to consider.
- 4. Simulation of the response of the dam in such anomalous scenarios.
- 5. Creation of a database including the loads the response of the dam at the location of the monitoring devices and a label for the corresponding case (normal or anomalous).
- 6. Training of a ML classifier. The parameters are fitted to part of the database (training set), then the model accuracy is evaluated by comparing the predictions with the known result for the remaining data (testing set).
The classifier takes as inputs both the loads and the response of the dam, then computes the predicted probability of such set of data of belonging to one of the pre-defined scenarios.
This procedure was applied to the identification of hypothetical anomalies in a 100-m high arch dam. Five anomaly scenarios were defined and the expected response computed in the form of displacements along X and Y axis at 28 locations within the dam body, where the deformation is actually measured by pendula (Fig. 4).
Figure 4. Numerical model considered for the test case with indication of the anomalies introduced: the mechanical boundary condition was modified in different parts of the foundation, with varying magnitude.
In this application, we used Random Forests as learning algorithm, since it is well-known to provide good results when many, highly-correlated inputs are involved. In this example, deformations in 28 locations, both in the X and Y directions, were taken as inputs.
The resulting model could identify the scenario associated to a set of measurements and loads with an average error of 5%. The wrong predicted classifications occurred for 0.5-mm imposed displacements, i.e., all cases for scenarios with 1-mm differential deformation were correctly identified. More details of this analysis can be found in (Salazar et al., 2019a)
This approach can be applied to other dam typologies and response variables, thanks to the high flexibility of RF models. The main drawback is that the anomalies need to be defined a priori and they have to be simulated with a numerical model, to compute the response pattern for the classifier to learn. To overcome such limitation, an open research line focuses on the identification of undefined anomalies with unsupervised learning techniques.
5 UNCERTAINTY QUANTIFICATION
5.1 Motivation
A deterministic approach has been traditionally followed in the design of dams. The relevant parameters governing the dam response are determined from experiments and considered as constant, i.e., valid for the whole domain. They are the grounds for the stability analysis in ordinary and extraordinary situations. The design is thus based on the computation of the factor of safety (FoS) and the verification of being above the values prescribed by the legislation for each scenario. However, there is always some uncertainty both in material properties and loading that should be accounted for: in certain settings, a higher FoS may be associated to higher risk scenarios (Hariri-Ardebili, 2018).
The need for uncertainty consideration is even greater when it comes to estimation of failure probability. Such studies are often performed for existing dams, which may have decades of service life, with limited information on the material properties and construction process. In such cases, also temporal effects can be relevant. All these factors increase the uncertainty.
In a risk analysis context, the probability of failure can be computed with one of the following approaches: (a) reliability techniques, (b) expert judgment, or (c) specific methodologies (SPANCOLD, 2013). Numerical modelling is a basic tool in most cases, either directly employed to calculate the probability of failure, or indirectly, as an aid to the analysis of a particular phenomenon that is subsequently evaluated by expert judgment. In this field, there is a consensus on the convenience of using numerical models with a stochastic approach, essential to obtain a quantitative estimate of the failure probability for a given model of uncertainty in those parameters related to materials and external loads (Altarejos et al., 2012).
This approach, which is widely accepted in the framework of risk management, is not so frequently applied in practice, or is used with highly simplified versions. It is limited by the need to perform a large number of calculations, which involve a long computational effort (Escuder et al., 2016), as well as the fact that methods such as Monte Carlo family and their proper interpretations (Schöbi and Sudret, 2017) are not still intimate to many practitioners.
On the other hand, numerical models have an additional uncertainty, which is often overlooked, due to intrinsic aspects of the calculation, such as mesh size, time step (in transient problems), boundary conditions (especially in thermo-mechanical problems), and constitutive model selection.
ML algorithms have shown their effectiveness in predicting dam behaviour, as well as to extract useful information for dam safety studies. In the context of risk analysis, these tools can be used in combination with others basically with two approaches:
- 1. The classification of a set of measures as corresponding to the normal situation or to a certain failure mode. Recently, some simple examples of similar procedures applied to detection of anomalies in dams have been published (Mata et al., 2014). In this case, the idea is to generate a database with a number of samples for the parameter values (according to their respective density function), and the corresponding responses (safe/failed). A ML-based classifier allows extending that database with multiple additional cases without the need to apply either a FEM model or an analytical function. Recent results show the benefits of machine learning in this context (Hariri-Ardebili and Pourkamali-Anaraki, 2018).
- 2. The estimation of certain results of complex numerical models (quantities of Interest, QoI) to reduce the global computational cost (Trehan et al., 2017). In the application of the Monte Carlo Method, which requires the execution of a large number of numerical models and the analysis of their results, it can be very advantageous - often inevitable - to calculate only a few cases and train a model with them (surrogate model, emulator or metamodel) that gives the system response for a set of input variables, without the need to perform a new complete calculation (Hariri-Ardebili and Boodagh, 2018). This approach can be extended to reduce different sources of uncertainties in the coupled system (Hariri-Ardebili and Pourkamali-Anaraki, 2019) This use of ML algorithms is also well known in other areas of engineering (e. g. Gorissen et al., 2010).
5.2 Methodology and results
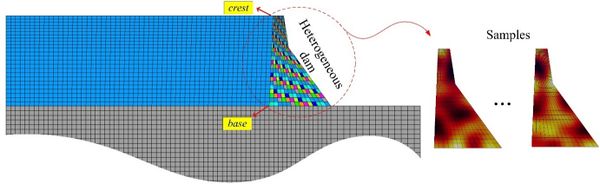
In an example application, we combined advanced numerical models with ML algorithms for the assessment of the stability of a pilot gravity dam with heterogeneous concrete (Salazar and Hariri-Ardebili, 2019). For that, a number of different numerical models were generated with the random field theory to reproduce variability in concrete properties along the dam body (Fig. 5). Each model was subjected to a dynamic seismic excitation and the response was computed in terms of maximum displacements and tensile stress (QoIs).
The first goal was to assess the prediction accuracy of ML-base models to approximate the selected QoIs on the basis of a reduced number of runs (i.e., only 100 simulations). We took 70 models for training and reserved the remaining 30 for testing. The inputs set in this case is formed by the values of the Young modulus of the concrete, which is different for each element within the mesh. This implies as many as 336 inputs. Since we only had 70 training cases, the setting is complex for a data-based ML model. In this conditions, RF are well known to provide good performance, thus were selected for the prediction task.
Indeed, the RF models allowed predicting the maximum displacement at the crest with an average error of 4.1 %, and the maximum stress with only 2.42 % error.
Figure 5. Finite element model of the coupled dam-reservoir-foundation system, including two sample realization of a heterogeneous dam.
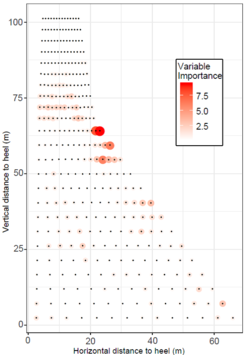
The analysis of these models offered more interesting results in this case. For better visualization, the importance of each input, as computed by the RF model, was depicted in Figure 6. The diameter of the circles is proportional to such model result. It can be seen that the most influential elements on dam displacement are those located around the neck. This finding is consistent with the physics of the problem in which the Koyna Dam has very long and unusual neck shape which makes this area vulnerable.
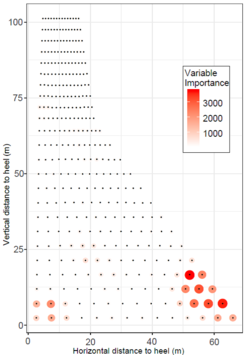
As for tensile stress, the most important elements are located around the toe and the heel. This is also in accordance with engineering knowledge, since a gravity dam is usually overstressed (in linear elastic analysis) in these areas when dynamic load is applied. Thus, they are the most sensitive areas to the first principal stress.
|
|
Figure 6. Variable importance of mesh elements on the maximum crest displacement (left) and tensile stress (right).
This result demonstrates the capability of RF models to identify the most relevant inputs in systems with many highly correlated variables. This case was particularly challenging, since the number of training cases (i.e., 70) was less than input variables.
6 BEHAVIOUR OF ARCH DAMS
6.1 Motivation
One of the most interesting features of ML models is their capability of discovering patterns in databases whose internal structure is not perfectly known. This can be used, in combination with tools for model interpretation, for investigating the performance of engineering systems. We used this possibility to investigate the effect of geotechnical and geometrical parameters in the response of double-curvature arch dams (Salazar et al, 2017c).
Arch dams have been studied for decades and engineering criteria have been proposed for pre-design. Some rules-of-thumb are well known as for the width-to-height ratio of the valley for an arch dam to be feasible, as well as for other design aspects. For instance, thermal load is acknowledged to be relevant when the base thickness to height ratio is lower than 0.2 (USBR, 2013). However, each dam is a case study with particular features regarding geometrical and geotechnical conditions. Other variables are also relevant such as the strength of the foundation (Romana, 2013), or the ratio between crest length and height (USACE, 1994), and their effect on dam response is not easy to identify a priori, since they influence on each other.
6.2 Methodology and results
To investigate the effect of geometry, geotechnical conditions and loads on the response of arch dams, we generated 3,000 different numerical models of arch dams with random parameters, including material properties of dam and foundation, as well as those involved in the geometrical definition of the structure (Vicente et al., 2017). Transient thermo-mechanical analyses were performed with realistic values of the evolution of the reservoir level and external temperature, also including some randomness. The maximum displacement at the crest and the maximum tensile stress at the heel were taken as QoI. For each of them, a ML-based predictive model was fitted based on RF to learn the relationship between the input parameters involved and the dam response.
Once fitted, the models were interpreted by analyzing the classification of the input variables and the partial dependence plots. For the maximum crest displacement, the results showed the crest chordal length as the most relevant parameter, followed by Young´s modulus of foundation. Thickness at the base was more influential than that at the crest, and the thermal properties featured lower influence.
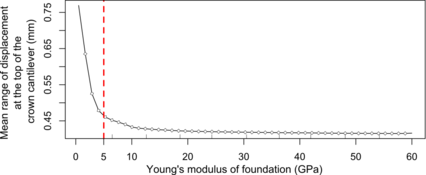
A further analysis of the partial dependence on the strength of the foundation (Fig. 7) showed that such effect was relevant for low values (below 5 GPa), with a much lower for higher, more conventional values for arch dams. This result was in accordance with the practical criterion proposed by Rocha for the minimum strength of foundation for arch dams (Rocha, 1964).
Figure 7. Partial dependence of dimensionless displacement at crown cantilever on Young’s modulus of foundation. The red dotted line shows the conventional lower threshold for appropriate foundation of arch dams. It can be seen that the effect of foundation on displacement is lower for conventional, higher values.
7 CONCLUSIONS
The results of the application of ML models in different problems related to dam engineering and safety showed the possibilities that arise from their use in combination with numerical modelling and engineering knowledge.
When used to generate behavior models based on monitoring data, ML allowed overcoming some of the limitations of traditional statistical models:
- 1. Different kind of response variables and dam typologies can be considered.
- 2. Correlation among acting loads can be accounted for.
- 3. Prediction accuracy can be improved in general, which results better control of the dam and allows early detection of anomalies.
- 4. Dam behavior can be interpreted by analyzing the fitted model.
ML classification models can also be used to identify behavior patterns by jointly analyzing a set of response variables and loads. This approach is in a preliminary stage of development and needs to be tested in practical settings, but the results obtained suggest that it can be useful as a complement to the independent analysis of each response variable to associate deviations between predicted and observed response to potential anomalies or failure modes.
In the field of quantitative risk analysis, the use of ML models as surrogate models to complement numerical simulations has great potential for widening the scope of probabilistic analysis. The reduction in computational cost of the whole process can be used to increase the number of random variables, even in complex numerical simulations such as transient thermomechanical or dynamic. In an additional research line, classification ML models are also being explored for similar purposes: in this case, a set of values for the random variables is presented to the model, which computes a prediction on the overall outcome of the system, considered as fail/no fail. This can also be used in Mote Carlo-like analysis.
Although ML models are often considered hard to interpret or analyze, the examples presented also showed that existing tools for interpretation are indeed useful for obtaining insight into the behavior of the system. In the case of heterogeneous concrete, where each element in the mesh takes a different value, the RF model correctly identified the most sensible areas to the QoIs defined.
The same feature was employed to investigate the effect of geometrical parameters, geotechnical conditions and loads on the performance of arch dams. Again, RF showed to be useful to separate the effect of the involved parameters, and the partial dependence plots showed interesting, non-linear effects of some of the variables involved.
In a slightly different case, regression ML models showed also benefits to generalize results of experimental campaigns on hydraulic structures. This is a more conventional application of regression models, which nonetheless opens the possibility for more efficient use of resources involved in laboratory testing for design optimization.
The main limitation of ML models, which applies to all the problems presented, is that results are in general non-reliable when predictions are made for cases out of the range of variation of the inputs in the training set. For instance, when monitoring data are used to fit a predictive ML model, predictions for extraordinary levels in the reservoir, higher than the maximum observed value in the training set, would be poor. This aspect should be always considered and is in fact a limitation.
Different ML algorithms can be used in general for a given prediction task. There is not a general rule as to which model performs better. Some features can be considered when making a decision, for which the results presented can be useful. In particular, techniques based on trees (RF and BRT) are flexible, reduce the need for variable classification and do not require pre-process. By contrast, NN performed better than RF for predicting the discharge coefficient in a pure regression analysis.
In all cases, engineering knowledge is essential to pose the problem, select the variables to consider, analyze the results and primarily for making decisions regarding design and safety assessment of dams.
ACKNOWLEDGEMENTS
The authors acknowledge the financial support to CIMNE via the CERCA Programme/Generalitat the Catalunya. This work was also partially funded by the Spanish Ministry of Science, Innovation and Universities (Ministerio de Ciencia, Innovación y Universidades) through the projects NUMA (RTC-2016-4859-5), COFRE (RTC-2017-6417-5) and TRISTAN (RTI2018-094785-B-I00).
REFERENCES
Altarejos-García, L., Escuder-Bueno, I., Serrano-Lombillo, A., & de Membrillera-Ortuño, M. G. 2012. Methodology for estimating the probability of failure by sliding in concrete gravity dams in the context of risk analysis. Structural Safety, 36, 1-13.
Crookston, B. M. Labyrinth weirs. Ph.D. Dissertation, Utah State University, Logan, Utah, 2010.
Crookston, B. M., & Tullis, B. P. (2012). Arced labyrinth weirs. Journal of Hydraulic Engineering, 138(6), 555-562.
Escuder-Bueno, I., & Halpin, E. 2016. Overcoming failure in infrastructure risk governance implementation: Large dams journey. J. of Risk Research, 1-18.
Gorissen, D., Couckuyt, I., Demeester, P., Dhaene, T., & Crombecq, K. 2010. A surrogate modelling and adaptive sampling toolbox for computer based design. Journal of Machine Learning Research, 11(Jul), 2051-2055.
Hariri-Ardebili, M. A. 2018. Risk, Reliability, Resilience (R3) and beyond in dam engineering: A state-of-the-art review. International Journal of Disaster Risk Reduction, 31, 806-831.
Hariri-Ardebili, M. A., & Boodagh, P. 2018. Taguchi design-based seismic reliability analysis of geostructures. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 1-19.
Hariri-Ardebili, M. A., & Pourkamali-Anaraki, F. 2018. Simplified reliability analysis of multi hazard risk in gravity dams via machine learning techniques. Archives of Civil and Mechanical Engineering, 18(2), 592-610.
Hariri-Ardebili, M. A., & Pourkamali-Anaraki, F. 2019. Matrix completion for cost reduction in finite element simulations under hybrid uncertainties. Applied Mathematical Modelling, 69, 164-180.
Mata, J. 2011. Interpretation of concrete dam behaviour with artificial neural network and multiple linear regression models. Engineering Structures, 33(3), 903-910.
Mata, J., Leitão, N. S., de Castro, A. T., & da Costa, J. S. 2014. Construction of decision rules for early detection of a developing concrete arch dam failure scenario. A discriminant approach. Computers & Structures, 142, 45-53.
Rocha, M. 1964. Statement of the physical problem of the arch dam. Proceedings. Symposium on the Theory of Arch Dams. Southampton. 1964.
Romana, M. 2003. DMR, a new geomechanics classification for use in dams foundations, adapted from RMR. 4th International Symposium on Roller Compacted Concrete (RCC) Dams, Madrid, Spain.
Salazar, F., Morán, R., Rossi, R., & Oñate, E. 2013. Analysis of the discharge capacity of radial-gated spillways using CFD and ANN–Oliana Dam case study. Journal of Hydraulic Research, 51(3), 244-252.
Salazar, F., San Mauro, J., Oñate, E., & Toledo, M. A. 2015. CFD analysis of flow pattern in labyrinth weirs. Dam Protections against Overtopping and Accidental Leakage, 287.
Salazar, F., Toledo, M. A., Oñate, E., & Morán, R. 2015. An empirical comparison of machine learning techniques for dam behaviour modelling. Structural Safety, 56, 9-17.
Salazar, F., Toledo, M. A., Oñate, E., & Suárez, B. 2016. Interpretation of dam deformation and leakage with boosted regression trees. Engineering Structures, 119, 230-251.
Salazar, F., Morán, R., Toledo, M. Á., & Oñate, E. 2017a. Data-based models for the prediction of dam behaviour: a review and some methodological considerations. Archives of computational methods in engineering, 24(1), 1-21.
Salazar, F., Toledo, M. Á., González, J. M., & Oñate, E. 2017b. Early detection of anomalies in dam performance: A methodology based on boosted regression trees. Structural Control and Health Monitoring, 24(11), e2012.
Salazar, F., Toledo, M., Vicente, D.V. 2017c. A systematic assessment of the influence of geometry and materials properties on the performance of arch dams. 14th International Benchmark Workshop on Numerical Analysis of Dams. Stockholm, Sep. 2017.
Salazar, F., & Crookston, B. M. 2019. A Performance Comparison of Machine Learning Algorithms for Arced Labyrinth Spillways. Water, 11(3), 544.
Salazar, F., Conde, A., Vicente, D.J. 2019a. Identification of dam behavior by means of machine learning classification models. 15th International Benchmark Workshop on Numerical Analysis of Dams. Milano, 9-11 Sep. 2019
Salazar, F., Kohler, A., Conde, A., Landstorfer, F. 2019b. Interpretation of dam monitoring data combining visualisation tools and machine learning. Eberlaste Dam Case Study. 15th International Benchmark Workshop on Numerical Analysis of Dams. Milano, 9-11 Sep. 2019
Salazar, F. & Hariri-Ardebili, M.A., 2019, Machine Learning Based Seismic Stability Assessment of Dams with Heterogeneous Concrete, 3rd Meeting of EWG Dams and Earthquakes, Lisbon, Portugal, May 06-09.
Schöbi, R., & Sudret, B. 2017. Structural reliability analysis for p-boxes using multi-level meta-models. Probabilistic. Engineering Mechanics, 48, 27-38.
SPANCOLD. Technical Guide for Operation of Dams and Reservoirs. Vol. I. Risk Analysis Applied to Dams and Reservoir Management. CICCP, CNEGP, 2013. (In Spanish)
Trehan, S., Carlberg, K. T., & Durlofsky, L. J. 2017. Error modeling for surrogates of dynamical systems using machine learning. International Journal for Numerical Methods in Engineering, 112(12), 1801-1827.
USACE – US Army Corps of Engineers, editor 1994. Arch Dam Design, chapter 8, pp. 1:15. USACE, Washington DC, USA.
USBR – US Bureau of Reclamation, editor, 2013. Design of Double-Curvature Arch Dams Planning, Appraisal, Feasability Level. Technical Memorandum No. EM36-86-68110.
Vicente, D.J., San Mauro, J., Salazar, F. and Baena, C. M. 2017. An Interactive Tool for Automatic Predimensioning and Numerical Modeling of Arch Dams. Mathematical Problems in Engineering, vol. 2017, Article ID 9856938, doi:10.1155/2017/9856938
Willm, G., Beaujoint, N. 1967. Les méthodes de surveillance des barrages au service de la production hydraulique d’Electricité de France-Problèmes ancients et solutions nouvelles. 9th ICOLD Congress, pp 529–550, q34-R30. [in French]
Document information
Published on 05/05/20
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?