AN INTERACTIVE TOOL FOR DATA ANALYSIS AND MACHINE-LEARNING MODEL FITTING WITH APPLICATION TO HYDRO-ENVIRONMENT SYSTEMS

ABSTRACT

The advances in sensors and communication technologies open great possibilities in the management and maintenance of engineering systems. In general, the performance of monitoring devices has undergone relevant improvements in terms of both accuracy and reliability, which have resulted in more information available on the behaviour of the structure under consideration. However, the investments made in the modernization of the monitoring systems are not recovered unless complemented by applications capable of handling such large and diverse information.

In this contribution, we present a software tool for importing, exploring, cleaning and analysing monitoring data. Also, it allows for fitting machine-learning behaviour models, as well as interpreting the response of the system to the actions or loads in operation. It was initially developed for dam safety assessment, but can be used -with minor changes- for other engineering systems.

The methodology and the overall structure can be categorized in two main sections: (i) the monitoring data can be uploaded, cleaned, completed and analysed and (ii) the machine-learning model can be fitted to predict the variables of interest of the system. The same model can then be used for online detection of anomalies by comparing predictions with recorded behaviour. For example, this allows the identification of abnormal displacements in dams for a given load combination.

The software can be equally run locally or in the cloud, with appropriate safe access. It has been written in the R language using the Shiny package for interactivity with the following functionalities: zooming and showing information for data exploration, selecting time periods to interpolate and choosing the training parameters to fit behaviour models.

Keywords: Data Visualization, Interactive Data Exploration, Data cleaning, Data pre-processing

1. INTRODUCTION

Data analysis is the basis of research studies in many hydro-environmental systems, such as hydrology, reservoir management or dam safety. Advances in measurement instruments as well as transmission and storage information techniques have undergone significant improvements in terms of accuracy and reliability, resulting in greater availability of information on the behaviour of the system under consideration. These advanced monitoring systems require applications capable of handling such large and diverse information. Conventional time-series plots and simple statistical methods are not appropriate to maximise the information extracted from these data.

The analysis of complex datasets often becomes the rate-limiting step in many engineering studies (Kotsiantis and Kanellopoulos, 2006). For both large and small data sets, real-time data interaction analysis is necessary on all resolution scales, from the complete data set to singular values (Thorvaldsdóttir et al., 2013). Although much of the analysis of databases can be automatically performed with specific software, the interpretation and experience of human technicians, based on a fast and flexible data visualization, are essential to distinguish among complex relationships between variables and errors or random noise (Guyon and Elisseeff, 2003).

Unfortunately, the size and diversity of the data sets produced by current systems often present great challenges for visualization applications. Although some specific tools have been developed that incorporate certain features (e. g. Mora et al., 2008), the tools used in engineering for the presentation and analysis of these data are often limited to conventional office software. Furthermore, data exploration is frequently restricted to observing time series evolution of each registered variable.

The measurements obtained from monitoring networks, whether manual or automatic, usually present errors that may be due to transcription or communication, as well as periods of missing data due to system interruptions of diverse origin. In addition, old manually recorded series and more recent digitalized data obtained from automatic systems frequently coexist in the same databases. The frequency of reading and the quality of these data are, in general, different, which results in heterogeneous series that require pre-processing actions to be standardized.

This communication presents a computer application developed in the programming language R (Team and R Development Core Team, 2018) that makes use for interactivity of the Shiny package (Chang et al., 2018) and can either be run locally or hosted in the cloud with adequate secure access. Its main objective is to treat monitoring data of hydro-environmental systems and it includes specific pre-process functionalities focused on the generation of a suitable database to subsequently adjust predictive models based on machine learning techniques. The first version was specifically developed to analyse dam behaviour, but it could also be applied, with small changes, to study other hydro-environmental processes such as leakage detection in water distribution networks or estimation of discharge flow in spillways based on experimental results.

2. DATA PREPROCESSING APP

2.1 Data exploration

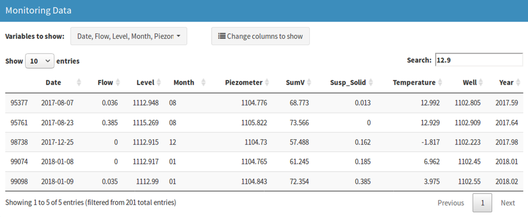
Data exploration is a fundamental preliminary step before analysing data. On the one hand, it allows knowing features of the data to analyse: available volume of data, ranges of variation, relationship between variables, etc. On the other hand, it is useful to identify errors such as anomalous data derived from measurement errors or periods of missing data. In addition, an expert with the adequate tools can draw a first idea of whether the behaviour responds to what was expected, observing clear changes in series trends, dispersion of the results, etc. The tool developed in this work allows the visualization of interactive data tables (Figure 1) where the user can see the values ordered by time, being able to choose the variables and the number of rows to be displayed, as well as searching for a specific value.

Figure 1. Table data showing the result of searching for “12.9”.

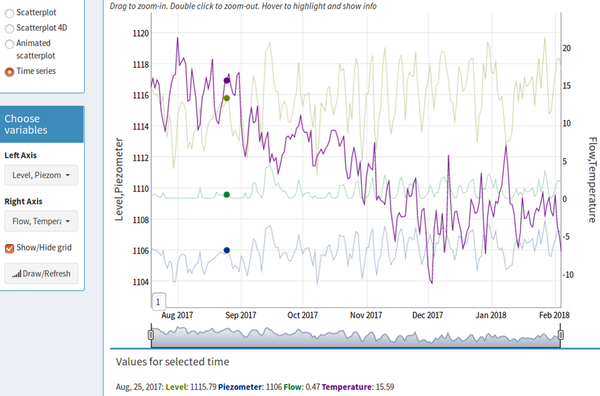
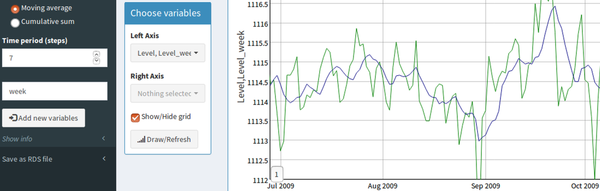
The second visualization option is a multivariate time series graph (Figure 2). In this plot, the user can select the variables to be represented using two independent axes. This enables their comparison in a single display when their range of variation is very different. Other visual options are zooming in both axes and shifting the image while maintaining the zoom. Moreover, when a specific instant is selected, the values of each variable are displayed in an additional table below the graph.

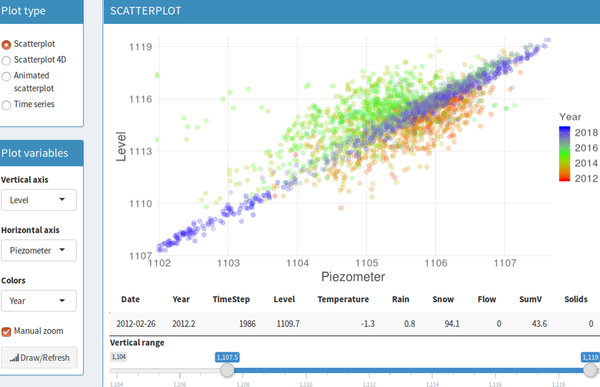
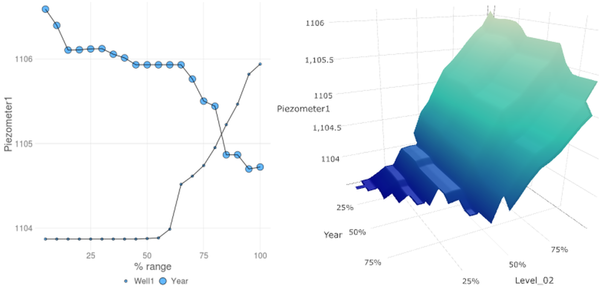
The data can also be displayed in a quasi-3D scatterplot, in which the user selects which variables to display on each axis, as well as a third one that controls the colour variation (Figure 3). In addition to zooming the two axes, it is also possible to choose the limits for the third variable; this functionality is very useful to analyse the relationship of two variables during specific periods of time. When a specific point is selected in the plot, a table below is shown with the values ​​for the selected entry and variables.

Figure 2. Time series plot with three variables in the left axis and two in the right one.

Figure 3. Scatterplot for three variables. In this example, the colours depend on the “Year” variable, hence the time evolution of the relation between the variables in both axes can be observed.

2.2 Fixing data

2.2.1 Missing data

Several methods can be useful to compensating missing data under specific circumstances, although imputing a high proportion of data may lead to a relevant problem as they call into question the credibility of the conclusions drawn (Little et al., 2012). When analysing variables with missing data is considered inappropriate, other alternatives need to be considered, such as the following ones:

1. Exclusion of the variables with missing data from the analysis.

2. Simple substitution methods: each missing value is filled in with a specific value of the same series such as the previous or the following observation;

3. Estimation methods when simple substitution can lead to biased effects (Molnar et al., 2009):

* Based on the same data series (e.g. mean value of a certain period);

* Based on data series of the same nature (i.e. measurement of other monitoring devices of the same phenomenon);

* Based on data series of variables of different nature but with a high correlation.

The suitability of each method depends on the mechanisms that led to missing data and the nature of the variable under consideration. Missing data can be completely random, i.e. not related to the variables of the study, or it can maintain some kind of relation with some variable. For example, the absence of rain data during winter should neither be replaced by the previous ones (autumn) nor be ignored by calculating the average of the rest of the year(since it might imply neglecting the rainy season).

Studying the reasons behind the missing data is useful to select an appropriate imputation method. For example, missing data can be estimated from some related variable. This technique results in lower bias than the analysis methods such as multiple imputation or estimation equations (Little et al., 2012).

After studying real cases, some of the most conventional procedures for data imputation have been implemented in the software. These procedures have been identified as useful for the case of dam monitoring, which, as mentioned above, has served as a reference for the development of the application. The following data imputation procedures are included:

• Linear interpolation between the previous and subsequent values;

• Interpolation of a parabola based on the closest correct previous value and two subsequent ones (if the user selected different groups of points at the same time, a different curve is used for each group);

• Replacement of each of the selected points by the average of the values registered the same calendar day (hour) for the previous and posterior year (day). This may be admissible in case of data with annual (daily) seasonality;

• Replacement of all selected points by a fixed value chosen by the user.

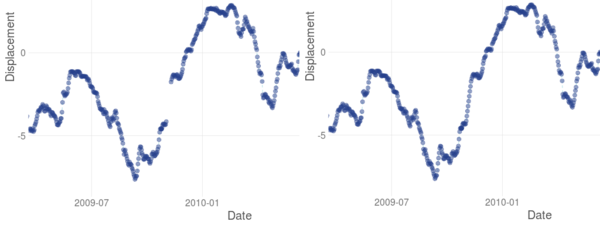
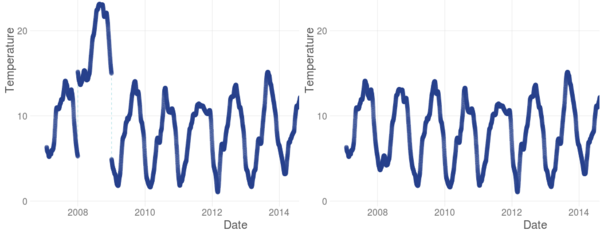
An example of filling missing values via linear interpolation is shown in Figure 4.

Figure 4. Original data (left). Imputation of missing data by lineal interpolation (right).

2.2.2 Data cleaning

The process of data cleaning consists of identifying corrupt, incorrect or irrelevant data from a database to later replace or eliminate them (Wu, 2013). These detected or eliminated inconsistencies may have been caused originally by the incorrect entry of data, by faults in the measurement sensors, transmission or storage errors, or by different definitions of the same variable.

The identification of outliers can be strict (such as rejecting any value that falls outside a certain range) or diffuse (such as correcting records that are within the global range but suppose a local variation above a certain value). The analysis of scatterplots is useful to observe any significant outliers in a data set.

This functionality has also been developed after observing many imperfections in the databases analysed, which come from dam monitoring systems. Other options can be implemented for application in other fields, according to the properties of the data series under consideration. In the current version, in addition to the options already mentioned for the missing data, the user can add a fixed value to the selected period, or delete certain values. Figure 5 shows an example in which it seems clear that the error is corrected by adding a fixed value.

Figure 5. Original data (left). Fixing errors by adding a fixed value (right).

2.3 Generation of derived variables

Once the data exploration has been carried out and the inaccurate values ​​have been corrected, and before fitting predictive models, variables derived from the raw records can be generated to enrich the input set. The decision of which variables to add corresponds to the user, and depends on the case study and the algorithm to be used. If the user wants to analyse the temporal evolution of the behaviour of the system, it is necessary to explicitly consider the time variable. The application automatically generates two new variables from the date: a categorical one with the months, to analyse the seasonality of the data, and a numerical one with the years (adding the decimal part) to facilitate the visualization of the evolution of the variables with time.

The main objective when adding new variables is to automatically obtain new features based on existing ones. For example, “n” moving averages are easy to perform and help to improve the signal/noise ratio of the data series by replacing each value of the series with the average of "n" previous values (Dilawari, 2018).

In this sense, the developed tool offers the possibility of adding moving averages or accumulated sums of existing variables. These two operations allow creating derived variables that reflect the main evolution of the base variable over time while hiding noise variations that can be non-relevant.

Figure 6. Time series of a variable and its weekly moving average.

Other transformations available include the selection of specific values of the original raw data or the aggregation of some of them under certain criteria, reducing the total amount of data per variable in the new series.

The use of databases with a high proportion of irrelevant and redundant information or noise to build predictive models is less efficient. The preparation and filtering of the data can save time for further processing and offer better results.

For example, series recorded with varying acquisition frequency can be reduced to a single value per day. The application also allows the reduction of data to one per week, fortnight or month. This reduction can be done with the following procedures:

• Taking as a daily value the one registered at a certain time of the day;

• Taking the maximum or minimum daily value for each period;

• Aggregating hourly values into longer time steps (day, week, fortnight or month), calculating either the average or the sum of the total measurements.

3. PREDICTIVE MODELS

The authors have previously used machine learning algorithms for generating predictive models of dam behaviour. In previous works, different algorithms were compared in terms of accuracy and ease of implementation (Salazar et al., 2015); the possibilities of interpretation of the models were analysed to draw conclusions about the behaviour of the system (Salazar et al., 2016) and a methodology for the application to the detection of anomalies was proposed. In addition, this methodology has also been applied to estimate the discharge capacity of gated spillways (Salazar et al., 2013) and labyrinth spillways (Salazar and Crookston, 2019). In these works, data pre-processing had a significant impact on the generalization performance of supervised machine learning algorithms.

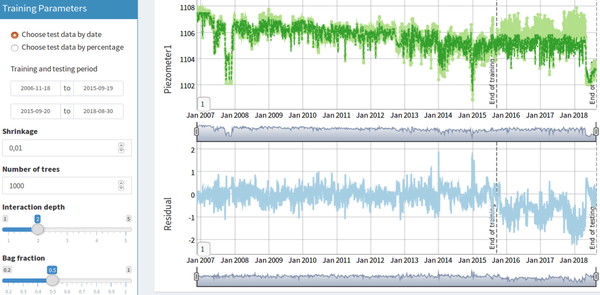
This prior knowledge has been applied to the development of a second application that allows using the data processed by the first one to adjust machine learning models of dam behaviour, as well as interpreting the response of the system to actions or loads in operation. With this approach, the reliability of the conclusions obtained through the application is related to the accuracy of the model predictions (Breiman, 2001). Therefore, the discrepancy between the predictions and the observations is calculated and shown, both for training and test sets (Figure 7).

Figure 7. Interface to fit and evaluate machine learning predictive models.

The user can select the predictor variables to be used and the target variable to be predicted, as well as the values ​​of the training parameters. It is also possible to calculate and compare several models with the same variables to verify the influence of the random component of the training algorithm. Figures 8 and 9 show an example of application to predict the level in a piezometer in an earth dam. A model is fitted with the external variables, which include original and moving average records of the reservoir level and snow thickness, as well as the accumulated rainfall in various periods and time (coded as "Year").

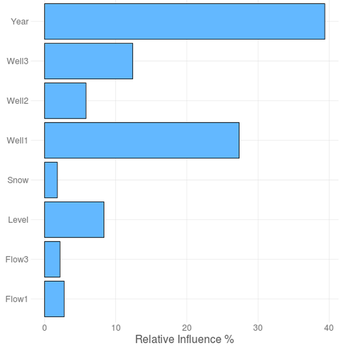
Figure 8 analyses the predictive model through a bar graph that shows the importance of the predictive variables (degree of association with the objective variable) in alphabetical order. In case several models are fitted, the mean value for the influence is shown. The partial influence of the most relevant inputs on the response can be also studied (Figure 9). In this example, it can be easily observed that the response increases with the reservoir level and with well01, and that it has decreased with time.

Figure 8. Influence of the predictor variables in the response.

Figure 9. Partial dependence plots for two predictors against the target: lines (left) and 3D surface (right).

4. CONCLUSIONS

Data-based predictive models are useful in many fields of science and engineering, in which there is an increase in the volume of available data. Expert judgment based on experience is essential for generating models, interpreting results, and making decisions. In this context, the models must be implemented in user-friendly applications with specific features for data exploration and pre-process.

A software tool has been developed for the interactive visual exploration of monitoring data that provides means for easy understanding of complex data sets and identifying the relationships between variables. The methodology is quite general: the monitoring data can be loaded, cleaned and analysed. This software contains:

• A flexible and dynamic graphic module to explore the data interactively;

• Tools for the pre-treatment of data: filter of anomalous values, completion of data series and calculation of modified variables.

A key feature of the application is the possibility of carrying out both a quick scan of parts of the data and the automation of operations on the complete data set. In addition to the capabilities of the usual visualization systems, it also includes specific libraries compatible with Shiny (Chang et al., 2018) for the automated design of sophisticated visualizations that integrate multiple options for analysis.

The authors are currently working on a specific version for the detection of leaks in water supply networks, as well as the integration of different machine learning algorithms.

REFERENCES

Breiman, L. (2001). Statistical Modeling: The Two Cultures. Statistical Science, 16(3), 199–231.

Chang, W., Cheng, J., Allaire, J., Xie, Y., & McPherson, J. (2018). Shiny: Web Application Framework for R. R package version 1.1.0 https://CRAN.R-project.org/package=shiny.

Dilawari, M. (2018). Forecasting models for the displacements and the piezometer levels in a concrete arch dam.

Guyon, I., & Elisseeff, A. (2003). An Introduction to Variable and Feature Selection. Journal of Machine Learning Research (JMLR), 3(3), 1157–1182. Special Issue on Variable and Feature Selection

Kotsiantis S., Kanellopoulos D., and P. P. (2006). Data Preprocessing for Supervised Learning. International Journal of Computer Science, 1(2), 111–117.

Little, R. J., D’Agostino, R., Cohen, M. L., Dickersin, K., Emerson, S. S., Farrar, J. T., … Stern, H. (2012). The Prevention and Treatment of Missing Data in Clinical Trials. New England Journal of Medicine, 367(14), 1355–1360.

Molnar, F. J., Man-Son-Hing, M., Hutton, B., & Fergusson, D. A. (2009). Have last-observation-carried-forward analyses caused us to favour more toxic dementia therapies over less toxic alternatives? A systematic review. Open Medicine, 3(2), 1–20.

Mora J., López E., and de Cea J. C. (2008). Estandarización en la gestión de datos de auscultación e informe anual en presas de titularidad estatal. In VIII Jornadas Españolas de Presas.

Salazar, F., Crookston, B. M. (2019). A performance comparison of machine learning algorithms for arced labyrinth spillways. Water. Special Issue “Machine Learning Applied to Hydraulic and Hydrological Modelling.”

Salazar, F., Morán, R., Rossi, R., & Oñate, E. (2013). Analysis of the discharge capacity of radial-gated spillways using CFD and ANN - Oliana Dam case study. Journal of Hydraulic Research, 51(3), 244–252.

Salazar, F., Toledo, M. A., Oñate, E., & Morán, R. (2015). An empirical comparison of machine learning techniques for dam behaviour modelling. Structural Safety, 56, 9–17.

Salazar, F., Toledo, M. T., Oñate, E., & Suárez, B. (2016). Interpretation of dam deformation and leakage with boosted regression trees. Engineering Structures, 119, 230–251.

Team, R. D. C., & R Development Core Team, R. (2018). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing (Vol. 1). Vienna.

Thorvaldsdóttir, H., Robinson, J. T., & Mesirov, J. P. (2013). Integrative Genomics Viewer (IGV): High-performance genomics data visualization and exploration. Briefings in Bioinformatics, 14(2), 178–192.

Wu, S. (2013). A review on coarse warranty data and analysis. Reliability Engineering and System Safety, 114(1), 1–11.