Analysis of MFS-DRM formulations for nonhomogeneous diffusion problems

Abstract

This paper presents tests and applications related to the Method of the Fundamental Solutions (MFS) for nonhomogeneous diffusion equations. The dual reciprocity method was applied to approximate the particular solution and different MSF were applied to solve the homogeneous equation. The computational accuracy for three different versions submitted to diverse geometries, initial, boundary and nonhomogeneous conditions is compared. The first version is the MFS, based on the fundamental solutions to the modified Helmholtz operator; the second and third versions are based on transient fundamental solutions proposed directly for the diffusion governing equation. This paper evaluates particularities for all methods proposed as the solution advances in time until steady-state solutions are reached. The developed computer codes are applied to several examples with the intention of demonstrating the methods’ effectiveness and applicability.

Keywords: Method of fundamental solutions, meshless methods, diffusion equations, transient diffusion

1. Introduction

The transient conduction problem, governed by the diffusion equations, appears in many areas of science and technology and simulates phenomena such as heat transfer, pollutants concentration, fluid flow, molecular movements, among others. These problems have been extensively treated in literature but, although analytical solutions can be found for some cases, when complex geometries and/or boundary conditions are prescribed, it is necessary to use numerical methods.

Generating a mesh for complicated geometries is time-consuming, requires great memory storage and takes a significant computational effort for classical methods, especially those based on a domain discretization. To overcome such problems, in the last decades there has been a significant increase in the use of meshless numerical methods for solving partial differential equations.

As for the classical methods, the meshless methods can be divided in two main categories: first, the domain-type methods such as the smoothed particle dynamics method (SPH) [1], the finite point method (FPM) [2], the element free Galerkin method (EFG) [3], the meshless local Petrov-Galerkin method (MLPG) [4], etc.; second, the boundary-type methods, as the boundary particle method (BPM) [5] and the method of fundamental solutions (MFS) [6], among others.

Due to the simplified formulation and implementation process, MSF has been largely used for different types of problems. The general concept of MFS is to approximate the solution by a linear combination of the fundamental solutions generated by source points that satisfies the governing equation in the interior domain, leaving only the boundary conditions to be satisfied. Unlike the boundary element method (BEM) in MFS, the solution in the interior domain does not require any additional integral equation. If a fundamental solution exists for the given governing equation, then the method of fundamental solutions can be utilized to obtain numerical solutions of the variable at a definite number of points in the domain [7].

The main issue in MFS is the source positioning in order obtain reasonable responses. The source points can be placed outside the problem domain, avoiding singularities over the space coordinates, and the solution can be approximated over time by Laplace transform [8,9,10] or by finite difference scheme [11], an interesting approach since MFS is well-posed problem in spatial domain. Otherwise, the source points can be placed at different time levels [7], and, by using transient fundamental solutions, they will not generate singularities in time and spatial domains, however generating an ill-posed problem.

For homogeneous diffusion equations, in Golberg et al. [12] for non-zero initial conditions, rectangular shaped domain and Dirichlet’s boundary conditions prescribed, the Laplace transform method and the finite difference method were studied. For both cases it leads to a non-homogeneous Helmholtz equation. Particular solutions, for different types of problems, are generally found by the dual reciprocity method (DRM), introduced by [13,14], that transform the domain integral into a boundary-type linear combination of radial basis functions (RBFs), and Golberg et al. [15] proposed particular solutions for Helmholtz-type operators. For a similar geometry, in Young et al. [7] transient fundamental solutions were applied for homogeneous Dirichlet’s boundary conditions with more complex initial conditions.

In Cao et al. [16], DRM-MFS based on the modified Helmholtz operator and DRM-Trefftz were applied for homogeneous diffusion equation with mixed boundary conditions and constant initial conditions, Chantasiriwan [17] compared MFS based on transient fundamental solutions with MFS based on the modified Helmholtz operator for a square with different types of boundary conditions.

To solve a linear diffusion equation with time-independent source terms, Young et al. [18] applied time-dependent fundamental solutions with DRM for a rectangular domain with different internal sources equations and in Wang and Qin [6] it was used MFS with the method of particular solutions (MPS) and with the eigenfunction expansion method (EEM) to solve several geometries.

In this article, MFS-DRM based on the modified Helmholtz operator with different types of RBFs is applied for different types of geometries, as well as for a set of different internal source terms and boundary conditions. Numerical solutions based on MFS-DRM with time-dependent fundamental solutions, that is, not using any integration techniques or requiring any kind of special geometric position for the source points, are obtained for comparison purposes. Nevertheless, in Young et al. [18] it was proposed a time moving collocation of source points, and in this paper a different approach for the sources is applied. All the described methods will be compared with each other and with the analytical solution in order to evaluate their accuracy and applicability.

This paper is organized as follows: governing equations and boundary conditions are described in Section 2; different formulations for the Method of Fundamental Solutions applied to the diffusion problem is in Section 3; numerical examples and their evaluations are in Section 4; and Section 5 consists of conclusions drawn based on the present study.

2. Governing equations

The transient diffusion equation in a domain ${\textstyle \Omega \left(X\right)}$ and a boundary ${\textstyle \Gamma \left(X\right)=}$${\Gamma }_{u}\left(X\right)+{\Gamma }_{q}\left(X\right)$ is given by:

${\frac {\partial U({\mathit {\boldsymbol {X}}},t)}{\partial t}}=k{\nabla }^{2}U\left({\mathit {\boldsymbol {X}}},t\right)+$$F({\mathit {\boldsymbol {X}}}),\,\,{\mathit {\boldsymbol {X}}}\,\in \Omega \left({\mathit {\boldsymbol {X}}}\right)$

(1)

in which ${\textstyle {\mathit {\boldsymbol {X\,}}}}$represents the spatial coordinates, ${\textstyle \,t}$ is time, ${\textstyle k}$ the thermal diffusivity, ${\textstyle U}$ is the potential under analysis, ${\textstyle F}$ is a spatial internal source function and ${\textstyle {\nabla }^{2}}$ is the Laplacian operator of partial derivatives. The initial condition of the problem is represented by:

$U\left({\mathit {\boldsymbol {X}}},0\right)={\overline {U}}\left({\mathit {\boldsymbol {X}}},0\right)=$${U}_{0},\,\,{\mathit {\boldsymbol {X}}}\,\in \Omega \left({\mathit {\boldsymbol {X}}}\right)$

(2)

Two boundary conditions can be prescribed. Dirichlet or necessary condition for the potential ${\textstyle U}$:

$U\left({\mathit {\boldsymbol {X}}},t\right)={\overline {U}}\left(X,t\right),\,\,{\mathit {\boldsymbol {X}}}\,\in {\Gamma }_{u}\left(X\right)$

(3)

and Neumann or nature condition for the potential flow:

${\frac {\partial U({\mathit {\boldsymbol {X}}},t)}{\partial n}}={\overline {Q}}\left({\mathit {\boldsymbol {X}}},t\right),\,\,{\mathit {\boldsymbol {X}}}\,\in {\Gamma }_{q}\left({\mathit {\boldsymbol {X}}}\right)$

(4)

where ${\textstyle {\Gamma }_{u}\left(X\right)\,}$ and ${\textstyle {\Gamma }_{q}\left(X\right)}$ are the boundary parts, where the Dirichlet and Neumann conditions respectively are prescribed, ${\textstyle {\mathit {\boldsymbol {n}}}}$ is the normal related to the boundary ${\textstyle {\Gamma }_{q}\left(X\right)}$ and ${\textstyle {U}_{0}}$, ${\textstyle {\overline {U}}\left({\mathit {\boldsymbol {X}}},t\right)}$, ${\textstyle {\overline {Q}}\left({\mathit {\boldsymbol {X}}},t\right)\,}$ are prescribed functions.

3. Numerical method

Based on the superposition principle of the linear systems, the solution of a nonhomogeneous diffusion problem with time-independent source terms can be represented as:

$U\left({\mathit {\boldsymbol {X}}},t\right)={U}_{h}\left({\mathit {\boldsymbol {X}}},t\right)+$${U}_{p}\left({\mathit {\boldsymbol {X}}}\right),\,\,{\mathit {\boldsymbol {X}}}\,\in \Omega \left({\mathit {\boldsymbol {X}}}\right)$

(5)

where ${\textstyle {U}_{h}}$ is the homogeneous solution and ${\textstyle {U}_{p}}$ is the particular solution. Depending on the time marching scheme, the particular solution should satisfy:

For the Laplacian operator

${\nabla }^{2}{U}_{p}\left({\mathit {\boldsymbol {X}}}\right)={\frac {-F\left({\mathit {\boldsymbol {X}}}\right)}{k}},\,\,{\mathit {\boldsymbol {X}}}\,\in \Omega \left({\mathit {\boldsymbol {X}}}\right)$

(6a)

For the modified Helmholtz operator

${(\nabla }^{2}-{\lambda }^{2}){U}_{p}\left({\mathit {\boldsymbol {X}}}\right)={\frac {-F\left({\mathit {\boldsymbol {X}}}\right)}{k}},\quad {\mathit {\boldsymbol {X}}}\,\in \Omega \left({\mathit {\boldsymbol {X}}}\right)$

(6b)

and the homogeneous solution satisfy:

${\frac {\partial {U}_{h}({\mathit {\boldsymbol {X}}},t)}{\partial t}}=k{\nabla }^{2}{U}_{h}\left({\mathit {\boldsymbol {X}}},t\right),\,\,{\mathit {\boldsymbol {X}}}\,\in \Omega \left({\mathit {\boldsymbol {X}}}\right)$ ${U}_{h}\left({\mathit {\boldsymbol {X}}},0\right)={U}_{0}-{U}_{p}\left({\mathit {\boldsymbol {X}}}\right),\,\,{\mathit {\boldsymbol {X}}}\,\in \Omega \left({\mathit {\boldsymbol {X}}}\right)$ ${U}_{h}\left({\mathit {\boldsymbol {X}}},t\right)={\overline {{U}_{h}}}\left(X,t\right)-$${U}_{p}\left({\mathit {\boldsymbol {X}}}\right),\,\,{\mathit {\boldsymbol {X}}}\,\in {\Gamma }_{u}\left(X\right)$ ${\frac {\partial {U}_{h}({\mathit {\boldsymbol {X}}},t)}{\partial n}}={\overline {{Q}_{h}}}\left({\mathit {\boldsymbol {X}}},t\right)-$${\frac {\partial {U}_{p}\left({\mathit {\boldsymbol {X}}}\right)}{\partial n}},\,\,{\mathit {\boldsymbol {X}}}\,\in {\Gamma }_{q}\left({\mathit {\boldsymbol {X}}}\right)$

(7)

In this paper, the particular solution is obtained by DRM with different radial basis functions (RBFs) and the homogeneous solutions are obtained by different MFS formulations.

3.1. Dual reciprocity method for particular solution

In order to obtain the particular solution ${\textstyle {U}_{p}\left({\mathit {\boldsymbol {X}}}\right)\,\,}$ with DRM, the term ${\textstyle F\left({\mathit {\boldsymbol {X}}}\right)}$ from the right-hand side of equation (6) is approximated by a RBF:

${\frac {-F\left({\mathit {\boldsymbol {X}}}\right)}{k}}=\,\sum _{j=1}^{N}{\alpha }_{j}{\varphi }_{j}({\mathit {\boldsymbol {X}}})\,\,$

(8)

where ${\textstyle N}$ is the number of collocation points, ${\textstyle {\alpha }_{i}}$ are the interpolation coefficients and ${\textstyle {\varphi }_{j}\left({\mathit {\boldsymbol {X}}}\right)=}$$\,\varphi \left(r\right)=\varphi (\left|X-{X}_{j}\right|)$ are functions based on the radial distance between collocation points with reference in ${\textstyle {X}_{j}}$. Depending on the method, the collocation points will be placed only in the domain [16] or both the domain and boundary [18,19].

After applying Eq. (8) at ${\textstyle N}$ collocation points, the interpolation coefficients ${\textstyle {\alpha }_{i}}$ are calculated. The particular solution is expressed:

${U}_{p}\left({\mathit {\boldsymbol {X}}}\right)=\,\sum _{j=1}^{N}{\alpha }_{j}{\psi }_{j}\left({\mathit {\boldsymbol {X}}}\right)+{\alpha }_{n+1}{\varphi }_{1}({\mathit {\boldsymbol {X}}})+$${\alpha }_{n+2}{\varphi }_{2}({\mathit {\boldsymbol {X}}})\,+{\alpha }_{n+3}{\varphi }_{3}({\mathit {\boldsymbol {X}}})\,$

(9)

where ${\textstyle {\psi }_{i}({\mathit {\boldsymbol {X}}})}$ is the approximate particular solutions in terms of RBF ${\textstyle {\varphi }_{i}({\mathit {\boldsymbol {X}}})}$. In order to obtain these solutions the following equations should be satisfied:

$\qquad \qquad {\begin{array}{l}{\nabla }^{2}{\psi }_{j}\left({\mathit {\boldsymbol {X}}}\right)={\varphi }_{j}\left({\mathit {\boldsymbol {X}}}\right)\\{{\nabla }^{2}\varphi }_{1}({\mathit {\boldsymbol {X}}})=1\,\\{{\nabla }^{2}\varphi }_{2}({\mathit {\boldsymbol {X}}})=x\,\\{{\nabla }^{2}\varphi }_{3}({\mathit {\boldsymbol {X}}})=y\,\end{array}}\qquad$ for the Laplacian operator

(10a)

$\qquad \qquad \qquad \qquad {\begin{array}{l}{(\nabla }^{2}-{\lambda }^{2}){\psi }_{j}({\mathit {\boldsymbol {X}}})={\varphi }_{j}({\mathit {\boldsymbol {X}}})\,\,\\{(\nabla }^{2}-{\lambda }^{2}){\varphi }_{1}\left({\mathit {\boldsymbol {X}}}\right)=1\,\\{{(\nabla }^{2}-{\lambda }^{2})\varphi }_{2}({\mathit {\boldsymbol {X}}})=x\,\,\\{{(\nabla }^{2}-{\lambda }^{2})\varphi }_{3}({\mathit {\boldsymbol {X}}})=y\end{array}}\qquad$ for the modified Helmholtz operator

(10b)

The typical approach is that ${\textstyle \varphi }$ is selected first, and then using Eq. (10) the corresponding particular solutions ${\textstyle \psi }$ are determined. For Eq. (10a) the particular solution in obtained by inverting the Laplace operator, only by repeated integration. For Eq. (10b), the particular solutions for the modified Helmholtz operator is not easy to obtain directly [20]. In this paper the RBF used was the thin plate splines (TPS) [1,20-22]:

$\varphi \left(r\right)=\,r\mathrm {ln} \,r\,\,$

(11)

and with solving the following linear system:

${\begin{matrix}{r}_{11}^{2}\mathrm {ln} \,{r}_{11}&{r}_{12}^{2}\mathrm {ln} \,{r}_{12}&{r}_{13}^{2}\mathrm {ln} \,{r}_{13}&\ldots &{r}_{1n}^{2}\mathrm {ln} \,{r}_{1n}&1&{x}_{1}&{y}_{1}&{\alpha }_{1}&&{\frac {-F\left(X\right)}{k}}\\{r}_{21}^{2}\mathrm {ln} \,{r}_{21}&{r}_{22}^{2}\mathrm {ln} \,{r}_{22}&{r}_{23}^{2}\mathrm {ln} \,{r}_{23}&\ldots &{r}_{2n}^{2}\mathrm {ln} \,{r}_{2n}&1&{x}_{2}&{y}_{2}&{\alpha }_{2}&&{\frac {-F\left(X\right)}{k}}\\\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &&\vdots \\{r}_{n1}^{2}\mathrm {ln} \,{r}_{n1}&{r}_{n2}^{2}\mathrm {ln} \,{r}_{n2}&{r}_{n3}^{2}\mathrm {ln} \,{r}_{n3}&\ldots &{r}_{nn}^{2}\mathrm {ln} \,{r}_{nn}&1&{x}_{n}&{y}_{n}&{\alpha }_{n}&=&{\frac {-F\left(X\right)}{k}}\\1&1&1&\ldots &1&0&0&0&{\alpha }_{n+1}&&0\\{x}_{1}&{x}_{2}&{x}_{3}&\ldots &{x}_{n}&0&0&0&{\alpha }_{n+2}&&0\\{y}_{1}&{y}_{2}&{y}_{3}&\ldots &{y}_{n}&0&0&0&{\alpha }_{n+3}&&0\end{matrix}}$

(12)

all unknown coefficients ${\textstyle \alpha }$ can be calculated, the corresponding ${\textstyle \psi }$ for the Laplacian operator:

$\psi \left(r\right)=\,\sum _{j=1}^{N}{\alpha }_{j}{\frac {{r}_{ij}^{2}\mathrm {(-2{r}_{ij}^{2}+4{r}_{ij}^{2}ln} \,{r}_{ij})\,}{6144}}+$${\alpha }_{n+1}{\frac {{x}^{3}}{6}}+{\alpha }_{n+2}{\frac {{y}^{3}}{6}}+{\alpha }_{n+3}{\frac {{x}^{2}+{y}^{2}}{4}},\quad$ for 2D

(13)

and for the modified Helmholtz operator:

$\psi \left(r\right)=\,\sum _{j=1}^{N}{\alpha }_{j}\left[-{\frac {4}{{\lambda }^{4}}}-{\frac {4\,ln{r}_{ij}}{{\lambda }^{4}}}-{\frac {{r}_{ij}^{2}\,ln{r}_{ij}}{{\lambda }^{2}}}-{\frac {4{K}_{0}\left(\lambda {r}_{ij}\right)}{{\lambda }^{2}}}\right]-$${\alpha }_{n+1}{\frac {1}{{\lambda }^{2}}}-{\alpha }_{n+2}{\frac {x}{{\lambda }^{2}}}-$${\alpha }_{n+3}{\frac {y}{{\lambda }^{2}}}\,,\quad$ for 2D and ${\textstyle r\not =0}$

(14a)

$\psi (r)=\,\sum _{j=1}^{N}{\alpha }_{j}\left[-{\frac {4}{{\lambda }^{4}}}-{\frac {4\,\gamma }{{\lambda }^{4}}}+\,{\frac {4\,}{{\lambda }^{4}}}\mathrm {ln} \,({\frac {\lambda }{2}})\right]-$${\alpha }_{n+1}{\frac {1}{{\lambda }^{2}}}-{\alpha }_{n+2}{\frac {x}{{\lambda }^{2}}}-$${\alpha }_{n+3}{\frac {y}{{\lambda }^{2}}},\quad$ for 2D and ${\textstyle r=}$$0$

(14b)

where ${\textstyle \gamma =0.5772156649015328}$is Euler’s constant and ${\textstyle {K}_{0}}$ is the modified Bessel function of the second kind order zero.

The next step is to calculate the homogenous solution with the modified conditions presented in Eq. (7). Here we consider two time-marching typical methods: the finite difference method and transient fundamental solutions, and also, for this last one, it is proposed a different approach considering the time collocation for the source points.

3.2. Modified Helmholtz operator for homogeneous solution

Using the finite difference method in Eq. (1) to approximate ${\textstyle {\frac {\partial U(X,t)}{\partial t}}}$ and ${\textstyle U\left(X,t\right)}$ with respect to time variable ${\textstyle t}$ within the interval ${\textstyle \left[{t}^{n},{t}^{n+1}\right]\subset [0,T]}$:

$U\left({\mathit {\boldsymbol {X,}}}t\right)=\,\theta {U}^{n+1}\left({\mathit {\boldsymbol {X}}}\right)+(1-$$\theta {)U}^{n+1}\left({\mathit {\boldsymbol {X}}}\right)$ ${\frac {\partial U({\mathit {\boldsymbol {X}}},t)}{\partial t}}=\,{\frac {{U}^{n+1}\left({\mathit {\boldsymbol {X}}}\right)+{U}^{n}\left({\mathit {\boldsymbol {X}}}\right)}{\Delta t}}$

(15)

where ${\textstyle \Delta t={t}^{n+1}-{t}^{n}}$ is time step size and ${\textstyle \theta =}$$1$ defining an implicit time marching method.

Substituting and rearranging terms of Eq. (16) in Eq. (1) and in conditions Eqs. (3)-(4) it yields to the modified Helmholtz equation:

${\nabla }^{2}{U}^{n+1}\left({\mathit {\boldsymbol {X}}}\right)-{\frac {{U}^{n+1}\left({\mathit {\boldsymbol {X}}}\right)}{k\Delta t}}=$$-{\frac {{U}^{n}\left({\mathit {\boldsymbol {X}}}\right)}{k\Delta t}}-{\frac {F({\mathit {\boldsymbol {X}}})}{k}}$

(16)

$U\left({\mathit {\boldsymbol {X}}},t\right)={\overline {U}}^{n+1}\left({\mathit {\boldsymbol {X}}},t\right),\,\,{\mathit {\boldsymbol {X}}}\,\in {\Gamma }_{u}\left(X\right)$ ${\frac {\partial U({\mathit {\boldsymbol {X}}},t)}{\partial n}}={\overline {Q}}^{n+1}\left({\mathit {\boldsymbol {X}}},t\right),\,\,{\mathit {\boldsymbol {X}}}\,\in {\Gamma }_{q}\left({\mathit {\boldsymbol {X}}}\right)$

(17)

Reducing Eq. (16) for a single-step formula:

${(\nabla }^{2}-{\lambda }^{2})U\left({\mathit {\boldsymbol {X}}}\right)=A\left({\mathit {\boldsymbol {X}}}\right)$

(18)

where ${\textstyle {\lambda }^{2}={\sqrt {\frac {1}{k\Delta t}}}}$ and ${\textstyle A\left({\mathit {\boldsymbol {X}}}\right)=}$$-{\frac {{U}^{n}\left({\mathit {\boldsymbol {X}}}\right)}{k\Delta t}}-{\frac {F({\mathit {\boldsymbol {X}}})}{k}}$ . It is worth noticing that the term ${\textstyle A\left({\mathit {\boldsymbol {X}}}\right)}$ is well defined and depends on the solution obtained from the previous time and the nonhomogenous condition, which is time-independent and is calculated by DRM proposed in Section 3.1. The initial condition should be applied in order to start the procedure.

By using MFS for every time step, the homogenous solution is approximated by:

${U}_{h}\left({\mathit {\boldsymbol {X}}}\right)=\,\sum _{j=1}^{{N}_{b}}{\beta }_{j}{U}_{j}^{\ast }\left({\mathit {\boldsymbol {X}}}\right)$ ${Q}_{h}\left({\mathit {\boldsymbol {X}}}\right)=\,\sum _{j=1}^{{N}_{b}}{\beta }_{j}{\frac {{\partial U}_{j}^{\ast }\left({\mathit {\boldsymbol {X}}}\right)}{\partial n}}$

(19)

where ${\textstyle {\beta }_{j}}$ are unknown coefficients, ${\textstyle \,{N}_{b}}$ are the source points placed only in the boundary outside the problem domain, ${\textstyle {U}_{j}^{\ast }}$ and ${\textstyle {\frac {{\partial U}_{j}^{\ast }\left({\mathit {\boldsymbol {X}}}\right)}{\partial n}}}$ are the fundamental solutions proposed for the modified Helmholtz operator:

${U}_{j}^{\ast }\left({\mathit {\boldsymbol {X}}}\right)=\,{\frac {1}{2\pi }}{K}_{0}(\lambda r)\,$ ${\frac {{\partial U}_{j}^{\ast }\left({\mathit {\boldsymbol {X}}}\right)}{\partial n}}=$$\,\left[{\frac {\lambda }{2\pi }}{K}_{1}(\lambda r)\,\right]{\frac {dr}{dn}}$

(20)

where ${\textstyle {K}_{0}}$ and ${\textstyle {K}_{1}}$ are the modified Bessel function of the second kind order zero and one, respectively.

By properly placing the source points (Figure 1) in order to avoid singularities, a well posed linear system with dimension ${\textstyle ({N}_{b}x{N}_{b})}$ is formed:

$\left[{A}_{ij}\right]\left\{{\beta }_{j}\right\}=\left\{{d}_{i}\right\}$

(21)

where ${\textstyle {A}_{ij}}$ is the matrix containing the fundamental solution (Eq. (20)) on an ${\textstyle i}$th field point generated by a ${\textstyle \,j}$th source and ${\textstyle {d}_{i}}$ are the prescribed boundary conditions (Eq. (7)).

By computing ${\textstyle {\beta }_{j}}$, the field points inside the domain can be obtained by Eq. (19). It is noteworthy that, for this method, sources and field points are at the same time level but in different geometrical positions, and it is well known that the source positioning outside the domain affects accuracy and stability. Typically, the response accuracy increase as the distance between the virtual and physical boundaries increase, but there is no definitive approach to this problem. In this article the sources geometrical position will be briefly evaluated.

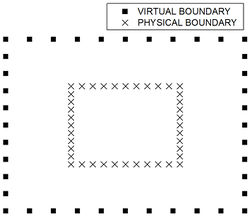
Figure 1. Source positions for MSF based on modified Helmholtz operator

3.3. Transient fundamental solutions for homogeneous solution

Applying the same concept described by Eq. (19), the general solution for Eq. (1) is now described as:

$U\left({\mathit {\boldsymbol {X}}},{t}_{F}\right)=\,\sum _{j=1}^{{N}_{i}+{N}_{b}}{\beta }_{j}{U}^{\ast }\left({\mathit {\boldsymbol {X}}},{t}_{F};{\mathit {\boldsymbol {\xi }}}_{\mathit {\boldsymbol {j}}},{t}_{j}\right)$ $Q\left({\mathit {\boldsymbol {X}}},{t}_{F}\right)=\,\sum _{j=1}^{{N}_{i}+{N}_{b}}{\beta }_{j}{Q}^{\ast }\left({\mathit {\boldsymbol {X,}}}{t}_{F};{\mathit {\boldsymbol {\xi }}}_{\mathit {\boldsymbol {j}}},{t}_{j}\right)$

(22)

it is known ${\textstyle {N}_{i}}$ is the number of initial sources (existing only in the domain), ${\textstyle {N}_{b}\,}$ is the number of sources in the boundary and ${\textstyle {\beta }_{j}}$ are the coefficients to be determined that represent the sources intensity. Inside the time step, ${\textstyle \Delta t=}$${t}^{n+1}-{t}^{n}$, ${\textstyle t}$ is the impulse application time at the source point and ${\textstyle {t}_{F}}$ is the field time, which are computed at intermediated levels for domain points and boundary points.

The fundamental solutions now are Green functions, which describe the potential field generated by a unit source applied to time ${\textstyle t}$ and point ${\textstyle {\boldsymbol {\xi }}}$:

${U}^{\ast }\left({\mathit {\boldsymbol {X}}},{\mathit {\boldsymbol {\xi }}};{t}_{F},t\right)=$$\,{\frac {1}{{\left(4\pi k\tau \right)}^{\frac {d}{2}}}}\exp \left[{\frac {-{r}^{2}\left({\mathit {\boldsymbol {X}}},{\mathit {\boldsymbol {\xi }}}\right)}{4k\tau }}\right]$ ${Q}^{\ast }\left({\mathit {\boldsymbol {X}}},{\mathit {\boldsymbol {\xi }}};{t}_{F},t\right)=$$\,{\frac {-r\left({\mathit {\boldsymbol {X}}},{\mathit {\boldsymbol {\xi }}}\right){\frac {\partial r\left({\mathit {\boldsymbol {X}}},{\mathit {\boldsymbol {\xi }}}\right)}{\partial n}}}{8\pi k{\tau }^{2}}}\exp \left[{\frac {-{r}^{2}\left({\mathit {\boldsymbol {X}}},{\mathit {\boldsymbol {\xi }}}\right)}{4k\tau }}\right]\,$

(23)

where ${\textstyle {\mathit {\boldsymbol {X}}}}$ is the field point coordinate, ${\textstyle \,{\boldsymbol {\xi }}}$ is the source point coordinate, ${\textstyle \,\tau =}$${t}_{F}-t$, ${\textstyle d}$ is the model dimension, ${\textstyle \,r\left(X,\xi \right)}$ is the radius measured between the source point and the field point in question, and ${\textstyle {\frac {\partial r\left(X,\xi \right)}{\partial n}}}$ is the projection of the radius projection over the normal-boundary.

In order to determine the sources intensities, the linear system must be solved:

$\left[{A}_{ij}\right]\left\{{\beta }_{j}\right\}=\left\{{d}_{i}\right\}$

(24)

where ${\textstyle {A}_{ij}}$ is a matrix with dimension (${\textstyle {N}_{i}+}$${N}_{b})\,x\,({N}_{i}+{N}_{b})$ containing the fundamental solutions, and ${\textstyle {d}_{i}}$ is the vector containing the initial conditions and prescribed boundary conditions (Eq. (7)).

When using fundamental solutions that are already transient, source and field points are at same geometrical positions but at different time levels even though inside the same time step. As the matrix is ill-conditioned, the difference between the time to which the source is applied in comparison with the time the field is calculated generates significant effect on the final response and will be investigated in this article.

The uniqueness of the matrix was approached through the technical use of Tikhonov’s Method:

$\left({\mathit {\boldsymbol {A}}}^{T}{\mathit {\boldsymbol {A+\lambda I}}}\right){\mathit {\boldsymbol {\alpha =\,}}}{\mathit {\boldsymbol {A}}}^{T}{\mathit {\boldsymbol {d}}}$

(25)

where ${\textstyle \lambda >0}$ is a regularization parameter whose values generally vary between ${\textstyle {10}^{-14}}$ and ${\textstyle {10}^{-1}}$ and ${\textstyle I\,}$ is the identity matrix.

3.3.1. Time sources positioning

Through Eq. (24) it is noted that both the matrix size and the vector size depend on the number of field points and source points chosen at each time step. However, it should be known that each time step is divided into intermediate steps where, firstly, the coefficients are determined by the points which the initial conditions are prescribed and then by the points where the boundary conditions are known.

In relation to the temporal coordinate of these sources, two forms of distribution would be tested: fixed source points (MFS1) and time moving source points (MFS2).

1) MFS1

In this paper, the scheme MFS1 is referred for fixed time source applications. On this proposal, even though the field points are obtained in a time box that advances through ${\textstyle [0,T]}$, the sources impulses are applied on the problem beginning, always at a same time level for domain sources and at another level for boundary sources. In order to avoid singularities, intermediate time levels are proposed as: the ${\textstyle (0-}$$b)\Delta t$ for domain sources, and ${\textstyle (0+b)\Delta t}$ for boundary sources, while field points will be placed at ${\textstyle (n-}$$1)\Delta t$ in interior domain and ${\textstyle (n+1)\Delta t}$ at the boundary. Figure 2 shows source placement during time steps.

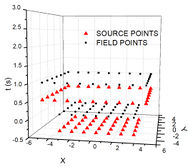
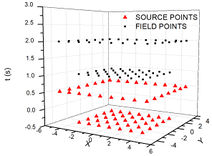
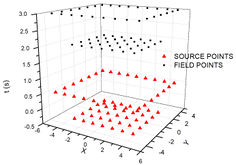
Figure 2. MSF1 evolutionary process

As the diffusion problem is an evolutionary problem, the impulse generated by maintaining the sources fixed at the beginning of the problem will be weakened as time progresses. Analogue to the geometrical distance, approximation increases accuracy as time evolves.

The matrix ${\textstyle A}$ exists when sources are applied before field nodes are calculated. For this approach, ${\textstyle A}$ will be fully completed, once domain source points generate fundamental solutions at domain and boundary field points, as well as, after the first time step, boundary source points also create responses on domain and boundary field points. After computing ${\textstyle \,A}$ and solving the linear system as in Eq. (24), the numerical response can be obtained using Eq. (22).

2) MFS2

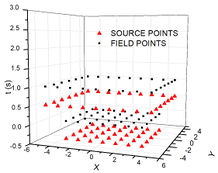
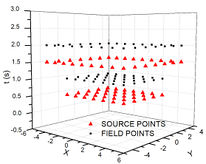
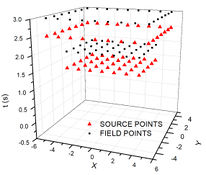
The scheme here referred as MSF2 makes use of [20,21] time-moving sources proposal. During the diffusion process, the field and source points are inside a time box that advances through ${\textstyle [0,T]}$, both field and sources are at different time levels on every time step. The time levels proposed are: the ${\textstyle (n-}$$b)\Delta t$ for domain sources, and ${\textstyle (n+b)\Delta t}$ for boundary sources while field points will be placed at ${\textstyle (n-}$$1)\Delta t$ in interior domain and ${\textstyle (n+1)\Delta t}$ at the boundary as showed in Figure 3.

Figure 3. MSF2 evolutionary process

Nevertheless, the ${\textstyle A}$ matrix will assume a different approach. Once boundary sources are applied after domain field points, it can only influence boundary field points. Inside a time step, the coefficient ${\textstyle b}$ that translates the distance between sources and field will now have an important role on the response accuracy. As in MSF1 the linear system Eq. (24) will be solved, and the potential Eq. (22) can be calculated at every time step until either the terminal time or the steady state solution is achieved.

4. Numerical results

In order to explore the methodologies potential and compare them with each other and with analytical solutions, three numerical examples were tested. As a way to evaluate the factors that influence the accuracy, several time increments, geometries, time coefficients and source positions were analyzed. Three types of internal sources were considered: constant, polynomial and senoidal for all proposed methods.

4.1. Example 1

Consider a unit circular disk, ${\textstyle k=1}$ with the following conditions:

$I.C.:\,U\left(x,y,t=0\right)=0$

$B.C.:\,U\left(x,y,t\right)=0$

$F\left(x,y\right)=\,{\frac {1}{m}}=10$

The analytical solution is given by:

$U\left(r,t\right)={\frac {1-{r}^{2}}{4m}}-{\frac {2}{m}}\sum _{n=1}^{\infty }{\frac {{J}_{0}({\lambda }_{n}r)}{{\lambda }_{n}^{3\,}{J}_{1}({\lambda }_{n})}}{e}^{-k{\lambda }_{n}^{2}t}$

where ${\textstyle {J}_{0}}$ and ${\textstyle {J}_{1}}$ are the Bessel functions first kind zero and one order, respectively. The parameters ${\textstyle {\lambda }_{n}}$ are the positive roots of ${\textstyle {J}_{0}\left({\lambda }_{n}\right)=}$$0$ and in this paper was used the first 100 roots.

In order to explore all methodologies nuances, three points in different geometrical positions (0,0), (0.4,0) and (0.8,0) were studied. In order to study the influence of source positions for the modified Helmholtz operator, different distances between virtual and physical boundary were proposed in Figure 4, and for MSF1 and MSF2 three different coefficient ${\textstyle b}$ were analyzed.

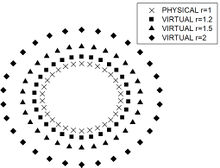
Figure 4. Physical and virtual boundary for example 1

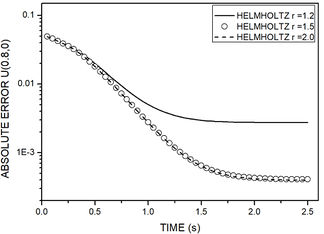
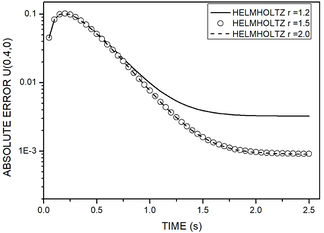
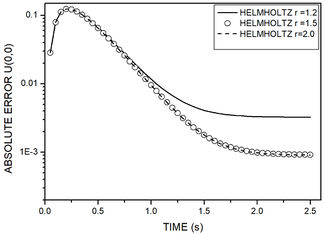
Figure 5 depicts the absolute error histograms for the modified Helmholtz operator for all the distances shown in Figure 4. As expected, it can be observed for all analyzed nodes that error and virtual boundary have an inverse relation, meaning that, until a distance is achieved, the error decrease as the distance increase. The method accuracy is also slightly better for nodes geometrically positioned closer to the physical boundary.

(a)

(b)

(c)

Figure 5. Time history of absolute error for example 1. Nodes coordinates are: (a) $x=0.8$, $y=0$. (b) $x=0.4$, $y=0$. (c) $x=0,\,y=0$

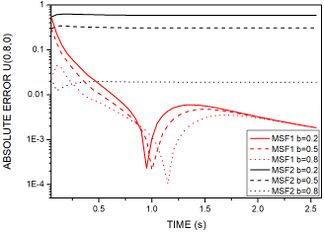
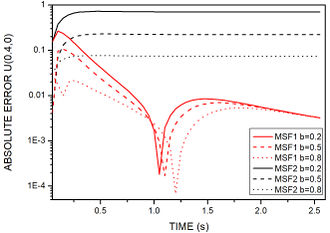
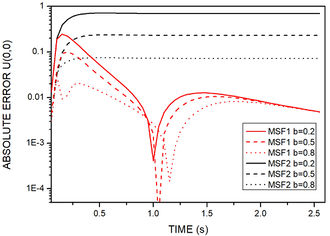
Figure 6 shows the absolute error histograms for MSF1 and MSF2 contemplating different time distances between sources and field nodes. In this example, for both methods, error decreases as the distance increases for all nodes. This relation shall not be generalized for different problems. Different parameters ${\textstyle b}$ should be tested for every problem. Joined with the time increment size, it affects ${\textstyle A}$ directly. It is worth mentioning that, for all nodes, MSF1 is less sensitive to the time distance between source and field and presented better performance when compared to MSF2.

(a)

(b)

(c)

Figure 6. Time history of absolute error for MSF1 and MSF2 for example 1. Nodes coordinates are: (a) $x=0.8$, $y=0$. (b) $x=0.4$, $y=0$. (c) $x=0,\,y=0$

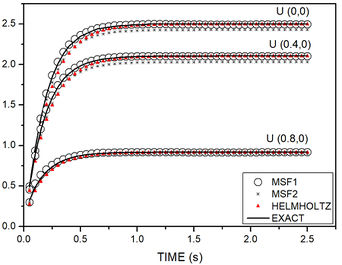
Figure 7 shows the time evolution history at (0,0), (0.4,0) and (0.8,0) for MSF1, MSF2 and MFS based on the modified Helmholtz operator, as well as the exact solution. For a circular domain, constant initial, boundary and nonhomogeneous conditions, accuracy decreases between the following methods: MSF based on the modified Helmholtz operator, MSF1 and MSF2. Although, in general, the results show good agreement with the analytical solution in different time stages.

Figure 7. Example 1 numerical results compared with analytical response

4.2. Example 2

Let a square plate of dimension $1\times 1$, with 256 nodes, ${\textstyle \Delta t=}$$0.2s$, ${\textstyle k=1}$ be submitted to the conditions:

$I.C.:\,U\left(x,y,t=0\right)=2\left[\cos \left(\pi x\right)+\sin \left(\pi y\right)\right]+$${\frac {{x}^{3}+{y}^{3}+{x}^{2}+y}{12}}$

$B.C.:\,U\left(x,y,t\right)=2\left[\cos \left(\pi x\right)+\sin \left(\pi y\right)\right]{e}^{-k{\pi }^{2}t}+$${\frac {{x}^{3}+{y}^{3}+{x}^{2}+y}{12}}$

$F\left(x,y\right)=\,{\frac {1}{m}}=-{\frac {6x+6y+2}{12}}$

The analytical solution is given by:

$U\left(x,y,t\right)=2\left[\cos \left(\pi x\right)+\sin \left(\pi y\right)\right]{e}^{-k{\pi }^{2}t}+$${\frac {{x}^{3}+{y}^{3}+{x}^{2}+y}{12}}$

In this example, for MSF1 and MSF2, the coefficient ${\textstyle b=0.5}$, and, for the modified Helmholtz operator, virtual sources are 0.5 from the physical boundary. In order to explore the methodologies, two different types of RBF were considered, referenced as RBF1 the TPS described on Section 3.1 and RBF2 the following functions [23]:

${\textstyle \varphi \left(r\right)=\,1+r\quad }$ and ${\textstyle \quad \psi \left(r\right)={\frac {{r}^{2}}{4}}+}$${\frac {{r}^{3}}{9}}\qquad$ for Laplacian operator

${\textstyle \varphi \left(r\right)=\,1+r-{\lambda }^{2}({\frac {{r}^{2}}{4}}+{\frac {{r}^{3}}{9}})\quad }$ and ${\textstyle \quad \psi \left(r\right)=}$${\frac {{r}^{2}}{4}}+{\frac {{r}^{3}}{9}}\qquad$ for modified Helmholtz operator

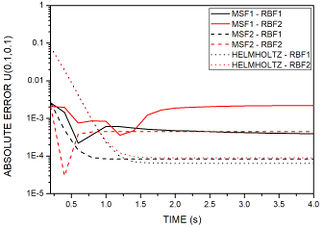
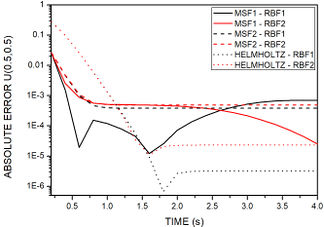
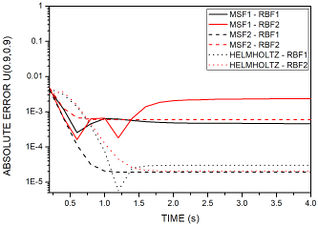
Figure 8 depicts the absolute error at nodes with distinct geometric positions for all methods proposed with RBF1 and RBF2. For all nodes, at initial stages, MSF1 and MSF2 presented better results. Moreover, between the radial basis functions, RBF1 showed greater accuracy. For senoidal and exponential initial and boundary conditions, polynomial non-homogeneous condition, MFS2-RBF1 revealed less error the closer the node is to the physical boundary, and MSF1 and MSF based on the modified Helmholtz operator revealed to be better the closer the node is to center domain.

(a)

(b)

(c)

Figure 8. Time history of absolute error for example 2. Nodes coordinates are: (a) $x=0.1,\,y=0.1$. (b) $x=0.5,\,y=0.5$. (c) $x=0.9,\,y=0.9$

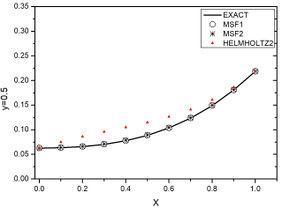
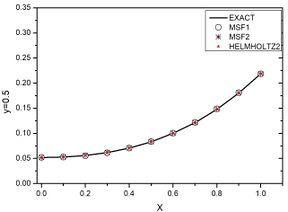
Figure 9 presents the results obtained by the three tested methods and the analytical solution for a line of nodes at ${\textstyle y=0.5}$ on initial stage and final stage. For initial stages MFS based on modified Helmholtz operator present less accuracy than MFS1 and MFS2, while at final times all methods present good precision. Figure 10 shows potential at all nodes at ${\textstyle t=3s}$.

(a)	(b)
Figure 9. Example 2 numerical results compared with analytical response. (a) Initial stage. (b) Final stage

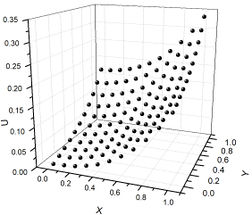
Figure 10. Example 2 potential for all nodes

4.3. Example 3

Consider a L-shaped irregular meshless MFS nodes, ${\textstyle k=1}$ with the following conditions:

$I.C.:\,U\left(x,y,t=0\right)=\mathrm {cos} \,\left(3x\right)\mathrm {sinh} \,\left(2y\right)xsin\left(y\right)$

$B.C.:\,U\left(x,y,t\right)=\mathrm {cos} \,\left(3x\right)\mathrm {sinh} \,\left(2y\right)\mathrm {exp} \,(-5t)+$$xsin(y)$

$F\left(x,y\right)=\,xsin(y)$

The analytical solution is given by:

$U\left(x,y,t\right)=\mathrm {cos} \,\left(3x\right)\mathrm {sinh} \,\left(2y\right)\mathrm {exp} \,(-5t)+$$xsin(y)$

In this example, two nodes –point A (1.03,0.56) and point B (0.35,1.36) depicted in Figure 11– and different time increments were tested to verify its influence on the final response.

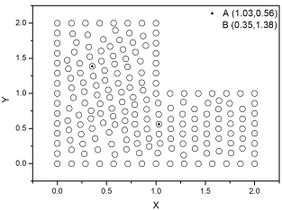
Figure 11. Meshless MFS nodes for example 3

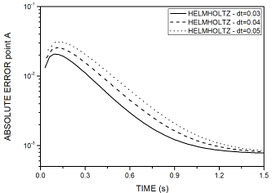
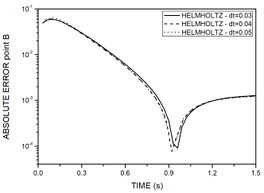
Figure 12 depicts absolute errors at nodes A and B, for different time steps in all methods. When compared, MSF1 and MSF based on the modified Helmholtz operator present better responses as time step decreases, and MSF2, a method that is known for its ill posed matrix, presents better results for a bigger time step. All methods showed to be sensitive concerning the field node geometrical position.

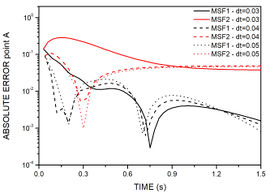
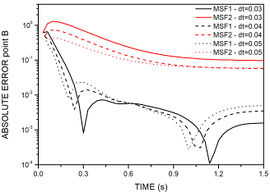
(a)	(b)
(c)	(d)
Figure 12. Time history of absolute error for example 3. (a) MSF1 and MSF2 for point A. (b) MSF1 and MSF2 for point B. (c) Helmholtz for point A. (d) Helmholtz for point B

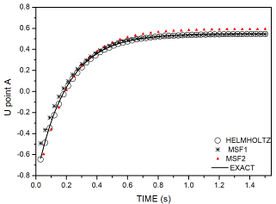
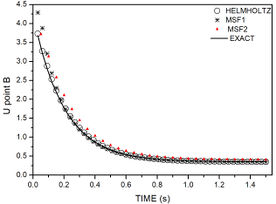
Figure 13 presents the results obtained by the three tested methods and the analytical solution at nodes A and B. For initial stages MFS1 presents less accuracy than the other methods. However, at final times MFS2 is worst. In general, for a senoidal non-homogeneous condition and trigonometrical initial and boundary conditions, all methods present reasonable results.

(a)	(b)
Figure 13. Example 3 numerical results compared with analytical response. (a) Node A. (b) Node B

5. Conclusions

Transient nonhomogeneous diffusion problems with different MFS methods and several types of initial, boundary and time-independent source functions were solved. The DRM technique was used to solve the nonhomogeneous equation, and different RBFs were analyzed. For the homogeneous solution, circular, squared and hard shaped meshes were tested, as well as different time increments and source positioning. It was described MFS based on the modified Helmholtz operator, MFS based on transient fundamental solutions, and it was proposed a variation of this last method.

The numerical procedures presented were validated by comparing results between methods and also with analytical solutions. The main issue for all methods is the sources positioning. For MFS modified Helmholtz operator, sources are geometrically positioned at a virtual boundary, and for MFS modified transient fundamental solutions, sources are time positioned at intermediate stages. In the proposed method sources are fixed in time, and its intensities, translated at ${\textstyle \beta }$ coefficients, are calculated for every time step.

Regarding the geometrical source position, the Helmholtz-based method showed to be sensitive until a certain distance between virtual and physical boundary is achieved, pattern that repeats for all mesh types. The so-called MSF1 showed to be less sensitive then MSF2 to temporal source positioning, although shape complexity interfered with the accuracy in both methods. Concerning time increments, MSF2 presented great discrepancies in accuracy between the times studied, mainly due to the disturbances generated when solving an ill-conditioned system, and for MFS1 and Helmholtz method, smaller time increments increase accuracy. The developed methods have a formulation that proved to be efficient in solving the various potential problems. Despite their limitations, it was realized that the methods present a controllable level of precision, versatility, computational gain and easy implementation.

Acknowledgements

The authors thankfully acknowledge the support of Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq). This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001.

References

[1] Gingold R.A., Monaghan J.J. Smoothed particle hydrodynamics: theory and application to non-spherical stars. Monthly notices of the royal astronomical society, 181(3):375-389, 1977.

[2] Oñate E., Idelsohn S., Zienkiewicz O.C., Taylor R.L. A finite point method in computational mechanics. Applications to convective transport and fluid flow. International Journal for Numerical Methods in Engineering, 39(22):3839-3866, 1996.

[3] Belytschko T., Lu Y.Y., Gu L. Element‐free Galerkin methods. International Journal for Numerical Methods in Engineering, 37(2):229-256, 1994.

[4] Atluri S.N., Zhu T. A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics. Computational Mechanics, 22(2):117-127, 1998.

[5] Chen W. Meshfree boundary particle method applied to Helmholtz problems. Engineering Analysis with Boundary Elements, 26(7):577-581, 2002.

[6] Wang H., Qin Q.H. Methods of fundamental solutions in solid mechanics. Elsevier, 2019.

[7] Young D.L., Tsai C.C., Murugesan K., Fan C.M., Chen C.W. Time-dependent fundamental solutions for homogeneous diffusion problems. Engineering Analysis with Boundary Elements, 28(12):1463-1473, 2004.

[8] Zhu S.P. Solving transient diffusion problems: time-dependent fundamental solution approaches versus LTDRM approaches. Engineering Analysis with Boundary Elements, 21(1):87-90, 1998.

[9] Zhu S.P., Liu H.W., Lu X.P. A combination of LTDRM and ATPS in solving diffusion problems. Engineering Analysis with Boundary Elements, 21(3):285-289, 1998.

[10] Sutradhar A., Paulino G.H., Gray L.J. Transient heat conduction in homogeneous and non-homogeneous materials by the Laplace transform Galerkin boundary element method. Engineering Analysis with Boundary Elements, 26(2):119-132, 2002.

[11] Bulgakov V., Šarler B., Kuhn G. Iterative solution of systems of equations in the dual reciprocity boundary element method for the diffusion equation. International Journal for Numerical Methods in Engineering, 43(4):713-732, 1998.

[12] Golberg M.A., Chen C.S., Muleshkov A.S. The method of fundamental solutions for time-dependent problems. WIT Transactions on Modelling and Simulation, 23, 1970.

[13] Nardini D., Brebbia C.A. A new approach to free vibration analysis using boundary elements. Applied Mathematical Modelling, 7(3):157-162, 1983.

[14] Partridge P.W., Brebbia C.A. Dual reciprocity boundary element method. Springer Science & Business Media, 2012.

[15] Golberg M.A., Chen C.S., Rashed Y.F. The annihilator method for computing particular solutions to partial differential equations. Engineering Analysis with Boundary Elements, 23(3):275-279, 1999.

[16] Cao L., Qin Q.H., Zhao N. Application of DRM-Trefftz and DRM-MFS to transient heat conduction analysis. Recent Patents on Space Technology, 2:41-50, 2010.

[17] Chantasiriwan S. Methods of fundamental solutions for time‐dependent heat conduction problems. International Journal for Numerical Methods in Engineering, 66(1):147-165, 2006.

[18] Young D.L., Tsai C.C., Fan C.M. Direct approach to solve nonhomogeneous diffusion problems using fundamental solutions and dual reciprocity methods. Journal of the Chinese Institute of Engineers, 27(4):597-609, 2004.

[19] Young D.L., Chen C.W., Fan C.M., Tsai C.C. The method of fundamental solutions with eigenfunction expansion method for nonhomogeneous diffusion equation. Numerical Methods for Partial Differential Equations: An International Journal, 22(5):1173-1196, 2006.

[20] Golberg M.A., Chen C.S. The theory of radial basis functions applied to the BEM for inhomogeneous partial differential equations. Boundary Elements Communications, 5(2):57-61, 1994.

[21] Chen C.S., Rashed Y.F. Evaluation of thin plate spline based particular solutions for Helmholtz-type operators for the DRM. Mechanics Research Communications, 25(2):195-201, 1998.

[22] Golberg M.A., Chen C.S. The method of fundamental solutions for potential, Helmholtz and diffusion problems. Boundary Integral Methods: Numerical and Mathematical Aspects, 1:103-176, 1998.

[23] Balakrishnan K., Sureshkumar R., Ramachandran P. A. An operator splitting-radial basis function method for the solution of transient nonlinear Poisson problems. Computers & Mathematics with Applications, 43(3-5):289-304, 2002.