FE Analysis of membrane systems including wrinkling and coupling

Published in Recent Advances in Textile Membranes and Inflatable Structures, Springer Verlag, pp. 89 - 108, 2005
DOI: 10.1007/1-4020-3317-6_6

1 Abstract

Current work summarizes the experience of the writer in the modeling of membrane systems. A first subsection describes an efficient membrane model, together with a reliable solution procedure. The following section addresses the simulation of the wrinkling phenomena providing details of a new solution procedure. The last one proposes an efficient technique to obtain the solution of the fluid structural interaction problem.

2 The Membrane Model

A membrane is basically a 2D solid which “lives” in a 3D environment. Given the lack of flexural stiffness, membranes can react to applied load only by using their in–plane resistance “choosing” the spatial disposition that is best suited to resist to the external forces. The consequence is that membrane structures tend naturally to find the optimal shape (compatible with the applied constraints) for any given load. In this “shape research”, they typically undergo large displacements and rotations.

From a numerical point of view, this reflects an intrinsic geometrical non–linearity that has to be taken in account in the formulation of the finite element model. In particular, an efficient Membrane Element should be able to represent correctly arbitrary rotations both of the element as a whole and internally to each element. The possibility of unrestricted rigid body motions constitutes a source of ill-conditioning or even of singularity of the tangent stiffness matrix introducing the need of carefully designed solution procedures.

2.1 Finite Element Model

Current section describes a finite element model that meets all of the requirements for the correct simulation of general membrane systems. The derivation makes use exclusively of orthogonal bases simplifying the calculations and allowing to express all the terms directly in Voigt Notation, which eases the implementation.

Einstein's sum on repeated indices is assumed unless specified otherwise

• ${\textstyle \mathbf {x_{I}} =\left\{x_{I},y_{I},z_{I}\right\}^{T}}$ is the position vector of the I–th node in the cartesian space (3D space)
• ${\textstyle \mathbf {\xi } =\left\{\xi ,\eta \right\}^{T}}$ describes the position of a point in the local system of coordinates
• Capital letter are used for addressing to the reference configuration
• ${\textstyle N_{I}(\mathbf {\xi } )}$ is the value of the shape function centered on node I on the point of local coordinates ${\textstyle \mathbf {\xi } }$

The use of the standard iso-parametric approach allows to express the position of any point as ${\textstyle \mathbf {x} (\mathbf {\xi } )=N_{I}(\mathbf {\xi } )\mathbf {x} _{I}}$.

In the usual assumptions of the continuum mechanics it is always possible to define the transformation between the local system of coordinates and the cartesian system as

$\left\{\xi {+}d\xi ,\eta \right\}^{T}-\left\{\xi ,\eta \right\}^{T}\rightarrow {\frac {\partial \mathbf {x} (\xi ,\eta )}{\partial \xi }}d\xi =\mathbf {g_{\xi }} d\xi$

(1)

$\left\{\xi ,\eta {+}d\eta \right\}^{T}-\left\{\xi ,\eta \right\}^{T}\rightarrow {\frac {\partial \mathbf {x} (\xi ,\eta )}{\partial \eta }}d\eta =\mathbf {g_{\eta }} d\eta$

(2)

in which we introduced the symbols

$\mathbf {g_{\xi }} ={\frac {\partial N_{I}(\xi ,\eta )}{\partial \xi }}\mathbf {x_{I}}$

(3)

$\mathbf {g_{\eta }} ={\frac {\partial N_{I}(\xi ,\eta )}{\partial \eta }}\mathbf {x_{I}}$

(4)

the vectors ${\textstyle \mathbf {g_{\xi }} }$ and ${\textstyle \mathbf {g_{\eta }} }$ of the 3D space, can be considered linearly independent (otherwise compenetration or self contact would manifest) follows immediately that they can be used in the construction of a base of the 3D space. In particular an orthogonal base can be defined as

$\mathbf {v_{1}} ={\frac {\mathbf {g_{\xi }} }{\left\|\mathbf {g_{\xi }} \right\|}}$

(5)

$\mathbf {n} ={\frac {\mathbf {\mathbf {\mathbf {g_{\xi }} } } \times \mathbf {\mathbf {\mathbf {g_{\eta }} } } }{\left\|\mathbf {\mathbf {\mathbf {g_{\xi }} } } \times \mathbf {\mathbf {\mathbf {g_{\eta }} } } \right\|}}\rightarrow \mathbf {v_{2}} =\mathbf {\mathbf {\mathbf {n} } } \times \mathbf {\mathbf {\mathbf {v_{1}} } }$

(6)

$\mathbf {v_{3}} =\mathbf {\mathbf {\mathbf {g_{\xi }} } } \times \mathbf {\mathbf {\mathbf {g_{\eta }} } }$

(7)

Vectors ${\textstyle \mathbf {v_{1}} }$ and ${\textstyle \mathbf {v_{2}} }$ describe the local tangent plane to the membrane while the third base vector is always orthogonal. Follows the possibility of defining a local transformation rule that links the local coordinates ${\textstyle \mathbf {\xi } }$ and the coordinates ${\textstyle \mathbf {\widehat {x}} }$ in the local tangent plane base. This can be achieved by considering that an increment ${\textstyle \left\{d\xi ,0\right\}}$ maps to the new base as

${\begin{pmatrix}d\xi \\0\end{pmatrix}}\rightarrow {\begin{pmatrix}\mathbf {\mathbf {\mathbf {g_{\xi }} } } \bullet \mathbf {\mathbf {\mathbf {v_{1}} } } \\\mathbf {\mathbf {\mathbf {g_{\xi }} } } \bullet \mathbf {\mathbf {\mathbf {v_{2}} } } \end{pmatrix}}d\xi \,;\,{\begin{pmatrix}0\\d\eta \end{pmatrix}}\rightarrow {\begin{pmatrix}\mathbf {\mathbf {\mathbf {g_{\eta }} } } \bullet \mathbf {\mathbf {\mathbf {v_{1}} } } \\\mathbf {\mathbf {\mathbf {g_{\eta }} } } \bullet \mathbf {\mathbf {\mathbf {v_{2}} } } \end{pmatrix}}d\eta$

(8)

this is sinthetized by the definition of the linear application

${\begin{pmatrix}d{\widehat {x}}_{1}\\d{\widehat {x}}_{2}\end{pmatrix}}={\begin{pmatrix}\mathbf {\mathbf {\mathbf {g_{\xi }} } } \bullet \mathbf {\mathbf {\mathbf {v_{1}} } } &\mathbf {\mathbf {\mathbf {g_{\eta }} } } \bullet \mathbf {\mathbf {\mathbf {v_{1}} } } \\\mathbf {\mathbf {\mathbf {g_{\xi }} } } \bullet \mathbf {\mathbf {\mathbf {v_{2}} } } &\mathbf {\mathbf {\mathbf {g_{\eta }} } } \bullet \mathbf {\mathbf {\mathbf {v_{2}} } } \end{pmatrix}}{\begin{pmatrix}d\xi \\d\eta \end{pmatrix}}\rightarrow d{\widehat {\mathbf {x} }}=\mathbf {j} d\mathbf {\xi }$

(9)

it should be noted that ${\textstyle \mathbf {\mathbf {\mathbf {g_{\xi }} } } \bullet \mathbf {\mathbf {\mathbf {v_{3}} } } }$ and ${\textstyle \mathbf {\mathbf {\mathbf {g_{\eta }} } } \bullet \mathbf {\mathbf {\mathbf {v_{3}} } } }$ are identically zero consequently no components are left apart in representing the membrane in the new coordinates system. Taking into account the definition of the base vectors the tensor ${\textstyle \mathbf {j} }$ becomes (after some calculations)

$\mathbf {j} ={\begin{pmatrix}\left\|\mathbf {g_{\xi }} \right\|&{\frac {\mathbf {\mathbf {\mathbf {g_{\xi }} } } \bullet \mathbf {\mathbf {\mathbf {g_{\eta }} } } }{\left\|\mathbf {g_{\xi }} \right\|}}\\0&{\frac {\left\|\mathbf {v_{3}} \right\|}{\left\|\mathbf {g_{\xi }} \right\|}}\end{pmatrix}}$

(10)

and its determinant

$det(\mathbf {j} )=\left\|\mathbf {v_{3}} \right\|=\left\|\mathbf {\mathbf {\mathbf {g_{\xi }} } } \times \mathbf {\mathbf {\mathbf {g_{\eta }} } } \right\|$

(11)

As the interest is focused on the purely membranal behavior, it is not needed to take in account the deformation of the structure over the thickness, as this can be calculated “a posteriori” once known the deformation of the mid–plane. On the base of this observation, the deformation gradient which describes the deformation of the membrane as a 3D body

$\mathbf {F} _{3\times {3}}={\frac {\partial \mathbf {x} }{\partial \mathbf {X} }}$

(12)

can be replaced by

$\mathbf {\widehat {F}} _{2\times {2}}={\frac {\partial \mathbf {\widehat {x}} }{\partial \mathbf {\widehat {X}} }}={\frac {\partial \mathbf {\widehat {x}} }{\partial \xi }}{\frac {\partial \xi }{\partial \mathbf {\widehat {X}} }}=\mathbf {j} \mathbf {J} ^{-1}$

(13)

taking in account the behavior over the thickness in the definition of the (two dimensional) constitutive model to be used (for example making the assumption of plane stress). The symbol ${\textstyle \mathbf {J} }$ is used here and in the following to indicate ${\textstyle \mathbf {j} }$ calculated in the reference position.

under this considerations the subsequent development of the finite element follows closely the standard procedure for a non–linear 2D finite element, the only difference being that the local base changes on all the domain, which makes the linearization slightly more involved.

To proceed further we need therefore to write the Right Cauchy Green Strain tensor ${\textstyle \mathbf {C} =\mathbf {F} ^{T}\mathbf {F} }$ which takes the form

$\mathbf {C} =\left(\mathbf {J} ^{-T}\mathbf {j} ^{T}\mathbf {j} \mathbf {J} ^{-1}\right)=\left(\mathbf {G} ^{T}\mathbf {g} \mathbf {G} \right)$

(14)

where we introduced the symbols ${\textstyle \mathbf {g} =\mathbf {j} ^{T}\mathbf {j} }$ and ${\textstyle \mathbf {G} =\mathbf {J} ^{-1}}$. Operator ${\textstyle \mathbf {g} }$ takes, after some calculations, the simple form

$\mathbf {g} ={\begin{pmatrix}\mathbf {\mathbf {\mathbf {g_{\xi }} } } \bullet \mathbf {\mathbf {\mathbf {g_{\xi }} } } &\mathbf {\mathbf {\mathbf {g_{\eta }} } } \bullet \mathbf {\mathbf {\mathbf {g_{\xi }} } } \\\mathbf {\mathbf {\mathbf {g_{\xi }} } } \bullet \mathbf {\mathbf {\mathbf {g_{\eta }} } } &\mathbf {\mathbf {\mathbf {g_{\eta }} } } \bullet \mathbf {\mathbf {\mathbf {g_{\eta }} } } \end{pmatrix}}$

(15)

From the definition of he Green Lagrange strain tensor ${\textstyle \mathbf {E} ={\frac {1}{2}}(\mathbf {C-I} )}$ we obtain immediately ${\textstyle \delta \mathbf {E} ={\frac {1}{2}}\delta \mathbf {C} }$. This allows to write the equation of virtual works in compact form as (taking in consideration only body forces and pressure forces)

$\delta W_{int}=\delta W_{ext}+\delta W_{press}$

(16)

${\frac {h_{0}}{2}}\int _{\Omega }{\delta \mathbf {C} :\mathbf {S} }=h_{0}\int _{\Omega }{\mathbf {\mathbf {\delta \mathbf {x} } } \bullet \mathbf {\mathbf {\mathbf {b} } } }+\int _{\omega }{p\mathbf {\mathbf {\delta \mathbf {x} } } \bullet \mathbf {\mathbf {\mathbf {n} } } }$

(17)

2.1.1 Internal Work

The term ${\textstyle {\frac {h_{0}}{2}}\int _{\Omega }{\delta \mathbf {C} :\mathbf {S} }}$ describes the work of internal forces during the deformation process. Operator ${\textstyle \mathbf {G} =\mathbf {J} ^{-1}}$ is referred to the reference configuration and is therefore strictly constant, follows immediately that

$\delta \mathbf {C} =\mathbf {G} ^{T}\delta \mathbf {g} \mathbf {G}$

(18)

The term ${\textstyle \delta \mathbf {C} :\mathbf {S} }$ becomes in Einstein's notation

${\frac {1}{2}}\delta \mathbf {C} :\mathbf {S} ={\frac {1}{2}}\delta C_{IJ}S_{IJ}={\frac {1}{2}}\delta g_{ij}G_{iI}G_{jJ}S_{IJ}$

(19)

introducing the symbols

${\frac {1}{2}}\delta g_{ij}\rightarrow {\frac {1}{2}}\delta \left\{\mathbf {g} \right\}={\frac {1}{2}}{\begin{pmatrix}\delta g_{11}\\\delta g_{22}\\2\delta g_{12}\end{pmatrix}}\,;\,S_{IJ}\rightarrow \left\{\mathbf {S} \right\}={\begin{pmatrix}S_{11}\\S_{22}\\S_{12}\end{pmatrix}}$

(20)

$G_{iI}G_{jJ}\rightarrow \left[\mathbf {Q} \right]^{T}={\begin{pmatrix}(G_{11})^{2}&(G_{12})^{2}&2G_{11}G_{12}\\0&(G_{22})^{2}&0\\0&G_{12}G_{22}&G_{11}G_{22}\end{pmatrix}}$

(21)

it is possible to express the (19) in Voigt form as

${\frac {1}{2}}\delta \mathbf {C} :\mathbf {S} ={\frac {1}{2}}\left\{\mathbf {\delta g} \right\}^{T}\left[\mathbf {Q} \right]^{T}\left\{\mathbf {S} \right\}={\frac {1}{2}}\left\{\mathbf {\delta g} \right\}^{T}\left\{\mathbf {s} \right\}\,;\,\left\{\mathbf {s} \right\}=\left[\mathbf {Q} \right]^{T}\left\{\mathbf {S} \right\}$

(22)

considering the definition(15), introducing the symbol ${\textstyle \left\{\mathbf {\delta x} \right\}^{T}={\begin{pmatrix}\left\{\mathbf {\delta x_{1}} \right\}^{T}&\ldots &\left\{\mathbf {\delta x_{k}} \right\}^{T}\end{pmatrix}}}$ and taking in account the isoparametric approximation one obtains

${\frac {1}{2}}\delta g_{11}={\frac {\partial N_{I}}{\partial \xi }}\delta \mathbf {\mathbf {\mathbf {x} _{I}} } \bullet \mathbf {\mathbf {\mathbf {g_{\xi }} } } =\left\{\mathbf {\delta x} \right\}^{T}{\begin{pmatrix}{\frac {\partial N_{1}}{\partial \xi }}\left\{\mathbf {\mathbf {g_{\xi }} } \right\}\\\ldots \\{\frac {\partial N_{k}}{\partial \xi }}\left\{\mathbf {\mathbf {g_{\xi }} } \right\}\end{pmatrix}}$

(23)

${\frac {1}{2}}\delta g_{22}={\frac {\partial N_{I}}{\partial \xi }}\delta \mathbf {\mathbf {\mathbf {x} _{I}} } \bullet \mathbf {\mathbf {\mathbf {g_{\eta }} } } =\left\{\mathbf {\delta x} \right\}^{T}{\begin{pmatrix}{\frac {\partial N_{1}}{\partial \eta }}\left\{\mathbf {\mathbf {g_{\eta }} } \right\}\\\ldots \\{\frac {\partial N_{k}}{\partial \eta }}\left\{\mathbf {\mathbf {g_{\eta }} } \right\}\end{pmatrix}}$

(24)

${\frac {1}{2}}\delta 2g_{12}={\frac {\partial N_{I}}{\partial \eta }}\delta \mathbf {\mathbf {\mathbf {x} _{I}} } \bullet \mathbf {\mathbf {\mathbf {g_{\xi }} } } +{\frac {\partial N_{I}}{\partial \xi }}\delta \mathbf {\mathbf {\mathbf {x} _{I}} } \bullet \mathbf {\mathbf {\mathbf {g_{\eta }} } } =\left\{\mathbf {\delta x} \right\}^{T}{\begin{pmatrix}{\frac {\partial N_{1}}{\partial \xi }}\left\{\mathbf {\mathbf {g_{\eta }} } \right\}+{\frac {\partial N_{1}}{\partial \eta }}\left\{\mathbf {\mathbf {g_{\xi }} } \right\}\\\ldots \\{\frac {\partial N_{k}}{\partial \xi }}\left\{\mathbf {\mathbf {g_{\eta }} } \right\}+{\frac {\partial N_{k}}{\partial \eta }}\left\{\mathbf {\mathbf {g_{\xi }} } \right\}\\\end{pmatrix}}$

(25)

by defining the matrix

$\left[\mathbf {b} \right]^{T}={\begin{pmatrix}{\frac {\partial N_{1}}{\partial \xi }}\left\{\mathbf {\mathbf {g_{\xi }} } \right\}&{\frac {\partial N_{1}}{\partial \eta }}\left\{\mathbf {\mathbf {g_{\eta }} } \right\}&{\frac {\partial N_{1}}{\partial \xi }}\left\{\mathbf {\mathbf {g_{\eta }} } \right\}+{\frac {\partial N_{1}}{\partial \eta }}\left\{\mathbf {\mathbf {g_{\xi }} } \right\}\\\ldots &\ldots &\ldots \\{\frac {\partial N_{k}}{\partial \xi }}\left\{\mathbf {\mathbf {g_{\xi }} } \right\}&{\frac {\partial N_{k}}{\partial \eta }}\left\{\mathbf {\mathbf {g_{\eta }} } \right\}&{\frac {\partial N_{k}}{\partial \xi }}\left\{\mathbf {\mathbf {g_{\eta }} } \right\}+{\frac {\partial N_{k}}{\partial \eta }}\left\{\mathbf {\mathbf {g_{\xi }} } \right\}\\\end{pmatrix}}$

(26)

it is then possible to write

${\frac {1}{2}}\left\{\mathbf {\delta C} \right\}^{T}\left\{\mathbf {S} \right\}=\left\{\mathbf {\delta E} \right\}^{T}\left\{\mathbf {S} \right\}=\left\{\mathbf {\delta x} \right\}^{T}\left[\mathbf {b} \right]^{T}\left[\mathbf {Q} \right]^{T}\left\{\mathbf {S} \right\}$

(27)

Defining the symbol ${\textstyle \left[\mathbf {B} \right]}$

$\left[\mathbf {B} \right]=\left[\mathbf {Q} \right]\left[\mathbf {b} \right]$

(28)

we finally obtain

$\left\{\mathbf {f_{int}} \right\}=\int _{\Omega }{h_{0}\left[\mathbf {B} \right]^{T}\left\{\mathbf {S} \right\}d\Omega }$ (29) $\delta W_{int}=\left\{\mathbf {\delta x} \right\}^{T}\left\{\mathbf {f_{int}} \right\}$ (30)

2.1.2 External Work

Derivation of the work of external conservative forces follows the standard procedure and can be found on any book on nonlinear finite elements. The expression of the work of follower forces (body forces) is on the other hand a little more involved. In the following the pressure is considered constant, the non linearity being introduced by the change of direction of the normal. For the derivation of the pressure contributions it is much easier to perform the integration over the actual domain then over the reference one.

$\delta W_{pr}=\int _{\omega }{p\mathbf {\mathbf {\delta \mathbf {x} } } \bullet \mathbf {\mathbf {\mathbf {n} } } }d\omega =\int _{\xi ,\eta }{p\mathbf {\mathbf {\delta \mathbf {x} } } \bullet \mathbf {\mathbf {\mathbf {n} } } }det(j)d\xi d\eta$

(31)

taking in account the definition of the base vectors (6)(7), and considering (11) we obtain immediately

$\left\{\mathbf {f_{I}} \right\}=\int _{\xi ,\eta }{N_{I}(\xi ,\eta )p(\xi ,\eta )\mathbf {v_{3}} (\xi ,\eta )d\xi d\eta }$

(32)

$\left\{\mathbf {f_{pr}} \right\}={\begin{pmatrix}\left\{\mathbf {f_{1}} \right\}^{T}&\ldots &\left\{\mathbf {f_{k}} \right\}^{T}\end{pmatrix}}^{T}$

(33)

$\delta W_{pr}=\left\{\mathbf {\delta \mathbf {x} } \right\}^{T}\left\{\mathbf {f_{pr}} \right\}$

(34)

2.1.3 Linearization

Equation (16) is nonlinear, its practical use needs therefore its linearization. The best rate of convergence is theoretically given by Newton-Raphson technique which guarantees quadratical convergence to the solution. Defining ${\textstyle \Psi =\delta W_{int}-\delta W_{ext}-\delta W_{pr}}$ each Newton–Raphson step takes the form

$d\Psi +\Psi =0$

(35)

The term ${\textstyle \Psi }$ can be explicitated using expression (30)(34) we therefore miss only the differential ${\textstyle d\Psi }$ that can be evaluated from the linearization of the different contributions

Linearization of internal work

The term connected to the internal works can be linearized as follows

$d\left(W_{int}\right)=d\left({\frac {h_{0}}{2}}\int _{\Omega }{\delta \mathbf {C} :\mathbf {S} }\right)=$ $={\frac {h_{0}}{2}}\int _{\Omega }{d\left(\delta \mathbf {C} \right):\mathbf {S} }+{\frac {h_{0}}{2}}\int _{\Omega }{\delta \mathbf {C} :d\left(\mathbf {S} \right)}$ (36)

the first terms gives, by using (22)

${\frac {h_{0}}{2}}\int _{\Omega }{d\left(\delta \mathbf {C} \right):\mathbf {S} }={\frac {h_{0}}{2}}\int _{\Omega }{d\left(\left\{\mathbf {\delta g} \right\}^{T}\right)\left\{\mathbf {s} \right\}}=$ $={\frac {h_{0}}{2}}\int _{\Omega }{d\left({\frac {\partial \left\{\mathbf {\delta g} \right\}^{T}}{\partial \left\{\mathbf {x} \right\}}}d\left\{\mathbf {x} \right\}\right)\left\{\mathbf {s} \right\}}$ (37)

now it can be seen that

$d\left({\frac {1}{2}}\left\{\mathbf {\delta g} \right\}^{T}\right)={\begin{pmatrix}\mathbf {\mathbf {\delta \mathbf {g_{\xi }} } } \bullet \mathbf {\mathbf {d\mathbf {g_{\xi }} } } &\mathbf {\mathbf {\delta \mathbf {g_{\eta }} } } \bullet \mathbf {\mathbf {d\mathbf {g_{\eta }} } } &\mathbf {\mathbf {\delta \mathbf {g_{\eta }} } } \bullet \mathbf {\mathbf {d\mathbf {g_{\xi }} } } +\mathbf {\mathbf {\delta \mathbf {g_{\xi }} } } \bullet \mathbf {\mathbf {d\mathbf {g_{\eta }} } } \end{pmatrix}}\left\{\mathbf {s} \right\}=$ $={\begin{pmatrix}s_{11}\mathbf {\mathbf {\delta \mathbf {g_{\xi }} } } \bullet \mathbf {\mathbf {d\mathbf {g_{\xi }} } } &s_{22}\mathbf {\mathbf {\delta \mathbf {g_{\eta }} } } \bullet \mathbf {\mathbf {d\mathbf {g_{\eta }} } } &s_{12}\left(\mathbf {\mathbf {\delta \mathbf {g_{\eta }} } } \bullet \mathbf {\mathbf {d\mathbf {g_{\xi }} } } +\mathbf {\mathbf {\delta \mathbf {g_{\xi }} } } \bullet \mathbf {\mathbf {d\mathbf {g_{\eta }} } } \right)\end{pmatrix}}$ (38)

substitution of the shape functions gives immediately a set of equalities in the form

$s_{11}\mathbf {\mathbf {\delta \mathbf {g_{\xi }} } } \bullet \mathbf {\mathbf {d\mathbf {g_{\xi }} } } =s_{11}{\frac {\partial N_{I}}{\partial \xi }}{\frac {\partial N_{J}}{\partial \xi }}\delta _{ij}\mathbf {\mathbf {\delta x_{I}} } \bullet \mathbf {\mathbf {dx_{jJ}} } =s_{11}{\frac {\partial N_{I}}{\partial \xi }}{\frac {\partial N_{J}}{\partial \xi }}\delta _{ij}\delta x_{iI}dx_{jJ}$

(39)

which makes possible to write

$d\left({\frac {1}{2}}\left\{\mathbf {\delta g} \right\}^{T}\right)$ $=\left(s_{11}{\frac {\partial N_{I}}{\partial \xi }}{\frac {\partial N_{J}}{\partial \xi }}+s_{22}{\frac {\partial N_{I}}{\partial \eta }}{\frac {\partial N_{J}}{\partial \eta }}+s_{12}\left({\frac {\partial N_{I}}{\partial \eta }}{\frac {\partial N_{J}}{\partial \xi }}+{\frac {\partial N_{I}}{\partial \xi }}{\frac {\partial N_{J}}{\partial \eta }}\right)\right)\delta _{ij}\delta x_{iI}dx_{jJ}$ (40)

introducing the vectors ${\textstyle \mathbf {a} ={\begin{pmatrix}{\frac {\partial N_{1}}{\partial \xi }}&\ldots &{\frac {\partial N_{k}}{\partial \xi }}\end{pmatrix}}}$ and ${\textstyle \mathbf {b} ={\begin{pmatrix}{\frac {\partial N_{1}}{\partial \eta }}&\ldots &{\frac {\partial N_{k}}{\partial \eta }}\end{pmatrix}}}$ together with the new tensor

$\mathbf {A} =\left(s_{11}\mathbf {a} \mathbf {a} +s_{22}\mathbf {b} \mathbf {b} +s_{12}\left(\mathbf {b} \mathbf {a} +\mathbf {a} \mathbf {b} \right)\right)\,;\,\mathbf {a} \mathbf {a} =\mathbf {a} \otimes \mathbf {a}$

(41)

we can simplify greatly the expression in the form

$d\left({\frac {1}{2}}\left\{\mathbf {\delta g} \right\}^{T}\right)$ $=A_{IJ}\delta {ij}\delta \mathbf {x_{iI}} d\mathbf {x_{jJ}}$

(42)

or, in Voigt form

$d\left({\frac {1}{2}}\left\{\mathbf {\delta g} \right\}^{T}\right)$ $={\begin{pmatrix}\left\{\mathbf {\delta x_{1}} \right\}^{T}&\ldots &\left\{\mathbf {\delta x_{k}} \right\}^{T}\end{pmatrix}}{\begin{pmatrix}A_{11}\left[\mathbf {I} \right]&\ldots &A_{1k}\left[\mathbf {I} \right]\\\ldots &\ldots &\ldots \\A_{k1}\left[\mathbf {I} \right]&\ldots &A_{kk}\left[\mathbf {I} \right]\\\end{pmatrix}}$ ${\begin{pmatrix}\left\{\mathbf {dx_{1}} \right\}\\\ldots \\\left\{\mathbf {dx_{k}} \right\}\end{pmatrix}}=\left\{\mathbf {\delta x} \right\}^{T}\left[\mathbf {K_{geo}} \right]\left\{\mathbf {dx} \right\}$ (43)

the derivation of the “material” contribution to the stiffness matrix follows the standard path. Assuming as normally

$d\mathbf {S} ={\frac {\partial \mathbf {S} }{\partial \mathbf {E} }}:d\mathbf {E} \rightarrow \left\{\mathbf {dS} \right\}=\left[\mathbf {D_{tan}} \right]\left\{\mathbf {dE} \right\}$

(44)

we obtain immediately

$\int _{\Omega }{{\frac {h_{0}}{2}}\delta \mathbf {C} :d\left(\mathbf {S} \right)}=\left(\int _{\Omega }{h_{0}\delta \left\{\mathbf {x} \right\}^{T}\left[\mathbf {B} \right]^{T}\left[\mathbf {D_{tan}} \right]\left[\mathbf {B} \right]d\Omega }\right)\left\{\mathbf {dx} \right\}$ $=\delta \left\{\mathbf {x} \right\}^{T}\left[\mathbf {K_{mat}} \right]\left\{\mathbf {dx} \right\}$

(45)

$\left[\mathbf {K_{mat}} \right]=\int _{\Omega }{h_{0}\left[\mathbf {B} \right]^{T}\left[\mathbf {D_{tan}} \right]\left[\mathbf {B} \right]d\Omega }$

(46)

Linearization of external forces The linearization of the work ${\textstyle W_{ext}}$ is not needed as it describes the work of constant forces. The only term missing is therefore the one relative to the work of the follower forces.

$d\left(\int _{\omega }{p\mathbf {\mathbf {\delta \mathbf {x} } } \bullet \mathbf {\mathbf {\mathbf {n} } } d\omega }\right)\rightarrow \delta \left\{\mathbf {x_{I}} \right\}^{T}d\mathbf {f_{I}} =\delta \left\{\mathbf {x_{I}} \right\}^{T}d\left(\int _{\omega }{pN_{I}\left\{\mathbf {\mathbf {\mathbf {\mathbf {g_{\xi }} } } \times \mathbf {\mathbf {\mathbf {g_{\eta }} } } } \right\}d\omega }\right)$

(47)

differentiating ${\textstyle pN_{I}\left\{\mathbf {\mathbf {\mathbf {\mathbf {g_{\xi }} } } \times \mathbf {\mathbf {\mathbf {g_{\eta }} } } } \right\}}$we obtain

$d\left(pN_{I}\left\{\mathbf {\mathbf {\mathbf {\mathbf {g_{\xi }} } } \times \mathbf {\mathbf {\mathbf {g_{\eta }} } } } \right\}\right)=pN_{I}\left\{\mathbf {\mathbf {\mathbf {d\mathbf {g_{\xi }} } } \times \mathbf {\mathbf {\mathbf {g_{\eta }} } } } \right\}+pN_{I}\left\{\mathbf {\mathbf {\mathbf {\mathbf {g_{\xi }} } } \times \mathbf {\mathbf {d\mathbf {g_{\eta }} } } } \right\}=$ $=pN_{I}\left\{\mathbf {\mathbf {\mathbf {\mathbf {g_{\xi }} } } \times \mathbf {\mathbf {d\mathbf {g_{\eta }} } } } \right\}-pN_{I}\left\{\mathbf {\mathbf {\mathbf {\mathbf {g_{\eta }} } } \times \mathbf {\mathbf {d\mathbf {g_{\xi }} } } } \right\}$ (48)

Considering that it is possible to write the cross product of two vectors in Voigt format as

$\mathbf {c} =\mathbf {\mathbf {a} } \times \mathbf {\mathbf {b} } \rightarrow {\begin{pmatrix}c_{1}\\c_{2}\\c_{3}\end{pmatrix}}={\begin{pmatrix}0&-a_{3}&a_{2}\\a_{3}&0&-a_{1}\\-a_{2}&a_{1}&0\end{pmatrix}}{\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}\rightarrow \left\{\mathbf {c} \right\}=\left[\mathbf {a\times } \right]\left\{\mathbf {b} \right\}$

(49)

and taking in account (3) and (4) we obtain

$d\left(pN_{I}\left\{\mathbf {\mathbf {\mathbf {\mathbf {g_{\xi }} } } \times \mathbf {\mathbf {\mathbf {g_{\eta }} } } } \right\}\right)=\left(pN_{I}{\frac {\partial N_{J}}{\partial \eta }}\left[\mathbf {\mathbf {g_{\xi }} \times } \right]-pN_{I}{\frac {\partial N_{J}}{\partial \xi }}\left[\mathbf {\mathbf {g_{\xi }} \times } \right]\right)\left\{\mathbf {dx_{J}} \right\}$

(50)

$\left[\mathbf {K_{pr}} \right]={\begin{pmatrix}K_{11}&\ldots &K_{1k}\\\ldots &\ldots &\ldots \\K_{k1}&\ldots &K_{kk}\end{pmatrix}}\,;\,\left[\mathbf {K_{IJ}} \right]=\left(pN_{I}{\frac {\partial N_{J}}{\partial \eta }}\left[\mathbf {\mathbf {g_{\xi }} \times } \right]-pN_{I}{\frac {\partial N_{J}}{\partial \xi }}\left[\mathbf {\mathbf {g_{\xi }} \times } \right]\right)$

(51)

$d(\delta W_{pr})=\left\{\mathbf {\delta x} \right\}^{T}\left[\mathbf {K_{pr}} \right]\left\{\mathbf {dx} \right\}$

(52)

Linearized formulation

The only step missing is to merge all the terms in (35) to find the final expression. The result of this operation is

$\left\{\mathbf {\delta x} \right\}^{T}\left(\left[\mathbf {K_{geo}} \right]+\left[\mathbf {K_{mat}} \right]-\left[\mathbf {K_{pr}} \right]\right)\left\{\mathbf {dx} \right\}=\left\{\mathbf {\delta x} \right\}^{T}\left(\left\{\mathbf {f_{ext}} \right\}-\left\{\mathbf {f_{int}} \right\}\right)$

(53)

invoking the arbitrariety of ${\textstyle \left\{\mathbf {\delta x} \right\}}$ and introducing the definitions

$\left[\mathbf {K_{tan}} \right]=\left[\mathbf {K_{geo}} \right]+\left[\mathbf {K_{mat}} \right]-\left[\mathbf {K_{pr}} \right]$

(54)

$\left\{\mathbf {R} \right\}=\left\{\mathbf {f_{ext}} \right\}-\left\{\mathbf {f_{int}} \right\}$

(55)

the principle of virtual works gives for each element

$\left[\mathbf {K_{tan}} \right]\left\{\mathbf {dx} \right\}=\left\{\mathbf {R} \right\}$

(56)

2.2 Solution procedure

As briefly outlined at the beginning of the section, membrane systems are possibly subjected to large rigid body motions which reflects in singular or ill-conditioned “static” stiffness matrices. In addition, convergence of the Newton–Raphson algorithm is often difficult as the final solution can be very “far” from the initial guess even for little variations of the applied loads.

Dynamic solution techniques on the other hand are not affected by such problems. Mass and damping contributions remove the singularities from the system and generally provide a better conditioning to the problem. The introduction of dynamic terms provides as well an excellent source of stabilization for the solution (physically the solution can't change much in a small time), ending up with better convergence properties inside each solution step.

Any standard (non–linear) time integration technique can be theoretically used in conjunction with the proposed FE model for the study of dynamic response of the systems of interest. Some care should be however taken in the choice because the high geometric non–linearities tend to challenge the stability of the time–integration scheme chosen.

Generally speaking, “statics” can be seen as the limit to which a dynamic process tends (under a given constant load). Dynamic systems show a “transient” phase that vanishes in time to reach the so called “steady state”; the presence of damping in the system reduces gradually the oscillations making the system tend to a constant configuration that is the “static” solution. The time needed for the system to reach this final configuration is controlled by the amount of damping. For values of system's damping exceeding a critical value, the transient phase disappears and the systems reaches directly the final solution without any oscillation.

In many situations the main engineering interest is focused on “static” solutions rather than on the complete dynamic analysis of the system. The previews considerations suggests immediately that “statics” could be obtained efficiently by studying the dynamics of over damped systems. This could be obtained by simply adding a fictitious damping source to the “standard” dynamic problem. The “only” problem is therefore the choice of an idoneous form for such damping. Unfortunately this choice is not trivial, however it possible to observe [1],[2] that the “steady state” solution of the system

$\mathbf {M} {\ddot {\mathbf {x} }}+\mathbf {D} {\dot {\mathbf {x} }}+\mathbf {K} \mathbf {x} =\mathbf {f} \left(\mathbf {x} \right)$

(57)

is (statically) equivalent to that of the system

$\mathbf {D} {\dot {\mathbf {x} }}+\mathbf {K} \mathbf {x} =\mathbf {f} \left(\mathbf {x} \right)$

(58)

which can be seen as the previews for the case of zero density. The advantage of this equivalent system is that the inertia terms are always zero, consequently the system converges smoothly in time to its solution. This final solution is not affected by the particular choice of the damping, however in the author's experience, an effective choice is ${\textstyle \mathbf {D} =\beta \mathbf {M} }$ as proposed by [1].

Table (1) gives the details of the proposed solution procedure, making use of Newmark's integration scheme. The procedure described differs from a “real” dynamics simulation only on the choice of the damping and of the mass matrix. Any other choice is possible for the time integration scheme to be used. It is of interest to observe that the system described is highly dissipative, energy stability of the time integration scheme is therefore not crucial.

Table. 1 Pseudo–Static solution procedure

for pseudo–static strategy: calculate the constant matrices $D=\beta \mathbf {M} \,$ set ${\textstyle \mathbf {M} =0}$ after initializing the damping matrix. (if ${\textstyle \mathbf {M} }$ is not set to 0, “real” dynamic simulation can be performed) choose Newmark constants: a classical choice is $\delta ={\frac {1}{2}}\,;\,\alpha ={\frac {1}{4}}$ evaluate the constants $a_{0}={\frac {1}{\alpha \Delta t^{2}}}\,;\,a_{1}={\frac {\delta }{\alpha \Delta t}}\,;\,a_{2}={\frac {1}{\alpha \Delta t}}$ $a_{3}={\frac {1}{2\alpha }}-1\,;\,a_{4}={\frac {\delta }{\alpha }}-1\,;\,a_{5}={\frac {\Delta t}{2}}\left({\frac {\delta }{\alpha }}-2\right)$ predict the solution at time ${\textstyle t+\Delta t}$ using for example $\mathbf {x} _{t+\Delta t}^{0}=\mathbf {x} _{t}+{\dot {\mathbf {x} }}_{t}\Delta t$ ${\dot {\mathbf {x} }}_{t+\Delta t}={\dot {\mathbf {x} }}_{t}$ ${\ddot {\mathbf {x} }}_{t+\Delta t}=0$ iterate until convergence calculate the system's contributions $\left[\mathbf {K_{tan}^{dyn}} \right]=\left[\mathbf {K_{tan}} \right]+a_{0}\left[\mathbf {M} \right]+a_{1}\left[\mathbf {D} \right]$ $\left\{\mathbf {R^{dyn}} \right\}=\left\{\mathbf {R} \right\}-\left[\mathbf {M} \right]\left\{\mathbf {{\ddot {\mathbf {x} }}_{t+\Delta t}^{i}} \right\}-\left[\mathbf {D} \right]\left\{\mathbf {{\dot {\mathbf {x} }}_{t+\Delta t}^{i}} \right\}$ solve the system for the correction ${\textstyle \mathbf {dx} }$ update the results as $\mathbf {x} _{t+\Delta t}^{i+1}=\mathbf {x} _{t+\Delta t}^{i}+\mathbf {dx}$ $\Delta \mathbf {x} =\mathbf {x} _{t+\Delta t}^{i+1}-\mathbf {x} _{t}$ ${\dot {\mathbf {x} }}_{t+\Delta t}=a_{1}\Delta \mathbf {x} -a_{4}{\dot {\mathbf {x} }}_{t}-a_{5}{\ddot {\mathbf {x} }}_{t}$ ${\ddot {\mathbf {x} }}_{t+\Delta t}=a_{0}\Delta \mathbf {x} -a_{2}{\dot {\mathbf {x} }}_{t}-a_{3}{\ddot {\mathbf {x} }}_{t}$ go to next time step

3 Wrinkling Simulation

Given the lack of flexural stiffness, membrane systems are easily subjected to buckling in presence of any compressive load. The idea is that when a compressive stress tends to appear on a part of a structure, it is immediately removed by local instability phenomena, that manifest with the formation of little "waves" of direction perpendicular to the direction of stresses. Prediction of the size of those "waves" commonly called "wrinkles" is not generally possible as their disposition is somehow random and connected to initial imperfections. However their average size is strictly connected to the bending stiffness meaning in particular that for the problems of interest the wrinkle tend to become quite little in comparison with the total size of the structure. It has been proved to be feasible [3] and [4] to describe correctly the formation of the wrinkles using extensively mesh refinement procedures together with low order thin-shell elements. An analogous approach using higher order shells and a fixed reference mesh, joint with some comparison with experimental data can be found in [5]. A key point to be taken in account is that this procedures need a mesh density inversely proportional to the expected size of the wrinkles. In other words the smaller are the wrinkles, the more elements are needed to correctly describe the phenomena. As in our structures, the thickness is very low compared to the other dimensions, the referenced approaches would become soon too expensive.

An alternative procedure is based on the "enrichment" of the elements involved in the simulation. The idea is to renounce to a description of the single wrinkle and to focus the analysis of the average stress and displacement field. This allows to consider in the analysis elements of size bigger then the expected wrinkle size introducing the effect of the local instability in the calculation of the stress or strain field at integration point level. We would like to stress that this approach is not necessarily less "precise" than the former. Indeed no information on the wrinkling size is provided, however the global stress field is correctly described. It is as well important to highlight how the position of the wrinkles is never known given its strong dependence on the initial imperfections, therefore the only reliable result is the individuation of the "wrinkled zone" that can be correctly described by both methods.

3.1 Enriched material model

Over the years many different proposals to perform the element enrichment were presented. Mainly two different approaches survived, one based on manipulations of the gradient of deformations, the second connected with a redefinition of the constitutive model.

The former, proposed by Roddeman in [6] and [7], is based on the definition of an effective deformation gradient obtained superimposing to the normal displacement field a term connected with the formation of wrinkles. This modification allows to describe correctly the shortening of the average plane of the membrane in presence of compressive stresses.

The latter is based on a modification of the stress-strain relationship, meaning that the constitutive law is modified not to allow compressive stresses. The main advantage of this second techniques, is to make the implementation completely independent from the element used, characteristic that makes them very attractive for the practical implementation.

A "new" material model, based on the modification of a standard linear material is introduced in current section. This formulation is based on the penalization of the elastic characteristics of the material in the system of the principal stresses. In simple words, the material is softened in the direction of the compressive stresses and keeps its characteristics in the other direction. This is achieved by a two step procedure, based on a phase of assessment of the state of the membrane and on a phase of modification of the material tangent matrix.

Many different choices are theoretically possible in combining the two different phases, however in the writer experience, iterative application of the wrinkling correction inside the same time step leads generally to a very slow or unstable convergence behavior. The proposed solution procedure is therefore based on a “explicit” approach in the form

• standard pseudo–static solution step
• check state of each element
• modify material
• go to next “time” step

This procedure is very efficient as it takes full advantage of the pseudo–static solution procedure the only additional cost being linked to the evaluation of the state and to the penalization of the constitutive matrix. As during each time step the material is "constant", no additional source of non-linearity is introduced therefore the element retains its convergence properties. The stabilization of the stress-field is guaranteed by the dynamic process that, together with the stabilization introduced in the material model effectively damps out the oscillations.

The reader should note that the aim of the proposed technique is to get a reliable static solution. There is absolutely no guarantee that “on the way” to the static solution the wrinkling procedure converges inside each time step, however, when all the movement is dissipated so the structure reached the final configuration, wrinkling arrived to a constant solution.

Assessment of the state of the membrane

One of the crucial steps in the procedure is the evaluation of the state of the membrane. In particular it is necessary to “decide” if the membrane is (or rather should be) in biaxial tension, in uniaxial tension or completely unstressed because of the formation of wrinkles. The assessment procedure, is based on the introduction of the fictitious stress ${\textstyle \mathbf {\sigma } ^{*}}$ that represents the stress that would exist on the membrane if formation of the wrinkles was not allowed. This is related to the total stress from the relation

$\left[\mathbf {\sigma ^{*}} \right]=\left[\mathbf {D_{original}} \right]:\left\{\mathbf {E} \right\}$

(59)

the principal direction of ${\textstyle \mathbf {\sigma } ^{*}}$ can be calculated as

$c_{1}=\sigma _{11}^{*}+\sigma _{22}^{*}\,;\,c_{2}=\sigma _{11}^{*}-\sigma _{22}^{*}\,;\,c_{3}={\sqrt {({\frac {c_{2}}{2}})^{2}+(\sigma _{12}^{*})^{2}}}$ $\sigma _{I}^{*}=c_{1}+c_{2}\,;\,\sigma _{II}^{*}=c_{1}-c_{2}\,;\,\alpha ^{*}=tan^{-1}\left({\frac {2\sigma _{12}^{*}}{c_{2}}}\right)\,;\,$

(60)

by introducing the tensors

$\left[\mathbf {E} \right]={\begin{pmatrix}\epsilon _{11}&{\frac {\gamma _{12}}{2}}\\{\frac {\gamma _{12}}{2}}&\epsilon _{22}\end{pmatrix}}\,;\,\left\{\mathbf {n_{\sigma ^{*}}} \right\}={\begin{pmatrix}cos(\alpha ^{*})\\sin(\alpha ^{*})\end{pmatrix}}$

(61)

it is possible to express the strain corresponding to the principal stresses as

$\left\{\mathbf {\epsilon ^{*}} \right\}=\left\{\mathbf {n_{\sigma ^{*}}} \right\}^{T}\left[\mathbf {E} \right]\left\{\mathbf {n_{\sigma ^{*}}} \right\}$

(62)

this strains can be used together with the corresponding principal stresses in assessing the state of the membrane, using the so called “mixed criteria”. The “decision” proceeds as follows:

• ${\textstyle (\sigma _{II}^{*}>0)}$ biaxial tension ${\textstyle \rightarrow }$ "taut state"
• ${\textstyle (\sigma _{II}^{*}<0)}$ and ${\textstyle (\epsilon _{sigma_{I}}>0)}$ uniaxial tension ${\textstyle \rightarrow }$ "wrinkled state"
• otherwise (all compressed) ${\textstyle \rightarrow }$ "slack state"

Modification of the material

Once known the state, the material has to be modified to remove undesired compression. This is obtained by modifying the directions in which direction appears, basically removing the stiffness contribution in that direction. The procedure is distinguished for the various cases:

• “taut case”: the ${\textstyle \left[\mathbf {D_{tan}} \right]}$ is the original matrix as the whole membrane is in tension and acts with its whole stiffness
• “wrinkled state” in this case one direction has to be penalized leaving the other unchanged. Introducing the matrix

${\begin{array}{c}{c}c=cos(\alpha ^{*})\\s=sin(\alpha ^{*})\end{array}}\,;\,\left[\mathbf {R(\alpha ^{*})} \right]={\begin{pmatrix}c^{2}&s^{2}&-2sc\\s^{2}&c^{2}&2sc\\sc&-sc&c^{2}-s^{2}\end{pmatrix}}$

(63)

the penalization can be applied following the steps

1. ${\textstyle \left[\mathbf {D_{rotated}} \right]=\left[\mathbf {R[-\alpha ]} \right]\left[\mathbf {D_{original}} \right]\left[\mathbf {R[-\alpha ]^{T}} \right]}$
2. ${\textstyle \left[\mathbf {D_{modified}} \right]={\begin{pmatrix}D_{rot_{11}}&PD_{rot_{12}}&D_{rot_{13}}\\PD_{rot_{21}}&PD_{rot_{22}}&PD_{rot_{23}}\\D_{rot_{31}}&PD_{rot_{32}}&D_{rot_{33}}\\\end{pmatrix}}}$
3. ${\textstyle \left[\mathbf {D_{modified}} \right]=\left[\mathbf {R[\alpha ]} \right]\left[\mathbf {D_{modified}} \right]\left[\mathbf {R[\alpha ]} \right]^{T}}$

• “slack state” the membrane is compressed in all directions. No contribution to the stiffness should be provided, consequently the whole constitutive matrix can be penalized as ${\textstyle \left[\mathbf {D_{modified}} \right]=P\left[\mathbf {D_{modified}} \right]}$

This modification procedure guarantees that the stress ${\textstyle \left\{\mathbf {S} \right\}=\left[\mathbf {D_{modified}} \right]\left\{\mathbf {E} \right\}}$ presents no compression.

The penalty factor "${\textstyle P}$" plays a central role in the stability of the wrinkling procedure. The problem is that when some parts of the structure are softened in some direction the stress redistributes, often causing a cyclic change of state of other parts of the structure. The use of a constant penalty factor as proposed for example in [8], causes some parts of the structure to be basically switched on and off when they change of state. An improvement can be obtained through the definition of a variable penalty factor, which makes the transition smoother helping the convergence. Introducing the parameter ${\textstyle \sigma _{max}}$ that indicates the maximum tolerable compression, ${\textstyle P_{max}}$ as the max penalty factor and defining ${\textstyle P_{\sigma }={\frac {\sigma _{max}}{\sigma }}}$ a suitable formulation for the penalty parameter can be obtained as

$P_{\sigma }<P_{max}\rightarrow P=P_{sigma}\,;\,$

(64)

$P_{\sigma }<0orP_{\sigma }>1\rightarrow P=1.0$

(65)

stability can be further improved by taking in account the loading history of each element. This should be considered as a purely numerical artifice to minimize oscillations of the stress field and can be expressed as:

$if(State\equiv OldState)\rightarrow {\hbox{leave P unchanged}}$

$otherwise\rightarrow P=P_{old}*coeff$

it should be however checked that the modified value for P is allowable.

3.2 validation

A few examples are proposed in current subsection to validate the procedure presented. Given the nature of the problem, it is very difficult to obtain an analytical or experimental prove of the effectiveness of the procedure, validation is therefore based on a set of numerical experiments.

It has already been highlighted that a realistic representation of the wrinkling behavior can be obtained using a sufficiently high number of elements; simulation can therefore be performed on dense meshes, introducing initial imperfections to initialize the formation of the wrinkles. This way the compressive stresses are correctly removed, and the results obtained can be used in validating the proposed wrinkling procedure.

A few test examples are proposed here showing the results obtained with the proposed approach.

(a) Plot of Principal PK2 stresses	(b) deformed VS reference configuration
(c) Plot of Principal PK2 stresses	(d) deformed VS reference configuration
(e) Plot of Principal PK2 stresses	(f) deformed VS reference configuration
Figure 1: Inflated Circular Airbag

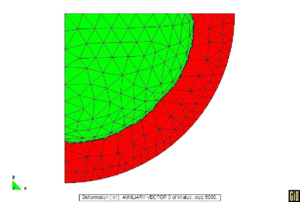
CIRCULAR AIRBAG: The circular airbag is probably one of the best examples to be used in testing the efficacy of the wrinkling procedure. The simulation proposed was carried using

$\rho =2700\left[{\frac {Kg}{m^{3}}}\right]\,;\,E=7000\left[{\frac {N}{mm^{3}}}\right]\,;\,\nu =0.3$

$Thickness=0.001\left[mm\right]\,;\,Radius=1000\left[mm\right]$

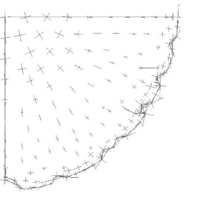
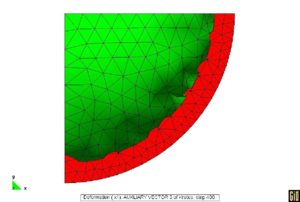
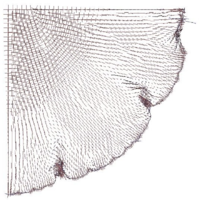
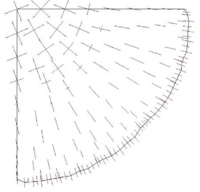
Symmetry boundary conditions were applied and the problem was evaluated with and without wrinkling algorithm. The same airbag was simulated using different meshes increasing progressively the mesh density. The results reported here refer to a coarse mesh of 236 elements and to a denser one of 4802 elements. For this example, a very dense mesh is needed to capture the formation of folds and wrinkles that eliminate the compression. Fig 1c and 1d suggests immediately how the formation of wrinkles and deep folds (larger wrinkles) correctly removes the compressive stresses. It is very relevant to highlight how the location of the folds changes in different simulations but their "distance" tends to be the same.

It can be easily checked how even different runs of the same structure with the same mesh can lead to different wrinkling patterns. The only realistic result is therefore the extension of the wrinkled zone.

The solution obtained on the coarse mesh without any improvement (see Fig. 1a,1b) is poor both in terms of stresses and displacements The introduction of the wrinkling correction allows to catch the correct behavior using a much coarser mesh. Considering the results on the dense mesh as the reference solution, Fig 1(e),1(f) clearly shows how a remarkable improvement is obtained both in terms of stresses and displacements using the wrinkling correction. Table 2 in particular highlights how the results of the analysis on the coarse mesh with the wrinkling correction are practically coincident to the reference solution confirming the efficacy of the approach.

Table. 2 Circular Airbag: Data sampled at center point

	Dense	Coarse No Correction	Coarse Corrected
Displacement: [m]	0.465	0.37	0.47
$S_{I}$: $\left[{\frac {N}{mm^{2}}}\right]$	9.55E7	11.2E7	9.51E7
$S_{II}$: $\left[{\frac {N}{mm^{2}}}\right]$	9.05E7	7.21E7	9.09E7

SHEAR TEST: A simple shear test is performed by imposing displacements on one side of a square membrane. The parameters used are the same as for the previews example. The dimension of the side is ${\textstyle 1000[mm]}$ and the imposed displacement is ${\textstyle 200[mm]}$. Two cases are considered the first (Fig. 2c, 2d) using the standard approach on a dense mesh, the second (Fig. 2a, 2b) applying the proposed correction on a coarser mesh. Local buckling is correctly reproduced by the first approach that is considered a representation of the "true" behavior of the membrane; this result is achieved imposing an initial imperfection in the form of a very small out-of-plane load. The formation of the tensile diagonal is correctly reproduced in the second simulation using the enriched material model. The improved procedure allows as well to describe correctly the deformed shape of the square (it can be easily checked that the “normal” solution has straight sides).

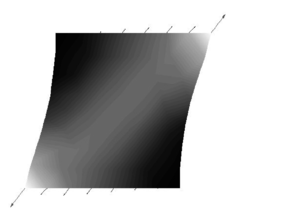
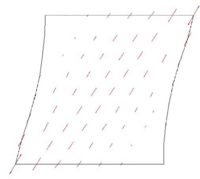
(a) Values of Principal PK2 Stresses	(b) Plot of Principal PK2 stresses
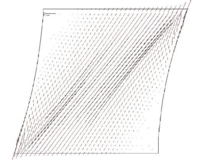
(c) Wrinkled configuration	(d) Plot of Principal PK2 stresses
Figure 2: quadrilatera under shear

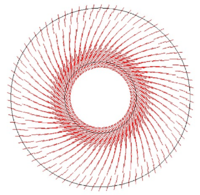
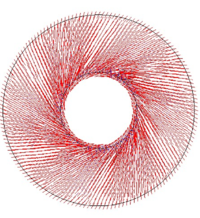
ANNULUS UNDER SHEAR: The last proposed example is an annulus under shear constituted by a thin membrane blocked by two rigid disks on the inner and outer boundaries. The inner disk is rotated by 10° counterclockwise causing the membrane to wrinkle. Fig 3(b) shows the results of the wrinkling procedure applied to a coarse mesh. Comparison with the reference results (Fig. 3d) shows excellent agreement in terms of principle PK2 stresses.

(a) Principal PK2 Stresses	(b) Values of First Principal PK2
(c) Principal PK2 Stresses	(d) Values of First Principal PK2
Figure 3: annulus subjected to torsion

4 Coupling issues - The case of the sails

Coupled fluid–membrane analysis is a challenging problem involving high non–linearities both on the side of the structure and of that of the fluid. The physical problem is however pretty clear: the membrane, is immersed in a fluid field. The presence of the structure influences the flow of the fluid, which exerts a force on the membrane. This force causes a deformation, changing the boundary conditions for the fluid flow and consequently the force exerted. Given the high flexibility of the structure, the coupling becomes strong.

This section addresses the coupled simulation of membrane systems, with particular reference to the “static” simulation of boat sails.

Figure 4: interaction of a genoa and a main sail - pressures at the end of the coupled analysis

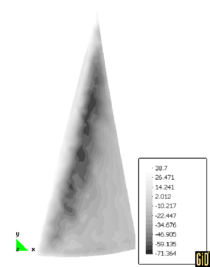
(a) genoa - leeward face	(b) genoa - windward face
Figure 5 pressure field on the genoa at the end of the coupled analysis

Before proceeding to the description of “our” method we should observe that sails are aerodynamic bodies which tend to a “stable” configuration with the fluid flow reaching a sort of steady state condition. The main engineering interest is therefore connected to the determination of this “final” configuration which represents a sort of “static solution” of the problem.

It is theoretically possible to deal with the coupled process using different strategies, including in particular “implicit (coupling) procedures” as proposed for example in [9] or “explicit” ones as described in [10]. Classical arguments in favor of one or of the other are connected to the numerical stability and computational efficiency of the different techniques. The traditional objection to the use of “explicit” ones is linked to the stringent requirements on the time step. Time step constraint for the stability of the coupling procedure is in fact normally more stringent than the one for the single-field solution. This strong requirement is connected to the lack of energy conservation at the interface between the various fields, which tends to introduce spurious energy contributions in the system.

It is however possible to observe that the pseudo–dynamic solution procedure presented in section  2 has very high dissipative properties and is perfectly suited for the research of coupled “static” solutions

The objection to the use of “explicit” coupling schemes is therefore no longer applicable as our artificial damping can easily remove any spurious energy contribution introduced by the couping process. Given this observation “explicit” procedures are much more efficient than the corresponding “implicit” ones as the single step is much cheaper. Table (3) proposes an efficient coupled solution strategy.

Fig. (4) presents the results of the coupled analysis of a genoa and main sail; a genoa alone is presented in Fig (5) The results obtained by this approach are presented in Fig. (4) in application to the simulation of a genoa and main sail.

Table. 3 “pseudo–static” coupling procedure

Predict Structural Solution Deform the mesh of the fluid domain According the predicted shape of the structure (variables needed for ALE formulation of the fluid should be calculated). The mesh–movement should keep the quality of the mesh, minimizing the deformation of the elements close to the structure, see [11] Advance in time the fluid on the deformed mesh transfer stresses FROM the fluid boundary TO the structural Boundary (stresses can be transferred as calculated) Advance the structure in using the pseudo–static solution technique proceed to next time step

References

[1] R.L. Taylor. (2001) "Finite Element Analysis of membrane structures". CIMNE

[2] R. Rossi. (2003) "A finite element formulation for 3D membrane structures including a wrinkling modified material model". CIMNE 226

[3] Cirak F., Ortiz M., Schroeder P. (2000) "Subdivision Surfaces: a new paradigm for thin shell finite element analysis", Volume 47. IJNME 2039–2072

[4] Cirak F., Ortiz M. (2001) "Fully C1 conforming subdivision elements for finite deformation thin shell analysis", Volume 51. IJNME 813–833

[5] Wong Y.W, Pellegrino S. (2002) "Computation of Wrinkling Amplitudes in Thin Membranes". 43rd AIAA/ASME/ASCE/AHS/ASC conference

[6] Roddeman D.G., Drukker J. et al. (1987) "The wrinkling of Thin Membranes: Part 1 - Theory", Volume 54. Journal of Applied Mechanics 884–887

[7] Roddeman D.G., Drukker J. et al. (1987) "The wrinkling of Thin Membranes: Part 2 - Numerical Analysis", Volume 54. Journal of Applied Mechanics 888-892

[8] Liu X., Jenkins C. Schur W. (2001) "Large deflecion Analysis of pneumatic envelopes using a penalty parametr modified material model", Volume 37. Finite Elements in Analysis and Design 233–251

[9] D.P. Mok, W.A. Wall. (2001) "Partitioned Analysis Schemes for the transient interaction of incompressible flows and nonlinear flexible structures". trends in computational structural mechanics

[10] S.Piperno, C.Farhat, B. Larroutorou. (1995) "Partitioned Procedures for the transient solution of coupled aeroelastic problems - Part2 - energy transfer analysis and three dimensional applications", Volume 124. Computer Methods in Applied Mechanics and Engineering 79-112

[11] E. Onate, J. Garcia, G.Bugeda, S.R. Idelsohn. (2002) "A general Stabilized formulation for incompressible fluid flow using Finite Calculus and the Finite Element method". Towards a New Fluid Dynamics with its challenges in Aeronautics