Automated in situ consolidation process for pre-impregnated carbon fibers: a cyber physical approach

1 Introduction

The concept of Cyber-Physical Systems (CPS) is related to machines involving integration of computation and control system by stablishing communication among them; this makes part of the fourth industrial revolution also knows as Industry 4.0, where the physical model of the process is used in a cyber-space to simulate scenarios using the sensors data [1], [2].

Consequently, the use of networked machines and sensors generates a high volume of data. This data can be used to develop intelligent systems, capable to give a more accurate response against production situations and at the same time, saving time and energy. This data volume has to be properly managed, applying a Big Data environment in order to bring intelligence to the shop floor [3], [4].

Considering the concept of Internet of Things (IoT) and the new Industrial Internet of Things (IIoT) [5], the communication protocol used in the CPS, the communications are not limited only to the company network. All the data, or some of it, can be available over a cloud, giving space to develop Enterprise Resources Planning (ERP) methodologies, and Manufacturing Execution Systems (MES) among others, making intelligent production systems[4].

An important part of the CPS, is the model employed in the computation system, which has to reflect, as good as possible, the physical system using mathematical methods, to help reduce costs and shorten development [6]. The growing of this industry 4.0 section is due to the increase of products and systems complexity. This represents a challenge when taking into account different phenomena into the same process, leading to a high non linearity level, requiring more advanced mathematical techniques to solve the problem, demanding not only more efficient algorithms but also good simulation and communication equipment[5], [7].

This paper focuses on the simulation of an in situ consolidation machine, for unidirectional carbon fibers pre impregnated with polyamide 6, presenting the simulation equations and a proposed communication dataflow for operation optimization. The objective is to optimize three operation parameters of the machine as a function of the desired heating temperature of the material.

First, the mechanical system is described, focusing on the machine head that will be the mechanism to handle the actuators and controllers. It follows with the presentation of the mathematical model used in this simulation, making emphasis in the fact of the radiation phenomena being nonlinear; causing that the solution of the equation system has to be in its explicit form to avoid iterating in each time step but, increasing the required simulation time.

The next section presented in this paper is the Artificial Bee Colony (ABC) algorithm; used to perform simulations of different working scenarios and taking the decisions for the operation parameters value.

As the entire system is going to be completely simulated, a communication protocol is proposed, to guarantee the safe data transmission and being a fully customizable protocol without losing any standardization. This means, that this work focuses in the mathematical model used in the cybernetic part of the CPS.

In addition, the simulations parameters and the physical properties for the composite are presented, as well as the optimization restrictions corresponding on the physical values of the machine.

The results of the simulation are presented in their evolution over the number of iterations needed in order to converge.

2 System description

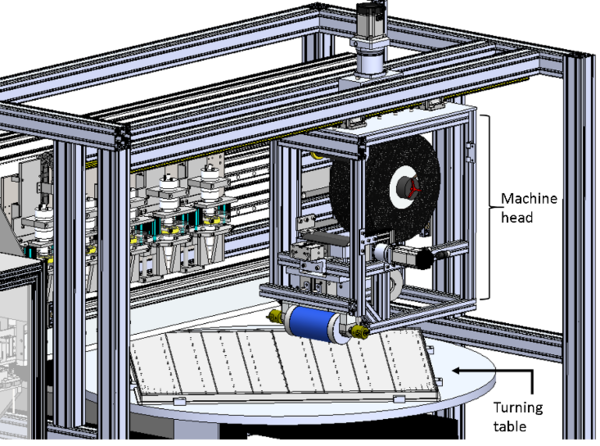
The in situ consolidation process that will be performed by this machine, consists on placing pre impregnated carbon fibers tapes in top of a turning table, see Figure 1, in order to create a composite blank, of a desired dimension and fiber orientation, to be stamped in a following process. Those tapes come in a width of 100 mm, a thickness of 5 mm and a variable length, from 30 meters to 100 meters.

Figure 1. CAD model overview of the machine, showing the in situ consolidation machine head and the turntable.

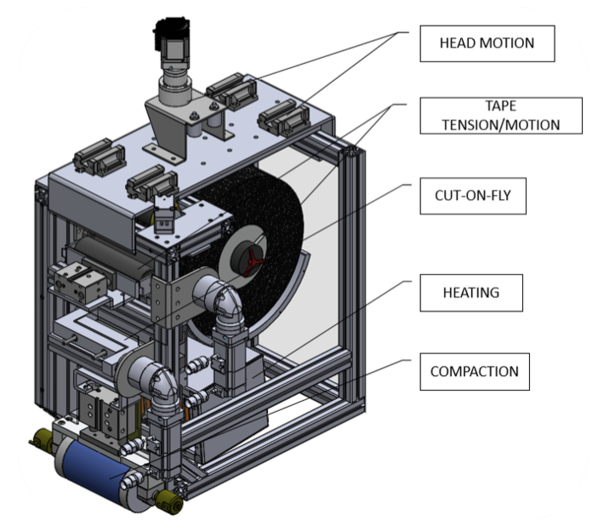
One of the main components is the tape feeder, which continuously unroll the material into a heating zone; this unroll mechanism has a tensioner system to keep the tape from wrinkling and to automatically feed new material after the blades cut the desired tape length.

Another relevant component is the ceramic heater used to raise the tape temperature. This temperature is relevant to ensure that the material matrix melts, without making any damage, to ensure that the new deployed material adheres to the already deployed one, or in the case of being the first layer, it adheres to the turning table.

The cooling roll is other relevant element in the system, it has two objectives, to lower the tape temperature solidifying the tape matrix and apply force (compaction), regulated by the pressure in its pneumatic cylinder actuator, ensuring that the material welds to the previous layer, or the turning table in the case of the first layer, seeFigure 2.

Figure 2. CAD overview of the machine head.

2.1 Heating element

To heat up the material, a ceramic heater is used due to the high temperatures its surface can reach in a short period; also, they are easily controllable using an ON/OFF strategy to regulate the temperature.

For most cases, the ceramic heater has a white surface finish, meaning that it covers the emission of a wide wavelength range, making them a general-purpose heating element. When the material optimal wavelength value is known, the surface color may change to adapt it to that particular wavelength emission. For this case, a general-purpose white heater element is used.

2.2 Cooling roller

The cooling process uses a cooling roller, in which interior circulates a cold fluid, in this case water, to ensure a constant temperature of its surface and at the same time, the roller compacts the new material layer against the previous one to weld the layers.

2.3 Control system

The temperature is a crucial parameter; the desired value has to be reached without any overshoot because it could cause material damages, in this case for the composite matrix. For that reason, an independent local temperature controller is used.

In the other hand, there are machine parameters such as material speed and heater position relative to the material surface, which can be defined in order to maximize the material velocity through the heating zone while maintaining the desired temperature; this allows a minimization of the process time without any other type of controller

In order to determine those parameter values, an algorithm runs in a server dedicated to perform optimization simulations according to the desired temperature, the material thickness, width and thermal characteristics of the tape being used. All those characteristics are sent to the optimization system and the results are sent back to the machine head controller to be applied.

3 Mathematical model

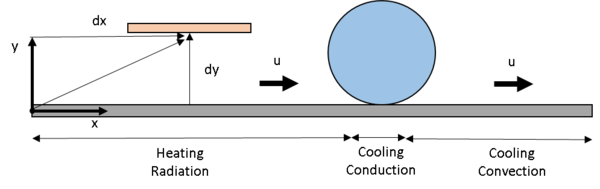
To model the process, the two dimensional heat diffusion equation is solved using finite differences in its explicit mode due to the high non linearity of the heating process, in this case radiation, involved. This model allows knowing the temperature profile along the tape, taking into account the radiation of the heating element, the cooling effect of the roller and the cooling effect due to the natural convection relative to the ambient temperature.

The three zones to simulate are shown in Figure 3 as: Heating Radiation, Cooling Conduction, and Cooling Convection.

Figure 3. Zones to simulate the temperature profile.

3.1 Main equation

The main equation is shown in (1), representing the general diffusion equation with a transport term in the ${\textstyle x}$ direction as presented in Figure 3.

${\textstyle {\frac {\partial T}{\partial t}}+U{\frac {\partial T}{\partial x}}=}$$\,{\propto }_{x}{\frac {{\partial }^{2}T}{{\partial x}^{2}}}+\,{\propto }_{y}{\frac {{\partial }^{2}T}{{\partial y}^{2}}}$

(1)

Where ${\textstyle U}$ stands for the material speed, ${\textstyle {\propto }_{x}}$ and ${\textstyle {\propto }_{y}}$ stands for the diffusion term in each direction according to the reference system shown in Figure 3.

3.1.1 Heating Radiation zone equation

For the heating zone, the energy source is the ceramic heater which, for simplicity of the model, its surface emits radiation in all directions as a white body. The equation used for this zone is shown in (2).

${\textstyle {q}_{radiation}=\,\,\sum _{}^{}{F}_{ij}\,\epsilon \,\sigma \,\,\left({T}_{i}^{4}-\,{T}_{j}^{4}\right)}$

(2)

Where the view factor term ${\textstyle {F}_{ij}}$ can be calculated using the expression in (3) for two parallel surfaces as shown in Figure 4. Where the subscript ${\textstyle i}$ stands for the heating element and ${\textstyle j}$ stands for the material element.

${\textstyle {F}_{ij}=\,{\frac {{\left({y}_{i}-\,{y}_{j}\right)}^{2}{Area}_{i}}{\pi \,{\sqrt {{\left({y}_{i}-\,{y}_{j}\right)}^{2}}}+\,{\left({x}_{i}-\,{x}_{j}\right)}^{2}}}}$ (3) ${\textstyle \,[[Image:Draft_{C}ompuestos_{1}19103723-image8.png|600px]]}$

Figure 4. Heater and Material discretization for the View Factor calculation.

3.1.2 Cooling Conduction zone.

To model the cooling zone, the heat transfer is calculated as conduction between two materials using the expression in (4) and the contact resistance between them, shown in equation (5).

${\textstyle {q}_{conduction}=\,{\frac {{T}_{surface\,1}-\,{T}_{surface\,2}}{{R}_{contact}}}}$

(4)

${\textstyle {R}_{contact}=\,{\frac {1}{{\frac {\Delta y}{2{\,k}_{cylinder}}}+{\frac {\Delta y}{2{\,k}_{material}}}\,}}}$

(5)

Where the cylinder conduction ${\textstyle {k}_{cylinder}}$ is a known parameter as well as the material conduction ${\textstyle {k}_{material}}$.

3.1.3 Cooling Convection zone.

The last zone is model as cooling by natural convection due to the air temperature using the expression in (6).

${\textstyle {q}_{convection}=h\,Area\,({T}_{\infty }-{T}_{material})}$

(6)

4 Optimization model

The optimization strategy to implement in this case will be the Artificial Bee Colony. This methodology was selected because does not need to work with functions derivatives, managing multidimensional problems [8], and is more likely to avoid local minimum by exploring the surroundings of a possible minimum and to compare values between several reached minimum situations and discard the worst scenarios while keeping the best ones and continue to explore for better ones [9].

This method was conceived to simulate the behavior of a honeybee swarm in search of honey sources, exploring the surroundings and giving information to other bees about the discovered honey source. The algorithm, colony, consists on three groups of bees [9][10][8][11]:

• Employed bees.

• Onlooker bees.

• Scout bees.

This method is usually employed in its unconstrained variation, this means, that all the variables involved could get any value. The constrained variation of this method employs the expression shown in (7) to accommodate all the variables to a confined space of values that makes sense for the physical system.

${\textstyle {x}_{ij}=\,{x}_{min,j}+rand\left[0,1\right]\left({x}_{max,j}-\right.}$$\left.{x}_{min,j}\right)$

(7)

The general idea of the method is that one employed bee is assigned to a food source so, lets define ${\textstyle SN}$ as the number of employed bees/food sources and define ${\textstyle D}$ as the dimensions of those food sources, this means, the amount of parameters involved on that source. These bees use the equation presented in (7) to define those parameters.

4.1 Employed bees

After the values are defined, the employed bees apply a greedy selection of their variables by perturb them using the expression presented in (8).

${\textstyle {v}_{ij}=\,{x}_{ij}+rand\left[-1,+1\right]\left({x}_{ij}-\right.}$$\left.\,{x}_{kj}\right)$

(8)

Where ${\textstyle j\,\in \,\left\{1,\,2,\,\ldots ,\,D\right\}}$ and ${\textstyle k\,\in \,\left\{1,\,2,\,\ldots ,\,D\right\}}$ and the random value is a scaling factor; it is mandatory that ${\textstyle k\,\not =j}$. The fitness of the new solution (the perturbed one) is also evaluated and a greedy selection is performed by choosing the food source out of the two.

4.1.1 Fitness equation

The fitness equation, for the minimization case, is presented in (9), where ${\textstyle {f}_{i}}$ is the quality of an individual source.

${\textstyle {fit}_{i}=\,\left\{{\begin{matrix}{\frac {1}{1+\,{f}_{i}}}&\left({f}_{i}\,\geq 0\right)\\1+\,\left|{f}_{i}\right|&\left({f}_{i}<0\right)\end{matrix}}\right.}$

(9)

4.2 Onlooker bees

The main objective of an onlooker bee is to select a food source (solution) based on a probability value of the source fitness given by the expression presented in (10).

${\textstyle {P}_{i}=\,{\frac {{fit}_{i}}{\sum _{n=1}^{SN}{fit}_{n}}}}$

(10)

The selection is made by comparing ${\textstyle {P}_{i}}$ against a random number, between [0,1], and the selection is approved if the calculated ${\textstyle {P}_{i}}$ value is greater than or equal to this random number. After an onlooker bee is assigned to a food source, it will perturb its source using the expression presented in (8) and perform a greedy selection.

4.3 Scouts bees

The task for the scouts bees is to find a new solution for those Employed bees, which did not pass the fitness test, expression (10), in order to assign new food sources to them and continue to explore for other solutions, using the expression (7).

4.4 Objective function

The Objective Function (OF) for this case, requires that the temperature of the material will not exceed a desired value and the process speed has to be has high as possible, according to the system capabilities. The OF to take into account is presented in (11).

${\textstyle OF=\,{\left({\overline {T}}-\,{T}^{\ast }\right)}^{2}\,K-}$$U$

(11)

Where ${\textstyle {\overline {T}}}$ stands for the desire material temperature, ${\textstyle {T}^{\ast }}$ stands for the maximum material temperature inside the Heating Radiation zone and ${\textstyle U}$ is the material speed. The term ${\textstyle K}$ is a penalty to the temperatures that adjusts the temperature values to a similar proportional magnitude as the speed in order for the mathematical operation to make any sense due to their physical units.

5 Communication strategy

5.1 Open Platform Communication Unified Architecture (OPC UA).

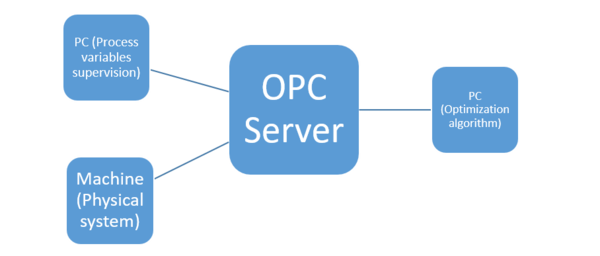
Open Platform Communication Unified Architecture is a data exchange standard (IEC 62541) widely used in industrial communication, offering a concept of secure data transfer and a multiplatform interconnection. This means that different equipment, such as an industrial Programmable Logic Controller (PLC), a Raspberry Pi based computer or a common Personal Computer, could have an OPC UA client to exchange data [4].

One important advantage is the that OPC UA protocols are implemented, among others, in the Python Programming Language, an Open Source language that allows to create custom OPC Servers and OPC Clients[12].

The communication architecture for the system is shown in Figure 5.

Figure 5. Communication architecture using the OPC protocol over Ethernet.

6 Simulation parameters

In order to simulate the material and the heating system, the necessary values, thermo-physical and geometric, are defined in order to solve the equations.

6.1 Composite

The physical properties of the pre impregnated carbon fibers used in this simulation are shown in Table 1.

Table 1. Physical properties of the pre impregnated composite[13]

Property	Value	Units
$\rho$	1400	${\frac {kg}{{m}^{3}}}$
${C}_{p}$	935	${\frac {J}{kg\,K}}$
${k}_{material}$	11.1	${\frac {W}{m\,K}}$
$\epsilon$	0.7

In addition, the geometric parameters are presented in Table 2

Table 2. Geometric parameters values

Parameter	Value	Units
${lenght}_{x\,axis}$	1	$m$
${lenght}_{y\,axis}$	0.005	$m$
${lenght}_{z\,axis}$	0.200	$m$

Other parameters relevant to the simulation are presented in Table 3.

Table 3. Additional parameters for the simulation

Property	Value	Units
Air convection coefficient ${\textstyle h}$	140	${\frac {W}{{m}^{2}\,K}}$
Cylinder conduction coefficient ${\textstyle {k}_{cylinder}}$	62.3	${\frac {W}{m\,K}}$

6.2 Parameters for the optimization simulation

In order to run the optimization algorithm, some parameters have to be defined. One of them is de desired temperature, set in this case as 260 ºC (533,15 ºK).

The initial onlooker bees are defined using a random function, but for repeatability purposes, the seed of the random function is fixed, so the entire simulation can be done again. In

Table 4 are presented those parameters.

Table 4. Optimization algorithm parameters

Parameter	Value
Number of bees	10
Number of iterations	100
Random seed 1	1530
Random seed 2	3060
Random seed 3	6120
Random seed 4	12240
Random seed 5	24480
Random seed 6	48960
Random seed 7	97920
Random seed 8	195840

The other parameters set to be defined are referenced to the test function, which are the resistance position and material speed limits. Those parameters are presented in Table 5.

Table 5. Optimization Test Function parameters

Parameter	Minimum value	Maximum value	Units
Resistance x position	0.1	0.26	$m$
Resistance y position	0.15	0.25	$m$
Material speed	0.01	0.05	${\frac {m}{s}}$

7 Results

The optimization algorithm performed 10 simulations, to have an overview of the possible local minimum, by starting the simulation from 10 different starting points’ combinations.

For stability issues in the explicit method and for simulation speed, in Table 6 are presented the parameters used in all the simulations.

Table 6. Explicit method parameters for stability

Parameter	Value	Units
Time step	0.01	$seconds$
Dimensional step	0.004975	$m$

7.1 Optimization algorithm results

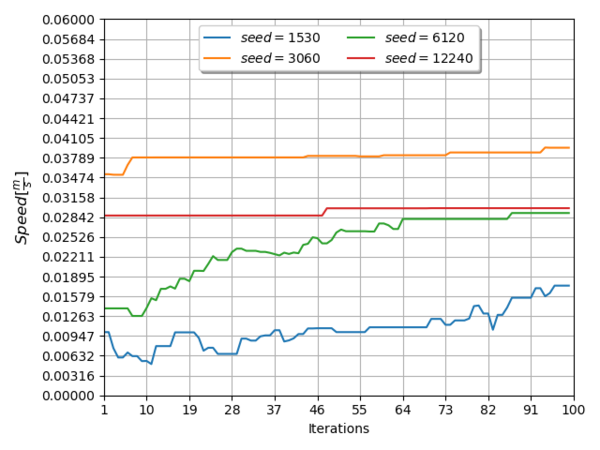
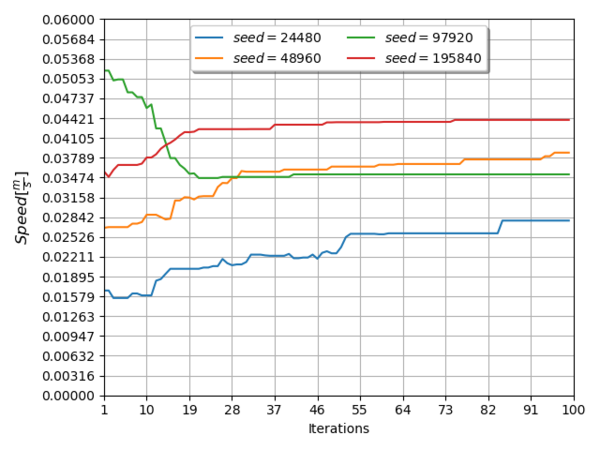
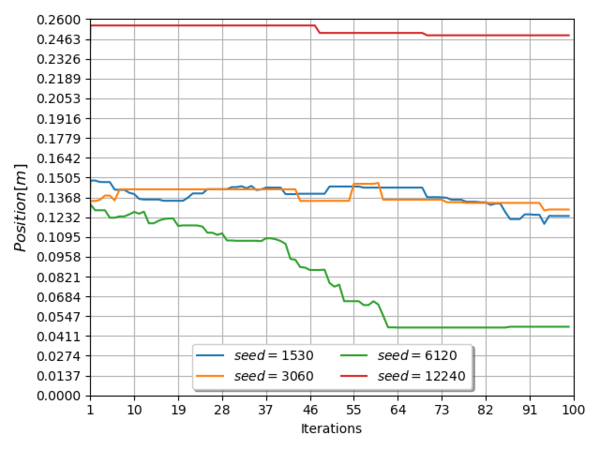
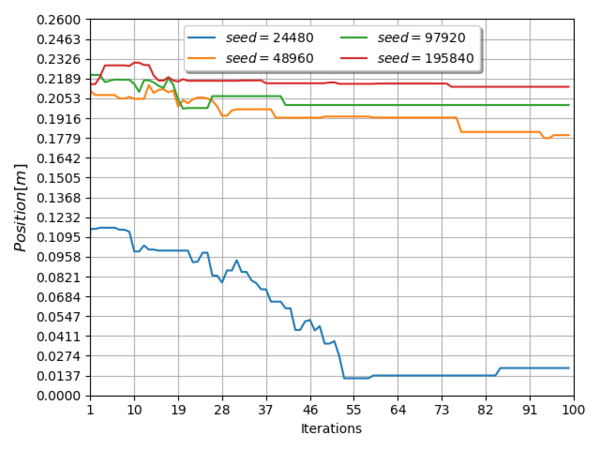
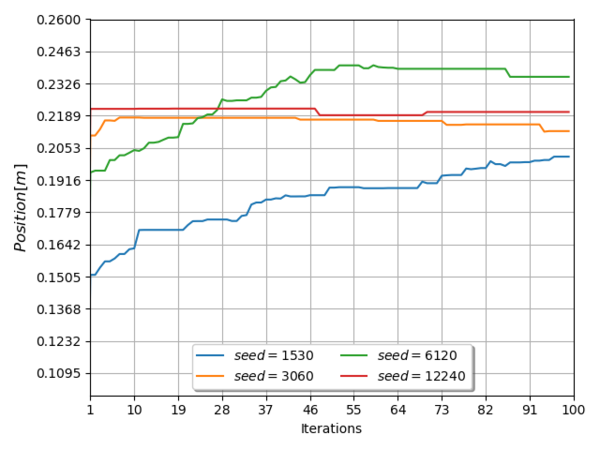
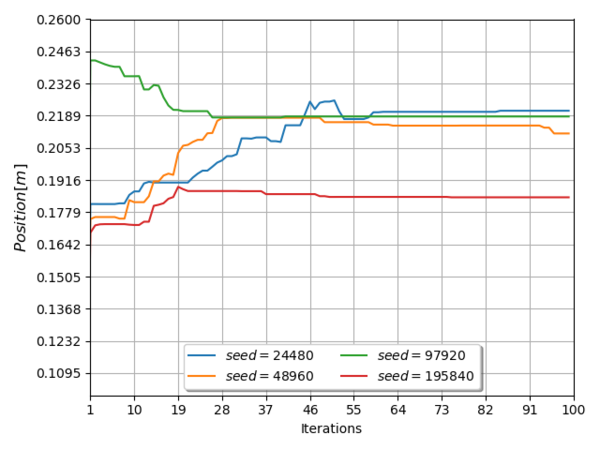
The process variables converged to a range of values presented in Table 7, and the evolution of them, along the entire simulation iterations, cab be seen in Figure 6 and Figure 7 for the speed parameter, in Figure 8 and Figure 9 for the heater x position and in Figure 10 and Figure 11 for the heater y position.

Table 7. Simulation optimized parameters

Parameter	Value minimum	Value maximum	Units
Speed	0.0175	0.0439	${\frac {m}{s}}$
Heater x position	0.01889	0.2489	$m$
Heater y position	0.1842	0.2355	$m$

The converge values for all the simulations seeds are shown in Table 8.

Table 8. Parameters convergence values for all the optimization seeds

Seed	Parameter	Value	Units
1530	Speed	0.0175	${\frac {m}{s}}$
	X Position	0.1240	$m$
	Y Position	0.2015	$m$
3060	Speed	0.0395	${\frac {m}{s}}$
	X Position	0.1285	$m$
	Y Position	0.2124	$m$
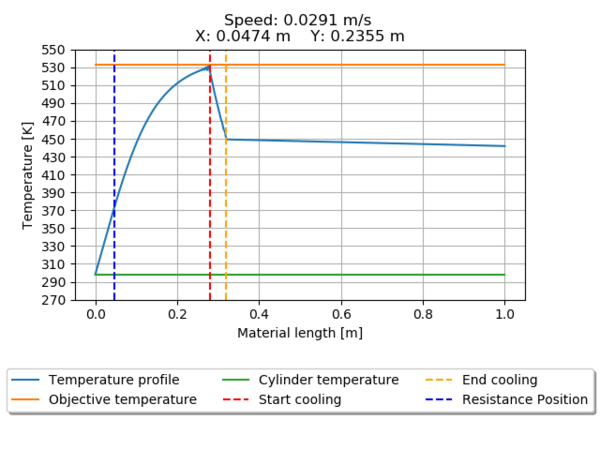
6120	Speed	0.0291	${\frac {m}{s}}$
	X Position	0.0474	$m$
	Y Position	0.2355	$m$
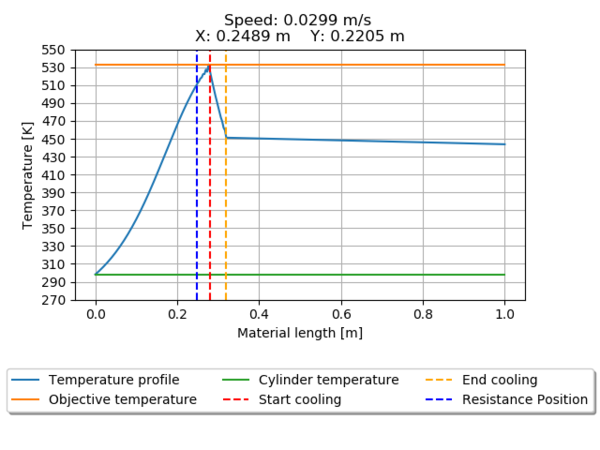
12240	Speed	0.0299	${\frac {m}{s}}$
	X Position	0.2489	$m$
	Y Position	0.2205	$m$
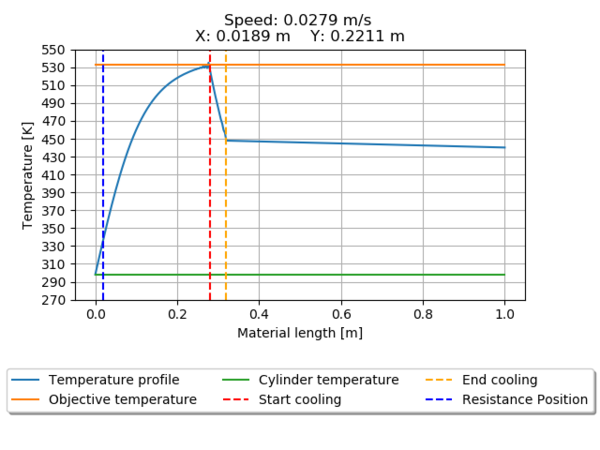
24480	Speed	0.0279	${\frac {m}{s}}$
	X Position	0.0189	$m$
	Y Position	0.2211	$m$
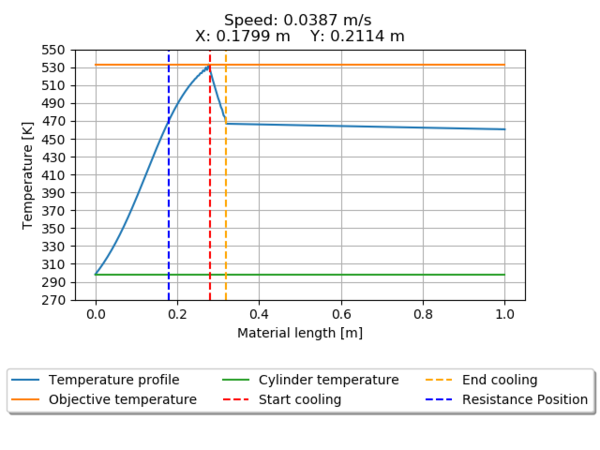
48960	Speed	0.0387	${\frac {m}{s}}$
	X Position	0.1799	$m$
	Y Position	0.2114	$m$
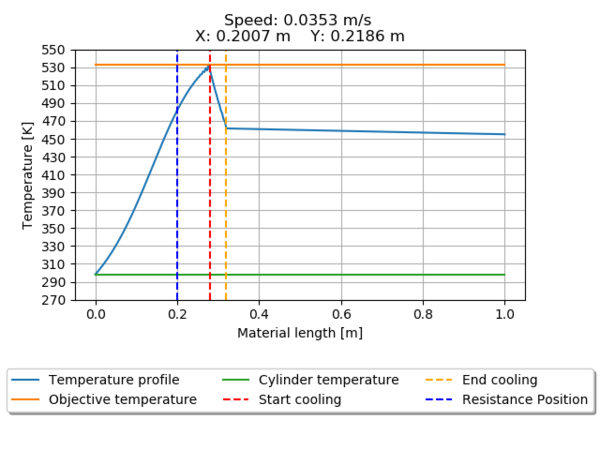
97920	Speed	0.0353	${\frac {m}{s}}$
	X Position	0.2007	$m$
	Y Position	0.2186	$m$
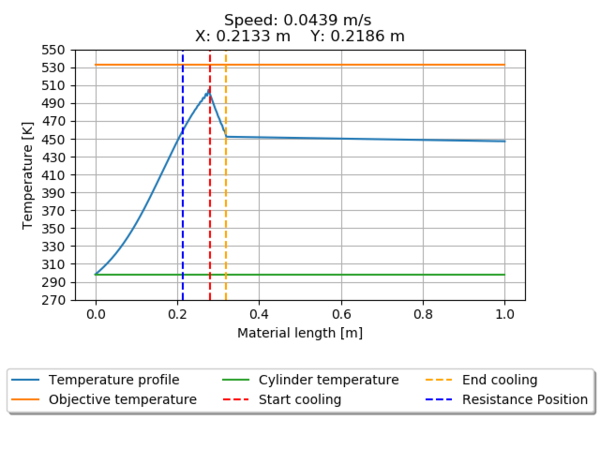
195840	Speed	0.0439	${\frac {m}{s}}$
	X Position	0.2133	$m$
	Y Position	0.2186	$m$

From Figure 6 through Figure 11, it can be seen that inside the variable domain exists more than one local minima, this means that the final decision is based on the minimum value for the objective function, presented in expression (11).

Figure 6. Speed parameter evolution for the first four seeds.

Figure 7. Speed parameter evolution for the last four seeds.

Figure 8. X position parameter evolution for the first four seeds.

Figure 9. X position parameter evolution for the last four seeds.

Figure 10. Y position parameter evolution for the first four seeds.

Figure 11. Y position parameter evolution for the last four seeds.

7.1.1 Objective function results

In order to select the best suitable parameters for the heater position and material speed, the lower objective function value is the indicator for the parameter combination selection. In Table 9 are presented the values of the objective function for the profile temperature stabilization.

Table 9. Objective function value for all the seeds tested

Seed	Objective function value
1530	19.3582
3060	-0.03829
6120	-0.02889
12240	-0.02986
24480	0.01594
48960	-0.03820
97920	-0.03475
195840	7.95567

7.2 Temperature profile simulation

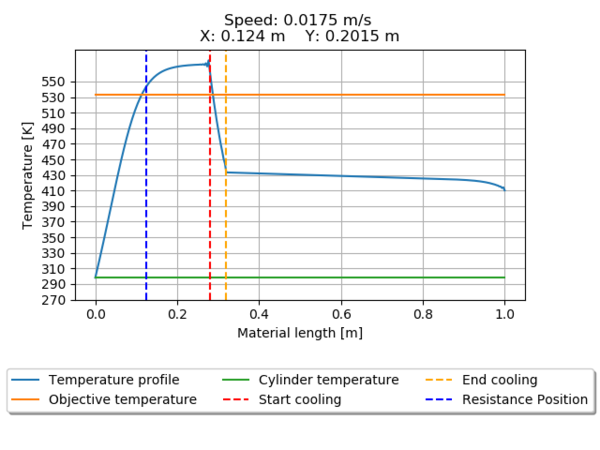
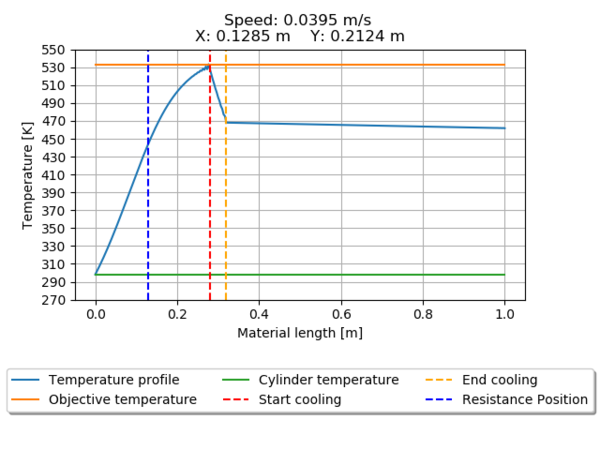
The temperature profile for all the seeds is presented from Figure 12 through Figure 19. Pointing the heater position relative to the beginning of the material entrance and the position of the cooling cylinder.

Seeds 1350 (Figure 12) and 195840 (Figure 19) does not meet the requirements of reaching the desired temperature, the first one over passes the value, leading to material damages, and the second one only reaches 96% of the desired temperature.

The optimal working parameters for the mechanical system are the ones produced by the second seed (3060), because has the lower objective function value and also the higher material speed without passing the desired temperature, minimizing the process time.

Figure 12. Temperature profile for seed 1530.

Figure 13. Temperature profile for seed 3060.

Figure 14. Temperature profile for seed 6120.

Figure 15. Temperature profile for seed 12240.

Figure 16. Temperature profile for seed 24480.

Figure 17. Temperature profile for seed 48960.

Figure 18. Temperature profile for seed 97920.

Figure 19. Temperature profile for seed 195840.

8 Conclusions

This work uses, in appropriate way, the concepts and tools linked with the fourth industrial revolution, which has developed a wide field of study, such as the Internet of Things (IoT), the Industrial Internet of Things (IIoT), Cyber-Physical Systems (CPS), and Information and Communication Technology (ICT), and this let to enhance the processes performance of automated systems.

This work focused on the field of CPS for an in situ consolidation machine, which handles pre impregnated material, in this case unidirectional carbon fibers tapes with polyamide 6, in order to create composite laminates. The physical model obtained, involved an unwinding system that feeds the tape into a turning table through a pressing mechanism, which has a radiation heater before and refrigeration during and after the presser, which proved to guarantee the composite temperature.

The objective of modelling and simulate the heating process before, during and after the pressing mechanism, is to allow to feed an optimization algorithm in order to calculate, within its boundaries, the optimal working parameters such as heater relative position to the material and the process speed; taking into account the temperatures of the tape, to avoid overheating and to improve the process time.

Having the optimal working parameters, makes that the heater own controller to perform minor corrections to the heating power, allowing a faster response avoiding undesired material temperatures.

The CPS proved that can handle different working scenarios and by learning during the consolidations process, improves the overall result, without the need of fully or partially reprogram the code, which is a main characteristic of the CPS.

Acnowldege

"This project has received funding from the European Union's Horizon 2020 research and innovation program under grant agreement No 768710".

“Authors gratefully acknowledge the funding of Project NORTE-01-0145-FEDER-000022 - SciTech - Science and Technology for Competitive and Sustainable Industries, cofinanced by Programa Operacional Regional do Norte (NORTE2020), through Fundo Europeu de Desenvolvimento Regional (FEDER).”

References

[1] B. Bagheri, S. Yang, H. A. Kao, and J. Lee, “Cyber-physical Systems Architecture for Self-Aware Machines in Industry 4.0 Environment,” IFAC-PapersOnLine, vol. 48, no. 3, pp. 1622–1627, Jan. 2015.

[2] J. Lee, B. Bagheri, and H. A. Kao, “A Cyber-Physical Systems architecture for Industry 4.0-based manufacturing systems,” Manuf. Lett., vol. 3, pp. 18–23, Jan. 2015.

[3] H. Meissner, R. Ilsen, and J. C. Aurich, “Analysis of Control Architectures in the Context of Industry 4.0,” in Procedia CIRP, 2017, vol. 62, pp. 165–169.

[4] M. Muller, E. Wings, and L. Bergmann, “Developing open source cyber-physical systems for service-oriented architectures using OPC UA,” Proc. - 2017 IEEE 15th Int. Conf. Ind. Informatics, INDIN 2017, pp. 83–88, 2017.

[5] F. Zezulka, P. Marcon, Z. Bradac, J. Arm, T. Benesl, and I. Vesely, “Communication Systems for Industry 4.0 and the IIoT,” IFAC-PapersOnLine, vol. 51, no. 6, pp. 150–155, Jan. 2018.

[6] B. Rodič, “Industry 4.0 and the New Simulation Modelling Paradigm,” Organizacija, vol. 50, no. 3, pp. 193–207, 2017.

[7] P. Palensky, E. Widl, and A. Elsheikh, “Simulating Cyber-Physical Energy Systems: Challenges, Tools and Methods,” IEEE Trans. Syst. Man, Cybern. Syst., vol. 44, no. 3, pp. 318–326, 2014.

[8] J. Krause, J. Cordeiro, R. S. Parpinelli, and H. S. A. Lopes, “A Survey of Swarm Algorithms Applied to Discrete Optimization Problems,” in Swarm Intelligence and Bio-Inspired Computation, Elsevier, 2013, pp. 169–191.

[9] A. Beatriz and D. S. Serapião, “Fundamentos de otimização por inteligência de enxames: uma visão geral,” vol. 20, no. 3, pp. 271–304, 2009.

[10] B. Nozohour-leilabady and B. Fazelabdolabadi, “On the application of artificial bee colony (ABC) algorithm for optimization of well placements in fractured reservoirs; efficiency comparison with the particle swarm optimization (PSO) methodology,” Petroleum, vol. 2, no. 1, pp. 79–89, Mar. 2016.

[11] G. Lindfield and J. Penny, “Artificial Bee and Ant Colony Optimization,” in Introduction to Nature-Inspired Optimization, Academic Press, 2017, pp. 119–140.

[12] V. Jirkovsky, P. Kadera, and M. Obitko, “OPC UA Realization of Cloud Cyber-Physical System,” Proc. - IEEE 16th Int. Conf. Ind. Informatics, INDIN 2018, pp. 115–120, 2018.

[13] F. P. INCROPERA, DAVID P. DEWITT, T. L. BERGMAN, and A. S. LAVINE, Fundamentals of Heat and Mass Transfer, Sixth Edit. Danvers, 2007.