Resumen
Introducción
En pacientes con estenosis carotídeas sintomáticas moderadas o asintomáticas severas, antes de realizar una endarterectomía se recomienda hacer un estudio detallado en que se incluya el mayor número posible de parámetros morfológicos y hemodinámicos.
Este trabajo analiza el efecto que la localización y la forma de la estenosis tienen sobre la distribución de las tensiones de cizallamiento y su repercusión en el diagnóstico clínico en estos casos.
Materiales y métodos
Se genera el modelo de la zona objeto de estudio y se realiza la simulación numérica. Se determinan las tensiones de cizallamiento, el índice de oscilación y el tiempo de exposición a dichas tensiones, y se analiza el riesgo de embolización o de crecimiento de la placa arterial. Se aplica la metodología a 3 carótidas idealizadas con diferente localización y pendiente de la estenosis y a un caso clínico.
Resultados
Para las carótidas idealizadas, se obtiene que la estenosis cercana a la bifurcación presenta un riesgo de embolización superior a la más alejada y tanto más riesgo cuanto más pendiente tiene la estenosis. Para el caso clínico, los resultados indican un riesgo alto de embolización por rotura cerca de la placa ateromatosa. Asimismo, también se concluye que el riesgo de que la placa continúe progresando es bajo.
Conclusiones
Los resultados obtenidos muestran que la localización de una estenosis moderada en relación con la bifurcación carotídea y su forma geométrica son factores que es bueno conocer para completar el diagnóstico y el pronóstico de la lesión.
Abstract
Introduction
In patients with moderate symptomatic or severe asymptomatic carotid stenosis, prior to an endarterectomy it is recommended to do a detailed study, in which the complet set of morphological and hemodynamic parameters are included.
In this work the effect that the location and shape of the stenosis has on the distribution of wall shear stresses and their impact on clinical diagnosis in these cases is analyzed.
Materials and methods
First the model of the area to study is generated and the numerical simulation is done. Then the wall shear stress, the oscilation index and the wall shear stress exposure time are established, and the impact of the results for embolization risk or the growth of arterial plaque because of intimal hiperpasia are analysed. The methodology is applied to three idealized carotids with different localization and geometrical slope of the stenosis.
Results
For the idealized carotids it is obtained that stenosis close to bifurcation present a higher embolization risk that the most distant one and has more risk as more stenosis slope it has. For the clinical case, the results show a high risk of embolization by break located near the atheromatous plaque. As well, it is obtained that the risk the arterial plaque to continue growing is low.
Conclusions
The results show that the location of a moderate stenosis related to carotid bifurcation and their geometry they are factors that aid to complete the diagnosis of lesion.
Palabras clave
Embolización ; Estenosis carotídea ; Hiperplasia de la íntima ; Índice de oscilación ; Simulación numérica ; Tensión de cizallamiento en la pared arterial ; Tiempo de exposición
Keywords
Embolization ; Carotid stenosis ; Intimal hyperplasia ; Oscillatory shear index ; Numerical simulation ; Wall shear stress ; Exposition time
1. Introducción
La presencia de placa ateromatosa en la zona carotídea es un factor importante de riesgo de ictus cerebral, así como de accidentes vasculares mayores como el infarto de miocardio [1] . Las causas básicas por las cuales se produce el ictus cerebral son: la obstrucción de los vasos por embolias provocadas por la ruptura de placa carotídea o una perfusión insuficiente debida a estenosis carotídeas significativas. El primer caso se da si la placa está fragmentada o ulcerada y sobre ella se registran valores elevados de las fuerzas de arrastre capaces de romperla y embolizarla. El segundo caso se produce con estenosis cuya reducción de la sección transversal del vaso es suficiente para disminuir el flujo sanguíneo de manera notable. En ambos casos, la hemodinámica juega un papel importante.
La elección del tipo de tratamiento a seguir en este tipo de patología se basa principalmente en el grado de estenosis carotídea y en la sintomatología neurológica asociada. La endarterectomía es uno de los posibles tratamientos en estos casos, su efecto beneficioso depende de si se trata de una estenosis sintomática o asintomática. Para estenosis carotídeas sintomáticas, los estudios de NASCET [2] y de ECST [3] concluyeron que, en pacientes con estenosis severa (>70%, según la medición de NASCET), la endarterectomía obtiene unos buenos resultados. En pacientes con estenosis inferiores al 50% no se obtiene beneficio alguno con la cirugía. En la franja de estenosis moderadas, es decir, entre el 50 y el 70%, el beneficio de la cirugía es moderado. En este caso, se recomienda hacer un estudio personalizado del paciente en el cual se incluya el mayor número posible de parámetros morfológicos y hemodinámicos.
Para estenosis carotídeas asintomáticas, los estudios de ECST [4] y de NASCET [5] concluyen que el riesgo de accidente cardiovascular es bajo, sea cual sea el grado de estenosis, y que el uso de la endarterectomía solo está justificado en estenosis severas.
En resumen, en estenosis sintomáticas moderadas y en estenosis asintomáticas severas, es aconsejable que la decisión de usar la endarterectomía como tratamiento vaya precedida de un estudio detallado de la zona afectada.
Para completar el diagnóstico en los casos en que se requiere un análisis detallado, puede ser de gran interés estudiar las fuerzas de arrastre que actúan directamente sobre el endotelio, es decir, las tensiones de cizallamiento en la pared arterial (Wall Shear Stress [WSS]). Si dichas tensiones de cizallamiento son altas, pueden provocar que la placa aterosclerótica se ulcere, se desencadene sobre ella la activación plaquetaria y, posteriormente, se rompa y se produzca la embolización [6] . Si son bajas y de carácter oscilatorio, pueden provocar que la estenosis continúe progresando por hiperplasia de la íntima (HI) [7] . Por tanto, el estudio directo de estas tensiones, para determinar su intensidad y su localización precisa, puede aportar una información adicional que ayude a clarificar y completar el diagnóstico.
Existen diversos procedimientos para calcular el WSS de manera no invasiva. Uno de ellos consiste en medir in vivo el perfil de velocidades cerca de la pared, lo cual se puede realizar mediante ultrasonidos o bien mediante angio-RM [8] and [9] . El inconveniente principal de la aplicación de este procedimiento en la zona carotídea es la baja resolución de los equipos. Un método alternativo no invasivo es la simulación numérica que consiste en reproducir mediante ordenador la hemodinámica del segmento arterial de interés, es decir, resolver las ecuaciones de movimiento del flujo sanguíneo y obtener la distribución de velocidades y magnitudes relacionadas como el WSS. Los datos necesarios para realizar la simulación numérica son la geometría del segmento arterial, las condiciones en la frontera de dicho segmento, y la densidad y viscosidad de la sangre, aunque para estos 2 últimos datos se pueden utilizar valores de referencia realizando una buena aproximación. La geometría se puede extraer a partir de la angio-TC o de la angio-RM y las condiciones en la frontera pueden ser datos de velocidad, obtenidos mediante ecografía Doppler.
En los últimos años, los estudios realizados mediante simulación numérica se han convertido en una herramienta muy útil para analizar los detalles hemodinámicos, en particular en la zona carotídea. Aunque existen numerosos trabajos con carótidas sanas o casi sanas [10] , [11] , [12] and [13] y, en menor medida, con estenosis severas [14] and [15] , conocemos muy pocos con estenosis moderadas y condiciones fisiológicas. Tang et al. [16] han investigado el efecto que la severidad y la asimetría de la estenosis tienen en diversos parámetros hemodinámicos utilizando, para ello, un modelo de tubo elástico. Groen et al. [17] establecen, en un estudio temporal para un paciente con estenosis carotídea moderada, que la ulceración de la placa se produce exclusivamente en la zona donde el WSS es alto. Jeong y Rhee [18] utilizan un segmento rectilíneo de arteria coronaria con estenosis moderada para analizar el efecto hemodinámico de la irregularidad superficial y de un modelo no-newtoniano.
En este trabajo se analiza mediante simulación numérica el efecto de la localización y la forma de la estenosis sobre las tensiones de cizallamiento y su repercusión en el diagnóstico clínico en una patología de estenosis carotídea moderada. Para ello, se estudian 3 modelos idealizados de carótidas con el mismo grado de estenosis pero con diferente localización y diferente forma geométrica. También se estudia un caso clínico sintomático.
2. Materiales y métodos
En virtud de un convenio de colaboración entre la Universidad Politécnica de Cataluña (UPC) y Althaia, la Red Asistencial Universitaria de Manresa, hemos establecido una metodología de trabajo para incorporar la simulación numérica al estudio de pacientes afectados de estenosis carotídea tributaria de endarterectomía.
El primer paso es la selección de la zona objeto de estudio. Se elige una segmento arterial centrado en la bifurcación carotídea y que contenga tramos lo más largos posible de la arteria carótida común (ACC), de la arteria carótida externa (ACE) y de la arteria carótida interna (ACI).
A continuación, se miden las velocidades mediante una ecografía Doppler (Eco Doppler Siemens Acuson, con transductor lineal de 7 MHz) en el centro de las secciones transversales de la frontera del modelo. Estos son los datos necesarios para realizar la simulación numérica, junto con la angio-TC o la angio-RM.
El paso siguiente es la obtención del modelo geométrico a partir de una angio-TC (TAC Siemens Somaton Definition AS de 20 coronas), mediante un proceso de segmentación. Para ello utilizamos el software de distribución libre ITK-SNAP y un procedimiento de segmentación manual. Del proceso de segmentación se obtiene un modelo geométrico en 3D en formato STL (estereolitografía).
Seguidamente, se realizan cortes transversales al eje del vaso en la entrada y en las salidas del modelo, se añaden extensiones cilíndricas en dirección axial y se cierran en los extremos con secciones planas para poder aplicar sobre ellas las condiciones de contorno que se describen más abajo. A continuación, se realiza un proceso de mallado sobre el modelo, con lo cual queda preparado para la simulación numérica. El proceso de mallado se realiza utilizando la herramienta snappyHexMesh, del software de distribución libre OpenFoam, y la malla obtenida es no estructurada y está formada por hexaedros y hexaedros truncados.
La simulación numérica consiste en imponer condiciones de contorno en la entrada de la ACC y en la salida de la ACE o de la ACI, con las velocidades medidas en la ecografía Doppler y suponiendo un perfil Womersley, que es el adecuado para un flujo pulsátil. En la salida, que no se impone velocidad, se supone presión cero. Seguidamente, se asignan valores para la viscosidad y la densidad de la sangre, y se resuelven las ecuaciones de movimiento (ecuaciones de Navier-Stokes, [NS]) para obtener la distribución de velocidades, el WSS y los parámetros relacionados. La resolución de las ecuaciones de movimiento se realiza mediante el método de volúmenes finitos utilizando el software OpenFoam. El algoritmo de resolución es el PISO (pressure implicit splitting of operators) . El Preconditioned bi-conjugate gradient linear solver (PBiCG) se utiliza para resolver las velocidades y el Preconditioned conjugate gradient linear solver (PCG), para la presión. Como criterios de convergencia, para la tolerancia de las velocidades y las presiones se toman de 10−5 y de 10−6 , respectivamente. El término convectivo en las ecuaciones NS se discretiza según el esquema linear upwind differencing , mientras que, para los términos de gradiente y de difusión, se utiliza el esquema de Gauss lineal. Dado que el flujo es pulsátil, para el término dependiente del tiempo se utiliza el esquema de primer orden Euler implícito. Se toma un tiempo de paso inicial de 5.0 · 10−4 s y, durante la simulación, se ajusta automáticamente de manera que el número de Curant se mantenga por debajo de 1. La validación in vitro de la metodología numérica puede verse en un trabajo anterior nuestro [19] .
Consideramos un modelo reológico newtoniano para la sangre, con una viscosidad cinemática (ν ) de 3, 6 · 10−6 m2 s−1 y una densidad de 994 kg/m3 . Las paredes arteriales se suponen rígidas. En diversos estudios, se ha analizado la importancia de considerar un modelo reológico no newtoniano para la sangre en las simulaciones con segmentos arteriales. Johnston et al. [20] concluyen que utilizar un modelo newtoniano es una aproximación adecuada para una simulación de flujo pulsátil en arterias coronarias incluso en la zona diastólica del periodo, que es cuando más podría diferir el modelo newtoniano del no-newtoniano. Groen et al. [17] utilizan la aproximación newtoniana en un estudio serial de estenosis carotídea moderada. Jeong y Rhee [18] analizan la diferencia entre el modelo newtoniano y el no-newtoniano en una estenosis arterial con un 48% de reducción del área y llegan a la conclusión de que el WSS promediado en un ciclo cardíaco es algo mayor para el modelo no-newtoniano que para un modelo newtoniano. Respecto a la elasticidad de las paredes arteriales en la simulación numérica, Seo [13] obtiene una diferencia del 5 al 11% en el promedio temporal del WSS entre considerar un modelo rígido y un modelo elástico en las simulaciones realizadas con carótidas.
Los resultados se visualizan y presentan mediante el software Paraview, de distribución libre.
Los parámetros hemodinámicos que se analizan son el WSS, el índice de oscilación (OSI) y el tiempo de exposición (TE) a valores altos del WSS. Como hemos dicho, el parámetro hemodinámico más significativo, pues afecta directamente el endotelio, es la tensión de cizallamiento en la pared arterial, que se define por
|
|
donde ts es el vector tensión tangencial en la superficie interna del vaso arterial. Generalmente, se analiza el valor promediado de WSS a lo largo de un ciclo cardíaco ( ):
|
|
donde T representa el período. En el sistema arterial humano, tiene un valor de 1,5 Pa, aproximadamente. El OSI es un parámetro derivado de la tensión tangencial que juega un papel fundamental sobre todo en la formación y en el desarrollo posterior de la placa aterosclerótica, y se define por:
|
|
Como se ve en la definición, el OSI tiene un rango de valores entre 0 y 0,5, y refleja el carácter oscilatorio de la tensión tangencial. El tercer parámetro que analizamos es el TE, definido como la fracción del período, en tanto por ciento, durante la cual el WSS es superior a un valor determinado.
Los valores altos de WSS, a partir de un umbral determinado, pueden provocar la activación plaquetaria y la formación de micropartículas, su acumulación y rotura posterior de la placa ateroesclerótica. Holme et al. [6] dan como valor típico una velocidad de cizallamiento de 10.500 s−1 , que corresponde, en nuestro caso, a una tensión de cizallamiento de 37,8 Pa, y concluyen que este proceso se ve potenciado cuando existe un tiempo prolongado de exposición a valores altos de WSS. En cambio, valores bajos de WSS, acompañados de un OSI alto, pueden provocar un aumento de la placa por HI [21] and [22] . Este proceso se produce para valores de la tensión de cizallamiento promediada en un ciclo cardíaco ( ) por debajo de 0,5 Pa [23] .
Una vez realizada la simulación, se analizan las distribuciones de , OSI y TE con el objetivo de determinar la posible obstrucción de los vasos sanguíneos, ya sea por aumento de placa arterial, o bien por trombosis y rotura posterior de la placa, y analizar de qué modo estos resultados pueden completar el diagnóstico clínico.
2.1. Modelos idealizados de carótidas
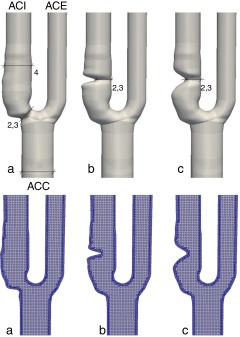
Se diseñan tres modelos idealizados de carótidas con una estenosis moderada y dimensiones parecidas al caso clínico que se describe en la sección siguiente (fig. 1 , izqda.). Para ello, se utiliza el software de distribución libre FreeCAD. En el modelo A, se diseña una estenosis situada al inicio de la carótida interna; en los modelos B y C, una estenosis situada a 5 mm de la bifurcación y con 2 perfiles geométricos diferentes: uno más abierto que el otro. Al igual que para el caso clínico, se realiza el proceso de mallaje y se obtienen aproximadamente unas 270.000 celdas y unos 380.000 nodos para cada uno de los modelos. En las secciones transversales, el número de celdas es de 20, aproximadamente, en la sección más delgada, y 30 o más en el resto (fig. 1 , dcha.).
|
|
|
Figura 1. Carótidas idealizadas. Arriba: modelos con dimensiones en milímetros. Abajo: secciones longitudinales de las mallas utilizadas. |
Se realiza la simulación numérica en los 3 modelos con el objetivo de analizar si un mismo grado de estenosis puede originar diferentes valores y distribuciones de WSS dependiendo de la localización más o menos cercana de la estenosis a la bifurcación o de la forma geométrica de dicha estenosis. Las velocidades que se imponen en la frontera de los 3 modelos son las mismas que las obtenidas para el caso clínico. Se aplica un perfil Womersley en la entrada de la ACC y en la salida de la ACI, y presión cero en la salida de la ACE.
2.2. Caso clínico
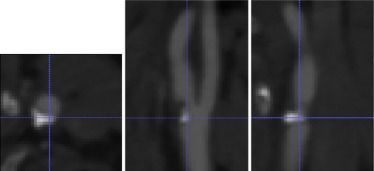
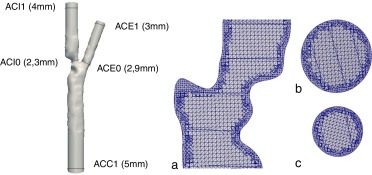
Se aplica la metodología expuesta a un paciente afectado de estenosis carotídea sintomática. En primer lugar, se realiza la angio-TC preoperatoria rutinaria de la zona afectada (fig. 2 ) y se obtiene el modelo tridimensional mediante el proceso de segmentación descrito en el apartado 2 . La malla obtenida en el proceso de mallaje contiene 152.918 celdas y 222.390 nodos, con unas 20 celdas en la sección transversal más delgada y más de 30 en el resto (fig. 3 ).
|
|
|
Figura 2. Caso clínico. Angio-TC de la zona cercana a la bifurcación carotídea, en escala de grises. De izquierda a derecha, vista axial, sagital y coronal. La resolución espacial es de 0, 58 × 0, 58 × 0, 4 mm. |
|
|
|
Figura 3. Caso clínico. Izquierda: modelo tridimensional segmentado a partir de la imagen angio-TC. Derecha: a) Sección longitudinal de la malla utilizada. b) Sección transversal en la ACC. c) Sección transversal en la ACI (en la ACE es similar). |
La medición directa de diámetros mediante la angio-TC proporciona un grado de estenosis del 42,5% según la definición utilizada en NASCET, es decir, queda ligeramente por debajo de la franja de estenosis moderadas (50-70%). Puesto que se dispone de un conjunto amplio de datos del paciente y que el grado de estenosis está cercano al límite inferior de las estenosis moderadas, se decide realizar el estudio mediante simulación numérica.
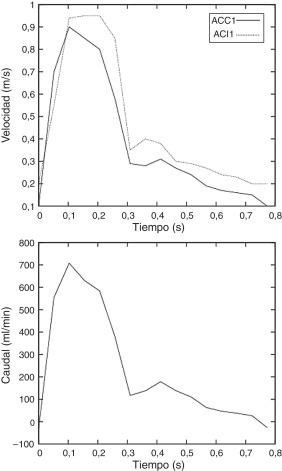
Se toman las velocidades mediante ecografía Doppler en el centro de las secciones transversales de la frontera del segmento ACC1, ACI1 y ACE1 (fig. 3 ). Las curvas de velocidad obtenidas en el centro de la entrada ACC1 y en el de la salida ACI1 son las que se imponen como condiciones de contorno en esas secciones suponiendo un perfil Womersley. Estas velocidades y el caudal resultante en la entrada de la ACC se ilustran en la figura 4 . En la salida ACE1, se impone presión 0.
|
|
|
Figura 4. Caso clínico. Izquierda: velocidad en el eje de entrada en la carótida común (ACC1) y en la salida de la carótida interna (ACI1). Derecha: caudal en la carótida común (ACC). |
También se toman las velocidades mediante una ecografía Doppler en la estenosis (sección ACI0) con el objeto de contrastar el grado de estenosis medido con diámetros mediante el angio-TAC con el obtenido a partir de las mediciones de velocidad. Las mediciones indican una velocidad sistólica máxima (VSM) en la estenosis de 1,23 m/s y una velocidad diastólica final (VDF) de 0,2 m/s. Dado que la VSM en la ACC medida es de 0,9 m/s, esto nos da un índice sistólico de 1,37. De acuerdo con [24] , tanto si se observa la VSM como la VDF o el índice sistólico, se obtiene un grado de estenosis ligeramente inferior al 50%, lo cual se corresponde bien con las medidas directas de diámetros mediante angio-TC (42,5%). Se toman también las velocidades en el inicio de la ACE (sección ACE0).
3. Resultados
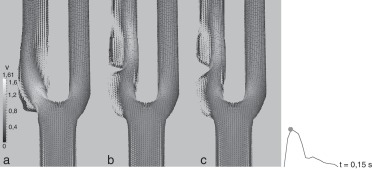
Con relación a las carótidas idealizadas, la figura 5 muestra el campo de velocidades para los 3 modelos en la sístole (t = 0, 15 s). En la tabla 1 se muestran la VSM y la VDF en la estenosis y los índices sistólicos (IS) correspondientes. De acuerdo con [24] , si observamos la VSM, los 3 modelos corresponden a un grado de estenosis entre el 50 y el 70%. Si observamos la VDF y el índice sistólico, corresponden a un grado de estenosis inferior al 50%, lo cual se aproxima más a las medidas directas de diámetros en los modelos (42,5%). En todo caso, los 3 modelos están en la misma franja de la clasificación en cuanto al grado de estenosis según los criterios hemodinámicos de signos directos y de índices. Se observa recirculación postestenótica en los 3 modelos y preestenótica, aunque más leve, en los modelos B y C, principalmente al final de la diástole.
|
|
|
Figura 5. Carótidas idealizadas. Velocidades en el plano de simetría en la sístole (m/s). |
| A | B | C | |
|---|---|---|---|
| VSM | 1,61 | 1,4 | 1,32 |
| VDF | 0,278 | 0,24 | 0,25 |
| IS | 1,79 | 1,55 | 1,46 |
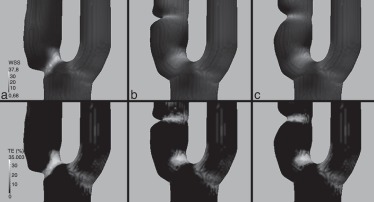
Los resultados del muestran (fig. 6 , sup.) valores altos de 37,76 Pa en el modelo A en la bifurcación y próximos a 20 Pa en los otros 2 modelos, siendo ligeramente más acentuados en el modelo B que en el C. En cuanto a los TE para WSS superiores a 30 Pa (fig. 6 , inf.) son más altos y abarcan una zona más extensa en el modelo A que en los modelos B y C. Estos valores de y del TE suponen, como ya se ha dicho, un riesgo de ulceración, trombosis y rompimiento posterior de placa. Por tanto, el modelo A implica un riesgo de embolización superior a los modelos B y C, siendo el B ligeramente superior al de C.
|
|
|
Figura 6. Carótidas idealizadas. Arriba: en Pa. Abajo: TE correspondiente a un WSS superior a 30 Pa, en porcentaje del período. |
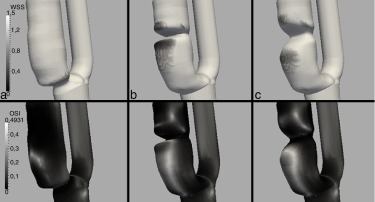
En la figura 7 se muestra el por debajo de 1,5 Pa y el OSI, con el objeto de analizar valores bajos y oscilantes simultáneamente de WSS que puedan ocasionar un riesgo de crecimiento de la placa por HI. Se observa que solo se registran en la parte distal de la estenosis en los modelos B y C. En ambos casos, el riesgo es bajo (no se sitúan claramente por debajo de 0,5 Pa), aunque algo superior en el modelo B que en el C, pues es más oscilante.
|
|
|
Figura 7. Carótidas idealizadas. Arriba: en Pa mostrando solo los valores por debajo de 1,5 Pa. Abajo: OSI. |
Con relación al caso clínico, la tabla 2 muestra las velocidades máxima y mínima en el centro de la ACI0 y de la ACE0 obtenidas en la simulación y las medidas con ecografía Doppler en esos mismos puntos de control. En general, se observa buena concordancia. Como se indica, la velocidad obtenida en la ACE0 y al final de la diástole se halla entre 0,1 y 0,2 m/s, pero con un flujo ligeramente retrógrado, lo cual no se observa en la medición Doppler. Estas discrepancias podrían ser debidas al supuesto de pared rígida en la simulación ya que, según concluyen Perktold y Rappitsch [25] , considerando pared rígida, la velocidad máxima en el instante sistólico aumenta ligeramente y la velocidad máxima al final de la diástole se hace ligeramente más retrógrada en algunas zonas. Esto podría afectar a la zona de la estenosis en menor grado, debido a la presencia de placa y la consiguiente rigidización de la zona.
| Simulación | Doppler | |
|---|---|---|
| ACI0 VSM | 1,41 | 1,23 |
| ACI0 VDF | 0,2 | 0,2 |
| ACE0 VSM | 1 | 0,87 |
| ACE0 VDF | 0,15 (ret.) | 0,12 |
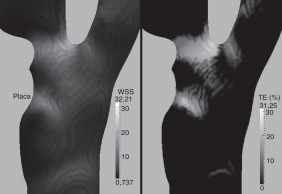
En la figura 8 se muestra el WSS promediado en un ciclo cardíaco, el y el TE con un umbral de 30 Pa. Como se observa, en la zona cercana a la placa se registran valores de altos, de hasta 32 Pa, con un TE del 31% a tensiones de cizallamiento superiores a 30 Pa. Estos valores implican un riesgo alto de embolización [26] and [6] . En cambio, no se dan valores de por debajo de 0,5 Pa, que es el umbral por debajo del cual hay riesgo de formación de placa [23] , lo cual implica que el riesgo de que la placa siga progresando es bajo.
|
|
|
Figura 8. Caso clínico. Izquierda: WSS medio en un ciclo cardíaco, en Pa. Derecha: TE correspondiente a un WSS superior a 30 Pa, en porcentaje del período. |
4. Discusión
Se ha analizado el efecto que tienen la localización y la forma de la estenosis sobre las tensiones de cizallamiento en una situación de estenosis tributaria de endarterectomía y cómo puede repercutir en su diagnóstico y pronóstico. Para ello, se ha establecido un procedimiento de trabajo y se ha aplicado a 3 modelos idealizados de carótidas con el mismo grado de estenosis moderada, una con la estenosis en la bifurcación carotídea y las otras 2 con la estenosis más alejada y con 2 pendientes geométricas diferentes, que se han analizado con las mismas condiciones de caudal fisiológico. Además, se ha estudiado un caso clínico con estenosis sintomática situada ligeramente por debajo de la franja moderada. Se ha realizado la simulación numérica a partir de los datos geométricos obtenidos con una angio-TC y de las velocidades obtenidas mediante ecografía Doppler.
Los resultados obtenidos en los modelos idealizados de carótidas muestran zonas de recirculación postestenótica y preestenótica, en que la postestenótica es más pronunciada y se produce principalmente en el final de la diástole. El análisis de las tensiones de cizallamiento y de los tiempos de exposición a valores altos de dichas tensiones muestra que el riesgo de embolización es superior si la estenosis se sitúa cerca de la bifurcación carotídea. Esto es debido a que la presencia de una estenosis hace aumentar el en la zona proximal y, si dicha estenosis se sitúa en una zona con valores altos de , aún sin estenosis, como es la zona próxima a la bifurcación [25] and [27] , el valor final de es superior al que se obtiene si la estenosis está situada donde los valores son inicialmente más bajos. Asimismo, se obtiene que el riesgo de embolización es ligeramente superior si la pendiente geométrica de la estenosis es más pronunciada. Se observa también que el riesgo de que la placa continúe en progresión es bajo en todos los casos, algo mayor si la pendiente de la estenosis es más pronunciada, y que previsiblemente el crecimiento de la placa se producirá en la parte distal de la estenosis. De acuerdo con los resultados de [18] , de haberse utilizado un modelo reológico no-newtoniano para la sangre, se habrían obtenido valores ligeramente superiores para las tensiones de cizallamiento medio, tanto en la zona proximal de la estenosis como en la zona distal, lo cual refuerza las conclusiones a que se ha llegado.
Para el caso clínico analizado, el análisis de las tensiones de cizallamiento y sus tiempos de exposición muestran que existe un riesgo elevado de embolización por rotura de la placa situada cerca de la bifurcación carotídea. Se obtiene también que el riesgo de que la placa aterosclerótica siga progresando es bajo. Estos resultados son coherentes con la sintomatología del paciente, que ya ha experimentado pequeños episodios de embolización, y contribuyen a completar y clarificar el diagnóstico inicial para la valoración de una intervención quirúrgica.
Los resultados obtenidos también son coherentes con la hipótesis de que un análisis de las tensiones de cizallamiento realizado mediante simulación numérica puede ayudar a completar el diagnóstico de las estenosis carotídeas sintomáticas moderadas o asintomáticas severas y a clarificar el riesgo de accidente cardiovascular. La limitación principal del estudio consiste en no haber considerado un número elevado de casos clínicos. El trabajo futuro se orientará en esta línea.
References
- [1] O. Joakimsen, K. Bø naa, E. Mathiesen, E. Stensland-Bugge, E. Arnesen; Prediction of mortality by ultrasound screening of a general population for carotid stenosis: The tromsø study; Stroke, 31 (2000), pp. 1871–1876
- [2] H.J. Barnett, D.W. Taylor, M. Eliasziw, A.J. Fox, G.G. Ferguson, R.B. Haynes, R.N. Rankin; Benefit of carotid endarterectomy in patiens with syntomatic, moderate or severe stenosis; N. Engl. J. Med., 339 (20) (1998), pp. 1415–1425
- [3] E.C.S.T.C. Group; Randomised trial of endarterectomy for recently symptomatic carotid stenosis: final results of the MRC european carotid surgery trial (ECST ) ; Lancet, 351 (1998), pp. 1379–1387
- [4] E.C.S.T.C. Group; Risk of stroke in the distribution of an asymptomatic carotid artery; Lancet, 345 (1995), pp. 209–212
- [5] D. Inzitari, M. Eliasziw, P. Gates, B.L. Sharpe, R.K. Chan, H.E. Meldrum, J. Barnett; The causes and risk of stroke in patients with asymptomatic internal-carotid-artery stenosis; N. Engl. J. Med., 342 (2000), pp. 1693–1700
- [6] P.A. Holme, U. Ø rvim, M. Hamers, N. Solum, F. Brosstad, R. Barstad, et al.; Shear-induced platelet activation and platelet microparticle formation at blood flow conditions as in arteries with a severe stenosis; Arterioscler Thromb Vasc Biol., 17 (1997), pp. 646–653
- [7] X.M. Li, S. Rittgers; Hemodynamic factors at the distal end-to-side anastomosis of a bypass graft different pos:dos flow ratios; J. Biomech. Eng.-T. ASME, 123 (2001), pp. 270–276
- [8] J.L.A. Carvalho, J.F. Nielsen, K.S. Nayak; Feasibility of in vivo measurement of carotid wall shear rate using spiral fourier velocity encoded mri; Magn. Reson. Med., 63 (2010), pp. 1537–1547
- [9] C. Wang, M. Chen, S. Liu, Y. Liu; Spatial distribution of wall shear stress in common carotid artery by color doppler flow imaging; J. Digit. Imaging., 26 (2013), pp. 466–471
- [10] D.A. Steinman, J.B. Thomas, H.M. Ladak, J.S. Milner, B.K. Rutt, J.D. Spence; Reconstruction of carotid bifurcation hemodynamics and wall thickness using computational fluid dynamics and MRI; Magn. Reson. Med., 47 (2002), pp. 149–159
- [11] S. Tada, J.M. Tarbell; A computational study of flow in a compliant carotid bifurcation-stress phase angle correlation with shear stress; Ann. Biomed. Eng., 33 (9) (2005), pp. 1202–1212
- [12] S. Lee, D.A. Steinman; On the relative importance of rheology for image-based cfd models of the carotid bifurcation; J. Biomech. Eng.-T. ASME, 129 (2007), pp. 273–278
- [13] T. Seo; Hemodynamic characteristics in the human carotid artery model induced by blood-arterial wall interactions, International Journal of Biological, Agricultural, Biosystems; Life Science and Engineering, 7 (5) (2013), pp. 153–158
- [14] J.S. Stroud, S.A. Berger, D. Saloner; Numerical analysis of flow through a severely stenotic carotid artery bifurcation; J. Biomech. Eng.-T. ASME, 124 (2002), pp. 9–20
- [15] C.M. Schirmer, A.M. Malek; Computational fluid dynamic characterization of carotid bifurcation stenosis in patient-based geometries; Brain Behav., 2 (1) (2012), pp. 42–52
- [16] D. Tang, C. Yang, D.N. Ku; A 3-D thin-wall model with fuid-structure interactions for blood flow in carotid arteries with symmetric and asymmetric stenoses; Comput. Struct., 72 (1999), pp. 357–377
- [17] H.C. Groen, F.J. Gijsen, A. van der Lugt, M.S. Ferguson, T.S. Hatsukami, A.F. van der Steen, et al.; Plaque rupture in the carotid artery is localized at the high shear stress region: a case report.; Stroke, 38 (2007), pp. 2379–2381
- [18] W.W. Jeong, K. Rhee; Effects of surface geometry and non-newtonian viscosity on the flow field in arterial stenoses; J. Mech. Sci. Technol., 23 (2009), pp. 2424–2433
- [19] J. Rivera, G. B. van der Graaf, J. R. Escudero, S. Bellmunt, F. van de Vosse, A CFD study on hemodynamics for different locations of the distal anastomosis of a bypass nearby a collateral vessel in the femoropopliteal area, Int. J. Numer. Meth. Biomed. Engng.
- [20] B.M. Johnston, P.R. Johnston, S. Corney, D. Kilpatrick; Non-newtonian blood flow in human right coronary arteries: Transient simulations; J. Biomech., 39 (2006), pp. 1116–1128
- [21] J.E. Moore Jr., C. Xu, S. Glagov, C.K. Zarins, D.N. Ku; Fluid wall shear stress measurements in a model of the human abdominal aorta: Oscillatory behavior and relationship to atherosclerosis; Atherosclerosis, 110 (1994), pp. 225–240
- [22] D.N. Ku, D.P. Giddens, C.K. Zarins, S. Glagov; Pulsatile flow and atherosclerosis in the human carotid bifurcation: positive correlation between plaque localization and low and oscillating shear stress; Arterioscler. Thromb. Vasc. Biol., 5 (1985), pp. 293–302
- [23] E. Sho, H. Nanjo, M. Sho, M. Kobayashi, M. Komatsu, K. Kawamura, et al.; Arterial enlargement, tortuosity and intimal thickening in response to sequential exposure to high and low wall shear stress; J. Vasc. Surg., 39 (2004), pp. 601–612
- [24] J. Serena, P. Irimia, S. Calleja, M. Blanco, J. Vivancos, O. Ayo-Martín; Ultrasound measurement of carotid stenosis: Recommendations from the Spanish society of neurosonology; Neurologia, 28 (7) (2013), pp. 435–442
- [25] K. Perktold, G. Rappitsch; Computer simulation of local blood flow and vessel mechanics in a compliant carotid artery bifurcation model; J. Biomech., 28 (7) (1995), pp. 845–856
- [26] L. Badimon, J.J. Badimon, A. Galvez, J.H. Chesebro, V. Fuster; Influence of arterial damage and wall shear rate on platelet deposition; Atherosclerosis, 6 (1986), pp. 312–320
- [27] S.Z. Zhao, X.Y. Xu, A.D. Hughes, S.A. Thom, A.V. Stanton, B. Ariff, Q. Long; Blood flow and vessel mechanics in a physiologically realistic model of a human carotid arterial bifurcation; J. Biomech., 33 (8) (2000), pp. 975–984
Document information
Published on 01/06/16
Accepted on 13/02/15
Submitted on 07/11/14
Volume 32, Issue 2, 2016
DOI: 10.1016/j.rimni.2015.02.005
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?