Abstract
The aim of this work is to investigate the soil water budget across China by means of hydrological modeling under current and future climate conditions and to evaluate the sensitivity to soil parameters. For this purpose, observed precipitation and temperature data (1981–2010) and climate simulations (2021–2050, 2071–2100) at high resolution (about 14 km) on a large part of China are used as weather forcing. The simulated weather forcing has been bias corrected by means of the distribution derived quantile mapping method to eliminate the effects of systematic biases in current climate modeling on water cycle components. As hydrological models, two 1D models are tested: TERRA-ML and HELP. Concerning soil properties, two datasets, provided respectively by Food and Agriculture Organization and U.S. Department of Agriculture, are separately tested. The combination of two hydrological models, two soil parameter datasets and three weather forcing inputs (observations, raw and bias corrected climate simulations) results in five different simulation chains.
The study highlights how the choice of some approaches or soil parameterizations can affect the results both in absolute and in relative terms and how these differences could be highly related to weather forcing in inputs or investigated soil. The analyses point out a decrease in average water content in the shallower part of the soil with different extents according to climate zone, concentration scenario and soil/cover features. Moreover, the projected increase in temperature and then in evapotranspirative demand do not ever result in higher actual evapotranspiration values, due to the concurrent variations in precipitation patterns.
Keywords
Water balance models ; Model comparison ; Bias correction ; Hydrological impacts ; Soil parameters ; China
1. Introduction
In recent years, some relevant studies have shown that the global warming could affect the precipitation patterns and the water cycle at the global and regional scale and at different time scales (Allen and Ingram, 2002 ; Held and Soden, 2006 ; Lenderink and van Meijgaard, 2010 ). However, under the current observational and modeling uncertainties, the Intergovernmental Panel on Climate Change (IPCC) assesses only with “medium confidence” the anthropogenic contribution to changes in precipitation patterns, although it recognizes as “virtual certain” the ongoing processes of global warming and the emerging of new evidences about the variations in global precipitation (IPCC, 2014 ).
This topic and its huge implications for the development of effective adaptation strategies in crucial sectors (agriculture, natural disaster mitigation, water resources, water supply) have meant numerous researches aimed to investigate how climate changes may affect the entire water cycle (Fischer et al., 2007 ). The main studies focus on:
- the potential intensification of water cycle (Easterling et al., 2000a ; Easterling et al., 2000b ; Huntington, 2006 ; Kyoung et al., 2011 ; Mason et al., 1999 ; Zollo et al., 2015 );
- the variations (mainly increases) in occurrence and magnitude of droughts (Piao et al., 2010 ; Qiu, 2010 ; Schiermeier, 2008 ; Zhai et al., 2010 ) and flood events (Kwon et al., 2011 ; Prudhomme et al., 2003 ; Vezzoli et al., 2015 ; Zhou et al., 2011 );
- the average trends and the associated effects on water resources (Arnell, 2004 ; Bates et al., 2008 ; Jackson et al., 2001 ; Obeysekera et al., 2011 ).
Of course, since the significance, extension and extreme geomorphological and climate heterogeneity, numerous studies have investigated such issues for China. China played indeed a key political and economic role in the mitigation of climate change and it is considered as one of the most vulnerable societies in terms of water resources and agriculture sustainability (IPCC, 2014 ; SC (State Council), 2011 ). Moreover, significant resources have been invested in climate change adaptation strategies and actions (SC, 2014 ). Concerning the topics already introduced, Wu et al. (2015) adopted the Soil and Water Assessment Tool (SWAT) model forced by available historical weather observation to assess the ongoing variations in the water cycle potentially induced by climate change for the Xiangjiang River Basin. On the same river basin, Luo et al. (2013) adopted the same tools for investigating the effect of current and planned scenarios of land use. Zhang et al. (2009) simulated evapotranspiration and soil water balance for different tillage systems on the 2010–2040 time span using as driver the monthly precipitation data provided by statistical downscaling of the Global Climate Model (GCM) HadCM3 projections. Wang et al. (2013) estimated the impacts of climate change on water demand for agriculture in ten basins covering the entire Chinese territory. They coupled the climate inputs provided by the Regional Climate Model (RCM) PRECIS (at 0.44° horizontal resolution; Yang et al., 2010 ) under A1B, A2 and B2 emission scenarios to the China Water Simulation Model (CWSM), assessing water demand and supply and allocating water among its users within the river basins. They showed how the effects could vary in function of severity of emission scenarios but, at the same time, proper adaptation strategies may satisfactorily cope with these issues.
However, for China, relatively much fewer studies have had as specific goal the investigation on potential changes induced by climate change in the soil moisture at local or regional scale. At local scale, e.g. Zhou et al. (2011) (again through the SWAT approach) assessed the effect of climate change on soil moisture dynamics and hydrological variables in an intact-forested watershed in southern China. Through the analysis of observed data, they show how current soil drying processes could be associated to relevant changes in weather forcing. Similarly, Jiang et al. (2007) perform an exhaustive comparison work analyzing the response of six different hydrological models in assessment of variations of soil hydrological balance induced by climate change (using hypothetical future scenarios) in the Dongjiang Basin (southern China).
On the other side, at country level (not only for China), this topic has been hardly investigated until now (Wu et al., 2015 ) also probably due to the limited availability of reliable and continuous soil moisture datasets around the world (Keshta et al., 2012 ). Among available studies, Komuscu et al. (1998) investigated the variations of soil moisture availability in the Southeast Anatolia (Turkey) both under the prescribed variations in weather forcing, and under those provided by the GCM, using a modified version of Thornthwaite water balance model. Naden and Watts (2001) evaluated the variations of monthly soil moisture in five typical areas of ecological interest in the United Kingdom taking into account the actual land covers and soil types. Bormann (2009) performed a sensitivity study for five different regions in Germany, aimed to understand the joined role of soil type and lower boundary conditions in response to variation of weather forcing induced by climate change. Keshta et al. (2012) adopted the Generic System Dynamics Watershed (GSDW) model (Keshta et al., 2009 ) to simulate the potential future soil moisture and evapotranspiration dynamics; the weather input forcing are obtained through the Statistical DownScaling Model (SDSM) proposed by Wilby et al. (2002) of Coupled General Circulation Model (CGCM3) under A2 and B1 emission scenarios. Finally, Bormann (2012) utilized the SIMULAT model (Bormann, 2008 ), a Soil Vegetation Atmosphere Transfer scheme (SVAT) for analysis of virtual soil columns, to assess the soil texture-specific sensitivity of simulated soil moisture to projected climate change. To this aim, he also took into account, in a simplified way, the role played by upper (land cover) and lower (shallow groundwater/free drainage) hydraulic boundary conditions of soil specimens.
Given the state of the art, the availability of climate projections at a very high resolution (0.125°, about 14 km) up to 2100 from RCM COSMO_CLM (Bucchignani et al., 2014 ) under RCP4.5 and RCP8.5 scenarios (Meinshausen et al., 2011 ) for a large part of the Chinese territory, grants an opportunity to attempt partly bridging such gap estimating the main variations assessed in soil water budget for the principal climate zones retrievable in the investigated domain.
The analysis are carried out adopting two hydrological models, two datasets for retrieving hydraulic and thermal soil properties, three weather forcing inputs. In this way, the effects of parameterizations and parameters on the assessment of seasonal and yearly soil water budget considering also the potential effect of soil type and land-use can be evaluated. Moreover, a first estimation about how current biases in weather forcing returned by climate simulations could affect the assessment of the soil water budget and its variation under climate change is also provided. The investigation is performed on five reference “boxes” located in four main climate areas; every box is selected as representative of the most widespread land cover and soil type in that area. Essentially, two time horizons are investigated: near time horizon 2021–2050 and long time horizon 2071–2100 under RCP4.5 and RCP8.5 scenarios. Then in the rest of this paper, firstly material and methods are displayed. Afterwards, attempting to estimate the main variations assessed in the soil water budget for the main climate zones identified in China, under the effect of climate change, and to quantify the reliability of the results under climate and hydrological modeling uncertainties, results are reported and commented in Section 3 . Finally, in conclusions, the main findings are reviewed and the possible future steps are identified.
2. Material and methods
2.1. Data description and investigated areas
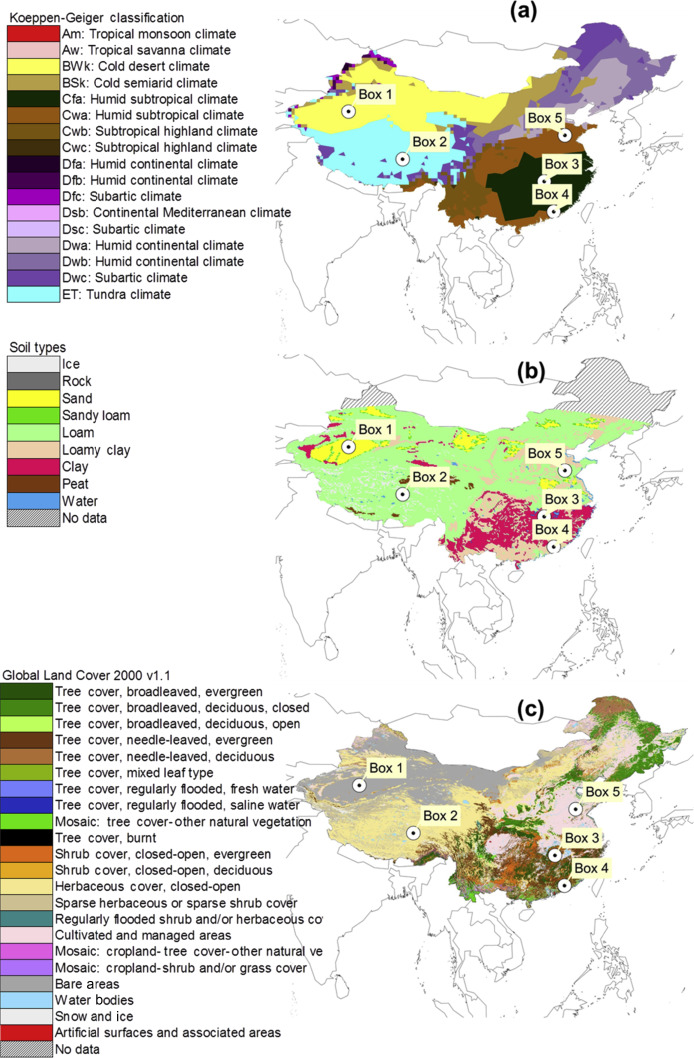
Given the great extension of China, climate features vary considerably among different areas. According to the Köppen–Geiger classification (Kottek et al., 2006 ), the Chinese territory is characterized by six climates (Fig. 1 a): cold desert climate (BWk) in the Northwest (NW), tundra climate (ET) in the Southwest (SW), humid subtropical climate (Cfa and Cwa) in the Southeast (SE), humid continental climate (Dwb) and subarctic climate (Dwc) in the Northeast (NE). In this study, we refer to the climate areas BWk, ET, Cfa and Cwa. Within each of these areas, a box, characterized by the dominant soil type (Fig. 1 b) and land cover (Fig. 1 c), is selected as representative of the area with the exception of the Cfa climate zone where the almost equal presence of two main different soil types (clay and loamy clay, see following sections for details) suggests analyzing two different boxes. As results, the effects of climate change on the water cycle are investigated on five boxes belonging to four different climate zones.
|
|
|
Fig. 1. Koppen–Geiger classification (a), soil type (b) and land cover (c) for the continental part of China. |
Concerning climate projections, in general, climate simulations over China return further growing temperatures (3–5 °C) while the average precipitation patterns are expected to vary in different ways. In this regard, further valuable details can be retrieved by the analysis performed by Bucchignani et al. (2014) . The adopted simulation chain in Bucchignani et al. (2014) is composed by the GCM CMCC_CM (Scoccimarro et al., 2011 ) with an horizontal resolution of about 0.75° and the RCM COSMO_CLM (Doms and Schättler, 2002 ; Rockel et al., 2008 ) at a very high resolution (0.125°, about 14 km); the former driving the latter as lateral boundary conditions. Both climate models are forced, as defined in IPCC-AR5, by the Coupled Model Intercomparison Project Phase 5 (CMIP5, Taylor et al., 2012 ) historical experiment up to 2006, and by the RCP4.5 and RCP8.5 emission scenarios from 2006 to 2100 (Meinshausen et al., 2011 ). Improvements associated to their optimized configuration and resolution increase are highlighted in Bucchignani et al. (2014) , where it is also pointed out how the lack of high resolution observational datasets may affect a proper validation, especially for high resolution simulations. According to the Bucchignani et al. (2014) projections, a general warming is expected over the whole area with values consistent with previous studies while an increase in precipitations could occur in the northern part of the domain (except in summer) with the exception of SE area where a precipitation reduction is expected, mainly in winter.
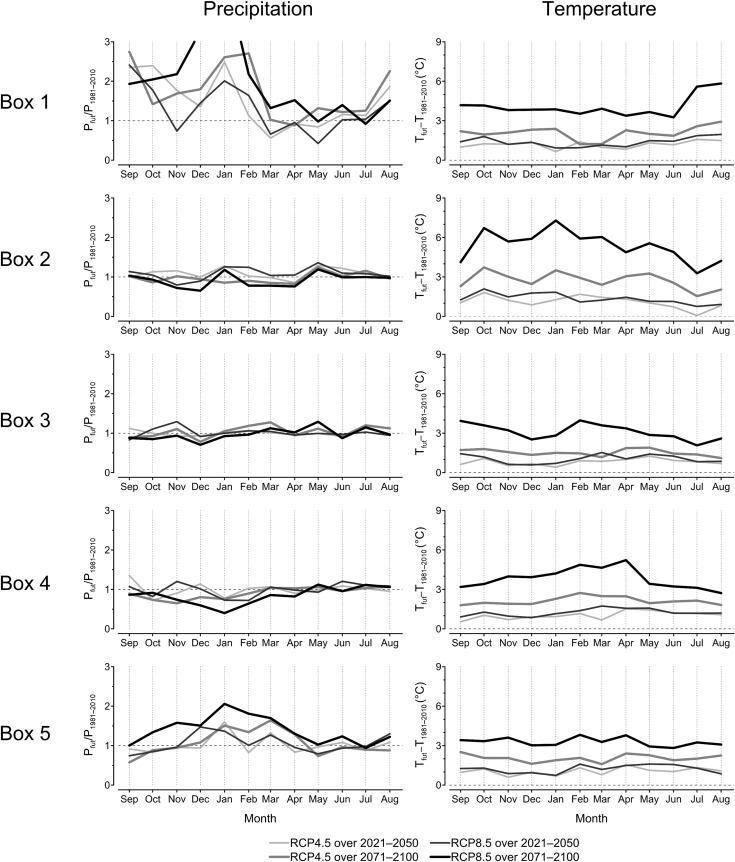
Fig. 2 shows the projected variations, according to Bucchignani et al. (2014) simulations, in monthly cumulative precipitations (as ratio) and temperatures (as difference) for the five boxes on the near (2021–2050) and long (2071–2100) time horizons under the RCP4.5 and RCP8.5 scenarios. In particular, concerning temperatures, a generalized increase is detected: on near term, slight variations are recognized between RCPs with growth for all locations of about 1 °C; on long term, more pronounced differences are returned: for the RCP4.5 scenario, the increase stands between 2 °C and 3 °C while it exceeds 3 °C in RCP8.5 (reaching 6 °C for the SE). Variations in precipitation patterns display more complex trends depending on seasonality and location. Box 1 (in the NW area) is characterized by scarce yearly precipitation values and slight future estimated variations. For box 2 (in the SW area), decreases are detected under RCP8.5 mainly in November and December (corresponding to the dry season in the area) while increases are estimated in the wet season (May–August mainly under RCP4.5). For boxes 3 and 4 (in the SE area), again, large decreases occur in the dry season (November–February) especially under RCP8.5 (up to 60%) while increases are obtained in the wetter time span. Finally, for box 5 (in the NE area), high variations (increases up to 100%) are assessed in the drier season (October–March) while they appear to be limited and fluctuating in the remaining months.
|
|
|
Fig. 2. Projected variations in monthly cumulative precipitation and temperature for the five boxes on near (2021–2050) and long (2071–2100) time horizon (relative to 1981–2010). |
Beyond the relevance of such data, the “strong non linearity” between climate forcing and soil water balance components and the presence of systematic biases in climate simulations altering quantitatively the expected weather forcing, entails that the climate projections cannot directly provide insights on future variations at the local scale of the soil water balance.
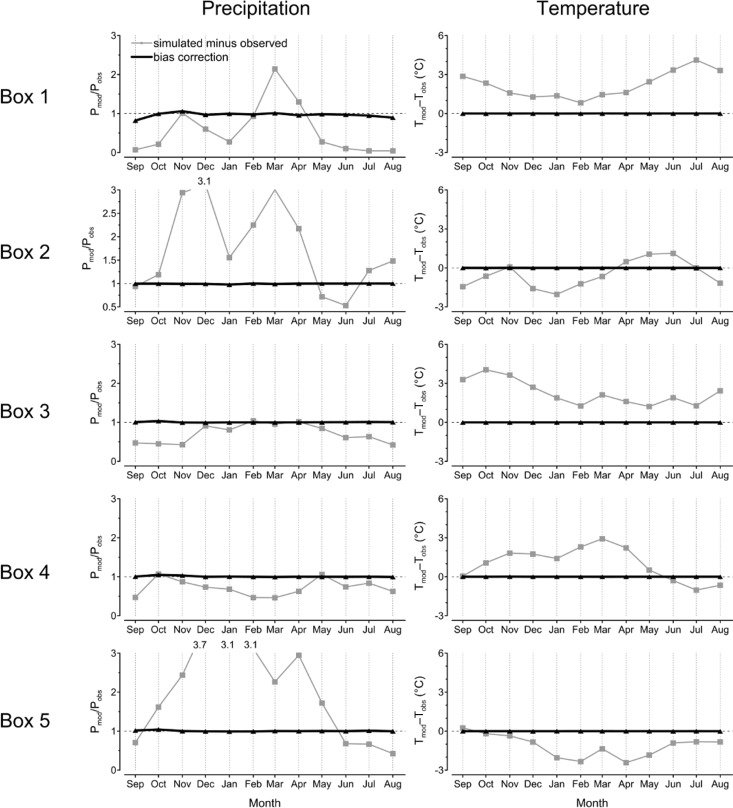
Although the improvements in the evaluation of weather forcing on the area achieved by Bucchignani et al. (2014) are mainly associated to higher horizontal resolutions and better representation of physical processes, biases remain as displayed in Fig. 3 , showing, for the five boxes and for the 1981–2010 control period, the ratio (difference) in monthly cumulative precipitations (temperatures) between observed (Wu and Gao, 2013 ) and simulated data (Bucchignani et al., 2014 ). Results show that precipitation biases are limited in the SE area and relevant (essentially in terms of overestimation in boxes 2 and 5) in the other cases. For temperatures in areas characterized by an overestimation of precipitations, an underestimation (1–2 °C) is detected. For other reference areas, biases stood on about +2 °C.
|
|
|
Fig. 3. Ratio in monthly cumulative precipitation, and difference in monthly average temperature for simulated against observed (grey line) and bias corrected simulated against observed (black curve) in 1981–2010. |
In this perspective, the adoption of a bias correction approach (Ehret et al., 2012 ; Piani et al., 2010 ; Teutschbein and Seibert, 2012 ; Teutschbein et al., 2011 ; Villani et al., 2015 ) is needed to investigate the soil water balance. To this aim, the non-parametric quantile mapping approach (Gudmundsson et al., 2012 ; Teutschbein and Seibert, 2012 ) is used to correct the precipitation and temperature values provided by numerical climate models. Bias correction approaches are based on a transfer function that imposes the equality in probability between observed and simulated data over a control period:
|
|
( 1) |
where FOBS and FCTRL are the cumulative distribution functions of daily observed and simulated variable X . Assuming that the transformation defined by Eq. (1) is valid over the whole simulation time period, the bias corrected value X∗ of the simulated variable X is obtained as
|
|
( 2) |
The main differences between the distribution mapping methods are due to h transformation. To this aim, theoretical distribution, parametric relationships quantile–quantile or directly the empirical quantiles are generally adopted. In this work, the last mentioned approach has been preferred ( Gudmundsson et al., 2012 ; Villani et al., 2015 ); it allows greater versatility and requires less a-priori assumptions about statistical distributions reproducing observed and simulated daily weather data. On the other side, higher caution should be paid in their adoption when used beyond the calibration intervals ( Gudmundsson et al., 2012 ; Villani et al., 2015 ).
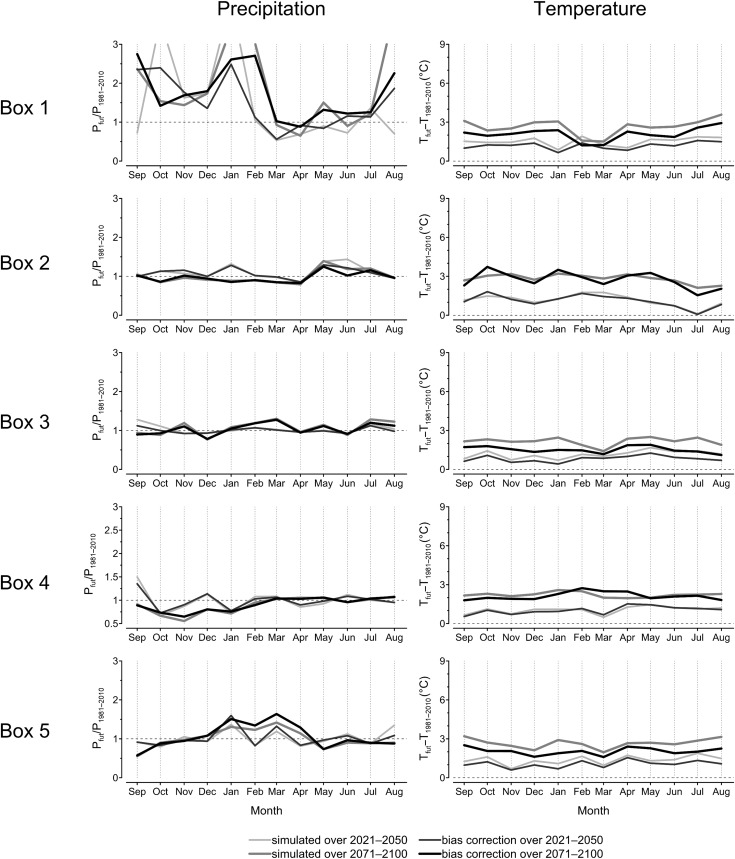
As it is evident in Fig. 3 , showing a comparison between bias corrected values and the observed data, the non-parametric quantile mapping approach succeeds in almost all cases in nullifying the biases of initial climate simulations. However, as it represents a further step in the simulation chain, additional assumptions should be taken into account (Ehret et al., 2012 ; Maraun, 2013 ). For example, its adoption could partly modify the climate signal returned by RCM simulations, as reported in Fig. 4 where the data for temperature and precipitation (again respectively in terms of difference and ratio) are shown for the two time horizons under RCP4.5 scenario.
|
|
|
Fig. 4. Climate signal returned by RCM simulations: ratio in monthly cumulative precipitation and difference in monthly average temperature for simulated and bias corrected simulated for the 2021–2050 and 2071–2100 time horizons under RCP4.5 scenario. |
Thus in this study, to take into account the spatial resolution of the RCM, each box includes nine grid cells (square 3 × 3) of the RCM. Fig. 4 illustrates the climate data that will be used to feed the hydrological models described in the following Section, in particular, the climate data that will be used are:
- observations in the period 1981–2010 (Wu and Gao, 2013 );
- climate simulation on the control period 1981–2010 (Bucchignani et al., 2014 );
- climate simulation on the near (2021–2050) and long time (2071–2100) period under both RCP4.5 and RCP8.5 scenarios (Bucchignani et al., 2014 );
- the bias corrected climate data obtained applying Eq. (2) to simulated values.
2.2. Hydrological models
The climate models described in the previous section represent the first element of the modeling chain. The second component is constituted by the hydrological model allowing the evaluation of soil water balance for current and future periods for a control volume in a given time interval. Generally, the main terms composing soil water balance, for a reference time, can be expressed as:
|
|
( 3) |
where : water storage variation (mm); P : precipitation (mm); R : runoff (mm); ET : evapotranspiration (mm); DD : deep drainage (mm).
On near time interval, additional terms can be considered. For example, during precipitation events a part can remain on the soil surface due to interception or ponding and after it is removed under evaporation or delayed infiltration. Moreover, on yearly scale, the variation in soil water storage on average tends to be small.
In this work, two hydrological models, TERRA_ML (ML means multi-layer) and HELP (Hydrologic Evaluation of Landfill Performance), are adopted and tested. Both models work on the strong assumption of 1D conditions, hence neglecting actual geomorphology or lateral superficial lost within soil intakes or leakages. In the following, they are briefly described.
2.2.1. TERRA_ML
TERRA_ML is the module currently adopted in the regional climate model COSMO_CLM (and also for its meteorological version: COSMO-LM) to assess the soil surface conditions in terms of water mass and temperature, constituting the lower boundaries for the atmospheric part (in this way, not only the effects of weather forcing on the soil are considered but also the corresponding soil-atmosphere feedbacks). To this aim, the assessment of the soil water/heat hydrological balance is required.
- Evapotranspiration results as the “weighted” sum of bare soil evaporation, plant transpiration, sublimation from snow and evaporation from the interception store (assumed as a reservoir for ponded water). Both bare soil evaporation and plant transpiration have been modeled according to the BATS (Biosphere Atmosphere Transfer) scheme proposed by Dickinson (1984) .
- Vertical water redistribution in unsaturated condition depends on gravity and capillary forces, and is described by the 1D Darcy equation (Dingman, 2002 ) as sum of drainage and diffusion. Drainage and diffusion are retrieved as function of hydraulic conductivity and hydraulic diffusivity, both depending on soil properties such as soil moisture, pore volume and air dryness point.
- Runoff occurs within each layer when the layer water content results greater than the field capacity or when the divergence of the fluxes in the layer results negative. Hence, two runoff mechanisms are detected: the former is a superficial runoff (Crawford and Linsley, 1966 ; Holtan, 1961 ); the latter represents deep runoff (sum of the runoff from each layer and deep drainage).
In the model, the water mass equation is linked to that for soil heat balance through the evaporation term regulating the latent heat flux. Furthermore, also the effect of snow cover assumed as a further upper layer is taken into account. The model works according to the time steps adopted for the atmospheric part.
2.2.2. HELP 3.95D
The code HELP (Schroeder et al., 1994 ) provides a simplified modeling of surface (such as snowmelt, interception by vegetation, surface runoff and surface evaporation) and subsurface processes (evaporation from soil profile, plant transpiration, unsaturated vertical drainage) returning at a daily scale the main components of the soil water balance at surface and within the shallower soil layer.
- Evapotranspiration is modeled by adopting, both for evaporation from bare soil and for plant transpiration, the Ritchie (1972) model. As patterned after Ritchie (1972) , the evaporation follows a two-stage pattern: in the first part, it is equal to the potential evaporation; in the second part the evaporation decreases, depending on the soil hydraulic conductivity and on the time root square. The plant transpiration, on the contrary, is assumed equal to the potential plant transpiration. Regarding the potential evapotranspiration, it is provided by the Penman (1963) equation and turned into potential evaporation and potential plant transpiration as function of LAI (Leaf Area Index).
- Vertical drainage is stated through the Darcy law, considering however only the gravitational forces. For this reason, it depends only on the soil hydraulic conductivity, carried out by adopting the Campbell (1974) approach. To take into account the effect of the vegetation on the hydraulic conductivity, this latter is increased in the top-half of the evaporative zone according to LAI.
- Infiltration/runoff is modeled by adopting the approach developed by the SCS (Soil Conservation Service) of U.S. Department of Agriculture (USDA) based on the curve number (CN) parameter (USDA, 1985 ) that takes into account the effects of hydraulic conductivity, land cover and roughly the soil wetness conditions antecedent the rainfall event.
2.2.3. Soil geometry and parameters
In order to make the soil water balance estimation obtained through TERRA_ML and that obtained through HELP comparable, the vertical dimension of the domain, the soil type (and then the thermal–hydraulic properties), the land cover and the bottom conditions (free drainage) are equal.
Regarding the soil column dimension, TERRA_ML adopts two different discretization schemes for soil heat and water budget. In the first case, the depth of the domain is 21.87 m, in the second case it is 2.43 m. In particular, soil thermal behavior is required to be assessed to provide surface temperatures constituting a lower boundary for atmospheric part of climate models. Specifically, it (with required soil thermal properties) contributes to assessment of evapotranspiration component (Dickinson, 1984 ). However, in HELP solving the water budget in isothermal conditions, the domain has been set equal to 2.43 m; indeed, HELP estimates evapotranspiration component through literature models (Ritchie, 1972 ; Penman, 1963 ) neglecting soil thermal behavior.
The predominant soil type and the land cover for the five reference boxes (Table 1 ) are retrieved by the datasets implemented in TERRA_ML, respectively Digital Soil Map of the World Food and Agriculture Organization and GLC2000 database (Global Land Cover, 2000; European Commission, Joint Research Centre). Related soil-thermo hydraulic parameters and land cover features (roughness length z0 , depth, min and max plant cover, min and max LAI) are borrowed from the TERRA_ML databases (Doms et al., 2011 ); however, as the HELP model also requires a value for curve number, such value is retrieved based on the soil texture (Table 1 ). Furthermore, as large uncertainties could affect the proper estimation of soil parameters as only function of the soil texture, the variations induced by adopting different databases for soil parameters have been investigated, considering for HELP also the USDA database (included in the software, values are reported in parentheses in Table 1 ) for simulations on current period 1981–2010, driven by raw climate simulations.
| Box | Climate zone | Soil type | Land cover | ωPV | ωFC | ωPWP | ωADP | ksat (cm h−1 ) | Ik2 (kg m−2 s−1 ) | D0 (cm2 h−1 ) | CN |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Box 1 | BWk | Sand | Bare soil | 0.364 (0.437) | 0.196 (0.062) | 0.042 (0.024) | 0.012 (−) | 17.24 (20.88) | 0.0035 (−) | 662.40 (−) | − (66) |
| Box 2 | ET | Loam | Herbaceous vegetation closed/open | 0.455 (0.463) | 0.340 (0.232) | 0.110 (0.116) | 0.035 (−) | 1.91 (1.35) | 0.001 (−) | 128.52 (−) | − (68) |
| Box 3 | Cfa | Clay | Cultivated and managed | 0.507 (0.475) | 0.463 (0.378) | 0.257 (0.265) | 0.065 (−) | 0.006 (0.06) | 0.0001 (−) | 15.19 (−) | − (85) |
| Box 4 | Cfa | Loamy clay | Cultivated and managed | 0.475 (0.464) | 0.370 (0.310) | 0.185 (0.187) | 0.060 (−) | 0.28 (0.23) | 0.0006 (−) | 42.48 (−) | − (81) |
| Box 5 | Cwa | Loam | Cultivated and managed | 0.455 (0.463) | 0.340 (0.232) | 0.110 (0.116) | 0.035 (−) | 1.91 (1.35) | 0.001 (−) | 128.52 (−) | − (53) |
ωPV = saturated water content (volume of voids); ωFC = field capacity; ωPWP = permanent wilting point; ωADP = residual water content (air dryness point); ksat = saturated hydraulic conductivity; Ik2 = minimum infiltration rate; D0 = hydraulic diffusivity parameter; CN = curve number. The parameters ωPV , ωFC , ωPWP , ωADP and CN are dimensionless.
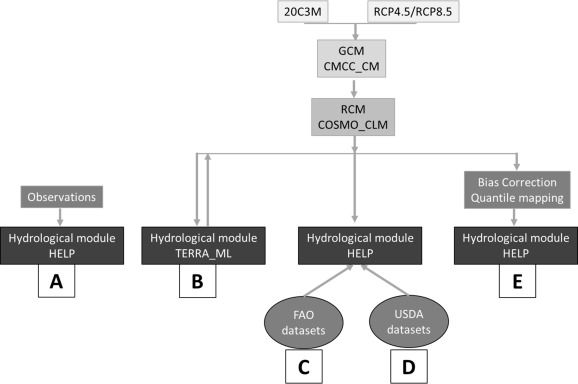
2.3. Modeling chains
Based on the elements mentioned above, five modeling chains are considered; they are summarized in Fig. 5 where they are identified through capital letters as follows.
- hydrological module HELP, driven by observed weather forcing;
- hydrological module TERRA_ML, driven by weather forcing provided by climate simulation chain;
- hydrological module HELP, driven by the weather forcing provided by the climate simulation chain adopting for characterization of soil and land cover the same parameters used in TERRA_ML (B);
- hydrological module HELP, driven by the weather forcing provided by the climate simulation chain adopting for characterization of soil and land cover the parameters retrieved by USDA dataset;
- hydrological module HELP, driven by the weather forcing provided by the climate simulation chain after bias correction, adopting for characterization of soil and land cover the same parameters used in TERRA_ML (B).
|
|
|
Fig. 5. Schematic representation of the five modeling chains adopted. |
Each modeling chain is tested for the five boxes over 1981–2010. Chains B, C and E are adopted to investigate the climate change effects on the soil water balance for the near and long time horizon under RCP4.5 and RCP8.5.
3. Results and discussion
3.1. Evaluation of surface water balance on current period according the different modeling chains
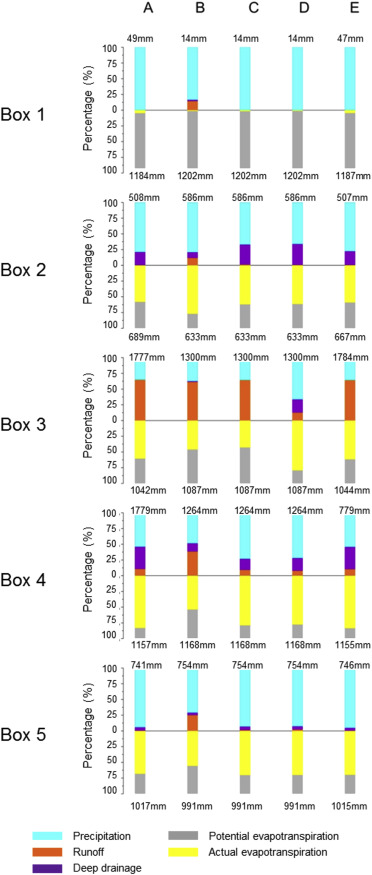
Fig. 6 shows, in the upper part, the percentages of average yearly surface runoff and deep drainage against cumulative precipitation and, in the lower part, the percentage of average yearly actual evapotranspiration against cumulative potential evapotranspiration. Results are carried out, for the five modeling chains and for each reference box, over 1981–2010. Furthermore, the cumulative values of atmospheric inward (precipitation) and outward (potential evapotranspiration) flows are marked; however, lacking observed data, comparisons can be only in relative terms between the chains.
|
|
|
Fig. 6. In the upper part, percentages of average yearly surface runoff and deep drainage against the precipitation (total amount indicated in mm per year); in the lower part percentages of average actual evapotranspiration against potential evapotranspiration (total amount indicated in mm per year). Results refer to 1981–2010. |
Firstly, results provided by modeling chain A driven by the observed data are considered. In box 1 the entire precipitation (however low) is assumed to fully enter the soil while only a tiny percentage of atmospheric evaporative demand (<10%) is fulfilled, probably due to low precipitation and coarse grained soils (sand). In box 2, the deep drainage takes values close to 20% while the actual evaporation covers about 75% of the atmospheric demand. The two values could be explained recalling, in the first case, the coarse soil texture that eases the water movement within the soil pores and, in the second one, the snowpack covering for a large part of the year (average temperature about −3 °C) the surface and that is able to satisfy the (albeit small) evaporative demand. In box 3, the clay soils (ksat = 0.006 cm h−1 ) induce runoff percentages higher than 60% (about 1100 mm) and quite similar values of actual evapotranspiration (about 650 mm) maintaining a large part of water in the shallower layer available to return in atmosphere through evapotranspiration. In the same climate areas and for similar weather forcing, but for more pervious (about 50 times) loamy clay soils (box 4), the runoff decreases to 10% with a considerable deep drainage (about 35%, 600 mm) while the actual evapotranspiration exceeds 900 mm (83%). Finally, for reference box 5 where more pervious loam soil is detected, surface runoff is assumed to be zero while about 10% of the precipitation reaches the deeper layers through bottom drainage where actual evapotranspiration is estimated as 70% of potential demand.
Very similar results are returned when the same hydrological tool is forced by the bias corrected weather data (modeling chain E). It reflects the capabilities of quantile mapping approaches in totally removing biases in the weather inputs provided by climate models. On the other hand, as the main components of soil water balance (e.g. actual evapotranspiration or infiltration) are a strong function of antecedent soil water conditions, such results display also how the climate modeling chain (in spite of quantitative biases) is able to satisfactorily reproduce weather patterns (e.g. temperature seasonal cycles, number of wet days, dry interarrival periods).
The comparison between values provided by E and C allows to evaluate the effects of weather inputs (either bias corrected or not) on the soil hydrological balance. Differences are small for box 1. For box 2, the bias in precipitation (+15%) entails a higher deep drainage for relatively pervious loam soil but comparable actual evaporation. For clay soil in box 3, the relative percentage between the surface runoff and overall precipitation is maintained in both analyses (about 64%) despite the relevant differences in average cumulative precipitation (1301 mm vs 1784 mm) while the actual evapotranspiration rate is greatly diminished (−20%), probably due to lower precipitation inputs sustaining the evaporative demand. For loamy clay (box 4), the lower water input results in smaller deep drainage. Finally, for box 5, the components of simulated and modeled soil water balance are similar since average water input and atmospheric demand were comparable. In general terms, biases in precipitation induce higher variations in all components of the soil water balance, compared to those associated to temperature, i.e. the main forcing of potential evapotranspiration. In this perspective, for example, the variations mentioned above in box 3 appear to be meaningful. On the other hand, the potential evapotranspiration estimated by the raw climate data range in between 92% and 97% of that computed through modeling chain A for boxes where the underestimation of the temperature stood at about 1 °C, while the potential discrepancy does not exceed 5% for boxes where the temperature is overestimated on average (up to 2.5 °C in box 3).
The impact of the adopted physical parameterizations in hydrological modules is taken into account considering values from C and B modeling chains. In box 2, for example, TERRA_ML returns a non-negligible surface runoff component (11%) not estimated through the CN approach used in HELP, where the deep drainage rate reaches values higher than 30%; moreover, the former estimates actual evapotranspirative losses covering 75% of the atmospheric demand while, in the second case it totaled 62%. For climate areas in the SE part of the country, while the models return similar results for clay soil (box 3), again they tend to diverge in reproducing the surface runoff components for loamy clay (box 4): 40% versus 10%. The higher infiltrated rate entails greater actual evaporation and deep drainage components. Analogous findings are then retrieved also for box 5, where the surface runoff reaches 24% in TERRA_ML and 1% for HELP model. Of course, the “intermediate” soils (in term of hydraulic properties) appear to be more sensitive to the approach adopted, while coarse (fine) grained soils for which the overwhelming part of precipitation infiltrate (runoff), are less affected.
At last, modeling chains C and D differ for the soil parameter datasets adopted. As it is clear from Fig. 6 and Table 2 , beyond the differences in intrinsic soil parameters accounting for porosity or field content, the higher the differences in soil permeability, the greater the variations in soil hydrological balance. For this reason, higher spreads are detectable for clay soil, due to a difference of one order of magnitude in ksat (box 3); the higher hydraulic conductivity suggested by USDA for clay soil induces a much lower estimated surface runoff (<10%) but, at the same time, higher evaporative losses and deep drainage components.
| Period | Chain | P (mm) | T (°C) | AE (mm) | R (mm) | DD (mm) |
|---|---|---|---|---|---|---|
| Box 1 1981–2010 | E | 46.6 | 12.6 | 54.0 | 0.0 | 0.0 |
| C | 13.7 | 14.8 | 20.8 | 0.0 | 0.0 | |
| B | 13.7 | 14.8 | 17.4 | 0.0 | 0.0 | |
| Box 1 RCP4.5 2021–2050 | E | 1.4 | 1.2 | 1.3 | 0.0 | 0.0 |
| C | 1.0 | 1.5 | 1.1 | 0.0 | 0.0 | |
| B | 1.0 | 1.5 | 0.7 | 0.0 | 0.0 | |
| Box 1 RCP4.5 2071–2100 | E | 1.6 | 2.1 | 1.5 | 0.0 | 0.0 |
| C | 1.4 | 2.6 | 1.3 | 0.0 | 0.0 | |
| B | 1.4 | 2.6 | 0.9 | 0.0 | 0.0 | |
| Box 1 RCP8.5 2021–2050 | E | 1.6 | 1.4 | 1.5 | 0.0 | 0.0 |
| C | 1.0 | 1.7 | 1.0 | 0.0 | 0.0 | |
| B | 1.0 | 1.7 | 0.7 | 0.0 | 0.0 | |
| Box 1 RCP8.5 2071–2100 | E | 1.5 | 4.1 | 1.4 | 0.0 | 0.0 |
| C | 1.8 | 5.2 | 1.6 | 0.0 | 0.0 | |
| B | 1.8 | 5.2 | 1.2 | 0.0 | 0.0 | |
| Box 2 1981–2010 | E | 506.9 | −2.9 | 393.8 | 1.9 | 111.6 |
| C | 586.4 | −3.4 | 393.1 | 6.4 | 187.3 | |
| B | 586.4 | −3.4 | 487.6 | 68.3 | 53.7 | |
| Box 2 RCP4.5 2021–2050 | E | 1.1 | 1.1 | 1.1 | 1.7 | 1.1 |
| C | 1.1 | 1.1 | 1.1 | 0.7 | 1.1 | |
| B | 1.1 | 1.1 | 1.1 | 1.0 | 1.2 | |
| Box 2 RCP4.5 2071–2100 | E | 1.0 | 2.7 | 1.2 | 0.1 | 0.6 |
| C | 1.1 | 2.8 | 1.1 | 0.5 | 0.9 | |
| B | 1.1 | 2.8 | 1.0 | 0.8 | 1.6 | |
| Box 2 RCP8.5 2021–2050 | E | 1.1 | 1.3 | 1.1 | 1.4 | 1.1 |
| C | 1.1 | 1.4 | 1.1 | 1.2 | 1.2 | |
| B | 1.1 | 1.4 | 1.1 | 1.0 | 1.5 | |
| Box 2 RCP8.5 2071–2100 | E | 1.0 | 5.4 | 1.1 | 0.1 | 0.7 |
| C | 1.0 | 5.4 | 1.1 | 0.3 | 0.9 | |
| B | 1.0 | 5.4 | 0.9 | 0.8 | 1.2 | |
| Box 3 1981–2010 | E | 1784.4 | 15.8 | 644.1 | 1144.3 | 0.0 |
| C | 1300.1 | 18.1 | 465.5 | 835.1 | 0.0 | |
| B | 1300.1 | 18.1 | 503.5 | 797.6 | 0.0 | |
| Box 3 RCP4.5 2021–2050 | E | 1.0 | 0.8 | 1.0 | 1.0 | 0.0 |
| C | 1.0 | 1.2 | 1.0 | 1.0 | 0.0 | |
| B | 1.0 | 1.2 | 1.0 | 1.0 | 0.0 | |
| Box 3 RCP4.5 2071–2100 | E | 1.1 | 1.5 | 1.0 | 1.1 | 0.0 |
| C | 1.1 | 2.2 | 1.0 | 1.1 | 0.0 | |
| B | 1.1 | 2.2 | 0.9 | 1.1 | 0.0 | |
| Box 3 RCP8.5 2021–2050 | E | 1.0 | 1.0 | 1.0 | 1.0 | 0.0 |
| C | 1.0 | 1.5 | 1.0 | 1.0 | 0.0 | |
| B | 1.0 | 1.5 | 0.9 | 1.0 | 0.0 | |
| Box 3 RCP8.5 2071–2100 | E | 1.0 | 3.1 | 0.9 | 1.1 | 0.0 |
| C | 1.1 | 4.3 | 0.9 | 1.1 | 0.0 | |
| B | 1.1 | 4.3 | 0.9 | 1.1 | 0.0 | |
| Box 4 1981–2010 | E | 1779.3 | 20.3 | 964.6 | 180.6 | 633.1 |
| C | 1264.1 | 21.3 | 921.8 | 114.5 | 224.3 | |
| B | 1264.1 | 21.3 | 629.1 | 488.4 | 171.4 | |
| Box 4 RCP4.5 2021–2050 | E | 1.0 | 1.0 | 1.2 | 1.2 | 0.8 |
| C | 1.0 | 1.0 | 1.0 | 1.1 | 0.9 | |
| B | 1.0 | 1.0 | 1.0 | 1.1 | 0.9 | |
| Box 4 RCP4.5 2071–2100 | E | 1.0 | 2.1 | 1.0 | 1.0 | 0.9 |
| C | 1.0 | 2.2 | 1.0 | 1.0 | 0.8 | |
| B | 1.0 | 2.2 | 0.9 | 1.0 | 0.8 | |
| Box 4 RCP8.5 2021–2050 | E | 1.0 | 1.2 | 1.0 | 1.2 | 1.0 |
| C | 1.0 | 1.3 | 1.0 | 1.2 | 1.0 | |
| B | 1.0 | 1.3 | 1.0 | 1.1 | 1.0 | |
| Box 4 RCP8.5 2071–2100 | E | 0.9 | 3.8 | 1.1 | 1.0 | 0.7 |
| C | 1.0 | 4.1 | 1.0 | 1.0 | 0.6 | |
| B | 1.0 | 4.1 | 0.9 | 1.0 | 0.9 | |
| Box 5 1981–2010 | E | 745.7 | 13.6 | 708 | 0.7 | 34.7 |
| C | 754 | 12.5 | 697.1 | 7.7 | 44.1 | |
| B | 754 | 12.5 | 551.7 | 186.3 | 32.2 | |
| Box 5 RCP4.5 2021–2050 | E | 1.0 | 1.1 | 1.0 | 2.5 | 0.7 |
| C | 1.0 | 1.4 | 1.0 | 0.4 | 0.4 | |
| B | 1.0 | 1.4 | 0.9 | 1.1 | 0.9 | |
| Box 5 RCP4.5 2071–2100 | E | 0.9 | 2.0 | 1.0 | 0.1 | 0.0 |
| C | 1.0 | 2.7 | 1.0 | 0.2 | 0.1 | |
| B | 1.0 | 2.7 | 0.9 | 0.9 | 0.7 | |
| Box 5 RCP8.5 2021–2050 | E | 1.0 | 1.2 | 1.0 | 1.7 | 1.1 |
| C | 1.0 | 1.6 | 1.0 | 0.5 | 0.8 | |
| B | 1.0 | 1.6 | 1.0 | 1.1 | 0.9 | |
| Box 5 RCP8.5 2071–2100 | E | 1.2 | 3.3 | 1.1 | 1.2 | 1.5 |
| C | 1.2 | 4.2 | 1.2 | 0.3 | 2.1 | |
| B | 1.2 | 4.2 | 1.1 | 1.5 | 1.4 |
3.2. Evaluation of future anomalies in weather forcing and in the main components of the soil water balance
The discussed values are reported for modeling chains B, C and E in Table 2 . In the same Table, future anomalies in main weather forcing (T and P) and principal components of the soil water budget are also given. For box 1 (NW), some issues for the bias correction approach in keeping the climate signal retrieved from climate models are detected not only for precipitations for which the cumulative values are very small, but also for mean temperatures (e.g. −1 °C for RCP8.5 in 2071–2100). On the other hand, much smaller differences between raw and bias corrected data arise if the temperature climate signal is evaluated in terms of relative variation; in this case, the discrepancies do not exceed 3%. However, due to the higher relative availability of soil water, a greater increase (in percentage) in actual evapotranspiration is returned using bias corrected weather inputs. On the other hand, for box 2 (SW), raw and bias corrected values are quite similar and the climate signal is wholly analogous; however, in this case, the discrepancies in hydrological modeling involve significant spreads in anomalies. For example, the actual evaporation is expected to be increasing (+10%) using HELP (driven by raw or bias corrected) while it is fluctuating for TERRA_ML. Such differences are much more evident for surface runoff and deep drainage components: in the first case, the abrupt variations between near and long time horizons using modeling chain E, induced by low runoff contributions, are not detected in the other analysis; for the deep drainage, TERRA_ML returns consistently a growth (up to 60%) between near and long time horizon, while through HELP, a sign variation is also detected (averagely from about 10% to about −20%). In this regard, it is worth noting that the average temperature values in box 2 are currently lower than zero while, under the effect of climate change, on the long time horizon they could move towards positive values, changing dramatically the snow duration and depth values and then with large variations of the whole soil surface water balance. For box 3 and box 4 (SE), in spite of the great differences in cumulative precipitation between raw and bias corrected values, the climate signal is maintained in a proper way, while for the temperature a decrease is evaluated (higher for box 3). Beyond such variations, components of the soil water balance are expected not to be affected in a significant way; a slight decrease in actual evapotranspiration (about 10% for the long time horizon) and increase in surface runoff (up to 10% for box 3 and 20% for box 4) are estimated while the deep drainage for box 4 is assessed as decreasing mainly on the long time horizon. For these boxes, it clearly arises how the compensation and smoothing effects could make the steps from the variations in weather forcing to the corresponding main components of the soil water balance non-trivial. Indeed, considering for example the farthest time horizons, the increases in temperature (in relative terms, 10% under RCP4.5 and 20% under RCP8.5) do not result in variations of equal magnitude in the actual evapotranspiration (which are often unchanged or slightly decreasing). On the other side, for box 4, under a quite similar cumulative precipitation amount, more consistent variations are returned in surface runoff and deep drainage probably due to variations in precipitation patterns (less wet days but characterized by higher intensities). At last, for box 5 (NE), remarks quite similar to those carried out for box 2 can be reiterated: in both cases, probably, the differences in reproducing surface runoff are associated to the features assumed for loam soil (more pervious according HELP modeling and then returning a greater infiltration rate), clearly revealing the crucial role and uncertainties potentially associated to soil parameters.
3.3. Assessment of seasonal cycles of cumulative water storage referring to shallower soil layer in current and future time spans
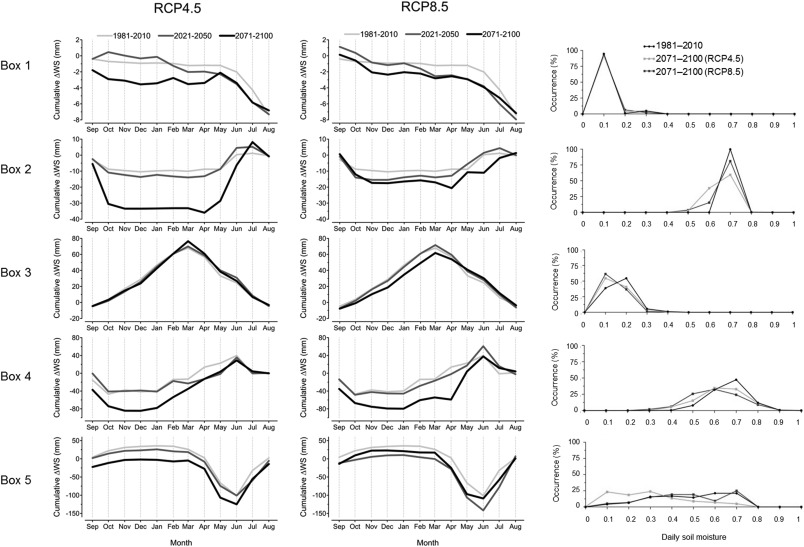
The overall effects of such variations are summed up in Fig. 7 . In the first two columns, one for each RCP considered, the seasonal cycles of cumulative soil water storage are displayed for the five boxes on three different time spans, control period 1981–2010, near term 2021–2050 and long term 2071–2100. The cumulative soil water storage is computed as the algebraic sum of cumulative values of water budget components from the initial instant t0 , corresponding to the beginning of the hydrological year (1st September) to the first day of the i -th month. Furthermore, in the third column, the relative frequencies of occurrence for daily soil moisture, ranging from the wilting point to saturation are displayed for the five boxes on 1981–2010 and 2071–2100 under both scenarios adopting modeling chain E. Concerning the RCP4.5 scenario, a general decrease of water availability in shallower layers is detected for all boxes except box 3 (more evident on the long time horizon); again, it is worth noting how grain texture can affect the soil response comparing cycles for box 3 and box 4 subjected to similar variations in weather forcing: while in clayey soils small variations arise, in the more pervious loamy clay a large reduction is estimated occurring (mainly on 2071–2100) for most of the year. The greater variations are localized in drier seasons (box 2, 4 and 5). Regarding RCP8.5, a minor decrease is expected in box 2 against a greater increase in temperature but where snow hydrology dynamics could play a relevant role. A slight decrease is estimated for box 3 while for box 4 (loamy clay) the variations between wet and dry seasons appear to be clearer. Finally, for box 5 the increase in precipitation is expected to partly counteract the correspondent higher actual evaporation, resulting in a less pronounced reduction of soil water storage during the entire year. In addition, the trends of the cumulative water storage curves point out clearly how larger variations in weather forcing could not result in larger differences in soil moisture due to the compensation and smoothing effects. In this regard, the land cover and soil act as a filter reducing the amplitude of variations of forcing at surface (precipitation and evapotranspiration demand). Finally, in terms of relative frequencies of occurrence of daily soil moisture, the distributions related to future time spans are characterized by a “backward shift” in the peak value in some cases (mainly for boxes 3 and 4) and generally by a higher data dispersion, consistent with what was shown above.
|
|
|
Fig. 7. Seasonal cycles of cumulative soil water storage on two different time spans (first two columns); relative frequencies of occurrence for daily soil moisture ranging from wilting point to saturation on 1981–2010 and 2071–2100 (third column; RCP4.5 and RCP8.5). |
4. Conclusions
The present work is aimed to investigate the main variations assessed in soil water budget for the main climate zones identified in China under the effect of climate change, and to quantify the reliability of the results under climate and hydrological modeling uncertainties. For this purpose, climate simulations at a high resolution (about 14 km) on a large part of China (Bucchignani et al., 2014 ) are used as weather forcing; furthermore, the adoption of two hydrological models, two soil parameter datasets, observed or modeled inputs (provided by raw or bias corrected climate simulations) result in five different simulation chains. The analyses are carried out on five boxes selected in the four main climate areas detected in the investigated domain; however, they should not be considered as strictly related to their location but as examples of potential future dynamics occurring in the different climate zones. Indeed, it is worth remembering that, generally, the soil datasets return parameters applicable at a global scale and estimated from the average features; the local geomorphological peculiarities could induce remarkable differences, in grain size and mainly in soil properties. In this perspective, this work is meant to display how the future impacts induced by variations of weather patterns could vary for different soils and land covers without expecting to represent the actual performance of current and future water balance in the boxes. Concerning the issue of investigating the role played by hydrological modeling and parameters in the evaluation of soil water budget components and their variation under the effect of climate change, the analysis highlights how the choice of some approaches or soil parameterizations can affect the results both in absolute and in relative terms (e.g., as variations between different time spans); moreover, the research shows how the differences could as well be highly related to weather forcing in inputs or investigated soil. Of course, the availability of observed data related to such components could allow for the evaluation of performances and then the selection between the different models; however, at the moment, the available datasets are few and often not adequate. Under these constraints, as currently carried out for climate models, the solution could be the adoption of ensembles multi or single-model with different soil parameter datasets. Moreover, as the processes regulating the soil water budget result as highly non-linear, the adoption of raw or bias corrected inputs can produce assessments different for magnitude and sign. Furthermore, the comparison between the analyses driven by observed and bias corrected values allows to appreciate the great capabilities in removing biases assumed as systematic in climate simulations. On the other hand, the further assumptions related to their use and the possible induced variations in the climate signal with respect to those provided by physically based climate modeling chains should be kept in mind.
Finally, the most evident findings retrieved by the analysis concern the substantial expected decrease in average water content in the shallower part of the soil with different extents according to climate zone, concentration scenario and soil/cover features. Moreover, the assessed increase in temperature and then in evapotranspirative demand do not ever result in higher actual evapotranspiration values, due to the concurrent variations in precipitation patterns. Despite the displayed current uncertainties, the results could represent a further tool in attempting to identify the most vulnerable future areas and what might be the priorities in future adaptation policies. To this aim, the adoption of a single climate simulation could represent a strong constraint while the ensemble simulation could be preferred.
Moreover, the performed analyses are essentially aimed to estimate variations in impacts on the soil, produced by changes in the average values of weather forcing due to climate change that could affect relevant sectors, as agriculture or water supply. On the other hand, special attention should be paid also to the effects of changes in extreme weather events that could entail, in different areas, a substantial increase in occurrence and magnitude of hydro meteorological hazards.
Acknowledgments
This work was developed within the framework of the GEMINA project, Work Package 7.1.6, “B action” (Italy–China cooperation on climate changes), funded by the Italian Ministry of Education, University, and Research and the Italian Ministry of the Environment, Land, and Sea .
References
- Allen and Ingram, 2002 M.R. Allen, W.J. Ingram; Constraints on future changes in climate and the hydrologic cycle; Nature, 419 (2002), pp. 224–232
- Arnell, 2004 N.W. Arnell; Climate change and global water resources: SRES emissions and socio-economic scenarios; Glob. Environ. Chang., 14 (1) (2004), pp. 31–52
- Bates et al., 2008 B.C. Bates, Z.W. Kundzewicz, S. Wu, et al.; Climate Change and Water, IPCC Secretariat, Geneva (2008)
- Bormann, 2008 H. Bormann; Sensitivity of a regionally applied soil vegetation atmosphere scheme to input data resolution and data classification; J. Hydrol., 351 (2008), pp. 154–169 http://dx.doi.org/10.1016/j.jhydrol.2007.12.011
- Bormann, 2009 H. Bormann; Analysis of possible impacts of climate change on the hydrological regimes of different regions in Germany; Adv. Geosci., 21 (2009), pp. 3–11
- Bormann, 2012 H. Bormann; Assessing the soil texture-specific sensitivity of simulated soil moisture to projected climate change by SVAT modelling; Geoderma, 185–186 (2012), pp. 73–83 http://dx.doi.org/10.1016/j.geoderma.2012.03.021
- Bucchignani et al., 2014 E. Bucchignani, M. Montesarchio, L. Cattaneo, et al.; Regional climate modeling over China with COSMO-CLM: performance assessment and climate projections; J. Geophys. Res. Atmos., 119 (2014), pp. 12,151–12,170 http://dx.doi.org/10.1002/jgrd.v119.21
- Campbell, 1974 G.S. Campbell; A simple method for determining unsaturated hydraulic conductivity from moisture retention data; Soil Sci., 117 (6) (1974), pp. 311–314
- Crawford and Linsley, 1966 N.H. Crawford, R.K. Linsley; Digital Simulation in Hydrology: Stanford Watershed Model IV; Department of Civil Engineering, Stanford University (1966)
- Dickinson, 1984 R. Dickinson; Modeling evapotranspiration for 3-dimensional global climate models; Washington DC AGU Geophys. Monogr. Ser., 29 (1984), pp. 58–72 http://dx.doi.org/10.1029/GM029p0058
- Dingman, 2002 S.L. Dingman; Physical Hydrology; (second ed.)Prentice Hall (2002)
- Doms and Schättler, 2002 G. Doms, U. Schättler; A description of the Nonhydrostatic Regional Model LM. Part 1: Dynamics and Numerics; Deutscher Wetterdienst, Offenbach, Germany (2002)
- Doms et al., 2011 G. Doms, J. Föister, E. Heise, et al.; A Description of the Nonhydrostatic Regional COSMO model. Part 2: Physical Parameterization; Deutscher Wetterdienst, Offenbach, Germany (2011)
- Easterling et al., 2000a D.R. Easterling, J.L. Evans, P.Y. Groisman, et al.; Observed variability and trends in extreme climate events: a brief review; Bull. Am. Meteorol. Soc., 81 (2000), pp. 417–425
- Easterling et al., 2000b D.R. Easterling, G.A. Meehl, C. Parmesan, et al.; Climate extremes: observations, modeling, and impacts; Science, 289 (5487) (2000), pp. 2068–2074 http://dx.doi.org/10.1126/science.289.5487.2068
- Ehret et al., 2012 U. Ehret, E. Zehe, V. Wulfmeyer, et al.; HESS opinions “Should we apply bias correction to global and regional climate model data?”; Hydrol. Earth Syst. Sci., 16 (9) (2012), pp. 3391–3404 http://dx.doi.org/10.5194/hess-16-3391-2012
- Fischer et al., 2007 E.M. Fischer, S.I. Seneviratne, P.L. Vidale, et al.; Soil moisture–atmosphere interactions during the 2003 european summer heat wave; J. Clim., 20 (2007), pp. 5081–5099
- Gudmundsson et al., 2012 L. Gudmundsson, J.B. Bremnes, J.E. Haugen, et al.; Technical note: downscaling RCM precipitation to the station scale using statistical transformations–a comparison of methods; Hydrol. Earth Syst. Sci., 16 (2012), pp. 3383–3390
- Held and Soden, 2006 I.M. Held, B.J. Soden; Robust responses of the hydrological cycle to global warming; J. Clim., 19 (2006), pp. 5686–5699 http://dx.doi.org/10.1175/JCLI3990.1
- Holtan, 1961 H.N. Holtan; A concept for infiltration estimates in watershed engineering, U.S. Department of Agriculture; Bulletin (1961), pp. 41–51 (U.S.)
- Huntington, 2006 T.G. Huntington; Evidence for intensification of the global water cycle: review and synthesis; J. Hydrol., 319 (2006), pp. 83–95 http://dx.doi.org/10.1016/j.jhydrol.2005.07.003
- IPCC, 2014 IPCC; Climate Change 2014: Impacts, Adaptation, and Vulnerability. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press, Cambridge and New York (2014)
- Jackson et al., 2001 R.B. Jackson, S.R. Carpenter, C.N. Dahm, et al.; Water in a changing world; Ecol. Appl., 11 (2001), pp. 1027–1045
- Jiang et al., 2007 T. Jiang, Y.D. Chen, C. Xu, et al.; Comparison of hydrological impacts of climate change simulated by six hydrological models in the Dongjiang Basin, South China; J. Hydrol., 336 (2007), pp. 316–333 http://dx.doi.org/10.1016/j.jhydrol.2007.01.010
- Keshta et al., 2009 N. Keshta, A. Elshorbagy, S. Carey; A generic system dynamics model for simulating and evaluating the hydrological performance of reconstructed watersheds; Hydrol. Earth Syst. Sci., 13 (6) (2009), pp. 865–881
- Keshta et al., 2012 N. Keshta, A. Elshorbagy, S. Carey; Impacts of climate change on soil moisture and evapotranspiration in reconstructed watersheds in northern Alberta, Canada; Hydrol. Process, 26 (2012), pp. 1321–1331
- Komuscu et al., 1998 A.U. Komuscu, A. Erkan, S. Oz; Possible impacts of climate change on soil moisture availability in the southeast Anatolia development project region (GAP): an analysis from an agricultural drought perspective; Clim. Change, 40 (1998), pp. 519–545
- Kottek et al., 2006 M. Kottek, J. Grieser, C. Beck, et al.; World map of the Koppen–Geiger climate classification updated; Meteorol. Z., 15 (3) (2006), pp. 259–263 http://dx.doi.org/10.1127/0941-2948/2006/0130
- Kwon et al., 2011 H.-H. Kwon, B. Sivakumar, Y.-I. Moon, et al.; Assessment of change in design flood frequency under climate change using a multivariate downscaling model and a precipitation-runoff model; Stoch. Environ. Res. Risk Assess., 25 (2011), pp. 567–581 http://dx.doi.org/10.1007/s00477-010-0422-z
- Kyoung et al., 2011 M.S. Kyoung, H.S. Kim, B. Sivakumar, et al.; Dynamic characteristics of monthly rainfall in the Korean Peninsula under climate change; Stoch. Environ. Res. Risk Assess., 25 (2011), pp. 613–625 http://dx.doi.org/10.1007/s00477-010-0425-9
- Lenderink and van Meijgaard, 2010 G. Lenderink, E. van Meijgaard; Linking increases in hourly precipitation extremes to atmospheric temperature and moisture changes; Environ. Res. Lett., 5 (2010) http://dx.doi.org/10.1088/1748–9326/5/2/025208
- Luo et al., 2013 Q. Luo, Y. Li, K. Wang, et al.; Application of the SWAT model to the Xiangjiang riverwatershed in subtropical central China; Water Sci. Technol., 67 (2013), pp. 2110–2116
- Maraun, 2013 D. Maraun; Bias correction, quantile mapping, and downscaling: revisiting the inflation issue; J. Clim., 26 (2013), pp. 2137–2143 http://dx.doi.org/10.1175/jcli-d-12-00821.1
- Mason et al., 1999 S.J. Mason, P.R. Waylen, G.M. Mimmack, et al.; Changes in extreme rainfall events in South Africa; Clim. Change, 41 (1999), pp. 249–257
- Meinshausen et al., 2011 M. Meinshausen, S.J. Smith, K. Calvin, et al.; The RCP greenhouse gas concentrations and their extensions from 1765 to 2300; Clim. Change, 109 (1) (2011), pp. 213–241
- Naden and Watts, 2001 P.S. Naden, C.D. Watts; Estimating climate-induced change in soil moisture at the landscape scale: an application to five areas of ecological interest in the UK; Clim. Change, 49 (4) (2001), pp. 411–440
- Obeysekera et al., 2011 J. Obeysekera, J. Park, M. Irizarry-Ortiz, et al.; Past and Projected Trends in Climate and Sea Level for South Florida. Hydrologic and Environmental Systems Modeling, Technical Report; (2011)
- Penman, 1963 H.L. Penman; Vegetation and Hydrology, Technical Communication 53 Harpenden; (1963) Herts, UK
- Piani et al., 2010 C. Piani, J. Haerter, E. Coppola; Statistical bias correction for daily precipitation in regional climate models over Europe; Theor. Appl. Clim., 99 (2010), pp. 187–192 http://dx.doi.org/10.1007/s00704-009-0134-9
- Piao et al., 2010 S. Piao, P. Ciasis, Y. Huang, et al.; The impacts of climate change on water resources and agriculture in China; Nature, 467 (2010), pp. 43–51 http://dx.doi.org/10.1038/nature09364
- Prudhomme et al., 2003 C. Prudhomme, D. Jakob, C. Svensson; Uncertainty and climate change impact on the flood regime of small UK catchments; J. Hydrol., 277 (1–2) (2003), pp. 1–23
- Qiu, 2010 J. Qiu; China drought highlights future climate threats; Nature, 465 (2010), pp. 142–143 http://dx.doi.org/10.1038/465142a
- Ritchie, 1972 J.T. Ritchie; Model for predicting evaporation from a row crop with incomplete cover; Water Resour. Res., 8 (1972), pp. 1204–1213
- Rockel et al., 2008 B. Rockel, A. Will, A. Hense; The regional Climate Model COSMO-CLM (CCLM); Meteorol. Z., 17 (2008), pp. 347–348 http://dx.doi.org/10.1127/0941-2948/2008/0309
- SC (State Council), 2011 SC (State Council); Chinas Policies and Actions on Climate Change; (2011) (in Chinese)
- SC (State Council), 2014 SC (State Council); Chinas Policies and Actions on Climate Change; (2014) (in Chinese)
- Schiermeier, 2008 Q. Schiermeier; Water: a long dry summer; Nature, 452 (2008), pp. 270–273 http://dx.doi.org/10.1038/452270a-
- Schroeder et al., 1994 P.R. Schroeder, T.S. Dozier, P.A. Zappi, et al.; The Hydrologic Evaluation of Landfill Performance (HELP) Model: Engineering Documentation for Version 3; US Environmental Protection Agency, Cincinnati, Ohio (1994)
- Scoccimarro et al., 2011 E. Scoccimarro, S. Gualdi, A. Bellucci, et al.; Effects of tropical cyclones on ocean heat transport in a high resolution coupled general circulation model; J. Clim., 24 (2011), pp. 4368–4384 http://dx.doi.org/10.1175/2011JCLI4104.1
- Taylor et al., 2012 K.E. Taylor, R.J. Stouffer, G.A. Meehl; An overview of CMIP5 and the experiment design; B. Am. Meteorol. Soc., 93 (4) (2012), pp. 485–498 http://dx.doi.org/10.1175/BAMS-D-11-00094.1
- Teutschbein and Seibert, 2012 C. Teutschbein, J. Seibert; Bias correction of regional climate model simulations for hydrological climate-change impact studies: review and evaluation of different methods; J. Hydrol., 456–457 (2012), pp. 12–29 http://dx.doi.org/10.1016/j.jhydrol.2012.05.052
- Teutschbein et al., 2011 C. Teutschbein, F. Wetterhall, J. Seibert; Evaluation of different downscaling techniques for hydrological climate-change impact studies at the catchment scale; Clim. Dynam., 37 (2011), pp. 2087–2105 http://dx.doi.org/10.1007/s00382-010-0979-8
- USDA (U.S. Department of Agriculture), 1985 USDA (U.S. Department of Agriculture); National Engineering Handbook; (U.S.) (1985)
- Vezzoli et al., 2015 R. Vezzoli, P. Mercogliano, S. Pecora, et al.; Hydrological simulation of Po River (North Italy) discharge under climate change scenarios using the RCM COSMO-CLM; Sci. Total Environ., 521–522 (2015), pp. 346–358 http://dx.doi.org/10.1016/j.scitotenv.2015.03.096
- Villani et al., 2015 V. Villani, G. Rianna, P. Mercogliano, et al.; Statistical approaches versus weather generator to downscale RCM outputs to slope scale for stability assessment: a comparison of performances; Electron. J. Geotech. Eng., 8 (2) (2015), pp. 1495–1515
- Wang et al., 2013 D. Wang, C. Menz, T. Simon, et al.; Regional dynamical downscaling with CCLM over East Asia; Meteorol. Atmos. Phys., 121 (2013), pp. 39–53 http://dx.doi.org/10.1007/s00703-013-0250-z
- Wilby et al., 2002 R.L. Wilby, C.W. Dawson, E.M. Barrow; SDSM–a decision support tool for the assessment of regional climate change impacts; Environ. Model. Softw., 17 (2002), pp. 147–159
- Wu and Gao, 2013 J. Wu, X.J. Gao; A gridded daily observation dataset over China region and comparison with the other datasets; Chin. J. Geophys., 56 (4) (2013), pp. 1102–1111 http://dx.doi.org/10.6038/cjg20130406 (in Chinese)
- Wu et al., 2015 Y. Wu, S. Liu, W. Yan, et al.; Climate change and consequences on the water cycle in the humid Xiangjiang River Basin, China; Stoch. Environ. Res. Risk Assess. (2015) http://dx.doi.org/10.1007/s00477-015-1073-x
- Yang et al., 2010 H.L. Yang, Y.L. Xu, L. Zhang, et al.; Projected change in heat waves over China using the PRECIS climate model; Clim. Res., 42 (2010), pp. 79–88
- Zhai et al., 2010 J.Q. Zhai, B. Liu, Hartmann, et al.; Dryness/wetness variations in ten large river basins of China during the first 50 years of the 21st century; Quat. Int., 226 (1–2) (2010), pp. 101–111 http://dx.doi.org/10.1016/j.quaint.2010.01.027
- Zhang et al., 2009 X.C. Zhang, W.Z. Liu, Z. Li, et al.; Simulating site-specific impacts of climate change on soil erosion and surface hydrology in southern Loess Plateau of China; Catena, 79 (3) (2009), pp. 237–242 http://dx.doi.org/10.1016/j.catena.2009.01.006
- Zhou et al., 2011 G. Zhou, X. Wei, Y. Wu, et al.; Quantifying the hydrological responses to climate change in an intact forested small watershed in Southern China; Glob. Change Biol., 17 (2011), pp. 3736–3746 http://dx.doi.org/10.1111/j.1365-2486.2011.02499.x
- Zollo et al., 2015 A.L. Zollo, V. Rillo, E. Bucchignani, et al.; Extreme temperature and precipitation events over Italy: assessment of high resolution simulations with COSMO-CLM and future scenarios; Int. J. Clim. (2015) http://dx.doi.org/10.1002/joc.4401
Document information
Published on 15/05/17
Submitted on 15/05/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?