Unsteady three-dimensional flow of Casson–Carreau fluids past a stretching surface

Abstract

In this study, we investigated the effects of nonlinear thermal radiation and non-uniform heat source/sink in unsteady three-dimensional flow of Carreau and Casson fluids past a stretching surface in the presence of homogeneous–heterogeneous reactions. The transformed governing equations are solved numerically using Runge–Kutta based shooting technique. We obtained good accuracy of the present results by comparing with the already published literature. The influence of dimensionless governing parameters on velocity, temperature and concentration profiles along with the friction factors, local Nusselt and Sherwood numbers is discussed and presented graphically. We presented dual solutions for flow, heat and mass transfer in Carreau and Casson fluids. It is found that the heat and mass transfer rate in Casson fluid is significantly high while compared with the Carreau fluid.

Keywords

MHD; Homogeneous–heterogeneous reaction; Nonlinear thermal radiation; Carreau fluid; Casson fluid; Non-uniform heat source/sink

Nomenclature

${\textstyle u{\mbox{,}}\quad v{\mbox{,}}\quad w}$- velocity components in ${\textstyle X{\mbox{,}}\quad Y\quad and\quad Z}$ directions respectively (${\textstyle {\mbox{m}}/{\mbox{s}}}$)

${\textstyle x}$- distance along the surface (${\textstyle {\mbox{m}}}$)

${\textstyle y}$- distance normal to the surface (${\textstyle {\mbox{m}}}$)

${\textstyle c_{p}}$- specific heat capacity at constant pressure (${\textstyle {\mbox{J}}/{\mbox{Kg}}\quad {\mbox{K}}}$)

${\textstyle f{\mbox{,}}g}$- dimensionless velocities

${\textstyle T}$- Temperature of the fluid (${\textstyle {\mbox{K}}}$)

${\textstyle C}$- concentration of the fluid (${\textstyle {\mbox{kg}}/{\mbox{m}}^{3}}$)

${\textstyle q^{'''}}$- non uniform heat source/sink (${\textstyle {\mbox{k}}/{\mbox{s}}}$)

${\textstyle g}$- acceleration due to gravity (${\textstyle {\mbox{m}}/{\mbox{s}}^{2}}$)

${\textstyle k}$- thermal conductivity (${\textstyle {\mbox{W}}/{\mbox{m}}\quad {\mbox{K}}}$)

${\textstyle \alpha }$- diffusion coefficient (${\textstyle {\mbox{m}}^{2}/{\mbox{s}}}$)

${\textstyle P}$- pressure (${\textstyle {\mbox{Pa}}\quad {\mbox{or}}\quad {\mbox{N}}/{\mbox{m}}}$)

${\textstyle \eta }$- similarity variable

${\textstyle \sigma }$- electrical conductivity (${\textstyle {\mbox{S}}/{\mbox{m}}}$)

${\textstyle {\sigma }^{_{\ast }}}$- Stefan–Boltzmann constant (${\textstyle {\mbox{W}}/{\mbox{m}}^{2}\quad {\mbox{K}}^{4}}$)

${\textstyle k^{_{\ast }}}$- mean absorption coefficient (${\textstyle {\mbox{m}}^{-1}}$)

${\textstyle {\beta }_{T}}$- volumetric thermal expansion (${\textstyle {\mbox{K}}^{-1}}$)

${\textstyle {\beta }_{C}}$- concentration expansion coefficient (${\textstyle {\mbox{K}}^{-1}}$)

${\textstyle \theta }$- dimensionless temperature

${\textstyle \rho }$- density (${\textstyle {\mbox{kg}}/{\mbox{m}}^{3}}$)

${\textstyle \nu }$- kinematic viscosity (${\textstyle {\mbox{m}}^{2}/{\mbox{s}}}$)

${\textstyle \mu }$- dynamic viscosity (${\textstyle {\mbox{N}}\quad {\mbox{s}}/{\mbox{m}}^{2}}$)

${\textstyle a{\mbox{,}}\quad b}$- rate constants

${\textstyle n}$- power-law index parameter

${\textstyle A^{_{\ast }}{\mbox{,}}\quad B^{_{\ast }}}$- non-uniform heat generation/absorption coefficients

${\textstyle {Cf}_{x}}$- skin friction coefficient in x-direction

${\textstyle {Cf}_{y}}$- skin friction coefficient in y-direction

${\textstyle {Nu}_{x}}$- local Nusselt number

${\textstyle {Sh}_{x}}$- local Sherwood number

${\textstyle {Re}_{x}}$- local Reynolds number

${\textstyle Pr}$- Prandtl number

${\textstyle Sc}$- Schmidt number

${\textstyle A}$- unsteadiness parameter

${\textstyle {\theta }_{w}}$- the ratio of temperatures

${\textstyle We}$- Weissenberg number

${\textstyle a_{0}}$- positive constant

${\textstyle D_{A}{\mbox{,}}\quad D_{B}}$- diffusion coefficients

${\textstyle a_{1}{\mbox{,}}\quad b_{1}}$- concentration of chemical species

${\textstyle k_{c}{\mbox{,}}\quad k_{s}}$- rate constants

${\textstyle \delta }$- ratio of diffusion coefficients

${\textstyle \beta }$- Casson fluid parameter

${\textstyle B_{0}}$- magnetic induction parameter

${\textstyle M}$- magnetic field parameter

${\textstyle \lambda }$- stretching ratio parameter

${\textstyle K_{s}}$- strength of heterogeneous reaction parameter

${\textstyle K}$- strength of homogeneous reaction parameter

Subscripts

${\textstyle f}$- fluid

${\textstyle w}$- condition at the wall

${\textstyle \infty }$- condition at the free stream

1. Introduction

Convection boundary layer flow over a stretching sheet has relevance in many engineering processes such as drawing of plastic films, tinning and annealing of copper wires and electrolyte paper production. Due to these applications Sakiadis [1] started an analysis on the flow past a stretching sheet. Thereafter, the researchers [2], [3], [4], [5] and [6] continued their research on the flow over a stretching sheet under various interesting aspects. On the other hand flow of non-Newtonian fluids encountered in several large-scale industrial applications including blood flows in micro-circulatory system, food and polymer processing, magma and ice flows. Due to flow diversity in the environment a single mathematical model does not overcome all the rheological fluid properties associated with non-Newtonian fluids. Thus various constitutive equations for such fluids are available in already existing literature [7] and [8]. Additionally, the power-law Carreau fluid is also one of the non-Newtonian fluids. Carreau fluid model is valid for viscous, high and low shear rates. Because of this advancement, it has benefitted in many technological and manufacturing flows. Keeping this into view, Zhu [9] discussed the mass transfer characteristics of Carreau fluid over a swarm of Newtonian drops. The time dependent Poiseuille flow of a Carreau fluid in the presence of slip effect was investigated by Georgiou [10] and concluded that the wavelength and amplitude of oscillations in radial direction are decreased with an increase in the slip effect. Abd El Naby et al. [11] considered the peristaltic flow characteristics of Carreau fluid in uniform tube and discussed the heat transfer characteristics of Carreau fluid.

Magnetohydrodynamic (MHD) is the mechanical property of fluids, which describes the motion of highly conducting fluid with existing magnetic field. The conducting fluids generate an electric current due to fluid flow and this force boosts up the mechanical properties of fluid. The peristaltic flow with induced magnetic field also has major applications in the psychological fluids: like peristaltic MHD compressor, blood pumping machines and the blood flows, and these were analytically studied by [12] and [13]. MHD convection flow of an unsteady EG-Nimonic nano fluid past a vertical plate was examined by Sandeep et al. [14]. Further, Raju et al. [15] extended this work for ferrofluids by considering the non-uniform heat source/sink and aligned magnetic field effects. The flow of peristaltic Carreau nanofluid past an asymmetric channel was numerically investigated by Akbar et al. [16] and found that increasing values of magnetic field parameter encourages the velocity profiles. Later on, the researchers [17], [18], [19] and [20] reported experimental and theoretical studies on non-Newtonian fluid flows with different flow configurations by considering different boundary conditions. Casson fluid is also a non-Newtonian fluid, which is a shear thinning liquid and exhibits the yield shear stresses. If yield stress is greater than the shear stress then it acts as a solid, whereas if yield stress lesser than the shear stress is applied then the fluid would start to move, for example honey, tomato sauce, fruit juices and human blood. It has various applications in fibrinogen, cancer homeo-therapy, protein and red blood cells form a chain type structure. Due to these applications many researchers are concentrating characteristics of Casson fluid, which are given in Refs. [21], [22] and [23].

The heat and mass transfer in the flows over a stretching sheet with homogeneous–heterogeneous reaction has a major role in metallurgy and chemical engineering industries, such as polymer production and food processing. Moreover, coupled heat and mass transfer problems in the presence of homogeneous–heterogeneous reaction are of importance in many processes, and therefore it is a considerable amount of attention in recent days. Therefore some of the possible applications can be found in the processes such as drying, damage of crops due to freezing, distribution of temperature and moisture over agricultural fields and groves of fruit trees, evaporation at the surface of a water body and energy transfer in a wet cooling tower. Hayat et al. [24] discussed Carreau fluid flow past a convectively heated stretching surface and concluded that the velocity profiles are improved with the material parameter. Convection flow of non-Newtonian MHD flow past a permeable exponentially stretching sheet was numerically investigated by Raju et al. [25]. The flow through stretching sheet has great attention due to its importance in various fields such as MHD accelerators, generators, pumps and flow meters, and design of cooling systems and these are given by Akbar et al. [26]. Jenny et al. [27] studied the Rayleigh–Benard flow for convection rolls in Carreau fluids and analyzed the momentum and heat transfer behavior of Carreau fluid. Jasmine Benazir et al. [31] examined an unsteady magnetohydrodynamic flow due to vertical cone with non-uniform heat generation/absorption. The variable conductivity effect on hydrodynamic convection flow due to cone in the presence of chemical reaction was investigated numerically by Rushikumar et al. [32]. Shehzad et al. [33] discussed the analytical solutions of slip effect on peristalsis flow over a curved channel in the presence of radial magnetic field. Dufour effect on radiative unsteady magnetohydrodynamic flow past a vertically accelerated wavy plate with variation of double diffusion effects was illustrated by Prakash et al. [34]. Recently, the researchers [35], [36], [37], [38] and [39] discussed the non-Newtonian fluid flow of stretching sheet with various effects and various boundary conditions. In these studies they found very interesting solutions as the non-uniform heat source/sink parameter has tendency to control the temperature profiles and also the non-Newtonian fluids are regulating the temperature profiles of the flow.

In most of the studies the radiation can be treated as a constant in the flow region. In real time it is very difficult to maintain the constant temperature entire flow region. But, in this study, we proposed a mathematical model for analyzing the effects of nonlinear thermal radiation on three-dimensional flow of Carreau and Casson fluids past a stretching surface with homogeneous–heterogeneous reactions and non-uniform heat source/sink. The nonlinear thermal radiation has importance in various industrial as well as science and technological applications. The transformed governing equations are solved numerically using Runge–Kutta based shooting technique. We presented dual solutions for the flow of Carreau and Casson fluids over a stretching sheet.

2. Formulation of the problem

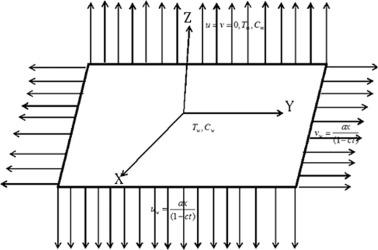
Consider an unsteady three dimensional flow of Carreau and Casson fluids past a stretching sheet in the presence of nonlinear thermal radiation and non-uniform heat source/sink. For improving mass transfer we also considered the homogeneous–heterogeneous reactions. The flow is restricted to z-direction as displayed in Fig. 1. In this study we skip the induced magnetic field and viscous dissipation effects. The flow is due to stretching surface. The rheological model for an isotropic flow of Casson fluid is [23] given as follows:

${\tau }^{1/n}={\tau }_{0}^{1/n}+\mu {\overset {\cdot }{\gamma }}^{1/n}$

(1)

${\tau }_{i{\mbox{,}}j}={\begin{array}{c}2({\mu }_{B}+p_{y}/{\sqrt {2\pi }})e_{ij}{\mbox{,}}\quad \pi \succ {\pi }_{c}\\2({\mu }_{B}+p_{y}/{\sqrt {2\pi }})e_{ij}{\mbox{,}}\quad \pi \prec {\pi }_{c}\end{array}}$

(2)

Figure 1. Schematic representation of physical model.

In the above equation ${\textstyle \pi =e_{ij}e_{ij}}$ and ${\textstyle e_{ij}}$ is the ${\textstyle \left(i{\mbox{,}}j\right)}$ th component of the deformation rate, ${\textstyle \pi }$ the product of the component of deformation rate with itself, ${\textstyle {\pi }_{c}}$ is a critical value of this product based on the non-Newtonian model, ${\textstyle {\pi }_{B}}$ is the plastic dynamic viscosity of non-Newtonian fluid, and ${\textstyle p_{y}}$ is the yield stress of the fluid. The anonymous researchers have suggested the value of n = 1. However, in many applications this value is n > 1.

The flow is generated due to the linear stretching sheet. The extra stress tensor for Carreau fluid is given by [26]

${\overline {{\tau }_{ij}}}={\eta }_{0}\left[1+{\frac {\left(n-1\right)}{2}}{\left(\Gamma {\overline {\overset {\cdot }{\gamma }}}\right)}^{2}{\overline {{\overset {\cdot }{\gamma }}_{ij}}}\right]$

(3)

Here ${\textstyle {\overline {{\tau }_{ij}}}}$ is the extra stress tensor, ${\textstyle {\eta }_{0}}$ is the zero shear rate viscosity, ${\textstyle \Gamma }$ is the time constant, ${\textstyle n}$ is the power-law index and ${\textstyle {\overline {\overset {\cdot }{\gamma }}}}$ is defined as

${\overline {\overset {\cdot }{\gamma }}}={\sqrt {{\frac {1}{2}}{\sum }_{i}{\sum }_{j}{\overline {{\overset {\cdot }{\gamma }}_{ij}}}{\overline {{\overset {\cdot }{\gamma }}_{ji}}}}}=$${\sqrt {\frac {1}{2}}}\Pi$

(4)

where Π is the second invariant strain tensor. According to above assumptions the flow analysis of Carreau and Casson fluids equations is given by

2.1. Flow analysis

${\frac {\partial u}{\partial x}}+{\frac {\partial v}{\partial y}}+$${\frac {\partial w}{\partial z}}=0{\mbox{,}}$

(5)

$\left({\frac {\partial u}{\partial t}}+u{\frac {\partial u}{\partial x}}+\right.$$\left.v{\frac {\partial u}{\partial y}}+w{\frac {\partial u}{\partial z}}\right)=$$\nu \left(\left(1+{\frac {1}{\beta }}\right){\frac {{\partial }^{2}u}{\partial z^{2}}}+\right.$$\left.{\frac {3(n-1)}{2}}{\Gamma }^{2}{\left({\frac {\partial u}{\partial z}}\right)}^{2}{\frac {{\partial }^{2}u}{\partial z^{2}}}\right)-$${\frac {\sigma B_{0}^{2}}{\rho }}u{\mbox{,}}$

(6)

$\left({\frac {\partial v}{\partial t}}+u{\frac {\partial v}{\partial x}}+\right.$$\left.v{\frac {\partial v}{\partial y}}+w{\frac {\partial v}{\partial z}}\right)=$$\nu \left(\left(1+{\frac {1}{\beta }}\right){\frac {{\partial }^{2}v}{\partial z^{2}}}+\right.$$\left.{\frac {3(n-1)}{2}}{\Gamma }^{2}{\left({\frac {\partial v}{\partial z}}\right)}^{2}{\frac {{\partial }^{2}v}{\partial z^{2}}}\right)-$${\frac {\sigma B_{0}^{2}}{\rho }}v{\mbox{,}}$

(7)

where ${\textstyle u{\mbox{,}}\quad v\quad {\mbox{and}}\quad w}$ are the velocity components along the ${\textstyle x{\mbox{,}}\quad y\quad {\mbox{and}}\quad z}$ directions respectively. ν   is the kinematic viscosity coefficient, ${\textstyle \beta }$ is the Casson fluid parameter, ${\textstyle \Gamma }$ is the time constant, ${\textstyle \rho }$ is the density of the fluid and ${\textstyle \sigma }$ is the electric conductivity with the boundary conditions

${\begin{array}{l}u=u_{w}(x)={\frac {ax}{\left(1-ct\right)}}{\mbox{,}}\quad v=v_{w}(x)={\frac {ax}{\left(1-ct\right)}}{\mbox{,}}\quad w=0{\mbox{,}}\quad {\mbox{at}}\quad z=0{\mbox{,}}\\u=v=0{\mbox{,}}\quad {\mbox{as}}\quad z\rightarrow \infty {\mbox{,}}\end{array}}$

(8)

here ${\textstyle u_{w}\quad {\mbox{and}}\quad v_{w}}$ are the stretching velocities near the surface. To convert the nonlinear partial differential equations for velocities, we are now introducing the similarity transformations as follows:

$u={\frac {bx}{\left(1-ct\right)}}f^{'}(\eta ){\mbox{,}}\quad v=$${\frac {by}{\left(1-ct\right)}}g^{'}(\eta ){\mbox{,}}\quad w=$$-{\frac {b\nu }{1-ct}}(f(\eta )+g(\eta )){\mbox{,}}\quad \eta =$$z{\sqrt {\frac {b}{{\upsilon }_{f}(1-ct)}}}{\mbox{,}}$

(9)

Here in Eq. (9)${\textstyle u{\mbox{,}}\quad v\quad {\mbox{and}}\quad w}$ automatically satisfy the continuity equation, and by using Eqs. (9), and (5), (6) and (7) are given by

$\left(1+{\frac {1}{\beta }}\right)f^{'''}+(f+g)f^{''}-$$f^{{'}2}-A\left(f^{'}+\eta {\frac {1}{2}}f^{''}\right)+$${\frac {3(n-1)}{2}}{Wef}^{{''}2}f^{'''}-{Mf}^{'}=$$0{\mbox{,}}$

(10)

$\left(1+{\frac {1}{\beta }}\right)g^{'''}+(f+g)g^{''}-$$g^{{'}2}-A\left(g^{'}+\eta {\frac {1}{2}}g^{''}\right)+$${\frac {3(n-1)}{2}}{Weg}^{{''}2}g^{'''}-{Mg}^{'}=$$0{\mbox{,}}$

(11)

The transformed boundary conditions are as follows:

${\begin{array}{l}f=0{\mbox{,}}\quad g=0{\mbox{,}}\quad f^{'}=\lambda {\mbox{,}}\quad g^{'}=\lambda {\mbox{,}}\quad {\mbox{at}}\quad \eta =0{\mbox{,}}\\f^{'}\rightarrow 0{\mbox{,}}\quad g^{'}\rightarrow 0{\mbox{,}}\quad {\mbox{as}}\quad \eta \rightarrow \infty {\mbox{,}}\end{array}}$

(12)

here A is the unsteadiness parameter, We is the Weissenberg number, M   is the magnetic field parameter and ${\textstyle \lambda }$ is the stretching ratio parameter.

$M={\frac {\sigma B_{0}^{2}}{{\rho }_{f}c}}{\mbox{,}}\quad We=$${\frac {{\Gamma }^{2}x^{2}b^{3}}{\nu {\left(1-ct\right)}^{3}}}{\mbox{,}}\quad \lambda =$${\frac {a}{b}}{\mbox{,}}\quad A={\frac {c}{b}}$

(13)

2.2. Heat transfer analysis

The boundary layer thermal energy equation with nonlinear thermal radiation and non-uniform heat source/sink is given by

${\frac {\partial T}{\partial t}}+u{\frac {\partial T}{\partial x}}+$$v{\frac {\partial T}{\partial y}}+w{\frac {\partial T}{\partial z}}=$$\alpha {\frac {{\partial }^{2}T}{\partial z^{2}}}+{\frac {16{\sigma }^{_{\ast }}}{3k\rho c_{p}}}{\frac {\partial T}{\partial z}}\left(T^{3}{\frac {\partial T}{\partial z}}\right)+$$q^{'''}{\mbox{,}}$

(14)

with the boundary conditions

$T=T_{w}{\mbox{,}}\quad {\mbox{at}}\quad z=0{\mbox{,}}\quad T\rightarrow T_{\infty }{\mbox{,}}\quad {\mbox{as}}\quad z\rightarrow \infty {\mbox{,}}$

(15)

The non-dimensional temperature parameters are given by

$T=T_{\infty }+(T_{w}-T_{\infty })\theta {\mbox{,}}\quad T=$$T_{\infty }(1+({\theta }_{w}-1)\theta )$

(16)

where T   is the fluid temperature, ${\textstyle T_{w}{\mbox{,}}\quad T_{\infty }}$ are near the fluid temperature and the far away from the fluid temperature, k   is the thermal conductivity of the fluid, ${\textstyle c_{p}}$ is the specific heat capacitance at constant pressure, ${\textstyle c_{s}}$ is the concentration susceptibility and ${\textstyle {\sigma }^{_{\ast }}}$ is the Stefan–Boltzmann constant.

The time dependent non-uniform heat source/sink ${\textstyle q^{'''}}$ is defined as follows:

$q^{'''}={\frac {k_{f}u_{w}(x)}{x\nu }}\left(A^{_{\ast }}(T_{w}-\right.$$\left.T_{\infty })f^{'}+B^{_{\ast }}(T-T_{\infty })\right){\mbox{,}}$

(17)

The positive values of ${\textstyle A^{_{\ast }}{\mbox{,}}\quad B^{_{\ast }}}$ of above equation correspond to heat generation and negative values corresponds to heat absorption.

Using Eqs. (16) and (17), (14) and (15) are reduced to

${\theta }^{''}+Pr(f+g){\theta }^{'}-(A/2)\eta {\theta }^{'}+$$A^{_{\ast }}f^{'}+B^{_{\ast }}\theta +R\left({\left(1+({\theta }_{w}-1)\theta \right)}^{3}{\theta }^{''}+\right.$$\left.3({\theta }_{w}-1){\theta }^{{'}2}{\left(1+({\theta }_{w}-1)\theta \right)}^{2}\right)=$$0{\mbox{,}}$

(18)

With the transformed boundary conditions

$\theta (0)=1{\mbox{,}}\quad \theta (\infty )=0{\mbox{,}}$

(19)

where Pr is the Prandtl number, A is the unsteadiness parameter, R   is the thermal radiation parameter, and ${\textstyle {\theta }_{w}}$ is the ratio of temperatures which are given by

$Pr={\frac {k}{\mu C_{p}}}{\mbox{,}}\quad R={\frac {16{\sigma }^{_{\ast }}T_{\infty }^{3}}{3{kk}^{_{\ast }}}}{\mbox{,}}\quad {\theta }_{w}=$${\frac {T_{\infty }}{T_{w}}}{\mbox{,}}$

2.3. Mass transfer analysis

The boundary layer equation for conservation of mass in the presence homogeneous–heterogeneous reactions is given by

${\frac {\partial a_{1}}{\partial t}}+u{\frac {\partial a_{1}}{\partial x}}+$$v{\frac {\partial a_{1}}{\partial y}}+w{\frac {\partial a_{1}}{\partial z}}=$$D_{A}{\frac {{\partial }^{2}a_{1}}{\partial z^{2}}}-k_{c}a_{1}b_{1}^{2}{\mbox{,}}$

(20)

${\frac {\partial b_{1}}{\partial t}}+u{\frac {\partial b_{1}}{\partial x}}+$$v{\frac {\partial b_{1}}{\partial y}}+w{\frac {\partial b_{1}}{\partial z}}=$$D_{B}{\frac {{\partial }^{2}b_{1}}{\partial z^{2}}}+k_{c}a_{1}b_{1}^{2}{\mbox{,}}$

(21)

The corresponding boundary conditions are

$D_{A}{\frac {\partial a_{1}}{\partial z}}=k_{\mbox{s}}a_{1}{\mbox{,}}\quad D_{B}{\frac {\partial b_{1}}{\partial z}}=$$-k_{\mbox{s}}a_{1}{\mbox{,}}\quad {\mbox{at}}\quad z=0{\mbox{,}}a_{1}\rightarrow a_{0}{\mbox{,}}\quad b_{1}\rightarrow 0{\mbox{,}}\quad {\mbox{as}}\quad z\rightarrow \infty {\mbox{,}}$

(22)

The non-dimensional are given by

$\phi (\eta )={\frac {a_{1}}{a_{0}}}{\mbox{,}}\quad H(\eta )=$${\frac {b_{1}}{a_{0}}}{\mbox{,}}$

(23)

where ${\textstyle D_{A}\quad {\mbox{and}}\quad D_{B}}$ are the diffusion coefficient of the species ${\textstyle A\quad {\mbox{and}}\quad B}$, ${\textstyle a_{0}}$ is the positive constant, ${\textstyle a_{1}{\mbox{,}}\quad b_{1}}$ are the concentrations of the chemical species, ${\textstyle k_{c}\quad {\mbox{and}}\quad k_{s}}$ are the rate constants, and we assume that both the chemical reactions are isothermal. Using similarity transforms (23), Eqs. (20) and (21) reduce to

${\frac {1}{Sc}}{\phi }^{''}+(f+g){\phi }^{'}-K\phi H^{2}=$$0{\mbox{,}}$

(24)

${\frac {\delta }{Sc}}H^{''}+(f+g)H^{'}+K\phi H^{2}=$$0{\mbox{,}}$

(25)

The corresponding boundary conditions are

${\phi }^{'}(0)=K_{s}\phi (0){\mbox{,}}\quad \delta H^{'}(0)=$$-K_{s}\phi (0)\quad {\mbox{at}}\quad \eta =0{\mbox{,}}\quad \phi =$$1{\mbox{,}}\quad H=0\quad {\mbox{as}}\quad \eta \rightarrow \infty {\mbox{,}}$

(26)

where Sc   is the Schmidt number, ${\textstyle K_{s}}$ is the strength of the heterogeneous-reaction parameter, δ is the ratio of diffusion coefficient, and K is the strength of the homogeneous reaction parameter, which are given by

$Sc={\frac {\nu }{D_{A}}}{\mbox{,}}\quad \delta ={\frac {D_{B}}{D_{A}}}{\mbox{,}}\quad K=$${\frac {k_{c}a_{0}^{2}}{\left(1-tc\right)}}{\mbox{,}}\quad K_{s}=$${\frac {k_{s}}{D_{A}}}{\left({\frac {\nu }{\left(1-tc\right)}}\right)}^{1/2}{\mbox{,}}$

(27)

For the most of real time practical applications we assume that chemical diffusion coefficients are almost same size. So diffusion coefficients are equal. Then ${\textstyle \delta =1}$ and in this case we get

$\phi (\eta )+H(\eta )=1{\mbox{,}}$

(28)

Then by substituting Eq. (25) in (21) and (22), we get

${\frac {1}{Sc}}{\phi }^{''}+(f+g){\phi }^{'}-K\phi {\left(1-\phi \right)}^{2}=$$0{\mbox{,}}$

(29)

Subject to the boundary conditions:

${\phi }^{'}(0)=K_{s}\phi (0){\mbox{,}}\quad \phi (\infty )=$$1{\mbox{,}}$

(30)

For physical quantities of interest the friction factor coefficients along ${\textstyle x{\mbox{,}}\quad y}$ directions, local Nusselt and Sherwood numbers are given by

$C_{fx}{Re}^{1/2}={\frac {{\tau }_{w}}{\rho u_{w}{\left(x\right)}^{2}}}{\mbox{,}}\quad {Re}^{1/2}C_{fy}=$${\frac {{\tau }_{w}}{\rho u_{w}{\left(y\right)}^{2}}}{\mbox{,}}$

(31)

$C_{fx}{Re}^{1/2}=\left[\left(1+{\frac {1}{\beta }}\right)f^{''}(0)+\right.$$\left.{\frac {(n-1)We}{2}}{\left(f^{''}(0)\right)}^{3}\right]{\mbox{,}}\quad {Re}^{1/2}C_{fy}=$$\left[\left(1+{\frac {1}{\beta }}\right)g^{''}(0)+{\frac {(n-1)We}{2}}{\left(g^{''}(0)\right)}^{3}\right]{\mbox{,}}$

(32)

${Re}^{-1/2}{Nu}_{x}=-{\theta }^{'}(0){\mbox{,}}\quad {Re}^{-1/2}{Sh}_{x}=$$-{\phi }^{'}(0){\mbox{.}}$

(33)

where ${\textstyle Re={\frac {{xu}_{w}(x)}{\nu }}}$ is the Reynolds number.

3. Results and discussion

The set of nonlinear ordinary differential Eqs. (10), (11), (18) and (29) corresponding to the boundary conditions (12), (19) and (30) are solved numerically using Runge–Kutta based shooting technique (Sandeep and Sulochana [30]). Results display the influence of non-dimensional governing parameters on velocity, temperature and concentration profiles along with the friction factors, local Nusselt and Sherwood numbers. For numerical results we considered the non-dimensional parameter values as ${\textstyle A=0.2{\mbox{,}}\quad M=2{\mbox{,}}\quad \eta =5{\mbox{,}}\quad n=}$$3{\mbox{,}}\quad \beta =0.2{\mbox{,}}\quad We=0.3$, ${\textstyle A^{_{\ast }}=0.1{\mbox{,}}\quad B^{_{\ast }}=0.2{\mbox{,}}\quad R=}$$0.3{\mbox{,}}\quad {\theta }_{w}=1.1{\mbox{,}}\quad Sc=0.6{\mbox{,}}\quad K=$$K_{s}=1{\mbox{,}}\quad Sc=0.5{\mbox{,}}\quad Pr=6.2{\mbox{.}}$ These values are kept as common in entire study except the variations in respective figures and tables. In graphical results red color profiles indicate the flow of Carreau fluid and green color profiles indicate the flow of Casson fluid.

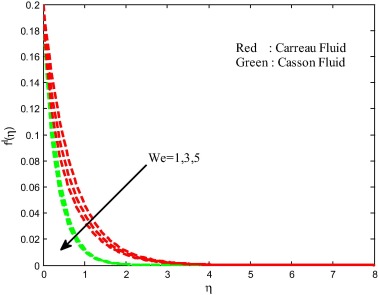
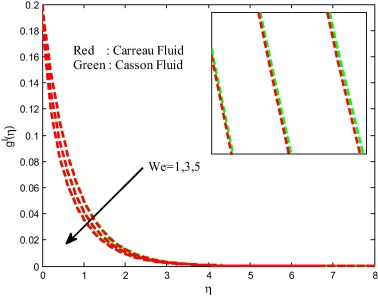
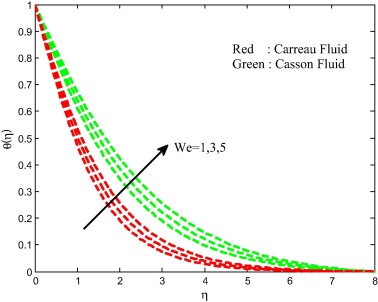
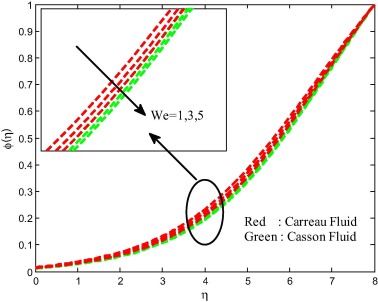
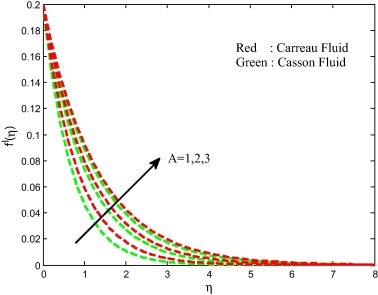
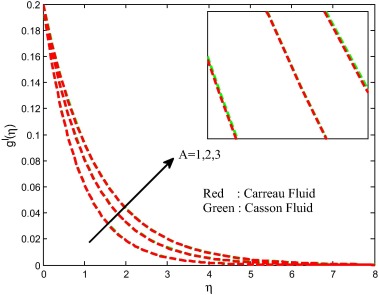
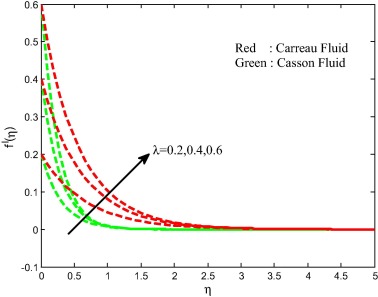
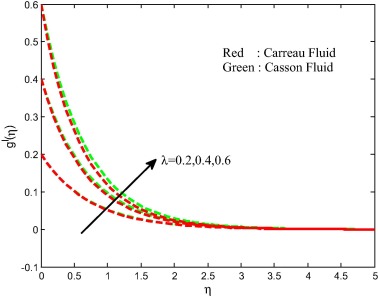
Figure 2, Figure 3, Figure 4 and Figure 5 depict the influence of Weissenberg number on velocity, temperature and concentration fields for both Carreau and Casson fluids. It is found that increasing values of the Weissenberg number enhances the thermal boundary layer and decreases the momentum concentration boundary layers. Physically, Weissenberg number is directly proportional to the time constant and inversely proportional to the viscosity. The time constant to viscosity ratio is higher for larger values of Weissenberg number. Hence, higher Weissenberg number causes to enhance the thermal boundary thickness.

Figure 2. Velocity filed for different values of Weissenberg number.

Figure 3. Velocity field for different values of Weissenberg number.

Figure 4. Temperature field for different values of the Weissenberg number.

Figure 5. Concentration field for different values of the Weissenberg number.

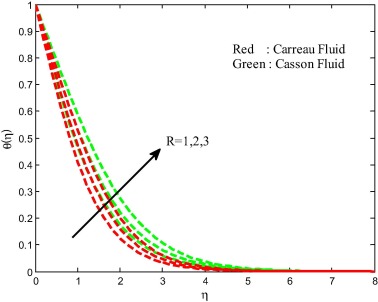
The dimensionless temperature distribution for different values of radiation parameter R is shown in Fig. 6 for both Carreau and Casson fluids. It reveals that the greater values of radiation parameter enhance the temperature boundary layer thickness. Generally, for higher values of radiation parameter produces more heat to working fluid that shows an enhancement in the temperature field. We have noticed an enhancement in the temperature profiles of both Carreau and Casson fluids due to increase in the radiation parameter. The ratio of temperature on temperature profiles is shown in Fig. 6. It is clear that increasing values of temperature ratio parameter improves the temperature profiles of the flow. This may happen due to increasing thermal conductivity of the flow (see Fig. 7).

Figure 6. Temperature field for different values of radiation parameter.

Figure 7. Temperature field for different values of ratio of temperature parameter.

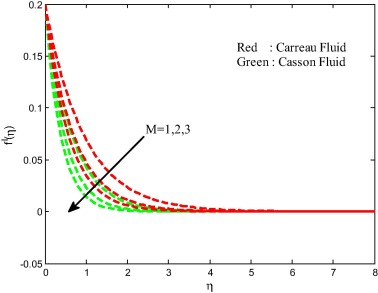
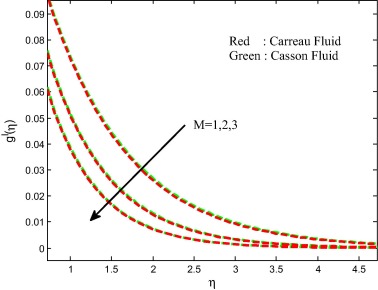
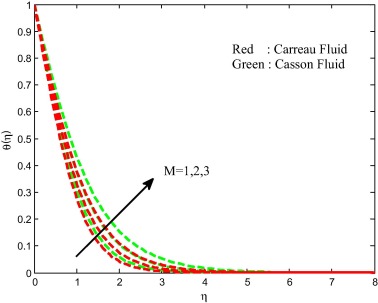
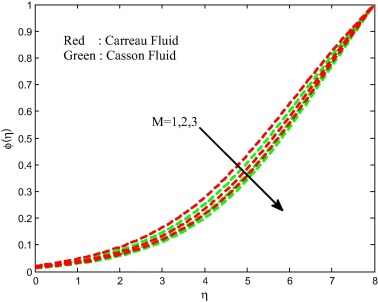
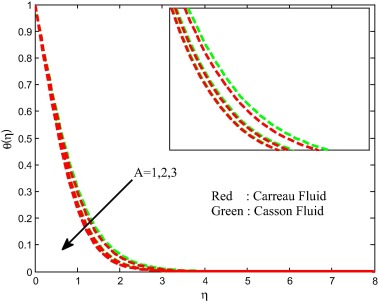
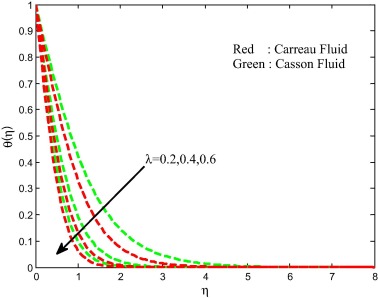
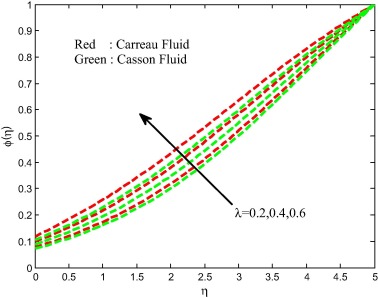
The effects of the magnetic field on velocity, temperature and concentration fields are displayed in Figure 8, Figure 9, Figure 10 and Figure 11. We observed depreciation in the velocity, concentration fields and enhancement in the temperature field for increasing values of magnetic field parameter. This proves the general physical behavior of M that improved values of M depreciate the velocity fields. Physically, the drag force increases with an increase in the magnetic field and as a result depreciation occurs in the velocity field. The influence of unsteadiness parameter on velocity, temperature and concentration fields is exhibited in Figure 12, Figure 13, Figure 14 and Figure 15 for both Carreau and Casson fluids. We detect from the figure that the velocity and concentration fields are enhanced and declined the temperature field with increasing values of unsteadiness parameter. Physically, increasing values of unsteadiness parameter causes the less heat to transfer to the sheet. This may be the reason for decreasing sense in the temperature filed.

Figure 8. Velocity field for different values of magnetic field parameter.

Figure 9. Velocity field for different values of magnetic field parameter.

Figure 10. Temperature field for different values of magnetic field parameter.

Figure 11. Concentration field for different values of magnetic field parameter.

Figure 12. Velocity field for different values of an unsteadiness parameter.

Figure 13. Velocity field for different values of an unsteadiness parameter.

Figure 14. Temperature field for different values of an unsteadiness parameter.

Figure 15. Concentration field for different values of an unsteadiness parameter.

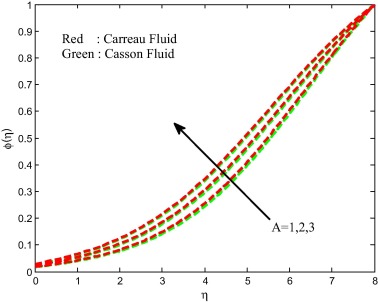
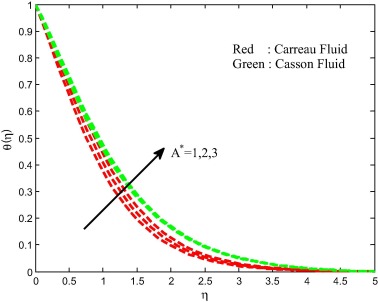
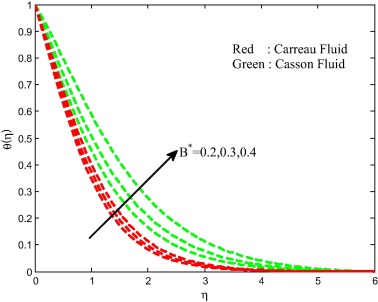
Figure 16, Figure 17, Figure 18 and Figure 19 present the effect of stretching ratio parameter on velocity, temperature and concentration fields for both Carreau and Casson fluid cases. The temperature field is suppressed and velocity and concentration fields are improved with increasing values of stretching ratio parameter. Generally, the stretching keeps more pressure on the sheet. Due to this reason we have seen a fall in temperature field and hike in velocity field. Figure 20 and Figure 21 demonstrate the effect of non-uniform heat source/sink parameter on temperature distribution of the flow for both Carreau and Casson fluid cases. It is clear that increasing values of space and temperature dependent heat source/sink parameters enhances the thermal boundary layer thickness of the flow over a stretching sheet for both Carreau fluid and Casson fluid cases. Physically, positive values of the non-uniform heat source/sink parameters act like a heat generator, which releases the heat energy to the flow and enhances the temperature profiles.

Figure 16. Velocity field for different values of stretching ratio parameter.

Figure 17. Velocity field for different values of stretching ratio parameter.

Figure 18. Temperature field for different values of stretching ratio parameter.

Figure 19. Concentration field for different values of stretching ratio parameter.

Figure 20. Temperature field for different values of non-uniform heat source/sink parameter.

Figure 21. Temperature field for different values of non-uniform heat source/sink parameter.

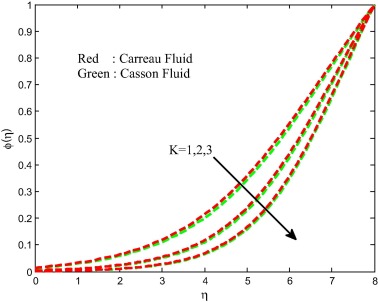
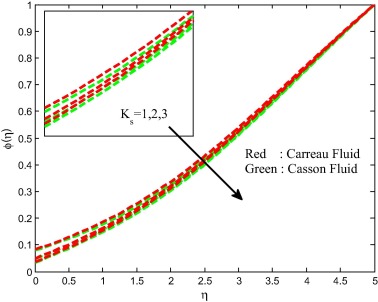
The strength of homogeneous and heterogeneous parameters on the concentration field is depicted in Figure 22 and Figure 23 for both Carreau and Casson fluids. It is clear that increasing values of homogeneous and heterogeneous parameters suppresses the concentration field for both cases. Physically, variation in the strength of homogeneous–heterogeneous reactions fluctuates the diffusivity of the flow. This causes to reduce the concentration profiles of the flow. Table 1 and Table 2 depict the validation of the present results by comparing with the existed literature under some special limited cases. We found a better agreement of the present results with the existed literature. This proves the validity of the present results along with the accuracy of the numerical technique we used in this study.

Figure 22. Concentration field for different values of strength of homogeneous reaction parameter.

Figure 23. Concentration field for different values of strength of heterogeneous reaction parameter.

Table 1. Validation of the present results by comparing with the published literature for skin friction coefficients when ${\textstyle We=\eta =R=A=A^{_{\ast }}=B^{_{\ast }}={\theta }_{w}=K=}$$K_{s}=Sc=Pr=0{\mbox{,}}\quad n=1$.

β	M	${\textstyle \lambda =0}$		${\textstyle \lambda =0.5}$
		Nadeem et al. [29]	Present results	Nadeem et al. [29]	Nadeem et al. [29]	Present results	Present results
		${\textstyle C_{fx}}$	${\textstyle C_{fx}}$	${\textstyle C_{fx}}$	${\textstyle C_{fy}}$	${\textstyle C_{fx}}$	${\textstyle C_{fy}}$
1	0	−1.4142	−1.4142	−1.5459	−0.6579	−1.5459	−0.6579
5		−1.0954	−1.0952	−1.1974	−0.5096	−1.1980	−0.5096
${\textstyle \infty }$		−1.0049	−1.0049	−1.0932	−0.4653	−1.0932	−0.4653
1	10	−4.6904	−4.6904	−4.7263	−2.3276	−4.7263	−2.3276
5		−3.6331	−3.6331	−3.6610	−1.8030	−3.6610	−1.8030
${\textstyle \infty }$		−3.3165	−3.3165	−3.3420	−1.6459	−3.3420	−1.6459
1	100	−14.2127	−14.212	−14.2244	−7.1004	−14.224	−7.1004
5		−11.0091	−11.009	−11.0182	−5.5000	−11.017	−5.4998
${\textstyle \infty }$		−10.0490	−10.049	−10.058	−5.0208	−10.058	−5.02079

Table 2. Validation of the present results by comparing with the existed literature for local Nusselt number when ${\textstyle \beta \rightarrow \infty {\mbox{,}}\quad We=\eta =R=}$$A=A^{_{\ast }}=B^{_{\ast }}={\theta }_{w}=K=K_{s}=Sc=0{\mbox{,}}\quad n=$$1$.

${\textstyle \lambda }$${\textstyle \downarrow }$	${\textstyle Pr=0.7}$			${\textstyle Pr=1}$
	Roy [28]	Raju et al.[20]	Present results	Roy [28]	Raju et al. [20]	Present results
0	0.4305	0.4769	0.4305	0.557294	0.5180	0.5572
1	0.6127	0.6004	0.6004	0.721982	0.7005	0.7219
10	1.0175	1.0097	1.0172	1.170983	1.1494	1.1709

Table 3 and Table 4 display the variations in the friction factors, local Nusselt and Sherwood numbers for Carreau and Casson fluids for various values of non-dimensional governing parameters. It is noticed from the tables that the hike in the values of unsteadiness parameter enhances the friction factor coefficients and heat transfer rate of both Carreau and Casson fluids. We have seen exactly opposite results for increasing values of magnetic field parameter and Weissenberg number. Rise in the values of non-uniform heat source/sink parameter does not influence the friction factor and mass transfer rate but it reduces the Nusselt number for both Carreau and Casson fluid cases. We have observed a similar type of results for increasing values of thermal radiation parameter. Rise in the homogeneous–heterogeneous parameters shows a mixed response in mass transfer rate. This concludes that the homogeneous–heterogeneous reaction parameters help to control the concentration profiles of the flow.

Table 3.

Physical parameter values of ${\textstyle f^{''}(0){\mbox{,}}\quad g^{''}(0){\mbox{,}}\quad -}$${\theta }^{'}(0)\quad {\mbox{and}}\quad -{\phi }^{'}(0)$ for Casson fluid.

M	R	K	${\textstyle K_{s}}$	A	We	${\textstyle \lambda }$	${\textstyle A^{_{\ast }}}$	${\textstyle f^{''}(0)}$	${\textstyle g^{''}(0)}$	${\textstyle -{\theta }^{'}(0)}$	${\textstyle -{\phi }^{'}(0)}$
1								−0.370542	−0.218615	0.806053	−0.018040
2								−0.626189	−0.324276	0.708147	−0.014499
3								−0.914227	−0.427845	0.630938	−0.012885
	1							−0.914227	−0.427845	0.563670	−0.012885
	2							−0.914227	−0.427845	0.464686	−0.012885
	3							−0.914227	−0.427845	0.395295	−0.012885
		1						−0.914227	−0.427845	0.630938	−0.012885
		2						−0.914227	−0.427845	0.630933	−0.004016
		3						−0.914227	−0.427845	0.630933	−0.001458
			1					−0.914227	−0.427845	0.636191	−0.079147
			2					−0.914227	−0.427845	0.636191	−0.094637
			3					−0.914227	−0.427845	0.636191	−0.101582
				1				−0.353005	−0.268963	0.790376	−0.017153
−0.022772					2				−0.218155	−0.194198	0.867563
				3				−0.172077	−0.160872	0.901181	−0.027919
					1			−5.929220	−0.799438	0.401890	−0.010760
					3			−8.094415	−1.335176	0.363705	−0.010528
					5			−10.63697	−2.366287	0.328190	−0.010329
						0.2		−1.356482	−0.323332	0.638757	−0.013330
						0.4		−8.613557	−1.097922	1.079688	−0.022118
						0.6		−32.08378	−2.980574	1.402644	−0.036072
							1	−0.368418	−0.331556	0.647340	−0.088065
							2	−0.368418	−0.331556	0.546861	−0.088065
							3	−0.368418	−0.331556	0.446312	−0.088065

Table 4. Physical parameter values of ${\textstyle f^{''}(0){\mbox{,}}\quad g^{''}(0){\mbox{,}}\quad -}$${\theta }^{'}(0)\quad {\mbox{and}}\quad -{\phi }^{'}(0)$ for Carreau fluid.

M	R	K	${\textstyle K_{s}}$	A	We	${\textstyle \lambda }$	${\textstyle A^{_{\ast }}}$	${\textstyle f^{''}(0)}$	${\textstyle g^{''}(0)}$	${\textstyle -{\theta }^{'}(0)}$	${\textstyle -{\phi }^{'}(0)}$
1								−0.234429	−0.221416	0.848403	−0.020765
2								−0.354917	−0.331612	0.767788	−0.016204
3								−0.478409	−0.443038	0.701860	−0.014134
	1							−0.478409	−0.443038	0.630469	−0.014134
	2							−0.478409	−0.443038	0.525606	−0.014134
	3							−0.478409	−0.443038	0.452131	−0.014134
		1						−0.478409	−0.443038	0.701860	−0.014134
		2						−0.478409	−0.443038	0.701861	−0.004388
		3						−0.478409	−0.443038	0.701861	−0.001587
			1					−0.499159	−0.442978	0.699096	−0.082839
			2					−0.499159	−0.442978	0.699096	−0.098872
			3					−0.499159	−0.442978	0.699096	−0.106066
				1				−0.281248	−0.271720	0.812987	−0.018332
				2				−0.198141	−0.194860	0.875240	−0.023661
				3				−0.162777	−0.161132	0.904927	−0.028765
					1			−0.880536	−0.802796	0.580387	−0.012285
					3			−1.473479	−1.342562	0.536358	−0.011855
					5			−2.595351	−2.380762	0.494735	−0.011495
						0.2		−0.354917	−0.331612	0.767788	−0.016204
						0.4		−1.409036	−1.273276	1.216572	−0.032431
						0.6		−5.205586	−4.614127	1.535326	−0.062058
							1	−1.356482	−0.323332	0.545206	−0.079966
							2	−1.356482	−0.323332	0.494005	−0.079966
							3	−1.356482	−0.323332	0.442794	−0.079966

4. Conclusions

In this study, we proposed a mathematical model for analyzing the effects of nonlinear thermal radiation on three-dimensional flow of Carreau and Casson fluids past a stretching surface with homogeneous–heterogeneous reactions and non-uniform heat source/sink. The nonlinear thermal radiation has importance in various industrial as well as science and technological applications. The transformed governing equations are solved numerically using Runge–Kutta based shooting technique. We presented dual solutions for the flow of Carreau and Casson fluids over a stretching sheet. The numerical findings are as follows:

• Heat and mass transfer rate in Casson fluid is significantly high while compared with the Carreau fluid
• Homogeneous–heterogeneous reaction parameters help to control the concentration boundary layer.
• Positive values of non-uniform heat source/sink parameter and nonlinear thermal radiation parameter help to reduce the Nusselt number for both Carreau Casson fluids.
• The Weissenberg number and magnetic field parameters have tendency to increase the mass transfer rate.
• Rise in unsteadiness parameter improves the friction factor coefficients and heat transfer rate.
• Momentum boundary layer of Carreau fluid is highly effective while compared with the momentum boundary layer of Casson fluid.

References

1. [1] B.C. Sakiadis; Boundary layer behavior on continuous solid surfaces; AICHE J., 7 (1) (1961), pp. 26–28
2. [2] L. Gosselin, A.K. da Silva; Combined heat transfer and power dissipation optimization of nanofluid flows; Appl. Phys. Lett., 85 (18) (2004), p. 4160
3. [3] N. Bachok, A. Ishak, I. Pop; Boundary-layer flow of nano fluids over a moving surface in a flowing fluid; Int. J. Therm. Sci., 49 (9) (2010), pp. 1663–1668
4. [4] A.J. Chamka, A.M. Aly; MHD free convection flow of a nanofluid past a vertical plate in the presence of heat generation or absorption effects; J. Chem. Eng. Commun., 198 (3) (2010), pp. 425–441
5. [5] L. Zheng, L. Wang, X. Zhang; Analytic solutions of unsteady boundary flow and heat transfer on a permeable stretching sheet with non-uniform heat source/sink; J. Commun. Nonlinear Sci. Numer. Simul., 16 (2) (2011), pp. 731–740
6. [6] M. Subhas Abel, P.G. Siddheshwar, N. Mahesha; Numerical solution of the momentum and heat transfer equations for a hydromantic flow due to a stretching sheet of a non-uniform property micropolar liquid; Appl. Math. Comput., 217 (12) (2011), pp. 5895–5909
7. [7] J. Harris; Rheology and Non-Newtonian Flow; Longman (1977)
8. [8] R.B. Bird, C.F. Curties, R.C. Armstrong, O. Hassager; Dynamics of Polymeric Liquids; Wiley (1987)
9. [9] J. Zhu; Drag and Mass transfer for flow of a Carreau fluid past a swarm of Newtonian drops; Int. J. Multiphase Flow, 21 (5) (1995), pp. 935–940
10. [10] G.C. Georgiou; The time-dependent, compressible poiseuille and extrudate-swell flows of a Carreau fluid with slip at the wall; J. Non-Newtonian Fluid Mech., 109 (2003), pp. 93–114
11. [11] A.H. Abd El Naby, A.E.M. Ei Misery, M.F. AbdEl Kareem; Separation in the flow through peristaltic motion of a Carreau fluid in uniform tube; Physica A, 343 (2004), pp. 1–14
12. [12] Kh.S. Mekheimer; Effect of the induced magnetic field on peristaltic flow of a couple stress fluid; Phys. Lett. A, 372 (2008), pp. 4271–4278
13. [13] T. Hayat, N. Saleem, N. Ali; Effect of induced magnetic field on peristaltic transport of a Carreau fluid; Commun. Nonlinear Sci. Numer. Simul., 15 (2010), pp. 2407–2423
14. [14] N. Sandeep, V. Sugunamma, P. Mohan Krishna; Effects of radiation on an unsteady natural convection flow of an EG-Nimonic 80a nanofluid past an infinite vertical plate; Adv. Phys. Theor. Appl., 23 (2013), pp. 36–43
15. [15] C.S.K. Raju, N. Sandeep, C. Sulochana, V. Sugunamma; Effects of aligned magnetic field and radiation on the flow of ferrofluids over a flat plate with non-uniform heat source/sink; Int. J. Sci. Eng., 8 (2) (2015), pp. 151–158
16. [16] N.S. Akbar, S. Nadeem, Z.H. Khan; Numerical simulation of peristaltic flow of a Carreau nanofluid in an asymmetric channel; Alex. Eng. J., 53 (2014), pp. 191–197
17. [17] E.F. EI-Shehawey, Z.A. Saleh Husseny; Peristaltic transport of a magneto fluid with porous boundaries; Appl. Math. Comput., 129 (2002), pp. 421–440
18. [18] R. Ellahi, A. Riaz; Analytical solution for MHD flow in a third grade fluid with variable viscosity; Math. Comput. Model, 52 (2010), pp. 1783–1793
19. [19] N. Ali, T. Hayat; Peristaltic motion of a Carreau fluid in an asymmetric channel; Appl. Math. Comput., 193 (2007), pp. 533–552
20. [20] C.S.K. Raju, M. Jayachandrababu, N. Sandeep; Chemically reacting radiative MHD Jefferey nanofluid flow over a cone in porous medium; Int. J. Eng. Res. Afr., 19 (2016), pp. 75–90
21. [21] M.N. Mahantesh, M. Subhas Abel, J. Tawade; Heat transfer in a Walter’s liquid B fluid over an impermeable stretching sheet with non-uniform heat source/sink and elastic deformation; J. Commun. Nonlinear Sci. Numer. Simul., 15 (7) (2010), pp. 1791–1802
22. [22] S.A. Shehzad, T. Hayat, A. Alsaedi; Three-dimensional MHD flow of Casson fluid in porous medium with heat generation; J. Appl. Fluid Mech., 9 (2016), pp. 215–223
23. [23] T. Hayat, M. Bilal Ashraf, S.A. Shehzad, A. Alsaedi; Mixed convection flow of Casson nanofluid over a stretching sheet with convectively heated chemical reaction and heat source/sink; J. Appl. Fluid Mech., 8 (2015), pp. 803–813
24. [24] T. Hayat, S. Asad, M. Mustafa, A. Alsaedi; Boundary layer flow of Carreau fluid over a convectively heated stretching sheet; Appl. Math. Comput., 246 (2014), pp. 12–22
25. [25] C.S.K. Raju, N. Sandeep, V. Sugunamma, M. Jayachandrababu, J.V. Ramanareddy; Heat and mass transfer in magnetohydrodynamic Casson fluid over an exponentially permeable stretching surface; Eng. Sci. Technol., Int. (2015) http://dx.doi.org/10.1016/j.jestch.2015.05.010
26. [26] N.S. Akbar, S. Nadeem, R.U.I. Haq, S. Ye; MHD stagnation point flow of Carreau fluid toward a permeable shrinking sheet: dual solutions; Ain Shams Eng. J., 5 (2014), pp. 1233–1239
27. [27] M. Jenny, E. Plaut, A. Briard; Numerical study of subcritical Rayleigh-Benard convection rolls in strong shear thinning Carreau fluids; J. Non-Newtonian Fluid Mech., 219 (2015), pp. 19–34
28. [28] D. Anilkumar, S. Roy; Unsteady mixed convection flow on a rotating cone in rotating fluid; Appl. Math. Comput., 155 (1963), pp. 545–561
29. [29] S. Nadeem, R.U.I. Haq, N.S. Akbar, Z.H. Khan; MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet; Alex. Eng. J., 52 (2013), pp. 577–582
30. [30] N. Sandeep, C. Sulochana; Dual solutions for unsteady mixed convection flow of MHD micropolar fluid over a stretching/shrinking sheet with non-uniform heat source/sink; Eng. Sci. Technol. Int. J., 18 (2015), pp. 738–745
31. [31] A. Jasmine Benazir, R. Sivaraj, O.D. Makinde; Unsteady MHD Casson fluid flow over a vertical cone and flat plate with non-uniform heat source/sink; Int. J. Eng. Res. Afr., 21 (2015), pp. 69–83
32. [32] B. Rushi Kumar, R. Sivaraj, A. Jasmine Benazir; Chemically reacting MHD free convective flow over a vertical cone with variable electric conductivity; Int. J. Pure Appl. Math., 101 (2015), pp. 821–828
33. [33] S.A. Shehzad, F.M. Abbasi, T. Hayat, F. Alsaedi, G. Mousa; Peristalsis in a curved channel with slip and radial magnetic field; Int. J. Heat Mass Transf., 91 (2015), pp. 562–569
34. [34] J. Prakash, B. Rushi Kumar, R. Sivaraj; Radiation and Dufour effects on unsteady MHD mixed convective flow in an accelerated vertical wavy plate with varying temperature and mass diffusion; Walailak J. Sci. Technol., 11 (2014), pp. 939–954
35. [35] C.S.K. Raju, N. Sandeep, M. Jayachandrababu, V. Sugunamma; Dual solutions for three-dimensional MHD flow of a nanofluid over a nonlinearly permeable stretching sheet; Alex. Eng. J., 55 (1) (2016), pp. 151–162
36. [36] R. Sivaraj, B. Rushi Kumar; Unsteady MHD dusty viscoelastic fluid Couette flow in an irregular channel with varying mass diffusion; Int. J. Heat Mass Transf., 55 (2012), pp. 3076–3089
37. [37] S.A. Shehzad, Z. Abdullah, A. Alsaedi, F.M. Abbasi, T. Hayat; Thermally radiative three-dimensional flow of Jeffrey nanofluid with internal heat generation and magnetic field; J. Magn. Magn. Mater., 397 (2016), pp. 108–114
38. [38] I.L. Annimasun, C.S.K. Raju, N. Sandeep; Unequal diffusivities case of homogeneous–heterogeneous reactions within viscoelastic fluid flow in the presence of induced magnetic-field and nonlinear thermal radiation; Alex. Eng. J., 55 (2) (2016), pp. 1595–1606
39. [39] S.A. Shehzad, Z. Abdullah, F.M. Abbasi, T. Hayat, A. Alsaedi; Magnetic field effect in three-dimensional flow of an Oldroyd-B nanofluid over a radiative surface; J. Magn. Magn. Mater., 399 (2016), pp. 97–108