Influência das superfícies sub-críticas no comprimento de reforços em estruturas de solos reforçados com geotêxteis ou geogrelhas

Resumo

No dimensionamento de taludes íngremes e de muros de contenção, reforçados com geotexteis ou geogrelhas, as verificações de estabilidade interna usualmente têm como referência uma superfície crítica, que determina a quantidade necessária de reforço. Na determinação do comprimento das camadas de reforço deve-se considerar a posição da superfície crítica e também das superfícies sub-críticas. Em relação a estas são verificados os comprimentos de ancoragem necessários para assegurar a resistência dos reforços ao arrancamento. Neste artigo é apresentado um estudo baseado em análise de equilíbrio limite, com superfície de ruptura bi-linear, para determinar a quantidade e o comprimento necessário das camadas de reforço. O modelo permite substituir as cartas de Jewell por meio de equações algébricas e processo iterativo de cálculo. Os resultados obtidos para o comprimento mínimo de reforços concordam com boa precisão para ângulos de atrito efetivo maiores ou iguais a 30° e indicam que podem ser usados comprimentos menores para materiais com ângulo de atrito efetivo menores do que 30°. São apresentadas também expressões para o cálculo do comprimento de ancoragem para os três casos possíveis: ancoragem em trecho sob projeção da face do talude, em parte sob a projeção da face do talude e trecho além da projeção da face do talude.

Palavras chave: Yalude, solo reforçado, geotêxtil, geogrelha, superfície sub-crítica, comprimento de reforço

Abstract

Design of steep slopes and retaining walls, reinforced with geotextile or geogrids, requires internal stability checks usually referred to a critical failure surface, which determines the amount of reinforcement required. In determining the length of the reinforcement layers the position of the critical surface and also of the sub-critical surfaces must be considered. In relation to these, are verified the anchorage lengths required to ensure the pullout resistance of the reinforcements. This paper presents a study based on limit equilibrium analysis, with bi-linear failure surface, to determine the amount and length of the reinforcement layers required. The model allows replacing Jewell charts by algebraic equations and iterative calculation processes. The results obtained for the minimum length of reinforcements agree with good accuracy for effective friction angles greater than or equal to 30° and indicate that shorter lengths can be used for materials with lower effective friction angle. Expressions for the calculation of the anchorage length are also presented for the three possible cases: anchorage in a section under the projection, part under the projection and beyond the horizontal projection of the slope face.

Keywords: Slope reinforced soil, geotextil, sub-critical surface, reinforcement length

1. Introdução

Apresenta-se no presente trabalho aspectos ligados ao projeto de taludes e de muros de solos reforçados com geotêxteis e geogrelhas. Usualmente se consideram como muros as estruturas com inclinação de face com ângulo maior ou igual a 70° com a horizontal. Ademais os muros de solo reforçado exigem alguma proteção de face. O dimensionamento de estruturas deste tipo envolve a determinação da quantidade de camadas de reforço e do comprimento necessário destas camadas para assegurar a estabilidade, levando em conta a ancoragem das camadas de reforço e a consideração de outros possíveis mecanismos de ruptura ou de instabilidade que possam ocorrer. No caso de muros as condições de estabilidade externa ao tombamento, ao deslizamento e de capacidade de carga da fundação permitem estabelecer um pré-dimensionamento do comprimento a utilizar para as camadas de reforço.

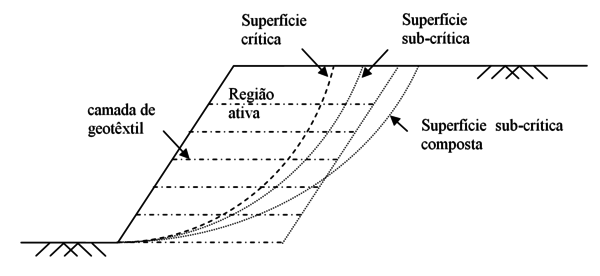
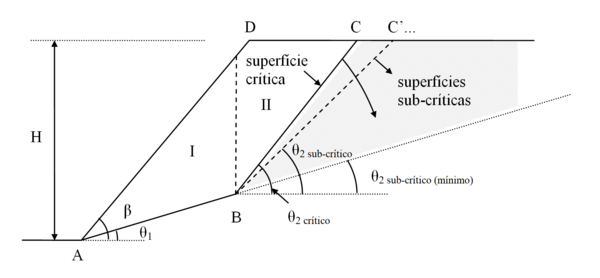
A quantidade necessária de reforços é dimensionada em função do máximo esforço exigido para estabilizar uma cunha de ruptura de massa de solo. Via de regra são testadas várias possíveis superfícies de ruptura para determinar a superfície de ruptura dita crítica, que leva a este esforço máximo. Esta superfície crítica estabelece a quantidade de reforço, mas não estabelece necessáriamente o comprimento das camadas de reforço, que pode ser condicionado pelas superfícies sub-críticas, que passam além da superfície crítica. Estas camadas sub-críticas podem interceptar todas as camadas de reforço ou somente parte delas, no caso das superfícies sub-críticas compostas. A Figura 1 ilustra de forma esquemática uma situação de superfície crítica e superfícies sub-críticas passantes pelo pé do talude. Na Figura 1 as camadas de reforço apresentam comprimentos iguais e espaçamentos verticais iguais. No estudo apresentado a seguir são abordados os casos de espaçamento dito ideal e de espaçamento constante entre camadas, para determinar o comprimento mínimo necessário de camadas de reforço de igual comprimento.

Figura 1. Cunha crítica de ruptura e cunhas sub-críticas de ruptura

O ponto específico aqui tratado é o exame da influência das superfícies sub-críticas na determinação do comprimento das camadas de reforço de geotêxteis, aspecto levantado em trabalho de Jewell [1]. Jewell apresentou solução para o problema indicando o emprego de uma expressão empírica, que produz o aumento do coeficiente de empuxo ${\textstyle K_{Req}}$, adiante apresentado, que é determinado para a superfície de ruptura capaz de produzir o máximo esforço necessário das camadas de reforço.

${K}_{d}=\displaystyle {\frac {{K}_{Req}}{1-\displaystyle {\frac {{L}_{B}}{{L}_{R}}}}}$

(1)

onde

${\textstyle K_{Req}}$ - coeficiente de empuxo determinado para a superfície crítica de ruptura;

${\textstyle L_{R}}$ – comprimento do reforço;

${\textstyle L_{B}}$ – comprimento de ancoragem na base do talude necessário para desenvolver o esforço admíssivel no reforço;

${\textstyle K_{d}}$ – valor de projeto do coeficiente de empuxo de cálculo determinado para a superfície crítica de ruptura.

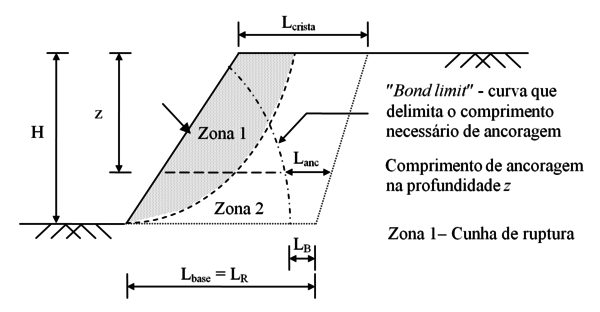
Desta forma é majorada a quantidade de reforço mantendo-se o comprimento das camadas do arranjo. A Figura 2 ilustra as dimensões de referência utilizadas em [1].

Figura 2. Comprimentos de referência utilizados em Jewell [1]

Os resultados obtidos por Jewell [1] continuam a ser empregados na prática, tendo sido referidos em [2,3]. No anexo estão reproduzidos os gráficos de Jewell [4] para a determinação do coeficiente de empuxo ${\textstyle K_{Req}}$ e da relação adimensional de comprimento de reforço ${\textstyle L/H}$, utilizando a citada expressão empírica de ajuste. Em trabalho mais recente [5], foi apresentado método de cálculo designado como método top-down, que usa uma análise extensiva de cálculo para determinar a variação do estado de tensão ao longo do comprimento de cada camada de reforço.

Mostra-se a seguir, por meio de análise de equilíbrio limite, como determinar de forma analítica mais simples e direta a influência das superfícies sub-críticas no comprimento a ser utilizado para as camadas de reforço. O processo apresentado pelos autores também permite conhecer o estado de tração nas camadas da estrutura de solo reforçado.

A determinação da superfície crítica pode ser feita com o emprego de superfícies circulares, arcos de espiral logarítmica [6,7], cunhas planas e cunhas com duas partes (two part wedge) [1,4]. Esta última forma é a empregada neste trabalho, de superfície de ruptura constituída por dois trechos retos, constituindo uma poligonal bi-linear. Em que pese a diversidade de enfoques empregadas por diversos autores, estas superfícies são razoavelmente coincidentes na definição da possível região crítica passível de ruptura e do esforço máximo exigido das camadas de reforço determinados em Jewell [1]. A norma britânica [8] permite o uso de superfícies planas de ruptura para projetos de muros de arrimo com inclinação entre 70° e 90°, e o uso de superfícies bilineares para taludes com inclinação entre 45° e 70°. Do estudo de Jewell [4], que empregou superfície de ruptura bi-linear, a faixa de inclinações de taludes foi ampliada de 30° até 90°, abrangendo o emprego de geogrelhas e geotexteis

2. Materiais e métodos

Empregando uma forma de cálculo adimensional, pode-se determinar o esforço máximo de tração necessário para assegurar a estabilidade, trabalhando com taludes de altura unitária e mesma inclinação do talude real, como apresentado em [9] e resumido a seguir.

Na dedução do esforço de cálculo é assumida superfície de ruptura bi-linear e formação de cunha de ruptura com duas partes, com interface vertical, sobre a qual o empuxo efetivo atuante e o empuxo decorrente de pressões neutras têm direção horizontal, como mostra a Figura 3. Nesta figura estão indicadas as componentes do esforço resultante ${\textstyle T}$ a ser resistido pelas camadas de reforço igual a ${\textstyle T=T_{1}+T_{2}}$ para um talude de altura ${\textstyle H}$ e inclinação ${\textstyle \beta }$.

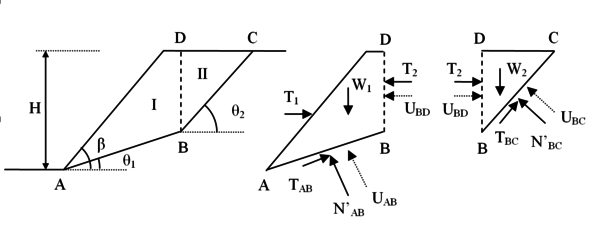
Figura 3. Superfície de ruptura bi-linear e partes I e II delimitadas por superfície vertical

Fazendo-se variar a posição do ponto ${\textstyle B}$, que define o ângulo ${\textstyle \theta _{1}}$ e do ponto ${\textstyle C}$, que define o ângulo ${\textstyle \theta _{2}}$, do equilíbrio estático das cunhas I e II obtém-se os valores de ${\textstyle T_{1}}$ e ${\textstyle T_{2}}$ e ao fim o valor do esforço resultante ${\textstyle T}$:

$T={\frac {{W}_{1}\left(tg{\theta }_{1}-tg\phi '\right)-\displaystyle {\frac {c'{l}_{AB}}{\cos {\theta }_{1}}}+{U}_{AB}\displaystyle {\frac {tg\phi '}{\cos {\theta }_{1}}}}{1+tg{\theta }_{1}.tg\phi '}}+$$\displaystyle {\frac {{W}_{2}\left(tg{\theta }_{2}-tg\phi '\right)-\displaystyle {\frac {c'{l}_{BC}}{\cos {\theta }_{2}}}+{U}_{BC}\displaystyle {\frac {tg\phi '}{\cos {\theta }_{2}}}}{1+tg{\theta }_{2}.tg\phi '}}$

(2)

onde

${W}_{1}$ e ${W}_{2}$ – peso total de solo da fatia I e da fatia II, que compõem a cunha de ruptura;

$c'$ e $\phi '$– coesão efetiva e ângulo de atrito efetivo do solo;

${l}_{AB}$ e ${l}_{BC}$ – comprimentos das bases das fatias I e II, respectivamente;

$\theta _{1}$ e $\theta _{2}$ – inclinações das bases das fatias I e II, respectivamente;

${U}_{AB}$ e ${U}_{BC}$ – resultante das pressões neutras atuantes sobre a a base das fatias I e da fatia II.

A resultante das pressões neutras é calculada com emprego do parâmetro de pressão neutra de Bishop – $r_{u}$. A pressão neutra $u$ à uma profundidade de solo $z$, para um solo com peso específico natural $\gamma$, é relacionada ao dito parâmetro pela expressão:

${r}_{u}={\frac {u}{\gamma .z}}$

(3)

As expressões para as resultantes das pressões neutras ${U}_{AB}$ e ${U}_{BC}$ utilizadas neste estudo estão reproduzidas no anexo, ao final deste artigo.

Do exame da Eq. (2) pode-se observar que esta pode ser escrita de forma genérica como:

$T=W{.f}_{1}\left(\phi ',{\theta }_{1},{\theta }_{2}\right)-c.{f}_{2}\left(\phi ',{\theta }_{1},{\theta }_{2}\right)+$$U.{f}_{3}\left(\phi ',{\theta }_{1},{\theta }_{2}\right)$

(4)

onde

$W$ – peso total da cunha de ruptura;

$U$ – resultante de pressões neutras sobre uma superfície vertical de altura H:

$U={\frac {1}{2}}.\gamma .r_{u}.H^{2}$;

$f_{1}$, $f_{2}$ e $f_{3}$ – funções dependentes da geometria da fatia e do ângulo de atrito efetivo.

Desprezando o efeito da contribuição da parcela devida à coesão, isto é, assumindo coesão efetiva $c'=0$ e assimilando o esforço $T$ a uma expressão de empuxo de Rakine, pode-se escrever:

$T={\frac {1}{2}}.\gamma .{H}^{2}.K$

(5)

Dividindo a Eq. (4) por $\gamma$, e colocando $c'=0$ obtém-se a Eq. (6):

${\frac {T}{\gamma }}={\frac {W}{\gamma }}{.f}_{1}\left(\phi ',{\theta }_{1},{\theta }_{2}\right)+$${\frac {U}{\gamma }}.{f}_{3}\left(\phi ',{\theta }_{1},{\theta }_{2}\right)$

(6)

E como $W/\gamma =A$ , área da seção transversal da cunha e $U/\gamma ={\frac {1}{2}}.r_{u}.H^{2}$ a Eq. (6) pode ainda ser simplificada para:

${\frac {1}{2}}.K.{H}^{2}=A.{f}_{1}\left(\phi ',{\theta }_{1},{\theta }_{2}\right)+$${\frac {1}{2}}.{r}_{u}.{H}^{2}.{f}_{3}\left(\phi ',{\theta }_{1},{\theta }_{2}\right)$

(7)

Por fim, assumindo $H=1$ e isolando o coeficiente de empuxo $K$, na Eq. (7) resulta a expressão do coeficiente de empuxo adimensional para o cálculo do esforço necessário dos reforços dado por Eq. (4), como:

$K={A}^{\ast }.{f}_{1}\left(\phi ',{\theta }_{1},{\theta }_{2}\right)+{r}_{u}.{f}_{3}\left(\phi ',{\theta }_{1},{\theta }_{2}\right)$

(8)

onde

${A}^{\ast }$ – área da seção transversal de cunha de ruptura de altura unitária $H=1$;

$f_{1}$ e $f_{3}$* – funções dependentes da geometria da fatia e do ângulo de atrito efetivo.

No método preconizado por Jewell [4] o ângulo de atrito $\phi '$ a ser utilizado, para a determinação do esforço total de tração $T$, deve ser o ângulo de atrito correspondente ao estado crítico, ou de volume constante $\phi '_{cs}$. A razão entre a resistência de pico $\phi '_{p}$ e a de estado crítico pode ser considerada, segundo Jewell, um fator de segurança concentrado sobre a resistência ao cisalhamento de pico, ou

${FS}_{s}={\frac {tg{\phi }_{p}^{'}}{tg{\phi }_{d}^{'}}}$

(9)

onde

${FS}_{s}=$ fator de segurança em relação ao parâmetro de resistência ao cisalhamento;

$\phi '_{p}$ = ângulo de atrito efetivo de resistência de pico;

$\phi '_{cs}$ = ângulo de atrito de estado crítico.

Desta forma o ângulo de atrito a ser utilizado nos gráficos de Jewell deve ser um ângulo de atrito efetivo de projeto $\phi '_{d}=\phi '_{cs}$, onde $\phi '_{d}=arc[(\tan \phi '_{p})/FS_{s}]$.

Na aplicação do método de Jewell determina-se o “coeficiente de empuxo” $K_{req}$, função da inclinação $\beta$ do talude, do ângulo de atrito efetivo de cálculo ${\phi }_{d}^{'}$ e do parâmetro de pressão neutra $r_{u}$. A seguir, com base nas demais cartas de Jewell [4], de estabilidade geral e de resistência ao deslizamento pela base, é definido o comprimento dos reforços $L_{R}$ (Figura 2). Na continuação, por tentativa e erro, ajusta-se o layout das camadas, estabelecendo o espaçamento em função da resistência do geossintético a ser empregado e determina-se o comprimento de ancoragem junto à base $L_{B}$ (Figura 2). E, por fim, o coeficiente de empuxo $K_{req}$ ainda recebe majoração por meio da expressão empírica (1) para compor o “coeficiente de empuxo” de cálculo $K_{d}$. Com este coeficiente de cálulo é feito um ajuste final no layout escolhido.

Assumindo que todas as camadas de reforço resistam a um mesmo valor de tração admissível - $T_{adm}$, o número mínimo necessário de camadas $n_{\min }$ para resistir ao esforço máximo é igual a:

${n}_{\min }\geq {\frac {T}{{T}_{adm}}}$

(10)

onde $T_{adm}$ é a resistência à tração de longo prazo, igual à resistência à ruptura, reduzida pela aplicação dos fatores de segurança à carga de longa duração, fluência, dano mecânico, degradação química, etc.

A resistência à tração de longo prazo $T_{adm}$ é obtida para os geossintéticos por meio da expressão (11) [2]:

${T}_{adm}={\frac {{T}_{\max }}{FRT}}={\frac {{T}_{\max }}{{FRP}_{FL}\times {FRP}_{DI}\times {FRP}_{MA}\times {FRP}_{AQ}}}$

(11)

onde

$T_{\max }$ – Resistência à tração indicada pelo fabricante;

FRT – Fator de redução global;

${FRP}_{FL}$ – Fator de redução para fluência em tração;

${FRP}_{DI}$ – Fator de redução parcial para danos mecânicos de instalação;

${FRP}_{MA}$ – Fator de redução parcial para degradação ambiental;

${FRP}_{AQ}$ – Fator de redução parcial para ataque químico.

Mostra-se a seguir, processo para determinar, com base nas equações de Montanelli e Recalcati [9], o comprimento necessário dos reforços resultante da análise de estabilidade interna. O dito comprimento pode ser obtido diretamente da determinação da superfície crítica e da verificação das superfícies sub-críticas, tendo em vista a segurança ao arrancamento dos reforços. Isto é feito a partir de uma escolha prévia de número de camadas e de forma de espaçamento entre elas. A resistência dos geossintéticos é escolhida de forma a atender à condição de segurança de ruptura à tração. No método de Jewell o dimensionamento do geossintético é determinado em função da tensão de face para a camada inferior do arranjo e de um espaçamento vertical $s_{v}$ escolhido com base na Eq. (12):

${T}_{adm}\geq {s}_{v}.{\gamma }_{d}.H.{K}_{d}$

(12)

onde

$s_{v}$ – espaçamento vertical adotado para a última camada;

${\gamma }_{d}$ – peso específico de cálculo;

$H$ – altura do muro ou talude:

$K_{d}$ – coeficiente de empuxo de cálculo (aqui mantido igual a $K_{req}$).

A definição de comprimento dos reforços com base na estabilidade externa deve ser feita obrigatoriamente, e comparada com a de estabilidade interna para estabelecer o comprimento final dos reforços no layout a ser utilizado na obra.

2.1 Algoritmo de busca da superfície crítica

A região de pesquisa para determinação da superfície crítica pode ser dividida segundo uma malha de pontos, de altura igual a $H=1$ e largura $B=2$, e inclinação igual à inclinação do muro ou talude de solo reforçado, conforme mostra a Figura 4.

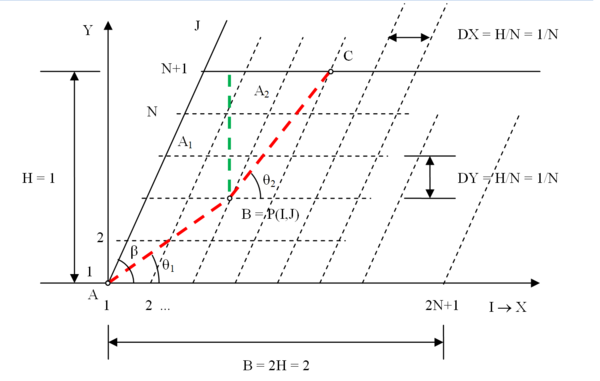
Figura 4. Esquema de referência para a determinação da superfície crítica

A determinação da superfície crítica é feita, construindo-se cunhas de ruptura bi-lineares, mantendo o ponto $A$ fixo no pé do talude, permitindo o deslocamento do ponto $B$ sobre os pontos da malha com índice $J$ variando entre 1 e $N$ e com variação do índice $I$ a partir de 2 na primeira linha e a partir de 1 para as linhas com $J\geq 2$. Neste processo o ponto $C$ desloca-se sobre os nós da malha da linha de índice $J=N+1$, sobre pontos de abcissa maior ou igual à do ponto $B$.

As componentes do peso da cunha considerada, $W_{1}$ e $W_{2}$ na Figura 3, são proporcionais às áreas $A_{1}$ e $A_{2}$ na Figura 4, que são determinadas a partir das coordenadas dos pontos A, B e C e das coordenadas do vértice do talude. As forças de sub-pressão $U_{AB}$ e $U_{BC}$, indicadas na Figura 3, são calculadas por meio das equações apresentadas no Anexo para os três casos possíveis esquematizados nas Figuras A6 a A8.

Do processo de varredura, com o uso reiterado de cálculo baseado na Eq. (2), resulta a definição da superfície crítica e a determinação do valor do maior “coeficiente de empuxo”, $K_{req}$.

2.2 Quantidade de reforço para as superfícies sub-críticas

Determinada a posição da superfície crítica devem ser examinadas as superfícies passantes além da superfície crítica. Neste estudo considerou-se como superfícies a serem examinadas, superfícies passantes pelo ponto $B$, referido na Figura 3, em que o segmento AB é mantido fixo e onde o ângulo $\theta _{2}$ vai sendo reduzido de grau em grau até atingir um ângulo igual à metade do ângulo de atrito interno ou igual à inclinação do ângulo $\theta _{1}$, o que resultar maior. A Figura 5 mostra o esquema utilizado no programa de cálculo com que foram obtidos os resultados apresentados no item 3. A justificativa para este procedimento é de que o ponto $B$, que funciona como um ponto de giro dos segmentos $BC$, se situa próximo da cota do pé do talude, com exceção de taludes com inclinação muito próxima de 90°. Para os casos de cálculo com pressões neutras diferentes de zero, isto é, para $r_{u}>\theta$, o ponto $B$, que se situa à direita do ponto $A$, em geral terá cota igual à do ponto $A$.

Figura 5. Superfície de ruptura bi-linear e partes I e II delimitadas por superfície vertical

Além deste caso geral, foram consideradas mais duas situações, que estão representadas de forma esquemática na Figura 6. Para muros com face vertical a superfície de ruptura da cunha crítica reduz-se a um plano, com segmentos AB e BC colineares ou quase colineares. Neste caso o ponto B é deslocado para o pé do talude, coincidindo com o ponto A e é permitido o giro da superfície em torno do ponto A, para a verificação das superfícies sub-críticas (Figura 6(a)). E, por fim, quando da aplicação do caso geral, ilustrado na Figura 5, o ângulo $\theta _{2}$ resultar igual ao ângulo $\theta _{2{\hbox{ sub-crítico}}}$ mínimo igual a $\theta _{1}$, o processo de verificação é continuado, com procedimento semelhante ao empregado para muro de face vertical, deslocando-se o ponto B para a posição do ponto A e permitindo o giro de uma superfície plana com $\theta _{2}$ variando entre $\theta _{1}$ e metade do ângulo de atrito efetivo (Figura 6(b)).

Figura 6. Situações complementares de verificação. (a) Para muros de face vertical. (b) Para situações em que o caso geral leva a superfície sub-crítica plana com inclinação $\theta _{1}$ maior do que $\phi '/2$

A determinação do esforço necessário de tração para as superfícies sub-críticas $ABC'$ é feita mantendo a fatia I (Figura 5) e variando a inclinação do segmento $BC$ da fatia II, obtendo-se sucessivos valores de $K$ sub-críticos ($K_{sc}$). E como o esforço de tração é proporcional ao coeficiente $K$, o número de camadas necessárias (Eq. (13)) é proporcional à razão $K_{sc}/K_{req}$ e é menor ou igual ao número da camadas $n_{\min }$

${n}_{nec}={n}_{\min }{\frac {{T}_{nec}}{T}}={n}_{\min }{\frac {{K}_{sc}}{{K}_{req}}}$

(13)

onde

${T}_{nec}$ – esforço total de tração necessário para a superfície sub-crítica;

${T}$ – esforço total de tração necessário para a superfície crítica;

${n}_{nec}$ – número de camadas de reforço que devem atuar para produzir o equilíbrio.

Se a Eq. (13) produzir um número inteiro, significa que todas as ${n}_{nec}$ camadas, que devem ser computadas de baixo para cima, devem atuar com o esforço máximo igual a ${T}_{adm}$. Se o número ${n}_{nec}$ resultar fracionário, a parte inteira de ${n}_{nec}$ camadas deve trabalhar sob esforço máximo igual a ${T}_{adm}$. O que restar da parte fracionária de ${n}_{nec}$, pode ser obtido pela operação:

${\Delta n}_{nec}={n}_{nec}-\,INT\left({n}_{nec}\right)$

(14)

onde

$INT({n}_{nec})$ – parte inteira de ${n}_{nec}$;

${\Delta n}_{nec}$ – parte fracionária do esforço de tração necessário para a camada complementar.

O esforço que deverá ser resistido por esta camada complementar será menor do que o esforço ${T}_{adm}$, e pode ser determinado pela Eq. (15):

${\Delta T}_{complementar}={\Delta n}_{nec}.{T}_{adm}$

(15)

onde ${\Delta T}_{complementar}$ é o esforço de tração requerido para a camada complementar.

Por exemplo, para um arranjo de 10 camadas de reforço, que devem resistir ao esforço máximo de tração relacionado à superfície crítica, se para uma dada superfície sub-crítica o esforço de tração exigir ${n}_{nec}=8.5$ camadas, então as 8 camadas inferiores deverão trabalhar sob um esforço de tração igual a ${T}_{adm}$, e a 9ª camada precisará resistir à metade do esforço de que é capaz, isto é, ${\Delta T}_{complementar}={\Delta n}_{nec}$. ${T}_{adm}=0.5{T}_{adm}$. A camada superior, isto é, a 10ª camada não é necessária para o equilíbrio da cunha de ruptura passante por esta superfície sub-crítica.

Para comparação dos resultados dos coeficientes de empuxo $K$ obtidos com o uso das equações de Montanelli e Recalcati [9] com os resultados das cartas de Jewell [4], apresentam-se no Anexo os gráficos de $K\times \phi '_{d}$ para valores do parâmetro de pressão neutra de Bishop $r_{u}=\theta$, $r_{u}=0.25$ e $r_{u}=0.5$. O valor de $r_{u}=0$ corresponde à situação de solo seco e $r_{u}=0.5$ à de solo praticamente saturado. Os resultados baseados em [9] dão boa concordância e em geral com valores ligeiramente a favor da segurança em relação aos valores apresentados em [4].

2.3 Comprimento das camadas de reforço para as superfícies críticas e sub-críticas

O comprimento necessário de cada camada de reforço é obtido da soma do trecho contido dentro da cunha de ruptura e do trecho de ancoragem além da superfície de ruptura. Para o caso da superfície crítica todas as camadas trabalham sujeitas a um mesmo esforço máximo de tração, aqui suposto em condição de número inteiro $n_{\min }$ de camadas necessárias, igual a ${T}_{adm}$ e, desta forma, todas necessitam de um comprimento de ancoragem capaz de resistir a um esforço máximo de tração igual a ${T}_{adm}$.

Para o caso das superfícies sub-críticas os comprimentos das camadas inferiores, que devem ser sujeitas a um esforço máximo de tração igual a ${T}_{adm}$, devem ter um trecho de ancoragem correspondente à este esforço. Para a camada complementar, que estará sujeita a um esforço menor do que ${T}_{adm}$ o comprimento de ancoragem deve ser o suficiente para resistir a este esforço de tração.

Para calcular o comprimento de ancoragem foram considerados três casos em que: (1) o comprimento de ancoragem se situa sobre a projeção da face do talude, (2) o comprimento de ancoragem se situa em parte sobre a projeção da face do talude, (3) o comprimento de ancoragem se situa além da projeção da face do talude. A Figura 7 mostra o esquema geral do cálculo do comprimento de ancoragem, considerando que no trecho de ancoragem atuam tensões resistentes na interface com o solo igual a $\tau _{r}$, onde esta tensão pode ser expressa pela Lei de Coulomb na forma:

${\begin{aligned}{\tau }_{r}&={\mu .\sigma }'_{v}\\{\tau }_{r}&=\left({f}_{b}.tg\phi '\right).\,\gamma .z\end{aligned}}$

(16)

onde

$\mu$ – coeficiente de atrito solo-geossintético;

$\sigma '_{v}$ – tensão vertical efetiva atuante sobre o geotêxtil à profundidade $z$;

$f_{b}$ – coeficiente de interação (bond adesão) entre solo e geossintético;

$z$ – profundidade do ponto considerado;

${\tau }_{r}$ – tensão de cisalhamento na interface solo-geosssintético.

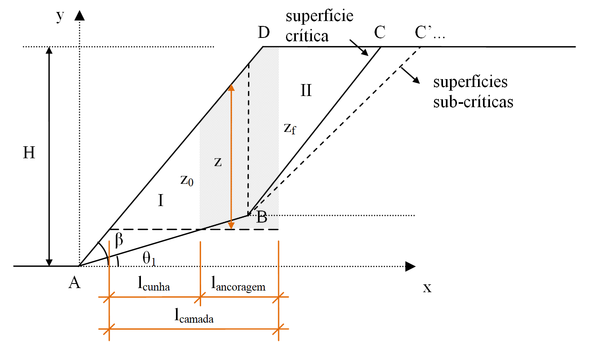
Figura 7. Esquema geral de cálculo do comprimento de camada de reforço

A dedução das expressões de cálculo do comprimento de ancoragem para os três casos antes citados está apresentada nos Anexos, com resultados finais transcritos a seguir, de forma adimensional em relação à altura do corte, isto é, na forma $(L/H)$:

Caso 1: Ancoragem situada sob a projeção da face do talude:

${\frac {{l}_{anc}}{H}}={\frac {-2.\left(\displaystyle {\frac {{z}_{0}}{H}}\right)+{\sqrt {4.{\left(\displaystyle {\frac {{z}_{0}}{H}}\right)}^{2}+2.\displaystyle {\frac {tg\beta }{n}}.\displaystyle {\frac {{K}_{req}}{tg\phi '.{f}_{b}.\left(1-{r}_{u}\right)}}}}}{2.tg\beta }}$

(17)

onde

$z_{0}$ – profundidade de solo acima da camada de reforço no início do trecho de ancoragem;

$n$ – número de camadas de reforço;

$\beta$ – ângulo de inclinação da face do talude;

$H$ – altura do talude;

$\phi '$ – ângulo de atrito efetivo de cálculo do solo, $\phi '=\phi '_{d}=\phi '_{cs}$;

$f_{b}$ – fator de interação solo-geossintético (bond – adesão);

${K}_{req}$ – coeficiente de empuxo correspondente à superfície crítica de ruptura;

$r_{u}$ – parâmetro de pressão neutra de Bishop;

$l_{anc}$ – comprimento de ancoragem do geossintético;

O fator de segurança ao arrancamento, no método de Jewell, já está aplicado no emprego do ângulo de atrito interno de cálculo (Eq. (9)) igual ao de estado crítico.

Caso 2: Ancoragem situada em parte sob a projeção da face do talude (Eq. (18)).

Este é o caso representado esquematicamente na Figura 7, antes apresentada

$\displaystyle {\frac {{l}_{anc}}{H}}=\left(\displaystyle {\frac {\displaystyle {\frac {{z}_{f}}{H}}-\displaystyle {\frac {{z}_{m}}{H}}}{\displaystyle {\frac {{z}_{f}}{H}}}}\right).\left(\displaystyle {\frac {{x}_{crista}}{H}}-\right.$$\left.\displaystyle {\frac {{x}_{0}}{H}}\right)+\displaystyle {\frac {1}{4n}}.{\frac {{K}_{req}}{{z}_{f}^{\ast }.tg{\phi '}.{f}_{b}.\left(1-{r}_{u}\right)}}$

(18)

onde

$z_{f}$ – profundidade de solo acima da camada de reforço no trecho final de ancoragem;

$z_{m}$ – profundidade média de solo no trecho final sob a face do talude $z_{m}=(z_{0}+z_{f})/2$;

${x}_{0}$ –abcissa das coordenadas do ponto de início do trecho de ancoragem;

${x}_{crista}$ –abcissa do ponto da crista do talude.

As demais variáveis na Eq. (18) são as mesmas envolvidas na Eq.(17).

Caso 3: Ancoragem situada além da projeção da face do talude:

$\displaystyle {\frac {{l}_{anc}}{H}}=\displaystyle {\frac {1}{4n}}.\displaystyle {\frac {{K}_{req}}{\left(\displaystyle {\frac {{z}_{f}}{H}}\right).tg\phi '.{f}_{b}.\left(1-{r}_{u}\right)}}$

(19)

onde $z_{f}$ é a profundidade de solo acima da camada de reforço no trecho final de ancoragem.

E novamente, as demais variáveis da Eq. (19) são as mesmas envolvidas na Eq. (17).

3. Resultados

Para a obtenção dos resultados apresentados a seguir foi feito uso da Eq. (2) para determinar os valores de ${K}_{req}$ para superfícies críticas e sub-críticas, para taludes onde se fez variar o ângulo de inclinação do talude $\beta$ de 30° a 90° e o ângulo de atrito efetivo $\phi$' de 20° a 50°.

Os valores obtidos estão plotados nos anexos, nas Figuras A1, A2 e A3, ao lado dos gráficos de Jewell, para comparação de resultados para os casos onde o parâmetro de pressão neutra é igual a $r_{u}=0$, a $0.25$ e $0.5$, respectivamente. Na obtenção destes resultados observou-se que a divisão da malha com 50 divisões em altura já é suficiente para garantir valores convergentes de “coeficientes de empuxo” com três casas decimais.

Para a verificação da influência das superfícies sub-críticas sobre o comprimento das camadas de reforço foi escolhido um arranjo com 20 camadas. Foram testadas duas formas de distribuição das camadas: com espaçamentos uniformes iguais a 1/20 da altura do talude e com espaçamentos variáveis correspondentes a espaçamentos ideais. A definição da segunda forma de espaçamento está ligada à distribuição linear de tensões horizontais sobre a face de muros de solo reforçado de tal forma que todas as camadas tenham igual esforço no ponto inicial da camada. Para uma tal condição, as camadas devem ter profundidade relativa dada pela Eq. (20):

${\frac {Z\left(i\right)}{H}}={\sqrt {\frac {i}{n}}}$

(20)

onde

$i$ – número de identificação da camada, partindo de cima para baixo;

$Z(i)$ – profundidade da camada de número $i$ medido da cota da crista do talude até à camada $i$;

$n$ – número de camadas do arranjo de reforços;

$H$ – altura do talude.

Exemplo 1

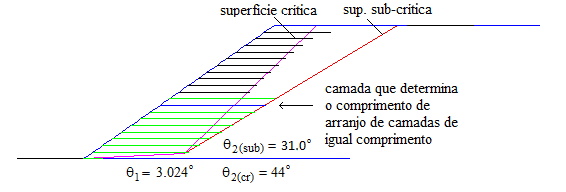
A Figura 8 mostra o esquema de distribuição vertical de camadas com espaçamento ideal, em saída de programa de cálculo, para ângulo $\beta =50$°, ângulo de atrito efetivo $\phi '=20$°, parâmetro $r_{u}=0$, coeficiente $f_{b}=0.5$ e $n=20$ camadas. O coeficiente de empuxo resultante é ${K}_{req}=0.2975$. As camadas de reforço mostram o comprimento mínimo necessário para estabilizar a cunha crítica de ruptura. Para arranjo de camadas de igual comprimento, o comprimento seria determinado pela camada de cima, que apresenta o maior comprimento com relação $(L/H)_{\hbox{crítica}}=0.622$. A superfície crítica de ruptura tem inclinações $\theta _{1}=0$° e $\theta _{2{\hbox{ crítica}}}=48.4$°. O vértice da superfície bi-linear de ruptura (ponto B nas Figuras 4 a 7) têm coordenadas $X_{B}=0.5$ H e $Y_{B}=0.0$ H. O ponto final da superfície de ruptura (ponto C nas Figuras 4 a 6) têm coordenadas $X_{C}=1.379$ H e $Y_{C}=1.0$ H.

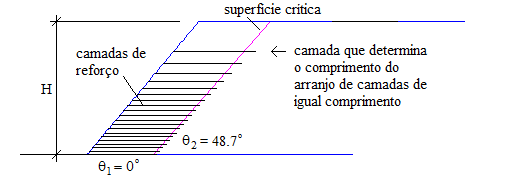
Figura 8. Esquema de distribuição de arranjo de 20 camadas com espaçamento ideal

A Figura 9 mostra resultado de processamento com os mesmos dados do exemplo mostrado na Figura 8, onde se vê a superfície crítica, a superfície sub-crítica determinante, e a camada, em particular, que necessita maior comprimento de reforço em relação à superfície sub-crítica, em azul. As demais camadas em verde complementam o arranjo necessário para a estabilidade da cunha sub-crítica determinante. O coeficiente de empuxo para a superfície sub-crítica é $K_{sc}=0.2154$, de forma que pela aplicação da Eq. (13) o número de camadas para assegurar a estabilidade é $n_{nec}=14.48$. O equilíbrio da cunha delimitada por esta superfície sub-crítica exige um esforço $T_{\max }$ das 14 camadas inferiores e 0.48 $T_{\max }$ da 15ª camada (ou sexta camada de cima para baixo). O equilíbrio da cunha definida pela superfície sub-crítica determinante exige o prolongamento das 14 camadas inferiores e de seus comprimentos de ancoragem além da superfície sub-crítica. Observe-se que estes comprimentos de ancoragem serão iguais ou menores do que os determinados em relação à superfície crítica pelo fato de que a tensão normal média sobre o comprimento de ancoragem ou se mantém constante ou aumenta.

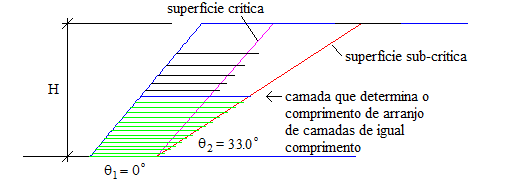
Figura 9. Seção transversal para talude com ângulo $\beta =50$°, ângulo de atrito efetivo $\phi '=20$°, parâmetro de pressão neutra $r_{u}=0$ e espaçamento ideal entre camadas

Neste exemplo a sexta camada a partir de cima controla o comprimento que deverá ter arranjo utilizando espaçamento ideal com todas as camadas de mesmo comprimento. A superfície sub-crítica tem ângulo de inclinação $\theta _{2{\hbox{ sub-crítica}}}=33.0$° e relação de comprimento $(L/H)_{\hbox{sub-crítica}}=0.835$, correspondente à sexta camada a partir de cima. Os comprimentos mostram que, neste caso, a superfície sub-crítica tem efeito significativo e exige comprimento 34.2% maior do que o determinado para a superfície crítica.

Para os mesmos dados utilizados neste primeiro exemplo, e portanto, para cunha crítica com ${K}_{req}=0.2975$, $\theta _{1}=0$° e $\theta _{2{\hbox{ crítica}}}=48.7$°, empregando espaçamento vertical uniforme entre camadas como mostrado na Figura 10, resulta relação $(L/H)_{\hbox{crítica}}=0.9467$.

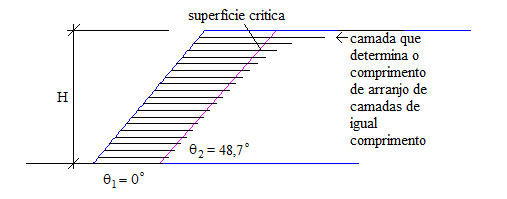
Figura 10. Esquema de distribuição de arranjo de 20 camadas com espaçamento uniforme

A Figura 11 mostra resultado de processamento para espaçamento uniforme, com os mesmos dados do exemplo mostrado na Figura 8, onde se vê a superfície crítica, a superfície sub-crítica, e a camada, em particular, que necessita maior comprimento de reforço em relação à superfície sub-crítica determinante, em azul. O coeficiente de empuxo para esta superfície sub-crítica é $K_{sc}=0.2026$, de forma que pela aplicação da Eq. (13) $n_{nec}=13.62$. O equilíbrio da cunha delimitada por esta superfície sub-crítica exige um esforço $T_{\max }$ das 13 camadas inferiores e 0.62 $T_{\max }$ da 14ª camada (ou sétima camada de cima para baixo).

A superfície sub-crítica determinante tem ângulo de inclinação $\theta _{2{\hbox{ crítica}}}=32.0$° e relação de comprimento $(L/H)_{\hbox{sub-crítica}}=1.0310$, correspondente à sétima camada a partir de cima.

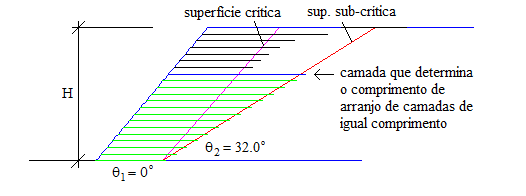
Figura 11. Seção transversal para talude com ângulo $\beta =50$°, ângulo de atrito efetivo $\phi '=20$°, parâmetro de pressão neutra $r_{u}=0$ e espaçamento uniforme entre camadas

Os resultados observados nas Figuras 8 a 11 mostram que o uso de espaçamento uniforme, com $(L/H)_{\hbox{sub-crítica}}=1.031$, para os dados deste exemplo, exigem comprimento 23.5% maior do que a solução com espaçamento ideal, com $(L/H)_{\hbox{sub-crítica}}=0.835$.

Exemplo 2

Um segundo exemplo de aplicação é apresentado na Figura 12, para esquema de distribuição vertical de camadas com espaçamento ideal, em saída de programa de cálculo, para ângulo ${\textstyle \beta =35}$°, ângulo de atrito efetivo ${\textstyle \phi '=30}$°, parâmetro ${\textstyle r_{u}=0.25}$, coeficiente ${\textstyle f_{b}=0.5}$ e ${\textstyle n=20}$ camadas. O coeficiente de empuxo resultante é ${\textstyle K_{req}=0.1370}$. A superfície crítica de ruptura tem inclinação ${\textstyle \theta _{1}=3.024}$° e ${\textstyle \theta _{2{\hbox{ crítica}}}=44.0}$°. O vértice da superfície bi-linear de ruptura (ponto B nas Figuras 4 a 6) têm coordenadas ${\textstyle X_{B}=0.7571}$ H e ${\textstyle Y_{B}=0.04}$ H. O ponto final da superfície de ruptura (ponto C nas Figuras 4 a 6) têm coordenadas ${\textstyle X_{C}=1.748}$ H e ${\textstyle Y_{C}=1.0}$ H.

As camadas de reforço mostram o comprimento mínimo necessário para estabilizar a cunha crítica de ruptura. Para arranjo de camadas de igual comprimento, o comprimento para assegurar a estabilidade da cunha crítica seria determinado pela 18ª camada de cima para baixo, que apresenta o maior comprimento com relação $(L/H)_{\hbox{crítica}}=0.712$.

O coeficiente de empuxo para a superfície sub-crítica determinante é $K_{sc}=0.0622$, de forma que pela aplicação da Eq. (13) $n_{nec}=9.08$. A superfície sub-crítica determinante tem inclinações ${\textstyle \theta _{1}=3.024}$° e ${\textstyle \theta _{2{\hbox{ crítica}}}=31.0}$°. A consideração da superfície sub-crítica exige comprimento com relação $(L/H)_{\hbox{sub-crítica}}=0.759$, passando a camada determinante do comprimento do arranjo a ser a 12ª camada de cima para baixo, em azul.

Figura 12. Seção transversal para talude com ângulo $\beta =35$°, ângulo de atrito efetivo $\phi '=30$°, parâmetro de pressão neutra $r_{u}=0.25$ e espaçamento uniforme entre camadas

De maneira análoga à do exemplo 1, para os mesmos dados iniciais utilizados no segundo exemplo, e portanto, para cunha crítica com ${\textstyle K_{req}=0.1370}$, e ângulos ${\textstyle \theta _{1}=3.024}$° e ${\textstyle \theta _{2{\hbox{ crítica}}}=44.0}$°, empregando espaçamento vertical uniforme entre camadas como mostrado na Figura 13, resulta relação $(L/H)_{\hbox{crítica}}=0.712$.

Figura 13. Seção transversal para talude com ângulo $\beta =35$°, ângulo de atrito efetivo $\phi '=30$°, parâmetro de pressão neutra $r_{u}=0.25$ e espaçamento uniforme entre camadas

Para a superfície sub-crítica determinante resulta ${\textstyle K_{req}=0.0622}$, de forma que pela aplicação da Eq. (13) $n_{nec}=9.08$. O equilíbrio da cunha delimitada por esta superfície sub-crítica exige um esforço $T_{\max }$ das 9 camadas inferiores e 0.08 $T_{\max }$ da 10ª camada, de baixo para cima. Da Figura 13 pode-se observar que a camada determinante do comprimento é a 12ª camada a partir de cima, camada esta que trabalha sob $T_{\max }$, e tem relação $(L/H)_{\hbox{sub-crítica}}=0.799$. A superfície sub-crítica determinante tem inclinações com ângulos ${\textstyle \theta _{1}=3.024}$° e ${\textstyle \theta _{2{\hbox{ crítica}}}=31.0}$°.

Neste segundo exemplo a solução com espaçamento uniforme que apresenta $(L/H)_{\hbox{sub-crítica}}=0.799$, exige comprimento 5.027 % maior do que a solução com espaçamento ideal, com $(L/H)_{\hbox{sub-crítica}}=0.759$.

A solução mais econômica, com espaçamento ideal, é usualmente ajustada no projeto final, dividindo o arranjo de camadas em três trechos de espaçamentos iguais, modulando estes espaçamentos em função de espessura de camada compactada a ser utilizada no campo. Esta orientação é indicada no manual de projeto [10] para taludes e muros com mais de 6 m de altura. Para alturas menores pode ser usado o espaçamento uniforme.

Outra forma de projeto é apresentada por Jewell [4], em exemplo de aplicação, no qual é utilizado um arranjo com espaçamento uniforme entre camadas, mas onde gradua-se a gramatura das camadas de forma a cobrir o diagrama de tensões sobre a face do muro. A definição do arranjo é feita por tentativas, onde a solução teórica ajuda a escolher o lay out de projeto mais eficiente.

3.1 Relações $(L/H)_{\hbox{crítica}}$ e $(L/H)_{\hbox{sub-crítica}}$ para espaçamento ideal3.1 Relações ( L / H ) crítica {\displaystyle (L/H) {\hbox{crítica}}} e ( L / H ) sub-crítica {\displaystyle (L/H) {\hbox{sub-crítica}}} para espaçamento ideal

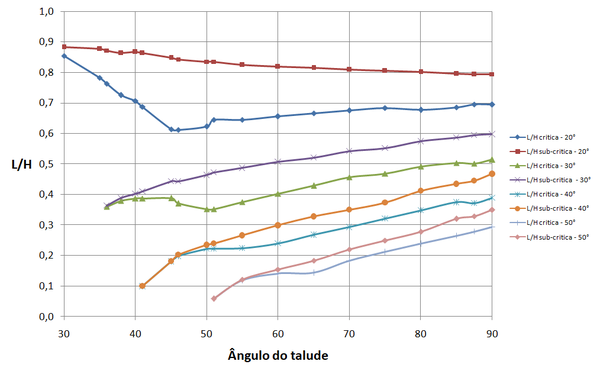
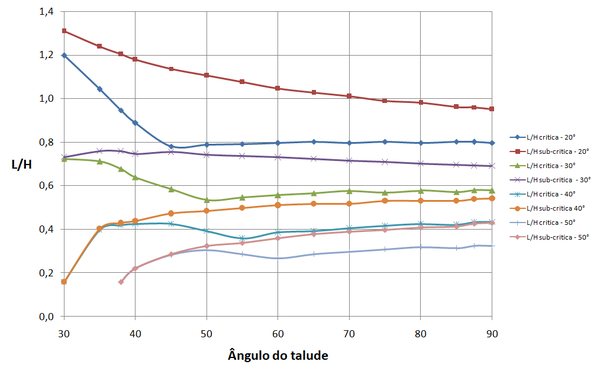
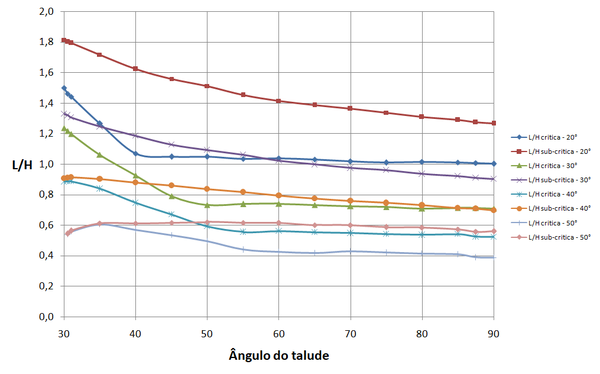
Os resultados apresentados a seguir se referem a arranjos de 20 camadas de reforço com espaçamento ideal. Foram testados arranjos com menor número de camadas tendo-se observado praticamente os mesmos valores de relações de comprimento $(L/H)_{\hbox{crítica}}$ e $(L/H)_{\hbox{sub-crítica}}$. Desta forma limitou-se, na exposição que se segue, ao caso de arranjo de 20 camadas. As Figuras 14 a 16 mostram os resultados das relações $(L/H)_{\hbox{crítica}}$ e $(L/H)_{\hbox{sub-crítica}}$ para ${\textstyle r_{u}=0}$, ${\textstyle r_{u}=0.25}$ e ${\textstyle r_{u}=0.5}$, respectivamente. Foi empregado fator de de interação entre solo e geossintético ${\textstyle f_{b}=0.5}$ (valor de ${\textstyle f_{b}}$ adotado nas cartas de Jewell [4] para geogrelhas), e ângulo de atrito efetivo igual ao de estado crítico $\phi '=\phi _{cs}$. O ângulo de arito considerado é indicado nas legendas das Figuras 14 a 22.

Figura 14. Relação comprimento de reforço para altura $(L/H)$ para ${\textstyle r_{u}=0.0}$

Figura 15. Relação comprimento de reforço para altura $(L/H)$ para ${\textstyle r_{u}=0.25}$

Figura 16. Relação comprimento de reforço para altura $(L/H)$ para ${\textstyle r_{u}=0.5}$

Para os arranjos com espaçamento ideal, as superfícies sub-críticas podem exigir comprimento dos reforços da ordem de 30% ou mais em relação ao exigido para as superfícies críticas.

3.2 Relações $(L/H)_{\hbox{crítica}}$ e $(L/H)_{\hbox{sub-crítica}}$ para espaçamento uniforme3.2 Relações ( L / H ) crítica {\displaystyle (L/H) {\hbox{crítica}}} e ( L / H ) sub-crítica {\displaystyle (L/H) {\hbox{sub-crítica}}} para espaçamento uniforme

As Figuras 17 a 19 mostram os resultados para ${\textstyle r_{u}=0}$, ${\textstyle r_{u}=0.25}$ e ${\textstyle r_{u}=0.5}$, para caso de espaçamento uniforme, respectivamente e demais dados iguais aos utilizados no item 3.1.

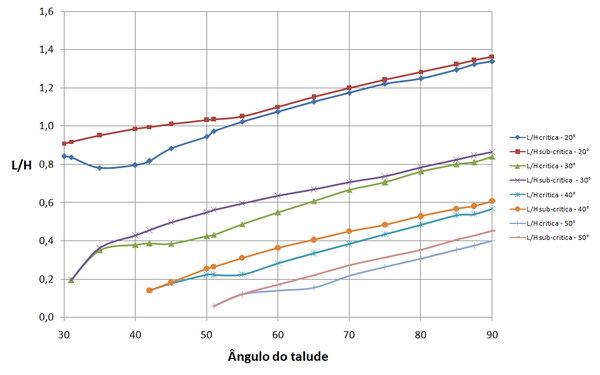
Figura 17. Relação comprimento de reforço para altura $(L/H)$ para ${\textstyle r_{u}=0.0}$

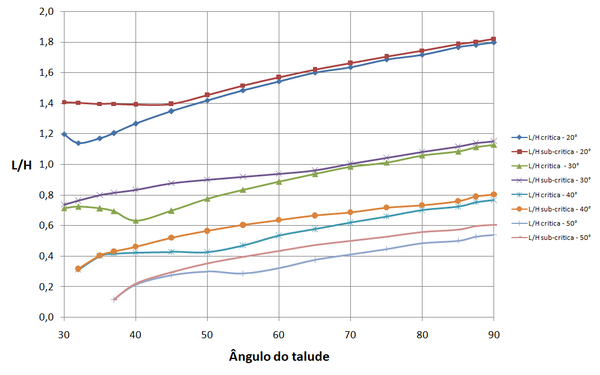
Figura 18. Relação comprimento de reforço para altura $(L/H)$ para ${\textstyle r_{u}=0.25}$

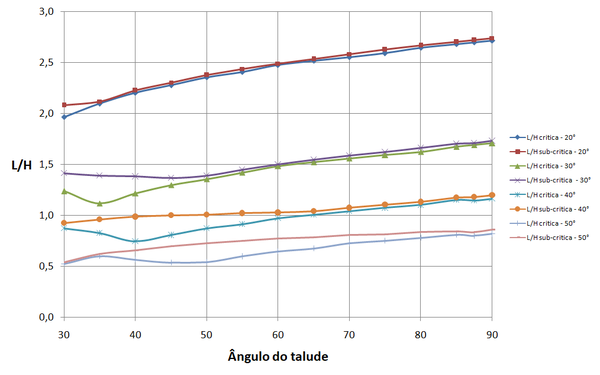
Figura 19. Relação comprimento de reforço para altura $(L/H)$ para ${\textstyle r_{u}=0.5}$

Para espaçamento uniforme, pode-se notar das Figuras 17 a 19, que os comprimentos necessários para as superfícies críticas e para as superfícies sub-críticas têm menores diferenças do que para o caso de espaçamento ideal. E, via de regra, arranjos com espaçamento uniforme exigem comprimentos maiores de reforços em relação ao necessário com uso de espaçamento ideal.

3.3 Análise de resultados

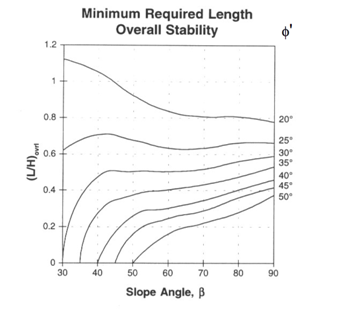
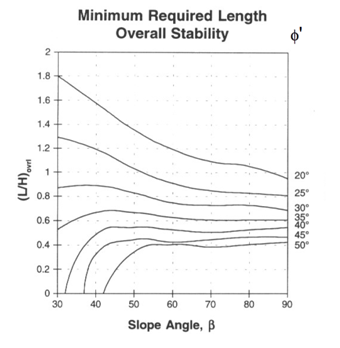
As Figuras 20 a 22 a seguir permitem a comparação entre os resultados obtidos neste trabalho, para relação de comprimento $(L/H)$ adimensional, com os gráficos de autoria de Jewell [4]. A análise é apresentada para o caso de espaçamento ideal, para ${\textstyle r_{u}=0}$, ${\textstyle r_{u}=0.25}$ e ${\textstyle r_{u}=0.5}$. Na obtenção destes resultados foi empregado coeficiente de interação solo-geossintético ${\textstyle f_{b}=0.5}$ e ângulo de atrito de cálculo $\phi '=\phi _{cs}$ para o cálculo dos comprimentos de ancoragem. Nas cartas de Jewell, que foram inicialmente obtidas para geogrelhas, é empregado para este fim ${\textstyle f_{b}=0.5}$, e o ângulo de atrito de cálculo $\phi '=\phi _{cs}$. No caso de emprego de geotextil pode-se usar valor maior para ${\textstyle f_{b}}$, por exemplo ${\textstyle f_{b}=0.8}$.

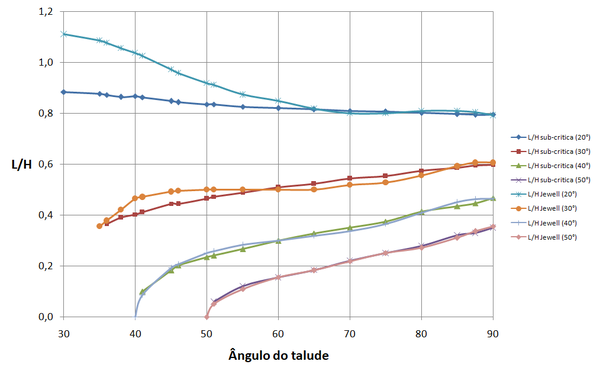
Figura 20. Relação comprimento de reforço/altura $(L/H)$ pelo processo indicado pelos autores $(L/H)_{sub}$ e por Jewell [4] $(L/H)$ Jewell para ${\textstyle r_{u}=0}$

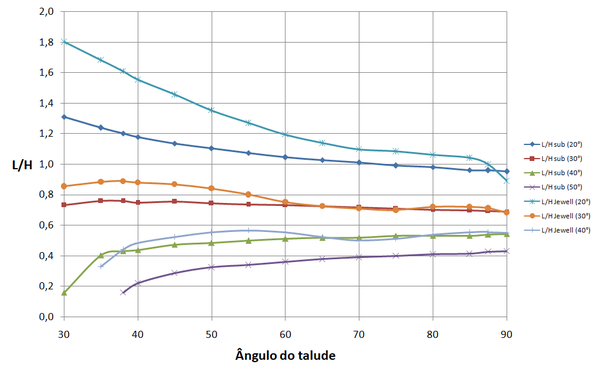
As curvas têm comportamento similar. Observa-se quase coincidência de valores para a curva correspondente a um ângulo de atrito $\phi '=50$°. À medida que o ângulo de atrito diminui cresce o afastamento entre as curvas, em termos absolutos.

Figura 21. Relação comprimento de reforço/altura $(L/H)$ pelo processo indicado pelos autores $(L/H)_{sub}$ e por Jewell [4] $(L/H)$ Jewell para ${\textstyle r_{u}=0.25}$

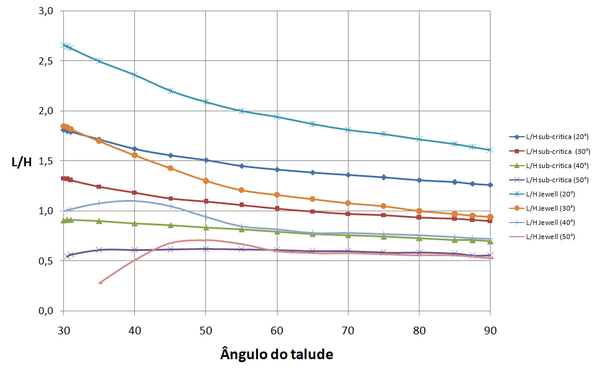
Figura 22. Relação comprimento de reforço/altura $(L/H)$ pelo processo indicado pelos autores $(L/H)_{sub}$ e por Jewell [4] $(L/H)$ Jewell para ${\textstyle r_{u}=0.5}$

Da comparação entre gráficos das Figuras 20 a 22 pode-se observar que as curvas apresentam tendências de variação semelhantes e razoável coincidência de valores numéricos. Os maiores afastamentos ocorrem para valor de ${\textstyle r_{u}=0.5}$ e para os mais baixos valores de ângulo de atrito.

4. Conclusões

O emprego de análise de equilíbrio-limite, com base nas equações de Montanelli e Recalcati [9], leva à determinação de coeficientes de empuxo ${\textstyle K_{req}}$ um pouco a favor da segurança e de comprimentos de reforços com tendência semelhante aos resultados obtidos por Jewell em [4].

O processo de cálculo aqui apresentado, que examina a estabilidade ao arrancamento das camadas de reforço, permite determinar, por processo iterativo, o comprimento necessário das camadas de reforços, prescindindo da utilização de coeficientes de correção empíricos, como empregado em [1] e [4].

A camada que exige o maior comprimento pode ser identificada no arranjo de camadas de reforço. E o processo de cálculo também permite determinar o estado de tração nas camadas da estrutura de solo reforçado.

A observância das superfícies de ruptura sub-críticas é particularmente importante para o caso de taludes de solo reforçado, ou seja, para os taludes com inclinação ${\textstyle \beta \leq 70}$°. No caso de projetos de muros de solo-reforçado, em que se deve verificar também condição de resistência ao deslizamento, tombamento e de não ocorrência de tensões de tração na base, é comum que a condição determinante do comprimento dos reforços seja de estabilidade externa e não de estabilidade interna da estrutura.

5. Considerações finais

O processo de cálculo aqui apresentado permite visualizar o mecanismo de segurança ao arrancamento das camadas de reforço, para os casos de espaçamento ideal e espaçamento uniforme entre camadas de reforço. Para a construção do layout de projeto do arranjo de camadas faz-se referência às orientações de Jewell [4] e da necessidade de atender um estado mínimo de tensões de face no topo do muro ou talude.

Em princípio, o procedimento apresentado neste artigo pode ser adaptado para terraplenos com inclinação e com sobrecargas sobre a superfície. A consideração das superfícies sub-críticas pode também, com as necessárias adequações de geometria, ser aplicada ao caso de dimensionamento de contenções com o uso de chumbadores, levando em conta a inclinação de instalação dos chumbadores em relação à horizontal.

Referências

[1] Jewell R.A. Strength and deformation in reinforced soil design. Soil Mechanics Report nº 117/91, University of Oxford, UK, 1991.

[2] Vertematti J.C. Manual brasileiro de geossintéticos. CTG-BAINT, Ed. Blücher, 2ª edição, Brasil, 2015.

[3] Vieira C.F. da Silva. Muros de taludes de solo reforçado com geossintéticos. Comportamento sísmico e metodologias de dimensionamento. Tese de Doutorado, FEUP Universidade do Porto, Portugal, 2008.

[4] Jewell R.A. Application of revised design charts for steep reinforced slopes. Geotextiles and Geomembranes, 10,(3):203-234, 1991.

[5] Leshchinsky D., Leshchinsky B., Leshchinsky O. Limit state design framework for geosynthetic-reinforced soil structures. Geotextiles and Geomembranes, 45(6), 642-652, 2017.

[6] Drucker D.C., Prager W. Soil mechanics and plastic analysis or limit design. Quarterly of Applied Mathematics, 10(2):157-165, 1952.

[7] Yamanouchi T., Fukuda N. Design and observation of steep reinforced embankments. Third International Conference on Case Histories in Geotechnical Engineering, Missouri University of Science and Technology, 1-6 June 1993.

[8] BS 8006-1:2010 Code of practice for strengthened/reinforced soils and other fills. British Standards Institution, ISBN 978-0-580-53842-1, 2010.

[9] Montanelli F., Recalcati P. The design of reinforced soil retaining walls using TENAX geogrids. Design Manual TENAX SPA, Geosynthetics Division, Italy, 2003.

[10] FHWA. Reinforced soil structures, design and construction guidelines. Volume I., U.S. Department of Transportation, Federal Highway Administration, USA, 152, 1990.

Anexo

A.1. Coeficientes de empuxo K_req

Os gráficos a seguir mostram a reprodução do cálculo dos valores do coeficiente de empuxo ${\textstyle K_{req}}$, obtidos com o uso da Eq. (2), extraída do trabalho de Montanelli e Recalcati [9] e os gráficos apresentados por Jewell [1,4].

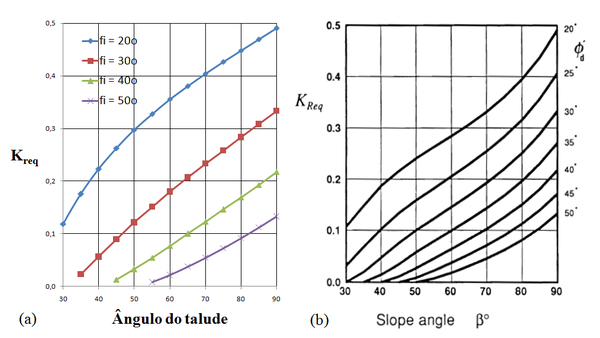
Figura A1. Coeficiente ${\textstyle K_{req}}$. (a) Montanelli e Recalcati [9]. (b) Jewell [1,4] para ${\textstyle r_{u}=0.0}$

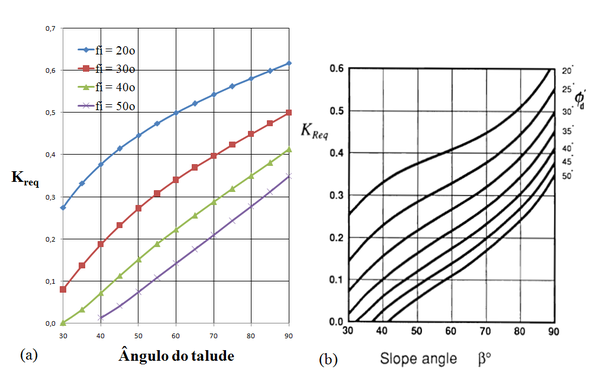
Figura A2. Coeficiente ${\textstyle K_{req}}$. (a) Montanelli e Recalcati [9]. (b) Jewell [1,4] para ${\textstyle r_{u}=0.25}$

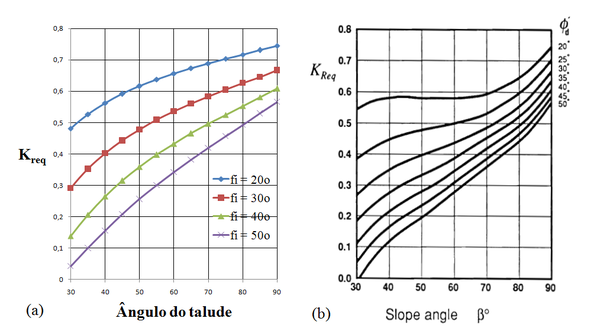
Figura A3. Coeficiente ${\textstyle K_{req}}$. (a) Montanelli e Recalcati [9]. (b) Jewell [1,4] para ${\textstyle r_{u}=0.5}$

A.2. Comprimentos de ancoragem

Caso 1: Ancoragem situada sob a projeção da face do talude

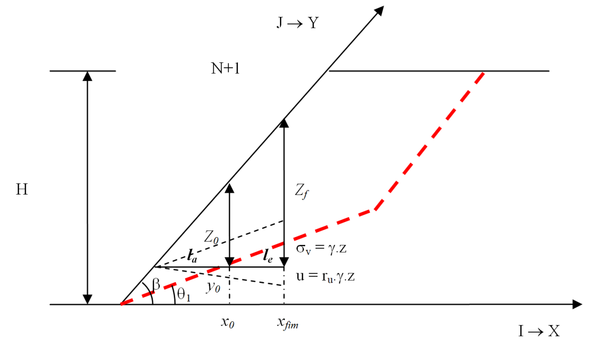
Figura A4. Primeiro caso de ancoragem – ancoragem sob a face do talude

Para um ponto a uma profundidade z no trecho de ancoragem a tensão vertical efetiva é igual a:

${\begin{aligned}{\sigma '}_{v}&=\gamma .z-{r}_{u}.\gamma .z\\{\sigma '}_{v}&=\left(1-{r}_{u}\right).\gamma .z\end{aligned}}$

Para uma camada de reforço o esforço no reforço é equilibrado pela resistência da ancoragem, assim

${\begin{aligned}&{T}_{adm}=2.\int _{0}^{{l}_{e}}{\tau }_{r}\left(l\right).dl\\&{\frac {{{\frac {1}{2}}K}_{req}.\gamma .{H}^{2}}{n}}=2.\int _{0}^{{l}_{e}}{\sigma '}_{v}.tg\phi '.{f}_{b}.dl\\&{\frac {{{\frac {1}{2}}K}_{req}.\gamma .{H}^{2}}{n}}=2.tg\phi '.{f}_{b}\int _{0}^{{l}_{e}}{\sigma '}_{v}.dl\\&{\frac {{{\frac {1}{2}}K}_{req}.\gamma .{H}^{2}}{n}}=2.tg\phi '.{f}_{b}.\left(1-{r}_{u}\right).\gamma \int _{0}^{{l}_{e}}z.dl\\&{\frac {{{\frac {1}{2}}K}_{req}.\gamma .{H}^{2}}{n}}=2.tg\phi '.{f}_{b}.\left(1-{r}_{u}\right).\gamma \int _{0}^{{l}_{e}}\left({z}_{0}+l.tg\beta \right).dl\\&{\frac {{K}_{req}}{4n}}.{\frac {1}{tg\phi '.{f}_{b}.\left(1-{r}_{u}\right)}}={\frac {{z}_{0}}{H}}.\left({\frac {{l}_{e}}{H}}\right)+{\frac {tg\beta }{2}}.{\left({\frac {{l}_{e}}{H}}\right)}^{2}\end{aligned}}$

Reordenando a equação do segundo grau e dividindo por 2, resulta:

$tg\beta .{\left({\frac {{l}_{e}}{H}}\right)}^{2}+{\frac {{2.z}_{0}}{H}}.\left({\frac {{l}_{e}}{H}}\right)-$${\frac {1}{2n}}.{\frac {{K}_{req}}{tg\phi '.{f}_{b}.\left(1-{r}_{u}\right)}}=0$

Onde colocando ${l}_{e}^{\ast }={\frac {{l}_{e}}{H}}$ e ${z}_{0}^{\ast }=$${\frac {{z}_{0}}{H}}\,$ fica:

$tg\beta .{\left({l}_{e}^{\ast }\right)}^{2}+2.{z}_{0}^{\ast }.\left({l}_{e}^{\ast }\right)-$${\frac {1}{2n}}.{\frac {{K}_{req}}{tg\phi '.{f}_{b}.\left(1-{r}_{u}\right)}}=0$

e

${l}_{e}^{\ast }={\frac {-2.{z}_{0}^{\ast }+{\sqrt {4.{\left({z}_{0}^{\ast }\right)}^{2}+4.tg\beta .{\frac {1}{2n}}.{\frac {{K}_{req}}{tg\phi '.{f}_{b}.\left(1-{r}_{u}\right)}}}}}{2.tg\beta }}$

Voltando às variáveis originais colocando ${\textstyle {l}_{e}={l}_{anc}}$ resulta:

${\frac {{l}_{anc}}{H}}={\frac {-2.{\frac {{z}_{0}}{H}}+{\sqrt {4.{\left({\frac {{z}_{0}}{H}}\right)}^{2}+4.tg\beta .{\frac {1}{2n}}.{\frac {{K}_{req}}{tg\phi '.{f}_{b}.\left(1-{r}_{u}\right)}}}}}{2.tg\beta }}$

(A1)

Caso 2: Ancoragem situada em parte sob a projeção da face do talude

Neste caso o trecho de ancoragem tem parte sujeita a tensão resistente de atrito variável (trecho $l_{e1}$) e parte sob tensão resistente de atrito constante (trecho $l_{e2}$). Isto é, um trecho tem tensão vertical variável (trecho $l_{e1}$) e o outro tem tensão vertical constante (trecho $l_{e2}$).

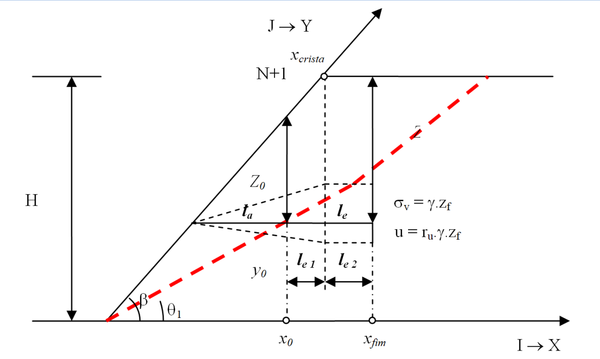
Figura A5. Segundo caso de ancoragem – ancoragem em parte sob a face do talude

Determina-se o trecho com tensão de aderência variável (trecho $l_{e1}$):

${l}_{e1}={x}_{crista\,\,}-{x}_{0}$

E determina-se a contribuição do trecho $l_{e1}$ para a força de ancoragem:

${\begin{aligned}&{z}_{m}={\frac {{z}_{0}+{z}_{f}\,}{2}}={\frac {{z}_{0}+\left(H-{y}_{0}\right)\,}{2}}\\&\sigma '_{vm}=\gamma .{z}_{m}-{r}_{u}.\gamma .{z}_{m}\\&\sigma '_{vm}=\left(1-{r}_{u}\right).\gamma .{z}_{m}\\&{\tau }_{m}{=\sigma '}_{vm\,}.tg\phi '.{f}_{b}\\&{\tau }_{m}=\gamma .{z}_{m}.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}\\&{\tau }_{m}=\gamma .\left[{\frac {{z}_{0}+\left(H-{y}_{0}\right)\,}{2}}\right].\left(1-{r}_{u}\right).tg\phi '.{f}_{b}\end{aligned}}$

E o esforço resistido pelo trecho $l_{e1}$ é igual a:

${F}_{r1}=2.{\tau }_{m}\,.{l}_{e1}$

${F}_{r1}=2\,.\left[\gamma .{\frac {\left({z}_{0}+{z}_{f}\right)}{2}}.\left(1-{r}_{u}\right)\,.tg\phi '.{f}_{b}\right].\left({x}_{crista\,\,}-{x}_{0}\right)$

O segundo trecho trabalha sob tensão de aderência constante, e assim:

$\left({F}_{ref}-\,{F}_{r1}\right)=2.\tau \,.{l}_{e2}$

${\begin{aligned}&{l}_{e2}={\frac {\left({F}_{ref}-\,{F}_{r1}\right)}{2.\tau }}\\&{l}_{e2}={\frac {\left({F}_{ref}-\,{F}_{r1}\right)}{2.\gamma .{z}_{f}.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}}}\end{aligned}}$

Onde o esforço para cada camada de reforço é igual a:

${F}_{ref}=\,{\frac {{{\frac {1}{2}}\,.\,K}_{req}.\gamma .{H}^{2}}{n}}={\frac {1}{2n}}\,.\,{K}_{req}\,.\,\gamma .{H}^{2}$

e, portanto

${\begin{aligned}&{l}_{e2}={\frac {{F}_{ref}}{2.\gamma .{z}_{f}.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}}}-{\frac {{F}_{r1}}{2.\gamma .{z}_{f}.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}}}\\&{l}_{e2}={\frac {{\frac {1}{2n}}\,.\,{K}_{req}\,.\,\gamma .{H}^{2}}{2.\gamma .{z}_{f}.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}}}\,-{\frac {2\,.\left[\gamma .{\frac {\left({z}_{0}+{z}_{f}\right)}{2}}.\left(1-{r}_{u}\right)\,.tg{\phi '}.{f}_{b}\right].\left({x}_{crista\,\,}-{x}_{0}\right)}{2.\gamma .{z}_{f}.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}}}\\&{l}_{e2}={\frac {1}{4n}}.{\frac {\,{K}_{req}\,.\,{H}^{2}}{{z}_{f}.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}}}\,-{\frac {{z}_{m}}{{z}_{f}}}\,.\left({x}_{crista\,\,}-{x}_{0}\right)\end{aligned}}$

E o comprimento de ancoragem do reforço é igual a:

${l}_{e}={l}_{e1}+\,{l}_{e2}$

Onde substituindo as expressões para $l_{e1}$ e $l_{e2}$, resulta:

${\begin{aligned}&{l}_{e}=\left({x}_{crista\,\,}-{x}_{0}\right)+{\frac {1}{4n}}.{\frac {\,{K}_{req}\,.\,{H}^{2}}{{z}_{f}.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}}}\,-\,{\frac {{z}_{m}}{{z}_{f}}}\,.\left({x}_{crista\,\,}-{x}_{0}\right)\\&{l}_{e}=\,\left({\frac {{z}_{f}-{z}_{m}}{{z}_{f}}}\right).\left({x}_{crista\,\,}-{x}_{0}\right)+{\frac {1}{4n}}.{\frac {\,{K}_{req}\,.\,{H}^{2}}{{z}_{f}.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}}}\end{aligned}}$

Onde colocando ${l}_{e}^{\ast }={\frac {{l}_{e}}{H}}$, ${z}_{f}^{\ast }={\frac {{z}_{f}}{H}}$, ${z}_{m}^{\ast }={\frac {{z}_{m}}{H}}$, ${x}_{crista}^{\ast }={\frac {{x}_{crista}}{H}}$ e ${x}_{0}^{\ast }={\frac {{x}_{0}}{H}}$ fica:

${l}_{e}^{\ast }=\,\left({\frac {{z}_{f}^{\ast }-{z}_{m}^{\ast }}{{z}_{f}^{\ast }}}\right).\left({x}_{crista}^{\ast }-\right.$$\left.{x}_{0}^{\ast }\right)+{\frac {1}{4n}}.{\frac {\,{K}_{req}\,}{{z}_{f}^{\ast }.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}}}$

E, por fim, voltando às variáveis originais, resulta:

${\frac {{l}_{anc}}{H}}=\,\left({\frac {{\frac {{z}_{f}}{H}}-{\frac {{z}_{m}}{H}}}{\frac {{z}_{f}}{H}}}\right).\left({\frac {{x}_{crista}}{H}}-{\frac {{x}_{0}}{H}}\right)+{\frac {1}{4n}}.{\frac {\,{K}_{req}\,}{{\frac {{z}_{f}}{H}}.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}}}$

(A2)

onde

${\textstyle z_{f}}$ – profundidade de solo acima da camada de reforço no trecho final de ancoragem;

${\textstyle z_{m}}$ – profundidade média de solo no trecho final sob a face do talude ${\textstyle z_{m}=(z_{0}+z_{f})/2}$;

${\textstyle x_{0}}$ –abcissa das coordenadas do ponto de início do trecho de ancoragem;

${\textstyle x_{crista}}$ –abcissa do ponto da crista do talude;

Caso 3: Ancoragem situada além da projeção da face do talude

Se o reforço tem ponto inicial após a projeção da crista do talude, a tensão de aderência atuante sobre o comprimento de ancoragem tem módulo constante.

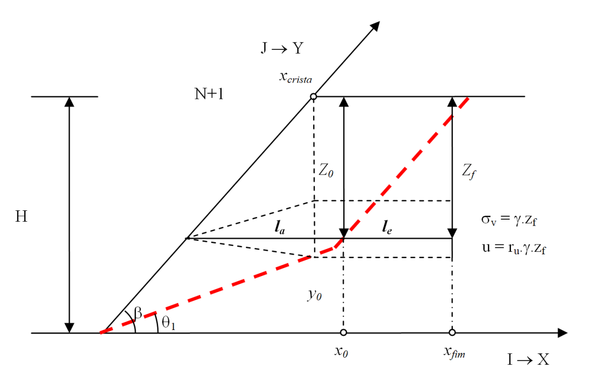
Figura A6. Terceiro caso de ancoragem – ancoragem totalmente sob o terrapleno

Neste caso, o ponto de intersecção do reforço com a cunha crítica tem $x_{0}>x_{crista}$

${\begin{aligned}&\sigma '_{v}=\gamma .{z}_{f}-{r}_{u}.\gamma .{z}_{f}\\&\sigma '_{v}=\left(1-{r}_{u}\right).\gamma .{z}_{f}\\&\tau =\sigma '_{v}.tg\phi '.{f}_{b}\\&\tau =\gamma .{z}_{f}.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}\end{aligned}}$

E o esforço resistido pelo trecho $l_{e}$ de ancoragem é igual a:

${F}_{ref}=2.\tau \,.{l}_{e}$

${\frac {1}{2n}}.{K}_{req}.\,\gamma .{H}^{2}=2.\left[\gamma .{z}_{f}.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}\right].{l}_{e}$

E o comprimento de ancoragem resulta:

${l}_{e}\,=\,{\frac {1}{4n}}.{\frac {{K}_{req}.\,\gamma .{H}^{2}}{\gamma .{z}_{f}.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}}}$

Onde colocando ${\textstyle {l}_{e}^{\ast }={\frac {{l}_{e}}{H}}}$ e ${\textstyle {z}_{f}^{\ast }=}$${\frac {{z}_{f}}{H}}\,$ fica:

${l}_{e}^{\ast }\,=\,{\frac {1}{4n}}.{\frac {{K}_{req}.}{\gamma .{z}_{f}^{\ast }.\left(1-{r}_{u}\right).tg\phi '.{f}_{b}}}$

E, por fim, retornando às variáveis originais, resulta

${\frac {{l}_{anc}}{H}}\,=\,{\frac {1}{4n}}.{\frac {{K}_{req}.}{\gamma .\left({\frac {{z}_{f}}{H}}\right).\left(1-{r}_{u}\right).tg\phi '.{f}_{b}}}$

(A3)

onde $z_{f}$ é a profundidade de solo acima da camada de reforço no trecho final de ancoragem.

A.3 Expressões para cálculo dos esforços de sub-pressão $U_{AB}$ e $U_{BC}$A.3 Expressões para cálculo dos esforços de sub-pressão U A B {\displaystyle U {AB}} e U B C {\displaystyle U {BC}}

As forças de sub-pressão $U_{AB}$ e $U_{BC}$ referidas no item 2 e indicadas esquematicamente na Figura 3, correspondem às forças denominadas a seguir como $U_{1}$ e $U_{2}$. O cálculo destas forcas pode recair em três casos dependendo da posição relativa do ponto de interseção $P(I,J)$ na malha de referência, em relação ao ponto da crista do talude $P(1,Np1)$. O índice Np1 = N+1.

Primeiro caso: $XP(I,J)\leq XP(1,Np1)$ e ponto final $XP(IT,Np1)=XP(1,Np1)$

Este é o caso representado na Figura A7, onde o ponto da crista do talude tem projeção situada à direita do ponto $P(I,J)$ e, portanto, a cunha de ruptura se situa sob a face do talude.

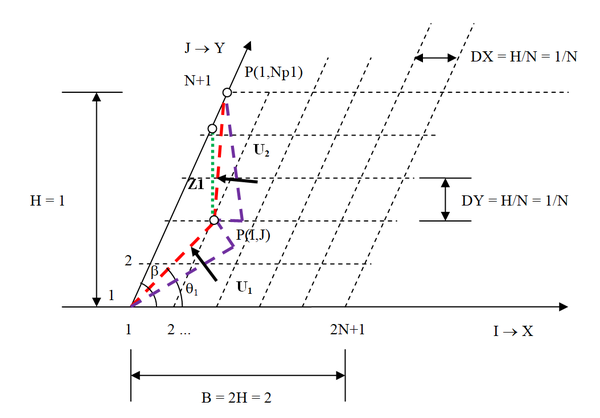
Figura A7. Determinação das forças de sub-pressão $U_{1}$ e $U_{2}$ – Caso 1

Designando como $Z_{1}$ a profundidade do ponto de interseção $P(I,J)$, medida a partir da face do talude, e $L_{1}$ e $L_{2}$ os comprimentos dos segmentos de reta que definem a cunha de ruptura, então:

${U}_{1}={\frac {{r}_{u}.{Z}_{1}.{L}_{1}}{2}}$	(A4)
${U}_{2}={\frac {{r}_{u}.{Z}_{1}.{L}_{2}}{2}}$	(A5)

onde

${\textstyle r_{u}}$ – parâmetro de pressão neutra de Bishop ;

$Z_{1}$ – altura de solo acima do ponto $P(I,J)$;

$L_{1}$ – distância do ponto $P(1,1)$ ao ponto $P(I,J)$;

$L_{2}$ – distância do ponto $P(I,J)$ ao ponto $P(1,Np1)$.

Segundo caso: $XP(I,J)\leq XP(1,Np1)$ e ponto final $XP(IT,Np1)>XP(1,Np1)$

Este é o caso representado na Figura A8, onde o ponto da crista do talude tem projeção situada à direita do ponto $P(I,J)$ e a cunha de ruptura termina adiante da crista do talude.

Neste caso o diagrama de pressões neutras que compõem $U_{1}$ tem trecho único e o diagrama de pressões neutras que compõem $U_{2}$ tem dois trechos.

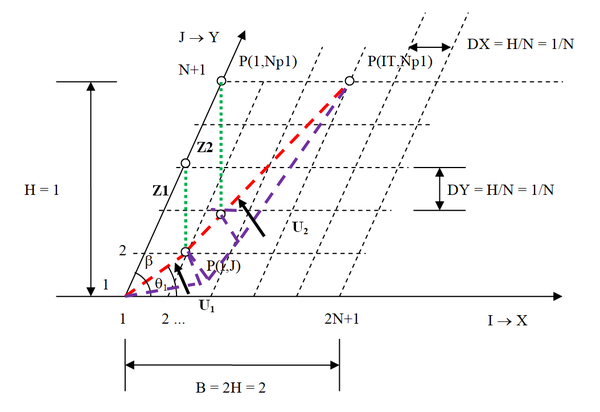
Figura A8. Determinação das forças de sub-pressão $U_{1}$ e $U_{2}$ – Caso 2

Determinados os comprimentos $L_{1}$ e $L_{2}$, o comprimento $L_{2}$ deve ainda ser subdividido em dois trechos, ${L}_{2A}$ e ${L}_{2B}$

${U}_{1}={\frac {{r}_{u}.{Z}_{1}.{L}_{1}}{2}}$	(A6)
${U}_{2}={\frac {{r}_{u}.\left({Z}_{1}+{Z}_{2}\right).{L}_{2A}}{2}}\,+\,{\frac {{r}_{u}.{Z}_{2}.{L}_{2B}}{2}}$	(A7)

onde

${\textstyle r_{u}}$ – parâmetro de pressão neutra de Bishop;

$Z_{1}$ – altura de solo acima do ponto $P(I,J)$;

$Z_{2}$ – altura de solo acima da base da cunha I até a crista do talude;

$L_{1}$ – distância do ponto $P(1,1)$ ao ponto $P(I,J)$;

$L_{2A}$ – distância do ponto $P(I,J)$ à projeção do ponto $P(1,Np1)$ sobre a base da cunha I;

$L_{2B}$ – distância do ponto correspondente à projeção do ponto $P(1,Np1)$ sobre a base da cunha I ao ponto $P(IT,Np1)$.

Terceiro caso: $XP(I,J)>XP(1,Np1)$

Este é o caso representado na Figura A9, onde o ponto da crista do talude tem projeção situada à esquerda do ponto $P(I,J)$ e a cunha de ruptura termina, portanto, adiante da crista do talude.

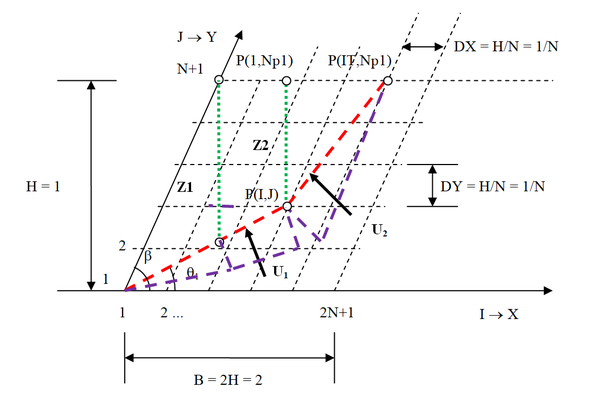
Figura A9. Determinação das forças de sub-pressão $U_{1}$ e $U_{2}$ – Caso 3

Determinados os comprimentos $L_{1}$ e $L_{2}$, o comprimento $L_{1}$ deve ainda ser subdividido em dois trechos, ${L}_{1A}$ e ${L}_{1B}$. E as expressões para $U_{1}$ e $U_{2}$, resultam

${U}_{1}={\frac {{r}_{u}.{Z}_{1}.{L}_{1A}}{2}}+\,{\frac {{r}_{u}.\left({Z}_{1}+{Z}_{2}\right).{L}_{1B}}{2}}$	(A8)
${U}_{2}={\frac {{r}_{u}.{Z}_{2}.{L}_{2}}{2}}$	(A9)

onde

$r_{u}$ – parâmetro de pressão neutra de Bishop;

$Z_{1}$ – altura de solo acima do ponto correspondente à projeção do ponto $P(1,Np1)$ até o ponto $P(1,Np1)$;

$Z_{2}$ – altura de solo acima do ponto $P(I,J)$ até a cota da crista do talude;

$L_{1A}$ – distância do ponto $P(1,1)$ ao ponto correspondente à projeção do ponto $P(1,Np1)$ sobre a base da cunha II;

$L_{1B}$ – distância do ponto correspondente à projeção do ponto $P(1,Np1)$ sobre a base da cunha II ao ponto $P(I,J)$;

$L_{2}$ – distância do ponto $P(I,J)$ ao ponto $P(IT,Np1)$.

A.4. Gráficos de Jewell

(a) (b)

Figura A10. Gráficos de relação $(L/H)$ de Jewell [1,4] para (a) ${\textstyle r_{u}=0}$ e (b) ${\textstyle r_{u}=0.25}$