In Computer Methods in Applied Mechanics and Engineering, Vol. 365, pp. 112984, 2020
DOI: 10.1016/j.cma.2020.112984
Abstract
In this paper we present a stabilized FIC-FEM formulation for the multidimensional transient advection-diffusion-absorption equation. The starting point is the non-local form of the governing equations for the multidimensional transient advection-diffusion-absorption problems obtained via the Finite Increment Calculus (FIC) procedure. The FIC governing equations have a residual form that introduces a characteristic length vector that depends on streamline, absorption and shock capturing stabilization parameters, as well as on a characteristic element size that ensures a stabilized numerical solution using a standard Galerkin FEM. The value of the stabilization parameters is obtained as an extension of the steady-state form. The accuracy of the FIC-FEM formulation is verified in the solution of several transient advection-diffusion-absorption problems using regular meshes of 3-noded triangles and 4-noded quadrilaterals.
Keywords: Advection-diffusion-absorption, transient solution, multidimensional, Finite element method, Finite increment calculus, FIC
1. Introduction
The numerical solution of the advection-diffusion-absorption equation by the Galerkin FEM can exhibit oscillations due to a number of reasons. For the stationary convection-dominated case global oscillations in the analysis can be found, as well as local Gibbs oscillations along the characteristic layers for 2D and 3D problems. Gibbs oscillations near the Dirichlet boundaries and in regions where the source term has an irregular distribution can also appear for stationary absorption-dominated problems. For transient problems dispersive oscillations can appear when the initial solution and/or the distributed source term are non regular [12,68].
A number of numerical procedures has been derived in recent decades aiming to overcome the above limitations of Galerkin FEM for solving advection-diffusion-absorption problems. The goal in all cases has been to obtain “stabilized” numerical solution that are free of spurious oscillations and have a physical meaning. Among the many procedures we can mention the family of streamline-upward Petrov-Galerkin (SUPG) methods. The original SUPG methods for advection-diffusion problems [5,25,26,33,35] where enhanced with the addition of non linear shock-capturing terms aiming to control the Gibbs oscillations across internal/boundary layers for advection-diffusion problems [7,10,13,14,20,32,34,36,51]. Other families of stabilized methods for this type of problems were based on Galerkin Least Squares (GLS) [27], Variational Multiscale (VMS) [28] and Characteristic split procedure [66,68]. Many of these methods are reviewed in [31].
Control over the dispersive oscillations for transient advection-diffusion problems via SUPG methods and space-time FEM were reported in [30] and [65], respectively.
Extensions of the SUPG method for advection-diffusion-reaction problems were reported in [6,29,64]. Other stabilization techniques for these problems were based in the GLS method [17,21], the addition of internal bubbles [1,2,3,4,18,19] and on variations of VMS procedure [9,22,23,24,63]. A review of some of these methods is presented in [8].
Oñate et al. [52,55] derived a non linear stabilization procedure for the steady state advection-diffusion-absorption problem using a single stabilization parameter via a Finite Increment Calculus (FIC) approach. Oñate and Felippa [15] used the variational FIC method for obtaining exact nodal solutions for 1D diffusion-reaction problems (including Helmholtz problems) using also a single linear stabilization parameter.
The homogeneous steady advection-diffusion-reaction equation has typically two fundamental solutions. This has lead the way to the derivation of linear stabilized methods that provide nodally exact solutions in 1D using two stabilization parameters via internal bubbles [4], SUPG [21] and VMS [24] procedures.
A particular class of two-parameter stabilized models for 1D and multidimensional steady and transient advection-diffusion production problems using the FIC approach and the FEM vas presented by Nadukandi, Oñate and García-Espinosa [37,38].
Starting from a different perspective, but still within the FIC framework, Oñate, Miquel and Nadukandi [61] presented a FIC-FEM formulation for the 1D steady-state and transient advection-diffusion-absorption equations using two linear stabilization parameters. The FIC-FEM formulation yielded exact nodal solution for 1D steady-state problems using regular meshes of 2-noded linear elements. Very accurate results were also obtained in [61] for 1D stationary problems solved with irregular meshes, as well as for 1D transient problems. The FIC-FEM formulation presented in [61] was extended by the same authors in [62] to multidimensional steady-state advection-diffusion-absorption problems. Good results were obtained for the problems analyzed using linear 3-noded triangles and bilinear 4-noded quadrilaterals.
In this work we extend to the multidimensional transient case the 1D FIC-FEM formulation presented in [62]. The lay-out of the paper is the following. In the next section we formulate the FIC form of the equations governing multidimensional transient convection-diffusion-absorption problems. The finite element discretization is then presented. The stabilization parameters are obtained as an extension of the expression for the stationary case [61]. The accuracy of the multidimensional transient FIC-FEM formulation is verified in the solution of a number of 2D transient advection-diffusion-absorption problems using uniform meshes of 3-noded triangles and 4-noded quadrilateral elements. Accurate solutions are obtained in all cases.
2. The multidimensional transient advection-diffusion-reaction problem
2.1 Governing equations
Transport balance
The transport balance equation in a domain of area/volume can be expressed as
|
|
(1.a) |
with
|
|
(1.b) |
For 3D problems,
|
|
(2) |
In Eqs.(1.a)–(1.b) is the transported variable (i.e., the temperature in a heat transfer problem or the concentration in a mass transfer problem), is the th component of the velocity vector ; and are the density, the specific flux parameter and the conductivity of the material along the th global direction, respectively and is the reaction parameter. In the following, and unless otherwise specified, we will assume that the velocity field is solenoidal and that the problem parameters () are constant over the analysis domain .
Boundary conditions
|
|
(3) |
|
|
(4) |
with
|
|
(5) |
where
|
|
(6) |
In Eqs.(3)–6 and are the prescribed values of the transported variable and the outgoing diffusive flux at the Dirichlet and Neumann boundaries and , respectively, with , being the total boundary of the domain and n is the unit vector normal to the boundary.
The definition of the problem is completed with the initial conditions
|
|
(7) |
where is the value of the transported variable at time .
In this work we will consider cases for which only. This includes the following particular problems:
- Advection-diffusion-absorption (, , ).
- Advection-diffusion (, , ).
- Diffusion-absorption (, , ).
- Advection-absorption (, , ).
In the above is the average difussion given by , where is the number of space dimensions (i.e. for 2D problems).
2.2 Finite increment calculus (FIC) expressions
The governing equations 1.a and 1.b and the boundary conditions 3-6 are expressed using the FIC theory as [55].
Transport balance
|
|
(8) |
with in 3D.
Boundary conditions
|
|
(9.a) |
|
|
(9.b) |
Eqs.(8) and (9.b) are obtained by expressing the balance of fluxes in an arbitrary prismatic space domain of size within the global problem domain and at the Neumann boundary, respectively. The distances are termed characteristic lengths of the FIC method. The variations of the transported variable within the balance domain are approximated by Taylor series expansions retaining one order higher terms than in the infinitesimal theory [40]. This higher order expansions lead to the underlined terms in Eqs.(8) and (2.2). These terms lead naturally to stabilized numerical schemes.
Note that as the characteristic length vector tends to zero the FIC governing equations gradually recover the standard infinitesimal form, giving in the limit (for ) in and .
The stability and accuracy of the numerical solution depends on the components of the characteristic length vector . At the discretization level the length of is usually expressed as a proportion of a typical grid dimension [40].
The FIC equations are the starting point for deriving different stabilized numerical methods. Combining the FIC equations with the Galerkin FEM leads to the so-called FIC-FEM procedure that has been successfully applied to the solution of many problems in convective transport, fluid and solid mechanics such as advection-diffusion [40,42,43,51], diffusion-absorption and Helmholtz [15], advection-diffusion-absorption [52,55], advection-diffusion-reaction [61], incompressible fluid flow [53,54,56,58,60], fluid-structure-interaction [45,49,57], particle-laden flows and standard and incompressible solid mechanics [47,50,59]. The FIC approach has also been applied to the solution of a variety of problems in mechanics using the meshless finite point method [39,41,44,46].
3. Definition of the characteristic length vector
The characteristic length vector is designed so that the expression for all the stabilization matrices and vectors reduce to those given for the 1D case as reported in [61].
With this objective in mind the following expression for the characteristic length vector has been chosen in this work
|
|
(10) |
The characteristic length vectors in the r.h.s. of Eq.10 are defined as follows.
Streamline characteristic length vector, hv
In Eq.10 is a length vector along the velocity direction defined as
|
|
(11) |
where is a streamline stabilization parameter, is a characteristic element dimension and is a unit velocity vector.
Absorption characteristic length vector, hr
In Eq.10 is a characteristic length vector induced by absorption effects and defined as
|
|
(12.a) |
where is an absorption stabilization parameter, and is the space residual defined as
|
|
(12.b) |
Matrix in Eq.12.a is defined for different element types as follows.
3-noded triangles and 4-noded tetrahedra:
|
|
(13) |
where is the vector joining the baricenter of the element and the th node, and is the number of nodes of the element.
The diffusion introduced by matrix takes care of the instabilities induced by the irregularity of the triangular mesh near boundaries that develop parabolic layes [62].
Any other element: Dₛ=[0]
Shock capturing characteristic length vector hsc
In Eq.10 is a shock-capturing characteristic length vector in the direction of the gradient of the solution. This vector accounts for the Gibbs oscillations across characteristic internal/boundary layers for advection-diffusion problems. It is defined as
|
|
(14.a) |
where is the unit gradient vector, and
|
|
(14.b) |
In Eq.14.b is a non linear parameter that depends on the angle between the velocity vector and the gradient vector. It is defined as
|
|
(14.c) |
where is a critical angle. In this work we have taken .
The parameter controls the amount of shock-capturing nonlinear diffusion active at any point of the domain [62]. When the gradient vector is parallel to the velocity vector then , vanishes and the linear stabilization terms suffice to diminish spurious numerical oscillations about the layers. The term in Eq.14.b gradually increases the magnitude of the shock-capturing term from zero, when the gradient vector is aligned to velocity vector, to a maximum value when the layer gradient is orthogonal to the velocity.
4. FIC-FEM formulation for the multidimensional transient advection-diffusion-absorption problem
4.1 Weighted residual form of the FIC equations
The weighted residual form of the FIC governing equations 8 and 2.2 is written as
|
|
(15) |
where are arbitrary weighting functions.
Integrating by parts the FIC term in the first integral of 15 gives
|
|
(16) |
Note that the FIC term has vanished from the boundary integral, as it usual in the FIC-FEM approach [40,48].
Let us substitute the expression for the characteristic vector of Eq.10 into Eq.16. This gives (using Eqs.11, 12.a and 14.a)
|
|
(17) |
The final step is the integration by parts of the diffusive term in the expression of in the first term of the first integral of Eq.17. This gives, after replacing the definition of in Eq.17 and grouping some terms, the following expression for the weak variational form of the FIC governing equations
|
|
(18) |
The space weighting function is given by
|
|
(19) |
The expression of the total diffusivity matrix in Eq.18 is
|
|
(20) |
where and are defined in Eqs.2 and 13, respectively, I is the unit matrix and
|
4.2 FIC-FEM equations
We interpolate the transported variable in the standard FEM fashion over a mesh of elements with nodes [67,68] as
|
|
(22) |
where are the space shape functions and the nodal variables.
Introducing Eq.22 into the FIC variational form 18 and using a Galerkin approach () gives the final system of discretized equations as
|
|
(23) |
where is the vector of nodal unknowns, with being total number of nodes in the mesh.
The rest of matrices and vector in Eq.23 are obtained in the standard FEM fashion by assembling the element contribution given by
|
We note that the second integral in Eq.25 vanishes for linear finite element approximations, such as those used in this work.
Good results have been obtained for the solution of the problems presented in this paper using a lumped form of matrix . An exception is the problem of the evolution of a concentration field presented in Section 7.6 for which using the consistent form of matrix is essential to reduce excessive diffusion.
5. Transient solution scheme
5.1 Implicit time integration scheme
We discretize in time the system of equations (23) using a Generalized Trapezoidal rule [11,67]. The solution for the nodal values at a time instant is found using an incremental iterative strategy as
|
|
(29) |
where is the increment of the nodal variables, is a non dimensional time parameter ( is required for the integration scheme to be unconditionally stable [11,67,68]), denotes values at time , denotes values at the th iteration and
|
|
(30) |
|
|
(31) |
In Eq.31 we define .
From the value of obtained from solving Eq.29 we compute the value of at the iteration as
|
|
(32) |
The iterative solution at , , is obtained as
|
|
(33) |
The non-linearity in the expression of matrix in Eq.30 is due to the dependence of the shock-capturing term in matrix via matrix (see Eq.21.b).
The iterations proceed until convergence is achieved for both the unknown and the residual measured in a norm. In the transient problems solved in this work, convergence within each time step was typically achieved in 2–3 iterations.
5.2 Explicit time integration scheme
If we rewrite the residual in Eq.31 choosing and defining now as leads to the following explicit solution scheme
|
|
(34) |
where denotes the lumped diagonal form of matrix .
In the expression of of Eq.34 the shock-capturing terms are taken as constant within a time step.
6. Computation of the stabilization parameters
6.1 General expression of the stabilization parameters
The optimal value of the stabilization parameters and giving nodally exact solutions is quite difficult in the transient case due to the multiple forms that the solution can take as it evolves in time. We present a procedure for computing a quasi-optimal value of and that has proved to yield accurate results for transient advection-diffusion-absorption problems evolving towards a steady state solution, as well as for solutions involving the pure advection of a discontinuous function. The method is an extension of the approach proposed and successfully tested for 1D transient problems in [61].
The transient equation (1.b) can be written as follows
|
|
(35) |
where
|
|
(36) |
Eq.(35) defines a pseudo-stationary problem in which a non linear reaction term has been introduced.
The non linear reaction term can be approximated as
|
|
(37) |
with
|
|
(38) |
The value of in Eq.37 has been limited in this work to a ten percent of the value of the actual absorption parameter .
From Eq.(36) we can define an equivalent Damköhler number as
|
|
(39) |
where is the Damköhler number defined in Eq.44 and is the element Courant number where is a characteristic element dimension. For 1D problems is taken as the element length. For 2D problems we have chosen where is the area of the element.
The following definition for has been chosen in the examples solved in this work
|
|
(40) |
where denotes the maximum value of within an element and is a positive number that controls the slope of the function that ranges from zero to one.
Function has been designed so that (and ) for a steady-state problem (or in zones where ), and (and ) for cases when suddenly changes from a zero value to a finite value at a node.
Good results were obtained in the transient problems solved using Eq.(40) with . The optimal choice of in terms of the nature of the transient solution is a matter that deserves further research.
We highlight that for the explicit time integration scheme we have used in the definition of and .
The stabilization parameters and in Eqs.11 and 12.a for the transient convection-diffusion-radiation problem are defined as follows
|
|
(41) |
with
|
|
(42) |
and
|
|
(43) |
In the above expressions
|
|
(44) |
The expressions of and in Eqs.41 and 43 are an extension of the values for the steady-state problem presented in [62].
In Eq.43 is a constant such that . The “exact” expression of for 1D problems requires choosing [62]. In our computations for 2D problems we have obtained good results using .
The characteristic length is defined as the size of the element in the direction of the velocity . Representing the element's edge joining nodes and with the vector , is computed as
|
|
(45) |
The characteristic length is generally defined as
|
|
(46) |
where is the element area. For elements belonging to the boundary in meshes of 3-noded triangles we have chosen
|
|
(47) |
The expression of in Eq.47 introduces a higher value of the shock-capturing term at the boundaries where sharp gradients exist in directions different from the velocity directions.
7. Examples
In the examples shown next the density and the specific flux c are chosen such that . We have also assumed an isotropic diffusion of value .
7.1 Transient advection-diffusion-absorption problem
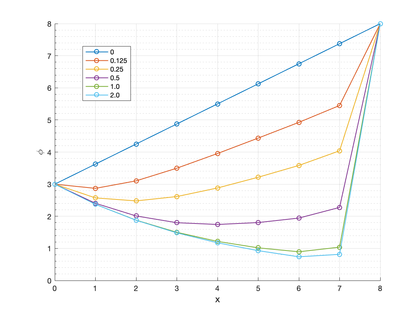
The analysis domain is discretised into a regular mesh of 3-noded triangles of unit rectangular side () (fig:dac_scheme). The advection, diffusion and reaction coefficients are chosen as , and . The transported variable is the temperature. The schematics of the problem can be seen in fig:dac_scheme. The problem data yields the dimensionless numbers and .
The Dirichlet boundary conditions and are employed. The initial solution is chosen to have a linear profile. The transient solution was obtained iteratively using the implicit scheme of Eqs.29–33 with and a time step of (fig:dac_results). This corresponds to an element Courant number . An exponential layer gradually develops at the right boundary which triggers a global instability in the Galerkin FEM. As there is not significant dispersive phenomena this global instability is successfully controlled by the SUPG method (well-known result) and the FIC-FEM method developed in this work. Figure 3 show a perspective view of the quasi-steady-state solution for the temperature for . The steady state solution matches the 1D result reported in [61].

|
| Figure 1: Transient advection-absorption problem. Square domain with linear velocity and zero source. |
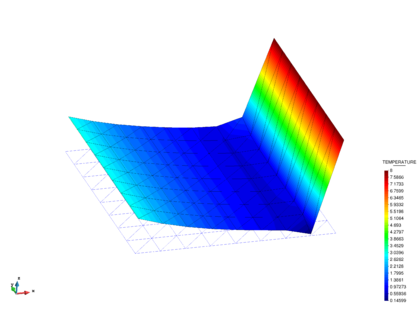
|
| Figure 3: Transient advection-diffusion-absorption problem. Solution obtained at t = 2 s. |
7.2 Skewed flow is a square domain with non-uniform boundary conditions
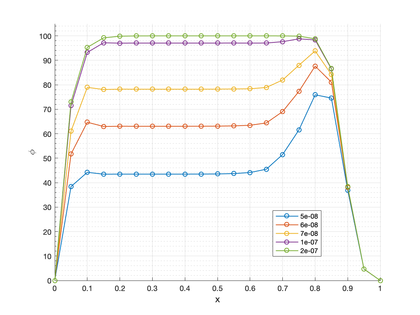
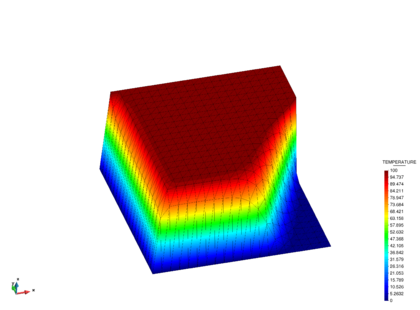
The domain is . The problem data is: , , , and . The transported variable is again the temperature. The boundary conditions are: on (, at () and on the rest of the boundary (fig:SC_scheme). The transient solution was obtained using the implicit scheme here presented with and a time step of e-09 s. Convergence within each time step was found in 2-3 iterations. The solution develops an exponential boundary layer at the outflow boundary and an internal characteristic layer (parabolic) which is skewed to the mesh and the boundary. Both layers are subgrid phenomena for the considered mesh resolution. Both the exponential and characteristic layers are reproduced in the FIC-FEM solution without spurious oscillations near the layers. The FIC-FEM result of the evolution of the solution in time towards steady state are shown in fig:SC_results. Figure 6 shows a perspective view of the quasi steady-state solution for e-07s. The steady-state solution agrees with that reported in [51,55,62].
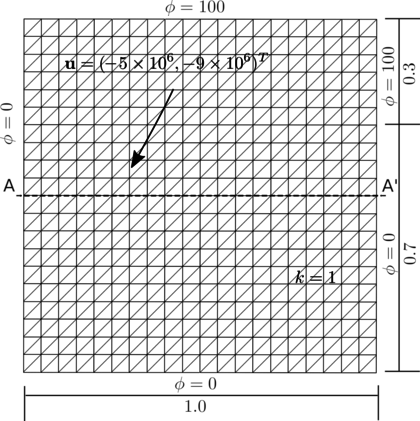
|
| Figure 4: Square domain with non-uniform Dirichlet conditions, downwards diagonal velocity and zero source. Mesh of three-noded triangles |
|
| Figure 5: Square domain with non-uniform Dirichlet conditions. FIC-FEM solution along line A-A'. The transient solutions are plotted at times 5e-08 s, 6e-08 s, 7e-08 s, 1e-07 s and 2e-07 s. |
|
| Figure 6: Square domain with non-uniform Dirichlet conditions. Solution at time 2e-07 s. |
7.3 Uniform advection problem with constant source
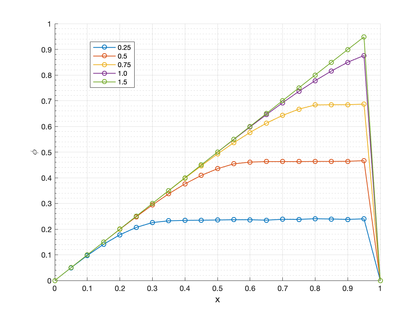
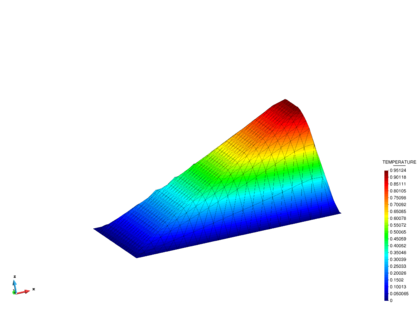
We study the uniform advection of a temperature field with a constant source term. The problem data is: , , , and . The homogeneous boundary condition is imposed everywhere as shown in fig:Q_source_scheme. The solution develops an exponential layer at the outflow boundary and parabolic layers at the boundaries and . The FIC-FEM results of the transient solution towards steady-state are shown in fig:Q_source_results. A perspective of the quasi steady-state solution at time is shown in Figure 9. Both layers are subgrid phenomena for the considered mesh resolution. The transient solution was obtained iteratively using the implicit scheme presented in the paper with and a time step of . Convergence within each time step was found in 2-3 iterations. The steady-state solution agrees with that reported in [62].

|
| Figure 7: Square domain with linear velocity and constant source. Structured mesh of three node triangles |
|
| Figure 8: Square domain with linear velocity and constant source. FIC solution obtained along line A-A'. The transient solutions are plotted at times 0.25 s, 0.5 s, 0.75 s, 1 s and 1.5 s. |
|
| Figure 9: Square domain with linear velocity and constant source. Solution at time 1.5 s. |
7.4 Advective-diffusive transport of the temperature in a rectangular domain with Neumann and non-uniform Dirichlet conditions, rotational velocity field and zero source
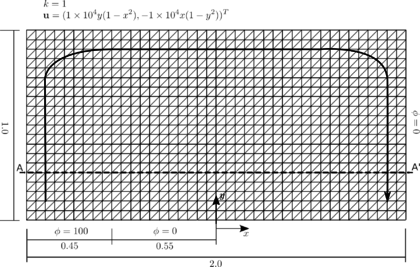
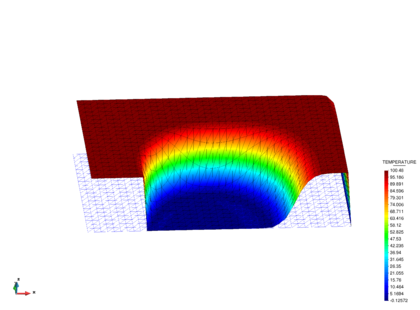
The rectangular domain of sides 1 2 units and the boundary conditions are shown in fig:rotational_scheme. The rotational velocity field is defined as . A unit isotropic diffusion is assumed. The value of the temperature () is prescribed at part of the domain sides as shown in fig:rotational_scheme. In the rest of the sides, the Neumann condition () is imposed. The problem was solved with the uniform mesh of 3-noded triangles shown in fig:rotational_scheme. The correct solution is a uniform plateau of with a boundary layer at the right hand side where the solution drops towards the prescribed value of and a circular sharp gradient region around the lower circular zone where the solution takes a zero value. The FIC-FEM results of the transient solution towards steady-state are shown in fig:rotational_results. A perspective of the quasi steady-state solution at time e-03s is shown in Figure 12. The transient solution was obtained using the implicit scheme presented in this work with and a time step of e-05s. Convergence within each time step was found in 2-3 iterations. The steady-state solution agrees with that reported in [51].

|
| Figure 11: FIC solution of the problem in Figure 10. The transient solutions are plotted along line A-A' at times 5e-05 s, 1e-04 s, 3e-04 s, 4e-04, 5e-04 and 1e-03 s. |
|
| Figure 12: Solution at 1e-03 s. |
7.5 Pure convection of a temperature plateau
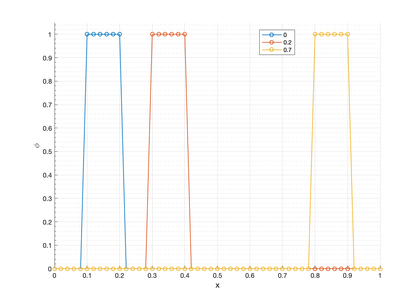
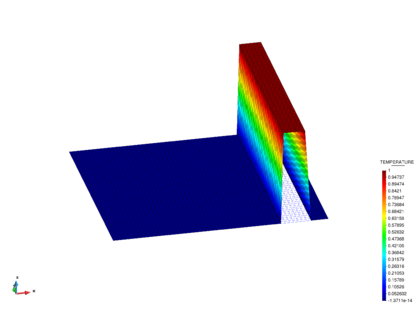
We study the pure convection of an initial temperature plateau. The domain dimensions are . The problem data is: , , , and . The homogeneous boundary condition is imposed at the left wall as shown in fig:explicit_wave_scheme. The temperature plateau is generated by imposing a value of the temperature from to . The problem has been solved using a regular mesh of four-noded quadrilateral elements. Figures 14 and 15 show that the initial solution maintains its shape through the domain. The transient solution was obtained using an explicit scheme and a time step of , giving an element Courant number of .

|
| Figure 13: Pure convection of a temperature plateau in a square domain with horizontal velocity. Structured mesh of 50 x 50 4-noded quadrilaterals. |
|
| Figure 14: Pure convection of a temperature plateau. FIC-FEM solution plotted along line A-A' at times 0 s, 0.2 s and 0.7 s. |
|
| Figure 15: Pure convective case. FIC-FEM solution at time 0.7 s. |
7.6 Advection-diffusion of a concentration field
In this problem we study the advection and diffusion of a concentration that is instantaneously released as a Dirac source in a point of a stream. This problem is generally known as the plume transport problem [16].
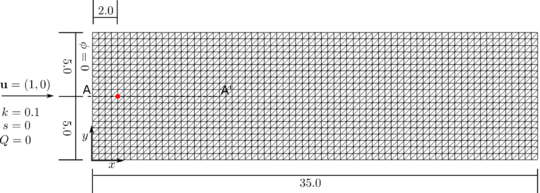
The domain dimensions are . The problem data is: , , , and . The homogeneous boundary condition is imposed on the left wall as shown in fig:plume_scheme. The value is imposed as a initial value of the concentration at the node .
The analytical solution for this 2D problem is [16]
|
|
(48.a) |
with
|
|
(48.b) |
In Eqs.7.6 is the initial value of the concentration that is dropped at the point with coordinates , is the vertical dimension of the analysis domain (in this problem we have taken ), and are the horizontal and vertical components of the velocity vector, respectively and where is the average diffusion defined in Section 2.1.
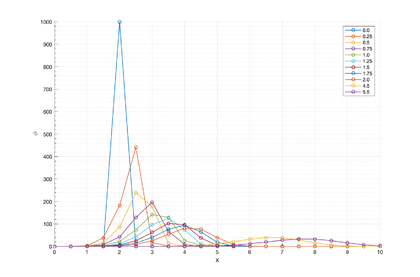
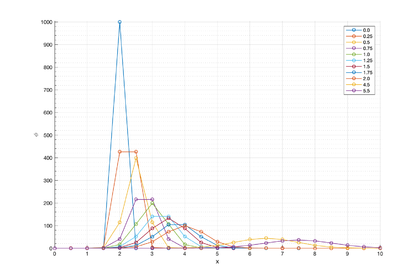
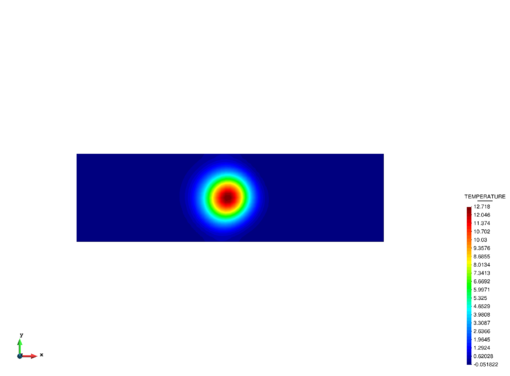
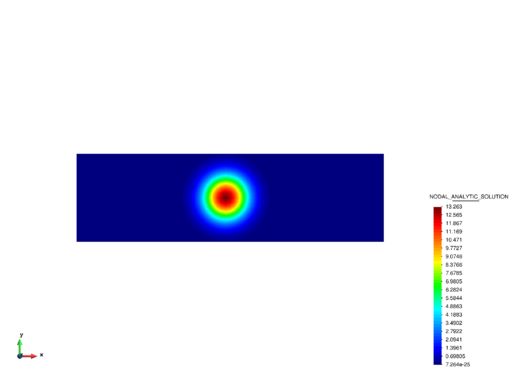
The transient solution was obtained using an implicit scheme with and a time step of , giving a Courant number of . We highlight that the shock-capturing terms were not taken into account for solving this problem. The use of the consistent form of the mass matrix was essential for obtaining good results for this problem. fig:plume_results_1 shows how the solution is advected and diffuses as time increases. The numerical results for the distribution of the contraction along line A-A' are in agreement with the analytical solution shown in fig:plume_results_2. The graphs are taken along the A-A' line, which goes from (0,5) to (10,5). A comparison of the contours of the numerical and analytical distributions of the concentration at can be seen in Figures 19 and 20, respectively.
|
| Figure 16: Advection-diffusion of a concentration field. Rectangular domain with horizontal velocity. Structured mesh of 2 x 70 x 20 three-noded triangles |
|
| Figure 17: Advection-diffusion of a concentration field. FIC-FEM solution along line A-A' obtained with the mesh of Figure 16. Structured mesh of 2 x 70 x 20 three-noded triangles. Solution at times 0 s, 0.25 s, 0.5 s, 0.75 s, 1.0 s, 1.25 s, 1.5 s, 1.75 s, 2.0 s, 4.5 s and 5.5 s. |
|
| Figure 18: Advection-diffusion of a concentration field. Analytical solution along line A-A' plotted on the structured mesh of Figure 16. Solution at times 0 s, 0.25 s, 0.5 s, 0.75 s, 1.0 s, 1.25 s, 1.5 s, 1.75 s, 2.0 s, 4.5 s and 5.5 s. |
|
| Figure 19: Advection-diffusion of a concentration field. Contours of the FIC-FEM results at t = 15s. |
|
| Figure 20: Advection-diffusion of a concentration field. Contours of the analytical results at t = 15s. |
8. Concluding remarks
In this work we have extended the steady-state multidimensional FIC-FEM formulation reported in [62] to the transient case. The stabilized variational expression has the standard residual form typical of the FIC-FEM procedure. The stabilized terms introduced by the FIC approach depend on a characteristic element length and two stabilization parameters which expression is obtained as an extension of the steady-state forms presented in [62]. A shock capturing term is introduced to account for the Gibbs oscillations across internal/boundary layers.
The good behavior of the FIC-FEM formulation has been verified for transient advection-diffusion-absorption problems with numerical solutions evolving to a steady-state, as well as to two fully transient problems.
The numerical results were obtained in most cases using an implicit scheme. An exception is the pure convection problem (Section 7.5) that was solved with an explicit scheme and a Courant number of . The shock capturing terms were not taken into account in the solution of the fully transient problems (Sections 7.5 and 7.6). We also remark the importance of using a consistent stabilized mass matrix in the concentration field example.
Acknowledgements
This research was partially funded by the PRECISE project (BIA2017-83805-R) of the Natural Research Plan of the Spanish Government. Support for this work was also provided from the Office for Naval Research Global (ONRG) of the US Navy through the NICE-SHIP project. We also acknowledge the financial support of the CERCA programme of the Generalitat de Catalunya.
References
[1] Baiocchi C, Brezzi F, Franca LP. Virtual bubbles and the GaLS. Computer Methods in Applied Mechanics and Engineering 1993; 105:125–141.
[2] Brezzi F, Bristeau MO, Franca LP, Mallet M, Rogé G. A relationship between stabilized finite element methods and the Galerkin method with bubble functions. Computer Methods in Applied Mechanics and Engineering 1992; 96:117–129.
[3] Brezzi F, Russo A. Choosing bubbles for advection-diffusion problems. Mathematical Models and Methods in Applied Sciences 1994; 4:571–587.
[4] Brezzi F, Hauke G, Marini LD, Sangalli G. Link-cutting bubbles for the stabilization of convection–diffusion–reaction problems. Mathematical Models and Methods in Applied Sciences 2003; 13(3):445–461.
[5] Brooks AN, Hughes TJR. Streamline Upwind/Petrov–Galerkin formulations for the convective dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Computer Methods in Applied Mechanics and Engineering 1982; 32 (1–3):199–259.
[6] Burman E, Ern A. Nonlinear diffusion and discrete maximum principle for stabilized Galerkin approximations of the convection–diffusion–reaction equation, Computer Methods in Applied Mechanics and Engineering 2002, 191:3833-3855.
[7] Codina R. A discontinuity-capturing crosswind-dissipation for the finite element solution of the convection-diffusion equation, Computer Methods in Applied Mechanics and Engineering 1993, 110:325-342.
[8] Codina R. Comparison of some finite element methods for solving the diffusion-convection-reaction equation, Computer Methods in Applied Mechanics and Engineering 1998, 156:185-210.
[9] Codina R. On stabilized finite element methods for linear systems of convection–diffusion–reaction equations, Computer Methods in Applied Mechanics and Engineering 2000a, 190:2681-2706.
[10] de Sampaio PAB, Coutinho ALGA. A natural derivation of discontinuity capturing operator for convection-diffusion problems, Computer Methods in Applied Mechanics and Engineering 2001, 190:6291-6308.
[11] Donea J. A Taylor-Galerkin method for convective transport problems, International Journal for Numerical Methods in Engineering 1984, 20:101-119.
[12] J. Donea, A. Huerta, Finite element method for flow problems. J. Wiley & Sons, 2003.
[13] Douglas J, Russell TF. Numerical methods for convection-dominated diffusion problems based on combining the method of characteristics with the finite element or finite difference procedures, SIAM Journal of Numerical Analysis 1982, 19:871-885.
[14] Dutra do Carmo EG, Alvarez GB. A new upwind function in stabilized finite element formulations, using linear and quadratic elements for the scalar convection-diffusion problems, Computer Methods in Applied Mechanics and Engineering 2004, 193:2383-2402.
[15] Felippa C, Oñate E. Nodally exact Ritz discretizations of the 1D diffusion-absorption and Helmholtz equations by variational FIC and modified equation methods, Computational Mechanics 2007, 39(2):91-111.
[16] Fisher H, List J, Koh C, Imberger J, Brooks N. Mixing in Inland and Coastal Waters, Elsevier, 2013.
[17] Franca LP, Dutra do Carmo EG. The Galerkin gradient least-squares method, Computer Methods in Applied Mechanics and Engineering 1989, 74:41-54.
[18] Franca LP, Farhat C. Bubble functions prompt unusual stabilized finite element methods, Computer Methods in Applied Mechanics and Engineering 1995, 123:299-308.
[19] Franca LP, Valentin F. On an improved unusual stabilized finite element method for the advective-reactive-diffusive equation, Computer Methods in Applied Mechanics and Engineering 2001, 190:1785-1800.
[20] Galeo AC, Dutra do Carmo EG. A consistent approximate upwind Petrov–Galerkin method for the convection-dominated problems. Computer Methods in Applied Mechanics and Engineering 1988, 68(1):83-95.
[21] Harari I, Hughes TJR. Stabilized finite element methods for steady advection-diffusion with production, Computer Methods in Applied Mechanics and Engineering 1994, 115:165-191.
[22] Hauke G, García-Olivares A. Variational subgrid scale formulations for the advection-diffusion–reaction equation, Computer Methods in Applied Mechanics and Engineering 2001, 190:6847-6865.
[23] Hauke G. A simple subgrid scale stabilized method for the advection-diffusion–reaction equation, Computer Methods in Applied Mechanics and Engineering 2002, 191:2925-2947.
[24] Hauke G, Sangalli G, Doweidar MH. Combining adjoint stabilized methods for the advection-diffusion–reaction problem, Mathematical Models and Methods in Applied Sciences 2007, 17(2):305-326.
[25] Hughes TJR, Brooks AN. A theoretical framework for Petrov–Galerkin methods, with discontinuous weighting functions: application to the streamline upwind procedure, in Gallagher RH, Norrie DM, Oden JT, Zienkiewicz OC (eds.), Finite Elements in Fluids 1982, IV,Wiley, Chichester.
[26] Hughes TJR, Mallet M. A new finite element formulations for computational fluid dynamics: III. The generalized streamline operator for multidimensional advective-diffusive systems. Comput Methods Appl. Mech. Engrg. 1986a, 58:305–328.
[27] Hughes TJR, Franca LP, Hulbert GM. A new finite element formulation for computational fluid dynamics: VIII. The Galerkin/least-squares method for advective-diffusive equations, Computer Methods in Applied Mechanics and Engineering 1989, 73:173-189.
[28] Hughes TJR, Feijoo GR, Mazzei L, Quincy JB. The variational multiscale method: a paradigm for computational mechanics, Computer Methods in Applied Mechanics and Engineering 1998, 166:3-24.
[29] Idelsohn SR, Nigro N, Storti M, Buscaglia G. A Petrov–Galerkin formulation for advective-reaction-diffusion problems, Computer Methods in Applied Mechanics and Engineering 1996, 136:27-46.
[30] Idelsohn SR, Heinrich JC, Oñate E. Petrov–Galerkin methods for the transient advective-diffusive equation with sharp gradients, International Journal for Numerical Methods in Engineering 1996, 39:1455-1473.
[31] John V, Knobloch P. On spurious oscillations at layers diminishing (SOLD) methods for convection-diffusion equations: Part I - A review, Computer Methods in Applied Mechanics and Engineering 2007, 196:2197–2215.
[32] Johnson C, Szepessy A, Hansbo P. On the convergence of shock-capturing streamline diffusion finite element methods for hyperbolic conservation laws, Mathematics of Computation 1990, 54:107-129.
[33] Kikuchi F, Ushijima T. Theoretical analysis of some finite element schemes for convective diffusion equations, in: R. Gallagher, D. Norrie, J. Oden, O. C. Zienkiewicz (Eds.), Finite Elements in Fluids, Vol. IV, John Wiley and Sons Ltd, Chichester, 1982.
[34] Knobloch P. Improvements of the Mizukami-Hughes method for convection-diffusion equations, Computer Methods in Applied Mechanics and Engineering 2006, 196:579-594.
[35] Löhner R, Morgan K, Zienkiewicz OC. The solution of non-linear hyperbolic equation systems by the finite element method, International Journal for Numerical Methods in Fluids 1984, 4:1043-1063.
[36] Mizukami A, Hughes TJR. A Petrov–Galerkin finite element method for convection-dominated flows: An accurate upwinding technique for satisfying the maximum principle, Computer Methods in Applied Mechanics and Engineering 1985, 50(2):181-193.
[37] Nadukandi P, Oñate E, García Espinosa J. A high-resolution Petrov-Galerkin method for the 1D convection-diffusion-reaction problem, Computer Methods in Applied Mechanics and Engineering 2010, 199(9–12):525-546.
[38] Nadukandi P, Oñate E, García Espinosa J. A high-resolution Petrov-Galerkin method for the convection-diffusion-reaction problem. Part II. A multidimensional extension, Computer Methods in Applied Mechanics and Engineering 2012, 213-216:327-352.
[39] Oñate E, Idelsohn SR, Zienkiewicz OC, TaylorRL, Sacco C. A stabilized finite point method for analysis of fluid mechanics problems. Computer Methods in Applied Mechanics and Engineering 1996, 139:315–346.
[40] Oñate E. Derivation of stabilized equations for numerical solution of advective-diffusive transport and fluid flow problems, Computer Methods in Applied Mechanics and Engineering 1998, 151:233-265.
[41] Oñate E, Idelsohn SR. A mesh-free finite point method for advective-diffusive transport and fluid flow problems. Comput. Mech. 1998, 23:283–292.
[42] Oñate E, Manzan M. A general procedure for deriving stabilized space-time finite element methods for advective-diffusive problems. Int. J. Num. Meth. Fluids 1999, 31:203–221.
[43] Oñate E, Manzan M. Stabilization techniques for finite element analysis of convection-diffusion problems, in Sundén B, Comini G. (eds.), Computational Analysis of Convection Heat Transfer 2000, 71-117, WIT Press, Southampton (UK), 2000.
[44] Oñate E, Sacco C, Idelsohn SR. A finite point method for incompressible flow problems. Computing and Visualization in Science 2000, 2:67–75.
[45] Oñate E, García J. A finite element method for fluid-structure interaction with surface waves using a finite calculus formulation. Computer Methods in Applied Mechanics and Engineering 2001, 191:635–660.
[46] Oñate E, Perazzo F, Miquel J. A finite point method for elasticity problems. Computers and Structures 2001, 79:2151–2163.
[47] Oñate E, Taylor RL, Zienkiewicz OC, Rojek J. A residual correction method based on finite calculus. Engineering Computations 2003, 20(5/6):629–658.
[48] Oñate E. Possibilities of finite calculus in computational mechanics. International Journal for Numerical Methods in Engineering 2004, 60(1), 255–281.
[49] Oñate E, Idelsohn SR, Del Pin F, Aubry R. The particle finite element method. An overview. International Journal of Computational Methods 2004, 1(2):267–307.
[50] Oñate E, Rojek J, Taylor RL Zienkiewicz OC. Finite calculus formulation for incompressible solids using linear triangles and tetrahedra. International Journal for Numerical Methods in Engineering 2004, 59:1473–1500.
[51] Oñate E, Zarate F, Idelsohn SR. Finite element formulation for the convective-diffusive problems with sharp gradients using finite calculus, Computer Methods in Applied Mechanics and Engineering 2006, 195:1793-1825.
[52] Oñate E, Miquel J, Hauke G. Stabilized formulation for the advection-diffusion-absorption equation using finite calculus and linear finite elements, Computer Methods in Applied Mechanics and Engineering 2006, 195(33–36):3926–3946.
[53] Oñate E, Valls A, García J. FIC/FEM formulation with matrix stabilizing terms for incompressible flows at low and high Reynolds numbers. Computational Mechanics 2006, 38(4-5):440–455.
[54] Oñate E, García J, Idelsohn SR, Del Pin F. FIC formulations for finite element analysis of incompressible flows. Eulerian, ALE and Lagrangian approaches. Computer Methods in Applied Mechanics and Engineering 2006, 195(23-24):3001–3037.
[55] Oñate E, Miquel J, Zarate F. Stabilized solution of the multidimensional advection-diffusion-absorption equation using linear finite elements, Computers and Fluids 2007, 36:92–112.
[56] Oñate E, Valls A, García J. Modeling incompressible flows at low and high Reynolds numbers via a finite calculus-finite element approach. Journal of Computational Physics 2007, 224:332–351.
[57] Oñate E, Idelsohn SR, Celigueta MA, Rossi R. Advances in the particle finite element method for the analysis of fluid-multibody interaction and bed erosion in free surface flows. Comput. Methods Appl. Mech. Engrg. 2008, 197(19-20):1777–-1800.
[58] Oñate E, Nadukandi P, Idelsohn S, García J, Felippa C. A family of residual-based stabilized finite element methods for Stokes flows. Int. J. Num. Meth. in Fluids 2011, 65 (1-3):106–134.
[59] Oñate E, Idelsohn SR, Felippa C. Consistent pressure Laplacian stabilization for incompressible continua via higher order finite calculus. International Journal for Numerical Methods in Engineering 2011, 87 (1-5):171–-195.
[60] Oñate E, Nadukandi P, Idelsohn S. P1/P0+ elements for incompressible flows with discontinuous material properties. Comput. Methods Appl. Mech. Engrg. 2014, 271:185–209
[61] Oñate E, Miquel J, Nadukandi P. An accurate FIC-FEM formulation for the 1D advection–diffusion–reaction equation. Comput. Methods Appl. Mech. Engrg. 2016, 298:373–406.
[62] Oñate E, Nadukandi P, Miquel J. Accurate FIC-FEM formulation for the multidimensional steady-state advection–diffusion–absorption equation. Comput. Methods Appl. Mech. Engrg. 2017, 327:352-368.
[63] J. Principe, R. Codina, [ On the stabilization parameter in the subgrid scale approximation of scalar convection–diffusion–reaction equations on distorted meshes], Computer Methods in Applied Mechanics and Engineering 2010, 199(21-22):1386–1402.
[64] Tezduyar TE, Park YJ. Discontinuity-capturing finite element formulations for nonlinear convection–diffusion–reaction equations. Computer Methods in Applied Mechanics and Engineering 1986; 59:307–325.
[65] Yu CC, Heinrich JC. Petrov–Galerkin methods for the time-dependent convective transport equations, International Journal for Numerical Methods in Engineering 1986, 23:883-901.
[66] Zienkiewicz OC, Codina R. A general algorithm for compressible and incompressible flows. Part I: the split, characteristic based scheme, International Journal for Numerical Methods in Fluids 1995, 20:869-885.
[67] Zienkiewicz OC, Taylor RL, Zhu JZ. The finite element method. The basis. 6th Ed., Elsevier, 2005.
[68] Zienkiewicz OC, Taylor RL, Nithiarasu P. The finite element method for fluid dynamics. 6th Ed., Elsevier, 2005.
Document information
Published on 01/01/2020
DOI: 10.1016/j.cma.2020.112984
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?