Using scaled physical model for assessment of mechanical damping of power plant boiler structure

Summary

To determine dynamic response of mechanical system is always a complex issue. One of the core inputs for such a task is a coefficient of logarithmic damping decrement. There is no way how to determine this coefficient analytically; it needs to be measured on the final product. There has been a large amount of dynamic tests carried out on common structures and the results have been incorporated in design codes. Nevertheless, power plant boiler structure differs significantly from common structures. To provide a large number of dynamic tests on real facility is very difficult for many reasons. Using a scaled model is a way how to achieve relevant data based on repeatable experiment.

Keywords

Physical model ; Scaling law ; Boiler ; Modal analysis ; Experiment

Foreword

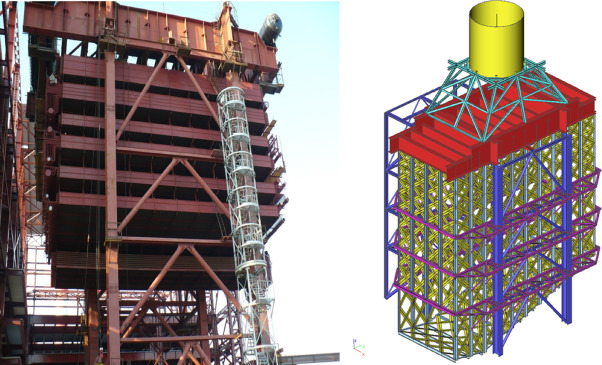
Structural conception of power plant boiler structure is driven by its technological purpose. According to boiler type there is a variety of types of boiler power plant structures. This article focuses to heat recovery steam boilers with vertical direction of flue gas (Fig. 1 ). This type of boiler is commonly known as a vertical HRSG boiler. Structural system of vertical HRSG boilers is quite simple and the differences compared to the common structure are well recognizable.

Fig. 1. Vertical HRSG boiler (real facility on the left, 3D FEM model on the right).

The majority of mass in structural system is made by tube modules and boiler casing. Either modules or boiler casing slang from boiler upmost part called “boiler ceiling”. Boiler ceiling is created by massive beams coming through the flue gas duct. These beams are in full contact with hot flue gas and that is why they cannot be fixed to the supporting structure. The suspended boiler body is fixed in its position by a system of vertical guiding and side stoppers. The detail of guiding allows thermal dilatation. This brief summary of boiler structure specifics shows that mechanical damping properties could have been bigger in HRSG structure compared to the common steel structure (Carpinteri et al., 2011 ).

Mechanical damping assessment is possible only by means of experimental testing (Cajka and Krejsa, 2013  and Li, 2010 ). Organizing this type of dynamic test on real facility is practically hardly feasible (Dusicka and Iwai, 2007 ). Moreover, the corresponding value of one unique dynamic test would have been limited. For that reason the solution on scaled physical model was chosen (Graczyk and Moan, 2011 ). Subject of the research was an experimental modal analysis carried out on one scaled physical model. This model was modified into five alternative designs during the testing. Three of the modifications represented one isolated specific in view. First and fifth modification represented simple steel structure without any technology. Logarithmic damping decrement applicable for real vertical HRSG boilers was determined on base of proportional change of property in view assessed for model with technology compared to a model without any technology (Maheedhara Reddy and Diwakar Reddy, 2014 ).

Similitude and dimensional analysis

Fundamental principle of theory of similitude between real product and its scaled model is a conversion of the technical task in view into its non-dimensional expression (Melcer and Kucharova, 2014 ). This way we can derive so called similitude invariant numbers which take the same value for both the product and its scaled model. The dimensional analysis of the specific task needs to be provided to perform these invariants. So the solution is not universal. There is a need to provide this type of analysis for every type of technical problems (Protivinsky and Krejsa, 2015 ).

Modal analysis on a scaled model

Modal analysis of mechanical systems is defined by nine mutually independent physical quantities (Merczel et al., 2013 ). By means of these quantities we can express the modal analysis problem in a perfect way. All nine relevant quantities with their expression in technical system LTM (length, time and mass) are provided in Table 1 (Salajka et al., 2013 ).

Table 1. Relevant physical quantities applicable for modal analysis.

Symbol	Scaled unit	Dimension in LTM
l	Characteristic length	L
ρ	Specific weight	ML−3
E	Modulus of elasticity	ML−1 T−2
t	Characteristic time	T
ω	Characteristic frequency	T−1
σ	Stress	ML−1 T−2
F	Force	MLT−2
a	Characteristic acceleration	LT−2
c	Coefficient of viscous damping	MT−1

On base of relevant quantities we can make up dimensional matrix of its exponents in LTM system. Determinant of sub-matrix composed from last three matrix columns is different from zero. Therefore the rank of the matrix is equal to three. In agreement with PI-Buckinghams theorem, the number of similitude invariant numbers is equal to the difference between the number of relevant quantities and the rank of dimensional matrix. Therefore the number of final similitude invariant numbers is equal to six. Representation of π -parameters will be provided by using the formula (1) solving unknown exponents x₁ to x₉ . Since there are just three quotations for estimating nine unknowns we are choosing six linear independent choices for the six redundant exponents x₄ to x₉ .

$\left[{\begin{array}{ccc}0&1&1\\1&-3&-1\\0&0&-2\end{array}}\right]\times \left({\begin{array}{c}x_{1}\\\vdots \\x_{3}\end{array}}\right)=(-1)\times \left[{\begin{array}{cccccc}0&0&1&1&0&1\\0&0&-1&1&1&0\\1&-1&-2&-2&-2&-1\end{array}}\right]\times \left({\begin{array}{c}x_{4}\\\vdots \\x_{9}\end{array}}\right)$

( 1)

By solving the Eq. (1) for i  = 6 exponent choices x₄ to x₉ we receive six dimensionless parameters π₁ to π₆ . Since the π -parameters are compound by relevant quantities and at the same time their numerical representation shall be equal for the original product, its scaled model can derive scaling laws for every relevant physical quantity just knowing π -parameters. Unfortunately the scaling laws computed from particular π -parameters contradict each other very often. It is on a researcher to neglect the weak laws not significant for main focus of his research. The contradiction comes from the fact that we choose a limited number of scales equal to the rank of dimensional matrix only. Moreover, choosing the length scale and model material we run out of all select scales. The rest of scales are computed.

Physical scaled model

PMMA material was chosen as the most suitable material for a physical model (Fig. 2 ). PMMA is a commonly used material in modeling practice (Protivinsky and Krejsa, 2012 ). PMMA has linear response to loading, quite small internal damping, and connections provided by the PMMA glue behaving as basic material (Pospisil et al., 2014 ). A brief summary of PMMA material properties is shown in Table 2 .

Fig. 2. Physical model (on the left – X direction view, on the right – Y direction view).

Table 2. PMMA material properties.

Symbol	Physical quantity	Value	Unit
ρ	Specific weight	1190	kgm−3
E	Modulus of elasticity	3200	MPa
fy	Yield point	60	MPa

Scaling laws of relevant physical quantities are shown in Table 3 . The gravity law was considered as weak law.

Table 3. Applicable scaling laws.

Symbol	Physical quantity	Scaling law (scale)	Note
L	Characteristic length	1:20 = 0.05	Geometry scale
P	Specific weight	1.19:7.85 = 0.15159	Determined by the material choice
E	Modulus of elasticity	3.2:210 = 0.015238	Determined by the material choice
T	Characteristic time	1:6.341 = 0.15770	Computed field
Ω	Characteristic frequency	6.341:1 = 6.341	Computed field
A	Characteristic acceleration	1:2 = 0.5	Computed field, considered as weak law

Experimental modal analysis

A complete set of dynamic tests was carried out in the experimental research center in ITAM Prague. Modal analysis was performed using industrial computer Dewetron DW 2010 and exciter Brüel&Kjaer, type 8202. The tests were carried out repeatedly on one single model in five particular modifications. A brief description of the model modifications is shown in Table 4 . There were twelve measurement tests for every single modification in each of horizontal directions. There were six accelerometric single-axial sensors fixed to the model. Location of fixing points was designed for evaluating both flexural shapes of natural vibration (Kralik, 2013 ).

Table 4. Model modifications.

Modification number	Model description
K1	Unloaded model – structure only
K2	Hanging technology fixed to structure by springs
K3	Hanging technology – no springs
K4	Hanging technology – no springs, beams supporting slung technology fixed on ball-bearing
K5	Unloaded model – structure only

Results and evaluations

Evaluation of the data recording of tail vibration shows that the PMMA scaled model is applicable for the specified task. In the first phase of tail there is significant mutual influence of adjacent natural shapes in evidence. Nevertheless, damping of the PMMA system is low enough to get in the late phase of tail where only the first dominant natural shape occurs.

Logarithmic decrement was determined from the late phase of tail according to formula (2) (Melcer and Kucharova, 2014 ).

$\theta ={\frac {1}{n}}\times ln{\frac {\nu _{0}(t)}{\nu _{0}(t+n\times T_{d})}}$

( 2)

The n in (2) formula represents number of periods and the v₀ represents amplitude of the measured physical quantity (Table 5 ).

Table 5. Logarithmic damping decrement.

Modification number	Logarithmic damping decrement	Rate to modification K1 (rate to common structure)
K1	0.059	1.0
K2	0.135	2.3
K3	0.154	2.6
K4	0.48	8.1
K5	0.065	1.1

Conclusion

This paper brings results of the first part of the experimental research on mechanical damping of power plant boiler structure. Time data recording of the vibration tail shows two phases of vibration tail. In the first phase there is visible significant mutual influence of the adjacent natural frequencies. In the second phase there is only one dominant natural frequency visible. All the evaluation was done on the basis of this second phase. The cardinal task for every research based on scaled physical models is how to converse the experimental results gained on scaled model to a real structural design. The methodology used in this case was very simple. The damping decrement gained for every particular model modification was divided by the decrement pertained for modification K₁ . This modification represents common steel structure. Every other modification represents some specific of vertical HRSG steel structure. This methodology is clear and universal. Results determined in this way are applicable for structural design of real vertical HRSG boiler structures ( Brozovsky and Dufka, 2014 , Jendzelovsky and Balaz, 2014 , Protivinsky and Krejsa, 2014 , Vican and Janik, 2014  and Protivinsky and Krejsa, 2015 ).

In next steps of this research it is planned to evaluate the vibrating tail from harmonic force with frequency of loading equal to first dominant natural ones. These measurements are to give countercheck of the recent conclusion. Moreover, it will be possible to evaluate the damping even based on the first phase of vibration tail.

Although there are some more tests ahead we can claim that vertical HRSG structures have significantly bigger damping than that applicable for common steel structures.

Conflict of interest

The authors declare that there is no conflict of interest.

Acknowledgements

This paper has been completed thanks to the financial support provided to VSB – Technical University of Ostrava by the Czech Ministry of Education, Youth and Sports from the budget for conceptual development of science, research and innovations for the year 2015.

References

1. Brozovsky and Dufka, 2014 J. Brozovsky, A. Dufka; To the problems of determination of dynamic elasticity modules of calcium silicate bricks by means of resonance method; Adv. Mater. Res., 897 (2014), pp. 139–143 http://dx.doi.org/10.4028/www.scientific.net/AMR.897.139
2. Cajka and Krejsa, 2013 R. Cajka, M. Krejsa; Validating a computational model of a rooflight steel structure by means of a load test; Appl. Mech. Mater., 501–504 (2013), pp. 592–598 http://dx.doi.org/10.4028/www.scientific.net/AMM.501-504.592
3. Carpinteri et al., 2011 A. Carpinteri, N. Pugno, A. Sapora; Dynamic response of damped von Koch antennas; J. Vib. Control, 17 (5) (2011), pp. 733–740 http://dx.doi.org/10.1177/1077546310375453
4. Dusicka and Iwai, 2007 P. Dusicka, R. Iwai; Development of linked column frame system for seismic lateral loads; Struct. Eng. Res. Front. (2007), pp. 1–13 http://dx.doi.org/10.1061/40944(249)63
5. Graczyk and Moan, 2011 M. Graczyk, T. Moan; Structural response to sloshing excitation in membrane LNG tank; J. Offshore Mech. Arct. Eng., 133 (2) (2011), p. 9 021103 http://dx.doi.org/10.1115/1.4001434 021103
6. Jendzelovsky and Balaz, 2014 N. Jendzelovsky, L. Balaz; Numerical modeling of cylindrical tank and compare with experiment; Appl. Mech. Mater., 617 (2014), pp. 148–151 http://dx.doi.org/10.4028/www.scientific.net/AMM.617.148
7. Kralik, 2013 J. Kralik; Deterministic and probabilistic analysis of steel frame bracing system efficiency; Appl. Mech. Mater., 390 (2013), pp. 172–177 http://dx.doi.org/10.4028/www.scientific.net/AMM.390.172
8. Li, 2010 X. Li; A scaling approach for the prediction of high-frequency mean responses of vibrating systems; J. Acoust. Soc. Am., 127 (5) (2010), pp. 209–214 http://dx.doi.org/10.1121/1.3397257
9. Maheedhara Reddy and Diwakar Reddy, 2014 G. Maheedhara Reddy, V. Diwakar Reddy; Theoretical investigations on dimensional analysis of ball bearing parameters by using Buckingham Pi-theorem; Procedia Eng., 97 (2014), pp. 1305–1311 http://dx.doi.org/10.1016/j.proeng.2014.12.410
10. Melcer and Kucharova, 2014 J. Melcer, D. Kucharova; Frequency response functions of a lorry; Adv. Mater. Res., 969 (2014), pp. 188–191 http://dx.doi.org/10.4028/www.scientific.net/AMR.969.188
11. Merczel et al., 2013 D.B. Merczel, H. Somja, J.-M. Aribert, J. Logo; On the behaviour of concentrically braced frames subjected to seismic loading; Period. Polytech. Civil Eng., 57 (2) (2013), pp. 113–122 http://dx.doi.org/10.3311/PPci.7167
12. Pospisil et al., 2014 S. Pospisil, C. Fischer, J. Naprstek; Experimental analysis of the influence of damping on the resonance behavior of a spherical pendulum; Nonlinear Dyn., 78 (1) (2014), pp. 371–390 http://dx.doi.org/10.1007/s11071-014-1446-6
13. Protivinsky and Krejsa, 2012 J. Protivinsky, M. Krejsa; Making use of the principle of energy dissipation in the seismic design of a steel structure of a steam boiler. Transaction of the VSB – Technical University of Ostrava; Civil Eng. Ser., 12 (2) (2012), pp. 143–152 http://dx.doi.org/10.2478/v10160-012-0028-0
14. Protivinsky and Krejsa, 2014 J. Protivinsky, M. Krejsa; Material study of a short seismic link in a dissipative structure of a vertical industrial boiler; Appl. Mech. Mater., 623 (2014), pp. 10–17 http://dx.doi.org/10.4028/www.scientific.net/AMM.623.10
15. Protivinsky and Krejsa, 2015 J. Protivinsky, M. Krejsa; Reliability assessment of the dissipative link in steel boiler structure with regard to seismic load; Proceedings of 4th International Conference on Materials Engineering for Advanced Technologies – ICMEAT (2015), pp. 202–206 ISBN: 978-1-60595-242-0
16. Salajka et al., 2013 V. Salajka, P. Hradil, J. Kala; Assess of the nuclear power plant structures residual life and earthquake resistance; Appl. Mech. Mater., 284–287 (2013), pp. 1247–1250 http://dx.doi.org/10.4028/www.scientific.net/AMM.284-287.1247
17. Vican and Janik, 2014 J. Vican, P. Janik; Experimental and numerical analysis of beam-column resistance; Procedia Eng., 91 (2014), pp. 280–285 http://dx.doi.org/10.1016/j.proeng.2014.12.060