Una metodología numérica sin malla para la resolución de las ecuaciones de elasticidad mediante el método de puntos finitos

A mi esposa y compañera Ivette, a mis lindos hijos Flavia y Gianluca, por todo el cariño y apoyo entregado durante la realización de este trabajo

Agradecimientos

Deseo expresar mi gratitud y agradecimiento en primer lugar a los profesores Dr. Eugenio Oñate Ibáñez de Navarra y Dr. Juan Miquel Canet, por toda la ayuda, orientación y apropiados consejos entregados durante la dirección de esta tesis. La palabra y motivación oportuna que me han entregado, posibilitó mi comprensión de los métodos sin malla en este apasionante mundo de la investigación.

Mi total gratitud también para mi esposa e hijos, por la paciencia y comprensión demostrada, también por el constante apoyo y en especial, el cariño y todas las alegrías que me han brindado. En estos instantes especiales de mi vida, deseo expresar y agradecer a mi padre Aldo Perazzo y mi madre María Maggi, el haberme enseñado el camino correcto para llegar a tan importante meta.

Mi más sincero agradecimiento para mi amigo Dr. Carlos Sacco, por su inusual característica de escuchar y atender siempre a mis dudas, sin duda echaré de menos todos los análisis y conversaciones que mantuvimos en el bar de la escuela, en torno al tema de los métodos sin malla.

Quiero agradecer también a todos mis amigos y compañeros que me han alentado y acompañado durante este largo camino, a los doctores Alex Hanganu y Juan Carlos Cante, y finalmente a Quino, Loli, Carlos, Dudiño y Fernando, a quienes les deseo toda la suerte del mundo.

Por último quiero tener una palabra de agradecimiento para con mis colegas del departamento de Ingeniería Mecánica de la UTFSM de Chile, a todo el personal del CIMNE y del Departamento de Resistencia de Materiales de la UPC en Barcelona, por todo el apoyo y confianza que me han brindado.

1 Introducción

El método de elementos finitos (MEF) ha sido durante los últimos 25 años, y sigue siendo, la herramienta numérica más utilizada para simular diversos problemas en mecánica computacional. El buen prestigio que ostenta el método se debe en gran medida a la fiabilidad de sus resultados, cuando este se utiliza adecuadamente, y la variada gama de problemas que permite simular. Sin embargo, en la última década se ha producido un avance importante en el conocimiento y posibilidades de aplicación de un nuevo tipo de método numérico denominado 'sin malla', en inglés meshless, gridless, element-free. Este método, que presenta ciertas particularidades desde el punto de vista de su formulación, es hoy en día objeto de numerosas investigaciones y lentamente se ha comenzado a posicionar como una alternativa de solución para problemas en donde los métodos tradicionales, como el de elementos finitos y volúmens finitos, presentan ciertas desventajas.

A pesar del auge experimentado en el último tiempo por esta técnica, su utilización y primeras aplicaciones corresponden a la década de los setenta en el campo de la astrofísica [59], principalmente para modelar determinados fenómenos como fisión de estrellas en rotación, donde intervienen masas de fluído en movimiento sin la presencia de contornos. Durante los siguientes diez años el método, bautizado con el acrónimo de SPH (smoothed-particle-hydrodynamics) pasó inadvertido hasta que su versatilidad y posible utilización en otros campos fué redescubierta [64], dando lugar al desarrollo de diversas variantes que han dado origen a otros tantos nuevos métodos sin malla.

Entre éstos se destacan aquellas técnicas en las que se construye la aproximación local, utilizando un polinomio interpolante mediante mínimos cuadrados, hoy en día, se reconoce al método DEM (diffuse-element.method) [69] como precursor en utilizar este tipo de técnica en conjunto con una formulación de Galekin. Sin embargo, al igual que en otros métodos sin malla, en el DEM es necesario recurrir a una malla de fondo o auxiliar para resolver la cuadratura numérica en su forma débil. Esto produce cierta confusión respecto de la idea de método sin malla planteada en un comienzo y, aunque el uso de una malla de fondo sea para propósitos de cuadratura numérica y no para construir la aproximación, se aparta de la filosofía o motivación original de este tipo de técnica.

Una forma alternativa de eliminar el uso de esta malla de fondo es utilizar un procedimiento de Colocación Puntual, el cual también se utiliza en el método SPH, empero, el método resultante puede presentar ciertas restricciones debido a la sensibilidad en la ubicación de estos puntos de colocación. Buscar una forma de atenuar esta sensibilidad o contar con una estrategia para corregirla, permitiría aprovechar en toda su potencialidad el procedimiento de colocación en el contexto de los métodos sin malla.

1.1 Motivación

En la utilización de todo método sin malla se busca que el modelo discreto sea completamente descrito por nodos. Con esto se consigue que los datos necesarios para describir el dominio de la solución sean simplemente las coordenadas de estos nodos y cierta información del contorno. La ausencia de una malla de elementos o elementos y sus conectividades, reporta ciertas ventajas respecto de los métodos tradicionales:

• La sencillez para discretizar el dominio de la solución en base a un conjunto de puntos distribuidos arbitrariamente, esta información por ejemplo se puede obtener a partir de cualquier sistema CAD

• No existe una conectividad fija entre los nodos que conforman el subdominio de interpolación y que permiten obtener la aproximación en forma local

• Menor tiempo empleado en la preparación de la información necesaria para el cálculo. Buena parte del tiempo total de una modelación compleja se invierte en realizar el modelo y la discretización por elementos o mallado, si bien los generadores de malla hoy en día son rápidos y eficientes en geometrías relativemente sencillas, lograr una malla de calidad en problemas tridimensionales sigue siendo una tarea ardua y no exenta de problemas. Por ejemplo, el proceso de generación de una malla en 3D puede tardar más tiempo que el tiempo de cálculo involucrado en la solución del sistema de ecuaciones discreto del modelo [84].

• Facilidad para realizar un procedimiento de solución adaptable, puesto que sólo es necesario agregar más nodos en las zonas de interés sin preocupase por la cercanía con los demás. En el MEF la cercanía entre dos nodos produce un fuerte gradiente en la función de forma, lo que origina errores numéricos en la solución [71].

• Facilidad para modelar problemas que involucren grandes deformaciones de la geometría o superfiicies en movimiento. Grandes distorsiones en los elementos de una malla hacen necesario realizar un procedimiento de remallado antes de efectuar el cálculo, esto conlleva un encarecimiento del coste computacional en aquellos problemas como conformado de metales o propagación de una grieta, que se caracterizan por un constante cambio en la geometría del dominio de análisis.

• Pueden proporcionar soluciones cuyas derivadas sean continuas. Es fácil construir funciones del tipo ${\textstyle {\mathcal {C}}^{1}}$, con lo cual el campo de deformaciones y tensiones en el dominio es continuo, haciendo innecesario el uso de técnicas de alisado que pueden resultar complicadas y costosas de implementar.

Para dimensionar el alcance real que pueden tener estas ventajas en un método sin malla, surge la necesidad de estudiar detenidamente su formulación matemática y evaluar las distintas alternativas que presenta su implementación para la resolución de las ecuaciones de la elasticidad lineal de sólidos. Esta ha sido la principal motivación para el desarrollo de la presente tesis, que nace dentro del las líneas de investigación en métodos sin malla que en forma conjunta llevan a cabo el Departamento de Resistencia de Materiales y Estructuras en la Ingeniería y el Centro Internacional de Métodos Numéricos en la Universidad Politécnica de Cataluña, En particular, se enfocará el estudio en el llamado 'Método de Puntos Finitos (MPF)' que ha sido la respuesta dada por estos centros de investigación a la iniciativa de formular un nuevo método sin malla.

Es pertinente mencionar en este apartado una breve aclaración respecto del nombre de Puntos Finitos, con el cual se ha denominado al método numérico objeto de investigación en esta tesis. El nombre se debe a las características particulares del método, es decir: una técnica numérica totalmente libre de malla en la cual el dominio se discretiza mediante un número finito de puntos.

1.2 Objetivos de la tesis

El objetivo principal de la tesis es obtener y desarrollar la formulación del Método de Puntos Finitos, como método totalmente libre de malla, para la resolución de las ecuaciones de la elasticidad en sólidos. Para cumplir este objetivo se pretende determinar y estudiar los aspectos relevantes de la fundamentación matemática del método, entre otros, la aproximación mediante mínimos cuadrados móviles, la función de ponderación y la técnica de colocación puntual. Para un completo análisis de las capacidades del método, se implementará un código que permita resolver diversos problemas, de índole mas bien académico, principalmente en 1D, 2D y en forma complementaria en 3D.

Como objetivos secundarios merecen ser destacados además, los siguientes:

• estudiar y analizar las principales propiedades de la aproximación, entre otras la consistencia y convergencia

• desarrollar una estrategia para seleccionar adecuadamente los puntos que conformarán la nube o subdominio de interpolación

• analizar la sensibilidad del método respecto de la adecuada colocación de los puntos en el dominio, tanto para discretizaciones regulares como irregulares de nodos

• evaluar la correcta implementación de las condiciones de contorno

• identificar aquellos aspectos relevantes que afecten y comprometan la exactitud de la aproximación, buscando plantear alternativas de solución para estos casos

Se pretende finalmente extender el desarrollo en la formulación del MPF para abarcar, además del análisis estático, algunos problemas de la dinámica lineal de sólidos.

1.3 Contenidos de la tesis

Para cumplir con los objetivos de este trabajo, la tesis se ha estructurado en 8 capítulos, el primero de ellos describe la motivación y el marco teórico en que esta se desarrollará. En el Capítulo 2 se entregan los principales fundamentos teóricos de los métodos sin malla bajo la perspectiva de las tres caracteristicas básicas que los distinguen como son, el tipo de aproximación, la función de ponderación y la forma de resolver el sistema discreto de ecuaciones. Bajo estos mismos conceptos, en el Capítulo 3 se presentan los aspectos matemáticos necesarios para comprender el Método de Puntos Finitos como método sin malla. Es en el Capítulo 4 donde se analiza en detalle la consistencia y convergencia del MPF, a través del desarrollo de diversos ejemplos de resolución de las ecuaciones de la elasticidad en sólidos, los resultados de este capítulo son fundamentales para comprender la importancia de plantear la estrategia que se presenta posteriormente. En el Capítulo 5 se formula una nueva metodología para mejorar la solución numérica de la aproximación por el MPF, principalmente en las zonas del contorno. Con los ejemplos de la elasticidad lineal de sólidos, estáticos y dinámicos, implementados en los Capítulos 6 y 7, se pretende comprobar la validez de la modificación propuesta. Se completa el estudio y análisis de la metodología sin malla formulada, con las conclusiones y las futuras líneas de investigación presentes en el Capítulo 8.

2 Revisión de los fundamentos teóricos de los métodos sin malla

Es conveniente especificar o definir globalmente, a manera de introducción y para aclarar conceptos, las características que posee una técnica numérica para que pueda ser interpretada como sin malla o libre de malla.

Duarte [25] entrega en su trabajo una primera propuesta para definir este tipo de técnica: un método se considera sin malla si las ecuaciones básicas que gobiernan el modelo discreto del problema de contorno no dependen de la disponibilidad de una malla bien definida. Sin embargo, como podrá constatarse en este capítulo, algunos métodos son aceptados como sin malla a pesar de tener una débil dependencia respecto de una malla utilizada para calcular la cuadratura numérica de las ecuaciones integrales que gobiernan el modelo discreto.

Con posterioridad, Oñate [74] formula en su trabajo una segunda propuesta al respecto, planteando que un procedimiento sin malla debiera satisfacer las siguientes condiciones:

2. La discretización de la función incógnita y sus derivadas deben poder ser definidas solamente en términos de la posición de los puntos localizados dentro del dominio de análisis y de los parámetros especificados en éstos.
3. La función de ponderación y sus derivadas deben poder ser definidas solamente en términos de la posición de los puntos localizados dentro del dominio de análisis.
5. No es necesario realizar ninguna integración de volumen o superficie, o
6. Cualquier integración de volumen o superficie debiera ser independiente del procedimiento de interpolación escogido.

Este último planteamiento es un buen punto de partida para comprender las características y funcionamiento de los distintos métodos numéricos mesh-free existentes, ya que entrega conceptos claves que son comunes a todos ellos: discretización de la función incógnita, función de ponderación, procedimiento de interpolación, e incorpora formalmente la posible utilización de una malla de fondo o celda de integración. Estos aspectos y la similitud que presentan estas técnicas, desde el punto de vista de su formulación matemática, ha sido objeto de análisis y estudio por parte de diversos grupos de trabajo [71] [25] [61] [11].

En el presente capítulo se exponen y examinan los diversos fundamentos matemáticos de las aproximaciones numéricas sin malla, para la resolución de sistemas de ecuaciones diferenciales en derivadas parciales sometidas a condiciones iniciales y de contorno conocidas. El análisis comprende cuatro etapas estrechamente relacionadas con el Método de Puntos Finitos: proceso de interpolación o de aproximación, uso de funciones de ponderación, discretización del sistema de ecuaciones diferenciales e implementación de las condiciones de contorno prescritas.

2.1 Aproximación y funciones de interpolación

Una característica importante de todo método sin malla es, sin lugar a dudas, la forma de obtener la aproximación de la función incógnita o desconocida en el dominio de análisis. Para este propósito, y en lo que resta de este capítulo, consideraremos que la aproximación ${\textstyle {\widehat {u}}(\mathbf {x} )}$ de la función ${\textstyle u(\mathbf {x} )}$ en el dominio ${\textstyle \Omega \subset {\mathbb {R} }^{d}}$,${\textstyle d=1}$,${\textstyle 2}$ o ${\textstyle 3}$, se obtiene mediante la siguiente combinación de funciones

$u(\mathbf {x} )\cong {\widehat {u}}(\mathbf {x} )={\stackrel {N}{\underset {I=1}{\sum }}}\phi _{I}(\mathbf {x} )u_{I}^{h}$

(2.1)

El dominio ${\textstyle \Omega }$ se discretiza por medio de un conjunto de nodos o puntos ${\textstyle \mathbf {x} _{I}}$, con ${\textstyle I=1}$,${\textstyle .....}$,${\textstyle N}$, siendo ${\textstyle N}$ el número total de puntos y ${\textstyle u_{I}^{h}}$ el valor aproximado de la función ${\textstyle u(\mathbf {x} )}$ en el punto ${\textstyle I}$, ${\textstyle u(\mathbf {x} _{I})\cong u_{I}^{h}}$. La función ${\textstyle \phi _{I}(\mathbf {x} )}$ se define localmente para cada subdominio ${\textstyle \Omega _{I}\subset \Omega }$, cumpliéndose:

${\begin{array}{l}\phi _{I}(\mathbf {x} )\neq 0{\hbox{ }}\forall {\hbox{ }}\mathbf {x} \in \Omega _{I}\\\phi _{I}(\mathbf {x} )=0{\hbox{ }}\forall {\hbox{ }}\mathbf {x} \notin \Omega _{I}\end{array}}$

(2.2)

En los métodos sin malla la función ${\textstyle \phi _{I}(\mathbf {x} )}$ se denomina indistintamente como función de forma o función de interpolación, quedando definida en el subdominio ${\textstyle \Omega _{I}}$ que contiene una cantidad ${\textstyle n}$ de puntos, tal que ${\textstyle n\ll N}$.

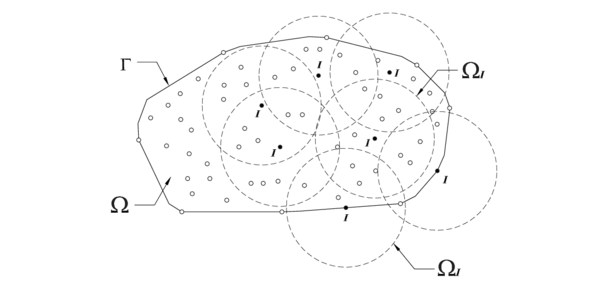
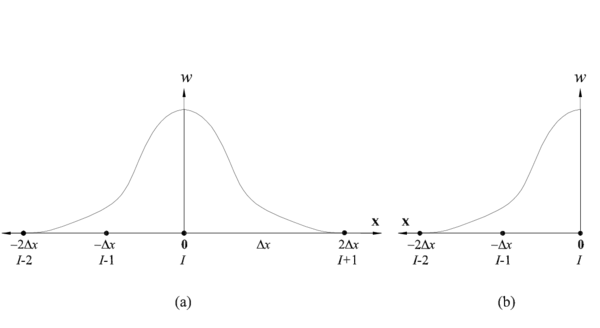
Para que la función de forma tenga un carácter local, es común en estos métodos el uso de una función de ponderación ${\textstyle w_{\overline {\mathbf {x} }}(\mathbf {x} )=w({\overline {\mathbf {x} }}-\mathbf {x} )}$ cuyo valor es distinto de cero, sobre el subdominio ${\textstyle \Omega _{\overline {\mathbf {x} }}}$ relativamente pequeño respecto del resto del dominio ${\textstyle \Omega }$. En el argumento de la función de ponderación: ${\textstyle \mathbf {x} }$ indica un punto cualquiera¹ del subdominio ${\textstyle \Omega _{\overline {\mathbf {x} }}}$, ${\textstyle {\overline {\mathbf {x} }}}$ referencia el punto donde se está efectuando la aproximación y donde la función de ponderación alcanza un máximo valor. El símbolo ${\textstyle \Omega _{I}}$ se reservará en esta tesis para indicar el subdominio asociado a un punto de coordenadas ${\textstyle \mathbf {x} _{I}}$ de la partición, sobre el cual se desea calcular o conocer los parámetros de la aproximación (figura 1). Dicho punto, en el léxico del MPF, se conoce como nodo estrella. Por otro lado, el símbolo ${\textstyle \Omega _{\mathbf {x} }}$ o ${\textstyle \Omega _{\overline {\mathbf {x} }}}$ indicará el subdominio asociado a un punto de coordenadas genéricas ${\textstyle \mathbf {x} }$ o ${\textstyle {\overline {\mathbf {x} }}}$ respectivamente.

Cada subdominio ${\textstyle \Omega _{I}}$, dominio de influencia o soporte de la función de ponderación, se define de manera que en 1D es siempre un intervalo, mientras que en 2D y 3D adopta la forma de disco y esfera respectivamente. También es posible emplear rectángulos o paralelepípedos, incluso es posible utilizar las dos geometrías circular y rectangular en un mismo modelo [11]². Para un caso en 2D, la figura 1 muestra el dominio de análisis ${\textstyle \Omega }$, su contorno ${\textstyle \Gamma }$ y algunos subdominios circulares ${\textstyle \Omega _{I}}$ asociados a su respectivo nodo estrella ${\textstyle I}$ (sean de interior o de contorno). Como para cada nodo de la partición existirá su correspondiente subdominio, la intersección o traslape existente entre ellos será mayor a la mostrada en la figura. Esta característica, que será analizada posteriormente, posibilita el hecho de que un mismo punto usualmente pertenezca a ${\textstyle 6}$ o más subdominios de interpolación

Figura 1: Modelo para un metodo sin malla basado en subdominios circulares

A continuación se describen y examinan los principales tipos de aproximación utilizados en los métodos sin malla, se analizarán sus propiedades y la conexión existente entre las distintas funciones de interpolación utilizadas. El análisis comprende fundamentalmente aquellas técnicas que por su construcción se asemejan al MPF, lo cual facilitará posteriormente su entendimiento desde el punto de vista de su mecánica operativa.

(¹) En el caso de las aproximaciones utilizadas en los metodos sin malla, este punto pertenece a la partición $\rightarrow x=x_{I}$

(²) Las funciones de ponderación que permiten generar este tipo de subdominios se analizan en el apartado 2.3

2.1.1 Aproximación por mínimos cuadrados ponderados

Una aproximación por mínimos cuadrados busca ajustar una curva o polinomio a los valores discretos de una función en unos puntos, de forma de minimizar el error cometido en la aproximación. A pesar que este tipo de aproximación difiere de lo que se conoce tradicionalmente como una interpolación, porque el polinomio no se iguala exactamente con los datos en los puntos, en la literatura de los métodos meshless los términos aproximación e interpolación suelen tratarse como sinónimos. Esta técnica ha sido utilizada en la resolución numérica de problemas de mecánica de sólidos y fluidos [68] [47] [6] , para aproximar el campo desconocido o incógnita a través de unos valores nodales. Sin embargo, tal como se demuestra en [71], el éxito de esta aproximación presenta una importante restricción o inconveniente. La aproximación se deteriora rápidamente en la medida que el número de puntos utilizados en la interpolación local, ${\textstyle n}$, aumenta o crece demasiado respecto del número de términos en el polinomio base de interpolación, ${\textstyle m}$. Para paliar este inconveniente se recurre al uso de una función de ponderación ${\textstyle w_{\overline {\mathbf {x} }}(\mathbf {x} )}$, que permite mejorar la aproximación por ejemplo, en la vecindad del punto ${\textstyle {\overline {\mathbf {x} }}}$ donde se requiere calcular la función o su derivada.

Una de las primeras aproximaciones por mínimos cuadrados, en la cual se introdujo el concepto de la función de ponderación, fue utilizada por Lancaster y Salkauskas [42] para representar o generar diversos tipos de superficies, a partir de la interpolación de una función base polinómica (interpolante) sobre un set de puntos aleatoriamente distribuidos en un dominio. Posteriormente este método, denominado por los autores como `interpolating moving least squares method' IMLS, ha sido ampliamente utilizado en el contexto de los métodos sin malla, para obtener una solución numérica aproximada a sistemas de ecuaciones en derivadas parciales [93]. Buen ejemplo de lo anterior, son las distintas familias de métodos sin malla que utilizan la técnica de interpolación tipo `moving least squares' (MLS), como: `diffuse element method' (DEM) [69], `element-free Galerkin methods' (EFGM) [9], `finite point method' (FPM) [71], `meshless local Petrov-Galerkin method' (MLPG) [3], `local boundary integral equation method' (LBIE) [105], y más recientemente `local point interpolation method' (LPIM) [49] y `least-squares collocation meshless method' (LSCMM) [103].

Construcción

En un método MLS, la aproximación local ${\textstyle {\widehat {u}}(\mathbf {x)} }$ de la función ${\textstyle u(\mathbf {x} )}$ para cada punto ${\textstyle {\overline {\mathbf {x} }}\in \Omega }$, se obtiene mediante una base de ${\textstyle m}$ funciones linealmente independientes ${\textstyle {\mathcal {P}}:=\left\{p_{1}(\mathbf {x} ),.....,p_{m}(\mathbf {x} )\right\}}$ y de un conjunto de ${\textstyle m}$ coeficientes desconocidos ${\textstyle {\mathcal {\alpha }}:=\left\{\alpha _{1}({\overline {\mathbf {x} }}),.....,\alpha _{m}({\overline {\mathbf {x} }})\right\}}$, de la siguiente manera

$u(\mathbf {x} )\cong {\widehat {u}}(\mathbf {x} ):={\stackrel {m}{\underset {i=1}{\sum }}}p_{i}(\mathbf {x} )\alpha _{i}({\overline {\mathbf {x} }})=\mathbf {p} ^{T}(\mathbf {x} )\mathbf {\alpha } ({\overline {\mathbf {x} }}){\hbox{ }}\forall \mathbf {\bar {x}} \in \Omega$

(2.3)

siendo el operador ${\textstyle L_{\overline {x}}}$ una aplicación

$L_{\overline {x}}:C^{0}(\Omega _{\overline {\mathbf {x} }})\rightarrow C^{m}(\Omega _{\overline {\mathbf {x} }})$

(2.4)

con los vectores

${\begin{array}{ll}\mathbf {p} ^{T}(\mathbf {x} )\mathbf {:=} \left[{\hbox{ }}p_{1}(\mathbf {x} ){\hbox{ }}p_{2}(\mathbf {x} ){\hbox{ .... }}p_{m}(\mathbf {x} ){\hbox{ }}\right]&{\hbox{ , }}\in Vec(m)\end{array}}$

(2.5)

${\begin{array}{rr}\mathbf {\alpha } ^{T}({\overline {\mathbf {x} }}):=\left[{\hbox{ }}\alpha _{1}({\overline {\mathbf {x} }}){\hbox{ }}\alpha _{2}({\overline {\mathbf {x} }}){\hbox{ ... }}\alpha _{m}({\overline {\mathbf {x} }}){\hbox{ }}\right]&{\hbox{ , }}\in Vec(m)\end{array}}$

(2.6)

La base de funciones contiene típicamente monomios que dependen de las coordenadas espaciales ${\textstyle \mathbf {x} ^{T}=\left[x,y\right]}$ (por ejemplo en 2D), mientras los coeficientes ${\textstyle \left\{\alpha _{i}({\overline {\mathbf {x} }})\right\}_{i=1}^{m}}$ dependen de la posición del punto ${\textstyle {\overline {\mathbf {x} }}}$. Como ejemplos, para el caso lineal y cuadrático respectivamente se tiene:

${\begin{array}{llllll}\mathbf {p} ^{T}(\mathbf {x} )=\left[1{\hbox{ }}x\right]&m=2&{\hbox{ y}}&\mathbf {p} ^{T}(\mathbf {x} )=\left[1{\hbox{ }}x{\hbox{ }}x^{2}\right]&m=3&{\hbox{ en 1D,}}\\\mathbf {p} ^{T}(\mathbf {x} )=\left[1{\hbox{ }}x{\hbox{ }}y\right]&m=3&{\hbox{ y}}&\mathbf {p} ^{T}(\mathbf {x} )=\left[1{\hbox{ }}x{\hbox{ }}y{\hbox{ }}x^{2}{\hbox{ }}xy{\hbox{ }}y^{2}\right]&m=6&{\hbox{ en 2D}}\end{array}}$

(2.7)

Es importante destacar la posibilidad de incluir otro tipo de funciones en la base, como por ejemplo, funciones que puedan tener singularidades o discontinuidades. Las bases así definidas, se han utilizado para la modelación de problemas en mecánica de fractura [8] [29] [91].

De acuerdo a la expresión 2.3 , para cada punto de la partición con coordenadas ${\textstyle \mathbf {x} _{I}}$ ${\textstyle \in {\mathcal {S}}({\overline {\mathbf {x} }})}$, siendo ${\textstyle {\mathcal {S}}({\overline {\mathbf {x} }})}$ el conjunto de ${\textstyle n}$ puntos pertenecientes al dominio de influencia del punto ${\textstyle {\overline {\mathbf {x} }}}$ donde ${\textstyle n\geq m}$, existirá una diferencia o error entre el valor de la función y el valor de la aproximación, que puede ser cuantificada mediante¹

$e(\mathbf {x} _{I},{\overline {\mathbf {x} }}):=u_{I}^{h}-{\widehat {u}}(\mathbf {x} _{I})=u_{I}^{h}-\mathbf {p} ^{T}(\mathbf {x} _{I})\mathbf {\alpha (} {\overline {\mathbf {x} }}){\hbox{, }}\forall \mathbf {x} _{I}\in {\mathcal {S}}({\overline {\mathbf {x} }})$

(2.8)

Se debe notar de 2.8 que el valor de la aproximación, consiste en los términos de la base evaluados en ${\textstyle \mathbf {x} _{I}}$ y sus respectivos coeficientes en ${\textstyle {\overline {\mathbf {x} }}}$. Para obtener el vector de parámetros desconocidos ${\textstyle \mathbf {\alpha } ({\overline {\mathbf {x} }})}$, se recurre a la minimización del siguiente funcional discreto

$J(\mathbf {\alpha } ({\overline {\mathbf {x} }})):={\underset {I\in {\mathcal {S}}({\overline {\mathbf {x} }})}{\sum }}w({\overline {\mathbf {x} }}-\mathbf {x} _{I})\left[e(\mathbf {x} _{I},{\overline {\mathbf {x} }})\right]^{2}$

(2.9)

cuya expresión compacta en forma matricial es

$J(\mathbf {\alpha } ({\overline {\mathbf {x} }}))=\mathbf {(u} ^{h}\mathbf {-P(x} _{I})\mathbf {\alpha (} {\overline {\mathbf {x} }}))^{T}{\hbox{ }}\mathbf {W(} {\overline {\mathbf {x} }}){\hbox{ }}(\mathbf {u} ^{h}\mathbf {-P(x} _{I})\mathbf {\alpha (} {\overline {\mathbf {x} }}))$

(2.10)

donde

$\mathbf {u} ^{h}:=\left[u_{1}^{h}{\hbox{ }}u_{2}^{h}{\hbox{ ...... }}u_{n}^{h}\right]^{T}{\hbox{ , }}\in Vec(n){\hbox{, }}n=card({\mathcal {S}}({\overline {\mathbf {x} }}))$

(2.11)

$\mathbf {P} (\mathbf {x} _{I}):=\left[{\begin{array}{cccc}p_{1}\left(\mathbf {x} _{1}\right)&p_{2}\left(\mathbf {x} _{1}\right)&\cdots &p_{m}\left(\mathbf {x} _{1}\right)\\p_{1}\left(\mathbf {x} _{2}\right)&p_{2}\left(\mathbf {x} _{2}\right)&\cdots &p_{m}\left(\mathbf {x} _{2}\right)\\\vdots &\vdots &\ddots &\vdots \\p_{1}\left(\mathbf {x} _{n}\right)&p_{2}\left(\mathbf {x} _{n}\right)&\cdots &p_{m}\left(\mathbf {x} _{n}\right)\end{array}}\right]{\hbox{ , }}\in Mat(n\times m)$

(2.12)

$\mathbf {W} ({\overline {\mathbf {x} }}):=\left[{\begin{array}{cccc}w({\overline {\mathbf {x} }}-\mathbf {x} _{1})&0&\cdots &0\\0&w({\overline {\mathbf {x} }}-\mathbf {x} _{2})&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &w({\overline {\mathbf {x} }}-\mathbf {x} _{n})\end{array}}\right]{\hbox{ }},{\hbox{ }}\in Mat(n\times n)$

(2.13)

La función de ponderación ${\textstyle w({\overline {\mathbf {x} }}-\mathbf {x} _{I})}$ en 2.9, al igual que en todos los métodos `mesh-free', confiere el carácter local a la aproximación. Esto significa que ${\textstyle {\widehat {u}}(\mathbf {x} )}$ se construirá únicamente con la información que aportan los valores ${\textstyle u_{I}^{h}}$, de los nodos que pertenezcan al subdominio para el cual ${\textstyle w({\overline {\mathbf {x} }}-\mathbf {x} _{I})}$ tenga un valor diferente de cero. Este subdominio o soporte de la función de ponderación, suele tener forma circular (disco o esfera) centrado en ${\textstyle {\overline {\mathbf {x} }}}$ y de radio ${\textstyle r_{\overline {\mathbf {x} }}}$.

Según [63], esta función debe cumplir las siguientes propiedades ${\textstyle \forall \varrho \in {\mathbb {R} }^{+}}$:

1. ${\textstyle w\left({\overline {\mathbf {x} }}-\mathbf {x} ,\varrho \right)>0}$ en un subdominio ${\textstyle \Omega _{\overline {\mathbf {x} }}}$ ${\textstyle \in }$ ${\textstyle \Omega }$,
2. ${\textstyle w\left({\overline {\mathbf {x} }}-\mathbf {x} ,\varrho \right)=0}$ fuera del subdominio ${\textstyle \Omega _{\overline {\mathbf {x} }}}$,
3. Propiedad de normalidad: ${\textstyle {\underset {\Omega }{\int }}w\left({\overline {\mathbf {x} }}-\mathbf {x} ,\varrho \right)dx=1}$,
4. ${\textstyle w\left(d,\varrho \right)}$ es una función monótonamente decreciente, donde ${\textstyle d=\left\|{\overline {\mathbf {x} }}-\mathbf {x} \right\|}$,
5. ${\textstyle w\left(d,\varrho \right)\rightarrow \delta \left(d\right)}$ cuando ${\textstyle \varrho \rightarrow 0}$, donde ${\textstyle \delta \left(d\right)}$ es la función delta de Dirac.

Desde ahora y en lo que resta de la tesis, cada vez que se haga referencia a una función de ponderación, se entenderá que esta cumple con las cinco propiedades anteriores. En el argumento de la función de ponderación ${\textstyle \varrho }$ es una medida del tamaño de su soporte². En el caso de la aproximación MLS, como consecuencia de las propiedades (i) y (ii), únicamente intervendrán en el cálculo de 2.3, aquellos puntos ${\textstyle \mathbf {x} _{I}\in {\mathcal {S}}({\overline {\mathbf {x} }})}$ que cumplan ${\textstyle \mid {\overline {\mathbf {x} }}-\mathbf {x} _{I}\mid <\varrho }$. En principio, para una distribución arbitraria de puntos, distintos valores de ${\textstyle \varrho }$ darán lugar a diferentes funciones de ponderación ${\textstyle w({\overline {\mathbf {x} }}-\mathbf {x} _{I})}$, lo que se traduce en la dificultad de no contar con una única manera de definirla globalmente.

Los parámetros desconocidos ${\textstyle \left\{\alpha _{i}({\overline {\mathbf {x} }})\right\}_{i=1}^{m}}$, que minimizan la expresión del error, se obtienen derivando vectorialmente 2.10 respecto del vector ${\textstyle \mathbf {\alpha (} {\overline {\mathbf {x} }})}$ e igualando a cero. Con esto se consigue un sistema lineal de ecuaciones

${\frac {\partial J(\mathbf {\alpha } ({\overline {\mathbf {x} }}))}{\partial \mathbf {\alpha } ({\overline {\mathbf {x} }})}}=0$

(2.14)

$\mathbf {A(} {\overline {\mathbf {x} }})\mathbf {\alpha } ({\overline {\mathbf {x} }})=\mathbf {B(} {\overline {\mathbf {x} }})\mathbf {u} ^{h}$

(2.15)

donde las matrices ${\textstyle \mathbf {A(} {\overline {\mathbf {x} }})}$ (matriz de momentos), y ${\textstyle \mathbf {B(} {\overline {\mathbf {x} }})}$ son

$\mathbf {A(} {\overline {\mathbf {x} }}):=\mathbf {P} ^{T}(\mathbf {x} _{I})\mathbf {W} ({\overline {\mathbf {x} }})\mathbf {P} (\mathbf {x} _{I}){\hbox{ , }}\in Mat(m\times m)$

(2.16)

$A_{ij}({\overline {\mathbf {x} }})={\underset {I\in {\mathcal {S}}({\overline {\mathbf {x} }})}{\sum }}p_{i}(\mathbf {x} _{I})w({\overline {\mathbf {x} }}-\mathbf {x} _{I})p_{j}(\mathbf {x} _{I}){\hbox{ , }}i,j=1,....,m$

(2.17)

$\mathbf {B} ({\overline {\mathbf {x} }}):=\mathbf {P} ^{T}(\mathbf {x} _{I})\mathbf {W} ({\overline {\mathbf {x} }}){\hbox{ , }}\in Mat(m\times n)$

(2.18)

$B_{jI}({\overline {\mathbf {x} }})=p_{j}(\mathbf {x} _{I})w({\overline {\mathbf {x} }}-\mathbf {x} _{I}){\hbox{ , }}j=1,...,m{\hbox{ }}I\in {\mathcal {S}}({\overline {\mathbf {x} }})$

(2.19)

De la ecuación 2.15 se puede obtener el vector ${\textstyle \mathbf {\alpha (} {\overline {\mathbf {x} }})}$ como

$\mathbf {\alpha (} {\overline {\mathbf {x} }})=\mathbf {A} ^{-1}\mathbf {(} {\overline {\mathbf {x} }})\mathbf {B(} {\overline {\mathbf {x} }})\mathbf {u} ^{h}:=\mathbf {C} ^{-1}({\overline {\mathbf {x} }})\mathbf {u} ^{h}{\hbox{ , con }}\mathbf {C} ^{-1}({\overline {\mathbf {x} }})\in Mat(m\times n)$

(2.20)

$\alpha _{i}({\overline {\mathbf {x} }})={\underset {I\in {\mathcal {S}}({\overline {\mathbf {x} }})}{\sum }}{\stackrel {m}{\underset {j=1}{\sum }}}A_{ij}^{-1}({\overline {\mathbf {x} }})B_{jI}({\overline {\mathbf {x} }})u_{I}^{h}{\hbox{ , }}i=1,....,m$

(2.21)

lo que permite obtener finalmente de 2.3 la expresión de la aproximación local en su forma compacta

${\widehat {u}}(\mathbf {x} )=\mathbf {p} ^{T}(\mathbf {x} )\mathbf {C} ^{-1}({\overline {\mathbf {x} }})\mathbf {u} ^{h}{\hbox{ , }}\forall \mathbf {x} \in \Omega _{\overline {\mathbf {x} }}$

(2.22)

y en forma desarrollada

${\widehat {u}}(\mathbf {x} )={\stackrel {m}{\underset {i=1}{\sum }}}p_{i}(\mathbf {x} )\alpha _{i}({\overline {\mathbf {x} }})={\underset {I\in {\mathcal {S}}({\overline {\mathbf {x} }})}{\sum }}{\stackrel {m}{\underset {k=1}{\sum }}}{\stackrel {m}{\underset {i=1}{\sum }}}p_{i}(\mathbf {x} )A_{ik}^{-1}({\overline {\mathbf {x} }})B_{kI}({\overline {\mathbf {x} }})u_{I}^{h}{\hbox{ , }}\forall \mathbf {x} \in \Omega _{\overline {\mathbf {x} }}$

(2.23)

La expresión de las funciones de forma se obtiene agrupando los términos que multiplican a ${\textstyle u_{I}^{h}}$ en 2.23

$\phi _{I}(\mathbf {x} )={\stackrel {m}{\underset {k=1}{\sum }}}{\stackrel {m}{\underset {i=1}{\sum }}}p_{i}(\mathbf {x} )A_{ik}^{-1}({\overline {\mathbf {x} }})B_{kI}({\overline {\mathbf {x} }}){\hbox{ , }}\forall \mathbf {x\in } \Omega _{\overline {\mathbf {x} }}{\hbox{, }}\forall I\in {\mathcal {S}}({\overline {\mathbf {x} }})$

(2.24)

Para extender la aproximación local 2.23 a todo el dominio, se introduce un operador global ${\textstyle G}$ tal que [63]

$u(\mathbf {x} )\cong Gu(\mathbf {x} ){\hbox{ , }}\forall \mathbf {x} \in \Omega$

(2.25)

donde

$G:C^{0}(\Omega )\rightarrow C^{m}(\Omega )$

(2.26)

lo que permite obtener en el límite ${\textstyle Gu(\mathbf {x} )={\widehat {u}}(\mathbf {x} )}$, siendo la aproximación global MLS en su forma compacta y desarrollada

$Gu(\mathbf {x} ):={\underset {{\overline {\mathbf {x} }}\rightarrow \mathbf {x} }{\lim }}{\widehat {u}}(\mathbf {x} )=\mathbf {p} ^{T}(\mathbf {x} )\mathbf {C} ^{-1}(\mathbf {x} )\mathbf {u} ^{h}{\hbox{ , }}\forall \mathbf {x} \in \Omega$

(2.27)

$Gu(\mathbf {x} )={\underset {I\in {\mathcal {S}}(\mathbf {x} )}{\sum }}{\stackrel {m}{\underset {k=1}{\sum }}}{\stackrel {m}{\underset {i=1}{\sum }}}p_{i}(\mathbf {x} )A_{ik}^{-1}(\mathbf {x} )B_{kI}(\mathbf {x} )u_{I}^{h}={\underset {I\in {\mathcal {S}}(\mathbf {x} )}{\sum }}\phi _{I}(\mathbf {x} )u_{I}^{h}{\hbox{ , }}\forall \mathbf {x} \in \Omega$

(2.28)

y la expresión de las funciones de forma

$\phi _{I}(\mathbf {x} )={\stackrel {m}{\underset {k=1}{\sum }}}{\stackrel {m}{\underset {i=1}{\sum }}}p_{i}(\mathbf {x} )A_{ik}^{-1}(\mathbf {x} )B_{kI}(\mathbf {x} ),\quad \forall \mathbf {x} \in \Omega ,\forall I\in {\mathcal {S}}(\mathbf {x} )$

(2.29)

(¹) La desigualdad $n\geq m$ se justificará cuando se analice la propiedad de existencia en la aproximación MLS

(²) Generalmente el parámetro $\varrho$ se omite como argumento de la función de ponderación

2.1.2 Interpolante de Shepard

Considérese el caso particular en que la función base de interpolación contiene como único elemento

${\mathcal {P}}=\left\{p_{i}(\mathbf {x} )\right\}_{i=1}^{m}=\left\{{\hbox{ }}1{\hbox{ }}\right\}{\hbox{ , }}\Rightarrow m=1$

(2.30)

en este caso las componentes de la matriz ${\textstyle \mathbf {A} (\mathbf {x} )}$ y ${\textstyle \mathbf {B(x)} }$ serán respectivamente (ver 2.17, 2.19)

$A(\mathbf {x} )={\underset {I\in {\mathcal {S}}(\mathbf {x)} }{\sum }}w(\mathbf {x} -\mathbf {x} _{I}\mathbf {)}$

(2.31)

$B_{1I}(\mathbf {x} )=w(\mathbf {x} -\mathbf {x} _{I}\mathbf {)} {\hbox{ , }}I\in {\mathcal {S}}(\mathbf {x)}$

(2.32)

quedando la aproximación global definida como

$Gu(\mathbf {x} )\mathbf {=} {\frac {{\underset {I\in {\mathcal {S}}(\mathbf {x)} }{\sum }}w(\mathbf {x} -\mathbf {x} _{I}\mathbf {)} u_{I}^{h}}{{\underset {J\in {\mathcal {S}}(\mathbf {x)} }{\sum }}w(\mathbf {x-x} _{J}\mathbf {)} }}$

(2.33)

y su correspondiente función de forma (recuérdese 2.29)

$\phi _{I}(\mathbf {x} )\mathbf {=} {\frac {w(\mathbf {x-x} _{I}\mathbf {)} }{{\underset {J\in {\mathcal {S}}(\mathbf {x)} }{\sum }}w(\mathbf {x-x} _{J}\mathbf {)} }}$

(2.34)

La aproximación global 2.33 recibe el nombre de interpolante de Shepard [90], y sus funciones de forma o funciones de Shepard cumplen las siguientes propiedades¹:

1. ${\textstyle 0<\phi _{I}(\mathbf {x} )\mathbf {<} 1}$
2. ${\textstyle {\stackrel {N}{\underset {I=1}{\sum }}}\phi _{I}(\mathbf {x} )\mathbf {=} 1}$ ${\textstyle \quad \forall \mathbf {x\in } \Omega }$

En el lenguaje matemático se dice que la colección de funciones que cumplen la propiedad (ii) representan una partición de la unidad [88].

(¹) Las funciones de forma que se construyen en el MEF también cumplen estas propiedades

2.1.3 Propiedades. Existencia de la aproximación.

La existencia de la aproximación MLS está condicionada a la resolución del sistema lineal de ecuaciones 2.20 , lo que se traduce en definitiva en calcular la inversa de la matriz de momentos. Recordando 2.17 , la matriz ${\textstyle \mathbf {A(} {\overline {\mathbf {x} }})}$ de un punto ${\textstyle {\overline {\mathbf {x} }}\in \Omega }$ para el cual existe un subdominio ${\textstyle \Omega _{\overline {\mathbf {x} }}}$ y un conjunto de puntos ${\textstyle \mathbf {x} _{I}\in {\mathcal {S}}({\overline {\mathbf {x} }}),}$ donde ${\textstyle n=card({\mathcal {S}}({\overline {\mathbf {x} }}))}$, puede escribirse como

$\mathbf {A(} {\overline {\mathbf {x} }})=\left[{\begin{array}{cccc}\left(p_{1},p_{1}\right)_{\overline {\mathbf {x} }}&\left(p_{1},p_{2}\right)_{\overline {\mathbf {x} }}&\cdots &\left(p_{1},p_{m}\right)_{\overline {\mathbf {x} }}\\\left(p_{2},p_{1}\right)_{\overline {\mathbf {x} }}&\left(p_{2},p_{2}\right)_{\overline {\mathbf {x} }}&\cdots &\left(p_{2},p_{m}\right)_{\overline {\mathbf {x} }}\\\vdots &\vdots &\ddots &\vdots \\\left(p_{m},p_{1}\right)_{\overline {\mathbf {x} }}&\left(p_{m},p_{2}\right)_{\overline {\mathbf {x} }}&\cdots &\left(p_{m},p_{m}\right)_{\overline {\mathbf {x} }}\end{array}}\right]$

(2.35)

donde ${\textstyle \left(p_{i},p_{j}\right)_{\overline {\mathbf {x} }}}$ corresponde al producto interno ponderado que depende del punto ${\textstyle {\overline {\mathbf {x} }}}$, definido por [42]

$\left(p_{i},p_{j}\right)_{\overline {\mathbf {x} }}:={\stackrel {n}{\underset {I=1}{\sum }}}p_{i}(\mathbf {x} _{I})w({\overline {\mathbf {x} }}-\mathbf {x} _{I})p_{j}(\mathbf {x} _{I})$

(2.36)

Como muestra 2.35 la matriz ${\textstyle \mathbf {A(} {\overline {\mathbf {x} }})}$ es simétrica por construcción, y definida positiva por la propiedad (i) de la función de ponderación estipulada del apartado 2.1.1, si además las funciones ${\textstyle \left\{p_{i}(\mathbf {x} )\right\}_{i=1}^{m}}$ son linealmente independientes, la matriz es invertible y la solución del sistema 2.20 existe y es única. No obstante, la independencia lineal de la base de polinomios ${\textstyle {\mathcal {P}}}$ no es condición suficiente para asegurar la no singularidad de la matriz ${\textstyle \mathbf {A(} {\overline {\mathbf {x} }})}$ y por consiguiente la existencia de su inversa. Para que la aproximación sea factible, deberán además respetarse unos requerimientos mínimos en la definición de los subdominios de interpolación, de cara a obtener una distribución admisible de puntos [56]. Una distribución admisible de puntos debe satisfacer los siguientes requerimientos:

1. El número de partículas ${\textstyle n}$ contenidas en el subdominio ${\textstyle \Omega _{\overline {\mathbf {x} }}}$ debe ser tal que

   $n_{\min .}\leq n\leq n_{\max .}$

   (2.37)

donde ${\textstyle n_{\min .}}$ es un número que garantiza la existencia de las funciones de forma o regularidad de la matriz ${\textstyle \mathbf {A(} {\overline {\mathbf {x} }})}$¹. Una condición necesaria para que ${\textstyle \mathbf {A(} {\overline {\mathbf {x} }})}$ sea una matriz regular es que ${\textstyle \forall }$ ${\textstyle {\overline {\mathbf {x} }}\in \Omega }$

$m=card({\mathcal {P}})\leq n=card({\mathcal {S}}({\overline {\mathbf {x} }}))$

(2.38)

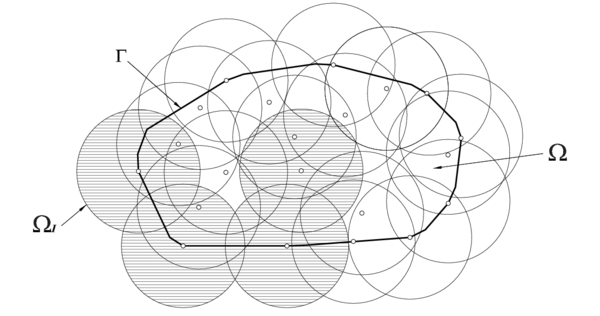
Recordando 2.13 y 2.16 se aprecia que el rango de la matriz ${\textstyle \mathbf {W} ({\overline {\mathbf {x} }})}$, y en consecuencia de ${\textstyle \mathbf {A(} {\overline {\mathbf {x} }})}$, puede ser como máximo igual a ${\textstyle n}$, por consiguiente para que ${\textstyle \mathbf {A(} {\overline {\mathbf {x} }})\in Mat(m\times m)}$ sea definida positiva es necesario que ${\textstyle n\geq m}$. Lo interesante de la propuesta 2.38 es la definición de un posible valor para ${\textstyle n_{\min .}}$. A título de ejemplo, si se elige como base de interpolación ${\textstyle {\mathcal {P}}=\left[1{\hbox{ }}x{\hbox{ }}y\right]}$, ${\textstyle m=3}$, la figura 2 muestra una serie de subdominios para los que no se satisface la condición ${\textstyle n\geq 3}$.

2. La distribución de puntos o partículas debe ser no degenerada , en concreto en 2D, significa que ${\textstyle \forall }$ ${\textstyle {\overline {\mathbf {x} }}\in \Omega }$ , un mínimo de 3 puntos deben pertenecer a ${\textstyle \Omega _{\overline {\mathbf {x} }}}$ y éstos no deben superponerse, es decir sus vectores de posición deben formar un elemento triangular no nulo.

Figura 2: Distribucion de puntos inadmisible. En los subdominios marcados n=card(S(x))<3math

(¹) El valor de $n_{\max .}$ sólo tiene sentido a efectos computacionales.

2.1.4 Consistencia

Cuando se estudia la convergencia de un método sin malla, la consistencia de la aproximación utilizada, es un aspecto que debe ser analizado con detenimiento. Entenderemos por orden de consistencia de una aproximación, al grado del polinomio que debe ser representado exactamente, de esta forma la capacidad de reproducir polinomios de grado ${\textstyle k}$ es equivalente a la consistencia de orden ${\textstyle k}$. Los requerimientos de consistencia dependen del orden de las ecuaciones diferenciales parciales que deben ser resueltas y del esquema de discretización empleado.

Para demostrar la consistencia de orden ${\textstyle k}$ de una aproximación MLS si la base de interpolación está completa en el polinomio de orden ${\textstyle k}$, considérese que se quieren aproximar simultáneamente el siguiente conjunto de funciones de la base, agrupadas en el vector ${\textstyle \mathbf {u} ^{T}\mathbf {(x)=p} ^{T}\mathbf {(x)=} \left[{\hbox{ }}p_{1}(\mathbf {x} ){\hbox{ }}p_{2}(\mathbf {x} ){\hbox{ .... }}p_{m}(\mathbf {x} ){\hbox{ }}\right]}$ , siendo esta vez la matriz con los valores de las funciones en los puntos ${\textstyle \mathbf {x} _{I}}$

$\mathbf {U} ^{T}:=\left[\mathbf {u} _{1}{\hbox{ }}\mathbf {u} _{2}{\hbox{ .........}}\mathbf {u} _{n}\right]=\left[{\begin{array}{cccc}p_{1}\left(\mathbf {x} _{1}\right)&p_{1}\left(\mathbf {x} _{2}\right)&\cdots &p_{1}\left(\mathbf {x} _{n}\right)\\p_{2}\left(\mathbf {x} _{1}\right)&p_{2}\left(\mathbf {x} _{2}\right)&\cdots &p_{2}\left(\mathbf {x} _{n}\right)\\\vdots &\vdots &\ddots &\vdots \\p_{m}\left(\mathbf {x} _{1}\right)&p_{m}\left(\mathbf {x} _{2}\right)&\cdots &p_{m}\left(\mathbf {x} _{n}\right)\end{array}}\right]{\hbox{ , }}\in Mat(m\times n)$

(2.39)

Supóngase como antes, que ${\textstyle {\overline {\mathbf {x} }}}$ es un punto arbitrario de ${\textstyle \Omega }$ para el cual existe un subdomino ${\textstyle \Omega _{\overline {\mathbf {x} }}}$, entonces para cada punto de la partición ${\textstyle \mathbf {x} _{I}\in {\mathcal {S}}({\overline {\mathbf {x} }}),}$ donde ${\textstyle n=card({\mathcal {S}}({\overline {\mathbf {x} }}))}$, la aproximación local 2.22 tendrá esta vez la siguiente expresión (recuérdese también exp. final vec. alfa , 2.18)

$L_{\overline {x}}\mathbf {u} ^{T}(\mathbf {x} )=\mathbf {p} ^{T}(\mathbf {x} )\mathbf {C} ^{-1}({\overline {\mathbf {x} }})\mathbf {U} =\mathbf {p} ^{T}(\mathbf {x} )\mathbf {A} ^{-1}\mathbf {(} {\overline {\mathbf {x} }})\mathbf {B(} {\overline {\mathbf {x} }})\mathbf {U} =$ (2.40) $=\mathbf {p} ^{T}(\mathbf {x} )\mathbf {A} ^{-1}\mathbf {(} {\overline {\mathbf {x} }})\mathbf {P} ^{T}(\mathbf {x} _{I})\mathbf {W} ({\overline {\mathbf {x} }})\mathbf {U=p} ^{T}(\mathbf {x} )\mathbf {A} ^{-1}\mathbf {(} {\overline {\mathbf {x} }})\mathbf {A(} {\overline {\mathbf {x} }})=\mathbf {p} ^{T}(\mathbf {x} )$

lo que demuestra el hecho de que cualquier función que aparezca en la base puede ser reproducida exactamente. Si por ejemplo, la base ${\textstyle \left\{p_{i}(\mathbf {x} )\right\}_{i=1}^{m}}$ contiene todos los términos constantes y monomios lineales, entonces el orden de consistencia de la aproximación MLS será lineal.

2.1.5 No interpolación

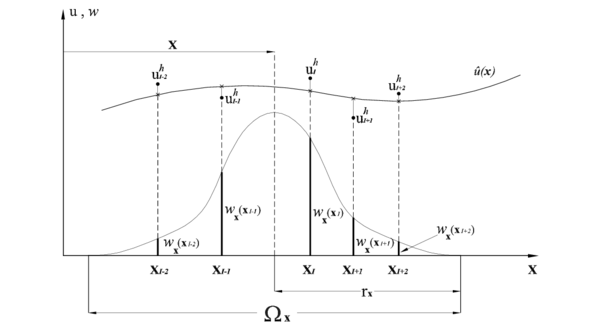
Sin duda el aspecto más destacado de las funciones de forma 2.29 que se acaban de deducir, presente además en todos los métodos sin malla que utilizan una interpolación por mínimos cuadrados, es el no cumplimiento de la propiedad de interpolación, es decir:

$\phi _{I}(\mathbf {x} _{J})\neq \delta _{IJ}$

(2.41)

siendo el símbolo ${\textstyle \delta _{IJ}}$ la delta de Kronecker. Como consecuencia de lo anterior, ver figura 3 , el valor de la función incógnita en el nodo ${\textstyle I}$ es distinto del valor de la aproximación en ese punto

$u(\mathbf {x} _{I})=u_{I}^{h}\neq {\widehat {u}}(\mathbf {x} _{I})$

(2.42)

Por este motivo, los parámetros ${\textstyle u_{I}^{h}}$ no deben ser tratados como valores nodales, sino como contribuciones nodales, en el entendido de que cada nodo ${\textstyle I}$ aporta su contribución ${\textstyle u_{I}^{h}}$ en la construcción de la aproximación ${\textstyle {\widehat {u}}(\mathbf {x)} }$. El subíndice que acompaña a la función de ponderación en la figura 3 indica el centro del subdominio de influencia y su argumento el punto donde esta se evalúa.

Figura 3: Aproximacion por minimos cuadrados ponderados tipo MLS

2.1.6 Continuidad y derivabilidad

La continuidad de la aproximación moving least squares está supeditada a la regularidad de las funciones de la base de interpolación ${\textstyle {\mathcal {P}}=:\left\{p_{i}(\mathbf {x} )\right\}_{i=1}^{m}}$ y de la función de ponderación ${\textstyle w(\mathbf {x-x} _{I})}$. Se puede comprobar sin mayor dificultad, que para un caso en que ${\textstyle \left\{p_{i}(\mathbf {x} )\right\}_{i=1}^{m}\in C^{q}(\Omega )}$ y ${\textstyle w(\mathbf {x-x} _{I})\in C^{r}(\Omega )}$, entonces la aproximación global MLS ${\textstyle Gu(\mathbf {x} )\in C^{\min(q,r)}}$.

La derivada parcial de la función de forma, en la aproximación MLS, se obtiene como (recuérdese la expresión 2.29):

$\phi _{I,j}\left(\mathbf {x} \right)={\stackrel {m}{\underset {k=1}{\sum }}}{\stackrel {m}{\underset {i=1}{\sum }}}p_{i,j}\left(\mathbf {x} \right)\left(A_{ik}^{-1}\left(\mathbf {x} \right)B_{kI}\left(\mathbf {x} \right)\right)+$ (2.43) $+p_{i}\left(\mathbf {x} \right)\left(A_{ik,j}^{-1}\left(\mathbf {x} \right)B_{kI}\left(\mathbf {x} \right)+A_{ik}^{-1}\left(\mathbf {x} \right)B_{kI,j}\left(\mathbf {x} \right)\right)$

donde

$A_{ik,j}^{-1}\left(\mathbf {x} \right)=-A_{ik}^{-1}\left(\mathbf {x} \right)A_{ik,j}\left(\mathbf {x} \right)A_{ik}^{-1}\left(\mathbf {x} \right)$

(2.44)

y el subíndice que sigue a la coma, representa la derivada respecto de la coordenada espacial ${\textstyle j-{\acute {e}}sima}$, es decir ${\textstyle \left({\hbox{ }}\right)_{,j}=\partial \left({\hbox{ }}\right)/\partial x^{j}}$. Las derivadas de orden superior se pueden obtener repitiendo el mismo procedimiento, sin embargo, a pesar del grado de sistematización que se puede lograr con este proceso, el coste computacional sigue siendo bastante elevado. Al respecto, vale la pena tener presente el hecho de que para calcular las derivadas parciales de las componentes de las matrices ${\textstyle A^{-1}(\mathbf {x)} }$ y ${\textstyle B(\mathbf {x)} }$, es necesario calcular previamente la derivada de la función de ponderación ${\textstyle w(\mathbf {x-x} _{I}\mathbf {)} }$.

Para lograr de forma más sencilla la derivada de la función de forma, Nayroles [69], primer investigador que utilizó la técnica MLS en el contexto de los métodos sin malla, propuso considerar constante el vector de parámetros desconocidos ${\textstyle \mathbf {\alpha } ({\overline {\mathbf {x} }})}$ en la aproximación 2.3. Como consecuencia de este planteamiento, la derivada de las función de forma se aproxima como

$\phi _{I,j}\left(\mathbf {x} \right)\approx {\stackrel {m}{\underset {k=1}{\sum }}}{\stackrel {m}{\underset {i=1}{\sum }}}p_{i,j}\left(\mathbf {x} \right)\left(A_{ik}^{-1}\left(\mathbf {x} \right)B_{kI}\left(\mathbf {x} \right)\right)$

(2.45)

lo que supone un considerable ahorro de cálculo en comparación con 2.43. Sin embargo, tal como se demuestra en [8], en el contexto del método sin malla (EFG), despreciar el término ${\textstyle \left(A_{ik,j}^{-1}\left(\mathbf {x} \right)B_{kI}\left(\mathbf {x} \right)+A_{ik}^{-1}\left(\mathbf {x} \right)B_{kI,j}\left(\mathbf {x} \right)\right)}$ cuando se utiliza una interpolación por MLS puede provocar errores que afectan la exactitud de la solución. Independiente del método sin malla que se utilice, lo que si parece estar claro es que, cuando se utiliza una interpolación por MLS se debe dedicar un esfuerzo adicional para desarrollar técnicas que permitan evaluar la derivada de la función de forma de una manera razonable, es decir, sin afectar la exactitud ni la versatilidad del método. Al respecto, en trabajos como [12] [41] y [17] se pueden encontrar técnicas que permiten obtener una reducción en el coste computacional de la derivación de la aproximación MLS.

2.1.7 Aproximación con función de ponderación smooth (SPH)

El método sin malla más antiguo que recoge la literatura científica se denomina smooth particle hydrodynamics method, también conocido con el acrónimo de SPH. Desde sus comienzos [59] [34] hasta hoy en día, el método ha sido desarrollado para simular fenómenos astrofísicos como la evolución, rotación y colisiones de estrellas, a partir de un set de puntos o partículas distribuidas de manera irregular. Si bien en sus inicios el método no estaba pensado para ser utilizado en medios continuos, pues la exactitud en sus resultados estaba condicionada a determinados tipos de problemas (número reducido de partículas y ausencia de contornos), paulatinamente se ha comenzado a investigar su utilización en la simulación dinámica de materiales que presentan fragmentación o fractura [87] y en la simulación de procesos de extrusión de metales [15].

En el método SPH la aproximación ${\textstyle {\widehat {u}}(\mathbf {x)} }$ , ${\textstyle L:C^{0}(\Omega )\rightarrow C^{m}(\Omega )}$ se define como [35] [63] [64] [65]:

${\widehat {u}}(\mathbf {x)} :={\underset {\Omega }{\int }}w(\mathbf {x-y} )u(\mathbf {y)} d\mathbf {y}$

(2.46)

donde ${\textstyle {\widehat {u}}(\mathbf {x)} }$ es la aproximación de la función ${\textstyle u(\mathbf {x)} }$ y ${\textstyle w(\mathbf {x-y} )}$ es la función de ponderación smooth. Es de interés destacar, que la aproximación en el método SPH coincide a efectos prácticos con la definición del producto de convolución de dos funciones

$u(\mathbf {x} )*w(\mathbf {x)} ={\stackrel {\infty }{\underset {-\infty }{\int }}}u(\mathbf {y} )w(\mathbf {x-y)} d\mathbf {y}$

(2.47)

en donde los límites de la integral pueden particularizarse para una zona de interés ${\textstyle \Omega }$, si la función ${\textstyle w(\mathbf {x-y)} }$ cumple los requisitos de la función de ponderación definidos en el apartado 2.1.1. En el método SPH, la función de ponderación utilizada se conoce como spline¹ SPH [63].

Para aproximar numéricamente la integral 2.46 el método considera el dominio de solución ${\textstyle \Omega }$, dividido en ${\textstyle N}$ partículas elementales de masas ${\textstyle m_{1}}$, ${\textstyle m_{2}}$, ....., ${\textstyle m_{N}}$, siendo la contribución a la integral de una partícula ${\textstyle I}$, cuyo volumen es ${\textstyle \Delta V_{I}}$, masa ${\textstyle m_{I}}$ y su centro de masa ubicado en ${\textstyle \mathbf {x} _{I}}$

$w(\mathbf {x} -\mathbf {x} _{I})u(\mathbf {x} _{I}){\frac {m_{I}}{\rho (\mathbf {x} _{I})}}$

(2.48)

donde ${\textstyle \rho (\mathbf {x} _{I})}$ es la densidad en el nodo ${\textstyle \mathbf {x} _{I}}$. De esta forma se obtiene la aproximación ${\textstyle {\widehat {u}}(\mathbf {x)} }$ en término de los valores nodales ${\textstyle u_{I}^{h}\equiv u(\mathbf {x} _{I})}$ de la siguiente manera

${\widehat {u}}(\mathbf {x)=} {\underset {I\in {\mathcal {S}}(\mathbf {x} )}{\sum }}w(\mathbf {x} -\mathbf {x} _{I})u_{I}^{h}\Delta V_{I}={\underset {I\in {\mathcal {S}}(\mathbf {x} )}{\sum }}\phi _{I}(\mathbf {x} )u_{I}^{h}$

(2.49)

donde ${\textstyle {\mathcal {S}}(\mathbf {x} )}$ representa el conjunto de puntos o nodos de la partición pertenecientes al dominio de influencia de ${\textstyle \mathbf {x} }$, tal que ${\textstyle \mathbf {x} _{I}\in }$ ${\textstyle \Omega _{\mathbf {x} }}$ , ${\textstyle \Delta V_{I}={\frac {m_{I}}{\rho (\mathbf {x} _{I})}}}$ y las funciones de forma de la aproximación SPH

$\phi _{I}(\mathbf {x} ):=w(\mathbf {x} -\mathbf {x} _{I})\Delta V_{I}$

(2.50)

Si bien es cierto, la aproximación 2.49 utilizada en el método SPH permite evaluar numéricamente la integral 2.46 sin la necesidad de una malla o una conexión fija entre los nodos, es necesario subdividir el dominio ${\textstyle \Omega }$ y contar con técnicas robustas que permitan asignar a cada nodo su correspondiente ${\textstyle \Delta V_{I}}$². Desarrollar estas técnicas resulta costoso y difícil de abordar, por ejemplo, en dominios 3D de geometrías irregulares.

(¹) Las características de esta función de ponderación se analizan en el apartado 2.2

(²) $\Delta V_{I}$ representa una medida del dominio que rodea al nodo $I$

2.1.8 Propiedades de la aproximación SPH

Al igual que en el caso de la aproximación MLS, el método SPH en general no cumple la propiedad de interpolación, es decir ${\textstyle u_{I}^{h}\neq {\widehat {u}}(\mathbf {x} _{I})}$, por lo que 2.50 no puede ser entendido como un verdadero interpolante. Sin embargo, es en la propiedad de consistencia de la aproximación donde el método SPH se resiente.

Que la aproximación 2.46 sea consistente, implica por ejemplo, que las funciones constantes y lineales deberán ser representadas de manera exacta. En una dimensión, tomando ${\textstyle u(y)=1}$ y ${\textstyle u(y)=y}$, significa que se deben verificar respectivamente las ecuaciones

${\underset {\Omega }{\int }}w(x-y)1dy=1$

(2.51)

${\underset {\Omega }{\int }}w(x-y\mathbf {)} ydy=x$

(2.52)

La ecuación 2.51 o consistencia de orden cero, se verifica automáticamente al coincidir con la propiedad (iii) de normalidad de la función de ponderación. Para aclarar si se verifica la consistencia lineal, es decir 2.52, adviértase que 2.51 implica

${\underset {\Omega }{\int }}w(x-y\mathbf {)} xdy\mathbf {=} x$

(2.53)

restando 2.53 de 2.52, se obtiene

${\underset {\Omega }{\int }}(x-y\mathbf {)} w(x-y\mathbf {)} dy\mathbf {=} 0$

(2.54)

La ecuación 2.54 es el momento de primer orden de la función de ponderación y su cumplimiento obliga a que esta sea simétrica respecto al origen. Como se verá posteriormente, la mayoría de funciones de ponderación satisfacen esta condición y, por lo tanto, la forma continua de la aproximación SPH con función de ponderación `smooth' posee consistencia de primer orden. Sin embargo, lo anterior no garantiza la consistencia lineal, ni siquiera en 1D, de la forma discreta 2.49.

En una dimensión, utilizando la regla del trapecio para la cuadratura numérica de 2.51 y 2.54, la versión discreta de las condiciones de consistencia son

${\underset {I\in {\mathcal {S}}\left(x\right)}{\sum }}w(x-x_{I})\Delta x_{I}={\underset {I\in {\mathcal {S}}\left(x\right)}{\sum }}\phi _{I}(x)=1$

(2.55)

${\underset {I\in {\mathcal {S}}\left(x\right)}{\sum }}(x-x_{I})w(x-x_{I})\Delta x_{I}={\underset {I\in {\mathcal {S}}\left(x\right)}{\sum }}(x-x_{I})\phi _{I}(x)=0$

(2.56)

donde para un set de nodos ${\textstyle x_{I}}$ numerados secuencialmente

$\Delta x_{I}={\frac {x_{I+1}-x_{I-1}}{2}}$

(2.57)

Se puede comprobar fácilmente, para una distribución no uniforme de nodos, que la ecuación 2.56 no se satisface. Considérese, por ejemplo, la disposición de cuatro nodos que se ilustra en la figura 4(a), donde se prescriben las condiciones de consistencia en ${\textstyle x=0}$. Particularizando 2.56 para el nodo ${\textstyle I}$, se tiene

${\underset {J\in {\mathcal {S}}\left(x_{I}\right)}{\sum }}(x_{I}-x_{J})w(x_{I}-x_{J})\Delta x_{J}=0$

(2.58)

lo que equivale a

$\left(-\Delta x\right)w_{I-1}\Delta x_{I-1}+\left(2\Delta x\right)w_{I+1}\Delta x_{I+1}=0$

(2.59)

Para una función de ponderación como el spline SPH, la expresión 2.59 es igual a ${\textstyle \Delta x/6\neq 0}$, por tanto, la condición de consistencia lineal no se satisface .

La situación se deteriora todavía más en el contorno. Para el caso de la figura 4(b), las condiciones de consistencia lineal en ${\textstyle I}$ exigen que

$\left(-\Delta x\right)w_{I-1}\Delta V_{I-1}=0$

(2.60)

lo que supone el cumplimiento de ${\textstyle w_{I-1}=0}$, sin embargo, esto es imposible de lograr con una función de ponderación que se ajuste a las condiciones (i) a (v) del apartado 2.1.1.

Figura 4: Consistencia lineal de la aproximacion SPH para una distribucion no uniforme de nodos

La derivada espacial de la aproximación SPH, respecto de la coordenada ${\textstyle x^{j}}$, se obtiene reemplazando ${\textstyle {\widehat {u}}_{,j}(\mathbf {x} )}$ por ${\textstyle {\widehat {u}}(\mathbf {x} )}$ en 2.46 y hallando el estimador de esta nueva relación como

${\widehat {u}}_{,j}(\mathbf {x} ):={\underset {\Omega }{\int }}w(\mathbf {x-y} )u_{,j}(\mathbf {y)} d\mathbf {y}$

(2.61)

Además se puede demostrar, después de cierta manipulación algebraica [87], que

${\widehat {u}}_{,j}(\mathbf {x} ):=-{\underset {\Omega }{\int }}w_{,j}(\mathbf {x-y} )u(\mathbf {y)} d\mathbf {y}$

(2.62)

por lo que la derivada de la aproximación, en su forma continua, se obtiene a partir de los valores de la función y de la derivada de la función de ponderación. Como antes, la forma discreta de 2.62 se obtiene a través de una suma sobre los puntos de interpolación

${\widehat {u}}_{,j}(\mathbf {x} )={\underset {I\in {\mathcal {S}}(\mathbf {x} )}{\sum }}w_{,j}(\mathbf {x-x} _{I})u_{I}^{h}\Delta V_{I}={\underset {I\in {\mathcal {S}}(\mathbf {x} )}{\sum }}\phi _{I,j}(\mathbf {x} )u_{I}^{h}$

(2.63)

Finalmente, en el método SPH, las expresiones 2.49 y 2.63 son colocadas en ${\textstyle \mathbf {x} _{I}}$ para obtener el sistema discreto de ecuaciones en derivadas parciales, cuya resolución permite obtener los coeficientes buscados ${\textstyle u_{I}^{h}}$.

2.1.9 Aproximación mediante el operador RK

El operador tipo reproducing kernel (RK) o núcleo generador es una clase de operador que permite, integrando sobre una función kernel ${\textstyle {\widehat {w}}(\mathbf {x-y,} r)}$, reproducir una función ${\textstyle u(\mathbf {x} )}$ como

$u(\mathbf {x} )\cong {\widehat {u}}(\mathbf {x)=} {\underset {\Omega }{\int }}{\widehat {w}}(\mathbf {x-y,} r){u}(\mathbf {y} )d\mathbf {y}$

(2.64)

Un ejemplo clásico de un operador tipo núcleo generador, que sirve para comprender el estudio y desarrollo del método sin malla denominado reproducing kernel particle method (RKPM)[50] [51] [54] [55], es la transformada de Fourier. El método RKPM surge como alternativa a la aproximación SPH, para corregir los problemas de consistencia y de precisión en la solución en los contornos o cuando se utiliza un número pequeño de partículas. De esta forma, la aproximación de la función incógnita sigue un planteamiento similar al presentado en el método SPH, utilizándose esta vez una función de ponderación modificada ${\textstyle {\widehat {w}}(\mathbf {x-y,} r)}$, o reproducing kernel, que incorpora las correcciones necesarias para mejorar la aproximación.

Para comprender el funcionamiento de la técnica de aproximación utilizada en el método RKPM, a continuación se ejemplifica su uso para reproducir la función ${\textstyle u(\mathbf {x)} }$, como una suma de funciones linealmente independientes, es decir

$u(\mathbf {x} )\cong {\widehat {u}}(\mathbf {x} )=\mathbf {p} ^{T}(\mathbf {x} )\mathbf {\alpha } (\mathbf {x} )$

(2.65)

donde los vectores ${\textstyle \mathbf {p} ^{T}(\mathbf {x} )}$ y ${\textstyle \mathbf {\alpha } (\mathbf {x} )}$ se definen como en 2.5 y 2.6. El vector de parámetros desconocidos ${\textstyle \mathbf {\alpha } (\mathbf {x} )}$, que en el apartado 2.1.1. se ha calculado mediante la técnica MLS, se obtiene multiplicando en ambos lados de 2.65 por ${\textstyle \mathbf {p} (\mathbf {y} )}$ y aplicando la integral de la función kernel ${\textstyle w_{r}\left({\frac {\mathbf {x-y} }{r}}\right)}$, es decir¹

${\underset {\Omega _{\mathbf {x} }}{\int }}\mathbf {p(y)u(y} )w_{r}\left({\frac {\mathbf {x-y} }{r}}\right)d\mathbf {y=} \left[{\underset {\Omega _{\mathbf {x} }}{\int }}\mathbf {p(y)p} ^{T}\mathbf {(y)} w_{r}\left({\frac {\mathbf {x-y} }{r}}\right)d\mathbf {y} \right]\mathbf {\alpha } (\mathbf {x} )$

(2.66)

donde se define la función

$\mathbf {c(x)=} {\underset {\Omega _{\mathbf {x} }}{\int }}\mathbf {p(y)p} ^{T}\mathbf {(y)} w_{r}\left({\frac {\mathbf {x-y} }{r}}\right)d\mathbf {y}$

(2.67)

que permite obtener

$\mathbf {\alpha } (\mathbf {x} )=\mathbf {c} ^{-1}\mathbf {(x)} {\underset {\Omega _{\mathbf {x} }}{\int }}\mathbf {p(y)} w_{r}\left({\frac {\mathbf {x-y} }{r}}\right)\mathbf {u(y} )d\mathbf {y}$

(2.68)

Reemplazando 2.68 en 2.65 se tiene finalmente

${\widehat {u}}(\mathbf {x} )={\underset {\Omega _{\mathbf {x} }}{\int }}\mathbf {p} ^{T}(\mathbf {x} )\mathbf {c} ^{-1}\mathbf {(x)p(y)} w_{r}\left({\frac {\mathbf {x-y} }{r}}\right)\mathbf {u(y} )d\mathbf {y=} {\underset {\Omega _{\mathbf {x} }}{\int }}\digamma \mathbf {(x,y)} w_{r}\left({\frac {\mathbf {x-y} }{r}}\right)\mathbf {u(y} )d\mathbf {y}$

(2.69)

donde la window function o función de ponderación modificada viene dada por

${\widehat {w}}(\mathbf {x-y,} r)=\digamma \mathbf {(x,y)} w_{r}\left({\frac {\mathbf {x-y} }{r}}\right)$

(2.70)

Debe destacarse, que si en la expresión 2.69 se escoge la función de corrección ${\textstyle \digamma \mathbf {(x,y)=} 1}$, entonces se recupera en su forma original la aproximación SPH. La función de ponderación ${\textstyle w_{r}}$ utilizada en la aproximación RKPM, a diferencia del método SPH, incorpora formalmente el radio de influencia o parámetro de dilatación ${\textstyle r}$ como argumento, siendo esta vez

$w_{r}={\frac {1}{r}}w({\frac {\mathbf {x-y} }{r}})$

(2.71)

A pesar de la diferente notación utilizada, ${\textstyle w_{r}}$ posee las mismas propiedades y características de la función de ponderación definidas en 2.1.1.

La función ${\textstyle \digamma \mathbf {(x,y)} }$ depende de los distintos momentos de la función de ponderación [50] [52], siendo para el caso unidimensional con una base polinómica lineal², ${\textstyle \mathbf {p} ^{T}(\mathbf {x} )=\left[1{\hbox{ }}x\right]}$,

$\digamma (x,y)=c_{1}(x)+c_{2}(x)\left({\frac {x-y}{r}}\right)$

(2.72)

con

$c_{1}(x)={\frac {m_{11}}{(m_{0}m_{11}-m_{1}^{2})}}$

(2.73)

$c_{2}(x)={\frac {m_{1}}{(m_{0}m_{11}-m_{1}^{2})}}$

(2.74)

y

$m_{0}(x)={\underset {\Omega _{\mathbf {x} }}{\int }}w_{r}({\frac {x-y}{r}})dy$

(2.75)

$m_{1}(x)={\underset {\Omega _{\mathbf {x} }}{\int }}(x-y)w_{r}({\frac {x-y}{r}})dy$

(2.76)

$m_{11}(x)={\underset {\Omega _{\mathbf {x} }}{\int }}(x-y)^{2}w_{r}({\frac {x-y}{r}})dy$

(2.77)

Incorporando las anteriores expresiones, en la forma continua de la aproximación RKPM 2.69, se obtiene finalmente para el caso unidimensional con una base de interpolación lineal

${\widehat {u}}(x)={\underset {\Omega _{\mathbf {x} }}{\int }}\left[c_{1}(x)+c_{2}(x)\left({\frac {x-y}{r}}\right)\right]w_{r}\left({\frac {x-y}{r}}\right)u\mathbf {(} y)dy$

(2.78)

expresión que pone de manifiesto, el distinto papel que juegan las funciones ${\textstyle c_{1}(x)}$ y ${\textstyle c_{2}(x)}$ en el interior del dominio y en los contornos. Al respecto vale la pena destacar que, mientras en el interior ${\textstyle c_{1}(x)=1}$ y ${\textstyle c_{2}(x)=0}$ (forma original SPH), en el contorno ${\textstyle c_{1}(x)\neq 1}$ y ${\textstyle c_{2}(x)\neq 0}$, lo que indica que la inclusión de la función de corrección ${\textstyle \digamma \mathbf {(x,y)} }$ en la aproximación RKPM juega un papel importante precisamente en los contornos, donde la consistencia la aproximación SPH se deteriora. Utilizando una cuadratura numérica como la regla del trapecio, la forma discreta de la aproximación RKPM 2.78 viene dada por

${\widehat {u}}(x)={\underset {I\in {\mathcal {S}}(\mathbf {x} )}{\sum }}\left[{\bar {c}}_{1}(x)+{\bar {c}}_{2}(x)\left({\frac {x-x_{I}}{r}}\right)\right]w_{r}\left({\frac {x-x_{I}}{r}}\right)u_{I}^{h}\Delta x_{I}={\underset {I\in {\mathcal {S}}(\mathbf {x} )}{\sum }}\phi _{I}(x)u_{I}^{h}$

(2.79)

siendo la función de forma

$\phi _{I}(x)=\left[{\bar {c}}_{1}(x)+{\bar {c}}_{2}(x)\left({\frac {x-x_{I}}{r}}\right)\right]w_{r}\left({\frac {x-x_{I}}{r}}\right)\Delta x_{I}$

(2.80)

de la misma manera, las funciones ${\textstyle {\bar {c}}_{1}(x)}$, ${\textstyle {\bar {c}}_{2}(x)}$ y los distintos momentos de la función de ponderación son esta vez

${\bar {c}}_{1}(x)={\frac {{\bar {m}}_{11}}{({\bar {m}}_{0}{\bar {m}}_{11}-{\bar {m}}_{1}^{2})}}$

(2.81)

${\bar {c}}_{2}(x)={\frac {{\bar {m}}_{1}}{({\bar {m}}_{0}{\bar {m}}_{11}-{\bar {m}}_{1}^{2})}}$

(2.82)

${\bar {m}}_{0}(x)={\underset {I\in {\mathcal {S(}}\mathbf {x} )}{\sum }}w_{r}({\frac {x-x_{I}}{r}})\Delta x_{I}$

(2.83)

${\bar {m}}_{1}(x)={\underset {I\in {\mathcal {S(}}\mathbf {x} )}{\sum }}(x-x_{I})w_{r}({\frac {x-x_{I}}{r}})\Delta x_{I}$

(2.84)

${\bar {m}}_{11}(x)={\underset {I\in {\mathcal {S(}}\mathbf {x} )}{\sum }}(x-x_{I})^{2}w_{r}({\frac {x-x_{I}}{r}})\Delta x_{I}$

(2.85)

(¹) Se introduce como variable de integración $\mathbf {y}$

(²) La obtención de la función $\digamma (\mathbf {x} ,\mathbf {y} )$ en un caso 2D o 3D, se consigue bajo el mismo procedimiento [51]

2.1.10 Propiedades de la aproximación RKPM

La continuidad de la aproximación RKPM, por su construcción, está supeditada a la regularidad de las funciones de la base de interpolación y de la window function, además, para el cómputo de las integrales deberá utilizarse una distribución admisible de puntos, tal como se estipuló en la aproximación MLS. La función de forma 2.80 de la aproximación RKPM no cumple con la identidad de la delta Kronecker, es decir ${\textstyle \phi _{I}(\mathbf {x} _{J})\neq \delta _{IJ}}$, puesto que su valor está ponderado por una función monótona decreciente que se anula únicamente fuera del dominio de influencia del nodo ${\textstyle \mathbf {x} _{J}}$. Sin embargo, la función de corrección permite introducir los cambios necesarios en la aproximación para que esta sea consistente, y así poder reproducir exactamente cualquier función que se incluya en la base de interpolación. Considérese por ejemplo, que se quiere aproximar un conjunto de funciones agrupadas en el vector ${\textstyle \mathbf {u} ^{T}\mathbf {(x)=p} ^{T}\mathbf {(x)=} \left[{\hbox{ }}p_{1}(\mathbf {x} ){\hbox{ }}p_{2}(\mathbf {x} ){\hbox{ .... }}p_{m}(\mathbf {x} ){\hbox{ }}\right]}$, aplicando 2.69 se tiene

$\mathbf {u} ^{T}\mathbf {(x)} ={\underset {\Omega _{\mathbf {x} }}{\int }}\mathbf {p} ^{T}(\mathbf {x} )\mathbf {c} ^{-1}\mathbf {(x)p(y)} w_{r}\left({\frac {\mathbf {x-y} }{r}}\right)\mathbf {u} ^{T}\mathbf {(y} )d\mathbf {y}$ (2.86) $=\mathbf {p} ^{T}(\mathbf {x} )\mathbf {c} ^{-1}\mathbf {(x)} {\underset {\Omega _{\mathbf {x} }}{\int }}\mathbf {p(y)p} ^{T}\mathbf {(y} )w_{r}\left({\frac {\mathbf {x-y} }{r}}\right)d\mathbf {y}$ $=\mathbf {p} ^{T}(\mathbf {x} )\mathbf {c} ^{-1}\mathbf {(x)c(x)}$ $=\mathbf {p} ^{T}(\mathbf {x} )$

La demostración anterior supone utilizar la misma cuadratura numérica para calcular ${\textstyle \mathbf {c} ^{-1}\mathbf {(x)} }$ y ${\textstyle \mathbf {c(x)} }$.

La derivada de la función de forma de la aproximación RKPM, para el caso 1D y base de interpolación lineal, se obtiene diferenciando 2.80 respecto de ${\textstyle x}$ como

$\phi _{I,x}(x)=\left[{\bar {c}}_{1,x}(x)+{\bar {c}}_{2,x}(x)\left({\frac {x-x_{I}}{r}}\right)+{\frac {{\bar {c}}_{2}(x)}{r}}\right]w_{r}\left({\frac {x-x_{I}}{r}}\right)\Delta x_{I}+$ $+\left[{\bar {c}}_{1}(x)+{\bar {c}}_{2}(x)\left({\frac {x-x_{I}}{r}}\right)\right]w_{r,x}(x-x_{I})\Delta x_{I}$

(2.87)

lo que supone calcular las derivadas de las funciones ${\textstyle {\bar {c}}_{1}(x)}$ y ${\textstyle {\bar {c}}_{2}(x)}$, es decir

${\bar {c}}_{1,x}(x)={\frac {{\bar {m}}_{11,x}}{({\bar {m}}_{0}{\bar {m}}_{11}-{\bar {m}}_{1}^{2})}}-{\frac {{\bar {m}}_{11}({\bar {m}}_{0,x}{\bar {m}}_{11}+{\bar {m}}_{0}{\bar {m}}_{11,x}-2{\bar {m}}_{1}{\bar {m}}_{1,x})}{({\bar {m}}_{0}{\bar {m}}_{11}-{\bar {m}}_{1}^{2})^{2}}}$

(2.88)

y

${\bar {c}}_{2,x}(x)={\frac {{\bar {m}}_{1,x}}{({\bar {m}}_{0}{\bar {m}}_{11}-{\bar {m}}_{1}^{2})}}-{\frac {{\bar {m}}_{1}({\bar {m}}_{0,x}{\bar {m}}_{11}+{\bar {m}}_{0}{\bar {m}}_{11,x}-2{\bar {m}}_{1}{\bar {m}}_{1,x})}{({\bar {m}}_{0}{\bar {m}}_{11}-{\bar {m}}_{1}^{2})^{2}}}$

(2.89)

además de la derivada de la función de ponderación. En las expresiones anteriores se ha utilizado la siguiente notación ${\textstyle \left({\hbox{ }}\right)_{,x}=d\left({\hbox{ }}\right)/dx}$.

Al igual que en el caso MLS, el coste computacional asociado al cálculo de la derivada de la función de forma, incluso en el caso anterior 1D, no es para nada despreciable (notar además que es necesario calcular la derivada de los distintos momentos de la función de ponderación ${\textstyle {\bar {m}}_{0,x}}$ , ${\textstyle {\bar {m}}_{1,x}}$ y ${\textstyle {\bar {m}}_{11,x}}$).

2.1.11 Aproximación mediante diferencias finitas generalizada (DFG)

Una forma alternativa de obtener la aproximación de la función incógnita y sus derivadas, en el contexto de los métodos sin malla, es mediante la expresión general de su desarrollo en serie de Taylor alrededor de un punto ${\textstyle {\overline {\mathbf {x} }}}$ del dominio. La técnica así desarrollada se conoce como diferencias finitas generalizadas [45] [47] y ha sido utilizada para resolver diversos tipos de problemas en mecánica aplicada [46] [96] [97]. Con posterioridad esta técnica ha sido utilizada por Liszka y Orkisz, en conjunto con el método de mínimos cuadrados ponderados, para la resolución de problemas de contorno mediante el método sin malla denominado hp-Meshless cloud method [48] [83]. Utilizando un esquema de diferencias finitas generalizadas, y con la notación empleada en esta tesis, la aproximación de la función ${\textstyle u(\mathbf {x)} }$ en un entorno del punto ${\textstyle {\overline {\mathbf {x} }}=\left[{\overline {x}},{\overline {y}}\right]}$ ${\textstyle \in \Omega }$ se construye como¹

${\widehat {u}}(\mathbf {x} )=u({\overline {\mathbf {x} }})+u_{,x}({\overline {\mathbf {x} }}\mathbf {)} ({\overline {x}}-x)+u_{,y}({\overline {\mathbf {x} }}\mathbf {)(} {\overline {y}}-y)+u_{,xx}({\overline {\mathbf {x} }}\mathbf {)} {\frac {({\overline {x}}-x)^{2}}{2}}+$ (2.90) $+u_{,xy}({\overline {\mathbf {x} }}\mathbf {)(} {\overline {x}}-x)({\overline {y}}-y)+u_{,yy}({\overline {\mathbf {x} }}\mathbf {)} {\frac {({\overline {y}}-y)^{2}}{2}}$ $={\stackrel {6}{\underset {i=1}{\sum }}}{\widehat {p}}_{i}(\mathbf {x} ){\widehat {\alpha }}_{i}({\overline {\mathbf {x} }})={\widehat {\mathbf {p} }}^{T}(\mathbf {x} ){\widehat {\mathbf {\alpha } }}({\overline {\mathbf {x} }})$

siendo los vectores

${\widehat {\mathbf {p} }}^{T}(\mathbf {x} )=\left[{\hbox{ }}1{\hbox{ }}({\overline {x}}-x){\hbox{ }}({\overline {y}}-y){\hbox{ }}{\frac {({\overline {x}}-x)^{2}}{2}}{\hbox{ }}({\overline {x}}-x)({\overline {y}}-y){\hbox{ }}{\frac {({\overline {y}}-y)^{2}}{2}}{\hbox{ }}\right]$

(2.91)

${\widehat {\mathbf {\alpha } }}^{T}({\overline {\mathbf {x} }})=\left[{\hbox{ }}u({\overline {\mathbf {x} }}){\hbox{ }}u_{,x}({\overline {\mathbf {x} }}\mathbf {)} {\hbox{ }}u_{,y}({\overline {\mathbf {x} }}\mathbf {)} {\hbox{ }}u_{,xx}({\overline {\mathbf {x} }}\mathbf {)} {\hbox{ }}u_{,xy}({\overline {\mathbf {x} }}\mathbf {)} {\hbox{ }}u_{,yy}({\overline {\mathbf {x} }}\mathbf {)} {\hbox{ }}\right]$

(2.92)

La expresión 2.90 puede ser interpretada como la expansión en serie de Taylor, de la aproximación ${\textstyle {\widehat {u}}(\mathbf {x} )}$, alrededor del punto ${\textstyle \mathbf {x=} {\overline {\mathbf {x} }}}$. El vector ${\textstyle {\widehat {\mathbf {\alpha } }}({\overline {\mathbf {x} }})}$, que contiene los valores de la función desconocida y sus derivadas en ${\textstyle {\overline {\mathbf {x} }}}$, se calcula empleando la técnica de mínimos cuadrados ponderados, de forma semejante a lo expuesto en el apartado 2.1.1. Esta vez, el funcional discreto que minimiza el error cuadrático ponderado es (recuérdese 2.9)

$J_{D}({\widehat {\mathbf {\alpha } }}({\overline {\mathbf {x} }})):={\underset {I\in {\mathcal {S}}({\overline {\mathbf {x} }})}{\sum }}w({\overline {\mathbf {x} }}-\mathbf {x} _{I})\left[u_{I}^{h}-{\stackrel {6}{\underset {i=1}{\sum }}}{\widehat {p}}_{i}(\mathbf {x} _{I}){\widehat {\alpha }}_{i}({\overline {\mathbf {x} }})\right]^{2}$

(2.93)

Derivando 2.93 respecto del vector ${\textstyle {\widehat {\mathbf {\alpha } }}({\overline {\mathbf {x} }})}$ e igualando a cero, se consigue un sistema lineal de ecuaciones que permite finalmente obtener los parámetros desconocidos ${\textstyle \left\{{\widehat {\alpha }}_{i}({\overline {\mathbf {x} }})\right\}_{i=1}^{6}}$. Como el proceso para obtener estos parámetros es semejante al utilizado en la aproximación MLS, no se ha estimado oportuno repetirlo nuevamente para este caso (DFG), además, si en el cálculo de 2.93 intervienen todos los nodos ${\textstyle \mathbf {x} _{I}}$ pertenecientes al subdominio de interpolación ${\textstyle \Omega _{\overline {\mathbf {x} }}}$, las aproximaciones 2.3 y 2.90 son equivalentes. Si por el contrario, no se utilizan todos los nodos que pertenecen al subdominio, las técnicas MLS y DFG entregarán distintas funciones de aproximación. Al respecto debe notarse, que en esta técnica la evaluación de los coeficientes desconocidos requieren de la conectividad de al menos 6 nodos.

(¹) Se ejemplificará, sin pérdida de generalidad, la utilización de DFG para un caso 2D

2.1.12 Aproximación tipo partición de la unidad (PU)

Utilizando el concepto de partición de la unidad, también es posible construir una aproximación de la función desconocida, para que pueda ser utilizada en un método sin malla. Este planteamiento, propuesto inicialmente por [24] y [5], permite además comprender bajo un aspecto más general el funcionamiento de los distintos métodos sin malla. En una partición de la unidad (PU), el dominio ${\textstyle \Omega }$ es cubierto por un número finito de subdominios ${\textstyle \Omega _{I}}$ que se superponen, asociándose a cada uno de ellos una función ${\textstyle \varphi _{I}(\mathbf {x} )}$ diferente de cero sólo sobre ${\textstyle \Omega _{I}}$ (notar la semejanza entre la proposición anterior y la definición de subdominios circulares utilizadas en los métodos sin malla, figura 1). Además, si el dominio ${\textstyle \Omega }$ se discretiza mediante un conjunto de puntos ${\textstyle \mathbf {x} _{I}}$, ${\textstyle I=1,...N}$, siendo ${\textstyle N}$ el número total de puntos, se dice que la familia de funciones ${\textstyle \left\{\varphi _{I}(\mathbf {x} )\right\}_{I=1}^{N}}$ representan una partición de la unidad respecto del conjunto de subdominios ${\textstyle \left\{\Omega _{I}\right\}_{I=1}^{N}}$ si

${\stackrel {N}{\underset {I=1}{\sum }}}\varphi _{I}(\mathbf {x} )=1$

(2.94)

Debe destacarse que la propiedad anterior de las funciones ${\textstyle \varphi _{I}(\mathbf {x} )}$, es idéntica a la condición de consistencia de orden cero (2.55) que deben cumplir las funciones de forma en una aproximación SPH. También las funciones de forma en una aproximación MLS son una partición de la unidad, puesto que por condición de consistencia cumplen

${\stackrel {N}{\underset {I=1}{\sum }}}\phi _{I}(\mathbf {x} )x_{I}^{p}=x^{p}$

(2.95)

siendo ${\textstyle p}$ el grado del monomio de la base de interpolación, en particular, si ${\textstyle p=0}$ (es decir función constante) se tiene

${\stackrel {N}{\underset {I=1}{\sum }}}\phi _{I}(\mathbf {x} )\cdot 1={\stackrel {N}{\underset {I=1}{\sum }}}\phi _{I}(\mathbf {x} )=1$

(2.96)

De esta forma, se pueden construir particiones de la unidad a partir de las aproximaciones tipo núcleo generador y MLS analizadas anteriormente. En particular, en el método denominado hp clouds [26], se utilizan las funciones de forma MLS (2.29) para construir la partición unitaria, formando subdominios o nubes asociadas a parámetros ${\textstyle h}$ y ${\textstyle p}$ que permiten plantear, al igual que en el MEF, procedimientos adaptativos de la solución aumentando el número de puntos utilizados en la discretización o por el contrario aumentando el grado del polinomio de interpolación. En el método hp, la aproximación de la función ${\textstyle u(\mathbf {x)} }$ viene dada por

${\widehat {u}}(\mathbf {x} )={\underset {I\in {\mathcal {S}}(\mathbf {x} )}{\sum }}\phi _{I}^{k}(\mathbf {x} )\left(u_{I}^{h}+{\stackrel {M}{\underset {i=1}{\sum }}}b_{Ii}L_{i}(\mathbf {x} )\right)={\underset {I\in {\mathcal {S}}(\mathbf {x} )}{\sum }}\left(\phi _{I}^{k}(\mathbf {x} )u_{I}^{h}+\phi _{I}^{k}(\mathbf {x} ){\stackrel {M}{\underset {i=1}{\sum }}}b_{Ii}L_{i}(\mathbf {x} )\right)$ $={\underset {I\in {\mathcal {S}}(\mathbf {x} )}{\sum }}\phi _{I}^{k}(\mathbf {x} )u_{I}^{h}+{\underset {I\in {\mathcal {S}}(\mathbf {x} )}{\sum }}\phi _{I}^{k}(\mathbf {x} ){\stackrel {M}{\underset {i=1}{\sum }}}b_{Ii}L_{i}(\mathbf {x} )$

(2.97)

donde el superíndice ${\textstyle k}$ de las funciones de forma indica el orden del polinomio base de interpolación¹, agregándose a la formulación clásica MLS, el conjunto de funciones ${\textstyle L_{i}(\mathbf {x} )}$ que constituyen la base extrínseca y que contienen polinomios² de orden superior al de las funciones ${\textstyle \phi _{I}^{k}(\mathbf {x} )}$ (base intrínseca), o cualquier otro tipo de función que se considere adecuada para la aproximación (enhancement functions). Debe destacarse que en el caso de la aproximación utilizada en el método ${\textstyle hp}$, además de calcular los ${\textstyle m}$ parámetros para la base intrínseca (recuérdese el proceso de inversión de la matriz ${\textstyle \mathbf {A(x} )}$ en la técnica MLS), es necesario resolver un sistema lineal de ecuaciones para obtener el conjunto de ${\textstyle M}$ parámetros ${\textstyle b_{Ii}}$ de la base extrínseca, lo que se traduce en definitiva en un aumento del coste computacional.

La idea principal de la formulación 2.97, es poder añadir elementos de forma jerárquica a la familia de funciones que representan la partición de la unidad ${\textstyle \left\{\phi _{I}^{k}(\mathbf {x} )\right\}_{I=1}^{N}}$, de manera que el nuevo set de funciones pueda reproducir polinomios de grado ${\textstyle p\geq k}$. Además, la base extrínseca puede ajustarse para cada nodo añadiendo términos extra, sin que las condiciones de continuidad y derivabilidad se vean afectadas [11], con ello se consigue la implementación de esquemas de refinamiento tipo ${\textstyle p}$. Para implementar un refinamiento tipo ${\textstyle h}$, los autores proponen un estimador del error en la solución a posteriori, que permite introducir nuevos nodos en aquellas zonas de interés del dominio [26].

Respecto de las propiedades de la aproximación tipo partición de la unidad, es fácil verificar que se deben respetar las mismas condiciones que garanticen la existencia de las funciones de la base intrínseca. Para el caso en que estas correspondan a las funciones de forma MLS, serán las indicadas en el apartado 2.1.1.

(¹) El caso particular $k=0$, corresponde a las funciones de forma del interpolanate de Shepard

(²) En [24] se utilizan polinomios de Legendre

2.2 Funciones de ponderación

Cuando se analizan las distintas características de las aproximaciones utilizadas en los métodos sin malla, es fácil identificar un aspecto común en todas ellas, esto es, la utilización de una función de ponderación ${\textstyle w(\mathbf {x-x} _{I})}$. Esta función, además de conferir el carácter local a la aproximación, permite distribuir o ponderar el error cometido en la interpolación, controlando el tamaño del subdominio o nube según su radio de acción. En principio su elección es arbitraria, siempre que se respeten las condiciones (i) a (v) del apartado 2.1.1 y que la función y sus derivadas sean continuas en el grado deseado. El grado de continuidad requerido dependerá, en general, del tipo de aproximación meshless que se utilice, del orden de la ecuación diferencial del problema y del esquema de discretización empleado.

La función de ponderación, por construcción, posee una forma bastante característica, es decir presenta un valor máximo en el entorno del punto ${\textstyle \mathbf {x} }$ donde se requiere evaluar la aproximación, con una tendencia decreciente a medida que aumenta la distancia al punto en cuestión. Recordando que las aproximaciones analizadas se encuentran asociadas a la minimización del error a través de un funcional, la interpretación práctica de esta tendencia o forma de la función de ponderación no es otra que buscar penalizar el error cometido en la interpolación, proporcionalmente a la distancia del punto donde se está evaluando. La forma y tamaño de la función de ponderación se pueden regular a través de ciertos parámetros, propios de cada función, que entre otras cosas deben además garantizar la no singularidad del problema. Uno de estos parámetros, que además proporciona una idea del tamaño de los subdominios, es el que se conoce como radio de influencia o parámetro de dilatación ${\textstyle r}$. El radio de influencia juega un papel importante en la selección de los subdominios ${\textstyle \Omega _{I}}$ controlando el número de puntos ${\textstyle n}$ que lo integran, de modo que ${\textstyle n\geq m}$, siendo ${\textstyle m}$ la dimensión de la base de interpolación, además su valor tiene una cota máxima para conseguir una mayor eficiencia computacional.

Para conseguir una completa y adecuada definición de todos los parámetros que intervienen en una función de ponderación, existen dos alternativas:

1. Definir a priori el número de puntos que componen el subdominio y a partir de aquí sacar los parámetros de la función (como por ejemplo el radio de influencia asociado a cada subdominio).
2. Determinar o fijar los parámetros y a partir de ellos obtener los puntos que componen el subdominio.

Cuando se utiliza una aproximación basada en MLS, la primera alternativa resulta más segura de cara a cerciorarse que se tendrá en todos los casos, el número de puntos suficientes en el subdominio garantizando de esta forma la no singularidad del problema, acorde con la dimensión de la base de interpolación. Esta alternativa, será la utilizada en el desarrollo de los ejemplos presentados en esta tesis.

2.2.1 Propiedades y construcción

Debido al carácter local de la aproximación, las funciones de ponderación deberán ser no nulas únicamente en un subdominio ${\textstyle \Omega _{\mathbf {x} }}$ cumpliéndose

$w(\mathbf {x-x} _{I})\equiv w(d)=\left\{{\begin{array}{ll}w(d)&{\hbox{ si }}d\leq r\\0&{\hbox{ si }}d>r\end{array}}\right.$

(2.98)

donde ${\textstyle d=\left\|\mathbf {x-x} _{I}\right\|}$ es la distancia entre el punto ${\textstyle \mathbf {x} }$ y un punto ${\textstyle \mathbf {x} _{I}}$ de la partición, pertenecientes al subdominio ${\textstyle \Omega _{\mathbf {x} }}$. En lo sucesivo ${\textstyle w_{I}}$ denotará la función de ponderación asociada a un nodo ${\textstyle \mathbf {x} _{I}}$, es decir cuyo valor máximo se encuentra en ${\textstyle \mathbf {x} =\mathbf {x} _{I}}$. Consultando los diversos desarrollo sobre métodos sin malla, las funciones de ponderación mayoritariamente utilizadas en la práctica resultan ser del tipo [8],[93]

$w(\mathbf {x} -\mathbf {x} _{I})\equiv w_{I}(d^{2k})$

(2.99)

con ${\textstyle w_{I}(d^{2k})}$ continua, así como sus ${\textstyle m-1}$ primeras derivadas. A continuación se estudian las condiciones que debe satisfacer ${\textstyle k}$ (entero positivo) para que las primeras ${\textstyle s}$ derivadas de la función de ponderación ${\textstyle w_{I}\left(d^{2k}\right)}$, con respecto a cada componente del vector ${\textstyle \mathbf {x} }$, sean continuas en dicho punto.

Considérese, en primer lugar, la derivada primera de la función ${\textstyle w_{I}\left(d^{2k}\right)}$ respecto de una componente cualquiera ${\textstyle x}$ del vector de posición ${\textstyle \mathbf {x} }$

$w_{I,x}=2kd^{2k-1}w_{I,d}d_{,x}=2k\left(x^{j}-x_{I}\right)d^{2k-2}w_{I,d}$

(2.100)

Adviértase que el límite de ${\textstyle \left(x-x_{I}\right)/d}$, a medida que ${\textstyle x}$ tiende a ${\textstyle x_{I}}$, no existe. Por consiguiente, la derivada primera sólo existirá para ${\textstyle k>1/2}$.

Para la derivada segunda, de la función de ponderación ${\textstyle w_{I}\left(d^{2k}\right)}$ respecto de ${\textstyle x}$, se tiene

$w_{I,xx}=2k\left(2k-2\right)\left(x-x_{I}\right)^{2}d^{2k-4}w_{I,d}+2kd^{2k-2}w_{I,d}+$ (2.101) $+2k\left(x-x_{I}\right)^{2}d^{4k-3}w_{I,dd}$

La derivada anterior existe siempre que ${\textstyle k>1}$ (para valores inferiores el segundo sumando del miembro derecho de 2.101 da lugar a problemas de continuidad). Por inducción, se puede demostrar que la derivada ${\textstyle n-}$ésima de la función de ponderación respecto de cada componente del vector ${\textstyle \mathbf {x} }$ existe si ${\textstyle k>n/2}$ [9].

2.2.2 Tipos de funciones de ponderación

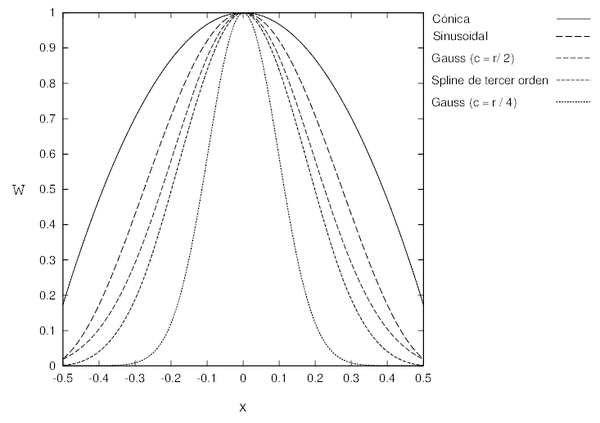
Habiendo revisado las principales características teóricas que han de verificar estas funciones, a continuación, se presentan las funciones de ponderación comunmente más utilizadas en las distintas aproximaciones sin malla. Considerando en primer término las funciones de ponderación cuyo soporte es circular o esférico (ver figuras 1,2), existe una función de interpolación que se aplica específicamente en la aproximación SPH, conocida como spline SPH [63], cuya expresión es

• Spline SPH

$w(q)={\frac {2}{3r}}\left\{{\begin{array}{ll}1-{\frac {3}{2}}\left(q\right)^{2}+{\frac {3}{4}}\left(q\right)^{3}&{\hbox{ si }}q\leq 1\\{\frac {1}{4}}\left(2-\left(q\right)^{3}\right)&{\hbox{ si }}1\leq q\leq 2\\0&{\hbox{ si }}q\geq 2\end{array}}\right.$

(2.102)

donde ${\textstyle q=d/\varrho }$ , siendo ${\textstyle \varrho }$ una medida del tamaño de su soporte.

Utilizando como argumento de la función de ponderación ${\textstyle {\overline {d}}=d/d_{\max }}$ (${\textstyle d_{\max }}$ se escoge igual al radio de influencia ${\textstyle r}$), además del spline SPH, se destacan por su mayor utilización las siguientes funciones de ponderación

• Función triangular

$w({\overline {d}})=1-{\overline {d}}$

(2.103)

la que ha pesar de su sencillez tiene la desventaja que su derivada no es continua en ${\textstyle d=0}$.

• Función cónica

$w({\overline {d}})=1-\left({\overline {d}}\right)^{2k}$

(2.104)

la que constituye una generalización de la función triangular, su continuidad aumenta paralelamente con el exponente ${\textstyle 2k}$, aunque en la práctica ${\textstyle k=1}$. Según Duarte [25], esta función da lugar a funciones de forma que pueden ser integradas con mayor precisión en el caso de utilizar como esquema de discretización el método de Galerkin¹.

• Función sinusoidal

$w({\overline {d}})={\frac {1}{2}}\left(1+\cos(\pi {\overline {d}})\right)$

(2.105)

• Spline de tercer orden

$w({\overline {d}})=\left\{{\begin{array}{ll}{\frac {2}{3}}-4\left({\overline {d}}\right)^{2}+4\left({\overline {d}}\right)^{3}&{\hbox{ si }}{\overline {d}}\leq {\frac {1}{2}}\\{\frac {4}{3}}-4\left({\overline {d}}\right)+4\left({\overline {d}}\right)^{2}-{\frac {4}{3}}\left({\overline {d}}\right)^{3}&{\hbox{ si }}{\frac {1}{2}}<{\overline {d}}\leq 1\\0&{\hbox{ si }}{\overline {d}}>1\end{array}}\right.$

(2.106)

• Spline de cuarto orden

$w({\overline {d}})=\left\{{\begin{array}{ll}1-6\left({\overline {d}}\right)^{2}+8\left({\overline {d}}\right)^{3}-3\left({\overline {d}}\right)^{4}&{\hbox{ si }}{\overline {d}}\leq 1\\0&{\hbox{ si }}{\overline {d}}>1\end{array}}\right.$

(2.107)

tanto el spline de tercer como de cuarto orden se utilizan para problemas en los que se requiere ${\textstyle C^{2}}$.

• Función exponencial o de Gauss

$w(d^{2k})=\left\{{\begin{array}{ll}{\frac {\exp(-(d/c)^{2k})-\exp(-(r/c)^{2k})}{(1-\exp(-(r/c)^{2k})}}&{\hbox{ si }}d\leq r\\0&{\hbox{ si }}d>r\end{array}}\right.$

(2.108)

el parámetro ${\textstyle c}$ (que se denomina factor de apuntamiento) y el exponente ${\textstyle k}$, determinan la forma de la función de ponderación, en definitiva los pesos relativos. En el caso del factor de apuntamiento, su valor determina por ejemplo, el que los pesos de la función de ponderación sean mayores, tanto cerca como lejos de ${\textstyle \mathbf {x} _{I}}$, en la medida en que ${\textstyle c}$ aumenta. En general, no existe un criterio o método para fijar ${\textstyle c}$, siendo su valor más bien arbitrario. En la literatura pueden encontrarse diversas proposiciones o recomendaciones para fijar su valor, así por ejemplo, Belytschko [8] sugiere

$c=\beta c_{I}{\hbox{ , }}1\leq \beta \leq 2$

(2.109)

con

$c_{I}=\max _{J\in S_{J}}\left\|\mathbf {x} _{J}-\mathbf {x} _{I}\right\|$

(2.110)

siendo ${\textstyle S_{J}}$ el menor conjunto de puntos necesarios para determinar un polígono alrededor de ${\textstyle \mathbf {x} _{I}}$. Oñate [74] propone determinar ${\textstyle c}$ en función del radio de influencia como

$c=\beta r{\hbox{ , }}\beta =0.5$

(2.111)

mientras que Hegen [36] utiliza

$c=\beta r{\hbox{ , }}\beta =0.25$

(2.112)

Con posterioridad Atluri [4] propone la utilización de la siguiente igualdad para la selección de los parámetros ${\textstyle c}$ y ${\textstyle r}$ de la función de Gauss

${\frac {r}{c}}={\frac {L}{2}}{\sqrt {\frac {\pi N}{mS}}}$

(2.113)

siendo ${\textstyle L}$, ${\textstyle S}$, una longitud característica y el area del dominio de análisis, ${\textstyle N}$ el número total de nodos utilizados y ${\textstyle m}$ como antes el número de términos utilizados en la función base de interpolación, para el caso de una aproximación MLS. Reordenando la expresión 2.113, el valor para el factor ${\textstyle \beta }$ resulta ser esta vez

$c=\beta r{\hbox{ , }}\beta ={\frac {2}{L}}{\sqrt {\frac {mS}{\pi N}}}$

(2.114)

La función de Gauss constituye en la práctica, junto con el spline de cuarto orden, una de las funciones de ponderación de mayor utilización en los diversos trabajos de investigación realizados sobre el desarrollo de métodos sin malla.

También es posible construir funciones de ponderación, a partir del producto tensorial de funciones como

$w(\mathbf {x-x} _{I})=w\left({\frac {\left\|x-x_{I}\right\|}{d_{\max }\left|_{x}\right.}}\right)w\left({\frac {\left\|y-y_{I}\right\|}{d_{\max }\left|_{y}\right.}}\right)w\left({\frac {\left\|z-z_{I}\right\|}{d_{\max }\left|_{z}\right.}}\right)$

(2.115)

donde esta vez el soporte de la función ${\textstyle w(\mathbf {x-x} _{I})}$ será de forma rectangular, con dimensiones ${\textstyle d_{\max }\left|_{x}\right.}$,${\textstyle d_{\max }\left|_{y}\right.}$ y ${\textstyle d_{\max }\left|_{z}\right.}$ en la dirección de los ejes coordenados ${\textstyle x}$,${\textstyle y}$ y ${\textstyle z}$ respectivamente. La función así definida ha sido utilizada principalmente, en el caso de dominios que por su geometría favorecen una discretización mediante una distribución regular de nodos. Finalmente, a modo de comparación, en la figura 5 se muestra una representacion de las diferentes funciones de ponderación para un caso 1D. Es de interés destacar, tal como lo indica la figura, la capacidad de la función de Gauss de poder representar, mediante una adecuada selección de los parámetros ${\textstyle c}$ y ${\textstyle r}$, algunas de las funciones de ponderación estudiadas anteriormente.

Figura 5: Funciones de ponderacion para un caso 1D

(¹) Véase apartado 2.3.1

2.3 Implementación numérica

Analizados los procedimientos para obtener la función aproximada en un método sin malla, a continuación se revisan las técnicas para obtener el sistema discreto de ecuaciones diferenciales, que permitirá la resolución numérica del problema de contorno asociado. Para el planteamiento del sistema discreto de ecuaciones, se han utilizado hasta la fecha, dos tipos de formulaciones:

• método de Galerkin

• método de colocación puntual

El optar por una u otra estrategia, como se verá, presenta sus ventajas e inconvenietes y condiciona el desarrollo de un método sin malla. Considérese la forma general de un problema vectorial gobernado por las siguientes ecuaciones diferenciales

${\mathcal {A}}\left(\mathbf {u} \right)=\mathbf {b} ,\mathbf {\quad x} \in \Omega$

(2.116)

con su condición de contorno de Neumann (natural)

${\mathcal {B}}\left(\mathbf {u} \right)=\mathbf {t} ,\quad \mathbf {x} \in \Gamma _{t}$

(2.117)

y condición de Dirichlet (esencial)

$\mathbf {u} -\mathbf {u} _{p}=\mathbf {0} ,\quad \mathbf {x} \in \Gamma _{u}$

(2.118)

que debe satisfacerse en un dominio ${\textstyle \Omega }$ con contorno ${\textstyle \Gamma :=\Gamma _{t}\cup \Gamma _{u}}$. En las expresiones anteriores, ${\textstyle {\mathcal {A}}}$ y ${\textstyle {\mathcal {B}}}$ son operadores diferenciales apropiados, ${\textstyle \mathbf {u=u} \left(\mathbf {x} \right)}$ será el vector de incógnitas (o campo de desplazamientos en el ámbito de la mecánica estructural) y ${\textstyle \mathbf {u} _{p}}$ el valor prescrito de ${\textstyle \mathbf {u} }$ a lo largo del contorno ${\textstyle \Gamma _{u}}$. Además ${\textstyle \mathbf {b} }$ y ${\textstyle \mathbf {t} }$, representan flujos o fuerzas externas actuando sobre el dominio ${\textstyle \Omega }$ y a lo largo del contorno ${\textstyle \Gamma _{t}}$, respectivamente.

Un procedimiento general para resolver numéricamente el problema de contorno anterior es el método de los residuos ponderados [106], cuya técnica permite obtener una solución aproximada, a partir de una ecuación integral equivalente al sistema de ecuaciones diferenciales del problema. Si la solución exacta ${\textstyle \mathbf {u} \left(\mathbf {x} \right)}$ se aproxima por ${\textstyle {\widehat {\mathbf {u} }}(\mathbf {x} )}$, por ejemplo utilizando cualquiera de las aproximaciones meshless estudiadas, es decir

$\mathbf {u} \left(\mathbf {x} \right)\cong {\widehat {\mathbf {u} }}\left(\mathbf {x} \right)={\underset {I=1}{\stackrel {N}{\sum }}}\phi _{I}\left(\mathbf {x} \right)\mathbf {u} _{I}^{h}$

(2.119)

se tiene que, en general, las ecuaciones 2.116, 2.117 y 2.118 no serán satisfechas, obteniéndose unos residuos o errores tanto en el dominio ${\textstyle \Omega }$ como en el contorno ${\textstyle \Gamma }$. La solución aproximada al problema de contorno original se consigue ponderando el error cometido en la aproximación mediante ${\textstyle N}$ funciones de prueba o de test como sigue

${\underset {\Omega }{\int }}\mathbf {v} _{I}\mathbf {(x)} \left({\mathcal {A}}\left({\widehat {\mathbf {u} }}\right)-\mathbf {b} \right)d\Omega +{\underset {\Gamma _{t}}{\int }}{\overline {\mathbf {v} }}_{I}(\mathbf {x} )\left({\mathcal {B}}\left({\widehat {\mathbf {u} }}\right)-\mathbf {t} \right)d\Gamma _{t}+{\underset {\Gamma _{u}}{\int }}{\overline {\overline {\mathbf {v} }}}_{I}(\mathbf {x)} \left({\widehat {\mathbf {u} }}-\mathbf {u} _{p}\right)d\Gamma _{u}=0$

(2.120)

$\forall \mathbf {v} _{I}\mathbf {(x} ),{\overline {\mathbf {v} }}_{I}(\mathbf {x} ),{\overline {\overline {\mathbf {v} }}}_{I}(\mathbf {x} )\in V,{\hbox{ }}I=1,...,N$

donde ${\textstyle \mathbf {v(x)} }$, ${\textstyle {\overline {\mathbf {v} }}(\mathbf {x} )}$, ${\textstyle {\overline {\overline {\mathbf {v} }}}(\mathbf {x} )}$ son las denominadas funciones de test, ${\textstyle V}$ es un subespacio finito de Sobolev y ${\textstyle N}$ el número de incógnitas del problemas. Tomando en consideración que los integrandos ${\textstyle {\mathcal {A}}\left({\widehat {\mathbf {u} }}\right)-\mathbf {b} }$, ${\textstyle {\mathcal {B}}\left({\widehat {\mathbf {u} }}\right)-\mathbf {t} }$, ${\textstyle {\widehat {\mathbf {u} }}-\mathbf {u} _{p}}$ representan el error cometido al sustituir la solución aproximada en la ecuación diferencial o en las condiciones de contorno, la expresión 2.120 puede entenderse como la integral ponderada de tales residuos.

2.3.1 Discretización mediante formulación de Galerkin

Esta formulación se basa en escoger como funciones de test, las funciones de forma utilizadas en la aproximación. Su formulación, en principio, no difiere sustancialmente de la utilizada en el método de elementos finitos, sin embargo, para poder imponer las condiciones de contorno escenciales o de Dirichlet es necesario implementar un procedimiento adicional. Para comprender las particularidades que presenta la formulación de Galerkin en una aproximación meshless, a continuación se desarrolla su implementación en un problema de contorno tipo, regido por la ecuación de Laplace en su versión escalar, es decir

$\Delta u=-b{\hbox{ }}\forall \mathbf {x} \in \Omega$

(2.121)

y condiciones de contorno Neumann¹

$u_{,n}=t{\hbox{ }}\forall \mathbf {x} \in \Gamma _{t}$

(2.122)

y condiciones de contorno Dirichlet

$u=u_{p}{\hbox{ }}\forall \mathbf {x} \in \Gamma _{u}$

(2.123)

Aplicando la ecuación de residuos ponderados 2.120, en este caso particular se tiene

${\underset {\Omega }{\int }}v\left(\Delta {\widehat {u}}+b\right)d\Omega +{\underset {\Gamma _{t}}{\int }}{\overline {v}}\left({\widehat {u}}_{,n}-t\right)d\Gamma _{t}+{\underset {\Gamma _{u}}{\int }}{\overline {\overline {v}}}\left({\widehat {u}}-u_{p}\right)d\Gamma _{u}=0{\hbox{ }}\forall v,{\overline {v}},{\overline {\overline {v}}}\in V$

(2.124)

integrando por partes y aplicando el teorema de la divergencia se obtiene la forma débil de la ecuación 2.124 como [106]

${\underset {\Omega }{\int }}\nabla v\cdot \nabla {\widehat {u}}d\Omega -{\underset {\Omega }{\int }}vbd\Omega -{\underset {\Gamma }{\int }}v{\widehat {u}}_{,n}d\Gamma -{\underset {\Gamma _{t}}{\int }}{\overline {v}}\left({\widehat {u}}_{,n}-t\right)d\Gamma _{t}+{\underset {\Gamma _{u}}{\int }}{\overline {\overline {v}}}\left({\widehat {u}}-u_{p}\right)d\Gamma _{u}=0$

(2.125)

donde ${\textstyle \Gamma =\Gamma _{t}\cup \Gamma _{u}}$. En principio, cualquiera de las aproximaciones meshless estudiadas en 2.1 puede ser utilizada en la expresión 2.125, sin embargo, el no cumplimiento de la condición de interpolación que caracteriza a estas aproximaciones, es decir

$\phi _{I}(\mathbf {x} _{J})\neq 0$

(2.126)

impide imponer las condiciones de contorno escenciales cuando ${\textstyle I\in \Omega \cup \Gamma _{t}}$ y ${\textstyle J\in \Gamma _{u}}$. Para hacer frente a este problema los investigadores han debido implementar diferentes soluciones, como por ejemplo, multiplicadores de Lagrange [9] [58] [66], acoplamiento con elementos finitos [10] [53] [36] [38] y métodos de penalización [104], [31]. Para tomar conciencia, del coste computacional adicional que significa tener que implementar un proceso para prescribir la condición de contorno de Dirichlet, a continuación se ejemplifica para el problema tipo, el uso de multiplicadores de Lagrange. Para ello se introduce la expresión de los multiplicadores de Lagrange, como función de los desplazamientos, es decir

$\lambda (\mathbf {x} )={\widehat {u}}_{,n}$

(2.127)

modificándose la expresión 2.125 como sigue

${\underset {\Omega }{\int }}\nabla v\cdot \nabla {\widehat {u}}d\Omega -{\underset {\Omega }{\int }}vbd\Omega -{\underset {\Gamma }{\int }}v\lambda d\Gamma -{\underset {\Gamma _{t}}{\int }}{\overline {v}}\left(\lambda -t\right)d\Gamma _{t}+{\underset {\Gamma _{u}}{\int }}{\overline {\overline {v}}}\left({\widehat {u}}-u_{p}\right)d\Gamma _{u}=0$

(2.128)

si se adoptan funciones de test de modo que ${\textstyle v=-{\overline {v}}}$, y ${\textstyle {\overline {\overline {v}}}}$ definida sobre ${\textstyle \Gamma _{u}}$ se tiene

${\underset {\Omega }{\int }}\nabla v\cdot \nabla {\widehat {u}}d\Omega -{\underset {\Omega }{\int }}vbd\Omega -{\underset {\Gamma _{u}}{\int }}v\lambda d\Gamma _{u}-{\underset {\Gamma _{t}}{\int }}vtd\Gamma _{t}+{\underset {\Gamma _{u}}{\int }}{\overline {\overline {v}}}\left({\widehat {u}}-u_{p}\right)d\Gamma _{u}=0$

(2.129)

donde los multiplicadores de Lagrange en conjunto con la función ${\textstyle {\widehat {u}}(\mathbf {x} )}$, pasan a ser las incógnitas del problema. Utilizando una aproximación meshless para la discretizar ${\textstyle {\widehat {u}}(\mathbf {x} )}$, una aproximación para ${\textstyle \lambda (\mathbf {x} )}$ basada en funciones de forma Lagrangianas, es decir

$\lambda (\mathbf {x} )\cong {\widehat {\lambda }}(\mathbf {x} )={\underset {K\in {\mathcal {G}}\left(\Gamma _{u}\right)}{\sum }}\Psi _{K}(s)\lambda _{K}^{h}{\hbox{ }}\mathbf {x} \in \Gamma _{u}$

(2.130)

donde ${\textstyle s}$ es una coordenada que mide la longitud de arco sobre el contorno y el conjunto ${\textstyle {\mathcal {G}}(\Gamma _{u})=\left\{K\mid \mathbf {x} _{K}\in \Gamma _{u}\right\}}$ y seleccionando las funciones test según el método de Galerkin

${\begin{array}{ll}v_{I}=\phi _{I}(\mathbf {x} )&I=1,...N\\{\overline {\overline {v}}}_{K}=\Psi _{K}(s)&K\in {\mathcal {G}}(\Gamma _{u})\end{array}}$

(2.131)

se obtiene finalmente el siguiente sistema de ecuaciones en forma matricial

$\left[{\begin{array}{ll}\mathbf {K} &\mathbf {G} \\\mathbf {G} ^{T}&\mathbf {0} \end{array}}\right]\left\{{\begin{array}{l}\mathbf {u} \\\mathbf {\lambda } \end{array}}\right\}=\left\{{\begin{array}{l}\mathbf {f} \\\mathbf {q} \end{array}}\right\}$

(2.132)

donde

$K_{IJ}={\underset {\Omega }{\int }}\nabla \phi _{I}\cdot \nabla \phi _{J}d\Omega {\hbox{ }}\mathbf {K\in } Mat\left(N\times N\right)$

(2.133)

$G_{IK}=-{\underset {\Gamma _{u}}{\int }}\phi _{I}\Psi _{K}d\Gamma _{u}{\hbox{ }}\mathbf {G\in } Mat(N\times card({\mathcal {G}}(\Gamma _{u})))$

(2.134)

$f_{I}={\underset {\Omega }{\int }}\phi _{I}bd\Omega +{\underset {\Gamma _{t}}{\int }}\phi _{I}td\Gamma _{t}{\hbox{ }}\mathbf {f\in } Vec(N)$

(2.135)

$q_{K}={\underset {\Gamma _{u}}{\int }}\Psi _{K}u_{p}d\Gamma _{u}{\hbox{ }}\mathbf {q} \in Vec(card({\mathcal {G}}(\Gamma _{u})))$

(2.136)

Como primera consecuencia, el uso de multiplicadores de Lagrange para imponer las condición de contorno escencial, supone un aumento del ancho de banda de la matriz ${\textstyle \mathbf {K} }$ respecto de la formulación de Galerkin utilizada en el método de elementos finitos. Esto, sumado al inconveniente de que la matriz final no es definida positiva, a pesar de su simetría [8], conlleva un encarecimiento del coste computacional asociado a la resolución del sistema.

(¹) $u_{,n}$ representa la derivada respecto de la normal

2.3.2 Evaluación numérica de las integrales

Una vez implementada la solución para imponer la condición de contorno, surge la necesidad de evaluar numéricamente las integrales 2.133, 2.134, 2.135 y 2.136, respetando en la medida de lo posible la filosofía de los métodos sin malla. Las estrategias que se han desarrollado para solucionar este dilema, pueden clasificarse en tres tipos:

1. Integración nodal, Integración por subdominios
2. Celda de integración
3. Malla auxiliar de elementos

La integración nodal es la más fácil y rápida de implementar. Al igual de lo que ocurre en las aproximaciones SPH, se aprovecha la misma partición de puntos del dominio para realizar la evaluación de las integrales, utilizándose expresiones del tipo

${\underset {\Omega }{\int }}g(\mathbf {x} )d\Omega ={\stackrel {N}{\underset {I=1}{\sum }}}g(\mathbf {x} _{I})\Delta V_{I}$

(2.137)

${\underset {\Gamma }{\int }}g(\mathbf {x} )d\Gamma ={\stackrel {N}{\underset {I=1}{\sum }}}g(\mathbf {x} _{I})\Delta S_{I}$

(2.138)

donde ${\textstyle \Delta V_{I}}$ y ${\textstyle \Delta S_{I}}$ son una medida del volúmen y superficie respectivamente, del entorno que rodea al punto ${\textstyle \mathbf {x} _{I}}$. Poder seleccionar y asignar adecuadamente estos parámetros no es para nada una tarea trivial, sobre todo en geometrías irregulares y en 3D, pero quizás el mayor inconveniente de la integración nodal sea la aparición de fenómenos de inestabilidad. Este tipo de inestabilidad, conocida como tensile instabilities, fue inicialmente identificada en las aproximaciones SPH por [92]. Con posterioridad este fenómeno ha sido objeto de estudio por parte de diferentes grupos de investigación, al respecto, referencias como [DYK 95] [28] [7] [87] [23] [15] [13], reflejan el esfuerzo dedicado por los investigadores en identificar el origen de estas inestabilidades y plantear posibles soluciones.

En el procedimiento de integración por subdominios, el cómputo de las integrales se realiza a través de una cuadratura numérica sobre un subdominio definido de forma local, el cual tiene generalmente una forma geométrica sencilla como una esfera, cubo o elipsoide para facilitar la integración [3] [104] [21] [49]. Si bien el método resultante se considera libre de malla, la definición de estos subdominios de integración, especialmente en el contorno, no es una tarea sencilla y requiere de técnicas especiales.

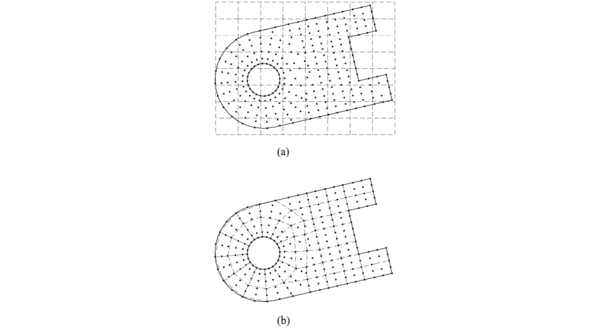
La segunda y tercera alternativa tienen la desventaja de que el método resultante no es verdaderamente un método sin malla, puesto que en ambos se recurre a una cuadratura numérica, como las conocidas cuadraturas de Gauss o regla del trapecio, para evaluar las integrales. Previamente, se debe definir una malla auxiliar formada por una red de celdas o elementos finitos, como se muestra en la figura 6, en donde se definen los puntos de integración . Se puede también observar de la figura, que en el caso de las celdas de integración estas se definen, independiente de la posición de los puntos, como un arreglo regular, a diferencia de la malla auxiliar de elementos finitos cuyos nodos coinciden con los vértices del elemento. A pesar que la evaluación de las integrales es independiente del proceso de interpolación elegido, el hecho de particionar el dominio ya sea con un CAD o con un mallador, ensombrece notablemente las posibles ventajas de los metodos sin malla. Además, en el caso de utilizar una cuadratura de Gauss, no existe un criterio respecto del número de celdas ${\textstyle n_{c}}$ y números de puntos ${\textstyle n_{g}}$ de la cuadratura a utilizar, adoptándose relaciones en función del número de nodos ${\textstyle N}$ y el número de nodos en cada celda ${\textstyle N_{c}}$ respectivamente, como [9] [58]

$n_{c}=N$

(2.139)

$n_{g}=\left({\sqrt {N_{c}}}+p\right)^{2}{\hbox{ con }}p=2,3$

(2.140)

La evaluación de las integrales, bajo estas alternativas, se realizan simbólicamente como

${\underset {\Omega }{\int }}g(\mathbf {x} )d\Omega ={\stackrel {n_{c}}{\sum }}{\stackrel {N_{c}}{\sum }}g(\mathbf {x} _{G})\omega _{G}$ ${\underset {\Gamma }{\int }}g(\mathbf {x} )d\Gamma ={\stackrel {n_{c}}{\sum }}{\stackrel {N_{c}}{\sum }}g(\mathbf {x} _{G})\gamma _{G}$

(2.141)

siendo ${\textstyle \mathbf {x} _{G}}$ un punto de integración y ${\textstyle \omega _{G}}$, ${\textstyle \gamma _{G}}$ los pesos de las cuadraturas de Gauss.

Figura 6: Cuadraturas numericas utilizadas en los metodos sin malla. (a) celda de integracion (b) malla auxiliar de elementos finitos

2.3.3 Discretización mediante colocación puntual

En el método de colocación puntual las funciones de test se escogen como (recuérdese 2.120)

$\mathbf {v} _{I}\mathbf {(x} )={\overline {\mathbf {v} }}_{I}(\mathbf {x} )={\overline {\overline {\mathbf {v} }}}_{I}(\mathbf {x} )=\delta (\mathbf {x-x} _{I}){\hbox{ }}I=1,...,N$

(2.142)

donde la función ${\textstyle \delta (\mathbf {x-x} _{I})}$ es la delta de Dirac, que cumple las propiedades siguientes

$\delta (\mathbf {x-x} _{I})=0{\hbox{ }}\forall \mathbf {x} \neq \mathbf {x} _{I}$ ${\underset {\Omega }{\int }}\delta (\mathbf {x-x} _{I})d\Omega =\mathbf {Id}$

(2.143)

Reemplazando los valores de las funciones de test en la ecuación integral de residuos ponderados 2.124, o forma fuerte, se obtiene el siguiente sistema de ecuaciones discretas

$\left(\Delta {\widehat {u}}+b\right)_{\mathbf {x} _{I}}=0{\hbox{ }}\forall \mathbf {x} _{I}\mathbf {\in } \Omega -\Gamma$ $\left({\widehat {u}}_{,n}-t\right)_{\mathbf {x} _{I}}=0{\hbox{ }}\forall \mathbf {x} _{I}\in \Gamma _{t}$ $\left({\widehat {u}}-u_{p}\right)_{\mathbf {x} _{I}}=0{\hbox{ }}\forall \mathbf {x} _{I}\in \Gamma _{u}$

(2.144)

lo que corresponde a hacer nulo el residuo en un determinado número de puntos del dominio, resultando innecesario cualquier proceso de integración [106]. El procedimiento anterior es aplicable para cualquiera de las aproximaciones meshless estudiadas, debe notarse, que en el caso de la ecuación de Laplace, la función interpolante debe tener continuidad ${\textstyle C^{2}}$, lo que también supone utilizar, en el caso de las aproximaciones MLS y SPH, una función de ponderación de clase ${\textstyle C^{2}}$. Reemplazando la aproximación 2.119 en el sistema de ecuaciones 2.144, se obtiene finalmente el conjunto de ecuaciones discretizadas cuya forma compacta es

$\mathbf {Ku} ^{h}=\mathbf {f}$

(2.145)

donde la matriz ${\textstyle \mathbf {K} \in Mat(N\times N)}$ contiene las funciones de forma ${\textstyle \phi _{I}(\mathbf {x} )}$, ${\textstyle \mathbf {u} ^{h}\in Vec(N)}$ contiene los parámetros desconocidos, o incógnitas del problema sin malla, y ${\textstyle \mathbf {f} \in Vec(N)}$ los términos que incluyen los valores prescritos de fuerzas ${\textstyle b}$, ${\textstyle t}$ y los desplazamientos ${\textstyle u_{p}}$. Recientemente, la capacidad de la técnica de colocación puntual ha sido explorada también con una aproximación tipo RKPM [1].

La implementación de un método sin malla con un esquema de colocación puntual, es un proceso rápido y sencillo. En principio, no requiere de un procedimiento especial para prescribir la condición de contorno de Neumann¹, ni se requiere de técnicas específicas para evaluar la cuadratura numérica de las integrales. En definitiva, es la técnica de discretización que mejor se adapta a los requerimientos de las aproximaciones sin malla. Quizás deba mencionarse como desventaja, desde el punto de vista del coste computacional, que en la técnica de colocación puntual se requiere calcular términos del mismo orden de los que intervienen en las ecuaciones diferenciales del problema, por ejemplo, de segundo orden para el problema de la ecuación de Laplace. Esto, como se mecionó oportunamente, influye en los requerimientos de consistencia que se le exigirá a la aproximación meshless, situación que contrasta con la técnica de Galerkin, donde la utilización de la ecuación integral en su forma débil, reduce en un orden de magnitud el grado de los términos que deben ser evaluados.

Por último, un aspecto importante que debe ser investigado cuando se utiliza el esquema de colocación puntual, tal como se verá más adelante, es el hecho de que el método resultante pueda ser sensible a dos cosas: la forma de seleccionar los subdominios o nubes, y sobre todo, respecto de la forma de imponer la condición de contorno de Neumann.

(¹) Esta idea deberá ser reformulada a la luz de los resultados del capítulo 4

2.4 Recapitulación de los principales métodos sin malla

Se han revisado los distintos aspectos teóricos que conforman un método meshless, es decir, tipo de aproximación, función de ponderación e implementación numérica, buscando comprender la importancia o el rol que cumple cada uno de ellos. Por separado, cada uno de estos aspectos puede ser visto como un ingrediente, que una vez seleccionados permiten la construcción y utilización de una nueva técnica numérica cuyo rasgo distintivo es ser libre de malla, o muy poco dependiente de ella. Si bien el método sin malla más antiguo que recoge la literatura es el Smooth Particle Hydrodynamics (SPH) [59] [34], concebido inicialmente para modelar determinados fenómenos astrofísicos en la década de los setenta, han debido transcurrir más de quince años para que éstos hayan sido nuevamente redescubiertos y utilizados en la resolución de problemas de contorno. Un buen estudio acerca del método SPH y sus bases teóricas, que sirvió para impulsar su aplicación en medios continuos, fue hecho por Monaghan en [64]. Con el transcurso del tiempo y por medio de diversas investigaciones, se ha ido comprobando que la sencillez y simplicidad del mismo, puede comprometer la exactitud de la solución y provocar fenómenos de inestabilidad [92] [DYK 95] [11] [14]. Esta situación ha propiciado un nuevo estudio y análisis del método por parte de los investigadores, continuándose hoy en dia la búsqueda de soluciones que permitan moderar o corregir las deficiencias originales de la aproximación [28] [15] [16].

En forma contemporánea al surgimiento del método SPH, Liszka [45] propone una interesante técnica de interpolación para un set de nodos distribuidos arbitrariamente, basada en el desarrollo de ecuaciones en diferencias finitas generalizadas. Inicialmente en este método, el número de nodos utilizados para construir la aproximación local era fijo y su elección no dependía del tamaño del soporte de una función de ponderación, lo que suponía contar con una aproximación discontinua a través del dominio. Esta situación, sumado al bajo grado de regularidad de la base de interpolación, parece haber influido en el hecho de que inicialmente este tipo de aproximación no fuera realmente considerada como una aproximación meshless. Trabajos posteriores desarrollados por los mismos autores [48] [83], han demostrado la manera de implementar la técnica de mínimos cuadrados ponderados para obtener la aproximación local, posibilitando bajo condiciones concretas que esta técnica basada en formulaciones de diferencias finitas generalizadas, pueda ser interpretada como una técnica MLS.

Otra vertiente desarrollada en los métodos sin malla surge como respuesta a los principales inconvenientes que presentaban las aproximaciones SPH, poca exactitud de la solución en los contornos para un número reducido de partículas. Para ello, Liu [50] recurre a la utilización de una función de corrección para plantear la aproximación local, dando lugar a nueva variante en los métodos sin malla conocida como Reproducing Kernel Particle Method (RKPM). Esta nueva proposición incorpora las ideas principales de las transformaciones wavelets [101] para reproducir una función, utilizando en la integral window transform una función kernel de soporte compacto, de manera que pueda ser trasladada a través del dominio. Por otro lado cuando la función de corrección se toma igual a la unidad, se recupera en su forma original la aproximación SPH, lo que permite considerar a esta ultima como un caso particular dentro del método RKPM.

En el caso de las aproximaciones por mínimos cuadrados, fue Nayroles [69] en el método sin malla bautizado como Diffuse Element Method (DEM), quien utilizó por primera vez la técnica MLS para resolver problemas de contorno. Con posterioridad esta técnica ha sido utilizada por diferentes investigadores, con modificaciones o planteamientos alternativos para implementar la discretización, dando lugar a un buen número de formulaciones meshless con aproximación MLS. Desde sus inicios hasta la fecha destacan, entre otras, la denominada Element-Free Galerkin Method (EFGM), propuesta por Belytschko [9] y Finite Point Method (FPM), propuesta por Oñate [71]. En este último método se recurre a la aproximación MLS con un esquema de colocación puntual para resolver el sistema de ecuaciones, dando origen a una técnica que desde sus inicios se ha caracterizado por ser totalmente libre de malla.

Otra línea de investigación y comprensión de estos métodos surge a partir de los trabajos desarrollados por Duarte [24] y Babuska [5], basados en el concepto matemático de partición de la unidad. Como resultado de estas investigaciones dos nuevos métodos, con ciertas similitudes entre ellos, son propuestos: Hp Clouds (HPC) y Partition of Unity Finite Element Method (PUFEM). Además, a estos autores se les reconoce el mérito de haber interpretado las aproximaciones MLS como un caso particular de una partición de la unidad y la posibilidad de contar con métodos sin malla capaces de realizar procedimientos adaptativos de la solución.

Desde la segunda mitad de la década de los noventa hasta hoy en dia, el fértil campo de utilización y aplicación de los métodos sin malla parece haber definitivamente llamado la atención de los investigadores, principalmente por el progresivo número de técnicas y sus variantes que han ido apareciendo. Al respecto, la figura 7 muestra una recopilación de los distintos métodos propuestos hasta la fecha¹ y la progresión experimentada por estos durante los últimos años, identificándose para cada uno de ellos las técnicas de aproximación y discretización utilizadas². Finalmente, si se piensa en las distintas alternativas que existen y que han sido analizadas en el presente capítulo para cada una de las 3 etapas fundamentales de los métodos sin malla (aproximación, función de ponderación y discretización), puede augurarse para el futuro una investigación sostenida en el estudio y utilización de estos en diversos campos de la ingeniería y otras disciplinas.

Figura 7: Principales metodos sin malla

(¹) La tabla sólo incluye los métodos sin malla más representativos, según los fundamentos teóricos estudiados en el capítulo

(²) Las funciones de ponderación mayoritariamente utilizadas son la de Gauss normalizada y el spline

3 Formulación del método de Puntos Finitos

Siguiendo la metodología utilizada en el capítulo anterior, a continuación se entregan los conceptos teóricos de la formulación del Método de Puntos Finitos (MPF) que permitirán comprender su funcionamiento y su posterior implementación, para la resolución de diversos problemas de contorno en elasticidad lineal de sólidos. Recordando la figura 7 se puede tener una primera noción acerca de las características principales del MPF (ó en ingles FPM) como técnica sin malla; aproximación local MLS, función de ponderación de Gauss y colocación puntual para evaluar las integrales. Sin embargo, aunque pertenece a la familia MLS, el tipo de aproximación específica utilizada en el MPF presenta algunas particularidades respecto de la formulación original. Estas y otras características propias del MPF serán analizadas a continuación.

3.1 Aproximación mediante mínimos cuadrados ponderados fijos

Como se mencionó oportunamente en el capítulo anterior, la técnica de interpolación MLS presenta dos grandes inconvenientes; en primer lugar la dificultad para establecer una definición global de la función de ponderación para cualquier punto ${\textstyle \mathbf {x} _{I}}$ de la partición, y en segundo término lo complejo que resulta obtener la derivada de la función de forma. En el método de puntos finitos [71] [74] [75] [78] se recurre al uso de una función de ponderación fija, procedimiento denominado fixed weighted least squares (FWLS), para solventar estos problemas. La idea detrás de este procedimiento es, definir la función de ponderación ${\textstyle w(\mathbf {x} -\mathbf {x} _{I})}$ solamente en los nodos ${\textstyle \mathbf {x} _{I}}$ donde se requiere calcular la función incógnita, y no en cualquier punto ${\textstyle \mathbf {x} }$ del dominio, limitándo de esta manera la validez de la aproximación al interior del subdominio o nube ${\textstyle \Omega _{I}}$. Utilizando la nomenclatura definida en esta tesis, la función de ponderación en el método de puntos finitos tendrá esta vez la siguiente forma: ${\textstyle w(\mathbf {x} _{I}-\mathbf {x} _{j})}$, es decir tendrá su máximo valor en el nodo ${\textstyle \mathbf {x} _{I}}$, denominado nodo estrella, atenuándose en la medida que aumenta la distancia entre un nodo ${\textstyle \mathbf {x} _{j}}$ de la nube y el nodo estrella. Esta vez ${\textstyle j=1,....n}$ ${\textstyle \mid n=card({\mathcal {S}}(\mathbf {x} _{I}))}$. Para comprender de mejor forma los cambios que introduce en la aproximación MLS el uso de una función de ponderación fija, en la figura 8 se representa la aproximación FWLS para una nube de 5 puntos (compárese con la figura 3).

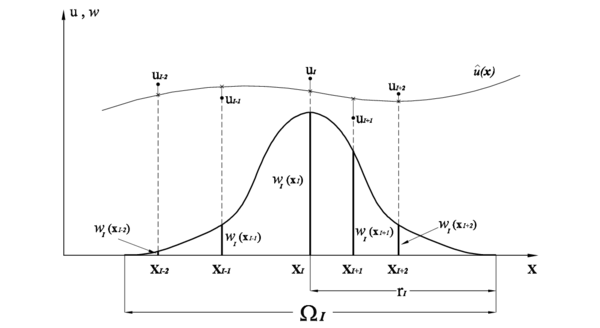
Figura 8: Aproximacion por minimos cuadrados ponderados tipo FWLS

3.1.1 Construcción

En el MPF, la aproximación FWLS de la función ${\textstyle u(\mathbf {x} )}$ en el subdominio o nube ${\textstyle \Omega _{I}}$ se construye de la siguiente forma

$u(\mathbf {x} )\cong {\widehat {u}}(\mathbf {x} )={\stackrel {m}{\underset {i=1}{\sum }}}p_{i}(\mathbf {x} )\alpha _{i}=\mathbf {p} ^{T}(\mathbf {x} )\mathbf {\alpha } {\hbox{ }}\forall \mathbf {x} _{I}\in \Omega {\hbox{, }}\forall \mathbf {x} \in \Omega _{I}$

(3.1)

siendo esta vez ${\textstyle \mathbf {\alpha } ^{T}\mathbf {=} \left[\alpha _{1}{\hbox{ }}\alpha _{2}........\alpha _{m}\right]}$ un vector de parámetros constantes, es decir válidos unicamente en la respectiva nube ${\textstyle \Omega _{I}}$ y que no dependen de las coordenadas espaciales ${\textstyle \mathbf {x} }$, y ${\textstyle \mathbf {p} ^{T}(\mathbf {x} )}$ es la base de interpolación que contiene típicamente monomios. Tal como en una interpolación por mínimos cuadrados, la condición ${\textstyle n\geq m}$ impide que la aproximación ${\textstyle {\widehat {u}}(\mathbf {x} )}$ pueda ajustarse a todos los valores nodales ${\textstyle u(\mathbf {x} _{j})=u_{j}^{h}}$ con ${\textstyle j=1,....,n}$, por esto se recurre a la minimización de la suma del error en cada punto, ponderado por una función fija como

$J_{I}={\stackrel {n}{\underset {j=1}{\sum }}}w(\mathbf {x} _{I}-\mathbf {x} _{j})\left(u_{j}^{h}-\mathbf {p} ^{T}(\mathbf {x} _{j})\mathbf {\alpha } \right)^{2}$

(3.2)

cuya forma compacta matricial es¹

$J_{I}=\left(\mathbf {u} ^{h}\mathbf {-P} (\mathbf {x} _{I})\mathbf {\alpha } \right)^{T}\mathbf {W} _{I}\left(\mathbf {u} ^{h}\mathbf {-P} (\mathbf {x} _{I})\mathbf {\alpha } \right)$

(3.3)

donde

$\mathbf {u} ^{h}=\left[u_{1}^{h}{\hbox{ }}u_{2}^{h}{\hbox{ }}........u_{n}^{h}\right]^{T},\in Vec(n),{\hbox{ }}n=card({\mathcal {S}}(\mathbf {x} _{I}))$

$\mathbf {P} (\mathbf {x} _{I})=\left[{\begin{array}{llll}p_{1}(\mathbf {x} _{1})&p_{2}(\mathbf {x} _{1})&\cdots &p_{m}(\mathbf {x} _{1})\\p_{1}(\mathbf {x} _{2})&p_{2}(\mathbf {x} _{2})&\cdots &p_{m}(\mathbf {x} _{2})\\\vdots &\vdots &\ddots &\vdots \\p_{1}(\mathbf {x} _{n})&p_{2}(\mathbf {x} _{n})&\cdots &p_{m}(\mathbf {x} _{n})\end{array}}\right],{\hbox{ }}\in Mat(n\times m)$

$\mathbf {W} _{I}=\left[{\begin{array}{cccc}w(\mathbf {x} _{I}-\mathbf {x} _{1})&0&\cdots &0\\0&w(\mathbf {x} _{I}-\mathbf {x} _{2})&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &w(\mathbf {x} _{I}-\mathbf {x} _{n})\end{array}}\right]{\hbox{ }},{\hbox{ }}\in Mat(n\times n)$

(3.4)

La minimización estándar del funcional 3.2 respecto del vector ${\textstyle \mathbf {\alpha } }$, permite obtener esta vez

$\mathbf {\alpha =} {\overline {\mathbf {C} }}_{I}^{-1}\mathbf {u} ^{h}{\hbox{ }},{\hbox{ con }}{\overline {\mathbf {C} }}_{I}^{-1}=\mathbf {A} _{I}^{-1}\mathbf {B} _{I}$

(3.5)

siendo ${\textstyle \mathbf {A} _{I}=\mathbf {A} \left(\mathbf {x} _{I}\right)}$ (matriz de momentos), y ${\textstyle \mathbf {B} _{I}=\mathbf {B} \left(\mathbf {x} _{I}\right)}$ respectivamente

$\mathbf {A} _{I}=\mathbf {P} ^{T}(\mathbf {x} _{I})\mathbf {W} _{I}\mathbf {P} (\mathbf {x} _{I})$

(3.6)

$\left[A_{I}\right]_{ij}={\underset {k=1}{\stackrel {n}{\sum }}}p_{i}(\mathbf {x} _{k})w(\mathbf {x} _{I}-\mathbf {x} _{k})p_{j}(\mathbf {x} _{k})\qquad i,j=1,....,m$

(3.7)

$\mathbf {B} _{I}=\mathbf {P} ^{T}(\mathbf {x} _{I})\mathbf {W} _{I}{\hbox{ }}$

(3.8)

$\left[B_{I}\right]_{ij}=p_{i}(\mathbf {x} _{j})w(\mathbf {x} _{I}-\mathbf {x} _{j}){\hbox{ }}i=1,...,m{\hbox{ }}j=1,...,n$

(3.9)

La aproximación final en el MPF se consigue reemplazando la expresión 3.5 en 3.1, con lo que se obtiene

$u(\mathbf {x} )\cong {\widehat {u}}(\mathbf {x} )=\mathbf {p} ^{T}(\mathbf {x} ){\overline {\mathbf {C} }}_{I}^{-1}\mathbf {u} ^{h}$ $={\stackrel {n}{\underset {i=1}{\sum }}}{\stackrel {m}{\underset {j=1}{\sum }}}{\stackrel {m}{\underset {k=1}{\sum }}}p_{k}(\mathbf {x} )\left[A_{I}\right]_{kj}^{-1}\left[B_{I}\right]_{ji}u_{i}^{h}{\hbox{ }}\forall \mathbf {x} \in \Omega _{I}{\hbox{ }}$

(3.10)

siendo las funciones de forma

$\phi _{I}^{i}(\mathbf {x} )=\mathbf {p} ^{T}(\mathbf {x} ){\overline {\mathbf {C} }}_{I}^{-1}=\mathbf {p} ^{T}(\mathbf {x} )\mathbf {A} _{I}^{-1}\mathbf {B} _{I}$ $={\stackrel {m}{\underset {j=1}{\sum }}}{\stackrel {m}{\underset {k=1}{\sum }}}p_{k}(\mathbf {x} )\left[A_{I}\right]_{kj}^{-1}\left[B_{I}\right]_{ji}{\hbox{ , }}i\in {\mathcal {S}}(\mathbf {x} _{I})$

(3.11)

Se debe notar, de acuerdo con la expresión 3.1, que la aproximación FWLS se define para cada subdominio de interpolación ${\textstyle \Omega _{I}}$. En consecuencia, un punto ${\textstyle i}$ que pertenezca a dos nubes ${\textstyle \Omega _{I}}$ y ${\textstyle \Omega _{J}}$ respectivamente, y entre las cuales exista cierto traslape, tendrá asociadas diferentes funciones de forma según si se adscribe a una u otra nube, lo que significa ${\textstyle \phi _{I}^{i}(\mathbf {x} )\neq \phi _{J}^{i}(\mathbf {x} )}$. La interpolación resulta ahora multievaluada en ${\textstyle i}$, por lo que es preciso tomar alguna decisión que limite la elección a un único valor. En el MPF, por ejemplo, esta disyuntiva se resuelve utilizando un procedimiento de colocación puntual [71] [74] [75] [78] [80] [81].

A continuación se muestran de forma gráfica, para un caso 1D, las pricipales características de la función de forma FWLS utilizada en el MPF. En primer término la figura 9 muestra las funciones de forma para el caso de nubes de 5 puntos (${\textstyle n=5}$), y una base de interpolación lineal, cuadrática y cúbica respectivamente, de seguida, la figura 10 muestra las distintas funciones de forma para una base de interpolación cuadrática (${\textstyle m=3}$), y nubes de ${\textstyle n=3}$,${\textstyle 5}$ y ${\textstyle 7}$ puntos.

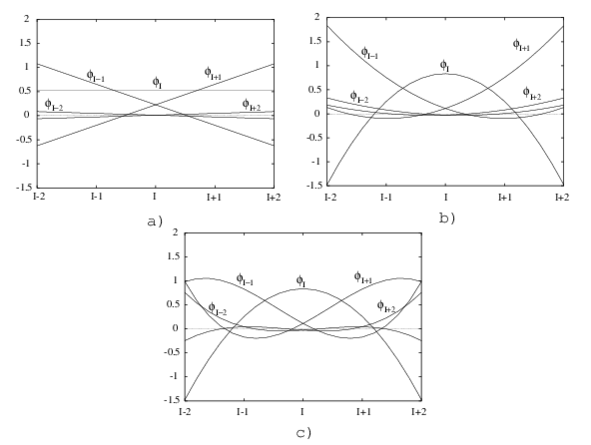
Figura 9: Funcion de forma FWLS para nubes de 5 puntos.a) m=2 b) m=3 c) m=4

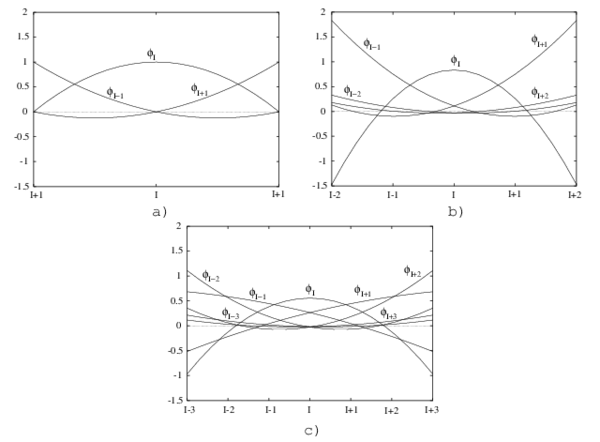
Figura 10: Funcion de forma FWLS para m=3. a) n=3 b) n=5 c) n=7

Puede visualizarse en ambas figuras, como era de esperar, el carácter no interpolatorio de la aproximación FWLS y los diferentes valores que adopta la función de forma, para un mismo punto, según se incluya en una u otra nube. Por otro lado, como muestra la figura 10, cuando el número de puntos de la nube coincide con el número de términos de la base de interpolación, en este caso ${\textstyle n=m=3}$, la función de forma cumple la condición de interpolación estándar del Método de Elementos Finitos.

(¹) Si en 3.2 se elige una función de ponderación igual a la unidad, se obtiene una aproximación por mínimos cuadrados estándar

3.1.2 Propiedades

La metodología para demostrar las propiedades de existencia y consistencia de la aproximación MLS, presentada en al apartado 2.1.1, es aplicable directamente para el caso FWLS si se reemplaza el punto ${\textstyle {\overline {\mathbf {x} }}}$ por ${\textstyle \mathbf {x} _{I}}$. Sin embargo, las condiciones para garantizar la inversa de la matriz de momentos y para reproducir cualquier función que se incluya en la base de interpolación, deberán restringirse al interior de cada subdominio de interpolación o nube ${\textstyle \Omega _{I}}$ y no al dominio ${\textstyle \Omega }$. La derivada parcial de la función de forma, en la aproximación FWLS, se obtiene derivando solamente los términos de la base de interpolación, pues a diferencia de lo que ocurre en el caso MLS, el vector de parámetros ${\textstyle \mathbf {\alpha } }$ contiene términos constantes que no dependen de la posición del punto donde se quiere evaluar la aproximación. Recordando 3.11, la derivada de la función de forma tiene la siguiente expresión

$\phi _{I,l}^{i}(\mathbf {x} )={\stackrel {m}{\underset {j=1}{\sum }}}{\stackrel {m}{\underset {k=1}{\sum }}}p_{k,l}(\mathbf {x} )\left[A_{I}\right]_{kj}^{-1}\left[B_{I}\right]_{ji}$

(3.12)

la cual coincide exactamente con la expresión 2.45, propuesta por Nayroles [69], cuando esta se evalúa en el nodo estrella; osea para ${\textstyle \mathbf {x} =\mathbf {x} _{I}}$ en 2.45 y 3.12, ${\textstyle i=I}$ en 3.12. Se debe notar que fuera del nodo ${\textstyle I}$, las derivadas no guardan ninguna relación, esto queda reflejado nítidamente si se visualizan ambas a través de una gráfica, tal como se ilustra en las figuras 11 y 12.

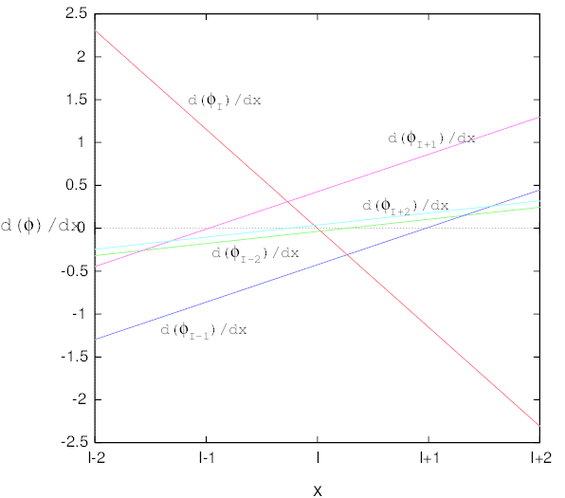
Figura 11: Derivada primera de la funcion de forma FWLS, m=3, n=5

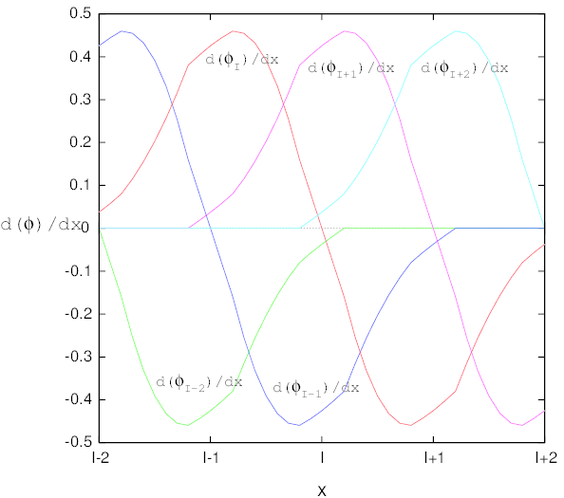
Figura 12: Derivada primera de la funcion de forma DLS, m=3, n=5

A diferencia de lo que ocurre en el MEF, en donde la presencia de dos nodos muy cercanos genera un fuerte gradiente de la función de forma y por consiguiente errores numéricos en la solución, en el MPF existe la posibilidad de incluir nuevos puntos independiente de la distancia que exista entre los nodos de la partición. La figura 13 muestra por ejemplo para una nube de 5 puntos, con dos de ellos situados a una distancia variable ${\textstyle \delta }$ del nodo estrella ${\textstyle I}$, de que manera las funciones de forma para estos tres nodos tienden a coincidir cuando la relación ${\textstyle d/\delta }$ aumenta.

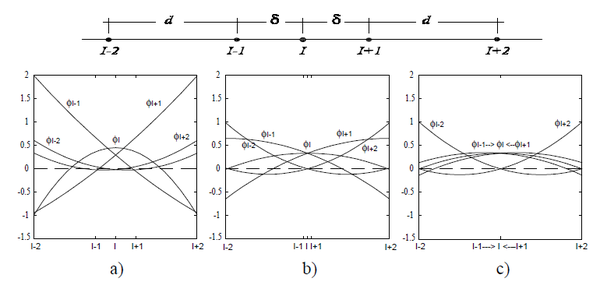
Figura 13: Funcion de forma FWLS para tres puntos muy cercanos (m=3). a)d/=2math b) d/=20math c) d/=100math

Considerando la discretización regular del dominio de la figura 14, se pueden visualizar también para un caso 2D, las distintas tendencias de la función de forma FWLS y su derivada. Por ejemplo, si se utiliza una base de interpolación cuadrática y nubes regulares de 9 puntos (${\textstyle n=6,m=9}$), las figuras 15, 16 y 17, muestran la forma típica de la función de forma y sus derivadas, para el nodo central ${\textstyle I}$ del dominio bidimensional. Además, las figuras 18 y 19 muestran la tendencia de la función de forma para los nodos del contorno ${\textstyle J}$ y ${\textstyle K}$ del dominio. Como era de esperar, al escoger una base de interpolación cuadrática, las superficies que representan las distintas funciones de forma muestran una tendencia parabólica, mientras que sus derivadas representan una superficie plana.

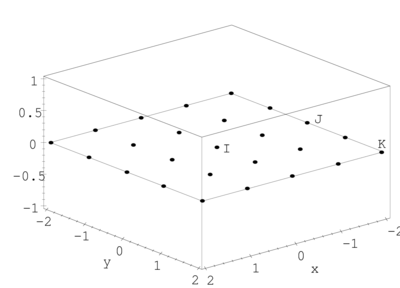
Figura 14: Discretizacion de un dominio bidimensional con 25 puntos

Figura 15: Funcion de forma del nodo central Imath para un dominio bidimensional

Figura 16: Derivada de la funcion de forma respecto a xmath, para el nodo Imath del dominio bidimensional

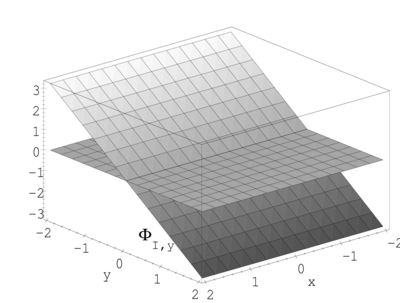
Figura 17: Derivada de la funcion de forma respecto de ymath, para el nodo Imath del dominio bidimensional

Figura 18: Funcion de forma para el nodo de contorno Jmath del dominio bidimensional

Figura 19: Funcion de forma para el nodo esquina Kmath del dominio bidimensional

3.2 Función de ponderación de Gauss

En el MPF se recurre al uso de la función de Gauss para conferir el carácter local a la interpolación [71] [74], por ello bastaría utilizar 2.108 en la expresión del funcional 3.2 para construir la aproximación FWLS. Esta función queda definida completamente en base a los parámetros ${\textstyle d}$ (norma euclídea de la diferencia de vectores de posición entre el nodo estrella y un nodo de la nube), el radio de influencia ${\textstyle r}$ y el exponente ${\textstyle k}$, recuérdese que el factor de apuntamiento ${\textstyle c}$ puede expresarse en función del radio de influencia. Por el momento, nada se ha dicho sobre la manera de calcular ${\textstyle r}$. En general, el radio de influencia se estima como el producto de una costante entera positiva por la máxima distancia entre los nodos del subdominio ${\textstyle \Omega _{I}}$ y el nodo estrella como

$r=q{\underset {J\in \Omega _{I}}{\max }}\left\|\mathbf {x} _{I}-\mathbf {x} _{J}\right\|=1.1d_{m{\acute {a}}x.}$

(3.13)

donde el uso de la constante se justifica para evitar la singularidad de la matriz de momentos ${\textstyle \mathbf {A} _{I{\hbox{ }}}}$, en el supuesto que ${\textstyle m=n}$. Tomar como radio de influencia la distancia entre el nodo estrella ${\textstyle \mathbf {x} _{I}}$ y el ${\textstyle n-}$ésimo punto más lejano, provoca que ${\textstyle w_{I}}$ se cancele en dicho punto o dicho de otra manera, que su peso relativo en el cálculo de las funciones de forma sea cero. Si se añade a esto, la posibilidad de que en esa nube ${\textstyle m=n}$, entonces uno de los coeficientes de la diagonal de ${\textstyle \mathbf {W} _{I}}$ sería nulo y por tanto ${\textstyle rango\left(\mathbf {A} _{I}\right)<m}$, la matriz ${\textstyle \mathbf {A} _{I}}$ no es invertible y la aproximación dejaría de existir. Por otro lado, se debe mencionar que si ${\textstyle r\rightarrow \infty }$ implica ${\textstyle w\left(\mathbf {x} _{I}-\mathbf {x} \right)\rightarrow 1}$, con lo cual la función de ponderación no juega ningún papel relevante en el cálculo de las funciones de forma, convirtiéndose el método para obtener la aproximación en una técnica de mínimos cuadrados estándar.

En el desarrollo de los distintos ejemplos que se presentan en la tesis, salvo se indique lo contrario, se utilizará como referencia para el cómputo de la función de ponderación de Gauss, ${\textstyle q=1.1}$, ${\textstyle k=1.0}$ y ${\textstyle c=0.25r}$, sin embargo, tal como muestran las figuras 20, 21 y 22 para un caso 1D, manipulando estos parámetros se pueden obtener distintas formas de la función y en consecuencia distintos valores útiles para la aproximación. Analizando ambas figuras, se deduce que la función de Gauss (y en consecuencia la aproximación final), presenta sensibilidad tanto a la variación del parámetro ${\textstyle c}$ como al valor de ${\textstyle k}$, existiendo un cierto compromiso entre ambos para el adecuado cómputo de las funciones de forma. Por último, en la figura 23 se muestra una representación en 3D de la función de Gauss para el nodo central ${\textstyle I}$ del dominio de 25 puntos de la figura 14.

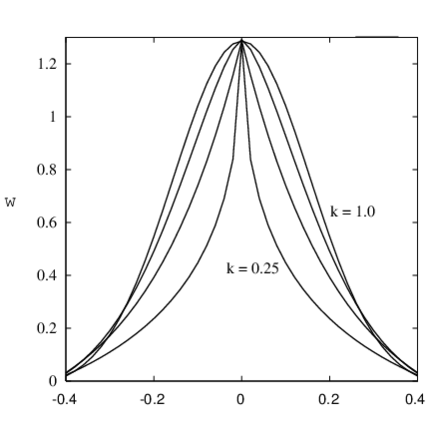
Figura 20: Representacion de la funcion de ponderacion para distintos valores del parametro kmath (c=0.25rmath , q=1.1math)

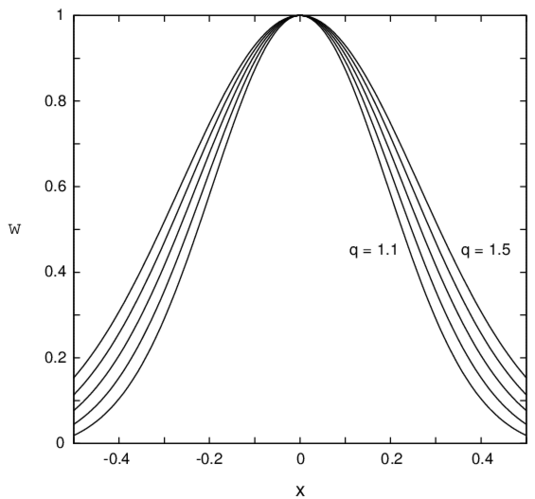
Figura 21: Representacion de la funcion de ponderacion de Gauss para distintos valores del parametro qmath (c=0.25rmath , k=1.0math)

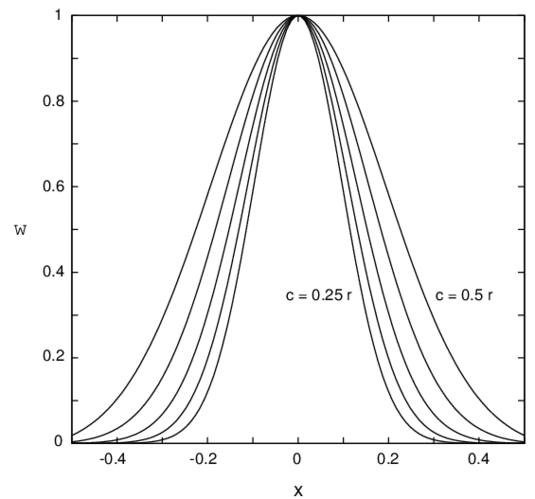
Figura 22: Representacion de la funcion de ponderacion de Gauss para distintos valores del factor de apuntamiento cmath (q=1.1,math k=1.0math)

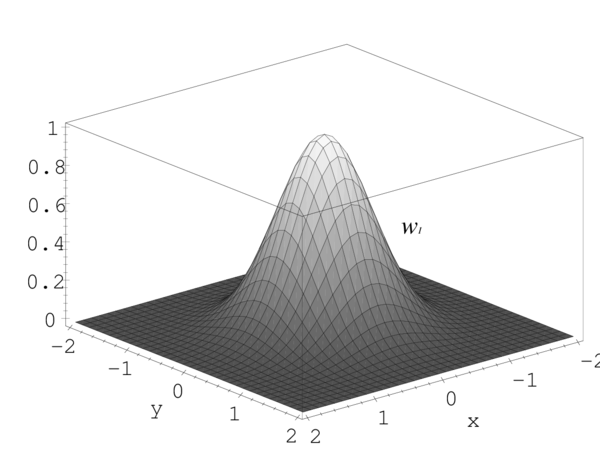
Figura 23: Representacion de la funcion de ponderacion de Gauss en 3D

3.3 Discretización mediante colocación puntual

El esquema de colocación puntual es la técnica de discretización que mejor se adapta al tipo de aproximación FWLS, puesto que permite superar el inconveniente de evaluación múltiple que presentan las funciones de forma y sus derivadas, circunscribe la validez de la aproximación al nodo estrella ${\textstyle \mathbf {x} _{I}}$ y también porque el sistema discreto de ecuaciones se obtiene sin utilizar un proceso de integración, lo que en definitiva permite conservar el carácter sin malla del método. En el contexto de los métodos sin malla, esta técnica ha sido empleada en conjunto con aproximaciones en diferencias finitas generalizadas [46], con posterioridad, se implementa por primera vez con una aproximación FWLS en el método de puntos finitos MPF [71] [72].

Considérese el sistema de ecuaciones diferenciales que gobierna el comportamiento de un sólido lineal elástico, cuyas fuerzas de inercias son despreciables, es decir, la ecuación de equilibrio

$\bigtriangledown \cdot \mathbf {\sigma (x} )+\rho \mathbf {b(x} )=\mathbf {0} {\hbox{ }}\forall \mathbf {x\in } \Omega$

(3.14)

con su correspondiente condición de Neumann

$\mathbf {\sigma (x} )\cdot \mathbf {n} ={\overline {\mathbf {t} }}(\mathbf {x} ){\hbox{ }}\forall \mathbf {x\in } \Gamma _{t}$

(3.15)

y condición de Dirichlet

$\mathbf {u(x} )\mathbf {=} {\overline {\mathbf {u} }}(\mathbf {x} ){\hbox{ }}\forall \mathbf {x} \in \Gamma _{u}$

(3.16)

siendo ${\textstyle \mathbf {\sigma } }$ el tensor de tensiones¹, ${\textstyle \rho }$ la densidad volumétrica del sólido, ${\textstyle \mathbf {b} }$ el vector de fuerzas másicas en el interior del sólido, ${\textstyle \mathbf {n} }$ el vector normal al contorno ${\textstyle \Gamma _{t}}$, ${\textstyle \mathbf {u} }$ el vector de desplazamientos y ${\textstyle {\overline {\mathbf {t} }}}$ , ${\textstyle {\overline {\mathbf {u} }}}$ los vectores de tracción y desplazamientos prescritos sobre el contorno ${\textstyle \Gamma _{t}}$ y ${\textstyle \Gamma _{u}}$ respectivamente. Para plantear el sistema únicamente en términos de los desplazamientos, se utilizan las relaciones fundamentales tensión-deformación (ecuación constitutiva) y deformación-desplazamientos (ecuación geométrica), dando lugar a las ecuaciones [60]

$(\lambda +\mu )\nabla (\nabla \cdot \mathbf {u} (\mathbf {x} ))+\mu \nabla ^{2}\mathbf {u} (\mathbf {x} )+\rho \mathbf {b(x} )=\mathbf {0} {\hbox{ }}\forall \mathbf {x\in } \Omega$ $\lambda (\nabla \cdot \mathbf {u} (\mathbf {x} ))\mathbf {n} +\mu (\mathbf {u} (\mathbf {x} )\otimes \nabla +\nabla \otimes \mathbf {u} (\mathbf {x} ))\cdot \mathbf {n} ={\overline {\mathbf {t} }}(\mathbf {x} ){\hbox{ }}\forall \mathbf {x\in } \Gamma _{t}$ $\mathbf {u(x} )={\overline {\mathbf {u} }}(\mathbf {x} ){\hbox{ }}\forall \mathbf {x} \in \Gamma _{u}$

Utilizando la aproximación FWLS de 3.1 para el campo de desplazamientos y la técnica de colocación puntual, se obtiene finalmente el siguiente sistema discreto

$(\lambda +\mu )\nabla (\nabla \cdot {\widehat {\mathbf {u} }}(\mathbf {x} _{I}))+\mu \nabla ^{2}{\widehat {\mathbf {u} }}(\mathbf {x} _{I})+\rho \mathbf {b(x} _{I})=\mathbf {0} \forall \mathbf {x} _{I}\in \mathbf {(} \Omega -\Gamma )$ $\lambda (\nabla \cdot {\widehat {\mathbf {u} }}(\mathbf {x} _{I}))\mathbf {n} +\mu ({\widehat {\mathbf {u} }}(\mathbf {x} _{I})\otimes \nabla +\nabla \otimes {\widehat {\mathbf {u} }}(\mathbf {x} _{I}))\cdot \mathbf {n} ={\overline {\mathbf {t} }}(\mathbf {x} _{I}){\hbox{ }}\forall \mathbf {x} _{I}\in \Gamma _{t}$ ${\widehat {\mathbf {u} }}(\mathbf {x} _{I})={\overline {\mathbf {u} }}(\mathbf {x} _{I}){\hbox{ }}\forall \mathbf {x} _{I}\in \Gamma _{u}$

(3.17)

del cual deben destacarse los siguientes aspectos relevantes:

1. La ecuación de equilibrio del problema se impone únicamente en los nodos interiores del dominio ${\textstyle \Omega }$ (${\textstyle \Gamma =\Gamma _{t}\cup \Gamma _{u}}$)
2. La condición de contorno de Neumann se impone también en los nodos sobre el contorno libre del sólido (donde el vector de tracciones prescrito ${\textstyle {\overline {\mathbf {t} }}(\mathbf {x} _{I})}$ sea nulo)
3. La condición de contorno de Dirichlet se impone de manera directa sin la necesidad de utilizar un procedimiento especial (como penalización en el método de Galerkin)

En el sistema 3.17 ${\textstyle \lambda }$, ${\textstyle \mu }$ son las constantes de Lamé que caracterizan el comportamiento elástico del material y ${\textstyle \otimes }$ el operdor gradiente.

(¹) El operador $\bigtriangledown \cdot$ en 3.14 es la divergencia

3.4 Implementación numérica

Sin pérdida de generalidad, a continuación se muestra el proceso para implementar numéricamente el MPF para un caso 2D de un sólido lineal elástico, similar procedimiento puede ser aplicado también tanto para un caso 1D como 3D. El sistema de ecuaciones en su forma desarrollada, que permite obtener como solución el campo de desplazamientos es (recuérdense 3.14, 3.15, 3.16)

Ecuación de equilibrio

$\sigma _{x,x}+\tau _{xy,y}+\rho b_{x}=0$ $\tau _{yx,x}+\sigma _{y,y}+\rho b_{y}=0$

(3.18)

Condición de Neumann

$\sigma _{x}n_{x}+\tau _{xy}n_{y}={\overline {t}}_{x}$ $\tau _{yx}n_{x}+\sigma _{y}n_{y}={\overline {t}}_{y}$

(3.19)

Condición de Dirichlet

$u={\overline {u}}$ $v={\overline {v}}$

que en forma compacta matricial puede expresarse como

$\mathbf {L} ^{T}\mathbf {\sigma +} \rho \mathbf {b} =\mathbf {0} {\hbox{ }}\forall \mathbf {x\in } \Omega -\Gamma$ $\mathbf {N} ^{T}\mathbf {\sigma } ={\overline {\mathbf {t} }}{\hbox{ }}\forall \mathbf {x\in } \Gamma _{t}$ $\mathbf {u} ={\overline {\mathbf {u} }}{\hbox{ }}\forall \mathbf {x\in } \Gamma _{u}$

(3.20)

siendo las matrices ${\textstyle \mathbf {L} }$, ${\textstyle \mathbf {N} }$

$\mathbf {L:=} \left[{\begin{array}{ll}{\frac {\partial }{\partial x}}&0\\0&{\frac {\partial }{\partial y}}\\{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial x}}\end{array}}\right]{\hbox{, }}\mathbf {N} :=\left[{\begin{array}{ll}n_{x}&0\\0&n_{y}\\n_{y}&n_{x}\end{array}}\right]$

los vectores ${\textstyle \mathbf {\sigma } }$ (${\textstyle \tau _{xy}=\tau _{yx}}$), ${\textstyle \mathbf {u} }$

$\mathbf {\sigma } :=\left[{\begin{array}{l}\sigma _{x}\\\sigma _{y}\\\tau _{xy}\end{array}}\right]{\hbox{, }}\mathbf {u} :=\left[{\begin{array}{l}u\\v\end{array}}\right]$

y los vectores ${\textstyle \mathbf {b} }$, ${\textstyle {\overline {\mathbf {t} }}}$ y ${\textstyle {\overline {\mathbf {u} }}}$ respectivamente

$\mathbf {b} :=\left[{\begin{array}{l}b_{x}\\b_{y}\end{array}}\right]{\hbox{, }}{\overline {\mathbf {t} }}:=\left[{\begin{array}{l}{\overline {t}}_{x}\\{\overline {t}}_{y}\end{array}}\right]{\hbox{, }}{\overline {\mathbf {u} }}:=\left[{\begin{array}{l}{\overline {u}}\\{\overline {v}}\end{array}}\right]$

Para obtener un sistema equivalente en términos de los desplazamientos, es necesario utilizar la relación tensión-deformación y la relación deformación-desplazamientos como sigue

$\mathbf {\sigma } =\mathbf {D\varepsilon }$ $\mathbf {\varepsilon } =\mathbf {Lu}$

(3.21)

donde la matriz ${\textstyle \mathbf {D} }$ (en un caso 2D)

$\mathbf {D=} \left[{\begin{array}{lll}d_{11}&d_{12}&d_{13}\\d_{21}&d_{22}&d_{23}\\d_{31}&d_{32}&d_{33}\end{array}}\right]$

representa la matriz simétrica constitutiva (o de constantes elásticas), cuyas componentes en el caso de un material elástico isótropo son [94]

$d_{11}=d_{22}={\frac {\overline {E}}{1-{\overline {\nu }}^{2}}}$ $d_{12}=d_{21}={\overline {\nu }}d_{11}$ $d_{33}={\frac {E}{2(1+\nu )}}$ $d_{13}=d_{23}=d_{31}=d_{32}=0$

con

${\overline {E}}\left\{{\begin{array}{ll}E&{\hbox{ tension plana}}\\E/(1-\nu )&{\hbox{ deformacion plana}}\end{array}}\right.$

${\overline {\nu }}\left\{{\begin{array}{ll}\nu &{\hbox{ tension plana}}\\\nu /(1-\nu )&{\hbox{ deformacion plana}}\end{array}}\right.$

siendo ${\textstyle E}$ y ${\textstyle \nu }$, dos parámteros que caracterizan el tipo de material y denominados módulo de elasticidad longitudinal y coeficiente de Poisson respectivamente. En 3.21 el vector ${\textstyle \mathbf {\varepsilon } }$ representa el vector de deformaciones.

Reemplazando 3.21 en 3.20 y utilizando la aproximación sin malla del MPF definida en 3.10, tanto para los desplazamientos en ${\textstyle u}$ como en ${\textstyle v}$ del vector de incógnitas ${\textstyle \mathbf {u} }$, es decir

$\mathbf {u} \cong {\widehat {\mathbf {u} }}=\left[{\begin{array}{l}{\widehat {u}}\\{\widehat {v}}\end{array}}\right]=\left[{\begin{array}{llllll}\phi _{I}^{1}(\mathbf {x} )&0&\cdots &&\phi _{I}^{n}(\mathbf {x} )&0\\0&\phi _{I}^{1}(\mathbf {x} )&\cdots &&0&\phi _{I}^{n}(\mathbf {x} )\end{array}}\right]\left[{\begin{array}{c}u_{1}^{h}\\v_{1}^{h}\\\vdots \\\\u_{n}^{h}\\v_{n}^{h}\end{array}}\right]$ $=\left[{\begin{array}{llll}\mathbf {\Phi } _{I}^{1}&\mathbf {\Phi } _{I}^{2}&\cdots &\mathbf {\Phi } _{I}^{n}\end{array}}\right]\mathbf {u} ^{h}{\hbox{ }}\mathbf {\Phi } _{I}^{i}\in Mat(2x2){\hbox{ , }}i=1,...,n$ $=\mathbf {\Phi u} ^{h}$

se obtiene el siguiente sistema de ecuaciones en forma matricial

$\left[\mathbf {L} ^{T}\mathbf {DL\Phi } \right]\mathbf {u} ^{h}=-\rho \mathbf {b} {\hbox{ }}\forall \mathbf {x\in } \Omega -\Gamma$ $\left[\mathbf {N} ^{T}\mathbf {DL\Phi } \right]\mathbf {u} ^{h}={\overline {\mathbf {t} }}{\hbox{ }}\forall \mathbf {x\in } \Gamma _{t}$ $\left[\mathbf {\Phi } \right]\mathbf {u} ^{h}={\overline {\mathbf {u} }}{\hbox{ }}\forall \mathbf {x\in } \Gamma _{u}$

o en su forma compacta

$\mathbf {K} _{I}\mathbf {u} ^{h}=\mathbf {f} _{I}{\hbox{ }}I=1,.....,N$

(3.22)

La matriz ${\textstyle \mathbf {K} _{I}}$ para cada punto ${\textstyle I}$ de la partición estará a su vez formada por ${\textstyle n}$ sub-matrices ${\textstyle \mathbf {K} _{I}^{i}\in Mat(2x2)}$

$\mathbf {K} _{I}=\left[{\begin{array}{llllll}\mathbf {K} _{I}^{1}&\mathbf {K} _{I}^{2}&\mathbf {K} _{I}^{3}&\cdots &\mathbf {K} _{I}^{n-1}&\mathbf {K} _{I}^{n}\end{array}}\right]$

donde el superíndice ${\textstyle i}$, ${\textstyle i=1,..n}$, indentifica el nodo en la nube perteneciente al nodo estrella ${\textstyle I}$. Dependiendo de si un punto pertenece al interior del dominio o al contorno, la manera de obtener los coeficientes de cada sub-matriz ${\textstyle \mathbf {K} _{I}^{i}}$ y su correspondiente vector de fuerzas independientes ${\textstyle \mathbf {f} _{I}\in Vec(2x1)}$ es la siguiente

• si ${\textstyle I\in \Omega -\Gamma }$

$\mathbf {K} _{I}^{i}\left\{{\begin{array}{l}\left[\mathbf {K} _{I}^{i}\right]_{11}=d_{11}\phi _{I,xx}^{i}+d_{33}\phi _{I,yy}^{i}\\\left[\mathbf {K} _{I}^{i}\right]_{12}=\phi _{I,xy}^{i}(d_{12}+d_{33})\\\left[\mathbf {K} _{I}^{i}\right]_{21}=\left[\mathbf {K} _{I}^{i}\right]_{12}\\\left[\mathbf {K} _{I}^{i}\right]_{22}=d_{22}\phi _{I,yy}^{i}+d_{33}\phi _{I,xx}^{i}\end{array}}\right.{\hbox{, }}\mathbf {f} _{I}=-\rho \mathbf {b}$

• si ${\textstyle I\in \Gamma _{t}}$

$\mathbf {K} _{I}^{i}\left\{{\begin{array}{l}\left[\mathbf {K} _{I}^{i}\right]_{11}=d_{11}\phi _{I,x}^{i}n_{x}+d_{33}\phi _{I,y}^{i}n_{y}\\\left[\mathbf {K} _{I}^{i}\right]_{12}=d_{12}\phi _{I,y}^{i}n_{x}+d_{33}\phi _{I,x}^{i}n_{y}\\\left[\mathbf {K} _{I}^{i}\right]_{21}=d_{33}\phi _{I,y}^{i}n_{x}+d_{12}\phi _{I,x}^{i}n_{y}\\\left[\mathbf {K} _{I}^{i}\right]_{22}=d_{33}\phi _{I,x}^{i}n_{x}+d_{22}\phi _{I,y}^{i}n_{y}\end{array}}\right.{\hbox{, }}\mathbf {f} _{I}={\overline {\mathbf {t} }}$

• si ${\textstyle I\in \Gamma _{u}}$

$\mathbf {K} _{I}^{i}\left\{{\begin{array}{l}\left[\mathbf {K} _{I}^{i}\right]_{11}=\left[\mathbf {\Phi } _{I}^{i}\right]_{11}\\\left[\mathbf {K} _{I}^{i}\right]_{12}=0\\\left[\mathbf {K} _{I}^{i}\right]_{21}=0\\\left[\mathbf {K} _{I}^{i}\right]_{22}=\left[\mathbf {K} _{I}^{i}\right]_{11}\end{array}}\right.{\hbox{, }}\mathbf {f} _{I}={\overline {\mathbf {u} }}$

La resolución del sistema matricial 3.22 que se obtiene de aplicar el MPF, permite encontrar el vector de parámetros ${\textstyle \mathbf {u} ^{h}}$ y posibilita el cálculo de la información necesaria para el post-proceso, en este caso el vector del campo de desplazamiento aproximado ${\textstyle {\widehat {\mathbf {u} }}}$, el vector de deformaciones ${\textstyle \mathbf {\varepsilon } }$ y el vector de tensiones ${\textstyle \mathbf {\sigma } }$.

Las expresiones desarrolladas en el presente apartado permiten implementar en un programa por ordenador el MPF para la resolución de problemas de elasticidad en 2D, sin embargo, el mismo procedimiento puede ser utilizado para la implementación en 1D o 3D de cualquier problema de contorno en elasticidad lineal, con las particularidades geométricas y físicas del problema en cuestión.

Para conseguir los objetivos de este trabajo de investigación, y para desarrollar los distintos ejemplos que se presentan en la tesis, se ha desarrollado e implementado un código en lenguaje FORTRAN para la resolución de las ecuaciones de elasticidad mediante el MPF. Como muestra la tabla 1, se ha subdividido el tratamiento de la información en tres etapas fundamentales; pre-proceso, cálculo y post-proceso, además se puede apreciar el tipo de información básica que maneja el código en cada etapa. Cabe mencionar que las etapas se han implementado de manera que puedan ser integradas en el software comercial de pre y post proceso gráfico denominado GID.

Tabla. 1 Principales etapas en la implementación del código de Puntos Finitos

3.4.1 Generación local de nubes

Una vez efectuada la etapa de pre-proceso y lectura de datos del problema, y como paso previo a la resolución del mismo, tiene lugar una etapa fundamental en todo método de puntos, esto es, la definición y generación de los subdominios locales de interpolación o nubes. La selección apropiada de los puntos que formarán cada nube, como también la adecuada discretización del dominio, tiene gran influencia en el resultado final de una modelación mediante colocación puntual. Intuitivamente y a pesar de no ser fácilmente cuantificables, se pueden establecer ciertos razonamientos para conformar una nube de buena calidad, por ejemplo:

1. el nodo central o nodo estrella completamente rodeado por los demás nodos de la nube
2. el centro de gravedad de la nube lo más cercano al nodo estrella

Inicialmente y por ser fácil de implementar, se probó un algoritmo de búsqueda y generación de las nubes basado en el criterio de la mínima distancia [40], en el cual, los puntos que conforman la nube, quedan dentro del círculo de radio ${\textstyle R_{I}}$ y centrado en el nodo estrella.

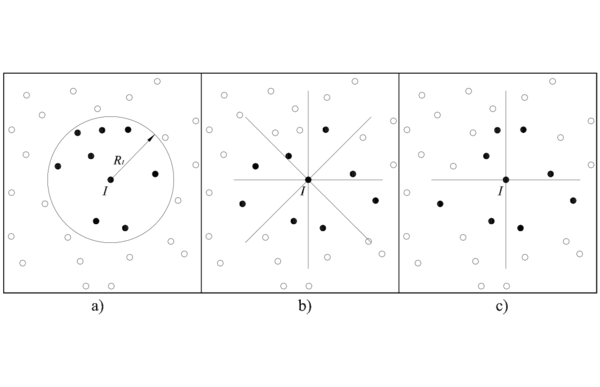
Figura 24: Generacion local de nubes en el dominio, a) criterio de la minima distancia b) criterio de ocho segmentos y c) criterio de cuatro cuadrantes

El valor de ${\textstyle R_{I}}$, debe ser el adecuado para que se obtengan nubes con el número suficiente de puntos para llevar a cabo la interpolación de mínimos cuadrados (${\textstyle 7}$ para un polinomio base cuadrático en 2D). A priori no es fácil definir este valor, sin embargo el mayor inconveniente de este procedimiento de generación de nubes es que, dependiendo de la densidad de puntos, puede producir nubes que no cumplen las condiciones geométricas mencionados anteriormente. A modo de ejemplo, la figura 24a muestra una nube generada con este criterio¹, como se aprecia, la información que aportan los puntos al nodo estrella proviene principalmente de la mitad superior del subdominio. Este tipo de nube, algo desbalanceada, propicia una deficiente interpolación local de la función aproximada y por consiguiente resultados poco precisos.

Una segunda técnica para generar las nubes, denominada por sus autores como eight segment criterion [85], consiste en subdividir el entorno que rodea al nodo estrella con ocho segmentos y seleccionar por cada sector generado el nodo más cercano. Un tercer método para seleccionar los nodos de la nube, denominado como four quadrant criterion [46], consiste en utilizar un sistema cartesiano de ejes en el nodo estrella y escoger los dos más cercanos a este por cada cuadrante. Con estos dos últimos métodos, tal como muestran las figuras 24b y 24c respectivamente, se pueden conseguir nubes de mejor calidad en el dominio, sin embargo, para minimizar la falta de simetría de las nubes y de cara a obtener también buenos resultados, estos criterios de búsqueda deben ser modificados cuando se utilizan en el contorno [48].

Para lograr los resultados que se presentan en esta tesis, se ha implementado un algoritmo de búsqueda y generación de nubes basado en una triangulación local de Delaunay. Esta técnica, ampliamente utilizada para la generación automática de mallas, permite conectar o relacionar un nodo con sus vecinos próximos mediante triángulos en 2D y tetrahedros en 3D, sin embargo, prescindiendo del tipo y calidad de los elementos generados esta técnica proporciona la información necesaria para generar localmente la nube de puntos. Aunque con anterioridad esta técnica también ha sido utilizada en el contexto del MPF [57], la versión implementada para la solución de los ejemplos que se muestran en esta tesis presenta algunas particularidades, por este motivo, a continuación se ejemplifica de una forma gráfica su uso para generar las nubes tanto en el dominio como el contorno, remitiéndose al lector interesado a referencias específicas como [32], [95] y [100] para un mayor detalle de los conceptos puntuales de la técnica de triangulación de Delaunay.

Los pasos importantes para generar las nubes en el dominio, según muestra la figura 25, son

1. definir un sistema local de ejes cartesianos, centrado en el nodo estrella, para identificar aquellos puntos más próximos al origen por cada cuadrante (figura 25a)
2. formar con el nodo estrella los cuatro triangulos iniciales para la búsqueda de puntos (figura 25b)
3. para cada triángulo generado se traza la circunsferencia circuscrita comprobándose si existe algún punto adicional en su interior, en caso de existir uno o más, se elimina el triángulo inicial y se forman dos nuevos con el punto más cercano al nodo estrella (25c y 25d). Esta operación se repite hasta que finalmente ningún círculo contenga puntos adicionales en su interior (figuras 25e y 25f)
4. se genera la nube del nodo estrella con los puntos obtenidos a partir de la triangulación
5. si la cantidad de puntos no es suficiente, o como se verá posteriormente, la calidad de la nube no es la adecuada, se van seleccionando nuevos puntos a partir de las nubes de los nodos iniciales de la triangulación

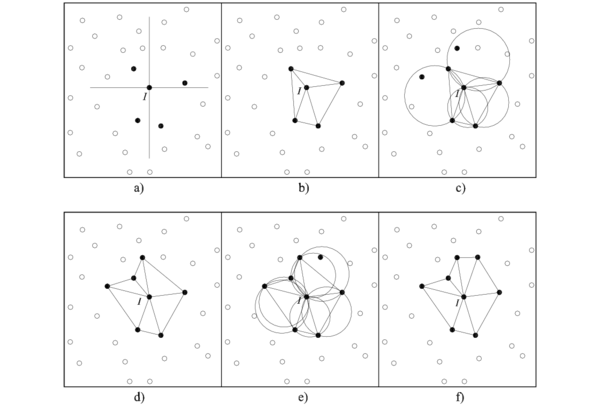
Figura 25: Ejemplo de generacion de una nube en el dominio mediante triangulacion de Delaunay

Para generar las nubes en el contorno, se puede emplear el procedimiento anterior pero poniendo atención en la generación inicial de los triángulos, los pasos a seguir en este caso son

1. seleccionar dos puntos adicionales al nodo estrella que pertenezcan al contorno (uno hacia cada lado) y buscar los nodos más cercanos por cuadrante (figura 26a)
2. generar los triángulos y trazar las circunsferencias circunscritas para buscar nodos adicionales (figuras 26b y 26c). De existir nodos adicionales se procede a eliminar el triángulo respectivo y se generan dos nuevos
3. en caso de no existir nodos adicionales, caso habitual en la práctica, se van agregando nodos a partir de las nubes de los puntos del interior (figuras 26d y 26e)
4. se debe repetir el paso anterior hasta cuando se logre el número suficiente de puntos (figura 26f)

Figura 26: Ejemplo de generacion de una nube en el contorno mediante triangulacion de Delaunay

El método de generación de nubes mediante triangulación de Delaunay, resuelve efectivamente los inconvenientes que presenta el método de búsqueda mediante la mínima distancia, tanto si se trata de discretizaciones en forma irregular como regular, incluso cuando se tiene diferente densidad de punto en ambas direcciones². A diferencia de las otras técnicas analizadas, y tal como muestra la figura 27, la triangulación de Delaunay permite obtener en estos casos la nube de puntos sin una modificación especial del algoritmo de búsqueda.

Figura 27: Ejemplo de generacion de una nube para un dominio regular y con diferente densidad de puntos, a) metodo de la minima distancia b) metodo de los ocho segmentos c) metodo de los cuatro cuadrantes, d) e) y f) triangulacion de Delaunay

(¹) En la figura 24 los nodos candidatos a pertenecer a la nube se indican con fondo sólido

(²) Este problema se puede presentar en discretizaciones de piezas delgadas o esbeltas

3.4.2 Polinomio base de interpolación y obtención de la función de forma

Uno de los aspectos importantes en toda aproximación por mínimos cuadrados, es la necesidad de invertir la matriz de momentos ${\textstyle \mathbf {A} _{I}}$ para obtener las funciones de forma en cada punto de la discretización. Si la matriz de momentos, que depende del polinomio base de interpolación (recuérdense las expresiones 3.6 y 3.11), se encuentra mal condicionada, pueden ocurrir errores en el proceso de inversión que afectarán directamente a los resultados numéricos de la aproximación. Analizando la matriz de momentos se puede distinguir claramente que ésta se obtiene a partir del producto de tres matrices como

$\mathbf {A} _{I}=\left[{\begin{array}{cccc}1&1&\cdots &1\\\mathbf {x} _{1}&\mathbf {x} _{2}&\cdots &\mathbf {x} _{n}\\\vdots &\vdots &\ddots &\vdots \\\left(\mathbf {x} _{1}\right)^{m-1}&\left(\mathbf {x} _{2}\right)^{m-1}&\cdots &\left(\mathbf {x} _{n}\right)^{m-1}\end{array}}\right]\left[{\begin{array}{ccc}w(\mathbf {x} _{I}-\mathbf {x} _{1})&\cdots &0\\\vdots &\ddots &\vdots \\0&\cdots &w(\mathbf {x} _{I}-\mathbf {x} _{n})\end{array}}\right]$ $\left[{\begin{array}{cccc}1&\mathbf {x} _{1}&\cdots &\left(\mathbf {x} _{1}\right)^{m-1}\\1&\mathbf {x} _{2}&\cdots &\left(\mathbf {x} _{2}\right)^{m-1}\\\vdots &\vdots &\ddots &\vdots \\1&\mathbf {x} _{n}&\cdots &\left(\mathbf {x} _{n}\right)^{m-1}\end{array}}\right]$

donde intervienen dos matrices de Vandermonde. La expresión anterior sirve para comprender el posible mal condicionamiento de la matriz ${\textstyle \mathbf {A} _{I}}$ cuando las coordenadas globales del punto se alejan del origen del sistema. Considérese por ejemplo el dominio 1D ${\textstyle \left[-95,95\right]}$ discretizado mediante una distribución equiespaciada de puntos, si se utiliza un polinomio de interpolación cuadrático ${\textstyle m=3}$ y nubes de ${\textstyle n=5}$ puntos, se obtienen como número de condición para un punto en el origen y otro situado en ${\textstyle x=90}$ los siguientes valores

${\begin{array}{ll}N{{}^{o}}_{cond.}(\mathbf {A} _{I})=4.1696&{\hbox{ para }}x_{I}=0\\N{{}^{o}}_{cond.}(\mathbf {A} _{I})=3.5717\times 10^{10}&{\hbox{ para }}x_{I}=90\end{array}}$

lo que nos detendría de efectuar cualquier interpolación con la función de forma para este segundo punto. Para evitar este tipo de mal condicionamiento conviene expresar la base polinómica de interpolación en forma local (centrada en el nodo estrella) y mediante coordenadas adimensionales, de esta forma la base se independiza de la geometría del dominio. Con esta modificación, una base cuadrática de interpolación para un caso 2D se expresaría como

$\mathbf {p} ^{T}\left(\mathbf {x} \right)=\left[1{\hbox{ }}{\frac {x_{I}-x}{{\underline {d}}d}}{\hbox{ }}{\frac {y_{I}-y}{{\underline {d}}d}}{\hbox{ }}\left({\frac {x_{I}-x}{{\underline {d}}d}}\right)^{2}{\hbox{ }}\left({\frac {\left(x_{I}-x\right)\left(y_{I}-y\right)}{{\underline {d}}d^{2}}}\right){\hbox{ }}\left({\frac {y_{I}-y}{{\underline {d}}d}}\right)^{2}\right]$

donde ${\textstyle \left(x_{I},y_{I}\right)}$ representan las coordenadas del nodo estrella y ${\textstyle {\underline {d}}d}$ una distancia característica de la nube. Se puede utilizar como distancia característica dentro de la nube el radio de influencia ${\textstyle r}$ [89], sin embargo, a través de los ejemplos desarrollados en esta tesis se ha podido comprobar que para discretizaciones de puntos como las indicadas en la figura 28 la solución numérica presenta algunas deficiencias. Para subsanar este inconveniente, detectado en discretizaciones donde

${\frac {dx_{m{\acute {a}}x.}}{dy_{m{\acute {a}}x.}}}\geq 4{\hbox{ o }}{\frac {dy_{m{\acute {a}}x.}}{dx_{m{\acute {a}}x.}}}\geq 4$

se ha propuesto utilizar como parámetro para adimensionalizar la base, las distancias máximas en la nube respecto del nodo estrella, es decir

$\mathbf {p} ^{T}\left(\mathbf {x} \right)=\left[1{\hbox{ }}{\frac {x_{I}-x}{dx_{m{\acute {a}}x.}}}{\hbox{ }}{\frac {y_{I}-y}{dy_{m{\acute {a}}x.}}}{\hbox{ }}\left({\frac {x_{I}-x}{dx_{m{\acute {a}}x.}}}\right)^{2}{\hbox{ }}\left({\frac {\left(x_{I}-x\right)\left(y_{I}-y\right)}{dx_{m{\acute {a}}x.}dy_{m{\acute {a}}x.}}}\right){\hbox{ }}\left({\frac {y_{I}-y}{dy_{m{\acute {a}}x.}}}\right)^{2}\right]$

Figura 28: Parametros para adimensionalizar la base de interpolacion en una nube

Otra forma de luchar contra el mal condicionamiento de la matriz ${\textstyle \mathbf {A} _{I}}$, que posibilita reducir el procedimiento para encontrar su inversa a una operación trivial, es convertirla en una matriz diagonal. Esta idea, propuesta por Lu [58] en el contexto del método EFG, consiste en ortogonalizar la base de interpolación mediante la técnica de Gram-Schmidt [37], en el MPF, esta técnica ha sido empleada con éxito pero conlleva un encarecimiento del coste computacional [99].

Como se ha visto, el proceso para invertir la matriz de momentos debe ser realizado con precaución para no afectar los resultados, por esto, se ha implementado en el código una estrategia para monitorear el número de condición de la matriz y comprobar la calidad de la función de forma y sus derivadas. Considerando un solver directo para invertir la matriz ${\textstyle \mathbf {A} _{I}}$, una nube será rechazada si el número de condición supera el valor de ${\textstyle 10^{7}}$, si es inferior se deberá además chequear, utilizando una función conocida como por ejemplo en 2D ${\textstyle u=x+y}$ y ${\textstyle u=x^{2}+y^{2}}$, el error existente entre las derivadas numéricas y las exactas. En este caso una nube será rechazada si la diferencia es mayor a ${\textstyle 10^{-10}}$. Para calcular el número de condición de la matriz se ha utilizado la norma siguiente

$Cond\left[\mathbf {A} _{I}\right]=\Vert \mathbf {A} _{I}\Vert _{\infty }\Vert \mathbf {A} _{I}^{-1}\Vert _{\infty }$

donde ${\textstyle \Vert \cdot \Vert _{\infty }}$ representa la norma infinita definida como

$\Vert \mathbf {A} _{I}\Vert _{\infty }=m{\acute {a}}x.{\stackrel {n}{\underset {j=1}{\sum }}}\mid A_{ij}\mid {\hbox{ , }}1\leq i\leq j$

4 Consistencia y convergencia del MPF

Para corroborar la técnica sin malla propuesta en los apartados anteriores, se desarrollan a continuación una serie de ejemplos prácticos que permiten analizar el comportamiento del método de puntos finitos bajo dos aspectos fundamentales, estos son la consistencia y convergencia. En primer término se utiliza el MPF para la resolución de problemas 1D de una barra sometida a una carga axial distribuida, seguidamente, se analizan diversos problemas de la ecuación de Poisson y Laplace, cuya solución analítica se conoce, finalizando el capítulo con ejemplos en 2D de diversas geometrías bajo un estado plano de tensiones y deformaciones. En todos los casos presentados, la solución numérica se obtiene luego de reemplazar la aproximación propia del MPF (recuérdese 3.10) en el sistema de ecuaciones del problema, además, siempre que exista una solución teórica, se utilizarán las siguientes relaciones para calcular el error relativo y global en la solución respectivamente

$e_{r}={\frac {\mathbf {\parallel } u_{I}-{\widehat {u}}_{I}\parallel }{u_{I}}}{\hbox{ , }}e_{g}={\sqrt {\frac {{\stackrel {N}{\underset {I=1}{\sum }}}\left(u_{I}-{\widehat {u}}_{I}\right)^{2}}{{\stackrel {N}{\underset {I=1}{\sum }}}\left(u_{I}\right)^{2}}}}$

siendo ${\textstyle u_{I}}$, ${\textstyle {\widehat {u}}_{I}}$, la solución teórica y numérica en el punto ${\textstyle I}$ de la partición del dominio, el cual se discretiza mediante un número finito de ${\textstyle N}$ puntos. En los distintos ejemplos analizados, la distancia entre puntos para una discretización regular vendrá dada por ${\textstyle h}$.

4.1 Resolución de problemas 1D

4.1.1 Barra bajo esfuerzos axiales

Particularizando las ecuaciones de Navier (recuérdese 3.17) para la geometría que muestra la figura 29, se puede obtener el sistema de ecuaciones diferenciales que rige el comportamiento de una barra sometida a un esfuerzo axial ${\textstyle \sigma _{0}}$ y sus correspondientes condiciones de contorno. En esta situación, el sistema de ecuaciones a resolver es [73]

$EA{\frac {d^{2}u(x)}{dx^{2}}}+p(x)=0{\hbox{ }}0<x<L$ $E{\frac {du(x)}{dx}}=\sigma _{0}={\frac {N}{A}}{\hbox{ }}x=L$ $u(x)=0{\hbox{ }}x=0$

donde los términos ${\textstyle p(x)}$, ${\textstyle E}$ y ${\textstyle A}$, representan la carga por unidad de longitud repartida, el módulo de elasticidad y el área tranversal de la barra.

Figura 29: Barra con una carga axial distribuida

Utilizando diferentes distribuciones para la carga repartida, se pueden obtener un buen número de soluciones prácticas para contrastar el MPF, en particular, se analizarán los casos indicados en la tabla tabla axial 1d, con los siguientes valores para los parámetros constantes

Tabla. 2 Tipo de carga repartida axial

${\textstyle {\hbox{Tipo de carga repartida }}p(x)}$	${\hbox{Solucion teorica}}$
${\textstyle {\frac {p}{L}}x}$	$u(x)={\frac {1}{EA}}\left[-{\frac {p}{6L}}x^{3}+{\frac {pL}{2}}x+Nx\right]$
${\textstyle p\sin({\frac {\pi }{L}}x)}$	$u(x)={\frac {1}{EA}}\left[{\frac {pL^{2}}{\pi ^{2}}}\sin({\frac {\pi }{L}}x)+({\frac {pL}{\pi }}+N)x\right]$

${\begin{array}{lllll}E=2.1e8[{\frac {kN}{m^{2}}}]&A=3.0e-3[m^{2}]&p=2.0e3[{\frac {kN}{m}}]&N=2.0e3[kN]&L=5.0[m]\end{array}}$

En ambos casos se utilizarán nubes de 5 puntos (${\textstyle n=5}$) y un polinomio cuadrático de interpolación (${\textstyle m=3}$), para discretizaciones regulares de 11, 26, 51 y 81 puntos. Adicionalmente en el caso de la carga repartida senoidal, se analiza la convergencia de la solución para una base de interpolación cúbica (${\textstyle m=4}$).

En primer término, la figura 30 muestra una correcta convergencia del MPF para las distintas discretizaciones utilizadas, cuando la carga axial se distribuye linealmente. Se destaca, que tanto para la aproximación de la solución (desplazamientos) como sus derivada (deformaciones), el error relativo máximo para una discretización con tan sólo 11 puntos es inferior al 1.8% (0.63% en el caso de los desplazamientos).

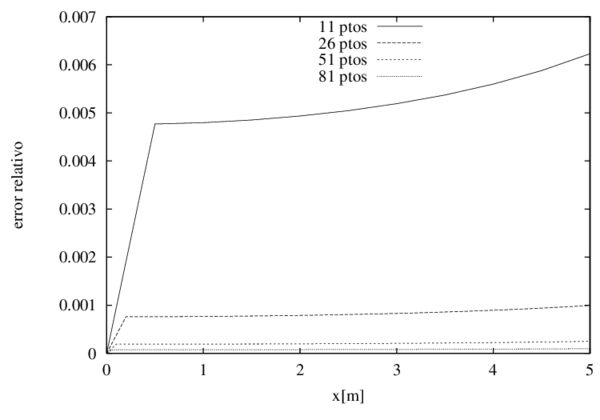
Figura 30: Distribucion del error relativo en desplazamientos. Problema de deformacion axial 1D, carga repartida lineal

La convergencia del error global de la solución y su derivada, figura 31, concuerda plenamente con los resultados anteriores y predice una velocidad de convergencia para los desplazamientos de ${\textstyle 2.0}$ y de ${\textstyle 1.97}$ las deformaciones.

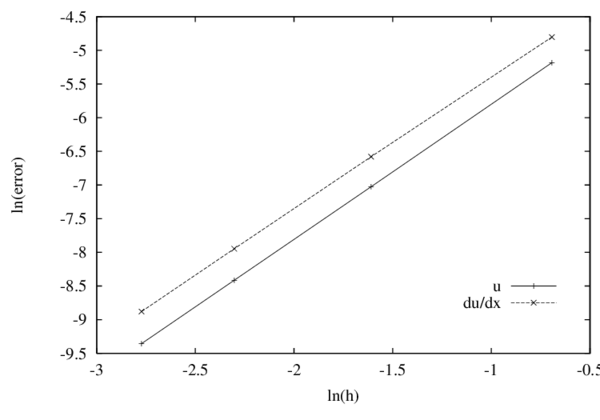
Figura 31: Convergencia del error global para el problema de deformacion axial 1D. Carga repartida lineal

Cuando la carga se reparte siguiendo una distribución senoidal, la figura 32 indica un aumento del error relativo en la solución respecto del caso lineal, para igual número de puntos utilizados en la discretización. Sin embargo, con una discretización de 26 puntos el error vuelve a ser inferior al 1% El análisis anterior sugiere que para obtener valores similares del error en la solución, se necesita una mayor discretización del dominio cuando la carga se reparte en forma senoidal. De todas formas, se debe tener en cuenta que la base de interpolación utilizada para aproximar la solución teórica, contiene solamente términos polinómicos. Al respecto, la figura 33 pone de manifiesto las ventajas que se obtienen, para este caso, cuando se utiliza una base de interpolación cúbica. Es de interés destacar en ambas situaciones que los valores máximos del error, aún siendo relativamente bajos, se concentran en la zona cercana al contorno de Neumann, con una clara tendencia a disminuir en la medida que se aumenta el número de puntos de la discretización.

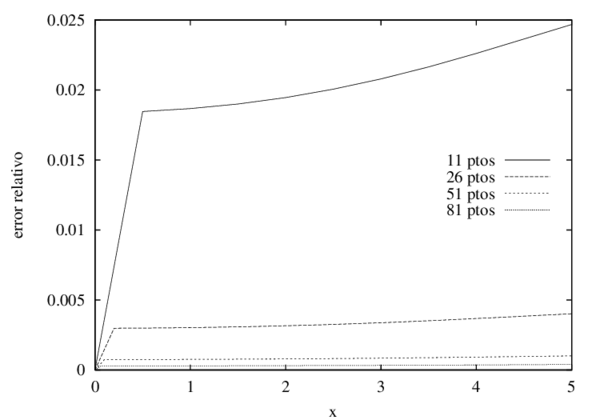
Figura 32: Distribucion del error relativo en desplazamientos. Problema de deformacion axial 1D, carga repartida senoidal

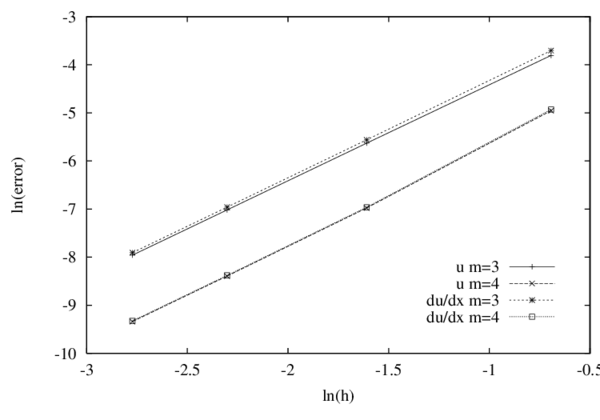
Figura 33: Convergencia del error global para el problema de deformacion axial 1D. Carga repartida senoidal

4.1.2 Solución de la ecuación de Poisson

Se puede estudiar también la convergencia y consistencia del MPF a través de la ecuación 1D de poisson, en particular se analizará la ecuación

${\frac {d^{2}u}{dx^{2}}}=-b(x){\hbox{ }}0<x<5$

(4.1)

sujeta a las condiciones que se indican en la tabla 3

Tabla. 3 Término independiente y condiciones de contorno de la ecuación de Poisson 1D

${\textstyle b(x)}$	$u(x=0)$	${\frac {du}{dx}}\mid _{x=5}$	${\hbox{Solucion teorica}}$
${\textstyle x}$	$0$	$0$	$-{\frac {1}{6}}x^{3}+{\frac {25}{2}}x$
${\textstyle \exp(x)}$	$9$	$1-\exp(5)$	$10+x-\exp(x)$

El ejemplo pretende además examinar cómo influye, en el resultado de la aproximación del MPF, el hecho de escoger nubes de forma asimétricas (ver figura 34).

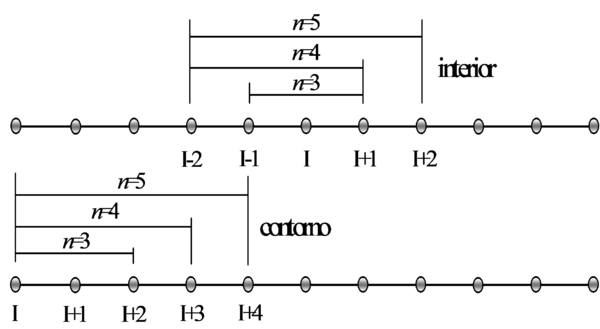
Figura 34: Disposicion de los puntos que conforman una nube interior y de contorno para un caso 1D

Para el caso del término independiente lineal, la figura 35 muestra la convergencia de la derivada de la solución, cuando se utiliza una discretización de 26, 51 y 81 puntos (${\textstyle n=5}$). Si bien el error relativo disminuye en la medida en que se aumenta el número de puntos, la figura muestra claramente que sólo cuando se incorpora el término cúbico en la base de interpolación, es decir ${\textstyle m=4}$, el error en la solución desaparece definitivamente.

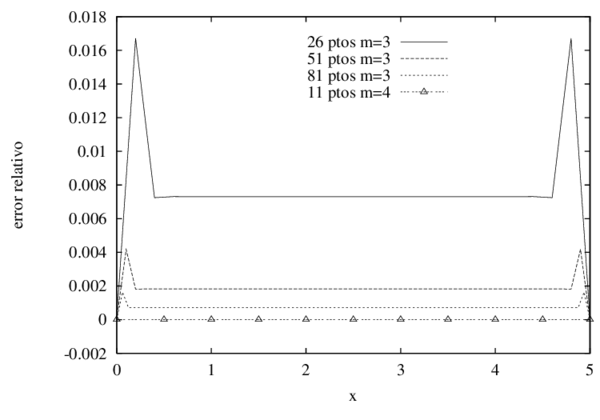
Figura 35: Distribucion del error relativo en derivadas. Problema 1D de la ecuacion de Poisson termino independiente lineal, nubes de 5 puntos

Siguiendo la misma tendencia, la figura 36 muestra la convergencia cuando se utilizan nubes de 4 puntos. Nuevamente se aprecia el efecto de agregar al polinomio base de interpolación el término cúbico. Para este ejemplo, como la solución teórica es una combinación lineal de los términos de la base, el MPF entrega los valores exactos de la solución en los puntos, lo que permite comprobar de una forma gráfica la consistencia del método. Si se comparan las gráficas para el caso de nubes de 5 y 4 puntos respectivamente, se nota un leve deterioro de la solución debido a la falta de simetría de la nube, de todas formas cuando ${\textstyle n=4}$ el error relativo máximo no supera el 2.6% El efecto de utilizar nubes de 4 puntos para este problema 1D, tal como indica la figura 37, supone un aumento del error global en la solución y también una disminución de la velocidad de convergencia cuando la nube está desbalanceada. La velocidad de convergencia para la solución numérica resulta ser 2.7 y 2.0, cuando se toman nubes de 5 y 4 puntos respectivamente.

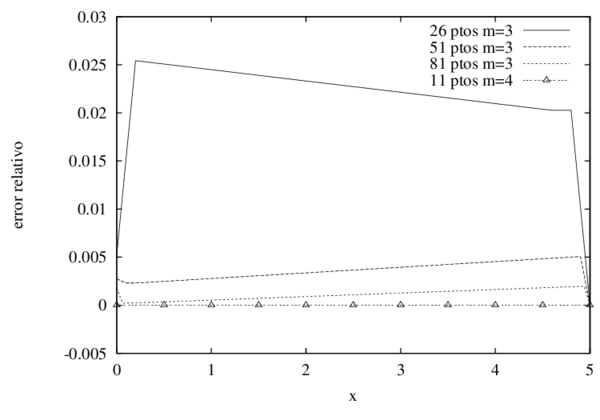
Figura 36: Distribucion del error relativo en derivadas. Problema 1D de la ecuacion de Poisson termino independiente lineal, nubes de 4 puntos

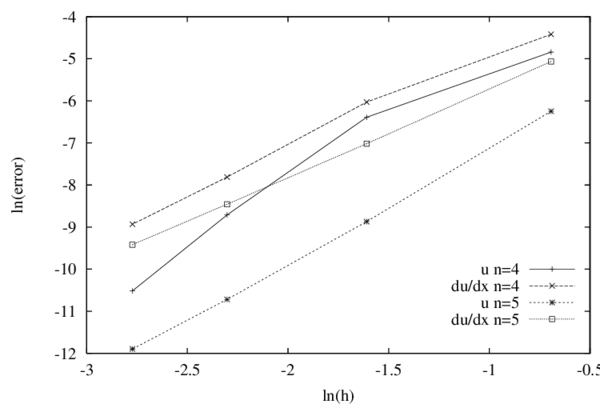
Figura 37: Convergencia del error global en la solucion para el problema de Poisson 1D, termino independiente lineal

Las figuras 38 y 39 muestran la convergencia de la solución, para discretizaciones de 6, 9, 11 y 26 puntos, cuando el término independiente de la ecuación de Poisson es exponencial y ${\textstyle n=5}$. Se aprecia de las figuras, que para este ejemplo se obtienen mejores resultados en la aproximación con el MPF cuando se utiliza una base de interpolación cuadrática ${\textstyle m=3}$. Este ejemplo permite comprobar el hecho de que, un aumento en el grado de la base de interpolación no comporta necesariamente una mejora de la solución numérica, cuando se mantiene constante el número de puntos en la nube.

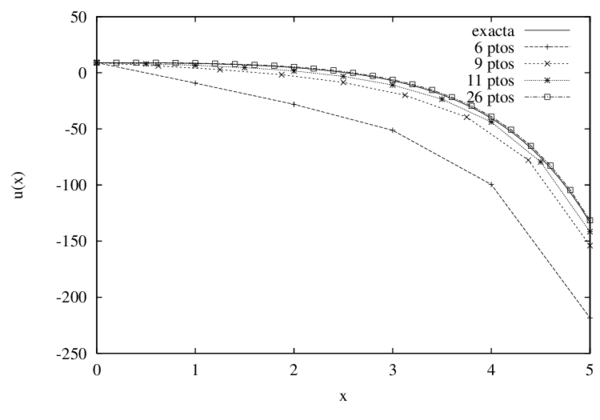
Figura 38: Convergencia de la solucion para el caso de la ecuacion de Poisson 1D, termino independiente exponencial, m=3math

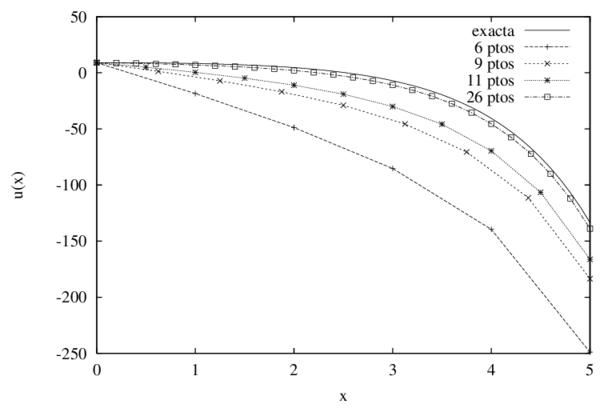
Figura 39: Convergencia de la solucion para el caso de la ecuacion de Poisson 1D, termino independiente exponencial, m=4math

Utilizando en la base de interpolación diferentes tipos de funciones linealmente independientes, se ha pretendido analizar una vez más la capacidad del MPF para capturar en forma local la solución teórica exacta. La figura 40 permite corroborar definitivamente, de una forma gráfica, la consistencia del MPF. Escogiendo esta vez 9 puntos para discretizar el dominio y ${\textstyle n=5}$, la aproximación reproduce exactamente la solución teórica sólo cuando se incorpora en la base de interpolación el término exponencial.

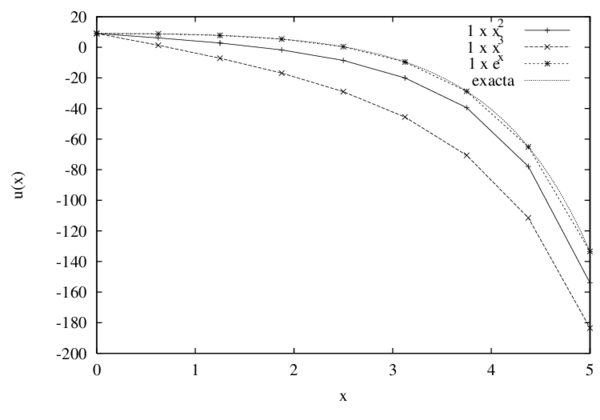
Figura 40: Convergencia de la solucion para distintas bases de interpolacion, termino independiente exponencial en la ecuacion de Poisson 1D

Para contrastar la convergencia del método, cuando se utiliza una distribución de puntos de forma irregular, se han generado para este ejemplo tres discretizaciones de 11, 26 y 41 puntos de forma aleatoria mediante una función random. Se puede apreciar de las figuras 41 y 42 que, al igual que cuando se utiliza una distribución de puntos regular, el error en la solución y su derivada disminuye en la medida que crece el número de puntos utilizados en la discretización. Sin embargo, para un número pequeño de puntos, los errores en la solución son mayores cuando se utiliza una distribución aleatoria. Esta alteración también se manifiesta en la convergencia del error global en la solución y su derivada, tal como indica la figura 43. En el caso de una distribución aleatoria, se ha utilizado la siguiente relación para obtener la distancia promedio entre puntos

$h={\frac {L}{N-1}}$

siendo ${\textstyle L}$ la longitud del dominio y ${\textstyle N}$ como antes el número total de puntos. Se debe tener presente al analizar los resultados, que éstos se obtuvieron utilizando una base cuadrática y nubes de 5 puntos, además, con una discretización aleatoria de 41 puntos, el error relativo en la solución y su derivada no supera en ningún punto el 1%

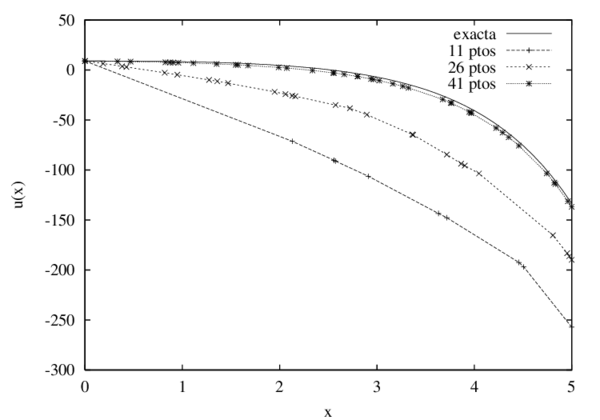
Figura 41: Convergencia de la solucion para una distribucion de puntos aleatoria, ejemplo1D de la ecuacion de Poisson, termino independiente exponencial.

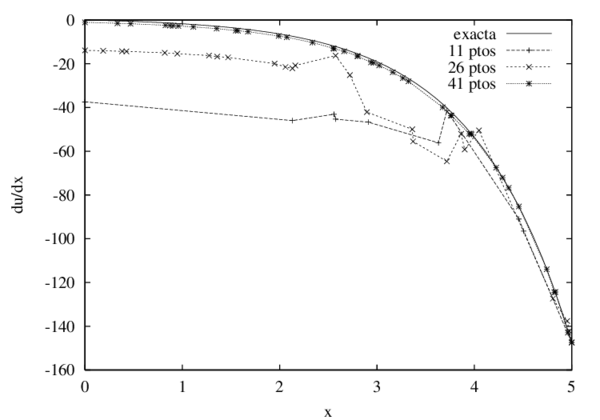
Figura 42: Convergencia de la derivada para una distribucion de puntos aleatoria, ejemplo1D de la ecuacion de Poisson, termino independiente exponencial.

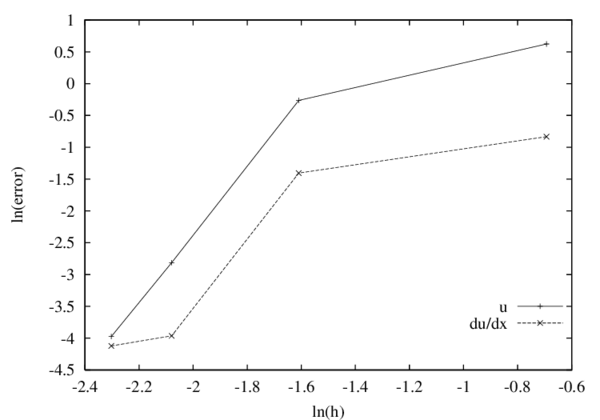
Figura 43: Convergencia del error global para una distribucion de puntos aleatoria, ejemplo 1D de la ecuacion de Poisson, termino independiente exponencial

4.1.3 Test con un gradiente de magnitud controlada

Un test para comprobar la convergencia de un método sin malla en 1D, ampliamente difundido en la literatura meshless (ver por ejemplo [24] y [56]), consiste en resolver una ecuación cuya solución analítica permita generar un gradiente de magnitud controlada en un punto concreto del dominio de análisis. Para el caso del MPF se propone resolver la ecuación de Poisson 1D en el intervalo ${\textstyle 0>x>1}$ (recordar expresión 4.1), cuyo término independiente y condiciones de contorno se ajustan a las características indicadas en la tabla 4.

Tabla. 4 Término independiente y condiciones de contorno de la ecuación de Poisson 1D con un gradiente controlado

${\textstyle b(x)}$	$u(x)\mid _{x=0}=u(x)\mid _{x=5}$
${\textstyle 2{\frac {\delta }{1+\delta ^{2}\left(x-x_{0}\right)^{2}}}+2\left(1-x\right){\frac {\delta ^{3}}{\left(1+\delta ^{2}\left(x-x_{0}\right)^{2}\right)^{2}}}\left(x-x_{0}\right)}$	$0$

Los parámetros que permiten controlar la magnitud del gradiente y el punto donde éste se genera son ${\textstyle \delta }$ y ${\textstyle x_{0}}$ respectivamente, en este caso concreto se utilizarán ${\textstyle \delta =60}$ y ${\textstyle x_{0}=0.5}$. Utilizando distribuciones regulares de 11, 21, 41 y 81 puntos, con nubes de 5 puntos y un polinomio cuadrático de interpolación, las figuras 44 y 45 muestran una correcta convergencia del MPF para este test, tanto para la solución numérica como su derivada. También se aprecia que la zona donde se producen los mayores errores en la solución y su derivada, corresponde precisamente con aquella donde se genera el gradiente en la solución (entorno del punto ${\textstyle x=0.5}$), en particular para este ejemplo, con una discretización de 11 puntos los errores superan el 100% en esa zona. La solución teórica para este problema es

$u(x)=(1-x)\left(\arctan \left(\delta \left(x-x_{0}\right)\right)+\arctan \left(\delta x_{0}\right)\right)$

y su derivada

$u_{,x}=-\arctan \delta \left(x-x_{0}\right)-\arctan \delta x_{0}+\left(1-x\right){\frac {\delta }{1+\delta ^{2}\left(x-x_{0}\right)^{2}}}$

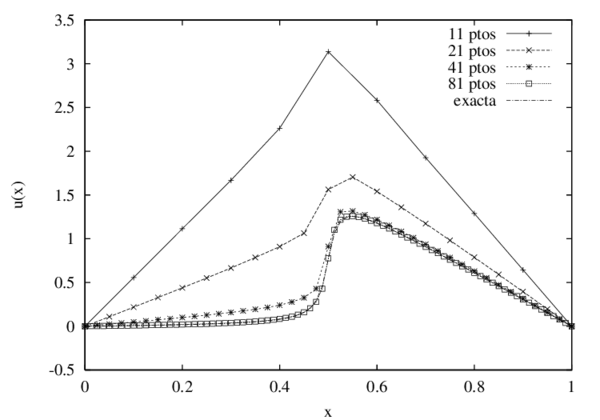
Figura 44: Convergencia de la solucion para un aumento del numero de puntos. Test 1D con un gradiente de magnitud controlada

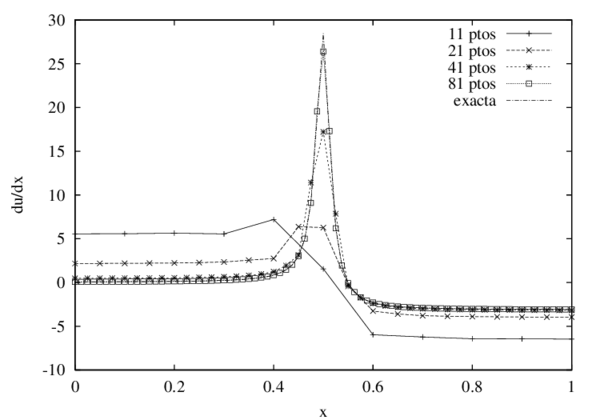
Figura 45: Convergencia de la derivada para un aumento del numero de puntos. Test 1D con un gradiente de magnitud controlada

El orden de convergencia del MPF para este test, se puede calcular a partir de los datos de la figura 46, obteniéndose un valor de 2.01 para la solución y 1.93 para su derivada. Estos valores concuerdan adecuadamente con los encontrados en anteriores ejemplos 1D.

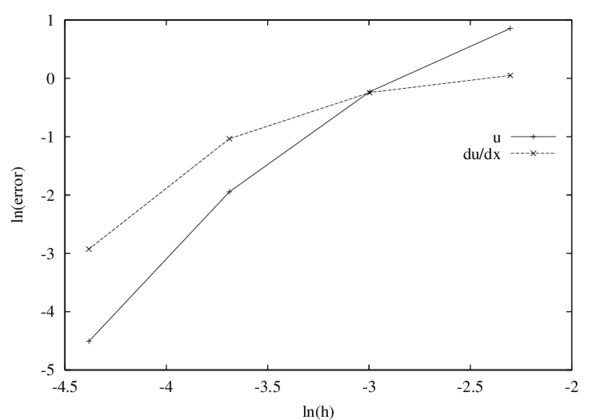
Figura 46: Convergencia del error global para un aumento del numero de puntos. Test 1D con un gradiente de magnitud controlada

4.2 Resolución de las ecuaciones de elasticidad en 2D

Una vez comprobada la consistencia y la convergencia del MPF para aplicaciones 1D, se pretende en este apartado utilizar la formulación sin malla desarrollada, para su aplicación en casos concretos de elasticidad bidimensional. Específicamente se quiere comprobar si la técnica del MPF, tal como se ha planteado, permite obtener resultados similares a los encontrados en los ejemplos 1D, o dicho de otra manera, si los resultados son extrapolables para situaciones de elasticidad 2D.

4.2.1 Test de la parcela y test de orden superior

Un primer ejemplo, como prueba necesaria para comprobar la convergencia del MPF en problemas de elasticidad 2D, consiste en resolver el test de la parcela simple, ampliamente utilizado para probar programas prácticos de elementos finitos. En referencias [39], [73] y [106] puede encontrarse un descripción más detallada de la utilización de este test en ejemplos de elasticidad lineal de sólidos. En el contexto de los métodos sin malla ha sido empleado también en [8] para demostrar la pérdida de consistencia de la aproximación, cuando no se utilizan multiplicadores de Lagrange para imponer las condiciones de contorno. Como primer test se propone resolver las ecuaciones de elasticidad en tensión plana, para el dominio cuadrado que muestra la figura 47. Se ha utilizado para el análisis una discretización uniforme de ${\textstyle 9}$ nodos y una aproximación cuadrática (${\textstyle m=6}$), con los valores para el módulo de Young y el coeficiente de Poisson de ${\textstyle E=1000}$ y ${\textstyle \nu =0.3}$ respectivamente.

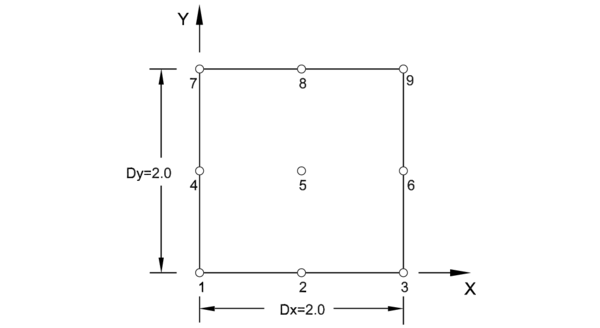
Figura 47: Test de la parcela con una distribucion regular de 9 puntos

Sobre los 8 nodos del contorno se prescriben desplazamientos ${\textstyle u=v=x+y}$, comprobándose la respuesta que se obtiene mediante el MPF para las distintas posiciones del punto central indicadas en la tabla 5.

Tabla. 5 Coordenadas del punto central para el test de la parcela con 9 puntos

Coordenadas del punto ${\textstyle 5}$

(${\textstyle 1.0,1.0}$)

(${\textstyle 1.2,0.35}$)

(${\textstyle 0.22,0.15}$)

(${\textstyle 0.3,1.76}$)

(${\textstyle 1.87,1.9}$)

En todas las situaciones, los valores numéricos del desplazamiento y esfuerzo del nodo interior coinciden de forma exacta con la solución teórica. Un segundo test consiste en utilizar la distribución irregular de 14 puntos mostrada en la figura 48, y calcular esta vez la respuesta en todos los puntos interiores del dominio. Como antes se prescriben los desplazamientos para los puntos sobre el contorno. Los requerimientos para satisfacer el test son por un lado que los desplazamientos en los nodos interiores sigan la misma distribución lineal prescrita en el contorno, y las deformaciones y esfuerzos sean constantes en la parcela.

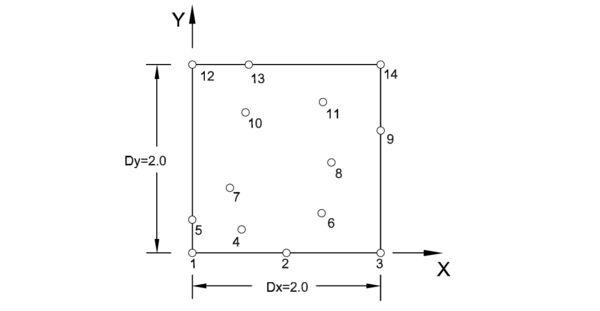
Figura 48: Test de la parcela para una distribucion irregular de 14 puntos

Como se aprecia en la tabla 6, donde se resumen los resultados numéricos para este test, en todos los puntos analizados se obtienen los valores exactos de la solución teórica, por consiguiente, el MPF cumple con el test de la parcela.

Tabla. 6 Resultados numéricos para el test de la parcela de 14 puntos

Puntos	Coordenadas	Desplazamientos (${\textstyle u=v}$)	$\sigma _{x}=\sigma _{y}$(${\textstyle \times 10^{3}}$)	$\tau _{xy}$(${\textstyle \times 10^{2}}$)
4	(${\textstyle 0.5,0.25}$)	$0.75$	$1.42857$	$7.6923$
6	(${\textstyle 1.38,0.45}$)	$1.83$	$1.42857$	$7.6923$
7	(${\textstyle 0.38,0.7}$)	$1.08$	$1.42857$	$7.6923$
8	(${\textstyle 1.5,1.0}$)	$2.5$	$1.42857$	$7.6923$
10	(${\textstyle 0.55,1.5}$)	$2.05$	$1.42857$	$7.6923$
11	(${\textstyle 1.4,1.6}$)	$3.0$	$1.42857$	$7.6923$

Si bien el test de la parcela resulta una prueba adecuada para comprobar la correcta programación del MPF, tal y como se ha propuesto no permite garantizar el correcto funcionamiento cuando se prescriben condiciones de contorno naturales o de Neumann. Para controlar lo anterior se construye un segundo test, de orden superior, en el que se incluyen este tipo de condiciones (ver figura 49). Para discretizar el dominio se ha utilizado una distribución regular de 28 puntos, asumiendo condiciones de tensión plana con valores de ${\textstyle E=1.0}$, ${\textstyle \nu =0.25}$ y espesor unitario. La solución teórica cuando el esfuerzo se distribuye uniformemente es [94] ${\textstyle u=x/E}$ y ${\textstyle v=-(\nu y)/E}$, mientras que para el caso de una distribución lineal se tiene ${\textstyle u=xy/E}$ , ${\textstyle v=-(x^{2}+\nu y^{2})/(2E)}$.

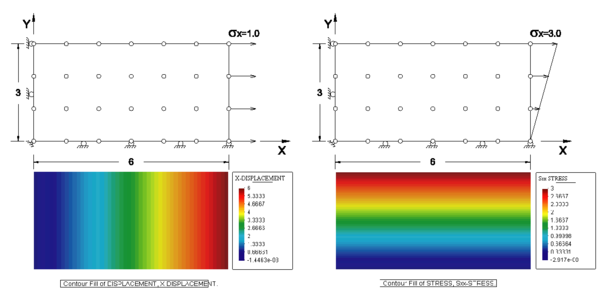
Figura 49: Dominio rectangular, discretizacion y resultados numericos para el test de la parcela de orden superior

Los resultados que se obtienen para este test, tanto desplazamientos como esfuerzos, coinciden nuevamente con la solución teórica para ambos casos de carga. En la figura 49 se aprecia la distribución del desplazamiento horizontal ${\textstyle u}$ y el esfuerzo ${\textstyle \sigma _{x}}$ para el caso de una tracción constante y lineal respectivamente, en los dos casos, la solución numérica se obtuvo utilizando un polinomio cuadrático de interpolación y nubes de 9 puntos.

4.2.2 Viga en cantilever

Siguiendo con el estudio de convergencia para ejemplos de elasticidad bidimensional, a continuación se resuelve un problema clásico en la literatura de los métodos meshless como es el de una viga en cantilever, se pretende también averiguar la convergencia del método para una distribución irregular de puntos. La figura 50 muestra la geometría de la viga para una distribución regular e irregular de 55 puntos, la carga total que actúa en el extremo se aplica mediante un esfuerzo tangencial que se distribye en forma parabólica, siendo su magnitud ${\textstyle P=1.0}$. El problema fué resuelto considerando condiciones de tensión plana y propiedades del material ${\textstyle E=1000}$ y ${\textstyle \nu =0.3}$, siendo su solución teórica [94]

$u=-{\frac {P}{6EI}}y\left[\left(6L-3x\right)x+\left(2+\nu \right)\left(y^{2}-{\frac {D^{2}}{4}}\right)\right]$ $v={\frac {P}{6EI}}\left[3\nu y^{2}\left(L-x\right)+\left(4+5\nu \right){\frac {D^{2}}{4}}x+\left(3L-x\right)x^{2}\right]$ $\sigma _{x}=-{\frac {P\left(L-x\right)}{I}}y{\hbox{ ; }}I={\frac {D^{3}}{12}}$ (4.2) $\sigma _{y}=0.0$ $\tau _{xy}={\frac {P}{2I}}\left({\frac {D^{2}}{4}}-y^{2}\right)$

con ${\textstyle I}$ el momento de inercia de la sección transversal, además, sobre el contorno ${\textstyle x=0}$, ${\textstyle y=\pm 0.5}$ se prescriben los desplazamientos de acuerdo con la solución teórica.

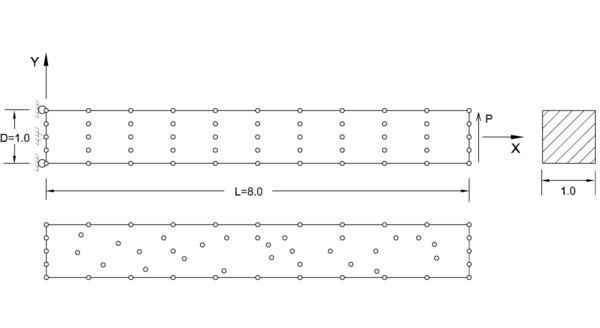
Figura 50: Viga en cantilever, geometria y distribucion regular e irregular de 55 puntos

Considerando una discretización regular, se analizó la respuesta del MPF con un total de 55, 165 y 333 puntos, para dos tipos de nubes distintas, en un primer caso las nubes contienen un número de puntos que varía entre 6 y 8, mientras que en el segundo el número de puntos se fija en 9 por nube (ver figura 51).

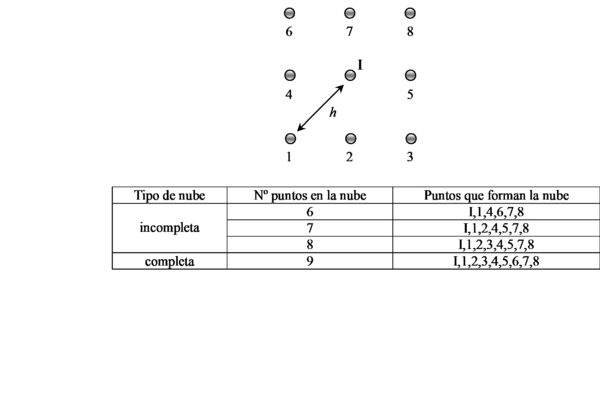
Figura 51: Eleccion de los nodos en las nubes para el ejemplo de la viga en cantilever, distribucion regular de puntos

Como indica la figura 52, cuando se utilizan nubes completas de 9 puntos el MPF muestra una correcta convergencia tanto en el desplazamiento horizontal como vertical, sin embargo, cuando se utilizan nubes incompletas de 6, 7 y 8 puntos existe un aumento del error global en la solución para la discretización con 165 puntos, lo que determina una menor velocidad de convergencia. Para obtener los resultados se han utilizado, en ambos casos, un polinomio cuadrático de interpolación (${\textstyle m=6}$) y ${\textstyle h}$ la distancia entre puntos indicada en la figura 51.

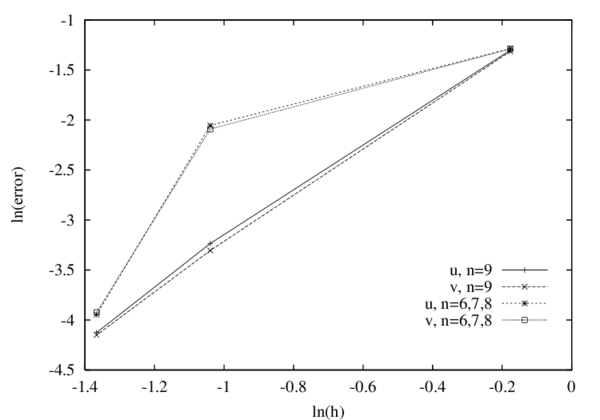
Figura 52: Convergencia del error global en la solucion para la viga en cantilever, distribucion regular de puntos

El aumento del error en la solución en el caso de nubes incompletas se debe a la falta de simetría de la nube, este fenómeno se acentúa aún más para las nubes de los puntos situados en el contorno. Además se ha constatado, tal como lo muestra la figura 53, que la utilización de nubes de forma asimétricas afectan también la simetría de la solución.

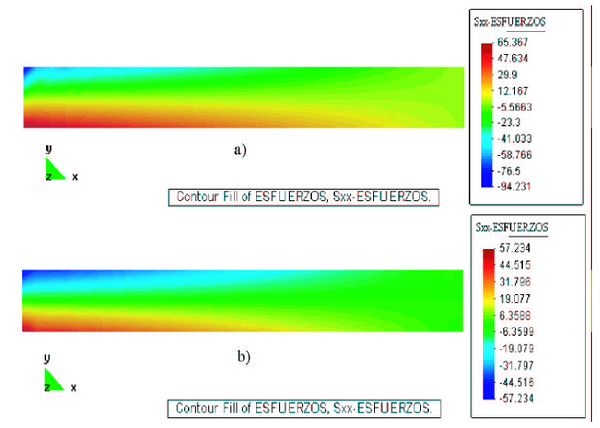
Figura 53: Distribucion del esfuerzo horizontal para la viga en cantilever discretizada en forma regular con 165math puntos, a) nubes incompletas n=6,7,8math y b) nubes completas n=9math

Analizando más en detalle el comportamiento anómalo de la solución, para el caso de nubes incompletas con 165 puntos, se ha comprobado también que en el caso de los esfuerzos horizontales en el contorno, la solución numérica presenta ciertas inestabilidades en la zona de máxima concentración del esfuerzo. La figura 54 permite corroborar esta tendencia, y muestra además cómo el error relativo se va atenuando en la medida que aumenta la distancia respecto del punto de máxima solicitación.

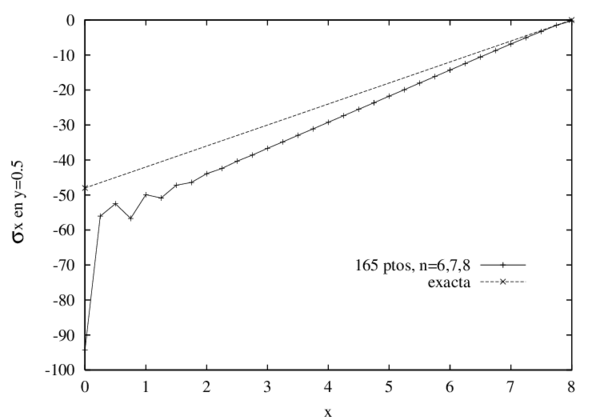
Figura 54: Esfuerzo horizontal _xmath a lo largo del contorno superior de la viga en cantilever discretizada en forma regular

Finalmente, la figura 55 muestra la convergencia del error para este ejemplo, cuando se utilizan discretizaciones irregulares de 55, 165 y 333 puntos. Aunque existe un aumento del error en la solución respecto del caso de utilizar una discretización regular, la velocidad de convergencia para los desplazamientos horizontales y verticales es similar en ambas situaciones, por ejemplo, en el caso de los desplazamientos horizontales se obtiene una convergencia de ${\textstyle 1.92}$ para discretizaciones irregulares y de ${\textstyle 2.0}$ para discretizaciones regulares.

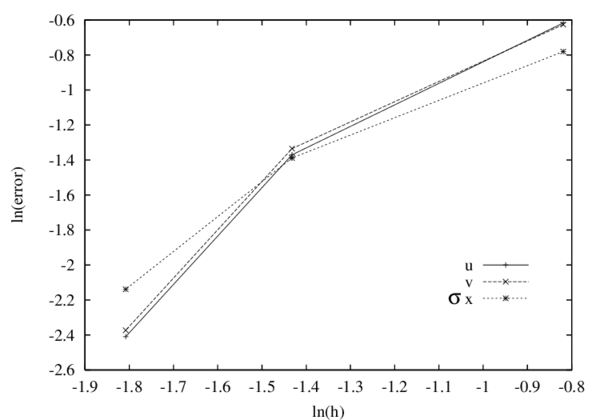
Figura 55: Convergencia del error global en la solucion para la viga en cantilever, distribucion irregular de puntos

4.2.3 Flexión de una viga simplemente apoyada

La figura 56 muestra la geometría de la viga con una discretización regular de 51 puntos. Sobre el contorno superior se aplica una carga uniformemente repartida de intensidad ${\textstyle q=1.0}$, bajo condiciones de tensión plana, con valores de ${\textstyle E=1000}$ y ${\textstyle \nu =0.3}$ para las propiedades del material. Sobre los apoyos se prescriben los desplazamientos según la solución teórica [94]

$u={\frac {q}{2EI}}\left[-y\left(L^{2}x-{\frac {x^{3}}{3}}\right)+x\left(-{\frac {2}{3}}y^{3}+{\frac {2}{5}}C^{2}y\right)+\nu x\left(-{\frac {1}{3}}y^{3}+C^{2}y+{\frac {2}{3}}C^{3}\right)\right]$ $v=-{\frac {q}{2EI}}\left[{\frac {y^{4}}{12}}-{\frac {C^{2}y^{2}}{2}}-{\frac {2}{3}}C^{3}y+\nu \left\{\left(L^{2}-x^{2}\right){\frac {y^{2}}{2}}+{\frac {y^{4}}{6}}-{\frac {1}{5}}C^{2}y^{2}\right\}\right]-$ ${\frac {q}{2EI}}\left[{\frac {L^{2}x^{2}}{2}}-{\frac {x^{4}}{12}}-{\frac {1}{5}}C^{2}x^{2}+\left(1+{\frac {1}{2}}\nu \right)C^{2}x^{2}\right]+0.6628$ $\sigma _{x}=-{\frac {q}{2I}}\left(L^{2}-x^{2}\right)y+{\frac {q}{2I}}\left({\frac {2}{5}}C^{2}y-{\frac {2}{3}}y^{3}\right)$ $\sigma _{y}={\frac {2}{2I}}\left({\frac {1}{3}}y^{3}-C^{2}y-{\frac {2}{3}}C^{3}\right)$ $\tau _{xy}=-{\frac {q}{2I}}\left(C^{2}-y^{2}\right)x$ $I={\frac {2}{3}}C^{3}$

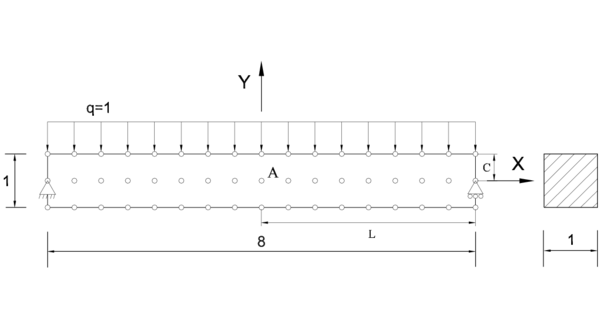
Figura 56: Viga simplemente apoyada, geometria y distribucion regular de 51 puntos

Para obtener los resultados se han analizado un total de ${\textstyle 5}$ configuraciones con una distribución regular de ${\textstyle 51,}$ ${\textstyle 105,}$ ${\textstyle 165,}$ ${\textstyle 343}$ y ${\textstyle 585}$ nodos, utilizándose un polinomio cuadrático de interpolación con nubes de ${\textstyle n=6,7}$ y ${\textstyle 8}$ puntos. La figura 57 muestra la convergencia del errror global para los desplazamientos y el esfuerzo horizontal, se advierten ciertas inestabilidades en la solución a medida que se aumenta el número de puntos, además, los errores que se obtienen con una discretización de ${\textstyle 51}$ puntos, son inferiores a los que entrega el método cuando se utilizan ${\textstyle 105}$ y ${\textstyle 165}$ puntos.

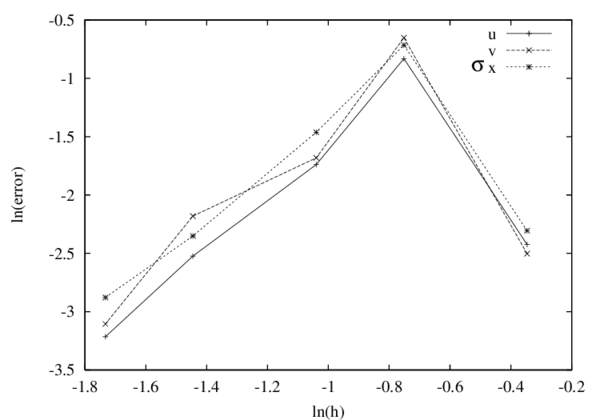
Figura 57: Convergencia del error global, viga simplemente apoyada con distribucion regular de puntos

Al igual que en el ejemplo anterior, se ha pretendido averiguar en que medida afecta a la solución, el hecho de utilizar nubes de forma asimétricas en los contornos, para ello, se ha evaluado numéricamente el esfuerzo horizontal ${\textstyle \sigma _{x}}$ a lo largo del contorno superior, es decir en ${\textstyle y=0.5}$. La figura 58, en concordancia con el resultado obtenido del análisis de convergencia, muestra en primer lugar un comportamiento errático de la distribución del esfuerzo en los extremos, este comportamiento oscilatorio tiende a disminuir, pero no desaparece, a medida que aumenta el número de puntos de la discretización. En segundo lugar, la solución que se obtiene con una distribución de 51 puntos parece más ádecuada respecto de las que se obtienen con 105 y 165 puntos respectivamente, lo que indicaría la no convergencia de la solución a su valor exacto. Un análisis posterior sobre todo el dominio, tal como muestran los contornos en desplazamientos y esfuerzos horizontales en las figuras 59 y 60, indica definitivamente que los resultados que se obtiene para estas últimas dos discretizaciones son erróneos.

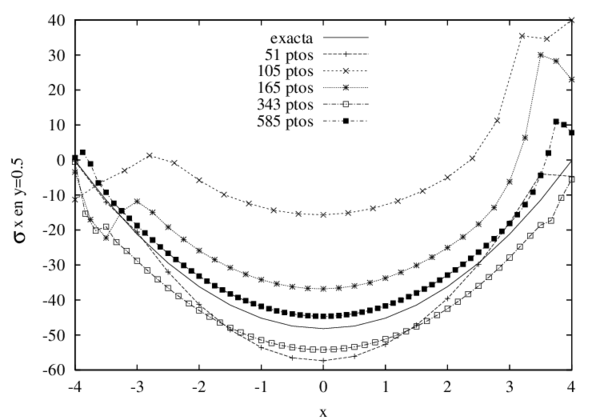
Figura 58: Convergencia del esfuerzo _xmath a lo largo del contorno y=0.5math, viga simplemente apoyada

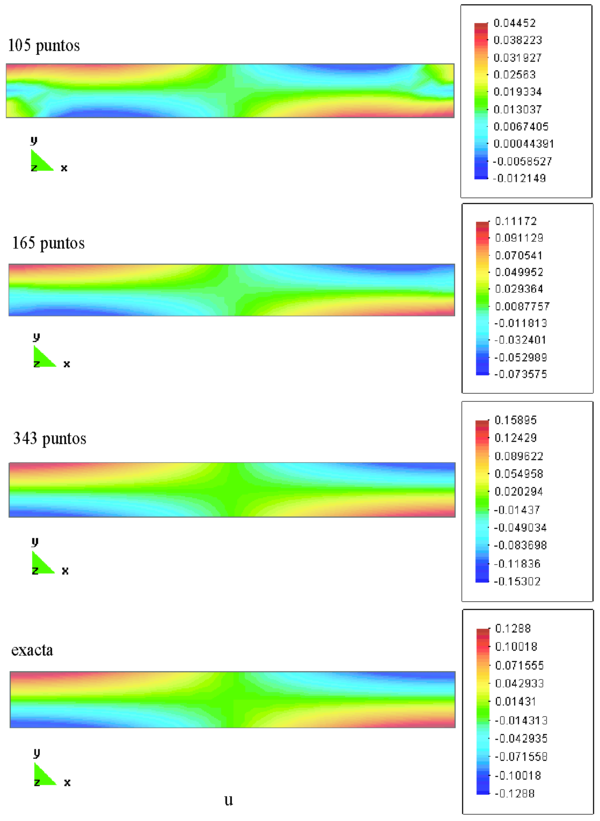
Figura 59: Contornos de desplazamiento horizontal umath, viga simplemente apoyada

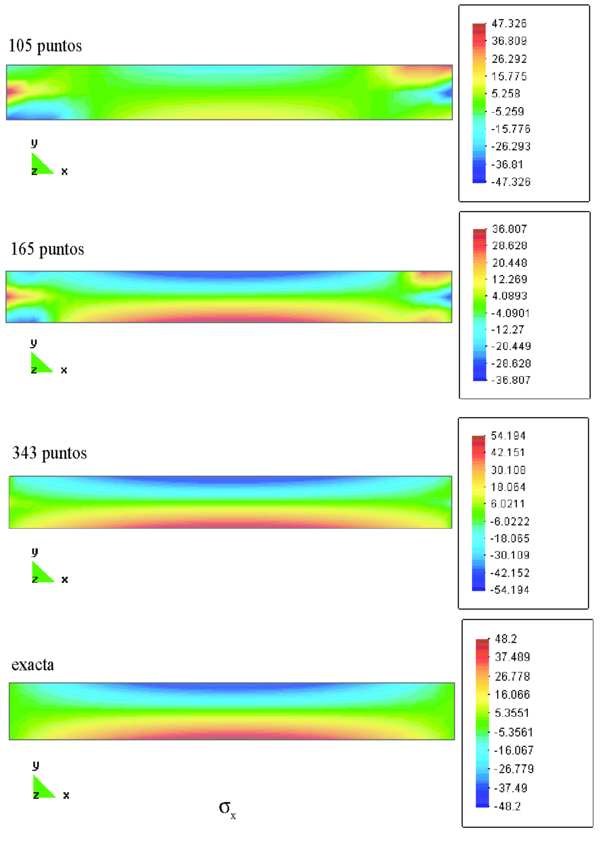
Figura 60: Contornos de esfuerzo horizontal _xmath, viga simplemente apoyada

4.2.4 Placa con agujero

Se ha analizado la convergencia del MPF, para la solución de la ecuaciones de la elasticidad, mediante el problema de una placa infinita en tensión con un agujero centrado en su origen y de radio ${\textstyle a}$ (ver figura 61).

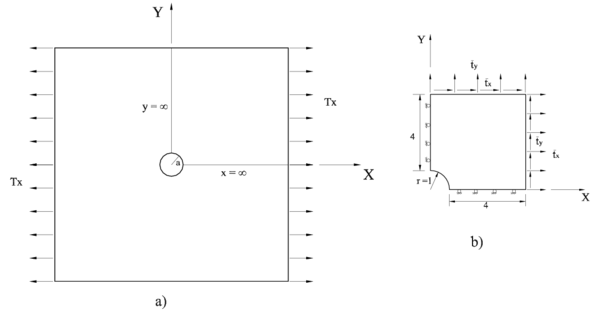
Figura 61: Geometria y condiciones de contorno a) placa infinita en tension y b) dominio de analisis

La solución analítica para el campo de tensiones es [94]

$\sigma _{x}=T_{x}\left[1-{\frac {a^{2}}{r^{2}}}\left({\frac {3}{2}}\cos(2\theta )+\cos(4\theta )\right)+{\frac {3a^{4}}{2r^{4}}}\cos(4\theta )\right]$ $\sigma _{y}=-T_{x}\left[{\frac {a^{2}}{r^{2}}}\left({\frac {1}{2}}\cos(2\theta )-\cos(4\theta )\right)+{\frac {3a^{4}}{2r^{4}}}\cos(4\theta )\right]$ (4.3) $\tau _{xy}=-T_{x}\left[{\frac {a^{2}}{r^{2}}}\left({\frac {1}{2}}\sin(2\theta )+\sin(4\theta )\right)+{\frac {3a^{4}}{2r^{4}}}\sin(4\theta )\right]$

donde ${\textstyle \left(r,\theta \right)}$ representan las coordenadas polares habituales. Debido a la simetría del problema, y, considerando un estado plano de deformación con ${\textstyle T_{x}=1.0}$, se ha modelado una región cuadrada cercana al origen (figura 61), sobre cuyos contornos (${\textstyle x=5.0}$ e ${\textstyle y=5.0}$) se prescriben condiciones de Neumann según la solución teórica 4.3. Las condiciones de contorno esenciales son

$u=0{\hbox{ en }}x=0,{\hbox{ }}1\leq y\leq 5$ $v=0{\hbox{ en }}y=0,{\hbox{ }}1\leq x\leq 5$

Se han realizado tres discretizaciones con 36, 48 y 60 puntos (figura 62), mediante una base de interpolación cuadrática y nubes de ${\textstyle 7,8}$ y ${\textstyle 9}$ nodos, asumiendo valores de ${\textstyle E=1000}$ y ${\textstyle \nu =0.3}$.

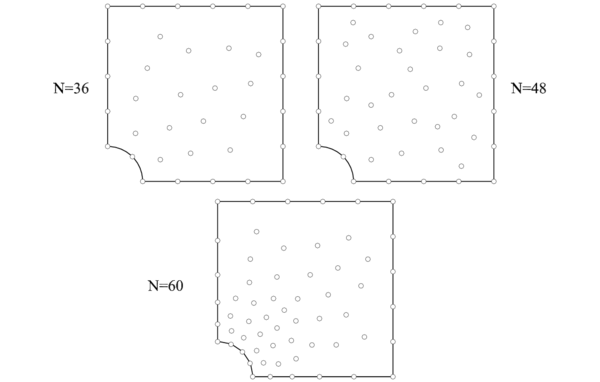
Figura 62: Distribuciones irregulares de puntos para el problema de la placa infinita en tension

La figura 63 muestra la distribución del esfuerzo ${\textstyle \sigma _{x}}$ a lo largo del contorno ${\textstyle x=0}$ para los tres arreglos de puntos analizados, como se aprecia, no existe un clara convergencia del método con un aumento del número de puntos, además, la solución numérica no entrega los valores adecuados del esfuerzo en la zona de máxima concentración.

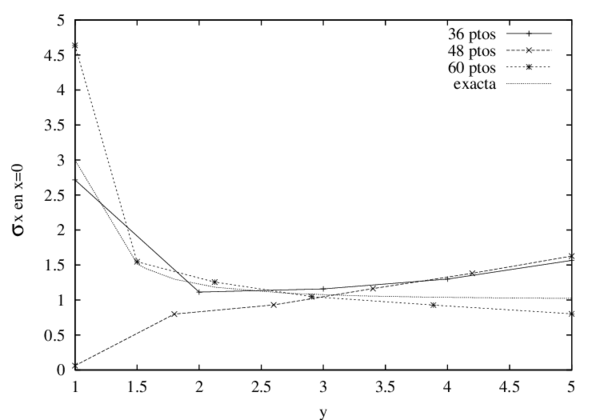
Figura 63: Distribucion del esfuerzo _xmath , en x=0math, para el problema de la placa con agujero

4.3 Resolución de las ecuaciones de elasticidad en 3D

La metodología desarrollada en el capítulo anterior puede extenderse sin mayor dificultad para su utilización en poblemas 3D de elasticidad lineal de sólidos. Como primer ejemplo se desarrolla el test de la parcela para el cubo de ${\textstyle 2}$ unidades de longitud mostrado en la figura 64, y sobre el que se prescriben los desplazamientos ${\textstyle u=x}$, ${\textstyle v=y}$ e ${\textstyle w=z}$ para los nodos del contorno. El dominio se discretiza mediante un total de 27 puntos, utilizándose una base de interpolación cuadrática (${\textstyle m=10}$) para obtener la solución numérica en el nodo central (nodo ${\textstyle 8}$). Tal como indica la figura 64, la respuesta que entrega el MPF, tanto en desplazamientos como en tensiones, coincide con la solución teórica por lo tanto el MPF supera sin dificultad el test de la parcela en 3D.

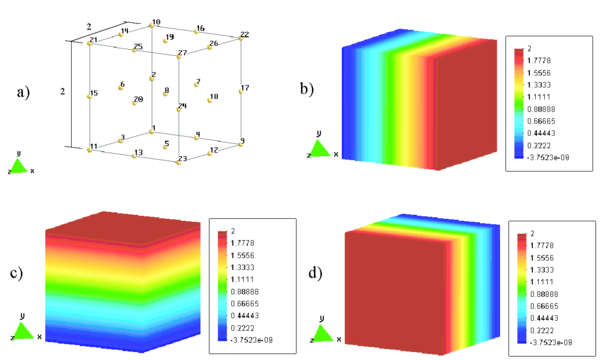
Figura 64: Test de la parcela en 3D, a) geometria y b) contornos de desplazamiento umath c) contornos de desplazamineto vmath y d) contornos de desplazamiento wmath

Se ha elaborado un segundo test, de orden superior, para comprobar el correcto comportamiento del MPF cuando se prescriben condiciones de contorno de Neumann sobre el dominio. Como muestra la figura 65, el test consiste en una barra prismática en flexión pura sobre cuyos extremos se prescribe un momento mediante un esfuerzo linealmente distribuido según ${\textstyle \sigma _{z}=x}$.

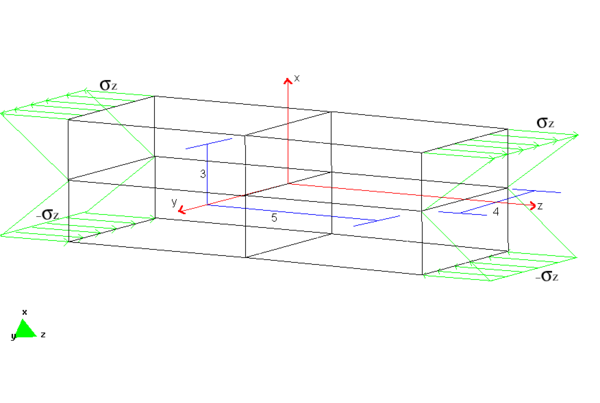
Figura 65: Barra prismatica en flexion, geometria y condiciones de carga

Se ha analizado dos arreglos de puntos, uno regular de 120 y otro irregular de 271 (ver figura 66), para modelar ${\textstyle 1/4}$ de la barra. Nuevamente se ha utilizado un polinomio base de interpolación cuadrático, con nubes que tienen 27 puntos en el caso de la discretización regular y entre 16 y 22 puntos para la no-regular. La solución teórica para este ejemplo es [94]

$u=-{\frac {M}{2EI_{yy}}}\left[z^{2}+\nu \left(x^{2}-y^{2}\right)\right]$ $v=-{\frac {\nu xyM}{EI_{yy}}}$ (4.4) $w={\frac {xzM}{EI_{yy}}}$ $M=2\int _{0}^{3}\sigma _{z}xdA$

con ${\textstyle M}$ e ${\textstyle I_{yy}}$, el momento flector y el momento de inercia de la sección respecto al eje ${\textstyle y}$. Se han utilizado como parámetros del material los valores siguientes, ${\textstyle E=1000}$ y ${\textstyle \nu =0.25}$.

Figura 66: Arreglo regular e irregular de 120 y 271 puntos, barra prismatica en flexion

Los resultados que se obtienen para este test, cuando se utiliza el arreglo regular de 120 puntos para modelar el comportamiento de la barra, se muestran en la figura 67. Se aprecia que la distribución, simetría y valores máximos de la solución no concuerdan plenamente con los valores teóricos. Tomando como ejemplo el caso de los desplazamientos ${\textstyle v}$ y ${\textstyle w}$, la figura muestra claramente que existe una variación de éstos respecto de las coordenadas ${\textstyle z}$ e ${\textstyle y}$ respectivamente, sin embargo, esto se contrapone con lo que predice la solución teórica. De la misma forma, los errores relativos respecto de los valores máximos de desplazamientos, en ambos casos, superan largamente el 100% En relación al esfuerzo ${\textstyle \sigma _{z}}$, cuya distribución es lineal respecto de la coordenada ${\textstyle x}$, la solución numérica no muestra un comportamiento adecuado, siendo el error relativo respecto del máximo valor nuevamente superior al 100%

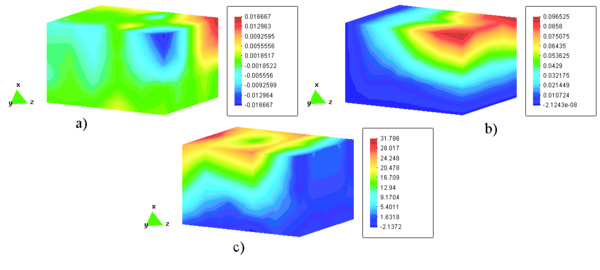
Figura 67: Barra prismatica en flexion, arreglo regular de 120 puntos, a) contornos de desplazamiento v math b) contornos de desplazamiento wmath y c) contornos de esfuerzo _zmath

Cuando se utiliza un arreglo irregular de puntos los problemas detectados anteriormente se acentúan, por lo que a pesar de usar un mayor número de puntos en la discretización (271), el MPF no es capaz de entregar solución alguna producto del mal condicionamiento de la matriz de rigidez global del sistema y la no convergencia del solver iterativo utilizado. Implementando un solver directo para resolver el sistema de ecuaciones, se ha podido comprobar el mal condicionamiento de la matriz y también obtener una solución para esta situación. Como era previsible, los resultados para este test (ver figura 68) ponen en evidencia la baja capacidad del método de puntos, tal como se ha formulado, para superar y satisfacer los requerimientos de las ecuaciones de elasticidad lineal en 3D.

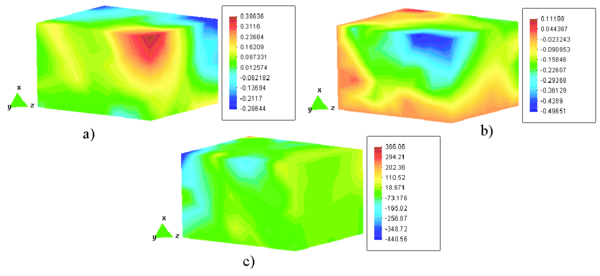
Figura 68: Barra prismatica en flexion, arreglo irregular de 271 puntos, a) contornos de desplazamiento vmath b) contornos de desplazamiento wmath y c) contornos de esfuerzo _zmath

4.4 Análisis de resultados

Se han desarrollado a lo largo del capítulo diversos ejemplos para analizar la consistencia y convergencia del MPF, tal como se demostró analíticamente, se ha comprobado que el método es consistente y por tanto capaz de reproducir en el grado deseado, cuando se utiliza la base de interpolación adecuada, cualquier polinomio o combinación lineal de éstos. Si bien es cierto, se ha podido comprobar en algunos ejemplos un orden de convergencia cuadrático para el método de puntos finitos, la respuesta numérica parece deteriorarse, principalmente en arreglos irregulares, cuando se utiliza un bajo número de puntos para discretizar el dominio. Este comportamiento no aparece claramente detectable en problemas unidimensionales, sin embargo, se aprecia con claridad en problemas bidimensionales en los que se ve afectada la convergencia de la solución. Un fenómeno que si se puede distinguir a través de las distintas modelaciones efectuadas, es la falta de precisión de la solución, y por consiguiente un mayor error respecto de la solución teórica, en los contornos donde se prescriben las condiciones de Neumann. En este comportamiento influye también, sin lugar a dudas, el hecho de que las nubes de los puntos del contorno sean completamente asimétricas.

El método sin malla de puntos finitos con un esquema de colocación puntual, tal como se mencionó en el capítulo de su formulación, entrega generalmente un sistema algebraico de ecuaciones cuya matriz de rigidez global se caracteriza por ser no simétrica ni definida positiva, pero además y dependiendo del problema, sus coeficientes pueden llegar a ser de diferentes órdenes de magnitud resultando una matriz mal condicionada. Como resultado de este mal condicionamiento, la técnica de colocación puntual suele producir resultados imprecisos e inestables tal como los encontrados a través de los ejemplos 2D y 3D analizados en la tesis. Esta característica del prodecimiento de colocación puntual también ha sido analizada y descrita en la formulación de otras técnicas sin malla, como por ejemplo en el método SPH [DYK 95] [15], en el método EFG con integración nodal [7], el método hp cloud [48], en el método DEM [18] y más recientemente en least-squares collocation meshless method [103].

Con los ejemplos numéricos desarrollados en esta tesis se demuestra por primera vez que el MPF para aplicaciones de la elasticidad lineal de sólidos, no está exento de las deficiencias del procedimiento de colocación puntual, por lo que se hace necesario implementar una técnica, similar a una estabilización, que permita superar y corregir estos inconvenientes, fundamentalmente en aquellas zonas del contorno donde la falta de simetría de las nubes acentúa estas deficiencias. A continuación se presenta y desarrolla una metodología, útil y fácil de implementar, para obtener una forma estable del sistema de ecuaciones en el MPF.

5 Estabilización del sistema de ecuaciones en el MPF

5.1 Introducción

En el MPF la discretización mediante colocación puntual presenta ciertas particularidades, respecto del método de Galerkin, en lo referente a la implementación de las condiciones de contorno. En el caso de la condición de contorno de Dirichlet, ésta se prescribe de una manera fácil y sencilla imponiendo el valor directamente en el punto y sin un tratamiento adicional del sistema de ecuaciones¹, sin embargo, la condición de Neumann (${\textstyle \mathbf {\sigma (x} )\cdot \mathbf {n} ={\overline {\mathbf {t} }}(\mathbf {x} )}$) se debe implementar en los puntos donde se conocen las componentes del vector de tracción externo ${\textstyle {\overline {\mathbf {t} }}(\mathbf {x} )}$ y adicionalmente en los puntos del contorno libre. Esto supone, además de calcular las normales en dichos puntos, preservar en la medida de lo posible la simetría de la nube para una adecuada discretización de las derivadas de la función incógnita, lamentablemente, esto es difícil de conseguir en las nubes de contorno. Otra particularidad del método de colocación puntual es que las ecuaciones de equilibrio sólo se imponen en los nodos interiores del dominio, lo que suele afectar la exactitud de los resultados cuando no se utiliza un número suficiente de puntos de colocación. Los ejemplos desarrollados han permitido corroborar estas dificultades, presentes en todos los casos bidimensionales estudiados, y ponen en evidencia la necesidad de implementar alguna modificación en el planteamiento del MPF para superar también el test en 3D con condiciones de contorno de Neumann.

(¹) Recuérdese el método de penalización ejemplificado en el apartado 2.3.1

5.2 Métodos sin malla con un esquema de colocación puntual modificado

Una forma intuitiva para obtener una mejora de la solución, cuando se utiliza una discretización con colocación puntual, es aumentar el número de grados de libertad del problema. En el caso del MPF se ha comprobado una reducción del error relativo en las zonas cercanas al contorno, para ejemplos unidimensionales, cuando se aumenta el número de puntos utilizado para discretizar el dominio [99]. Sin embargo, como se ha verificado en esta tesis, en problemas bidimensionales no siempre se consigue una mejora de la solución cuando se aumenta el número de puntos (ver entre otros, ejemplo viga simplemente apoyada).

Otra manera de reducir los errores de la solución en el contorno, ampliamente utilizada en el método de diferencias finitas, se basa en la utilización de un nodo ficticio fuera del dominio para prescribir la derivada en el contorno [2], [62], sin embargo, la técnica utilizada en los métodos sin malla, basados en aproximaciones de diferencias finitas generalizadas [48], [83], consiste en imponer sobre los nodos del contorno dos ecuaciones: una resultante de las condiciones de contorno y la segunda proveniente de las ecuaciones de equilibrio del problema (igual que en el interior del dominio).

Una tercera alternativa, utilizada en un método sin malla con aproximación de mínimos cuadrados ponderados [103], consiste en emplear un número ${\textstyle N_{a}}$ de puntos adicionales a los puntos de colocación (ver figura 69), llamados puntos auxiliares, sobre los que también se satisfacen las ecuaciones de equilibrio pero en el sentido de los mínimos cuadrados.

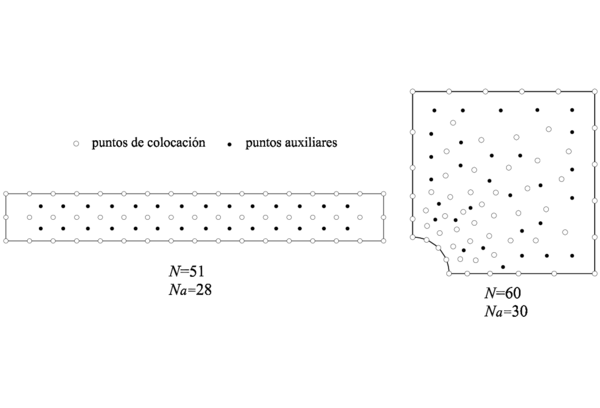
Figura 69: Ejemplo de geometrias discretizadas mediante Nmath puntos de colocacion y N_amath puntos auxiliares

Para comprender los cambios que introduce esta modificación en el método de colocación puntual estándar, a continuación se ejemplifica la forma de obtener el sistema discreto de ecuaciones diferenciales con esta técnica y su posterior resolución. Considérese, como antes, la aproximación ${\textstyle {\widehat {\mathbf {u} }}(\mathbf {x} )}$ de la función incógnita ${\textstyle \mathbf {u} (\mathbf {x} )}$, esta vez el sistema discreto de ecuaciones diferenciales a resolver es (recuérdense 2.116,2.117 y 2.118)

${\mathcal {A}}({\widehat {\mathbf {u} }}_{j})=\mathbf {b} _{j}{\hbox{ }}j=1,......,N+N_{a}$ ${\mathcal {B}}({\widehat {\mathbf {u} }}_{j})=\mathbf {t} _{j}{\hbox{ }}j=1,.......,N_{t}$ (5.1) ${\widehat {\mathbf {u} }}_{j}=\mathbf {u} _{p}{}_{j}{\hbox{ }}j=1,......,N_{u}$

donde ${\textstyle N=N_{\Omega }+N_{t}+N_{u}}$ es el número total de puntos de colocación utilizados para obtener la función aproximada ${\textstyle {\widehat {\mathbf {u} }}(\mathbf {x} )}$ mediante mínimos cuadrados ponderados, mientras ${\textstyle N_{\Omega }}$, ${\textstyle N_{t}}$ y ${\textstyle N_{u}}$, representan el número de puntos en el interior del dominio, sobre el contorno de Neumann ${\textstyle \Gamma _{t}}$ y sobre el contorno de Dirichlet ${\textstyle \Gamma _{u}}$, respectivamente. El sistema 5.1 constituye un set de ${\textstyle N+N_{a{\hbox{ }}}+N_{t}+N_{u}}$ número de ecuaciones para un total de ${\textstyle N}$ incógnitas, por consiguiente, debe ser resuelto utilizando un procedimiento de mínimos cuadrados. Utilizando una aproximación sin malla¹ como las definidas en el capítulo 2, es decir ${\textstyle {\widehat {\mathbf {u} }}(\mathbf {x} )=\mathbf {\Phi u} ^{h}}$, reagrupando las incógnitas correspondientes a los puntos colocados en el contorno (${\textstyle N_{t}+N_{u}}$) y en el interior del dominio (${\textstyle N_{\Omega }}$) en los vectores ${\textstyle \mathbf {u} _{1}^{h}}$ y ${\textstyle \mathbf {u} _{2}^{h}}$ respectivamente, se obtiene el siguiente sistema

$\mathbf {K} _{11}\mathbf {u} _{1}^{h}+\mathbf {K} _{12}\mathbf {u} _{2}^{h}=\mathbf {f} _{1}$ (5.2) $\mathbf {K} _{21}\mathbf {u} _{1}^{h}+\mathbf {K} _{22}\mathbf {u} _{2}^{h}=\mathbf {f} _{2}$ (5.3)

o en forma matricial

$\left[{\begin{array}{ll}\mathbf {K} _{11}&\mathbf {K} _{12}\\\mathbf {K} _{21}&\mathbf {K} _{22}\end{array}}\right]\left[{\begin{array}{l}\mathbf {u} _{1}^{h}\\\mathbf {u} _{2}^{h}\end{array}}\right]=\left[{\begin{array}{l}\mathbf {f} _{1}\\\mathbf {f} _{2}\end{array}}\right]$

(5.4)

Para resolver este sistema se puede despejar el vector ${\textstyle \mathbf {u} _{1}^{h}}$ de 5.2 y reemplazarlo en la segunda ecuación 5.3, dando lugar finalmente a

$\mathbf {K} ^{^{\prime }}\mathbf {u} _{2}^{h}=\mathbf {f} ^{^{\prime }}$

(5.5)

en donde ${\textstyle \mathbf {K} ^{^{\prime }}=\mathbf {K} _{22}-\mathbf {K} _{21}\mathbf {K} _{11}^{-1}\mathbf {K} _{12}}$, ${\textstyle \mathbf {f} ^{^{\prime }}=\mathbf {f} _{2}-\mathbf {K} _{21}\mathbf {K} _{11}^{-1}\mathbf {f} _{1}}$ y de donde se puede encontrar ${\textstyle \mathbf {u} _{2}^{h}}$. Se debe notar nuevamente que el sistema 5.5 contiene un número de ${\textstyle N+N_{a}}$ ecuaciones con tan sólo ${\textstyle N_{\Omega }}$ incógnitas², además, ${\textstyle \mathbf {u} _{1}^{h}}$ se puede obtener a partir de 5.2 una vez resuelto 5.5. Tal como ha sido propuesta, la técnica combina dos de las posibles soluciones mencionadas anteriormente para mejorar la aproximación cuando se utiliza colocación puntual, por un lado se aumenta el número de puntos de colocación (puntos auxiliares) y por otro se imponen las ecuaciones de equilibrio del dominio también en los puntos situados en el contorno. Según sus autores, con este procedimiento de colocación modificado se pueden atenuar las inestabilidades, como por ejemplo las encontradas a través de los ejemplos del capítulo 4, sin un aumento considerable del coste computacional. Sin embargo, no existe información de cómo afecta a la solución el hecho de utilizar una discretización irregular de puntos, además, no está totalmente definido cúantos puntos auxiliares son necesarios para obtener una solución estable como tampoco cuál es la distribución adecuada de éstos.

(¹) En principio se podría utilizar cualquiera de la aproximaciones meshless estudiadas. En su trabajo original los autores utilizan una aproximación tipo MLS [103]

(²) Esta vez será preciso invertir dos matrices ($\mathbf {K} _{11}$ y $\mathbf {K} ^{^{\prime }}$) para resolver el sistema global de ecuaciones

5.3 Estabilización mediante el procedimiento de Cálculo Finitesimal

Una forma diferente de abordar las inestabilidades en los contornos que introduce el procedimiento de colocación puntual, consiste en modificar el sistema final de ecuaciones agregando nuevos términos que son función de las ecuaciones originales de gobierno del problema. La técnica para obtener este nuevo sistema de ecuaciones, similar a una estabilización, está basada en el procedimiento de Cálculo Finitesimal (CF), en inglés Finite Increment Calculus (FIC) [76], y será la utilizada en la solución de los ejemplos que se presentan en el siguiente capítulo. La implementación y verificación con resultados de esta metodología constituyen una de las principales aportaciones de esta tesis, además, su utilización representa una novedad en la aplicación del MPF, como método totalmente libre de malla, para problemas de elasticidad lineal de sólidos [79] [81]. En el mismo contexto, los principios fundamentales del procedimiento de CF se han utilizado recientemente para desarrollar una forma estabilizada del método SPH [16].

Las conceptos claves del Cálculo Finitesimal, utilizados también para obtener la forma estabilizada de las ecuaciones de convección-difusión y de dinámica de fluidos mediante el MEF, se pueden sintetizar en

1. imponer las ecuaciones de equilibrio o balance sobre un dominio de tamaño finito
2. aproximar el campo desconocido o incógnita del problema utilizando una expansión en serie de Taylor
3. conservar los términos de un orden superior que aquellos utilizados en una aproximación infinitesimal estándar

Teniendo presente estas ideas, a continuación se desarrolla el proceso para obtener las ecuaciones estabilizadas, utilizando FIC, para el problema 1D de la barra bajo esfuerzos axiales. Se pretende con este ejemplo dejar sentadas las bases teóricas que permitirán obtener posteriormente, con un planteamiento similar, el sistema final para la resolución de las ecuaciones de la elasticidad en 2D o 3D mediante el MPF estabilizado.

5.3.1 Ejemplo 1D de la barra bajo esfuerzos axiales

Considérese el problema planteado en el apartado 4.1.1 para la barra bajo una carga axial repartida, esta vez, para obtener el sistema de ecuaciones diferenciales a resolver, plantearemos las condiciones de equilibrio sobre el dominio finito de longitud ${\textstyle h}$ de la figura 70 además de sus correspondientes condiciones de contorno.

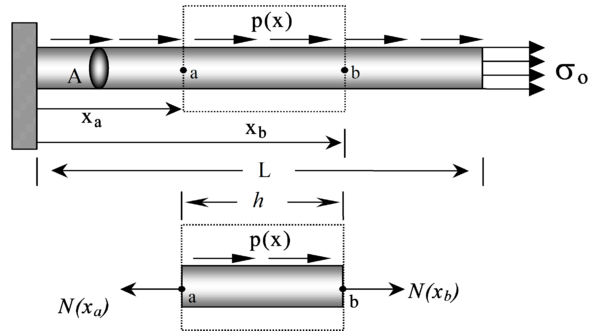
Figura 70: Dominio finito de equilibrio abmath para barra bajo esfuerzos axiales

Planteando sumatoria de fuerzas sobre el dominio finito se tiene¹

$N\left(x_{b}\right)-N\left(x_{a}\right)+p(x)h=0$

(5.6)

donde la normal ${\textstyle N\left(x_{a}\right)}$ en términos de la normal en el punto ${\textstyle \left(x_{b}=x_{a}+h\right)}$ mediante desarrollo en serie de Taylor de segundo orden es

$N\left(x_{a}\right)=N\left(x_{b}-h\right)=N\left(x_{b}\right)-h\left({\frac {dN}{dx}}\right)_{x_{b}}+0h^{2}$

(5.7)

reemplazando 5.7 en 5.6 se obtiene luego de simplificar²

$\left({\frac {dN}{dx}}\right)+p(x)=0$

Recordando que la fuerza normal puede expresarse en términos de los desplazamientos como

$N\left(x\right)=EA{\frac {du(x)}{dx}}$

el sistema de ecuaciones a resolver, considerando las correspondientes condiciones de contorno, es³

$EA{\frac {d^{2}u(x)}{dx^{2}}}+p(x)=0{\hbox{ }}0<x<L$ $E{\frac {du(x)}{dx}}=\sigma _{0}{\hbox{ }}x=L$ (5.8) $u(x)=0{\hbox{ }}x=0$

(¹) Considerando la carga repartida por unidad de longitud $p(x)$ constante sobre el dominio $ab$

(²) Siendo la posición del punto $b$ arbitraria, la ecuación es válida para cualquier $x_{b}=x$

(³) Coincide exactamente con el sistema utilizado en 4.1.1

5.3.2 Obtención del sistema de ecuaciones estabilizado. Estabilización en el dominio.

Supóngase que existe una variación importante del esfuerzo y la carga axial repartida sobre el dominio finito ${\textstyle ab}$, esta vez, considerando una variación lineal de ${\textstyle p(x)}$, la ecuación de equilibrio es (ver figura 71)

$N\left(x_{b}\right)-N\left(x_{a}\right)+p(x_{a})h+{\frac {1}{2}}\left(p\left(x_{b}\right)-p(x_{a})\right)h=0$ $N\left(x_{b}\right)-N\left(x_{a}\right)+{\frac {h}{2}}\left(p\left(x_{a}\right)-p\left(x_{b}\right)\right)=0$

(5.9)

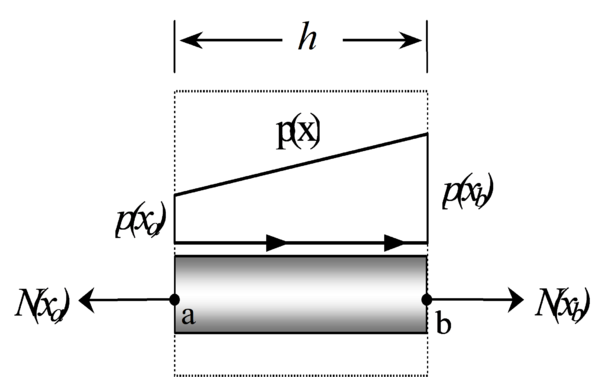
Figura 71: Dominio finito de equilibrio abmath con una variacion lineal de la carga axial repartida

para poder capturar esa variación y, considerando nuevamente la posición del punto ${\textstyle b}$ arbitraria, la fuerza normal ${\textstyle N(x_{a})}$ se expresará mediante una expansión en serie de hasta tercer orden como

$N\left(x_{a}\right)=N\left(x_{b}-h\right)=N(x-h)=N\left(x\right)-h\left({\frac {dN}{dx}}\right)+{\frac {h^{2}}{2}}\left({\frac {d^{2}N}{dx^{2}}}\right)-0h^{3}$

(5.10)

Utilizando un expansión de segundo orden para expresar la carga repartida, es decir

$p(x_{a})=p(x_{b}-h)=p(x-h)=p(x)-h{\frac {dp}{dx}}+0h^{2}$

(5.11)

se obtiene luego de reemplazar 5.10 y 5.11 en 5.9 la siguiente ecuación de equilibrio en el dominio

$\left({\frac {dN}{dx}}\right)+p(x)-{\frac {h}{2}}\left[{\frac {d^{2}N}{dx^{2}}}+{\frac {dp(x)}{dx}}\right]=0$

o en términos de los desplazamientos

$EA{\frac {d^{2}u(x)}{dx^{2}}}+p(x)-{\frac {h}{2}}\left[EA{\frac {d^{3}u(x)}{dx^{3}}}+{\frac {dp(x)}{dx}}\right]=0$

(5.12)

La ecuación 5.12 se puede expresar en forma compacta como

$r-{\frac {h}{2}}{\frac {dr}{dx}}=0$

(5.13)

con

$r=EA{\frac {d^{2}u(x)}{dx^{2}}}+p(x)$

5.3.3 Estabilización de la condición de contorno de Neumann

Para obtener la ecuación estabilizada se sigue la misma metodología empleada en el dominio, esto es, plantear el equilibrio sobre un dominio finito ubicado en el contorno de Neumann tal como muestra la figura 72.

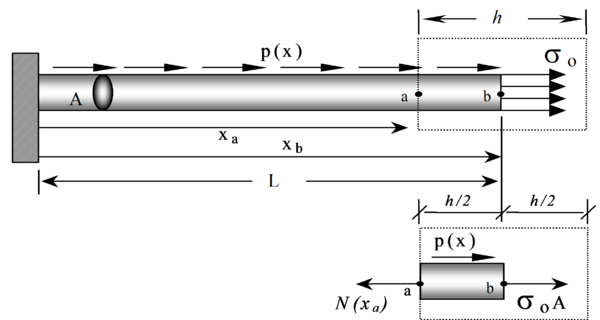
Figura 72: Dominio finito de equilibrio abmath en el contorno para barra bajo esfuerzos axiales

Realizando una sumatoria de fuerzas, esta vez sobre el dominio de longitud ${\textstyle h/2}$, se obtiene

$\sigma _{0}A-N\left(x_{a}\right)+p(x){\frac {h}{2}}=0$

(5.14)

donde la fuerza normal en el punto ${\textstyle a}$ se puede expresar mediante un desarrollo en serie de Taylor de segundo orden como

$N\left(x_{a}\right)=N\left(x_{b}-{\frac {h}{2}}\right)=N\left(x_{b}\right)-{\frac {h}{2}}\left({\frac {dN}{dx}}\right)_{x_{b}}+0h^{2}$

(5.15)

Reemplazando la expresión 5.15 en 5.14 se tiene luego se simplificar¹

$N\left(x\right)-\sigma _{0}A-{\frac {h}{2}}\left[{\frac {dN}{dx}}+p(x)\right]=0{\hbox{ para }}x=L$ $EA{\frac {du(x)}{dx}}-\sigma _{0}A-{\frac {h}{2}}\left[EA{\frac {d^{2}u(x)}{dx^{2}}}+p(x)\right]=0{\hbox{ para }}x=L$

(5.16)

o en forma más compacta

$EA{\frac {du(x)}{dx}}-\sigma _{0}A-{\frac {h}{2}}r=0$

(5.17)

El conjunto de ecuaciones 5.13, 5.17 y la condición de contorno de Dirichlet, corresponden al sistema de ecuaciones estabilizado mediante la técnica de CF que permitirá encontrar una solución numérica al problema de la barra 1D bajo esfuerzos axiales. Este sistema, que expresado en forma compacta es

$r-{\frac {h}{2}}{\frac {dr}{dx}}=0{\hbox{ }}0<x<L$ $EA{\frac {du(x)}{dx}}-\sigma _{0}A-{\frac {h}{2}}r=0{\hbox{ }}x=L$ (5.18) $u(x)=0x=0$

constituye el punto de partida para obtener un buen número de esquemas de estabilización utilizando el procedimiento del CF [76]. Se debe notar que cuando ${\textstyle h\rightarrow 0}$ en 5.18, se recupera exactamente el sistema 5.8 encontrado mediante el análisis infinitesimal.

La adecuada selección del parámetro ${\textstyle h}$ o longitud característica, cuando se utiliza el MPF², constituye un asunto crucial de cara a obtener resultados correctos y con la adecuada exactitud en los contornos, por esto, en el siguiente capítulo se expone la metología empleada en esta tesis para obtener este parámetro de estabilización, como también la formulación para generalizar el uso de la técnica del CF en la resolución de las ecuaciones de elasticidad mediante el MPF.

(¹) La posición del punto $b$ corresponde a la coordenada $x=L$

(²) En referencia [77] se expone la técnica apropiada para obtener el valor de $h$ cuando se utiliza un análisis por el MEF.

6 Solución de las ecuaciones de la elasticidad mediante el MPF estabilizado (MPFE)

6.1 Introducción

La utilización de la técnica de Cálculo Finitesimal, presentada en el capítulo anterior, introduce de forma natural ciertos términos adicionales al sistema original lo que permite, tal como se ejemplificará más adelante, aprovechar en toda su potencialidad la discretización mediante colocación puntual en el contexto del MPF. Estos términos, de un orden superior a los que se obtienen por el procedimiento infinitesimal estándar, son fundamentales para el correcto funcionamiento del método, y posibilitan la utilización de una técnica totalmente libre de malla para la resolución de las ecuaciones de la elasticidad, tal como se ha planteado en los objetivos de esta tesis. De entre estos destaca claramente el tamaño del dominio de equilibrio (vector ${\textstyle \mathbf {h} }$ en 2D), el cual deberá ser evaluado para poder obtener la solución al sistema. Se presenta a continuación la formulación para obtener este sistema en un problema de elasticidad lineal, la extensión para el caso 3D es inmediata.

6.2 Formulación del problema de elasticidad

Considérese en primer término el dominio finito mostrado el la figura 73 y sobre el que se plantea un equilibrio de fuerzas en ambas direcciones, suponiendo además una distribución lineal de los esfuerzos normales y esfuerzos cortantes sobre las caras del dominio, de espesor unitario, con dimensiones ${\textstyle h_{x}\times h_{y}}$ se obtiene para el interior del cuerpo¹

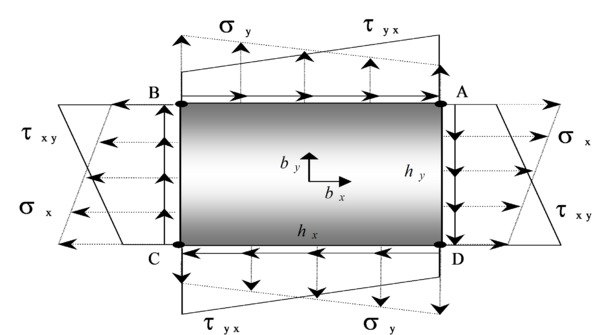
Figura 73: Dominio finito ABCD para el planteamiento de equilibrio de fuerzas en el interior del cuerpo

equilibrio de fuerzas horizontales

${\frac {h_{y}}{2}}\left[\left(\sigma _{x}\right)_{A}+\left(\sigma _{x}\right)_{D}\right]-{\frac {h_{y}}{2}}\left[\left(\sigma _{x}\right)_{C}+\left(\sigma _{x}\right)_{B}\right]+{\frac {h_{x}}{2}}\left[\left(\tau _{yx}\right)_{A}+\left(\tau _{yx}\right)_{B}\right]-$

$-{\frac {h_{x}}{2}}\left[\left(\tau _{yx}\right)_{C}+\left(\tau _{yx}\right)_{D}\right]=-h_{x}h_{y}\rho b_{x}$

(6.1)

equilibrio de fuerzas verticales

${\frac {h_{x}}{2}}\left[\left(\sigma _{y}\right)_{B}+\left(\sigma _{y}\right)_{A}\right]-{\frac {h_{x}}{2}}\left[\left(\sigma _{y}\right)_{D}+\left(\sigma _{y}\right)_{C}\right]+{\frac {h_{y}}{2}}\left[\left(\tau _{xy}\right)_{B}+\left(\tau _{xy}\right)_{C}\right]-$

$-{\frac {h_{y}}{2}}\left[\left(\tau _{xy}\right)_{D}+\left(\tau _{xy}\right)_{A}\right]=-h_{x}h_{y}\rho b_{y}$

(6.2)

utilizando una expansión en serie de Taylor de tercer orden para los esfuerzos en B, C y D se tiene respectivamente

$\left(\circ \right)_{B}=\left(\circ \right)_{A}-h_{x}{\frac {\partial }{\partial x}}\left(\circ \right)+{\frac {h_{x}^{2}}{2}}{\frac {\partial ^{2}}{\partial x^{2}}}\left(\circ \right)-0h_{x}^{3}$ $\left(\circ \right)_{C}=\left(\circ \right)_{A}-h_{x}{\frac {\partial }{\partial x}}\left(\circ \right)-h_{y}{\frac {\partial }{\partial y}}\left(\circ \right)+{\frac {h_{x}^{2}}{2}}{\frac {\partial ^{2}}{\partial x^{2}}}\left(\circ \right)+{\frac {h_{y}^{2}}{2}}{\frac {\partial ^{2}}{\partial y^{2}}}\left(\circ \right)+h_{x}h_{y}{\frac {\partial ^{2}}{\partial x\partial y}}\left(\circ \right)-$ $-0(h_{x}^{3},h_{y})$ $\left(\circ \right)_{D}=\left(\circ \right)_{A}-h_{y}{\frac {\partial }{\partial y}}\left(\circ \right)+{\frac {h_{y}^{2}}{2}}{\frac {\partial ^{2}}{\partial y^{2}}}\left(\circ \right)-0h_{y}^{3}$

(6.3)

Reemplazando las expresiones 6.3 en 6.1 y 6.2, se encuentra luego de simplificar

$h_{x}h_{y}\left[{\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{yx}}{\partial y}}+\rho b_{x}\right]-{\frac {h_{x}^{2}h_{y}}{2}}\left[{\frac {\partial ^{2}\sigma _{x}}{\partial x^{2}}}+{\frac {\partial ^{2}\tau _{yx}}{\partial x\partial y}}\right]-{\frac {h_{x}h_{y}^{2}}{2}}\left[{\frac {\partial ^{2}\sigma _{x}}{\partial x\partial y}}+{\frac {\partial ^{2}\tau _{yx}}{\partial y^{2}}}\right]=0$ $h_{x}h_{y}\left[{\frac {\partial \sigma _{y}}{\partial y}}+{\frac {\partial \tau _{xy}}{\partial x}}+\rho b_{y}\right]-{\frac {h_{x}^{2}h_{y}}{2}}\left[{\frac {\partial ^{2}\sigma _{y}}{\partial x\partial y}}+{\frac {\partial ^{2}\tau _{xy}}{\partial x^{2}}}\right]-{\frac {h_{x}h_{y}^{2}}{2}}\left[{\frac {\partial ^{2}\sigma _{x}}{\partial y^{2}}}+{\frac {\partial ^{2}\tau _{xy}}{\partial x\partial y}}\right]=0$

que luego de dividir por el producto ${\textstyle \left(h_{x}h_{y}\right)}$ se convierten en

$\left[{\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{yx}}{\partial y}}+\rho b_{x}\right]-{\frac {h_{x}}{2}}\left[{\frac {\partial ^{2}\sigma _{x}}{\partial x^{2}}}+{\frac {\partial ^{2}\tau _{yx}}{\partial x\partial y}}\right]-{\frac {h_{y}}{2}}\left[{\frac {\partial ^{2}\sigma _{x}}{\partial x\partial y}}+{\frac {\partial ^{2}\tau _{yx}}{\partial y^{2}}}\right]=0$ $\left[{\frac {\partial \sigma _{y}}{\partial y}}+{\frac {\partial \tau _{xy}}{\partial x}}+\rho b_{y}\right]-{\frac {h_{x}}{2}}\left[{\frac {\partial ^{2}\sigma _{y}}{\partial x\partial y}}+{\frac {\partial ^{2}\tau _{xy}}{\partial x^{2}}}\right]-{\frac {h_{y}}{2}}\left[{\frac {\partial ^{2}\sigma _{x}}{\partial y^{2}}}+{\frac {\partial ^{2}\tau _{xy}}{\partial x\partial y}}\right]=0$

(6.4)

el cual se diferencia con el sistema sin estabilizar², ya que en este caso se incluyen los términos de la longitud característica del dominio de equilibrio y las derivadas de las ecuaciones originales. El sistema 6.4 se puede expresar en forma más compacta como

$r_{1}-{\frac {1}{2}}\mathbf {h} ^{T}\cdot \mathbf {\nabla } r_{1}=0$ $r_{2}-{\frac {1}{2}}\mathbf {h} ^{T}\cdot \mathbf {\nabla } r_{2}=0$

(6.5)

donde³

$r_{1}={\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{xy}}{\partial y}}+\rho b_{x}$ $r_{2}={\frac {\partial \sigma _{y}}{\partial y}}+{\frac {\partial \tau _{xy}}{\partial x}}+\rho b_{y}$

siendo ${\textstyle \mathbf {\nabla } }$ el operador gradiente y el vector ${\textstyle \mathbf {h} }$

$\mathbf {h} =\left[{\begin{array}{l}h_{x}\\h_{y}\end{array}}\right]{\hbox{ }}$

Para encontrar la forma estabilizada de las ecuaciones que representan la condición de contorno de Neumann, se debe plantear el equilibrio de fuerzas sobre el prisma triangular mostrado en la figura 74, en este caso, se adopta una distribución constante de los esfuerzos sobre las caras del elemento.

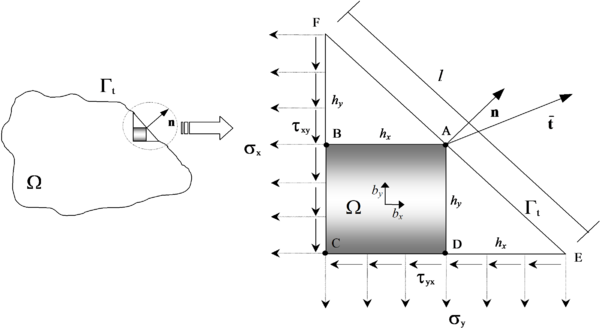
Figura 74: Dominio finito CEF para el planteamiento de equilibrio de fuerzas en el contorno de Neumann

Como antes, se plantea un equilibrio de fuerzas horizontales y verticales para obtener

$\sum F_{x}=\left(\sigma _{x}\right)_{B}2h_{y}+\left(\tau _{yx}\right)_{D}2h_{x}-{\frac {4}{2}}h_{x}h_{y}\rho b_{x}-{\overline {t}}_{x}l=0$ $\sum F_{y}=\left(\sigma _{y}\right)_{D}2h_{x}+\left(\tau _{xy}\right)_{B}2h_{y}-{\frac {4}{2}}h_{x}h_{y}\rho b_{y}-{\overline {t}}_{y}l=0$

(6.6)

utilizando una expansión en serie de Taylor de segundo orden para los esfuerzos en B y D se tiene respectivamente

$\left(\circ \right)_{B}=\left(\circ \right)_{A}-h_{x}{\frac {\partial \left(\circ \right)}{\partial x}}$ $\left(\circ \right)_{D}=\left(\circ \right)_{A}-h_{y}{\frac {\partial \left(\circ \right)}{\partial y}}$

reemplazando estas últimas expresiones en 6.6 y agrupando términos se obtiene

$\sigma _{x}{\frac {2h_{y}}{l}}+\tau _{yx}{\frac {2h_{x}}{l}}-{\overline {t}}_{x}-{\frac {2h_{x}h_{y}}{l}}\left[{\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{yx}}{\partial y}}+\rho b_{x}\right]=0$ $\sigma _{y}{\frac {2h_{x}}{l}}+\tau _{xy}{\frac {2h_{y}}{l}}-{\overline {t}}_{y}-{\frac {2h_{x}h_{y}}{l}}\left[{\frac {\partial \sigma _{y}}{\partial y}}+{\frac {\partial \tau _{xy}}{\partial x}}+\rho b_{y}\right]=0$

(6.7)

Advirtiendo que las componentes de la normal unitaria en el punto A del contorno son

$n_{x}={\frac {2h_{y}}{l}}{\hbox{ }},{\hbox{ }}n_{y}={\frac {2h_{x}}{l}}$

y que

${\frac {2h_{x}h_{y}}{l}}={\frac {h_{x}h_{y}}{l}}+{\frac {h_{x}h_{y}}{l}}={\frac {h_{x}n_{x}}{2}}+{\frac {h_{y}n_{y}}{2}}={\frac {1}{2}}\left[h_{x}n_{x}+h_{y}n_{y}\right]$

se tiene finalmente en 6.7 el siguiente sistema

$\sigma _{x}n_{x}+\tau _{yx}n_{y}-{\overline {t}}_{x}-{\frac {1}{2}}\left[h_{x}n_{x}+h_{y}n_{y}\right]\left[{\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{yx}}{\partial y}}+\rho b_{x}\right]=0$ $\sigma _{x}n_{y}+\tau _{xy}n_{x}-{\overline {t}}_{y}-{\frac {1}{2}}\left[h_{x}n_{x}+h_{y}n_{y}\right]\left[{\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{yx}}{\partial y}}+\rho b_{x}\right]=0$

que puede ser expresado en forma compacta como

$\left(\sigma _{x}n_{x}+\tau _{xy}n_{y}-{\overline {t}}_{x}\right)-{\frac {1}{2}}\mathbf {h} ^{T}\cdot \mathbf {n} \left[r_{1}\right]=0$ $\left(\sigma _{x}n_{y}+\tau _{xy}n_{x}-{\overline {t}}_{y}\right)-{\frac {1}{2}}\mathbf {h} ^{T}\cdot \mathbf {n} \left[r_{2}\right]=0$

(6.8)

siendo el vector normal ${\textstyle \mathbf {n} }$

$\mathbf {n} =\left[{\begin{array}{l}n_{x}\\n_{y}\end{array}}\right]$

El conjunto de ecuaciones 6.5 y 6.8 más las condiciones de contorno de Dirichlet, constituyen un nuevo sistema de ecuaciones (estabilizado), que permite ser resuelto utilizando el MPF sin los inconvenientes propios de la técnica de colocación puntual. Se debe notar de este sistema que cuando ${\textstyle \mathbf {h} }$ tiende a cero se recuperan las ecuaciones originales encontradas mediante el procedimiento infinitesimal. Así mismo es interesante destacar, respecto de la condición de contorno de Neumann, que la técnica del CF introduce de una manera natural la ecuación de equilibrio característica de los puntos del adyacentes al contorno (puntos C y D de la figura 74), que como era de esperar no es otra que la ecuación de equilibrio en el dominio (términos ${\textstyle r_{1}}$ y ${\textstyle r_{2}}$).

(¹) La notación utilizada es consistente con la del capítulo 3

(²) Recuérdese ecuaciones 3.18

(³) Se asume $\tau _{xy}=\tau _{yx}$

6.3 Implementación computacional

Una vez que se obtiene el nuevo sistema de escuaciones, resta por definir la manera de calcular los parámetros de estabilización y la forma de encontrar la solución al sistema global de ecuaciones. Tomando como ejemplo el caso 2D, este sistema, una vez aplicada la discretización mediante colocación, estará formado por el siguiente set de ecuaciones

${\begin{array}{l}r_{1}-{\frac {1}{2}}\mathbf {h} ^{T}\cdot \mathbf {\nabla } r_{1}=0\\r_{2}-{\frac {1}{2}}\mathbf {h} ^{T}\cdot \mathbf {\nabla } r_{2}=0\end{array}}{\hbox{ }}\forall \mathbf {x} _{I}\in (\Omega -\Gamma )$

${\begin{array}{l}\left(\sigma _{x}n_{x}+\tau _{xy}n_{y}-{\overline {t}}_{x}\right)-{\frac {1}{2}}h_{n}\left[r_{1}\right]=0\\\left(\sigma _{x}n_{y}+\tau _{xy}n_{x}-{\overline {t}}_{y}\right)-{\frac {1}{2}}h_{n}\left[r_{2}\right]=0\end{array}}{\hbox{ }}\forall \mathbf {x} _{I}\in \Gamma _{t}$

(6.9)

${\begin{array}{l}u={\overline {u}}\\v={\overline {v}}\end{array}}{\hbox{ }}\forall \mathbf {x} _{I}\in \Gamma _{u}$

donde el término ${\textstyle h_{n}}$ corresponde a la proyección del vector ${\textstyle \mathbf {h} }$ en la dirección de la normal ${\textstyle \mathbf {n} }$, es decir

$h_{n}=\mathbf {h} ^{T}\cdot \mathbf {n=(} h_{x}n_{x}+h_{y}n_{y})$

6.3.1 Parámetros de estabilización

Como se aprecia en 6.9, para que la técnica de colocación puntual sea competitiva y proporcione buenos resultados en el MPF, resulta fundamental obtener el valor adecuado de la longitud característica del dominio finito de balance. En referencia [77] se desarrolla una técnica iterativa, basada en la reducción de un residuo, que permite obtener las componentes del vector ${\textstyle \mathbf {h} }$ cuando se utiliza el MEF en problemas de convección difusión. Recientemente y para este mismo tipo de problemas, Oñate y colaboradores [82] han presentado un nuevo procedimiento para el cálculo de este vector basado en la descomposición de ${\textstyle \mathbf {h} }$ como la suma dos vectores

$\mathbf {h} =\mathbf {h} _{s}+\mathbf {h} _{t}$

donde ${\textstyle \mathbf {h} _{s}}$ y ${\textstyle \mathbf {h} _{t}}$ son los vectores de las longitudes características en la dirección de la velocidad y en la dirección transversal a ella, respectivamente.

Se ha determinado, a través del presente trabajo de investigación, que se pueden conseguir resultados estables de la solución en el MPF, para problemas de elasticidad lineal de sólidos, escogiendo ${\textstyle \mathbf {h} }$ en términos de un parámetro geométrico de la nube de interpolación. Siguiendo estas ideas, el parámetro en cuestión adoptado en los ejemplos que se desarrollan en el presente capítulo, así como en el siguiente, ha sido la distancia mínima característica de la nube ${\textstyle \mathbf {d} _{I}^{\min }=\left[d_{IX}^{\min }{\hbox{ }}d_{IY}^{\min }\right]^{T}}$(ver figura 75).

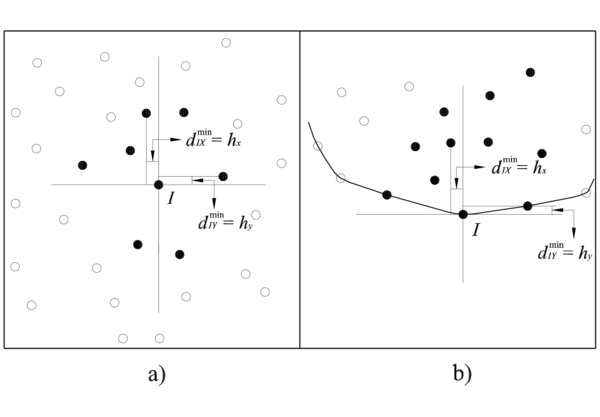
Figura 75: Definicion del vector hmath para a) una nube en el interior del dominio y b) una nube del contorno

6.3.2 Solución del sistema de ecuaciones

Utilizando la notación matricial compacta para expresar el sistema de ecuaciones estabilizado 6.9, se obtiene esta vez

$\left\{\left[\mathbf {L} ^{T}\mathbf {DL\Phi } \right]-{\frac {1}{2}}\mathbf {h} ^{T}\cdot \mathbf {\nabla } \left[\mathbf {L} ^{T}\mathbf {DL\Phi } \right]\right\}\mathbf {u} ^{h}=-\rho \mathbf {b} {\hbox{ }}\forall \mathbf {x\in } \Omega -\Gamma$ $\left\{\left[\mathbf {N} ^{T}\mathbf {DL\Phi } \right]-{\frac {1}{2}}h_{n}\left[\mathbf {L} ^{T}\mathbf {DL\Phi } \right]\right\}\mathbf {u} ^{h}={\overline {\mathbf {t} }}+{\frac {1}{2}}h_{n}\rho \mathbf {b} {\hbox{ }}\forall \mathbf {x\in } \Gamma _{t}$ (6.10) $\left[\mathbf {\Phi } \right]\mathbf {u} ^{h}={\overline {\mathbf {u} }}{\hbox{ }}\forall \mathbf {x\in } \Gamma _{u}$

siendo las matrices ${\textstyle \mathbf {N} }$, ${\textstyle \mathbf {D} }$, ${\textstyle \mathbf {L} }$ y ${\textstyle \mathbf {\Phi } }$ las definidas en el apartado 3.3. El sistema anterior se puede expresar en la conocida forma ${\textstyle \mathbf {Ku} ^{h}=\mathbf {f} }$, de donde se encuentra finalmente el vector de parámetros desconocidos ${\textstyle \mathbf {u} ^{h}}$. Conviene destacar el hecho de que, al igual que en el sistema sin estabilizar, la matriz ${\textstyle \mathbf {K} }$ resulta ser no simétrica ni definida positiva, por lo que se ha implementado un solver iterativo de Gradientes Bi-Conjugados para resolver el sistema de ecuaciones. Este método corresponde a una generalización del método de Gradientes Conjugados, donde la solución se obtiene minimizando el error de un funcional, pero aplicable específicamente a matrices no simétricas ni definidas positivas [30], [98].

6.4 Ejemplos numéricos

A continuación se desarrollan algunos de los ejemplos resueltos en el capítulo 4 (MPF sin estabilizar), principalmente aquellos que presentan un comportamiento erróneo respecto de la solución teórica, para validar la efectividad de la técnica de estabilización propuesta. También se incluyen otros ejemplos de interés práctico, fundamentalmente en 2D, que muestran esta vez una correcta convergencia del método y una nula sensibilidad a la prescripción de la condición de contorno de Neumann.

6.4.1 Ejemplos 1-D

Como primer caso se analiza la distribución del error relativo en desplazamientos, para el problema de deformación axial, cuando la carga se reparte de manera lineal. La figura 76 muestra la importante disminución del error relativo en desplazamientos que se consigue mediante la técnica de estabilización propuesta. Se debe notar el hecho de que aun manteniéndose la ubicación de los valores picos del error (zonas cercanas a los bordes), la disminución que se consigue es superior al 100%, siendo esta vez el valor máximo con sólo 11 puntos inferior al 0.3%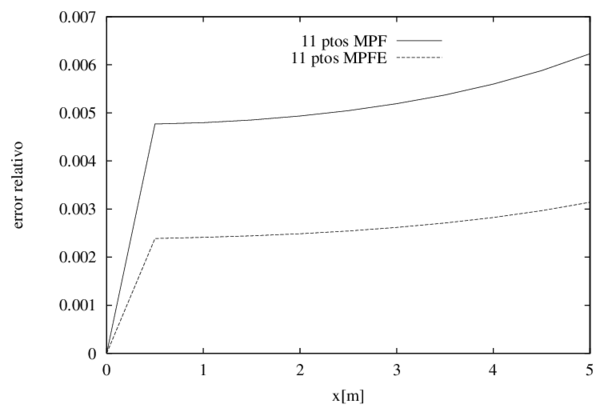

Figura 76: Distribucion del error relativo en desplazamientos. Problema de deformacion axial 1D, MPFE

Las gráficas con 26, 51 y 81 puntos presentan la misma tendencia anterior, por lo que no se ha estimado oportuno repetirlas, sin embargo, para corroborar la mejora que se obtiene en este ejemplo se presenta también la figura 77. En esta se compara la convergencia del error, con y sin estabilización, para los deplazamientos y su derivada. Notar como en ambos casos se consigue una disminución del error respecto de la solución teórica.

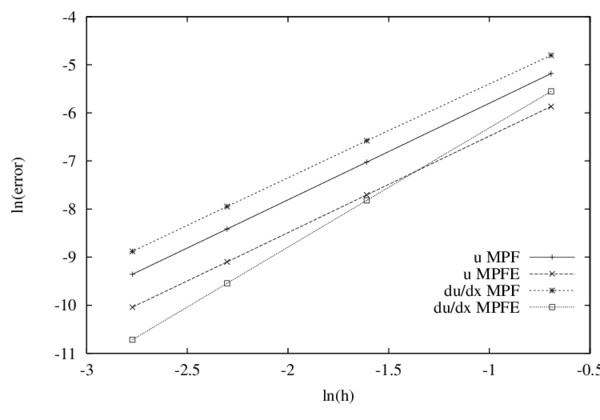
Figura 77: Convergencia del error para el problema de deformacion axial 1D. Carga repartida lineal, MPFE

Se puede verificar la mejor convergencia del solver de gradientes biconjugados, cuando el problema se estabiliza, haciendo un estudio del residuo v/s número de iteraciones. Tomando como ejemplo la discretización con 81 puntos y, considerando que el algoritmo de resolución del sistema de ecuaciones es de terminación finita (la solución de logra con un número de iteraciones menor o igual al número de incógnitas), la figura 78 muestra cómo es la evolución del residuo y cómo en el caso del MPFE la solución se alcanza en un menor número de iteraciones.

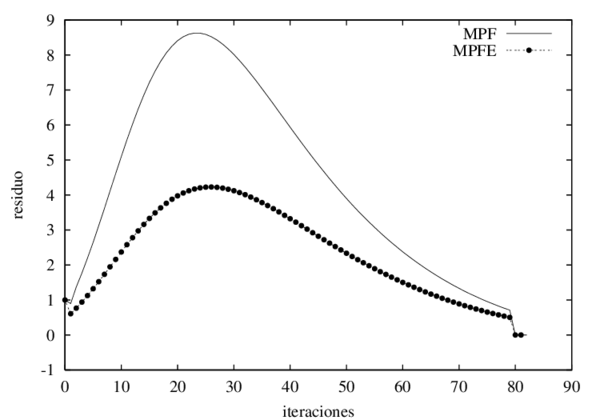
Figura 78: Evolucion del residuo en el solver de gradientes biconjugados, problema de deformacion axial 1D carga repartida lineal

6.4.2 Ejemplos 2-D de tensión plana y deformación plana. Viga en cantilever.

Se analiza el comportamiento de la viga en cantilever del apartado 4.2.2 (ver figura 50), para mostrar las mejoras que se consiguen utilizando la técnica de estabilización del CF. Por ser este un ejemplo donde se ha detectado que la falta de simetría de la nube (nubes incompletas) afecta la convergencia de la solución, se pretende comprobar si con el MPFE este fenómeno se consigue atenuar, verificando además el comportamiento de la solución en la zona de máxima distribución del esfuerzo horizontal. Como se puede apreciar de la figura 79, la convergencia del error en desplazamientos para el caso de utilizar nubes incompletas de 6, 7 y 8 puntos, con una distribución regular de puntos, mejora significativamente y desaparece el cambio brusco en la tendencia que muestra la solución sin estabilizar (s/e), cuando se pasa de una discretización de 165 a 333 puntos.

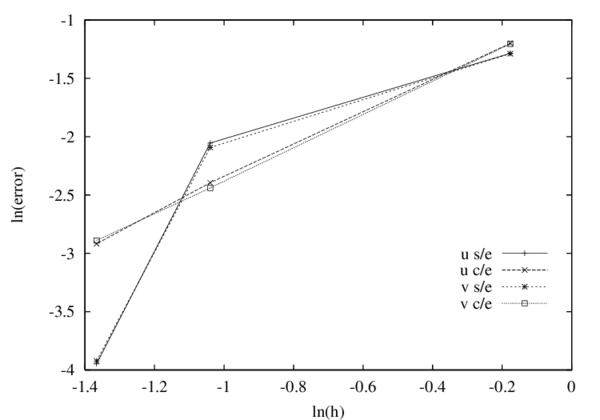
Figura 79: Comparacion de la convergencia del error global en desplazamientos para la viga en cantilever, distribucion regular de puntos, nubes de 6, 7 y 8 puntos

Cuando se utilizan nubes completas de 9 puntos y una discretización regular, el efecto usar o no la estabilización se aprecia en el error global de la solución. Tal como muestra la figura 80 y para todas las discretizaciones utilizadas (55, 165 y 333 puntos), existe una disminución del error para ambos desplazamientos de alrededor de un 20% como promedio.

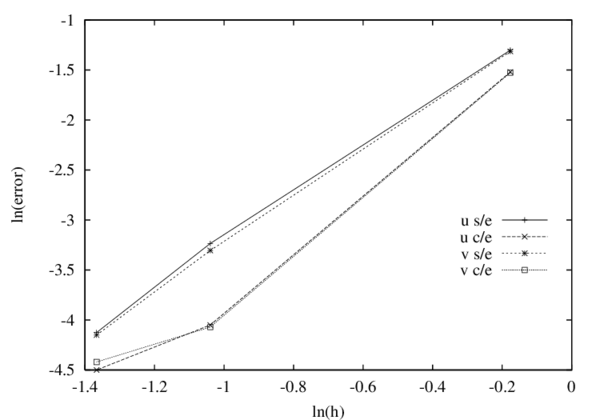
Figura 80: Comparacion de la convergencia del error global en desplazamientos para la viga en cantilever, distribucion regular de puntos, nubes de 9 puntos

En el caso de utilizar una distribución irregular de puntos, la respuesta del MPFE también ha mostrado una mejora de la solución tanto a nivel global como local. En forma comparativa estos resultados se pueden visualizar en las figuras 81, 82 y 83. En la primera de ellas se aprecia nuevamente cómo la solución estabilizada entrega un menor valor del error global para cada discretización, observándose esta vez un incremento en la velocidad de convergencia (cambio de la pendiente de las rectas).

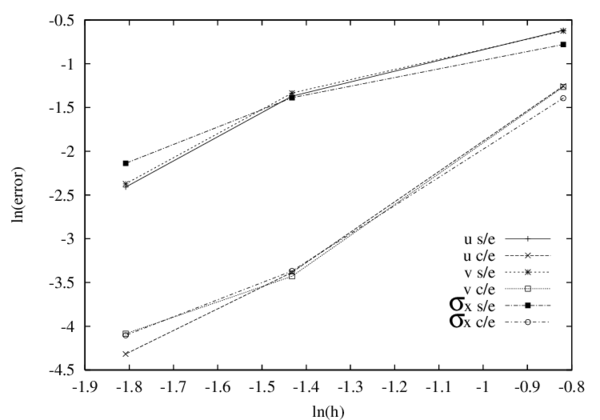
Figura 81: Comparacion de la convergencia del error global para la viga en cantilever, distribucion irregular de puntos

La segunda muestra una falta de simetría de la solución, cuando se utiliza el MPF y una discretización irregular de 165 puntos (82a), además de elevados errores en las zonas de máxima concentración del esfuerzo. Este comportamiento cambia en forma radical y se compara favorablemente con la solución teórica cuando se utiliza el MPFE (82b).

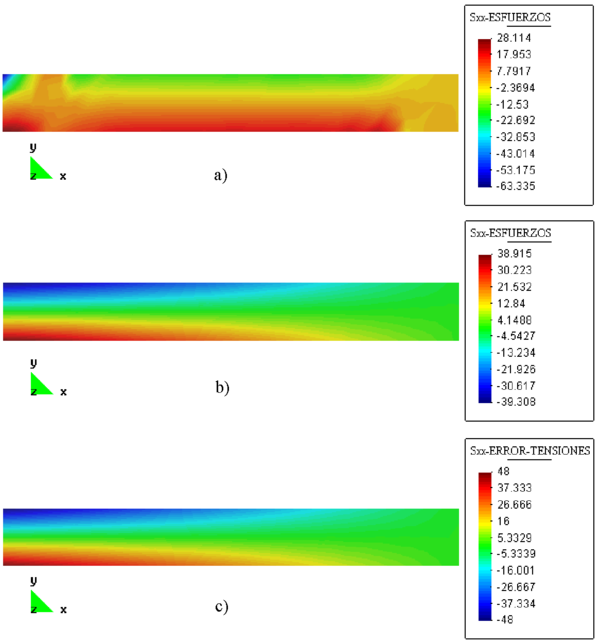
Figura 82: Contornos de esfuerzo horizontal _xmath para viga en cantilever con una discretizacion irregular de 165 puntos, a) solucion sin estabilizar, b)solucion estabilizada y c) solucion teorica

La baja sensibilidad del MPFE para una distribución irregular se puede apreciar también cuando se analiza la figura 83. En esta se muestra cómo varía el esfuerzo ${\textstyle \sigma _{x}}$ a lo largo de la viga, para la coordenada ${\textstyle y=0.5}$, con una discretización de 165 puntos. Aunque existe una tendencia a disminuir, en la medida que aumenta la distancia a la zona de máxima solicitación, los valores del esfuerzos en el MPF no reflejan claramente una variación lineal acorde con los de la solución teórica. Este comportamiento, más bien oscilatorio, no está presente en el MPFE. Cabe hacer presente que el error relativo respecto de la solución teórica, en la zona del máximo esfuerzo horizontal, es de un 31% en el caso del MPF y cercano al 18% en el MPFE.

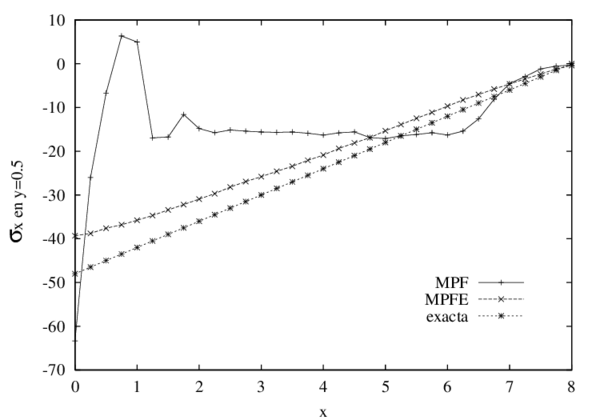
Figura 83: Esfuerzo horizontal _xmath a lo largo del contorno superior de la viga, discretizacion irregular de 165 puntos

6.4.3 Análisis de la solución cerca del rango de incompresibilidad

Se ha utilizado el ejemplo de la viga en cantilever, para analizar la respuesta numérica del MPF en problemas de deformación plana cerca del rango de incompresibilidad del material. Como se sabe, en el MEF el elemento CST con seis grados de libertad muestra un pobre comportamiento ante esta situación [106]. Los valores de la geometría y cargas utilizadas, según la figura 50, son esta vez ${\textstyle D=12}$, ${\textstyle L=48}$ y ${\textstyle P=40000}$. Las propiedades del material ${\textstyle E=3.0\times 10^{7}}$ y un módulo de poisson ${\textstyle \nu }$ variable. Esta vez la solución para el campo de desplazamiento horizontal (${\textstyle u}$) y desplazamiento vertical (${\textstyle v}$) se encuentra reemplazando los valores de ${\textstyle E}$ y ${\textstyle \nu }$ en las ecuaciones 4.2, por ${\textstyle E/\left(1-\nu ^{2}\right)}$ y ${\textstyle \nu /\left(1-\nu \right)}$, respectivamente[94].

En primer término la tabla 7 muestra el resultado, para distintos valores de ${\textstyle \nu }$, del cuociente entre el desplazamiento numérico y el teórico para una discretización de 85 puntos (equivale a malla de ${\textstyle 4\times 16}$). Todos los valores mostrados corresponden al punto de máximo desplazamiento, es decir, ${\textstyle \left(x,y\right)=\left(48,0\right)}$ para ${\textstyle v}$, ${\textstyle \left(x,y\right)=\left(48,\pm 6\right)}$ para ${\textstyle u}$.

Tabla. 7 Desplazamientos para la viga en cantilever, deformación plana

Los resultados que se obtienen para este ejemplo, cuando se aumenta el número de puntos, se muestran en la tabla 8. Se aprecia en ambos casos, que el MPFE resulta ser bastante flexible ya que permite obtener buenos resultados, incluso en el rango cercano a la incompresibilidad del material (${\textstyle \nu =0.4999}$), sin recurrir a ninguna estrategia para modificar su formulación.

Tabla. 8 Convergencia del desplazamiento para la viga en cantilever, deformación plana

Respecto a la convergencia de la solución para este problema con el MEF, en condiciones de tensión plana, la tabla 9 compara la respuesta en el punto de máximo desplazamiento vertical para distintos tipos de elementos encontrada por Piltner [86]¹. Para poder comparar la respuesta que se obtiene con el presente método sin malla, se han agregado a la tabla las columnas que contienen los valores encontrados en la modelación con el MPF y MPFE.

Tabla. 9 Desplazamiento vertical para la viga en cantilever, tensión plana

Tal como muestra la figura 84, se puede decir que para problemas donde el comportamiento sea predominantemente de flexión, tanto el MPF como el MPFE muestran una mejor respuesta que el elemento CST en el MEF², por otro lado, los resultados que se obtienen con el MPFE se comparan favorablemente con los encontrados por Piltner en [86], cuando se utiliza el MEF y los elementos triangulares mejorados TE4 propuestos por los autores.

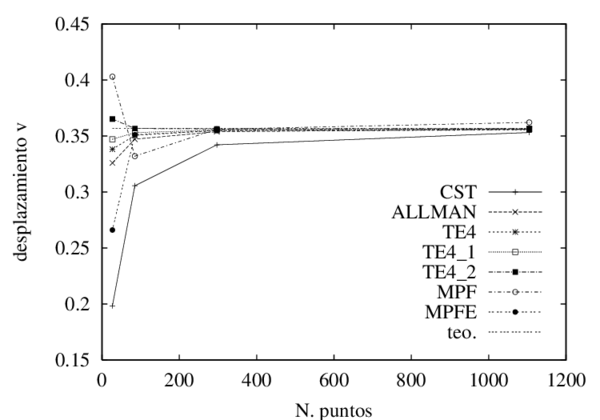
Figura 84: Convergencia del desplazamiento vertical para la viga en cantilever utilizando el MEF(diferentes elementos), MPF y el MPFE

(¹) La publicación contiene una descripción más detallada acerca de las características de los distintos elementos TE4, TE4_ y TE4_

(²) En parte esto era previsible debido a la excesiva rigidez que presenta el elemento CST

6.4.4 Flexión de una viga simplemente apoyada

A pesar de haberse utilizado una discretización regular de puntos para modelar la viga (ver apartado 4.2.3), es en este ejemplo donde se manifiesta con mayor claridad la importancia que tiene el tratamiento de la condición de contorno de Neumann. A diferencia del caso de la viga en cantilever, donde la condición de Neumann se impone sobre unos pocos puntos, esta vez existe en forma proporcional una mayor cantidad de puntos del dominio en los que se impone la carga prescrita (todo el contorno superior) y, por consiguiente, una menor cantidad de puntos que soportan la ecuación de equilibrio del problema. Sin embargo, tal como indican las figuras 85 y 86, el MPFE muestra una correcta convergencia del error global en la solución y del esfuerzo ${\textstyle \sigma _{x}}$ a lo largo del contorno superior. Se debe notar también, el cambio significativo en la tendencia de éstas gráficas respecto de las encontradas anteriormente (ver figuras 57 y 58). Notar asimismo cómo, para el caso del esfuerzo ${\textstyle \sigma _{x}}$, desaparecen en forma definitiva las oscilaciones en las zonas en los extremos y se obtiene adecuadamente la tendencia parabólica de los valores teóricos en todas las discretizaciones modeladas.

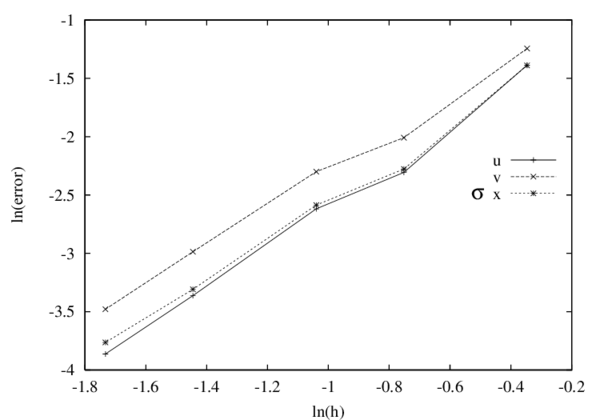
Figura 85: Convergencia del error global utilizando el MPFE, viga simplemente apoyada

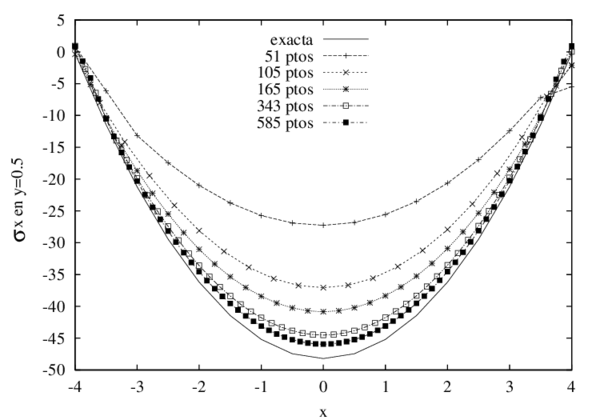
Figura 86: Convergencia del esfuerzo _xmath a lo largo del contorno y=0.5math con el MPFE, viga simplemente apoyada

Con el propósito de poder comparar y también complementar de una forma gráfica la respuesta del MPFE en este ejemplo, se ha decidido plotear nuevamente los contornos en desplazamientos y esfuerzos horizontales en la viga (figuras 87 y 88). A diferencia de lo encontrado anteriormente (compárese con las figuras 59 y 60), se aprecia una correcta distribución, simetría y convergencia de la solución en todas las discretizaciones.

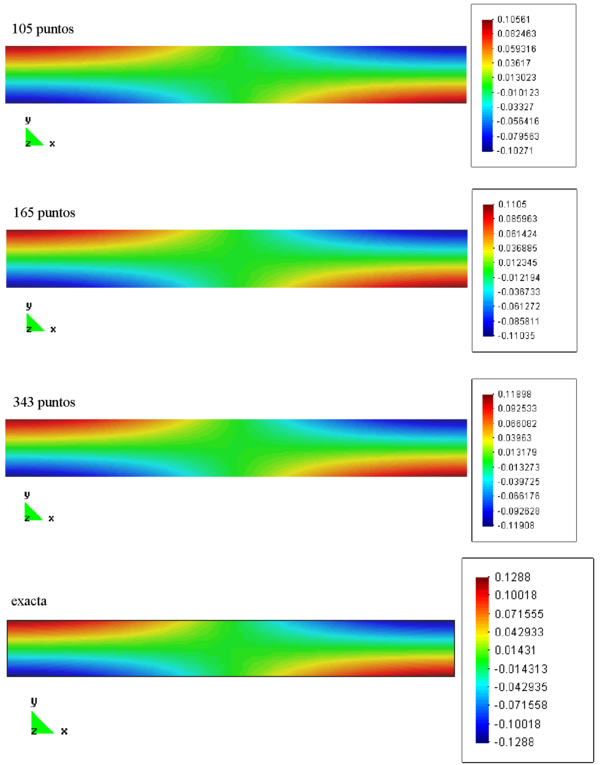
Figura 87: Contornos de desplazamiento horizontal umath con el MPFE, viga simplemente apoyada

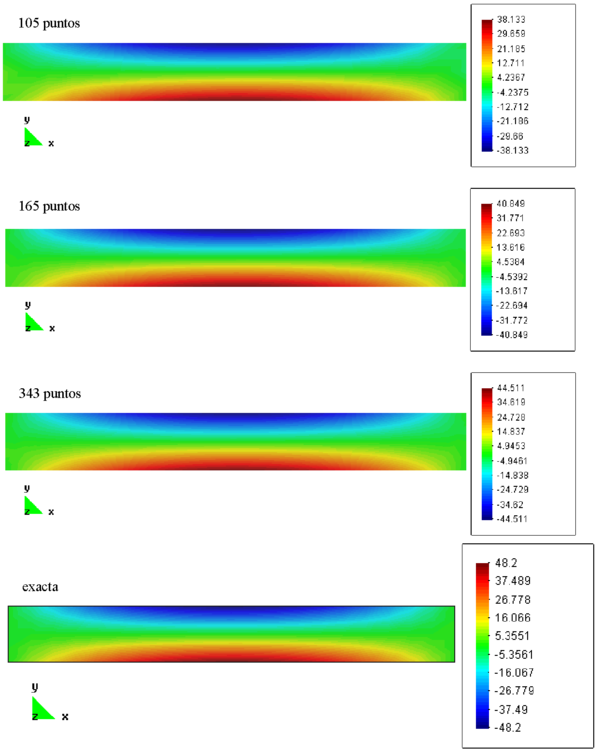
Figura 88: Contornos de esfuerzo horizontal _xmath con el MPFE, viga simplemente apoyada

Finalmente, a modo de comparación, se ha resuelto el ejemplo mediante un código comercial de elementos finitos utilizando las mismas discretizaciones que en el método de puntos. Tal como muestran las figuras 89 y 90, la respuesta del MPFE se compara favorablemente con la del MEF (elemento CST). Más aun, para discretizaciones con bajo número de puntos, el error respecto del valor teórico de la flecha máxima (punto A de la figura 56) y el esfuerzo horizontal, es menor en el MPFE. Notar nuevamente el efecto favorable que se logra cuando se estabiliza el sistema de ecuaciones.

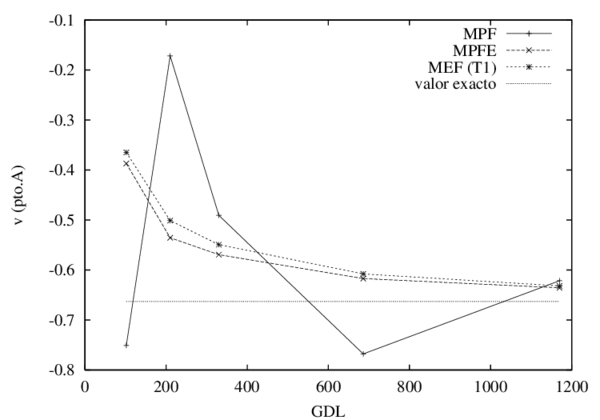
Figura 89: Convergencia del maximo desplazamiento vertical vmath en funcion del numero de puntos, viga simplemente apoyada

Figura 90: Convergencia del maximo esfuerzo horizontal _xmath en funcion del numero de puntos, viga simplemente apoyada

6.4.5 Placa con agujero

Utilizando las mismas discretizaciones irregulares analizadas en el apartado 4.2.4, pero con la técnica FIC, la respuesta del MPF muestra una correcta convergencia de la solución (ver figura 91) y una mejor capacidad para capturar el valor adecuado del esfuerzo horizontal en la zona superior del agujero (zona de máxima concentración del esfuerzo horizontal).

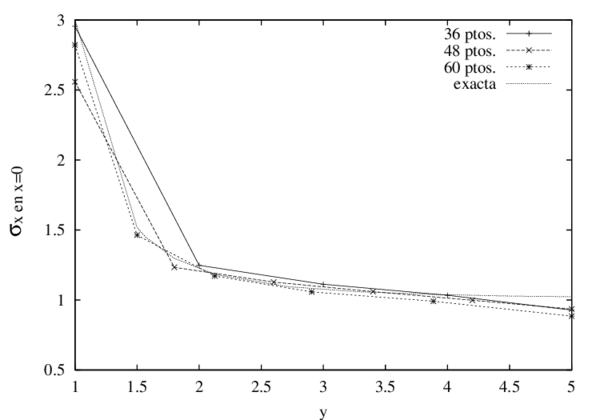
Figura 91: Distribucion del esfuerzo _xmath , en x=0math, para el problema de la placa con agujero

También, a modo de comparación, se ha resuelto el ejemplo mediante el MEF utilizando elementos tipo CST (triángulo lineal). Estos resultados se incluyen en las gráficas de la figura 92, junto a los contornos de esfuerzo horizontal, tanto para el caso del MPF como para el MPFE. Tal como se aprecia en la figura, los resultados que se obtienen para el máximo esfuerzo horizontal con el MPFE, se comparan favorablemente tanto con los que entrega la solución teórica ${\textstyle \sigma _{x}=3.0}$ [94] como con los del MEF. Por ejemplo, considerando 36 puntos para discretizar el dominio (50 elementos CST), el error respecto de la solución teórica es de 6% en el MPFE y de un 38% en el MEF. Cuando se utilizan 60 puntos (94 elementos CST) , el error disminuye a un 1.5% en el MPFE y a un 20% en el MEF¹.

Figura 92: Placa en tension con agujero circular, arreglos de 36 y 60 puntos. a) Contornos de esfuerzo horizontal _xmath para el MPF, b) contornos de esfuerzo horizontal _xmath para la geometria deformada con el MPFE y c) distribucion del esfuerzo horizontal sobre la linea x=0math

(¹) Similares resultados se obtienen también para la discretización irregular de 48 puntos (figura 62)

6.4.6 Ejemplos NAFEMS

La agencia NAFEMS (National Agency for Finite Element Methods and Standards), con el propósito de promover el uso seguro y fiable de la tecnología de elementos finitos, ha propuesto una serie de test para poder validar la respuesta que entrega un código basado en este tipo aproximación numérica [67]. Con el objeto de poder comparar la eficiencia del MPFE, para problemas bidimensionales de tensión plana, se han modelado 2 de estos test utilizando arreglos regulares e irregulares de puntos. Los resultados que se muestran a continuación permiten comprobar que el MPFE supera sin dificultad este tipo de test.

6.4.7 Test IC1 (Placa en tensión con carga normal)

La geometría del dominio y el tipo de carga se aprecia en la figura 93. La placa tiene un espesor de ${\textstyle e=0.1\left[m\right]}$ y sobre el contorno FC se prescriben condiciones de contorno de Neumann en forma de una carga distribuida según P ${\textstyle =10\left[{\frac {MN}{m}}\right]}$, sobre el contorno ED se prescriben condiciones de Dirichlet restringiendo el movimiento en la dirección del eje X. Adicionalmente para el punto A (punto medio del contorno ED) se restringe el movimiento en la dirección Y. Las propiedades del material utilizadas en la modelación son ${\textstyle E=2.1\times 10^{5}\left[MPa\right]}$ y ${\textstyle \nu =0.3}$.

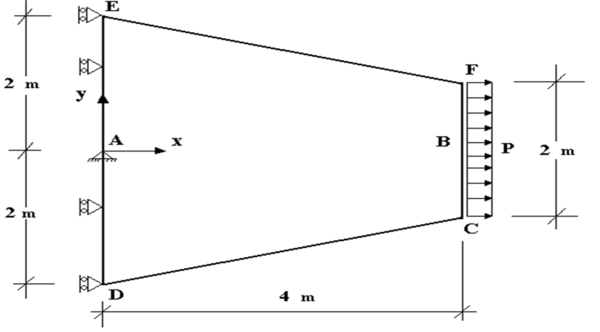
Figura 93: Geometria, condiciones de contorno y de carga para el test NAFEMS IC1

Los resultados que se buscan para este test son el desplazamiento en el punto B (punto medio del contorno FC) ${\textstyle u_{B}=0.00144\left[m\right]}$, y el esfuerzo horizontal en A, ${\textstyle \sigma _{x}=61.3\left[MPa\right]}$, respectivamente. Como información adicional se ha calculado la fuerza de reacción sobre el contorno ED, cuyo valor teórico es de ${\textstyle R_{x}=20\left[MN\right]}$, mediante la relación

$R_{x}=\int _{-2}^{2}\sigma _{x}dA=\int _{-2}^{2}\sigma _{x}edy$

Se han analizado un total de 7 configuraciones para arreglos regulares de puntos y 8 con arreglos irregulares, tanto para el MPF como el MPFE, obteniéndose los resultados que se muestran en la tablas tabla IC1 reg y 11, además, la figuras 94 y 95 muestran algunas de las configuraciones analizadas.

Tabla. 10 Principales resultados test IC1, discretización regular

Tabla. 11 Principales resultados test IC1, discretización irregular

Figura 94: Discretizacion regular de puntos para el test IC1

Figura 95: Discretizacion irregular de puntos para el test IC1

La convergencia hacia la solución esperada, cuando se utilizan nubes de puntos regulares, se puede ver en las gráficas 96, 97 y 98, de ellas se aprecia el correcto comportamiento del MPF con estabilización (MPF c/e), para un determinado incremento del número de puntos. Por otro lado las gráficas sugieren que, a excepción de cuando se utilizan 49 puntos, la respuesta no se deteriora significativamente con el MPF sin estabilización (MPF s/e).

Un tipo de información cuantitativa, que permite tener una idea aproximada de la rapidez con que se alcanza la solución del sistema global de ecuaciones, es el número de iteraciones que realiza el solver de gradientes bi-conjugados que se ha implementado en el código. Esta información, que se incluye en las tablas tabla IC1 reg y 11, predice un mayor número de iteraciones en todos los casos para el MPF, lo que indicaría de alguna forma lo mal condicionada que se encuentra la matriz de rigidez global. Por el contrario, y tal como corresponde a un solver de terminación finita, en el MPFE la solución se logra con un número de iteraciones inferior al número de incógnitas.

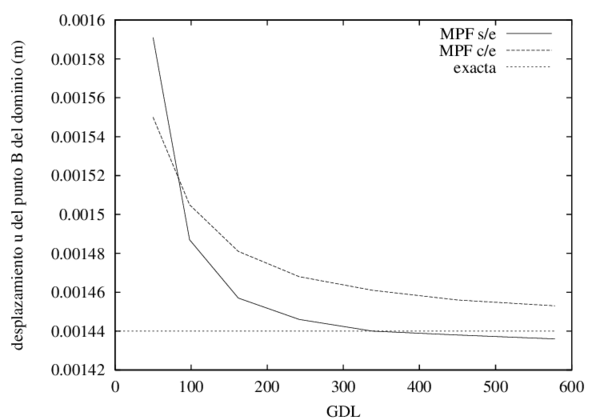
Figura 96: Convergencia del desplazamiento horizontal en B para un arreglo regular de puntos, test IC1

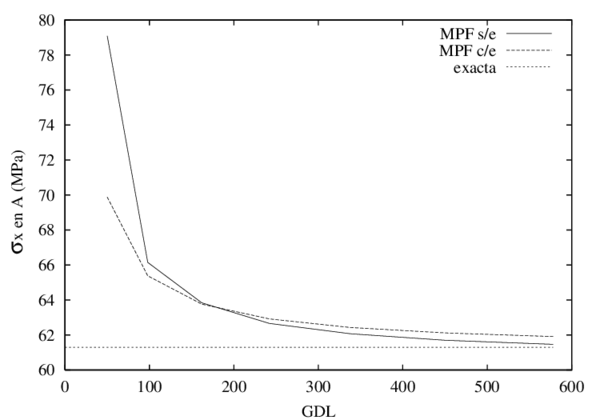
Figura 97: Convergencia del esfuerzo horizontal en A para un arreglo regular de puntos, test IC1

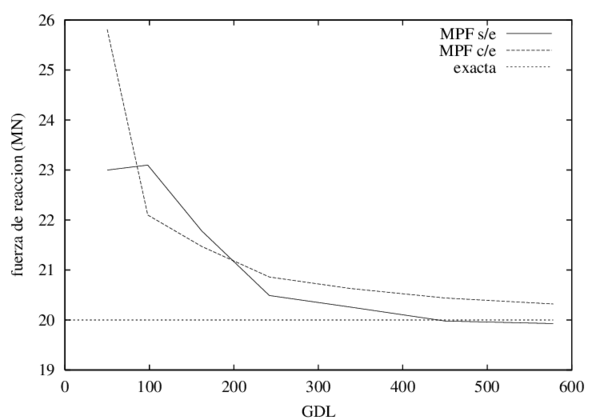
Figura 98: Convergencia de la fuerza de reaccion en el extremo ED para un arreglo regular de puntos, test IC1

En las figuras 99, 100 y 101, se aprecia cómo es la convergencia de la solución en este test, para el caso de las discretizaciones de puntos irregulares. A diferencia del caso anterior, las gráficas muestran esta vez un comportamiento oscilatorio de la solución en el MPF a medida que se aumenta el número de puntos. Además, la solución numérica difiere significativamente del valor buscado en algunas configuraciones, por ejemplo, para 122 puntos, el error relativo en el esfuerzo ${\textstyle \sigma _{x}}$ es de 60% mientras que para la fuerza de reacción ${\textstyle R_{x}}$ supera el 100%

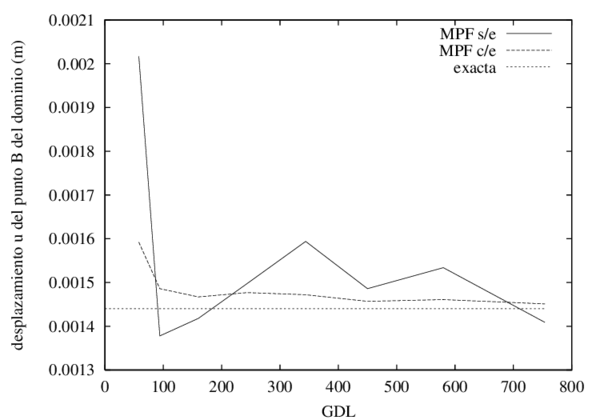
Figura 99: Convergencia del desplazamiento horizontal en B para un arreglo irregular de puntos, test IC1

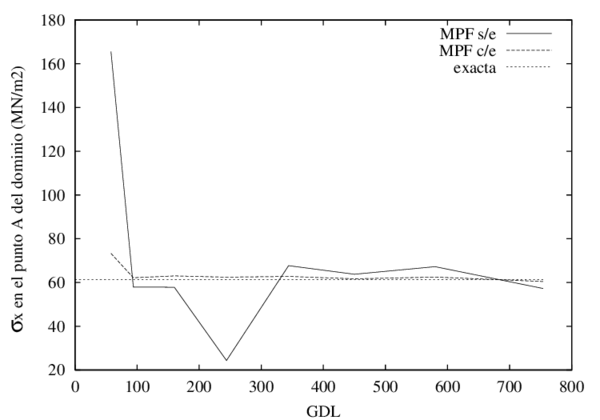
Figura 100: Convergencia del esfuerzo horizontal en A para un arreglo irregular de puntos, test IC1

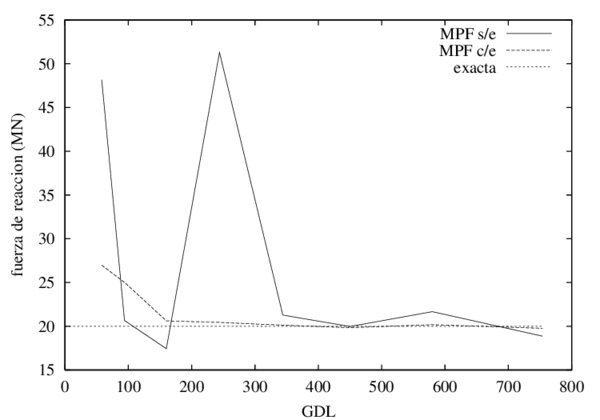
Figura 101: Convergencia de la fuerza de reaccion en el extremo ED para un arreglo irregular de puntos, test IC1

Con el objetivo de comparar los resultados que se obtienen para este test, es conveniente plotear los contornos de desplazamiento y esfuerzo horizontal en el dominio, y tener así una visión global de la respuesta como método sin malla. A modo de ejemplo, analizando la configuración irregular de 290 puntos, se tiene que los errores para el desplazamiento y esfuerzo, en los puntos buscados, son de 6.2% y 9.7% cuando se utiliza el MPF. Sin embargo, estos valores que puntualmente pueden indicar un correcto comportamiento de la solución numérica, no reflejan realmente lo que ocurre en otras zonas de la placa. Las figuras 102 y 103 permiten corroborar esta situación. Nótese tanto la falta de simetría de la solución como la ubicación errónea de los valores extremos del desplazamiento y del esfuerzo.

Por el contrario, cuando se utiliza el MPFE, se recuperan tanto la simetría como la zona donde se localizan estos valores extremos, además, la solución se compara favorablemente con la que entrega el MEF utilizando elementos CST. Para esta situación, y como era previsible, los errores para el desplazamiento y el esfuerzo disminuyen a un 1.4% y 1.9%, respectivamente.

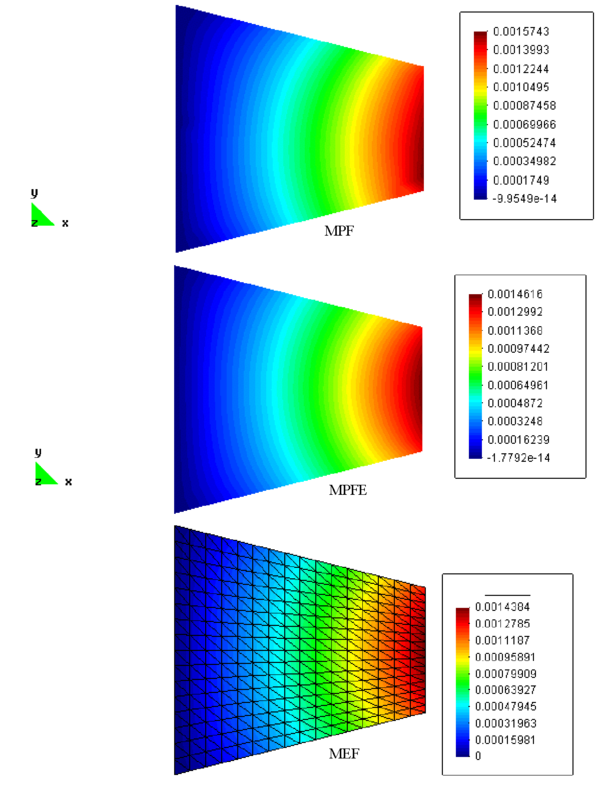
Figura 102: Contornos de desplazamiento horizontal para arreglo irregular de 290 puntos, test IC1

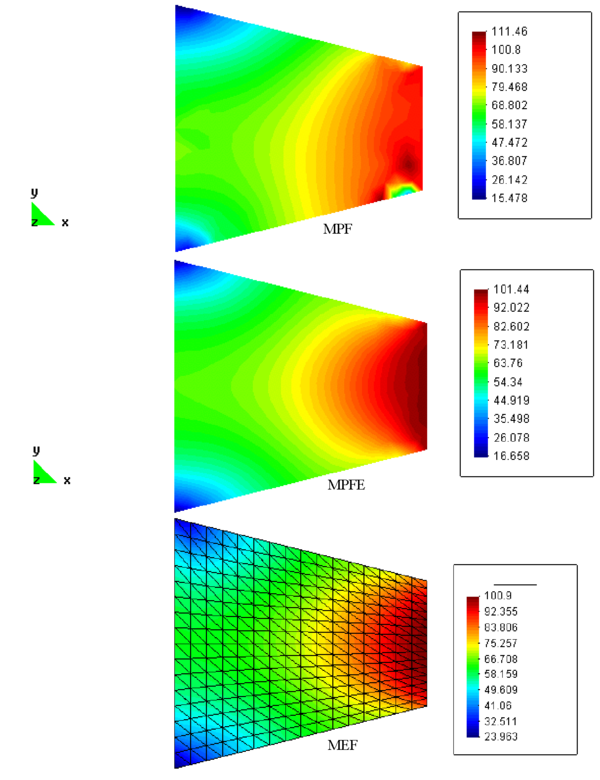
Figura 103: Contornos de esfuerzo horizontal para arreglo irregular de 290 puntos, test IC1

6.4.8 Test IC2 (Placa bajo peso propio)

La geometría y dirección en la que actúa la fuerza de gravedad se aprecian en la figura 104, la placa tiene un espesor de ${\textstyle e=0.1\left[m\right]}$ y sobre el contorno CD se prescriben condiciones de Dirichlet restringiendo el movimiento en la dirección del eje Y. Adicionalmente para el punto A (punto medio del contorno CD) se restringe el movimiento en la dirección X. Las propiedades del material utilizadas en la modelación son ${\textstyle E=2.1\times 10^{5}\left[MPa\right]}$, ${\textstyle \nu =0.3}$ y un peso específico de ${\textstyle \gamma =0.07\left[{\frac {MN}{m^{3}}}\right]}$. Los valores buscados en la modelación corresponden al desplazamiento vertical en el punto B, ${\textstyle v_{B}=-2.26\times 10^{-6}\left[m\right]}$, el esfuerzo vertical en A, ${\textstyle \sigma _{y}=0.247\left[MPa\right]}$, y la fuerza de reacción ${\textstyle R_{y}=0.084\left[MN\right]}$ (equivalente al peso de la placa) en el contorno CD, respectivamente.

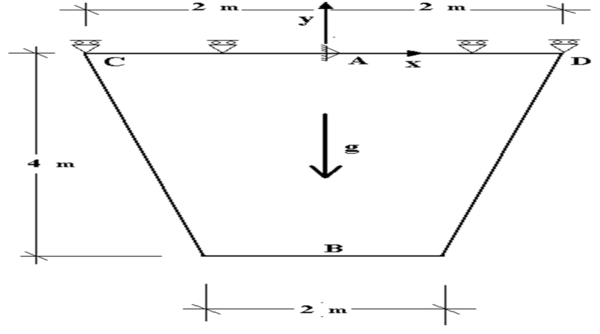
Figura 104: Geometria, condiciones de contorno y de carga para el test NAFEMS IC2

Se han modelado un total de 15 configuraciones, con discretizaciones regulares e irregulares de puntos, obteniéndose los resultados que muestran las tablas tabla IC2 irreg y 13.

Tabla. 12 Principales resultados test IC2, discretización irregular

Tabla. 13 Principales resultados test IC2, discretización regular

Considerando los resultados para las discretizaciones regulares de puntos, excepto para el caso de la fuerza de reacción, el MPF no muestra una clara tendencia hacia los valores buscados de la solución NAFEMS. Esto no ocurre así para el MPFE donde, a pesar del mayor error respecto de la solución que sugieren las figuras 105, 106 y 107, existe una clara convergencia con el aumento del número de puntos.

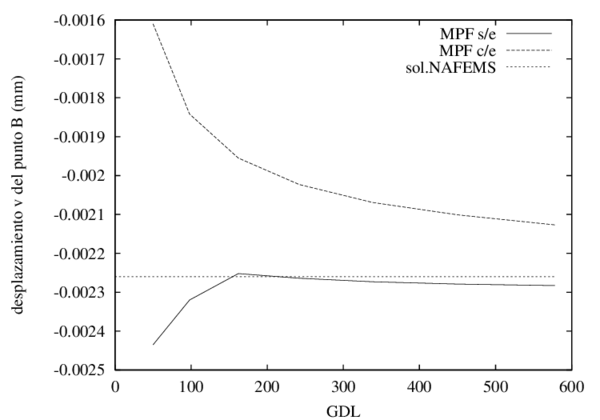
Figura 105: Convergencia del desplazamiento vertical en B para un arreglo regular de puntos, test IC2

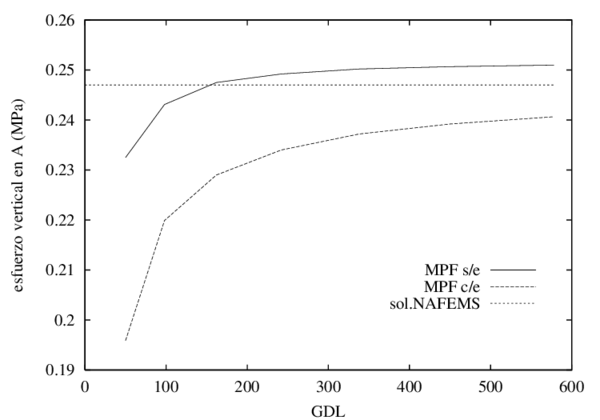
Figura 106: Convergencia del esfuerzo vertical en A para un arreglo regular de puntos, test IC2

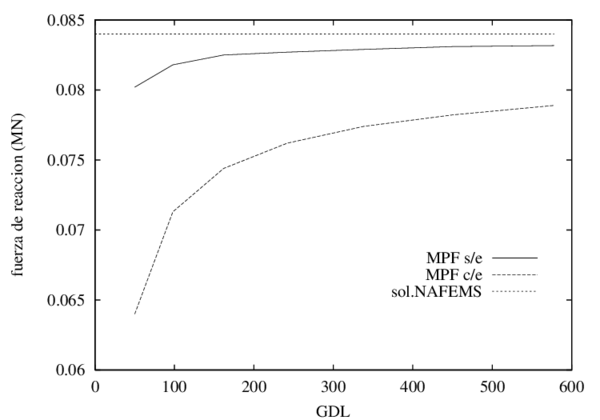
Figura 107: Convergencia de la fuerza de reaccion en el extremo CD para un arreglo regular de puntos, test IC2

En las figuras 108, 109 y 110, se aprecia la convergencia de la solución para este test cuando se utilizan discretizaciones de puntos irregulares. Nuevamente existe una gran diferencia en la tendencia que muestra el MPF y el MPFE, por ejemplo, para la zona comprendida entre 94 y 344 GDL, existe un pico del error importante de un 27% para el esfuerzo vertical y 57% para la fuerza de reacción en el MPF. Por contra, el error para los mismos parámetros en el MPFE no supera el 27% con la mínima discretización, y, disminuye de manera constante hasta un mínimo de 5% para la geometría con el mayor número de puntos.

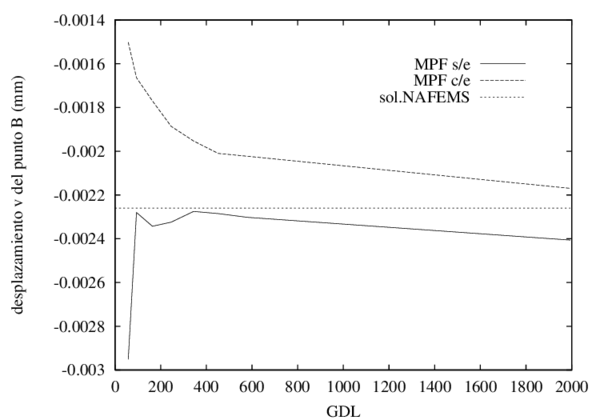
Figura 108: Convergencia del desplazamiento vertical en B para un arreglo irregular de puntos, test IC2

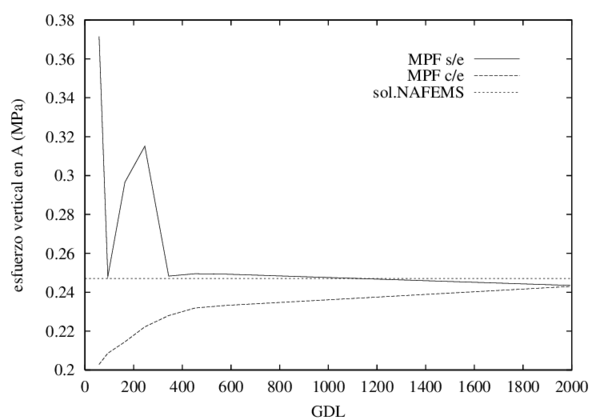
Figura 109: Convergencia del esfuerzo vertical en A para un arreglo irregular de puntos, test IC2

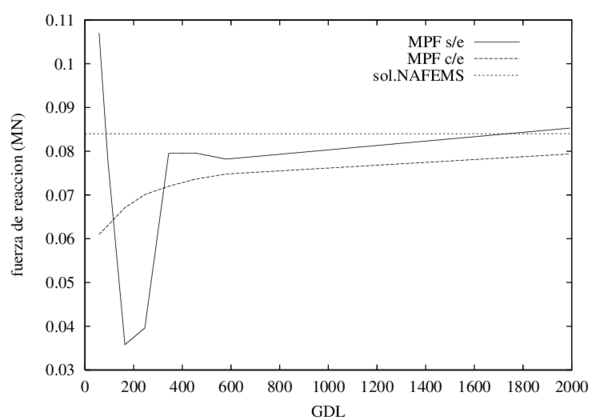
Figura 110: Convergencia de la fuerza de reaccion en el extremo CD para un arreglo irregular de puntos, test IC2

Por último, para la distribución irregular de 290 puntos y, para tener una comparación de lo que ocurre en todo el dominio, la figura 111 muestra los contornos de esfuerzo ${\textstyle \sigma _{y}}$ sobre la geometría deformada que se obtienen para el test IC2. Notar la diferencia en la distribución de los valores para el caso del MPF en contraste con lo encontrado para el MPFE y el MEF(elementos CST).

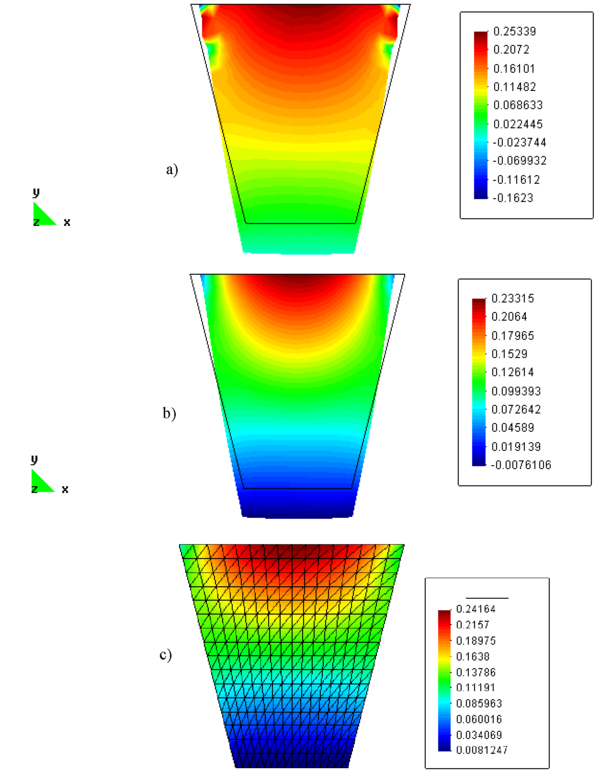
Figura 111: Contornos de esfuerzos _ymath en el test IC2, para una distribucion de 290 puntos, a) MPF b) MPFE y c) MEF

6.4.9 Cilindro de pared gruesa con presión uniforme

En la figura 112 se muestra la geometría del cilindro y la distribución de la presión interna y externa, debido a la simetría del problema se ha modelado un cuarto de cilindro. El problema fue resuelto bajo condiciones de tensión plana y con un espesor unitario. Se han utilizado para el presente ejemplo ${\textstyle a=5}$, ${\textstyle b=8}$, ${\textstyle p_{i}=1}$, ${\textstyle p_{0}=0}$ y una interpolación cuadrática (${\textstyle m=6}$), con nubes de un mínimo de 7 nodos. La solución teórica del esfuerzo radial para este problema es [94]

$\sigma _{r}={\frac {a^{2}b^{2}\left(p_{0}-p_{i}\right)}{b^{2}-a^{2}}}\cdot {\frac {1}{r}}+{\frac {p_{i}a^{2}-p_{0}b^{2}}{b^{2}-a^{2}}}$

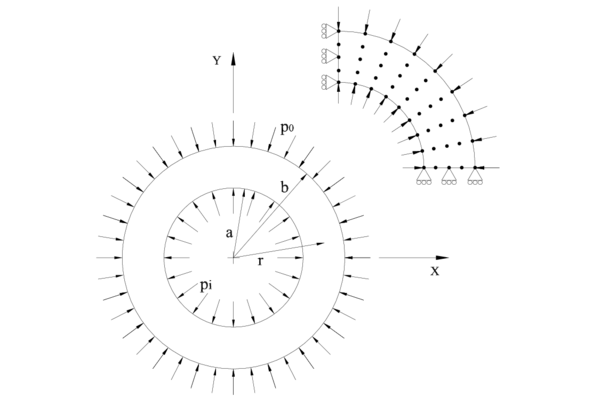
Figura 112: Geometria y discretizacion para el cilindro de pared gruesa con presion uniforme

En la figura 113 se puede apreciar el comportamiento del MPFE y el MPF (sin estabilización), para el esfuerzo radial en el eje ${\textstyle y=0}$ cuando se utilizan 45 puntos. Como indica el gráfico, la solución se deteriora y presenta un comportamiento errático mientras no se emplee el procedimiento del CF, este comportamiento se manifiesta también para otras configuraciones de puntos analizadas. Se puede visualizar mejor esta tendencia ploteando la distribución del esfuerzo radial sobre el cuerpo, se debe notar que la solución teórica predice una distribución que depende únicamente de la coordenada radial¹. En las figuras 114 y 115 se pueden apreciar ambas distribuciones, comprobándose nuevamente el efecto favorable que tiene sobre la solución numérica el uso de la técnica de estabilización propuesta, al respecto, mencionar que con tan sólo 45 puntos, los errores sobre el eje ${\textstyle y=0}$ no superan el 15% Notar además cómo la falta de exactitud de la solución, en el caso sin estabilizar, se presenta de manera importante sobre los contornos del cilindro.

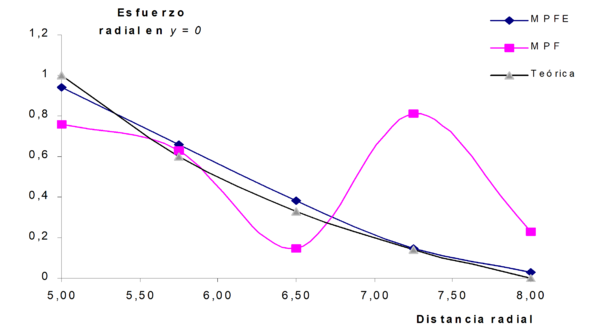
Figura 113: Variacion del esfuerzo radial en el cilindro de pared gruesa

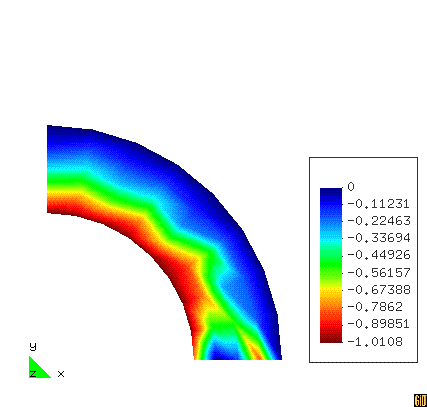
Figura 114: Distribucion del esfuerzo radial _rmath sobre el cilindro utilizando el MPF

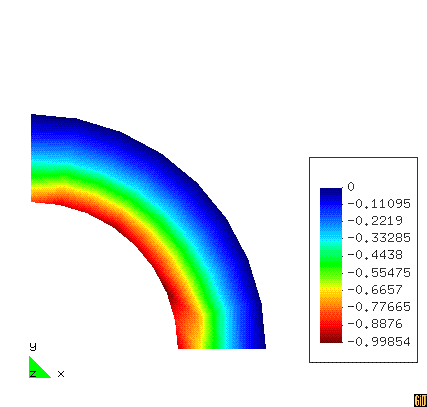
Figura 115: Distribucion del esfuerzo radial _rmath sobre el cilindro utilizando el MPFE

(¹) La solución teórica de este problema supone el uso del sistema de coordenadas polares habituales $\left(r,\theta \right)$

6.4.10 Ejemplo 3-D

Se pretende comprobar en este apartado la validez del procedimiento de estabilización, para el caso 3D, mediante la resolución del ejemplo de la barra prismática en flexión del apartado 4.3. En primer lugar, para el test de nubes regulares de 120 puntos, la figura 116 presenta los contornos de desplazamientos y esfuerzo ${\textstyle \sigma _{z}}$. Esta vez y tal como muestran las ecuaciones teóricas 4.4 para los desplazamientos ${\textstyle v}$, cuya solución no depende de la coordenada ${\textstyle z}$, y ${\textstyle w}$, que no depende de ${\textstyle y}$, la respuesta numérica es un fiel reflejo de la solución teórica.

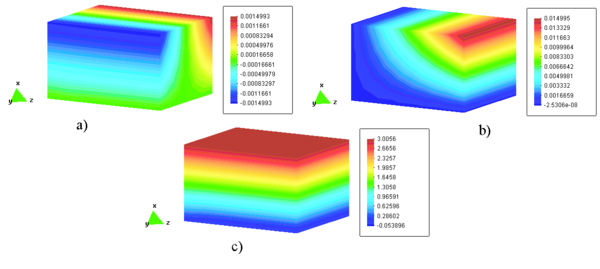
Figura 116: Barra prismatica en flexion, arreglo de 120 puntos para el MPFE, a) contornos de desplazamiento vmath b) contornos de desplazamientos wmath y c) contornos de esfuerzo _zmath

Para comprobar la exactitud de la solución se han graficado los desplazamientos y el esfuerzo ${\textstyle \sigma _{z}}$ en los planos donde se produce su máximo valor, notar que estos planos coinciden con los contornos de la barra (ver figura 116). Los resultados muestran claramente que la solución numérica en el MPF (MPF s/e) no concuerda con los valores teóricos, por contra, en el MPFE (MPF c/e) los errores desaparecen o disminuyen de manera importante (ver figuras 117, 118 y 119).

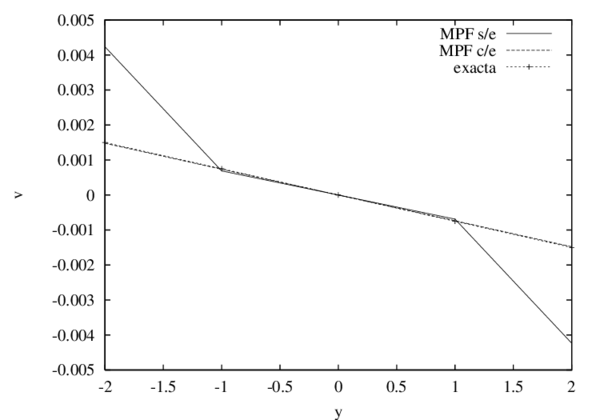
Figura 117: Desplazamiento vmath para el plano x=3math de la barra prismatica

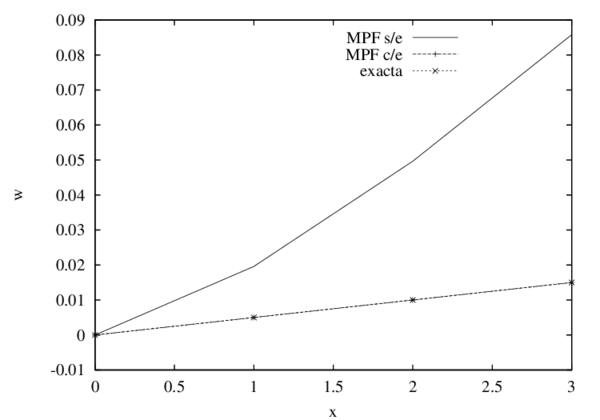
Figura 118: Desplazamiento wmath para el plano z=5math de la barra prismatica

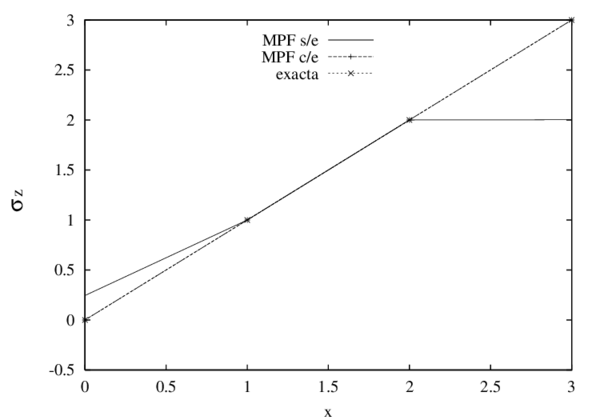
Figura 119: Distribucion del esfuerzo _zmath en la barra prismatica

La buena respuesta que se obtuvo para la discretización con 120 puntos con el MPFE, se ha encontrado también para la configuración irregular de 271 puntos. Los principales resultados se muestran en la figura 120, éstos indican una total equivalencia con la solución teórica y con los encontrados anteriormente (compárese con la figura 116).

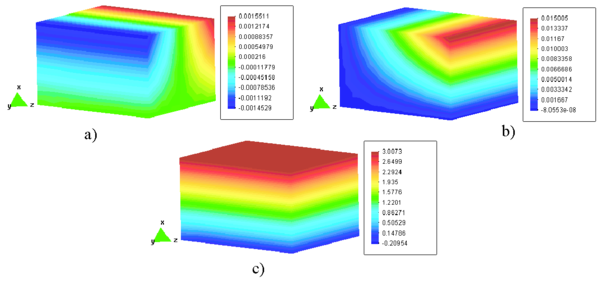
Figura 120: Barra prismatica en flexion, arreglo de 271 puntos para el MPFE, a) contornos de desplazamiento vmath b) contornos de desplazamientos wmath y c) contornos de esfuerzo _zmath

Finalmente la tabla 14 muestra una comparación con los valores que entrega la solución teórica de referencia [94] y los principales resultados numéricos que se han obtenido para este test.

Tabla. 14 Resultados numéricos y teóricos para la barra prismática en flexión

6.5 Análisis de resultados

Se han desarrollado en el presente capítulo diversos problemas, principalemente en 2D, para verificar y validar la técnica de estabilización que permite utilizar en toda su potencialidad el procedimiento de colocación puntual en el Método de Puntos Finitos. Los resultados indican que el procedimiento mejora los resultados numéricos, de forma importante, en aquellos ejemplos donde el dominio se ha discretizado de una manera no-regular o irregular y con un bajo número de puntos. También se ha podido comprobar que para un método basado en la técnica de colocación puntual, como lo es el MPF, la forma como se impone la condición de contorno de Neumann afecta significativamente la respuesta del método. En este sentido, la utilización de la técnica del CF permite contar con una estrategia para imponer esta condición de manera sencilla y con buenos resultados.

Aunque no se ha realizado un estudio de los tiempos involucrados en la solución de los problemas, se ha podido establecer que, basándose principalmente en parámetros del solver (residuo, número de iteraciones), la técnica propuesta no aumenta significativamente el esfuerzo de cálculo, por lo que puede ser atractiva para problemas en donde exista un elevado número de grados de libertad, además se debe agregar a esta consideración, el hecho de que todavía es posible mejorar aspectos en la programación del código fortran del método.

Si se compara por ejemplo la respuesta del MPFE en los distintos problemas de flexión analizados, se puede distinguir una buena respuesta del método ante este tipo de solicitación, lo cual constituye una alternativa para los métodos tradicionales en donde, si se emplean elementos de bajo orden, se deben utilizar mallas muy densas para obtener resultados aceptables. También, la buena respuesta que se obtuvo para problemas de flexión en el rango cercano a la incompresibilidad permiten demostrar la flexibilidad que presenta el MPF y abren nuevas vías de investigación en este campo.

7 Aplicación del MPF en problemas de la dinámica lineal elástica

7.1 Introducción

A continuación se desarrolla la formulación del MPF para su aplicación en ejemplos de elastodinámica de sólidos. Se pretende de esta manera extender el campo de utilización del MPF a problemas en donde intervienen fuerzas de inercia, pero sin considerar fuerzas de amortiguamiento. Conceptualmente el tipo de aproximación meshless que se utiliza es la misma que se ha estudiado a través de este trabajo, sin embargo, el planteamiento y resolución del sistema final de ecuaciones claramente difiere del utilizado para el caso estático. Principalmente la solución depende del tiempo o del intervalo de tiempo considerado, por lo que es necesario contar con un esquema de integración temporal del sistema de ecuaciones diferenciales. En este trabajo se ha utilizado e implementado un sistema de integración explícito, basado en diferencias centradas, para resolver esta cuestión.

7.2 Formulación del problema dinámico

En el caso dinámico la formulación del sistema de ecuaciones estabilizado sigue la misma metodología descrita en el apartado 6.2, sin embargo, esta vez se deben incluir los efectos de las fuerzas de inercia. En primer término se plantea el equilibrio de fuerzas en ambas direcciones, en el interior del cuerpo, para el dominio finito de espesor unitario mostrado en la figura 121¹.

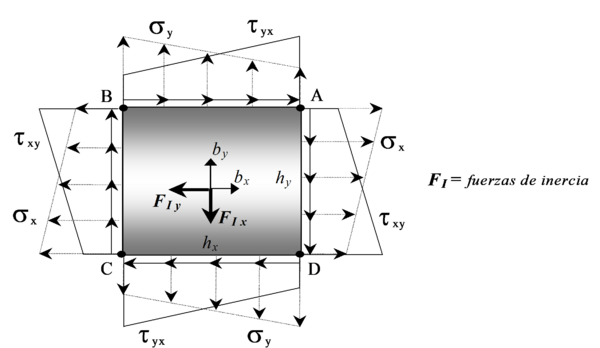
Figura 121: Dominio finito ABCD para el planteamiento de equilibrio dinamico en el interior del cuerpo

El sistema de ecuaciones que se obtiene en esta condición es

${\frac {h_{y}}{2}}\left[\left(\sigma _{x}\right)_{A}+\left(\sigma _{x}\right)_{D}\right]-{\frac {h_{y}}{2}}\left[\left(\sigma _{x}\right)_{C}+\left(\sigma _{x}\right)_{B}\right]+{\frac {h_{x}}{2}}\left[\left(\tau _{yx}\right)_{A}+\left(\tau _{yx}\right)_{B}\right]-$

$-{\frac {h_{x}}{2}}\left[\left(\tau _{yx}\right)_{C}+\left(\tau _{yx}\right)_{D}\right]+h_{x}h_{y}\rho b_{x}=m{\stackrel {..}{u}}$

(7.1)

para el eje ${\textstyle x}$

${\frac {h_{x}}{2}}\left[\left(\sigma _{y}\right)_{B}+\left(\sigma _{y}\right)_{A}\right]-{\frac {h_{x}}{2}}\left[\left(\sigma _{y}\right)_{D}+\left(\sigma _{y}\right)_{C}\right]+{\frac {h_{y}}{2}}\left[\left(\tau _{xy}\right)_{B}+\left(\tau _{xy}\right)_{C}\right]-$

$-{\frac {h_{y}}{2}}\left[\left(\tau _{xy}\right)_{D}+\left(\tau _{xy}\right)_{A}\right]+h_{x}h_{y}\rho b_{y}=m{\stackrel {..}{v}}$

(7.2)

para el eje ${\textstyle y}$, respectivamente². Las fuerzas de inercia han sido reemplazadas por el producto de la masa ${\textstyle m}$ del dominio y la correspondiente aceleración ${\textstyle {\stackrel {..}{u}}}$ o ${\textstyle {\stackrel {..}{v}}}$.

Utilizando nuevamente una expansión en serie de Taylor de tercer orden para los esfuerzos en B, C, D (ver ecuaciones 6.3) y reemplazando estas expresiones en 7.1 y 7.2, se obtiene

$h_{x}h_{y}\left[{\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{yx}}{\partial y}}+\rho b_{x}\right]-{\frac {h_{x}^{2}h_{y}}{2}}\left[{\frac {\partial ^{2}\sigma _{x}}{\partial x^{2}}}+{\frac {\partial ^{2}\tau _{yx}}{\partial x\partial y}}\right]-{\frac {h_{x}h_{y}^{2}}{2}}\left[{\frac {\partial ^{2}\sigma _{x}}{\partial x\partial y}}+{\frac {\partial ^{2}\tau _{yx}}{\partial y^{2}}}\right]=m{\stackrel {..}{u}}$ $h_{x}h_{y}\left[{\frac {\partial \sigma _{y}}{\partial y}}+{\frac {\partial \tau _{xy}}{\partial x}}+\rho b_{y}\right]-{\frac {h_{x}^{2}h_{y}}{2}}\left[{\frac {\partial ^{2}\sigma _{y}}{\partial x\partial y}}+{\frac {\partial ^{2}\tau _{xy}}{\partial x^{2}}}\right]-{\frac {h_{x}h_{y}^{2}}{2}}\left[{\frac {\partial ^{2}\sigma _{x}}{\partial y^{2}}}+{\frac {\partial ^{2}\tau _{xy}}{\partial x\partial y}}\right]=m{\stackrel {..}{v}}$

las cuales una vez simplificadas por el producto ${\textstyle \left(h_{x}h_{y}\right)}$ se convierten en

$\left[{\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{yx}}{\partial y}}+\rho b_{x}\right]-{\frac {h_{x}}{2}}\left[{\frac {\partial ^{2}\sigma _{x}}{\partial x^{2}}}+{\frac {\partial ^{2}\tau _{yx}}{\partial x\partial y}}\right]-{\frac {h_{y}}{2}}\left[{\frac {\partial ^{2}\sigma _{x}}{\partial x\partial y}}+{\frac {\partial ^{2}\tau _{yx}}{\partial y^{2}}}\right]=\rho {\stackrel {..}{u}}$ $\left[{\frac {\partial \sigma _{y}}{\partial y}}+{\frac {\partial \tau _{xy}}{\partial x}}+\rho b_{y}\right]-{\frac {h_{x}}{2}}\left[{\frac {\partial ^{2}\sigma _{y}}{\partial x\partial y}}+{\frac {\partial ^{2}\tau _{xy}}{\partial x^{2}}}\right]-{\frac {h_{y}}{2}}\left[{\frac {\partial ^{2}\sigma _{x}}{\partial y^{2}}}+{\frac {\partial ^{2}\tau _{xy}}{\partial x\partial y}}\right]=\rho {\stackrel {..}{v}}$

Este sistema se puede expresar en forma más compacta como

$r_{3}-{\frac {1}{2}}\mathbf {h} ^{T}\cdot \mathbf {\nabla } r_{3}=0$ $r_{4}-{\frac {1}{2}}\mathbf {h} ^{T}\cdot \mathbf {\nabla } r_{4}=0$

(7.3)

donde³

$r_{3}={\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{xy}}{\partial y}}+\rho b_{x}-\rho {\stackrel {..}{u}}$ $r_{4}={\frac {\partial \sigma _{y}}{\partial y}}+{\frac {\partial \tau _{xy}}{\partial x}}+\rho b_{y}-\rho {\stackrel {..}{v}}$

siendo ${\textstyle \mathbf {\nabla } }$ el operador gradiente y el vector ${\textstyle \mathbf {h} }$

$\mathbf {h} =\left[{\begin{array}{l}h_{x}\\h_{y}\end{array}}\right]{\hbox{ }}$

El sistema de ecuaciones 7.3 se puede particularizar para los casos que se ejemplificarán más adelante, es decir cuando no existen fuerzas másicas y se utiliza un polinomio base de interpolación cuadrático en 2D, osea ${\textstyle m=6}$. Bajo estos supuestos el sistema final de ecuaciones en el dominio, para el caso dinámico, es

$r_{3}=0$ $r_{4}=0$

(7.4)

donde

$r_{3}={\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{xy}}{\partial y}}-\rho {\stackrel {..}{u}}$ $r_{4}={\frac {\partial \sigma _{y}}{\partial y}}+{\frac {\partial \tau _{xy}}{\partial x}}-\rho {\stackrel {..}{v}}$

Para obtener el sistema de ecuaciones estabilizado en el contorno de Neumann, se plantea el equilibrio de fuerzas horizontales y verticales sobre el prisma de espesor unitario mostrado en la figura 122.

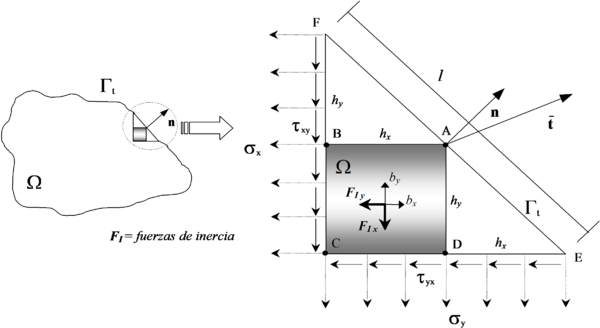
Figura 122: Dominio finito CEF para el planteamiento de equilibrio dinamico de fuerzas en el contorno de Neumann

Reemplazando los términos de las fuerzas de inercia como antes, el sistema adopta la siguiente forma

$\sum F_{x}=\left(\sigma _{x}\right)_{B}2h_{y}+\left(\tau _{yx}\right)_{D}2h_{x}-{\frac {4}{2}}h_{x}h_{y}\rho b_{x}-{\overline {t}}_{x}l+m{\stackrel {..}{u}}=0$ $\sum F_{y}=\left(\sigma _{y}\right)_{D}2h_{x}+\left(\tau _{xy}\right)_{B}2h_{y}-{\frac {4}{2}}h_{x}h_{y}\rho b_{y}-{\overline {t}}_{y}l+m{\stackrel {..}{v}}=0$

(7.5)

utilizando una expansión en serie de Taylor de segundo orden para los esfuerzos en B, D y reemplazando estas expresiones en 7.5 se tiene

$\sigma _{x}{\frac {2h_{y}}{l}}+\tau _{yx}{\frac {2h_{x}}{l}}-{\overline {t}}_{x}-{\frac {2h_{x}h_{y}}{l}}\left[{\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{yx}}{\partial y}}+\rho b_{x}-\rho {\stackrel {..}{u}}\right]=0$ $\sigma _{y}{\frac {2h_{x}}{l}}+\tau _{xy}{\frac {2h_{y}}{l}}-{\overline {t}}_{y}-{\frac {2h_{x}h_{y}}{l}}\left[{\frac {\partial \sigma _{y}}{\partial y}}+{\frac {\partial \tau _{xy}}{\partial x}}+\rho b_{y}-\rho {\stackrel {..}{v}}\right]=0$

(7.6)

Advirtiendo que las componentes de la normal unitaria en el punto A del contorno son

$n_{x}={\frac {2h_{y}}{l}}{\hbox{ }},{\hbox{ }}n_{y}={\frac {2h_{x}}{l}}$

y que

${\frac {2h_{x}h_{y}}{l}}={\frac {h_{x}h_{y}}{l}}+{\frac {h_{x}h_{y}}{l}}={\frac {h_{x}n_{x}}{2}}+{\frac {h_{y}n_{y}}{2}}={\frac {1}{2}}\left[h_{x}n_{x}+h_{y}n_{y}\right]$

se tiene finalmente en 7.6 el siguiente sistema⁴

$\sigma _{x}n_{x}+\tau _{yx}n_{y}-{\overline {t}}_{x}-{\frac {1}{2}}\left[h_{x}n_{x}+h_{y}n_{y}\right]\left[{\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{yx}}{\partial y}}-\rho {\stackrel {..}{u}}\right]=0$ $\sigma _{x}n_{y}+\tau _{xy}n_{x}-{\overline {t}}_{y}-{\frac {1}{2}}\left[h_{x}n_{x}+h_{y}n_{y}\right]\left[{\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau _{yx}}{\partial y}}-\rho {\stackrel {..}{v}}\right]=0$

el cual puede ser expresado en forma compacta como

$\left(\sigma _{x}n_{x}+\tau _{xy}n_{y}-{\overline {t}}_{x}\right)-{\frac {1}{2}}\mathbf {h} ^{T}\cdot \mathbf {n} \left[r_{3}\right]=0$ $\left(\sigma _{x}n_{y}+\tau _{xy}n_{x}-{\overline {t}}_{y}\right)-{\frac {1}{2}}\mathbf {h} ^{T}\cdot \mathbf {n} \left[r_{4}\right]=0$

(7.7)

siendo el vector normal ${\textstyle \mathbf {n} }$

$\mathbf {n} =\left[{\begin{array}{l}n_{x}\\n_{y}\end{array}}\right]$

Es interesante destacar nuevamente cómo el sistema de ecuaciones 7.7 incluye el efecto de los puntos adyacentes al contorno de Neumann, términos ${\textstyle r_{3}}$ y ${\textstyle r_{4}}$ respectivamente.

(¹) Se puede aplicar la misma metodología para extender la formulación al caso 3D

(²) La notación es consistente con la empleada en el capítulo 6

(³) Se asume $\tau _{xy}=\tau _{yx}$

(⁴) Cuando no existen fuerzas de cuerpo

7.2.1 Implementación Computacional

La solución al problema dinámico se encuentra resolviendo para cada instante de tiempo el sistema que forman 7.4 y 7.7, más las condiciones de contorno de Dirichlet. Esta vez para resolver el sistema final de ecuaciones, además de reemplazar las relaciones tensión-deformación y deformación-desplazamientos para un material elástico lineal, es necesario implementar un esquema de integración temporal para obtener los desplazamientos en un determinado paso de tiempo. Utilizando un esquema explícito de diferencias centradas, se tiene que los desplazamientos en el intervalo de tiempo ${\textstyle (t+\Delta t)}$ se calcularán recursivamente como [70]

$u_{(t+\Delta t)}=2u_{(t)}-u_{(t-\Delta t)}+\Delta t^{2}{\stackrel {..}{u}}_{(t)}$ $v_{(t+\Delta t)}=2v_{(t)}-v_{(t-\Delta t)}+\Delta t^{2}{\stackrel {..}{v}}_{(t)}$

(7.8)

lo que supone conocer o calcular el desplazamiento y la aceleración actual ${\textstyle \left(u_{(t)},{\stackrel {..}{u}}_{(t)}\right)}$, pero también el desplazamiento previo ${\textstyle u_{(t-\Delta t)}}$. Para esto se utiliza la siguiente relación¹

$u_{(t-\Delta t)}=u_{(t)}-\Delta t{\stackrel {.}{u}}_{(t)}+{\frac {\Delta t^{2}}{2}}{\stackrel {..}{u}}_{(t)}$

(7.9)

donde la velocidad es

${\stackrel {.}{u}}_{(t)}={\frac {u_{(t+\Delta t)}-u_{(t-\Delta t)}}{2\Delta t}}$

Se debe tener presente que en el inicio, es decir en ${\textstyle t=0}$, es necesario calcular ${\textstyle u_{(-\Delta t)}}$ mediante la relación 7.9 para que de comienzo el algoritmo 7.8. Esto supone conocer como dato inicial el desplazamiento y la velocidad en ${\textstyle t=0}$ ${\textstyle (u_{0}}$ y ${\textstyle v_{0})}$. Notar en este caso que la aceleración en ${\textstyle t=0}$ ${\textstyle ({\stackrel {..}{u}}_{0})}$ se obtiene resolviendo inicialmente el sistema que forman 7.4 y 7.7.

Tal como se ha explicado en el capítulo 6, para obtener las componentes del vector ${\textstyle \mathbf {h} }$ se utilizan los conceptos de las distancias mínimas características en la nube.

(¹) Similar relación se emplea para $v_{\left(t-\Delta t\right)}$

7.3 Ejemplos numéricos

7.3.1 Propagación de una onda 1D

Como primer ejemplo, se analiza el comportamiento del MPF para el problema de propagación de una onda en un medio unidimensional. La figura 123 muestra las características geométricas del modelo, siendo las propiedades mecánicas del material ${\textstyle E=3.0\times 10^{7}\left[psi\right]}$, ${\textstyle \rho =7.35\times 10^{-4}[slug/in^{3}]}$, y el área de la barra ${\textstyle A=1[in^{2}]}$. La barra se somete a un esfuerzo axil impulsivo, constante en el tiempo, de ${\textstyle \sigma _{0}=1000[psi]}$. Para obtener la solución numérica en el caso del MPF, se utilizado un paso de tiempo ${\textstyle \Delta t=\left(L_{\min .}/c\right)}$, donde ${\textstyle L_{\min .}}$ es la distancia mínima entre dos puntos y ${\textstyle c=\left(E/\rho \right)^{1/2}}$ la velocidad de propagación de la onda en el cuerpo.

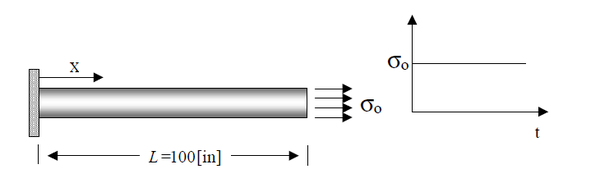
Figura 123: Geometria para la barra sometida a carga impulsiva

La solución teórica para este ejemplo viene dada por[20]

$u(x,t)={\frac {8\sigma _{0}L}{\pi ^{2}E}}{\stackrel {\infty }{\underset {n=1}{\sum }}}\left\{\pm \left({\frac {1-\cos \left[\left({\frac {2n-1}{2}}\right)\pi {\frac {ct}{L}}\right]}{\left(2n-1\right)^{2}}}\right)\sin \left[{\frac {\left(2n-1\right)}{2}}\pi {\frac {x}{L}}\right]\right\}$

(7.10)

expresión que permite además encontrar la velocidad ${\textstyle {\stackrel {.}{u}}}$ , y la deformación ${\textstyle u_{,x}}$.

Las figuras que se muestran a continuación indican el correcto comportamiento del método, tanto en desplazamientos como en tensión, para las distintas discretizaciones utilizadas. En todos los casos se han utilizado nubes de ${\textstyle n=5}$ puntos y una base de interpolación cuadrática ${\textstyle (m=3)}$. Por ejemplo, las figuras 124, 125 y 126 muestran la convergencia hacia la solución teórica del desplazamiento, la velocidad y el esfuerzo, para un punto ubicado en el centro de la barra (${\textstyle x=50}$). En el caso de los desplazamientos se comprueba que con 33 puntos la solución numérica coincide con la expresión 7.10, esta buena correlación con los valores teóricos también se logra para la velocidad y el esfuerzo con tan sólo 41 puntos.

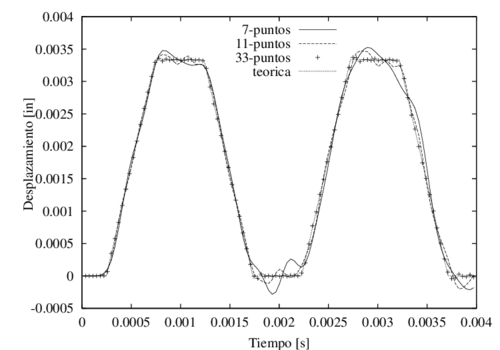
Figura 124: Desplazamiento del punto central en la barra para distintas discretizaciones

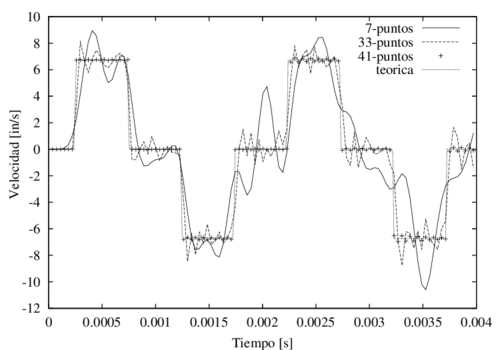
Figura 125: Velocidad del punto central en la barra para distintas discretizaciones

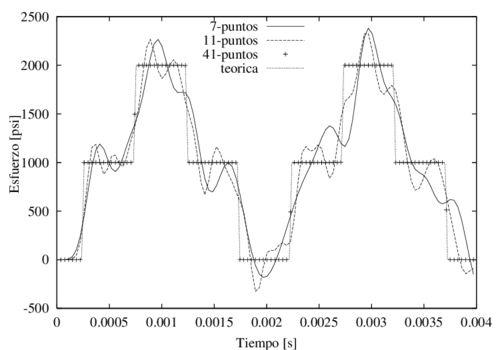
Figura 126: Esfuerzo en el punto central de la barra para distintas discretizaciones

Se ha efectuado una comparación de la solución que entrega el MPF con los valores que se obtienen para este ejemplo utilizando el MEF. Para igual número de puntos en los modelos (21 puntos ó 10 elementos), la figura 127 indica un comportamiento similar para ambos métodos respecto del valor teórico, sin embargo, aumentando el número de puntos (41 puntos ó 20 elementos) las figuras 128 y 129 muestran que la solución con el método de puntos, a diferencia del MEF, concuerda exactamente con la solución teórica.

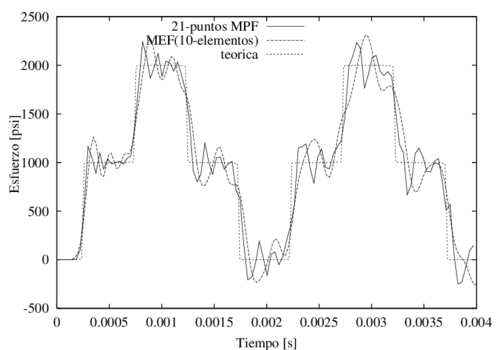
Figura 127: Esfuerzo en el nodo central de la barra para una discretizacion con 21 puntos (10 elementos)

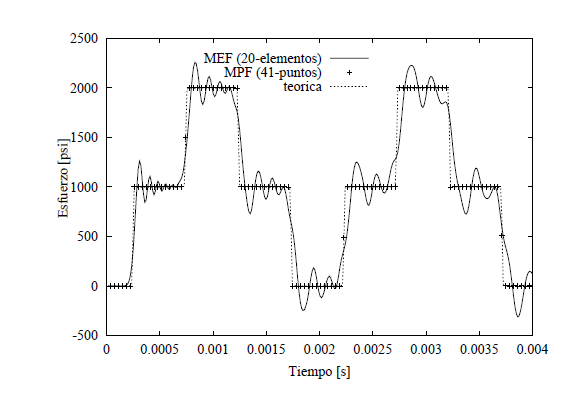
Figura 128: Esfuerzo en el nodo central de la barra para una discretizacion con 41 puntos (20 elementos)

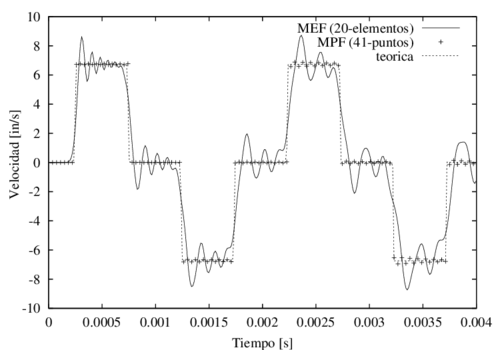
Figura 129: Velocidad en el nodo central de la barra para una discretizacion con 41 puntos (20 elementos)

Finalmente la figura 130 muestra la posición de la onda de ${\textstyle 1000[psi]}$ en un instante de tiempo, durante su viaje de propagación a través de la barra. Se aprecia claramente cómo el perfil de la onda comienza a definirse en la medida que se aumenta el numero de puntos, lográndose ya con 41 puntos el perfil esperado.

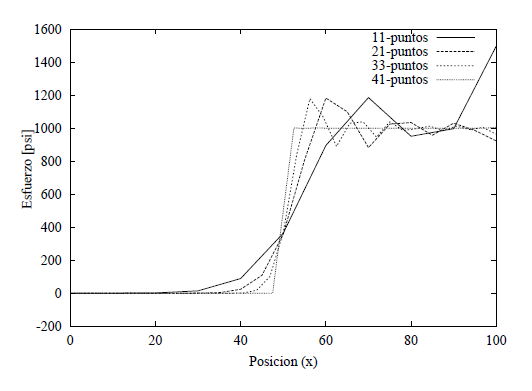
Figura 130: Distribucion del esfuerzo axil en el vigesimo paso de tiempo

7.3.2 Ejemplo 2-D. Ménsula sometida a carga impulsiva.

La ménsula de la figura 131 está sometida en su extremo libre a una carga impulsiva de magnitud ${\textstyle P_{0}=1000[lb]}$. Sobre el empotramiento se prescriben los desplazamientos de acuerdo a la solución teórica para un caso estático [94], utilizándose una discretización regular de 27, 95 y 175 puntos. Para las propiedades del material se han utilizado los siguientes valores, módulo de elasticidad ${\textstyle E=2.08\times 10^{6}[psi]}$, coeficiente de Poisson ${\textstyle \nu =0.3}$ y densidad ${\textstyle \rho =7.35\times 10^{-4}[slug/in^{3}]}$. El problema se ha resuelto considerando condiciones de deformación plana, una base de interpolación cuadrática y nubes de 9 puntos.

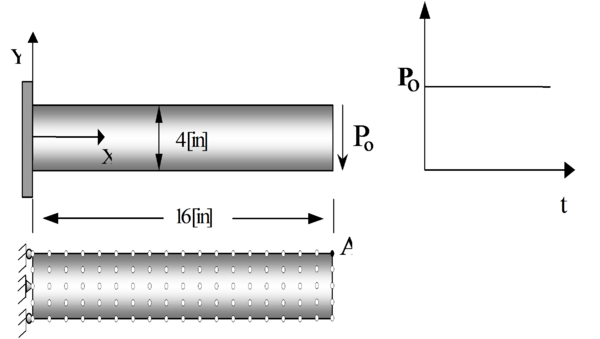
Figura 131: Mensula sometida a carga impulsiva. Geometria y discretizacion de puntos

Como no se tiene una respuesta teórica para este ejemplo, se ha efectuado una modelación mediante un código comercial de elementos finitos (Abaqus) para comparar los resultados, también en referencia [39] se analiza la respuesta para este ejemplo usando otro código de elementos finitos. Los resultados que se obtienen para las tres configuraciones de puntos muestran un adecuado comportamiento respecto de la modelación con el MEF, a continuación se muestran los principales resultados para el arreglo regular de 95 puntos.

Las figuras 132 y 133 muestran la variación temporal del desplazamiento en el punto A de la ménsula, para un tiempo total de análisis de 0.025 [s]. Esta vez el paso de tiempo se ha calculado como ${\textstyle \Delta t=0.1(L_{\min .}/c)}$. En ambos casos, los resultados que se obtienen con el MPF se comparan favorablemente con aquellos que entrega el código comercial de elementos finitos Abaqus, usando elementos CST.

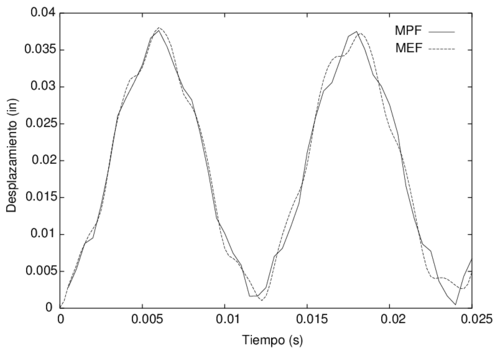
Figura 132: Mensula bajo carga impulsiva, variacion temporal del desplazamiento horizontal en el punto A

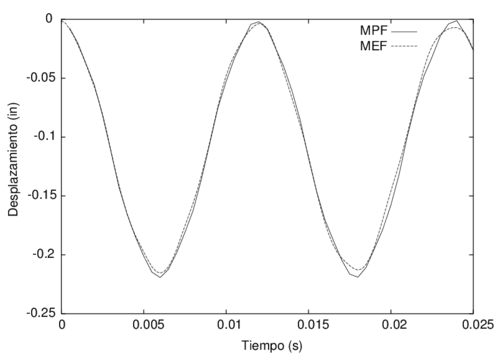
Figura 133: Mensula bajo carga impulsiva, variacion temporal del desplazamiento vertical en el punto A

Se ha podido establecer, para el análisis con el MPF, un período fundamental de ${\textstyle 0.0123[s]}$ para la ménsula (ver 132 y 133), valor que se compara también favorablemente con los ${\textstyle 0.0124[s]}$ que se obtienen en [39].

La figura 134 muestra la variación del esfuerzo horizontal en el extremo A de la barra para ambos métodos, si bien los valores del esfuerzo parecen concordar durante el primer período, existe posteriormente un desfase en la solución que puede tener una explicación en el diferente esquema de integración (implícito) que utiliza Abaqus.

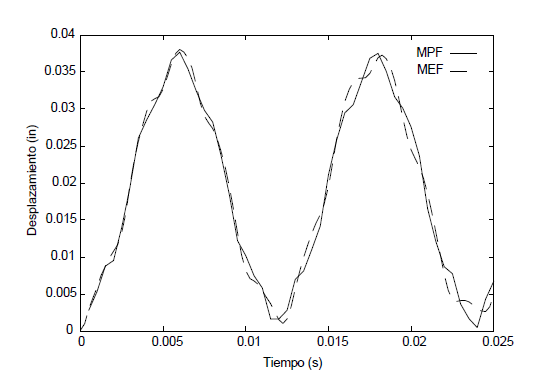
Figura 134: Mensula bajo carga impulsiva, variacion temporal del esfuerzo horizontal en el punto A

Como se sabe, el esquema de integración de diferencias centradas que se utilizó para el MPF es condicionalmente estable, esto supone calcular un intervalo de tiempo ${\textstyle \Delta t}$ crítico para prevenir, tal como indica la figura 135, posibles problemas de estabilidad. Además, este ${\textstyle \Delta t}$ crítico debiera ser recalculado cada cierto número de incrementos de tiempo.

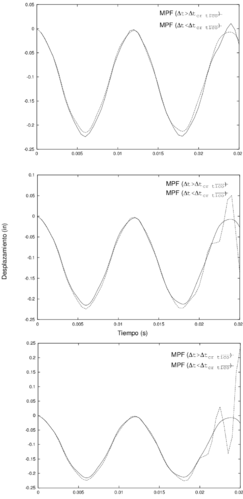
Figura 135: Desplazamiento vertical en el punto A de la mensula para distintos valores de tmath critico

La importancia de estabilizar las ecuaciones, principalmente en el contorno, también se manifiesta en el análisis dinámico. No ha sido posible obtener un resultado comparable con los anteriores, para ninguna discretización, cuando se escoge ${\textstyle \mathbf {h=0} }$ en las ecuaciones 7.7. Para corroborar esto la figura 136 indica el comportamiento, con 95 puntos, del desplazamiento vertical en el punto A de la ménsula bajo esta situación. Como se observa, los valores y la tendencia de la curva no guardan relación alguna con lo esperado.

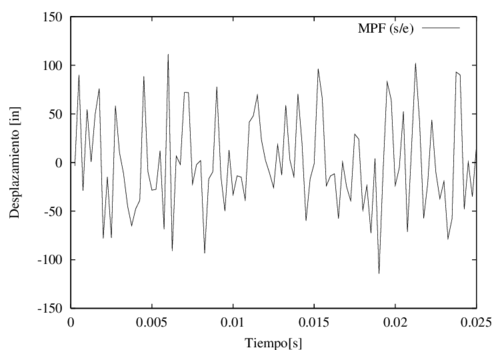
Figura 136: Desplazamiento vertical en el punto A de la mensula para el MPF sin estabilizar

7.4 Análisis de resultados

Se ha desarrollado la formulación de las ecuaciones estabilizadas que rigen el comportamiento dinámico 2D, de un sólido lineal elástico, para ser implementadas numéricamente en el método de puntos finitos. Este desarrollo puede ser extendido sin dificultad para un caso 3D.

Los resultados preliminares de los ejemplos 1D y 2D muestran una adecuada convergencia del método y se comparan favorablemente con los que entrega el MEF. En el caso 1D, el método de puntos muestra una convergencia más rápida que el MEF para las diferentes discretizaciones analizadas. En el caso 2D el método de puntos y el MEF muestran una convergencia similar, sin embargo, el intervalo de tiempo crítico condiciona notablemente los resultados en el MPF.

8 Conclusiones

8.1 De la formulación del MPF y su aplicación a problemas de elasticidad

Se han establecido las bases matemáticas para la comprensión del Método de Puntos Finitos, como método sin malla, contrastando el tipo de aproximación, función de ponderación y tipo de discretización utilizada, con la que ofrecen otros métodos meshless. Principalmente el MPF se caracteriza por:

• una interpolación de mínimos cuadrados con función de ponderación fija y colocación puntual para discretizar el sistema de ecuaciones.

La utilización de una función de ponderación fija permite evaluar de una manera más fácil y sencilla las derivadas de la función de forma, mientras que un esquema de colocación puntual permite contar con un método totalmente libre de malla, para la resolución de las ecuaciones de la elasticidad lineal de sólidos.

Tal como ha sido propuesto originalmente, el MPF permite resolver una variada gama de problemas en 1D y 2D con arreglos de puntos regulares, sin embargo, cuando la discretización de puntos es irregular el método se resiente y muestra problemas en cuanto a la exactitud de la solución, principalmente en los contornos. Estas falencias también se han manifestado en arreglos regulares con discretizaciones de bajo número de puntos. Se han analizado las causas de estas dificultades, estableciéndose que el método es sensible a la forma como se construye la aproximación local y la ubicación de los puntos de colocación. Para resolver estas cuestiones, se han propuesto y analizado soluciones que se implementaron en el MPFE (Método de Puntos Finitos Estabilizados), comprobándose la validez de estas a través de diversos ejemplos desarrollados.

Respecto a su aplicación para la solución de problemas de elasticidad, la investigación desarrollada permite extraer las siguientes conclusiones:

• Es necesario contar con un procedimiento para comprobar la calidad de la función de forma que se obtiene y para formular el problema de interpolación en la nube en términos de las coordenadas locales adimensionales.

• En problemas con discretizacion irregular de puntos, la implementacion de la cc. de Neumann con el procedimiento del Cálculo Finitesimal resulta fundamental para obtener resultados adecuados. La metodología desarrollada permite aprovechar en toda su potencialidad el proceso de colocación puntual y no aumenta significativamente los costes de cálculo.

• Es importante contar con un método eficiente para generar las nubes y comprobar aspectos de calidad de la nube.

• La imposiciónde las condiciones de contorno en el MPF se realiza de manera sencilla y fácil de implementar.

• Es posible utilizar diferentes bases de interpolación para costruir la aproximación local, empleando también distinto número de puntos por cada nube.

• Los resultados de los ejemplos en donde el tipo de carga es principalmente de flexión, muestran que la respuesta numérica que se obtiene con el MPF reporta ventaja frente a la utilización del MEF con elementos de bajo orden.

• El MPF resulta ser bastante flexible, incluso en problemas donde el módulo de Poisson se encuentran cerca del límite de incompresibilidad del material. Esto constituye una potencialidad del método y tema para futuras investigaciones.

• El MPF es consistente y muestra un orden de convergencia cuadrático en 2D, cuando se utiliza una base de interpolación completa de grado mínimo (${\textstyle m=6}$).

• El MPF resulta ser una técnica sin malla totalmente flexible y fácil de implementar, para la solución de las ecuaciones de la elasticidad en sólidos.

• En los ejemplos de dinámica que se han implementado, los resultados que entrega el método se ven afectados por el paso de tiempo ${\textstyle \Delta t}$ utilizado en el esquema de integración explícita, por lo que es necesario desarrollar procedimientos para obtener su valor crítico o implementar algoritmos de integración implícita.

• El esquema de estabilización propuesto, basado en el criterio de imponer las condiciones de equilibrio sobre un dominio de tamaño finito, permite salvar con éxitos los problemas típicos que presenta una discretización mediante colocación puntual.

8.2 Principales aportaciones de la tesis

Las principales aportaciones de la tesis se pueden circunscribir a los siguientes ámbitos:

• Por un lado explicar y desarrollar la formulación del MPF para su utilización en problemas de la elasticidad lineal de sólidos. Hasta la fecha no se contaba con un análisis completo de la formulación del método, además no se contaba con un código que permitiese evaluar la respuesta del método en problemas 2D de tensión plana y deformación plana.

• Se ha propuesto una técnica para paliar las deficiencias de trabajar con una aproximación expresada en coordenadas globales. Para esto se adimensionaliza la base de interpolación por medio de la máxima distancia al nodo estrella en la nube. Adicionalmente se comprueba la calidad de la aproximación evaluando el número de condición de la matriz de momentos y evaluando las derivadas de la función de forma.

• Por otro lado el desarrollo y comprobación de una técnica para implementar adecuadamente las condiciones de contorno bajo un esquema de colocación puntual. Tal como se ha podido comprobar el método es sensible a la ubicación de los puntos de colocación en el dominio, sobre todo en problemas con bajo número de puntos. Sin embargo, para aprovechar las ventajas que ofrece la técnica de colocación en los métodos sin malla, se ha debido desarrollar una técnica, similar a una estabilización, para mejorar la aproximación. Para esto se ha utilizado, de forma original, la técnica del Cálculo Finitesimal.

• Adicionalmente, la formulación del problema estático y dinámico mediante el MPF, permitirá enfrentar con éxito futuros desarrollos del método, puesto que para realizar la interpolación local y la generación de nubes ya se cuenta inicialmente con los códigos que se han implementado para esta tesis.

8.3 Futuras líneas de investigación

El trabajo de investigación que se ha llevado a cabo, ha permitido establecer las bases teóricas y los fundamentos matemáticos para el completo entendimiento del MPF como método sin malla, esto permitirá en el futuro poder extender las aplicaciones del método a otro tipo de problemas. Por citar algunos temas, donde se visualiza interesante desarrollar nuevas aplicaciones del MPF, se pueden mencionar: problemas de mecánica de fractura, problemas de estática y dinámica no-lineal de sólidos, problemas que involucren grandes deformaciones en la geometría del dominio.

Un tema que debiera abordarse en futuras investigaciones es el de realizar un estudio comparativo, respecto a otros métodos sin malla, de los tiempos de pre-proceso y cálculo involucrados en el MPF. Antes de abordar esta cuestión debiera optimizarse todo lo concerniente a la programación del método, aspecto que en esta tesis no se ha puesto demasiado énfasis pues el código se ha planteado para resolver inicialmente problemas en el ámbito académico.

Existen otros temas que han debido ser resueltos para el correcto funcionamiento del MPF, y que subyacen en su formulación e implementación, los cuales merecen ser objeto de un análisis y desarrollo más profundo. De entre estos se puede mencionar:

• La generación de las nubes o puntos que conforman el subdominio de interpolación. Si bien es cierto hoy en día algunos programas de pre y post-proceso comienzan a ofrecer la posibilidad de discretizar el dominio en base a un conjunto de puntos [33], es necesario, para aprovechar esta capacidad, contar con un programa que permita formar las nubes en el dominio y el contorno de manera eficiente y, adicionalmente, permita controlar variables como la cantidad de puntos por nube y la posibilidad de agregar o sacar puntos de la misma.
• La estimación del error cometido en la aproximación. La cuantificación del error que se ha realizado a través de los ejemplos, supone la contrastación con un valor teórico de referencia, sin embargo, y pensando en futuras aplicaciones del MPF a procesos industriales, sería conveniente tener un estimador del error para poder desarrollar criterios de solución adaptable.
• La posibilidad de extender la capacidad del MPF para modelar materiales heterogéneos o con diferentes propiedades mecánicas.
• La capacidad de modelar piezas y geometrías en 3D. El estudio debiera abarcar además el desarrollo de un generador de puntos eficiente para estos casos.
• La resolución del sistema global de ecuaciones. Se ha implementado un solver de gradientes bi-conjugado para resolver el sistema de ecuaciones, dadas las características particulares de falta de simetría que este presenta. Contar con solver más eficientes permitiría disminuir los tiempos involucrados en el cálculo, de manera importante para aquellos problemas donde se hace necesario discretizar el dominio con una gran cantidad de puntos [44], [98].

Finalmente, existen diversos aspectos teóricos que es necesario abordar en futuros trabajos, como la utilización de otras bases de interpolación o funciones de ponderación, sin embargo, considerando los temas que se han debido solucionar e implementar para comprender y valorizar en su justa medida el método de puntos finitos, se puede afirmar que la sencillez y flexibilidad que presenta el método son las principales ventajas de este. Por lo tanto, son precisamente estas características las que deben ser explotadas para consolidar el método en futuras aplicaciones.

BIBLIOGRAFÍA

[1] Aluru N. R. (2000), A point collocation method based on reproducing kernel approximations. International Journal for Numerical Methods in Engineering, 47, 1083-1121.

[2] Anderson D. A., Tannehill J. C. & Pletcher R. H. (1984), Computational Fluid Mechanics and Heat Transfer, Hemisphere Publishing Group eds.

[3] Atluri S.N.& Zhu T. (1998), A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics. Computational Mechanics, 22, 117-127.

[4] Atluri S.N., Sladek J., Sladek V. & Zhu T. (2000), The local boundary integral equation (LBIE) and its meshless implementation for linear elasticity. Computational Mechanics, 25, 180-198.

[5] Babuska I. & Melenk J. M. (1996), The partition of unity finite element method: Basic theory and applications. Computer Methods in Applied Mechanics and Engineering, 139, 289-314.

[6] Batina, J. (1993), A gridless Euler/Navier-Stokes solution algorithm for complex aircraft aplications. AIAA 93-0333, Reno NV, Enero 11-14.

[7] Beissel S. & Belytschko T. (1996), Nodal integration of the element-free Galerkin method. Computer Methods in Applied Mechanics and Engineering, 139, 49-74.

[8] Belytschko T., Gu L. & Lu L. (1994), Fracture and crack growth by element-free Galerkin methods. Modelling and Simulation in Material Science and Engineering, 2, 519-534.

[9] Belytschko T., Lu Y. Y. & Gu L. (1994), Element-free Galerkin methods. International Journal for Numerical Methods in Engineering, 37, 229-256.

[10] Belytschko T., Krongauz Y., Organ D., Fleming M. & Krysl P. (1995), A coupled finite element-free Galerkin method. Computational Mechanics, 17, 186-195.

[11] Belytschko T., Krongauz Y., Organ D., Fleming M. & Krysl P. (1996), Meshless Methods: An Overview and Recent Developments. Computer Methods in Applied Mechanics and Engineering, 139, 3-47.

[12] Belytschko T., Krongauz Y., Fleming M., Organ D. & Liu W. K. (1996), Smoothing and Accelerated computations in the element-free Galerkin method. Journal of Computational and Applied Mathematics, 74, 111-126.

[13] Belytschko T., Guo Y., Liu W.K. & Xiao S.P. (2000), A Unified Stability Analysis of Meshless Particle Methods. International Journal for Numerical Methods in Engineering, 48, 1359-1400.

[14] Bonet J. & Loc T.S.L. (1999), Variational and momentum preservation aspects of Smooth Particle Hydrodynamic formulations. Computer Methods in Applied Mechanics and Engineering, 180, 97-115.

[15] Bonet J. & Kulasegaram S. (2000), Correction and Stabilization of Smooth Particle Hydrodynamics Method with Applications in Metal Forming Simulations. International Journal for Numerical Methods in Engineering, 47, 1189-1214.

[16] Bonet J.& Kulasegaram S. (2000), Finite increment gradient stabilization of point integrated meshless method for elliptic equations. Communications in Numerical Methods in Engineering, 16, 475-483.

[17] Breitkopf P., Rassineux A., Touzot G. & Villon P. (2000), Explicit form and efficient computation of MLS shape functions an their derivatives. International Journal for Numerical Methods in Engineering, 48, 451-466.

[18] Breitkopf P., Touzot G. & Villon P. (2000), Double grid diffuse collocation method. Computational Mechanics, 25, 199-206.

[19] Burden R.L., Faires J.D. (1985), Análisis Numérico, 3rd. ed. Grupo Editorial Iberoamérica, México, D.F.

[20] Clough R.W. & Penzien J. (1993), Dinamics of Structures, 2d. ed. McGraw-Hill.

[21] De S. & Bathe K.J. (2000), The method of finite spheres. Computational Mechanics, 25, 329-345.

[22] De S. & Bathe K.J. (2001), The method of finite spheres with improved numerical integration. Computers & Structures, 79, 2183-2196.

[23] Dilts G.A. (1999), Moving-Least-Squares-Particle-Hydrodynamics: I. Consistency and Stability. International Journal for Numerical Methods in Engineering, 44, 1115-1155.

[24] Duarte C.A. & Oden J. T. (1995), Hp Clouds–-A Meshless Method to Solve Boundary-Value Problems. Technical Report 95-05, TICAM, The University of Texas at Austin.

[25] Duarte C.A. (1995), A Review of Some Meshless Methods to Solve Partial Differential Equations. Technical Report 95-06, TICAM, The University of Texas at Austin.

[26] Duarte C.A.& Oden J. T. (1996), An h-p adaptive method using clouds. Computer Methods in Applied Mechanics and Engineering, 139, 237-262.

[27] Dyka C.T. & Ingel R.P. (1995), An Approach for Tension Instability in Smoothed Particle Hydrodynamics (SPH). Computers & Structures, 57, 573-580.

[28] Dyka C.T., Randles P.W. & Ingel R.P. (1997), Stress Points for Tension Instability in SPH. International Journal for Numerical Methods in Engineering, 40, 2325-2341.

[29] Fleming M., Chu Y.A., Moran B. & Belytschko T. (1997), Enriched element-free Galerkin methods for crack tip field. International Journal for Numerical Methods in Engineering, 40, 1483-1504.

[30] Fletcher R. (1975), Conjugate gradient methods for indefinite system. Proceedings of the Dundee Bienal Conference in Numerical Analysis, G. Watson Eds., 73-89.

[31] Gavete L., Benito J.J., Falco S. & Ruiz A. (2000), Implementation of essential boundary conditions in a meshless method, Communications in Numerical Methods in Engineering, 16, 409-421.

[32] George P.L. & Borouchaki H. (1998), Delaunay Triangulation and Meshing, ed. Hermes, Paris.

[33] GID, personal pre and post processor, version 7. CIMNE, Barcelona España.(http://gid.cimne.upc.es)

[34] Gingold R.A. & Monaghan J.J. (1977), Smooth Particle Hydrodynamics: Theory and Applications to Non-spherical Stars. Monthly Notices Royal Astr. Soc., 181, 375-389.

[35] Gingold R.A. & Monaghan J.J. (1982), Kernel Estimates as a Basis for General Particle Methods in Hydrodynamics. Journal of Computational Physics, 46, 429-453.

[36] Hegen D. (1996), Element-free Galerkin methods in combination with finite element approaches. Computer Methods in Applied Mechanics and Engineering, 135, 143-166.

[37] Horn R.A. & Johnson C.R.(1990), Matrix Analysis, 3rd. ed. Cambridge University Press, New York, USA.

[38] Huerta A.. & Fernández S. (2000), Enrichment and Coupling of the Finite Element and Meshless Methods. International Journal for Numerical Methods in Engineering, 48, 1615-1636.

[39] Hughes T.J.R. (1987), The Finite Element Method: linear static and dynamic finite element analysis. Prentice-Hall.

[40] Jensen P.S. (1972), Finite difference technique for variable grids. Computers & Structures, 2, 17-29.

[41] Krongauz Y. & Belytschko T. (1997), Consistent pseudo-derivatives in meshless methods. Computer Methods in Applied Mechanics and Engineering, 146, 371-386.

[42] Lancaster P. & Salkauskas K. (1981), Surfaces generated by moving least-squares. Mathematics of Computation, 37, 141-158.

[43] Lawson C. L. & Hanson R. J. (1974), Solving least squares problems. Prentice-Hall, Series in Automatic Computation.

[44] Lin H., Yang D. Y. & Chieng C. C. (1995), Variants of Bi-Conjugate Method for Compressible Navier-Stoke Solver. AIAA J., 33, 1177-1184.

[45] Liszka T. & Orkisz J. (1977), Finite difference method for arbitrary irregular meshes in nonlinear problems of applied mechanics. In IV SMiRt, San Francisco.

[46] Liszka T. & Orkisz J. (1980), The finite difference method at arbitrary irregular grids and its application in applied mechanics. Computers and Structures, 11: 83-95.

[47] Liszka T. & Orkisz J. (1984), An interpolation method for an irregular net of nodes. International Journal for Numerical Methods in Engineering, 20, 1599-1612.

[48] Liszka T., Duarte C.A. & Tworzydlo W. (1996), hp-Meshless cloud method. Computer Methods in Applied Mechanics and Engineering, 139, 263-288.

[49] Liu G.R. & Gu Y.T. (2001), A point interpolation method for two-dimensional solids. International Journal for Numerical Methods in Engineering, 50, 937-951.

[50] Liu W. K., Adee J. & Jun S. (1993), Reproducing kernel particle methods for elastic and plastic problems. Advanced Computational Methods for Material Modeling, Benson D.J. y Asaro A. (eds.), ASME, 268, 175-190.

[51] Liu W. K., Jun S. & Zhang Y. F. (1995), Reproducing Kernel Particle Methods. International Journal for Numerical Methods in Fluids, 20, 1081-1106.

[52] Liu W. K. & Chen Y. F. (1995), Wavelet and multiple scale reproducing kernel methods. International Journal for Numerical Methods in Fluids, 21, 901-933.

[53] Liu W. K., Chen Y. F. & Uras (1995), Enrichment of the finite element method with the reproducing kernel particle method. In J. J. F. Cory & J. L. Gordon (Eds.). Current Topics in Computational Mechanics, 305: 253-258.

[54] Liu W. K., Jun S., Li S. Adee J. & Belytschko T. (1995), Reproducing kernel particle methods for structural dynamics. International Journal for Numerical Methods in Engineering, 38, 1655-1679.

[55] Liu W. L., Chen Y., Uras R. A. & Chang C. T. (1996), Generalized multiple scale reproducing kernel particle methods. Computer Methods in Applied Mechanics and Engineering, 139, 91-157.

[56] Liu W. K., Li S. & Belytschko T. (1997), Moving least-square reproducing kernel methods. (I) Methodology and convergence. Computer Methods in Applied Mechanics and Engineering, 143, 113-154.

[57] Löhner R., Sacco C., Oñate E. & Idelsohn S. (2002), A finite point method for compressible flow. International Journal for Numerical Methods in Engineering, 53, 1765-1779.

[58] Lu Y. Y., BelytschkoT. & Gu L. (1994), A new implementation of the element free Galerkin method. Computer Methods in Applied Mechanics and Engineering, 113, 397-414.

[59] Lucy, L. B. (1977), A numerical approach to the testing of the fission hypothesis. The Astronomical Journal, 82(12), 1013-1024.

[60] Malvern L.E. (1969), Introduction to the Mechanics of a Continuous Medium, Prentice-Hall

[61] Melenk J. M.& Babuska I. (1996), The partition of unity finite element method: Basic theory and applications. Computer Methods in Applied Mechanics and Engineering, 139, 289-314.

[62] Mitchell A. R. & Griffiths D. F. (1987), The Finite Difference Method in Partial Differential Equations, Wiley & Sons, Norwich.

[63] Monaghan J.J. (1982), Why particle methods work. SIAM Journal of Scientific and Statistical Computing, 3(4), 422-433.

[64] Monaghan J.J. (1988), An introduction to sph. Computer Physics Communications, 48, 89-96.

[65] Monaghan J.J.(1992), Smoothed particle hydrodynamics. Annual Review of Astronomy and Astrophysics, 30, 543-574.

[66] Mukherjee Y. X.& Mukherjee S. (1997), On boundary conditions in the element-free Galerkin, Computational Mechanics, 19, 264-270.

[67] National Agency for Finite Element Methods and Standards (1987), Linear statics benchmarks, vol.1, October.

[68] Nay R.A. & Utku S. (1972), An alternative for the finite element method. Variational Method in Engineering, Vol. 1, Univ. of Southampton.

[69] Nayroles B., Touzot G. & Villon P. (1992), Generalizing the finite element method: diffuse approximation and diffuse elements. Computational Mechanics, 10, 307-318.

[70] Oller S.(2002), Dinámica no-lineal. Monografía CIMNE.

[71] Oñate E., Idelsohn S. & Zienkiewicz O.C. (1995), Finite point methods in computational mechanics. Research Report, 67 , CIMNE.

[72] Oñate E., Idelsohn S., Zienkiewicz O.C. & Fisher T. (1995), A finite point method for analysis of fluid flow problems. Proceedings of the 9th International Conference on Finite Element Methods in Fluids, 15-21 October, Venize, Italy.

[73] Oñate E. (1995), Cálculo de Estructuras por el Método de Elementos Finitos, 2rd. ed. CIMNE, Barcelona España.

[74] Oñate E., Idelsohn S., Zienkiewicz O.C. & Taylor R.L. (1996), A finite point method in computational mechanics. Applications to convective transporte and fluid flow. International Journal for Numerical Methods in Engineering, 39, 3839-3866.

[75] Oñate E., Idelsohn S., Zienkiewicz O.C., Taylor R.L. & Sacco C. (1996), A stabilized finite point method for analysis of fluid mechanics problems. Computer Methods in Applied Mechanics and Engineering, 139, 315-346.

[76] Oñate E. (1996), On the stabilization of numerical solution for advective-diffusive transport and fluid flow problems. Publication N${\textstyle {{}^{o}}}$ 81, CIMNE, Barcelona-Spain.

[77] Oñate E., García J. & Idelsohn S. (1997), Computation of the stabilization parameter for the finite element solution of advective-diffusive problems. International Journal for Numerical Methods in Fluids, 25, 1385-1407.

[78] Oñate E. & Idelsohn S. (1998), A mesh free finite point method for advective-diffusive transport and fluid flow problems. Computational Mechanics, 21, 283-292.

[79] Oñate E., Perazzo F. & Miquel J. (1999), Advances in the stabilized finite point method for structural mechanics. Publication N${\textstyle {{}^{o}}}$ 164, CIMNE, Barcelona-Spain, also in W.Wunderlich et al., editor. European Conference on Computational Mechanics (ECCM'99), 31 August-3 September-3, Munich, Germany.

[80] Oñate E., Sacco C. & Idelsohn S. (2000), A finite point method for incompressible flow problems. Computer Visual Science, 3, 67-75.

[81] Oñate E., Perazzo F. & Miquel J. (2001), A finite point method for elasticity problems. Computers & Structures, 79, 2151-2163.

[82] Oñate E. & Arraez J.A. (2002) Avances del cálculo finitesimal en mecánica computacional, J.M. Goicolea et al. editores. V Congreso de Métodos Numéricos en Ingeniería (V COMNI), 3-6 Junio, Madrid, España.

[83] Orkisz J. (1998), Meshless finite difference method. I Basic approach. II Adaptative approach. Proceedings of the IACM-Fourth World Congress of Computational Mechanics, Idelsohn-Oñate-Dvorkin Eds. CIMNE, Barcelona-Spain.

[84] Peraire J, Peiro J., Formaggia L, Morgan K.& Zienkiewicz O.C. (1988), Finite element Euler computations in three dimensions. International Journal for Numerical Methods in Engineering, 26, 2135-2159.

[85] Perrone N. & Kao R. (1975), A general finite difference method for arbitrary meshes. Computers & Structures, 5, 45-58.

[86] Piltner R. & Taylor R. (2000), Triangular finite elements with rotational degrees of freedom and enhanced strain modes. Computers & Structures, 75, 361-368.

[87] Randles P.W. & Libersky L.D. (1996), Smoothed Particle Hydrodynamics: Some recent improvement and applications. Computer Methods in Applied Mechanics and Engineering, 139, 375-384.

[88] Rudin W. (1976), Principles of Mathematical Analysis, 3rd. ed. McGraw-Hill, New York.

[89] Sacco C. (2002), Desarrollo del Método de Puntos Finitos en Mecánica de Fluidos, Tesis doctoral, Escola Técnica Superior d'Enginyers de Camins, Canals i Ports, Universitat Politécnica de Catalunya, Barcelona.

[90] Shepard D. (1968), A two dimensional function for irregularly spaced points. In ACM National Conference, 517-524.

[91] Sukumar N., Moran B., Black T. & Belytschko T. (1997), An element-free Galerkin method for three-dimensional fracture mechanics. Computational Mechanics, 20, 170-175.

[92] Swegle J.W., Hicks D.L. & Attaway S.W. (1995), Smoothed Particle Hydrodynamics Stability Analysis. Journal of Computational Physics, 116, 123-134.

[93] Taylor R.L., Zienkiewicz O.C., Oñate E. & Idelsohn S. (1995), Moving least square approximations for solution of differential equations. Research Report, 74, CIMNE.

[94] Timoshenko S. P. & Goodier J. N. (1970), Theory of Elasticity. McGraw-Hill, New York.

[95] Topping B.H.V., Muylle J., Putanowicz R. & Cheng B. (2001), Finite Element Mesh Generation, Saxe-Coburg Publications, Edinburgh.

[96] Tworzydlo W. (1987), Analysis of large deformations of membrane shells by the generalized finite difference method. Computers & Structures, 27, 39-59.

[97] Tworzydlo W. (1989), The fdm in arbitrary curvilinear co-ordinates formulation, numerical approach and applications. International Journal for Numerical Methods in Engineering, 28, 261-277.

[98] Van der Vorst H.A.(1992), Bi-CGSTAB: A fast and smoothly converging variant of Bi-CG for the solution of non-symmetric linear system. SIAM Journal on Scientific Computing, 13(2), 631-644.

[99] Vericat i Roure M. (2000), Análisis de Estructuras en el Campo Elástico Mediante Métodos sin Malla, Tesina final, Escola Técnica Superior d'Enginyers de Camins, Canals i Ports, Universitat Politécnica de Catalunya, Barcelona.

[100] Weatherill N., Morgan K., Hassan O. (2002), An Introduction to Mesh Generation, John Wiley & Sons.

[101] William J.R. & Amaratunga K. (1994), Introduction to Wavelets in Engineering. International Journal for Numerical Methods in Engineering, 37, 2365-2388.

[102] Yagawa G. & Furukawa T. (2000), Recent developments of free mesh method. International Journal for Numerical Methods in Engineering, 47, 1419-1443.

[103] Zhang X., Liu X.H., Song K.Z.& Lu M.W. (2001), Least-squares collocation meshless method. International Journal for Numerical Methods in Engineering, 51, 1089-1100.

[104] Zhu T. & Atluri S.N. (1998), A modified collocation & a penalty formulation for enforcing the essential boundary conditions in the element free Galerkin method. Computational Mechanics, 21, 211-222.

[105] Zhu T., Zhang J.D.& Atluri S.N. (1998), A local boundary integral equation (LBIE) method in computational mechanics, and a meshless discretization approach. Computational Mechanics, 21, 223-235.

[106] Zienkiewicz O.C. & Taylor R.L. (1994), El Método de Elementos Finitos, volúmen 1 y 2, 4rd. ed. McGraw-Hill, CIMNE, Barcelona España.