Comparative analysis between the maxent and the weighted least square shape functions in a collocation meshless method

Resumen

En el presente artículo se analiza el comportamiento de la función de forma basada en el principio de máxima entropía (maxent), en el contexto de un método sin malla con un esquema de colocación, comparando su resultado con la función de forma tradicional basada en mínimos cuadrados ponderados fijos (FWLS). La función de forma maxent considerada en el presente trabajo posee ciertas propiedades deseables para formulaciones sin malla basadas en un esquema de colocación, como lo son su positividad, suavidad y aspecto uniforme, para distintos tipos de discretizaciones. Además, en los contornos, la aproximación no depende de las funciones de forma de los nodos interiores del dominio, propiedad que se conoce como reducción de la función de forma sobre el contorno. Para comparar este tipo de funciones se han desarrollado ejemplos que incluyen la resolución de ecuaciones elípticas de segundo orden, en 1D y 2D. Los resultados numéricos muestran un mejor comportamiento de la función de forma maxent en comparación con la de FWLS, en particular en cuanto a la convergencia y estabilidad del método sin malla de colocación resultante.

Abstract

In this article the behavior of a shape function based on the maximum entropy principle (maxent) is analyzed in a meshless collocation method, compared with a traditional fixed weighted least square shape function (FWLS). The maxent shape function used in this work has certain properties that are desired in a meshless collocation method, for example the positivity, the smooth and uniform aspect for different discretizations. Further, in the boundary, the approximation not depends of the shape function of the interior nodes, this property is know as a reduction of the shape function on the boundary. To compare this type of function, it was developed examples that include the solution of eliptical second order equations in 1D and 2D. The numerical results shown a better behavior of the maxent shape function compared with the FWLS, particularly in terms of the convergence and stability of the meshless collocations method that result.

Palabras clave

Función de forma;Principio de máxima entropía;Colocación;Métodos sin malla

Keywords

Shape function;Maximum entropy principle;Collocation;Meshless

1. Introducción

En los últimos años, dentro del contexto de los métodos sin malla, se ha establecido un claro predominio en el uso, aplicación e investigación de los métodos de formulación tipo débil o Galerkin (FG) en contraposición a los métodos basados en una formulación fuerte o de colocación (FC) [1]; [2] ;  [3]. Esta situación se debe al hecho de que los FG han demostrado ser metodologías estables y robustas; teniendo solo el inconveniente de las dificultades originadas por el proceso de sub-integración, hecho reconocido e investigado por distintos autores [4] ;  [5]. Diferente es el caso de las FC en las cuales existen problemas documentados de inestabilidad y robustez en la aproximación, aun cuando diversos investigadores han planteado metodologías para solventarlos [6]; [7]; [8]; [9] ;  [10]. Uno de los principales factores responsables de esta situación corresponde al operador diferencial, el cual se caracteriza por ser un amplificador de los errores numéricos [1]. Otro inconveniente de estas técnicas FC es la dificultad en la imposición de las condiciones de contorno en derivadas o también conocidas como tipo Neumann, pues deben cumplir con una ecuación distinta a la impuesta en el dominio, pudiendo generar un mal condicionamiento en el sistema final de ecuaciones a resolver. Esta situación ha sido analizada por varios autores [2]; [3]; [11]; [12] ;  [13]. Las soluciones propuestas para tratar este tipo de inestabilidades se han enfocado, entre otras, en la forma como se seleccionan los sub-dominios locales o nubes de interpolación [14], en la imposición de ecuaciones adicionales en el contorno de Neumann [15] y en la estabilización del sistema de ecuaciones a resolver mediante el procedimiento del Cálculo Finitesimal [6]; [16] ;  [17]. En el presente trabajo se desarrolla una solución alternativa a este problema la que supone el uso de una nueva función de forma. Esta, a diferencia de la comúnmente utilizada en los FC basada en el principio de mínimos cuadrados ponderados (FWLS), se construye minimizando un funcional sujeto a ciertas restricciones tal como en un problema de optimización convexa. Para obtener esta función de forma se utiliza el principio de Máxima Entropía (maxent) [18] ;  [19], el cual también se ha utilizado en otros ámbitos como por ejemplo computación gráfica, modelación geométrica y procesamiento de imágenes. En el contexto de las funciones de aproximación, el principio maxent fue utilizado por Sukumar en [20] ;  [21] para el desarrollo de una función con consistencia de primer orden para aproximaciones baricéntricas en dominios convexos. Posteriormente, Arroyo en [22] plantea por primera vez el uso de este tipo de función maxent, de carácter local, en un método sin malla tipo FG. Tratando de remediar el proceso de sub-integración presente en los métodos sin malla tipo FG, esta función ha sido probada con éxito para resolver problemas del ámbito de la elasticidad lineal de sólidos cuasi incompresibles [23]. La formulación maxent, también ha sido utilizada en el ámbito de la dinámica de fluidos por ejemplo para simular el comportamiento de un flujo viscoplástico [24]. Otras aplicaciones recientes incluyen, entre otros, la resolución de problemas de grandes deformaciones [25], solución adaptiva de problemas lineales y no lineales con métodos sin malla [26]; [27] ;  [28] y estudio de mecánica de la fractura lineal en cáscaras delgadas [29]. Las funciones de forma tipo maxent presentan ciertas propiedades atractivas de cara a su utilización en un método sin malla de formulación FC, como por ejemplo son suaves, sus valores son siempre positivos y tienen la propiedad de que los nodos interiores no tienen influencia en su valor cuando esta se calcula sobre el contorno del dominio [22]. Otras propiedades, tan relevantes como las anteriores, son su variación decreciente (la aproximación no genera valores extremos) y su monotonicidad [30]. Esto permite que la función de forma en todo su dominio presente valores positivos, lo cual corresponde al primer criterio de positividad señalado en [10] para metodologías sin malla tipo FC, situación que no ocurre en el caso de las funciones de forma que se obtienen mediante FWLS. Para probar las ventajas del uso de estas funciones en un método sin malla FC, en el presente trabajo se desarrolla su formulación para consistencia de primer y segundo orden tal como se propone en [21] y [30], respectivamente. En lo que sigue, la estructura del artículo se desarrolla de la siguiente manera. En el primer apartado se muestra la formulación de los métodos sin malla tipo colocación, para a continuación desarrollar la función de forma maxent utilizada en este trabajo como alternativa a la tradicional FWLS. En el apartado siguiente se realizan ejemplos que muestran el comportamiento de la propuesta presentada. Finalmente se realiza un análisis comparativo de resultados entre la función maxent y FWLS, planteándose las principales conclusiones como también las futuras líneas de investigación.

2. Métodos sin malla de formulación fuerte

La técnica de residuos ponderados es una estrategia que permite la obtención de metodologías numéricas para aproximar ecuaciones diferenciales [3]. Al respecto, considérese la siguiente ecuación diferencial de la forma,

$F(u)-b=0\in \Omega$

(1)

donde F es un operador diferencial que se aplica sobre una función escalar o vectorial u, y b una función que representa al campo diferencial dentro de un dominio Ω. Por otro lado para el contorno del dominio, ∂Ω, se tendrá,

$G(u)-g=0\in \partial \Omega$

(2)

con G el operador diferencial que aplica en el contorno, y g la función de campo respectiva.

La función u se puede aproximar mediante una combinación lineal de la forma,

$u^{h}(x)=\sum _{i=1}^{n}{\boldsymbol {\phi }}_{i}(x)u_{i}$

(3)

donde ϕ_i(x) se conoce como la función de forma asociada al nodo i-ésimo de la discretización del dominio, siendo u_i coeficientes desconocidos y n el número total de nodos de la discretización del dominio. Estas funciones de forma se obtienen a partir de parámetros geométricos de la discretización, existiendo diversas alternativas para esto.

Al reemplazar la ecuación (3) en (1) y (2), en general, no se cumplirá la igualdad por lo que se obtiene un residuo R de la forma

$R_{d}=F(u^{h})-b$

(4)

$R_{s}=G(u^{h})-g$

(5)

donde R_d y R_s corresponden al residuo en el dominio y su contorno, respectivamente. La solución aproximada del problema de contorno original se consigue ponderando el error cometido mediante funciones de prueba como:

${\int }_{\Omega }W_{i}R_{d}d\Omega +{\int }_{\partial \Omega }V_{i}R_{s}d\Gamma =$$0$

(6a)

${\int }_{\Omega }W_{i}(F\lbrace {\boldsymbol {\phi }}_{i}{\boldsymbol {\mbox{u}}}_{i}\rbrace -$$b)d\Omega +{\int }_{\partial \Omega }V_{i}(G\lbrace {\boldsymbol {\phi }}_{i}{\boldsymbol {\mbox{u}}}_{i}\rbrace -$$g)d\Gamma =0$

(6b)

donde W_i y V_i son un conjunto de funciones de ponderación para cada uno de los residuos R_Ω y R_∂Ω respectivamente. Esta metodología se conoce como “métodos de los residuos ponderados”, sirve como base para el desarrollo del método de elementos finitos y además entrega nociones de los errores involucrados en la aproximación [31]. A lo anterior se suma el hecho de que mediante esta técnica es posible transformar ecuaciones diferenciales, ya sean ordinarias o parciales, a una forma integral que desde el punto de vista numérico puede considerarse con una mayor estabilidad y exactitud [3]. Cabe señalar que las distintas metodologías quedarán en gran medida determinadas por la selección de las funciones de ponderación W_i y V_i que se plantee utilizar. En una formulación fuerte o de colocación las funciones de ponderación corresponden a la función “Delta de Dirac” centrada en los nodos, es decir,

$W_{i}=\delta (x-x_{i})$

(7)

$V_{i}=\delta (x-x_{i})$

(8)

Utilizando las ecuaciones (7) y (8) en (6b) se obtiene,

${\int }_{\Omega }\delta (x-x_{i})(F\lbrace {\boldsymbol {\phi }}_{i}{\boldsymbol {\mbox{u}}}_{i}\rbrace -$$b)d\Omega +{\int }_{\partial \Omega }\delta (x-x_{i})(G\lbrace {\boldsymbol {\phi }}_{i}{\boldsymbol {\mbox{u}}}_{i}\rbrace -$$g)d\Gamma =0$

(9)

lo que equivale a,

$(F\lbrace {\boldsymbol {\phi }}_{i}{\boldsymbol {\mbox{u}}}_{i}\rbrace -$$b)+(G\lbrace {\boldsymbol {\phi }}_{i}{\boldsymbol {\mbox{u}}}_{i}\rbrace -$$g)=0$

(10)

Al observar la ecuación (10) queda de manifiesto que los métodos de colocación en general fuerzan a que el residuo sea cero en los nodos del dominio y del contorno. Esto es distinto al planteamiento integral en cuyo caso se busca que en promedio el residuo sea cero. Si además el cálculo de la función de forma no depende de la discretización del dominio en una subdivisión de elementos, se obtiene lo que se denomina un método sin malla, en este caso de formulación fuerte. Un claro ejemplo de este tipo de metodología es el método de puntos finitos [6] ;  [16], en el cual las funciones de forma se obtienen utilizando el procedimiento de mínimos cuadrados ponderados (FWLS) [7] ;  [8]. En el presente trabajo se propone una estrategia diferente para obtener la función de forma, basada en el principio de máxima entropía, la cual se presenta en la siguiente sección.

3. Función de forma maxent

En general el principio de máxima entropía (maxent), se puede entender como una técnica para estimar la probabilidad de un evento en forma generalizada. Como resultado del procedimiento se obtiene una distribución de probabilidad del evento en cuestión, la cual responde en forma coherente a las restricciones probabilísticas que se conocen del problema, quedando definidas como medias o también en valores futuros esperados [18]. La solución que se obtiene de este modo tiene como característica principal que posee la menor incertidumbre posible para la información disponible. A pesar de que el principio puede ser aplicado en diversos campos, en sus orígenes fue pensado para su uso en física estadística, en un esfuerzo por relacionar las propiedades macroscópicas medibles de un sistema físico con lo que ocurre a nivel molecular y atómico [32]. Su utilidad práctica en este campo radica en que a nivel molecular y atómico solo es posible establecer distribuciones de probabilidad de las distintas propiedades que describen al sistema.

Para formular el principio maxent, Jaynes propuso maximizar el siguiente funcional [18] ;  [19],

$Maximizar\quad \left[{\boldsymbol {\mbox{H}}}(p_{1},...,p_{n})=\right.$$\left.-\sum _{i=1}^{n}p_{i}lnp_{i}\right]$

(11)

sujeto a,

$\sum _{i=1}^{n}p_{i}=1$

(12a)

$\sum _{i=1}^{n}p_{i}g_{r}(x_{i})=\left\langle g_{r}(x)\right\rangle$

(12b)

donde H corresponde a la definición de entropía utilizada por Shannon [33] como una medida de la incerteza en la información, p_i la probabilidad de ocurrencia de un evento x_i, y 〈g_r(x)〉 una función de distribución de probabilidad conocida. Se debe destacar, que esta definición de entropía no corresponde a la utilizada en Termodinámica, además, las ecuaciones (12a) y (12b) representan la probabilidad total de un espacio muestral, y la conformación de valores esperados de los cuales se conoce su distribución de probabilidad respectivamente.

Observando las ecuaciones (11) ;  (12a) y (12b) es posible establecer ciertas similitudes entre una distribución de probabilidad y una función de forma, si se reescribe el problema clásico de maxent por uno equivalente de funciones de forma como:

$Maximizar\quad \left[{\boldsymbol {\mbox{H}}}({\phi }_{1},...,{\phi }_{n})=\right.$$\left.-\sum _{i=1}^{n}{\phi }_{i}ln{\phi }_{i}\right]$

(13)

sujeto a,

$\sum _{i=1}^{n}{\phi }_{i}=1$

(14a)

$\sum _{i=1}^{n}{\phi }_{i}x_{i}=x$

(14b)

donde esta vez las ecuaciones (14a) y (14b) representan el criterio de partición de la unidad y la consistencia de primer orden de una función de forma, respectivamente. La analogía con el caso de las probabilidades es aun más evidente, si se considera el hecho de que estas nunca toman valores negativos, y, como se mencionó anteriormente, este es justamente un aspecto deseable para toda función de forma que se utilice en un método sin malla tipo FC. Esta forma de interpretar el principio maxent, en el ámbito de las aproximaciones numéricas, también fue utilizado por Sukumar [20] pero para obtener las funciones base utilizadas en aproximaciones baricéntricas.

3.1. Formulación de primer orden

Como se mencionó anteriormente, en el presente trabajo se propone utilizar las funciones de forma que se obtienen del sistema de ecuaciones (13) ;  (14a) y (14b), en un método sin malla tipo FC. Una de las características de las funciones de forma utilizadas en los métodos sin malla, es su grado de localidad. El carácter local de la misma se puede establecer mediante el uso de una función de ponderación, siendo las más utilizadas en los métodos sin malla, las del tipo ”spline” y exponencial o de Gauss [1]; [2] ;  [3]. Se puede incorporar el carácter local de la aproximación, en el caso de maxent, modificando la ecuación (13) mediante el uso de una función acotada como por ejemplo la función de Gauss siguiente;

$m_{i}({\boldsymbol {\mbox{x}}})=exp(-{\beta }_{i}\quad \Vert {\boldsymbol {\mbox{x}}}_{i}-$${\boldsymbol {\mbox{x}}}{\Vert }^{2}),{\beta }_{i}={\frac {\gamma }{h_{i}^{2}}}$

(15)

donde γ es el parámetro mediante el cual se controla el tamaño del soporte de las función en cada nodo i, y h_i, corresponde a la longitud característica relativa al nodo i. En el caso particular de que m_i(x) sea igual a la unidad, se tiene el problema convencional en donde todo el dominio interviene en la aproximación para cada nodo de campo.

De este modo, se puede plantear un problema de optimización convexa para la búsqueda de la funciones de forma como,

$max{\boldsymbol {\mbox{H}}}\left({\phi }_{1},{\phi }_{2},...,{\phi }_{n}\right)=$$-\sum _{i=1}^{n}{\phi }_{i}({\boldsymbol {\mbox{x}}})ln{\frac {{\phi }_{i}({\boldsymbol {\mbox{x}}})}{m_{i}({\boldsymbol {\mbox{x}}})}},s.a.$

(16a)

${\begin{array}{ccc}\sum _{i=1}^{n}{\phi }_{i}({\boldsymbol {\mbox{x}}})&=&1\\\sum _{i=1}^{n}{\phi }_{i}({\boldsymbol {\mbox{x}}}){\tilde {\boldsymbol {\mbox{x}}}}_{i}&=&0\end{array}}$

(16b)

donde en la ecuación (16b), ${\textstyle {\tilde {\boldsymbol {\mbox{x}}}}_{i}={\boldsymbol {\mbox{x}}}_{i}-}$${\boldsymbol {\mbox{x}}}$ corresponde a las coordenadas nodales desplazadas, y centradas en el nodo de campo i, lo cual permite una forma más robusta del problema de optimización a resolver desde un punto de vista numérico. Un problema de optimización convexa sujeto a restricciones, puede ser resuelto mediante la metodología Dual de Lagrange, considerando las condiciones óptimas y la “Función Conjugada”. Mayores antecedentes sobre los procedimientos para resolver casos de optimización convexa se pueden revisar en [34]. El funcional de Lagrange correspondiente al problema de optimización que se presenta en ecuaciones 16, puede ser escrito como,

$L(\phi ,\lambda ,x)=\sum _{i=1}^{n}{\phi }_{i}ln{\frac {{\phi }_{i}}{m_{i}}}+$${\lambda }_{0}\left(\sum _{i=1}^{n}{\phi }_{i}-1\right)+{\lambda }^{T}\left(\sum _{i=1}^{n}{\phi }_{i}({\boldsymbol {\mbox{x}}}_{i}-\right.$$\left.{\boldsymbol {\mbox{x}}})\right)$

(17)

expresión que puede ser diferenciada con respecto a cada una de las funciones de forma ϕ_i para i ∈ (1, . . . n), con lo que se obtiene

${\frac {\partial L}{\partial {\phi }_{j}}}=ln\left({\frac {{\phi }_{j}}{m_{j}}}\right)+$$1+{\lambda }_{0}+{\lambda }^{T}({\boldsymbol {\mbox{x}}}_{j}-$${\boldsymbol {\mbox{x}}})=0$

(18a)

$ln\left({\frac {{\phi }_{j}}{m_{j}}}\right)=-1-{\lambda }_{0}-$${\lambda }^{T}({\boldsymbol {\mbox{x}}}_{j}-{\boldsymbol {\mbox{x}}})$

(18b)

A pesar de no conocer aún los multiplicadores de Lagrange (λ₀ y λ), es posible despejar las funciones de forma ϕ_i (siendo i igual a j), obteniéndose,

${\phi }_{i}=m_{i}exp\left(-1-{\lambda }_{0}-{\lambda }^{T}({\boldsymbol {\mbox{x}}}_{i}-\right.$$\left.{\boldsymbol {\mbox{x}}})\right)$

(19a)

${\phi }_{i}=m_{i}{\frac {exp\left(-{\lambda }^{T}({\boldsymbol {\mbox{x}}}_{i}-{\boldsymbol {\mbox{x}}})\right)}{exp\left({\lambda }_{0}+1\right)}}$

(19b)

Para encontrar los multiplicadores desconocidos se utiliza el problema dual de Lagrange considerando la función conjugada,

$f^{\ast }({\boldsymbol {\mbox{y}}})={\underset {x\in \Omega }{sup}}\left(y^{T}x-\right.$$\left.f(x)\right)$

(20)

aplicada sobre la función objetivo H(ϕ, m) y cuyo argumento en este caso corresponde a

${\boldsymbol {\mbox{y}}}=-{\lambda }_{0}^{T}{\boldsymbol {1}}-$${\lambda }^{T}({\boldsymbol {\mbox{x}}}_{i}-{\boldsymbol {\mbox{x}}})$

(21)

dando como resultado,

$f^{\ast }({\boldsymbol {\mbox{y}}})=\sum _{i=1}^{n}m_{i}exp(y_{i}-$$1)$

(22)

Con lo anterior es posible plantear la función del problema dual como

$g({\lambda }_{0},\lambda )=-{\lambda }_{0}-f^{\ast }({\boldsymbol {\mbox{y}}})$

(23a)

$g({\lambda }_{0},\lambda )=-{\lambda }_{0}-\sum _{i=1}^{n}m_{i}exp(-$${\lambda }_{0}^{T}{\boldsymbol {1}}-{\lambda }^{T}({\boldsymbol {\mbox{x}}}_{i}-$${\boldsymbol {\mbox{x}}})-1)$

(23b)

$g({\lambda }_{0},\lambda )=-{\lambda }_{0}-exp(-{\lambda }_{0}^{T}{\boldsymbol {1}}-$$1)\sum _{i=1}^{n}m_{i}exp(-{\lambda }^{T}({\boldsymbol {\mbox{x}}}_{i}-$${\boldsymbol {\mbox{x}}}))$

(23c)

Maximizando 23 con respecto a λ₀ es posible encontrar una expresión equivalente para ${\textstyle exp({\lambda }_{0}^{T}{\boldsymbol {1}}+1)}$, la cual se conoce como función partición Z(λ, x)

$Z(\lambda ,x)=exp({\lambda }_{0}^{T}{\boldsymbol {1}}+1)=$$\sum _{i=1}^{n}m_{i}exp(-{\lambda }^{T}({\boldsymbol {\mbox{x}}}_{i}-$${\boldsymbol {\mbox{x}}}))$

(24)

Reemplazando (24) en (23c), es posible escribir la función dual como,

${\overset {\mbox{ˆ}}{g}}(\lambda )=-$$lnZ(\lambda ,x)$

(25)

La solución buscada es el resultado de minimizar la función ${\textstyle -{\overset {\mbox{ˆ}}{g}}(\lambda )}$ para encontrar el valor de λ^*, conocido como óptimo. La existencia de este multiplicador óptimo está asegurada por el teorema de “Karush - Kuhn - Tucker” en el caso de x ∈ convex(Ω) [34]. Reemplazando los resultados anteriores la función de forma puede ser escrita como,

${\phi }_{i}=m_{i}{\frac {exp\left(-{\left({\lambda }^{\ast }\right)}^{T}({\boldsymbol {\mbox{x}}}_{i}-{\boldsymbol {\mbox{x}}})\right)}{Z({\lambda }^{\ast },x)}}$

(26)

La obtención del λ^* óptimo se realiza mediante el problema de minimización no restrictiva ${\textstyle -{\overset {\mbox{ˆ}}{g}}(\lambda )}$, aprovechando las coordenadas desplazadas consideradas anteriormente, mediante la utilización de un algoritmo de búsqueda de raíces de punto fijo. En el presente trabajo como metodología de búsqueda se ha utilizado un algoritmo de Newton - Raphson.

La derivada de la función de forma se obtiene a partir de (26), con lo cual

$\nabla {\phi }_{i}({\boldsymbol {\mbox{x}}})={\phi }_{i}\left({\boldsymbol {\mbox{x}}}_{i}\left({\boldsymbol {\mbox{He}}}^{-1}-\right.\right.$$\left.\left.{\boldsymbol {\mbox{He}}}^{-1}\sum _{j=1}^{n}{\phi }_{j}{\tilde {{\boldsymbol {\mbox{x}}}_{j}}}\otimes {\frac {\nabla m_{j}}{m_{j}}}\right)+\right.$$\left.{\frac {\nabla m_{i}}{m_{i}}}-\sum _{j=1}^{n}{\phi }_{j}{\frac {\nabla m_{j}}{m_{j}}}\right)$

(27)

donde la matriz Hessiana He es,

${\boldsymbol {\mbox{He}}}=\sum _{j=1}^{n}{\phi }_{j}{\tilde {{\boldsymbol {\mbox{x}}}_{j}}}\otimes {\tilde {{\boldsymbol {\mbox{x}}}_{j}}}$

(28)

En la ecuación (27) es posible observar que el gradiente de la función de forma contiene términos ya calculados anteriormente, con lo cual su evaluación no representa un costo computacional elevado.

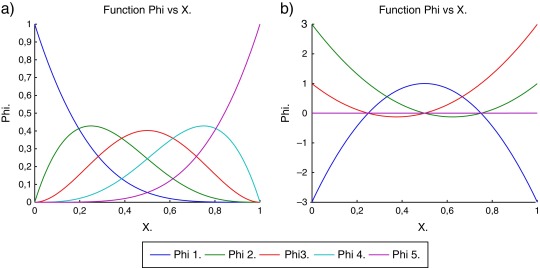
En la figura 1 es posible apreciar la diferencia existente entre una función de forma calculada mediante la metodología maxent y la de mínimos cuadrados ponderados FWLS, para un dominio unidimensional y 5 nodos de discretización. En primer lugar se hace evidente la positividad de las funciones de forma maxent, situación contrapuesta a las FWLS, en donde estas pueden tomar valores tanto positivos como negativos sin ningún tipo de restricción. A lo anterior se suma la regularidad en la forma de las funciones maxent. Otro aspecto a destacar, corresponde al cumplimiento de la condición delta de Kronecker en el borde, ya que como queda de manifiesto en la figura, los nodos del dominio no tienen influencia sobre el valor de la función de forma en el borde.

Figura 1. Función de forma 1D de 5 nodos. a) maxent b) FWLS.

4. Ejemplos

Con el objeto de poder realizar una comparación, se calculan los indicadores para el error global de la solución numérica y su derivada, L₂ y H₂ respectivamente. Estos indicadores se definen como:

$L_{2}={\sqrt {\frac {{\sum }_{i=1}^{N}{\left(u_{i}^{teo}-u_{i}^{\acute {num}}\right)}^{2}}{{\sum }_{i=1}^{N}{\left(u_{i}^{teo}\right)}^{2}}}}$

(29)

donde ${\textstyle u_{i}^{teo}}$ y ${\textstyle u_{i}^{\acute {num}}}$ corresponden a la solución teórica y numérica respectivamente

$H_{2}={\sqrt {\frac {{\sum }_{i=1}^{N}{\left(u_{i,x}^{teo}-u_{i,x}^{\acute {num}}\right)}^{2}}{{\sum }_{i=1}^{N}{\left(u_{i,x}^{teo}\right)}^{2}}}}$

(30)

y ${\textstyle u_{i,x}^{teo}}$ y ${\textstyle u_{i,x}^{\acute {num}}}$ corresponden a la derivada de la solución teórica y numérica respectivamente.

En los ejemplos se considera en el caso de FWLS bases cuadráticas completas de aproximación, además de nubes de 5 puntos. En el presente trabajo se ha utilizado como función de ponderación la función de Gauss, la cual se define como

$w_{i}({\boldsymbol {x}}_{j})={\frac {e^{-\left({\frac {{\boldsymbol {d}}_{j}}{\xi }}\right)}-e^{-\left({\frac {\beta }{\xi }}\right)}}{1-e^{-\left({\frac {\beta }{\xi }}\right)}}}$

(31)

donde d_j es la distancia existente entre un nodo x_j cualquiera de la nube Ω_i y el nodo estrella x_i, β = κd_max siendo d_max la distancia entre el nodo estrella y el nodo más alejado del subdominio. El factor κ es una constante que debe ser ligeramente mayor a la unidad, con el propósito de asegurar que la función de ponderación no se anule en los puntos extremos del subdominio. Finalmente se define ξ = β/ω con ω un parámetro de control para la ponderación asignada a los puntos que componen la nube. Su valor en este caso corresponde a 3.5.

4.1. Test de Rachford-Wheeler

Para comprobar el adecuado comportamiento e implementación de la función de forma maxent en un caso unidimensional, se propone resolver el test de Rachford-Wheeler [35]. Este test ha sido ampliamente utilizado en la investigación de métodos sin malla para probar la correcta convergencia de las propuestas presentadas [6]; [13]; [36] ;  [37]. El problema consiste en resolver una ecuación de Poisson, cuya solución analítica permite generar un gradiente de magnitud controlada en un punto del dominio. Para este ejemplo se propone además incluir condiciones de borde en derivadas o de tipo Neummann. La ecuación a resolver se puede expresar como,

$-u^{''}+u=f(x),x\in (0,1),$

(32)

sujeto a,

$u^{'}(0)={\frac {\alpha }{1+{\alpha }^{2}{\overline {x}}^{2}}},$

(33a)

$u^{'}(1)=[arctan(\alpha (1-{\overline {x}})+$$arctan(\alpha {\overline {x}})].$

(33b)

y cuya solución teórica es:

$u(x)=(1-x)[arctan(\alpha (x-{\overline {x}}))+$$arctan(\alpha {\overline {x}})].$

(34)

El parámetro α   se utiliza para controlar la magnitud del gradiente. En la medida que su valor disminuye la solución se suaviza, mientras que un valor elevado del mismo, en el punto ${\textstyle {\overline {x}}}$, genera un salto y la solución adopta una forma similar a la de una cuña. En el caso del presente ejemplo, se ha considerado un valor de α   igual 50.0 y un ${\textstyle {\overline {x}}}$ de 0.40. El problema se resuelve para una discretización regular e irregular de puntos.

Para la realización del ejemplo, tanto para el caso de nubes de forma regular e irregular, se ha considerado en el caso de la aproximación mediante FWLS una base de interpolación cuadrática de m=3 términos según,

$p^{T}(x)=\left[{\begin{array}{ccc}1&x&x^{2}\end{array}}\right]$

(35)

Además, se han utilizado nubes de 5 puntos siendo los parámetros de función de ponderación (ecuación (31)) κ = 1.1 y ω = 3.5. Para obtener estos parámetros se realizó un estudio de sensibilidad siguiendo los lineamientos dados en [38].

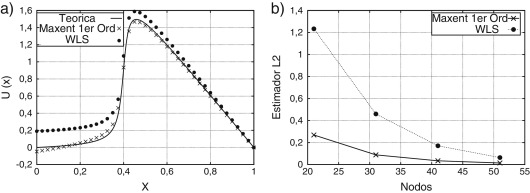
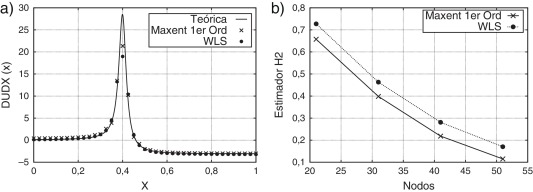
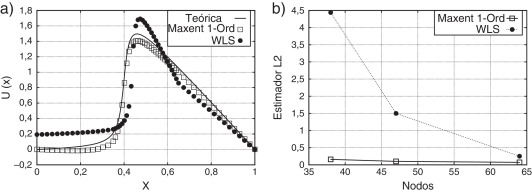
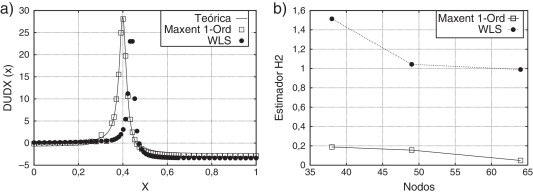
En el caso de una distribución uniforme de puntos, tal como se muestra en las figuras 2a y 3a, tanto la solución como su derivada muestran un mejor comportamiento respecto del valor teórico, cuando se utiliza la función de forma maxent. Esta situación se refleja también en las figuras 2b y 3b en donde se aprecia la tendencia del error global de la solución y su derivada. En el caso de la figura 2a, además, es posible apreciar como la solución numérica que se obtiene mediante maxent, a diferencia de la que se obtiene con FWLS, puede aproximar de buena manera la solución teórica en x=0.0 donde se imponen condiciones tipo Neumann. Esto indica que las funciones de forma maxent presentan un mejor comportamiento ante la presencia de este tipo de condiciones de borde. Está situación también se repite para otras discretizaciones, tal como se muestra en la figura 4. Al respecto la tabla 1 muestra la tendencia del error global de la solución numérica, tanto en la norma L2 como H2, cuando se utiliza una discretización con 21, 31, 41 y 51 nodos. La longitud característica h se obtiene a partir de

$h={\frac {L}{N-1}}$

(36)

donde L y N son la longitud del dominio y el número total de nodos de la discretización respectivamente, lo cual corresponde a un refinamiento uniforme.

Figura 2. Solución numérica utilizando 41 puntos distribuidos en forma regular. a) u(x) b) Estimador L2.

Figura 3. Solución numérica utilizando 41 puntos distribuidos en forma regular. a) du/dx b) Estimador H2.

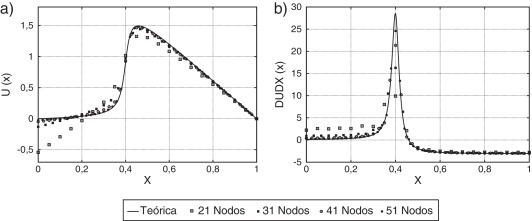
Figura 4. Solución numérica para una distribución regular de puntos utilizando función de forma maxent de primer orden. a) u(x) b) du/dx.

Tabla 1. Comparación de la tendencia del error global

N° puntos	Longitud característica h	L2	H2
21	5.000e-02	2.688e-01	6.575e-01
31	3.333e-02	8.811e-02	3.982e-01
41	2.500e-02	3.448e-02	2.183e-01
51	2.000e-02	1.446e-02	1.149e-01

Considerando el abrupto cambio de la solución y su derivada en el entorno del punto x=0.4, el test de Rachford-Wheeler resulta un buen ejemplo para verificar el comportamiento de la solución numérica cuando se utiliza una distribución irregular de puntos. En las figuras 5 y 6 se puede apreciar el resultado de la metodología propuesta utilizando maxent en comparación a la función de forma mediante FWLS. Para 64 puntos distribuidos de manera no uniforme, en el caso de maxent, la solución numérica captura apropiadamente la magnitud del cambio y el lugar donde este se ubica. Lo anterior no ocurre en el caso de FWLS, donde se visualiza un desfase y un valor más elevado de la solución en el entorno del punto x=0.4. Este comportamiento se replica de igual manera en el caso de la derivada de la solución. En las mismas figuras, además, es posible verificar que para un mismo número de nodos la solución con maxent siempre presenta un menor error global respecto de FWLS, siendo notorio además la falta de exactitud de esta solución en el contorno x=0.0. Si bien en el caso de la figura 3b, para una distribución regular de puntos, las tasas de convergencia en derivadas parecen similares entre ambos métodos, para el caso de una distribución irregular (figura 6b) si existen diferencias. En el presente test la función de forma maxent siempre muestra un mejor comportamiento respecto de los estimadores L₂ y H₂.

Figura 5. Solución numérica utilizando una distribución irregular de 64 puntos. a) u(x) b) Estimador L2.

Figura 6. Solución numérica utilizando una distribución irregular de 64 puntos. a) du/dx b) Estimador H2.

4.2. Problema de Poisson con fuentes localizadas

Para comprobar la calidad de la función de forma maxent en un método sin malla de formulación fuerte, esta vez en un caso 2D, se desarrolla el ejemplo correspondiente a un problema de Poisson con cuatro fuentes localizadas. En este caso, para realizar las comparaciones respecto de la solución teórica, se ha considerado la utilización del estimador L₂ pero en su versión bidimensional. El objetivo de este problema es poder evaluar la convergencia de la solución numérica en un caso 2D. La formulación del problema se puede expresar matemáticamente como,

$-\nabla \cdot (k\nabla u)=s(x,y),\quad \in [0,1]x[0,1],$

(37a)

$u={\overline {u}}\quad \in x=0,x=1,y=0,$

(37b)

$\nabla u\cdot n=0\quad \in y=1.$

(37c)

$u(x,y)=\sum _{i=1}^{4}A_{i}exp(-{\beta }_{i}{\left((x-x_{i}\right)}^{2}+$${\left(y-y_{i}\right)}^{2}))$

(38)

donde s(x, y  ) y ${\textstyle {\overline {u}}}$ corresponden a la segunda derivada y a la solución u(x, y) evaluadas en el borde respectivamente. Para el caso del presente ejemplo se ha considerado un k = 1. Los coeficientes necesarios para poder evaluar la solución teórica a partir de la ecuación (38) se obtienen de la tabla 2,

Tabla 2. Coeficientes para el problema de Poisson con fuentes localizadas

i	Ai	βi	xi	yi
1	10	180	0,51	0,52
2	50	450	0,31	0,34
3	100	800	0,73	0,71
4	50	1000	0,28	0,72

Para la realización de presente ejemplo se ha considerado, en el caso de la aproximación mediante FWLS, una base de interpolación cuadrática de m=6 términos según,

$p^{T}(x)=\left[{\begin{array}{cccccc}1&x&y&x^{2}&xy&y^{2}\end{array}}\right]$

(39)

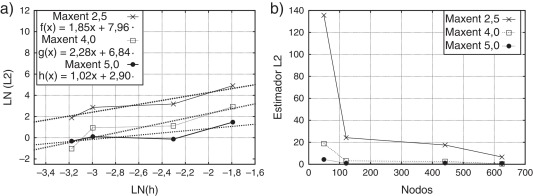
Además, se han utilizado nubes de 9 puntos siendo los parámetros de función de ponderación (ecuación (31)) κ = 1.1 y ω = 3.5. De la misma forma que en el test de Rachford-Wheeler, los resultados numéricos muestran que las aproximaciones maxent de primer orden son convergentes a la solución exacta, para el caso de una distribución regular de nodos. En las figuras 7a y 7b se aprecia una correcta convergencia de la aproximación para diferente número de nodos de la discretización. Los valores de 2.5, 4.0 y 5.0 corresponden al parámetro γ, de acuerdo a la ecuación (15), e indican el grado de localidad que tendrá la función de forma. Se aprecia que el párametro γ para un valor de 2.5, en una discretización de 49 puntos, presenta un error mayor al esperado, lo cual se explica por el bajo número de puntos que se utiliza en la aproximación local de la función maxent. Sin embargo, con γ igual a 4.0 y 5.0, este efecto desaparece para la misma discretización, debido a que esta vez se considera un mayor número de puntos en la nube. Al aumentar el número total de nodos de la discretización, el valor de γ se vuelve menos sensible a la cantidad de puntos utilizados en la aproximación local. En la tabla 3 se aprecia una comparación del error global entre la solución maxent y FWLS. Al respecto conviene resaltar que a diferencia de la solución mediante una función de forma FWLS, el error global L2 cuando se utiliza maxent es decreciente con el número de nodos, situación que contrasta con el carácter no estable de FWLS. De la misma manera la magnitud del error es siempre menor en el caso de maxent para todas las discretizaciones utilizadas, siendo en algunos casos hasta dos órdenes menor. Además, la tabla presenta los tiempos en segundos de cómputo empleado en el cálculo de las funciones de forma maxent y FWLS. Al respecto, no se aprecia una diferencia significativa en el coste de generar las aproximaciones.

Figura 7. Estimador del error L2. a) Estimador L2 v/s longitud característica h b) Estimador L2 v/s número de nodos.

Tabla 3. Comparación entre maxent con γ = 4.0 y FWLS

N° Puntos	L2 - maxent	L2 - FWLS	Tiempo [s] - maxent	Tiempo [s] - FWLS
49	1,880E+01	8,436E+02	0,6402	0,6777
121	3,047E+00	2,880E+02	2,7406	2,9069
441	2,551E+00	2,444E+03	32,0418	32,7002
625	3,545E-01	9,564E+01	63,4109	64,2872

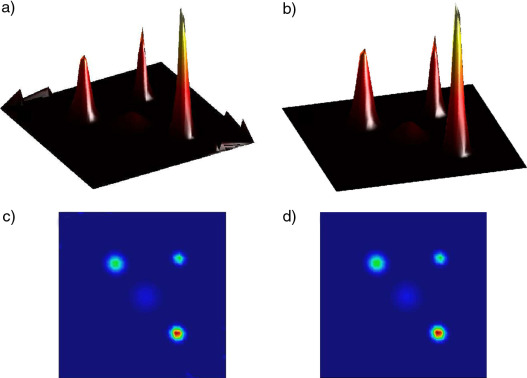
Con el objetivo de visualizar la solución numérica, se presentan en la figura 8 las superficies del campo u(x), además de las curvas de nivel respectivas. Considerando que tan solo se utilizan 441 puntos, no se aprecian diferencias significativas entre la solución teórica y numérica. Esto demuestra un comportamiento convergente hacia la solución real del problema, y la capacidad de la metodología para capturar altos gradientes localizados en un dominio determinado. Las fuentes, se aprecian correctamente ubicadas respecto a la solución teórica en la figuras 8 c) y d) incluso considerando el hecho de que en este problema tres de los contornos corresponden a condiciones de Neumman.

Figura 8. Comparación entre la solución numérica mediante maxent y teórica para una discretización regular. a) Vista isométrica solución numérica. b) Vista isométrica solución teórica. c) Vista en planta solución numérica con 441 puntos. d) Vista en planta solución teórica con 1600 puntos.

5. Conclusiones

En el presente trabajo se analiza el comportamiento de la función de forma tipo maxent, cuando se utiliza en un método sin malla con un esquema de colocación. Esta función se obtiene mediante el principio de máxima entropía y, en contraposición con la función de forma calculada mediante mínimos cuadrados ponderados fijos, posee interesantes características como lo son su positividad y suavidad, requerimientos deseados en todo esquema de colocación. La función de forma tipo maxent posee además la ventaja de que los nodos interiores del dominio no influyen sobre su valor en el contorno, es decir, se calcula únicamente con la información de los nodos del contorno. Dado que estas funciones resultan de un proceso de optimización convexa, representan la mejor aproximación considerando la información realmente disponible en el problema. Los ejemplos desarrollados muestran que en el contexto de un método sin malla de colocación, la solución numérica que se obtiene utilizando maxent, posee una mejor convergencia y estabilidad cuando se la compara con la aproximación mediante FWLS, inclusive para una distribución irregular de nodos. Si bien el cálculo de la derivada de este tipo de función de forma resulta un poco más laboriosa de implementar, el esfuerzo se ve recompensado por la calidad de la misma como también su posibilidad de poder utilizarla con éxito para casos 3D en el ámbito de la mecánica de sólidos. Futuros trabajos de investigación se deberán desarrollar en este sentido, teniendo presente que su utilización no requiere de ningún tipo de interconexión entre los nodos para el proceso de cálculo, lo cual mantiene la idea original de un verdadero método sin malla. Respecto al costo computacional para el cálculo de la función de forma en un método sin malla de colocación mediante maxent, y tal como se presenta en el ejemplo 2D para distintas discretizaciones, este no presenta un aumento con respecto al utilizado por FWLS. Finalmente otra de las líneas de investigación corresponderá al desarrollo de la metodología para consistencias de segundo u orden superior.

Agradecimientos

Los autores agradecen el financiamiento para la realización del presente trabajo al proyecto DGIP 25.15.55 de la Universidad Técnica Federico Santa María, de Valparaíso, Chile, al Aula DIMEC-CIMNE perteneciente a la Asociación Internacional de Aulas CIMNE (AIAC) del Centro Internacional de Métodos Numéricos en Ingeniería, de Barcelona, España, como también al Capital Semilla UGM-VRA 10117.

References

1. [1] G. Liu; Meshfree Methods: Moving Beyond the F inite Element Method, Vol. I, CRC Press LLC (2003)
2. [2] S. Li, W. Liu; Meshfree Particle Method, Vol. I, Springer-Verlag (2004)
3. [3] G. Liu, Y. Gu; An Introduction to Meshfree Methods and Their Programming; Springer (2005)
4. [4] Q. Duan, X. Li, H. Zhang, T. Belytschko; Second-order accurate derivatives and integration schemes for meshfree methods; International Journal for Numerical Methods in Engineering, 92 (2012), pp. 399–424
5. [5] J. Chen, M. Hillman, M. Rüter; An arbitrary order variationally consistent integration for Galerkin meshfree methods; International Journal for Numerical Methods in Engineering, 95 (2013), pp. 387–418
6. [6] E. Oñate, F. Perazzo, J. Miquel; A finite point method for elasticity problems; Computers and Structures, 79 (2001), pp. 2151–2163
7. [7] F. Perazzo, E. Oñate, J. Miquel; El método de puntos finitos para problemas de la dinámica de sólidos; Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 20 (3) (2004), pp. 235–246
8. [8] F. Perazzo, S. Oller, J. Miquel, E. Oñate; Avances en el método de puntos finitos para la mecánica de sólidos; Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 22 (2006), pp. 153–167
9. [9] G. Liu, Y. Gu; A local radial point interpolation method (lr-pim) for free vibration analyses of 2-d solids; Journal of Sound Vibration, 246-1 (2001), pp. 29–46
10. [10] J. Xiaozhong, L. Gang, N. Aluru; Positivity conditions in meshless collocation methods; Computer methods in applied mechanics and engineering, 193 (2004), pp. 1171–1202
11. [11] S. Patankar; Numerical Heat Transfer and Fluid Flow; Hemisphere (1980)
12. [12] T. Belytschko, Y. Lu, L. Gu; Element Free Galerkin Methods; International Journal for Numerical Methods in Engineering, 37 (1994), pp. 229–256
13. [13] W. Liu, S. Li, T. Belytschko; Moving Least Square Reproducing Kernel Methods. Part (I): Methodology and Convergence; Computer Methods in Applied Mechanics and Engineering, 143 (1997), pp. 422–453
14. [14] T. Liszka, C. Duarte, W. Tworzydlo; Hp-meshless cloud method; Computer Methods in Applied Mechanics and Engineering, 139 (1996), pp. 263–288
15. [15] X. Zhang, X. Liu, K. Song, M. Lu; Least-squares collocation meshless method; International Journal for Numerical Methods in Engineering, 51 (2001), pp. 1089–1100
16. [16] E. Oñate, S. Idelsohn, O. Zienkiewicz, R. Taylor, C. Sacco; A finite point method in computational mechanics. Applications to convective transport and fluid flow; International Journal for Numerical Methods in Engineering, 39 (1996), pp. 3839–3866
17. [17] F. Perazzo, R. Löhner, L. Pérez-Pozo; Adaptive methodology for meshless finite point method; Advances in Engineering Software, 39 (2008), pp. 156–166
18. [18] E. Jaynes; Information theory and statistical mechanics; Physical Review, 106 (1957), pp. 620–630
19. [19] E. Jaynes; Information theory and statistical mechanics. II; Physical Review, 108 (1957), pp. 171–190
20. [20] N. Sukumar; Construction of polygonal interpolants: a maximum entropy approach; International Journal for Numerical Methods in Engineering, 61 (2004), pp. 2159–2181
21. [21] N. Sukumar, R. Wright; Overview and construction of meshfree basis functions: from moving least ssquare to entropy approximants; International Journal for Numerical Methods in Engineering, 70 (2) (2007), pp. 181–205
22. [22] M. Arroyo, M. Ortiz; Local maximum-entropy approximation schemes: a seamless bridge between finite elements and meshfree methods; International Journal for Numerical Methods in Engineering, 65 (2006), pp. 2167–2202
23. [23] A. Ortiz, M. Puso, N. Sukumar; Maximum-entropy meshfree method for compressible and near-incompressible elasticity; Computer Methods in Applied Mechanics and Engineering, 199 (2010), pp. 1859–1871
24. [24] F. Greco, L. Filice, C. Peco, M. Arroyo; A stabilized formulation with maximum entropy meshfree approximants for viscoplastic flow simulation in metal forming; International Journal of Material Forming, 8 (3) (2015), pp. 341–353
25. [25] C. Peco, D. Millán, A. Rosolen, M. Arroyo; Efficient implementation of galerkin meshfree methods for large-scale problems with and emphasis on maximum entropy approximants; Computers and Structures, 150 (2015), pp. 52–62
26. [26] Z. Ullah, W. Coombs, C. Augarde; An adaptive finite element/meshless coupled method based on local maximum entropy shape functions for linear and non-linear problems; Computer methods in applied mechanics and engineering, 267 (2013), pp. 111–132
27. [27] A. Rosolen, C. Peco, M. Arroyo; An adaptive meshfree method for phase-field models of biomembranes. part i: approximation with maximum entropy approximants; Journal of Computational Physics, 249 (2013), pp. 303–319
28. [28] C. Wu, D. Young, H. Hong; Adaptive meshless local maximum-entropy finite element method for convection-diffusion problems; Computational Mechanics, 53 (2014), pp. 189–200
29. [29] F. Amiri, D. Millán, Y. Shen, T. Rabczuk, M. Arroyo; Phase-field modelling of fracture mechanics in linear thin shells; Theoretical and Applied Fracture Mechanics, 69 (2014), pp. 102–109
30. [30] C. Cyron, M. Arroyo, M. Ortiz; Smooth, second order, non-negative meshfree approximants selected by maximum entropy; International Journal for Numerical Methods in Engineering, 79 (2009), pp. 1605–1632
31. [31] T.-J. Hughes; The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Publications (2000)
32. [32] E. Jaynes; Paper on Probability, Statistics and Statistical Physics; Kluwer Academic (1989)
33. [33] C. Shannon; A mathematical theory of communication; The Bell System Technical Journal, 27 (1948), pp. 379–423
34. [34] S. Boyd, L. Vandenberghe; Convex Optimization; Cambridge University Press (2004)
35. [35] H. Rachford, M. Wheeler; An H⁻¹-galerkin procedure for the two-point boundary value problem; Carl de Boor (Ed.), Mathematical Aspects of Finite Elements in Partial Differential Equations, Academic Press (1974), pp. 353–382
36. [36] C. Duarte, J. Oden; An hp adaptive method using clouds; Computer Methods in Applied Mechanics and Engineering, 139 (1996), pp. 237–262
37. [37] I. Babuska, J. Melenk; The partition of unity finite element method: basic theory and applications; Computer Methods in Applied Mechanics and Engineering, 139 (1996), pp. 289–314
38. [38] E. Ortega; Método de Puntos F initos: Un análisis de los parámetros que definen las nubes en aproximaciones de segundo y cuarto orden; ,in: G. Buscaglia, E. Dari, Zamonsky (Eds.), Mecánica Computacional, Vol.23 (2004), pp. 3273–3291